name: Введение в формальную криптографию goal: Глубокое введение в науку и практику криптографии. objectives:
- Изучите шифры Била и современные криптографические методы, чтобы понять основные и исторические концепции криптографии.
- Углубитесь в теорию чисел, групп и полей, чтобы освоить ключевые математические понятия, лежащие в основе криптографии.
- Изучите потоковый шифр RC4 и AES со 128-битным ключом, чтобы узнать о симметричных криптографических алгоритмах.
- Изучите криптосистему RSA, распределение ключей и хэш-функции для изучения асимметричной криптографии.
Глубокое погружение в криптографию
Трудно найти много материалов, которые предлагают хорошую середину в обучении криптографии.
С одной стороны, есть длинные формальные трактаты, доступные только тем, кто хорошо знает математику, логику или другие формальные дисциплины. С другой стороны, есть очень высокоуровневые введения, которые действительно скрывают слишком много деталей для любого, кто хотя бы немного любопытен.
Это введение в криптографию стремится занять промежуточную позицию. Хотя оно должно быть относительно сложным и подробным для тех, кто только начинает изучать криптографию, это не кроличья нора типичного фундаментального трактата.
Введение
Обзор курса
bb8a8b73-7fb2-50da-bf4e-98996d79887b Добро пожаловать на курс CYP302!
Эта книга предлагает глубокое введение в науку и практику криптографии. Там, где это возможно, основное внимание уделяется концептуальному, а не формальному изложению материала.
Этот образовательный контент адаптирован из книги и repo JWBurgers. Хотя автор любезно разрешил его использование в образовательных целях, все права интеллектуальной собственности остаются за первоначальным создателем.
Мотивация и цели
Трудно найти много материалов, которые предлагают хорошую середину в обучении криптографии.
С одной стороны, есть длинные формальные трактаты, доступные только тем, кто хорошо знает математику, логику или другие формальные дисциплины. С другой стороны, есть очень высокоуровневые введения, которые действительно скрывают слишком много деталей для любого, кто хотя бы немного любопытен.
Это введение в криптографию стремится занять промежуточную позицию. Хотя оно должно быть относительно сложным и подробным для тех, кто только начинает изучать криптографию, это не кроличья нора типичного фундаментального трактата.
Целевая аудитория
От разработчиков до интеллектуально любопытных - эта книга будет полезна всем, кто хочет получить более чем поверхностное понимание криптографии. Если ваша цель - освоить криптографию, то эта книга также станет хорошей отправной точкой.
Рекомендации по чтению
В настоящее время книга содержит семь глав: "Что такое криптография?" (глава 1), "Математические основы криптографии I" (глава 2), "Математические основы криптографии II" (глава 3), "Симметричная криптография" (глава 4), "RC4 и AES" (глава 5), "Асимметричная криптография" (глава 6) и "Криптосистема RSA" (глава 7). Еще будет добавлена последняя глава "Криптография на практике". Она посвящена различным криптографическим приложениям, включая безопасность транспортного уровня, луковую маршрутизацию и систему обмена ценностями Bitcoin.
Если вы не имеете сильного математического образования, теория чисел, вероятно, является самой сложной темой в этой книге. Я предлагаю обзор этой темы в главе 3, она также присутствует в изложении AES в главе 5 и криптосистемы RSA в главе 7.
Если вам действительно трудно разобраться с формальными деталями в этих частях книги, я рекомендую в первый раз остановиться на их прочтении на высоком уровне.
Благодарности
Самой влиятельной книгой в формировании этого курса стала книга Джонатана Каца и Иегуды Линделла Introduction to Modern Cryptography, CRC Press (Boca Raton, FL), 2015. Сопровождающий курс доступен на Coursera под названием "Криптография"
Основными дополнительными источниками, которые были полезны при создании обзора в этой книге, являются Саймон Сингх, The Code Book, Fourth Estate (London, 1999); Кристоф Паар и Ян Пельцль, Understanding Cryptography, Springer (Heidelberg, 2010) и курс на основе книги Паара под названием "Введение в криптографию"; и Брюс Шнайер, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons).
Я буду приводить только очень конкретную информацию и результаты, почерпнутые из этих источников, но хочу отметить, что в целом я в долгу перед ними.
Тем читателям, которые захотят получить более глубокие знания по криптографии после этого введения, я настоятельно рекомендую книгу Каца и Линделла. Курс Каца на Coursera несколько доступнее, чем книга.
Взносы
Пожалуйста, загляните в файл взносов в репозитории, чтобы узнать, как поддержать проект.
Условные обозначения
Ключевые термины:
Ключевые термины в праймерах вводятся жирным шрифтом. Например, введение шифра Rijndael в качестве ключевого термина будет выглядеть следующим образом: шифр Rijndael.
Ключевые термины определены в явном виде, если только они не являются именами собственными или их значение не очевидно из обсуждения.
Определение обычно дается при введении ключевого термина, хотя иногда удобнее оставить определение на более поздний срок.
*Подчеркнутые слова и фразы:
Слова и фразы выделяются курсивом. Например, фраза "Запомните свой пароль" будет выглядеть следующим образом: Remember your password.
Формальные обозначения:
Формальные обозначения в основном касаются переменных, случайных величин и множеств.
- Переменные: Обычно их обозначают просто строчной буквой (например, "x" или "y"). Иногда для наглядности их пишут с заглавной буквы (например, "М" или "К").
- Случайные переменные: Они всегда обозначаются заглавной буквой (например, "X" или "Y")
- Наборы: Они всегда обозначаются жирными заглавными буквами (например, S)
Готовы исследовать увлекательный мир криптографии? Вперёд!
Что такое криптография?
Шифры Била
Давайте начнем наше исследование области криптографии с одного из самых очаровательных и забавных эпизодов в ее истории - шифров Била. [1]
История шифров Била, на мой взгляд, скорее вымысел, чем реальность. Но якобы все происходило следующим образом.
Зимой 1820 и 1822 годов человек по имени Томас Дж. Бил останавливался в гостинице, принадлежавшей Роберту Моррису в Линчбурге (штат Вирджиния). В конце второго пребывания Бил передал Моррису на хранение железный ящик с ценными бумагами.
Через несколько месяцев Моррисс получил письмо от Била, датированное 9 мая 1822 года. В нем подчеркивалась огромная ценность содержимого железного ящика и содержались некоторые инструкции для Моррисса: если ни Биль, ни кто-либо из его помощников никогда не придут за ящиком, он должен открыть его ровно через десять лет со дня написания письма (то есть 9 мая 1832 года). Некоторые из бумаг внутри были бы написаны обычным текстом. Однако некоторые другие были бы "неразборчивы без помощи ключа" Этот "ключ" должен был быть доставлен Моррису неназванным другом Била в июне 1832 года.
Несмотря на четкие инструкции, Моррисс не открыл шкатулку в мае 1832 года, а таинственный друг Била так и не появился в июне того же года. Только в 1845 году трактирщик наконец решился открыть шкатулку. В ней Моррисс обнаружил записку, в которой объяснялось, как Бил и его помощники нашли на Западе золото и серебро и закопали их вместе с драгоценностями для сохранности. Кроме того, в шкатулке находились три шифротекста, то есть написанные кодом тексты, для разгадки которых требуется криптографический ключ, или секрет, и сопутствующий алгоритм. Процесс разблокировки шифртекста называется дешифрованием, а процесс блокировки - шифрованием. (Как объясняется в главе 3, термин "шифр" может принимать различные значения. В названии "шифры Била" это сокращение от шифротекстов)
Три шифротекста, которые Моррисс нашел в железном ящике, состоят из ряда цифр, разделенных запятыми. Согласно записке Била, в этих шифротекстах отдельно указывается местонахождение клада, его содержимое, а также список имен законных наследников клада и их долей (последняя информация актуальна на случай, если Бил и его соратники так и не придут за шкатулкой).
Моррис пытался расшифровать три шифротекста в течение двадцати лет. При наличии ключа это было бы легко. Но ключа у Морриса не было, и его попытки восстановить оригинальные тексты, или простые тексты, как их обычно называют в криптографии, не увенчались успехом.
Ближе к концу жизни, в 1862 году, Моррисс передал шкатулку своему другу. Этот друг впоследствии опубликовал памфлет в 1885 году под псевдонимом Дж. Б. Уорд. В ней содержалось описание (предполагаемой) истории шкатулки, трех шифротекстов и найденного им решения для второго шифротекста. (Судя по всему, для каждого шифротекста существует свой ключ, а не один ключ, который работает со всеми тремя шифротекстами, как первоначально предполагал Бил в своем письме Моррису)
Второй шифртекст вы можете увидеть на Рисунке 2 ниже. [2] Ключом к этому шифртексту является Декларация независимости Соединенных Штатов. Процедура расшифровки сводится к применению следующих двух правил:
- Для любого числа n в шифротексте найдите n-ое слово в Декларации независимости Соединенных Штатов
- Замените цифру n первой буквой найденного слова
Рисунок 1: Шифр Била №. 2

Например, первое число второго шифротекста - 115. 115-е слово Декларации независимости - "instituted", поэтому первая буква открытого текста - "i" В шифротексте нет прямого указания на интервал между словами и капитализацию. Но, расшифровав первые несколько слов, можно сделать логический вывод, что первым словом открытого текста было просто "I" (Открытый текст начинается с фразы "Я вложил деньги в округе Бедфорд")
После расшифровки во втором сообщении подробно описывается содержимое клада (золото, серебро и драгоценности), а также говорится, что он был зарыт в железных горшках и засыпан камнями в округе Бедфорд (штат Вирджиния). Люди любят хорошие загадки, поэтому много усилий было потрачено на расшифровку двух других шифров Била, особенно того, который описывает местонахождение сокровищ. Даже различные известные криптографы пробовали свои силы. Однако до сих пор никому не удалось расшифровать два других шифротекста.
Примечания:
[1] Хорошее краткое изложение этой истории см. в Simon Singh, The Code Book, Fourth Estate (London, 1999), pp. 82-99. Эндрю Аллен снял короткометражный фильм по этой истории в 2010 году. Вы можете найти фильм "Шифр Томаса Била" на его сайте.
[2] Это изображение доступно на странице Википедии, посвященной шифрам Била.
Современная криптография
Красочные истории, подобные истории шифров Била, - это то, что ассоциируется у большинства из нас с криптографией. Однако современная криптография отличается от подобных исторических примеров как минимум четырьмя важными аспектами.
Во-первых, исторически криптография занималась только секретностью (или конфиденциальностью). [3] Шифртексты создавались для того, чтобы гарантировать, что только определенные стороны могут быть посвящены в информацию, содержащуюся в открытых текстах, как в случае с шифрами Била. Чтобы схема шифрования хорошо служила этой цели, расшифровка шифротекста должна быть осуществима только при наличии ключа.
Современная криптография занимается более широким кругом вопросов, чем просто секретность. К ним относятся, прежде всего, (1) целостность сообщения - гарантия того, что сообщение не было изменено; (2) подлинность сообщения - гарантия того, что сообщение действительно пришло от конкретного отправителя; и (3) неотрицание - гарантия того, что отправитель не сможет впоследствии ложно отрицать, что он отправил сообщение. [4]
Таким образом, следует помнить о важном различии между схемой шифрования и криптографической схемой. Схема шифрования занимается только обеспечением секретности. Хотя схема шифрования - это криптографическая схема, обратное не верно. Криптографическая схема может служить и для других основных тем криптографии, включая целостность, подлинность и неотказуемость.
Темы целостности и подлинности так же важны, как и секретность. Наши современные системы связи не смогли бы функционировать без гарантий целостности и подлинности сообщений. Неотрицание также является важной задачей, например, для цифровых контрактов, но в криптографических приложениях оно требуется не так часто, как секретность, целостность и подлинность.
Во-вторых, классические схемы шифрования, такие как шифры Била, всегда предполагают использование одного ключа, который делится между всеми заинтересованными сторонами. Однако во многих современных криптографических схемах используется не один, а два ключа: частный и общественный. В то время как первый должен оставаться закрытым в любых приложениях, второй, как правило, является общедоступным (отсюда и соответствующие названия). В сфере шифрования открытый ключ может использоваться для шифрования сообщения, а закрытый - для дешифрования.
Раздел криптографии, в котором рассматриваются схемы, в которых все стороны используют один ключ, известен как симметричная криптография. Единственный ключ в такой схеме обычно называется приватным ключом (или секретным ключом). Ветвь криптографии, которая занимается схемами, требующими пары закрытый-публичный ключ, известна как асимметричная криптография. Иногда эти отрасли также называют криптографией с закрытым ключом и криптографией с открытым ключом соответственно (хотя это может вызвать путаницу, поскольку криптографические схемы с открытым ключом также имеют закрытые ключи).
Появление асимметричной криптографии в конце 1970-х годов стало одним из важнейших событий в истории криптографии. Без нее большинство современных коммуникационных систем, включая биткойн, были бы невозможны или, по крайней мере, очень непрактичны.
Важно отметить, что современная криптография - это не только изучение криптографических схем с симметричными и ассиметричными ключами (хотя это и охватывает большую часть области). Например, криптография также занимается хэш-функциями и генераторами псевдослучайных чисел, и на этих примитивах можно строить приложения, не связанные с криптографией симметричных или ассиметричных ключей.
В-третьих, классические схемы шифрования, как и те, что использовались в шифрах Била, были скорее искусством, чем наукой. Их предполагаемая безопасность в значительной степени основывалась на интуиции относительно их сложности. Обычно их исправляли, когда узнавали о новой атаке на них, или полностью отказывались от них, если атака была особенно серьезной. Современная криптография, однако, является строгой наукой с формальным, математическим подходом к разработке и анализу криптографических схем. [5]
В частности, современная криптография сосредоточена на формальных доказательствах безопасности. Любое доказательство безопасности криптографической схемы проходит в три этапа:
Изложение криптографического определения безопасности, то есть набора целей безопасности и угрозы, исходящей от злоумышленника.
Изложение любых математических предположений относительно вычислительной сложности схемы. Например, криптографическая схема может содержать генератор псевдослучайных чисел. Хотя мы не можем доказать, что они существуют, мы можем предположить, что они существуют.
Изложение математического доказательства безопасности схемы на основе формального понятия безопасности и любых математических предположений.
В-четвертых, если раньше криптография использовалась в основном в военных целях, то в цифровую эпоху она проникает в нашу повседневную деятельность. Неважно, осуществляете ли вы банковские операции в Интернете, публикуете сообщения в социальных сетях, покупаете товар на Amazon с помощью кредитной карты или даете другу биткоины, криптография - непременное условие нашей цифровой эпохи.
Учитывая эти четыре аспекта современной криптографии, мы можем охарактеризовать современную криптографию как науку, занимающуюся формальной разработкой и анализом криптографических схем для защиты цифровой информации от вражеских атак. [6] Безопасность здесь следует понимать в широком смысле как предотвращение атак, нарушающих секретность, целостность, аутентификацию и/или неотказуемость в коммуникациях.
Криптографию лучше всего рассматривать как поддисциплину кибербезопасности, которая занимается предотвращением краж, повреждений и неправомерного использования компьютерных систем. Обратите внимание, что многие проблемы кибербезопасности имеют мало или лишь частичную связь с криптографией.
Например, если компания размещает дорогостоящие серверы на локальном уровне, она может быть озабочена защитой этого оборудования от кражи и повреждения. Хотя это и относится к кибербезопасности, к криптографии это имеет мало отношения.
Например, фишинговые атаки - распространенная проблема в наше время. В ходе этих атак людей пытаются обманом заставить отказаться от конфиденциальной информации, такой как пароли или номера кредитных карт, с помощью электронной почты или других средств связи. Хотя криптография в определенной степени может помочь в борьбе с фишинговыми атаками, комплексный подход требует не только использования некоторых видов криптографии.
Примечания:
[3] Если быть точным, важные приложения криптографических схем были связаны с секретностью. Дети, например, часто используют простые криптографические схемы для "забавы". В таких случаях секретность не имеет особого значения.
[4] Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons), p. 2.
[5] Хорошее описание см. в Jonathan Katz and Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), esp. pp. 16-23.
[6] Ср. Katz and Lindell, ibid., p. 3. Я считаю, что их характеристика имеет некоторые проблемы, поэтому представляю здесь несколько иную версию их высказывания.
Открытые коммуникации
Современная криптография призвана обеспечить гарантии безопасности в условиях открытых коммуникаций. Если наш канал связи настолько хорошо защищен, что у подслушивающих нет шансов манипулировать нашими сообщениями или даже просто наблюдать за ними, то криптография излишня. Однако большинство наших каналов связи вряд ли так хорошо защищены.
Основой связи в современном мире является массивная сеть оптоволоконных кабелей. Телефонные звонки, просмотр телепередач и веб-страниц в современном доме, как правило, зависят от этой сети оптоволоконных кабелей (в небольшом проценте случаев - от спутников). Правда, в вашем доме могут быть разные соединения для передачи данных: коаксиальный кабель, (асимметричная) цифровая абонентская линия и оптоволоконный кабель. Но, по крайней мере в развитых странах мира, эти различные среды передачи данных быстро соединяются за пределами вашего дома с узлом в массивной сети оптоволоконных кабелей, которая соединяет весь земной шар. Исключение составляют некоторые отдаленные районы развитых стран, например США и Австралия, где трафик данных все еще может проходить значительные расстояния по традиционным медным телефонным проводам.
Невозможно предотвратить физический доступ потенциальных злоумышленников к этой сети кабелей и ее вспомогательной инфраструктуре. На самом деле мы уже знаем, что большая часть наших данных перехватывается различными национальными спецслужбами на важнейших перекрестках Интернета.[7] Сюда входит все - от сообщений в Facebook до адресов сайтов, которые вы посещаете.
Если для масштабного наблюдения за данными требуется мощный противник, например национальная разведка, то злоумышленники, располагающие лишь небольшими ресурсами, могут легко попытаться шпионить в более локальных масштабах. Хотя это может происходить на уровне прослушивания проводов, гораздо проще просто перехватить беспроводные коммуникации.
Большинство данных в локальной сети - дома, в офисе или в кафе - теперь передается по радиоволнам к беспроводным точкам доступа на универсальных маршрутизаторах, а не по физическим кабелям. Поэтому злоумышленнику не нужно много ресурсов, чтобы перехватить любой ваш локальный трафик. Это особенно тревожно, поскольку большинство людей мало что делают для защиты данных, проходящих через их локальные сети. Кроме того, потенциальные злоумышленники могут атаковать наши мобильные широкополосные соединения, такие как 3G, 4G и 5G. Все эти беспроводные коммуникации - легкая мишень для злоумышленников.
Таким образом, идея сохранения тайны связи путем защиты канала связи является безнадежно бредовым стремлением для большей части современного мира. Все, что мы знаем, требует жесткой паранойи: вы всегда должны предполагать, что кто-то вас подслушивает. И криптография - это главный инструмент, которым мы располагаем, чтобы добиться хоть какой-то безопасности в этой современной среде.
Примечания:
[7] Например, Ольга Хазан, "Жуткая, давняя практика прослушивания подводных кабелей", The Atlantic, 16 июля 2013 г. (доступно по адресу The Atlantic).
Математические основы криптографии 1
Случайные величины
Криптография опирается на математику. И если вы хотите получить более чем поверхностное понимание криптографии, вам нужно быть в курсе этой математики.
В этой главе мы познакомим вас с основными математическими понятиями, с которыми вы столкнетесь при изучении криптографии. Среди тем - случайные величины, операции по модулю, операции XOR и псевдослучайность. Для любого не поверхностного понимания криптографии вам следует освоить материал этих разделов.
В следующем разделе рассматривается теория чисел, которая гораздо сложнее.
Случайные величины
Случайная величина обычно обозначается нежирной заглавной буквой. Так,
например, мы можем говорить о случайной переменной X, случайной переменной Y или
случайной переменной Z. Это
обозначение я буду использовать и в дальнейшем.
Переменная случайная величина может принимать два или более возможных значений, каждое из которых имеет определенную положительную вероятность. Возможные значения перечислены в наборе результатов.
Каждый раз, когда вы выбираете случайную переменную, вы берете определенное значение из ее набора исходов в соответствии с заданными вероятностями.
Обратимся к простому примеру. Предположим, что переменная X определена следующим образом:
- X имеет множество исходов
\{1,2\}
Pr[X = 1] = 0.5Pr[X = 2] = 0.5Легко видеть, что X - это
случайная переменная. Во-первых, существует два или более возможных
значения, которые может принимать X, а именно 1 и 2. Во-вторых, каждое из
возможных значений имеет положительную вероятность появления при любом
образце X, а именно 0,5.
Все, что требуется от случайной величины, - это набор исходов с двумя или более возможностями, где каждая возможность имеет положительную вероятность появления при выборке. В принципе, случайная величина может быть определена абстрактно, без какого-либо контекста. В этом случае "выборку" можно представить как проведение естественного эксперимента по определению значения случайной переменной.
Переменная X выше была
определена абстрактно. Таким образом, вы можете представить выборку
переменной X как
подбрасывание честной монеты и присвоение "2" в случае голов и "1" в случае
решки. Для каждой выборки X вы
снова подбрасываете монету.
В качестве альтернативы можно представить выборку X как бросание честного кубика и присвоение "2" в случае выпадения 1, 3 или 4, и присвоение "1" в
случае выпадения 2, 5 или 6. Каждый раз при выборке X вы бросаете кубик снова.
Действительно, любой естественный эксперимент, который позволил бы
определить вероятности возможных значений X выше, можно представить в отношении рисунка.
Однако часто случайные величины вводятся не просто абстрактно. Вместо этого набор возможных значений исходов имеет явное значение в реальном мире (а не просто как числа). Кроме того, эти значения исходов могут быть определены для какого-то конкретного типа эксперимента (а не как любой естественный эксперимент с этими значениями).
Теперь рассмотрим пример переменной X, которая не определена абстрактно. Для того чтобы определить, какая из
двух команд начнет футбольный матч, X определяется следующим образом:
- у
Xесть множество исходов {красный отбивает, синий отбивает} - Подбросьте монету
C: решка = "красный выбивает"; голова = "синий выбивает"
Pr [X = \text{red kicks off}] = 0.5Pr [X = \text{blue kicks off}] = 0.5В этом случае набор исходов X имеет конкретное значение, а именно, какая
команда начнет игру в футбол. Кроме того, возможные исходы и связанные с
ними вероятности определяются конкретным экспериментом, а именно
подбрасыванием определенной монеты C.
При обсуждении криптографии случайные величины обычно вводятся в сравнение с каким-либо набором результатов, имеющим реальное значение. Это может быть множество всех сообщений, которые могут быть зашифрованы, известное как пространство сообщений, или множество всех ключей, из которых могут выбирать стороны, использующие шифрование, известное как пространство ключей.
Случайные величины в дискуссиях о криптографии, однако, обычно определяются не на основе какого-то конкретного естественного эксперимента, а на основе любого эксперимента, который может дать правильное распределение вероятностей.
Случайные величины могут иметь дискретное или непрерывное распределение
вероятности. Случайные величины с дискретным распределением вероятности - то есть дискретные случайные величины - имеют конечное число возможных
исходов. В обоих приведенных примерах случайная величина X была дискретной.
Непрерывные случайные величины могут принимать значения в одном или нескольких интервалах. Например, можно сказать, что случайная величина после выборки примет любое вещественное значение между 0 и 1, и что каждое вещественное число в этом интервале равновероятно. Внутри этого интервала существует бесконечно много возможных значений.
Для обсуждения криптографии вам понадобится только понимание дискретных случайных величин. Поэтому любое обсуждение случайных величин с этого момента следует понимать как относящееся к дискретным случайным величинам, если специально не оговорено иное.
Построение графиков случайных величин
Возможные значения и связанные с ними вероятности для случайной переменной
можно легко представить в виде графика. Например, рассмотрим случайную
переменную X из предыдущего
раздела с набором исходов \{1, 2\}, и Pr [X = 1] = 0,5 и Pr [X = 2] = 0,5. Обычно мы
отображаем такую случайную переменную в виде гистограммы, как на рисунке 1.
Рисунок 1: Случайная переменная X
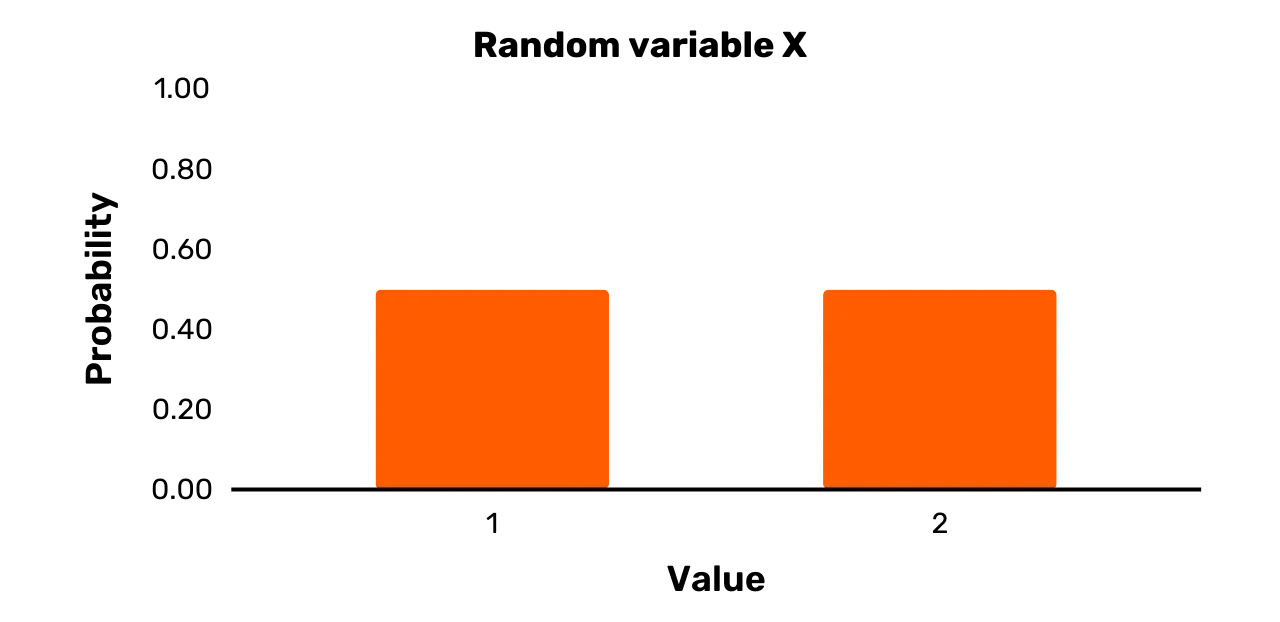
Широкие полосы на Рисунке 1, очевидно, не означают, что случайная
переменная X на самом деле непрерывна.
Напротив, широкие полосы сделаны для того, чтобы быть более визуально привлекательными
(прямая линия вверх дает менее интуитивную визуализацию).
Равномерные переменные
В выражении "случайная величина" термин "случайный" означает просто "вероятностный". Другими словами, это означает, что два или более возможных исхода переменной происходят с определенной вероятностью. Однако эти исходы не обязательно должны быть одинаково вероятными (хотя термин "случайный" действительно может иметь такое значение в других контекстах).
Равномерная переменная** - это частный случай случай случайной переменной.
Она может принимать два или более значений с одинаковой вероятностью.
Случайная величина X,
изображенная на рисунке 1, явно является равномерной величиной,
поскольку оба возможных исхода происходят с вероятностью 0,5. Однако существует
множество случайных величин, которые не являются экземплярами равномерных
переменных.
Рассмотрим, например, случайную переменную Y. Она имеет набор исходов {1, 2, 3, 8, 10} и следующее
распределение вероятностей:
\Pr[Y = 1] = 0.25\Pr[Y = 2] = 0.35\Pr[Y = 3] = 0.1\Pr[Y = 8] = 0.25\Pr[Y = 10] = 0.05Хотя два возможных исхода действительно имеют равную вероятность
наступления, а именно 1 и 8, Y также может принимать определенные значения с вероятностями, отличными от 0,25 при выборке. Следовательно, хотя Y действительно является случайной
величиной, она не является равномерной.
Графическое изображение Y представлено на Рисунке 2.
Рисунок 2: Случайная переменная Y
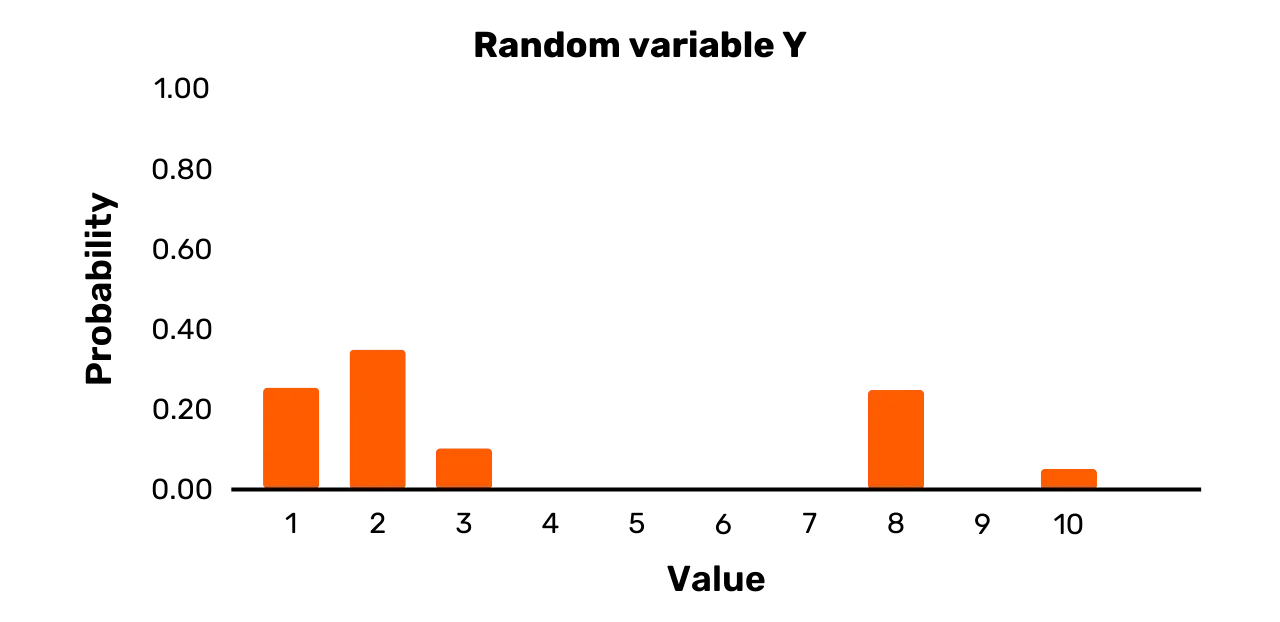
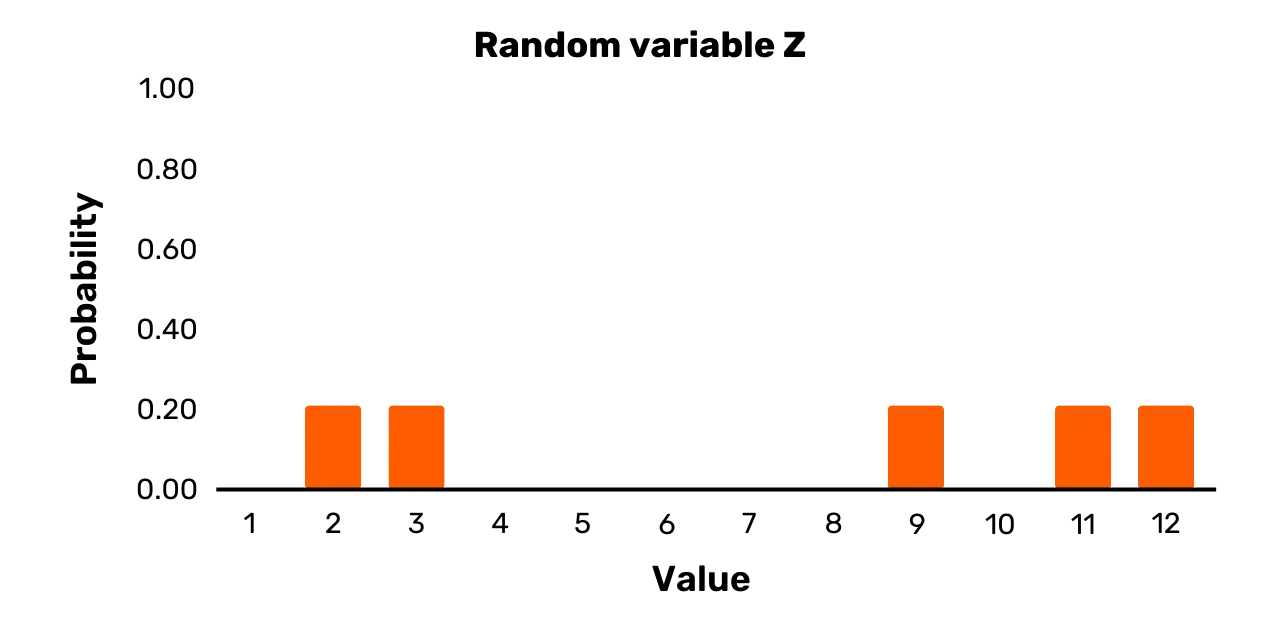
В качестве последнего примера рассмотрим случайную переменную Z. Она имеет набор исходов {1,3,7,11,12} и следующее распределение вероятностей:
\Pr[Z = 2] = 0.2\Pr[Z = 3] = 0.2\Pr[Z = 9] = 0.2\Pr[Z = 11] = 0.2\Pr[Z = 12] = 0.2Вы можете увидеть это на Рисунке 3. Случайная величина Z, в отличие от Y, является равномерной, так как все вероятности возможных значений при выборке равны.
Рисунок 3: Случайная переменная Z
Условная вероятность
Предположим, что Боб намерен равномерно выбрать день из последнего календарного года. Какова вероятность того, что выбранный день придется на лето?
Если мы считаем, что процесс Боба будет действительно равномерным, мы должны заключить, что вероятность того, что Боб выберет день летом, равна 1/4. Это условная вероятность того, что случайно выбранный день окажется летним.
Предположим теперь, что вместо равномерного выбора календарного дня Боб выбирает равномерно только те дни, в которые температура в полдень в Кристал-Лейк (Нью-Джерси) была 21 градус Цельсия или выше. Учитывая эту дополнительную информацию, какой вывод мы можем сделать о вероятности того, что Боб выберет день летом?
Мы действительно должны сделать другой вывод, чем раньше, даже без дополнительной конкретной информации (например, температуры в полдень каждого дня в прошлом календарном году).
Зная, что Хрустальное озеро находится в Нью-Джерси, мы, конечно, не ожидаем, что зимой температура в полдень будет 21 градус по Цельсию или выше. Напротив, гораздо вероятнее, что это будет теплый день весной или осенью, или день где-то летом. Таким образом, зная, что температура в полдень в Кристалл-Лейк в выбранный день была 21 градус Цельсия или выше, вероятность того, что день, выбранный Бобом, приходится на лето, становится гораздо выше. Это условная вероятность того, что случайно выбранный день окажется летним, учитывая, что полуденная температура в Кристал-Лейк была 21 градус Цельсия или выше.
В отличие от предыдущего примера, вероятности двух событий могут быть совершенно не связаны между собой. В этом случае мы говорим, что они независимы.
Предположим, например, что некая честная монета упала головой вниз. Учитывая этот факт, какова вероятность того, что завтра пойдет дождь? Условная вероятность в данном случае должна быть такой же, как и безусловная вероятность того, что завтра пойдет дождь, поскольку подбрасывание монеты, как правило, не оказывает никакого влияния на погоду.
Для записи условных выражений вероятности мы используем символ "|".
Например, вероятность события A при условии, что произошло событие B, может быть записана
следующим образом:
Pr[A|B]Итак, когда два события, A и B, независимы, то:
Pr[A|B] = Pr[A] \text{ and } Pr[B|A] = Pr[B]Условие независимости можно упростить следующим образом:
Pr[A, B] = Pr[A] \cdot Pr[B]Ключевой результат в теории вероятностей известен как теорема Бэйса. В основном она гласит, что Pr[A|B] можно переписать следующим
образом:
Pr[A|B] = \frac{Pr[B|A] \cdot Pr[A]}{Pr[B]}Вместо того чтобы использовать условные вероятности для конкретных событий,
мы можем рассмотреть условные вероятности для двух или более случайных
величин на множестве возможных событий. Предположим, есть две случайные
величины, X и Y. Мы можем обозначить любое
возможное значение для X через x, а любое возможное
значение для Y через y. Тогда можно сказать, что
две случайные величины независимы, если выполняется следующее утверждение:
Pr[X = x, Y = y] = Pr[X = x] \cdot Pr[Y = y]для всех x и y.
Давайте немного уточним, что означает это утверждение.
Предположим, что множества исходов для X и Y определены следующим
образом: X = \{x_1, x_2, \ldots, x_i, \ldots, x_n\} и Y = \{y_1, y_2, \ldots, y_i, \ldots, y_m\}. (Обычно наборы значений выделяются жирным шрифтом и прописными буквами)
Теперь предположим, что вы взяли выборку Y и наблюдаете y_1.
Вышеприведенное утверждение говорит нам, что вероятность получить x_1 из выборки X точно такая же,
как если бы мы никогда не наблюдали y_1. Это верно для любых y_i, которые мы могли бы
получить из нашей первоначальной выборки Y. Наконец, это верно не
только для x_1. Для любого x_i вероятность появления не зависит от результатов выборки Y. Все это относится и к
случаю, когда сначала берется выборка X.
Давайте закончим нашу дискуссию на несколько более философском моменте. В любой реальной ситуации вероятность того или иного события всегда оценивается с учетом определенного набора информации. Не существует "безусловной вероятности" в любом строгом смысле этого слова.
Например, предположим, я спрашиваю вас о вероятности того, что свиньи будут летать к 2030 году. Хотя я не даю вам никакой дополнительной информации, вы явно знаете о мире много такого, что может повлиять на ваше суждение. Вы никогда не видели, как летают свиньи. Вы знаете, что большинство людей не ожидают, что они будут летать. Вы знаете, что на самом деле они не созданы для полетов. И так далее.
Поэтому, когда мы говорим о "безусловной вероятности" какого-то события в реальном мире, этот термин действительно может иметь смысл только в том случае, если мы понимаем под ним что-то вроде "вероятность без какой-либо дополнительной явной информации". Любое понимание "условной вероятности" должно, таким образом, всегда пониматься в сравнении с какой-то конкретной информацией.
Например, я могу спросить вас о вероятности того, что свиньи будут летать к 2030 году, после того как приведу доказательства того, что некоторые козы в Новой Зеландии научились летать после нескольких лет обучения. В этом случае вы, вероятно, скорректируете свое суждение о вероятности того, что свиньи будут летать к 2030 году. Итак, вероятность того, что свиньи будут летать к 2030 году, зависит от этого свидетельства о козах в Новой Зеландии.
Операция модуло
Модуль
Самое простое выражение с операцией модуло имеет следующий
вид: x \mod y.
Переменная x называется
делителем, а переменная y - делимым.
Чтобы выполнить операцию модуляции с положительным делителем и положительным
делимым, нужно просто определить остаток от деления.
Например, рассмотрим выражение 25 \mod 4. Число 4 входит в число 25 в общей сложности 6 раз. Остаток от этого
деления равен 1. Следовательно, 25 \mod 4 равно 1. Аналогичным
образом мы можем оценить выражения, приведенные ниже:
29 \mod 30 = 29(так как 30 входит в 29 всего 0 раз, а остаток равен 29)42 \mod 2 = 0(так как 2 входит в 42 всего 21 раз, а остаток равен 0)12 \mod 5 = 2(так как 5 входит в 12 всего 2 раза, а остаток равен 2)20 \mod 8 = 4(так как 8 входит в 20 всего 2 раза, а остаток равен 4)
Когда делимое или делитель отрицательны, операции модуляции могут обрабатываться языками программирования по-разному.
Вам обязательно встретятся случаи с отрицательными дивидендами в криптографии. В этих случаях типичный подход следующий:
- Сначала определите ближайшее значение меньше или равно делимого,
на которое делитель делится с остатком, равным нулю. Назовите это значение
p. - Если дивиденд равен
x, то результатом операции modulo будет значениеx - p.
Например, предположим, что делимое равно -20, а делитель - 3. Ближайшее значение, меньшее или равное -20, на которое равномерно
делится 3, - -21. Значение x - p в этом случае равно -20 - (-21). Это равно 1, и,
следовательно, -20 \mod 3 равно
1. Аналогичным образом мы можем оценить выражения, приведенные ниже:
-8 \mod 5 = 2-19 \mod 16 = 13-14 \mod 6 = 4
Что касается обозначений, то обычно встречаются следующие типы выражений: x = [y \mod z]. Из-за скобок операция модуляции в этом случае применяется только к правой
части выражения. Если, например, y равно 25, а z равно 4, то x будет равна 1.
Без скобок операция modulo действует на обе стороны выражения.
Предположим, например, следующее выражение: x = y \mod z. Если y равно 25, а z равно 4, то
все, что мы знаем, это то, что x \mod 4 оценивается в 1. Это соответствует любому значению для x из множества \{\ldots,-7, -3, 1, 5, 9,\ldots\}.
Раздел математики, включающий операции модуляции над числами и выражениями, называется модульной арифметикой. Эту ветвь можно рассматривать как арифметику для случаев, когда числовая линия не является бесконечно длинной. Хотя в криптографии мы обычно сталкиваемся с операциями модуляции для (положительных) целых чисел, вы также можете выполнять операции модуляции с любыми вещественными числами.
Шифр сдвига
Операция modulo часто встречается в криптографии. Для примера рассмотрим одну из самых известных исторических схем шифрования - шифр сдвига.
Давайте сначала определим его. Пусть имеется словарь D, который
приравнивает все буквы английского алфавита по порядку к набору чисел \{0, 1, 2, \ldots, 25\}. Предположим, что имеется пространство сообщений M. Тогда шифр сдвига - это схема шифрования, определяемая следующим образом:
- Равномерно выбрать ключ
kиз пространства ключей K, где K =\{0, 1, 2, \ldots, 25\}[1] - Зашифруйте сообщение
m \in \mathbf{M}следующим образом:- Разделите
mна отдельные буквыm_0, m_1, \ldots, m_i, \ldots, m_l - Преобразуйте каждое
m_iв число в соответствии с D - Для каждого
m_i,c_i = [(m_i + k)\mod 26] - Преобразуйте каждый
c_iв букву в соответствии с D - Затем объедините
c_0, c_1, \ldots, c_l, чтобы получить шифротекстc
- Разделите
- Расшифруйте шифротекст
cследующим образом:- Преобразуйте каждый
c_iв число в соответствии с D - Для каждого
c_i,m_i = [(c_i - k)\mod 26] - Преобразуйте каждый
m_iв букву в соответствии с D - Затем объедините
m_0, m_1, \ldots, m_l, чтобы получить исходное сообщениеm
- Преобразуйте каждый
Оператор modulo в шифре сдвига обеспечивает обводку букв, так что все буквы шифротекста определены. Для примера рассмотрим применение шифра сдвига к слову "DOG".
Предположим, что вы равномерно выбрали ключ, значение которого равно 17.
Буква "О" равна 15. Без операции модуляции при сложении этого числа
открытого текста с ключом получилось бы число шифртекста 32. Однако это
число нельзя превратить в букву шифротекста, поскольку в английском алфавите
всего 26 букв. Операция модуляции гарантирует, что число шифртекста на самом
деле равно 6 (результат 32 \mod 26), что соответствует букве шифртекста "G".
Полный шифр слова "DOG" со значением ключа 17 выглядит следующим образом:
- Сообщение = DOG = D,O,G = 3,15,6
c_0 = [(3 + 17)\mod 26] = [(20)\mod 26] = 20 = Uc_1 = [(15 + 17)\mod 26] = [(32)\mod 26] = 6 = Gc_2 = [(6 + 17)\mod 26] = [(23)\mod 26] = 23 = Xc = UGX
Каждый может интуитивно понять, как работает шифр сдвига, и, вероятно, использовать его самостоятельно. Однако для развития ваших знаний в области криптографии важно начать более комфортно относиться к формализации, так как схемы станут намного сложнее. Именно поэтому шаги шифра сдвига были формализованы.
Примечания:
[1] Мы можем точно определить это утверждение, используя терминологию из
предыдущего раздела. Пусть однородная переменная K имеет K в качестве множества возможных
исходов. Таким образом:
Pr[K = 0] = \frac{1}{26}Pr[K = 1] = \frac{1}{26}...и т.д. Сделайте выборку однородной переменной K один раз, чтобы получить конкретный ключ.
Операция XOR
Все компьютерные данные обрабатываются, хранятся и передаются по сетям на уровне битов. Любые криптографические схемы, применяемые к компьютерным данным, также работают на уровне битов.
Например, предположим, что вы набрали письмо в своем почтовом приложении. Любое шифрование, которое вы применяете, не происходит непосредственно с ASCII-символами вашего письма. Вместо этого оно применяется к битовому представлению букв и других символов в вашем письме.
Ключевой математической операцией, которую необходимо понимать для
современной криптографии, помимо операции модуляции, является операция XOR, или "исключающее или". Эта операция принимает на вход два бита и выдает
на выходе другой бит. Операция XOR будет обозначаться просто "XOR". Она дает
0, если два бита одинаковые, и 1, если два бита разные. Ниже показаны четыре
варианта. Символ \oplus обозначает
"XOR":
0 \oplus 0 = 00 \oplus 1 = 11 \oplus 0 = 11 \oplus 1 = 0
Для примера предположим, что у вас есть сообщение m_1 (01111001) и сообщение m_2 (01011001).
Операция XOR для этих двух сообщений показана ниже.
m_1 \oplus m_2 = 01111001 \oplus 01011001 = 00100000
Процесс прост. Сначала вы XOR крайние левые биты m_1 и m_2. В данном случае это 0 \oplus 0 = 0. Затем
выполняется XOR второй пары битов слева. В данном случае это 1 \oplus 1 = 0. Вы
продолжаете этот процесс до тех пор, пока не выполните операцию XOR для
крайних правых битов.
Легко видеть, что операция XOR является коммутативной, а именно, что m_1 \oplus m_2 = m_2 \oplus m_1. Кроме того, операция XOR также является ассоциативной. То есть (m_1 \oplus m_2) \oplus m_3 = m_1 \oplus (m_2 \oplus m_3).
Операция XOR над двумя строками разной длины может иметь различные интерпретации в зависимости от контекста. Здесь мы не будем рассматривать операции XOR над строками разной длины.
Операция XOR эквивалентна частному случаю выполнения операции сложения битов по модулю, когда делитель равен 2. Эквивалентность можно увидеть в следующих результатах:
(0 + 0)\mod 2 = 0 \oplus 0 = 0(1 + 0)\mod 2 = 1 \oplus 0 = 1(0 + 1)\mod 2 = 0 \oplus 1 = 1(1 + 1)\mod 2 = 1 \oplus 1 = 0
Псевдослучайность
При обсуждении случайных и равномерных величин мы провели конкретное различие между "случайными" и "равномерными". Это различие обычно сохраняется на практике при описании случайных величин. Однако в нашем текущем контексте это различие необходимо отменить и использовать синонимы "случайная" и "равномерная". В конце раздела я объясню, почему.
Начнем с того, что двоичную строку длины n можно назвать случайной (или равномерной),
если она получена в результате выборки равномерной переменной S, которая дает каждой
двоичной строке такой длины n равную вероятность выбора.
Пусть, например, множество всех двоичных строк длины 8: \{0000\ 0000, 0000\ 0001, \ldots, 1111\ 1111\}. (Обычно 8-битная строка записывается в виде двух квартетов, каждый из
которых называется ниббл) Назовем этот набор строк S_8.
Согласно приведенному выше определению, мы можем назвать конкретную двоичную
строку длины 8 случайной (или равномерной), если она является результатом
выборки равномерной переменной S, которая дает каждой строке в S_8 равную вероятность выбора. Учитывая, что множество S_8 включает 2^8 элементов,
вероятность выбора по выборке должна быть 1/2^8 для каждой строки в этом
множестве.
Ключевым аспектом случайности двоичной строки является то, что она определяется в зависимости от процесса, с помощью которого она была выбрана. Поэтому форма любой конкретной двоичной строки сама по себе ничего не говорит о ее случайности при выборе.
Например, многие люди интуитивно думают, что такая строка, как 1111\ 1111, не могла быть выбрана случайным образом. Но это явно неверно.
Если задать равномерную переменную S над всеми двоичными строками длины 8, то вероятность выбора 1111\ 1111 из множества S_8 будет такой же, как и для строки 0111\ 0100. Таким образом,
нельзя ничего сказать о случайности строки, просто анализируя саму строку.
Мы также можем говорить о случайных строках, не имея в виду двоичные строки.
Например, мы можем говорить о случайной шестнадцатеричной строке AF\ 02\ 82. В этом случае строка была бы выбрана случайным образом из множества всех
шестнадцатеричных строк длины 6. Это эквивалентно случайному выбору двоичной
строки длины 24, поскольку каждая шестнадцатеричная цифра представляет собой
4 бита.
Обычно выражение "случайная строка", без оговорок, означает строку, случайно
выбранную из множества всех строк одинаковой длины. Именно так я описал его
выше. Конечно, строка длины n может быть выбрана случайным образом и из другого множества. Например, из
подмножества всех строк длины n, или из множества,
включающего строки разной длины. В этих случаях, однако, мы не будем
называть его "случайной строкой", а скорее "строкой, выбранной случайным
образом из некоторого множества S".
Ключевым понятием в криптографии является понятие псевдослучайности.
Псевдослучайная строка** длины n выглядит так, как будто она является результатом выборки однородной
переменной S, которая дает
каждой строке в S_n равную вероятность выбора. На самом деле, однако, строка является
результатом выборки однородной переменной S', которая определяет
распределение вероятностей - не обязательно с равными вероятностями для всех
возможных исходов - на подмножестве S_n.
Решающим моментом здесь является то, что никто не сможет отличить выборки из S и S', даже если вы возьмете
их много.
Предположим, например, что имеется случайная величина S. Ее множество исходов - S_{256}, это множество всех двоичных строк длины 256. Это множество содержит 2^{256} элементов. Каждый элемент имеет равную вероятность выбора, 1/2^{256}, при
выборке.
Кроме того, предположим, что имеется случайная переменная S'. Ее набор исходов включает только двоичные строки длиной 256 долларов. Она
имеет некоторое распределение вероятностей по этим строкам, но это
распределение не обязательно равномерное.
Предположим, что теперь я взял 1000 выборок из S и 1000 выборок из S' и
передал вам два набора результатов. Я говорю вам, какой набор исходов связан
с какой случайной переменной. Далее я беру выборку из одной из двух
случайных величин. Но на этот раз я не говорю вам, какую случайную
переменную я беру в качестве образца. Если бы S' было псевдослучайным, то идея заключалась бы в том, что вероятность того,
что вы правильно угадаете, какую случайную переменную я выбрал, практически
не лучше, чем 1/2.
Обычно псевдослучайная строка длины n получается путем случайного выбора строки размера n - x, где x - целое положительное число, и использования ее в качестве входных данных
для алгоритма расширения. Эта случайная строка размера n - x известна как семя.
Псевдослучайные строки - это ключевая концепция для практического применения криптографии. Рассмотрим, например, потоковые шифры. В потоковом шифре случайно выбранный ключ вставляется в расширяющий алгоритм, чтобы получить гораздо большую псевдослучайную строку. Затем эта псевдослучайная строка объединяется с открытым текстом с помощью операции XOR для получения шифротекста.
Если бы мы не смогли создать такую псевдослучайную строку для потокового шифра, то для его безопасности нам понадобился бы ключ, длина которого была бы равна длине сообщения. В большинстве случаев это не очень практичный вариант.
Понятие псевдослучайности, рассмотренное в этом разделе, можно определить более формально. Оно также распространяется на другие контексты. Но здесь нам не нужно углубляться в это обсуждение. Все, что вам действительно нужно интуитивно понимать для большей части криптографии, - это разницу между случайной и псевдослучайной строкой. [2]
Причина отказа от различия между "случайным" и "равномерным" в нашем
обсуждении теперь также должна быть понятна. На практике все используют
термин "псевдослучайная" для обозначения строки, которая выглядит **так, как
если бы она была результатом выборки однородной переменной S. Строго говоря, мы должны называть такую строку "псевдооднородной",
переняв наш прежний язык. Поскольку термин "псевдооднородная" и громоздок, и
никем не используется, мы не будем вводить его здесь для ясности. Вместо
этого мы просто отбросим различие между "случайным" и "равномерным" в
текущем контексте.
Примечания
[2] Если вас интересует более формальное изложение этих вопросов, вы можете обратиться к книге Катца и Линделла Введение в современную криптографию, особенно к главе 3.
Математические основы криптографии 2
Что такое теория чисел?
В этой главе рассматривается более продвинутая тема математических основ криптографии - теория чисел. Хотя теория чисел важна для симметричной криптографии (например, в шифре Rijndael), она особенно важна в криптографии с открытым ключом.
Если детали теории чисел кажутся вам громоздкими, я бы рекомендовал в первый раз читать на высоком уровне. Вы всегда сможете вернуться к нему позже.
Можно охарактеризовать теорию чисел как изучение свойств целых чисел и математических функций, которые работают с целыми числами.
Рассмотрим, например, что любые два числа a и N являются копиями (или относительными примами), если их наибольший общий
делитель равен 1. Предположим теперь, что существует определенное целое
число N. Сколько целых чисел,
меньших N, являются копримами
с N? Можем ли мы сделать
общие утверждения об ответах на этот вопрос? Это типичные вопросы, на
которые стремится ответить теория чисел.
Современная теория чисел опирается на инструменты абстрактной алгебры. Область абстрактной алгебры - это субдисциплина математики, в которой основными объектами анализа являются абстрактные объекты, известные как алгебраические структуры. Алгебраическая структура** - это набор элементов, соединенных одной или несколькими операциями, который удовлетворяет определенным аксиомам. С помощью алгебраических структур математики могут получить представление о конкретных математических проблемах, абстрагируясь от их деталей.
Область абстрактной алгебры иногда также называют современной алгеброй. Вы также можете встретить понятие абстрактная математика (или чистая математика). Этот последний термин не относится к абстрактной алгебре, а скорее означает изучение математики ради нее самой, а не только с целью поиска потенциальных приложений.
Множества из абстрактной алгебры могут иметь дело со многими типами объектов, от преобразований, сохраняющих форму равностороннего треугольника, до рисунков на обоях. В теории чисел мы рассматриваем только наборы элементов, содержащие целые числа, или функции, работающие с целыми числами.
Группы
Базовым понятием в математике является понятие множества элементов. Множество обычно обозначается знаками ударения, а элементы разделяются запятыми.
Например, множество всех целых чисел - \{..., -2, -1, 0, 1, 2, ...\}. Эллипсы здесь означают, что определенная закономерность продолжается в
определенном направлении. Таким образом, множество всех целых чисел также
включает 3, 4, 5, 6 и так
далее, а также 3, -4, -5, -6 и так далее. Это множество всех целых чисел обычно обозначается \mathbb{Z}.
Другой пример множества - \mathbb{Z} \mod 11, или множество всех целых чисел по модулю 11. В отличие от всего множества \mathbb{Z}, это
множество содержит только конечное число элементов, а именно \{0, 1, \ldots, 9, 10\}.
Частая ошибка - думать, что множество \mathbb{Z} \mod 11 на самом деле является \{-10, -9, \ldots, 0, \ldots, 9, 10\}. Но это не так, учитывая то, как мы определили операцию модуляции ранее.
Любые отрицательные целые числа, уменьшенные по модулю 11, сворачиваются в \{0, 1, \ldots, 9, 10\}. Например, выражение -2 \mod 11 сворачивается в 9, а
выражение -27 \mod 11 сворачивается в 5.
Еще одно базовое понятие в математике - бинарная операция. Это любая операция, при которой из двух элементов получается третий. Например, из основ арифметики и алгебры вам знакомы четыре фундаментальные бинарные операции: сложение, вычитание, умножение и деление.
Эти два базовых математических понятия, множества и бинарные операции, используются для определения понятия группы - самой важной структуры в абстрактной алгебре.
В частности, предположим некоторую бинарную операцию \circ. Кроме того, предположим некоторое множество элементов S,
оснащенное этой операцией. Все, что здесь означает "оснащен", это то, что
операция \circ может быть
выполнена между любыми двумя элементами из множества S.
Комбинация \langle \mathbf{S}, \circ \rangle является группой, если она удовлетворяет четырем
определенным условиям, известным как аксиомы группы.
Для любых
aиb, которые являются элементами\mathbf{S},a \circ bтакже является элементом\mathbf{S}. Это известно как условие закрытия.Для любых
a,bиc, являющихся элементами\mathbf{S}, справедливо утверждение, что(a \circ b) \circ c = a \circ (b \circ c). Это известно как условие ассоциативности.Существует единственный элемент
eв\mathbf{S}, такой, что для каждого элементаaв\mathbf{S}выполняется следующее уравнение:e \circ a = a \circ e = a. Поскольку существует только один такой элементe, он называется идентичным элементом. Это условие известно как условие тождества.Для каждого элемента
aв\mathbf{S}существует элементbв\mathbf{S}, такой, что выполняется следующее уравнение:a \circ b = b \circ a = e, гдеe- элемент тождества. Элементbздесь известен как обратный элемент, и его принято обозначать какa^{-1}. Это условие известно как обратное условие или условие инвертируемости.
Давайте изучим группы немного дальше. Обозначим множество всех целых чисел
через \mathbb{Z}.
Это множество в сочетании со стандартным сложением, или \langle \mathbb{Z}, + \rangle, явно подходит под определение группы, поскольку отвечает четырем
аксиомам, приведенным выше.
Для любых
xиy, которые являются элементами\mathbb{Z},x + yтакже являются элементами\mathbb{Z}. Значит,\langle \mathbb{Z}, + \rangleудовлетворяет условию замкнутости.Для любых
x,yиz, являющихся элементами\mathbb{Z},(x + y) + z = x + (y + z). Таким образом,\langle \mathbb{Z}, + \rangleудовлетворяет условию ассоциативности.В
\langle \mathbb{Z}, + \rangleсуществует элемент тождества, а именно 0. Для любогоxв\mathbb{Z}имеет место то, что:0 + x = x + 0 = x. Таким образом,\langle \mathbb{Z}, + \rangleудовлетворяет условию тождества.Наконец, для каждого элемента
xв\mathbb{Z}найдется такойy, чтоx + y = y + x = 0. Например, еслиxравно 10, тоyбудет равно-10(в случае, когдаxравно 0,yтакже равно 0). Значит,\langle \mathbb{Z}, + \rangleудовлетворяет обратному условию.
Важно отметить, что то, что множество целых чисел со сложением представляет
собой группу, не означает, что оно представляет собой группу с умножением. В
этом можно убедиться, проверив \langle \mathbb{Z}, \cdot \rangle на соответствие четырем аксиомам групп (где \cdot означает стандартное умножение).
Очевидно, что первые две аксиомы справедливы. Кроме того, при умножении
элемент 1 может служить элементом тождества. Любое целое число x, умноженное на 1, дает именно x. Однако \langle \mathbb{Z}, \cdot \rangle не удовлетворяет обратному условию. То есть для каждого x в \mathbb{Z} не
существует единственного элемента y в \mathbb{Z},
такого, что x \cdot y = 1.
Например, предположим, что x = 22. Какое значение y из
множества \mathbb{Z},
умноженное на x, даст элемент
тождества 1? Сработало бы значение 1/22, но его нет в множестве \mathbb{Z}.
Фактически, вы столкнетесь с этой проблемой для любого целого числа x, кроме значений 1 и -1 (где y должно быть равно 1 и -1 соответственно).
Если мы допустим для нашего множества вещественные числа, то наши проблемы в
значительной степени исчезнут. Для любого элемента x в наборе умножение на 1/x дает
1. Поскольку дроби входят в набор действительных чисел, для каждого действительного
числа можно найти обратное. Исключение составляет ноль, поскольку любое умножение
на ноль никогда не даст тождественного элемента 1. Следовательно, множество ненулевых
вещественных чисел, снабженных умножением, действительно является группой.
Некоторые группы удовлетворяют пятому общему условию, известному как условие коммутативности. Это условие заключается в следующем:
- Пусть есть группа
Gс множеством S и бинарным оператором\circ. Предположим, чтоaиbявляются элементами S. Если для любых двух элементовaиbиз S справедливо, чтоa \circ b = b \circ a, тоGудовлетворяет условию коммутативности.
Любая группа, удовлетворяющая условию коммутативности, называется коммутативной группой, или абелевой группой (в честь Нильса Хенрика Абеля). Легко убедиться, что множество вещественных чисел над сложением и множество целых чисел над умножением являются абелевыми группами. Множество целых чисел при умножении вообще не является группой, поэтому ipso facto не может быть абелевой группой. Множество ненулевых вещественных чисел при умножении, напротив, также является абелевой группой.
Вам следует обратить внимание на два важных условных обозначения. Во-первых, для обозначения групповых операций часто используются знаки "+" или "×", даже если элементы не являются числами. В этих случаях не следует понимать эти знаки как стандартное арифметическое сложение или умножение. Вместо этого они представляют собой операции, имеющие лишь абстрактное сходство с этими арифметическими операциями.
Если вы не имеете в виду арифметическое сложение или умножение, проще
использовать такие символы, как \circ и \diamond для групповых операций,
так как они не имеют слишком укоренившихся культурных коннотаций.
Во-вторых, по той же причине, по которой "+" и "×" часто используются для
обозначения неарифметических операций, тождественные элементы групп часто
обозначаются символами "0" и "1", даже если элементы в этих группах не
являются числами. Если вы не имеете в виду тождественный элемент группы с
числами, проще использовать более нейтральный символ, например "e", для обозначения тождественного элемента.
Множество различных и очень важных в математике наборов значений, оснащенных определенными бинарными операциями, являются группами. Криптографические приложения, однако, работают только с множествами целых чисел или, по крайней мере, с элементами, которые описываются целыми числами, то есть в пределах области теории чисел. Таким образом, множества с вещественными числами, отличными от целых чисел, не используются в криптографических приложениях.
В заключение приведем пример элементов, которые могут быть "описаны целыми числами", хотя они не являются целыми числами. Хороший пример - точки эллиптических кривых. Хотя любая точка на эллиптической кривой явно не является целым числом, такая точка действительно описывается двумя целыми числами.
Эллиптические кривые, например, имеют решающее значение для Bitcoin. Любая стандартная пара закрытых и открытых ключей Bitcoin выбирается из набора точек, определяемых следующей эллиптической кривой:
x^3 + 7 = y^2 \mod 2^{256} – 2^{32} – 29 – 28 – 27 – 26 - 24 - 1(наибольшее простое число, меньшее, чем 2^{256}). Координата x - это
закрытый ключ, а координата y - ваш открытый ключ.
Транзакции в Bitcoin обычно связаны с блокировкой выхода на один или несколько открытых ключей. Затем стоимость, полученная в результате этих транзакций, может быть разблокирована с помощью цифровых подписей с соответствующими закрытыми ключами.
Циклические группы
Основное различие можно провести между бесконечной и бесконечной группой. Первая имеет конечное число элементов, а вторая - бесконечное. Количество элементов в любой конечной группе называется порядком группы. Вся практическая криптография, связанная с использованием групп, опирается на конечные (теоретико-числовые) группы.
В криптографии с открытым ключом особое значение имеет определенный класс конечных абелевых групп, известных как циклические группы. Для того чтобы понять, что такое циклические группы, нам сначала нужно понять концепцию экспоненции элементов группы.
Пусть есть группа G с
групповой операцией \circ, и a - элемент G. Тогда выражение a^n следует интерпретировать как элемент a, объединенный с самим собой
в общей сложности n - 1 раз.
Например, a^2 означает a \circ a, a^3 - a \circ a \circ a, и так
далее. (Обратите внимание, что экспоненция здесь - это не обязательно
экспоненция в стандартном арифметическом смысле)
Обратимся к примеру. Предположим, что G = \langle \mathbb{Z} \mod 7, + \rangle, и что наше значение a равно 4. В этом случае a^2 = [4 + 4 \mod 7] = [8 \mod 7] = 1 \mod 7. В качестве альтернативы, a^4 будет представлять собой [4 + 4 + 4 + 4 \mod 7] = [16 \mod 7] = 2 \mod 7.
В некоторых абелевых группах есть один или несколько элементов, которые могут дать все остальные элементы группы путем продолжения экспоненты. Такие элементы называются генераторами или примитивными элементами.
Важным классом таких групп является \langle \mathbb{Z}^* \mod N, \cdot \rangle, где N - простое число.
Обозначение \mathbb{Z}^* здесь означает, что группа содержит все ненулевые положительные целые числа,
меньшие N. Поэтому такая
группа всегда имеет N - 1 элементов.
Рассмотрим, например, G = \langle \mathbb{Z}^* \mod 11, \cdot \rangle. Эта группа состоит из следующих элементов: \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. Порядок этой группы равен 10 (что действительно равно 11 - 1).
Давайте рассмотрим экспоненцию элемента 2 из этой группы. Вычисления до 2^{12} показаны ниже. Обратите внимание, что в левой части уравнения экспонента относится
к экспоненте элемента группы. В нашем конкретном примере это действительно связано
с арифметическим экспоненцированием в правой части уравнения (но могло бы быть
и, например, со сложением). Чтобы прояснить ситуацию, я выписал повторную операцию,
а не форму экспоненты в правой части.
2^1 = 2 \mod 112^2 = 2 \cdot 2 \mod 11 = 4 \mod 112^3 = 2 \cdot 2 \cdot 2 \mod 11 = 8 \mod 112^4 = 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 16 \mod 11 = 5 \mod 112^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 32 \mod 11 = 10 \mod 112^6 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 64 \mod 11 = 9 \mod 112^7 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 128 \mod 11 = 7 \mod 112^8 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 256 \mod 11 = 3 \mod 112^9 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 512 \mod 11 = 6 \mod 112^{10} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 1024 \mod 11 = 1 \mod 112^{11} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 2048 \mod 11 = 2 \mod 112^{12} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 4096 \mod 11 = 4 \mod 11
Если внимательно присмотреться, то можно увидеть, что экспоненция элемента 2
проходит через все элементы \langle \mathbb{Z}^* \mod 11, \cdot \rangle в следующем порядке: 2, 4, 8, 5, 10, 9, 7, 3, 6, 1. После 2^{10} продолжение экспонирования элемента 2 снова проходит через все элементы и в
том же порядке. Следовательно, элемент 2 является генератором в \langle \mathbb{Z}^* \mod 11, \cdot \rangle.
Хотя \langle \mathbb{Z}^* \mod 11, \cdot \rangle имеет множество генераторов, не все элементы этой группы являются генераторами.
Рассмотрим, например, элемент 3. Пробежавшись по первым 10 экспонентам, не показывая
громоздких вычислений, мы получаем следующие результаты:
3^1 = 3 \mod 113^2 = 9 \mod 113^3 = 5 \mod 113^4 = 4 \mod 113^5 = 1 \mod 113^6 = 3 \mod 113^7 = 9 \mod 113^8 = 5 \mod 113^9 = 4 \mod 113^{10} = 1 \mod 11
Вместо того чтобы перебирать все значения в \langle \mathbb{Z}^* \mod 11, \cdot \rangle, экспоненция элемента 3 приводит только к подмножеству этих значений: 3,
9, 5, 4 и 1. После пятой экспоненты эти значения начинают повторяться.
Теперь мы можем определить циклическую группу как любую группу с хотя бы одним генератором. То есть существует хотя бы один элемент группы, из которого можно получить все остальные элементы группы путем экспоненцирования.
Возможно, вы заметили в нашем примере выше, что и 2^{10}, и 3^{10} равны 1 \mod 11. На самом деле,
хотя мы не будем производить вычисления, экспоненция на 10 любого элемента
группы \langle \mathbb{Z}^* \mod 11, \cdot \rangle даст 1 \mod 11. Почему так
происходит?
Это важный вопрос, но для ответа на него нужно потрудиться.
Для начала возьмем два положительных целых числа a и N. Важная теорема в теории
чисел гласит, что a имеет
мультипликативную обратную величину по модулю N (то есть целое число b такое,
что a \cdot b = 1 \mod N)
тогда и только тогда, когда наибольший общий делитель между a и N равен 1. То есть, если a и N являются копримами.
Таким образом, для любой группы целых чисел, оснащенной умножением по модулю N, в набор входят только меньшие копримы с N. Мы можем обозначить это
множество через \mathbb{Z}^c \mod N.
Например, предположим, что число N равно 10. Только целые числа 1, 3, 7 и 9 совпадают с 10. Поэтому множество \mathbb{Z}^c \mod 10 включает только \{1, 3, 7, 9\}. Вы
не можете создать группу с целочисленным умножением по модулю 10, используя
любые другие целые числа от 1 до 10. Для этой конкретной группы обратными
являются пары 1 и 9, а также 3 и 7.
В случае, когда N само по
себе простое, все целые числа от 1 до N - 1 являются копримами с N. Такая
группа, таким образом, имеет порядок N - 1. Используя наши прежние
обозначения, \mathbb{Z}^c \mod N равно \mathbb{Z}^* \mod N, когда N простое. Группа,
которую мы выбрали для нашего предыдущего примера, \langle \mathbb{Z}^* \mod 11, \cdot \rangle, является частным случаем этого класса групп.
Далее, функция \phi(N) вычисляет количество копримов до числа N и известна как функция Эйлера Phi. [1] Согласно теореме Эйлера, когда два целых числа a и N являются копримами, имеет
место следующее:
a^{\phi(N)} \mod N = 1 \mod N
Это имеет важное следствие для класса групп \langle \mathbb{Z}^* \mod N, \cdot \rangle, где N простое. Для этих
групп экспоненция элементов группы представляет собой арифметическую
экспоненцию. То есть, a^{\phi(N)} \mod N представляет собой арифметическую операцию a^{\phi(N)} \mod N.
Поскольку любой элемент a в
этих мультипликативных группах соизмерим с N, это означает, что a^{\phi(N)} \mod N = a^{N - 1} \mod N = 1 \mod N.
Теорема Эйлера - очень важный результат. Начнем с того, что из нее следует,
что все элементы в \langle \mathbb{Z}^* \mod N, \cdot \rangle могут циклически проходить только через такое число значений экспоненты,
которое делится на N - 1. В
случае \langle \mathbb{Z}^* \mod 11, \cdot \rangle, это означает, что каждый элемент может циклически пройти только через 2,
5 или 10 элементов. Группа значений, через которую циклически проходит любой
элемент при экспоненте, называется порядком элемента.
Элемент с порядком, эквивалентным порядку группы, является генератором.
Кроме того, из теоремы Эйлера следует, что мы всегда можем узнать результат a^{N - 1} \mod N для любой группы \langle \mathbb{Z}^* \mod N, \cdot \rangle, где N простое. Это так, независимо
от того, насколько сложными могут быть фактические вычисления.
Например, предположим, что наша группа - это \mathbb{Z}^* \mod 160 481 182 (где 160 481 182 - действительно простое число). Мы знаем, что все целые
числа от 1 до 160 481 181 должны быть элементами этой группы, и что \phi(n) = 160 481 181. Хотя
мы не можем выполнить все вычисления, мы знаем, что такие выражения, как 514^{160,481,181}, 2,005^{160,481,181} и 256,212^{160,481,181} должны равняться 1 \mod 160,481,182.
Примечания:
[1] Функция работает следующим образом. Любое целое число N можно разложить в произведение простых чисел. Предположим, что конкретное N разлагается следующим образом: p_1^{e1} \cdot p_2^{e2} \cdot \ldots \cdot
p_m^{em}, где все p - простые числа,
а все e - целые числа, большие
или равные 1. Тогда:
\phi(N) = \sum_{i=1}^m \left[p_i^{e_i} - p_i^{e_i - 1}\right]Формула функции Phi Эйлера для простой факторизации N.
Поля
Группа - это основная алгебраическая структура в абстрактной алгебре, но существует множество других. Единственная алгебраическая структура, с которой вы должны быть знакомы, - это поле, в частности бесконечное поле. Этот тип алгебраической структуры часто используется в криптографии, например, в Advanced Encryption Standard. Последний является основной схемой симметричного шифрования, с которой вы столкнетесь на практике.
Поле является производным от понятия группы. В частности, поле - это множество элементов S, снабженное двумя бинарными
операторами \circ и \diamond, которое
удовлетворяет следующим условиям:
Множество S, снабженное
\circ, является абелевой группой.Множество S, оснащенное
\diamond, является абелевой группой для "ненулевых" элементов.Множество S, снабженное двумя операторами, удовлетворяет так называемому условию дистрибутивности: Предположим, что
a,bиcявляются элементами S. Тогда S с двумя операторами удовлетворяет дистрибутивному свойству, еслиa \circ (b \diamond c) = (a \circ b) \diamond (a \circ c).
Обратите внимание, что, как и в случае с группами, определение поля является
очень абстрактным. Оно не содержит никаких утверждений ни о типах элементов
в S, ни об операциях \circ и \diamond. Оно просто
утверждает, что поле - это любое множество элементов с двумя операциями, для
которых выполняются три вышеприведенных условия. (Нулевой элемент во второй
абелевой группе может быть абстрактно интерпретирован)
Что же может быть примером поля? Хорошим примером является множество \mathbb{Z} \mod 7, или \{0, 1, \ldots, 7\}, определенное через стандартное сложение (вместо \circ выше) и стандартное умножение (вместо \diamond выше).
Во-первых, \mathbb{Z} \mod 7 удовлетворяет условию принадлежности к абелевой группе по сложению, а также
удовлетворяет условию принадлежности к абелевой группе по умножению, если рассматривать
только ненулевые элементы. Во-вторых, комбинация множества с двумя операторами
удовлетворяет условию дистрибутивности.
С дидактической точки зрения целесообразно исследовать эти утверждения на
примере некоторых конкретных значений. Возьмем экспериментальные значения 5,
2 и 3, некоторые случайно выбранные элементы из множества \mathbb{Z} \mod 7, для проверки поля \langle \mathbb{Z} \mod 7, +, \cdot \rangle. Мы будем использовать эти три значения по порядку, по мере необходимости
для изучения конкретных условий.
Давайте сначала выясним, является ли \mathbb{Z} \mod 7 с дополнением является абелевой группой.
Условие закрытия: Возьмем в качестве значений 5 и 2. Тогда
[5 + 2] \mod 7 = 7 \mod 7 = 0. Это действительно элемент\mathbb{Z} \mod 7, поэтому результат согласуется с условием закрытия.Условие ассоциативности: Возьмем в качестве значений 5, 2 и 3. Тогда
[(5 + 2) + 3] \mod 7 = [5 + (2 + 3)] \mod 7 = 10 \mod 7 = 3. Это соответствует условию ассоциативности.Условие идентичности: Возьмем 5 в качестве значения. В этом случае
[5 + 0] \mod 7 = [0 + 5] \mod 7 = 5. Таким образом, 0 является тождественным элементом для сложения.Инверсное условие: Рассмотрим обратное число от 5. Должно быть так, чтобы
[5 + d] \mod 7 = 0, при некотором значенииd. В этом случае единственное значение из\mathbb{Z} \mod 7, удовлетворяющее этому условию, равно 2.Условие коммутативности: Возьмем в качестве значений 5 и 3. Тогда
[5 + 3] \mod 7 = [3 + 5] \mod 7 = 1. Это соответствует условию коммутативности.
Множество \mathbb{Z} \mod 7, снабженное дополнением, очевидно, является абелевой группой. Теперь
давайте выясним, является ли \mathbb{Z} \mod 7,
оснащенное умножением, является абелевой группой для всех ненулевых
элементов.
Условие закрытия: Возьмем в качестве значений 5 и 2. Тогда
[5 \cdot 2] \mod 7 = 10 \mod 7 = 3. Это также элемент\mathbb{Z} \mod 7, поэтому результат согласуется с условием закрытия.Условие ассоциативности: Возьмем в качестве значений 5, 2 и 3. Тогда
[(5 \cdot 2) \cdot 3] \mod 7 = [5 \cdot (2 \cdot 3)] \mod 7 = 30 \mod 7 = 2. Это соответствует условию ассоциативности.Условие идентичности: Возьмем 5 в качестве значения. В этом случае
[5 \cdot 1] \mod 7 = [1 \cdot 5] \mod 7 = 5. Таким образом, 1 является тождественным элементом для умножения.Инверсное условие: Рассмотрим обратное число от 5. Должно быть так, чтобы
[5 \cdot d] \mod 7 = 1, для некоторого значенияd. Единственное значение из\mathbb{Z} \mod 7, удовлетворяющее этому условию, равно 3. Это соответствует обратному условию.Условие коммутативности: Возьмем в качестве значений 5 и 3. Тогда
[5 \cdot 3] \mod 7 = [3 \cdot 5] \mod 7 = 15 \mod 7 = 1. Это соответствует условию коммутативности.
Множество \mathbb{Z} \mod 7 явно удовлетворяет правилам абелевой группы, если его объединить со сложением
или умножением ненулевых элементов.
Наконец, этот набор в сочетании с обоими операторами, похоже, удовлетворяет
условию дистрибутивности. Возьмем в качестве значений 5, 2 и 3. Мы видим,
что [5 \cdot (2 + 3)] \mod 7 = [5 \cdot 2 + 5 \cdot 3] \mod 7 = 25 \mod 7 = 4.
Теперь мы убедились, что \mathbb{Z} \mod 7 со сложением и умножением удовлетворяет аксиомам для конечного поля при проверке
с определенными значениями. Конечно, мы можем показать это и в общем случае,
но не будем этого делать.
Ключевое различие заключается в двух типах полей: конечных и бесконечных.
К бесконечному полю относится поле, в котором множество S бесконечно велико. Примером бесконечного поля является множество
вещественных чисел \mathbb{R},
оснащенное сложением и умножением. Бесконечное поле**, также известное как
поле Галуа, - это поле, в котором множество S конечное. В нашем примере \langle \mathbb{Z} \mod 7, +, \cdot \rangle является конечным полем.
В криптографии нас в первую очередь интересуют конечные поля. В общем случае
можно показать, что конечное поле существует для некоторого множества
элементов S тогда и только тогда, когда оно имеет p^m элементов, где p - простое
число, а m - целое
положительное число, большее или равное единице. Другими словами, если
порядок некоторого множества S - простое число (p^m, где m = 1) или некоторая
простая мощность (p^m, где m > 1), то можно найти два
оператора \circ и \diamond, такие, что условия
для поля выполняются.
Если некоторое конечное поле имеет простое число элементов, то оно называется простым полем. Если число элементов в конечном поле является простым, то поле называется экстенсивным полем. В криптографии нас интересуют как простые, так и расширенные поля. [2]
Основные простые поля, представляющие интерес для криптографии, - это те, в
которых множество всех целых чисел модулируется некоторым простым числом, а
операторами являются стандартные сложение и умножение. К этому классу
конечных полей относятся \mathbb{Z} \mod 2, \mathbb{Z} \mod 3, \mathbb{Z} \mod 5, \mathbb{Z} \mod 7, \mathbb{Z} \mod 11, \mathbb{Z} \mod 13,
и так далее. Для любого простого поля \mathbb{Z} \mod p,
множество целых чисел этого поля выглядит следующим образом: \{0, 1, \ldots, p - 2, p - 1\}.
В криптографии нас также интересуют поля расширения, в частности, любые поля
с 2^m элементами, где m > 1. Такие конечные поля,
например, используются в шифре Rijndael, который лежит в основе Advanced
Encryption Standard. Хотя простые поля относительно интуитивно понятны, эти
поля расширения основания 2, вероятно, не для тех, кто не знаком с
абстрактной алгеброй.
Начнем с того, что любому набору целых чисел с элементами 2^m можно поставить в соответствие два оператора, которые сделают их комбинацию
полем (при условии, что m - целое
положительное число). Однако то, что поле существует, вовсе не означает, что
его легко обнаружить или что оно особенно практично для определенных приложений.
Как выяснилось, в криптографии особенно применимы поля расширения 2^m, определенные над определенными наборами полиномиальных выражений, а не
над некоторым набором целых чисел.
Например, предположим, что нам нужно поле расширения с 2^3(то есть 8) элементами в наборе. Хотя для полей такого размера может
существовать множество различных наборов, один из таких наборов включает
все уникальные многочлены видаa_2x^2 + a_1x + a_0, где каждый коэффициентa_i$ равен либо 0, либо 1. Следовательно, это множество S включает следующие элементы:
0: Случай, когдаa_2 = 0,a_1 = 0иa_0 = 0.1: Случай, когдаa_2 = 0,a_1 = 0иa_0 = 1.x: Случай, когдаa_2 = 0,a_1 = 1иa_0 = 0.x + 1: Случай, когдаa_2 = 0,a_1 = 1иa_0 = 1.x^2: Случай, когдаa_2 = 1,a_1 = 0иa_0 = 0.x^2 + 1: Случай, когдаa_2 = 1,a_1 = 0иa_0 = 1.x^2 + x: Случай, когдаa_2 = 1,a_1 = 1иa_0 = 0.x^2 + x + 1: Случай, когдаa_2 = 1,a_1 = 1иa_0 = 1.
Таким образом, S будет множеством \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}. Какие две операции можно определить над этим набором элементов, чтобы их
комбинация была полем?
Первая операция над множеством S (\circ) может быть определена как стандартное сложение многочленов по модулю 2.
Все, что вам нужно сделать, это сложить многочлены обычным образом, а затем
применить модулор 2 к каждому из коэффициентов полученного многочлена. Вот
несколько примеров:
[(x^2) + (x^2 + x + 1)] \mod 2 = [2x^2 + x + 1] \mod 2 = x + 1[(x^2 + x) + (x)] \mod 2 = [x^2 + 2x] \mod 2 = x^2[(x + 1) + (x^2 + x + 1)] \mod 2 = [x^2 + 2x + 2] \mod 2 = x^2 + 1
Вторая операция над множеством S (\diamond), которая необходима для создания поля, более сложная. Это своего рода
умножение, но не стандартное умножение из арифметики. Вместо этого вы должны
рассматривать каждый элемент как вектор и понимать операцию как умножение
этих двух векторов по модулю невыводимого многочлена.
Сначала обратимся к идее несводимого многочлена. Невыводимый многочлен** - это многочлен, который нельзя разложить на составляющие (так же как простое число нельзя разложить на составляющие, отличные от 1 и самого простого числа). Для наших целей нас интересуют полиномы, которые являются несводимыми относительно множества всех целых чисел. (Обратите внимание, что вы можете разложить некоторые многочлены, например, по действительным или комплексным числам, даже если вы не можете разложить их по целым числам)
Например, рассмотрим многочлен x^2 - 3x + 2. Его можно переписать как (x - 1)(x - 2).
Следовательно, он не является несводимым. Теперь рассмотрим многочлен x^2 + 1. Используя только
целые числа, это выражение невозможно разложить на множители. Следовательно,
это несводимый многочлен по отношению к целым числам.
Далее обратимся к понятию векторного умножения. Мы не будем углубленно рассматривать эту тему, но вам просто необходимо понять основное правило: Любое векторное деление может иметь место до тех пор, пока делимое имеет степень, большую или равную степени делителя. Если делимое имеет меньшую степень, чем делитель, то делимое уже не может делиться на делитель.
Например, рассмотрим выражение x^6 + x + 1 \mod x^5 + x^2. Оно явно уменьшается, так как степень делимого, 6, больше степени
делителя, 5. Теперь рассмотрим выражение x^5 + x + 1 \mod x^5 + x^2.
Оно также уменьшается, так как степени делимого и делителя 5 равны.
Однако теперь рассмотрим выражение x^4 + x + 1 \mod x^5 + x^2. Оно не сокращается дальше, так как степень делителя, 4, меньше степени
делимого, 5.
Основываясь на этой информации, мы готовы найти вторую операцию для
множества \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.
Я уже говорил, что вторую операцию следует понимать как умножение векторов по модулю некоторого несводимого многочлена. Этот несводимый многочлен должен гарантировать, что вторая операция определяет абелеву группу над S и согласуется с условием дистрибутивности. Каким же должен быть этот несводимый многочлен?
Поскольку все векторы в наборе имеют степень 2 или ниже, то невыводимый многочлен должен быть степени 3. Если при умножении двух векторов в наборе получается многочлен степени 3 или выше, то мы знаем, что по модулю многочлен степени 3 всегда дает многочлен степени 2 или ниже. Это так, потому что любой многочлен степени 3 или выше всегда делится на многочлен степени 3. Кроме того, многочлен, выступающий в роли делителя, должен быть несводимым.
Оказывается, существует несколько несводимых многочленов степени 3, которые
мы могли бы использовать в качестве делителя. Каждый из этих многочленов
определяет свое поле в сочетании с нашим множеством S и
сложением по модулю 2. Это означает, что у вас есть несколько вариантов
использования полей расширения 2^m в криптографии.
Для примера выберем многочлен x^3 + x + 1. Он действительно является несводимым, поскольку его нельзя разложить на
множители, используя целые числа. Кроме того, он гарантирует, что любое
умножение двух элементов даст многочлен степени 2 или меньше.
Давайте рассмотрим пример второй операции, используя многочлен x^3 + x + 1 в качестве делителя, чтобы проиллюстрировать, как она работает. Предположим,
что вы умножаете элементы x^2 + 1 на x^2 + x в нашем множестве S. Тогда нам нужно вычислить выражение [(x^2 + 1)\cdot (x^2 + x)] \mod x^3 + x + 1. Это можно упростить следующим образом:
[(x^2 + 1)\cdot (x^2 + x)] \mod x^3 + x + 1 =[x^2 \cdot x^2 + x^2 \cdot x + 1 \cdot x^2 + 1 \cdot x] \mod x^3 + x + 1 =[x^4 + x^3 + x^2 + x] \mod x^3 + x + 1
Мы знаем, что [x^4 + x^3 + x^2 + x] \mod x^3 + x + 1 можно сократить, так как делимое имеет более высокую степень (4), чем делитель
(3).
Для начала вы увидите, что выражение x^3 + x + 1 переходит в x^4 + x^3 + x^2 + x в общей сложности x раз. Вы
можете убедиться в этом, умножив x^3 + x + 1 на x, что составляет x^4 + x^2 + x. Поскольку
последний член имеет ту же степень, что и делитель, а именно 4, мы знаем,
что это работает. Остаток от деления на x можно вычислить следующим образом:
[(x^4 + x^3 + x^2 + x) - (x^4 + x^2 + x)] \mod x^3 + x + 1 =[x^3] \mod x^3 + x + 1 =x^3
Таким образом, после деления x^4 + x^3 + x^2 + x на x^3 + x + 1 в общей
сложности x раз, у нас есть
остаток x^3. Можно ли его
разделить еще на x^3 + x + 1?
Интуитивно может показаться привлекательным сказать, что x^3 больше нельзя делить на x^3 + x + 1, потому что
последний член кажется больше. Однако вспомните нашу дискуссию о делении
векторов. Пока делитель имеет степень, большую или равную делимому,
выражение можно сократить. В частности, выражение x^3 + x + 1 может перейти в x^3 ровно 1 раз.
Остаток вычисляется следующим образом:
[(x^3) - (x^3 + x + 1)] \mod x^3 + x + 1 = [x + 1] \mod x^3 + x + 1 = x + 1Вам может быть интересно, почему (x^3) - (x^3 + x + 1) оценивается в x + 1, а не в -x - 1. Помните, что первая
операция нашего поля определена по модулю 2. Следовательно, вычитание двух
векторов дает точно такой же результат, как и сложение двух векторов.
Суммируем умножение x^2 + 1 и x^2 + x: При умножении этих
двух членов получается многочлен степени 4, x^4 + x^3 + x^2 + x, который
нужно сократить по модулю x^3 + x + 1. Многочлен
степени 4 делится на x^3 + x + 1 ровно x + 1 раз. Остаток
после деления x^4 + x^3 + x^2 + x на x^3 + x + 1 ровно x + 1 раз равен x + 1. Это
действительно элемент нашего множества \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.
Почему расширение полей с основанием 2 над наборами многочленов, как в примере выше, может быть полезно для криптографии? Причина в том, что коэффициенты в многочленах таких наборов, равные 0 или 1, можно рассматривать как элементы двоичных строк определенной длины. Например, множество S в нашем примере выше можно рассматривать как множество S, включающее все двоичные строки длины 3 (от 000 до 111). Тогда операции над S также могут быть использованы для выполнения операций над этими двоичными строками и получения двоичной строки той же длины.
Примечания:
[2] Поля расширения оказываются весьма контринтуитивными. Вместо элементов из целых чисел они содержат наборы многочленов. Кроме того, любые операции выполняются по модулю некоторого несводимого многочлена.
Абстрактная алгебра на практике
Несмотря на формальный язык и абстрактность обсуждения, понятие группы не должно быть слишком сложным для понимания. Это просто набор элементов вместе с бинарной операцией, где выполнение этой бинарной операции над этими элементами удовлетворяет четырем общим условиям. Абелева группа просто имеет дополнительное условие, известное как коммутативность. Циклическая группа, в свою очередь, является особым видом абелевой группы, а именно той, которая имеет генератор. Поле - это просто более сложная конструкция из базового понятия группы.
Но если вы человек практичный, вы можете задаться вопросом: А какая разница? Имеет ли какое-либо значение в реальном мире знание того, что некоторый набор элементов с оператором является группой, или даже абелевой или циклической группой? А знание того, что что-то является полем?
Не вдаваясь в излишние подробности, ответ - "да". Впервые группы были созданы в XIX веке французским математиком Эваристом Галуа. Он использовал их, чтобы сделать выводы о решении полиномиальных уравнений степени выше пяти.
С тех пор понятие группы помогло пролить свет на ряд проблем в математике и других областях. На их основе, например, физик Мюррей-Геллман смог предсказать существование частицы до того, как она была замечена в экспериментах. [3] Например, химики используют теорию групп для классификации форм молекул. Математики даже использовали понятие группы, чтобы сделать выводы о такой конкретной вещи, как обои!
По сути, показать, что набор элементов с некоторым оператором является группой, означает, что то, что вы описываете, обладает определенной симметрией. Не симметрия в обычном понимании этого слова, а более абстрактная форма. И это может дать существенное представление о конкретных системах и проблемах. Более сложные понятия из абстрактной алгебры просто дают нам дополнительную информацию.
Самое главное, вы увидите важность теоретико-числовых групп и полей на практике через их применение в криптографии, особенно в криптографии с открытым ключом. При обсуждении полей мы уже видели, например, как поля расширения используются в шифре Rijndael. Мы разберем этот пример в главе 5.
Для дальнейшего обсуждения абстрактной алгебры я бы рекомендовал отличную серию видео по абстрактной алгебре от Socratica. [4] Я бы особенно рекомендовал следующие видео: "Что такое абстрактная алгебра?", "Определение группы (расширенное)", "Определение кольца (расширенное)" и "Определение поля (расширенное)" Эти четыре видеоролика дадут вам дополнительное представление о многом из того, что обсуждалось выше. (Мы не обсуждали кольца, но поле - это просто особый тип кольца)
Для дальнейшего обсуждения современной теории чисел вы можете обратиться к многим продвинутым дискуссиям по криптографии. Я бы предложил для дальнейшего обсуждения книгу Джонатана Каца и Иегуды Линделла "Введение в современную криптографию" или книгу Кристофа Паара и Яна Пельцля "Понимание криптографии". [5]
Примечания:
[3] Смотрите Видео YouTube
[4] Socratica, Абстрактная алгебра
[5] Katz and Lindell, Introduction to Modern Cryptography, 2nd edn, 2015 (CRC Press: Boca Raton, FL). Paar and Pelzl, Understanding Cryptography, 2010 (Springer-Verlag: Berlin).
Симметричная криптография
Алиса и Боб
Одной из двух основных ветвей криптографии является симметричная криптография. Она включает в себя схемы шифрования, а также схемы, связанные с аутентификацией и целостностью. До 1970-х годов вся криптография состояла из схем симметричного шифрования.
Основное обсуждение начинается с рассмотрения схем симметричного шифрования и проведения важного различия между потоковыми и блочными шифрами. Затем мы переходим к кодам аутентификации сообщений, которые представляют собой схемы обеспечения целостности и подлинности сообщений. Наконец, мы исследуем, как симметричные схемы шифрования и коды аутентификации сообщений могут быть объединены для обеспечения безопасной связи.
В этой главе вскользь рассматриваются различные симметричные криптографические схемы из практики. В следующей главе подробно рассматривается шифрование с помощью потокового и блочного шифров, а именно RC4 и AES соответственно.
Прежде чем начать обсуждение симметричной криптографии, я хочу сделать несколько замечаний по поводу иллюстраций Алисы и Боба в этой и последующих главах.
Иллюстрируя принципы криптографии, люди часто опираются на примеры с участием Алисы и Боба. Я тоже буду это делать.
Особенно если вы новичок в криптографии, важно понимать, что эти примеры Алисы и Боба служат лишь иллюстрацией криптографических принципов и конструкций в упрощенной среде. Однако эти принципы и конструкции применимы к гораздо более широкому кругу реальных ситуаций.
Ниже приведены пять ключевых моментов, которые следует учитывать при рассмотрении примеров с участием Алисы и Боба в криптографии:
Их можно легко перенести на примеры с другими типами действующих лиц, такими как компании или государственные организации.
Их можно легко расширить, включив в них трех и более актеров.
В примерах Боб и Алиса обычно активно участвуют в создании каждого сообщения и в применении к нему криптографических схем. Но в реальности электронные коммуникации в значительной степени автоматизированы. Например, когда вы посещаете веб-сайт, использующий защиту транспортного уровня, криптографией обычно занимаются ваш компьютер и веб-сервер.
В контексте электронной коммуникации "сообщения", которые передаются по каналу связи, обычно представляют собой пакеты TCP/IP. Они могут относиться к электронной почте, сообщению в Facebook, телефонному разговору, передаче файлов, веб-сайту, загрузке программного обеспечения и так далее. Они не являются сообщениями в традиционном смысле этого слова. Тем не менее, криптографы часто упрощают эту реальность, заявляя, что сообщение - это, например, электронная почта.
Примеры, как правило, посвящены электронной коммуникации, но их можно распространить и на традиционные формы общения, такие как письма.
Симметричные схемы шифрования
Мы можем дать свободное определение симметричной схемы шифрования как любой криптографической схемы с тремя алгоритмами:
Алгоритм генерации ключей, который генерирует закрытый ключ.
Алгоритм шифрования, который принимает на вход закрытый ключ и открытый текст и выдает на выходе шифротекст.
Алгоритм дешифрования, который принимает на вход закрытый ключ и шифртекст и выдает исходный открытый текст.
Как правило, схема шифрования - симметричная или асимметричная - предлагает шаблон для шифрования на основе основного алгоритма, а не точную спецификацию.
Например, рассмотрим Salsa20, схему симметричного шифрования. Она может использоваться как со 128-, так и с 256-битной длиной ключа. Выбор длины ключа влияет на некоторые мелкие детали алгоритма (точнее, на количество раундов в алгоритме).
Но нельзя сказать, что использование Salsa20 со 128-битным ключом - это другая схема шифрования, чем Salsa20 с 256-битным ключом. Основной алгоритм остается неизменным. Только когда основной алгоритм меняется, мы можем говорить о двух разных схемах шифрования.
Схемы симметричного шифрования обычно полезны в двух случаях: (1) когда два или более агента общаются на расстоянии и хотят сохранить содержимое своих сообщений в тайне; и (2) когда один агент хочет сохранить содержимое сообщения в тайне на протяжении всего времени.
Изображение ситуации (1) можно увидеть на Рисунке 1 ниже. Боб хочет
отправить Алисе сообщение M на
расстояние, но не хочет, чтобы другие могли прочитать это сообщение.
Сначала Боб шифрует сообщение M с помощью закрытого ключа K.
Затем он отправляет шифротекст C Алисе. Получив шифротекст, Алиса может расшифровать его с помощью ключа K и прочитать открытый текст. При хорошей схеме шифрования любой
злоумышленник, перехвативший шифротекст C, не сможет узнать ничего
действительно важного о сообщении M.
Изображение ситуации (2) можно увидеть на Рисунке 2 ниже. Боб хочет запретить другим просматривать определенную информацию. Типичная ситуация может заключаться в том, что Боб - сотрудник, хранящий на своем компьютере конфиденциальные данные, которые не должны читать ни посторонние, ни его коллеги.
Боб шифрует сообщение M в
момент времени T_0 с помощью
ключа K, чтобы получить
шифротекст C. В момент
времени T_1 ему снова нужно
это сообщение, и он расшифровывает шифротекст C с помощью ключа K. Любой
злоумышленник, которому за это время мог попасться шифротекст C, не должен был выудить из
него ничего существенного о M.
Рисунок 1: Секретность в пространстве

Рисунок 2: Секретность во времени

Пример: Шифр сдвига
В главе 2 мы познакомились с шифром сдвига, который является примером очень простой схемы симметричного шифрования. Давайте рассмотрим ее еще раз.
Предположим, что существует словарь D, который приравнивает все
буквы английского алфавита по порядку к набору чисел \{0,1,2,\dots,25\}.
Предположим, что существует множество возможных сообщений M. Тогда шифр сдвига - это схема шифрования, определяемая
следующим образом:
- Выберите случайным образом ключ
kиз множества возможных ключей K, где K =\{0,1,2,\dots,25\} - Зашифруйте сообщение
m \inM следующим образом:- Разделите
mна отдельные буквыm_0, m_1,\dots, m_i, \dots, m_l - Преобразуйте каждое
m_iв число в соответствии с D - Для каждого
m_i,c_i = [(m_i + k)\mod 26] - Преобразуйте каждый
c_iв букву в соответствии с D - Затем объедините
c_0, c_1,\dots, c_l, чтобы получить шифротекстc
- Разделите
- Расшифруйте шифротекст
cследующим образом:- Преобразуйте каждый
c_iв число в соответствии с D - Для каждого
c_i,m_i = [(c_i - k)\mod 26] - Преобразуйте каждый
m_iв букву в соответствии с D - Затем объедините
m_0, m_1,\dots, m_l, чтобы получить исходное сообщениеm
- Преобразуйте каждый
Шифр сдвига относится к симметричным схемам шифрования потому, что один и тот же ключ используется как для шифрования, так и для дешифрования. Например, предположим, что вы хотите зашифровать сообщение "DOG" с помощью шифра сдвига, а в качестве ключа наугад выбрали "24". Зашифровав сообщение с помощью этого ключа, вы получите "BME". Единственный способ получить исходное сообщение - использовать тот же ключ "24" для расшифровки.
Этот шифр Шифта является примером моноалфавитного подстановочного шифра: схемы шифрования, в которой алфавит шифротекста фиксирован (т.е. используется только один алфавит). Если предположить, что алгоритм расшифровки детерминирован, то каждый символ в подстановочном шифротексте может соответствовать не более чем одному символу в открытом тексте.
До 1700-х годов многие приложения шифрования в значительной степени опирались на моноалфавитные подстановочные шифры, хотя зачастую они были гораздо сложнее, чем шифр Шифта. Например, можно было случайным образом выбрать букву из алфавита для каждой буквы оригинального текста при ограничении, что каждая буква встречается в алфавите шифротекста только один раз. Это означает, что у вас будет факториал 26 возможных закрытых ключей, что было огромной величиной в докомпьютерную эпоху.
Обратите внимание, что в криптографии вы часто встречаете термин шифр. Имейте в виду, что у этого термина есть разные значения. На самом деле, я знаю как минимум пять различных значений этого термина в криптографии.
В некоторых случаях он относится к схеме шифрования, как, например, в шифре Шифта и моноалфавитном подстановочном шифре. Однако этот термин может относиться и к алгоритму шифрования, закрытому ключу или просто к шифртексту любой такой схемы шифрования.
Наконец, термин "шифр" может также означать основной алгоритм, на основе которого можно строить криптографические схемы. К ним могут относиться различные алгоритмы шифрования, а также другие типы криптографических схем. Этот смысл термина становится актуальным в контексте блочных шифров (см. раздел "Блочные шифры" ниже).
Вы также можете встретить термины шифровать или дешифровать. Эти термины - всего лишь синонимы шифрования и дешифрования.
Атаки методом грубой силы и принцип Керкхоффа
Шифр сдвига - очень ненадежная схема симметричного шифрования, по крайней мере в современном мире. [1] Злоумышленник может просто попытаться расшифровать любой шифротекст с помощью всех 26 возможных ключей, чтобы увидеть, какой результат имеет смысл. Такой тип атаки, когда злоумышленник просто перебирает ключи, чтобы посмотреть, что получится, известен как атака грубой силы или исчерпывающий поиск ключей.
Чтобы любая схема шифрования удовлетворяла минимальному понятию безопасности, она должна иметь набор возможных ключей, или пространство ключей, настолько большой, чтобы атаки методом перебора были неосуществимы. Все современные схемы шифрования отвечают этому стандарту. Он известен как принцип достаточного пространства ключей. Аналогичный принцип обычно применяется в различных типах криптографических схем.
Чтобы понять, насколько велики размеры ключевого пространства в современных
схемах шифрования, предположим, что файл был зашифрован 128-битным ключом с
использованием расширенного стандарта шифрования. Это означает, что у
злоумышленника есть набор ключей размером 2^{128}, которые ему нужно перебрать для атаки методом грубой силы. Для успеха в
0,78% при использовании этой стратегии злоумышленнику потребуется перебрать
примерно 2,65 \times 10^{36} ключей.
Оптимистично предположим, что злоумышленник может пробовать 10^{16} ключей в секунду (т.е. 10 квадриллионов ключей в секунду). Чтобы проверить
0,78 % всех ключей в пространстве ключей, ее атака должна длиться 2,65 \times 10^{20} секунд. Это примерно 8,4 триллиона лет. Таким образом, даже атака грубой силой
со стороны абсурдно мощного противника нереальна для современной 128-битной схемы
шифрования. Это и есть принцип достаточного ключевого пространства.
Является ли шифр сдвига более безопасным, если злоумышленник не знает алгоритма шифрования? Возможно, но не намного.
В любом случае, современная криптография всегда исходит из того, что безопасность любой симметричной схемы шифрования зависит только от сохранения в тайне закрытого ключа. Предполагается, что злоумышленнику известны все остальные детали, включая пространство сообщений, пространство ключей, пространство шифротекстов, алгоритм выбора ключа, алгоритм шифрования и алгоритм дешифрования.
Идея о том, что безопасность симметричной схемы шифрования может зависеть только от секретности закрытого ключа, известна как принцип Керкхоффа.
По первоначальному замыслу Керкхоффа, этот принцип применим только к схемам симметричного шифрования. Однако более общая версия принципа применима и ко всем другим современным типам криптографических схем: Для того чтобы любая криптографическая схема была безопасной, ее конструкция не должна быть секретной; секретность может распространяться только на некоторые строки (строки) информации, как правило, на закрытый ключ.
Принцип Керкхоффса занимает центральное место в современной криптографии по четырем причинам. [2] Во-первых, существует лишь ограниченное количество криптографических схем для определенных типов приложений. Например, большинство современных приложений симметричного шифрования используют шифр Rijndael. Таким образом, ваша секретность в отношении дизайна схемы очень ограничена. Однако гораздо больше гибкости в том, чтобы держать в секрете некоторый закрытый ключ для шифра Rijndael.
Во-вторых, проще заменить какую-то строку информации, чем всю криптографическую схему. Предположим, что у всех сотрудников компании есть одно и то же программное обеспечение для шифрования, и у каждого из них есть закрытый ключ для конфиденциального общения. Компрометация ключей в этом сценарии - неприятность, но, по крайней мере, компания может сохранить программное обеспечение при таких нарушениях безопасности. Если бы компания полагалась на секретность схемы, то любое нарушение этой секретности потребовало бы замены всего программного обеспечения.
В-третьих, принцип Керкхоффса позволяет обеспечить стандартизацию и совместимость криптографических схем между пользователями. Это дает огромные преимущества в плане эффективности. Например, трудно представить, как миллионы людей могли бы безопасно подключаться к веб-серверам Google каждый день, если бы для обеспечения безопасности требовалось хранить криптографические схемы в секрете.
В-четвертых, принцип Керкхоффа позволяет публично проверять криптографические схемы. Такая проверка абсолютно необходима для создания безопасных криптографических схем. Например, основной базовый алгоритм симметричной криптографии, шифр Rijndael, стал результатом конкурса, организованного Национальным институтом стандартов и технологий в период с 1997 по 2000 год.
Любая система, которая пытается достичь безопасности за счет неизвестности, - это система, которая полагается на сохранение в тайне деталей своей разработки и/или реализации. В криптографии это, в частности, система, которая полагается на сохранение в тайне деталей конструкции криптографической схемы. Таким образом, безопасность за счет неизвестности прямо противоречит принципу Керкхоффа.
Способность открытости повышать качество и безопасность также распространяется на цифровой мир шире, чем просто криптография. Свободные дистрибутивы Linux с открытым исходным кодом, такие как Debian, например, обычно имеют ряд преимуществ перед аналогами Windows и MacOS в плане конфиденциальности, стабильности, безопасности и гибкости. Хотя это может быть вызвано множеством причин, наиболее важным принципом, вероятно, является то, что, как выразился Эрик Рэймонд в своем знаменитом эссе "Собор и базар", "при достаточном количестве глаз все ошибки неглубоки" [3] Именно этот принцип мудрости толпы обеспечил Linux самый значительный успех.
Никогда нельзя однозначно утверждать, что криптографическая схема является "безопасной" или "небезопасной" Вместо этого существуют различные понятия безопасности для криптографических схем. Каждое определение криптографической безопасности должно определять (1) цели безопасности, а также (2) возможности злоумышленника. Анализ криптографических схем в соответствии с одним или несколькими конкретными понятиями безопасности дает представление об их применении и ограничениях.
Хотя мы не будем вдаваться во все подробности различных понятий криптографической безопасности, вы должны знать, что два предположения являются вездесущими для всех современных криптографических представлений о безопасности, относящихся к симметричным и асимметричным схемам (и в той или иной форме к другим криптографическим примитивам):
- Знания злоумышленника о схеме соответствуют принципу Керкхоффса.
- Злоумышленник не может осуществить атаку грубой силой на схему. В частности, модели угроз криптографических представлений о безопасности обычно даже не допускают атак грубой силы, поскольку предполагают, что они не являются релевантными.
Примечания:
[1] Согласно Сеутониусу, шифр сдвига с постоянным значением ключа 3 использовался Юлием Цезарем в его военных сообщениях. Таким образом, A всегда становилось D, B - E, C - F и так далее. Эта версия шифра сдвига стала известна как шифр Цезаря (хотя на самом деле это не шифр в современном понимании этого слова, поскольку значение ключа постоянно). Шифр Цезаря мог быть безопасным в первом веке до нашей эры, если враги Рима не были знакомы с шифрованием. Но в наше время это явно не очень надежная схема.
[2] Jonathan Katz and Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), p. 7f.
[3] Эрик Реймонд, "Собор и базар", доклад был представлен на Linux Kongress, Вюрцбург, Германия (27 мая 1997 года). Существует несколько последующих версий, а также книга. Мои цитаты взяты со страницы 30 в книге: Eric Raymond, The Cathedral and the Bazaar: Размышления о Linux и Open Source случайного революционера, пересмотренное изд. (2001), O'Reilly: Себастополь, Калифорния.
Потоковые шифры
Схемы симметричного шифрования стандартно подразделяются на два типа: потоковые шифры и блочные шифры. Однако это различие вызывает некоторые затруднения, поскольку люди используют эти термины непоследовательно. В следующих нескольких разделах я изложу это различие так, как считаю нужным. Однако вы должны знать, что многие люди будут использовать эти термины несколько иначе, чем я излагаю.
Сначала обратимся к потоковым шифрам. Потоковый шифр** - это симметричная схема шифрования, в которой шифрование состоит из двух этапов.
Сначала с помощью закрытого ключа создается строка длиной с открытый текст. Эта строка называется keystream.
Затем поток ключей математически комбинируется с открытым текстом для
получения шифротекста. Обычно это сочетание представляет собой операцию XOR.
Для расшифровки можно просто изменить операцию на противоположную. (Обратите
внимание, что A \oplus B = B \oplus A в случае, когда A и B являются битовыми строками. Таким образом, порядок операции XOR в потоковом
шифре не имеет значения для результата. Это свойство известно как коммутативность)
Типичный потоковый шифр XOR изображен на Рисунке 3. Сначала вы
берете закрытый ключ K и
используете его для генерации потока ключей. Затем поток ключей объединяется
с открытым текстом с помощью операции XOR для получения шифротекста. Любой
агент, получивший шифротекст, может легко его расшифровать, если у него есть
ключ K. Для этого достаточно
создать поток ключей такой же длины, как и шифротекст, в соответствии с
заданной схемой процедурой и выполнить XOR с шифротекстом.
Рисунок 3: Потоковый шифр XOR
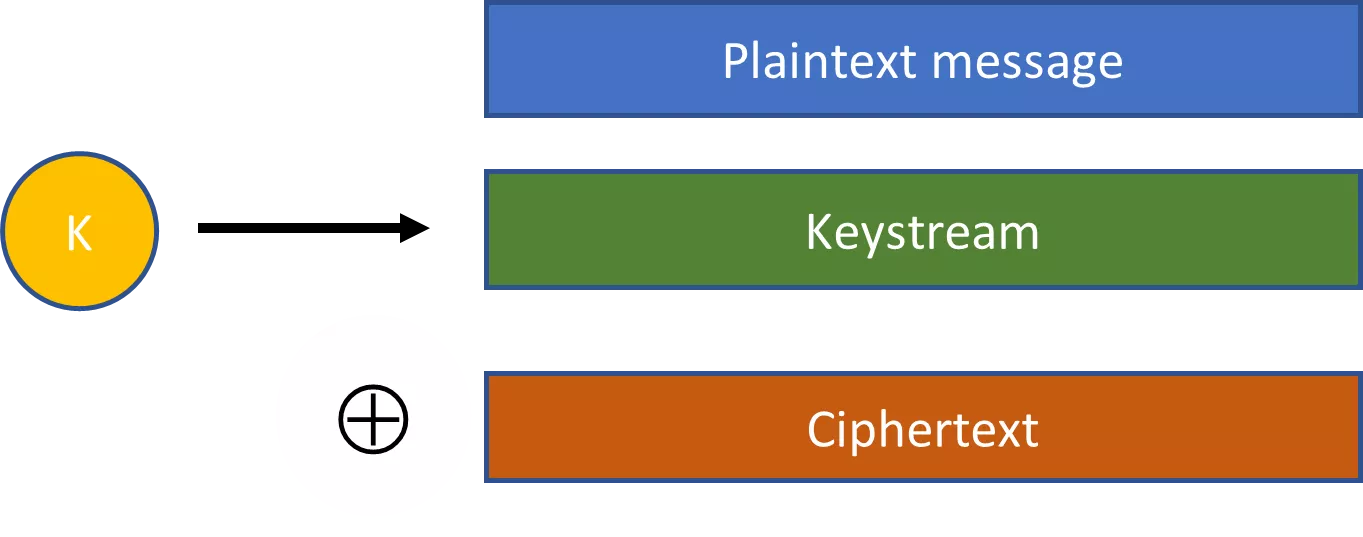
Помните, что схема шифрования - это, как правило, шаблон для шифрования с одним и тем же основным алгоритмом, а не точная спецификация. В свою очередь, потоковый шифр - это шаблон для шифрования, в котором можно использовать ключи разной длины. Хотя длина ключа может влиять на некоторые мелкие детали схемы, она не влияет на ее суть.
Шифр сдвига - это пример очень простого и небезопасного поточного шифра. Используя одну букву (закрытый ключ), вы можете получить строку букв длиной в сообщение (поток ключей). Затем этот поток ключей объединяется с открытым текстом с помощью операции модуляции для получения шифротекста. (Эта операция модуляции может быть упрощена до операции XOR при представлении букв в битах).
Другим известным примером потокового шифра является шифр Виженера, по имени Блеза де Виженера, который полностью разработал его в конце XVI века (хотя до него многое было сделано другими). Это пример полиалфавитного подстановочного шифра: схема шифрования, в которой алфавит шифротекста для символа открытого текста меняется в зависимости от его положения в тексте. В отличие от моноалфавитного подстановочного шифра, символы шифртекста могут быть связаны с более чем одним символом открытого текста.
По мере того как шифрование набирало популярность в Европе эпохи Возрождения, развивался и криптоанализ, то есть взлом шифртекстов, в частности, с помощью частотного анализа. Этот метод, использующий статистические закономерности нашего языка для взлома шифротекстов, был открыт арабскими учеными еще в IX веке. Эта техника особенно хорошо работает с длинными текстами. И даже самые сложные моноалфавитные подстановочные шифры к 1700-м годам в Европе перестали быть достаточными для борьбы с частотным анализом, особенно в военной сфере и в сфере безопасности. Поскольку шифр Виженера обеспечивал значительное повышение безопасности, он стал популярным в этот период и получил широкое распространение к концу 1700-х годов.
Неформально говоря, схема шифрования работает следующим образом:
Выберите многобуквенное слово в качестве закрытого ключа.
Для любого сообщения примените шифр сдвига к каждой букве сообщения, используя в качестве сдвига соответствующую букву в ключевом слове.
Если вы перебрали все ключевые слова, но все еще не полностью зашифровали открытый текст, снова примените буквы ключевого слова в качестве шифра сдвига к соответствующим буквам в оставшейся части текста.
Продолжайте этот процесс, пока все сообщение не будет зашифровано.
Для примера предположим, что ваш закрытый ключ - "GOLD", и вы хотите зашифровать сообщение "CRYPTOGRAPHY". В этом случае в соответствии с шифром Виженера вы поступите следующим образом:
c_0 = [(2 + 6)\mod 26] = 8 = Ic_1 = [(17 + 14)\mod 26] = 5 = Fc_2 = [(24 + 11)\mod 26] = 9 = Jc_3 = [(15 + 3)\mod 26] = 18 = Sc_4 = [(19 + 6)\mod 26] = 25 = Zc_5 = [(14 + 14)\mod 26] = 2 = Cc_6 = [(6 + 11)\mod 26] = 17 = Rc_7 = [(17 + 3)\mod 26] = 20 = Uc_8 = [(0 + 6)\mod 26] = 6 = Gc_9 = [(15 + 14)\mod 26] = 3 = Dc_{10} = [(7 + 11)\mod 26] = 18 = Sc_{11} = [(24 + 3)\mod 26] = 1 = B
Таким образом, шифротекст c =
"IFJSZCRUGDSB".
Другим известным примером потокового шифра является одноразовый блокнот. В одноразовом шифре вы просто создаете строку случайных битов длиной с открытое сообщение и получаете шифротекст с помощью операции XOR. Таким образом, закрытый ключ и поток ключей эквивалентны одноразовому шифру.
В то время как шифры Шифта и Виженера очень небезопасны в современную эпоху, одноразовый блокнот очень безопасен при правильном использовании. Вероятно, самым известным применением одноразового шифра было, по крайней мере до 1980-х годов, использование его для вашингтонско-московской горячей линии. [4]
Горячая линия - это прямая связь между Вашингтоном и Москвой для решения неотложных вопросов, которая была установлена после Кубинского ракетного кризиса. За прошедшие годы технология ее создания претерпела изменения. В настоящее время она включает в себя прямой оптоволоконный кабель, а также два спутниковых канала (для резервирования), которые позволяют обмениваться электронными и текстовыми сообщениями. Связь заканчивается в разных местах США. Известны такие конечные точки, как Пентагон, Белый дом и гора Рейвен-Рок. Вопреки распространенному мнению, горячая линия никогда не использовала телефоны.
По сути, схема одноразового блокнота работала следующим образом. И Вашингтон, и Москва имели два набора случайных чисел. Один набор случайных чисел, созданный русскими, относился к шифрованию и дешифрованию любых сообщений на русском языке. Один набор случайных чисел, созданный американцами, относился к шифрованию и дешифрованию любых сообщений на английском языке. Время от времени доверенные курьеры доставляли на другую сторону дополнительные случайные числа.
Вашингтон и Москва могли тайно общаться, используя эти случайные числа для создания одноразовых прокладок. Каждый раз, когда вам нужно было связаться, вы использовали следующую порцию случайных чисел для своего сообщения.
Несмотря на высокую степень безопасности, одноразовый блокнот имеет существенные практические ограничения: ключ должен быть таким же длинным, как и сообщение, и ни одна часть одноразового блокнота не может быть использована повторно. Это означает, что вам нужно отслеживать, где вы находитесь в одноразовом блокноте, хранить огромное количество битов и время от времени обмениваться случайными битами с вашими контрагентами. Как следствие, одноразовый блокнот не часто используется на практике.
Вместо этого на практике преобладают псевдослучайные потоковые шифры. Salsa20 и близкий к нему вариант под названием ChaCha являются примерами широко используемых псевдослучайных потоковых шифров.
При использовании этих псевдослучайных потоковых шифров вы сначала случайным образом выбираете ключ K, длина которого меньше длины открытого текста. Такой случайный ключ K обычно создается нашим компьютером на основе непредсказуемых данных, которые он собирает с течением времени, например, времени между сетевыми сообщениями, движениями мыши и так далее.
Этот случайный ключ K затем вставляется
в алгоритм расширения, который создает псевдослучайный поток ключей такой же
длины, как и сообщение. Вы можете указать, какой именно длины должен быть поток
ключей (например, 500 бит, 1000 бит, 1200 бит, 29 117 бит и т. д.).
Псевдослучайный поток ключей выглядит так, как будто он был выбран совершенно случайно из множества всех строк одинаковой длины. Следовательно, шифрование с помощью псевдослучайного потока ключей выглядит так, как если бы оно было выполнено с помощью одноразового блокнота. Но это, конечно, не так.
Поскольку наш закрытый ключ короче потока ключей, а наш алгоритм расширения должен быть детерминированным, чтобы процесс шифрования/дешифрования работал, не каждый поток ключей такой длины мог бы стать выходом нашей операции расширения.
Предположим, например, что наш закрытый ключ имеет длину 128 бит и что мы
можем вставить его в расширительный алгоритм, чтобы создать гораздо более
длинный поток ключей, скажем, в 2 500 бит. Поскольку наш расширительный
алгоритм должен быть детерминированным, он может выбрать не более 1/2^{128} строк длиной 2 500 бит. Поэтому такой поток ключей никогда не может быть выбран
полностью случайным образом из всех строк одинаковой длины.
Наше определение потокового шифра состоит из двух аспектов: (1) поток ключей длиной до открытого текста генерируется с помощью закрытого ключа; и (2) этот поток ключей объединяется с открытым текстом, обычно с помощью операции XOR, для получения шифротекста.
Иногда условие (1) определяют более строго, утверждая, что поток ключей должен быть именно псевдослучайным. Это означает, что ни шифр сдвига, ни одноразовый блокнот не будут считаться потоковыми шифрами.
На мой взгляд, более широкое определение условия (1) обеспечивает более простой способ организации схем шифрования. Кроме того, это означает, что нам не придется перестать называть конкретную схему шифрования потоковым шифром только потому, что мы узнаем, что на самом деле она не опирается на псевдослучайные ключевые потоки.
Примечания:
[4] Crypto Museum, "Горячая линия Вашингтон-Москва", 2013, доступно на https://www.cryptomuseum.com/crypto/hotline/index.htm.
Блочные шифры
Первый способ, которым блочный шифр обычно понимается как нечто более примитивное, чем поточный шифр: Основной алгоритм, выполняющий сохраняющее длину преобразование строки подходящей длины с помощью ключа. Этот алгоритм может быть использован для создания схем шифрования и, возможно, других типов криптографических схем.
Часто блочный шифр может принимать на вход строки различной длины, например 64, 128 или 256 бит, а также ключи различной длины, например 128, 192 или 256 бит. Хотя некоторые детали алгоритма могут меняться в зависимости от этих переменных, основной алгоритм не меняется. Если бы это было так, мы бы говорили о двух разных блочных шифрах. Обратите внимание, что терминология основного алгоритма здесь такая же, как и для схем шифрования.
Принцип работы блочного шифра показан на рисунке 4* ниже. Сообщение M длины L и ключ K служат входами для блочного шифра. На выходе получается сообщение M' длины L. Для большинства
блочных шифров ключ не обязательно должен быть той же длины, что и M и M'.
Рисунок 4: Блочный шифр

Сам по себе блочный шифр не является схемой шифрования. Но блочный шифр может быть использован с различными режимами работы для создания различных схем шифрования. Режим работы просто добавляет некоторые дополнительные операции за пределами блочного шифра.
Чтобы проиллюстрировать, как это работает, предположим, что блочный шифр (БШ) требует 128-битной входной строки и 128-битного закрытого ключа. На рисунке 5 ниже показано, как этот блочный шифр может быть использован с режимом электронной кодовой книги (ECB mode) для создания схемы шифрования. (Многоточие справа указывает на то, что вы можете повторять эту схему столько, сколько потребуется).
Рисунок 5: Блочный шифр с режимом ECB
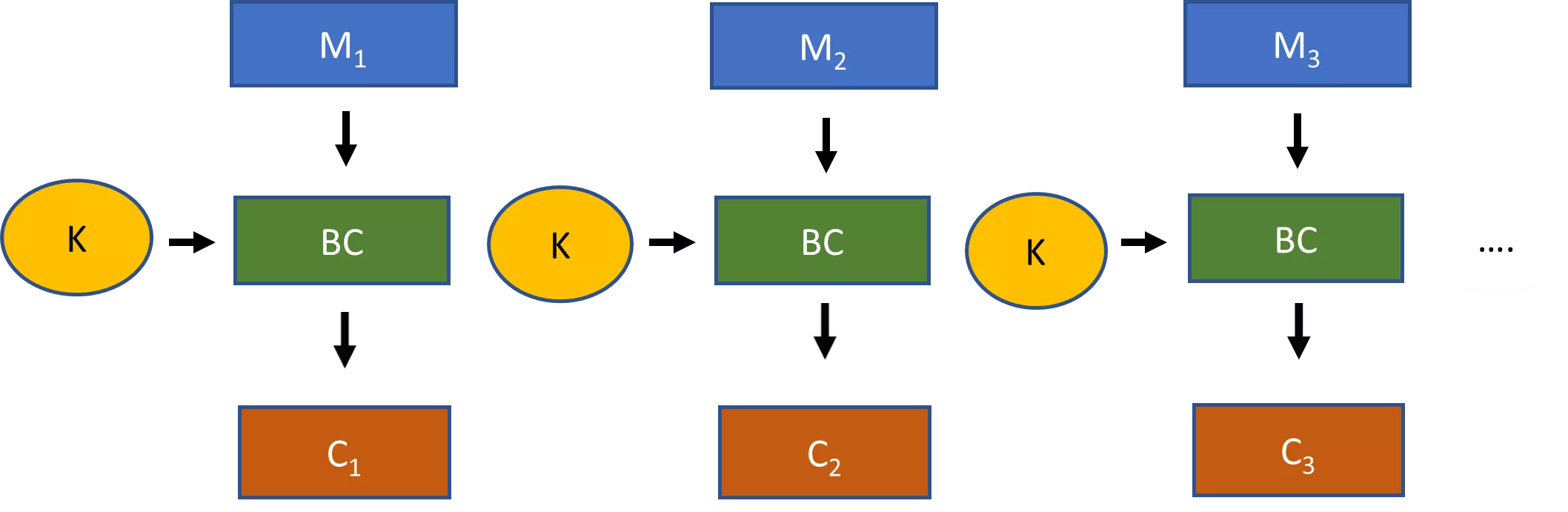
Процесс шифрования электронной кодовой книги с помощью блочного шифра выглядит следующим образом. Проверьте, можно ли разделить сообщение с открытым текстом на 128-битные блоки. Если нет, добавьте к сообщению падинг, чтобы результат можно было равномерно разделить на блок размером 128 бит. Это и есть ваши данные, используемые в процессе шифрования.
Теперь разделите данные на фрагменты 128-битных строк (M_1, M_2, M_3 и так далее). Пропустите каждую 128-битную строку через блочный шифр с вашим
128-битным ключом, чтобы получить 128-битные фрагменты шифротекста (C_1, C_2, C_3 и так далее). Эти фрагменты
при повторном объединении образуют полный шифротекст.
Расшифровка - это обратный процесс, хотя получателю нужен какой-то узнаваемый способ удалить из расшифрованных данных любую подложку, чтобы получить оригинальное сообщение с открытым текстом.
Несмотря на относительную простоту, блочный шифр с режимом электронной кодовой книги не обладает достаточной безопасностью. Это связано с тем, что он приводит к детерминированному шифрованию. Любые две одинаковые 128-битные строки данных шифруются одинаково. Эта информация может быть использована.
Вместо этого любая схема шифрования, построенная на основе блочного шифра,
должна быть вероятностной: то есть шифрование любого
сообщения M или любого
конкретного фрагмента M должно
каждый раз приводить к разным результатам. [5]
Режим цепления блоков шифра (CBC-режим) - это, пожалуй, самый распространенный режим, используемый с блочным шифром. При правильном сочетании получается вероятностная схема шифрования. Изображение этого режима работы можно увидеть на Рисунке 6 ниже.
Рисунок 6: Блочный шифр с режимом CBC
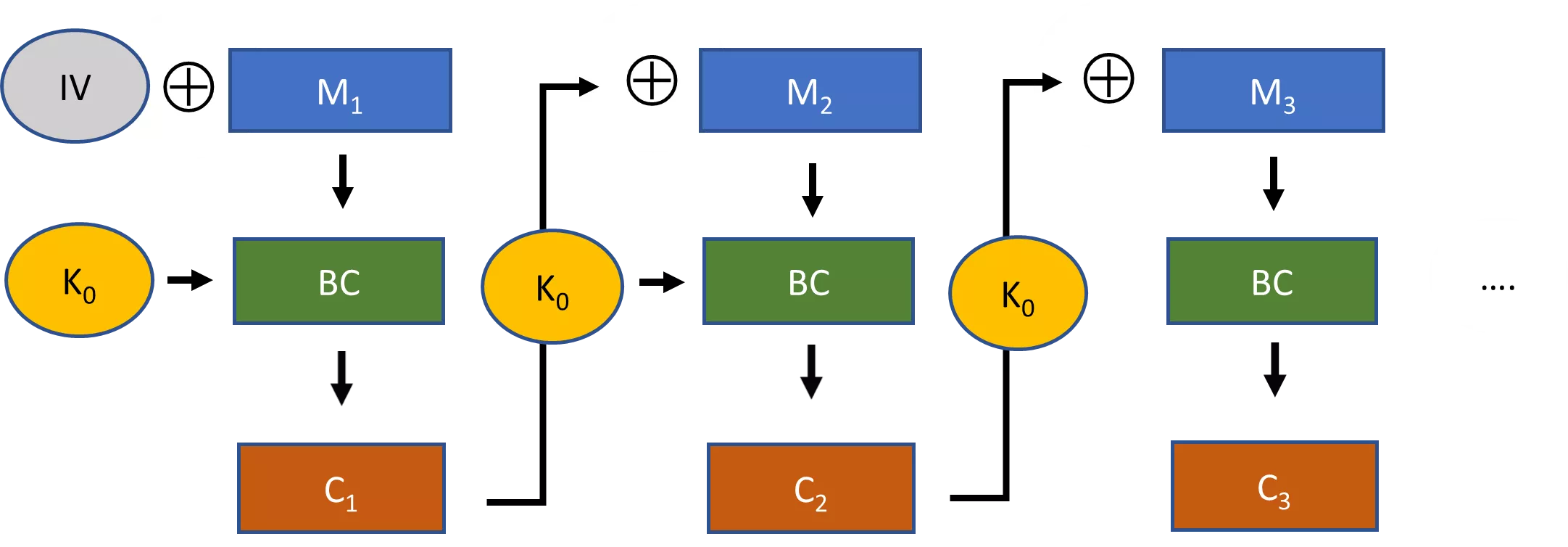
Предположим, что размер блока снова равен 128 битам. Для начала вам снова нужно убедиться, что исходное сообщение с открытым текстом получило необходимую прокладку.
Затем вы XORируете первую 128-битную часть открытого текста с вектором инициализации из 128 бит. Результат помещается в блочный шифр для получения шифротекста первого блока. Для второго блока из 128 бит сначала выполняется XOR открытого текста с шифртекстом из первого блока, а затем он помещается в блочный шифр. Этот процесс продолжается до тех пор, пока не будет зашифровано все сообщение с открытым текстом.
После завершения вы отправляете зашифрованное сообщение вместе с незашифрованным вектором инициализации получателю. Получатель должен знать вектор инициализации, иначе он не сможет расшифровать шифрованный текст.
При правильном использовании эта конструкция гораздо надежнее, чем режим электронной кодовой книги. Прежде всего, необходимо убедиться, что вектор инициализации является случайной или псевдослучайной строкой. Кроме того, при каждом использовании этой схемы шифрования следует применять другой вектор инициализации.
Другими словами, вектор инициализации должен быть случайным или псевдослучайным nonce, где nonce означает "число, которое используется только один раз" Если вы будете придерживаться этой практики, то режим CBC с блочным шифром гарантирует, что любые два одинаковых блока открытого текста будут каждый раз зашифрованы по-разному.
Наконец, обратим внимание на режим обратной связи по выходу (OFB mode). Изображение этого режима можно увидеть на Рисунке 7.
Рисунок 7: Блочный шифр с режимом OFB
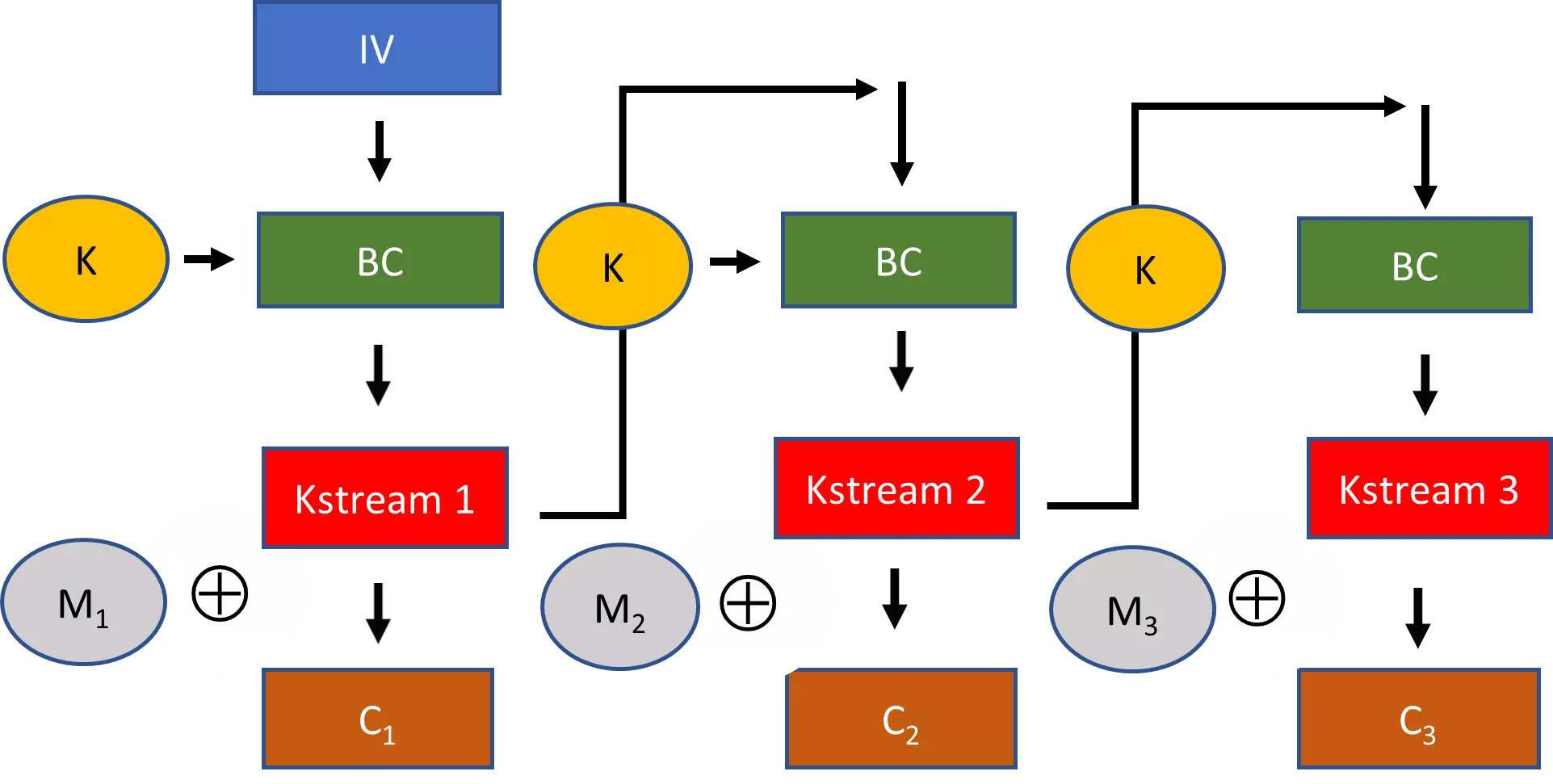
В режиме OFB вы также выбираете вектор инициализации. Но здесь для первого блока вектор инициализации непосредственно вставляется в блочный шифр вместе с вашим ключом. Полученные 128 бит рассматриваются как поток ключей. Этот поток ключей переписывается с открытым текстом, чтобы получить шифротекст для блока. Для последующих блоков вы используете поток ключей из предыдущего блока в качестве входа в блочный шифр и повторяете все шаги.
Если присмотреться, то из блочного шифра с режимом OFB получился поточный шифр. Вы генерируете порции ключевого потока по 128 бит, пока не получите длину открытого текста (отбрасывая ненужные биты из последней 128-битной порции ключевого потока). Затем вы выполняете XOR потока ключей с открытым текстом, чтобы получить шифротекст.
В предыдущем разделе, посвященном потоковым шифрам, я говорил о том, что поток ключей создается с помощью закрытого ключа. Точнее говоря, он должен создаваться не только с помощью закрытого ключа. Как вы можете видеть в режиме OFB, поток ключей создается при поддержке как закрытого ключа, так и вектора инициализации.
Обратите внимание, что, как и в случае с режимом CBC, при использовании блочного шифра в режиме OFB важно каждый раз выбирать псевдослучайный или случайный nonce для вектора инициализации. В противном случае одна и та же 128-битная строка сообщения, отправленная в разных сообщениях, будет зашифрована одинаково. Это один из способов создания вероятностного шифрования с помощью потокового шифра.
Некоторые потоковые шифры используют закрытый ключ только для создания потока ключей. Для таких потоковых шифров важно использовать случайный nonce для выбора закрытого ключа для каждого случая связи. В противном случае результаты шифрования с помощью этих потоковых шифров также будут детерминированными, что приведет к проблемам безопасности.
Самым популярным современным блочным шифром является шифр Rijndael. Он стал победителем из пятнадцати заявок на конкурсе, проводившемся Национальным институтом стандартов и технологий (NIST) с 1997 по 2000 год с целью замены более старого стандарта шифрования, стандарта шифрования данных (DES).
Шифр Rijndael может использоваться с различными спецификациями длины ключа и размера блока, а также в различных режимах работы. Комитет по проведению конкурса NIST принял ограниченную версию шифра Rijndael - а именно ту, которая требует 128-битного размера блока и длины ключа либо 128 бит, либо 192 бит, либо 256 бит - в качестве части advanced encryption standard (AES). Это действительно основной стандарт для приложений симметричного шифрования. Он настолько безопасен, что даже АНБ, по-видимому, готово использовать его с 256-битными ключами для совершенно секретных документов. [6]
Блочный шифр AES будет подробно рассмотрен в главе 5.
Примечания:
[5] Важность вероятностного шифрования впервые была подчеркнута Шафи Голдвассером и Сильвио Микали, "Вероятностное шифрование", Journal of Computer and System Sciences, 28 (1984), 270-99.
[6] См. NSA, "Commercial National Security Algorithm Suite", https://apps.nsa.gov/iaarchive/programs/iad-initiatives/cnsa-suite.cfm.
Устранение путаницы
Путаница с различием между блочными и потоковыми шифрами возникает потому, что иногда люди понимают термин блочный шифр как относящийся именно к блочному шифру с блочным режимом шифрования.
Рассмотрим режимы ECB и CBC в предыдущем разделе. Они требуют, чтобы данные для шифрования были кратны размеру блока (это означает, что вам придется использовать прокладку для исходного сообщения). Кроме того, данные в этих режимах обрабатываются блочным шифром напрямую (а не просто комбинируются с результатом операции блочного шифрования, как в режиме OFB).
Таким образом, в качестве альтернативы можно определить блочный шифр как любую схему шифрования, которая оперирует блоками сообщения фиксированной длины за раз (при этом любой блок должен быть длиннее байта, иначе он сворачивается в потоковый шифр). И данные для шифрования, и шифротекст должны равномерно делиться на этот размер блока. Обычно размер блока составляет 64, 128, 192 или 256 бит. Потоковый шифр, напротив, может шифровать любые сообщения фрагментами по одному биту или байту за раз.
При таком более конкретном понимании блочного шифра можно утверждать, что современные схемы шифрования являются либо потоковыми, либо блочными шифрами. С этого момента я буду использовать термин блочный шифр в более общем смысле, если не указано иное.
Обсуждение режима OFB в предыдущем разделе также поднимает еще один интересный вопрос. Некоторые потоковые шифры создаются на основе блочных шифров, например Rijndael с OFB. Некоторые, такие как Salsa20 и ChaCha, не создаются из блочных шифров. Последние можно назвать примитивными потоковыми шифрами. (На самом деле не существует стандартного термина для обозначения таких потоковых шифров)
Когда люди говорят о преимуществах и недостатках потоковых и блочных шифров, они обычно сравнивают примитивные потоковые шифры со схемами шифрования на основе блочных шифров.
Если из блочного шифра всегда можно легко построить поточный шифр, то из примитивного поточного шифра обычно очень сложно построить какую-либо конструкцию с блочным режимом шифрования (например, с режимом CBC).
Из этого обсуждения вы должны понять Рисунок 8. На нем представлен обзор схем симметричного шифрования. Мы используем три вида схем шифрования: примитивные потоковые шифры, потоковые шифры с блочным шифрованием и блочные шифры в блочном режиме (на рисунке они также называются "блочными шифрами").
Рисунок 8: Обзор схем симметричного шифрования
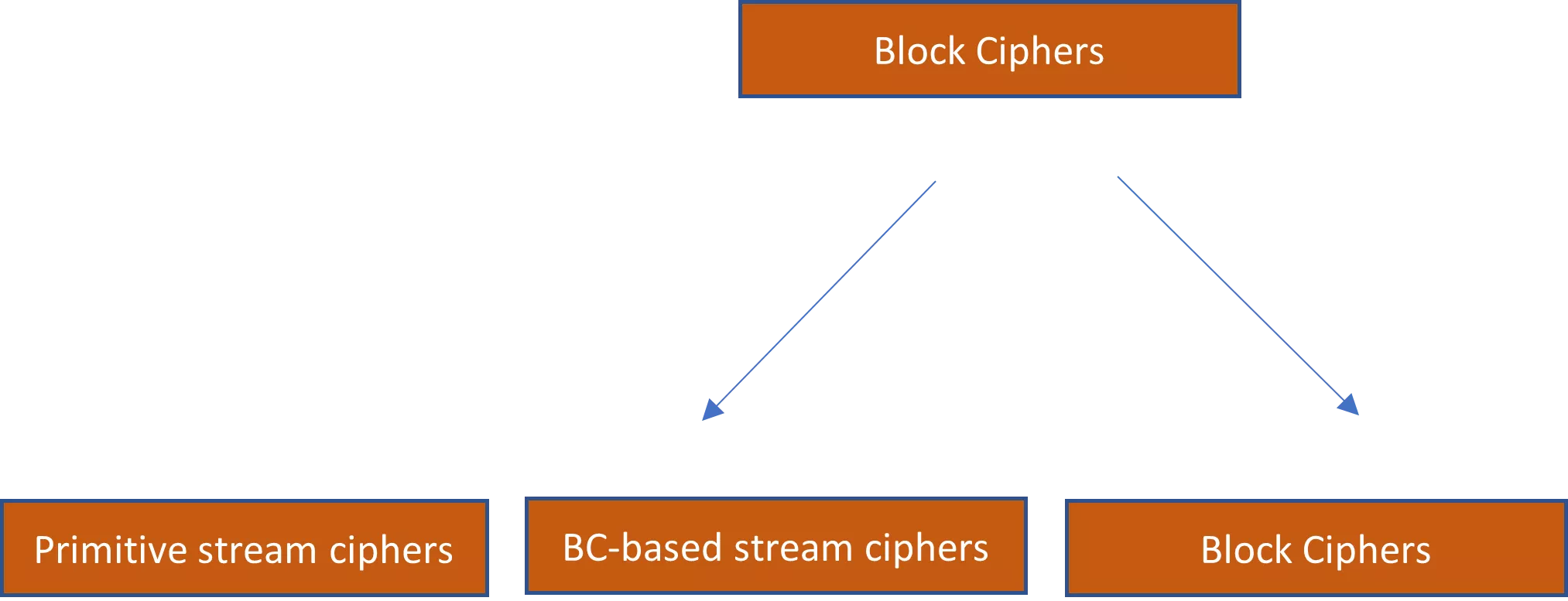
Коды аутентификации сообщений
Шифрование связано с обеспечением секретности. Но криптография также занимается более широкими темами, такими как целостность, подлинность и неотрицание сообщений. Так называемые коды аутентификации сообщений (MACs) - это криптографические схемы с симметричным ключом, которые поддерживают аутентичность и целостность сообщений.
Почему в общении необходимо что-либо, кроме секретности? Предположим, что Боб отправляет Алисе сообщение, используя практически невзламываемое шифрование. Любой злоумышленник, перехвативший это сообщение, не сможет получить никаких существенных сведений о его содержании. Однако у злоумышленника остается как минимум два других доступных ему вектора атаки:
Она может перехватить шифротекст, изменить его содержимое и отправить измененный шифротекст Алисе.
Она может полностью заблокировать сообщение Боба и отправить свой собственный шифртекст.
В обоих этих случаях злоумышленник может не иметь никакого представления о содержимом шифротекстов (1) и (2). Но он все равно может нанести значительный ущерб таким образом. Вот здесь-то и становятся важными коды аутентификации сообщений.
Коды аутентификации сообщений определяются как симметричные криптографические схемы с тремя алгоритмами: алгоритмом генерации ключа, алгоритмом генерации метки и алгоритмом верификации. Безопасный MAC гарантирует, что метки экзистенциально неподделываемы для любого злоумышленника - то есть, он не может успешно создать метку на сообщении, которое проверяет, если только у него нет закрытого ключа.
Боб и Алиса могут бороться с манипуляциями с конкретным сообщением с помощью MAC. Предположим, что на данный момент им не важна секретность. Они лишь хотят убедиться, что сообщение, полученное Алисой, действительно от Боба и никак не изменено.
Этот процесс изображен на рисунке 9. Чтобы использовать MAC (код аутентификации сообщений), сначала генерируется закрытый ключ K, который делится между
ними. Боб создает метку T для
сообщения, используя закрытый ключ K. Затем он отправляет
сообщение и метку Алисе. Алиса может проверить, что Боб действительно создал
метку, пропустив закрытый ключ, сообщение и метку через алгоритм проверки.
Рисунок 9: Обзор схем симметричного шифрования
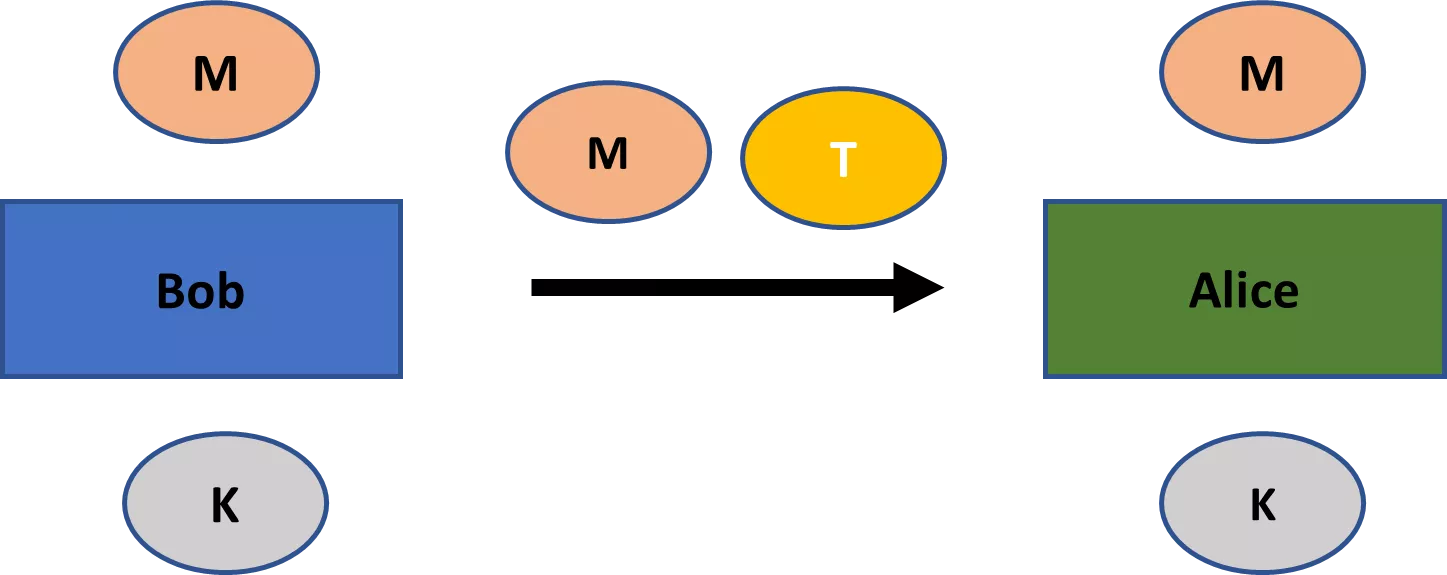
В силу экзистенциальной неустранимости злоумышленник не
может каким-либо образом изменить сообщение M или создать собственное сообщение с действительной меткой. Это так, даже
если злоумышленник наблюдает за метками многих сообщений между Бобом и
Алисой, в которых используется один и тот же закрытый ключ. В крайнем
случае, злоумышленник может заблокировать получение Алисой сообщения M (проблема, которую криптография
решить не может).
MAC гарантирует, что сообщение действительно было создано Бобом. Эта аутентичность автоматически подразумевает целостность сообщения - то есть если Боб создал какое-то сообщение, то, ipso facto, оно не было изменено злоумышленником. Таким образом, с этого момента любая забота об аутентификации должна автоматически подразумевать заботу о целостности.
Хотя в своем обсуждении я проводил различие между аутентичностью и целостностью сообщений, обычно эти термины используются как синонимы. Они относятся к идее сообщений, которые были созданы определенным отправителем и не подвергались никаким изменениям. В этом духе коды аутентификации сообщений часто также называют кодами целостности сообщений.
Аутентифицированное шифрование
Обычно требуется гарантировать как секретность, так и подлинность связи, поэтому схемы шифрования и MAC обычно используются вместе.
Схема аутентифицированного шифрования - это схема, которая сочетает шифрование с MAC в очень безопасной манере. В частности, она должна удовлетворять стандартам экзистенциальной неустранимости, а также очень сильному понятию секретности, а именно устойчивости к атакам с выбором шифртекста. [7]
Для того чтобы схема шифрования была устойчива к атакам с выбором шифртекста, она должна удовлетворять стандартам нерасщепляемости: то есть любая модификация шифртекста злоумышленником должна приводить либо к недействительному шифртексту, либо к такому, который расшифровывается в открытый текст, не имеющий ничего общего с исходным. [8]
Поскольку аутентифицированная схема шифрования гарантирует, что шифртекст, созданный злоумышленником, всегда будет недействительным (так как метка не будет проверена), она удовлетворяет стандартам стойкости к атакам с выбором шифртекста. Интересно, что можно доказать, что аутентифицированная схема шифрования всегда может быть создана из комбинации экзистенциально неподделываемого MAC и схемы шифрования, которая удовлетворяет менее сильным представлениям о безопасности, известным как безопасность атаки по выбранному шифртексту.
Мы не будем вдаваться во все подробности построения аутентифицированных схем шифрования. Но важно знать две детали их построения.
Во-первых, схема аутентифицированного шифрования сначала выполняет шифрование, а затем создает метку сообщения на шифротексте. Оказывается, что другие подходы - например, объединение шифротекста с меткой на открытом тексте или сначала создание метки, а затем шифрование как открытого текста, так и метки - небезопасны. Кроме того, для обеих операций необходимо иметь свой собственный случайно выбранный закрытый ключ, иначе ваша безопасность будет серьезно подорвана.
Вышеупомянутый принцип применим и в более общем случае: при комбинировании основных криптографических схем всегда следует использовать отдельные ключи.
Схема аутентифицированного шифрования изображена на Рисунке 10.
Сначала Боб создает шифротекст C из сообщения M, используя
случайно выбранный ключ K_C.
Затем он создает метку сообщения T, пропуская шифротекст и
другой случайно выбранный ключ K_T через алгоритм генерации меток.
И шифротекст, и метка сообщения отправляются Алисе.
Теперь Алиса сначала проверяет, действительна ли метка, учитывая шифротекст C и ключ K_T. Если она
действительна, она может расшифровать сообщение, используя ключ K_C. Она не только уверена в
очень сильном понятии секретности их связи, но и знает, что сообщение было
создано Бобом.
Рисунок 10: Схема аутентифицированного шифрования

Как создаются MAC? Хотя MAC могут быть созданы несколькими способами, распространенным и эффективным способом их создания являются криптографические хэш-функции.
Более подробно мы познакомимся с криптографическими хэш-функциями в главе 6. Пока же просто знайте, что хэш-функция - это эффективно вычисляемая функция, которая принимает входные данные произвольного размера и выдает выходные данные фиксированной длины. Например, популярная хэш-функция SHA-256 (secure hash algorithm 256) всегда генерирует 256-битный выход независимо от размера входа. Некоторые хэш-функции, такие как SHA-256, находят полезное применение в криптографии.
Наиболее распространенным типом метки, создаваемой с помощью
криптографической хэш-функции, является код аутентификации сообщений на основе хэша (HMAC). Этот процесс изображен на рисунке 11. Сторона производит
два разных ключа из закрытого ключа K, внутренний ключ K_1 и внешний ключ K_2. Затем
открытый текст M или
шифротекст C хэшируется с
помощью внутреннего ключа. Результат T' хэшируется внешним ключом для получения метки сообщения T.
Существует палитра хэш-функций, которые могут быть использованы для создания HMAC. Наиболее часто используемой хэш-функцией является SHA-256.
Рисунок 11: HMAC
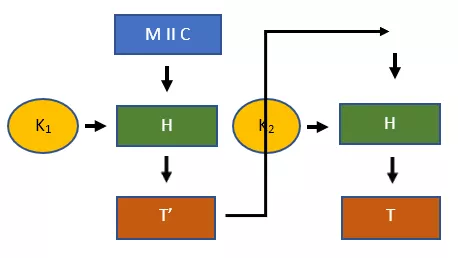
Примечания:
[7] Конкретные результаты, обсуждаемые в этом разделе, взяты из Katz and Lindell, pp. 131-47.
[8] Технически, определение атак на выбранный шифртекст отличается от понятия нерасщепляемости. Но можно показать, что эти два понятия безопасности эквивалентны.
Безопасные сеансы связи
Предположим, что две стороны находятся в сеансе связи, и они отправляют несколько сообщений туда и обратно.
Схема шифрования с аутентификацией позволяет получателю сообщения убедиться, что оно было создано его партнером по сеансу связи (при условии, что закрытый ключ не просочился). Это достаточно хорошо работает для одного сообщения. Однако обычно две стороны пересылают сообщения туда и обратно в рамках сеанса связи. И в таких условиях простая схема шифрования с аутентификацией, описанная в предыдущем разделе, не может обеспечить безопасность.
Основная причина заключается в том, что аутентифицированная схема шифрования не дает никаких гарантий того, что сообщение действительно было отправлено агентом, который его создал в рамках сеанса связи. Рассмотрим следующие три вектора атаки:
Атака переигрывания: Злоумышленник повторно отправляет шифротекст и метку, которые он перехватил между двумя сторонами в более ранний момент времени.
Атака с перестановкой порядка: Злоумышленник перехватывает два сообщения в разное время и отправляет их получателю в обратном порядке.
Атака с отражением: Злоумышленник наблюдает за сообщением, отправленным из A в B, и также отправляет это сообщение в A.
Хотя злоумышленник не знает шифртекста и не может создавать поддельные шифртексты, описанные выше атаки все равно могут нанести значительный ущерб коммуникациям.
Предположим, например, что конкретное сообщение между двумя сторонами связано с переводом финансовых средств. Атака на воспроизведение может перевести эти средства во второй раз. Ванильная схема шифрования с аутентификацией не имеет защиты от таких атак.
К счастью, эти виды атак можно легко предотвратить во время сеанса связи, используя идентификаторы и индикаторы относительного времени.
Идентификаторы могут быть добавлены к открытому тексту сообщения перед шифрованием. Это предотвратит любые атаки на отражение. Индикатором относительного времени может быть, например, номер последовательности в конкретном сеансе связи. Каждая сторона добавляет номер последовательности к сообщению перед шифрованием, поэтому получатель знает, в каком порядке были отправлены сообщения. Это исключает возможность атак с перестановкой порядковых номеров. Это также исключает атаки повторного воспроизведения. Любое сообщение, отправленное злоумышленником по линии связи, будет иметь старый порядковый номер, и получатель будет знать, что не следует обрабатывать это сообщение снова.
Чтобы проиллюстрировать, как работают защищенные сеансы связи, предположим, что Алиса и Боб снова общаются. Они отправляют в общей сложности четыре сообщения туда и обратно. Ниже на Рисунке 11 показано, как будет работать схема аутентифицированного шифрования с идентификаторами и порядковыми номерами.
Сеанс связи начинается с того, что Боб отправляет Алисе шифротекст C_{0,B} с меткой сообщения T_{0,B}. Шифротекст
содержит сообщение, а также идентификатор (BOB) и порядковый номер (0).
Метка T_{0,B} ставится
на весь шифротекст. В своих последующих сообщениях Алиса и Боб поддерживают этот
протокол, обновляя поля по мере необходимости.
Рисунок 12: Безопасный сеанс связи
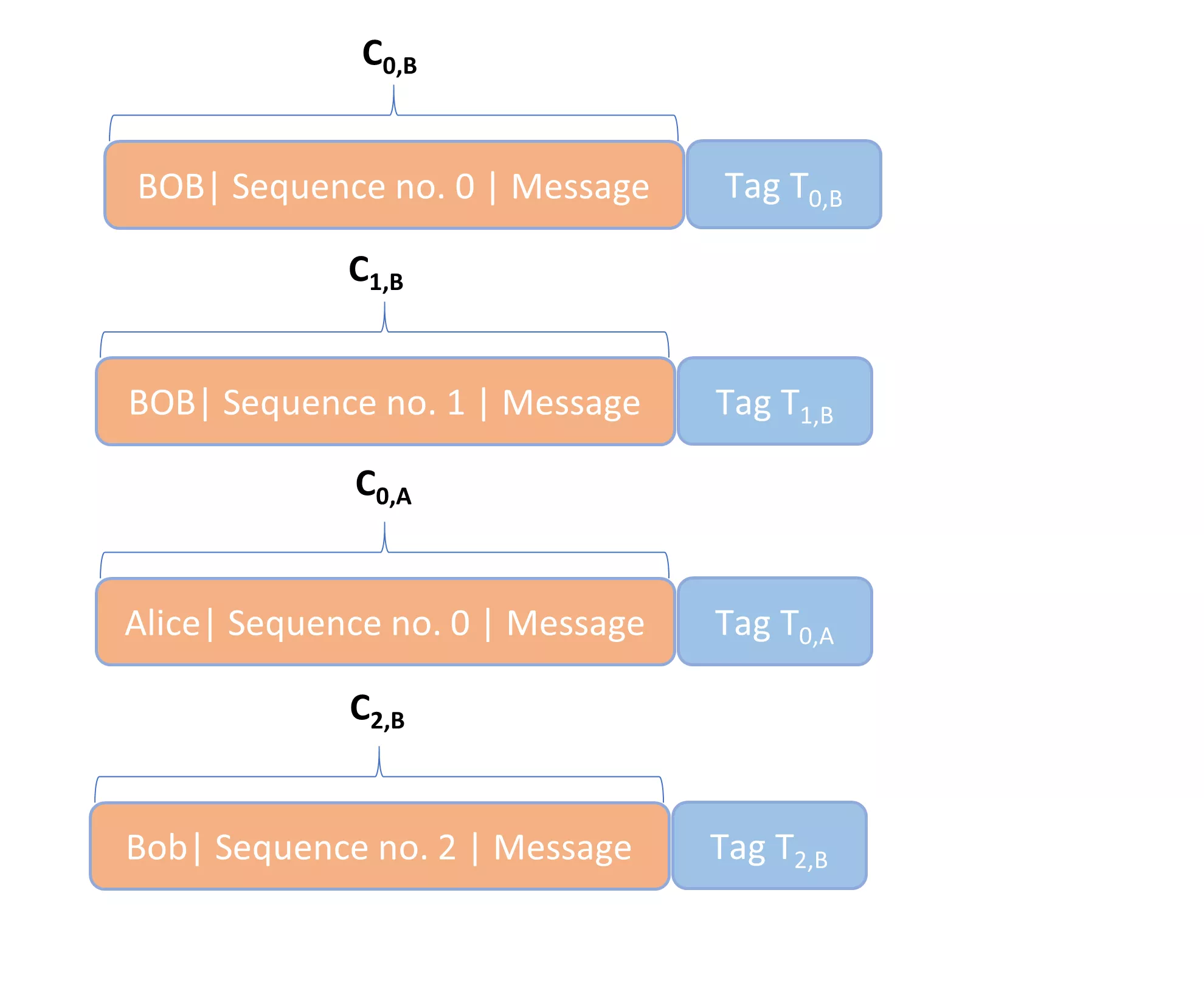
RC4 и AES
Потоковый шифр RC4
В этой главе мы рассмотрим детали схемы шифрования с использованием современного примитивного потокового шифра RC4 (или "шифра Ривеста 4") и современного блочного шифра AES. В то время как шифр RC4 утратил свою популярность как метод шифрования, AES является стандартом современного симметричного шифрования. Эти два примера должны дать лучшее представление о том, как работает симметричное шифрование.
Чтобы получить представление о том, как работают современные псевдослучайные потоковые шифры, я остановлюсь на потоковом шифре RC4. Это псевдослучайный потоковый шифр, который использовался в протоколах безопасности беспроводных точек доступа WEP и WAP, а также в TLS. Поскольку RC4 имеет множество доказанных слабых мест, он попал в немилость. Фактически, Internet Engineering Task Force теперь запрещает использование наборов RC4 клиентскими и серверными приложениями во всех экземплярах TLS. Тем не менее, он хорошо подходит в качестве примера, иллюстрирующего работу примитивного потокового шифра.
Для начала я покажу, как зашифровать сообщение с открытым текстом с помощью детского шифра RC4. Предположим, что наш открытый текст - это "SOUP" Тогда шифрование с помощью детского шифра RC4 происходит в четыре этапа.
Шаг 1
Сначала определите массив S с S[0] = 0 до S[7] = 7. Массив здесь
означает просто изменяемую коллекцию значений, организованных по индексу,
также называемую списком в некоторых языках программирования (например,
Python). В данном случае индекс начинается от 0 до 7, и значения также
начинаются от 0 до 7. Таким образом, S выглядит следующим образом:
S = [0, 1, 2, 3, 4, 5, 6, 7]
Значения здесь - это не ASCII-числа, а десятичные представления 1-байтовых
строк. Так, значение 2 будет равно 0000 \ 0011. Таким образом, длина массива S составляет 8 байт.
Шаг 2
Во-вторых, определите массив ключей K длиной 8 байт, выбрав ключ длиной от 1 до 8 байт (не допускается дробное число байт). Поскольку каждый байт состоит из 8 бит, вы можете выбрать любое число от 0 до 255 для каждого байта вашего ключа.
Предположим, что мы выбрали ключ k в виде [14, 48, 9], чтобы его длина
составляла 3 байта. Тогда каждый индекс нашего массива ключей
устанавливается в соответствии с десятичным значением для данного элемента
ключа, по порядку. Если вы пробежались по всему ключу, начните с самого
начала, пока не заполните все 8 слотов массива ключей. Таким образом, наш
массив ключей выглядит следующим образом:
K = [14, 48, 9, 14, 48, 9, 14, 48]
Шаг 3
В-третьих, мы преобразуем массив S, используя массив ключей K, в процессе, известном как планирование ключей. В псевдокоде этот процесс выглядит следующим образом:
- Создайте переменные j и i
- Установите переменную
j = 0 - Для каждого
iот 0 до 7:- Пусть
j = (j + S[i] + K[i])\mod 8 - Поменяйте местами
S[i]иS[j]
- Пусть
Преобразование массива S отражено в Таблице 1.
Для начала вы можете представить начальное состояние S как [0, 1, 2, 3, 4, 5, 6, 7] с начальным значением 0 для j. Оно будет преобразовано с
помощью массива ключей [14, 48, 9, 14, 48, 9, 14, 48].
Цикл for начинается с i = 0.
Согласно нашему псевдокоду выше, новое значение j становится 6 (j = (j + S[0] + K[0])\mod 8 = (0 + 0 + 14)\mod 8 = 6 \mod 8). Поменяв местами S[0] и S[6], состояние S после 1 раунда становится [6, 1, 2, 3, 4, 5, 0, 7].
В следующей строке i = 1.
Снова проходя через цикл for, j получает значение 7 (j = (j + S[1] + K[1])\mod 8 = (6 + 1 + 48)\mod 8 = 55 \mod 8 = 7 \mod 8). Поменяв местами S[1] и S[7] из текущего состояния S, [6, 1, 2, 3, 4, 5, 0, 7], мы
получим [6, 7, 2, 3, 4, 5, 0, 1] после
второго раунда.
Мы продолжаем этот процесс, пока не получим последнюю строку внизу для
массива S, [6, 4, 1, 0, 3, 7, 5, 2].
Таблица 1: Таблица ключевых расписаний
| Round | i | j | S[0] | S[1] | S[2] | S[3] | S[4] | S[5] | S[6] | S[7] | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 1 | 0 | 6 | 6 | 1 | 2 | 3 | 4 | 5 | 0 | 7 | |
| 2 | 1 | 7 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 3 | 2 | 2 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 4 | 3 | 3 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 5 | 4 | 3 | 6 | 7 | 2 | 0 | 3 | 5 | 4 | 1 | |
| 6 | 5 | 6 | 6 | 4 | 2 | 0 | 3 | 7 | 5 | 1 | |
| 7 | 6 | 1 | 6 | 4 | 2 | 0 | 3 | 7 | 5 | 2 | |
| 8 | 7 | 2 | 6 | 4 | 1 | 0 | 3 | 7 | 5 | 2 |
Шаг 4
На четвертом этапе мы создаем keystream. Это псевдослучайная строка длиной, равной длине сообщения, которое мы хотим отправить. Она будет использована для шифрования исходного сообщения "SOUP" Поскольку ключевой поток должен быть такой же длины, как и сообщение, нам нужен такой, который содержит 4 байта.
Поток ключей создается с помощью следующего псевдокода:
- Создайте переменные j, i и t.
- Установите
j = 0. - Для каждого
iоткрытого текста, начиная сi = 1и доi = 4, каждый байт потока ключей производится следующим образом:j = (j + S[i])\mod 8- Поменяйте местами
S[i]иS[j]. t = (S[i] + S[j])\mod 8- Байт
i^{th}потока ключей =S[t]
Вы можете проследить за расчетами в Таблице 2.
Начальное состояние S равно S = [6, 4, 1, 0, 3, 7, 5, 2].
Если задать i = 1, то
значение j станет равным 4 (j = (j + S[i])\mod 8 = (0 + 4)\mod 8 = 4). Затем поменяем местами S[1] и S[4], чтобы получить
преобразование S во втором ряду, [6, 3, 1, 0, 4, 7, 5, 2].
Тогда значение t равно 7 (t = (S[i] + S[j])\mod 8 = (3 + 4)\mod 8 = 7). Наконец, байт для потока ключей равен S[7], или 2.
Затем мы продолжаем получать остальные байты, пока не получим следующие четыре байта: 2, 6, 3 и 7. Каждый из этих байтов может быть использован для шифрования каждой буквы открытого текста "SOUP".
Для начала, используя таблицу ASCII, мы видим, что "SOUP", закодированный десятичными значениями базовых байтовых строк, - это "83 79 85 80". Комбинация с ключевым потоком "2 6 3 7" дает "85 85 88 87", который остается неизменным после операции modulo 256. В ASCII шифротекст "85 85 88 87" равен "UUXW".
Что произойдет, если слово, которое нужно зашифровать, будет длиннее массива S? В этом случае массив S просто продолжает преобразовываться таким образом, как показано выше, для каждого байта i открытого текста, пока количество байтов в потоке ключей не станет равным количеству букв в открытом тексте.
Таблица 2: Генерация ключевого потока
| i | j | t | Keystream | S[0] | S[1] | S[2] | S[3] | S[4] | S[5] | S[6] | S[7] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 4 | 1 | 0 | 3 | 7 | 5 | 2 | |||
| 1 | 4 | 7 | 2 | 6 | 3 | 1 | 0 | 4 | 7 | 5 | 2 |
| 2 | 5 | 0 | 6 | 6 | 3 | 7 | 0 | 4 | 1 | 5 | 2 |
| 3 | 5 | 1 | 3 | 6 | 3 | 7 | 1 | 4 | 0 | 5 | 2 |
| 4 | 1 | 7 | 2 | 6 | 4 | 7 | 1 | 3 | 0 | 5 | 2 |
Пример, который мы только что рассмотрели, является лишь уменьшенной версией потокового шифра RC4. Настоящий потоковый шифр RC4 имеет массив S длиной 256 байт, а не 8 байт, и ключ, который может быть от 1 до 256 байт, а не от 1 до 8 байт. Массив ключей и ключевые потоки создаются с учетом 256-байтовой длины массива S. Вычисления значительно усложняются, но принципы остаются прежними. Используя тот же ключ [14,48,9] со стандартным шифром RC4, сообщение "SOUP" зашифровывается как 67 02 ed df в шестнадцатеричном формате.
Потоковый шифр, в котором поток ключей обновляется независимо от сообщения открытого текста или шифротекста, является синхронным потоковым шифром. Поток ключей зависит только от ключа. Очевидно, что RC4 является примером синхронного потокового шифра, поскольку поток ключей не связан ни с открытым текстом, ни с шифротекстом. Все наши примитивные потоковые шифры, упомянутые в предыдущей главе, включая шифр сдвига, шифр Виженера и одноразовый блокнот, также относятся к синхронному типу.
В отличие от него, асинхронный потоковый шифр имеет поток ключей, который создается как ключом, так и предыдущими элементами шифротекста. Этот тип шифра также называется самосинхронизирующимся шифром.
Важно отметить, что поток ключей, созданный с помощью RC4, следует рассматривать как одноразовый блокнот, и вы не сможете создать поток ключей точно таким же образом в следующий раз. Вместо того чтобы каждый раз менять ключ, практическим решением является объединение ключа с nonce для создания байтстрима.
AES со 128-битным ключом
Как уже упоминалось в предыдущей главе, Национальный институт стандартов и технологий (NIST) в период с 1997 по 2000 год проводил конкурс на определение нового стандарта симметричного шифрования. Победителем оказался шифр Rijndael. Название представляет собой игру слов с именами бельгийских создателей, Винсента Риймена и Джоан Демен.
Шифр Rijndael - это блочный шифр, то есть существует основной алгоритм, который можно использовать с различными спецификациями длины ключа и размера блока. Таким образом, вы можете использовать его с различными режимами работы для построения схем шифрования.
Комитет конкурса NIST принял ограниченную версию шифра Rijndael - а именно ту, которая требует 128-битного размера блока и длины ключа либо 128 бит, либо 192 бит, либо 256 бит - в качестве части Advanced Encryption Standard (AES). Эта ограниченная версия шифра Rijndael также может использоваться в нескольких режимах работы. Спецификация стандарта известна как Advanced Encryption Standard (AES).
Чтобы показать, как работает шифр Rijndael, лежащий в основе AES, я проиллюстрирую процесс шифрования с 128-битным ключом. Размер ключа влияет на количество раундов, проводимых для каждого блока шифрования. Для 128-битных ключей требуется 10 раундов. При 192 и 256 битах это было бы 12 и 14 раундов соответственно.
Кроме того, я буду считать, что AES используется в ECB-режиме. Это несколько упрощает изложение и не имеет значения для алгоритма Rijndael. На практике режим ECB не является безопасным, поскольку приводит к детерминированному шифрованию. Наиболее часто в AES используется безопасный режим CBC (Cipher Block Chaining).
Назовем ключ K_0. Тогда
конструкция с указанными параметрами выглядит так, как показано на Рисунок 1, где M_i обозначает часть открытого текста сообщения размером 128 бит, а C_i - часть шифротекста размером
128 бит. Если открытый текст не может быть равномерно разделен на размер блока,
то к открытому тексту добавляется прокладка для последнего блока.
Рисунок 1: AES-ECB со 128-битным ключом
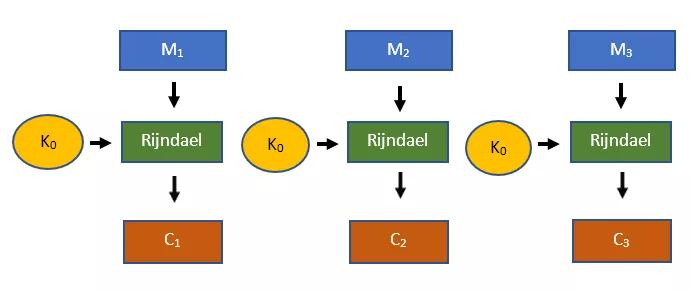
Каждый 128-битный блок текста проходит десять раундов в схеме шифрования
Rijndael. Для каждого раунда (с K_1 по K_{10})
требуется отдельный ключ. Они создаются для каждого раунда из исходного
128-битного ключа K_0 с
помощью алгоритма расширения ключа. Таким образом, для
шифрования каждого блока текста мы будем использовать исходный ключ K_0, а также десять отдельных
раундовых ключей. Обратите внимание, что эти же 11 ключей используются для
каждого 128-битного блока открытого текста, требующего шифрования.
Алгоритм расширения ключа длинный и сложный. Работа над ним не имеет особой
дидактической пользы. При желании вы можете самостоятельно ознакомиться с
алгоритмом расширения ключа. После получения ключей раунда шифр Rijndael
будет манипулировать первым 128-битным блоком открытого текста, M_1, как показано на Рисунке 2. Теперь мы проделаем все эти шаги.
Рисунок 2: Манипуляция с M_1 с помощью шифра Rijndael:
Раунд 0:
- XOR
M_1иK_0для полученияS_0
Раунд n для n = {1,...,9}:
- XOR
S_{n-1}иK_n - Подстановка байтов
- Сдвиговые ряды
- Смешать колонки
- XOR
SиK_nдля полученияS_n
10 раунд:
- XOR
S_9иK_{10} - Подстановка байтов
- Переключение рядов
- XOR
SиK_{10}для полученияS_{10} S_{10}=C_1
Раунд 0
Раунд 0 шифра Rijndael очень прост. Массив S_0 образуется в результате операции XOR между 128-битным открытым текстом и закрытым
ключом. То есть,
S_0 = M_1 \oplus K_0
Раунд 1
В первом раунде массив S_0 сначала объединяется с ключом раунда K_1 с помощью операции XOR. В результате образуется новое состояние S.
Во-вторых, операция замены байта выполняется над текущим
состоянием S. Она выполняется
путем взятия каждого байта 16-байтового массива S и замены его байтом из массива, называемого Rijndael's S-box. Каждый байт имеет уникальное
преобразование, и в результате получается новое состояние S. S-box Рейндаля показан на рисунке 3.
Рисунок 3: S-бокс Rijndael
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 0A | 0B | 0C | 0D | 0E | 0F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 63 | 7C | 77 | 7B | F2 | 6B | 6F | C5 | 30 | 01 | 67 | 2B | FE | D7 | AB | 76 |
| 10 | CA | 82 | C9 | 7D | FA | 59 | 47 | F0 | AD | D4 | A2 | AF | 9C | A4 | 72 | C0 |
| 20 | B7 | FD | 93 | 26 | 36 | 3F | F7 | CC | 34 | A5 | E5 | F1 | 71 | D8 | 31 | 15 |
| 30 | 04 | C7 | 23 | C3 | 18 | 96 | 05 | 9A | 07 | 12 | 80 | E2 | EB | 27 | B2 | 75 |
| 40 | 09 | 83 | 2C | 1A | 1B | 6E | 5A | A0 | 52 | 3B | D6 | B3 | 29 | E3 | 2F | 84 |
| 50 | 53 | D1 | 00 | ED | 20 | FC | B1 | 5B | 6A | CB | BE | 39 | 4A | 4C | 58 | CF |
| 60 | D0 | EF | AA | FB | 43 | 4D | 33 | 85 | 45 | F9 | 02 | 7F | 50 | 3C | 9F | A8 |
| 70 | 51 | A3 | 40 | 8F | 92 | 9D | 38 | F5 | BC | B6 | DA | 21 | 10 | FF | F3 | D2 |
| 80 | CD | 0C | 13 | EC | 5F | 97 | 44 | 17 | C4 | A7 | 7E | 3D | 64 | 5D | 19 | 73 |
| 90 | 60 | 81 | 4F | DC | 22 | 2A | 90 | 88 | 46 | EE | B8 | 14 | DE | 5E | 0B | DB |
| A0 | E0 | 32 | 3A | 0A | 49 | 06 | 24 | 5C | C2 | D3 | AC | 62 | 91 | 95 | E4 | 79 |
| B0 | E7 | C8 | 37 | 6D | 8D | D5 | 4E | A9 | 6C | 56 | F4 | EA | 65 | 7A | AE | 08 |
| C0 | BA | 78 | 25 | 2E | 1C | A6 | B4 | C6 | E8 | DD | 74 | 1F | 4B | BD | 8B | 8A |
| D0 | 70 | 3E | B5 | 66 | 48 | 03 | F6 | 0E | 61 | 35 | 57 | B9 | 86 | C1 | 1D | 9E |
| E0 | E1 | F8 | 98 | 11 | 69 | D9 | 8E | 94 | 9B | 1E | 87 | E9 | CE | 55 | 28 | DF |
| F0 | 8C | A1 | 89 | 0D | BF | E6 | 42 | 68 | 41 | 99 | 2D | 0F | B0 | 54 | BB | 16 |
Этот S-Box - одно из мест, где абстрактная алгебра вступает в игру в шифре Rijndael, а именно поля Галуа.
Для начала определите каждый возможный элемент байта с 00 по FF как 8-битный
вектор. Каждый такой вектор является элементом поля Галуа GF(2^8), где неприводимый многочлен для операции modulo равен x^8 + x^4 + x^3 + x + 1. Поле
Галуа с такими характеристиками также называется Конечным полем Рейндаля.
Далее для каждого возможного элемента поля мы создаем так называемый Nyberg S-Box. В этом ящике каждый байт отображается на свою многозначную обратную величину (т. е. так, чтобы их произведение равнялось 1). Затем мы переносим значения из S-бокса Найберга в S-бокс Rijndael с помощью аффинного преобразования.
Третья операция над массивом S - это операция сдвиг строк. Она принимает состояние S и перечисляет все шестнадцать байт в матрицу. Заполнение матрицы начинается сверху слева и идет сверху вниз, а затем, каждый раз, когда столбец заполняется, сдвигается на один столбец вправо и вверх.
После построения матрицы S четыре строки сдвигаются. Первая строка остается неизменной. Вторая строка сдвигается на одну строку влево. Третья сдвигается на два влево. Четвертый сдвигается на три влево. Пример этого процесса приведен на Рисунке 4. Сверху показано исходное состояние S, а под ним - результирующее состояние после операции сдвига строк.
Рисунок 4: Операция сдвига строк
| F1 | A0 | B1 | 23 |
|---|---|---|---|
| 59 | EF | 09 | 82 |
| 97 | 01 | B0 | CC |
| D4 | 72 | 04 | 21 |
| F1 | A0 | B1 | 23 |
|---|---|---|---|
| EF | 09 | 82 | 59 |
| B0 | CC | 97 | 01 |
| 21 | D4 | 72 | 04 |
На четвертом шаге снова появляются поля Галуа. Для начала
каждый столбец матрицы S умножается на столбец матрицы 4 x
4, показанной на рисунке 5. Но вместо обычного умножения матриц это
векторное умножение модуля невыводимого многочлена, x^8 + x^4 + x^3 + x + 1.
Коэффициенты результирующего вектора представляют собой отдельные биты
байта.
Рисунок 5: Матрица смешанных колонок
| 02 | 03 | 01 | 01 |
|---|---|---|---|
| 01 | 02 | 03 | 01 |
| 01 | 01 | 02 | 03 |
| 03 | 01 | 01 | 02 |
Умножение первого столбца матрицы S на матрицу 4 x 4, приведенную выше, дает результат на рисунке 6.
Рисунок 6: Умножение первого столбца:
\begin{matrix}
02 \cdot F1 + 03 \cdot EF + 01 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 02 \cdot EF + 03 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 01 \cdot EF + 02 \cdot B0 + 03 \cdot 21 \\
03 \cdot F1 + 01 \cdot EF + 01 \cdot B0 + 02 \cdot 21
\end{matrix}На следующем этапе все члены матрицы нужно превратить в полиномы. Например,
F1 представляет собой 1 байт и станет x^7 + x^6 + x^5 + x^4 + 1, а 03 представляет собой 1 байт и станет x + 1.
Затем все умножения выполняются модульно x^8 + x^4 + x^3 + x + 1. Это
приводит к сложению четырех многочленов в каждой из четырех ячеек столбца.
После выполнения этих сложений modulo 2 вы получите четыре
многочлена. Каждый из этих многочленов представляет собой 8-битную строку,
или 1 байт, числа S. Мы не будем выполнять все эти
вычисления для матрицы на рисунке 6, поскольку они очень объемны.
После обработки первого столбца аналогичным образом обрабатываются остальные три столбца матрицы S. В конечном итоге получится матрица с шестнадцатью байтами, которую можно преобразовать в массив.
На последнем этапе массив S снова объединяется с круглым
ключом в операцию XOR. В результате получается состояние S_1. То есть,
S_1 = S \oplus K_0
Раунды со 2 по 10
Раунды со 2 по 9 - это просто повторение раунда 1, mutatis mutandis. Последний раунд очень похож на предыдущие, за исключением того, что шаг перемешать столбцы исключен. То есть раунд 10 выполняется следующим образом:
S_9 \oplus K_{10}- Подстановка байтов
- Переключение рядов
S_{10} = S \oplus K_{10}
Теперь состояние S_{10} установлено на C_1, первые
128 бит шифротекста. Пройдя через оставшиеся 128-битные блоки открытого
текста, вы получите полный шифртекст C.
Операции шифра Rijndael
Чем обусловлены различные операции, используемые в шифре Rijndael?
Не вдаваясь в подробности, схемы шифрования оцениваются по степени запутанности и диффузности. Если схема шифрования имеет высокую степень запутанности, это означает, что шифротекст выглядит кардинально иначе, чем открытый текст. Если схема шифрования имеет высокую степень диффузии, это означает, что любое небольшое изменение открытого текста приводит к кардинальному изменению шифротекста.
Причина, по которой операции, лежащие в основе шифра Rijndael, приводят к высокой степени запутанности и диффузии. Путаницу создает операция подстановки байта, а диффузию - операции сдвига строк и смешивания столбцов.
Асимметричная криптография
Проблема распределения и управления ключами
Как и в симметричной криптографии, асимметричные схемы могут использоваться для обеспечения как секретности, так и аутентификации. Однако, в отличие от них, эти схемы используют не один, а два ключа: закрытый и открытый.
Мы начнем наше исследование с открытия асимметричной криптографии, в частности с проблем, которые послужили толчком к ее появлению. Далее мы обсудим, как работают асимметричные схемы шифрования и аутентификации на высоком уровне. Затем мы представляем хэш-функции, которые являются ключевыми для понимания асимметричных схем аутентификации, а также имеют значение в других криптографических контекстах, например, для кодов аутентификации сообщений на основе хэша, которые мы обсуждали в главе 4.
Предположим, что Боб хочет купить новый дождевик в Jim's Sporting Goods, онлайн-магазине спортивных товаров с миллионами покупателей в Северной Америке. Это будет его первая покупка у них, и он хочет воспользоваться своей кредитной картой. Поэтому Бобу сначала нужно создать учетную запись в Jim's Sporting Goods, для чего необходимо отправить личные данные, такие как адрес и информация о кредитной карте. После этого он сможет выполнить все действия, необходимые для покупки дождевика.
Боб и Jim's Sporting Goods захотят обеспечить безопасность своих коммуникаций на протяжении всего этого процесса, учитывая, что Интернет - это открытая система связи. Например, они захотят убедиться, что ни один потенциальный злоумышленник не сможет узнать данные кредитной карты и адрес Боба, а также повторить его покупки или создать поддельные от его имени.
Усовершенствованная схема шифрования с аутентификацией, о которой шла речь в предыдущей главе, безусловно, могла бы сделать переписку между Бобом и Jim's Sporting Goods безопасной. Однако для реализации такой схемы существуют очевидные практические препятствия.
Чтобы проиллюстрировать эти практические препятствия, предположим, что мы живем в мире, в котором существуют только инструменты симметричной криптографии. Что тогда могут сделать Jim's Sporting Goods и Боб, чтобы обеспечить безопасную связь?
В таких обстоятельствах безопасная связь обойдется им очень дорого. Поскольку Интернет - это открытая коммуникационная система, они не могут просто обменяться набором ключей через нее. Поэтому Бобу и представителю Jim's Sporting Goods придется обмениваться ключами лично.
Одна из возможностей заключается в том, что Jim's Sporting Goods создает специальные места обмена ключами, где Боб и другие новые покупатели могут получить набор ключей для безопасной связи. Очевидно, что это потребует значительных организационных затрат и значительно снизит эффективность совершения покупок новыми клиентами.
Кроме того, Jim's Sporting Goods может отправить Бобу пару ключей с надежным курьером. Это, вероятно, более эффективно, чем организация мест обмена ключами. Но это все равно потребует значительных затрат, особенно если многие покупатели совершают всего одну или несколько покупок.
Далее, симметричная схема аутентифицированного шифрования также вынуждает Jim's Sporting Goods хранить отдельные наборы ключей для всех своих клиентов. Это было бы серьезной практической проблемой для тысяч клиентов, не говоря уже о миллионах.
Чтобы понять этот последний момент, предположим, что Jim's Sporting Goods предоставляет каждому клиенту одну и ту же пару ключей. Это позволит каждому клиенту - или любому другому, кто сможет получить эту пару ключей, - читать и даже манипулировать всеми сообщениями между Jim's Sporting Goods и ее клиентами. В таком случае вы можете вообще не использовать криптографию в своих сообщениях.
Даже повторение набора ключей только для некоторых клиентов - это ужасная практика безопасности. Любой потенциальный злоумышленник может попытаться использовать эту особенность схемы (помните, что в соответствии с принципом Керкхоффса предполагается, что злоумышленники знают о схеме все, кроме ключей)
Таким образом, Jim's Sporting Goods придется хранить пару ключей для каждого клиента, независимо от того, как эти пары ключей будут распределены. Это создает несколько практических проблем.
- Jim's Sporting Goods пришлось бы хранить миллионы пар ключей, по одному на каждого покупателя.
- Эти ключи должны быть надлежащим образом защищены, поскольку они станут надежной мишенью для хакеров. Любые нарушения безопасности потребуют повторения дорогостоящих обменов ключами либо в специальных местах обмена, либо с курьером.
- Любой покупатель Jim's Sporting Goods должен надежно хранить пару ключей дома. Потери и кражи будут иметь место, что потребует повторного обмена ключами. Подобный процесс придется пройти и покупателям других интернет-магазинов или других организаций, с которыми они хотят общаться и совершать сделки через Интернет.
Эти две только что описанные проблемы были весьма фундаментальными до конца 1970-х годов. Они были известны как проблема распределения ключей и проблема управления ключами, соответственно.
Конечно, эти проблемы существовали всегда и часто создавали головную боль в прошлом. Например, военным приходилось постоянно распространять книги с ключами для безопасной связи среди персонала в полевых условиях, что было сопряжено с большими рисками и затратами. Но эти проблемы усугублялись по мере того, как мир все больше переходил к цифровой связи на большие расстояния, особенно для неправительственных организаций.
Если бы эти проблемы не были решены в 1970-х годах, эффективных и безопасных покупок в Jim's Sporting Goods, скорее всего, не существовало бы. На самом деле, большая часть нашего современного мира с практичной и безопасной электронной почтой, онлайн-банкингом и покупками, вероятно, была бы лишь далекой фантазией. Что-либо, даже напоминающее биткойн, вообще не могло бы существовать.
Что же произошло в 1970-х годах? Как стало возможным, что мы можем мгновенно совершать покупки в Интернете и безопасно просматривать страницы Всемирной паутины? Как стало возможным, что мы можем мгновенно отправлять биткойны по всему миру со своих смартфонов?
Новые направления в криптографии
К 1970-м годам проблемы распределения и управления ключами привлекли внимание группы американских ученых-криптографов: Уитфилда Диффи, Мартина Хеллмана и Ральфа Меркла. Перед лицом жесткого скептицизма со стороны большинства коллег они решились разработать решение этой проблемы.
По крайней мере, одним из основных мотивов их начинания было предвидение того, что открытые компьютерные коммуникации окажут глубокое влияние на наш мир. Как отмечают Диффи и Хелманн в 1976 году,
Развитие сетей связи, управляемых компьютерами, обещает легкие и недорогие контакты между людьми или компьютерами на противоположных концах света, заменяя большую часть почты и многие экскурсии телекоммуникациями. Для многих приложений эти контакты должны быть защищены как от подслушивания, так и от передачи нелегитимных сообщений. Однако в настоящее время решение проблем безопасности значительно отстает от других областей коммуникационных технологий. Современная криптография не в состоянии удовлетворить предъявляемые требования, поскольку ее использование налагает на пользователей системы такие серьезные неудобства, что сводит на нет многие преимущества телеобработки [1]
Упорство Диффи, Хеллмана и Меркла принесло свои плоды. Первой публикацией их результатов стала работа Диффи и Хеллмана 1976 года под названием "Новые направления в криптографии" В ней они представили два оригинальных способа решения проблем распределения и управления ключами.
Первым решением, которое они предложили, был удаленный протокол обмена ключами, то есть набор правил для обмена одним или несколькими симметричными ключами по незащищенному каналу связи. Этот протокол сегодня известен как обмен ключами Диффи-Хельмана или обмен ключами Диффи-Хельмана-Меркле. [2]
При обмене ключами Диффи-Хельмана две стороны сначала обмениваются некоторой информацией в открытом виде по незащищенному каналу, например в Интернете. Затем на основе этой информации они независимо друг от друга создают симметричный ключ (или пару симметричных ключей) для безопасной связи. Хотя обе стороны создают свои ключи независимо друг от друга, информация, которой они поделились публично, гарантирует, что этот процесс создания ключа даст одинаковый результат для них обоих.
Важно отметить, что хотя все могут наблюдать за информацией, которой стороны открыто обмениваются по незащищенному каналу, только две стороны, участвующие в обмене информацией, могут создавать на ее основе симметричные ключи.
Это, конечно, звучит совершенно нелогично. Как две стороны могут публично обменяться некоторой информацией, которая позволит только им создать на ее основе симметричные ключи? Почему кто-то другой, наблюдающий за обменом информацией, не сможет создать такие же ключи?
Конечно, он опирается на красивую математику. Обмен ключами Диффи-Хельмана работает через одностороннюю функцию с люком. Давайте по очереди обсудим значение этих двух терминов.
Предположим, что вам дана некоторая функция f(x) и результат f(a) = y, где a - конкретное значение x. Мы
говорим, что f(x) является односторонней функцией, если легко вычислить значение y при заданных a и f(x), но вычислить значение a при заданных y и f(x) вычислительно невыполнимо. Название односторонняя функция,
конечно, происходит от того, что такую функцию можно вычислить только в
одном направлении.
Некоторые односторонние функции имеют так называемую ловушку. Хотя практически невозможно вычислить a, имея только y и f(x), существует
определенная часть информации Z, которая делает вычисление a по y вычислительно
осуществимым. Эта часть информации Z известна как ловушка. Односторонние функции, в которых есть
люк, называются люками.
Мы не будем вдаваться в подробности обмена ключами Диффи-Хельмана. Но по сути каждый участник создает некоторую информацию, часть которой выкладывается в открытый доступ, а часть остается в секрете. Затем каждая сторона берет свою секретную часть информации и открытую информацию, которой поделилась другая сторона, чтобы создать закрытый ключ. И каким-то чудесным образом обе стороны в итоге получат один и тот же закрытый ключ.
Любая сторона, наблюдающая только общедоступную информацию между двумя сторонами в обмене ключами Диффи-Хельмана, не может воспроизвести эти вычисления. Для этого им потребуется закрытая информация от одной из сторон.
Хотя базовая версия обмена ключами Диффи-Хелмана, представленная в работе 1976 года, не очень безопасна, усовершенствованные версии базового протокола, безусловно, используются и сегодня. Что особенно важно, каждый протокол обмена ключами в последней версии протокола безопасности транспортного уровня (версия 1.3) по сути является усовершенствованной версией протокола, представленного Диффи и Хеллманом в 1976 году. Протокол безопасности транспортного уровня является основным протоколом для безопасного обмена информацией, отформатированной в соответствии с протоколом передачи гипертекста (http), стандартом для обмена веб-контентом.
Важно отметить, что обмен ключами Диффи-Хельмана не является асимметричной схемой. Строго говоря, она относится к области криптографии с симметричными ключами. Но поскольку и обмен ключами Диффи-Хельмана, и асимметричная криптография основаны на односторонних теоретико-числовых функциях с дверями-ловушками, их обычно обсуждают вместе.
Второй способ, который Диффи и Гельман предложили для решения проблемы распределения и управления ключами в своей работе 1976 года, - это, конечно же, асимметричная криптография.
В отличие от своего представления обмена ключами Диффи-Хеллмана, они представили лишь общие контуры того, как могут быть построены асимметричные криптографические схемы. Они не предложили никакой односторонней функции, которая могла бы конкретно выполнить условия, необходимые для разумной безопасности в таких схемах.
Однако практическая реализация асимметричной схемы была найдена годом позже тремя разными академическими криптографами и математиками: Рональдом Ривестом, Ади Шамиром и Леонардом Адлеманом. [3] Представленная ими криптосистема стала известна как RSA-криптосистема (по их фамилиям).
Функции-ловушки, используемые в асимметричной криптографии (и обмене ключами Диффи-Хельмана), связаны с двумя основными вычислительно трудными проблемами: факторизацией простых чисел и вычислением дискретных логарифмов.
Простая факторизация требует, как следует из названия, разложения целого числа на простые множители. Проблема RSA - это, безусловно, самый известный пример криптосистемы, связанной с простой факторизацией.
Проблема дискретного логарифма - это проблема, возникающая в циклических группах. При задании генератора в определенной циклической группе требуется вычислить уникальную экспоненту, необходимую для получения из генератора другого элемента группы.
Схемы на основе дискретного логарифма опираются на два основных вида циклических групп: мультипликативные группы целых чисел и группы, включающие точки на эллиптических кривых. Оригинальный обмен ключами Диффи-Хельмана, представленный в книге "Новые направления в криптографии", работает с циклической мультипликативной группой целых чисел. Алгоритм цифровой подписи Bitcoin и недавно представленная схема подписи Шнорра (2021) основаны на задаче дискретного логарифма для определенной циклической группы эллиптических кривых.
Далее мы перейдем к обзору секретности и аутентификации в асимметричной среде. Однако перед этим нам необходимо сделать краткую историческую справку.
Теперь кажется правдоподобным, что группа британских криптографов и математиков, работавших в Штабе правительственной связи (GCHQ), независимо друг от друга сделала вышеупомянутые открытия несколькими годами ранее. В эту группу входили Джеймс Эллис, Клиффорд Кокс и Малкольм Уильямсон.
По их собственным данным и данным GCHQ, именно Джеймс Эллис впервые разработал концепцию криптографии с открытым ключом в 1969 году. Предположительно, Клиффорд Кокс открыл криптографическую систему RSA в 1973 году, а Малкольм Уильямсон - концепцию обмена ключами Диффи-Хельмана в 1974 году. [4] Однако их открытия, как утверждается, были раскрыты только в 1997 году, учитывая секретный характер работы, проводимой в GCHQ.
Примечания:
[1] Уитфилд Диффи и Мартин Хеллман, "Новые направления в криптографии", IEEE Transactions on Information Theory IT-22 (1976), pp. 644-654, at p. 644.
[2] Ральф Меркл также обсуждает протокол обмена ключами в статье "Secure communications over insecure channels", Communications of the Association for Computing Machinery, 21 (1978), 294-99. Хотя Меркл представил эту работу до появления статьи Диффи и Хеллмана, она была опубликована позже. Решение Меркла не является экспоненциально безопасным, в отличие от решения Диффи-Хеллмана.
[3] Рон Ривест, Ади Шамир и Леонард Адлеман, "Метод получения цифровых подписей и криптосистемы с открытым ключом", Communications of the Association for Computing Machinery, 21 (1978), pp. 120-26.
[4] Хорошую историю этих открытий дает Саймон Сингх, The Code Book, Fourth Estate (London, 1999), глава 6.
Асимметричное шифрование и аутентификация
Обзор асимметричного шифрования на примере Боба и Алисы представлен на рисунке 1.
Сначала Алиса создает пару ключей, состоящую из одного открытого (K_P) и одного закрытого (K_S),
где "P" в K_P означает
"public", а "S" в K_S -
"secret". Затем она свободно распространяет этот открытый ключ среди других
людей. Мы вернемся к деталям этого процесса распространения немного позже. А
пока предположим, что любой человек, включая Боба, может безопасно получить
открытый ключ Алисы K_P.
В какой-то момент Боб хочет написать Алисе сообщение M. Поскольку оно содержит конфиденциальную информацию, он хочет, чтобы его
содержимое оставалось секретным для всех, кроме Алисы. Поэтому Боб сначала
шифрует свое сообщение M с
помощью K_P. Затем он
отправляет полученный шифротекст C Алисе, которая расшифровывает C с помощью K_S, чтобы получить
исходное сообщение M.
Рисунок 1: Асимметричное шифрование
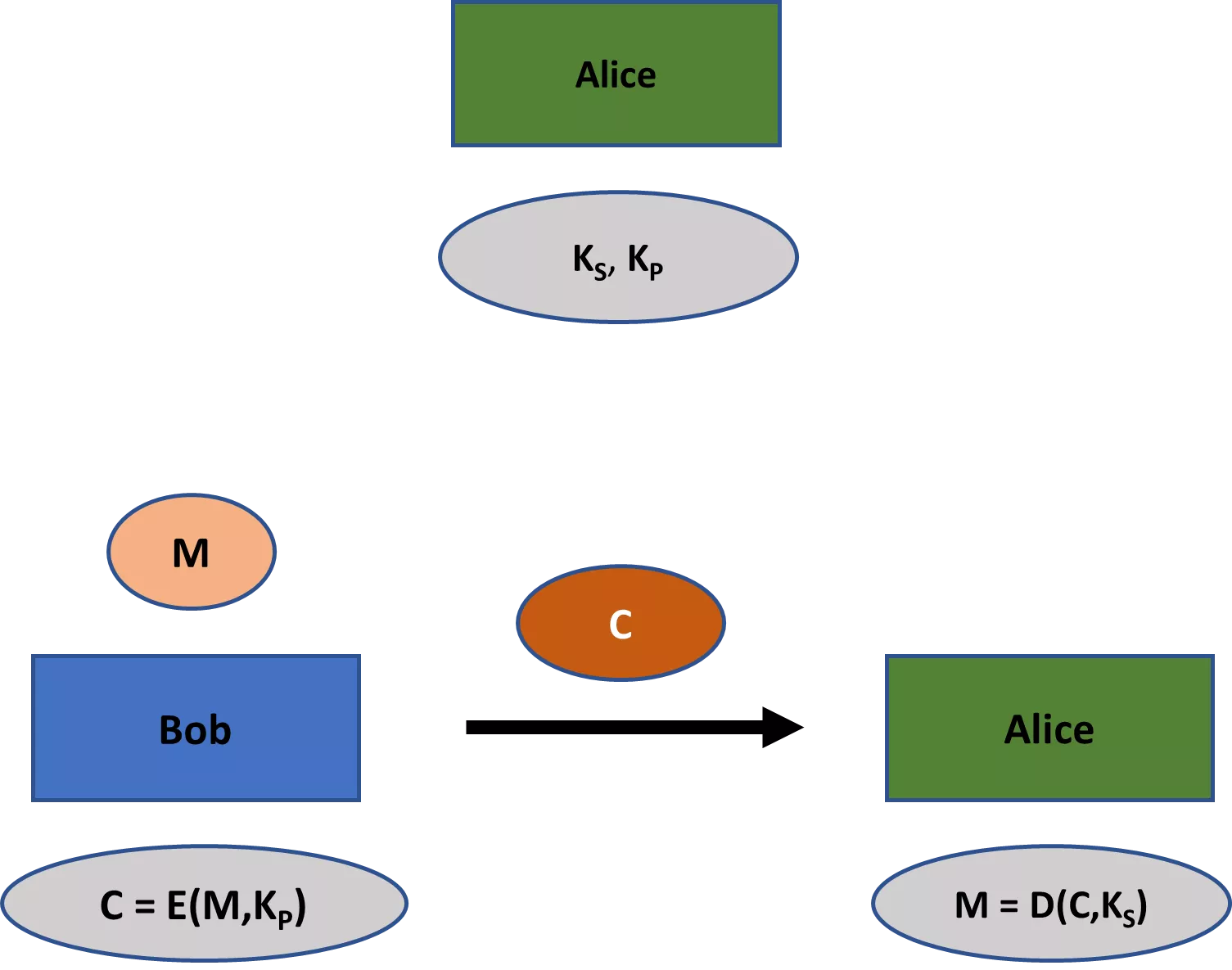
Любой противник, прослушивающий общение Боба и Алисы, может наблюдать C. Она также знает K_P и
алгоритм шифрования E(\cdot).
Важно, однако, что эта информация не позволяет злоумышленнику практически
расшифровать шифротекст C.
Для расшифровки требуется K_S, которым злоумышленник не
обладает.
Схемы симметричного шифрования, как правило, должны быть защищены от злоумышленника, который может правильно зашифровать сообщение с открытым текстом (так называемая защита от атаки с выбором шифртекста). Однако они не предназначены для того, чтобы позволить злоумышленнику или кому-либо еще создавать такие правильные шифртексты.
Это резко отличается от асимметричной схемы шифрования, где вся цель состоит в том, чтобы позволить любому, в том числе и злоумышленникам, создавать правильные шифротексты. Поэтому асимметричные схемы шифрования можно назвать шифрами многократного доступа.
Чтобы лучше понять, что происходит, представьте, что вместо электронной отправки сообщения Боб хочет тайно отправить физическое письмо. Одним из способов обеспечения секретности было бы послать Алисе надежный висячий замок, а ключ для его отпирания оставить себе. Написав письмо, Боб мог бы положить его в ящик и закрыть его на висячий замок Алисы. Затем он может отправить запертый ящик с письмом Алисе, у которой есть ключ, чтобы его открыть.
Хотя Боб способен запереть висячий замок, ни он, ни любой другой человек, перехвативший ящик, не сможет снять его, если он действительно надежно заперт. Только Алиса может отпереть его и увидеть содержимое письма Боба, потому что у нее есть ключ.
Асимметричная схема шифрования - это, грубо говоря, цифровая версия этого процесса. Висячий замок похож на открытый ключ, а ключ от замка - на закрытый ключ. Однако, поскольку замок цифровой, Алисе гораздо проще и не так дорого распространить его среди всех, кто захочет отправить ей секретные сообщения.
Для аутентификации в асимметричной среде мы используем цифровые подписи. Таким образом, они выполняют ту же функцию, что и коды аутентификации сообщений в симметричной системе. Обзор цифровых подписей представлен на Рисунке 2.
Сначала Боб создает пару ключей, состоящую из открытого ключа (K_P) и закрытого ключа (K_S), и
распространяет свой открытый ключ. Когда он хочет отправить Алисе
аутентифицированное сообщение, он сначала берет свое сообщение M и свой закрытый ключ, чтобы создать цифровую подпись D. Затем Боб отправляет Алисе
свое сообщение вместе с цифровой подписью.
Алиса вставляет сообщение, открытый ключ и цифровую подпись в алгоритм проверки. Этот алгоритм выдает либо true для действительной подписи, либо false для недействительной подписи.
Цифровая подпись - это, как ясно из названия, цифровой эквивалент письменной подписи на письмах, контрактах и так далее. На самом деле цифровая подпись обычно гораздо надежнее. Приложив некоторые усилия, можно подделать письменную подпись; этот процесс облегчается тем, что письменные подписи часто не проверяются. Однако защищенная цифровая подпись, как и защищенный код аутентификации сообщения, экзистенциально не подделывается: то есть при использовании схемы защищенной цифровой подписи никто не сможет создать подпись для сообщения, которое пройдет процедуру проверки, если только у него нет закрытого ключа.
Рисунок 2: Асимметричная аутентификация
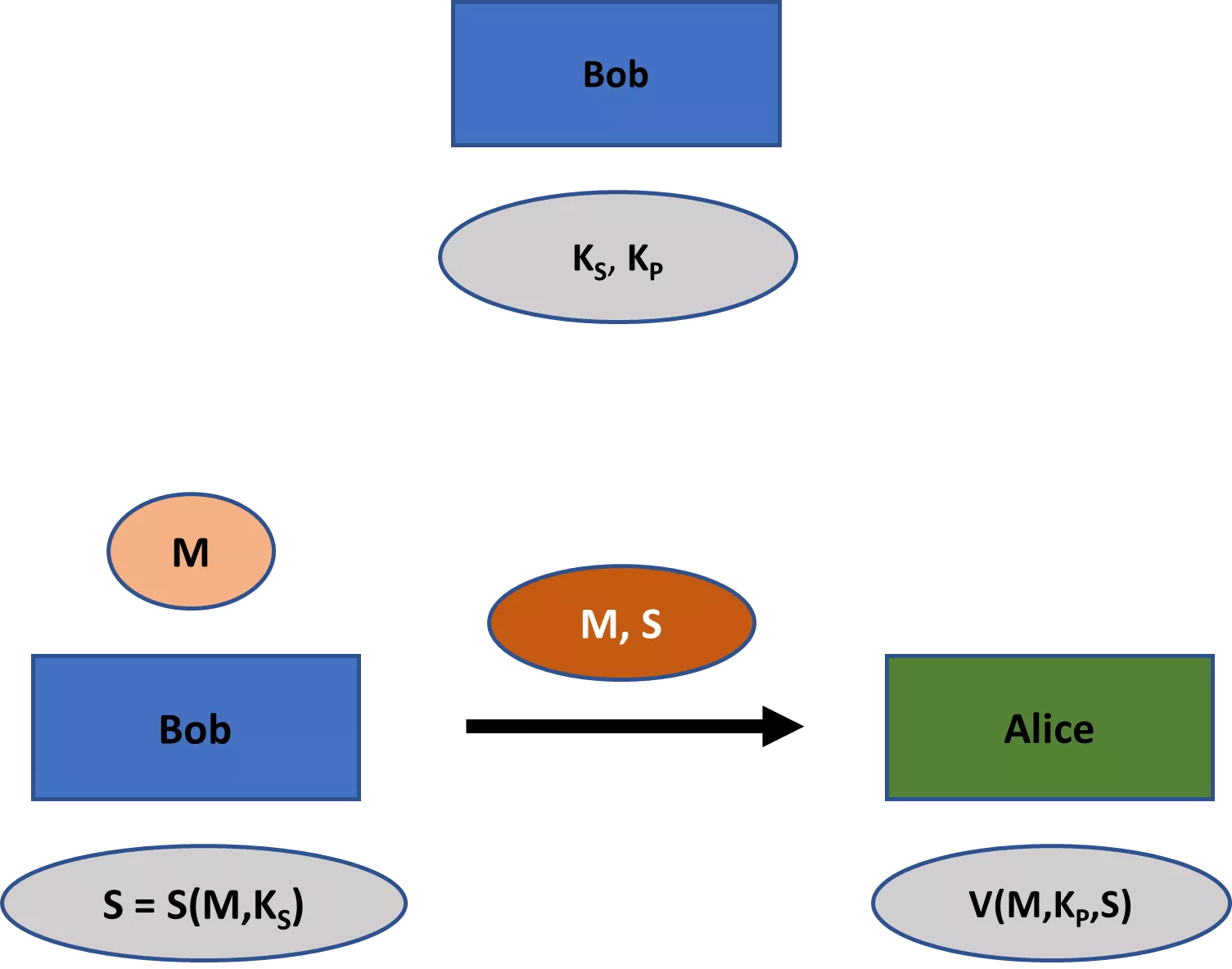
Как и в случае с асимметричным шифрованием, мы видим интересный контраст
между цифровыми подписями и кодами аутентификации сообщений. В последнем
случае алгоритм проверки может быть использован только одной из сторон,
имеющей доступ к защищенному сообщению. Это связано с тем, что для него
требуется закрытый ключ. Однако в асимметричном случае любой может проверить
цифровую подпись S, сделанную
Бобом.
Все это делает цифровые подписи чрезвычайно мощным инструментом. Например,
на ее основе можно создавать подписи под контрактами, которые могут быть
проверены в юридических целях. Если в ходе вышеописанного обмена Боб
поставил подпись под контрактом, Алиса может предъявить сообщение M, контракт и подпись S в суде.
Затем суд может проверить подпись с помощью открытого ключа Боба. [5]
Например, цифровые подписи являются важным аспектом безопасного распространения программного обеспечения и его обновлений. Такой тип публичной верификации невозможно создать, используя только коды аутентификации сообщений.
В качестве последнего примера силы цифровых подписей рассмотрим биткойн. Одно из самых распространенных заблуждений о биткойне, особенно в средствах массовой информации, заключается в том, что транзакции шифруются: это не так. Вместо этого в транзакциях Bitcoin для обеспечения безопасности используются цифровые подписи.
Биткойны существуют в виде пачек, называемых неизрасходованными транзакционными выходами (или UTXO's). Предположим, вы получили три платежа на определенный адрес биткойна по 2 биткойна каждый. Технически у вас теперь нет 6 биткойнов на этом адресе. Вместо этого у вас есть три партии по 2 биткойна, которые заблокированы криптографической проблемой, связанной с этим адресом. Для любого платежа вы можете использовать одну, две или все три партии, в зависимости от того, сколько вам нужно для транзакции.
Подтверждение права собственности на неизрасходованные транзакции обычно осуществляется с помощью одной или нескольких цифровых подписей. Биткойн работает именно потому, что действительные цифровые подписи на неизрасходованных результатах транзакций вычислительно невыполнимы, если только вы не владеете секретной информацией, необходимой для их создания.
В настоящее время транзакции биткоина прозрачно включают всю информацию, которая должна быть проверена участниками сети, например, происхождение неизрасходованных транзакционных выходов, использованных в транзакции. Хотя можно скрыть часть этой информации и при этом обеспечить возможность проверки (как это делают некоторые альтернативные криптовалюты, например Monero), это также создает определенные риски для безопасности.
Иногда возникает путаница между цифровыми подписями и письменными подписями, выполненными в цифровом виде. В последнем случае вы делаете снимок своей письменной подписи и вставляете его в электронный документ, например в трудовой договор. Однако это не цифровая подпись в криптографическом смысле. Последняя представляет собой длинное число, которое можно получить, только владея закрытым ключом.
Как и в случае с симметричным ключом, вы можете использовать асимметричные схемы шифрования и аутентификации вместе. При этом действуют аналогичные принципы. Прежде всего, для шифрования и создания цифровых подписей следует использовать разные пары закрытых и открытых ключей. Кроме того, сначала нужно зашифровать сообщение, а затем проверить его подлинность.
Важно отметить, что во многих приложениях асимметричная криптография не используется на протяжении всего процесса обмена данными. Вместо этого она обычно используется только для обмена симметричными ключами между сторонами, с помощью которых они будут общаться.
Так происходит, например, при покупке товаров в Интернете. Зная открытый ключ продавца, он может отправлять вам сообщения с цифровой подписью, которые вы можете проверить на подлинность. Исходя из этого, вы можете использовать один из множества протоколов обмена симметричными ключами для безопасного взаимодействия.
Основная причина частоты использования вышеупомянутого подхода заключается в том, что асимметричная криптография гораздо менее эффективна, чем симметричная, в обеспечении определенного уровня безопасности. Это одна из причин, почему нам по-прежнему нужна криптография с симметричным ключом наряду с открытой криптографией. Кроме того, криптография с симметричным ключом гораздо более естественна в конкретных приложениях, например, когда пользователь компьютера шифрует свои собственные данные.
Как же именно цифровые подписи и шифрование с открытым ключом решают проблемы распределения и управления ключами?
Здесь нет единого ответа. Асимметричная криптография - это инструмент, и не существует единого способа его применения. Но давайте возьмем наш предыдущий пример с Jim's Sporting Goods, чтобы показать, как обычно решаются проблемы в этом примере.
Для начала Jim's Sporting Goods, вероятно, обратится в центр сертификации, организацию, которая занимается распространением открытых ключей. Центр сертификации зарегистрирует некоторые сведения о компании Jim's Sporting Goods и предоставит ей открытый ключ. Затем он отправит компании Jim's Sporting Goods сертификат, известный как TLS/SSL-сертификат, с открытым ключом Jim's Sporting Goods, подписанным цифровой подписью с использованием собственного открытого ключа центра сертификации. Таким образом, центр сертификации подтверждает, что конкретный открытый ключ действительно принадлежит компании Jim's Sporting Goods.
Ключевым моментом в понимании этого процесса с сертификатами TLS/SSL является то, что, хотя открытый ключ Jim's Sporting Goods обычно не хранится где-либо на вашем компьютере, открытые ключи признанных центров сертификации действительно хранятся в вашем браузере или в вашей операционной системе. Они хранятся в так называемых корневых сертификатах.
Поэтому, когда Jim's Sporting Goods предоставляет вам свой сертификат TLS/SSL, вы можете проверить цифровую подпись центра сертификации с помощью корневого сертификата в своем браузере или операционной системе. Если подпись действительна, вы можете быть уверены, что открытый ключ сертификата действительно принадлежит Jim's Sporting Goods. Исходя из этого, можно легко настроить протокол для безопасной связи с Jim's Sporting Goods.
Теперь распределение ключей стало намного проще для Jim's Sporting Goods. Нетрудно заметить, что управление ключами также значительно упростилось. Вместо того чтобы хранить тысячи ключей, компании Jim's Sporting Goods достаточно хранить только закрытый ключ, который позволяет делать подписи для открытого ключа SSL-сертификата. Каждый раз, когда клиент заходит на сайт Jim's Sporting Goods, он может установить защищенный сеанс связи с помощью этого открытого ключа. Клиентам также не нужно хранить какую-либо информацию (кроме открытых ключей признанных центров сертификации в операционной системе и браузере).
Примечания:
[5] Любые схемы, пытающиеся достичь безответственности, - еще одна тема, которую мы обсуждали в главе 1, - в своей основе должны включать цифровые подписи.
Хэш-функции
Хэш-функции повсеместно используются в криптографии. Они не являются ни симметричными, ни асимметричными схемами, а относятся к самостоятельной криптографической категории.
Мы уже сталкивались с хэш-функциями в главе 4 при создании сообщений аутентификации на основе хэша. Они также важны в контексте цифровых подписей, хотя и по несколько иной причине: Цифровые подписи обычно создаются именно над хэш-значением некоторого (зашифрованного) сообщения, а не над самим сообщением. В этом разделе я предложу более подробное введение в хэш-функции.
Начнем с определения хэш-функции. Хэш-функция - это любая эффективно вычисляемая функция, которая принимает входные данные произвольного размера и выдает выходные данные фиксированной длины.
Криптографическая хэш-функция** - это просто хэш-функция, полезная для применения в криптографии. Выходные данные криптографической хэш-функции обычно называются хэш, хэш-значение или дайджест сообщения.
В контексте криптографии под "хэш-функцией" обычно подразумевается криптографическая хэш-функция. В дальнейшем я буду придерживаться этой практики.
Примером популярной хэш-функции является SHA-256 (безопасный хэш-алгоритм 256). Независимо от размера входных данных (например, 15 бит, 100 бит или 10 000 бит), эта функция выдает 256-битное хэш-значение. Ниже приведено несколько примеров вывода функции SHA-256.
"Привет": 185f8db32271fe25f561a6fc938b2e264306ec304eda518007d1764826381969
"52398": a3b14d2bf378c1bd47e7f8eaec63b445150a3d7a80465af16dd9fd319454ba90
"Криптография - это весело": 3cee2a5c7d2cc1d62db4893564c34ae553cc88623992d994e114e344359b146c
Все выходные данные представляют собой ровно 256 бит, записанных в шестнадцатеричном формате (каждая шестнадцатеричная цифра может быть представлена четырьмя двоичными цифрами). Поэтому даже если бы вы вставили в функцию SHA-256 книгу Толкиена Властелин колец, выходной результат все равно был бы равен 256 битам.
Хэш-функции, такие как SHA-256, используются в криптографии для различных целей. Какие свойства требуются от хэш-функции, зависит от контекста конкретного приложения. Существует два основных свойства, которые обычно требуются от хэш-функций в криптографии: [6]
Устойчивость к столкновениям
Скрыть
Хэш-функция H считается устойчивой к коллизиям, если невозможно найти два значения, x и y, такие, что x \neq y, но H(x) = H(y).
Устойчивые к столкновениям хэш-функции важны, например, при проверке программного обеспечения. Предположим, вы хотите загрузить Windows-версию Bitcoin Core 0.21.0 (серверное приложение для обработки сетевого трафика биткоина). Для проверки легитимности этого программного обеспечения вам потребуется выполнить следующие основные действия:
Сначала вам нужно загрузить и импортировать открытые ключи одного или нескольких участников Bitcoin Core в программное обеспечение, которое может проверять цифровые подписи (например, Kleopetra). Вы можете найти эти открытые ключи здесь. Рекомендуется проверять программное обеспечение Bitcoin Core с помощью открытых ключей от нескольких контрибьюторов.
Далее необходимо проверить открытые ключи, которые вы импортировали. По крайней мере один из шагов, который вы должны сделать, - это проверить, что найденные вами открытые ключи совпадают с опубликованными в различных других местах. Например, вы можете обратиться к личным веб-страницам, страницам в Twitter или Github людей, чьи открытые ключи вы импортировали. Обычно такое сравнение открытых ключей выполняется путем сравнения короткого хэша открытого ключа, известного как отпечаток пальца.
Далее вам нужно загрузить исполняемый файл для Bitcoin Core с их веб-сайта. Там будут доступны пакеты для операционных систем Linux, Windows и MAC.
Далее вам нужно найти два файла релиза. Первый содержит официальный хэш SHA-256 для загруженного вами исполняемого файла вместе с хэшами всех остальных пакетов, которые были выпущены. Другой файл релиза будет содержать подписи различных авторов над файлом релиза с хэшами пакетов. Оба этих файла релиза должны находиться на сайте Bitcoin Core.
Далее вам нужно вычислить хэш SHA-256 исполняемого файла, загруженного с сайта Bitcoin Core, на своем компьютере. Затем сравните этот результат с хэшем официального пакета для исполняемого файла. Они должны быть одинаковыми.
Наконец, вам нужно будет проверить, что одна или несколько цифровых подписей над файлом релиза с официальными хэшами пакета действительно соответствуют одному или нескольким импортированным вами открытым ключам (релизы Bitcoin Core не всегда подписываются всеми). Это можно сделать с помощью такого приложения, как Kleopetra.
Этот процесс проверки программного обеспечения имеет два основных преимущества. Во-первых, он гарантирует, что при загрузке с сайта Bitcoin Core не было ошибок в передаче данных. Во-вторых, он гарантирует, что злоумышленники не могли заставить вас загрузить модифицированный вредоносный код, либо взломав сайт Bitcoin Core, либо перехватив трафик.
Как именно вышеописанный процесс проверки программного обеспечения защищает от этих проблем?
Если вы тщательно проверили открытые ключи, которые импортировали, то можете быть уверены, что эти ключи действительно принадлежат им и не были скомпрометированы. Учитывая, что цифровые подписи обладают экзистенциальной неизменяемостью, вы знаете, что только эти участники могли сделать цифровую подпись под хэшами официальных пакетов в файле релиза.
Предположим, что подписи на загруженном файле выпуска проверены. Теперь вы можете сравнить хэш-значение, вычисленное вами локально для загруженного исполняемого файла Windows, со значением, содержащимся в правильно подписанном файле релиза. Как вы знаете, хэш-функция SHA-256 устойчива к коллизиям, и совпадение означает, что ваш исполняемый файл точно такой же, как и официальный.
Перейдем ко второму общему свойству хэш-функций: скрытие.
Говорят, что любая хэш-функция H обладает свойством сокрытия, если для любого случайно выбранного x из очень большого диапазона найти x, имея только H(x), не представляется
возможным.
Ниже показан вывод SHA-256 для сообщения, которое я написал. Чтобы обеспечить достаточную случайность, в конце сообщения содержится случайно сгенерированная строка символов. Учитывая, что SHA-256 обладает свойством скрытия, никто не сможет расшифровать это сообщение.
b194221b37fa4cd1cfce15aaef90351d70de17a98ee6225088b523b586c32ded
Но я не буду оставлять вас в напряжении, пока SHA-256 не станет слабее. Первоначально я написал следующее сообщение:
- "Это очень случайное послание, ну или вроде того. Начало - нет, но я закончу некоторыми относительно случайными символами, чтобы обеспечить непредсказуемость сообщения. XLWz4dVG3BxUWm7zQ9qS".
Обычно хэш-функции со свойством сокрытия используются в управлении паролями (устойчивость к столкновениям также важна для этого приложения). Любой приличный онлайн-сервис, основанный на учетных записях, такой как Facebook или Google, не будет хранить ваши пароли непосредственно для управления доступом к учетной записи. Вместо этого они будут хранить только хэш этого пароля. Каждый раз, когда вы вводите пароль в браузере, сначала вычисляется хэш. Только этот хэш отправляется на сервер поставщика услуг и сравнивается с хэшем, хранящимся в внутренней базе данных. Свойство сокрытия позволяет злоумышленникам не восстанавливать пароль по его хэш-значению.
Управление паролями с помощью хэшей, конечно, работает только в том случае, если пользователи действительно выбирают сложные пароли. Свойство сокрытия предполагает, что x выбирается случайным образом из очень большого диапазона. Выбор таких паролей, как "1234", "mypassword" или дата вашего дня рождения, не обеспечит никакой реальной безопасности. Существуют длинные списки распространенных паролей и их хэшей, которые злоумышленники могут использовать, если им удастся получить хэш вашего пароля. Такие атаки известны как словарные атаки. Если злоумышленникам известны некоторые ваши личные данные, они также могут попытаться сделать несколько обоснованных догадок. Поэтому вам всегда нужны длинные, надежные пароли (лучше всего длинные, случайные строки из менеджера паролей).
Иногда приложению может потребоваться хэш-функция, обладающая одновременно устойчивостью к столкновениям и скрытием. Но, конечно, не всегда. Например, процесс проверки программного обеспечения, который мы обсуждали, требует, чтобы хэш-функция демонстрировала только устойчивость к столкновениям, скрытие не имеет значения.
Хотя устойчивость к столкновениям и сокрытие являются основными свойствами, которые требуются от хэш-функций в криптографии, в некоторых приложениях могут быть желательны и другие типы свойств.
Примечания:
[6] Терминология "сокрытия" не является общепринятой, а взята из книги Арвинда Нараянана, Джозефа Бонно, Эдварда Фелтена, Эндрю Миллера и Стивена Голдфедера, Биткоин и криптовалютные технологии, Princeton University Press (Princeton, 2016), глава 1.
Криптосистема RSA
Проблема факторизации
Если симметричная криптография обычно достаточно интуитивно понятна для большинства людей, то с асимметричной криптографией дело обстоит иначе. Хотя вы, скорее всего, знакомы с высокоуровневым описанием, предложенным в предыдущих разделах, вам, вероятно, интересно, что именно представляют собой односторонние функции и как именно они используются для построения асимметричных схем.
В этой главе я сниму часть таинственности с асимметричной криптографии, более глубоко рассмотрев конкретный пример, а именно криптосистему RSA. В первом разделе я представлю проблему факторизации, на которой основана проблема RSA. Затем будет рассмотрен ряд ключевых результатов из теории чисел. В последнем разделе мы объединим эту информацию, чтобы объяснить проблему RSA и то, как она может быть использована для создания асимметричных криптографических схем.
Добавить эту глубину в наше обсуждение - задача не из легких. Она требует введения довольно большого количества теорем и предложений из теории чисел. Но пусть математика вас не разочаровывает. Работа над этим обсуждением значительно улучшит ваше понимание того, что лежит в основе асимметричной криптографии, и это достойное вложение средств.
Теперь обратимся к задаче факторизации.
При умножении двух чисел, скажем, a и b, числа a и b называют факторами, а результат - продуктом.
Попытка записать число N в
виде умножения двух или более факторов называется факторизацией или факторизацией. [1] Любую задачу, требующую этого, можно
назвать задачей факторизации.
Около 2 500 лет назад греческий математик Евклид Александрийский открыл ключевую теорему о факторизации целых чисел. Она называется единственной теоремой факторизации и гласит следующее:
Теорема 1. Каждое целое число N, которое больше 1, либо
является простым числом, либо может быть выражено как произведение простых
факторов.
Последняя часть этого утверждения означает, что вы можете взять любое не
простое целое число N больше 1
и записать его как умножение простых чисел. Ниже приведено несколько примеров
целых не простых чисел, записанных в виде произведения простых факторов.
18 = 2 \cdot 3 \cdot 3 = 2 \cdot 3^284 = 2 \cdot 2 \cdot 3 \cdot 7 = 2^2 \cdot 3 \cdot 7144 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 = 2^4 \cdot 3^2
Для всех трех приведенных выше целых чисел вычислить их простые коэффициенты
довольно просто, даже если вам дано всего N. Вы начинаете с наименьшего простого числа, а именно 2, и смотрите,
сколько раз целое число N делится на него. Затем вы переходите к проверке делимости N на 3, 5, 7 и так далее. Вы продолжаете этот процесс до тех пор, пока целое
число N не будет записано как
произведение только простых чисел.
Возьмем, к примеру, целое число 84. Ниже показан процесс определения его простых множителей. На каждом шаге мы убираем наименьший оставшийся простой множитель (слева) и определяем остаток, который нужно разложить на множители. Так продолжается до тех пор, пока оставшийся член не станет простым числом. На каждом шаге текущая факторизация числа 84 отображается в крайнем правом углу.
- Первообразная = 2: остаток = 42 (
84 = 2 \cdot 42) - Первообразная = 2: остаток = 21 (
84 = 2 \cdot 2 \cdot 21) - Первообразная = 3: остаток = 7 (
84 = 2 \cdot 2 \cdot 3 \cdot 7) - Поскольку 7 - простое число, результат равен
2 \cdot 2 \cdot 3 \cdot 7, или2^2 \cdot 3 \cdot 7.
Предположим, что N очень
велико. Насколько сложно будет сократить N до простых коэффициентов?
Это зависит от числа N.
Предположим, например, что N равно
50 450 400. Хотя это число выглядит пугающе, вычисления не так уж сложны и могут
быть легко выполнены вручную. Как и в предыдущем случае, начните с 2 и двигайтесь
дальше. Ниже вы можете увидеть результат этого процесса.
- 2: 25,225,200 (
50,450,400 = 2 \cdot 25,225,200) - 2: 12,612,600 (
50,450,400 = 2^2 \cdot 12,612,600) - 2: 6,306,300 (
50,450,400 = 2^3 \cdot 6,306,300) - 2: 3,153,150 (
50,450,400 = 2^4 \cdot 3,153,150) - 2: 1,576,575 (
50,450,400 = 2^5 \cdot 1,576,575) - 3: 525,525 (
50,450,400 = 2^5 \cdot 3 \cdot 525,525) - 3: 175,175 (
50,450,400 = 2^5 \cdot 3^2 \cdot 175,175) - 5: 35,035 (
50,450,400 = 2^5 \cdot 3^2 \cdot 5 \cdot 35,035) - 5: 7,007 (
50,450,400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7,007) - 7: 1,001 (
50,450,400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7 \cdot 1,001) - 7: 143 (
50,450,400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 143) - 11: 13 (
50,450,400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13) - Поскольку 13 - простое число, результат равен
2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13.
Решение этой задачи вручную занимает некоторое время. Компьютер, конечно, может сделать все это за малую долю секунды. Более того, часто компьютер может даже факторизовать очень большие целые числа за доли секунды.
Однако есть и исключения. Предположим, что сначала мы случайным образом
выбираем два очень больших простых числа. Обычно их принято обозначать p и q, и здесь я буду
придерживаться этого правила.
Для конкретности предположим, что p и q - это 1024-битные простые
числа, и что для их представления действительно требуется не менее 1024
битов (поэтому первый бит должен быть 1). Так, например, 37 не может быть
одним из простых чисел. Вы, конечно, можете представить 37 с помощью 1024
битов. Но очевидно, что вам не нужно столько бит для его
представления. Вы можете представить 37 любой строкой, содержащей 6 или
более бит. (В 6 битах 37 будет представлено как 100101).
Важно понимать, насколько велики p и q, если они выбраны в
соответствии с приведенными выше условиями. В качестве примера ниже я выбрал
случайное простое число, для представления которого требуется не менее 1024
бит.
- 14,752,173,874,503,595,484,930,006,383,670,759,559,764,562,721,397,166,747,289,220,945,457,932,666,751,048,198,854,920,097,085,690,793,755,254,946,188,163,753,506,778,089,706,699,671,722,089,715,624,760,049,594,106,189,662,669,156,149,028,900,805,928,183,585,427,782,974,951,355,515,394,807,209,836,870,484,558,332,897,443,152,653,214,483,870,992,618,171,825,921,582,253,023,974,514,209,142,520,026,807,636,589
Предположим, что после случайного выбора простых чисел p и q мы перемножим их, чтобы
получить целое число N. Это
целое число, таким образом, является 2048-битным числом, для представления
которого требуется не менее 2048 битов. Оно намного, намного больше, чем p или q.
Предположим, вы даете компьютеру N и просите его найти два 1024-битных простых фактора N. Вероятность того, что
компьютер найдет p и q, крайне мала. Можно
сказать, что это невозможно для всех практических целей. Это так, даже если
бы вы использовали суперкомпьютер или даже сеть суперкомпьютеров.
Для начала предположим, что компьютер пытается решить задачу, перебирая 1024
битовых числа, проверяя в каждом случае, являются ли они простыми и являются
ли они факторами N. Тогда
набор проверяемых простых чисел составляет примерно 1,265 \cdot 10^{305}. [2]
Даже если взять все компьютеры на планете и заставить их попытаться найти и
проверить 1024-битные простые числа таким образом, то для того, чтобы с
вероятностью 1 к миллиарду успешно найти простой множитель N, потребуется период вычислений, намного превышающий возраст Вселенной.
На практике компьютер может работать лучше, чем только что описанная грубая процедура. Существует несколько алгоритмов, которые компьютер может применить, чтобы быстрее прийти к факторизации. Однако дело в том, что даже при использовании этих более эффективных алгоритмов задача компьютера все равно остается вычислительно невыполнимой. [3]
Важно отметить, что сложность факторизации при только что описанных условиях основывается на предположении, что не существует эффективных с точки зрения вычислений алгоритмов для вычисления простых факторов. На самом деле мы не можем доказать, что эффективного алгоритма не существует. Тем не менее, это предположение очень правдоподобно: несмотря на обширные усилия, продолжающиеся сотни лет, мы до сих пор не нашли такого эффективного алгоритма.
Следовательно, при определенных обстоятельствах проблему факторизации можно
с полным основанием считать трудной задачей. В частности, когда p и q - очень большие простые
числа, их произведение N несложно вычислить; но факторизация только с учетом N практически невозможна.
Примечания:
[1] Факторизация также может быть важна для работы не только с числами, но и
с другими типами математических объектов. Например, она может быть полезна
для факторизации полиномиальных выражений, таких как x^2 - 2x + 1. В нашем обсуждении мы сосредоточимся только на факторизации чисел, а
именно целых чисел.
[2] Согласно теореме о простых числах, количество простых
чисел, меньших или равных N,
равно примерно N/\ln(N). Это
означает, что количество простых чисел длиной 1024 бита можно приблизительно
определить следующим образом:
\frac{2^{1024}}{\ln(2^{1024})} -
\frac{2^{1023}}{\ln(2^{1023})}
...что равно примерно 1,265 \times 10^{305}.
[3] То же самое справедливо и для задач дискретного логарифма. Отсюда следует, что асимметричные конструкции работают с гораздо большими ключами, чем симметричные криптографические конструкции.
Результаты теории чисел
К сожалению, проблема факторизации не может быть напрямую использована для асимметричных криптографических схем. Однако мы можем использовать для этого более сложную, но родственную проблему - проблему RSA.
Чтобы разобраться в проблеме RSA, нам потребуется понять ряд теорем и предложений из теории чисел. В этом разделе они представлены в трех подразделах: (1) порядок N, (2) инвертируемость по модулю N и (3) теорема Эйлера.
Часть материала, изложенного в этих трех подразделах, уже была представлена в главе 3. Но для удобства я изложу этот материал заново.
Порядок N
Целое число a является простым или относительно простым с целым числом N, если наибольший общий
делитель между ними равен 1. Хотя 1 по условию не является простым числом,
оно является простым для каждого целого числа (как и -1).
Например, рассмотрим случай, когда a = 18 и N = 37. Это явно копримы.
Наибольшее целое число, которое делится и на 18, и на 37, равно 1. Напротив,
рассмотрим случай, когда a = 42 и N = 16. Очевидно, что они
не являются копримами. Оба числа делятся на 2, что больше 1.
Теперь мы можем определить порядок N следующим образом. Предположим, что N - целое число, большее 1. Тогда порядок N - это число всех
копримов с N, таких, что для
каждого коприма a выполняется
следующее условие: 1 \leq a < N.
Например, если N = 12, то 1,
5, 7 и 11 - единственные копирайты, удовлетворяющие вышеуказанному
требованию. Следовательно, порядок 12 равен 4.
Предположим, что N - простое
число. Тогда любое целое число, меньшее N, но большее или равное 1,
сопряжено с ним. К ним относятся все элементы следующего множества: \{1,2,3,....,N - 1\}. Следовательно, когда N простое, порядок N равен N - 1. Это утверждается в
предложении 1, где \phi(N) обозначает порядок N.
Предположение 1. \phi(N) = N - 1, если N простое
Предположим, что число N не
является простым. Тогда вы можете вычислить его порядок с помощью функции Эйлера Phi. Если вычисление порядка небольшого
целого числа относительно просто, то функция Эйлера Phi становится особенно
важной для больших целых чисел. Ниже приводится предложение функции Эйлера
Phi.
Теорема 2. Пусть N равно p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot
p_i^{e_i} \cdot \ldots \cdot p_n^{e_n}, где множество \{p_i\} состоит из всех различных простых факторов N, а каждое e_i указывает, сколько раз простой фактор p_i встречается для N. Тогда,
\phi(N) = p_1^{e_1 - 1} \cdot (p_1 - 1)\cdot p_2^{e_2 -
1} \cdot (p_2 - 1)\cdot \ldots \cdot p_n^{e_n - 1} \cdot
(p_n - 1)
Теорема 2 показывает, что, разложив любое не простое число N на его отдельные простые факторы, можно легко вычислить порядок числа N.
Например, предположим, что N = 270. Это явно не простое число. Разложив N на простые множители, получим выражение: 2 \cdot 3^3 \cdot 5. Согласно
функции Эйлера Phi, порядок N выглядит следующим образом:
\phi(N) = 2^{1 - 1} \cdot (2 - 1) + 3^{3 - 1} \cdot
(3 - 1) + 5^{1 - 1} \cdot (5 - 1) = 1 \cdot 1 + 9 \cdot 2 + 1
\cdot 4 = 1 + 18 + 4 = 23
Предположим, что N - это
произведение двух простых, p и q. тогда Теорема 2, приведенная выше, утверждает, что порядок N следующий:
p^{1 - 1} \cdot (p - 1)\cdot q^{1 - 1} \cdot (q - 1)
= (p - 1) \cdot (q - 1)
Это ключевой результат, в частности, для проблемы RSA, и он изложен в Предложении 2 ниже.
Предложение 2. Если N - произведение двух простых чисел, p и q, то порядок N равен произведению (p - 1)\cdot (q - 1).
Для примера предположим, что N = 119. Это целое число можно разложить на два простых числа, а именно 7 и 17.
Следовательно, функция Эйлера Phi предполагает, что порядок 119 будет
следующим:
\phi(119) = (7 - 1)\cdot (17 - 1) = 6 \cdot 16 = 96
Другими словами, целое число 119 имеет 96 копримов в диапазоне от 1 до 119. Фактически, это множество включает все целые числа от 1 до 119, которые не кратны ни 7, ни 17.
В дальнейшем будем обозначать множество копримов, определяющих порядок N, как C_N. Для нашего
примера, где N = 119,
множество C_{119} слишком
велико, чтобы перечислить его полностью. Но некоторые его элементы можно перечислить
следующим образом:
C_{119} = \{1, 2, \dots, 6, 8, \dots, 13, 15, 16, 18,
\dots, 33, 35, \dots, 96\}
Инвертируемость по модулю N
Можно сказать, что целое число a является инвертируемым по модулю N, если существует хотя бы
одно целое число b, такое,
что a \cdot b \mod N = 1 \mod N.
Любое такое целое число b называется инверсным (или мультипликативным обратным) от a с учетом сокращения по модулю N.
Предположим, например, что a = 5 и N = 11. Существует
множество целых чисел, на которые можно умножить 5, так что 5 \cdot b \mod 11 = 1 \mod 11. Рассмотрим, например, целые числа 20 и 31. Легко видеть, что оба этих
числа являются инверсиями 5 при уменьшении по модулю 11.
5 \cdot 20 \mod 11 = 100 \mod 11 = 1 \mod 115 \cdot 31 \mod 11 = 155 \mod 11 = 1 \mod 11
Хотя у 5 есть много обратных, уменьшаемых по модулю 11, можно показать, что существует только один положительный обратный 5, который меньше 11. На самом деле, это не уникальный для нашего конкретного примера, а общий результат.
Предположение 3. Если целое число a инвертируемо по модулю N, то
должно быть так, что ровно одна положительная обратная a меньше N. (Таким образом, эта
единственная обратная a должна происходить из множества \{1, \dots, N - 1\}).
Обозначим единственную обратную величину a из Предложения 3 как a^{-1}. Для случая,
когда a = 5 и N = 11, видно, что a^{-1} = 9,
учитывая, что 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11.
Обратите внимание, что значение 9 для a^{-1} в нашем примере можно также получить, просто уменьшив любое другое обратное
число a по модулю 11.
Например, 20 \mod 11 = 31 \mod 11 = 9 \mod 11. Таким образом, если целое число a > N является инвертируемым по модулю N, то a \mod N также должно быть инвертируемым по модулю N.
Не обязательно, что обратное число a существует, уменьшаясь по модулю N. Предположим, например, что a = 2 и N = 8. Не существует ни b, ни какого-либо a^{-1}, такого, что 2 \cdot b \mod 8 = 1 \mod 8.
Это связано с тем, что любое значение b всегда будет кратно 2, поэтому
деление на 8 никогда не даст остатка, равного 1.
Как узнать, есть ли у некоторого целого числа a обратная величина для данного N? Как вы могли заметить в
примере выше, наибольший общий делитель между 2 и 8 больше 1, а именно 2. И
это на самом деле иллюстрирует следующий общий результат:
Предположение 4. Существует обратная величина целого числа a, приведенного к модулю N, а именно единственная
положительная обратная величина меньше N, тогда и только тогда,
когда наибольший общий делитель между a и N равен 1 (то есть, если они
являются копримами).
Для случая, когда a = 5 и N = 11, мы пришли к выводу,
что a^{-1} = 9,
учитывая, что 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11. Важно отметить, что обратное тоже верно. То есть, если a = 9 и N = 11, то a^{-1} = 5.
Теорема Эйлера
Прежде чем перейти к решению проблемы RSA, нам необходимо понять еще одну важнейшую теорему, а именно теорему Эйлера. Она гласит следующее:
Теорема 3. Предположим, что два целых числа a и N являются копримами. Тогда a^{\phi(N)} \mod N = 1 \mod N.
Это замечательный результат, но поначалу немного запутанный. Давайте обратимся к примеру, чтобы понять его.
Предположим, что a = 5 и N = 7. Это действительно
простые числа, как того требует теорема Эйлера. Мы знаем, что порядок 7
равен 6, учитывая, что 7 - простое число (см. Предположение 1).
Теперь теорема Эйлера утверждает, что 5^6 \mod 7 должно быть равно 1 \mod 7.
Ниже приведены вычисления, показывающие, что это действительно так.
5^6 \mod 7 = 15,625 \mod 7 = 1 \mod N
Целое число 7 делится на 15 624 в общей сложности 2 233 раза. Следовательно, остаток от деления 16 625 на 7 равен 1.
Далее, используя функцию Эйлера Phi, Теорема 2, можно вывести Предположение 5, приведенное ниже.
Предположение 5. \phi(a \cdot b) = \phi(a) \cdot \phi(b) для любых положительных целых чисел a и b.
Мы не будем показывать, почему это так. Просто отметим, что вы уже видели
доказательство этого утверждения в том, что \phi(p \cdot q) = \phi(p) \cdot \phi(q) = (p - 1) \cdot (q - 1), когда p и q являются простыми, как указано в Предложении 2.
Теорема Эйлера в сочетании с предложением 5 имеет важные
следствия. Посмотрите, что происходит, например, в приведенных ниже
выражениях, где a и N - соправители.
a^{2 \cdot \phi(N)} \mod N = a^{\phi(N)} \cdot a^{\phi(N)} \mod N = 1 \cdot 1 \mod N = 1 \mod Na^{\phi(N) + 1} \mod N = a^{\phi(N)} \cdot a^1 \mod N = 1 \cdot a^1 \mod N = a \mod Na^{8 \cdot \phi(N) + 3} \mod N = a^{8 \cdot \phi(N)} \cdot a^3 \mod N = 1 \cdot a^3 \mod N = a^3 \mod N
Таким образом, сочетание теоремы Эйлера и предложения 5 позволяет просто вычислить ряд выражений. В общем случае мы можем обобщить это понимание в предложении 6.
Предположение 6. a^x \mod N = a^{x \mod \phi(N)}
Осталось собрать все воедино на последнем сложном этапе.
Так же как у N есть порядок \phi(N), включающий элементы
множества C_N, мы знаем, что
целое число \phi(N) в свою
очередь тоже должно иметь порядок и множество копримов. Зададим \phi(N) = R. Тогда мы знаем,
что существует также значение \phi(R) и множество копримов C_R.
Предположим, что теперь мы выберем целое число e из множества C_R. Из Предложения 3 известно, что это целое число e имеет только одну единственную положительную обратную величину меньше R. То есть e имеет одну единственную обратную величину из множества C_R. Назовем эту обратную
величину d. Учитывая
определение обратной величины, это означает, что e \cdot d = 1 \mod R.
С помощью этого результата мы можем сделать утверждение о нашем исходном
целом N. Это кратко изложено
в Предложении 7.
Предположение 7. Предположим, что e \cdot d \mod \phi(N) = 1 \mod \phi(N). Тогда для любого элемента a множества C_N должно быть
так, что a^{e \cdot d \mod \phi(N)} = a^{1 \mod \phi(N)} = a
\mod N.
Теперь у нас есть все результаты теории чисел, необходимые для четкой постановки задачи RSA.
Криптосистема RSA
Теперь мы готовы сформулировать проблему RSA. Предположим, вы создали набор
переменных, состоящий из p, q, N, \phi(N), e, d и y. Назовем этот набор \Pi. Он создается следующим
образом:
Сгенерируйте два случайных простых числа
pиqодинакового размера и вычислите их произведениеN.Вычислите порядок
N,\phi(N), по следующему произведению:(p - 1) \cdot (q - 1).Выберите
e > 2, такое, что оно меньше и соизмеримо с\phi(N).Вычислите
d, задавe \cdot d \mod \phi(N) = 1.Выберите случайную величину
y, меньшую и простую по отношению кN.
Задача RSA состоит в том, чтобы найти такое число x, что x^e = y, имея при этом
только подмножество информации о \Pi, а именно переменные N, e и y. Когда p и q очень велики, обычно рекомендуется,
чтобы их размер составлял 1024 бита, проблема RSA считается трудной. Теперь вы
можете понять, почему это так, учитывая предыдущее обсуждение.
Легкий способ вычислить x,
когда x^e \mod N = y \mod N,
- это просто вычислить y^d \mod N. Мы знаем, что y^d \mod N = x \mod N из следующих
вычислений:
y^d \mod N = x^{e \cdot d} \mod N = x^{e \cdot d \mod
\phi(N)} \mod N = x^{1 \mod \phi(N)} \mod N = x \mod N.
Проблема в том, что мы не знаем значения d, так как оно не задано в задаче. Следовательно, мы не можем напрямую
вычислить y^d \mod N, чтобы
получить x \mod N.
Однако мы могли бы косвенно вычислить d из порядка N, \phi(N), поскольку знаем, что e \cdot d \mod \phi(N) = 1 \mod \phi(N). Но по предположению задача не дает значения и для \phi(N).
Наконец, порядок можно было бы вычислить косвенно с помощью простых факторов p и q, чтобы в итоге вычислить d. Но, по предположению,
значения p и q также не были нам предоставлены.
Строго говоря, даже если проблема факторизации в рамках проблемы RSA является трудной, мы не можем доказать, что проблема RSA также является трудной. Могут существовать и другие способы решения проблемы RSA, кроме факторизации. Однако принято считать, что если проблема факторизации внутри проблемы RSA трудна, то и сама проблема RSA трудна.
Если проблема RSA действительно трудна, то она порождает одностороннюю
функцию с "черным ходом". В данном случае это функция f(g) = g^e \mod N. Зная f(g), любой может
легко вычислить значение y для конкретного g = x. Однако
вычислить конкретное значение x, зная только значение y и функцию f(g), практически
невозможно. Исключением является случай, когда вам дана часть информации d - "люк". В этом случае вы можете просто вычислить y^d, чтобы получить x.
Давайте рассмотрим конкретный пример, иллюстрирующий проблему RSA. Я не могу выбрать задачу RSA, которая считалась бы трудной при вышеуказанных условиях, так как цифры были бы громоздкими. Вместо этого я привожу пример, чтобы проиллюстрировать, как в целом работает проблема RSA.
Для начала предположим, что вы выбрали два случайных простых числа 13 и 31.
Таким образом, p = 13 и q = 31. Произведение N этих двух простых чисел равно 403. Мы можем легко вычислить порядок числа
403. Он эквивалентен (13 - 1)\cdot (31 - 1) = 360.
Далее, как предписывает шаг 3 задачи RSA, нам нужно выбрать для 360 число, которое больше 2 и меньше 360. Мы не должны выбирать это значение случайным образом. Предположим, что мы выберем 103. Это число совпадает с 360, так как его наибольший общий делитель с 103 равен 1.
Теперь шаг 4 требует вычисления значения d, такого, что 103 \cdot d \mod 360 = 1. Это
нелегко сделать вручную, если значение N велико. Для этого нужно использовать процедуру, называемую расширенным евклидовым алгоритмом.
Хотя я не показываю здесь эту процедуру, она дает значение 7, когда e = 103. Вы можете убедиться, что пара значений 103 и 7 действительно
удовлетворяет общему условию e \cdot d \mod \phi(n) = 1,
выполнив следующие вычисления.
103 \cdot 7 \mod 360 = 721 \mod 360 = 1 \mod 360
Важно отметить, что, учитывая предложение 4, мы знаем, что никакое
другое целое число от 1 до 360 для d не приведет к результату, что 103 \cdot d = 1 \mod 360.
Кроме того, из этого предложения следует, что выбор другого значения e приведет к другому уникальному значению d.
На шаге 5 задачи RSA нам нужно выбрать некоторое целое положительное число y, которое является меньшим копримом 403. Предположим, что мы зададим y = 2^{103}.
Экспонирование 2 на 103 дает следующий результат.
2^{103} \mod 403 = 10,141,204,801,825,835,211,973,625,643,008 \mod 403 = 349 \mod 403
Задача RSA в этом конкретном примере выглядит следующим образом: У вас есть N = 403, e = 103 и y = 349 \mod 403. Теперь вам
нужно вычислить x так, чтобы x^{103} = 349 \mod 403. То есть вы должны найти, что исходное значение до экспоненцирования на
103 было равно 2.
Вычислить x было бы легко (по
крайней мере, для компьютера), если бы мы знали, что d = 7. В этом случае вы могли
бы просто определить x, как
показано ниже.
x = y^7 \mod 403 = 349^7 \mod 403 = 630,634,881,591,804,949 \mod 403 = 2 \mod 403
Проблема в том, что вам не предоставили информацию о том, что d = 7. Конечно, вы можете вычислить d из того факта, что 103 \cdot d = 1 \mod 360.
Проблема в том, что вам также не предоставлена информация о том, что порядок N = 360. Наконец, вы также
могли бы вычислить порядок 403, вычислив следующее произведение: (p - 1)\cdot (q - 1). Но вам
также не сообщили, что p = 13 и q = 31.
Конечно, компьютер все еще может решить проблему RSA для этого примера относительно легко, потому что простые числа невелики. Но когда простые числа становятся очень большими, перед ним встает практически невыполнимая задача.
Теперь мы представили проблему RSA, набор условий, при которых она трудна, и математические основы. Как все это может помочь в асимметричной криптографии? В частности, как мы можем превратить трудность проблемы RSA при определенных условиях в схему шифрования или схему цифровой подписи?
Один из подходов заключается в том, чтобы взять проблему RSA и построить
схемы простым способом. Например, предположим, что вы сгенерировали набор
переменных \Pi, как описано в
задаче RSA, и убедились, что p и q достаточно велики. Вы
устанавливаете свой открытый ключ равным (N, e) и сообщаете эту информацию всему миру. Как описано выше, вы держите в
секрете значения p, q, \phi(n) и d. Фактически, d - это ваш закрытый ключ.
Любой, кто захочет отправить вам сообщение m, являющееся элементом C_N,
может просто зашифровать его следующим образом: c = m^e \mod N. (Шифротекст c здесь эквивалентен значению y в задаче RSA.) Вы можете легко расшифровать это сообщение, просто вычислив c^d \mod N.
Аналогичным образом можно попытаться создать схему цифровой подписи.
Предположим, вы хотите отправить кому-то сообщение m с цифровой подписью S. Вы
можете просто задать S = m^d \mod N и отправить пару (m,S) получателю. Любой человек может проверить цифровую подпись, просто проверив,
что S^e \mod N = m \mod N.
Однако любому злоумышленнику будет очень сложно создать действительную S для сообщения, учитывая, что он не обладает d.
К сожалению, превращение сложной проблемы RSA в криптографическую схему не
так просто. Для прямой схемы шифрования вы можете выбрать в качестве
сообщений только копримы из N. Это не оставляет нам много возможных сообщений, и уж точно не достаточно
для стандартной коммуникации. Кроме того, эти сообщения должны быть выбраны
случайным образом. Это кажется несколько непрактичным. Наконец, любое
сообщение, выбранное дважды, будет содержать один и тот же шифротекст. Это
крайне нежелательно в любой схеме шифрования и не соответствует никаким
строгим современным стандартным представлениям о безопасности шифрования.
Проблемы становятся еще более серьезными для нашей простой схемы цифровой
подписи. В нынешнем виде любой злоумышленник может легко подделать цифровую
подпись, просто выбрав в качестве подписи число, кратное N, а затем вычислив соответствующее оригинальное сообщение. Это явно
нарушает требование экзистенциальной неизменяемости.
Тем не менее, добавив немного сложности, проблему RSA можно использовать для создания безопасной схемы шифрования с открытым ключом, а также безопасной схемы цифровой подписи. Мы не будем здесь вдаваться в подробности таких конструкций. [4] Важно, однако, что эта дополнительная сложность не меняет фундаментальной проблемы RSA, на которой основаны эти схемы.
Примечания:
[4] См. например, Jonathan Katz and Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), pp. 410-32 о шифровании RSA и pp. 444-41 о цифровых подписях RSA.
Заключительный раздел
Обзор & Оценка
366d6fd0-ceb2-4299-bf37-8c6dfcb681d5 true
Итоговый Экзамен
44882d2b-63cd-4fde-8485-f76f14d8b2fe true
Заключение
f1905f78-8cf7-5031-949a-dfa8b76079b4 true