name: Introdução à criptografia formal goal: Uma introdução aprofundada à ciência e à prática da criptografia. objectives:

Mergulhar na criptografia

É difícil encontrar muitos materiais que ofereçam um bom meio-termo no ensino da criptografia.

Por um lado, há tratados longos e formais, acessíveis apenas a quem tem uma sólida formação em matemática, lógica ou qualquer outra disciplina formal. Por outro lado, há introduções de muito alto nível que escondem demasiados pormenores para qualquer pessoa minimamente curiosa.

Esta introdução à criptografia procura captar o meio-termo. Embora deva ser relativamente desafiadora e detalhada para qualquer pessoa nova na criptografia, não é a toca do coelho de um típico tratado fundamental.

Introdução

Visão geral do curso

bb8a8b73-7fb2-50da-bf4e-98996d79887b Bem-vindo ao curso CYP302!

Este livro oferece uma introdução aprofundada à ciência e à prática da criptografia. Sempre que possível, centra-se na exposição concetual, em vez de formal, do material.

Este conteúdo educacional é adaptado do livro e repo JWBurgers. Embora o autor tenha gentilmente permitido seu uso educacional, todos os direitos de propriedade intelectual permanecem com o criador original.

Motivação e objectivos

É difícil encontrar muitos materiais que ofereçam um bom meio-termo no ensino da criptografia.

Por um lado, há tratados longos e formais, acessíveis apenas a quem tem uma sólida formação em matemática, lógica ou qualquer outra disciplina formal. Por outro lado, há introduções de muito alto nível que escondem demasiados pormenores para qualquer pessoa minimamente curiosa.

Esta introdução à criptografia procura captar o meio-termo. Embora deva ser relativamente desafiadora e detalhada para qualquer pessoa nova na criptografia, não é a toca do coelho de um típico tratado fundamental.

Público-alvo

Desde programadores a curiosos intelectuais, este livro é útil para qualquer pessoa que pretenda mais do que uma compreensão superficial da criptografia. Se o seu objetivo é dominar o campo da criptografia, então este livro é também um bom ponto de partida.

Orientações de leitura

O livro contém atualmente sete capítulos: "O que é criptografia?" (Capítulo 1), "Fundamentos matemáticos da criptografia I" (Capítulo 2), "Fundamentos matemáticos da criptografia II" (Capítulo 3), "Criptografia simétrica" (Capítulo 4), "RC4 e AES" (Capítulo 5), "Criptografia assimétrica" (Capítulo 6) e "O criptossistema RSA" (Capítulo 7). Um último capítulo, "Criptografia na prática", será ainda acrescentado. Este capítulo centra-se em várias aplicações criptográficas, incluindo a segurança da camada de transporte, o onion routing e o sistema de troca de valores da Bitcoin.

A menos que tenha uma sólida formação em matemática, a teoria dos números é provavelmente o tópico mais difícil deste livro. Apresento uma visão geral no Capítulo 3, e também aparece na exposição do AES no Capítulo 5 e do criptossistema RSA no Capítulo 7.

Se tiver dificuldades com os pormenores formais destas partes do livro, recomendo que se contente com uma leitura de alto nível da primeira vez.

Agradecimentos

O livro mais influente na formação deste foi o Introduction to Modern Cryptography de Jonathan Katz e Yehuda Lindell, CRC Press (Boca Raton, FL), 2015. Um curso de acompanhamento está disponível no Coursera chamado "Cryptography"

As principais fontes adicionais que foram úteis para criar a visão geral deste livro são Simon Singh, The Code Book, Fourth Estate (Londres, 1999); Christof Paar e Jan Pelzl, Understanding Cryptography, Springer (Heidelberg, 2010) e um curso baseado no livro de Paar chamado "Introduction to Cryptography"; e Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons).

Apenas citarei informações e resultados muito específicos que retiro destas fontes, mas quero reconhecer aqui a minha dívida geral para com elas.

Para os leitores que desejam procurar conhecimentos mais avançados sobre criptografia após esta introdução, recomendo vivamente o livro de Katz e Lindell. O curso de Katz no Coursera é um pouco mais acessível do que o livro.

Contribuições

Por favor, consulte o ficheiro de contribuições no repositório para obter algumas orientações sobre como apoiar o projeto.

Notação

**Termos-chave

Os termos-chave nas cartilhas são introduzidos a negrito. Por exemplo, a introdução da cifra Rijndael como termo-chave seria a seguinte: Cifra Rijndael.

Os termos-chave são explicitamente definidos, exceto se se tratar de nomes próprios ou se o seu significado for óbvio na discussão.

A definição é geralmente dada aquando da introdução de um termo-chave, embora por vezes seja mais conveniente deixar a definição para um momento posterior.

Palavras e frases sublinhadas:

As palavras e frases são realçadas através de itálico. Por exemplo, a frase "Lembre-se da sua palavra-passe" teria o seguinte aspeto: Lembre-se da sua palavra-passe.

Notação formal:

A notação formal refere-se principalmente a variáveis, variáveis aleatórias e conjuntos.

Pronto para explorar o fascinante universo da criptografia? Vamos lá!

O que é a criptografia?

As cifras de Beale

Comecemos a nossa investigação no domínio da criptografia com um dos episódios mais encantadores e divertidos da sua história: o das cifras de Beale. [1]

A história das cifras de Beale é, na minha opinião, mais suscetível de ser ficção do que realidade. Mas supostamente aconteceu o seguinte.

Tanto no inverno de 1820 como no de 1822, um homem chamado Thomas J. Beale hospedou-se numa estalagem pertencente a Robert Morriss, em Lynchburg (Virgínia). No final da sua segunda estadia, Beale entregou a Morriss uma caixa de ferro com documentos valiosos para serem guardados.

Alguns meses mais tarde, Morriss recebeu uma carta de Beale, datada de 9 de maio de 1822. Esta carta sublinhava o grande valor do conteúdo da caixa de ferro e dava algumas instruções a Morriss: se nem Beale nem nenhum dos seus associados viesse reclamar a caixa, ele deveria abri-la precisamente dez anos após a data da carta (ou seja, 9 de maio de 1832). Alguns dos papéis dentro da caixa estariam escritos em texto normal. Vários outros, porém, seriam "ininteligíveis sem o auxílio de uma chave" Essa "chave" seria, então, entregue a Morriss por um amigo não identificado de Beale em junho de 1832.

Apesar das instruções claras, Morriss não abriu a caixa em maio de 1832 e o misterioso amigo de Beale nunca apareceu em junho desse ano. Só em 1845 é que o estalajadeiro decidiu finalmente abrir a caixa. Nela, Morriss encontrou uma nota que explicava como Beale e os seus associados descobriram ouro e prata no Oeste e os enterraram, juntamente com algumas jóias, para os guardar. Além disso, a caixa continha três textos de cifra: isto é, textos escritos em código que requerem uma chave criptográfica, ou um segredo, e um algoritmo de acompanhamento para serem desbloqueados. Este processo de desbloqueio de um texto cifrado é conhecido como desencriptação, enquanto o processo de bloqueio é conhecido como encriptação. (Como explicado no Capítulo 3, o termo cifra pode assumir vários significados. No nome "Beale ciphers", é a abreviatura de ciphertexts)

Os três textos cifrados que Morriss encontrou na caixa de ferro são constituídos por uma série de números separados por vírgulas. De acordo com a nota de Beale, estes textos cifrados fornecem separadamente a localização do tesouro, o conteúdo do tesouro e uma lista de nomes com os herdeiros legítimos do tesouro e as suas acções (sendo esta última informação relevante no caso de Beale e os seus associados nunca virem reclamar a caixa).

Morris tentou decifrar os três textos cifrados durante vinte anos. Isto teria sido fácil com a chave. Mas Morriss não tinha a chave e não teve sucesso nas suas tentativas de recuperar os textos originais, ou textos simples, como são normalmente designados em criptografia.

Já perto do fim da sua vida, Morriss passou a caixa a um amigo em 1862. Este amigo publicou posteriormente um panfleto em 1885, sob o pseudónimo J.B. Ward. Incluía uma descrição da (alegada) história da caixa, os três textos cifrados e uma solução que ele tinha encontrado para o segundo texto cifrado. (Aparentemente, há uma chave para cada texto cifrado, e não uma chave que funciona para todos os três textos cifrados, como Beale parece ter sugerido originalmente em sua carta a Morriss)

Pode ver-se o segundo texto cifrado na Figura 2 abaixo. [2] A chave para este texto cifrado é a Declaração de Independência dos Estados Unidos. O processo de descodificação resume-se à aplicação das duas regras seguintes:

Figura 1: Cifra Beale n.º. 2

Figure 1: Beale cipher no 2.

Por exemplo, o primeiro número do segundo texto cifrado é 115. A 115ª palavra da Declaração de Independência é "instituído", pelo que a primeira letra do texto simples é "i" O texto cifrado não indica diretamente o espaçamento entre palavras e a capitalização. Mas depois de decifrar as primeiras palavras, pode logicamente deduzir que a primeira palavra do texto simples era simplesmente "I" (O texto simples começa com a frase "Depositei no condado de Bedford.")

Após a descodificação, a segunda mensagem fornece o conteúdo detalhado do tesouro (ouro, prata e jóias) e sugere que foi enterrado em potes de ferro e coberto com pedras no condado de Bedford (Virgínia). As pessoas adoram um bom mistério, pelo que foram feitos grandes esforços para decifrar as outras duas cifras de Beale, especialmente a que descreve a localização do tesouro. Até vários criptógrafos de renome tentaram decifrá-las. No entanto, até à data, ninguém conseguiu decifrar os outros dois textos cifrados.

Notas:

[1] Para um bom resumo da história, ver Simon Singh, The Code Book, Fourth Estate (Londres, 1999), pp. 82-99. Um pequeno filme da história foi realizado por Andrew Allen em 2010. Pode encontrar o filme, "The Thomas Beale Cipher", no seu sítio Web.

[2] Esta imagem está disponível na página da Wikipédia sobre as cifras de Beale.

Criptografia moderna

Histórias coloridas, como a das cifras de Beale, são o que a maioria de nós associa à criptografia. No entanto, a criptografia moderna difere em pelo menos quatro aspectos importantes deste tipo de exemplos históricos.

Em primeiro lugar, historicamente, a criptografia tem-se preocupado apenas com o secreto (ou confidencialidade)[3]. Os textos cifrados seriam criados para garantir que apenas certas partes poderiam ter acesso à informação contida nos textos simples, como no caso das cifras de Beale. Para que um esquema de encriptação sirva bem este propósito, decifrar o texto cifrado só deve ser possível se se tiver a chave.

A criptografia moderna preocupa-se com uma gama mais vasta de temas do que apenas o segredo. Estes temas incluem principalmente (1) integridade da mensagem-isto é, garantir que uma mensagem não foi alterada; (2) autenticidade da mensagem-isto é, garantir que uma mensagem veio efetivamente de um determinado remetente; e (3) não repúdio-isto é, garantir que um remetente não pode negar falsamente mais tarde que enviou uma mensagem. [4]

Uma distinção importante a ter em conta é, portanto, entre um esquema de encriptação e um esquema criptográfico. Um esquema de encriptação só diz respeito ao segredo. Embora um esquema de cifragem seja um esquema criptográfico, o inverso não é verdadeiro. Um esquema criptográfico pode também servir os outros temas principais da criptografia, incluindo a integridade, a autenticidade e o não-repúdio.

Os temas da integridade e da autenticidade são tão importantes como o do sigilo. Os nossos sistemas de comunicação modernos não poderiam funcionar sem garantias relativamente à integridade e autenticidade das comunicações. O não-repúdio é também uma preocupação importante, como no caso dos contratos digitais, mas é menos necessário em aplicações criptográficas do que o segredo, a integridade e a autenticidade.

Em segundo lugar, os esquemas de encriptação clássicos, como as cifras de Beale, envolvem sempre uma chave que foi partilhada entre todas as partes relevantes. No entanto, muitos esquemas criptográficos modernos envolvem não apenas uma, mas duas chaves: uma privada e uma chave pública. Enquanto a primeira deve permanecer privada em todas as aplicações, a segunda é normalmente do conhecimento público (daí os seus respectivos nomes). No domínio da encriptação, a chave pública pode ser utilizada para encriptar a mensagem, enquanto a chave privada pode ser utilizada para a desencriptação.

O ramo da criptografia que lida com esquemas em que todas as partes partilham uma chave é conhecido como criptografia assimétrica. A chave única num esquema deste tipo é normalmente designada por chave privada (ou chave secreta). O ramo da criptografia que lida com esquemas que requerem um par de chaves privada-pública é conhecido como criptografia assimétrica. Estes ramos são por vezes também referidos como criptografia de chave privada e criptografia de chave pública, respetivamente (embora isto possa gerar confusão, uma vez que os esquemas criptográficos de chave pública também têm chaves privadas).

O advento da criptografia assimétrica no final da década de 1970 foi um dos eventos mais importantes na história da criptografia. Sem ela, a maioria dos nossos sistemas de comunicação modernos, incluindo a Bitcoin, não seria possível ou, pelo menos, seria muito impraticável.

É importante notar que a criptografia moderna não é exclusivamente o estudo de esquemas criptográficos de chave simétrica e assimétrica (embora isso abranja grande parte do domínio). Por exemplo, a criptografia também se ocupa das funções de hash e dos geradores de números pseudo-aleatórios, e é possível criar aplicações com base nestas primitivas que não estão relacionadas com a criptografia de chave simétrica ou assimétrica.

Em terceiro lugar, os esquemas de cifragem clássicos, como os utilizados nas cifras Beale, eram mais arte do que ciência. A sua perceção de segurança baseava-se em grande medida em intuições relativas à sua complexidade. Normalmente, eram corrigidos quando se descobria um novo ataque contra eles ou abandonados por completo se o ataque fosse particularmente grave. A criptografia moderna, no entanto, é uma ciência rigorosa com uma abordagem formal e matemática tanto para desenvolver como para analisar esquemas criptográficos. [5]

Especificamente, a criptografia moderna centra-se em provas formais de segurança. Qualquer prova de segurança para um esquema criptográfico procede em três passos:

  1. A declaração de uma definição criptográfica de segurança, ou seja, um conjunto de objectivos de segurança e a ameaça representada pelo atacante.

  2. A declaração de quaisquer pressupostos matemáticos no que respeita à complexidade computacional do sistema. Por exemplo, um esquema criptográfico pode conter um gerador de números pseudo-aleatórios. Embora não possamos provar que estes existem, podemos assumir que sim.

  3. A exposição de uma prova de segurança matemática do sistema com base na noção formal de segurança e em quaisquer pressupostos matemáticos.

Em quarto lugar, embora historicamente a criptografia tenha sido utilizada principalmente em contextos militares, passou a permear as nossas actividades diárias na era digital. Quer esteja a fazer operações bancárias em linha, a publicar nas redes sociais, a comprar um produto na Amazon com o seu cartão de crédito ou a dar uma gorjeta de bitcoin a um amigo, a criptografia é a condição sine qua non da nossa era digital.

Tendo em conta estes quatro aspectos da criptografia moderna, podemos caraterizar a criptografia moderna como a ciência que se ocupa do desenvolvimento formal e da análise de esquemas criptográficos para proteger a informação digital contra ataques adversários. [6] Neste contexto, a segurança deve ser entendida como a prevenção de ataques que prejudiquem o sigilo, a integridade, a autenticação e/ou o não-repúdio nas comunicações.

A criptografia é melhor vista como uma subdisciplina da segurança cibernética, que se preocupa com a prevenção do roubo, danos e utilização indevida de sistemas informáticos. Note-se que muitos problemas de cibersegurança têm pouca ou apenas uma ligação parcial à criptografia.

Por exemplo, se uma empresa aloja localmente servidores dispendiosos, pode estar preocupada em proteger este hardware contra roubo e danos. Embora esta seja uma preocupação de cibersegurança, tem pouco a ver com criptografia.

Por exemplo, os ataques de phishing são um problema comum na nossa era moderna. Estes ataques tentam enganar as pessoas através de uma mensagem de correio eletrónico ou de outro meio de mensagem, levando-as a ceder informações sensíveis, como palavras-passe ou números de cartões de crédito. Embora a criptografia possa ajudar a resolver os ataques de phishing até um certo ponto, uma abordagem abrangente exige mais do que apenas a utilização de alguma criptografia.

Notas:

Para ser exato, as aplicações importantes dos esquemas criptográficos têm sido relacionadas com o segredo. As crianças, por exemplo, utilizam frequentemente esquemas criptográficos simples para se "divertirem". Nestes casos, o segredo não é uma preocupação real.

[4] Bruce Schneier, Applied Cryptography, 2.ª ed., 2015 (Indianapolis, IN: John Wiley & Sons), p. 2.

[5] Para uma boa descrição, ver Jonathan Katz e Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), especialmente pp. 16-23.

[6] Cf. Katz e Lindell, ibid., p. 3. Penso que a sua caraterização tem alguns problemas, pelo que apresento aqui uma versão ligeiramente diferente da sua declaração.

Comunicações abertas

A criptografia moderna foi concebida para fornecer garantias de segurança num ambiente de comunicações abertas. Se o nosso canal de comunicação estiver tão bem protegido que os espiões não tenham qualquer hipótese de manipular ou mesmo apenas observar as nossas mensagens, então a criptografia é supérflua. No entanto, a maior parte dos nossos canais de comunicação não estão assim tão bem guardados.

A espinha dorsal da comunicação no mundo moderno é uma enorme rede de cabos de fibra ótica. Fazer chamadas telefónicas, ver televisão e navegar na Web numa casa moderna depende geralmente desta rede de cabos de fibra ótica (uma pequena percentagem pode depender exclusivamente de satélites). É verdade que pode haver diferentes ligações de dados em sua casa, como o cabo coaxial, a linha de assinante digital (assimétrica) e o cabo de fibra ótica. Mas, pelo menos no mundo desenvolvido, estes diferentes meios de transmissão de dados ligam-se rapidamente, fora de casa, a um nó de uma enorme rede de cabos de fibra ótica que liga todo o globo. As excepções são algumas zonas remotas do mundo desenvolvido, como nos Estados Unidos e na Austrália, onde o tráfego de dados pode ainda percorrer distâncias substanciais através dos tradicionais fios telefónicos de cobre.

Seria impossível impedir que potenciais atacantes acedessem fisicamente a esta rede de cabos e à sua infraestrutura de apoio. De facto, já sabemos que a maior parte dos nossos dados é interceptada por várias agências de informação nacionais em intersecções cruciais da Internet[7], o que inclui tudo, desde mensagens do Facebook a endereços de sítios Web que visitamos.

Embora a vigilância de dados a uma escala maciça exija um adversário poderoso, como uma agência nacional de informações, os atacantes com poucos recursos podem facilmente tentar bisbilhotar a uma escala mais local. Embora isto possa acontecer ao nível da escuta de fios, é muito mais fácil intercetar comunicações sem fios.

A maior parte dos dados da nossa rede local - seja em casa, no escritório ou num café - viaja agora através de ondas de rádio para pontos de acesso sem fios em routers tudo-em-um, em vez de passar por cabos físicos. Assim, um atacante precisa de poucos recursos para intercetar qualquer tráfego local. Isto é particularmente preocupante porque a maioria das pessoas faz muito pouco para proteger os dados que circulam nas suas redes locais. Além disso, os potenciais atacantes podem também visar as nossas ligações móveis de banda larga, como as 3G, 4G e 5G. Todas estas comunicações sem fios são um alvo fácil para os atacantes.

Assim, a ideia de manter as comunicações secretas através da proteção do canal de comunicação é uma aspiração irremediavelmente delirante para grande parte do mundo moderno. Tudo o que sabemos justifica uma paranoia severa: deve sempre assumir-se que alguém está a ouvir. E a criptografia é a principal ferramenta de que dispomos para obter qualquer tipo de segurança neste ambiente moderno.

Notas:

[7] Ver, por exemplo, Olga Khazan, "The creepy, long-standing practice of undersea cable tapping", The Atlantic, 16 de julho de 2013 (disponível em The Atlantic).

Fundamentos matemáticos da criptografia 1

Variáveis aleatórias

A criptografia baseia-se na matemática. E se quiser construir mais do que uma compreensão superficial da criptografia, precisa de se sentir confortável com essa matemática.

Este capítulo introduz a maior parte da matemática básica que irá encontrar na aprendizagem da criptografia. Os tópicos incluem variáveis aleatórias, operações de módulo, operações XOR e pseudo-aleatoriedade. Deve dominar o material destas secções para qualquer compreensão não superficial da criptografia.

A secção seguinte trata da teoria dos números, que é muito mais difícil.

Variáveis aleatórias

Uma variável aleatória é normalmente denotada por uma letra maiúscula, sem negrito. Assim, por exemplo, podemos falar de uma variável aleatória X, uma variável aleatória Y, ou uma variável aleatória Z. Esta é a notação que também utilizarei daqui para a frente.

Uma variável aleatória pode assumir dois ou mais valores possíveis, cada um com uma certa probabilidade positiva. Os valores possíveis estão listados no conjunto de resultados.

Cada vez que se amostra uma variável aleatória, retira-se um determinado valor do seu conjunto de resultados de acordo com as probabilidades definidas.

Vejamos um exemplo simples. Suponhamos que uma variável X é definida da seguinte forma:

Pr[X = 1] = 0.5
Pr[X = 2] = 0.5

É fácil ver que X é uma variável aleatória. Primeiro, há dois ou mais valores possíveis que X pode assumir, nomeadamente 1 e 2. Em segundo lugar, cada valor possível tem uma probabilidade positiva de ocorrer sempre que se faz uma amostragem de X, nomeadamente 0,5.

Tudo o que uma variável aleatória requer é um conjunto de resultados com duas ou mais possibilidades, em que cada possibilidade tem uma probabilidade positiva de ocorrer aquando da amostragem. Em princípio, uma variável aleatória pode ser definida de forma abstrata, sem qualquer contexto. Neste caso, pode pensar-se em "amostragem" como a realização de uma experiência natural para determinar o valor da variável aleatória.

A variável X acima foi definida de forma abstrata. Pode, portanto, pensar na amostragem da variável X acima como lançar uma moeda ao ar e atribuir "2" no caso de cara e "1" no caso de coroa. Para cada amostra de X, lança-se novamente a moeda ao ar.

Alternativamente, também pode pensar em amostrar X, como lançar um dado justo e atribuir "2" no caso de o dado sair 1, 3 ou 4, e atribuir "1" no caso de o dado sair 2, 5 ou 6. De cada vez que se faz uma amostra de X, lança-se o dado novamente.

Na verdade, qualquer experiência natural que permita definir as probabilidades dos valores possíveis de X acima referidos pode ser imaginada em relação ao desenho.

Frequentemente, no entanto, as variáveis aleatórias não são introduzidas apenas de forma abstrata. Em vez disso, o conjunto de valores de resultados possíveis tem um significado explícito no mundo real (e não apenas como números). Além disso, estes valores de resultados podem ser definidos em relação a um tipo específico de experiência (e não como qualquer experiência natural com esses valores).

Consideremos agora um exemplo de variável X que não é definida abstratamente. X é definida da seguinte forma para determinar qual das duas equipas começa um jogo de futebol:

Pr [X = \text{red kicks off}] = 0.5
Pr [X = \text{blue kicks off}] = 0.5

Neste caso, o conjunto de resultados de X tem um significado concreto, nomeadamente qual a equipa que começa num jogo de futebol. Além disso, os resultados possíveis e as suas probabilidades associadas são determinados por uma experiência concreta, nomeadamente o lançamento de uma determinada moeda C.

Nas discussões sobre criptografia, as variáveis aleatórias são normalmente introduzidas num conjunto de resultados com significado no mundo real. Pode ser o conjunto de todas as mensagens que podem ser encriptadas, conhecido como o espaço de mensagens, ou o conjunto de todas as chaves que as partes que utilizam a encriptação podem escolher, conhecido como o espaço de chaves.

As variáveis aleatórias nas discussões sobre criptografia não são, no entanto, normalmente definidas em relação a uma experiência natural específica, mas em relação a qualquer experiência que possa produzir as distribuições de probabilidade corretas.

As variáveis aleatórias podem ter distribuições de probabilidade discretas ou contínuas. As variáveis aleatórias com uma distribuição de probabilidade discreta - isto é, variáveis aleatórias discretas - têm um número finito de resultados possíveis. A variável aleatória X em ambos os exemplos dados até agora era discreta.

As variáveis aleatórias contínuas podem, em vez disso, assumir valores num ou mais intervalos. Pode dizer-se, por exemplo, que uma variável aleatória, após amostragem, assumirá qualquer valor real entre 0 e 1, e que cada número real neste intervalo é igualmente provável. Dentro deste intervalo, existem infinitos valores possíveis.

Para as discussões criptográficas, apenas será necessário compreender as variáveis aleatórias discretas. Qualquer discussão sobre variáveis aleatórias a partir de agora deve, portanto, ser entendida como referindo-se a variáveis aleatórias discretas, a menos que seja especificamente indicado o contrário.

Gráficos de variáveis aleatórias

Os valores possíveis e as probabilidades associadas a uma variável aleatória podem ser facilmente visualizados através de um gráfico. Por exemplo, considere a variável aleatória X da secção anterior com um conjunto de resultados de \{1, 2\}, e Pr [X = 1] = 0,5 e Pr [X = 2] = 0,5. Normalmente, apresentaríamos uma variável aleatória deste tipo sob a forma de um gráfico de barras, como na Figura 1.

Figura 1: Variável aleatória X

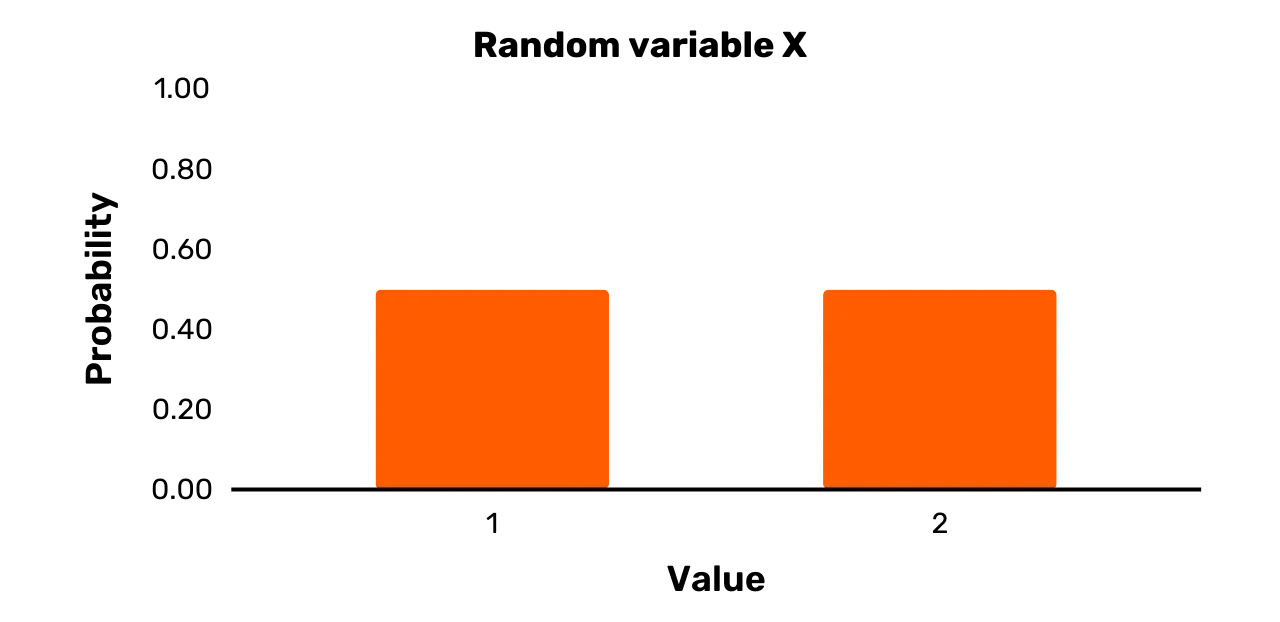
Figure 1: Random variable X.

As barras largas na Figura 1 não pretendem obviamente sugerir que a variável aleatória X é efetivamente contínua. Em vez disso, as barras são largas para serem visualmente mais apelativas (apenas uma linha reta para cima proporciona uma visualização menos intuitiva).

Variáveis uniformes

Na expressão "variável aleatória", o termo "aleatório" significa apenas "probabilístico". Por outras palavras, significa apenas que dois ou mais resultados possíveis da variável ocorrem com determinadas probabilidades. Estes resultados, no entanto, não têm necessariamente de ser igualmente prováveis (embora o termo "aleatório" possa ter esse significado noutros contextos).

Uma variável uniforme é um caso especial de uma variável aleatória. Pode assumir dois ou mais valores, todos com a mesma probabilidade. A variável aleatória X representada na Figura 1 é claramente uma variável uniforme, uma vez que ambos os resultados possíveis ocorrem com uma probabilidade de 0,5. Existem, no entanto, muitas variáveis aleatórias que não são instâncias de variáveis uniformes.

Considere, por exemplo, a variável aleatória Y. Tem um conjunto de resultados {1, 2, 3, 8, 10} e a seguinte distribuição de probabilidade:

\Pr[Y = 1] = 0.25
\Pr[Y = 2] = 0.35
\Pr[Y = 3] = 0.1
\Pr[Y = 8] = 0.25
\Pr[Y = 10] = 0.05

Embora dois resultados possíveis tenham, de facto, a mesma probabilidade de ocorrer, nomeadamente 1 e 8, Y também pode assumir certos valores com probabilidades diferentes de 0,25 após a amostragem. Assim, embora Y seja de facto uma variável aleatória, não é uma variável uniforme.

A Figura 2 apresenta uma representação gráfica de Y.

Figura 2: Variável aleatória Y

Figure 2: Random variable Y.

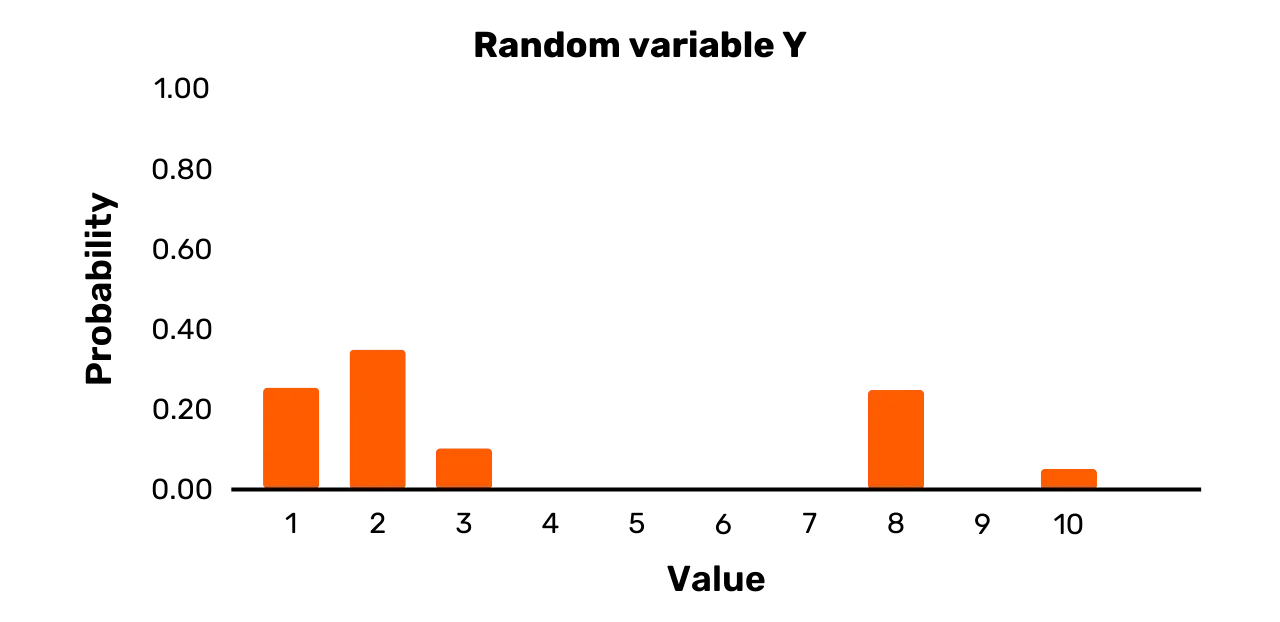
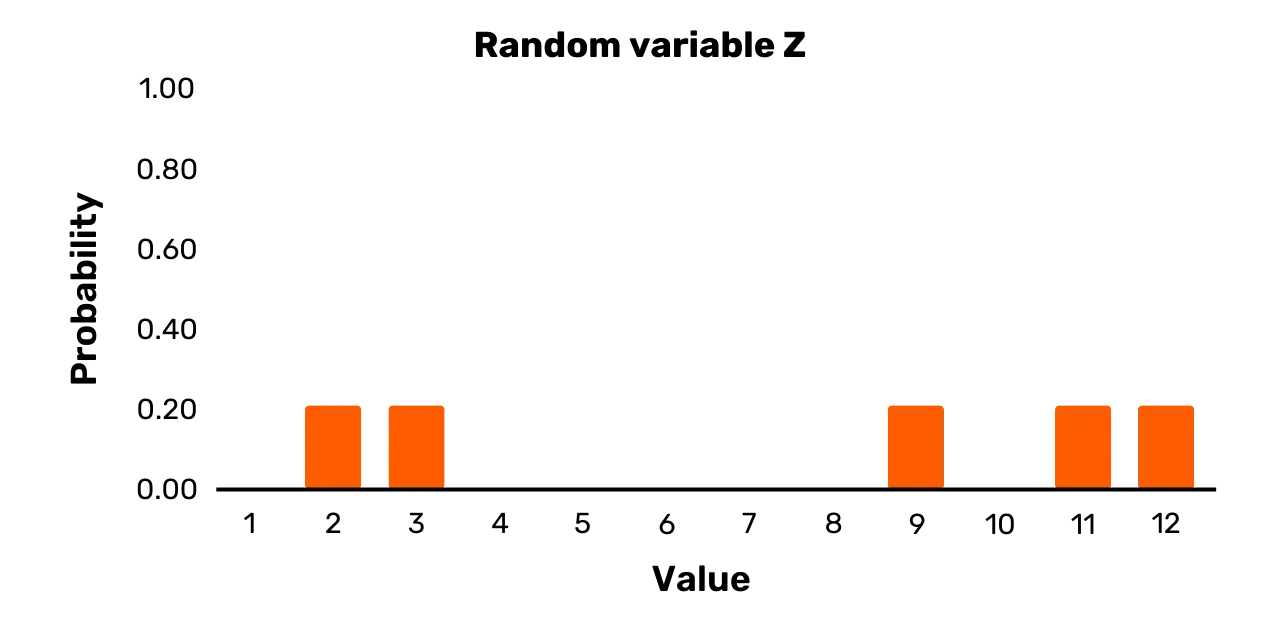
Para um exemplo final, considere a variável aleatória Z. Tem o conjunto de resultados {1,3,7,11,12} e a seguinte distribuição de probabilidade:

\Pr[Z = 2] = 0.2
\Pr[Z = 3] = 0.2
\Pr[Z = 9] = 0.2
\Pr[Z = 11] = 0.2
\Pr[Z = 12] = 0.2

Pode vê-lo representado na Figura 3. A variável aleatória Z é, ao contrário de Y, uma variável uniforme, uma vez que todas as probabilidades dos valores possíveis após a amostragem são iguais.

Figura 3: Variável aleatória Z

Figure 3: Random variable Z.

Probabilidade condicional

Suponha que o Bob pretende selecionar uniformemente um dia do último ano civil. Qual é a probabilidade de o dia selecionado ser um dia de verão?

Desde que pensemos que o processo do Bob será de facto verdadeiramente uniforme, devemos concluir que existe uma probabilidade de 1/4 de o Bob selecionar um dia no verão. Esta é a probabilidade incondicional de o dia selecionado aleatoriamente ser no verão.

Suponha agora que, em vez de selecionar uniformemente um dia do calendário, o Bob apenas seleciona uniformemente entre os dias em que a temperatura ao meio-dia em Crystal Lake (Nova Jérsia) foi igual ou superior a 21 graus Celsius. Dada esta informação adicional, o que podemos concluir sobre a probabilidade de o Bob selecionar um dia de verão?

Deveríamos, de facto, chegar a uma conclusão diferente da anterior, mesmo sem qualquer outra informação específica (por exemplo, a temperatura ao meio-dia de cada dia do último ano civil).

Sabendo que Crystal Lake fica em Nova Jérsia, não seria de esperar que a temperatura ao meio-dia fosse de 21 graus Celsius ou mais no inverno. Em vez disso, é muito mais provável que seja um dia quente na primavera ou no outono, ou um dia algures no verão. Assim, sabendo que a temperatura ao meio-dia em Crystal Lake no dia selecionado era de 21 graus Celsius ou superior, a probabilidade de o dia selecionado pelo Bob ser no verão torna-se muito maior. Esta é a probabilidade condicional de o dia selecionado aleatoriamente ser no verão, dado que a temperatura ao meio-dia em Crystal Lake era de 21 graus Celsius ou superior.

Ao contrário do exemplo anterior, as probabilidades de dois acontecimentos também podem ser completamente independentes. Nesse caso, dizemos que são independentes.

Suponha-se, por exemplo, que uma determinada moeda justa saiu cara. Tendo em conta este facto, qual é a probabilidade de chover amanhã? A probabilidade condicional neste caso deve ser a mesma que a probabilidade incondicional de chover amanhã, uma vez que o lançamento de uma moeda ao ar não tem, em geral, qualquer impacto no estado do tempo.

Utilizamos o símbolo "|" para escrever as declarações de probabilidade condicional. Por exemplo, a probabilidade do evento A dado que o evento B ocorreu pode ser escrita da seguinte forma:

Pr[A|B]

Assim, quando dois acontecimentos, A e B, são independentes, então:

Pr[A|B] = Pr[A] \text{ and } Pr[B|A] = Pr[B]

A condição de independência pode ser simplificada da seguinte forma:

Pr[A, B] = Pr[A] \cdot Pr[B]

Um resultado fundamental na teoria das probabilidades é conhecido como Teorema de Bayes. Basicamente, afirma que Pr[A|B] pode ser reescrito da seguinte forma:

Pr[A|B] = \frac{Pr[B|A] \cdot Pr[A]}{Pr[B]}

Em vez de utilizar probabilidades condicionais com acontecimentos específicos, também podemos olhar para as probabilidades condicionais envolvidas com duas ou mais variáveis aleatórias num conjunto de acontecimentos possíveis. Suponha duas variáveis aleatórias, X e Y. Podemos designar qualquer valor possível para X por x e qualquer valor possível para Y por y. Podemos dizer, então, que duas variáveis aleatórias são independentes se a seguinte afirmação for válida:

Pr[X = x, Y = y] = Pr[X = x] \cdot Pr[Y = y]

para todos os x e y.

Vamos ser um pouco mais explícitos sobre o significado desta afirmação.

Suponha que os conjuntos de resultados para X e Y são definidos da seguinte forma: X = \{x_1, x_2, \ldots, x_i, \ldots, x_n\} e Y = \{y_1, y_2, \ldots, y_i, \ldots, y_m\}. (É típico indicar conjuntos de valores por letras maiúsculas e a negrito)

Agora, suponha que amostra Y e observa y_1. A afirmação acima diz-nos que a probabilidade de obter agora x_1 a partir da amostragem de X é exatamente a mesma que se nunca tivéssemos observado y_1. Isto é verdade para qualquer y_i que pudéssemos ter obtido da nossa amostragem inicial de Y. Finalmente, isto é verdade não apenas para x_1. Para qualquer x_i, a probabilidade de ocorrência não é influenciada pelo resultado de uma amostragem de Y. Tudo isto também se aplica ao caso em que X é amostrado primeiro.

Vamos terminar a nossa discussão com um ponto um pouco mais filosófico. Em qualquer situação do mundo real, a probabilidade de um acontecimento é sempre avaliada em função de um determinado conjunto de informações. Não existe uma "probabilidade incondicional" num sentido muito estrito da palavra.

Por exemplo, suponha que lhe pergunto qual a probabilidade de os porcos voarem até 2030. Embora não lhe dê mais nenhuma informação, é evidente que sabe muito sobre o mundo que pode influenciar o seu julgamento. Nunca viu porcos a voar. Sabe que a maioria das pessoas não espera que eles voem. Sabe que eles não foram feitos para voar. E assim por diante.

Assim, quando falamos de uma "probabilidade incondicional" de um acontecimento num contexto do mundo real, esse termo só pode ter significado se o entendermos como "a probabilidade sem qualquer outra informação explícita". Qualquer entendimento de uma "probabilidade condicional" deve, então, ser sempre entendido em relação a uma informação específica.

Posso, por exemplo, perguntar-lhe qual a probabilidade de os porcos voarem até 2030, depois de lhe ter dado provas de que algumas cabras na Nova Zelândia aprenderam a voar após alguns anos de treino. Neste caso, provavelmente ajustará o seu juízo sobre a probabilidade de os porcos voarem até 2030. Assim, a probabilidade de os porcos voarem até 2030 está condicionada a esta prova sobre cabras na Nova Zelândia.

A operação de módulo

Módulo

A expressão mais básica com a operação módulo tem a seguinte forma: x \mod y.

A variável x é designada por dividendo e a variável y por divisor. Para efetuar uma operação de módulo com um dividendo positivo e um divisor positivo, basta determinar o resto da divisão.

Por exemplo, considere a expressão 25 \mod 4. O número 4 entra no número 25 um total de 6 vezes. O resto dessa divisão é 1. Portanto, 25 \mod 4 é igual a 1. De maneira semelhante, podemos avaliar as expressões abaixo:

Quando o dividendo ou divisor é negativo, as operações de módulo podem ser tratadas de forma diferente pelas linguagens de programação.

De certeza que vai encontrar casos com um dividendo negativo na criptografia. Nestes casos, a abordagem típica é a seguinte:

Por exemplo, suponha que o dividendo é -20 e o divisor 3. O valor mais próximo inferior ou igual a -20 em que 3 se divide uniformemente é -21. O valor de x - p neste caso é -20 - (-21). Este valor é igual a 1 e, portanto, -20 \mod 3 é igual a 1. De forma semelhante, podemos calcular as expressões abaixo:

No que diz respeito à notação, verá normalmente os seguintes tipos de expressões: x = [y \mod z]. Devido aos parêntesis, a operação de módulo neste caso só se aplica ao lado direito da expressão. Se y é igual a 25 e z é igual a 4, por exemplo, então x é igual a 1.

Sem parênteses, a operação de módulo actua em ambos os lados de uma expressão. Suponha, por exemplo, a seguinte expressão: x = y \mod z. Se y é igual a 25 e z é igual a 4, então tudo o que sabemos é que x \mod 4 vale 1. Isto é consistente com qualquer valor para x do conjunto \{\ldots,-7, -3, 1, 5, 9,\ldots\}.

O ramo da matemática que envolve operações de módulo em números e expressões é designado por aritmética modular. Pode pensar neste ramo como aritmética para casos em que a linha numérica não é infinitamente longa. Apesar de, em criptografia, nos depararmos normalmente com operações de módulo para números inteiros (positivos), também é possível efetuar operações de módulo utilizando quaisquer números reais.

A cifra de deslocamento

A operação de módulo é frequentemente utilizada em criptografia. Para ilustrar, consideremos um dos mais famosos esquemas históricos de encriptação: a cifra de deslocamento.

Comecemos por defini-lo. Suponhamos um dicionário D que equaciona todas as letras do alfabeto inglês, por ordem, com o conjunto de números \{0, 1, 2, \ldots, 25\}. Suponha-se um espaço de mensagem M. A cifra de deslocamento é, então, um esquema de encriptação definido da seguinte forma:

O operador de módulo na cifra de deslocamento assegura que as letras se envolvem, de modo a que todas as letras do texto cifrado sejam definidas. Para ilustrar, considere a aplicação da cifra de deslocamento na palavra "DOG".

Suponha que selecionou uniformemente uma chave para ter o valor de 17. A letra "O" equivale a 15. Sem a operação de módulo, a adição deste número de texto simples com a chave resultaria num número de texto cifrado de 32. No entanto, esse número de texto cifrado não pode ser transformado numa letra de texto cifrado, uma vez que o alfabeto inglês só tem 26 letras. A operação de módulo garante que o número do texto cifrado é efetivamente 6 (o resultado de 32 \mod 26), o que equivale à letra de texto cifrado "G".

A encriptação completa da palavra "DOG" com um valor de chave de 17 é a seguinte:

Toda a gente consegue compreender intuitivamente como funciona a cifra de deslocamento e, provavelmente, utilizá-la. No entanto, para avançar os seus conhecimentos de criptografia, é importante começar a sentir-se mais confortável com a formalização, pois os esquemas tornar-se-ão muito mais difíceis. Por isso, os passos da cifra de deslocamento foram formalizados.

Notas:

[1] Podemos definir esta afirmação com exatidão, utilizando a terminologia da secção anterior. Seja uma variável uniforme K e tenha K como o seu conjunto de resultados possíveis. Então:

Pr[K = 0] = \frac{1}{26}
Pr[K = 1] = \frac{1}{26}

...e assim por diante. Amostrar a variável uniforme K uma vez para obter uma determinada chave.

A operação XOR

Todos os dados informáticos são processados, armazenados e enviados através de redes ao nível dos bits. Quaisquer esquemas criptográficos que sejam aplicados a dados informáticos também funcionam ao nível dos bits.

Por exemplo, suponhamos que escreveu uma mensagem de correio eletrónico na sua aplicação de correio eletrónico. Qualquer encriptação que aplique não ocorre diretamente nos caracteres ASCII da sua mensagem de correio eletrónico. Em vez disso, é aplicada à representação em bits das letras e outros símbolos da mensagem de correio eletrónico.

Uma operação matemática fundamental a compreender para a criptografia moderna, para além da operação de módulo, é a operação XOR, ou operação "exclusive or". Esta operação recebe como entrada dois bits e produz como saída outro bit. A operação XOR será simplesmente designada por "XOR". A operação produz 0 se os dois bits forem iguais e 1 se os dois bits forem diferentes. Pode ver as quatro possibilidades abaixo. O símbolo \oplus representa "XOR" :

Para ilustrar, suponha que tem uma mensagem m_1 (01111001) e uma mensagem m_2 (01011001). A operação XOR destas duas mensagens pode ser vista abaixo.

O processo é simples. Primeiro, faz o XOR dos bits mais à esquerda de m_1 e m_2. Neste caso, isto é 0 \oplus 0 = 0. De seguida, faz-se XOR do segundo par de bits a partir da esquerda. Neste caso, isto é 1 \oplus 1 = 0. Continua este processo até ter efectuado a operação XOR nos bits mais à direita.

É fácil ver que a operação XOR é comutativa, nomeadamente que m_1 \oplus m_2 = m_2 \oplus m_1. Para além disso, a operação XOR também é associativa. Ou seja, (m_1 \oplus m_2) \oplus m_3 = m_1 \oplus (m_2 \oplus m_3).

Uma operação XOR em duas cadeias de caracteres de comprimentos alternativos pode ter diferentes interpretações, consoante o contexto. Não nos preocuparemos aqui com quaisquer operações XOR sobre cadeias de caracteres de comprimentos diferentes.

Uma operação XOR é equivalente ao caso especial de efetuar uma operação de módulo na adição de bits quando o divisor é 2. Pode ver a equivalência nos resultados seguintes:

Pseudorandomicidade

Na nossa discussão sobre variáveis aleatórias e uniformes, estabelecemos uma distinção específica entre "aleatório" e "uniforme". Essa distinção é normalmente mantida na prática quando se descrevem variáveis aleatórias. No entanto, no nosso contexto atual, esta distinção tem de ser abandonada e "aleatório" e "uniforme" são utilizados como sinónimos. Explicarei porquê no final da secção.

Para começar, podemos chamar a uma cadeia binária de comprimento n aleatória (ou uniforme), se for o resultado da amostragem de uma variável uniforme S que dá a cada cadeia binária de tal comprimento n uma probabilidade igual de seleção.

Suponhamos, por exemplo, o conjunto de todas as cadeias binárias com comprimento 8: \{0000\ 0000, 0000\ 0001, \ldots, 1111\ 1111\}. (É típico escrever uma cadeia de 8 bits em dois quartetos, cada um chamado nibble) Chamemos a este conjunto de cadeias S_8.

De acordo com a definição acima, podemos, então, chamar aleatória (ou uniforme) a uma determinada cadeia binária de comprimento 8, se for o resultado da amostragem de uma variável uniforme S que dá a cada cadeia em S_8 uma probabilidade igual de seleção. Dado que o conjunto S_8 inclui 2^8 elementos, a probabilidade de seleção após amostragem teria de ser 1/2^8 para cada cadeia do conjunto.

Um aspeto fundamental da aleatoriedade de uma cadeia binária é que ela é definida com referência ao processo pelo qual foi selecionada. A forma de qualquer cadeia binária em particular, por si só, não revela nada sobre a sua aleatoriedade na seleção.

Por exemplo, muitas pessoas têm intuitivamente a ideia de que uma cadeia como 1111\ 1111 não pode ter sido selecionada aleatoriamente. Mas isso é claramente falso.

Definindo uma variável uniforme S sobre todas as cadeias binárias de comprimento 8, a probabilidade de selecionar 1111\ 1111 do conjunto S_8 é a mesma que a de uma cadeia como 0111\ 0100. Assim, não se pode dizer nada sobre a aleatoriedade de uma cadeia, apenas analisando a própria cadeia.

Também podemos falar de cadeias aleatórias sem nos referirmos especificamente a cadeias binárias. Podemos, por exemplo, falar de uma cadeia hexadecimal aleatória AF\ 02\ 82. Neste caso, a cadeia teria sido selecionada aleatoriamente do conjunto de todas as cadeias hexadecimais de comprimento 6. Isto é equivalente a selecionar aleatoriamente uma cadeia binária de comprimento 24, uma vez que cada dígito hexadecimal representa 4 bits.

Normalmente, a expressão "uma cadeia aleatória", sem qualificação, refere-se a uma cadeia selecionada aleatoriamente do conjunto de todas as cadeias com o mesmo comprimento. Foi assim que a descrevi acima. Uma cadeia de comprimento n também pode, naturalmente, ser selecionada aleatoriamente de um conjunto diferente. Um, por exemplo, que constitua apenas um subconjunto de todas as cordas de comprimento n, ou talvez um conjunto que inclua cordas de comprimento variável. Nesses casos, no entanto, não nos referiríamos a ela como uma "cadeia aleatória", mas sim como "uma cadeia que é selecionada aleatoriamente de um conjunto S".

Um conceito chave na criptografia é o da pseudo-aleatoriedade. Uma cadeia pseudo-aleatória de comprimento n aparece como se fosse o resultado da amostragem de uma variável uniforme S que dá a cada cadeia em S_n uma probabilidade igual de seleção. De facto, no entanto, a cadeia é o resultado da amostragem de uma variável uniforme S' que apenas define uma distribuição de probabilidade - não necessariamente uma com probabilidades iguais para todos os resultados possíveis - num subconjunto de S_n. O ponto crucial aqui é que ninguém pode realmente distinguir entre amostras de S e S', mesmo que se recolha muitas delas.

Suponhamos, por exemplo, uma variável aleatória S. O seu conjunto de resultados é S_{256}, isto é, o conjunto de todas as cadeias binárias de comprimento 256. Este conjunto tem 2^{256} elementos. Cada elemento tem uma probabilidade igual de seleção, 1/2^{256}, na amostragem.

Além disso, suponha uma variável aleatória S'. O seu conjunto de resultados inclui apenas 2^{128} cadeias binárias de comprimento 256. Tem uma distribuição de probabilidades sobre essas cadeias, mas essa distribuição não é necessariamente uniforme.

Suponha que eu recolhia agora 1000 amostras de S e 1000 amostras de S' e lhe dava os dois conjuntos de resultados. Digo-lhe que conjunto de resultados está associado a que variável aleatória. De seguida, retiro uma amostra de uma das duas variáveis aleatórias. Mas, desta vez, não lhe digo qual a variável aleatória que retiro. Se S' fosse pseudo-aleatória, então a ideia é que a sua probabilidade de adivinhar corretamente qual a variável aleatória que eu retirei é praticamente igual a 1/2.

Normalmente, uma cadeia pseudo-aleatória de comprimento n é produzida selecionando aleatoriamente uma cadeia de tamanho n - x, em que x é um número inteiro positivo, e utilizando-a como entrada para um algoritmo de expansão. Esta cadeia aleatória de tamanho n - x é conhecida como a semente.

As cadeias de caracteres pseudo-aleatórias são um conceito chave para tornar a criptografia prática. Consideremos, por exemplo, as cifras de fluxo. Com uma cifra de fluxo, uma chave selecionada aleatoriamente é ligada a um algoritmo de expansão para produzir uma cadeia pseudo-aleatória muito maior. Esta cadeia pseudo-aleatória é então combinada com o texto simples através de uma operação XOR para produzir um texto cifrado.

Se não fosse possível produzir este tipo de cadeia pseudo-aleatória para uma cifra de fluxo, então precisaríamos de uma chave tão longa quanto a mensagem para a sua segurança. Esta não é uma opção muito prática na maioria dos casos.

A noção de pseudo-aleatoriedade abordada nesta secção pode ser definida de forma mais formal. Também se estende a outros contextos. Mas não precisamos de nos aprofundar nessa discussão aqui. Tudo o que precisa de compreender intuitivamente para grande parte da criptografia é a diferença entre uma cadeia aleatória e uma pseudo-aleatória. [2]

A razão para abandonar a distinção entre "aleatório" e "uniforme" na nossa discussão deve agora ser clara. Na prática, toda a gente usa o termo pseudo-aleatório para indicar uma cadeia que aparece como se fosse o resultado da amostragem de uma variável uniforme S. Em rigor, devemos chamar a essa cadeia "pseudo-uniforme", adoptando a nossa linguagem de há pouco. Como o termo "pseudo-uniforme" é pouco prático e não é usado por ninguém, não o introduziremos aqui por uma questão de clareza. Em vez disso, deixamos de fazer a distinção entre "aleatório" e "uniforme" no contexto atual.

**Notas

[2] Se estiver interessado numa exposição mais formal sobre estas questões, pode consultar o livro Introduction to Modern Cryptography de Katz e Lindell, especialmente o capítulo 3.

Fundamentos matemáticos da criptografia 2

O que é a teoria dos números?

Este capítulo aborda um tópico mais avançado sobre os fundamentos matemáticos da criptografia: a teoria dos números. Embora a teoria dos números seja importante para a criptografia simétrica (como na cifra Rijndael), é particularmente importante no contexto da criptografia de chave pública.

Se os pormenores da teoria dos números lhe parecerem complicados, recomendo uma leitura de alto nível numa primeira fase. Pode sempre voltar a ela mais tarde.

Pode caraterizar-se a teoria dos números como o estudo das propriedades dos números inteiros e das funções matemáticas que funcionam com números inteiros.

Consideremos, por exemplo, que dois números a e N são coprimes (ou primos relativos) se o seu maior divisor comum for igual a 1. Suponhamos agora um determinado número inteiro N. Quantos números inteiros menores que N são coprimários de N? Podemos fazer afirmações gerais sobre as respostas a esta pergunta? Estes são os tipos típicos de questões a que a teoria dos números procura responder.

A teoria moderna dos números baseia-se nas ferramentas da álgebra abstrata. O campo da álgebra abstrata é uma subdisciplina da matemática em que os principais objectos de análise são objectos abstractos conhecidos como estruturas algébricas. Uma estrutura algébrica é um conjunto de elementos conjugados com uma ou mais operações, que satisfaz certos axiomas. Através das estruturas algébricas, os matemáticos podem obter informações sobre problemas matemáticos específicos, abstraindo dos seus pormenores.

O campo da álgebra abstrata é por vezes também designado por álgebra moderna. Pode também encontrar o conceito de matemática abstrata (ou matemática pura). Este último termo não é uma referência à álgebra abstrata, mas significa antes o estudo da matemática por si só, e não apenas com vista a potenciais aplicações.

Os conjuntos da álgebra abstrata podem lidar com muitos tipos de objectos, desde as transformações que preservam a forma de um triângulo equilátero até aos padrões de papel de parede. Para a teoria dos números, apenas consideramos conjuntos de elementos que contêm números inteiros ou funções que funcionam com números inteiros.

Grupos

Um conceito básico em matemática é o de um conjunto de elementos. Um conjunto é geralmente denotado por sinais de adição com os elementos separados por vírgulas.

Por exemplo, o conjunto de todos os números inteiros é \{..., -2, -1, 0, 1, 2, ...\}. As elipses aqui significam que um determinado padrão continua numa determinada direção. Assim, o conjunto de todos os números inteiros também inclui 3, 4, 5, 6 e assim por diante, bem como -3, -4, -5, -6 e assim por diante. Este conjunto de todos os números inteiros é tipicamente designado por \mathbb{Z}.

Outro exemplo de um conjunto é \mathbb{Z} \mod 11, ou o conjunto de todos os números inteiros módulo 11. Ao contrário do conjunto completo \mathbb{Z}, este conjunto contém apenas um número finito de elementos, nomeadamente \{0, 1, \ldots, 9, 10\}.

Um erro comum é pensar que o conjunto \mathbb{Z} \mod 11 é de facto \{-10, -9, \ldots, 0, \ldots, 9, 10\}. Mas este não é o caso, dada a forma como definimos a operação de módulo anteriormente. Quaisquer números inteiros negativos reduzidos pelo módulo 11 são envolvidos em \{0, 1, \ldots, 9, 10\}. Por exemplo, a expressão -2 \mod 11 envolve-se em 9, enquanto a expressão -27 \mod 11 envolve-se em 5.

Outro conceito básico em matemática é o de operação binária. Trata-se de qualquer operação que utiliza dois elementos para produzir um terceiro. Por exemplo, a partir da aritmética e da álgebra básicas, conhece quatro operações binárias fundamentais: adição, subtração, multiplicação e divisão.

Estes dois conceitos matemáticos básicos, conjuntos e operações binárias, são utilizados para definir a noção de grupo, a estrutura mais essencial da álgebra abstrata.

Especificamente, suponhamos uma operação binária \circ. Além disso, suponha um conjunto de elementos S equipado com essa operação. Tudo o que "equipado" significa aqui é que a operação \circ pode ser efectuada entre quaisquer dois elementos do conjunto S.

A combinação \langle \mathbf{S}, \circ \rangle é, então, um grupo se satisfizer quatro condições específicas, conhecidas como axiomas de grupo.

  1. Para quaisquer a e b que sejam elementos de \mathbf{S}, a \circ b é também um elemento de \mathbf{S}. Isto é conhecido como a condição de fecho.

  2. Para quaisquer a, b e c que sejam elementos de \mathbf{S}, é o caso de (a \circ b) \circ c = a \circ (b \circ c). Isto é conhecido como a condição de associatividade.

  3. Existe um único elemento e em \mathbf{S}, tal que, para cada elemento a em \mathbf{S}, se verifica a seguinte equação: e \circ a = a \circ e = a. Como só existe um elemento deste género e, chama-se o elemento de identidade. Esta condição é conhecida como a condição de identidade.

  4. Para cada elemento a em \mathbf{S}, existe um elemento b em \mathbf{S}, tal que a seguinte equação é válida: a \circ b = b \circ a = e, onde e é o elemento identidade. O elemento b é aqui conhecido como o elemento inverso, e é normalmente denotado por a^{-1}. Esta condição é conhecida como a condição inversa ou a condição de invertibilidade.

Vamos explorar os grupos um pouco mais. Denotemos o conjunto de todos os números inteiros por \mathbb{Z}. Este conjunto combinado com a adição padrão, ou \langle \mathbb{Z}, + \rangle, encaixa-se claramente na definição de grupo, uma vez que cumpre os quatro axiomas acima.

  1. Para quaisquer x e y que sejam elementos de \mathbb{Z}, x + y é também um elemento de \mathbb{Z}. Então \langle \mathbb{Z}, + \rangle satisfaz a condição de fecho.

  2. Para quaisquer x, y e z que sejam elementos de \mathbb{Z}, (x + y) + z = x + (y + z). Então \langle \mathbb{Z}, + \rangle satisfaz a condição de associatividade.

  3. Há um elemento de identidade em \langle \mathbb{Z}, + \rangle, nomeadamente 0. Para qualquer x em \mathbb{Z}, é válido que: 0 + x = x + 0 = x. Então \langle \mathbb{Z}, + \rangle satisfaz a condição de identidade.

  4. Finalmente, para cada elemento x em \mathbb{Z}, existe um y de modo que x + y = y + x = 0. Se x fosse 10, por exemplo, y seria -10 (no caso em que x é 0, y também é 0). Assim, \langle \mathbb{Z}, + \rangle satisfaz a condição inversa.

É importante notar que o facto de o conjunto dos números inteiros com adição constituir um grupo não significa que constitua um grupo com multiplicação. Pode verificar isto testando \langle \mathbb{Z}, \cdot \rangle contra os quatro axiomas de grupo (onde \cdot significa multiplicação padrão).

Os dois primeiros axiomas são obviamente válidos. Além disso, na multiplicação, o elemento 1 pode servir como elemento de identidade. Qualquer inteiro x multiplicado por 1, nomeadamente, dá x. No entanto, \langle \mathbb{Z}, \cdot \rangle não satisfaz a condição inversa. Ou seja, não existe um único elemento y em \mathbb{Z} para cada x em \mathbb{Z}, de modo que x \cdot y = 1.

Por exemplo, suponha que x = 22. Que valor y do conjunto \mathbb{Z} multiplicado por x produziria o elemento de identidade 1? O valor de 1/22 funcionaria, mas este não está no conjunto \mathbb{Z}. De facto, este problema coloca-se para qualquer número inteiro x, exceto para os valores 1 e -1 (em que y teria de ser 1 e -1 respetivamente).

Se admitirmos números reais para o nosso conjunto, então os nossos problemas desaparecem em grande parte. Para qualquer elemento x do conjunto, a multiplicação por 1/x dá 1. Como as fracções estão incluídas no conjunto dos números reais, é possível encontrar um inverso para cada número real. A exceção é o zero, pois qualquer multiplicação por zero nunca produzirá o elemento de identidade 1. Assim, o conjunto dos números reais não nulos equipados com multiplicação é de facto um grupo.

Alguns grupos satisfazem uma quinta condição geral, conhecida como a condição de comutatividade. Esta condição é a seguinte:

Qualquer grupo que satisfaça a condição de comutatividade é conhecido como um grupo comutativo, ou um grupo abeliano (em homenagem a Niels Henrik Abel). É fácil verificar que tanto o conjunto dos números reais sobre a adição como o conjunto dos números inteiros sobre a adição são grupos abelianos. O conjunto dos números inteiros sobre a multiplicação não é de todo um grupo, pelo que, ipso facto, não pode ser um grupo abeliano. O conjunto dos números reais não nulos sobre a multiplicação, pelo contrário, é também um grupo abeliano.

Deve ter em atenção duas convenções importantes sobre notação. Em primeiro lugar, os sinais "+" ou "×" são frequentemente utilizados para simbolizar operações de grupo, mesmo quando os elementos não são, de facto, números. Nestes casos, não se deve interpretar estes sinais como adição ou multiplicação aritméticas normais. Em vez disso, são operações que têm apenas uma semelhança abstrata com estas operações aritméticas.

A menos que se esteja a referir especificamente à adição ou multiplicação aritméticas, é mais fácil utilizar símbolos como \circ e \diamond para operações de grupo, uma vez que estes não têm conotações muito enraizadas culturalmente.

Em segundo lugar, pela mesma razão que "+" e "×" são frequentemente utilizados para indicar operações não aritméticas, os elementos de identidade dos grupos são frequentemente simbolizados por "0" e "1", mesmo quando os elementos desses grupos não são números. A menos que se esteja a referir ao elemento de identidade de um grupo com números, é mais fácil utilizar um símbolo mais neutro, como "e", para indicar o elemento de identidade.

Muitos conjuntos de valores diferentes e muito importantes em matemática, equipados com certas operações binárias, são grupos. As aplicações criptográficas, no entanto, só funcionam com conjuntos de números inteiros ou, pelo menos, com elementos que são descritos por números inteiros, ou seja, no domínio da teoria dos números. Assim, os conjuntos com números reais que não sejam inteiros não são utilizados em aplicações criptográficas.

Para terminar, vamos dar um exemplo de elementos que podem ser "descritos por números inteiros", apesar de não serem inteiros. Um bom exemplo são os pontos de curvas elípticas. Embora qualquer ponto de uma curva elíptica não seja claramente um número inteiro, esse ponto é de facto descrito por dois números inteiros.

As curvas elípticas são, por exemplo, cruciais para a Bitcoin. Qualquer par de chaves públicas e privadas padrão da Bitcoin é selecionado a partir do conjunto de pontos definido pela seguinte curva elíptica:

x^3 + 7 = y^2 \mod 2^{256} – 2^{32} – 29 – 28 – 27 – 26 - 24 - 1

(o maior número primo menor que 2^{256}). A coordenada x é a chave privada e a coordenada y é a sua chave pública.

As transacções em Bitcoin envolvem tipicamente o bloqueio de saídas para uma ou mais chaves públicas de alguma forma. O valor destas transacções pode, então, ser desbloqueado através de assinaturas digitais com as chaves privadas correspondentes.

Grupos cíclicos

Uma distinção importante que podemos fazer é entre um grupo finito e um grupo infinito. O primeiro tem um número finito de elementos, enquanto o segundo tem um número infinito de elementos. O número de elementos de qualquer grupo finito é conhecido como a ordem do grupo. Toda a criptografia prática que envolve a utilização de grupos baseia-se em grupos finitos (teóricos dos números).

Na criptografia de chave pública, uma certa classe de grupos abelianos finitos conhecidos como grupos cíclicos são particularmente importantes. Para compreendermos os grupos cíclicos, precisamos primeiro de compreender o conceito de exponenciação de elementos de grupo.

Suponhamos um grupo G com uma operação de grupo \circ, e que a é um elemento de G. A expressão a^n deve, então, ser interpretada como o elemento a combinado consigo próprio um total de n - 1 vezes. Por exemplo, a^2 significa a \circ a, a^3 significa a \circ a \circ a, e assim por diante. (Note-se que a exponenciação aqui não é necessariamente exponenciação no sentido aritmético padrão)

Vejamos um exemplo. Suponhamos que G = \langle \mathbb{Z} \mod 7, + \rangle, e que o nosso valor para a é igual a 4. Neste caso, a^2 = [4 + 4 \mod 7] = [8 \mod 7] = 1 \mod 7. Em alternativa, a^4 representaria [4 + 4 + 4 + 4 + 4 \mod 7] = [16 \mod 7] = 2 \mod 7.

Alguns grupos abelianos têm um ou mais elementos, que podem produzir todos os outros elementos do grupo através de exponenciação contínua. Estes elementos são chamados geradores ou elementos primitivos.

Uma classe importante de tais grupos é \langle \mathbb{Z}^* \mod N, \cdot \rangle, onde N é um número primo. A notação \mathbb{Z}^* significa que o grupo contém todos os números inteiros positivos não nulos menores que N. Portanto, um grupo deste género tem sempre elementos N - 1.

Consideremos, por exemplo, G = \langle \mathbb{Z}^* \mod 11, \cdot \rangle. Este grupo tem os seguintes elementos: \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. A ordem deste grupo é 10 (que é de facto igual a 11 - 1).

Vamos explorar a exponenciação do elemento 2 deste grupo. Os cálculos até 2^{12} são mostrados abaixo. Note-se que no lado esquerdo da equação, o expoente refere-se à exponenciação do elemento do grupo. No nosso exemplo particular, isto envolve de facto a exponenciação aritmética no lado direito da equação (mas também poderia ter envolvido, por exemplo, adição). Para clarificar, escrevi a operação repetida, em vez da forma de expoente do lado direito.

Se olharmos com atenção, podemos ver que a exponenciação do elemento 2 percorre todos os elementos de \langle \mathbb{Z}^* \mod 11, \cdot \rangle pela seguinte ordem: 2, 4, 8, 5, 10, 9, 7, 3, 6, 1: 2, 4, 8, 5, 10, 9, 7, 3, 6, 1. Depois de 2^{10}, a exponenciação continuada do elemento 2 percorre todos os elementos de novo e pela mesma ordem. Logo, o elemento 2 é um gerador em \langle \mathbb{Z}^* \mod 11, \cdot \rangle.

Embora \langle \mathbb{Z}^* \mod 11, \cdot \rangle tenha múltiplos geradores, nem todos os elementos deste grupo são geradores. Consideremos, por exemplo, o elemento 3. Percorrendo as primeiras 10 exponenciações, sem mostrar os cálculos incómodos, obtemos os seguintes resultados:

Em vez de percorrer todos os valores em \langle \mathbb{Z}^* \mod 11, \cdot \rangle, a exponenciação do elemento 3 apenas conduz a um subconjunto desses valores: 3, 9, 5, 4 e 1. Após a quinta exponenciação, estes valores começam a repetir-se.

Podemos agora definir um grupo cíclico como qualquer grupo com pelo menos um gerador. Ou seja, existe pelo menos um elemento do grupo a partir do qual é possível produzir todos os outros elementos do grupo através de exponenciação.

Deve ter reparado no nosso exemplo acima que tanto 2^{10} como 3^{10} são iguais a 1 \mod 11. De facto, apesar de não irmos efetuar os cálculos, a exponenciação por 10 de qualquer elemento do grupo \langle \mathbb{Z}^* \mod 11, \cdot \rangle produzirá 1 \mod 11. Porque é que isto acontece?

Esta é uma questão importante, mas requer algum trabalho para a responder.

Para começar, suponha dois inteiros positivos a e N. Um teorema importante na teoria dos números afirma que a tem um inverso multiplicativo módulo N (ou seja, um inteiro b de modo a que a \cdot b = 1 \mod N) se e só se o maior divisor comum entre a e N for igual a 1. Ou seja, se a e N são coprimes.

Assim, para qualquer grupo de inteiros equipado com multiplicação modulo N, apenas os menores coprimes com N estão incluídos no conjunto. Podemos designar este conjunto por \mathbb{Z}^c \mod N.

Por exemplo, suponhamos que N é 10. Apenas os inteiros 1, 3, 7 e 9 são coprimes de 10. Assim, o conjunto \mathbb{Z}^c \mod 10 inclui apenas \{1, 3, 7, 9\}. Não é possível criar um grupo com multiplicação de números inteiros módulo 10 utilizando quaisquer outros números inteiros entre 1 e 10. Para este grupo em particular, os inversos são os pares 1 e 9, e 3 e 7.

No caso em que N é primo, todos os números inteiros de 1 a N - 1 são coprimos de N. Um tal grupo tem, portanto, uma ordem de N - 1. Usando a nossa notação anterior, \mathbb{Z}^c \mod N é igual a \mathbb{Z}^* \mod N quando N é primo. O grupo que selecionámos para o nosso exemplo anterior, \langle \mathbb{Z}^* \mod 11, \cdot \rangle, é um exemplo particular desta classe de grupos.

A seguir, a função \phi(N) calcula o número de coprimes até um número N, e é conhecida como função Phi de Euler. [1] De acordo com o Teorema de Euler, sempre que dois inteiros a e N são coprimos, tem-se o seguinte:

Isto tem uma implicação importante para a classe de grupos \langle \mathbb{Z}^* \mod N, \cdot \rangle onde N é primo. Para estes grupos, a exponenciação de elementos de grupo representa a exponenciação aritmética. Ou seja, a^{\phi(N)} \mod N representa a operação aritmética a^{\phi(N)} \mod N. Como qualquer elemento a nestes grupos multiplicativos é coprimo de N, significa que a^{\phi(N)} \mod N = a^{N - 1} \mod N = 1 \mod N.

O teorema de Euler é um resultado muito importante. Para começar, implica que todos os elementos em \langle \mathbb{Z}^* \mod N, \cdot \rangle só podem percorrer um número de valores por exponenciação que se divide em N - 1. No caso de \langle \mathbb{Z}^* \mod 11, \cdot \rangle, isto significa que cada elemento só pode percorrer 2, 5 ou 10 elementos. O grupo de valores que qualquer elemento percorre após a exponenciação é conhecido como a ordem do elemento. Um elemento com uma ordem equivalente à ordem de um grupo é um gerador.

Além disso, o teorema de Euler implica que podemos sempre saber o resultado de a^{N - 1} \mod N para qualquer grupo \langle \mathbb{Z}^* \mod N, \cdot \rangle onde N é primo. Isto é assim independentemente de quão complicados possam ser os cálculos actuais.

Por exemplo, suponhamos que o nosso grupo é \mathbb{Z}^* \mod 160,481,182 (onde 160,481,182 é de facto um número primo). Sabemos que todos os inteiros de 1 a 160,481,181 têm de ser elementos deste grupo, e que \phi(n) = 160,481,181. Apesar de não podermos efetuar todos os passos dos cálculos, sabemos que expressões como 514^{160,481,181}, 2,005^{160,481,181} e 256,212^{160,481,181} têm de ser todas iguais a 1 \mod 160,481,182.

Notas:

[1] A função funciona da seguinte forma. Qualquer número inteiro N pode ser facturado num produto de números primos. Suponha que um determinado N é facturado da seguinte forma: p_1^{e1} \cdot p_2^{e2} \cdot \ldots \cdot p_m^{em} onde todos os p são números primos e todos os e são inteiros maiores ou iguais a 1. Então:

\phi(N) = \sum_{i=1}^m \left[p_i^{e_i} - p_i^{e_i - 1}\right]

A fórmula da função Phi de Euler para a factorização prima de N.

Campos

Um grupo é a estrutura algébrica básica da álgebra abstrata, mas existem muitas mais. A única outra estrutura algébrica com que precisa de estar familiarizado é a de um campo, especificamente a de um campo finito. Este tipo de estrutura algébrica é frequentemente utilizado em criptografia, como por exemplo no Advanced Encryption Standard. Este último é o principal esquema de encriptação simétrica que encontrará na prática.

Um campo é derivado da noção de grupo. Especificamente, um campo é um conjunto de elementos S equipado com dois operadores binários \circ e \diamond, que satisfaz as seguintes condições:

  1. O conjunto S equipado com \circ é um grupo abeliano.

  2. O conjunto S equipado com \diamond é um grupo abeliano para os elementos "não nulos".

  3. O conjunto S equipado com os dois operadores satisfaz o que é conhecido como a condição distributiva: Suponhamos que a, b e c são elementos de S. Então S equipado com os dois operadores satisfaz a propriedade distributiva quando a \circ (b \diamond c) = (a \circ b) \diamond (a \circ c).

Note-se que, tal como no caso dos grupos, a definição de um campo é muito abstrata. Não faz afirmações sobre os tipos de elementos em S, ou sobre as operações \circ e \diamond. Diz apenas que um campo é qualquer conjunto de elementos com duas operações para as quais as três condições acima se verificam. (O elemento "zero" no segundo grupo Abeliano pode ser interpretado abstratamente)

Então, o que é que pode ser um exemplo de um campo? Um bom exemplo é o conjunto \mathbb{Z} \mod 7, ou \{0, 1, \ldots, 7\} definido por adição padrão (em vez de \circ acima) e multiplicação padrão (em vez de \diamond acima).

Primeiro, \mathbb{Z} \mod 7 satisfaz a condição para ser um grupo abeliano sobre a adição, e satisfaz a condição para ser um grupo abeliano sobre a multiplicação se considerarmos apenas os elementos não nulos. Em segundo lugar, a combinação do conjunto com os dois operadores satisfaz a condição distributiva.

Vale a pena, didaticamente, explorar estas afirmações utilizando alguns valores particulares. Tomemos os valores experimentais 5, 2 e 3, alguns elementos selecionados aleatoriamente do conjunto \mathbb{Z} \mod 7, para inspecionar o campo \langle \mathbb{Z} \mod 7, +, \cdot \rangle. Utilizaremos estes três valores por ordem, conforme necessário para explorar condições particulares.

Comecemos por explorar se \mathbb{Z} \mod 7 equipado com adição é um grupo abeliano.

  1. Condição de fecho: Vamos tomar 5 e 2 como nossos valores. Nesse caso, [5 + 2] \mod 7 = 7 \mod 7 = 0. Este é de facto um elemento de \mathbb{Z} \mod 7, pelo que o resultado é consistente com a condição de fecho.

  2. Condição de associatividade: Vamos tomar 5, 2 e 3 como nossos valores. Nesse caso, [(5 + 2) + 3] \mod 7 = [5 + (2 + 3)] \mod 7 = 10 \mod 7 = 3. Isto é consistente com a condição de associatividade.

  3. Condição de identidade: Tomemos 5 como o nosso valor. Nesse caso, [5 + 0] \mod 7 = [0 + 5] \mod 7 = 5. Portanto, 0 parece ser o elemento de identidade para a adição.

  4. Condição inversa: Consideremos o inverso de 5. Tem de acontecer que [5 + d] \mod 7 = 0, para algum valor de d. Neste caso, o único valor de \mathbb{Z} \mod 7 que satisfaz esta condição é 2.

  5. Condição de comutatividade: Tomemos 5 e 3 como os nossos valores. Nesse caso, [5 + 3] \mod 7 = [3 + 5] \mod 7 = 1. Isto é consistente com a condição de comutatividade.

O conjunto \mathbb{Z} \mod 7 equipado com adição parece claramente ser um grupo abeliano. Vamos agora explorar se \mathbb{Z} \mod 7 equipado com multiplicação é um grupo abeliano para todos os elementos não nulos.

  1. Condição de fecho: Vamos tomar 5 e 2 como nossos valores. Nesse caso, [5 \cdot 2] \mod 7 = 10 \mod 7 = 3. Este é também um elemento de \mathbb{Z} \mod 7, pelo que o resultado é consistente com a condição de fecho.

  2. Condição de associatividade: Vamos tomar 5, 2 e 3 como nossos valores. Nesse caso, [(5 \cdot 2) \cdot 3] \mod 7 = [5 \cdot (2 \cdot 3)] \mod 7 = 30 \mod 7 = 2. Isto é consistente com a condição de associatividade.

  3. Condição de identidade: Vamos tomar 5 como o nosso valor. Nesse caso, [5 \cdot 1] \mod 7 = [1 \cdot 5] \mod 7 = 5. Portanto, 1 parece ser o elemento de identidade para a multiplicação.

  4. Condição inversa: Consideremos o inverso de 5. Tem de acontecer que [5 \cdot d] \mod 7 = 1, para algum valor de d. O único valor de \mathbb{Z} \mod 7 que satisfaz esta condição é 3. Isto é consistente com a condição inversa.

  5. Condição de comutatividade: Vamos tomar 5 e 3 como nossos valores. Nesse caso, [5 \cdot 3] \mod 7 = [3 \cdot 5] \mod 7 = 15 \mod 7 = 1. Isto é consistente com a condição de comutatividade.

O conjunto \mathbb{Z} \mod 7 parece satisfazer claramente as regras para ser um grupo abeliano quando combinado com a adição ou a multiplicação sobre os elementos não nulos.

Finalmente, este conjunto combinado com ambos os operadores parece satisfazer a condição distributiva. Tomemos 5, 2 e 3 como os nossos valores. Podemos ver que [5 \cdot (2 + 3)] \mod 7 = [5 \cdot 2 + 5 \cdot 3] \mod 7 = 25 \mod 7 = 4.

Vimos agora que \mathbb{Z} \mod 7 equipado com adição e multiplicação cumpre os axiomas para um campo finito quando testado com valores particulares. Claro que também podemos mostrar isso de forma geral, mas não o faremos aqui.

Uma distinção fundamental é entre dois tipos de campos: campos finitos e infinitos.

Um campo infinito é um campo em que o conjunto S é infinitamente grande. O conjunto dos números reais \mathbb{R} equipados com adição e multiplicação é um exemplo de um campo infinito. Um campo finito, também conhecido por campo de Galois, é um campo em que o conjunto S é finito. O nosso exemplo acima de \langle \mathbb{Z} \mod 7, +, \cdot \rangle é um campo finito.

Em criptografia, estamos principalmente interessados em campos finitos. Em geral, pode demonstrar-se que existe um campo finito para um conjunto de elementos S se e só se tiver p^m elementos, em que p é um número primo e m um número inteiro positivo maior ou igual a um. Por outras palavras, se a ordem de um conjunto S for um número primo (p^m onde m = 1) ou uma potência prima (p^m onde m > 1), então é possível encontrar dois operadores \circ e \diamond de modo a que as condições para um campo sejam satisfeitas.

Se um campo finito tem um número primo de elementos, então chama-se campo primo. Se o número de elementos do campo finito for uma potência de primo, então o campo chama-se campo de extensão. Em criptografia, estamos interessados tanto em campos primos como em campos de extensão. [2]

Os principais campos primos de interesse em criptografia são aqueles em que o conjunto de todos os números inteiros é modulado por um número primo e os operadores são a adição e a multiplicação normais. Esta classe de campos finitos incluiria \mathbb{Z} \mod 2, \mathbb{Z} \mod 3, \mathbb{Z} \mod 5, \mathbb{Z} \mod 7, \mathbb{Z} \mod 11, \mathbb{Z} \mod 13, e assim por diante. Para qualquer campo primo \mathbb{Z} \mod p, o conjunto dos números inteiros do campo é o seguinte: \{0, 1, \ldots, p - 2, p - 1\}.

Em criptografia, também estamos interessados em campos de extensão, particularmente quaisquer campos com 2^m elementos onde m > 1. Estes campos finitos são, por exemplo, utilizados na cifra Rijndael, que constitui a base do Advanced Encryption Standard. Embora os campos primos sejam relativamente intuitivos, estes campos de extensão de base 2 não são provavelmente para quem não esteja familiarizado com álgebra abstrata.

Para começar, é de facto verdade que a qualquer conjunto de números inteiros com 2^m elementos podem ser atribuídos dois operadores que fariam da sua combinação um campo (desde que m seja um número inteiro positivo). No entanto, o facto de um campo existir não significa necessariamente que seja fácil de descobrir ou particularmente prático para certas aplicações.

Como se verifica, os campos de extensão de 2^m particularmente aplicáveis em criptografia são aqueles definidos sobre conjuntos particulares de expressões polinomiais, em vez de um conjunto de inteiros.

Por exemplo, suponhamos que queríamos um campo de extensão com 2^3 (i.e., 8) elementos no conjunto. Embora possam existir muitos conjuntos diferentes que possam ser usados para campos dessa dimensão, um desses conjuntos inclui todos os polinómios únicos da forma a_2x^2 + a_1x + a_0, em que cada coeficiente a_i é 0 ou 1. Assim, este conjunto S inclui os seguintes elementos:

  1. 0: O caso em que a_2 = 0, a_1 = 0, e a_0 = 0.

  2. 1: O caso em que a_2 = 0, a_1 = 0, e a_0 = 1.

  3. x: O caso em que a_2 = 0, a_1 = 1, e a_0 = 0.

  4. x + 1: O caso em que a_2 = 0, a_1 = 1, e a_0 = 1.

  5. x^2: O caso em que a_2 = 1, a_1 = 0, e a_0 = 0.

  6. x^2 + 1: O caso em que a_2 = 1, a_1 = 0, e a_0 = 1.

  7. x^2 + x: O caso em que a_2 = 1, a_1 = 1, e a_0 = 0.

  8. x^2 + x + 1: O caso em que a_2 = 1, a_1 = 1, e a_0 = 1.

Então S seria o conjunto \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}. Que duas operações podem ser definidas sobre este conjunto de elementos para garantir que a sua combinação é um campo?

A primeira operação no conjunto S (\circ) pode ser definida como uma adição polinomial padrão módulo 2. Tudo o que tem de fazer é adicionar os polinómios como faria normalmente, e depois aplicar o módulo 2 a cada um dos coeficientes do polinómio resultante. Aqui estão alguns exemplos:

A segunda operação no conjunto S (\diamond) que é necessária para criar o campo é mais complicada. É uma espécie de multiplicação, mas não a multiplicação normal da aritmética. Em vez disso, temos de ver cada elemento como um vetor e entender a operação como a multiplicação desses dois vectores módulo de um polinómio irredutível.

Comecemos por abordar a ideia de um polinómio irredutível. Um polinómio irredutível é um polinómio que não pode ser factorizado (tal como um número primo não pode ser factorizado em componentes diferentes de 1 e do próprio número primo). Para o nosso objetivo, estamos interessados em polinómios irredutíveis em relação ao conjunto dos números inteiros. (Note-se que pode ser capaz de fatorizar certos polinómios, por exemplo, através de números reais ou complexos, mesmo que não os consiga fatorizar através de números inteiros)

Por exemplo, considere o polinómio x^2 - 3x + 2. Este pode ser reescrito como (x - 1)(x - 2). Logo, não é irredutível. Consideremos agora o polinómio x^2 + 1. Utilizando apenas números inteiros, não há forma de fatorizar esta expressão. Portanto, este é um polinómio irredutível em relação aos inteiros.

Em seguida, vamos abordar o conceito de multiplicação de vectores. Não vamos aprofundar este tema, mas basta compreender uma regra básica: Qualquer divisão vetorial pode ter lugar desde que o dividendo tenha um grau maior ou igual ao do divisor. Se o dividendo tiver um grau menor que o do divisor, então o dividendo já não pode ser dividido pelo divisor.

Por exemplo, considere a expressão x^6 + x + 1 \mod x^5 + x^2. Isto reduz-se claramente, uma vez que o grau do dividendo, 6, é superior ao grau do divisor, 5. Considere agora a expressão x^5 + x + 1 \mod x^5 + x^2. Esta também se reduz ainda mais, pois o grau do dividendo, 5, e o do divisor, 5, são iguais.

No entanto, considere agora a expressão x^4 + x + 1 \mod x^5 + x^2. Esta não se reduz mais, pois o grau do dividendo, 4, é menor que o grau do divisor, 5.

Com base nesta informação, estamos agora prontos para encontrar a nossa segunda operação para o conjunto \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.

Já disse que a segunda operação deve ser entendida como multiplicação de vectores módulo de um polinómio irredutível. Este polinómio irredutível deve garantir que a segunda operação define um grupo abeliano sobre S e é consistente com a condição distributiva. Então qual deve ser esse polinómio irredutível?

Como todos os vectores do conjunto são de grau 2 ou inferior, o polinómio irredutível deve ser de grau 3. Se qualquer multiplicação de dois vectores do conjunto resultar num polinómio de grau 3 ou superior, sabemos que o módulo de um polinómio de grau 3 resulta sempre num polinómio de grau 2 ou inferior. Isto acontece porque qualquer polinómio de grau 3 ou superior é sempre divisível por um polinómio de grau 3. Além disso, o polinómio que funciona como divisor tem de ser irredutível.

Acontece que há vários polinómios irredutíveis de grau 3 que poderíamos usar como divisor. Cada um destes polinómios define um campo diferente em conjunto com o nosso conjunto S e a adição módulo 2. Isto significa que tem múltiplas opções quando utiliza campos de extensão 2^m em criptografia.

Para o nosso exemplo, suponhamos que seleccionamos o polinómio x^3 + x + 1. Este é irredutível, porque não pode ser factorizado com números inteiros. Além disso, garante que qualquer multiplicação de dois elementos dará origem a um polinómio de grau 2 ou inferior.

Vamos dar um exemplo da segunda operação utilizando o polinómio x^3 + x + 1 como divisor para ilustrar o seu funcionamento. Suponhamos que multiplicamos os elementos x^2 + 1 por x^2 + x no nosso conjunto S. Precisamos, então, de calcular a expressão [(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1. Isto pode ser simplificado da seguinte forma:

Sabemos que [x^4 + x^3 + x^2 + x] \mod x^3 + x + 1 pode ser reduzido pois o dividendo tem um grau maior (4) que o divisor (3).

Para começar, pode ver que a expressão x^3 + x + 1 entra em x^4 + x^3 + x^2 + x um total de x vezes. Pode verificar este facto multiplicando x^3 + x + 1 por x, que é x^4 + x^2 + x. Como o último termo é do mesmo grau que o dividendo, nomeadamente 4, sabemos que funciona. Pode calcular o resto desta divisão por x da seguinte forma:

Assim, depois de dividir x^4 + x^3 + x^2 + x por x^3 + x + 1 um total de x vezes, temos um resto de x^3. Este pode ser dividido por x^3 + x + 1?

Intuitivamente, pode ser apelativo dizer que x^3 já não pode ser dividido por x^3 + x + 1, porque o último termo parece maior. No entanto, lembre-se da nossa discussão anterior sobre divisão de vectores. Desde que o dividendo tenha um grau maior ou igual ao do divisor, a expressão pode ser reduzida. Especificamente, a expressão x^3 + x + 1 pode entrar em x^3 exatamente 1 vez. O resto é calculado da seguinte forma:

[(x^3) - (x^3 + x + 1)] \mod x^3 + x + 1 = [x + 1] \mod x^3 + x + 1 = x + 1

Poderá estar a perguntar-se porque é que (x^3) - (x^3 + x + 1) resulta em x + 1 e não em -x - 1. Lembre-se que a primeira operação do nosso campo é definida no módulo 2. Assim, a subtração de dois vectores produz exatamente o mesmo resultado que a adição de dois vectores.

Para resumir a multiplicação de x^2 + 1 e x^2 + x: Quando se multiplicam estes dois termos, obtém-se um polinómio de grau 4, x^4 + x^3 + x^2 + x, que precisa de ser reduzido ao módulo x^3 + x + 1. O polinómio de grau 4 é divisível por x^3 + x + 1 exatamente x + 1 vezes. O resto depois de dividir x^4 + x^3 + x^2 + x por x^3 + x + 1 exatamente x + 1 vezes é x + 1. Este é, de facto, um elemento do nosso conjunto \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.

Porque é que os campos de extensão de base 2 sobre conjuntos de polinómios, como no exemplo acima, são úteis para a criptografia? A razão é que se pode ver os coeficientes dos polinómios desses conjuntos, 0 ou 1, como elementos de cadeias binárias com um determinado comprimento. O conjunto S no nosso exemplo acima, por exemplo, pode ser visto como um conjunto S que inclui todas as cadeias binárias de comprimento 3 (000 a 111). As operações sobre S, então, também podem ser utilizadas para efetuar operações sobre estas cadeias binárias e produzir uma cadeia binária do mesmo comprimento.

Notas:

[2] Os campos de extensão tornam-se muito contra-intuitivos. Em vez de terem elementos de números inteiros, têm conjuntos de polinómios. Além disso, todas as operações são efectuadas no módulo de um polinómio irredutível.

Álgebra abstrata na prática

Apesar da linguagem formal e do carácter abstrato da discussão, o conceito de grupo não deve ser demasiado difícil de apreender. Trata-se apenas de um conjunto de elementos juntamente com uma operação binária, em que a realização dessa operação binária sobre esses elementos satisfaz quatro condições gerais. Um grupo abeliano tem apenas uma condição extra conhecida como comutatividade. Um grupo cíclico, por sua vez, é um tipo especial de grupo abeliano, nomeadamente um grupo que tem um gerador. Um campo é apenas uma construção mais complexa a partir da noção básica de grupo.

Mas se for uma pessoa com inclinações práticas, pode perguntar-se nesta altura: O que é que isso interessa? Será que saber que um conjunto de elementos com um operador é um grupo, ou mesmo um grupo abeliano ou cíclico, tem alguma relevância no mundo real? Será que saber que algo é um campo?

Sem entrar em demasiados pormenores, a resposta é "sim". Os grupos foram criados pela primeira vez no século XIX pelo matemático francês Evariste Galois. Ele utilizou-os para tirar conclusões sobre a resolução de equações polinomiais de grau superior a cinco.

Desde então, o conceito de grupo tem ajudado a esclarecer uma série de problemas em matemática e noutros domínios. Com base neles, por exemplo, o físico Murray-Gellman foi capaz de prever a existência de uma partícula antes de esta ser efetivamente observada em experiências[3]. [3] Por outro lado, os químicos utilizam a teoria dos grupos para classificar as formas das moléculas. Os matemáticos chegaram mesmo a utilizar o conceito de grupo para tirar conclusões sobre algo tão concreto como o papel de parede!

Essencialmente, mostrar que um conjunto de elementos com algum operador é um grupo significa que o que está a descrever tem uma simetria particular. Não uma simetria no sentido comum da palavra, mas numa forma mais abstrata. E isso pode fornecer informações substanciais sobre sistemas e problemas específicos. As noções mais complexas da álgebra abstrata apenas nos dão informação adicional.

Mais importante ainda, verá a importância dos grupos e campos da teoria dos números na prática através da sua aplicação na criptografia, particularmente na criptografia de chave pública. Já vimos na nossa discussão sobre campos, por exemplo, como os campos de extensão são empregues na cifra Rijndael. Iremos trabalhar esse exemplo no Capítulo 5.

Para uma discussão mais aprofundada sobre álgebra abstrata, recomendo a excelente série de vídeos sobre álgebra abstrata da Socratica. [4] Recomendo particularmente os seguintes vídeos: "O que é a álgebra abstrata?", "Definição de grupo (expandida)", "Definição de anel (expandida)" e "Definição de campo (expandida)" Estes quatro vídeos dar-lhe-ão uma visão adicional de grande parte do que foi discutido acima. (Não falámos de anéis, mas um campo é apenas um tipo especial de anel)

Para uma discussão mais aprofundada sobre a teoria moderna dos números, pode consultar muitas discussões avançadas sobre criptografia. Sugiro como sugestões Jonathan Katz e Yehuda Lindell's Introduction to Modern Cryptography ou Christof Paar e Jan Pelzl's Understanding Cryptography para uma discussão mais aprofundada. [5]

Notas:

[3] Ver Vídeo do YouTube

[4] Socratica, Álgebra Abstrata

[5] Katz e Lindell, Introduction to Modern Cryptography, 2.ª ed., 2015 (CRC Press: Boca Raton, FL). Paar e Pelzl, Understanding Cryptography, 2010 (Springer-Verlag: Berlim).

Criptografia simétrica

Alice e Bob

Um dos dois principais ramos da criptografia é a criptografia simétrica. Inclui esquemas de cifragem, bem como esquemas relacionados com a autenticação e a integridade. Até à década de 1970, toda a criptografia consistia em esquemas de cifragem simétrica.

A discussão principal começa por analisar os sistemas de cifragem simétrica e fazer a distinção crucial entre cifras de fluxo e cifras de bloco. De seguida, abordamos os códigos de autenticação de mensagens, que são esquemas para garantir a integridade e a autenticidade das mensagens. Finalmente, exploramos o modo como os esquemas de cifragem simétrica e os códigos de autenticação de mensagens podem ser combinados para garantir uma comunicação segura.

Este capítulo aborda, de passagem, vários esquemas criptográficos simétricos da prática. O capítulo seguinte apresenta uma exposição pormenorizada da encriptação com uma cifra de fluxo e uma cifra de bloco da prática, nomeadamente o RC4 e o AES, respetivamente.

Antes de iniciarmos a nossa discussão sobre criptografia simétrica, gostaria de fazer algumas observações breves sobre as ilustrações da Alice e do Bob neste capítulo e nos seguintes.

Para ilustrar os princípios da criptografia, recorre-se frequentemente a exemplos que envolvem Alice e Bob. É o que farei também.

Especialmente se for novo na criptografia, é importante perceber que estes exemplos de Alice e Bob servem apenas para ilustrar os princípios e construções criptográficas num ambiente simplificado. Os princípios e construções, no entanto, são aplicáveis a uma gama muito maior de contextos da vida real.

Seguem-se cinco pontos-chave a ter em conta sobre exemplos que envolvem Alice e Bob em criptografia:

  1. Podem ser facilmente transpostas para exemplos com outros tipos de actores, como empresas ou organizações governamentais.

  2. Podem ser facilmente alargados para incluir três ou mais actores.

  3. Nos exemplos, Bob e Alice são normalmente participantes activos na criação de cada mensagem e na aplicação de esquemas criptográficos a essa mensagem. Mas, na realidade, as comunicações electrónicas são em grande parte automatizadas. Quando se visita um sítio Web que utiliza a segurança da camada de transporte, por exemplo, a criptografia é normalmente toda tratada pelo computador e pelo servidor Web.

  4. No contexto da comunicação eletrónica, as "mensagens" que são enviadas através de um canal de comunicação são normalmente pacotes TCP/IP. Estes podem pertencer a um e-mail, uma mensagem do Facebook, uma conversa telefónica, uma transferência de ficheiros, um sítio Web, um carregamento de software, etc. Não são mensagens no sentido tradicional. No entanto, os criptógrafos simplificam frequentemente esta realidade, afirmando que a mensagem é, por exemplo, um correio eletrónico.

  5. Os exemplos centram-se normalmente na comunicação eletrónica, mas também podem ser alargados às formas tradicionais de comunicação, como as cartas.

Esquemas de encriptação simétrica

Podemos definir vagamente um esquema de encriptação assimétrica como qualquer esquema criptográfico com três algoritmos:

  1. Um algoritmo de geração de chaves, que gera uma chave privada.

  2. Um algoritmo de encriptação, que recebe a chave privada e um texto simples como entradas e produz um texto cifrado.

  3. Um algoritmo de decifração, que recebe a chave privada e o texto cifrado como entradas e produz o texto simples original.

Normalmente, um esquema de cifragem - simétrico ou assimétrico - oferece um modelo de cifragem baseado num algoritmo central, em vez de uma especificação exacta.

Por exemplo, considere o Salsa20, um esquema de encriptação simétrica. Pode ser utilizado com chaves de 128 e 256 bits. A escolha do comprimento da chave tem impacto em alguns detalhes menores do algoritmo (o número de rondas no algoritmo, para ser exato).

Mas não se pode dizer que utilizar o Salsa20 com uma chave de 128 bits é um esquema de encriptação diferente do Salsa20 com uma chave de 256 bits. O algoritmo de base permanece o mesmo. Só quando o algoritmo central muda é que se fala realmente de dois esquemas de encriptação diferentes.

Os esquemas de cifragem simétrica são normalmente úteis em dois tipos de casos: (1) aqueles em que dois ou mais agentes estão a comunicar à distância e querem manter o conteúdo das suas comunicações em segredo; e (2) aqueles em que um agente quer manter o conteúdo de uma mensagem em segredo ao longo do tempo.

Pode ver uma representação da situação (1) na Figura 1 abaixo. Bob quer enviar uma mensagem M para Alice à distância, mas não quer que outras pessoas possam ler essa mensagem.

O Bob começa por cifrar a mensagem M com a chave privada K. De seguida, envia o texto cifrado C para a Alice. Quando Alice recebe o texto cifrado, pode decifrá-lo utilizando a chave K e ler o texto simples. Com um bom esquema de encriptação, qualquer atacante que intercepte o texto cifrado C não deve ser capaz de aprender nada de realmente significativo sobre a mensagem M.

Pode ver uma representação da situação (2) na Figura 2 abaixo. O Bob quer impedir que outras pessoas vejam determinadas informações. Uma situação típica pode ser o facto de Bob ser um empregado que guarda dados sensíveis no seu computador, que não é suposto serem lidos por estranhos nem pelos seus colegas.

O Bob encripta a mensagem M no tempo T_0 com a chave K para produzir o texto cifrado C. No momento T_1 ele precisa novamente da mensagem e decifra o texto cifrado C com a chave K. Qualquer atacante que possa ter encontrado o texto cifrado C entretanto não deve ter sido capaz de deduzir nada de significativo sobre M a partir dele.

Figura 1: Sigilo no espaço

Figure 1: Secrecy across space

Figura 2: Sigilo ao longo do tempo

Figure 2: Secrecy across time

Um exemplo: A cifra de deslocamento

No Capítulo 2, encontrámos a cifra de deslocamento, que é um exemplo de um esquema de encriptação simétrica muito simples. Vamos voltar a vê-lo aqui.

Suponha um dicionário D que equaciona todas as letras do alfabeto inglês, por ordem, com o conjunto de números \{0,1,2,\dots,25\}. Suponha-se um conjunto de mensagens possíveis M. A cifra de deslocamento é, então, um esquema de encriptação definido da seguinte forma:

O que torna a cifra de deslocamento um esquema de encriptação simétrico é o facto de a mesma chave ser utilizada tanto para o processo de encriptação como para o de desencriptação. Por exemplo, suponha que pretende encriptar a mensagem "DOG" utilizando a cifra de deslocamento e que selecionou aleatoriamente "24" como chave. A encriptação da mensagem com esta chave produziria "BME". A única forma de recuperar a mensagem original é utilizando a mesma chave, "24", para o processo de desencriptação.

Esta cifra Shift é um exemplo de uma cifra de substituição monoalfabética: um esquema de encriptação em que o alfabeto do texto cifrado é fixo (ou seja, é utilizado apenas um alfabeto). Assumindo que o algoritmo de desencriptação é determinístico, cada símbolo no texto cifrado de substituição pode, no máximo, pertencer a um símbolo no texto simples.

Até aos anos 1700, muitas aplicações de cifragem baseavam-se fortemente em cifras de substituição monoalfabéticas, embora estas fossem frequentemente muito mais complexas do que a cifra Shift. Por exemplo, podia-se selecionar aleatoriamente uma letra do alfabeto para cada letra do texto original, com a condição de que cada letra ocorresse apenas uma vez no alfabeto do texto cifrado. Isso significa que teríamos um fatorial de 26 chaves privadas possíveis, o que era enorme na era pré-computador.

Note que vai encontrar o termo cifra muitas vezes em criptografia. Esteja ciente de que este termo tem vários significados. De facto, conheço pelo menos cinco significados distintos do termo no âmbito da criptografia.

Nalguns casos, refere-se a um esquema de cifragem, como acontece na cifra Shift e na cifra de substituição monoalfabética. No entanto, o termo pode também referir-se especificamente ao algoritmo de encriptação, à chave privada ou apenas ao texto cifrado de qualquer esquema de encriptação.

Por último, o termo cifra pode também referir-se a um algoritmo central a partir do qual se podem construir esquemas criptográficos. Estes podem incluir vários algoritmos de encriptação, mas também outros tipos de esquemas criptográficos. Este sentido do termo torna-se relevante no contexto das cifras de bloco (ver a secção "Cifras de bloco" abaixo).

Pode também encontrar os termos encriptar ou decifrar. Estes termos são apenas sinónimos de encriptação e desencriptação.

Ataques de força bruta e princípio de Kerckhoff

A cifra shift é um esquema de encriptação simétrica muito inseguro, pelo menos no mundo moderno[1]. Um atacante pode simplesmente tentar desencriptar qualquer texto cifrado com todas as 26 chaves possíveis para ver qual o resultado que faz sentido. Este tipo de ataque, em que o atacante está apenas a percorrer as chaves para ver o que funciona, é conhecido como brute force attack ou exhaustive key search.

Para que qualquer esquema de encriptação cumpra uma noção mínima de segurança, deve ter um conjunto de chaves possíveis, ou espaço de chaves, que seja tão grande que os ataques de força bruta sejam inviáveis. Todos os esquemas de encriptação modernos cumprem esta norma. É conhecido como o princípio do espaço de chaves suficiente. Um princípio semelhante aplica-se tipicamente em diferentes tipos de esquemas criptográficos.

Para ter uma ideia do enorme espaço de chaves dos esquemas de encriptação modernos, suponha que um ficheiro foi encriptado com uma chave de 128 bits utilizando a norma de encriptação avançada. Isto significa que um atacante tem um conjunto de 2^{128} chaves que precisa de percorrer para um ataque de força bruta. Uma hipótese de 0,78% de sucesso com esta estratégia exigiria que o atacante percorresse cerca de 2,65 \times 10^{36} chaves.

Suponhamos que assumimos optimisticamente que um atacante pode tentar 10^{16} chaves por segundo (i.e., 10 quadriliões de chaves por segundo). Para testar 0,78% de todas as chaves no espaço de chaves, o seu ataque teria de durar 2,65 \times 10^{20} segundos. Isto é cerca de 8,4 triliões de anos. Assim, mesmo um ataque de força bruta por um adversário absurdamente poderoso não é realista com um esquema de encriptação moderno de 128 bits. Este é o princípio do espaço de chave suficiente em ação.

A cifra de deslocamento é mais segura se o atacante não conhecer o algoritmo de encriptação? Talvez, mas não muito.

De qualquer modo, a criptografia moderna parte sempre do princípio de que a segurança de qualquer esquema de cifragem simétrica assenta apenas na manutenção do segredo da chave privada. Parte-se sempre do princípio de que o atacante conhece todos os outros pormenores, incluindo o espaço da mensagem, o espaço da chave, o espaço do texto cifrado, o algoritmo de seleção da chave, o algoritmo de cifragem e o algoritmo de decifragem.

A ideia de que a segurança de um esquema de encriptação simétrica só pode depender do segredo da chave privada é conhecida como princípio de Kerckhoffs.

Tal como pretendido originalmente por Kerckhoffs, o princípio aplica-se apenas a esquemas de encriptação simétrica. Uma versão mais geral do princípio, no entanto, também se aplica a todos os outros tipos de esquemas criptográficos actuais: A conceção de qualquer esquema criptográfico não deve exigir segredo para que seja seguro; o segredo só pode estender-se a algumas cadeias de informação, normalmente uma chave privada.

O princípio de Kerckhoffs é fundamental para a criptografia moderna por quatro razões. [2] Em primeiro lugar, existe apenas um número limitado de esquemas criptográficos para determinados tipos de aplicações. Por exemplo, a maior parte das aplicações modernas de encriptação simétrica utilizam a cifra Rijndael. Assim, o seu sigilo relativamente à conceção de um esquema é muito limitado. Existe, no entanto, muito mais flexibilidade em manter em segredo uma chave privada para a cifra Rijndael.

Em segundo lugar, é mais fácil substituir uma cadeia de informação do que todo um esquema criptográfico. Suponhamos que todos os empregados de uma empresa têm o mesmo software de encriptação e que cada dois empregados têm uma chave privada para comunicar confidencialmente. O comprometimento das chaves é um incómodo neste cenário, mas pelo menos a empresa pode manter o software com essas falhas de segurança. Se a empresa estivesse a confiar no segredo do esquema, então qualquer quebra desse segredo exigiria a substituição de todo o software.

Em terceiro lugar, o princípio de Kerckhoffs permite a normalização e a compatibilidade entre os utilizadores de esquemas criptográficos. Este facto traz enormes benefícios em termos de eficiência. Por exemplo, é difícil imaginar como é que milhões de pessoas se poderiam ligar em segurança aos servidores Web da Google todos os dias, se essa segurança exigisse manter em segredo os esquemas criptográficos.

Em quarto lugar, o princípio de Kerckhoff permite o escrutínio público dos esquemas criptográficos. Este tipo de controlo é absolutamente necessário para obter esquemas criptográficos seguros. A título de exemplo, o principal algoritmo central da criptografia simétrica, a cifra Rijndael, foi o resultado de um concurso organizado pelo National Institute of Standards and Technology entre 1997 e 2000.

Qualquer sistema que tente alcançar a segurança por obscuridade é um sistema que se baseia em manter secretos os detalhes da sua conceção e/ou implementação. Na criptografia, isto seria especificamente um sistema que se baseia em manter secretos os pormenores da conceção do esquema criptográfico. Assim, a segurança por obscuridade está em contraste direto com o princípio de Kerckhoffs.

A capacidade da abertura para reforçar a qualidade e a segurança também se estende mais amplamente ao mundo digital do que apenas à criptografia. As distribuições Linux livres e de código aberto, como a Debian, por exemplo, têm geralmente várias vantagens sobre as suas congéneres Windows e MacOS em termos de privacidade, estabilidade, segurança e flexibilidade. Embora isso possa ter várias causas, o princípio mais importante é provavelmente, como Eric Raymond expressou no seu famoso ensaio "The Cathedral and the Bazaar", que "com olhos suficientes, todos os bugs são superficiais" [3] É este princípio do tipo sabedoria das multidões que deu ao Linux seu sucesso mais significativo.

Nunca se pode afirmar sem ambiguidade que um esquema criptográfico é "seguro" ou "inseguro" Em vez disso, existem várias noções de segurança para esquemas criptográficos. Cada definição de segurança criptográfica deve especificar (1) os objectivos de segurança, bem como (2) as capacidades de um atacante. A análise de esquemas criptográficos em relação a uma ou mais noções específicas de segurança fornece informações sobre as suas aplicações e limitações.

Embora não nos aprofundemos em todos os pormenores das várias noções de segurança criptográfica, deve saber que dois pressupostos são omnipresentes em todas as noções criptográficas modernas de segurança relativas a esquemas simétricos e assimétricos (e, de alguma forma, a outras primitivas criptográficas):

Notas:

[1] De acordo com Seutónio, uma cifra de deslocamento com um valor de chave constante de 3 foi usada por Júlio César nas suas comunicações militares. Assim, A tornar-se-ia sempre D, B sempre E, C sempre F, e assim por diante. Esta versão particular da cifra de deslocamento tornou-se, assim, conhecida como a Cifra de César (embora não seja realmente uma cifra no sentido moderno da palavra, uma vez que o valor da chave é constante). A cifra de César pode ter sido segura no século I a.C., se os inimigos de Roma não estivessem muito familiarizados com a encriptação. Mas claramente não seria um esquema muito seguro nos tempos modernos.

[2] Jonathan Katz e Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), p. 7f.

[3] Eric Raymond, "The Cathedral and the Bazaar", artigo apresentado no Linux Kongress, Würzburg, Alemanha (27 de maio de 1997). Há uma série de versões subsequentes disponíveis, bem como um livro. As minhas citações são da página 30 do livro: Eric Raymond, The Cathedral and the Bazaar: Musings on Linux and Open Source by an Accidental Revolutionary, revised edn. (2001), O'Reilly: Sebastopol, CA.

Cifras de fluxo

Os esquemas de cifragem simétrica são normalmente subdivididos em dois tipos: cifras de fluxo e cifras de bloco. Esta distinção é, no entanto, um pouco problemática, uma vez que as pessoas utilizam estes termos de forma inconsistente. Nas próximas secções, estabelecerei a distinção da forma que considero mais adequada. No entanto, deve estar ciente de que muitas pessoas utilizarão estes termos de forma um pouco diferente da que eu defini.

Vamos primeiro falar de cifras de fluxo. Uma cifra de fluxo é um esquema de encriptação simétrica em que a encriptação consiste em dois passos.

Em primeiro lugar, é produzida uma cadeia de caracteres com o comprimento do texto simples através de uma chave privada. Esta cadeia é designada por keystream.

De seguida, o fluxo de chaves é combinado matematicamente com o texto simples para produzir um texto cifrado. Esta combinação é normalmente uma operação XOR. Para a desencriptação, basta inverter a operação. (Note-se que A \oplus B = B \oplus A, no caso de A e B serem cadeias de bits. Assim, a ordem de uma operação XOR numa cifra de fluxo não é importante para o resultado. Esta propriedade é conhecida como comutatividade)

Uma cifra de fluxo XOR típica é representada na Figura 3. Primeiro, pega numa chave privada K e utiliza-a para gerar um fluxo de chaves. O fluxo de chaves é, então, combinado com o texto simples através de uma operação XOR para produzir o texto cifrado. Qualquer agente que receba o texto cifrado pode decifrá-lo facilmente se tiver a chave K. Tudo o que precisa de fazer é criar um fluxo de chaves tão longo como o texto cifrado, de acordo com o procedimento especificado no esquema, e combiná-lo com o texto cifrado.

Figura 3: Uma cifra de fluxo XOR

Figure 3: An XOR stream cipher

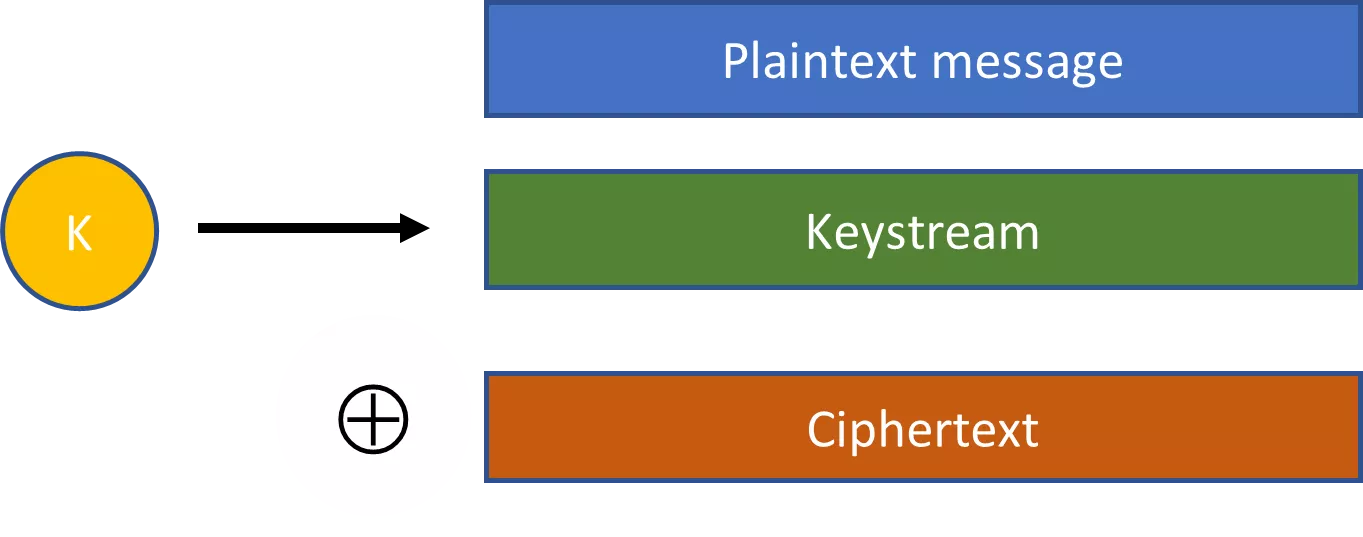
Lembre-se que um esquema de encriptação é tipicamente um modelo para encriptação com o mesmo algoritmo principal, em vez de uma especificação exacta. Por extensão, uma cifra de fluxo é tipicamente um modelo para encriptação em que se podem usar chaves de diferentes comprimentos. Embora o comprimento da chave possa afetar alguns detalhes menores do esquema, não afectará a sua forma essencial.

A cifra de deslocamento é um exemplo de uma cifra de fluxo muito simples e insegura. Utilizando uma única letra (a chave privada), é possível produzir uma sequência de letras com o comprimento da mensagem (o fluxo de chaves). Esta cadeia de chaves é, então, combinada com o texto simples através de uma operação de módulo para produzir um texto cifrado. (Esta operação de módulo pode ser simplificada para uma operação XOR quando se representam as letras em bits).

Outro exemplo famoso de uma cifra de fluxo é a Cifra de Vigenere, em homenagem a Blaise de Vigenere, que a desenvolveu completamente no final do século XVI (embora outros tenham feito muito trabalho anterior). É um exemplo de uma cifra de substituição polialfabética: um esquema de cifragem em que o alfabeto do texto cifrado para um símbolo do texto simples muda consoante a sua posição no texto. Ao contrário de uma cifra de substituição monoalfabética, os símbolos de texto cifrado podem ser associados a mais do que um símbolo de texto simples.

À medida que a encriptação ganhava popularidade na Europa renascentista, o mesmo acontecia com a análise de cifras, ou seja, a quebra de textos cifrados, em particular, utilizando a análise de frequências. Esta última utiliza regularidades estatísticas na nossa língua para quebrar textos cifrados, e foi descoberta por académicos árabes já no século IX. É uma técnica que funciona particularmente bem com textos mais longos. E mesmo as mais sofisticadas cifras monoalfabéticas de substição já não eram suficientes contra a análise de frequências por volta de 1700 na Europa, particularmente em contextos militares e de segurança. Uma vez que a cifra Vigenere oferecia um avanço significativo em termos de segurança, tornou-se popular neste período e estava generalizada no final do século XVIII.

Em termos informais, o esquema de encriptação funciona da seguinte forma:

  1. Selecione uma palavra com várias letras como chave privada.

  2. Para qualquer mensagem, aplicar a cifra de deslocamento a cada letra da mensagem utilizando a letra correspondente na palavra-chave como deslocamento.

  3. Se tiver passado pela palavra-chave mas ainda não tiver cifrado totalmente o texto simples, aplique novamente as letras da palavra-chave como uma cifra de deslocamento às letras correspondentes no restante texto.

  4. Continuar este processo até que toda a mensagem tenha sido cifrada.

Para ilustrar, suponhamos que a sua chave privada é "GOLD" e que pretende cifrar a mensagem "CRYPTOGRAPHY". Nesse caso, procederia da seguinte forma, de acordo com a cifra de Vigenère:

Assim, o texto cifrado c = "IFJSZCRUGDSB".

Outro exemplo famoso de uma cifra de fluxo é o one-time pad. Com o one-time pad, basta criar uma cadeia de bits aleatórios tão longa como a mensagem de texto simples e produzir o texto cifrado através da operação XOR. Assim, a chave privada e o fluxo de chaves são equivalentes com um one-time pad.

Enquanto a cifra Shift e as cifras Vigenere são muito inseguras na era moderna, o bloco de tempo único é muito seguro se utilizado corretamente. Provavelmente, a aplicação mais famosa do bloco de tempo único foi, pelo menos até aos anos 80, para a linha direta Washington-Moscovo. [4]

A linha direta é uma ligação de comunicação direta entre Washington e Moscovo para assuntos urgentes que foi instalada após a crise dos mísseis de Cuba. A tecnologia para a linha direta foi-se transformando ao longo dos anos. Atualmente, inclui um cabo direto de fibra ótica, bem como duas ligações por satélite (para redundância), que permitem o envio de mensagens de correio eletrónico e de texto. A ligação termina em vários locais nos EUA. O Pentágono, a Casa Branca e a montanha Raven Rock são pontos de chegada conhecidos. Contrariamente à opinião popular, a linha direta nunca envolveu telefones.

Na sua essência, o esquema do bloco único funcionava da seguinte forma. Tanto Washington como Moscovo teriam dois conjuntos de números aleatórios. Um conjunto de números aleatórios, criado pelos russos, dizia respeito à encriptação e desencriptação de quaisquer mensagens em língua russa. Um conjunto de números aleatórios, criado pelos americanos, dizia respeito à cifragem e decifragem de quaisquer mensagens em língua inglesa. De tempos a tempos, mais números aleatórios eram entregues ao outro lado por correios de confiança.

Washington e Moscovo puderam, então, comunicar secretamente utilizando estes números aleatórios para criar blocos de acesso único. De cada vez que era necessário comunicar, utilizava-se a porção seguinte de números aleatórios para a mensagem.

Embora altamente seguro, o bloco de tempo único enfrenta limitações práticas significativas: a chave tem de ser tão longa como a mensagem e nenhuma parte de um bloco de tempo único pode ser reutilizada. Isto significa que é necessário manter um registo da sua posição no bloco de tempo único, armazenar um número enorme de bits e trocar bits aleatórios com as suas contrapartes de tempos a tempos. Consequentemente, o bloco de notas de uso único não é frequentemente utilizado na prática.

Em vez disso, as cifras de fluxo predominantes utilizadas na prática são cifras de fluxo pseudo-aleatórias. A Salsa20 e uma variante intimamente relacionada chamada ChaCha são exemplos de cifras de fluxo pseudo-aleatórias comummente utilizadas.

Com estas cifras de fluxo pseudo-aleatórias, começa-se por selecionar aleatoriamente uma chave K que é mais curta do que o comprimento do texto simples. Essa chave aleatória K é normalmente criada pelo nosso computador com base em dados imprevisíveis que recolhe ao longo do tempo, como o tempo entre mensagens de rede, movimentos do rato, etc.

Esta chave aleatória K é então inserida num algoritmo de expansão que cria um fluxo de chave pseudo-aleatório tão longo quanto a mensagem. Pode especificar exatamente o comprimento do fluxo de chaves (por exemplo, 500 bits, 1000 bits, 1200 bits, 29.117 bits, etc.).

Uma cadeia de chaves pseudo-aleatória aparece como se tivesse sido escolhida completamente ao acaso do conjunto de todas as cadeias de caracteres com o mesmo comprimento. Assim, a encriptação com uma cadeia de chaves pseudo-aleatória aparece como se tivesse sido feita com um bloco de tempo único. Mas é claro que não é esse o caso.

Uma vez que a nossa chave privada é mais curta do que o fluxo de chaves e o nosso algoritmo de expansão tem de ser determinístico para que o processo de encriptação/desencriptação funcione, nem todos os fluxos de chaves com esse comprimento específico poderiam ter resultado da nossa operação de expansão.

Suponhamos, por exemplo, que a nossa chave privada tem um comprimento de 128 bits e que podemos inseri-la num algoritmo de expansão para criar uma cadeia de chaves muito mais longa, digamos de 2.500 bits. Como o nosso algoritmo de expansão tem de ser determinístico, o nosso algoritmo pode, no máximo, selecionar cadeias de 1/2^{128} com um comprimento de 2500 bits. Assim, uma tal cadeia de chaves nunca poderia ser selecionada de forma totalmente aleatória a partir de todas as cadeias com o mesmo comprimento.

A nossa definição de uma cifra de fluxo tem dois aspectos: (1) um fluxo de chaves desde que o texto simples seja gerado com a ajuda de uma chave privada; e (2) este fluxo de chaves é combinado com o texto simples, normalmente através de uma operação XOR, para produzir o texto cifrado.

Por vezes, as pessoas definem a condição (1) de forma mais rigorosa, afirmando que o fluxo de chaves deve ser especificamente pseudo-aleatório. Isto significa que nem a cifra de deslocamento, nem o bloco de tempo único seriam considerados cifras de fluxo.

Na minha opinião, definir a condição (1) de uma forma mais ampla facilita a organização dos sistemas de cifragem. Além disso, significa que não temos de deixar de chamar a um determinado esquema de cifragem uma cifra de fluxo só porque descobrimos que não se baseia efetivamente em fluxos de chaves pseudo-aleatórios.

Notas:

[4] Crypto Museum, "Washington-Moscow hotline," 2013, disponível em https://www.cryptomuseum.com/crypto/hotline/index.htm.

Cifras de bloco

A primeira forma como uma cifra de bloco é normalmente entendida é como algo mais primitivo do que uma cifra de fluxo: Um algoritmo central que efectua uma transformação que preserva o comprimento numa cadeia de um comprimento adequado com a ajuda de uma chave. Este algoritmo pode ser utilizado para criar esquemas de cifragem e talvez outros tipos de esquemas criptográficos.

Frequentemente, uma cifra de bloco pode receber cadeias de entrada de vários comprimentos, como 64, 128 ou 256 bits, bem como chaves de vários comprimentos, como 128, 192 ou 256 bits. Embora alguns pormenores do algoritmo possam mudar em função destas variáveis, o algoritmo principal não muda. Se assim fosse, estaríamos a falar de duas cifras de bloco diferentes. Note-se que a utilização da terminologia do algoritmo de base é a mesma que para os esquemas de encriptação.

Uma representação do funcionamento de uma cifra de bloco pode ser vista na Figura 4 abaixo. Uma mensagem M de comprimento L e uma chave K servem como entradas para a cifra de bloco. O resultado é uma mensagem M' de comprimento L. A chave não precisa necessariamente de ter o mesmo comprimento que M e M' para a maioria das cifras de bloco.

Figura 4: Uma cifra de bloco

Figure 4: A block cipher

Uma cifra de bloco por si só não é um esquema de encriptação. Mas uma cifra de bloco pode ser utilizada com vários modos de funcionamento para produzir diferentes esquemas de encriptação. Um modo de operação simplesmente acrescenta algumas operações adicionais fora da cifra de bloco.

Para ilustrar como isto funciona, suponhamos uma cifra de bloco (BC) que requer uma cadeia de entrada de 128 bits e uma chave privada de 128 bits. A figura 5 abaixo mostra como essa cifra de bloco pode ser utilizada com o modo electronic code book (ECB mode) para criar um esquema de encriptação. (As elipses à direita indicam que pode repetir este padrão o tempo que for necessário).

Figura 5: Uma cifra de bloco com o modo ECB

Figure 5: A block cipher with ECB mode

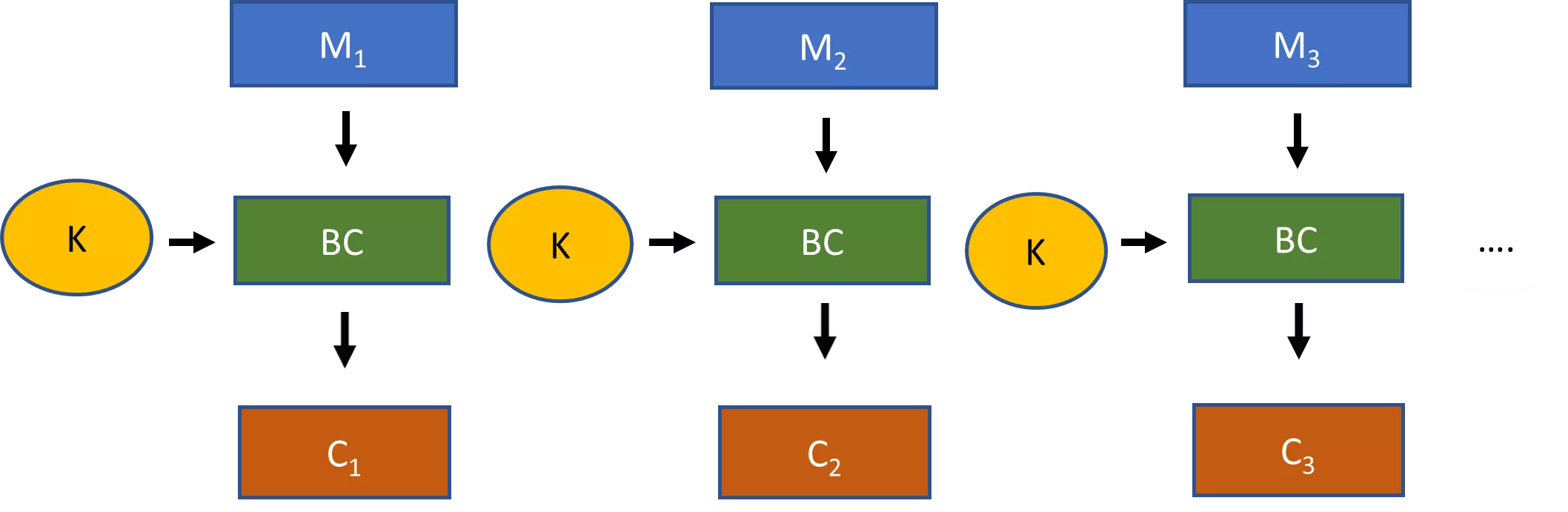
O processo de encriptação de livros de códigos electrónicos com a cifra de bloco é o seguinte. Veja se consegue dividir a sua mensagem de texto simples em blocos de 128 bits. Se não for possível, adicione padding à mensagem, de modo a que o resultado possa ser dividido uniformemente pelo tamanho do bloco de 128 bits. Estes são os dados utilizados para o processo de encriptação.

Agora, divida os dados em blocos de cadeias de 128 bits (M_1, M_2, M_3, etc.). Passe cada cadeia de 128 bits pela cifra de bloco com a sua chave de 128 bits para produzir blocos de texto cifrado de 128 bits (C_1, C_2, C_3, etc.). Estes pedaços, quando combinados novamente, formam o texto cifrado completo.

A desencriptação é apenas o processo inverso, embora o destinatário necessite de uma forma reconhecível de retirar qualquer preenchimento dos dados desencriptados para produzir a mensagem de texto simples original.

Embora relativamente simples, uma cifra de bloco com modo de livro de códigos eletrónico carece de segurança. Isto deve-se ao facto de conduzir a uma encriptação determinística. Quaisquer duas cadeias de dados idênticas de 128 bits são encriptadas exatamente da mesma forma. Essa informação pode ser explorada.

Em vez disso, qualquer esquema de encriptação construído a partir de uma cifra de bloco deve ser probabilístico: ou seja, a encriptação de qualquer mensagem M, ou de qualquer parte específica de M, deve geralmente produzir um resultado diferente de cada vez. [5]

O modo de encadeamento de blocos de cifra (modo CBC) é provavelmente o modo mais comum utilizado com uma cifra de bloco. A combinação, se bem feita, produz um esquema de encriptação probabilístico. Pode ver uma representação deste modo de funcionamento na Figura 6 abaixo.

Figura 6: Uma cifra de bloco com modo CBC

Figure 6: A block cipher with CBC mode

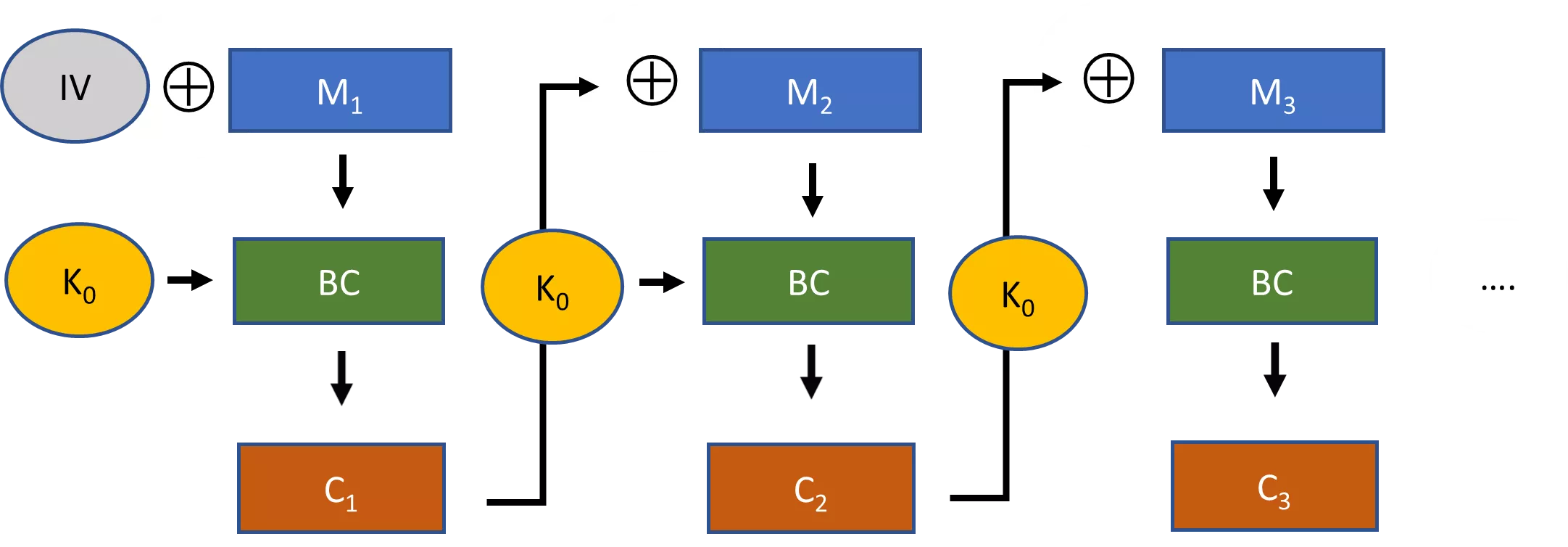
Suponhamos que o tamanho do bloco é novamente de 128 bits. Assim, para começar, teria novamente de garantir que a sua mensagem de texto simples original recebe o preenchimento necessário.

Depois, faz XOR da primeira porção de 128 bits do seu texto simples com um vetor de inicialização de 128 bits. O resultado é colocado na cifra de bloco para produzir um texto cifrado para o primeiro bloco. Para o segundo bloco de 128 bits, primeiro faz XOR do texto simples com o texto cifrado do primeiro bloco, antes de o inserir na cifra de bloco. Continua este processo até ter encriptado toda a sua mensagem de texto simples.

Quando terminar, envia a mensagem cifrada juntamente com o vetor de inicialização não cifrado para o destinatário. O destinatário tem de conhecer o vetor de inicialização, caso contrário não pode desencriptar o texto cifrado.

Esta construção é muito mais segura do que o modo de livro de códigos eletrónico quando utilizado corretamente. Deve-se, em primeiro lugar, assegurar que o vetor de inicialização é uma string aleatória ou pseudo-aleatória. Além disso, deve utilizar um vetor de inicialização diferente de cada vez que utilizar este esquema de encriptação.

Por outras palavras, o seu vetor de inicialização deve ser um nonce aleatório ou pseudo-aleatório, onde um nonce significa "um número que só é usado uma vez" Se mantiver esta prática, então o modo CBC com uma cifra de bloco garante que quaisquer dois blocos de texto simples idênticos serão geralmente encriptados de forma diferente de cada vez.

Por fim, vamos debruçar-nos sobre o modo de feedback de saída (modo OFB). Pode ver uma representação deste modo na Figura 7.

Figura 7: Uma cifra de bloco com modo OFB

Figure 7: A block cipher with OFB mode

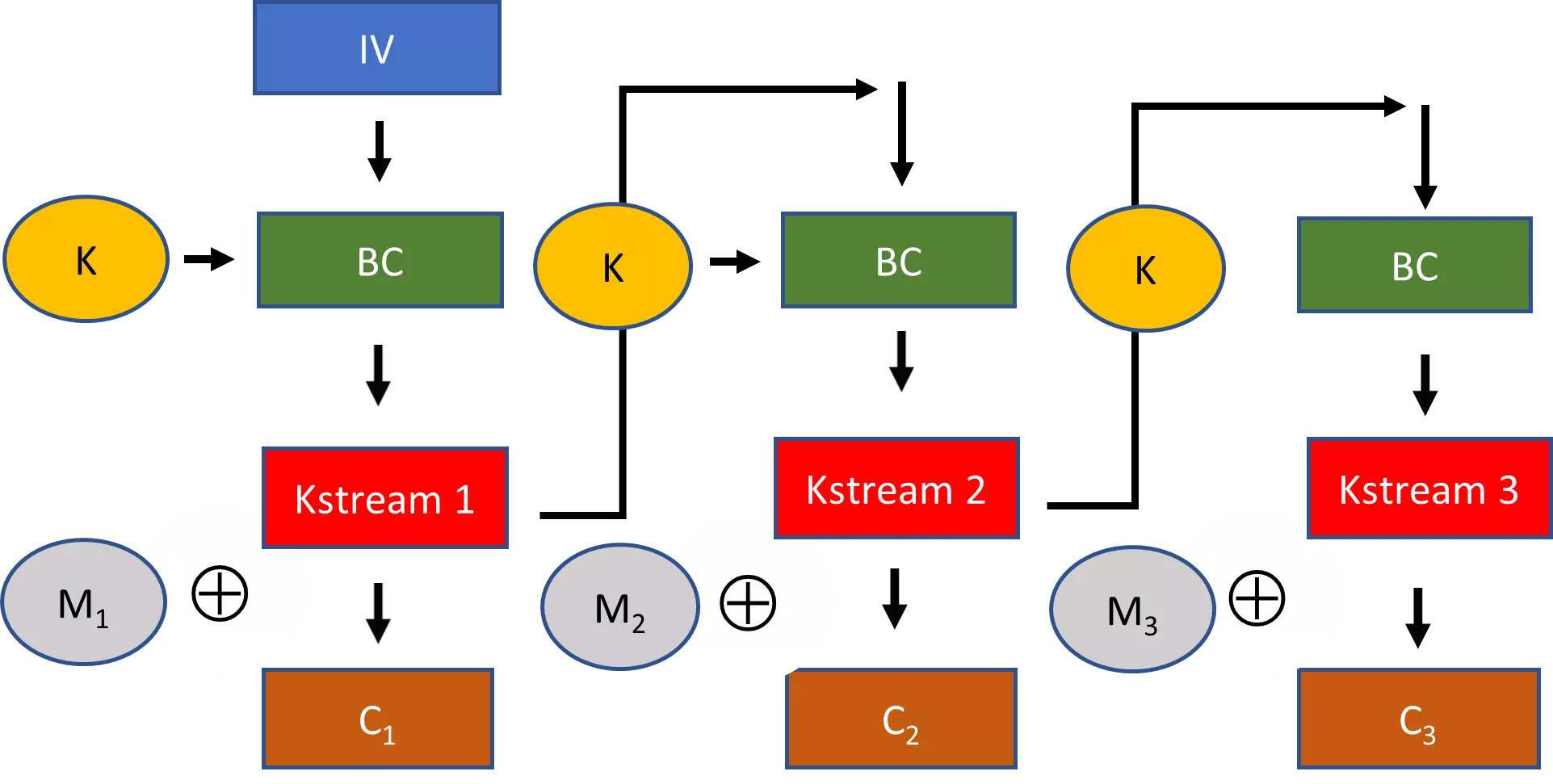
Com o modo OFB também se seleciona um vetor de inicialização. Mas aqui, para o primeiro bloco, o vetor de inicialização é diretamente inserido na cifra de bloco com a sua chave. Os 128 bits resultantes são, então, tratados como um fluxo de chaves. Este keystream é XORed com o texto simples para produzir o texto cifrado para o bloco. Para os blocos subsequentes, utiliza-se o fluxo de chaves do bloco anterior como entrada na cifra de bloco e repetem-se os passos.

Se reparar bem, o que foi efetivamente criado aqui a partir da cifra de bloco com o modo OFB é uma cifra de fluxo. Gera porções de keystream de 128 bits até obter o comprimento do texto simples (descartando os bits de que não precisa da última porção de keystream de 128 bits). De seguida, faz XOR do fluxo de chaves com a sua mensagem de texto simples para obter o texto cifrado.

Na secção anterior sobre cifras de fluxo, afirmei que se produz um fluxo de chaves com a ajuda de uma chave privada. Para ser exato, não tem de ser criado apenas com uma chave privada. Como se pode ver no modo OFB, o fluxo de chaves é produzido com o apoio de uma chave privada e de um vetor de inicialização.

Note que, tal como no modo CBC, é importante selecionar um nonce pseudo-aleatório ou aleatório para o vetor de inicialização sempre que utilizar uma cifra de bloco no modo OFB. Caso contrário, a mesma cadeia de mensagens de 128 bits enviada em diferentes comunicações será encriptada da mesma forma. Esta é uma forma de criar encriptação probabilística com uma cifra de fluxo.

Algumas cifras de fluxo utilizam apenas uma chave privada para criar um fluxo de chaves. Para essas cifras de fluxo, é importante que utilize um nonce aleatório para selecionar a chave privada para cada instância de comunicação. Caso contrário, os resultados da encriptação com essas cifras de fluxo também serão determinísticos, levando a problemas de segurança.

A cifra de bloco moderna mais popular é a cifra Rijndael. Foi a vencedora entre quinze candidaturas a um concurso realizado pelo National Institute of Standards and Technology (NIST) entre 1997 e 2000, com o objetivo de substituir uma norma de encriptação mais antiga, a data encryption standard (DES).

A cifra Rijndael pode ser utilizada com diferentes especificações para comprimentos de chave e tamanhos de bloco, bem como em diferentes modos de funcionamento. O comité para o concurso do NIST adoptou uma versão restrita da cifra Rijndael - nomeadamente uma que requer tamanhos de bloco de 128 bits e comprimentos de chave de 128 bits, 192 bits ou 256 bits - como parte do advanced encryption standard (AES). Esta é realmente a norma principal para aplicações de encriptação simétrica. É tão seguro que até a NSA está aparentemente disposta a usá-lo com chaves de 256 bits para documentos ultra-secretos. [6]

A cifra de bloco AES será explicada em pormenor no Capítulo 5.

Notas:

[5] A importância da encriptação probabilística foi salientada pela primeira vez por Shafi Goldwasser e Silvio Micali, "Probabilistic encryption," Journal of Computer and System Sciences, 28 (1984), 270-99.

[6] Ver NSA, "Commercial National Security Algorithm Suite", https://apps.nsa.gov/iaarchive/programs/iad-initiatives/cnsa-suite.cfm.

Esclarecer a confusão

A confusão sobre a distinção entre cifras de bloco e cifras de fluxo surge porque, por vezes, as pessoas entendem o termo cifra de bloco como referindo-se especificamente a uma cifra de bloco com um modo de encriptação em bloco.

Considere os modos ECB e CBC na secção anterior. Estes modos requerem especificamente que os dados para encriptação sejam divisíveis pelo tamanho do bloco (o que significa que poderá ser necessário utilizar enchimento para a mensagem original). Além disso, os dados nestes modos são também operados diretamente pela cifra de bloco (e não apenas combinados com o resultado de uma operação de cifra de bloco como no modo OFB).

Assim, em alternativa, pode definir-se uma cifra de bloco como qualquer esquema de encriptação que opere em blocos de comprimento fixo da mensagem de cada vez (em que qualquer bloco tem de ser maior do que um byte, caso contrário transforma-se numa cifra de fluxo). Tanto os dados para encriptação como o texto cifrado devem dividir-se uniformemente neste tamanho de bloco. Normalmente, o tamanho do bloco é de 64, 128, 192 ou 256 bits de comprimento. Em contrapartida, uma cifra de fluxo pode encriptar quaisquer mensagens em blocos de um bit ou byte de cada vez.

Com este entendimento mais específico de cifra de bloco, é possível afirmar que os esquemas de encriptação modernos são cifras de fluxo ou de bloco. Daqui em diante, usarei o termo cifra de bloco no sentido mais geral, exceto quando especificado em contrário.

A discussão sobre o modo OFB na secção anterior também levanta outro ponto interessante. Algumas cifras de fluxo são criadas a partir de cifras de bloco, como o Rijndael com OFB. Algumas, como a Salsa20 e a ChaCha, não são criadas a partir de cifras de bloco. A estas últimas pode chamar-se cifras de fluxo primitivas. (Não existe um termo normalizado para designar estas cifras de fluxo)

Quando as pessoas falam das vantagens e desvantagens das cifras de fluxo e das cifras de bloco, estão normalmente a comparar cifras de fluxo primitivas com esquemas de encriptação baseados em cifras de bloco.

Embora seja sempre possível construir facilmente uma cifra de fluxo a partir de uma cifra de bloco, é normalmente muito difícil construir algum tipo de cifra com um modo de encriptação de bloco (como o modo CBC) a partir de uma cifra de fluxo primitiva.

A partir desta discussão, deve agora compreender a Figura 8. Esta fornece uma visão geral dos esquemas de encriptação simétrica. Utilizamos três tipos de esquemas de encriptação: cifras de fluxo primitivas, cifras de fluxo com cifra de bloco e cifras de bloco em modo de bloco (também chamadas "cifras de bloco" no diagrama).

Figura 8: Panorâmica dos sistemas de cifragem simétrica

Figure 8: Overview of symmetric encryption schemes

Códigos de autenticação de mensagens

A encriptação diz respeito ao segredo. Mas a criptografia também se preocupa com temas mais vastos, como a integridade da mensagem, a autenticidade e o não-repúdio. Os chamados códigos de autenticação de mensagens (MAC) são esquemas criptográficos de chave simétrica que suportam a autenticidade e a integridade das comunicações.

Por que razão é necessário qualquer coisa, exceto o sigilo, na comunicação? Suponhamos que Bob envia a Alice uma mensagem utilizando uma encriptação praticamente inquebrável. Qualquer atacante que intercepte esta mensagem não será capaz de obter qualquer informação significativa sobre o seu conteúdo. No entanto, o atacante tem ainda à sua disposição pelo menos dois outros vectores de ataque:

  1. Ela poderia intercetar o texto cifrado, alterar o seu conteúdo e enviar o texto cifrado alterado para Alice.

  2. Ela poderia bloquear completamente a mensagem de Bob e enviar o seu próprio texto cifrado criado.

Em ambos os casos, o atacante pode não ter qualquer conhecimento do conteúdo dos textos cifrados (1) e (2). Mas, mesmo assim, poderia causar danos significativos desta forma. É aqui que os códigos de autenticação de mensagens se tornam importantes.

Os códigos de autenticação de mensagens são definidos livremente como esquemas criptográficos simétricos com três algoritmos: um algoritmo de geração de chaves, um algoritmo de geração de etiquetas e um algoritmo de verificação. Um MAC seguro garante que as etiquetas são existencialmente não falsificáveis para qualquer atacante - ou seja, não podem criar com sucesso uma etiqueta na mensagem que verifica, a menos que tenham a chave privada.

Bob e Alice podem combater a manipulação de uma determinada mensagem utilizando um MAC. Suponhamos que, de momento, não se preocupam com o secretismo. Apenas querem garantir que a mensagem recebida por Alice é efetivamente de Bob e não foi alterada de forma alguma.

O processo é ilustrado na Figura 9. Para utilizar um MAC (Message Authentication Code - Código de Autenticação de Mensagens), primeiro geram uma chave privada K que é partilhada entre os dois. Bob cria uma etiqueta T para a mensagem utilizando a chave privada K. De seguida, envia a mensagem e a etiqueta da mensagem à Alice. Esta pode então verificar que Bob criou efetivamente a etiqueta, passando a chave privada, a mensagem e a etiqueta por um algoritmo de verificação.

Figura 9: Panorâmica dos sistemas de cifragem simétrica

Figure 9: Overview of symmetric encryption schemes

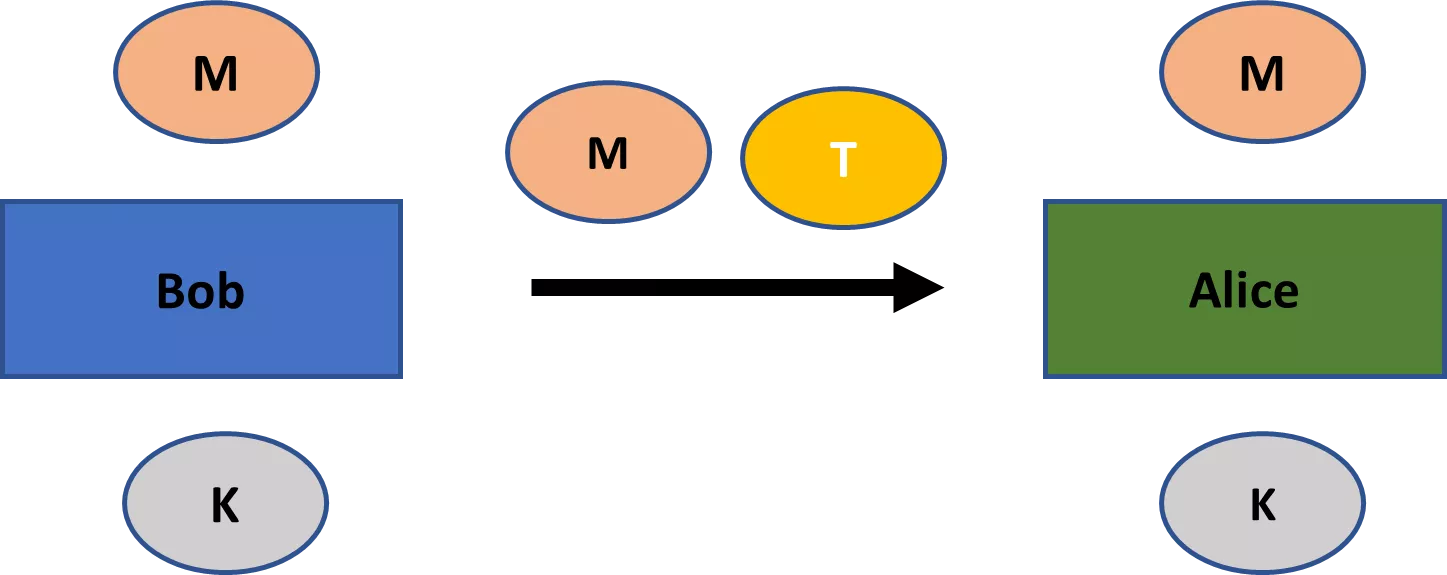
Devido à infalibilidade existencial, um atacante não pode alterar a mensagem M de forma alguma ou criar uma mensagem própria com uma etiqueta válida. Isto é assim, mesmo que o atacante observe as etiquetas de muitas mensagens entre Bob e Alice que usam a mesma chave privada. No máximo, um atacante poderia impedir Alice de receber a mensagem M (um problema que a criptografia não pode resolver).

Um MAC garante que uma mensagem foi efetivamente criada por Bob. Esta autenticidade implica automaticamente a integridade da mensagem - ou seja, se Bob criou uma mensagem, então, ipso facto, ela não foi alterada de forma alguma por um atacante. Assim, daqui em diante, qualquer preocupação com a autenticação deve ser automaticamente entendida como implicando uma preocupação com a integridade.

Embora eu tenha feito uma distinção entre autenticidade e integridade da mensagem na minha discussão, também é comum utilizar estes termos como sinónimos. Referem-se, portanto, à ideia de mensagens que foram criadas por um determinado remetente e que não foram alteradas de forma alguma. Neste espírito, os códigos de autenticação de mensagens são também frequentemente designados por códigos de integridade de mensagens.

Encriptação autenticada

Normalmente, pretende-se garantir tanto o sigilo como a autenticidade da comunicação, pelo que os sistemas de cifragem e os sistemas MAC são normalmente utilizados em conjunto.

Um esquema de encriptação autenticado é um esquema que combina a encriptação com um MAC de uma forma altamente segura. Especificamente, tem de cumprir as normas de não falsificabilidade existencial, bem como uma noção muito forte de sigilo, nomeadamente uma que seja resistente a ataques de texto cifrado escolhido. [7]

Para que um esquema de cifragem seja resistente a ataques de escolha de texto cifrado, tem de cumprir as normas de não maleabilidade: ou seja, qualquer modificação de um texto cifrado por um atacante deve produzir um texto cifrado inválido ou um texto que decifre para um texto simples sem qualquer relação com o original. [8]

Como um esquema de encriptação autenticado garante que um texto cifrado criado por um atacante é sempre inválido (uma vez que a etiqueta não será verificada), cumpre as normas de resistência a ataques de texto cifrado escolhido. Curiosamente, é possível provar que um esquema de encriptação autenticado pode sempre ser criado a partir da combinação de um MAC existencialmente não-codificável e de um esquema de encriptação que satisfaça uma noção menos forte de segurança, conhecida como segurança de ataque de texto escolhido.

Não vamos entrar em todos os pormenores da construção de esquemas de encriptação autenticados. Mas é importante conhecer dois pormenores da sua construção.

Em primeiro lugar, um esquema de encriptação autenticado trata primeiro da encriptação e depois cria uma etiqueta de mensagem no texto cifrado. Acontece que outras abordagens - como combinar o texto cifrado com uma etiqueta no texto simples, ou criar primeiro uma etiqueta e depois encriptar tanto o texto simples como a etiqueta - são inseguras. Além disso, ambas as operações têm a sua própria chave privada selecionada aleatoriamente, caso contrário a sua segurança fica gravemente comprometida.

O princípio acima mencionado aplica-se de forma mais geral: deve utilizar sempre chaves distintas ao combinar esquemas criptográficos básicos.

Um esquema de encriptação autenticada é representado na Figura 10. Bob cria primeiro um texto cifrado C a partir da mensagem M utilizando uma chave selecionada aleatoriamente K_C. Em seguida, cria uma etiqueta de mensagem T executando o texto cifrado e uma chave diferente selecionada aleatoriamente K_T através do algoritmo de geração de etiquetas. Tanto o texto cifrado como a etiqueta da mensagem são enviados para a Alice.

A Alice começa por verificar se a etiqueta é válida, tendo em conta o texto cifrado C e a chave K_T. Se for válida, ela pode então desencriptar a mensagem utilizando a chave K_C. Não só lhe é garantida uma noção muito forte de sigilo nas suas comunicações, como também sabe que a mensagem foi criada pelo Bob.

Figura 10: Um sistema de cifragem autenticado

Figure 10: An authenticated encryption scheme

Como são criados os MACs? Embora os MACs possam ser criados através de vários métodos, uma forma comum e eficiente de os criar é através de funções hash criptográficas.

Iremos introduzir as funções hash criptográficas mais detalhadamente no Capítulo 6. Por enquanto, basta saber que uma função hash é uma função computável de forma eficiente que recebe entradas de tamanho arbitrário e produz saídas de comprimento fixo. Por exemplo, a popular função de hash SHA-256 (algoritmo de hash seguro 256) sempre gera uma saída de 256 bits, independentemente do tamanho da entrada. Algumas funções de hash, como o SHA-256, têm aplicações úteis em criptografia.

O tipo mais comum de etiqueta produzida com uma função de hash criptográfico é o código de autenticação de mensagem baseado em hash (HMAC). O processo está representado na Figura 11. Uma parte produz duas chaves distintas a partir de uma chave privada K, a chave interna K_1 e a chave externa K_2. O texto simples M ou o texto cifrado C é então submetido a hash juntamente com a chave interna. O resultado T' é então misturado com a chave externa para produzir a etiqueta de mensagem T.

Existe uma paleta de funções de hash que podem ser utilizadas para criar um HMAC. A função de hash mais comummente utilizada é a SHA-256.

Figura 11: HMAC

Figure 11: HMAC

Notas:

[7] Os resultados específicos discutidos nesta secção são retirados de Katz e Lindell, pp. 131-47.

[8] Tecnicamente, a definição de ataques de texto cifrado escolhido é diferente da noção de não maleabilidade. Mas é possível mostrar que estas duas noções de segurança são equivalentes.

Sessões de comunicação seguras

Suponha que duas partes estão numa sessão de comunicação, pelo que enviam várias mensagens para trás e para a frente.

Um esquema de encriptação autenticado permite a um destinatário de uma mensagem verificar que esta foi criada pelo seu parceiro na sessão de comunicação (desde que a chave privada não tenha sido divulgada). Isto funciona suficientemente bem para uma única mensagem. No entanto, normalmente, duas partes estão a enviar mensagens para trás e para a frente numa sessão de comunicação. Nesse caso, um esquema de encriptação autenticada simples, como o descrito na secção anterior, não oferece segurança suficiente.

A principal razão é que um esquema de encriptação autenticado não oferece quaisquer garantias de que a mensagem também foi efetivamente enviada pelo agente que a criou numa sessão de comunicação. Considere os três vectores de ataque seguintes:

  1. Ataque de repetição: Um atacante reenvia um texto cifrado e uma etiqueta que interceptou entre duas partes num momento anterior.

  2. Ataque de reordenação: Um atacante intercepta duas mensagens em momentos diferentes e envia-as para o destinatário pela ordem inversa.

  3. Ataque de reflexão: Um atacante observa uma mensagem enviada de A para B e também envia essa mensagem para A.

Embora o atacante não tenha conhecimento do texto cifrado e não possa criar textos cifrados falsos, os ataques acima referidos podem ainda assim causar danos significativos nas comunicações.

Suponhamos, por exemplo, que uma determinada mensagem entre as duas partes envolve a transferência de fundos financeiros. Um ataque de repetição pode transferir os fundos uma segunda vez. Um esquema de encriptação autenticado simples não tem defesa contra esses ataques.

Felizmente, este tipo de ataques pode ser facilmente mitigado numa sessão de comunicação utilizando identificadores e indicadores de tempo relativo.

Os identificadores podem ser adicionados à mensagem de texto simples antes da encriptação. Isto impediria qualquer ataque de reflexão. Um indicador de tempo relativo pode, por exemplo, ser um número de sequência numa determinada sessão de comunicação. Cada parte acrescenta um número de sequência a uma mensagem antes da cifragem, para que o destinatário saiba por que ordem as mensagens foram enviadas. Isto elimina a possibilidade de ataques de reordenação. Também elimina os ataques de repetição. Qualquer mensagem que um atacante envie ao longo da linha terá um número de sequência antigo, e o destinatário saberá que não deve processar a mensagem novamente.

Para ilustrar o funcionamento das sessões de comunicação segura, suponhamos novamente Alice e Bob. Enviam um total de quatro mensagens para trás e para a frente. Pode ver como funcionaria um esquema de encriptação autenticado com identificadores e números de sequência na Figura 11.

A sessão de comunicação começa com o Bob a enviar um texto cifrado C_{0,B} para a Alice com uma etiqueta de mensagem T_{0,B}. O texto cifrado contém a mensagem, bem como um identificador (BOB) e um número de sequência (0). A etiqueta T_{0,B} é feita sobre todo o texto cifrado. Nas suas comunicações subsequentes, Alice e Bob mantêm este protocolo, actualizando os campos conforme necessário.

Figura 12: Uma sessão de comunicação segura

Figure 12: A secure communication session

RC4 e AES

A cifra de fluxo RC4

Neste capítulo, discutiremos os detalhes de um esquema de criptografia com uma cifra de fluxo primitiva moderna, RC4 (ou "Rivest cipher 4"), e uma cifra de bloco moderna, AES. Embora a cifra RC4 tenha caído em desuso como método de encriptação, o AES é o padrão para a encriptação simétrica moderna. Estes dois exemplos devem dar uma ideia melhor de como a encriptação simétrica funciona por baixo do capô.

Para ter uma noção de como funcionam as cifras de fluxo pseudo-aleatórias modernas, vou concentrar-me na cifra de fluxo RC4. Trata-se de uma cifra de fluxo pseudo-aleatória que foi utilizada nos protocolos de segurança de pontos de acesso sem fios WEP e WAP, bem como no TLS. Como o RC4 tem muitas fraquezas comprovadas, caiu em desgraça. De facto, a Internet Engineering Task Force proíbe agora a utilização de suites RC4 por aplicações cliente e servidor em todas as instâncias do TLS. No entanto, funciona bem como um exemplo para ilustrar como funciona uma cifra de fluxo primitiva.

Para começar, vou mostrar como encriptar uma mensagem de texto simples com uma cifra RC4 para bebés. Suponhamos que a nossa mensagem de texto simples é "SOUP" A encriptação com a nossa cifra RC4 para bebés processa-se, então, em quatro passos.

Passo 1

Primeiro, defina uma matriz S com S[0] = 0 a S[7] = 7. Um array aqui significa simplesmente uma coleção mutável de valores organizada por um índice, também chamada de lista em algumas linguagens de programação (por exemplo, Python). Neste caso, o índice vai de 0 a 7, e os valores também vão de 0 a 7. Então S é o seguinte:

Os valores aqui não são números ASCII, mas as representações de valores decimais de cadeias de 1 byte. Assim, o valor 2 seria igual a 0000 \ 0011. O comprimento da matriz S é, portanto, 8 bytes.

Passo 2

Em segundo lugar, defina um conjunto de chaves K de 8 bytes de comprimento, escolhendo uma chave entre 1 e 8 bytes (não são permitidas fracções de bytes). Como cada byte tem 8 bits, pode selecionar qualquer número entre 0 e 255 para cada byte da sua chave.

Suponhamos que escolhemos a nossa chave k como [14, 48, 9], de modo a que tenha um comprimento de 3 bytes. Cada índice da nossa matriz de chaves é, então, definido de acordo com o valor decimal para esse elemento específico da chave, por ordem. Se percorrermos toda a chave, recomeçamos do início, até preenchermos as 8 posições do conjunto de chaves. Assim, o nosso conjunto de chaves é o seguinte:

Passo 3

Em terceiro lugar, vamos transformar a matriz S utilizando a matriz de chaves K, num processo conhecido como programação de chaves. O processo é o seguinte em pseudocódigo:

A transformação da matriz S é captada pelo Quadro 1.

Para começar, pode ver o estado inicial de S como [0, 1, 2, 3, 4, 5, 6, 7] com um valor inicial de 0 para j. Isto será transformado utilizando o conjunto de chaves [14, 48, 9, 14, 48, 9, 14, 48].

O ciclo for começa com i = 0. De acordo com o nosso pseudocódigo acima, o novo valor de j torna-se 6 (j = (j + S[0] + K[0]) \mod 8 = (0 + 0 + 14) \mod 8 = 6 \mod 8). Trocando S[0] e S[6], o estado de S após 1 ronda passa a ser [6, 1, 2, 3, 4, 5, 0, 7].

Na linha seguinte, i = 1. Passando novamente pelo laço for, j obtém um valor de 7 (j = (j + S[1] + K[1]) \mod 8 = (6 + 1 + 48) \mod 8 = 55 \mod 8 = 7 \mod 8). Trocando S[1] e S[7] do estado atual de S, [6, 1, 2, 3, 4, 5, 0, 7], obtém-se [6, 7, 2, 3, 4, 5, 0, 1] após a ronda 2.

Continuamos com este processo até produzirmos a linha final na parte inferior da matriz S, [6, 4, 1, 0, 3, 7, 5, 2].

Quadro 1: Quadro de programação de chaves

RoundijS[0]S[1]S[2]S[3]S[4]S[5]S[6]S[7]
Initial001234567
10661234507
21767234501
32267234501
43367234501
54367203541
65664203751
76164203752
87264103752

Passo 4

Como quarto passo, produzimos o keystream. Esta é a string pseudo-aleatória de comprimento igual à mensagem que queremos enviar. Esta será usada para encriptar a mensagem original "SOUP" Como a keystream precisa de ser tão longa como a mensagem, precisamos de uma que tenha 4 bytes.

O keystream é produzido pelo seguinte pseudocódigo:

Pode seguir os cálculos no Quadro 2.

O estado inicial de S é S = [6, 4, 1, 0, 3, 7, 5, 2]. Definindo i = 1, o valor de j torna-se 4 (j = (j + S[i]) \mod 8 = (0 + 4) \mod 8 = 4). Trocamos então S[1] e S[4] para produzir a transformação de S na segunda linha, [6, 3, 1, 0, 4, 7, 5, 2]. O valor de t é então 7 (t = (S[i] + S[j]) \mod 8 = (3 + 4) \mod 8 = 7). Finalmente, o byte para o keystream é S[7], ou 2.

Depois continuamos a produzir os outros bytes até termos os seguintes quatro bytes: 2, 6, 3 e 7. Cada um destes bytes pode então ser usado para encriptar cada letra do texto simples, "SOUP".

Para começar, usando uma tabela ASCII, podemos ver que "SOUP" codificado pelos valores decimais das cadeias de bytes subjacentes é "83 79 85 80". A combinação com o fluxo de chaves "2 6 3 7" produz "85 85 88 87", que permanece o mesmo após uma operação de módulo 256. Em ASCII, o texto cifrado "85 85 88 87" é igual a "UUXW".

O que aconteceria se a palavra a encriptar fosse maior do que a matriz S? Nesse caso, o array S continua a transformar-se da forma apresentada acima para cada byte i do texto simples, até termos um número de bytes no keystream igual ao número de letras do texto simples.

Quadro 2: Geração de fluxos principais

ijtKeystreamS[0]S[1]S[2]S[3]S[4]S[5]S[6]S[7]
064103752
147263104752
250663704152
351363714052
417264713052

O exemplo que acabámos de discutir é apenas uma versão diluída do RC4 stream cipher. A verdadeira cifra de fluxo RC4 tem uma matriz S de 256 bytes de comprimento, não 8 bytes, e uma chave que pode ter entre 1 e 256 bytes, não entre 1 e 8 bytes. O array de chaves e os keystreams são então todos produzidos considerando o comprimento de 256 bytes do array S. Os cálculos tornam-se imensamente mais complexos, mas os princípios permanecem os mesmos. Usando a mesma chave, 14,48,9, com a cifra RC4 padrão, a mensagem de texto simples "SOUP" é encriptada como 67 02 ed df em formato hexadecimal.

Uma cifra de fluxo em que o fluxo de chaves é atualizado independentemente da mensagem de texto simples ou do texto cifrado é uma cifra de fluxo síncrona. O keystream depende apenas da chave. Claramente, o RC4 é um exemplo de uma cifra de fluxo síncrono, uma vez que o fluxo de chaves não tem qualquer relação com o texto simples ou o texto cifrado. Todas as nossas cifras de fluxo primitivas mencionadas no capítulo anterior, incluindo a cifra de deslocamento, a cifra de Vigenère e o bloco de tempo único, eram também da variedade síncrona.

Em contrapartida, uma cifra de fluxo assíncrono tem um fluxo de chaves que é produzido tanto pela chave como pelos elementos anteriores do texto cifrado. Este tipo de cifra é também designado por cifra auto-sincronizadora.

É importante notar que o fluxo de chaves produzido com RC4 deve ser tratado como um bloco de tempo único, e não é possível produzir o fluxo de chaves exatamente da mesma forma na próxima vez. Em vez de alterar a chave de cada vez, a solução prática é combinar a chave com um nonce para produzir o bytestream.

AES com uma chave de 128 bits

Como mencionado no capítulo anterior, o National Institute of Standards and Technology (NIST) organizou um concurso entre 1997 e 2000 para determinar uma nova norma de encriptação simétrica. A cifra Rijndael acabou por ser a vencedora. O nome é um jogo de palavras com os nomes dos criadores belgas, Vincent Rijmen e Joan Daemen.

A cifra Rijndael é uma cifra de bloco, o que significa que existe um algoritmo central, que pode ser utilizado com diferentes especificações para comprimentos de chave e tamanhos de bloco. Pode, então, utilizá-lo com diferentes modos de operação para construir esquemas de encriptação.

O comité para o concurso do NIST adoptou uma versão restrita da cifra Rijndael - nomeadamente uma que requer tamanhos de bloco de 128 bits e comprimentos de chave de 128 bits, 192 bits ou 256 bits - como parte do Advanced Encryption Standard (AES). Esta versão restrita da cifra Rijndael também pode ser utilizada em vários modos de funcionamento. A especificação da norma é conhecida como Advanced Encryption Standard (AES).

Para mostrar como funciona a cifra Rijndael, o núcleo do AES, vou ilustrar o processo de encriptação com uma chave de 128 bits. O tamanho da chave tem um impacto no número de rondas realizadas para cada bloco de encriptação. Para chaves de 128 bits, são necessárias 10 rondas. Com 192 bits e 256 bits, seriam necessárias 12 e 14 rondas, respetivamente.

Para além disso, assumirei que o AES é utilizado no modo ECB. Isto torna a exposição ligeiramente mais fácil e não tem importância para o algoritmo Rijndael. É certo que o modo ECB não é seguro na prática porque conduz a uma encriptação determinística. O modo de segurança mais comummente utilizado com o AES é o CBC (Cipher Block Chaining).

Chamemos à chave K_0. A construção com os parâmetros acima referidos tem então o aspeto da Figura 1, em que M_i representa uma parte da mensagem de texto simples de 128 bits e C_i uma parte do texto cifrado de 128 bits. O preenchimento é adicionado ao texto simples para o último bloco, se o texto simples não puder ser dividido uniformemente pelo tamanho do bloco.

Figura 1: AES-ECB com uma chave de 128 bits

Figure 1: AES-ECB with a 128-bit key

Cada bloco de texto de 128 bits passa por dez rondas no esquema de encriptação Rijndael. Isto requer uma chave de ronda separada para cada ronda (K_1 até K_{10}). Estas são produzidas para cada ronda a partir da chave original de 128 bits K_0 utilizando um algoritmo de expansão de chaves. Assim, para cada bloco de texto a ser encriptado, usaremos a chave original K_0 assim como dez chaves de ronda separadas. Note-se que estas mesmas 11 chaves são utilizadas para cada bloco de 128 bits de texto simples que requer encriptação.

O algoritmo de expansão de chaves é longo e complexo. Trabalhar com ele não tem grande utilidade didática. Se desejar, pode analisar o algoritmo de expansão de chaves por si próprio. Uma vez produzidas as chaves redondas, a cifra Rijndael manipulará o primeiro bloco de 128 bits de texto simples, M_1, como se vê na Figura 2. Vamos agora percorrer estes passos.

Figura 2: A manipulação de M_1 com a cifra Rijndael:

Ronda 0:

Ronda n para n = {1,...,9}:

Ronda 10:

Ronda 0

A ronda 0 da cifra Rijndael é simples. Uma matriz S_0 é produzida por uma operação XOR entre o texto simples de 128 bits e a chave privada. Ou seja,

Primeira ronda

Na ronda 1, a matriz S_0 é primeiro combinada com a chave da ronda K_1 utilizando uma operação XOR. Isto produz um novo estado de S.

Segundo, a operação de substituição de bytes é executada no estado atual de S. Funciona pegando em cada byte do array de 16 bytes S e substituindo-o por um byte de um array chamado Rijndael's S-box. Cada byte tem uma transformação única, e um novo estado de S é produzido como resultado. A S-box de Rijndael é apresentada na Figura 3.

Figura 3: S-Box do Rijndael

000102030405060708090A0B0C0D0E0F
00637C777BF26B6FC53001672BFED7AB76
10CA82C97DFA5947F0ADD4A2AF9CA472C0
20B7FD9326363FF7CC34A5E5F171D83115
3004C723C31896059A071280E2EB27B275
4009832C1A1B6E5AA0523BD6B329E32F84
5053D100ED20FCB15B6ACBBE394A4C58CF
60D0EFAAFB434D338545F9027F503C9FA8
7051A3408F929D38F5BCB6DA2110FFF3D2
80CD0C13EC5F974417C4A77E3D645D1973
9060814FDC222A908846EEB814DE5E0BDB
A0E0323A0A4906245CC2D3AC629195E479
B0E7C8376D8DD54EA96C56F4EA657AAE08
C0BA78252E1CA6B4C6E8DD741F4BBD8B8A
D0703EB5664803F60E613557B986C11D9E
E0E1F8981169D98E949B1E87E9CE5528DF
F08CA1890DBFE6426841992D0FB054BB16

Esta S-Box é um dos locais onde a álgebra abstrata entra em jogo na cifra Rijndael, especificamente os campos de Galois.

Para começar, define-se cada elemento de byte possível de 00 a FF como um vetor de 8 bits. Cada um desses vectores é um elemento do campo de Galois GF(2^8) onde o polinómio irredutível para a operação de módulo é x^8 + x^4 + x^3 + x + 1. O campo de Galois com estas especificações é também chamado Campo Finito de Rijndael.

Em seguida, para cada elemento possível no campo, criamos o que é chamado de Nyberg S-Box. Nesta caixa, cada byte é mapeado para o seu inverso multiplicativo (ou seja, para que o seu produto seja igual a 1). Em seguida, mapeamos esses valores da caixa S de Nyberg para a caixa S de Rijndael usando a transformação afim.

A terceira operação na matriz S é a operação shift rows. Esta pega no estado de S e lista todos os dezasseis bytes numa matriz. O preenchimento da matriz começa no canto superior esquerdo e segue o seu caminho indo de cima para baixo e, de cada vez que uma coluna é preenchida, desloca uma coluna para a direita e para cima.

Uma vez construída a matriz de S, as quatro linhas são deslocadas. A primeira linha permanece a mesma. A segunda linha desloca-se uma para a esquerda. A terceira move duas para a esquerda. A quarta desloca três para a esquerda. Um exemplo do processo é apresentado na Figura 4. O estado original de S é mostrado na parte superior e o estado resultante após a operação de deslocação de linhas é mostrado por baixo.

Figura 4: Operação de deslocação de linhas

F1A0B123
59EF0982
9701B0CC
D4720421
F1A0B123
EF098259
B0CC9701
21D47204

No quarto passo, os campos de Galois voltam a aparecer. Para começar, cada coluna da matriz S é multiplicada pela coluna da matriz 4 x 4 vista na Figura 5. Mas em vez de ser uma multiplicação matricial normal, é uma multiplicação vetorial módulo de um polinómio irredutível, x^8 + x^4 + x^3 + x + 1. Os coeficientes do vetor resultante representam os bits individuais de um byte.

Figura 5: Matriz de colunas mistas

02030101
01020301
01010203
03010102

A multiplicação da primeira coluna da matriz S com a matriz 4 x 4 acima produz o resultado na Figura 6.

Figura 6: Multiplicação da primeira coluna:

\begin{matrix}
02 \cdot F1 + 03 \cdot EF + 01 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 02 \cdot EF + 03 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 01 \cdot EF + 02 \cdot B0 + 03 \cdot 21 \\
03 \cdot F1 + 01 \cdot EF + 01 \cdot B0 + 02 \cdot 21
\end{matrix}

Como passo seguinte, todos os termos da matriz teriam de ser transformados em polinómios. Por exemplo, F1 representa 1 byte e tornar-se-ia x^7 + x^6 + x^5 + x^4 + 1, e 03 representa 1 byte e tornar-se-ia x + 1.

Todas as multiplicações são então efectuadas módulo x^8 + x^4 + x^3 + x + 1. Isto resulta na adição de quatro polinómios em cada uma das quatro células da coluna. Depois de efetuar essas adições módulo 2, obtém-se quatro polinómios. Cada um destes polinómios representa uma cadeia de 8 bits, ou 1 byte, de S. Não vamos efetuar todos estes cálculos aqui na matriz da Figura 6 porque são extensos.

Quando a primeira coluna tiver sido processada, as outras três colunas da matriz S são processadas da mesma forma. Eventualmente, isto produzirá uma matriz com dezasseis bytes que pode ser transformada numa matriz.

Como passo final, a matriz S é novamente combinada com a chave de ronda numa operação XOR. Isto produz o estado S_1. Ou seja,

Rodadas 2 a 10

As rondas 2 a 9 são apenas uma repetição da ronda 1, mutatis mutandis. A ronda final é muito semelhante às rondas anteriores, exceto que o passo misturar colunas é eliminado. Ou seja, a ronda 10 é executada da seguinte forma:

O estado S_{10} está agora definido para C_1, os primeiros 128 bits do texto cifrado. Prosseguindo através dos restantes blocos de texto simples de 128 bits obtém-se o texto cifrado completo C.

As operações da cifra Rijndael

Qual é o raciocínio subjacente às diferentes operações observadas na cifra Rijndael?

Sem entrar em pormenores, os esquemas de cifragem são avaliados com base na medida em que criam confusão e difusão. Se o esquema de cifragem tiver um elevado grau de confusão, isso significa que o texto cifrado tem um aspeto drasticamente diferente do texto simples. Se o esquema de cifragem tiver um elevado grau de difusão, significa que qualquer pequena alteração ao texto simples produz um texto cifrado drasticamente diferente.

O raciocínio para as operações subjacentes à cifra Rijndael é o facto de produzirem um elevado grau de confusão e difusão. A confusão é produzida pela operação de substituição de bytes, enquanto a difusão é produzida pelas operações de deslocação de linhas e mistura de colunas.

Criptografia assimétrica

O problema da distribuição e gestão de chaves

Tal como na criptografia simétrica, os esquemas assimétricos podem ser utilizados para garantir tanto o secretismo como a autenticação. No entanto, em contrapartida, estes esquemas utilizam duas chaves em vez de uma: uma chave privada e uma chave pública.

Começamos a nossa investigação com a descoberta da criptografia assimétrica, em particular os problemas que a estimularam. Em seguida, discutimos como funcionam os esquemas assimétricos de encriptação e autenticação a um nível elevado. Introduzimos então as funções de hash, que são fundamentais para compreender os esquemas de autenticação assimétricos e que também têm relevância noutros contextos criptográficos, como no caso dos códigos de autenticação de mensagens baseados em hash que discutimos no Capítulo 4.

Suponha que o Bob quer comprar um novo impermeável na Jim's Sporting Goods, um retalhista de artigos desportivos em linha com milhões de clientes na América do Norte. Esta será a sua primeira compra e ele quer utilizar o seu cartão de crédito. Assim, o Bob terá primeiro de criar uma conta na Jim's Sporting Goods, o que requer o envio de dados pessoais, como a morada e a informação do cartão de crédito. Em seguida, ele pode seguir os passos necessários para comprar a capa de chuva.

O Bob e a Jim's Sporting Goods vão querer garantir que as suas comunicações são seguras durante todo este processo, considerando que a Internet é um sistema de comunicações aberto. Por exemplo, devem assegurar-se de que nenhum potencial atacante pode obter os dados do cartão de crédito e da morada do Bob e que nenhum potencial atacante pode repetir as suas compras ou criar compras falsas em seu nome.

Um esquema avançado de encriptação autenticada, como discutido no capítulo anterior, poderia certamente tornar seguras as comunicações entre o Bob e a Jim's Sporting Goods. Mas há claramente obstáculos práticos à implementação desse esquema.

Para ilustrar estes obstáculos práticos, suponhamos que vivíamos num mundo em que apenas existiam as ferramentas da criptografia simétrica. O que é que a Jim's Sporting Goods e o Bob poderiam então fazer para garantir uma comunicação segura?

Nessas circunstâncias, teriam de suportar custos substanciais para comunicar de forma segura. Como a Internet é um sistema de comunicações aberto, não podem simplesmente trocar um conjunto de chaves através dela. Assim, o Bob e um representante da Jim's Sporting Goods terão de efetuar uma troca de chaves pessoalmente.

Uma possibilidade é que a Jim's Sporting Goods crie locais especiais de troca de chaves, onde Bob e outros novos clientes possam obter um conjunto de chaves para comunicação segura. Obviamente, isto implicaria custos organizacionais substanciais e reduziria muito a eficiência com que os novos clientes podem efetuar compras.

Em alternativa, a Jim's Sporting Goods pode enviar ao Bob um par de chaves através de um estafeta de elevada confiança. Isto é provavelmente mais eficiente do que organizar locais de troca de chaves. No entanto, isto teria custos substanciais, especialmente se muitos clientes fizerem apenas uma ou poucas compras.

Em seguida, um esquema simétrico para encriptação autenticada também obriga a Jim's Sporting Goods a armazenar conjuntos separados de chaves para todos os seus clientes. Este seria um desafio prático significativo para milhares de clientes, quanto mais para milhões.

Para compreender este último ponto, suponhamos que a Jim's Sporting Goods fornece a cada cliente o mesmo par de chaves. Isto permitiria a cada cliente - ou a qualquer outra pessoa que pudesse obter este par de chaves - ler e até manipular todas as comunicações entre a Jim's Sporting Goods e os seus clientes. Assim, mais valia não utilizar criptografia nas suas comunicações.

Mesmo a repetição de um conjunto de chaves apenas para alguns clientes é uma prática de segurança terrível. Qualquer potencial atacante poderia tentar explorar essa caraterística do esquema (lembre-se que se assume que os atacantes sabem tudo sobre um esquema exceto as chaves, de acordo com o princípio de Kerckhoffs)

Assim, a Jim's Sporting Goods teria de armazenar um par de chaves para cada cliente, independentemente da forma como esses pares de chaves são distribuídos. Isto apresenta claramente vários problemas práticos.

Estes dois desafios principais que acabámos de descrever eram preocupações muito fundamentais até ao final da década de 1970. Eram conhecidos como o problema da distribuição de chaves e o problema da gestão de chaves, respetivamente.

Estes problemas sempre existiram, é claro, e muitas vezes criaram dores de cabeça no passado. As forças militares, por exemplo, tinham de distribuir constantemente livros com chaves para comunicações seguras ao pessoal no terreno, com grandes riscos e custos. Mas estes problemas estavam a agravar-se à medida que o mundo se transformava cada vez mais num mundo de comunicações digitais a longa distância, sobretudo para as entidades não governamentais.

Se estes problemas não tivessem sido resolvidos na década de 1970, as compras eficientes e seguras na Jim's Sporting Goods não teriam provavelmente existido. De facto, a maior parte do nosso mundo moderno, com correio eletrónico prático e seguro, serviços bancários em linha e compras, seria provavelmente apenas uma fantasia distante. Qualquer coisa que se assemelhasse ao Bitcoin poderia nem sequer ter existido.

O que é que aconteceu nos anos 70? Como é que é possível fazermos compras online instantaneamente e navegarmos em segurança na World Wide Web? Como é possível que possamos enviar instantaneamente Bitcoins para todo o mundo a partir dos nossos smartphones?

Novas direcções na criptografia

Na década de 1970, os problemas de distribuição e gestão de chaves tinham atraído a atenção de um grupo de criptógrafos académicos americanos: Whitfield Diffie, Martin Hellman e Ralph Merkle. Perante o grande ceticismo da maioria dos seus pares, aventuraram-se a conceber uma solução para o problema.

Pelo menos uma das principais motivações para o seu empreendimento foi a previsão de que as comunicações abertas por computador iriam afetar profundamente o nosso mundo. Como referem Diffie e Helmann em 1976,

O desenvolvimento de redes de comunicação controladas por computador promete um contacto sem esforço e pouco dispendioso entre pessoas ou computadores em lados opostos do mundo, substituindo a maior parte do correio e muitas excursões por telecomunicações. Para muitas aplicações, estes contactos devem ser seguros, tanto contra a escuta como contra a injeção de mensagens ilegítimas. Atualmente, porém, a solução dos problemas de segurança está muito atrasada em relação a outros domínios da tecnologia das comunicações. A criptografia contemporânea não é capaz de satisfazer os requisitos, na medida em que a sua utilização imporia inconvenientes tão graves aos utilizadores do sistema que eliminaria muitos dos benefícios do teleprocessamento. [1]

A tenacidade de Diffie, Hellman e Merkle deu frutos. A primeira publicação dos seus resultados foi um artigo de Diffie e Helmann em 1976 intitulado "New Diretions in Cryptography" Nele, apresentaram duas formas originais de resolver os problemas de distribuição de chaves e de gestão de chaves.

A primeira solução que propuseram foi um protocolo de troca de chaves remoto, ou seja, um conjunto de regras para a troca de uma ou mais chaves simétricas através de um canal de comunicação inseguro. Este protocolo é atualmente conhecido como Diffie-Helmann key exchange ou Diffie-Helmann-Merkle key exchange. [2]

Com a troca de chaves Diffie-Helmann, duas partes começam por trocar algumas informações publicamente num canal inseguro, como a Internet. Com base nessa informação, criam de seguida, de forma independente, uma chave simétrica (ou um par de chaves simétricas) para uma comunicação segura. Embora ambas as partes criem as suas chaves de forma independente, a informação que partilharam publicamente garante que este processo de criação de chaves produz o mesmo resultado para ambas.

É importante notar que, embora toda a gente possa observar a informação trocada publicamente pelas partes através do canal inseguro, apenas as duas partes envolvidas na troca de informação podem criar chaves simétricas a partir dessa informação.

Isto, claro, parece completamente contra-intuitivo. Como é que duas partes poderiam trocar informações publicamente que só elas poderiam criar chaves simétricas a partir delas? Porque é que qualquer outra pessoa que observasse a troca de informações não seria capaz de criar as mesmas chaves?

É claro que se baseia numa bela matemática. A troca de chaves Diffie-Helmann funciona através de uma função unidirecional com um alçapão. Vamos discutir o significado destes dois termos de cada vez.

Suponha que lhe é dada uma função f(x) e o resultado f(a) = y, onde a é um valor particular para x. Dizemos que f(x) é uma função unidirecional se é fácil calcular o valor y quando são dados a e f(x), mas é computacionalmente inviável calcular o valor a quando são dados y e f(x). O nome função unidirecional deriva, naturalmente, do facto de uma função deste tipo só poder ser calculada num sentido.

Algumas funções unidireccionais têm aquilo a que se chama um trapdoor. Embora seja praticamente impossível calcular a dado apenas y e f(x), existe uma certa informação Z que torna o cálculo de a a partir de y computacionalmente viável. Este pedaço de informação Z é conhecido como trapdoor. As funções unidireccionais que têm uma porta de armadilha são conhecidas como funções de porta de armadilha.

Não entraremos aqui nos pormenores da troca de chaves Diffie-Helmann. Mas, essencialmente, cada participante cria alguma informação, da qual uma parte é partilhada publicamente e outra permanece secreta. Cada parte, então, pega na sua parte secreta da informação e na informação pública partilhada pela outra parte para criar uma chave privada. E, de forma algo miraculosa, ambas as partes acabam por ter a mesma chave privada.

Qualquer parte que observe apenas a informação partilhada publicamente entre as duas partes numa troca de chaves Diffie Helmann não pode replicar estes cálculos. Para o fazer, necessitaria da informação privada de uma das duas partes.

Embora a versão básica da troca de chaves Diffie-Helmann apresentada no documento de 1976 não seja muito segura, ainda hoje são utilizadas versões sofisticadas do protocolo básico. Mais importante ainda, cada protocolo de troca de chaves na última versão do protocolo de segurança da camada de transporte (versão 1.3) é essencialmente uma versão enriquecida do protocolo apresentado por Diffie e Hellman em 1976. O protocolo de segurança da camada de transporte é o protocolo predominante para o intercâmbio seguro de informações formatadas de acordo com o protocolo de transferência de hipertexto (http), a norma para o intercâmbio de conteúdos da Web.

É importante notar que a troca de chaves Diffie-Helmann não é um esquema assimétrico. Em termos estritos, pertence ao domínio da criptografia de chave simétrica. Mas como tanto a troca de chaves Diffie-Helmann como a criptografia assimétrica se baseiam em funções teóricas de números unidireccionais com alçapões, são normalmente discutidas em conjunto.

A segunda forma que Diffie e Helmann propuseram para resolver o problema da distribuição e gestão de chaves no seu documento de 1976 foi, evidentemente, através da criptografia assimétrica.

Em contraste com a sua apresentação da troca de chaves Diffie-Hellman, apenas forneceram os contornos gerais de como os esquemas criptográficos assimétricos poderiam ser construídos de forma plausível. Não apresentaram qualquer função unidirecional que pudesse preencher especificamente as condições necessárias para uma segurança razoável em tais esquemas.

No entanto, um ano mais tarde, três criptógrafos e matemáticos académicos diferentes encontraram uma implementação prática de um esquema assimétrico: Ronald Rivest, Adi Shamir e Leonard Adleman. [3] O criptosistema que introduziram ficou conhecido como RSA cryptosystem (depois dos seus apelidos).

As funções de alçapão utilizadas na criptografia assimétrica (e na troca de chaves Diffie Helmann) estão todas relacionadas com dois problemas principais computacionalmente difíceis: a factorização de primos e o cálculo de logaritmos discretos.

A factorização de primos requer, como o nome indica, a decomposição de um número inteiro nos seus factores primos. O problema RSA é, de longe, o exemplo mais conhecido de um criptossistema relacionado com a factorização de primos.

O problema do logaritmo discreto é um problema que ocorre em grupos cíclicos. Dado um gerador num determinado grupo cíclico, requer o cálculo do expoente único necessário para produzir outro elemento no grupo a partir do gerador.

Os esquemas baseados em logaritmos discretos baseiam-se em dois tipos principais de grupos cíclicos: grupos multiplicativos de inteiros e grupos que incluem os pontos em curvas elípticas. A troca de chaves Diffie Helmann original, apresentada em "New Diretions in Cryptography", funciona com um grupo cíclico multiplicativo de inteiros. O algoritmo de assinatura digital da Bitcoin e o esquema de assinatura Schnorr recentemente introduzido (2021) baseiam-se ambos no problema do logaritmo discreto para um determinado grupo cíclico de curvas elípticas.

De seguida, passaremos a uma visão geral de alto nível do sigilo e da autenticação no contexto assimétrico. Antes de o fazermos, porém, precisamos de fazer uma breve nota histórica.

Atualmente, parece plausível que um grupo de criptógrafos e matemáticos britânicos que trabalhavam para o Government Communications Headquarters (GCHQ) tenha feito, de forma independente, as descobertas acima mencionadas alguns anos antes. Este grupo era constituído por James Ellis, Clifford Cocks e Malcolm Williamson.

De acordo com os seus próprios relatos e os do GCHQ, foi James Ellis quem primeiro concebeu o conceito de criptografia de chave pública em 1969. Supostamente, Clifford Cocks descobriu depois o sistema criptográfico RSA em 1973 e Malcolm Williamson o conceito de troca de chaves Diffie Helmann em 1974[4]. No entanto, as suas descobertas só foram reveladas em 1997, dado o carácter secreto do trabalho realizado no GCHQ.

Notas:

[1] Whitfield Diffie e Martin Hellman, "New diretions in cryptography," IEEE Transactions on Information Theory IT-22 (1976), pp. 644-654, na p. 644.

[2] Ralph Merkle também discute um protocolo de troca de chaves em "Secure communications over insecure channels", Communications of the Association for Computing Machinery, 21 (1978), 294-99. Embora Merkle tenha apresentado este trabalho antes do trabalho de Diffie e Hellman, foi publicado mais tarde. A solução de Merkle não é exponencialmente segura, ao contrário da de Diffie-Hellman.

[3] Ron Rivest, Adi Shamir e Leonard Adleman, "A method for obtaining digital signatures and public-key cryptosystems", Communications of the Association for Computing Machinery, 21 (1978), pp. 120-26.

[4] Uma boa história destas descobertas é fornecida por Simon Singh, The Code Book, Fourth Estate (Londres, 1999), Capítulo 6.

Encriptação e autenticação assimétricas

Na Figura 1 é apresentada uma visão geral da encriptação assimétrica com a ajuda de Bob e Alice.

Alice começa por criar um par de chaves, constituído por uma chave pública (K_P) e uma chave privada (K_S), em que o "P" em K_P significa "público" e o "S" em K_S significa "secreto". A chave pública é então distribuída livremente a outras pessoas. Voltaremos aos pormenores deste processo de distribuição um pouco mais tarde. Mas, para já, suponhamos que qualquer pessoa, incluindo o Bob, pode obter de forma segura a chave pública da Alice K_P.

Mais tarde, o Bob quer escrever uma mensagem M para a Alice. Como esta inclui informação sensível, ele quer que o conteúdo permaneça secreto para todos, exceto para Alice. Assim, Bob começa por cifrar a sua mensagem M utilizando K_P. Em seguida, envia o texto cifrado resultante C para Alice, que decifra C com K_S para produzir a mensagem original M.

Figura 1: Encriptação assimétrica

Figure 1: Asymmetric encryption

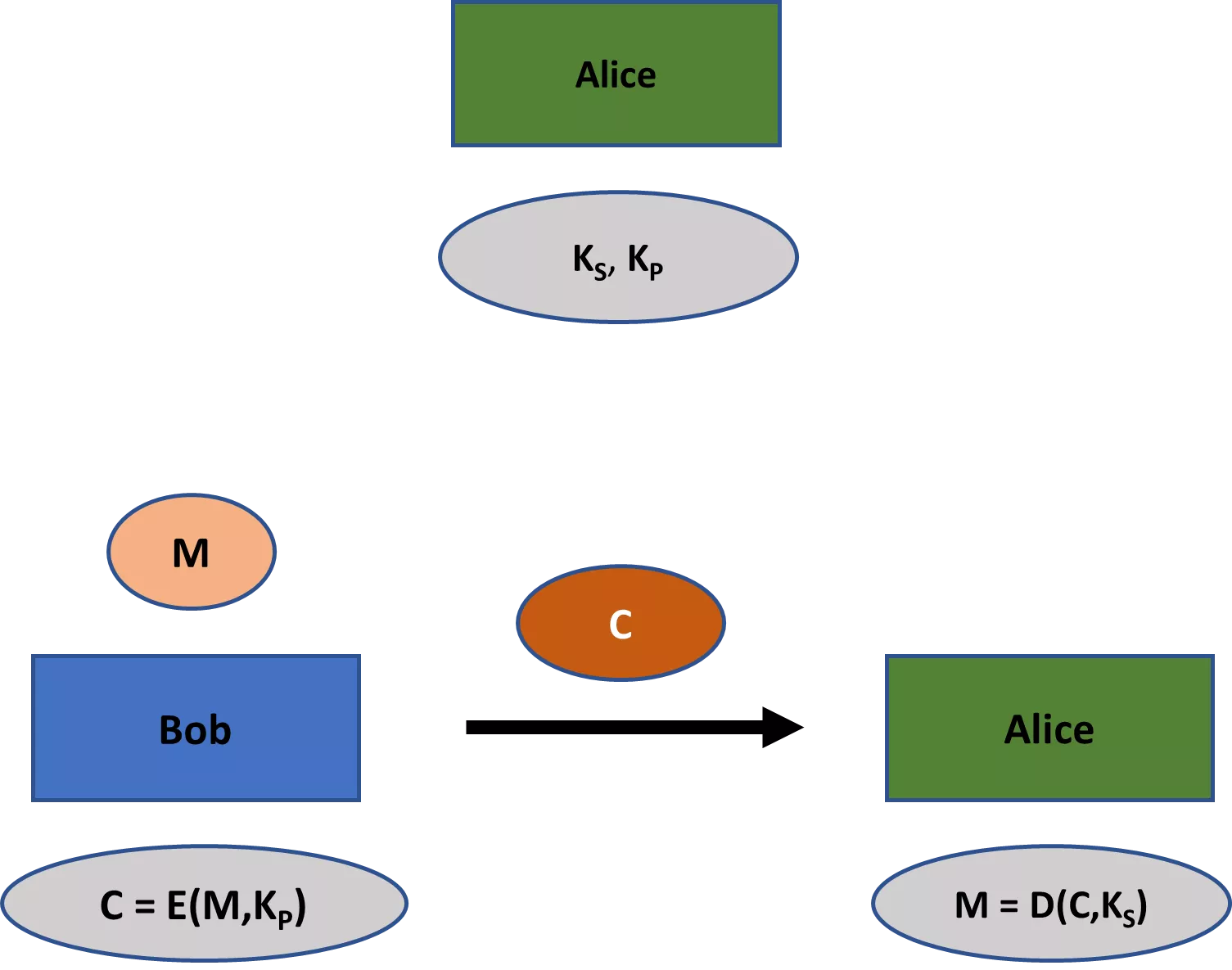
Qualquer adversário que escute a comunicação do Bob e da Alice pode observar C. Também conhece K_P e o algoritmo de encriptação E(\cdot). No entanto, é importante referir que esta informação não permite ao atacante decifrar o texto cifrado C. A desencriptação requer especificamente K_S, que o atacante não possui.

Os sistemas de cifragem simétrica precisam geralmente de ser seguros contra um atacante que possa cifrar validamente mensagens de texto simples (conhecido como segurança de ataque de texto cifrado escolhido). No entanto, não foi concebido com o objetivo explícito de permitir a criação de tais textos cifrados válidos por um atacante ou por qualquer outra pessoa.

Isto contrasta fortemente com um esquema de encriptação assimétrica, em que o seu objetivo é permitir que qualquer pessoa, incluindo os atacantes, produza textos cifrados válidos. Os esquemas de encriptação assimétrica podem, portanto, ser rotulados como cifras de acesso múltiplo.

Para compreender melhor o que se passa, imagine que, em vez de enviar uma mensagem por via eletrónica, Bob queria enviar uma carta física em segredo. Uma forma de garantir o sigilo seria a Alice enviar um cadeado seguro ao Bob, mas ficar com a chave para o abrir. Depois de escrever a sua carta, Bob poderia colocá-la numa caixa e fechá-la com o cadeado de Alice. Pode, então, enviar a caixa fechada com a mensagem a Alice, que tem a chave para a abrir.

Embora o Bob consiga fechar o cadeado, nem ele nem qualquer outra pessoa que intercepte a caixa podem abrir o cadeado, se este estiver efetivamente seguro. Só a Alice pode abrir o cadeado e ver o conteúdo da carta do Bob porque tem a chave.

Um esquema de encriptação assimétrica é, grosso modo, uma versão digital deste processo. O cadeado é semelhante à chave pública e a chave do cadeado é semelhante à chave privada. No entanto, como o cadeado é digital, é muito mais fácil e não tão dispendioso para Alice distribuí-lo a qualquer pessoa que queira enviar-lhe mensagens secretas.

Para a autenticação na configuração assimétrica, utilizamos assinaturas digitais. Estas têm, portanto, a mesma função que os códigos de autenticação de mensagens na configuração simétrica. Na Figura 2 é apresentada uma panorâmica das assinaturas digitais.

O Bob começa por criar um par de chaves, constituído pela chave pública (K_P) e pela chave privada (K_S), e distribui a sua chave pública. Quando quer enviar uma mensagem autenticada à Alice, começa por pegar na sua mensagem M e na sua chave privada para criar uma assinatura digital D. O Bob envia então a sua mensagem à Alice juntamente com a assinatura digital.

Alice insere a mensagem, a chave pública e a assinatura digital num algoritmo de verificação. Este algoritmo produz verdadeiro para uma assinatura válida, ou falso para uma assinatura inválida.

Uma assinatura digital é, como o nome indica claramente, o equivalente digital de uma assinatura escrita em cartas, contratos, etc. De facto, uma assinatura digital é normalmente muito mais segura. Com algum esforço, é possível falsificar uma assinatura escrita; um processo facilitado pelo facto de as assinaturas escritas não serem frequentemente verificadas de perto. Uma assinatura digital segura, no entanto, é, tal como um código de autenticação de mensagem segura, existencialmente não falsificável: ou seja, com um esquema de assinatura digital segura, ninguém pode criar uma assinatura para uma mensagem que passe no procedimento de verificação, a menos que tenha a chave privada.

Figura 2: Autenticação assimétrica

Figure 2: Asymmetric authentication

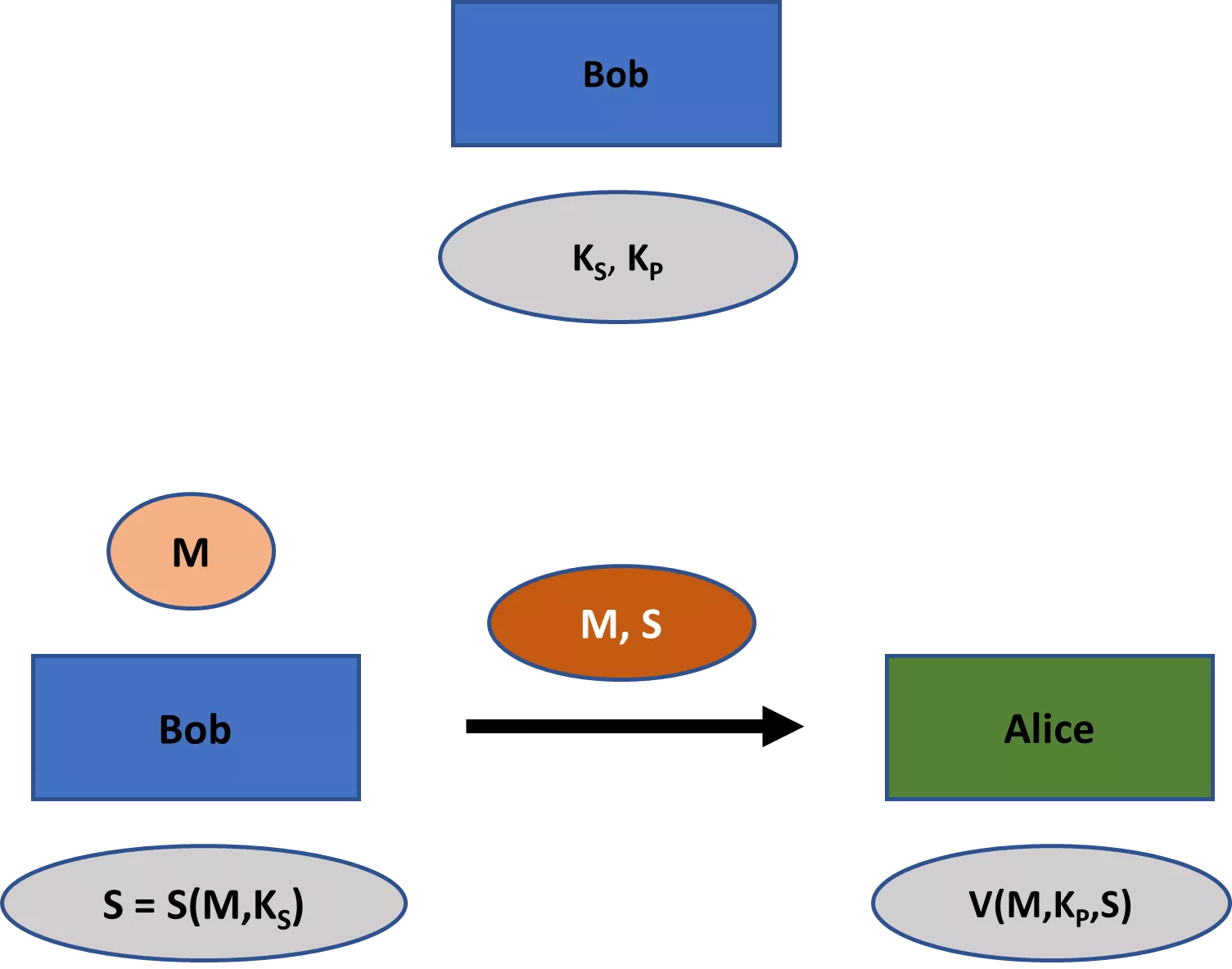
Tal como acontece com a cifragem assimétrica, vemos um contraste interessante entre as assinaturas digitais e os códigos de autenticação de mensagens. No caso destes últimos, o algoritmo de verificação só pode ser empregue por uma das partes que tem conhecimento da comunicação segura. Isto deve-se ao facto de ser necessária uma chave privada. Na configuração assimétrica, no entanto, qualquer pessoa pode verificar uma assinatura digital S feita por Bob.

Tudo isto faz das assinaturas digitais uma ferramenta extremamente poderosa. Constitui a base, por exemplo, da criação de assinaturas em contratos que podem ser verificadas para fins legais. Se o Bob tiver assinado um contrato na troca acima, a Alice pode mostrar a mensagem M, o contrato e a assinatura S a um tribunal. O tribunal pode, então, verificar a assinatura utilizando a chave pública de Bob. [5]

Por outro exemplo, as assinaturas digitais são um aspeto importante da distribuição segura de software e de actualizações de software. Este tipo de verificabilidade pública nunca poderia ser criado utilizando apenas códigos de autenticação de mensagens.

Como último exemplo do poder das assinaturas digitais, considere-se a Bitcoin. Uma das ideias erradas mais comuns sobre a Bitcoin, sobretudo nos meios de comunicação social, é que as transacções são encriptadas: não são. Em vez disso, as transacções Bitcoin funcionam com assinaturas digitais para garantir a segurança.

Os bitcoins existem em lotes chamados outputs de transacções não gastas (ou UTXO's). Suponha que você receba três pagamentos num determinado endereço Bitcoin de 2 bitcoins cada. Tecnicamente, não tem agora 6 bitcoins nesse endereço. Em vez disso, tem três lotes de 2 bitcoins que estão bloqueados por um problema criptográfico associado a esse endereço. Para qualquer pagamento que faça, pode usar um, dois ou todos os três lotes, dependendo de quanto precisa para a transação.

A prova de propriedade sobre os resultados de transacções não gastas é normalmente apresentada através de uma ou mais assinaturas digitais. A Bitcoin funciona precisamente porque as assinaturas digitais válidas sobre os resultados de transacções não gastas são computacionalmente inviáveis de fazer, a menos que se esteja na posse da informação secreta necessária para as fazer.

Atualmente, as transacções Bitcoin incluem de forma transparente toda a informação que precisa de ser verificada pelos participantes na rede, como a origem dos outputs de transação não gastos utilizados na transação. Embora seja possível ocultar algumas dessas informações e ainda assim permitir a verificação (como fazem algumas criptomoedas alternativas, como a Monero), isso também cria riscos de segurança específicos.

Por vezes, surge a confusão entre assinaturas digitais e assinaturas escritas capturadas digitalmente. Neste último caso, o utilizador captura uma imagem da sua assinatura escrita e cola-a num documento eletrónico, como um contrato de trabalho. No entanto, isto não é uma assinatura digital no sentido criptográfico. Esta última é apenas um número longo que só pode ser produzido se estiver na posse de uma chave privada.

Tal como na definição de chave simétrica, também é possível utilizar esquemas de encriptação e autenticação assimétricos em conjunto. Aplicam-se princípios semelhantes. Em primeiro lugar, deve utilizar diferentes pares de chaves públicas e privadas para encriptar e fazer assinaturas digitais. Além disso, deve começar por encriptar uma mensagem e depois autenticá-la.

É importante notar que, em muitas aplicações, a criptografia assimétrica não é utilizada durante todo o processo de comunicação. Em vez disso, normalmente só é utilizada para trocar chaves simétricas entre as partes através das quais estas irão efetivamente comunicar.

É o que acontece, por exemplo, quando se compram produtos em linha. Conhecendo a chave pública do vendedor, este pode enviar-lhe mensagens assinadas digitalmente, cuja autenticidade pode ser verificada por si. Nesta base, pode seguir um dos vários protocolos de troca de chaves simétricas para comunicar de forma segura.

A principal razão para a frequência da abordagem acima referida é o facto de a criptografia assimétrica ser muito menos eficiente do que a criptografia simétrica na produção de um determinado nível de segurança. Esta é uma das razões pelas quais continuamos a precisar de criptografia de chave simétrica a par da criptografia pública. Além disso, a criptografia de chave simétrica é muito mais natural em aplicações específicas, como a de um utilizador de computador que cifra os seus próprios dados.

Então, como é que as assinaturas digitais e a encriptação de chave pública resolvem exatamente os problemas de distribuição e gestão de chaves?

Não há uma resposta única. A criptografia assimétrica é uma ferramenta e não existe uma única forma de a utilizar. Mas vamos pegar no nosso exemplo anterior da Jim's Sporting Goods para mostrar como as questões seriam normalmente abordadas neste exemplo.

Para começar, a Jim's Sporting Goods abordaria provavelmente uma autoridade de certificação, uma organização que apoia a distribuição de chaves públicas. A autoridade de certificação registaria alguns detalhes sobre a Jim's Sporting Goods e conceder-lhe-ia uma chave pública. De seguida, enviaria à Jim's Sporting Goods um certificado, conhecido como certificado TLS/SSL, com a chave pública da Jim's Sporting Goods assinada digitalmente utilizando a chave pública da própria autoridade de certificação. Desta forma, a autoridade de certificação afirma que uma determinada chave pública pertence efetivamente à Jim's Sporting Goods.

A chave para compreender este processo com certificados TLS/SSL é que, embora geralmente não tenha a chave pública da Jim's Sporting Goods armazenada em qualquer parte do seu computador, as chaves públicas das autoridades de certificação reconhecidas estão de facto armazenadas no seu browser ou no seu sistema operativo. Estas são armazenadas nos chamados certificados de raiz.

Assim, quando a Jim's Sporting Goods lhe fornece o seu certificado TLS/SSL, pode verificar a assinatura digital da autoridade de certificação através de um certificado de raiz no seu browser ou sistema operativo. Se a assinatura for válida, pode estar relativamente seguro de que a chave pública do certificado pertence efetivamente à Jim's Sporting Goods. Nesta base, é fácil estabelecer um protocolo para uma comunicação segura com a Jim's Sporting Goods.

A distribuição de chaves tornou-se agora muito mais simples para a Jim's Sporting Goods. Não é difícil perceber que a gestão de chaves também se tornou muito simplificada. Em vez de ter de armazenar milhares de chaves, a Jim's Sporting Goods só precisa de armazenar uma chave privada que lhe permita efetuar assinaturas para a chave pública no seu certificado SSL. Sempre que um cliente acede ao site da Jim's Sporting Goods, pode estabelecer uma sessão de comunicação segura a partir desta chave pública. Os clientes também não precisam de armazenar qualquer informação (para além das chaves públicas das autoridades de certificação reconhecidas no seu sistema operativo e browser).

Notas:

[5] Qualquer sistema que tente obter o não repúdio, o outro tema que discutimos no Capítulo 1, terá de envolver assinaturas digitais na sua base.

Funções de hash

As funções de hash são omnipresentes na criptografia. Não são esquemas simétricos nem assimétricos, mas pertencem a uma categoria criptográfica por direito próprio.

Já nos deparámos com funções de hash no Capítulo 4 com a criação de mensagens de autenticação baseadas em hash. São também importantes no contexto das assinaturas digitais, embora por uma razão ligeiramente diferente: As assinaturas digitais são tipicamente feitas sobre o valor hash de uma mensagem (encriptada), em vez da própria mensagem (encriptada). Nesta secção, farei uma introdução mais aprofundada às funções de hash.

Vamos começar por definir uma função hash. Uma função hash é qualquer função computável de forma eficiente que recebe entradas de tamanho arbitrário e produz saídas de comprimento fixo.

Uma função hash criptográfica é apenas uma função hash que é útil para aplicações em criptografia. O resultado de uma função hash criptográfica é tipicamente chamado de hash, valor hash ou digestão de mensagem.

No contexto da criptografia, uma "função hash" refere-se tipicamente a uma função hash criptográfica. Adoptarei essa prática daqui em diante.

Um exemplo de uma função de hash popular é o SHA-256 (algoritmo de hash seguro 256). Independentemente do tamanho da entrada (por exemplo, 15 bits, 100 bits ou 10.000 bits), esta função produzirá um valor de hash de 256 bits. Abaixo pode ver alguns exemplos de resultados da função SHA-256.

"Olá": 185f8db32271fe25f561a6fc938b2e264306ec304eda518007d1764826381969

"52398": a3b14d2bf378c1bd47e7f8eaec63b445150a3d7a80465af16dd9fd319454ba90

"A criptografia é divertida": 3cee2a5c7d2cc1d62db4893564c34ae553cc88623992d994e114e344359b146c

Todos os resultados são exatamente 256 bits escritos em formato hexadecimal (cada dígito hexadecimal pode ser representado por quatro dígitos binários). Assim, mesmo que tivesse inserido o livro O Senhor dos Anéis de Tolkien na função SHA-256, o resultado continuaria a ser 256 bits.

As funções de hash, como o SHA-256, são utilizadas para vários fins na criptografia. As propriedades que são necessárias numa função de hash dependem realmente do contexto de uma determinada aplicação. Há duas propriedades principais geralmente desejadas das funções de hash em criptografia: [6]

  1. Resistência à colisão

  2. Esconderijo

Diz-se que uma função de hash H é resistente a colisões se for inviável encontrar dois valores, x e y, tais que x \neq y, mas H(x) = H(y).

As funções hash resistentes a colisões são importantes, por exemplo, na verificação de software. Suponhamos que queria descarregar a versão Windows do Bitcoin Core 0.21.0 (uma aplicação de servidor para processar o tráfego da rede Bitcoin). Os principais passos que teria de dar, para verificar a legitimidade do software, são os seguintes:

  1. Primeiro, é necessário descarregar e importar as chaves públicas de um ou mais contribuidores Bitcoin Core para um software que possa verificar assinaturas digitais (por exemplo, Kleopetra). Pode encontrar estas chaves públicas aqui. Recomenda-se que verifique o software Bitcoin Core com as chaves públicas de vários contribuidores.

  2. De seguida, é necessário verificar as chaves públicas que importou. Pelo menos um passo que deve dar é verificar se as chaves públicas que encontrou são as mesmas que foram publicadas em vários outros locais. Pode, por exemplo, consultar as páginas Web pessoais, as páginas do Twitter ou as páginas do Github das pessoas cujas chaves públicas importou. Normalmente, esta comparação de chaves públicas é efectuada através da comparação de um hash curto da chave pública, conhecido como impressão digital.

  3. Em seguida, é necessário descarregar o executável para o Bitcoin Core a partir do seu website. Haverá pacotes disponíveis para os sistemas operativos Linux, Windows e MAC.

  4. A seguir, tem de localizar dois ficheiros de lançamento. O primeiro contém o hash SHA-256 oficial para o executável que descarregou juntamente com os hashes de todos os outros pacotes que foram lançados. Outro ficheiro de lançamento conterá as assinaturas de vários contribuidores sobre o ficheiro de lançamento com os hashes dos pacotes. Ambos os ficheiros de lançamento devem estar localizados no site do Bitcoin Core.

  5. Em seguida, você precisaria calcular o hash SHA-256 do executável que você baixou do site do Bitcoin Core em seu próprio computador. Depois, compara este resultado com o resultado do hash do pacote oficial para o executável. Eles devem ser os mesmos.

  6. Finalmente, teria de verificar se uma ou mais assinaturas digitais sobre o ficheiro de lançamento com os hashes oficiais do pacote correspondem efetivamente a uma ou mais chaves públicas que importou (os lançamentos do Bitcoin Core nem sempre são assinados por todos). Pode fazer isto com uma aplicação como a Kleopetra.

Este processo de verificação de software tem dois benefícios principais. Primeiro, ele garante que não houve erros na transmissão durante o download do site do Bitcoin Core. Em segundo lugar, garante que nenhum atacante poderia ter feito com que você baixasse um código modificado e malicioso, seja invadindo o site do Bitcoin Core ou interceptando o tráfego.

Como é que o processo de verificação de software acima descrito protege exatamente contra estes problemas?

Se você verificou diligentemente as chaves públicas que importou, então você pode ter certeza que essas chaves são realmente deles e não foram comprometidas. Dado que as assinaturas digitais têm uma imprevisibilidade existencial, você sabe que apenas estes contribuidores poderiam ter feito uma assinatura digital sobre os hashes oficiais do pacote no ficheiro de lançamento.

Suponha que as assinaturas no ficheiro de lançamento que descarregou são verificadas. Pode agora comparar o valor de hash que calculou localmente para o executável do Windows que descarregou com o valor incluído no ficheiro de lançamento devidamente assinado. Como sabe, a função de hash SHA-256 é resistente a colisões, uma correspondência significa que o seu executável é exatamente o mesmo que o executável oficial.

Passemos agora à segunda propriedade comum das funções hash: esconder. Diz-se que uma função hash H tem a propriedade de ocultação se, para qualquer x selecionado aleatoriamente de um intervalo muito grande, for inviável encontrar x quando se dá apenas H(x).

Abaixo, você pode ver a saída SHA-256 de uma mensagem que escrevi. Para garantir aleatoriedade suficiente, a mensagem incluía uma sequência de caracteres gerada aleatoriamente no final. Dado que o SHA-256 tem a propriedade de ocultação, ninguém seria capaz de decifrar esta mensagem.

Mas não vos deixarei em suspense até que o SHA-256 se torne mais fraco. A mensagem original que escrevi era a seguinte:

Uma forma comum de utilizar funções hash com a propriedade de ocultação é na gestão de palavras-passe (a resistência à colisão também é importante para esta aplicação). Qualquer serviço online decente baseado em contas, como o Facebook ou o Google, não guarda as suas palavras-passe diretamente para gerir o acesso à sua conta. Em vez disso, guardam apenas um hash da palavra-passe. De cada vez que preenche a sua palavra-passe num browser, é primeiro calculado um hash. Apenas esse hash é enviado para o servidor do fornecedor de serviços e comparado com o hash armazenado na base de dados back-end. A propriedade de ocultação pode ajudar a garantir que os atacantes não possam recuperá-la a partir do valor do hash.

A gestão de senhas através de hashes, obviamente, só funciona se os utilizadores escolherem realmente senhas difíceis. A propriedade de ocultação assume que x é escolhido aleatoriamente a partir de um intervalo muito grande. Selecionar palavras-passe como "1234", "mypassword" ou a data do seu aniversário não oferece qualquer segurança real. Existem longas listas de palavras-passe comuns e respectivos hashes que os atacantes podem utilizar se alguma vez obtiverem o hash da sua palavra-passe. Estes tipos de ataques são conhecidos como ataques de dicionário. Se os atacantes conhecerem alguns dos seus dados pessoais, podem também tentar algumas tentativas de adivinhação informada. Por isso, são sempre necessárias palavras-passe longas e seguras (de preferência, cadeias longas e aleatórias de um gestor de palavras-passe).

Por vezes, uma aplicação pode necessitar de uma função hash que seja simultaneamente resistente à colisão e oculta. Mas certamente nem sempre. O processo de verificação de software que discutimos, por exemplo, apenas requer que a função hash apresente resistência à colisão, a ocultação não é importante.

Embora a resistência à colisão e a ocultação sejam as principais propriedades procuradas nas funções de hash em criptografia, em determinadas aplicações podem também ser desejáveis outros tipos de propriedades.

Notas:

[6] A terminologia "esconder" não é linguagem comum, mas foi retirada especificamente de Arvind Narayanan, Joseph Bonneau, Edward Felten, Andrew Miller e Steven Goldfeder, Bitcoin and Cryptocurrency Technologies, Princeton University Press (Princeton, 2016), Capítulo 1.

O sistema de criptografia RSA

O problema da factorização

Enquanto a criptografia simétrica é normalmente bastante intuitiva para a maioria das pessoas, o mesmo não acontece com a criptografia assimétrica. Embora provavelmente se sinta confortável com a descrição de alto nível apresentada nas secções anteriores, deve estar a perguntar-se o que são exatamente funções unidireccionais e como são utilizadas para construir esquemas assimétricos.

Neste capítulo, vou eliminar algum do mistério que rodeia a criptografia assimétrica, analisando mais profundamente um exemplo específico, nomeadamente o criptossistema RSA. Na primeira secção, introduzirei o problema da factorização em que se baseia o problema RSA. Em seguida, abordaremos uma série de resultados importantes da teoria dos números. Na última secção, juntaremos esta informação para explicar o problema RSA e como este pode ser utilizado para criar esquemas criptográficos assimétricos.

Acrescentar esta profundidade à nossa discussão não é uma tarefa fácil. Requer a introdução de alguns teoremas e proposições da teoria dos números. Mas não deixe que a matemática o dissuada. Trabalhar nesta discussão irá melhorar significativamente a sua compreensão do que está subjacente à criptografia assimétrica e é um investimento que vale a pena.

Passemos agora ao problema da factorização.

Sempre que se multiplicam dois números, digamos a e b, referimo-nos aos números a e b como factores, e ao resultado como produto. A tentativa de escrever um número N na multiplicação de dois ou mais factores chama-se factorização ou factoring. [1] A qualquer problema que exija isto pode chamar-se um problema de factorização.

Há cerca de 2.500 anos, o matemático grego Euclides de Alexandria descobriu um teorema fundamental sobre a factorização de números inteiros. É vulgarmente designado por teorema da factorização única e afirma o seguinte:

Teorema 1. Todo o número inteiro N que é maior que 1 é um número primo ou pode ser expresso como um produto de factores primos.

Tudo o que a última parte desta afirmação significa é que se pode pegar em qualquer número inteiro não primo N maior que 1 e escrevê-lo como uma multiplicação de números primos. Abaixo estão vários exemplos de números inteiros não-primos escritos como o produto de factores primos.

Para os três números inteiros acima referidos, o cálculo dos seus factores primos é relativamente fácil, mesmo que só lhe sejam dados N. Começa-se pelo número primo mais pequeno, o 2, e verifica-se quantas vezes o inteiro N é divisível por ele. De seguida, passa a testar a divisibilidade de N por 3, 5, 7, e assim sucessivamente. Continua este processo até que o número inteiro N seja escrito como o produto de apenas números primos.

Tomemos, por exemplo, o número inteiro 84. Abaixo pode ver o processo de determinação dos seus factores primos. Em cada passo, retiramos o menor fator primo restante (à esquerda) e determinamos o termo restante a ser factorizado. Continuamos até que o termo restante seja também um número primo. Em cada passo, a factorização atual de 84 é apresentada na extrema direita.

Suponhamos agora que N é muito grande. Qual seria a dificuldade de reduzir N aos seus factores primos?

Isso depende realmente de N. Suponhamos, por exemplo, que N é 50.450.400. Embora este número pareça intimidante, os cálculos não são assim tão complicados e podem ser facilmente efectuados à mão. Tal como acima, basta começar com 2 e ir avançando. Abaixo, pode ver o resultado deste processo de uma forma semelhante à anterior.

Resolver este problema à mão demora algum tempo. Um computador, claro, pode fazer tudo isto numa pequena fração de segundo. De facto, um computador pode, frequentemente, até fatorizar números inteiros extremamente grandes numa fração de segundo.

Existem, no entanto, algumas excepções. Suponhamos que começamos por selecionar aleatoriamente dois números primos muito grandes. É habitual rotulá-los de p e q, e vou adotar essa convenção aqui.

Para sermos concretos, digamos que p e q são ambos números primos de 1024 bits e que, de facto, necessitam de pelo menos 1024 bits para serem representados (pelo que o primeiro bit tem de ser 1). Assim, por exemplo, 37 não pode ser um dos números primos. Pode certamente representar 37 com 1024 bits. Mas claramente não precisa de tantos bits para o representar. Pode representar 37 por qualquer string que tenha 6 bits ou mais. (Em 6 bits, 37 seria representado por 100101).

É importante apreciar o tamanho de p e q se forem selecionados nas condições acima. A título de exemplo, selecionei um número primo aleatório que necessita de pelo menos 1024 bits para ser representado.

Suponhamos agora que, depois de seleccionarmos aleatoriamente números primos p e q, os multiplicamos para obter um número inteiro N. Este último número inteiro é, portanto, um número de 2048 bits que requer pelo menos 2048 bits para a sua representação. É muito, muito maior que p ou q.

Suponha-se que se dá a um computador N e se lhe pede para encontrar os dois factores primos de 1024 bits de N. A probabilidade de o computador descobrir p e q é extremamente pequena. Pode dizer-se que é impossível para todos os efeitos práticos. Isto é assim, mesmo que se utilizasse um supercomputador ou mesmo uma rede de supercomputadores.

Para começar, suponha que o computador tenta resolver o problema percorrendo 1024 números de bits, testando em cada caso se são primos e se são factores de N. O conjunto de números primos a testar é então aproximadamente 1.265 \cdot 10^{305}. [2]

Mesmo que pegássemos em todos os computadores do planeta e os puséssemos a tentar encontrar e testar números primos de 1024 bits desta forma, uma hipótese de 1 em mil milhões de encontrar com sucesso um fator primo de N exigiria um período de cálculo muito superior à idade do Universo.

Na prática, um computador pode fazer melhor do que o procedimento aproximado que acabámos de descrever. Existem vários algoritmos que o computador pode aplicar para chegar a uma factorização mais rapidamente. A questão, no entanto, é que mesmo usando estes algoritmos mais eficientes, a tarefa do computador continua a ser computacionalmente inviável. [3]

É importante notar que a dificuldade da factorização nas condições que acabámos de descrever assenta no pressuposto de que não existem algoritmos computacionalmente eficientes para calcular factores primos. De facto, não podemos provar que não existe um algoritmo eficiente. No entanto, este pressuposto é muito plausível: apesar dos esforços de centenas de anos, ainda não encontrámos um algoritmo computacionalmente eficiente.

Assim, o problema da factorização, em determinadas circunstâncias, pode ser plausivelmente considerado um problema difícil. Especificamente, quando p e q são números primos muito grandes, o seu produto N não é difícil de calcular; mas a factorização apenas dado N é praticamente impossível.

Notas:

[1] A factorização também pode ser importante para trabalhar com outros tipos de objectos matemáticos para além dos números. Por exemplo, pode ser útil fatorizar expressões polinomiais como x^2 - 2x + 1. Na nossa discussão, iremos focar-nos apenas na factorização de números, especificamente de números inteiros.

[2] De acordo com o teorema dos números primos, o número de números primos menores ou iguais a N é aproximadamente N/\ln(N). Isto significa que se pode aproximar o número de primos de comprimento 1024 bits por:

\frac{2^{1024}}{\ln(2^{1024})} - \frac{2^{1023}}{\ln(2^{1023})}

...o que equivale a aproximadamente 1,265 \times 10^{305}.

O mesmo se aplica aos problemas de logaritmos discretos. É por isso que as construções assimétricas funcionam com chaves muito maiores do que as construções criptográficas simétricas.

Resultados da teoria dos números

Infelizmente, o problema da factorização não pode ser utilizado diretamente para esquemas criptográficos assimétricos. No entanto, podemos utilizar um problema mais complexo mas relacionado com este efeito: o problema RSA.

Para compreender o problema do RSA, precisamos de compreender uma série de teoremas e proposições da teoria dos números. Estes são apresentados nesta secção em três subsecções: (1) a ordem de N, (2) a invertibilidade módulo N e (3) o teorema de Euler.

Parte do material das três subsecções já foi introduzido no Capítulo 3. Mas, por uma questão de conveniência, vou apresentar novamente esse material.

A ordem de N

Um número inteiro a é coprimo ou primo relativo com um número inteiro N, se o maior divisor comum entre eles for 1. Embora 1 não seja, por convenção, um número primo, é um coprimo de qualquer número inteiro (tal como -1).

Por exemplo, considere o caso em que a = 18 e N = 37. Estes são claramente coprimes. O maior número inteiro que divide 18 e 37 é 1. Por outro lado, considere o caso em que a = 42 e N = 16. Estes números não são claramente coprimários. Ambos os números são divisíveis por 2, que é maior do que 1.

Podemos agora definir a ordem de N da seguinte forma. Suponhamos que N é um número inteiro maior que 1. A ordem de N é, então, o número de todos os coprimos com N tais que, para cada coprimo a, se verifica a seguinte condição: 1 \leq a < N.

Por exemplo, se N = 12, então 1, 5, 7 e 11 são os únicos coprimes que satisfazem o requisito acima. Logo, a ordem de 12 é igual a 4.

Suponhamos que N é um número primo. Então qualquer número inteiro menor que N mas maior ou igual a 1 é coprimo com ele. Isto inclui todos os elementos do seguinte conjunto: \{1,2,3,....,N - 1\}. Assim, quando N é primo, a ordem de N é N - 1. Isto é afirmado na proposição 1, onde \phi(N) denota a ordem de N.

Proposição 1. \phi(N) = N - 1 quando N é primo

Suponha que N não é primo. Pode, então, calcular a sua ordem usando a função Phi de Euler. Embora o cálculo da ordem de um número inteiro pequeno seja relativamente simples, a função Phi de Euler torna-se particularmente importante para números inteiros maiores. A proposição da função Phi de Euler é apresentada a seguir.

Teorema 2. Seja N igual a p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot p_i^{e_i} \cdot \ldots \cdot p_n^{e_n}, onde o conjunto \{p_i\} consiste em todos os factores primos distintos de N e cada e_i indica quantas vezes o fator primo p_i ocorre para N. Então,

\phi(N) = p_1^{e_1 - 1} \cdot (p_1 - 1) \cdot p_2^{e_2 - 1} \cdot (p_2 - 1) \cdot \ldots \cdot p_n^{e_n - 1} \cdot (p_n - 1)

O Teorema 2 mostra que, uma vez decomposto qualquer N não primo nos seus distintos factores primos, é fácil calcular a ordem de N.

Por exemplo, suponhamos que N = 270. Este não é claramente um número primo. Decompondo N nos seus factores primos, obtém-se a expressão: 2 \cdot 3^3 \cdot 5. De acordo com a função Phi de Euler, a ordem de N é então a seguinte:

\phi(N) = 2^{1 - 1} \cdot (2 - 1) + 3^{3 - 1} \cdot (3 - 1) + 5^{1 - 1} \cdot (5 - 1) = 1 \cdot 1 + 9 \cdot 2 + 1 \cdot 4 = 1 + 18 + 4 = 23

Suponhamos de seguida que N é um produto de dois primos, p e q. O Teorema 2 acima, então, afirma que a ordem de N é a seguinte:

p^{1 - 1} \cdot (p - 1) \cdot q^{1 - 1} \cdot (q - 1) = (p - 1) \cdot (q - 1)

Este é um resultado fundamental para o problema RSA em particular, e é apresentado na Proposição 2 abaixo.

Proposição 2. Se N é o produto de dois números primos, p e q, a ordem de N é o produto (p - 1) \cdot (q - 1).

Para ilustrar, suponha que N = 119. Este número inteiro pode ser dividido em dois números primos, nomeadamente 7 e 17. Assim, a função Phi de Euler sugere que a ordem de 119 é a seguinte:

\phi(119) = (7 - 1) \cdot (17 - 1) = 6 \cdot 16 = 96

Por outras palavras, o número inteiro 119 tem 96 coprimes no intervalo de 1 a 119. De facto, este conjunto inclui todos os números inteiros de 1 a 119 que não são múltiplos de 7 ou 17.

A partir daqui, vamos designar por C_N o conjunto dos coprimes que determina a ordem de N. Para o nosso exemplo em que N = 119, o conjunto C_{119} é demasiado grande para ser listado completamente. Mas alguns dos seus elementos são os seguintes:

C_{119} = \{1, 2, \dots 6, 8 \dots 13, 15, 16, 18, \dots 33, 35 \dots 96\}

Invertibilidade módulo N

Podemos dizer que um número inteiro a é inversível módulo N, se existir pelo menos um número inteiro b tal que a \cdot b \mod N = 1 \mod N. Um tal número inteiro b é referido como um inverso (ou inverso multiplicativo) de a dada a redução por módulo N.

Suponha, por exemplo, que a = 5 e N = 11. Há muitos números inteiros pelos quais se pode multiplicar 5, de modo que 5 \cdot b \mod 11 = 1 \mod 11. Consideremos, por exemplo, os números inteiros 20 e 31. É fácil ver que estes dois números inteiros são inversos de 5 para a redução módulo 11.

Embora 5 tenha muitas reduções inversas módulo 11, é possível mostrar que só existe um único inverso positivo de 5 que é menor que 11. De facto, isto não é exclusivo do nosso exemplo particular, mas um resultado geral.

Proposição 3. Se o inteiro a é invertível modulo N, tem de haver exatamente um inverso positivo de a que seja menor que N. (Assim, este único inverso de a tem de vir do conjunto \{1, \dots, N - 1\}).

Denotemos o único inverso de a da Proposição 3 por a^{-1}. Para o caso em que a = 5 e N = 11, pode ver-se que a^{-1} = 9, dado que 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11.

Repare que também pode obter o valor 9 para a^{-1} no nosso exemplo reduzindo simplesmente qualquer outro inverso de a pelo módulo 11. Por exemplo, 20 \mod 11 = 31 \mod 11 = 9 \mod 11. Assim, sempre que um inteiro a > N é inversível no módulo N, então a \mod N também tem de ser inversível no módulo N.

Não é necessariamente o caso de existir uma redução do inverso de a modulo N. Suponhamos, por exemplo, que a = 2 e N = 8. Não existe b, ou qualquer a^{-1} especificamente, tal que 2 \cdot b \mod 8 = 1 \mod 8. Isto acontece porque qualquer valor de b produzirá sempre um múltiplo de 2, pelo que nenhuma divisão por 8 pode produzir um resto igual a 1.

Como é que sabemos exatamente se um número inteiro a tem um inverso para um dado N? Como deve ter reparado no exemplo acima, o maior divisor comum entre 2 e 8 é superior a 1, nomeadamente 2. E isto ilustra o seguinte resultado geral:

Proposição 4. Existe uma inversa de um inteiro a dada a redução modulo N, e especificamente uma única inversa positiva menor que N, se e só se o maior divisor comum entre a e N for 1 (isto é, se forem coprimes).

Para o caso em que a = 5 e N = 11, concluímos que a^{-1} = 9, dado que 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11. É importante notar que o inverso também é verdadeiro. Ou seja, quando a = 9 e N = 11, acontece que a^{-1} = 5.

Teorema de Euler

Antes de passarmos ao problema RSA, precisamos de compreender mais um teorema crucial, nomeadamente o Teorema de Euler. Este teorema diz o seguinte:

Teorema 3. Suponha que dois inteiros a e N são coprimos. Então, a^{\phi(N)} \mod N = 1 \mod N.

Este é um resultado notável, mas um pouco confuso no início. Vamos recorrer a um exemplo para o compreender.

Suponhamos que a = 5 e N = 7. Estes são, de facto, coprimes, como o teorema de Euler exige. Sabemos que a ordem de 7 é igual a 6, dado que 7 é um número primo (ver Proposição 1).

O que o teorema de Euler afirma agora é que 5^6 \mod 7 deve ser igual a 1 \mod 7. Abaixo estão os cálculos para mostrar que isto é de facto verdade.

O número inteiro 7 divide-se em 15 624 um total de 2 233 vezes. Logo, o resto da divisão de 16.625 por 7 é 1.

Em seguida, utilizando a função Phi de Euler, Teorema 2, pode derivar a Proposição 5 abaixo.

Proposição 5. \phi(a \cdot b) = \phi(a) \cdot \phi(b) para quaisquer inteiros positivos a e b.

Não vamos mostrar porque é que isto é assim. Mas basta notar que já viu uma prova desta proposição pelo facto de \phi(p \cdot q) = \phi(p) \cdot \phi(q) = (p - 1) \cdot (q - 1) quando p e q são primos, como se afirma na Proposição 2.

O teorema de Euler em conjunto com a Proposição 5 tem implicações importantes. Veja o que acontece, por exemplo, nas expressões abaixo, onde a e N são coprimos.

Assim, a combinação do teorema de Euler e da Proposição 5 permite-nos calcular simplesmente um certo número de expressões. Em geral, podemos resumir o conhecimento como na Proposição 6.

Proposta 6. a^x \mod N = a^{x \mod \phi(N)}

Agora temos de juntar tudo numa última etapa complicada.

Tal como N tem uma ordem \phi(N) que inclui os elementos do conjunto C_N, sabemos que o inteiro \phi(N) deve por sua vez ter também uma ordem e um conjunto de coprimes. Fixemos \phi(N) = R. Sabemos então que existe também um valor para \phi(R) e um conjunto de coprimes C_R.

Suponhamos que agora seleccionamos um inteiro e do conjunto C_R. Sabemos pela Proposição 3 que este inteiro e só tem um único inverso positivo menor que R. Ou seja, e tem um único inverso do conjunto C_R. Chamemos a este inverso d. Dada a definição de inverso, isto significa que e \cdot d = 1 \mod R.

Podemos usar este resultado para fazer uma afirmação sobre o nosso inteiro original N. Isto está resumido na Proposição 7.

Proposição 7. Suponha-se que e \cdot d \mod \phi(N) = 1 \mod \phi(N). Então para qualquer elemento a do conjunto C_N tem de ser o caso que a^{e \cdot d \mod \phi(N)} = a^{1 \mod \phi(N)} = a \mod N.

Dispomos agora de todos os resultados da teoria dos números necessários para enunciar claramente o problema RSA.

O sistema de criptografia RSA

Estamos agora prontos para apresentar o problema RSA. Suponha que cria um conjunto de variáveis que consiste em p, q, N, \phi(N), e, d e y. Chame a este conjunto \Pi. É criado da seguinte forma:

  1. Gerar dois números primos aleatórios p e q de igual tamanho e calcular o seu produto N.

  2. Calcule a ordem de N, \phi(N), através do seguinte produto: (p - 1) \cdot (q - 1).

  3. Selecionar um e > 2 tal que seja menor e coprimo de \phi(N).

  4. Calcule d definindo e \cdot d \mod \phi(N) = 1.

  5. Selecione um valor aleatório y que seja menor e coprimo de N.

O problema RSA consiste em encontrar um x tal que x^e = y, tendo apenas um subconjunto de informações sobre \Pi, nomeadamente as variáveis N, e e y. Quando p e q são muito grandes, tipicamente recomenda-se que tenham 1024 bits de tamanho, o problema RSA é considerado difícil. Pode ver agora porque é que isto acontece, dada a discussão anterior.

Uma maneira fácil de calcular x quando x^e \mod N = y \mod N é simplesmente calculando y^d \mod N. Sabemos que y^d \mod N = x \mod N pelos seguintes cálculos:

y^d \mod N = x^{e \cdot d} \mod N = x^{e \cdot d \mod \phi(N)} \mod N = x^{1 \mod \phi(N)} \mod N = x \mod N.

O problema é que não sabemos o valor d, pois não é dado no problema. Assim, não podemos calcular diretamente y^d \mod N para produzir x \mod N.

Poderemos, no entanto, ser capazes de calcular indiretamente d a partir da ordem de N, \phi(N), pois sabemos que e \cdot d \mod \phi(N) = 1 \mod \phi(N). Mas, por hipótese, o problema também não dá um valor para \phi(N).

Finalmente, a ordem poderia ser calculada indiretamente com os factores primos p e q, de modo a podermos eventualmente calcular d. Mas, por hipótese, os valores p e q também não nos foram fornecidos.

Estritamente falando, mesmo que o problema de factorização dentro de um problema RSA seja difícil, não podemos provar que o problema RSA também é difícil. Pode, nomeadamente, haver outras formas de resolver o problema RSA sem ser através da factorização. No entanto, é geralmente aceite e assumido que, se o problema de factorização dentro do problema RSA for difícil, o problema RSA em si também é difícil.

Se o problema RSA é de facto difícil, então produz uma função unidirecional com um alçapão. A função aqui é f(g) = g^e \mod N. Com o conhecimento de f(g), qualquer pessoa poderia facilmente calcular um valor y para um determinado g = x. No entanto, é praticamente impossível calcular um determinado valor x apenas conhecendo o valor y e a função f(g). A exceção é quando lhe é dada uma informação d, o alçapão. Nesse caso, pode simplesmente calcular y^d para obter x.

Vamos analisar um exemplo específico para ilustrar o problema RSA. Não posso selecionar um problema de RSA que seja considerado difícil nas condições acima referidas, pois os números seriam muito pesados. Em vez disso, este exemplo serve apenas para ilustrar o funcionamento geral do problema RSA.

Para começar, suponha que seleciona dois números primos aleatórios 13 e 31. Então p = 13 e q = 31. O produto N destes dois números primos é igual a 403. Podemos calcular facilmente a ordem de 403. É equivalente a (13 - 1) \cdot (31 - 1) = 360.

Em seguida, como ditado pelo passo 3 do problema RSA, temos de selecionar um coprimo para 360 que seja maior do que 2 e menor do que 360. Não é necessário selecionar este valor aleatoriamente. Suponhamos que seleccionamos 103. Este é um coprimo de 360, pois o seu maior divisor comum com 103 é 1.

O passo 4 requer agora que calculemos um valor d tal que 103 \cdot d \mod 360 = 1. Esta não é uma tarefa fácil quando o valor de N é grande. É necessário utilizar um procedimento chamado algoritmo euclidiano alargado.

Embora eu não mostre o procedimento aqui, ele produz o valor 7 quando e = 103. Pode verificar que o par de valores 103 e 7 satisfaz de facto a condição geral e \cdot d \mod \phi(n) = 1 através dos cálculos abaixo.

É importante notar que, dada a Proposição 4, sabemos que nenhum outro número inteiro entre 1 e 360 para d produzirá o resultado que 103 \cdot d = 1 \mod 360. Adicionalmente, a proposição implica que selecionar um valor diferente para e, produzirá um valor único diferente para d.

No passo 5 do problema RSA, temos de selecionar um número inteiro positivo y que seja um coprimo menor de 403. Suponhamos que definimos y = 2^{103}. A exponenciação de 2 por 103 dá o resultado abaixo.

O problema RSA neste exemplo específico é agora o seguinte: São-lhe fornecidos N = 403, e = 103 e y = 349 \mod 403. Tem agora de calcular x de modo a que x^{103} = 349 \mod 403. Ou seja, tens de descobrir que o valor original antes da exponenciação por 103 era 2.

Seria fácil (pelo menos para um computador) calcular x se soubéssemos que d = 7. Nesse caso, bastava determinar x da seguinte forma.

O problema é que não lhe foi dada a informação de que d = 7. Poderia, evidentemente, calcular d a partir do facto de que 103 \cdot d = 1 \mod 360. O problema é que também não lhe foi dada a informação de que a ordem de N = 360. Finalmente, também poderias calcular a ordem de 403 calculando o seguinte produto: (p - 1) \cdot (q - 1). Mas também não lhe é dito que p = 13 e q = 31.

É claro que um computador pode resolver o problema do RSA para este exemplo com relativa facilidade, porque os números primos envolvidos não são grandes. Mas quando os números primos se tornam muito grandes, o computador enfrenta uma tarefa praticamente impossível.

Apresentámos agora o problema do RSA, um conjunto de condições em que é difícil e a matemática subjacente. Como é que isto ajuda na criptografia assimétrica? Especificamente, como podemos transformar a dificuldade do problema RSA sob certas condições num esquema de encriptação ou num esquema de assinatura digital?

Uma abordagem é pegar no problema RSA e construir esquemas de uma forma simples. Por exemplo, suponha que gerou um conjunto de variáveis \Pi como descrito no problema RSA e que p e q são suficientemente grandes. Define a sua chave pública como (N, e) e partilha esta informação com o mundo. Como descrito acima, mantém os valores de p, q, \phi(n) e d em segredo. De facto, d é a sua chave privada.

Qualquer pessoa que queira enviar-lhe uma mensagem m que seja um elemento de C_N pode simplesmente encriptá-la da seguinte forma: c = m^e \mod N. (O texto cifrado c aqui é equivalente ao valor y no problema RSA.) Pode facilmente desencriptar esta mensagem calculando apenas c^d \mod N.

Pode tentar criar um esquema de assinatura digital da mesma forma. Suponha que quer enviar a alguém uma mensagem m com uma assinatura digital S. Pode simplesmente definir S = m^d \mod N e enviar o par (m,S) para o destinatário. Qualquer pessoa pode verificar a assinatura digital apenas verificando se S^e \mod N = m \mod N. Qualquer atacante, no entanto, teria muita dificuldade em criar um S válido para uma mensagem, dado que não possui d.

Infelizmente, transformar o que é por si só um problema difícil, o problema RSA, num esquema criptográfico não é assim tão simples. Para o esquema de encriptação simples, só é possível selecionar coprimes de N como mensagens. Isto não nos deixa com muitas mensagens possíveis, certamente não as suficientes para uma comunicação normal. Além disso, estas mensagens têm de ser selecionadas aleatoriamente. Isto parece pouco prático. Finalmente, qualquer mensagem que seja selecionada duas vezes produzirá exatamente o mesmo texto cifrado. Isto é extremamente indesejável em qualquer esquema de encriptação e não corresponde a qualquer noção moderna e rigorosa de segurança na encriptação.

Os problemas tornam-se ainda piores para o nosso esquema de assinatura digital simples. Tal como está, qualquer atacante pode facilmente falsificar assinaturas digitais apenas selecionando primeiro um coprimo de N como assinatura e depois calculando a mensagem original correspondente. Este facto quebra claramente o requisito da não falsificabilidade existencial.

No entanto, com a adição de um pouco de complexidade inteligente, o problema RSA pode ser utilizado para criar um esquema seguro de encriptação de chave pública, bem como um esquema seguro de assinatura digital. Não entraremos aqui nos pormenores de tais construções. [4] No entanto, é importante notar que esta complexidade adicional não altera o problema fundamental do RSA em que estes esquemas se baseiam.

Notas:

[4] Ver, por exemplo, Jonathan Katz e Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), pp. 410-32 sobre a encriptação RSA e pp. 444-41 sobre as assinaturas digitais RSA.

Seção final

Revisão & Avaliação

366d6fd0-ceb2-4299-bf37-8c6dfcb681d5 true

Exame Final

44882d2b-63cd-4fde-8485-f76f14d8b2fe true

Conclusão

f1905f78-8cf7-5031-949a-dfa8b76079b4 true