name: O Funcionamento Interno das Carteiras de Bitcoin goal: Mergulhar nos princípios criptográficos que alimentam as carteiras de Bitcoin. objectives:
- Definir as noções teóricas necessárias para entender os algoritmos criptográficos usados no Bitcoin.
- Compreender completamente a construção de uma carteira determinística e hierárquica.
- Saber como identificar e reduzir os riscos associados à gestão de uma carteira.
- Entender os princípios das funções de hash, chaves criptográficas e assinaturas digitais.
Uma Jornada ao Coração das Carteiras de Bitcoin
Descubra os segredos das carteiras de Bitcoin determinísticas e hierárquicas com nosso curso CYP201! Seja você um usuário regular ou um entusiasta procurando aprofundar seu conhecimento, este curso oferece uma imersão completa no funcionamento dessas ferramentas que todos usamos diariamente.
Aprenda sobre os mecanismos das funções de hash, assinaturas digitais (ECDSA e Schnorr), frases mnemônicas, chaves criptográficas e a criação de endereços de recebimento, tudo isso enquanto explora estratégias avançadas de segurança.
Este treinamento não só o equipará com o conhecimento para entender a estrutura de uma carteira de Bitcoin, mas também o preparará para mergulhar mais fundo no mundo empolgante da criptografia.
Com uma pedagogia clara, mais de 60 diagramas explicativos e exemplos concretos, o CYP201 permitirá que você entenda de A a Z como sua carteira funciona, para que você possa navegar pelo universo do Bitcoin com confiança. Tome controle dos seus UTXOs hoje, entendendo como funcionam as carteiras HD!
Introdução
Introdução ao Curso
Bem-vindo ao curso CYP201, onde exploraremos em profundidade o funcionamento das carteiras HD de Bitcoin. Este curso é projetado para qualquer pessoa que queira entender os fundamentos técnicos do uso do Bitcoin, seja eles usuários casuais, entusiastas esclarecidos ou futuros especialistas.
O objetivo deste treinamento é dar-lhe as chaves para dominar as ferramentas que você usa diariamente. As carteiras HD de Bitcoin, que estão no coração da sua experiência de usuário, são baseadas em conceitos às vezes complexos, que tentaremos tornar acessíveis. Juntos, vamos desmistificá-los!
Antes de mergulharmos nos detalhes da construção e operação das carteiras de
Bitcoin, começaremos com alguns capítulos sobre as primitivas criptográficas
a saber para o que segue. Começaremos com funções de hash criptográficas,
fundamentais tanto para as carteiras quanto para o próprio protocolo
Bitcoin. Você descobrirá suas principais características, as funções
específicas usadas no Bitcoin e, em um capítulo mais técnico, aprenderá em
detalhes sobre o funcionamento da rainha das funções de hash: SHA256. 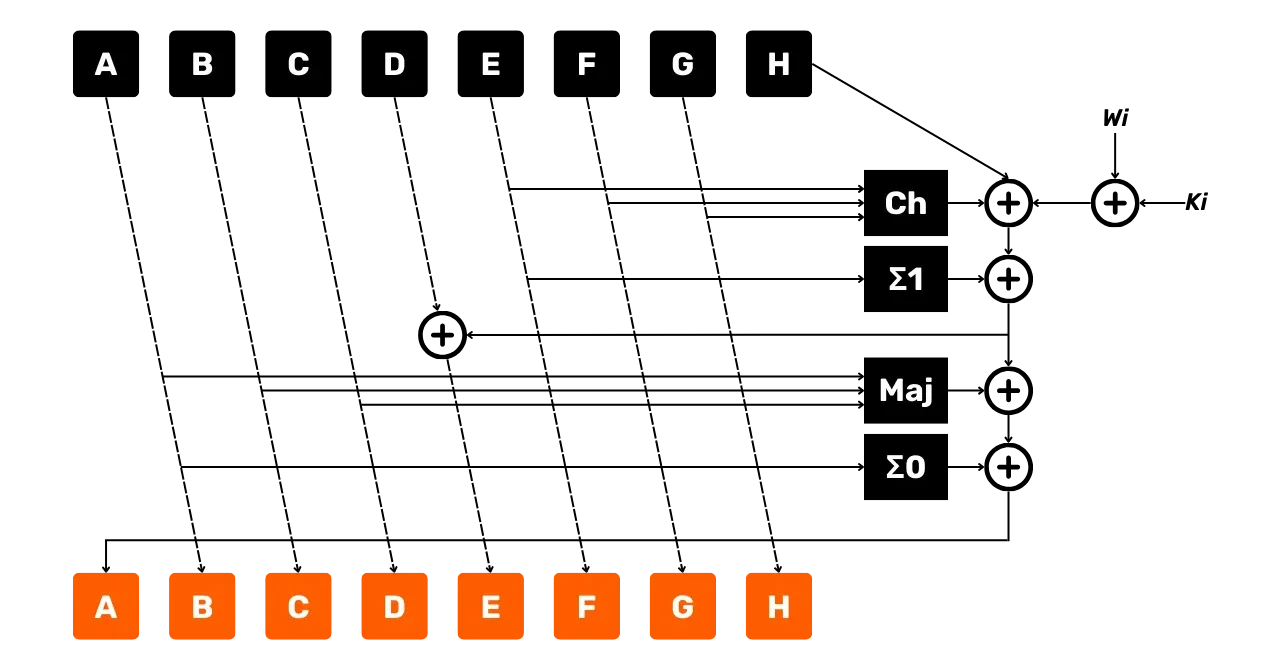
Em seguida, discutiremos o funcionamento dos algoritmos de assinatura digital que você usa todos os dias para proteger seus UTXOs. O Bitcoin usa dois: ECDSA e o protocolo Schnorr. Você aprenderá quais primitivas matemáticas subjazem a esses algoritmos e como eles garantem a segurança das transações.
Uma vez que tenhamos uma boa compreensão desses elementos de criptografia, finalmente passaremos para o coração do treinamento: carteiras determinísticas e hierárquicas! Primeiro, há uma seção dedicada a frases mnemônicas, essas sequências de 12 ou 24 palavras que permitem criar e restaurar suas carteiras. Você descobrirá como essas palavras são geradas a partir de uma fonte de entropia e como facilitam o uso do Bitcoin.
 O treinamento continuará com o estudo da frase-senha BIP39, a semente (não confundir
com a frase mnemônica), o código da cadeia mestre e a chave mestra. Veremos em
detalhes o que são esses elementos, seus respectivos papéis e como são calculados.
O treinamento continuará com o estudo da frase-senha BIP39, a semente (não confundir
com a frase mnemônica), o código da cadeia mestre e a chave mestra. Veremos em
detalhes o que são esses elementos, seus respectivos papéis e como são calculados. 
Finalmente, a partir da chave mestra, descobriremos como pares de chaves criptográficas são derivados de maneira determinística e hierárquica até os endereços de recebimento.

Este treinamento permitirá que você use seu software de carteira com confiança, ao mesmo tempo em que aprimora suas habilidades para identificar e mitigar riscos. Prepare-se para se tornar um verdadeiro especialista em carteiras Bitcoin!
Funções de Hash
Introdução às Funções de Hash
O primeiro tipo de algoritmos criptográficos usados no Bitcoin engloba as funções de hash. Elas desempenham um papel essencial em diferentes níveis do protocolo, mas também dentro das carteiras Bitcoin. Vamos descobrir juntos o que é uma função de hash e para que serve no Bitcoin.
Definição e Princípio do Hashing
Hashing é um processo que transforma informações de comprimento arbitrário em outra peça de informação de comprimento fixo por meio de uma função de hash criptográfica. Em outras palavras, uma função de hash recebe uma entrada de qualquer tamanho e a converte em uma impressão digital de tamanho fixo, chamada de "hash". O hash também pode ser referido às vezes como "digest", "condensado", ou "hashed".
Por exemplo, a função de hash SHA256 produz um hash de comprimento fixo de 256 bits. Assim, se usarmos a entrada "PlanB", uma mensagem de comprimento arbitrário, o hash gerado será a seguinte impressão digital de 256 bits:
24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688

Características das Funções de Hash
Essas funções de hash criptográficas têm várias características essenciais que as tornam particularmente úteis no contexto do Bitcoin e de outros sistemas computacionais:
- Irreversibilidade (ou resistência à imagem prévia)
- Resistência à adulteração (efeito avalanche)
- Resistência à colisão
- Resistência à segunda imagem prévia
1. Irreversibilidade (resistência à imagem prévia):
A irreversibilidade significa que é fácil calcular o hash a partir da informação de entrada, mas que o cálculo inverso, ou seja, encontrar a entrada a partir do hash, é praticamente impossível. Essa propriedade torna as funções de hash perfeitas para criar impressões digitais únicas sem comprometer a informação original.
No exemplo dado, obter o hash 24f1b9… sabendo a entrada "PlanB" é simples e rápido. No entanto, encontrar a mensagem "PlanB"
apenas sabendo 24f1b9… é impossível.

Portanto, é impossível encontrar uma imagem prévia m para um hash h tal que h = \text{HASH}(m),
onde \text{HASH} é uma
função de hash criptográfica.
2. Resistência à adulteração (efeito avalanche)
A segunda característica é a resistência à adulteração, também conhecida como efeito avalanche. Esta característica é observada em uma função de hash se uma pequena alteração na mensagem de entrada resulta em uma mudança radical no hash de saída. Se voltarmos ao nosso exemplo com a entrada "PlanB" e a função SHA256, vimos que o hash gerado é o seguinte:
24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688
Se fizermos uma alteração muito leve na entrada, usando desta vez "Planb", então simplesmente mudar de um "B" maiúsculo para um "b" minúsculo altera completamente o hash de saída do SHA256:
bb038b4503ac5d90e1205788b00f8f314583c5e22f72bec84b8735ba5a36df3f

Esta propriedade garante que até mesmo uma alteração menor da mensagem original é imediatamente detectável, pois não apenas muda uma pequena parte do hash, mas o hash inteiro. Isso pode ser de interesse em vários campos para verificar a integridade de mensagens, software ou até mesmo transações de Bitcoin.
3. Resistência à Colisão
A terceira característica é a resistência à colisão. Uma função de hash é
resistente à colisão se for computacionalmente impossível encontrar 2
mensagens diferentes que produzam o mesmo hash a partir da função.
Formalmente, é difícil encontrar duas mensagens distintas m_1 e m_2 tal que:
\text{HASH}(m_1) = \text{HASH}(m_2)
Na realidade, é matematicamente inevitável que existam colisões para funções
de hash, porque o tamanho das entradas pode ser maior que o tamanho das
saídas. Isso é conhecido como o princípio da gaveta de Dirichlet: se n objetos são distribuídos em m gavetas, com m < n,
então pelo menos uma gaveta necessariamente conterá dois ou mais objetos.
Para uma função de hash, este princípio se aplica porque o número de
mensagens possíveis é (quase) infinito, enquanto o número de hashes
possíveis é finito (2^{256} no caso do SHA256).
Assim, esta característica não significa que não existam colisões para
funções de hash, mas sim que uma boa função de hash torna a probabilidade de
encontrar uma colisão negligenciável. Esta característica, por exemplo, já
não é verificada nos algoritmos SHA-0 e SHA-1, predecessores do SHA-2, para
os quais colisões foram encontradas. Essas funções são, portanto, agora
desaconselhadas e muitas vezes consideradas obsoletas. Para uma função de
hash de n bits, a resistência
à colisão é da ordem de 2^{\frac{n}{2}}, de acordo com o ataque de aniversário. Por exemplo, para SHA256 (n = 256), a complexidade de encontrar uma colisão é da ordem de 2^{128} tentativas. Em termos práticos, isso significa que se passar 2^{128} mensagens diferentes
pela função, é provável encontrar uma colisão.
4. Resistência à Segunda Pré-imagem
A resistência à segunda pré-imagem é outra característica importante das
funções de hash. Ela afirma que, dado uma mensagem m_1 e seu hash h, é
computacionalmente inviável encontrar outra mensagem m_2 \neq m_1 tal que:
\text{HASH}(m_1) = \text{HASH}(m_2)Portanto, a resistência à segunda pré-imagem é um pouco semelhante à
resistência à colisão, exceto que aqui, o ataque é mais difícil porque o
atacante não pode escolher livremente m_1.

Aplicações de Funções Hash no Bitcoin
A função hash mais usada no Bitcoin é SHA256 ("Secure Hash Algorithm 256 bits"). Projetada no início dos anos 2000 pela NSA e padronizada pelo NIST, ela produz uma saída de hash de 256 bits.
Esta função é usada em muitos aspectos do Bitcoin. No nível do protocolo, ela está envolvida no mecanismo de Prova de Trabalho, onde é aplicada em duplo hash para buscar uma colisão parcial entre o cabeçalho de um bloco candidato, criado por um minerador, e o alvo de dificuldade. Se essa colisão parcial é encontrada, o bloco candidato torna-se válido e pode ser adicionado à blockchain.
SHA256 também é usado na construção de uma árvore de Merkle, que é notavelmente o acumulador usado para registrar transações em blocos. Esta estrutura também é encontrada no protocolo Utreexo, que permite reduzir o tamanho do Conjunto UTXO. Além disso, com a introdução do Taproot em 2021, SHA256 é explorado em MAST (Merkelised Alternative Script Tree), que permite revelar apenas as condições de gasto realmente usadas em um script, sem divulgar as outras opções possíveis. Ele também é usado no cálculo de identificadores de transação, na transmissão de pacotes pela rede P2P, em assinaturas eletrônicas... Finalmente, e isso é de particular interesse neste treinamento, SHA256 é usado no nível de aplicação para a construção de carteiras Bitcoin e a derivação de endereços.
Na maioria das vezes, quando você se depara com o uso de SHA256 no Bitcoin, será na verdade um duplo hash SHA256, notado "HASH256", que simplesmente consiste em aplicar SHA256 duas vezes sucessivamente: HASH256(m) = SHA256(SHA256(m))
Esta prática de duplo hash adiciona uma camada extra de segurança contra certos ataques potenciais, mesmo que um único SHA256 seja hoje considerado criptograficamente seguro.
Outra função de hash disponível na linguagem Script e usada para derivar endereços de recebimento é a função RIPEMD160. Esta função produz um hash de 160 bits (portanto, mais curto que SHA256). Geralmente, ela é combinada com SHA256 para formar a função HASH160:
\text{HASH160}(m) = \text{RIPEMD160}(\text{SHA256}(m))Esta combinação é usada para gerar hashes mais curtos, notavelmente na criação de certos endereços Bitcoin que representam hashes de chaves ou hashes de script, bem como para produzir impressões digitais de chaves.
Finalmente, apenas no nível de aplicação, a função SHA512 às vezes também é usada, que indiretamente desempenha um papel na derivação de chaves para carteiras. Esta função é muito semelhante ao SHA256 em sua operação; ambos pertencem à mesma família SHA2, mas SHA512 produz, como seu nome indica, um hash de 512 bits, comparado a 256 bits para SHA256. Detalharemos seu uso nos próximos capítulos.
Agora você conhece os conceitos básicos essenciais sobre funções de hash para o que segue. No próximo capítulo, proponho descobrir em mais detalhes o funcionamento da função que está no coração do Bitcoin: SHA256. Vamos dissecá-la para entender como ela alcança as características que descrevemos aqui. Este próximo capítulo é bastante longo e técnico, mas não é essencial para seguir o restante do treinamento. Então, se você tiver dificuldade em entendê-lo, não se preocupe e passe diretamente para o capítulo seguinte, que será muito mais acessível.
O Funcionamento Interno do SHA256
905eb320-f15b-5fb6-8d2d-5bb447337deb Anteriormente, vimos que as funções de hashing possuem características importantes que justificam seu uso no Bitcoin. Vamos agora examinar os mecanismos internos dessas funções de hashing que lhes conferem essas propriedades, e para fazer isso, proponho dissecar o funcionamento do SHA256. As funções SHA256 e SHA512 pertencem à mesma família SHA2. Seu mecanismo é baseado em uma construção específica chamada construção de Merkle-Damgård. RIPEMD160 também usa esse mesmo tipo de construção.
Como lembrete, temos uma mensagem de tamanho arbitrário como entrada para o SHA256, e vamos passá-la pela função para obter um hash de 256 bits como saída.
Pré-processamento da entrada
Para começar, precisamos preparar nossa mensagem de entrada m para que ela tenha um comprimento padrão que seja múltiplo de 512 bits. Esta
etapa é crucial para o funcionamento adequado do algoritmo posteriormente.
Para fazer isso, começamos com a etapa de bits de preenchimento. Primeiro,
adicionamos um bit separador 1 à mensagem, seguido por um certo
número de bits 0. O número de bits 0 adicionados é
calculado para que o comprimento total da mensagem após essa adição seja
congruente a 448 módulo 512. Assim, o comprimento L da mensagem com os bits de preenchimento
é igual a:
L \equiv 448 \mod 512\text{mod}, para
módulo, é uma operação matemática que, entre dois inteiros, retorna o resto
da divisão euclidiana do primeiro pelo segundo. Por exemplo: 16 \mod 5 = 1. É uma operação
amplamente utilizada em criptografia.
Aqui, a etapa de preenchimento garante que, após adicionar os 64 bits na
próxima etapa, o comprimento total da mensagem equalizada será um múltiplo
de 512 bits. Se a mensagem inicial tem um comprimento de M bits, o número (N) de bits 0 a ser adicionado é assim:
N = (448 - (M + 1) \mod 512) \mod 512Por exemplo, se a mensagem inicial for de 950 bits, o cálculo seria o seguinte:
\begin{align*}
M & = 950 \\
M + 1 & = 951 \\
(M + 1) \mod 512 & = 951 \mod 512 \\
& = 951 - 512 \cdot \left\lfloor \frac{951}{512} \right\rfloor \\
& = 951 - 512 \cdot 1 \\
& = 951 - 512 \\
& = 439 \\
\\
448 - (M + 1) \mod 512 & = 448 - 439 \\
& = 9 \\
\\
N & = (448 - (M + 1) \mod 512) \mod 512 \\
N & = 9 \mod 512 \\
& = 9
\end{align*}Assim, teríamos 9 0s além do separador 1. Nossos
bits de preenchimento a serem adicionados diretamente após nossa mensagem M seriam assim:
1000 0000 00
Após adicionar os bits de preenchimento à nossa mensagem M, também adicionamos uma representação de 64 bits do comprimento original
da mensagem M, expressa em
binário. Isso permite que a função de hash seja sensível à ordem dos bits e
ao comprimento da mensagem. Se voltarmos ao nosso exemplo com uma mensagem
inicial de 950 bits, convertemos o número decimal 950 para
binário, o que nos dá 1110 1101 10. Completamos esse número com
zeros na base para fazer um total de 64 bits. No nosso exemplo, isso resulta
em:
0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0011 1011 0110
Este tamanho de preenchimento é adicionado seguindo o preenchimento de bits. Portanto, a mensagem após nosso pré-processamento consiste em três partes:
- A mensagem original
M; - Um bit
1seguido por vários bits0para formar o preenchimento de bits; - Uma representação de 64 bits do comprimento de
Mpara formar o preenchimento com o tamanho.

Inicialização de Variáveis
SHA256 usa oito variáveis de estado inicial, denotadas de A a H, cada uma de 32 bits.
Essas variáveis são inicializadas com constantes específicas, que são as
partes fracionárias das raízes quadradas dos primeiros oito números primos.
Usaremos esses valores subsequentemente durante o processo de hash:
A = 0x6a09e667B = 0xbb67ae85C = 0x3c6ef372D = 0xa54ff53aE = 0x510e527fF = 0x9b05688cG = 0x1f83d9abH = 0x5be0cd19
SHA256 também usa outras 64 constantes, denotadas de K_0 a K_{63}, que são
as partes fracionárias das raízes cúbicas dos primeiros 64 números primos:
K[0 \ldots 63] = \begin{pmatrix}
0x428a2f98, & 0x71374491, & 0xb5c0fbcf, & 0xe9b5dba5, \\
0x3956c25b, & 0x59f111f1, & 0x923f82a4, & 0xab1c5ed5, \\
0xd807aa98, & 0x12835b01, & 0x243185be, & 0x550c7dc3, \\
0x72be5d74, & 0x80deb1fe, & 0x9bdc06a7, & 0xc19bf174, \\
0xe49b69c1, & 0xefbe4786, & 0x0fc19dc6, & 0x240ca1cc, \\
0x2de92c6f, & 0x4a7484aa, & 0x5cb0a9dc, & 0x76f988da, \\
0x983e5152, & 0xa831c66d, & 0xb00327c8, & 0xbf597fc7, \\
0xc6e00bf3, & 0xd5a79147, & 0x06ca6351, & 0x14292967, \\
0x27b70a85, & 0x2e1b2138, & 0x4d2c6dfc, & 0x53380d13, \\
0x650a7354, & 0x766a0abb, & 0x81c2c92e, & 0x92722c85, \\
0xa2bfe8a1, & 0xa81a664b, & 0xc24b8b70, & 0xc76c51a3, \\
0xd192e819, & 0xd6990624, & 0xf40e3585, & 0x106aa070, \\
0x19a4c116, & 0x1e376c08, & 0x2748774c, & 0x34b0bcb5, \\
0x391c0cb3, & 0x4ed8aa4a, & 0x5b9cca4f, & 0x682e6ff3, \\
0x748f82ee, & 0x78a5636f, & 0x84c87814, & 0x8cc70208, \\
0x90befffa, & 0xa4506ceb, & 0xbef9a3f7, & 0xc67178f2
\end{pmatrix}Divisão da Entrada
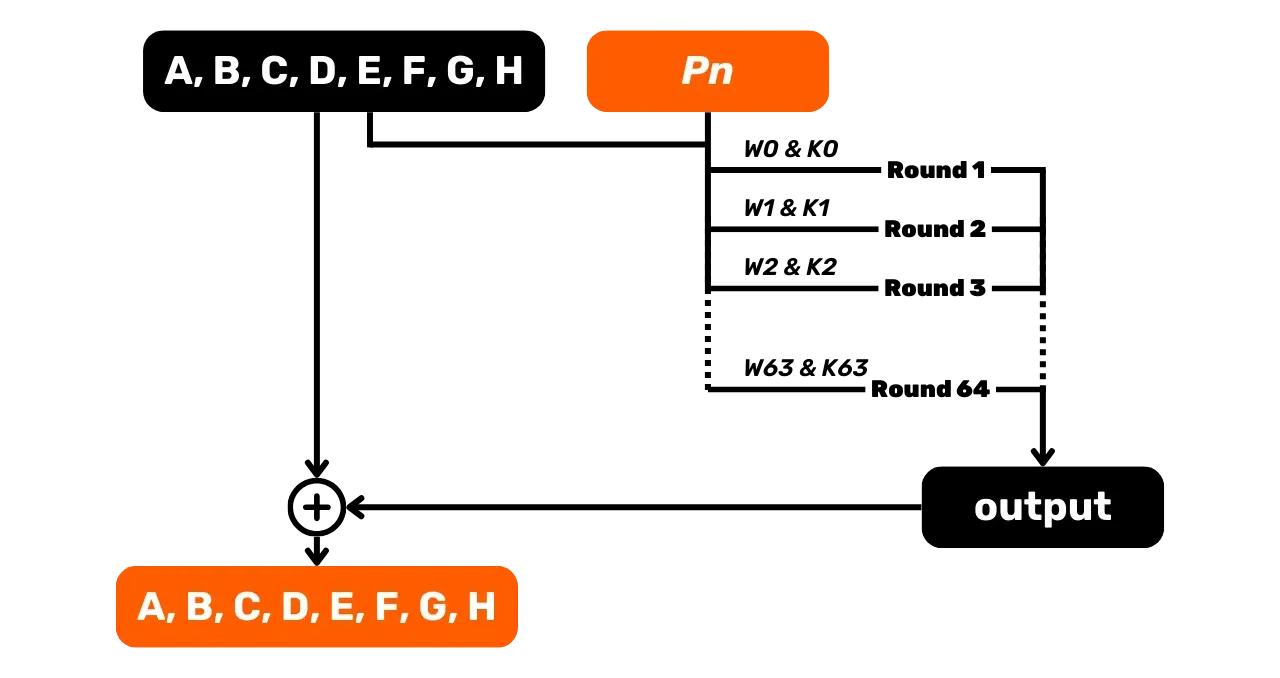
Agora que temos uma entrada equalizada, vamos agora avançar para a fase principal de processamento do algoritmo SHA256: a função de compressão. Esta etapa é muito importante, pois é principalmente o que confere à função hash suas propriedades criptográficas que estudamos no capítulo anterior.
Primeiro, começamos dividindo nossa mensagem equalizada (resultado das
etapas de pré-processamento) em vários blocos P de 512 bits cada. Se nossa mensagem equalizada tem um tamanho total de n \times 512 bits, teremos, portanto, n blocos, cada um de 512 bits. Cada bloco de 512 bits será processado
individualmente pela função de compressão, que consiste em 64 rodadas de
operações sucessivas. Vamos nomear esses blocos P_1, P_2, P_3...
Operações Lógicas
Antes de explorar a função de compressão em detalhes, é importante entender as operações lógicas básicas usadas nela. Essas operações, baseadas na álgebra booleana, operam no nível de bit. As operações lógicas básicas usadas são:
- Conjunção (AND): denotada
\land, corresponde a um "E" lógico. - Disjunção (OR): denotada
\lor, corresponde a um "OU" lógico. - Negação (NOT): denotada
\lnot, corresponde a um "NÃO" lógico.
A partir dessas operações básicas, podemos definir operações mais complexas,
como o "OU Exclusivo" (XOR) denotado \oplus, que é amplamente usado em criptografia. Cada operação lógica pode ser
representada por uma tabela verdade, que indica o resultado para todas as
combinações possíveis de valores de entrada binários (dois operandos p e q). Para XOR (\oplus):
p | q | p \oplus q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Para AND (\land):
p | q | p \land q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Para NOT (\lnot p):
p | \lnot p |
|---|---|
| 0 | 1 |
| 1 | 0 |
Vamos pegar um exemplo para entender a operação de XOR ao nível de bit. Se temos dois números binários em 6 bits:
a = 101100b = 001000
Então:
a \oplus b = 101100 \oplus 001000 = 100100
Aplicando XOR bit a bit:
| Posição do Bit | a | b | a \oplus b |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 1 | 0 | 1 |
| 5 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 |
O resultado é, portanto, 100100.
Além das operações lógicas, a função de compressão usa operações de deslocamento de bits, que desempenharão um papel essencial na difusão de bits no algoritmo.
Primeiro, há a operação de deslocamento lógico para a direita, denotada ShR_n(x), que desloca todos os bits de x para a direita por n posições,
preenchendo os bits vagos à esquerda com zeros.
Por exemplo, para x = 101100001 (em 9 bits) e n = 4:
ShR_4(101100001) = 000010110
Esquematicamente, a operação de deslocamento para a direita pode ser vista assim:
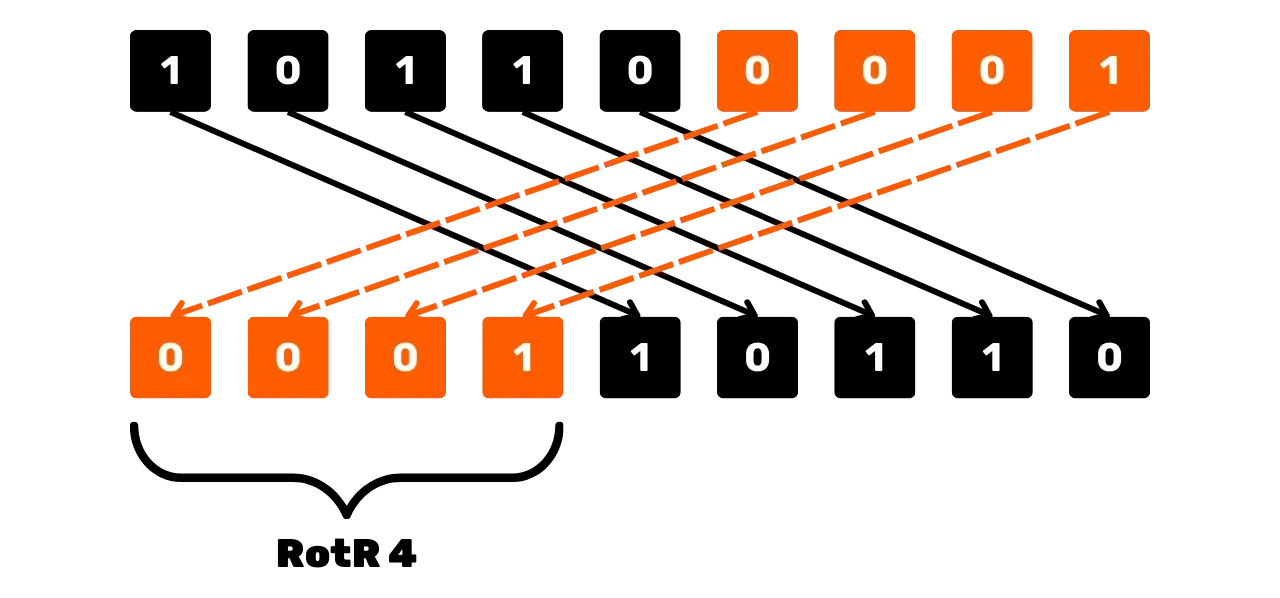
 Outra operação usada no SHA256 para manipulação de bits é a rotação circular
à direita, denotada
Outra operação usada no SHA256 para manipulação de bits é a rotação circular
à direita, denotada RotR_n(x), que desloca os
bits de x para a direita por n posições, reinserindo os bits deslocados no início da string. Por exemplo,
para x = 101100001 (em 9
bits) e n = 4:
RotR_4(101100001) = 000110110
Esquematicamente, a operação de rotação circular à direita pode ser vista assim:
Função de Compressão
Agora que entendemos as operações básicas, vamos examinar a função de compressão SHA256 em detalhes.
Na etapa anterior, dividimos nossa entrada em várias peças de 512 bits P. Para cada bloco de 512 bits P, temos:
- As palavras da mensagem
W_i: paraide 0 a 63. - As constantes
K_i: paraide 0 a 63, definidas na etapa anterior. - As variáveis de estado
A, B, C, D, E, F, G, H: inicializadas com os valores da etapa anterior. As primeiras 16 palavras,W_0atéW_{15}, são extraídas diretamente do bloco processado de 512 bitsP. Cada palavraW_iconsiste em 32 bits consecutivos do bloco. Então, por exemplo, pegamos nossa primeira peça de entradaP_1, e a dividimos em pedaços menores de 32 bits que chamamos de palavras. As próximas 48 palavras (W_{16}atéW_{63}) são geradas usando a seguinte fórmula:
W_i = W_{i-16} + \sigma*0(W_{i-15}) + W_{i-7} + \sigma_1(W_{i-2}) \mod 2^{32}
Com:
\sigma_0(x) = RotR_7(x) \oplus RotR_{18}(x) \oplus ShR_3(x)\sigma_1(x) = RotR_{17}(x) \oplus RotR_{19}(x) \oplus ShR_{10}(x)
Neste caso, x é igual a W_{i-15} para \sigma_0(x) e W_{i-2} para \sigma_1(x).
Uma vez que determinamos todas as palavras W_i para nossa peça de 512 bits, podemos prosseguir para a função de compressão,
que consiste em realizar 64 rodadas.
 Para cada rodada
Para cada rodada i de 0 a 63,
temos três tipos diferentes de entradas. Primeiro, o W_i que acabamos de determinar, consistindo parcialmente de nossa peça de
mensagem P_n. Em seguida, as
64 constantes K_i.
Finalmente, usamos as variáveis de estado A, B, C, D, E, F, G e H, que evoluirão ao longo
do processo de hashing e serão modificadas a cada função de compressão. No
entanto, para a primeira peça P_1, usamos as constantes
iniciais dadas anteriormente. Então, realizamos as seguintes operações em
nossas entradas:
- Função
\Sigma_0:
\Sigma*0(A) = RotR_2(A) \oplus RotR_{13}(A) \oplus RotR\_{22}(A)
- Função
\Sigma_1:
\Sigma*1(E) = RotR_6(E) \oplus RotR_{11}(E) \oplus RotR\_{25}(E)
- Função
Ch("Escolha"):
Ch(E, F, G) = (E \land F) \oplus (\lnot E \land G)
- Função
Maj("Maioria"):
Maj(A, B, C) = (A \land B) \oplus (A \land C) \oplus (B \land C)
Em seguida, calculamos 2 variáveis temporárias:
temp1:
temp1 = H + \Sigma_1(E) + Ch(E, F, G) + K_i + W_i \mod 2^{32}
temp2:
temp2 = \Sigma_0(A) + Maj(A, B, C) \mod 2^{32}
A seguir, atualizamos as variáveis de estado da seguinte forma:
\begin{cases}
H = G \\
G = F \\
F = E \\
E = D + temp1 \mod 2^{32} \\
D = C \\
C = B \\
B = A \\
A = temp1 + temp2 \mod 2^{32}
\end{cases}
O diagrama a seguir representa uma rodada da função de compressão SHA256 como acabamos de descrever:

- As setas indicam o fluxo de dados;
- As caixas representam as operações realizadas;
- O
+cercado representa a adição módulo2^{32}.
Já podemos observar que esta rodada produz novas variáveis de estado A, B, C, D, E, F, G e H. Essas novas variáveis
servirão como entrada para a próxima rodada, que por sua vez produzirá novas
variáveis A, B, C, D, E, F, G e H, a serem usadas na rodada
seguinte. Esse processo continua até a 64ª rodada. Após as 64 rodadas,
atualizamos os valores iniciais das variáveis de estado adicionando-os aos
valores finais ao final da rodada 64:
\begin{cases}
A = A_{\text{inicial}} + A \mod 2^{32} \\
B = B_{\text{inicial}} + B \mod 2^{32} \\
C = C_{\text{inicial}} + C \mod 2^{32} \\
D = D_{\text{inicial}} + D \mod 2^{32} \\
E = E_{\text{inicial}} + E \mod 2^{32} \\
F = F_{\text{inicial}} + F \mod 2^{32} \\
G = G_{\text{inicial}} + G \mod 2^{32} \\
H = H_{\text{inicial}} + H \mod 2^{32}
\end{cases}Esses novos valores de A, B, C, D, E, F, G e H servirão como os valores
iniciais para o próximo bloco, P_2. Para este bloco P_2, replicamos o mesmo
processo de compressão com 64 rodadas, depois atualizamos as variáveis para
o bloco P_3, e assim por
diante até o último bloco de nossa entrada equalizada.
Após processar todos os blocos de mensagem, concatenamos os valores finais
das variáveis A, B, C, D, E, F, G e H para formar o hash final de
256 bits de nossa função de hash:
\text{Hash} = A \Vert B \Vert C \Vert D \Vert E \Vert F \Vert G \Vert HCada variável é um inteiro de 32 bits, então sua concatenação sempre resulta em um resultado de 256 bits, independentemente do tamanho da nossa entrada de mensagem para a função de hash.
Justificação das Propriedades Criptográficas
Mas então, como essa função é irreversível, resistente a colisões e resistente a adulterações?
Para a resistência a adulterações, é bastante simples de entender. São
realizados tantos cálculos em cascata, que dependem tanto da entrada quanto
das constantes, que a menor modificação da mensagem inicial muda
completamente o caminho tomado, e assim, muda completamente o hash de saída.
Isso é o que se chama de efeito avalanche. Essa propriedade é parcialmente
assegurada pela mistura dos estados intermediários com os estados iniciais
para cada peça. A seguir, ao discutir uma função de hash criptográfica, o
termo "irreversibilidade" geralmente não é usado. Em vez disso, falamos
sobre "resistência à pré-imagem", que especifica que para qualquer y dado, é difícil encontrar um x tal que h(x) = y. Esta
resistência à pré-imagem é garantida pela complexidade algébrica e pela
forte não-linearidade das operações realizadas na função de compressão, bem
como pela perda de certas informações no processo. Por exemplo, para um dado
resultado de uma adição módulo, existem vários operandos possíveis:$$ 3+2
\mod 10 = 5 \ 7+8 \mod 10 = 5 \ 5+10 \mod 10 = 5
Neste exemplo, sabendo apenas o módulo usado (10) e o resultado (5), não se pode determinar com certeza quais são os operandos corretos usados na adição. Diz-se que existem múltiplas congruências módulo 10.
Para a operação XOR, enfrentamos o mesmo problema. Lembre-se da tabela verdade para esta operação: qualquer saída de 1 bit pode ser determinada por duas configurações de entrada diferentes que têm exatamente a mesma probabilidade de serem os valores corretos. Portanto, não se pode determinar com certeza os operandos de um XOR sabendo apenas seu resultado. Se aumentarmos o tamanho dos operandos do XOR, o número de entradas possíveis sabendo apenas o resultado aumenta exponencialmente. Além disso, o XOR é frequentemente usado junto com outras operações a nível de bit, como a operação $\text{RotR}$, que adiciona ainda mais possíveis interpretações ao resultado.
A função de compressão também usa a operação $\text{ShR}$. Esta operação remove uma parte da informação básica, que depois se torna impossível de recuperar. Mais uma vez, não há meios algébricos para reverter esta operação. Todas essas operações unidirecionais e de perda de informação são usadas muito frequentemente em funções de compressão. O número de entradas possíveis para uma saída dada é quase infinito, e cada tentativa de cálculo reverso levaria a equações com um número muito alto de incógnitas, que aumentaria exponencialmente a cada etapa.
Finalmente, para a característica de resistência à colisão, vários parâmetros entram em jogo. O pré-processamento da mensagem original desempenha um papel essencial. Sem este pré-processamento, poderia ser mais fácil encontrar colisões na função. Embora, teoricamente, colisões existam (devido ao princípio da casa dos pombos), a estrutura da função de hash, combinada com as propriedades mencionadas, torna a probabilidade de encontrar uma colisão extremamente baixa.
Para que uma função de hash seja resistente à colisão, é essencial que:
- A saída seja imprevisível: Qualquer previsibilidade pode ser explorada para encontrar colisões mais rapidamente do que com um ataque de força bruta. A função garante que cada bit da saída dependa de uma maneira não trivial da entrada. Em outras palavras, a função é projetada de modo que cada bit do resultado final tenha uma probabilidade independente de ser 0 ou 1, mesmo que esta independência não seja absoluta na prática.
- A distribuição dos hashes seja pseudo-aleatória: Isso garante que os hashes sejam uniformemente distribuídos.
- O tamanho do hash seja substancial: quanto maior o espaço possível para resultados, mais difícil é encontrar uma colisão.
Os criptógrafos projetam essas funções avaliando os melhores ataques possíveis para encontrar colisões, ajustando então os parâmetros para tornar esses ataques ineficazes.
### Construção de Merkle-Damgård
A estrutura do SHA256 é baseada na construção de Merkle-Damgård, que permite transformar uma função de compressão em uma função de hash que pode processar mensagens de comprimento arbitrário. É exatamente isso que vimos neste capítulo.
No entanto, algumas funções de hash antigas como SHA1 ou MD5, que usam essa construção específica, são vulneráveis a ataques de extensão de comprimento. Esta é uma técnica que permite a um atacante que conhece o hash de uma mensagem $M$ e o comprimento de $M$ (sem conhecer a própria mensagem) calcular o hash de uma mensagem $M'$ formada pela concatenação de $M$ com conteúdo adicional.
SHA256, mesmo utilizando o mesmo tipo de construção, é teoricamente resistente a este tipo de ataque, ao contrário de SHA1 e MD5. Isso pode explicar o mistério da dupla hash implementada em todo o Bitcoin por Satoshi Nakamoto. Para evitar esse tipo de ataque, Satoshi pode ter preferido usar um duplo SHA256:
\text{HASH256}(m) = \text{SHA256}(\text{SHA256}(m))
Isso aumenta a segurança contra ataques potenciais relacionados à construção de Merkle-Damgård, mas não aumenta a segurança do processo de hash em termos de resistência à colisão. Além disso, mesmo que SHA256 fosse vulnerável a este tipo de ataque, isso não teria um impacto sério, pois todos os casos de uso de funções de hash no Bitcoin envolvem dados públicos. No entanto, o ataque de extensão de comprimento só seria útil para um atacante se os dados hashados fossem privados e o usuário tivesse usado a função de hash como um mecanismo de autenticação para esses dados, semelhante a um MAC. Assim, a implementação da dupla hash permanece um mistério no design do Bitcoin.
Agora que examinamos em detalhes o funcionamento das funções de hash, particularmente SHA256, que é amplamente utilizado no Bitcoin, vamos focar mais especificamente nos algoritmos de derivação criptográfica usados no nível de aplicação, especialmente para derivar as chaves para sua carteira.
## Os algoritmos usados para derivação
<chapterId>cc668121-7789-5e99-bf5e-1ba085f4f5f2</chapterId>
No Bitcoin, no nível de aplicação, além das funções de hash, algoritmos de derivação criptográfica são usados para gerar dados seguros a partir de entradas iniciais. Embora esses algoritmos dependam de funções de hash, eles servem a propósitos diferentes, especialmente em termos de autenticação e geração de chaves. Esses algoritmos retêm algumas das características das funções de hash, como irreversibilidade, resistência a adulteração e resistência a colisões.
Em carteiras de Bitcoin, principalmente 2 algoritmos de derivação são usados:
- **HMAC (*Código de Autenticação de Mensagem Baseado em Hash*)**
- **PBKDF2 (*Função de Derivação de Chave Baseada em Senha 2*)**
Vamos explorar juntos o funcionamento e o papel de cada um deles.
### HMAC-SHA512
HMAC é um algoritmo criptográfico que calcula um código de autenticação com base em uma combinação de uma função de hash e uma chave secreta. O Bitcoin usa HMAC-SHA512, a variante do HMAC que usa a função de hash SHA512. Já vimos no capítulo anterior que SHA512 faz parte da mesma família de funções de hash que SHA256, mas produz uma saída de 512 bits.
Aqui está seu esquema geral de operação com $m$ sendo a mensagem de entrada e $K$ uma chave secreta:
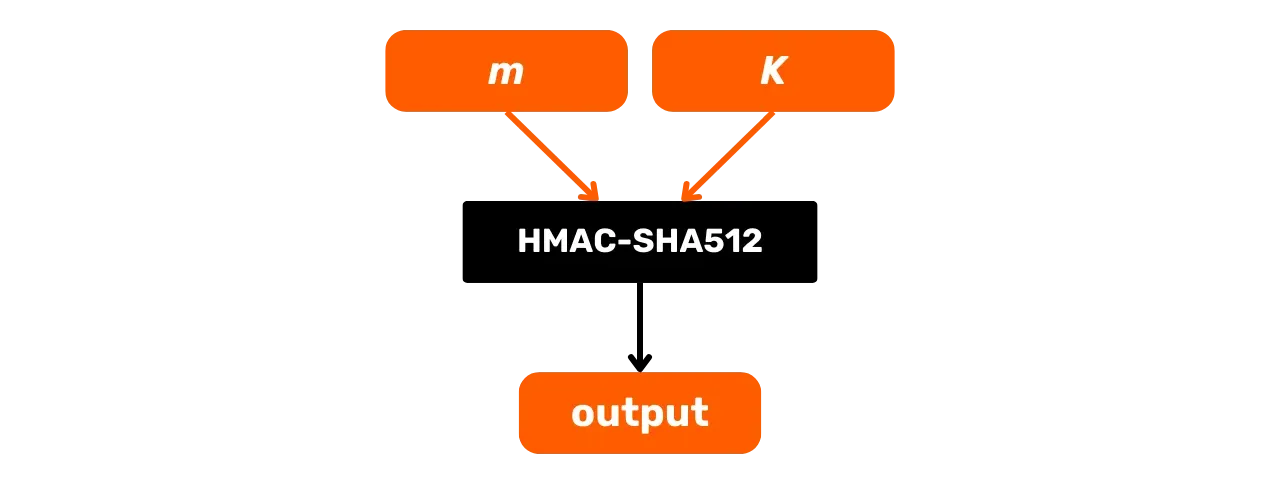
Vamos estudar em mais detalhes o que acontece nesta caixa preta HMAC-SHA512. A função HMAC-SHA512 com:
- $m$: a mensagem de tamanho arbitrário escolhida pelo usuário (primeira entrada);
- $K$: a chave secreta arbitrária escolhida pelo usuário (segunda entrada);
- $K'$: a chave $K$ ajustada ao tamanho $B$ dos blocos da função de hash (1024 bits para SHA512, ou 128 bytes);
- $\text{SHA512}$: a função de hash SHA512;
- $\oplus$: a operação XOR (ou exclusivo);
- $\Vert$: o operador de concatenação, ligando cadeias de bits de ponta a ponta;
- $\text{opad}$: constante composta pelo byte $0x5c$ repetido 128 vezes
- $\text{ipad}$: constante composta pelo byte $0x36$ repetido 128 vezes
Antes de calcular o HMAC, é necessário igualar a chave e as constantes de acordo com o tamanho do bloco $B$. Por exemplo, se a chave $K$ for menor que 128 bytes, ela é preenchida com zeros até atingir o tamanho $B$. Se $K$ for maior que 128 bytes, ela é comprimida usando SHA512, e então zeros são adicionados até que atinja 128 bytes. Desta forma, obtém-se uma chave equalizada denominada $K'$.
Os valores de $\text{opad}$ e $\text{ipad}$ são obtidos repetindo seu byte base ($0x5c$ para $\text{opad}$, $0x36$ para $\text{ipad}$) até que o tamanho $B$ seja alcançado. Assim, com $B = 128$ bytes, temos:
\text{opad} = \underbrace{0x5c5c\ldots5c}_{128 , \text{bytes}}
Uma vez feito o pré-processamento, o algoritmo HMAC-SHA512 é definido pela seguinte equação:
\text {HMAC-SHA512}_K(m) = \text{SHA512} \left( (K' \oplus \text{opad}) \parallel \text{SHA512} \left( (K' \oplus \text{ipad}) \parallel m \right) \right)
Esta equação é dividida nos seguintes passos:
- XOR da chave ajustada $K'$ com $\text{ipad}$ para obter $\text{iKpad}$;
- XOR da chave ajustada $K'$ com $\text{opad}$ para obter $\text{oKpad}$;
- Concatenar $\text{iKpad}$ com a mensagem $m$.
- Fazer o hash deste resultado com SHA512 para obter um hash intermediário $H_1$.
- Concatenar $\text{oKpad}$ com $H_1$.
- Fazer o hash deste resultado com SHA512 para obter o resultado final $H_2$.
Estes passos podem ser resumidos esquematicamente da seguinte forma:
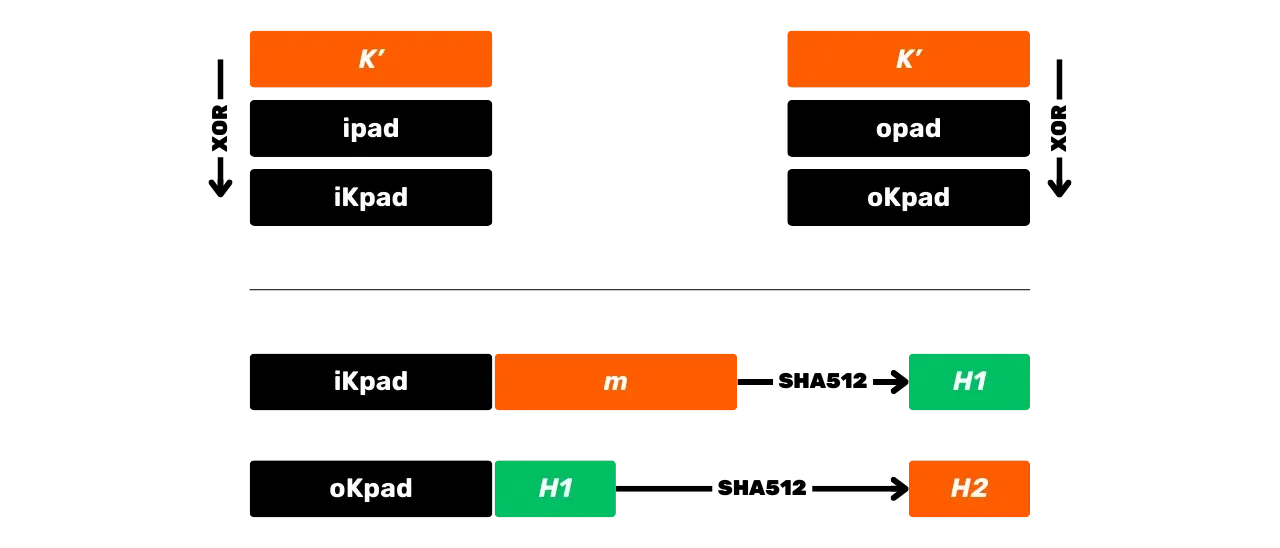
O HMAC é usado no Bitcoin notavelmente para a derivação de chaves em carteiras HD (Hierarchical Deterministic) (falaremos sobre isso com mais detalhes nos próximos capítulos) e como um componente do PBKDF2.
### PBKDF2
PBKDF2 (*Password-Based Key Derivation Function 2*) é um algoritmo de derivação de chave projetado para aumentar a segurança de senhas. O algoritmo aplica uma função pseudo-aleatória (aqui HMAC-SHA512) em uma senha e um sal criptográfico, e então repete esta operação um certo número de vezes para produzir uma chave de saída.
No Bitcoin, o PBKDF2 é usado para gerar a semente de uma carteira HD a partir de uma frase mnemônica e uma passphrase (mas falaremos sobre isso com mais detalhes nos próximos capítulos).
O processo do PBKDF2 é o seguinte, com:
- $m$: a frase mnemônica do usuário;
- $s$: a passphrase opcional para aumentar a segurança (campo vazio se não houver passphrase);
- $n$: o número de iterações da função, no nosso caso, são 2048.
A função PBKDF2 é definida iterativamente. Cada iteração pega o resultado da anterior, passa-o pelo HMAC-SHA512 e combina os resultados sucessivos para produzir a chave final:\text{PBKDF2}(m, s) = \text{HMAC-SHA512}^{2048}(m, s)
Esquematicamente, o PBKDF2 pode ser representado da seguinte forma:
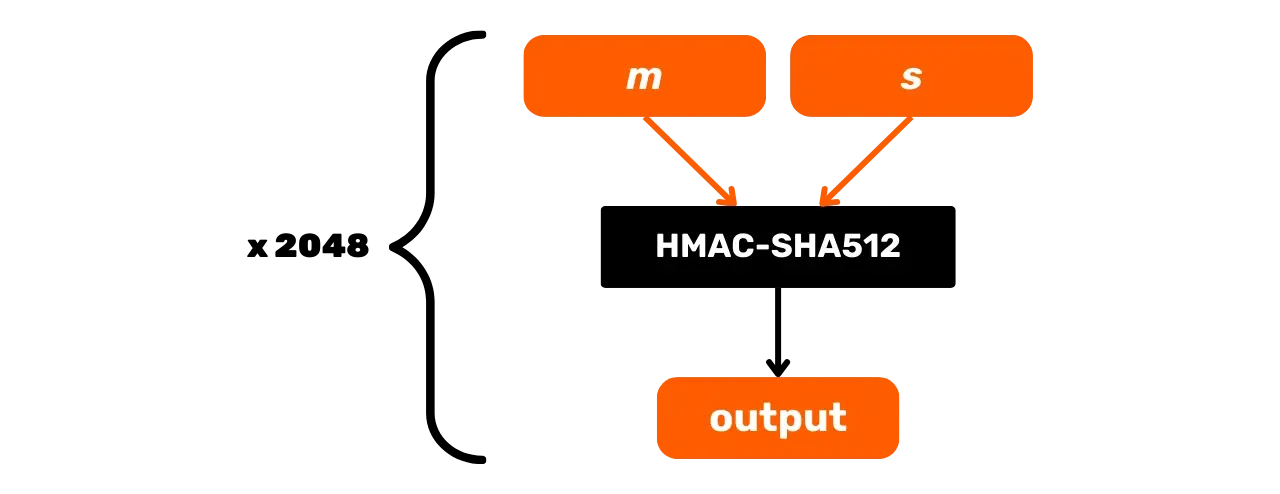
Neste capítulo, exploramos as funções HMAC-SHA512 e PBKDF2, que usam funções de hash para garantir a integridade e segurança das derivações de chaves no protocolo Bitcoin. Na próxima parte, vamos olhar para as assinaturas digitais, outro método criptográfico amplamente utilizado no Bitcoin.
# Assinaturas Digitais
<partId>76b58a00-0c18-54b9-870d-6b7e34029db8</partId>
## Assinaturas Digitais e Curvas Elípticas
<chapterId>c9dd9672-6da1-57f8-9871-8b28994d4c1a</chapterId>
O segundo método criptográfico usado no Bitcoin envolve algoritmos de assinatura digital. Vamos explorar o que isso implica e como funciona.
### Bitcoins, UTXOs e Condições de Gasto
O termo "*carteira*" em Bitcoin pode ser bastante confuso para iniciantes. De fato, o que é chamado de carteira Bitcoin é um software que não guarda diretamente seus bitcoins, ao contrário de uma carteira física que pode conter moedas ou cédulas. Bitcoins são simplesmente unidades de conta. Esta unidade de conta é representada por **UTXO** (*Unspent Transaction Outputs*), que são saídas de transações não gastas. Se essas saídas não são gastas, significa que pertencem a um usuário. UTXOs são, de certa forma, pedaços de bitcoins, de tamanho variável, pertencentes a um usuário.
O protocolo Bitcoin é distribuído e opera sem uma autoridade central. Portanto, não é como os registros bancários tradicionais, onde os euros que pertencem a você são simplesmente associados à sua identidade pessoal. No Bitcoin, seus UTXOs pertencem a você porque são protegidos por condições de gasto especificadas na linguagem Script. Para simplificar, existem dois tipos de scripts: o script de bloqueio (*scriptPubKey*), que protege um UTXO, e o script de desbloqueio (*scriptSig*), que permite desbloquear um UTXO e, assim, gastar as unidades de bitcoin que ele representa.
A operação inicial do Bitcoin com scripts P2PK envolve usar uma chave pública para bloquear fundos, especificando em um *scriptPubKey* que a pessoa que deseja gastar este UTXO deve fornecer uma assinatura válida com a chave privada correspondente a esta chave pública. Para desbloquear este UTXO, é necessário fornecer uma assinatura válida no *scriptSig*. Como seus nomes sugerem, a chave pública é conhecida por todos, pois é transmitida na blockchain, enquanto a chave privada é conhecida apenas pelo legítimo proprietário dos fundos.
Esta é a operação básica do Bitcoin, mas com o tempo, essa operação se tornou mais complexa. Primeiro, Satoshi também introduziu scripts P2PKH, que usam um endereço de recebimento no *scriptPubKey*, que representa o hash da chave pública. Depois, o sistema se tornou ainda mais complexo com a chegada do SegWit e, em seguida, do Taproot. No entanto, o princípio geral permanece fundamentalmente o mesmo: uma chave pública ou uma representação desta chave é usada para bloquear UTXOs, e uma chave privada correspondente é necessária para desbloqueá-los e, assim, gastá-los.
Um usuário que deseja realizar uma transação com Bitcoin deve, portanto, criar uma assinatura digital usando sua chave privada na transação em questão. A assinatura pode ser verificada por outros participantes da rede. Se for válida, isso significa que o usuário que iniciou a transação é de fato o proprietário da chave privada e, portanto, o proprietário dos bitcoins que deseja gastar. Outros usuários podem então aceitar e propagar a transação.
Como resultado, um usuário que possui bitcoins protegidos com uma chave pública deve encontrar uma maneira de armazenar de forma segura o que permite desbloquear seus fundos: a chave privada. Uma carteira de Bitcoin é precisamente um dispositivo que permitirá que você mantenha todas as suas chaves sem que outras pessoas tenham acesso a elas. Portanto, é mais como um chaveiro do que uma carteira.
A ligação matemática entre uma chave pública e uma chave privada, bem como a capacidade de realizar uma assinatura para provar a posse de uma chave privada sem revelá-la, são possibilitadas por um algoritmo de assinatura digital. No protocolo Bitcoin, são usados 2 algoritmos de assinatura: **ECDSA** (*Elliptic Curve Digital Signature Algorithm*) e o **esquema de assinatura Schnorr**. ECDSA é o protocolo de assinatura digital usado no Bitcoin desde seus inícios. Schnorr é mais recente no Bitcoin, pois foi introduzido em novembro de 2021 com a atualização Taproot.
Esses dois algoritmos são bastante semelhantes em seus mecanismos. Ambos são baseados na criptografia de curva elíptica. A principal diferença entre esses dois protocolos reside na estrutura da assinatura e em algumas propriedades matemáticas específicas. Portanto, estudaremos o funcionamento desses algoritmos, começando com o mais antigo: ECDSA.
### Criptografia de Curva Elíptica
Criptografia de Curva Elíptica (ECC) é um conjunto de algoritmos que usam uma curva elíptica por suas várias propriedades matemáticas e geométricas para fins criptográficos. A segurança desses algoritmos depende da dificuldade do problema do logaritmo discreto em curvas elípticas. Curvas elípticas são notavelmente usadas para trocas de chaves, criptografia assimétrica ou para criar assinaturas digitais.
Uma propriedade importante dessas curvas é que elas são simétricas em relação ao eixo x. Assim, qualquer linha não vertical que corte a curva em dois pontos distintos sempre intersectará a curva em um terceiro ponto. Além disso, qualquer tangente à curva em um ponto não singular intersectará a curva em outro ponto. Essas propriedades serão úteis para definir operações na curva.
Aqui está uma representação de uma curva elíptica sobre o campo dos números reais:
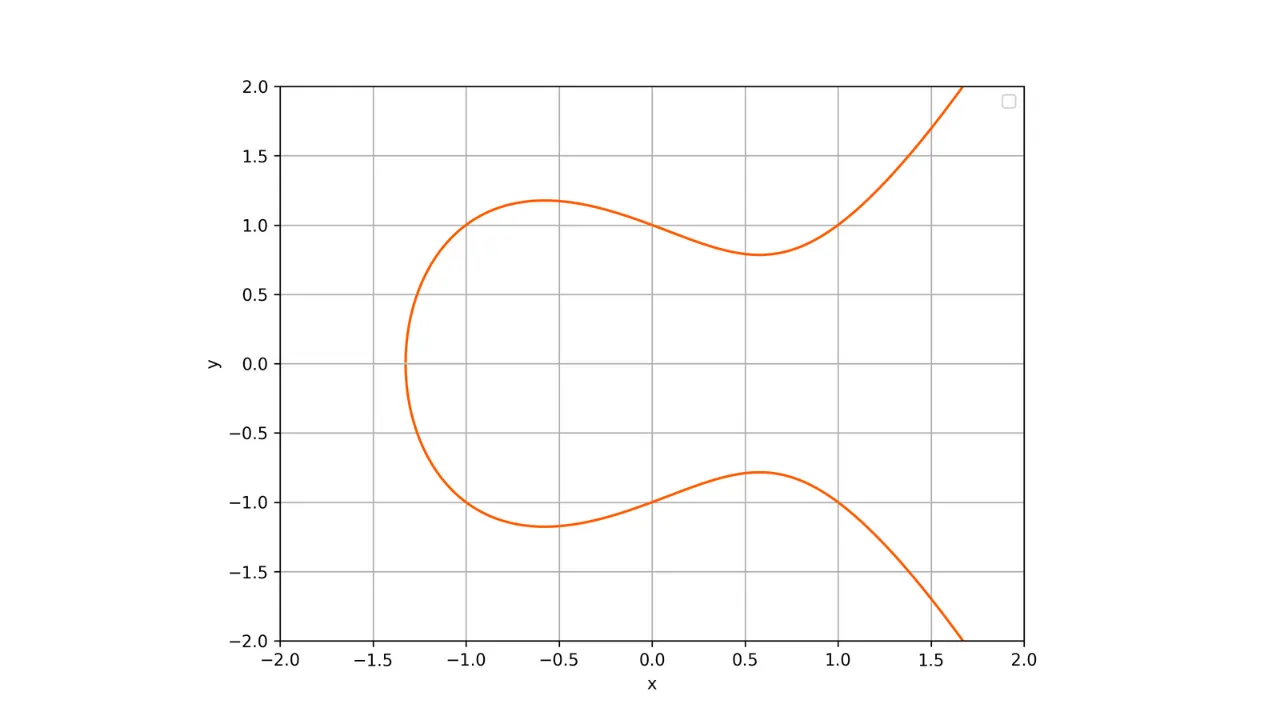
Cada curva elíptica é definida por uma equação da forma:
y^2 = x^3 + ax + b
### secp256k1
Para usar ECDSA ou Schnorr, deve-se escolher os parâmetros da curva elíptica, isto é, os valores de $a$ e $b$ na equação da curva. Existem diferentes padrões de curvas elípticas que são reputados como seguros criptograficamente. O mais conhecido é a curva *secp256r1*, definida e recomendada pelo NIST (*National Institute of Standards and Technology*).
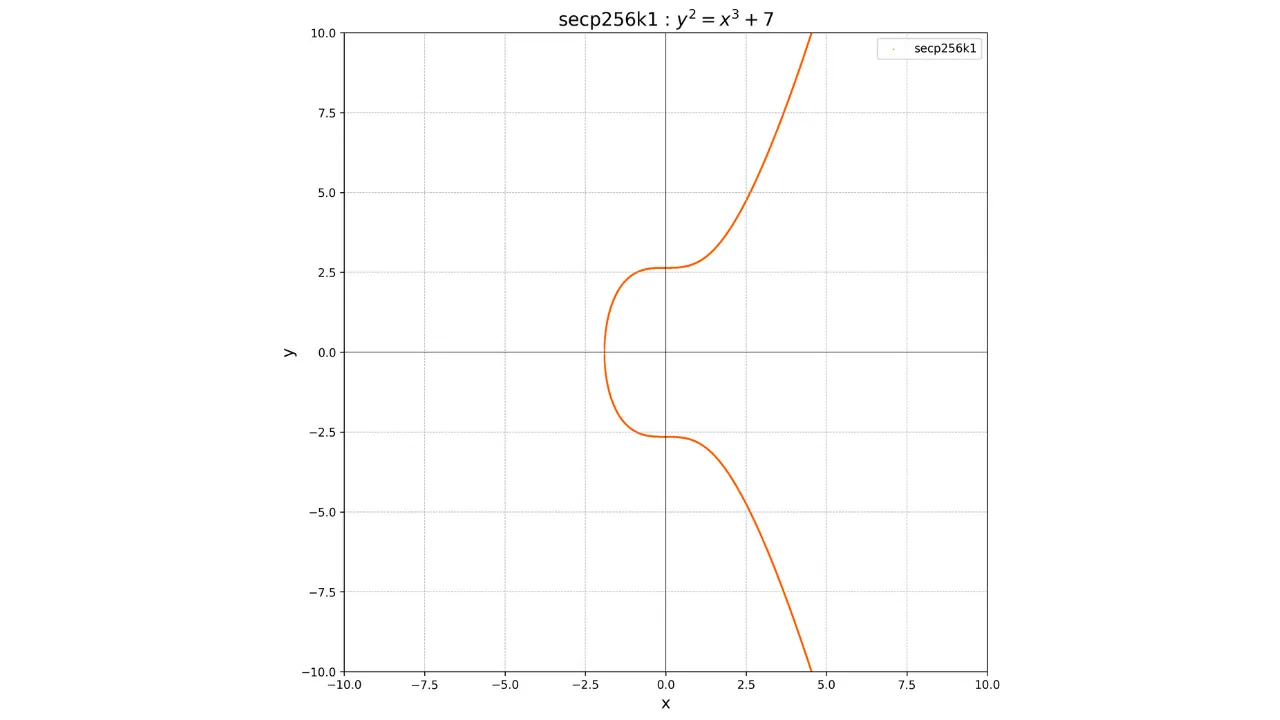
Apesar disso, Satoshi Nakamoto, o inventor do Bitcoin, optou por não usar essa curva. A razão dessa escolha é desconhecida, mas alguns acreditam que ele preferiu encontrar uma alternativa porque os parâmetros dessa curva poderiam potencialmente conter uma porta dos fundos. Em vez disso, o protocolo Bitcoin usa a curva padrão ***secp256k1***. Esta curva é definida pelos parâmetros $a = 0$ e $b = 7$. Sua equação é, portanto:
y^2 = x^3 + 7
Sua representação gráfica sobre o campo dos números reais é assim:
No entanto, em criptografia, trabalhamos com conjuntos finitos de números. Mais especificamente, trabalhamos no campo finito $\mathbb{F}_p$, que é o campo dos inteiros módulo um número primo $p$.
**Definição**: Um número primo é um inteiro natural maior ou igual a 2 que possui apenas dois divisores inteiros positivos distintos: 1 e ele mesmo. Por exemplo, o número 7 é um número primo, pois só pode ser dividido por 1 e 7. Por outro lado, o número 8 não é primo porque pode ser dividido por 1, 2, 4 e 8.
No Bitcoin, o número primo $p$ usado para definir o campo finito é muito grande. É escolhido de tal forma que a ordem do campo (ou seja, o número de elementos em $\mathbb{F}_p$) seja suficientemente grande para garantir a segurança criptográfica.
O número primo $p$ usado é:
```txt
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
```
Na notação decimal, isso corresponde a:
p = 2^{256} - 2^{32} - 977
Assim, a equação da nossa curva elíptica é na verdade:
y^2 \equiv x^3 + 7 \mod p
Dado que esta curva é definida sobre o campo finito $\mathbb{F}_p$, ela não se assemelha mais a uma curva contínua, mas sim a um conjunto discreto de pontos. Por exemplo, aqui está como a curva usada no Bitcoin parece para um $p$ muito pequeno, $p = 17$:
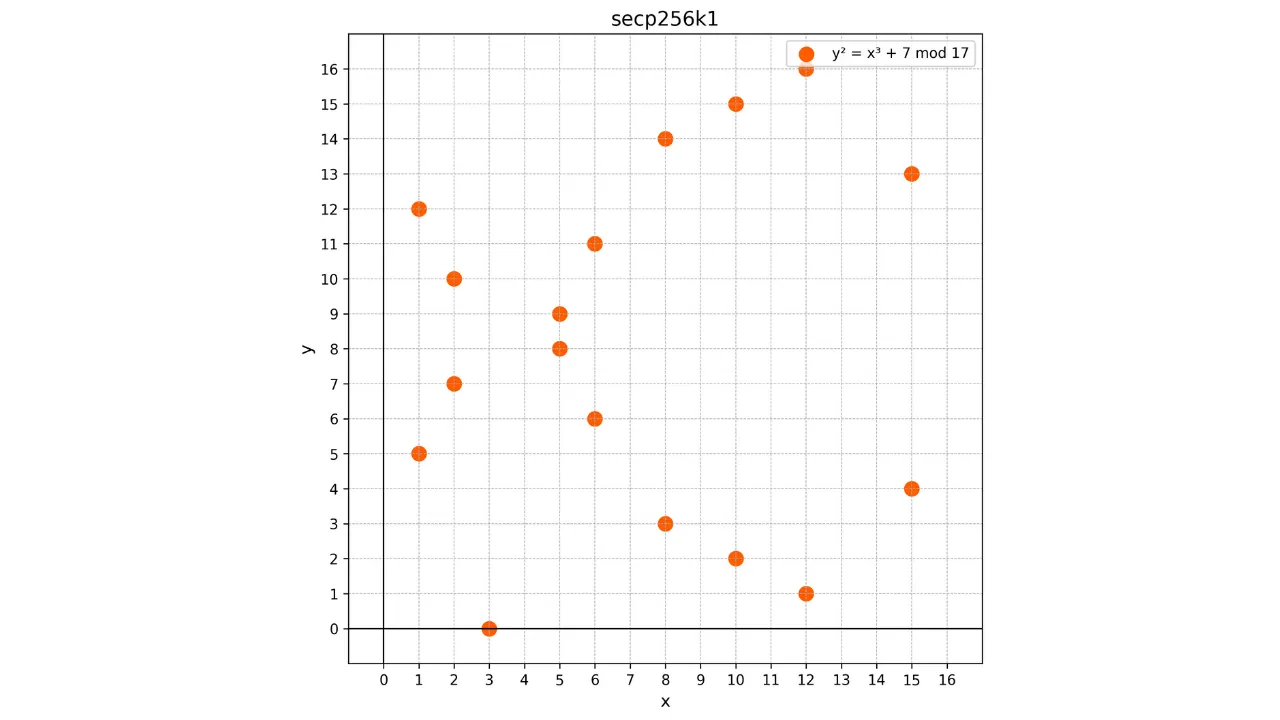
Neste exemplo, limitei intencionalmente o campo finito a $p = 17$ por razões educacionais, mas deve-se imaginar que o usado no Bitcoin é imensamente maior, quase $2^{256}$.
Usamos um campo finito de inteiros módulo $p$ para garantir a precisão das operações na curva. De fato, curvas elípticas sobre o campo dos números reais estão sujeitas a imprecisões devido a erros de arredondamento durante cálculos computacionais. Se muitas operações são realizadas na curva, esses erros se acumulam e o resultado final pode ser incorreto ou difícil de reproduzir. O uso exclusivo de inteiros positivos garante a precisão perfeita dos cálculos e, assim, a reprodutibilidade do resultado.
A matemática das curvas elípticas sobre campos finitos é análoga àquela sobre o campo dos números reais, com a adaptação de que todas as operações são realizadas módulo $p$. Para simplificar as explicações, continuaremos nos capítulos seguintes a ilustrar conceitos usando uma curva definida sobre números reais, mantendo em mente que, na prática, a curva é definida sobre um campo finito.
Se você deseja aprender mais sobre os fundamentos matemáticos da criptografia moderna, também recomendo consultar este outro curso na Plan ₿ Network:
https://planb.network/courses/d2fd9fc0-d9ed-4a87-9fa3-0fdbb3937e28
## Calculando a Chave Pública a partir da Chave Privada
<chapterId>fcb2bd58-5dda-5ecf-bb8f-ad1a0561ab4a</chapterId>
Como visto anteriormente, os algoritmos de assinatura digital no Bitcoin são baseados em um par de chaves privadas e públicas que estão matematicamente vinculadas. Vamos explorar juntos qual é esse vínculo matemático e como elas são geradas.
### A Chave Privada
A chave privada é simplesmente um número aleatório ou pseudoaleatório. No caso do Bitcoin, esse número tem 256 bits de tamanho. O número de possibilidades para uma chave privada do Bitcoin é, portanto, teoricamente $2^{256}$.
**Nota**: Um "número pseudoaleatório" é um número que possui propriedades próximas às de um número verdadeiramente aleatório, mas é gerado por um algoritmo determinístico.
No entanto, na prática, existem apenas $n$ pontos distintos na nossa curva elíptica secp256k1, onde $n$ é a ordem do ponto gerador $G$ da curva. Veremos mais tarde a que este número corresponde, mas simplesmente lembre-se de que uma chave privada válida é um inteiro entre $1$ e $n-1$, sabendo que $n$ é um número próximo, mas ligeiramente menor que $2^{256}$. Portanto, existem alguns números de 256 bits que não são válidos para se tornarem uma chave privada no Bitcoin, especificamente, todos os números entre $n$ e $2^{256}$. Se a geração do número aleatório (a chave privada) produzir um valor $k$ tal que $k \geq n$, ele é considerado inválido, e um novo valor aleatório deve ser gerado.
O número de possibilidades para uma chave privada de Bitcoin é, portanto, cerca de $n$, que é um número próximo a $1.158 \times 10^{77}$. Este número é tão grande que, se você escolher uma chave privada aleatoriamente, é estatisticamente quase impossível cair em uma chave privada de outro usuário. Para lhe dar uma ideia da escala, o número de chaves privadas possíveis no Bitcoin é de uma ordem de magnitude próxima à do número estimado de átomos no universo observável.
Como veremos nos próximos capítulos, hoje, a maioria das chaves privadas usadas no Bitcoin não são geradas aleatoriamente, mas são o resultado da derivação determinística de uma frase mnemônica, ela mesma pseudoaleatória (esta é a famosa frase de 12 ou 24 palavras). Esta informação não muda nada para o uso de algoritmos de assinatura como o ECDSA, mas ajuda a refocar nossa popularização no Bitcoin.
Para a continuação da explicação, a chave privada será denotada pela letra minúscula $k$.
### A Chave Pública
A chave pública é um ponto na curva elíptica, denotado pela letra maiúscula $K$, e é calculada a partir da chave privada $k$. Este ponto $K$ é representado por um par de coordenadas $(x, y)$ na curva elíptica, cada coordenada sendo um inteiro módulo $p$, o número primo que define o campo finito $\mathbb{F}_p$.
Na prática, uma chave pública não comprimida é representada por 512 bits (ou 64 bytes), correspondendo a dois números de 256 bits ($x$ e $y$) colocados lado a lado. Estes números são a abscissa ($x$) e a ordenada ($y$) do nosso ponto na secp256k1. Se adicionarmos o prefixo, a chave pública totaliza 520 bits.
No entanto, também é possível representar a chave pública de forma comprimida usando apenas 33 bytes (264 bits) mantendo apenas a abscissa $x$ do nosso ponto na curva e um byte indicando a paridade de $y$. Isso é o que se conhece como uma chave pública comprimida. Falarei mais sobre isso nos últimos capítulos deste treinamento. Mas o que você precisa lembrar é que uma chave pública $K$ é um ponto descrito por $x$ e $y$.
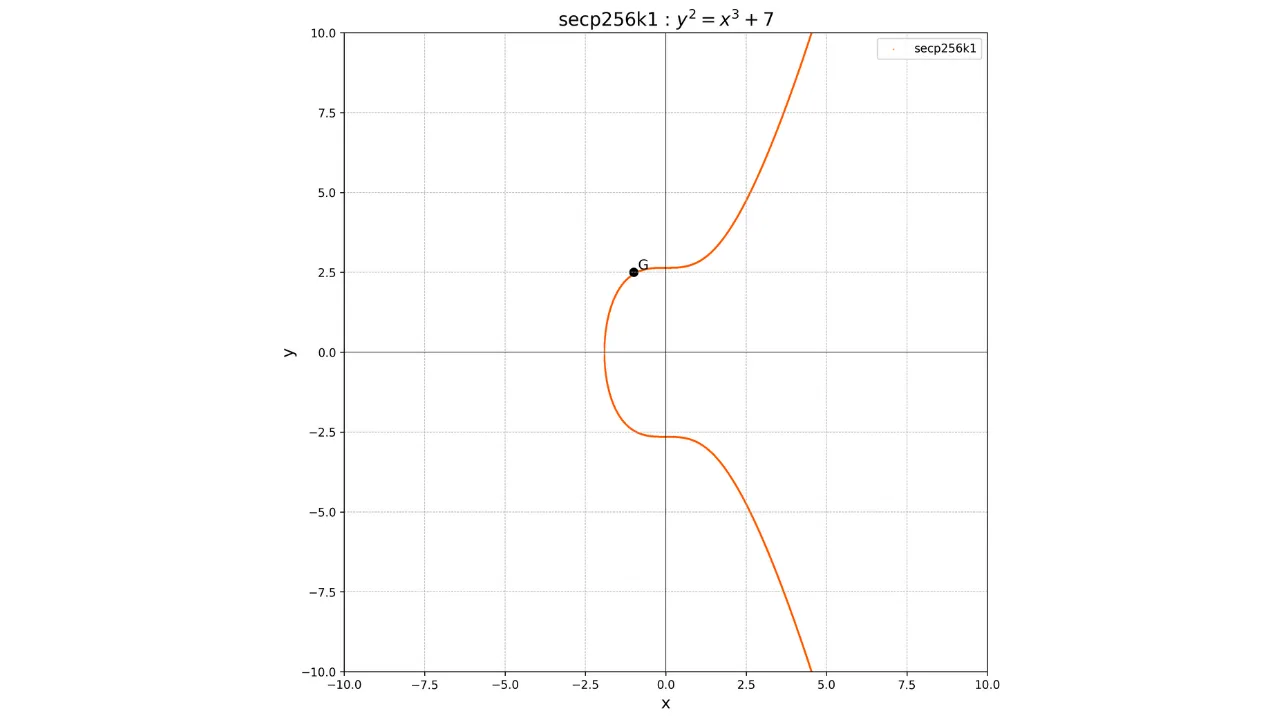
Para calcular o ponto $K$ que corresponde à nossa chave pública, usamos a operação de multiplicação escalar em curvas elípticas, definida como uma adição repetida ($k$ vezes) do ponto gerador $G$:
K = k \cdot G
onde:
- $k$ é a chave privada (um inteiro aleatório entre $1$ e $n-1$);
- $G$ é o ponto gerador da curva elíptica usado por todos os participantes da rede Bitcoin; - $\cdot$ representa a multiplicação escalar na curva elíptica, que é equivalente a adicionar o ponto $G$ a si mesmo $k$ vezes.
O fato de que este ponto $G$ é comum a todas as chaves públicas no Bitcoin nos permite ter certeza de que a mesma chave privada $k$ sempre nos dará a mesma chave pública $K$:
A principal característica desta operação é que ela é uma função unidirecional. É fácil calcular a chave pública $K$ conhecendo a chave privada $k$ e o ponto gerador $G$, mas é praticamente impossível calcular a chave privada $k$ conhecendo apenas a chave pública $K$ e o ponto gerador $G$. Encontrar $k$ a partir de $K$ e $G$ equivale a resolver o problema do logaritmo discreto em curvas elípticas, um problema matematicamente difícil para o qual não se conhece algoritmo eficiente. Mesmo os calculadores mais poderosos atuais são incapazes de resolver este problema em um tempo razoável.

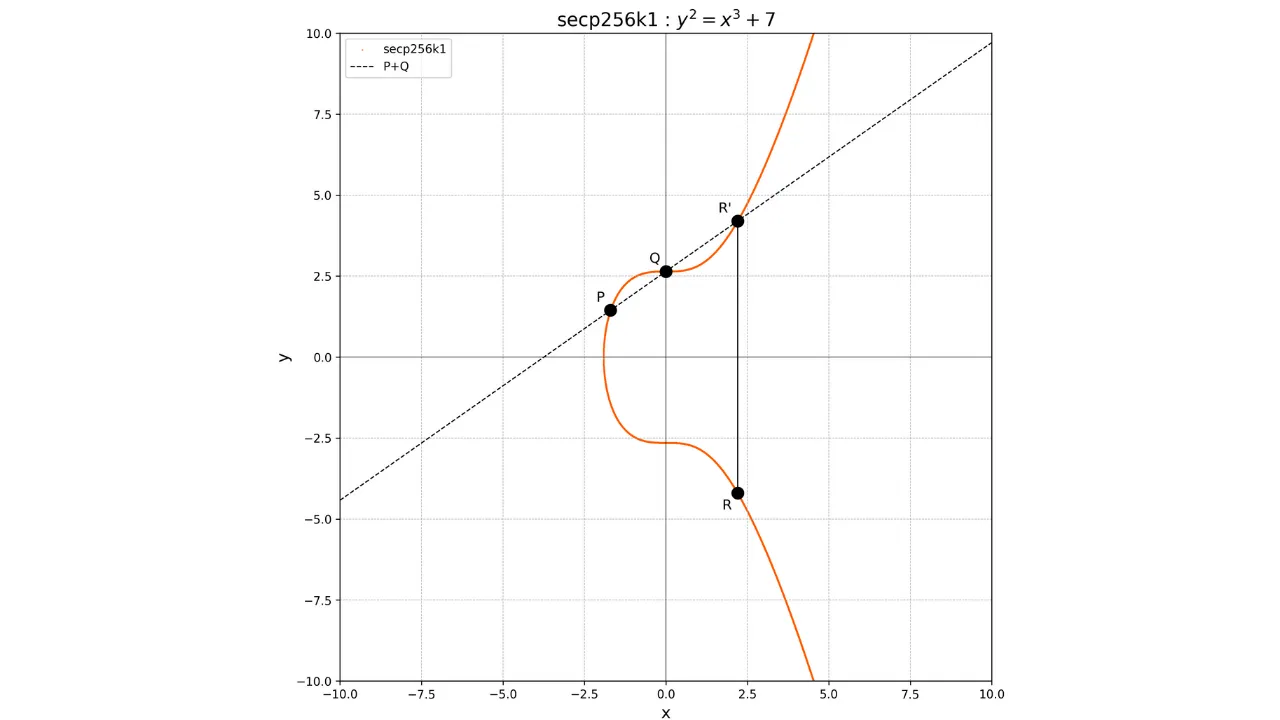
### Adição e Dobramento de Pontos em Curvas Elípticas
O conceito de adição em curvas elípticas é definido geometricamente. Se temos dois pontos $P$ e $Q$ na curva, a operação $P + Q$ é calculada desenhando uma linha que passa por $P$ e $Q$. Esta linha necessariamente intersectará a curva em um terceiro ponto $R'$. Em seguida, tomamos a imagem espelhada deste ponto em relação ao eixo x para obter o ponto $R$, que é o resultado da adição:
P + Q = R
Graficamente, isso pode ser representado da seguinte forma:
Para o dobramento de um ponto, isto é, a operação $P + P$, desenhamos a tangente à curva no ponto $P$. Esta tangente intersecta a curva em outro ponto $S'$. Em seguida, tomamos a imagem espelhada deste ponto em relação ao eixo x para obter o ponto $S$, que é o resultado do dobramento:
2P = S
Graficamente, isso é mostrado como:
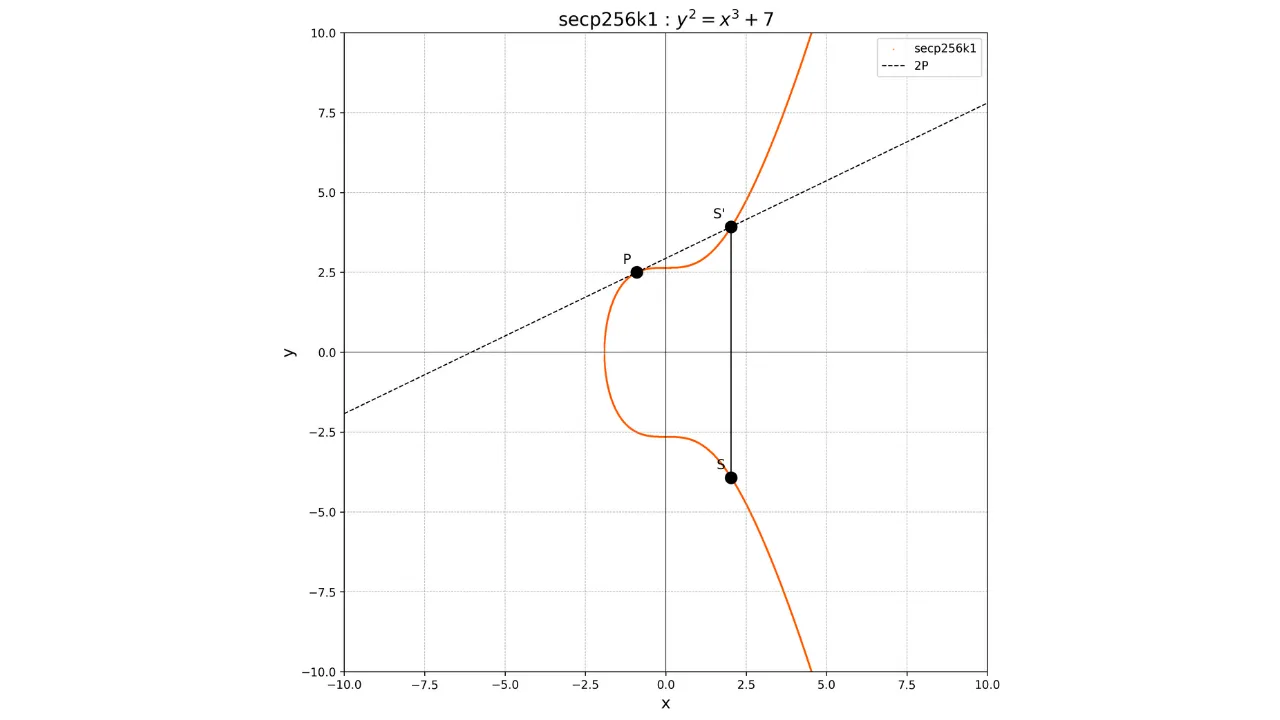
Usando essas operações de adição e dobramento, podemos realizar a multiplicação escalar de um ponto por um inteiro $k$, denotado $kP$, realizando dobramentos e adições repetidas.
Por exemplo, suponha que escolhemos uma chave privada $k = 4$. Para calcular a chave pública associada, realizamos:
K = k \cdot G = 4G
Graficamente, isso corresponde a realizar uma série de adições e dobramentos:
- Calcular $2G$ dobrando $G$.
- Calcular $4G$ dobrando $2G$.

Se desejarmos, por exemplo, calcular o ponto $3G$, devemos primeiro calcular o ponto $2G$ dobrando o ponto $G$, depois adicionar $G$ e $2G$. Para adicionar $G$ e $2G$, basta desenhar a linha conectando esses dois pontos, recuperar o ponto único $-3G$ na interseção entre esta linha e a curva elíptica, e então determinar $3G$ como o oposto de $-3G$.
Teremos:
G + G = 2G
2G + G = 3G
Graficamente, isso seria representado da seguinte forma:
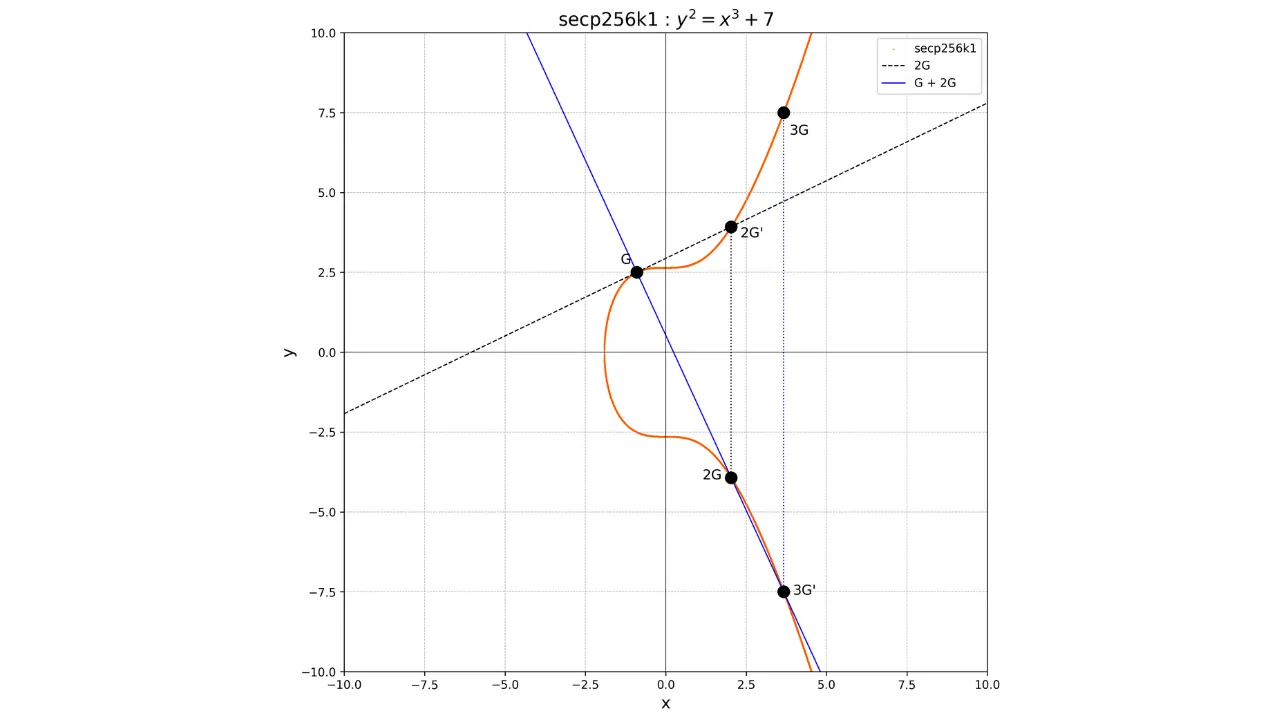
### Função Unidirecional
Graças a essas operações, podemos entender por que é fácil derivar uma chave pública a partir de uma chave privada, mas o inverso é praticamente impossível.
Vamos voltar ao nosso exemplo simplificado. Com uma chave privada $k = 4$. Para calcular a chave pública associada, realizamos:
K = k \cdot G = 4G
Assim, fomos capazes de calcular facilmente a chave pública $K$ conhecendo $k$ e $G$.
Agora, se alguém conhece apenas a chave pública $K$, enfrenta o problema do logaritmo discreto: encontrar $k$ tal que $K = k \cdot G$. Este problema é considerado difícil porque não existe um algoritmo eficiente para resolvê-lo em curvas elípticas. Isso garante a segurança dos algoritmos ECDSA e Schnorr.
Claro, neste exemplo simplificado com $k = 4$, seria possível encontrar $k$ por tentativa e erro, já que o número de possibilidades é baixo. No entanto, na prática no Bitcoin, $k$ é um inteiro de 256 bits, tornando o número de possibilidades astronomicamente grande (cerca de $1.158 \times 10^{77}$). Portanto, é inviável encontrar $k$ por força bruta.
## Assinando com a Chave Privada
<chapterId>bb07826f-826e-5905-b307-3d82001fb778</chapterId>
Agora que você sabe como derivar uma chave pública a partir de uma chave privada, você já pode receber bitcoins usando esse par de chaves como condição de gasto. Mas como gastá-los? Para gastar bitcoins, você precisará desbloquear o _scriptPubKey_ anexado ao seu UTXO para provar que você é de fato seu legítimo proprietário. Para fazer isso, você deve produzir uma assinatura $s$ que corresponda à chave pública $K$ presente no _scriptPubKey_ usando a chave privada $k$ que foi inicialmente usada para calcular $K$. A assinatura digital é, portanto, prova irrefutável de que você está na posse da chave privada associada à chave pública que você reivindica.
### Parâmetros da Curva Elíptica
Para realizar uma assinatura digital, todos os participantes devem primeiro concordar com os parâmetros da curva elíptica usada. No caso do Bitcoin, os parâmetros do **secp256k1** são os seguintes:
O campo finito $\mathbb{Z}_p$ definido por:
p = 2^{256} - 2^{32} - 977
```txt
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
```
$p$ é um número primo muito grande, ligeiramente menor que $2^{256}$.
A curva elíptica $y^2 = x^3 + ax + b$ sobre $\mathbb{Z}_p$ definida por:
a = 0, \quad b = 7
O ponto gerador ou ponto de origem $G$:
```txt
G = 0x0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
```
Este número é a forma comprimida que fornece apenas a abscissa do ponto $G$. O prefixo `02` no início determina qual dos dois valores com esta abscissa $x$ deve ser usado como o ponto gerador.
A ordem $n$ de $G$ (o número de pontos existentes) e o cofator $h$:
```txt
n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
```
$n$ é um número muito grande, ligeiramente menor que $p$.
h=1
$h$ é o cofator ou o número de subgrupos. Não vou me aprofundar no que isso representa aqui, pois é bastante complexo, e no caso do Bitcoin, não precisamos levar isso em conta, já que é igual a $1$.
Todas essas informações são públicas e conhecidas por todos os participantes. Graças a elas, os usuários podem fazer uma assinatura digital e verificá-la.
### Assinatura com ECDSA
O algoritmo ECDSA permite que um usuário assine uma mensagem usando sua chave privada, de tal forma que qualquer pessoa que conheça a chave pública correspondente possa verificar a validade da assinatura, sem que a chave privada seja revelada. No contexto do Bitcoin, a mensagem a ser assinada depende do _sighash_ escolhido pelo usuário. É este _sighash_ que determinará quais partes da transação são cobertas pela assinatura. Falarei mais sobre isso no próximo capítulo.
Aqui estão os passos para gerar uma assinatura ECDSA:
Primeiro, calculamos o hash ($e$) da mensagem que precisa ser assinada. A mensagem $m$ é, portanto, passada por uma função de hash criptográfica, geralmente SHA256 ou duplo SHA256 no caso do Bitcoin:
e = \text{HASH}(m)
Em seguida, calculamos um nonce. Em criptografia, um nonce é simplesmente um número gerado de maneira aleatória ou pseudoaleatória que é usado apenas uma vez. Ou seja, cada vez que uma nova assinatura digital é feita com este par de chaves, será muito importante usar um nonce diferente, caso contrário, comprometerá a segurança da chave privada. Portanto, é suficiente determinar um inteiro aleatório e único $r$ tal que $1 \leq r \leq n-1$, onde $n$ é a ordem do ponto gerador $G$ da curva elíptica.
Então, calcularemos o ponto $R$ na curva elíptica com as coordenadas $(x_R, y_R)$ tal que:
R = r \cdot G
Extraímos o valor da abscissa do ponto $R$ ($x_R$). Este valor representa a primeira parte da assinatura. E, finalmente, calculamos a segunda parte da assinatura $s$ desta maneira:
s = r^{-1} \left( e + k \cdot x_R \right) \mod n
onde:
- $r^{-1}$ é o inverso modular de $r$ módulo $n$, ou seja, um inteiro tal que $r \cdot r^{-1} \equiv 1 \mod n$;
- $k$ é a chave privada do usuário;
- $e$ é o hash da mensagem;
- $n$ é a ordem do ponto gerador $G$ da curva elíptica.
A assinatura é então simplesmente a concatenação de $x_R$ e $s$:
\text{SIG} = x_R \Vert s
### Verificação da Assinatura ECDSA
Para verificar uma assinatura $(x_R, s)$, qualquer pessoa que conheça a chave pública $K$ e os parâmetros da curva elíptica pode proceder da seguinte maneira:
Primeiro, verifique se $x_R$ e $s$ estão dentro do intervalo $[1, n-1]$. Isso garante que a assinatura respeita as restrições matemáticas do grupo elíptico. Se não for o caso, o verificador rejeita imediatamente a assinatura como inválida.
Em seguida, calcule o hash da mensagem:
e = \text{HASH}(m)
Calcule o inverso modular de $s$ módulo $n$:
s^{-1} \mod n
Calcule dois valores escalares $u_1$ e $u_2$ desta forma:
\begin{align*} u_1 &= e \cdot s^{-1} \mod n \ u_2 &= x_R \cdot s^{-1} \mod n \end{align*}
E finalmente, calcule o ponto $V$ na curva elíptica tal que:
V = u_1 \cdot G + u_2 \cdot K
A assinatura é válida apenas se $x_V \equiv x_R \mod n$, onde $x_V$ é a coordenada $x$ do ponto $V$. De fato, combinando $u_1 \cdot G$ e $u_2 \cdot K$, obtém-se um ponto $V$ que, se a assinatura for válida, deve corresponder ao ponto $R$ usado durante a assinatura (módulo $n$).
### Assinatura com o Protocolo Schnorr
O esquema de assinatura Schnorr é uma alternativa ao ECDSA que oferece muitas vantagens. Tem sido possível usá-lo no Bitcoin desde 2021 e a introdução do Taproot, com os padrões de script P2TR. Como o ECDSA, o esquema Schnorr permite assinar uma mensagem usando uma chave privada, de tal forma que a assinatura possa ser verificada por qualquer pessoa que conheça a chave pública correspondente.
No caso do Schnorr, a mesma curva que o ECDSA é usada com os mesmos parâmetros. No entanto, as chaves públicas são representadas de forma ligeiramente diferente em comparação com o ECDSA. De fato, elas são designadas apenas pela coordenada $x$ do ponto na curva elíptica. Ao contrário do ECDSA, onde chaves públicas comprimidas são representadas por 33 bytes (com o byte de prefixo indicando a paridade de $y$), Schnorr usa chaves públicas de 32 bytes, correspondendo apenas à coordenada $x$ do ponto $K$, e presume-se que $y$ seja par por padrão. Esta representação simplificada reduz o tamanho das assinaturas e facilita certas otimizações nos algoritmos de verificação.
A chave pública é então a coordenada $x$ do ponto $K$:
\text{pk} = K_x
O primeiro passo para gerar uma assinatura é fazer o hash da mensagem. Mas, ao contrário do ECDSA, isso é feito com outros valores e uma função de hash rotulada é usada para evitar colisões em diferentes contextos. Uma função de hash rotulada simplesmente envolve adicionar um rótulo arbitrário às entradas da função de hash junto com os dados da mensagem.
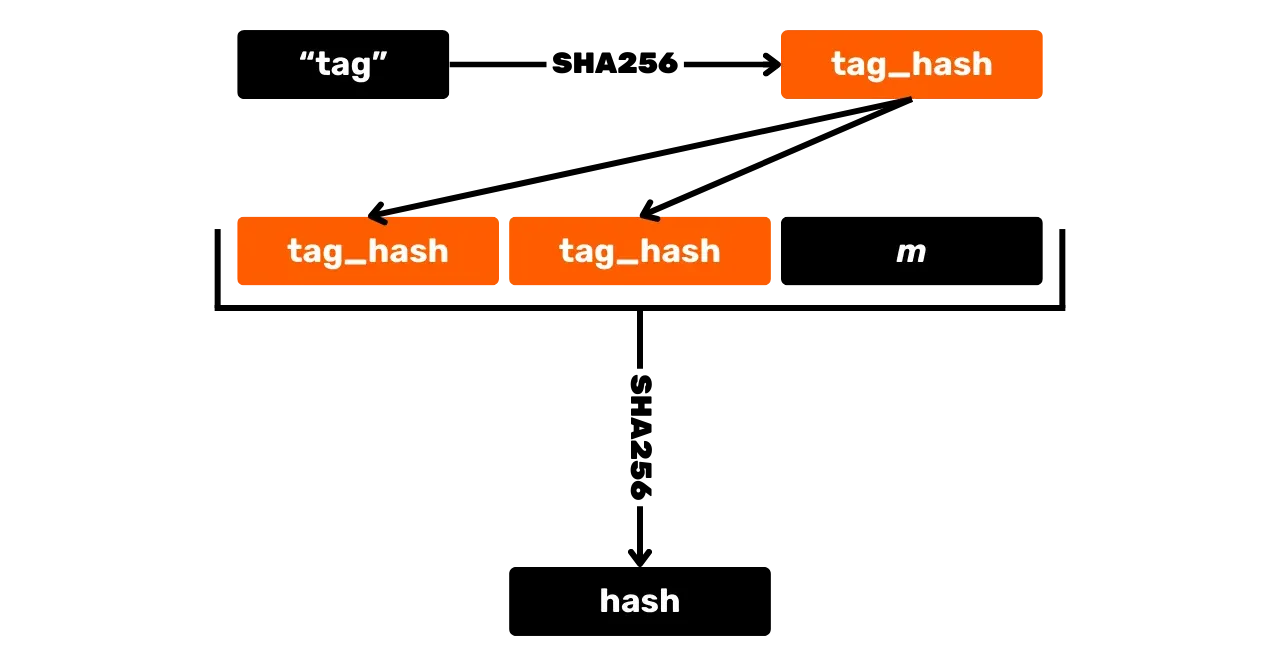
Além da mensagem, a coordenada $x$ da chave pública $K_x$, bem como um ponto $R$ calculado a partir do nonce $r$ ($R=r \cdot G$) que é ele mesmo um inteiro único para cada assinatura, calculado deterministicamente a partir da chave privada e da mensagem para evitar vulnerabilidades relacionadas à reutilização de nonce, também são passados para a função rotulada. Assim como para a chave pública, apenas a coordenada $x$ do ponto nonce $R_x$ é retida para descrever o ponto.
O resultado deste hash, notado $e$, é chamado de "desafio":
e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod n$$
Aqui, $\text{HASH}$ é a função de hash SHA256, e $\text{``BIP0340/challenge''}$ é a tag específica para o hashing.
Finalmente, o parâmetro $s$ é calculado desta maneira a partir da chave privada $k$, do nonce $r$ e do desafio $e$:
s = (r + e \cdot k) \mod n
A assinatura é então simplesmente o par $Rx$ e $s$.
\text{SIG} = R_x \Vert s
### Verificação da Assinatura Schnorr
A verificação de uma assinatura Schnorr é mais simples do que a de uma assinatura ECDSA. Aqui estão os passos para verificar a assinatura $(R_x, s)$ com a chave pública $K_x$ e a mensagem $m$:
Primeiro, verificamos se $K_x$ é um inteiro válido e menor que $p$. Se for o caso, recuperamos o ponto correspondente na curva com $K_y$ sendo par. Também extraímos $R_x$ e $s$ separando a assinatura $\text{SIG}$. Então, verificamos que $R_x < p$ e $s < n$ (a ordem da curva).
Em seguida, calculamos o desafio $e$ da mesma maneira que o emissor da assinatura:
e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod n
Depois, calculamos um ponto de referência na curva desta maneira:
R' = s \cdot G - e \cdot K
Finalmente, verificamos se $R'_x = R_x$. Se as duas coordenadas x coincidirem, então a assinatura $(R_x, s)$ é de fato válida com a chave pública $K_x$.
### Por que isso funciona?
O signatário calculou $s = r + e \cdot k \mod n$, então $R' = s \cdot G - e \cdot K$ deve ser igual ao ponto original $R$, porque:
s \cdot G = (r + e \cdot k) \cdot G = r \cdot G + e \cdot k \cdot G
Como $K = k \cdot G$, temos $e \cdot k \cdot G = e \cdot K$. Assim:
R' = r \cdot G = R
Portanto, temos:
R'_x = R_x
### As vantagens das assinaturas Schnorr
O esquema de assinatura Schnorr oferece várias vantagens para o Bitcoin em relação ao algoritmo ECDSA original. Primeiro, Schnorr permite a agregação de chaves e assinaturas. Isso significa que várias chaves públicas podem ser combinadas em uma única chave.
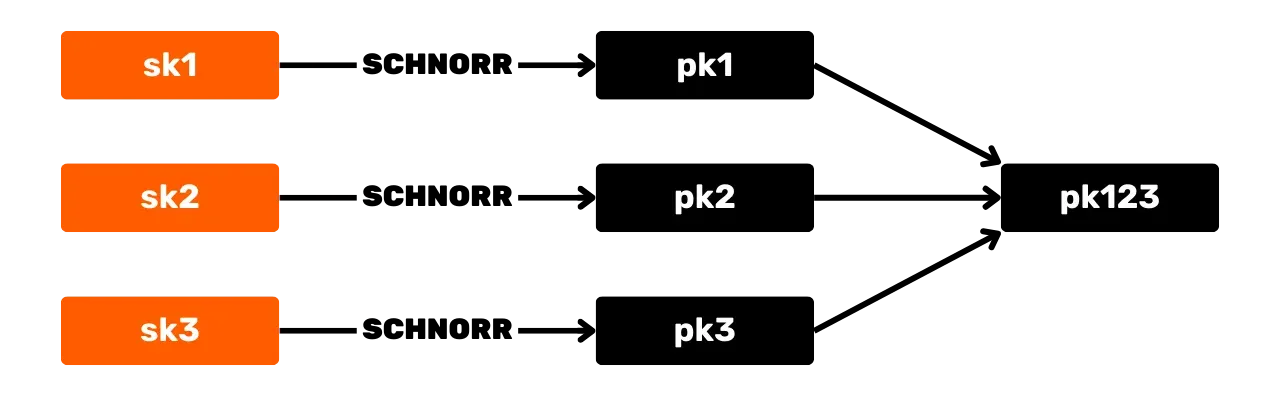
E da mesma forma, várias assinaturas podem ser agregadas em uma única assinatura válida. Assim, no caso de uma transação de assinatura múltipla, um conjunto de participantes pode assinar com uma única assinatura e uma única chave pública agregada. Isso reduz significativamente os custos de armazenamento e computação para a rede, pois cada nó só precisa verificar uma única assinatura.

Além disso, a agregação de assinaturas melhora a privacidade. Com Schnorr, torna-se impossível distinguir uma transação de assinatura múltipla de uma transação de assinatura única padrão. Essa homogeneidade torna a análise de cadeia mais difícil, pois limita a capacidade de identificar impressões digitais de carteiras.
Finalmente, Schnorr também oferece a possibilidade de verificação em lote. Ao verificar múltiplas assinaturas simultaneamente, os nós podem ganhar eficiência, especialmente para blocos contendo muitas transações. Esta otimização reduz o tempo e os recursos necessários para validar um bloco. Além disso, as assinaturas Schnorr não são maleáveis, ao contrário das assinaturas produzidas com ECDSA. Isso significa que um atacante não pode modificar uma assinatura válida para criar outra assinatura válida para a mesma mensagem e a mesma chave pública. Essa vulnerabilidade estava anteriormente presente no Bitcoin e impediu notavelmente a implementação segura da Lightning Network. Foi resolvida para ECDSA com o softfork SegWit em 2017, que envolve mover as assinaturas para um banco de dados separado das transações para prevenir sua maleabilidade.
### Por que Satoshi escolheu ECDSA?
Como vimos, Satoshi inicialmente escolheu implementar ECDSA para assinaturas digitais no Bitcoin. No entanto, também vimos que Schnorr é superior ao ECDSA em muitos aspectos, e este protocolo foi criado por Claus-Peter Schnorr em 1989, 20 anos antes da invenção do Bitcoin.
Bem, não sabemos realmente por que Satoshi não o escolheu, mas uma hipótese provável é que este protocolo estava sob patente até 2008. Embora o Bitcoin tenha sido criado um ano depois, em janeiro de 2009, não havia uma padronização de código aberto para assinaturas Schnorr disponível naquela época. Talvez Satoshi tenha considerado mais seguro usar ECDSA, que já era amplamente utilizado e testado em software de código aberto e tinha várias implementações reconhecidas (notavelmente a biblioteca OpenSSL usada até 2015 no Bitcoin Core, depois substituída por libsecp256k1 na versão 0.10.0). Ou talvez ele simplesmente não estivesse ciente de que essa patente iria expirar em 2008. De qualquer forma, a hipótese mais provável parece estar relacionada a essa patente e ao fato de que ECDSA tinha um histórico comprovado e era mais fácil de implementar.
## Os flags de sighash
<chapterId>231c41a2-aff2-4655-9048-47b6d2d83d64</chapterId>
Como vimos em capítulos anteriores, assinaturas digitais são frequentemente usadas para desbloquear o script de uma entrada. No processo de assinatura, é necessário incluir os dados assinados no cálculo, designados em nossos exemplos pela mensagem $m$. Esses dados, uma vez assinados, não podem ser modificados sem invalidar a assinatura. De fato, seja para ECDSA ou Schnorr, o verificador da assinatura deve incluir em seu cálculo a mesma mensagem $m$. Se ela difere da mensagem $m$ inicialmente usada pelo assinante, o resultado será incorreto e a assinatura será considerada inválida. Diz-se então que uma assinatura cobre certos dados e os protege, de certa forma, contra modificações não autorizadas.
### O que é um flag de sighash?
No caso específico do Bitcoin, vimos que a mensagem $m$ corresponde à transação. No entanto, na realidade, é um pouco mais complexo. De fato, graças aos flags de sighash, é possível selecionar dados específicos dentro da transação que serão ou não cobertos pela assinatura.
O "flag de sighash" é, portanto, um parâmetro adicionado a cada entrada, permitindo a determinação dos componentes de uma transação que são cobertos pela assinatura associada. Esses componentes são as entradas e as saídas. A escolha do flag de sighash determina, assim, quais entradas e quais saídas da transação são fixadas pela assinatura e quais ainda podem ser modificadas sem invalidá-la. Este mecanismo permite que as assinaturas comprometam dados da transação de acordo com as intenções do assinante.
Obviamente, uma vez que a transação é confirmada na blockchain, ela se torna imutável, independentemente dos flags de sighash usados. A possibilidade de modificação por meio dos flags de sighash é limitada ao período entre a assinatura e a confirmação.
Geralmente, o software de carteira não oferece a opção de modificar manualmente o flag de sighash de suas entradas quando você constrói uma transação. Por padrão, `SIGHASH_ALL` é definido. Pessoalmente, só conheço o Sparrow Wallet que permite essa modificação a partir da interface do usuário.
### Quais são os flags de sighash existentes no Bitcoin?
No Bitcoin, existem primeiramente 3 flags de sighash básicos:
- `SIGHASH_ALL` (`0x01`): A assinatura aplica-se a todas as entradas e todas as saídas da transação. A transação é, portanto, inteiramente coberta pela assinatura e não pode mais ser modificada. `SIGHASH_ALL` é o sighash mais comumente usado em transações do dia a dia quando se deseja simplesmente realizar uma transação sem que ela possa ser modificada.

Em todos os diagramas deste capítulo, a cor laranja representa os elementos cobertos pela assinatura, enquanto a cor preta indica aqueles que não estão.
- `SIGHASH_NONE` (`0x02`): A assinatura cobre todas as entradas, mas nenhuma das saídas, permitindo assim a modificação das saídas após a assinatura. Na prática, isso é semelhante a um cheque em branco. O signatário desbloqueia os UTXOs nas entradas, mas deixa o campo das saídas inteiramente modificável. Qualquer pessoa que conheça esta transação pode, assim, adicionar a saída de sua escolha, por exemplo, especificando um endereço de recebimento para coletar os fundos consumidos pelas entradas, e então transmitir a transação para recuperar os bitcoins. A assinatura do proprietário das entradas não será invalidada, pois cobre apenas as entradas.

- `SIGHASH_SINGLE` (`0x03`): A assinatura cobre todas as entradas, bem como uma única saída, correspondendo ao índice da entrada assinada. Por exemplo, se a assinatura desbloqueia o _scriptPubKey_ da entrada #0, então ela também cobre a saída #0. A assinatura também protege todas as outras entradas, que não podem mais ser modificadas. No entanto, qualquer pessoa pode adicionar uma saída adicional sem invalidar a assinatura, desde que a saída #0, que é a única coberta por ela, não seja modificada.

Além desses três flags de sighash, existe também o modificador `SIGHASH_ANYONECANPAY` (`0x80`). Este modificador pode ser combinado com um flag de sighash básico para criar três novos flags de sighash:
- `SIGHASH_ALL | SIGHASH_ANYONECANPAY` (`0x81`): A assinatura cobre uma única entrada, incluindo todas as saídas da transação. Este flag de sighash combinado permite, por exemplo, a criação de uma transação de financiamento coletivo. O organizador prepara a saída com seu endereço e o valor alvo, e cada investidor pode então adicionar entradas para financiar essa saída. Uma vez que fundos suficientes são reunidos nas entradas para satisfazer a saída, a transação pode ser transmitida.

- `SIGHASH_NONE | SIGHASH_ANYONECANPAY` (`0x82`): A assinatura cobre uma única entrada, sem se comprometer com qualquer saída;

- `SIGHASH_SINGLE | SIGHASH_ANYONECANPAY` (`0x83`): A assinatura cobre uma única entrada, bem como a saída que tem o mesmo índice que esta entrada. Por exemplo, se a assinatura desbloqueia o _scriptPubKey_ da entrada #3, ela também cobrirá a saída #3. O restante da transação permanece modificável, tanto em termos de outras entradas quanto de outras saídas.

### Projetos para Adicionar Novas Bandeiras Sighash
Atualmente (2024), apenas as bandeiras sighash apresentadas na seção anterior são utilizáveis no Bitcoin. No entanto, alguns projetos estão considerando a adição de novas bandeiras sighash. Por exemplo, o BIP118, proposto por Christian Decker e Anthony Towns, introduz duas novas bandeiras sighash: `SIGHASH_ANYPREVOUT` e `SIGHASH_ANYPREVOUTANYSCRIPT` (_AnyPrevOut = "Qualquer Saída Anterior"_).
Essas duas bandeiras sighash ofereceriam uma possibilidade adicional no Bitcoin: criar assinaturas que não cobrem nenhuma entrada específica da transação.

Essa ideia foi inicialmente formulada por Joseph Poon e Thaddeus Dryja no White Paper do Lightning. Antes de ser renomeada, essa bandeira sighash era chamada de `SIGHASH_NOINPUT`.
Se essa bandeira sighash for integrada ao Bitcoin, ela permitirá o uso de covenants, mas também é um pré-requisito obrigatório para a implementação do Eltoo, um protocolo geral para camadas secundárias que define como gerenciar conjuntamente a propriedade de um UTXO. O Eltoo foi especificamente projetado para resolver os problemas associados aos mecanismos de negociação do estado dos canais Lightning, ou seja, entre a abertura e o fechamento.
Para aprofundar seu conhecimento sobre a Lightning Network, após o curso CYP201, eu recomendo fortemente o curso LNP201 por Fanis Michalakis, que aborda o tópico em detalhes:
https://planb.network/courses/34bd43ef-6683-4a5c-b239-7cb1e40a4aeb
Na próxima parte, proponho descobrir como funciona a frase mnemônica na base da sua carteira Bitcoin.
# A frase mnemônica
<partId>4070af16-c8a2-58b5-9871-a22c86c07458</partId>
## Evolução das carteiras Bitcoin
<chapterId>9d9acd5d-a0e5-5dfd-b544-f043fae8840f</chapterId>
Agora que exploramos o funcionamento das funções hash e assinaturas digitais, podemos estudar como as carteiras Bitcoin funcionam. O objetivo será imaginar como uma carteira no Bitcoin é construída, como ela é decomposta e quais as diferentes peças de informação que a constituem são usadas. Este entendimento dos mecanismos da carteira permitirá que você melhore seu uso do Bitcoin em termos de segurança e privacidade.
Antes de mergulhar nos detalhes técnicos, é essencial esclarecer o que se entende por "carteira Bitcoin" e entender sua utilidade.
### O que é uma carteira Bitcoin?
Ao contrário das carteiras tradicionais, que permitem armazenar cédulas e moedas físicas, uma carteira Bitcoin não "contém" bitcoins per se. De fato, os bitcoins não existem em uma forma física ou digital que possa ser armazenada, mas são representados por unidades de conta retratadas no sistema na forma de **UTXOs** (_Unspent Transaction Output_).
Os UTXOs representam, assim, fragmentos de bitcoins, de tamanhos variados, que podem ser gastos desde que seu _scriptPubKey_ seja satisfeito. Para gastar seus bitcoins, um usuário deve fornecer um _scriptSig_ que desbloqueia o _scriptPubKey_ associado ao seu UTXO. Essa prova é geralmente feita por meio de uma assinatura digital, gerada a partir da chave privada correspondente à chave pública presente no _scriptPubKey_. Assim, o elemento crucial que o usuário deve proteger é a chave privada. O papel de uma carteira Bitcoin é precisamente gerenciar essas chaves privadas de forma segura. Na realidade, seu papel é mais semelhante ao de um chaveiro do que uma carteira no sentido tradicional.
### Carteiras JBOK (_Just a Bunch Of Keys_)
As primeiras carteiras usadas no Bitcoin foram as carteiras JBOK (_Just a Bunch Of Keys_), que agrupavam chaves privadas geradas independentemente e sem qualquer ligação entre elas. Essas carteiras operavam em um modelo simples onde cada chave privada poderia desbloquear um endereço Bitcoin único para recebimento.
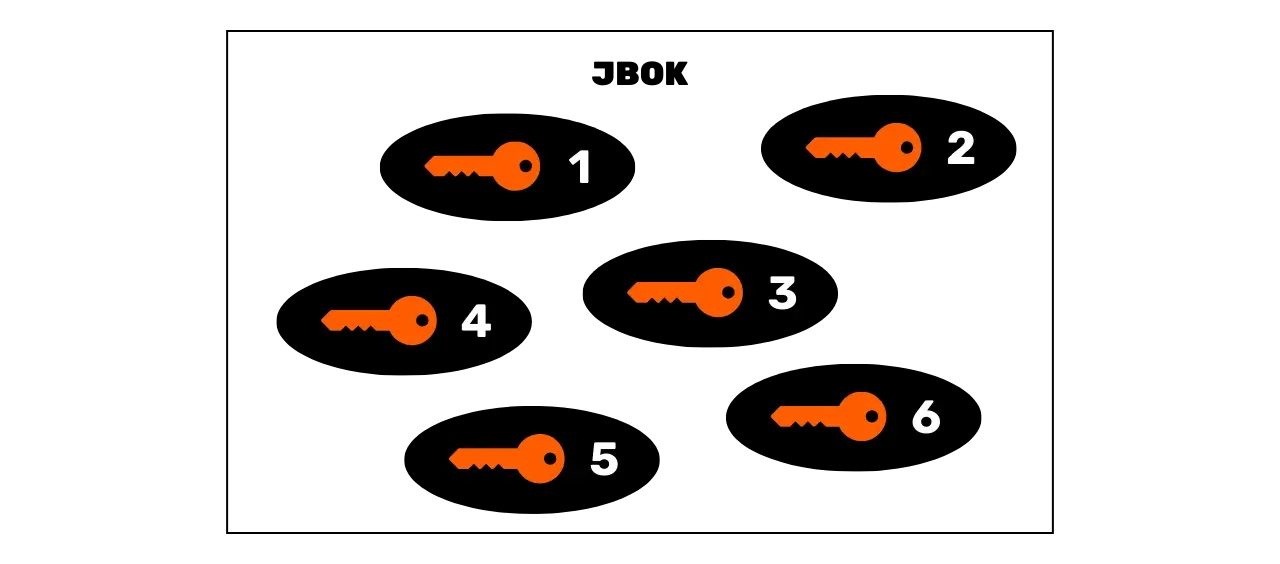
Se alguém desejasse usar múltiplas chaves privadas, então era necessário fazer tantos backups quanto necessário para garantir o acesso aos fundos em caso de problemas com o dispositivo que hospeda a carteira. Se usar uma única chave privada, essa estrutura de carteira pode ser suficiente, já que um único backup é o bastante. No entanto, isso apresenta um problema: no Bitcoin, é fortemente aconselhado contra o uso sempre da mesma chave privada. De fato, uma chave privada está associada a um endereço único, e os endereços de recebimento Bitcoin são normalmente projetados para uso único. Cada vez que você recebe fundos, você deve gerar um novo endereço em branco.
Essa restrição decorre do modelo de privacidade do Bitcoin. Ao reutilizar o mesmo endereço, torna-se mais fácil para observadores externos rastrear todas as minhas transações Bitcoin. É por isso que a reutilização de um endereço de recebimento é fortemente desencorajada. No entanto, para ter múltiplos endereços e separar publicamente nossas transações, é necessário gerenciar múltiplas chaves privadas. No caso das carteiras JBOK, isso implica criar tantos backups quantos forem os novos pares de chaves, uma tarefa que pode rapidamente se tornar complexa e difícil de manter para os usuários.
Para aprender mais sobre o modelo de privacidade do Bitcoin e descobrir métodos para proteger sua privacidade, também recomendo seguir meu curso BTC204 na Rede Plan ₿:
https://planb.network/courses/65c138b0-4161-4958-bbe3-c12916bc959c
### Carteiras HD (_Hierarchical Deterministic_)
Para abordar a limitação das carteiras JBOK, uma nova estrutura de carteira foi posteriormente utilizada. Em 2012, Pieter Wuille introduziu uma melhoria com o BIP32, que introduz carteiras determinísticas hierárquicas. O princípio de uma carteira HD é derivar todas as chaves privadas de uma única fonte de informação, chamada de semente, de maneira determinística e hierárquica. Essa semente é gerada aleatoriamente quando a carteira é criada e constitui um backup único que permite a recriação de todas as chaves privadas da carteira. Assim, o usuário pode gerar um número muito grande de chaves privadas para evitar a reutilização de endereços e preservar sua privacidade, enquanto só precisa fazer um único backup de sua carteira via semente.
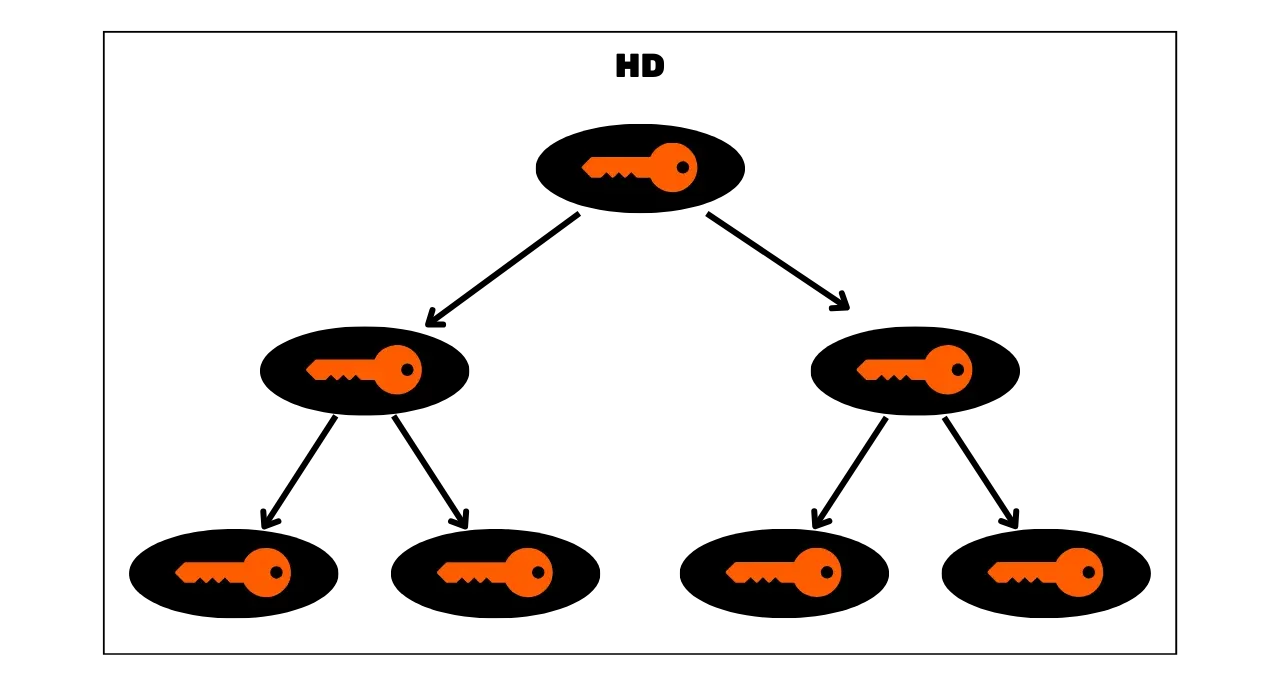
Nas carteiras HD, a derivação de chaves é realizada de acordo com uma estrutura hierárquica que permite que as chaves sejam organizadas em subespaços de derivação, cada subespaço sendo ainda mais subdividível, para facilitar a gestão de fundos e a interoperabilidade entre diferentes softwares de carteira. Atualmente, esse padrão é adotado pela grande maioria dos usuários de Bitcoin. Por essa razão, examinaremos isso em detalhe nos próximos capítulos.
### O Padrão BIP39: A Frase Mnemônica
Além do BIP32, o BIP39 padroniza o formato da semente como uma frase mnemônica, para facilitar o backup e a legibilidade pelos usuários. A frase mnemônica, também chamada de frase de recuperação ou frase de 24 palavras, é uma sequência de palavras retiradas de uma lista predefinida que codifica de forma segura a semente da carteira.
A frase mnemônica simplifica muito o backup para o usuário. Em caso de perda, dano ou roubo do dispositivo que hospeda a carteira, simplesmente saber essa frase mnemônica permite a recriação da carteira e a recuperação do acesso a todos os fundos assegurados por ela.
Nos próximos capítulos, exploraremos os funcionamentos internos das carteiras HD, incluindo mecanismos de derivação de chaves e as diferentes estruturas hierárquicas possíveis. Isso permitirá que você entenda melhor as fundações criptográficas nas quais a segurança dos fundos em Bitcoin se baseia. E para começar, no próximo capítulo, proponho que descubramos o papel da entropia na base da sua carteira.
## Entropia e Número Aleatório
<chapterId>b43c715d-affb-56d8-a697-ad5bc2fffd63</chapterId>
As carteiras HD modernas (determinísticas e hierárquicas) dependem de uma única peça inicial de informação chamada "entropia" para gerar deterministicamente todo o conjunto de chaves da carteira. Esta entropia é um número pseudoaleatório cujo nível de caos determina em parte a segurança da carteira.
### Definição de Entropia
Entropia, no contexto da criptografia e informação, é uma medida quantitativa da incerteza ou imprevisibilidade associada a uma fonte de dados ou um processo aleatório. Ela desempenha um papel importante na segurança dos sistemas criptográficos, especialmente na geração de chaves e números aleatórios. Alta entropia garante que as chaves geradas sejam suficientemente imprevisíveis e resistentes a ataques de força bruta, onde um atacante tenta todas as combinações possíveis para adivinhar a chave.
No contexto do Bitcoin, a entropia é usada para gerar a semente. Ao criar uma carteira determinística e hierárquica, a construção da frase mnemônica é feita a partir de um número aleatório, derivado de uma fonte de entropia. A frase é então usada para gerar múltiplas chaves privadas, de maneira determinística e hierárquica, para criar condições de gasto em UTXOs.
### Métodos de Geração de Entropia
A entropia inicial usada para uma carteira HD é geralmente de 128 bits ou 256 bits, onde:
- **128 bits de entropia** correspondem a uma frase mnemônica de **12 palavras**;
- **256 bits de entropia** correspondem a uma frase mnemônica de **24 palavras**.
Na maioria dos casos, esse número aleatório é gerado automaticamente pelo software da carteira usando um PRNG (_Pseudo-Random Number Generator_). PRNGs são uma categoria de algoritmos usados para gerar sequências de números a partir de um estado inicial, que têm características que se aproximam daquelas de um número aleatório, sem realmente ser um. Um bom PRNG deve ter propriedades como uniformidade de saída, imprevisibilidade e resistência a ataques preditivos. Diferentemente dos geradores de números aleatórios verdadeiros (TRNG), os PRNGs são determinísticos e reprodutíveis.
Uma alternativa é gerar manualmente a entropia, o que oferece melhor controle, mas também é muito mais arriscado. Eu aconselho fortemente contra a geração da entropia para sua carteira HD por conta própria.
No próximo capítulo, veremos como passamos de um número aleatório para uma frase mnemônica de 12 ou 24 palavras.
## A Frase Mnemônica
<chapterId>8f9340c1-e6dc-5557-a2f2-26c9669987d5</chapterId>
A frase mnemônica, também chamada de "frase-semente", "frase de recuperação", "frase secreta" ou "frase de 24 palavras", é uma sequência geralmente composta por 12 ou 24 palavras, que é gerada a partir de entropia. É usada para derivar deterministicamente todas as chaves de uma carteira HD. Isso significa que, a partir desta frase, é possível gerar e recriar deterministicamente todas as chaves privadas e públicas da carteira Bitcoin, e consequentemente acessar os fundos que estão protegidos com ela. O propósito da frase mnemônica é fornecer um meio de backup e recuperação de bitcoins que seja seguro e fácil de usar. Foi introduzida nos padrões em 2013 com o BIP39.
Vamos descobrir juntos como passar de entropia para uma frase mnemônica.
### O Checksum
Para transformar entropia em uma frase mnemônica, deve-se primeiro adicionar um checksum (ou "soma de controle") ao final da entropia. Este checksum é uma curta sequência de bits que garante a integridade dos dados verificando que nenhuma modificação acidental foi introduzida.
Para calcular o checksum, a função hash SHA256 é aplicada à entropia (apenas uma vez; este é um dos raros casos no Bitcoin onde um único hash SHA256 é usado em vez de um hash duplo). Esta operação produz um hash de 256 bits. O checksum consiste nos primeiros bits deste hash, e seu comprimento depende do da entropia, de acordo com a seguinte fórmula:
\text{CS} = \frac{\text{ENT}}{32}
onde $\text{ENT}$ representa o comprimento da entropia em bits, e $\text{CS}$ o comprimento do checksum em bits.
Por exemplo, para uma entropia de 256 bits, os primeiros 8 bits do hash são tomados para formar o checksum:
\text{CS} = \frac{256}{32} = 8 \text{ bits}
Uma vez calculado o checksum, ele é concatenado com a entropia para obter uma sequência de bits estendida notada $\text{ENT} \Vert \text{CS}$ ("concatenar" significa colocar um ao lado do outro).

### Correspondência entre a Entropia e a Frase Mnemônica
O número de palavras na frase mnemônica depende do tamanho da entropia inicial, como ilustrado na tabela a seguir com:
- $\text{ENT}$: o tamanho em bits da entropia;
- $\text{CS}$: o tamanho em bits do checksum;
- $w$: o número de palavras na frase mnemônica final.
\begin{array}{|c|c|c|c|} \hline \text{ENT} & \text{CS} & \text{ENT} \Vert \text{CS} & w \ \hline 128 & 4 & 132 & 12 \ 160 & 5 & 165 & 15 \ 192 & 6 & 198 & 18 \ 224 & 7 & 231 & 21 \ 256 & 8 & 264 & 24 \ \hline \end{array}
Por exemplo, para uma entropia de 256 bits, o resultado $\text{ENT} \Vert \text{CS}$ é de 264 bits e gera uma frase mnemônica de 24 palavras.
### Conversão da Sequência Binária em uma Frase Mnemônica
A sequência de bits $\text{ENT} \Vert \text{CS}$ é então dividida em segmentos de 11 bits. Cada segmento de 11 bits, uma vez convertido para decimal, corresponde a um número entre 0 e 2047, que designa a posição de uma palavra [em uma lista de 2048 palavras padronizadas pelo BIP39](https://github.com/Planb-Network/bitcoin-educational-content/blob/dev/resources/bet/bip39-wordlist//courses/cyp201/assets/BIP39-WORDLIST.pdf).
Por exemplo, para uma entropia de 128 bits, o checksum é de 4 bits, e assim a sequência total mede 132 bits. Ela é dividida em 12 segmentos de 11 bits (os bits laranjas designam o checksum):

Cada segmento é então convertido em um número decimal que representa uma palavra na lista. Por exemplo, o segmento binário `01011010001` é equivalente em decimal a `721`. Ao adicionar 1 para alinhar com a indexação da lista (que começa em 1 e não 0), isso dá o rank da palavra `722`, que é "*focus*" na lista.

Esta correspondência é repetida para cada um dos 12 segmentos, a fim de obter uma frase de 12 palavras.

### Características da Lista de Palavras BIP39
Uma particularidade da lista de palavras BIP39 é que nenhuma palavra compartilha as mesmas quatro primeiras letras na mesma ordem com outra palavra. Isso significa que anotar apenas as quatro primeiras letras de cada palavra é suficiente para salvar a frase mnemônica. Isso pode ser interessante para economizar espaço, especialmente para aqueles que desejam gravá-la em um suporte de metal.
Esta lista de 2048 palavras existe em vários idiomas. Estas não são simples traduções, mas palavras distintas para cada idioma. No entanto, é fortemente recomendado manter a versão em inglês, pois as versões em outros idiomas geralmente não são suportadas pelo software de carteira.
### Qual Comprimento Escolher para Sua Frase Mnemônica?
Para determinar o comprimento ótimo da sua frase mnemônica, deve-se considerar a segurança real que ela proporciona. Uma frase de 12 palavras garante 128 bits de segurança, enquanto uma frase de 24 palavras oferece 256 bits.
No entanto, essa diferença no nível de segurança da frase não melhora a segurança geral de uma carteira Bitcoin, pois as chaves privadas derivadas dessa frase só se beneficiam de 128 bits de segurança. De fato, como vimos anteriormente, as chaves privadas do Bitcoin são geradas a partir de números aleatórios (ou derivadas de uma fonte aleatória) variando entre $1$ e $n-1$, onde $n$ representa a ordem do ponto gerador $G$ da curva secp256k1, um número ligeiramente menor que $2^{256}$. Pode-se, portanto, pensar que essas chaves privadas oferecem 256 bits de segurança. No entanto, sua segurança reside na dificuldade de encontrar uma chave privada a partir de sua chave pública associada, uma dificuldade estabelecida pelo problema matemático do logaritmo discreto em curvas elípticas (*ECDLP*). Até o momento, o algoritmo mais conhecido para resolver esse problema é o algoritmo rho de Pollard, que reduz o número de operações necessárias para quebrar uma chave para a raiz quadrada de seu tamanho.
Para chaves de 256 bits, como as usadas no Bitcoin, o algoritmo rho de Pollard reduz assim a complexidade para $2^{128}$ operações:
O(\sqrt{2^{256}}) = O(2^{128})
Portanto, considera-se que uma chave privada usada no Bitcoin oferece 128 bits de segurança.
Como resultado, escolher uma frase de 24 palavras não proporciona proteção adicional para a carteira, pois 256 bits de segurança na frase são inúteis se as chaves derivadas só oferecem 128 bits de segurança. Para ilustrar esse princípio, é como ter uma casa com duas portas: uma porta de madeira antiga e uma porta reforçada. No caso de um arrombamento, a porta reforçada não seria útil, já que o intruso passaria pela porta de madeira. Esta é uma situação análoga aqui.
Uma frase de 12 palavras, que também oferece 128 bits de segurança, é, portanto, atualmente suficiente para proteger seus bitcoins contra qualquer tentativa de roubo. Enquanto o algoritmo de assinatura digital não mudar para usar chaves maiores ou depender de um problema matemático diferente do ECDLP, uma frase de 24 palavras permanece supérflua. Além disso, uma frase mais longa aumenta o risco de perda durante o backup: um backup que é duas vezes mais curto é sempre mais fácil de gerenciar.
Para ir além e aprender concretamente como gerar manualmente uma frase mnemônica de teste, aconselho você a descobrir este tutorial:
https://planb.network/tutorials/wallet/backup/generate-mnemonic-phrase-47507d90-e6af-4cac-b01b-01a14d7a8228
Antes de continuar com a derivação da carteira a partir desta frase mnemônica, vou apresentar a você, no capítulo seguinte, a passphrase BIP39, pois ela desempenha um papel no processo de derivação, e está no mesmo nível que a frase mnemônica.
## A passphrase
<chapterId>6a51b397-f3b5-5084-b151-cef94bc9b93f</chapterId>
Como acabamos de ver, as carteiras HD são geradas a partir de uma frase mnemônica tipicamente consistindo de 12 ou 24 palavras. Esta frase é muito importante porque permite a restauração de todas as chaves de uma carteira em caso de perda do seu dispositivo físico (como uma carteira de hardware, por exemplo). No entanto, ela constitui um único ponto de falha, porque se for comprometida, um atacante poderia roubar todos os bitcoins. É aqui que a passphrase BIP39 entra em jogo.
### O que é uma passphrase BIP39?
A passphrase é uma senha opcional, que você pode escolher livremente, que é adicionada à frase mnemônica no processo de derivação da chave para aumentar a segurança da carteira.
Cuidado, a passphrase não deve ser confundida com o código PIN da sua carteira de hardware ou a senha usada para desbloquear o acesso à sua carteira no seu computador. Ao contrário de todos esses elementos, a passphrase desempenha um papel na derivação das chaves da sua carteira. **Isso significa que sem ela, você nunca será capaz de recuperar seus bitcoins.**
A passphrase trabalha em conjunto com a frase mnemônica, modificando a semente da qual as chaves são geradas. Assim, mesmo que alguém obtenha sua frase de 12 ou 24 palavras, sem a passphrase, não podem acessar seus fundos. Usar uma passphrase essencialmente cria uma nova carteira com chaves distintas. Modificar (mesmo que levemente) a passphrase gerará uma carteira diferente.

### Por que você deve usar uma passphrase?
A passphrase é arbitrária e pode ser qualquer combinação de caracteres escolhida pelo usuário. Usar uma passphrase, portanto, oferece várias vantagens. Primeiramente, reduz todos os riscos associados ao comprometimento da frase mnemônica exigindo um segundo fator para acessar os fundos (roubo, acesso à sua casa, etc.).
Em seguida, pode ser usada estrategicamente para criar uma carteira isca, para enfrentar restrições físicas para roubar seus fundos como o infame "_ataque da chave inglesa de $5_". Neste cenário, a ideia é ter uma carteira sem passphrase contendo apenas uma pequena quantidade de bitcoins, o suficiente para satisfazer um potencial agressor, enquanto se tem uma carteira oculta. Esta última usa a mesma frase mnemônica mas é protegida com uma passphrase adicional.
Finalmente, o uso de uma passphrase é interessante quando se deseja controlar a aleatoriedade da geração da semente da carteira HD.
### Como escolher uma boa passphrase?
Para que a passphrase seja eficaz, ela deve ser suficientemente longa e aleatória. Assim como uma senha forte, recomendo escolher uma passphrase que seja o mais longa e aleatória possível, com uma diversidade de letras, números e símbolos para tornar qualquer ataque de força bruta impossível.
É também importante salvar corretamente essa passphrase, da mesma forma que a frase mnemônica. **Perdê-la significa perder o acesso aos seus bitcoins**. Eu aconselho fortemente contra tentar lembrá-la apenas de cor, pois isso aumenta de forma irrazoável o risco de perda. O ideal é anotá-la em um meio físico (papel ou metal) separado da frase mnemônica. Este backup deve, obviamente, ser armazenado em um local diferente de onde sua frase mnemônica está guardada para evitar que ambos sejam comprometidos simultaneamente.
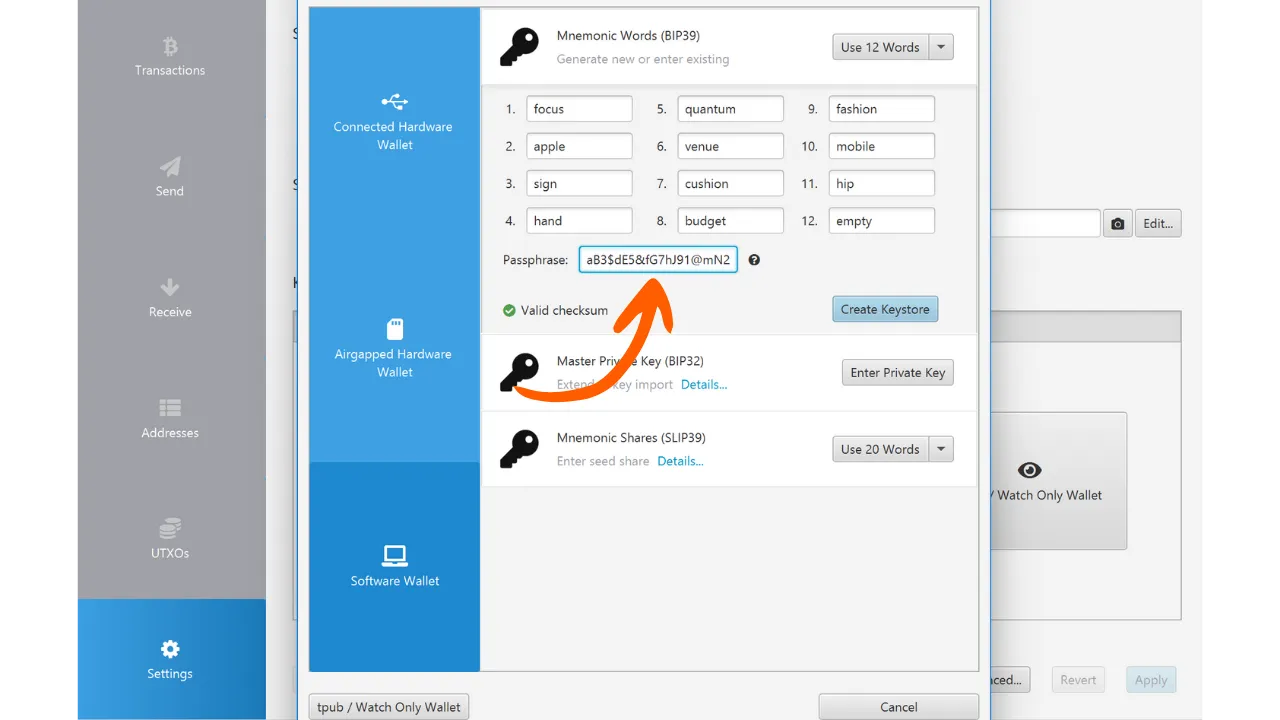
Na seção seguinte, descobriremos como esses dois elementos na base da sua carteira — a frase mnemônica e a passphrase — são usados para derivar os pares de chaves usados no *scriptPubKey* que bloqueiam seus UTXOs.
# Criação de Carteiras Bitcoin
<partId>9c25e767-7eae-50b8-8c5f-679d8fc83bab</partId>
## Criação da Semente e Chave Mestra
<chapterId>63093760-2010-5691-8d0e-9a04732ae557</chapterId>
Uma vez que a frase mnemônica e a passphrase opcional são geradas, o processo de derivação de uma carteira Bitcoin HD pode começar. A frase mnemônica é primeiro convertida em uma semente que constitui a base de todas as chaves da carteira.
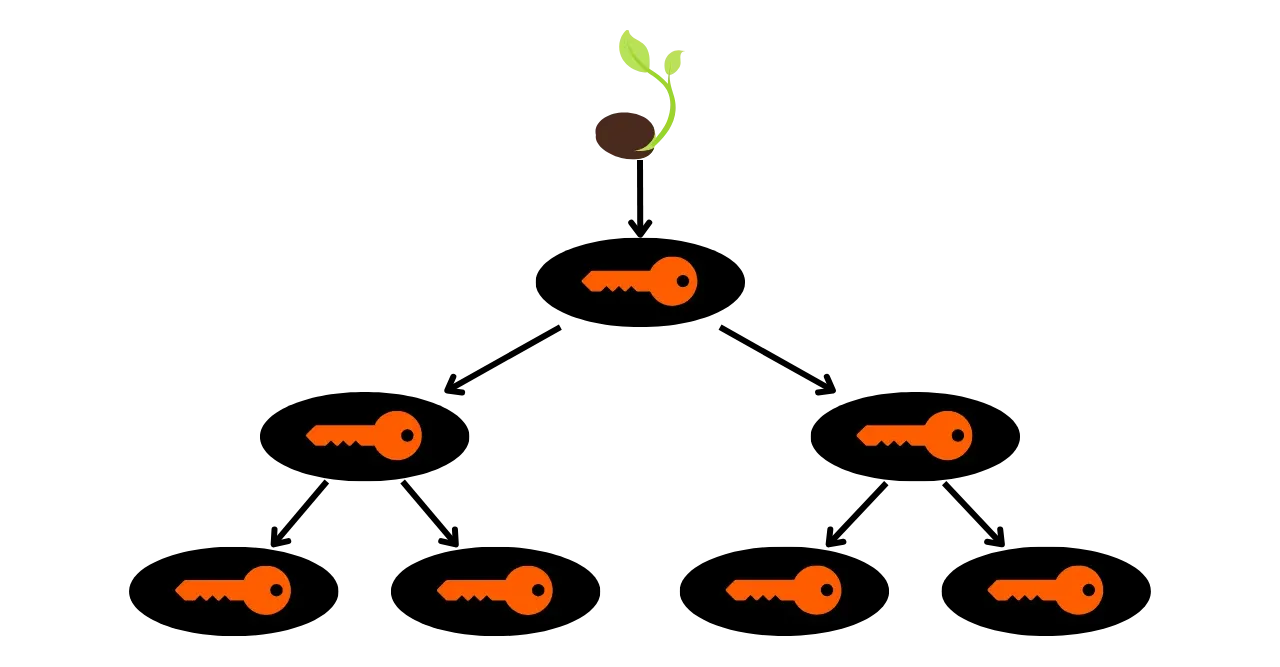
### A Semente de uma Carteira HD
O padrão BIP39 define a semente como uma sequência de 512 bits, que serve como ponto de partida para a derivação de todas as chaves de uma carteira HD. A semente é derivada da frase mnemônica e da possível passphrase usando o algoritmo **PBKDF2** (*Password-Based Key Derivation Function 2*) que já discutimos no capítulo 3.3. Nesta função de derivação, usaremos os seguintes parâmetros:
- $m$ : a frase mnemônica;
- $p$ : uma passphrase opcional escolhida pelo usuário para aumentar a segurança da semente. Se não houver passphrase, este campo é deixado em branco;
- $\text{PBKDF2}$ : a função de derivação com $\text{HMAC-SHA512}$ e $2048$ iterações;
- $s$: a semente da carteira de 512 bits.
Independentemente do comprimento da frase mnemônica escolhida (132 bits ou 264 bits), a função PBKDF2 sempre produzirá uma saída de 512 bits, e a semente, portanto, sempre será deste tamanho.
### Esquema de Derivação da Semente com PBKDF2
A seguinte equação ilustra a derivação da semente a partir da frase mnemônica e da passphrase:
s = \text{PBKDF2}_{\text{HMAC-SHA512}}(m, p, 2048)

O valor da semente é assim influenciado pelo valor da frase mnemônica e da passphrase. Ao mudar a passphrase, obtém-se uma semente diferente. No entanto, com a mesma frase mnemônica e passphrase, a mesma semente é sempre gerada, já que o PBKDF2 é uma função determinística. Isso garante que os mesmos pares de chaves possam ser recuperados através de nossos backups.
**Nota:** No linguajar comum, o termo "semente" muitas vezes se refere, por uso indevido da linguagem, à frase mnemônica. De fato, na ausência de uma passphrase, uma é simplesmente a codificação da outra. No entanto, como vimos, na realidade técnica das carteiras, a semente e a frase mnemônica são de fato dois elementos distintos.
Agora que temos nossa semente, podemos continuar com a derivação de nossa carteira Bitcoin.
### A Chave Mestra e o Código da Cadeia Mestra
Uma vez obtida a semente, o próximo passo na derivação de uma carteira HD envolve o cálculo da chave privada mestra e do código da cadeia mestra, que representarão a profundidade 0 da nossa carteira.
Para obter a chave privada mestra e o código da cadeia mestra, a função HMAC-SHA512 é aplicada à semente, usando uma chave fixa "*Bitcoin Seed*" idêntica para todos os usuários do Bitcoin. Esta constante é escolhida para garantir que as derivações de chave sejam específicas para o Bitcoin. Aqui estão os elementos:
- $\text{HMAC-SHA512}$: a função de derivação;
- $s$: a semente da carteira de 512 bits;
- $\text{"Bitcoin Seed"}$: a constante de derivação comum para todas as carteiras Bitcoin.
\text{output} = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)
O resultado desta função é, portanto, de 512 bits. Ele é então dividido em 2 partes:
- Os 256 bits à esquerda formam a **chave privada mestra**;
- Os 256 bits à direita formam o **código da cadeia mestra**.
Matematicamente, esses dois valores podem ser notados da seguinte forma, com $k_M$ sendo a chave privada mestra e $C_M$ o código da cadeia mestra:k_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[:256]}
C_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[256:]}

### Papel da Chave Mestra e do Código da Cadeia
A chave privada mestra é considerada a chave pai, da qual todas as chaves privadas derivadas — filhos, netos, bisnetos, etc. — serão geradas. Ela representa o nível zero na hierarquia de derivação.
O código da cadeia mestra, por outro lado, introduz uma fonte adicional de entropia no processo de derivação de chave para os filhos, a fim de contrariar certos ataques potenciais. Além disso, na carteira HD, cada par de chaves tem um código de cadeia único associado a ele, que também é usado para derivar chaves filhas deste par, mas discutiremos isso com mais detalhes nos próximos capítulos.
Antes de continuar com a derivação da carteira HD com os elementos seguintes, desejo, no próximo capítulo, apresentá-lo às chaves estendidas, que são frequentemente confundidas com a chave mestra. Veremos como elas são construídas e qual papel desempenham na carteira Bitcoin.
## Chaves Estendidas
<chapterId>8dcffce1-31bd-5e0b-965b-735f5f9e4602</chapterId>
Uma chave estendida é simplesmente a concatenação de uma chave (seja privada ou pública) e seu código de cadeia associado. Este código de cadeia é essencial para a derivação de chaves filhas porque, sem ele, é impossível derivar chaves filhas de uma chave pai, mas descobriremos esse processo com mais precisão no próximo capítulo. Essas chaves estendidas permitem, assim, agregar todas as informações necessárias para derivar chaves filhas, simplificando assim a gestão de contas dentro de uma carteira HD.
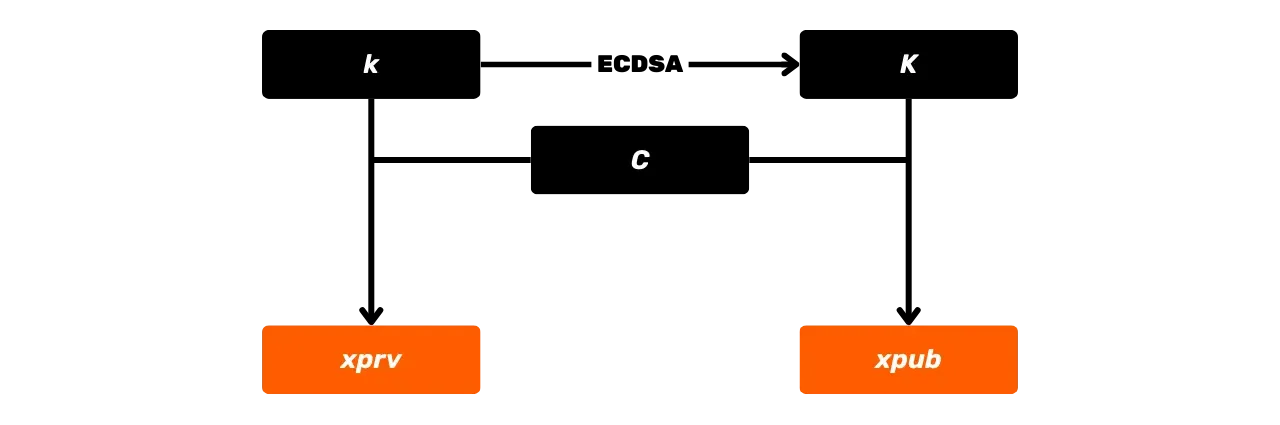
A chave estendida consiste em duas partes:
- O payload, que contém a chave privada ou pública, bem como o código de cadeia associado;
- Os metadados, que são várias peças de informação para facilitar a interoperabilidade entre softwares e melhorar a compreensão para o usuário.
### Como Funcionam as Chaves Estendidas
Quando a chave estendida contém uma chave privada, ela é referida como uma chave privada estendida. É reconhecida pelo seu prefixo que contém a menção `prv`. Além da chave privada, a chave privada estendida também contém o código de cadeia associado. Com este tipo de chave estendida, é possível derivar todos os tipos de chaves privadas filhas, e, portanto, pela adição e duplicação de pontos em curvas elípticas, também permite a derivação de todas as chaves públicas filhas.
Quando a chave estendida não contém uma chave privada, mas sim, uma chave pública, ela é referida como uma chave pública estendida. É reconhecida pelo seu prefixo que contém a menção `pub`. Obviamente, além da chave, ela também contém o código de cadeia associado. Diferente da chave privada estendida, a chave pública estendida permite a derivação apenas de chaves públicas filhas "normais" (o que significa que não pode derivar chaves filhas "blindadas"). Veremos no capítulo seguinte o que esses qualificadores "normal" e "blindado" significam.
Mas, em qualquer caso, a chave pública estendida não permite a derivação de chaves privadas filhas. Portanto, mesmo se alguém tiver acesso a um `xpub`, não será capaz de gastar os fundos associados, pois não terá acesso às chaves privadas correspondentes. Eles só podem derivar chaves públicas filhas para observar as transações associadas.
Para o seguinte, adotaremos a seguinte notação:
- $K_{\text{PAR}}$: uma chave pública pai;
- $k_{\text{PAR}}$: uma chave privada pai;
- $C_{\text{PAR}}$: um código de cadeia pai;
- $C_{\text{CHD}}$: um código de cadeia filho;
- $K_{\text{CHD}}^n$: uma chave pública filha normal;
- $k_{\text{CHD}}^n$: uma chave privada filha normal;
- $K_{\text{CHD}}^h$: uma chave pública filha blindada;
- $k_{\text{CHD}}^h$: uma chave privada filha blindada.

### Construção de uma Chave Estendida
Uma chave estendida é estruturada da seguinte forma:
- **Versão**: Código de versão para identificar a natureza da chave (`xprv`, `xpub`, `yprv`, `ypub`...). Veremos no final deste capítulo o que as letras `x`, `y` e `z` correspondem.
- **Profundidade**: Nível hierárquico na carteira HD relativo à chave mestre (0 para a chave mestre).
- **Impressão Digital do Pai**: Os primeiros 4 bytes do hash HASH160 da chave pública pai usada para derivar a chave presente no payload.
- **Número do Índice**: Identificador da chave filha entre chaves irmãs, isto é, entre todas as chaves no mesmo nível de derivação que têm as mesmas chaves pais.
- **Código de Cadeia**: Um código único de 32 bytes para derivar chaves filhas.
- **Chave**: A chave privada (prefixada por 1 byte para tamanho) ou a chave pública.
- **Checksum**: Um checksum calculado com a função HASH256 (duplo SHA256) também é adicionado, o que permite a verificação da integridade da chave estendida durante sua transmissão ou armazenamento.
O formato completo de uma chave estendida é, portanto, 78 bytes sem o checksum, e 82 bytes com o checksum. Em seguida, é convertido para Base58 para produzir uma representação facilmente legível pelos usuários. O formato Base58 é o mesmo que o usado para endereços de recebimento *Legacy* (antes do *SegWit*).
| Elemento | Descrição | Tamanho |
| ----------------- | ------------------------------------------------------------------------------------------------------------------ | --------- |
| Versão | Indica se a chave é pública (`xpub`, `ypub`) ou privada (`xprv`, `zprv`), bem como a versão da chave estendida | 4 bytes |
| Profundidade | Nível na hierarquia relativo à chave mestra | 1 byte |
| Impressão Digital do Pai | Os primeiros 4 bytes do HASH160 da chave pública pai | 4 bytes |
| Número do Índice | Posição da chave na ordem dos filhos | 4 bytes |
| Código da Cadeia | Usado para derivar chaves filhas | 32 bytes |
| Chave | A chave privada (com um prefixo de 1 byte) ou a chave pública | 33 bytes |
| Soma de Verificação | Soma de verificação para verificar a integridade | 4 bytes |
Se um byte é adicionado apenas à chave privada, é porque a chave pública comprimida é mais longa que a chave privada por um byte. Este byte adicional, adicionado no início da chave privada como `0x00`, iguala o tamanho delas, garantindo que o payload da chave estendida tenha o mesmo comprimento, seja ela uma chave pública ou privada.
### Prefixos de Chaves Estendidas
Como acabamos de ver, as chaves estendidas incluem um prefixo que indica tanto a versão da chave estendida quanto sua natureza. A notação `pub` indica que se refere a uma chave pública estendida, e a notação `prv` indica uma chave privada estendida. A letra adicional na base da chave estendida ajuda a indicar se o padrão seguido é Legacy, SegWit v0, SegWit v1, etc.
Aqui está um resumo dos prefixos usados e seus significados:
| Base 58 Prefix | Base 16 Prefix | Network | Purpose | Associated Scripts | Derivation | Key Type |
| --------------- | --------------- | ------- | ------------------- | ------------------- | --------------------- | ------------ |
| `xpub` | `0488b21e` | Mainnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/0'`, `m/86'/0'` | public |
| `xprv` | `0488ade4` | Mainnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/0'`, `m/86'/0'` | private |
| `tpub` | `043587cf` | Testnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/1'`, `m/86'/1'` | public |
| `tprv` | `04358394` | Testnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/1'`, `m/86'/1'` | private |
| `ypub` | `049d7cb2` | Mainnet | Nested SegWit | P2WPKH in P2SH | `m/49'/0'` | public |
| `yprv` | `049d7878` | Mainnet | Nested SegWit | P2WPKH in P2SH | `m/49'/0'` | private |
| `upub` | `049d7cb2` | Testnet | Nested SegWit | P2WPKH in P2SH | `m/49'/1'` | public |
| `uprv` | `044a4e28` | Testnet | Nested SegWit | P2WPKH in P2SH | `m/49'/1'` | private |
| `zpub` | `04b24746` | Mainnet | SegWit V0 | P2WPKH | `m/84'/0'` | public |
| `zprv` | `04b2430c` | Mainnet | SegWit V0 | P2WPKH | `m/84'/0'` | private |
| `vpub` | `045f1cf6` | Testnet | SegWit V0 | P2WPKH | `m/84'/1'` | public |
| `vprv` | `045f18bc` | Testnet | SegWit V0 | P2WPKH | `m/84'/1'` | private |
### Detalhes dos Elementos de uma Chave Estendida
Para entender melhor a estrutura interna de uma chave estendida, vamos pegar uma como exemplo e desmembrá-la. Aqui está uma chave estendida:
- **Em Base58**:
```txt
xpub6CTNzMUkzpurBWaT4HQoYzLP4uBbGJuWY358Rj7rauiw4rMHCyq3Rfy9w4kyJXJzeFfyrKLUar2rUCukSiDQFa7roTwzjiAhyQAdPLEjqHT
```
- **Em hexadecimal**:
```txt
0488B21E036D5601AD80000000C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A89303772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF50658051F067C3A
```
Esta chave estendida se desdobra em vários elementos distintos:
- **Versão**: `0488B21E`
Os primeiros 4 bytes são a versão. Aqui, corresponde a uma chave pública estendida no Mainnet com um propósito de derivação de _Legacy_ ou _SegWit v1_.
- **Profundidade**: `03`
Este campo indica o nível hierárquico da chave dentro da carteira HD. Neste caso, uma profundidade de `03` significa que esta chave está três níveis de derivação abaixo da chave mestre.
- **Impressão digital do pai**: `6D5601AD`
Estes são os primeiros 4 bytes do hash HASH160 da chave pública pai que foi usada para derivar este `xpub`.
- **Número do Índice**: `80000000`
Este índice indica a posição da chave entre os filhos de seu pai. O prefixo `0x80` indica que a chave é derivada de maneira endurecida (hardened), e como o restante é preenchido com zeros, indica que esta chave é a primeira entre seus possíveis irmãos.
- **Código da Cadeia**: `C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A893`
- **Chave Pública**: `03772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF5065805`
- **Checksum**: `1F067C3A`
O checksum corresponde aos primeiros 4 bytes do hash (SHA256 duplo) de tudo o mais.
Neste capítulo, descobrimos que existem dois tipos diferentes de chaves filhas. Também aprendemos que a derivação dessas chaves filhas requer uma chave (seja privada ou pública) e seu código da cadeia. No próximo capítulo, examinaremos em detalhes a natureza desses diferentes tipos de chaves e como derivá-las de sua chave pai e código da cadeia.
## Derivação de Pares de Chaves Filhas
<chapterId>61c0807c-845b-5076-ad06-7f395b36adfd</chapterId>
A derivação de pares de chaves filhas em carteiras HD do Bitcoin depende de uma estrutura hierárquica que permite gerar um grande número de chaves, enquanto organiza esses pares em diferentes grupos através de ramos. Cada par filho derivado de um par pai pode ser usado diretamente em um _scriptPubKey_ para bloquear bitcoins, ou como ponto de partida para gerar mais chaves filhas, e assim por diante, para criar uma árvore de chaves.
Todas essas derivações começam com a chave mestre e o código da cadeia mestre, que são os primeiros pais no nível de profundidade 0. Eles são, de certa forma, o Adão e Eva das chaves da sua carteira, ancestrais comuns de todas as chaves derivadas.
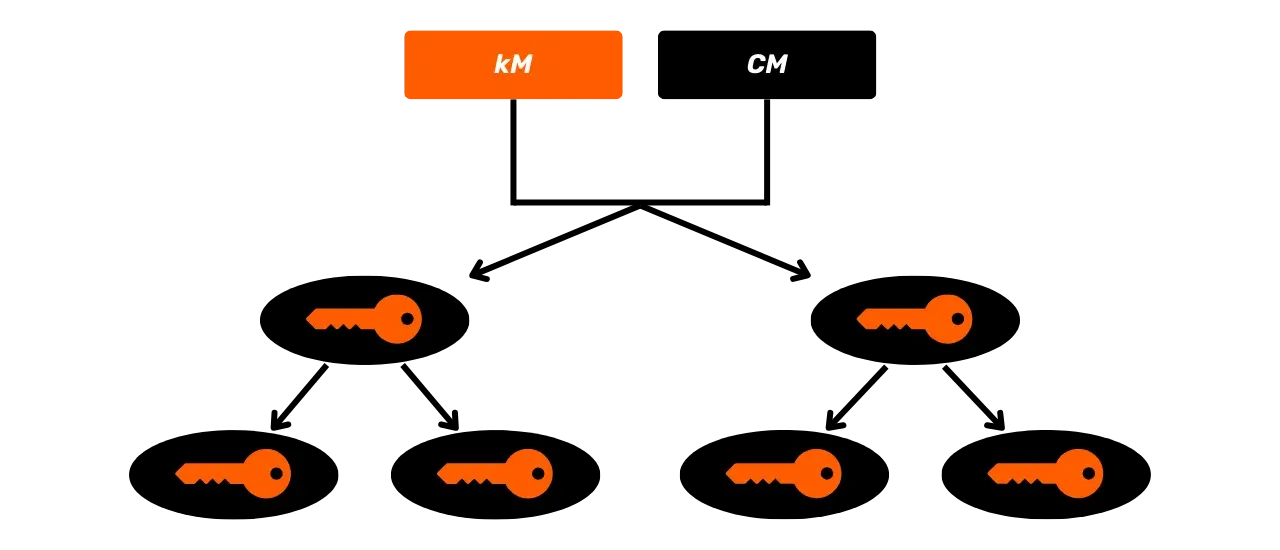
Vamos explorar como essa derivação determinística funciona.
### Os Diferentes Tipos de Derivações de Chaves Filhas
Como tocamos brevemente no capítulo anterior: as chaves filhas são divididas em dois tipos principais:
- **Chaves filhas normais** ($k_{\text{CHD}}^n, K_{\text{CHD}}^n$): São derivadas da chave pública estendida ($K_{\text{PAR}}$), ou da chave privada estendida ($k_{\text{PAR}}$), derivando primeiro a chave pública.
- **Chaves filhas endurecidas** ($k_{\text{CHD}}^h, K_{\text{CHD}}^h$): Só podem ser derivadas da chave privada estendida ($k_{\text{PAR}}$) e, portanto, são invisíveis para observadores que só têm a chave pública estendida.
Cada par de chaves filho é identificado por um **índice** de 32 bits (denominado $i$ em nossos cálculos). Os índices para chaves normais variam de $0$ a $2^{31}-1$, enquanto aqueles para chaves endurecidas (hardened) variam de $2^{31}$ a $2^{32}-1$. Esses números são usados para distinguir pares de chaves irmãs durante a derivação. De fato, cada par de chaves pai deve ser capaz de derivar múltiplos pares de chaves filho. Se aplicássemos o mesmo cálculo sistematicamente a partir das chaves pai, todas as chaves irmãs obtidas seriam idênticas, o que não é desejável. O índice, portanto, introduz uma variável que modifica o cálculo de derivação, permitindo que cada par irmão seja diferenciado. Exceto por uso específico em certos protocolos e padrões de derivação, geralmente começamos derivando a primeira chave filho com o índice `0`, a segunda com o índice `1`, e assim por diante.
### Processo de Derivação com HMAC-SHA512
A derivação de cada chave filho é baseada na função HMAC-SHA512, que discutimos na Seção 2 sobre funções de hash. Ela recebe dois inputs: o código de cadeia pai $C_{\text{PAR}}$ e a concatenação da chave pai (seja a chave pública $K_{\text{PAR}}$ ou a chave privada $k_{\text{PAR}}$, dependendo do tipo de chave filho desejado) e o índice. A saída do HMAC-SHA512 é uma sequência de 512 bits, dividida em duas partes:
- **Os primeiros 32 bytes** (ou $h_1$) são usados para calcular o novo par filho.
- **Os últimos 32 bytes** (ou $h_2$) servem como o novo código de cadeia $C_{\text{CHD}}$ para o par filho.
Em todos os nossos cálculos, vou denotar $\text{hash}$ a saída da função HMAC-SHA512.
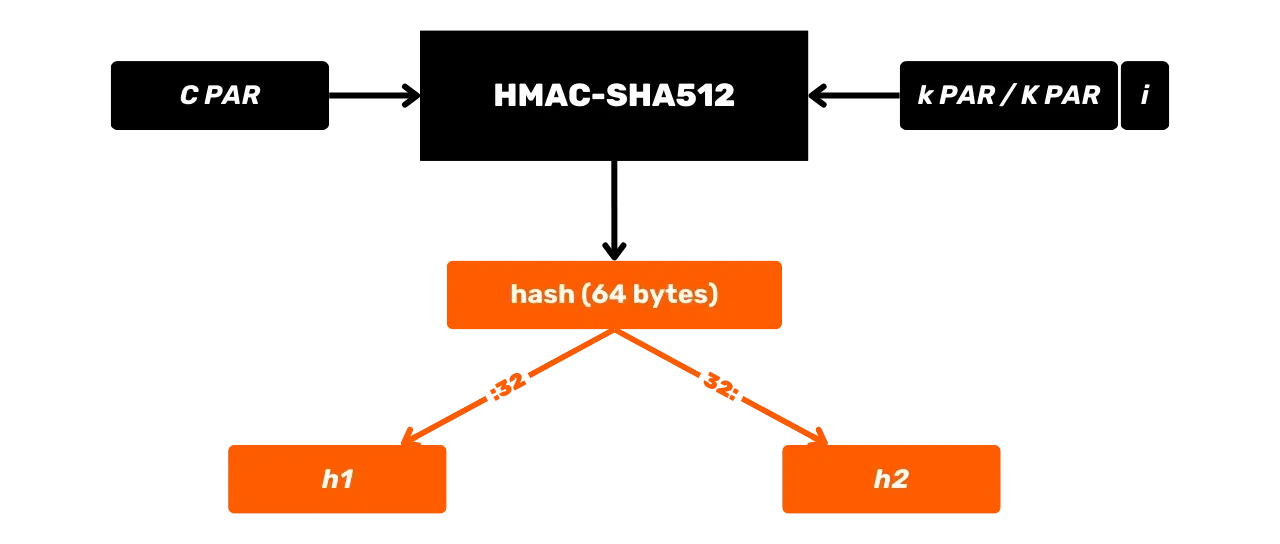
#### Derivação de uma Chave Privada Filho a partir de uma Chave Privada Pai
Para derivar uma chave privada filho $k_{\text{CHD}}$ a partir de uma chave privada pai $k_{\text{PAR}}$, dois cenários são possíveis dependendo se uma chave endurecida ou normal é desejada.
Para uma **chave filho normal** ($i < 2^{31}$), o cálculo de $\text{hash}$ é o seguinte:
\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, G \cdot k_{\text{PAR}} \Vert i)
Neste cálculo, observamos que nossa função HMAC recebe dois inputs: primeiro, o código de cadeia pai, e depois a concatenação do índice com a chave pública associada à chave privada pai. A chave pública pai é usada aqui porque estamos procurando derivar uma chave filho normal, não uma endurecida.
Agora temos um $\text{hash}$ de 64 bytes que dividiremos em 2 partes de 32 bytes cada: $h_1$ e $h_2$:
\text{hash} = h_1 \Vert h_2
h1 = \text{hash}_{[:32]} \quad, \quad h2 = \text{hash}_{[32:]}
A chave privada filho $k_{\text{CHD}}^n$ é então calculada da seguinte forma:
k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n
Neste cálculo, a operação $\text{parse256}(h_1)$ consiste em interpretar os primeiros 32 bytes do $\text{hash}$ como um inteiro de 256 bits. Esse número é então adicionado à chave privada pai, tudo tomado modulo $n$ para permanecer dentro da ordem da curva elíptica, como vimos na seção 3 sobre assinaturas digitais. Assim, para derivar uma chave privada filha normal, embora a chave pública pai seja usada como base para cálculo nas entradas da função HMAC-SHA512, é sempre necessário ter a chave privada pai para finalizar o cálculo.
A partir desta chave privada filha, é possível derivar a chave pública correspondente aplicando ECDSA ou Schnorr. Desta forma, obtemos um par completo de chaves.
Então, a segunda parte do $\text{hash}$ é simplesmente interpretada como sendo o código de cadeia para o par de chaves filho que acabamos de derivar:
C_{\text{CHD}} = h_2
Aqui está uma representação esquemática da derivação geral:
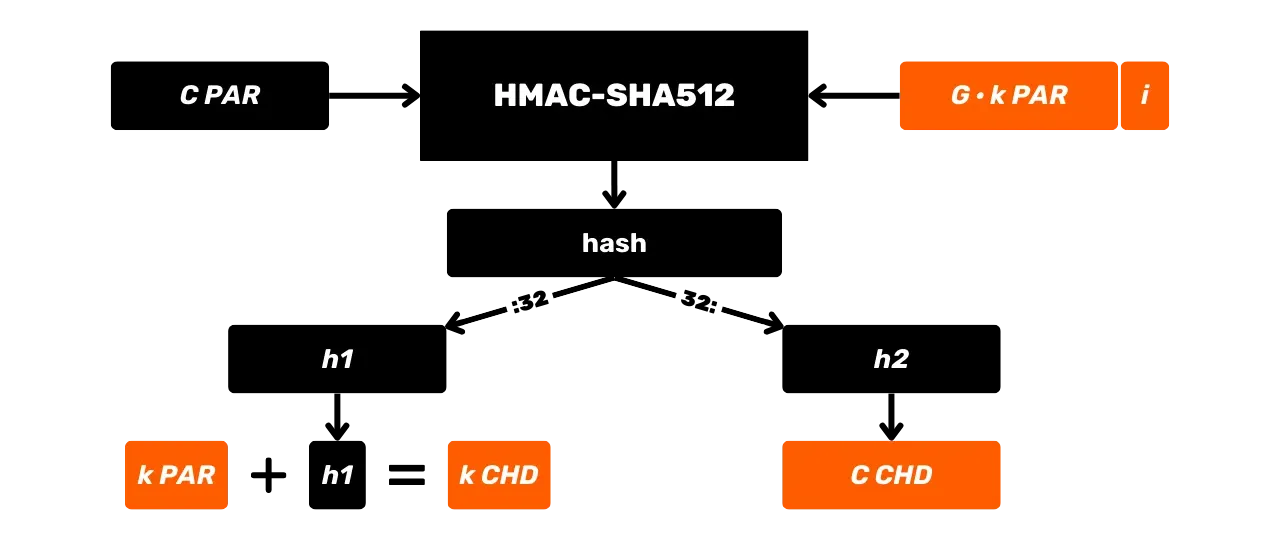
Para uma **chave filha endurecida** ($i \geq 2^{31}$), o cálculo do $\text{hash}$ é o seguinte:
hash = \text{HMAC-SHA512}(C_{\text{PAR}}, 0x00 \Vert k_{\text{PAR}} \Vert i)
Neste cálculo, observamos que nossa função HMAC recebe dois inputs: primeiro, o código de cadeia pai, e depois a concatenação do índice com a chave privada pai. A chave privada pai é usada aqui porque estamos procurando derivar uma chave filha endurecida. Além disso, um byte igual a `0x00` é adicionado no início da chave. Esta operação iguala seu comprimento para corresponder ao de uma chave pública comprimida.
Então, agora temos um $\text{hash}$ de 64 bytes que dividiremos em 2 partes de 32 bytes cada: $h_1$ e $h_2$:
\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}[:32] \quad, \quad h_2 = \text{hash}[32:]
A chave privada filha $k_{\text{CHD}}^h$ é então calculada da seguinte forma:
k_{\text{CHD}}^h = \text{parse256}(h_1) + k_{\text{PAR}} \mod n
Em seguida, simplesmente interpretamos a segunda parte do $\text{hash}$ como sendo o código de cadeia para o par de chaves filho que acabamos de derivar:
C_{\text{CHD}} = h_2
Aqui está uma representação esquemática da derivação geral:

Podemos ver que a derivação normal e a derivação endurecida funcionam da mesma maneira, com esta diferença: a derivação normal usa a chave pública pai como entrada para a função HMAC, enquanto a derivação endurecida usa a chave privada pai.
#### Derivando uma chave pública filha a partir de uma chave pública pai
Se conhecemos apenas a chave pública pai $K_{\text{PAR}}$ e o código de cadeia associado $C_{\text{PAR}}$, isto é, uma chave pública estendida, é possível derivar chaves públicas filhas $K_{\text{CHD}}^n$, mas apenas para chaves filhas normais (não endurecidas). Este princípio permite notavelmente monitorar os movimentos de uma conta em uma carteira Bitcoin a partir do `xpub` (_somente visualização_).
Para realizar este cálculo, vamos computar o $\text{hash}$ com um índice $i < 2^{31}$ (derivação normal):
\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, K_{\text{PAR}} \Vert i)
Neste cálculo, observamos que nossa função HMAC recebe dois inputs: primeiro o código de cadeia pai, depois a concatenação do índice com a chave pública pai.
Então, agora temos um $hash$ de 64 bytes que vamos dividir em 2 partes de 32 bytes cada: $h_1$ e $h_2$:
\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}[:32] \quad, \quad h_2 = \text{hash}[32:]
A chave pública filha $K_{\text{CHD}}^n$ é então calculada da seguinte forma:
K_{\text{CHD}}^n = G \cdot \text{parse256}(h_1) + K_{\text{PAR}}
Se $\text{parse256}(h_1) \geq n$ (ordem da curva elíptica) ou se $K_{\text{CHD}}^n$ é o ponto no infinito, a derivação é inválida, e outro índice deve ser escolhido.
Neste cálculo, a operação $\text{parse256}(h_1)$ envolve interpretar os primeiros 32 bytes do $\text{hash}$ como um inteiro de 256 bits. Este número é usado para calcular um ponto na curva elíptica através da adição e duplicação a partir do ponto gerador $G$. Este ponto é então adicionado à chave pública pai para obter a chave pública filha normal. Assim, para derivar uma chave pública filha normal, apenas a chave pública pai e o código de cadeia pai são necessários; a chave privada pai nunca entra neste processo, ao contrário do cálculo da chave privada filha que vimos anteriormente.
A seguir, o código de cadeia filha é simplesmente:
C_{\text{CHD}} = h_2
Aqui está uma representação esquemática da derivação geral:
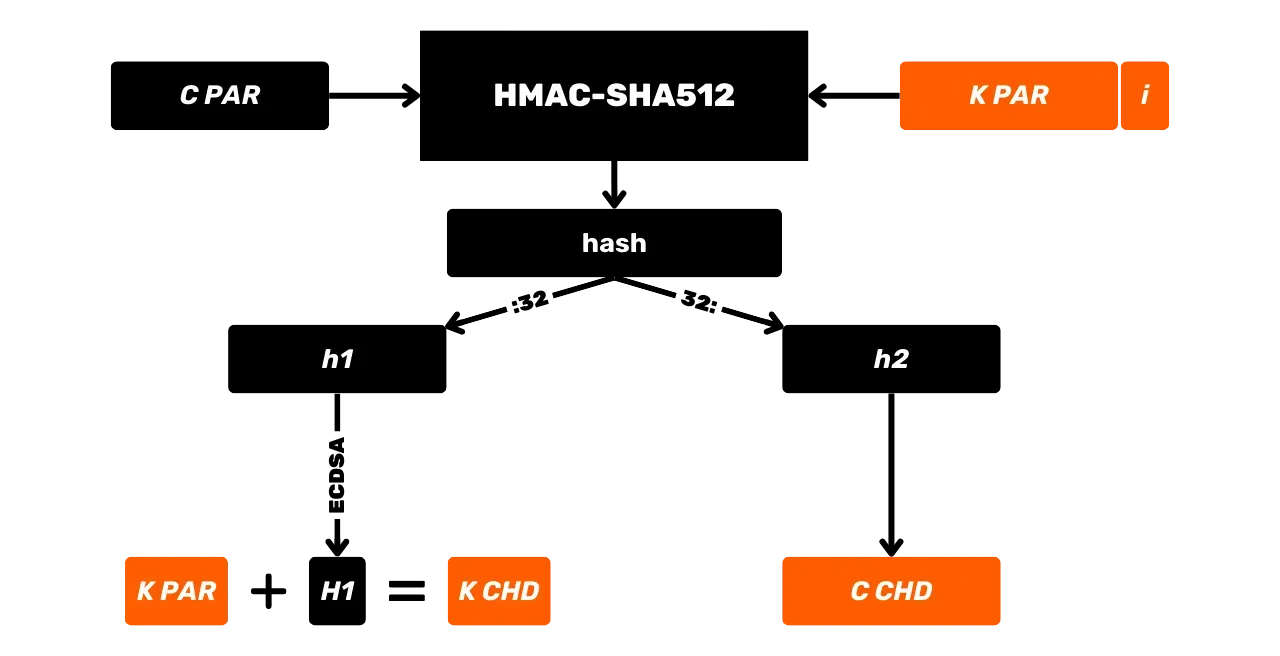
### Correspondência entre chaves públicas e privadas filhas
Uma questão que pode surgir é como uma chave pública filha normal derivada de uma chave pública pai pode corresponder a uma chave privada filha normal derivada da chave privada pai correspondente. Este link é precisamente garantido pelas propriedades das curvas elípticas. De fato, para derivar uma chave pública filha normal, o HMAC-SHA512 é aplicado da mesma maneira, mas seu output é usado de forma diferente:
- **Chave privada filha normal**: $k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n$
- **Chave pública filha normal**: $K_{\text{CHD}}^n = G \cdot \text{parse256}(h_1) + K_{\text{PAR}}$
Graças às operações de adição e duplicação na curva elíptica, ambos os métodos produzem resultados consistentes: a chave pública derivada da chave privada filha é idêntica à chave pública filha derivada diretamente da chave pública pai.
### Resumo dos tipos de derivação
Para resumir, aqui estão os diferentes tipos possíveis de derivações:
\begin{array}{|c|c|c|c|} \hline \rightarrow & \text{PAR} & \text{CHD} & \text{n/h} \ \hline k_{\text{PAR}} \rightarrow k_{\text{CHD}} & k_{\text{PAR}} & { k_{\text{CHD}}^n, k_{\text{CHD}}^h } & { n, h } \ k_{\text{PAR}} \rightarrow K_{\text{CHD}} & k_{\text{PAR}} & { K_{\text{CHD}}^n, K_{\text{CHD}}^h } & { n, h } \ K_{\text{PAR}} \rightarrow k_{\text{CHD}} & K_{\text{PAR}} & \times & \times \ K_{\text{PAR}} \rightarrow K_{\text{CHD}} & K_{\text{PAR}} & K_{\text{CHD}}^n & n \ \hline \end{array}
Para resumir, até agora você aprendeu a criar os elementos básicos da carteira HD: a frase mnemônica, a semente e, então, a chave mestra e o código da cadeia mestre. Você também descobriu como derivar pares de chaves filhas neste capítulo. No próximo capítulo, exploraremos como essas derivações são organizadas em carteiras Bitcoin e qual estrutura seguir para obter concretamente os endereços de recebimento, bem como os pares de chaves usados no _scriptPubKey_ e _scriptSig_.
## Estrutura da Carteira e Caminhos de Derivação
<chapterId>34e1bbda-67de-5493-b268-1fded8d67689</chapterId>
A estrutura hierárquica das carteiras HD no Bitcoin permite a organização de pares de chaves de várias maneiras. A ideia é derivar, a partir da chave privada mestre e do código da cadeia mestre, vários níveis de profundidade. Cada nível adicionado corresponde à derivação de um par de chaves filha de um par de chaves pai.
Com o tempo, diferentes BIPs introduziram padrões para esses caminhos de derivação, visando padronizar seu uso em diferentes softwares. Então, neste capítulo, descobriremos o significado de cada nível de derivação em carteiras HD, de acordo com esses padrões.
### As Profundidades de Derivação de uma Carteira HD
Os caminhos de derivação são organizados em camadas de profundidade, variando da profundidade 0, que representa a chave mestre e o código da cadeia mestre, até camadas de subníveis para derivar endereços usados para bloquear UTXOs. Os BIPs (_Propostas de Melhoria do Bitcoin_) definem os padrões para cada camada, o que ajuda a harmonizar práticas em diferentes softwares de gestão de carteiras.
Um caminho de derivação, portanto, refere-se à sequência de índices usados para derivar chaves filhas de uma chave mestre.
**Profundidade 0: Chave Mestre (BIP32)**
Esta profundidade corresponde à chave privada mestre da carteira e ao código da cadeia mestre. É representada pela notação $m/$.
**Profundidade 1: Propósito (BIP43)**
O objetivo determina a estrutura lógica de derivação. Por exemplo, um endereço P2WPKH terá $/84'/$ na profundidade 1 (de acordo com o BIP84), enquanto um endereço P2TR terá $/86'/$ (de acordo com o BIP86). Esta camada facilita a compatibilidade entre carteiras ao indicar números de índice correspondentes aos números BIP.
Em outras palavras, uma vez que você tenha a chave mestra e o código da cadeia mestre, estes servem como um par de chaves pai para derivar um par de chaves filho. O índice usado nesta derivação pode ser, por exemplo, $/84'/$ se a carteira for destinada a usar scripts do tipo SegWit v0. Este par de chaves está então na profundidade 1. Seu papel não é bloquear bitcoins, mas simplesmente servir como um ponto de passagem na hierarquia de derivação.
**Profundidade 2: Tipo de Moeda (BIP44)**
A partir do par de chaves na profundidade 1, uma nova derivação é realizada para obter o par de chaves na profundidade 2. Esta profundidade permite diferenciar contas Bitcoin de outras criptomoedas dentro da mesma carteira.
Cada moeda tem um índice único para garantir a compatibilidade entre carteiras multi-moedas. Por exemplo, para Bitcoin, o índice é $/0'/$ (ou `0x80000000` em notação hexadecimal). Índices de moedas são escolhidos na faixa de $2^{31}$ a $2^{32}-1$ para garantir derivação reforçada.
Para dar outros exemplos, aqui estão os índices de algumas moedas:
- $1'$ (`0x80000001`) para bitcoins de testnet;
- $2'$ (`0x80000002`) para Litecoin;
- $60'$ (`0x8000003c`) para Ethereum...
**Profundidade 3: Conta (BIP32)**
Cada carteira pode ser dividida em várias contas, numeradas a partir de $2^{31}$, e representadas na profundidade 3 por $/0'/$ para a primeira conta, $/1'/$ para a segunda, e assim por diante. Geralmente, quando se refere a uma chave estendida `xpub`, refere-se a chaves nesta profundidade de derivação.
Esta separação em diferentes contas é opcional. Tem como objetivo simplificar a organização da carteira para os usuários. Na prática, muitas vezes apenas uma conta é usada, geralmente a primeira por padrão. No entanto, em alguns casos, se deseja claramente distinguir pares de chaves para diferentes usos, isso pode ser útil. Por exemplo, é possível criar uma conta pessoal e uma conta profissional a partir da mesma semente, com grupos completamente distintos de chaves a partir desta profundidade de derivação.
**Profundidade 4: Cadeia (BIP32)**
Cada conta definida na profundidade 3 é então estruturada em duas cadeias:
- **A cadeia externa**: Nesta cadeia, o que são conhecidos como endereços "públicos" são derivados. Estes endereços de recebimento são destinados a bloquear UTXOs provenientes de transações externas (ou seja, originadas do consumo de UTXOs que não pertencem a você). Simplificando, esta cadeia externa é usada sempre que se deseja receber bitcoins. Quando você clica em "_receber_" no software da sua carteira, é sempre um endereço da cadeia externa que é oferecido a você. Esta cadeia é representada por um par de chaves derivado com o índice $/0/$.
- **A cadeia interna (troco)**: Esta cadeia é reservada para endereços de recebimento que bloqueiam bitcoins provenientes do consumo de UTXOs que pertencem a você, em outras palavras, endereços de troco. É identificada pelo índice $/1/$.
**Profundidade 5: Índice de Endereço (BIP32)**
Finalmente, a profundidade 5 representa o último passo da derivação na carteira. Embora seja tecnicamente possível continuar indefinidamente, os padrões atuais param aqui. Nesta profundidade final, os pares de chaves que serão realmente usados para bloquear e desbloquear os UTXOs são derivados. Cada índice permite distinguir entre pares de chaves irmãs: assim, o primeiro endereço de recebimento usará o índice $/0/$, o segundo o índice $/1/$, e assim por diante.
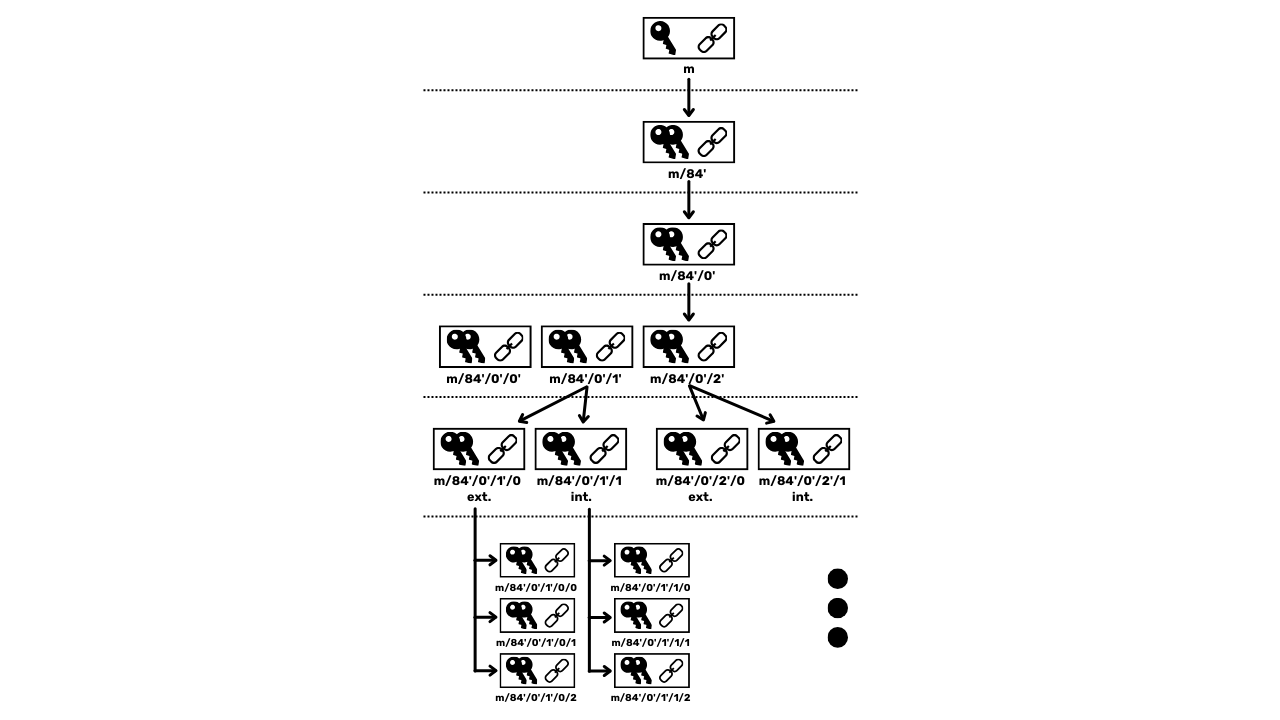
### Notação dos Caminhos de Derivação
O caminho de derivação é escrito separando cada nível com uma barra ($/$). Cada barra indica, assim, uma derivação de um par de chaves pai ($k_{\text{PAR}}$, $K_{\text{PAR}}$, $C_{\text{PAR}}$) para um par de chaves filho ($k_{\text{CHD}}$, $K_{\text{CHD}}$, $C_{\text{CHD}}$). O número anotado em cada profundidade corresponde ao índice usado para derivar esta chave de seus pais. O apóstrofo ($'$) às vezes colocado à direita do índice indica uma derivação endurecida ($k_{\text{CHD}}^h$, $K_{\text{CHD}}^h$). Às vezes, este apóstrofo é substituído por um $h$. Na ausência de um apóstrofo ou $h$, trata-se, portanto, de uma derivação normal ($k_{\text{CHD}}^n$, $K_{\text{CHD}}^n$).
Como vimos nos capítulos anteriores, os índices de chaves endurecidas começam de $2^{31}$, ou `0x80000000` em hexadecimal. Portanto, quando um índice é seguido por um apóstrofo em um caminho de derivação, $2^{31}$ deve ser adicionado ao número indicado para obter o valor real usado na função HMAC-SHA512. Por exemplo, se o caminho de derivação especifica $/44'/$, o índice real será:
i = 44 + 2^{31} = 2,147,483,692
Em hexadecimal, isso é `0x8000002C`.
Agora que entendemos os princípios principais dos caminhos de derivação, vamos tomar um exemplo! Aqui está o caminho de derivação para um endereço de recebimento Bitcoin:
m / 84' / 0' / 1' / 0 / 7
Neste exemplo:
- $84'$ indica o padrão P2WPKH (SegWit v0);
- $0'$ indica a moeda Bitcoin na mainnet;
- $1'$ corresponde à segunda conta na carteira;
- $0$ indica que o endereço está na cadeia externa;
- $7$ indica o 8º endereço externo desta conta.
### Resumo da estrutura de derivação
| Profundidade | Descrição | Exemplo Padrão |
| ------------ | ------------------ | -------------------------------- |
| 0 | Chave Mestra | $m/$ |
| 1 | Propósito | $/86'/$ (P2TR) |
| 2 | Moeda | $/0'/$ (Bitcoin) |
| 3 | Conta | $/0'/$ (Primeira conta) |
| 4 | Cadeia | $/0/$ (externa) ou $/1/$ (troco) |
| 5 | Índice de Endereço | $/0/$ (primeiro endereço) |
No próximo capítulo, descobriremos o que são os "_output script descriptors_", uma inovação recentemente introduzida no Bitcoin Core que simplifica o backup de uma carteira Bitcoin.
## Output script descriptors
<chapterId>e4f1c2d3-9b8a-4d3e-8f2a-7b6c5d4e3f2a</chapterId>
Frequentemente, é dito que a frase mnemônica sozinha é suficiente para recuperar o acesso a uma carteira. Na realidade, as coisas são um pouco mais complexas. No capítulo anterior, examinamos a estrutura de derivação da carteira HD, e você pode ter notado que esse processo é bastante complexo. Os caminhos de derivação indicam ao software qual direção seguir para derivar as chaves do usuário. No entanto, ao recuperar uma carteira Bitcoin, se não se conhece esses caminhos, a frase mnemônica sozinha não é suficiente. Ela permite obter a chave mestra e o código da cadeia mestre, mas é necessário saber os índices usados para alcançar as chaves filhas.
Teoricamente, seria necessário salvar não apenas a frase mnemônica da nossa carteira, mas também os caminhos para as contas que usamos. Na prática, muitas vezes é possível recuperar o acesso às chaves filhas sem essa informação, desde que os padrões tenham sido seguidos. Testando cada padrão um por um, geralmente é possível recuperar o acesso aos bitcoins. No entanto, isso não é garantido e é especialmente complicado para iniciantes. Além disso, com a diversificação dos tipos de script e o surgimento de configurações mais complexas, essa informação poderia se tornar difícil de extrapolar, transformando esses dados em informações privadas e difíceis de recuperar por força bruta. É por isso que uma inovação foi recentemente introduzida e está começando a ser integrada ao seu software de carteira favorito: os _output script descriptors_.
### O que é um "descriptor"?
Os "_output script descriptors_", ou simplesmente "_descriptors_", são expressões estruturadas que descrevem completamente um script de saída (_scriptPubKey_) e fornecem todas as informações necessárias para seguir as transações associadas a um script específico. Eles facilitam o gerenciamento de chaves em carteiras HD, oferecendo uma descrição padronizada e completa da estrutura da carteira e dos tipos de endereços usados.
A principal vantagem dos descriptors reside na sua capacidade de encapsular todas as informações essenciais para restaurar uma carteira em uma única string (além da frase de recuperação). Ao salvar um descriptor com as frases mnemônicas associadas, torna-se possível restaurar as chaves privadas sabendo precisamente sua posição na hierarquia. Para carteiras multisig, cujo backup inicialmente era mais complexo, o descriptor inclui o `xpub` de cada fator, garantindo assim a possibilidade de regenerar os endereços em caso de problema.
### Construção de um descriptor
Um descriptor consiste em vários elementos:
- Funções de script como `pk` (_Pay-to-PubKey_), `pkh` (_Pay-to-PubKey-Hash_), `wpkh` (_Pay-to-Witness-PubKey-Hash_), `sh` (_Pay-to-Script-Hash_), `wsh` (_Pay-to-Witness-Script-Hash_), `tr` (_Pay-to-Taproot_), `multi` (_Multisignature_), e `sortedmulti` (_Multisignature com chaves ordenadas_);
- Caminhos de derivação, por exemplo, `[d34db33f/44h/0h/0h]` que indica um caminho de conta derivada e uma impressão digital de chave mestra específica;
- Chaves em vários formatos, como chaves públicas hexadecimais ou chaves públicas estendidas (`xpub`);
- Um checksum, precedido por um sinal de hash, para verificar a integridade do descriptor.
Por exemplo, um descritor para uma carteira P2WPKH (SegWit v0) poderia parecer assim:
```text
wpkh([cdeab12f/84h/0h/0h]xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U/<0;1>/*)#jy0l7nr4
```
Neste descritor, a função de derivação `wpkh` indica um tipo de script _Pay-to-Witness-Public-Key-Hash_. É seguido pelo caminho de derivação que contém:
- `cdeab12f`: a impressão digital da chave mestra;
- `84h`: que significa o uso de um propósito BIP84, destinado a endereços SegWit v0;
- `0h`: que indica que é uma moeda BTC na mainnet;
- `0h`: que se refere ao número específico da conta usada na carteira.
O descritor também inclui a chave pública estendida usada nesta carteira:
```text
xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U
```
Em seguida, a notação `/<0;1>/*` especifica que o descritor pode gerar endereços da cadeia externa (`0`) e da cadeia interna (`1`), com um curinga (`*`) permitindo a derivação sequencial de múltiplos endereços de maneira configurável, semelhante ao gerenciamento de um "limite de lacuna" em softwares de carteira tradicionais.
Finalmente, `#jy0l7nr4` representa o checksum para verificar a integridade do descritor.
Agora você sabe tudo sobre o funcionamento da carteira HD no Bitcoin e o processo de derivação de pares de chaves. No entanto, nos últimos capítulos, limitamo-nos à geração de chaves privadas e públicas, sem abordar a construção de endereços de recebimento. Este será precisamente o assunto do próximo capítulo!
## Endereços de Recebimento
<chapterId>ca80a89d-f8da-4e09-8c35-43179b65bced</chapterId>
Endereços de recebimento são pedaços de informação embutidos em _scriptPubKey_ para bloquear UTXOs recém-criados. Simplificando, um endereço serve para receber bitcoins. Vamos explorar seu funcionamento em conexão com o que estudamos nos capítulos anteriores.
### O Papel dos Endereços Bitcoin em Scripts
Como explicado anteriormente, o papel de uma transação é transferir a propriedade de bitcoins de entradas para saídas. Esse processo envolve consumir UTXOs como entradas enquanto cria novos UTXOs como saídas. Esses UTXOs são protegidos por scripts, que definem as condições necessárias para desbloquear os fundos.
Quando um usuário recebe bitcoins, o remetente cria uma saída UTXO e a bloqueia com um _scriptPubKey_. Esse script contém as regras que especificam tipicamente as assinaturas e chaves públicas necessárias para desbloquear este UTXO. Para gastar este UTXO em uma nova transação, o usuário deve fornecer as informações solicitadas via _scriptSig_. A execução de _scriptSig_ em combinação com _scriptPubKey_ deve retornar "true" ou `1`. Se essa condição for atendida, o UTXO pode ser gasto para criar um novo UTXO, ele mesmo bloqueado por um novo _scriptPubKey_, e assim por diante.

É precisamente no _scriptPubKey_ que os endereços de recebimento são encontrados. No entanto, o uso deles varia dependendo do padrão de script adotado. Aqui está uma tabela resumida das informações contidas no _scriptPubKey_ de acordo com o padrão usado, bem como as informações esperadas no _scriptSig_ para desbloquear o _scriptPubKey_.
| Padrão | _scriptPubKey_ | _scriptSig_ | _script de resgate_ | _testemunha_ |
| ------------------------ | ----------------------------------------------------------- | ------------------------------------------ | ------------------- | --------------------------------------------------- |
| P2PK | `<pubkey> OP_CHECKSIG` | `<assinatura>` | | |
| P2PKH | `OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG` | `<assinatura> <chave pública>` | | |
| P2SH | `OP_HASH160 <scriptHash> OP_EQUAL` | `<empurrões de dados> <script de resgate>` | Dados arbitrários | |
| P2WPKH | `0 <pubKeyHash>` | | | `<assinatura> <chave pública>` |
| P2WSH | `0 <witnessScriptHash>` | | | `<empurrões de dados> <script de testemunha>` |
| P2SH-P2WPKH | `OP_HASH160 <redeemScriptHash> OP_EQUAL` | `<script de resgate>` | `0 <pubKeyHash>` | `<assinatura> <chave pública>` |
| P2SH-P2WSH | `OP_HASH160 <redeemScriptHash> OP_EQUAL` | `<script de resgate>` | `0 <scriptHash>` | `<empurrões de dados> <script de testemunha>` |
| P2TR (caminho da chave) | `1 <chave pública>` | | | `<assinatura>` |
| P2TR (caminho do script) | `1 <chave pública>` | | | `<empurrões de dados> <script> <bloco de controle>` |
_Fonte: Bitcoin Core PR review club, 7 de julho de 2021 - Gloria Zhao_
Os opcodes usados em um script são projetados para manipular informações e, se necessário, para comparar ou testá-las. Vamos tomar o exemplo de um script P2PKH, que é o seguinte:
```txt
OP_DUP OP_HASH160 OP_PUSHBYTES_20 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG
```
Como veremos neste capítulo, `<pubKeyHash>` representa na verdade o payload do endereço de recebimento usado para bloquear o UTXO. Para desbloquear este _scriptPubKey_, é necessário fornecer um _scriptSig_ contendo:
```txt
<assinatura> <chave pública>
```
Em linguagem de script, a "pilha" é uma estrutura de dados "_LIFO_" ("_Last In, First Out_" ou "Último a Entrar, Primeiro a Sair") usada para armazenar temporariamente elementos durante a execução do script. Cada operação de script manipula essa pilha, onde elementos podem ser adicionados (_push_) ou removidos (_pop_). Scripts usam essas pilhas para avaliar expressões, armazenar variáveis temporárias e gerenciar condições.
A execução do script que acabei de dar como exemplo segue este processo:
- Temos o _scriptSig_, o _ScriptPubKey_ e a pilha:

- O _scriptSig_ é colocado na pilha:

- `OP_DUP` duplica a chave pública fornecida no _scriptSig_ na pilha:

- `OP_HASH160` retorna o hash da chave pública que acabou de ser duplicada:
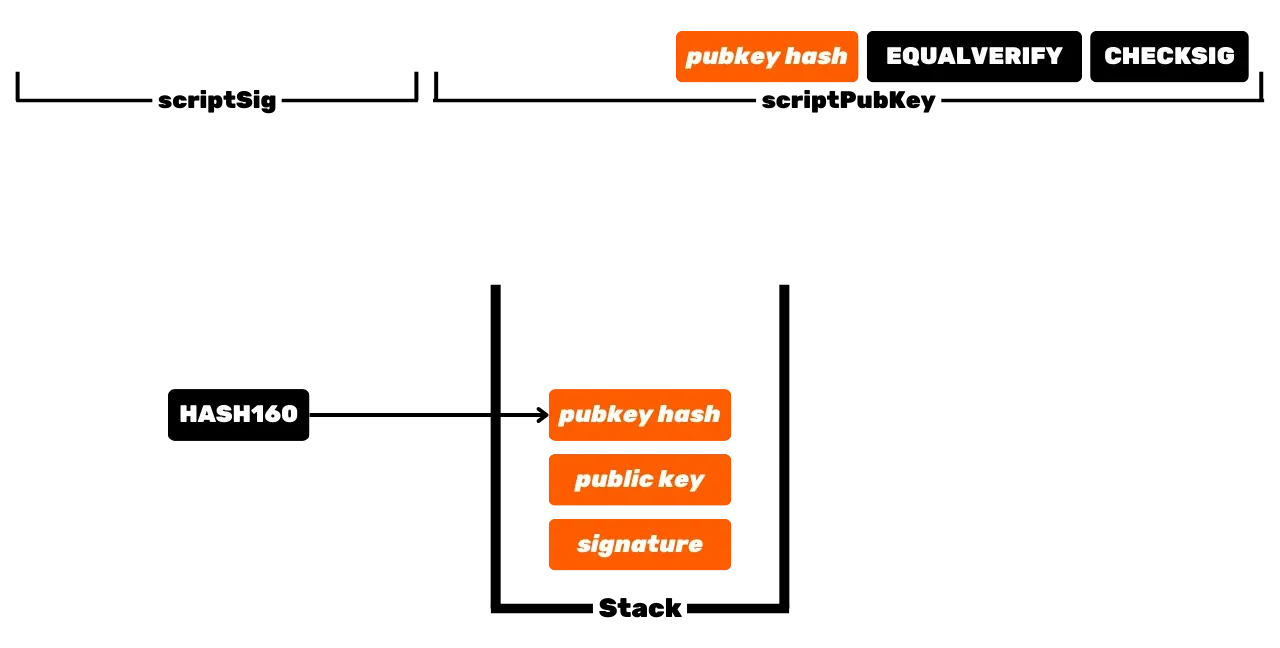
- `OP_PUSHBYTES_20 <pubKeyHash>` coloca o endereço Bitcoin contido no _scriptPubKey_ na pilha:

- `OP_EQUALVERIFY` verifica se a chave pública hashada corresponde ao endereço de recebimento fornecido:

`OP_CHECKSIG` verifica a assinatura contida no _scriptSig_ usando a chave pública. Este opcode essencialmente realiza uma verificação de assinatura como descrevemos na parte 3 deste treinamento:

- Se `1` permanecer na pilha, então o script é válido:
Portanto, para resumir, este script permite verificar, com a ajuda da assinatura digital, que o usuário reivindicando a propriedade deste UTXO e desejando gastá-lo de fato possui a chave privada associada ao endereço de recebimento usado durante a criação deste UTXO.
### Os diferentes tipos de endereços Bitcoin
Ao longo da evolução do Bitcoin, vários modelos de script padrão foram adicionados. Cada um deles usa um tipo distinto de endereço de recebimento. Aqui está uma visão geral dos principais modelos de script disponíveis até o momento:
**P2PK (_Pay-to-PubKey_)**:
Este modelo de script foi introduzido na primeira versão do Bitcoin por Satoshi Nakamoto. O script P2PK bloqueia bitcoins diretamente usando uma chave pública bruta (assim, nenhum endereço de recebimento é usado com este modelo). Sua estrutura é simples: contém uma chave pública e requer uma assinatura digital correspondente para desbloquear os fundos. Este script faz parte do padrão "_Legacy_".
**P2PKH (_Pay-to-PubKey-Hash_)**:
Assim como o P2PK, o script P2PKH foi introduzido no lançamento do Bitcoin. Diferentemente de seu predecessor, ele bloqueia os bitcoins usando o hash da chave pública, em vez de usar diretamente a chave pública bruta. O _scriptSig_ deve então fornecer a chave pública associada ao endereço de recebimento, bem como uma assinatura válida. Os endereços correspondentes a este modelo começam com `1` e são codificados em _base58check_. Este script também pertence ao padrão "_Legacy_".
**P2SH (_Pay-to-Script-Hash_)**:
Introduzido em 2012 com o BIP16, o modelo P2SH permite o uso do hash de um script arbitrário no _scriptPubKey_. Este script hash, chamado de "_redeemScript_", contém as condições para desbloquear os fundos. Para gastar um UTXO bloqueado com P2SH, é necessário fornecer um _scriptSig_ contendo o _redeemScript_ original, bem como os dados necessários para validá-lo. Este modelo é notavelmente usado para multisigs antigos. Os endereços associados ao P2SH começam com `3` e são codificados em _base58check_. Este script também pertence ao padrão "_Legacy_".
**P2WPKH (_Pay-to-Witness-PubKey-Hash_)**:
Este script é semelhante ao P2PKH, pois também bloqueia bitcoins usando o hash de uma chave pública. No entanto, ao contrário do P2PKH, o _scriptSig_ é movido para uma seção separada chamada "_Witness_". Isso é às vezes referido como "_scriptWitness_" para denotar o conjunto composto pela assinatura e pela chave pública. Cada entrada SegWit tem seu próprio _scriptWitness_, e a coleção de _scriptWitnesses_ constitui o campo _Witness_ da transação. Esse movimento dos dados de assinatura é uma inovação introduzida pela atualização SegWit, visando especialmente prevenir a maleabilidade das transações devido às assinaturas ECDSA.
Endereços P2WPKH usam codificação _bech32_ e sempre começam com `bc1q`. Este tipo de script corresponde às saídas SegWit versão 0.
**P2WSH (_Pay-to-Witness-Script-Hash_)**:
O modelo P2WSH também foi introduzido com a atualização SegWit em agosto de 2017. Semelhante ao modelo P2SH, ele bloqueia bitcoins usando o hash de um script. A principal diferença reside em como assinaturas e scripts são incorporados à transação. Para gastar bitcoins bloqueados com este tipo de script, o destinatário deve fornecer o script original, chamado _witnessScript_ (equivalente ao _redeemScript_ em P2SH), junto com os dados necessários para validar este _witnessScript_. Este mecanismo permite a implementação de condições de gasto mais complexas, como multisigs.
Endereços P2WSH usam codificação _bech32_ e sempre começam com `bc1q`. Este script também corresponde às saídas SegWit versão 0.
**P2TR (_Pay-to-Taproot_)**:
O modelo P2TR foi introduzido com a implementação do Taproot em novembro de 2021. Ele é baseado no protocolo Schnorr para agregação de chaves criptográficas, bem como em uma árvore Merkle para scripts alternativos, chamada MAST (_Merkelized Alternative Script Tree_). Diferentemente de outros tipos de scripts, onde as condições de gasto são expostas publicamente (seja no recebimento ou no gasto), P2TR permite o ocultamento de scripts complexos atrás de uma única chave pública aparente.
Tecnicamente, um script P2TR bloqueia bitcoins em uma chave pública Schnorr única, denotada como $Q$. Esta chave $Q$ é na verdade um agregado de uma chave pública $P$ e uma chave pública $M$, sendo esta última calculada a partir da raiz Merkle de uma lista de _scriptPubKey_. Bitcoins bloqueados com este tipo de script podem ser gastos de duas maneiras:
- Publicando uma assinatura para a chave pública $P$ (_caminho da chave_).
- Satisfazendo um dos scripts contidos na árvore Merkle (_caminho do script_).
O P2TR oferece grande flexibilidade, pois permite bloquear bitcoins com uma chave pública única, com vários scripts de escolha, ou ambos simultaneamente. A vantagem dessa estrutura de árvore de Merkle é que apenas o script de gasto usado é revelado durante a transação, mas todos os outros scripts alternativos permanecem secretos. 
O P2TR corresponde às saídas SegWit versão 1, o que significa que as assinaturas para entradas P2TR são armazenadas na seção _Witness_ da transação, e não no _scriptSig_. Os endereços P2TR usam a codificação _bech32m_ e começam com `bc1p`, mas são bastante únicos porque não usam uma função de hash para sua construção. De fato, eles representam diretamente a chave pública $Q$ que é simplesmente formatada com metadados. Portanto, é um modelo de script próximo ao P2PK.
Agora que cobrimos a teoria, vamos passar para a prática! No capítulo seguinte, proponho derivar tanto um endereço SegWit v0 quanto um endereço SegWit v1 a partir de um par de chaves.
## Derivação de Endereço
<chapterId>3ebdc750-4135-4881-b07e-08965941b93e</chapterId>
Vamos explorar juntos como gerar um endereço de recebimento a partir de um par de chaves localizado, por exemplo, na profundidade 5 de uma carteira HD. Esse endereço pode então ser usado em um software de carteira para bloquear um UTXO.
Como o processo de geração de um endereço depende do modelo de script adotado, vamos nos concentrar em dois casos específicos: gerar um endereço SegWit v0 em P2WPKH e um endereço SegWit v1 em P2TR. Esses dois tipos de endereços cobrem a grande maioria dos usos hoje.
### Compressão da Chave Pública
Após realizar todas as etapas de derivação da chave mestra até a profundidade 5 usando os índices apropriados, obtemos um par de chaves ($k$, $K$) com $K = k \cdot G$. Embora seja possível usar essa chave pública como está para bloquear fundos com o padrão P2PK, esse não é nosso objetivo aqui. Em vez disso, nosso objetivo é criar um endereço em P2WPKH em primeira instância, e depois em P2TR para outro exemplo.
O primeiro passo é comprimir a chave pública $K$. Para entender bem esse processo, vamos primeiro relembrar alguns fundamentos cobertos na parte 3.
Uma chave pública no Bitcoin é um ponto $K$ localizado em uma curva elíptica. Ela é representada na forma $(x, y)$, onde $x$ e $y$ são as coordenadas do ponto. Em sua forma não comprimida, essa chave pública mede 520 bits: 8 bits para um prefixo (valor inicial de `0x04`), 256 bits para a coordenada $x$ e 256 bits para a coordenada $y$.
No entanto, curvas elípticas têm uma propriedade de simetria em relação ao eixo x: para uma coordenada $x$ dada, existem apenas dois valores possíveis para $y$: $y$ e $-y$. Esses dois pontos estão localizados de um lado e do outro do eixo x. Em outras palavras, se sabemos $x$, é suficiente especificar se $y$ é par ou ímpar para identificar o ponto exato na curva.
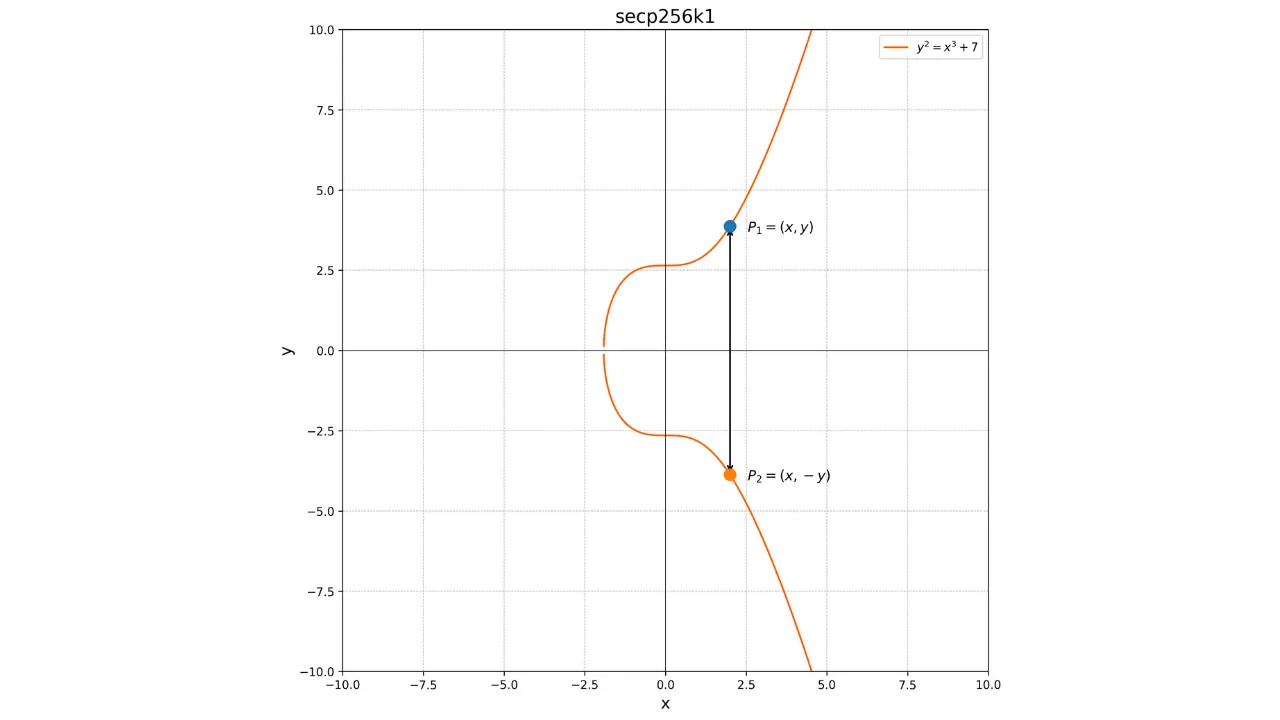
Para comprimir uma chave pública, apenas $x$ é codificado, o que ocupa 256 bits, e um prefixo é adicionado para especificar a paridade de $y$. Este método reduz o tamanho da chave pública para 264 bits em vez dos iniciais 520. O prefixo `0x02` indica que $y$ é par, e o prefixo `0x03` indica que $y$ é ímpar.
Vamos tomar um exemplo para entender bem, com uma chave pública crua em representação não comprimida:
```txt
K = 04678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f
```
Se descompusermos esta chave, temos:
- O prefixo: `04`;
- $x$: `678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6`;
- $y$: `49f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f`
O último caractere hexadecimal de $y$ é `f`. Em base 10, `f = 15`, o que corresponde a um número ímpar. Portanto, $y$ é ímpar, e o prefixo será `0x03` para indicar isso.
A chave pública comprimida torna-se:
```txt
K = 03678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6
```
Esta operação aplica-se a todos os modelos de script baseados em ECDSA, ou seja, todos exceto P2TR que usa Schnorr. No caso de Schnorr, como explicado na parte 3, retemos apenas o valor de $x$, sem adicionar um prefixo para indicar a paridade de $y$, ao contrário do ECDSA. Isso é possível pelo fato de uma paridade única ser arbitrariamente escolhida para todas as chaves. Isso permite uma ligeira redução no espaço de armazenamento necessário para chaves públicas.
### Derivação de um endereço SegWit v0 (bech32)
Agora que obtivemos nossa chave pública comprimida, podemos derivar dela um endereço de recebimento SegWit v0.
O primeiro passo é aplicar a função de hash HASH160 à chave pública comprimida. HASH160 é uma composição de duas funções de hash sucessivas: SHA256, seguido por RIPEMD160:
\text{HASH160}(K) = \text{RIPEMD160}(\text{SHA256}(K))
Primeiro, passamos a chave por SHA256:
```txt
SHA256(K) = C489EBD66E4103B3C4B5EAFF462B92F5847CA2DCE0825F4997C7CF57DF35BF3A
```
Em seguida, passamos o resultado por RIPEMD160:
```txt
RIPEMD160(SHA256(K)) = 9F81322CC88622CA4CCB2A52A21E2888727AA535
```
Obtivemos um hash de 160 bits da chave pública, que constitui o que é chamado de payload do endereço. Este payload representa a parte central e mais importante do endereço. Ele também é usado no _scriptPubKey_ para bloquear os UTXOs. No entanto, para tornar este payload mais facilmente utilizável por humanos, metadados são adicionados a ele. O próximo passo envolve codificar este hash em grupos de 5 bits em decimal. Esta transformação decimal será útil para conversão em _bech32_, usado por endereços pós-SegWit. O hash binário de 160 bits é, assim, dividido em 32 grupos de 5 bits:
\begin{array}{|c|c|} \hline \text{5 bits} & \text{Decimal} \ \hline 10011 & 19 \ 11110 & 30 \ 00000 & 0 \ 10011 & 19 \ 00100 & 4 \ 01011 & 11 \ 00110 & 6 \ 01000 & 8 \ 10000 & 16 \ 11000 & 24 \ 10001 & 17 \ 01100 & 12 \ 10100 & 20 \ 10011 & 19 \ 00110 & 6 \ 01011 & 11 \ 00101 & 5 \ 01001 & 9 \ 01001 & 9 \ 01010 & 10 \ 00100 & 4 \ 00111 & 7 \ 10001 & 17 \ 01000 & 8 \ 10001 & 17 \ 00001 & 1 \ 11001 & 25 \ 00111 & 7 \ 10101 & 21 \ 00101 & 5 \ 00101 & 5 \ 10101 & 21 \ \hline \end{array}
Então, temos:
```txt
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
```
Uma vez que o hash é codificado em grupos de 5 bits, um checksum é adicionado ao endereço. Este checksum é usado para verificar que o payload do endereço não foi alterado durante seu armazenamento ou transmissão. Por exemplo, ele permite que um software de carteira garanta que você não cometeu um erro ao digitar um endereço de recebimento. Sem essa verificação, você poderia acidentalmente enviar bitcoins para um endereço incorreto, resultando em uma perda permanente de fundos, já que você não possui a chave pública ou privada associada. Portanto, o checksum é uma proteção contra erros humanos.
Para os antigos endereços Bitcoin _Legacy_, o checksum era simplesmente calculado a partir do início do hash do endereço com a função HASH256. Com a introdução do SegWit e do formato _bech32_, códigos BCH (_Bose, Ray-Chaudhuri e Hocquenghem_) são agora utilizados. Esses códigos de correção de erros são usados para detectar e corrigir erros em sequências de dados. Eles garantem que a informação transmitida chegue intacta ao seu destino, mesmo no caso de alterações menores. Códigos BCH são usados em muitos campos, como SSDs, DVDs e códigos QR. Por exemplo, graças a esses códigos BCH, um código QR parcialmente obscurecido ainda pode ser lido e decodificado.
No contexto do Bitcoin, códigos BCH oferecem um melhor compromisso entre tamanho e capacidade de detecção de erros em comparação com as funções de hash simples usadas para endereços _Legacy_. No entanto, no Bitcoin, códigos BCH são usados apenas para detecção de erros, não correção. Assim, o software de carteira sinalizará um endereço de recebimento incorreto, mas não o corrigirá automaticamente. Esta limitação é deliberada: permitir a correção automática reduziria a capacidade de detecção de erros.
Para calcular o checksum com códigos BCH, precisamos preparar vários elementos:
- **A Parte Legível por Humanos (HRP - _Human Readable Part_)**: Para a mainnet do Bitcoin, o HRP é `bc`;
O HRP deve ser expandido separando cada caractere em duas partes:
- Pegando os caracteres do HRP em ASCII:
- `b`: `01100010`
- `c`: `01100011`
- Extraindo os 3 bits mais significativos e os 5 bits menos significativos:
- 3 bits mais significativos: `011` (3 em decimal)
- 3 bits mais significativos: `011` (3 em decimal)
- 5 bits menos significativos: `00010` (2 em decimal)
- 5 bits menos significativos: `00011` (3 em decimal)
Com o separador `0` entre os dois caracteres, a extensão do HRP é, portanto:
```txt
03 03 00 02 03
```
- **A versão do testemunho (witness version)**: Para a versão 0 do SegWit, é `00`;
- **O payload**: Os valores decimais do hash da chave pública;
- **A reserva para o checksum**: Adicionamos 6 zeros `[0, 0, 0, 0, 0, 0]` no final da sequência.
Todos os dados combinados para inserir no programa para calcular o checksum são os seguintes:
```txt
HRP = 03 03 00 02 03
SEGWIT v0 = 00
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
CHECKSUM = 00 00 00 00 00 00
INPUT = 03 03 00 02 03 00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 00 00 00 00 00 00
```
O cálculo do checksum é bastante complexo. Envolve aritmética de campo finito polinomial. Não detalharemos este cálculo aqui e passaremos diretamente para o resultado. Em nosso exemplo, o checksum obtido em decimal é:
```txt
10 16 11 04 13 18
```
Agora podemos construir o endereço de recebimento concatenando na ordem os seguintes elementos:
- **A versão do SegWit**: `00`
- **O payload**: O hash da chave pública
- **O checksum**: Os valores obtidos na etapa anterior (`10 16 11 04 13 18`)
Isso nos dá em decimal:
```txt
00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 10 16 11 04 13 18
```
Então, cada valor decimal deve ser mapeado para seu caractere _bech32_ usando a seguinte tabela de conversão:
\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \ \hline +0 & q & p & z & r & y & 9 & x & 8 \ \hline +8 & g & f & 2 & t & v & d & w & 0 \ \hline +16 & s & 3 & j & n & 5 & 4 & k & h \ \hline +24 & c & e & 6 & m & u & a & 7 & l \ \hline \end{array}
Para converter um valor em um caractere _bech32_ usando esta tabela, basta localizar os valores na primeira coluna e na primeira linha que, quando somados, resultam no valor desejado. Em seguida, recupere o caractere correspondente. Por exemplo, o número decimal `19` será convertido na letra `n`, porque $19 = 16 + 3$.
Mapeando todos os nossos valores, obtemos o seguinte endereço:
```
qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj
```
Tudo o que resta é adicionar o HRP `bc`, que indica que se trata de um endereço para a rede principal do Bitcoin, bem como o separador `1`, para obter o endereço de recebimento completo:
```
bc1qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj
```
A particularidade deste alfabeto _bech32_ é que ele inclui todos os caracteres alfanuméricos exceto `1`, `b`, `i` e `o` para evitar confusão visual entre caracteres similares, especialmente durante sua digitação ou leitura por humanos.
Para resumir, aqui está o processo de derivação:
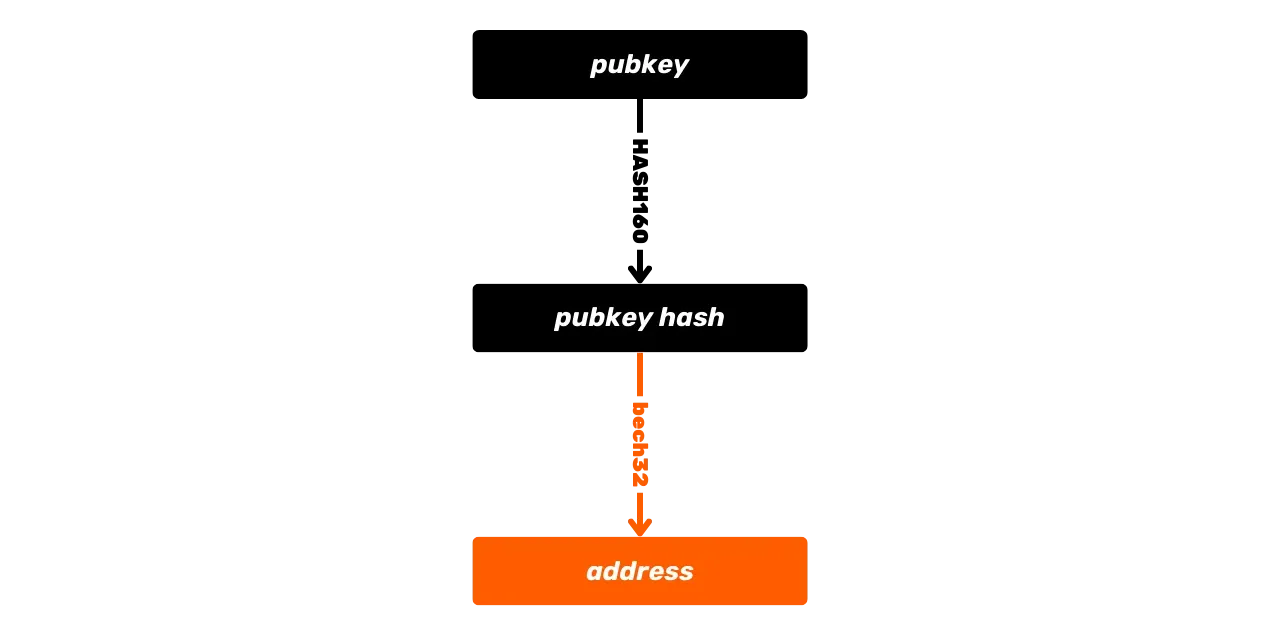
É assim que se deriva um endereço de recebimento P2WPKH (SegWit v0) a partir de um par de chaves. Vamos agora passar para os endereços P2TR (SegWit v1 / Taproot) e descobrir seu processo de geração.
### Derivação de um Endereço SegWit v1 (bech32m)
Para endereços Taproot, o processo de geração difere ligeiramente. Vamos ver isso juntos!
Desde a etapa de compressão da chave pública, uma primeira distinção aparece em comparação com ECDSA: as chaves públicas usadas para Schnorr no Bitcoin são representadas apenas pela sua abscissa ($x$). Portanto, não há prefixo, e a chave comprimida mede exatamente 256 bits.
Como vimos no capítulo anterior, um script P2TR bloqueia bitcoins em uma chave pública Schnorr única, designada por $Q$. Esta chave $Q$ é um agregado de duas chaves públicas: $P$, uma chave pública interna principal, e $M$, uma chave pública derivada da raiz de Merkle de uma lista de _scriptPubKey_. Os bitcoins bloqueados com este tipo de script podem ser gastos de duas maneiras:
- Publicando uma assinatura para a chave pública $P$ (_caminho da chave_);
- Satisfazendo um dos scripts incluídos na árvore de Merkle (_caminho do script_).
Na realidade, essas duas chaves não são verdadeiramente "agregadas". A chave $P$ é, em vez disso, modificada pela chave $M$. Em criptografia, "modificar" uma chave pública significa alterar essa chave aplicando um valor aditivo chamado de "tweak". Esta operação permite que a chave modificada permaneça compatível com a chave privada original e o tweak. Tecnicamente, um tweak é um valor escalar $t$ que é adicionado à chave pública inicial. Se $P$ é a chave pública original, a chave modificada torna-se:
P' = P + tG
Onde $G$ é o gerador da curva elíptica usada. Esta operação produz uma nova chave pública derivada da chave original, mantendo propriedades criptográficas que permitem seu uso.
Se você não precisa adicionar scripts alternativos (gastando exclusivamente através do _caminho da chave_), você pode gerar um endereço Taproot baseado unicamente na chave pública presente no nível 5 da sua carteira. Neste caso, é necessário criar um script não gastável para o _caminho do script_, a fim de satisfazer os requisitos da estrutura. O ajuste $t$ é então calculado aplicando uma função de hash etiquetada, **`TapTweak`**, na chave pública interna $P$:
t = \text{H}_{\text{TapTweak}}(P)
onde:
- **$\text{H}_{\text{TapTweak}}$** é uma função de hash SHA256 etiquetada com a tag `TapTweak`. Se você não está familiarizado com o que é uma função de hash etiquetada, convido você a consultar o capítulo 3.3;
- $P$ é a chave pública interna, representada em seu formato comprimido de 256 bits, usando apenas a coordenada $x$.
A chave pública Taproot $Q$ é então calculada adicionando o ajuste $t$, multiplicado pelo gerador da curva elíptica $G$, à chave pública interna $P$:
Q = P + t \cdot G
Uma vez que a chave pública Taproot $Q$ é obtida, podemos gerar o endereço de recebimento correspondente. Diferentemente de outros formatos, os endereços Taproot não são estabelecidos em um hash da chave pública. Portanto, a chave $Q$ é inserida diretamente no endereço, de maneira bruta.
Para começar, extraímos a coordenada $x$ do ponto $Q$ para obter uma chave pública comprimida. Neste payload, um checksum é calculado usando códigos BCH, como com endereços SegWit v0. No entanto, o programa usado para endereços Taproot difere ligeiramente. De fato, após a introdução do formato _bech32_ com SegWit, um bug foi descoberto: quando o último caractere de um endereço é um `p`, inserir ou remover `q`s logo antes deste `p` não torna o checksum inválido. Embora este bug não tenha consequências no SegWit v0 (graças a uma restrição de tamanho), ele poderia representar um problema no futuro. Este bug foi, portanto, corrigido para endereços Taproot, e o novo formato corrigido é chamado "_bech32m_".
O endereço Taproot é gerado codificando a coordenada $x$ de $Q$ no formato _bech32m_, com os seguintes elementos:
- **O HRP (_Human Readable Part_)**: `bc`, para indicar a rede principal do Bitcoin;
- **A versão**: `1` para indicar Taproot / SegWit v1;
- **O checksum**.
O endereço final terá, portanto, o formato:
```
bc1p[Qx][checksum]
```
Por outro lado, se você deseja adicionar scripts alternativos além de gastar com a chave pública interna (_caminho do script_), o cálculo do endereço de recebimento será ligeiramente diferente. Você precisará incluir o hash dos scripts alternativos no cálculo do ajuste. No Taproot, cada script alternativo, localizado no final da árvore de Merkle, é chamado de "folha".
Uma vez que os diferentes scripts alternativos são escritos, você deve passá-los individualmente por uma função de hash etiquetada `TapLeaf`, acompanhada de alguns metadados:
\text{h}{\text{leaf}} = \text{H}{\text{TapLeaf}} (v \Vert sz \Vert S)
Com:
- $v$: o número da versão do script (padrão `0xC0` para Taproot);
- $sz$: o tamanho do script codificado no formato _CompactSize_;
- $S$: o script.
Os diferentes hashes de script ($\text{h}_{\text{leaf}}$) são primeiramente ordenados em ordem lexicográfica. Em seguida, eles são concatenados em pares e passados através de uma função de hash etiquetada `TapBranch`. Esse processo é repetido iterativamente para construir, passo a passo, a árvore de Merkle:\text{h}{\text{branch}} = \text{H}{\text{TapBranch}}(\text{h}{\text{leaf1}} \Vert \text{h}{\text{leaf2}})
Continuamos então concatenando os resultados dois a dois, passando-os a cada etapa pela função de hash etiquetada `TapBranch`, até obtermos a raiz da árvore de Merkle:
Uma vez calculada a raiz de Merkle $h_{\text{root}}$, podemos calcular o tweak. Para isso, concatenamos a chave pública interna da carteira $P$ com a raiz $h_{\text{root}}$ e passamos o resultado pela função hash marcada `TapTweak`:
t = \text{H}{\text{TapTweak}}(P \Vert h{\text{root}})
Finalmente, como antes, a chave pública Taproot $Q$ é obtida somando a chave pública interna $P$ ao produto do tweak $t$ pelo ponto gerador $G$:
Q = P + t \cdot G
A geração do endereço segue então o mesmo processo, utilizando a chave pública bruta $Q$ como carga útil, juntamente com alguns metadados adicionais.
E é isso! Chegamos ao fim deste curso CYP201. Se você achou este curso útil, ficaria muito grato se você pudesse dedicar alguns momentos para dar uma boa avaliação no capítulo de avaliação a seguir. Sinta-se livre também para compartilhá-lo com seus entes queridos ou em suas redes sociais. Finalmente, se você deseja obter seu diploma para este curso, você pode fazer o exame final logo após o capítulo de avaliação.
# Seção final
<partId>58111408-b734-54db-9ea7-0d5b67f99f99</partId>
## Avaliações & Notas
<chapterId>0cd71541-a7fd-53db-b66a-8611b6a28b04</chapterId>
<isCourseReview>true</isCourseReview>
## Exame final
<chapterId>a53ea27d-0f84-56cd-b37c-a66210a4b31d</chapterId>
<isCourseExam>true</isCourseExam>
## Conclusão
<chapterId>d291428b-3cfa-5394-930e-4b514be82d5a</chapterId>
<isCourseConclusion>true</isCourseConclusion>