name: Wprowadzenie do kryptografii formalnej goal: Dogłębne wprowadzenie do nauki i praktyki kryptografii. objectives:

Głębokie zagłębienie się w kryptografię

Trudno jest znaleźć wiele materiałów, które oferują dobry środek w edukacji kryptograficznej.

Z jednej strony istnieją długie, formalne traktaty, naprawdę dostępne tylko dla osób z silnym doświadczeniem w matematyce, logice lub innej dyscyplinie formalnej. Z drugiej strony, istnieją bardzo szczegółowe wprowadzenia, które naprawdę ukrywają zbyt wiele szczegółów dla każdego, kto jest choć trochę ciekawy.

To wprowadzenie do kryptografii ma na celu uchwycenie środka. Chociaż powinno być stosunkowo trudne i szczegółowe dla każdego, kto jest nowy w kryptografii, nie jest to królicza nora typowego fundamentalnego traktatu.

Wprowadzenie

Przegląd kursu

Witamy na kursie CYP302!

Książka ta oferuje dogłębne wprowadzenie do nauki i praktyki kryptografii. Tam, gdzie to możliwe, koncentruje się na koncepcyjnej, a nie formalnej ekspozycji materiału.

Ta treść edukacyjna jest adaptacją książki i repo JWBurgers. Chociaż autor łaskawie zezwolił na jej wykorzystanie edukacyjne, wszystkie prawa własności intelektualnej pozostają przy pierwotnym twórcy.

Motywacja i cele

Trudno jest znaleźć wiele materiałów, które oferują dobry środek w edukacji kryptograficznej.

Z jednej strony istnieją długie, formalne traktaty, naprawdę dostępne tylko dla osób z silnym doświadczeniem w matematyce, logice lub innej dyscyplinie formalnej. Z drugiej strony, istnieją bardzo szczegółowe wprowadzenia, które naprawdę ukrywają zbyt wiele szczegółów dla każdego, kto jest choć trochę ciekawy.

To wprowadzenie do kryptografii ma na celu uchwycenie środka. Chociaż powinno być stosunkowo trudne i szczegółowe dla każdego, kto jest nowy w kryptografii, nie jest to królicza nora typowego fundamentalnego traktatu.

Docelowi odbiorcy

Od programistów po intelektualnie ciekawskich, ta książka jest przydatna dla każdego, kto chce czegoś więcej niż tylko powierzchownego zrozumienia kryptografii. Jeśli Twoim celem jest opanowanie dziedziny kryptografii, ta książka jest również dobrym punktem wyjścia.

Wytyczne do czytania

Książka zawiera obecnie siedem rozdziałów: "Czym jest kryptografia?" (rozdział 1), "Matematyczne podstawy kryptografii I" (rozdział 2), "Matematyczne podstawy kryptografii II" (rozdział 3), "Kryptografia symetryczna" (rozdział 4), "RC4 i AES" (rozdział 5), "Kryptografia asymetryczna" (rozdział 6) oraz "Kryptosystem RSA" (rozdział 7). Ostatni rozdział, "Kryptografia w praktyce", zostanie jeszcze dodany. Skupia się on na różnych zastosowaniach kryptograficznych, w tym bezpieczeństwie transportu Layer, routingu cebulowym i systemie Bitcoin o wartości Exchange.

O ile nie masz silnego zaplecza matematycznego, teoria liczb jest prawdopodobnie najtrudniejszym tematem w tej książce. Przedstawiam jej przegląd w rozdziale 3, a także pojawia się ona w opisie AES w rozdziale 5 i kryptosystemu RSA w rozdziale 7.

Jeśli naprawdę zmagasz się z formalnymi szczegółami w tych częściach książki, radzę zadowolić się czytaniem ich na wysokim poziomie za pierwszym razem.

Podziękowania

Najbardziej wpływową książką, która wpłynęła na ukształtowanie tego tematu, jest Introduction to Modern Cryptography Jonathana Katza i Yehudy Lindella, CRC Press (Boca Raton, FL), 2015. Kurs towarzyszący jest dostępny na Coursera pod nazwą "Kryptografia"

Głównymi dodatkowymi źródłami, które były pomocne w tworzeniu przeglądu w tej książce, są Simon Singh, The Code Book, Fourth Estate (Londyn, 1999); Christof Paar i Jan Pelzl, Understanding Cryptography, Springer (Heidelberg, 2010) i kurs oparty na książce Paara zatytułowany "Wprowadzenie do kryptografii"; oraz Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons).

Przytoczę tylko bardzo konkretne informacje i wyniki, które zaczerpnąłem z tych źródeł, ale chcę tutaj wyrazić moje ogólne uznanie dla nich.

Czytelnikom, którzy po zapoznaniu się z tym wprowadzeniem chcieliby poszukać bardziej zaawansowanej wiedzy na temat kryptografii, gorąco polecam książkę Katza i Lindella. Kurs Katza na Coursera jest nieco bardziej przystępny niż książka.

Wkład

Prosimy o zapoznanie się z [plikiem wkładu w repozytorium] (https://github.com/JWBurgers/An_Introduction_to_Cryptography/blob/master/Contributions.md) w celu uzyskania wskazówek, jak wspierać projekt.

Notacja

Kluczowe pojęcia:

Kluczowe terminy w elementarzach są wprowadzane poprzez ich pogrubienie. Na przykład wprowadzenie szyfru Rijndael jako terminu kluczowego wyglądałoby następująco: Szyfr Rijndael.

Kluczowe terminy są wyraźnie zdefiniowane, chyba że są to nazwy własne lub ich znaczenie jest oczywiste z dyskusji.

Każda definicja jest zwykle podawana po wprowadzeniu kluczowego terminu, choć czasami wygodniej jest pozostawić definicję do późniejszego punktu.

Podkreślone słowa i zwroty:

Słowa i frazy są podkreślone kursywą. Na przykład fraza "Zapamiętaj swoje hasło" wyglądałaby następująco: Zapamiętaj hasło.

Formalny zapis:

Formalna notacja dotyczy głównie zmiennych, zmiennych losowych i zbiorów.

Gotowy na poznanie fascynującego świata kryptografii? Do dzieła!

Czym jest kryptografia?

Szyfry Beale'a

Zacznijmy nasze badanie dziedziny kryptografii od jednego z bardziej uroczych i zabawnych epizodów w jej historii: szyfrów Beale'a. [1]

Historia szyfrów Beale'a jest moim zdaniem bardziej fikcją niż rzeczywistością. Ale podobno wyglądało to następująco.

Zimą 1820 i 1822 roku niejaki Thomas J. Beale zatrzymał się w gospodzie należącej do Roberta Morrissa w Lynchburgu (Wirginia). Pod koniec drugiego pobytu Beale przekazał Morrissowi żelazną skrzynię z cennymi dokumentami na przechowanie.

Kilka miesięcy później Morriss otrzymał list od Beale'a datowany na 9 maja 1822 roku. Podkreślał on wielką wartość zawartości żelaznej skrzyni i zawierał pewne instrukcje dla Morrissa: jeśli ani Beale, ani żaden z jego współpracowników nigdy nie zgłosi się po skrzynię, powinien ją otworzyć dokładnie dziesięć lat od daty listu (tj. 9 maja 1832 r.). Niektóre z dokumentów w środku byłyby napisane zwykłym tekstem. Kilka innych byłoby jednak "niezrozumiałych bez pomocy klucza" Ten "klucz" miał zostać dostarczony Morrissowi przez nienazwanego przyjaciela Beale'a w czerwcu 1832 roku.

Pomimo jasnych instrukcji, Morriss nie otworzył skrzynki w maju 1832 roku, a tajemniczy przyjaciel Beale'a nigdy nie pojawił się w czerwcu tego samego roku. Dopiero w 1845 roku właściciel zajazdu zdecydował się w końcu otworzyć skrzynkę. Morriss znalazł w niej notatkę wyjaśniającą, w jaki sposób Beale i jego współpracownicy odkryli złoto i srebro na Zachodzie i zakopali je wraz z biżuterią na przechowanie. Ponadto pudełko zawierało trzy szyfrogramy, czyli teksty napisane kodem, które wymagają klucza kryptograficznego lub sekretu i towarzyszącego mu algorytmu do odblokowania. Proces odblokowywania szyfrogramu znany jest jako decryption, podczas gdy proces blokowania znany jest jako encryption. (Jak wyjaśniono w rozdziale 3, termin szyfr może przybierać różne znaczenia. W nazwie "szyfry Beale'a" jest to skrót od ciphertexts)

Trzy szyfrogramy, które Morriss znalazł w żelaznej skrzyni, składają się z serii liczb oddzielonych przecinkami. Zgodnie z notatką Beale'a, szyfrogramy te oddzielnie podają lokalizację skarbu, zawartość skarbu oraz listę nazwisk prawowitych spadkobierców skarbu i ich udziałów (ta ostatnia informacja jest istotna na wypadek, gdyby Beale i jego współpracownicy nigdy nie odebrali skrzyni).

Morris próbował odszyfrować trzy szyfrogramy przez dwadzieścia lat. Z kluczem byłoby to łatwe. Ale Morriss nie miał klucza i nie udało mu się odzyskać oryginalnych tekstów lub plaintexts, jak są one zwykle nazywane w kryptografii.

Pod koniec życia Morriss przekazał skrzynkę przyjacielowi w 1862 roku. Przyjaciel ten opublikował następnie w 1885 roku broszurę pod pseudonimem J.B. Ward. Zawierała ona opis (rzekomej) historii skrzynki, trzech szyfrogramów i rozwiązania, które znalazł dla drugiego szyfrogramu. (Najwyraźniej istnieje jeden klucz dla każdego szyfrogramu, a nie jeden klucz, który działa na wszystkie trzy szyfrogramy, jak pierwotnie sugerował Beale w swoim liście do Morrissa)

Drugi szyfrogram można zobaczyć na Rysunku 2 poniżej. [Kluczem do tego szyfrogramu jest Deklaracja Niepodległości Stanów Zjednoczonych. Procedura deszyfrowania sprowadza się do zastosowania następujących dwóch zasad:

Rysunek 1: Szyfr Beale'a nr. 2

Figure 1: Beale cipher no 2.

Na przykład pierwsza liczba drugiego szyfrogramu to 115. 115. słowo Deklaracji Niepodległości to "ustanowiony", więc pierwszą literą tekstu jawnego jest "i" Szyfrogram nie wskazuje bezpośrednio odstępów między wyrazami i wielkich liter. Jednak po odszyfrowaniu kilku pierwszych słów można logicznie wywnioskować, że pierwszym słowem tekstu jawnego było po prostu "I" (Zwykły tekst zaczyna się od frazy "Zdeponowałem w hrabstwie Bedford")

Po odszyfrowaniu druga wiadomość zawiera szczegółową zawartość skarbu (złoto, srebro i klejnoty) i sugeruje, że został on zakopany w żelaznych garnkach i przykryty skałami w hrabstwie Bedford (Wirginia). Ludzie uwielbiają dobre tajemnice, więc włożono wiele wysiłku w odszyfrowanie pozostałych dwóch szyfrów Beale'a, zwłaszcza tego opisującego lokalizację skarbu. Swoich sił próbowali nawet różni wybitni kryptografowie. Jednak jak dotąd nikomu nie udało się odszyfrować pozostałych dwóch szyfrogramów.

Uwagi:

[1] Dobre podsumowanie tej historii można znaleźć w Simon Singh, The Code Book, Fourth Estate (Londyn, 1999), s. 82-99. Krótki film przedstawiający tę historię został nakręcony przez Andrew Allena w 2010 roku. Można go znaleźć pod tytułem "The Thomas Beale Cipher" [na jego stronie internetowej] (http://www.thomasbealecipher.com/).

[2] Ten obraz jest dostępny na stronie Wikipedii poświęconej szyfrom Beale'a.

Nowoczesna kryptografia

Barwne historie, takie jak ta o szyfrach Beale'a, są tym, co większość z nas kojarzy z kryptografią. Jednak współczesna kryptografia różni się od tego typu historycznych przykładów na co najmniej cztery ważne sposoby.

Po pierwsze, historycznie kryptografia zajmowała się wyłącznie tajemnicą (lub poufnością)[3]. [Szyfrogramy były tworzone w celu zapewnienia, że tylko niektóre strony mogą być wtajemniczone w informacje zawarte w tekstach jawnych, tak jak w przypadku szyfrów Beale'a. Aby schemat szyfrowania dobrze służył temu celowi, odszyfrowanie szyfrogramu powinno być możliwe tylko wtedy, gdy masz klucz.

Nowoczesna kryptografia zajmuje się szerszym zakresem tematów niż tylko tajność. Tematy te obejmują przede wszystkim (1) integralność wiadomości - czyli zapewnienie, że wiadomość nie została zmieniona; (2) autentyczność wiadomości - czyli zapewnienie, że wiadomość rzeczywiście pochodzi od określonego nadawcy; oraz (3) niezaprzeczalność - czyli zapewnienie, że nadawca nie może później fałszywie zaprzeczyć, że wysłał wiadomość. [4]

Ważnym rozróżnieniem, o którym należy pamiętać, jest zatem rozróżnienie między schematem szyfrowania a schematem kryptograficznym. Schemat szyfrowania dotyczy tylko tajności. Podczas gdy schemat szyfrowania jest schematem kryptograficznym, nie jest to prawdą. Schemat kryptograficzny może również służyć innym głównym tematom kryptografii, w tym integralności, autentyczności i niezaprzeczalności.

Zagadnienia integralności i autentyczności są równie ważne jak tajność. Nasze nowoczesne systemy komunikacyjne nie byłyby w stanie funkcjonować bez gwarancji dotyczących integralności i autentyczności komunikacji. Niezaprzeczalność jest również ważną kwestią, na przykład w przypadku umów cyfrowych, ale jest mniej potrzebna w zastosowaniach kryptograficznych niż tajność, integralność i autentyczność.

Po drugie, klasyczne schematy szyfrowania, takie jak szyfry Beale'a, zawsze obejmują jeden klucz, który był współdzielony przez wszystkie odpowiednie strony. Jednak wiele nowoczesnych schematów kryptograficznych obejmuje nie tylko jeden, ale dwa klucze: prywatny i publiczny. Podczas gdy ten pierwszy powinien pozostać prywatny we wszystkich zastosowaniach, drugi jest zazwyczaj wiedzą publiczną (stąd ich nazwy). W dziedzinie szyfrowania, klucz publiczny może być użyty do zaszyfrowania wiadomości, podczas gdy klucz prywatny może być użyty do odszyfrowania.

Gałąź kryptografii zajmująca się schematami, w których wszystkie strony dzielą jeden klucz, znana jest jako kryptografia symetryczna. Pojedynczy klucz w takim schemacie jest zwykle nazywany kluczem prywatnym (lub kluczem tajnym). Gałąź kryptografii, która zajmuje się schematami wymagającymi pary kluczy prywatny-publiczny, znana jest jako kryptografia asymetryczna. Gałęzie te są czasami nazywane odpowiednio kryptografią klucza prywatnego i kryptografią klucza publicznego (choć może to powodować zamieszanie, ponieważ schematy kryptograficzne z kluczem publicznym mają również klucze prywatne).

Pojawienie się kryptografii asymetrycznej pod koniec lat 70. było jednym z najważniejszych wydarzeń w historii kryptografii. Bez niej większość naszych nowoczesnych systemów komunikacyjnych, w tym Bitcoin, nie byłaby możliwa lub przynajmniej bardzo niepraktyczna.

Co ważne, współczesna kryptografia nie polega wyłącznie na badaniu schematów kryptograficznych z kluczem symetrycznym i asymetrycznym (choć obejmuje to znaczną część dziedziny). Na przykład kryptografia zajmuje się również funkcjami Hash i generatorami liczb pseudolosowych, a na tych prymitywach można budować aplikacje, które nie są związane z kryptografią kluczy symetrycznych lub asymetrycznych.

Po trzecie, klasyczne schematy szyfrowania, takie jak te stosowane w szyfrach Beale'a, były bardziej sztuką niż nauką. Ich postrzegane bezpieczeństwo było w dużej mierze oparte na intuicjach dotyczących ich złożoności. Zazwyczaj były one łatane, gdy poznano nowy atak na nie, lub całkowicie porzucane, jeśli atak był szczególnie poważny. Współczesna kryptografia jest jednak rygorystyczną nauką z formalnym, matematycznym podejściem zarówno do opracowywania, jak i analizowania schematów kryptograficznych. [5]

W szczególności, nowoczesna kryptografia koncentruje się na formalnych dowodach bezpieczeństwa. Każdy dowód bezpieczeństwa dla schematu kryptograficznego przebiega w trzech krokach:

  1. Określenie kryptograficznej definicji bezpieczeństwa, czyli zestawu celów bezpieczeństwa i zagrożenia stwarzanego przez atakującego.

  2. Określenie wszelkich założeń matematycznych w odniesieniu do złożoności obliczeniowej schematu. Na przykład, schemat kryptograficzny może zawierać generator liczb pseudolosowych. Chociaż nie możemy udowodnić ich istnienia, możemy założyć, że tak jest.

  3. Ekspozycja matematycznego dowodu bezpieczeństwa schematu na podstawie formalnego pojęcia bezpieczeństwa i dowolnych założeń matematycznych.

Po czwarte, podczas gdy w przeszłości kryptografia była wykorzystywana głównie w środowisku wojskowym, w erze cyfrowej przeniknęła ona do naszych codziennych czynności. Niezależnie od tego, czy korzystasz z bankowości internetowej, publikujesz posty w mediach społecznościowych, kupujesz produkt w Amazon za pomocą karty kredytowej, czy dajesz napiwek znajomemu Bitcoin, kryptografia jest warunkiem sine qua non naszej ery cyfrowej.

Biorąc pod uwagę te cztery aspekty nowoczesnej kryptografii, możemy scharakteryzować nowoczesną kryptografię jako naukę zajmującą się formalnym rozwojem i analizą schematów kryptograficznych w celu zabezpieczenia informacji cyfrowych przed atakami przeciwnika [6]. [Bezpieczeństwo powinno być tutaj szeroko rozumiane jako zapobieganie atakom, które niszczą tajność, integralność, uwierzytelnianie i/lub niezaprzeczalność w komunikacji.

Kryptografię najlepiej postrzegać jako subdyscyplinę cyberbezpieczeństwa, która zajmuje się zapobieganiem kradzieży, uszkodzeniom i niewłaściwemu wykorzystaniu systemów komputerowych. Należy pamiętać, że wiele kwestii związanych z cyberbezpieczeństwem ma niewielki lub tylko częściowy związek z kryptografią.

Na przykład, jeśli firma przechowuje drogie serwery lokalnie, może być zaniepokojona zabezpieczeniem tego sprzętu przed kradzieżą i uszkodzeniem. Chociaż jest to kwestia cyberbezpieczeństwa, nie ma ona wiele wspólnego z kryptografią.

Innym przykładem są ataki phishingowe, które są powszechnym problemem w dzisiejszych czasach. Ataki te próbują oszukać ludzi za pośrednictwem wiadomości e-mail lub innego środka przekazu, aby zrzec się poufnych informacji, takich jak hasła lub numery kart kredytowych. Podczas gdy kryptografia może w pewnym stopniu pomóc w atakach phishingowych Address, kompleksowe podejście wymaga czegoś więcej niż tylko użycia kryptografii.

Uwagi:

[3] Mówiąc dokładniej, ważne zastosowania schematów kryptograficznych dotyczyły tajności. Na przykład dzieci często używają prostych schematów kryptograficznych do "zabawy". W takich przypadkach tajność nie ma większego znaczenia.

[4] Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons), s. 2.

[5] Patrz Jonathan Katz i Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), szczególnie s. 16-23, dla dobrego opisu.

[6] Por. Katz i Lindell, tamże, s. 3. Uważam, że ich charakterystyka ma pewne problemy, dlatego przedstawiam tutaj nieco inną wersję ich stwierdzenia.

Otwarta komunikacja

Nowoczesna kryptografia została zaprojektowana w celu zapewnienia bezpieczeństwa w otwartym środowisku komunikacyjnym. Jeśli nasz kanał komunikacyjny jest tak dobrze chroniony, że podsłuchujący nie mają szans na manipulowanie lub nawet tylko obserwowanie naszych wiadomości, wówczas kryptografia jest zbędna. Większość naszych kanałów komunikacyjnych nie jest jednak tak dobrze strzeżona.

Szkieletem komunikacji we współczesnym świecie jest ogromna sieć kabli światłowodowych. Wykonywanie połączeń telefonicznych, oglądanie telewizji i przeglądanie stron internetowych w nowoczesnym gospodarstwie domowym zazwyczaj opiera się na sieci kabli światłowodowych (niewielki procent może polegać wyłącznie na satelitach). Prawdą jest, że możesz mieć różne połączenia danych w domu, takie jak kabel koncentryczny, (asymetryczna) cyfrowa linia abonencka i kabel światłowodowy. Jednak, przynajmniej w rozwiniętym świecie, te różne nośniki danych szybko łączą się poza domem z węzłem w ogromnej sieci kabli światłowodowych, która łączy cały świat. Wyjątkiem są niektóre odległe obszary rozwiniętego świata, takie jak Stany Zjednoczone i Australia, gdzie ruch danych może nadal pokonywać znaczne odległości za pomocą tradycyjnych miedzianych przewodów telefonicznych.

Niemożliwe byłoby uniemożliwienie potencjalnym atakującym fizycznego dostępu do tej sieci kabli i jej infrastruktury pomocniczej[7]. W rzeczywistości wiemy już, że większość naszych danych jest przechwytywana przez różne krajowe agencje wywiadowcze na kluczowych skrzyżowaniach Internetu[7]. Obejmuje to wszystko, od wiadomości na Facebooku po adresy odwiedzanych stron internetowych.

Podczas gdy inwigilacja danych na masową skalę wymaga potężnego przeciwnika, takiego jak krajowa agencja wywiadowcza, atakujący z niewielkimi zasobami mogą z łatwością próbować szpiegować na bardziej lokalną skalę. Chociaż może się to zdarzyć na poziomie podsłuchiwania przewodów, znacznie łatwiej jest po prostu przechwycić komunikację bezprzewodową.

Większość naszych lokalnych danych sieciowych - czy to w naszych domach, w biurze, czy w kawiarni - podróżuje teraz za pośrednictwem fal radiowych do bezprzewodowych punktów dostępowych na routerach typu all-in-one, a nie przez fizyczne kable. Atakujący potrzebuje więc niewielkich zasobów, aby przechwycić ruch lokalny. Jest to szczególnie niepokojące, ponieważ większość ludzi robi bardzo niewiele, aby chronić dane przesyłane przez ich sieci lokalne. Ponadto potencjalni atakujący mogą również atakować nasze mobilne połączenia szerokopasmowe, takie jak 3G, 4G i 5G. Wszystkie te połączenia bezprzewodowe są łatwym celem dla atakujących.

Dlatego też idea utrzymywania komunikacji w tajemnicy poprzez ochronę kanału komunikacyjnego jest beznadziejnie złudnym dążeniem większości współczesnego świata. Wszystko, co wiemy, uzasadnia poważną paranoję: zawsze należy zakładać, że ktoś nas podsłuchuje. A kryptografia jest głównym narzędziem, jakie mamy do uzyskania jakiegokolwiek rodzaju bezpieczeństwa w tym nowoczesnym środowisku.

Uwagi:

[7] Zob. na przykład Olga Khazan, "The creepy, long-standing practice of undersea cable tapping", The Atlantic, 16 lipca 2013 r. (dostępny pod adresem The Atlantic).

Matematyczne podstawy kryptografii 1

Zmienne losowe

Kryptografia opiera się na matematyce. A jeśli chcesz zbudować coś więcej niż powierzchowne zrozumienie kryptografii, musisz czuć się komfortowo z tą matematyką.

W tym rozdziale przedstawiono większość podstawowych zagadnień matematycznych, z którymi można się zetknąć podczas nauki kryptografii. Tematy te obejmują zmienne losowe, operacje modulo, operacje XOR i pseudolosowość. Powinieneś opanować materiał zawarty w tych sekcjach, aby zrozumieć kryptografię w stopniu innym niż powierzchowny.

Następna sekcja dotyczy teorii liczb, która jest znacznie bardziej wymagająca.

Zmienne losowe

Zmienna losowa jest zwykle oznaczana niepogrubioną, wielką literą. Możemy więc na przykład mówić o zmiennej losowej X, zmiennej losowej Y lub zmiennej losowej Z. Jest to notacja, którą będę stosował w dalszej części artykułu.

Zmienna losowa może przyjmować dwie lub więcej możliwych wartości, każda z określonym dodatnim prawdopodobieństwem. Możliwe wartości są wymienione w zestawie wyników.

Za każdym razem, gdy próbkujesz zmienną losową, losujesz określoną wartość z jej zbioru wyników zgodnie z określonymi prawdopodobieństwami.

Przejdźmy do prostego przykładu. Załóżmy, że zmienna X jest zdefiniowana w następujący sposób:

Pr[X = 1] = 0.5
Pr[X = 2] = 0.5

Łatwo zauważyć, że X jest zmienną losową. Po pierwsze, istnieją co najmniej dwie możliwe wartości, które może przyjąć X, a mianowicie 1 i 2. Po drugie, każda możliwa wartość ma dodatnie prawdopodobieństwo wystąpienia za każdym razem, gdy próbkujesz X, a mianowicie 0,5.

Wszystko, czego wymaga zmienna losowa, to zbiór wyników z dwiema lub więcej możliwościami, gdzie każda możliwość ma dodatnie prawdopodobieństwo wystąpienia po pobraniu próbki. Zasadniczo zmienną losową można więc zdefiniować abstrakcyjnie, bez żadnego kontekstu. W tym przypadku można myśleć o "próbkowaniu" jako przeprowadzaniu naturalnego eksperymentu w celu określenia wartości zmiennej losowej.

Powyższa zmienna X została zdefiniowana abstrakcyjnie. Możesz więc myśleć o próbkowaniu zmiennej X powyżej jako o rzucaniu uczciwą monetą i przypisywaniu "2" w przypadku głów i "1" w przypadku reszek. Dla każdej próbki X, rzucasz monetą ponownie.

Alternatywnie, można również myśleć o próbkowaniu X, jako rzucaniu sprawiedliwą kością i przypisywaniu "2" w przypadku, gdy kość wyrzuci 1, 3 lub 4, oraz przypisywaniu "1" w przypadku, gdy kość wyrzuci 2, 5 lub 6. Za każdym razem, gdy próbkujesz X, ponownie rzucasz kością.

W rzeczywistości każdy naturalny eksperyment, który pozwoliłby określić prawdopodobieństwa możliwych wartości X powyżej, można sobie wyobrazić w odniesieniu do rysunku.

Często jednak zmienne losowe nie są po prostu wprowadzane abstrakcyjnie. Zamiast tego zestaw możliwych wartości wyników ma wyraźne znaczenie w świecie rzeczywistym (a nie tylko jako liczby). Ponadto te wartości wyników mogą być zdefiniowane w odniesieniu do określonego rodzaju eksperymentu (a nie jako dowolny naturalny eksperyment z tymi wartościami).

Rozważmy teraz przykład zmiennej X, która nie jest zdefiniowana abstrakcyjnie. X jest zdefiniowana w następujący sposób, aby określić, która z dwóch drużyn rozpocznie mecz piłki nożnej:

Pr [X = \text{red kicks off}] = 0.5
Pr [X = \text{blue kicks off}] = 0.5

W tym przypadku zbiór wyników X ma konkretne znaczenie, a mianowicie to, która drużyna rozpocznie mecz piłki nożnej. Ponadto, możliwe wyniki i związane z nimi prawdopodobieństwa są określane przez konkretny eksperyment, a mianowicie rzucanie konkretną monetą C.

W dyskusjach na temat kryptografii zmienne losowe są zwykle wprowadzane w odniesieniu do zbioru wyników o znaczeniu w świecie rzeczywistym. Może to być zbiór wszystkich wiadomości, które można zaszyfrować, znany jako przestrzeń wiadomości, lub zbiór wszystkich kluczy, z których mogą wybierać strony korzystające z szyfrowania, znany jako przestrzeń kluczy.

Zmienne losowe w dyskusjach na temat kryptografii nie są jednak zwykle definiowane w odniesieniu do konkretnego naturalnego eksperymentu, ale w odniesieniu do dowolnego eksperymentu, który może przynieść odpowiednie rozkłady prawdopodobieństwa.

Zmienne losowe mogą mieć dyskretne lub ciągłe rozkłady prawdopodobieństwa. Zmienne losowe o dyskretnym rozkładzie prawdopodobieństwa - czyli dyskretne zmienne losowe - mają skończoną liczbę możliwych wyników. Zmienna losowa X w obu dotychczas podanych przykładach była dyskretna.

Ciągłe zmienne losowe mogą zamiast tego przyjmować wartości w jednym lub więcej przedziałach. Można na przykład powiedzieć, że zmienna losowa po pobraniu próbki przyjmie dowolną wartość rzeczywistą z przedziału od 0 do 1, a każda liczba rzeczywista w tym przedziale jest równie prawdopodobna. W tym przedziale istnieje nieskończenie wiele możliwych wartości.

Do dyskusji na temat kryptografii wystarczy rozumieć dyskretne zmienne losowe. Wszelkie dyskusje na temat zmiennych losowych od tego momentu należy zatem rozumieć jako odnoszące się do dyskretnych zmiennych losowych, chyba że wyraźnie zaznaczono inaczej.

Wykresy zmiennych losowych

Możliwe wartości i związane z nimi prawdopodobieństwa dla zmiennej losowej można łatwo zwizualizować za pomocą wykresu. Dla przykładu, rozważmy zmienną losową X z poprzedniej sekcji ze zbiorem wyników \{1, 2\} oraz Pr [X = 1] = 0.5 i Pr [X = 2] = 0.5. Zazwyczaj wyświetlamy taką zmienną losową w postaci wykresu słupkowego, jak na Rysunku 1.

Rysunek 1: Zmienna losowa X

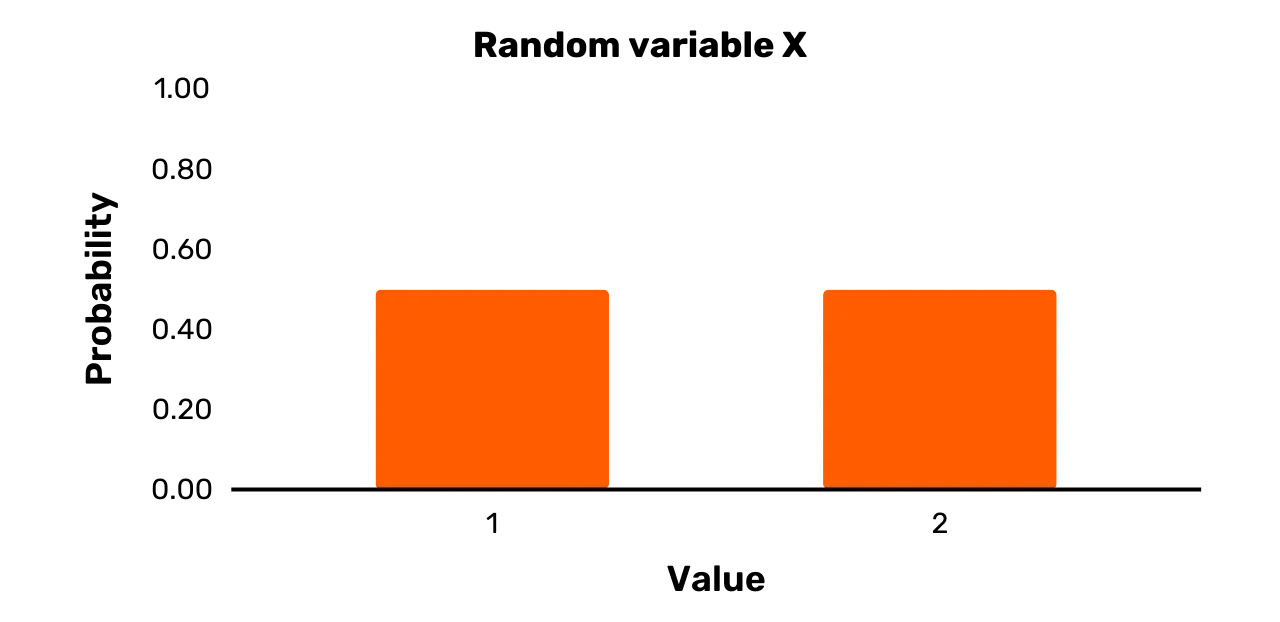
Figure 1: Random variable X.

Szerokie słupki na Rysunku 1 oczywiście nie sugerują, że zmienna losowa X jest ciągła. Zamiast tego słupki są szerokie, aby były bardziej atrakcyjne wizualnie (tylko linia prosto w górę zapewnia mniej intuicyjną wizualizację).

Zmienne jednolite

W wyrażeniu "zmienna losowa" termin "losowy" oznacza po prostu "probabilistyczny". Innymi słowy, oznacza to, że dwa lub więcej możliwych wyników zmiennej występuje z pewnym prawdopodobieństwem. Wyniki te jednak nie muszą być równie prawdopodobne (choć termin "losowy" może mieć takie znaczenie w innych kontekstach).

Zmienna jednorodna jest szczególnym przypadkiem zmiennej losowej. Może ona przyjmować dwie lub więcej wartości z jednakowym prawdopodobieństwem. Zmienna losowa X przedstawiona na Rysunku 1 jest wyraźnie zmienną jednorodną, ponieważ oba możliwe wyniki występują z prawdopodobieństwem 0,5. Istnieje jednak wiele zmiennych losowych, które nie są instancjami zmiennych jednorodnych.

Rozważmy na przykład zmienną losową Y. Ma ona zbiór wyników {1, 2, 3, 8, 10} i następujący rozkład prawdopodobieństwa:

\Pr[Y = 1] = 0.25
\Pr[Y = 2] = 0.35
\Pr[Y = 3] = 0.1
\Pr[Y = 8] = 0.25
\Pr[Y = 10] = 0.05

Podczas gdy dwa możliwe wyniki rzeczywiście mają równe prawdopodobieństwo wystąpienia, a mianowicie 1 i 8, Y może również przyjmować pewne wartości z innym prawdopodobieństwem niż 0,25 podczas próbkowania. W związku z tym, choć Y jest zmienną losową, nie jest zmienną jednorodną.

Graficzne przedstawienie Y znajduje się na Rysunku 2.

Rysunek 2: Zmienna losowa Y

Figure 2: Random variable Y.

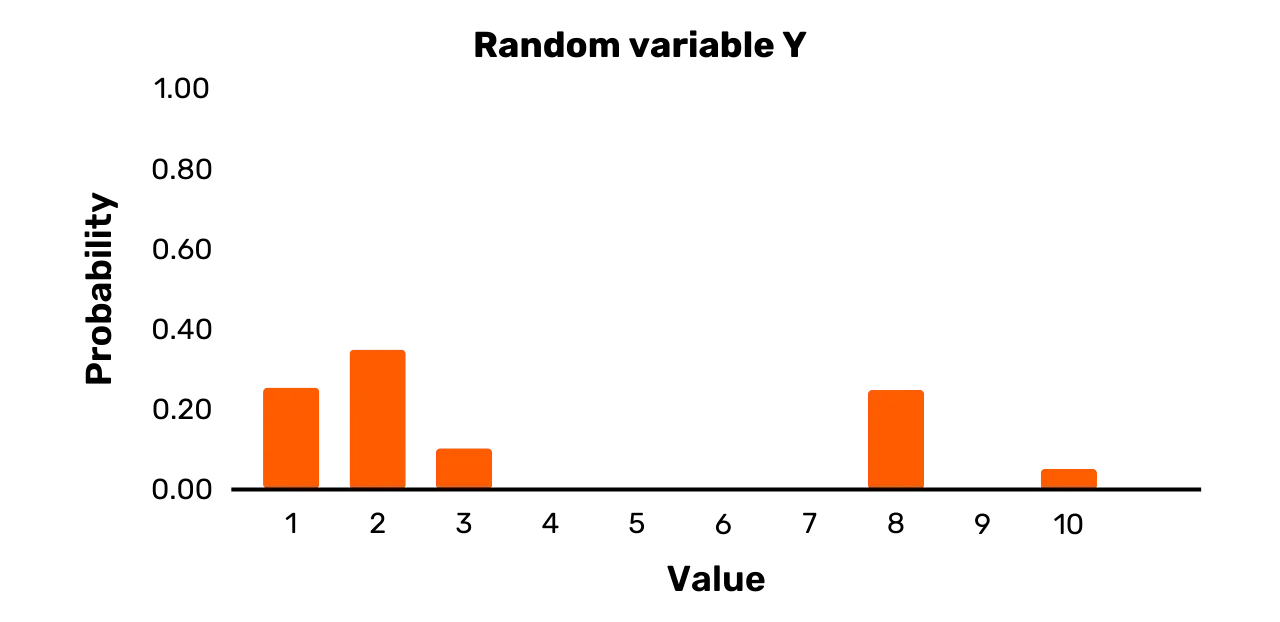
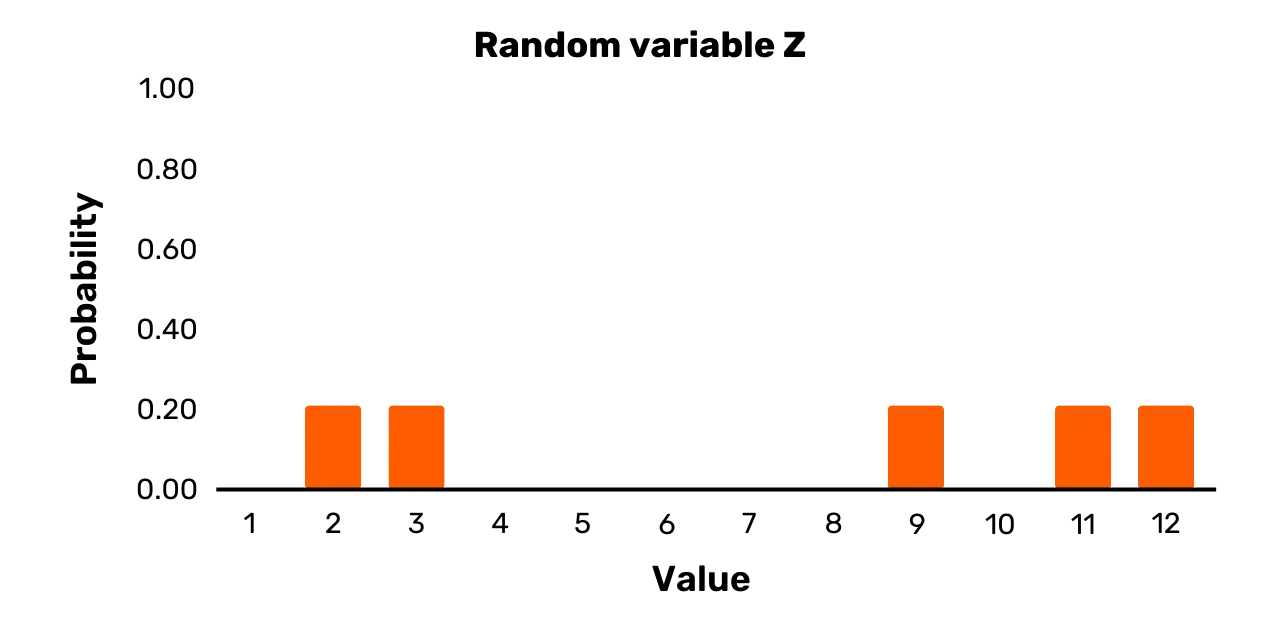
W ostatnim przykładzie rozważmy zmienną losową Z. Ma ona zbiór wyników {1,3,7,11,12} i następujący rozkład prawdopodobieństwa:

\Pr[Z = 2] = 0.2
\Pr[Z = 3] = 0.2
\Pr[Z = 9] = 0.2
\Pr[Z = 11] = 0.2
\Pr[Z = 12] = 0.2

Można to zobaczyć na Rysunku 3. Zmienna losowa Z jest, w przeciwieństwie do Y, zmienną jednorodną, ponieważ wszystkie prawdopodobieństwa możliwych wartości po pobraniu próbki są równe.

Rysunek 3: Zmienna losowa Z

Figure 3: Random variable Z.

Prawdopodobieństwo warunkowe

Załóżmy, że Bob zamierza wybrać jeden dzień z ostatniego roku kalendarzowego. Jakie jest prawdopodobieństwo, że wybrany dzień będzie latem?

Tak długo, jak uważamy, że proces Boba będzie rzeczywiście jednolity, powinniśmy dojść do wniosku, że istnieje 1/4 prawdopodobieństwa, że Bob wybierze dzień w lecie. Jest to bezwarunkowe prawdopodobieństwo, że losowo wybrany dzień będzie latem.

Załóżmy teraz, że zamiast losować dzień kalendarzowy, Bob wybiera tylko spośród tych dni, w których temperatura w południe w Crystal Lake (New Jersey) wynosiła 21 stopni Celsjusza lub więcej. Biorąc pod uwagę te dodatkowe informacje, co możemy wywnioskować o prawdopodobieństwie, że Bob wybierze dzień w lecie?

Powinniśmy naprawdę wyciągnąć inny wniosek niż wcześniej, nawet bez dalszych szczegółowych informacji (np. temperatura w południe każdego dnia w ubiegłym roku kalendarzowym).

Wiedząc, że Crystal Lake znajduje się w New Jersey, z pewnością nie spodziewalibyśmy się, że temperatura w południe wyniesie 21 stopni Celsjusza lub więcej w zimie. Zamiast tego jest znacznie bardziej prawdopodobne, że będzie to ciepły dzień wiosną lub jesienią, lub dzień gdzieś latem. W związku z tym, wiedząc, że temperatura w południe nad jeziorem Crystal Lake w wybranym dniu wynosiła 21 stopni Celsjusza lub więcej, prawdopodobieństwo, że dzień wybrany przez Boba jest latem, staje się znacznie wyższe. Jest to warunkowe prawdopodobieństwo, że losowo wybrany dzień będzie latem, biorąc pod uwagę, że temperatura w południe nad jeziorem Crystal Lake wynosiła 21 stopni Celsjusza lub więcej.

W przeciwieństwie do poprzedniego przykładu, prawdopodobieństwa dwóch zdarzeń mogą być całkowicie niepowiązane. W takim przypadku mówimy, że są one niezależne.

Załóżmy na przykład, że w pewnej uczciwej monecie wypadł reszka. Biorąc pod uwagę ten fakt, jakie jest prawdopodobieństwo, że jutro będzie padać? Prawdopodobieństwo warunkowe w tym przypadku powinno być takie samo jak prawdopodobieństwo bezwarunkowe, że jutro będzie padać, ponieważ rzut monetą nie ma żadnego wpływu na pogodę.

Używamy symbolu "|" do zapisywania warunkowych stwierdzeń prawdopodobieństwa. Na przykład, prawdopodobieństwo zdarzenia A przy założeniu, że wystąpiło zdarzenie B można zapisać w następujący sposób:

Pr[A|B]

Tak więc, gdy dwa zdarzenia, A i B, są niezależne, to:

Pr[A|B] = Pr[A] \text{ and } Pr[B|A] = Pr[B]

Warunek niezależności można uprościć w następujący sposób:

Pr[A, B] = Pr[A] \cdot Pr[B]

Kluczowy wynik w teorii prawdopodobieństwa jest znany jako Twierdzenie Bayesa. Stwierdza ono, że Pr[A|B] można zapisać w następujący sposób:

Pr[A|B] = \frac{Pr[B|A] \cdot Pr[A]}{Pr[B]}

Zamiast używać prawdopodobieństw warunkowych dla określonych zdarzeń, możemy również spojrzeć na prawdopodobieństwa warunkowe związane z dwiema lub więcej zmiennymi losowymi w zbiorze możliwych zdarzeń. Załóżmy, że mamy dwie zmienne losowe, X i Y. Każdą możliwą wartość dla X możemy oznaczyć przez x, a każdą możliwą wartość dla Y przez y. Możemy zatem powiedzieć, że dwie zmienne losowe są niezależne, jeśli zachodzi następujące stwierdzenie:

Pr[X = x, Y = y] = Pr[X = x] \cdot Pr[Y = y]

dla wszystkich x i y.

Wyjaśnijmy nieco dokładniej, co oznacza to stwierdzenie.

Załóżmy, że zbiory wyników dla X i Y są zdefiniowane następująco: X = \{x_1, x_2, \ldots, x_i, \ldots, x_n\} oraz Y = \{y_1, y_2, \ldots, y_i, \ldots, y_m\}. (Typowe jest oznaczanie zestawów wartości pogrubionymi, dużymi literami)

Załóżmy teraz, że próbkujemy Y i obserwujemy y_1. Powyższe stwierdzenie mówi nam, że prawdopodobieństwo uzyskania x_1 z próby X jest dokładnie takie samo, jak gdybyśmy nigdy nie zaobserwowali y_1. Jest to prawdą dla każdego y_i, który moglibyśmy wylosować z naszego początkowego próbkowania Y. Wreszcie, jest to prawdą nie tylko dla x_1. Dla każdego x_i prawdopodobieństwo wystąpienia nie zależy od wyniku próbkowania Y. Wszystko to odnosi się również do przypadku, w którym próbka X jest pobierana jako pierwsza.

Zakończmy naszą dyskusję na nieco bardziej filozoficznym punkcie. W każdej rzeczywistej sytuacji prawdopodobieństwo jakiegoś zdarzenia jest zawsze oceniane na podstawie określonego zestawu informacji. Nie istnieje "bezwarunkowe prawdopodobieństwo" w ścisłym znaczeniu tego słowa.

Załóżmy na przykład, że zapytałem cię o prawdopodobieństwo, że świnie będą latać do 2030 roku. Mimo że nie podaję żadnych dodatkowych informacji, najwyraźniej wiesz dużo o świecie, co może wpłynąć na twoją ocenę. Nigdy nie widziałeś latających świń. Wiesz, że większość ludzi nie spodziewa się, że będą latać. Wiesz, że tak naprawdę nie są stworzone do latania. I tak dalej.

Dlatego też, gdy mówimy o "bezwarunkowym prawdopodobieństwie" jakiegoś zdarzenia w kontekście świata rzeczywistego, termin ten może mieć znaczenie tylko wtedy, gdy przyjmiemy, że oznacza coś w rodzaju "prawdopodobieństwa bez żadnych dalszych wyraźnych informacji". Każde rozumienie "prawdopodobieństwa warunkowego" powinno być zatem zawsze rozumiane w odniesieniu do jakiejś konkretnej informacji.

Mógłbym, na przykład, zapytać cię o prawdopodobieństwo, że świnie będą latać do 2030 roku, po przedstawieniu ci dowodów na to, że niektóre kozy w Nowej Zelandii nauczyły się latać po kilku latach treningu. W takim przypadku prawdopodobnie skorygujesz swoją ocenę prawdopodobieństwa, że świnie będą latać do 2030 roku. Tak więc prawdopodobieństwo, że świnie będą latać do 2030 roku jest uzależnione od dowodów dotyczących kóz w Nowej Zelandii.

Operacja modulo

Modulo

Najbardziej podstawowe wyrażenie z operacją modulo ma następującą postać: x \mod y.

Zmienna x nazywana jest dywidendą, a zmienna y dzielnikiem. Aby wykonać operację modulo z dodatnią dzielną i dodatnim dzielnikiem, wystarczy określić resztę z dzielenia.

Na przykład, rozważmy wyrażenie 25 \mod 4. Liczba 4 jest dzielona przez liczbę 25 łącznie 6 razy. Reszta z tego dzielenia wynosi 1. Stąd 25 \mod 4 równa się 1. W podobny sposób możemy obliczyć poniższe wyrażenia:

Gdy dzielna lub dzielnik są ujemne, operacje modulo mogą być obsługiwane w różny sposób przez języki programowania.

Na pewno natkniesz się na przypadki z negatywną dywidendą w kryptografii. W takich przypadkach typowe podejście jest następujące:

Załóżmy na przykład, że dzielna wynosi -20, a dzielnik 3. Najbliższą wartością mniejszą lub równą -20, na którą dzieli się 3, jest -21. Wartość x - p w tym przypadku wynosi -20 - (-21). Jest ona równa 1, a zatem -20 \ mod 3 jest równe 1. W podobny sposób możemy obliczyć poniższe wyrażenia:

Jeśli chodzi o notację, zazwyczaj można spotkać się z następującymi typami wyrażeń: x = [y \mod z]. Ze względu na nawiasy, operacja modulo w tym przypadku dotyczy tylko prawej strony wyrażenia. Jeśli y równa się 25, a z równa się 4, to x ma wartość 1.

Bez nawiasów, operacja modulo działa na obu stronach wyrażenia. Załóżmy na przykład następujące wyrażenie: x = y \mod z. Jeśli y jest równe 25, a z jest równe 4, to wiemy tylko, że x \mod 4 jest równe 1. Jest to zgodne z dowolną wartością dla x ze zbioru \{\ldots,-7, -3, 1, 5, 9,\ldots\}.

Gałąź matematyki, która obejmuje operacje modulo na liczbach i wyrażeniach, nazywana jest modułową arytmetyką. Można o niej myśleć jako o arytmetyce dla przypadków, w których linia liczbowa nie jest nieskończenie długa. Chociaż zazwyczaj spotykamy się z operacjami modulo dla (dodatnich) liczb całkowitych w kryptografii, można również wykonywać operacje modulo przy użyciu dowolnych liczb rzeczywistych.

Szyfr przesunięcia

Operacja modulo jest często spotykana w kryptografii. Aby to zilustrować, rozważmy jeden z najbardziej znanych historycznych schematów szyfrowania: szyfr przesunięcia.

Najpierw ją zdefiniujmy. Załóżmy słownik D, który zrównuje wszystkie litery alfabetu angielskiego, w kolejności, ze zbiorem liczb \{0, 1, 2, \ldots, 25\}. Przyjmijmy przestrzeń wiadomości M. Szyfr przesunięcia** jest zatem schematem szyfrowania zdefiniowanym w następujący sposób:

Operator modulo w szyfrze przestawieniowym zapewnia zawijanie liter, dzięki czemu wszystkie litery szyfrogramu są zdefiniowane. Aby to zilustrować, rozważmy zastosowanie szyfru przestawieniowego na słowie "DOG".

Załóżmy, że jednolicie wybrano klucz o wartości 17. Litera "O" jest równa 15. Bez operacji modulo, dodanie tej liczby tekstu jawnego do klucza dałoby liczbę szyfrogramu równą 32. Jednak ta liczba szyfrogramu nie może zostać przekształcona w literę szyfrogramu, ponieważ alfabet angielski ma tylko 26 liter. Operacja modulo zapewnia, że liczba szyfrogramu wynosi w rzeczywistości 6 (wynik 32 \mod 26), co odpowiada literze szyfrogramu "G".

Całe szyfrowanie słowa "DOG" z wartością klucza 17 wygląda następująco:

Każdy może intuicyjnie zrozumieć, jak działa szyfr przestawieniowy i prawdopodobnie sam go używać. Aby jednak pogłębić swoją wiedzę na temat kryptografii, ważne jest, aby zacząć czuć się bardziej komfortowo z formalizacją, ponieważ schematy staną się znacznie trudniejsze. Dlatego też kroki szyfru przestawieniowego zostały sformalizowane.

Uwagi:

[1] Możemy dokładnie zdefiniować to stwierdzenie, używając terminologii z poprzedniej sekcji. Niech jednolita zmienna K ma K jako zbiór możliwych wyników. Zatem:

Pr[K = 0] = \frac{1}{26}
Pr[K = 1] = \frac{1}{26}

i tak dalej. Jednokrotne próbkowanie jednolitej zmiennej K w celu uzyskania określonego klucza.

Operacja XOR

Wszystkie dane komputerowe są przetwarzane, przechowywane i przesyłane przez sieci na poziomie bitów. Wszelkie schematy kryptograficzne stosowane do danych komputerowych również działają na poziomie bitów.

Załóżmy na przykład, że użytkownik wpisał wiadomość e-mail w aplikacji pocztowej. Każde zastosowane szyfrowanie nie dotyczy bezpośrednio znaków ASCII wiadomości e-mail. Zamiast tego jest stosowane do bitowej reprezentacji liter i innych symboli w wiadomości e-mail.

Kluczową operacją matematyczną, którą należy zrozumieć w nowoczesnej kryptografii, oprócz operacji modulo, jest operacja XOR, czyli operacja "exclusive or". Operacja ta przyjmuje jako dane wejściowe dwa bity i daje jako dane wyjściowe inny bit. Operacja XOR będzie po prostu oznaczana jako "XOR". Daje ona 0, jeśli dwa bity są takie same i 1, jeśli dwa bity są różne. Poniżej przedstawiono cztery możliwości. Symbol \oplus reprezentuje "XOR":

Aby to zilustrować, załóżmy, że masz wiadomość m_1 (01111001) i wiadomość m_2 (01011001). Operację XOR tych dwóch wiadomości można zobaczyć poniżej.

Proces ten jest prosty. Najpierw należy wykonać XOR lewych bitów m_1 i m_2. W tym przypadku jest to 0 \oplus 0 = 0. Następnie wykonujemy XOR drugiej pary bitów od lewej. W tym przypadku jest to 1 \oplus 1 = 0. Kontynuuj ten proces, aż wykonasz operację XOR na najbardziej wysuniętych na prawo bitach.

Łatwo zauważyć, że operacja XOR jest komutatywna, a mianowicie, że m_1 \oplus m_2 = m_2 \oplus m_1. Ponadto, operacja XOR jest również asocjatywna. Oznacza to, że (m_1 \oplus m_2) \oplus m_3 = m_1 \oplus (m_2 \oplus m_3).

Operacja XOR na dwóch łańcuchach o różnych długościach może mieć różne interpretacje, w zależności od kontekstu. Nie będziemy się tutaj zajmować żadnymi operacjami XOR na ciągach o różnych długościach.

Operacja XOR jest równoważna specjalnemu przypadkowi wykonywania operacji modulo na dodawaniu bitów, gdy dzielnik wynosi 2. Równoważność można zobaczyć w poniższych wynikach:

Pseudolosowość

W naszej dyskusji na temat zmiennych losowych i jednorodnych dokonaliśmy konkretnego rozróżnienia między "losowymi" i "jednorodnymi". Rozróżnienie to jest zwykle utrzymywane w praktyce przy opisywaniu zmiennych losowych. Jednak w naszym obecnym kontekście rozróżnienie to należy porzucić, a "losowy" i "jednolity" są używane jako synonimy. Wyjaśnię dlaczego na końcu tej sekcji.

Na początek możemy nazwać ciąg binarny o długości n losowym (lub jednolitym), jeśli był on wynikiem próbkowania jednolitej zmiennej S, która daje każdemu ciągowi binarnemu o takiej długości n równe prawdopodobieństwo wyboru.

Załóżmy na przykład zbiór wszystkich ciągów binarnych o długości 8: \{0000\ 0000, 0000\ 0001, \ldots, 1111\ 1111\}. (Typowe jest zapisywanie 8-bitowego ciągu w dwóch kwartetach, z których każdy nazywany jest nibble) Nazwijmy ten zestaw ciągów S_8.

Zgodnie z powyższą definicją, możemy zatem nazwać konkretny ciąg binarny o długości 8 losowym (lub jednolitym), jeśli był on wynikiem próbkowania jednolitej zmiennej S, która daje każdemu ciągowi w S_8 równe prawdopodobieństwo wyboru. Biorąc pod uwagę, że zbiór S_8 zawiera 2^8 Elements, prawdopodobieństwo wyboru po pobraniu próbki musiałoby wynosić 1/2^8 dla każdego ciągu w zbiorze.

Kluczowym aspektem losowości ciągu binarnego jest to, że jest ona definiowana w odniesieniu do procesu, w którym została wybrana. Forma dowolnego konkretnego ciągu binarnego sama w sobie nie ujawnia zatem nic na temat jego losowości w wyborze.

Na przykład, wiele osób intuicyjnie uważa, że ciąg znaków taki jak 1111\1111 nie mógł zostać wybrany losowo. Jest to jednak oczywista nieprawda.

Definiując jednolitą zmienną S nad wszystkimi ciągami binarnymi o długości 8, prawdopodobieństwo wybrania 1111\1111 ze zbioru S_8 jest takie samo jak prawdopodobieństwo wybrania ciągu takiego jak 0111\0100. Nie można więc powiedzieć nic o losowości ciągu, analizując tylko sam ciąg.

Możemy również mówić o losowych ciągach, nie mając na myśli konkretnie ciągów binarnych. Możemy na przykład mówić o losowym ciągu szesnastkowym AF\ 02\ 82. W tym przypadku ciąg zostałby wybrany losowo ze zbioru wszystkich ciągów szesnastkowych o długości 6. Jest to równoważne losowemu wybraniu ciągu binarnego o długości 24, ponieważ każda cyfra szesnastkowa reprezentuje 4 bity.

Zazwyczaj wyrażenie "losowy ciąg", bez kwalifikacji, odnosi się do ciągu losowo wybranego ze zbioru wszystkich ciągów o tej samej długości. Tak właśnie opisałem to powyżej. Ciąg o długości n może być oczywiście losowo wybrany z innego zbioru. Na przykład takiego, który stanowi tylko podzbiór wszystkich ciągów o długości n, lub być może zbioru zawierającego ciągi o różnej długości. W takich przypadkach nie będziemy jednak mówić o "losowym ciągu", ale raczej o "ciągu losowo wybranym z pewnego zbioru S".

Kluczowym pojęciem w kryptografii jest pseudolosowość. Pseudolosowy ciąg o długości n wygląda jakby był wynikiem próbkowania jednolitej zmiennej S, która daje każdemu ciągowi w S_n równe prawdopodobieństwo wyboru. W rzeczywistości jednak ciąg ten jest wynikiem próbkowania jednolitej zmiennej S', która definiuje jedynie rozkład prawdopodobieństwa - niekoniecznie taki, który ma równe prawdopodobieństwa dla wszystkich możliwych wyników - na podzbiorze S_n. Kluczową kwestią jest to, że nikt tak naprawdę nie jest w stanie rozróżnić próbek z S i S', nawet jeśli pobierze się ich wiele.

Załóżmy na przykład zmienną losową S. Jej zbiorem wynikowym jest S_{256}, czyli zbiór wszystkich ciągów binarnych o długości 256. Zbiór ten ma 2^{256} Elements. Każdy element ma równe prawdopodobieństwo wyboru, 1/2^{256}, podczas próbkowania.

Ponadto załóżmy, że zmienna losowa S'. Jej zbiór wyników zawiera tylko 2^{128} ciągów binarnych o długości 256. Ma ona pewien rozkład prawdopodobieństwa nad tymi ciągami, ale rozkład ten niekoniecznie jest jednostajny.

Załóżmy, że pobrałem teraz 1000 próbek z S i 1000 próbek z S' i przekazałem ci dwa zestawy wyników. Powiem ci, który zestaw wyników jest powiązany z którą zmienną losową. Następnie pobieram próbkę z jednej z dwóch zmiennych losowych. Ale tym razem nie mówię, którą zmienną losową próbkuję. Jeśli S' byłoby pseudolosowe, to prawdopodobieństwo trafnego odgadnięcia, którą zmienną losową próbkuję, jest praktycznie nie lepsze niż 1/2.

Zazwyczaj ciąg pseudolosowy o długości n jest tworzony poprzez losowe wybranie ciągu o rozmiarze n - x, gdzie x jest dodatnią liczbą całkowitą, i użycie go jako danych wejściowych dla algorytmu rozszerzającego. Ten losowy ciąg o rozmiarze n - x jest znany jako seed.

Ciągi pseudolosowe są kluczową koncepcją, dzięki której kryptografia jest praktyczna. Rozważmy na przykład szyfry strumieniowe. W przypadku szyfru strumieniowego losowo wybrany klucz jest podłączany do algorytmu rozszerzającego w celu uzyskania znacznie większego ciągu pseudolosowego. Ten pseudolosowy ciąg jest następnie łączony z tekstem jawnym za pomocą operacji XOR w celu utworzenia szyfrogramu.

Jeśli nie bylibyśmy w stanie wytworzyć tego typu pseudolosowego ciągu dla szyfru strumieniowego, to dla jego bezpieczeństwa potrzebowalibyśmy klucza o długości równej długości wiadomości. W większości przypadków nie jest to zbyt praktyczna opcja.

Pojęcie pseudolosowości omówione w tej sekcji można zdefiniować bardziej formalnie. Rozciąga się ono również na inne konteksty. Nie musimy jednak zagłębiać się w tę dyskusję. Wszystko, czego naprawdę potrzebujesz, aby intuicyjnie zrozumieć większość kryptografii, to różnica między ciągiem losowym a pseudolosowym. [2]

Powód porzucenia rozróżnienia między "losowym" i "jednolitym" w naszej dyskusji powinien być teraz również jasny. W praktyce wszyscy używają terminu pseudolosowy, aby wskazać ciąg, który wygląda jakby był wynikiem próbkowania jednolitej zmiennej S. Ściśle rzecz biorąc, powinniśmy nazwać taki ciąg "pseudo-jednolitym", przyjmując nasz język z wcześniej. Ponieważ termin "pseudo-jednolity" jest zarówno niezgrabny, jak i nieużywany przez nikogo, nie będziemy go tutaj wprowadzać dla jasności. Zamiast tego porzucamy rozróżnienie między "losowym" i "jednolitym" w obecnym kontekście.

Uwagi

[2] Jeśli jesteś zainteresowany bardziej formalną ekspozycją tych kwestii, możesz zapoznać się z Introduction to Modern Cryptography Katza i Lindella, zwłaszcza z rozdziałem 3.

Matematyczne podstawy kryptografii 2

Czym jest teoria liczb?

Niniejszy rozdział obejmuje bardziej zaawansowany temat matematycznych podstaw kryptografii: teorię liczb. Chociaż teoria liczb jest ważna dla kryptografii symetrycznej (takiej jak szyfr Rijndael), jest ona szczególnie istotna w kryptografii klucza publicznego.

Jeśli uważasz, że szczegóły teorii liczb są uciążliwe, polecam lekturę na wysokim poziomie za pierwszym razem. Zawsze możesz do niej wrócić w późniejszym czasie.

Można scharakteryzować teorię liczb jako badanie właściwości liczb całkowitych i funkcji matematycznych, które działają na liczbach całkowitych.

Rozważmy na przykład, że dowolne dwie liczby a i N są coprimes (lub relative primes), jeśli ich największy wspólny dzielnik jest równy 1. Załóżmy teraz, że dana jest liczba całkowita N. Ile liczb całkowitych mniejszych od N jest liczbami pierwszymi z N? Czy możemy sformułować ogólne stwierdzenia dotyczące odpowiedzi na to pytanie? Są to typowe pytania, na które stara się odpowiedzieć teoria liczb.

Współczesna teoria liczb opiera się na narzędziach algebry abstrakcyjnej. Dziedzina algebry abstrakcyjnej jest subdyscypliną matematyki, w której głównymi obiektami analizy są abstrakcyjne obiekty znane jako struktury algebraiczne. Struktura algebraiczna** to zbiór Elements połączony z jedną lub więcej operacjami, który spełnia pewne aksjomaty. Dzięki strukturom algebraicznym matematycy mogą uzyskać wgląd w konkretne problemy matematyczne, abstrahując od ich szczegółów.

Dziedzina algebry abstrakcyjnej jest czasami nazywana również nowoczesną algebrą. Można również spotkać się z pojęciem matematyki abstrakcyjnej (lub czystej matematyki). Ten ostatni termin nie odnosi się do algebry abstrakcyjnej, ale oznacza raczej badanie matematyki dla niej samej, a nie tylko z myślą o potencjalnych zastosowaniach.

Zbiory z algebry abstrakcyjnej mogą dotyczyć wielu rodzajów obiektów, od przekształceń zachowujących kształt trójkąta równobocznego po wzory tapet. W przypadku teorii liczb rozważamy tylko zbiory Elements, które zawierają liczby całkowite lub funkcje działające na liczbach całkowitych.

Grupy

Podstawowym pojęciem w matematyce jest zbiór Elements. Zbiór jest zwykle oznaczany znakami wyróżnienia z Elements oddzielonymi przecinkami.

Na przykład zbiór wszystkich liczb całkowitych to \{..., -2, -1, 0, 1, 2, ...\}. Elipsy oznaczają tutaj, że pewien wzór jest kontynuowany w określonym kierunku. Tak więc zbiór wszystkich liczb całkowitych obejmuje również 3, 4, 5, 6 i tak dalej, a także 3, -4, -5, -6 i tak dalej. Ten zbiór wszystkich liczb całkowitych jest zwykle oznaczany przez \mathbb{Z}.

Innym przykładem zbioru jest \mathbb{Z} \mod 11, czyli zbiór wszystkich liczb całkowitych modulo 11. W przeciwieństwie do całego zbioru \mathbb{Z}, zbiór ten zawiera tylko skończoną liczbę Elements, a mianowicie \{0, 1, \ldots, 9, 10\}.

Częstym błędem jest myślenie, że zbiór \mathbb{Z} \mod 11 faktycznie wynosi \{-10, -9, \ldots, 0, \ldots, 9, 10\}. Ale tak nie jest, biorąc pod uwagę sposób, w jaki wcześniej zdefiniowaliśmy operację modulo. Wszelkie ujemne liczby całkowite zredukowane przez modulo 11 zawijają się do \{0, 1, \ldots, 9, 10\}. Na przykład, wyrażenie -2 \mod 11 zawija się do 9, podczas gdy wyrażenie -27 \mod 11 zawija się do 5.

Innym podstawowym pojęciem w matematyce jest operacja binarna. Jest to każda operacja, która wymaga dwóch Elements, aby uzyskać trzecią. Na przykład, z podstawowej arytmetyki i algebry, znasz cztery podstawowe operacje binarne: dodawanie, odejmowanie, mnożenie i dzielenie.

Te dwa podstawowe pojęcia matematyczne, zbiory i operacje binarne, są używane do zdefiniowania pojęcia grupy, najważniejszej struktury w algebrze abstrakcyjnej.

W szczególności, załóżmy pewną operację binarną \circ. Ponadto załóżmy, że pewien zbiór Elements S jest wyposażony w tę operację. "Wyposażony" oznacza tutaj jedynie, że operacja \circ może być wykonana pomiędzy dowolnymi dwoma Elements w zbiorze S.

Kombinacja \langle \mathbf{S}, \circ \rangle jest zatem grupą, jeśli spełnia cztery określone warunki, znane jako aksjomaty grupy.

  1. Dla dowolnych a i b, które są Elements \mathbf{S}, a \circ b jest również elementem \mathbf{S}. Jest to znane jako warunek domknięcia.

  2. Dla dowolnych a, b i c, które są Elements z \mathbf{S}, zachodzi przypadek, że (a \circ b) \circ c = a \circ (b \circ c). Jest to znane jako warunek asocjatywności.

  3. Istnieje unikalny element e w \mathbf{S}, taki, że dla każdego elementu a w \mathbf{S} zachodzi następujące równanie: e \circ a = a \circ e = a. Ponieważ istnieje tylko jeden taki element e, jest on nazywany elementem tożsamości. Warunek ten jest znany jako warunek tożsamości.

  4. Dla każdego elementu a w \mathbf{S} istnieje element b w \mathbf{S}, taki, że zachodzi następujące równanie: a \circ b = b \circ a = e, gdzie e jest elementem tożsamości. Element b jest tutaj znany jako element odwrotny i jest powszechnie oznaczany jako a^{-1}. Warunek ten znany jest jako warunek odwrotności lub warunek odwracalności.

Przyjrzyjmy się grupom nieco bliżej. Oznaczmy zbiór wszystkich liczb całkowitych przez \mathbb{Z}. Ten zbiór w połączeniu ze standardowym dodawaniem, czyli \kąt \mathbb{Z}, + \kąt, wyraźnie pasuje do definicji grupy, ponieważ spełnia cztery powyższe aksjomaty.

  1. Dla dowolnych x i y, które są Elements \mathbb{Z}, x + y jest również elementem \mathbb{Z}. Zatem \kąt \mathbb{Z}, + \kąt spełnia warunek domknięcia.

  2. Dla dowolnych x, y i z, które są Elements \mathbb{Z}, (x + y) + z = x + (y + z). Zatem \kąt \mathbb{Z}, + \kąt spełnia warunek asocjatywności.

  3. Istnieje element tożsamości w \kąt \mathbb{Z}, + \kąt, mianowicie 0. Dla dowolnego x w \mathbb{Z} zachodzi mianowicie zależność: 0 + x = x + 0 = x. Zatem \kąt \mathbb{Z}, + \kąt spełnia warunek tożsamości.

  4. Wreszcie, dla każdego elementu x w \mathbb{Z} istnieje y taki, że x + y = y + x = 0. Gdyby x wynosiło na przykład 10, y wynosiłoby -10 (w przypadku, gdy x wynosi 0, y również wynosi 0). Zatem \kąt \mathbb{Z}, + \kąt spełnia warunek odwrotności.

Co ważne, fakt, że zbiór liczb całkowitych z dodawaniem stanowi grupę, nie oznacza, że stanowi on grupę z mnożeniem. Można to zweryfikować testując \langle \mathbb{Z}, \cdot \rangle względem czterech aksjomatów grupy (gdzie \cdot oznacza standardowe mnożenie).

Pierwsze dwa aksjomaty są oczywiście prawdziwe. Ponadto, przy mnożeniu element 1 może służyć jako element tożsamości. Każda liczba całkowita x pomnożona przez 1 daje x. Jednak \langle \mathbb{Z}, \cdot \rangle nie spełnia warunku odwrotności. Oznacza to, że nie istnieje unikalny element y w \mathbb{Z} dla każdego x w \mathbb{Z}, tak aby x \cdot y = 1.

Załóżmy na przykład, że x = 22. Jaka wartość y ze zbioru \mathbb{Z} pomnożona przez x dałaby pierwiastek tożsamości 1? Wartość 1/22 zadziałałaby, ale nie należy ona do zbioru \mathbb{Z}. W rzeczywistości problem ten występuje dla każdej liczby całkowitej x, poza wartościami 1 i -1 (gdzie y musiałoby wynosić odpowiednio 1 i -1).

Jeśli dopuścimy liczby rzeczywiste do naszego zbioru, to nasze problemy w dużej mierze znikną. Dla dowolnego elementu x w zbiorze, mnożenie przez 1/x daje 1. Ponieważ ułamki należą do zbioru liczb rzeczywistych, dla każdej liczby rzeczywistej można znaleźć jej odwrotność. Wyjątkiem jest zero, ponieważ każde mnożenie przez zero nigdy nie da pierwiastka tożsamości 1. Zatem zbiór niezerowych liczb rzeczywistych wyposażonych w mnożenie jest rzeczywiście grupą.

Niektóre grupy spełniają piąty ogólny warunek, znany jako warunek przemienności. Warunek ten jest następujący:

Każda grupa spełniająca warunek komutatywności jest znana jako grupa komutatywna lub grupa abelowa (od nazwiska Nielsa Henrika Abla). Łatwo zweryfikować, że zarówno zbiór liczb rzeczywistych nad dodawaniem, jak i zbiór liczb całkowitych nad dodawaniem są grupami abelowymi. Zbiór liczb całkowitych nad mnożeniem nie jest w ogóle grupą, więc ipso facto nie może być grupą abelową. Natomiast zbiór niezerowych liczb rzeczywistych nad mnożeniem jest również grupą abelową.

Należy zwrócić uwagę na dwie ważne konwencje dotyczące notacji. Po pierwsze, znaki "+" lub "×" będą często używane do symbolizowania operacji grupowych, nawet jeśli Elements nie są w rzeczywistości liczbami. W takich przypadkach nie należy interpretować tych znaków jako standardowego dodawania lub mnożenia arytmetycznego. Zamiast tego są to operacje o jedynie abstrakcyjnym podobieństwie do tych operacji arytmetycznych.

O ile nie chodzi konkretnie o dodawanie lub mnożenie arytmetyczne, łatwiej jest używać symboli takich jak \circ i \diamond dla operacji grupowych, ponieważ nie mają one bardzo zakorzenionych kulturowo konotacji.

Po drugie, z tego samego powodu, dla którego "+" i "×" są często używane do oznaczania operacji niearytmetycznych, tożsamościowe Elements grup są często symbolizowane przez "0" i "1", nawet jeśli Elements w tych grupach nie są liczbami. Jeśli nie odnosimy się do elementu tożsamości grupy z liczbami, łatwiej jest użyć bardziej neutralnego symbolu, takiego jak "e", aby wskazać element tożsamości.

Wiele różnych i bardzo ważnych zbiorów wartości w matematyce wyposażonych w pewne operacje binarne to grupy. Aplikacje kryptograficzne działają jednak tylko ze zbiorami liczb całkowitych lub przynajmniej Elements, które są opisane przez liczby całkowite, czyli w domenie teorii liczb. Dlatego też zbiory liczb rzeczywistych innych niż liczby całkowite nie są wykorzystywane w zastosowaniach kryptograficznych.

Zakończmy podając przykład Elements, które mogą być "opisane przez liczby całkowite", mimo że nie są liczbami całkowitymi. Dobrym przykładem są punkty krzywych eliptycznych. Chociaż dowolny punkt na krzywej eliptycznej nie jest liczbą całkowitą, taki punkt jest rzeczywiście opisany przez dwie liczby całkowite.

Krzywe eliptyczne są na przykład kluczowe dla Bitcoin. Każda standardowa para kluczy prywatnych i publicznych Bitcoin jest wybierana ze zbioru punktów zdefiniowanych przez następującą krzywą eliptyczną:

x^3 + 7 = y^2 \mod 2^{256} – 2^{32} – 29 – 28 – 27 – 26 - 24 - 1

(największa liczba pierwsza mniejsza niż 2^{256}). Współrzędna x to klucz prywatny, a współrzędna y to klucz publiczny.

Transakcje w Bitcoin zazwyczaj obejmują blokowanie danych wyjściowych do jednego lub więcej kluczy publicznych w jakiś sposób. Wartość z tych transakcji można następnie odblokować, wykonując podpisy cyfrowe za pomocą odpowiednich kluczy prywatnych.

Grupy cykliczne

Głównym rozróżnieniem, które możemy narysować, jest rozróżnienie między nieskończoną i nieskończoną grupą. Pierwsza z nich ma skończoną liczbę Elements, podczas gdy druga ma nieskończoną liczbę Elements. Liczba Elements w dowolnej skończonej grupie jest znana jako porządek grupy. Cała praktyczna kryptografia, która wymaga użycia grup, opiera się na grupach skończonych (liczbowo-teoretycznych).

W kryptografii klucza publicznego szczególnie ważna jest pewna klasa skończonych grup abelowych znanych jako grupy cykliczne. Aby zrozumieć grupy cykliczne, musimy najpierw zrozumieć pojęcie potęgowania elementów grupy.

Załóżmy, że istnieje grupa G z operacją grupową \circ i że a jest elementem G. Wyrażenie a^n powinno być interpretowane jako element a połączony z samym sobą łącznie n - 1 razy. Na przykład, a^2 oznacza a \circ a, a^3 oznacza a \circ a \circ a, i tak dalej. (Zwróć uwagę, że potęgowanie tutaj niekoniecznie jest potęgowaniem w standardowym sensie arytmetycznym)

Przejdźmy do przykładu. Załóżmy, że G = \langle \mathbb{Z} \mod 7, + \rangle, i że nasza wartość dla a jest równa 4. W tym przypadku a^2 = [4 + 4 \mod 7] = [8 \mod 7] = 1 \mod 7. Alternatywnie, a^4 reprezentowałoby [4 + 4 + 4 + 4 \mod 7] = [16 \mod 7] = 2 \mod 7.

Niektóre grupy abelowe mają jeden lub więcej Elements, które mogą dać wszystkie inne Elements grupy poprzez ciągłe potęgowanie. Te Elements są nazywane generatorami lub prymitywnymi Elements.

Ważną klasą takich grup jest \langle \mathbb{Z}^* \mod N, \cdot \rangle, gdzie N jest liczbą pierwszą. Zapis \mathbb{Z}^* oznacza, że grupa zawiera wszystkie niezerowe, dodatnie liczby całkowite mniejsze niż N. Taka grupa ma zatem zawsze N - 1 Elements.

Rozważmy na przykład G = \langle \mathbb{Z}^* \mod 11, \cdot \rangle. Grupa ta ma następujące Elements: \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. Rząd tej grupy wynosi 10 (co jest równe 11 - 1).

Przyjrzyjmy się wykładniczemu pierwiastkowi 2 z tej grupy. Obliczenia do 2^{12} są pokazane poniżej. Zwróć uwagę, że po lewej stronie równania wykładnik odnosi się do potęgowania elementu grupy. W naszym konkretnym przykładzie, po prawej stronie równania rzeczywiście mamy do czynienia z wykładnikiem arytmetycznym (ale równie dobrze mogłoby to być na przykład dodawanie). Aby to wyjaśnić, wypisałem powtarzaną operację, a nie formę wykładnika po prawej stronie.

Przyglądając się uważnie, można zauważyć, że potęgowanie pierwiastka 2 przechodzi przez wszystkie Elements \langle \mathbb{Z}^* \mod 11, \cdot \rangle w następującej kolejności: 2, 4, 8, 5, 10, 9, 7, 3, 6, 1. Po 2^{10} dalsze potęgowanie pierwiastka 2 ponownie przechodzi przez wszystkie Elements w tej samej kolejności. Stąd pierwiastek 2 jest generatorem w \langle \mathbb{Z}^* \mod 11, \cdot \rangle.

Chociaż \langle \mathbb{Z}^* \mod 11, \cdot \rangle ma wiele generatorów, nie wszystkie Elements tej grupy są generatorami. Rozważmy na przykład element 3. Przeprowadzenie pierwszych 10 potęgowań, bez pokazywania kłopotliwych obliczeń, daje następujące wyniki:

Zamiast przechodzić przez wszystkie wartości w \langle \mathbb{Z}^* \mod 11, \cdot \rangle, potęgowanie pierwiastka 3 prowadzi tylko do podzbioru tych wartości: 3, 9, 5, 4 i 1. Po piątym potęgowaniu wartości te zaczynają się powtarzać.

Możemy teraz zdefiniować grupę cykliczną jako dowolną grupę z co najmniej jednym generatorem. Oznacza to, że istnieje co najmniej jeden element grupy, z którego można utworzyć wszystkie inne Elements poprzez potęgowanie.

Być może zauważyłeś w naszym powyższym przykładzie, że zarówno 2^{10}, jak i 3^{10} są równe 1 \mod 11. W rzeczywistości, choć nie będziemy wykonywać obliczeń, potęgowanie przez 10 dowolnego elementu w grupie \langle \mathbb{Z}^* \mod 11, \cdot \rangle da 1 \mod 11. Dlaczego tak się dzieje?

To ważne pytanie, ale odpowiedź na nie wymaga trochę pracy.

Na początek załóżmy, że mamy dwie dodatnie liczby całkowite a i N. Ważne twierdzenie w teorii liczb mówi, że liczba a ma multiplikatywną odwrotność modulo N (czyli liczbę całkowitą b taką, że a \cdot b = 1 \mod N) wtedy i tylko wtedy, gdy największy wspólny dzielnik liczb a i N jest równy 1. To znaczy, jeśli a i N są liczbami całkowitymi.

Tak więc, dla dowolnej grupy liczb całkowitych wyposażonych w mnożenie modulo N, w zbiorze znajdują się tylko mniejsze liczby całkowite z N. Możemy oznaczyć ten zbiór przez \mathbb{Z}^c \mod N.

Załóżmy na przykład, że N wynosi 10. Tylko liczby całkowite 1, 3, 7 i 9 są pierwiastkami z 10. Zatem zbiór \mathbb{Z}^c \mod 10 zawiera tylko \{1, 3, 7, 9\}. Nie można utworzyć grupy z mnożeniem liczb całkowitych modulo 10 przy użyciu innych liczb całkowitych z przedziału od 1 do 10. W przypadku tej konkretnej grupy odwrotnościami są pary 1 i 9 oraz 3 i 7.

W przypadku, gdy N jest liczbą pierwszą, wszystkie liczby całkowite od 1 do N - 1 są koprimami z N. Taka grupa ma zatem rząd N - 1. Używając naszej wcześniejszej notacji, \mathbb{Z}^c \mod N równa się \mathbb{Z}^* \mod N, gdy N jest liczbą pierwszą. Grupa, którą wybraliśmy dla naszego wcześniejszego przykładu, \langle \mathbb{Z}^* \mod 11, \cdot \rangle, jest szczególnym przykładem tej klasy grup.

Następnie, funkcja \phi(N) oblicza liczbę liczb całkowitych aż do liczby N i jest znana jako funkcja Phi Eulera. [1] Zgodnie z Twierdzeniem Eulera, gdy dwie liczby całkowite a i N są liczbami całkowitymi, zachodzi następująca zależność:

Ma to ważną implikację dla klasy grup \langle \mathbb{Z}^* \mod N, \cdot \rangle, gdzie N jest liczbą pierwszą. Dla tych grup, potęgowanie elementów grupy reprezentuje potęgowanie arytmetyczne. Oznacza to, że a^{\phi(N)} \mod N reprezentuje operację arytmetyczną a^{\phi(N)} \mod N. Ponieważ dowolny element a w tych grupach multiplikatywnych jest podzielny przez N, oznacza to, że a^{\phi(N)} \mod N = a^{N - 1} \mod N = 1 \mod N.

Twierdzenie Eulera jest naprawdę ważnym wynikiem. Na początek, wynika z niego, że wszystkie Elements w \langle \mathbb{Z}^* \mod N, \cdot \rangle mogą cyklicznie przechodzić tylko przez taką liczbę wartości przez potęgowanie, która dzieli się na N - 1. W przypadku \langle \mathbb{Z}^* \mod 11, \cdot \rangle oznacza to, że każdy element może przejść tylko przez 2, 5 lub 10 Elements. Grupa wartości, przez które przechodzi każdy element po potęgowaniu, jest znana jako porządek elementu. Element o porządku równoważnym porządkowi grupy jest generatorem.

Co więcej, twierdzenie Eulera implikuje, że zawsze możemy znać wynik a^{N - 1} \mod N dla dowolnej grupy \langle \mathbb{Z}^* \mod N, \cdot \rangle, gdzie N jest liczbą pierwszą. Jest tak niezależnie od tego, jak skomplikowane mogą być rzeczywiste obliczenia.

Załóżmy na przykład, że nasza grupa to \mathbb{Z}^* \mod 160,481,182 (gdzie 160,481,182 jest liczbą pierwszą). Wiemy, że wszystkie liczby całkowite od 1 do 160,481,181 muszą być Elements tej grupy i że \phi(n) = 160,481,181. Chociaż nie możemy wykonać wszystkich kroków w obliczeniach, wiemy, że wyrażenia takie jak 514^{160,481,181}, 2,005^{160,481,181} i 256,212^{160,481,181} muszą być równe 1 \mod 160,481,182.

Uwagi:

[1] Funkcja działa w następujący sposób. Dowolną liczbę całkowitą N można rozłożyć na iloczyn liczb pierwszych. Załóżmy, że konkretna liczba N jest podzielna w następujący sposób: p_1^{e1} \cdot p_2^{e2} \cdot \ldots \cdot p_m^{em}, gdzie wszystkie p są liczbami pierwszymi, a wszystkie e są liczbami całkowitymi większymi lub równymi 1:

\phi(N) = \sum_{i=1}^m \left[p_i^{e_i} - p_i^{e_i - 1}\right]

Wzór na funkcję Phi Eulera dla pierwszej faktoryzacji N.

Pola

Grupa jest podstawową strukturą algebraiczną w algebrze abstrakcyjnej, ale istnieje wiele innych. Jedyną inną strukturą algebraiczną, którą należy znać, jest pole, a konkretnie pole nieskończone. Ten typ struktury algebraicznej jest często wykorzystywany w kryptografii, na przykład w Advanced Encryption Standard. Ten ostatni jest głównym schematem szyfrowania symetrycznego, z którym spotkasz się w praktyce.

Pole wywodzi się z pojęcia grupy. W szczególności, pole jest zbiorem Elements S wyposażonym w dwa binarne operatory \circ i \diamond, który spełnia następujące warunki:

  1. Zbiór S wyposażony w \circ jest grupą abelową.

  2. Zbiór S wyposażony w \diamond jest grupą abelową dla "niezerowego" Elements.

  3. Zbiór S wyposażony w te dwa operatory spełnia tak zwany warunek dystrybutywności: Załóżmy, że a, b i c są Elements zbioru S. Wtedy S wyposażony w te dwa operatory spełnia warunek dystrybutywności, gdy a \circ (b \diamond c) = (a \circ b) \diamond (a \circ c).

Należy zauważyć, że podobnie jak w przypadku grup, definicja pola jest bardzo abstrakcyjna. Nie zawiera ona żadnych twierdzeń o typach Elements w S, ani o operacjach \circ i \diamond. Stwierdza jedynie, że polem jest dowolny zbiór Elements z dwiema operacjami, dla których spełnione są trzy powyższe warunki. (Element "zero" w drugiej grupie abelowej można interpretować abstrakcyjnie)

Co może być przykładem pola? Dobrym przykładem jest zbiór \mathbb{Z} \mod 7, lub \{0, 1, \ldots, 7\} zdefiniowany przez standardowe dodawanie (zamiast \circ powyżej) i standardowe mnożenie (zamiast \diamond powyżej).

Po pierwsze, \mathbb{Z} \mod 7 spełnia warunek bycia grupą abelową nad dodawaniem i spełnia warunek bycia grupą abelową nad mnożeniem, jeśli weźmiemy pod uwagę tylko niezerowe Elements. Po drugie, kombinacja zbioru z dwoma operatorami spełnia warunek rozdzielności.

Z dydaktycznego punktu widzenia warto zbadać te twierdzenia, używając pewnych konkretnych wartości. Weźmy eksperymentalne wartości 5, 2 i 3, losowo wybrane Elements ze zbioru \mathbb{Z} \mod 7, aby zbadać pole \langle \mathbb{Z} \mod 7, +, \cdot \rangle. Będziemy używać tych trzech wartości w kolejności, w zależności od potrzeb, aby zbadać określone warunki.

Zbadajmy najpierw, czy \mathbb{Z} \mod 7 wyposażona w dodawanie jest grupą abelową.

  1. Warunek zamknięcia: Przyjmijmy 5 i 2 jako nasze wartości. W takim przypadku [5 + 2] \mod 7 = 7 \mod 7 = 0. Jest to rzeczywiście element \mathbb{Z} \mod 7, więc wynik jest zgodny z warunkiem domknięcia.

  2. Warunek asocjatywności: Przyjmijmy 5, 2 i 3 jako nasze wartości. W takim przypadku [(5 + 2) + 3] \mod 7 = [5 + (2 + 3)] \mod 7 = 10 \mod 7 = 3. Jest to zgodne z warunkiem asocjatywności.

  3. Warunek tożsamości: Przyjmijmy 5 jako naszą wartość. W takim przypadku [5 + 0] \mod 7 = [0 + 5] \mod 7 = 5. Wygląda więc na to, że 0 jest elementem tożsamości dla dodawania.

  4. Warunek odwrotny: Rozważmy odwrotność liczby 5. Musi być tak, że [5 + d] \mod 7 = 0, dla pewnej wartości d. W tym przypadku unikalna wartość z \mathbb{Z} \mod 7, która spełnia ten warunek jest 2.

  5. Warunek przemienności: Przyjmijmy 5 i 3 jako nasze wartości. W takim przypadku [5 + 3] \mod 7 = [3 + 5] \mod 7 = 1. Jest to zgodne z warunkiem przemienności.

Zbiór \mathbb{Z} \mod 7 wyposażony w dodawanie wyraźnie wydaje się być grupą abelową. Zbadajmy teraz, czy \mathbb{Z} \mod 7 wyposażony w mnożenie jest grupą abelową dla wszystkich niezerowych Elements.

  1. Warunek zamknięcia: Przyjmijmy 5 i 2 jako nasze wartości. W takim przypadku [5 \cdot 2] \mod 7 = 10 \mod 7 = 3. Jest to również element \mathbb{Z} \mod 7, więc wynik jest zgodny z warunkiem domknięcia.

  2. Warunek asocjatywności: Przyjmijmy 5, 2 i 3 jako nasze wartości. W takim przypadku [(5 \cdot 2) \cdot 3] \mod 7 = [5 \cdot (2 \cdot 3)] \mod 7 = 30 \mod 7 = 2. Jest to zgodne z warunkiem asocjatywności.

  3. Warunek tożsamości: Przyjmijmy 5 jako naszą wartość. W takim przypadku [5 \cdot 1] \mod 7 = [1 \cdot 5] \mod 7 = 5. Wygląda więc na to, że 1 jest elementem tożsamości dla mnożenia.

  4. Warunek odwrotny: Rozważmy odwrotność liczby 5. Musi być tak, że [5 \cdot d] \mod 7 = 1, dla pewnej wartości d. Unikalna wartość z \mathbb{Z} \mod 7, która spełnia ten warunek jest 3. Jest to zgodne z warunkiem odwrotności.

  5. Warunek przemienności: Przyjmijmy 5 i 3 jako nasze wartości. W takim przypadku [5 \cdot 3] \mod 7 = [3 \cdot 5] \mod 7 = 15 \mod 7 = 1. Jest to zgodne z warunkiem przemienności.

Zbiór \mathbb{Z} \mod 7 wydaje się wyraźnie spełniać zasady bycia grupą abelową, gdy jest połączony z dodawaniem lub mnożeniem nad niezerowym Elements.

Wreszcie, ten zestaw w połączeniu z obydwoma operatorami wydaje się spełniać warunek rozdzielności. Przyjmijmy 5, 2 i 3 jako nasze wartości. Widzimy, że [5 \cdot (2 + 3)] \mod 7 = [5 \cdot 2 + 5 \cdot 3] \mod 7 = 25 \mod 7 = 4.

Przekonaliśmy się teraz, że \mathbb{Z} \mod 7 wyposażona w dodawanie i mnożenie spełnia aksjomaty dla skończonego pola przy testowaniu z konkretnymi wartościami. Oczywiście możemy pokazać to także w ogólności, ale nie będziemy tego tutaj robić.

Kluczowym rozróżnieniem są dwa rodzaje pól: skończone i nieskończone.

Pole nieskończone obejmuje pole, w którym zbiór S jest nieskończenie duży. Zbiór liczb rzeczywistych \mathbb{R} wyposażony w dodawanie i mnożenie jest przykładem pola nieskończonego. Pole nieskończone, znane również jako pole Galois, to pole, w którym zbiór S jest skończony. Nasz powyższy przykład \langle \mathbb{Z} \mod 7, +, \cdot \rangle jest polem skończonym.

W kryptografii interesują nas przede wszystkim pola skończone. Ogólnie rzecz biorąc, można wykazać, że pole skończone istnieje dla pewnego zbioru Elements S wtedy i tylko wtedy, gdy ma p^m Elements, gdzie p jest liczbą pierwszą, a m dodatnią liczbą całkowitą większą lub równą jeden. Innymi słowy, jeśli rząd pewnego zbioru S jest liczbą pierwszą (p^m gdzie m = 1) lub potęgą liczby pierwszej (p^m gdzie m > 1), to można znaleźć dwa operatory \circ i \diamond takie, że warunki dla pola są spełnione.

Jeśli jakieś skończone pole ma liczbę pierwszą Elements, to nazywamy je pierwszym polem. Jeśli liczba Elements w polu skończonym jest potęgą liczby pierwszej, wówczas pole to nazywane jest polem rozszerzającym. W kryptografii jesteśmy zainteresowani zarówno polami pierwszymi, jak i rozszerzeniami. [2]

Głównymi polami pierwszymi interesującymi w kryptografii są te, w których zbiór wszystkich liczb całkowitych jest modulowany przez pewną liczbę pierwszą, a operatorami są standardowe dodawanie i mnożenie. Ta klasa pól skończonych obejmuje \mathbb{Z} \mod 2, \mathbb{Z} \mod 3, \mathbb{Z} \mod 5, \mathbb{Z} \mod 7, \mathbb{Z} \mod 11, \mathbb{Z} \mod 13 i tak dalej. Dla dowolnego pola pierwszego \mathbb{Z} \mod p, zbiór liczb całkowitych tego pola jest następujący: \{0, 1, \ldots, p - 2, p - 1\}.

W kryptografii interesują nas również pola rozszerzeń, w szczególności dowolne pola z 2^m Elements, gdzie m > 1. Takie skończone pola są na przykład wykorzystywane w szyfrze Rijndael, który stanowi podstawę Advanced Encryption Standard. Podczas gdy pola pierwsze są względnie intuicyjne, te pola rozszerzenia bazy 2 prawdopodobnie nie są dla nikogo, kto nie jest zaznajomiony z algebrą abstrakcyjną.

Na początek, prawdą jest, że każdemu zbiorowi liczb całkowitych z 2^m Elements można przypisać dwa operatory, które sprawią, że ich kombinacja będzie polem (o ile m jest dodatnią liczbą całkowitą). Jednak sam fakt, że pole istnieje, niekoniecznie oznacza, że jest ono łatwe do odkrycia lub szczególnie praktyczne w niektórych zastosowaniach.

Jak się okazuje, w kryptografii szczególnie przydatne są pola rozszerzeń 2^m zdefiniowane na określonych zbiorach wyrażeń wielomianowych, a nie na pewnych zbiorach liczb całkowitych.

Załóżmy na przykład, że chcemy mieć pole rozszerzenia z 2^3 (tj. 8) Elements w zbiorze. Chociaż może istnieć wiele różnych zbiorów, które mogą być użyte dla pól tego rozmiaru, jeden z takich zbiorów zawiera wszystkie unikalne wielomiany postaci a_2x^2 + a_1x + a_0, gdzie każdy współczynnik a_i wynosi 0 lub 1. Stąd ten zbiór S zawiera następujące Elements:

  1. 0: Przypadek, w którym a_2 = 0, a_1 = 0 i a_0 = 0.

  2. 1: Przypadek, w którym a_2 = 0, a_1 = 0 i a_0 = 1.

  3. x: Przypadek, w którym a_2 = 0, a_1 = 1 i a_0 = 0.

  4. x + 1: Przypadek, w którym a_2 = 0, a_1 = 1 i a_0 = 1.

  5. x^2: Przypadek, w którym a_2 = 1, a_1 = 0 i a_0 = 0.

  6. x^2 + 1: Przypadek, w którym a_2 = 1, a_1 = 0 i a_0 = 1.

  7. x^2 + x: Przypadek, w którym a_2 = 1, a_1 = 1 i a_0 = 0.

  8. x^2 + x + 1: Przypadek, w którym a_2 = 1, a_1 = 1 i a_0 = 1.

Zatem S byłby zbiorem \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}. Jakie dwie operacje można zdefiniować na tym zbiorze Elements, aby ich kombinacja była polem?

Pierwszą operację na zbiorze S (\circ) można zdefiniować jako standardowe dodawanie wielomianów modulo 2. Wszystko, co musisz zrobić, to dodać wielomiany w normalny sposób, a następnie zastosować modulo 2 do każdego ze współczynników wynikowego wielomianu. Oto kilka przykładów:

Druga operacja na zbiorze S (\diamond), która jest potrzebna do utworzenia pola, jest bardziej skomplikowana. Jest to rodzaj mnożenia, ale nie jest to standardowe mnożenie arytmetyczne. Zamiast tego należy postrzegać każdy element jako wektor i rozumieć operację jako mnożenie tych dwóch wektorów modulo nieredukowalny wielomian.

Zajmijmy się najpierw pojęciem wielomianu nieredukowalnego. Wielomian nieredukowalny to taki, który nie może być rozłożony na czynniki pierwsze (tak jak liczba pierwsza nie może być rozłożona na składniki inne niż 1 i sama liczba pierwsza). Dla naszych celów interesują nas wielomiany, które są nieredukowalne względem zbioru wszystkich liczb całkowitych. (Zauważ, że możesz być w stanie rozłożyć niektóre wielomiany na czynniki, na przykład przez liczby rzeczywiste lub zespolone, nawet jeśli nie możesz ich rozłożyć na czynniki przy użyciu liczb całkowitych)

Rozważmy na przykład wielomian x^2 - 3x + 2. Można go zapisać jako (x - 1)(x - 2). Stąd nie jest on nieredukowalny. Rozważmy teraz wielomian x^2 + 1. Używając tylko liczb całkowitych, nie ma możliwości dalszego dzielenia tego wyrażenia. Jest to więc wielomian nieredukowalny względem liczb całkowitych.

Następnie przejdźmy do koncepcji mnożenia wektorów. Nie będziemy dogłębnie analizować tego tematu, ale wystarczy zrozumieć podstawową zasadę: Każde dzielenie wektorowe może mieć miejsce, o ile dzielna ma stopień wyższy lub równy dzielnikowi. Jeśli dzielna ma niższy stopień niż dzielnik, wówczas dzielna nie może być dzielona przez dzielnik.

Na przykład, rozważmy wyrażenie x^6 + x + 1 \mod x^5 + x^2. To wyraźnie zmniejsza się dalej, ponieważ stopień dywidendy, 6, jest wyższy niż stopień dzielnika, 5. Teraz rozważ wyrażenie x^5 + x + 1 \mod x^5 + x^2. To również ulega dalszej redukcji, ponieważ stopień dzielnej, 5, i dzielnika, 5, są równe.

Rozważmy jednak wyrażenie x^4 + x + 1 \mod x^5 + x^2. To nie redukuje się dalej, ponieważ stopień dzielnika, 4, jest niższy niż stopień dzielnika, 5.

Na podstawie tych informacji jesteśmy teraz gotowi do znalezienia drugiej operacji dla zbioru \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.

Powiedziałem już, że druga operacja powinna być rozumiana jako mnożenie wektorowe modulo pewien nieredukowalny wielomian. Ten nieredukowalny wielomian powinien zapewnić, że druga operacja definiuje grupę abelową nad S i jest zgodna z warunkiem dystrybucyjnym. Jaki więc powinien być ten nieredukowalny wielomian?

Ponieważ wszystkie wektory w zbiorze są stopnia 2 lub niższego, nieredukowalny wielomian powinien być stopnia 3. Jeśli każde mnożenie dwóch wektorów w zbiorze daje wielomian stopnia 3 lub wyższego, wiemy, że modulo wielomian stopnia 3 zawsze daje wielomian stopnia 2 lub niższego. Dzieje się tak, ponieważ każdy wielomian stopnia 3 lub wyższego jest zawsze podzielny przez wielomian stopnia 3. Ponadto wielomian, który działa jako dzielnik, musi być nieredukowalny.

Okazuje się, że istnieje kilka nieredukowalnych wielomianów stopnia 3, których możemy użyć jako dzielników. Każdy z tych wielomianów definiuje inne pole w połączeniu z naszym zbiorem S i dodawaniem modulo 2. Oznacza to, że w kryptografii mamy wiele możliwości wykorzystania pól rozszerzenia 2^m.

Dla naszego przykładu załóżmy, że wybieramy wielomian x^3 + x + 1. Jest on rzeczywiście nieredukowalny, ponieważ nie można go rozłożyć na czynniki przy użyciu liczb całkowitych. Ponadto zapewni to, że każde mnożenie dwóch Elements da wielomian stopnia 2 lub mniejszego.

Przeanalizujmy przykład drugiej operacji, używając wielomianu x^3 + x + 1 jako dzielnika, aby zilustrować jej działanie. Załóżmy, że mnożymy Elements x^2 + 1 z x^2 + x w naszym zbiorze S. Następnie musimy obliczyć wyrażenie [(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1. Można to uprościć w następujący sposób:

Wiemy, że [x^4 + x^3 + x^2 + x] \mod x^3 + x + 1 można zredukować, ponieważ dywidenda ma wyższy stopień (4) niż dzielnik (3).

Na początek można zauważyć, że wyrażenie x^3 + x + 1 przechodzi w x^4 + x^3 + x^2 + x łącznie x razy. Można to sprawdzić mnożąc x^3 + x + 1 przez x, czyli x^4 + x^2 + x. Ponieważ ten ostatni wyraz jest tego samego stopnia co dywidenda, czyli 4, wiemy, że to działa. Resztę z dzielenia przez x można obliczyć w następujący sposób:

Zatem po podzieleniu x^4 + x^3 + x^2 + x przez x^3 + x + 1 w sumie x razy, otrzymujemy resztę x^3. Czy można ją dalej podzielić przez x^3 + x + 1?

Intuicyjnie, może być atrakcyjne stwierdzenie, że x^3 nie może być dzielone przez x^3 + x + 1, ponieważ ten drugi człon wydaje się większy. Przypomnijmy sobie jednak naszą wcześniejszą dyskusję na temat dzielenia wektorowego. Tak długo, jak dzielna ma stopień większy lub równy dzielnikowi, wyrażenie może być dalej redukowane. W szczególności, wyrażenie x^3 + x + 1 może przejść do x^3 dokładnie 1 raz. Resztę oblicza się w następujący sposób:

[(x^3) - (x^3 + x + 1)] \mod x^3 + x + 1 = [x + 1] \mod x^3 + x + 1 = x + 1

Być może zastanawiasz się, dlaczego (x^3) - (x^3 + x + 1) ma wartość x + 1, a nie -x - 1. Pamiętajmy, że pierwsza operacja naszego pola jest zdefiniowana modulo 2. Stąd odejmowanie dwóch wektorów daje dokładnie taki sam wynik jak dodawanie dwóch wektorów.

Podsumowując mnożenie x^2 + 1 i x^2 + x: Po pomnożeniu tych dwóch wyrażeń otrzymamy wielomian stopnia 4, x^4 + x^3 + x^2 + x, który należy zredukować modulo x^3 + x + 1. Wielomian stopnia 4 jest podzielny przez x^3 + x + 1 dokładnie x + 1 razy. Reszta z dzielenia x^4 + x^3 + x^2 + x przez x^3 + x + 1 dokładnie x + 1 razy wynosi x + 1. Jest to rzeczywiście element naszego zbioru \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.

Dlaczego pola rozszerzeń o podstawie 2 nad zbiorami wielomianów, jak w powyższym przykładzie, miałyby być przydatne w kryptografii? Powodem jest to, że współczynniki w wielomianach takich zbiorów, 0 lub 1, można postrzegać jako Elements ciągów binarnych o określonej długości. Na przykład zbiór S w naszym powyższym przykładzie może być postrzegany jako zbiór S, który zawiera wszystkie ciągi binarne o długości 3 (od 000 do 111). Operacje na S mogą być również wykorzystane do wykonywania operacji na tych ciągach binarnych i tworzenia ciągów binarnych o tej samej długości.

Uwagi:

[2] Pola rozszerzeń stają się bardzo sprzeczne z intuicją. Zamiast mieć Elements liczb całkowitych, mają zbiory wielomianów. Ponadto wszelkie operacje są wykonywane modulo pewnego nieredukowalnego wielomianu.

Algebra abstrakcyjna w praktyce

Pomimo formalnego języka i abstrakcyjności dyskusji, pojęcie grupy nie powinno być zbyt trudne do zrozumienia. Jest to po prostu zbiór Elements wraz z operacją binarną, gdzie wykonanie tej operacji binarnej na tych Elements spełnia cztery ogólne warunki. Grupa abelowa ma tylko dodatkowy warunek znany jako przemienność. Z kolei grupa cykliczna jest szczególnym rodzajem grupy abelowej, a mianowicie taką, która ma generator. Pole jest jedynie bardziej złożoną konstrukcją z podstawowego pojęcia grupy.

Ale jeśli jesteś osobą o praktycznych skłonnościach, możesz się w tym momencie zastanawiać: Kogo to obchodzi? Czy wiedza o tym, że jakiś zbiór Elements z operatorem jest grupą, a nawet grupą abelową lub cykliczną, ma jakiekolwiek znaczenie w świecie rzeczywistym? Czy wiedza o tym, że coś jest polem?

Nie wdając się w zbytnie szczegóły, odpowiedź brzmi "tak". Grupy zostały po raz pierwszy stworzone w XIX wieku przez francuskiego matematyka Evariste Galois. Wykorzystał je do wyciągnięcia wniosków na temat rozwiązywania równań wielomianowych stopnia wyższego niż pięć.

Od tego czasu pojęcie grupy pomogło rzucić światło na wiele problemów w matematyce i nie tylko. Na ich podstawie, na przykład, fizyk Murray-Gellman był w stanie przewidzieć istnienie cząstki, zanim została ona faktycznie zaobserwowana w eksperymentach[3]. [Innym przykładem jest to, że chemicy wykorzystują teorię grup do klasyfikowania kształtów cząsteczek. Matematycy wykorzystali nawet pojęcie grupy do wyciągnięcia wniosków na temat czegoś tak konkretnego jak papier ścienny!

Zasadniczo wykazanie, że zbiór Elements z pewnym operatorem jest grupą, oznacza, że to, co opisujesz, ma określoną symetrię. Nie symetrię w powszechnym znaczeniu tego słowa, ale w bardziej abstrakcyjnej formie. A to może zapewnić istotny wgląd w konkretne systemy i problemy. Bardziej złożone pojęcia z algebry abstrakcyjnej dają nam tylko dodatkowe informacje.

Co najważniejsze, zobaczysz znaczenie grup i pól teorii liczb w praktyce poprzez ich zastosowanie w kryptografii, w szczególności w kryptografii klucza publicznego. W naszej dyskusji na temat pól widzieliśmy już na przykład, w jaki sposób pola rozszerzeń są wykorzystywane w szyfrze Rijndael. Omówimy ten przykład w Rozdziale 5.

Do dalszej dyskusji na temat algebry abstrakcyjnej polecam doskonałą serię filmów na temat algebry abstrakcyjnej autorstwa Socratica. [4] Szczególnie polecam następujące filmy: "Czym jest algebra abstrakcyjna?", "Definicja grupy (rozszerzona)", "Definicja pierścienia (rozszerzona)" i "Definicja pola (rozszerzona)" Te cztery filmy dadzą ci dodatkowy wgląd w wiele z powyższej dyskusji. (Nie omawialiśmy pierścieni, ale pole jest po prostu specjalnym typem pierścienia)

W celu dalszej dyskusji na temat współczesnej teorii liczb można zapoznać się z wieloma zaawansowanymi dyskusjami na temat kryptografii. Jako sugestie do dalszej dyskusji proponuję Jonathana Katza i Yehudę Lindella Introduction to Modern Cryptography lub Christofa Paara i Jana Pelzla Understanding Cryptography. [5]

Uwagi:

[3] Zobacz YouTube Video

[4] Socratica, Abstract Algebra

[5] Katz i Lindell, Introduction to Modern Cryptography, 2nd edn, 2015 (CRC Press: Boca Raton, FL). Paar i Pelzl, Understanding Cryptography, 2010 (Springer-Verlag: Berlin).

Kryptografia symetryczna

Alice i Bob

Jedną z dwóch głównych gałęzi kryptografii jest kryptografia symetryczna. Obejmuje ona schematy szyfrowania, a także schematy związane z uwierzytelnianiem i integralnością. Do lat 70. ubiegłego wieku cała kryptografia składała się z symetrycznych schematów szyfrowania.

Główna dyskusja rozpoczyna się od przyjrzenia się symetrycznym schematom szyfrowania i dokonania kluczowego rozróżnienia między szyframi strumieniowymi a szyframi blokowymi. Następnie przechodzimy do kodów uwierzytelniania wiadomości, które są schematami zapewniającymi integralność i autentyczność wiadomości. Na koniec zbadamy, w jaki sposób symetryczne schematy szyfrowania i kody uwierzytelniania wiadomości mogą być łączone w celu zapewnienia bezpiecznej komunikacji.

W tym rozdziale omówiono różne symetryczne schematy kryptograficzne z praktyki. Następny rozdział zawiera szczegółowe omówienie szyfrowania za pomocą szyfru strumieniowego i szyfru blokowego z praktyki, a mianowicie odpowiednio RC4 i AES.

Przed rozpoczęciem naszej dyskusji na temat kryptografii symetrycznej, chciałbym pokrótce przedstawić kilka uwag na temat ilustracji Alice i Boba w tym i kolejnych rozdziałach.

Ilustrując zasady kryptografii, ludzie często opierają się na przykładach z udziałem Alicji i Boba. Ja również to zrobię.

Zwłaszcza jeśli jesteś nowy w kryptografii, ważne jest, aby zdać sobie sprawę, że te przykłady Alice i Boba mają służyć jedynie jako ilustracje zasad i konstrukcji kryptograficznych w uproszczonym środowisku. Zasady i konstrukcje mają jednak zastosowanie w znacznie szerszym zakresie rzeczywistych kontekstów.

Poniżej znajduje się pięć kluczowych punktów, o których należy pamiętać w przypadku przykładów z udziałem Alice i Boba w kryptografii:

  1. Można je łatwo przełożyć na przykłady z innymi rodzajami podmiotów, takimi jak firmy lub organizacje rządowe.

  2. Można je łatwo rozszerzyć na trzech lub więcej aktorów.

  3. W podanych przykładach Bob i Alice są zazwyczaj aktywnymi uczestnikami tworzenia każdej wiadomości i stosowania schematów kryptograficznych do tej wiadomości. W rzeczywistości jednak komunikacja elektroniczna jest w dużej mierze zautomatyzowana. Na przykład, gdy odwiedzasz stronę internetową korzystającą z zabezpieczeń transportowych Layer, kryptografia jest zwykle obsługiwana przez twój komputer i serwer WWW.

  4. W kontekście komunikacji elektronicznej "wiadomości" wysyłane przez kanał komunikacyjny to zazwyczaj pakiety TCP/IP. Mogą one należeć do wiadomości e-mail, wiadomości na Facebooku, rozmowy telefonicznej, transferu plików, strony internetowej, przesyłania oprogramowania itp. Nie są to wiadomości w tradycyjnym sensie. Niemniej jednak kryptografowie często upraszczają tę rzeczywistość, stwierdzając, że wiadomość jest na przykład wiadomością e-mail.

  5. Przykłady zazwyczaj koncentrują się na komunikacji elektronicznej, ale można je również rozszerzyć na tradycyjne formy komunikacji, takie jak listy.

Symetryczne schematy szyfrowania

Możemy luźno zdefiniować symetryczny schemat szyfrowania jako dowolny schemat kryptograficzny z trzema algorytmami:

  1. Algorytm generowania klucza, który generuje klucz prywatny.

  2. Algorytm szyfrowania, który pobiera klucz prywatny i zwykły tekst jako dane wejściowe i wyprowadza szyfrogram.

  3. Algorytm deszyfrowania, który pobiera klucz prywatny i szyfrogram jako dane wejściowe i wyprowadza oryginalny tekst jawny.

Zazwyczaj schemat szyfrowania - symetryczny lub asymetryczny - oferuje szablon szyfrowania oparty na podstawowym algorytmie, a nie dokładną specyfikację.

Rozważmy na przykład Salsa20, symetryczny schemat szyfrowania. Można go używać zarówno z kluczami o długości 128, jak i 256 bitów. Wybór długości klucza wpływa na pewne drobne szczegóły algorytmu (a dokładniej na liczbę rund w algorytmie).

Nie można jednak powiedzieć, że użycie Salsa20 z kluczem 128-bitowym jest innym schematem szyfrowania niż Salsa20 z kluczem 256-bitowym. Podstawowy algorytm pozostaje taki sam. Tylko wtedy, gdy podstawowy algorytm ulega zmianie, możemy mówić o dwóch różnych schematach szyfrowania.

Schematy szyfrowania symetrycznego są zazwyczaj przydatne w dwóch rodzajach przypadków: (1) tych, w których dwóch lub więcej agentów komunikuje się na odległość i chce zachować treść swojej komunikacji w tajemnicy; oraz (2) tych, w których jeden agent chce zachować treść wiadomości w tajemnicy w czasie.

Sytuację (1) można zobaczyć na Rysunku 1 poniżej. Bob chce wysłać wiadomość M do Alicji na odległość, ale nie chce, aby inni mogli ją odczytać.

Bob najpierw szyfruje wiadomość M za pomocą klucza prywatnego K. Następnie wysyła szyfrogram C do Alicji. Gdy Alicja otrzyma szyfrogram, może go odszyfrować za pomocą klucza K i odczytać tekst jawny. Przy dobrym schemacie szyfrowania każdy atakujący, który przechwyci szyfrogram C, nie powinien być w stanie dowiedzieć się niczego istotnego o wiadomości M.

Sytuację (2) można zobaczyć na Rysunku 2 poniżej. Bob chce uniemożliwić innym przeglądanie pewnych informacji. Typowa sytuacja może być taka, że Bob jest pracownikiem przechowującym poufne dane na swoim komputerze, których ani osoby postronne, ani jego koledzy nie powinni czytać.

Bob szyfruje wiadomość M w czasie T_0 kluczem K w celu uzyskania szyfrogramu C. W czasie T_1 ponownie potrzebuje wiadomości i odszyfrowuje szyfrogram C za pomocą klucza K. Każdy atakujący, który mógł natknąć się na szyfrogram C w międzyczasie, nie powinien być w stanie wywnioskować z niego niczego istotnego o M.

Rysunek 1: Tajność w przestrzeni

Figure 1: Secrecy across space

Rysunek 2: Tajność w czasie

Figure 2: Secrecy across time

Przykład: Szyfr przesunięcia

W rozdziale 2 spotkaliśmy się z szyfrem przestawieniowym, który jest przykładem bardzo prostego schematu szyfrowania symetrycznego. Przyjrzyjmy się mu jeszcze raz.

Załóżmy słownik D, który utożsamia wszystkie litery alfabetu angielskiego, w kolejności, ze zbiorem liczb \{0,1,2,\dots,25\}. Przyjmijmy zbiór możliwych wiadomości M. Szyfr przestawieniowy jest zatem schematem szyfrowania zdefiniowanym w następujący sposób:

To, co sprawia, że szyfr przesunięcia jest symetrycznym schematem szyfrowania, to fakt, że ten sam klucz jest używany zarówno do szyfrowania, jak i deszyfrowania. Dla przykładu, załóżmy, że chcesz zaszyfrować wiadomość "DOG" przy użyciu szyfru przestawieniowego i losowo wybrałeś "24" jako klucz. Zaszyfrowanie wiadomości tym kluczem dałoby wynik "BME". Jedynym sposobem na odzyskanie oryginalnej wiadomości jest użycie tego samego klucza, "24", w procesie deszyfrowania.

Ten szyfr Shift jest przykładem monoalfabetycznego szyfru podstawieniowego: schematu szyfrowania, w którym alfabet szyfrogramu jest stały (tj. używany jest tylko jeden alfabet). Zakładając, że algorytm deszyfrujący jest deterministyczny, każdy symbol w szyfrogramie podstawieniowym może odnosić się co najwyżej do jednego symbolu w tekście jawnym.

Do XVIII wieku wiele zastosowań szyfrowania opierało się w dużej mierze na monoalfabetycznych szyfrach podstawieniowych, choć często były one znacznie bardziej złożone niż szyfr Shift. Można było na przykład losowo wybrać literę z alfabetu dla każdej litery oryginalnego tekstu przy założeniu, że każda litera występuje tylko raz w alfabecie szyfrogramu. Oznacza to, że istniałoby 26 możliwych kluczy prywatnych, co było ogromną liczbą w erze przedkomputerowej.

Należy pamiętać, że termin cipher jest często używany w kryptografii. Należy pamiętać, że termin ten ma różne znaczenia. W rzeczywistości znam co najmniej pięć różnych znaczeń tego terminu w kryptografii.

W niektórych przypadkach odnosi się do schematu szyfrowania, tak jak w przypadku szyfru Shift i monoalfabetycznego szyfru podstawieniowego. Jednak termin ten może również odnosić się konkretnie do algorytmu szyfrowania, klucza prywatnego lub po prostu szyfrogramu dowolnego takiego schematu szyfrowania.

Wreszcie, termin szyfr może również odnosić się do podstawowego algorytmu, na podstawie którego można konstruować schematy kryptograficzne. Mogą one obejmować różne algorytmy szyfrowania, ale także inne rodzaje schematów kryptograficznych. Takie znaczenie tego terminu staje się istotne w kontekście szyfrów blokowych (patrz sekcja "Szyfry blokowe" poniżej).

Możesz również natknąć się na terminy szyfrować lub odszyfrowywać. Terminy te są jedynie synonimami szyfrowania i deszyfrowania.

Ataki siłowe i zasada Kerckhoffa

Szyfr przestawieniowy jest bardzo niepewnym schematem szyfrowania symetrycznego, przynajmniej we współczesnym świecie[1]. [Atakujący może po prostu spróbować odszyfrować dowolny szyfrogram za pomocą wszystkich 26 możliwych kluczy, aby zobaczyć, który wynik ma sens. Ten rodzaj ataku, w którym atakujący po prostu przechodzi przez klucze, aby zobaczyć, co działa, jest znany jako brute force attack lub exhaustive key search.

Aby każdy schemat szyfrowania spełniał minimalne pojęcie bezpieczeństwa, musi mieć zestaw możliwych kluczy lub przestrzeń kluczy, która jest tak duża, że ataki siłowe są niewykonalne. Wszystkie nowoczesne schematy szyfrowania spełniają ten standard. Jest to znane jako zasada wystarczającej przestrzeni klucza. Podobna zasada ma zazwyczaj zastosowanie w różnych typach schematów kryptograficznych.

Aby wyobrazić sobie ogromny rozmiar przestrzeni kluczy w nowoczesnych schematach szyfrowania, załóżmy, że plik został zaszyfrowany 128-bitowym kluczem przy użyciu zaawansowanego standardu szyfrowania. Oznacza to, że atakujący ma zestaw 2^{128}kluczy, przez które musi przejść w celu przeprowadzenia ataku siłowego. Szansa na 0,78% sukcesu przy tej strategii wymagałaby od atakującego przejścia przez około 2,65 \ razy 10^{36} kluczy.

Załóżmy optymistycznie, że atakujący może próbować 10^{16}kluczy na sekundę (tj. 10 kwadrylionów kluczy na sekundę). Aby przetestować 0,78% wszystkich kluczy w przestrzeni kluczy, jej atak musiałby trwać 2,65 \ razy 10^{20} sekund. To około 8,4 biliona lat. Tak więc nawet atak siłowy przeprowadzony przez absurdalnie potężnego przeciwnika nie jest realistyczny w przypadku nowoczesnego 128-bitowego schematu szyfrowania. Jest to zasada wystarczającej przestrzeni klucza.

Czy szyfr przesunięcia jest bezpieczniejszy, jeśli atakujący nie zna algorytmu szyfrowania? Być może, ale niewiele.

W każdym razie nowoczesna kryptografia zawsze zakłada, że bezpieczeństwo dowolnego symetrycznego schematu szyfrowania opiera się wyłącznie na utrzymaniu klucza prywatnego w tajemnicy. Zakłada się, że atakujący zawsze zna wszystkie inne szczegóły, w tym przestrzeń wiadomości, przestrzeń klucza, przestrzeń szyfrogramu, algorytm wyboru klucza, algorytm szyfrowania i algorytm deszyfrowania.

Pomysł, że bezpieczeństwo symetrycznego schematu szyfrowania może opierać się wyłącznie na tajności klucza prywatnego, znany jest jako zasada Kerckhoffa.

Zgodnie z pierwotnymi założeniami Kerckhoffsa, zasada ta ma zastosowanie wyłącznie do symetrycznych schematów szyfrowania. Bardziej ogólna wersja tej zasady ma jednak również zastosowanie do wszystkich innych współczesnych typów schematów kryptograficznych: Projekt dowolnego schematu kryptograficznego nie może być tajny, aby był bezpieczny; tajność może obejmować tylko niektóre ciągi (ciągi) informacji, zazwyczaj klucz prywatny.

Zasada Kerckhoffsa ma kluczowe znaczenie dla współczesnej kryptografii z czterech powodów. [Po pierwsze, istnieje tylko ograniczona liczba schematów kryptograficznych dla określonych typów aplikacji. Przykładowo, większość nowoczesnych aplikacji szyfrowania symetrycznego wykorzystuje szyfr Rijndael. Tak więc tajemnica dotycząca projektu schematu jest po prostu bardzo ograniczona. Istnieje jednak znacznie większa elastyczność w utrzymywaniu w tajemnicy klucza prywatnego dla szyfru Rijndael.

Po drugie, łatwiej jest zastąpić jakiś ciąg informacji niż cały schemat kryptograficzny. Załóżmy, że wszyscy pracownicy firmy mają to samo oprogramowanie szyfrujące, a każdy z nich ma klucz prywatny do poufnej komunikacji. Naruszenie klucza jest w tym scenariuszu kłopotliwe, ale przynajmniej firma może zachować oprogramowanie z takimi naruszeniami bezpieczeństwa. Gdyby firma polegała na tajności systemu, wówczas każde naruszenie tej tajności wymagałoby wymiany całego oprogramowania.

Po trzecie, zasada Kerckhoffsa pozwala na standaryzację i kompatybilność między użytkownikami schematów kryptograficznych. Ma to ogromne korzyści dla wydajności. Na przykład, trudno sobie wyobrazić, jak miliony ludzi mogłyby bezpiecznie łączyć się z serwerami internetowymi Google każdego dnia, gdyby bezpieczeństwo to wymagało utrzymywania schematów kryptograficznych w tajemnicy.

Po czwarte, zasada Kerckhoffa pozwala na publiczną kontrolę schematów kryptograficznych. Ten rodzaj kontroli jest absolutnie niezbędny do osiągnięcia bezpiecznych schematów kryptograficznych. Przykładowo, główny algorytm w kryptografii symetrycznej, szyfr Rijndael, był wynikiem konkursu zorganizowanego przez National Institute of Standards and Technology w latach 1997-2000.

Każdy system, który próbuje osiągnąć bezpieczeństwo przez zaciemnienie to taki, który opiera się na utrzymaniu w tajemnicy szczegółów jego projektu i/lub implementacji. W kryptografii byłby to w szczególności system, który opiera się na utrzymywaniu w tajemnicy szczegółów projektu schematu kryptograficznego. Tak więc bezpieczeństwo przez zaciemnienie jest bezpośrednim przeciwieństwem zasady Kerckhoffa.

Zdolność otwartości do zwiększania jakości i bezpieczeństwa rozciąga się również szerzej na świat cyfrowy niż tylko na kryptografię. Wolne i otwarte dystrybucje Linuksa, takie jak na przykład Debian, mają generalnie kilka zalet w stosunku do swoich odpowiedników z systemami Windows i MacOS pod względem prywatności, stabilności, bezpieczeństwa i elastyczności. Chociaż może to mieć wiele przyczyn, najważniejszą zasadą jest prawdopodobnie, jak sformułował to Eric Raymond w swoim słynnym eseju "The Cathedral and the Bazaar", że "biorąc pod uwagę wystarczającą liczbę gałek ocznych, wszystkie błędy są płytkie" [3] [To właśnie ta zasada mądrości tłumów zapewniła Linuksowi największy sukces.

Nigdy nie można jednoznacznie stwierdzić, że schemat kryptograficzny jest "bezpieczny" lub "niezabezpieczony" Zamiast tego istnieją różne pojęcia bezpieczeństwa dla schematów kryptograficznych. Każda definicja bezpieczeństwa kryptograficznego musi określać (1) cele bezpieczeństwa, a także (2) możliwości atakującego. Analiza schematów kryptograficznych pod kątem jednego lub więcej konkretnych pojęć bezpieczeństwa zapewnia wgląd w ich zastosowania i ograniczenia.

Chociaż nie będziemy zagłębiać się we wszystkie szczegóły różnych pojęć bezpieczeństwa kryptograficznego, powinieneś wiedzieć, że dwa założenia są wszechobecne we wszystkich współczesnych kryptograficznych pojęciach bezpieczeństwa odnoszących się do schematów symetrycznych i asymetrycznych (oraz w pewnej formie do innych prymitywów kryptograficznych):

Uwagi:

[1] Według Seutoniusa, szyfr przestawieniowy ze stałą wartością klucza wynoszącą 3 był używany przez Juliusza Cezara w jego komunikacji wojskowej. Tak więc A zawsze stawało się D, B zawsze E, C zawsze F i tak dalej. Ta konkretna wersja szyfru przestawieniowego stała się znana jako szyfr Cezara (choć tak naprawdę nie jest to szyfr we współczesnym znaczeniu tego słowa, ponieważ wartość klucza jest stała). Szyfr Cezara mógł być bezpieczny w I wieku p.n.e., jeśli wrogowie Rzymu nie znali się na szyfrowaniu. Jednak w dzisiejszych czasach nie byłby to zbyt bezpieczny schemat.

[2] Jonathan Katz i Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), s. 7f.

[3] Eric Raymond, "The Cathedral and the Bazaar", referat wygłoszony na Linux Kongress, Würzburg, Niemcy (27 maja 1997). Dostępnych jest wiele kolejnych wersji, a także książka. Moje cytaty pochodzą ze strony 30 książki: Eric Raymond, The Cathedral and the Bazaar: Musings on Linux and Open Source by an Accidental Revolutionary, revised edn. (2001), O'Reilly: Sebastopol, CA.

Szyfry strumieniowe

Schematy szyfrowania symetrycznego są standardowo podzielone na dwa typy: szyfry strumieniowe i szyfry blokowe. To rozróżnienie jest jednak nieco kłopotliwe, ponieważ ludzie używają tych terminów w niespójny sposób. W następnych kilku sekcjach przedstawię to rozróżnienie w sposób, który uważam za najlepszy. Należy jednak pamiętać, że wiele osób będzie używać tych terminów nieco inaczej niż ja.

Przejdźmy najpierw do szyfrów strumieniowych. Szyfr strumieniowy** to symetryczny schemat szyfrowania, w którym szyfrowanie składa się z dwóch etapów.

Najpierw za pomocą klucza prywatnego tworzony jest ciąg o długości tekstu jawnego. Ciąg ten nazywany jest keystream.

Następnie strumień klucza jest matematycznie łączony z tekstem jawnym w celu utworzenia szyfrogramu. Ta kombinacja jest zazwyczaj operacją XOR. W celu odszyfrowania można po prostu odwrócić tę operację. (Należy pamiętać, że A \oplus B = B \oplus A, w przypadku gdy A i B są ciągami bitów. Tak więc kolejność operacji XOR w szyfrze strumieniowym nie ma znaczenia dla wyniku. Właściwość ta znana jest jako komutatywność)

Typowy szyfr strumieniowy XOR został przedstawiony na Rysunku 3. Najpierw bierze się klucz prywatny K i używa go do generate strumienia klucza. Strumień klucza jest następnie łączony z tekstem jawnym za pomocą operacji XOR w celu utworzenia szyfrogramu. Każdy agent, który otrzyma szyfrogram, może go łatwo odszyfrować, jeśli posiada klucz K. Wszystko, co musi zrobić, to utworzyć strumień klucza tak długi jak szyfrogram zgodnie z określoną procedurą schematu i XOR go z szyfrogramem.

Rysunek 3: Szyfr strumieniowy XOR

Figure 3: An XOR stream cipher

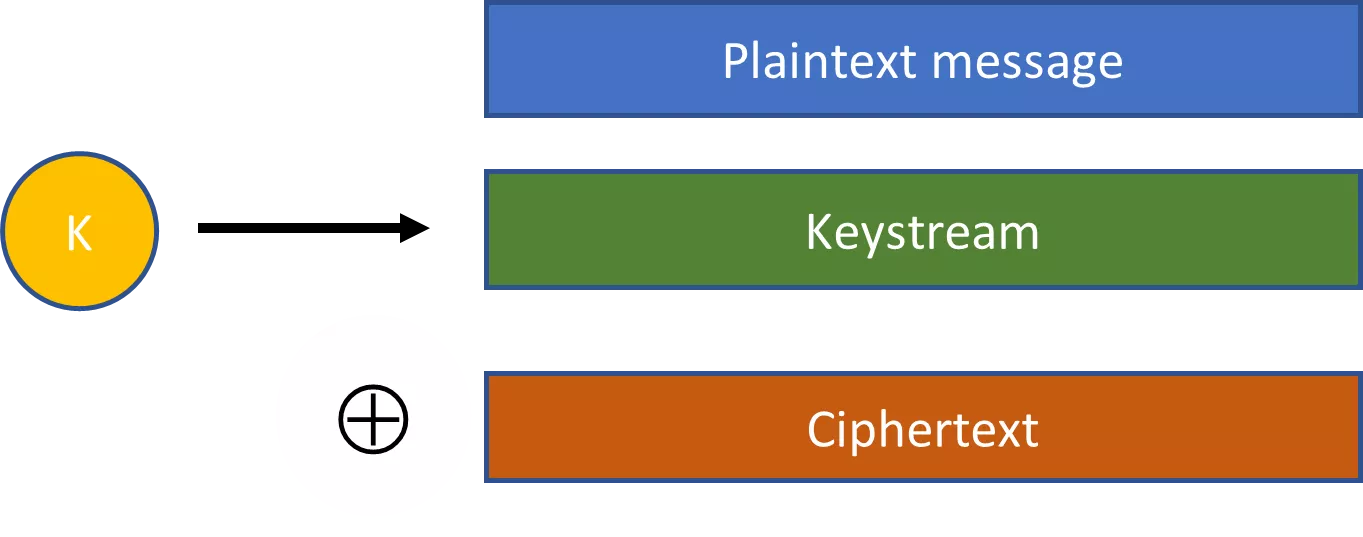
Należy pamiętać, że schemat szyfrowania jest zazwyczaj szablonem dla szyfrowania z tym samym podstawowym algorytmem, a nie dokładną specyfikacją. W związku z tym szyfr strumieniowy jest zazwyczaj szablonem szyfrowania, w którym można używać kluczy o różnych długościach. Chociaż długość klucza może wpływać na niektóre drobne szczegóły schematu, nie wpłynie to na jego zasadniczą formę.

Szyfr przesunięcia jest przykładem bardzo prostego i niezabezpieczonego szyfru strumieniowego. Używając pojedynczej litery (klucza prywatnego), można utworzyć ciąg liter o długości wiadomości (strumień klucza). Ten strumień klucza jest następnie łączony z tekstem jawnym za pomocą operacji modulo w celu utworzenia szyfrogramu. (Ta operacja modulo może być uproszczona do operacji XOR, gdy litery są reprezentowane w bitach).

Innym znanym przykładem szyfru strumieniowego jest szyfr Vigenere'a, od nazwiska Blaise'a de Vigenere'a, który w pełni opracował go pod koniec XVI wieku (choć inni wykonali wiele wcześniejszych prac). Jest to przykład polialfabetycznego szyfru podstawieniowego: schematu szyfrowania, w którym alfabet szyfrogramu dla symbolu tekstu jawnego zmienia się w zależności od jego pozycji w tekście. W przeciwieństwie do monoalfabetycznego szyfru podstawieniowego, symbole szyfrogramu mogą być powiązane z więcej niż jednym symbolem tekstu jawnego.

Wraz ze wzrostem popularności szyfrowania w renesansowej Europie, pojawiła się również kryptoanaliza, czyli łamanie szyfrogramów - w szczególności przy użyciu analizy częstotliwości. Ta ostatnia wykorzystuje statystyczne prawidłowości w naszym języku do łamania szyfrogramów i została odkryta przez arabskich uczonych już w IX wieku. Jest to technika, która działa szczególnie dobrze w przypadku dłuższych tekstów. Nawet najbardziej wyrafinowane monoalfabetyczne szyfry podstawieniowe nie były już wystarczające przeciwko analizie częstotliwości w 1700 roku w Europie, szczególnie w środowiskach wojskowych i bezpieczeństwa. Ponieważ szyfr Vigenere oferował znaczny postęp w zakresie bezpieczeństwa, stał się popularny w tym okresie i był szeroko rozpowszechniony pod koniec XVIII wieku.

Mówiąc nieformalnie, schemat szyfrowania działa w następujący sposób:

  1. Wybierz wieloliterowe słowo jako klucz prywatny.

  2. Dla dowolnej wiadomości zastosuj szyfr przesunięcia do każdej litery wiadomości, używając odpowiedniej litery w słowie kluczowym jako przesunięcia.

  3. Jeśli przeszedłeś przez słowo kluczowe, ale nadal nie całkowicie zaszyfrowałeś tekst jawny, ponownie zastosuj litery słowa kluczowego jako szyfr przesunięcia do odpowiednich liter w pozostałej części tekstu.

  4. Kontynuuj ten proces, aż cała wiadomość zostanie zaszyfrowana.

Aby to zilustrować, załóżmy, że twój klucz prywatny to "GOLD" i chcesz zaszyfrować wiadomość "CRYPTOGRAPHY". W takim przypadku należy postępować w następujący sposób zgodnie z szyfrem Vigenère'a:

Zatem szyfrogram c = "IFJSZCRUGDSB".

Innym znanym przykładem szyfru strumieniowego jest one-time pad. W przypadku tego szyfru wystarczy utworzyć ciąg losowych bitów o długości równej długości tekstu jawnego i utworzyć szyfrogram za pomocą operacji XOR. W związku z tym klucz prywatny i strumień klucza są równoważne z jednorazowym padem.

Podczas gdy szyfr Shift i szyfr Vigenere są bardzo niepewne w dzisiejszych czasach, one-time pad jest bardzo bezpieczny, jeśli jest używany prawidłowo. Prawdopodobnie najbardziej znanym zastosowaniem szyfru jednorazowego było, przynajmniej do lat 80. ubiegłego wieku, gorąca linia Waszyngton-Moskwa. [4]

Gorąca linia to bezpośrednie połączenie komunikacyjne między Waszyngtonem a Moskwą w pilnych sprawach, które zostało zainstalowane po kubańskim kryzysie rakietowym. Technologia tego połączenia zmieniała się na przestrzeni lat. Obecnie obejmuje bezpośredni kabel światłowodowy, a także dwa łącza satelitarne (dla redundancji), które umożliwiają wysyłanie wiadomości e-mail i wiadomości tekstowych. Łącze kończy się w różnych miejscach w USA. Pentagon, Biały Dom i Raven Rock Mountain są znanymi punktami końcowymi. Wbrew powszechnej opinii, gorąca linia nigdy nie obejmowała telefonów.

Zasadniczo schemat jednorazowego padu działał w następujący sposób. Zarówno Waszyngton, jak i Moskwa miały dwa zestawy liczb losowych. Jeden zestaw liczb losowych, stworzony przez Rosjan, odnosił się do szyfrowania i deszyfrowania wszelkich wiadomości w języku rosyjskim. Jeden zestaw liczb losowych, stworzony przez Amerykanów, odnosił się do szyfrowania i deszyfrowania wszelkich wiadomości w języku angielskim. Od czasu do czasu kolejne losowe liczby były dostarczane drugiej stronie przez zaufanych kurierów.

Waszyngton i Moskwa były więc w stanie komunikować się potajemnie, wykorzystując te losowe liczby do tworzenia jednorazowych blokad. Za każdym razem, gdy trzeba było się komunikować, używano kolejnej porcji liczb losowych do przesłania wiadomości.

Mimo wysokiego poziomu bezpieczeństwa, one-time pad napotyka na poważne ograniczenia praktyczne: klucz musi być tak długi, jak wiadomość, a żadna część one-time pada nie może być ponownie użyta. Oznacza to, że musisz śledzić, gdzie jesteś w one-time pad, przechowywać ogromną liczbę bitów i Exchange losowych bitów ze swoimi kontrahentami od czasu do czasu. W związku z tym one-time pad nie jest często wykorzystywany w praktyce.

Zamiast tego, dominującymi szyframi strumieniowymi stosowanymi w praktyce są pseudolosowe szyfry strumieniowe. Salsa20 i blisko spokrewniony wariant o nazwie ChaCha są przykładami powszechnie stosowanych pseudolosowych szyfrów strumieniowych.

W przypadku tych pseudolosowych szyfrów strumieniowych należy najpierw losowo wybrać klucz K, który jest krótszy niż długość tekstu jawnego. Taki losowy klucz K jest zwykle tworzony przez nasz komputer na podstawie nieprzewidywalnych danych, które gromadzi w czasie, takich jak czas między wiadomościami sieciowymi, ruchy myszy itp.

Ten losowy klucz K jest następnie wstawiany do algorytmu rozszerzającego, który tworzy pseudolosowy strumień klucza o długości równej długości wiadomości. Można dokładnie określić, jak długi ma być strumień kluczy (np. 500 bitów, 1000 bitów, 1200 bitów, 29 117 bitów itd.).

Pseudolosowy strumień klucza wygląda tak, jakby został wybrany całkowicie losowo ze zbioru wszystkich ciągów o tej samej długości. W związku z tym szyfrowanie za pomocą pseudolosowego strumienia klucza wygląda tak, jakby zostało wykonane za pomocą jednorazowego pada. Ale tak oczywiście nie jest.

Ponieważ nasz klucz prywatny jest krótszy niż strumień klucza, a nasz algorytm rozszerzający musi być deterministyczny, aby proces szyfrowania/deszyfrowania działał, nie każdy strumień klucza o tej konkretnej długości mógł być wynikiem naszej operacji rozszerzającej.

Załóżmy na przykład, że nasz klucz prywatny ma długość 128 bitów i możemy wstawić go do algorytmu rozszerzającego, aby utworzyć znacznie dłuższy strumień klucza, powiedzmy 2500 bitów. Ponieważ nasz algorytm rozszerzający musi być deterministyczny, nasz algorytm może co najwyżej wybrać ciągi 1/2^{128} o długości 2500 bitów. Tak więc taki strumień kluczy nigdy nie mógłby zostać wybrany całkowicie losowo spośród wszystkich ciągów o tej samej długości.

Nasza definicja szyfru strumieniowego obejmuje dwa aspekty: (1) strumień klucza o długości tekstu jawnego jest generowany za pomocą klucza prywatnego; oraz (2) ten strumień klucza jest łączony z tekstem jawnym, zazwyczaj za pomocą operacji XOR, w celu uzyskania szyfrogramu.

Czasami ludzie definiują warunek (1) bardziej rygorystycznie, twierdząc, że strumień klucza musi być pseudolosowy. Oznacza to, że ani szyfr przestawieniowy, ani szyfr jednorazowy nie byłyby uważane za szyfry strumieniowe.

Moim zdaniem szersze zdefiniowanie warunku (1) zapewnia łatwiejszy sposób organizacji schematów szyfrowania. Ponadto oznacza to, że nie musimy przestać nazywać konkretnego schematu szyfrowania szyfrem strumieniowym tylko dlatego, że dowiedzieliśmy się, że w rzeczywistości nie opiera się on na pseudolosowych strumieniach kluczy.

Uwagi:

[4] Crypto Museum, "Washington-Moscow hotline", 2013, dostępne pod adresem https://www.cryptomuseum.com/crypto/hotline/index.htm.

Szyfry blokowe

Pierwszy sposób, w jaki szyfr blokowy jest powszechnie rozumiany, to coś bardziej prymitywnego niż szyfr strumieniowy: Podstawowy algorytm, który wykonuje transformację z zachowaniem długości na ciągu o odpowiedniej długości za pomocą klucza. Algorytm ten może być używany do tworzenia schematów szyfrowania i być może innych rodzajów schematów kryptograficznych.

Często szyfr blokowy może przyjmować ciągi wejściowe o różnej długości, takie jak 64, 128 lub 256 bitów, a także klucze o różnej długości, takie jak 128, 192 lub 256 bitów. Chociaż niektóre szczegóły algorytmu mogą się zmieniać w zależności od tych zmiennych, podstawowy algorytm się nie zmienia. Gdyby tak było, mówilibyśmy o dwóch różnych szyfrach blokowych. Należy zauważyć, że terminologia dotycząca podstawowego algorytmu jest tutaj taka sama, jak w przypadku schematów szyfrowania.

Przedstawienie działania szyfru blokowego można zobaczyć na Rysunku 4 poniżej. Wiadomość M o długości L i klucz K służą jako dane wejściowe do szyfru blokowego. Na wyjściu otrzymujemy wiadomość M' o długości L. Klucz nie musi być tej samej długości co M i M' dla większości szyfrów blokowych.

Rysunek 4: Szyfr blokowy

Figure 4: A block cipher

Szyfr blokowy sam w sobie nie jest schematem szyfrowania. Ale szyfr blokowy może być używany z różnymi trybami działania w celu stworzenia różnych schematów szyfrowania. Tryb działania po prostu dodaje pewne dodatkowe operacje poza szyfrem blokowym.

Aby zilustrować, jak to działa, załóżmy szyfr blokowy (BC), który wymaga 128-bitowego ciągu wejściowego i 128-bitowego klucza prywatnego. Rysunek 5 poniżej pokazuje, w jaki sposób ten szyfr blokowy może być użyty z trybem elektronicznej książki kodowej (trybECB) do stworzenia schematu szyfrowania. (Elipsy po prawej stronie wskazują, że można powtarzać ten schemat tak długo, jak jest to potrzebne).

Rysunek 5: Szyfr blokowy z trybem ECB

Figure 5: A block cipher with ECB mode

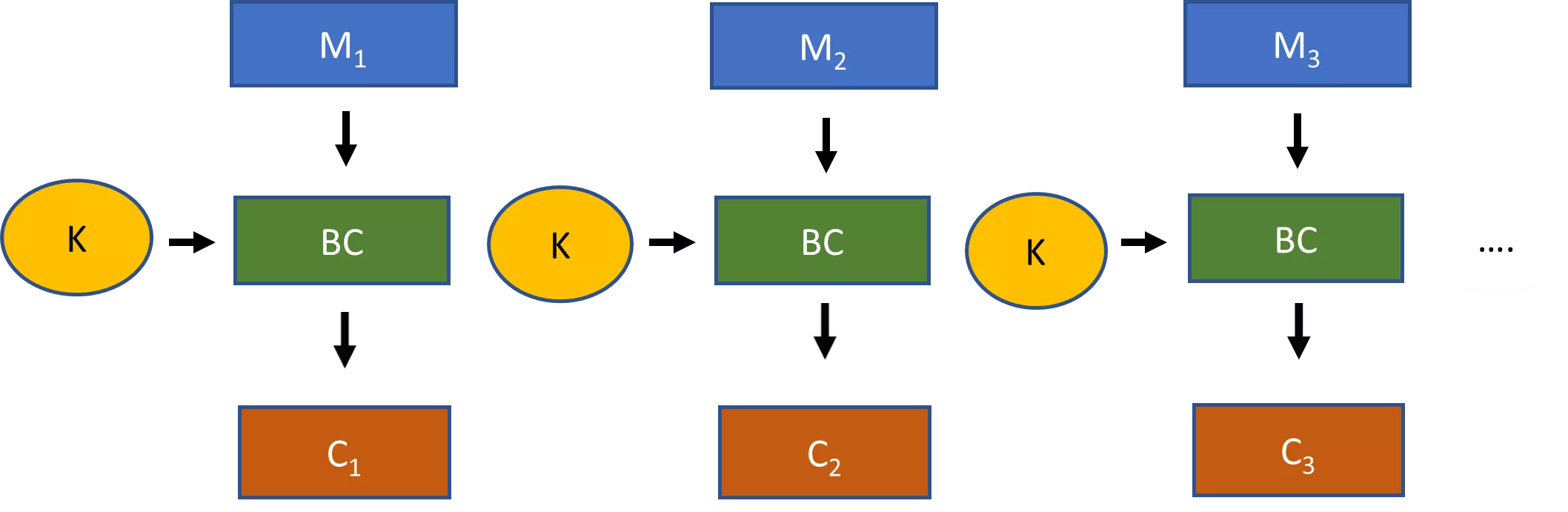
Proces szyfrowania elektronicznej książki kodowej za pomocą szyfru blokowego wygląda następująco. Sprawdź, czy możesz podzielić swój zwykły tekst na 128-bitowe bloki. Jeśli nie, dodaj padding do wiadomości, tak aby wynik mógł być równomiernie podzielony przez rozmiar bloku 128 bitów. Są to dane używane w procesie szyfrowania.

Teraz podziel dane na fragmenty 128-bitowych ciągów (M_1, M_2, M_3 itd.). Przeprowadź każdy 128-bitowy ciąg przez szyfr blokowy za pomocą 128-bitowego klucza, aby utworzyć 128-bitowe fragmenty szyfrogramu (C_1, C_2, C_3 itd.). Te fragmenty, po ponownym połączeniu, tworzą pełny szyfrogram.

Deszyfrowanie jest procesem odwrotnym, choć odbiorca potrzebuje jakiegoś rozpoznawalnego sposobu na usunięcie wszelkich wypełnień z odszyfrowanych danych w celu uzyskania oryginalnej wiadomości w postaci zwykłego tekstu.

Choć stosunkowo prosty, szyfr blokowy z trybem elektronicznej książki kodowej nie jest bezpieczny. Dzieje się tak, ponieważ prowadzi to do deterministycznego szyfrowania. Dowolne dwa identyczne 128-bitowe ciągi danych są szyfrowane dokładnie w ten sam sposób. Informacja ta może zostać wykorzystana.

Zamiast tego, każdy schemat szyfrowania zbudowany z szyfru blokowego powinien być probabilistyczny: to znaczy, że szyfrowanie dowolnej wiadomości M lub dowolnego określonego fragmentu M powinno generalnie dawać inny wynik za każdym razem. [5]

Tryb cipher block chaining (tryb CBC) jest prawdopodobnie najczęściej używanym trybem z szyfrem blokowym. Kombinacja ta, jeśli jest wykonana prawidłowo, tworzy probabilistyczny schemat szyfrowania. Ten tryb działania można zobaczyć na Rysunku 6 poniżej.

Rysunek 6: Szyfr blokowy z trybem CBC

Figure 6: A block cipher with CBC mode

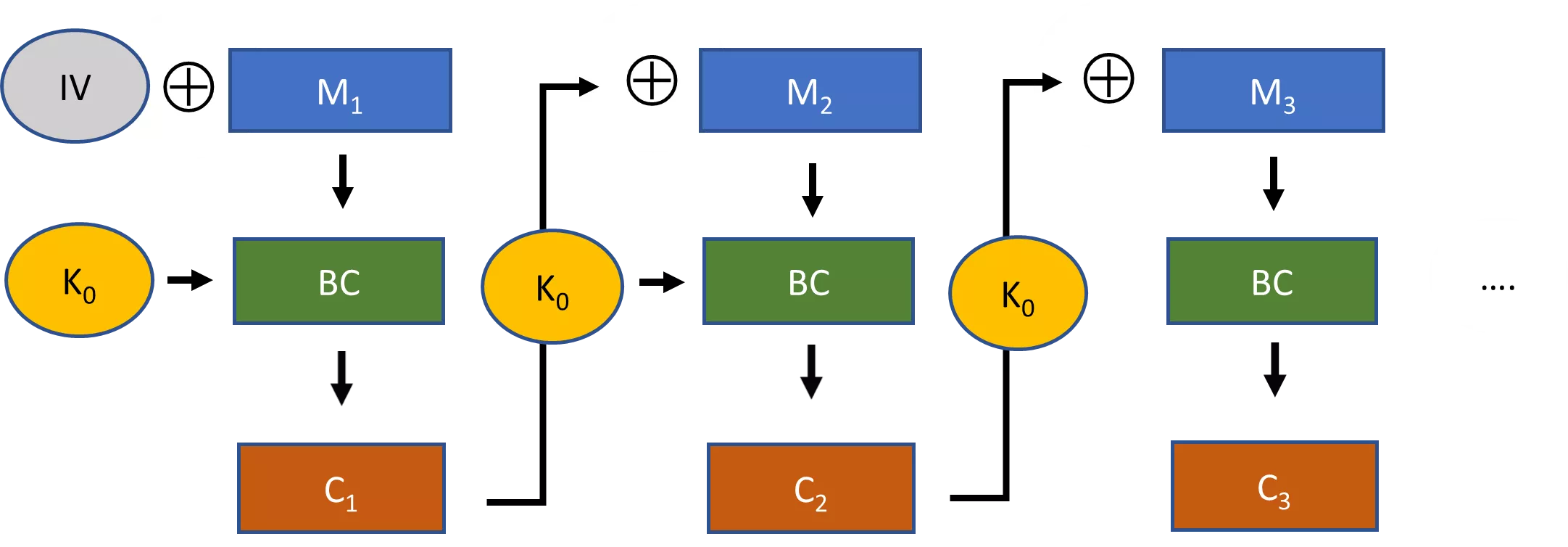
Załóżmy, że rozmiar bloku wynosi ponownie 128 bitów. Aby rozpocząć, należy ponownie upewnić się, że oryginalna wiadomość w postaci zwykłego tekstu otrzyma niezbędne wypełnienie.

Następnie wykonujemy XOR pierwszej 128-bitowej części tekstu jawnego z wektorem inicjującym składającym się ze 128 bitów. Wynik jest umieszczany w szyfrze blokowym w celu utworzenia szyfrogramu dla pierwszego bloku. Dla drugiego bloku 128 bitów, najpierw XOR zwykłego tekstu z szyfrogramem z pierwszego bloku, przed wstawieniem go do szyfru blokowego. Proces ten jest kontynuowany do momentu zaszyfrowania całej wiadomości z tekstem jawnym.

Po zakończeniu wysyłasz zaszyfrowaną wiadomość wraz z niezaszyfrowanym wektorem inicjującym do odbiorcy. Odbiorca musi znać wektor inicjujący, w przeciwnym razie nie będzie mógł odszyfrować szyfrogramu.

Ta konstrukcja jest znacznie bezpieczniejsza niż tryb elektronicznej książki kodów, jeśli jest używana poprawnie. Po pierwsze, należy upewnić się, że wektor inicjujący jest ciągiem losowym lub pseudolosowym. Ponadto należy używać innego wektora inicjalizacji za każdym razem, gdy używany jest ten schemat szyfrowania.

Innymi słowy, wektor inicjujący powinien być losowym lub pseudolosowym Nonce, gdzie Nonce oznacza "liczbę, która jest używana tylko raz" Jeśli zachowasz tę praktykę, tryb CBC z szyfrem blokowym zapewni, że dowolne dwa identyczne bloki tekstu jawnego będą generalnie szyfrowane inaczej za każdym razem.

Na koniec zwróćmy uwagę na tryb wyjściowego sprzężenia zwrotnego (trybOFB). Obraz tego trybu można zobaczyć na Rysunku 7.

Rysunek 7: Szyfr blokowy z trybem OFB

Figure 7: A block cipher with OFB mode

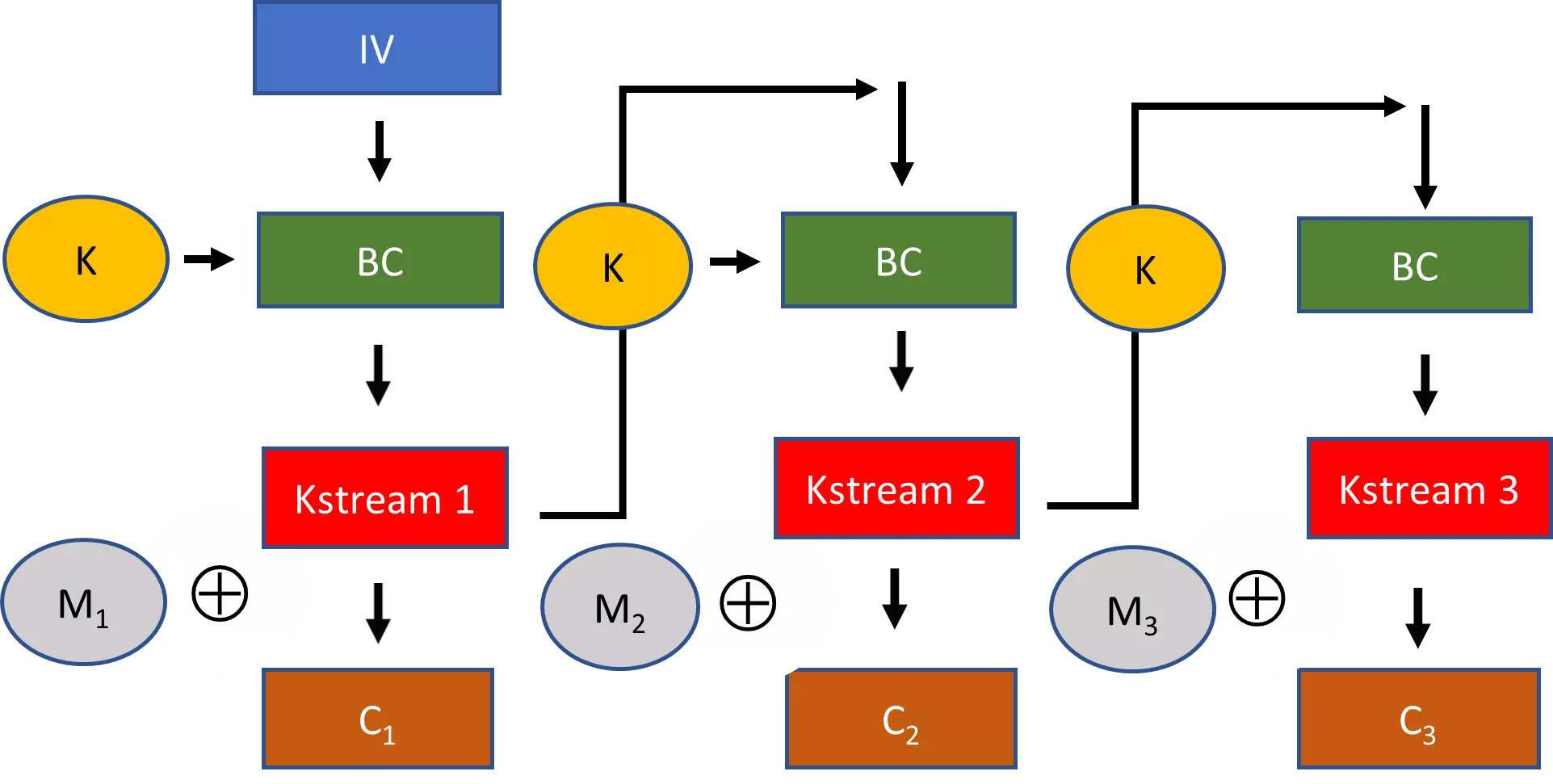
W trybie OFB użytkownik również wybiera wektor inicjujący. Ale tutaj, dla pierwszego bloku, wektor inicjujący jest bezpośrednio wstawiany do szyfru blokowego wraz z kluczem. Wynikowe 128 bitów jest następnie traktowane jako strumień klucza. Ten strumień klucza jest XORowany z tekstem jawnym w celu utworzenia szyfrogramu dla bloku. W przypadku kolejnych bloków używa się strumienia klucza z poprzedniego bloku jako danych wejściowych do szyfru blokowego i powtarza kroki.

Jeśli przyjrzeć się uważnie, to to, co faktycznie zostało tutaj utworzone z szyfru blokowego z trybem OFB, jest szyfrem strumieniowym. Tworzysz generate porcje strumienia klucza o długości 128 bitów, aż uzyskasz długość tekstu jawnego (odrzucając niepotrzebne bity z ostatniej 128-bitowej porcji strumienia klucza). Następnie XOR strumienia klucza z wiadomością tekstu jawnego w celu uzyskania szyfrogramu.

W poprzedniej sekcji dotyczącej szyfrów strumieniowych stwierdziłem, że strumień klucza tworzy się za pomocą klucza prywatnego. Gwoli ścisłości, nie musi on być tworzony wyłącznie za pomocą klucza prywatnego. Jak widać w trybie OFB, strumień klucza jest tworzony przy użyciu zarówno klucza prywatnego, jak i wektora inicjalizacyjnego.

Należy pamiętać, że podobnie jak w przypadku trybu CBC, ważne jest, aby wybrać pseudolosowy lub losowy Nonce dla wektora inicjalizacji za każdym razem, gdy używany jest szyfr blokowy w trybie OFB. W przeciwnym razie ten sam 128-bitowy ciąg wiadomości wysłany w różnych komunikatach zostanie zaszyfrowany w ten sam sposób. Jest to jeden ze sposobów tworzenia szyfrowania probabilistycznego za pomocą szyfru strumieniowego.

Niektóre szyfry strumieniowe używają tylko klucza prywatnego do utworzenia strumienia klucza. W przypadku tych szyfrów strumieniowych ważne jest, aby użyć losowego Nonce do wybrania klucza prywatnego dla każdej instancji komunikacji. W przeciwnym razie wyniki szyfrowania za pomocą tych szyfrów strumieniowych będą również deterministyczne, co prowadzi do problemów z bezpieczeństwem.

Najpopularniejszym współczesnym szyfrem blokowym jest szyfr Rijndael. Był to zwycięski szyfr spośród piętnastu zgłoszonych do konkursu organizowanego przez National Institute of Standards and Technology (NIST) w latach 1997-2000 w celu zastąpienia starszego standardu szyfrowania, standardu szyfrowania danych (DES).

Szyfr Rijndael może być używany z różnymi specyfikacjami długości kluczy i rozmiarów bloków, a także w różnych trybach działania. Komitet konkursu NIST przyjął ograniczoną wersję szyfru Rijndael - mianowicie taką, która wymaga 128-bitowych rozmiarów bloków i długości kluczy 128 bitów, 192 bitów lub 256 bitów - jako część zaawansowanego standardu szyfrowania (AES). Jest to tak naprawdę główny standard dla aplikacji szyfrowania symetrycznego. Jest tak bezpieczny, że nawet NSA jest skłonna używać go z 256-bitowymi kluczami do ściśle tajnych dokumentów. [6]

Szyfr blokowy AES zostanie szczegółowo wyjaśniony w Rozdziale 5.

Uwagi:

[5] Znaczenie szyfrowania probabilistycznego zostało po raz pierwszy podkreślone przez Shafi Goldwasser i Silvio Micali, "Probabilistic encryption," Journal of Computer and System Sciences, 28 (1984), 270-99.

[6] Zob. NSA, "Commercial National Security Algorithm Suite", https://apps.nsa.gov/iaarchive/programs/iad-initiatives/cnsa-suite.cfm.

Wyjaśnienie nieporozumień

Zamieszanie związane z rozróżnieniem między szyframi blokowymi a szyframi strumieniowymi wynika z tego, że czasami ludzie rozumieją termin szyfr blokowy jako odnoszący się konkretnie do szyfru blokowego z blokowym trybem szyfrowania.

Rozważmy tryby ECB i CBC z poprzedniej sekcji. W szczególności wymagają one, aby dane do szyfrowania były podzielne przez rozmiar bloku (co oznacza, że może być konieczne użycie wypełnienia dla oryginalnej wiadomości). Ponadto dane w tych trybach są również obsługiwane bezpośrednio przez szyfr blokowy (a nie tylko łączone z wynikiem operacji szyfru blokowego, jak w trybie OFB).

Stąd, alternatywnie, można zdefiniować szyfr blokowy jako dowolny schemat szyfrowania, który działa na blokach wiadomości o stałej długości w danym czasie (gdzie każdy blok musi być dłuższy niż bajt, w przeciwnym razie zapada się w szyfr strumieniowy). Zarówno dane do szyfrowania, jak i szyfrogram muszą równomiernie dzielić się na ten rozmiar bloku. Zazwyczaj rozmiar bloku wynosi 64, 128, 192 lub 256 bitów. Z kolei szyfr strumieniowy może szyfrować dowolne wiadomości w kawałkach po jednym bicie lub bajcie na raz.

Dzięki temu bardziej szczegółowemu rozumieniu szyfru blokowego można rzeczywiście twierdzić, że nowoczesne schematy szyfrowania są albo szyframi strumieniowymi, albo blokowymi. Od tego momentu będę miał na myśli termin szyfr blokowy w bardziej ogólnym znaczeniu, chyba że określono inaczej.

Dyskusja na temat trybu OFB w poprzedniej sekcji porusza również inną interesującą kwestię. Niektóre szyfry strumieniowe są zbudowane z szyfrów blokowych, jak Rijndael z OFB. Niektóre, takie jak Salsa20 i ChaCha, nie są tworzone z szyfrów blokowych. Te ostatnie można nazwać prymitywnymi szyframi strumieniowymi. (Tak naprawdę nie istnieje ustandaryzowany termin odnoszący się do takich szyfrów strumieniowych)

Kiedy ludzie mówią o zaletach i wadach szyfrów strumieniowych i blokowych, zazwyczaj porównują prymitywne szyfry strumieniowe do schematów szyfrowania opartych na szyfrach blokowych.

Podczas gdy zawsze można łatwo zbudować szyfr strumieniowy z szyfru blokowego, zwykle bardzo trudno jest zbudować jakąś konstrukcję z blokowym trybem szyfrowania (takim jak tryb CBC) z prymitywnego szyfru strumieniowego.

Z tej dyskusji powinieneś teraz zrozumieć Rysunek 8. Przedstawia on przegląd symetrycznych schematów szyfrowania. Używamy trzech rodzajów schematów szyfrowania: prymitywnych szyfrów strumieniowych, szyfrów blokowych szyfrów strumieniowych i szyfrów blokowych w trybie blokowym (zwanych również "szyframi blokowymi" na diagramie).

Rysunek 8: Przegląd schematów szyfrowania symetrycznego

Figure 8: Overview of symmetric encryption schemes

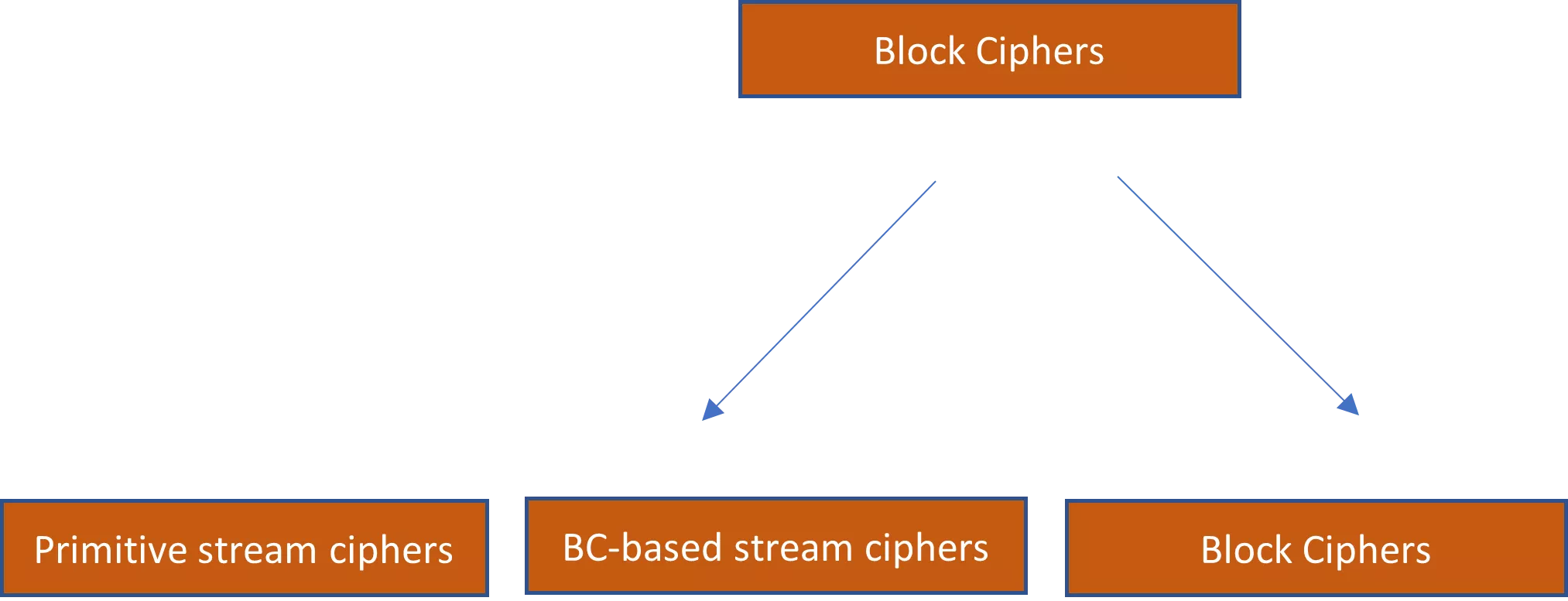
Kody uwierzytelniania wiadomości

Szyfrowanie dotyczy tajności. Ale kryptografia zajmuje się również szerszymi zagadnieniami, takimi jak integralność wiadomości, autentyczność i niezaprzeczalność. Tak zwane kody uwierzytelniania wiadomości (MAC) to schematy kryptograficzne z kluczem symetrycznym, które wspierają autentyczność i integralność w komunikacji.

Dlaczego w komunikacji potrzebne jest cokolwiek poza tajnością? Załóżmy, że Bob wysyła Alicji wiadomość przy użyciu praktycznie niemożliwego do złamania szyfrowania. Każdy atakujący, który przechwyci tę wiadomość, nie będzie w stanie uzyskać żadnych istotnych informacji na temat jej treści. Atakujący ma jednak do dyspozycji co najmniej dwa inne wektory ataku:

  1. Mogłaby przechwycić szyfrogram, zmienić jego zawartość i wysłać zmieniony szyfrogram do Alice.

  2. Mogłaby całkowicie zablokować wiadomość Boba i wysłać swój własny szyfrogram.

W obu tych przypadkach atakujący może nie mieć żadnego wglądu w zawartość szyfrogramów (1) i (2). Ale nadal może spowodować znaczne szkody w ten sposób. W tym miejscu ważne stają się kody uwierzytelniania wiadomości.

Kody uwierzytelniania wiadomości są luźno zdefiniowane jako symetryczne schematy kryptograficzne z trzema algorytmami: algorytmem generowania klucza, algorytmem generowania znacznika i algorytmem weryfikacji. Bezpieczny MAC zapewnia, że znaczniki są istniejąco nie do sfałszowania dla każdego atakującego - to znaczy, że nie może on pomyślnie utworzyć znacznika na wiadomości, która weryfikuje, chyba że posiada klucz prywatny.

Bob i Alice mogą zwalczać manipulację konkretną wiadomością za pomocą MAC. Załóżmy na chwilę, że nie zależy im na tajności. Chcą jedynie upewnić się, że wiadomość otrzymana przez Alicję rzeczywiście pochodzi od Boba i nie została w żaden sposób zmieniona.

Proces ten został przedstawiony na Rysunku 9. Aby użyć MAC (Message Authentication Code), najpierw generate klucz prywatny K, który jest współdzielony między nimi. Bob tworzy znacznik T dla wiadomości przy użyciu klucza prywatnego K. Następnie wysyła wiadomość wraz z tagiem do Alicji. Może ona następnie zweryfikować, czy Bob rzeczywiście utworzył znacznik, uruchamiając klucz prywatny, wiadomość i znacznik za pomocą algorytmu weryfikacji.

Rysunek 9: Przegląd schematów szyfrowania symetrycznego

Figure 9: Overview of symmetric encryption schemes

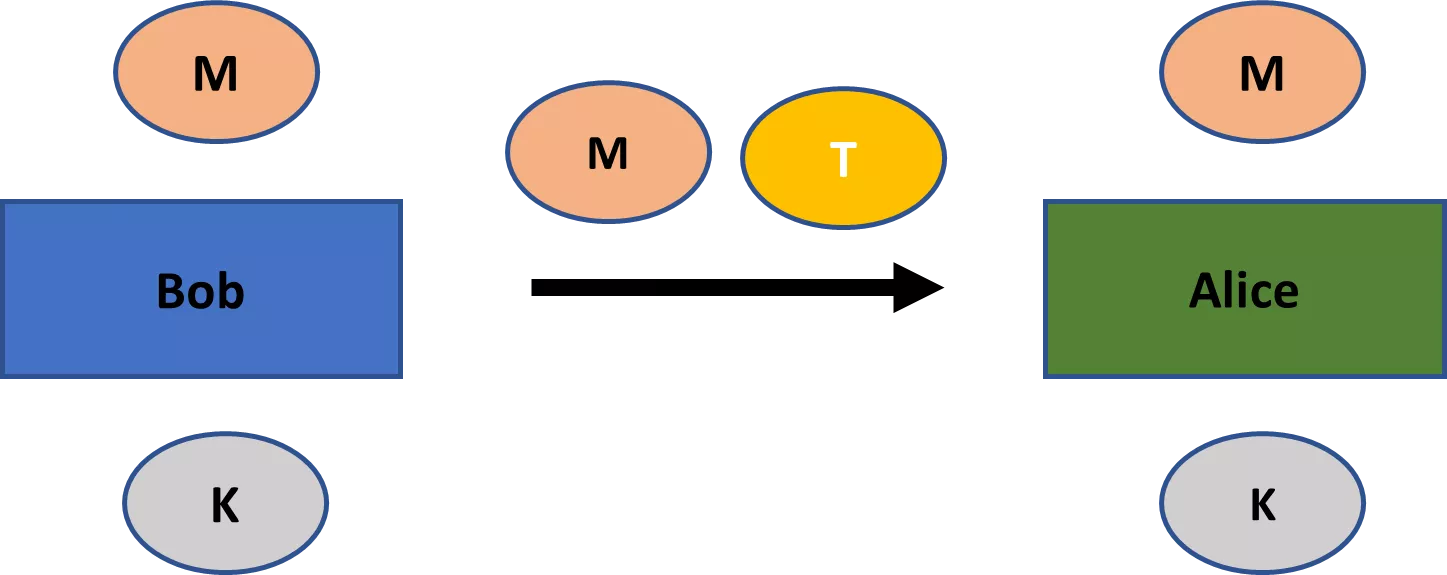
Ze względu na istniejącą niezmienność, atakujący nie może w żaden sposób zmienić wiadomości M ani utworzyć własnej wiadomości z prawidłowym znacznikiem. Dzieje się tak, nawet jeśli atakujący obserwuje znaczniki wielu wiadomości między Bobem i Alicją, które używają tego samego klucza prywatnego. Atakujący może co najwyżej zablokować Alicji możliwość odebrania wiadomości M (problem, którego kryptografia nie może Address).

MAC gwarantuje, że wiadomość została faktycznie utworzona przez Boba. Ta autentyczność automatycznie implikuje integralność wiadomości - to znaczy, że jeśli Bob stworzył jakąś wiadomość, to ipso facto nie została ona w żaden sposób zmieniona przez atakującego. Tak więc od tego momentu każda troska o uwierzytelnianie powinna być automatycznie rozumiana jako troska o integralność.

Chociaż w mojej dyskusji dokonałem rozróżnienia między autentycznością a integralnością wiadomości, powszechne jest również używanie tych terminów jako synonimów. Odnoszą się one zatem do idei wiadomości, które zostały stworzone przez konkretnego nadawcę i nie zostały w żaden sposób zmienione. W tym duchu kody uwierzytelniania wiadomości są często nazywane również kodami integralności wiadomości.

Uwierzytelnione szyfrowanie

Zazwyczaj chce się zagwarantować zarówno tajność, jak i autentyczność komunikacji, a zatem schematy szyfrowania i schematy MAC są zwykle używane razem.

Uwierzytelniony schemat szyfrowania to schemat, który łączy szyfrowanie z MAC w wysoce bezpieczny sposób. W szczególności, musi on spełniać standardy egzystencjalnej niefałszowalności, jak również bardzo silnego pojęcia tajności, a mianowicie takiego, które jest odporne na ataki z wybranym tekstem szyfrującym. [7]

Aby schemat szyfrowania był odporny na ataki z użyciem wybranego szyfrogramu, musi on spełniać standardy non-malleability: to znaczy, że każda modyfikacja szyfrogramu przez atakującego powinna dawać albo nieważny szyfrogram, albo taki, który odszyfrowuje się do tekstu jawnego nie mającego żadnego związku z oryginalnym. [8]

Ponieważ uwierzytelniony schemat szyfrowania zapewnia, że szyfrogram utworzony przez atakującego jest zawsze nieważny (ponieważ znacznik nie zostanie zweryfikowany), spełnia on standardy odporności na ataki z użyciem wybranego szyfrogramu. Co ciekawe, można udowodnić, że uwierzytelniony schemat szyfrowania można zawsze utworzyć z kombinacji egzystencjalnie niemożliwego do sfałszowania MAC i schematu szyfrowania, który spełnia mniej silne pojęcie bezpieczeństwa, znane jako bezpieczeństwo ataku z użyciem wybranego tekstu jawnego.

Nie będziemy zagłębiać się we wszystkie szczegóły konstruowania uwierzytelnionych schematów szyfrowania. Ważne jest jednak, aby znać dwa szczegóły ich budowy.

Po pierwsze, uwierzytelniony schemat szyfrowania najpierw obsługuje szyfrowanie, a następnie tworzy znacznik wiadomości na szyfrogramie. Okazuje się, że inne podejścia - takie jak łączenie szyfrogramu ze znacznikiem na zwykłym tekście lub najpierw tworzenie znacznika, a następnie szyfrowanie zarówno zwykłego tekstu, jak i znacznika - są niezabezpieczone. Ponadto, obie operacje muszą mieć swój własny losowo wybrany klucz prywatny, w przeciwnym razie bezpieczeństwo jest poważnie zagrożone.

Powyższa zasada ma bardziej ogólne zastosowanie: podczas łączenia podstawowych schematów kryptograficznych należy zawsze używać odrębnych kluczy.

Uwierzytelniony schemat szyfrowania został przedstawiony na Rysunku 10. Bob najpierw tworzy szyfrogram C z wiadomości M przy użyciu losowo wybranego klucza K_C. Następnie tworzy znacznik wiadomości T, uruchamiając szyfrogram i inny losowo wybrany klucz K_T przez algorytm generowania znaczników. Zarówno szyfrogram, jak i znacznik wiadomości są wysyłane do Alicji.

Alice sprawdza teraz najpierw, czy znacznik jest ważny, biorąc pod uwagę szyfrogram C i klucz K_T. Jeśli jest ważny, może odszyfrować wiadomość przy użyciu klucza K_C. Nie tylko ma pewność, że jej komunikacja jest bardzo tajna, ale wie również, że wiadomość została stworzona przez Boba.

Rysunek 10: Uwierzytelniony schemat szyfrowania

Figure 10: An authenticated encryption scheme

W jaki sposób tworzone są MAC? Chociaż MAC mogą być tworzone za pomocą wielu metod, powszechnym i skutecznym sposobem ich tworzenia są kryptograficzne funkcje Hash.

Kryptograficzne funkcje Hash przedstawimy dokładniej w Rozdziale 6. Na razie wystarczy wiedzieć, że funkcja Hash jest efektywnie obliczalną funkcją, która przyjmuje dane wejściowe o dowolnym rozmiarze i daje dane wyjściowe o stałej długości. Na przykład, popularna funkcja Hash SHA-256 (bezpieczny algorytm Hash 256) zawsze generuje 256-bitowe wyjście niezależnie od rozmiaru wejścia. Niektóre funkcje Hash, takie jak SHA-256, mają przydatne zastosowania w kryptografii.

Najczęstszym typem znacznika produkowanego z kryptograficzną funkcją Hash jest kod uwierzytelniania wiadomości oparty na Hash (HMAC). Proces ten został przedstawiony na Rysunku 11. Strona tworzy dwa różne klucze z klucza prywatnego K, klucz wewnętrzny K_1 i klucz zewnętrzny K_2. Tekst jawny M lub szyfrogram C jest następnie hashowany wraz z kluczem wewnętrznym. Wynik T' jest następnie mieszany z kluczem zewnętrznym w celu uzyskania znacznika wiadomości T.

Istnieje paleta funkcji Hash, których można użyć do utworzenia HMAC. Najczęściej stosowaną funkcją Hash jest SHA-256.

Rysunek 11: HMAC

Figure 11: HMAC

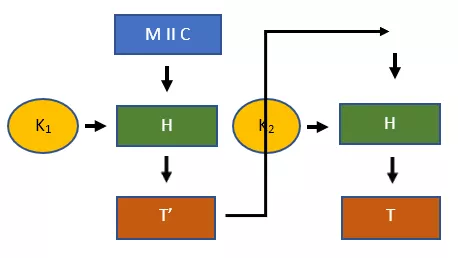
Uwagi:

[7] Konkretne wyniki omówione w tej sekcji pochodzą z Katz i Lindell, s. 131-47.

[8] Technicznie rzecz biorąc, definicja ataków z użyciem wybranego tekstu zaszyfrowanego jest inna niż pojęcie braku równoległości. Można jednak pokazać, że te dwa pojęcia bezpieczeństwa są równoważne.

Bezpieczne sesje komunikacyjne

Załóżmy, że dwie strony są w sesji komunikacyjnej, więc wysyłają wiele wiadomości tam i z powrotem.

Uwierzytelniony schemat szyfrowania pozwala odbiorcy wiadomości zweryfikować, że została ona utworzona przez jego partnera w sesji komunikacyjnej (o ile klucz prywatny nie wyciekł). Działa to wystarczająco dobrze w przypadku pojedynczej wiadomości. Zazwyczaj jednak dwie strony wysyłają wiadomości tam i z powrotem w sesji komunikacyjnej. W takim przypadku zwykły uwierzytelniony schemat szyfrowania, opisany w poprzedniej sekcji, nie zapewnia bezpieczeństwa.

Głównym powodem jest to, że uwierzytelniony schemat szyfrowania nie daje żadnych gwarancji, że wiadomość została faktycznie wysłana przez agenta, który ją utworzył w ramach sesji komunikacyjnej. Rozważmy następujące trzy wektory ataku:

  1. Atak odtwarzający: Atakujący ponownie wysyła szyfrogram i znacznik, które przechwycił między dwiema stronami we wcześniejszym momencie.

  2. Atak polegający na zmianie kolejności: Atakujący przechwytuje dwie wiadomości w różnym czasie i wysyła je do odbiorcy w odwrotnej kolejności.

  3. Atak odbiciowy: Atakujący obserwuje wiadomość wysłaną z A do B i również wysyła tę wiadomość do A.

Chociaż atakujący nie ma wiedzy o szyfrogramie i nie może tworzyć fałszywych szyfrogramów, powyższe ataki mogą nadal powodować znaczne szkody w komunikacji.

Załóżmy na przykład, że konkretna wiadomość między dwiema stronami obejmuje transfer środków finansowych. Atak typu replay może spowodować przekazanie środków po raz drugi. Uwierzytelniony schemat szyfrowania waniliowego nie chroni przed takimi atakami.

Na szczęście tego rodzaju ataki można łatwo ograniczyć w sesji komunikacyjnej przy użyciu identyfikatorów i wskaźników czasu względnego.

Identyfikatory mogą być dodawane do zwykłej wiadomości przed jej zaszyfrowaniem. Uniemożliwiłoby to wszelkie ataki z odbicia. Względnym wskaźnikiem czasu może być na przykład numer sekwencji w danej sesji komunikacyjnej. Każda ze stron dodaje numer sekwencji do wiadomości przed jej zaszyfrowaniem, dzięki czemu odbiorca wie, w jakiej kolejności wiadomości zostały wysłane. Eliminuje to możliwość ataków polegających na zmianie kolejności. Eliminuje to również ataki typu replay. Każda wiadomość wysłana przez atakującego będzie miała stary numer sekwencji, a odbiorca będzie wiedział, aby nie przetwarzać wiadomości ponownie.

Aby zilustrować, jak działają bezpieczne sesje komunikacyjne, załóżmy ponownie, że Alice i Bob. Wysyłają oni w sumie cztery wiadomości tam i z powrotem. Schemat uwierzytelnionego szyfrowania z identyfikatorami i numerami sekwencyjnymi można zobaczyć poniżej na Rysunku 11.

Sesja komunikacyjna rozpoczyna się od wysłania przez Boba szyfrogramu C_{0,B} do Alicji ze znacznikiem wiadomości T_{0,B}. Szyfrogram zawiera wiadomość, a także identyfikator (BOB) i numer sekwencyjny (0). Znacznik T_{0,B} jest tworzony dla całego szyfrogramu. W późniejszej komunikacji Alicja i Bob utrzymują ten protokół, aktualizując pola w razie potrzeby.

Rysunek 12: Sesja bezpiecznej komunikacji

Figure 12: A secure communication session

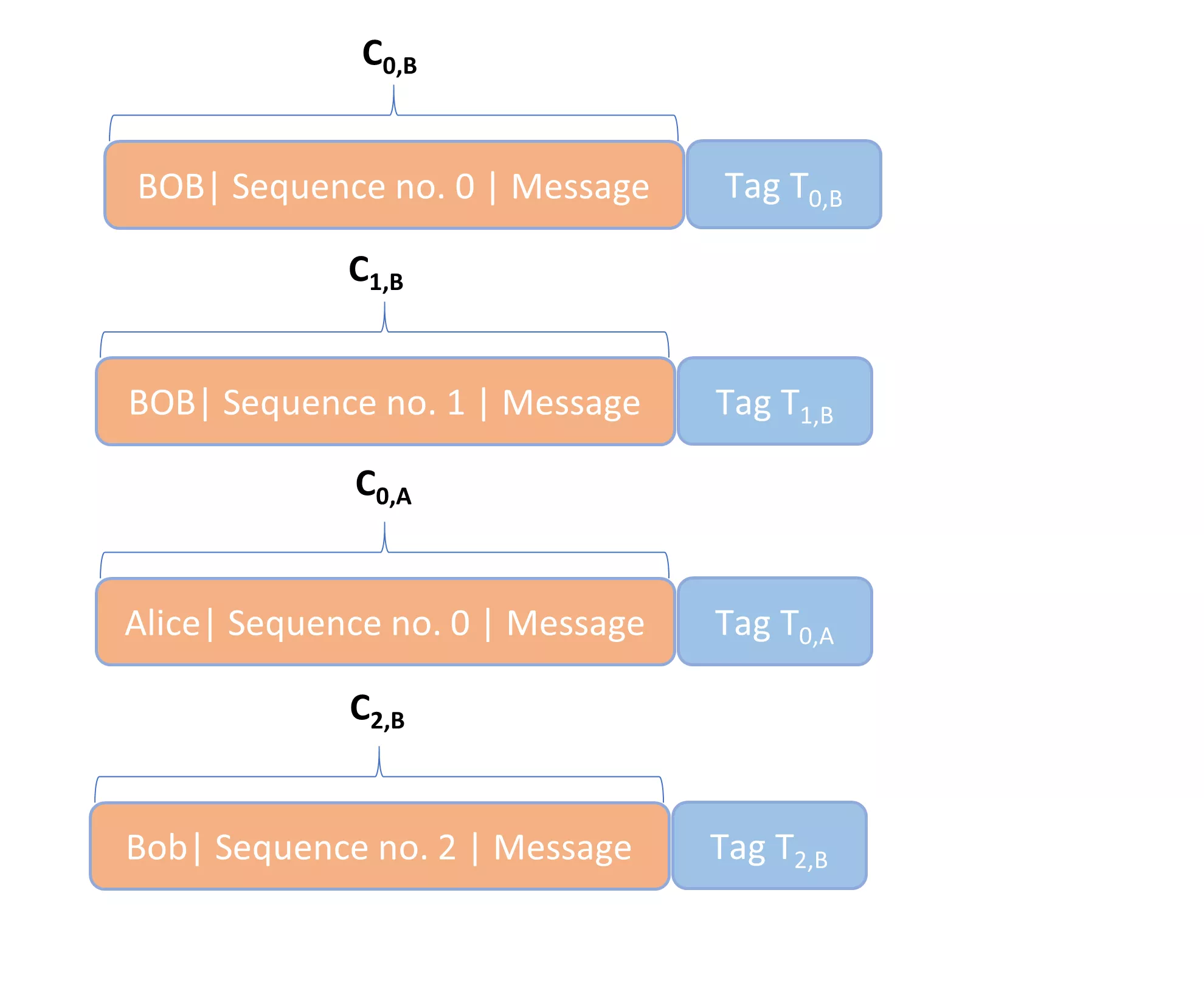
RC4 i AES

Szyfr strumieniowy RC4

W tym rozdziale omówimy szczegóły schematu szyfrowania z nowoczesnym prymitywnym szyfrem strumieniowym RC4 (lub "szyfrem Rivesta 4") i nowoczesnym szyfrem blokowym AES. Podczas gdy szyfr RC4 popadł w niełaskę jako metoda szyfrowania, AES jest standardem nowoczesnego szyfrowania symetrycznego. Te dwa przykłady powinny dać lepsze wyobrażenie o tym, jak działa szyfrowanie symetryczne pod maską.

Aby zrozumieć, jak działają nowoczesne pseudolosowe szyfry strumieniowe, skupię się na szyfrze strumieniowym RC4. Jest to pseudolosowy szyfr strumieniowy, który był używany w protokołach bezpieczeństwa bezprzewodowych punktów dostępowych WEP i WAP, a także w TLS. Ponieważ RC4 ma wiele udowodnionych słabości, popadł w niełaskę. W rzeczywistości Internet Engineering Task Force zabrania obecnie używania pakietów RC4 przez aplikacje klienckie i serwerowe we wszystkich instancjach TLS. Niemniej jednak dobrze sprawdza się jako przykład ilustrujący działanie prymitywnego szyfru strumieniowego.

Na początek pokażę, jak zaszyfrować zwykłą wiadomość za pomocą szyfru RC4. Załóżmy, że nasza wiadomość to "SOUP" Szyfrowanie za pomocą naszego szyfru RC4 przebiega w czterech krokach.

Krok 1

Najpierw zdefiniuj tablicę S od S[0] = 0 do S[7] = 7. Tablica oznacza tutaj po prostu zmienną kolekcję wartości uporządkowanych według indeksu, zwaną także listą w niektórych językach programowania (np. Python). W tym przypadku indeks wynosi od 0 do 7, a wartości również wynoszą od 0 do 7. Tak więc S wygląda następująco:

Wartości tutaj nie są liczbami ASCII, ale reprezentacjami wartości dziesiętnych 1-bajtowych ciągów. Tak więc wartość 2 będzie równa 0000 \ 0011. Długość tablicy S wynosi zatem 8 bajtów.

Krok 2

Po drugie, zdefiniuj tablicę kluczy K o długości 8 bajtów, wybierając klucz od 1 do 8 bajtów (bez dopuszczalnych ułamków bajtów). Ponieważ każdy bajt ma 8 bitów, można wybrać dowolną liczbę od 0 do 255 dla każdego bajtu klucza.

Załóżmy, że wybieramy nasz klucz k jako [14, 48, 9], tak aby miał długość 3 bajtów. Każdy indeks naszej tablicy kluczy jest następnie ustawiany zgodnie z wartością dziesiętną dla danego elementu klucza, w kolejności. Jeśli przejdziesz przez cały klucz, zacznij od początku, aż wypełnisz 8 slotów tablicy kluczy. Stąd nasza tablica kluczy wygląda następująco:

Krok 3

Po trzecie, przekształcimy tablicę S przy użyciu tablicy kluczy K, w procesie znanym jako planowanie kluczy. Proces ten wygląda następująco w pseudokodzie:

Transformacja tablicy S została przedstawiona w Tabeli 1.

Na początek można zobaczyć początkowy stan S jako [0, 1, 2, 3, 4, 5, 6, 7] z początkową wartością 0 dla j. Zostanie on przekształcony przy użyciu tablicy kluczy [14, 48, 9, 14, 48, 9, 14, 48].

Pętla for rozpoczyna się od i = 0. Zgodnie z powyższym pseudokodem, nowa wartość j wynosi 6 (j = (j + S[0] + K[0]) \mod 8 = (0 + 0 + 14) \mod 8 = 6 \mod 8). Zamieniając S[0] i S[6], stan S po 1 rundzie staje się [6, 1, 2, 3, 4, 5, 0, 7].

W następnym wierszu i = 1. Przechodząc ponownie przez pętlę for, j uzyskuje wartość 7 (j = (j + S[1] + K[1]) \mod 8 = (6 + 1 + 48) \mod 8 = 55 \mod 8 = 7 \mod 8). Zamiana S[1] i S[7] z bieżącego stanu S, [6, 1, 2, 3, 4, 5, 0, 7], daje [6, 7, 2, 3, 4, 5, 0, 1] po rundzie 2.

Kontynuujemy ten proces, aż otrzymamy ostatni wiersz na dole dla tablicy S, [6, 4, 1, 0, 3, 7, 5, 2].

Tabela 1: Tabela kluczowych harmonogramów

RoundijS[0]S[1]S[2]S[3]S[4]S[5]S[6]S[7]
Initial001234567
10661234507
21767234501
32267234501
43367234501
54367203541
65664203751
76164203752
87264103752

Krok 4

W czwartym kroku tworzymy keystream. Jest to pseudolosowy ciąg o długości równej wiadomości, którą chcemy wysłać. Zostanie on użyty do zaszyfrowania oryginalnej wiadomości "SOUP" Ponieważ strumień klucza musi być tak długi jak wiadomość, potrzebujemy takiego, który ma 4 bajty.

Strumień klucza jest generowany przez następujący pseudokod:

Obliczenia można prześledzić w Tabeli 2.

Początkowy stan S to S = [6, 4, 1, 0, 3, 7, 5, 2]. Ustawiając i = 1, wartość j wynosi 4 (j = (j + S[i]) \mod 8 = (0 + 4) \mod 8 = 4). Następnie zamieniamy S[1] i S[4], aby uzyskać transformację S w drugim rzędzie, [6, 3, 1, 0, 4, 7, 5, 2]. Wartość t wynosi wtedy 7 (t = (S[i] + S[j]) \mod 8 = (3 + 4) \mod 8 = 7). Ostatecznie bajt dla strumienia klucza to S[7], czyli 2.

Następnie kontynuujemy tworzenie innych bajtów, aż uzyskamy następujące cztery bajty: 2, 6, 3 i 7. Każdy z tych bajtów może być następnie użyty do zaszyfrowania każdej litery tekstu jawnego "SOUP".

Na początek, używając tabeli ASCII, możemy zobaczyć, że "SOUP" zakodowany przez wartości dziesiętne bazowych ciągów bajtów to "83 79 85 80". Połączenie ze strumieniem klucza "2 6 3 7" daje "85 85 88 87", który pozostaje taki sam po operacji modulo 256. W ASCII szyfrogram "85 85 88 87" jest równy "UUXW".

Co by się stało, gdyby słowo do zaszyfrowania było dłuższe niż tablica S? W takim przypadku tablica S po prostu przekształca się w sposób pokazany powyżej dla każdego bajtu i tekstu jawnego, dopóki nie uzyskamy liczby bajtów w strumieniu klucza równej liczbie liter w tekście jawnym.

Tabela 2: Generowanie strumienia klucza

ijtKeystreamS[0]S[1]S[2]S[3]S[4]S[5]S[6]S[7]
064103752
147263104752
250663704152
351363714052
417264713052

Przykład, który właśnie omówiliśmy, jest jedynie rozwodnioną wersją szyfru strumieniowego RC4. Rzeczywisty szyfr strumieniowy RC4 ma tablicę S o długości 256 bajtów, a nie 8 bajtów i klucz, który może mieć od 1 do 256 bajtów, a nie od 1 do 8 bajtów. Tablica kluczy i strumienie kluczy są następnie tworzone z uwzględnieniem 256-bajtowej długości tablicy S. Obliczenia stają się znacznie bardziej złożone, ale zasady pozostają takie same. Używając tego samego klucza, [14,48,9], ze standardowym szyfrem RC4, zwykła wiadomość "SOUP" jest szyfrowana jako 67 02 ed df w formacie szesnastkowym.

Szyfr strumieniowy, w którym strumień klucza aktualizuje się niezależnie od wiadomości tekstowej lub szyfrogramu, jest synchronicznym szyfrem strumieniowym. Strumień klucza jest zależny tylko od klucza. Oczywiście RC4 jest przykładem synchronicznego szyfru strumieniowego, ponieważ strumień klucza nie ma związku z tekstem jawnym lub szyfrogramem. Wszystkie nasze prymitywne szyfry strumieniowe wspomniane w poprzednim rozdziale, w tym szyfr przestawieniowy, szyfr Vigenère'a i szyfr jednokrotnego zapisu, były również odmianą synchroniczną.

Dla kontrastu, asynchroniczny szyfr strumieniowy ma strumień klucza, który jest wytwarzany zarówno przez klucz, jak i poprzedni Elements szyfrogramu. Ten typ szyfru jest również nazywany samosynchronizującym się szyfrem.

Co ważne, strumień klucza wytworzony za pomocą RC4 powinien być traktowany jako jednorazowa podkładka i nie można wytworzyć strumienia klucza w dokładnie taki sam sposób następnym razem. Zamiast zmieniać klucz za każdym razem, praktycznym rozwiązaniem jest połączenie klucza z Nonce w celu utworzenia strumienia bajtowego.

AES z kluczem 128-bitowym

Jak wspomniano w poprzednim rozdziale, Narodowy Instytut Standardów i Technologii (NIST) przeprowadził konkurs w latach 1997-2000 w celu określenia nowego standardu szyfrowania symetrycznego. Zwycięzcą okazał się szyfr Rijndael. Nazwa jest grą słów od nazwisk belgijskich twórców, Vincenta Rijmena i Joana Daemena.

Szyfr Rijndael jest szyfrem blokowym, co oznacza, że istnieje podstawowy algorytm, który może być używany z różnymi specyfikacjami długości kluczy i rozmiarów bloków. Można go zatem używać z różnymi trybami działania do tworzenia schematów szyfrowania.

Komitet konkursu NIST przyjął ograniczoną wersję szyfru Rijndael - mianowicie taką, która wymaga 128-bitowych rozmiarów bloków i długości klucza 128 bitów, 192 bitów lub 256 bitów - jako część Advanced Encryption Standard (AES). Ta ograniczona wersja szyfru Rijndael może być również używana w wielu trybach działania. Specyfikacja tego standardu jest znana jako Advanced Encryption Standard (AES).

Aby pokazać, jak działa szyfr Rijndael, rdzeń AES, zilustruję proces szyfrowania 128-bitowym kluczem. Rozmiar klucza ma wpływ na liczbę rund wykonywanych dla każdego bloku szyfrowania. W przypadku kluczy 128-bitowych wymagane jest 10 rund. W przypadku kluczy 192-bitowych i 256-bitowych byłoby to odpowiednio 12 i 14 rund.

Ponadto założę, że AES jest używany w trybie ECB. Ułatwia to nieco ekspozycję i nie ma znaczenia dla algorytmu Rijndael. Z pewnością tryb ECB nie jest bezpieczny w praktyce, ponieważ prowadzi do deterministycznego szyfrowania. Najczęściej używanym bezpiecznym trybem z AES jest CBC (Cipher Block Chaining).

Nazwijmy klucz K_0. Konstrukcja z powyższymi parametrami wygląda jak na Rysunku 1, gdzie M_i oznacza część tekstu jawnego o długości 128 bitów, a C_i część szyfrogramu o długości 128 bitów. Padding jest dodawany do tekstu jawnego dla ostatniego bloku, jeśli tekst jawny nie może być równo podzielony przez rozmiar bloku.

Rysunek 1: AES-ECB z kluczem 128-bitowym

Figure 1: AES-ECB with a 128-bit key

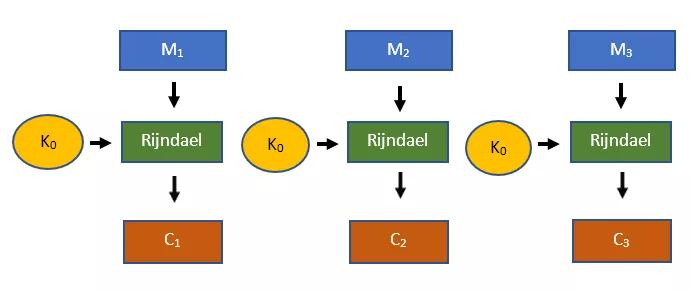
Każdy 128-bitowy blok tekstu przechodzi przez dziesięć rund w schemacie szyfrowania Rijndael. Wymaga to osobnego klucza dla każdej rundy (od K_1 do K_{10}). Są one tworzone dla każdej rundy z oryginalnego 128-bitowego klucza K_0 przy użyciu algorytmu rozszerzania klucza. W związku z tym, dla każdego bloku tekstu, który ma zostać zaszyfrowany, użyjemy oryginalnego klucza K_0, a także dziesięciu oddzielnych kluczy rundowych. Należy pamiętać, że te same 11 kluczy jest używanych dla każdego 128-bitowego bloku tekstu jawnego, który wymaga szyfrowania.

Algorytm rozszerzania klucza jest długi i złożony. Praca nad nim ma niewielką wartość dydaktyczną. Jeśli chcesz, możesz samodzielnie zapoznać się z algorytmem rozszerzania klucza. Po utworzeniu okrągłych kluczy, szyfr Rijndael będzie manipulował pierwszym 128-bitowym blokiem tekstu jawnego, M_1, jak widać na Rysunku 2. Przejdziemy teraz przez te kroki.

Rysunek 2: Manipulacja M_1 za pomocą szyfru Rijndael:

Runda 0:

Runda n dla n = {1,...,9}:

Runda 10:

Runda 0

Runda 0 szyfru Rijndael jest prosta. Tablica S_0 jest tworzona przez operację XOR między 128-bitowym tekstem jawnym a kluczem prywatnym. To znaczy,

Runda 1

W rundzie 1 tablica S_0 jest najpierw łączona z kluczem rundy K_1 przy użyciu operacji XOR. W ten sposób powstaje nowy stan S.

Po drugie, operacja zastępowania bajtów jest wykonywana na bieżącym stanie S. Działa ona poprzez pobranie każdego bajtu z 16-bajtowej tablicy S i zastąpienie go bajtem z tablicy zwanej Rijndael's S-box. Każdy bajt ma unikalną transformację, a w rezultacie powstaje nowy stan S. S-box Rijndaela jest przedstawiony na Rysunku 3.

Rysunek 3: S-Box Rijndael'a

000102030405060708090A0B0C0D0E0F
00637C777BF26B6FC53001672BFED7AB76
10CA82C97DFA5947F0ADD4A2AF9CA472C0
20B7FD9326363FF7CC34A5E5F171D83115
3004C723C31896059A071280E2EB27B275
4009832C1A1B6E5AA0523BD6B329E32F84
5053D100ED20FCB15B6ACBBE394A4C58CF
60D0EFAAFB434D338545F9027F503C9FA8
7051A3408F929D38F5BCB6DA2110FFF3D2
80CD0C13EC5F974417C4A77E3D645D1973
9060814FDC222A908846EEB814DE5E0BDB
A0E0323A0A4906245CC2D3AC629195E479
B0E7C8376D8DD54EA96C56F4EA657AAE08
C0BA78252E1CA6B4C6E8DD741F4BBD8B8A
D0703EB5664803F60E613557B986C11D9E
E0E1F8981169D98E949B1E87E9CE5528DF
F08CA1890DBFE6426841992D0FB054BB16

Ten S-Box jest jednym z miejsc, w których abstrakcyjna algebra wchodzi do gry w szyfrze Rijndael, a konkretnie pola Galois.

Na początek definiujemy każdy możliwy element bajtu od 00 do FF jako 8-bitowy wektor. Każdy taki wektor jest elementem pola Galois GF(2^8), gdzie nieredukowalnym wielomianem dla operacji modulo jest x^8 + x^4 + x^3 + x + 1. Pole Galois z tymi specyfikacjami jest również nazywane Rijndael's Finite Field.

Następnie, dla każdego możliwego elementu w polu, tworzymy tak zwane Nyberg S-Box. W tym polu każdy bajt jest mapowany na jego multiplikatywną odwrotność (tj. tak, aby ich iloczyn był równy 1). Następnie mapujemy te wartości z S-box Nyberga do S-Box Rijndaela przy użyciu transformacji afinicznej.

Trzecią operacją na tablicy S jest operacja shift rows. Pobiera ona stan S i wyświetla wszystkie szesnaście bajtów w macierzy. Wypełnianie macierzy rozpoczyna się od lewego górnego rogu i działa od góry do dołu, a następnie, za każdym razem, gdy kolumna jest wypełniana, przesuwa jedną kolumnę w prawo i do góry.

Po skonstruowaniu macierzy S cztery wiersze są przesuwane. Pierwszy rząd pozostaje bez zmian. Drugi wiersz przesuwa się o jeden w lewo. Trzeci przesuwa dwa w lewo. Czwarty wiersz przesuwa trzy wiersze w lewo. Przykład tego procesu przedstawiono na Rysunku 4. Oryginalny stan S jest pokazany na górze, a stan wynikowy po operacji przesunięcia wierszy jest pokazany poniżej.

Rysunek 4: Operacja przesunięcia wierszy

F1A0B123
59EF0982
9701B0CC
D4720421
F1A0B123
------------------------
EF098259
B0CC9701
21D47204

W czwartym kroku ponownie pojawiają się pola Galois. Na początek każda kolumna macierzy S jest mnożona przez kolumnę macierzy 4 x 4 widocznej na Rysunku 5. Ale zamiast zwykłego mnożenia macierzy, jest to mnożenie wektorowe modulo nieredukowalnego wielomianu, x^8 + x^4 + x^3 + x + 1. Wynikowe współczynniki wektora reprezentują poszczególne bity bajtu.

Rysunek 5: Macierz kolumn mieszania

02030101
01020301
01010203
03010102

Mnożenie pierwszej kolumny macierzy S z powyższą macierzą 4 x 4 daje wynik przedstawiony na Rysunku 6.

Rysunek 6: Mnożenie pierwszej kolumny:

\begin{matrix}
02 \cdot F1 + 03 \cdot EF + 01 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 02 \cdot EF + 03 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 01 \cdot EF + 02 \cdot B0 + 03 \cdot 21 \\
03 \cdot F1 + 01 \cdot EF + 01 \cdot B0 + 02 \cdot 21
\end{matrix}

W kolejnym kroku wszystkie wyrazy w macierzy musiałyby zostać przekształcone w wielomiany. Na przykład F1 reprezentuje 1 bajt i stałoby się x^7 + x^6 + x^5 + x^4 + 1, a 03 reprezentuje 1 bajt i stałoby się x + 1.

Wszystkie mnożenia są następnie wykonywane modulo x^8 + x^4 + x^3 + x + 1. Skutkuje to dodaniem czterech wielomianów w każdej z czterech komórek kolumny. Po wykonaniu tych dodawań modulo 2, otrzymamy cztery wielomiany. Każdy z tych wielomianów reprezentuje 8-bitowy ciąg lub 1 bajt S. Nie będziemy tutaj wykonywać wszystkich tych obliczeń na macierzy na Rysunku 6, ponieważ są one obszerne.

Po przetworzeniu pierwszej kolumny, pozostałe trzy kolumny macierzy S są przetwarzane w ten sam sposób. Ostatecznie da to macierz z szesnastoma bajtami, którą można przekształcić w tablicę.

W ostatnim kroku tablica S jest ponownie łączona z okrągłym kluczem w operacji XOR. W ten sposób powstaje stan S_1. To znaczy,

Rundy od 2 do 10

Rundy od 2 do 9 są po prostu powtórzeniem rundy 1, mutatis mutandis. Ostatnia runda wygląda bardzo podobnie do poprzednich, z tym wyjątkiem, że krok mieszania kolumn jest wyeliminowany. Oznacza to, że runda 10 jest wykonywana w następujący sposób:

Stan S_{10} jest teraz ustawiony na C_1, pierwsze 128 bitów szyfrogramu. Przejście przez pozostałe 128-bitowe bloki tekstu jawnego daje pełny szyfrogram C.

Operacje szyfru Rijndael

Jakie jest uzasadnienie różnych operacji w szyfrze Rijndael?

Bez wchodzenia w szczegóły, schematy szyfrowania są oceniane na podstawie stopnia, w jakim powodują zamieszanie i rozprzestrzenianie się. Jeśli schemat szyfrowania ma wysoki stopień zamieszania, oznacza to, że szyfrogram wygląda drastycznie inaczej niż tekst jawny. Jeśli schemat szyfrowania ma wysoki stopień dyfuzji, oznacza to, że każda niewielka zmiana w tekście jawnym powoduje drastycznie inny szyfrogram.

Uzasadnieniem dla operacji stojących za szyfrem Rijndael jest to, że powodują one zarówno wysoki stopień dezorientacji, jak i dyfuzji. Dezorientacja jest wytwarzana przez operację podstawiania bajtów, podczas gdy dyfuzja jest wytwarzana przez operacje przesuwania wierszy i mieszania kolumn.

Kryptografia asymetryczna

Problem dystrybucji kluczy i zarządzania nimi

Podobnie jak w przypadku kryptografii symetrycznej, schematy asymetryczne mogą być wykorzystywane do zapewnienia zarówno tajności, jak i uwierzytelniania. Jednak w przeciwieństwie do nich, schematy te wykorzystują dwa klucze zamiast jednego: klucz prywatny i klucz publiczny.

Rozpoczynamy nasze badanie od odkrycia kryptografii asymetrycznej, a zwłaszcza problemów, które ją pobudziły. Następnie omawiamy, jak asymetryczne schematy szyfrowania i uwierzytelniania działają na wysokim poziomie. Następnie wprowadzamy funkcje Hash, które są kluczem do zrozumienia asymetrycznych schematów uwierzytelniania, a także mają znaczenie w innych kontekstach kryptograficznych, takich jak kody uwierzytelniania wiadomości oparte na Hash, które omówiliśmy w rozdziale 4.

Załóżmy, że Bob chce kupić nowy płaszcz przeciwdeszczowy od Jim's Sporting Goods, internetowego sprzedawcy artykułów sportowych z milionami klientów w Ameryce Północnej. Będzie to jego pierwszy zakup w tym sklepie i chce użyć swojej karty kredytowej. Bob będzie więc musiał najpierw utworzyć konto w Jim's Sporting Goods, co wymaga przesłania danych osobowych, takich jak Address i informacje o karcie kredytowej. Następnie może przejść przez kroki niezbędne do zakupu płaszcza przeciwdeszczowego.

Bob i Jim's Sporting Goods będą chcieli upewnić się, że ich komunikacja jest bezpieczna podczas tego procesu, biorąc pod uwagę, że Internet jest otwartym systemem komunikacji. Będą chcieli na przykład upewnić się, że żaden potencjalny atakujący nie może ustalić danych karty kredytowej Boba i Address oraz że żaden potencjalny atakujący nie może powtórzyć jego zakupów lub stworzyć fałszywych zakupów w jego imieniu.

Zaawansowany uwierzytelniony schemat szyfrowania, omówiony w poprzednim rozdziale, z pewnością mógłby sprawić, że komunikacja między Bobem a Jim's Sporting Goods byłaby bezpieczna. Istnieją jednak praktyczne przeszkody w implementacji takiego schematu.

Aby zilustrować te praktyczne przeszkody, załóżmy, że żyjemy w świecie, w którym istnieją tylko narzędzia kryptografii symetrycznej. Co mogliby zrobić Jim's Sporting Goods i Bob, aby zapewnić bezpieczną komunikację?

W takich okolicznościach musieliby ponieść znaczne koszty bezpiecznej komunikacji. Ponieważ Internet jest otwartym systemem komunikacji, nie mogą po prostu Exchange zestawu kluczy za jego pośrednictwem. Dlatego Bob i przedstawiciel Jim's Sporting Goods będą musieli osobiście wykonać klucz Exchange.

Jedną z możliwości jest to, że Jim's Sporting Goods tworzy specjalne kluczowe lokalizacje Exchange, w których Bob i inni nowi klienci mogą pobrać zestaw kluczy do bezpiecznej komunikacji. Wiązałoby się to oczywiście ze znacznymi kosztami organizacyjnymi i znacznie zmniejszyłoby wydajność, z jaką nowi klienci mogą dokonywać zakupów.

Alternatywnie, Jim's Sporting Goods może wysłać Bobowi parę kluczy wysoce zaufanym kurierem. Jest to prawdopodobnie bardziej efektywne niż organizowanie kluczowych lokalizacji Exchange. Jednak nadal wiązałoby się to ze znacznymi kosztami, zwłaszcza jeśli wielu klientów dokona tylko jednego lub kilku zakupów.

Następnie, symetryczny schemat uwierzytelnionego szyfrowania zmusza również Jim's Sporting Goods do przechowywania oddzielnych zestawów kluczy dla wszystkich swoich klientów. Byłoby to znaczące wyzwanie praktyczne dla tysięcy klientów, nie mówiąc już o milionach.

Aby zrozumieć ten ostatni punkt, załóżmy, że Jim's Sporting Goods zapewnia każdemu klientowi tę samą parę kluczy. Umożliwiłoby to każdemu klientowi - lub komukolwiek innemu, kto mógłby uzyskać tę parę kluczy - odczytanie, a nawet manipulowanie całą komunikacją między Jim's Sporting Goods a jego klientami. Równie dobrze można więc w ogóle nie używać kryptografii w komunikacji.

Nawet powtarzanie zestawu kluczy tylko dla niektórych klientów jest fatalną praktyką bezpieczeństwa. Każdy potencjalny atakujący może próbować wykorzystać tę cechę schematu (należy pamiętać, że zgodnie z zasadą Kerckhoffa zakłada się, że atakujący wiedzą wszystko o schemacie oprócz kluczy)

Tak więc Jim's Sporting Goods musiałby przechowywać parę kluczy dla każdego klienta, niezależnie od tego, w jaki sposób te pary kluczy są dystrybuowane. Wiąże się to z kilkoma praktycznymi problemami.

Te dwa główne wyzwania były bardzo podstawowymi problemami aż do późnych lat 70-tych. Były one znane odpowiednio jako problem dystrybucji kluczy i problem zarządzania kluczami.

Problemy te oczywiście zawsze istniały i w przeszłości często przyprawiały o ból głowy. Siły wojskowe, na przykład, musiały stale dystrybuować książki z kluczami do bezpiecznej komunikacji dla personelu w terenie, co wiązało się z dużym ryzykiem i kosztami. Problemy te stawały się jednak coraz poważniejsze, ponieważ świat w coraz większym stopniu przechodził na długodystansową komunikację cyfrową, szczególnie w przypadku podmiotów pozarządowych.

Gdyby te problemy nie zostały rozwiązane w latach 70-tych, sprawne i bezpieczne zakupy w Jim's Sporting Goods prawdopodobnie by nie istniały. W rzeczywistości większość naszego współczesnego świata z praktyczną i bezpieczną pocztą elektroniczną, bankowością internetową i zakupami byłaby prawdopodobnie tylko odległą fantazją. Cokolwiek nawet przypominającego Bitcoin mogłoby w ogóle nie istnieć.

Co więc wydarzyło się w latach siedemdziesiątych? Jak to możliwe, że możemy błyskawicznie dokonywać zakupów online i bezpiecznie przeglądać sieć WWW? Jak to możliwe, że możemy błyskawicznie wysyłać Bitcoiny na cały świat z naszych smartfonów?

Nowe kierunki w kryptografii

W latach 70. problemy dystrybucji kluczy i zarządzania kluczami przyciągnęły uwagę grupy amerykańskich kryptografów akademickich: Whitfield Diffie, Martin Hellman i Ralph Merkle. W obliczu poważnego sceptycyzmu ze strony większości swoich kolegów, odważyli się oni opracować rozwiązanie tego problemu.

Przynajmniej jedną z głównych motywacji dla ich przedsięwzięcia było przewidywanie, że otwarta komunikacja komputerowa głęboko wpłynie na nasz świat. Jak zauważają Diffie i Helmann w 1976 roku,

Rozwój sterowanych komputerowo sieci komunikacyjnych obiecuje łatwy i tani kontakt między ludźmi lub komputerami po przeciwnych stronach świata, zastępując większość poczty i wiele wycieczek telekomunikacją. W wielu zastosowaniach kontakty te muszą być zabezpieczone zarówno przed podsłuchiwaniem, jak i wprowadzaniem nielegalnych wiadomości. Obecnie jednak rozwiązanie problemów bezpieczeństwa pozostaje daleko w tyle za innymi obszarami technologii komunikacyjnej. Współczesna kryptografia nie jest w stanie sprostać stawianym jej wymaganiom, ponieważ jej zastosowanie wiązałoby się z tak poważnymi niedogodnościami dla użytkowników systemu, że wyeliminowałoby wiele korzyści płynących z teleprzetwarzania [1]

Wytrwałość Diffiego, Hellmana i Merkle'a opłaciła się. Pierwszą publikacją ich wyników był artykuł Diffiego i Helmanna z 1976 roku zatytułowany "New Directions in Cryptography" Przedstawili w nim dwa oryginalne sposoby na rozwiązanie problemów z dystrybucją i zarządzaniem kluczami w Address.

Pierwszym zaproponowanym przez nich rozwiązaniem był zdalny protokół klucza Exchange, czyli zestaw reguł dla Exchange jednego lub więcej kluczy symetrycznych przez niezabezpieczony kanał komunikacyjny. Protokół ten jest obecnie znany jako Diffie-Helmann key Exchange lub Diffie-Helmann-Merkle key Exchange. [2]

W przypadku klucza Diffiego-Helmanna Exchange, dwie strony najpierw publicznie Exchange pewne informacje na niezabezpieczonym kanale, takim jak Internet. Następnie na podstawie tych informacji niezależnie tworzą klucz symetryczny (lub parę kluczy symetrycznych) do bezpiecznej komunikacji. Podczas gdy obie strony tworzą swoje klucze niezależnie, informacje, które udostępniły publicznie, zapewniają, że proces tworzenia klucza daje taki sam wynik dla obu stron.

Co ważne, podczas gdy każdy może obserwować informacje wymieniane publicznie przez strony za pośrednictwem niezabezpieczonego kanału, tylko dwie strony angażujące się w informacje Exchange mogą tworzyć z nich klucze symetryczne.

Brzmi to oczywiście całkowicie sprzecznie z intuicją. W jaki sposób dwie strony Exchange mogłyby upublicznić pewne informacje, które pozwoliłyby tylko im na tworzenie z nich kluczy symetrycznych? Dlaczego ktokolwiek inny obserwujący informacje Exchange nie byłby w stanie stworzyć tych samych kluczy?

Opiera się on oczywiście na pięknej matematyce. Klucz Diffiego-Helmanna Exchange działa poprzez funkcję jednokierunkową z zapadnią. Omówmy po kolei znaczenie tych dwóch terminów.

Załóżmy, że dana jest funkcja f(x) i wynik f(a) = y, gdzie a jest konkretną wartością dla x. Mówimy, że f(x) jest funkcją jednokierunkową, jeśli łatwo jest obliczyć wartość y, gdy dane są a i f(x), ale obliczeniowo niewykonalne jest obliczenie wartości a, gdy dane są y i f(x). Nazwa funkcja jednokierunkowa wynika oczywiście z faktu, że taką funkcję można obliczyć tylko w jednym kierunku.

Niektóre funkcje jednokierunkowe posiadają tak zwaną pułapkę. Podczas gdy praktycznie niemożliwe jest obliczenie a biorąc pod uwagę tylko y i f(x), istnieje pewna informacja Z, która sprawia, że obliczenie a z y jest wykonalne obliczeniowo. Ta część informacji Z jest znana jako pułapka. Funkcje jednokierunkowe, które mają zasuwę, są znane jako funkcje zasuwowe.

Nie będziemy tutaj zagłębiać się w szczegóły klucza Diffie-Helmanna Exchange. Zasadniczo jednak każdy uczestnik tworzy pewne informacje, z których część jest udostępniana publicznie, a część pozostaje tajna. Następnie każda ze stron bierze swoją tajną część informacji i informacje publiczne udostępnione przez drugą stronę, aby utworzyć klucz prywatny. I jakimś cudem obie strony otrzymają ten sam klucz prywatny.

Każda strona obserwująca tylko publicznie udostępnione informacje między dwiema stronami w Exchange klucza Diffiego Helmanna nie jest w stanie odtworzyć tych obliczeń. Aby to zrobić, potrzebowałby prywatnych informacji od jednej z dwóch stron.

Chociaż podstawowa wersja klucza Diffiego-Helmanna Exchange przedstawiona w artykule z 1976 roku nie jest zbyt bezpieczna, wyrafinowane wersje podstawowego protokołu są z pewnością nadal w użyciu. Co najważniejsze, każdy kluczowy protokół Exchange w najnowszej wersji transportowego protokołu bezpieczeństwa Layer (wersja 1.3) jest zasadniczo wzbogaconą wersją protokołu przedstawionego przez Diffiego i Hellmana w 1976 roku. Transportowy protokół bezpieczeństwa Layer jest dominującym protokołem do bezpiecznej wymiany informacji sformatowanych zgodnie z protokołem transferu hipertekstu (http), standardem wymiany treści internetowych.

Co ważne, klucz Diffiego-Helmanna Exchange nie jest schematem asymetrycznym. Ściśle rzecz biorąc, prawdopodobnie należy on do sfery kryptografii kluczy symetrycznych. Ponieważ jednak zarówno klucz Diffiego-Helmanna Exchange, jak i kryptografia asymetryczna opierają się na jednokierunkowych funkcjach liczbowo-teoretycznych z zapadniami, są one zwykle omawiane razem.

Drugim sposobem, w jaki Diffie i Helmann zaproponowali Address rozwiązanie problemu dystrybucji i zarządzania kluczami w swoim artykule z 1976 roku, była oczywiście kryptografia asymetryczna.

W przeciwieństwie do prezentacji klucza Diffiego-Hellmana w Exchange, przedstawili oni jedynie ogólne kontury tego, w jaki sposób asymetryczne schematy kryptograficzne mogłyby zostać skonstruowane. Nie zaproponowali żadnej funkcji jednokierunkowej, która mogłaby spełnić warunki potrzebne do zapewnienia odpowiedniego bezpieczeństwa w takich schematach.

Praktyczna implementacja schematu asymetrycznego została jednak znaleziona rok później przez trzech różnych akademickich kryptografów i matematyków: Ronald Rivest, Adi Shamir i Leonard Adleman. [Wprowadzony przez nich kryptosystem stał się znany jako kryptosystem RSA (od ich nazwisk).

Funkcje trapdoor używane w kryptografii asymetrycznej (i kluczu Diffiego Helmanna Exchange) są związane z dwoma głównymi problemami obliczeniowymi Hard: faktoryzacją liczb pierwszych i obliczaniem logarytmów dyskretnych.

Faktoryzacja liczb pierwszych wymaga, jak sama nazwa wskazuje, rozłożenia liczby całkowitej na czynniki pierwsze. Problem RSA jest zdecydowanie najbardziej znanym przykładem kryptosystemu związanego z faktoryzacją liczb pierwszych.

Problem logarytmu dyskretnego** jest problemem występującym w grupach cyklicznych. Biorąc pod uwagę generator w danej grupie cyklicznej, wymaga on obliczenia unikalnego wykładnika potrzebnego do wytworzenia innego elementu w grupie z generatora.

Schematy oparte na logarytmach dyskretnych opierają się na dwóch głównych rodzajach grup cyklicznych: multiplikatywnych grupach liczb całkowitych i grupach obejmujących punkty na krzywych eliptycznych. Oryginalny klucz Diffie Helmanna Exchange przedstawiony w "New Directions in Cryptography" działa z cykliczną multiplikatywną grupą liczb całkowitych. Algorytm podpisu cyfrowego Bitcoin i niedawno wprowadzony schemat podpisu Schnorra (2021) opierają się na problemie logarytmu dyskretnego dla określonej grupy cyklicznej krzywej eliptycznej.

Następnie przejdziemy do ogólnego przeglądu tajności i uwierzytelniania w środowisku asymetrycznym. Zanim jednak to zrobimy, musimy poczynić krótką wzmiankę historyczną.

Obecnie wydaje się prawdopodobne, że grupa brytyjskich kryptografów i matematyków pracujących dla Government Communications Headquarters (GCHQ) niezależnie dokonała wspomnianych odkryć kilka lat wcześniej. Grupa ta składała się z Jamesa Ellisa, Clifforda Cocksa i Malcolma Williamsona.

Według ich własnych relacji i relacji GCHQ, to James Ellis jako pierwszy opracował koncepcję kryptografii klucza publicznego w 1969 roku. Rzekomo Clifford Cocks odkrył następnie system kryptograficzny RSA w 1973 roku, a Malcolm Williamson koncepcję klucza Diffie Helmanna Exchange w 1974 roku[4]. [Ich odkrycia zostały jednak rzekomo ujawnione dopiero w 1997 roku, biorąc pod uwagę tajny charakter pracy wykonanej w GCHQ.

Uwagi:

[1] Whitfield Diffie i Martin Hellman, "New directions in cryptography", IEEE Transactions on Information Theory IT-22 (1976), s. 644-654, s. 644.

[2] Ralph Merkle omawia również kluczowy protokół Exchange w "Secure communications over insecure channels", Communications of the Association for Computing Machinery, 21 (1978), 294-99. Chociaż Merkle faktycznie przedłożył ten artykuł przed artykułem Diffiego i Hellmana, został on opublikowany później. Rozwiązanie Merkle'a nie jest wykładniczo bezpieczne, w przeciwieństwie do rozwiązania Diffiego-Hellmana.

[3] Ron Rivest, Adi Shamir i Leonard Adleman, "A method for obtaining digital signatures and public-key cryptosystems", Communications of the Association for Computing Machinery, 21 (1978), s. 120-26.

[4] Dobrą historię tych odkryć przedstawia Simon Singh, The Code Book, Fourth Estate (Londyn, 1999), rozdział 6.

Asymetryczne szyfrowanie i uwierzytelnianie

Przegląd szyfrowania asymetrycznego z pomocą Boba i Alicji przedstawiono na Rysunku 1.

Alice najpierw tworzy parę kluczy, składającą się z jednego klucza publicznego (K_P) i jednego klucza prywatnego (K_S), gdzie "P" w K_P oznacza "publiczny", a "S" w K_S oznacza "tajny". Następnie swobodnie rozpowszechnia ten klucz publiczny wśród innych osób. Do szczegółów tego procesu dystrybucji powrócimy nieco później. Na razie jednak załóżmy, że każdy, w tym Bob, może bezpiecznie uzyskać klucz publiczny K_P Alicji.

W pewnym momencie Bob chce napisać wiadomość M do Alicji. Ponieważ zawiera ona poufne informacje, Bob chce, aby jej treść pozostała tajna dla wszystkich poza Alicją. Zatem Bob najpierw szyfruje swoją wiadomość M przy użyciu K_P. Następnie wysyła wynikowy szyfrogram C do Alicji, która odszyfrowuje C za pomocą K_S, aby uzyskać oryginalną wiadomość M.

Rysunek 1: Szyfrowanie asymetryczne

Figure 1: Asymmetric encryption

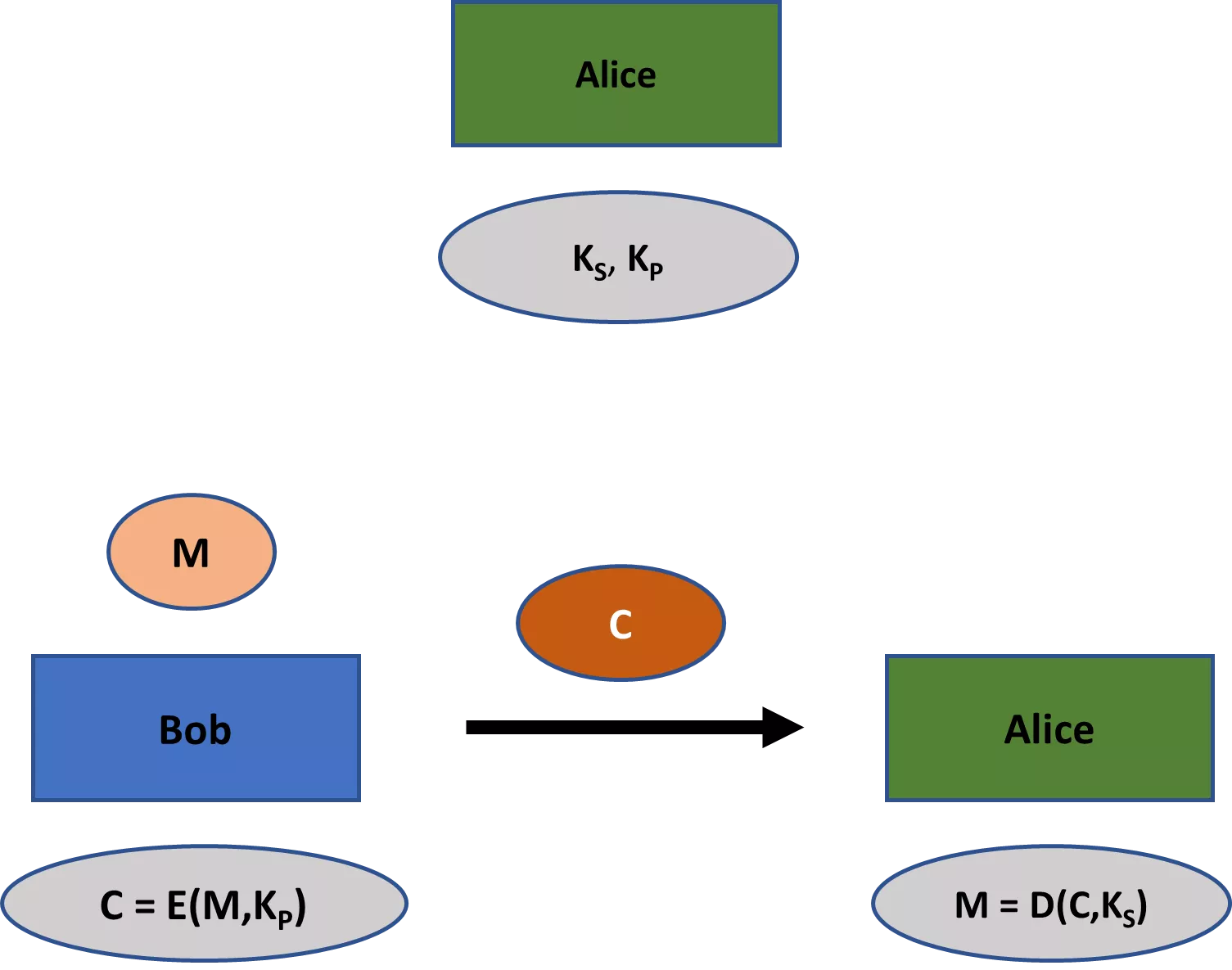
Każdy przeciwnik, który podsłuchuje komunikację Boba i Alicji, może obserwować C. Zna również K_P i algorytm szyfrowania E(\cdot). Co ważne, informacje te nie pozwalają atakującemu na odszyfrowanie szyfrogramu C. Odszyfrowanie wymaga w szczególności K_S, którego atakujący nie posiada.

Schematy szyfrowania symetrycznego zasadniczo muszą być zabezpieczone przed atakującym, który może prawidłowo zaszyfrować wiadomości z tekstem jawnym (znane jako bezpieczeństwo ataku z wybranym szyfrogramem). Nie został on jednak zaprojektowany z wyraźnym celem umożliwienia tworzenia takich ważnych szyfrogramów przez atakującego lub kogokolwiek innego.

Jest to wyraźne przeciwieństwo asymetrycznego schematu szyfrowania, w którym jego celem jest umożliwienie każdemu, w tym atakującym, tworzenia prawidłowych szyfrogramów. Schematy szyfrowania asymetrycznego można zatem określić jako szyfry wielodostępne.

Aby lepiej zrozumieć, co się dzieje, wyobraźmy sobie, że zamiast wysyłać wiadomość elektronicznie, Bob chce wysłać fizyczny list w tajemnicy. Jednym ze sposobów zapewnienia tajemnicy byłoby wysłanie przez Alicję bezpiecznej kłódki do Boba, ale zachowanie klucza do jej otwarcia. Po napisaniu listu Bob mógłby umieścić go w skrzynce i zamknąć na kłódkę Alicji. Następnie mógłby wysłać zamkniętą skrzynkę z wiadomością do Alicji, która ma klucz do jej otwarcia.

Podczas gdy Bob jest w stanie zamknąć kłódkę, ani on, ani żadna inna osoba, która przechwyci skrzynkę, nie może otworzyć kłódki, jeśli jest ona rzeczywiście zabezpieczona. Tylko Alicja może ją otworzyć i zobaczyć zawartość listu Boba, ponieważ ma klucz.

Asymetryczny schemat szyfrowania jest, z grubsza rzecz biorąc, cyfrową wersją tego procesu. Kłódka jest podobna do klucza publicznego, a klucz do kłódki jest podobny do klucza prywatnego. Ponieważ jednak kłódka jest cyfrowa, znacznie łatwiej i nie jest tak kosztowne dla Alicji dystrybuowanie jej do każdego, kto może chcieć wysłać do niej tajne wiadomości.

Do uwierzytelniania w ustawieniu asymetrycznym używamy podpisów cyfrowych. Pełnią one zatem tę samą funkcję, co kody uwierzytelniania wiadomości w ustawieniu symetrycznym. Przegląd podpisów cyfrowych przedstawiono na Rysunku 2.

Bob najpierw tworzy parę kluczy, składającą się z klucza publicznego (K_P) i klucza prywatnego (K_S), i rozpowszechnia swój klucz publiczny. Kiedy chce wysłać uwierzytelnioną wiadomość do Alicji, najpierw bierze swoją wiadomość M i swój klucz prywatny, aby utworzyć podpis cyfrowy D. Następnie Bob wysyła Alicji swoją wiadomość wraz z podpisem cyfrowym.

Alice wstawia wiadomość, klucz publiczny i podpis cyfrowy do algorytmu weryfikacji. Algorytm ten daje prawdę dla prawidłowego podpisu lub fałsz dla nieprawidłowego podpisu.

Podpis cyfrowy jest, jak sama nazwa wskazuje, cyfrowym odpowiednikiem pisemnego podpisu na listach, umowach itp. W rzeczywistości podpis cyfrowy jest zwykle znacznie bezpieczniejszy. Przy odrobinie wysiłku można sfałszować podpis pisemny; proces ten ułatwia fakt, że podpisy pisemne często nie są dokładnie weryfikowane. Bezpieczny podpis cyfrowy jest jednak, podobnie jak bezpieczny kod uwierzytelniania wiadomości, egzystencjalnie nie do sfałszowania: to znaczy, w przypadku schematu bezpiecznego podpisu cyfrowego, nikt nie może stworzyć podpisu dla wiadomości, która przejdzie procedurę weryfikacji, chyba że posiada klucz prywatny.

Rysunek 2: Uwierzytelnianie asymetryczne

Figure 2: Asymmetric authentication

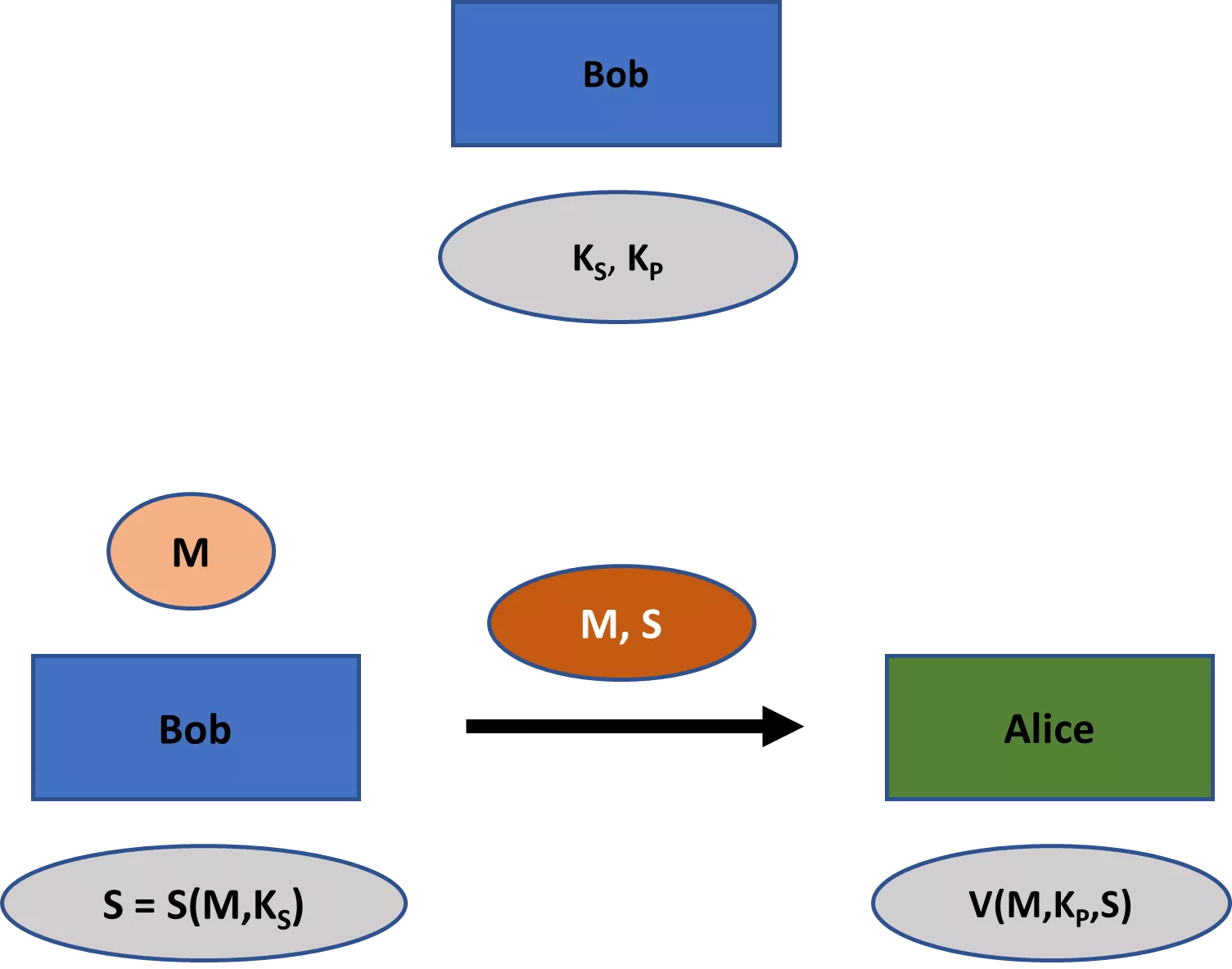
Podobnie jak w przypadku szyfrowania asymetrycznego, widzimy interesujący kontrast między podpisami cyfrowymi a kodami uwierzytelniania wiadomości. W przypadku tych drugich algorytm weryfikacji może być zastosowany tylko przez jedną ze stron mających dostęp do bezpiecznej komunikacji. Wymaga to bowiem klucza prywatnego. W asymetrycznym ustawieniu każdy może jednak zweryfikować podpis cyfrowy S złożony przez Boba.

Wszystko to sprawia, że podpis cyfrowy jest niezwykle potężnym narzędziem. Stanowi on podstawę, na przykład, do tworzenia podpisów na umowach, które mogą być weryfikowane do celów prawnych. Jeśli Bob złożył podpis na Contract w Exchange powyżej, Alicja może pokazać sądowi wiadomość M, Contract i podpis S. Sąd może następnie zweryfikować podpis przy użyciu klucza publicznego Boba. [5]

Innym przykładem są podpisy cyfrowe, które są ważnym aspektem bezpiecznej dystrybucji oprogramowania i aktualizacji oprogramowania. Ten rodzaj publicznej weryfikowalności nigdy nie mógłby zostać stworzony przy użyciu samych kodów uwierzytelniania wiadomości.

Ostatnim przykładem potęgi podpisów cyfrowych jest Bitcoin. Jednym z najczęstszych błędnych przekonań na temat Bitcoin, szczególnie w mediach, jest to, że transakcje są szyfrowane: nie są. Zamiast tego transakcje Bitcoin współpracują z podpisami cyfrowymi w celu zapewnienia bezpieczeństwa.

Bitcoiny istnieją w partiach zwanych niewydanymi transakcjami (lub UTXO). Załóżmy, że otrzymałeś trzy płatności na konkretnym Bitcoin Address po 2 bitcoiny każda. Technicznie rzecz biorąc, nie masz teraz 6 bitcoinów na tym Address. Zamiast tego masz trzy partie po 2 bitcoiny, które są zablokowane przez problem kryptograficzny związany z tym Address. Do każdej płatności możesz użyć jednej, dwóch lub wszystkich trzech partii, w zależności od tego, ile potrzebujesz do transakcji.

Dowód Ownership na niewydanych wynikach transakcji jest zwykle przedstawiany za pomocą jednego lub więcej podpisów cyfrowych. Bitcoin działa właśnie dlatego, że prawidłowe podpisy cyfrowe na niewydanych wynikach transakcji są obliczeniowo niewykonalne, chyba że jesteś w posiadaniu tajnych informacji wymaganych do ich wykonania.

Obecnie transakcje Bitcoin w przejrzysty sposób zawierają wszystkie informacje, które muszą zostać zweryfikowane przez uczestników sieci, takie jak pochodzenie niewydanych wyników transakcji wykorzystanych w transakcji. Chociaż możliwe jest ukrycie niektórych z tych informacji i nadal umożliwienie weryfikacji (jak robią to niektóre alternatywne kryptowaluty, takie jak Monero), stwarza to również szczególne zagrożenie dla bezpieczeństwa.

Niekiedy dochodzi do nieporozumień związanych z podpisami cyfrowymi i podpisami pisemnymi składanymi cyfrowo. W tym drugim przypadku użytkownik przechwytuje obraz swojego podpisu pisemnego i wkleja go do dokumentu elektronicznego, takiego jak Contract. Nie jest to jednak podpis cyfrowy w sensie kryptograficznym. Ten ostatni jest po prostu długą liczbą, którą można uzyskać tylko będąc w posiadaniu klucza prywatnego.

Podobnie jak w przypadku ustawienia klucza symetrycznego, można również używać asymetrycznych schematów szyfrowania i uwierzytelniania. Obowiązują podobne zasady. Przede wszystkim należy używać różnych par kluczy prywatno-publicznych do szyfrowania i składania podpisów cyfrowych. Ponadto należy najpierw zaszyfrować wiadomość, a następnie ją uwierzytelnić.

Co ważne, w wielu zastosowaniach kryptografia asymetryczna nie jest wykorzystywana w całym procesie komunikacji. Zamiast tego, będzie ona zazwyczaj używana tylko do Exchange kluczy symetrycznych między stronami, za pomocą których będą się one faktycznie komunikować.

Dzieje się tak na przykład w przypadku zakupu towarów online. Znając klucz publiczny sprzedawcy, może on wysyłać podpisane cyfrowo wiadomości, których autentyczność można zweryfikować. Na tej podstawie można skorzystać z jednego z wielu protokołów wymiany kluczy symetrycznych w celu bezpiecznej komunikacji.

Głównym powodem częstotliwości stosowania wspomnianego podejścia jest fakt, że kryptografia asymetryczna jest znacznie mniej wydajna niż kryptografia symetryczna w zapewnianiu określonego poziomu bezpieczeństwa. Jest to jeden z powodów, dla których nadal potrzebujemy kryptografii z kluczem symetrycznym obok kryptografii publicznej. Ponadto kryptografia z kluczem symetrycznym jest znacznie bardziej naturalna w określonych zastosowaniach, takich jak szyfrowanie własnych danych przez użytkownika komputera.

W jaki więc sposób podpisy cyfrowe i szyfrowanie kluczem publicznym Address rozwiązują problemy związane z dystrybucją kluczy i zarządzaniem nimi?

Nie ma tu jednej odpowiedzi. Kryptografia asymetryczna jest narzędziem i nie ma jednego sposobu na wykorzystanie tego narzędzia. Weźmy jednak nasz wcześniejszy przykład z Jim's Sporting Goods, aby pokazać, w jaki sposób kwestie te byłyby zazwyczaj rozwiązywane w tym przykładzie.

Aby rozpocząć, Jim's Sporting Goods prawdopodobnie zwróciłby się do urzędu certyfikacji, organizacji, która wspiera dystrybucję kluczy publicznych. Urząd certyfikacji zarejestrowałby pewne szczegóły dotyczące Jim's Sporting Goods i przyznał mu klucz publiczny. Następnie wysłałby Jim's Sporting Goods certyfikat, znany jako certyfikat TLS/SSL, z kluczem publicznym Jim's Sporting Goods podpisanym cyfrowo przy użyciu własnego klucza publicznego urzędu certyfikacji. W ten sposób urząd certyfikacji potwierdza, że określony klucz publiczny rzeczywiście należy do Jim's Sporting Goods.

Kluczem do zrozumienia tego procesu w przypadku certyfikatów TLS/SSL jest to, że chociaż generalnie nie będziesz mieć klucza publicznego Jim's Sporting Goods przechowywanego w dowolnym miejscu na komputerze, klucze publiczne uznanych urzędów certyfikacji są rzeczywiście przechowywane w przeglądarce lub w systemie operacyjnym. Są one przechowywane w tak zwanych certyfikatach głównych.

Dlatego też, gdy Jim's Sporting Goods udostępnia swój certyfikat TLS/SSL, można zweryfikować podpis cyfrowy urzędu certyfikacji za pomocą certyfikatu głównego w przeglądarce lub systemie operacyjnym. Jeśli podpis jest ważny, możesz być stosunkowo pewny, że klucz publiczny w certyfikacie rzeczywiście należy do Jim's Sporting Goods. Na tej podstawie można łatwo skonfigurować protokół bezpiecznej komunikacji z Jim's Sporting Goods.

Dystrybucja kluczy stała się teraz znacznie prostsza dla Jim's Sporting Goods. Nie jest Hard, aby zobaczyć, że zarządzanie kluczami również stało się znacznie uproszczone. Zamiast przechowywać tysiące kluczy, Jim's Sporting Goods musi jedynie przechowywać klucz prywatny, który umożliwia mu składanie podpisów pod kluczem publicznym w certyfikacie SSL. Za każdym razem, gdy klient odwiedza witrynę Jim's Sporting Goods, może ustanowić bezpieczną sesję komunikacyjną z tego klucza publicznego. Klienci nie muszą również przechowywać żadnych informacji (innych niż klucze publiczne uznanych urzędów certyfikacji w ich systemie operacyjnym i przeglądarce).

Uwagi:

[Wszelkie schematy próbujące osiągnąć niezaprzeczalność, inny temat omówiony w rozdziale 1, będą musiały opierać się na podpisach cyfrowych.

Funkcje Hash

Funkcje Hash są wszechobecne w kryptografii. Nie są one ani schematami symetrycznymi, ani asymetrycznymi, ale same w sobie należą do kategorii kryptograficznej.

Z funkcjami Hash zetknęliśmy się już w rozdziale 4 przy okazji tworzenia komunikatów uwierzytelniających opartych na Hash. Są one również ważne w kontekście podpisów cyfrowych, choć z nieco innego powodu: Podpisy cyfrowe są mianowicie zazwyczaj tworzone na podstawie wartości Hash jakiejś (zaszyfrowanej) wiadomości, a nie na podstawie samej (zaszyfrowanej) wiadomości. W tej sekcji przedstawię bardziej szczegółowe wprowadzenie do funkcji Hash.

Zacznijmy od zdefiniowania funkcji Hash. Funkcja Hash to dowolna efektywnie obliczalna funkcja, która przyjmuje dane wejściowe o dowolnym rozmiarze i daje dane wyjściowe o stałej długości.

Kryptograficzna funkcja Hash to po prostu funkcja Hash, która jest przydatna do zastosowań w kryptografii. Wynik funkcji kryptograficznej Hash jest zwykle nazywany Hash, wartością Hash lub skrótem wiadomości.

W kontekście kryptografii "funkcja Hash" zazwyczaj odnosi się do kryptograficznej funkcji Hash. Przyjmę tę praktykę od teraz.

Przykładem popularnej funkcji Hash jest SHA-256 (bezpieczny algorytm Hash 256). Niezależnie od rozmiaru danych wejściowych (np. 15 bitów, 100 bitów lub 10 000 bitów), funkcja ta da 256-bitową wartość Hash. Poniżej znajduje się kilka przykładowych wyników funkcji SHA-256.

"Hello": 185f8db32271fe25f561a6fc938b2e264306ec304eda518007d1764826381969

"52398": a3b14d2bf378c1bd47e7f8eaec63b445150a3d7a80465af16dd9fd319454ba90

"Kryptografia jest fajna": 3cee2a5c7d2cc1d62db4893564c34ae553cc88623992d994e114e344359b146c

Wszystkie dane wyjściowe to dokładnie 256 bitów zapisanych w formacie szesnastkowym (każda cyfra szesnastkowa może być reprezentowana przez cztery cyfry binarne). Więc nawet gdybyś wstawił książkę Tolkiena Władca Pierścieni do funkcji SHA-256, wynik nadal wynosiłby 256 bitów.

Funkcje Hash, takie jak SHA-256, są wykorzystywane do różnych celów w kryptografii. To, jakie właściwości są wymagane od funkcji Hash, zależy tak naprawdę od kontekstu konkretnego zastosowania. Istnieją dwie główne właściwości ogólnie pożądane od funkcji Hash w kryptografii: [6]

  1. Odporność na kolizje

  2. Ukrywanie

O funkcji Hash H mówi się, że jest odporna na kolizje, jeśli nie jest możliwe znalezienie dwóch wartości, x i y, takich, że x \neq y, a H(x) = H(y).

Odporne na kolizje funkcje Hash są ważne na przykład przy weryfikacji oprogramowania. Załóżmy, że chcesz pobrać wersję Bitcoin Core 0.21.0 dla systemu Windows (aplikacja serwerowa do przetwarzania ruchu sieciowego Bitcoin). Główne kroki, które należałoby wykonać, aby zweryfikować legalność oprogramowania, są następujące:

  1. Najpierw należy pobrać i zaimportować klucze publiczne jednego lub więcej współtwórców Bitcoin Core do oprogramowania, które może weryfikować podpisy cyfrowe (np. Kleopetra). Te klucze publiczne można znaleźć [tutaj] (https://github.com/Bitcoin/Bitcoin/blob/master/contrib/builder-keys/keys.txt). Zaleca się zweryfikowanie oprogramowania Bitcoin Core za pomocą kluczy publicznych od wielu dostawców.

  2. Następnie należy zweryfikować zaimportowane klucze publiczne. Przynajmniej jednym krokiem, który powinieneś podjąć, jest sprawdzenie, czy znalezione klucze publiczne są takie same, jak opublikowane w różnych innych lokalizacjach. Możesz na przykład zapoznać się z osobistymi stronami internetowymi, stronami Twittera lub stronami Github osób, których klucze publiczne zaimportowałeś. Zazwyczaj porównanie kluczy publicznych odbywa się poprzez porównanie krótkiego Hash klucza publicznego znanego jako odcisk palca.

  3. Następnie należy pobrać plik wykonywalny dla Bitcoin Core z ich [strony internetowej] (www.bitcoincore.org). Dostępne będą pakiety dla systemów operacyjnych Linux, Windows i MAC.

  4. Następnie należy zlokalizować dwa pliki wydania. Pierwszy z nich zawiera oficjalny SHA-256 Hash dla pobranego pliku wykonywalnego wraz ze skrótami wszystkich innych wydanych pakietów. Kolejny plik wydania będzie zawierał podpisy różnych współtwórców nad plikiem wydania wraz ze skrótami pakietów. Oba te pliki powinny znajdować się na stronie Bitcoin Core.

  5. Następnie należy obliczyć SHA-256 Hash pliku wykonywalnego pobranego ze strony Bitcoin Core na własnym komputerze. Następnie należy porównać ten wynik z oficjalnym pakietem Hash dla pliku wykonywalnego. Powinny one być takie same.

  6. Na koniec należy zweryfikować, czy jeden lub więcej podpisów cyfrowych nad plikiem wydania z oficjalnymi skrótami pakietów rzeczywiście odpowiada jednemu lub więcej zaimportowanym kluczom publicznym (wydania Bitcoin Core nie zawsze są podpisywane przez wszystkich). Można to zrobić za pomocą aplikacji takiej jak Kleopetra.

Ten proces weryfikacji oprogramowania ma dwie główne zalety. Po pierwsze, gwarantuje, że podczas pobierania ze strony Bitcoin Core nie wystąpiły błędy w transmisji. Po drugie, gwarantuje, że żaden atakujący nie mógł nakłonić użytkownika do pobrania zmodyfikowanego, złośliwego kodu, ani poprzez włamanie na stronę Bitcoin Core, ani poprzez przechwycenie ruchu.

Jak dokładnie powyższy proces weryfikacji oprogramowania chroni przed tymi problemami?

Jeśli starannie zweryfikowałeś zaimportowane klucze publiczne, możesz być całkiem pewny, że te klucze są rzeczywiście ich i nie zostały naruszone. Biorąc pod uwagę, że podpisy cyfrowe mają egzystencjalną niemożliwość podrobienia, wiesz, że tylko ci współtwórcy mogli złożyć podpis cyfrowy nad oficjalnymi skrótami pakietów w pliku wydania.

Załóżmy, że podpisy na pobranym pliku wydania zostały sprawdzone. Możesz teraz porównać wartość Hash obliczoną lokalnie dla pobranego pliku wykonywalnego Windows z wartością zawartą w prawidłowo podpisanym pliku wydania. Jak wiadomo, funkcja SHA-256 Hash jest odporna na kolizje, a zgodność oznacza, że plik wykonywalny jest dokładnie taki sam jak oficjalny plik wykonywalny.

Przejdźmy teraz do drugiej wspólnej właściwości funkcji Hash: ukrywanie. O dowolnej funkcji Hash H mówi się, że ma własność ukrywania, jeśli dla dowolnego losowo wybranego x z bardzo dużego przedziału, znalezienie x jest niewykonalne, gdy tylko dana jest H(x).

Poniżej znajduje się wynik SHA-256 napisanej przeze mnie wiadomości. Aby zapewnić wystarczającą losowość, wiadomość zawierała losowo wygenerowany ciąg znaków na końcu. Biorąc pod uwagę, że SHA-256 ma właściwość ukrywania, nikt nie byłby w stanie odszyfrować tej wiadomości.

Ale nie pozostawię was w niepewności, dopóki SHA-256 nie stanie się słabszy. Oryginalna wiadomość, którą napisałem, brzmiała następująco:

Powszechnym sposobem wykorzystania funkcji Hash z właściwością ukrywania jest zarządzanie hasłami (odporność na kolizje jest również ważna dla tego zastosowania). Każda przyzwoita usługa online oparta na koncie, taka jak Facebook lub Google, nie będzie przechowywać haseł bezpośrednio w celu zarządzania dostępem do konta. Zamiast tego będą przechowywać tylko Hash tego hasła. Za każdym razem, gdy wpisujesz hasło w przeglądarce, najpierw obliczany jest Hash. Tylko ten Hash jest wysyłany do serwera usługodawcy i porównywany z Hash przechowywanym w bazie danych zaplecza. Właściwość ukrywania może pomóc zapewnić, że atakujący nie będą mogli odzyskać jej z wartości Hash.

Zarządzanie hasłami za pomocą skrótów działa oczywiście tylko wtedy, gdy użytkownicy faktycznie wybierają trudne hasła. Właściwość ukrywania zakłada, że x jest wybierane losowo z bardzo dużego zakresu. Wybieranie haseł takich jak "1234", "mypassword" lub data urodzin nie zapewni żadnego realnego bezpieczeństwa. Istnieją długie listy popularnych haseł i ich skrótów, które atakujący mogą wykorzystać, jeśli kiedykolwiek uzyskają Hash hasła. Tego typu ataki znane są jako ataki słownikowe. Jeśli atakujący znają niektóre z twoich danych osobowych, mogą również próbować zgadywać. Dlatego zawsze potrzebujesz długich, bezpiecznych haseł (najlepiej długich, losowych ciągów z menedżera haseł).

Czasami aplikacja może potrzebować funkcji Hash, która ma zarówno odporność na kolizje, jak i ukrywanie. Ale z pewnością nie zawsze. Na przykład proces weryfikacji oprogramowania, który omówiliśmy, wymaga jedynie, aby funkcja Hash wykazywała odporność na kolizje, ukrywanie nie jest ważne.

Podczas gdy odporność na kolizje i ukrywanie są głównymi właściwościami poszukiwanymi przez funkcje Hash w kryptografii, w niektórych zastosowaniach pożądane mogą być również inne rodzaje właściwości.

Uwagi:

[6] Terminologia "ukrywania" nie jest językiem potocznym, ale została zaczerpnięta z książki Arvinda Narayanana, Josepha Bonneau, Edwarda Feltena, Andrew Millera i Stevena Goldfedera, Bitcoin and Cryptocurrency Technologies, Princeton University Press (Princeton, 2016), rozdział 1.

Kryptosystem RSA

Problem z faktoringiem

Podczas gdy kryptografia symetryczna jest zwykle dość intuicyjna dla większości ludzi, zwykle nie jest tak w przypadku kryptografii asymetrycznej. Mimo, że prawdopodobnie nie masz problemu z wysokopoziomowym opisem przedstawionym w poprzednich sekcjach, prawdopodobnie zastanawiasz się, czym dokładnie są funkcje jednokierunkowe i jak dokładnie są one wykorzystywane do konstruowania schematów asymetrycznych.

W tym rozdziale rozwieję część tajemnic związanych z kryptografią asymetryczną, analizując bardziej szczegółowo konkretny przykład, a mianowicie kryptosystem RSA. W pierwszej sekcji przedstawię problem faktoryzacji, na którym opiera się problem RSA. Następnie omówię kilka kluczowych wyników z teorii liczb. W ostatniej sekcji połączymy te informacje, aby wyjaśnić problem RSA i sposób, w jaki można go wykorzystać do tworzenia asymetrycznych schematów kryptograficznych.

Dodanie tej głębi do naszej dyskusji nie jest łatwym zadaniem. Wymaga to wprowadzenia kilku twierdzeń i propozycji z zakresu teorii liczb. Nie pozwól jednak, by matematyka cię zniechęciła. Praca nad tą dyskusją znacznie poprawi twoje zrozumienie tego, co leży u podstaw kryptografii asymetrycznej i jest wartą zachodu inwestycją.

Przejdźmy teraz do problemu faktoryzacji.

Ilekroć mnożymy dwie liczby, powiedzmy a i b, liczby a i b nazywamy czynnikami, a wynik produktem. Próba zapisania liczby N w postaci mnożenia dwóch lub więcej czynników nazywana jest faktoryzacją lub faktoryzacją. [1] Każdy problem, który tego wymaga można nazwać problemem faktoryzacji.

Około 2500 lat temu grecki matematyk Euklides z Aleksandrii odkrył kluczowe twierdzenie dotyczące faktoryzacji liczb całkowitych. Jest ono powszechnie nazywane unikalnym twierdzeniem o faktoryzacji i stwierdza, co następuje:

Twierdzenie 1. Każda liczba całkowita N, która jest większa od 1, jest liczbą pierwszą lub może być wyrażona jako iloczyn czynników pierwszych.

Ostatnia część tego stwierdzenia oznacza, że można wziąć dowolną liczbę całkowitą N większą od 1 i zapisać ją jako iloczyn liczb pierwszych. Poniżej znajduje się kilka przykładów liczb całkowitych innych niż pierwsze zapisanych jako iloczyn czynników pierwszych.

Dla wszystkich trzech powyższych liczb całkowitych, obliczenie ich czynników pierwszych jest stosunkowo łatwe, nawet jeśli masz tylko N. Zaczynamy od najmniejszej liczby pierwszej, czyli 2, i sprawdzamy, ile razy liczba całkowita N jest przez nią podzielna. Następnie przechodzimy do testowania podzielności N przez 3, 5, 7 itd. Proces ten należy kontynuować do momentu, gdy liczba całkowita N zostanie zapisana jako iloczyn wyłącznie liczb pierwszych.

Weźmy na przykład liczbę całkowitą 84. Poniżej przedstawiono proces wyznaczania jej czynników pierwszych. W każdym kroku usuwamy najmniejszy pozostały czynnik pierwszy (po lewej) i określamy resztę, która ma zostać poddana faktoryzacji. Kontynuujemy aż do momentu, gdy reszta również będzie liczbą pierwszą. W każdym kroku po prawej stronie wyświetlana jest bieżąca faktoryzacja liczby 84.

Załóżmy teraz, że liczba N jest bardzo duża. Jak trudno byłoby rozłożyć N na czynniki pierwsze?

To naprawdę zależy od N. Załóżmy na przykład, że N wynosi 50 450 400. Choć liczba ta wygląda onieśmielająco, obliczenia nie są aż tak skomplikowane i można je łatwo wykonać ręcznie. Podobnie jak powyżej, wystarczy zacząć od 2 i pracować dalej. Poniżej możesz zobaczyć wynik tego procesu w podobny sposób jak powyżej.

Ręczne rozwiązywanie tego problemu zajmuje trochę czasu. Komputer mógłby oczywiście zrobić to wszystko w ułamku sekundy. W rzeczywistości, komputer często może nawet faktoryzować bardzo duże liczby całkowite w ułamku sekundy.

Istnieją jednak pewne wyjątki. Załóżmy, że najpierw losowo wybieramy dwie bardzo duże liczby pierwsze. Typowe jest oznaczanie tych liczb p i q i taką konwencję przyjmę tutaj.

Dla uściślenia, powiedzmy, że p i q są 1024-bitowymi liczbami pierwszymi i że rzeczywiście wymagają co najmniej 1024 bitów, aby mogły być reprezentowane (więc pierwszy bit musi wynosić 1). Tak więc, na przykład, 37 nie może być jedną z liczb pierwszych. Z pewnością można przedstawić 37 za pomocą 1024 bitów. Ale najwyraźniej nie potrzebujesz tylu bitów do jej reprezentacji. Liczbę 37 można przedstawić za pomocą dowolnego ciągu, który ma 6 lub więcej bitów. (W 6 bitach, 37 byłoby reprezentowane jako 100101).

Ważne jest, aby docenić, jak duże są p i q, jeśli zostaną wybrane zgodnie z powyższymi warunkami. Jako przykład wybrałem losową liczbę pierwszą, która wymaga co najmniej 1024 bitów do reprezentacji poniżej.

Załóżmy teraz, że po losowym wybraniu liczb pierwszych p i q, mnożymy je w celu uzyskania liczby całkowitej N. Ta ostatnia liczba całkowita jest zatem liczbą 2048-bitową, która wymaga co najmniej 2048 bitów do swojej reprezentacji. Jest ona znacznie, znacznie większa niż p lub q.

Załóżmy, że dajemy komputerowi tylko N i prosimy go o znalezienie dwóch 1024-bitowych czynników pierwszych liczby N. Prawdopodobieństwo, że komputer odkryje p i q jest niezwykle małe. Można powiedzieć, że jest to niemożliwe ze względów praktycznych. Dzieje się tak nawet w przypadku zastosowania superkomputera lub nawet sieci superkomputerów.

Na początek załóżmy, że komputer próbuje rozwiązać problem, przechodząc przez 1024 bitowe liczby, sprawdzając w każdym przypadku, czy są one pierwsze i czy są czynnikami N. Zbiór liczb pierwszych do przetestowania wynosi wtedy około 1,265 \cdot 10^{305}. [2]

Nawet jeśli weźmiemy wszystkie komputery na planecie i poprosimy je o próbę znalezienia i przetestowania 1024-bitowych liczb pierwszych w ten sposób, szansa 1 na miliard na pomyślne znalezienie czynnika pierwszego N wymagałaby okresu obliczeń znacznie dłuższego niż wiek Wszechświata.

W praktyce komputer radzi sobie lepiej niż opisana przed chwilą przybliżona procedura. Istnieje kilka algorytmów, które komputer może zastosować, aby szybciej uzyskać faktoryzację. Chodzi jednak o to, że nawet przy użyciu tych bardziej wydajnych algorytmów, zadanie komputera jest nadal niewykonalne obliczeniowo. [3]

Co ważne, trudność faktoryzacji w opisanych warunkach opiera się na założeniu, że nie istnieją efektywne obliczeniowo algorytmy obliczania czynników pierwszych. Nie możemy udowodnić, że efektywny algorytm nie istnieje. Niemniej jednak założenie to jest bardzo prawdopodobne: pomimo intensywnych wysiłków trwających setki lat, nie udało nam się jeszcze znaleźć takiego efektywnego obliczeniowo algorytmu.

W związku z tym, problem faktoryzacji, w pewnych okolicznościach, może zostać uznany za problem Hard. W szczególności, gdy p i q są bardzo dużymi liczbami pierwszymi, ich iloczyn N nie jest trudny do obliczenia; ale faktoryzacja tylko N jest praktycznie niemożliwa.

Uwagi:

[1] Faktoryzacja może być również ważna przy pracy z innymi typami obiektów matematycznych niż liczby. Na przykład, przydatne może być faktoryzowanie wyrażeń wielomianowych, takich jak x^2 - 2x + 1. W naszej dyskusji skupimy się tylko na faktoryzacji liczb, w szczególności liczb całkowitych.

[2] Zgodnie z twierdzeniem o liczbach pierwszych, liczba liczb pierwszych mniejszych lub równych N wynosi w przybliżeniu N/\LN(N). Oznacza to, że można przybliżyć liczbę liczb pierwszych o długości 1024 bitów przez:

\frac{2^{1024}}{\LN(2^{1024})} - \frac{2^{1023}}{\LN(2^{1023})}

...co równa się w przybliżeniu 1,265 razy 10^{305}.

to samo dotyczy problemów logarytmu dyskretnego [3]. Dlatego też konstrukcje asymetryczne działają z dużo większymi kluczami niż symetryczne konstrukcje kryptograficzne.

Wyniki teorii liczb

Niestety, problem faktoryzacji nie może być bezpośrednio wykorzystany w asymetrycznych schematach kryptograficznych. Możemy jednak wykorzystać w tym celu bardziej złożony, ale pokrewny problem: problem RSA.

Aby zrozumieć problem RSA, będziemy musieli zrozumieć szereg twierdzeń i propozycji z teorii liczb. Zostały one przedstawione w tej sekcji w trzech podrozdziałach: (1) porządek N, (2) odwracalność modulo N i (3) twierdzenie Eulera.

Część materiału zawartego w tych trzech podrozdziałach została już przedstawiona w Rozdziale 3. Ale dla wygody powtórzę ten materiał tutaj.

Kolejność N

Liczba całkowita a jest coprime lub relative prime z liczbą całkowitą N, jeśli największy wspólny dzielnik między nimi wynosi 1. Chociaż 1 nie jest umownie liczbą pierwszą, jest ona coprime każdej liczby całkowitej (podobnie jak -1).

Dla przykładu, rozważmy przypadek, gdy a = 18 i N = 37. Są to liczby całkowite. Największą liczbą całkowitą, która dzieli zarówno 18, jak i 37 jest 1. Dla kontrastu, rozważmy przypadek, gdy a = 42 i N = 16. Wyraźnie nie są to liczby całkowite. Obie liczby są podzielne przez 2, czyli większe niż 1.

Możemy teraz zdefiniować rząd N w następujący sposób. Przypuśćmy, że N jest liczbą całkowitą większą od 1. Porządek N jest zatem liczbą wszystkich koprimów z N takich, że dla każdego koprimu a zachodzi następujący warunek: 1 \leq a < N.

Na przykład, jeśli N = 12, to 1, 5, 7 i 11 są jedynymi liczbami całkowitymi spełniającymi powyższy warunek. Stąd rząd 12 jest równy 4.

Załóżmy, że N jest liczbą pierwszą. Wtedy każda liczba całkowita mniejsza od N, ale większa lub równa 1, jest z nią współliniowa. Obejmuje to wszystkie Elements w następującym zbiorze: \{1,2,3,....,N - 1\}. Stąd, gdy N jest liczbą pierwszą, rząd N wynosi N - 1. Stwierdza to teza 1, gdzie \phi(N) oznacza rząd N.

Propozycja 1. \phi(N) = N - 1, gdy N jest liczbą pierwszą

Załóżmy, że N nie jest liczbą pierwszą. Można wtedy obliczyć jego rząd za pomocą funkcji Phi Eulera. Podczas gdy obliczenie rzędu małej liczby całkowitej jest stosunkowo proste, funkcja Phi Eulera staje się szczególnie ważna dla większych liczb całkowitych. Twierdzenie o funkcji Phi Eulera przedstawiono poniżej.

Twierdzenie 2. Niech N będzie równe p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot p_i^{e_i} \cdot \ldots \cdot p_n^{e_n}, gdzie zbiór \{p_i\} składa się ze wszystkich różnych czynników pierwszych N, a każde e_i wskazuje, ile razy czynnik pierwszy p_i występuje dla N. Następnie,

\phi(N) = p_1^{e_1 - 1} \cdot (p_1 - 1) \cdot p_2^{e_2 - 1} \cdot (p_2 - 1) \cdot \ldots \cdot p_n^{e_n - 1} \cdot (p_n - 1)

Twierdzenie 2 pokazuje, że po rozłożeniu dowolnej liczby nie pierwszej N na czynniki pierwsze, łatwo jest obliczyć rząd liczby N.

Załóżmy na przykład, że N = 270. Nie jest to oczywiście liczba pierwsza. Rozkładając N na czynniki pierwsze otrzymamy wyrażenie: 2 \cdot 3^3 \cdot 5. Zgodnie z funkcją Phi Eulera, rząd liczby N jest następujący:

\phi(N) = 2^{1 - 1} \cdot (2 - 1) + 3^{3 - 1} \cdot (3 - 1) + 5^{1 - 1} \cdot (5 - 1) = 1 \cdot 1 + 9 \cdot 2 + 1 \cdot 4 = 1 + 18 + 4 = 23

Załóżmy następnie, że N jest iloczynem dwóch liczb pierwszych, p i q. powyższe Twierdzenie 2 stwierdza, że porządek N jest następujący:

p^{1 - 1} \cdot (p - 1) \cdot q^{1 - 1} \cdot (q - 1) = (p - 1) \cdot (q - 1)

Jest to kluczowy wynik w szczególności dla problemu RSA i został przedstawiony w Propozycji 2 poniżej.

Propozycja 2. Jeśli N jest iloczynem dwóch liczb pierwszych, p i q, to rząd N jest iloczynem (p - 1) \cdot (q - 1).

Aby to zilustrować, załóżmy, że N = 119. Ta liczba całkowita może być podzielona na dwie liczby pierwsze, a mianowicie 7 i 17. Stąd funkcja Phi Eulera sugeruje, że kolejność 119 jest następująca:

\phi(119) = (7 - 1) \cdot (17 - 1) = 6 \cdot 16 = 96

Innymi słowy, liczba całkowita 119 ma 96 wielokrotności w zakresie od 1 do 119. W rzeczywistości zbiór ten obejmuje wszystkie liczby całkowite od 1 do 119, które nie są wielokrotnościami liczby 7 lub 17.

Od tego momentu oznaczmy zbiór liczb całkowitych, które określają kolejność N jako C_N. Dla naszego przykładu, gdzie N = 119, zbiór C_{119} jest zbyt duży, by go w całości wyliczyć. Ale niektóre z Elements są następujące:

C_{119} = \{1, 2, \punkty 6, 8 \punkty 13, 15, 16, 18, \punkty 33, 35 \punkty 96\}

Odwracalność modulo N

Możemy powiedzieć, że liczba całkowita a jest odwracalna modulo N, jeśli istnieje co najmniej jedna liczba całkowita b taka, że a \cdot b \mod N = 1 \mod N. Każda taka liczba całkowita b jest nazywana odwrotnością (lub multiplikatywną odwrotnością) liczby a przy redukcji przez modulo N.

Załóżmy na przykład, że a = 5 i N = 11. Istnieje wiele liczb całkowitych, przez które można pomnożyć 5, tak aby 5 \cdot b \mod 11 = 1 \mod 11. Rozważmy na przykład liczby całkowite 20 i 31. Łatwo zauważyć, że obie te liczby całkowite są odwrotnościami 5 dla redukcji modulo 11.

Podczas gdy 5 ma wiele odwrotności redukujących się modulo 11, można pokazać, że istnieje tylko jedna dodatnia odwrotność 5, która jest mniejsza niż 11. W rzeczywistości nie jest to unikalne dla naszego konkretnego przykładu, ale ogólny wynik.

Propozycja 3. Jeśli liczba całkowita a jest odwracalna modulo N, to musi zachodzić przypadek, że dokładnie jedna dodatnia odwrotność liczby a jest mniejsza niż N. (Zatem ta jedyna odwrotność liczby a musi pochodzić ze zbioru \{1, \dots, N - 1\}).

Oznaczmy unikalną odwrotność a z Propozycji 3 jako a^{-1}. Dla przypadku, gdy a = 5 i N = 11, można zauważyć, że a^{-1} = 9, biorąc pod uwagę, że 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11.

Zauważ, że wartość 9 dla a^{-1} w naszym przykładzie można również uzyskać po prostu redukując dowolną inną odwrotność a przez modulo 11. Na przykład, 20 \mod 11 = 31 \mod 11 = 9 \mod 11. Jeśli więc liczba całkowita a > N jest odwracalna modulo N, to a \mod N również musi być odwracalna modulo N.

Niekoniecznie jest tak, że odwrotność a istnieje w redukcji modulo N. Załóżmy na przykład, że a = 2 i N = 8. Nie istnieje b, ani konkretnie a^{-1}, dla którego 2 \cdot b \mod 8 = 1 \mod 8. Dzieje się tak dlatego, że każda wartość b zawsze daje wielokrotność 2, więc żadne dzielenie przez 8 nie może dać reszty równej 1.

Skąd dokładnie wiemy, czy jakaś liczba całkowita a ma odwrotność dla danego N? Jak być może zauważyłeś w powyższym przykładzie, największy wspólny dzielnik między 2 a 8 jest większy niż 1, a mianowicie 2. Jest to ilustracja następującego ogólnego wyniku:

Propozycja 4. Istnieje odwrotność liczby całkowitej a przy danej redukcji modulo N, a w szczególności unikalna dodatnia odwrotność mniejsza niż N, wtedy i tylko wtedy, gdy największy wspólny dzielnik liczb a i N wynosi 1 (to znaczy, gdy są one koprimami).

Dla przypadku, gdy a = 5 i N = 11, doszliśmy do wniosku, że a^{-1} = 9, biorąc pod uwagę, że 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11. Ważne jest, aby zauważyć, że sytuacja odwrotna jest również prawdziwa. Oznacza to, że gdy a = 9 i N = 11, to a^{-1} = 5.

Twierdzenie Eulera

Zanim przejdziemy do problemu RSA, musimy zrozumieć jeszcze jedno kluczowe twierdzenie, a mianowicie twierdzenie Eulera. Stwierdza ono, co następuje:

Twierdzenie 3. Załóżmy, że dwie liczby całkowite a i N są liczbami całkowitymi. Wtedy a^{\phi(N)} \mod N = 1 \mod N.

Jest to niezwykły wynik, ale na początku nieco mylący. Aby to zrozumieć, posłużmy się przykładem.

Załóżmy, że a = 5 i N = 7. Są to rzeczywiście liczby pierwsze, jak wymaga tego twierdzenie Eulera. Wiemy, że rząd 7 jest równy 6, biorąc pod uwagę, że 7 jest liczbą pierwszą (patrz Propozycja 1).

Twierdzenie Eulera mówi, że 5^6 \mod 7 musi być równe 1 \mod 7. Poniżej znajdują się obliczenia pokazujące, że jest to prawdą.

Liczba całkowita 7 dzieli się przez 15 624 łącznie 2 233 razy. Stąd reszta z dzielenia 16 625 przez 7 wynosi 1.

Następnie, używając funkcji Phi Eulera, Twierdzenie 2, można wyprowadzić Propozycję 5 poniżej.

Propozycja 5. \phi(a \cdot b) = \phi(a) \cdot \phi(b) dla dowolnych dodatnich liczb całkowitych a i b.

Nie będziemy pokazywać, dlaczego tak jest. Zauważmy tylko, że już widzieliśmy dowód tej tezy w postaci faktu, że \phi(p \cdot q) = \phi(p) \cdot \phi(q) = (p - 1) \cdot (q - 1), gdy p i q są liczbami pierwszymi, jak stwierdzono w Propozycji 2.

Twierdzenie Eulera w połączeniu z Propozycją 5 ma ważne implikacje. Zobaczmy, co dzieje się na przykład w poniższych wyrażeniach, gdzie a i N są liczbami całkowitymi.

Stąd połączenie twierdzenia Eulera i Propozycji 5 pozwala nam po prostu obliczyć szereg wyrażeń. Ogólnie rzecz biorąc, możemy podsumować ten wniosek tak, jak w Propozycji 6.

Propozycja 6. a^x \mod N = a^{x \mod \phi(N)}

Teraz musimy połączyć wszystko razem w trudnym, ostatnim kroku.

Tak jak N ma porządek \phi(N), który zawiera Elements zbioru C_N, tak wiemy, że liczba całkowita \phi(N) również musi mieć porządek i zbiór coprimów. Przyjmijmy, że \phi(N) = R. Wiemy wtedy, że istnieje również wartość \phi(R) i zbiór koprimów C_R.

Przypuśćmy, że wybierzemy teraz liczbę całkowitą e ze zbioru C_R. Z Propozycji 3 wiemy, że ta liczba całkowita e ma tylko jeden unikalny dodatni odwrotność mniejszą niż R. Oznacza to, że e ma jedną unikalną odwrotność ze zbioru C_R. Nazwijmy tę odwrotność d. Biorąc pod uwagę definicję odwrotności, oznacza to, że e \cdot d = 1 \mod R.

Możemy wykorzystać ten wynik do sformułowania twierdzenia o naszej pierwotnej liczbie całkowitej N. Jest to podsumowane w Propozycji 7.

Propozycja 7. Przypuśćmy, że e \cdot d \mod \phi(N) = 1 \mod \phi(N). Wtedy dla dowolnego elementu a zbioru C_N musi zachodzić przypadek, że a^{e \cdot d \mod \phi(N)} = a^{1 \mod \phi(N)} = a \mod N.

Mamy teraz wszystkie wyniki teorii liczb potrzebne do jasnego określenia problemu RSA.

Kryptosystem RSA

Jesteśmy teraz gotowi do sformułowania problemu RSA. Załóżmy, że tworzymy zbiór zmiennych składający się z p, q, N, \phi(N), e, d i y. Nazwij ten zbiór \Pi. Jest on tworzony w następujący sposób:

  1. generate dwie losowe liczby pierwsze p i q równej wielkości i obliczyć ich iloczyn N.

  2. Oblicz rząd N, \phi(N), za pomocą następującego iloczynu: (p - 1) \cdot (q - 1).

  3. Wybierz liczbę e > 2 taką, że jest ona mniejsza i większa od \phi(N).

  4. Oblicz d ustawiając e \cdot d \mod \phi(N) = 1.

  5. Wybierz losową wartość y, która jest mniejsza i większa od N.

Problem RSA polega na znalezieniu x takiego, że x^e = y, mając do dyspozycji jedynie podzbiór informacji dotyczących \Pi, a mianowicie zmienne N, e i y. Gdy p i q są bardzo duże, zazwyczaj zaleca się, aby miały rozmiar 1024 bitów, problem RSA jest uważany za Hard. Można teraz zobaczyć, dlaczego tak jest, biorąc pod uwagę powyższą dyskusję.

Łatwym sposobem na obliczenie x, gdy x^e \mod N = y \mod N jest po prostu obliczenie y^d \mod N. Z poniższych obliczeń wiemy, że y^d \mod N = x \mod N:

y^d \mod N = x^{e \cdot d} \mod N = x^{e \cdot d \mod \phi(N)} \mod N = x^{1 \mod \phi(N)} \mod N = x \mod N.

Problem polega na tym, że nie znamy wartości d, ponieważ nie została ona podana w zadaniu. Nie możemy więc bezpośrednio obliczyć y^d \mod N, aby otrzymać x \mod N.

Moglibyśmy jednak pośrednio obliczyć d na podstawie rzędu N, \phi(N), ponieważ wiemy, że e \cdot d \mod \phi(N) = 1 \mod \phi(N). Ale z założenia problem nie daje też wartości dla \phi(N).

Wreszcie, kolejność można obliczyć pośrednio za pomocą czynników pierwszych p i q, aby ostatecznie obliczyć d. Z założenia jednak wartości p i q również nie zostały nam dostarczone.

Ściśle rzecz biorąc, nawet jeśli problem faktoryzacji w ramach problemu RSA jest Hard, nie możemy udowodnić, że problem RSA jest również Hard. Mogą bowiem istnieć inne sposoby rozwiązania problemu RSA niż faktoryzacja. Jednak ogólnie przyjmuje się, że jeśli problem faktoryzacji w ramach problemu RSA jest Hard, to sam problem RSA jest również Hard.

Jeśli problem RSA jest rzeczywiście Hard, to daje on funkcję jednokierunkową z zasuwą. Funkcja ta ma postać f(g) = g^e \mod N. Znając f(g), każdy mógłby łatwo obliczyć wartość y dla konkretnego g = x. Jednak praktycznie niemożliwe jest obliczenie konkretnej wartości x tylko na podstawie znajomości wartości y i funkcji f(g). Wyjątkiem jest sytuacja, w której otrzymujemy informację d, będącą zapadnią. W takim przypadku można po prostu obliczyć y^d, aby otrzymać x.

Przejdźmy przez konkretny przykład, aby zilustrować problem RSA. Nie mogę wybrać problemu RSA, który byłby uważany za Hard w powyższych warunkach, ponieważ liczby byłyby nieporęczne. Zamiast tego, ten przykład ma jedynie zilustrować, jak ogólnie działa problem RSA.

Na początek załóżmy, że wybierzemy dwie losowe liczby pierwsze 13 i 31. Zatem p = 13 i q = 31. Iloczyn N tych dwóch liczb pierwszych jest równy 403. Możemy łatwo obliczyć rząd liczby 403. Jest on równy (13 - 1) \cdot (31 - 1) = 360.

Następnie, zgodnie z krokiem 3 problemu RSA, musimy wybrać koprim dla 360, który jest większy niż 2 i mniejszy niż 360. Nie musimy wybierać tej wartości losowo. Załóżmy, że wybierzemy 103. Jest to liczba większa od 360, ponieważ jej największy wspólny dzielnik ze 103 wynosi 1.

Krok 4 wymaga teraz obliczenia wartości d takiej, że 103 \cdot d \mod 360 = 1. Nie jest to łatwe zadanie, gdy wartość N jest duża. Wymaga to użycia procedury zwanej rozszerzonym algorytmem euklidesowym.

Chociaż nie pokazuję tutaj procedury, daje ona wartość 7, gdy e = 103. Możesz zweryfikować, że para wartości 103 i 7 rzeczywiście spełnia ogólny warunek e \cdot d \mod \phi(n) = 1 poprzez poniższe obliczenia.

Co ważne, biorąc pod uwagę Propozycję 4, wiemy, że żadna inna liczba całkowita z przedziału od 1 do 360 dla d nie da wyniku, że 103 \cdot d = 1 \mod 360. Dodatkowo, propozycja ta implikuje, że wybranie innej wartości dla e, da inną unikalną wartość dla d.

W kroku 5 problemu RSA, musimy wybrać pewną dodatnią liczbę całkowitą y, która jest mniejszym koprimem od 403. Przyjmijmy, że y = 2^{103}. Potęgowanie 2 przez 103 daje poniższy wynik.

Problem RSA w tym konkretnym przykładzie wygląda następująco: Mamy N = 403, e = 103 i y = 349 \mod 403. Musisz teraz obliczyć x takie, że x^{103} = 349 \mod 403. Oznacza to, że oryginalna wartość przed potęgowaniem przez 103 wynosiła 2.

Obliczenie x byłoby łatwe (przynajmniej dla komputera), gdybyśmy wiedzieli, że d = 7. W takim przypadku można po prostu wyznaczyć x jak poniżej.

Problem polega na tym, że nie otrzymałeś informacji, że d = 7. Mógłbyś oczywiście obliczyć d na podstawie faktu, że 103 \cdot d = 1 \mod 360. Problem w tym, że nie otrzymałeś informacji, że rząd N = 360. Wreszcie, można również obliczyć rząd 403 obliczając następujący iloczyn: (p - 1) \cdot (q - 1). Nie podano jednak informacji, że p = 13 i q = 31.

Oczywiście, komputer nadal mógłby stosunkowo łatwo rozwiązać problem RSA dla tego przykładu, ponieważ liczby pierwsze nie są duże. Ale gdy liczby pierwsze stają się bardzo duże, zadanie staje się praktycznie niewykonalne.

Przedstawiliśmy teraz problem RSA, zestaw warunków, w których jest on Hard, oraz leżącą u jego podstaw matematykę. W jaki sposób może to pomóc w kryptografii asymetrycznej? W szczególności, jak możemy przekształcić twardość problemu RSA w pewnych warunkach w schemat szyfrowania lub schemat podpisu cyfrowego?

Jednym z podejść jest przyjęcie problemu RSA i zbudowanie schematów w prosty sposób. Załóżmy na przykład, że wygenerowałeś zestaw zmiennych \Pi, jak opisano w problemie RSA, i upewniłeś się, że p i q są wystarczająco duże. Ustawiasz swój klucz publiczny równy (N, e) i dzielisz się tą informacją ze światem. Jak opisano powyżej, wartości p, q, \phi(n) i d pozostają tajne. W rzeczywistości, d jest kluczem prywatnym.

Każdy, kto chce wysłać ci wiadomość m, która jest elementem C_N, może po prostu zaszyfrować ją w następujący sposób: c = m^e \mod N. (Szyfrogram c jest tutaj równoważny wartości y w problemie RSA.) Możesz łatwo odszyfrować tę wiadomość, po prostu obliczając c^d \mod N.

W ten sam sposób można spróbować utworzyć schemat podpisu cyfrowego. Załóżmy, że chcemy wysłać komuś wiadomość m z podpisem cyfrowym S. Mógłbyś po prostu ustawić S = m^d \mod N i wysłać parę (m,S) do odbiorcy. Każdy może zweryfikować podpis cyfrowy po prostu sprawdzając, czy S^e \mod N = m \mod N. Każdy atakujący miałby jednak naprawdę trudny czas na stworzenie ważnego S dla wiadomości, biorąc pod uwagę, że nie posiada d.

Niestety, przekształcenie tego, co samo w sobie jest problemem Hard, problemem RSA, w schemat kryptograficzny nie jest takie proste. W przypadku prostego schematu szyfrowania, jako wiadomości można wybierać tylko coprimes of N. To nie pozostawia nam wielu możliwych wiadomości, z pewnością niewystarczających do standardowej komunikacji. Co więcej, wiadomości te muszą być wybierane losowo. Wydaje się to nieco niepraktyczne. Wreszcie, każda wiadomość, która zostanie wybrana dwukrotnie, da dokładnie ten sam szyfrogram. Jest to bardzo niepożądane w każdym schemacie szyfrowania i nie spełnia żadnego rygorystycznego współczesnego standardowego pojęcia bezpieczeństwa szyfrowania.

Problemy stają się jeszcze gorsze w przypadku naszego prostego schematu podpisu cyfrowego. W obecnej postaci, każdy atakujący może z łatwością sfałszować podpisy cyfrowe, po prostu wybierając jako podpis potęgę N, a następnie obliczając odpowiadającą jej oryginalną wiadomość. To wyraźnie łamie wymóg egzystencjalnej niepodrabialności.

Niemniej jednak, dodając nieco sprytnej złożoności, problem RSA można wykorzystać do stworzenia bezpiecznego schematu szyfrowania klucza publicznego, a także bezpiecznego schematu podpisu cyfrowego. Nie będziemy tutaj wchodzić w szczegóły takich konstrukcji. [Co ważne, ta dodatkowa złożoność nie zmienia fundamentalnego problemu RSA, na którym opierają się te schematy.

Uwagi:

[4] Zob. na przykład Jonathan Katz i Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), s. 410-32 na temat szyfrowania RSA i s. 444-41 na temat podpisów cyfrowych RSA.

Sekcja końcowa

Recenzje i oceny

true

Egzamin końcowy

true

Wnioski

true