name: Wewnętrzne działanie portfeli Bitcoin goal: Zanurz się w zasadach kryptograficznych, które zasilają portfele Bitcoin. objectives:

Zdefiniowanie pojęć teoretycznych niezbędnych do zrozumienia algorytmów kryptograficznych używanych w Bitcoin.
Pełne zrozumienie budowy deterministycznego i hierarchicznego Wallet.
Wie, jak zidentyfikować i ograniczyć ryzyko związane z zarządzaniem Wallet.
Zrozumienie zasad działania funkcji Hash, kluczy kryptograficznych i podpisów cyfrowych.

Podróż do serca portfeli Bitcoin

Odkryj sekrety deterministycznych i hierarchicznych portfeli Bitcoin dzięki naszemu kursowi CYP201! Niezależnie od tego, czy jesteś zwykłym użytkownikiem, czy entuzjastą, który chce pogłębić swoją wiedzę, ten kurs oferuje pełne zanurzenie w działaniu tych narzędzi, z których wszyscy korzystamy na co dzień.

Dowiedz się więcej o mechanizmach funkcji Hash, podpisach cyfrowych (ECDSA i Schnorr), frazach Mnemonic, kluczach kryptograficznych i tworzeniu adresów odbiorczych, jednocześnie badając zaawansowane strategie bezpieczeństwa.

Szkolenie to nie tylko wyposaży Cię w wiedzę umożliwiającą zrozumienie struktury Bitcoin Wallet, ale także przygotuje Cię do głębszego zanurzenia się w ekscytującym świecie kryptografii.

Dzięki jasnej pedagogice, ponad 60 diagramom wyjaśniającym i konkretnym przykładom, CYP201 pozwoli ci zrozumieć od A do Z, jak działa twój Wallet, dzięki czemu będziesz mógł pewnie poruszać się po wszechświecie Bitcoin. Przejmij kontrolę nad swoimi UTXO już dziś, rozumiejąc, jak działają portfele HD!

Wprowadzenie

Wprowadzenie do kursu

Witamy w kursie CYP201, w którym dogłębnie zbadamy działanie portfeli HD Bitcoin. Ten kurs jest przeznaczony dla każdego, kto chce zrozumieć techniczne podstawy korzystania z Bitcoin, niezależnie od tego, czy są zwykłymi użytkownikami, oświeconymi entuzjastami, czy przyszłymi ekspertami.

Celem tego szkolenia jest przekazanie ci kluczy do opanowania narzędzi, z których korzystasz na co dzień. Portfele HD Bitcoin, które są sercem doświadczenia użytkownika, opierają się na czasami skomplikowanych koncepcjach, które postaramy się przedstawić w przystępny sposób. Wspólnie je zdemistyfikujemy!

Zanim zagłębimy się w szczegóły budowy i działania portfeli Bitcoin, zaczniemy od kilku rozdziałów na temat prymitywów kryptograficznych, które warto znać.

Zaczniemy od kryptograficznych funkcji Hash, fundamentalnych zarówno dla portfeli, jak i samego protokołu Bitcoin. Odkryjesz ich główne cechy, konkretne funkcje używane w Bitcoin, a w bardziej technicznym rozdziale poznasz szczegółowo działanie królowej funkcji Hash: SHA256.

Następnie omówimy działanie algorytmów podpisu cyfrowego, których używasz na co dzień do zabezpieczania swoich UTXO. Bitcoin wykorzystuje dwa z nich: ECDSA i protokół Schnorra. Dowiesz się, jakie prymitywy matematyczne leżą u podstaw tych algorytmów i w jaki sposób zapewniają one bezpieczeństwo transakcji.

Kiedy już dobrze zrozumiemy te Elements kryptografii, przejdziemy wreszcie do sedna szkolenia: deterministycznych i hierarchicznych portfeli! Po pierwsze, istnieje sekcja poświęcona frazom Mnemonic, tym sekwencjom 12 lub 24 słów, które pozwalają tworzyć i przywracać portfele. Dowiesz się, w jaki sposób słowa te są generowane ze źródła entropii i jak ułatwiają korzystanie z Bitcoin.

Szkolenie będzie kontynuowane wraz z badaniem BIP39 passphrase, seed (nie mylić z frazą Mnemonic), głównego kodu łańcucha i klucza głównego. Zobaczymy szczegółowo, czym są te Elements, jakie są ich role i jak są obliczane.

Wreszcie, na podstawie klucza głównego odkryjemy, w jaki sposób pary kluczy kryptograficznych są wyprowadzane w sposób deterministyczny i hierarchiczny aż do adresów odbiorczych.

Szkolenie to pozwoli ci pewnie korzystać z oprogramowania Wallet, jednocześnie zwiększając swoje umiejętności w zakresie identyfikacji i ograniczania ryzyka. Przygotuj się, aby stać się prawdziwym ekspertem w dziedzinie portfeli Bitcoin!

Funkcje Hash

Wprowadzenie do funkcji Hash

Pierwszy rodzaj algorytmów kryptograficznych wykorzystywanych w Bitcoin obejmuje funkcje Hash. Odgrywają one istotną rolę na różnych poziomach protokołu, ale także w portfelach Bitcoin. Odkryjmy razem, czym jest funkcja Hash i do czego służy w Bitcoin.

Definicja i zasada Hashingu

Hashing to proces przekształcania informacji o dowolnej długości w inną informację o stałej długości za pomocą kryptograficznej funkcji Hash. Innymi słowy, funkcja Hash pobiera dane wejściowe o dowolnym rozmiarze i przekształca je w odcisk palca o stałym rozmiarze, zwany "Hash".

Hash może być również czasami określany jako "skrót", "kondensat", "skondensowany" lub "hashowany".

Na przykład, funkcja SHA256 Hash generuje Hash o stałej długości 256 bitów. Tak więc, jeśli użyjemy wejścia "PlanB", wiadomości o dowolnej długości, wygenerowany Hash będzie następującym 256-bitowym odciskiem palca:

24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688

Charakterystyka funkcji Hash

Te kryptograficzne funkcje Hash mają kilka istotnych cech, które czynią je szczególnie użytecznymi w kontekście Bitcoin i innych systemów komputerowych:

Nieodwracalność (lub odporność na obraz wstępny)
Odporność na manipulacje (efekt lawinowy)
Odporność na kolizje
Druga odporność na obraz wstępny

1. Nieodwracalność (odporność na obraz wstępny):

Nieodwracalność oznacza, że łatwo jest obliczyć Hash na podstawie informacji wejściowych, ale odwrotne obliczenie, czyli znalezienie danych wejściowych na podstawie Hash, jest praktycznie niemożliwe. Ta właściwość sprawia, że funkcje Hash są idealne do tworzenia unikalnych cyfrowych odcisków palców bez naruszania oryginalnych informacji. Cecha ta jest często określana jako funkcja jednokierunkowa.

W podanym przykładzie, uzyskanie Hash 24f1b9... znając dane wejściowe "PlanB" jest proste i szybkie. Jednak znalezienie wiadomości "PlanB" znając tylko 24f1b9... jest niemożliwe.

Dlatego niemożliwe jest znalezienie preobrazu $m$ dla Hash $h$ takiego, że $h = \text{Hash}(m)$ , gdzie $\text{Hash}$ jest kryptograficzną funkcją Hash.

2. Odporność na manipulacje (efekt lawinowy)

Drugą cechą jest odporność na sabotaż, znana również jako efekt lawinowy. Cecha ta jest obserwowana w funkcji Hash, jeśli niewielka zmiana w komunikacie wejściowym powoduje radykalną zmianę w wyjściowym Hash.

Jeśli wrócimy do naszego przykładu z danymi wejściowymi "PlanB" i funkcją SHA256, zobaczymy, że wygenerowany Hash wygląda następująco:

24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688

Jeśli wprowadzimy bardzo niewielką zmianę w danych wejściowych, używając tym razem "Planb", to zwykła zmiana z dużej litery "B" na małą literę "b" całkowicie zmieni wyjściowy kod SHA256 Hash:

bb038b4503ac5d90e1205788b00f8f314583c5e22f72bec84b8735ba5a36df3f

Ta właściwość zapewnia, że nawet niewielka zmiana oryginalnej wiadomości jest natychmiast wykrywalna, ponieważ nie zmienia ona tylko niewielkiej części Hash, ale cały Hash. Może to być interesujące w różnych dziedzinach w celu weryfikacji integralności wiadomości, oprogramowania, a nawet transakcji Bitcoin.

3. Odporność na kolizje

Trzecią cechą jest odporność na kolizje. Funkcja Hash jest odporna na kolizje, jeśli obliczeniowo niemożliwe jest znalezienie 2 różnych komunikatów, które dają ten sam wynik Hash z funkcji. Formalnie, trudno jest znaleźć dwa różne komunikaty $m_1$ i $m_2$ takie, że:

 $\text{HASH}(m_1) = \text{HASH}(m_2)$

W rzeczywistości jest matematycznie nieuniknione, że kolizje istnieją dla funkcji Hash, ponieważ rozmiar wejść może być większy niż rozmiar wyjść. Jest to znane jako zasada szuflady Dirichleta: jeśli $n$ obiektów jest rozmieszczonych w $m$ szufladach, z $m < n$ , to co najmniej jedna szuflada będzie musiała zawierać dwa lub więcej obiektów. W przypadku funkcji Hash zasada ta ma zastosowanie, ponieważ liczba możliwych wiadomości jest (prawie) nieskończona, podczas gdy liczba możliwych skrótów jest skończona ( $2^{256}$ w przypadku SHA256).

W związku z tym cecha ta nie oznacza, że nie ma kolizji dla funkcji Hash, ale raczej, że dobra funkcja Hash sprawia, że prawdopodobieństwo znalezienia kolizji jest znikome. Cecha ta, na przykład, nie jest już weryfikowana w algorytmach SHA-0 i SHA-1, poprzednikach SHA-2, dla których znaleziono kolizje. Dlatego też funkcje te są obecnie odradzane i często uważane za przestarzałe.

Dla funkcji Hash składającej się z $n$ bitów, odporność na kolizję jest rzędu $2^{\frac{n}{2}}$ , zgodnie z atakiem urodzinowym. Na przykład, dla SHA256 ( $n = 256$ ), złożoność znalezienia kolizji jest rzędu $2^{128}$ prób. W praktyce oznacza to, że jeśli ktoś przepuści przez funkcję 2^{128}$ różnych wiadomości, to prawdopodobnie znajdzie kolizję.

4. Odporność na drugi obraz

Odporność na drugi obraz jest kolejną ważną cechą funkcji Hash. Stwierdza ona, że biorąc pod uwagę wiadomość $m_1$ i jej Hash $h$ , znalezienie innej wiadomości $m_2 \neq m_1$ takiej, że:

 $\text{HASH}(m_1) = \text{HASH}(m_2)$

W związku z tym odporność na drugi preimage jest nieco podobna do odporności na kolizję, z tą różnicą, że tutaj atak jest trudniejszy, ponieważ atakujący nie może dowolnie wybrać $m_1$ .

Zastosowania funkcji Hash w Bitcoin

Najczęściej używaną funkcją Hash w Bitcoin jest SHA256 ("Secure Hash Algorithm 256 bits"). Zaprojektowana na początku XXI wieku przez NSA i ustandaryzowana przez NIST, generuje 256-bitowy wynik Hash.

Funkcja ta jest wykorzystywana w wielu aspektach Bitcoin. Na poziomie protokołu jest zaangażowana w mechanizm Proof-of-Work, gdzie jest stosowana w podwójnym haszowaniu w celu wyszukania częściowej kolizji między nagłówkiem bloku kandydującego, utworzonego przez Miner, a celem trudności. Jeśli taka częściowa kolizja zostanie znaleziona, blok kandydujący staje się ważny i może zostać dodany do Blockchain.

SHA256 jest również używany w konstrukcji Merkle Tree, który jest w szczególności akumulatorem używanym do rejestrowania transakcji w blokach. Struktura ta znajduje się również w protokole Utreexo, co pozwala na zmniejszenie rozmiaru zestawu UTXO. Dodatkowo, wraz z wprowadzeniem Taproot w 2021 r., SHA256 jest wykorzystywany w MAST (Merkelised Alternative Script Tree), co pozwala na ujawnienie tylko warunków wydatków faktycznie użytych w skrypcie, bez ujawniania innych możliwych opcji. Jest on również wykorzystywany do obliczania identyfikatorów transakcji, w transmisji pakietów przez sieć P2P, w podpisach elektronicznych... Wreszcie, co jest szczególnie interesujące w tym szkoleniu, SHA256 jest używany na poziomie aplikacji do budowy portfeli Bitcoin i wyprowadzania adresów.

W większości przypadków, gdy natkniesz się na użycie SHA256 w Bitcoin, będzie to w rzeczywistości podwójny Hash SHA256, oznaczony jako "HASH256", który po prostu polega na dwukrotnym zastosowaniu SHA256:

 $\text{HASH256}(m) = \text{SHA256}(\text{SHA256}(m))$

Ta praktyka podwójnego haszowania dodaje dodatkowy Layer zabezpieczenia przed niektórymi potencjalnymi atakami, mimo że pojedynczy SHA256 jest obecnie uważany za bezpieczny kryptograficznie.

Inną funkcją haszującą dostępną w języku skryptowym i używaną do uzyskiwania adresów odbiorczych jest funkcja RIPEMD160. Funkcja ta tworzy 160-bitowy Hash (a więc krótszy niż SHA256). Zazwyczaj jest ona łączona z SHA256 w celu utworzenia funkcji HASH160:

 $\text{HASH160}(m) = \text{RIPEMD160}(\text{SHA256}(m))$

Ta kombinacja jest używana do generate krótszych skrótów, zwłaszcza w tworzeniu niektórych adresów Bitcoin, które reprezentują skróty kluczy lub skróty skryptów, a także do tworzenia kluczowych odcisków palców.

Wreszcie, tylko na poziomie aplikacji, czasami używana jest również funkcja SHA512, która pośrednio odgrywa rolę w wyprowadzaniu kluczy dla portfeli. Funkcja ta jest bardzo podobna do SHA256 w swoim działaniu; obie należą do tej samej rodziny SHA2, ale SHA512 wytwarza, jak wskazuje jej nazwa, 512-bitowy Hash, w porównaniu do 256 bitów dla SHA256. Szczegółowo opiszemy jego użycie w kolejnych rozdziałach.

Teraz znasz już podstawowe podstawy funkcji haszujących. W następnym rozdziale proponuję bardziej szczegółowo odkryć działanie funkcji, która jest sercem Bitcoin: SHA256. Przeanalizujemy ją, aby zrozumieć, w jaki sposób osiąga ona cechy, które tutaj opisaliśmy. Następny rozdział jest dość długi i techniczny, ale nie jest niezbędny do śledzenia reszty szkolenia. Jeśli więc masz trudności z jego zrozumieniem, nie przejmuj się i przejdź bezpośrednio do następnego rozdziału, który będzie znacznie bardziej przystępny.

Wewnętrzne działanie SHA256

Wcześniej widzieliśmy, że funkcje haszujące mają ważne cechy, które uzasadniają ich użycie w Bitcoin. Przeanalizujmy teraz wewnętrzne mechanizmy tych funkcji haszujących, które nadają im te właściwości, a w tym celu proponuję przeanalizować działanie SHA256.

Funkcje SHA256 i SHA512 należą do tej samej rodziny SHA2. Ich mechanizm opiera się na specyficznej konstrukcji zwanej konstrukcją Merkle-Damgård. RIPEMD160 również wykorzystuje ten sam typ konstrukcji.

Dla przypomnienia, mamy wiadomość o dowolnym rozmiarze jako dane wejściowe do SHA256 i przekażemy ją przez funkcję, aby uzyskać 256-bitowy Hash jako dane wyjściowe.

Wstępne przetwarzanie danych wejściowych

Na początek musimy przygotować naszą wiadomość wejściową $m$ tak, aby miała standardową długość będącą wielokrotnością 512 bitów. Ten krok jest kluczowy dla prawidłowego funkcjonowania algorytmu.

Aby to zrobić, zaczynamy od kroku bitów dopełniających. Najpierw dodajemy bit separatora 1 do wiadomości, a następnie pewną liczbę bitów 0. Liczba dodanych bitów 0 jest obliczana tak, aby całkowita długość wiadomości po tym dodaniu była zgodna z 448 modulo 512. Zatem długość $L$ wiadomości z bitami dopełniającymi jest równa:

 $L \equiv 448 \mod 512$

$\text{mod}$ , czyli modulo, to operacja matematyczna, która między dwiema liczbami całkowitymi zwraca resztę z euklidesowego dzielenia pierwszej przez drugą. Na przykład: $16 \mod 5 = 1$ . Jest to operacja szeroko stosowana w kryptografii.

Krok uzupełniania zapewnia, że po dodaniu 64 bitów w następnym kroku, całkowita długość wyrównanej wiadomości będzie wielokrotnością 512 bitów. Jeśli początkowa wiadomość ma długość $M$ bitów, to liczba ( $N$ ) bitów 0 do dodania wynosi:

 $N = (448 - (M + 1) \mod 512) \mod 512$

Na przykład, jeśli początkowa wiadomość ma 950 bitów, obliczenia będą następujące:

 $\begin{align*} M & = 950 \\ M + 1 & = 951 \\ (M + 1) \mod 512 & = 951 \mod 512 \\ & = 951 - 512 \cdot \left\lfloor \frac{951}{512} \right\rfloor \\ & = 951 - 512 \cdot 1 \\ & = 951 - 512 \\ & = 439 \\ \\ 448 - (M + 1) \mod 512 & = 448 - 439 \\ & = 9 \\ \\ N & = (448 - (M + 1) \mod 512) \mod 512 \\ N & = 9 \mod 512 \\ & = 9 \end{align*}$

W ten sposób mielibyśmy 9 0 oprócz separatora 1. Nasze bity wypełniające, które zostaną dodane bezpośrednio po naszej wiadomości $M$ , będą zatem następujące:

1000 0000 00

Po dodaniu bitów dopełnienia do naszej wiadomości $M$ , dodajemy również 64-bitową reprezentację oryginalnej długości wiadomości $M$ , wyrażoną w systemie binarnym. Dzięki temu funkcja Hash jest wrażliwa na kolejność bitów i długość wiadomości.

Jeśli wrócimy do naszego przykładu z początkową wiadomością składającą się z 950 bitów, przekonwertujemy liczbę dziesiętną 950 na binarną, co da nam 1110 1101 10. Uzupełniamy tę liczbę zerami w podstawie, aby uzyskać łącznie 64 bity. W naszym przykładzie daje to:

0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0011 1011 0110

Ten rozmiar dopełnienia jest dodawany po dopełnieniu bitowym. Dlatego wiadomość po wstępnym przetworzeniu składa się z trzech części:

Oryginalna wiadomość $M$ ;
Bit 1, po którym następuje kilka bitów 0 tworzących bit padding;
64-bitowa reprezentacja długości $M$ w celu utworzenia wypełnienia z rozmiarem.

Inicjalizacja zmiennych

SHA256 wykorzystuje osiem początkowych zmiennych stanu, oznaczonych od $A$ do $H$ , każda po 32 bity. Zmienne te są inicjowane określonymi stałymi, które są ułamkowymi częściami pierwiastków kwadratowych pierwszych ośmiu liczb pierwszych. Będziemy używać tych wartości później podczas procesu haszowania:

$A = 0x6a09e667$
$B = 0xbb67ae85$
$C = 0x3c6ef372$
$D = 0xa54ff53a$
$E = 0x510e527f$
$F = 0x9b05688c$
$G = 0x1f83d9ab$
$H = 0x5be0cd19$

SHA256 wykorzystuje również 64 inne stałe, oznaczone od $K_0$ do $K_{63}$ , które są ułamkowymi częściami pierwiastków sześciennych z 64 liczb pierwszych:

 $K[0 \ldots 63] = \begin{pmatrix} 0x428a2f98, & 0x71374491, & 0xb5c0fbcf, & 0xe9b5dba5, \\ 0x3956c25b, & 0x59f111f1, & 0x923f82a4, & 0xab1c5ed5, \\ 0xd807aa98, & 0x12835b01, & 0x243185be, & 0x550c7dc3, \\ 0x72be5d74, & 0x80deb1fe, & 0x9bdc06a7, & 0xc19bf174, \\ 0xe49b69c1, & 0xefbe4786, & 0x0fc19dc6, & 0x240ca1cc, \\ 0x2de92c6f, & 0x4a7484aa, & 0x5cb0a9dc, & 0x76f988da, \\ 0x983e5152, & 0xa831c66d, & 0xb00327c8, & 0xbf597fc7, \\ 0xc6e00bf3, & 0xd5a79147, & 0x06ca6351, & 0x14292967, \\ 0x27b70a85, & 0x2e1b2138, & 0x4d2c6dfc, & 0x53380d13, \\ 0x650a7354, & 0x766a0abb, & 0x81c2c92e, & 0x92722c85, \\ 0xa2bfe8a1, & 0xa81a664b, & 0xc24b8b70, & 0xc76c51a3, \\ 0xd192e819, & 0xd6990624, & 0xf40e3585, & 0x106aa070, \\ 0x19a4c116, & 0x1e376c08, & 0x2748774c, & 0x34b0bcb5, \\ 0x391c0cb3, & 0x4ed8aa4a, & 0x5b9cca4f, & 0x682e6ff3, \\ 0x748f82ee, & 0x78a5636f, & 0x84c87814, & 0x8cc70208, \\ 0x90befffa, & 0xa4506ceb, & 0xbef9a3f7, & 0xc67178f2 \end{pmatrix}$

Podział wejścia

Teraz, gdy mamy już wyrównane dane wejściowe, przejdziemy do głównej fazy przetwarzania algorytmu SHA256: funkcji kompresji. Ten krok jest bardzo ważny, ponieważ to przede wszystkim on nadaje funkcji Hash jej właściwości kryptograficzne, które badaliśmy w poprzednim rozdziale.

Po pierwsze, zaczynamy od podzielenia naszej wyrównanej wiadomości (wynik wstępnego przetwarzania) na kilka bloków $P$ po 512 bitów każdy. Jeśli nasza zrównoleglona wiadomość ma całkowity rozmiar $n \ razy 512$ bitów, będziemy mieli $n$ bloków, każdy po 512 bitów. Każdy 512-bitowy blok będzie przetwarzany indywidualnie przez funkcję kompresji, która składa się z 64 rund kolejnych operacji. Nazwijmy te bloki $P_1$ , $P_2$ , $P_3$ ....

Operacje logiczne

Przed szczegółowym zbadaniem funkcji kompresji ważne jest, aby zrozumieć podstawowe operacje logiczne w niej używane. Operacje te, oparte na algebrze Boole'a, działają na poziomie bitów. Podstawowe operacje logiczne to:

Koniunkcja (AND)**: oznaczana $\land$ , odpowiada logicznemu "AND".
Dysjunkcja (OR)**: oznaczana $\lor$ , odpowiada logicznemu "OR".
Negacja (NOT)**: oznaczana $\lnot$ , odpowiada logicznemu "NOT".

Na podstawie tych podstawowych operacji możemy zdefiniować bardziej złożone operacje, takie jak "Exclusive OR" (XOR) oznaczane $\oplus$ , które jest szeroko stosowane w kryptografii.

Każda operacja logiczna może być reprezentowana przez tablicę prawdy, która wskazuje wynik dla wszystkich możliwych kombinacji binarnych wartości wejściowych (dwa operandy $p$ i $q$ ).

Dla XOR ( $\oplus$ ):

$p$	$q$	$p \oplus q$
0	0	0
0	1	1
1	0	1
1	1	0

Dla AND ( $\land$ ):

$p$	$q$	$p \land q$
0	0	0
0	1	0
1	0	0
1	1	1

Dla NOT ( $\lnot p$ ):

$p$	$\lnot p$
0	1
1	0

Weźmy przykład, aby zrozumieć działanie XOR na poziomie bitów. Jeśli mamy dwie liczby binarne na 6 bitach:

$a = 101100$
$b = 001000$

Następnie:

 $a \oplus b = 101100 \oplus 001000 = 100100$

Stosując XOR bit po bicie:

Bit Position	$a$	$b$	$a \oplus b$
1	1	0	1
2	0	0	0
3	1	1	0
4	1	0	1
5	0	0	0
6	0	0	0

Wynik wynosi zatem 100100 USD.

Oprócz operacji logicznych, funkcja kompresji wykorzystuje operacje przesuwania bitów, które będą odgrywać istotną rolę w dyfuzji bitów w algorytmie.

Po pierwsze, istnieje logiczna operacja przesunięcia w prawo, oznaczana $ShR_n(x)$ , która przesuwa wszystkie bity $x$ w prawo o $n$ pozycji, wypełniając wolne bity po lewej stronie zerami.

Na przykład dla $x = 101100001$ (na 9 bitach) i $n = 4$ :

 $ShR_4(101100001) = 000010110$

Schematycznie, operacja przesunięcia w prawo może wyglądać następująco:

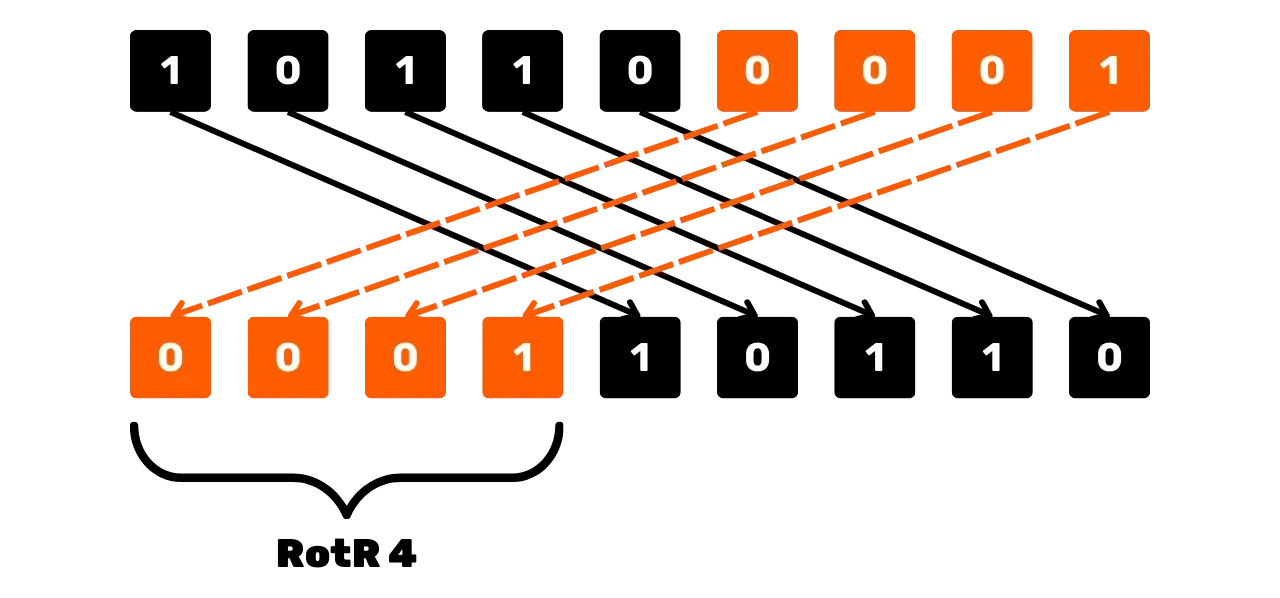
Inną operacją używaną w SHA256 do manipulacji bitami jest rotacja kołowa w prawo, oznaczana $RotR_n(x)$ , która przesuwa bity $x$ w prawo o $n$ pozycji, ponownie wstawiając przesunięte bity na początku ciągu.

Na przykład dla $x = 101100001$ (ponad 9 bitów) i $n = 4$ :

 $RotR_4(101100001) = 000110110$

Schematycznie, operacja przesunięcia w prawo może wyglądać następująco:

Funkcja kompresji

Teraz, gdy zrozumieliśmy już podstawowe operacje, przyjrzyjmy się szczegółowo funkcji kompresji SHA256.

W poprzednim kroku podzieliliśmy nasze dane wejściowe na kilka 512-bitowych bloków $P$ . Dla każdego 512-bitowego bloku $P$ mamy:

Słowa wiadomości $W_i$ **: dla $i$ od 0 do 63.
Stałe $K_i$ **: dla $i$ od 0 do 63, zdefiniowane w poprzednim kroku.
Zmienne stanu $A, B, C, D, E, F, G, H$ **: inicjowane wartościami z poprzedniego kroku.

Pierwsze 16 słów, od $W_0$ do $W_{15}$ , jest wyodrębnianych bezpośrednio z przetwarzanego 512-bitowego bloku $P$ . Każde słowo $W_i$ składa się z 32 kolejnych bitów z bloku. Przykładowo, bierzemy pierwszy fragment danych wejściowych $P_1$ i dzielimy go na mniejsze 32-bitowe fragmenty, które nazywamy słowami.

Kolejne 48 słów (od $W_{16}$ do $W_{63}$ ) generowanych jest przy użyciu następującego wzoru:

 $W_i = W_{i-16} + \sigma_0(W_{i-15}) + W_{i-7} + \sigma_1(W_{i-2}) \mod 2^{32}$

$\sigma_0(x) = RotR_7(x) \oplus RotR_{18}(x) \oplus ShR_3(x)$
$\sigma_1(x) = RotR_{17}(x) \oplus RotR_{19}(x) \oplus ShR_{10}(x)$

W tym przypadku $x$ jest równe $W_{i-15}$ dla $\sigma_0(x)$ i $W_{i-2}$ dla $\sigma_1(x)$ .

Po określeniu wszystkich słów $W_i$ dla naszego 512-bitowego fragmentu, możemy przejść do funkcji kompresji, która polega na wykonaniu 64 rund.

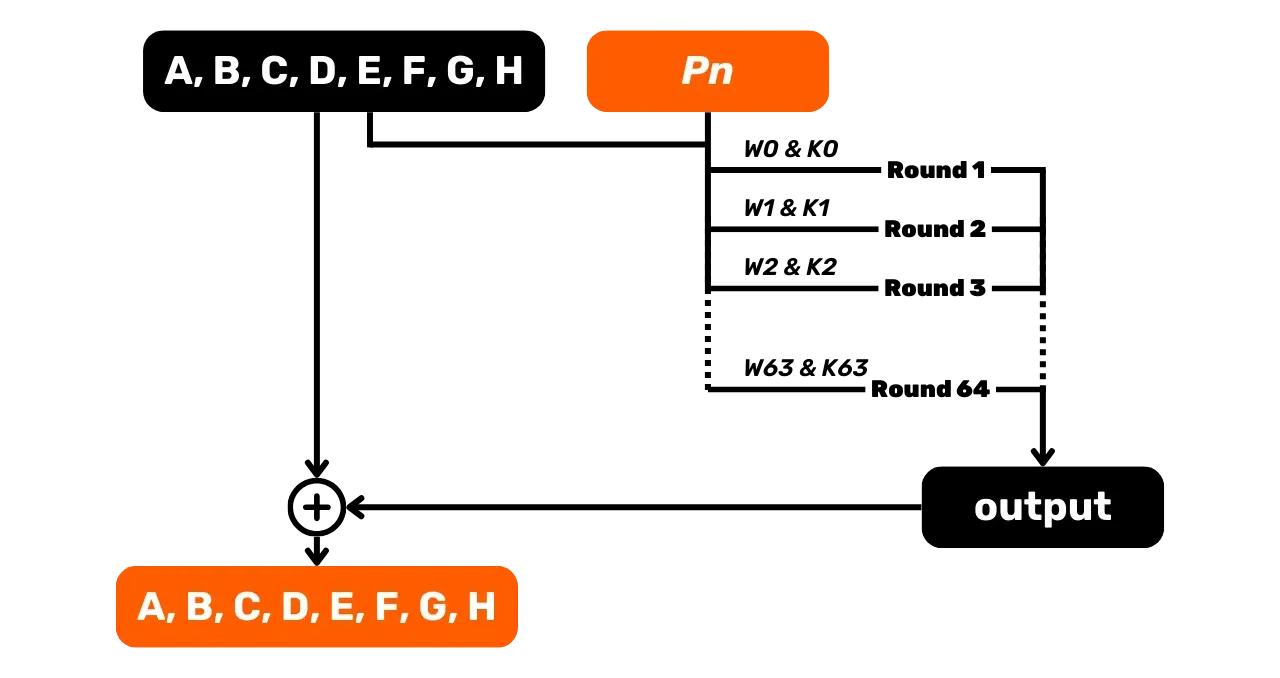
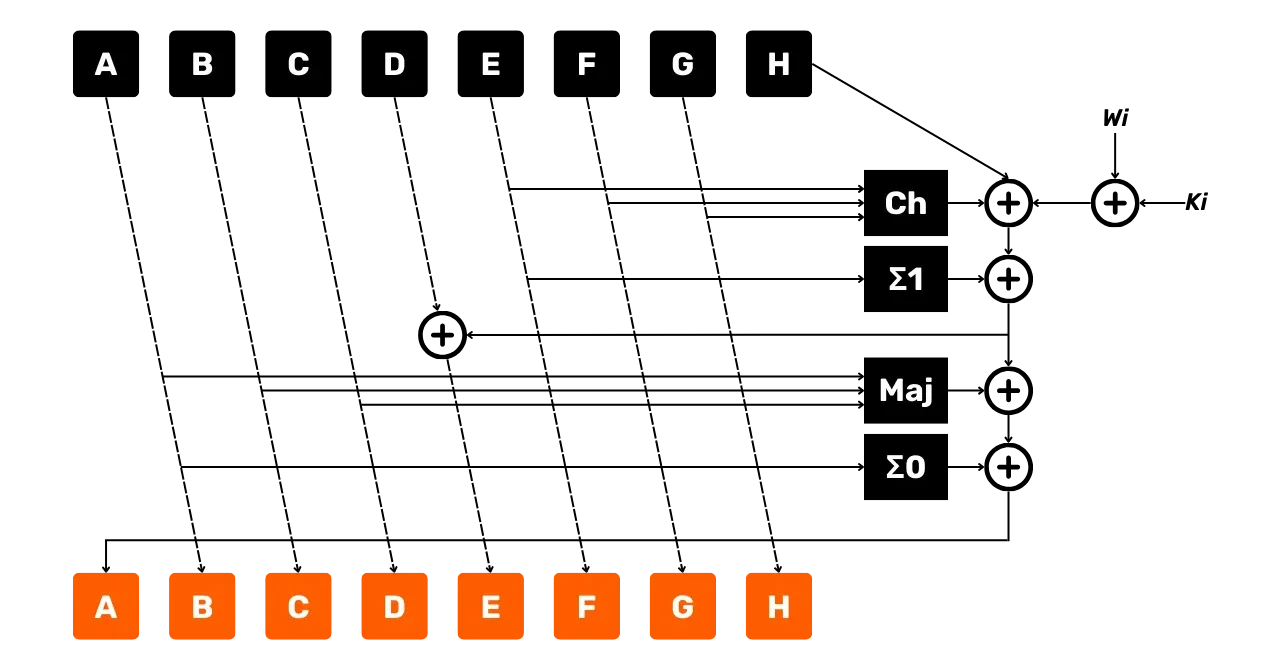
Dla każdej rundy $i$ od 0 do 63 mamy trzy różne rodzaje danych wejściowych. Po pierwsze, $W_i$ , który właśnie ustaliliśmy, częściowo składający się z naszego fragmentu wiadomości $P_n$ . Następnie 64 stałe $K_i$ . Wreszcie, używamy zmiennych stanu $A$ , $B$ , $C$ , $D$ , $E$ , $F$ , $G$ i $H$ , które będą ewoluować przez cały proces haszowania i będą modyfikowane przy każdej funkcji kompresji. Jednak dla pierwszego elementu $P_1$ używamy początkowych stałych podanych wcześniej.

Następnie wykonujemy następujące operacje na naszych danych wejściowych:

Funkcja $\Sigma_0$ :**

 $\Sigma_0(A) = RotR_2(A) \oplus RotR_{13}(A) \oplus RotR_{22}(A)$

Funkcja $\Sigma_1$ :**

 $\Sigma_1(E) = RotR_6(E) \oplus RotR_{11}(E) \oplus RotR_{25}(E)$

Funkcja $Ch$ ("Choose"):**

 $Ch(E, F, G) = (E \land F) \oplus (\lnot E \land G)$

Funkcja $Maj$ ("Majority"):**

 $Maj(A, B, C) = (A \land B) \oplus (A \land C) \oplus (B \land C)$

Następnie obliczamy 2 zmienne tymczasowe:

$temp1$ :

 $temp1 = H + \Sigma_1(E) + Ch(E, F, G) + K_i + W_i \mod 2^{32}$

$temp2$ :

 $temp2 = \Sigma_0(A) + Maj(A, B, C) \mod 2^{32}$

Następnie aktualizujemy zmienne stanu w następujący sposób:

 $\begin{cases} H = G \\ G = F \\ F = E \\ E = D + temp1 \mod 2^{32} \\ D = C \\ C = B \\ B = A \\ A = temp1 + temp2 \mod 2^{32} \end{cases}$

Poniższy diagram przedstawia rundę funkcji kompresji SHA256, którą właśnie opisaliśmy:

Strzałki wskazują przepływ danych;
Pola reprezentują wykonane operacje;
Otoczone $+$ reprezentują dodawanie modulo $2^{32}$ .

Możemy już zaobserwować, że ta runda generuje nowe zmienne stanu $A$ , $B$ , $C$ , $D$ , $E$ , $F$ , $G$ i $H$ . Te nowe zmienne posłużą jako dane wejściowe dla następnej rundy, która z kolei wygeneruje nowe zmienne $A$ , $B$ , $C$ , $D$ , $E$ , $F$ , $G$ i $H$ , które zostaną wykorzystane w następnej rundzie. Proces ten trwa aż do 64. rundy.

Po 64 rundach aktualizujemy początkowe wartości zmiennych stanu, dodając je do wartości końcowych na koniec rundy 64:

 $\begin{cases} A = A_{\text{initial}} + A \mod 2^{32} \\ B = B_{\text{initial}} + B \mod 2^{32} \\ C = C_{\text{initial}} + C \mod 2^{32} \\ D = D_{\text{initial}} + D \mod 2^{32} \\ E = E_{\text{initial}} + E \mod 2^{32} \\ F = F_{\text{initial}} + F \mod 2^{32} \\ G = G_{\text{initial}} + G \mod 2^{32} \\ H = H_{\text{initial}} + H \mod 2^{32} \end{cases}$

Te nowe wartości $A$ , $B$ , $C$ , $D$ , $E$ , $F$ , $G$ i $H$ posłużą jako wartości początkowe dla następnego bloku, $P_2$ . Dla tego bloku $P_2$ powielamy ten sam proces kompresji z 64 rundami, a następnie aktualizujemy zmienne dla bloku $P_3$ i tak dalej, aż do ostatniego bloku naszego wyrównanego wejścia.

Po przetworzeniu wszystkich bloków wiadomości, łączymy końcowe wartości zmiennych $A$ , $B$ , $C$ , $D$ , $E$ , $F$ , $G$ i $H$ , aby utworzyć ostateczny 256-bitowy Hash naszej funkcji haszującej:

 $\text{Hash} = A \Vert B \Vert C \Vert D \Vert E \Vert F \Vert G \Vert H$

Każda zmienna jest 32-bitową liczbą całkowitą, więc ich konkatenacja zawsze daje 256-bitowy wynik, niezależnie od rozmiaru naszej wiadomości wejściowej do funkcji haszującej.

Uzasadnienie właściwości kryptograficznych

Ale w jaki sposób ta funkcja jest nieodwracalna, odporna na kolizje i manipulacje?

W przypadku odporności na manipulacje jest to dość proste do zrozumienia. Istnieje tak wiele obliczeń wykonywanych kaskadowo, które zależą zarówno od danych wejściowych, jak i stałych, że najmniejsza modyfikacja początkowej wiadomości całkowicie zmienia obraną ścieżkę, a tym samym całkowicie zmienia wyjściowy Hash. Nazywa się to efektem lawiny. Właściwość ta jest częściowo zapewniona przez mieszanie stanów pośrednich ze stanami początkowymi dla każdego elementu.

Następnie, podczas omawiania kryptograficznej funkcji Hash, termin "nieodwracalność" nie jest powszechnie używany. Zamiast tego mówimy o "odporności na obraz wstępny", która określa, że dla dowolnego $y$ trudno jest znaleźć $x$ takie, że $h(x) = y$ . Ta odporność na preimage jest gwarantowana przez złożoność algebraiczną i silną nieliniowość operacji wykonywanych w funkcji kompresji, a także przez utratę pewnych informacji w tym procesie. Na przykład, dla danego wyniku dodawania modulo istnieje kilka możliwych operandów:

 $3+2 \mod 10 = 5 \\ 7+8 \mod 10 = 5 \\ 5+10 \mod 10 = 5$

W tym przykładzie, znając tylko użyte modulo (10) i wynik (5), nie można z całą pewnością określić, które operandy są poprawne w dodawaniu. Mówi się, że istnieje wiele kongruencji modulo 10.

W przypadku operacji XOR mamy do czynienia z tym samym problemem. Przypomnijmy sobie tabelę prawdy dla tej operacji: każde 1-bitowe wyjście może być określone przez dwie różne konfiguracje wejściowe, które mają dokładnie takie samo prawdopodobieństwo bycia poprawnymi wartościami. Dlatego nie można z całą pewnością określić operandów operacji XOR, znając tylko jej wynik. Jeśli zwiększymy rozmiar operandów XOR, liczba możliwych wejść, znając tylko wynik, wzrośnie wykładniczo. Co więcej, XOR jest często używany wraz z innymi operacjami na poziomie bitowym, takimi jak operacja $\text{RotR}$ , które dodają jeszcze więcej możliwych interpretacji do wyniku.

Funkcja kompresji wykorzystuje również operację $\text{ShR}$ . Operacja ta usuwa część podstawowych informacji, których późniejsze odzyskanie jest niemożliwe. Ponownie, nie ma algebraicznego sposobu na odwrócenie tej operacji. Wszystkie te operacje jednokierunkowe i operacje utraty informacji są bardzo często używane w funkcjach kompresji. Liczba możliwych danych wejściowych dla danego wyjścia jest więc prawie nieskończona, a każda próba obliczenia odwrotnego prowadziłaby do równań z bardzo dużą liczbą niewiadomych, które rosłyby wykładniczo na każdym kroku.

Wreszcie, jeśli chodzi o charakterystykę odporności na kolizje, w grę wchodzi kilka parametrów. Istotną rolę odgrywa wstępne przetwarzanie oryginalnej wiadomości. Bez tego wstępnego przetwarzania łatwiej byłoby znaleźć kolizje w funkcji. Chociaż teoretycznie kolizje istnieją (ze względu na zasadę gołębnika), struktura funkcji Hash w połączeniu z wyżej wymienionymi właściwościami sprawia, że prawdopodobieństwo znalezienia kolizji jest niezwykle niskie.

Aby funkcja Hash była odporna na kolizje, konieczne jest, aby

Wynik jest nieprzewidywalny: Każda przewidywalność może zostać wykorzystana do znalezienia kolizji szybciej niż w przypadku ataku siłowego. Funkcja zapewnia, że każdy bit wyniku zależy w nietrywialny sposób od danych wejściowych. Innymi słowy, funkcja jest zaprojektowana tak, aby każdy bit wyniku końcowego miał niezależne prawdopodobieństwo bycia 0 lub 1, nawet jeśli ta niezależność nie jest absolutna w praktyce.
Dystrybucja skrótów jest pseudolosowa: Gwarantuje to, że skróty są równomiernie rozłożone.
Rozmiar Hash jest znaczący: im większa możliwa przestrzeń wyników, tym trudniej jest znaleźć kolizję.

Kryptografowie projektują te funkcje, oceniając najlepsze możliwe ataki w celu znalezienia kolizji, a następnie dostosowując parametry, aby uczynić te ataki nieskutecznymi.

Merkle-Damgård Construction

Struktura SHA256 opiera się na konstrukcji Merkle-Damgård, która umożliwia przekształcenie funkcji kompresji w funkcję Hash, która może przetwarzać wiadomości o dowolnej długości. To jest dokładnie to, co widzieliśmy w tym rozdziale.

Jednak niektóre stare funkcje Hash, takie jak SHA1 lub MD5, które wykorzystują tę konkretną konstrukcję, są podatne na ataki polegające na wydłużeniu długości. Jest to technika, która pozwala atakującemu, który zna Hash wiadomości $M$ i długość $M$ (bez znajomości samej wiadomości), obliczyć Hash wiadomości $M'$ utworzonej przez połączenie $M$ z dodatkową zawartością.

SHA256, mimo że wykorzystuje ten sam typ konstrukcji, jest teoretycznie odporny na tego typu ataki, w przeciwieństwie do SHA1 i MD5. Może to wyjaśniać tajemnicę podwójnego haszowania zaimplementowanego w Bitcoin przez Satoshi Nakamoto. Aby uniknąć tego typu ataków, Satoshi mógł preferować użycie podwójnego SHA256:

 $\text{HASH256}(m) = \text{SHA256}(\text{SHA256}(m))$

Zwiększa to bezpieczeństwo przed potencjalnymi atakami związanymi z konstrukcją Merkle-Damgård, ale nie zwiększa bezpieczeństwa procesu mieszania pod względem odporności na kolizje. Co więcej, nawet gdyby SHA256 był podatny na tego typu ataki, nie miałoby to poważnego wpływu, ponieważ wszystkie przypadki użycia funkcji Hash w Bitcoin dotyczą danych publicznych. Atak polegający na wydłużeniu długości może być jednak przydatny dla atakującego tylko wtedy, gdy zaszyfrowane dane są prywatne, a użytkownik użył funkcji Hash jako mechanizmu uwierzytelniania tych danych, podobnego do MAC. Tak więc implementacja podwójnego haszowania pozostaje tajemnicą w projekcie Bitcoin.

Teraz, gdy szczegółowo przyjrzeliśmy się działaniu funkcji Hash, w szczególności SHA256, który jest szeroko stosowany w Bitcoin, skupimy się bardziej szczegółowo na algorytmach derywacji kryptograficznej stosowanych na poziomie aplikacji, zwłaszcza do wyprowadzania kluczy dla Wallet.

Algorytmy używane do wyprowadzania

W Bitcoin na poziomie aplikacji, oprócz funkcji Hash, kryptograficzne algorytmy pochodne są wykorzystywane do generate zabezpieczania danych przed początkowymi danymi wejściowymi. Chociaż algorytmy te opierają się na funkcjach Hash, służą innym celom, zwłaszcza w zakresie uwierzytelniania i generowania kluczy. Algorytmy te zachowują niektóre cechy funkcji Hash, takie jak nieodwracalność, odporność na manipulacje i odporność na kolizje.

W portfelach Bitcoin stosowane są głównie 2 algorytmy derywacji:

HMAC (Hash-based Message Authentication Code)**
PBKDF2 (Password-Based Key Derivation Function 2)**

Wspólnie zbadamy funkcjonowanie i rolę każdego z nich.

HMAC-SHA512

HMAC to algorytm kryptograficzny, który oblicza kod uwierzytelniający na podstawie kombinacji funkcji Hash i tajnego klucza. Bitcoin wykorzystuje HMAC-SHA512, wariant HMAC, który wykorzystuje funkcję SHA512 Hash. Widzieliśmy już w poprzednim rozdziale, że SHA512 jest częścią tej samej rodziny funkcji Hash co SHA256, ale daje 512-bitowy wynik.

Oto jego ogólny schemat działania, w którym $m$ jest wiadomością wejściową, a $K$ tajnym kluczem:

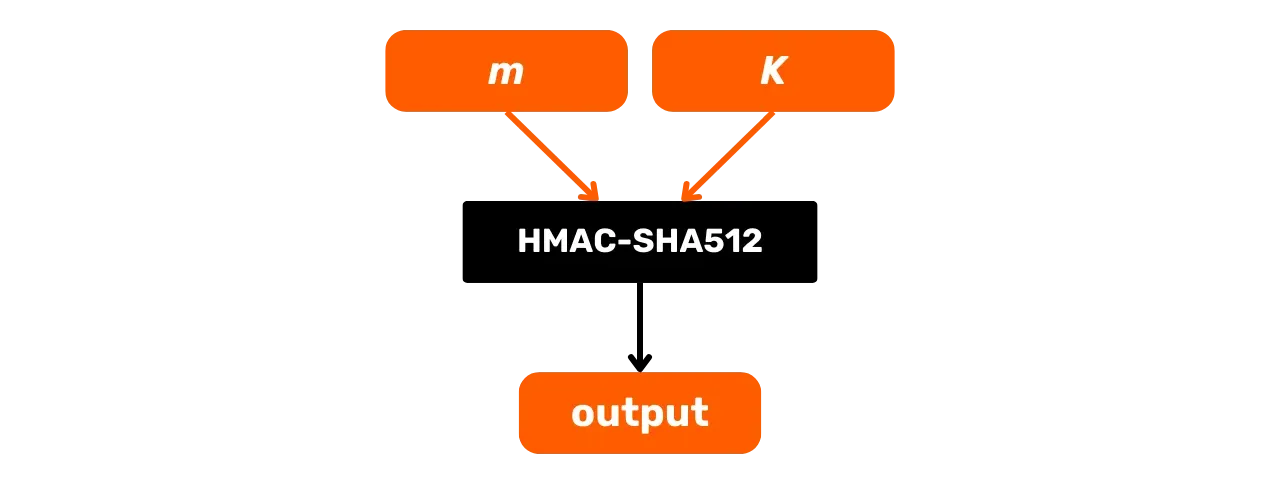
Przeanalizujmy bardziej szczegółowo, co dzieje się w tej czarnej skrzynce HMAC-SHA512. Funkcja HMAC-SHA512 z:

$m$ : wiadomość o dowolnym rozmiarze wybrana przez użytkownika (pierwsze wejście);
$K$ : dowolny tajny klucz wybrany przez użytkownika (drugie wejście);
$K'$ : klucz $K$ dostosowany do rozmiaru $B$ bloków funkcyjnych Hash (1024 bity dla SHA512 lub 128 bajtów);
$\text{SHA512}$ : funkcja SHA512 Hash;
$\oplus$ : operacja XOR (exclusive or);
$\Vert$ : operator konkatenacji, łączący ciągi bitów od końca do końca;
$\text{opad}$ : stała składająca się z bajtu $0x5c$ powtórzonego 128 razy
$\text{ipad}$ : stała składająca się z bajtu $0x36$ powtórzonego 128 razy.

Przed obliczeniem HMAC konieczne jest wyrównanie klucza i stałych zgodnie z rozmiarem bloku $B$ . Na przykład, jeśli klucz $K$ jest krótszy niż 128 bajtów, jest on uzupełniany zerami, aby osiągnąć rozmiar $B$ . Jeśli $K$ jest dłuższy niż 128 bajtów, jest kompresowany przy użyciu SHA512, a następnie dodawane są zera, aż osiągnie 128 bajtów. W ten sposób uzyskuje się zrównoleglony klucz o nazwie $K'$ . Wartości $\text{opad}$ i $\text{ipad}$ są uzyskiwane poprzez powtarzanie ich bajtu bazowego ( $0x5c$ dla $\text{opad}$ , $0x36$ dla $\text{ipad}$ ), aż do osiągnięcia rozmiaru $B$ . Tak więc, przy $B = 128$ bajtów, mamy:

 $\text{opad} = \underbrace{0x5c5c\ldots5c}\_{128 \ \text{bytes}}$

Po zakończeniu przetwarzania wstępnego algorytm HMAC-SHA512 jest zdefiniowany przez następujące równanie:

 $\text{HMAC-SHA512}(K,m) = \text{SHA512} \left( (K' \oplus \text{opad}) \parallel \text{SHA512} \left( (K' \oplus \text{ipad}) \parallel m \right) \right)$

Równanie to jest podzielone na następujące kroki:

XOR skorygowanego klucza $K'$ z $\text{ipad}$ w celu uzyskania $\text{iKpad}$ ;
XOR skorygowanego klucza $K'$ z $\text{opad}$ w celu uzyskania $\text{oKpad}$ ;
Konkatenacja $\text{iKpad}$ z wiadomością $m$ .
Hash ten wynik z SHA512, aby uzyskać pośredni Hash $H_1$ .
Złącz $\text{oKpad}$ z $H_1$ .
Hash ten wynik z SHA512, aby uzyskać ostateczny wynik $H_2$ .

Kroki te można podsumować schematycznie w następujący sposób:

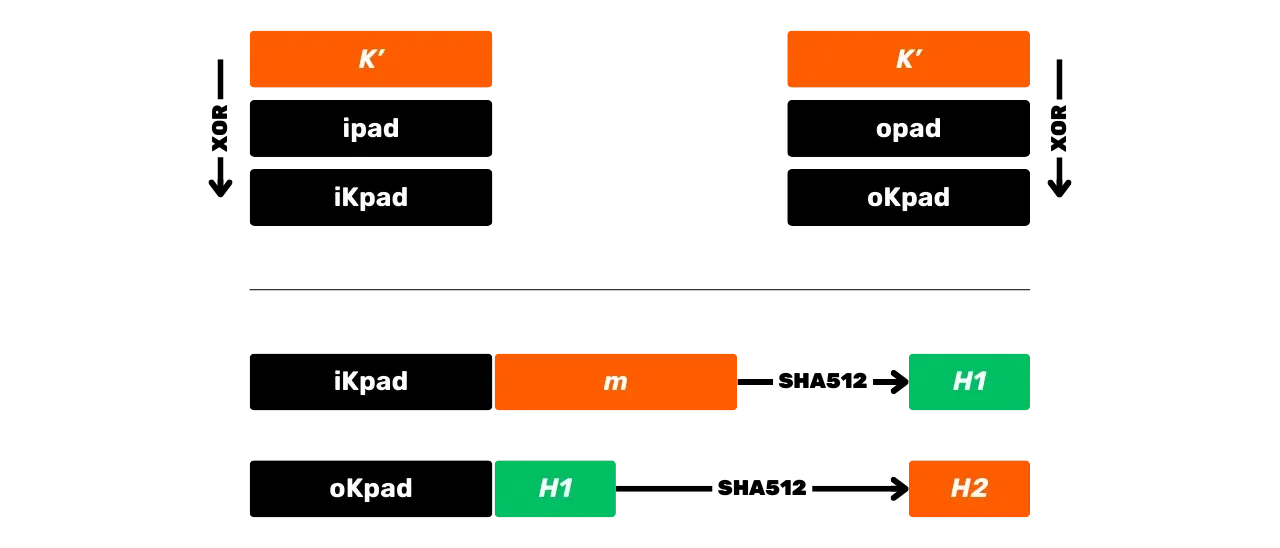
HMAC jest używany w Bitcoin w szczególności do wyprowadzania kluczy w portfelach HD (Hierarchical Deterministic) (omówimy to bardziej szczegółowo w kolejnych rozdziałach) oraz jako składnik PBKDF2.

PBKDF2

PBKDF2 (Password-Based Key Derivation Function 2) to algorytm wyprowadzania klucza zaprojektowany w celu zwiększenia bezpieczeństwa haseł. Algorytm stosuje funkcję pseudolosową (tutaj HMAC-SHA512) do hasła i soli kryptograficznej, a następnie powtarza tę operację określoną liczbę razy w celu uzyskania klucza wyjściowego.

W Bitcoin, PBKDF2 jest używany do generate seed HD Wallet z frazy Mnemonic i passphrase (ale omówimy to bardziej szczegółowo w kolejnych rozdziałach).

Proces PBKDF2 wygląda następująco:

$m$ : fraza Mnemonic użytkownika;
$s$ : opcjonalny passphrase w celu zwiększenia bezpieczeństwa (puste pole w przypadku braku passphrase);
$n$ : liczba iteracji funkcji, w naszym przypadku jest to 2048.

Funkcja PBKDF2 jest zdefiniowana iteracyjnie. Każda iteracja pobiera wynik poprzedniej, przepuszcza go przez HMAC-SHA512 i łączy kolejne wyniki w celu uzyskania klucza końcowego:

 $\text{PBKDF2}(m, s) = \text{HMAC-SHA512}^{2048}(m, s)$

Schematycznie PBKDF2 można przedstawić w następujący sposób:

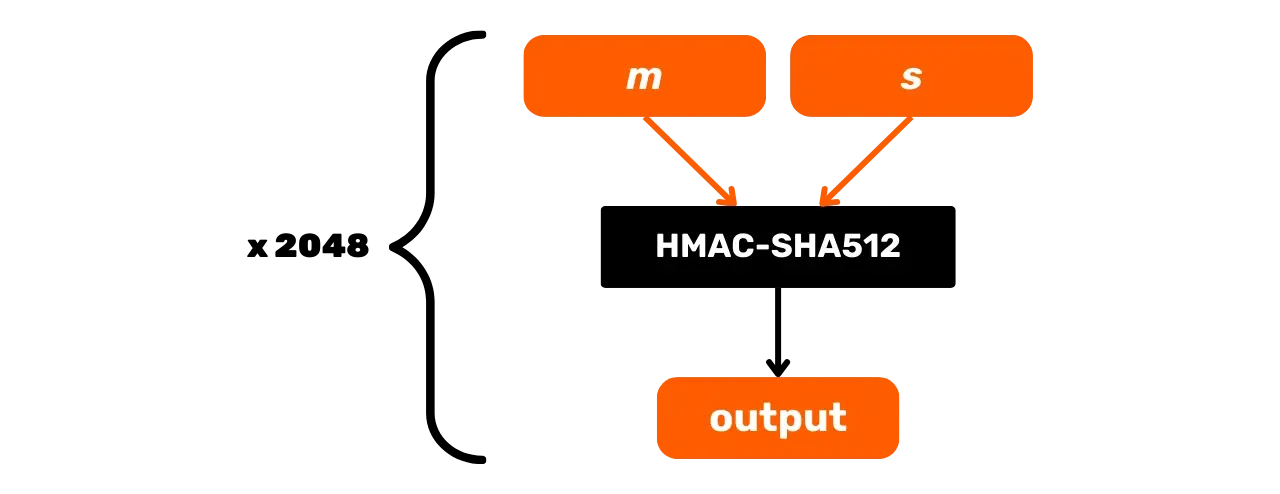
W tym rozdziale przeanalizowaliśmy funkcje HMAC-SHA512 i PBKDF2, które wykorzystują funkcje haszujące w celu zapewnienia integralności i bezpieczeństwa wyprowadzania kluczy w protokole Bitcoin. W następnej części przyjrzymy się podpisom cyfrowym, innej metodzie kryptograficznej szeroko stosowanej w Bitcoin.

Podpisy cyfrowe

Podpisy cyfrowe i krzywe eliptyczne

Druga metoda kryptograficzna stosowana w Bitcoin obejmuje algorytmy podpisu cyfrowego. Przyjrzyjmy się, co to oznacza i jak to działa.

Bitcoiny, UTXO i warunki wydawania pieniędzy

Termin "wallet" w Bitcoin może być dość mylący dla początkujących. W rzeczywistości to, co nazywa się Bitcoin Wallet, jest oprogramowaniem, które nie przechowuje bezpośrednio bitcoinów, w przeciwieństwie do fizycznego Wallet, który może przechowywać monety lub banknoty. Bitcoiny są po prostu jednostkami rozliczeniowymi. Ta jednostka konta jest reprezentowana przez UTXO (Unspent Transaction Outputs), które są niewydanymi wyjściami transakcji. Jeśli te wyjścia są niewydane, oznacza to, że należą do użytkownika. UTXO są w pewnym sensie kawałkami bitcoinów o zmiennej wielkości, należącymi do użytkownika.

Protokół Bitcoin jest rozproszony i działa bez centralnego organu. Dlatego nie przypomina tradycyjnych rejestrów bankowych, w których euro należące do użytkownika są po prostu powiązane z jego tożsamością. W Bitcoin twoje UTXO należą do ciebie, ponieważ są chronione przez warunki wydawania określone w języku skryptów. Upraszczając, istnieją dwa rodzaje skryptów: skrypt blokujący (scriptPubKey), który chroni UTXO, oraz skrypt odblokowujący (scriptSig), który umożliwia odblokowanie UTXO, a tym samym wydawanie reprezentowanych przez niego jednostek Bitcoin.

Początkowe działanie Bitcoin ze skryptami P2PK polega na użyciu klucza publicznego do zablokowania środków, określając w scriptPubKey, że osoba, która chce wydać ten UTXO, musi dostarczyć ważny podpis z kluczem prywatnym odpowiadającym temu kluczowi publicznemu. Aby odblokować ten UTXO, konieczne jest zatem dostarczenie ważnego podpisu w scriptSig. Jak sugerują ich nazwy, klucz publiczny jest znany wszystkim, ponieważ jest nadawany na Blockchain, podczas gdy klucz prywatny jest znany tylko prawowitemu właścicielowi funduszy.

Jest to podstawowa operacja Bitcoin, ale z czasem operacja ta stała się bardziej złożona. Po pierwsze, Satoshi wprowadził również skrypty P2PKH, które używają odbiorczego Address w scriptPubKey, który reprezentuje Hash klucza publicznego. Następnie system stał się jeszcze bardziej złożony wraz z pojawieniem się SegWit, a następnie Taproot. Jednak ogólna zasada pozostaje zasadniczo taka sama: klucz publiczny lub reprezentacja tego klucza jest używana do blokowania UTXO, a odpowiedni klucz prywatny jest wymagany do ich odblokowania, a tym samym ich wydania.

Użytkownik, który chce dokonać transakcji Bitcoin, musi zatem utworzyć podpis cyfrowy przy użyciu swojego klucza prywatnego na transakcji. Podpis ten może zostać zweryfikowany przez innych uczestników sieci. Jeśli jest on prawidłowy, oznacza to, że użytkownik inicjujący transakcję jest rzeczywiście właścicielem klucza prywatnego, a tym samym właścicielem bitcoinów, które chce wydać. Inni użytkownicy mogą następnie zaakceptować i propagować transakcję.

W rezultacie użytkownik posiadający bitcoiny zablokowane kluczem publicznym musi znaleźć sposób na bezpieczne przechowywanie tego, co umożliwia odblokowanie jego środków: klucza prywatnego. Bitcoin Wallet to właśnie urządzenie, które pozwoli ci łatwo przechowywać wszystkie klucze bez dostępu do nich innych osób. Przypomina więc bardziej brelok do kluczy niż Wallet.

Matematyczne powiązanie między kluczem publicznym a kluczem prywatnym, a także możliwość wykonania podpisu w celu udowodnienia posiadania klucza prywatnego bez jego ujawniania, są możliwe dzięki algorytmowi podpisu cyfrowego. W protokole Bitcoin stosowane są dwa algorytmy podpisu: ECDSA (Elliptic Curve Digital Signature Algorithm) oraz Schnorr signature scheme. ECDSA jest protokołem podpisu cyfrowego używanym w Bitcoin od jego początków. Schnorr jest nowszy w Bitcoin, ponieważ został wprowadzony w listopadzie 2021 r. wraz z aktualizacją Taproot.

Te dwa algorytmy są dość podobne w swoich mechanizmach. Oba opierają się na kryptografii krzywej eliptycznej. Główna różnica między tymi dwoma protokołami polega na strukturze podpisu i pewnych specyficznych właściwościach matematycznych. Przeanalizujemy zatem działanie tych algorytmów, zaczynając od najstarszego: ECDSA.

Kryptografia krzywych eliptycznych

Kryptografia krzywych eliptycznych (ECC) to zestaw algorytmów wykorzystujących krzywą eliptyczną ze względu na jej różne właściwości matematyczne i geometryczne do celów kryptograficznych. Bezpieczeństwo tych algorytmów opiera się na trudności problemu logarytmu dyskretnego na krzywych eliptycznych. Krzywe eliptyczne są w szczególności wykorzystywane do wymiany kluczy, szyfrowania asymetrycznego lub tworzenia podpisów cyfrowych.

Ważną właściwością tych krzywych jest to, że są one symetryczne względem osi x. Zatem każda linia niepionowa przecinająca krzywą w dwóch różnych punktach zawsze będzie przecinać krzywą w trzecim punkcie. Co więcej, każda styczna do krzywej w niesymetrycznym punkcie będzie przecinać krzywą w innym punkcie. Właściwości te będą przydatne do definiowania operacji na krzywej.

Oto reprezentacja krzywej eliptycznej w dziedzinie liczb rzeczywistych:

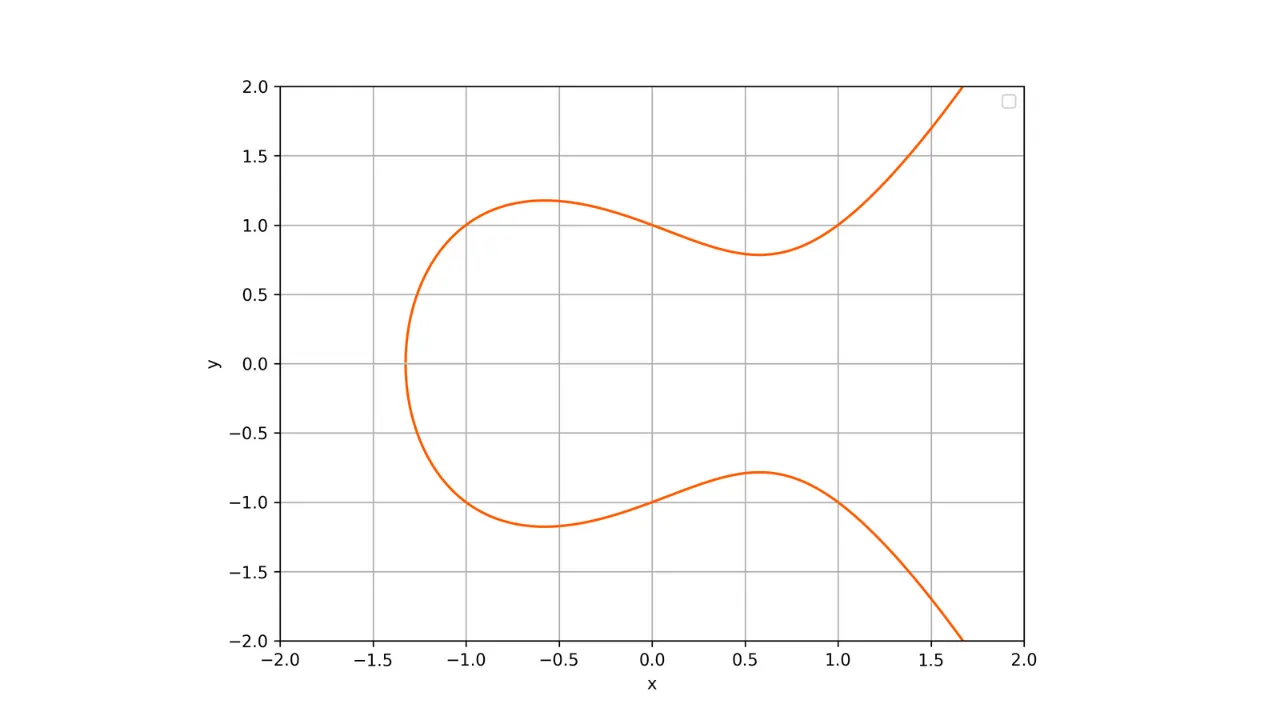
Każda krzywa eliptyczna jest zdefiniowana przez równanie postaci:

 $y^2 = x^3 + ax + b$

secp256k1

Aby użyć ECDSA lub Schnorr, należy wybrać parametry krzywej eliptycznej, czyli wartości $a$ i $b$ w równaniu krzywej. Istnieją różne standardy krzywych eliptycznych, które są uważane za bezpieczne kryptograficznie. Najbardziej znana jest krzywa secp256r1, zdefiniowana i zalecana przez NIST (National Institute of Standards and Technology).

Pomimo tego Satoshi Nakamoto, wynalazca Bitcoin, zdecydował się nie używać tej krzywej. Powód tego wyboru jest nieznany, ale niektórzy uważają, że wolał znaleźć alternatywę, ponieważ parametry tej krzywej mogłyby potencjalnie zawierać backdoora. Zamiast tego protokół Bitcoin wykorzystuje standardową krzywą secp256k1. Krzywa ta jest zdefiniowana przez parametry $a = 0$ i $b = 7$ . Jej równanie ma zatem postać:

 $y^2 = x^3 + 7$

Jego graficzna reprezentacja na polu liczb rzeczywistych wygląda następująco:

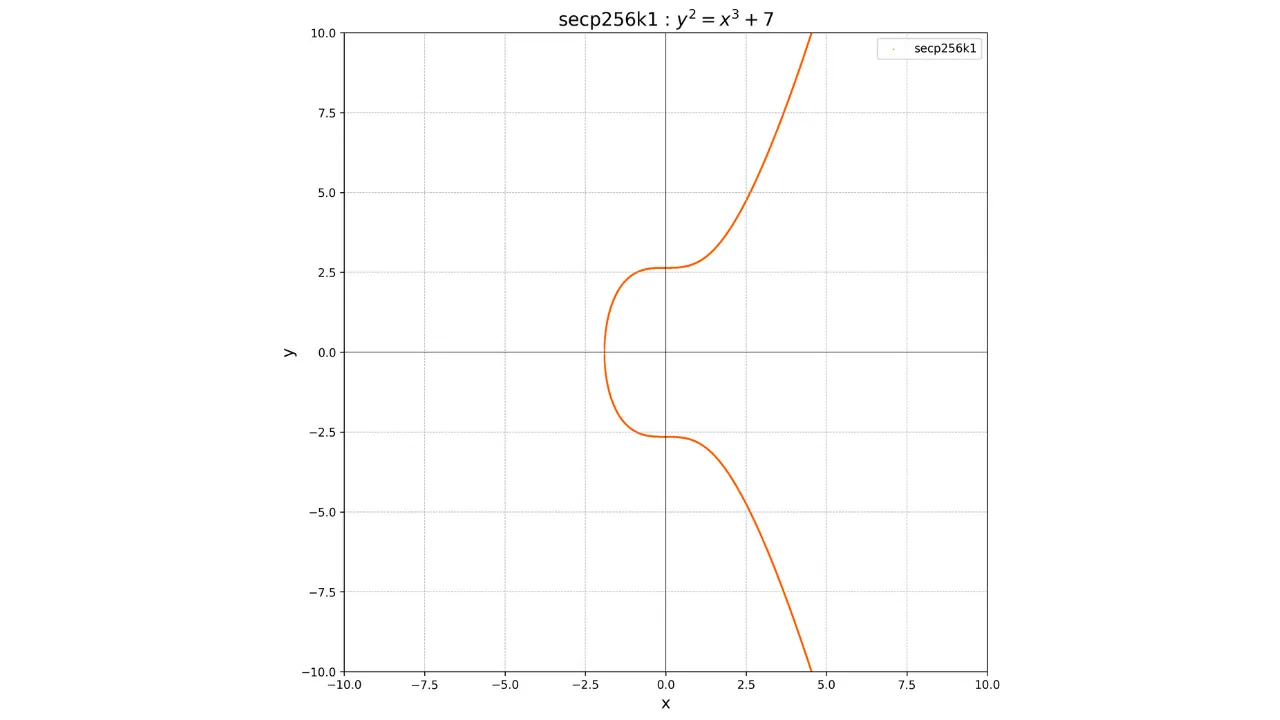
Jednak w kryptografii pracujemy ze skończonymi zbiorami liczb. Mówiąc dokładniej, pracujemy na skończonym polu $\mathbb{F}_p$ , które jest polem liczb całkowitych modulo liczba pierwsza $p$ .

Definicja: Liczba pierwsza to naturalna liczba całkowita większa lub równa 2, która ma tylko dwa różne dzielniki całkowite dodatnie: 1 i samą siebie. Na przykład, liczba 7 jest liczbą pierwszą, ponieważ może być podzielna tylko przez 1 i 7. Z drugiej strony, liczba 8 nie jest liczbą pierwszą, ponieważ może być podzielna przez 1, 2, 4 i 8.

W Bitcoin liczba pierwsza $p$ użyta do zdefiniowania skończonego pola jest bardzo duża. Jest ona wybierana w taki sposób, aby porządek pola (tj. liczba Elements w $\mathbb{F}_p$ ) był wystarczająco duży, aby zapewnić bezpieczeństwo kryptograficzne.

Użyta liczba pierwsza $p$ to:

p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F

W notacji dziesiętnej odpowiada to:

 $p = 2^{256} - 2^{32} - 977$

Zatem równanie naszej krzywej eliptycznej to:

 $y^2 \equiv x^3 + 7 \mod p$

Biorąc pod uwagę, że krzywa ta jest zdefiniowana na skończonym polu $\mathbb{F}_p$ , nie przypomina ona już krzywej ciągłej, ale raczej dyskretny zbiór punktów. Na przykład, oto jak wygląda krzywa użyta w Bitcoin dla bardzo małego $p = 17$ :

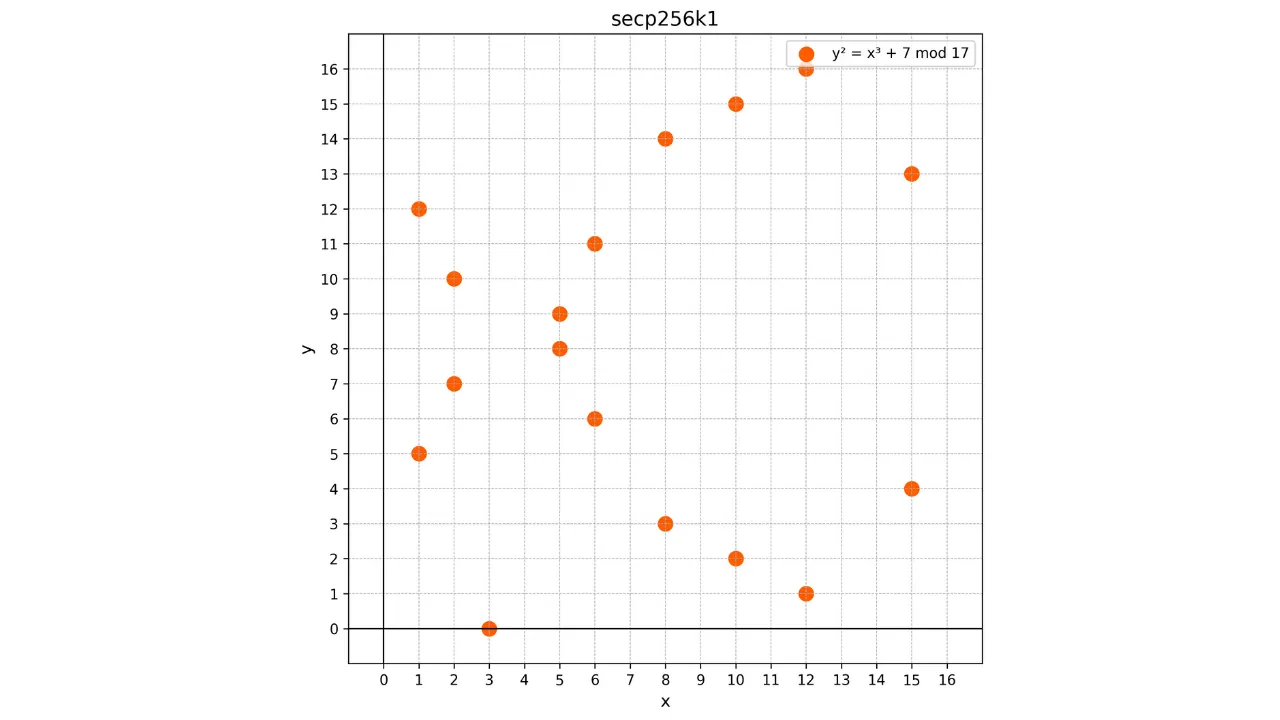
W tym przykładzie celowo ograniczyłem skończone pole do $p = 17$ ze względów edukacyjnych, ale należy sobie wyobrazić, że to użyte w Bitcoin jest znacznie większe, prawie $2^{256}$ .

Używamy skończonego pola liczb całkowitych modulo $p$ , aby zapewnić dokładność operacji na krzywej. Rzeczywiście, krzywe eliptyczne na polu liczb rzeczywistych są narażone na niedokładności wynikające z błędów zaokrągleń podczas obliczeń. Jeśli na krzywej wykonywanych jest wiele operacji, błędy te kumulują się, a ostateczny wynik może być nieprawidłowy lub trudny do odtworzenia. Wyłączne użycie dodatnich liczb całkowitych zapewnia doskonałą dokładność obliczeń, a tym samym powtarzalność wyniku.

Matematyka krzywych eliptycznych nad skończonymi polami jest analogiczna do tych nad polem liczb rzeczywistych, z tą różnicą, że wszystkie operacje są wykonywane modulo $p$ . Aby uprościć wyjaśnienia, w kolejnych rozdziałach będziemy kontynuować ilustrowanie pojęć za pomocą krzywej zdefiniowanej na liczbach rzeczywistych, pamiętając jednocześnie, że w praktyce krzywa jest zdefiniowana na skończonym polu.

Jeśli chcesz dowiedzieć się więcej o matematycznych podstawach współczesnej kryptografii, polecam również zapoznanie się z tym innym kursem na Plan ₿ Network:

https://planb.network/courses/d2fd9fc0-d9ed-4a87-9fa3-0fdbb3937e28

Obliczanie klucza publicznego na podstawie klucza prywatnego

Jak już wcześniej wspomniano, algorytmy podpisu cyfrowego w Bitcoin opierają się na parze kluczy prywatnych i publicznych, które są ze sobą powiązane matematycznie. Zbadajmy razem, czym jest to matematyczne powiązanie i jak są one generowane.

Klucz prywatny

Klucz prywatny jest po prostu liczbą losową lub pseudolosową. W przypadku Bitcoin liczba ta ma rozmiar 256 bitów. Liczba możliwości dla klucza prywatnego Bitcoin wynosi zatem teoretycznie $2^{256}$ .

Uwaga: "Liczba pseudolosowa" to liczba, która ma właściwości zbliżone do liczby prawdziwie losowej, ale jest generowana przez algorytm deterministyczny.

Jednak w praktyce istnieje tylko $n$ różnych punktów na naszej krzywej eliptycznej secp256k1, gdzie $n$ jest rzędem punktu generatora $G$ krzywej. Zobaczymy później, czemu odpowiada ta liczba, ale wystarczy pamiętać, że prawidłowy klucz prywatny jest liczbą całkowitą z przedziału od $1$ do $n-1$ , wiedząc, że $n$ jest liczbą bliską, ale nieco mniejszą niż $2^{256}$ . Dlatego istnieją pewne 256-bitowe liczby, które nie są ważne, aby stać się kluczem prywatnym w Bitcoin, w szczególności wszystkie liczby między $n$ a $2^{256}$ . Jeśli podczas generowania liczby losowej (klucza prywatnego) wygenerowana zostanie wartość $k$ taka, że $k \geq n$ , jest ona uznawana za nieważną i konieczne jest wygenerowanie nowej wartości losowej.

Liczba możliwości dla klucza prywatnego Bitcoin wynosi zatem około $n$ , co jest liczbą zbliżoną do $1,158 \ razy 10^{77}$ . Liczba ta jest tak duża, że jeśli wybierzesz klucz prywatny losowo, statystycznie prawie niemożliwe jest trafienie na klucz prywatny innego użytkownika. Aby dać ci wyobrażenie o skali, liczba możliwych kluczy prywatnych w Bitcoin jest rzędu wielkości zbliżonej do szacowanej liczby atomów w obserwowalnym wszechświecie.

Jak zobaczymy w kolejnych rozdziałach, obecnie większość kluczy prywatnych używanych w Bitcoin nie jest generowana losowo, ale jest wynikiem deterministycznego wyprowadzenia z frazy Mnemonic, która sama w sobie jest pseudolosowa (jest to słynna fraza 12 lub 24 słów). Ta informacja nie zmienia niczego w kwestii stosowania algorytmów podpisu takich jak ECDSA, ale pomaga przeorientować naszą popularyzację w Bitcoin.

W dalszej części wyjaśnienia klucz prywatny będzie oznaczany małą literą $k$ .

Klucz publiczny

Klucz publiczny jest punktem na krzywej eliptycznej, oznaczonym wielką literą $K$ i jest obliczany na podstawie klucza prywatnego $k$ . Punkt $K$ jest reprezentowany przez parę współrzędnych $(x, y)$ na krzywej eliptycznej, z których każda jest liczbą całkowitą modulo $p$ , liczbą pierwszą definiującą skończone pole $\mathbb{F}_p$ .

W praktyce nieskompresowany klucz publiczny jest reprezentowany przez 520 bitów (lub 65 bajtów), co odpowiada dwóm 256-bitowym liczbom ( $x$ i $y$ ) umieszczonym od końca do końca, poprzedzonym 8-bitowym prefiksem $0x04$ .

Możliwe jest jednak również przedstawienie klucza publicznego w skompresowanej formie przy użyciu tylko 33 bajtów (264 bitów), zachowując tylko odciętą $x$ naszego punktu na krzywej i bajt wskazujący parzystość $y$ . Jest to tak zwany skompresowany klucz publiczny. Więcej na ten temat opowiem w ostatnich rozdziałach tego szkolenia. Należy jednak pamiętać, że klucz publiczny $K$ to punkt opisany przez $x$ i $y$ .

Aby obliczyć punkt $K$ odpowiadający naszemu kluczowi publicznemu, wykorzystujemy operację mnożenia skalarnego na krzywych eliptycznych, zdefiniowaną jako wielokrotne dodawanie ( $k$ razy) punktu generatora $G$ :

 $K = k \cdot G$

gdzie:

$k$ to klucz prywatny (losowa liczba całkowita z przedziału od $1$ do $n-1$ );
$G$ jest punktem generatora krzywej eliptycznej używanej przez wszystkich uczestników sieci Bitcoin;
$\cdot$ reprezentuje mnożenie skalarne na krzywej eliptycznej, które jest równoważne dodaniu punktu $G$ do siebie $k$ razy.

Fakt, że ten punkt $G$ jest wspólny dla wszystkich kluczy publicznych w Bitcoin pozwala nam mieć pewność, że ten sam klucz prywatny $k$ zawsze da nam ten sam klucz publiczny $K$ :

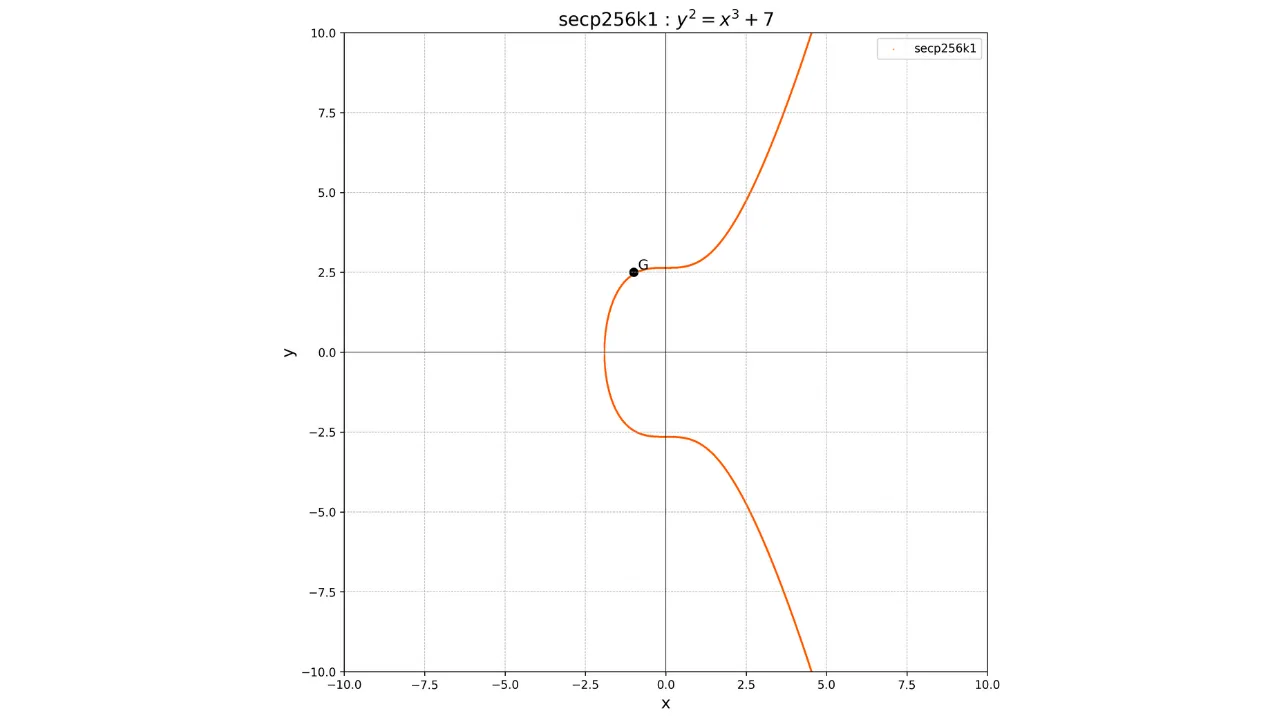
Główną cechą tej operacji jest to, że jest to funkcja jednokierunkowa. Łatwo jest obliczyć klucz publiczny $K$ znając klucz prywatny $k$ i punkt generatora $G$ , ale praktycznie niemożliwe jest obliczenie klucza prywatnego $k$ znając tylko klucz publiczny $K$ i punkt generatora $G$ . Znalezienie $k$ na podstawie $K$ i $G$ sprowadza się do rozwiązania problemu logarytmu dyskretnego na krzywych eliptycznych, trudnego matematycznie problemu, dla którego nie jest znany żaden skuteczny algorytm. Nawet najpotężniejsze obecne kalkulatory nie są w stanie rozwiązać tego problemu w rozsądnym czasie.

Dodawanie i podwajanie punktów na krzywych eliptycznych

Koncepcja dodawania na krzywych eliptycznych jest zdefiniowana geometrycznie. Jeśli mamy dwa punkty $P$ i $Q$ na krzywej, operacja $P + Q$ jest obliczana poprzez narysowanie linii przechodzącej przez $P$ i $Q$ . Linia ta z konieczności przetnie krzywą w trzecim punkcie $R'$ . Następnie bierzemy lustrzane odbicie tego punktu względem osi x, aby uzyskać punkt $R$ , który jest wynikiem dodawania:

 $P + Q = R$

Graficznie można to przedstawić w następujący sposób:

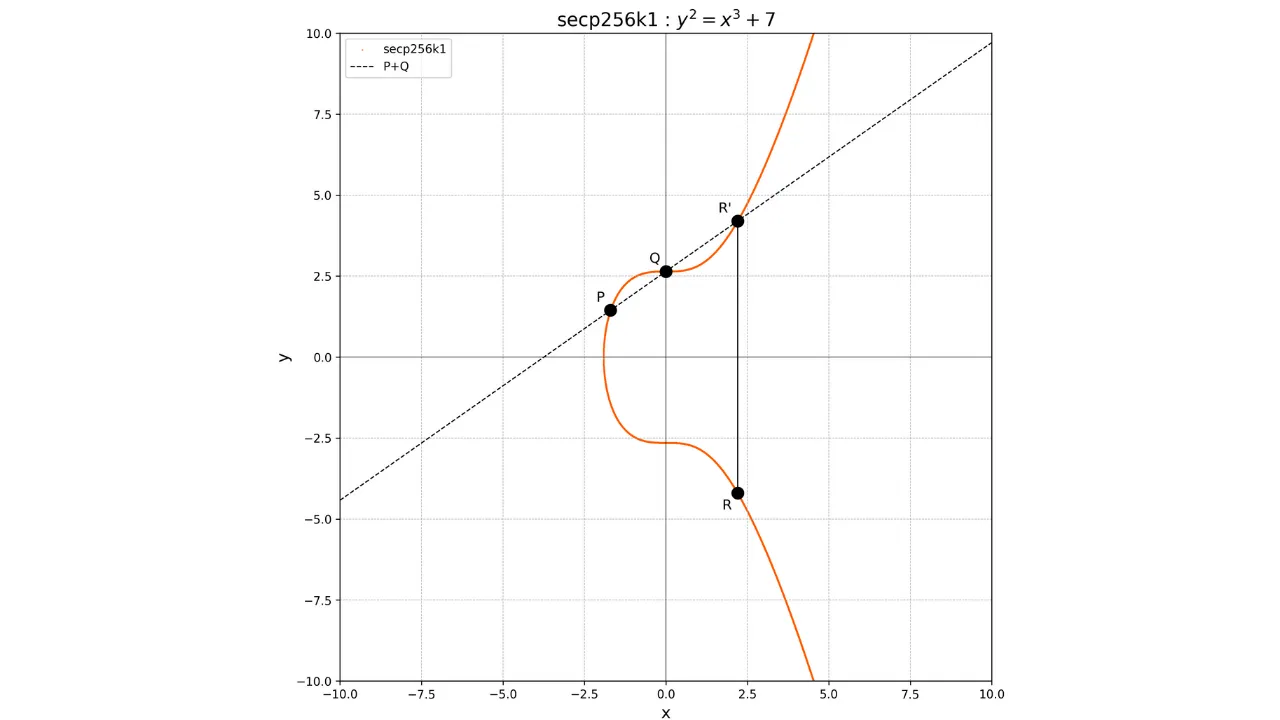
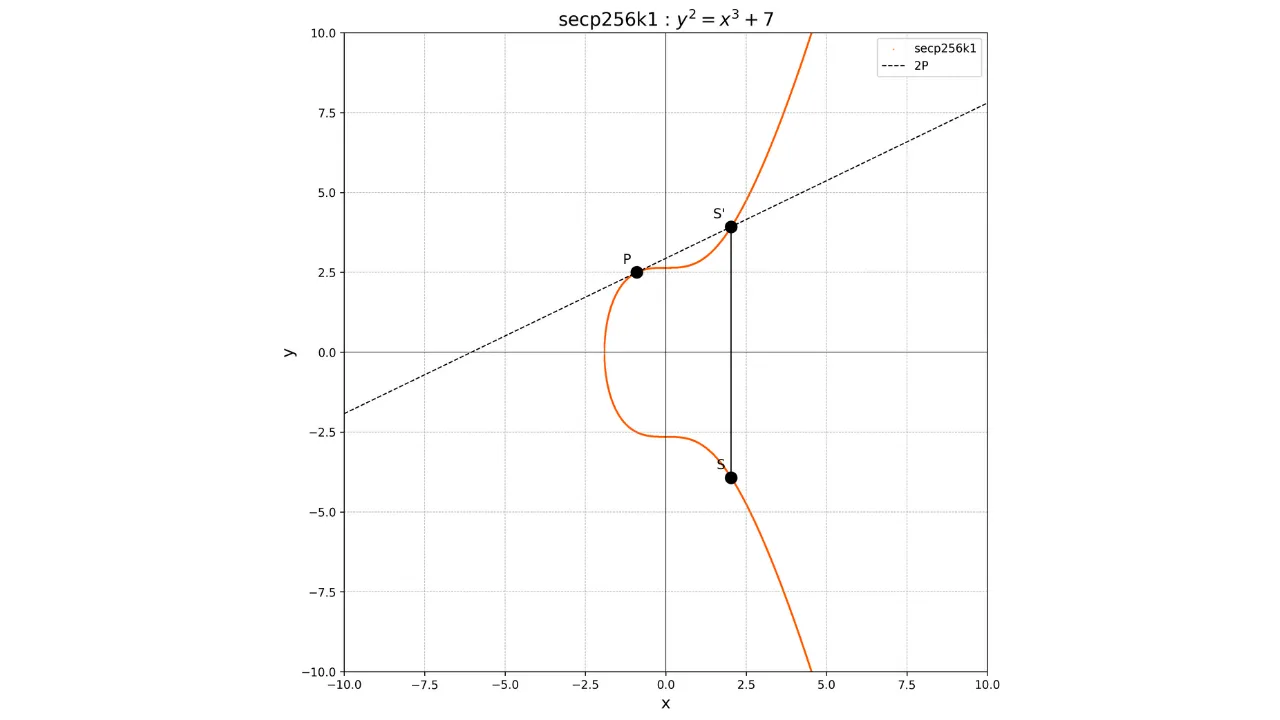
W przypadku podwojenia punktu, czyli operacji $P + P$ , rysujemy styczną do krzywej w punkcie $P$ . Ta styczna przecina krzywą w innym punkcie $S'$ . Następnie bierzemy lustrzane odbicie tego punktu względem osi x, aby uzyskać punkt $S$ , który jest wynikiem podwojenia:

 $2P = S$

Graficznie jest to przedstawione jako:

Korzystając z tych operacji dodawania i podwajania, możemy wykonać skalarne mnożenie punktu przez liczbę całkowitą $k$ , oznaczoną jako $kP$ , poprzez wielokrotne podwajanie i dodawanie.

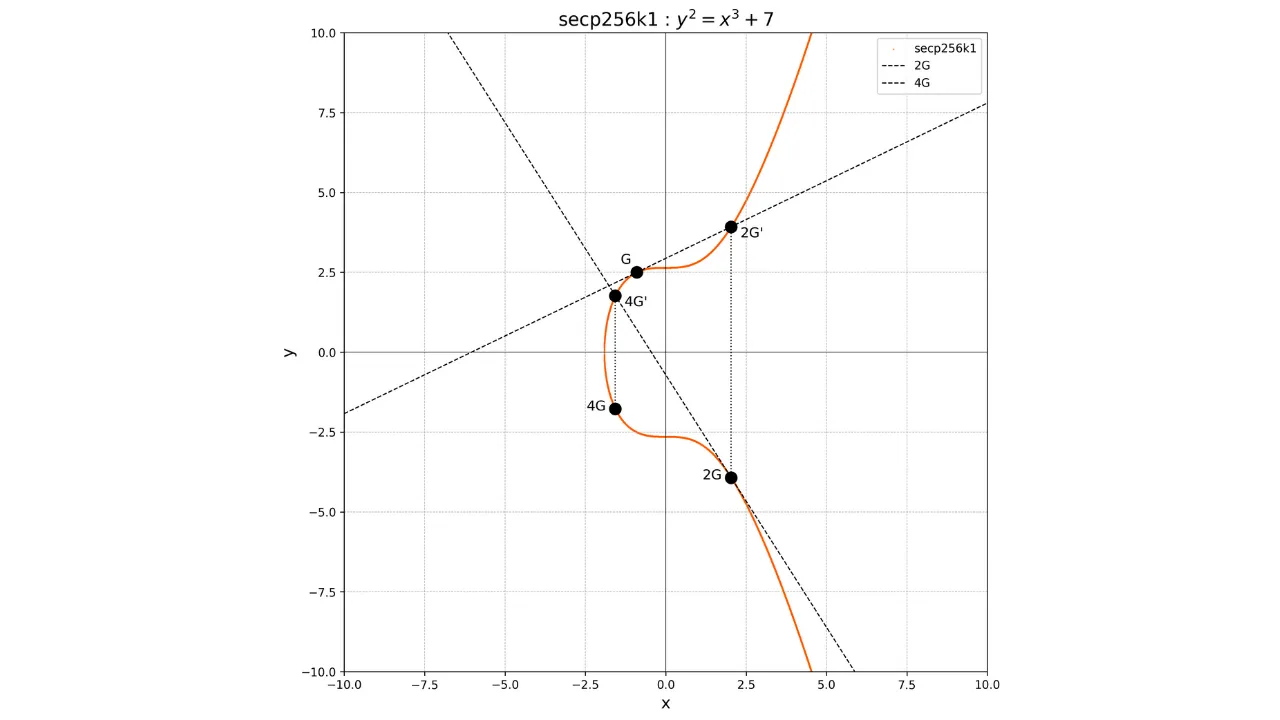
Załóżmy na przykład, że wybraliśmy klucz prywatny $k = 4$ . Aby obliczyć powiązany klucz publiczny, wykonujemy następujące czynności:

 $K = k \cdot G = 4G$

Graficznie odpowiada to wykonaniu serii dodawań i podwojeń:

Oblicz $2G$ podwajając $G$ .
Oblicz $4G$ podwajając $2G$ .

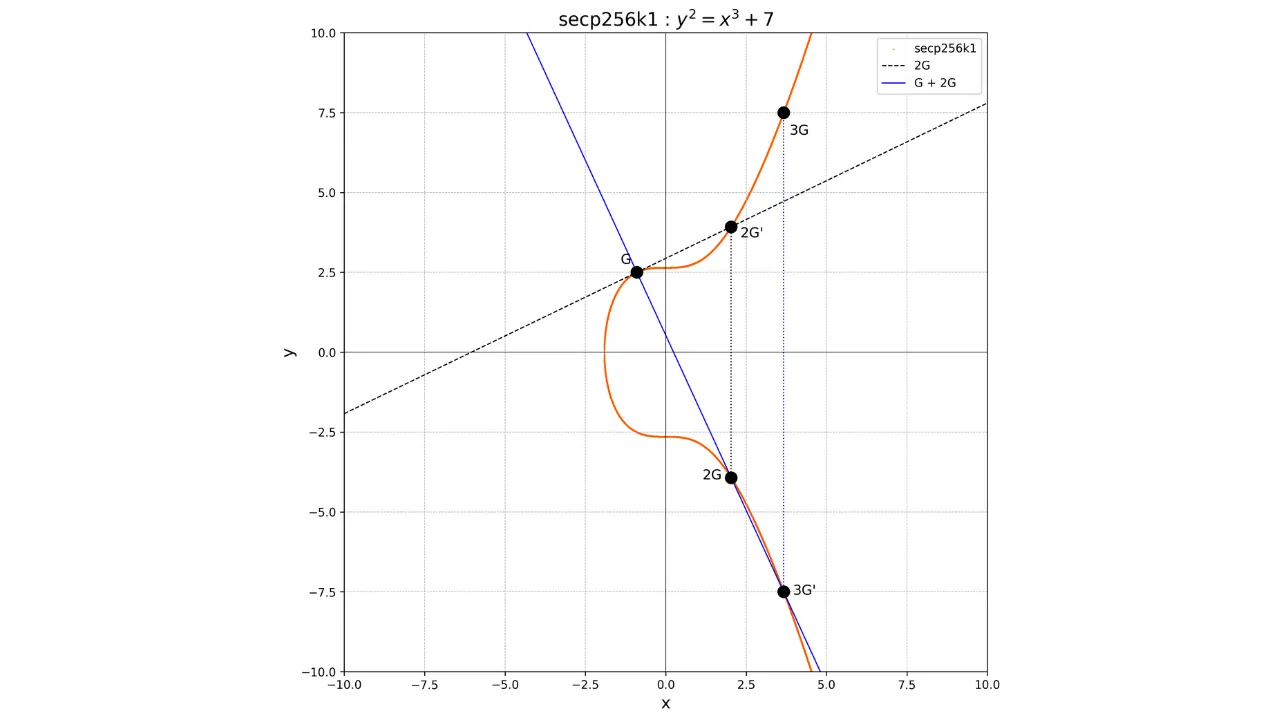
Jeśli chcemy na przykład obliczyć punkt $3G$ , musimy najpierw obliczyć punkt $2G$ poprzez podwojenie punktu $G$ , a następnie dodać $G$ i $2G$ . Aby dodać $G$ i $2G$ , wystarczy narysować linię łączącą te dwa punkty, znaleźć unikalny punkt $-3G$ na przecięciu tej linii z krzywą eliptyczną, a następnie wyznaczyć $3G$ jako przeciwieństwo $-3G$ .

Będziemy mieć:

 $G + G = 2G$

 $2G + G = 3G$

Graficznie można to przedstawić w następujący sposób:

Funkcja jednokierunkowa

Dzięki tym operacjom możemy zrozumieć, dlaczego łatwo jest wyprowadzić klucz publiczny z klucza prywatnego, ale odwrotna sytuacja jest praktycznie niemożliwa.

Wróćmy do naszego uproszczonego przykładu. Z kluczem prywatnym $k = 4$ . Aby obliczyć powiązany klucz publiczny, wykonujemy:

 $K = k \cdot G = 4G$

W ten sposób byliśmy w stanie łatwo obliczyć klucz publiczny $K$ znając $k$ i $G$ .

Teraz, jeśli ktoś zna tylko klucz publiczny $K$ , staje przed problemem logarytmu dyskretnego: znalezienie $k$ takiego, że $K = k \cdot G$ . Problem ten jest uważany za trudny, ponieważ nie istnieje skuteczny algorytm rozwiązujący go na krzywych eliptycznych. Zapewnia to bezpieczeństwo algorytmów ECDSA i Schnorr.

Oczywiście, w tym uproszczonym przykładzie z $k = 4$ , możliwe byłoby znalezienie $k$ metodą prób i błędów, ponieważ liczba możliwości jest niska. Jednak w praktyce $k$ jest 256-bitową liczbą całkowitą, co sprawia, że liczba możliwości jest astronomicznie duża (około 1,158 \ razy 10^{77} $). Dlatego znalezienie$ k$ metodą siłową jest niewykonalne.

Podpisywanie za pomocą klucza prywatnego

Teraz, gdy już wiesz, jak wyprowadzić klucz publiczny z klucza prywatnego, możesz już otrzymywać bitcoiny, używając tej pary kluczy jako warunku wydawania. Ale jak je wydać? Aby wydać bitcoiny, musisz odblokować scriptPubKey dołączony do UTXO, aby udowodnić, że rzeczywiście jesteś jego prawowitym właścicielem. Aby to zrobić, musisz stworzyć podpis $s$ , który pasuje do klucza publicznego $K$ obecnego w scriptPubKey przy użyciu klucza prywatnego $k$ , który został pierwotnie użyty do obliczenia $K$ . Podpis cyfrowy jest zatem niepodważalnym dowodem na to, że jesteś w posiadaniu klucza prywatnego powiązanego z kluczem publicznym, o który się ubiegasz.

Parametry krzywej eliptycznej

Aby złożyć podpis cyfrowy, wszyscy uczestnicy muszą najpierw uzgodnić parametry używanej krzywej eliptycznej. W przypadku Bitcoin parametry secp256k1 są następujące:

Skończone pole $\mathbb{Z}_p$ zdefiniowane przez:

 $p = 2^{256} - 2^{32} - 977$

p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F

$p$ jest bardzo dużą liczbą pierwszą, nieco mniejszą niż $2^{256}$ .

Krzywa eliptyczna $y^2 = x^3 + ax + b$ nad $\mathbb{Z}_p$ zdefiniowana przez:

 $a = 0, \quad b = 7$

Punkt generatora lub punkt początkowy $G$ :

G = 0x0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798

Liczba ta jest skompresowaną formą, która podaje tylko odciętą punktu $G$ . Przedrostek 02 na początku określa, która z dwóch wartości o tym odciętym $x$ ma być użyta jako punkt generujący.

Porządek $n$ w $G$ (liczba istniejących punktów) i kofaktor $h$ :

n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141

$n$ jest bardzo dużą liczbą nieco mniejszą niż $p$ .

 $h=1$

$h$ jest kofaktorem lub liczbą podgrup. Nie będę się tutaj rozwodził nad tym, co to reprezentuje, ponieważ jest to dość skomplikowane, a w przypadku Bitcoin nie musimy go brać pod uwagę, ponieważ jest równy $1$ .

Wszystkie te informacje są publiczne i znane wszystkim uczestnikom. Dzięki nim użytkownicy są w stanie złożyć podpis cyfrowy i zweryfikować go.

Podpis ECDSA

Algorytm ECDSA umożliwia użytkownikowi podpisanie wiadomości przy użyciu jego klucza prywatnego w taki sposób, że każdy znający odpowiedni klucz publiczny może zweryfikować ważność podpisu, bez ujawniania klucza prywatnego. W kontekście Bitcoin, podpisywana wiadomość zależy od sighash wybranego przez użytkownika. To właśnie ten sighash określa, które części transakcji są objęte podpisem. Więcej na ten temat opowiem w następnym rozdziale.

Oto kroki do generate podpisu ECDSA:

Najpierw obliczamy Hash ( $e$ ) wiadomości, która ma zostać podpisana. Wiadomość $m$ jest zatem przekazywana przez kryptograficzną funkcję Hash, zazwyczaj SHA256 lub podwójną SHA256 w przypadku Bitcoin:

 $e = \text{HASH}(m)$

Następnie obliczamy Nonce. W kryptografii Nonce jest po prostu liczbą generowaną w sposób losowy lub pseudolosowy, która jest używana tylko raz. Oznacza to, że za każdym razem, gdy składany jest nowy podpis cyfrowy za pomocą tej pary kluczy, bardzo ważne będzie użycie innego Nonce, w przeciwnym razie zagrozi to bezpieczeństwu klucza prywatnego. Wystarczy zatem określić losową i unikalną liczbę całkowitą $r$ taką, że $1 \leq r \leq n-1$ , gdzie $n$ jest rzędem punktu generującego $G$ krzywej eliptycznej.

Następnie obliczymy punkt $R$ na krzywej eliptycznej o współrzędnych $(x_R, y_R)$ takich, że:

 $R = r \cdot G$

Wyodrębniamy wartość odciętej punktu $R$ ( $x_R$ ). Wartość ta reprezentuje pierwszą część sygnatury. Na koniec obliczamy drugą część sygnatury $s$ w ten sposób:

 $s = r^{-1} \left( e + k \cdot x_R \right) \mod n$

gdzie:

$r^{-1}$ jest modularną odwrotnością $r$ modulo $n$ , czyli liczbą całkowitą taką, że $r \cdot r^{-1} \equiv 1 \mod n$ ;
$k$ to klucz prywatny użytkownika;
$e$ to Hash wiadomości;
$n$ jest rzędem punktu generatora $G$ krzywej eliptycznej.

Sygnatura jest wtedy po prostu konkatenacją $x_R$ i $s$ :

 $\text{SIG} = x_R \Vert s$

Weryfikacja podpisu ECDSA

Aby zweryfikować podpis $(x_R, s)$ , każdy znający klucz publiczny $K$ i parametry krzywej eliptycznej może postępować w ten sposób:

Najpierw należy sprawdzić, czy $x_R$ i $s$ należą do przedziału $[1, n-1]$ . Gwarantuje to, że podpis jest zgodny z matematycznymi ograniczeniami grupy eliptycznej. Jeśli tak nie jest, weryfikator natychmiast odrzuca podpis jako nieprawidłowy.

Następnie należy obliczyć Hash wiadomości:

 $e = \text{HASH}(m)$

Oblicz odwrotność modularną $s$ modulo $n$ :

 $s^{-1} \mod n$

Oblicz w ten sposób dwie wartości skalarne $u_1$ i $u_2$ :

 $\begin{align*} u_1 &= e \cdot s^{-1} \mod n \\ u_2 &= x_R \cdot s^{-1} \mod n \end{align*}$

Na koniec oblicz punkt $V$ na krzywej eliptycznej taki, że:

 $V = u_1 \cdot G + u_2 \cdot K$

Sygnatura jest poprawna tylko wtedy, gdy $x_V \equiv x_R \mod n$ , gdzie $x_V$ jest współrzędną $x$ punktu $V$ . Rzeczywiście, łącząc $u_1 \cdot G$ i $u_2 \cdot K$ , otrzymujemy punkt $V$ , który, jeśli podpis jest ważny, musi odpowiadać punktowi $R$ użytemu podczas podpisu (modulo $n$ ).

Podpis z protokołem Schnorra

Schemat podpisu Schnorra jest alternatywą dla ECDSA, która oferuje wiele zalet. Można go używać w Bitcoin od 2021 r. i wprowadzenia Taproot, z wzorcami skryptów P2TR. Podobnie jak ECDSA, schemat Schnorra umożliwia podpisanie wiadomości przy użyciu klucza prywatnego w taki sposób, że podpis może zostać zweryfikowany przez każdego, kto zna odpowiedni klucz publiczny.

W przypadku Schnorra używana jest dokładnie ta sama krzywa co w ECDSA z tymi samymi parametrami. Klucze publiczne są jednak reprezentowane nieco inaczej niż w przypadku ECDSA. W rzeczywistości są one oznaczone tylko współrzędną $x$ punktu na krzywej eliptycznej. W przeciwieństwie do ECDSA, gdzie skompresowane klucze publiczne są reprezentowane przez 33 bajty (z bajtem prefiksu wskazującym parzystość $y$ ), Schnorr używa 32-bajtowych kluczy publicznych, odpowiadających jedynie współrzędnej $x$ punktu $K$ i zakłada się, że $y$ jest domyślnie parzyste. Ta uproszczona reprezentacja zmniejsza rozmiar podpisów i ułatwia pewne optymalizacje w algorytmach weryfikacji.

Klucz publiczny jest wtedy współrzędną $x$ punktu $K$ :

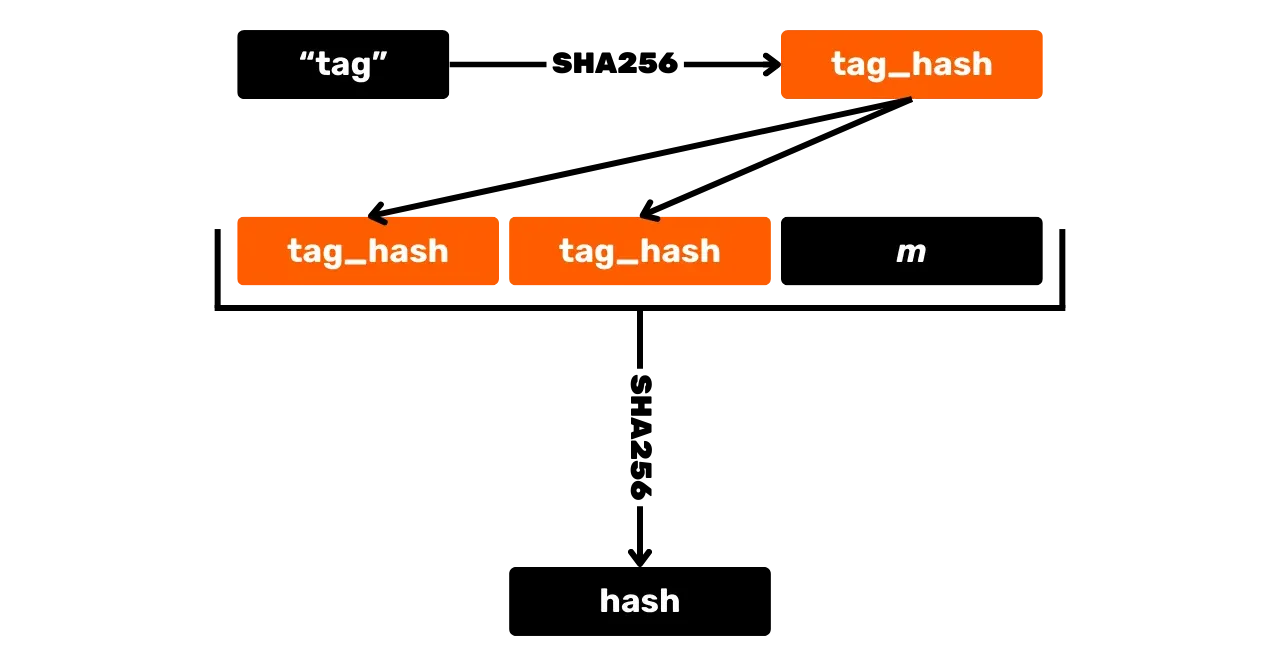
 $\text{pk} = K_x$

Pierwszym krokiem do generate podpisu jest Hash wiadomości. Ale w przeciwieństwie do ECDSA, odbywa się to z innymi wartościami, a oznaczona funkcja Hash jest używana w celu uniknięcia kolizji w różnych kontekstach. Oznaczona funkcja Hash polega po prostu na dodaniu dowolnej etykiety do wejść funkcji Hash wraz z danymi wiadomości.

Oprócz wiadomości, współrzędna $x$ klucza publicznego $K_x$ , a także punkt $R = r \cdot G$ , obliczony na podstawie Nonce $r$ (który sam w sobie jest unikalną liczbą całkowitą dla każdego podpisu, obliczaną deterministycznie na podstawie klucza prywatnego i wiadomości, aby uniknąć luk w zabezpieczeniach związanych z ponownym użyciem Nonce), są również przekazywane do funkcji oznaczonej. Podobnie jak w przypadku klucza publicznego, tylko współrzędna $x$ punktu Nonce $R_x$ jest przechowywana w celu opisania punktu.

Wynik tego haszowania odnotowany w $e$ nazywany jest "wyzwaniem":

 $e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod n$

Tutaj $\text{Hash}$ jest funkcją SHA256 Hash, a $\text{``BIP0340/challenge'}$ jest specyficznym tagiem dla haszowania.

Wreszcie, parametr $s$ jest obliczany na podstawie klucza prywatnego $k$ , Nonce $r$ i wyzwania $e$ w następujący sposób:

 $s = (r + e \cdot k) \mod n$

Sygnatura jest wtedy po prostu parą $R_x$ i $s$ .

 $\text{SIG} = R_x \Vert s$

Weryfikacja podpisu Schnorr

Weryfikacja podpisu Schnorra jest prostsza niż weryfikacja podpisu ECDSA. Oto kroki weryfikacji podpisu $(R_x, s)$ z kluczem publicznym $K_x$ i wiadomością $m$ .

Najpierw sprawdzamy, czy $K_x$ jest poprawną liczbą całkowitą mniejszą od $p$ . Jeśli tak jest, pobieramy odpowiedni punkt na krzywej, gdzie $K_y$ jest parzysty. Wyodrębniamy również $R_x$ i $s$ , dzieląc sygnaturę $\text{SIG}$ . Następnie sprawdzamy, czy $R_x < p$ i $s < n$ (rząd krzywej).

Następnie obliczamy wyzwanie $e$ w taki sam sposób, jak wystawca podpisu:

 $e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod n$

Następnie obliczamy punkt odniesienia na krzywej w ten sposób:

 $R' = s \cdot G - e \cdot K$

Na koniec sprawdzamy, czy $R'_x = R_x$ . Jeśli dwie współrzędne x są zgodne, to podpis $(R_x, s)$ jest rzeczywiście ważny z kluczem publicznym $K_x$ .

Dlaczego to działa?

Sygnatariusz obliczył $s = r + e \cdot k \mod n$ , więc $R' = s \cdot G - e \cdot K$ powinno być równe oryginalnemu punktowi $R$ , ponieważ:

 $s \cdot G = (r + e \cdot k) \cdot G = r \cdot G + e \cdot k \cdot G$

Ponieważ $K = k \cdot G$ , mamy $e \cdot k \cdot G = e \cdot K$ . Zatem:

 $R' = r \cdot G = R$

W związku z tym mamy:

 $R'_x = R_x$

Zalety podpisów Schnorr

Schemat podpisu Schnorra oferuje kilka korzyści dla Bitcoin w porównaniu z oryginalnym algorytmem ECDSA. Po pierwsze, Schnorr pozwala na agregację kluczy i podpisów. Oznacza to, że wiele kluczy publicznych można połączyć w jeden klucz.

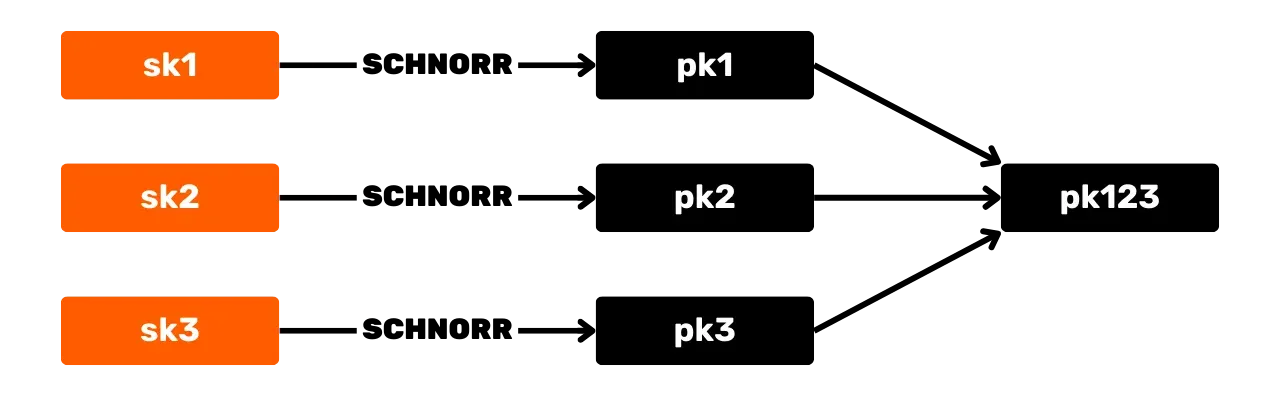
Podobnie, wiele podpisów można zagregować w jeden ważny podpis. Tak więc, w przypadku transakcji z wieloma podpisami, zestaw uczestników może podpisać się jednym podpisem i jednym zagregowanym kluczem publicznym. Znacząco zmniejsza to koszty przechowywania i obliczeń w sieci, ponieważ każdy węzeł musi zweryfikować tylko jeden podpis.

Co więcej, agregacja podpisów poprawia prywatność. W przypadku Schnorra niemożliwe staje się odróżnienie transakcji z wieloma podpisami od standardowej transakcji z jednym podpisem. Ta jednorodność utrudnia analizę łańcucha, ponieważ ogranicza możliwość identyfikacji odcisków palców Wallet.

Wreszcie, Schnorr oferuje również możliwość weryfikacji wsadowej. Weryfikując wiele podpisów jednocześnie, węzły mogą zyskać na wydajności, szczególnie w przypadku bloków zawierających wiele transakcji. Ta optymalizacja zmniejsza czas i zasoby potrzebne do walidacji bloku.

Ponadto podpisy Schnorra nie są plastyczne, w przeciwieństwie do podpisów tworzonych za pomocą ECDSA. Oznacza to, że atakujący nie może zmodyfikować ważnego podpisu, aby utworzyć inny ważny podpis dla tej samej wiadomości i tego samego klucza publicznego. Luka ta występowała wcześniej w Bitcoin i w szczególności uniemożliwiała bezpieczną implementację Lightning Network. Została ona rozwiązana dla ECDSA za pomocą softforka SegWit w 2017 roku, który polega na przeniesieniu podpisów do oddzielnej bazy danych niż transakcje, aby zapobiec możliwości ich modyfikacji.

Dlaczego Satoshi wybrał ECDSA?

Jak widzieliśmy, Satoshi początkowo zdecydował się na implementację ECDSA dla podpisów cyfrowych w Bitcoin. Jednak widzieliśmy również, że Schnorr jest lepszy od ECDSA w wielu aspektach, a protokół ten został stworzony przez Clausa-Petera Schnorra w 1989 roku, 20 lat przed wynalezieniem Bitcoin.

Cóż, tak naprawdę nie wiemy, dlaczego Satoshi go nie wybrał, ale prawdopodobną hipotezą jest to, że protokół ten był opatentowany do 2008 roku. Chociaż Bitcoin został stworzony rok później, w styczniu 2009 roku, żadna standaryzacja open-source dla podpisów Schnorra nie była dostępna w tym czasie. Być może Satoshi uznał, że bezpieczniej jest użyć ECDSA, który był już szeroko stosowany i testowany w oprogramowaniu open-source i miał kilka uznanych implementacji (w szczególności bibliotekę OpenSSL używaną do 2015 roku w Bitcoin Core, a następnie zastąpioną przez libsecp256k1 w wersji 0.10.0). A może po prostu nie wiedział, że patent ten wygaśnie w 2008 roku. W każdym razie najbardziej prawdopodobna hipoteza wydaje się związana z tym patentem i faktem, że ECDSA miała sprawdzoną historię i była łatwiejsza do wdrożenia.

Flagi westchnień

Jak widzieliśmy w poprzednich rozdziałach, podpisy cyfrowe są często używane do odblokowania skryptu danych wejściowych. W procesie podpisywania konieczne jest uwzględnienie podpisanych danych w obliczeniach, oznaczonych w naszych przykładach komunikatem $m$ . Dane te, po podpisaniu, nie mogą być modyfikowane bez unieważnienia podpisu. Rzeczywiście, czy to w przypadku ECDSA, czy Schnorra, weryfikator podpisu musi uwzględnić w swoich obliczeniach tę samą wiadomość $m$ . Jeśli różni się ona od wiadomości $m$ pierwotnie użytej przez podpisującego, wynik będzie nieprawidłowy, a podpis zostanie uznany za nieważny. Mówi się zatem, że podpis obejmuje pewne dane i chroni je w pewien sposób przed nieautoryzowanymi modyfikacjami.

Czym jest flaga sighash?

W konkretnym przypadku Bitcoin widzieliśmy, że wiadomość $m$ odpowiada transakcji. W rzeczywistości jest to jednak nieco bardziej złożone. Rzeczywiście, dzięki flagom sighash, możliwe jest wybranie określonych danych w ramach transakcji, które będą objęte lub nie podpisem.

"Flaga sighash" jest zatem parametrem dodawanym do każdego wejścia, umożliwiającym określenie składników transakcji, które są objęte powiązanym podpisem. Te komponenty to wejścia i wyjścia. Wybór flagi sighash określa zatem, które dane wejściowe i wyjściowe transakcji są ustalone przez sygnaturę, a które mogą być nadal modyfikowane bez jej unieważniania. Mechanizm ten pozwala podpisom na zatwierdzanie danych transakcji zgodnie z intencjami podpisującego.

Oczywiście po potwierdzeniu transakcji na Blockchain staje się ona niezmienna, niezależnie od użytych flag sighash. Możliwość modyfikacji za pomocą flag sighash jest ograniczona do okresu między podpisaniem a potwierdzeniem.

Ogólnie rzecz biorąc, oprogramowanie Wallet nie oferuje opcji ręcznej modyfikacji flagi sighash danych wejściowych podczas konstruowania transakcji. Domyślnie ustawiona jest wartość SIGHASH_ALL. Osobiście znam tylko Sparrow Wallet, który pozwala na tę modyfikację od użytkownika Interface.

Jakie są istniejące flagi sighash w Bitcoin?

W Bitcoin istnieją przede wszystkim 3 podstawowe flagi sighash:

SIGHASH_ALL (0x01): Podpis dotyczy wszystkich wejść i wszystkich wyjść transakcji. Transakcja jest więc całkowicie objęta sygnaturą i nie może być już modyfikowana. SIGHASH_ALL jest najczęściej używanym sighashem w codziennych transakcjach, gdy chcemy po prostu dokonać transakcji bez możliwości jej modyfikacji.

Na wszystkich diagramach w tym rozdziale kolor pomarańczowy reprezentuje Elements objęte sygnaturą, podczas gdy kolor czarny oznacza te, które nie są objęte sygnaturą.

SIGHASH_NONE (0x02): Podpis obejmuje wszystkie wejścia, ale żadnego z wyjść, pozwalając w ten sposób na modyfikację wyjść po podpisie. Konkretnie, jest to podobne do czeku in blanco. Sygnatariusz odblokowuje UTXO na wejściach, ale pozostawia pole wyjść całkowicie modyfikowalne. Każdy, kto zna tę transakcję, może zatem dodać wybrane przez siebie wyjście, na przykład określając odbierający Address, aby zebrać środki zużyte przez wejścia, a następnie transmitować transakcję w celu odzyskania bitcoinów. Podpis właściciela danych wejściowych nie zostanie unieważniony, ponieważ obejmuje tylko dane wejściowe.

SIGHASH_SINGLE (0x03): Sygnatura obejmuje wszystkie wejścia, jak również pojedyncze wyjście, odpowiadające indeksowi podpisanego wejścia. Na przykład, jeśli podpis odblokowuje scriptPubKey wejścia #0, to obejmuje również wyjście #0. Podpis chroni również wszystkie inne wejścia, których nie można już modyfikować. Jednak każdy może dodać dodatkowe wyjście bez unieważniania podpisu, pod warunkiem, że wyjście #0, które jest jedynym objętym podpisem, nie zostanie zmodyfikowane.

Oprócz tych trzech flag sighash, istnieje również modyfikator SIGHASH_ANYONECANPAY (0x80). Modyfikator ten można połączyć z podstawową flagą sighash, aby utworzyć trzy nowe flagi sighash:

SIGHASH_ALL | SIGHASH_ANYONECANPAY (0x81): Podpis obejmuje pojedyncze wejście, jednocześnie uwzględniając wszystkie wyjścia transakcji. Ta połączona flaga sighash pozwala na przykład na utworzenie transakcji crowdfundingowej. Organizator przygotowuje wynik ze swoim Address i kwotą docelową, a każdy inwestor może następnie dodać dane wejściowe, aby sfinansować ten wynik. Po zebraniu wystarczających środków w postaci wkładów, aby zaspokoić wynik, transakcja może zostać wyemitowana.

SIGHASH_NONE | SIGHASH_ANYONECANPAY (0x82): Sygnatura obejmuje pojedyncze wejście, bez zobowiązywania się do jakiegokolwiek wyjścia;

SIGHASH_SINGLE | SIGHASH_ANYONECANPAY (0x83): Sygnatura obejmuje pojedyncze wejście, a także wyjście o tym samym indeksie co to wejście. Na przykład, jeśli sygnatura odblokuje scriptPubKey wejścia #3, obejmie również wyjście #3. Reszta transakcji pozostaje modyfikowalna, zarówno pod względem innych wejść, jak i innych wyjść.

Projekty dodające nowe flagi Sighash

Obecnie (2024 r.) w Bitcoin można używać tylko flag sighash przedstawionych w poprzedniej sekcji. Jednak niektóre projekty rozważają dodanie nowych flag sighash. Na przykład BIP118, zaproponowany przez Christiana Deckera i Anthony'ego Townsa, wprowadza dwie nowe flagi sighash: SIGHASH_ANYPREVOUT i SIGHASH_ANYPREVOUTANYSCRIPT (AnyPrevOut = "Any Previous Output").

Te dwie flagi sighash oferują dodatkową możliwość w Bitcoin: tworzenie podpisów, które nie obejmują żadnego konkretnego wejścia transakcji.

Pomysł ten został początkowo sformułowany przez Josepha Poona i Thaddeusa Dryję w białej księdze Lightning. Przed zmianą nazwy, ta flaga sighash nosiła nazwę SIGHASH_NOINPUT.

Jeśli ta flaga sighash zostanie zintegrowana z Bitcoin, umożliwi to korzystanie z przymierzy, ale jest również obowiązkowym warunkiem wstępnym do wdrożenia Eltoo, ogólnego protokołu dla warstw drugich, który definiuje sposób wspólnego zarządzania Ownership UTXO. Eltoo został specjalnie zaprojektowany w celu rozwiązania problemów związanych z mechanizmami negocjowania stanu kanałów Lightning, czyli między ich otwieraniem i zamykaniem.

Aby pogłębić swoją wiedzę na temat Lightning Network, po kursie CYP201 gorąco polecam kurs LNP201 autorstwa Fanisa Michalakisa, który szczegółowo omawia ten temat:

https://planb.network/courses/34bd43ef-6683-4a5c-b239-7cb1e40a4aeb

W następnej części proponuję odkryć, jak działa fraza Mnemonic u podstawy Bitcoin Wallet.

Zwrot Mnemonic

Ewolucja portfeli Bitcoin

Teraz, gdy zbadaliśmy działanie funkcji Hash i podpisów cyfrowych, możemy zbadać, jak działają portfele Bitcoin. Celem będzie opisanie, w jaki sposób skonstruowany jest Wallet w Bitcoin, jak jest dekomponowany i do czego służą różne informacje, które go tworzą. Zrozumienie mechanizmów Wallet pozwoli ci ulepszyć korzystanie z Bitcoin pod względem bezpieczeństwa i prywatności.

Zanim zagłębimy się w szczegóły techniczne, należy wyjaśnić, co oznacza termin "Bitcoin Wallet" i zrozumieć jego użyteczność.

Co to jest Bitcoin Wallet?

W przeciwieństwie do tradycyjnych portfeli, które umożliwiają przechowywanie fizycznych banknotów i monet, Bitcoin Wallet nie "zawiera" bitcoinów jako takich. W rzeczywistości bitcoiny nie istnieją w formie fizycznej lub cyfrowej, którą można przechowywać, ale są reprezentowane przez jednostki rozliczeniowe przedstawione w systemie Bitcoin w postaci UTXO (Unspent Transaction Outputs).

UTXO reprezentują fragmenty bitcoinów o różnej wielkości, które można wydać pod warunkiem, że ich scriptPubKey jest spełniony. Aby wydać swoje bitcoiny, użytkownik musi dostarczyć scriptSig, który odblokuje scriptPubKey powiązany z jego UTXO. Dowód ten jest zazwyczaj składany za pomocą podpisu cyfrowego, generowanego z klucza prywatnego odpowiadającego kluczowi publicznemu obecnemu w scriptPubKey. Zatem kluczowym elementem, który użytkownik musi zabezpieczyć, jest klucz prywatny.

Rolą Bitcoin Wallet jest właśnie bezpieczne zarządzanie tymi kluczami prywatnymi. W rzeczywistości jego rola jest bardziej zbliżona do roli pęku kluczy niż Wallet w tradycyjnym znaczeniu.

Portfele JBOK

Pierwszymi portfelami używanymi w Bitcoin były portfele JBOK (Just a Bunch Of Keys), które grupowały klucze prywatne wygenerowane niezależnie i bez żadnych powiązań między nimi. Portfele te działały w oparciu o prosty model, w którym każdy klucz prywatny mógł odblokować unikalny Bitcoin otrzymujący Address.

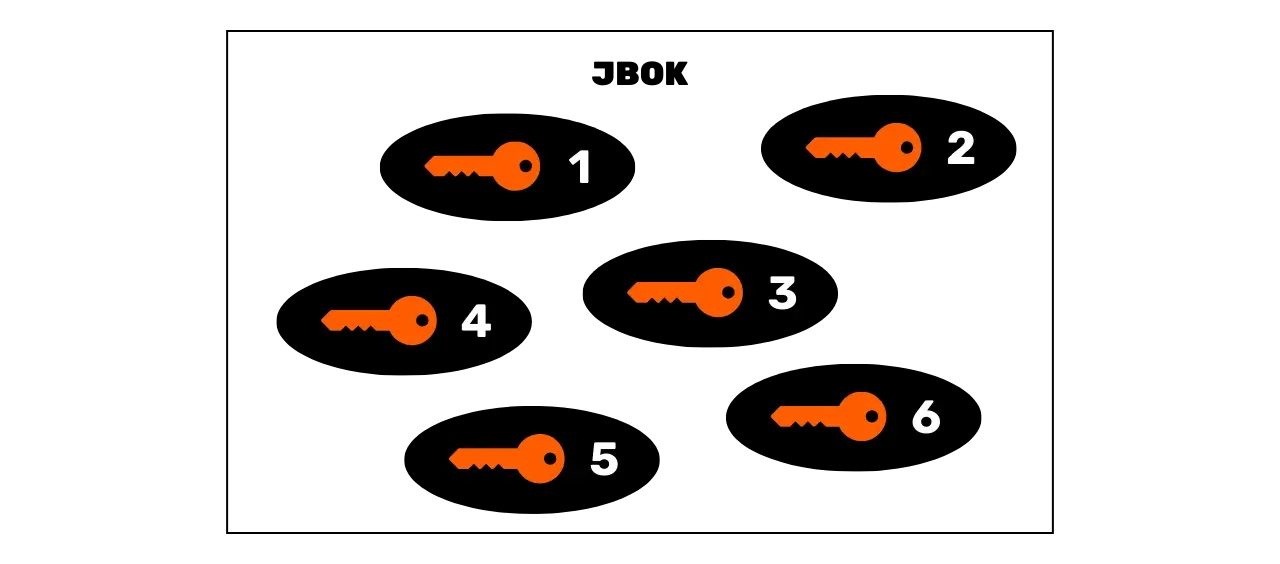
Jeśli ktoś chciał użyć wielu kluczy prywatnych, konieczne było utworzenie tylu kopii zapasowych, aby zapewnić dostęp do środków w przypadku problemów z urządzeniem obsługującym Wallet. W przypadku korzystania z jednego klucza prywatnego taka struktura Wallet może być wystarczająca, ponieważ wystarczy jedna kopia zapasowa. Wiąże się to jednak z pewnym problemem: w Bitcoin zdecydowanie odradza się używanie zawsze tego samego klucza prywatnego. Klucz prywatny jest bowiem powiązany z unikalnym Address, a adresy odbiorcze Bitcoin są zwykle przeznaczone do jednorazowego użytku. Za każdym razem, gdy otrzymujesz środki, powinieneś generate nowy pusty Address.

Ograniczenie to wynika z modelu prywatności Bitcoin. Ponowne użycie tego samego Address ułatwia zewnętrznym obserwatorom śledzenie transakcji Bitcoin. Dlatego też ponowne użycie otrzymującego Address jest zdecydowanie odradzane. Aby jednak mieć wiele adresów i publicznie oddzielić nasze transakcje, konieczne jest zarządzanie wieloma kluczami prywatnymi. W przypadku portfeli JBOK oznacza to tworzenie tylu kopii zapasowych, ile jest nowych par kluczy, co może szybko stać się skomplikowane i trudne w utrzymaniu dla użytkowników.

Aby dowiedzieć się więcej o modelu prywatności Bitcoin i odkryć metody ochrony swojej prywatności, polecam również śledzenie mojego kursu BTC204 na temat Plan ₿ Network:

https://planb.network/courses/65c138b0-4161-4958-bbe3-c12916bc959c

Portfele HD

W celu Address ograniczenia portfeli JBOK, wykorzystano następnie nową strukturę Wallet. W 2012 roku Pieter Wuille zaproponował ulepszenie BIP32, które wprowadza portfele HD (Hierarchical Deterministic). Zasada HD Wallet polega na wyprowadzeniu wszystkich kluczy prywatnych z jednego źródła informacji, zwanego seed, w sposób deterministyczny i hierarchiczny. Ten seed jest generowany losowo podczas tworzenia Wallet i stanowi unikalną kopię zapasową, która pozwala na odtworzenie wszystkich kluczy prywatnych Wallet. W ten sposób użytkownik może utworzyć generate bardzo dużej liczby kluczy prywatnych, aby uniknąć ponownego użycia Address i zachować swoją prywatność, a jednocześnie musi wykonać tylko jedną kopię zapasową swojego Wallet za pośrednictwem seed.

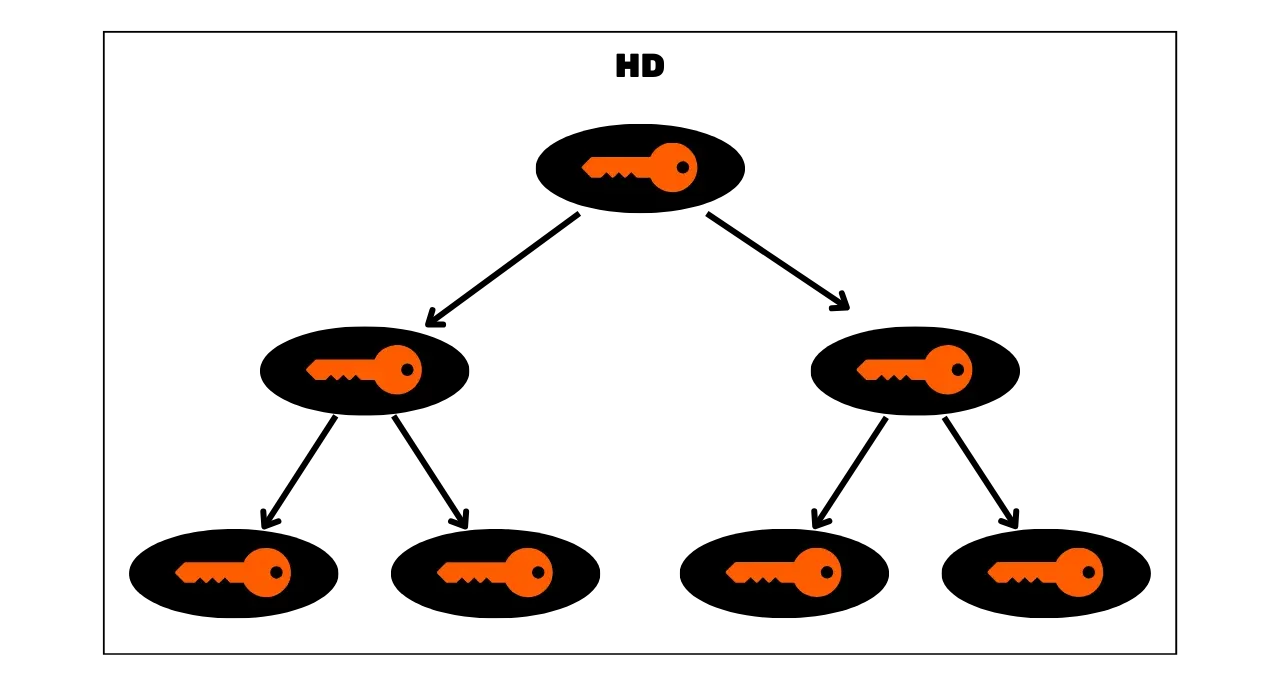
W portfelach HD wyprowadzanie kluczy odbywa się zgodnie z hierarchiczną strukturą, która umożliwia organizowanie kluczy w podprzestrzenie wyprowadzania, przy czym każda podprzestrzeń może być dalej dzielona, aby ułatwić zarządzanie funduszami i interoperacyjność między różnymi programami Wallet. Obecnie standard ten jest stosowany przez zdecydowaną większość użytkowników Bitcoin. Z tego powodu przeanalizujemy go szczegółowo w kolejnych rozdziałach.

Standard BIP39: Zwrot Mnemonic

Oprócz BIP32, BIP39 standaryzuje format seed jako frazę Mnemonic, aby ułatwić tworzenie kopii zapasowych i czytelność dla użytkowników. Fraza Mnemonic, zwana również frazą odzyskiwania lub frazą 24-słowną, jest sekwencją słów wyciągniętych z predefiniowanej listy, która bezpiecznie koduje Wallet seed.

Fraza Mnemonic znacznie upraszcza użytkownikowi tworzenie kopii zapasowych. W przypadku utraty, uszkodzenia lub kradzieży urządzenia obsługującego Wallet, wystarczy znać frazę Mnemonic, aby odtworzyć Wallet i odzyskać dostęp do wszystkich zabezpieczonych przez niego środków.

W nadchodzących rozdziałach zbadamy wewnętrzne działanie portfeli HD, w tym mechanizmy wyprowadzania kluczy i różne możliwe struktury hierarchiczne. Pozwoli to lepiej zrozumieć podstawy kryptograficzne, na których opiera się bezpieczeństwo środków w Bitcoin. Na początek, w następnym rozdziale, proponuję odkryć rolę entropii u podstaw Wallet.

Entropia i liczby losowe

Nowoczesne portfele HD polegają na pojedynczej początkowej informacji zwanej "entropią" w celu deterministycznego generate całego zestawu kluczy Wallet. Ta entropia jest liczbą pseudolosową, która częściowo określa bezpieczeństwo Wallet.

Definicja entropii

Entropia, w kontekście kryptografii i informacji, jest ilościową miarą niepewności lub nieprzewidywalności związanej ze źródłem danych lub procesem losowym. Odgrywa ona ważną rolę w bezpieczeństwie systemów kryptograficznych, zwłaszcza w generowaniu kluczy i liczb losowych. Wysoka entropia zapewnia, że wygenerowane klucze są wystarczająco nieprzewidywalne i odporne na ataki siłowe, w których atakujący próbuje wszystkich możliwych kombinacji, aby odgadnąć klucz.

W kontekście Bitcoin, entropia jest używana do generate seed. Podczas tworzenia HD Wallet, konstrukcja frazy Mnemonic jest wykonywana z liczby losowej, która sama pochodzi ze źródła entropii. Fraza jest następnie wykorzystywana do generate wielu kluczy prywatnych, w deterministyczny i hierarchiczny sposób, w celu stworzenia warunków wydatków na UTXO.

Metody generowania entropii

Początkowa entropia używana dla HD Wallet wynosi zazwyczaj 128 bitów lub 256 bitów, gdzie:

128 bitów entropii** odpowiada frazie Mnemonic składającej się z 12 słów;
256 bitów entropii** odpowiada frazie Mnemonic składającej się z 24 słów.

W większości przypadków ta liczba losowa jest generowana automatycznie przez oprogramowanie Wallet przy użyciu PRNG (Pseudo-Random Number Generator). PRNG to kategoria algorytmów używanych do generate sekwencji liczb ze stanu początkowego, które mają cechy zbliżone do liczb losowych, ale w rzeczywistości nimi nie są. Dobry PRNG musi mieć takie właściwości, jak jednorodność wyjścia, nieprzewidywalność i odporność na ataki predykcyjne. W przeciwieństwie do prawdziwych generatorów liczb losowych (TRNG), PRNG są deterministyczne i powtarzalne.

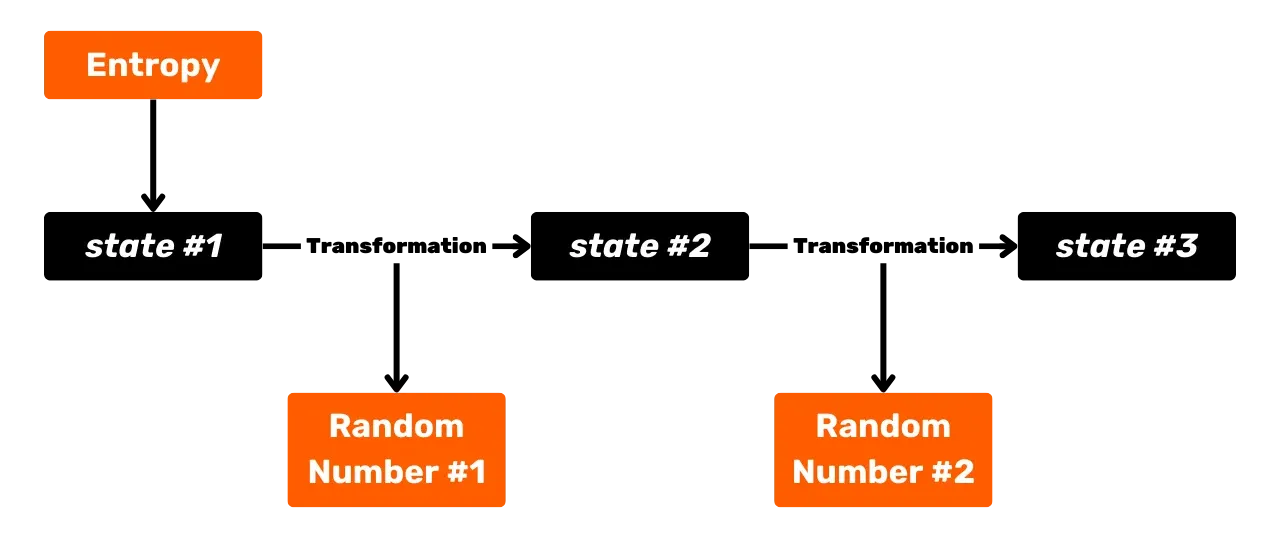
Alternatywą jest ręczne generate entropii, co zapewnia lepszą kontrolę, ale jest również znacznie bardziej ryzykowne. Zdecydowanie odradzam samodzielne generowanie entropii dla HD Wallet.

W następnym rozdziale zobaczymy, jak przejść od losowej liczby do frazy Mnemonic składającej się z 12 lub 24 słów.

Zwrot Mnemonic

Fraza Mnemonic, zwana również "frazą seed", "frazą odzyskiwania", "tajną frazą" lub "24-słowną frazą", to sekwencja składająca się zwykle z 12 lub 24 słów, która jest generowana na podstawie entropii. Jest ona używana do deterministycznego wyprowadzenia wszystkich kluczy HD Wallet. Oznacza to, że na podstawie tej frazy możliwe jest deterministyczne generate i odtworzenie wszystkich kluczy prywatnych i publicznych Bitcoin Wallet, a w konsekwencji uzyskanie dostępu do chronionych nim środków. Celem frazy Mnemonic jest zapewnienie sposobu tworzenia kopii zapasowych i odzyskiwania bitcoinów, który jest zarówno bezpieczny, jak i łatwy w użyciu. Został on wprowadzony w 2013 roku wraz ze standardem BIP39.

Odkryjmy razem, jak przejść od entropii do frazy Mnemonic.

Suma kontrolna

Aby przekształcić entropię we frazę Mnemonic, należy najpierw dodać sumę kontrolną (lub "sumę kontrolną") na końcu entropii. Suma kontrolna to krótka sekwencja bitów, która zapewnia integralność danych poprzez sprawdzenie, czy nie wprowadzono żadnych przypadkowych modyfikacji.

Aby obliczyć sumę kontrolną, funkcja SHA256 Hash jest stosowana do entropii (tylko raz; jest to jeden z rzadkich przypadków w Bitcoin, w którym używany jest pojedynczy SHA256 Hash zamiast podwójnego Hash). W wyniku tej operacji powstaje 256-bitowy Hash. Suma kontrolna składa się z pierwszych bitów tego Hash, a jej długość zależy od entropii, zgodnie z następującym wzorem:

 $\text{CS} = \frac{\text{ENT}}{32}$

gdzie $\text{ENT}$ reprezentuje długość entropii w bitach, a $\text{CS}$ długość sumy kontrolnej w bitach.

Na przykład, dla entropii 256 bitów, pierwsze 8 bitów Hash jest brane do utworzenia sumy kontrolnej:

 $\text{CS} = \frac{256}{32} = 8 \text{ bits}$

Po obliczeniu sumy kontrolnej jest ona konkatenowana z entropią w celu uzyskania rozszerzonej sekwencji bitów zapisanej $\text{ENT} \Vert \text{CS}$ ("concatenate" oznacza połączenie od końca do końca).

Zgodność między entropią a frazą Mnemonic

Liczba słów we frazie Mnemonic zależy od wielkości początkowej entropii, jak pokazano w poniższej tabeli:

$\text{ENT}$ : rozmiar entropii w bitach;
$\text{CS}$ : rozmiar sumy kontrolnej w bitach;
$w$ : liczba słów w końcowej frazie Mnemonic.

 $\begin{array}{|c|c|c|c|} \hline \text{ENT} & \text{CS} & \text{ENT} \Vert \text{CS} & w \\ \hline 128 & 4 & 132 & 12 \\ 160 & 5 & 165 & 15 \\ 192 & 6 & 198 & 18 \\ 224 & 7 & 231 & 21 \\ 256 & 8 & 264 & 24 \\ \hline \end{array}$

Na przykład, dla 256-bitowej entropii, wynik $\text{ENT} \Vert \text{CS}$ wynosi 264 bity i daje frazę Mnemonic składającą się z 24 słów.

Konwersja sekwencji binarnej na frazę Mnemonic

Sekwencja bitów $\text{ENT} \Vert \text{CS}$ jest następnie dzielony na segmenty po 11 bitów. Każdy 11-bitowy segment, po przekonwertowaniu na liczbę dziesiętną, odpowiada liczbie od 0 do 2047, która wyznacza pozycję słowa [na liście 2048 słów znormalizowanej przez BIP39] (https://github.com/Planb-Network/Bitcoin-educational-content/blob/dev/resources/bet/bip39-wordlist//courses/cyp201/assets/BIP39-WORDLIST.pdf).

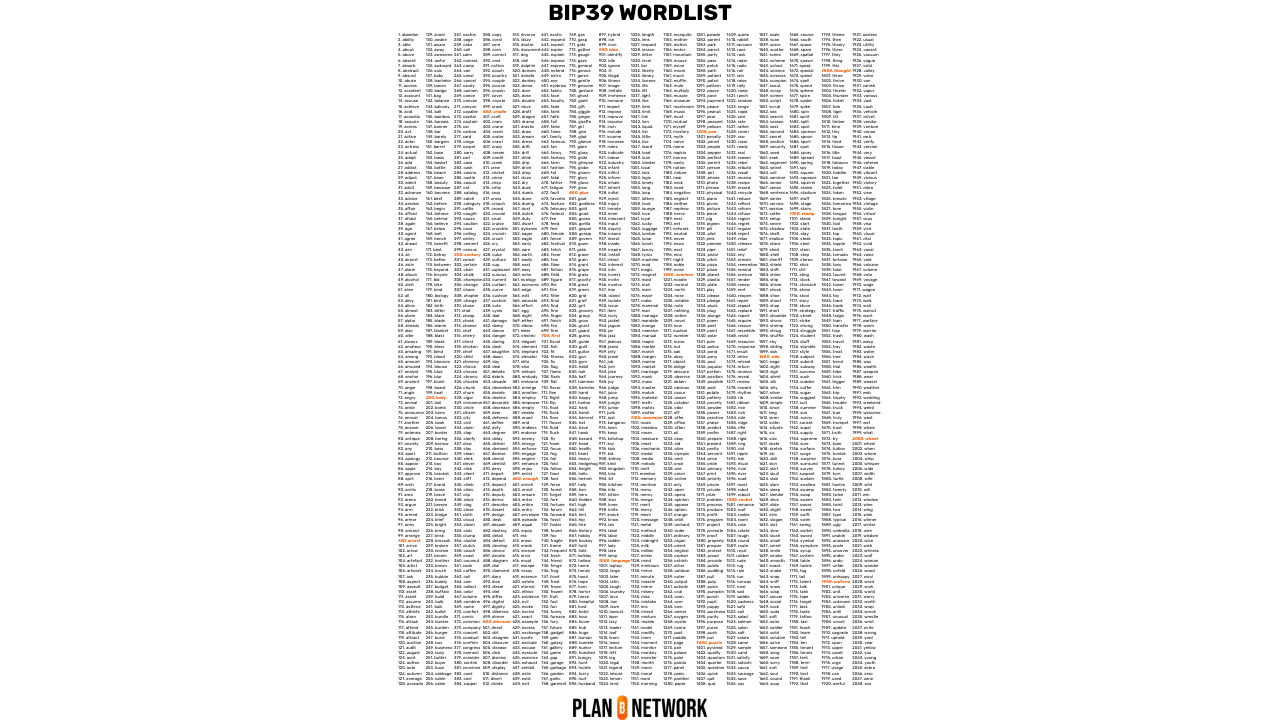
Na przykład dla 128-bitowej entropii suma kontrolna wynosi 4 bity, a zatem całkowita sekwencja ma 132 bity. Jest on podzielony na 12 segmentów po 11 bitów (pomarańczowe bity oznaczają sumę kontrolną):

Każdy segment jest następnie konwertowany na liczbę dziesiętną, która reprezentuje słowo na liście. Na przykład, segment binarny 01011010001 jest odpowiednikiem dziesiętnym 721. Dodając 1, aby dostosować się do indeksowania listy (która zaczyna się od 1, a nie 0), daje to słowo o randze 722, które jest "focus" na liście.

Ta korespondencja jest powtarzana dla każdego z 12 segmentów w celu uzyskania 12-wyrazowej frazy.

Charakterystyka listy słów BIP39

Szczególną cechą listy słów BIP39 jest to, że żadne słowo nie ma tych samych czterech pierwszych liter w tej samej kolejności z innym słowem. Oznacza to, że do zapisania frazy Mnemonic wystarczą tylko cztery pierwsze litery każdego słowa. Może to być interesujące ze względu na oszczędność miejsca, zwłaszcza dla tych, którzy chcą wygrawerować je na metalowym wsporniku.

Ta lista 2048 słów istnieje w kilku językach. Nie są to proste tłumaczenia, ale odrębne słowa dla każdego języka. Zdecydowanie zaleca się jednak trzymanie się wersji angielskiej, ponieważ wersje w innych językach nie są zazwyczaj obsługiwane przez oprogramowanie Wallet.

Jaką długość frazy Mnemonic wybrać?

Aby określić optymalną długość frazy Mnemonic, należy wziąć pod uwagę rzeczywiste bezpieczeństwo, jakie zapewnia. 12-wyrazowa fraza zapewnia 128 bitów bezpieczeństwa, podczas gdy 24-wyrazowa fraza oferuje 256 bitów.

Jednak ta różnica w bezpieczeństwie na poziomie frazy nie poprawia ogólnego bezpieczeństwa Bitcoin Wallet, ponieważ klucze prywatne pochodzące z tej frazy korzystają tylko ze 128 bitów bezpieczeństwa. Rzeczywiście, jak widzieliśmy wcześniej, klucze prywatne Bitcoin są generowane z liczb losowych (lub pochodzących ze źródła losowego) w zakresie od $1$ do $n-1$ , gdzie $n$ reprezentuje rząd punktu generatora $G$ krzywej secp256k1, liczbę nieco mniejszą niż $2^{256}$ . Można by zatem pomyśleć, że te klucze prywatne oferują 256 bitów bezpieczeństwa. Jednak ich bezpieczeństwo leży w trudności znalezienia klucza prywatnego z powiązanego z nim klucza publicznego, trudności ustalonej przez matematyczny problem dyskretnego logarytmu na krzywych eliptycznych (ECDLP). Do tej pory najbardziej znanym algorytmem rozwiązującym ten problem jest algorytm rho Pollarda, który redukuje liczbę operacji potrzebnych do złamania klucza do pierwiastka kwadratowego z jego rozmiaru.

W przypadku 256-bitowych kluczy, takich jak te używane w Bitcoin, algorytm rho Pollarda zmniejsza złożoność do 2^{128}$ operacji:

 $O(\sqrt{2^{256}}) = O(2^{128})$

Dlatego uważa się, że klucz prywatny używany w Bitcoin zapewnia 128 bitów bezpieczeństwa.

W rezultacie wybór 24-wyrazowej frazy nie zapewnia dodatkowej ochrony dla Wallet, ponieważ 256 bitów bezpieczeństwa na frazie jest bezcelowe, jeśli klucze pochodne oferują tylko 128 bitów bezpieczeństwa. Aby zilustrować tę zasadę, to tak, jakby mieć dom z dwoma drzwiami: starymi drewnianymi drzwiami i wzmocnionymi drzwiami. W przypadku włamania, wzmocnione drzwi byłyby bezużyteczne, ponieważ intruz przeszedłby przez drewniane drzwi. Analogiczna sytuacja ma miejsce w tym przypadku.

12-wyrazowa fraza, która również oferuje 128 bitów bezpieczeństwa, jest zatem obecnie wystarczająca do ochrony bitcoinów przed wszelkimi próbami kradzieży. Dopóki algorytm podpisu cyfrowego nie zmieni się w celu użycia większych kluczy lub polegania na problemie matematycznym innym niż ECDLP, 24-słowna fraza pozostaje zbędna. Co więcej, dłuższa fraza zwiększa ryzyko utraty podczas tworzenia kopii zapasowej: dwukrotnie krótsza kopia zapasowa jest zawsze łatwiejsza w zarządzaniu.

Aby przejść dalej i dowiedzieć się konkretnie, jak ręcznie generate frazę testową Mnemonic, radzę zapoznać się z tym samouczkiem:

https://planb.network/tutorials/wallet/backup/generate-mnemonic-phrase-47507d90-e6af-4cac-b01b-01a14d7a8228

Przed kontynuowaniem wyprowadzania Wallet z tej frazy Mnemonic, w następnym rozdziale przedstawię ci BIP39 passphrase, ponieważ odgrywa on rolę w procesie wyprowadzania i jest na tym samym poziomie co fraza Mnemonic.

passphrase

Jak właśnie zauważyliśmy, portfele HD są generowane na podstawie frazy Mnemonic składającej się zazwyczaj z 12 lub 24 słów. Fraza ta jest bardzo ważna, ponieważ pozwala na przywrócenie wszystkich kluczy Wallet w przypadku utraty jego fizycznego urządzenia (na przykład Hardware Wallet). Stanowi jednak pojedynczy punkt awarii, ponieważ jeśli zostanie naruszony, atakujący może ukraść wszystkie bitcoiny. W tym miejscu do gry wkracza BIP39 passphrase.

Co to jest BIP39 passphrase?

passphrase to opcjonalne hasło, które można dowolnie wybrać, które jest dodawane do frazy Mnemonic w procesie wyprowadzania klucza w celu zwiększenia bezpieczeństwa Wallet.

Należy uważać, aby nie pomylić passphrase z kodem PIN Hardware Wallet lub hasłem używanym do odblokowania dostępu do Wallet na komputerze. W przeciwieństwie do wszystkich Elements, passphrase odgrywa rolę w tworzeniu kluczy Wallet. **Oznacza to, że bez niego nigdy nie będziesz w stanie odzyskać swoich bitcoinów

passphrase działa w tandemie z frazą Mnemonic, modyfikując seed, z którego generowane są klucze. Tak więc, nawet jeśli ktoś uzyska 12- lub 24-wyrazową frazę, bez passphrase nie będzie mógł uzyskać dostępu do środków. Użycie passphrase zasadniczo tworzy nowy Wallet z odrębnymi kluczami. Modyfikacja (nawet niewielka) passphrase spowoduje, że generate będzie innym Wallet.

Dlaczego warto używać passphrase?

passphrase jest dowolny i może być dowolną kombinacją znaków wybraną przez użytkownika. Korzystanie z passphrase ma zatem kilka zalet. Po pierwsze, zmniejsza wszelkie ryzyko związane z naruszeniem frazy Mnemonic, wymagając drugiego czynnika w celu uzyskania dostępu do środków (włamanie, dostęp do domu itp.).

Następnie można go wykorzystać strategicznie do stworzenia wabika Wallet, aby stawić czoła fizycznym ograniczeniom w celu kradzieży środków, takich jak niesławny "atak kluczem $5". W tym scenariuszu chodzi o posiadanie Wallet bez passphrase zawierającego tylko niewielką ilość bitcoinów, wystarczającą do zaspokojenia potencjalnego agresora, przy jednoczesnym posiadaniu ukrytego Wallet. Ten ostatni wykorzystuje tę samą frazę Mnemonic, ale jest zabezpieczony dodatkowym passphrase.

Wreszcie, użycie passphrase jest interesujące, gdy chcemy kontrolować losowość generowania seed z HD Wallet.

Jak wybrać dobry passphrase?

Aby hasło passphrase było skuteczne, musi być wystarczająco długie i losowe. Podobnie jak w przypadku silnego hasła, zalecam wybranie passphrase, który jest tak długi i losowy, jak to możliwe, z różnorodnością liter, cyfr i symboli, aby uniemożliwić atak siłowy.

Ważne jest również prawidłowe zapisanie tego passphrase, w taki sam sposób jak frazy Mnemonic. Jego utrata oznacza utratę dostępu do bitcoinów. Zdecydowanie odradzam zapamiętywanie go tylko na pamięć, ponieważ nadmiernie zwiększa to ryzyko utraty. Idealnym rozwiązaniem jest zapisanie go na fizycznym nośniku (papierowym lub metalowym) oddzielnie od frazy Mnemonic. Ta kopia zapasowa musi być oczywiście przechowywana w innym miejscu niż fraza Mnemonic, aby zapobiec jednoczesnemu naruszeniu obu.

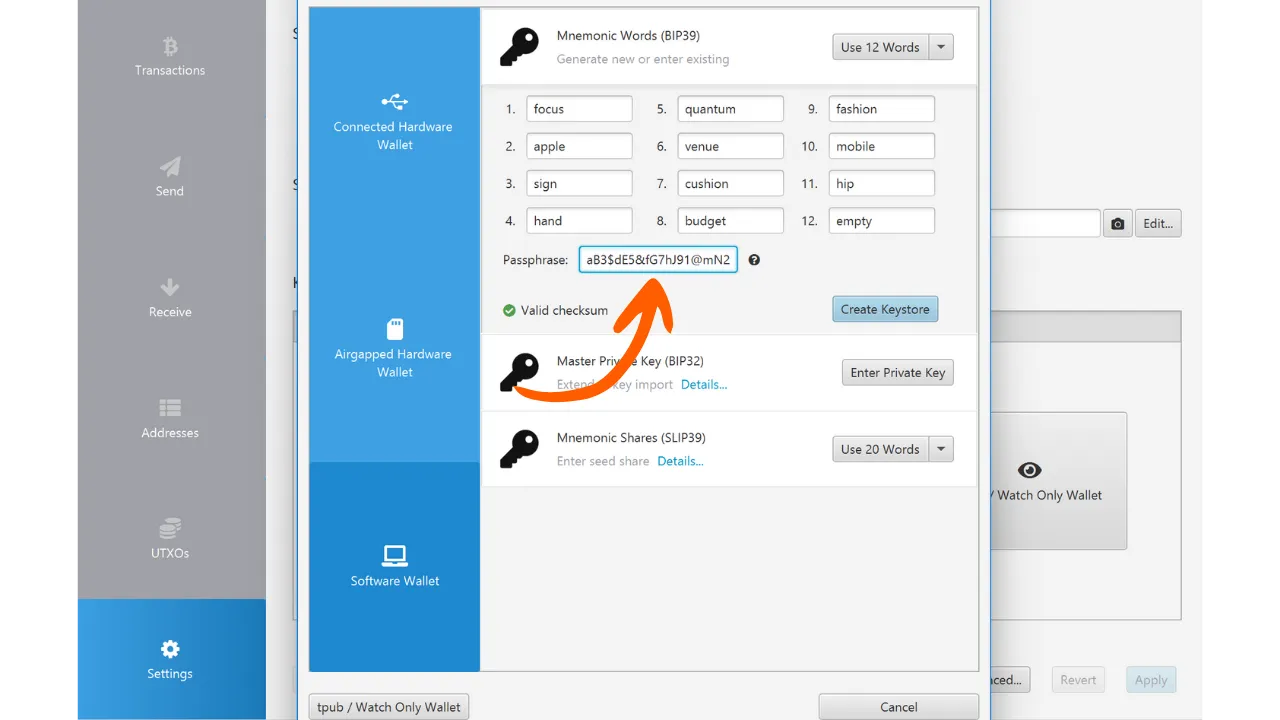
W następnej sekcji dowiemy się, w jaki sposób te dwa Elements u podstawy Wallet - fraza Mnemonic i passphrase - są używane do wyprowadzania par kluczy używanych w scriptPubKey, które blokują UTXO.

Tworzenie portfeli Bitcoin

Utworzenie seed i klucza głównego

Po wygenerowaniu frazy Mnemonic i opcjonalnego passphrase można rozpocząć proces wyprowadzania Bitcoin HD Wallet. Fraza Mnemonic jest najpierw konwertowana na seed, który stanowi podstawę wszystkich kluczy Wallet.

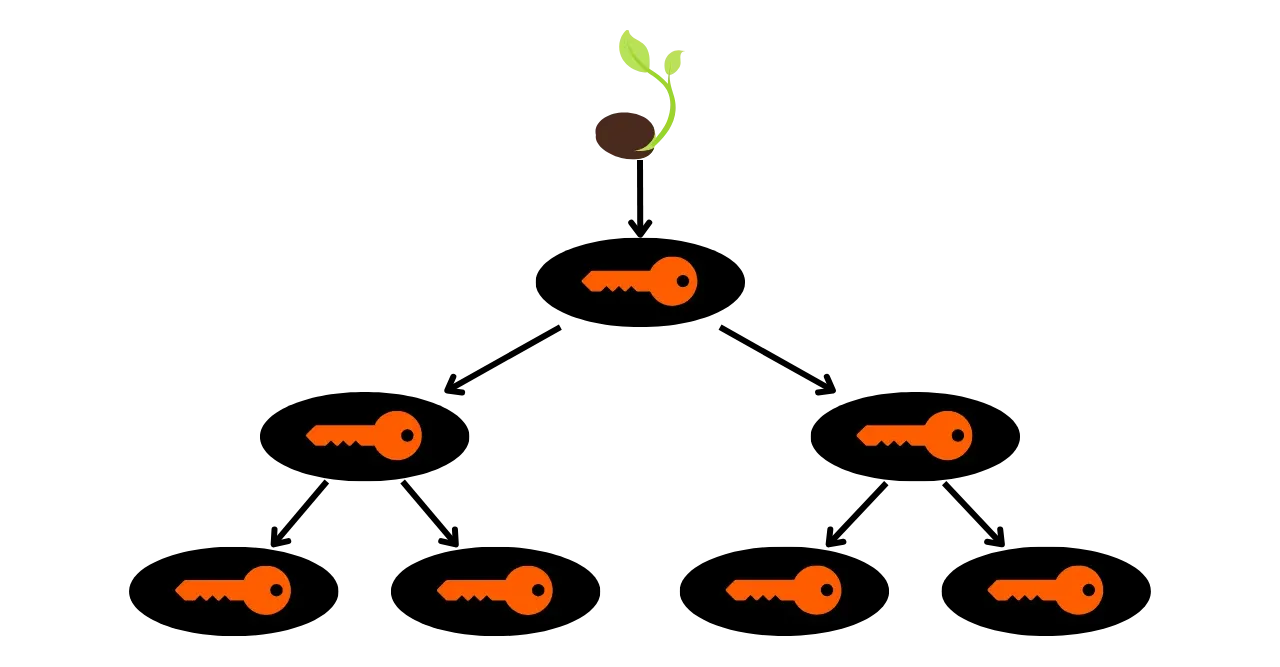
seed z HD Wallet

Standard BIP39 definiuje seed jako 512-bitową sekwencję, która służy jako punkt wyjścia do wyprowadzenia wszystkich kluczy HD Wallet. seed jest wyprowadzany z frazy Mnemonic i możliwego passphrase przy użyciu algorytmu PBKDF2 (Password-Based Key Derivation Function 2), który omówiliśmy już w rozdziale 3.3. W tej funkcji wyprowadzania użyjemy następujących parametrów:

$m$ : fraza Mnemonic;
$p$ : opcjonalny passphrase wybrany przez użytkownika w celu zwiększenia bezpieczeństwa seed. Jeśli nie ma passphrase, pole to pozostaje puste;
$\text{PBKDF2}$ : funkcja wyprowadzania z $\text{HMAC-SHA512}$ i $2048$ iteracji;
$s$ : 512-bitowy Wallet seed.

Niezależnie od wybranej długości frazy Mnemonic (132 bity lub 264 bity), funkcja PBKDF2 zawsze wygeneruje 512-bitowy wynik, a zatem seed zawsze będzie miał taki rozmiar.

Schemat pochodnej seed z PBKDF2

Poniższe równanie ilustruje wyprowadzenie seed z frazy Mnemonic i passphrase:

 $s = \text{PBKDF2}_{\text{HMAC-SHA512}}(m, p, 2048)$

Na wartość seed wpływa zatem wartość frazy Mnemonic i passphrase. Zmieniając passphrase, uzyskuje się inny seed. Jednak przy tej samej frazie Mnemonic i passphrase zawsze generowany jest ten sam seed, ponieważ PBKDF2 jest funkcją deterministyczną. Gwarantuje to, że te same pary kluczy można odzyskać za pomocą naszych kopii zapasowych.

Uwaga: W języku potocznym termin "seed" często odnosi się, przez niewłaściwe użycie języka, do frazy Mnemonic. Rzeczywiście, w przypadku braku passphrase, jeden jest po prostu kodowaniem drugiego. Jednakże, jak widzieliśmy, w technicznej rzeczywistości portfeli, fraza seed i Mnemonic są w rzeczywistości dwoma odrębnymi Elements.

Teraz, gdy mamy już nasz seed, możemy kontynuować wyprowadzanie naszego Bitcoin Wallet.

Klucz główny i kod łańcucha głównego

Po uzyskaniu seed, następnym krokiem w uzyskaniu HD Wallet jest obliczenie głównego klucza prywatnego i głównego kodu łańcucha, który będzie reprezentował głębokość 0 naszego Wallet.

Aby uzyskać główny klucz prywatny i główny kod łańcucha, funkcja HMAC-SHA512 jest stosowana do seed, przy użyciu stałego klucza "Bitcoin Seed" identycznego dla wszystkich użytkowników Bitcoin. Ta stała została wybrana w celu zapewnienia, że pochodne klucza są specyficzne dla Bitcoin. Oto Elements:

$\text{HMAC-SHA512}$ : funkcja wyprowadzania;
$s$ : 512-bitowy Wallet seed;
$\text{"Bitcoin seed"}$ : wspólna stała pochodna dla wszystkich portfeli Bitcoin.

 $\text{output} = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)$

Wyjście tej funkcji ma zatem 512 bitów. Jest on następnie dzielony na 2 części:

Pozostałe 256 bitów tworzy główny klucz prywatny;
Prawe 256 bitów tworzy główny kod łańcucha.

Matematycznie, te dwie wartości można zapisać w następujący sposób, gdzie $k_M$ jest głównym kluczem prywatnym, a $C_M$ głównym kodem łańcucha:

 $k_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[:256]}$

 $C_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[256:]}$

Rola klucza głównego i kodu łańcuchowego

Główny klucz prywatny jest uważany za klucz nadrzędny, z którego będą generowane wszystkie pochodne klucze prywatne - dzieci, wnuki, prawnuki itp. Reprezentuje on poziom zerowy w hierarchii derywacji.

Z drugiej strony, główny kod łańcucha wprowadza dodatkowe źródło entropii do procesu wyprowadzania kluczy dla dzieci, aby przeciwdziałać niektórym potencjalnym atakom. Co więcej, w HD Wallet każda para kluczy ma przypisany unikalny kod łańcucha, który jest również używany do wyprowadzania kluczy potomnych z tej pary, ale omówimy to bardziej szczegółowo w kolejnych rozdziałach.

Przed kontynuowaniem wyprowadzania HD Wallet z następującym Elements, chciałbym w następnym rozdziale przedstawić klucze rozszerzone, które często są mylone z kluczem głównym. Zobaczymy, jak są zbudowane i jaką rolę odgrywają w Bitcoin Wallet.

Rozszerzone klucze

Klucz rozszerzony jest po prostu połączeniem klucza (prywatnego lub publicznego) i powiązanego z nim kodu łańcuchowego. Ten kod łańcucha jest niezbędny do wyprowadzenia kluczy podrzędnych, ponieważ bez niego niemożliwe jest wyprowadzenie kluczy podrzędnych z klucza nadrzędnego, ale proces ten omówimy dokładniej w następnym rozdziale. Te rozszerzone klucze umożliwiają zatem agregowanie wszystkich niezbędnych informacji w celu uzyskania kluczy podrzędnych, upraszczając w ten sposób zarządzanie kontami w HD Wallet.

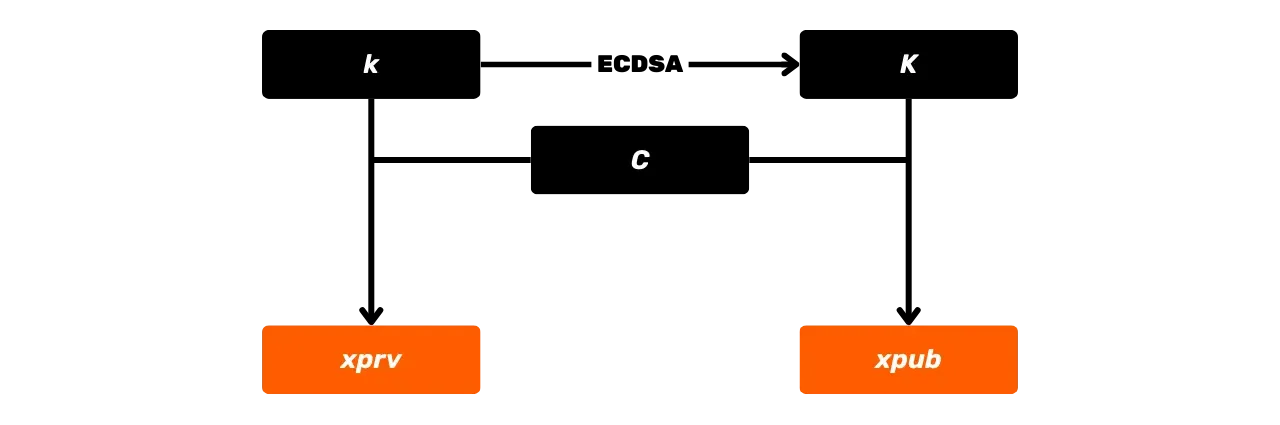
Klucz rozszerzony składa się z dwóch części:

Ładunek, który zawiera klucz prywatny lub publiczny, a także powiązany kod łańcucha;
Metadane, które są różnymi informacjami ułatwiającymi interoperacyjność między oprogramowaniem i poprawiającymi zrozumienie dla użytkownika.

Jak działają klucze rozszerzone

Gdy klucz rozszerzony zawiera klucz prywatny, jest on określany jako rozszerzony klucz prywatny. Jest on rozpoznawany po prefiksie, który zawiera identyfikator prv. Oprócz klucza prywatnego, rozszerzony klucz prywatny zawiera również powiązany kod łańcucha. Z tego typu rozszerzonego klucza możliwe jest wyprowadzenie wszystkich typów podrzędnych kluczy prywatnych. W związku z tym, poprzez dodawanie i podwajanie punktów na krzywych eliptycznych, pozwala on również na wyprowadzanie podrzędnych kluczy publicznych.

Gdy klucz rozszerzony nie zawiera klucza prywatnego, ale zamiast tego klucz publiczny, jest on określany jako rozszerzony klucz publiczny. Jest on rozpoznawany przez swój prefiks, który zawiera identyfikator pub. Oczywiście, oprócz klucza, zawiera on również powiązany kod łańcucha. W przeciwieństwie do rozszerzonego klucza prywatnego, rozszerzony klucz publiczny pozwala na wyprowadzanie tylko "normalnych" podrzędnych kluczy publicznych (co oznacza, że nie może wyprowadzać "wzmocnionych" kluczy podrzędnych). W następnym rozdziale zobaczymy, co oznaczają te "normalne" i "wzmocnione" kwalifikatory.

W każdym razie, rozszerzony klucz publiczny nie pozwala na wyprowadzenie podrzędnych kluczy prywatnych. Dlatego nawet jeśli ktoś ma dostęp do xpub, nie będzie mógł wydać powiązanych środków, ponieważ nie będzie miał dostępu do odpowiednich kluczy prywatnych. Może jedynie wyprowadzić podrzędne klucze publiczne, aby obserwować powiązane transakcje.

W dalszej części przyjmiemy następującą notację:

$K_{\text{PAR}}$ : nadrzędny klucz publiczny;
$k_{\text{PAR}}$ : nadrzędny klucz prywatny;
$C_{\text{PAR}}$ : kod łańcucha nadrzędnego;
$C_{\text{CHD}}$ : kod łańcucha podrzędnego;
$K_{\text{CHD}}^n$ : zwykły podrzędny klucz publiczny;
$k_{\text{CHD}}^n$ : normalny klucz prywatny dziecka;
$K_{\text{CHD}}^h$ : wzmocniony klucz publiczny dziecka;
$k_{\text{CHD}}^h$ : wzmocniony klucz prywatny dziecka.

Budowa klucza rozszerzonego

Klucz rozszerzony ma następującą strukturę:

Version**: Kod wersji identyfikujący naturę klucza (xprv, xpub, yprv, ypub...). Na końcu tego rozdziału zobaczymy, co oznaczają litery x, y i z.
Głębokość**: Poziom hierarchiczny w HD Wallet względem klucza głównego (0 dla klucza głównego).
Parent Fingerprint**: Pierwsze 4 bajty HASH160 Hash nadrzędnego klucza publicznego używanego do wyprowadzenia klucza obecnego w ładunku.
Numer indeksu**: Identyfikator elementu podrzędnego wśród kluczy rodzeństwa, czyli wśród wszystkich kluczy na tym samym poziomie pochodnym, które mają te same klucze nadrzędne.
Kod łańcucha**: Unikalny 32-bajtowy kod do wyprowadzania kluczy podrzędnych.
Klucz**: Klucz prywatny (poprzedzony 1 bajtem w celu określenia rozmiaru) lub klucz publiczny.
Suma kontrolna**: Dodawana jest również suma kontrolna obliczana za pomocą funkcji HASH256 (podwójny SHA256), która umożliwia weryfikację integralności klucza rozszerzonego podczas jego przesyłania lub przechowywania.

Kompletny format klucza rozszerzonego to zatem 78 bajtów bez sumy kontrolnej i 82 bajty z sumą kontrolną. Jest on następnie konwertowany do Base58, aby uzyskać reprezentację, która jest łatwa do odczytania przez użytkowników. Format Base58 jest taki sam jak ten używany dla adresów odbiorczych Legacy (przed SegWit).

Element	Description	Size
Version	Indicates whether the key is public (`xpub`, `ypub`) or private (`xprv`, `zprv`), as well as the version of the extended key	4 bytes
Depth	Level in the hierarchy relative to the master key	1 byte
Parent Fingerprint	The first 4 bytes of HASH160 of the parent public key	4 bytes
Index Number	Position of the key in the order of children	4 bytes
Chain Code	Used to derive child keys	32 bytes
Key	The private key (with a 1-byte prefix) or the public key	33 bytes
Checksum	Checksum to verify integrity	4 bytes

Jeśli jeden bajt jest dodawany tylko do klucza prywatnego, to dlatego, że skompresowany klucz publiczny jest dłuższy od klucza prywatnego o jeden bajt. Ten dodatkowy bajt, dodany na początku klucza prywatnego jako 0x00, wyrównuje ich rozmiar, zapewniając, że ładunek rozszerzonego klucza ma taką samą długość, niezależnie od tego, czy jest to klucz publiczny, czy prywatny.

Rozszerzone prefiksy kluczy

Jak właśnie zauważyliśmy, klucze rozszerzone zawierają prefiks, który wskazuje zarówno wersję klucza rozszerzonego, jak i jego naturę. Notacja pub wskazuje, że odnosi się do rozszerzonego klucza publicznego, a notacja prv wskazuje na rozszerzony klucz prywatny. Dodatkowa litera u podstawy klucza rozszerzonego pomaga wskazać, czy zastosowany standard to Legacy, SegWit v0, SegWit v1 itd.

Poniżej znajduje się podsumowanie używanych przedrostków i ich znaczeń:

Base 58 Prefix	Base 16 Prefix	Network	Purpose	Associated Scripts	Derivation	Key Type
`xpub`	`0488b21e`	Mainnet	Legacy and SegWit V1	P2PK / P2PKH / P2TR	`m/44'/0'`, `m/86'/0'`	public
`xprv`	`0488ade4`	Mainnet	Legacy and SegWit V1	P2PK / P2PKH / P2TR	`m/44'/0'`, `m/86'/0'`	private
`tpub`	`043587cf`	Testnet	Legacy and SegWit V1	P2PK / P2PKH / P2TR	`m/44'/1'`, `m/86'/1'`	public
`tprv`	`04358394`	Testnet	Legacy and SegWit V1	P2PK / P2PKH / P2TR	`m/44'/1'`, `m/86'/1'`	private
`ypub`	`049d7cb2`	Mainnet	Nested SegWit	P2WPKH in P2SH	`m/49'/0'`	public
`yprv`	`049d7878`	Mainnet	Nested SegWit	P2WPKH in P2SH	`m/49'/0'`	private
`upub`	`049d7cb2`	Testnet	Nested SegWit	P2WPKH in P2SH	`m/49'/1'`	public
`uprv`	`044a4e28`	Testnet	Nested SegWit	P2WPKH in P2SH	`m/49'/1'`	private
`zpub`	`04b24746`	Mainnet	SegWit V0	P2WPKH	`m/84'/0'`	public
`zprv`	`04b2430c`	Mainnet	SegWit V0	P2WPKH	`m/84'/0'`	private
`vpub`	`045f1cf6`	Testnet	SegWit V0	P2WPKH	`m/84'/1'`	public
`vprv`	`045f18bc`	Testnet	SegWit V0	P2WPKH	`m/84'/1'`	private

Szczegóły klucza rozszerzonego Elements

Aby lepiej zrozumieć wewnętrzną strukturę klucza rozszerzonego, weźmy jeden jako przykład i podzielmy go. Oto klucz rozszerzony:

W Base58**:

xpub6CTNzMUkzpurBWaT4HQoYzLP4uBbGJuWY358Rj7rauiw4rMHCyq3Rfy9w4kyJXJzeFfyrKLUar2rUCukSiDQFa7roTwzjiAhyQAdPLEjqHT

W systemie szesnastkowym**:

0488B21E036D5601AD80000000C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A89303772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF50658051F067C3A

Ten rozszerzony klucz dzieli się na kilka różnych Elements:

1.Wersja: 0488B21E

Pierwsze 4 bajty to wersja. W tym przypadku odpowiada to rozszerzonemu kluczowi publicznemu na Mainnet z celem derywacji Legacy lub SegWit v1.

2.Głębokość: 03

To pole wskazuje hierarchiczny poziom klucza w HD Wallet. W tym przypadku głębokość 03 oznacza, że klucz ten znajduje się trzy poziomy poniżej klucza głównego.

3.Parent fingerprint: 6D5601AD

Są to pierwsze 4 bajty HASH160 Hash nadrzędnego klucza publicznego, który został użyty do wyprowadzenia tego xpub.

4.Numer indeksu: 80000000

Indeks ten wskazuje pozycję klucza wśród dzieci jego rodzica. Prefiks 0x80 wskazuje, że klucz jest wyprowadzany w sposób zahartowany, a ponieważ reszta jest wypełniona zerami, oznacza to, że ten klucz jest pierwszym wśród jego możliwego rodzeństwa.

5.Kod łańcucha: C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A893

6.Klucz publiczny: 03772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF5065805

7.Checksum: 1F067C3A

Suma kontrolna odpowiada pierwszym 4 bajtom Hash (podwójny SHA256) całej reszty.

W tym rozdziale dowiedzieliśmy się, że istnieją dwa różne typy kluczy potomnych. Dowiedzieliśmy się również, że wyprowadzenie tych kluczy potomnych wymaga klucza (prywatnego lub publicznego) i jego kodu łańcuchowego. W następnym rozdziale szczegółowo przeanalizujemy naturę tych różnych typów kluczy i sposób ich wyprowadzania z klucza nadrzędnego i kodu łańcuchowego.

Tworzenie par kluczy podrzędnych

Wyprowadzanie par kluczy potomnych w portfelach Bitcoin HD opiera się na hierarchicznej strukturze, która umożliwia generowanie dużej liczby kluczy, jednocześnie organizując te pary w różne grupy za pomocą gałęzi. Każda para potomna wywodząca się z pary nadrzędnej może być użyta bezpośrednio w scriptPubKey do zablokowania bitcoinów lub jako punkt wyjścia do generate kolejnych kluczy potomnych, i tak dalej, w celu utworzenia drzewa kluczy.

Wszystkie te pochodne zaczynają się od klucza głównego i głównego kodu łańcucha, które są pierwszymi rodzicami na poziomie głębokości 0. Są to w pewnym sensie Adam i Ewa kluczy Wallet, wspólni przodkowie wszystkich kluczy pochodnych.

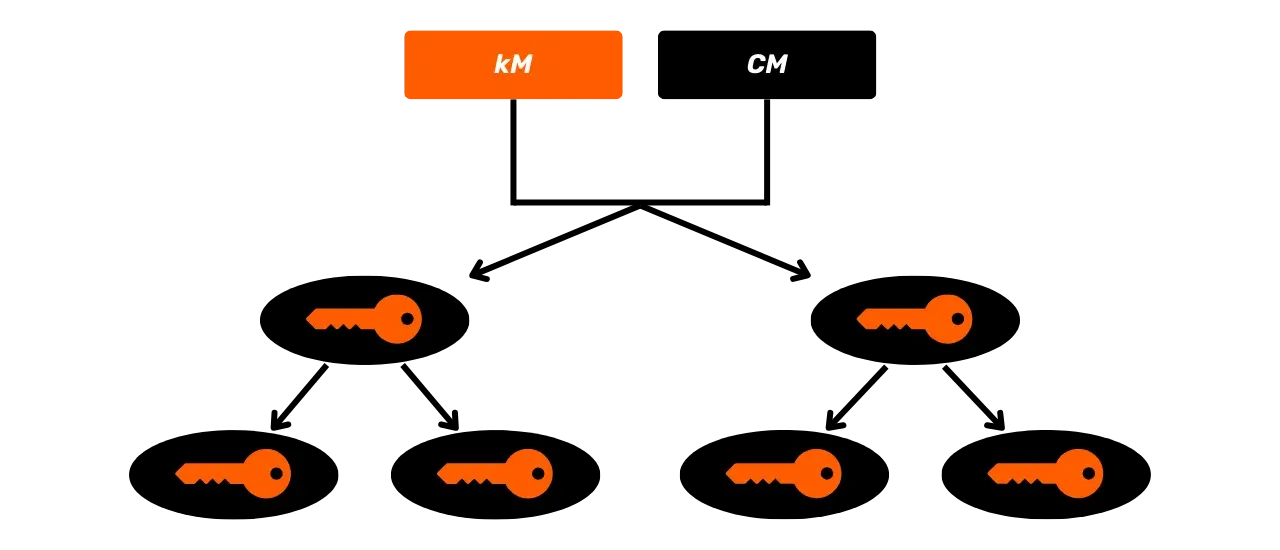
Przyjrzyjmy się, jak działa ta deterministyczna pochodna.

Różne rodzaje pochodnych kluczy podrzędnych

Jak pokrótce wspomnieliśmy w poprzednim rozdziale, klucze podrzędne dzielą się na dwa główne typy.

Normalne klucze podrzędne** ( $k_{\text{CHD}}^n, K_{\text{CHD}}^n$ ): Są one wyprowadzane z rozszerzonego klucza publicznego ( $K_{\text{PAR}}$ ) lub rozszerzonego klucza prywatnego ( $k_{\text{PAR}}$ ), najpierw wyprowadzając klucz publiczny.
Utwardzone klucze podrzędne** ( $k_{\text{CHD}}^h, K_{\text{CHD}}^h$ ): Można je wyprowadzić tylko z rozszerzonego klucza prywatnego ( $k_{\text{PAR}}$ ) i dlatego są niewidoczne dla obserwatorów, którzy mają tylko rozszerzony klucz publiczny.

Każda para kluczy potomnych jest identyfikowana przez 32-bitowy indeks (nazwany $i$ w naszych obliczeniach). Indeksy dla normalnych kluczy mieszczą się w zakresie od $0$ do $2^{31}-1$ , podczas gdy te dla kluczy wzmocnionych mieszczą się w zakresie od $2^{31}$ do $2^{32}-1$ . Numery te są używane do rozróżniania par kluczy rodzeństwa podczas wyprowadzania. Rzeczywiście, każda para kluczy nadrzędnych musi być w stanie wyprowadzić wiele par kluczy podrzędnych. Jeśli zastosowalibyśmy to samo obliczenie systematycznie od kluczy nadrzędnych, wszystkie uzyskane klucze rodzeństwa byłyby identyczne, co nie jest pożądane. Indeks wprowadza zatem zmienną, która modyfikuje obliczenia wyprowadzania, umożliwiając rozróżnienie każdej pary rodzeństwa. Z wyjątkiem szczególnych zastosowań w niektórych protokołach i standardach wyprowadzania, zazwyczaj zaczynamy od wyprowadzenia pierwszego klucza potomnego z indeksem 0, drugiego z indeksem 1 i tak dalej.

Proces wyprowadzania z HMAC-SHA512

Derywacja każdego klucza podrzędnego opiera się na funkcji HMAC-SHA512, którą omówiliśmy w sekcji 2 dotyczącej funkcji Hash. Przyjmuje ona dwa dane wejściowe: kod łańcucha nadrzędnego $C_{\text{PAR}}$ i konkatenację klucza nadrzędnego (albo klucza publicznego $K_{\text{PAR}}$ , albo klucza prywatnego $k_{\text{PAR}}$ , w zależności od typu pożądanego klucza podrzędnego) z indeksem. Wynikiem HMAC-SHA512 jest 512-bitowa sekwencja podzielona na dwie części:

Pierwsze 32 bajty** (lub $h_1$ ) są używane do obliczenia nowej pary dzieci.
Ostatnie 32 bajty** (lub $h_2$ ) służą jako nowy kod łańcucha $C_{\text{CHD}}$ dla pary podrzędnej.

We wszystkich naszych obliczeniach będę oznaczał $\text{Hash}$ jako wynik funkcji HMAC-SHA512.

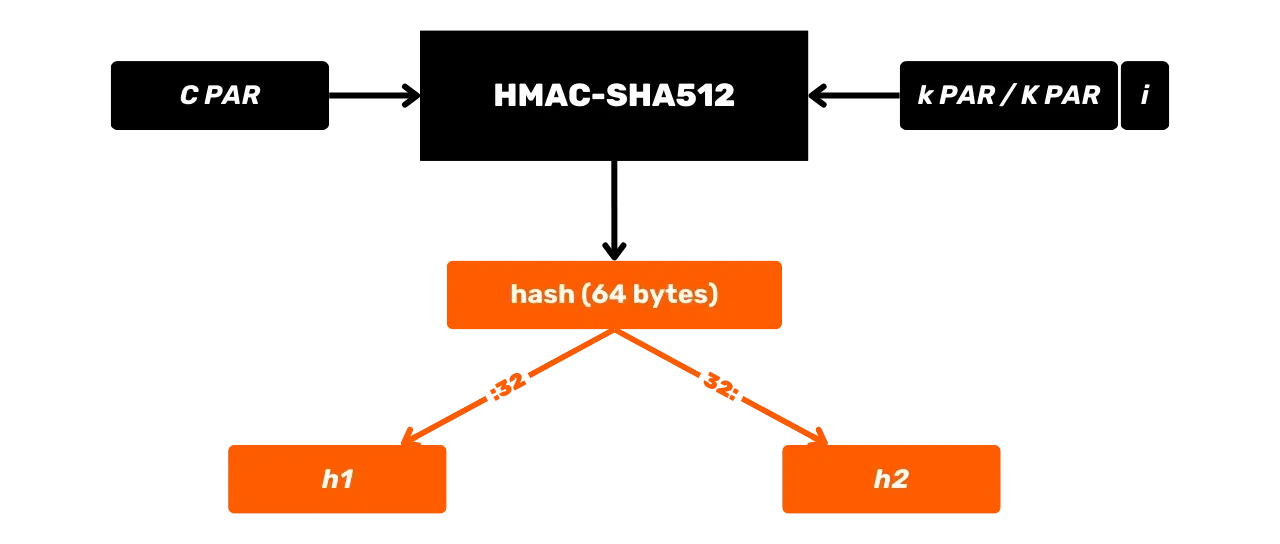
Wywiedzenie podrzędnego klucza prywatnego z nadrzędnego klucza prywatnego

Aby wyprowadzić podrzędny klucz prywatny $k_{\text{CHD}} z nadrzędnego klucza prywatnego$ k_{\text{PAR}}, możliwe są dwa scenariusze, w zależności od tego, czy pożądany jest klucz wzmocniony czy normalny.

Dla normalnego klucza podrzędnego ( $i < 2^{31}$ ), obliczenie $\text{Hash}$ jest następujące:

 $\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, k_{\text{PAR}} \cdot G \Vert i)$

W tym obliczeniu zauważamy, że nasza funkcja HMAC pobiera dwa dane wejściowe: najpierw kod łańcucha nadrzędnego, a następnie konkatenację indeksu z kluczem publicznym powiązanym z kluczem prywatnym nadrzędnym. Klucz publiczny rodzica jest tutaj używany, ponieważ chcemy uzyskać normalny klucz podrzędny, a nie klucz wzmocniony.

Mamy teraz 64-bajtowy $\text{Hash}$ , który podzielimy na 2 części po 32 bajty, $h_1$ i $h_2$ :

 $\text{hash} = h_1 \Vert h_2$

 $h_1 = \text{hash}_{[:32]} \quad, \quad h_2 = \text{hash}_{[32:]}$

Klucz prywatny dziecka $k_{\text{CHD}}^n$ jest następnie obliczany w następujący sposób:

 $k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n$

W tym obliczeniu operacja $\text{parse256}(h_1)$ polega na interpretacji pierwszych 32 bajtów $\text{Hash}$ jako 256-bitowej liczby całkowitej. Liczba ta jest następnie dodawana do nadrzędnego klucza prywatnego, a wszystko to modulo $n$ , aby pozostać w porządku krzywej eliptycznej, jak widzieliśmy w sekcji 3 dotyczącej podpisów cyfrowych. Tak więc, aby uzyskać normalny klucz prywatny dziecka, chociaż klucz publiczny rodzica jest używany jako podstawa do obliczeń w danych wejściowych funkcji HMAC-SHA512, zawsze konieczne jest posiadanie klucza prywatnego rodzica, aby zakończyć obliczenia.

Z tego klucza prywatnego dziecka można wyprowadzić odpowiadający mu klucz publiczny, stosując ECDSA lub Schnorr. W ten sposób otrzymujemy kompletną parę kluczy.

Następnie druga część $\text{Hash}$ jest po prostu interpretowana jako kod łańcucha dla pary kluczy potomnych, którą właśnie wyprowadziliśmy:

 $C_{\text{CHD}} = h_2$

Poniżej znajduje się schemat ogólnego wyprowadzenia:

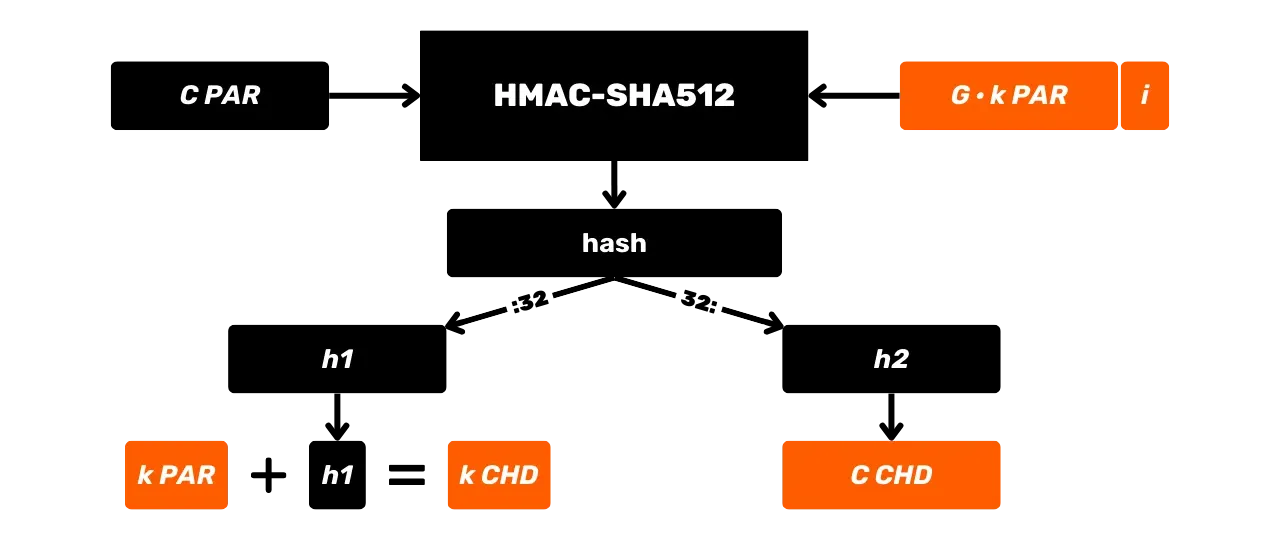
Dla hardened child key ( $i \geq 2^{31}$ ), obliczenie $\text{Hash}$ jest następujące:

 $\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, 0x00 \Vert k_{\text{PAR}} \Vert i)$

W tym obliczeniu zauważamy, że nasza funkcja HMAC pobiera dwa dane wejściowe: najpierw kod łańcucha rodzica, a następnie konkatenację indeksu z kluczem prywatnym rodzica. Klucz prywatny rodzica jest tutaj używany, ponieważ chcemy uzyskać wzmocniony klucz potomny. Co więcej, na początku klucza dodawany jest bajt równy 0x00. Ta operacja wyrównuje jego długość, aby pasowała do skompresowanego klucza publicznego.

Mamy więc teraz 64-bajtowy $\text{Hash}$ , który podzielimy na 2 części po 32 bajty każda, $h_1$ i $h_2$ :

 $\text{hash} = h_1 \Vert h_2$

 $h_1 = \text{hash}[:32] \quad, \quad h_2 = \text{hash}[32:]$

Klucz prywatny dziecka $k_{\text{CHD}}^h$ jest następnie obliczany w następujący sposób:

 $k_{\text{CHD}}^h = \text{parse256}(h_1) + k_{\text{PAR}} \mod n$

Następnie po prostu interpretujemy drugą część $\text{Hash}$ jako kod łańcucha dla pary kluczy potomnych, które właśnie wyprowadziliśmy:

 $C_{\text{CHD}} = h_2$

Poniżej znajduje się schemat ogólnego wyprowadzenia:

Widzimy, że normalna derywacja i utwardzona derywacja działają w ten sam sposób, z tą różnicą: normalna derywacja wykorzystuje nadrzędny klucz publiczny jako dane wejściowe do funkcji HMAC, podczas gdy utwardzona derywacja wykorzystuje nadrzędny klucz prywatny.

Uzyskanie podrzędnego klucza publicznego z nadrzędnego klucza publicznego

Jeśli znamy tylko nadrzędny klucz publiczny $K_{\text{PAR}}$ i powiązany z nim kod łańcucha $C_{\text{PAR}}$ , czyli rozszerzony klucz publiczny, możliwe jest wyprowadzenie podrzędnych kluczy publicznych $K_{\text{CHD}}^n$ , ale tylko dla normalnych (niehartowanych) kluczy podrzędnych. Zasada ta pozwala w szczególności na monitorowanie ruchów konta w Bitcoin Wallet z xpub (watch-only).

Aby wykonać te obliczenia, obliczymy $\text{Hash}$ z indeksem $i < 2^{31}$ (normalna pochodna):

 $\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, K_{\text{PAR}} \Vert i)$

W tym obliczeniu zauważamy, że nasza funkcja HMAC pobiera dwa dane wejściowe: najpierw kod łańcucha nadrzędnego, a następnie konkatenację indeksu z nadrzędnym kluczem publicznym.

Mamy więc teraz $\text{Hash}$ o rozmiarze 64 bajtów, który podzielimy na 2 części po 32 bajty każda, $h_1$ i $h_2$ :

 $\text{hash} = h_1 \Vert h_2$

 $h_1 = \text{hash}[:32] \quad, \quad h_2 = \text{hash}[32:]$

Klucz publiczny dziecka $K_{\text{CHD}}^n$ jest następnie obliczany w następujący sposób:

 $K_{\text{CHD}}^n = \text{parse256}(h_1) \cdot G + K_{\text{PAR}}$

Jeśli $\text{parse256}(h_1) \geq n$ (rząd krzywej eliptycznej) lub jeśli $K_{\text{CHD}}^n$ jest punktem w nieskończoności, wyprowadzenie jest nieprawidłowe i należy wybrać inny indeks.

W tym obliczeniu operacja $\text{parse256}(h_1)$ obejmuje interpretację pierwszych 32 bajtów $\text{Hash}$ jako 256-bitowej liczby całkowitej. Liczba ta jest używana do obliczenia punktu na krzywej eliptycznej poprzez dodawanie i podwajanie od punktu generatora $G$ . Punkt ten jest następnie dodawany do nadrzędnego klucza publicznego w celu uzyskania normalnego podrzędnego klucza publicznego. Tak więc, aby uzyskać normalny klucz publiczny dziecka, potrzebny jest tylko klucz publiczny rodzica i kod łańcucha rodzica; klucz prywatny rodzica nigdy nie wchodzi w ten proces, w przeciwieństwie do obliczania klucza prywatnego dziecka, który widzieliśmy wcześniej.

Następnie kod łańcucha podrzędnego jest prosty:

 $C_{\text{CHD}} = h_2$

Poniżej znajduje się schemat ogólnego wyprowadzenia:

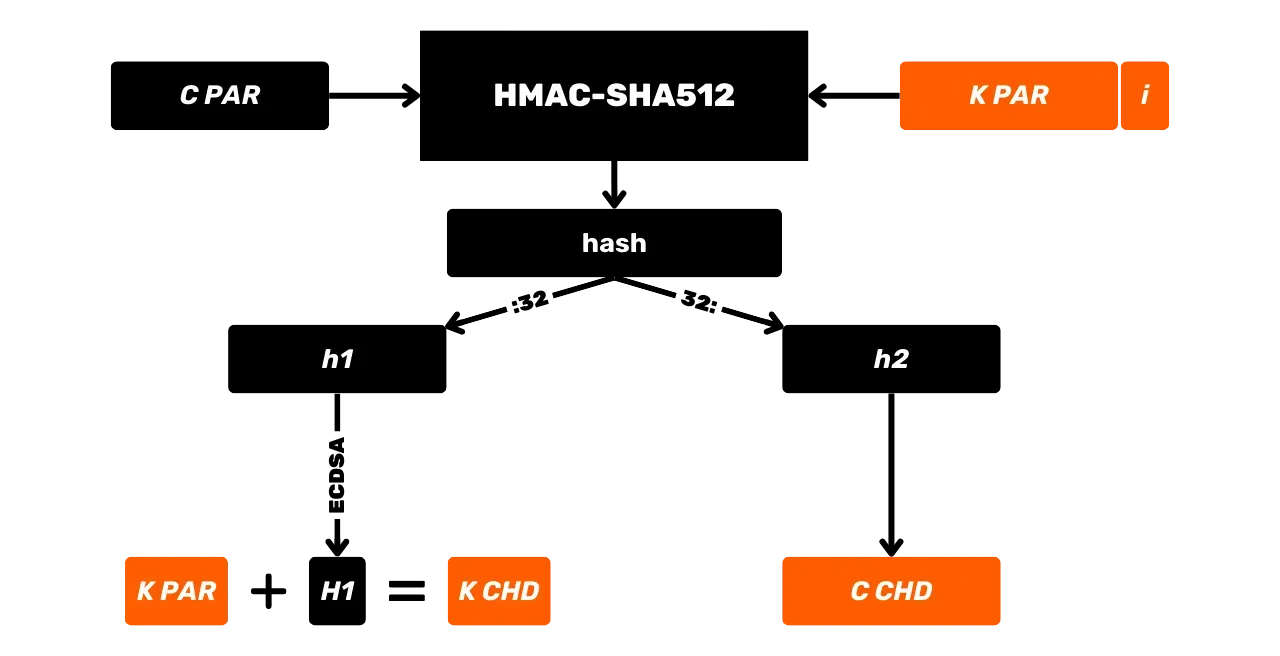
Zgodność między kluczami publicznymi i prywatnymi dziecka

Może pojawić się pytanie, w jaki sposób normalny klucz publiczny potomka wyprowadzony z nadrzędnego klucza publicznego może odpowiadać normalnemu kluczowi prywatnemu potomka wyprowadzonemu z odpowiedniego nadrzędnego klucza prywatnego. Związek ten jest dokładnie zapewniony przez właściwości krzywych eliptycznych. Rzeczywiście, aby uzyskać normalny klucz publiczny dziecka, HMAC-SHA512 jest stosowany w ten sam sposób, ale jego dane wyjściowe są używane w inny sposób:

Zwykły klucz prywatny dziecka**: $k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n$
Zwykły klucz publiczny dziecka**: $K_{\text{CHD}}^n = \text{parse256}(h_1) \cdot G + K_{\text{PAR}}$

Dzięki operacjom dodawania i podwajania na krzywej eliptycznej, obie metody dają spójne wyniki: klucz publiczny wyprowadzony z podrzędnego klucza prywatnego jest identyczny z podrzędnym kluczem publicznym wyprowadzonym bezpośrednio z nadrzędnego klucza publicznego.

Podsumowanie typów pochodnych

Podsumowując, oto różne możliwe typy pochodnych:

 $\begin{array}{|c|c|c|c|} \hline \rightarrow & \text{PAR} & \text{CHD} & \text{n/h} \\ \hline k_{\text{PAR}} \rightarrow k_{\text{CHD}} & k_{\text{PAR}} & \{ k_{\text{CHD}}^n, k_{\text{CHD}}^h \} & \{ n, h \} \\ k_{\text{PAR}} \rightarrow K_{\text{CHD}} & k_{\text{PAR}} & \{ K_{\text{CHD}}^n, K_{\text{CHD}}^h \} & \{ n, h \} \\ K_{\text{PAR}} \rightarrow k_{\text{CHD}} & K_{\text{PAR}} & \times & \times \\ K_{\text{PAR}} \rightarrow K_{\text{CHD}} & K_{\text{PAR}} & K_{\text{CHD}}^n & n \\ \hline \end{array}$

Do tej pory nauczyłeś się tworzyć podstawowy Elements z HD Wallet: frazę Mnemonic, seed, a następnie klucz główny i kod łańcucha głównego. W tym rozdziale dowiedziałeś się również, jak wyprowadzać pary kluczy podrzędnych. W następnym rozdziale zbadamy, jak te pochodne są zorganizowane w portfelach Bitcoin i jaką strukturę należy zastosować, aby konkretnie uzyskać adresy odbiorcze, a także pary kluczy używane w scriptPubKey i scriptSig.

Struktura Wallet i ścieżki pochodne

Hierarchiczna struktura portfeli HD w Bitcoin pozwala na organizację par kluczy na różne sposoby. Pomysł polega na wyprowadzeniu, z głównego klucza prywatnego i głównego kodu łańcucha, kilku poziomów głębokości. Każdy dodany poziom odpowiada wyprowadzeniu pary kluczy podrzędnych z pary kluczy nadrzędnych.

Z biegiem czasu różne BIP wprowadziły standardy dla tych ścieżek derywacji, mając na celu standaryzację ich wykorzystania w różnych programach. W tym rozdziale odkryjemy znaczenie każdego poziomu derywacji w portfelach HD, zgodnie z tymi standardami.

Głębokość pochodnej HD Wallet

Ścieżki wyprowadzania są zorganizowane w warstwy głębokości, począwszy od głębokości 0, która reprezentuje klucz główny i kod łańcucha głównego, do warstw podpoziomów do wyprowadzania adresów używanych do blokowania UTXO. BIPs (Bitcoin Improvement Proposals) definiują standardy dla każdego Layer, co pomaga zharmonizować praktyki w różnych oprogramowaniach do zarządzania Wallet.

Ścieżka derywacji odnosi się zatem do sekwencji indeksów używanych do wyprowadzania kluczy podrzędnych z klucza głównego.

Głębokość 0: Klucz główny (BIP32)

Głębokość ta odpowiada głównemu kluczowi prywatnemu Wallet i głównemu kodowi łańcucha. Jest ona reprezentowana przez notację $m/$ .

Głębokość 1: Cel (BIP43)

Cel określa logiczną strukturę derywacji. Na przykład P2WPKH Address będzie miał $/84'/$ na głębokości 1 (zgodnie z BIP84), podczas gdy P2TR Address będzie miał $/86'/$ (zgodnie z BIP86). Ten Layer ułatwia kompatybilność między portfelami, wskazując numery indeksów odpowiadające numerom BIP.

Innymi słowy, po uzyskaniu klucza głównego i kodu łańcucha głównego służą one jako para kluczy nadrzędnych do wyprowadzenia pary kluczy podrzędnych. Indeksem używanym w tej derywacji może być na przykład $/84'/$ , jeśli Wallet ma używać skryptów typu SegWit v0. Ta para kluczy znajduje się wtedy na głębokości 1. Jej rolą nie jest blokowanie bitcoinów, ale po prostu służenie jako punkt orientacyjny w hierarchii derywacji.

Głębokość 2: Typ waluty (BIP44)

Z pary kluczy na głębokości 1 wykonywana jest nowa derywacja w celu uzyskania pary kluczy na głębokości 2. Głębokość ta pozwala odróżnić konta Bitcoin od innych kryptowalut w ramach tego samego Wallet.

Każda waluta ma unikalny indeks, aby zapewnić kompatybilność z portfelami wielowalutowymi. Na przykład dla Bitcoin indeks to $/0'/$ (lub 0x80000000 w zapisie szesnastkowym). Indeksy walut są wybierane w zakresie od $2^{31}$ do $2^{32}-1$ , aby zapewnić wzmocnioną derywację.

Aby podać inne przykłady, oto indeksy niektórych walut:

$1'$ (0x800001) za bitcoiny Testnet;
$2'$ (0x80000002) dla Litecoin;
60'$ (0x8000003c) za Ethereum...

Głębokość 3: Konto (BIP32)

Każdy Wallet może być podzielony na kilka kont, ponumerowanych od $2^{31}$ i reprezentowanych na głębokości 3 przez $/0'/$ dla pierwszego konta, $/1'/$ dla drugiego i tak dalej. Generalnie, odnosząc się do klucza rozszerzonego xpub, odnosi się on do kluczy na tej głębokości derywacji.

Ten podział na różne konta jest opcjonalny. Ma to na celu uproszczenie organizacji Wallet dla użytkowników. W praktyce często używane jest tylko jedno konto, zwykle domyślnie pierwsze. Jednak w niektórych przypadkach, jeśli chcemy wyraźnie rozróżnić pary kluczy do różnych zastosowań, może to być przydatne. Na przykład możliwe jest utworzenie konta osobistego i konta profesjonalnego z tego samego seed, z całkowicie odrębnymi grupami kluczy z tej głębokości derywacji.

Głębokość 4: Łańcuch (BIP32)

Każdy rachunek zdefiniowany na głębokości 3 jest następnie podzielony na dwa łańcuchy:

Łańcuch zewnętrzny**: W tym łańcuchu wyprowadzane są tak zwane adresy "publiczne". Te adresy odbiorcze są przeznaczone do blokowania UTXO pochodzących z transakcji zewnętrznych (czyli pochodzących z konsumpcji UTXO, które nie należą do ciebie). Mówiąc prościej, ten zewnętrzny łańcuch jest używany za każdym razem, gdy ktoś chce otrzymać bitcoiny. Po kliknięciu "odbierz" w oprogramowaniu Wallet, zawsze oferowany jest Address z zewnętrznego łańcucha. Łańcuch ten jest reprezentowany przez parę kluczy o indeksie $/0/$ .
Łańcuch wewnętrzny (zmiana)**: Ten łańcuch jest zarezerwowany do odbierania adresów, które blokują bitcoiny pochodzące z konsumpcji UTXO należących do użytkownika, innymi słowy, adresów zmiany. Jest on identyfikowany przez indeks $/1/$ .

Głębokość 5: Indeks Address (BIP32)

Wreszcie, głębokość 5 stanowi ostatni krok derywacji w Wallet. Chociaż technicznie możliwe jest kontynuowanie w nieskończoność, obecne standardy zatrzymują się tutaj. Na tej ostatniej głębokości wyprowadzane są pary kluczy, które będą faktycznie używane do blokowania i odblokowywania UTXO. Każdy indeks umożliwia rozróżnienie między parami kluczy rodzeństwa: w ten sposób pierwszy odbierający Address użyje indeksu $/0/$ , drugi indeksu $/1/$ i tak dalej.

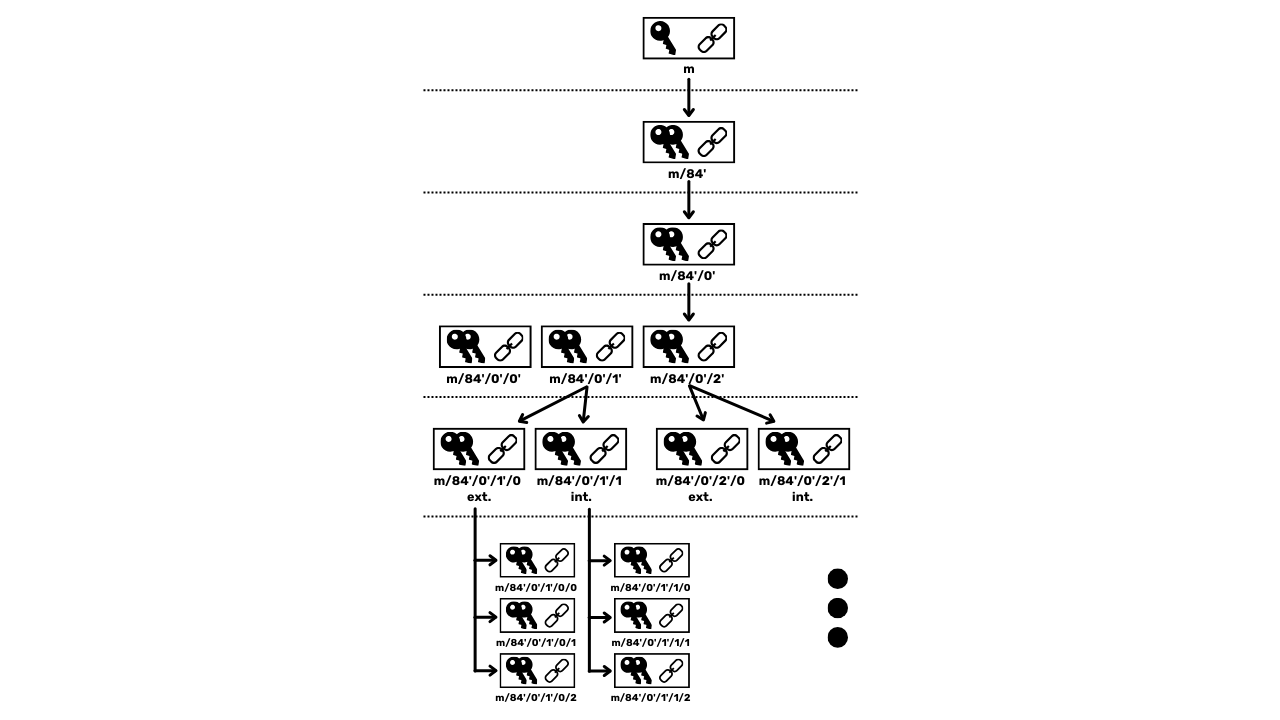
Notacja ścieżek pochodnych

Ścieżka derywacji jest zapisywana poprzez oddzielenie każdego poziomu ukośnikiem ( $/$ ). Każdy ukośnik oznacza zatem wyprowadzenie pary kluczy nadrzędnych ( $k_{\text{PAR}}$ , $K_{\text{PAR}}$ , $C_{\text{PAR}}$ ) do pary kluczy podrzędnych ( $k_{\text{CHD}}$ , $K_{\text{CHD}}$ , $C_{\text{CHD}}$ ). Liczba odnotowana na każdej głębokości odpowiada indeksowi użytemu do wyprowadzenia tego klucza z jego rodziców. Apostrof ( $'$ ) czasami umieszczany po prawej stronie indeksu wskazuje na utwardzone wyprowadzenie ( $k_{\text{CHD}}^h$ , $K_{\text{CHD}}^h$ ). Czasami ten apostrof jest zastępowany przez $h$ . W przypadku braku apostrofu lub $h$ , jest to zatem normalna derywacja ( $k_{\text{CHD}}^n$ , $K_{\text{CHD}}^n$ ).

Jak widzieliśmy w poprzednich rozdziałach, utwardzone indeksy kluczy zaczynają się od $2^{31}$ , lub 0x80000000 w systemie szesnastkowym. Dlatego też, gdy po indeksie następuje apostrof w ścieżce pochodnej, $2^{31}$ musi zostać dodane do wskazanej liczby, aby uzyskać rzeczywistą wartość używaną w funkcji HMAC-SHA512. Na przykład, jeśli ścieżka pochodna określa $/44'/$ , rzeczywisty indeks będzie następujący:

 $i = 44 + 2^{31} = 2\,147\,483\,692$

W systemie szesnastkowym jest to 0x8000002C.

Teraz, gdy zrozumieliśmy główne zasady ścieżek derywacji, weźmy przykład! Oto ścieżka wyprowadzania dla Bitcoin odbierającego Address:

 $m / 84' / 0' / 1' / 0 / 7$

W tym przykładzie:

$84'$ oznacza standard P2WPKH (SegWit v0);
$0'$ wskazuje walutę Bitcoin na Mainnet;
$1'$ odpowiada drugiemu rachunkowi w Wallet;
$0$ wskazuje, że Address znajduje się w zewnętrznym łańcuchu;
$7$ oznacza 8. zewnętrzny Address dla tego konta.

Podsumowanie struktury pochodnej

Depth	Description	Standard Example
0	Master Key	$m/$
1	Purpose	$/86'/$ (P2TR)
2	Currency	$/0'/$ (Bitcoin)
3	Account	$/0'/$ (First account)
4	Chain	$/0/$ (external) or $/1/$ (change)
5	Address Index	$/0/$ (first address)

W następnym rozdziale odkryjemy, czym są "* deskryptory skryptu wyjścia*", niedawno wprowadzona innowacja w Bitcoin Core, która upraszcza tworzenie kopii zapasowych Bitcoin Wallet.

Deskryptory skryptu wyjściowego

Często mówi się, że sama fraza Mnemonic jest wystarczająca do odzyskania dostępu do Wallet. W rzeczywistości sprawy są nieco bardziej złożone. W poprzednim rozdziale przyjrzeliśmy się strukturze derywacji HD Wallet i być może zauważyłeś, że proces ten jest dość złożony. Ścieżki derywacji informują oprogramowanie, w którym kierunku należy podążać, aby uzyskać klucze użytkownika. Jednak podczas odzyskiwania Bitcoin Wallet, jeśli ktoś nie zna tych ścieżek, sama fraza Mnemonic nie wystarczy. Umożliwia ona uzyskanie klucza głównego i kodu łańcucha głównego, ale konieczna jest znajomość indeksów użytych do uzyskania kluczy podrzędnych.

Teoretycznie konieczne byłoby zapisanie nie tylko frazy Mnemonic naszego Wallet, ale także ścieżek do kont, z których korzystamy. W praktyce często możliwe jest odzyskanie dostępu do kluczy podrzędnych bez tych informacji, pod warunkiem przestrzegania standardów. Testując każdy standard po kolei, zazwyczaj można odzyskać dostęp do bitcoinów. Nie jest to jednak gwarantowane i jest szczególnie skomplikowane dla początkujących. Ponadto, wraz z dywersyfikacją typów skryptów i pojawieniem się bardziej złożonych konfiguracji, informacje te mogą stać się trudne do ekstrapolacji, zmieniając w ten sposób te dane w informacje prywatne i trudne do odzyskania za pomocą brutalnej siły. Właśnie dlatego niedawno wprowadzono innowację, która zaczyna być integrowana z ulubionym oprogramowaniem Wallet: * deskryptory skryptów wyjściowych*.

Co to jest "deskryptor"?

"deskryptory skryptu wyjściowego", lub po prostu "deskryptory", są ustrukturyzowanymi wyrażeniami, które w pełni opisują skrypt wyjściowy (scriptPubKey) i dostarczają wszystkich niezbędnych informacji do śledzenia transakcji związanych z konkretnym skryptem. Ułatwiają one zarządzanie kluczami w portfelach HD, oferując znormalizowany i kompletny opis struktury Wallet i typów używanych adresów.

Główną zaletą deskryptorów jest ich zdolność do zawarcia wszystkich niezbędnych informacji do przywrócenia Wallet w jednym ciągu (oprócz frazy odzyskiwania). Zapisując deskryptor z powiązanymi frazami Mnemonic, możliwe staje się przywrócenie kluczy prywatnych, znając dokładnie ich pozycję w hierarchii. W przypadku portfeli Multisig, których kopia zapasowa była początkowo bardziej złożona, deskryptor zawiera xpub każdego czynnika, zapewniając w ten sposób możliwość regeneracji adresów w przypadku wystąpienia problemu.

Budowa deskryptora

Deskryptor składa się z kilku Elements:

Funkcje skryptowe takie jak pk (Pay-to-PubKey), pkh (Pay-to-PubKey-Hash), wpkh (Pay-to-Witness-PubKey-Hash), sh (Pay-to-Script-Hash), wsh (Pay-to-Witness-Script-Hash), tr (Pay-to-Taproot), multi (Multisignature) i sortedmulti (Multisignature with sorted keys);
Ścieżki pochodne, na przykład [d34db33f/44h/0h/0h], która wskazuje pochodną ścieżkę konta i określony odcisk palca klucza głównego;
Klucze w różnych formatach, takich jak szesnastkowe klucze publiczne lub rozszerzone klucze publiczne (xpub);
Suma kontrolna poprzedzona znakiem Hash w celu weryfikacji integralności deskryptora.

Na przykład deskryptor dla P2WPKH (SegWit v0) Wallet może wyglądać następująco:

wpkh([cdeab12f/84h/0h/0h]xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U/<0;1>/*)#jy0l7nr4

W tym deskryptorze funkcja pochodna wpkh wskazuje skrypt typu Pay-to-Witness-Public-Key-Hash. Po niej następuje ścieżka pochodna, która zawiera:

cdeab12f: odcisk palca klucza głównego;
84h: co oznacza użycie celu BIP84, przeznaczonego dla adresów SegWit v0;
0h: co wskazuje, że jest to waluta BTC na Mainnet;
0h: który odnosi się do konkretnego numeru konta używanego w Wallet.

Deskryptor zawiera również rozszerzony klucz publiczny używany w tym Wallet:

xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U

Następnie notacja /<0;1>/* określa, że deskryptor może zawierać adresy generate z zewnętrznego łańcucha (0) i wewnętrznego łańcucha (1), z symbolem wieloznacznym (*) pozwalającym na sekwencyjne wyprowadzanie wielu adresów w konfigurowalny sposób, podobny do zarządzania "limitem luk" w tradycyjnym oprogramowaniu Wallet.

Wreszcie, #jy0l7nr4 reprezentuje sumę kontrolną w celu weryfikacji integralności deskryptora.

Wiesz już wszystko o działaniu portfeli HD w Bitcoin i procesie tworzenia par kluczy. Jednak w ostatnich rozdziałach ograniczyliśmy się do generowania kluczy prywatnych i publicznych, nie zajmując się konstrukcją adresów odbiorczych. To właśnie będzie tematem następnego rozdziału!

Adresy odbiorcze

Adresy odbiorcze to informacje osadzone w scriptPubKey w celu zablokowania nowo utworzonych UTXO. Mówiąc prościej, Address służy do odbierania bitcoinów. Przeanalizujmy ich działanie w połączeniu z tym, co studiowaliśmy w poprzednich rozdziałach.

Rola adresów Bitcoin w skryptach

Jak wyjaśniono wcześniej, rolą transakcji jest przeniesienie Ownership bitcoinów z wejść do wyjść. Proces ten obejmuje zużywanie UTXO jako danych wejściowych przy jednoczesnym tworzeniu nowych UTXO jako danych wyjściowych. Te UTXO są zabezpieczone przez skrypty, które definiują warunki niezbędne do odblokowania środków.

Gdy użytkownik otrzymuje bitcoiny, nadawca tworzy UTXO i blokuje go za pomocą scriptPubKey. Skrypt ten zawiera reguły odblokowania UTXO, zazwyczaj określając wymagane podpisy i klucze publiczne. Aby wydać UTXO w nowej transakcji, użytkownik musi dostarczyć wymagane informacje za pośrednictwem scriptSig. Wykonanie scriptSig w połączeniu z scriptPubKey musi zwrócić "true" lub 1. Jeśli ten warunek zostanie spełniony, UTXO może zostać wydany w celu utworzenia nowego UTXO, zablokowanego przez nowy scriptPubKey, i tak dalej.

To właśnie w scriptPubKey znajdują się adresy odbiorcze. Ich wykorzystanie różni się jednak w zależności od przyjętego standardu skryptu. Poniżej znajduje się tabela podsumowująca informacje zawarte w scriptPubKey w zależności od używanego standardu, a także informacje oczekiwane w scriptSig w celu odblokowania scriptPubKey.

Standard	scriptPubKey	scriptSig	redeem script	witness
P2PK	`<pubkey> OP_CHECKSIG`	`<signature>`
P2PKH	`OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG`	`<signature> <public key>`
P2SH	`OP_HASH160 <scriptHash> OP_EQUAL`	`<data pushes> <redeem script>`	Arbitrary data
P2WPKH	`0 <pubKeyHash>`			`<signature> <public key>`
P2WSH	`0 <witnessScriptHash>`			`<data pushes> <witness script>`
P2SH-P2WPKH	`OP_HASH160 <redeemScriptHash> OP_EQUAL`	`<redeem script>`	`0 <pubKeyHash>`	`<signature> <public key>`
P2SH-P2WSH	`OP_HASH160 <redeemScriptHash> OP_EQUAL`	`<redeem script>`	`0 <scriptHash>`	`<data pushes> <witness script>`
P2TR (key path)	`1 <public key>`			`<signature>`
P2TR (script path)	`1 <public key>`			`<data pushes> <script> <control block>`

Źródło: Klub przeglądowy Bitcoin Core PR, 7 lipca 2021 r. - Gloria Zhao

Kody operacyjne używane w skrypcie są przeznaczone do manipulowania informacjami oraz, w razie potrzeby, do ich porównywania lub testowania. Weźmy przykład skryptu P2PKH, który wygląda następująco:

OP_DUP OP_HASH160 OP_PUSHBYTES_20 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG

Jak zobaczymy w tym rozdziale, <pubKeyHash> w rzeczywistości reprezentuje ładunek otrzymanego Address używanego do zablokowania UTXO. Aby odblokować ten scriptPubKey, konieczne jest dostarczenie scriptSig zawierającego:

<signature> <public key>

W języku skryptowym stos jest strukturą danych LIFO ("Last In, First Out") używaną do tymczasowego przechowywania Elements podczas wykonywania skryptu. Każda operacja skryptu manipuluje tym stosem, gdzie Elements może być dodawany (push) lub usuwany (pop). Skrypty używają stosu do oceny wyrażeń, przechowywania zmiennych tymczasowych i zarządzania warunkami.

Wykonanie skryptu, który właśnie podałem jako przykład, przebiega zgodnie z tym procesem:

Mamy scriptSig, scriptPubKey i stos:

Wartość scriptSig jest umieszczana na stosie:

OP_DUP duplikuje klucz publiczny podany w scriptSig na stosie:

OP_HASH160 zwraca Hash klucza publicznego, który został właśnie zduplikowany:

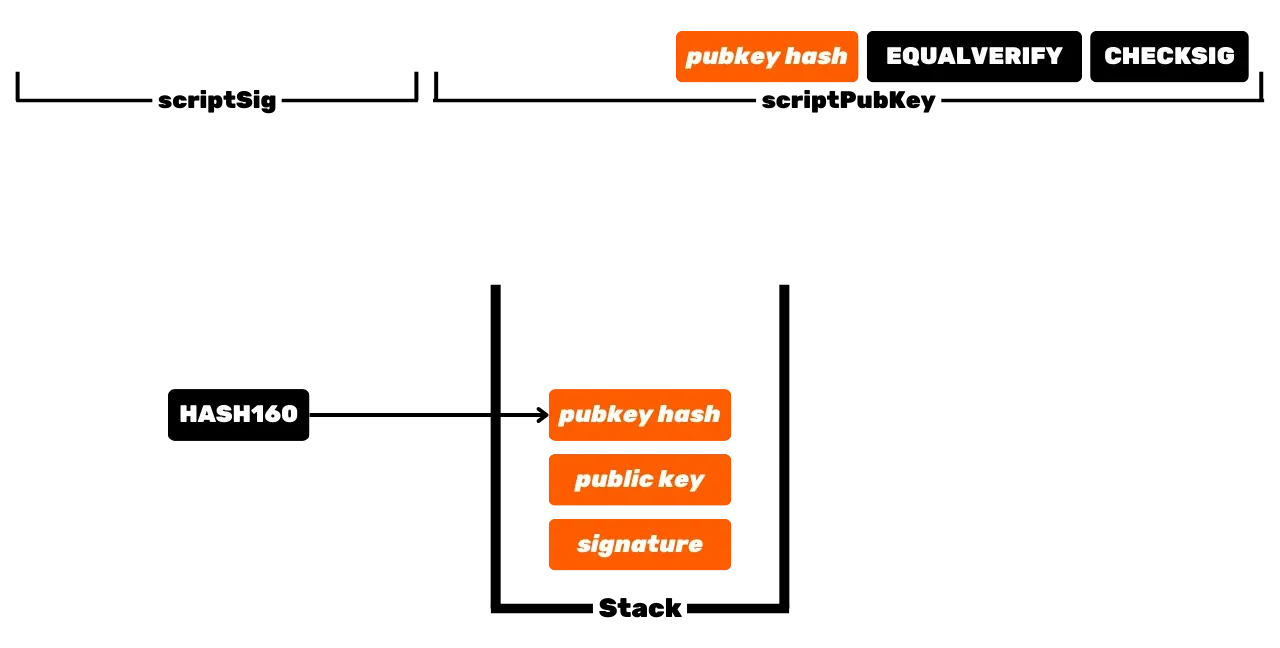
OP_PUSHBYTES_20 <pubKeyHash> przesuwa Bitcoin Address zawarty w scriptPubKey na stos:

OP_EQUALVERIFY weryfikuje, czy zaszyfrowany klucz publiczny pasuje do dostarczonego odbiorczego Address:

OP_CHECKSIG sprawdza podpis zawarty w scriptSig przy użyciu klucza publicznego. Ten kod operacyjny zasadniczo wykonuje weryfikację podpisu, jak opisaliśmy w części 3 tego szkolenia:

Jeśli 1 pozostaje na stosie, skrypt jest poprawny:

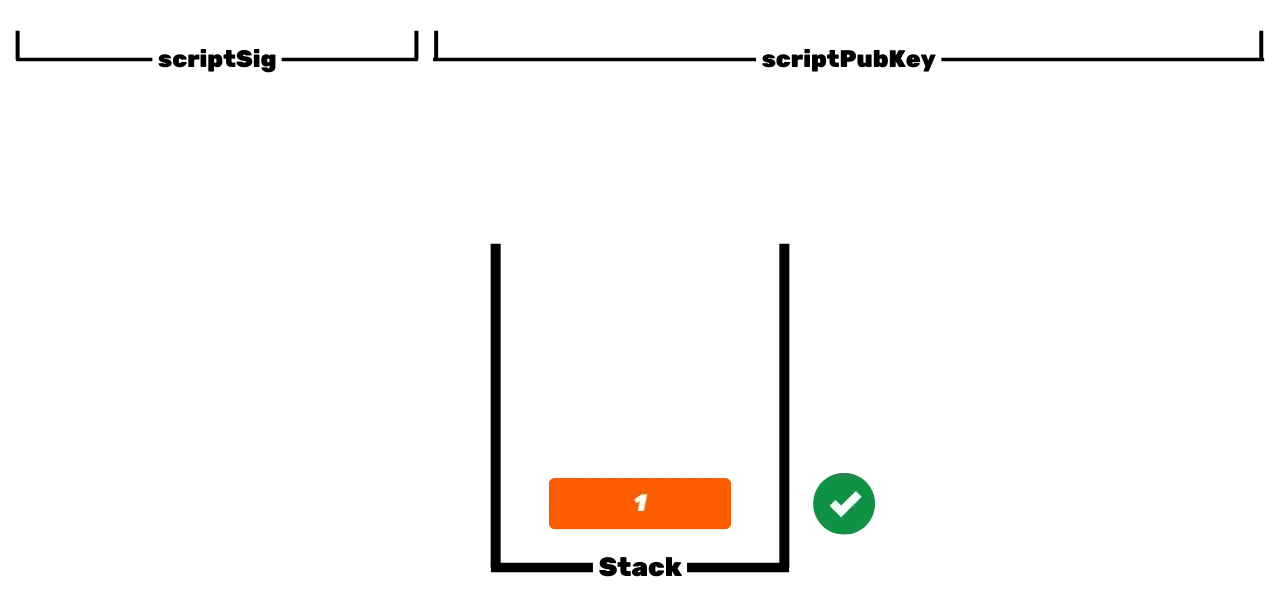
Podsumowując, skrypt ten pozwala zweryfikować, za pomocą podpisu cyfrowego, że użytkownik zgłaszający Ownership tego UTXO i chcący go wydać rzeczywiście posiada klucz prywatny powiązany z otrzymanym Address użytym podczas tworzenia tego UTXO.

Różne typy adresów Bitcoin

W trakcie ewolucji Bitcoin dodano kilka standardowych modeli skryptów. Każdy z nich wykorzystuje inny typ odbioru Address. Poniżej znajduje się przegląd głównych modeli skryptów dostępnych do tej pory:

P2PK (Pay-to-PubKey):

Ten model skryptu został wprowadzony w pierwszej wersji Bitcoin przez Satoshi Nakamoto. Skrypt P2PK blokuje bitcoiny bezpośrednio przy użyciu nieprzetworzonego klucza publicznego (dlatego w tym modelu nie stosuje się odbierania Address). Jego struktura jest prosta: zawiera klucz publiczny i wymaga odpowiedniego podpisu cyfrowego w celu odblokowania środków. Skrypt ten jest częścią standardu "Legacy".

P2PKH (Pay-to-PubKey-Hash):

Podobnie jak P2PK, skrypt P2PKH został wprowadzony podczas premiery Bitcoin. W przeciwieństwie do swojego poprzednika, blokuje on bitcoiny przy użyciu Hash klucza publicznego, a nie bezpośrednio przy użyciu surowego klucza publicznego. scriptSig musi następnie dostarczyć klucz publiczny powiązany z odbierającym Address, a także ważny podpis. Adresy odpowiadające temu modelowi zaczynają się od 1 i są zakodowane w base58check. Skrypt ten należy również do standardu "Legacy".

P2SH (Pay-to-Script-Hash):

Wprowadzony w 2012 roku wraz z BIP16, model P2SH pozwala na użycie Hash dowolnego skryptu w scriptPubKey. Ten zaszyfrowany skrypt, zwany "redeemscript", zawiera warunki odblokowania środków. Aby wydać UTXO zablokowany za pomocą P2SH, konieczne jest dostarczenie scriptSig zawierającego oryginalny redeemscript, a także dane niezbędne do jego walidacji. Ten model jest szczególnie używany w przypadku starych multisigów. Adresy związane z P2SH zaczynają się od 3 i są zakodowane w base58check. Ten skrypt również należy do standardu "Legacy".

P2WPKH (Pay-to-Witness-PubKey-Hash):

Ten skrypt jest podobny do P2PKH, ponieważ również blokuje bitcoiny za pomocą Hash klucza publicznego. Jednak w przeciwieństwie do P2PKH, scriptSig jest przenoszony do oddzielnej sekcji o nazwie "Witness". Jest to czasami określane jako "scriptWitness", aby oznaczyć zestaw zawierający podpis i klucz publiczny. Każde wejście SegWit ma swój własny scriptWitness, a zbiór scriptWitnesses stanowi pole Witness transakcji. Ten ruch danych podpisu jest innowacją wprowadzoną przez aktualizację SegWit, mającą na celu w szczególności zapobieganie zniekształceniom transakcji z powodu podpisów ECDSA.

Adresy P2WPKH używają kodowania bech32 i zawsze zaczynają się od bc1q. Ten typ skryptu odpowiada wyjściom SegWit w wersji 0.

P2WSH (Pay-to-Witness-Script-Hash):

Model P2WSH został również wprowadzony wraz z aktualizacją SegWit w sierpniu 2017 roku. Podobnie jak model P2SH, blokuje on bitcoiny przy użyciu Hash skryptu. Główna różnica polega na sposobie, w jaki podpisy i skrypty są włączane do transakcji. Aby wydać bitcoiny zablokowane za pomocą tego typu skryptu, odbiorca musi dostarczyć oryginalny skrypt, zwany witnessScript (odpowiednik redeemscript w P2SH), wraz z danymi niezbędnymi do walidacji tego witnessScript. Mechanizm ten pozwala na implementację bardziej złożonych warunków wydawania, takich jak multisigs.

Adresy P2WSH używają kodowania bech32 i zawsze zaczynają się od bc1q. Ten skrypt odpowiada również wyjściom SegWit w wersji 0.

P2TR (Pay-to-Taproot):

Model P2TR został wprowadzony wraz z wdrożeniem Taproot w listopadzie 2021 roku. Opiera się on na protokole Schnorra do agregacji kluczy kryptograficznych, a także na Merkle Tree dla alternatywnych skryptów, zwanych MAST (Merkelized Alternative Script Tree). W przeciwieństwie do innych rodzajów skryptów, w których warunki wydatków są publicznie ujawniane (przy odbiorze lub przy wydatkowaniu), P2TR pozwala na ukrycie złożonych skryptów za pojedynczym, pozornym kluczem publicznym.

Technicznie rzecz biorąc, skrypt P2TR blokuje bitcoiny na unikalnym kluczu publicznym Schnorra, oznaczonym jako $Q$ . Klucz $Q$ jest w rzeczywistości agregatem klucza publicznego $P$ i klucza publicznego $M$ , przy czym ten ostatni jest obliczany na podstawie Merkle Root listy scriptPubKey. Bitcoiny zablokowane za pomocą tego typu skryptu można wydać na dwa sposoby:

Publikując podpis dla klucza publicznego $P$ (ścieżka klucza).
Spełniając jeden ze skryptów zawartych w Merkle Tree (ścieżka skryptu).

P2TR oferuje zatem dużą elastyczność, ponieważ umożliwia blokowanie bitcoinów za pomocą unikalnego klucza publicznego, kilku wybranych skryptów lub obu jednocześnie. Zaletą tej struktury Merkle Tree jest to, że podczas transakcji ujawniany jest tylko używany skrypt wydatków, ale wszystkie inne alternatywne skrypty pozostają tajne.

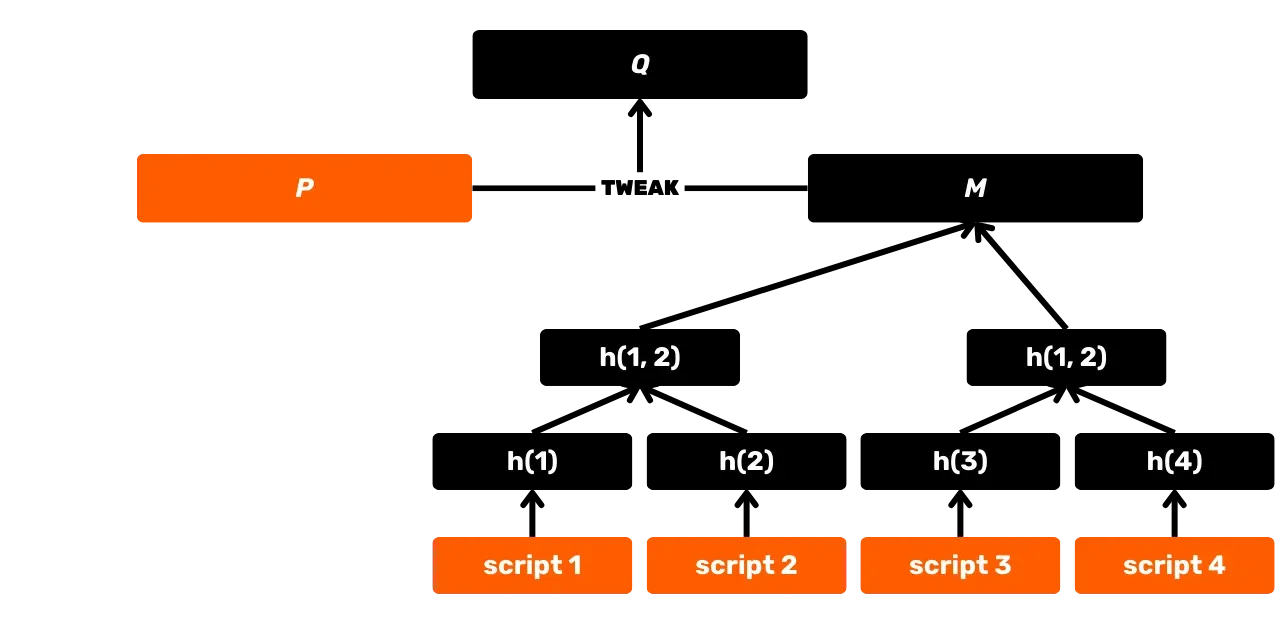
P2TR odpowiada wyjściom SegWit w wersji 1, co oznacza, że podpisy dla wejść P2TR są przechowywane w sekcji Witness transakcji, a nie w scriptSig. Adresy P2TR używają kodowania bech32m i zaczynają się od bc1p, ale są dość unikalne, ponieważ nie używają funkcji Hash do ich budowy. W rzeczywistości reprezentują one bezpośrednio klucz publiczny $Q$ , który jest po prostu sformatowany za pomocą metadanych. Jest to zatem model skryptu zbliżony do P2PK.

Skoro omówiliśmy już teorię, przejdźmy do praktyki! W następnym rozdziale proponuję wyprowadzenie zarówno SegWit v0 Address, jak i SegWit v1 Address z pary kluczy.

Pochodna Address

Przeanalizujmy razem, w jaki sposób generate może odebrać Address z pary kluczy znajdujących się na przykład na głębokości 5 w HD Wallet. Ten Address może być następnie użyty w oprogramowaniu Wallet do zablokowania UTXO.

Ponieważ proces generowania Address zależy od przyjętego modelu skryptu, skupmy się na dwóch konkretnych przypadkach: generowaniu SegWit v0 Address w P2WPKH i SegWit v1 Address w P2TR. Te dwa typy adresów obejmują zdecydowaną większość dzisiejszych zastosowań.

Kompresja klucza publicznego

Po wykonaniu wszystkich kroków derywacji od klucza głównego do głębokości 5 przy użyciu odpowiednich indeksów, otrzymujemy parę kluczy ( $k$ , $K$ ) z $K = k \cdot G$ . Chociaż możliwe jest użycie tego klucza publicznego do blokowania środków w standardzie P2PK, nie jest to naszym celem. Zamiast tego chcemy utworzyć Address w P2WPKH w pierwszej kolejności, a następnie w P2TR dla innego przykładu.

Pierwszym krokiem jest skompresowanie klucza publicznego $K$ . Aby dobrze zrozumieć ten proces, przypomnijmy sobie najpierw kilka podstaw omówionych w części 3.

Klucz publiczny w Bitcoin to punkt $K$ znajdujący się na krzywej eliptycznej. Jest on reprezentowany w postaci $(x, y)$ , gdzie $x$ i $y$ są współrzędnymi punktu. W nieskompresowanej formie ten klucz publiczny mierzy 520 bitów: 8 bitów na prefiks (wartość początkowa 0x04), 256 bitów na współrzędną $x$ i 256 bitów na współrzędną $y$ .

Krzywe eliptyczne mają jednak właściwość symetrii względem osi x: dla danej współrzędnej $x$ istnieją tylko dwie możliwe wartości dla $y$ : $y$ i $-y$ . Te dwa punkty znajdują się po obu stronach osi x. Innymi słowy, jeśli znamy $x$ , wystarczy określić, czy $y$ jest parzyste czy nieparzyste, aby zidentyfikować dokładny punkt na krzywej.

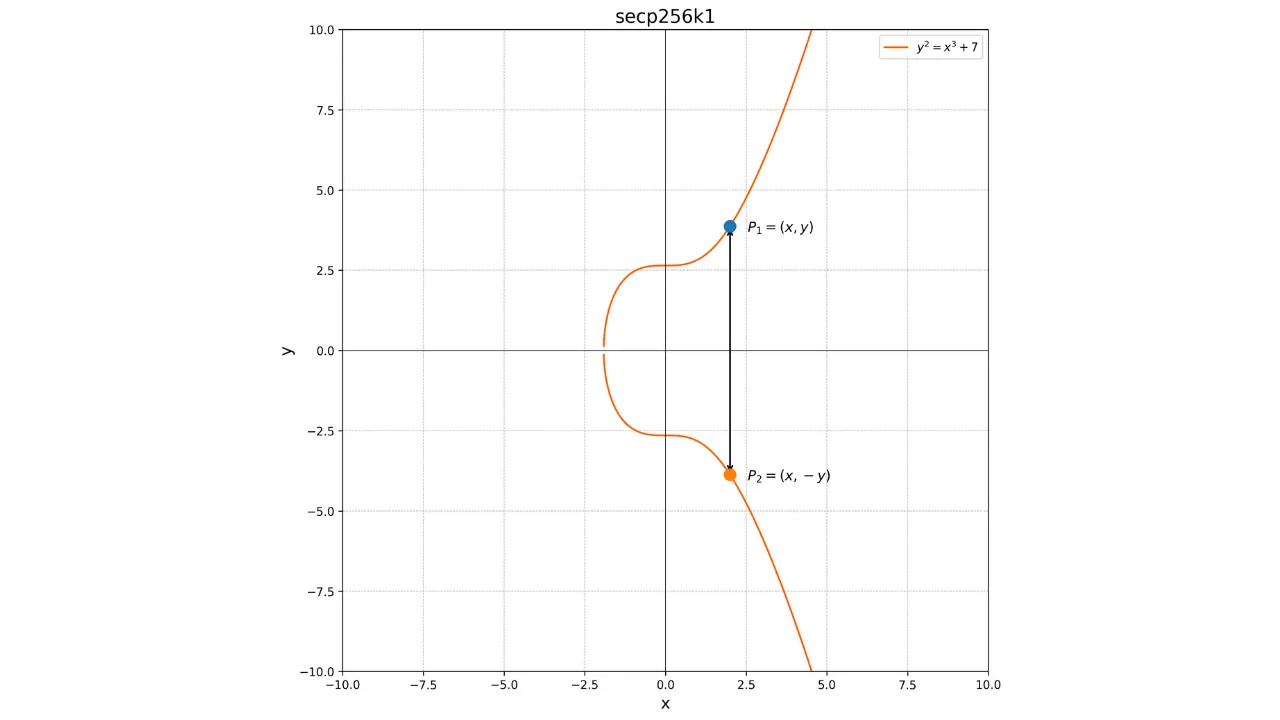
Aby skompresować klucz publiczny, kodowane jest tylko $x$ , które zajmuje 256 bitów, a prefiks jest dodawany w celu określenia parzystości $y$ . Ta metoda zmniejsza rozmiar klucza publicznego do 264 bitów zamiast początkowych 520. Prefiks 0x02 wskazuje, że $y$ jest parzyste, a prefiks 0x03 wskazuje, że $y$ jest nieparzyste.

Weźmy przykład, aby dobrze zrozumieć, z surowym kluczem publicznym w nieskompresowanej reprezentacji:

K = 04678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f

Jeśli zdekomponujemy ten klucz, otrzymamy:

Prefiks: 04;
$x$ : 678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6;
$y$ : 49f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f

Ostatnim szesnastkowym znakiem $y$ jest f. W podstawie 10, f = 15, co odpowiada liczbie nieparzystej. Dlatego $y$ jest nieparzyste, a prefiksem będzie 0x03, aby to wskazać.

Skompresowany klucz publiczny staje się:

K = 03678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6

Ta operacja ma zastosowanie do wszystkich modeli skryptów opartych na ECDSA, czyli wszystkich z wyjątkiem P2TR, który używa Schnorra. W przypadku Schnorra, jak wyjaśniono w części 3, zachowujemy tylko wartość $x$ , bez dodawania prefiksu wskazującego parzystość $y$ , w przeciwieństwie do ECDSA. Jest to możliwe dzięki temu, że unikalna parzystość jest arbitralnie wybierana dla wszystkich kluczy. Pozwala to na nieznaczne zmniejszenie przestrzeni dyskowej wymaganej dla kluczy publicznych.

Pochodna SegWit v0 (bech32) Address

Teraz, gdy uzyskaliśmy nasz skompresowany klucz publiczny, możemy wyprowadzić z niego SegWit v0 otrzymujący Address.

Pierwszym krokiem jest zastosowanie funkcji HASH160 Hash do skompresowanego klucza publicznego. HASH160 jest kompozycją dwóch kolejnych funkcji Hash: SHA256, a następnie RIPEMD160:

 $\text{HASH160}(K) = \text{RIPEMD160}(\text{SHA256}(K))$

Najpierw przepuszczamy klucz przez SHA256:

SHA256(K) = C489EBD66E4103B3C4B5EAFF462B92F5847CA2DCE0825F4997C7CF57DF35BF3A

Następnie przekazujemy wynik przez RIPEMD160:

RIPEMD160(SHA256(K)) = 9F81322CC88622CA4CCB2A52A21E2888727AA535

Uzyskaliśmy 160-bitowy Hash klucza publicznego, który stanowi tak zwany ładunek Address. Ten ładunek stanowi centralną i najważniejszą część Address. Jest on również używany w scriptPubKey do blokowania UTXO.

Aby jednak ten ładunek był łatwiejszy do wykorzystania przez ludzi, dodawane są do niego metadane. Następnym krokiem jest zakodowanie Hash w grupy po 5 bitów w systemie dziesiętnym. Ta transformacja dziesiętna będzie przydatna do konwersji na bech32, używany przez adresy post-SegWit. 160-bitowy binarny Hash jest zatem podzielony na 32 grupy po 5 bitów:

 $\begin{array}{|c|c|} \hline \text{5 bits} & \text{Decimal} \\ \hline 10011 & 19 \\ 11110 & 30 \\ 00000 & 0 \\ 10011 & 19 \\ 00100 & 4 \\ 01011 & 11 \\ 00110 & 6 \\ 01000 & 8 \\ 10000 & 16 \\ 11000 & 24 \\ 10001 & 17 \\ 01100 & 12 \\ 10100 & 20 \\ 10011 & 19 \\ 00110 & 6 \\ 01011 & 11 \\ 00101 & 5 \\ 01001 & 9 \\ 01001 & 9 \\ 01010 & 10 \\ 00100 & 4 \\ 00111 & 7 \\ 10001 & 17 \\ 01000 & 8 \\ 10001 & 17 \\ 00001 & 1 \\ 11001 & 25 \\ 00111 & 7 \\ 10101 & 21 \\ 00101 & 5 \\ 00101 & 5 \\ 10101 & 21 \\ \hline \end{array}$

Mamy więc:

HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21

Po zakodowaniu Hash w grupy po 5 bitów, do Address dodawana jest suma kontrolna. Ta suma kontrolna służy do weryfikacji, czy ładunek Address nie został zmieniony podczas jego przechowywania lub transmisji. Na przykład, pozwala to oprogramowaniu Wallet upewnić się, że nie popełniono literówki podczas wprowadzania odbieranego Address. Bez tej weryfikacji użytkownik mógłby przypadkowo wysłać bitcoiny do nieprawidłowego Address, co skutkowałoby trwałą utratą środków, ponieważ nie jest właścicielem powiązanego klucza publicznego lub prywatnego. Dlatego suma kontrolna stanowi ochronę przed błędami ludzkimi.

Dla starych adresów Bitcoin Legacy, suma kontrolna była po prostu obliczana od początku Address Hash z funkcją HASH256. Wraz z wprowadzeniem SegWit i formatu bech32, używane są teraz kody BCH (Bose, Ray-Chaudhuri i Hocquenghem). Kody te służą do wykrywania i korygowania błędów w sekwencjach danych. Zapewniają one, że przesyłane informacje dotrą do miejsca przeznaczenia w nienaruszonym stanie, nawet w przypadku drobnych zmian. Kody BCH są wykorzystywane w wielu dziedzinach, takich jak dyski SSD, DVD i kody QR. Na przykład, dzięki tym kodom BCH, częściowo zasłonięty kod QR może być nadal odczytywany i dekodowany.

W kontekście Bitcoin, kody BCH oferują lepszy kompromis między rozmiarem a możliwościami wykrywania błędów w porównaniu do prostych funkcji Hash używanych dla adresów Legacy. Jednak w Bitcoin kody BCH są używane tylko do wykrywania błędów, a nie do korekcji. Dlatego oprogramowanie Wallet zasygnalizuje nieprawidłowy odbiór Address, ale nie skoryguje go automatycznie. Ograniczenie to jest celowe: zezwolenie na automatyczną korektę zmniejszyłoby możliwości wykrywania błędów.

Aby obliczyć sumę kontrolną za pomocą kodów BCH, musimy przygotować kilka Elements.

HRP (Część czytelna dla człowieka)**: Dla Bitcoin Mainnet, HRP to bc;

HRP należy rozszerzyć, rozdzielając każdy znak na dwie części:

Pobieranie znaków HRP w ASCII:
b: 01100010
c: 01100011
Wyodrębnienie 3 najbardziej znaczących bitów i 5 najmniej znaczących bitów:
- 3 najbardziej znaczące bity: 011 (3 w zapisie dziesiętnym)
- 3 najbardziej znaczące bity: 011 (3 w zapisie dziesiętnym)
- 5 najmniej znaczących bitów: 00010 (2 w zapisie dziesiętnym)
- 5 najmniej znaczących bitów: 00011 (3 w zapisie dziesiętnym)

Z separatorem 0 pomiędzy dwoma znakami, rozszerzenie HRP ma zatem postać:

03 03 00 02 03

Wersja świadka**: Dla SegWit w wersji 0 jest to 00;
Ładunek**: Wartości dziesiętne klucza publicznego Hash;
Zastrzeżenie dla sumy kontrolnej**: Dodajemy 6 zer [0, 0, 0, 0, 0] na końcu sekwencji.

Wszystkie dane, które należy wprowadzić do programu w celu obliczenia sumy kontrolnej, są następujące:

HRP = 03 03 00 02 03
SEGWIT v0 = 00
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
CHECKSUM = 00 00 00 00 00 00

INPUT = 03 03 00 02 03 00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 00 00 00 00 00 00

Obliczanie sumy kontrolnej jest dość skomplikowane. Obejmuje wielomianową arytmetykę pól skończonych. Nie będziemy tutaj szczegółowo opisywać tych obliczeń i przejdziemy bezpośrednio do wyniku. W naszym przykładzie suma kontrolna otrzymana w zapisie dziesiętnym to:

10 16 11 04 13 18

Możemy teraz skonstruować odbierający Address, łącząc w kolejności następujące Elements:

Wersja SegWit**: 00
Ładunek**: Klucz publiczny Hash
Suma kontrolna**: Wartości uzyskane w poprzednim kroku (10 16 11 04 13 18)

Daje nam to wartość dziesiętną:

00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 10 16 11 04 13 18

Następnie każda wartość dziesiętna musi zostać odwzorowana na znak bech32 przy użyciu poniższej tabeli konwersji:

 $\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline +0 & q & p & z & r & y & 9 & x & 8 \\ \hline +8 & g & f & 2 & t & v & d & w & 0 \\ \hline +16 & s & 3 & j & n & 5 & 4 & k & h \\ \hline +24 & c & e & 6 & m & u & a & 7 & l \\ \hline \end{array}$

Aby przekonwertować wartość na znak bech32 przy użyciu tej tabeli, wystarczy zlokalizować wartości w pierwszej kolumnie i pierwszym wierszu, które po zsumowaniu dają pożądany wynik. Następnie należy pobrać odpowiedni znak. Na przykład, liczba dziesiętna 19 zostanie przekonwertowana na literę n, ponieważ $19 = 16 + 3$ .

Mapując wszystkie nasze wartości, otrzymujemy następujący Address:

qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj

Pozostaje tylko dodać HRP bc, który wskazuje, że jest to Address dla Bitcoin Mainnet, a także separator 1, aby uzyskać kompletny odbiorczy Address:

bc1qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj

Szczególną cechą tego alfabetu bech32 jest to, że zawiera on wszystkie znaki alfanumeryczne z wyjątkiem 1, b, i i o, aby uniknąć wizualnej pomyłki między podobnymi znakami, zwłaszcza podczas ich wprowadzania lub odczytywania przez ludzi.

Podsumowując, oto proces derywacji:

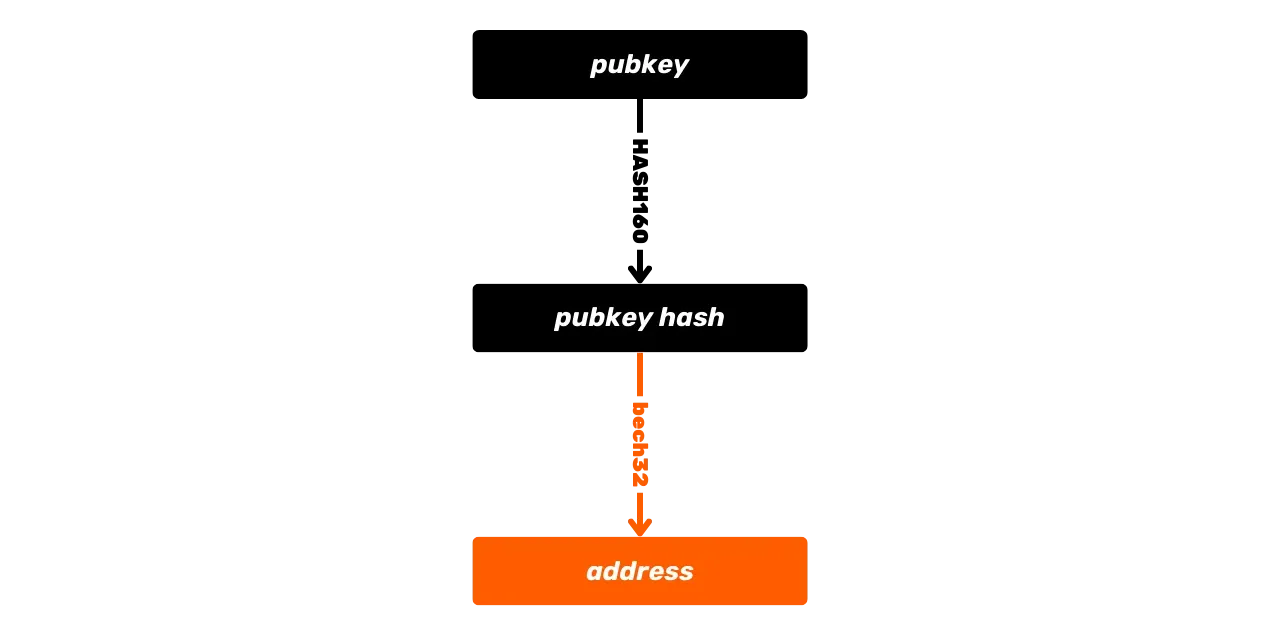
Oto jak wyprowadzić P2WPKH (SegWit v0) otrzymujący Address z pary kluczy. Przejdźmy teraz do adresów P2TR (SegWit v1 / Taproot) i odkryjmy proces ich generowania.

Pochodna SegWit v1 (bech32m) Address

W przypadku adresów Taproot proces generowania różni się nieznacznie. Przyjrzyjmy się temu razem!

Od etapu kompresji klucza publicznego pojawia się pierwsza różnica w porównaniu do ECDSA: klucze publiczne używane dla Schnorra w Bitcoin są reprezentowane tylko przez ich odciętą ( $x$ ). Dlatego nie ma prefiksu, a skompresowany klucz mierzy dokładnie 256 bitów.

Jak widzieliśmy w poprzednim rozdziale, skrypt P2TR blokuje bitcoiny na unikalnym kluczu publicznym Schnorra, oznaczonym jako $Q$ . Klucz $Q$ jest agregatem dwóch kluczy publicznych: $P$ , głównego wewnętrznego klucza publicznego, oraz $M$ , klucza publicznego pochodzącego z Merkle Root listy scriptPubKey. Bitcoiny zablokowane za pomocą tego typu skryptu można wydać na dwa sposoby:

Publikując podpis dla klucza publicznego $P$ (ścieżka klucza);
Wykonując jeden ze skryptów zawartych w Merkle Tree (ścieżka skryptu).

W rzeczywistości te dwa klucze nie są tak naprawdę "zagregowane" Klucz $P$ jest zamiast tego modyfikowany przez klucz $M$ . W kryptografii "tweakowanie" klucza publicznego oznacza modyfikowanie tego klucza poprzez zastosowanie wartości addytywnej zwanej "tweakiem" Ta operacja pozwala zmodyfikowanemu kluczowi pozostać kompatybilnym z oryginalnym kluczem prywatnym i tweakiem. Technicznie rzecz biorąc, tweak jest skalarną wartością $t$ , która jest dodawana do początkowego klucza publicznego. Jeśli $P$ jest oryginalnym kluczem publicznym, zmodyfikowany klucz staje się:

 $P' = P + t \cdot G$

Gdzie $G$ jest generatorem użytej krzywej eliptycznej. Ta operacja tworzy nowy klucz publiczny pochodzący z oryginalnego klucza, zachowując właściwości kryptograficzne umożliwiające jego użycie.

Jeśli nie ma potrzeby dodawania alternatywnych skryptów (wydawanie wyłącznie poprzez ścieżkę key), można generate Taproot Address ustanowić wyłącznie na kluczu publicznym obecnym na głębokości 5 Wallet. W tym przypadku konieczne jest utworzenie skryptu bez możliwości wydawania dla ścieżki script, aby spełnić wymagania struktury. Tweak $t$ jest następnie obliczany przez zastosowanie oznaczonej funkcji Hash, TapTweak, na wewnętrznym kluczu publicznym $P$ :

 $t = \text{H}_{\text{TapTweak}}(P)$

gdzie:

$\text{H}_{\text{TapTweak}}$ ** jest funkcją SHA256 Hash oznaczoną tagiem TapTweak. Jeśli nie wiesz, czym jest oznaczona funkcja Hash, zapraszam do zapoznania się z rozdziałem 3.3;
$P$ to wewnętrzny klucz publiczny, reprezentowany w skompresowanym 256-bitowym formacie, przy użyciu tylko współrzędnej $x$ .

Klucz publiczny Taproot $Q$ jest następnie obliczany poprzez dodanie tweaku $t$ , pomnożonego przez generator krzywej eliptycznej $G$ , do wewnętrznego klucza publicznego $P$ :

 $Q = P + t \cdot G$

Po uzyskaniu Taproot klucza publicznego $Q$ , możemy generate odpowiadający odbierający Address. W przeciwieństwie do innych formatów, adresy Taproot nie są ustalane na podstawie Hash klucza publicznego. Dlatego klucz $Q$ jest wstawiany bezpośrednio do Address, w sposób nieprzetworzony.

Na początek wyodrębniamy współrzędną $x$ punktu $Q$ , aby uzyskać skompresowany klucz publiczny. Na tym ładunku obliczana jest suma kontrolna przy użyciu kodów BCH, podobnie jak w przypadku adresów SegWit v0. Jednak program używany dla adresów Taproot różni się nieznacznie. Rzeczywiście, po wprowadzeniu formatu bech32 z SegWit, odkryto błąd: gdy ostatnim znakiem Address jest p, wstawienie lub usunięcie q tuż przed tym p nie powoduje, że suma kontrolna jest nieważna. Chociaż błąd ten nie ma konsekwencji dla SegWit v0 (dzięki ograniczeniu rozmiaru), może on stanowić problem w przyszłości. W związku z tym błąd ten został poprawiony dla adresów Taproot, a nowy poprawiony format nosi nazwę "bech32m".

Taproot Address jest generowany przez kodowanie współrzędnej $x$ $Q$ w formacie bech32m, z następującym Elements:

HRP (Human Readable Part)**: bc, aby wskazać główną sieć Bitcoin;
Wersja**: 1, aby wskazać Taproot / SegWit v1;
Suma kontrolna**.

Ostateczny Address będzie miał zatem format:

bc1p[Qx][checksum]

Z drugiej strony, jeśli chcesz dodać alternatywne skrypty oprócz wydatków z wewnętrznym kluczem publicznym (script path), obliczenie otrzymanego Address będzie nieco inne. Konieczne będzie uwzględnienie Hash alternatywnych skryptów w obliczeniach ulepszenia. W Taproot każdy alternatywny skrypt, znajdujący się na końcu Merkle Tree, nazywany jest "liściem".

Po napisaniu różnych alternatywnych skryptów, należy przekazać je indywidualnie przez oznaczoną funkcję Hash TapLeaf, wraz z pewnymi metadanymi:

 $\text{h}_{\text{leaf}} = \text{H}_{\text{TapLeaf}} (v \Vert sz \Vert S)$

$v$ : numer wersji skryptu (domyślnie 0xC0 dla Taproot);
$sz$ : rozmiar skryptu zakodowany w formacie CompactSize;
$S$ : skrypt.

Różne skróty skryptów ( $\text{h}_{\text{leaf}}$ ) są najpierw sortowane w porządku leksykograficznym. Następnie są one łączone w pary i przekazywane przez oznaczoną funkcję Hash TapBranch. Proces ten jest powtarzany iteracyjnie, aby krok po kroku zbudować Merkle Tree:

 $\text{h}_{\text{branch}} = \text{H}_{\text{TapBranch}}(\text{h}_{\text{leaf1}} \Vert \text{h}_{\text{leaf2}})$

Następnie kontynuujemy, łącząc wyniki dwa po dwa, przekazując je na każdym kroku przez oznaczoną funkcję Hash TapBranch, aż do uzyskania korzenia Merkle Tree:

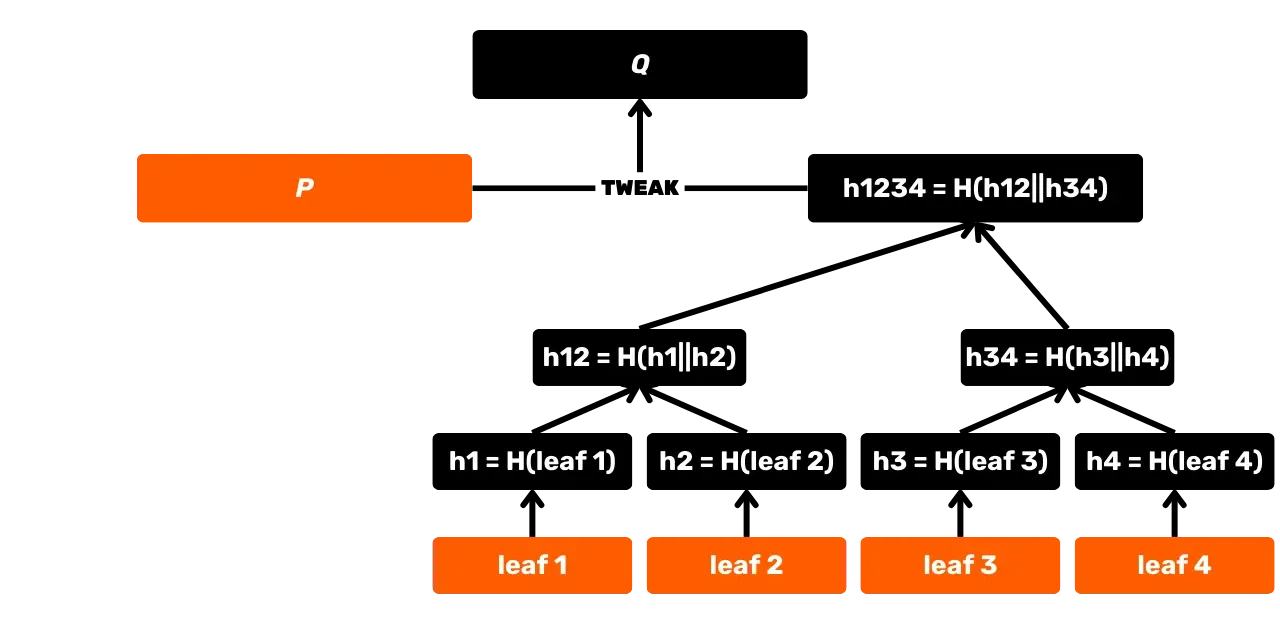
Po obliczeniu Merkle Root $h_{\text{root}}$ , możemy obliczyć tweak. W tym celu łączymy wewnętrzny klucz publiczny Wallet $P$ z rootem $h_{\text{root}}$ , a następnie przekazujemy całość przez oznaczoną funkcję Hash TapTweak:

 $t = \text{H}_{\text{TapTweak}}(P \Vert h_{\text{root}})$

Wreszcie, tak jak poprzednio, klucz publiczny $Q$ Taproot jest uzyskiwany przez dodanie wewnętrznego klucza publicznego $P$ do iloczynu tweaku $t$ przez punkt generatora $G$ :

 $Q = P + t \cdot G$

Następnie generowanie Address odbywa się w ten sam sposób, przy użyciu nieprzetworzonego klucza publicznego $Q$ jako ładunku, któremu towarzyszą dodatkowe metadane.

I gotowe! Dotarliśmy do końca tego kursu CYP201. Jeśli uznałeś ten kurs za pomocny, byłbym bardzo wdzięczny, gdybyś poświęcił kilka chwil na wystawienie mu dobrej oceny w poniższym rozdziale oceny. Zapraszam również do podzielenia się nim z bliskimi lub w sieciach społecznościowych. Wreszcie, jeśli chcesz uzyskać dyplom za ten kurs, możesz przystąpić do egzaminu końcowego zaraz po rozdziale oceny.

Sekcja końcowa

Recenzje i oceny

true

Egzamin końcowy

true

Wnioski

true