name: Introduzione alla crittografia formale goal: Un'introduzione approfondita alla scienza e alla pratica della crittografia. objectives:
- Esplorare i cifrari di Beale e i moderni metodi crittografici per comprendere i concetti fondamentali e storici della crittografia.
- Approfondite la teoria dei numeri, i gruppi e i campi per padroneggiare i concetti matematici chiave alla base della crittografia.
- Studiare il cifrario a flusso RC4 e AES con chiave a 128 bit per conoscere gli algoritmi crittografici simmetrici.
- Analizzare il crittosistema RSA, la distribuzione delle chiavi e le funzioni hash per esplorare la crittografia asimmetrica.
Un'immersione nella crittografia
È difficile trovare molti materiali che offrano una buona via di mezzo nell'educazione alla crittografia.
Da un lato, ci sono lunghi trattati formali, accessibili solo a chi ha un solido background in matematica, logica o altre discipline formali. Dall'altro lato, ci sono introduzioni di altissimo livello che nascondono troppi dettagli per chiunque sia almeno un po' curioso.
Questa introduzione alla crittografia cerca di cogliere la via di mezzo. Pur essendo relativamente impegnativa e dettagliata per chiunque sia alle prime armi con la crittografia, non è la tana del coniglio di un tipico trattato di fondamenti.
Introduzione
Panoramica del corso
bb8a8b73-7fb2-50da-bf4e-98996d79887b Benvenuto al corso CYP302!
Questo libro offre un'introduzione approfondita alla scienza e alla pratica della crittografia. Dove possibile, si concentra sull'esposizione concettuale piuttosto che formale del materiale.
Questo contenuto educativo è adattato dal libro e repo JWBurgers. Sebbene l'autore ne abbia gentilmente concesso l'uso educativo, tutti i diritti di proprietà intellettuale rimangono del creatore originale.
Motivazione e obiettivi
È difficile trovare molti materiali che offrano una buona via di mezzo nell'educazione alla crittografia.
Da un lato, ci sono lunghi trattati formali, accessibili solo a chi ha un solido background in matematica, logica o altre discipline formali. Dall'altro lato, ci sono introduzioni di altissimo livello che nascondono troppi dettagli per chiunque sia almeno un po' curioso.
Questa introduzione alla crittografia cerca di cogliere la via di mezzo. Pur essendo relativamente impegnativa e dettagliata per chiunque sia alle prime armi con la crittografia, non è la tana del coniglio di un tipico trattato di fondamenti.
Pubblico di riferimento
Dagli sviluppatori ai curiosi, questo libro è utile per tutti coloro che desiderano una comprensione più che superficiale della crittografia. Se il vostro obiettivo è quello di padroneggiare il campo della crittografia, questo libro è anche un buon punto di partenza.
Linee guida per la lettura
Il libro contiene attualmente sette capitoli: "Che cos'è la crittografia?" (Capitolo 1), "Fondamenti matematici della crittografia I" (Capitolo 2), "Fondamenti matematici della crittografia II" (Capitolo 3), "Crittografia simmetrica" (Capitolo 4), "RC4 e AES" (Capitolo 5), "Crittografia asimmetrica" (Capitolo 6) e "Il crittosistema RSA" (Capitolo 7). Verrà inoltre aggiunto un capitolo finale, "La crittografia nella pratica". Si concentra su varie applicazioni crittografiche, tra cui la sicurezza del livello di trasporto, il routing a cipolla e il sistema di scambio di valore di Bitcoin.
A meno che non abbiate una solida preparazione matematica, la teoria dei numeri è probabilmente l'argomento più difficile di questo libro. Ne offro una panoramica nel Capitolo 3, e compare anche nell'esposizione di AES nel Capitolo 5 e del crittosistema RSA nel Capitolo 7.
Se vi trovate in difficoltà con i dettagli formali di queste parti del libro, vi consiglio di accontentarvi di una lettura di alto livello la prima volta.
Ringraziamenti
Il libro più influente per la formazione di questo è stato Introduction to Modern Cryptography di Jonathan Katz e Yehuda Lindell, CRC Press (Boca Raton, FL), 2015. Su Coursera è disponibile un corso di accompagnamento intitolato "Cryptography"
Le principali fonti aggiuntive che sono state utili per creare la panoramica di questo libro sono Simon Singh, The Code Book, Fourth Estate (Londra, 1999); Christof Paar e Jan Pelzl, Understanding Cryptography, Springer (Heidelberg, 2010) e un corso basato sul libro di Paar chiamato "Introduction to Cryptography"; e Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons).
Citerò solo le informazioni e i risultati specifici che ho tratto da queste fonti, ma voglio riconoscere il mio debito generale nei loro confronti.
Per i lettori che desiderano approfondire le conoscenze sulla crittografia dopo questa introduzione, consiglio vivamente il libro di Katz e Lindell. Il corso di Katz su Coursera è un po' più accessibile del libro.
Contributi
Si prega di dare un'occhiata a il file dei contributi nel repository per alcune linee guida su come sostenere il progetto.
Notazione
Termini chiave:
I termini chiave dei primer sono introdotti in grassetto. Ad esempio, l'introduzione del cifrario Rijndael come termine chiave si presenta come segue: Cifrario Rijndael.
I termini chiave sono definiti esplicitamente, a meno che non si tratti di nomi propri o il loro significato sia evidente dalla discussione.
La definizione viene solitamente fornita al momento dell'introduzione di un termine chiave, anche se a volte è più conveniente rimandare la definizione a un momento successivo.
Parole e frasi sottolineate:
Le parole e le frasi sono sottolineate dal corsivo. Ad esempio, la frase "Ricorda la tua password" si presenta come segue: Ricorda la tua password.
Notazione formale:
La notazione formale riguarda principalmente variabili, variabili casuali e insiemi.
- Variabili: Di solito sono indicate con una lettera minuscola (ad esempio, "x" o "y"). A volte vengono indicate con la lettera maiuscola per chiarezza (ad esempio, "M" o "K").
- Variabili casuali: Sono sempre indicate con una lettera maiuscola (ad esempio, "X" o "Y")
- Insiemi: Sono sempre indicati con lettere maiuscole e in grassetto (ad esempio, S)
Pronto a esplorare l'affascinante universo della crittografia? Andiamo!
Che cos'è la crittografia?
I cifrari di Beale
Iniziamo la nostra indagine sul campo della crittografia con uno degli episodi più affascinanti e divertenti della sua storia: quello dei cifrari di Beale. [1]
La storia dei codici cifrati di Beale è, a mio parere, più probabile che sia una finzione che una realtà. Ma si suppone che sia andata come segue.
Sia nell'inverno del 1820 che in quello del 1822, un uomo di nome Thomas J. Beale soggiornò in una locanda di proprietà di Robert Morriss a Lynchburg (Virginia). Alla fine del secondo soggiorno, Beale consegnò a Morriss una scatola di ferro con documenti di valore da custodire.
Qualche mese dopo, Morriss ricevette una lettera di Beale datata 9 maggio 1822. In essa si sottolineava il grande valore del contenuto della cassetta di ferro e si davano alcune istruzioni a Morriss: se né Beale né alcuno dei suoi soci fosse mai venuto a reclamare la cassetta, egli avrebbe dovuto aprirla esattamente dieci anni dopo la data della lettera (cioè il 9 maggio 1832). Alcuni dei documenti all'interno sarebbero stati scritti in modo regolare. Molti altri, invece, sarebbero "incomprensibili senza l'aiuto di una chiave" Questa "chiave" sarebbe stata consegnata a Morriss da un amico innominato di Beale nel giugno del 1832.
Nonostante le chiare istruzioni, Morriss non aprì la scatola nel maggio del 1832 e il misterioso amico di Beale non si fece vivo nel giugno dello stesso anno. Solo nel 1845 l'oste si decise finalmente ad aprire la scatola. Al suo interno, Morriss trovò una nota che spiegava come Beale e i suoi soci avessero scoperto oro e argento nel West e li avessero seppelliti, insieme ad alcuni gioielli, per custodirli. Inoltre, la scatola conteneva tre cifrari: cioè testi scritti in codice che per essere sbloccati richiedono una chiave crittografica, o un segreto, e un algoritmo di accompagnamento. Il processo di sblocco di un testo cifrato è noto come decrittazione, mentre il processo di blocco è noto come crittografia. (Come spiegato nel Capitolo 3, il termine cifrario può assumere diversi significati. Nel nome "Beale ciphers", è l'abbreviazione di ciphertexts)
I tre testi cifrati che Morriss trovò nella scatola di ferro consistono ciascuno in una serie di numeri separati da virgole. Secondo la nota di Beale, questi testi cifrati forniscono separatamente l'ubicazione del tesoro, il contenuto del tesoro e un elenco di nomi con gli eredi legittimi del tesoro e le loro quote (quest'ultima informazione è rilevante nel caso in cui Beale e i suoi soci non venissero mai a reclamare la scatola).
Morris tentò di decifrare i tre testi cifrati per vent'anni. Con la chiave sarebbe stato facile. Ma Morriss non aveva la chiave e non riuscì nei suoi tentativi di recuperare i testi originali, o plaintexts come vengono tipicamente chiamati in crittografia.
Verso la fine della sua vita, Morriss passò la scatola a un amico nel 1862. Questo amico pubblicò poi un opuscolo nel 1885, con lo pseudonimo di J.B. Ward. L'opuscolo includeva una descrizione della (presunta) storia della scatola, i tre testi cifrati e una soluzione che aveva trovato per il secondo testo cifrato. (A quanto pare, esiste una chiave per ogni testo cifrato, e non una chiave che funziona su tutti e tre i testi cifrati, come sembra aver suggerito Beale nella sua lettera a Morriss)
Il secondo testo cifrato è visibile nella Figura 2 qui sotto. La chiave di questo testo cifrato è la Dichiarazione di Indipendenza degli Stati Uniti. La procedura di decrittazione si riduce all'applicazione delle due regole seguenti:
- Per qualsiasi numero n nel testo cifrato, individuare l'ennesima parola della Dichiarazione d'Indipendenza degli Stati Uniti
- Sostituire il numero n con la prima lettera della parola trovata
Figura 1: Cifrario di Beale n. 2

Per esempio, il primo numero del secondo testo cifrato è 115. La 115a parola della Dichiarazione di Indipendenza è "istituito", quindi la prima lettera del testo in chiaro è "i" Il testo cifrato non indica direttamente la spaziatura e la capitalizzazione delle parole. Ma dopo aver decifrato le prime parole, si può logicamente dedurre che la prima parola del testo in chiaro era semplicemente "I" (Il testo in chiaro inizia con la frase "Ho depositato nella contea di Bedford")
Dopo la decrittazione, il secondo messaggio fornisce il contenuto dettagliato del tesoro (oro, argento e gioielli) e suggerisce che era sepolto in vasi di ferro e coperto di rocce nella Contea di Bedford (Virginia). Le persone amano i misteri, quindi sono stati compiuti grandi sforzi per decriptare gli altri due messaggi cifrati di Beale, in particolare quello che descrive l'ubicazione del tesoro. Anche diversi crittografi di spicco si sono cimentati nell'impresa. Tuttavia, a tutt'oggi, nessuno è riuscito a decifrare gli altri due cifrari.
Note:
[1] Per un buon riassunto della storia, si veda Simon Singh, The Code Book, Fourth Estate (Londra, 1999), pp. 82-99. Un breve filmato della storia è stato realizzato da Andrew Allen nel 2010. Il filmato, "The Thomas Beale Cipher", è disponibile sul suo sito web (http://www.thomasbealecipher.com/).
[2] Questa immagine è disponibile nella pagina di Wikipedia dedicata ai cifrari di Beale.
Crittografia moderna
Storie colorate come quella dei cifrari di Beale sono ciò che la maggior parte di noi associa alla crittografia. Tuttavia, la crittografia moderna si differenzia per almeno quattro aspetti importanti da questi esempi storici.
In primo luogo, storicamente la crittografia si è occupata solo di segretezza (o riservatezza). I crittogrammi verrebbero creati per garantire che solo alcuni soggetti possano essere a conoscenza delle informazioni contenute nei testi in chiaro, come nel caso dei cifrari di Beale. Affinché uno schema di crittografia serva bene a questo scopo, la decrittazione del testo cifrato deve essere possibile solo se si possiede la chiave.
La crittografia moderna si occupa di una gamma di temi più ampia della semplice segretezza. Questi temi includono principalmente (1) l'integrità del messaggio, cioè la garanzia che un messaggio non sia stato modificato; (2) l'autenticità del messaggio, cioè la garanzia che un messaggio provenga realmente da un determinato mittente; e (3) il non ripudio, cioè la garanzia che un mittente non possa falsamente negare in seguito di aver inviato un messaggio. [4]
Una distinzione importante da tenere a mente è quindi quella tra uno sistema di crittografia e uno sistema crittografico. Uno schema di crittografia riguarda solo la segretezza. Mentre uno schema di crittografia è uno schema crittografico, non è vero il contrario. Uno schema crittografico può anche servire gli altri temi principali della crittografia, tra cui l'integrità, l'autenticità e il non ripudio.
I temi dell'integrità e dell'autenticità sono importanti quanto la segretezza. I nostri moderni sistemi di comunicazione non potrebbero funzionare senza garanzie di integrità e autenticità delle comunicazioni. Anche il non ripudio è un aspetto importante, ad esempio per i contratti digitali, ma è meno richiesto nelle applicazioni crittografiche rispetto a segretezza, integrità e autenticità.
In secondo luogo, gli schemi di crittografia classici, come i cifrari di Beale, prevedono sempre una chiave condivisa tra tutte le parti interessate. Tuttavia, molti schemi crittografici moderni prevedono non solo una, ma due chiavi: una privata e una pubblica. Mentre la prima dovrebbe rimanere privata in qualsiasi applicazione, la seconda è tipicamente di dominio pubblico (da qui i rispettivi nomi). Nell'ambito della crittografia, la chiave pubblica può essere utilizzata per crittografare il messaggio, mentre la chiave privata può essere utilizzata per decifrarlo.
La branca della crittografia che si occupa di schemi in cui tutte le parti condividono una chiave è nota come crittografia simmetrica. La singola chiave in un tale schema è solitamente chiamata chiave privata (o chiave segreta). La branca della crittografia che si occupa di schemi che richiedono una coppia di chiavi private e pubbliche è nota come crittografia asimmetrica. Questi rami sono talvolta indicati anche come crittografia a chiave privata e crittografia a chiave pubblica, rispettivamente (anche se questo può generare confusione, poiché gli schemi di crittografia a chiave pubblica hanno anche chiavi private).
L'avvento della crittografia asimmetrica alla fine degli anni '70 è stato uno degli eventi più importanti nella storia della crittografia. Senza di essa, la maggior parte dei nostri moderni sistemi di comunicazione, compreso Bitcoin, non sarebbe possibile, o perlomeno molto poco pratica.
È importante notare che la crittografia moderna non è esclusivamente lo studio degli schemi crittografici a chiave simmetrica e assimetrica (anche se questo copre gran parte del campo). Per esempio, la crittografia si occupa anche di funzioni hash e generatori di numeri pseudorandom, e su queste primitive si possono costruire applicazioni che non sono legate alla crittografia a chiave simmetrica o assimetrica.
In terzo luogo, gli schemi di crittografia classici, come quelli utilizzati nei cifrari di Beale, erano più arte che scienza. La loro sicurezza percepita si basava in gran parte su intuizioni relative alla loro complessità. In genere, venivano modificati quando si veniva a conoscenza di un nuovo attacco, o abbandonati del tutto se l'attacco era particolarmente grave. La crittografia moderna, invece, è una scienza rigorosa con un approccio formale e matematico allo sviluppo e all'analisi degli schemi crittografici. [5]
In particolare, la crittografia moderna è incentrata sulle prove di sicurezza formali. Qualsiasi prova di sicurezza per uno schema crittografico procede in tre fasi:
L'enunciazione di una definizione crittografica della sicurezza, cioè un insieme di obiettivi di sicurezza e la minaccia rappresentata dall'attaccante.
La dichiarazione di eventuali ipotesi matematiche relative alla complessità computazionale dello schema. Ad esempio, uno schema crittografico può contenere un generatore di numeri pseudorandom. Sebbene non si possa dimostrare l'esistenza di questi ultimi, è possibile ipotizzarne l'esistenza.
L'esposizione di una prova di sicurezza matematica dello schema sulla base della nozione formale di sicurezza e di eventuali ipotesi matematiche.
In quarto luogo, mentre storicamente la crittografia veniva utilizzata principalmente in ambito militare, nell'era digitale è arrivata a permeare le nostre attività quotidiane. Che si tratti di effettuare operazioni bancarie online, di postare sui social media, di acquistare un prodotto su Amazon con la carta di credito o di dare una mancia in bitcoin a un amico, la crittografia è la conditio sine qua non della nostra era digitale.
Considerati questi quattro aspetti della crittografia moderna, potremmo definire la crittografia moderna come la scienza che si occupa dello sviluppo e dell'analisi formale di schemi crittografici per proteggere le informazioni digitali da attacchi avversari. La sicurezza deve essere intesa in senso lato come la prevenzione di attacchi che danneggiano la segretezza, l'integrità, l'autenticazione e/o il non ripudio delle comunicazioni.
La crittografia è vista come una sottodisciplina della cbersicurezza, che si occupa di prevenire il furto, il danneggiamento e l'uso improprio dei sistemi informatici. Si noti che molti problemi di cybersecurity hanno una connessione minima o parziale con la crittografia.
Ad esempio, se un'azienda possiede server costosi a livello locale, potrebbe preoccuparsi di proteggere questo hardware da furti e danni. Pur trattandosi di un problema di cybersecurity, questo ha poco a che fare con la crittografia.
Per fare un altro esempio, gli attacchi di phishing sono un problema comune nella nostra epoca moderna. Questi attacchi tentano di ingannare le persone tramite un'e-mail o un altro mezzo di comunicazione, spingendole a cedere informazioni sensibili come password o numeri di carte di credito. Sebbene la crittografia possa aiutare ad affrontare gli attacchi di phishing fino a un certo punto, un approccio completo richiede qualcosa di più del semplice utilizzo della crittografia.
Note:
[3] Per essere precisi, le applicazioni più importanti degli schemi crittografici hanno riguardato la segretezza. I bambini, ad esempio, usano spesso semplici schemi crittografici per "divertimento". In questi casi la segretezza non è un problema.
[4] Bruce Schneier, Crittografia applicata, 2a ed., 2015 (Indianapolis, IN: John Wiley & Sons), pag. 2.
[5] Per una buona descrizione si veda Jonathan Katz e Yehuda Lindell, Introduzione alla crittografia moderna, CRC Press (Boca Raton, FL: 2015), in particolare le pagine 16-23.
[6] Cfr. Katz e Lindell, ibidem, p. 3. Ritengo che la loro caratterizzazione abbia qualche problema, per cui presento qui una versione leggermente diversa della loro affermazione.
Comunicazioni aperte
La crittografia moderna è stata progettata per fornire garanzie di sicurezza in un ambiente di comunicazioni aperte. Se il nostro canale di comunicazione è così ben protetto che chi origlia non ha alcuna possibilità di manipolare o anche solo osservare i nostri messaggi, allora la crittografia è superflua. La maggior parte dei nostri canali di comunicazione, tuttavia, non sono così ben protetti.
La spina dorsale delle comunicazioni nel mondo moderno è costituita da un'enorme rete di cavi in fibra ottica. Telefonare, guardare la televisione e navigare sul web in una casa moderna si basa generalmente su questa rete di cavi in fibra ottica (una piccola percentuale può affidarsi esclusivamente ai satelliti). È vero che in casa si possono avere diverse connessioni dati, come il cavo coassiale, la linea digitale ad abbonamento (asimmetrica) e la fibra ottica. Ma, almeno nel mondo sviluppato, questi diversi mezzi di trasmissione dati si uniscono rapidamente all'esterno della casa a un nodo di un'enorme rete di cavi in fibra ottica che collega l'intero globo. Fanno eccezione alcune aree remote del mondo sviluppato, come gli Stati Uniti e l'Australia, dove il traffico di dati può ancora percorrere distanze considerevoli sui tradizionali cavi telefonici in rame.
Sarebbe impossibile impedire a potenziali aggressori di accedere fisicamente a questa rete di cavi e alla sua infrastruttura di supporto. In realtà, sappiamo già che la maggior parte dei nostri dati viene intercettata da varie agenzie di intelligence nazionali in corrispondenza di intersezioni cruciali di Internet[7]. Questo include tutto, dai messaggi di Facebook agli indirizzi dei siti web visitati.
Mentre per sorvegliare i dati su vasta scala è necessario un avversario potente, come un'agenzia di intelligence nazionale, gli aggressori che dispongono di poche risorse possono facilmente tentare di ficcare il naso su scala più locale. Sebbene ciò possa avvenire a livello di intercettazione di cavi, è molto più semplice intercettare le comunicazioni wireless.
La maggior parte dei dati della nostra rete locale, a casa, in ufficio o in un bar, oggi viaggia tramite onde radio verso i punti di accesso wireless dei router all-in-one, anziché attraverso cavi fisici. Un aggressore ha quindi bisogno di poche risorse per intercettare il traffico locale. Questo aspetto è particolarmente preoccupante perché la maggior parte delle persone fa ben poco per proteggere i dati che viaggiano attraverso le proprie reti locali. Inoltre, i potenziali aggressori possono prendere di mira anche le nostre connessioni mobili a banda larga, come 3G, 4G e 5G. Tutte queste comunicazioni wireless sono un facile bersaglio per gli aggressori.
Pertanto, l'idea di mantenere segrete le comunicazioni proteggendo il canale di comunicazione è un'aspirazione irrimediabilmente illusoria per gran parte del mondo moderno. Tutto ciò che sappiamo giustifica una forte paranoia: si deve sempre presumere che qualcuno stia ascoltando. E la crittografia è lo strumento principale che abbiamo per ottenere qualsiasi tipo di sicurezza in questo ambiente moderno.
Note:
[7] Si veda, ad esempio, Olga Khazan, "The creepy, long-standing practice of undersea cable tapping", The Atlantic, 16 luglio 2013 (disponibile su The Atlantic).
Fondamenti matematici della crittografia 1
Variabili casuali
La crittografia si basa sulla matematica. E se si vuole ottenere una comprensione più che superficiale della crittografia, è necessario essere a proprio agio con la matematica.
Questo capitolo introduce la maggior parte della matematica di base che si incontra nell'apprendimento della crittografia. Gli argomenti comprendono le variabili casuali, le operazioni modulo, le operazioni XOR e la pseudorandomicità. Per una comprensione non superficiale della crittografia è necessario padroneggiare il materiale di queste sezioni.
La sezione successiva tratta la teoria dei numeri, che è molto più impegnativa.
Variabili casuali
Una variabile casuale è tipicamente indicata con una lettera maiuscola non
in grassetto. Ad esempio, si può parlare di una variabile casuale X, di una variabile casuale Y o di una variabile casuale Z.
Questa è la notazione che utilizzerò anche d'ora in poi.
Una variabile casuale può assumere due o più valori possibili, ciascuno con una certa probabilità positiva. I valori possibili sono elencati nell'insieme dei risultati.
Ogni volta che si campiona una variabile casuale, si estrae un particolare valore dal suo insieme di risultati in base alle probabilità definite.
Passiamo a un semplice esempio. Supponiamo che una variabile X sia definita come segue:
- X ha l'insieme di risultati
{1,2}
Pr[X = 1] = 0.5Pr[X = 2] = 0.5È facile capire che X è una
variabile casuale. Innanzitutto, ci sono due o più valori possibili che X può assumere, ossia 1 e 2. In secondo luogo, ogni
possibile valore ha una probabilità positiva di verificarsi ogni volta che
si campiona X, ovvero 0,5.
Tutto ciò che richiede una variabile casuale è un insieme di risultati con due o più possibilità, dove ogni possibilità ha una probabilità positiva di verificarsi al momento del campionamento. In linea di principio, quindi, una variabile casuale può essere definita astrattamente, senza alcun contesto. In questo caso, si potrebbe pensare al "campionamento" come all'esecuzione di un esperimento naturale per determinare il valore della variabile casuale.
La variabile X di cui sopra è
stata definita in modo astratto. Si può quindi pensare di campionare la
variabile X come se si
lanciasse una moneta equa e si assegnasse "2" in caso di testa e "1" in caso
di croce. Per ogni campione di X, si lancia nuovamente la
moneta.
In alternativa, si può anche pensare di campionare X, come se si lanciasse un dado equo e si assegnasse "2" nel caso in cui il
dado colpisca 1, 3 o 4, e si assegnasse "1" nel
caso in cui il dado colpisca 2, 5 o 6. Ogni volta che si
campiona X, si tira di nuovo
il dado.
In realtà, qualsiasi esperimento naturale che permetta di definire le
probabilità dei possibili valori di X di cui sopra può essere immaginato rispetto al disegno.
Spesso, tuttavia, le variabili casuali non vengono introdotte in modo astratto. Al contrario, l'insieme dei possibili valori di risultato ha un esplicito significato nel mondo reale (piuttosto che essere solo numeri). Inoltre, questi valori di risultato possono essere definiti rispetto a un tipo specifico di esperimento (piuttosto che come qualsiasi esperimento naturale con quei valori).
Consideriamo ora un esempio di variabile X che non è definita astrattamente. Per determinare quale delle due squadre inizia
una partita di calcio, X viene definita come segue:
Xha l'insieme di esiti {il rosso si spegne, il blu si spegne}- Lancio di una moneta particolare
C: croce = "il rosso viene espulso"; testa = "il blu viene espulso"
Pr [X = \text{red kicks off}] = 0.5Pr [X = \text{blue kicks off}] = 0.5In questo caso, l'insieme dei risultati di X ha un significato concreto,
ovvero quale squadra inizia in una partita di calcio. Inoltre, i possibili
esiti e le relative probabilità sono determinati da un esperimento concreto,
ovvero il lancio di una particolare moneta C.
Nelle discussioni sulla crittografia, le variabili casuali vengono solitamente introdotte rispetto a un insieme di risultati con un significato reale. Può trattarsi dell'insieme di tutti i messaggi che possono essere crittografati, noto come spazio dei messaggi, o dell'insieme di tutte le chiavi che le parti che utilizzano la crittografia possono scegliere, noto come spazio delle chiavi.
Le variabili casuali nelle discussioni sulla crittografia, tuttavia, non sono solitamente definite rispetto a uno specifico esperimento naturale, ma rispetto a qualsiasi esperimento che possa produrre le giuste distribuzioni di probabilità.
Le variabili casuali possono avere distribuzioni di probabilità discrete o
continue. Le variabili casuali con una distribuzione di probabilità discreta, cioè le variabili casuali discrete, hanno un numero finito di esiti
possibili. La variabile casuale X in entrambi gli esempi fatti
finora era discreta.
Le variabili casuali continue possono invece assumere valori in uno o più intervalli. Si può dire, per esempio, che una variabile casuale, al momento del campionamento, assumerà qualsiasi valore reale compreso tra 0 e 1, e che ogni numero reale in questo intervallo ha la stessa probabilità. All'interno di questo intervallo, ci sono infiniti valori possibili.
Per le discussioni sulla crittografia, è sufficiente comprendere le variabili casuali discrete. Qualsiasi discussione sulle variabili casuali da qui in avanti deve quindi essere intesa come riferita a variabili casuali discrete, a meno che non sia specificato diversamente.
Grafici di variabili casuali
I possibili valori e le probabilità associate a una variabile casuale
possono essere facilmente visualizzati attraverso un grafico. Ad esempio, si
consideri la variabile casuale X della sezione precedente con un insieme di risultati di {1, 2} e Pr [X = 1] = 0,5 e Pr [X = 2] = 0,5. Una
variabile casuale di questo tipo viene tipicamente visualizzata sotto forma
di grafico a barre come nella Figura 1.
Figura 1: Variabile casuale X
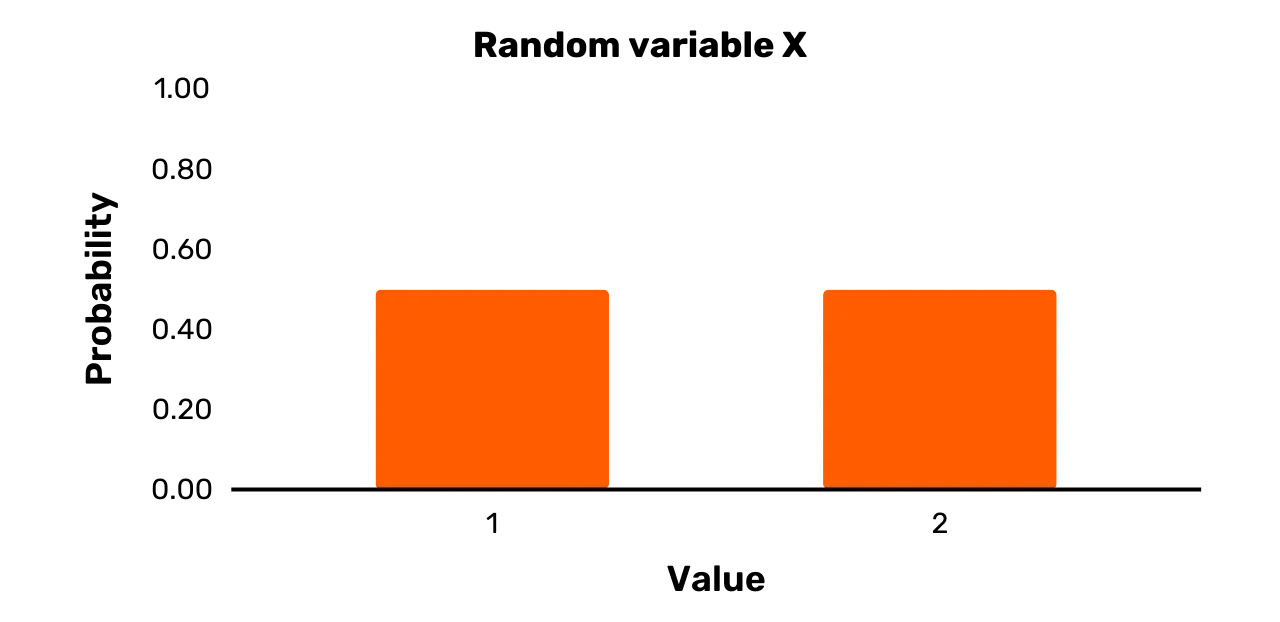
Le barre larghe della Figura 1 non intendono ovviamente suggerire
che la variabile casuale X sia
effettivamente continua. Al contrario, le barre sono state rese larghe per essere
più attraenti dal punto di vista visivo (una semplice linea retta verso l'alto
fornisce una visualizzazione meno intuitiva).
Variabili uniformi
Nell'espressione "variabile casuale", il termine "casuale" significa semplicemente "probabilistico". In altre parole, significa semplicemente che due o più possibili esiti della variabile si verificano con determinate probabilità. Questi esiti, tuttavia, non devono * necessariamente* avere la stessa probabilità (anche se il termine "casuale" può avere questo significato in altri contesti).
Una variabile uniforme è un caso speciale di variabile
casuale. Può assumere due o più valori, tutti con la stessa probabilità. La
variabile casuale X rappresentata nella Figura 1 è chiaramente una variabile uniforme,
poiché entrambi i possibili risultati si verificano con una probabilità di 0,5. Esistono tuttavia molte
variabili casuali che non sono istanze di variabili uniformi.
Consideriamo, ad esempio, la variabile casuale Y. Essa ha un insieme di risultati {1, 2, 3, 8, 10} e la
seguente distribuzione di probabilità:
\Pr[Y = 1] = 0.25\Pr[Y = 2] = 0.35\Pr[Y = 3] = 0.1\Pr[Y = 8] = 0.25\Pr[Y = 10] = 0.05Mentre due possibili esiti hanno una probabilità uguale di verificarsi, cioè 1 e 8, Y può anche assumere certi valori con probabilità diverse da 0,25 al momento del campionamento. Quindi, sebbene Y sia effettivamente una variabile
casuale, non è una variabile uniforme.
Una rappresentazione grafica di Y è riportata nella Figura 2.
Figura 2: Variabile casuale Y
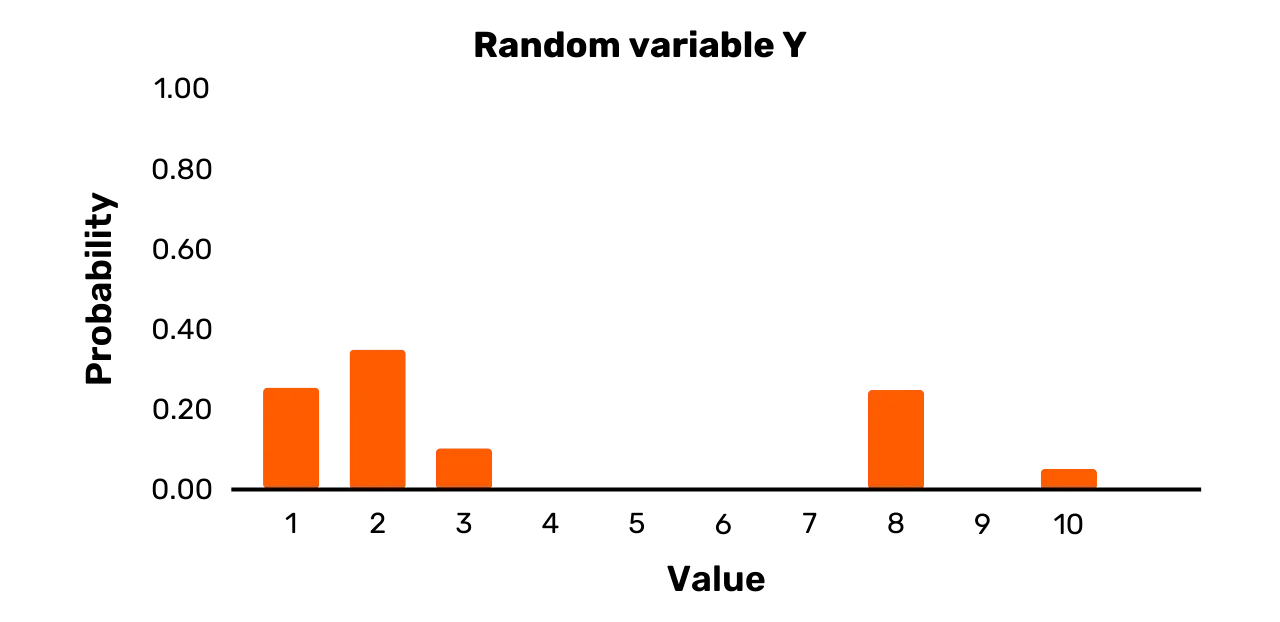
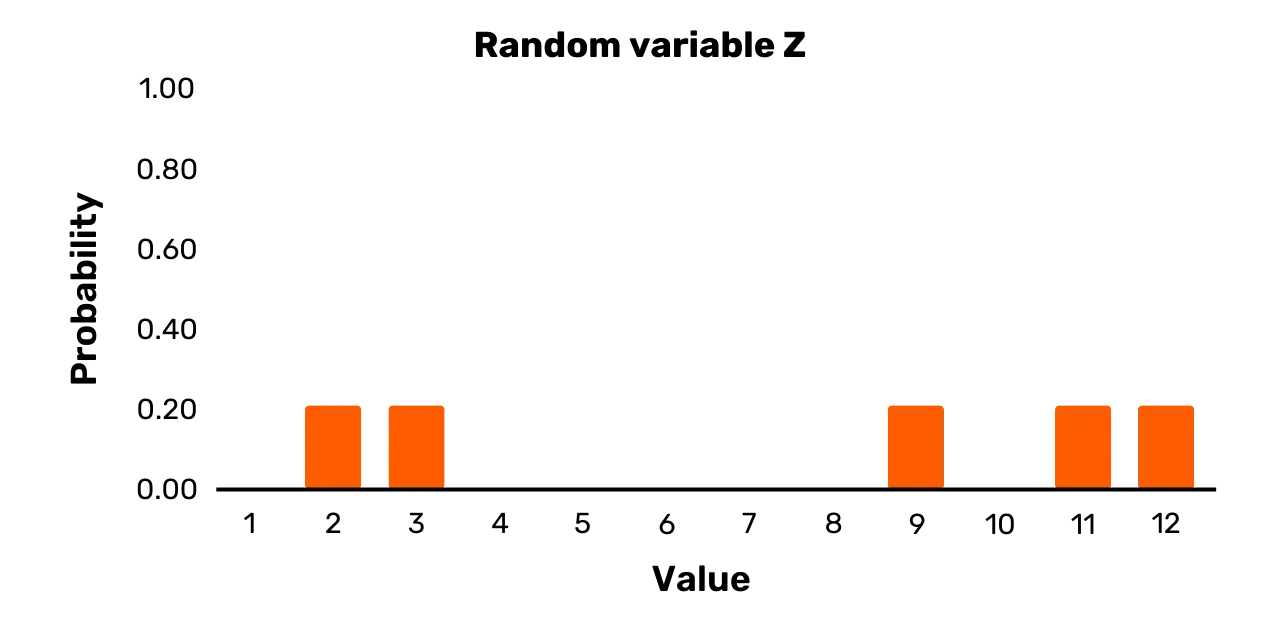
Per un ultimo esempio, consideriamo la variabile casuale Z. Essa ha l'insieme di risultati {1,3,7,11,12} e la seguente distribuzione di probabilità:
\Pr[Z = 2] = 0.2\Pr[Z = 3] = 0.2\Pr[Z = 9] = 0.2\Pr[Z = 11] = 0.2\Pr[Z = 12] = 0.2Lo si può vedere rappresentato nella Figura 3. La variabile casuale Z è, a differenza di Y, una variabile uniforme, in quanto tutte le probabilità per i possibili valori al momento del campionamento sono uguali.
Figura 3: Variabile casuale Z
Probabilità condizionata
Supponiamo che Bob intenda selezionare uniformemente un giorno dell'ultimo anno solare. Qual è la probabilità che il giorno selezionato sia in estate?
Finché pensiamo che il processo di Bob sarà davvero uniforme, dovremmo concludere che c'è una probabilità di 1/4 che Bob scelga un giorno in estate. Questa è la probabilità incondizionata che il giorno selezionato a caso sia in estate.
Supponiamo ora che, invece di estrarre uniformemente un giorno del calendario, Bob scelga uniformemente solo tra i giorni in cui la temperatura di mezzogiorno a Crystal Lake (New Jersey) era di 21 gradi Celsius o superiore. Data questa informazione aggiuntiva, cosa possiamo concludere sulla probabilità che Bob scelga un giorno d'estate?
Dovremmo davvero trarre una conclusione diversa rispetto a prima, anche senza ulteriori informazioni specifiche (ad esempio, la temperatura a mezzogiorno di ogni giorno dell'ultimo anno solare).
Sapendo che Crystal Lake si trova nel New Jersey, non ci aspetteremmo certo che la temperatura a mezzogiorno sia di 21 gradi Celsius o superiore in inverno. È invece molto più probabile che si tratti di una giornata calda in primavera o in autunno, o di una giornata estiva. Quindi, sapendo che la temperatura di mezzogiorno a Crystal Lake nel giorno selezionato era di 21 gradi Celsius o superiore, la probabilità che il giorno scelto da Bob sia in estate diventa molto più alta. Questa è la probabilità condizionata che il giorno selezionato a caso sia in estate, dato che la temperatura di mezzogiorno a Crystal Lake era di 21 gradi Celsius o superiore.
A differenza dell'esempio precedente, le probabilità di due eventi possono anche essere completamente indipendenti. In questo caso, si dice che sono indipendenti.
Supponiamo, ad esempio, che una certa moneta equa sia uscita testa. Data questa circostanza, qual è la probabilità che domani piova? La probabilità condizionata in questo caso dovrebbe essere la stessa della probabilità incondizionata che domani piova, poiché il lancio di una moneta non ha generalmente alcun impatto sul tempo.
Per scrivere gli enunciati di probabilità condizionale si usa il simbolo
"|". Ad esempio, la probabilità dell'evento A dato che l'evento B si è verificato
può essere scritta come segue:
Pr[A|B]Quindi, quando due eventi, A e B, sono indipendenti,
allora:
Pr[A|B] = Pr[A] \text{ and } Pr[B|A] = Pr[B]La condizione di indipendenza può essere semplificata come segue:
Pr[A, B] = Pr[A] \cdot Pr[B]Un risultato chiave della teoria della probabilità è noto come Teorema di Bayes. Esso afferma sostanzialmente che Pr[A|B] può essere riscritto come
segue:
Pr[A|B] = \frac{Pr[B|A] \cdot Pr[A]}{Pr[B]}Invece di utilizzare le probabilità condizionali con eventi specifici,
possiamo anche considerare le probabilità condizionali relative a due o più
variabili casuali su un insieme di eventi possibili. Supponiamo due
variabili casuali, X e Y. Possiamo indicare ogni
possibile valore di X con x e ogni possibile valore di Y con y. Possiamo dire che due
variabili casuali sono indipendenti se vale la seguente affermazione:
Pr[X = x, Y = y] = Pr[X = x] \cdot Pr[Y = y]per tutti gli x e gli y.
Cerchiamo di essere un po' più espliciti sul significato di questa affermazione.
Supponiamo che gli insiemi di risultati per X e Y siano definiti come
segue: X = \{x_1, x_2, \ldots, x_i, \ldots, x_n\} e Y = \{y_1, y_2, \ldots, y_i, \ldots, y_m\}. (È tipico indicare gli insiemi di valori con lettere maiuscole e in
grassetto)
Supponiamo ora di campionare Y e di osservare y_1.
L'affermazione precedente ci dice che la probabilità di ottenere x_1 dal campionamento di X è
esattamente la stessa che avremmo se non avessimo mai osservato y_1. Questo è vero per
qualsiasi y_i che avremmo
potuto ricavare dal nostro campionamento iniziale di Y. Infine, questo vale non
solo per x_1. Per qualsiasi x_i, la probabilità di
verificarsi non è influenzata dal risultato del campionamento di Y. Tutto questo vale anche
nel caso in cui X venga campionato
per primo.
Concludiamo la nostra discussione su un punto leggermente più filosofico. In qualsiasi situazione del mondo reale, la probabilità di un evento viene sempre valutata in base a un particolare insieme di informazioni. Non esiste una "probabilità incondizionata" in senso stretto.
Per esempio, supponiamo che vi chieda la probabilità che i maiali volino entro il 2030. Anche se non vi fornisco altre informazioni, è chiaro che conoscete molte cose sul mondo che possono influenzare il vostro giudizio. Non avete mai visto volare i maiali. Sa che la maggior parte delle persone non si aspetta che volino. Sa che non sono costruiti per volare. E così via.
Pertanto, quando parliamo di "probabilità incondizionata" di un evento in un contesto reale, questo termine può avere un significato solo se lo intendiamo come "la probabilità senza ulteriori informazioni esplicite". Qualsiasi comprensione di una "probabilità condizionale" deve quindi essere sempre intesa rispetto a qualche informazione specifica.
Potrei, per esempio, chiedervi la probabilità che i maiali volino entro il 2030, dopo avervi dato la prova che alcune capre in Nuova Zelanda hanno imparato a volare dopo alcuni anni di addestramento. In questo caso, probabilmente modificherete il vostro giudizio sulla probabilità che i maiali volino entro il 2030. Quindi la probabilità che i maiali volino entro il 2030 è condizionata da questa evidenza sulle capre in Nuova Zelanda.
L'operazione modulo
Modulo
L'espressione più elementare con l'operazione modulo è
della forma seguente: x \mod y.
La variabile x è chiamata
dividendo e la variabile y divisore.
Per eseguire un'operazione modulo con un dividendo positivo e un divisore positivo,
basta determinare il resto della divisione.
Ad esempio, si consideri l'espressione 25 ´mod 4. Il numero 4 entra nel numero 25 per un totale di 6 volte. Il resto di
questa divisione è 1. Quindi, 25 ´mod 4 è uguale a 1. In modo
analogo, possiamo valutare le espressioni seguenti:
29 ´mod 30 = 29(poiché 30 entra in 29 per un totale di 0 volte e il resto è 29)42 \mod 2 = 0(poiché 2 entra in 42 per un totale di 21 volte e il resto è 0)12 ´mod 5 = 2(poiché 5 entra in 12 per un totale di 2 volte e il resto è 2)20 ´mod 8 = 4(poiché 8 entra in 20 per un totale di 2 volte e il resto è 4)
Quando il dividendo o il divisore è negativo, le operazioni modulo possono essere gestite in modo diverso dai linguaggi di programmazione.
Si incontreranno sicuramente casi con un dividendo negativo in crittografia. In questi casi, l'approccio tipico è il seguente:
- Determinare innanzitutto il valore più vicino inferiore o uguale al dividendo in cui il divisore si divide con un resto pari a zero.
Chiamiamo questo valore
p. - Se il dividendo è
x, il risultato dell'operazione modulo è il valore dix - p.
Per esempio, supponiamo che il dividendo sia 20 e il divisore 3. Il valore più vicino inferiore o uguale a 20 in cui 3 si divide uniformemente è 21. Il valore di x - p in questo caso è -20 - (-21).
Questo valore è uguale a 1 e, quindi, -20 \mod 3 è uguale a 1. In modo
analogo, possiamo valutare le espressioni seguenti:
-8 \mod 5 = 2-19 \mod 16 = 13-14 \mod 6 = 4
Per quanto riguarda la notazione, in genere si vedono i seguenti tipi di
espressioni: x = [y \mod z].
A causa delle parentesi, in questo caso l'operazione modulo si applica solo
al lato destro dell'espressione. Se y è uguale a 25 e z è uguale a
4, ad esempio, allora x è valutato
1.
Senza parentesi, l'operazione modulo agisce su entrambi i lati di
un'espressione. Supponiamo, ad esempio, la seguente espressione: x = y \mod z. Se y è uguale a 25 e z è uguale a
4, tutto ciò che sappiamo è che x \mod 4 è valutato 1. Questo è coerente con qualsiasi valore di x dell'insieme {\ldots,-7, -3, 1, 5, 9,\ldots}
Il ramo della matematica che coinvolge le operazioni modulo su numeri ed espressioni è denominato aritmetica modulare. Si può pensare a questo ramo come all'aritmetica per i casi in cui la linea dei numeri non è infinitamente lunga. Sebbene in crittografia le operazioni modulo siano tipicamente eseguite con numeri interi (positivi), è possibile eseguire operazioni modulo anche con qualsiasi numero reale.
Il cifrario a turni
L'operazione modulo si incontra spesso in crittografia. Per illustrarla, consideriamo uno degli schemi di crittografia storici più famosi: il cifrario a turni.
Definiamolo innanzitutto. Supponiamo un dizionario D che equipara
tutte le lettere dell'alfabeto inglese, in ordine, con l'insieme dei numeri {0, 1, 2, \ldots, 25}. Si assuma uno spazio dei messaggi M. Il cifrario a spostamento è, quindi, uno schema di cifratura definito
come segue:
- Selezionare uniformemente una chiave
kdallo spazio delle chiavi K, dove K ={0, 1, 2, \ldots, 25}[1] - Crittografare un messaggio
m \ in \mathbf{M}, come segue:- Separare
mnelle sue singole letterem_0, m_1, \ldots, m_i, \ldots, m_l - Convertire ogni
m_iin un numero secondo D - Per ogni
m_i,c_i = [(m_i + k) ´mod 26] - Convertire ogni
c_iin una lettera secondo D - Quindi combinare
c_0, c_1, \ldots, c_lper ottenere il testo cifratoc
- Separare
- Decifrare un testo cifrato
ccome segue:- Convertire ogni
c_iin un numero secondo D - Per ogni
c_i,m_i = [(c_i - k) ´mod 26] - Convertire ogni
m_iin una lettera secondo D - Quindi combinare
m_0, m_1, \ldots, m_lper ottenere il messaggio originalem
- Convertire ogni
L'operatore modulo nel cifrario a turni assicura che le lettere si avvolgano su se stesse, in modo che tutte le lettere del testo cifrato siano definite. A titolo di esempio, si consideri l'applicazione del cifrario a turni alla parola "CANE".
Supponiamo di aver selezionato in modo uniforme una chiave che abbia il
valore 17. La lettera "O" equivale a 15. Senza l'operazione modulo,
l'addizione di questo numero del testo in chiaro con la chiave darebbe come
risultato un numero di testo cifrato pari a 32. Tuttavia, questo numero del
testo in chiaro non può essere trasformato in una lettera del testo in
chiaro, poiché l'alfabeto inglese ha solo 26 lettere. L'operazione modulo
assicura che il numero del testo cifrato sia effettivamente 6 (il risultato
di 32 ´mod 26), che equivale
alla lettera "G" del testo cifrato.
L'intera codifica della parola "DOG" con un valore chiave di 17 è la seguente:
- Messaggio = DOG = D,O,G = 3,15,6
c_0 = [(3 + 17) \mod 26] = [(20) \mod 26] = 20 = Uc_1 = [(15 + 17) \mod 26] = [(32) \mod 26] = 6 = Gc_2 = [(6 + 17) \mod 26] = [(23) \mod 26] = 23 = Xc = UGX
Tutti sono in grado di capire intuitivamente come funziona il cifrario a turni e probabilmente lo usano da soli. Per progredire nella conoscenza della crittografia, tuttavia, è importante iniziare a prendere confidenza con la formalizzazione, poiché gli schemi diventeranno molto più difficili. Ecco perché i passaggi del cifrario a turni sono stati formalizzati.
Note:
[1] Possiamo definire esattamente questa affermazione, utilizzando la
terminologia della sezione precedente. Che una variabile uniforme K abbia K come insieme di possibili
risultati. Quindi:
Pr[K = 0] = \frac{1}{26}Pr[K = 1] = \frac{1}{26}... e così via. Campionare una volta la variabile uniforme K per ottenere una particolare chiave.
L'operazione XOR
Tutti i dati informatici vengono elaborati, memorizzati e inviati attraverso le reti a livello di bit. Anche gli schemi crittografici applicati ai dati informatici operano a livello di bit.
Ad esempio, supponiamo di aver digitato un'e-mail nella nostra applicazione di posta elettronica. La crittografia applicata non riguarda direttamente i caratteri ASCII dell'e-mail. Viene invece applicata alla rappresentazione in bit delle lettere e degli altri simboli dell'e-mail.
Un'operazione matematica chiave da comprendere per la crittografia moderna,
oltre all'operazione modulo, è quella dell'operazione XOR,
o operazione "esclusiva o". Questa operazione prende in ingresso due bit e
produce in uscita un altro bit. L'operazione XOR viene indicata
semplicemente come "XOR". Essa produce 0 se i due bit sono uguali e 1 se i
due bit sono diversi. Di seguito sono riportate le quattro possibilità. Il
simbolo oplus rappresenta lo "XOR":
0 \oplus 0 = 00 \oplus 1 = 11 \oplus 0 = 11 \oplus 1 = 0
A titolo di esempio, si supponga di avere un messaggio m_1 (01111001) e un messaggio m_2 (01011001). L'operazione XOR di questi due messaggi può essere vista qui sotto.
m_1 \oplus m_2 = 01111001 \oplus 01011001 = 00100000
Il processo è semplice. Per prima cosa si esegue lo XOR dei bit più a
sinistra di m_1 e m_2. In questo caso si tratta
di 0 ´oplus 0 = 0. Poi si
esegue lo XOR della seconda coppia di bit da sinistra. In questo caso è 1 \oplus 1 = 0. Si continua
con questo procedimento fino a quando non si è eseguita l'operazione XOR sui
bit più a destra.
È facile vedere che l'operazione XOR è commutativa, ovvero che m_1 \oplus m_2 = m_2 \oplus m_1. Inoltre, l'operazione XOR è anche associativa. Ovvero, (m_1 \oplus m_2) \oplus m_3 = m_1 \oplus (m_2 \oplus m_3).
Un'operazione XOR su due stringhe di lunghezza diversa può avere interpretazioni diverse, a seconda del contesto. In questa sede non ci occuperemo di operazioni XOR su stringhe di lunghezza diversa.
Un'operazione XOR è equivalente al caso speciale di eseguire un'operazione modulo sull'addizione di bit quando il divisore è 2. L'equivalenza è visibile nei risultati seguenti:
(0 + 0) \mod 2 = 0 \oplus 0 = 0(1 + 0) \mod 2 = 1 \oplus 0 = 1(0 + 1) \mod 2 = 0 \oplus 1 = 1(1 + 1) \mod 2 = 1 \oplus 1 = 0
Pseudorandomia
Nella nostra discussione sulle variabili casuali e uniformi, abbiamo fatto una distinzione specifica tra "casuale" e "uniforme". Questa distinzione viene tipicamente mantenuta nella pratica quando si descrivono variabili casuali. Tuttavia, nel nostro contesto attuale, questa distinzione deve essere abbandonata e "casuale" e "uniforme" sono usati come sinonimi. Ne spiegherò il motivo alla fine della sezione.
Per cominciare, possiamo chiamare una stringa binaria di lunghezza n casuale (o uniforme), se è il risultato
del campionamento di una variabile uniforme S che dà a ogni stringa binaria di tale lunghezza n un'uguale probabilità di selezione.
Supponiamo, ad esempio, l'insieme di tutte le stringhe binarie di lunghezza
8: \{0000\ 0000, 0000\ 0001, \ldots, 1111\ 1111\}. (È tipico scrivere una stringa a 8 bit in due quartine, ciascuna chiamata nibble) Chiamiamo questo insieme di stringhe S_8.
In base alla definizione precedente, possiamo quindi chiamare casuale (o
uniforme) una particolare stringa binaria di lunghezza 8, se è il risultato
del campionamento di una variabile uniforme S che dà a ogni stringa in S_8 un'uguale probabilità di selezione. Dato che l'insieme S_8 comprende 2^8 elementi, la
probabilità di selezione al momento del campionamento dovrebbe essere 1/2^8 per ogni stringa dell'insieme.
Un aspetto fondamentale della casualità di una stringa binaria è che essa è definita in riferimento al processo con cui è stata selezionata. La forma di una particolare stringa binaria di per sé, quindi, non rivela nulla sulla sua casualità nella selezione.
Ad esempio, molte persone hanno l'idea che una stringa come 1111$ non possa essere stata selezionata a caso. Ma questo è chiaramente falso.
Definendo una variabile uniforme S su tutte le stringhe binarie di lunghezza 8, la probabilità di selezionare 1111\ 1111 dall'insieme S_8 è la stessa di una stringa come 0111\ 0100. Pertanto, non si
può dire nulla sulla casualità di una stringa, solo analizzando la stringa
stessa.
Possiamo anche parlare di stringhe casuali senza intendere specificamente le
stringhe binarie. Ad esempio, possiamo parlare di una stringa esadecimale
casuale AF 02 82. In questo
caso, la stringa sarebbe stata selezionata a caso dall'insieme di tutte le
stringhe esadecimali di lunghezza 6. Ciò equivale a selezionare casualmente
una stringa binaria di lunghezza 24, poiché ogni cifra esadecimale
rappresenta 4 bit.
In genere l'espressione "una stringa casuale", senza alcuna qualificazione,
si riferisce a una stringa selezionata a caso dall'insieme di tutte le
stringhe con la stessa lunghezza. È così che l'ho descritta sopra. Una
stringa di lunghezza n può,
ovviamente, essere selezionata a caso da un insieme diverso. Un insieme, per
esempio, che costituisce solo un sottoinsieme di tutte le stringhe di
lunghezza n, o magari un
insieme che include stringhe di lunghezza variabile. In questi casi,
tuttavia, non si parlerebbe di "stringa casuale", ma piuttosto di "stringa
selezionata casualmente da un insieme S".
Un concetto chiave della crittografia è quello di pseudorandomicità. Una
stringa pseudorandom di lunghezza n appare come se fosse il risultato del campionamento di una
variabile uniforme S che dà a
ogni stringa in S_n un'uguale probabilità di selezione. In realtà, però, la stringa è il
risultato del campionamento di una variabile uniforme S' che definisce solo una distribuzione di probabilità - non necessariamente
con probabilità uguali per tutti i risultati possibili - su un sottoinsieme
di S_n. Il
punto cruciale qui è che nessuno può realmente distinguere tra i campioni di S e S', anche se se ne prendono
molti.
Supponiamo, ad esempio, una variabile casuale S. Il suo insieme di risultati è S_{256}, cioè l'insieme di tutte le stringhe binarie di lunghezza 256. Questo
insieme ha 2^{256} elementi. Questo insieme ha 2^{256} elementi. Ogni elemento ha un'uguale probabilità di selezione, 1/2^{256}, al
momento del campionamento.
Inoltre, supponiamo una variabile casuale S'. Il suo insieme di risultati comprende solo 2^{128} stringhe binarie
di lunghezza 256. Ha una certa distribuzione di probabilità su queste stringhe,
ma questa distribuzione non è necessariamente uniforme.
Supponiamo che ora io prenda 1000 campioni da S e 1000 campioni da S' e che
vi dia le due serie di risultati. Vi dico quale serie di risultati è
associata a quale variabile casuale. Poi prendo un campione da una delle due
variabili casuali. Ma questa volta non vi dico quale variabile casuale
campionare. Se S' fosse
pseudorandom, la probabilità di indovinare quale variabile casuale ho
campionato non sarebbe praticamente migliore di 1/2.
In genere, una stringa pseudorandom di lunghezza n viene prodotta selezionando casualmente una stringa di dimensione n - x, dove x è un intero positivo, e utilizzandola come input per un algoritmo di
espansione. Questa stringa casuale di dimensione n - x è nota come seme.
Le stringhe pseudorandom sono un concetto chiave per rendere pratica la crittografia. Si pensi, ad esempio, ai cifrari a flusso. Con un cifrario a flusso, una chiave selezionata a caso viene inserita in un algoritmo di espansione per produrre una stringa pseudorandom molto più grande. Questa stringa pseudorandom viene poi combinata con il testo in chiaro tramite un'operazione XOR per produrre un testo cifrato.
Se non fossimo in grado di produrre questo tipo di stringa pseudorandom per un cifrario a flusso, avremmo bisogno di una chiave lunga quanto il messaggio per garantire la sicurezza. Questa non è un'opzione molto pratica nella maggior parte dei casi.
La nozione di pseudorandomicità discussa in questa sezione può essere definita in modo più formale. Si estende anche ad altri contesti. Ma non è necessario addentrarsi in questa discussione. Tutto ciò che è necessario capire intuitivamente per gran parte della crittografia è la differenza tra una stringa casuale e una pseudorandom. [2]
Ora dovrebbe essere chiaro anche il motivo per cui abbiamo abbandonato la
distinzione tra "casuale" e "uniforme" nella nostra discussione. In pratica,
tutti usano il termine pseudorandom per indicare una stringa che appare come se fosse il risultato del campionamento di una variabile uniforme S. A rigore, dovremmo
chiamare tale stringa "pseudo-uniforme", adottando il linguaggio di prima.
Poiché il termine "pseudo-uniforme" è goffo e non è usato da nessuno, non lo
introdurremo qui per chiarezza. Al contrario, ci limitiamo a eliminare la
distinzione tra "casuale" e "uniforme" nel contesto attuale.
Note
[2] Se si è interessati a un'esposizione più formale di questi argomenti, si può consultare Introduzione alla crittografia moderna di Katz e Lindell, in particolare il capitolo 3.
Fondamenti matematici della crittografia 2
Che cos'è la teoria dei numeri?
Questo capitolo tratta un argomento più avanzato delle basi matematiche della crittografia: la teoria dei numeri. Sebbene la teoria dei numeri sia importante per la crittografia simmetrica (come nel Cifrario Rijndael), è particolarmente importante nell'ambito della crittografia a chiave pubblica.
Se i dettagli della teoria dei numeri vi appesantiscono, vi consiglio una lettura di alto livello per la prima volta. Potrete sempre tornarci sopra in un secondo momento.
Si potrebbe definire la teoria dei numeri come lo studio delle proprietà dei numeri interi e delle funzioni matematiche che operano con i numeri interi.
Si consideri, ad esempio, che due numeri a e N sono coprimari (o primi relativi) se il loro massimo comune divisore è
uguale a 1. Supponiamo ora un particolare numero intero N. Quanti numeri interi più
piccoli di N sono coprimari
di N? Possiamo fare
affermazioni generali sulle risposte a questa domanda? Questi sono i tipici
tipi di domande a cui la teoria dei numeri cerca di rispondere.
La moderna teoria dei numeri si basa sugli strumenti dell'algebra astratta. Il campo dell'algebra astratta è una sottodisciplina della matematica in cui i principali oggetti di analisi sono oggetti astratti noti come strutture algebriche. Una struttura algebrica è un insieme di elementi abbinati a una o più operazioni, che soddisfa determinati assiomi. Attraverso le strutture algebriche, i matematici possono ottenere approfondimenti su specifici problemi matematici, astraendo dai loro dettagli.
Il campo dell'algebra astratta è talvolta chiamato anche algebra moderna. È possibile imbattersi anche nel concetto di matematica astratta (o matematica pura). Quest'ultimo termine non si riferisce all'algebra astratta, ma indica piuttosto lo studio della matematica in sé e per sé, non solo in vista di potenziali applicazioni.
Gli insiemi dell'algebra astratta possono trattare molti tipi di oggetti, dalle trasformazioni che preservano la forma di un triangolo equilatero ai modelli di carta da parati. Per la teoria dei numeri, consideriamo solo insiemi di elementi che contengono numeri interi o funzioni che lavorano con i numeri interi.
Gruppi
Un concetto fondamentale in matematica è quello di insieme di elementi. Un insieme è solitamente indicato da segni di riconoscimento con gli elementi separati da virgole.
Ad esempio, l'insieme di tutti i numeri interi è \{..., -2, -1, 0, 1, 2, ...\}. Le ellissi qui significano che un certo schema continua in una
particolare direzione. Quindi l'insieme di tutti i numeri interi comprende
anche 3, 4, 5, 6 e così via,
così come -3, -4, -5, -6 e
così via. Questo insieme di tutti i numeri interi è tipicamente indicato con \mathbb{Z}.
Un altro esempio di insieme è \mathbb{Z} \mod 11, ovvero l'insieme di tutti i numeri interi modulo 11. A differenza dell'intero
insieme \mathbb{Z},
questo insieme contiene solo un numero finito di elementi, ovvero \{0, 1, \ldots, 9, 10\}.
Un errore comune è pensare che l'insieme \mathbb{Z} \mod 11 sia in realtà \{-10, -9, \ldots, 0, \ldots, 9, 10\}. Ma non è questo il caso, dato il modo in cui abbiamo definito
l'operazione modulo in precedenza. Qualsiasi intero negativo ridotto con
modulo 11 si avvolge su \{0, 1, \ldots, 9, 10\}. Per esempio, l'espressione -2 \mod 11 si avvolge su 9, mentre
l'espressione -27 \mod 11 si
avvolge su 5.
Un altro concetto fondamentale della matematica è quello di operazione binaria. Si tratta di qualsiasi operazione che prende due elementi per produrne un terzo. Per esempio, dall'aritmetica e dall'algebra di base si conoscono le quattro operazioni binarie fondamentali: addizione, sottrazione, moltiplicazione e divisione.
Questi due concetti matematici di base, gli insiemi e le operazioni binarie, sono utilizzati per definire la nozione di gruppo, la struttura più essenziale dell'algebra astratta.
In particolare, supponiamo un'operazione binaria circ. Inoltre, supponiamo un insieme di elementi S dotato di
tale operazione. "Dotato" significa solo che l'operazione circ può essere eseguita tra due elementi qualsiasi dell'insieme S.
La combinazione \langle \mathbf{S}, \circ \rangle è, quindi, un gruppo se soddisfa quattro condizioni specifiche,
note come assiomi di gruppo.
Per ogni
aebche sono elementi di\mathbf{S},a \circ bè anche un elemento di\mathbf{S}. Questa è nota come condizione di chiusura.Per qualsiasi
a,becche siano elementi di\mathbf{S}, si ha che(a \circ b) \circ c = a \circ (b \circ c). Questa è nota come condizione di associabilità.Esiste un unico elemento
ein\mathbf{S}, tale che per ogni elementoain\mathbf{S}, vale la seguente equazione:e \circ a = a \circ e = a. Poiché esiste un solo elemento di questo tipo,eè chiamato elemento di identità. Questa condizione è nota come condizione di identità.Per ogni elemento
ain\mathbf{S}, esiste un elementobin\mathbf{S}, tale che la seguente equazione sia valida:a \circ b = b \circ a = e, doveeè l'elemento identità. L'elementobè noto come elemento inverso e viene comunemente indicato comea^{-1}. Questa condizione è nota come condizione inversa o condizione di invertibilità.
Esploriamo ulteriormente i gruppi. Si consideri l'insieme di tutti gli
interi con \mathbb{Z}. Questo insieme, combinato con l'addizione standard, ovvero \langle \mathbb{Z}, + \rangle, corrisponde chiaramente alla definizione di gruppo, in quanto soddisfa i
quattro assiomi di cui sopra.
Per ogni
xeyche sono elementi di\mathbb{Z}, anchex + yè un elemento di\mathbb{Z}. Quindi\langle \mathbb{Z}, + \ranglesoddisfa la condizione di chiusura.Per ogni
x,yezche sono elementi di\mathbb{Z},(x + y) + z = x + (y + z). Pertanto,\langle \mathbb{Z}, + \ranglesoddisfa la condizione di associatività.Esiste un elemento di identità in
\langle \mathbb{Z}, + \rangle, cioè0. Per qualsiasixin\mathbb{Z}, vale cioè che:0 + x = x + 0 = x. Quindi\langle \mathbb{Z}, + \ranglesoddisfa la condizione di identità.Infine, per ogni elemento
xin\mathbb{Z}, esiste unytale chex + y = y + x = 0. Sexfosse10, per esempio,ysarebbe-10(nel caso in cuixsia0, ancheyè0). Quindi\langle \mathbb{Z}, + \ranglesoddisfa la condizione inversa.
È importante notare che il fatto che l'insieme dei numeri interi con
l'addizione costituisca un gruppo non significa che costituisca un gruppo
con la moltiplicazione. Lo si può verificare testando \langle \mathbb{Z}, \cdot \rangle con i quattro assiomi di gruppo (dove \cdot significa moltiplicazione
standard).
I primi due assiomi sono ovviamente validi. Inoltre, in caso di
moltiplicazione, l'elemento 1 può fungere da elemento identità. Qualsiasi intero x moltiplicato per 1, produce x. Tuttavia, \langle \mathbb{Z}, \cdot \rangle non soddisfa la condizione inversa. Cioè, non esiste un elemento unico y in \mathbb{Z} per
ogni x in \mathbb{Z}, in modo
che x \cdot y = 1.
Per esempio, supponiamo che x = 22. Quale valore di y dell'insieme \mathbb{Z} moltiplicato per x darebbe
l'elemento identità 1? Il
valore 1/22 funzionerebbe, ma
non è compreso nell'insieme \mathbb{Z}. In
effetti, il problema si presenta per qualsiasi intero x, a parte i valori 1 e -1 (dove y dovrebbe essere rispett
Se ammettiamo i numeri reali per il nostro insieme, i problemi scompaiono in
gran parte. Per qualsiasi elemento x dell'insieme, la moltiplicazione per 1/x dà come risultato 1. Poiché
le frazioni sono incluse nell'insieme dei numeri reali, è possibile trovare un
inverso per ogni numero reale. L'eccezione è rappresentata dallo zero, in quanto
qualsiasi moltiplicazione con lo zero non produrrà mai l'elemento identità 1.
Quindi, l'insieme dei numeri reali non nulli dotati di moltiplicazione è effettivamente
un gruppo.
Alcuni gruppi soddisfano una quinta condizione generale, nota come condizione di commutatività. Questa condizione è la seguente:
- Supponiamo un gruppo
Gcon un insieme S e un operatore binariocirc. Supponiamo cheaebsiano elementi di S. Se si verifica chea \circ b = b \circ aper due qualsiasi elementiaebin S, alloraGsoddisfa la condizione di commutatività.
Ogni gruppo che soddisfa la condizione di commutatività è noto come gruppo commutativo, o gruppo abeliano (dal nome di Niels Henrik Abel). È facile verificare che sia l'insieme dei numeri reali per addizione sia l'insieme dei numeri interi per addizione sono gruppi abeliani. L'insieme dei numeri interi sulla moltiplicazione non è affatto un gruppo, quindi ipso facto non può essere un gruppo abeliano. L'insieme dei numeri reali non nulli sulla moltiplicazione, invece, è anch'esso un gruppo abeliano.
È necessario rispettare due importanti convenzioni sulla notazione. In primo luogo, i segni "+" o "×" saranno spesso utilizzati per simboleggiare le operazioni di gruppo, anche quando gli elementi non sono, di fatto, numeri. In questi casi, non bisogna interpretare questi segni come le normali addizioni o moltiplicazioni aritmetiche. Si tratta invece di operazioni che hanno solo una somiglianza astratta con le operazioni aritmetiche.
A meno che non ci si riferisca specificamente all'addizione o alla
moltiplicazione aritmetica, è più facile usare simboli come circ e diamond per le operazioni di
gruppo, poiché non hanno una connotazione culturalmente molto radicata.
In secondo luogo, per lo stesso motivo per cui "+" e "×" sono spesso
utilizzati per indicare operazioni non aritmetiche, gli elementi identitari
dei gruppi sono spesso simboleggiati con "0" e "1", anche quando gli
elementi di questi gruppi non sono numeri. A meno che non ci si riferisca
all'elemento identico di un gruppo con numeri, è più facile usare un simbolo
più neutro come "e" per
indicare l'elemento identico.
Molti insiemi di valori diversi e molto importanti in matematica, dotati di determinate operazioni binarie, sono gruppi. Le applicazioni crittografiche, tuttavia, funzionano solo con insiemi di numeri interi o almeno con elementi che sono descritti da numeri interi, cioè nel dominio della teoria dei numeri. Pertanto, gli insiemi di numeri reali diversi dai numeri interi non sono utilizzati nelle applicazioni crittografiche.
Concludiamo fornendo un esempio di elementi che possono essere "descritti da numeri interi", anche se non sono numeri interi. Un buon esempio sono i punti delle curve ellittiche. Sebbene qualsiasi punto di una curva ellittica non sia chiaramente un numero intero, un tale punto è effettivamente descritto da due numeri interi.
Le curve ellittiche sono, ad esempio, fondamentali per Bitcoin. Qualsiasi coppia di chiavi private e pubbliche standard di Bitcoin viene selezionata dall'insieme di punti definiti dalla seguente curva ellittica:
x^3 + 7 = y^2 \mod 2^{256} – 2^{32} – 29 – 28 – 27 – 26 - 24 - 1(il più grande numero primo inferiore a 2^{256}). La coordinata x è la
chiave privata e la coordinata y è la chiave pubblica.
Le transazioni in Bitcoin comportano tipicamente il blocco degli output a una o più chiavi pubbliche in qualche modo. Il valore di queste transazioni può poi essere sbloccato tramite firme digitali con le corrispondenti chiavi private.
Gruppi ciclici
Una distinzione importante che possiamo fare è tra un gruppo finito e un gruppo infinito. Il primo ha un numero finito di elementi, mentre il secondo ha un numero infinito di elementi. Il numero di elementi di un gruppo finito è noto come ordine del gruppo. Tutta la crittografia pratica che implica l'uso di gruppi si basa su gruppi finiti (numerici).
Nell'ambito della crittografia a chiave pubblica, una certa classe di gruppi abeliani finiti noti come gruppi ciclici è particolarmente importante. Per comprendere i gruppi ciclici, occorre innanzitutto capire il concetto di esponenziazione degli elementi del gruppo.
Supponiamo un gruppo G con
un'operazione di gruppo \circ e che a sia un elemento di G. L'espressione a^n va quindi interpretata come l'elemento a combinato con se stesso per un totale di n - 1 volte. Ad esempio, a^2 significa a \circ a, a^3 significa a \circ a \circ a,
e così via. (Si noti che l'esponenziazione in questo caso non è
necessariamente un'esponenziazione in senso aritmetico standard)
Facciamo un esempio. Supponiamo che G = \langle \mathbb{Z} \mod 7, + \rangle, e che il nostro valore per a sia uguale a 4. In questo
caso, a^2 = [4 + 4 \mod 7] = [8 \mod 7] = 1 \mod 7. In alternativa, a^4 rappresenterebbe [4 + 4 + 4 + 4 \mod 7] = [16 \mod 7] = 2 \mod 7.
Alcuni gruppi abeliani hanno uno o più elementi che possono generare tutti gli altri elementi del gruppo attraverso l'esponenziazione continua. Questi elementi sono chiamati generatori o elementi primitivi.
Un'importante classe di tali gruppi è quella dei \mathbb{Z}^* \mod N, \cdot \rangle, dove N è un numero primo.
La notazione \mathbb{Z}^* significa che il gruppo contiene tutti i numeri interi positivi non nulli
minori di N. Un gruppo di
questo tipo, quindi, ha sempre N - 1 elementi.
Consideriamo, ad esempio, G = \langle \mathbb{Z}^* \mod 11, \cdot \rangle. Questo gruppo ha i seguenti elementi: \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. L'ordine di questo gruppo è 10 (che è appunto uguale a 11 - 1).
Esploriamo l'esponenziazione dell'elemento 2 di questo gruppo. I calcoli
fino a 2^{12} sono mostrati
di seguito. Si noti che sul lato sinistro dell'equazione, l'esponente si riferisce
all'esponenziazione dell'elemento del gruppo. Nel nostro esempio particolare,
si tratta effettivamente di un'esponenziazione aritmetica sul lato destro dell'equazione
(ma potrebbe anche trattarsi, per esempio, di un'addizione). Per chiarire, ho
scritto l'operazione ripetuta, piuttosto che la forma dell'esponente sul lato
destro.
2^1 = 2 \mod 112^2 = 2 \cdot 2 \mod 11 = 4 \mod 112^3 = 2 \cdot 2 \cdot 2 \mod 11 = 8 \mod 112^4 = 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 16 \mod 11 = 52^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 32 \mod 11 = 102^6 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 64 \mod 11 = 92^7 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 128 \mod 11 = 72^8 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 256 \mod 11 = 32^9 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 512 \mod 11 = 62^{10} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 1024 \mod 11 = 12^{11} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 2048 \mod 11 = 22^{12} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 4096 \mod 11 = 4
Se si osserva attentamente, si può notare che l'esponenziazione
dell'elemento 2 attraversa
tutti gli elementi del \langle \mathbb{Z}^* \mod 11, \cdot \rangle nel seguente ordine: 2, 4, 8, 5, 10, 9, 7, 3, 6, 1. Dopo 2^{10},
l'esponenziazione continua dell'elemento 2 attraversa nuovamente tutti gli elementi nello stesso ordine. Quindi,
l'elemento 2 è un generatore
in \langle \mathbb{Z}^* \mod 11, \cdot \rangle.
Sebbene il \langle \mathbb{Z}^* \mod 11, \cdot \rangle abbia più generatori, non tutti gli elementi di questo gruppo sono
generatori. Consideriamo, ad esempio, l'elemento 3. Eseguendo le prime 10 esponenziazioni, senza mostrare
i complicati calcoli, si ottengono i seguenti risultati:
3^1 = 3 \mod 113^2 = 9 \mod 113^3 = 5 \mod 113^4 = 4 \mod 113^5 = 1 \mod 113^6 = 3 \mod 113^7 = 9 \mod 113^8 = 5 \mod 113^9 = 4 \mod 113^{10} = 1 \mod 11
Invece di scorrere tutti i valori in \langle \mathbb{Z}^* \mod 11, \cdot \rangle, l'esponenziazione dell'elemento 3 porta solo a un sottoinsieme di questi valori: 3, 9, 5, 4 e 1. Dopo la quinta
esponenziazione, questi valori iniziano a ripetersi.
Possiamo ora definire un gruppo ciclico come qualsiasi gruppo con almeno un generatore. Cioè, esiste almeno un elemento del gruppo dal quale è possibile produrre tutti gli altri elementi del gruppo attraverso l'esponenziazione.
Avrete notato nell'esempio precedente che sia 2^{10} che 3^{10} sono
uguali a 1 \mod 11. In
effetti, anche se non eseguiremo i calcoli, l'esponenziazione per 10 di qualsiasi elemento del gruppo \langle \mathbb{Z}^* \mod 11, \cdot \rangle darà come risultato 1 \mod 11. Perché è così?
Si tratta di una domanda importante, ma la risposta richiede un po' di lavoro.
Per iniziare, supponiamo due numeri interi positivi a e N. Un importante teorema
della teoria dei numeri afferma che a ha un inverso moltiplicativo modulo N (cioè un intero b tale che a \cdot b = 1 \mod N) se e
solo se il massimo comun divisore tra a e N è uguale a 1. Ovvero, se a e N sono coprimari.
Quindi, per qualsiasi gruppo di interi dotato di moltiplicazione modulo N, solo i coprimeri minori con N sono inclusi nell'insieme. Possiamo indicare questo insieme con \mathbb{Z}^c \mod N.
Ad esempio, supponiamo che N sia 10. Solo i numeri interi 1, 3, 7 e 9 sono coprimari di 10. Quindi l'insieme \mathbb{Z}^c \mod 10 include solo \{1, 3, 7, 9\}. Non
è possibile creare un gruppo con moltiplicazione intera modulo 10 usando altri numeri interi tra 1 e 10. Per questo particolare
gruppo, gli inversi sono le coppie 1 e 9 e 3 e 7.
Nel caso in cui N stesso sia
primo, tutti i numeri interi da 1 a N - 1 sono coprimari di N. Un gruppo di questo tipo
ha quindi un ordine di N - 1.
Utilizzando la notazione precedente, \mathbb{Z}^c \mod N equivale a \mathbb{Z}^* \mod N quando N è primo. Il gruppo
scelto per l'esempio precedente, \langle \mathbb{Z}^* \mod 11, \cdot \rangle, è un'istanza particolare di questa classe di gruppi.
Successivamente, la funzione \phi(N) calcola il numero di coprimi fino a un numero N, ed è nota come funzione Phi di Eulero. Secondo il teorema di Eulero, quando due numeri interi a e N sono coprimi, vale quanto
segue:
a^{\phi(N)} \mod N = 1 \mod N
Ciò ha un'importante implicazione per la classe di gruppi \langle \mathbb{Z}^* \mod N, \cdot \rangle dove N è primo. Per questi
gruppi, l'esponenziazione degli elementi del gruppo rappresenta
l'esponenziazione aritmetica. Cioè, a^{\phi(N)} \mod N rappresenta l'operazione aritmetica a^{\phi(N)} \mod N.
Poiché qualsiasi elemento a in questi gruppi moltiplicativi è coprimo con N, significa che a^{\phi(N)} \mod N = a^{N - 1} \mod N = 1 \mod N.
Il teorema di Eulero è un risultato molto importante. Per cominciare,
implica che tutti gli elementi del \langle \mathbb{Z}^* \mod N, \cdot \rangle possono passare attraverso un numero di valori per esponenziazione che si
divide in N - 1. Nel caso del \langle \mathbb{Z}^* \mod 11, \cdot \rangle, ciò significa che ogni elemento può percorrere solo 2, 5 o 10 elementi. Il gruppo di
valori attraverso i quali un elemento può passare attraverso
l'esponenziazione è noto come ordine dell'elemento. Un
elemento con un ordine equivalente all'ordine di un gruppo è un generatore.
Inoltre, il teorema di Eulero implica che possiamo sempre conoscere il
risultato di a^{N - 1} \mod N per qualsiasi gruppo \langle \mathbb{Z}^* \mod N, \cdot \rangle dove N è primo. Questo vale indipendentemente
dalla complessità dei calcoli effettivi.
Per esempio, supponiamo che il nostro gruppo sia \mathbb{Z}^* \mod 160,481,182 (dove 160,481,182 è
effettivamente un numero primo). Sappiamo che tutti gli interi da 1 a 160,481,181 devono essere
elementi di questo gruppo e che \phi(n) = 160,481,181. Anche
se non possiamo fare tutti i calcoli, sappiamo che espressioni come 514^{160,481,181}, 2,005^{160,481,181} e 256,212^{160,481,181} devono essere tutte valutate come 1 \mod 160,481,182.
Note:
[1] La funzione funziona come segue. Qualsiasi intero N può essere fattorizzato in un prodotto di primi. Supponiamo che un
particolare N sia
fattorizzato come segue: p_1^{e1} \cdot p_2^{e2} \cdot \ldots \cdot
p_m^{em} dove tutti i p sono numeri
primi e tutti gli e sono numeri
interi maggiori o uguali a 1. Allora:
\phi(N) = \sum_{i=1}^m \left[p_i^{e_i} - p_i^{e_i - 1}\right]Formula della funzione Phi di Eulero per la fattorizzazione dei primi di N.
Campi
Un gruppo è la struttura algebrica di base dell'algebra astratta, ma ne esistono molte altre. L'unica altra struttura algebrica con cui è necessario avere familiarità è quella di un campo, in particolare di un campo finito. Questo tipo di struttura algebrica è spesso utilizzata in crittografia, come ad esempio nell'Advanced Encryption Standard. Quest'ultimo è il principale schema di crittografia simmetrica che si incontra nella pratica.
Un campo deriva dalla nozione di gruppo. In particolare, un campo è un insieme di elementi S dotato di due operatori binari \circ e \diamond, che soddisfa le
seguenti condizioni:
L'insieme S dotato di
\circè un gruppo abeliano.L'insieme S dotato di
\diamondè un gruppo abeliano per gli elementi "non nulli".L'insieme S dotato dei due operatori soddisfa la cosiddetta condizione distributiva: Supponiamo che
a,becsiano elementi di S. Allora S dotato dei due operatori soddisfa la proprietà distributiva quandoa \circ (b \diamond c) = (a \circ b) \diamond (a \circ c).
Si noti che, come per i gruppi, la definizione di campo è molto astratta.
Non fa affermazioni sui tipi di elementi in S, né sulle
operazioni \circ e \diamond. Si limita ad
affermare che un campo è un qualsiasi insieme di elementi con due operazioni
per il quale valgono le tre condizioni di cui sopra. (L'elemento "zero" del
secondo gruppo abeliano può essere interpretato astrattamente)
Quale potrebbe essere un esempio di campo? Un buon esempio è l'insieme \mathbb{Z} \mod 7, ovvero \{0, 1, \ldots, 6\} definito su addizione standard (al posto del precedente \circ) e moltiplicazione
standard (al posto del precedente \diamond).
Innanzitutto, \mathbb{Z} \mod 7 soddisfa la condizione di gruppo abeliano per addizione, e soddisfa la condizione
di gruppo abeliano per moltiplicazione se si considerano solo gli elementi non
nulli. In secondo luogo, la combinazione dell'insieme con i due operatori soddisfa
la condizione distributiva.
È didatticamente utile esplorare queste affermazioni utilizzando alcuni
valori particolari. Prendiamo i valori sperimentali 5, 2 e 3, elementi scelti a caso
dall'insieme \mathbb{Z} \mod 7,
per ispezionare il campo \langle \mathbb{Z} \mod 7, +, \cdot \rangle. Utilizzeremo questi tre valori in ordine sparso, secondo le necessità,
per esplorare condizioni particolari.
Cerchiamo innanzitutto di capire se \mathbb{Z} \mod 7 dotato di addizione è un gruppo abeliano.
Condizione di chiusura: Prendiamo
5e2come valori. In questo caso,[5 + 2] \mod 7 = 7 \mod 7 = 0. Questo è effettivamente un elemento di\mathbb{Z} \mod 7, quindi il risultato è coerente con la condizione di chiusura.Condizione di associabilità: Prendiamo 5, 2 e 3 come valori. In questo caso,
[(5 + 2) + 3] \mod 7 = [5 + (2 + 3)] \mod 7 = 10 \mod 7 = 3. Questo è coerente con la condizione di associatività.Condizione di identità: Prendiamo 5 come valore. In questo caso,
[5 + 0] \mod 7 = [0 + 5] \mod 7 = 5. Quindi 0 sembra essere l'elemento di identità per l'addizione.Condizione inversa: Consideriamo l'inverso di 5. Deve verificarsi che
[5 + d] \mod 7 = 0, per qualche valore did. In questo caso, l'unico valore dimathbb{Z} \mod 7che soddisfa questa condizione è 2.Condizione di commutatività: Prendiamo 5 e 3 come valori. In questo caso,
[5 + 3] \mod 7 = [3 + 5] \mod 7 = 1. Questo è coerente con la condizione di commutatività.
L'insieme \mathbb{Z} \mod 7 dotato di addizione appare chiaramente come un gruppo abeliano. Vediamo ora
se \mathbb{Z} \mod 7 dotato
di moltiplicazione è un gruppo abeliano per tutti gli elementi non nulli.
Condizione di chiusura: Prendiamo 5 e 2 come valori. In questo caso,
[5 \cdot 2] \mod 7 = 10 \mod 7 = 3. Anche questo è un elemento dimathbb{Z} \mod 7, quindi il risultato è coerente con la condizione di chiusura.Condizione di associabilità: Prendiamo 5, 2 e 3 come valori. In questo caso,
[(5 \cdot 2) \cdot 3] \mod 7 = [5 \cdot (2 \cdot 3)] \mod 7 = 30 \cdot 7 = 2. Questo è coerente con la condizione di associatività.Condizione di identità: Prendiamo 5 come valore. In questo caso,
[5 \cdot 1] \mod 7 = [1 \cdot 5] \mod 7 = 5. Quindi 1 sembra essere l'elemento di identità per la moltiplicazione.Condizione inversa: Consideriamo l'inverso di
5. Deve essere il caso che[5 \cdot d] \mod 7 = 1, per qualche valore did. L'unico valore di\mathbb{Z} \mod 7che soddisfa questa condizione è3. Questo è coerente con la condizione inversa.Condizione di commutatività: Prendiamo 5 e 3 come valori. In questo caso,
[5 \cdot 3] \mod 7 = [3 \cdot 5] \mod 7 = 15 \mod 7 = 1. Questo è coerente con la condizione di commutatività.
L'insieme \mathbb{Z} \mod 7 sembra chiaramente soddisfare le regole per essere un gruppo abeliano se combinato
con l'addizione o la moltiplicazione sugli elementi non nulli.
Infine, questo insieme combinato con entrambi gli operatori sembra
soddisfare la condizione distributiva. Prendiamo 5, 2 e 3 come valori.
Vediamo che [5 \cdot (2 + 3)] \mod 7 = [5 \cdot 2 + 5 \cdot 3] \mod 7 = 25 \mod 7 = 4.
Abbiamo visto che \mathbb{Z} \mod 7 dotato di addizione e moltiplicazione soddisfa gli assiomi per un campo finito
quando viene testato con valori particolari. Naturalmente possiamo anche dimostrarlo
in generale, ma non lo faremo qui.
Una distinzione fondamentale è tra due tipi di campi: campi finiti e campi infiniti.
Un campo infinito è un campo in cui l'insieme S è infinitamente grande. L'insieme dei numeri reali \mathbb{R} dotato di addizione e moltiplicazione è un esempio di campo infinito. Un campo finito, noto anche come campo di Galois, è un campo in cui l'insieme S è finito. L'esempio precedente del \langle \mathbb{Z} \mod 7, +, \cdot \rangle è un campo finito.
In crittografia, siamo principalmente interessati ai campi finiti. In
generale, si può dimostrare che un campo finito esiste per un certo insieme
di elementi S se e solo se ha p^m elementi, dove p è un numero
primo e m un intero positivo
maggiore o uguale a uno. In altre parole, se l'ordine di un insieme S è un numero primo (p^m dove m = 1) o una potenza prima (p^m dove m > 1), è possibile
trovare due operatori \circ e \diamond tali da soddisfare le
condizioni per un campo.
Se un campo finito ha un numero di elementi primi, si chiama campo primo. Se il numero di elementi del campo finito è una potenza prima, allora il campo è chiamato campo di estensione. In crittografia, siamo interessati sia ai campi primi che a quelli di estensione. [2]
I principali campi primi di interesse per la crittografia sono quelli in cui
l'insieme di tutti i numeri interi è modulato da qualche numero primo e gli
operatori sono l'addizione e la moltiplicazione standard. Questa classe di
campi finiti comprende \mathbb{Z} \mod 2, \mathbb{Z} \mod 3, \mathbb{Z} \mod 5, \mathbb{Z} \mod 7, \mathbb{Z} \mod 11, \mathbb{Z} \mod 13,
e così via. Per qualsiasi campo primo \mathbb{Z} \mod p,
l'insieme dei numeri interi del campo è il seguente: \{0, 1, \ldots, p - 2, p - 1\}.
In crittografia, ci interessano anche i campi di estensione, in particolare
i campi con 2^m elementi dove m > 1. Tali campi finiti sono
utilizzati, ad esempio, nel cifrario Rijndael, che costituisce la base
dell'Advanced Encryption Standard. Mentre i campi primi sono relativamente
intuitivi, questi campi di estensione in base 2 non sono probabilmente
adatti a chi non ha familiarità con l'algebra astratta.
Per cominciare, è vero che a qualsiasi insieme di interi con 2^m elementi si possono assegnare due operatori che rendono la loro combinazione
un campo (purché m sia un intero
positivo). Tuttavia, il fatto che un campo esista non significa necessariamente
che sia facile da scoprire o particolarmente pratico per certe applicazioni.
Come si è visto, i campi di estensione di 2^m particolarmente applicabili in crittografia sono quelli definiti su particolari
insiemi di espressioni polinomiali, piuttosto che su un insieme di numeri interi.
Per esempio, supponiamo di volere un campo di estensione con 2^3 (cioè 8) elementi
nell'insieme. Sebbene esistano molti insiemi diversi che possono essere
utilizzati per campi di queste dimensioni, uno di questi include tutti i
polinomi unici della forma a_2x^2 + a_1x + a_0, dove
ogni coefficiente a_i è 0 o 1. Quindi, questo insieme S include i seguenti elementi:
0: Il caso in cuia_2 = 0,a_1 = 0ea_0 = 0.1: Il caso in cuia_2 = 0,a_1 = 0ea_0 = 1.x: Il caso in cuia_2 = 0,a_1 = 1ea_0 = 0.x + 1: Il caso in cuia_2 = 0,a_1 = 1ea_0 = 1.x^2: Il caso in cuia_2 = 1,a_1 = 0ea_0 = 0.x^2 + 1: Il caso in cuia_2 = 1,a_1 = 0ea_0 = 1.x^2 + x: Il caso in cuia_2 = 1,a_1 = 1ea_0 = 0.x^2 + x + 1: Il caso in cuia_2 = 1,a_1 = 1ea_0 = 1.
Quindi S sarebbe l'insieme {0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1}. Quali operazioni si possono definire su questo insieme di elementi per
garantire che la loro combinazione sia un campo?
La prima operazione sull'insieme S (\circ) può essere definita come una normale addizione di polinomi modulo 2. Tutto ciò che si deve fare
è sommare i polinomi come si farebbe normalmente e poi applicare il modulo 2 a ciascun coefficiente risultante. Tutto ciò che si deve fare è sommare i
polinomi come si farebbe normalmente, e poi applicare il modulo 2 a ciascuno dei coefficienti
del polinomio risultante. Ecco alcuni esempi:
[(x^2) + (x^2 + x + 1)] \mod 2 = [2x^2 + x + 1] \mod 2 = x + 1[(x^2 + x) + (x)] \mod 2 = [x^2 + 2x] \mod 2 = x^2[(x + 1) + (x^2 + x + 1)] \mod 2 = [x^2 + 2x + 2] \mod 2 = x^2 + 1
La seconda operazione sull'insieme S (\diamond), necessaria per creare il campo, è più complicata. È una sorta di
moltiplicazione, ma non la moltiplicazione standard dell'aritmetica. Bisogna
invece vedere ogni elemento come un vettore e intendere l'operazione come la
moltiplicazione di questi due vettori modulo un polinomio irriducibile.
Per prima cosa parliamo dell'idea di polinomio irriducibile. Un polinomio irriducibile è un polinomio che non può essere fattorizzato (così come un numero primo non può essere fattorizzato in componenti diverse da 1 e dal numero primo stesso). Per i nostri scopi, siamo interessati ai polinomi irriducibili rispetto all'insieme di tutti i numeri interi. (Si noti che si può essere in grado di fattorizzare alcuni polinomi, ad esempio con i numeri reali o complessi, anche se non è possibile farlo con i numeri interi)
Ad esempio, si consideri il polinomio x^2 - 3x + 2. Questo può essere riscritto come (x - 1)(x - 2). Quindi, non è
irriducibile. Consideriamo ora il polinomio x^2 + 1. Utilizzando solo
numeri interi, non c'è modo di fattorizzare ulteriormente questa
espressione. Si tratta quindi di un polinomio irriducibile rispetto agli
interi.
Passiamo ora al concetto di moltiplicazione vettoriale. Non approfondiremo questo argomento, ma è sufficiente comprendere una regola di base: Qualsiasi divisione vettoriale può avvenire a condizione che il dividendo abbia un grado superiore o uguale a quello del divisore. Se il dividendo ha un grado inferiore a quello del divisore, allora il dividendo non può più essere diviso per il divisore.
Ad esempio, si consideri l'espressione x^6 + x + 1 \mod x^5 + x^2. Questa chiaramente si riduce ulteriormente, poiché il grado del
dividendo, 6, è maggiore del grado del divisore, 5. Consideriamo ora
l'espressione x^5 + x + 1 \mod x^5 + x^2.
Anche questa si riduce ulteriormente, poiché il grado del dividendo, 5, e
del divisore, 5, sono uguali.
Tuttavia, consideriamo ora l'espressione x^4 + x + 1 \mod x^5 + x^2. Questa espressione non si riduce ulteriormente, poiché il grado del
dividendo, 4, è inferiore al
grado del divisore, 5.
Sulla base di queste informazioni, siamo ora pronti a trovare la nostra
seconda operazione per l'insieme \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.
Ho già detto che la seconda operazione deve essere intesa come una moltiplicazione vettoriale modulo qualche polinomio irriducibile. Questo polinomio irriducibile dovrebbe garantire che la seconda operazione definisca un gruppo abeliano su S e sia coerente con la condizione distributiva. Quale dovrebbe essere questo polinomio irriducibile?
Poiché tutti i vettori dell'insieme sono di grado 2 o inferiore, il polinomio irriducibile deve essere di grado 3. Se qualsiasi moltiplicazione di due vettori dell'insieme produce un polinomio di grado 3 o superiore, sappiamo che modulo un polinomio di grado 3 produce sempre un polinomio di grado 2 o inferiore. Questo perché qualsiasi polinomio di grado 3 o superiore è sempre divisibile per un polinomio di grado 3. Inoltre, il polinomio che funge da divisore deve essere irriducibile.
Si scopre che esistono diversi polinomi irriducibili di grado 3 che potremmo
usare come divisore. Ognuno di questi polinomi definisce un campo diverso in
combinazione con il nostro insieme S e l'addizione modulo
2. Questo significa che si hanno più opzioni quando si usa il campo di
estensione 2^m in
crittografia. Ciò significa che si hanno diverse opzioni quando si
utilizzano i campi di estensione 2^m in crittografia.
Per il nostro esempio, supponiamo di scegliere il polinomio x^3 + x + 1. Questo polinomio è irriducibile, perché non può essere fattorizzato con i
numeri interi. Inoltre, garantisce che qualsiasi moltiplicazione di due
elementi produca un polinomio di grado 2 o inferiore.
Vediamo un esempio della seconda operazione utilizzando il polinomio x^3 + x + 1 come divisore per illustrarne il funzionamento. Supponiamo di moltiplicare
gli elementi x^2 + 1 con x^2 + x nel nostro insieme S. Dobbiamo quindi calcolare
l'espressione [(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1. Questa operazione può essere semplificata come segue:
[(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1 =[x^2 \cdot x^2 + x^2 \cdot x + 1 \cdot x^2 + 1 \cdot x] \mod x^3 + x + 1 =[x^4 + x^3 + x^2 + x] \mod x^3 + x + 1
Sappiamo che [x^4 + x^3 + x^2 + x] \mod x^3 + x + 1 può essere ridotto poiché il dividendo ha un grado superiore (4) rispetto al
divisore (3).
Per cominciare, si può notare che l'espressione x^3 + x + 1 entra in x^4 + x^3 + x^2 + x per un totale di x volte. Lo
si può verificare moltiplicando x^3 + x + 1 per x, che è x^4 + x^2 + x. Poiché
quest'ultimo termine ha lo stesso grado del dividendo, cioè 4, sappiamo che
funziona. È possibile calcolare il resto di questa divisione per x come segue:
[(x^4 + x^3 + x^2 + x) - (x^4 + x^2 + x)] \mod (x^3 + x + 1) =[x^3] \mod (x^3 + x + 1) =x^3
Quindi, dopo aver diviso x^4 + x^3 + x^2 + x per x^3 + x + 1 per un totale
di x volte, abbiamo un resto
di x^3. È possibile dividerlo
ulteriormente per x^3 + x + 1?
Intuitivamente, potrebbe essere interessante dire che x^3 non può più essere diviso per x^3 + x + 1, perché
quest'ultimo termine sembra più grande. Tuttavia, ricordiamo la nostra
discussione sulla divisione vettoriale. Finché il dividendo ha un grado
maggiore o uguale al divisore, l'espressione può essere ulteriormente
ridotta. In particolare, l'espressione x^3 + x + 1 può entrare in x^3 esattamente
1 volta. Il resto si calcola come segue:
[(x^3) - (x^3 + x + 1)] \mod x^3 + x + 1 = [x + 1] \mod x^3 + x + 1 = x + 1Ci si potrebbe chiedere perché (x^3) - (x^3 + x + 1) valuti x + 1 e non -x - 1. Ricordiamo che la
prima operazione del nostro campo è definita modulo 2. Quindi, la
sottrazione di due vettori dà esattamente lo stesso risultato dell'addizione
di due vettori.
Riassumiamo la moltiplicazione di x^2 + 1 e x^2 + x: Moltiplicando
questi due termini, si ottiene un polinomio di grado 4, x^4 + x^3 + x^2 + x, che deve
essere ridotto modulo x^3 + x + 1. Il polinomio di
grado 4 è divisibile per x^3 + x + 1 esattamente x + 1 volte. Il
resto dopo aver diviso x^4 + x^3 + x^2 + x per x^3 + x + 1 esattamente x + 1 volte è x + 1. Questo è
infatti un elemento del nostro insieme {0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1}.
Perché i campi di estensione con base 2 su insiemi di polinomi, come nell'esempio precedente, sarebbero utili per la crittografia? Il motivo è che è possibile vedere i coefficienti dei polinomi di tali insiemi, 0 o 1, come elementi di stringhe binarie con una particolare lunghezza. L'insieme S dell'esempio precedente, ad esempio, potrebbe essere visto come un insieme S che include tutte le stringhe binarie di lunghezza 3 (da 000 a 111). Le operazioni su S, quindi, possono essere utilizzate anche per eseguire operazioni su queste stringhe binarie e produrre una stringa binaria della stessa lunghezza.
Note:
[2] I campi di estensione diventano molto controintuitivi. Invece di avere elementi di numeri interi, hanno insiemi di polinomi. Inoltre, tutte le operazioni vengono eseguite in modulo di un polinomio irriducibile.
Algebra astratta in pratica
Nonostante il linguaggio formale e l'astrattezza della discussione, il concetto di gruppo non dovrebbe essere troppo difficile da afferrare. Si tratta semplicemente di un insieme di elementi insieme a un'operazione binaria, dove l'esecuzione di tale operazione binaria su tali elementi soddisfa quattro condizioni generali. Un gruppo abeliano ha solo una condizione in più, nota come commutatività. Un gruppo ciclico, a sua volta, è un tipo speciale di gruppo abeliano, cioè quello che ha un generatore. Un campo è semplicemente un costrutto più complesso della nozione di gruppo di base.
Ma se siete persone inclini alla pratica, a questo punto potreste chiedervi: Chi se ne frega? Sapere che un insieme di elementi con un operatore è un gruppo, o anche un gruppo abeliano o ciclico, ha qualche rilevanza nel mondo reale? Sapere che qualcosa è un campo?
Senza entrare troppo nei dettagli, la risposta è "sì". I gruppi furono creati per la prima volta nel XIX secolo dal matematico francese Evariste Galois. Egli li utilizzò per trarre conclusioni sulla risoluzione di equazioni polinomiali di grado superiore a cinque.
Da allora il concetto di gruppo ha contribuito a far luce su una serie di problemi in matematica e altrove. Sulla loro base, ad esempio, il fisico Murray-Gellman è stato in grado di prevedere l'esistenza di una particella prima che fosse effettivamente osservata negli esperimenti. [3] Per un altro esempio, i chimici utilizzano la teoria dei gruppi per classificare le forme delle molecole. I matematici hanno persino utilizzato il concetto di gruppo per trarre conclusioni su qualcosa di così concreto come la carta da parati!
In sostanza, dimostrare che un insieme di elementi con un certo operatore è un gruppo significa che ciò che si sta descrivendo ha una particolare simmetria. Non una simmetria nel senso comune del termine, ma in una forma più astratta. E questo può fornire intuizioni sostanziali su sistemi e problemi particolari. Le nozioni più complesse dell'algebra astratta forniscono solo informazioni aggiuntive.
Soprattutto, vedrete l'importanza dei gruppi e dei campi della teoria dei numeri nella pratica attraverso la loro applicazione nella crittografia, in particolare nella crittografia a chiave pubblica. Nella nostra discussione sui campi abbiamo già visto, ad esempio, come i campi di estensione siano impiegati nel Cifrario Rijndael. Questo esempio verrà elaborato nel Capitolo 5.
Per ulteriori discussioni sull'algebra astratta, raccomando l'eccellente serie di video sull'algebra astratta di Socratica. [4] In particolare raccomando i seguenti video: "Cos'è l'algebra astratta?", "Definizione di gruppo (estesa)", "Definizione di anello (estesa)" e "Definizione di campo (estesa)" Questi quattro video vi daranno una visione aggiuntiva di gran parte della discussione precedente. (Non abbiamo parlato degli anelli, ma un campo è solo un tipo speciale di anello)
Per approfondire la teoria moderna dei numeri, è possibile consultare molte discussioni avanzate sulla crittografia. Per ulteriori approfondimenti, suggerisco l'Introduzione alla crittografia moderna di Jonathan Katz e Yehuda Lindell o il libro Understanding Cryptography di Christof Paar e Jan Pelzl. [5]
Note:
[3] Vedere Video YouTube
[4] Socratica, Algebra astratta
[5] Katz e Lindell, Introduzione alla crittografia moderna, 2a ed., 2015 (CRC Press: Boca Raton, FL). Paar e Pelzl, Understanding Cryptography, 2010 (Springer-Verlag: Berlino).
Crittografia simmetrica
Alice e Bob
Uno dei due rami principali della crittografia è la crittografia simmetrica. Essa comprende schemi di crittografia e schemi di autenticazione e integrità. Fino agli anni '70, tutta la crittografia consisteva in schemi di crittografia simmetrica.
La discussione principale inizia esaminando gli schemi di crittografia simmetrica e facendo la distinzione cruciale tra cifrari a flusso e cifrari a blocchi. Si passa poi ai codici di autenticazione dei messaggi, che sono schemi per garantire l'integrità e l'autenticità dei messaggi. Infine, esploriamo come gli schemi di crittografia simmetrica e i codici di autenticazione dei messaggi possano essere combinati per garantire una comunicazione sicura.
In questo capitolo vengono discussi di sfuggita vari schemi di crittografia simmetrica. Il capitolo successivo offre un'esposizione dettagliata della crittografia con un cifrario a flusso e un cifrario a blocchi, rispettivamente RC4 e AES.
Prima di iniziare la discussione sulla crittografia simmetrica, vorrei fare alcune brevi osservazioni sulle illustrazioni di Alice e Bob in questo e nei capitoli successivi.
Nell'illustrare i principi della crittografia, ci si basa spesso su esempi che coinvolgono Alice e Bob. Lo farò anch'io.
Soprattutto se si è alle prime armi con la crittografia, è importante rendersi conto che questi esempi di Alice e Bob servono solo a illustrare i principi e le costruzioni crittografiche in un ambiente semplificato. I principi e le costruzioni, tuttavia, sono applicabili a una gamma molto più ampia di contesti reali.
Di seguito sono riportati cinque punti chiave da tenere a mente sugli esempi che coinvolgono Alice e Bob nella crittografia:
Possono essere facilmente tradotti in esempi con altri tipi di attori, come aziende o organizzazioni governative.
Possono essere facilmente estesi per includere tre o più attori.
Negli esempi, Bob e Alice sono tipicamente partecipanti attivi nella creazione di ogni messaggio e nell'applicazione degli schemi crittografici a quel messaggio. Ma in realtà le comunicazioni elettroniche sono in gran parte automatizzate. Quando si visita un sito Web che utilizza la sicurezza del livello di trasporto, ad esempio, la crittografia è in genere gestita dal computer e dal server Web.
Nel contesto della comunicazione elettronica, i "messaggi" inviati attraverso un canale di comunicazione sono solitamente pacchetti TCP/IP. Questi possono appartenere a un'e-mail, a un messaggio di Facebook, a una conversazione telefonica, a un trasferimento di file, a un sito web, a un caricamento di software e così via. Non sono messaggi nel senso tradizionale del termine. Tuttavia, i crittografi spesso semplificano questa realtà affermando che il messaggio è, ad esempio, un'e-mail.
Gli esempi si concentrano in genere sulla comunicazione elettronica, ma possono essere estesi anche alle forme di comunicazione tradizionali, come le lettere.
Schemi di crittografia simmetrica
Possiamo definire in modo approssimativo uno schema di crittografia simmetrica come qualsiasi schema crittografico con tre algoritmi:
Un algoritmo di generazione di chiavi, che genera una chiave privata.
Un algoritmo di cifratura che prende in ingresso la chiave privata e un testo in chiaro e produce un testo cifrato.
Un algoritmo di decrittazione che prende in ingresso la chiave privata e il testo cifrato e restituisce il testo in chiaro originale.
In genere uno schema di crittografia - simmetrico o asimmetrico - offre un modello di crittografia basato su un algoritmo di base, piuttosto che una specifica esatta.
Ad esempio, consideriamo Salsa20, uno schema di crittografia simmetrica. Può essere utilizzato con chiavi di lunghezza pari a 128 e 256 bit. La scelta della lunghezza della chiave influisce su alcuni dettagli minori dell'algoritmo (per l'esattezza, il numero di cicli dell'algoritmo).
Ma non si può dire che utilizzare Salsa20 con una chiave a 128 bit sia uno schema di crittografia diverso da Salsa20 con una chiave a 256 bit. L'algoritmo di base rimane lo stesso. Solo quando l'algoritmo di base cambia si può parlare di due schemi di crittografia diversi.
Gli schemi di crittografia simmetrica sono tipicamente utili in due tipi di casi: (1) quelli in cui due o più agenti comunicano a distanza e vogliono mantenere segreto il contenuto delle loro comunicazioni; e (2) quelli in cui un agente vuole mantenere segreto il contenuto di un messaggio nel tempo.
Una rappresentazione della situazione (1) è riportata nella Figura 1 qui sotto. Bob vuole inviare un messaggio M ad Alice a distanza, ma non
vuole che altri possano leggerlo.
Bob cripta prima il messaggio M con la chiave privata K.
Quindi invia il testo cifrato C ad Alice. Una volta ricevuto il testo cifrato, Alice può decifrarlo
utilizzando la chiave K e
leggere il testo in chiaro. Con un buon schema di crittografia, qualsiasi
aggressore che intercetti il testo cifrato C non dovrebbe essere in grado di apprendere nulla di veramente significativo
sul messaggio M.
Una rappresentazione della situazione (2) è riportata nella Figura 2 qui sotto. Bob vuole impedire ad altri di visualizzare determinate informazioni. Una situazione tipica potrebbe essere quella di un dipendente che memorizza sul suo computer dati sensibili che non devono essere letti né da estranei né dai suoi colleghi.
Bob cripta il messaggio M al
tempo T_0 con la chiave K per produrre il testo cifrato C. Al tempo T_1 ha bisogno di nuovo del messaggio e decifra il testo cifrato C con la chiave K. Qualsiasi
aggressore che nel frattempo si sia imbattuto nel testo cifrato C non dovrebbe essere in grado di dedurne nulla di significativo su M.
Figura 1: Segretezza nello spazio

Figura 2: Segretezza nel tempo

Un esempio: Il cifrario a turni
Nel Capitolo 2 abbiamo incontrato il cifrario a turni, che è un esempio di schema di crittografia simmetrica molto semplice. Riportiamolo qui di seguito.
Supponiamo un dizionario D che equipara tutte le lettere
dell'alfabeto inglese, in ordine, con l'insieme di numeri {0,1,2,\dots,25}.
Si supponga un insieme di possibili messaggi M. Il cifrario
a turni è quindi uno schema di crittografia definito come segue:
- Selezionare casualmente una chiave
kdall'insieme delle possibili chiavi K, dove K ={0,1,2,\dots,25}. - Crittografare un messaggio
m \inM, come segue:- Separare
mnelle sue singole letterem_0, m_1, \dots, m_i, \dots, m_l - Convertire ogni
m_iin un numero secondo D - Per ogni
m_i,c_i = [(m_i + k) \mod 26] - Convertire ogni
c_iin una lettera secondo D - Quindi, combinando
c_0, c_1, \dots, c_lsi ottiene il testo cifratoc
- Separare
- Decifrare un testo cifrato
ccome segue:- Convertire ogni
c_iin un numero secondo D - Per ogni
c_i,m_i = [(c_i - k) \mod 26] - Convertire ogni
m_iin una lettera secondo D - Quindi combinare
m_0, m_1, \dots, m_lper ottenere il messaggio originalem
- Convertire ogni
Ciò che rende il cifrario a turni uno schema di crittografia simmetrica è che la stessa chiave viene utilizzata sia per il processo di crittografia che per quello di decrittografia. Per esempio, supponiamo di voler criptare il messaggio "DOG" utilizzando il cifrario a turni e di aver scelto a caso "24" come chiave. Cifrando il messaggio con questa chiave si otterrebbe "BME". L'unico modo per recuperare il messaggio originale è utilizzare la stessa chiave, "24", per il processo di decifrazione.
Questo cifrario Shift è un esempio di cifrario di sostituzione monoalfabetico: uno schema di crittografia in cui l'alfabeto del testo cifrato è fisso (cioè viene utilizzato un solo alfabeto). Assumendo che l'algoritmo di decifrazione sia deterministico, ogni simbolo del testo cifrato di sostituzione può corrispondere al massimo a un simbolo del testo in chiaro.
Fino al 1700, molte applicazioni di crittografia si basavano su cifrari monoalfabetici di sostituzione, anche se spesso erano molto più complessi del cifrario Shift. Si poteva, ad esempio, selezionare a caso una lettera dell'alfabeto per ogni lettera del testo originale, con il vincolo che ogni lettera ricorresse una sola volta nell'alfabeto del testo cifrato. Ciò significa che si avrebbe un fattoriale di 26 possibili chiavi private, un numero enorme nell'era dei precomputer.
Si noti che nella crittografia si incontra spesso il termine cipher. Sappiate che questo termine ha diversi significati. In effetti, conosco almeno cinque significati distinti del termine nell'ambito della crittografia.
In alcuni casi si riferisce a uno schema di crittografia, come nel caso del cifrario a turni e del cifrario a sostituzione monoalfabetica. Tuttavia, il termine può anche riferirsi specificamente all'algoritmo di crittografia, alla chiave privata o semplicemente al testo cifrato di uno schema di crittografia.
Infine, il termine cifrario può anche riferirsi a un algoritmo di base a partire dal quale è possibile costruire schemi crittografici. Questi possono includere vari algoritmi di crittografia, ma anche altri tipi di schemi crittografici. Questa accezione del termine diventa rilevante nel contesto dei cifrari a blocchi (si veda la sezione "Cifrari a blocchi").
Potreste anche imbattervi nei termini enciclare o decifrare. Questi termini non sono altro che sinonimi di crittografia e decrittografia.
Attacchi di forza bruta e principio di Kerckhoff
Il cifrario a turni è uno schema di crittografia simmetrica molto insicuro, almeno nel mondo moderno. [1] Un aggressore potrebbe semplicemente tentare di decifrare qualsiasi testo cifrato con tutte le 26 chiavi possibili per vedere quale risultato ha senso. Questo tipo di attacco, in cui l'attaccante si limita a scorrere le chiavi per vedere quale funziona, è noto come attacco di forza o ricerca esaustiva di chiavi.
Affinché un sistema di crittografia soddisfi una nozione minima di sicurezza, deve avere un insieme di chiavi possibili, o spazio delle chiavi, talmente ampio da rendere impraticabili gli attacchi di forza bruta. Tutti i moderni schemi di crittografia soddisfano questo standard. È noto come principio dello spazio chiave sufficiente. Un principio simile si applica in genere a diversi tipi di schemi crittografici.
Per avere un'idea delle enormi dimensioni dello spazio delle chiavi nei
moderni schemi di crittografia, supponiamo che un file sia stato
crittografato con una chiave a 128 bit utilizzando lo standard di
crittografia avanzato. Ciò significa che un attaccante dispone di una serie
di chiavi da 2^{128} che deve scorrere per un attacco a forza bruta. Per avere una probabilità di
successo dello 0,78% con questa strategia, l'attaccante dovrebbe utilizzare
circa 2,65 volte 10^{36} chiavi.
Supponiamo ottimisticamente che un attaccante possa tentare 10^{16} chiavi al secondo (cioè 10 quadrilioni di chiavi al secondo). Per testare lo
0,78% di tutte le chiavi nello spazio delle chiavi, il suo attacco dovrebbe
durare 2,65 ´times 10^{20} secondi. Ciò
equivale a circa 8,4 trilioni di anni. Quindi anche un attacco a forza bruta
da parte di un avversario assurdamente potente non è realistico con un moderno
schema di crittografia a 128 bit. Questo è il principio dello spazio sufficiente
per le chiavi.
Il cifrario a turni è più sicuro se l'attaccante non conosce l'algoritmo di crittografia? Forse, ma non di molto.
In ogni caso, la crittografia moderna presuppone sempre che la sicurezza di qualsiasi schema di crittografia simmetrica si basi solo sul mantenimento del segreto della chiave privata. Si presume sempre che l'attaccante conosca tutti gli altri dettagli, tra cui lo spazio dei messaggi, lo spazio delle chiavi, lo spazio dei testi cifrati, l'algoritmo di selezione delle chiavi, l'algoritmo di crittografia e l'algoritmo di decrittografia.
L'idea che la sicurezza di uno schema di crittografia simmetrica possa basarsi solo sulla segretezza della chiave privata è nota come principio di Kerckhoffs.
Secondo le intenzioni originarie di Kerckhoffs, il principio si applica solo agli schemi di crittografia simmetrica. Una versione più generale del principio, tuttavia, si applica anche a tutti gli altri tipi di schemi crittografici moderni: Non è necessario che il progetto di uno schema crittografico sia segreto perché sia sicuro; la segretezza può estendersi solo ad alcune stringhe di informazioni, tipicamente una chiave privata.
Il principio di Kerckhoffs è centrale nella crittografia moderna per quattro motivi. [2] In primo luogo, esiste solo un numero limitato di schemi crittografici per particolari tipi di applicazioni. Ad esempio, la maggior parte delle moderne applicazioni di crittografia simmetrica utilizza il cifrario Rijndael. Quindi la segretezza sulla progettazione di uno schema è molto limitata. È invece molto più flessibile mantenere segreta una chiave privata per il cifrario Rijndael.
In secondo luogo, è più facile sostituire una stringa di informazioni che un intero schema crittografico. Supponiamo che i dipendenti di un'azienda abbiano tutti lo stesso software di crittografia e che ogni due dipendenti abbiano una chiave privata per comunicare in modo riservato. La compromissione delle chiavi è una seccatura in questo scenario, ma almeno l'azienda potrebbe conservare il software con tali violazioni della sicurezza. Se l'azienda si affidasse alla segretezza dello schema, qualsiasi violazione di tale segretezza richiederebbe la sostituzione di tutto il software.
In terzo luogo, il principio di Kerckhoffs consente la standardizzazione e la compatibilità tra gli utenti degli schemi crittografici. Ciò comporta enormi vantaggi in termini di efficienza. Ad esempio, è difficile immaginare come milioni di persone possano connettersi in modo sicuro ai server web di Google ogni giorno, se per garantire la sicurezza è necessario mantenere segreti gli schemi crittografici.
In quarto luogo, il principio di Kerckhoff consente il controllo pubblico degli schemi crittografici. Questo tipo di controllo è assolutamente necessario per ottenere schemi crittografici sicuri. Ad esempio, il principale algoritmo della crittografia simmetrica, il cifrario Rijndael, è stato il risultato di un concorso organizzato dal National Institute of Standards and Technology tra il 1997 e il 2000.
Qualsiasi sistema che tenta di raggiungere la sicurezza per oscurità è un sistema che si basa sul mantenere segreti i dettagli della sua progettazione e/o implementazione. In crittografia, questo sarebbe specificamente un sistema che si basa sul mantenere segreti i dettagli del progetto dello schema crittografico. La sicurezza per oscurità è quindi in diretto contrasto con il principio di Kerckhoff.
La capacità dell'apertura di rafforzare la qualità e la sicurezza si estende anche al mondo digitale in modo più ampio rispetto alla sola crittografia. Le distribuzioni Linux libere e open source come Debian, ad esempio, presentano generalmente numerosi vantaggi rispetto alle controparti Windows e MacOS in termini di privacy, stabilità, sicurezza e flessibilità. Anche se le cause possono essere molteplici, il principio più importante è probabilmente, come ha detto Eric Raymond nel suo famoso saggio "La cattedrale e il bazar", che "se ci sono abbastanza occhi, tutti i bug sono superficiali" [3] È questo principio di saggezza delle folle che ha dato a Linux il suo successo più significativo.
Non si può mai affermare senza ambiguità che uno schema crittografico sia "sicuro" o "insicuro" Esistono invece varie nozioni di sicurezza per gli schemi crittografici. Ogni definizione di sicurezza crittografica deve specificare (1) gli obiettivi di sicurezza e (2) le capacità di un attaccante. L'analisi degli schemi crittografici rispetto a una o più nozioni specifiche di sicurezza fornisce indicazioni sulle loro applicazioni e sui loro limiti.
Anche se non ci addentreremo in tutti i dettagli delle varie nozioni di sicurezza crittografica, è bene sapere che due presupposti sono onnipresenti in tutte le moderne nozioni di sicurezza crittografica relative agli schemi simmetrici e asimmetrici (e in qualche forma ad altre primitive crittografiche):
- La conoscenza dello schema da parte dell'attaccante è conforme al principio di Kerckhoffs.
- L'attaccante non può eseguire un attacco di forza bruta allo schema. In particolare, i modelli di minaccia delle nozioni di sicurezza crittografica di solito non ammettono nemmeno gli attacchi a forza bruta, in quanto presuppongono che non siano una considerazione rilevante.
Note:
[1] Secondo Seutonio, un cifrario a turni con un valore costante della chiave di 3 fu utilizzato da Giulio Cesare nelle sue comunicazioni militari. Quindi A diventava sempre D, B sempre E, C sempre F e così via. Questa particolare versione del cifrario a turni è diventata nota come Cifrario di Cesare (anche se non si tratta di un vero e proprio cifrario nel senso moderno del termine, poiché il valore della chiave è costante). Il cifrario di Cesare poteva essere sicuro nel primo secolo a.C., se i nemici di Roma non avevano molta dimestichezza con la crittografia. Ma chiaramente non sarebbe uno schema molto sicuro in tempi moderni.
[2] Jonathan Katz e Yehuda Lindell, Introduzione alla crittografia moderna, CRC Press (Boca Raton, FL: 2015), pag. 7f.
[3] Eric Raymond, "The Cathedral and the Bazaar", documento presentato al Linux Kongress, Würzburg, Germania (27 maggio 1997). Sono disponibili diverse versioni successive e un libro. Le mie citazioni sono tratte da pagina 30 del libro: Eric Raymond, La cattedrale e il bazar: Musings on Linux and Open Source by an Accidental Revolutionary, ed. riveduta. (2001), O'Reilly: Sebastopol, CA.
Cifrari di flusso
Gli schemi di crittografia simmetrica si suddividono in due tipi: cifrari a flusso e cifrari a blocco. Questa distinzione, tuttavia, è alquanto problematica, in quanto le persone utilizzano questi termini in modo incoerente. Nelle prossime sezioni esporrò la distinzione nel modo che ritengo migliore. È bene sapere, tuttavia, che molte persone useranno questi termini in modo diverso da come li ho descritti.
Parliamo innanzitutto dei cifrari a flusso. Un cifrario a flusso è uno schema di crittografia simmetrica in cui la crittografia consiste in due fasi.
In primo luogo, viene prodotta una stringa della lunghezza del testo in chiaro tramite una chiave privata. Questa stringa è chiamata keystream.
Successivamente, il flusso di chiavi viene combinato matematicamente con il
testo in chiaro per produrre un testo cifrato. Questa combinazione è in
genere un'operazione XOR. Per la decrittazione, è sufficiente invertire
l'operazione. (Si noti che A \oplus B = B \oplus A, nel caso in cui A e B siano stringhe di bit. Quindi l'ordine di un'operazione XOR in un cifrario a
flusso non ha importanza per il risultato. Questa proprietà è nota come commutatività)
Un tipico cifrario a flusso XOR è rappresentato in Figura 3. Per
prima cosa si prende una chiave privata K e la si usa per generare un flusso di chiavi. Il flusso di chiavi viene
quindi combinato con il testo in chiaro mediante un'operazione XOR per
produrre il testo cifrato. Qualsiasi agente che riceve il testo cifrato può
facilmente decifrarlo se possiede la chiave K. Tutto ciò che deve fare è
creare un flusso di chiavi lungo quanto il testo in chiaro secondo la
procedura specificata dallo schema e fare lo XOR con il testo in chiaro.
Figura 3: Cifrario a flusso XOR
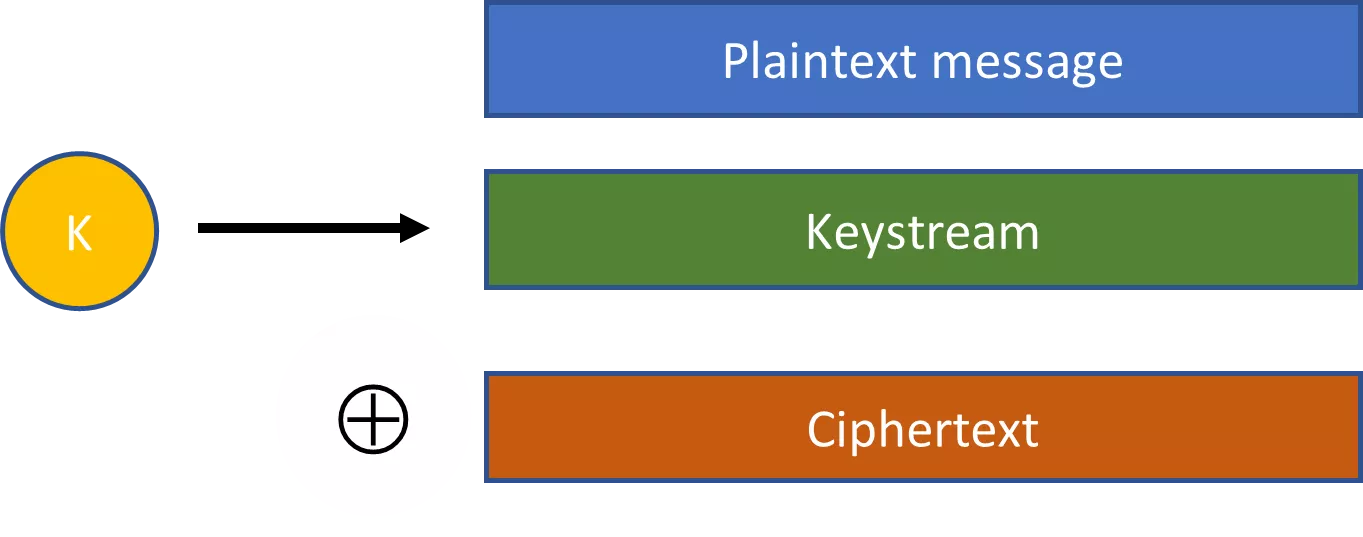
Si ricorda che uno schema di crittografia è in genere un modello di crittografia con lo stesso algoritmo di base, piuttosto che una specifica esatta. Per estensione, un cifrario a flusso è tipicamente un modello di crittografia in cui è possibile utilizzare chiavi di lunghezza diversa. Sebbene la lunghezza della chiave possa influire su alcuni dettagli minori dello schema, non influisce sulla sua forma essenziale.
Il cifrario a turni è un esempio di cifrario a flusso molto semplice e insicuro. Utilizzando una singola lettera (la chiave privata), è possibile produrre una stringa di lettere della lunghezza del messaggio (la keystream). Questo flusso di chiavi viene poi combinato con il testo in chiaro tramite un'operazione modulo per produrre un testo cifrato. (Questa operazione modulo può essere semplificata in un'operazione XOR quando si rappresentano le lettere in bit).
Un altro famoso esempio di cifrario a flusso è il cifrario di Vigenere, dal nome di Blaise de Vigenere che lo sviluppò completamente alla fine del XVI secolo (anche se altri avevano fatto molto lavoro in precedenza). È un esempio di cifrario a sostituzione polialfabetica: uno schema di crittografia in cui l'alfabeto del testo cifrato per un simbolo del testo in chiaro cambia a seconda della sua posizione nel testo. A differenza di un cifrario di sostituzione monoalfabetico, i simboli del testo cifrato possono essere associati a più di un simbolo del testo in chiaro.
Con l'affermarsi della crittografia nell'Europa rinascimentale, si diffuse anche la cryptanalysis, cioè la decifrazione dei testi cifrati, in particolare con l'ausilio dell'analisi delle frequenze. Quest'ultima sfrutta le regolarità statistiche della nostra lingua per decifrare i testi cifrati ed è stata scoperta dagli studiosi arabi già nel IX secolo. È una tecnica che funziona particolarmente bene con i testi più lunghi. E anche i più sofisticati cifrari monoalfabetici a sostituzione non erano più sufficienti contro l'analisi delle frequenze già nel 1700 in Europa, soprattutto in ambito militare e di sicurezza. Poiché il cifrario di Vigenere offriva un significativo progresso in termini di sicurezza, divenne popolare in questo periodo e si diffuse alla fine del 1700.
In termini informali, lo schema di crittografia funziona come segue:
Selezionare una parola di più lettere come chiave privata.
Per qualsiasi messaggio, applicare il cifrario a turni a ogni lettera del messaggio utilizzando come turno la lettera corrispondente nella parola chiave.
Se si è proceduto con la parola chiave ma non si è ancora riusciti a cifrare completamente il testo in chiaro, applicare nuovamente le lettere della parola chiave come cifrario a turni alle lettere corrispondenti del resto del testo.
Continuare questo processo fino a quando l'intero messaggio è stato cifrato.
A titolo di esempio, si supponga che la propria chiave privata sia "ORO" e che si voglia criptare il messaggio "CRIPTOGRAFIA". In questo caso, si procederà come segue secondo il cifrario di Vigenère:
c_0 = [(2 + 6) \mod 26] = 8 = Ic_1 = [(17 + 14) ´mod 26] = 5 = Fc_2 = [(24 + 11) ´mod 26] = 9 = Jc_3 = [(15 + 3) \mod 26] = 18 = Sc_4 = [(19 + 6) \mod 26] = 25 = Zc_5 = [(14 + 14) \mod 26] = 2 = Cc_6 = [(6 + 11) \mod 26] = 17 = Rc_7 = [(17 + 3) \mod 26] = 20 = Uc_8 = [(0 + 6) \mod 26] = 6 = Gc_9 = [(15 + 14) \mod 26] = 3 = Dc_{10} = [(7 + 11) \mod 26] = 18 = Sc_{11} = [(24 + 3) \mod 26] = 1 = B
Pertanto, il testo cifrato c =
"IFJSZCRUGDSB".
Un altro famoso esempio di cifrario a flusso è il one-time pad. Con il one-time pad, è sufficiente creare una stringa di bit casuali lunga quanto il messaggio in chiaro e produrre il testo cifrato tramite l'operazione XOR. Pertanto, la chiave privata e il flusso di chiavi sono equivalenti con un one-time pad.
Mentre il cifrario Shift e il cifrario Vigenere sono molto insicuri nell'era moderna, il one-time pad è molto sicuro se usato correttamente. Probabilmente l'applicazione più famosa del one-time pad è stata, almeno fino agli anni '80, quella della Washington-Moscow hotline. [4]
La hotline è un collegamento diretto tra Washington e Mosca per le comunicazioni urgenti, istituito dopo la crisi dei missili di Cuba. La tecnologia della linea si è trasformata nel corso degli anni. Attualmente comprende un cavo diretto in fibra ottica e due collegamenti satellitari (per la ridondanza), che consentono di inviare e-mail e messaggi di testo. Il collegamento termina in vari luoghi degli Stati Uniti. Il Pentagono, la Casa Bianca e Raven Rock Mountain sono punti terminali noti. Contrariamente all'opinione comune, la linea diretta non ha mai coinvolto i telefoni.
In sostanza, lo schema one-time pad funzionava come segue. Sia Washington che Mosca disponevano di due serie di numeri casuali. Una serie di numeri casuali, creata dai russi, riguardava la crittografia e la decrittografia di qualsiasi messaggio in lingua russa. Una serie di numeri casuali, creata dagli americani, riguardava la crittografia e la decrittografia di qualsiasi messaggio in lingua inglese. Di tanto in tanto, altri numeri casuali venivano consegnati all'altra parte da corrieri fidati.
Washington e Mosca erano quindi in grado di comunicare segretamente utilizzando questi numeri casuali per la creazione di blocchi una tantum. Ogni volta che si doveva comunicare, si utilizzava la porzione successiva di numeri casuali per il messaggio.
Pur essendo altamente sicuro, il one-time pad presenta notevoli limitazioni pratiche: la chiave deve essere lunga quanto il messaggio e nessuna parte di un one-time pad può essere riutilizzata. Ciò significa che è necessario tenere traccia della propria posizione nel one-time pad, memorizzare un numero enorme di bit e scambiare di volta in volta bit casuali con le controparti. Di conseguenza, l'one-time pad non viene utilizzato di frequente nella pratica.
Invece, i cifrari a flusso predominanti utilizzati nella pratica sono i cifrari a flusso pseudorandom. Salsa20 e una variante strettamente correlata chiamata ChaCha sono esempi di cifrari a flusso pseudorandom comunemente utilizzati.
Con questi cifrari a flusso pseudorandom, si sceglie innanzitutto in modo casuale una chiave K che è più corta della lunghezza del testo in chiaro. Tale chiave casuale K viene solitamente creata dal nostro computer sulla base di dati imprevedibili che raccoglie nel tempo, come l'intervallo tra i messaggi di rete, i movimenti del mouse e così via.
Questa chiave casuale K viene
quindi inserita in un algoritmo di espansione che crea un flusso di chiavi pseudorandom
lungo quanto il messaggio. È possibile specificare con precisione la lunghezza
del flusso di chiavi (ad esempio, 500 bit, 1000 bit, 1200 bit, 29.117 bit e così
via).
Un flusso di chiavi pseudorandom appare come se fosse stato scelto in modo completamente casuale dall'insieme di tutte le stringhe della stessa lunghezza. Di conseguenza, la crittografia con un flusso di chiavi pseudorandom appare come se fosse stata eseguita con un pad a tempo unico. Ma naturalmente non è così.
Poiché la nostra chiave privata è più corta del flusso di chiavi e il nostro algoritmo di espansione deve essere deterministico per far funzionare il processo di crittografia/decrittografia, non tutti i flussi di chiavi di quella particolare lunghezza potrebbero risultare come output della nostra operazione di espansione.
Supponiamo, ad esempio, che la nostra chiave privata abbia una lunghezza di
128 bit e che possiamo inserirla in un algoritmo di espansione per creare un
flusso di chiavi molto più lungo, ad esempio di 2.500 bit. Poiché il nostro
algoritmo espansivo deve essere deterministico, esso può al massimo
selezionare 1/2^{128} stringhe con una lunghezza di 2.500 bit. Quindi un tale flusso di chiavi non
potrebbe mai essere selezionato in modo del tutto casuale tra tutte le stringhe
della stessa lunghezza.
La nostra definizione di cifrario a flusso ha due aspetti: (1) un flusso di chiavi lungo quanto il testo in chiaro viene generato con l'aiuto di una chiave privata; e (2) questo flusso di chiavi viene combinato con il testo in chiaro, tipicamente tramite un'operazione XOR, per produrre il testo cifrato.
A volte si definisce la condizione (1) in modo più rigoroso, affermando che il flusso di chiavi deve essere specificamente pseudorandom. Ciò significa che né il cifrario a turni né il one-time pad sarebbero considerati cifrari a flusso.
A mio avviso, definire la condizione (1) in modo più ampio offre un modo più semplice di organizzare gli schemi di crittografia. Inoltre, ciò significa che non dobbiamo smettere di chiamare un particolare schema di crittografia un cifrario a flusso solo perché scopriamo che in realtà non si basa su flussi di chiavi pseudorandom.
Note:
[4] Crypto Museum, "Washington-Moscow hotline", 2013, disponibile su https://www.cryptomuseum.com/crypto/hotline/index.htm.
Cifrari a blocchi
Il primo modo in cui un cifrario a blocchi viene comunemente inteso è come qualcosa di più primitivo di un cifrario a flusso: Un algoritmo di base che esegue una trasformazione che preserva la lunghezza su una stringa di lunghezza adeguata con l'aiuto di una chiave. Questo algoritmo può essere utilizzato per creare schemi di crittografia e forse altri tipi di schemi crittografici.
Spesso un cifrario a blocchi può accettare stringhe di input di lunghezza variabile, come 64, 128 o 256 bit, e chiavi di lunghezza variabile, come 128, 192 o 256 bit. Sebbene alcuni dettagli dell'algoritmo possano cambiare a seconda di queste variabili, l'algoritmo di base non cambia. Se così fosse, si parlerebbe di due cifrari a blocchi diversi. Si noti che l'uso della terminologia dell'algoritmo di base è lo stesso degli schemi di crittografia.
Una rappresentazione del funzionamento di un cifrario a blocchi può essere
vista nella Figura 4 qui sotto. Un messaggio M di lunghezza L e una chiave K sono gli input del cifrario a blocchi. Il cifrario a blocchi produce un
messaggio M' di lunghezza L. Per la maggior parte dei
cifrari a blocchi, la chiave non deve necessariamente avere la stessa
lunghezza di M e M'.
Figura 4: Un cifrario a blocchi

Un cifrario a blocchi da solo non è uno schema di crittografia. Ma un cifrario a blocchi può essere utilizzato con varie modalità di funzionamento per produrre diversi schemi di crittografia. Una modalità di funzionamento aggiunge semplicemente alcune operazioni aggiuntive al di fuori del cifrario a blocchi.
Per illustrare il funzionamento, si supponga un cifrario a blocchi (BC) che richieda una stringa di ingresso di 128 bit e una chiave privata di 128 bit. La Figura 5 mostra come questo cifrario a blocchi possa essere utilizzato con la modalità codice elettronico (modalità ECB) per creare uno schema di cifratura. (Le ellissi sulla destra indicano che è possibile ripetere questo schema per tutto il tempo necessario).
Figura 5: Cifrario a blocchi con modalità ECB
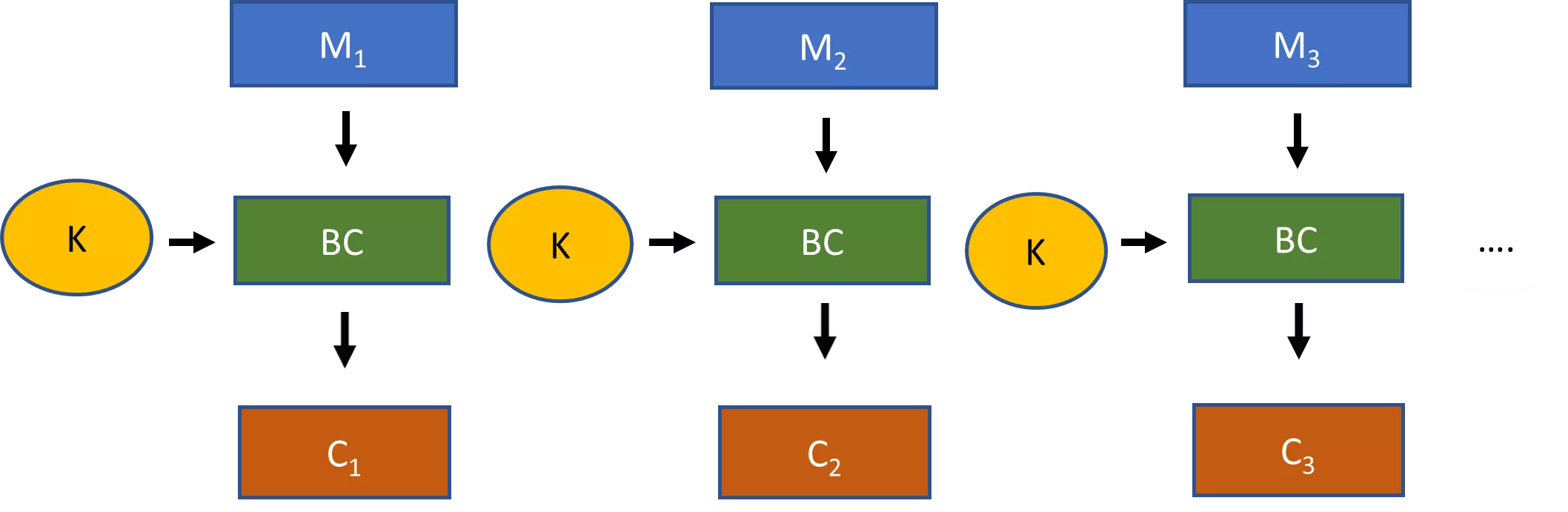
Il processo di crittografia elettronica con il cifrario a blocchi è il seguente. Verificare se è possibile dividere il messaggio in chiaro in blocchi di 128 bit. In caso contrario, aggiungete un padding al messaggio, in modo che il risultato possa essere diviso uniformemente per la dimensione del blocco di 128 bit. Questi sono i dati utilizzati per il processo di crittografia.
Ora dividete i dati in pezzi di stringhe a 128 bit (M_1, M_2, M_3 e così via). Eseguite ogni stringa di 128 bit attraverso il cifrario a
blocchi con la vostra chiave di 128 bit per produrre pezzi di testo cifrato
di 128 bit (C_1, C_2, C_3 e così via). Questi pezzi,
una volta ricombinati, formano il testo cifrato completo.
La decrittazione è semplicemente il processo inverso, anche se il destinatario ha bisogno di un modo riconoscibile per eliminare il padding dai dati decifrati e ottenere il messaggio originale in chiaro.
Sebbene sia relativamente semplice, un cifrario a blocchi con modalità di cifratura elettronica manca di sicurezza. Questo perché porta a una crittografia deterministica. Due stringhe di dati identiche a 128 bit vengono crittografate esattamente allo stesso modo. Questa informazione può essere sfruttata.
Al contrario, qualsiasi schema di crittografia costruito a partire da un
cifrario a blocchi dovrebbe essere probabilistico: cioè, la
crittografia di qualsiasi messaggio M, o di qualsiasi specifica
porzione di M, dovrebbe in
genere dare ogni volta un risultato diverso. [5]
La modalità cipher block chaining (modalità CBC) è probabilmente la modalità più comunemente utilizzata con un cifrario a blocchi. La combinazione, se eseguita correttamente, produce uno schema di crittografia probabilistico. Una rappresentazione di questa modalità di funzionamento è riportata nella Figura 6 qui sotto.
Figura 6: Cifrario a blocchi con modalità CBC
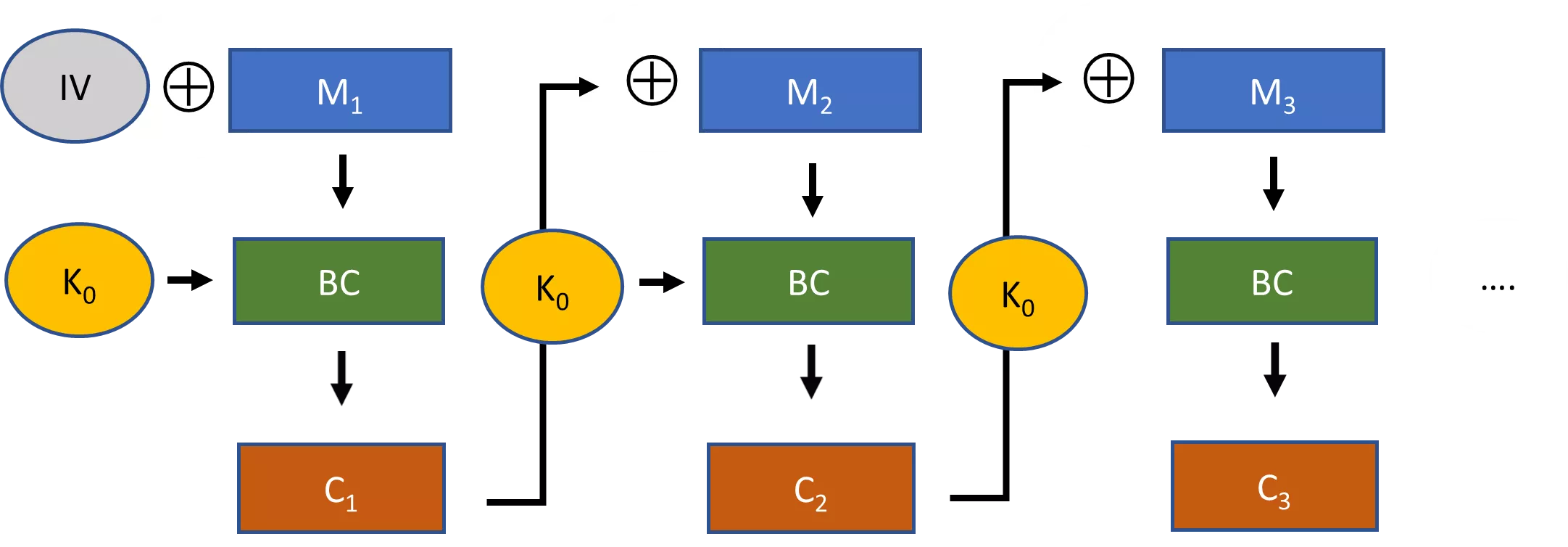
Supponiamo che la dimensione del blocco sia di nuovo di 128 bit. Per iniziare, è necessario assicurarsi che il messaggio in chiaro originale riceva il padding necessario.
Quindi, si esegue lo XOR della prima porzione di 128 bit del testo in chiaro con un vettore di inizializzazione di 128 bit. Il risultato viene inserito nel cifrario a blocchi per produrre un testo cifrato per il primo blocco. Per il secondo blocco di 128 bit, si esegue lo XOR del testo in chiaro con il testo cifrato del primo blocco, prima di inserirlo nel cifrario a blocchi. Si continua questo processo fino a quando non si è cifrato l'intero messaggio in chiaro.
Al termine, si invia al destinatario il messaggio cifrato insieme al vettore di inizializzazione non cifrato. Il destinatario deve conoscere il vettore di inizializzazione, altrimenti non potrà decifrare il testo cifrato.
Questa costruzione, se usata correttamente, è molto più sicura della modalità del cifrario elettronico. È necessario innanzitutto assicurarsi che il vettore di inizializzazione sia una stringa casuale o pseudorandom. Inoltre, è necessario utilizzare un vettore di inizializzazione diverso ogni volta che si utilizza questo schema di crittografia.
In altre parole, il vettore di inizializzazione dovrebbe essere un nonce casuale o pseudorandom, dove nonce sta per "un numero che viene usato una sola volta" Se si segue questa pratica, la modalità CBC con un cifrario a blocchi garantisce che due blocchi di testo in chiaro identici vengano generalmente crittografati ogni volta in modo diverso.
Infine, passiamo alla modalità output feedback (modalità OFB). Una rappresentazione di questa modalità è riportata nella Figura 7.
Figura 7: Cifrario a blocchi con modalità OFB
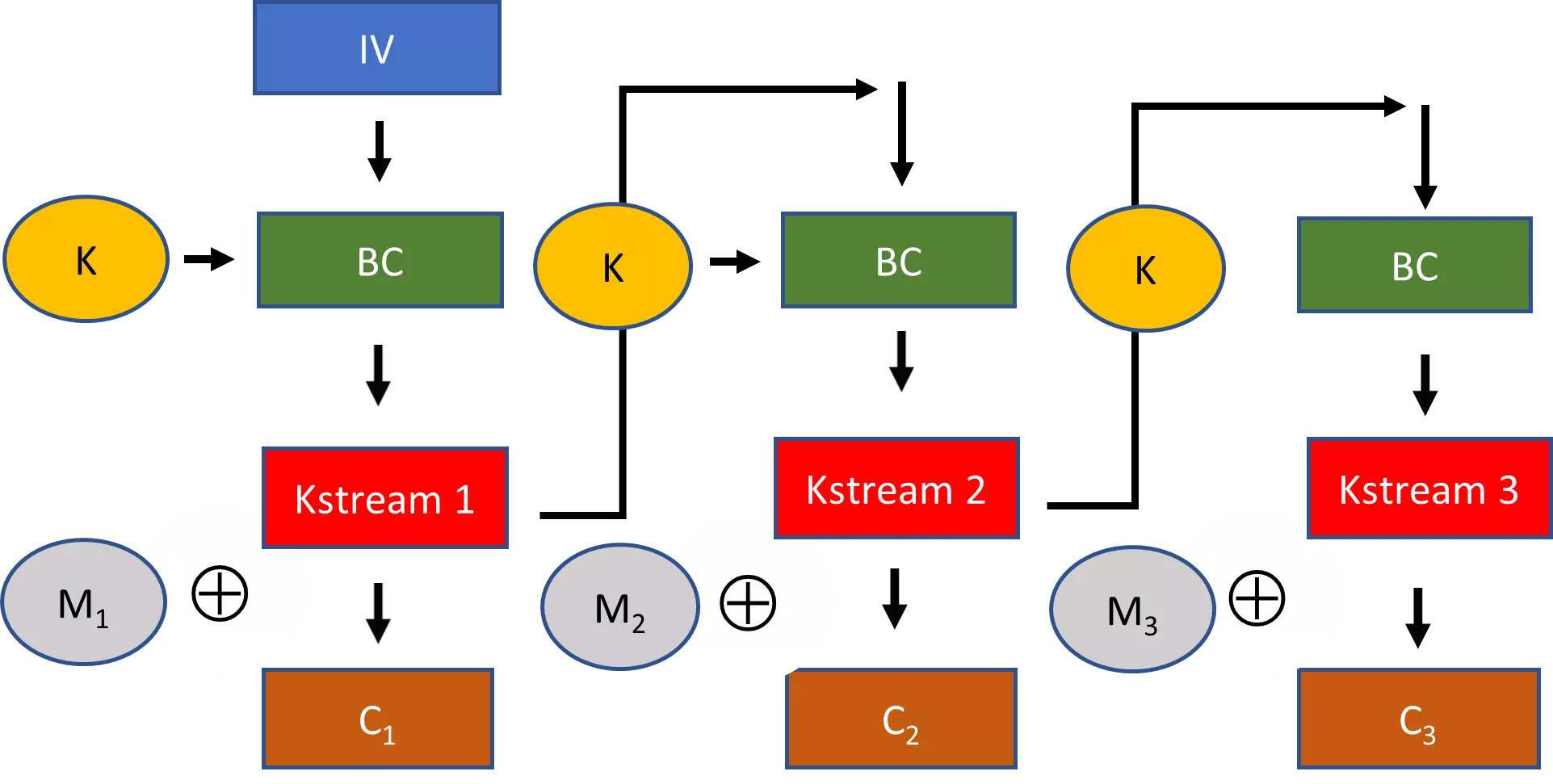
Con la modalità OFB si seleziona anche un vettore di inizializzazione. Ma in questo caso, per il primo blocco, il vettore di inizializzazione viene inserito direttamente nel cifrario a blocchi con la chiave. I 128 bit risultanti vengono quindi trattati come un flusso di chiavi. Questo flusso di chiavi viene sottoposto a XOR con il testo in chiaro per produrre il testo cifrato del blocco. Per i blocchi successivi, si utilizza il flusso di chiavi del blocco precedente come ingresso nel cifrario a blocchi e si ripete la procedura.
Se si osserva attentamente, ciò che è stato creato qui dal cifrario a blocchi con modalità OFB è un cifrario a flusso. Si generano porzioni di keystream di 128 bit fino a ottenere la lunghezza del testo in chiaro (scartando i bit non necessari dall'ultima porzione di keystream di 128 bit). Quindi si esegue lo XOR tra il flusso di chiavi e il messaggio in chiaro per ottenere il testo cifrato.
Nella sezione precedente sui cifrari a flusso, ho affermato che si produce un flusso di chiavi con l'aiuto di una chiave privata. Per essere precisi, non deve essere creato solo con una chiave privata. Come si può vedere in modalità OFB, il flusso di chiavi viene prodotto con il supporto di una chiave privata e di un vettore di inizializzazione.
Come per la modalità CBC, è importante selezionare un nonce pseudorandom o casuale per il vettore di inizializzazione ogni volta che si utilizza un cifrario a blocchi in modalità OFB. In caso contrario, la stessa stringa di messaggio a 128 bit inviata in comunicazioni diverse verrà crittografata allo stesso modo. Questo è un modo per creare una crittografia probabilistica con un cifrario a flusso.
Alcuni cifrari a flusso utilizzano solo una chiave privata per creare un flusso di chiavi. Per questi cifrari a flusso, è importante utilizzare un nonce casuale per selezionare la chiave privata per ogni istanza di comunicazione. In caso contrario, anche i risultati della crittografia con questi cifrari a flusso saranno deterministici, con conseguenti problemi di sicurezza.
Il più popolare cifrario a blocchi moderno è il cifrario Rijndael. È stato il vincitore di un concorso indetto dal National Institute of Standards and Technology (NIST) tra il 1997 e il 2000 per sostituire un vecchio standard di crittografia, il data encryption standard (DES).
Il cifrario Rijndael può essere utilizzato con diverse specifiche per la lunghezza delle chiavi e la dimensione dei blocchi, nonché in diverse modalità di funzionamento. Il comitato del concorso NIST ha adottato una versione ristretta del cifrario Rijndael, che richiede blocchi di 128 bit e chiavi di 128, 192 o 256 bit, come parte dello standard di crittografia avanzata (AES). Si tratta dello standard principale per le applicazioni di crittografia simmetrica. È così sicuro che persino l'NSA è disposta a usarlo con chiavi a 256 bit per i documenti top secret. [6]
Il cifrario a blocchi AES sarà spiegato in dettaglio nel capitolo 5.
Note:
[5] L'importanza della crittografia probabilistica è stata sottolineata per la prima volta da Shafi Goldwasser e Silvio Micali, "Probabilistic encryption," Journal of Computer and System Sciences, 28 (1984), 270-99.
[6] Vedi NSA, "Commercial National Security Algorithm Suite", https://apps.nsa.gov/iaarchive/programs/iad-initiatives/cnsa-suite.cfm.
Chiarire la confusione
La confusione sulla distinzione tra cifrari a blocchi e cifrari a flusso nasce dal fatto che a volte si intende il termine cifrario a blocchi come se si riferisse specificamente a un cifrario a blocchi con una modalità di crittografia a blocchi.
Si considerino le modalità ECB e CBC della sezione precedente. Queste modalità richiedono specificamente che i dati per la crittografia siano divisibili per la dimensione del blocco (il che significa che potrebbe essere necessario utilizzare un padding per il messaggio originale). Inoltre, in queste modalità, i dati vengono anche utilizzati direttamente dal cifrario a blocchi (e non solo combinati con il risultato di un'operazione di cifratura a blocchi come nella modalità OFB).
Quindi, in alternativa, è possibile definire un cifrario a blocchi come qualsiasi schema di crittografia che opera su blocchi di lunghezza fissa del messaggio alla volta (dove ogni blocco deve essere più lungo di un byte, altrimenti collassa in un cifrario a flusso). Sia i dati da crittografare che il testo cifrato devono dividersi uniformemente in questa dimensione di blocco. In genere, la dimensione del blocco è di 64, 128, 192 o 256 bit. Al contrario, un cifrario a flusso può crittografare qualsiasi messaggio in blocchi di un bit o di un byte alla volta.
Con questa comprensione più specifica del concetto di cifrario a blocchi, si può effettivamente affermare che i moderni schemi di crittografia sono cifrari a flusso o a blocchi. D'ora in poi, salvo diversa indicazione, intenderò il termine cifrario a blocchi nel senso più generale del termine.
La discussione sulla modalità OFB nella sezione precedente solleva anche un altro punto interessante. Alcuni cifrari a flusso sono costruiti a partire da cifrari a blocchi, come Rijndael con OFB. Alcuni, come Salsa20 e ChaCha, non sono creati a partire da cifrari a blocchi. Questi ultimi potrebbero essere chiamati cifrari di flusso primitivi. (Non esiste un termine standardizzato per indicare tali cifrari di flusso)
Quando si parla di vantaggi e svantaggi dei cifrari a flusso e dei cifrari a blocchi, in genere si confrontano i cifrari a flusso primitivi con gli schemi di crittografia basati sui cifrari a blocchi.
Mentre è sempre possibile costruire facilmente un cifrario a flusso da un cifrario a blocchi, è in genere molto difficile costruire un qualche tipo di costrutto con una modalità di crittografia a blocchi (come la modalità CBC) da un cifrario a flusso primitivo.
Da questa discussione si dovrebbe comprendere la Figura 8. Essa fornisce una panoramica sugli schemi di crittografia simmetrica. Utilizziamo tre tipi di schemi di crittografia: i cifrari a flusso primitivi, i cifrari a flusso con cifratura a blocchi e i cifrari a blocco in modalità a blocchi (chiamati anche "cifrari a blocco" nel diagramma).
Figura 8: Panoramica degli schemi di crittografia simmetrica
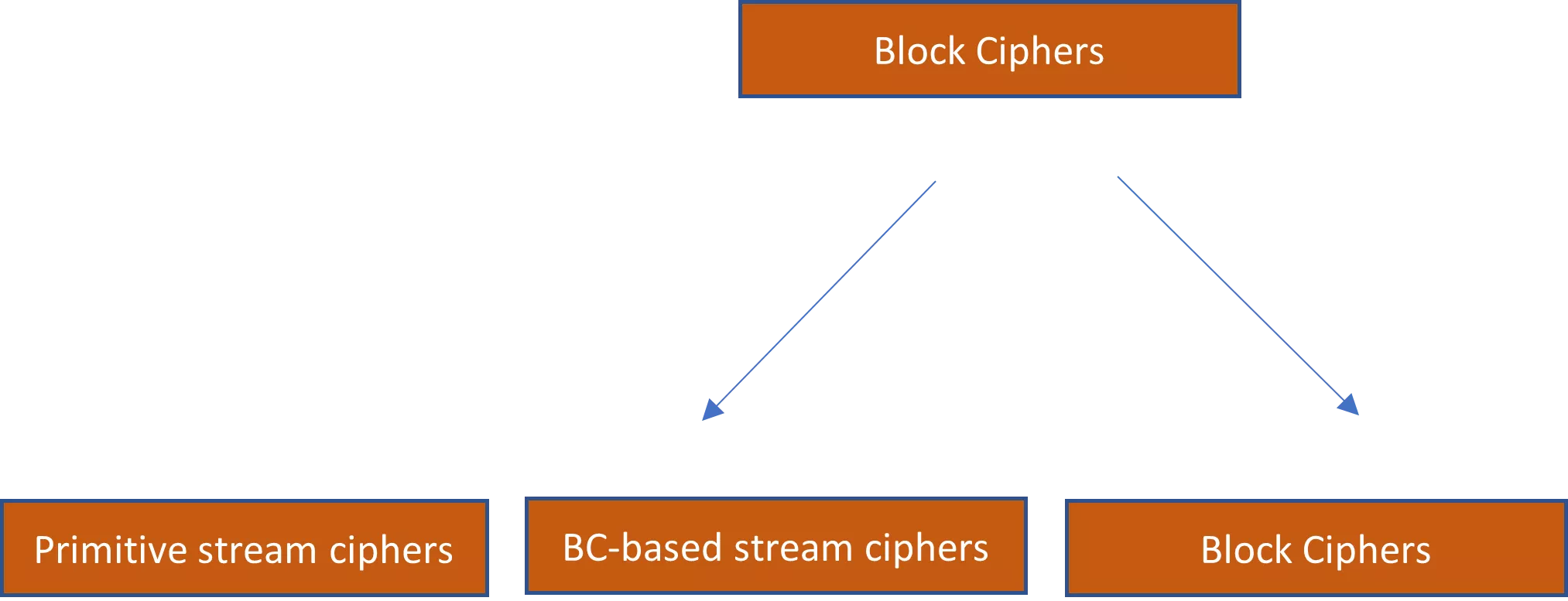
Codici di autenticazione dei messaggi
La crittografia si occupa della segretezza. Ma la crittografia si occupa anche di temi più ampi, come l'integrità dei messaggi, l'autenticità e il non ripudio. I cosiddetti codici di autenticazione dei messaggi (MAC) sono schemi crittografici a chiave simmetrica che supportano l'autenticità e l'integrità delle comunicazioni.
Perché nella comunicazione è necessaria solo la segretezza? Supponiamo che Bob invii ad Alice un messaggio utilizzando una crittografia praticamente infrangibile. Qualsiasi aggressore che intercetti questo messaggio non sarà in grado di ottenere informazioni significative sul suo contenuto. Tuttavia, l'aggressore ha ancora a disposizione almeno altri due vettori di attacco:
Potrebbe intercettare il testo cifrato, alterarne il contenuto e inviarlo ad Alice.
Potrebbe bloccare completamente il messaggio di Bob e inviare un proprio testo cifrato.
In entrambi i casi, l'aggressore potrebbe non avere alcuna conoscenza dei contenuti dei cifrari (1) e (2). Ma potrebbe comunque causare danni significativi in questo modo. È qui che i codici di autenticazione dei messaggi diventano importanti.
I codici di autenticazione dei messaggi sono definiti in modo generico come schemi crittografici simmetrici con tre algoritmi: un algoritmo di generazione della chiave, un algoritmo di generazione del tag e un algoritmo di verifica. Un MAC sicuro garantisce che i tag siano inesistenti per qualsiasi attaccante, ovvero che non possa creare un tag sul messaggio che verifica, a meno che non abbia la chiave privata.
Bob e Alice possono contrastare la manipolazione di un particolare messaggio utilizzando un MAC. Supponiamo per il momento che non si preoccupino della segretezza. Vogliono solo assicurarsi che il messaggio ricevuto da Alice provenga effettivamente da Bob e non sia stato modificato in alcun modo.
Il processo è illustrato nella Figura 9. Per utilizzare un MAC (Message Authentication Code), i due devono prima generare una chiave
privata K condivisa tra loro.
Bob crea un tag T per il
messaggio utilizzando la chiave privata K. Quindi invia il messaggio
e l'etichetta del messaggio ad Alice. Quest'ultima può quindi verificare che
Bob abbia effettivamente creato l'etichetta, facendo passare la chiave
privata, il messaggio e l'etichetta attraverso un algoritmo di verifica.
Figura 9: Panoramica degli schemi di crittografia simmetrica
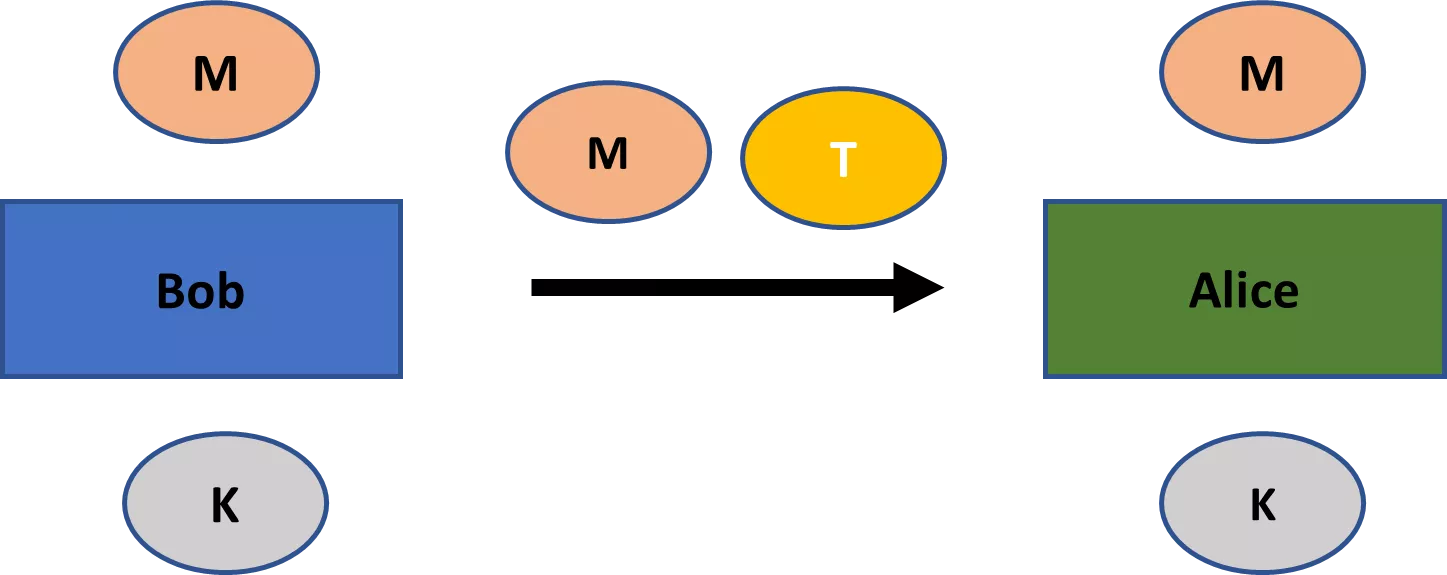
A causa dell'inforcabilità esistenziale, un aggressore non
può alterare in alcun modo il messaggio M o creare un proprio messaggio con un tag valido. Questo vale anche se
l'aggressore osserva i tag di molti messaggi tra Bob e Alice che utilizzano
la stessa chiave privata. Al massimo, un aggressore potrebbe impedire ad
Alice di ricevere il messaggio M (un problema che la crittografia
non può risolvere).
Un MAC garantisce che un messaggio è stato effettivamente creato da Bob. Questa autenticità implica automaticamente l'integrità del messaggio, vale a dire che se Bob ha creato un messaggio, allora, ipso facto, non è stato alterato in alcun modo da un aggressore. Quindi, d'ora in poi, qualsiasi preoccupazione per l'autenticazione dovrebbe essere automaticamente intesa come una preoccupazione per l'integrità.
Sebbene nella mia trattazione abbia fatto una distinzione tra autenticità e integrità dei messaggi, è anche comune usare questi termini come sinonimi. Essi si riferiscono all'idea di messaggi creati da un particolare mittente e non alterati in alcun modo. In questo spirito, i codici di autenticazione dei messaggi sono spesso chiamati anche codici di integrità dei messaggi.
Crittografia autenticata
In genere, si desidera garantire sia la segretezza che l'autenticità della comunicazione e, pertanto, gli schemi di crittografia e gli schemi MAC sono tipicamente utilizzati insieme.
Uno schema di crittografia autenticata è uno schema che combina la crittografia con un MAC in modo altamente sicuro. In particolare, deve soddisfare gli standard per l'inesigibilità esistenziale e una nozione molto forte di segretezza, ossia resistente agli attacchi chosen-ciphertext. [7]
Affinché uno schema di crittografia sia resistente agli attacchi di tipo chosen-ciphertext, deve soddisfare gli standard di non-malleabilità: cioè, qualsiasi modifica di un testo cifrato da parte di un attaccante deve produrre un testo cifrato non valido o che si decifra in un testo in chiaro che non ha alcuna relazione con quello originale. [8]
Poiché uno schema di crittografia autenticato garantisce che un testo cifrato creato da un attaccante sia sempre invalido (poiché il tag non sarà verificato), soddisfa gli standard di resistenza agli attacchi di tipo chosen-ciphertext. È interessante notare che è possibile dimostrare che uno schema di crittografia autenticato può sempre essere creato dalla combinazione di un MAC esistenzialmente non falsificabile e di uno schema di crittografia che soddisfa una nozione di sicurezza meno forte, nota come sicurezza dell'attacco del testo scelto.
Non ci addentreremo in tutti i dettagli della costruzione di schemi di crittografia autenticati. Ma è importante conoscere due dettagli della loro costruzione.
In primo luogo, uno schema di crittografia autenticata gestisce prima la crittografia e poi crea un tag di messaggio sul testo in chiaro. È emerso che altri approcci, come la combinazione del testo cifrato con un tag sul testo in chiaro o la creazione di un tag e la successiva crittografia del testo in chiaro e del tag, non sono sicuri. Inoltre, entrambe le operazioni devono avere una propria chiave privata selezionata casualmente, altrimenti la sicurezza è gravemente compromessa.
Il principio sopra menzionato si applica più in generale: si dovrebbero sempre usare chiavi distinte quando si combinano schemi crittografici di base.
Uno schema di crittografia autenticata è rappresentato in Figura 10. Bob crea innanzitutto un testo cifrato C dal messaggio M utilizzando
una chiave K_C scelta a caso.
Quindi crea un tag messaggio T facendo passare il testo cifrato e un'altra chiave selezionata a caso K_T attraverso l'algoritmo di
generazione del tag. Sia il testo cifrato che l'etichetta del messaggio vengono
inviati ad Alice.
Alice verifica innanzitutto se il tag è valido dato il testo cifrato C e la chiave K_T. Se è valida,
può decifrare il messaggio usando la chiave K_C. In questo modo non solo
si assicura un concetto di segretezza molto forte nelle loro comunicazioni,
ma sa anche che il messaggio è stato creato da Bob.
Figura 10: Schema di crittografia autenticata

Come vengono creati i MAC? I MAC possono essere creati con diversi metodi, ma un modo comune ed efficiente per crearli è quello delle funzioni hash crittografiche.
Introdurremo le funzioni hash crittografiche in modo più approfondito nel capitolo 6. Per ora, è sufficiente sapere che una funzione hash è una funzione calcolabile in modo efficiente che accetta input di dimensioni arbitrarie e produce output di lunghezza fissa. Ad esempio, la popolare funzione di hash SHA-256 (secure hash algorithm 256) genera sempre un output a 256 bit indipendentemente dalle dimensioni dell'input. Alcune funzioni hash, come SHA-256, hanno applicazioni utili in crittografia.
Il tipo più comune di tag prodotto con una funzione hash crittografica è il codice di autenticazione dei messaggi basato su hash (HMAC). Il processo è illustrato nella Figura 11. Una parte produce
due chiavi distinte da una chiave privata K, la chiave interna K_1 e la chiave esterna K_2. Il
testo in chiaro M o il testo
cifrato C viene quindi
sottoposto a hash con la chiave interna. Il risultato T' viene quindi sottoposto a hashing con la chiave esterna per produrre il tag
del messaggio T.
Esiste una serie di funzioni hash che possono essere utilizzate per creare un HMAC. La funzione di hash più comunemente utilizzata è SHA-256.
Figura 11: HMAC
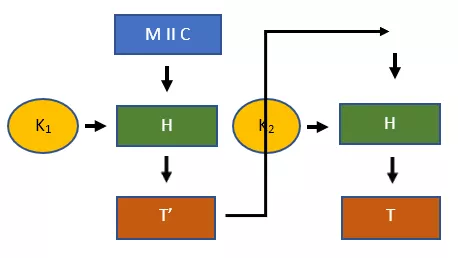
Note:
[7] I risultati specifici discussi in questa sezione sono tratti da Katz e Lindell, pp. 131-47.
[8] Tecnicamente, la definizione di attacchi a testo cifrato scelto è diversa dalla nozione di non-malleabilità. Ma è possibile dimostrare che queste due nozioni di sicurezza sono equivalenti.
Sessioni di comunicazione sicure
Supponiamo che due parti siano in una sessione di comunicazione e che inviino più messaggi avanti e indietro.
Uno schema di crittografia autenticata consente al destinatario di un messaggio di verificare che sia stato creato dal suo interlocutore durante la sessione di comunicazione (a condizione che la chiave privata non sia trapelata). Questo sistema funziona abbastanza bene per un singolo messaggio. In genere, tuttavia, due parti inviano messaggi avanti e indietro in una sessione di comunicazione. In questo caso, uno schema di crittografia autenticata semplice come quello descritto nella sezione precedente non è in grado di garantire la sicurezza.
Il motivo principale è che uno schema di crittografia autenticata non fornisce alcuna garanzia che il messaggio sia stato effettivamente inviato anche dall'agente che lo ha creato all'interno di una sessione di comunicazione. Si considerino i seguenti tre vettori di attacco:
attacco Replay: Un attaccante invia nuovamente un testo cifrato e un tag che ha intercettato tra due parti in un momento precedente.
Attacco di riordino: Un aggressore intercetta due messaggi in momenti diversi e li invia al destinatario nell'ordine inverso.
Attacco di riflessione: Un utente malintenzionato osserva un messaggio inviato da A a B e lo invia anche ad A.
Anche se l'attaccante non è a conoscenza del testo cifrato e non può creare testi cifrati spoofed, gli attacchi di cui sopra possono comunque causare danni significativi alle comunicazioni.
Supponiamo, ad esempio, che un particolare messaggio tra le due parti preveda il trasferimento di fondi finanziari. Un attacco replay potrebbe trasferire i fondi una seconda volta. Uno schema di crittografia autenticata semplice non ha alcuna difesa contro tali attacchi.
Fortunatamente, questo tipo di attacchi può essere facilmente mitigato in una sessione di comunicazione utilizzando identificatori e indicatori di tempo relativo.
Gli identificatori possono essere aggiunti al messaggio in chiaro prima della crittografia. Questo impedirebbe qualsiasi attacco di riflessione. Un indicatore temporale relativo può essere, ad esempio, un numero di sequenza in una particolare sessione di comunicazione. Ciascuna parte aggiunge un numero di sequenza a un messaggio prima della crittografia, in modo che il destinatario sappia in quale ordine sono stati inviati i messaggi. In questo modo si elimina la possibilità di attacchi di riordino. Elimina anche gli attacchi di replay. Qualsiasi messaggio inviato da un attaccante lungo la linea avrà un vecchio numero di sequenza e il destinatario saprà di non doverlo elaborare di nuovo.
Per illustrare il funzionamento delle sessioni di comunicazione sicure, supponiamo di nuovo Alice e Bob. Essi inviano un totale di quattro messaggi avanti e indietro. La figura 11 illustra il funzionamento di uno schema di crittografia autenticata con identificatori e numeri di sequenza.
La sessione di comunicazione inizia con l'invio da parte di Bob di un testo
cifrato C_{0,B} ad
Alice con un tag di messaggio T_{0,B}. Il testo
cifrato contiene il messaggio, un identificatore (BOB) e un numero di
sequenza (0). Il tag T_{0,B} viene applicato
all'intero testo cifrato. Nelle comunicazioni successive, Alice e Bob mantengono
questo protocollo, aggiornando i campi secondo necessità.
Figura 12: Una sessione di comunicazione sicura
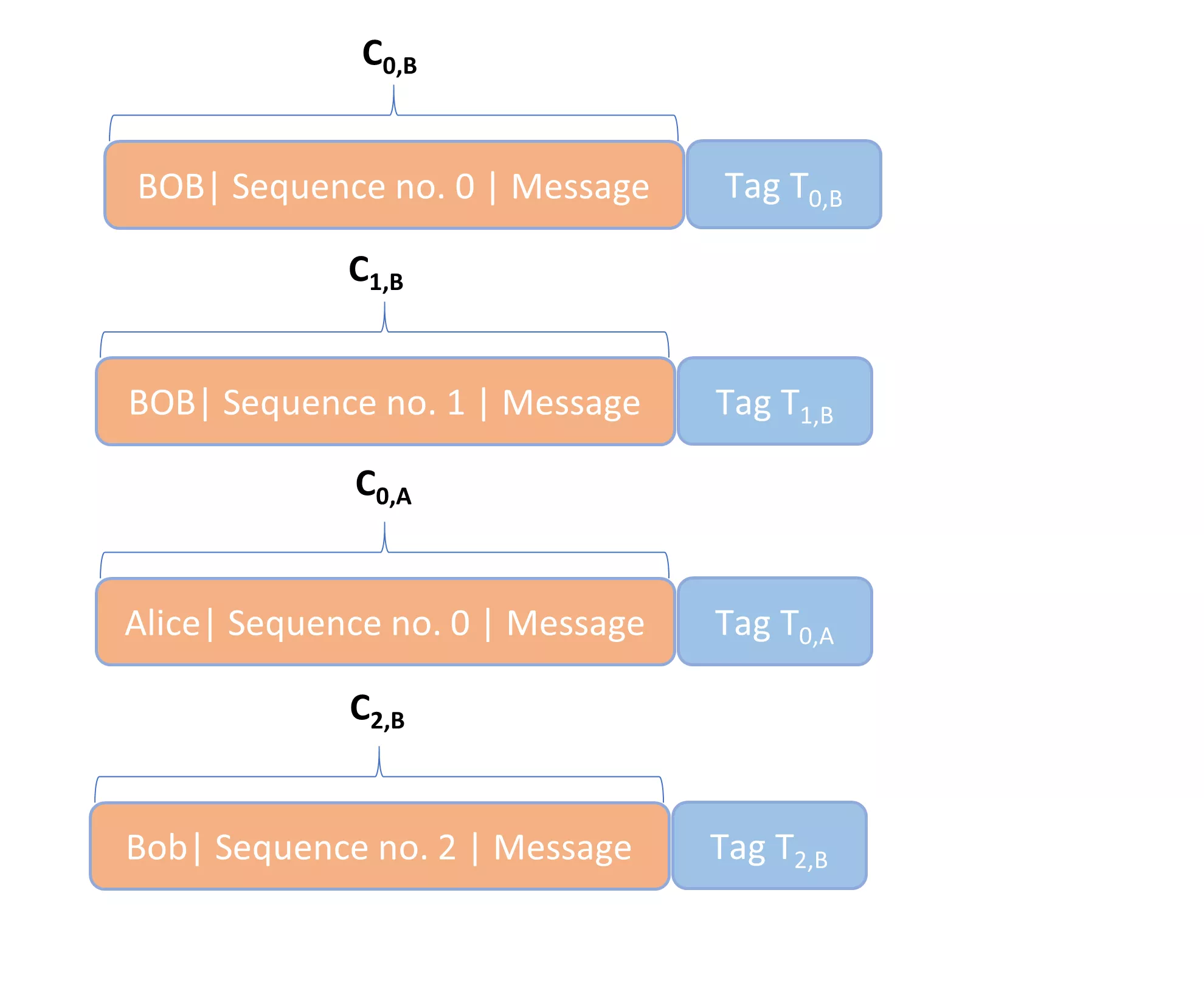
RC4 e AES
Il cifrario a flusso RC4
In questo capitolo discuteremo i dettagli di uno schema di crittografia con un moderno cifrario a flusso primitivo, RC4 (o "cifrario Rivest 4"), e un moderno cifrario a blocchi, AES. Mentre il cifrario RC4 è caduto in disgrazia come metodo di crittografia, AES è lo standard per la moderna crittografia simmetrica. Questi due esempi dovrebbero dare un'idea più precisa del funzionamento della crittografia simmetrica.
Per avere un'idea del funzionamento dei moderni cifrari a flusso pseudorandom, mi concentrerò sul cifrario a flusso RC4. Si tratta di un cifrario a flusso pseudorandom utilizzato nei protocolli di sicurezza WEP e WAP per i punti di accesso wireless e in TLS. Poiché l'RC4 presenta molte debolezze comprovate, è caduto in disgrazia. Infatti, l'Internet Engineering Task Force vieta l'uso delle suite RC4 da parte delle applicazioni client e server in tutte le istanze di TLS. Tuttavia, funziona bene come esempio per illustrare il funzionamento di un cifrario a flusso primitivo.
Per cominciare, mostrerò come criptare un messaggio in chiaro con un piccolo cifrario RC4. Supponiamo che il nostro messaggio in chiaro sia "SOUP" La crittografia con il nostro cifrario RC4 procede in quattro fasi.
Passo 1
Innanzitutto, definiamo un array S con S[0] = 0 e S[7] = 7. Per array si
intende semplicemente un insieme mutevole di valori organizzati da un
indice, chiamato anche lista in alcuni linguaggi di programmazione (ad
esempio, Python). In questo caso, l'indice va da 0 a 7 e anche i valori
vanno da 0 a 7. Quindi S è come segue:
S = [0, 1, 2, 3, 4, 5, 6, 7]
I valori qui non sono numeri ASCII, ma rappresentazioni decimali di stringhe
a 1 byte. Quindi il valore 2 sarebbe uguale a 0000 \ 0011. La lunghezza dell'array S è quindi di 8 byte.
Passo 2
In secondo luogo, definire un array di chiavi K della lunghezza di 8 byte scegliendo una chiave compresa tra 1 e 8 byte (non sono ammesse frazioni di byte). Poiché ogni byte è di 8 bit, è possibile selezionare qualsiasi numero compreso tra 0 e 255 per ogni byte della chiave.
Supponiamo di scegliere la chiave k come [14, 48, 9], in modo che
abbia una lunghezza di 3 byte. Ogni indice del nostro array di chiavi viene
quindi impostato in base al valore decimale di quel particolare elemento
della chiave, in ordine. Se si percorre l'intera chiave, si ricomincia
dall'inizio, finché non si sono riempiti gli 8 slot dell'array di chiavi.
Quindi, il nostro array di chiavi è il seguente:
K = [14, 48, 9, 14, 48, 9, 14, 48]
Passo 3
In terzo luogo, trasformeremo l'array S utilizzando l'array di chiavi K, in un processo noto come schedulazione delle chiavi. Il processo è il seguente in pseudocodice:
- Creare le variabili j e i
- Impostare la variabile $j = 0
- Per ogni
ida 0 a 7:- Impostare
j = (j + S[i] + K[i]) ´modulo 8 - Scambio di
S[i]eS[j]
- Impostare
La trasformazione dell'array S è rappresentata dalla Tabella 1.
Per iniziare, si può vedere lo stato iniziale di S come [0, 1, 2, 3, 4, 5, 6, 7] con un valore iniziale di 0 per j. Questo verrà trasformato
utilizzando l'array di chiavi [14, 48, 9, 14, 48, 9, 14, 48].
Il ciclo for inizia con i = 0. Secondo il nostro pseudocodice precedente, il nuovo valore di j diventa 6 (j = (j + S[0] + K[0]) \mod 8 = (0 + 0 + 14) \mod 8 = 6 \mod 8). Scambiando S[0] e S[6], lo stato di S dopo 1 round diventa [6, 1, 2, 3, 4, 5, 0, 7].
Nella riga successiva, i = 1.
Eseguendo nuovamente il ciclo for, j ottiene il valore 7 (j = (j + S[1] + K[1]) \mod 8 = (6 + 1 + 48) \mod 8 = 55 \mod 8 = 7 \mod 8). Scambiando S[1] e S[7] dallo stato attuale di S, [6, 1, 2, 3, 4, 5, 0, 7], si
ottiene [6, 7, 2, 3, 4, 5, 0, 1] dopo
il secondo round.
Continuiamo con questo processo fino a produrre la riga finale in basso per
l'array S, [6, 4, 1, 0, 3, 7, 5, 2].
Tabella 1: Tabella delle chiavi di programmazione
| Round | i | j | S[0] | S[1] | S[2] | S[3] | S[4] | S[5] | S[6] | S[7] | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Iniziale | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 0 | 6 | 6 | 1 | 2 | 3 | 4 | 5 | 0 | 7 | |
| 2 | 1 | 7 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 3 | 2 | 2 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 4 | 3 | 3 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 5 | 4 | 3 | 6 | 7 | 2 | 0 | 3 | 5 | 4 | 1 | |
| 6 | 5 | 6 | 6 | 4 | 2 | 0 | 3 | 7 | 5 | 1 | |
| 7 | 6 | 1 | 6 | 4 | 2 | 0 | 3 | 7 | 5 | 2 | |
| 8 | 7 | 2 | 6 | 4 | 1 | 0 | 3 | 7 | 5 | 2 |
Passo 4
Come quarto passo, produciamo il keystream. Si tratta di una stringa pseudorandom di lunghezza pari al messaggio che vogliamo inviare. Verrà utilizzata per criptare il messaggio originale "SOUP" Poiché il flusso di chiavi deve essere lungo quanto il messaggio, ne serve uno di 4 byte.
Il flusso di chiavi viene prodotto dal seguente pseudocodice:
- Creare le variabili j, i e t.
- Impostare
j = 0. - Per ogni
idel testo in chiaro, a partire dai = 1e fino ai = 4, ogni byte del flusso di chiavi viene prodotto come segue: j = (j + S[i]) \mod 8- Scambiare
S[i]eS[j]. t = (S[i] + S[j]) \mod 8- Il byte
i^{th}del flusso di chiavi =S[t]
I calcoli sono riportati nella Tabella 2.
Lo stato iniziale di S è S = [6, 4, 1, 0, 3, 7, 5, 2].
Impostando i = 1, il valore
di j diventa 4 (j = (j + S[i]) \mod 8 = (0 + 4) \mod 8 = 4). Scambiamo quindi S[1] e S[4] per produrre la trasformazione di S nella seconda riga, [6, 3, 1, 0, 4, 7, 5, 2]. Il
valore di t è quindi 7 (t = (S[i] + S[j]) \mod 8 = (3 + 4) \mod 8 = 7). Infine, il byte per il flusso di chiavi è S[7], ovvero 2.
Continuiamo quindi a produrre gli altri byte fino a ottenere i seguenti quattro byte: 2, 6, 3 e 7. Ciascuno di questi byte può essere utilizzato per crittografare ogni lettera del testo in chiaro, "SOUP".
Per cominciare, utilizzando una tabella ASCII, possiamo vedere che "SOUP" codificato dai valori decimali delle stringhe di byte sottostanti è "83 79 85 80". La combinazione con il flusso di chiavi "2 6 3 7" produce "85 85 88 87", che rimane invariato dopo l'operazione modulo 256. In ASCII, il testo cifrato "85 85 88 87" equivale a "UUXW".
Cosa succede se la parola da criptare fosse più lunga dell'array S? In questo caso, l'array S continua a trasformarsi nel modo mostrato sopra per ogni byte i del testo in chiaro, finché non si ottiene un numero di byte nel flusso di chiavi pari al numero di lettere del testo in chiaro.
Tabella 2: Generazione del flusso di chiavi
| i | j | t | Keystream | S[0] | S[1] | S[2] | S[3] | S[4] | S[5] | S[6] | S[7] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 4 | 1 | 0 | 3 | 7 | 5 | 2 | |||
| 1 | 4 | 7 | 2 | 6 | 3 | 1 | 0 | 4 | 7 | 5 | 2 |
| 2 | 5 | 0 | 6 | 6 | 3 | 7 | 0 | 4 | 1 | 5 | 2 |
| 3 | 5 | 1 | 3 | 6 | 3 | 7 | 1 | 4 | 0 | 5 | 2 |
| 4 | 1 | 7 | 2 | 6 | 4 | 7 | 1 | 3 | 0 | 5 | 2 |
L'esempio appena discusso è solo una versione annacquata del codificatore di flusso RC4. Il vero cifrario di flusso RC4 ha un array S di 256 byte di lunghezza, non di 8 byte, e una chiave che può essere compresa tra 1 e 256 byte, non tra 1 e 8 byte. L'array di chiavi e i flussi di chiavi vengono quindi prodotti considerando la lunghezza di 256 byte dell'array S. I calcoli diventano immensamente più complessi, ma i principi rimangono gli stessi. Utilizzando la stessa chiave, 14,48,9, con il cifrario RC4 standard, il messaggio in chiaro "SOUP" viene cifrato come 67 02 ed df in formato esadecimale.
Un cifrario a flusso in cui il flusso di chiavi si aggiorna indipendentemente dal messaggio in chiaro o dal testo cifrato è un cifrario a flusso sincrono. Il flusso di chiavi dipende solo dalla chiave. Chiaramente, l'RC4 è un esempio di cifrario a flusso sincrono, poiché il flusso di chiavi non ha alcuna relazione con il testo in chiaro o il testo cifrato. Tutti i cifrari a flusso primitivi menzionati nel capitolo precedente, tra cui il cifrario a turni, il cifrario di Vigenère e il one-time pad, erano anch'essi di tipo sincrono.
Al contrario, un cifrario a flusso asincrono ha un flusso di chiavi che viene prodotto sia dalla chiave che dagli elementi precedenti del testo cifrato. Questo tipo di cifrario è anche chiamato cifrario autosincronizzante.
È importante notare che il flusso di chiavi prodotto con l'RC4 deve essere trattato come un pad una tantum, e non è possibile produrre il flusso di chiavi esattamente nello stesso modo la volta successiva. Piuttosto che cambiare la chiave ogni volta, la soluzione pratica è quella di combinare la chiave con un nonce per produrre il bytestream.
AES con chiave a 128 bit
Come accennato nel capitolo precedente, tra il 1997 e il 2000 il National Institute of Standards and Technology (NIST) ha indetto un concorso per determinare un nuovo standard di crittografia simmetrica. Il cifrario Rijndael risultò essere il vincitore. Il nome è un gioco di parole con i nomi dei creatori belgi, Vincent Rijmen e Joan Daemen.
Il cifrario Rijndael è un cifrario a blocchi, il che significa che esiste un algoritmo di base che può essere utilizzato con diverse specifiche per le lunghezze delle chiavi e le dimensioni dei blocchi. È quindi possibile utilizzarlo con diverse modalità di funzionamento per costruire schemi di crittografia.
Il comitato del concorso NIST ha adottato una versione ristretta del cifrario Rijndael, che richiede blocchi di 128 bit e chiavi di 128, 192 o 256 bit, come parte dell'Advanced Encryption Standard (AES). Questa versione ristretta del cifrario Rijndael può essere utilizzata anche in più modalità operative. Le specifiche dello standard sono note come Advanced Encryption Standard (AES).
Per mostrare il funzionamento del cifrario Rijndael, il cuore di AES, illustrerò il processo di crittografia con una chiave a 128 bit. La dimensione della chiave ha un impatto sul numero di round per ogni blocco di crittografia. Per le chiavi a 128 bit sono necessari 10 cicli. Con 192 bit e 256 bit, sarebbero stati necessari rispettivamente 12 e 14 cicli.
Inoltre, assumerò che AES sia utilizzato in modalità ECB. Questo semplifica leggermente l'esposizione e non ha importanza per l'algoritmo Rijndael. La modalità ECB non è sicura nella pratica perché porta a una crittografia deterministica. La modalità sicura più comunemente utilizzata con AES è CBC (Cipher Block Chaining).
Chiamiamo la chiave K_0. La
costruzione con i parametri di cui sopra si presenta quindi come in Figura 1, dove M_i sta per una parte del messaggio in chiaro di 128 bit e C_i per una parte del testo cifrato
di 128 bit. Il padding viene aggiunto al testo in chiaro per l'ultimo blocco,
se il testo in chiaro non può essere diviso uniformemente per la dimensione del
blocco.
Figura 1: AES-ECB con una chiave a 128 bit
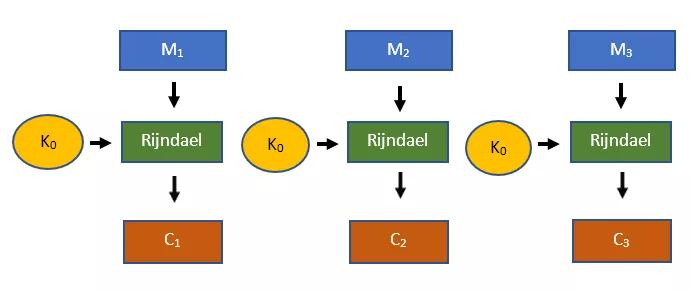
Ogni blocco di testo a 128 bit viene sottoposto a dieci round nello schema
di crittografia Rijndael. Ciò richiede una chiave separata per ogni round
(da K_1 a K_{10}). Queste
vengono prodotte per ogni round dalla chiave originale di 128 bit K_0 utilizzando un algoritmo di espansione della chiave.
Quindi, per ogni blocco di testo da crittografare, utilizzeremo la chiave
originale K_0 e dieci chiavi separate
per i round. Si noti che le stesse 11 chiavi vengono utilizzate per ogni blocco
di testo in chiaro a 128 bit che deve essere crittografato.
L'algoritmo di espansione della chiave è lungo e complesso. Lavorare su di
esso non ha grandi vantaggi didattici. Se lo desiderate, potete esaminare
l'algoritmo di espansione della chiave da soli. Una volta prodotte le chiavi
circolari, il cifrario Rijndael manipolerà il primo blocco di 128 bit di
testo in chiaro, M_1, come si
vede nella Figura 2. Eseguiamo ora questi passaggi.
Figura 2: La manipolazione di M_1 con il cifrario Rijndael:
Round 0:
- XOR di
M_1eK_0per produrreS_0
Round n per n = {1,...,9}:
- XOR
S_{n-1}eK_n - Sostituzione di byte
- Spostare le righe
- Colonne di miscelazione
- XOR
SeK_nper produrreS_n
Round 10:
- XOR
S_9eK_{10} - Sostituzione di byte
- Spostare le righe
- XOR
SeK_{10}per produrreS_{10} S_{10}=C_1
Round 0
Il round 0 del cifrario Rijndael è semplice. Un array S_0 è prodotto da un'operazione XOR tra il testo in chiaro a 128 bit e la chiave
privata. Ovvero,
S_0 = M_1 \oplus K_0
1° turno
Nel round 1, l'array S_0 viene prima combinato con la chiave del round K_1 utilizzando un'operazione XOR. Questo produce un nuovo stato di S.
In secondo luogo, l'operazione sostituzione di byte viene
eseguita sullo stato corrente di S. Funziona prendendo ogni
byte dell'array di 16 byte S e sostituendolo con un byte di un array chiamato Scatola di Rijndael. Ogni byte ha una trasformazione unica
e il risultato è un nuovo stato di S. La S-box di Rijndael è
mostrata nella Figura 3.
Figura 3: S-Box di Rijndael
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 0A | 0B | 0C | 0D | 0E | 0F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 63 | 7C | 77 | 7B | F2 | 6B | 6F | C5 | 30 | 01 | 67 | 2B | FE | D7 | AB | 76 |
| 10 | CA | 82 | C9 | 7D | FA | 59 | 47 | F0 | AD | D4 | A2 | AF | 9C | A4 | 72 | C0 |
| 20 | B7 | FD | 93 | 26 | 36 | 3F | F7 | CC | 34 | A5 | E5 | F1 | 71 | D8 | 31 | 15 |
| 30 | 04 | C7 | 23 | C3 | 18 | 96 | 05 | 9A | 07 | 12 | 80 | E2 | EB | 27 | B2 | 75 |
| 40 | 09 | 83 | 2C | 1A | 1B | 6E | 5A | A0 | 52 | 3B | D6 | B3 | 29 | E3 | 2F | 84 |
| 50 | 53 | D1 | 00 | ED | 20 | FC | B1 | 5B | 6A | CB | BE | 39 | 4A | 4C | 58 | CF |
| 60 | D0 | EF | AA | FB | 43 | 4D | 33 | 85 | 45 | F9 | 02 | 7F | 50 | 3C | 9F | A8 |
| 70 | 51 | A3 | 40 | 8F | 92 | 9D | 38 | F5 | BC | B6 | DA | 21 | 10 | FF | F3 | D2 |
| 80 | CD | 0C | 13 | EC | 5F | 97 | 44 | 17 | C4 | A7 | 7E | 3D | 64 | 5D | 19 | 73 |
| 90 | 60 | 81 | 4F | DC | 22 | 2A | 90 | 88 | 46 | EE | B8 | 14 | DE | 5E | 0B | DB |
| A0 | E0 | 32 | 3A | 0A | 49 | 06 | 24 | 5C | C2 | D3 | AC | 62 | 91 | 95 | E4 | 79 |
| B0 | E7 | C8 | 37 | 6D | 8D | D5 | 4E | A9 | 6C | 56 | F4 | EA | 65 | 7A | AE | 08 |
| C0 | BA | 78 | 25 | 2E | 1C | A6 | B4 | C6 | E8 | DD | 74 | 1F | 4B | BD | 8B | 8A |
| D0 | 70 | 3E | B5 | 66 | 48 | 03 | F6 | 0E | 61 | 35 | 57 | B9 | 86 | C1 | 1D | 9E |
| E0 | E1 | F8 | 98 | 11 | 69 | D9 | 8E | 94 | 9B | 1E | 87 | E9 | CE | 55 | 28 | DF |
| F0 | 8C | A1 | 89 | 0D | BF | E6 | 42 | 68 | 41 | 99 | 2D | 0F | B0 | 54 | BB | 16 |
Questa S-Box è uno dei punti in cui l'algebra astratta entra in gioco nel cifrario Rijndael, in particolare i campi di Galileois.
Per iniziare, si definisce ogni possibile elemento di byte da 00 a FF come
un vettore a 8 bit. Ogni vettore è un elemento del campo di Galois GF(2^8) dove il polinomio irriducibile per l'operazione modulo è x^8 + x^4 + x^3 + x + 1. Il
campo di Galois con queste specifiche è anche chiamato Campo finito di Rijndael.
Quindi, per ogni possibile elemento del campo, creiamo quella che viene chiamata Nyberg S-Box. In questa scatola, ogni byte è mappato sul suo inverso moltiplicativo (cioè, in modo che il loro prodotto sia uguale a 1). Quindi mappiamo i valori dalla S-Box di Nyberg alla S-Box di Rijndael usando la trasformazione affine.
La terza operazione sulla matrice S è l'operazione shift rows. Essa prende lo stato di S ed elenca tutti i sedici byte in una matrice. Il riempimento della matrice inizia in alto a sinistra e procede dall'alto verso il basso e poi, ogni volta che una colonna viene riempita, si sposta di una colonna a destra e in alto.
Una volta costruita la matrice di S, le quattro righe vengono spostate. La prima riga rimane invariata. La seconda riga si sposta di uno a sinistra. La terza si sposta di due a sinistra. La quarta si sposta di tre a sinistra. Un esempio del processo è riportato nella Figura 4. Lo stato originale di S è mostrato in alto, mentre lo stato risultante dopo l'operazione di spostamento delle righe è mostrato sotto.
Figura 4: Operazione di spostamento delle righe
| F1 | A0 | B1 | 23 |
|---|---|---|---|
| 59 | EF | 09 | 82 |
| 97 | 01 | B0 | CC |
| D4 | 72 | 04 | 21 |
| F1 | A0 | B1 | 23 |
|---|---|---|---|
| EF | 09 | 82 | 59 |
| B0 | CC | 97 | 01 |
| 21 | D4 | 72 | 04 |
Nella quarta fase, i campi di Galois fanno di nuovo la loro
comparsa. Per iniziare, ogni colonna della matrice S viene
moltiplicata per la colonna della matrice 4 x 4 vista in Figura 5.
Ma invece di essere una normale moltiplicazione matriciale, si tratta di una
moltiplicazione vettoriale modulo di un polinomio irriducibile, x^8 + x^4 + x^3 + x + 1. I
coefficienti del vettore risultante rappresentano i singoli bit di un byte.
Figura 5: Matrice delle colonne di miscela
| 02 | 03 | 01 | 01 |
|---|---|---|---|
| 01 | 02 | 03 | 01 |
| 01 | 01 | 02 | 03 |
| 03 | 01 | 01 | 02 |
La moltiplicazione della prima colonna della matrice S con la matrice 4 x 4 di cui sopra dà il risultato della Figura 6.
Figura 6: moltiplicazione della prima colonna:
\begin{matrix}
02 \cdot F1 + 03 \cdot EF + 01 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 02 \cdot EF + 03 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 01 \cdot EF + 02 \cdot B0 + 03 \cdot 21 \\
03 \cdot F1 + 01 \cdot EF + 01 \cdot B0 + 02 \cdot 21
\end{matrix}Come passo successivo, tutti i termini della matrice devono essere
trasformati in polinomi. Ad esempio, F1 rappresenta 1 byte e diventerebbe x^7 + x^6 + x^5 + x^4 + 1, mentre 03 rappresenta 1 byte e diventerebbe x + 1.
Tutte le moltiplicazioni vengono quindi eseguite modulo x^8 + x^4 + x^3 + x + 1. Il
risultato è l'addizione di quattro polinomi in ciascuna delle quattro celle
della colonna. Dopo aver eseguito queste addizioni modulo 2, si otterranno quattro polinomi. Ognuno di questi
polinomi rappresenta una stringa di 8 bit, o 1 byte, di S.
Non eseguiremo qui tutti questi calcoli sulla matrice di Figura 6 perché
sono molto estesi.
Una volta elaborata la prima colonna, le altre tre colonne della matrice S vengono elaborate allo stesso modo. Alla fine si ottiene una matrice di sedici byte che può essere trasformata in una matrice.
Come passo finale, l'array S viene nuovamente combinato con
la chiave circolare in un'operazione XOR. Questo produce lo
stato S_1. Ovvero,
S_1 = S \oplus K_0
Giri da 2 a 10
I round da 2 a 9 sono solo una ripetizione del round 1, mutatis mutandis. L'ultimo round è molto simile ai precedenti, tranne per il fatto che viene eliminata la fase di miscelazione delle colonne. In altre parole, il round 10 viene eseguito come segue:
S_9 \oplus K_{10}- Sostituzione di byte
- Spostare le righe
S_{10} = S \oplus K_{10}
Lo stato S_{10} è
ora impostato su C_1, i primi
128 bit del testo cifrato. Procedendo attraverso i restanti blocchi di testo
in chiaro a 128 bit si ottiene il testo cifrato completo C.
Le operazioni del cifrario Rijndael
Qual è il ragionamento alla base delle diverse operazioni viste nel cifrario Rijndael?
Senza entrare nei dettagli, gli schemi di crittografia vengono valutati in base alla misura in cui creano confusione e diffusione. Se lo schema di crittografia ha un alto grado di confusione, significa che il testo cifrato appare drasticamente diverso dal testo in chiaro. Se lo schema di crittografia ha un alto grado di diffusione, significa che qualsiasi piccola modifica al testo in chiaro produce un testo cifrato drasticamente diverso.
Il motivo delle operazioni alla base del cifrario Rijndael è che producono un alto grado di confusione e di diffusione. La confusione è prodotta dall'operazione di sostituzione dei byte, mentre la diffusione è prodotta dalle operazioni di spostamento delle righe e di miscelazione delle colonne.
Crittografia asimmetrica
Il problema della distribuzione e della gestione delle chiavi
Come per la crittografia simmetrica, gli schemi asimmetrici possono essere utilizzati per garantire sia la segretezza che l'autenticazione. Tuttavia, questi schemi utilizzano due chiavi anziché una: una chiave privata e una pubblica.
Iniziamo la nostra indagine con la scoperta della crittografia asimmetrica, in particolare con i problemi che l'hanno stimolata. Successivamente, discutiamo il funzionamento degli schemi asimmetrici di crittografia e autenticazione ad alto livello. Introduciamo quindi le funzioni hash, che sono fondamentali per comprendere gli schemi di autenticazione asimmetrica e che hanno rilevanza anche in altri contesti crittografici, come ad esempio per i codici di autenticazione dei messaggi basati su hash di cui abbiamo parlato nel Capitolo 4.
Supponiamo che Bob voglia acquistare una nuova giacca da pioggia da Jim's Sporting Goods, un rivenditore online di articoli sportivi con milioni di clienti in Nord America. Questo sarà il suo primo acquisto da loro e vuole usare la sua carta di credito. Per questo motivo, Bob dovrà innanzitutto creare un account presso Jim's Sporting Goods, il che richiede l'invio di dati personali come l'indirizzo e i dati della carta di credito. Poi potrà seguire i passi necessari per l'acquisto dell'impermeabile.
Bob e Jim's Sporting Goods vorranno assicurarsi che le loro comunicazioni siano sicure durante tutto questo processo, considerando che Internet è un sistema di comunicazione aperto. Ad esempio, vorranno assicurarsi che nessun potenziale aggressore possa conoscere i dati della carta di credito e dell'indirizzo di Bob e che nessun potenziale aggressore possa ripetere i suoi acquisti o crearne di falsi per suo conto.
Uno schema avanzato di crittografia autenticata, come quello discusso nel capitolo precedente, potrebbe certamente rendere sicure le comunicazioni tra Bob e Jim's Sporting Goods. Ma ci sono chiaramente ostacoli pratici all'implementazione di un tale schema.
Per illustrare questi ostacoli pratici, supponiamo di vivere in un mondo in cui esistano solo gli strumenti della crittografia simmetrica. Cosa potrebbero fare Jim's Sporting Goods e Bob per garantire una comunicazione sicura?
In queste circostanze, la comunicazione sicura comporterebbe costi notevoli. Poiché Internet è un sistema di comunicazione aperto, non possono semplicemente scambiarsi una serie di chiavi. Pertanto, Bob e un rappresentante di Jim's Sporting Goods dovranno effettuare uno scambio di chiavi di persona.
Una possibilità è che Jim's Sporting Goods crei delle postazioni speciali per lo scambio di chiavi, dove Bob e altri nuovi clienti possano recuperare una serie di chiavi per comunicare in modo sicuro. Questo ovviamente comporterebbe notevoli costi organizzativi e ridurrebbe notevolmente l'efficienza con cui i nuovi clienti possono fare acquisti.
In alternativa, Jim's Sporting Goods può inviare a Bob un paio di chiavi con un corriere di fiducia. Questa soluzione è probabilmente più efficiente dell'organizzazione dei luoghi di scambio delle chiavi. Ma ciò comporterebbe comunque costi notevoli, soprattutto se molti clienti effettuano solo uno o pochi acquisti.
Inoltre, uno schema simmetrico per la crittografia autenticata costringe Jim's Sporting Goods a conservare serie di chiavi separate per tutti i suoi clienti. Questa sarebbe una sfida pratica significativa per migliaia di clienti, per non parlare di milioni.
Per capire quest'ultimo punto, supponiamo che Jim's Sporting Goods fornisca a ogni cliente la stessa coppia di chiavi. Ciò consentirebbe a ciascun cliente, o a chiunque altro possa ottenere questa coppia di chiavi, di leggere e persino manipolare tutte le comunicazioni tra Jim's Sporting Goods e i suoi clienti. Quindi, tanto vale non usare affatto la crittografia nelle vostre comunicazioni.
Anche la ripetizione di una serie di chiavi solo per alcuni clienti è una pessima pratica di sicurezza. Qualsiasi potenziale attaccante potrebbe tentare di sfruttare questa caratteristica dello schema (ricordate che si presume che gli attaccanti conoscano tutto di uno schema tranne le chiavi, secondo il principio di Kerckhoffs)
Quindi, Jim's Sporting Goods dovrebbe memorizzare una coppia di chiavi per ogni cliente, indipendentemente da come queste coppie di chiavi sono distribuite. Questo presenta chiaramente diversi problemi pratici.
- Jim's Sporting Goods dovrebbe memorizzare milioni di coppie di chiavi, un set per ogni cliente.
- Queste chiavi dovrebbero essere adeguatamente protette, in quanto sarebbero un bersaglio sicuro per gli hacker. Eventuali violazioni della sicurezza richiederebbero la ripetizione di costosi scambi di chiavi, sia in apposite sedi che tramite corriere.
- Ogni cliente di Jim's Sporting Goods dovrebbe conservare in modo sicuro un paio di chiavi a casa. Si verificheranno smarrimenti e furti, che richiederanno la ripetizione dello scambio di chiavi. I clienti dovrebbero seguire questa procedura anche per qualsiasi altro negozio online o altro tipo di entità con cui desiderano comunicare e fare transazioni su Internet.
Queste due sfide principali appena descritte erano problemi fondamentali fino alla fine degli anni Settanta. Erano note rispettivamente come problema della distribuzione delle chiavi e problema della gestione delle chiavi.
Questi problemi sono sempre esistiti, naturalmente, e spesso hanno creato grattacapi in passato. Le forze militari, ad esempio, dovevano costantemente distribuire al personale sul campo libri con le chiavi per la comunicazione sicura, con grandi rischi e costi. Ma questi problemi si stavano aggravando con il progressivo passaggio a un mondo di comunicazioni digitali a distanza, in particolare per le entità non governative.
Se questi problemi non fossero stati risolti negli anni '70, probabilmente gli acquisti efficienti e sicuri da Jim's Sporting Goods non sarebbero esistiti. In effetti, la maggior parte del nostro mondo moderno, con e-mail pratiche e sicure, operazioni bancarie online e acquisti, sarebbe probabilmente solo una lontana fantasia. Qualcosa di simile a Bitcoin non sarebbe mai esistito.
Cosa è successo negli anni '70? Com'è possibile che possiamo fare istantaneamente acquisti online e navigare in sicurezza nel World Wide Web? Come è possibile che possiamo inviare istantaneamente Bitcoin in tutto il mondo dai nostri smartphone?
Nuove direzioni della crittografia
Negli anni '70, i problemi di distribuzione e gestione delle chiavi avevano attirato l'attenzione di un gruppo di crittografi accademici americani: Whitfield Diffie, Martin Hellman e Ralph Merkle. Di fronte al forte scetticismo della maggior parte dei loro colleghi, si cimentarono nell'ideazione di una soluzione.
Almeno una delle motivazioni principali della loro impresa è stata la previsione che le comunicazioni informatiche aperte avrebbero influenzato profondamente il nostro mondo. Come notano Diffie e Helmann nel 1976,
Lo sviluppo di reti di comunicazione controllate da computer promette contatti senza sforzo e a basso costo tra persone o computer che si trovano ai lati opposti del mondo, sostituendo la maggior parte della posta e molte escursioni con le telecomunicazioni. Per molte applicazioni questi contatti devono essere resi sicuri sia contro le intercettazioni che contro l'immissione di messaggi illegittimi. Attualmente, tuttavia, la soluzione dei problemi di sicurezza è in ritardo rispetto ad altre aree della tecnologia delle comunicazioni. La crittografia contemporanea non è in grado di soddisfare i requisiti, in quanto il suo utilizzo imporrebbe gravi inconvenienti agli utenti del sistema, tanto da eliminare molti dei vantaggi della teleelaborazione. [1]
La tenacia di Diffie, Hellman e Merkle fu ripagata. La prima pubblicazione dei loro risultati fu un articolo di Diffie e Helmann del 1976 intitolato "New Directions in Cryptography" In esso presentavano due modi originali per affrontare i problemi di distribuzione e gestione delle chiavi.
La prima soluzione offerta è stata un protocollo di scambio di chiavi a distanza, ovvero un insieme di regole per lo scambio di una o più chiavi simmetriche su un canale di comunicazione non sicuro. Questo protocollo è oggi noto come scambio di chiavi di Diffie-Helmann o scambio di chiavi di Diffie-Helmann-Merkle. [2]
Con lo scambio di chiavi Diffie-Helmann, due parti si scambiano prima alcune informazioni pubblicamente su un canale non sicuro come Internet. Sulla base di queste informazioni, poi, creano indipendentemente una chiave simmetrica (o una coppia di chiavi simmetriche) per una comunicazione sicura. Sebbene entrambe le parti creino le proprie chiavi in modo indipendente, le informazioni condivise pubblicamente garantiscono che il processo di creazione delle chiavi produca lo stesso risultato per entrambe.
È importante notare che, mentre tutti possono osservare le informazioni scambiate pubblicamente dalle parti attraverso il canale insicuro, solo le due parti coinvolte nello scambio di informazioni possono creare chiavi simmetriche a partire da esse.
Questo, ovviamente, sembra del tutto controintuitivo. Come possono due parti scambiarsi pubblicamente alcune informazioni che permettono solo a loro di creare chiavi simmetriche? Perché chiunque altro osservi lo scambio di informazioni non sarebbe in grado di creare le stesse chiavi?
Naturalmente si basa su una bella matematica. Lo scambio di chiavi Diffie-Helmann funziona tramite una funzione unidirezionale con una trapdoor. Discutiamo a turno il significato di questi due termini.
Si supponga di ricevere una funzione f(x) e il risultato f(a) = y, dove a è un particolare valore di x.
Diciamo che f(x) è una funzione unidirezionale se è facile calcolare il valore y quando vengono dati a e f(x), ma è computazionalmente
impossibile calcolare il valore a quando vengono dati y e f(x). Il nome funzione unidirezionale, ovviamente, deriva dal fatto che
una funzione di questo tipo può essere calcolata solo in una direzione.
Alcune funzioni unidirezionali presentano la cosiddetta porta trappola. Sebbene sia praticamente impossibile calcolare a con solo y e f(x), esiste una certa
informazione Z che rende
computabile il calcolo di a a
partire da y. Questa
informazione Z è nota come trapdoor. Le funzioni unidirezionali che hanno una botola
sono note come funzioni botola.
Non ci addentreremo qui nei dettagli dello scambio di chiavi Diffie-Helmann. Ma essenzialmente ogni partecipante crea delle informazioni, di cui una parte è condivisa pubblicamente e una parte rimane segreta. Ciascuna parte, quindi, prende la propria informazione segreta e l'informazione pubblica condivisa dall'altra parte per creare una chiave privata. E, un po' miracolosamente, entrambe le parti si ritroveranno con la stessa chiave privata.
Chiunque osservi solo le informazioni condivise pubblicamente tra le due parti in uno scambio di chiavi Diffie Helmann non è in grado di replicare questi calcoli. Per farlo avrebbe bisogno delle informazioni private di una delle due parti.
Sebbene la versione di base dello scambio di chiavi Diffie-Helmann presentata nel 1976 non sia molto sicura, versioni sofisticate del protocollo di base sono certamente ancora in uso oggi. Soprattutto, ogni protocollo di scambio di chiavi nell'ultima versione del protocollo di sicurezza del livello di trasporto (versione 1.3) è essenzialmente una versione arricchita del protocollo presentato da Diffie e Hellman nel 1976. Il protocollo di sicurezza del livello di trasporto è il protocollo predominante per lo scambio sicuro di informazioni formattate secondo il protocollo di trasferimento di ipertesti (http), lo standard per lo scambio di contenuti Web.
È importante notare che lo scambio di chiavi Diffie-Helmann non è uno schema asimmetrico. A rigore, si può dire che appartiene al regno della crittografia a chiave simmetrica. Tuttavia, poiché sia lo scambio di chiavi Diffie-Helmann che la crittografia asimmetrica si basano su funzioni teoriche numeriche unidirezionali con trapdoor, in genere vengono discussi insieme.
Il secondo modo proposto da Diffie e Helmann per risolvere il problema della distribuzione e della gestione delle chiavi nel loro articolo del 1976 era, ovviamente, la crittografia asimmetrica.
A differenza della loro presentazione dello scambio di chiavi Diffie-Hellman, hanno fornito solo i contorni generali di come gli schemi crittografici asimmetrici potrebbero essere plausibilmente costruiti. Non hanno proposto alcuna funzione unidirezionale che potesse soddisfare specificamente le condizioni necessarie per una ragionevole sicurezza in tali schemi.
Un'implementazione pratica di uno schema asimmetrico fu tuttavia trovata un anno dopo da tre diversi crittografi e matematici accademici: Ronald Rivest, Adi Shamir e Leonard Adleman. [3] Il sistema di crittografia da loro introdotto divenne noto come crittosistema RSA (dal nome dei loro cognomi).
Le funzioni trapdoor utilizzate nella crittografia asimmetrica (e nello scambio di chiavi Diffie Helmann) sono tutte legate a due problemi principali difficili dal punto di vista computazionale: la fattorizzazione dei primi e il calcolo dei logaritmi discreti.
*La fattorizzazione dei primi richiede, come dice il nome, la scomposizione di un intero nei suoi fattori primi. Il problema RSA è di gran lunga l'esempio più noto di crittosistema legato alla fattorizzazione dei primi.
Il problema del logaritmo discreto è un problema che si presenta nei gruppi ciclici. Dato un generatore in un particolare gruppo ciclico, richiede il calcolo dell'esponente unico necessario per produrre un altro elemento del gruppo a partire dal generatore.
Gli schemi basati sui logaritmi discreti si basano su due tipi principali di gruppi ciclici: i gruppi moltiplicativi di numeri interi e i gruppi che includono i punti delle curve ellittiche. Lo scambio di chiavi Diffie Helmann originale, presentato in "New Directions in Cryptography", funziona con un gruppo ciclico moltiplicativo di numeri interi. L'algoritmo di firma digitale di Bitcoin e lo schema di firma Schnorr recentemente introdotto (2021) si basano entrambi sul problema del logaritmo discreto per un particolare gruppo ciclico di curve ellittiche.
In seguito, passeremo a una panoramica di alto livello sulla segretezza e l'autenticazione nel contesto asimmetrico. Prima di farlo, tuttavia, è necessario fare una breve nota storica.
Sembra ora plausibile che un gruppo di crittografi e matematici britannici che lavoravano per il Government Communications Headquarters (GCHQ) avesse fatto in modo indipendente le scoperte di cui sopra qualche anno prima. Il gruppo era composto da James Ellis, Clifford Cocks e Malcolm Williamson.
Secondo i loro stessi racconti e quelli del GCHQ, fu James Ellis a ideare per primo il concetto di crittografia a chiave pubblica nel 1969. Clifford Cocks avrebbe poi scoperto il sistema crittografico RSA nel 1973 e Malcolm Williamson il concetto di scambio di chiavi Diffie Helmann nel 1974. [4] Le loro scoperte, tuttavia, sarebbero state rivelate solo nel 1997, data la natura segreta del lavoro svolto al GCHQ.
Note:
[1] Whitfield Diffie e Martin Hellman, "New directions in cryptography", IEEE Transactions on Information Theory IT-22 (1976), pp. 644-654, a p. 644.
[2] Anche Ralph Merkle discute un protocollo di scambio di chiavi in "Secure communications over insecure channels", Communications of the Association for Computing Machinery, 21 (1978), 294-99. Sebbene Merkle abbia presentato questo documento prima di quello di Diffie e Hellman, è stato pubblicato successivamente. La soluzione di Merkle non è esponenzialmente sicura, a differenza di quella di Diffie-Hellman.
[3] Ron Rivest, Adi Shamir e Leonard Adleman, "A method for obtaining digital signatures and public-key cryptosystems", Communications of the Association for Computing Machinery, 21 (1978), pp. 120-26.
[4] Una buona storia di queste scoperte è fornita da Simon Singh, The Code Book, Fourth Estate (Londra, 1999), capitolo 6.
Crittografia e autenticazione asimmetrica
Una panoramica della crittografia asimmetrica con l'aiuto di Bob e Alice è riportata nella Figura 1.
Alice crea innanzitutto una coppia di chiavi, composta da una chiave
pubblica (K_P) e una privata
(K_S), dove la "P" di K_P sta per "pubblica" e la "S" di K_S per "segreta". La chiave pubblica viene poi distribuita liberamente ad
altri. Torneremo sui dettagli di questo processo di distribuzione poco più
avanti. Per ora, però, supponiamo che chiunque, compreso Bob, possa ottenere
in modo sicuro la chiave pubblica K_P di Alice.
In un secondo momento, Bob vuole scrivere un messaggio M ad Alice. Poiché contiene informazioni sensibili, vuole che il contenuto
rimanga segreto per tutti tranne che per Alice. Pertanto, Bob cripta prima
il suo messaggio M utilizzando K_P. Poi invia il
testo cifrato risultante C ad
Alice, che decifra C con K_S per ottenere il messaggio originale M.
Figura 1: crittografia asimmetrica
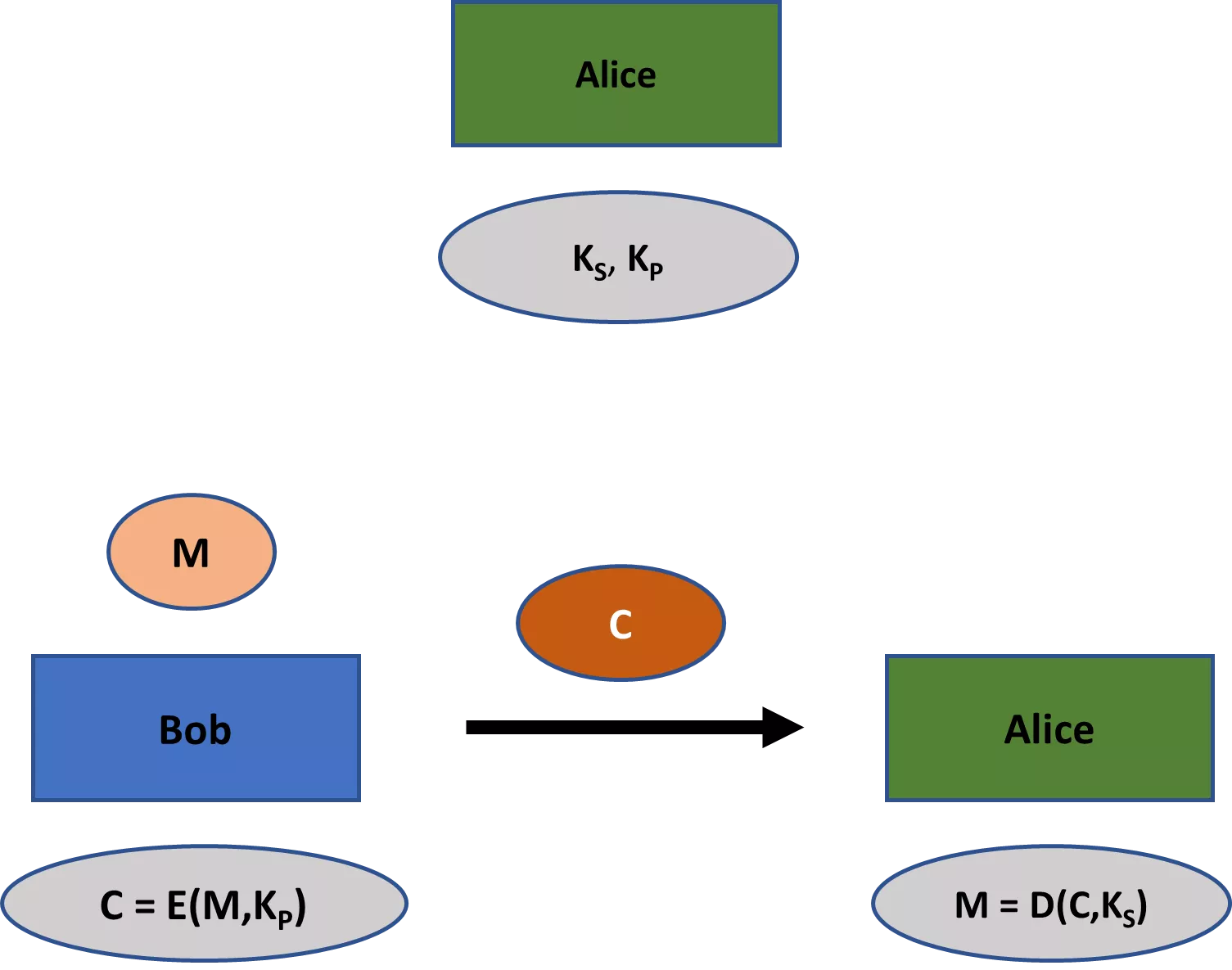
Qualsiasi avversario che ascolti le comunicazioni di Bob e Alice può
osservare C. Conosce anche K_P e l'algoritmo di cifratura E(\cdot). Tuttavia, è
importante notare che queste informazioni non consentono all'attaccante di
decifrare il testo cifrato C.
La decrittazione richiede specificamente K_S, che l'attaccante non
possiede.
Gli schemi di crittografia simmetrica in genere devono essere sicuri contro un aggressore in grado di crittografare validamente i messaggi in chiaro (noto come sicurezza dell'attacco chosen-ciphertext). Tuttavia, non è stato progettato con lo scopo esplicito di consentire la creazione di tali cifrari validi da parte di un attaccante o di chiunque altro.
Ciò è in netto contrasto con uno schema di crittografia asimmetrica, il cui scopo è consentire a chiunque, compresi gli aggressori, di produrre cifrari validi. Gli schemi di crittografia asimmetrica possono quindi essere definiti cifrari ad accesso multiplo.
Per capire meglio cosa sta succedendo, immaginiamo che Bob, invece di inviare un messaggio elettronico, voglia spedire una lettera fisica in segreto. Un modo per garantire la segretezza sarebbe che Alice inviasse a Bob un lucchetto sicuro, ma tenesse la chiave per sbloccarlo. Dopo aver scritto la lettera, Bob potrebbe metterla in una scatola e chiuderla con il lucchetto di Alice. Potrebbe quindi inviare la scatola chiusa con il messaggio ad Alice, che ha la chiave per aprirla.
Sebbene Bob sia in grado di bloccare il lucchetto, né lui né qualsiasi altra persona che intercetti la scatola può sbloccare il lucchetto, se è effettivamente sicuro. Solo Alice può sbloccarlo e vedere il contenuto della lettera di Bob perché possiede la chiave.
Uno schema di crittografia asimmetrica è, grosso modo, una versione digitale di questo processo. Il lucchetto è simile alla chiave pubblica e la chiave del lucchetto è simile alla chiave privata. Poiché il lucchetto è digitale, tuttavia, è molto più facile e meno costoso per Alice distribuirlo a chiunque voglia inviarle messaggi segreti.
Per l'autenticazione in ambito asimmetrico si utilizzano le firme digitali. Queste hanno quindi la stessa funzione dei codici di autenticazione dei messaggi nell'impostazione simmetrica. Una panoramica delle firme digitali è riportata nella Figura 2.
Bob crea innanzitutto una coppia di chiavi, composta dalla chiave pubblica (K_P) e dalla chiave privata (K_S), e distribuisce la sua chiave pubblica. Quando vuole inviare un messaggio
autenticato ad Alice, prende prima il suo messaggio M e la sua chiave privata per creare una firma digitale D. Bob invia quindi ad Alice
il suo messaggio insieme alla firma digitale.
Alice inserisce il messaggio, la chiave pubblica e la firma digitale in un algoritmo di verifica. Questo algoritmo produce vero se la firma è valida, oppure falso se la firma non è valida.
La firma digitale è, come dice chiaramente il nome, l'equivalente digitale della firma scritta su lettere, contratti e così via. In realtà, una firma digitale è solitamente molto più sicura. Con un certo sforzo, è possibile falsificare una firma scritta; un processo reso più facile dal fatto che le firme scritte spesso non vengono verificate da vicino. Una firma digitale sicura, tuttavia, è, proprio come un codice di autenticazione sicura dei messaggi, inesigibile: in altre parole, con uno schema di firma digitale sicura, nessuno può creare una firma per un messaggio che superi la procedura di verifica, a meno che non sia in possesso della chiave privata.
Figura 2: Autenticazione asimmetrica
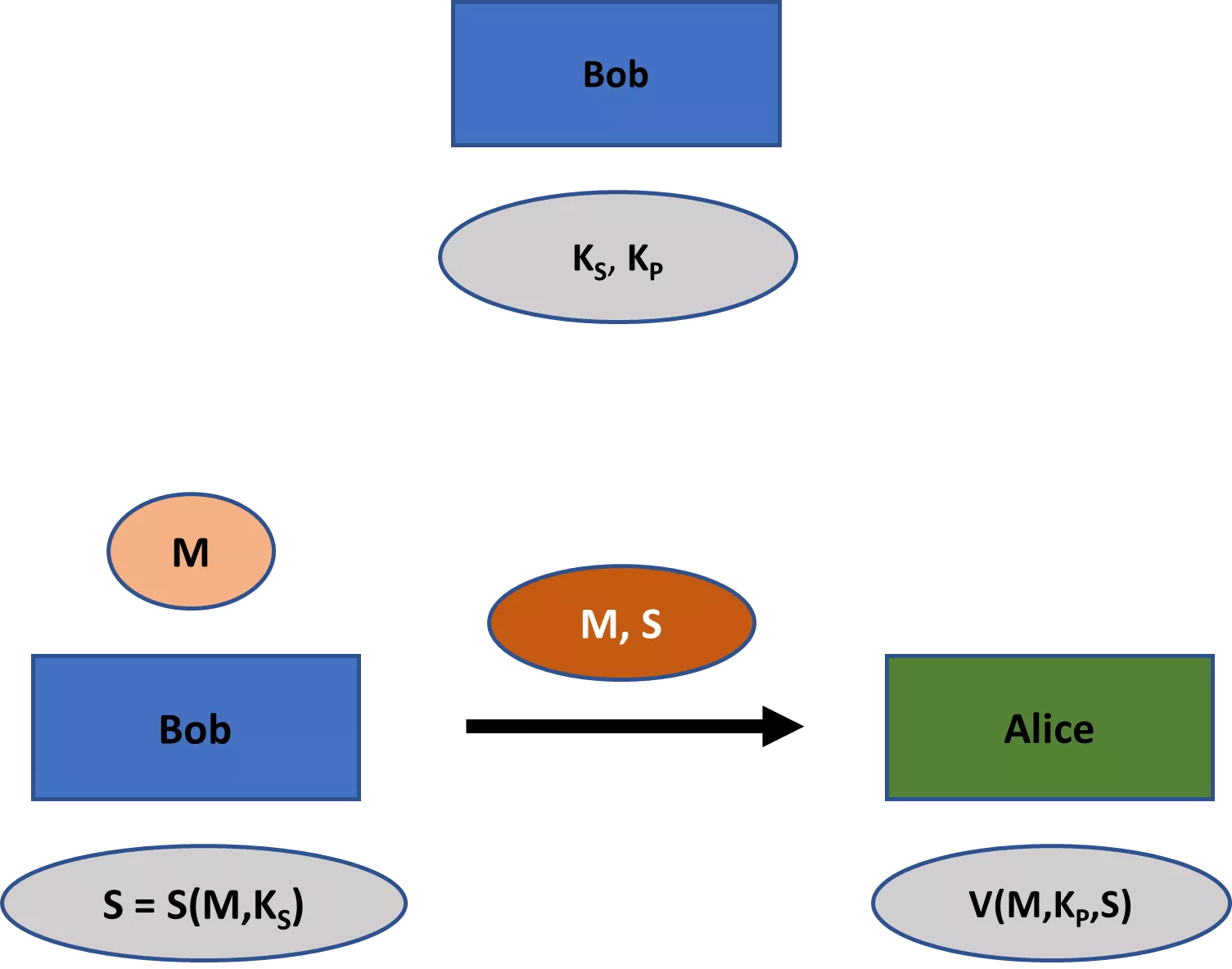
Come nel caso della crittografia asimmetrica, si nota un interessante
contrasto tra le firme digitali e i codici di autenticazione dei messaggi.
Per questi ultimi, l'algoritmo di verifica può essere utilizzato solo da una
delle parti a conoscenza della comunicazione sicura. Questo perché richiede
una chiave privata. Nell'impostazione asimmetrica, invece, chiunque può
verificare una firma digitale S apposta da Bob.
Tutto ciò rende la firma digitale uno strumento estremamente potente. È la
base, ad esempio, per creare firme su contratti che possono essere
verificati a fini legali. Se Bob ha apposto una firma su un contratto nello
scambio di cui sopra, Alice può mostrare il messaggio M, il contratto e la firma S a
un tribunale. Il tribunale può quindi verificare la firma utilizzando la chiave
pubblica di Bob. [5]
Per fare un altro esempio, le firme digitali sono un aspetto importante della distribuzione sicura di software e aggiornamenti software. Questo tipo di verificabilità pubblica non potrebbe mai essere creata utilizzando solo i codici di autenticazione dei messaggi.
Come ultimo esempio della potenza delle firme digitali, consideriamo il Bitcoin. Una delle idee sbagliate più comuni sul Bitcoin, soprattutto nei media, è che le transazioni siano criptate: non è così. Al contrario, le transazioni Bitcoin funzionano con le firme digitali per garantire la sicurezza.
I Bitcoin esistono in lotti chiamati output di transazione non spesi (o UTXO). Supponiamo di aver ricevuto tre pagamenti su un particolare indirizzo Bitcoin per 2 bitcoin ciascuno. Tecnicamente non avete 6 bitcoin su quell'indirizzo. Al contrario, avete tre lotti di 2 bitcoin che sono bloccati da un problema crittografico associato a quell'indirizzo. Per ogni pagamento effettuato, è possibile utilizzare uno, due o tutti e tre questi lotti, a seconda della quantità necessaria per la transazione.
La prova della proprietà dei risultati delle transazioni non spesi è solitamente fornita da una o più firme digitali. Il Bitcoin funziona proprio perché le firme digitali valide sui risultati delle transazioni non spese sono computazionalmente impossibili da realizzare, a meno che non si sia in possesso delle informazioni segrete necessarie per realizzarle.
Attualmente, le transazioni Bitcoin includono in modo trasparente tutte le informazioni che devono essere verificate dai partecipanti alla rete, come ad esempio l'origine degli output non spesi utilizzati nella transazione. Sebbene sia possibile nascondere alcune di queste informazioni e consentire comunque la verifica (come fanno alcune criptovalute alternative come Monero), ciò crea particolari rischi per la sicurezza.
A volte si crea confusione tra la firma digitale e la firma scritta acquisita digitalmente. In quest'ultimo caso, si cattura un'immagine della propria firma scritta e la si incolla su un documento elettronico come un contratto di lavoro. Questa, tuttavia, non è una firma digitale in senso crittografico. Quest'ultima è solo un lungo numero che può essere prodotto solo se si è in possesso di una chiave privata.
Come per l'impostazione a chiave simmetrica, è possibile utilizzare insieme schemi di crittografia e autenticazione asimmetrici. Si applicano principi simili. Innanzitutto, è necessario utilizzare coppie di chiavi private e pubbliche diverse per la crittografia e la creazione di firme digitali. Inoltre, è necessario prima criptare un messaggio e poi autenticarlo.
È importante notare che in molte applicazioni la crittografia asimmetrica non viene utilizzata per l'intero processo di comunicazione. Al contrario, in genere viene utilizzata solo per lo scambio di chiavi simmetriche tra le parti che comunicheranno effettivamente.
È il caso, ad esempio, degli acquisti online. Conoscendo la chiave pubblica del venditore, quest'ultimo può inviarvi messaggi firmati digitalmente di cui potete verificare l'autenticità. Su questa base, è possibile seguire uno dei numerosi protocolli per lo scambio di chiavi simmetriche per comunicare in modo sicuro.
La ragione principale della frequenza di questo approccio è che la crittografia asimmetrica è molto meno efficiente di quella simmetrica nel produrre un determinato livello di sicurezza. Questo è uno dei motivi per cui abbiamo ancora bisogno della crittografia a chiave simmetrica accanto alla crittografia pubblica. Inoltre, la crittografia a chiave simmetrica è molto più naturale in applicazioni particolari, come la crittografia dei propri dati da parte di un utente di computer.
In che modo la firma digitale e la crittografia a chiave pubblica risolvono esattamente i problemi di distribuzione e gestione delle chiavi?
Non esiste una risposta univoca. La crittografia asimmetrica è uno strumento e non esiste un solo modo di utilizzarlo. Ma prendiamo l'esempio precedente di Jim's Sporting Goods per mostrare come si affronterebbero i problemi in questo esempio.
Per iniziare, Jim's Sporting Goods probabilmente si rivolge a una autorità di certificazione, un'organizzazione che supporta la distribuzione di chiavi pubbliche. L'autorità di certificazione registrerebbe alcuni dettagli su Jim's Sporting Goods e gli concederebbe una chiave pubblica. Quindi invierebbe a Jim's Sporting Goods un certificato, noto come certificato TLS/SSL, con la chiave pubblica di Jim's Sporting Goods firmata digitalmente utilizzando la chiave pubblica dell'autorità di certificazione. In questo modo, l'autorità di certificazione afferma che una determinata chiave pubblica appartiene effettivamente a Jim's Sporting Goods.
La chiave per comprendere questo processo con i certificati TLS/SSL è che, mentre in genere la chiave pubblica di Jim's Sporting Goods non è memorizzata da nessuna parte sul vostro computer, le chiavi pubbliche delle autorità di certificazione riconosciute sono effettivamente memorizzate nel vostro browser o nel vostro sistema operativo. Queste sono memorizzate nei cosiddetti certificati radice.
Pertanto, quando Jim's Sporting Goods vi fornisce il suo certificato TLS/SSL, potete verificare la firma digitale dell'autorità di certificazione tramite un certificato root nel vostro browser o sistema operativo. Se la firma è valida, si può essere relativamente sicuri che la chiave pubblica del certificato appartenga effettivamente a Jim's Sporting Goods. Su questa base, è facile impostare un protocollo per una comunicazione sicura con Jim's Sporting Goods.
La distribuzione delle chiavi è diventata molto più semplice per Jim's Sporting Goods. Non è difficile capire che anche la gestione delle chiavi è diventata molto più semplice. Invece di dover memorizzare migliaia di chiavi, Jim's Sporting Goods deve solo memorizzare una chiave privata che gli consenta di apporre le firme alla chiave pubblica del suo certificato SSL. Ogni volta che un cliente visita il sito di Jim's Sporting Goods, può stabilire una sessione di comunicazione sicura a partire da questa chiave pubblica. Inoltre, i clienti non devono memorizzare alcuna informazione (a parte le chiavi pubbliche delle autorità di certificazione riconosciute nel loro sistema operativo e nel loro browser).
Note:
[5] Qualsiasi schema che tenti di ottenere il non ripudio, l'altro tema trattato nel Capitolo 1, dovrà essere basato sulla firma digitale.
Funzioni di hash
Le funzioni di hash sono onnipresenti in crittografia. Non sono schemi simmetrici o asimmetrici, ma rientrano in una categoria crittografica a sé stante.
Abbiamo già incontrato le funzioni hash nel Capitolo 4, con la creazione di messaggi di autenticazione basati su hash. Sono importanti anche nel contesto delle firme digitali, anche se per un motivo leggermente diverso: Le firme digitali, infatti, sono tipicamente realizzate sul valore di hash di un messaggio (crittografato), piuttosto che sul messaggio stesso (crittografato). In questa sezione offrirò un'introduzione più approfondita delle funzioni hash.
Iniziamo con il definire una funzione hash. Una funzione hash è una qualsiasi funzione calcolabile in modo efficiente che accetta input di dimensioni arbitrarie e produce output di lunghezza fissa.
Una funzione hash crittografica è semplicemente una funzione hash utile per le applicazioni in crittografia. L'output di una funzione hash crittografica è tipicamente chiamato hash, valore hash o digesto del messaggio.
Nel contesto della crittografia, una "funzione hash" si riferisce tipicamente a una funzione hash crittografica. D'ora in poi adotterò questa prassi.
Un esempio di funzione hash molto diffusa è SHA-256 (secure hash algorithm 256). Indipendentemente dalla dimensione dell'input (ad esempio, 15 bit, 100 bit o 10.000 bit), questa funzione produce un valore hash a 256 bit. Di seguito sono riportati alcuni esempi di output della funzione SHA-256.
"Ciao": 185f8db32271fe25f561a6fc938b2e264306ec304eda518007d1764826381969
"52398": a3b14d2bf378c1bd47e7f8eaec63b445150a3d7a80465af16dd9fd319454ba90
"La crittografia è divertente": 3cee2a5c7d2cc1d62db4893564c34ae553cc88623992d994e114e344359b146c
Tutti gli output sono esattamente 256 bit scritti in formato esadecimale (ogni cifra esadecimale può essere rappresentata da quattro cifre binarie). Quindi, anche se si fosse inserito il libro Il Signore degli Anelli di Tolkien nella funzione SHA-256, l'output sarebbe stato comunque di 256 bit.
Le funzioni di hash, come SHA-256, sono utilizzate per vari scopi nella crittografia. Le proprietà richieste a una funzione hash dipendono dal contesto di una particolare applicazione. Esistono due proprietà principali generalmente richieste alle funzioni hash in crittografia: [6]
Resistenza alle collisioni
Nascondersi
Una funzione hash H si dice resistente alle collisioni se è impossibile trovare due valori, x e y, tali che x sia uguale a y, ma H(x) = H(y).
Le funzioni hash resistenti alle collisioni sono importanti, ad esempio, nella verifica del software. Supponiamo di voler scaricare la versione Windows di Bitcoin Core 0.21.0 (un'applicazione server per l'elaborazione del traffico di rete Bitcoin). I passi principali da compiere per verificare la legittimità del software sono i seguenti:
Per prima cosa è necessario scaricare e importare le chiavi pubbliche di uno o più collaboratori di Bitcoin Core in un software in grado di verificare le firme digitali (ad esempio Kleopetra). È possibile trovare queste chiavi pubbliche qui. Si raccomanda di verificare il software Bitcoin Core con le chiavi pubbliche di più collaboratori.
Successivamente, è necessario verificare le chiavi pubbliche importate. Almeno uno dei passi da compiere è verificare che le chiavi pubbliche trovate siano le stesse pubblicate in altri luoghi. Ad esempio, si possono consultare le pagine web personali, le pagine Twitter o le pagine Github delle persone di cui si sono importate le chiavi pubbliche. In genere, il confronto tra le chiavi pubbliche viene effettuato confrontando un breve hash della chiave pubblica, noto come impronta digitale.
Successivamente, è necessario scaricare l'eseguibile per Bitcoin Core dal loro sito web. Sono disponibili pacchetti per i sistemi operativi Linux, Windows e MAC.
Successivamente, è necessario individuare due file di rilascio. Il primo contiene l'hash SHA-256 ufficiale dell'eseguibile scaricato insieme agli hash di tutti gli altri pacchetti rilasciati. Un altro file di rilascio conterrà le firme dei vari collaboratori sul file di rilascio con gli hash dei pacchetti. Entrambi i file di rilascio si trovano sul sito web di Bitcoin Core.
Successivamente, è necessario calcolare l'hash SHA-256 dell'eseguibile scaricato dal sito web di Bitcoin Core sul proprio computer. Confrontare poi questo risultato con quello dell'hash del pacchetto ufficiale dell'eseguibile. Dovrebbero essere uguali.
Infine, dovrete verificare che una o più firme digitali sul file di rilascio con gli hash ufficiali del pacchetto corrispondano effettivamente a una o più chiavi pubbliche importate (i rilasci di Bitcoin Core non sono sempre firmati da tutti). È possibile farlo con un'applicazione come Kleopetra.
Questo processo di verifica del software ha due vantaggi principali. In primo luogo, garantisce che non vi siano stati errori di trasmissione durante il download dal sito web di Bitcoin Core. In secondo luogo, garantisce che nessun aggressore abbia potuto farvi scaricare codice modificato e dannoso, violando il sito web di Bitcoin Core o intercettando il traffico.
In che modo il processo di verifica del software sopra descritto protegge da questi problemi?
Se avete verificato diligentemente le chiavi pubbliche che avete importato, allora potete essere abbastanza certi che queste chiavi siano effettivamente le loro e non siano state compromesse. Dato che le firme digitali hanno un'incancellabilità esistenziale, si sa che solo questi collaboratori avrebbero potuto apporre una firma digitale sugli hash dei pacchetti ufficiali presenti nel file di rilascio.
Supponiamo che le firme sul file di rilascio scaricato siano state verificate. È ora possibile confrontare il valore hash calcolato localmente per l'eseguibile Windows scaricato con quello incluso nel file di rilascio correttamente firmato. Come sapete, la funzione di hash SHA-256 è resistente alle collisioni; una corrispondenza significa che il vostro eseguibile è esattamente identico all'eseguibile ufficiale.
Passiamo ora alla seconda proprietà comune delle funzioni hash: nascondersi. Si dice che una funzione hash H ha la proprietà di nascondersi se, per qualsiasi x scelto a caso da un intervallo molto ampio, non è possibile trovare x se si dà solo H(x).
Qui sotto potete vedere l'output SHA-256 di un messaggio che ho scritto. Per garantire una sufficiente casualità, il messaggio includeva una stringa di caratteri generati a caso alla fine. Dato che SHA-256 ha la proprietà di nascondersi, nessuno sarebbe in grado di decifrare questo messaggio.
b194221b37fa4cd1cfce15aaef90351d70de17a98ee6225088b523b586c32ded
Ma non vi lascerò in sospeso finché SHA-256 non diventerà più debole. Il messaggio originale che ho scritto era il seguente:
- "Questo è un messaggio molto casuale, o meglio un po' casuale. Questa parte iniziale non lo è, ma finirò con alcuni caratteri relativamente casuali per garantire un messaggio molto imprevedibile. XLWz4dVG3BxUWm7zQ9qS".
Un modo comune in cui vengono utilizzate le funzioni hash con la proprietà di nascondimento è la gestione delle password (anche la resistenza alle collisioni è importante per questa applicazione). Qualsiasi servizio online decente basato su un account, come Facebook o Google, non memorizza direttamente le password per gestire l'accesso all'account. Al contrario, memorizzeranno solo un hash della password. Ogni volta che si inserisce la password in un browser, viene prima calcolato un hash. Solo questo hash viene inviato al server del fornitore di servizi e confrontato con quello memorizzato nel database di back-end. La proprietà di nascondere la password può aiutare a garantire che gli aggressori non possano recuperarla dal valore dell'hash.
La gestione delle password tramite hash, ovviamente, funziona solo se gli utenti scelgono effettivamente password difficili. La proprietà di occultamento presuppone che x sia scelto in modo casuale da una gamma molto ampia. Scegliere password come "1234", "mypassword" o la data del proprio compleanno non garantisce una reale sicurezza. Esistono lunghi elenchi di password comuni e dei relativi hash che gli aggressori possono sfruttare se riescono a ottenere l'hash della password. Questi tipi di attacchi sono noti come attacchi al dizionario. Se gli aggressori conoscono alcuni dei vostri dati personali, potrebbero anche tentare delle ipotesi informate. Per questo motivo, è sempre necessario disporre di password lunghe e sicure (preferibilmente stringhe lunghe e casuali provenienti da un gestore di password).
A volte un'applicazione potrebbe aver bisogno di una funzione hash che abbia sia la resistenza alle collisioni che la nascondimento. Ma certamente non sempre. Il processo di verifica del software di cui abbiamo parlato, ad esempio, richiede solo che la funzione hash mostri una resistenza alle collisioni, l'occultamento non è importante.
Sebbene la resistenza alle collisioni e l'occultamento siano le principali proprietà richieste alle funzioni hash in crittografia, in alcune applicazioni potrebbero essere desiderabili anche altri tipi di proprietà.
Note:
[6] La terminologia "nascondere" non è di uso comune, ma è tratta specificamente da Arvind Narayanan, Joseph Bonneau, Edward Felten, Andrew Miller e Steven Goldfeder, Bitcoin and Cryptocurrency Technologies, Princeton University Press (Princeton, 2016), capitolo 1.
Il crittosistema RSA
Il problema della fattorizzazione
Mentre la crittografia simmetrica è di solito abbastanza intuitiva per la maggior parte delle persone, non è così per la crittografia asimmetrica. Anche se probabilmente vi sentite a vostro agio con la descrizione di alto livello offerta nelle sezioni precedenti, vi starete chiedendo cosa siano esattamente le funzioni unidirezionali e come vengano utilizzate per costruire schemi asimmetrici.
In questo capitolo, eliminerò alcuni dei misteri che circondano la crittografia asimmetrica, approfondendo un esempio specifico, ovvero il crittosistema RSA. Nella prima sezione, introdurrò il problema della fattorizzazione su cui si basa il problema RSA. In seguito, tratterò una serie di risultati chiave della teoria dei numeri. Nell'ultima sezione, metteremo insieme queste informazioni per spiegare il problema RSA e come questo possa essere utilizzato per creare schemi crittografici asimmetrici.
Aggiungere questa profondità alla nostra discussione non è un compito facile. Richiede l'introduzione di alcuni teoremi e proposizioni di teoria dei numeri. Ma non lasciatevi scoraggiare dalla matematica. La trattazione di questo argomento migliorerà in modo significativo la comprensione di ciò che sta alla base della crittografia asimmetrica e rappresenta un investimento proficuo.
Passiamo ora al problema della fattorizzazione.
Quando si moltiplicano due numeri, ad esempio a e b, ci si riferisce ai
numeri a e b come fattori, e al risultato come prodotto. Il tentativo di scrivere un numero N nella moltiplicazione di due o più fattori è chiamato fattorizzazione o fattorizzazione. [1] Ogni problema che richiede questa
operazione può essere definito un problema di fattorizzazione.
Circa 2.500 anni fa, il matematico greco Euclide di Alessandria scoprì un teorema chiave sulla fattorizzazione dei numeri interi. È comunemente chiamato teorema della fattorizzazione unica e afferma quanto segue:
Teorema 1. Ogni intero N maggiore di 1 è un numero primo
o può essere espresso come prodotto di fattori primi.
L'ultima parte di questa affermazione significa che è possibile prendere
qualsiasi intero non primo N maggiore
di 1 e scriverlo come una moltiplicazione di numeri primi. Di seguito sono riportati
diversi esempi di numeri interi non primi scritti come prodotto di fattori primi.
18 = 2 \cdot 3 \cdot 3 = 2 \cdot 3^284 = 2 \cdot 2 \cdot 3 \cdot 7 = 2^2 \cdot 3 \cdot 7144 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 = 2^4 \cdot 3^2
Per tutti e tre i numeri interi di cui sopra, calcolare i loro fattori primi
è relativamente facile, anche se si dispone solo di N. Si inizia con il numero primo più piccolo, cioè 2, e si vede quante volte
il numero intero N è
divisibile per esso. Si passa poi a verificare la divisibilità di N per 3, 5, 7 e così via. Continuate questo processo finché il vostro intero N non sarà scritto come il prodotto
di soli numeri primi.
Prendiamo ad esempio il numero intero 84. Di seguito viene illustrato il procedimento per determinare i suoi fattori primi. A ogni passo, si estrae il più piccolo fattore primo rimanente (a sinistra) e si determina il termine residuo da fattorizzare. Continuiamo fino a quando anche il termine rimanente è un numero primo. A ogni passo, la fattorizzazione attuale di 84 viene visualizzata all'estrema destra.
- Fattore primo = 2: termine residuo = 42 (
84 = 2 \cdot 42) - Fattore primo = 2: termine residuo = 21 (
84 = 2 \cdot 2 \cdot 21) - Fattore primo = 3: termine residuo = 7 (
84 = 2 \cdot 2 \cdot 3 \cdot 7) - Poiché 7 è un numero primo, il risultato è
2 \cdot 2 \cdot 3 \cdot 7, o2^2 \cdot 3 \cdot 7.
Supponiamo ora che N sia
molto grande. Quanto sarebbe difficile ridurre N in fattori primi?
Questo dipende da N.
Supponiamo, ad esempio, che N sia pari a 50.450.400. Anche se questo numero sembra spaventoso, i calcoli non
sono così complicati e possono essere facilmente eseguiti a mano. Come sopra,
è sufficiente iniziare con 2 e proseguire. Di seguito, è possibile vedere il
risultato di questo processo in modo simile a quello descritto sopra.
- 2:
25.225.200(50.450.400 = 2 \cdot 25.225.200) - 2:
12.612.600(50.450.400 = 2^2 \cdot 12.612.600) - 2:
6.306.300(50.450.400 = 2^3 \cdot 6.306.300) - 2:
3.153.150(50.450.400 = 2^4 \cdot 3.153.150) - 2:
1.576.575(50.450.400 = 2^5 \cdot 1.576.575) - 3:
525.525(50.450.400 = 2^5 \cdot 3 \cdot 525.525) - 3:
175.175(50.450.400 = 2^5 \cdot 3^2 \cdot 175.175) - 5:
35.035(50.450.400 = 2^5 \cdot 3^2 \cdot 5 \cdot 35.035) - 5:
7.007(50.450.400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7.007) - 7:
1.001(50.450.400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7 \cdot 1.001) - 7:
143(50.450.400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 143) - 11:
13(50.450.400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13) - Poiché 13 è un numero primo, il risultato è
2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13.
Risolvere questo problema a mano richiede un po' di tempo. Un computer, ovviamente, potrebbe fare tutto questo in una piccola frazione di secondo. Anzi, spesso un computer può persino fattorizzare numeri interi estremamente grandi in una frazione di secondo.
Esistono tuttavia alcune eccezioni. Supponiamo di scegliere a caso due
numeri primi molto grandi. È tipico etichettare questi due numeri p e q, e adotterò questa
convenzione in questa sede.
Per concretezza, diciamo che p e q sono entrambi numeri
primi a 1024 bit e che richiedono almeno 1024 bit per essere rappresentati
(quindi il primo bit deve essere 1). Quindi, ad esempio, 37 non può essere
uno dei numeri primi. È certamente possibile rappresentare 37 con 1024 bit.
Ma chiaramente non è necessario un numero così elevato di bit per
rappresentarlo. È possibile rappresentare 37 con qualsiasi stringa che abbia
6 bit o più. (In 6 bit, 37 sarebbe rappresentato come 100101).
È importante capire quanto siano grandi p e q se selezionati nelle condizioni
di cui sopra. A titolo di esempio, ho selezionato un numero primo casuale che
necessita di almeno 1024 bit per essere rappresentato.
- 14,752,173,874,503,595,484,930,006,383,670,759,559,764,562,721,397,166,747,289,220,945,457,932,666,751,048,198,854,920,097,085,690,793,755,254,946,188,163,753,506,778,089,706,699,671,722,089,715,624,760,049,594,106,189,662,669,156,149,028,900,805,928,183,585,427,782,974,951,355,515,394,807,209,836,870,484,558,332,897,443,152,653,214,483,870,992,618,171,825,921,582,253,023,974,514,209,142,520,026,807,636,589
Supponiamo ora che, dopo aver selezionato casualmente i numeri primi p e q, li moltiplichiamo per
ottenere un numero intero N.
Quest'ultimo numero intero, quindi, è un numero a 2048 bit che richiede
almeno 2048 bit per la sua rappresentazione. È molto, molto più grande di p e q.
Supponiamo di dare a un computer solo N e di chiedergli di trovare i due fattori primi a 1024 bit di N. La probabilità che il
computer scopra p e q è estremamente piccola. Si può
dire che è impossibile per tutti gli scopi pratici. Questo è vero anche se si
dovesse impiegare un supercomputer o addirittura una rete di supercomputer.
Per iniziare, supponiamo che il computer cerchi di risolvere il problema
scorrendo 1024 numeri di bit, verificando in ogni caso se sono primi e se
sono fattori di N. L'insieme
dei numeri primi da testare è circa 1,265 \cdot 10^{305}. [2]
Anche se si prendono tutti i computer del pianeta e si fa in modo che
tentino di trovare e testare numeri primi a 1024 bit in questo modo, una
possibilità su un miliardo di trovare con successo un fattore primo di N richiederebbe un periodo di calcolo molto più lungo dell'età dell'Universo.
In pratica, un computer può fare meglio della procedura approssimativa appena descritta. Esistono diversi algoritmi che il computer può applicare per arrivare più rapidamente a una fattorizzazione. Il punto, tuttavia, è che anche utilizzando questi algoritmi più efficienti, il compito del computer è ancora computazionalmente impossibile. [3]
È importante notare che la difficoltà della fattorizzazione nelle condizioni appena descritte si basa sull'ipotesi che non esistano algoritmi computazionalmente efficienti per il calcolo dei fattori primi. In realtà non possiamo dimostrare che non esista un algoritmo efficiente. Tuttavia, questa ipotesi è molto plausibile: nonostante gli sforzi estesi per centinaia di anni, non abbiamo ancora trovato un algoritmo efficiente dal punto di vista computazionale.
Pertanto, il problema della fattorizzazione, in determinate circostanze, può
essere plausibilmente assunto come un problema difficile. In particolare,
quando p e q sono numeri primi molto grandi, il loro prodotto N non è difficile da calcolare; ma la fattorizzazione solo con N è praticamente impossibile.
Note:
[1] La fattorizzazione può essere importante anche per lavorare con oggetti
matematici diversi dai numeri. Ad esempio, può essere utile per fattorizzare
espressioni polinomiali come x^2 - 2x + 1. Nella nostra trattazione ci concentreremo solo sulla fattorizzazione dei
numeri, in particolare dei numeri interi.
[2] Secondo il teorema dei numeri primi, il numero di primi
minori o uguali a N è
approssimativamente N/\ln(N).
Ciò significa che è possibile approssimare il numero di primi di lunghezza
1024 bit con:
\frac{2^{1024}}{\ln(2^{1024})} -
\frac{2^{1023}}{\ln(2^{1023})}
...che equivale a circa 1,265 \times 10^{305}.
[3] Lo stesso vale per i problemi di logaritmo discreto. Ecco perché le costruzioni asimmetriche funzionano con chiavi molto più grandi rispetto alle costruzioni crittografiche simmetriche.
Risultati della teoria dei numeri
Purtroppo, il problema della fattorizzazione non può essere utilizzato direttamente per gli schemi crittografici asimmetrici. Tuttavia, possiamo utilizzare a questo scopo un problema più complesso ma correlato: il problema RSA.
Per capire il problema RSA, è necessario comprendere una serie di teoremi e proposizioni della teoria dei numeri. In questa sezione vengono presentati in tre sottosezioni: (1) l'ordine di N, (2) l'invertibilità modulo N e (3) il teorema di Eulero.
Parte del materiale delle tre sottosezioni è già stato introdotto nel capitolo 3. Tuttavia, per comodità, lo ripeterò qui.
L'ordine di N
Un intero a è coprimo o primo relativo di un intero N, se il massimo comun
divisore tra loro è 1. Sebbene 1 non sia per convenzione un numero primo, è
un coprimario di ogni intero (come lo è -1).
Ad esempio, si consideri il caso in cui a = 18 e N = 37. Si tratta
chiaramente di numeri coprimari. Il più grande intero che si divide in 18 e
37 è 1. Consideriamo invece il caso in cui a = 42 e N = 16. È evidente che non
si tratta di numeri coprimari. Entrambi i numeri sono divisibili per 2, che
è maggiore di 1.
Possiamo ora definire l'ordine di N come segue. Supponiamo che N sia un intero maggiore di 1. L'ordine di N è, allora, il
numero di tutti i coprimeri con N tali che, per ogni coprimero a, vale la seguente
condizione: 1 \leq a < N.
Ad esempio, se N = 12, 1, 5,
7 e 11 sono gli unici numeri coprimari che soddisfano il requisito
precedente. Quindi, l'ordine di 12 è uguale a 4.
Supponiamo che N sia un
numero primo. Allora ogni intero minore di N ma maggiore o uguale a 1 è coprimo con esso. Questo include tutti gli
elementi del seguente insieme: \{1,2,3,....,N - 1\}. Quindi, quando N è primo,
l'ordine di N è N - 1. Ciò è affermato nella
proposizione 1, dove \phi(N) indica l'ordine di N.
Proposizione 1.
phi(N) = N - 1$ quando $N$ è primo
Supponiamo che N non sia
primo. È quindi possibile calcolare il suo ordine utilizzando la funzione Phi di Eulero. Mentre il calcolo dell'ordine di un
intero piccolo è relativamente semplice, la funzione Phi di Eulero diventa
particolarmente importante per gli interi più grandi. La proposizione della
funzione Phi di Eulero è riportata di seguito.
Teorema 2. Sia N uguale a p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot
p_i^{e_i} \cdot \ldots \cdot p_n^{e_n}, dove l'insieme \{p_i\} è costituito da tutti i fattori primi distinti di N e ogni e_i indica quante
volte il fattore primo p_i ricorre per N. Allora,
\phi(N) = p_1^{e_1 - 1} \cdot (p_1 - 1) \cdot p_2^{e_2 -
1} \cdot (p_2 - 1) \cdot \ldots \cdot p_n^{e_n - 1} \cdot
(p_n - 1)
il teorema 2 dimostra che, una volta scomposto un
qualsiasi N non primo nei
suoi fattori primi distinti, è facile calcolare l'ordine di N.
Ad esempio, supponiamo che N = 270. Questo non è chiaramente un numero primo. Scomponendo N nei suoi fattori primi si ottiene l'espressione: 2 \cdot 3^3 \cdot 5. Secondo
la funzione Phi di Eulero, l'ordine di N è quindi il seguente:
\phi(N) = 2^{1 - 1} \cdot (2 - 1) + 3^{3 - 1} \cdot
(3 - 1) + 5^{1 - 1} \cdot (5 - 1) = 1 \cdot 1 + 9 \cdot 2 + 1
\cdot 4 = 1 + 18 + 4 = 23
Supponiamo poi che N sia il
prodotto di due primi, p e q. il precedente teorema 2 afferma che l'ordine di N è il
seguente:
p^{1 - 1} \cdot (p - 1) \cdot q^{1 - 1} \cdot (q - 1)
= (p - 1) \cdot (q - 1)
Si tratta di un risultato fondamentale, in particolare per il problema RSA, e viene enunciato nella Proposizione 2 che segue.
Proposizione 2. Se N è il prodotto di due primi, p e q, l'ordine di N è il prodotto (p - 1) \cdot (q - 1).
Per illustrare, supponiamo che N = 119. Questo numero intero può essere scomposto in due numeri primi, 7 e 17.
Quindi, la funzione Phi di Eulero suggerisce che l'ordine di 119$ è il
seguente:
\phi(119) = (7 - 1) \cdot (17 - 1) = 6 \cdot 16 = 96
In altre parole, l'intero 119 ha 96 coprimeri nell'intervallo da 1 a 119. In effetti, questo insieme comprende tutti i numeri interi da 1 a 119 che non sono multipli di 7 o di 17.
D'ora in poi, indicheremo l'insieme dei coprimeri che determina l'ordine di N come C_N. Per il nostro
esempio in cui N = 119,
l'insieme C_{119} è
troppo grande per essere elencato completamente. Ma alcuni degli elementi sono
i seguenti:
C_{119} = \{1, 2, \dots, 6, 8, \dots, 13, 15, 16, 18,
\dots, 33, 35, \dots, 96\}
Invertibilità modulo N
Possiamo dire che un intero a è invertibile modulo N, se esiste almeno un intero b tale che a \cdot b \mod N = 1 \mod N.
Un tale intero b viene
definito inverso (o inverso moltiplicativo) di a, data la riduzione per
modulo di N.
Supponiamo, ad esempio, che a = 5 e N = 11. Esistono molti
numeri interi per i quali è possibile moltiplicare 5, in modo che 5 \cdot b \mod 11 = 1 \mod 11. Si considerino, ad esempio, i numeri interi 20 e 31. È facile vedere che
entrambi questi numeri interi sono inversi di 5 per la riduzione modulo 11.
5 \cdot 20 \mod 11 = 100 \mod 11 = 1 \mod 115 \cdot 31 \mod 11 = 155 \mod 11 = 1 \mod 11
Mentre 5 ha molte riduzioni di inversi modulo 11, è possibile dimostrare che esiste un solo inverso positivo di 5 che è minore di 11. In realtà, questo non è un risultato unico per il nostro esempio particolare, ma generale.
Proposizione 3. Se l'intero a è invertibile modulo N, deve
esserci esattamente un inverso positivo di a minore di N (quindi, questo
unico inverso di a deve
provenire dall'insieme \{1, \dots, N - 1\}).
Indichiamo l'inverso unico di a dalla Proposizione 3 come a^{-1}. Per il caso
in cui a = 5 e N = 11, si può vedere che a^{-1} = 9, dato
che 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11.
Si noti che è possibile ottenere il valore 9 per a^{-1} nel nostro esempio anche riducendo semplicemente qualsiasi altro inverso di a per modulo 11. Ad esempio, 20 \mod 11 = 31 \modulo 11 = 9 \mod 11.
Quindi, ogni volta che un intero a > N è invertibile modulo N,
allora anche a \mod N deve
essere invertibile modulo N.
Non è detto che esista una riduzione dell'inverso di a modulo N. Supponiamo, ad
esempio, che a = 2 e N = 8. Non esiste b, o qualsiasi a^{-1} in particolare, tale che 2 \cdot b \mod 8 = 1 \mod 8. Questo perché
qualsiasi valore di b produrrà
sempre un multiplo di 2, quindi nessuna divisione per 8 potrà mai produrre un
resto uguale a 1.
Come facciamo a sapere se un intero a ha un inverso per un dato N?
Come avrete notato nell'esempio precedente, il massimo comun divisore tra 2
e 8 è maggiore di 1, cioè 2. E questo è in realtà esemplificativo del
seguente risultato generale:
Proposizione 4. Esiste un inverso di un intero a dato ridotto modulo N, e in
particolare un unico inverso positivo minore di N, se e solo se il massimo
comun divisore tra a e N è 1 (cioè se sono coprimari).
Per il caso in cui a = 5 e N = 11, abbiamo concluso che a^{-1} = 9, dato
che 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11. È importante notare che è vero anche il contrario. Cioè, quando a = 9 e N = 11, si ha che a^{-1} = 5.
Teorema di Eulero
Prima di passare al problema RSA, dobbiamo comprendere un altro teorema cruciale, il teorema di Eulero. Esso afferma quanto segue:
Teorema 3. Supponiamo che due numeri interi a e N siano coprimari. Allora a^{\phi(N)} \mod N = 1 \mod N.
Si tratta di un risultato notevole, ma all'inizio un po' confuso. Vediamo un esempio per capirlo.
Supponiamo che a = 5 e N = 7. Si tratta
effettivamente di numeri coprimi, come richiesto dal teorema di Eulero.
Sappiamo che l'ordine di 7 è uguale a 6, dato che 7 è un numero primo (vedi Proposizione 1).
Il teorema di Eulero afferma che 5^6 ´mod 7 deve essere uguale a 1 ´mod 7. Di seguito sono
riportati i calcoli che dimostrano che ciò è effettivamente vero.
5^6 \mod 7 = 15.625 \mod 7 = 1 \mod N
Il numero intero 7 si divide in 15.624 per un totale di 2.233 volte. Quindi, il resto della divisione di 16.625 per 7 è 1.
Quindi, utilizzando la funzione Phi di Eulero, Teorema 2, si può ricavare la Proposizione 5 che segue.
Proposizione 5. \varphi(a \cdot b) = \varphi(a) \cdot \varphi(b) per qualsiasi numero intero positivo a e b.
Non mostreremo perché questo è il caso. Ma ci limitiamo a notare che la
prova di questa proposizione è già stata data dal fatto che \varphi(p \cdot q) = \varphi(p) \cdot \varphi(q) = (p - 1) \cdot (q - 1) quando p e q sono primi, come affermato nella Proposizione 2.
Il teorema di Eulero, insieme alla Proposizione 5, ha
importanti implicazioni. Si veda, ad esempio, cosa accade nelle espressioni
seguenti, dove a e N sono coprimari.
a^{2 \cdot \phi(N)} \mod N = a^{\phi(N)} \cdot a^{\phi(N)} \mod N = 1 \cdot 1 \mod N = 1 \mod Na^{\phi(N) + 1} \cdot N = a^{\phi(N)} \cdot a^1 \cdot N = 1 \cdot a^1 \cdot N = a \cdot Na^{8 \cdot \phi(N) + 3} \mod N = a^{8 \cdot \phi(N)} \cdot a^3 \mod N = 1 \cdot a^3 \mod N = a^3 \mod N
Quindi, la combinazione del teorema di Eulero e della Proposizione 5 ci permette di calcolare semplicemente una serie di espressioni. In generale, possiamo riassumere l'intuizione come nella Proposizione 6.
Proposizione 6. a^x \mod N = a^{x \mod \varphi(N)}
Ora dobbiamo mettere tutto insieme in un ultimo complicato passaggio.
Così come N ha un ordine \phi(N) che include gli elementi dell'insieme C_N, sappiamo che l'intero \phi(N) deve a sua volta avere un ordine e un insieme di coprimeri. Poniamo \phi(N) = R. Allora sappiamo
che esiste anche un valore per \phi(R) e un insieme di coprimeri C_R.
Supponiamo di scegliere un intero e dall'insieme C_R. Dalla Proposizione 3 sappiamo che questo intero e ha un solo inverso positivo minore di R. Cioè, e ha un unico inverso dell'insieme C_R. Chiamiamo questo inverso d. Data la definizione di
inverso, ciò significa che e \cdot d = 1 \mod R.
Possiamo usare questo risultato per fare un'affermazione sul nostro intero
originale N. Ciò è riassunto
nella Proposizione 7.
Proposizione 7. Supponiamo che e \cdot d \mod \phi(N) = 1 \mod \phi(N). Allora per qualsiasi elemento a dell'insieme C_N si deve
verificare che a^{e \cdot d \mod \phi(N)} = a^{1 \mod \phi(N)} = a
\mod N.
Ora disponiamo di tutti i risultati di teoria dei numeri necessari per enunciare chiaramente il problema RSA.
Il crittosistema RSA
Siamo ora pronti per enunciare il problema RSA. Si supponga di creare un
insieme di variabili composto da p, q, N, \phi(N), e, d e y. Chiamiamo questo insieme Pi. Viene creato come segue:
Generare due primi casuali
peqdi uguale dimensione e calcolare il loro prodottoN.Calcolare l'ordine di
N,\phi(N), mediante il seguente prodotto:(p - 1) \cdot (q - 1).Scegliere un
e > 2tale che sia minore e coprimario di\phi(N).Calcolare
dimpostandoe \cdot d \mod \phi(N) = 1.Selezionare un valore casuale
ypiù piccolo e coprimario diN.
Il problema RSA consiste nel trovare un x tale che x^e = y, pur avendo
a disposizione solo un sottoinsieme di informazioni riguardanti Pi, ovvero le variabili N, e e y. Quando p e q sono molto grandi, in genere
si raccomanda che siano di 1024 bit, il problema RSA è considerato difficile.
Si può capire perché questo è il caso, data la discussione precedente.
Un modo semplice per calcolare x quando x^e \mod N = y \mod N è semplicemente calcolare y^d \mod N. Sappiamo che y^d \mod N = x \mod N grazie ai
seguenti calcoli:
y^d \mod N = x^{e \cdot d} \mod N = x^{e \cdot d \mod
\phi(N)} \mod N = x^{1 \mod \phi(N)} \mod N = x \mod N.
Il problema è che non conosciamo il valore d, poiché non è indicato nel problema. Pertanto, non possiamo calcolare
direttamente y^d \mod N per
produrre x \mod N.
Potremmo tuttavia essere in grado di calcolare indirettamente d dall'ordine di N, \phi(N), poiché sappiamo che e \cdot d \mod \phi(N) = 1 \mod \phi(N). Ma per ipotesi il problema non fornisce un valore nemmeno per \phi(N).
Infine, l'ordine potrebbe essere calcolato indirettamente con i fattori
primi p e q, in modo da poter
eventualmente calcolare d. Ma
per ipotesi, anche i valori p e q non ci sono stati forniti.
A rigore, anche se il problema della fattorizzazione all'interno di un problema RSA è difficile, non possiamo dimostrare che anche il problema RSA è difficile. Potrebbero infatti esistere altri modi per risolvere il problema RSA oltre alla fattorizzazione. Tuttavia, è generalmente accettato e assunto che se il problema di fattorizzazione all'interno del problema RSA è difficile, anche il problema RSA stesso è difficile.
Se il problema RSA è effettivamente difficile, allora produce una funzione
unidirezionale con una trapdoor. La funzione in questo caso è f(g) = g^e \mod N. Conoscendo f(g), chiunque
potrebbe facilmente calcolare un valore y per un particolare g = x.
Tuttavia, è praticamente impossibile calcolare un particolare valore x solo conoscendo il valore y e
la funzione f(g). L'eccezione
è data da un'informazione d,
la botola. In questo caso, è sufficiente calcolare y^d per ottenere x.
Vediamo un esempio specifico per illustrare il problema RSA. Non posso scegliere un problema RSA che sarebbe considerato difficile in base alle condizioni di cui sopra, perché i numeri sarebbero ingombranti. Questo esempio serve invece a illustrare il funzionamento generale del problema RSA.
Per iniziare, supponiamo di selezionare due numeri primi casuali 13 e 31.
Quindi p = 13 e q = 31. Il prodotto N di questi due primi è uguale a 403. Possiamo facilmente calcolare l'ordine
di 403. È equivalente a (13 - 1) \cdot (31 - 1) = 360.
Quindi, come previsto dal passo 3 del problema RSA, dobbiamo selezionare un coprimetro per 360 che sia maggiore di 2 e minore di 360. Non dobbiamo scegliere questo valore a caso. Questo valore non deve essere scelto a caso. Supponiamo di scegliere 103. Si tratta di un coprimotore di 360, poiché il suo massimo comun divisore con 103 è 1.
Il passo 4 richiede ora di calcolare un valore d tale che 103 \cdot d \mod 360 = 1.
Questo non è un compito facile se il valore di N è grande. È necessario utilizzare una procedura chiamata algoritmo euclideo esteso.
Sebbene non mostri qui la procedura, essa produce il valore 7 quando e = 103. Potete verificare che la coppia di valori 103 e 7 soddisfa effettivamente
la condizione generale e \cdot d \mod \phi(n) = 1 attraverso
i calcoli che seguono.
103 \cdot 7 \mod 360 = 721 \mod 360 = 1 \mod 360
Inoltre, data la Proposizione 4, sappiamo che nessun altro intero
compreso tra 1 e 360 per d produrrà il risultato che 103 \cdot d = 1 \mod 360.
Inoltre, la proposizione implica che selezionando un valore diverso per e, si otterrà un valore unico
diverso per d.
Nel passo 5 del problema RSA, dobbiamo scegliere un intero positivo y che sia un coprimetro minore di 403. Supponiamo di impostare y = 2^{103}.
L'esponenziazione di 2 per 103 dà il risultato seguente.
2^{103} \mod 403 = 10.141.204.801.825.835.211.973.625.643.008 \mod 403 = 349 \mod 403
Il problema RSA in questo particolare esempio è ora il seguente: Si dispone
di N = 403, e = 103 e y = 349 \mod 403. Ora si
deve calcolare x in modo che x^{103} = 349 \mod 403. In altre parole, bisogna trovare che il valore originale prima
dell'esponenziazione per 103 era 2.
Sarebbe facile (almeno per un computer) calcolare x se sapessimo che d = 7. In
tal caso, si potrebbe determinare x come segue.
x = y^7 \mod 403 = 349^7 \mod 403 = 630,634,881,591,804,949 \mod 403 = 2 \mod 403
Il problema è che non è stata fornita l'informazione che d = 7. Si potrebbe ovviamente calcolare d dal fatto che 103 \cdot d = 1 \mod 360. Il
problema è che non vi è stata fornita l'informazione che l'ordine di N = 360. Infine, si potrebbe
anche calcolare l'ordine di 403 calcolando il seguente prodotto: (p - 1) \cdot (q - 1). Ma non
vi viene detto che p = 13 e q = 31.
Naturalmente, un computer potrebbe ancora risolvere il problema RSA per questo esempio con relativa facilità, perché i numeri primi coinvolti non sono grandi. Ma quando i numeri primi diventano molto grandi, si trova di fronte a un compito praticamente impossibile.
Abbiamo presentato il problema RSA, una serie di condizioni che lo rendono difficile e la matematica sottostante. In che modo tutto questo può essere utile per la crittografia asimmetrica? In particolare, come possiamo trasformare la durezza del problema RSA in determinate condizioni in uno schema di crittografia o di firma digitale?
Un approccio consiste nel prendere il problema RSA e costruire schemi in
modo semplice. Per esempio, supponiamo di aver generato un insieme di
variabili \Pi come descritto
nel problema RSA, e di assicurarci che p e q siano sufficientemente
grandi. Si imposta la propria chiave pubblica pari a (N, e) e si condivide questa informazione con il mondo. Come descritto in
precedenza, si mantengono segreti i valori di p, q, \phi(n) e d. Infatti, d è la vostra chiave privata.
Chiunque voglia inviarvi un messaggio m che è un elemento di C_N può
semplicemente cifrarlo come segue: (Il testo cifrato c è equivalente al valore y nel
problema RSA). Si può facilmente decifrare questo messaggio calcolando c^d \mod N.
Si potrebbe tentare di creare uno schema di firma digitale nello stesso
modo. Supponiamo di voler inviare a qualcuno un messaggio m con una firma digitale S. Si
potrebbe semplicemente impostare S = m^d \mod N e inviare la coppia (m,S) al
destinatario. Chiunque può verificare la firma digitale semplicemente
controllando se S^e \mod N = m \mod N. Per un
attaccante, invece, sarebbe molto difficile creare una S valida per un messaggio, dato che non possiede d.
Purtroppo, trasformare quello che di per sé è un problema difficile, il
problema RSA, in uno schema crittografico non è così semplice. Per uno
schema di crittografia semplice, si possono scegliere solo coprimeri di N come messaggi. Questo non ci lascia molti messaggi possibili, certamente non
abbastanza per una comunicazione standard. Inoltre, questi messaggi devono essere
selezionati in modo casuale. Questo sembra poco pratico. Infine, qualsiasi messaggio
selezionato due volte produrrà lo stesso identico testo cifrato. Questo è estremamente
indesiderabile in qualsiasi schema di crittografia e non soddisfa nessuna nozione
moderna e rigorosa di sicurezza nella crittografia.
I problemi diventano ancora più gravi per il nostro schema di firma digitale
semplice. Allo stato attuale, qualsiasi aggressore può facilmente
falsificare le firme digitali semplicemente scegliendo prima un coprimetro
di N come firma e poi calcolando
il messaggio originale corrispondente. Questo rompe chiaramente il requisito
di falsificabilità esistenziale.
Tuttavia, aggiungendo un po' di complessità intelligente, il problema RSA può essere utilizzato per creare uno schema sicuro di crittografia a chiave pubblica e uno schema sicuro di firma digitale. Non entreremo nei dettagli di tali costruzioni in questa sede. [4] Tuttavia, è importante notare che questa complessità aggiuntiva non modifica il problema RSA fondamentale su cui si basano questi schemi.
Note:
[4] Si veda, ad esempio, Jonathan Katz e Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), pp. 410-32 sulla crittografia RSA e pp. 444-41 per le firme digitali RSA.
Sezione finale
Recensioni & Valutazioni
366d6fd0-ceb2-4299-bf37-8c6dfcb681d5 true
Esame Finale
44882d2b-63cd-4fde-8485-f76f14d8b2fe true
Conclusione
f1905f78-8cf7-5031-949a-dfa8b76079b4 true