name: Introduction à la cryptographie formelle goal: Une introduction approfondie à la science et à la pratique de la cryptographie. objectives:

Plongée dans la cryptographie

Il est difficile de trouver beaucoup de matériel qui offre un juste milieu dans l'enseignement de la cryptographie.

D'une part, il existe de longs papiers formels qui ne sont accessibles qu'aux personnes ayant une solide formation en mathématiques, en logique ou dans une autre discipline formelle. D'autre part, il y a des introductions de très haut niveau qui cachent trop de détails pour quiconque est un tant soit peu curieux.

Cette introduction à la cryptographie cherche à se situer à mi-chemin. Bien qu'elle soit relativement stimulante et détaillée pour toute personne débutant dans le domaine de la cryptographie, elle n'est pas le trou du lapin d'un ouvrage académique typique.

Introduction

Aperçu du cours

bb8a8b73-7fb2-50da-bf4e-98996d79887b Bienvenue dans le cours CYP302 !

Ce livre propose une introduction approfondie à la science et à la pratique de la cryptographie. Dans la mesure du possible, il se concentre sur l'exposition conceptuelle plutôt que formelle de la matière.

Ce contenu éducatif est adapté du livre et repo JWBurgers. Bien que l'auteur ait gracieusement autorisé son utilisation pédagogique, tous les droits de propriété intellectuelle restent la propriété du créateur original.

Motivation et objectifs

Il est difficile de trouver beaucoup de matériel qui offre un juste milieu dans l'enseignement de la cryptographie.

D'une part, il existe de longs traités formels qui ne sont accessibles qu'aux personnes ayant une solide formation en mathématiques, en logique ou dans une autre discipline formelle. D'autre part, il y a des introductions de très haut niveau qui cachent trop de détails pour quiconque est un tant soit peu curieux.

Cette introduction à la cryptographie cherche à se situer à mi-chemin. Bien qu'elle soit relativement stimulante et détaillée pour toute personne débutant dans le domaine de la cryptographie, elle n'est pas le trou du lapin d'un traité fondamental typique.

Public cible

Des développeurs aux personnes intellectuellement curieuses, ce livre est utile à tous ceux qui veulent plus qu'une compréhension superficielle de la cryptographie. Si votre objectif est de maîtriser le domaine de la cryptographie, ce livre est également un bon point de départ.

Guide de lecture

Le livre contient actuellement sept chapitres : "Qu'est-ce que la cryptographie ?" (partie 2), "Fondements mathématiques de la cryptographie I" (partie 3), "Fondements mathématiques de la cryptographie II" (partie 4), "Cryptographie symétrique" (partie 5), "RC4 et AES" (partie 6), "Cryptographie asymétrique" (partie 7) et "Le système cryptographique RSA" (partie 8). Un dernier chapitre, "La cryptographie en pratique", sera encore ajouté. Il se concentre sur diverses applications cryptographiques, notamment la sécurité de la couche transport, le routage en oignon et le système d'échange de valeur de Bitcoin.

À moins que vous n'ayez une solide formation en mathématiques, la théorie des nombres est probablement le sujet le plus difficile de ce livre. J'en propose une vue d'ensemble au chapitre 3, et elle apparaît également dans l'exposé de l'AES au chapitre 5 et du système de chiffrement RSA au chapitre 7.

Si vous avez vraiment du mal avec les détails formels de ces parties du livre, je vous recommande de vous contenter d'une lecture de haut niveau la première fois.

Remerciements

L'ouvrage qui a le plus influencé la conception de ce cours est Introduction to Modern Cryptography de Jonathan Katz et Yehuda Lindell, CRC Press (Boca Raton, FL), 2015. Un cours d'accompagnement intitulé "Cryptography" est disponible sur Coursera

Les principales sources supplémentaires qui ont été utiles pour créer la vue d'ensemble de ce livre sont Simon Singh, The Code Book, Fourth Estate (Londres, 1999) ; Christof Paar et Jan Pelzl, Understanding Cryptography, Springer (Heidelberg, 2010) et un cours basé sur le livre de Paar intitulé "Introduction to Cryptography" ; et Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN : John Wiley & Sons).

Je ne citerai que les informations et les résultats très spécifiques que je tire de ces sources, mais je tiens à reconnaître ici ma dette générale à leur égard.

Pour les lecteurs qui souhaitent acquérir des connaissances plus avancées sur la cryptographie après cette introduction, je recommande vivement le livre de Katz et Lindell. Le cours de Katz sur Coursera est un peu plus accessible que le livre.

Contributions

Veuillez consulter le fichier des contributions dans le dépôt pour obtenir des indications sur la manière de soutenir le projet.

Notation

Termes clés:

Les termes clés des abécédaires sont introduits en les mettant en gras. Par exemple, l'introduction du chiffrement Rijndael en tant que terme clé se présenterait comme suit : Chiffrement Rijndael.

Les termes clés sont explicitement définis, sauf s'il s'agit de noms propres ou si leur signification est évidente dans la discussion.

Une définition est généralement donnée lors de l'introduction d'un terme clé, bien qu'il soit parfois plus pratique de laisser la définition à un stade ultérieur.

Mots et phrases mis en exergue:

Les mots et les phrases sont mis en évidence par l'italique. Par exemple, la phrase "Retenez votre mot de passe" se présenterait comme suit : Mémorisez votre mot de passe.

Notation formelle:

La notation formelle concerne principalement les variables, les variables aléatoires et les ensembles.

Prêt à explorer l'univers fascinant de la cryptographie ? C'est parti !

Qu'est-ce que la cryptographie ?

Les chiffres de Beale

Commençons notre exploration du domaine de la cryptographie par l'un des épisodes les plus charmants et divertissants de son histoire : celui des chiffres de Beale. [1]

L'histoire des chiffres de Beale est, à mon avis, plus susceptible d'être une fiction qu'une réalité. Mais elle est censée s'être déroulée comme suit.

À la fois durant l'hiver de 1820 et de 1822, un homme nommé Thomas J. Beale séjourna dans une auberge tenue par Robert Morriss à Lynchburg (Virginie). À la fin de son second séjour, Beale remit à Morriss une boîte en fer contenant des documents précieux à des fins de protection.

Quelques mois plus tard, Morriss reçut une lettre de Beale datée du 9 mai 1822. Elle soulignait la grande valeur du contenu de la boîte en fer et comportait quelques instructions pour Morriss : si ni Beale ni aucun de ses associés ne revenaient jamais réclamer la boîte, il devait l'ouvrir précisément dix ans après la date de la lettre (soit le 9 mai 1832). Certains des documents à l'intérieur seraient écrits en texte ordinaire. Plusieurs autres, cependant, seraient "inintelligibles sans l'aide d'une clé". Cette "clé" devait ensuite être remise à Morriss par un ami non identifié de Beale en juin 1832.

Malgré les instructions claires, Morriss n'ouvrit pas la boîte en mai 1832 et l'ami mystérieux de Beale n'apparut jamais en juin de cette année. Ce n'est qu'en 1845 que l'aubergiste décida enfin d'ouvrir la boîte. À l'intérieur, Morriss trouva une note expliquant comment Beale et ses associés avaient découvert de l'or et de l'argent dans l'Ouest et les avaient enterrés, avec quelques bijoux, pour les protéger. En outre, la boîte contenait trois textes chiffrés : c'est-à-dire des textes écrits en code nécessitant une clé cryptographique, ou un secret, et un algorithme associé pour les déverrouiller. Ce processus de déverrouillage d'un texte chiffré est appelé déchiffrement, tandis que le processus de verrouillage est appelé chiffrement. (Comme expliqué au chapitre 3, le terme "chiffre" peut revêtir plusieurs significations. Dans l'expression "chiffres de Beale", il s'agit d'une abréviation pour textes chiffrés.)

Les trois textes chiffrés trouvés par Morriss dans la boîte en fer sont chacun constitués d'une série de nombres séparés par des virgules. Selon la note de Beale, ces textes chiffrés fournissent séparément l'emplacement du trésor, le contenu du trésor, et une liste de noms avec les héritiers légitimes du trésor et leurs parts (ces dernières informations étant pertinentes au cas où Beale et ses associés ne viendraient jamais réclamer la boîte).

Morriss tenta de déchiffrer les trois textes chiffrés pendant vingt ans. Cela aurait été facile avec la clé. Mais Morriss ne possédait pas la clé et ne parvint pas à récupérer les textes originaux, ou textes en clair comme on les appelle généralement en cryptographie.

Vers la fin de sa vie, Morriss transmit la boîte à un ami en 1862. Cet ami publia ensuite un pamphlet en 1885, sous le pseudonyme J.B. Ward. Il contenait une description de l'histoire (supposée) de la boîte, des trois textes chiffrés, et une solution qu'il avait trouvée pour le deuxième texte chiffré. (Apparemment, il existe une clé pour chaque texte chiffré, et non une clé unique fonctionnant pour les trois textes chiffrés comme Beale semblait initialement l'indiquer dans sa lettre à Morriss.)

Vous pouvez voir le deuxième texte chiffré dans la Figure 2 ci-dessous. [2] La clé de ce texte chiffré est la Déclaration d'Indépendance des États-Unis. La procédure de déchiffrement revient à appliquer les deux règles suivantes :

Figure 1 : Chiffre de Beale n°2

Figure 1 : Chiffre de Beale n°2.

Par exemple, le premier nombre du deuxième texte chiffré est 115. Le 115e mot de la Déclaration d'Indépendance est "instituted", donc la première lettre du texte en clair est "i". Le texte chiffré n'indique pas directement les espaces entre les mots et les majuscules. Cependant, après avoir déchiffré les premiers mots, on peut logiquement en déduire que le premier mot du texte en clair était simplement "I". (Le texte en clair commence par la phrase "I have deposited in the county of Bedford.")

Après déchiffrement, le second message fournit le contenu détaillé du trésor (or, argent et bijoux), et suggère qu'il a été enterré dans des pots en fer et recouvert de pierres dans le comté de Bedford (Virginie). Les gens adorent un bon mystère, et de grands efforts ont été déployés pour déchiffrer les deux autres chiffres de Beale, notamment celui décrivant l'emplacement du trésor. Même divers cryptographes de renom ont tenté leur chance. Cependant, à ce jour, personne n'a réussi à déchiffrer les deux autres textes chiffrés.

Notes :

[1] Pour un bon résumé de l'histoire, voir Simon Singh, The Code Book, Fourth Estate (Londres, 1999), pp. 82-99. Un court métrage sur l'histoire a été réalisé par Andrew Allen en 2010. Vous pouvez trouver le film, "The Thomas Beale Cipher", sur son site Web.

[2] Cette image est disponible sur la page Wikipédia dédiée aux chiffres de Beale.

Cryptographie moderne

Les histoires pittoresques comme celle des chiffres de Beale sont ce à quoi la plupart d'entre nous associent la cryptographie. Cependant, la cryptographie moderne diffère d'au moins quatre manières importantes de ces exemples historiques.

Premièrement, historiquement, la cryptographie ne s'est préoccupée que de la confidentialité (ou du secret). [3] Les textes chiffrés étaient créés pour s'assurer que seules certaines parties pouvaient avoir accès aux informations des textes en clair, comme dans le cas des chiffres de Beale. Pour qu'un schéma de chiffrement serve bien cet objectif, déchiffrer le texte chiffré ne doit être réalisable que si l'on possède la clé.

La cryptographie moderne s'intéresse à un éventail plus large de thèmes que la simple confidentialité. Ces thèmes incluent principalement (1) l'intégrité des messages — c'est-à-dire garantir qu'un message n'a pas été modifié ; (2) l'authenticité des messages — c'est-à-dire garantir qu'un message provient réellement d'un expéditeur particulier ; et (3) la non-répudiation — c'est-à-dire garantir qu'un expéditeur ne peut pas nier faussement plus tard qu'il a envoyé un message. [4]

Il est donc important de bien distinguer un schéma de chiffrement d'un schéma cryptographique. Un schéma de chiffrement ne concerne que la confidentialité. Bien qu'un schéma de chiffrement soit un schéma cryptographique, l'inverse n'est pas vrai. Un schéma cryptographique peut également servir les autres objectifs principaux de la cryptographie, notamment l'intégrité, l'authenticité et la non-répudiation.

Les thèmes de l'intégrité et de l'authenticité sont tout aussi importants que celui de la confidentialité. Nos systèmes de communication modernes ne pourraient pas fonctionner sans garanties concernant l'intégrité et l'authenticité des communications. La non-répudiation est également une préoccupation importante, par exemple pour les contrats numériques, mais elle est moins nécessaire de manière généralisée dans les applications cryptographiques que la confidentialité, l'intégrité et l'authenticité.

Deuxièmement, les schémas de chiffrement classiques comme les chiffres de Beale impliquaient toujours une clé partagée entre toutes les parties concernées. Cependant, de nombreux schémas cryptographiques modernes impliquent non pas une seule, mais deux clés : une clé privée et une clé publique. Alors que la première doit rester privée dans toutes les applications, la seconde est généralement une information publique (d'où leurs noms respectifs). Dans le domaine du chiffrement, la clé publique peut être utilisée pour chiffrer le message, tandis que la clé privée peut être utilisée pour le déchiffrer.

La branche de la cryptographie qui traite des schémas où toutes les parties partagent une clé est appelée cryptographie symétrique. La clé unique dans un tel schéma est généralement appelée clé privée (ou clé secrète). La branche de la cryptographie qui traite des schémas nécessitant une paire clé privée-clé publique est connue sous le nom de cryptographie asymétrique. Ces branches sont parfois également appelées respectivement cryptographie à clé secrète et cryptographie à clé publique (bien que cela puisse prêter à confusion, car les schémas de cryptographie à clé publique possèdent également des clés privées).

L'avènement de la cryptographie asymétrique à la fin des années 1970 a été l'un des événements les plus importants de l'histoire de la cryptographie. Sans elle, la plupart de nos systèmes de communication modernes, y compris Bitcoin, ne seraient pas possibles, ou du moins très impraticables.

Il est important de noter que la cryptographie moderne ne se limite pas exclusivement à l'étude des schémas de cryptographie symétrique et asymétrique (bien que cela couvre une grande partie du domaine). Par exemple, la cryptographie s'intéresse également aux fonctions de hachage et aux générateurs de nombres pseudo-aléatoires, et vous pouvez construire des applications sur ces primitives qui ne sont pas liées à la cryptographie symétrique ou asymétrique.

Troisièmement, les schémas de chiffrement classiques, comme ceux utilisés dans les chiffres de Beale, relevaient davantage de l'art que de la science. Leur sécurité perçue reposait principalement sur des intuitions concernant leur complexité. Ils étaient généralement corrigés lorsqu'une nouvelle attaque contre eux était découverte, ou totalement abandonnés si l'attaque était particulièrement grave. Cependant, la cryptographie moderne est une science rigoureuse avec une approche formelle et mathématique pour le développement et l'analyse des schémas cryptographiques. [5]

Plus précisément, la cryptographie moderne se concentre sur les preuves formelles de sécurité. Toute preuve de sécurité pour un schéma cryptographique suit trois étapes :

  1. Énoncer une définition cryptographique de la sécurité, c'est-à-dire un ensemble d'objectifs de sécurité et la menace posée par l'attaquant.
  2. Énoncer toutes les hypothèses mathématiques concernant la complexité computationnelle du schéma. Par exemple, un schéma cryptographique peut contenir un générateur de nombres pseudo-aléatoires. Bien que nous ne puissions pas prouver leur existence, nous pouvons supposer qu'ils existent.
  3. Exposer une preuve mathématique de sécurité du schéma sur la base de la notion formelle de sécurité et de toute hypothèse mathématique.

Quatrièmement, alors qu'historiquement la cryptographie était principalement utilisée dans des contextes militaires, elle a progressivement imprégné nos activités quotidiennes à l'ère numérique. Que vous fassiez des transactions bancaires en ligne, que vous postiez sur les réseaux sociaux, que vous achetiez un produit sur Amazon avec votre carte de crédit, ou que vous envoyiez des bitcoins à un ami, la cryptographie est le sine qua non de notre ère numérique.

Compte tenu de ces quatre aspects de la cryptographie moderne, on pourrait caractériser la cryptographie moderne comme la science qui se consacre au développement formel et à l'analyse des schémas cryptographiques visant à sécuriser les informations numériques contre les attaques adverses. [6] La sécurité doit être comprise au sens large comme la prévention des attaques compromettant la confidentialité, l'intégrité, l'authentification et/ou la non-répudiation dans les communications.

La cryptographie doit être considérée comme une sous-discipline de la cybersécurité, qui vise à prévenir le vol, les dommages et l'utilisation abusive des systèmes informatiques. Notez que de nombreux aspects de la cybersécurité ont peu ou seulement partiellement de rapport avec la cryptographie.

Par exemple, si une entreprise héberge localement des serveurs coûteux, elle peut être préoccupée par la sécurité de ce matériel contre le vol et les dommages. Bien que ce soit un problème de cybersécurité, cela n'a que peu de rapport avec la cryptographie.

Autre exemple, les attaques par hameçonnage (phishing) sont un problème courant dans notre ère moderne. Ces attaques tentent de tromper les gens via un e-mail ou un autre moyen de communication pour leur soutirer des informations sensibles telles que des mots de passe ou des numéros de carte de crédit. Bien que la cryptographie puisse aider à limiter les attaques par hameçonnage dans une certaine mesure, une approche globale nécessite bien plus que l'utilisation de la cryptographie.

Notes :

[3] Pour être précis, les applications importantes des schémas cryptographiques ont concerné la confidentialité. Les enfants, par exemple, utilisent fréquemment des schémas cryptographiques simples pour "s'amuser". La confidentialité n'est pas réellement une préoccupation dans ces cas.

[4] Bruce Schneier, Applied Cryptography, 2e éd., 2015 (Indianapolis, IN : John Wiley & Sons), p. 2.

[5] Voir Jonathan Katz et Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL : 2015), en particulier pp. 16-23, pour une bonne description.

[6] Cf. Katz et Lindell, ibid., p. 3. Je pense que leur caractérisation présente certains problèmes, donc j'en propose une version légèrement différente ici.

Communications ouvertes

La cryptographie moderne est conçue pour fournir des garanties de sécurité dans un environnement de communications ouvertes. Si notre canal de communication est si bien protégé que les espions n'ont aucune chance de manipuler ou même d'observer nos messages, alors la cryptographie est superflue. Cependant, la plupart de nos canaux de communication sont loin d'être aussi bien protégés.

L'infrastructure de communication dans le monde moderne repose sur un vaste réseau de câbles en fibre optique. Passer des appels téléphoniques, regarder la télévision et naviguer sur Internet dans un foyer moderne dépendent généralement de ce réseau de câbles en fibre optique (un faible pourcentage peut reposer uniquement sur des satellites). Il est vrai que vous pouvez disposer de différentes connexions de données chez vous, comme des câbles coaxiaux, des lignes d'abonnés numériques (asymétriques) (DSL) et des câbles en fibre optique. Mais, du moins dans les pays développés, ces différents supports de données rejoignent rapidement un nœud à l'extérieur de votre maison, intégré dans un vaste réseau de câbles en fibre optique qui relie l'ensemble du globe. Les exceptions concernent certaines zones reculées des pays développés, comme aux États-Unis et en Australie, où le trafic de données peut encore parcourir de longues distances via des fils téléphoniques en cuivre traditionnels.

Il serait impossible d'empêcher des attaquants potentiels d'accéder physiquement à ce réseau de câbles et à son infrastructure de soutien. En fait, nous savons déjà que la plupart de nos données sont interceptées par diverses agences nationales de renseignement aux intersections cruciales d'Internet. [7] Cela inclut tout, des messages Facebook aux adresses de sites Web que vous visitez.

Alors que la surveillance massive des données nécessite un adversaire puissant, comme une agence nationale de renseignement, des attaquants disposant de peu de ressources peuvent facilement tenter d'espionner à une échelle plus locale. Bien que cela puisse se faire en piratant des fils, il est beaucoup plus facile d'intercepter les communications sans fil.

La plupart de nos données réseau locales — que ce soit chez nous, au bureau ou dans un café — transitent désormais par des ondes radio vers des points d'accès sans fil sur des routeurs tout-en-un, plutôt que par des câbles physiques. Ainsi, un attaquant a besoin de peu de ressources pour intercepter l'ensemble de votre trafic local. Cela est particulièrement préoccupant, car la plupart des gens ne protègent que très peu les données qui transitent par leurs réseaux locaux. De plus, les attaquants potentiels peuvent également cibler nos connexions haut débit mobiles, telles que la 3G, la 4G et la 5G. Toutes ces communications sans fil sont une cible facile pour les attaquants.

Ainsi, l'idée de garder les communications secrètes en protégeant le canal de communication est une aspiration désespérément illusoire pour une grande partie du monde moderne. Tout ce que nous savons justifie une paranoïa sévère : vous devez toujours supposer que quelqu'un écoute. Et la cryptographie est le principal outil dont nous disposons pour obtenir une quelconque sécurité dans cet environnement moderne.

Notes :

[7] Voir, par exemple, Olga Khazan, “The creepy, long-standing practice of undersea cable tapping”, The Atlantic, 16 juillet 2013 (disponible sur The Atlantic).

Fondements Mathématiques de la Cryptographie 1

Variables aléatoires

La cryptographie repose sur les mathématiques. Et si vous souhaitez acquérir une compréhension approfondie de la cryptographie, vous devez être à l'aise avec ces mathématiques.

Ce chapitre présente la plupart des notions mathématiques de base que vous rencontrerez en apprenant la cryptographie. Les sujets abordés comprennent les variables aléatoires, les opérations modulo, les opérations XOR et la pseudo-aléatoire. Vous devez maîtriser ces notions pour toute compréhension non superficielle de la cryptographie.

La prochaine section traitera de la théorie des nombres, qui est bien plus complexe.

Variables aléatoires

Une variable aléatoire est généralement notée par une lettre majuscule non en gras. Par exemple, nous pourrions parler d'une variable aléatoire X, d'une variable aléatoire Y ou d'une variable aléatoire Z. C'est la notation que j'utiliserai désormais.

Une variable aléatoire peut prendre deux ou plusieurs valeurs possibles, chacune avec une probabilité positive donnée. Les valeurs possibles sont répertoriées dans l'ensemble des résultats.

Chaque fois que vous échantillonnez une variable aléatoire, vous tirez une valeur particulière de son ensemble de résultats selon les probabilités définies.

Prenons un exemple simple. Supposons une variable X définie comme suit :

Pr[X = 1] = 0.5
Pr[X = 2] = 0.5

Il est facile de voir que X est une variable aléatoire. Premièrement, il y a deux ou plusieurs valeurs possibles que X peut prendre, à savoir 1 et 2. Deuxièmement, chaque valeur possible a une probabilité positive de se produire lors de l'échantillonnage de X, à savoir 0.5.

Tout ce qu'une variable aléatoire exige, c'est un ensemble de résultats avec deux possibilités ou plus, où chaque possibilité a une probabilité positive de se produire lors de l'échantillonnage. En principe, une variable aléatoire peut donc être définie de manière abstraite, sans aucun contexte. Dans ce cas, vous pouvez considérer l’« échantillonnage » comme l’exécution d’une expérience naturelle pour déterminer la valeur de la variable aléatoire.

La variable X ci-dessus a été définie de manière abstraite. Vous pourriez ainsi considérer l'échantillonnage de la variable X comme le fait de lancer une pièce équitable et d’attribuer « 2 » en cas de face et « 1 » en cas de pile. Pour chaque échantillon de X, vous lancez à nouveau la pièce.

Alternativement, vous pourriez aussi considérer l'échantillonnage de X comme le fait de lancer un dé équitable et d’attribuer « 2 » si le dé tombe sur 1, 3 ou 4, et « 1 » s'il tombe sur 2, 5 ou 6. Chaque fois que vous échantillonnez X, vous lancez à nouveau le dé.

En réalité, toute expérience naturelle qui permettrait de définir les probabilités des valeurs possibles de X peut être imaginée en ce qui concerne le tirage.

Cependant, les variables aléatoires ne sont pas toujours introduites de manière abstraite. L'ensemble des valeurs possibles a souvent une signification concrète dans le monde réel (plutôt que de simples nombres). De plus, ces valeurs peuvent être définies par rapport à un type spécifique d'expérience (plutôt que par toute expérience naturelle ayant ces valeurs).

Prenons maintenant un exemple de variable X qui n'est pas définie abstraitement. X est définie comme suit pour déterminer laquelle de deux équipes commence un match de football :

Pr [X = \text{rouge engage}] = 0.5
Pr [X = \text{bleu engage}] = 0.5

Dans ce cas, l'ensemble des résultats de X est fourni avec une signification concrète, à savoir quelle équipe commence un match de football. De plus, les résultats possibles et leurs probabilités associées sont déterminés par une expérience concrète, à savoir le lancement d'une pièce particulière C.

En cryptographie, les variables aléatoires sont généralement introduites avec un ensemble de résultats ayant une signification réelle. Il peut s'agir de l'ensemble de tous les messages pouvant être chiffrés, connu sous le nom d’espace des messages, ou de l'ensemble de toutes les clés que les parties utilisant le chiffrement peuvent choisir, connu sous le nom d’espace des clés.

Les variables aléatoires dans les discussions cryptographiques ne sont cependant généralement pas définies par rapport à une expérience naturelle spécifique, mais par rapport à toute expérience pouvant produire les bonnes distributions de probabilité.

Les variables aléatoires peuvent avoir des distributions de probabilité discrètes ou continues. Les variables aléatoires ayant une distribution de probabilité discrète — c'est-à-dire des variables aléatoires discrètes — ont un nombre fini de résultats possibles. La variable aléatoire X dans les deux exemples donnés jusqu'à présent était discrète.

Les variables aléatoires continues peuvent, au contraire, prendre des valeurs dans un ou plusieurs intervalles. Par exemple, vous pourriez dire qu'une variable aléatoire, lors de l'échantillonnage, prendra une valeur réelle quelconque entre 0 et 1, et que chaque nombre réel dans cet intervalle est également probable. Dans cet intervalle, il y a une infinité de valeurs possibles.

Pour les discussions cryptographiques, vous n'avez besoin de comprendre que les variables aléatoires discrètes. Toute discussion sur les variables aléatoires à partir de maintenant doit donc être comprise comme se référant aux variables aléatoires discrètes, sauf indication contraire.

Représentation graphique des variables aléatoires

Les valeurs possibles et les probabilités associées pour une variable aléatoire peuvent être facilement visualisées par un graphique. Par exemple, considérons la variable aléatoire X de la section précédente avec un ensemble de résultats \{1, 2\}, et Pr [X = 1] = 0.5 et Pr [X = 2] = 0.5. Nous représenterions généralement une telle variable aléatoire sous forme de diagramme en barres comme dans la Figure 1.

Figure 1 : Variable aléatoire X

Figure 1 : Variable aléatoire X.

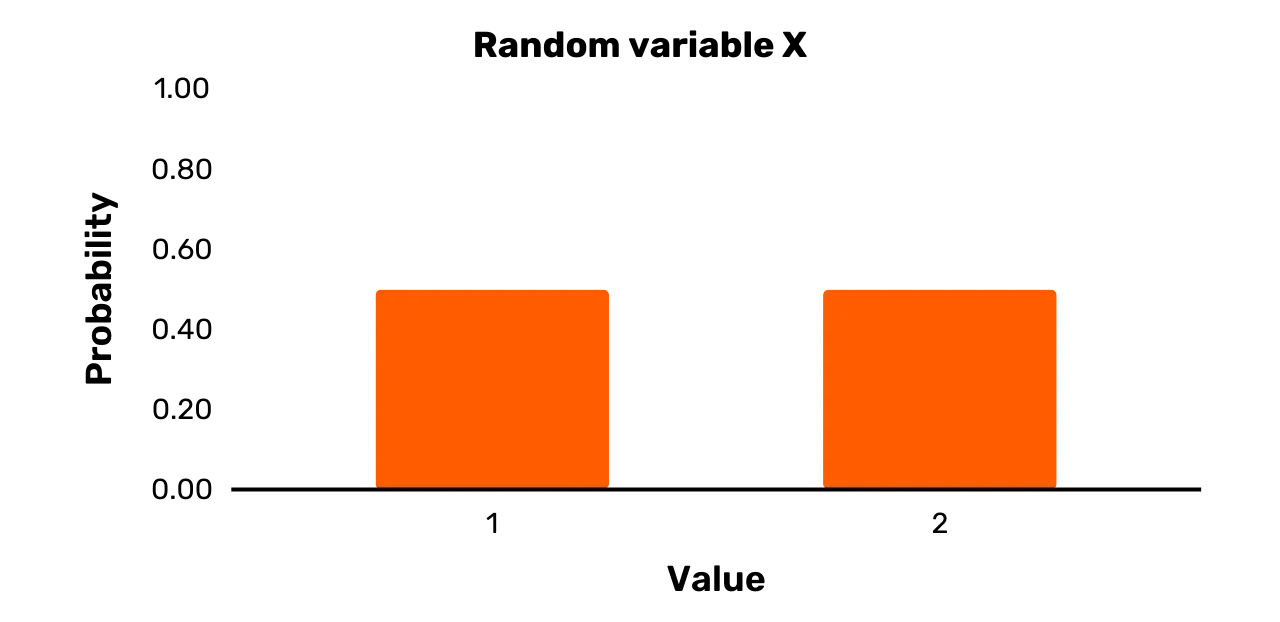
Les barres larges dans la Figure 1 ne suggèrent évidemment pas que la variable aléatoire X est en réalité continue. Les barres sont rendues larges afin d'être plus esthétiques visuellement (une simple ligne verticale serait moins intuitive à visualiser).

Variables uniformes

Dans l'expression « variable aléatoire », le terme « aléatoire » signifie simplement « probabiliste ». En d'autres termes, cela signifie simplement que deux ou plusieurs résultats possibles de la variable se produisent avec certaines probabilités. Cependant, ces résultats ne doivent pas nécessairement être également probables (même si le terme « aléatoire » peut effectivement avoir ce sens dans d'autres contextes).

Une variable uniforme est un cas particulier de variable aléatoire. Elle peut prendre deux valeurs ou plus, toutes avec une probabilité égale. La variable aléatoire X représentée dans la Figure 1 est clairement une variable uniforme, puisque les deux résultats possibles se produisent avec une probabilité de 0.5. Il existe cependant de nombreuses variables aléatoires qui ne sont pas des instances de variables uniformes.

Considérons, par exemple, la variable aléatoire Y. Elle a un ensemble de résultats \{1, 2, 3, 8, 10\} et la distribution de probabilité suivante :

\Pr[Y = 1] = 0.25
\Pr[Y = 2] = 0.35
\Pr[Y = 3] = 0.1
\Pr[Y = 8] = 0.25
\Pr[Y = 10] = 0.05

Bien que deux résultats possibles aient effectivement une probabilité égale de se produire, à savoir 1 et 8, Y peut également prendre certaines valeurs avec des probabilités différentes de 0.25 lors de l'échantillonnage. Ainsi, bien que Y soit bien une variable aléatoire, ce n'est pas une variable uniforme.

Une représentation graphique de Y est fournie dans la Figure 2.

Figure 2 : Variable aléatoire Y

Figure 2 : Variable aléatoire Y.

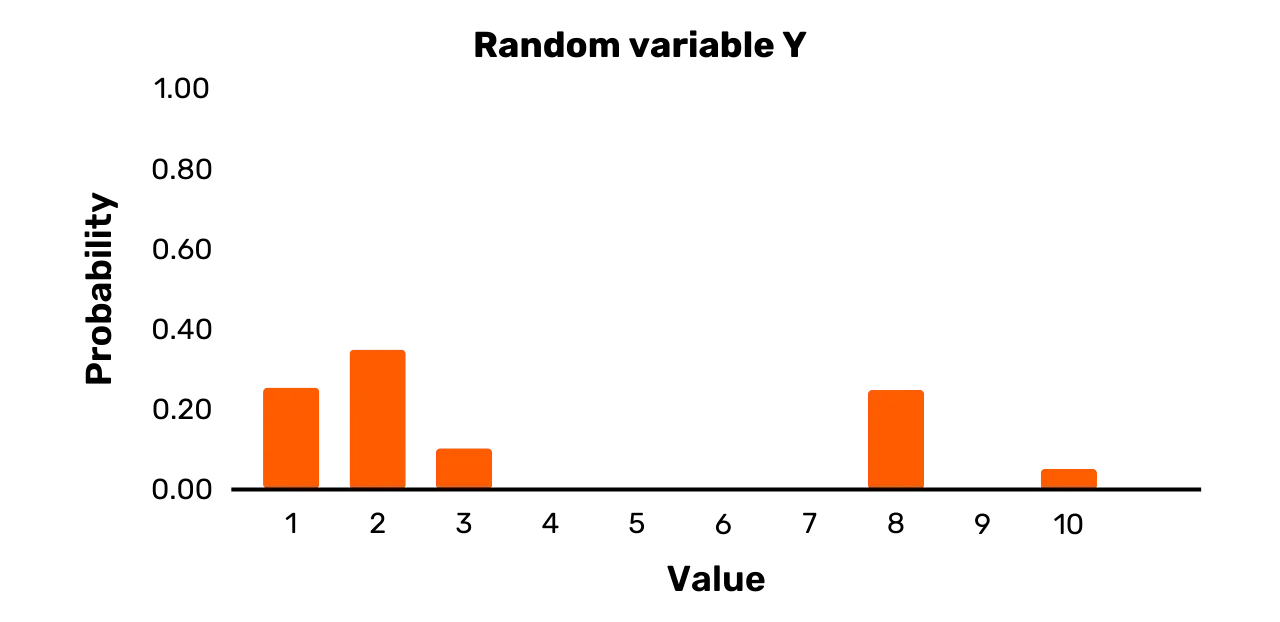
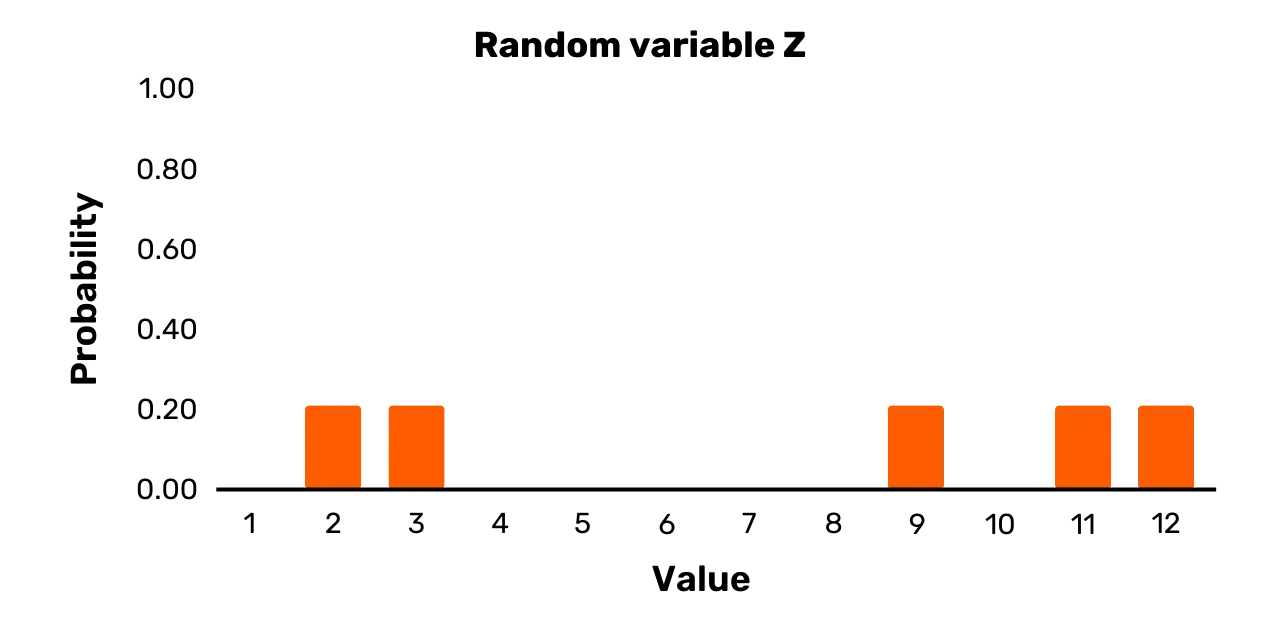
Pour un dernier exemple, considérons la variable aléatoire Z. Elle a l'ensemble de résultats \{1,3,7,11,12\} et la distribution de probabilité suivante :

\Pr[Z = 2] = 0.2
\Pr[Z = 3] = 0.2
\Pr[Z = 9] = 0.2
\Pr[Z = 11] = 0.2
\Pr[Z = 12] = 0.2

Vous pouvez voir sa représentation dans la Figure 3. La variable aléatoire Z est, contrairement à Y, une variable uniforme, puisque toutes les probabilités pour les valeurs possibles lors de l'échantillonnage sont égales.

Figure 3 : Variable aléatoire Z

Figure 3 : Variable aléatoire Z.

Probabilité conditionnelle

Supposons que Bob souhaite sélectionner uniformément un jour de l'année civile précédente. Que devons-nous conclure sur la probabilité que le jour sélectionné soit en été ?

Tant que nous pensons que le processus de Bob est réellement uniforme, nous devons conclure qu'il y a une probabilité de 1/4 que Bob sélectionne un jour en été. C'est la probabilité inconditionnelle du jour sélectionné au hasard étant en été.

Supposons maintenant qu'au lieu de tirer uniformément un jour du calendrier, Bob ne sélectionne uniformément qu'entre les jours où la température à midi au Crystal Lake (New Jersey) était de 21 degrés Celsius ou plus. Compte tenu de cette information supplémentaire, que pouvons-nous conclure sur la probabilité que Bob sélectionne un jour en été ?

Nous devrions parvenir à une conclusion différente de celle précédemment énoncée, même sans informations supplémentaires spécifiques (par exemple, la température à midi chaque jour de l'année précédente).

Sachant que Crystal Lake est situé dans le New Jersey, nous n’attendons certainement pas à ce que la température à midi atteigne 21 degrés Celsius ou plus en hiver. Au contraire, il est beaucoup plus probable qu'il s'agisse d'un jour chaud au printemps ou en automne, ou d'un jour situé quelque part en été. Par conséquent, sachant que la température à midi au Crystal Lake le jour sélectionné était de 21 degrés Celsius ou plus, la probabilité que le jour sélectionné par Bob se situe en été devient beaucoup plus élevée. C'est la probabilité conditionnelle du jour sélectionné au hasard étant en été, sachant que la température à midi au Crystal Lake était de 21 degrés Celsius ou plus.

Contrairement à l'exemple précédent, les probabilités de deux événements peuvent également être totalement indépendantes. Dans ce cas, nous disons qu'ils sont indépendants.

Supposons, par exemple, qu'une certaine pièce équitable soit tombée sur face. Étant donné ce fait, quelle est alors la probabilité qu'il pleuve demain ? La probabilité conditionnelle, dans ce cas, devrait être la même que la probabilité inconditionnelle qu'il pleuve demain, car un lancer de pièce n'a généralement aucune influence sur la météo.

Nous utilisons le symbole "|" pour écrire des énoncés de probabilité conditionnelle. Par exemple, la probabilité de l'événement A étant donné que l'événement B s'est produit peut s'écrire comme suit :

Pr[A|B]

Ainsi, lorsque deux événements, A et B, sont indépendants, alors :

Pr[A|B] = Pr[A] \text{ et } Pr[B|A] = Pr[B]

La condition d'indépendance peut être simplifiée comme suit :

Pr[A, B] = Pr[A] \cdot Pr[B]

Un résultat clé en théorie des probabilités est connu sous le nom de Théorème de Bayes. Il indique essentiellement que Pr[A|B] peut être réécrit comme suit :

Pr[A|B] = \frac{Pr[B|A] \cdot Pr[A]}{Pr[B]}

Au lieu d'utiliser des probabilités conditionnelles avec des événements spécifiques, nous pouvons également examiner les probabilités conditionnelles impliquées avec deux ou plusieurs variables aléatoires sur un ensemble d'événements possibles. Supposons deux variables aléatoires, X et Y. Nous pouvons désigner toute valeur possible pour X par x, et toute valeur possible pour Y par y. Nous pourrions dire alors que deux variables aléatoires sont indépendantes si l'énoncé suivant est vérifié :

Pr[X = x, Y = y] = Pr[X = x] \cdot Pr[Y = y]

pour tous x et y.

Soyons un peu plus explicites sur ce que cet énoncé signifie.

Supposons que les ensembles de résultats pour X et Y sont définis comme suit : X = \{x_1, x_2, \ldots, x_i, \ldots, x_n\} et Y = \{y_1, y_2, \ldots, y_i, \ldots, y_m\}. (Il est habituel d'indiquer les ensembles de valeurs par des lettres majuscules en gras.)

Maintenant, supposons que vous échantillonnez Y et observez y_1. L’énoncé ci-dessus nous dit que la probabilité d’obtenir maintenant x_1 en échantillonnant X est exactement la même que si nous n’avions jamais observé y_1. Cela est vrai pour tout y_i que nous aurions pu tirer lors de notre échantillonnage initial de Y. Enfin, cela s'applique non seulement à x_1, mais pour tout x_i, la probabilité de se produire n'est pas influencée par le résultat d'un échantillonnage de Y. Tout cela s'applique également au cas où X est échantillonné en premier.

Terminons notre discussion sur un point légèrement plus philosophique. Dans toute situation réelle, la probabilité d'un événement est toujours évaluée par rapport à un ensemble particulier d'informations. Il n'y a pas de « probabilité inconditionnelle » dans un sens très strict du terme.

Par exemple, supposons que je vous demande quelle est la probabilité que les cochons volent d'ici 2030. Bien que je ne vous donne pas d'informations supplémentaires, vous savez clairement beaucoup de choses sur le monde qui peuvent influencer votre jugement. Vous n'avez jamais vu de cochons voler. Vous savez que la plupart des gens ne s'attendront pas à ce qu'ils volent. Vous savez qu'ils ne sont pas vraiment faits pour voler. Et ainsi de suite.

Ainsi, lorsque nous parlons d'une « probabilité inconditionnelle » d'un événement dans un contexte réel, ce terme ne peut vraiment avoir de sens que si nous le comprenons comme signifiant quelque chose comme « la probabilité sans aucune information supplémentaire explicite ». Toute compréhension d'une « probabilité conditionnelle » doit alors toujours être comprise par rapport à une information spécifique.

Je pourrais, par exemple, vous demander quelle est la probabilité que les cochons volent d'ici 2030, après vous avoir fourni une preuve que certaines chèvres en Nouvelle-Zélande ont appris à voler après quelques années d'entraînement. Dans ce cas, vous ajusterez probablement votre jugement sur la probabilité que les cochons volent d'ici 2030. Ainsi, la probabilité que les cochons volent d'ici 2030 est conditionnelle à cette preuve concernant les chèvres en Nouvelle-Zélande.

L'opération modulo

Modulo

L'expression la plus basique de l’opération modulo est de la forme suivante : x \mod y.

La variable x est appelée le dividende et la variable y le diviseur. Pour effectuer une opération modulo avec un dividende positif et un diviseur positif, il suffit de déterminer le reste de la division.

Par exemple, considérons l'expression 25 \mod 4. Le nombre 4 rentre dans le nombre 25 un total de 6 fois. Le reste de cette division est 1. Ainsi, 25 \mod 4 est égal à 1. De la même manière, nous pouvons évaluer les expressions ci-dessous :

Lorsque le dividende ou le diviseur est négatif, les opérations modulo peuvent être traitées différemment par les langages de programmation.

Vous rencontrerez certainement des cas avec un dividende négatif en cryptographie. Dans ces cas, l'approche typique est la suivante :

Par exemple, supposons que le dividende soit –20 et le diviseur 3. La valeur la plus proche inférieure ou égale à –20 dans laquelle 3 se divise exactement est –21. La valeur de x – p dans ce cas est –20 – (–21). Cela équivaut à 1, et donc –20 \mod 3 est égal à 1. De la même manière, nous pouvons évaluer les expressions ci-dessous :

En ce qui concerne la notation, vous verrez généralement des expressions de ce type : x = [y \mod z]. En raison des crochets, l'opération modulo dans ce cas ne s'applique qu'au côté droit de l'expression. Si y vaut 25 et z vaut 4, par exemple, alors x vaut 1.

Sans crochets, l'opération modulo agit sur les deux côtés d'une expression. Supposons, par exemple, l'expression suivante : x = y \mod z. Si y vaut 25 et z vaut 4, alors tout ce que nous savons, c'est que x \mod 4 vaut 1. Cela est cohérent avec toute valeur de x appartenant à l'ensemble \{\ldots,–7, –3, 1, 5, 9,\ldots\}.

La branche des mathématiques qui traite des opérations modulo sur les nombres et les expressions est appelée arithmétique modulaire. Vous pouvez considérer cette branche comme une arithmétique pour les cas où la ligne des nombres n'est pas infiniment longue. Bien que nous rencontrions généralement des opérations modulo pour des entiers positifs en cryptographie, vous pouvez également effectuer des opérations modulo en utilisant n'importe quel nombre réel.

Le chiffre de décalage

L'opération modulo est fréquemment rencontrée en cryptographie. Pour illustrer cela, considérons l'un des schémas de chiffrement historiques les plus célèbres : le chiffre de décalage.

Définissons-le d'abord. Supposons un dictionnaire D qui associe toutes les lettres de l'alphabet anglais, dans l'ordre, à l'ensemble des nombres \{0, 1, 2, \ldots, 25\}. Supposons un espace de messages M. Le chiffre de décalage est alors un schéma de chiffrement défini comme suit :

L'opérateur modulo dans le chiffre de décalage garantit que les lettres bouclent, de sorte que toutes les lettres du texte chiffré soient définies. Pour illustrer, considérons l'application du chiffre de décalage sur le mot « DOG ».

Supposons que vous ayez sélectionné uniformément une clé ayant la valeur de 17. La lettre « O » correspond à 15. Sans l'opération modulo, l’addition de ce nombre de texte en clair avec la clé donnerait un nombre chiffré égal à 32. Cependant, ce nombre ne peut pas être converti en une lettre chiffrée, puisque l'alphabet anglais ne comporte que 26 lettres. L'opération modulo garantit que le nombre chiffré est en réalité 6 (le résultat de 32 \mod 26), ce qui correspond à la lettre chiffrée « G ».

Le chiffrement complet du mot « DOG » avec une clé de valeur 17 est le suivant :

Tout le monde peut comprendre intuitivement comment fonctionne le chiffre de décalage et probablement l'utiliser lui-même. Cependant, pour progresser en cryptographie, il est important de commencer à se familiariser avec la formalisation, car les schémas deviendront beaucoup plus complexes. C'est pourquoi les étapes du chiffre de décalage ont été formalisées.

Notes :

[1] Nous pouvons définir cette déclaration de manière précise, en utilisant la terminologie de la section précédente. Supposons une variable uniforme K ayant K comme ensemble de résultats possibles. Ainsi :

Pr[K = 0] = \frac{1}{26}
Pr[K = 1] = \frac{1}{26}

...et ainsi de suite. Échantillonner la variable uniforme K une fois pour obtenir une clé particulière.

L'opération XOR

Toutes les données informatiques sont traitées, stockées et transmises sur les réseaux au niveau des bits. Tous les schémas cryptographiques appliqués aux données informatiques fonctionnent également au niveau des bits.

Par exemple, supposons que vous ayez tapé un e-mail dans votre application de messagerie. Tout chiffrement que vous appliquez ne se produit pas directement sur les caractères ASCII de votre e-mail. Il est plutôt appliqué à la représentation binaire des lettres et autres symboles de votre e-mail.

Une opération mathématique essentielle à comprendre pour la cryptographie moderne, en plus de l'opération modulo, est celle de l’opération XOR ou « ou exclusif ». Cette opération prend en entrée deux bits et produit en sortie un autre bit. L'opération XOR sera simplement notée "XOR". Elle produit 0 si les deux bits sont identiques et 1 s'ils sont différents. Vous pouvez voir les quatre possibilités ci-dessous. Le symbole \oplus représente "XOR" :

Pour illustrer, supposons que vous ayez un message m_1 (01111001) et un message m_2 (01011001). L'opération XOR de ces deux messages est montrée ci-dessous :

Le processus est simple. Vous effectuez d'abord l'opération XOR sur les bits les plus à gauche de m_1 et m_2. Dans ce cas, cela donne 0 \oplus 0 = 0. Ensuite, vous appliquez XOR sur la deuxième paire de bits en partant de la gauche. Dans ce cas, cela donne 1 \oplus 1 = 0. Vous continuez ce processus jusqu'à ce que vous ayez effectué l'opération XOR sur les bits les plus à droite.

Il est facile de voir que l'opération XOR est commutative, c'est-à-dire que m_1 \oplus m_2 = m_2 \oplus m_1. De plus, l'opération XOR est également associative. C'est-à-dire que (m_1 \oplus m_2) \oplus m_3 = m_1 \oplus (m_2 \oplus m_3).

Une opération XOR sur deux chaînes de longueurs différentes peut avoir des interprétations différentes, selon le contexte. Nous ne nous préoccuperons pas ici des opérations XOR sur des chaînes de longueurs différentes.

Une opération XOR est équivalente au cas particulier de l'exécution d'une opération modulo sur l'addition de bits lorsque le diviseur est 2. Vous pouvez voir l'équivalence dans les résultats suivants :

Pseudoaléatoire

Dans notre discussion sur les variables aléatoires et uniformes, nous avons établi une distinction spécifique entre « aléatoire » et « uniforme ». Cette distinction est généralement maintenue en pratique lorsqu’on décrit des variables aléatoires. Cependant, dans notre contexte actuel, cette distinction doit être abandonnée et les termes « aléatoire » et « uniforme » sont utilisés de manière synonyme. Je vais expliquer pourquoi à la fin de cette section.

Pour commencer, nous pouvons qualifier une chaîne binaire de longueur n de chaîne aléatoire (ou uniforme), si elle est le résultat de l’échantillonnage d’une variable uniforme S qui donne à chaque chaîne binaire de longueur n une probabilité égale d’être sélectionnée.

Prenons par exemple l’ensemble de toutes les chaînes binaires de longueur 8 : \{0000\ 0000, 0000\ 0001, \ldots, 1111\ 1111\}. (Il est courant d’écrire une chaîne de 8 bits en deux quatuors, chacun appelé un nibble.) Appelons cet ensemble de chaînes S_8.

Selon la définition ci-dessus, une chaîne binaire particulière de longueur 8 peut être qualifiée d'aléatoire (ou uniforme), si elle résulte de l'échantillonnage d'une variable uniforme S qui attribue à chaque chaîne de S_8 une probabilité égale d'être sélectionnée. Étant donné que l'ensemble S_8 contient 2^8 éléments, la probabilité de sélection lors de l'échantillonnage serait de 1/2^8 pour chaque chaîne de l'ensemble.

Un aspect essentiel de l’aléatoirité d’une chaîne binaire est qu’elle est définie par rapport au processus par lequel elle a été sélectionnée. La forme d'une chaîne binaire particulière, en elle-même, ne révèle donc rien sur son caractère aléatoire lors de sa sélection.

Par exemple, beaucoup de gens ont l'intuition qu'une chaîne comme 1111\ 1111 ne pourrait pas avoir été sélectionnée de manière aléatoire. Mais c'est clairement faux.

En définissant une variable uniforme S sur l'ensemble de toutes les chaînes binaires de longueur 8, la probabilité de sélectionner 1111\ 1111 parmi l'ensemble S_8 est la même que celle de sélectionner une chaîne comme 0111\ 0100. Par conséquent, il est impossible de déterminer si une chaîne est aléatoire simplement en l’analysant.

On peut également parler de chaînes aléatoires sans nécessairement faire référence à des chaînes binaires. Par exemple, nous pourrions parler d'une chaîne hexadécimale aléatoire AF\ 02\ 82. Dans ce cas, la chaîne aurait été sélectionnée aléatoirement parmi l'ensemble de toutes les chaînes hexadécimales de longueur 6. Cela revient à sélectionner aléatoirement une chaîne binaire de longueur 24, chaque chiffre hexadécimal représentant 4 bits.

En général, l’expression « une chaîne aléatoire », sans précision supplémentaire, se réfère à une chaîne sélectionnée aléatoirement parmi l’ensemble de toutes les chaînes de même longueur. C’est ainsi que nous l’avons décrite ci-dessus. Une chaîne de longueur n peut, bien sûr, être sélectionnée aléatoirement à partir d'un ensemble différent. Par exemple, un ensemble qui ne constitue qu'un sous-ensemble de toutes les chaînes de longueur n, ou peut-être un ensemble qui comprend des chaînes de longueurs variées. Dans ces cas, cependant, nous ne parlerions pas d'une « chaîne aléatoire », mais plutôt d'une « chaîne sélectionnée aléatoirement dans un ensemble S ».

Un concept clé en cryptographie est celui de pseudoaléatoirité. Une chaîne pseudoaléatoire de longueur n semble comme si elle résultait de l’échantillonnage d’une variable uniforme S qui attribue à chaque chaîne de S_n une probabilité égale d'être sélectionnée. En réalité, cependant, la chaîne résulte de l’échantillonnage d’une variable uniforme S' qui définit uniquement une distribution de probabilité — pas nécessairement uniforme — sur un sous-ensemble de S_n. L’élément crucial ici est qu’il est pratiquement impossible de distinguer des échantillons provenant de S de ceux provenant de S', même si vous en prenez de nombreux.

Supposons, par exemple, une variable aléatoire S. Son ensemble de résultats est S_{256}, qui correspond à l’ensemble de toutes les chaînes binaires de longueur 256. Cet ensemble comporte 2^{256} éléments. Chaque élément a une probabilité égale d'être sélectionné, soit 1/2^{256}, lors de l'échantillonnage.

En outre, supposons une variable aléatoire S'. Son ensemble de résultats ne comprend que 2^{128} chaînes binaires de longueur 256. Elle a une distribution de probabilité sur ces chaînes, mais cette distribution n'est pas nécessairement uniforme.

Imaginons maintenant que je prenne des milliers d’échantillons de S et des milliers d’échantillons de S', et que je vous remette ces deux ensembles de résultats. Je vous indique quel ensemble de résultats est associé à quelle variable aléatoire. Ensuite, je prends un échantillon d'une des deux variables aléatoires, sans vous dire laquelle. Si S' est pseudoaléatoire, alors votre probabilité de deviner correctement de quelle variable aléatoire provient l’échantillon est pratiquement équivalente à 1/2.

En général, une chaîne pseudoaléatoire de longueur n est produite en sélectionnant aléatoirement une chaîne de taille n - x, où x est un entier positif, et en l’utilisant comme entrée pour un algorithme d’expansion. Cette chaîne aléatoire de taille n - x est appelée la graine.

Les chaînes pseudoaléatoires sont un concept clé pour rendre la cryptographie pratique. Prenons, par exemple, les chiffrements par flot. Avec un chiffrement par flot, une clé aléatoirement sélectionnée est insérée dans un algorithme d’expansion pour produire une chaîne pseudoaléatoire beaucoup plus grande. Cette chaîne pseudoaléatoire est ensuite combinée avec le texte en clair via une opération XOR pour produire un texte chiffré.

Si nous étions incapables de produire ce type de chaîne pseudoaléatoire pour un chiffrement par flot, nous aurions besoin d’une clé aussi longue que le message pour garantir sa sécurité. Ce qui n'est pas une option pratique dans la plupart des cas.

La notion de pseudoaléatoirité abordée dans cette section peut être définie de manière plus formelle et s’étend à d’autres contextes. Cependant, nous n’avons pas besoin d’approfondir cette discussion ici. Il vous suffit de comprendre intuitivement la différence entre une chaîne aléatoire et une chaîne pseudoaléatoire. [2]

La raison de l’abandon de la distinction entre « aléatoire » et « uniforme » devrait maintenant être claire. En pratique, tout le monde utilise le terme pseudoaléatoire pour désigner une chaîne qui semble comme si elle résultait de l'échantillonnage d'une variable uniforme S. Strictement parlant, nous devrions appeler une telle chaîne « pseudo-uniforme », en adoptant notre langage précédent. Mais comme ce terme est lourd et peu utilisé, nous ne l’introduirons pas ici pour plus de clarté. Nous abandonnons donc la distinction entre « aléatoire » et « uniforme » dans ce contexte.

Notes

[2] Pour une exposition plus formelle de ces notions, vous pouvez consulter Introduction to Modern Cryptography de Katz et Lindell, notamment le chapitre 3.

Fondements mathématiques de la cryptographie 2

Qu'est-ce que la théorie des nombres ?

Ce chapitre traite d'un sujet plus avancé sur les fondements mathématiques de la cryptographie : la théorie des nombres. Bien que la théorie des nombres soit importante pour la cryptographie symétrique (comme dans le chiffrement Rijndael), elle joue un rôle particulièrement essentiel dans le cadre de la cryptographie à clé publique.

Si vous trouvez les détails de la théorie des nombres fastidieux, je vous recommande d’en faire une première lecture globale. Vous pourrez toujours y revenir plus tard pour approfondir votre compréhension.

La théorie des nombres peut être décrite comme l'étude des propriétés des entiers et des fonctions mathématiques qui opèrent sur ces entiers.

Considérons, par exemple, deux nombres a et N. Ces nombres sont dits copremiers (ou premiers entre eux) si leur plus grand diviseur commun est égal à 1. Imaginons maintenant un entier particulier N. Combien d'entiers inférieurs à N sont copremiers avec N ? Pouvons-nous formuler des déclarations générales pour répondre à cette question ? Ce sont précisément le genre de questions auxquelles la théorie des nombres cherche à répondre.

La théorie moderne des nombres s'appuie sur les outils de l’algèbre abstraite. L’algèbre abstraite est une branche des mathématiques où les principaux objets d’analyse sont des entités abstraites appelées structures algébriques. Une structure algébrique est un ensemble d’éléments associé à une ou plusieurs opérations qui satisfont certains axiomes. Grâce à ces structures, les mathématiciens peuvent acquérir une meilleure compréhension de problèmes mathématiques spécifiques, en faisant abstraction de leurs détails concrets.

Le domaine de l’algèbre abstraite est parfois appelé algèbre moderne. Vous rencontrerez peut-être aussi l’expression mathématiques abstraites (ou mathématiques pures). Ce dernier terme ne désigne pas spécifiquement l’algèbre abstraite, mais englobe plutôt l’étude des mathématiques pour elles-mêmes, sans considération immédiate pour des applications pratiques.

Les ensembles étudiés en algèbre abstraite peuvent traiter de nombreux types d’objets, allant des transformations préservant la forme d’un triangle équilatéral aux motifs réguliers tels que les frises ou les pavages. En ce qui concerne la théorie des nombres, cependant, nous nous limitons aux ensembles contenant des entiers ou aux fonctions qui opèrent sur ces entiers.

Groupes

Un concept fondamental en mathématiques est celui d'un ensemble d’éléments. Un ensemble est généralement noté par des accolades avec les éléments séparés par des virgules.

Par exemple, l'ensemble de tous les entiers est \{…, -2, -1, 0, 1, 2, …\}. Les points de suspension indiquent ici qu'un certain motif se poursuit dans une direction particulière. Ainsi, l'ensemble de tous les entiers comprend également 3, 4, 5, 6, et ainsi de suite, ainsi que -3, -4, -5, -6, et ainsi de suite. Cet ensemble de tous les entiers est habituellement noté par \mathbb{Z}.

Un autre exemple d'ensemble est \mathbb{Z} \mod 11, c'est-à-dire l'ensemble de tous les entiers modulo 11. Contrairement à l'ensemble infini \mathbb{Z}, cet ensemble ne contient qu'un nombre fini d'éléments, à savoir \{0, 1, \ldots, 9, 10\}.

Une erreur courante consiste à penser que l'ensemble \mathbb{Z} \mod 11 est en réalité \{-10, -9, \ldots, 0, \ldots, 9, 10\}. Mais ce n'est pas le cas, en raison de la définition de l'opération modulo évoquée précédemment. Tout entier négatif réduit par modulo 11 se replie sur \{0, 1, \ldots, 9, 10\}. Par exemple, l'expression -2 \mod 11 se réduit à 9, tandis que l'expression -27 \mod 11 se réduit à 5.

Un autre concept fondamental en mathématiques est celui d'une opération binaire. Il s'agit de toute opération qui prend deux éléments pour en produire un troisième. Par exemple, en arithmétique et en algèbre de base, vous êtes familier avec quatre opérations binaires fondamentales : l'addition, la soustraction, la multiplication et la division.

Ces deux concepts mathématiques fondamentaux, les ensembles et les opérations binaires, sont utilisés pour définir la notion de groupe, la structure la plus essentielle en algèbre abstraite.

Plus précisément, supposons une opération binaire \circ. De plus, supposons qu’un ensemble d’éléments S soit équipé de cette opération. Lorsque l'on dit qu'un ensemble est "équipé" d'une opération, cela signifie simplement que l'opération \circ peut être effectuée entre n'importe quels deux éléments de l'ensemble S.

La combinaison \langle \mathbf{S}, \circ \rangle est alors un groupe si elle satisfait quatre conditions spécifiques, appelées les axiomes de groupe.

  1. Pour tout a et b appartenant à \mathbf{S}, a \circ b est également un élément de \mathbf{S}. C'est ce que l'on appelle la condition de fermeture.
  2. Pour tout a, b et c appartenant à \mathbf{S}, on a (a \circ b) \circ c = a \circ (b \circ c). C'est ce que l'on appelle la condition d'associativité.
  3. Il existe un élément unique e dans \mathbf{S} tel que, pour tout élément a de \mathbf{S}, l'équation suivante est vérifiée : e \circ a = a \circ e = a. Puisqu'il n'y a qu'un seul élément de ce type, il est appelé élément neutre. Cette condition est connue sous le nom de condition d'identité.
  4. Pour chaque élément a de \mathbf{S}, il existe un élément b dans \mathbf{S} tel que l'équation suivante est vérifiée : a \circ b = b \circ a = e, où e est l’élément neutre. L’élément b est appelé élément inverse, et il est couramment noté a^{-1}. Cette condition est appelée condition d'inverse ou condition d'inversibilité.

Explorons un peu plus les groupes. Notons l'ensemble de tous les entiers par \mathbb{Z}. Cet ensemble, combiné avec l’addition standard, soit \langle \mathbb{Z}, + \rangle, répond clairement à la définition d’un groupe puisqu'il satisfait aux quatre axiomes mentionnés ci-dessus.

  1. Pour tout x et y appartenant à \mathbb{Z}, x + y est aussi un élément de \mathbb{Z}. Ainsi, \langle \mathbb{Z}, + \rangle satisfait la condition de fermeture.
  2. Pour tout x, y et z appartenant à \mathbb{Z}, (x + y) + z = x + (y + z). Donc, \langle \mathbb{Z}, + \rangle satisfait la condition d'associativité.
  3. Il existe un élément neutre dans \langle \mathbb{Z}, + \rangle, à savoir 0. Pour tout x dans \mathbb{Z}, on a : 0 + x = x + 0 = x. Ainsi, \langle \mathbb{Z}, + \rangle satisfait la condition d'identité.
  4. Enfin, pour chaque élément x dans \mathbb{Z}, il existe un y tel que x + y = y + x = 0. Si x est égal à 10, alors y serait -10 (dans le cas où x est 0, y est aussi 0). Ainsi, \langle \mathbb{Z}, + \rangle satisfait la condition d'inverse.

Il est important de noter que le fait que l'ensemble des entiers avec l'addition constitue un groupe ne signifie pas qu'il en constitue un avec la multiplication. Vous pouvez vérifier cela en testant \langle \mathbb{Z}, \cdot \rangle par rapport aux quatre axiomes de groupe (où \cdot représente la multiplication standard).

Les deux premiers axiomes sont évidemment vérifiés. De plus, pour ce qui est de la multiplication, l’élément 1 peut servir d’élément neutre. En effet, tout entier x multiplié par 1 donne x. Cependant, \langle \mathbb{Z}, \cdot \rangle ne satisfait pas la condition d'inverse. Autrement dit, il n’existe pas d’élément unique y dans \mathbb{Z} pour chaque x appartenant à \mathbb{Z} tel que x \cdot y = 1.

Par exemple, supposons que x = 22. Quelle valeur y de l'ensemble \mathbb{Z} multipliée par x donnerait l’élément neutre 1 ? La valeur 1/22 conviendrait, mais cela n’appartient pas à l’ensemble \mathbb{Z}. En fait, ce problème se pose pour tout entier x, à l’exception de 1 et -1 (pour lesquels y doit être respectivement 1 et -1).

Si nous permettons aux nombres réels de faire partie de notre ensemble, alors ces problèmes disparaissent en grande partie. Pour tout élément x dans l'ensemble, la multiplication par 1/x donne 1. Comme les fractions sont incluses dans l'ensemble des nombres réels, un inverse peut être trouvé pour chaque nombre réel. L’exception est zéro, car toute multiplication par zéro ne donnera jamais l’élément neutre 1. Ainsi, l'ensemble des nombres réels non nuls muni de l'opération de multiplication est bel et bien un groupe.

Certains groupes respectent une cinquième condition générale, connue sous le nom de condition de commutativité. Cette condition est formulée comme suit :

Tout groupe qui respecte la condition de commutativité est appelé un groupe commutatif, ou un groupe abélien (d’après Niels Henrik Abel). Il est facile de vérifier que l'ensemble des nombres réels muni de l’addition et l'ensemble des entiers muni de l’addition sont tous deux des groupes abéliens. En revanche, l'ensemble des entiers muni de la multiplication n'est pas un groupe du tout, donc il ne peut pas être un groupe abélien. L'ensemble des nombres réels non nuls muni de la multiplication, en revanche, est également un groupe abélien.

Il est important de prêter attention à deux conventions courantes en matière de notation. Premièrement, les signes “+” ou “×” sont fréquemment utilisés pour symboliser des opérations de groupe, même lorsque les éléments ne sont pas, en réalité, des nombres. Dans ces cas, il ne faut pas interpréter ces signes comme une addition ou une multiplication arithmétique classique. Au lieu de cela, il s’agit d’opérations ayant seulement une similitude abstraite avec ces opérations arithmétiques.

À moins de se référer spécifiquement à l’addition ou la multiplication arithmétique, il est préférable d'utiliser des symboles comme \circ et \diamond pour désigner des opérations de groupe, car ces symboles n’ont pas les connotations culturelles profondément ancrées des signes “+” et “×”.

Deuxièmement, pour la même raison que les signes “+” et “×” sont souvent utilisés pour indiquer des opérations non arithmétiques, les éléments neutres des groupes sont fréquemment symbolisés par “0” et “1”, même lorsque les éléments de ces groupes ne sont pas des nombres. Sauf si l’on se réfère à l’élément neutre d’un groupe de nombres, il est préférable d'utiliser un symbole plus neutre tel que “e” pour désigner l’élément neutre.

De nombreux ensembles différents et très importants en mathématiques, équipés de certaines opérations binaires, sont des groupes. Les applications cryptographiques, cependant, fonctionnent uniquement avec des ensembles d'entiers ou au moins avec des éléments qui peuvent être décrits par des entiers, c'est-à-dire dans le domaine de la théorie des nombres. Par conséquent, les ensembles contenant des nombres réels autres que des entiers ne sont pas utilisés dans les applications cryptographiques.

Terminons par un exemple d’éléments qui peuvent être “décrits par des entiers”, même s’ils ne sont pas eux-mêmes des entiers. Un bon exemple est celui des points sur des courbes elliptiques. Bien qu’un point sur une courbe elliptique ne soit clairement pas un entier, un tel point est effectivement décrit par deux entiers.

Les courbes elliptiques sont, par exemple, essentielles au fonctionnement de Bitcoin. Toute paire de clés privée et publique standard en Bitcoin est sélectionnée à partir de l'ensemble des points définis par la courbe elliptique suivante :

x^3 + 7 = y^2 \mod 2^{256} – 2^{32} – 29 – 28 – 27 – 26 - 24 - 1

(qui est le plus grand nombre premier inférieur à 2^{256}). La coordonnée x représente la clé privée, et la coordonnée y représente la clé publique.

Les transactions en Bitcoin consistent généralement à verrouiller des sorties (outputs) sur une ou plusieurs clés publiques d'une certaine manière. La valeur de ces transactions peut alors être déverrouillée en créant des signatures numériques avec les clés privées correspondantes.

Groupes cycliques

Une distinction majeure que l'on peut établir est celle entre un groupe fini et un groupe infini. Le premier possède un nombre fini d’éléments, tandis que le second en possède un nombre infini. Le nombre d’éléments dans tout groupe fini est appelé ordre du groupe. Toute cryptographie pratique utilisant des groupes repose sur des groupes finis (issus de la théorie des nombres).

En cryptographie à clé publique, une certaine classe de groupes finis abéliens, appelés groupes cycliques, est particulièrement importante. Pour comprendre les groupes cycliques, nous devons d’abord comprendre le concept d’exponentiation d’éléments de groupe.

Supposons un groupe G avec une opération de groupe \circ, et que a soit un élément de G. L'expression a^n doit alors être interprétée comme l’élément a combiné avec lui-même un total de n - 1 fois. Par exemple, a^2 signifie a \circ a, a^3 signifie a \circ a \circ a, et ainsi de suite. (Il est important de noter que l'exponentiation ici n'est pas nécessairement l'exponentiation au sens arithmétique standard.)

Prenons un exemple. Supposons que G = \langle \mathbb{Z} \mod 7, + \rangle, et que notre valeur de a soit égale à 4. Dans ce cas :

Certains groupes abéliens possèdent un ou plusieurs éléments qui, par exponentiation continue, peuvent produire tous les autres éléments du groupe. Ces éléments sont appelés générateurs ou éléments primitifs.

Une classe importante de tels groupes est \langle \mathbb{Z}^* \mod N, \cdot \rangle, où N est un nombre premier. La notation \mathbb{Z}^* signifie ici que le groupe contient tous les entiers positifs non nuls inférieurs à N. Ainsi, ce groupe contient toujours N - 1 éléments.

Prenons par exemple G = \langle \mathbb{Z}^* \mod 11, \cdot \rangle. Ce groupe contient les éléments suivants : \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. L’ordre de ce groupe est de 10 (ce qui est bien égal à 11 - 1).

Examinons maintenant l'exponentiation de l’élément 2 de ce groupe. Les calculs jusqu’à 2^{12} sont présentés ci-dessous. Notez que, dans cet exemple particulier, l'exponentiation de groupe correspond effectivement à l'exponentiation arithmétique sur le côté droit de l’équation (mais cela pourrait aussi impliquer, par exemple, une addition). Pour plus de clarté, j'ai détaillé l'opération répétée au lieu d'utiliser la forme exponentielle sur la partie droite.

En examinant attentivement, on constate que l’exponentiation de l’élément 2 parcourt tous les éléments de \langle \mathbb{Z}^* \mod 11, \cdot \rangle dans l’ordre suivant : 2, 4, 8, 5, 10, 9, 7, 3, 6, 1. Après 2^{10}, l’exponentiation continue de l’élément 2 parcourt à nouveau tous les éléments, dans le même ordre. Par conséquent, l’élément 2 est un générateur dans \langle \mathbb{Z}^* \mod 11, \cdot \rangle.

Bien que \langle \mathbb{Z}^* \mod 11, \cdot \rangle possède plusieurs générateurs, tous les éléments de ce groupe ne sont pas des générateurs. Prenons par exemple l’élément 3. En parcourant les dix premières exponentiations, sans montrer les calculs détaillés, on obtient les résultats suivants :

Au lieu de parcourir toutes les valeurs de \langle \mathbb{Z}^* \mod 11, \cdot \rangle, l’exponentiation de l’élément 3 ne produit qu’un sous-ensemble de ces valeurs : 3, 9, 5, 4, et 1. Après la cinquième exponentiation, ces valeurs commencent à se répéter.

Nous pouvons maintenant définir un groupe cyclique comme étant tout groupe possédant au moins un générateur. C'est-à-dire qu'il existe au moins un élément du groupe à partir duquel on peut obtenir tous les autres éléments du groupe par exponentiation.

Vous avez peut-être remarqué dans notre exemple précédent que 2^{10} et 3^{10} sont tous deux égaux à 1 \mod 11. En fait, bien que nous n'effectuions pas tous les calculs, l’exponentiation par 10 de n'importe quel élément du groupe \langle \mathbb{Z}^* \mod 11, \cdot \rangle donnera 1 \mod 11. Pourquoi en est-il ainsi ?

C'est une question importante, mais y répondre demande un peu de travail.

Pour commencer, supposons deux entiers positifs a et N. Un théorème important en théorie des nombres indique que a possède un inverse multiplicatif modulo N (c'est-à-dire un entier b tel que a \cdot b = 1 \mod N) si et seulement si le plus grand commun diviseur entre a et N est égal à 1. Autrement dit, si a et N sont premiers entre eux (ou copremiers).

Ainsi, pour tout groupe d'entiers muni de la multiplication modulo N, seuls les entiers qui sont copremiers avec N sont inclus dans l'ensemble. Nous pouvons désigner cet ensemble par \mathbb{Z}^c \mod N.

Par exemple, supposons que N soit 10. Seuls les entiers 1, 3, 7, et 9 sont copremiers avec 10. Ainsi, l'ensemble \mathbb{Z}^c \mod 10 contient uniquement \{1, 3, 7, 9\}. On ne peut pas créer un groupe avec la multiplication des entiers modulo 10 en utilisant d'autres entiers entre 1 et 10. Pour ce groupe particulier, les inverses sont les paires 1 et 9, ainsi que 3 et 7.

Dans le cas où N est lui-même un nombre premier, tous les entiers de 1 à N - 1 sont copremiers avec N. Ainsi, ce groupe a un ordre de N - 1. Avec notre notation précédente, \mathbb{Z}^c \mod N est équivalent à \mathbb{Z}^* \mod N lorsque N est premier. Le groupe que nous avons choisi pour notre exemple précédent, \langle \mathbb{Z}^* \mod 11, \cdot \rangle, est un cas particulier de cette classe de groupes.

Ensuite, la fonction \phi(N) calcule le nombre d’entiers qui sont copremiers avec un nombre N, et elle est connue sous le nom de fonction Phi d’Euler. [1] Selon le théorème d’Euler, lorsque deux entiers a et N sont copremiers, la relation suivante est vérifiée :

Cela a une implication importante pour la classe de groupes \langle \mathbb{Z}^* \mod N, \cdot \rangle où N est premier. Pour ces groupes, l'exponentiation d’éléments de groupe correspond à l’exponentiation arithmétique. C'est-à-dire que a^{\phi(N)} \mod N représente l'opération arithmétique a^{\phi(N)} \mod N. Comme tout élément a dans ces groupes multiplicatifs est copremier avec N, cela signifie que a^{\phi(N)} \mod N = a^{N - 1} \mod N = 1 \mod N.

Le théorème d’Euler est un résultat essentiel. Pour commencer, il implique que tous les éléments de \langle \mathbb{Z}^* \mod N, \cdot \rangle ne peuvent parcourir qu'un certain nombre de valeurs par exponentiation qui divise N - 1. Dans le cas de \langle \mathbb{Z}^* \mod 11, \cdot \rangle, cela signifie que chaque élément peut parcourir 2, 5 ou 10 éléments. Les valeurs du groupe qu'un élément parcourt par exponentiation sont appelées ordre de l’élément. Un élément dont l'ordre est équivalent à l'ordre du groupe est un générateur.

De plus, le théorème d’Euler implique que nous pouvons toujours connaître le résultat de a^{N - 1} \mod N pour tout groupe \langle \mathbb{Z}^* \mod N, \cdot \rangle où N est premier. Cela reste valable même si les calculs eux-mêmes peuvent être très complexes.

Par exemple, supposons que notre groupe soit \mathbb{Z}^* \mod 160,481,182 (où 160,481,182 est effectivement un nombre premier). Nous savons que tous les entiers de 1 à 160,481,181 sont des éléments de ce groupe, et que \phi(N) = 160,481,181. Bien que nous ne puissions pas effectuer tous les calculs, nous savons que des expressions telles que 514^{160,481,181}, 2,005^{160,481,181}, et 256,212^{160,481,181} doivent toutes être égales à 1 \mod 160,481,182.

Notes :

[1] La fonction s’applique comme suit. Tout entier N peut être factorisé en un produit de nombres premiers. Supposons qu’un certain N soit factorisé de la manière suivante : p_1^{e1} \cdot p_2^{e2} \cdot \ldots \cdot p_m^{em} où tous les p sont des nombres premiers et tous les e sont des entiers supérieurs ou égaux à 1. Ainsi :

\phi(N) = \sum_{i=1}^m \left[p_i^{e_i} - p_i^{e_i - 1}\right]

Formule de la fonction Phi d’Euler pour la factorisation en nombres premiers de N.

Corps

Un groupe est la structure algébrique de base en algèbre abstraite, mais il en existe beaucoup d’autres. La seule autre structure algébrique dont vous devez être familier est celle d’un corps, en particulier celle d’un corps fini. Ce type de structure algébrique est fréquemment utilisé en cryptographie, par exemple dans l’algorithme Advanced Encryption Standard (AES), qui est le principal schéma de chiffrement symétrique utilisé en pratique.

Un corps est dérivé de la notion de groupe. Plus précisément, un corps est un ensemble d’éléments S équipé de deux opérateurs binaires \circ et \diamond, qui satisfait les conditions suivantes :

  1. L’ensemble S équipé de \circ est un groupe abélien.
  2. L’ensemble S équipé de \diamond est un groupe abélien pour les éléments non nuls.
  3. L’ensemble S équipé des deux opérateurs satisfait ce que l’on appelle la condition de distributivité : Supposons que a, b et c sont des éléments de S. Alors S satisfait la propriété distributive lorsque a \circ (b \diamond c) = (a \circ b) \diamond (a \circ c).

Il est important de noter que, comme pour les groupes, la définition d’un corps est très abstraite. Elle ne précise rien sur les types d’éléments de S, ni sur les opérations \circ et \diamond. Elle indique simplement qu’un corps est un ensemble d’éléments muni de deux opérations pour lesquelles les trois conditions ci-dessus sont vérifiées. (L’élément “zéro” dans le deuxième groupe abélien peut être interprété de manière abstraite.)

Quel pourrait être un exemple de corps ? Un bon exemple est l’ensemble \mathbb{Z} \mod 7, soit \{0, 1, \ldots, 6\}, défini avec l’addition standard (remplaçant \circ) et la multiplication standard (remplaçant \diamond).

Premièrement, \mathbb{Z} \mod 7 satisfait la condition pour être un groupe abélien sur l’addition, et il satisfait également la condition pour être un groupe abélien sur la multiplication si l’on considère uniquement les éléments non nuls. Deuxièmement, la combinaison de l’ensemble avec les deux opérateurs satisfait la condition de distributivité.

Il est utile pédagogiquement d’explorer ces affirmations en utilisant des valeurs particulières. Prenons les valeurs expérimentales 5, 2 et 3, des éléments sélectionnés aléatoirement de l’ensemble \mathbb{Z} \mod 7, pour inspecter le corps \langle \mathbb{Z} \mod 7, +, \cdot \rangle. Nous allons utiliser ces trois valeurs dans l'ordre, en fonction des conditions à vérifier.

Explorons d’abord si \mathbb{Z} \mod 7 équipé de l’addition est un groupe abélien.

  1. Condition de fermeture : Prenons 5 et 2 comme valeurs. Dans ce cas, [5 + 2] \mod 7 = 7 \mod 7 = 0. Cela appartient bien à l’ensemble \mathbb{Z} \mod 7, donc le résultat est conforme à la condition de fermeture.
  2. Condition d’associativité : Prenons 5, 2 et 3 comme valeurs. Dans ce cas, [(5 + 2) + 3] \mod 7 = [5 + (2 + 3)] \mod 7 = 10 \mod 7 = 3. Cela satisfait la condition d’associativité.
  3. Condition d’identité : Prenons 5 comme valeur. Dans ce cas, [5 + 0] \mod 7 = [0 + 5] \mod 7 = 5. Ainsi, 0 semble être l’élément neutre pour l’addition.
  4. Condition d’inverse : Considérons l’inverse de 5. Il faut que [5 + d] \mod 7 = 0, pour une certaine valeur de d. La valeur unique de \mathbb{Z} \mod 7 qui satisfait cette condition est 2.
  5. Condition de commutativité : Prenons 5 et 3 comme valeurs. Dans ce cas, [5 + 3] \mod 7 = [3 + 5] \mod 7 = 1. Cela satisfait la condition de commutativité.

L’ensemble \mathbb{Z} \mod 7 équipé de l’addition semble clairement être un groupe abélien. Explorons maintenant si \mathbb{Z} \mod 7 équipé de la multiplication est un groupe abélien pour tous les éléments non nuls.

  1. Condition de fermeture : Prenons 5 et 2 comme valeurs. Dans ce cas, [5 \cdot 2] \mod 7 = 10 \mod 7 = 3. Cela appartient bien à l’ensemble \mathbb{Z} \mod 7, donc le résultat est conforme à la condition de fermeture.
  2. Condition d’associativité : Prenons 5, 2 et 3 comme valeurs. Dans ce cas, [(5 \cdot 2) \cdot 3] \mod 7 = [5 \cdot (2 \cdot 3)] \mod 7 = 30 \mod 7 = 2. Cela satisfait la condition d’associativité.
  3. Condition d’identité : Prenons 5 comme valeur. Dans ce cas, [5 \cdot 1] \mod 7 = [1 \cdot 5] \mod 7 = 5. Ainsi, 1 semble être l’élément neutre pour la multiplication.
  4. Condition d’inverse : Considérons l’inverse de 5. Il faut que [5 \cdot d] \mod 7 = 1, pour une certaine valeur de d. La valeur unique de \mathbb{Z} \mod 7 qui satisfait cette condition est 3. Cela satisfait la condition d’inversibilité.
  5. Condition de commutativité : Prenons 5 et 3 comme valeurs. Dans ce cas, [5 \cdot 3] \mod 7 = [3 \cdot 5] \mod 7 = 15 \mod 7 = 1. Cela satisfait la condition de commutativité.

L’ensemble \mathbb{Z} \mod 7 semble clairement répondre aux règles pour être un groupe abélien lorsqu'il est combiné avec l’addition ou avec la multiplication appliquée uniquement aux éléments non nuls.

Enfin, cet ensemble combiné avec les deux opérateurs semble satisfaire la condition de distributivité. Prenons 5, 2 et 3 comme valeurs. On peut constater que [5 \cdot (2 + 3)] \mod 7 = [5 \cdot 2 + 5 \cdot 3] \mod 7 = 25 \mod 7 = 4.

Nous avons maintenant montré que \mathbb{Z} \mod 7 muni de l’addition et de la multiplication satisfait les axiomes d’un corps fini lorsqu’on teste avec des valeurs particulières. Bien sûr, cela peut aussi être démontré de manière générale, mais nous ne le ferons pas ici.

Une distinction clé existe entre deux types de corps : les corps finis et les corps infinis.

Un corps infini est un corps où l’ensemble S est infiniment grand. Par exemple, l’ensemble des nombres réels \mathbb{R} muni de l’addition et de la multiplication est un corps infini. Un corps fini, également connu sous le nom de corps de Galois, est un corps où l’ensemble S est fini. Notre exemple précédent \langle \mathbb{Z} \mod 7, +, \cdot \rangle est un corps fini.

En cryptographie, nous nous intéressons principalement aux corps finis. En général, il peut être démontré qu’un corps fini existe pour un certain ensemble d’éléments S si et seulement si cet ensemble contient p^m éléments, où p est un nombre premier et m est un entier positif supérieur ou égal à 1. En d’autres termes, si l’ordre de l’ensemble S est un nombre premier (p^m où m = 1) ou une puissance de nombre premier (p^m où m > 1), alors on peut trouver deux opérateurs \circ et \diamond tels que les conditions pour un corps soient satisfaites.

Si un corps fini a un nombre premier d’éléments, on l’appelle un corps premier. Si le nombre d’éléments du corps fini est une puissance d’un nombre premier, alors le corps est appelé un corps d’extension. En cryptographie, nous nous intéressons à la fois aux corps premiers et aux corps d’extension. [2]

Les principaux corps premiers d’intérêt en cryptographie sont ceux où l’ensemble de tous les entiers est modulé par un nombre premier, et les opérateurs sont l’addition et la multiplication standard. Cette classe de corps finis comprendrait \mathbb{Z} \mod 2, \mathbb{Z} \mod 3, \mathbb{Z} \mod 5, \mathbb{Z} \mod 7, \mathbb{Z} \mod 11, \mathbb{Z} \mod 13, etc. Pour tout corps premier \mathbb{Z} \mod p, l’ensemble des entiers du corps est : \{0, 1, \ldots, p - 2, p - 1\}.

En cryptographie, nous nous intéressons également aux corps d’extension, en particulier aux corps contenant 2^m éléments où m > 1. Ces corps finis sont, par exemple, utilisés dans le chiffrement Rijndael, qui constitue la base de l’Advanced Encryption Standard (AES). Bien que les corps premiers soient relativement intuitifs, ces corps d’extension en base 2 peuvent sembler beaucoup moins intuitifs pour ceux qui ne sont pas familiers avec l’algèbre abstraite.

Pour commencer, il est effectivement vrai que tout ensemble d’entiers contenant 2^m éléments peut être associé à deux opérateurs qui en feront un corps (tant que m est un entier positif). Cependant, le fait qu'un corps existe ne signifie pas nécessairement qu'il est facile à découvrir ou particulièrement pratique pour certaines applications.

Il se trouve que les corps d’extension de 2^m particulièrement utiles en cryptographie sont ceux définis sur des ensembles particuliers d'expressions polynomiales, plutôt que sur un ensemble d’entiers.

Par exemple, supposons que nous voulions un corps d’extension contenant 2^3 (c’est-à-dire 8) éléments dans l’ensemble. Bien qu'il puisse exister de nombreux ensembles qui peuvent être utilisés pour des corps de cette taille, un ensemble particulier inclut tous les polynômes uniques de la forme a_2x^2 + a_1x + a_0, où chaque coefficient a_i est soit 0, soit 1. Ainsi, cet ensemble S comprend les éléments suivants :

  1. 0 : Le cas où a_2 = 0, a_1 = 0, et a_0 = 0.
  2. 1 : Le cas où a_2 = 0, a_1 = 0, et a_0 = 1.
  3. x : Le cas où a_2 = 0, a_1 = 1, et a_0 = 0.
  4. x + 1 : Le cas où a_2 = 0, a_1 = 1, et a_0 = 1.
  5. x^2 : Le cas où a_2 = 1, a_1 = 0, et a_0 = 0.
  6. x^2 + 1 : Le cas où a_2 = 1, a_1 = 0, et a_0 = 1.
  7. x^2 + x : Le cas où a_2 = 1, a_1 = 1, et a_0 = 0.
  8. x^2 + x + 1 : Le cas où a_2 = 1, a_1 = 1, et a_0 = 1.

L'ensemble S serait donc : \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}. Quelles sont les deux opérations qui peuvent être définies sur cet ensemble d’éléments pour garantir que leur combinaison forme un corps ?

La première opération sur l'ensemble S (\circ) peut être définie comme l’addition polynomiale standard modulo 2. Il suffit d’additionner les polynômes normalement, puis d’appliquer le modulo 2 à chacun des coefficients du polynôme résultant. Voici quelques exemples :

La deuxième opération sur l'ensemble S (\diamond) nécessaire pour créer le corps est plus complexe. Il s’agit d’une sorte de multiplication, mais pas de la multiplication standard en arithmétique. Au lieu de cela, chaque élément doit être considéré comme un vecteur, et l’opération doit être comprise comme une multiplication de vecteurs modulo un polynôme irréductible.

Passons d’abord à l’idée d’un polynôme irréductible. Un polynôme irréductible est un polynôme qui ne peut pas être factorisé (de la même manière qu’un nombre premier ne peut pas être décomposé en d’autres éléments que 1 et lui-même). Pour notre cas, nous nous intéressons aux polynômes irréductibles par rapport à l'ensemble de tous les entiers. (Il est à noter que certains polynômes peuvent être factorisés par exemple avec les nombres réels ou complexes, même s’ils ne peuvent pas l’être avec les entiers.)

Par exemple, considérons le polynôme x^2 - 3x + 2. Celui-ci peut être réécrit comme (x - 1)(x - 2). Ainsi, il n’est pas irréductible. Maintenant, considérons le polynôme x^2 + 1. En utilisant uniquement les entiers, il est impossible de factoriser cette expression. Ainsi, ce polynôme est irréductible par rapport aux entiers.

Ensuite, considérons la multiplication de vecteurs. Nous n’allons pas explorer ce sujet en profondeur, mais il est important de comprendre une règle fondamentale : Toute division de vecteur peut avoir lieu tant que le dividende a un degré supérieur ou égal à celui du diviseur. Si le degré du dividende est inférieur au degré du diviseur, alors la division est impossible.

Par exemple, considérons l’expression x^6 + x + 1 \mod x^5 + x^2. Celle-ci peut être réduite car le degré du dividende, 6, est supérieur au degré du diviseur, 5. Maintenant, considérons l’expression x^5 + x + 1 \mod x^5 + x^2. Celle-ci peut également être réduite, car les degrés du dividende et du diviseur sont égaux (5 chacun).

Cependant, si nous considérons l’expression x^4 + x + 1 \mod x^5 + x^2, elle ne peut pas être simplifiée davantage, car le degré du dividende, 4, est inférieur au degré du diviseur, 5.

Sur la base de ces informations, nous sommes maintenant prêts à définir notre deuxième opération pour l’ensemble \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.

J’ai déjà mentionné que la deuxième opération doit être comprise comme une multiplication de vecteurs modulo un polynôme irréductible. Ce polynôme irréductible doit garantir que l'opération définit un groupe abélien sur S et est cohérente avec la condition de distributivité. Alors, quel devrait être ce polynôme irréductible ?

Comme tous les vecteurs de l’ensemble ont un degré 2 ou inférieur, le polynôme irréductible doit être de degré 3. Si une multiplication de deux vecteurs dans l'ensemble produit un polynôme de degré 3 ou supérieur, nous savons que la réduction modulo un polynôme de degré 3 donnera toujours un polynôme de degré 2 ou inférieur. Cela est vrai parce que tout polynôme de degré 3 ou supérieur est toujours divisible par un polynôme de degré 3. De plus, le polynôme qui sert de diviseur doit être irréductible.

Il se trouve qu’il existe plusieurs polynômes irréductibles de degré 3 que nous pourrions utiliser comme diviseur. Chacun de ces polynômes définit un corps différent en conjonction avec notre ensemble S et l’addition modulo 2. Cela signifie que vous disposez de plusieurs options lorsque vous utilisez des corps d’extension 2^m en cryptographie.

Pour notre exemple, supposons que nous sélectionnons le polynôme x^3 + x + 1. Celui-ci est effectivement irréductible, car il est impossible de le factoriser en utilisant des entiers. De plus, il garantit que toute multiplication de deux éléments donnera un polynôme de degré 2 ou moins.

Travaillons maintenant sur un exemple de la deuxième opération en utilisant le polynôme x^3 + x + 1 comme diviseur pour illustrer comment cela fonctionne. Supposons que vous multipliez les éléments x^2 + 1 avec x^2 + x dans notre ensemble S. Nous devons alors calculer l’expression suivante :

Nous savons que [x^4 + x^3 + x^2 + x] \mod x^3 + x + 1 peut être réduit car le dividende a un degré supérieur (4) au diviseur (3).

Pour commencer, vous pouvez constater que l'expression x^3 + x + 1 divise x^4 + x^3 + x^2 + x un total de x fois. Vous pouvez vérifier cela en multipliant x^3 + x + 1 par x, ce qui donne x^4 + x^2 + x. Comme ce terme est du même degré que le dividende, à savoir 4, nous savons que cela fonctionne. Vous pouvez calculer le reste de cette division par x comme suit :

Après avoir divisé x^4 + x^3 + x^2 + x par x^3 + x + 1 un total de x fois, il reste un reste de x^3. Ce reste peut-il être divisé davantage par x^3 + x + 1 ?

Intuitivement, il pourrait sembler que x^3 ne puisse plus être divisé par x^3 + x + 1, car ce dernier terme semble plus grand. Cependant, rappelez-vous notre discussion sur la division des vecteurs. Tant que le dividende a un degré supérieur ou égal à celui du diviseur, l'expression peut être réduite davantage. Plus précisément, l'expression x^3 + x + 1 peut diviser x^3 exactement une fois. Le reste est calculé comme suit :

[(x^3) - (x^3 + x + 1)] \mod x^3 + x + 1 = [x + 1] \mod x^3 + x + 1 = x + 1

Vous vous demandez peut-être pourquoi (x^3) - (x^3 + x + 1) donne x + 1 au lieu de -x - 1. Rappelez-vous que la première opération de notre corps est définie modulo 2. Par conséquent, la soustraction de deux vecteurs donne exactement le même résultat que l’addition de ces deux vecteurs.

Pour résumer la multiplication de x^2 + 1 par x^2 + x : Lorsque vous multipliez ces deux termes, vous obtenez un polynôme de degré 4, x^4 + x^3 + x^2 + x, qui doit être réduit modulo x^3 + x + 1. Le polynôme de degré 4 est divisible par x^3 + x + 1 exactement x + 1 fois. Le reste après avoir divisé x^4 + x^3 + x^2 + x par x^3 + x + 1 exactement x + 1 fois est x + 1. Ce résultat est effectivement un élément de notre ensemble \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.

Pourquoi les corps d’extension en base 2 sur des ensembles de polynômes, comme dans l’exemple ci-dessus, sont-ils utiles en cryptographie ? La raison est que vous pouvez considérer les coefficients dans les polynômes de tels ensembles, qui sont soit 0 soit 1, comme des éléments de chaînes binaires d'une certaine longueur. L’ensemble S dans notre exemple ci-dessus pourrait par exemple être considéré comme un ensemble S qui comprend toutes les chaînes binaires de longueur 3 (de 000 à 111). Les opérations sur S peuvent alors également être utilisées pour effectuer des opérations sur ces chaînes binaires et produire une chaîne binaire de la même longueur.

Notes :

[2] Les corps d’extension peuvent être très contre-intuitifs. Au lieu d’avoir des éléments constitués d’entiers, ils sont composés d’ensembles de polynômes. De plus, toutes les opérations sont effectuées modulo un polynôme irréductible.

Algèbre abstraite en pratique

Bien que le langage formel et l’abstraction de la discussion puissent sembler complexes, le concept de groupe ne devrait pas être trop difficile à comprendre. Il s'agit simplement d'un ensemble d’éléments accompagné d’une opération binaire, où l’application de cette opération sur ces éléments respecte quatre conditions générales. Un groupe abélien possède simplement une condition supplémentaire appelée commutativité. Un groupe cyclique, quant à lui, est un type particulier de groupe abélien, à savoir celui qui possède un générateur. Un corps est simplement une construction plus complexe issue de la notion fondamentale de groupe.

Mais si vous êtes une personne orientée vers la pratique, vous pourriez vous demander à ce stade : En quoi cela est-il utile ? Le fait de savoir qu’un ensemble d’éléments avec un opérateur est un groupe, ou même un groupe abélien ou cyclique, a-t-il une réelle importance pratique ? Le fait de savoir qu'il s'agit d'un corps est-il pertinent ?

Sans entrer dans trop de détails, la réponse est « oui ». Les groupes ont été créés au XIXe siècle par le mathématicien français Évariste Galois. Il les a utilisés pour tirer des conclusions sur la résolution des équations polynomiales d’un degré supérieur à cinq.

Depuis lors, le concept de groupe a permis de clarifier de nombreux problèmes en mathématiques et ailleurs. Par exemple, le physicien Murray Gell-Mann a pu prédire l'existence d'une particule avant même qu'elle ne soit effectivement observée lors d’expériences. [3] Autre exemple, les chimistes utilisent la théorie des groupes pour classifier les formes des molécules. Les mathématiciens ont même utilisé le concept de groupe pour tirer des conclusions sur quelque chose de concret comme les motifs des papiers peints !

Montrer essentiellement qu’un ensemble d’éléments avec un certain opérateur est un groupe signifie que ce que vous décrivez possède une certaine symétrie. Pas une symétrie au sens courant du terme, mais sous une forme plus abstraite. Cela peut apporter des éclairages considérables sur certains systèmes et problèmes. Les notions plus complexes issues de l’algèbre abstraite ne font que fournir des informations supplémentaires.

Surtout, vous verrez l’importance des groupes et des corps issus de la théorie des nombres en pratique grâce à leur application en cryptographie, en particulier la cryptographie à clé publique. Nous avons déjà vu dans notre discussion sur les corps comment les corps d’extension sont utilisés dans l’algorithme Rijndael. Nous détaillerons cet exemple dans le Chapitre 5.

Pour approfondir la discussion sur l’algèbre abstraite, je recommande l'excellente série de vidéos sur l'algèbre abstraite proposée par Socratica. [4] Je recommande particulièrement les vidéos suivantes : « What is abstract algebra? », « Group definition (expanded) », « Ring definition (expanded) », et « Field definition (expanded) ». Ces quatre vidéos vous apporteront des informations supplémentaires sur une grande partie de ce qui a été discuté ci-dessus. (Nous n’avons pas abordé les anneaux, mais un corps est simplement un type particulier d’anneau.)

Pour aller plus loin sur la théorie moderne des nombres, vous pouvez consulter de nombreuses discussions avancées sur la cryptographie. Je suggère notamment Introduction to Modern Cryptography de Jonathan Katz et Yehuda Lindell, ou Understanding Cryptography de Christof Paar et Jan Pelzl pour une étude plus approfondie. [5]

Notes :

[3] Voir Vidéo YouTube

[4] Socratica, Algèbre Abstraite

[5] Katz et Lindell, Introduction to Modern Cryptography, 2e éd., 2015 (CRC Press : Boca Raton, FL). Paar et Pelzl, Understanding Cryptography, 2010 (Springer-Verlag : Berlin).

Cryptographie symétrique

Alice et Bob

L'une des deux principales branches de la cryptographie est la cryptographie symétrique. Elle comprend les schémas de chiffrement ainsi que les schémas relatifs à l’authentification et à l’intégrité. Jusqu’aux années 1970, toute la cryptographie se limitait aux schémas de chiffrement symétrique.

La discussion principale commence par l'examen des schémas de chiffrement symétrique et par l'établissement de la distinction cruciale entre les chiffrements par flot et les chiffrements par bloc. Ensuite, nous aborderons les codes d’authentification de message (MAC), qui sont des schémas destinés à garantir l’intégrité et l’authenticité des messages. Enfin, nous verrons comment les schémas de chiffrement symétrique et les MAC peuvent être combinés pour assurer une communication sécurisée.

Ce chapitre aborde en passant divers schémas cryptographiques symétriques utilisés en pratique. Le chapitre suivant propose une exposition détaillée du chiffrement à l'aide d'un chiffrement par flot (RC4) et d'un chiffrement par bloc (AES).

Avant de commencer notre discussion sur la cryptographie symétrique, je souhaite faire quelques remarques sur les illustrations d’Alice et Bob qui seront utilisées dans ce chapitre et les suivants.

Pour illustrer les principes de la cryptographie, les exemples impliquant Alice et Bob sont souvent utilisés. Je les utiliserai également.

Surtout si vous êtes nouveau en cryptographie, il est important de comprendre que ces exemples d’Alice et Bob ne servent qu’à illustrer des principes et des constructions cryptographiques dans un environnement simplifié. Cependant, ces principes et constructions sont applicables à un éventail beaucoup plus large de contextes réels.

Voici cinq points clés à garder à l’esprit concernant les exemples impliquant Alice et Bob en cryptographie :

  1. Ils peuvent facilement être transposés à des exemples impliquant d’autres types d’acteurs comme des entreprises ou des organisations gouvernementales.
  2. Ils peuvent facilement être étendus pour inclure trois acteurs ou plus.
  3. Dans les exemples, Bob et Alice sont généralement des participants actifs dans la création de chaque message et dans l’application des schémas cryptographiques sur ce message. Mais en réalité, les communications électroniques sont largement automatisées. Par exemple, lorsque vous visitez un site web utilisant la sécurité de la couche de transport (TLS), la cryptographie est généralement gérée intégralement par votre ordinateur et le serveur web.
  4. Dans le contexte de la communication électronique, les « messages » qui sont transmis via un canal de communication sont généralement des paquets TCP/IP. Ces paquets peuvent appartenir à un e-mail, un message Facebook, une conversation téléphonique, un transfert de fichier, un site web, un téléchargement de logiciel, etc. Ils ne sont pas des messages au sens traditionnel. Néanmoins, les cryptographes simplifient souvent cette réalité en affirmant que le message est, par exemple, un e-mail.
  5. Les exemples se concentrent généralement sur la communication électronique, mais ils peuvent également être appliqués aux formes traditionnelles de communication comme les lettres.

Schémas de chiffrement symétrique

On peut définir grossièrement un schéma de chiffrement symétrique comme tout schéma cryptographique composé de trois algorithmes :

  1. Un algorithme de génération de clé, qui génère une clé privée.
  2. Un algorithme de chiffrement, qui prend en entrée la clé privée et un message en clair, et produit un texte chiffré.
  3. Un algorithme de déchiffrement, qui prend en entrée la clé privée et le texte chiffré, et produit le message en clair d'origine.

En général, un schéma de chiffrement — qu'il soit symétrique ou asymétrique — offre un modèle de chiffrement basé sur un algorithme de base, plutôt qu'une spécification exacte.

Par exemple, considérons Salsa20, un schéma de chiffrement symétrique. Il peut être utilisé avec des clés de longueur de 128 bits ou 256 bits. Le choix de la longueur de la clé influence certains détails mineurs de l'algorithme (notamment le nombre de tours de l’algorithme).

Cependant, on ne dirait pas que l’utilisation de Salsa20 avec une clé de 128 bits est un schéma de chiffrement différent de celui utilisant une clé de 256 bits. L’algorithme de base reste le même. Ce n’est que lorsque l’algorithme de base change que l’on peut réellement parler de deux schémas de chiffrement différents.

Les schémas de chiffrement symétrique sont généralement utiles dans deux types de cas : (1) Ceux dans lesquels deux ou plusieurs agents communiquent à distance et souhaitent garder le contenu de leurs communications secret ; et (2) ceux dans lesquels un agent souhaite garder le contenu d’un message secret au fil du temps.

Vous pouvez voir une représentation de la situation (1) dans la Figure 1 ci-dessous. Bob veut envoyer un message M à Alice à distance, mais il ne veut pas que d’autres puissent lire ce message.

Bob chiffre d’abord le message M avec la clé privée K. Il envoie ensuite le texte chiffré C à Alice. Une fois qu’Alice a reçu le texte chiffré, elle peut le déchiffrer en utilisant la clé K et lire le message en clair. Avec un bon schéma de chiffrement, tout attaquant qui intercepterait le texte chiffré C ne devrait pas pouvoir déduire quoi que ce soit de significatif sur le message M.

Vous pouvez voir une représentation de la situation (2) dans la Figure 2 ci-dessous. Bob souhaite empêcher d’autres personnes de consulter certaines informations. Une situation typique pourrait être celle où Bob est un employé qui stocke des données sensibles sur son ordinateur, que ni des tiers extérieurs ni ses collègues ne sont censés lire.

Bob chiffre le message M à un moment donné T_0 avec la clé K pour produire le texte chiffré C. À un moment ultérieur T_1, il a besoin d'accéder au message à nouveau, et déchiffre le texte chiffré C avec la clé K. Tout attaquant qui aurait pu trouver le texte chiffré C entre-temps ne devrait pas avoir été capable de déduire quoi que ce soit de significatif concernant M.

Figure 1 : Secret à travers l'espace

Figure 1 : Secret à travers l'espace

Figure 2 : Secret à travers le temps

Figure 2 : Secret à travers le temps

Un exemple : Le chiffre de décalage

Dans le Chapitre 2, nous avons rencontré le chiffre de décalage, qui est un exemple très simple de schéma de chiffrement symétrique. Examinons-le à nouveau ici.

Supposons un dictionnaire D qui associe toutes les lettres de l’alphabet anglais, dans l’ordre, à l’ensemble de nombres \{0,1,2,\ldots,25\}. On suppose un ensemble de messages possibles M. Le chiffre de décalage est alors un schéma de chiffrement défini comme suit :

Ce qui fait du chiffre de décalage un schéma de chiffrement symétrique, c’est que la même clé est utilisée à la fois pour le chiffrement et pour le déchiffrement. Par exemple, supposons que vous souhaitiez chiffrer le message "DOG" en utilisant le chiffre de décalage, et que vous ayez choisi aléatoirement la clé "24". Le chiffrement du message avec cette clé donnerait "BME". La seule manière de récupérer le message original est d’utiliser la même clé, "24", pour le processus de déchiffrement.

Ce chiffre de décalage est un exemple de chiffre de substitution monoalphabétique : un schéma de chiffrement où l'alphabet du texte chiffré est fixe (c'est-à-dire qu'un seul alphabet est utilisé). En supposant que l’algorithme de déchiffrement soit déterministe, chaque symbole du texte chiffré par substitution peut au maximum correspondre à un seul symbole du texte en clair.

Jusqu’aux années 1700, de nombreuses applications du chiffrement reposaient largement sur des chiffres de substitution monoalphabétiques, bien que ceux-ci fussent souvent beaucoup plus complexes que le chiffre de décalage. Par exemple, on pouvait sélectionner aléatoirement une lettre de l’alphabet pour chaque lettre du texte original sous la contrainte que chaque lettre n’apparaisse qu’une seule fois dans l’alphabet du texte chiffré. Cela signifie qu'il y aurait 26! (factorielle de 26) clés privées possibles, ce qui représentait une quantité énorme à l’époque préinformatique.

Il convient de noter que vous rencontrerez souvent le terme chiffre en cryptographie. Soyez conscient que ce terme a plusieurs significations. En fait, il existe au moins cinq sens distincts de ce terme en cryptographie.

Dans certains cas, il se réfère à un schéma de chiffrement, comme c'est le cas pour le chiffre de décalage et le chiffre de substitution monoalphabétique. Cependant, le terme peut également désigner spécifiquement l’algorithme de chiffrement, la clé privée, ou simplement le texte chiffré d’un tel schéma de chiffrement.

Enfin, le terme chiffre peut aussi désigner un algorithme de base à partir duquel on peut construire des schémas cryptographiques. Cela peut inclure divers algorithmes de chiffrement, mais aussi d’autres types de schémas cryptographiques. Ce sens du terme devient pertinent dans le contexte des chiffrements par bloc (voir la section « Chiffrements par bloc » ci-dessous).

Vous pourriez également rencontrer les termes chiffrer ou déchiffrer.

Attaques par force brute et principe de Kerckhoffs

Le chiffre de décalage est un schéma de chiffrement symétrique très peu sécurisé, du moins dans le monde moderne. [1] Un attaquant pourrait simplement tenter de déchiffrer n'importe quel texte chiffré en testant les 26 clés possibles pour voir laquelle produit un résultat cohérent. Ce type d’attaque, où l’attaquant teste toutes les clés possibles jusqu’à trouver la bonne, est appelé une attaque par force brute ou recherche exhaustive de clés.

Pour qu'un schéma de chiffrement réponde à une notion minimale de sécurité, il doit posséder un ensemble de clés possibles, ou espace de clés, suffisamment vaste pour rendre les attaques par force brute irréalistes. Tous les schémas de chiffrement modernes respectent ce critère. Ce principe est connu sous le nom de principe d'espace de clés suffisant. Un principe similaire s'applique généralement aux différents types de schémas cryptographiques.

Pour vous donner une idée de l’énormité de l’espace de clés des schémas de chiffrement modernes, supposons qu’un fichier ait été chiffré avec une clé de 128 bits en utilisant l’Advanced Encryption Standard (AES). Cela signifie qu’un attaquant doit tester un ensemble de 2^{128} clés pour réussir une attaque par force brute. Obtenir une probabilité de succès de 0,78 % avec cette stratégie nécessiterait de tester environ 2,65 \times 10^{36} clés.

Supposons de manière optimiste qu'un attaquant puisse tester 10^{16} clés par seconde (soit 10 quadrillions de clés par seconde). Pour tester 0,78 % de toutes les clés de l'espace de clés, son attaque devrait durer environ 2,65 \times 10^{20} secondes. Cela représente environ 8,4 billions d'années. Ainsi, même une attaque par force brute menée par un adversaire extrêmement puissant est irréaliste avec un schéma de chiffrement moderne utilisant une clé de 128 bits. C'est ainsi que s'applique le principe d'espace de clés suffisant.

Le chiffre de décalage est-il plus sécurisé si l’attaquant ne connaît pas l’algorithme de chiffrement ? Peut-être, mais pas de manière significative.

En tout cas, la cryptographie moderne suppose toujours que la sécurité de tout schéma de chiffrement symétrique repose uniquement sur le secret de la clé privée. On suppose toujours que l’attaquant connaît tous les autres détails, y compris l’espace des messages, l’espace des clés, l’espace des textes chiffrés, l’algorithme de sélection de clé, l’algorithme de chiffrement et l’algorithme de déchiffrement.

L’idée selon laquelle la sécurité d’un schéma de chiffrement symétrique ne peut reposer que sur le secret de la clé privée est connue sous le nom de principe de Kerckhoffs.

Tel qu’il a été initialement conçu par Kerckhoffs, ce principe ne s’applique qu’aux schémas de chiffrement symétrique. Une version plus générale du principe, cependant, s’applique également à tous les autres types modernes de schémas cryptographiques : La conception d’un schéma cryptographique ne doit pas avoir besoin d’être secrète pour être sécurisée ; la confidentialité ne peut s’étendre qu’à une ou plusieurs chaînes d’informations, généralement une clé privée.

Le principe de Kerckhoffs est fondamental en cryptographie moderne pour quatre raisons. [2] Premièrement, il existe un nombre limité de schémas cryptographiques pour des applications spécifiques. Par exemple, la plupart des applications modernes de chiffrement symétrique utilisent le chiffre de Rijndael (AES). Ainsi, la confidentialité concernant la conception d’un schéma est très limitée. En revanche, il est beaucoup plus facile de garder une clé privée pour le chiffre de Rijndael secrète.

Deuxièmement, il est plus facile de remplacer une chaîne d'informations qu'un schéma cryptographique entier. Supposons que les employés d'une entreprise utilisent tous le même logiciel de chiffrement, et que chaque paire d’employés dispose d'une clé privée pour communiquer de manière confidentielle. Si une clé privée est compromise dans ce scénario, cela pose problème, mais au moins l'entreprise peut continuer à utiliser le logiciel malgré de telles failles de sécurité. Si la sécurité de l'entreprise reposait sur le secret du schéma lui-même, toute compromission de ce secret nécessiterait le remplacement complet du logiciel.

Troisièmement, le principe de Kerckhoffs permet la standardisation et la compatibilité entre les utilisateurs des schémas cryptographiques. Cela présente des avantages considérables en termes d'efficacité. Par exemple, il est difficile d'imaginer comment des millions de personnes pourraient se connecter de manière sécurisée aux serveurs web de Google chaque jour, si cette sécurité exigeait de garder les schémas cryptographiques secrets.

Quatrièmement, le principe de Kerckhoffs permet l’examen public des schémas cryptographiques. Ce type de vérification est absolument essentiel pour atteindre un niveau de sécurité adéquat. À titre d’illustration, l’algorithme central de la cryptographie symétrique, le chiffre de Rijndael (AES), est le résultat d’un concours organisé par le National Institute of Standards and Technology (NIST) entre 1997 et 2000.

Tout système qui cherche à atteindre une sécurité par l'obscurité repose sur le maintien du secret des détails de sa conception et/ou de sa mise en œuvre. En cryptographie, cela correspondrait spécifiquement à un système qui repose sur le secret des détails de conception du schéma cryptographique. La sécurité par l'obscurité est donc en contradiction directe avec le principe de Kerckhoffs.

La capacité de l'ouverture à renforcer la qualité et la sécurité s'étend au-delà de la cryptographie pour englober le monde numérique en général. Par exemple, les distributions Linux libres et open source telles que Debian offrent généralement plusieurs avantages par rapport à leurs homologues sous Windows et MacOS en termes de confidentialité, de stabilité, de sécurité et de flexibilité. Bien que cela puisse être dû à de multiples facteurs, le principe le plus important est probablement, comme l’a formulé Eric Raymond dans son célèbre essai "The Cathedral and the Bazaar", que "dès lors qu'un nombre suffisant de regards sont tournés vers un problème, tous les bogues deviennent superficiels." [3] C'est ce principe fondé sur la sagesse collective qui a contribué au succès majeur de Linux.

On ne peut jamais affirmer de manière non équivoque qu'un schéma cryptographique est « sécurisé » ou « non sécurisé ». Il existe plutôt diverses notions de sécurité pour les schémas cryptographiques. Chaque définition de la sécurité cryptographique doit spécifier (1) les objectifs de sécurité, ainsi que (2) les capacités d'un attaquant. L'analyse des schémas cryptographiques en fonction d'une ou plusieurs notions spécifiques de sécurité permet de comprendre leurs applications et leurs limites.

Bien que nous n'entrions pas dans tous les détails des différentes notions de sécurité cryptographique, vous devez savoir que deux hypothèses sont omniprésentes dans toutes les notions modernes de sécurité cryptographique relatives aux schémas symétriques et asymétriques (et sous une forme ou une autre pour d'autres primitives cryptographiques) :

Notes :

[1] Selon Suétone, un chiffre de décalage avec une valeur de clé constante de 3 était utilisé par Jules César dans ses communications militaires. Ainsi, A devenait toujours D, B devenait toujours E, C devenait toujours F, etc. Cette version particulière du chiffre de décalage est ainsi devenue connue sous le nom de Chiffre de César (bien qu'il ne s'agisse pas vraiment d'un chiffre au sens moderne du terme, puisque la valeur de la clé est constante). Le chiffre de César pouvait être sécurisé au Ier siècle avant J.-C., si les ennemis de Rome étaient très peu familiers avec le chiffrement. Mais il ne s’agirait manifestement pas d’un schéma sécurisé de nos jours.

[2] Jonathan Katz et Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL : 2015), p. 7f.

[3] Eric Raymond, « The Cathedral and the Bazaar », article présenté au Linux Kongress, Würzburg, Allemagne (27 mai 1997). Il existe plusieurs versions ultérieures disponibles ainsi qu'un livre. Les citations sont extraites de la page 30 du livre : Eric Raymond, The Cathedral and the Bazaar: Musings on Linux and Open Source by an Accidental Revolutionary, édition révisée (2001), O’Reilly : Sebastopol, CA.

Chiffrements par flot

Les schémas de chiffrement symétrique sont couramment subdivisés en deux types : les chiffrements par flot et les chiffrements par bloc. Cependant, cette distinction peut poser problème, car ces termes sont parfois utilisés de manière incohérente. Dans les prochaines sections, je présenterai cette distinction de la manière qui me semble la plus appropriée. Il est néanmoins important de noter que de nombreuses personnes peuvent employer ces termes différemment.

Commençons par les chiffrements par flot. Un chiffrement par flot est un schéma de chiffrement symétrique dans lequel le chiffrement consiste en deux étapes.

Tout d’abord, une chaîne de caractères de la même longueur que le texte en clair est produite à l’aide d’une clé privée. Cette chaîne est appelée flux de clé (keystream).

Ensuite, le flux de clé est combiné mathématiquement avec le texte en clair pour produire un texte chiffré. Cette combinaison est généralement effectuée via une opération XOR. Pour déchiffrer, il suffit d’inverser l’opération. (Notez que A \oplus B = B \oplus A, lorsque A et B sont des chaînes de bits. Ainsi, l’ordre d’une opération XOR dans un chiffrement par flot n’a pas d’importance sur le résultat. Cette propriété est appelée commutativité.)

Un chiffrement par flot basé sur XOR est représenté dans la Figure 3. Vous commencez par prendre une clé privée K et l’utilisez pour générer un flux de clé. Le flux de clé est ensuite combiné avec le texte en clair via une opération XOR pour produire le texte chiffré. Toute personne qui reçoit le texte chiffré peut facilement le déchiffrer si elle possède la clé K. Tout ce qu’elle doit faire est de recréer un flux de clé de la même longueur que le texte chiffré selon la procédure spécifiée par le schéma, puis d’appliquer une opération XOR au texte chiffré.

Figure 3 : Un chiffrement par flot basé sur XOR

Figure 3 : Un chiffrement par flot basé sur XOR

Rappelons qu'un schéma de chiffrement est généralement un modèle de chiffrement utilisant un même algorithme de base, plutôt qu’une spécification exacte. Par extension, un chiffrement par flot est typiquement un modèle de chiffrement dans lequel on peut utiliser des clés de différentes longueurs. Bien que la longueur de la clé puisse modifier certains détails mineurs du schéma, elle n’affecte pas sa forme essentielle.

Le chiffre de décalage est un exemple très simple et peu sûr de chiffrement par flot. En utilisant une seule lettre (la clé privée), vous pouvez produire une chaîne de lettres de la même longueur que le message (le flux de clé). Ce flux de clé est ensuite combiné avec le texte en clair par une opération de modulo pour produire un texte chiffré. (Cette opération de modulo peut être simplifiée en une opération XOR lorsque les lettres sont représentées en bits).

Un autre exemple célèbre de chiffrement par flot est le chiffre de Vigenère, nommé d'après Blaise de Vigenère, qui l'a pleinement développé à la fin du XVIe siècle (bien que d'autres aient fait un travail préparatoire important). C'est un exemple de chiffrement par substitution polyalphabétique : un schéma de chiffrement où l’alphabet du texte chiffré pour un symbole donné dépend de sa position dans le texte. Contrairement à un chiffre de substitution monoalphabétique, les symboles du texte chiffré peuvent être associés à plusieurs symboles du texte en clair.

À mesure que le chiffrement gagnait en popularité dans l'Europe de la Renaissance, il en allait de même pour la cryptanalyse — c'est-à-dire, la détection des textes chiffrés — en particulier à l'aide de l'analyse de fréquence. Cette dernière exploite les régularités statistiques de notre langage pour casser les textes chiffrés, une technique découverte par des érudits arabes dès le IXe siècle. Elle est particulièrement efficace sur des textes longs. Même les chiffres de substitution monoalphabétiques les plus sophistiqués n’étaient plus suffisants contre l'analyse de fréquence dès les années 1700 en Europe, en particulier dans les contextes militaires et de sécurité. Comme le chiffre de Vigenère offrait une avancée significative en matière de sécurité, il est devenu populaire à cette époque et était largement utilisé à la fin du XVIIIe siècle.

De manière informelle, le fonctionnement de ce schéma de chiffrement est le suivant :

  1. Choisir un mot de plusieurs lettres comme clé privée.
  2. Pour n'importe quel message, appliquer le chiffre de décalage à chaque lettre du message en utilisant la lettre correspondante du mot-clé comme décalage.
  3. Si vous avez parcouru toutes les lettres du mot-clé sans avoir entièrement chiffré le texte en clair, réutiliser les lettres du mot-clé comme chiffre de décalage pour les lettres restantes du texte.
  4. Continuer ce processus jusqu’à ce que le message entier soit chiffré.

Pour illustrer, supposons que votre clé privée soit "GOLD" et que vous souhaitiez chiffrer le message "CRYPTOGRAPHY". Selon le chiffre de Vigenère, vous procéderiez comme suit :

Ainsi, le texte chiffré c obtenu est : "IFJSZCRUGDSB".

Un autre exemple célèbre de chiffrement par flot est le One-Time Pad (chiffrement à usage unique). Avec ce système, vous créez simplement une chaîne de bits aléatoires de la même longueur que le message en clair, et vous produisez le texte chiffré via une opération XOR. Ainsi, dans le cas du One-Time Pad, la clé privée et le flux de clé sont équivalents.

Alors que le chiffre de décalage et les chiffres de Vigenère sont très peu sécurisés à notre époque, le One-Time Pad est extrêmement sécurisé s’il est utilisé correctement. L’application la plus connue du One-Time Pad était, au moins jusqu’aux années 1980, pour la ligne directe Washington-Moscou. [4]

Cette ligne directe est un lien de communication entre Washington et Moscou destiné aux urgences, installé après la crise des missiles de Cuba. La technologie a évolué au fil des années. Aujourd’hui, elle inclut une connexion par fibre optique directe ainsi que deux liaisons par satellite (pour la redondance), permettant l’envoi d’e-mails et de messages texte. Cette connexion se termine en plusieurs endroits aux États-Unis, dont le Pentagone, la Maison Blanche et Raven Rock Mountain. Contrairement à ce que l’on croit souvent, cette ligne n’a jamais impliqué de téléphones.

Essentiellement, le fonctionnement du One-Time Pad était le suivant : Washington et Moscou disposaient chacun de deux ensembles de nombres aléatoires. Un ensemble de nombres aléatoires, créé par les Russes, servait au chiffrement et au déchiffrement de tous les messages en langue russe. Un ensemble de nombres aléatoires, créé par les Américains, servait au chiffrement et au déchiffrement de tous les messages en langue anglaise. De temps à autre, de nouveaux nombres aléatoires étaient envoyés à l'autre partie par des coursiers de confiance.

Washington et Moscou pouvaient alors communiquer secrètement en utilisant ces nombres aléatoires pour créer des One-Time Pads. Chaque fois qu'ils devaient communiquer, ils utilisaient la portion suivante des nombres aléatoires pour leur message.

Bien que très sécurisé, le One-Time Pad présente des limitations pratiques importantes : la clé doit être aussi longue que le message, et aucune partie d'un One-Time Pad ne peut être réutilisée. Cela signifie qu'il faut suivre précisément l’endroit où l’on se trouve dans le One-Time Pad, stocker une quantité massive de bits, et échanger des bits aléatoires avec les autres parties de manière périodique. En conséquence, le One-Time Pad est rarement utilisé en pratique.

À la place, les chiffrements par flot prédominants en pratique sont les chiffrements par flot pseudorandomisés. Salsa20 et sa variante étroitement liée appelée ChaCha sont des exemples courants de chiffrements par flot pseudorandomisés.

Avec ces chiffrements par flot pseudorandomisés, vous commencez par sélectionner aléatoirement une clé K plus courte que la longueur du message en clair. Une telle clé aléatoire K est généralement créée par votre ordinateur à partir de données imprévisibles qu'il collecte au fil du temps, telles que le temps écoulé entre les messages réseau, les mouvements de la souris, etc.

Cette clé aléatoire K est ensuite insérée dans un algorithme d’expansion qui génère un flux de clé pseudorandomisé aussi long que le message. Vous pouvez spécifier précisément la longueur du flux de clé nécessaire (par exemple, 500 bits, 1000 bits, 1200 bits, 29 117 bits, etc.).

Un flux de clé pseudorandomisé semble avoir été choisi comme si il l’avait été entièrement au hasard parmi l’ensemble de toutes les chaînes de la même longueur. Ainsi, le chiffrement avec un flux de clé pseudorandomisé semble avoir été effectué avec un One-Time Pad. Mais ce n’est évidemment pas le cas.

Comme notre clé privée est plus courte que le flux de clé et que notre algorithme d’expansion doit être déterministe pour que le processus de chiffrement/déchiffrement fonctionne, tous les flux de clé possibles de cette longueur particulière ne peuvent pas être produits par notre algorithme d’expansion.

Supposons, par exemple, que notre clé privée ait une longueur de 128 bits et que nous puissions l'insérer dans un algorithme d'expansion pour créer un flux de clé beaucoup plus long, disons de 2 500 bits. Étant donné que notre algorithme d’expansion doit être déterministe, notre algorithme ne pourra sélectionner au maximum que 1/2^{128} chaînes de longueur 2 500 bits. Un tel flux de clé ne pourrait donc jamais être sélectionné de manière entièrement aléatoire parmi toutes les chaînes de même longueur.

Notre définition d’un chiffre par flot comporte deux aspects : (1) un flux de clé aussi long que le texte en clair est généré à l’aide d’une clé privée ; et (2) ce flux de clé est combiné avec le texte en clair, généralement par une opération XOR, pour produire le texte chiffré.

Parfois, certaines personnes définissent la condition (1) de manière plus stricte, en affirmant que le flux de clé doit être spécifiquement pseudorandomisé. Cela signifie que ni le chiffre de décalage, ni le One-Time Pad ne seraient considérés comme des chiffrements par flot.

De mon point de vue, définir la condition (1) de manière plus large permet de mieux organiser les schémas de chiffrement. De plus, cela signifie que l'on n'est pas obligé de cesser d’appeler un schéma de chiffrement particulier un chiffre par flot simplement parce qu’on apprend qu’il ne repose pas réellement sur des flux de clé pseudorandomisés.

Notes :

[4] Crypto Museum, « Washington-Moscow hotline », 2013, disponible sur : https://www.cryptomuseum.com/crypto/hotline/index.htm.

Chiffrements par bloc

La première manière de comprendre un chiffrement par bloc est de le considérer comme quelque chose de plus élémentaire qu’un chiffre par flot : un algorithme de base qui réalise une transformation préservant la longueur d’une chaîne de caractères de longueur appropriée, à l’aide d’une clé. Cet algorithme peut être utilisé pour créer des schémas de chiffrement ou peut-être d’autres types de schémas cryptographiques.

Un chiffre par bloc peut généralement accepter des chaînes d’entrée de longueurs variables, telles que 64, 128 ou 256 bits, ainsi que des clés de longueurs variables, telles que 128, 192 ou 256 bits. Bien que certains détails de l’algorithme puissent changer en fonction de ces variables, l’algorithme de base lui-même ne change pas. Si c'était le cas, on parlerait alors de deux chiffrements par bloc différents. Notez que l'utilisation du terme algorithme de base est la même que pour les schémas de chiffrement.

Un schéma illustrant le fonctionnement d'un chiffre par bloc est présenté à la Figure 4 ci-dessous. Un message M de longueur L et une clé K servent d’entrées au chiffre par bloc. Il produit un message M' de longueur L. La clé n'a pas nécessairement besoin d'être de la même longueur que M et M' pour la plupart des chiffrements par bloc.

Figure 4 : Un chiffrement par bloc

Figure 4 : Un chiffrement par bloc

Un chiffre par bloc seul n'est pas un schéma de chiffrement. Mais il peut être utilisé avec divers modes de fonctionnement pour produire différents schémas de chiffrement. Un mode de fonctionnement ajoute simplement des opérations supplémentaires en dehors du chiffre par bloc.

Pour illustrer comment cela fonctionne, supposons un chiffre par bloc (BC) qui nécessite une chaîne d’entrée de 128 bits et une clé privée de 128 bits. La Figure 5 ci-dessous montre comment ce chiffre par bloc peut être utilisé avec le mode Electronic Code Book (mode ECB) pour créer un schéma de chiffrement. (Les points de suspension à droite indiquent que ce schéma peut être répété autant de fois que nécessaire).

Figure 5 : Un chiffrement par bloc avec le mode ECB

Figure 5 : Un chiffrement par bloc avec le mode ECB

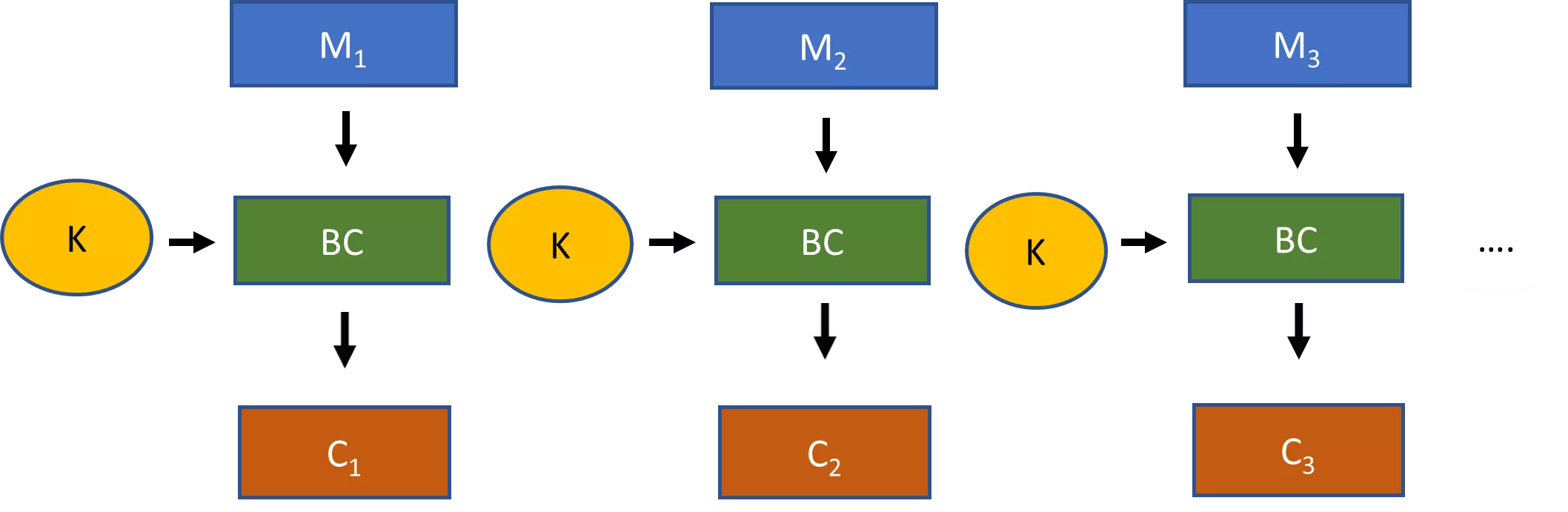
Le processus de chiffrement en mode Electronic Code Book (ECB) avec un chiffre par bloc est le suivant. Voyez si vous pouvez diviser votre message en clair en blocs de 128 bits. Si ce n'est pas possible, ajoutez un padding (remplissage) au message, de sorte que le résultat puisse être divisé en blocs de 128 bits. Cela constitue vos données utilisées pour le processus de chiffrement.

Ensuite, divisez les données en segments de chaînes de 128 bits (M_1, M_2, M_3, etc.). Faites passer chaque chaîne de 128 bits à travers le chiffre par bloc avec votre clé de 128 bits pour produire des segments de texte chiffré de 128 bits (C_1, C_2, C_3, etc.). Ces segments, une fois combinés, forment le texte chiffré complet.

Le déchiffrement est simplement le processus inverse, bien que le destinataire ait besoin d'un moyen de reconnaître le padding (remplissage) du message déchiffré pour retrouver le message en clair d'origine.

Bien que relativement simple, un chiffrement par bloc en mode Electronic Code Book (ECB) manque de sécurité. Cela est dû au fait qu'il conduit à un chiffrement déterministe. Deux chaînes de données identiques de 128 bits sont chiffrées exactement de la même manière. Cette particularité peut être exploitée.

Au lieu de cela, tout schéma de chiffrement construit à partir d'un chiffre par bloc devrait être probabiliste : c'est-à-dire que le chiffrement de tout message M, ou de tout segment spécifique de M, devrait généralement produire un résultat différent à chaque fois. [5]

Le mode de chaînage par blocs de chiffrement (mode CBC) est probablement le mode le plus courant utilisé avec un chiffre par bloc. La combinaison, si elle est bien faite, produit un schéma de chiffrement probabiliste. Un schéma illustrant ce mode de fonctionnement est présenté dans la Figure 6 ci-dessous.

Figure 6 : Un chiffrement par bloc avec le mode CBC

Figure 6 : Un chiffrement par bloc avec le mode CBC

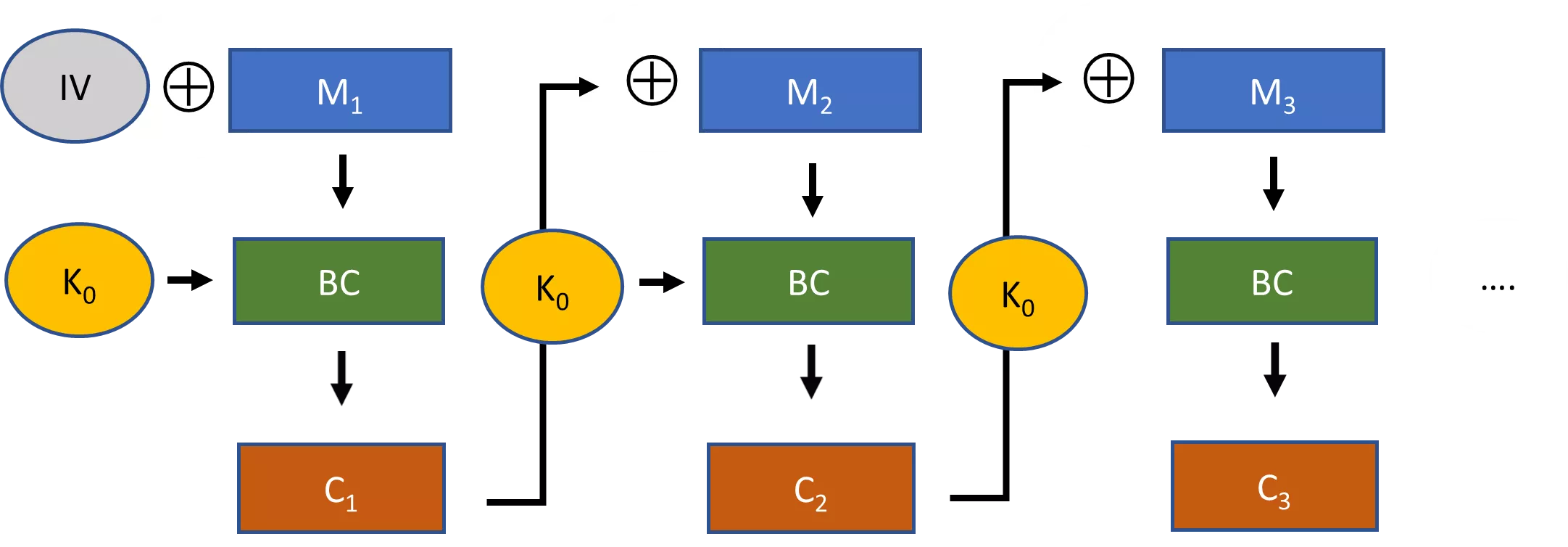
Supposons que la taille des blocs soit à nouveau de 128 bits. Pour commencer, vous devez vous assurer que votre message en clair d’origine reçoit le padding nécessaire.

Ensuite, vous appliquez une opération XOR au premier bloc de 128 bits de votre message en clair avec un vecteur d’initialisation (Initialization Vector - IV) de 128 bits. Le résultat est placé dans le chiffre par bloc pour produire un texte chiffré pour le premier bloc. Pour le deuxième bloc de 128 bits, vous appliquez d’abord une opération XOR au texte en clair avec le texte chiffré du premier bloc, avant de l'insérer dans le chiffre par bloc. Vous continuez ce processus jusqu’à ce que vous ayez chiffré l'intégralité de votre message en clair.

Une fois terminé, vous envoyez le message chiffré accompagné du vecteur d’initialisation non chiffré au destinataire. Le destinataire doit connaître ce vecteur d’initialisation, sinon il ne pourra pas déchiffrer le texte chiffré.

Cette construction est bien plus sécurisée que le mode Electronic Code Book (ECB) lorsqu'elle est utilisée correctement. Tout d'abord, vous devez vous assurer que le vecteur d’initialisation (IV) est une chaîne aléatoire ou pseudorandomisée. De plus, vous devez utiliser un vecteur d’initialisation différent chaque fois que vous utilisez ce schéma de chiffrement.

En d'autres termes, votre vecteur d’initialisation doit être un nombre aléatoire ou pseudorandomisé appelé nonce (pour "number used once" ou "nombre utilisé une seule fois"). Si vous respectez cette pratique, alors le mode CBC avec un chiffre par bloc garantit que deux blocs de texte en clair identiques seront généralement chiffrés différemment chaque fois.

Passons maintenant au mode de rétroaction de sortie (Output Feedback Mode - OFB Mode). Une illustration de ce mode est présentée dans la Figure 7.

Figure 7 : Un chiffrement par bloc avec le mode OFB

Figure 7 : Un chiffrement par bloc avec le mode OFB

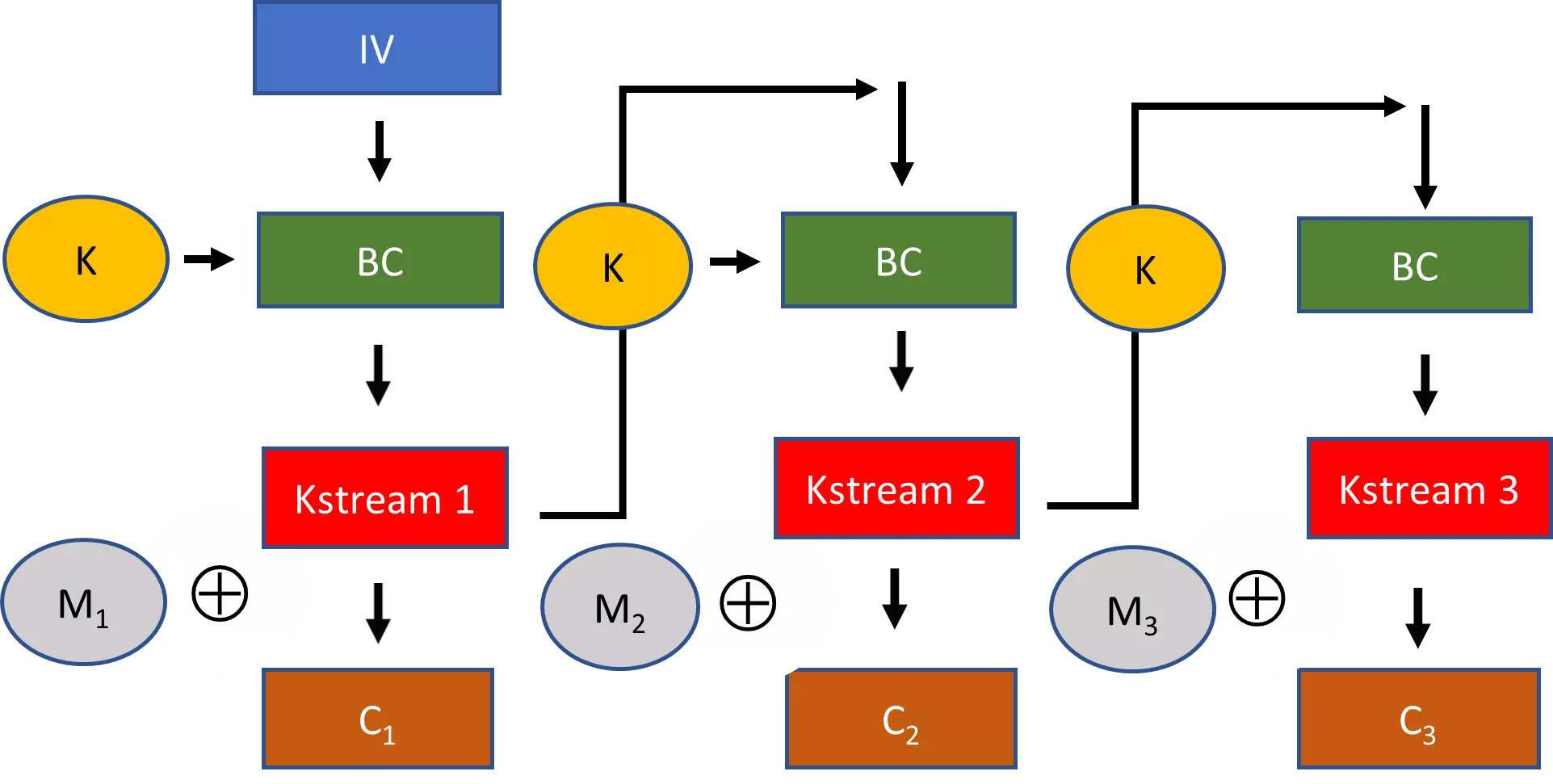
Avec le mode OFB, vous sélectionnez également un vecteur d’initialisation. Mais ici, pour le premier bloc, le vecteur d’initialisation est directement inséré dans le chiffre par bloc avec votre clé. Les 128 bits résultants sont alors traités comme un flux de clé. Ce flux de clé est ensuite combiné par une opération XOR avec le texte en clair pour produire le texte chiffré correspondant au bloc. Pour les blocs suivants, vous utilisez le flux de clé du bloc précédent comme entrée du chiffre par bloc, puis vous répétez les étapes.

En y regardant de plus près, ce qui a réellement été créé ici à partir du chiffre par bloc avec le mode OFB est un chiffrement par flot. Vous générez des portions de flux de clé de 128 bits jusqu'à obtenir une longueur totale correspondant au texte en clair (en éliminant les bits dont vous n'avez pas besoin provenant de la dernière portion de 128 bits du flux de clé). Vous appliquez ensuite une opération XOR entre le flux de clé et votre message en clair pour obtenir le texte chiffré.

Dans la section précédente sur les chiffres par flot, j'ai mentionné que vous produisez un flux de clé avec l'aide d'une clé privée. Pour être précis, il n'est pas nécessaire qu'il soit créé uniquement avec une clé privée. Comme vous pouvez le constater avec le mode OFB, le flux de clé est produit avec l'aide d'une clé privée et d'un vecteur d’initialisation.

Notez qu’à l’instar du mode CBC, il est important de sélectionner un nonce pseudorandomisé ou aléatoire comme vecteur d’initialisation chaque fois que vous utilisez un chiffre par bloc en mode OFB. Sinon, la même chaîne de message de 128 bits envoyée dans des communications différentes sera chiffrée de la même manière. C'est une façon de créer un chiffrement probabiliste avec un chiffre par flot.

Certains chiffres par flot utilisent uniquement une clé privée pour créer un flux de clé. Pour ces chiffres par flot, il est essentiel d'utiliser un nonce aléatoire pour sélectionner la clé privée pour chaque instance de communication. Sinon, les résultats du chiffrement avec ces chiffres par flot seront également déterministes, ce qui entraînera des problèmes de sécurité.

Le chiffre par bloc moderne le plus populaire est le chiffre de Rijndael. Il a été sélectionné parmi quinze soumissions lors d'un concours organisé par le National Institute of Standards and Technology (NIST) entre 1997 et 2000 afin de remplacer un ancien standard de chiffrement, le Data Encryption Standard (DES).

Le chiffre de Rijndael peut être utilisé avec différentes spécifications de longueurs de clé et de tailles de bloc, ainsi qu'avec différents modes de fonctionnement. Le comité du concours du NIST a adopté une version restreinte du chiffre de Rijndael — à savoir celle qui requiert des blocs de 128 bits et des clés de longueur 128 bits, 192 bits ou 256 bits — dans le cadre de la norme appelée Advanced Encryption Standard (AES). Il s'agit vraiment de la norme principale pour les applications de chiffrement symétrique. Elle est si sécurisée que même la NSA semble prête à l'utiliser avec des clés de 256 bits pour les documents classés Top Secret. [6]

Le chiffre par bloc AES sera expliqué en détail dans le Chapitre 5.

Notes :

[5] L’importance du chiffrement probabiliste a été soulignée pour la première fois par Shafi Goldwasser et Silvio Micali, « Probabilistic encryption », Journal of Computer and System Sciences, 28 (1984), 270–99.

[6] Voir NSA, "Commercial National Security Algorithm Suite", https://apps.nsa.gov/iaarchive/programs/iad-initiatives/cnsa-suite.cfm.

Dissiper la confusion

La confusion concernant la distinction entre les chiffrements par bloc et les chiffrements par flot provient du fait que certaines personnes comprennent parfois le terme chiffrement par bloc comme faisant spécifiquement référence à un chiffrement par bloc utilisant un mode de chiffrement par bloc.

Considérons les modes ECB et CBC mentionnés dans la section précédente. Ceux-ci exigent spécifiquement que les données à chiffrer puissent être divisées par la taille du bloc (ce qui signifie que vous devrez peut-être utiliser un remplissage pour le message d'origine). De plus, les données dans ces modes sont également traitées directement par le chiffre par bloc (et non pas simplement combinées avec le résultat d'une opération de chiffre par bloc comme dans le mode OFB).

Ainsi, de manière alternative, vous pouvez définir un chiffrement par bloc comme tout schéma de chiffrement qui fonctionne sur des blocs de longueur fixe du message à la fois (où chaque bloc doit être plus long qu'un octet, sinon il se réduit à un chiffre par flot). À la fois les données à chiffrer et le texte chiffré doivent pouvoir être divisés uniformément selon cette taille de bloc. En général, la taille des blocs est de 64, 128, 192 ou 256 bits. Par contraste, un chiffre par flot peut chiffrer des messages de toute longueur en les découpant en morceaux de 1 bit ou 1 octet à la fois.

Avec cette compréhension plus spécifique d'un chiffrement par bloc, vous pouvez effectivement affirmer que les schémas de chiffrement modernes sont soit des chiffrements par flot, soit des chiffrements par bloc. À partir de maintenant, j'utiliserai le terme chiffrement par bloc dans son sens général, sauf indication contraire.

La discussion sur le mode OFB dans la section précédente soulève également un autre point intéressant. Certains chiffres par flot sont construits à partir de chiffres par bloc, comme Rijndael avec le mode OFB. D'autres, comme Salsa20 et ChaCha, ne sont pas créés à partir de chiffres par bloc. Vous pouvez appeler ces derniers des chiffrements par flot primitifs. (Il n'existe pas vraiment de terme standardisé pour désigner ces chiffres par flot.)

Lorsque les gens parlent des avantages et des inconvénients des chiffrements par flot et des chiffrements par bloc, ils comparent généralement des chiffrements par flot primitifs à des schémas de chiffrement basés sur des chiffres par bloc.

Bien que vous puissiez toujours construire facilement un chiffre par flot à partir d'un chiffre par bloc, il est généralement très difficile de construire une sorte de structure avec un mode de chiffrement par bloc (comme avec le mode CBC) à partir d'un chiffre par flot primitif.

Grâce à cette discussion, vous devriez maintenant comprendre la Figure 8. Elle fournit un aperçu des schémas de chiffrement symétriques. Nous utilisons trois types de schémas de chiffrement : les chiffrements par flot primitifs, les chiffrements par flot basés sur des chiffres par bloc, et les chiffrements par bloc avec un mode de chiffrement par bloc (également appelés « chiffres par bloc » dans le diagramme).

Figure 8 : Aperçu des schémas de chiffrement symétriques

Figure 8 : Aperçu des schémas de chiffrement symétriques

Codes d’authentification de message (MAC)

Le chiffrement concerne la confidentialité. Mais la cryptographie traite également de thèmes plus larges, tels que l’intégrité des messages, l’authenticité et la non-répudiation. Les codes d’authentification de message (MAC) sont des schémas cryptographiques symétriques qui soutiennent l’authenticité et l’intégrité dans les communications.

Pourquoi serait-il nécessaire de garantir autre chose que la confidentialité dans une communication ? Supposons que Bob envoie un message à Alice en utilisant un chiffrement pratiquement incassable. Tout attaquant interceptant ce message ne pourra pas obtenir d’informations significatives sur son contenu. Cependant, l’attaquant dispose tout de même d’au moins deux autres vecteurs d’attaque possibles :

  1. Elle pourrait intercepter le texte chiffré, en modifier le contenu, puis transmettre le texte chiffré altéré à Alice.
  2. Elle pourrait bloquer entièrement le message de Bob et envoyer son propre texte chiffré créé de toutes pièces.

Dans ces deux cas, l’attaquant n’a peut-être aucune idée du contenu des textes chiffrés (1) et (2). Mais elle pourrait tout de même causer des dommages importants de cette manière. C’est là que les codes d’authentification de message (MAC) deviennent essentiels.

Les codes d’authentification de message (MAC) sont définis de manière approximative comme des schémas cryptographiques symétriques comprenant trois algorithmes : un algorithme de génération de clé, un algorithme de génération de tag, et un algorithme de vérification. Un MAC sécurisé garantit que les tags sont existentiellement infalsifiables pour tout attaquant — c’est-à-dire qu'il est impossible de créer un tag valide pour un message sans posséder la clé privée.

Bob et Alice peuvent contrer la manipulation d’un message particulier en utilisant un MAC. Supposons pour le moment qu’ils ne se préoccupent pas de la confidentialité. Ils veulent simplement s’assurer que le message reçu par Alice provient bien de Bob et n’a pas été modifié de quelque manière que ce soit.

Le processus est illustré dans la Figure 9. Pour utiliser un MAC (Code d’Authentification de Message), ils commencent par générer une clé privée K qui est partagée entre eux deux. Bob crée un tag T pour le message en utilisant la clé privée K. Il envoie ensuite le message ainsi que le tag du message à Alice. Elle peut alors vérifier que Bob a bien généré le tag en passant la clé privée, le message et le tag dans un algorithme de vérification.

Figure 9 : Vue d'ensemble des schémas de chiffrement symétrique

Figure 9 : Vue d'ensemble des schémas de chiffrement symétrique

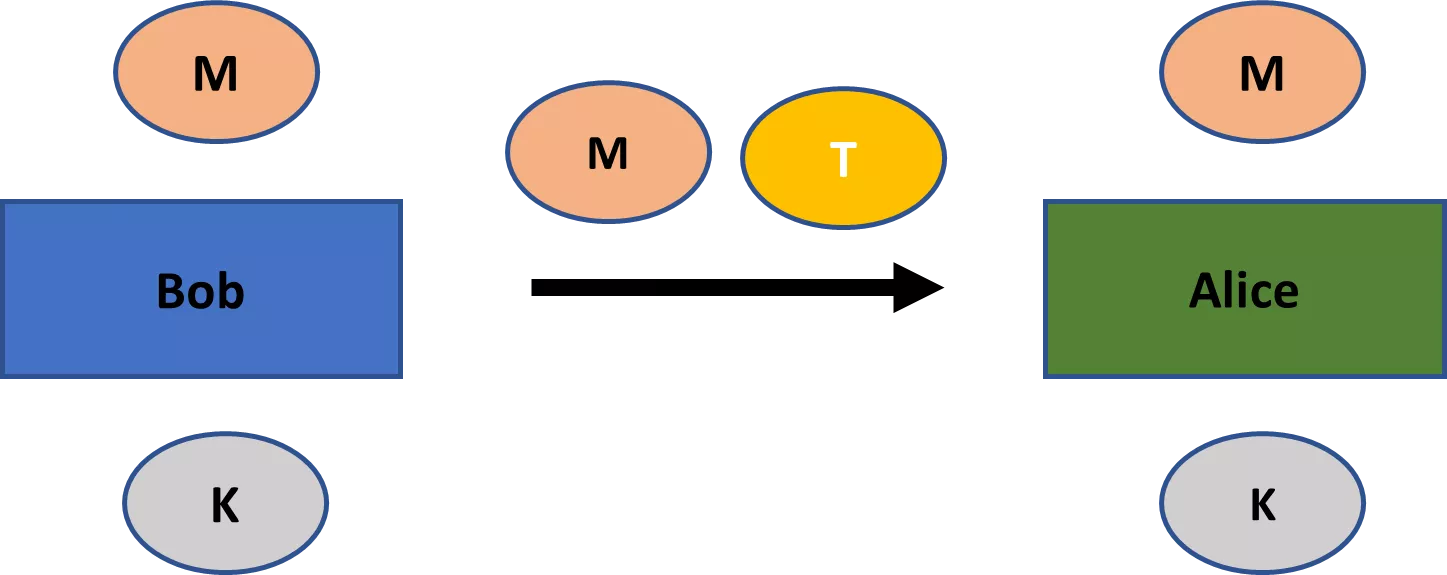
En raison de l’existentielle infalsifiabilité, un attaquant ne peut ni modifier le message M, ni créer son propre message avec un tag valide. Cela reste vrai même si l’attaquant observe les tags de nombreux messages échangés entre Bob et Alice utilisant la même clé privée. Au mieux, un attaquant pourrait bloquer Alice pour l’empêcher de recevoir le message M (un problème que la cryptographie ne peut pas résoudre).

Un MAC garantit qu’un message a bien été créé par Bob. Cette authenticité implique automatiquement l’intégrité du message — c’est-à-dire que si Bob a créé un message, alors, ipso facto, il n’a pas été altéré de quelque manière que ce soit par un attaquant. À partir de maintenant, toute préoccupation concernant l’authenticité doit être automatiquement comprise comme impliquant une préoccupation pour l’intégrité.

Bien que j’aie distingué l’authenticité des messages et l’intégrité dans ma discussion, il est également courant d’utiliser ces termes comme synonymes. Ils désignent alors l’idée que les messages ont été à la fois créés par un expéditeur particulier et qu’ils n’ont pas été modifiés de quelque manière que ce soit. Dans cet esprit, les codes d’authentification de message (MAC) sont fréquemment appelés aussi codes d’intégrité de message.

Chiffrement authentifié

En général, vous souhaitez garantir à la fois la confidentialité et l’authenticité dans une communication, c’est pourquoi les schémas de chiffrement et les schémas de MAC sont souvent utilisés ensemble.

Un schéma de chiffrement authentifié est un schéma qui combine le chiffrement avec un MAC de manière hautement sécurisée. Spécifiquement, il doit répondre aux normes d’existentielle infalsifiabilité ainsi qu’à une notion très stricte de confidentialité, à savoir une résistance aux attaques par texte chiffré choisi. [7]

Pour qu’un schéma de chiffrement résiste aux attaques par texte chiffré choisi, il doit répondre aux critères de non-malléabilité : c’est-à-dire que toute modification d’un texte chiffré par un attaquant doit soit produire un texte chiffré invalide, soit se déchiffrer en un texte clair qui n’a aucun rapport avec l’original. [8]

Comme un schéma de chiffrement authentifié garantit qu’un texte chiffré créé par un attaquant est toujours invalide (puisque le tag ne sera pas vérifié), il répond aux critères de résistance aux attaques par texte chiffré choisi. Il est intéressant de noter que l’on peut démontrer qu’un schéma de chiffrement authentifié peut toujours être créé en combinant un MAC existentiellement infalsifiable et un schéma de chiffrement répondant à une notion de sécurité moins stricte, appelée sécurité contre les attaques par texte clair choisi.

Nous n’entrerons pas dans tous les détails de la construction des schémas de chiffrement authentifié. Cependant, il est important de connaître deux points essentiels de leur construction.

Premièrement, un schéma de chiffrement authentifié procède d’abord au chiffrement, puis génère un tag de message sur le texte chiffré. Il s’avère que d’autres approches — telles que combiner le texte chiffré avec un tag basé sur le texte clair, ou créer d’abord un tag puis chiffrer à la fois le texte clair et le tag — sont peu sécurisées. De plus, chaque opération doit disposer de sa propre clé privée sélectionnée aléatoirement, sans quoi la sécurité est gravement compromise.

Ce principe s’applique de manière plus générale : vous devez toujours utiliser des clés distinctes lorsque vous combinez des schémas cryptographiques de base.

Un schéma de chiffrement authentifié est illustré dans la Figure 10. Bob crée d’abord un texte chiffré C à partir du message M en utilisant une clé aléatoire K_C. Il génère ensuite un tag de message T en passant le texte chiffré et une autre clé aléatoire K_T par l’algorithme de génération de tag. Bob envoie ensuite le texte chiffré et le tag de message à Alice.

Alice commence par vérifier si le tag est valide, en tenant compte du texte chiffré C et de la clé K_T. Si le tag est valide, elle peut ensuite déchiffrer le message en utilisant la clé K_C. Non seulement elle est assurée d’une confidentialité robuste dans leur communication, mais elle sait aussi que le message a bien été créé par Bob.

Figure 10 : Un schéma de chiffrement authentifié

Figure 10 : Un schéma de chiffrement authentifié

Comment sont créés les MAC ?

Bien que les MAC puissent être créés par plusieurs méthodes, une manière courante et efficace de les générer est via les fonctions de hachage cryptographiques.

Nous introduirons les fonctions de hachage cryptographiques de manière plus détaillée dans le Chapitre 6. Pour l’instant, sachez simplement qu’une fonction de hachage est une fonction calculable efficacement qui prend en entrée des données de taille arbitraire et produit une sortie de longueur fixe. Par exemple, la fonction de hachage populaire SHA-256 (Secure Hash Algorithm 256) génère toujours une sortie de 256 bits, quelle que soit la taille de l’entrée. Certaines fonctions de hachage, telles que SHA-256, ont des applications utiles en cryptographie.

Le type de tag le plus couramment produit par une fonction de hachage cryptographique est le code d’authentification de message basé sur un hachage (HMAC). Le processus est illustré dans la Figure 11. Une partie génère deux clés distinctes à partir d’une clé privée K, une clé interne K_1 et une clé externe K_2. Le texte clair M ou le texte chiffré C est ensuite haché avec la clé interne. Le résultat T’ est ensuite haché avec la clé externe pour produire le tag de message T.

Il existe un ensemble de fonctions de hachage qui peuvent être utilisées pour créer un HMAC. La fonction de hachage la plus couramment utilisée est SHA-256.

Figure 11 : HMAC

Figure 11 : HMAC

Notes :

[7] Les résultats spécifiques discutés dans cette section proviennent de Katz et Lindell, pp. 131–47.

[8] Techniquement, la définition des attaques par texte chiffré choisi est différente de celle de la notion de non-malléabilité. Cependant, il est possible de montrer que ces deux notions de sécurité sont équivalentes.

Sessions de communication sécurisées

Supposons que deux parties soient engagées dans une session de communication où elles échangent plusieurs messages successivement.

Un schéma de chiffrement authentifié permet au destinataire d'un message de vérifier qu'il a bien été créé par son partenaire au cours de la session de communication (à condition que la clé privée ne soit pas compromise). Cela fonctionne correctement pour un seul message. Toutefois, lorsque deux parties échangent plusieurs messages au sein d’une session de communication, un simple schéma de chiffrement authentifié tel que décrit dans la section précédente ne suffit pas à garantir une sécurité adéquate.

La principale raison est qu’un schéma de chiffrement authentifié ne garantit pas que le message a réellement été envoyé par l’agent qui l’a créé au sein de la session de communication. Considérons les trois vecteurs d’attaque suivants :

  1. Attaque par rejeu : Un attaquant renvoie un texte chiffré et un tag qu'il a interceptés entre deux parties à un moment antérieur.
  2. Attaque par réorganisation : Un attaquant intercepte deux messages à des moments différents et les transmet au destinataire dans un ordre inversé.
  3. Attaque par réflexion : Un attaquant observe un message envoyé de A vers B, puis envoie ce même message à A.

Même si l’attaquant n’a aucune connaissance du texte chiffré et ne peut pas générer de textes chiffrés falsifiés, ces attaques peuvent tout de même causer des dommages importants dans les communications.

Imaginons, par exemple, qu’un message spécifique entre les deux parties implique un transfert de fonds. Une attaque par rejeu pourrait entraîner un transfert supplémentaire des fonds. Un simple schéma de chiffrement authentifié ne fournit aucune défense contre de telles attaques.

Heureusement, ces types d’attaques peuvent être efficacement contrés dans une session de communication en utilisant des identifiants et des indicateurs de temps relatifs.

Les identifiants peuvent être ajoutés au message en clair avant son chiffrement. Cela permet d'empêcher les attaques par réflexion. Un indicateur de temps relatif peut, par exemple, être un numéro de séquence dans une session de communication particulière. Chaque partie ajoute un numéro de séquence à un message avant de le chiffrer, permettant au destinataire de connaître l'ordre d'envoi des messages. Cela élimine la possibilité d’attaques par réorganisation et d’attaques par rejeu. Tout message qu’un attaquant essaierait de transmettre plus tard aurait un ancien numéro de séquence, ce qui permettrait au destinataire de savoir qu’il ne doit pas traiter ce message à nouveau.

Pour illustrer comment fonctionnent les sessions de communication sécurisées, prenons à nouveau l’exemple d’Alice et Bob. Ils échangent au total quatre messages. Le schéma de chiffrement authentifié avec identifiants et numéros de séquence fonctionne comme décrit ci-dessous dans la Figure 12.

La session de communication commence par Bob qui envoie un texte chiffré C_{0,B} à Alice accompagné d’un tag de message T_{0,B}. Le texte chiffré contient le message, ainsi qu'un identifiant (BOB) et un numéro de séquence (0). Le tag T_{0,B} est calculé sur l'ensemble du texte chiffré. Lors de leurs communications suivantes, Alice et Bob suivent ce protocole en mettant à jour les champs nécessaires.

Figure 12 : Une session de communication sécurisée

Figure 12 : Une session de communication sécurisée

RC4 et AES

Le chiffrement par flot RC4

Dans ce chapitre, nous allons examiner en détail un schéma de chiffrement utilisant un chiffrement par flot primitif moderne, RC4 (ou "Rivest Cipher 4"), ainsi qu'un chiffrement par bloc moderne, AES. Bien que le chiffrement RC4 soit aujourd'hui considéré comme peu sûr pour le chiffrement, AES est la norme actuelle pour le chiffrement symétrique moderne. Ces deux exemples permettront de mieux comprendre le fonctionnement interne du chiffrement symétrique.

Pour comprendre comment fonctionnent les chiffrements par flot pseudorandomisés modernes, nous allons nous concentrer sur le chiffrement par flot RC4. C'est un chiffrement par flot pseudorandomisé qui a été utilisé dans les protocoles de sécurité pour les points d'accès sans fil WEP et WAP ainsi que dans TLS. Cependant, RC4 présente de nombreuses faiblesses avérées, ce qui a entraîné son abandon progressif. En effet, l’Internet Engineering Task Force interdit désormais l’utilisation de suites RC4 par les applications clientes et serveurs dans tous les cas de TLS. Néanmoins, RC4 reste un bon exemple pour illustrer le fonctionnement d’un chiffrement par flot primitif.

Pour commencer, nous allons chiffrer un message en clair en utilisant une version simplifiée du chiffrement RC4. Supposons que notre message en clair soit “SOUP”. Le chiffrement avec notre version simplifiée de RC4 se déroule en quatre étapes.

Étape 1

Tout d’abord, définissons un tableau S avec S[0] = 0 à S[7] = 7. Un tableau est simplement une collection modifiable de valeurs organisées par un index, également appelé une liste dans certains langages de programmation (comme Python). Dans ce cas, l’index va de 0 à 7, et les valeurs également de 0 à 7. Ainsi, S est le suivant :

Ces valeurs ne sont pas des nombres ASCII, mais des représentations décimales de chaînes d'un octet. Par exemple, la valeur 2 correspond à 0000 \ 0011. La longueur du tableau S est donc de 8 octets.

Étape 2

Deuxièmement, définissons un tableau de clé K de longueur 8 octets en choisissant une clé comprise entre 1 et 8 octets (aucune fraction d’octet n’est permise). Comme chaque octet représente 8 bits, vous pouvez sélectionner n'importe quel nombre compris entre 0 et 255 pour chaque octet de votre clé.

Supposons que nous choisissions notre clé k comme [14, 48, 9], ce qui correspond à une longueur de 3 octets. Chaque index de notre tableau de clé est ensuite défini en fonction de la valeur décimale de cet élément particulier de la clé, dans l'ordre. Si vous avez parcouru toute la clé, recommencez au début jusqu'à remplir les 8 emplacements du tableau de clé. Ainsi, notre tableau de clé est le suivant :

Étape 3

Troisièmement, nous allons transformer le tableau S en utilisant le tableau de clé K, dans un processus appelé ordonnancement de clé (key scheduling). Le processus se déroule comme suit en pseudocode :

La transformation du tableau S est capturée par le Tableau 1.

Au départ, vous pouvez voir l'état initial de S comme étant [0, 1, 2, 3, 4, 5, 6, 7] avec une valeur initiale de 0 pour j. Cela sera transformé en utilisant le tableau de clé [14, 48, 9, 14, 48, 9, 14, 48].

La boucle commence avec i = 0. Selon notre pseudocode ci-dessus, la nouvelle valeur de j devient 6 (j = (j + S[0] + K[0]) \mod 8 = (0 + 0 + 14) \mod 8 = 6 \mod 8). En échangeant S[0] et S[6], l’état de S après la première ronde devient [6, 1, 2, 3, 4, 5, 0, 7].

À la ligne suivante, i = 1. En poursuivant la boucle, j obtient une valeur de 7 (j = (j + S[1] + K[1]) \mod 8 = (6 + 1 + 48) \mod 8 = 55 \mod 8 = 7 \mod 8). En échangeant S[1] et S[7] à partir de l’état actuel de S, [6, 1, 2, 3, 4, 5, 0, 7], on obtient [6, 7, 2, 3, 4, 5, 0, 1] après la deuxième ronde.

Nous poursuivons ce processus jusqu'à obtenir l'état final du tableau S : [6, 4, 1, 0, 3, 7, 5, 2].

Tableau 1 : Tableau d'ordonnancement de clé

RondeijS[0]S[1]S[2]S[3]S[4]S[5]S[6]S[7]
Initial001234567
10661234507
21767234501
32267234501
43367234501
54367203541
65664203751
76164203752
87264103752

Étape 4

En quatrième étape, nous produisons le keystream (flux de clé). Il s'agit d'une chaîne pseudorandomisée de longueur égale au message que nous souhaitons envoyer. Cette chaîne sera utilisée pour chiffrer le message original “SOUP”. Puisque le keystream doit avoir la même longueur que le message, nous avons besoin ici de 4 octets.

Le keystream est produit par le pseudocode suivant :

Vous pouvez suivre les calculs dans le Tableau 2.

L'état initial de S est S = [6, 4, 1, 0, 3, 7, 5, 2]. En prenant i = 1, la valeur de j devient 4 (j = (j + S[i]) \mod 8 = (0 + 4) \mod 8 = 4). Nous échangeons ensuite S[1] et S[4], ce qui produit la transformation de S visible dans la deuxième ligne : [6, 3, 1, 0, 4, 7, 5, 2]. La valeur de t est ensuite 7 (t = (S[i] + S[j]) \mod 8 = (3 + 4) \mod 8 = 7). Enfin, l’octet du keystream est S[7], soit 2.

Nous continuons à produire les autres octets jusqu'à obtenir les quatre octets suivants : 2, 6, 3, et 7. Chacun de ces octets est ensuite utilisé pour chiffrer chaque lettre du message en clair, "SOUP".

Pour commencer, en utilisant une table ASCII, nous voyons que “SOUP” encodé par les valeurs décimales des chaînes d'octets sous-jacentes est “83 79 85 80”. La combinaison avec le keystream “2 6 3 7” donne “85 85 88 87”, ce qui reste identique après une opération modulo 256. En ASCII, le texte chiffré “85 85 88 87” correspond à “UUXW”.

Que se passe-t-il si le mot à chiffrer est plus long que le tableau S ? Dans ce cas, le tableau S continue de se transformer de cette manière pour chaque octet i du texte en clair, jusqu'à ce que nous ayons un nombre d'octets dans le keystream équivalent au nombre de lettres dans le texte en clair.

Tableau 2 : Génération du Keystream

ijtKeystreamS[0]S[1]S[2]S[3]S[4]S[5]S[6]S[7]
064103752
147263104752
250663704152
351363714052
417264713052

L’exemple que nous venons de décrire n’est qu’une version simplifiée du chiffrement par flot RC4. Le véritable chiffrement RC4 possède un tableau S d'une longueur de 256 octets, et non pas de 8 octets, ainsi qu'une clé qui peut être comprise entre 1 et 256 octets, au lieu d’être limitée entre 1 et 8 octets. Le tableau de clé et les keystreams sont ensuite tous produits en tenant compte de la longueur de 256 octets du tableau S. Les calculs deviennent beaucoup plus complexes, mais les principes restent les mêmes. En utilisant la même clé, [14,48,9], avec le chiffrement RC4 standard, le message en clair "SOUP" est chiffré sous la forme 67 02 ed df en format hexadécimal.

Un chiffrement par flot dont le keystream est mis à jour indépendamment du message en clair ou du texte chiffré est un chiffrement par flot synchrone. Le keystream ne dépend que de la clé. Il est évident que RC4 est un exemple de chiffrement par flot synchrone, puisque le keystream n’a aucun lien avec le message en clair ou le texte chiffré. Tous les chiffrements par flot primitifs mentionnés dans le chapitre précédent, y compris le chiffrement par décalage, le chiffre de Vigenère, et le masque jetable (one-time pad), sont également de type synchrone.

En revanche, un chiffrement par flot asynchrone génère un keystream qui dépend à la fois de la clé et d’éléments précédents du texte chiffré. Ce type de chiffrement est également appelé un chiffrement auto-synchronisé.

Il est important de noter que le keystream produit avec RC4 doit être traité comme un masque jetable, et il ne doit pas être produit de la même manière lors d’une prochaine utilisation. Plutôt que de changer de clé à chaque fois, la solution pratique consiste à combiner la clé avec un nonce pour produire le flux d’octets.

AES avec une clé de 128 bits

Comme mentionné dans le chapitre précédent, le National Institute of Standards and Technology (NIST) a organisé un concours entre 1997 et 2000 pour déterminer une nouvelle norme de chiffrement symétrique. Le chiffre de Rijndael s'est avéré être l'entrée gagnante. Son nom est un jeu de mots basé sur les noms de ses créateurs belges, Vincent Rijmen et Joan Daemen.

Le chiffre de Rijndael est un chiffrement par bloc, ce qui signifie qu'il s'agit d'un algorithme de base pouvant être utilisé avec différentes spécifications pour les tailles de clés et de blocs. Il peut ensuite être utilisé avec différents modes d’opération pour construire des schémas de chiffrement.

Le comité du concours du NIST a adopté une version restreinte du chiffre de Rijndael — spécifiquement celle qui nécessite des blocs de 128 bits et des clés de longueur de 128 bits, 192 bits ou 256 bits — dans le cadre de la norme de chiffrement avancée (AES). Cette version restreinte du chiffre de Rijndael peut également être utilisée avec plusieurs modes d’opération. La spécification pour la norme est ce que l’on appelle la norme de chiffrement avancée (AES).

Pour montrer comment fonctionne le chiffre de Rijndael, qui constitue le cœur de l'AES, j’illustrerai le processus de chiffrement avec une clé de 128 bits. La taille de la clé a un impact sur le nombre de tours effectués pour chaque bloc de chiffrement. Pour les clés de 128 bits, 10 tours sont nécessaires. Avec des clés de 192 bits et 256 bits, il aurait fallu respectivement 12 et 14 tours.

De plus, je suppose que l’AES est utilisé en mode ECB (Electronic Code Book). Cela simplifie légèrement l'explication et ne change rien au fonctionnement de l’algorithme de Rijndael. Il est important de noter que le mode ECB n'est pas sécurisé en pratique car il entraîne un chiffrement déterministe. Le mode sécurisé le plus couramment utilisé avec l’AES est le mode CBC (Cipher Block Chaining).

Appelons la clé K_0. La construction avec les paramètres ci-dessus ressemble alors à ce qui est montré dans la Figure 1, où M_i représente une partie du message en clair de 128 bits et C_i une partie du texte chiffré de 128 bits. Un remplissage (padding) est ajouté au texte en clair pour le dernier bloc si celui-ci ne peut pas être divisé de manière égale par la taille de bloc.

Figure 1 : AES-ECB avec une clé de 128 bits

Figure 1 : AES-ECB avec une clé de 128 bits

Chaque bloc de texte de 128 bits passe par dix tours dans le schéma de chiffrement de Rijndael. Cela nécessite une clé de tour distincte pour chaque tour (K_1 à K_{10}). Ces clés sont produites pour chaque tour à partir de la clé originale de 128 bits K_0 en utilisant un algorithme d'expansion de clé. Ainsi, pour chaque bloc de texte à chiffrer, nous utiliserons la clé originale K_0 ainsi que dix clés de tour distinctes. Notez que ces 11 clés sont utilisées pour chaque bloc de texte en clair de 128 bits nécessitant un chiffrement.

L’algorithme d'expansion de clé est long et complexe. Le parcourir en détail présente peu d'intérêt didactique. Vous pouvez examiner l’algorithme d'expansion de clé par vous-même si vous le souhaitez. Une fois les clés de tour produites, le chiffre de Rijndael va manipuler le premier bloc de texte en clair de 128 bits, M_1, comme illustré dans la Figure 2. Nous allons maintenant détailler ces étapes.

Figure 2 : La manipulation de M_1 avec le chiffre de Rijndael :

Tour 0 :

Tour n pour n = {1,...,9} :

Tour 10 :

Tour 0

Le tour 0 du chiffre de Rijndael est simple. Un tableau S_0 est produit par une opération XOR entre le texte en clair de 128 bits et la clé privée. C'est-à-dire,

Tour 1

Lors du tour 1, le tableau S_0 est d'abord combiné avec la clé de tour K_1 à l'aide d'une opération XOR. Cela produit un nouvel état de S.

Ensuite, l’opération de substitution d’octets est effectuée sur l’état actuel de S. Elle consiste à prendre chaque octet des 16 octets du tableau S et à le substituer par un octet issu d’un tableau appelé S-box de Rijndael. Chaque octet subit une transformation unique, ce qui produit un nouvel état de S. La S-box de Rijndael est présentée dans la Figure 3.

Figure 3 : S-Box de Rijndael

000102030405060708090A0B0C0D0E0F
00637C777BF26B6FC53001672BFED7AB76
10CA82C97DFA5947F0ADD4A2AF9CA472C0
20B7FD9326363FF7CC34A5E5F171D83115
3004C723C31896059A071280E2EB27B275
4009832C1A1B6E5AA0523BD6B329E32F84
5053D100ED20FCB15B6ACBBE394A4C58CF
60D0EFAAFB434D338545F9027F503C9FA8
7051A3408F929D38F5BCB6DA2110FFF3D2
80CD0C13EC5F974417C4A77E3D645D1973
9060814FDC222A908846EEB814DE5E0BDB
A0E0323A0A4906245CC2D3AC629195E479
B0E7C8376D8DD54EA96C56F4EA657AAE08
C0BA78252E1CA6B4C6E8DD741F4BBD8B8A
D0703EB5664803F60E613557B986C11D9E
E0E1F8981169D98E949B1E87E9CE5528DF
F08CA1890DBFE6426841992D0FB054BB16

Cette S-box est l’un des endroits où l’algèbre abstraite entre en jeu dans le chiffre de Rijndael, en particulier les corps de Galois.

Pour commencer, chaque élément d'octet possible allant de 00 à FF est défini comme un vecteur de 8 bits. Chacun de ces vecteurs est un élément du corps de Galois GF(2^8) où le polynôme irréductible pour l'opération modulo est x^8 + x^4 + x^3 + x + 1. Le corps de Galois avec ces spécifications est également appelé corps fini de Rijndael.

Ensuite, pour chaque élément possible du corps, nous créons ce que l'on appelle la S-box de Nyberg. Dans cette boîte, chaque octet est mappé sur son inverse multiplicatif (c’est-à-dire que leur produit est égal à 1). Nous mappons ensuite ces valeurs depuis la S-box de Nyberg vers la S-box de Rijndael à l'aide de la transformation affine.

La troisième opération sur le tableau S est l'opération de décalage des lignes (Shift Rows). Cette étape consiste à prendre l'état de S et à disposer les seize octets dans une matrice. Le remplissage de la matrice commence en haut à gauche et progresse en allant de haut en bas, puis, chaque fois qu'une colonne est remplie, il passe à la colonne suivante, en remontant en haut.

Une fois que la matrice de S est construite, les quatre lignes sont décalées de la manière suivante :

Un exemple du processus est présenté dans la Figure 4. L'état initial de S est montré en haut, et l'état résultant après l'opération de décalage des lignes est affiché ci-dessous.

Figure 4 : Opération de décalage des lignes (Shift Rows)

F1A0B123
59EF0982
9701B0CC
D4720421
F1A0B123
EF098259
B0CC9701
21D47204

Dans la quatrième étape, les champs de Galois apparaissent de nouveau. Chaque colonne de la matrice S est multipliée par la colonne de la matrice 4 x 4 présentée dans la Figure 5. Cependant, il ne s'agit pas d'une multiplication matricielle classique, mais d'une multiplication vectorielle modulo un polynôme irréductible, x^8 + x^4 + x^3 + x + 1. Les coefficients des vecteurs résultants représentent les bits individuels d’un octet.

Figure 5 : Matrice de mélange des colonnes (Mix Columns)

02030101
01020301
01010203
03010102

La multiplication de la première colonne de la matrice S par la matrice 4 x 4 ci-dessus produit le résultat montré dans la Figure 6.

Figure 6 : Multiplication de la première colonne :

\begin{matrix}
02 \cdot F1 + 03 \cdot EF + 01 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 02 \cdot EF + 03 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 01 \cdot EF + 02 \cdot B0 + 03 \cdot 21 \\
03 \cdot F1 + 01 \cdot EF + 01 \cdot B0 + 02 \cdot 21
\end{matrix}

L'étape suivante consiste à convertir tous les termes de la matrice en polynômes. Par exemple, F1 représente un octet qui devient x^7 + x^6 + x^5 + x^4 + 1, et 03 représente un octet qui devient x + 1.

Toutes les multiplications sont alors effectuées modulo x^8 + x^4 + x^3 + x + 1. Cela aboutit à l'addition de quatre polynômes dans chacune des quatre cellules de la colonne. Après avoir effectué ces additions modulo 2, on obtient quatre polynômes. Chacun de ces polynômes représente une chaîne de 8 bits, soit un octet de S. Nous n'effectuerons pas ici tous ces calculs sur la matrice de la Figure 6, car ils sont trop longs.

Une fois la première colonne traitée, les trois autres colonnes de la matrice S sont traitées de la même manière. Cela produit finalement une matrice contenant seize octets qui peuvent être transformés en un tableau.

En guise d'étape finale, le tableau S est combiné à nouveau avec la clé de tour dans une opération d’XOR. Cela produit l'état S_1. C'est-à-dire,

Tours 2 à 10

Les tours 2 à 9 sont simplement une répétition du tour 1, mutatis mutandis. Le dernier tour diffère légèrement des précédents, car l'étape de mixage des colonnes (Mix Columns) est supprimée. Ainsi, le tour 10 est exécuté comme suit :

L'état S_{10} est maintenant défini comme C_1, les premiers 128 bits du texte chiffré. La progression à travers les blocs restants de 128 bits du texte en clair produit le texte chiffré complet C.

Les opérations du chiffrement Rijndael

Quelle est la logique derrière les différentes opérations présentes dans le chiffrement Rijndael ?

Sans entrer dans les détails, les schémas de chiffrement sont évalués en fonction de leur capacité à créer de la confusion et de la diffusion. Si le chiffrement présente un haut degré de confusion, cela signifie que le texte chiffré semble radicalement différent du texte en clair. Si le chiffrement présente un haut degré de diffusion, cela signifie que toute petite modification apportée au texte en clair produit un texte chiffré complètement différent.

La logique des opérations derrière le chiffrement Rijndael est qu'elles produisent à la fois un haut degré de confusion et de diffusion. La confusion est générée par l’opération de substitution d’octets (Byte Substitution), tandis que la diffusion est produite par les opérations de décalage des lignes (Shift Rows) et de mélange des colonnes (Mix Columns).

Cryptographie asymétrique

Le problème de la distribution et de la gestion des clés

Comme pour la cryptographie symétrique, les schémas asymétriques peuvent être utilisés pour garantir à la fois la confidentialité et l’authentification. Cependant, contrairement aux schémas symétriques, ceux-ci utilisent deux clés au lieu d’une : une clé privée et une clé publique.

Nous commençons notre exploration par la découverte de la cryptographie asymétrique, en particulier les problèmes qui ont motivé son développement. Ensuite, nous expliquons comment les schémas asymétriques de chiffrement et d’authentification fonctionnent de manière générale. Puis, nous introduisons les fonctions de hachage, qui sont essentielles pour comprendre les schémas d’authentification asymétrique, et qui ont également leur importance dans d'autres contextes cryptographiques, comme les codes d’authentification de messages basés sur des hachages dont nous avons parlé au chapitre 4.

Imaginons que Bob souhaite acheter un nouvel imperméable chez Jim’s Sporting Goods, un détaillant en ligne d’articles de sport qui compte des millions de clients en Amérique du Nord. Ce sera son premier achat chez eux, et il souhaite utiliser sa carte de crédit. Bob doit donc commencer par créer un compte chez Jim’s Sporting Goods, ce qui nécessite l’envoi d’informations personnelles telles que son adresse et les détails de sa carte de crédit. Il pourra alors procéder aux étapes nécessaires pour acheter l’imperméable.

Bob et Jim’s Sporting Goods souhaitent que leurs communications soient sécurisées tout au long de ce processus, étant donné qu’Internet est un système de communication ouvert. Ils veulent notamment s’assurer qu’aucun attaquant potentiel ne puisse obtenir les informations relatives à la carte de crédit et à l’adresse de Bob, ni qu’il puisse répéter ses achats ou en créer de faux en son nom.

Un schéma avancé de chiffrement authentifié, comme celui décrit dans le chapitre précédent, pourrait certainement rendre les communications entre Bob et Jim’s Sporting Goods sécurisées. Cependant, il existe des obstacles pratiques évidents à la mise en œuvre d’un tel schéma.

Pour illustrer ces obstacles pratiques, imaginons que nous vivions dans un monde où seuls les outils de cryptographie symétrique existent. Que pourraient alors faire Jim’s Sporting Goods et Bob pour garantir une communication sécurisée ?

Dans de telles circonstances, ils seraient confrontés à des coûts considérables pour communiquer de manière sécurisée. Étant donné qu’Internet est un système de communication ouvert, ils ne peuvent pas simplement échanger une série de clés via celui-ci. Par conséquent, Bob et un représentant de Jim’s Sporting Goods devraient procéder à un échange de clés en personne.

Une possibilité serait que Jim’s Sporting Goods établisse des points d’échange de clés spéciaux, où Bob et d’autres nouveaux clients pourraient récupérer une série de clés pour une communication sécurisée. Cela entraînerait évidemment des coûts organisationnels considérables et réduirait considérablement l'efficacité avec laquelle de nouveaux clients peuvent effectuer des achats.

Alternativement, Jim’s Sporting Goods pourrait envoyer à Bob une paire de clés par l’intermédiaire d’un coursier hautement fiable. Cela serait probablement plus efficace que d’organiser des lieux spécifiques d’échange de clés. Cependant, cela entraînerait toujours des coûts considérables, en particulier si de nombreux clients n’effectuent qu’un ou quelques achats seulement.

Ensuite, un schéma symétrique de chiffrement authentifié obligerait également Jim’s Sporting Goods à stocker des ensembles de clés distincts pour chacun de ses clients. Cela représenterait un défi pratique important pour des milliers de clients, et encore plus pour des millions.

Pour comprendre ce dernier point, supposons que Jim’s Sporting Goods fournisse à chaque client la même paire de clés. Cela permettrait à chaque client — ou à toute personne capable d’obtenir cette paire de clés — de lire et même de manipuler toutes les communications entre Jim’s Sporting Goods et ses clients. Autant dire qu’il serait alors inutile d’utiliser la cryptographie dans vos communications.

Répéter un ensemble de clés pour seulement certains clients est également une pratique de sécurité désastreuse. Tout attaquant potentiel pourrait tenter d’exploiter cette faiblesse du schéma (rappelez-vous que les attaquants sont supposés connaître tous les détails d’un schéma sauf les clés, conformément au principe de Kerckhoffs).

Par conséquent, Jim’s Sporting Goods devrait stocker une paire de clés pour chaque client, indépendamment de la manière dont ces paires de clés sont distribuées. Cela pose clairement plusieurs problèmes pratiques :

Ces deux défis majeurs décrits ci-dessus étaient des préoccupations fondamentales jusqu’à la fin des années 1970. Ils étaient connus sous le nom de problème de distribution des clés et de problème de gestion des clés, respectivement.

Ces problèmes avaient toujours existé, bien sûr, et avaient souvent provoqué de sérieux désagréments dans le passé. Par exemple, les forces militaires devaient constamment distribuer des livres contenant des clés pour des communications sécurisées au personnel sur le terrain, ce qui impliquait des coûts et des risques importants. Mais ces problèmes prenaient une ampleur croissante à mesure que le monde se dirigeait vers un modèle de communication numérique à longue distance, en particulier pour des entités non gouvernementales.

Si ces problèmes n’avaient pas été résolus dans les années 1970, les achats en ligne efficaces et sécurisés chez Jim’s Sporting Goods n’auraient probablement jamais vu le jour. En fait, la majorité de notre monde moderne avec des e-mails sécurisés, des opérations bancaires en ligne et des achats sur Internet ne serait probablement qu’une utopie lointaine. Et quelque chose même approchant de près ou de loin à Bitcoin n’aurait jamais pu exister.

Alors, que s’est-il passé dans les années 1970 ? Comment est-il possible que nous puissions effectuer des achats en ligne instantanément et naviguer en toute sécurité sur le World Wide Web ? Comment est-il possible que nous puissions envoyer instantanément des bitcoins à travers le monde depuis nos smartphones ?

Nouvelles directions en cryptographie

Dans les années 1970, les problèmes de distribution et de gestion des clés ont attiré l'attention d'un groupe de cryptographes académiques américains : Whitfield Diffie, Martin Hellman et Ralph Merkle. Malgré un scepticisme sévère de la part de la majorité de leurs pairs, ils ont entrepris de trouver une solution à ces problèmes.

Au moins une des principales motivations de leur recherche était la prévoyance selon laquelle les communications informatiques ouvertes allaient profondément transformer notre monde. Comme le notaient Diffie et Hellman en 1976 :

Le développement de réseaux de communication contrôlés par ordinateur promet un contact sans effort et peu coûteux entre des personnes ou des ordinateurs situés à l'autre bout du monde, remplaçant la plupart des courriers et de nombreux déplacements par des télécommunications. Pour de nombreuses applications, ces contacts doivent être protégés contre l'écoute clandestine et l'injection de messages illégitimes. Actuellement, cependant, la résolution des problèmes de sécurité accuse un retard considérable par rapport aux autres domaines de la technologie des communications. La cryptographie contemporaine est incapable de répondre aux exigences, car son utilisation imposerait des inconvénients si sévères aux utilisateurs du système qu'elle éliminerait une grande partie des avantages de la télécommunication. [1]

La persévérance de Diffie, Hellman et Merkle a fini par porter ses fruits. Leurs premiers résultats ont été publiés dans un article de Diffie et Hellman en 1976 intitulé “New Directions in Cryptography.” Ils y présentaient deux manières originales d’aborder les problèmes de distribution et de gestion des clés.

La première solution qu'ils ont proposée était un protocole d'échange de clés à distance, c'est-à-dire un ensemble de règles permettant l'échange d'une ou plusieurs clés symétriques via un canal de communication non sécurisé. Ce protocole est désormais connu sous le nom d’échange de clés de Diffie-Hellman ou échange de clés de Diffie-Hellman-Merkle. [2]

Avec l'échange de clés de Diffie-Hellman, deux parties échangent d'abord des informations publiquement sur un canal non sécurisé comme Internet. Sur la base de ces informations, elles créent ensuite indépendamment une clé symétrique (ou une paire de clés symétriques) pour une communication sécurisée. Bien que les deux parties créent leurs clés de manière indépendante, les informations qu'elles ont partagées publiquement garantissent que ce processus de création de clés produit le même résultat pour les deux.

De manière importante, bien que tout le monde puisse observer les informations échangées publiquement par les parties sur le canal non sécurisé, seules les deux parties impliquées dans l'échange peuvent créer des clés symétriques à partir de ces informations.

Cela semble évidemment complètement contre-intuitif. Comment deux parties peuvent-elles échanger des informations publiquement, permettant ainsi uniquement à elles deux de créer des clés symétriques à partir de celles-ci ? Pourquoi toute personne observant l'échange d'informations ne pourrait-elle pas créer les mêmes clés ?

Cela repose évidemment sur des mathématiques élégantes. L'échange de clés de Diffie-Hellman repose sur une fonction à sens unique avec une porte dérobée (ou trapdoor). Expliquons ce que signifient ces deux termes.

Supposons que l'on dispose d'une fonction f(x) et du résultat f(a) = y, où a est une valeur particulière de x. On dit que f(x) est une fonction à sens unique si le calcul de la valeur y à partir de a et de f(x) est facile, mais si le calcul de la valeur a à partir de y et de f(x) est pratiquement impossible. Le nom de fonction à sens unique vient bien sûr du fait qu'une telle fonction n'est pratiquement calculable que dans un seul sens.

Certaines fonctions à sens unique possèdent ce que l’on appelle une porte dérobée (trapdoor). Bien qu’il soit pratiquement impossible de calculer a en connaissant seulement y et f(x), il existe une certaine information Z qui rend le calcul de a à partir de y réalisable. Cette information Z est appelée la porte dérobée. Les fonctions à sens unique qui possèdent une porte dérobée sont appelées fonctions à porte dérobée (trapdoor functions).

Nous n’allons pas entrer dans les détails de l’échange de clés de Diffie-Hellman ici. Mais essentiellement, chaque participant crée une certaine information, dont une partie est partagée publiquement et dont une autre partie reste secrète. Chaque partie utilise ensuite son information secrète ainsi que l’information publique partagée par l’autre partie pour créer une clé privée. Et de manière assez étonnante, les deux parties obtiendront exactement la même clé privée.

Toute partie observant uniquement les informations échangées publiquement entre les deux participants lors d’un échange de clés Diffie-Hellman est incapable de reproduire ces calculs. Elle aurait besoin des informations privées d’une des deux parties pour y parvenir.

Bien que la version de base de l'échange de clés Diffie-Hellman présentée dans l'article de 1976 ne soit pas très sécurisée, des versions sophistiquées de ce protocole de base sont encore largement utilisées aujourd'hui. Plus important encore, tous les protocoles d'échange de clés dans la dernière version du protocole de sécurité de la couche de transport (Transport Layer Security ou TLS, version 1.3) sont essentiellement des versions enrichies du protocole présenté par Diffie et Hellman en 1976. Le protocole TLS est le principal protocole utilisé pour échanger de manière sécurisée des informations formatées selon le protocole de transfert hypertexte (HTTP), la norme pour l'échange de contenu Web.

Il est important de noter que l'échange de clés Diffie-Hellman n'est pas un schéma asymétrique. En toute rigueur, il appartient plutôt au domaine de la cryptographie à clé symétrique. Cependant, comme l'échange de clés Diffie-Hellman et la cryptographie asymétrique reposent sur des fonctions mathématiques à sens unique avec portes dérobées (trapdoors), ils sont généralement abordés ensemble.

La deuxième méthode proposée par Diffie et Hellman dans leur article de 1976 pour résoudre les problèmes de distribution et de gestion des clés reposait bien entendu sur la cryptographie asymétrique.

Contrairement à leur présentation de l'échange de clés Diffie-Hellman, ils n'ont fourni que les grandes lignes de la manière dont des schémas cryptographiques asymétriques pouvaient être plausiblement construits. Ils n'ont pas proposé de fonction à sens unique pouvant concrètement remplir les conditions nécessaires pour assurer une sécurité raisonnable dans de tels schémas.

Une implémentation pratique d'un schéma asymétrique a toutefois été découverte un an plus tard par trois cryptographes et mathématiciens académiques différents : Ronald Rivest, Adi Shamir et Leonard Adleman. [3] Le système cryptographique qu'ils ont introduit est devenu connu sous le nom de système RSA (d'après les initiales de leurs noms).

Les fonctions à porte dérobée utilisées en cryptographie asymétrique (ainsi que dans l'échange de clés Diffie-Hellman) sont toutes liées à deux principaux problèmes calculatoires complexes : la factorisation des entiers et le calcul des logarithmes discrets.

La factorisation des entiers consiste, comme son nom l'indique, à décomposer un nombre entier en ses facteurs premiers. Le problème RSA est de loin l'exemple le plus connu d'un système cryptographique reposant sur la difficulté de la factorisation des entiers.

Le problème du logarithme discret est un problème qui survient dans les groupes cycliques. Étant donné un générateur d'un groupe cyclique particulier, il s'agit de calculer l'exposant unique nécessaire pour produire un autre élément du groupe à partir du générateur.

Les schémas basés sur les logarithmes discrets reposent sur deux principaux types de groupes cycliques : les groupes multiplicatifs d'entiers et les groupes constitués des points sur des courbes elliptiques. L'échange de clés Diffie-Hellman original, tel que présenté dans New Directions in Cryptography, fonctionne avec un groupe cyclique multiplicatif d'entiers. L'algorithme de signature numérique de Bitcoin et le schéma de signature Schnorr introduit récemment (2021) reposent tous deux sur le problème du logarithme discret pour un groupe cyclique particulier défini sur une courbe elliptique.

Ensuite, nous allons examiner une vue d'ensemble des mécanismes de confidentialité et d'authentification dans le contexte asymétrique. Cependant, avant cela, nous devons faire une brève note historique.

Il semble maintenant plausible qu'un groupe de cryptographes et de mathématiciens britanniques travaillant pour le Government Communications Headquarters (GCHQ) ait découvert indépendamment les concepts mentionnés ci-dessus quelques années auparavant. Ce groupe comprenait James Ellis, Clifford Cocks et Malcolm Williamson.

Selon leurs propres témoignages et celui du GCHQ, c'est James Ellis qui aurait d'abord conçu le concept de cryptographie à clé publique en 1969. Clifford Cocks aurait ensuite découvert le système cryptographique RSA en 1973, et Malcolm Williamson le concept de l'échange de clés Diffie-Hellman en 1974. [4] Leurs découvertes auraient cependant été gardées secrètes jusqu'en 1997, en raison de la nature confidentielle du travail effectué au GCHQ.

Notes :

[1] Whitfield Diffie et Martin Hellman, « New directions in cryptography », IEEE Transactions on Information Theory IT-22 (1976), pp. 644–654, p. 644.

[2] Ralph Merkle évoque également un protocole d'échange de clés dans « Secure communications over insecure channels », Communications of the Association for Computing Machinery, 21 (1978), 294–99. Bien que Merkle ait soumis cet article avant celui de Diffie et Hellman, il a été publié plus tard. La solution proposée par Merkle n'est pas exponentiellement sécurisée, contrairement à celle de Diffie-Hellman.

[3] Ron Rivest, Adi Shamir et Leonard Adleman, « A method for obtaining digital signatures and public-key cryptosystems », Communications of the Association for Computing Machinery, 21 (1978), pp. 120–26.

[4] Un bon historique de ces découvertes est fourni par Simon Singh, The Code Book, Fourth Estate (Londres, 1999), Chapitre 6.

Chiffrement et authentification asymétriques

Un aperçu de la cryptographie asymétrique avec l'aide de Bob et Alice est présenté dans Figure 1.

Alice commence par créer une paire de clés, composée d'une clé publique (K_P) et d'une clé privée (K_S), où le “P” dans K_P signifie “publique” et le “S” dans K_S signifie “secrète”. Elle distribue ensuite librement cette clé publique à d'autres utilisateurs. Nous reviendrons plus tard sur les détails de ce processus de distribution. Pour l'instant, supposons que quiconque, y compris Bob, peut obtenir en toute sécurité la clé publique K_P d'Alice.

À un moment ultérieur, Bob souhaite écrire un message M à Alice. Comme il contient des informations sensibles, il veut que le contenu reste secret pour tout le monde sauf Alice. Ainsi, Bob commence par chiffrer son message M en utilisant K_P. Il envoie ensuite le ciphertext résultant C à Alice, qui déchiffre C avec K_S pour retrouver le message original M.

Figure 1 : Cryptographie asymétrique

Figure 1 : Cryptographie asymétrique

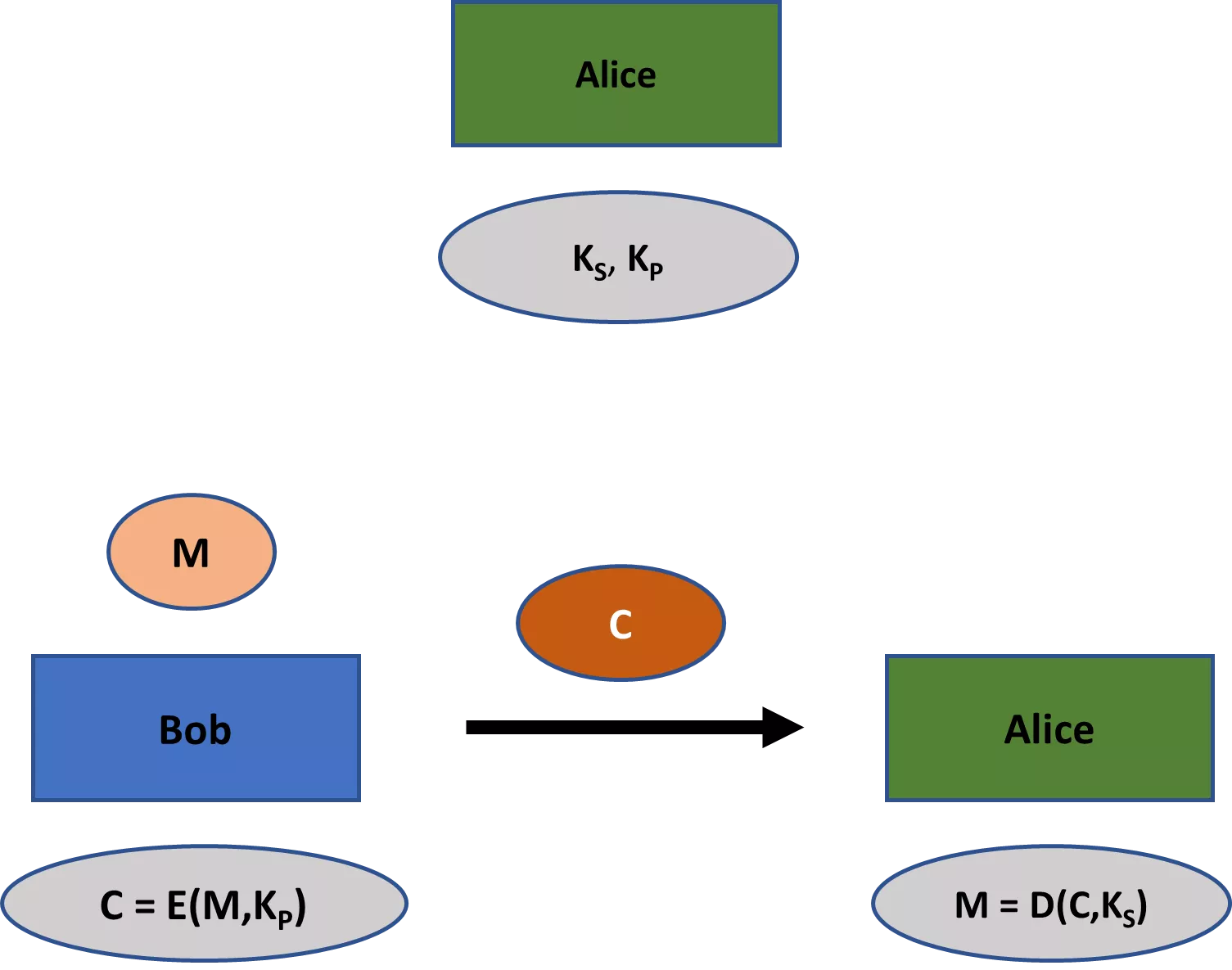
Tout adversaire qui écoute la communication entre Bob et Alice peut observer C. Il connaît également K_P et l'algorithme de chiffrement E(\cdot). Cependant, cette information ne permet pas à l'attaquant de déchiffrer C de manière faisable. Le déchiffrement nécessite spécifiquement K_S, que l'attaquant ne possède pas.

Les schémas de chiffrement symétrique doivent généralement être sécurisés contre un attaquant qui peut valablement chiffrer des messages en clair (c'est ce que l'on appelle la sécurité contre les attaques par texte chiffré choisi). Toutefois, ces schémas ne sont pas conçus avec l'objectif explicite de permettre à un attaquant ou à quiconque de créer de tels textes chiffrés valides.

Cela contraste fortement avec un schéma de chiffrement asymétrique, dont l'objectif est justement de permettre à n'importe qui, y compris les attaquants, de produire des textes chiffrés valides. Les schémas de chiffrement asymétrique peuvent donc être qualifiés de chiffrements à accès multiple.

Pour mieux comprendre ce qui se passe, imaginons qu'au lieu d'envoyer un message par voie électronique, Bob souhaite envoyer une lettre physique en toute confidentialité. Une façon d'assurer la confidentialité serait qu'Alice envoie un cadenas sécurisé à Bob, mais qu'elle garde la clé qui permet de l'ouvrir. Après avoir écrit sa lettre, Bob pourrait la placer dans une boîte et la fermer avec le cadenas d'Alice. Il pourrait ensuite envoyer la boîte verrouillée avec le message à Alice, qui possède la clé pour l'ouvrir.

Alors que Bob est capable de verrouiller le cadenas, ni lui ni aucune autre personne qui intercepte la boîte ne peuvent déverrouiller le cadenas si celui-ci est effectivement sécurisé. Seule Alice peut le déverrouiller et lire le contenu de la lettre de Bob parce qu'elle possède la clé.

Un schéma de chiffrement asymétrique est, en termes simples, une version numérique de ce processus. Le cadenas est analogue à la clé publique et la clé du cadenas est analogue à la clé privée. Cependant, comme le cadenas est numérique, il est beaucoup plus facile et moins coûteux pour Alice de le distribuer à quiconque souhaite lui envoyer des messages secrets.

Pour l'authentification dans le cadre asymétrique, nous utilisons des signatures numériques. Celles-ci remplissent donc la même fonction que les codes d'authentification de message (MAC) dans le cadre symétrique. Un aperçu des signatures numériques est présenté dans Figure 2.

Bob commence par créer une paire de clés, composée de la clé publique (K_P) et de la clé privée (K_S), puis distribue sa clé publique. Lorsqu'il souhaite envoyer un message authentifié à Alice, il prend d'abord son message M et sa clé privée pour créer une signature numérique D. Bob envoie ensuite son message à Alice accompagné de la signature numérique.

Alice insère le message, la clé publique et la signature numérique dans un algorithme de vérification. Cet algorithme produit soit vrai pour une signature valide, soit faux pour une signature invalide.

Une signature numérique est, comme son nom l'indique clairement, l'équivalent numérique d'une signature manuscrite sur des lettres, des contrats, etc. En fait, une signature numérique est généralement beaucoup plus sécurisée. Avec un certain effort, il est possible de falsifier une signature manuscrite ; un processus facilité par le fait que les signatures manuscrites ne sont souvent pas rigoureusement vérifiées. Cependant, une signature numérique sécurisée est, tout comme un code d'authentification de message sécurisé, existentiellement infalsifiable : c'est-à-dire qu'avec un schéma de signature numérique sécurisé, personne ne peut créer de manière faisable une signature pour un message qui passe la procédure de vérification, à moins de posséder la clé privée.

Figure 2 : Authentification asymétrique

Figure 2 : Authentification asymétrique

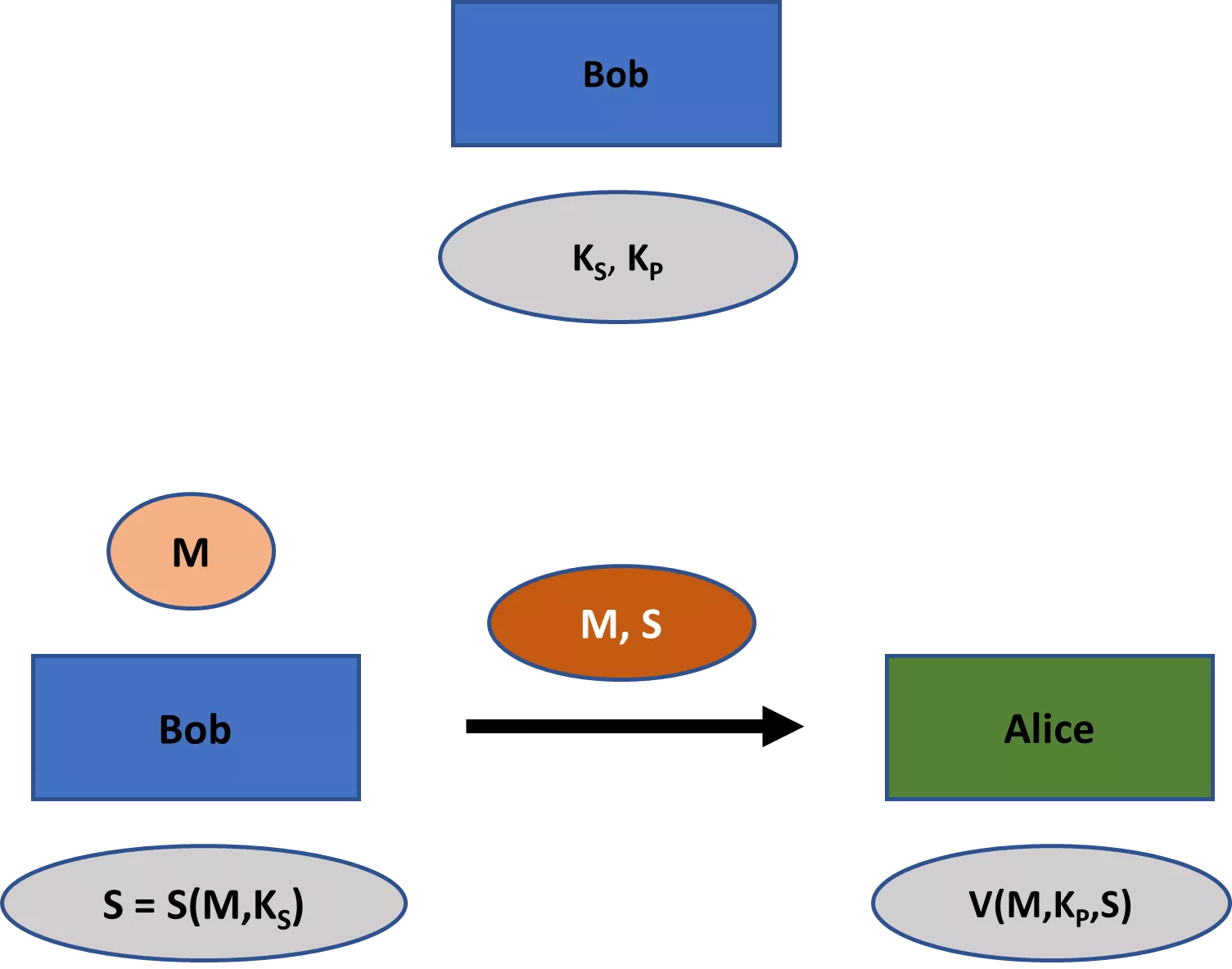
Comme pour le chiffrement asymétrique, nous voyons un contraste intéressant entre les signatures numériques et les codes d'authentification de message. Pour ces derniers, l'algorithme de vérification ne peut être utilisé que par l'une des parties participant à la communication sécurisée, car il nécessite une clé privée. Dans le cadre asymétrique, cependant, n'importe qui peut vérifier une signature numérique S réalisée par Bob.

Tout cela fait des signatures numériques un outil extrêmement puissant. Elles constituent, par exemple, la base de la création de signatures sur des contrats pouvant être vérifiées à des fins légales. Si Bob avait apposé une signature sur un contrat dans l'exemple précédent, Alice pourrait montrer le message M, le contrat et la signature S à un tribunal. Le tribunal pourrait alors vérifier la signature en utilisant la clé publique de Bob. [5]

Un autre exemple est l'utilisation des signatures numériques pour la distribution sécurisée de logiciels et de mises à jour logicielles. Ce type de vérification publique ne pourrait jamais être réalisé en utilisant uniquement des codes d'authentification de message.

Enfin, considérons un exemple pertinent pour Bitcoin. L'une des idées fausses les plus courantes à propos de Bitcoin, en particulier dans les médias, est que les transactions sont chiffrées : elles ne le sont pas. Au lieu de cela, les transactions Bitcoin utilisent des signatures numériques pour garantir leur sécurité.

Les bitcoins existent sous forme de lots appelés sorties de transaction non dépensées (ou UTXO, pour Unspent Transaction Outputs). Supposons que vous receviez trois paiements sur une adresse Bitcoin particulière de 2 bitcoins chacun. Techniquement, vous n'avez pas 6 bitcoins sur cette adresse. Au lieu de cela, vous avez trois lots de 2 bitcoins qui sont verrouillés par un problème cryptographique associé à cette adresse. Pour tout paiement que vous effectuez, vous pouvez utiliser un, deux ou les trois lots, selon le montant dont vous avez besoin pour la transaction.

La preuve de possession des sorties de transaction non dépensées est généralement fournie par une ou plusieurs signatures numériques. Bitcoin fonctionne précisément parce que produire des signatures numériques valides sur des sorties de transaction non dépensées est pratiquement impossible, sauf si vous possédez l'information secrète nécessaire pour les générer.

Actuellement, les transactions Bitcoin incluent de manière transparente toutes les informations qui doivent être vérifiées par les participants du réseau, telles que l'origine des sorties de transaction non dépensées utilisées dans la transaction. Bien qu'il soit possible de masquer certaines de ces informations tout en permettant la vérification (comme le font certaines cryptomonnaies alternatives telles que Monero), cela entraîne également certains risques de sécurité.

Il existe parfois une confusion entre les signatures numériques et les signatures manuscrites capturées numériquement. Dans ce dernier cas, il s'agit simplement d'une image de votre signature manuscrite collée dans un document électronique tel qu'un contrat de travail. Cependant, cela ne constitue pas une signature numérique au sens cryptographique. Une véritable signature numérique est un nombre long qui ne peut être produit qu'en étant en possession d'une clé privée.

Tout comme dans le cadre de la cryptographie symétrique, il est également possible d'utiliser conjointement des schémas de chiffrement et d'authentification asymétriques. Des principes similaires s'appliquent. Tout d'abord, il convient d'utiliser des paires de clés privées-publiques différentes pour le chiffrement et pour la création de signatures numériques. En outre, il est recommandé de chiffrer d'abord un message avant de l'authentifier.

Il est important de noter que, dans de nombreuses applications, la cryptographie asymétrique n'est pas utilisée tout au long du processus de communication. En réalité, elle est généralement employée uniquement pour échanger des clés symétriques entre les parties qui vont réellement communiquer.

C'est notamment le cas lorsque vous achetez des biens en ligne. En connaissant la clé publique du vendeur, celui-ci peut vous envoyer des messages signés numériquement que vous pouvez vérifier pour en confirmer l’authenticité. Sur cette base, vous pouvez suivre un des nombreux protocoles d'échange de clés symétriques pour communiquer de manière sécurisée.

La principale raison de cette approche courante est que la cryptographie asymétrique est beaucoup moins efficace que la cryptographie symétrique pour atteindre un certain niveau de sécurité. C'est l'une des raisons pour lesquelles nous avons toujours besoin de la cryptographie symétrique en complément de la cryptographie publique. En outre, la cryptographie symétrique est beaucoup plus adaptée pour certaines applications spécifiques, comme lorsqu'un utilisateur d'ordinateur chiffre ses propres données.

Alors, comment exactement les signatures numériques et le chiffrement à clé publique résolvent-ils les problèmes de distribution et de gestion des clés ?

Il n'existe pas une réponse unique à cette question. La cryptographie asymétrique est un outil, et il n'existe pas une seule manière de l'utiliser. Cependant, reprenons notre exemple précédent de Jim’s Sporting Goods pour montrer comment ces problèmes seraient généralement traités dans ce cas précis.

Pour commencer, Jim’s Sporting Goods ferait probablement appel à une autorité de certification, une organisation qui facilite la distribution de clés publiques. L'autorité de certification enregistrerait certaines informations sur Jim’s Sporting Goods et lui attribuerait une clé publique. Elle lui enverrait ensuite un certificat, appelé certificat TLS/SSL, contenant la clé publique de Jim’s Sporting Goods signée numériquement à l'aide de la clé publique de l'autorité de certification. De cette manière, l'autorité de certification affirme qu'une clé publique donnée appartient bien à Jim’s Sporting Goods.

L'élément clé pour comprendre ce processus avec les certificats TLS/SSL est que, bien que vous n'ayez généralement pas la clé publique de Jim’s Sporting Goods stockée sur votre ordinateur, les clés publiques des autorités de certification reconnues sont effectivement stockées dans votre navigateur ou votre système d'exploitation. Elles sont enregistrées dans ce que l'on appelle des certificats racine.

Ainsi, lorsque Jim’s Sporting Goods vous fournit son certificat TLS/SSL, vous pouvez vérifier la signature numérique de l'autorité de certification grâce à un certificat racine présent dans votre navigateur ou votre système d'exploitation. Si la signature est valide, vous pouvez être raisonnablement sûr que la clé publique figurant sur le certificat appartient bien à Jim’s Sporting Goods. Sur cette base, il est facile d'établir un protocole de communication sécurisée avec Jim’s Sporting Goods.

La distribution des clés est désormais considérablement simplifiée pour Jim’s Sporting Goods. Il est également évident que la gestion des clés a été grandement simplifiée. Au lieu de devoir stocker des milliers de clés, Jim’s Sporting Goods n'a besoin que de stocker une clé privée qui lui permet de créer des signatures pour la clé publique figurant sur son certificat SSL. Chaque fois qu'un client se rend sur le site de Jim’s Sporting Goods, il peut établir une session de communication sécurisée à partir de cette clé publique. Les clients n'ont également pas besoin de stocker d'informations spécifiques (autre que les clés publiques des autorités de certification reconnues présentes dans leur système d'exploitation et leur navigateur).

Notes :

[5] Tout schéma visant à atteindre la non-répudiation, le thème que nous avons discuté au Chapitre 1, devra nécessairement inclure l'utilisation de signatures numériques.

Fonctions de hachage

Les fonctions de hachage sont omniprésentes en cryptographie. Elles ne relèvent ni de la cryptographie symétrique ni de la cryptographie asymétrique, mais appartiennent à une catégorie cryptographique qui leur est propre.

Nous avons déjà rencontré les fonctions de hachage au Chapitre 4, lors de la création de codes d’authentification basés sur des hachages. Elles sont également importantes dans le contexte des signatures numériques, bien que pour une raison légèrement différente : les signatures numériques sont en effet généralement créées sur la valeur de hachage d’un message (chiffré) plutôt que sur le message (chiffré) lui-même. Dans cette section, nous allons fournir une introduction plus approfondie aux fonctions de hachage.

Commençons par définir ce qu’est une fonction de hachage. Une fonction de hachage est toute fonction calculable efficacement qui prend en entrée des données de taille arbitraire et produit une sortie de longueur fixe.

Une fonction de hachage cryptographique est simplement une fonction de hachage qui est utile pour des applications en cryptographie. La sortie d’une fonction de hachage cryptographique est généralement appelée le hachage, la valeur de hachage ou le digest du message.

En cryptographie, le terme « fonction de hachage » fait généralement référence à une fonction de hachage cryptographique. Nous adopterons cette convention pour la suite.

Un exemple de fonction de hachage populaire est SHA-256 (Secure Hash Algorithm 256). Quelle que soit la taille de l’entrée (par exemple, 15 bits, 100 bits ou 10 000 bits), cette fonction produira une valeur de hachage de 256 bits. Voici quelques exemples de sorties de la fonction SHA-256.

Toutes les sorties sont exactement de 256 bits, écrites en format hexadécimal (chaque chiffre hexadécimal peut être représenté par quatre chiffres binaires). Ainsi, même si vous insériez l’intégralité du livre Le Seigneur des Anneaux de Tolkien dans la fonction SHA-256, la sortie serait toujours de 256 bits.

Les fonctions de hachage comme SHA-256 sont utilisées à diverses fins en cryptographie. Les propriétés requises d'une fonction de hachage dépendent du contexte d'une application particulière. Cependant, il existe deux propriétés principales généralement attendues des fonctions de hachage en cryptographie : [6]

  1. Résistance aux collisions
  2. Masquage

Une fonction de hachage H est dite résistante aux collisions s’il est impossible de trouver deux valeurs, x et y, telles que x \neq y, mais H(x) = H(y).

Les fonctions de hachage résistantes aux collisions sont importantes, par exemple, dans la vérification de logiciels. Supposons que vous souhaitiez télécharger la version Windows de Bitcoin Core 0.21.0 (une application serveur permettant de traiter le trafic du réseau Bitcoin). Voici les principales étapes à suivre pour vérifier la légitimité du logiciel :

  1. Vous devez d’abord télécharger et importer les clés publiques d'un ou plusieurs contributeurs de Bitcoin Core dans un logiciel permettant de vérifier les signatures numériques (par exemple, Kleopatra). Vous pouvez trouver ces clés publiques ici. Il est recommandé de vérifier le logiciel Bitcoin Core avec les clés publiques de plusieurs contributeurs.
  2. Ensuite, vous devez vérifier les clés publiques que vous avez importées. Au minimum, vous devriez vérifier que les clés publiques que vous avez trouvées sont les mêmes que celles publiées à divers endroits. Par exemple, vous pourriez consulter les pages personnelles, les comptes Twitter ou les pages GitHub des personnes dont vous avez importé les clés publiques. En général, cette comparaison de clés publiques est effectuée en comparant un court hachage de la clé publique connu sous le nom d’empreinte numérique (ou fingerprint).
  3. Ensuite, vous devez télécharger l’exécutable de Bitcoin Core depuis leur site officiel. Des packages seront disponibles pour les systèmes d’exploitation Linux, Windows et Mac.
  4. Ensuite, vous devez localiser deux fichiers de publication. Le premier contient le hachage officiel SHA-256 de l’exécutable que vous avez téléchargé, ainsi que les hachages de tous les autres packages qui ont été publiés. Un autre fichier de publication contiendra les signatures de divers contributeurs sur le fichier de publication contenant les hachages des packages. Ces deux fichiers de publication devraient se trouver sur le site officiel de Bitcoin Core.
  5. Ensuite, vous devez calculer le hachage SHA-256 de l’exécutable que vous avez téléchargé depuis le site officiel de Bitcoin Core sur votre propre ordinateur. Vous devez alors comparer ce résultat avec celui du hachage officiel du package correspondant à l’exécutable. Les deux valeurs devraient être identiques.
  6. Enfin, vous devez vérifier qu'une ou plusieurs des signatures numériques sur le fichier de publication contenant les hachages officiels des packages correspondent bien à une ou plusieurs clés publiques que vous avez importées (les publications de Bitcoin Core ne sont pas toujours signées par tous les contributeurs). Vous pouvez effectuer cette vérification avec une application comme Kleopatra.

Ce processus de vérification des logiciels présente deux avantages principaux. Premièrement, il garantit qu'il n'y a pas eu d'erreurs de transmission lors du téléchargement depuis le site officiel de Bitcoin Core. Deuxièmement, il assure qu'aucun attaquant n'a pu vous amener à télécharger un code modifié et malveillant, soit en piratant le site de Bitcoin Core, soit en interceptant le trafic.

Comment exactement ce processus de vérification protège-t-il contre ces problèmes ?

Si vous avez scrupuleusement vérifié les clés publiques que vous avez importées, vous pouvez être raisonnablement certain que ces clés leur appartiennent réellement et n'ont pas été compromises. Étant donné que les signatures numériques sont dotées de l’inforgeabilité existentielle, vous savez que seuls ces contributeurs ont pu créer une signature numérique sur les hachages officiels des packages présents dans le fichier de publication.

Supposons que les signatures du fichier de publication que vous avez téléchargé soient valides. Vous pouvez alors comparer la valeur de hachage que vous avez calculée localement pour l'exécutable Windows que vous avez téléchargé avec celle incluse dans le fichier de publication correctement signé. Comme vous savez que la fonction de hachage SHA-256 est résistante aux collisions, une correspondance signifie que votre exécutable est exactement le même que l'exécutable officiel.

Passons maintenant à la deuxième propriété courante des fonctions de hachage : le masquage (hiding). Une fonction de hachage H est considérée comme possédant la propriété de masquage si, pour toute valeur x choisie au hasard dans un ensemble très large, il est pratiquement impossible de retrouver x en ne connaissant que H(x).

Vous trouverez ci-dessous la sortie SHA-256 d'un message que j'ai rédigé. Pour garantir une randomisation suffisante, le message comprend une chaîne de caractères générée aléatoirement à la fin. Étant donné que SHA-256 possède la propriété de masquage, personne ne pourrait déchiffrer ce message.

Mais je ne vais pas vous laisser dans l'expectative jusqu'à ce que SHA-256 devienne plus faible. Le message original que j'ai écrit était le suivant :

Une manière courante d'utiliser des fonctions de hachage possédant la propriété de masquage est la gestion des mots de passe (la résistance aux collisions est également importante pour cette application). Tout service en ligne basé sur un compte décent, comme Facebook ou Google, ne stockera pas vos mots de passe directement pour gérer l'accès à votre compte. Au lieu de cela, il ne stockera qu'un hachage de ce mot de passe. Chaque fois que vous saisissez votre mot de passe sur un navigateur, un hachage est d'abord calculé. Seul ce hachage est envoyé au serveur du prestataire de services et comparé au hachage stocké dans la base de données du serveur. La propriété de masquage permet de garantir que les attaquants ne peuvent pas retrouver le mot de passe à partir de la valeur de hachage.

La gestion des mots de passe par hachage, bien sûr, ne fonctionne que si les utilisateurs choisissent réellement des mots de passe complexes. La propriété de masquage suppose que x est choisi aléatoirement dans un ensemble très large. Choisir des mots de passe comme « 1234 », « motdepasse » ou votre date de naissance n'offrira aucune sécurité réelle. Il existe de longues listes de mots de passe courants et de leurs hachages que les attaquants peuvent exploiter s'ils obtiennent le hachage de votre mot de passe. Ces types d'attaques sont appelées attaques par dictionnaire. Si les attaquants connaissent certaines de vos informations personnelles, ils peuvent également tenter des suppositions informées. Ainsi, vous devez toujours choisir des mots de passe longs et sécurisés (de préférence des chaînes longues et aléatoires générées par un gestionnaire de mots de passe).

Parfois, une application peut nécessiter une fonction de hachage qui possède à la fois la résistance aux collisions et le masquage. Mais ce n'est certainement pas toujours le cas. Par exemple, le processus de vérification des logiciels que nous avons décrit n'exige que la résistance aux collisions, tandis que le masquage n'est pas essentiel.

Bien que la résistance aux collisions et le masquage soient les principales propriétés recherchées des fonctions de hachage en cryptographie, d'autres types de propriétés peuvent également être souhaitables dans certaines applications.

Notes :

[6] Le terme « masquage » (traduit depuis l'anglais) n’est pas un langage courant, mais il est spécifiquement emprunté à Arvind Narayanan, Joseph Bonneau, Edward Felten, Andrew Miller, et Steven Goldfeder, Bitcoin and Cryptocurrency Technologies, Princeton University Press (Princeton, 2016), Chapitre 1.

Le système cryptographique RSA

Le problème de la factorisation

Bien que la cryptographie symétrique soit généralement assez intuitive pour la plupart des gens, ce n'est généralement pas le cas de la cryptographie asymétrique. Bien que vous soyez probablement à l'aise avec la description générale présentée dans les sections précédentes, vous vous demandez probablement ce que sont précisément les fonctions à sens unique et comment elles sont utilisées pour construire des systèmes asymétriques.

Dans ce chapitre, je vais lever une partie du mystère entourant la cryptographie asymétrique, en examinant plus en détail un exemple spécifique, à savoir le système cryptographique RSA. Dans la première section, je vais introduire le problème de la factorisation sur lequel repose le problème RSA. Ensuite, j'aborderai un certain nombre de résultats clés issus de la théorie des nombres. Dans la dernière section, nous mettrons ensemble ces informations pour expliquer le problème RSA, et comment celui-ci peut être utilisé pour créer des schémas cryptographiques asymétriques.

Approfondir cette discussion n'est pas une tâche facile. Cela nécessite l'introduction de nombreux théorèmes et propositions de la théorie des nombres. Mais ne laissez pas les mathématiques vous décourager. Travailler sur cette discussion améliorera considérablement votre compréhension des bases de la cryptographie asymétrique et constituera un investissement précieux.

Commençons donc par examiner le problème de la factorisation.

Chaque fois que vous multipliez deux nombres, disons a et b, nous appelons ces nombres a et b des facteurs, et le résultat le produit. Tenter d'écrire un nombre N comme la multiplication de deux ou plusieurs facteurs est appelé factorisation ou décomposition en facteurs premiers. [1] Tout problème nécessitant cela peut être appelé un problème de factorisation.

Il y a environ 2 500 ans, le mathématicien grec Euclide d'Alexandrie a découvert un théorème clé sur la factorisation des entiers. Il est couramment appelé le théorème de la factorisation unique et énonce ce qui suit :

Théorème 1. Tout entier N supérieur à 1 est soit un nombre premier, soit peut être exprimé comme un produit de facteurs premiers.

La seconde partie de cette affirmation signifie simplement que vous pouvez prendre n'importe quel entier non premier N supérieur à 1, et l'écrire comme une multiplication de nombres premiers. Voici plusieurs exemples d'entiers non premiers écrits comme produit de facteurs premiers.

Pour tous ces exemples, calculer leurs facteurs premiers est relativement simple, même si vous ne disposez que de N. Vous commencez par le plus petit nombre premier, c'est-à-dire 2, et vous voyez combien de fois l'entier N est divisible par celui-ci. Ensuite, vous passez à tester la divisibilité de N par 3, 5, 7, et ainsi de suite. Vous poursuivez ce processus jusqu'à ce que votre entier N soit écrit comme produit uniquement de nombres premiers.

Prenons par exemple l'entier 84. Vous pouvez voir ci-dessous le processus pour déterminer ses facteurs premiers. À chaque étape, nous prenons le plus petit facteur premier restant (à gauche) et déterminons le reste à factoriser. Nous continuons jusqu'à ce que le reste soit également un nombre premier. À chaque étape, la factorisation actuelle de 84 est affichée à droite.

Supposons maintenant que N soit très grand. Quelle serait la difficulté de réduire N en ses facteurs premiers ?

Cela dépend vraiment de N. Supposons, par exemple, que N soit égal à 50 450 400. Bien que ce nombre semble intimidant, les calculs ne sont pas si compliqués et peuvent facilement être effectués à la main. Comme ci-dessus, vous commencez simplement par 2 et continuez. Vous trouverez ci-dessous le résultat de ce processus de manière similaire à l'exemple précédent.

Réaliser cette décomposition en facteurs premiers à la main prend un certain temps. Un ordinateur, bien sûr, pourrait effectuer tous ces calculs en une fraction de seconde. En fait, un ordinateur peut fréquemment factoriser des entiers extrêmement grands en une fraction de seconde.

Il existe cependant certaines exceptions. Supposons que nous sélectionnions d'abord aléatoirement deux nombres premiers très grands. Il est courant de les désigner par p et q, et j'adopterai cette convention ici.

Pour être concret, disons que p et q sont tous deux des nombres premiers de 1024 bits, et qu'ils nécessitent effectivement au moins 1024 bits pour être représentés (donc le premier bit doit être égal à 1). Par exemple, 37 ne pourrait pas être l'un de ces nombres premiers. Vous pouvez certainement représenter 37 avec 1024 bits, mais il est clair que vous n'avez pas besoin d'autant de bits pour le représenter. Vous pouvez représenter 37 par n'importe quelle chaîne ayant au moins 6 bits. (En 6 bits, 37 serait représenté par 100101).

Il est important de comprendre à quel point p et q sont grands s'ils sont sélectionnés selon les conditions ci-dessus. Par exemple, voici un nombre premier aléatoire qui nécessite au moins 1024 bits pour être représenté :

Supposons maintenant qu'après avoir sélectionné aléatoirement les nombres premiers p et q, nous les multiplions pour obtenir un entier N. Ce dernier entier est donc un nombre de 2048 bits qui nécessite au moins 2048 bits pour être représenté. Il est beaucoup, beaucoup plus grand que p ou q.

Supposons que vous fournissiez uniquement l'entier N à un ordinateur, et que vous lui demandiez de trouver les deux facteurs premiers de 1024 bits de N. La probabilité que l'ordinateur découvre p et q est extrêmement faible. Vous pouvez dire qu'il est impossible de les trouver pour des raisons pratiques. Cela reste vrai même si vous utilisiez un superordinateur ou même un réseau de superordinateurs.

Pour commencer, supposons que l'ordinateur tente de résoudre le problème en parcourant tous les nombres de 1024 bits, en testant à chaque fois s'ils sont premiers et s'ils sont facteurs de N. L'ensemble des nombres premiers à tester est alors approximativement égal à 1.265 \cdot 10^{305}. [2]

Même si vous preniez tous les ordinateurs de la planète et les faisiez essayer de trouver et de tester les nombres premiers de 1024 bits de cette manière, une chance sur un milliard de réussir nécessiterait une période de calcul bien plus longue que l'âge de l'Univers.

En pratique, un ordinateur peut faire mieux que la procédure approximative décrite ci-dessus. Il existe plusieurs algorithmes que l'ordinateur peut appliquer pour parvenir à une factorisation plus rapidement. Cependant, même en utilisant ces algorithmes plus efficaces, la tâche reste toujours computationnellement infaisable. [3]

Il est important de noter que la difficulté de la factorisation dans les conditions décrites repose sur l'hypothèse qu'il n'existe pas d'algorithmes efficaces pour calculer les facteurs premiers. Nous ne pouvons pas réellement prouver qu'un algorithme efficace n'existe pas. Néanmoins, cette hypothèse est très plausible : malgré des efforts considérables qui s'étendent sur des centaines d'années, nous n'avons toujours pas trouvé un tel algorithme qui soit efficace en pratique.

Par conséquent, le problème de la factorisation, dans certaines conditions, peut raisonnablement être supposé être un problème difficile. Plus précisément, lorsque p et q sont des nombres premiers très grands, leur produit N n'est pas difficile à calculer ; mais la factorisation de N sans connaître p ou q est pratiquement impossible.

Notes :

[1] La factorisation peut également être importante pour travailler avec d'autres types d'objets mathématiques que les nombres. Par exemple, il peut être utile de factoriser des expressions polynomiales telles que x^2 - 2x + 1. Dans notre discussion, nous nous concentrerons uniquement sur la factorisation des nombres, en particulier des entiers.

[2] Selon le théorème des nombres premiers, le nombre de nombres premiers inférieurs ou égaux à N est approximativement égal à N/\ln(N). Cela signifie que vous pouvez approximer le nombre de nombres premiers de longueur 1024 bits par :

\frac{2^{1024}}{\ln(2^{1024})} - \frac{2^{1023}}{\ln(2^{1023})}

...ce qui est approximativement égal à 1.265 \times 10^{305}.

[3] La même chose est vraie pour les problèmes de logarithmes discrets. C'est pourquoi les constructions asymétriques nécessitent des clés beaucoup plus longues que les constructions cryptographiques symétriques.

Résultats en théorie des nombres

Malheureusement, le problème de la factorisation ne peut pas être utilisé directement pour les systèmes cryptographiques asymétriques. Cependant, nous pouvons utiliser un problème plus complexe mais lié : le problème RSA.

Pour comprendre le problème RSA, nous devons assimiler un certain nombre de théorèmes et propositions issus de la théorie des nombres. Ceux-ci sont présentés dans cette section en trois sous-sections : (1) l'ordre de N, (2) l'inversibilité modulo N, et (3) le théorème d'Euler.

Certains des éléments abordés dans ces trois sous-sections ont déjà été introduits au Chapitre 3. Cependant, nous les réexposons ici par souci de commodité.

L'ordre de N

Un entier a est premier avec ou un co-premier d'un entier N, si le plus grand diviseur commun entre eux est 1. Bien que 1 ne soit pas considéré comme un nombre premier par convention, il est co-premier avec tout entier (tout comme -1).

Par exemple, considérons le cas où a = 18 et N = 37. Ces nombres sont clairement co-premiers. Le plus grand entier qui divise à la fois 18 et 37 est 1. En revanche, considérons le cas où a = 42 et N = 16. Ces nombres ne sont pas co-premiers, car ils sont tous deux divisibles par 2, qui est supérieur à 1.

Nous pouvons maintenant définir l'ordre de N de la manière suivante. Supposons que N est un entier supérieur à 1. L'ordre de N est alors le nombre de tous les co-premiers avec N tels que pour chaque co-premier a, la condition suivante est vérifiée : 1 \leq a < N.

Par exemple, si N = 12, alors 1, 5, 7, et 11 sont les seuls co-premiers qui répondent à la condition ci-dessus. Par conséquent, l'ordre de 12 est égal à 4.

Supposons maintenant que N soit un nombre premier. Alors, tout entier inférieur à N mais supérieur ou égal à 1 est co-premier avec celui-ci. Cela inclut tous les éléments de l'ensemble suivant : \{1,2,3,....,N - 1\}. Par conséquent, lorsque N est premier, l'ordre de N est N - 1. Cela est énoncé dans la Proposition 1, où \phi(N) désigne l'ordre de N.

Proposition 1. \phi(N) = N - 1 lorsque N est premier.

Supposons maintenant que N ne soit pas premier. Vous pouvez alors calculer son ordre en utilisant la fonction Phi d'Euler. Bien que calculer l'ordre d'un petit entier soit relativement simple, la fonction Phi d'Euler devient particulièrement importante pour les grands entiers. La proposition de la fonction Phi d'Euler est énoncée ci-dessous.

Théorème 2. Soit N égal à p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot p_i^{e_i} \cdot \ldots \cdot p_n^{e_n}, où l'ensemble \{p_i\} est constitué de tous les facteurs premiers distincts de N et chaque e_i indique combien de fois le facteur premier p_i apparaît pour N. Alors,

\phi(N) = p_1^{e_1 - 1} \cdot (p_1 - 1) \cdot p_2^{e_2 - 1} \cdot (p_2 - 1) \cdot \ldots \cdot p_n^{e_n - 1} \cdot (p_n - 1)

Le Théorème 2 montre qu'une fois que vous avez décomposé un entier non premier N en ses facteurs premiers distincts, il devient facile de calculer l'ordre de N.

Par exemple, supposons que N = 270. Il est clair que ce n'est pas un nombre premier. Sa décomposition en facteurs premiers donne l'expression suivante : 2 \cdot 3^3 \cdot 5. Selon la fonction Phi d'Euler, l'ordre de N est alors :

\phi(N) = 2^{1 - 1} \cdot (2 - 1) \cdot 3^{3 - 1} \cdot (3 - 1) \cdot 5^{1 - 1} \cdot (5 - 1) = 1 \cdot 1 \cdot 9 \cdot 2 \cdot 1 \cdot 4 = 1 + 18 + 4 = 23

Supposons maintenant que N soit le produit de deux nombres premiers, p et q. Le Théorème 2 ci-dessus indique alors que l'ordre de N est le suivant :

p^{1 - 1} \cdot (p - 1) \cdot q^{1 - 1} \cdot (q - 1) = (p - 1) \cdot (q - 1)

C'est un résultat clé pour le problème RSA en particulier, et il est énoncé dans la Proposition 2 ci-dessous.

Proposition 2. Si N est le produit de deux nombres premiers, p et q, l'ordre de N est le produit (p - 1) \cdot (q - 1).

Pour illustrer, supposons que N = 119. Cet entier peut être factorisé en deux nombres premiers, à savoir 7 et 17. Par conséquent, la fonction Phi d'Euler suggère que l'ordre de 119 est :

\phi(119) = (7 - 1) \cdot (17 - 1) = 6 \cdot 16 = 96

En d'autres termes, l'entier 119 possède 96 co-premiers dans l'intervalle allant de 1 à 119. En fait, cet ensemble comprend tous les entiers de 1 à 119 qui ne sont pas des multiples de 7 ou de 17.

Désormais, désignons par C_N l'ensemble des co-premiers qui déterminent l'ordre de N. Pour notre exemple où N = 119, l'ensemble C_{119} est bien trop grand pour être énuméré complètement. Cependant, certains des éléments sont les suivants :

C_{119} = \{1, 2, \ldots, 6, 8, \ldots, 13, 15, 16, 18, \ldots, 33, 35, \ldots, 96\}

Inversibilité modulo N

On dit qu'un entier a est inversible modulo N, s'il existe au moins un entier b tel que a \cdot b \mod N = 1 \mod N. Tout entier b qui satisfait cette condition est appelé un inverse (ou inverse multiplicatif) de a pour une réduction par modulo N.

Supposons, par exemple, que a = 5 et N = 11. Il existe plusieurs entiers par lesquels vous pouvez multiplier 5, de sorte que 5 \cdot b \mod 11 = 1 \mod 11. Considérons, par exemple, les entiers 20 et 31. Il est facile de vérifier que ces deux entiers sont des inverses de 5 pour une réduction modulo 11.

Bien que 5 ait de nombreux inverses en réduction modulo 11, vous pouvez démontrer qu'il n'existe qu'un seul inverse positif de 5 qui soit inférieur à 11. En fait, ce résultat est valable de manière générale.

Proposition 3. Si l'entier a est inversible modulo N, il doit exister un seul inverse positif de a inférieur à N. (Cet inverse unique de a doit donc appartenir à l'ensemble \{1, \ldots, N - 1\}).

Désignons l'inverse unique de a de la Proposition 3 par a^{-1}. Dans le cas où a = 5 et N = 11, on constate que a^{-1} = 9, puisque 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11.

Remarquez que vous pouvez également obtenir la valeur 9 pour a^{-1} dans notre exemple en réduisant simplement tout autre inverse de a par modulo 11. Par exemple, 20 \mod 11 = 31 \mod 11 = 9 \mod 11. Ainsi, chaque fois qu'un entier a > N est inversible modulo N, alors a \mod N doit aussi être inversible modulo N.

Cependant, il n'est pas toujours garanti qu'un inverse de a existe en réduction modulo N. Supposons, par exemple, que a = 2 et N = 8. Il n'existe aucun b, ni même aucun a^{-1}, tel que 2 \cdot b \mod 8 = 1 \mod 8. Cela s'explique par le fait que toute valeur de b produira toujours un multiple de 2, de sorte qu'aucune division par 8 ne pourra jamais donner un reste égal à 1.

Comment savoir exactement si un entier a possède un inverse pour un N donné ? Comme vous l'avez peut-être remarqué dans l'exemple ci-dessus, le plus grand diviseur commun entre 2 et 8 est supérieur à 1, à savoir 2. Et cela illustre en fait le résultat général suivant :

Proposition 4. Un inverse d'un entier a pour une réduction modulo N existe, et spécifiquement un unique inverse positif inférieur à N, si et seulement si le plus grand diviseur commun entre a et N est 1 (c'est-à-dire s'ils sont co-premiers).

Dans le cas où a = 5 et N = 11, nous avons conclu que a^{-1} = 9, puisque 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11. Il est important de noter que l'inverse est également vrai. C'est-à-dire que lorsque a = 9 et N = 11, on a a^{-1} = 5.

Théorème d'Euler

Avant de passer au problème RSA, nous devons comprendre un dernier théorème crucial, à savoir le théorème d'Euler. Celui-ci énonce ce qui suit :

Théorème 3. Supposons que deux entiers a et N sont copremiers. Alors, a^{\phi(N)} \mod N = 1 \mod N.

Ce résultat est remarquable, mais peut paraître déroutant au premier abord. Prenons un exemple pour mieux le comprendre.

Supposons que a = 5 et N = 7. Ces deux nombres sont effectivement copremiers, comme l'exige le théorème d'Euler. Nous savons que l'ordre de 7 est égal à 6, étant donné que 7 est un nombre premier (voir Proposition 1).

Le théorème d'Euler indique maintenant que 5^6 \mod 7 doit être égal à 1 \mod 7. Voici les calculs qui montrent que cela est effectivement vrai.

L'entier 7 divise 15 624 un total de 2 233 fois. Par conséquent, le reste de la division de 15 625 par 7 est 1.

Ensuite, en utilisant la fonction Phi d'Euler (Théorème 2), vous pouvez dériver la Proposition 5 ci-dessous.

Proposition 5. \phi(a \cdot b) = \phi(a) \cdot \phi(b) pour tous les entiers positifs a et b.

Nous n'allons pas démontrer pourquoi c'est le cas. Il suffit de noter que vous avez déjà vu une preuve de cette proposition par le fait que \phi(p \cdot q) = \phi(p) \cdot \phi(q) = (p - 1) \cdot (q - 1) lorsque p et q sont des nombres premiers, comme énoncé dans la Proposition 2.

Le théorème d'Euler, associé à la Proposition 5, a des implications importantes. Voyez ce qui se passe, par exemple, dans les expressions ci-dessous, où a et N sont copremiers.

Ainsi, la combinaison du théorème d'Euler et de la Proposition 5 permet de simplifier le calcul d'un certain nombre d'expressions. En général, nous pouvons résumer ce principe par la Proposition 6.

Proposition 6. a^x \mod N = a^{x \mod \phi(N)}

Nous devons maintenant assembler toutes ces connaissances dans une dernière étape délicate.

Tout comme N possède un ordre \phi(N) qui inclut les éléments de l'ensemble C_N, nous savons que l'entier \phi(N) doit lui-même avoir un ordre et un ensemble de copremiers. Appelons \phi(N) = R. Il existe donc également une valeur pour \phi(R) et un ensemble de copremiers C_R.

Supposons maintenant que nous sélectionnions un entier e dans l'ensemble C_R. Nous savons d'après la Proposition 3 que cet entier e possède un unique inverse positif inférieur à R. C'est-à-dire que e a un seul inverse unique dans l'ensemble C_R. Appelons cet inverse d. D'après la définition d'un inverse, cela signifie que e \cdot d = 1 \mod R.

Nous pouvons utiliser ce résultat pour formuler une assertion concernant notre entier d'origine N. Cela est résumé dans la Proposition 7.

Proposition 7. Supposons que e \cdot d \mod \phi(N) = 1 \mod \phi(N). Alors, pour tout élément a de l'ensemble C_N, il doit être vrai que a^{e \cdot d \mod \phi(N)} = a^{1 \mod \phi(N)} = a \mod N.

Nous disposons maintenant de tous les résultats issus de la théorie des nombres nécessaires pour énoncer clairement le problème RSA.

Le système cryptographique RSA

Nous sommes maintenant prêts à énoncer le problème RSA. Supposons que vous créez un ensemble de variables composé de p, q, N, \phi(N), e, d, et y. Appelons cet ensemble \Pi. Il est créé comme suit :

  1. Générez deux nombres premiers aléatoires p et q de taille égale et calculez leur produit N.
  2. Calculez l'ordre de N, \phi(N), à l'aide du produit suivant : (p - 1) \cdot (q - 1).
  3. Choisissez un e > 2 tel qu'il soit plus petit que \phi(N) et copremier avec \phi(N).
  4. Calculez d en définissant e \cdot d \mod \phi(N) = 1.
  5. Sélectionnez une valeur aléatoire y qui est inférieure à N et copremière avec N.

Le problème RSA consiste à trouver un x tel que x^e = y, tout en ne disposant que d'un sous-ensemble d'informations concernant \Pi, à savoir les variables N, e, et y. Lorsque p et q sont très grands, généralement de l'ordre de 1024 bits chacun, on considère que le problème RSA est difficile. Vous comprenez maintenant pourquoi c'est le cas, compte tenu de notre discussion précédente.

Une méthode simple pour calculer x lorsque x^e \mod N = y \mod N est de calculer y^d \mod N. Nous savons que y^d \mod N = x \mod N par les calculs suivants :

y^d \mod N = x^{e \cdot d} \mod N = x^{e \cdot d \mod \phi(N)} \mod N = x^{1 \mod \phi(N)} \mod N = x \mod N.

Le problème est que nous ne connaissons pas la valeur de d, car elle n'est pas donnée dans le problème. Par conséquent, nous ne pouvons pas calculer directement y^d \mod N pour obtenir x \mod N.

Nous pourrions toutefois, indirectement, calculer d à partir de l'ordre de N, \phi(N), car nous savons que e \cdot d \mod \phi(N) = 1 \mod \phi(N). Mais par hypothèse, le problème ne fournit pas non plus de valeur pour \phi(N).

Enfin, l'ordre pourrait être calculé indirectement à partir des facteurs premiers p et q, afin que nous puissions finalement calculer d. Mais par hypothèse, les valeurs p et q ne sont pas non plus fournies.

En toute rigueur, même si le problème de factorisation dans un problème RSA est difficile, nous ne pouvons pas prouver que le problème RSA lui-même est difficile. Il peut en effet exister d'autres méthodes pour résoudre le problème RSA que par la factorisation. Cependant, il est généralement admis et supposé que si le problème de factorisation dans le problème RSA est difficile, alors le problème RSA lui-même l'est aussi.

Si le problème RSA est effectivement difficile, alors il produit une fonction à sens unique avec une porte dérobée. La fonction ici est f(g) = g^e \mod N. Avec la connaissance de f(g), n'importe qui pourrait facilement calculer une valeur y pour une valeur particulière g = x. Cependant, il est pratiquement impossible de calculer une valeur particulière x simplement en connaissant la valeur y et la fonction f(g). L'exception est lorsque vous disposez d'une information d, la porte dérobée. Dans ce cas, vous pouvez simplement calculer y^d pour obtenir x.

Voyons un exemple spécifique pour illustrer le problème RSA. Je ne peux pas sélectionner un problème RSA qui serait considéré comme difficile dans les conditions décrites ci-dessus, car les nombres seraient trop volumineux. Cet exemple est donc simplement destiné à illustrer comment fonctionne généralement le problème RSA.

Pour commencer, supposons que vous sélectionnez deux nombres premiers aléatoires 13 et 31. Ainsi, p = 13 et q = 31. Le produit N de ces deux nombres premiers est égal à 403. Nous pouvons facilement calculer l'ordre de 403. Il est équivalent à (13 - 1) \cdot (31 - 1) = 360.

Ensuite, comme indiqué à l'étape 3 du problème RSA, nous devons sélectionner un copremier de 360 qui est supérieur à 2 et inférieur à 360. Il n'est pas nécessaire de choisir cette valeur au hasard. Supposons que nous choisissions 103. Il s'agit bien d'un copremier de 360, car leur plus grand diviseur commun est 1.

L'étape 4 exige maintenant que nous calculions une valeur d telle que 103 \cdot d \mod 360 = 1. Ce n'est pas une tâche facile à effectuer à la main lorsque la valeur de N est grande. Cela nécessite d'utiliser une procédure appelée algorithme d'Euclide étendu.

Bien que je ne montre pas ici la procédure, elle donne la valeur 7 lorsque e = 103. Vous pouvez vérifier que la paire de valeurs 103 et 7 satisfait bien la condition générale e \cdot d \mod \phi(n) = 1 grâce aux calculs suivants :

Il est important de noter qu'étant donné la Proposition 4, nous savons qu'aucun autre entier compris entre 1 et 360 pour d ne produira le résultat 103 \cdot d = 1 \mod 360. De plus, la proposition implique que la sélection d'une valeur différente pour e donnera une valeur unique différente pour d.

À l'étape 5 du problème RSA, nous devons sélectionner un entier positif y qui est un copremier de 403. Supposons que nous fixions y = 2^{103}. L'exponentiation de 2 par 103 donne le résultat suivant :

Le problème RSA dans cet exemple particulier est maintenant le suivant : On vous fournit N = 403, e = 103 et y = 349 \mod 403. Vous devez maintenant calculer x tel que x^{103} = 349 \mod 403. Autrement dit, vous devez trouver que la valeur d'origine avant l'exponentiation par 103 était 2.

Il serait facile (pour un ordinateur du moins) de calculer x si nous savions que d = 7. Dans ce cas, vous pourriez déterminer x comme suit :

Le problème est que vous n'avez pas reçu l'information que d = 7. Vous pourriez bien sûr calculer d à partir du fait que 103 \cdot d = 1 \mod 360. Le problème est que vous ne disposez pas non plus de l'information que l'ordre de N = 360. Enfin, vous pourriez aussi calculer l'ordre de 403 en déterminant le produit : (p - 1) \cdot (q - 1). Mais on ne vous a pas dit que p = 13 et q = 31.

Bien entendu, un ordinateur pourrait encore résoudre facilement le problème RSA pour cet exemple, car les nombres premiers impliqués ne sont pas grands. Mais lorsque les nombres premiers deviennent très grands, cela devient une tâche pratiquement impossible.

Nous avons maintenant présenté le problème RSA, un ensemble de conditions sous lesquelles il est difficile, ainsi que les mathématiques sous-jacentes. Comment cela aide-t-il concrètement à la cryptographie asymétrique ? Plus précisément, comment pouvons-nous transformer la difficulté du problème RSA dans certaines conditions en un schéma de chiffrement ou un schéma de signature numérique ?

Une approche consiste à prendre le problème RSA et à construire des schémas de manière directe. Par exemple, supposons que vous ayez généré un ensemble de variables \Pi tel que décrit dans le problème RSA, en vous assurant que p et q sont suffisamment grands. Vous définissez votre clé publique comme étant (N, e) et vous partagez cette information avec le monde. Comme décrit ci-dessus, vous conservez les valeurs p, q, \phi(n) et d secrètes. En fait, d est votre clé privée.

Toute personne qui souhaite vous envoyer un message m qui est un élément de C_N pourrait simplement le chiffrer comme suit : c = m^e \mod N. (Le texte chiffré c ici est équivalent à la valeur y dans le problème RSA.) Vous pouvez facilement déchiffrer ce message en calculant simplement c^d \mod N.

Vous pourriez essayer de créer un schéma de signature numérique de la même manière. Supposons que vous vouliez envoyer un message m accompagné d'une signature numérique S. Vous pourriez simplement définir S = m^d \mod N et envoyer la paire (m, S) au destinataire. N'importe qui peut vérifier la signature numérique en vérifiant si S^e \mod N = m \mod N. Tout attaquant, cependant, aurait beaucoup de mal à créer une valeur valide S pour un message donné, puisqu'il ne possède pas d.

Malheureusement, transformer un problème intrinsèquement difficile, le problème RSA, en un schéma cryptographique n'est pas aussi simple. Pour le schéma de chiffrement simple décrit ci-dessus, vous ne pouvez sélectionner que des copremiers de N comme messages. Cela ne laisse pas beaucoup de messages possibles, certainement pas assez pour une communication standard. De plus, ces messages doivent être choisis de manière aléatoire, ce qui semble peu pratique. Enfin, tout message sélectionné deux fois produira exactement le même texte chiffré. Ceci est extrêmement indésirable dans tout schéma de chiffrement et ne répond pas aux normes modernes rigoureuses de sécurité en chiffrement.

Les problèmes deviennent encore pires pour notre schéma de signature numérique simplifié. En l'état, tout attaquant peut facilement falsifier des signatures numériques en sélectionnant d'abord un copremier de N comme signature, puis en calculant le message original correspondant. Cela viole clairement l'exigence d'inforgeabilité existentielle.

Cependant, en ajoutant une certaine complexité astucieuse, le problème RSA peut être utilisé pour créer un schéma de chiffrement par clé publique sécurisé ainsi qu'un schéma de signature numérique sécurisé. Nous n'entrerons pas dans les détails de ces constructions ici. [4] Il est important de noter, cependant, que cette complexité supplémentaire ne change pas le problème RSA fondamental sur lequel ces schémas sont basés.

Notes :

[4] Voir par exemple Jonathan Katz et Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL : 2015), pp. 410–32 pour le chiffrement RSA et pp. 444–41 pour les signatures numériques RSA.

Section finale

Avis & Notes

366d6fd0-ceb2-4299-bf37-8c6dfcb681d5 true

Examen Final

44882d2b-63cd-4fde-8485-f76f14d8b2fe true

Conclusion

f1905f78-8cf7-5031-949a-dfa8b76079b4 true