name: Les rouages des portefeuilles Bitcoin goal: Plongez dans les principes cryptographiques qui font fonctionner les portefeuilles Bitcoin. objectives:
- Définir les notions théoriques nécessaires à la compréhension des algorithmes cryptographiques utilisés sur Bitcoin.
- Comprendre en intégralité la construction d'un portefeuille déterministe et hiérachique.
- Savoir identifier et réduire les risques liés à la gestion d’un portefeuille.
- Comprendre les principes des fonctions de hachage, des clés cryptographiques et des signatures numériques.
Un voyage au cœur des portefeuilles Bitcoin
Découvrez les secrets des portefeuilles Bitcoin déterministes et hiérarchiques avec notre formation CYP201 ! Que vous soyez un utilisateur régulier ou un passionné cherchant à approfondir vos connaissances, ce cours vous offre une immersion complète dans les rouages de ces outils que nous utilisons tous au quotidien.
Découvrez les mécanismes des fonctions de hachage, des signatures numériques (ECDSA et Schnorr), de la phrase mnémonique, des clés cryptographiques et de la création des adresses de réception, tout en explorant des stratégies de sécurisation avancées.
Cette formation vous dotera non seulement des connaissances pour comprendre la structure d'un portefeuille Bitcoin, mais vous préparera également à plonger plus profondément dans le passionnant univers de la cryptographie.
Grâce à une pédagogie claire, plus de 60 schémas explicatifs et des exemples concrets, CYP201 vous permettra de comprendre de A à Z comment fonctionne votre portefeuille, afin de naviguer dans l’univers de Bitcoin en toute confiance. Reprenez le contrôle sur vos UTXOs dès aujourd'hui en comprenant comment fonctionnent les portefeuilles HD !
Introduction
Introduction de la formation
Bienvenue dans la formation CYP201, dans laquelle nous allons explorer en profondeur le fonctionnement des portefeuilles Bitcoin HD. Ce cours s’adresse à tous ceux qui souhaitent comprendre les bases techniques de l'utilisation de Bitcoin, qu’ils soient simples utilisateurs, amateurs éclairés ou futurs experts.
L’objectif de cette formation est de vous donner les clés pour maîtriser les outils que vous utilisez au quotidien. Les portefeuilles Bitcoin HD, qui sont au cœur de votre expérience utilisateur, reposent sur des concepts parfois complexes, que nous allons essayer de rendre accessibles. Ensemble, nous allons les démystifier !
Avant d’entrer dans le détail de la construction et du fonctionnement des portefeuilles Bitcoin, nous commencerons avec quelques chapitres sur les primitives cryptographiques à connaître pour la suite.
Nous débuterons avec les fonctions de hachage cryptographique, fondamentales tant pour les portefeuilles que pour le protocole Bitcoin lui-même. Vous découvrirez leurs principales caractéristiques, les fonctions spécifiques utilisées dans Bitcoin, et dans un chapitre plus technique, vous découvrirez en détail les rouages de la reine des fonctions de hachage : SHA256.
Ensuite, nous aborderons le fonctionnement des algorithmes de signature numérique que vous utilisez au quotidien pour sécuriser vos UTXOs. Bitcoin en utilise deux : ECDSA et le protocole de Schnorr. Vous apprendrez quelles primitives mathématiques sous-tendent ces algorithmes et comment ils garantissent la sécurité des transactions.
Une fois que nous aurons bien compris ces quelques éléments sur la cryptographie, nous passerons enfin au cœur de la formation : les portefeuilles déterministes et hiérarchiques ! Il y a tout d'abord une section dédiée aux phrases mnémoniques, ces suites de 12 ou 24 mots qui permettent de créer et de restaurer vos portefeuilles. Vous découvrirez comment ces mots sont générés à partir d’une source d’entropie et en quoi ils facilitent l’utilisation de Bitcoin.

La formation continuera avec l’étude de la passphrase BIP39, de la graine (à ne pas confondre avec la phrase mnémonique), du code chaîne maître et de la clé maîtresse. Nous verrons en détail ce que sont ces éléments, leurs rôles respectifs et la manière dont ils sont calculés.

Enfin, à partir de la clé maîtresse, nous découvrirons comment les paires de clés cryptographiques sont dérivées de manière déterministe et hiérarchique jusqu’aux adresses de réception.

Cette formation vous permettra d’utiliser vos logiciels de portefeuille en toute confiance, tout en renforçant vos compétences pour identifier et atténuer les risques. Préparez-vous à devenir un véritable expert des portefeuilles Bitcoin !
Les fonctions de hachage
Introduction aux fonctions de hachage
Le premier type d'algorithmes cryptographiques utilisé sur Bitcoin regroupe les fonctions de hachage. Elles jouent un rôle essentiel à différents niveaux du protocole, mais également au sein des portefeuilles Bitcoin. Découvrons ensemble ce qu'est une fonction de hachage et à quoi ça sert sur Bitcoin.
Définition et principe du hachage
Le hachage est un procédé qui permet de transformer une information de longueur arbitraire en une autre information de longueur fixe par le biais d'une fonction de hachage cryptographique. Autrement dit, une fonction de hachage prend une entrée de taille quelconque et la convertit en une empreinte de taille fixe, appelée "hash".
Le hash peut également parfois être désigné par les termes "digest", "condensat", "condensé" ou "haché".
Par exemple, la fonction de hachage SHA256 produit un hash d'une longueur fixe de 256 bits. Ainsi, si l’on utilise l’entrée "PlanB", un message de longueur arbitraire, le hash généré sera l'empreinte de 256 bits suivante :
24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688

Caractéristiques des fonctions de hachage
Ces fonctions de hachage cryptographiques possèdent plusieurs caractéristiques essentielles qui les rendent particulièrement utiles dans le contexte de Bitcoin et d'autres systèmes informatiques :
- L'irréversibilité (ou résistance à la préimage)
- La résistance à la falsification (effet avalanche)
- La résistance aux collisions
- La résistance à la seconde préimage
1. L'irréversibilité (résistance à la préimage) :
L'irréversibilité signifie qu'il est facile de calculer le hash à partir de l'information en entrée, mais que le calcul inverse, c'est-à-dire retrouver l'entrée à partir du hash, est pratiquement impossible. Cette propriété rend les fonctions de hachage parfaites pour créer des empreintes numériques uniques sans compromettre les informations d'origine.
Dans l'exemple donné, obtenir le hash 24f1b9… en connaissant
l'entrée "PlanB" est simple et rapide. Toutefois, retrouver le
message "PlanB" en connaissant uniquement 24f1b9… est impossible.

Il est donc impossible de trouver une préimage m pour un hash h tel que h = \text{HASH}(m),
où \text{HASH} est une
fonction de hachage cryptographique.
2. La résistance à la falsification (effet avalanche)
La deuxième caractéristique est la résistance à la falsification, également connue sous le nom d'effet avalanche. Cette caractéristique s'observe sur une fonction de hachage si une petite modification du message d'entrée entraîne une modification radicale du hash de sortie.
Si l'on reprend notre exemple avec l’entrée "PlanB" et la fonction SHA256, nous avons vu que le hash généré est le suivant :
24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688
Si l'on modifie très légèrement l'entrée en utilisant cette fois "Planb", alors le simple passage d'un "B" majuscule à un "b" minuscule modifie complètement le hash en sortie de SHA256 :
bb038b4503ac5d90e1205788b00f8f314583c5e22f72bec84b8735ba5a36df3f

Cette propriété garantit que même une altération minime du message original est immédiatement détectable, car cela ne modifie pas seulement une petite partie du hash, mais bien tout le hash. Cela pourra nous intéresser dans divers domaines pour vérifier l'intégrité de messages, de logiciels ou encore, de transactions Bitcoin.
3. La résistance aux collisions
La troisième caractéristique est la résistance aux collisions. Une fonction
de hachage est résistante aux collisions s'il est computationnellement
impossible de trouver 2 messages différents qui produisent le même hash en
sortie de la fonction. Formellement, il est difficile de trouver deux
messages distincts m_1 et m_2 tels que :
\text{HASH}(m_1) = \text{HASH}(m_2)
En réalité, il est mathématiquement inévitable que des collisions existent
pour les fonctions de hachage, car la taille des entrées peut être
supérieure à celle des sorties. C'est ce que l'on appelle le principe des
tiroirs de Dirichlet : si n objets sont répartis dans m tiroirs, avec m < n,
alors au moins un tiroir contiendra forcément deux objets ou plus. Pour une
fonction de hachage, ce principe s'applique, car le nombre de messages
possibles est (presque) infini, tandis que le nombre de hash possibles est
fini (2^{256} dans le
cas de SHA256).
Ainsi, cette caractéristique ne signifie pas qu'il n'existe aucune collision pour les fonctions de hachage, mais plutôt qu'une bonne fonction de hachage rend la probabilité de trouver une collision négligeable. Cette caractéristique n’est par exemple plus vérifiée sur les algorithmes SHA-0 et SHA-1, prédécesseurs des SHA-2, pour lesquels des collisions ont été trouvées. Ces fonctions sont donc aujourd’hui déconseillées et souvent considérées comme désuètes.
Pour une fonction de hachage de n bits, la résistance aux collisions est de l'ordre de 2^{\frac{n}{2}}, conformément à l'attaque de l'anniversaire. Par exemple, pour SHA256 (n = 256), la complexité de trouver une collision est de l'ordre de 2^{128} essais. Concrètement, cela veut dire que si l'on passe 2^{128} messages différents
dans la fonction, on va probablement trouver une collision.
4. La résistance à la seconde préimage
La résistance à la seconde préimage est une autre caractéristique importante
des fonctions de hachage. Elle stipule qu'étant donné un message m_1 et son hash h, il est
computationnellement infaisable de trouver un autre message m_2 \neq m_1 tel que :
\text{HASH}(m_1) = \text{HASH}(m_2)La résistance à la seconde préimage est donc un petit peu similaire à la
résistance à la collision, sauf qu'ici, l'attaque est plus difficile car
l'attaquant ne peut pas choisir librement m_1.

Applications des fonctions de hachage dans Bitcoin
La fonction de hachage la plus utilisée dans Bitcoin est SHA256 ("Secure Hash Algorithm 256 bits"). Conçue au début des années 2000 par la NSA et standardisée par le NIST, elle produit un hash de 256 bits en sortie.
Cette fonction est utilisée dans de nombreux aspects de Bitcoin. Au niveau protocolaire, elle intervient dans le mécanisme de Proof-of-Work, où elle est appliquée en double hachage pour rechercher une collision partielle entre l'en-tête d'un bloc candidat, créé par un mineur, et la cible de difficulté. Si cette collision partielle est trouvée, le bloc candidat devient valide et peut être ajouté à la blockchain.
SHA256 est également utilisée dans la construction d'un arbre de Merkle, qui est notamment l'accumulateur utilisé pour l'enregistrement des transactions dans les blocs. On retrouve aussi cette structure dans le protocole Utreexo qui permet de réduire la taille de l'UTXO Set. Aussi, avec l'introduction de Taproot en 2021, SHA256 est exploitée dans les MAST (Merkelised Alternative Script Tree), qui permettent de ne révéler que les conditions de dépense effectivement utilisées dans un script, sans divulguer les autres options possibles. On la retrouve également dans le calcul de l'identifiant des transactions, dans la transmission des paquets sur le réseau P2P, dans les signatures électroniques... Enfin, et c'est ce qui nous intéressera particulièrement dans cette formation, SHA256 est utilisée au niveau applicatif pour la construction des portefeuilles Bitcoin et la dérivation des adresses.
La plupart du temps, lorsque vous croiserez l'utilisation de SHA256 sur Bitcoin, ce sera en réalité un double hachage SHA256, noté "HASH256", et qui consiste simplement à appliquer SHA256 deux fois successivement :
\text{HASH256}(m) = \text{SHA256}(\text{SHA256}(m))Cette pratique du double hachage ajoute une couche supplémentaire de sécurité contre certaines attaques potentielles, même si un SHA256 simple est aujourd'hui considéré comme sûr cryptographiquement.
Une autre fonction de hachage disponible dans le langage de Script et utilisée pour la dérivation des adresses de réception est la fonction RIPEMD160. Cette fonction produit un hash de 160 bits (donc plus court que SHA256). Elle est généralement combinée avec SHA256 pour former la fonction HASH160 :
\text{HASH160}(m) = \text{RIPEMD160}(\text{SHA256}(m))Cette combinaison est employée pour générer des hash plus courts, notamment dans la création de certaines adresses Bitcoin qui représentent des hachages de clés ou des hachages de script, ainsi que pour produire des empreintes de clés.
Enfin, au niveau applicatif uniquement, on utilise parfois également la fonction SHA512, qui intervient de manière indirecte dans la dérivation de clés pour les portefeuilles. Cette fonction est très similaire à SHA256 dans son fonctionnement ; toutes deux appartiennent à la même famille SHA2, mais SHA512 produit, comme son nom l'indique, un hash de 512 bits, contre 256 bits pour SHA256. Nous détaillerons son utilisation dans les chapitres suivants.
Vous connaissez maintenant les bases indispensables sur les fonctions de hachage pour la suite. Dans le chapitre suivant, je vous propose de découvrir plus en détail le fonctionnement de la fonction qui est au cœur de Bitcoin : SHA256. Nous allons la décortiquer pour comprendre comment elle parvient à obtenir les caractéristiques que nous avons décrites ici. Ce prochain chapitre est assez long et technique, mais il n'est pas indispensable pour suivre la suite de la formation. Donc, si vous avez des difficultés à le comprendre, ne vous inquiétez pas et passez directement au chapitre suivant, qui, lui, sera bien plus accessible.
Les rouages de SHA256
Nous avons vu précédemment que les fonctions de hachage possèdent des caractéristiques importantes qui justifient leur utilisation sur Bitcoin. Examinons maintenant les mécanismes internes de ces fonctions de hachage qui leur confèrent ces propriétés, et pour ce faire, je vous propose de décortiquer le fonctionnement de SHA256.
Les fonctions SHA256 et SHA512 appartiennent à la même famille des SHA2. Leur mécanisme est basé sur une construction spécifique appelée construction de Merkle-Damgård. RIPEMD160 utilise également ce même type de construction.
Pour rappel, nous avons donc un message de taille arbitraire en entrée de SHA256, et nous allons le passer dans la fonction pour obtenir un hash de 256 bits en sortie.
Pré-traitement de l'input
Pour commencer, il faut préparer notre message m en entrée afin qu'il ait une longueur standard qui est un multiple de 512 bits.
Cette étape est importante pour le bon fonctionnement de l'algorithme par la
suite.
Pour ce faire, on commence avec l'étape des bits de rembourrage. On ajoute
d'abord un bit séparateur 1 au message, suivi d'un certain
nombre de bits 0. Le nombre de bits 0 ajoutés est
calculé de manière à ce que la longueur totale du message après cet ajout
soit congrue à 448 modulo 512. On a donc la longueur L du message avec les bits de
rembourrage qui est égale à :
L \equiv 448 \mod 512\text{mod}, pour
modulo, est une opération mathématique qui, entre deux nombres entiers,
renvoie le reste de la division euclidienne du premier par le second. Par
exemple : 16 \mod 5 = 1.
C'est une opération très utilisée en cryptographie.
Ici, l'étape du rembourrage garantit que, après l'ajout des 64 bits de
l'étape suivante, la longueur totale du message égalisé sera un multiple de
512 bits. Si le message initial a une longueur de M bits, le nombre (N) de bits 0 à ajouter est donc :
N = (448 - (M + 1) \mod 512) \mod 512Par exemple, si le message initial mesure 950 bits, le calcul sera le suivant :
\begin{align*}
M & = 950 \\
M + 1 & = 951 \\
(M + 1) \mod 512 & = 951 \mod 512 \\
& = 951 - 512 \cdot \left\lfloor \frac{951}{512} \right\rfloor \\
& = 951 - 512 \cdot 1 \\
& = 951 - 512 \\
& = 439 \\
\\
448 - (M + 1) \mod 512 & = 448 - 439 \\
& = 9 \\
\\
N & = (448 - (M + 1) \mod 512) \mod 512 \\
N & = 9 \mod 512 \\
& = 9
\end{align*}Nous aurions ainsi 9 0 en plus du séparateur 1.
Nos bits de rembourrage à ajouter directement après notre message M seraient donc :
1000 0000 00
Après avoir ajouté les bits de rembourrage à notre message M, on ajoute également une représentation de 64 bits de la longueur
originale du message M,
exprimée en binaire. Cela permet à la fonction de hachage d'être sensible à
l'ordre des bits et à la longueur du message.
Si l'on reprend notre exemple avec un message initial de 950 bits, on va
convertir le nombre décimal 950 en nombre binaire ce qui nous
donne 1110 1101 10. On complète ce nombre avec des zéros à la
base pour faire 64 bits au total. Dans notre exemple, cela donne :
0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0011 1011 0110
Ce rembourrage de la taille est ajouté à la suite du rembourrage des bits. Le message après notre pré-traitement se compose donc de trois parties :
- Le message original
M; - Un bit
1suivi de plusieurs bits0pour former le rembourrage des bits ; - Une représentation de 64 bits de la longueur de
Mpour former le rembourrage avec la taille.

Initialisation des variables
SHA256 utilise huit variables d'état initiales, notées A à H, chacune de 32 bits. Ces
variables sont initialisées avec des constantes spécifiques, qui sont les
parties fractionnaires des racines carrées des huit premiers nombres
premiers. Nous allons utiliser ces valeurs par la suite durant le processus
du hachage :
A = 0x6a09e667B = 0xbb67ae85C = 0x3c6ef372D = 0xa54ff53aE = 0x510e527fF = 0x9b05688cG = 0x1f83d9abH = 0x5be0cd19
SHA256 utilise également 64 autres constantes, notées K_0 à K_{63}, qui sont
les parties fractionnaires des racines cubiques des 64 premiers nombres
premiers :
K[0 \ldots 63] = \begin{pmatrix}
0x428a2f98, & 0x71374491, & 0xb5c0fbcf, & 0xe9b5dba5, \\
0x3956c25b, & 0x59f111f1, & 0x923f82a4, & 0xab1c5ed5, \\
0xd807aa98, & 0x12835b01, & 0x243185be, & 0x550c7dc3, \\
0x72be5d74, & 0x80deb1fe, & 0x9bdc06a7, & 0xc19bf174, \\
0xe49b69c1, & 0xefbe4786, & 0x0fc19dc6, & 0x240ca1cc, \\
0x2de92c6f, & 0x4a7484aa, & 0x5cb0a9dc, & 0x76f988da, \\
0x983e5152, & 0xa831c66d, & 0xb00327c8, & 0xbf597fc7, \\
0xc6e00bf3, & 0xd5a79147, & 0x06ca6351, & 0x14292967, \\
0x27b70a85, & 0x2e1b2138, & 0x4d2c6dfc, & 0x53380d13, \\
0x650a7354, & 0x766a0abb, & 0x81c2c92e, & 0x92722c85, \\
0xa2bfe8a1, & 0xa81a664b, & 0xc24b8b70, & 0xc76c51a3, \\
0xd192e819, & 0xd6990624, & 0xf40e3585, & 0x106aa070, \\
0x19a4c116, & 0x1e376c08, & 0x2748774c, & 0x34b0bcb5, \\
0x391c0cb3, & 0x4ed8aa4a, & 0x5b9cca4f, & 0x682e6ff3, \\
0x748f82ee, & 0x78a5636f, & 0x84c87814, & 0x8cc70208, \\
0x90befffa, & 0xa4506ceb, & 0xbef9a3f7, & 0xc67178f2
\end{pmatrix}Division de l'input
Maintenant que nous avons un input égalisé, nous allons maintenant aborder la phase de traitement principale de l'algorithme SHA256 : la fonction de compression. Cette étape est très importante, car c'est principalement elle qui confère à la fonction de hachage ses propriétés cryptographiques que nous avons étudiées dans le chapitre précédent.
Tout d'abord, on commence par diviser notre message égalisé (résultat des
étapes de pré-traitement) en plusieurs blocs P de 512 bits chacun. Si notre message égalisé a une taille totale de n \times 512 bits, nous aurons donc n blocs, chacun de 512 bits. Chaque bloc de 512 bits sera traité
individuellement par la fonction de compression, qui consiste en 64 tours
d'opérations successives. Nommons ces blocs P_1, P_2, P_3...
Opérations logiques
Avant d'explorer en détail la fonction de compression, il est important de comprendre les opérations logiques de base utilisées dans celle-ci. Ces opérations, basées sur l'algèbre de Boole, s'opèrent au niveau des bits. Les opérations logiques de base utilisées sont :
- La conjonction (AND) : notée
\land, correspond à un "ET" logique. - La disjonction (OR) : notée
\lor, correspond à un "OU" logique. - La négation (NOT) : notée
\lnot, correspond à un "NON" logique.
À partir de ces opérations de base, nous pouvons définir des opérations plus
complexes, telles que le "OU exclusif" (XOR) noté \oplus, qui est très utilisé en cryptographie.
Chaque opération logique peut être représentée par une table de vérité, qui
indique le résultat pour toutes les combinaisons possibles des valeurs
d'entrée en binaire (deux opérandes p et q).
Pour le XOR (\oplus) :
p | q | p \oplus q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Pour le AND (\land) :
p | q | p \land q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Pour le NOT (\lnot p) :
p | \lnot p |
|---|---|
| 0 | 1 |
| 1 | 0 |
Prenons un exemple pour bien comprendre le fonctionnement de l'opération XOR au niveau des bits. Si nous avons deux nombres binaires sur 6 bits :
a = 101100b = 001000
Alors :
a \oplus b = 101100 \oplus 001000 = 100100En appliquant le XOR bit par bit :
| Position du bit | a | b | a \oplus b |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 1 | 0 | 1 |
| 5 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 |
Le résultat est donc 100100.
En plus des opérations logiques, la fonction de compression utilise des opérations de décalage de bits, qui vont jouer un rôle essentiel pour la diffusion des bits dans l'algorithme.
Tout d'abord il y a l'opération de décalage logique à droite, notée ShR_n(x), qui décale tous les bits de x vers la droite de n positions,
en complétant les bits vacants à gauche par des zéros.
Par exemple, pour x = 101100001 (sur 9 bits) et n = 4 :
ShR_4(101100001) = 000010110Schématiquement, l'opération de décalage à droite pourrait être vue comme cela :

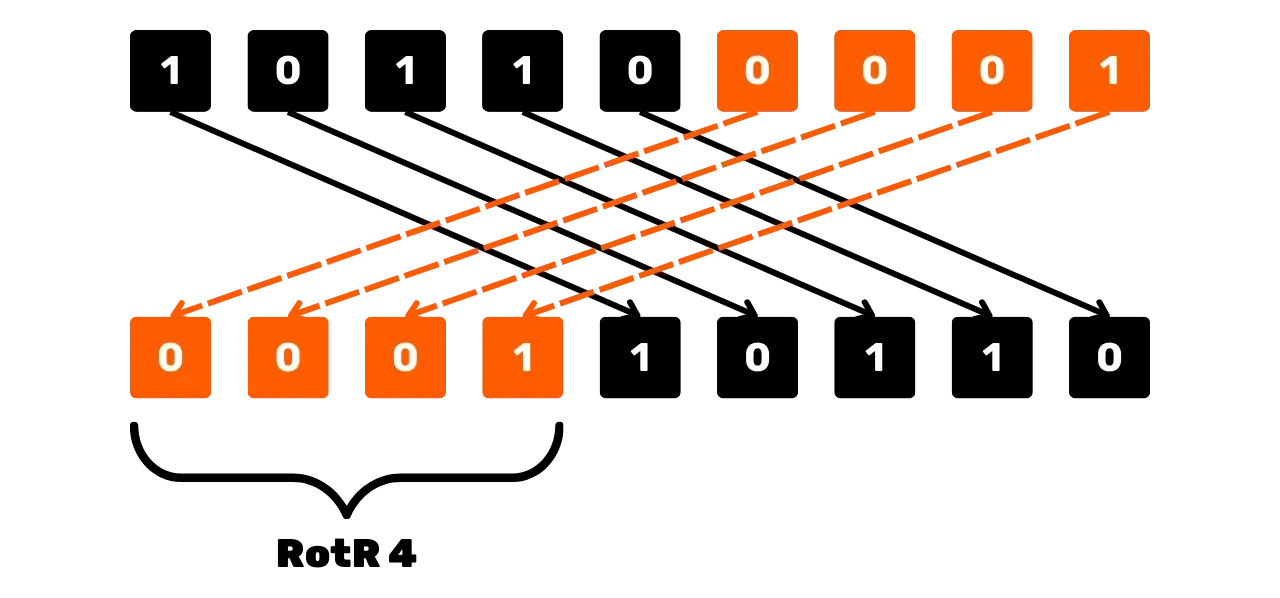
Une autre opération que l'on utilise dans SHA256 pour manier les bits est
celle de la rotation circulaire à droite, notée RotR_n(x), qui décale les bits de x vers la droite de n positions,
en réinsérant les bits décalés à droite au début de la chaîne.
Par exemple, pour x = 101100001 (sur 9 bits) et n = 4 :
RotR_4(101100001) = 000110110Schématiquement, l'opération de décalage circulaire à droite pourrait être vue comme cela :
Fonction de compression
Maintenant que nous avons compris les opérations de base, examinons la fonction de compression de SHA256 en détail.
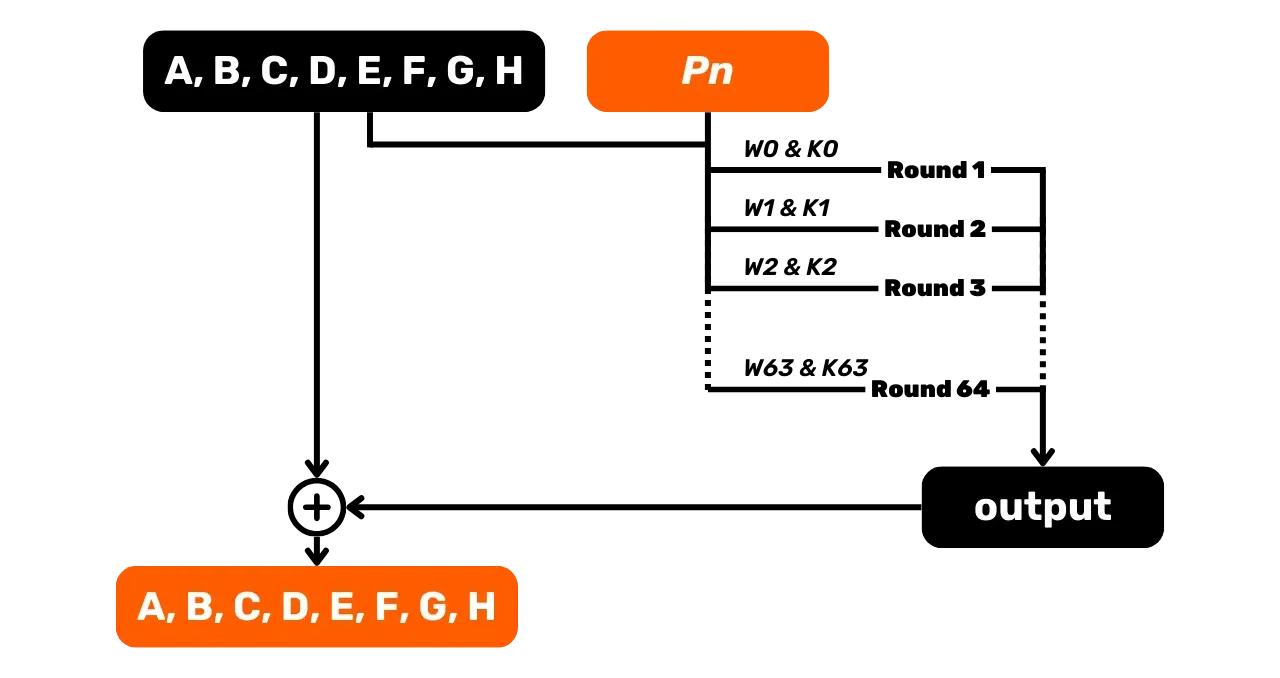
À l'étape précédente, nous avons donc divisé notre input en plusieurs
morceaux P de 512 bits
chacun. Pour chaque bloc P de
512 bits, nous avons :
- Les mots de message
W_i: pouride 0 à 63. - Les constantes
K_i: pouride 0 à 63, définies à l'étape précédente. - Les variables d'état
A, B, C, D, E, F, G, H: initialisées avec les valeurs de l'étape précédente.
Les 16 premiers mots, W_0 à W_{15}, sont
directement extraits du bloc P de 512 bits traité. Chaque mot W_i est constitué de 32 bits consécutifs du bloc. On prend donc par exemple
notre premier morceau de l'input P_1, et on le divise encore
en de plus petits morceaux de 32 bits chacun que l'on appelle les mots.
Les 48 mots suivants (W_{16} à W_{63}) sont
générés à l'aide de la formule suivante :
W_i = W_{i-16} + \sigma_0(W_{i-15}) + W_{i-7} + \sigma_1(W_{i-2}) \mod 2^{32}Avec :
\sigma_0(x) = RotR_7(x) \oplus RotR_{18}(x) \oplus ShR_3(x)\sigma_1(x) = RotR_{17}(x) \oplus RotR_{19}(x) \oplus ShR_{10}(x)
Dans ce cas, x est égal à W_{i-15} pour \sigma_0(x) et W_{i-2} pour \sigma_1(x).
Une fois que nous avons déterminé tous les mots W_i pour notre morceau de 512 bits, nous pouvons passer à la fonction de compression
qui consiste à effectuer 64 tours.
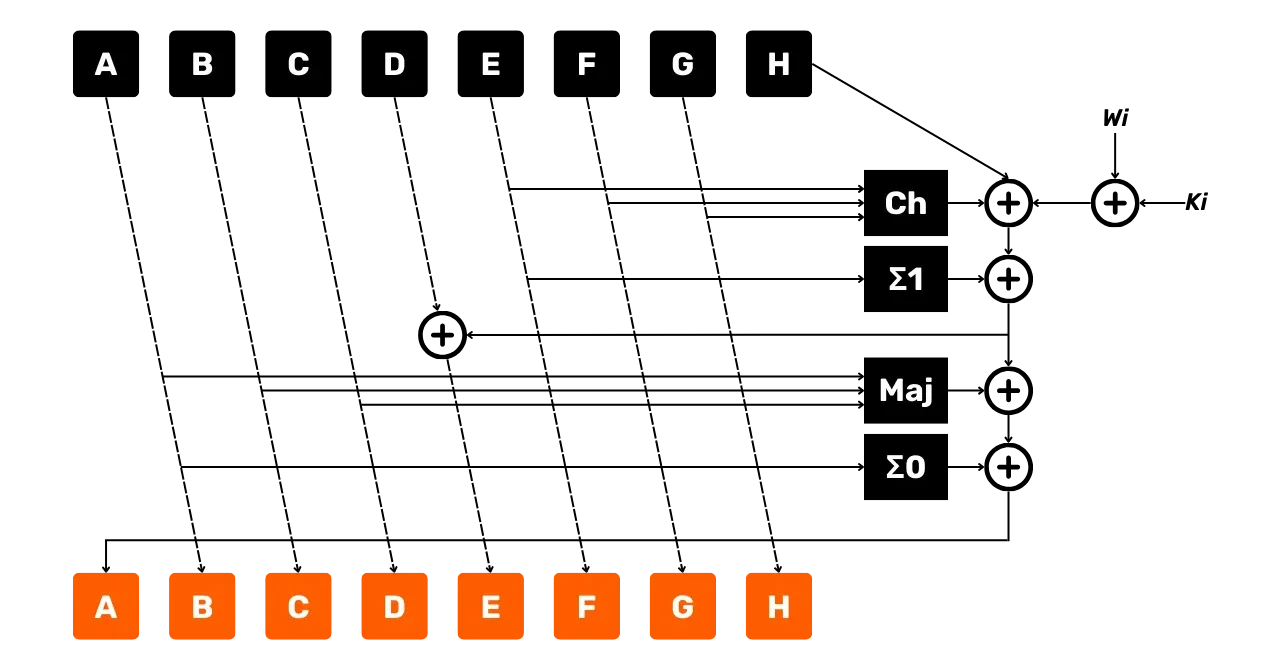
Pour chaque tour i de 0 à 63,
nous avons donc 3 types d'inputs différents. D'abord, les W_i que nous venons de déterminer, constitués en partie de notre morceau P_n du message. Ensuite, les 64 constantes K_i. Enfin, nous utilisons
les variables d'état A, B, C, D, E, F, G, et H, qui vont évoluer tout au
long du processus de hachage et être modifiées à chaque fonction de
compression. Cependant, pour le premier morceau P_1, on utilise les
constantes initiales données précédemment.
Nous effectuons donc les opérations suivantes sur nos inputs :
- Fonction
\Sigma_0:
\Sigma_0(A) = RotR_2(A) \oplus RotR_{13}(A) \oplus RotR_{22}(A)- Fonction
\Sigma_1:
\Sigma_1(E) = RotR_6(E) \oplus RotR_{11}(E) \oplus RotR_{25}(E)- Fonction
Ch("Choose") :
Ch(E, F, G) = (E \land F) \oplus (\lnot E \land G)- Fonction
Maj("Majority") :
Maj(A, B, C) = (A \land B) \oplus (A \land C) \oplus (B \land C)Nous calculons ensuite 2 variables temporaires :
temp1:
temp1 = H + \Sigma_1(E) + Ch(E, F, G) + K_i + W_i \mod 2^{32}temp2:
temp2 = \Sigma_0(A) + Maj(A, B, C) \mod 2^{32}Ensuite, nous mettons à jour les variables d'état comme suit :
\begin{cases}
H = G \\
G = F \\
F = E \\
E = D + temp1 \mod 2^{32} \\
D = C \\
C = B \\
B = A \\
A = temp1 + temp2 \mod 2^{32}
\end{cases}Le schéma suivant représente un tour de la fonction de compression de SHA256 comme nous venons de le décrire :

- Les flèches indiquent le flux des données ;
- Les boîtes représentent les opérations effectuées ;
- Les
+entourés représentent l'addition modulo2^{32}.
On peut déjà observer que ce tour nous donne en sortie de nouvelles
variables d'état A, B, C, D, E, F, G, et H. Ces nouvelles variables
serviront d’entrée pour le tour suivant, qui produira à son tour de
nouvelles variables A, B, C, D, E, F, G, et H, que l'on utilisera pour le
tour d'après. Ce processus se poursuit ainsi jusqu'au 64ème tour.
Après les 64 tours, nous mettons à jour les valeurs initiales des variables d'état en les additionnant aux valeurs finales en sortie du tour n°64 :
\begin{cases}
A = A_{\text{initial}} + A \mod 2^{32} \\
B = B_{\text{initial}} + B \mod 2^{32} \\
C = C_{\text{initial}} + C \mod 2^{32} \\
D = D_{\text{initial}} + D \mod 2^{32} \\
E = E_{\text{initial}} + E \mod 2^{32} \\
F = F_{\text{initial}} + F \mod 2^{32} \\
G = G_{\text{initial}} + G \mod 2^{32} \\
H = H_{\text{initial}} + H \mod 2^{32}
\end{cases}Ces nouvelles valeurs de A, B, C, D, E, F, G, et H serviront de valeurs initiales pour le bloc suivant, P_2. Pour ce bloc P_2, on reproduit le même
processus de compression avec 64 tours, puis on met à jour les variables
pour le bloc P_3, et ainsi de
suite jusqu'au dernier bloc de notre input égalisé.
Après avoir traité tous les blocs du message, nous concaténons les valeurs
finales des variables A, B, C, D, E, F, G, et H pour former le hash final de
256 bits de notre fonction de hachage :
\text{Hash} = A \Vert B \Vert C \Vert D \Vert E \Vert F \Vert G \Vert HChaque variable est un entier de 32 bits, donc leur concaténation donne bien toujours un résultat de 256 bits, et ce, quelle que soit la taille de notre message en input de la fonction de hachage.
Justification des propriétés cryptographiques
Mais alors, en quoi cette fonction est-elle irréversible, résistante aux collisions et résistante à la falsification ?
Pour la résistance à la falsification, c’est assez simple à comprendre. Il y a tellement de calculs effectués en cascade, qui dépendent à la fois de l’input et des constantes, que la moindre modification du message initial change complètement le chemin parcouru, et donc change complètement le hash en sortie. C'est ce que l'on appelle l'effet avalanche. Cette propriété est en partie assurée par le mélange des états intermédiaires avec les états initiaux pour chaque morceau.
Ensuite, lorsque l’on parle d’une fonction de hachage cryptographique, le
terme "irréversibilité" n’est généralement pas utilisé. À la place, on parle
de “résistance à la préimage” qui spécifie que pour tout y donné, il est difficile de trouver un x tel que h(x) = y. Cette
résistance à la préimage, quant à elle, est garantie par la complexité
algébrique et la forte non-linéarité des opérations effectuées dans la
fonction de compression, ainsi que par la perte de certaines informations
dans le processus. Par exemple, pour un résultat donné à une addition
modulo, il existe plusieurs opérandes possibles :
3+2 \mod 10 = 5 \\
7+8 \mod 10 = 5 \\
5+10 \mod 10 = 5On voit bien dans cet exemple qu’en connaissant uniquement le modulo utilisé (10) et le résultat (5), on ne peut pas déterminer avec certitude quels sont les deux bons opérandes utilisés dans l’addition. On dit qu’il existe plusieurs congrus modulo 10.
Pour l’opération XOR, on est confronté au même problème. Rappelez-vous de la
table de vérité de cette opération : toute sortie de 1 bit peut être
déterminée par deux configurations différentes en entrées qui ont exactement
la même probabilité d’être les bonnes valeurs. On ne peut donc pas
déterminer avec certitude les opérandes d’un XOR en connaissant uniquement
son résultat. Si on augmente la taille des opérandes du XOR, le nombre de
possibles entrées en connaissant uniquement le résultat augmente de façon
exponentielle. De plus, le XOR est souvent utilisé aux côtés d’autres
opérations au niveau du bit, comme l’opération \text{RotR}, qui viennent ajouter encore plus d’interprétations possibles au résultat.
On utilise également au sein de la fonction de compression l’opération \text{ShR}. Celle-ci vient supprimer une partie de l’information de base qui est donc
impossible à retrouver par la suite. Il n’y a encore une fois pas de moyen
algébrique pour inverser cette opération. Toutes ces opérations à sens
unique et ces opérations de perte d’information sont utilisées à de très
nombreuses reprises dans les fonctions de compression. Le nombre de
possibles entrées pour une sortie donnée est donc presque infini, et chaque
tentative de calcul inverse mènerait à des équations avec un nombre
d’inconnus très élevé qui augmenterait exponentiellement à chaque étape.
Enfin, pour la caractéristique de résistance aux collisions, plusieurs paramètres entrent en compte. Le pré-traitement du message d’origine tient un rôle essentiel. Sans ce pré-traitement, il pourrait être plus facile de trouver des collisions sur la fonction. Bien que, théoriquement, des collisions existent (en raison du principe des tiroirs), la structure de la fonction de hachage, combinée aux propriétés précédentes, rend la probabilité de trouver une collision extrêmement faible.
Pour qu'une fonction de hachage soit résistante aux collisions, il est essentiel que :
- La sortie soit imprévisible : Toute prévisibilité peut être exploitée pour trouver des collisions plus rapidement qu'avec une attaque par force brute. La fonction assure que chaque bit de la sortie dépend de façon non triviale de l'entrée. En d'autres termes, la fonction est conçue pour que chaque bit du résultat final ait une probabilité indépendante d'être 0 ou 1, même si cette indépendance n'est pas absolue en pratique.
- La distribution des hash soit pseudo-aléatoire : Cela assure que les hash sont répartis de manière uniforme.
- La taille du hash soit conséquente : au plus l'espace possible pour les résultats est grand, au plus il est difficile de trouver une collision.
Les cryptographes conçoivent ces fonctions en évaluant les meilleures attaques possibles pour trouver des collisions, puis en ajustant les paramètres pour rendre ces attaques inefficaces.
Construction de Merkle-Damgård
La structure de SHA256 est basée sur la construction de Merkle-Damgård, qui permet de transformer une fonction de compression en une fonction de hachage pouvant traiter des messages de longueur arbitraire. C'est justement ce que nous venons de voir dans ce chapitre.
Cependant, certaines vieilles fonctions de hachage comme SHA1 ou MD5, qui
utilisent cette construction spécifique, sont vulnérables aux attaques par
extension de longueur. C'est une technique qui permet à un attaquant qui
connaît le hash d’un message M et la longueur de M (sans
connaître le message lui-même) de calculer le hash d’un message M' formé de M concaténé avec un contenu
supplémentaire.
SHA256, même si elle utilise le même type de construction, est en théorie résistante à ce type d'attaque, contrairement à SHA1 et MD5. C'est peut-être ce qui pourrait expliquer le mystère du double hachage implémenté partout dans Bitcoin par Satoshi Nakamoto. Pour éviter ce type d'attaque, il est possible que Satoshi ait préféré utiliser un double SHA256 :
\text{HASH256}(m) = \text{SHA256}(\text{SHA256}(m))Cela renforce la sécurité contre les attaques potentielles liées à la construction de Merkle-Damgård, mais cela n'augmente absolument pas la sécurité du processus de hachage en termes de résistance aux collisions. De plus, même si SHA256 avait été vulnérable à ce type d'attaque, cela n'aurait pas eu d'impact grave, car tous les cas d'utilisation des fonctions de hachage dans Bitcoin concernent des données publiques. Or, l'attaque par extension de longueur peut n'être utile pour un attaquant que si les données hachées sont privées et que l'utilisateur a utilisé la fonction de hachage comme un mécanisme d'authentification pour ces données, à la manière d'un MAC. Ainsi, l'implémentation du double hachage reste un mystère dans la conception de Bitcoin.
Maintenant que nous avons vu en détail le fonctionnement des fonctions de hachage, et notamment de SHA256, utilisée partout dans Bitcoin, nous allons nous pencher plus spécifiquement sur les algorithmes de dérivation employés au niveau applicatif, notamment pour dériver les clés de votre portefeuille.
Les algorithmes utilisés pour la dérivation
Sur Bitcoin au niveau applicatif, en complément des fonctions de hachage, on utilise des algorithmes de dérivation cryptographiques permettant de générer des données sécurisées à partir d'entrées initiales. Bien que ces algorithmes reposent sur des fonctions de hachage, ils répondent à des objectifs différents, notamment en termes d'authentification et de génération de clés. Ces algorithmes conservent en partie les caractéristiques des fonctions de hachage, telles que l'irréversibilité, la résistance à la falsification et la résistance aux collisions.
Sur les portefeuilles Bitcoin, on utilise principalement 2 algorithmes de dérivation :
- HMAC (Hash-based Message Authentication Code)
- PBKDF2 (Password-Based Key Derivation Function 2)
Nous allons explorer ensemble le fonctionnement et le rôle de chacun d'eux.
HMAC-SHA512
HMAC est un algorithme cryptographique permettant de calculer un code d'authentification basé sur une combinaison d’une fonction de hachage et d’une clé secrète. Bitcoin utilise HMAC-SHA512, soit la variante de HMAC utilisant la fonction de hachage SHA512. Nous avons déjà vu dans le chapitre précédent que SHA512 fait partie de la même famille de fonctions de hachage que SHA256, mais elle produit un output de 512 bits.
Voici son schéma de fonctionnement général avec m le message en entrée et K une
clé secrète :
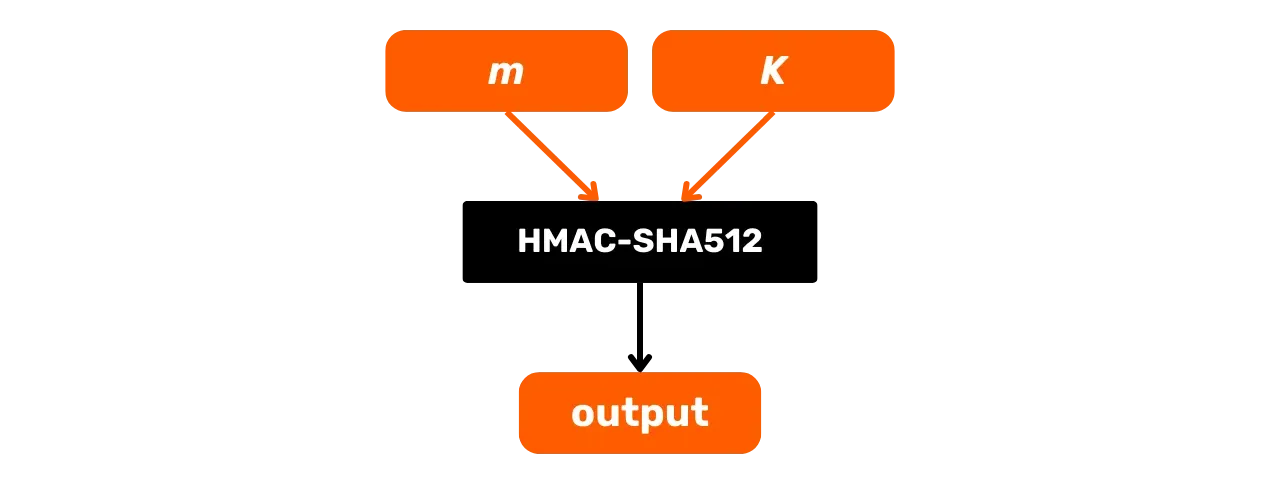
Étudions plus en détail ce qu’il se passe dans cette boîte noire HMAC-SHA512. Soit la fonction HMAC-SHA512 avec :
m: le message de taille arbitraire choisi par l’utilisateur (premier input) ;K: la clé secrète arbitraire choisie par l’utilisateur (second input) ;K': la cléKajustée à la tailleBdes blocs de la fonction de hachage (1024 bits pour SHA512, soit 128 octets) ;\text{SHA512}: la fonction de hachage SHA512 ;\oplus: l'opération XOR (ou exclusif) ;\Vert: l’opérateur de concaténation, reliant les chaînes de bits bout-à-bout ;\text{opad}: constante composée de l’octet0x5crépété 128 fois\text{ipad}: constante composée de l’octet0x36répété 128 fois
Avant de calculer le HMAC, il est nécessaire d'égaliser la clé et les
constantes selon la taille du bloc B. Par exemple, si la clé K est plus courte que 128 octets, on la complète avec des zéros pour obtenir
la taille B. Si K est plus longue que 128 octets, on la compresse avec SHA512, puis on ajoute
des zéros jusqu'à atteindre 128 octets. De cette manière on obtient une clé
égalisée nommée K'.
Les valeurs de \text{opad} et \text{ipad} sont
obtenues en répétant leur octet de base (0x5c pour \text{opad}, 0x36 pour \text{ipad} )
jusqu'à atteindre la taille B. Ainsi, avec B = 128 octets, on a :
\text{opad} = \underbrace{0x5c5c\ldots5c}_{128 \, \text{bytes}}Une fois le prétraitement réalisé, l'algorithme HMAC-SHA512 est défini par l'équation suivante :
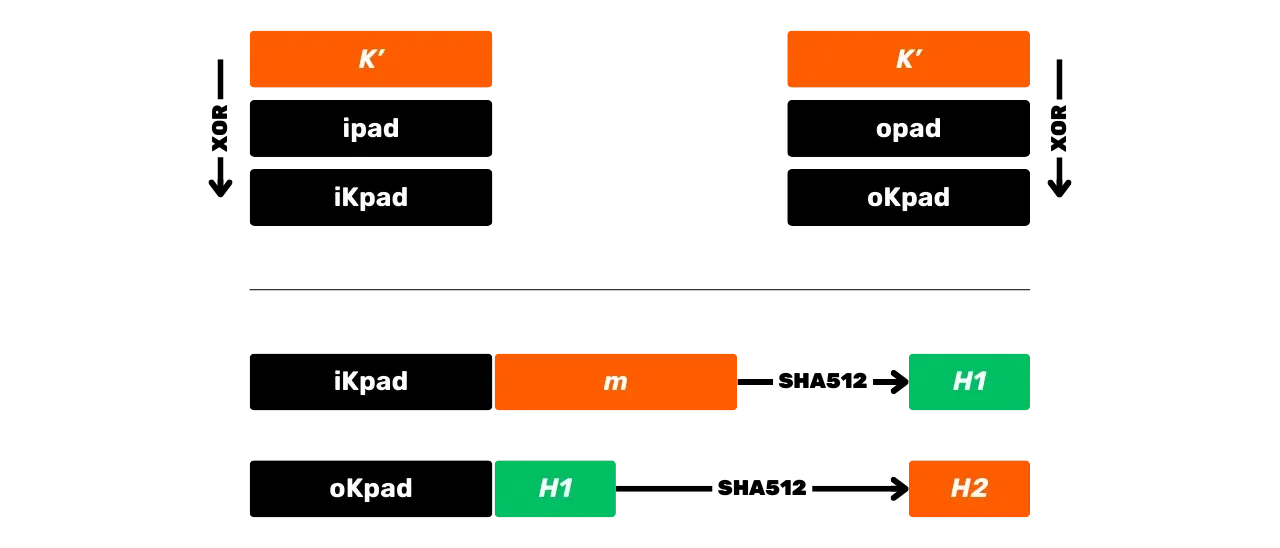
\text {HMAC-SHA512}_K(m) = \text{SHA512} \left( (K' \oplus \text{opad}) \parallel \text{SHA512} \left( (K' \oplus \text{ipad}) \parallel m \right) \right)Cette équation se décompose avec les étapes suivantes :
- On XOR la clé ajustée
K'avec\text{ipad}pour obtenir\text{iKpad}; - On XOR la clé ajustée
K'avec\text{opad}pour obtenir\text{oKpad}; - On concatène
\text{iKpad}avec le messagem. - On hache ce résultat avec SHA512 pour obtenir un hash intermédiaire
H_1. - On concatène
\text{oKpad}avecH_1. - On hache ce résultat avec SHA512 pour obtenir le résultat final
H_2.
Ces étapes peuvent être résumées schématiquement comme suit :
HMAC est utilisé dans Bitcoin notamment pour la dérivation des clés dans les portefeuilles HD (nous en parlerons plus en détail dans les prochains chapitres) et comme composant de PBKDF2.
PBKDF2
PBKDF2 (Password-Based Key Derivation Function 2) est un algorithme de dérivation de clé destiné à renforcer la sécurité des mots de passe. L'algorithme applique une fonction pseudo-aléatoire (ici HMAC-SHA512) sur un mot de passe et un sel cryptographique, puis répète cette opération un certain nombre de fois pour obtenir une clé en sortie.
Dans Bitcoin, PBKDF2 est utilisé pour générer la graine d'un portefeuille HD à partir d’une phrase mnémonique et d'une passphrase (mais nous en parlerons plus en détail dans les prochains chapitres).
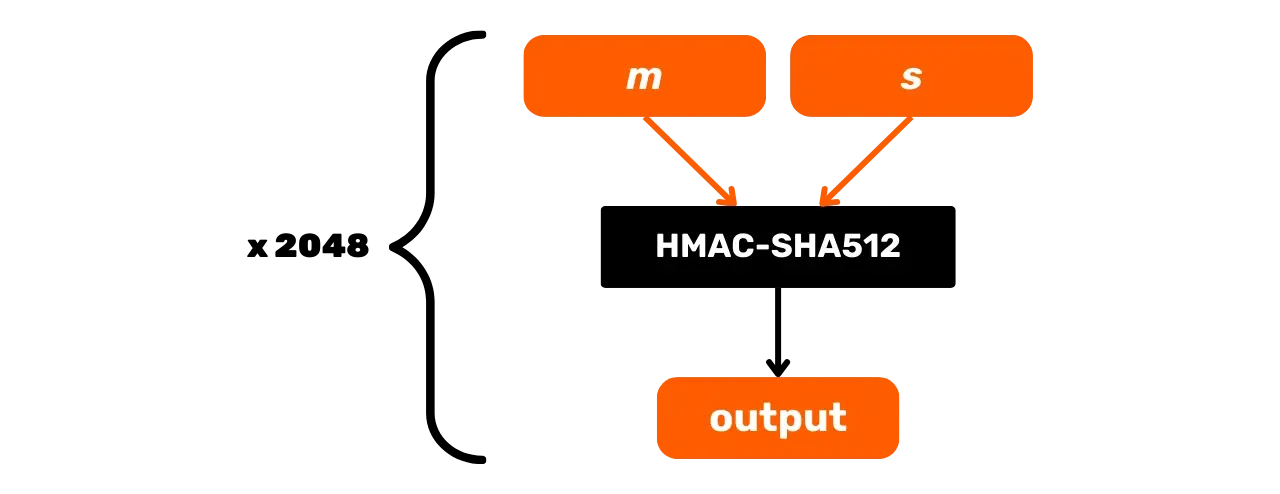
Le processus de PBKDF2 est le suivant, avec :
m: la phrase mnémonique de l'utilisateur ;s: la passphrase optionnelle pour augmenter la sécurité (champs vide si pas de passphrase) ;n: le nombre d'itérations de la fonction, dans notre cas c'est 2048.
La fonction PBKDF2 est définie de manière itérative. Chaque itération prend en entrée le résultat de la précédente, le passe dans HMAC-SHA512, et combine les résultats successifs pour produire la clé finale :
\text{PBKDF2}(m, s) = \text{HMAC-SHA512}^{2048}(m, s)Schématiquement, PBKDF2 peut être représenté comme suit :
Dans ce chapitre, nous avons exploré les fonctions HMAC-SHA512 et PBKDF2, qui utilisent les fonctions de hachage pour garantir l'intégrité et la sécurité des dérivations de clés dans le protocole Bitcoin. Dans la prochaine partie, nous allons nous pencher sur les signatures numériques, une autre méthode cryptographique largement utilisée sur Bitcoin.
Les signatures numériques
Signatures numériques et courbes elliptiques
La deuxième méthode cryptographique utilisée dans Bitcoin concerne les algorithmes de signatures numériques. Examinons ensemble en quoi cela consiste et comment cela fonctionne.
Bitcoins, UTXOs et conditions de dépense
Le terme "wallet" sur Bitcoin est assez déroutant pour les débutants. En effet, ce que l'on appelle un portefeuille Bitcoin est un logiciel qui ne conserve pas directement vos bitcoins, contrairement à un portefeuille physique qui permet de conserver des pièces ou des billets. Les bitcoins sont simplement des unités de compte. Cette unité de compte est représentée par des UTXO (Unspent Transaction Outputs), qui sont des sorties de transactions non dépensées. Si ces sorties ne sont pas dépensées, cela signifie qu'elles appartiennent à un utilisateur. Les UTXOs sont donc en quelque sorte des morceaux de bitcoins, d'une taille variable, appartenant à un utilisateur.
Le protocole Bitcoin est distribué et fonctionne sans autorité centrale. On ne peut donc pas faire comme dans les registres bancaires traditionnels, où les euros qui vous appartiennent sont simplement associés à votre identité personnelle. Sur Bitcoin, vos UTXOs vous appartiennent car ils sont protégés par des conditions de dépense spécifiées dans le langage Script. Pour simplifier, il existe deux types de scripts : le script de verrouillage (scriptPubKey), qui protège un UTXO, et le script de déverrouillage (scriptSig), qui permet de déverrouiller un UTXO et ainsi de dépenser les unités de bitcoins qu'il représente.
Le fonctionnement initial de Bitcoin avec les scripts P2PK consiste à utiliser une clé publique pour verrouiller les fonds, en spécifiant dans un scriptPubKey que la personne souhaitant dépenser cet UTXO doit fournir une signature valide avec la clé privée correspondant à cette clé publique. Pour déverrouiller cet UTXO, il est donc nécessaire de fournir une signature valide dans le scriptSig. Comme leurs noms l'indiquent, la clé publique est connue de tous puisqu'elle est diffusée sur la blockchain, tandis que la clé privée est uniquement connue du propriétaire légitime des fonds.
Ça, c'est le fonctionnement de base de Bitcoin, mais au fil des mises à jour, ce fonctionnement s'est complexifié. D'abord, Satoshi a également introduit les scripts P2PKH, qui utilisent une adresse de réception dans le scriptPubKey, laquelle représente le hachage de la clé publique. Puis, le système s'est encore complexifié avec l'arrivée de SegWit puis de Taproot. Cependant, le principe général reste fondamentalement le même : une clé publique ou une représentation de cette clé sert à verrouiller les UTXOs, et une clé privée correspondante est requise pour les déverrouiller et donc les dépenser.
L'utilisateur qui souhaite faire une transaction Bitcoin doit donc établir une signature numérique à l'aide de sa clé privée sur la transaction en question. La signature pourra être vérifiée par les autres participants du réseau. Si elle est valide, cela signifie que l'utilisateur qui lance la transaction est bien le propriétaire de la clé privée, et donc qu'il est bien le propriétaire des bitcoins qu'il souhaite dépenser. Les autres utilisateurs pourront alors accepter et propager la transaction.
En conséquence, un utilisateur qui possède des bitcoins verrouillés avec une clé publique doit trouver un moyen de stocker de manière sécurisée ce qui permet de débloquer ses fonds : la clé privée. Un portefeuille Bitcoin est justement un dispositif qui va vous permettre de conserver facilement toutes vos clés sans que d'autres personnes y aient accès. Cela ressemble donc plus à un porte-clés qu'à un portefeuille.
Le lien mathématique entre une clé publique et une clé privée, ainsi que la possibilité de réaliser une signature pour prouver la possession d'une clé privée sans la dévoiler, sont rendus possibles par un algorithme de signature numérique. Dans le protocole Bitcoin, on utilise 2 algorithmes de signature : ECDSA (Elliptic Curve Digital Signature Algorithm) et le schéma de signature de Schnorr. ECDSA est le protocole de signature numérique utilisé dans Bitcoin depuis ses débuts. Schnorr est plus récent dans Bitcoin, puisqu'il a été introduit en novembre 2021 avec la mise à jour Taproot.
Ces deux algorithmes sont assez similaires dans leurs mécanismes. Ils sont tous deux basés sur la cryptographie sur les courbes elliptiques. La différence majeure entre ces deux protocoles réside dans la structure de la signature et certaines propriétés mathématiques spécifiques. Nous allons donc étudier le fonctionnement de ces algorithmes en commençant par le plus ancien : ECDSA.
La cryptographie sur les courbes elliptiques
La cryptographie sur les courbes elliptiques (ECC) est un ensemble d'algorithmes qui utilisent une courbe elliptique pour ses différentes propriétés mathématiques et géométriques dans un objectif cryptographique. La sécurité de ces algorithmes repose sur la difficulté du problème du logarithme discret sur les courbes elliptiques. Les courbes elliptiques sont notamment utilisées pour réaliser des échanges de clés, du chiffrement asymétrique, ou encore pour réaliser des signatures numériques.
Une propriété importante de ces courbes est qu'elles sont symétriques par rapport à l'axe des abscisses. Ainsi, toute droite non verticale coupant la courbe en deux points distincts intersectera toujours la courbe en un troisième point. De plus, toute tangente à la courbe en un point non singulier recoupera la courbe en un autre point. Ces propriétés seront utiles pour définir les opérations sur la courbe.
Voici une représentation d'une courbe elliptique sur le corps des réels :
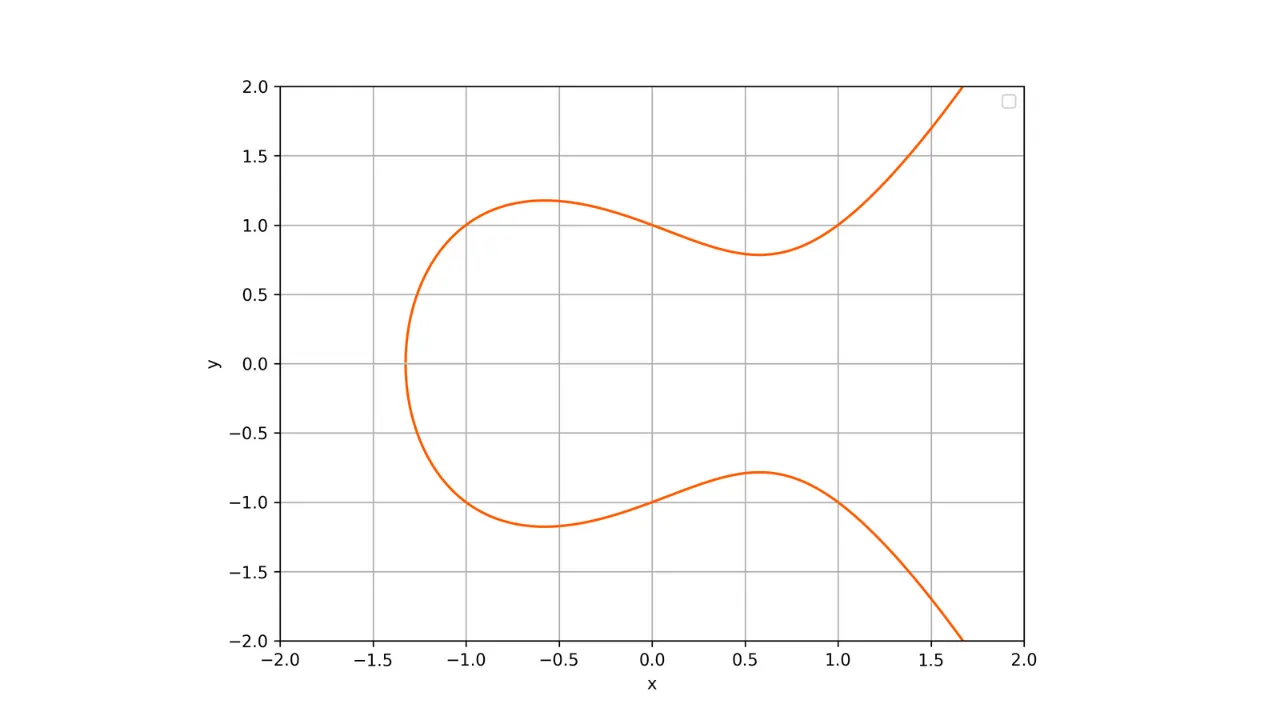
Toute courbe elliptique est définie par une équation de la forme :
y^2 = x^3 + ax + bsecp256k1
Pour utiliser ECDSA ou Schnorr, il faut choisir les paramètres de la courbe
elliptique, c'est-à-dire les valeurs de a et de b dans l'équation de la
courbe. Il existe différents standards de courbes elliptiques réputées
cryptographiquement sûres. La plus connue est la courbe secp256r1,
définie et recommandée par le NIST (National Institute of Standards and Technology).
Malgré cela, Satoshi Nakamoto, l'inventeur de Bitcoin, a choisi de ne pas
utiliser cette courbe. La raison de ce choix est inconnue, mais certains
pensent qu'il a préféré trouver une alternative car les paramètres de cette
courbe pourraient potentiellement contenir une backdoor. À la place, le
protocole Bitcoin utilise la courbe standard secp256k1. Cette courbe est définie par les paramètres a = 0 et b = 7. Son équation est
donc :
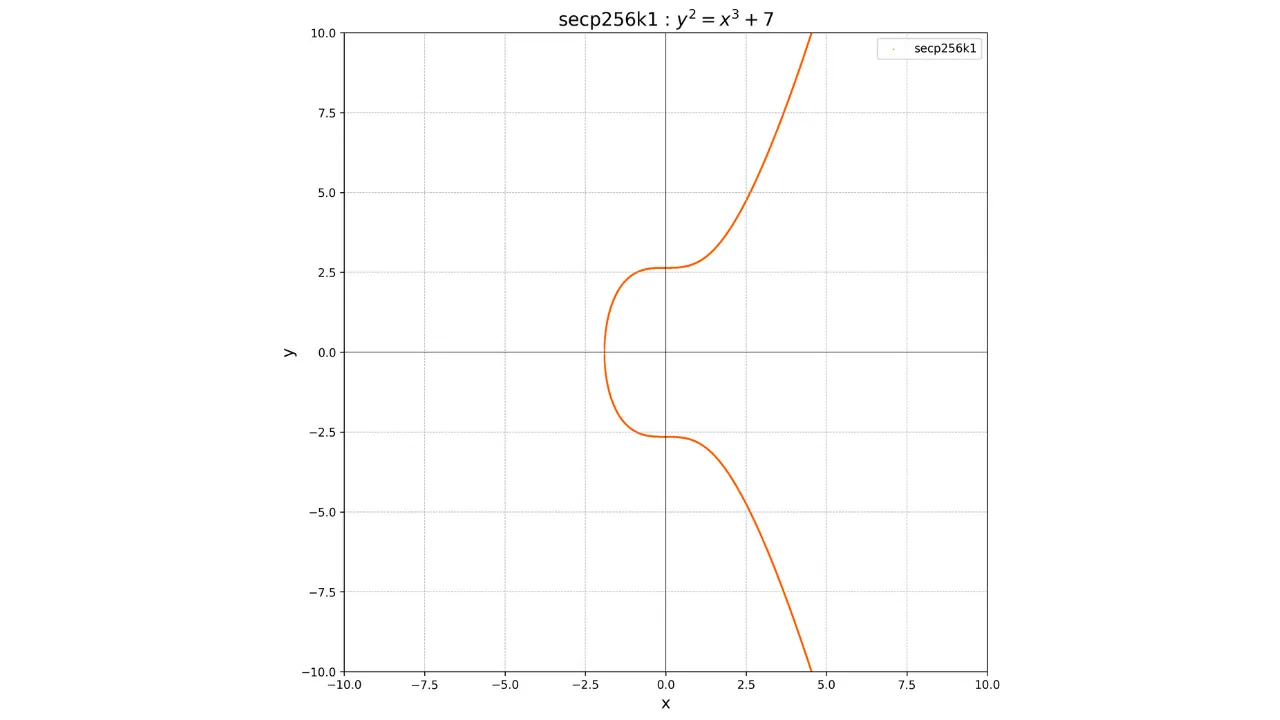
y^2 = x^3 + 7Sa représentation graphique sur le corps des réels ressemble à ceci :
Cependant, en cryptographie, nous travaillons sur des ensembles finis de
nombres. Plus précisément, nous travaillons sur le corps fini \mathbb{F}_p, qui est le corps des entiers modulo un nombre premier p.
Définition : Un nombre premier est un entier naturel supérieur ou égal à 2 qui n'admet que deux diviseurs entiers positifs distincts : 1 et lui-même. Par exemple, le nombre 7 est un nombre premier puisqu'il ne peut être divisé que par 1 et 7. En revanche, le nombre 8 n'est pas premier, car il peut être divisé par 1, 2, 4 et 8.
Dans Bitcoin, le nombre premier p utilisé pour définir le corps fini est très grand. Il est choisi de manière
à ce que l'ordre du corps (c'est-à-dire le nombre d'éléments dans \mathbb{F}_p) soit
suffisamment grand pour assurer la sécurité cryptographique.
Le nombre premier p utilisé est
:
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
En notation décimale, cela correspond à :
p = 2^{256} - 2^{32} - 977Ainsi, l'équation de notre courbe elliptique est en réalité :
y^2 \equiv x^3 + 7 \mod pÉtant donné que cette courbe est définie sur le corps fini \mathbb{F}_p, elle ne ressemble plus à une courbe continue mais plutôt à un ensemble
discret de points. Par exemple, voici à quoi ressemble la courbe utilisée
dans Bitcoin pour un tout petit p = 17 :
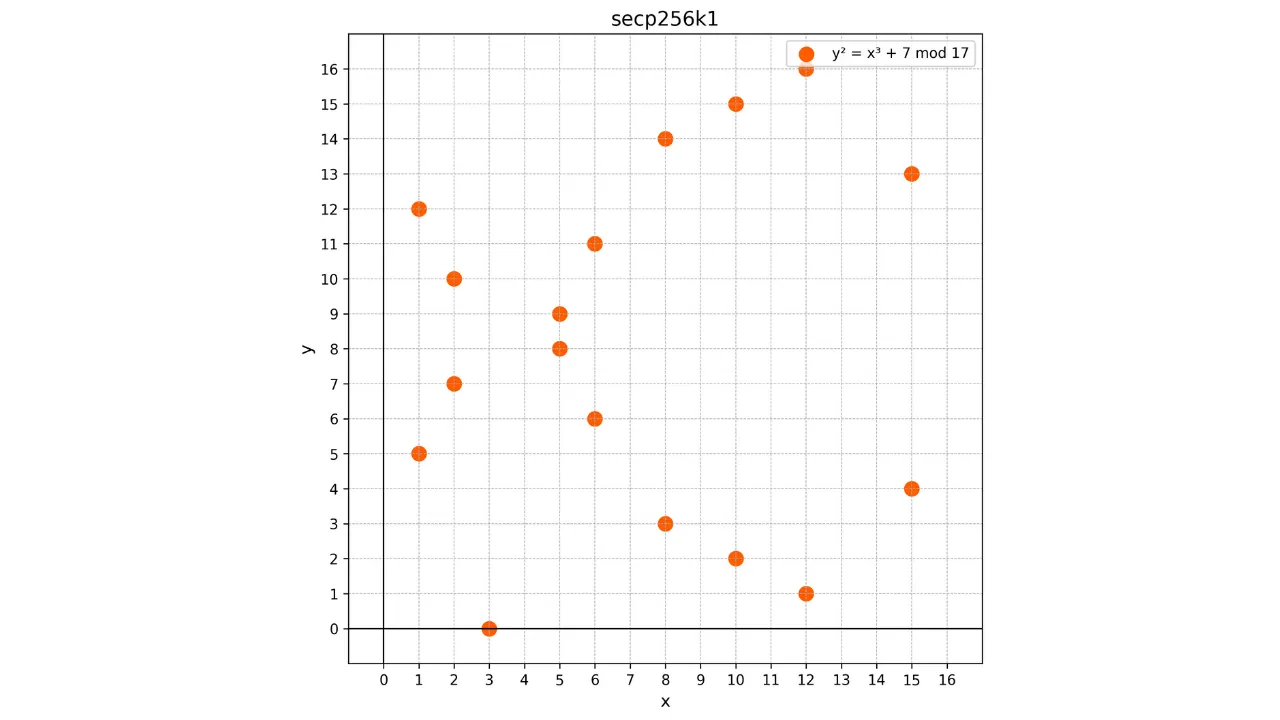
Dans cet exemple, j'ai intentionnellement limité le corps fini à p = 17 pour des raisons pédagogiques, mais il faut imaginer que celui utilisé dans
Bitcoin est immensément plus grand, presque 2^{256}.
Nous utilisons un corps fini d'entiers modulo p afin d'assurer la précision des opérations sur la courbe. En effet, les courbes
elliptiques sur le corps des réels sont sujettes à des imprécisions dues aux
erreurs d'arrondi lors des calculs informatiques. Si l'on effectue de nombreuses
opérations sur la courbe, ces erreurs s'accumulent et le résultat final peut
être incorrect ou difficilement reproductible. L'utilisation exclusive d'entiers
positifs permet d'assurer une précision parfaite des calculs et donc une reproductibilité
du résultat.
Les mathématiques des courbes elliptiques sur les corps finis sont analogues
à celles sur le corps des réels, avec l'adaptation que toutes les opérations
sont effectuées modulo p.
Pour simplifier les explications, nous continuerons dans les prochains
chapitres à illustrer les concepts en utilisant une courbe définie sur les
nombres réels, tout en gardant à l'esprit que, dans la pratique, la courbe
est définie sur un corps fini.
Si vous souhaitez en savoir plus sur les bases mathématiques de la cryptographie moderne, je vous conseille par la suite de consulter également cette autre formation sur Plan ₿ Network :
https://planb.network/courses/d2fd9fc0-d9ed-4a87-9fa3-0fdbb3937e28
Calculer la clé publique à partir de la clé privée
Comme vu précédemment, les algorithmes de signature numérique sur Bitcoin sont basés sur un couple clé privée / clé publique qui sont liées mathématiquement. Découvrons ensemble quel est ce lien mathématique et comment elles sont générées.
La clé privée
La clé privée est simplement un nombre aléatoire ou pseudo-aléatoire. Dans
le cas de Bitcoin, ce nombre est d'une taille de 256 bits. Le nombre de
possibilités pour une clé privée Bitcoin est donc théoriquement de 2^{256}.
Remarque : Un "nombre pseudo-aléatoire" est un nombre qui possède des propriétés s'approchant de celles d'un nombre véritablement aléatoire, mais qui est généré par un algorithme déterministe.
Cependant, en pratique, il existe seulement n points distincts sur notre courbe elliptique secp256k1, où n est l'ordre du point générateur G de la courbe. Nous verrons plus tard à quoi correspond ce nombre, mais
retenez simplement qu'une clé privée valide est un nombre entier compris
entre 1 et n-1, en sachant que n est un nombre proche mais légèrement plus petit que 2^{256}. Il existe
donc certains nombres de 256 bits qui ne sont pas valides pour devenir une
clé privée dans Bitcoin, en l'occurrence, ce sont tous les nombres compris
entre n et 2^{256}. Si la
génération du nombre aléatoire (la clé privée) produit une valeur k telle que k \geq n, celle-ci
est considérée comme invalide, et il faudra générer une nouvelle valeur
aléatoire.
Le nombre de possibilités pour une clé privée Bitcoin est donc d'environ n, qui est un nombre proche de 1.158 \times 10^{77}. C'est un nombre tellement grand que si vous choisissez une clé privée
aléatoirement, il est statistiquement presque impossible de tomber sur la
clé privée d'un autre utilisateur. Pour vous donner un ordre de grandeur, le
nombre de clés privées possibles sur Bitcoin est d’un ordre de magnitude
proche de celui des atomes estimés dans l'univers observable.
Comme nous le verrons dans les prochains chapitres, aujourd'hui, la majorité des clés privées utilisées sur Bitcoin ne sont pas générées aléatoirement mais sont le résultat d'une dérivation déterministe depuis une phrase mnémonique, elle-même pseudo-aléatoire (c'est la fameuse phrase de 12 ou 24 mots). Cette information ne change rien pour l'utilisation des algorithmes de signature comme ECDSA, mais elle permet de recentrer notre vulgarisation sur Bitcoin.
Pour la suite de l'explication, la clé privée sera notée par la lettre
minuscule k.
La clé publique
La clé publique est un point sur la courbe elliptique, noté par la lettre
majuscule K, et est calculée
à partir de la clé privée k.
Ce point K est représenté par
une paire de coordonnées (x, y) sur la courbe elliptique, chaque coordonnée étant un entier modulo p, le nombre premier
définissant le corps fini \mathbb{F}_p.
En pratique, une clé publique non compressée est représentée par 512 bits
(ou 64 octets), correspondant à deux nombres mis bout-à-bout de 256 bits (x et y). Ces nombres, ce sont
l'abscisse (x) et l'ordonnée
(y) de notre point sur
secp256k1. Si l'on ajoute le préfixe, la clé publique fait au total 520
bits.
Cependant, il est aussi possible de représenter la clé publique de manière
compressée en utilisant seulement 33 octets (264 bits) en conservant
uniquement l'abscisse x de
notre point sur la courbe et un octet indiquant la parité de y. C'est ce qu'on appelle une
clé publique compressée. Je vous en parlerai plus en détail dans les
derniers chapitres de cette formation. Mais ce qu'il faut retenir, c'est
qu'une clé publique K est un
point décrit par x et y.
Pour calculer le point K qui
correspond à notre clé publique, nous utilisons l'opération de
multiplication scalaire sur les courbes elliptiques, définie comme une
addition répétée (k fois) du
point générateur G :
K = k \cdot Goù :
kest la clé privée (un entier aléatoire compris entre1etn-1) ;Gest le point générateur de la courbe elliptique utilisé par tous les participants du réseau Bitcoin ;\cdotreprésente la multiplication scalaire sur la courbe elliptique, qui équivaut à ajouter le pointGà lui-mêmekfois.
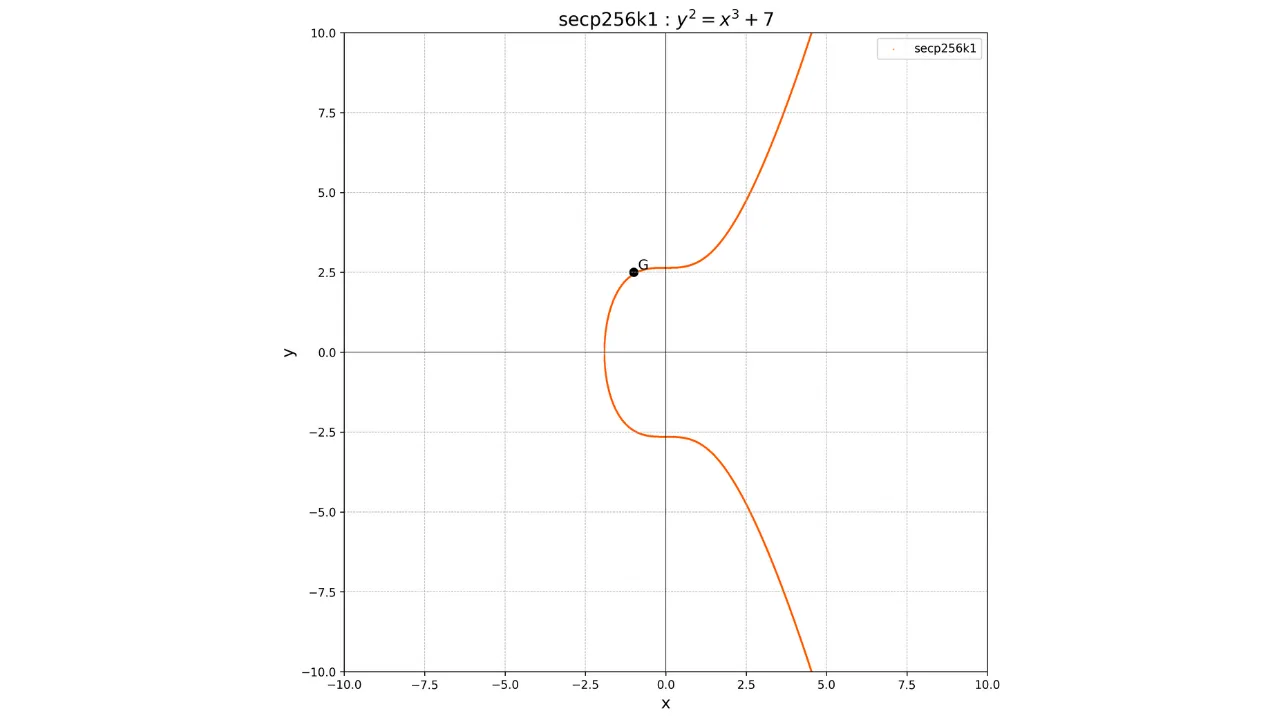
Le fait que ce point G soit
commun à toutes les clés publiques sur Bitcoin nous permet d'être sûr qu'une
même clé privée k nous
donnera toujours la même clé publique K :
La principale caractéristique de cette opération est qu'elle est une
fonction à sens unique. Il est facile de calculer la clé publique K en connaissant la clé privée k et le point générateur G,
mais il est pratiquement impossible de calculer la clé privée k en connaissant seulement la clé publique K et le point générateur G.
Trouver k à partir de K et G revient à résoudre le problème
du logarithme discret sur les courbes elliptiques, un problème mathématiquement
difficile pour lequel il n'existe pas d'algorithme efficace connu. Même les calculateurs
les plus puissants actuels sont incapables de résoudre ce problème dans un temps
raisonnable.

Addition et doublement de points sur les courbes elliptiques
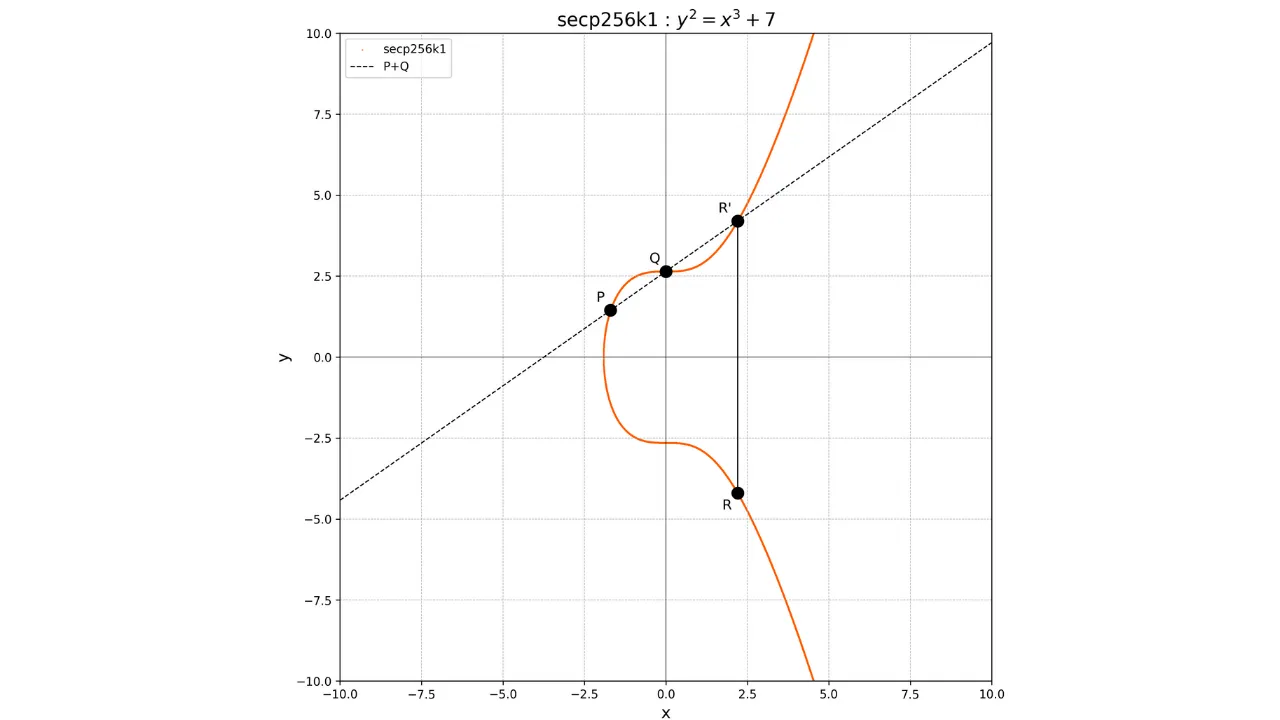
La notion d'addition sur les courbes elliptiques est définie de manière
géométrique. Si nous avons deux points P et Q sur la courbe,
l'opération P + Q est
calculée en traçant la droite passant par P et Q. Cette droite coupera
forcément la courbe en un troisième point R'. Nous prenons alors le
symétrique de ce point par rapport à l'axe des abscisses pour obtenir le
point R, qui est le résultat
de l'addition :
P + Q = RGraphiquement, cela peut être représenté comme suit :
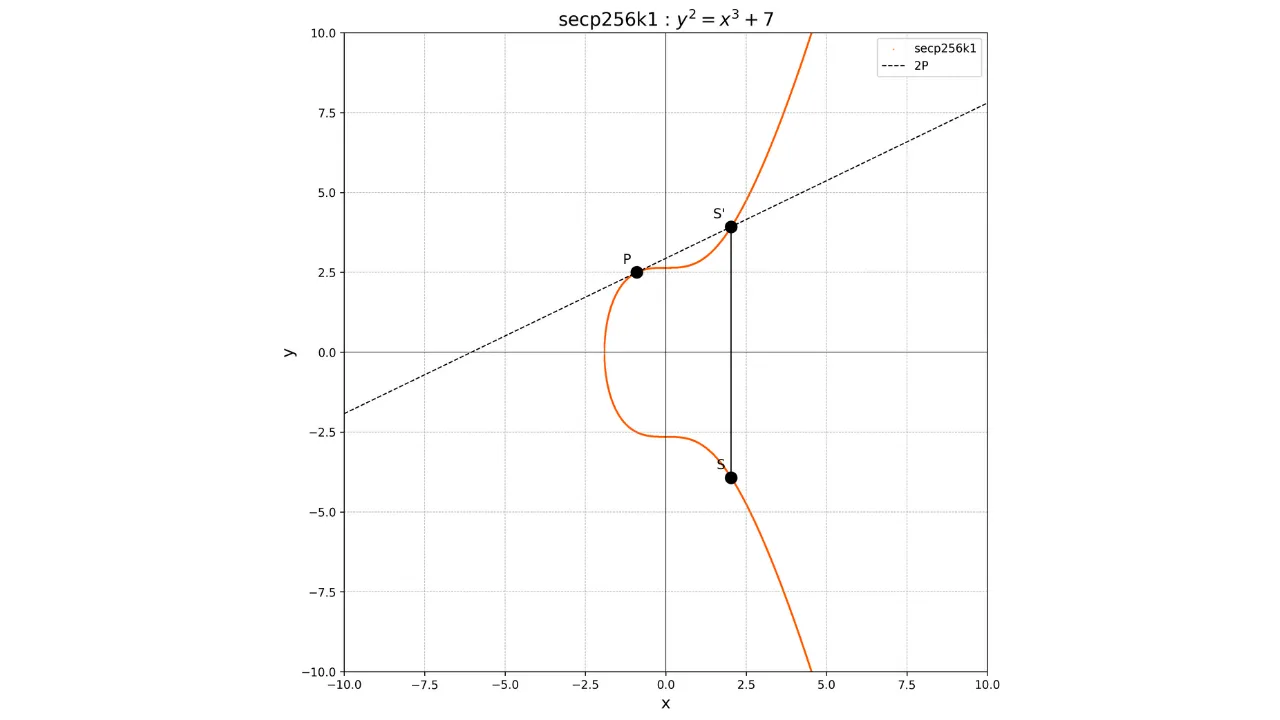
Pour le doublement d'un point, c'est-à-dire l'opération P + P, nous traçons la tangente à la courbe en ce point P. Cette tangente coupe la
courbe en un autre point S'.
Nous prenons alors le symétrique de ce point par rapport à l'axe des
abscisses pour obtenir le point S, qui est le résultat du
doublement :
2P = SGraphiquement, cela donne :
En utilisant ces opérations d'addition et de doublement, nous pouvons
effectuer la multiplication scalaire d'un point par un entier k, notée kP, en effectuant
des doublements répétés et des additions.
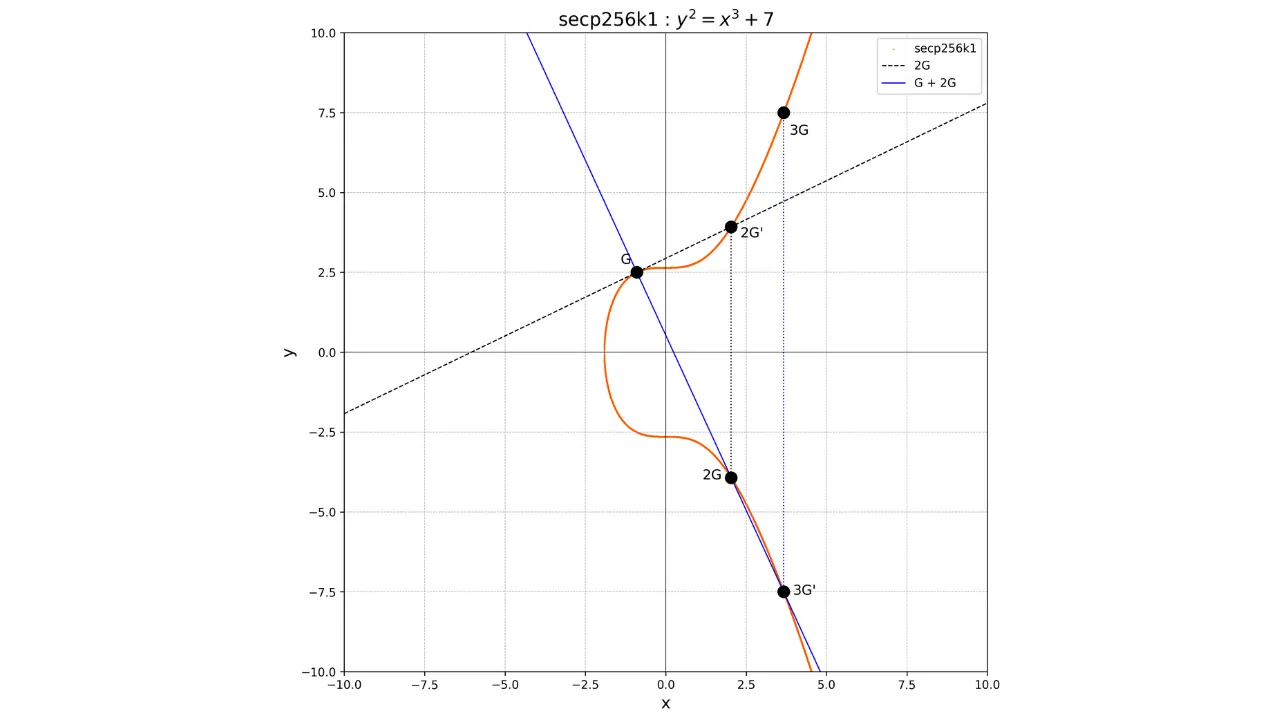
Par exemple, supposons que nous ayons choisi une clé privée k = 4. Pour calculer la clé publique associée, nous effectuons :
K = k \cdot G = 4GGraphiquement, cela correspond à effectuer une série d'additions et de doublements :
- Calculer
2Gen doublantG. - Calculer
4Gen doublant2G.

Si l’on souhaite, par exemple, calculer le point 3G, nous devons d’abord calculer le point 2G en doublant le point G, puis
additionner G et 2G. Pour additionner G et 2G, il suffit de tracer la
droite reliant ces deux points, de récupérer le point unique -3G à l’intersection entre cette droite et la courbe elliptique, puis de
déterminer 3G comme l’opposé
de -3G.
Nous aurons donc :
G + G = 2G2G + G = 3GGraphiquement, cela se représenterait ainsi :
Fonction à sens unique
Grâce à ces opérations, nous pouvons comprendre pourquoi il est facile de dériver une clé publique à partir d'une clé privée, mais l'inverse est pratiquement impossible.
Reprenons notre exemple simplifié. Avec une clé privée k = 4. Pour calculer la clé publique associée, nous effectuons :
K = k \cdot G = 4GNous avons donc pu facilement calculer la clé publique K en connaissant k et G.
Maintenant, si quelqu'un connaît uniquement la clé publique K, il est confronté au problème du logarithme discret : trouver k tel que K = k \cdot G. Ce
problème est considéré comme difficile car il n'existe pas d'algorithme
efficace pour le résoudre sur les courbes elliptiques. Cela assure la
sécurité des algorithmes ECDSA et Schnorr.
Bien sûr, dans cet exemple simplifié avec k = 4, il serait possible de trouver k par essai successif, car le nombre de possibilités est faible. Cependant, en
pratique sur Bitcoin, k est
un entier de 256 bits, ce qui rend le nombre de possibilités
astronomiquement grand (environ 1.158 \times 10^{77}). Il est donc infaisable de trouver k par force brute.
Signer avec la clé privée
Maintenant que vous savez dériver une clé publique à partir d’une clé
privée, vous pouvez déjà recevoir des bitcoins en utilisant cette paire de
clés comme condition de dépense. Mais comment les dépenser ? Pour dépenser
des bitcoins, il va falloir déverrouiller le scriptPubKey apposé
sur votre UTXO pour prouver que vous en êtes bien le propriétaire légitime.
Pour ce faire, il faut produire une signature s qui correspond à la clé publique K présente dans le scriptPubKey à l'aide de la clé privée k qui a servi initialement à calculer K. La signature numérique est
ainsi une preuve irréfutable que vous êtes bien en possession de la clé
privée associée à la clé publique que vous revendiquez.
Les paramètres de la courbe elliptique
Pour réaliser une signature numérique, il faut tout d’abord que tous les participants se mettent d'accord sur les paramètres de la courbe elliptique utilisée. Dans le cas de Bitcoin, les paramètres de secp256k1 sont les suivants :
Le champ fini \mathbb{Z}_p défini par :
p = 2^{256} - 2^{32} - 977p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
p est un nombre premier très
grand légèrement inférieur à 2^{256}.
La courbe elliptique y^2 = x^3 + ax + b sur \mathbb{Z}_p définie
par :
a = 0, \quad b = 7Le point générateur ou point d'origine G :
G = 0x0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
Ce nombre est la forme compressée qui donne uniquement l’abscisse du point G. Le préfixe 02 au départ permet de déterminer laquelle des
deux valeurs ayant cette abscisse x est à utiliser comme point générateur.
L'ordre n de G (le nombre de points existants) et le cofacteur h :
n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
n est un nombre très grand
légèrement inférieur à p.
h=1h est le cofacteur ou le
nombre de sous-groupes. Je ne vais pas développer ce que cela représente
ici, car c’est assez complexe, et dans le cas de Bitcoin, nous n’avons pas
besoin de le prendre en compte puisqu’il est égal à 1.
Toutes ces informations sont publiques et connues de tous les participants. Grâce à elles, les utilisateurs sont en capacité de réaliser une signature numérique et de la vérifier.
Signature avec ECDSA
L'algorithme ECDSA permet à un utilisateur de signer un message en utilisant sa clé privée, de manière à ce que toute personne connaissant la clé publique correspondante puisse vérifier la validité de la signature, sans que la clé privée soit jamais révélée. Dans le contexte de Bitcoin, le message à signer dépend du sighash choisi par l'utilisateur. C'est ce sighash qui va déterminer quelles parties de la transaction sont couvertes par la signature. Je vous en parlerai plus en détail dans le chapitre suivant.
Voici les étapes pour générer une signature ECDSA :
Tout d'abord on va calculer le hash (e) du message qui doit être signé. Le message m est donc passé dans une fonction
de hachage cryptographique, généralement SHA256 ou double SHA256 dans le cas
de Bitcoin :
e = \text{HASH}(m)Ensuite, on va calculer un nonce. En cryptographie, un nonce est simplement
un nombre généré de manière aléatoire ou pseudo-aléatoire qui est utilisé
une seule fois. C'est-à-dire qu'à chaque fois que l'on réalise une nouvelle
signature numérique avec cette paire de clés, il sera très important
d'utiliser un nonce différent, sinon cela compromettra la sécurité de la clé
privée. Il suffit donc de déterminer un entier aléatoire et unique r tel que 1 \leq r \leq n-1, où n est l'ordre du point générateur G de la courbe elliptique.
Puis, nous allons calculer le point R sur la courbe elliptique avec les coordonnées (x_R, y_R) tel que :
R = r \cdot GOn extrait la valeur de l'abscisse du point R (x_R). Cette valeur
représente la première partie de la signature. Et enfin, on calcule la
seconde partie de la signature s de cette manière :
s = r^{-1} \left( e + k \cdot x_R \right) \mod noù :
r^{-1}est l'inverse modulaire dermodulon, c'est-à-dire un entier tel quer \cdot r^{-1} \equiv 1 \mod n;kest la clé privée de l'utilisateur ;eest le hash du message ;nest l'ordre du point générateurGde la courbe elliptique.
La signature est alors simplement la concaténation de x_R et de s :
\text {SIG} = x_R \Vert sVérification de la signature ECDSA
Pour vérifier une signature (x_R, s), toute personne connaissant la clé publique K et les paramètres de la courbe
elliptique peut procéder de cette façon :
Tout d'abord, on vérifie que x_R et s sont bien dans
l'intervalle [1, n-1]. Cela
garantit que la signature respecte les contraintes mathématiques du groupe
elliptique. Si ce n’est pas le cas, le vérificateur rejette immédiatement la
signature comme invalide.
Puis, on calcule le hash du message :
e = \text{HASH}(m)On calcule l'inverse modulaire de s modulo n :
s^{-1} \mod nOn calcule deux valeurs scalaires u_1 et u_2 de cette manière :
\begin{align*}
u_1 &= e \cdot s^{-1} \mod n \\
u_2 &= x_R \cdot s^{-1} \mod n
\end{align*}Et enfin, on calcule le point V sur la courbe elliptique tel que :
V = u_1 \cdot G + u_2 \cdot KLa signature est valide uniquement si x_V \equiv x_R \mod n, où x_V est la coordonnée x du point V. En effet, en
combinant u_1 \cdot G et u_2 \cdot K, on obtient un
point V qui, si la signature
est valide, doit correspondre au point R utilisé lors de la signature (modulo n).
Signature avec le protocole de Schnorr
Le schéma de signature de Schnorr est une alternative à ECDSA qui offre de nombreux avantages. Il est possible de l'utiliser sur Bitcoin depuis 2021 et l'introduction de Taproot, avec les modèles de script P2TR. Comme ECDSA, le schéma de Schnorr permet de signer un message en utilisant une clé privée, de manière à ce que la signature puisse être vérifiée par toute personne connaissant la clé publique correspondante.
Dans le cas de Schnorr on utilise exactement la même courbe que ECDSA avec
les mêmes paramètres. En revanche, les clés publiques sont représentées
légèrement différemment par rapport à ECDSA. En effet, on les désigne
uniquement par la coordonnée x du point sur la courbe elliptique. Contrairement à ECDSA, où les clés
publiques compressées sont représentées par 33 octets (avec l'octet de
préfixe indiquant la parité de y), Schnorr utilise des clés
publiques de 32 octets, correspondant uniquement à la coordonnée x du point K, et on considère
que y est pair par défaut. Cette
représentation simplifiée permet de réduire la taille des signatures et facilite
certaines optimisations dans les algorithmes de vérification.
La clé publique est alors la coordonnée x du point K :
\text{pk} = K_xLa première étape pour générer une signature est de hacher le message. Mais contrairement à ECDSA, on va le faire avec d'autres valeurs et on va utiliser une fonction de hachage étiquetée pour éviter les collisions dans différents contextes. Une fonction de hachage étiquetée consiste simplement à ajouter une étiquette arbitraire dans les inputs de la fonction de hachage aux côtés des données du message.
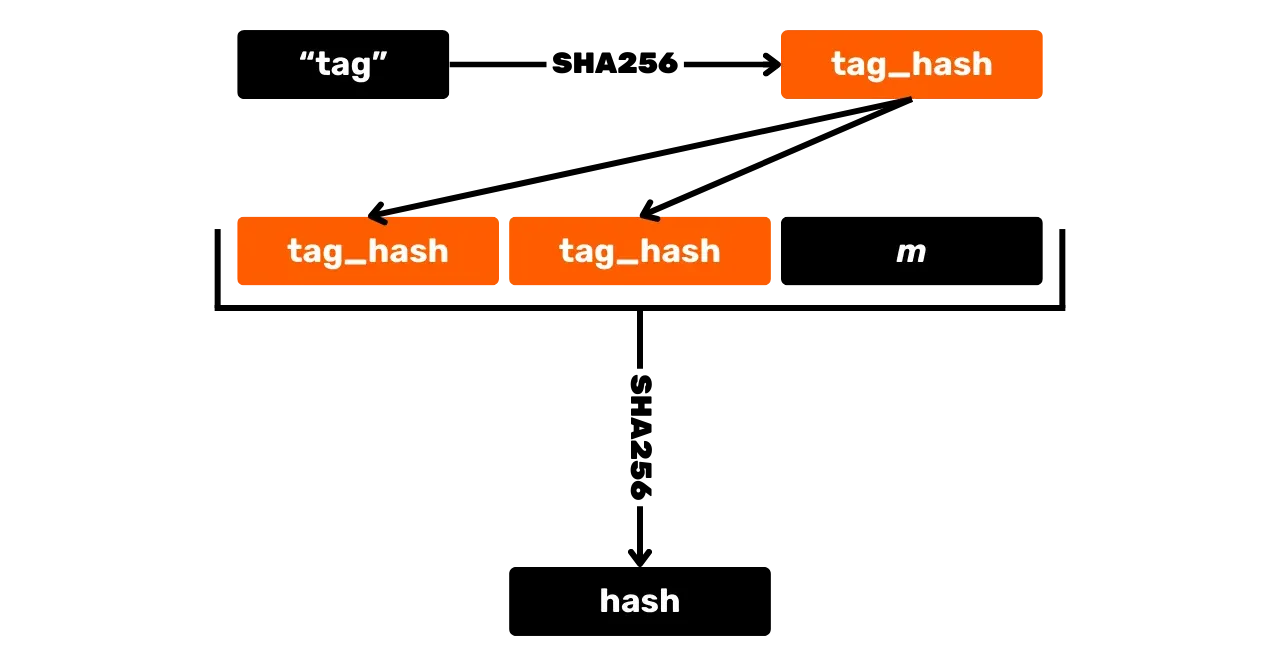
En plus du message, on va également passer dans la fonction étiquetée
l'abscisse de la clé publique K_x, ainsi qu'un point R calculé à partir du nonce r (R=r \cdot G) qui est
lui-même un entier unique pour chaque signature, calculé de manière
déterministe à partir de la clé privée et du message pour éviter les
vulnérabilités liées à la réutilisation du nonce. De la même manière que
pour la clé publique, seule l'abscisse du point du nonce R_x est conservée pour décrire
le point.
Le résultat de ce hachage noté e s'appelle le "challenge" :
e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod nIci, \text{HASH} est la fonction de hachage SHA256, et \text{``BIP0340/challenge''} est le tag spécifique pour le hachage.
Et enfin, on calcule le paramètre s de cette manière à partir de la clé privée k, du nonce r et du challenge e :
s = (r + e \cdot k) \mod nLa signature est ensuite simplement le couple Rx et s.
\text{SIG} = R_x \Vert sVérification de la signature Schnorr
La vérification d'une signature Schnorr est plus simple que celle d'une
signature ECDSA. Voici les étapes pour vérifier la signature (R_x, s) avec la clé publique K_x et
le message m :
Tout d'abord, on vérifie que K_x est un entier valide et inférieur à p. Si c'est le cas, on
récupère le point correspondant sur la courbe avec K_y pair. On va également extraire R_x et s en séparant la signature \text{SIG}. Puis,
nous vérifions que R_x < p et s < n (l'ordre de la courbe).
Ensuite, on calcule le challenge e de la même manière que l'a fait l'émetteur de la signature :
e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod nPuis, on calcule un point de référence sur la courbe de cette façon :
R' = s \cdot G - e \cdot KEnfin, on vérifie que R'_x = R_x. Si les deux abscisses correspondent, alors la signature (R_x, s) est bien valide avec la clé publique K_x.
Pourquoi cela fonctionne-t-il ?
Le signataire a calculé s = r + e \cdot k \mod n, donc R' = s \cdot G - e \cdot K devrait être égal au point R original,
car :
s \cdot G = (r + e \cdot k) \cdot G = r \cdot G + e \cdot k \cdot GPuisque K = k \cdot G, on a e \cdot k \cdot G = e \cdot K. Ainsi :
R' = r \cdot G = ROn a donc bien :
R'_x = R_xLes avantages des signatures de Schnorr
Le schéma de signature de Schnorr présente plusieurs avantages pour Bitcoin par rapport à l'algorithme original ECDSA. Tout d’abord, Schnorr permet l'agrégation des clés et des signatures. Cela signifie que plusieurs clés publiques peuvent être combinées en une seule clé.
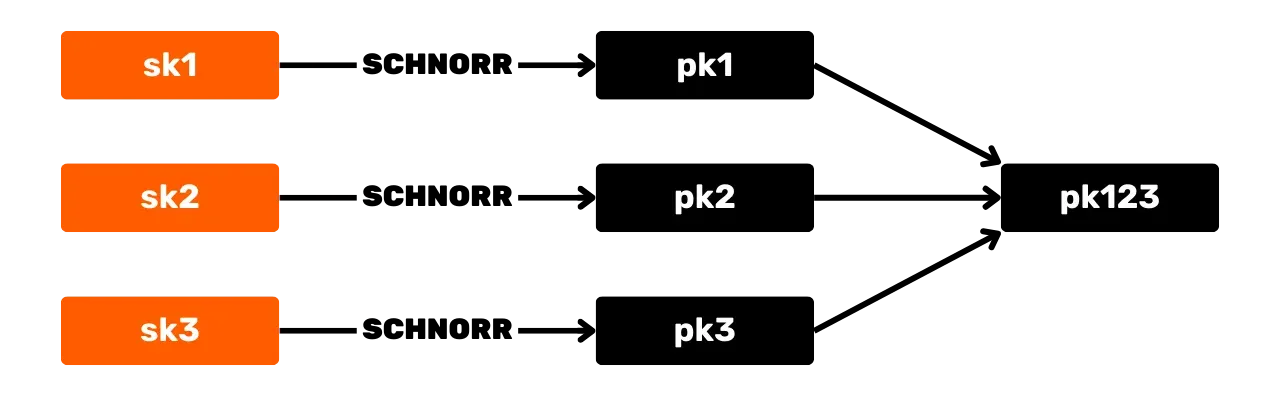
Et de même, plusieurs signatures peuvent être agrégées en une seule signature valide. Ainsi, dans le cas d'une transaction multisignatures, un ensemble de participants peut signer avec une seule signature et une seule clé publique agrégée. Cela réduit considérablement les coûts de stockage et de calcul pour le réseau, car chaque nœud n’a besoin de vérifier qu'une seule signature.

De plus, l’agrégation des signatures améliore la confidentialité. Avec Schnorr, il devient impossible de distinguer une transaction multisignature d'une transaction standard à une seule signature. Cette homogénéité rend les analyses de la chaîne plus difficiles, car elle limite la possibilité d'identifier des empreintes de portefeuille.
Enfin, Schnorr offre également la possibilité de vérification par lot. En vérifiant plusieurs signatures simultanément, les nœuds peuvent gagner en efficacité, surtout pour les blocs contenant de nombreuses transactions. Cette optimisation réduit le temps et les ressources nécessaires pour valider un bloc.
Aussi, les signatures Schnorr ne sont pas malléables, contrairement aux signatures produites avec ECDSA. Cela signifie qu'un attaquant ne peut pas modifier une signature valide pour créer une autre signature valide pour le même message et la même clé publique. Cette vulnérabilité était présente auparavant sur Bitcoin et empêchait notamment la mise en place de manière sécurisée du Lightning Network. Elle a été résolue pour ECDSA avec le softfork SegWit en 2017, qui consiste à déplacer les signatures dans une base de données séparée des transactions afin d'empêcher leur malléabilité.
Pourquoi Satoshi a-t-il choisi ECDSA ?
Nous l'avons vu, Satoshi a initialement choisi d'implémenter ECDSA pour les signatures numériques sur Bitcoin. Pourtant, nous avons également vu que Schnorr est bien supérieur à ECDSA sur de nombreux aspects, et ce protocole a été créé par Claus-Peter Schnorr en 1989, soit 20 ans avant l'invention de Bitcoin.
Et bien, on ne sait pas vraiment pourquoi Satoshi ne l'a pas choisi, mais une hypothèse probable est que ce protocole était sous brevet jusqu'en 2008. Bien que Bitcoin ait vu le jour un an plus tard, en janvier 2009, aucune standardisation open-source pour les signatures de Schnorr n'était alors disponible. Peut-être que Satoshi a jugé plus sûr d'utiliser ECDSA, qui était déjà largement utilisé et testé dans des logiciels open-source et bénéficiait de plusieurs implémentations reconnues (notamment la bibliothèque OpenSSL utilisée jusqu'en 2015 sur Bitcoin Core, puis remplacée par libsecp256k1 dans la version 0.10.0). Ou alors, peut-être qu'il n'avait tout simplement pas connaissance du fait que ce brevet allait expirer en 2008. Dans tous les cas, l'hypothèse la plus probable semble liée à ce brevet et au fait qu'ECDSA avait alors un historique éprouvé et était plus facile à implémenter.
Les sighash flags
Comme nous l'avons vu dans les chapitres précédents, les signatures
numériques sont souvent utilisées pour déverrouiller le script d'un input.
Dans le processus de signature, il est nécessaire d’inclure la donnée signée
dans le calcul, désignée dans nos exemples par le message m. Cette donnée, une fois signée, ne peut plus être modifiée sans rendre la
signature invalide. En effet, que ce soit pour ECDSA ou pour Schnorr, le
vérificateur de la signature doit inclure dans son calcul le même message m. Si celui-ci diffère du
message m utilisé initialement
par le signataire, le résultat sera incorrect et la signature sera jugée invalide.
On dit alors qu'une signature couvre une certaine donnée et la protège en quelque
sorte contre les modifications non autorisées.
C'est quoi un sighash flag ?
Dans le cas spécifique de Bitcoin, nous avons vu que le message m correspond à la transaction. Mais en réalité, c'est un peu plus complexe. En
effet, il est possible, grâce aux sighash flags, de sélectionner les données
spécifiques dans la transaction qui seront couvertes ou non par la signature.
Le "sighash flag" est donc un paramètre ajouté à chaque input, permettant de déterminer les composants d'une transaction qui sont couverts par la signature associée. Ces composants sont les inputs et les outputs. Le choix du sighash flag détermine ainsi quels inputs et quels outputs de la transaction sont figés par la signature et lesquels peuvent encore être modifiés sans invalider celle-ci. Ce mécanisme permet aux signatures d'engager les données de transaction selon les intentions du signataire.
Évidemment, une fois la transaction confirmée sur la blockchain, elle devient immuable, quels que soient les sighash flags utilisés. La possibilité de modification via les sighash flags est limitée à la période entre la signature et la confirmation.
Généralement, les logiciels de portefeuille ne vous proposent pas de
modifier manuellement le sighash flag de vos inputs lorsque vous construisez
une transaction. Par défaut, c'est le SIGHASH_ALL qui est paramétré.
Personnellement, je ne connais que Sparrow Wallet qui permette de faire cette
modification depuis l'interface utilisateur.
Quels sont les sighash flags existants sur Bitcoin ?
Sur Bitcoin, il y a tout d'abord 3 sighash flags de base :
SIGHASH_ALL(0x01) : La signature s'applique à tous les inputs et à tous les outputs de la transaction. La transaction est donc entièrement couverte par la signature et ne peut plus être modifiée.SIGHASH_ALLest le sighash le plus couramment utilisé dans les transactions au quotidien, lorsque l'on souhaite simplement faire une transaction sans qu'elle puisse être modifiée.

Dans tous les schémas de ce chapitre, la couleur orange représente les éléments couverts par la signature, tandis que la couleur noire indique ceux qui ne le sont pas.
SIGHASH_NONE(0x02) : La signature couvre tous les inputs mais aucun output, ce qui permet ainsi la modification des outputs après la signature. Concrètement, il s’agit d’un chèque en blanc. Le signataire déverrouille les UTXOs en inputs, mais laisse le champ des outputs entièrement modifiable. N'importe qui connaissant cette transaction peut donc y ajouter l’output de son choix, par exemple en spécifiant une adresse de réception pour récupérer les fonds consommés par les inputs, puis diffuser la transaction pour récupérer les bitcoins. La signature du propriétaire des inputs ne sera pas invalidée, car elle couvre uniquement les inputs.

SIGHASH_SINGLE(0x03) : La signature couvre tous les inputs ainsi qu’un seul output, correspondant à l’index de l’input signé. Par exemple, si la signature déverrouille le scriptPubKey de l'input #0, alors elle couvre également l'output #0. La signature protège également tous les autres inputs, qui ne peuvent plus être modifiés. Cependant, n'importe qui peut ajouter un output supplémentaire sans invalider la signature, à condition de ne pas modifier l'output #0, qui est le seul couvert par celle-ci.

En complément de ces trois sighash flags, il existe également le
modificateur SIGHASH_ANYONECANPAY (0x80). Ce
modificateur peut être combiné avec un sighash flag de base pour créer trois
nouveaux sighash flags :
SIGHASH_ALL | SIGHASH_ANYONECANPAY(0x81) : La signature couvre un seul input tout en incluant l'intégralité des outputs de la transaction. Ce sighash flag combiné permet, par exemple, de créer une transaction de financement participatif. L’organisateur prépare l'output avec son adresse et le montant cible, et chaque investisseur peut ensuite ajouter des inputs pour financer cet output. Une fois les fonds suffisants réunis en inputs pour satisfaire l'output, la transaction peut être diffusée.

SIGHASH_NONE | SIGHASH_ANYONECANPAY(0x82) : La signature couvre un seul input, sans engager aucun output ;

SIGHASH_SINGLE | SIGHASH_ANYONECANPAY(0x83) : La signature couvre un seul input ainsi que l'output ayant le même index que cet input. Par exemple, si la signature déverrouille le scriptPubKey de l'input #3, elle couvrira également l'output #3. Le reste de la transaction demeure modifiable, tant au niveau des autres inputs que des autres outputs.

Les projets d'ajout de nouveaux sighash flags
Actuellement (2024), seuls les sighash flags présentés dans la section
précédente sont utilisables sur Bitcoin. Cependant, certains projets
envisagent l’ajout de nouveaux sighash flags. Par exemple, le BIP118,
proposé par Christian Decker et Anthony Towns, introduit deux nouveaux
sighash flags : SIGHASH_ANYPREVOUT et SIGHASH_ANYPREVOUTANYSCRIPT (AnyPrevOut = "Any Previous Output").
Ces deux sighash flags offriraient une possibilité supplémentaire sur Bitcoin : créer des signatures qui ne couvrent aucun input spécifique de la transaction.

Cette idée a initialement été formulée par Joseph Poon et Thaddeus Dryja
dans le White Paper de Lightning. Avant son renommage, ce sighash flag
portait le nom de SIGHASH_NOINPUT.
Si ce sighash flag est intégré à Bitcoin, il permettra l'utilisation de covenants, mais c'est aussi un prérequis obligatoire pour implémenter Eltoo, un protocole généraliste pour les secondes couches qui définit la manière de gérer conjointement la propriété d'un UTXO. Eltoo a notamment été conçu pour résoudre les problèmes associés aux mécanismes de négociation de l'état des canaux Lightning, c'est-à-dire entre l'ouverture et la fermeture.
Pour approfondir vos connaissances sur le Lightning Network, après la formation CYP201, je vous recommande vivement la formation LNP201 de Fanis Michalakis, qui aborde le sujet en détail :
https://planb.network/courses/34bd43ef-6683-4a5c-b239-7cb1e40a4aeb
Dans la prochaine partie, je vous propose de découvrir comment fonctionne la phrase mnémonique à la base de votre portefeuille Bitcoin.
La phrase mnémonique
Évolution des portefeuilles Bitcoin
Maintenant que nous avons découvert les rouages des fonctions de hachages et des signatures numériques, nous allons pouvoir étudier le fonctionnement des portefeuilles Bitcoin. L’objectif va être de pouvoir imaginer comment se construit un portefeuille sur Bitcoin, comment il se décompose et à quoi servent les différentes informations qui le constituent. Cette compréhension des mécanismes du portefeuille vous permettra par la suite d'améliorer votre utilisation de Bitcoin en termes de sécurisation et de confidentialité.
Avant d'entrer dans les détails techniques, il est essentiel de clarifier ce que l'on entend par "portefeuille Bitcoin" et de comprendre son utilité.
Qu'est-ce qu'un portefeuille Bitcoin ?
Contrairement aux portefeuilles classiques, qui permettent de stocker des billets et des pièces physiques, un portefeuille Bitcoin ne "contient" pas de bitcoins à proprement parler. En effet, les bitcoins n'existent pas sous forme physique ou numérique stockable, mais sont représentés par des unités de compte représentées sur le système sous forme d'UTXOs (Unspent Transaction Output).
Les UTXOs représentent donc des fragments de bitcoins, de tailles variables, pouvant être dépensés à condition que leur scriptPubKey soit satisfait. Pour dépenser ses bitcoins, un utilisateur doit fournir un scriptSig qui déverrouille le scriptPubKey associé à son UTXO. Cette preuve se fait généralement par une signature numérique, générée à partir de la clé privée correspondant à la clé publique présente dans le scriptPubKey. Ainsi, l'élément crucial que l’utilisateur doit sécuriser est la clé privée.
Le rôle d’un portefeuille Bitcoin est précisément de gérer de manière sécurisée ces clés privées. En réalité, son rôle se rapproche donc davantage de celui d’un porte-clés que d’un portefeuille au sens classique.
Les portefeuilles JBOK (Just a Bunch Of Keys)
Les premiers portefeuilles utilisés sur Bitcoin étaient des portefeuilles JBOK (Just a Bunch Of Keys), qui regroupaient des clés privées générées de manière indépendante et sans aucun lien entre elles. Ces portefeuilles fonctionnaient sur un modèle simple où chaque clé privée permettait de déverrouiller une adresse de réception Bitcoin unique.
Si l’on souhaitait utiliser plusieurs clés privées, il fallait alors effectuer autant de sauvegardes pour garantir l’accès aux fonds en cas de problème avec l’appareil hébergeant le portefeuille. Si l’on utilise une seule clé privée, cette structure de portefeuille peut convenir, puisqu’une seule sauvegarde suffit. Cependant, cela pose un problème : sur Bitcoin, il est fortement déconseillé d’utiliser toujours la même clé privée. En effet, une clé privée est associée à une adresse unique, et les adresses de réception sur Bitcoin sont normalement conçues pour un usage unique. À chaque fois que vous recevez des fonds, vous devriez générer une nouvelle adresse vierge.
Cette contrainte découle du modèle de confidentialité de Bitcoin. En réutilisant une même adresse, on facilite le travail des observateurs externes qui peuvent alors retracer l’ensemble de mes transactions Bitcoin. C’est pourquoi la réutilisation d’une adresse de réception est fortement déconseillée. Or, pour disposer de plusieurs adresses et séparer publiquement nos transactions, il est nécessaire de gérer de multiples clés privées. Dans le cas des portefeuilles JBOK, cela implique de créer autant de sauvegardes qu'il y a de nouvelles paires de clés, une tâche qui peut rapidement devenir complexe et difficile à maintenir pour les utilisateurs.
Pour en savoir plus sur le modèle de confidentialité de Bitcoin et découvrir les méthodes pour protéger votre vie privée, je vous recommande également de suivre ma formation BTC204 sur Plan ₿ Network :
https://planb.network/courses/65c138b0-4161-4958-bbe3-c12916bc959c
Les portefeuilles HD (Hierarchical Deterministic)
Pour résoudre cette limitation des portefeuilles JBOK, on a ensuite utilisé une nouvelle structure de portefeuille. En 2012, Pieter Wuille propose une amélioration avec le BIP32, qui introduit les portefeuilles déterministes hiérarchiques. Le principe d’un portefeuille HD est de dériver l'ensemble des clés privées d'une unique source d'information, appelée graine (ou "seed"), de façon déterministe et hiérarchique. Cette graine est générée de manière aléatoire lors de la création du portefeuille et constitue une unique sauvegarde qui permet de recréer l'ensemble des clés privées du portefeuille. Ainsi, l'utilisateur peut générer un très grand nombre de clés privées pour éviter la réutilisation d'adresse et préserver sa confidentialité, tout en ne faisant qu'une seule sauvegarde de son portefeuille via la graine.
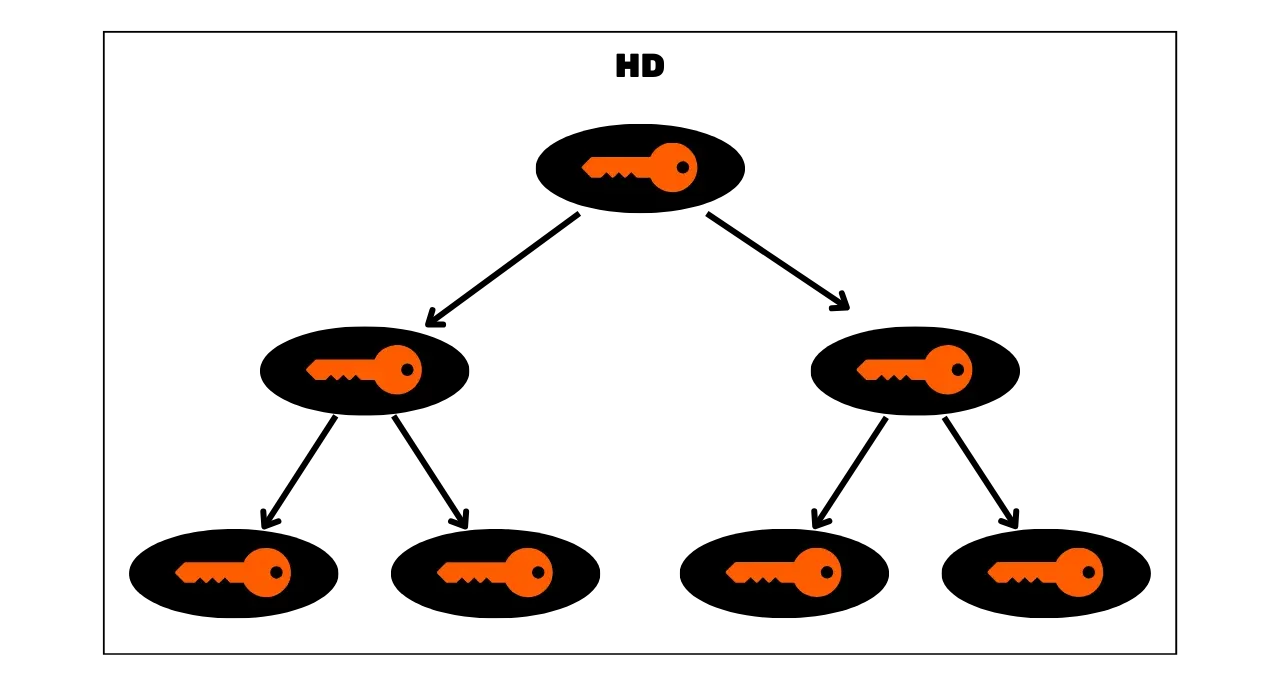
Dans les portefeuilles HD, la dérivation de clés est réalisée selon une structure hiérarchique qui permet d'organiser les clés en sous-espaces de dérivation, chaque sous-espace pouvant lui-même être subdivisé, afin de faciliter la gestion des fonds et l'interopérabilité entre les différents logiciels de portefeuille. De nos jours, ce standard est adopté par l'immense majorité des utilisateurs de Bitcoin. Pour cette raison, nous allons l'examiner en détail dans les chapitres suivants.
Le standard BIP39 : La phrase mnémonique
En complément du BIP32, le BIP39 standardise le format de la graine sous forme de phrase mnémonique, afin de faciliter la sauvegarde et la lisibilité par les utilisateurs. La phrase mnémonique, également appelée phrase de récupération ou phrase de 24 mots, est une séquence de mots tirée d'une liste prédéfinie qui encode de manière sécurisée la graine du portefeuille.
La phrase mnémonique simplifie grandement la sauvegarde pour l’utilisateur. En cas de perte, de casse ou de vol du support hébergeant le portefeuille, la simple connaissance de cette phrase mnémonique permet de recréer le portefeuille et de récupérer l’accès à l’ensemble des fonds sécurisés par celui-ci.
Dans les prochains chapitres, nous explorerons le fonctionnement interne des portefeuilles HD, notamment les mécanismes de dérivation des clés et les différentes structures hiérarchiques possibles. Cela vous permettra de mieux comprendre les bases cryptographiques sur lesquelles repose la sécurité des fonds sur Bitcoin. Et pour commencer, dans le chapitre suivant, je vous propose de découvrir le rôle de l'entropie à la base de votre portefeuille.
Entropie et nombre aléatoire
Les portefeuilles HD modernes (déterministes et hiérarchiques) reposent sur une unique information initiale appelée "entropie" pour générer de manière déterministe l’ensemble des clés du portefeuille. Cette entropie est un nombre pseudo-aléatoire dont le niveau de chaos détermine en partie la sécurité du portefeuille.
Définition de l’entropie
L'entropie, dans le contexte de la cryptographie et de l'information, est une mesure quantitative de l'incertitude ou de l'imprévisibilité associée à une source de données ou à un processus aléatoire. Elle joue un rôle important dans la sécurité des systèmes cryptographiques, notamment dans la génération de clés et de nombres aléatoires. Une entropie élevée garantit que les clés générées sont suffisamment imprévisibles et résistantes aux attaques par force brute, où un attaquant essaie toutes les combinaisons possibles pour deviner la clé.
Dans le contexte de Bitcoin, l'entropie est utilisée pour générer la graine. Lors de la création d'un portefeuille déterministe et hiérarchique, la construction de la phrase mnémonique se fait à partir d'un nombre aléatoire, lui-même issu d'une source d'entropie. La phrase est ensuite utilisée pour générer plusieurs clés privées, de manière déterministe et hiérarchique, afin de créer des conditions de dépense sur des UTXOs.
Les méthodes de génération de l’entropie
L’entropie initiale utilisée pour un portefeuille HD est généralement de 128 bits ou 256 bits, où :
- 128 bits d’entropie correspondent à une phrase mnémonique de 12 mots ;
- 256 bits d’entropie correspondent à une phrase mnémonique de 24 mots.
Dans la plupart des cas, ce nombre aléatoire est généré automatiquement par le logiciel de portefeuille grâce à un PRNG (Pseudo-Random Number Generator). Les PRNG sont une catégorie d'algorithmes utilisés pour générer des séquences de nombres à partir d'un état initial, qui disposent de caractéristiques s'approchant d'un nombre aléatoire, sans pour autant en être. Un bon PRNG doit avoir des propriétés telles que l'uniformité des sorties, l'imprévisibilité et la résistance aux attaques prédictives. Contrairement aux générateurs de nombres véritablement aléatoires (TRNG), les PRNG sont en revanche déterministes et reproduisibles.
Une alternative consiste à générer manuellement l’entropie, ce qui offre un meilleur contrôle mais est également beaucoup plus risqué. Je vous déconseille d'ailleurs fortement de générer vous-même l'entropie à la base de votre portefeuille HD.
Dans le prochain chapitre, nous allons voir comment est-ce que l'on passe d'un nombre aléatoire à une phrase mnémonique de 12 ou 24 mots.
La phrase mnémonique
La phrase mnémonique, aussi appelée "seed phrase", "phrase de récupération", "phrase secrète", ou "phrase de 24 mots", est une séquence composée habituellement de 12 ou de 24 mots, qui est générée à partir de l'entropie. Elle est utilisée pour dériver de façon déterministe l'intégralité des clés d'un portefeuille HD. Cela signifie qu’à partir de cette phrase, il est possible de générer et de recréer déterministiquement l'ensemble des clés privées et publiques du portefeuille Bitcoin, et par conséquent d'accéder aux fonds qui sont protégés avec. La raison d'être de la phrase mnémonique est de fournir un moyen de sauvegarde et de récupération des bitcoins qui est à la fois sécurisé et facile à utiliser. Elle a été introduite dans les standards en 2013 avec le BIP39.
Découvrons ensemble comment passer d'une entropie à une phrase mnémonique.
La checksum
Pour transformer une entropie en phrase mnémonique, il faut d’abord ajouter une checksum (ou "somme de contrôle") à la fin de l’entropie. Cette checksum est une courte séquence de bits qui assure l’intégrité des données en vérifiant qu’aucune modification accidentelle n’a été introduite.
Pour calculer la checksum, on applique la fonction de hachage SHA256 à l’entropie (une seule fois ; c'est d'ailleurs l'un des rares cas dans Bitcoin où l'on utilise un SHA256 simple au lieu d'un double hachage). Cette opération produit un hash de 256 bits. La checksum est constituée des premiers bits de ce hash, et sa longueur dépend de celle de l’entropie, selon la formule suivante :
\text{CS} = \frac{\text{ENT}}{32}où \text{ENT} représente la longueur de l’entropie en bits, et \text{CS} la longueur
de la checksum en bits.
Par exemple, pour une entropie de 256 bits, on va prendre les 8 premiers bits du hash pour former la checksum :
\text{CS} = \frac{256}{32} = 8 \text{ bits}Une fois la checksum calculée, on la concatène avec l’entropie pour obtenir
une séquence étendue de bits notée \text{ENT} \Vert \text{CS} ("concaténer" signifie mettre bout-à-bout).

Correspondance entre l’entropie et la phrase mnémonique
Le nombre de mots dans la phrase mnémonique dépend de la taille de l’entropie initiale, comme illustré dans le tableau suivant avec :
\text{ENT}: la taille en bits de l'entropie ;\text{CS}: la taille en bits de la checksum ;w: le nombre de mots dans la phrase mnémonique finale.
\begin{array}{|c|c|c|c|}
\hline
\text{ENT} & \text{CS} & \text{ENT} \Vert \text{CS} & w \\
\hline
128 & 4 & 132 & 12 \\
160 & 5 & 165 & 15 \\
192 & 6 & 198 & 18 \\
224 & 7 & 231 & 21 \\
256 & 8 & 264 & 24 \\
\hline
\end{array}Par exemple, pour une entropie de 256 bits, le résultat \text{ENT} \Vert \text{CS} fait 264 bits et donne une phrase mnémonique de 24 mots.
Conversion de la séquence binaire en une phrase mnémonique
La séquence de bits \text{ENT} \Vert \text{CS} est ensuite découpée en segments de 11 bits. Chaque segment de 11 bits, une
fois converti en décimal, correspond à un nombre compris entre 0 et 2047,
qui désigne la position d’un mot dans une liste de 2048 mots standardisée par le BIP39.
Par exemple, pour une entropie de 128 bits, la checksum est de 4 bits, et donc la séquence totale mesure 132 bits. Elle est découpée en 12 segments de 11 bits (les bits oranges désignent la checksum) :

Chaque segment est ensuite converti en un nombre décimal qui représente un
mot dans la liste. Par exemple, le segment binaire 01011010001 est équivalent en décimal à 721. En ajoutant 1 pour aligner
avec l’indexation de la liste (qui commence par 1 et non pas par 0), cela
donne le mot de rang 722, qui est "focus" dans la
liste.

On répète cette correspondance pour chacun des 12 segments, afin d'obtenir une phrase de 12 mots.

Caractéristiques de la liste de mots du BIP39
Une particularité de la liste de mots du BIP39 est qu'aucun mot ne partage les quatre premières lettres dans le même ordre avec un autre mot. Cela signifie que noter seulement les quatre premières lettres de chaque mot suffit pour sauvegarder la phrase mnémonique. Cela peut être intéressant pour gagner de la place, notamment pour ceux qui souhaitent la graver sur un support en métal.
Cette liste de 2048 mots existe en plusieurs langues. Ce ne sont pas de simples traductions, mais des mots distincts pour chaque langue. Cependant, il est fortement recommandé de se limiter à la version anglaise, car les versions dans d'autres langues ne sont généralement pas prises en charge par les logiciels de portefeuille.
Quelle longueur choisir pour sa phrase mnémonique ?
Pour déterminer la longueur optimale de sa phrase mnémonique, il faut considérer la sécurité effective qu'elle offre. Une phrase de 12 mots assure 128 bits de sécurité, tandis qu'une phrase de 24 mots en offre 256 bits.
Cependant, cette différence de sécurité au niveau de la phrase n’améliore
pas la sécurité globale d’un portefeuille Bitcoin, car les clés privées
dérivées depuis cette phrase ne bénéficient que de 128 bits de sécurité. En
effet, comme nous l’avons vu précédemment, les clés privées Bitcoin sont
générées à partir de nombres aléatoires (ou dérivés d’une source aléatoire)
compris entre 1 et n-1, où n représente l’ordre du point générateur G de la courbe secp256k1, un nombre légèrement inférieur à 2^{256}. On
pourrait donc penser que ces clés privées offrent une sécurité de 256 bits.
Cependant, leur sécurité réside dans la difficulté à retrouver une clé
privée depuis sa clé publique associée, une difficulté établie par le
problème mathématique du logarithme discret sur les courbes elliptiques (ECDLP). À ce jour, le meilleur algorithme connu pour résoudre ce problème est
l’algorithme rho de Pollard, qui diminue le nombre d’opérations nécessaires
pour casser une clé à la racine carrée de sa taille.
Pour des clés de 256 bits, comme celles utilisées sur Bitcoin, l’algorithme
rho de Pollard réduit donc la complexité à 2^{128} opérations :
O(\sqrt{2^{256}}) = O(2^{128})Ainsi, on considère qu’une clé privée utilisée sur Bitcoin offre 128 bits de sécurité.
En conséquence, choisir une phrase de 24 mots n’apporte pas de protection supplémentaire pour le portefeuille, car une sécurité de 256 bits sur la phrase est inutile si les clés dérivées n'offrent que 128 bits de sécurité. Pour illustrer ce principe, c'est comme si une maison possédait deux portes : une vieille porte en bois et une porte blindée. En cas de cambriolage, la porte blindée ne serait d'aucune utilité, puisque l'intrus passerait par la porte en bois. C'est une situation analogue ici.
Une phrase de 12 mots, qui offre également 128 bits de sécurité, est donc actuellement suffisante pour protéger vos bitcoins contre toute tentative de vol. Tant que l’algorithme de signature numérique ne change pas pour utiliser des clés plus grandes ou bien pour reposer sur un autre problème mathématique que l'ECDLP, une phrase de 24 mots demeure superflue. De plus, une phrase plus longue augmente le risque de perte lors de la sauvegarde : une sauvegarde deux fois plus courte est toujours plus facile à gérer.
Pour aller plus loin et découvrir concrètement comment générer manuellement une phrase mnémonique de test, je vous conseille de découvrir ce tutoriel :
Avant de poursuivre la dérivation du portefeuille à partir de cette phrase mnémonique, je vais vous présenter, dans le chapitre suivant, la passphrase BIP39, car celle-ci joue un rôle dans la dérivation, et elle se situe au même niveau que la phrase mnémonique.
La passphrase
Comme nous venons de le voir, les portefeuilles HD sont générés à partir d’une phrase mnémonique constituée généralement de 12 ou de 24 mots. Cette phrase est très importante, car elle permet de restaurer l'ensemble des clés d'un portefeuille en cas de perte de son support (comme un hardware wallet par exemple). Cependant, elle constitue un point de défaillance unique, car si elle est compromise, un attaquant pourrait voler l'intégralité des bitcoins. C'est ici qu'intervient la passphrase BIP39.
C'est quoi une passphrase BIP39 ?
La passphrase est un mot de passe optionnel, que vous pouvez choisir librement, qui s'ajoute à la phrase mnémonique dans la dérivation des clés pour renforcer la sécurité du portefeuille.
Attention, la passphrase ne doit pas être confondue avec le code PIN de votre hardware wallet ou le mot de passe permettant de déverrouiller l'accès à votre portefeuille sur votre ordinateur. Contrairement à tous ces éléments, la passphrase joue un rôle dans la dérivation des clés de votre portefeuille. Cela signifie que sans elle, vous ne pourrez jamais récupérer vos bitcoins.
La passphrase fonctionne en tandem avec la phrase mnémonique, en modifiant la graine à partir de laquelle sont générées les clés. Ainsi, même si une personne obtient votre phrase de 12 ou de 24 mots, sans la passphrase, elle ne peut pas accéder à vos fonds. L'utilisation d'une passphrase crée essentiellement un nouveau portefeuille avec des clés distinctes. Modifier (même légèrement) la passphrase générera un portefeuille différent.

Pourquoi devriez-vous utiliser une passphrase ?
La passphrase est arbitraire et peut être n'importe quelle combinaison de caractères choisie par l'utilisateur. L'utilisation d'une passphrase offre ainsi plusieurs avantages. Tout d'abord, elle réduit tous les risques liés à la compromission de la phrase mnémonique en nécessitant un second facteur pour accéder aux fonds (cambriolage, accès à votre domicile…).
Ensuite, elle peut être utilisée stratégiquement pour créer un portefeuille d’appât, afin de faire face à des contraintes physiques pour voler vos fonds comme la fameuse "$5 wrench attack". Dans ce scénario, l'idée est d'avoir un portefeuille sans passphrase contenant seulement une petite quantité de bitcoins, suffisante pour satisfaire un agresseur potentiel, tout en disposant d'un portefeuille caché. Ce dernier utilise la même phrase mnémonique, mais est sécurisé avec une passphrase additionnelle.
Enfin, l'utilisation d'une passphrase est intéressante lorsque l’on souhaite maitriser le caractère aléatoire de la génération de la graine du portefeuille HD.
Comment choisir une bonne passphrase ?
Pour que la passphrase soit efficace, elle doit être suffisamment longue et aléatoire. Comme pour un mot de passe fort, je vous recommande de choisir une passphrase la plus longue et aléatoire possible, avec une diversité de lettres, de chiffres et de symboles pour rendre toute attaque par brute force impossible.
Il est également important de bien sauvegarder cette passphrase, de la même manière que la phrase mnémonique. La perdre revient à perdre l’accès aux bitcoins. Je vous déconseille fortement de la retenir uniquement de tête, car cela augmente irraisonnablement les risques de perte. L’idéal est de la noter sur un support physique (en papier ou en métal) séparé de la phrase mnémonique. Cette sauvegarde devra évidemment être stockée dans un lieu différent de celui où est stockée votre phrase mnémonique pour éviter que les deux soient compromis simultanément.
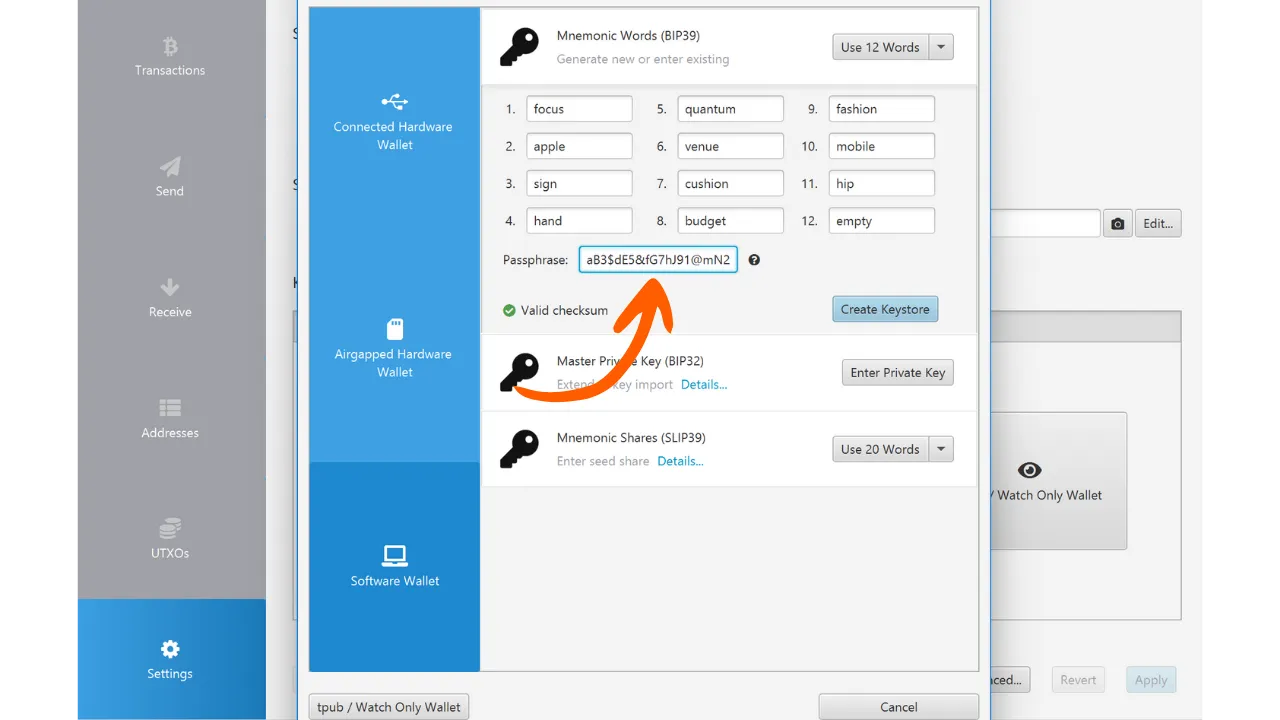
Dans la section suivante, nous découvrirons comment ces deux éléments à la base de votre portefeuille — la phrase mnémonique et la passphrase — sont employés pour dériver les paires de clés utilisées dans les scriptPubKey qui verrouillent vos UTXOs.
Création des portefeuilles Bitcoin
Création de la graine et de la clé maîtresse
Une fois la phrase mnémonique et l'optionnelle passphrase générées, le processus de dérivation d’un portefeuille HD Bitcoin peut commencer. La phrase mnémonique est d'abord convertie en une graine qui constitue la base de toutes les clés du portefeuille.
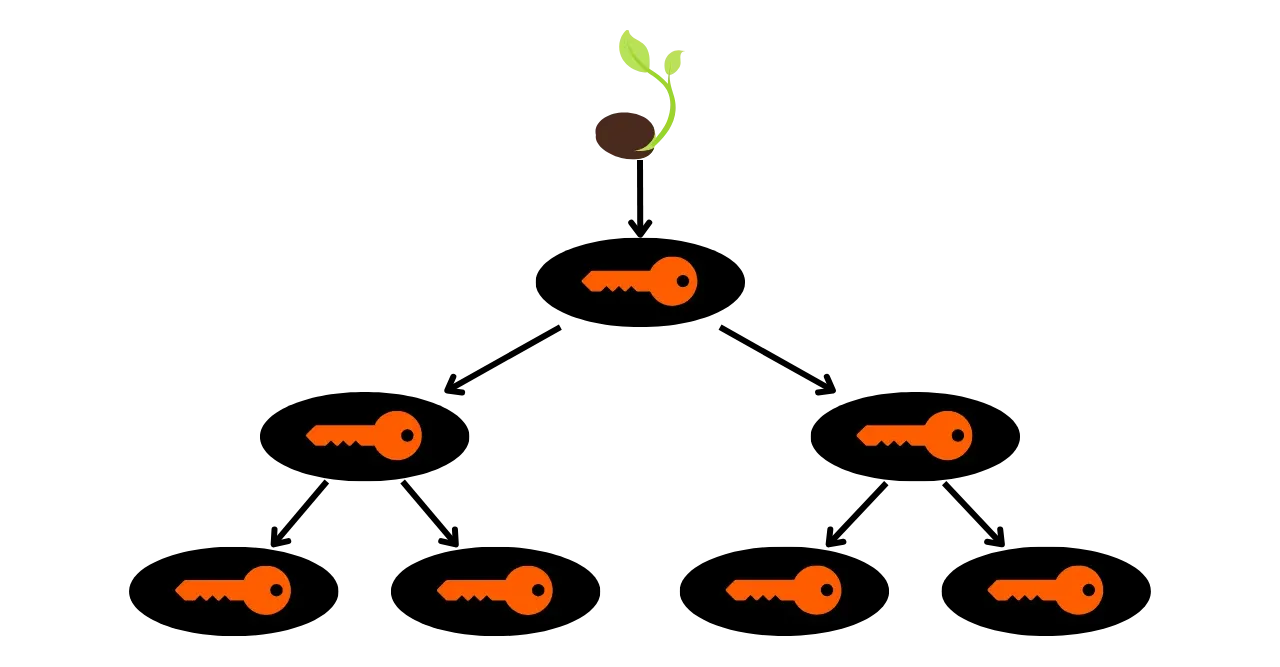
La graine d'un portefeuille HD
Le standard BIP39 définit la graine comme une séquence de 512 bits, qui sert de point de départ pour la dérivation de toutes les clés d’un portefeuille HD. La graine est dérivée de la phrase mnémonique et de l'éventuelle passphrase en utilisant l’algorithme PBKDF2 (Password-Based Key Derivation Function 2) dont nous avons déjà parlé dans le chapitre 3.3. Dans cette fonction de dérivation, on va utiliser les paramètres suivants :
m: la phrase mnémonique ;p: une passphrase optionnelle choisie par l’utilisateur pour renforcer la sécurité de la graine. S'il n'y a pas de passphrase, ce champ est laissé vide ;\text{PBKDF2}: la fonction de dérivations avec\text{HMAC-SHA512}et2048itérations ;s: la graine du portefeuille de 512 bits.
Quelle que soit la longueur de la phrase mnémonique choisie (132 bits ou 264 bits), la fonction PBKDF2 produira toujours un output de 512 bits et la graine sera donc toujours de cette taille.
Schéma de dérivation de la graine avec PBKDF2
L’équation suivante illustre la dérivation de la graine à partir de la phrase mnémonique et de la passphrase :
s = \text{PBKDF2}_{\text{HMAC-SHA512}}(m, p, 2048)
La valeur de la graine est ainsi influencée par la valeur de la phrase mnémonique et de la passphrase. En modifiant la passphrase, on obtient une graine différente. En revanche, avec une phrase mnémonique et une passphrase identiques, on génère toujours la même graine, puisque PBKDF2 est une fonction déterministe. Cela garantit que l’on peut retrouver les mêmes paires de clés grâce à nos sauvegardes.
Remarque : Dans le langage courant, le terme "graine" désigne souvent, par abus de langage, la phrase mnémonique. En effet, en l'absence de passphrase, l'une est simplement l'encodage de l'autre. Cependant, comme nous l'avons vu, dans la réalité technique des portefeuilles, la graine et la phrase mnémonique sont bien deux éléments distincts.
Maintenant que nous disposons de notre graine, nous pouvons continuer la dérivation de notre portefeuille Bitcoin.
La clé maîtresse et le code de chaîne maître
Une fois la graine obtenue, la prochaine étape de la dérivation d'un portefeuille HD consiste à calculer la clé privée maîtresse et le code de chaîne maître, qui représenteront la profondeur 0 de notre portefeuille.
Pour obtenir la clé privée maîtresse et le code de chaîne maître, on applique la fonction HMAC-SHA512 à la graine, en utilisant une clé fixe "Bitcoin Seed" identique pour tous les utilisateurs de Bitcoin. Cette constante est choisie pour garantir que les dérivations de clé sont spécifiques à Bitcoin. Voici les éléments :
\text{HMAC-SHA512}: la fonction de dérivations ;s: la graine du portefeuille de 512 bits ;\text{"Bitcoin Seed"}: la constante de dérivation commune à tous les portefeuilles Bitcoin.
\text{output} = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)La sortie de cette fonction est donc de 512 bits. Elle est ensuite divisée en 2 parties :
- Les 256 bits de gauche forment la clé privée maîtresse ;
- Les 256 bits de droite forment le code de chaîne maître.
Mathématiquement, on peut noter ces deux valeurs comme suit avec k_M la clé privée maîtresse et C_M le code de chaîne maître :
k_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[:256]}C_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[256:]}
Rôle de la clé maîtresse et du code de chaîne
La clé privée maîtresse est considérée comme la clé parent, à partir de laquelle toutes les clés privées dérivées — enfants, petits-enfants, arrière-petits-enfants, etc. — seront générées. Elle représente le niveau zéro dans la hiérarchie de dérivation.
Le code de chaîne maître, pour sa part, introduit une source d’entropie supplémentaire dans le processus de dérivation des clés enfants, afin de contrer certaines attaques potentielles. D’ailleurs, dans le portefeuille HD, chaque paire de clés possède un code de chaîne unique associé, qui est utilisé lui aussi pour dériver des clés enfants à partir de cette paire, mais nous en parlerons plus en détail dans les prochains chapitres.
Avant de poursuivre la dérivation du portefeuille HD avec les éléments suivants, je souhaite, dans le prochain chapitre, vous présenter les clés étendues, qui sont souvent confondues avec la clé maîtresse. Nous allons voir comment elles sont construites et quel rôle elles jouent dans le portefeuille Bitcoin.
Les clés étendues
Une clé étendue est simplement la concaténation d’une clé (qu’elle soit privée ou publique) et de son code de chaîne associé. Ce code de chaîne est indispensable pour la dérivation des clés enfants car, sans lui, il est impossible de dériver les clés enfants d’une clé parent, mais nous découvrirons plus précisément ce processus dans le chapitre suivant. Ces clés étendues permettent ainsi d’agréger toutes les informations nécessaires pour dériver des clés enfants, et donc de simplifier la gestion des comptes au sein d'un portefeuille HD.
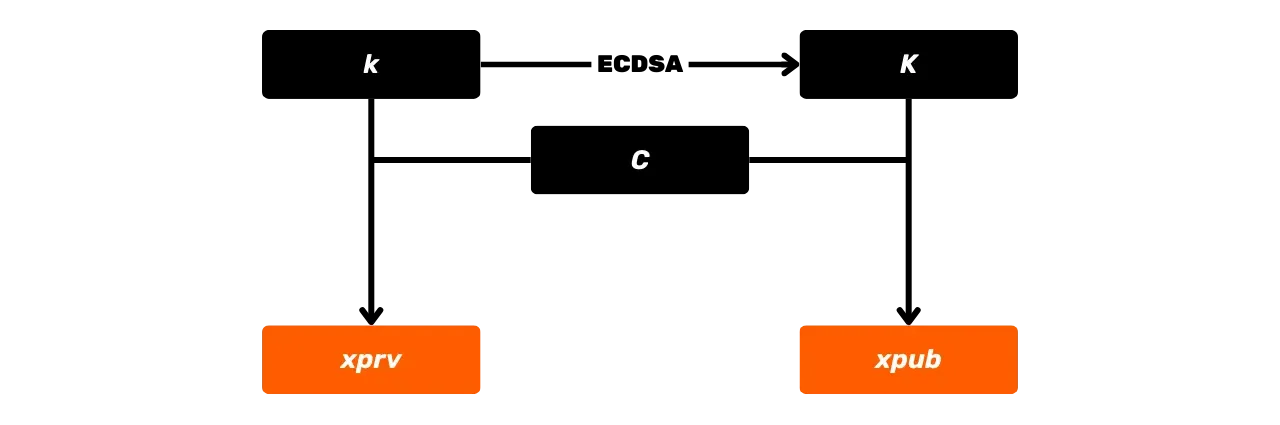
La clé étendue se compose de deux parties :
- La charge utile, qui contient la clé privée ou la clé publique ainsi que le code de chaîne associé ;
- Les métadonnées, qui sont diverses informations pour faciliter l'interopérabilité entre les logiciels et améliorer la compréhension pour l’utilisateur.
Fonctionnement des clés étendues
Lorsque la clé étendue contient une clé privée, on dit que c'est une clé
privée étendue. Elle se reconnait par son préfixe qui contient la mention prv. En plus de la clé privée, la clé privée étendue contient donc également
le code chaîne associé à la clé. Avec ce type de clé étendue, il est
possible de dériver tous les types de clés privées enfants, et donc par
addition et doublement de points sur les courbes elliptiques, elle permet
également de dériver l’intégralité des clés publiques enfants.
Lorsque la clé étendue ne contient pas une clé privée, mais à la place, une
clé publique, on dit que c'est une clé publique étendue. Elle se reconnait
par son préfixe qui contient la mention pub. Évidemment, en
plus de la clé, elle contient également le code de chaîne associé.
Contrairement à la clé privée étendue, la clé publique étendue permet de
dériver uniquement les clés publiques enfants dites "normales" (c'est-à-dire
qu'elle ne peut pas dériver les clés enfants "endurcies"). Nous verrons dans
le chapitre suivant ce que signifient ces qualificatifs "normale" et
"endurcie".
Mais dans tous les cas, la clé publique étendue ne permet pas de dériver des
clés privées enfants. Par conséquent, même si une personne a accès à une xpub, elle ne pourra pas dépenser les fonds associés, car elle n’aura pas accès
aux clés privées correspondantes. Elle pourra seulement dériver les clés
publiques enfant pour observer les transactions associées.
Pour la suite, nous adopterons la notation suivante :
K_{\text{PAR}}: une clé publique parent ;k_{\text{PAR}}: une clé privée parent ;C_{\text{PAR}}: un code chaîne parent ;C_{\text{CHD}}: un code chaîne enfant ;K_{\text{CHD}}^n: une clé publique enfant normale ;k_{\text{CHD}}^n: une clé privée enfant normale ;K_{\text{CHD}}^h: une clé publique enfant endurcie ;k_{\text{CHD}}^h: une clé privée enfant endurcie.

Construction d'une clé étendue
Une clé étendue est structurée comme suit :
- Version : Code de version pour identifier la nature de la
clé (
xprv,xpub,yprv,ypub...). Nous verrons à la fin de ce chapitre à quoi correspondent les lettresx,yetz. - Profondeur : Niveau hiérarchique dans le portefeuille HD par rapport à la clé maîtresse (0 pour la clé maîtresse).
- Empreinte parent : Les 4 premiers octets du hash HASH160 de la clé publique parent ayant servi à dériver la clé présente dans la charge utile.
- Numéro d'index : Identifiant de l'enfant parmi les clés sœurs, c'est-à-dire parmi toutes les clés au même étage de dérivation qui ont les mêmes clés parent.
- Code de chaîne : Code unique de 32 octets pour la dérivation des clés enfants.
- Clé : La clé privée (préfixée par 1 octet pour la taille) ou la clé publique.
- Somme de contrôle : On ajoute également une checksum calculée avec la fonction HASH256 (double SHA256), qui permet de vérifier l’intégrité de la clé étendue lors de sa transmission ou de son stockage.
Le format complet d’une clé étendue est donc de 78 octets sans la checksum, et de 82 octets avec la checksum. Elle est ensuite convertie en Base58 pour produire une représentation facilement lisible par les utilisateurs. Le format Base58 est le même que celui utilisé pour les adresses de réception Legacy (avant SegWit).
| Élément | Description | Taille |
|---|---|---|
| Version | Indique si la clé est publique (xpub, ypub)
ou privée (xprv, zprv), ainsi que la version
de la clé étendue | 4 octets |
| Profondeur | Niveau dans la hiérarchie par rapport à la clé maîtresse | 1 octet |
| Empreinte parent | Les 4 premiers octets de HASH160 de la clé publique parent | 4 octets |
| Numéro d'index | Position de la clé dans l’ordre des enfants | 4 octets |
| Code de chaîne | Utilisé pour dériver les clés enfants | 32 octets |
| Clé | La clé privée (avec un préfixe de 1 octet) ou la clé publique | 33 octets |
| Somme de contrôle | Checksum pour vérifier l'intégrité | 4 octets |
Si l'on ajoute un octet à la clé privée uniquement, c’est parce que la clé
publique compressée est plus longue que la clé privée d’un octet. Cet octet
supplémentaire, ajouté au début de la clé privée sous la forme 0x00, permet d’égaliser leur taille, ce qui assure d'avoir une charge utile de
clé étendue de même longueur, qu’il s’agisse d’une clé publique ou d'une clé
privée.
Préfixes des clés étendues
Comme nous venons de le voir, les clés étendues incluent un préfixe qui
indique d'une part la version de la clé étendue, mais également sa nature.
La notation pub indique que l'on à affaires à une clé publique
étendue et la notation prv indique une clé privée étendue. La lettre
supplémentaire qui se trouve à la base de la clé étendue permet d'indiquer si
le standard suivi est Legacy, SegWit v0, SegWit v1...
Voici donc un récapitulatif des préfixes utilisés et de leur signification :
| Préfixe base 58 | Préfixe base 16 | Réseau | Objectif | Scripts associés | Dérivation | Type de clé |
|---|---|---|---|---|---|---|
xpub | 0488b21e | Mainnet | Legacy et SegWit V1 | P2PK / P2PKH / P2TR | m/44'/0', m/86'/0' | publique |
xprv | 0488ade4 | Mainnet | Legacy et SegWit V1 | P2PK / P2PKH / P2TR | m/44'/0', m/86'/0' | privée |
tpub | 043587cf | Testnet | Legacy et SegWit V1 | P2PK / P2PKH / P2TR | m/44'/1', m/86'/1' | publique |
tprv | 04358394 | Testnet | Legacy et SegWit V1 | P2PK / P2PKH / P2TR | m/44'/1', m/86'/1' | privée |
ypub | 049d7cb2 | Mainnet | Nested SegWit | P2WPKH in P2SH | m/49'/0' | publique |
yprv | 049d7878 | Mainnet | Nested SegWit | P2WPKH in P2SH | m/49'/0' | privée |
upub | 049d7cb2 | Testnet | Nested SegWit | P2WPKH in P2SH | m/49'/1' | publique |
uprv | 044a4e28 | Testnet | Nested SegWit | P2WPKH in P2SH | m/49'/1' | privée |
zpub | 04b24746 | Mainnet | SegWit V0 | P2WPKH | m/84'/0' | publique |
zprv | 04b2430c | Mainnet | SegWit V0 | P2WPKH | m/84'/0' | privée |
vpub | 045f1cf6 | Testnet | SegWit V0 | P2WPKH | m/84'/1' | publique |
vprv | 045f18bc | Testnet | SegWit V0 | P2WPKH | m/84'/1' | privée |
Détail des éléments d'une clé étendue
Pour mieux comprendre la structure interne d'une clé étendue, nous allons en prendre une pour exemple et la décomposer. Voici une clé étendue :
- En Base58 :
xpub6CTNzMUkzpurBWaT4HQoYzLP4uBbGJuWY358Rj7rauiw4rMHCyq3Rfy9w4kyJXJzeFfyrKLUar2rUCukSiDQFa7roTwzjiAhyQAdPLEjqHT
- En hexadécimal :
0488B21E036D5601AD80000000C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A89303772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF50658051F067C3A
Cette clé étendue se décompose en plusieurs éléments distincts :
- Version :
0488B21E
Les 4 premiers octets sont la version. Ici, cela correspond à une clé publique étendue sur le Mainnet avec un objectif de dérivation soit Legacy, soit SegWit v1.
- Profondeur :
03
Ce champ indique le niveau hiérarchique de la clé dans le portefeuille HD.
Dans ce cas, une profondeur de 03 signifie que cette clé est à trois
niveaux de dérivation en dessous de la clé maîtresse.
- Empreinte parent :
6D5601AD
Ce sont les 4 premiers octets du hash HASH160 de la clé publique parent
ayant servi à dériver cette xpub.
- Numéro d'index :
80000000
Cet index indique la position de la clé parmi les enfants de ses clés
parent. Le préfixe 0x80 indique que la clé est dérivée de manière
endurcie, et puisque le reste est rempli de zéros, cela indique que cette clé
est la première parmi ses éventuelles sœurs.
Code de chaîne :
C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A893Clé publique :
03772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF5065805Somme de contrôle :
1F067C3A
La checksum correspond aux 4 premiers octets du hachage (double SHA256) de tout le reste.
Dans ce chapitre, nous avons découvert qu’il existe deux types de clés enfants différents. Nous avons également appris que la dérivation de ces clés enfants nécessite une clé (privée ou publique) et son code de chaîne. Dans le chapitre suivant, nous examinerons en détail la nature de ces différents types de clés et la manière de les dériver à partir de leur clé et code de chaîne parent.
Dérivation des paires de clés enfants
La dérivation des paires de clés enfants dans les portefeuilles HD Bitcoin repose sur une structure hiérarchique permettant de générer un grand nombre de clés, tout en organisant ces paires en différents groupes via des branches. Chaque paire enfant dérivée depuis une paire parent peut être utilisée soit directement dans un scriptPubKey pour verrouiller des bitcoins, soit comme point de départ pour générer d’autres clés enfants, et ainsi de suite, afin de créer une arborescence de clés.
Toutes ces dérivations débutent avec la clé maîtresse et le code de chaîne maître, qui sont les premiers parents au niveau de profondeur 0. Ce sont, en quelque sorte, les Adam et Ève des clés de votre portefeuille, ancêtres communs de toutes les clés dérivées.
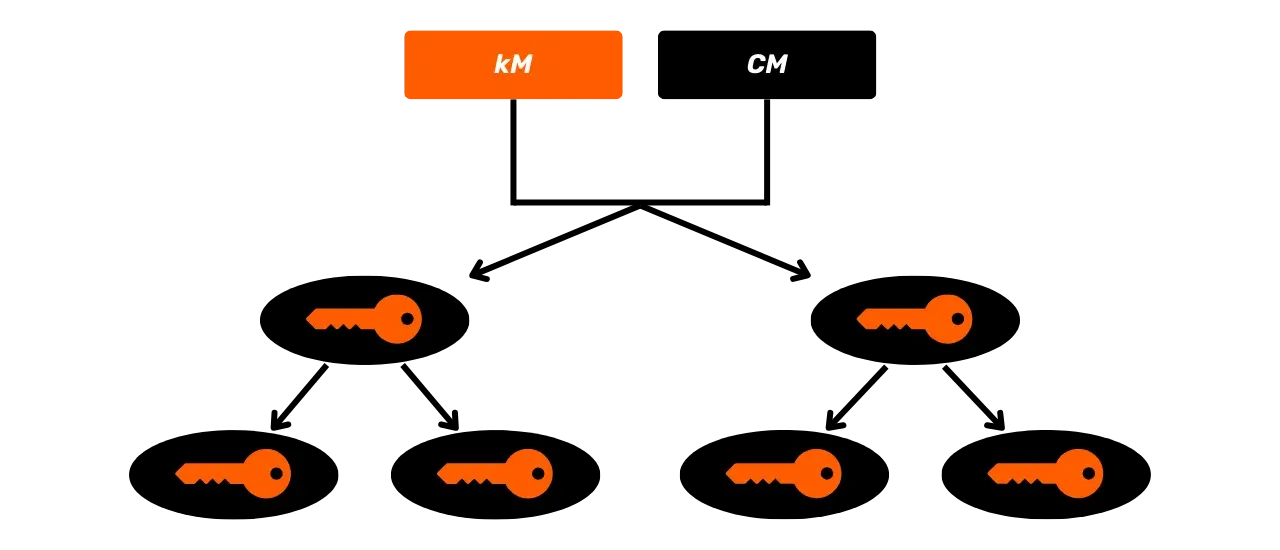
Découvrons ensemble comment fonctionne cette dérivation déterministe.
Les différents types de dérivations de clés enfants
Nous l'avons abordé rapidement dans le chapitre précédent : les clés enfants se divisent en deux types principaux :
- Les clés enfants normales (
k_{\text{CHD}}^n, K_{\text{CHD}}^n) : Elles sont dérivées à partir de la clé publique étendue parent (K_{\text{PAR}}), ou de la clé privée étendue (k_{\text{PAR}}), en dérivant d'abord la clé publique. - Les clés enfants endurcies (
k_{\text{CHD}}^h, K_{\text{CHD}}^h) : Elles ne peuvent être dérivées qu'à partir de la clé privée étendue (k_{\text{PAR}}) et sont donc invisibles aux observateurs disposant uniquement de la clé publique étendue.
Chaque paire de clés enfant est identifiée par un index de
32 bits (nommé i dans nos
calculs). Les index pour les clés normales vont de 0 à 2^{31}-1, tandis
que ceux des clés endurcies vont de 2^{31} à 2^{32}-1. Ces
numéros servent à distinguer les paires de clés sœurs lors de la dérivation.
En effet, chaque paire de clés parent doit être capable de dériver plusieurs
paires de clés enfants. Si l’on appliquait systématiquement le même calcul
depuis les clés parent, toutes les clés sœurs obtenues seraient identiques,
ce qui n’est pas souhaitable. L’index introduit donc une variable qui
modifie le calcul de dérivation, permettant ainsi de différencier chaque
paire sœur. Sauf utilisation spécifique dans certains protocoles et
standards de dérivation, on commence généralement par dériver la première
clé enfant avec l’index 0, la seconde avec l’index 1, et ainsi de suite.
Processus de dérivation avec HMAC-SHA512
La dérivation de chaque clé enfant repose sur la fonction HMAC-SHA512 dont
nous avons parlé dans la section 2 sur les fonctions de hachage. Elle prend
en entrée 2 éléments : le code de chaîne parent C_{\text{PAR}} et la concaténation de la clé parent (soit la clé publique K_{\text{PAR}}, soit la clé privée k_{\text{PAR}} en fonction du type de clé enfant souhaité) et de l’index. La sortie du HMAC-SHA512
est une séquence de 512 bits, séparée en deux parties :
- Les 32 premiers octets (ou
h_1) servent à calculer la nouvelle paire enfant. - Les 32 derniers octets (ou
h_2) servent de nouveau code de chaîneC_{\text{CHD}}pour la paire enfant.
Dans tous nos calculs, je noterai \text{hash} l'output de la fonction HMAC-SHA512.
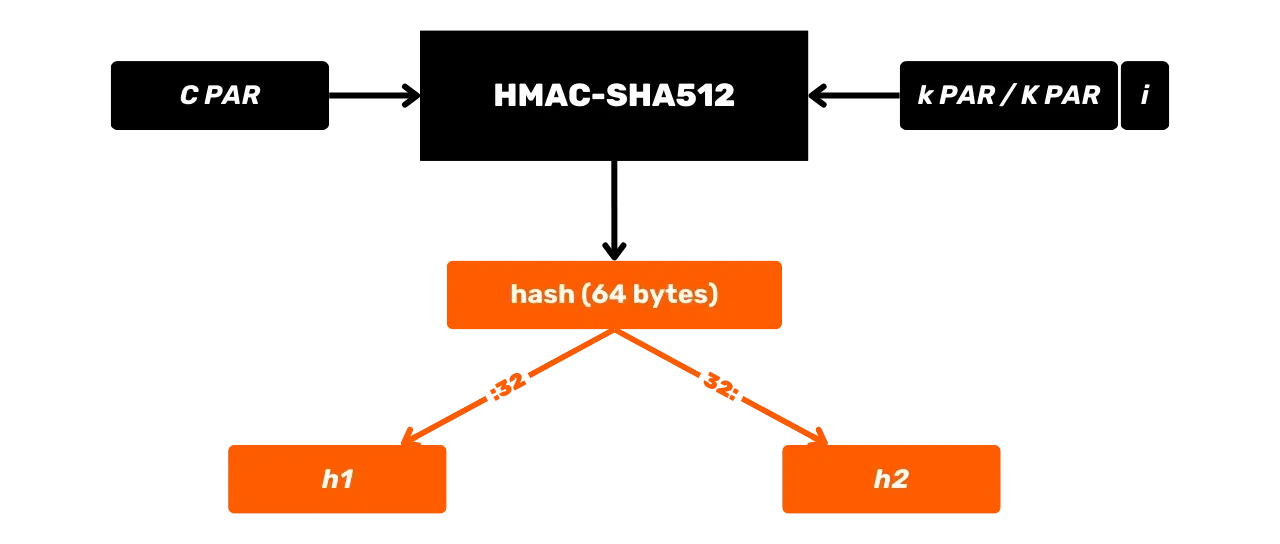
Dérivation d'une clé privée enfant à partir d’une clé privée parent
Pour dériver une clé privée enfant k_{\text{CHD}} à partir d’une clé privée parent k_{\text{PAR}}, deux scénarios sont possibles en fonction de si l'on veut avoir une clé
endurcie ou normale.
Pour une clé enfant normale (i < 2^{31}), le calcul de \text{hash} est le suivant
:
\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, G \cdot k_{\text{PAR}} \Vert i)Dans ce calcul, on observe que notre fonction HMAC prend deux entrées : d’abord le code de chaîne parent, puis la concaténation de l’index avec la clé publique associée à la clé privée parent. La clé publique parent est utilisée ici car nous cherchons à dériver une clé enfant normale, et non endurcie.
On a donc maintenant un \text{hash} de 64 octets que l'on va séparer en 2 parties de 32 octets chacune : h_1 et h_2 :
\text{hash} = h_1 \Vert h_2h_1 = \text{hash}_{[:32]} \quad, \quad h_2 = \text{hash}_{[32:]}La clé privée enfant k_{\text{CHD}}^n est alors calculée comme cela :
k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod nDans ce calcul, l’opération \text{parse256}(h_1) consiste à interpréter les 32 premiers octets du \text{hash} comme un entier de 256 bits. Ce nombre est ensuite additionné à la clé
privée parent, le tout étant pris modulo n pour rester dans l’ordre de
la courbe elliptique, comme nous l’avons vu dans la section 3 sur les signatures
électroniques. Ainsi, pour dériver une clé privée enfant normale, bien que la
clé publique parent soit utilisée comme base de calcul dans les entrées de la
fonction HMAC-SHA512, il est toujours nécessaire de disposer de la clé privée
parent pour finaliser le calcul.
À partir de cette clé privée enfant, il est possible de dériver la clé publique correspondante en appliquant ECDSA ou Schnorr. Nous obtiendrons ainsi une paire de clés complète.
Ensuite, on interprète simplement la seconde partie du \text{hash} comme étant le code chaîne pour la paire de clés enfants que l'on vient de
dériver :
C_{\text{CHD}} = h_2Voici une représentation schématique de la dérivation globale :
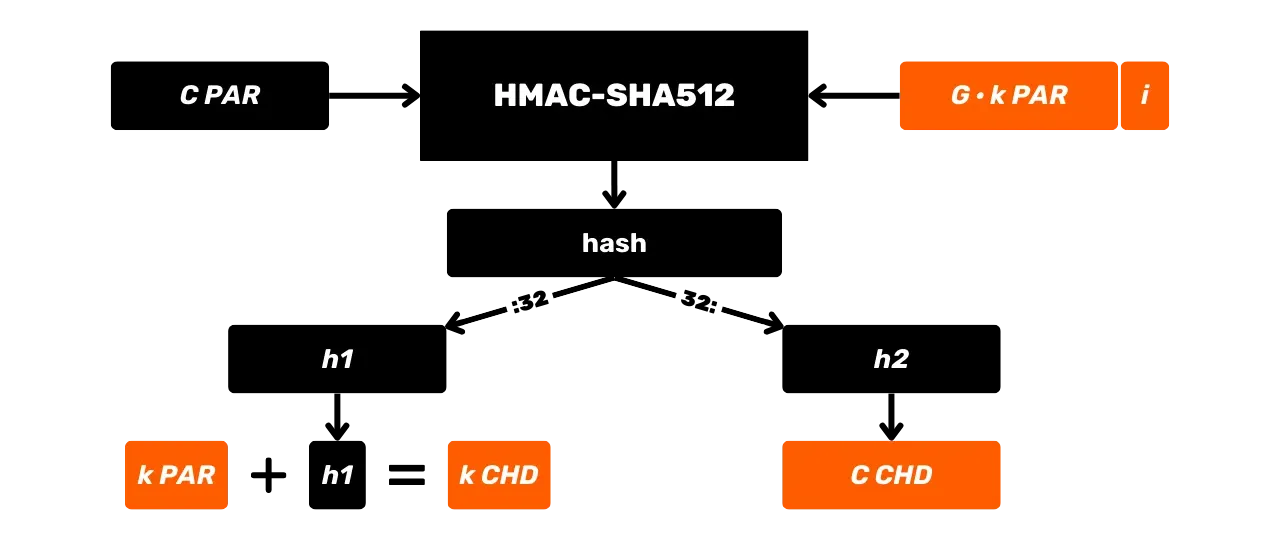
Pour une clé enfant endurcie (i \geq 2^{31}), le calcul de \text{hash} est le suivant
:
hash = \text{HMAC-SHA512}(C_{\text{PAR}}, 0x00 \Vert k_{\text{PAR}} \Vert i)Dans ce calcul, on observe que notre fonction HMAC prend deux entrées :
d’abord le code de chaîne parent, puis la concaténation de l’index avec la
clé privée parent. La clé privée parent est utilisée ici car nous cherchons
à dériver une clé enfant endurcie. De plus, un octet égal à 0x00 est ajouté au début de la clé. Cette opération permet d'égaliser sa longueur
pour correspondre à celle d'une clé publique compressée.
On a donc maintenant un \text{hash} de 64 octets que l'on va séparer en 2 parties de 32 octets chacune : h_1 et h_2 :
\text{hash} = h_1 \Vert h_2h_1 = \text{hash}_{[:32]} \quad, \quad h_2 = \text{hash}_{[32:]}La clé privée enfant k_{\text{CHD}}^h est alors calculée comme cela :
k_{\text{CHD}}^h = \text{parse256}(h_1) + k_{\text{PAR}} \mod nEnsuite, on interprète simplement la seconde partie de \text{hash} comme étant le code chaîne pour la paire de clés enfants que l'on vient de
dériver :
C_{\text{CHD}} = h_2Voici une représentation schématique de la dérivation globale :

On peut donc constater que la dérivation normale et la dérivation endurcie fonctionnent de manière identique, à cette différence près : la dérivation normale utilise en entrée de la fonction HMAC la clé publique parent, tandis que la dérivation renforcée utilise la clé privée parent.
Dérivation d'une clé publique enfant à partir d’une clé publique parent
Si l'on n'a connaissance que de la clé publique parent K_{\text{PAR}} et du code de chaîne associé C_{\text{PAR}}, c'est-à-dire une clé publique étendue, il est possible de dériver des
clés publiques enfant K_{\text{CHD}}^n, mais seulement pour des clés enfants normales (non endurcies). Ce
principe permet notamment de pouvoir surveiller les mouvements d'un compte
dans un portefeuille Bitcoin à partir de la xpub (watch-only).
Pour réaliser ce calcul, on va calculer le \text{hash} avec un index i < 2^{31} (dérivation
normale) :
\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, K_{\text{PAR}} \Vert i)Dans ce calcul, on observe que notre fonction HMAC prend deux entrées : d’abord le code de chaîne parent, puis la concaténation de l’index avec la clé publique parent.
On a donc maintenant un hash de 64 octets que l'on va séparer en 2 parties de 32 octets chacune : h_1 et h_2 :
\text{hash} = h_1 \Vert h_2h_1 = \text{hash}_{[:32]} \quad, \quad h_2 = \text{hash}_{[32:]}La clé publique enfant K_{\text{CHD}}^n est alors calculée comme cela :
K_{\text{CHD}}^n = G \cdot \text{parse256}(h_1) + K_{\text{PAR}}Si \text{parse256}(h_1) \geq n (ordre de la courbe elliptique) ou si K_{\text{CHD}}^n est le point à l'infini, la dérivation est invalide, et un autre index doit
être choisi.
Dans ce calcul, l’opération \text{parse256}(h_1) consiste à interpréter les 32 premiers octets du \text{hash} comme un entier de 256 bits. On utilise ce nombre pour calculer un point sur
la courbe elliptique par addition et doublement depuis le point générateur G. Ce point est ensuite
additionné à la clé publique parent pour obtenir la clé publique enfant
normale. Ainsi, pour dériver une clé publique enfant normale, seules la clé
publique parent et le code de chaîne parent sont nécessaires ; la clé privée
parent n'intervient jamais dans ce processus, contrairement au calcul de la
clé privée enfant que nous avons vu précédemment.
Ensuite, le code de chaîne enfant est simplement :
C_{\text{CHD}} = h_2Voici une représentation schématique de la dérivation globale :
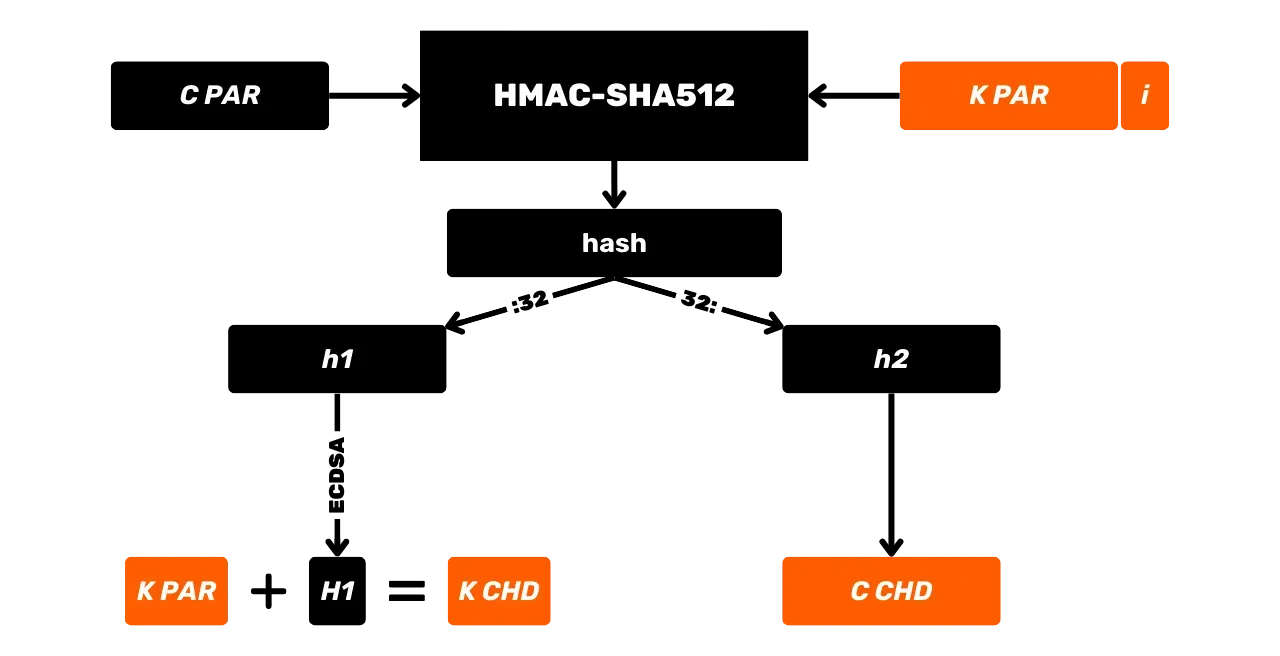
Correspondance entre les clés publiques et privées enfants
Une question que l'on peut se poser est de comprendre comment une clé publique enfant normale dérivée d’une clé publique parent peut correspondre à une clé privée enfant normale dérivée de la clé privée parent correspondante. Ce lien est justement assuré par les propriétés des courbes elliptiques. En effet, pour dériver une clé publique enfant normale, HMAC-SHA512 est appliquée de la même manière, mais sa sortie est utilisée différemment :
- Clé privée enfant normale :
k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n - Clé publique enfant normale :
K_{\text{CHD}}^n = G \cdot \text{parse256}(h_1) + K_{\text{PAR}}
Grâce aux opérations d’addition et de doublement sur la courbe elliptique, les deux méthodes produisent des résultats cohérents : la clé publique dérivée de la clé privée enfant est identique à la clé publique enfant dérivée directement de la clé publique parent.
Résumé des types de dérivations
Pour résumer, voici les différents types de dérivations possibles :
\begin{array}{|c|c|c|c|}
\hline
\rightarrow & \text{PAR} & \text{CHD} & \text{n/h} \\
\hline
k_{\text{PAR}} \rightarrow k_{\text{CHD}} & k_{\text{PAR}} & \{ k_{\text{CHD}}^n, k_{\text{CHD}}^h \} & \{ n, h \} \\
k_{\text{PAR}} \rightarrow K_{\text{CHD}} & k_{\text{PAR}} & \{ K_{\text{CHD}}^n, K_{\text{CHD}}^h \} & \{ n, h \} \\
K_{\text{PAR}} \rightarrow k_{\text{CHD}} & K_{\text{PAR}} & \times & \times \\
K_{\text{PAR}} \rightarrow K_{\text{CHD}} & K_{\text{PAR}} & K_{\text{CHD}}^n & n \\
\hline
\end{array}Si je résume, vous avez appris jusqu’à présent à créer les éléments de base du portefeuille HD : la phrase mnémonique, la graine, puis la clé maîtresse et le code de chaîne maître. Vous avez également découvert comment dériver des paires de clés enfants dans ce chapitre. Dans le prochain chapitre, nous découvrirons comment ces dérivations s’organisent dans les portefeuilles Bitcoin et quelle structure suivre pour obtenir concrètement les adresses de réception ainsi que les paires de clés utilisées dans le scriptPubKey et le scriptSig.
Structure du portefeuille et chemins de dérivation
La structure hiérarchique des portefeuilles HD sur Bitcoin permet d'organiser les paires de clés de diverses façons. L'idée est de dériver, depuis la clé privée maîtresse et le code de chaîne maître, plusieurs niveaux de profondeur. Chaque niveau ajouté correspond à la dérivation d’une paire de clés enfants à partir d’une paire de clés parent.
Au fil du temps, différents BIP ont introduit des normes pour ces chemins de dérivation, visant à standardiser leur usage entre les différents logiciels. Nous allons donc découvrir dans ce chapitre la signification de chaque niveau de dérivation dans les portefeuilles HD, en fonction de ces standards.
Les profondeurs de dérivation d’un portefeuille HD
Les chemins de dérivation sont organisés en couches de profondeur, allant de la profondeur 0, qui représente la clé maîtresse et le code de chaîne maître, jusqu'à des couches de sous-niveaux pour dériver les adresses utilisées pour verrouiller des UTXOs. Les BIPs (Bitcoin Improvement Proposals) définissent les normes de chaque couche, ce qui permet d'harmoniser les pratiques entre les différents logiciels de gestion de portefeuille.
Un chemin de dérivation désigne donc la séquence d'index utilisée pour dériver des clés enfants à partir d'une clé maîtresse.
Profondeur 0 : Clé maîtresse (BIP32)
Cette profondeur correspond à la clé privée maîtresse et au code de chaîne
maître du portefeuille. Elle est représentée par la notation m/.
Profondeur 1 : Objectif (BIP43)
L’objectif détermine la structure logique de dérivation. Par exemple, une
adresse P2WPKH aura /84'/ en
profondeur 1 (selon le BIP84), tandis qu’une adresse P2TR aura /86'/ (selon le BIP86). Cette
couche facilite la compatibilité entre les portefeuilles, en indiquant des numéros
d’index correspondant aux numéros des BIPs.
Autrement dit, une fois que l’on dispose de la clé maîtresse et du code de
chaîne maître, ceux-ci servent de paire de clés parent pour dériver une
paire de clés enfant. L’index utilisé dans cette dérivation peut être, par
exemple, /84'/ si le portefeuille
est destiné à utiliser des scripts de type SegWit v0. Cette paire de clés se
situe alors en profondeur 1. Elle n’a pas pour rôle de verrouiller des bitcoins,
mais simplement de servir de point de passage dans la hiérarchie de dérivation.
Profondeur 2 : Type de devise (BIP44)
À partir de la paire de clés en profondeur 1, on effectue une nouvelle dérivation pour obtenir la paire de clés en profondeur 2. Cette profondeur permet de différencier les comptes Bitcoin des autres crypto-monnaies au sein d'un même portefeuille.
Chaque devise possède un index unique pour assurer la compatibilité sur des
portefeuilles multi-devises. Par exemple, pour Bitcoin, l’index est /0'/ (ou 0x80000000 en notation hexadécimale). Les index des devises
sont choisis dans l’intervalle de 2^{31} à 2^{32}-1 pour garantir
une dérivation endurcie.
Pour vous donner d'autres exemples, voici les index de quelques devises :
1'(0x80000001) pour les bitcoins testnet ;2'(0x80000002) pour Litecoin ;60'(0x8000003c) pour Ethereum...
Profondeur 3 : Compte (BIP32)
Chaque portefeuille peut être divisé en plusieurs comptes, numérotés à
partir de 2^{31},
et représentés en profondeur 3 par /0'/ pour le premier compte, /1'/ pour le second, et ainsi de suite. En général, lorsqu’on fait référence à
une clé étendue xpub, il s’agit des clés situées à cette
profondeur de dérivation.
Cette séparation en différents comptes est optionnelle. Elle vise à simplifier l’organisation du portefeuille pour les utilisateurs. En pratique, on utilise souvent un seul compte, généralement le premier par défaut. Cependant, dans certains cas, si l’on souhaite bien distinguer les paires de clés pour différents usages, cela peut s’avérer utile. Par exemple, il est possible de créer un compte personnel et un compte professionnel à partir de la même graine, avec des groupes de clés complètement distincts à partir de cette profondeur de dérivation.
Profondeur 4 : Chaîne (BIP32)
Chaque compte défini en profondeur 3 est ensuite structuré en deux chaînes :
- La chaîne externe : Dans cette chaîne, on dérive les
adresses dites "publiques". Ces adresses de réception sont destinées à
verrouiller des UTXOs provenant de transactions extérieures (c'est-à-dire
qui proviennent de la consommation d'UTXOs qui ne vous appartiennent pas).
Pour le dire plus simplement, cette chaîne externe est utilisée à chaque
fois que l'on souhaite recevoir des bitcoins. Lorsque vous cliquez sur "recevoir" dans votre logiciel de portefeuille, c’est toujours une adresse de la
chaîne externe qui vous est proposée. Cette chaîne est représentée par une
paire de clés dérivée avec l’index
/0/. - La chaîne interne (change) : Cette chaîne est réservée
aux adresses de réception qui verrouillent des bitcoins provenant de la
consommation d’UTXOs vous appartenant, autrement dit, les adresses de
change. Elle est identifiée par l’index
/1/.
Profondeur 5 : Index d’adresse (BIP32)
Enfin, la profondeur 5 représente la dernière étape de dérivation dans le
portefeuille. Bien qu’il soit techniquement possible de continuer
indéfiniment, les standards actuels s’arrêtent ici. À cette profondeur
finale, on dérive donc les paires de clés qui seront effectivement utilisées
pour verrouiller et déverrouiller les UTXOs. Chaque index permet de
distinguer les paires de clés sœurs : ainsi, la première adresse de
réception utilisera l’index /0/, la seconde l’index /1/, et
ainsi de suite.
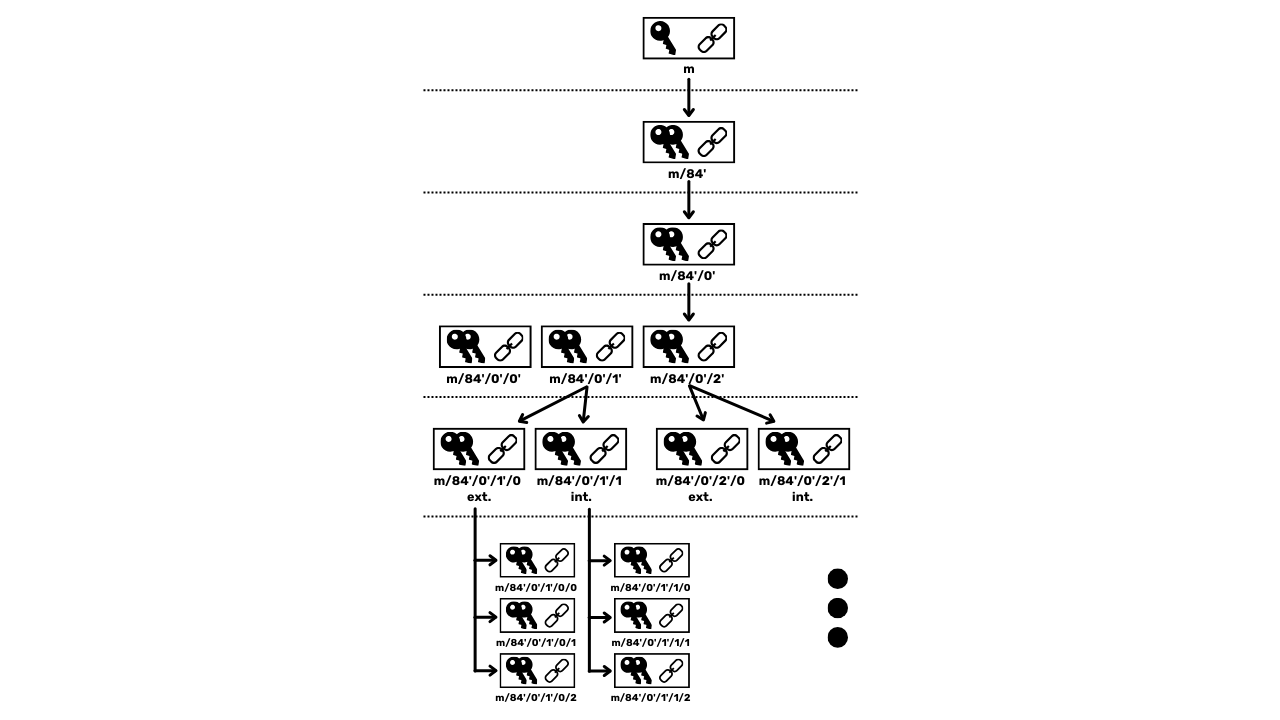
Notation des chemins de dérivation
Le chemin de dérivation s’écrit en séparant chaque niveau par une barre
oblique (/). Chaque barre
oblique indique ainsi une dérivation d'une paire de clés parent (k_{\text{PAR}}, K_{\text{PAR}}, C_{\text{PAR}}) vers une paire de clés enfant (k_{\text{CHD}}, K_{\text{CHD}}, C_{\text{CHD}}). Le nombre noté à chaque profondeur correspond à l'index utilisé pour
dériver cette clé à partir de ses parents. L’apostrophe (') située parfois à droite de l'index indique une dérivation endurcie (k_{\text{CHD}}^h, K_{\text{CHD}}^h). Parfois, cette apostrophe est remplacée par un h. En l'absence d'apostrophe
ou de h, il s'agit donc d'une
dérivation normale (k_{\text{CHD}}^n, K_{\text{CHD}}^n).
Comme nous l’avons vu dans les chapitres précédents, les index des clés
endurcies commencent à partir de 2^{31}, soit 0x80000000 en hexadécimal. Par conséquent, lorsqu'un
index est accompagné d'une apostrophe dans un chemin de dérivation, il faut
ajouter 2^{31} au
nombre indiqué pour obtenir la valeur réelle utilisée dans la fonction
HMAC-SHA512. Par exemple, si le chemin de dérivation spécifie /44'/, l’index réel sera :
i = 44 + 2^{31} = 2\,147\,483\,692En hexadécimal, cela donne 0x8000002C.
Maintenant que nous avons compris les grands principes des chemins de dérivation, prenons un exemple ! Voici le chemin de dérivation d'une adresse de réception Bitcoin :
m / 84' / 0' / 1' / 0 / 7Dans cet exemple :
84'indique le standard P2WPKH (SegWit v0) ;0'indique la devise Bitcoin sur le mainnet ;1'correspond au deuxième compte dans le portefeuille ;0désigne que l'adresse est sur la chaîne externe ;7désigne la 8ème adresse externe de ce compte.
Résumé de la structure de dérivation
| Profondeur | Description | Exemple standard |
|---|---|---|
| 0 | Clé maîtresse | m/ |
| 1 | Objectif | /86'/ (P2TR) |
| 2 | Devise | /0'/ (Bitcoin) |
| 3 | Compte | /0'/ (Premier compte) |
| 4 | Chaîne | /0/ (externe) ou /1/ (change) |
| 5 | Index de l’adresse | /0/ (première adresse) |
Dans le prochain chapitre, nous allons découvrir ce que sont les "output script descriptors", une innovation récemment introduite dans Bitcoin Core qui simplifie la sauvegarde d'un portefeuille Bitcoin.
Output script descriptors
On vous dit souvent que la phrase mnémonique seule suffit pour récupérer l’accès à un portefeuille. En réalité, les choses sont un peu plus complexes. Dans le chapitre précédent, nous avons vu la structure de dérivation du portefeuille HD, et vous avez peut-être constaté que ce processus est assez complexe. Les chemins de dérivation indiquent à un logiciel la direction à suivre pour dériver les clés de l’utilisateur. Cependant, lors de la récupération d’un portefeuille Bitcoin, si l’on ne connaît pas ces chemins, la phrase mnémonique seule ne suffit pas. Elle permet d’obtenir la clé maîtresse et le code de chaîne maître, mais il est ensuite nécessaire de connaître les index utilisés pour atteindre les clés enfant.
Théoriquement, il faudrait donc sauvegarder non seulement la phrase mnémonique de notre portefeuille, mais aussi les chemins vers les comptes que l’on utilise. En pratique, on parvient souvent à retrouver l’accès aux clés enfant sans cette information, à condition d’avoir suivi les standards. En testant un à un chaque standard, on parvient généralement à retrouver l’accès aux bitcoins. Cependant, cela n’est pas garanti et c'est surtout compliqué pour les débutants. Aussi, avec la diversification des types de scripts et l’émergence de configurations plus complexes, ces informations pourraient devenir difficiles à extrapoler, transformant ainsi ces données en informations privées et difficilement récupérables par brute force. C’est pourquoi une innovation a récemment été introduite et commence à être intégrée dans vos logiciels de portefeuille préférés : les output script descriptors.
C'est quoi un "descriptor" ?
Les "output script descriptors", ou simplement "descriptors", sont des expressions structurées qui décrivent intégralement un script de sortie (scriptPubKey) et fournissent toutes les informations nécessaires pour suivre les transactions associées à un script particulier. Ils facilitent la gestion des clés dans les portefeuilles HD en offrant une description standardisée et complète de la structure du portefeuille et des types d’adresses utilisés.
L’avantage principal des descriptors réside dans leur capacité à encapsuler
toutes les informations essentielles pour restaurer un portefeuille dans une
seule chaîne de caractères (en complément de la phrase de récupération). En
sauvegardant un descriptor avec les phrases mnémoniques associées, il
devient possible de restaurer les clés privées en connaissant précisément
leur position dans la hiérarchie. Pour les portefeuilles multisig, dont la
sauvegarde était initialement plus complexe, le descriptor inclut les xpub de chaque facteur, ce qui garantit ainsi la possibilité de régénérer les adresses
en cas de problème.
Construction d'un descriptor
Un descriptor se compose de plusieurs éléments :
- Des fonctions de script comme
pk(Pay-to-PubKey),pkh(Pay-to-PubKey-Hash),wpkh(Pay-to-Witness-PubKey-Hash),sh(Pay-to-Script-Hash),wsh(Pay-to-Witness-Script-Hash),tr(Pay-to-Taproot),multi(Multisignature) etsortedmulti(Multisignature avec clés triées) ; - Des chemins de dérivation, par exemple
[d34db33f/44h/0h/0h]qui indique un chemin de compte dérivé et une empreinte de clé maîtresse spécifique ; - Des clés en divers formats tels que des clés publiques en hexadécimal ou
des clés publiques étendues (
xpub) ; - Une somme de contrôle, précédée d'un dièse, pour vérifier l'intégrité du descriptor.
Par exemple, un descriptor pour un portefeuille P2WPKH (SegWit v0) pourrait ressembler à :
wpkh([cdeab12f/84h/0h/0h]xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U/<0;1>/*)#jy0l7nr4
Dans ce descriptor, la fonction de dérivation wpkh indique un
type de script Pay-to-Witness-Public-Key-Hash. Elle est suivie par
le chemin de dérivation qui contient :
cdeab12f: l'empreinte de la clé maîtresse ;84h: qui signifie l'utilisation d'un objectif BIP84, destiné aux adresses SegWit v0 ;0h: qui indique qu'il s'agit d'une devise BTC sur le mainnet ;0h: qui fait référence au numéro de compte spécifique utilisé dans le portefeuille.
Le descriptor inclut également la clé publique étendue utilisée sur ce portefeuille :
xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U
Ensuite, la notation /<0;1>/* spécifie que le descriptor
peut générer des adresses à partir de la chaîne externe (0) et
interne (1), avec un wildcard (*) permettant la
dérivation séquentielle de plusieurs adresses de manière paramétrable,
similaire à la gestion d'un « gap limit » sur des logiciels de
portefeuille classiques.
Enfin, #jy0l7nr4 représente la somme de contrôle pour vérifier l'intégrité
du descriptor.
Vous savez désormais tout sur le fonctionnement du portefeuille HD sur Bitcoin et sur le processus de dérivation des paires de clés. Cependant, dans les derniers chapitres, nous nous sommes limités à la génération des clés privées et publiques, sans aborder la construction des adresses de réception. Ce sera justement l’objet du prochain chapitre !
Les adresses de réception
Les adresses de réception sont des informations intégrées dans les scriptPubKey pour verrouiller des UTXOs nouvellement créés. En termes simples, une adresse sert à recevoir des bitcoins. Explorons leur fonctionnement en lien avec ce que nous avons étudié dans les chapitres précédents.
Le rôle des adresses Bitcoin dans les scripts
Comme expliqué précédemment, une transaction a pour rôle de transférer la possession des bitcoins des inputs vers les outputs. Ce processus consiste à consommer des UTXOs en inputs tout en créant de nouveaux UTXOs en outputs. Ces UTXOs sont sécurisés par des scripts, qui définissent les conditions nécessaires pour débloquer les fonds.
Lorsqu’un utilisateur reçoit des bitcoins, l’expéditeur crée un UTXO en
output et le verrouille avec un scriptPubKey. Ce script contient
les règles spécifiant généralement les signatures et clés publiques requises
pour débloquer cet UTXO. Pour dépenser cet UTXO dans une nouvelle
transaction, l’utilisateur doit fournir les informations demandées via un scriptSig. L’exécution du scriptSig en combinaison avec le scriptPubKey doit retourner "vrai" ou 1. Si cette condition est remplie,
l’UTXO peut être dépensé pour créer un nouvel UTXO, lui-même verrouillé par
un nouveau scriptPubKey, et ainsi de suite.

C’est précisément dans le scriptPubKey que se trouvent les adresses de réception. Leur utilisation varie cependant en fonction du standard de script adopté. Voici un tableau récapitulatif des informations contenues dans le scriptPubKey selon le standard utilisé, ainsi que des informations attendues dans le scriptSig pour déverrouiller le scriptPubKey.
| Standard | scriptPubKey | scriptSig | redeem script | witness |
|---|---|---|---|---|
| P2PK | <pubkey> OP_CHECKSIG | <signature> | ||
| P2PKH | OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG | <signature> <public key> | ||
| P2SH | OP_HASH160 <scriptHash> OP_EQUAL | <data pushes> <redeem script> | Données arbitraires | |
| P2WPKH | 0 <pubKeyHash> | <signature> <public key> | ||
| P2WSH | 0 <witnessScriptHash> | <data pushes> <witness script> | ||
| P2SH-P2WPKH | OP_HASH160 <redeemScriptHash> OP_EQUAL | <redeem script> | 0 <pubKeyHash> | <signature> <public key> |
| P2SH-P2WSH | OP_HASH160 <redeemScriptHash> OP_EQUAL | <redeem script> | 0 <scriptHash> | <data pushes> <witness script> |
| P2TR (key path) | 1 <public key> | <signature> | ||
| P2TR (script path) | 1 <public key> | <data pushes> <script> <control block> |
Source : Bitcoin Core PR review club du 7 juillet 2021 - Gloria Zhao
Les opcodes utilisés dans un script permettent de manipuler les informations, et, si nécessaire, de les comparer ou de les tester. Prenons l’exemple d’un script P2PKH, qui a la forme suivante :
OP_DUP OP_HASH160 OP_PUSHBYTES_20 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG
Comme nous allons le voir dans la suite de ce chapitre, <pubKeyHash> représente en réalité la charge utile de l’adresse de réception utilisée
pour verrouiller l’UTXO. Pour déverrouiller ce scriptPubKey, il est
nécessaire de fournir un scriptSig contenant :
<signature> <public key>
Dans le langage script, la "pile" est une structure de données de type "LIFO" ("Last In, First Out") utilisée pour stocker temporairement des éléments pendant l'exécution du script. Chaque opération du script manipule cette pile, où les éléments peuvent être ajoutés (push) ou retirés (pop). Les scripts exploitent ces piles pour évaluer des expressions, stocker des variables temporaires et gérer des conditions.
L'exécution du script que je viens de vous donner en exemple suit donc ce processus :
- On a le scriptSig, le ScriptPubKey et la pile :

- Le scriptSig est poussé sur la pile :

OP_DUPduplique la clé publique fournie dans le scripSig sur la pile :

OP_HASH160renvoie le hachage de la clé publique qui vient d'être dupliquée :
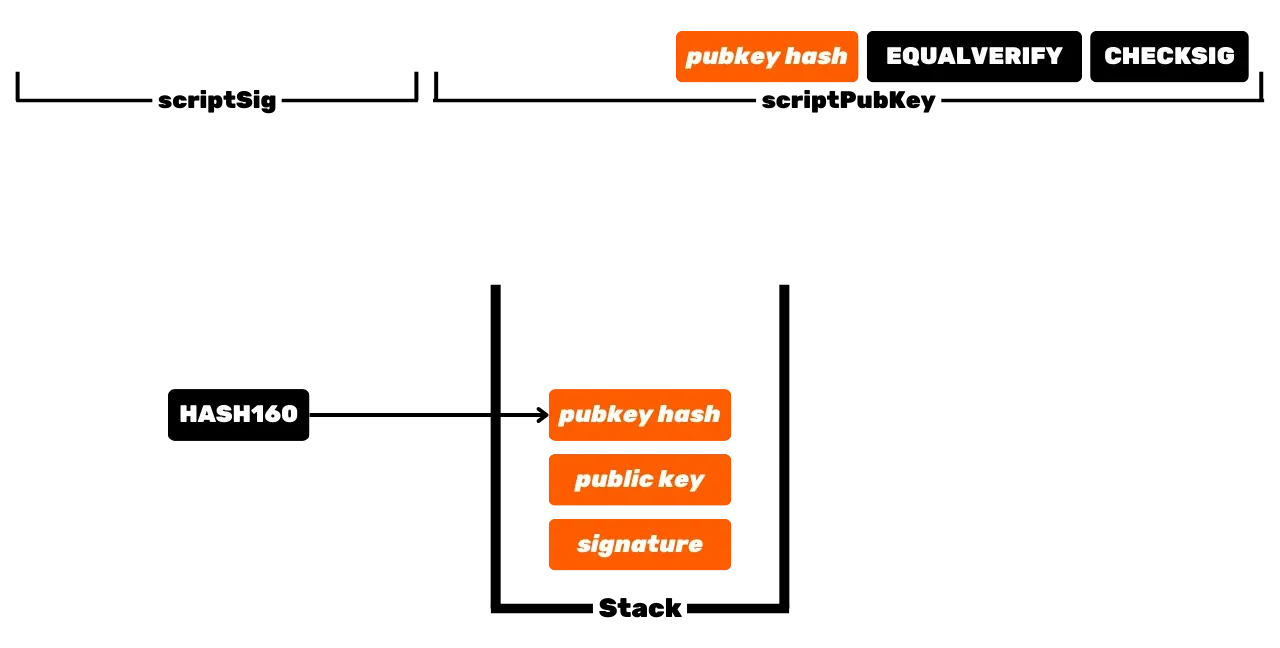
OP_PUSHBYTES_20 <pubKeyHash>pousse l'adresse Bitcoin contenue dans le scriptPubKey sur la pile :

OP_EQUALVERIFYvérifie que la clé publique hachée correspond à l'adresse de réception fournie :

OP_CHECKSIGvérifie la signature contenue dans le scriptSig à partir de la clé publique. Cet opcode exécute essentiellement une vérification de signature telle que nous l'avons décrite dans la partie 3 de cette formation :

- S'il reste
1sur la pile, alors le script est valide :
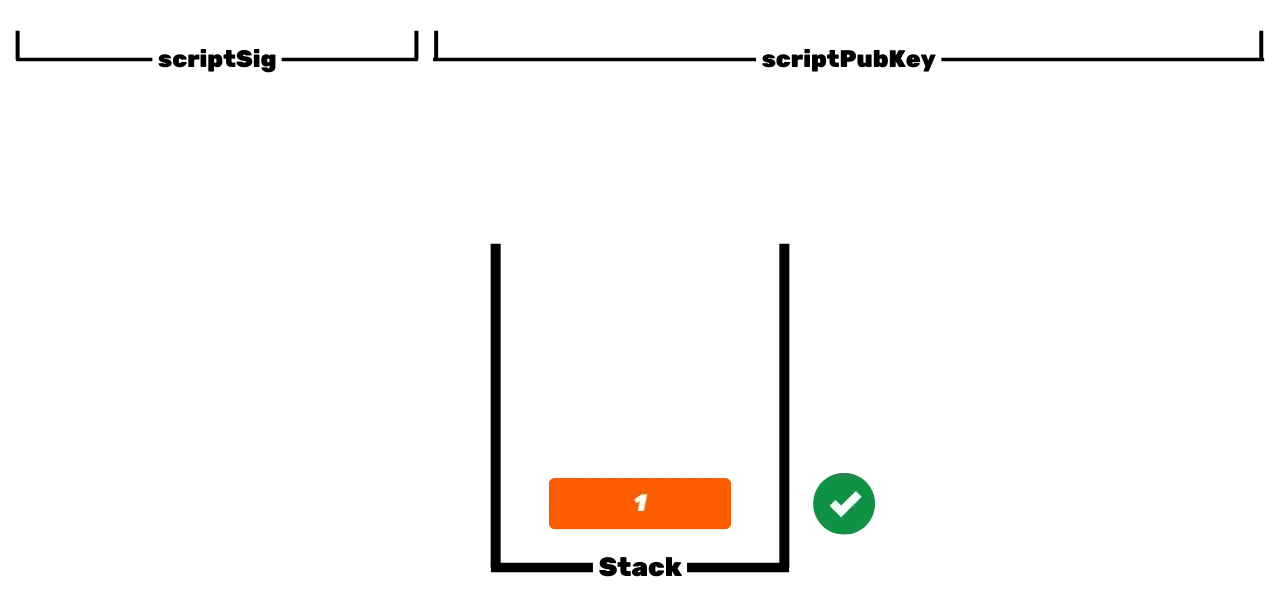
Donc pour résumer, ce script permet de vérifier, à l’aide de la signature numérique, que l’utilisateur revendiquant la propriété de cet UTXO et souhaitant le dépenser possède bien la clé privée associée à l’adresse de réception utilisée lors de la création de cet UTXO.
Les différents types d'adresses Bitcoin
Au fil de l’évolution de Bitcoin, plusieurs modèles de script standards ont été ajoutés. Chacun d’entre eux utilise un type d’adresse de réception distinct. Voici un aperçu des principaux modèles de script disponibles à ce jour :
P2PK (Pay-to-PubKey) :
Ce modèle de script a été introduit dès la première version de Bitcoin par Satoshi Nakamoto. Le script P2PK verrouille des bitcoins directement à l’aide d’une clé publique brute (on n'utilise donc pas d'adresse de réception avec ce modèle). Sa structure est simple : il contient une clé publique et requiert une signature numérique correspondante pour déverrouiller les fonds. Ce script fait partie du standard "Legacy".
P2PKH (Pay-to-PubKey-Hash) :
Comme pour P2PK, le script P2PKH a été introduit dès le lancement de
Bitcoin. Contrairement à son prédécesseur, il verrouille les bitcoins à
l’aide du hash de la clé publique, plutôt que d’utiliser directement la clé
publique brute. Le scriptSig doit alors fournir la clé publique
associée à l’adresse de réception, ainsi qu’une signature valide. Les
adresses correspondant à ce modèle commencent par 1 et sont
encodées en base58check. Ce script appartient également au standard
"Legacy".
P2SH (Pay-to-Script-Hash) :
Introduit en 2012 avec le BIP16, le modèle P2SH permet d’utiliser le hash
d’un script arbitraire dans le scriptPubKey. Ce script haché,
appelé "redeemScript", contient les conditions de déverrouillage
des fonds. Pour dépenser un UTXO verrouillé avec P2SH, il est nécessaire de
fournir un scriptSig contenant le redeemScript original
ainsi que les données nécessaires pour le valider. Ce modèle est notamment
utilisé pour les vieux multisigs. Les adresses associées à P2SH commencent
par 3 et sont encodées en base58check. Ce script
appartient également au standard "Legacy".
P2WPKH (Pay-to-Witness-PubKey-Hash) :
Ce script est similaire au P2PKH, car il verrouille également des bitcoins en utilisant le hash d’une clé publique. Cependant, contrairement à P2PKH, le scriptSig est déplacé dans une section distincte appelée "Witness". On parle parfois de "scriptWitness" pour désigner cet ensemble comprenant la signature et la clé publique. Chaque input SegWit possède son propre scriptWitness, et l’ensemble des scriptWitness constitue le champ Witness de la transaction. Ce déplacement des données de signature est une innovation introduite par la mise à jour SegWit, visant notamment à empêcher la malléabilité des transactions à cause des signatures ECDSA.
Les adresses P2WPKH utilisent l’encodage bech32 et commencent
toujours par bc1q. Ce type de script correspond aux sorties
SegWit de version 0.
P2WSH (Pay-to-Witness-Script-Hash) :
Le modèle P2WSH a également été introduit avec la mise à jour SegWit en août 2017. Similaire au modèle P2SH, il verrouille des bitcoins en utilisant le hash d’un script. La principale différence réside dans la manière dont les signatures et les scripts sont intégrés dans la transaction. Pour dépenser des bitcoins verrouillés avec ce type de script, le bénéficiaire doit fournir le script original, appelé witnessScript (équivalent du redeemScript dans P2SH), ainsi que les données nécessaires pour valider ce witnessScript. Ce mécanisme permet de mettre en place des conditions de dépense plus complexes, comme des multisigs.
Les adresses P2WSH utilisent l’encodage bech32 et commencent
toujours par bc1q. Ce script correspond également aux sorties
SegWit de version 0.
P2TR (Pay-to-Taproot) :
Le modèle P2TR a été introduit avec l’implémentation de Taproot en novembre 2021. Il repose sur le protocole de Schnorr pour l’agrégation de clés cryptographiques, ainsi que sur un arbre de Merkle pour des scripts alternatifs, appelé MAST (Merkelized Alternative Script Tree). Contrairement aux autres types de scripts, où les conditions de dépense sont exposées publiquement (soit à la réception, soit à la dépense), P2TR permet de masquer des scripts complexes derrière une clé publique unique et apparente.
Techniquement, un script P2TR verrouille des bitcoins sur une clé publique
Schnorr unique, dénommée Q.
Cette clé Q est en réalité un
agrégat d’une clé publique P et d’une clé publique M,
cette dernière étant calculée à partir de la racine de Merkle d’une liste de scriptPubKey. Les bitcoins verrouillés avec ce type de script
peuvent être dépensés de deux manières :
- En publiant une signature pour la clé publique
P(key path). - En satisfaisant l’un des scripts contenus dans l’arbre de Merkle (script path).
P2TR offre ainsi une grande flexibilité, car il permet de verrouiller des bitcoins soit avec une clé publique unique, soit avec plusieurs scripts au choix, soit les deux simultanément. L'avantage de cette structure en arbre de Merkle est que seul le script de dépense utilisé est révélé lors de la transaction, mais tous les autres scripts alternatifs restent secrets.
P2TR correspond aux sorties SegWit de version 1, ce qui signifie que les
signatures pour les entrées P2TR sont stockées dans le témoin (Witness) d’une transaction, et non dans le scriptSig. Les adresses P2TR
utilisent l’encodage bech32m et commencent par bc1p,
mais elles sont assez particulières, car on n'utilise pas de fonction de
hachage pour les construire. En effet, elles représentent directement la clé
publique Q qui est simplement
mise en forme avec des métadonnées. C'est donc un modèle de script proche de
P2PK.
Maintenant que nous avons vu la théorie, passons à la pratique ! Je vous propose dans le chapitre suivant de dériver une adresse SegWit v0 et une adresse SegWit v1 à partir d’une paire de clés.
Dérivation des adresses
Découvrons ensemble comment générer une adresse de réception à partir d’une paire de clés située, par exemple, en profondeur 5 d’un portefeuille HD. Cette adresse pourra ensuite être utilisée dans un logiciel de portefeuille pour verrouiller un UTXO.
Puisque le processus de génération d’une adresse dépend du modèle de script adopté, concentrons-nous sur deux cas spécifiques : la génération d’une adresse SegWit v0 en P2WPKH et celle d’une adresse SegWit v1 en P2TR. Ces deux types d’adresses couvrent aujourd’hui l’immense majorité des usages.
Compression de la clé publique
Après avoir effectué toutes les étapes de dérivation depuis la clé maîtresse
jusqu’à la profondeur 5 en utilisant les index appropriés, nous obtenons une
paire de clés (k, K) avec K = k \cdot G. Bien qu’il
soit possible d’utiliser cette clé publique telle quelle pour verrouiller
des fonds avec le standard P2PK, ce n’est pas ce que nous cherchons à faire
ici. Nous souhaitons plutôt créer une adresse en P2WPKH dans un premier
temps, puis en P2TR pour un autre exemple.
La première étape consiste à compresser la clé publique K. Pour bien comprendre ce processus, rappelons d’abord quelques
fondamentaux abordés dans la partie 3.
Une clé publique sur Bitcoin est un point K situé sur une courbe elliptique. Elle est représentée sous la forme (x, y), où x et y sont les coordonnées du
point. Dans sa forme non compressée, cette clé publique mesure 520 bits : 8
bits pour un préfixe (valeur initiale de 0x04), 256 bits pour
la coordonnée x, et 256 bits
pour la coordonnée y.
Cependant, les courbes elliptiques possèdent une propriété de symétrie par
rapport à l’axe des abscisses : pour une coordonnée x donnée, il n’existe que deux valeurs possibles pour y : y et -y. Ces deux points se
trouvent de part et d’autre de l’axe des abscisses. En d’autres termes, si
nous connaissons x, il suffit
de préciser si y est pair ou impair
pour identifier le point exact sur la courbe.
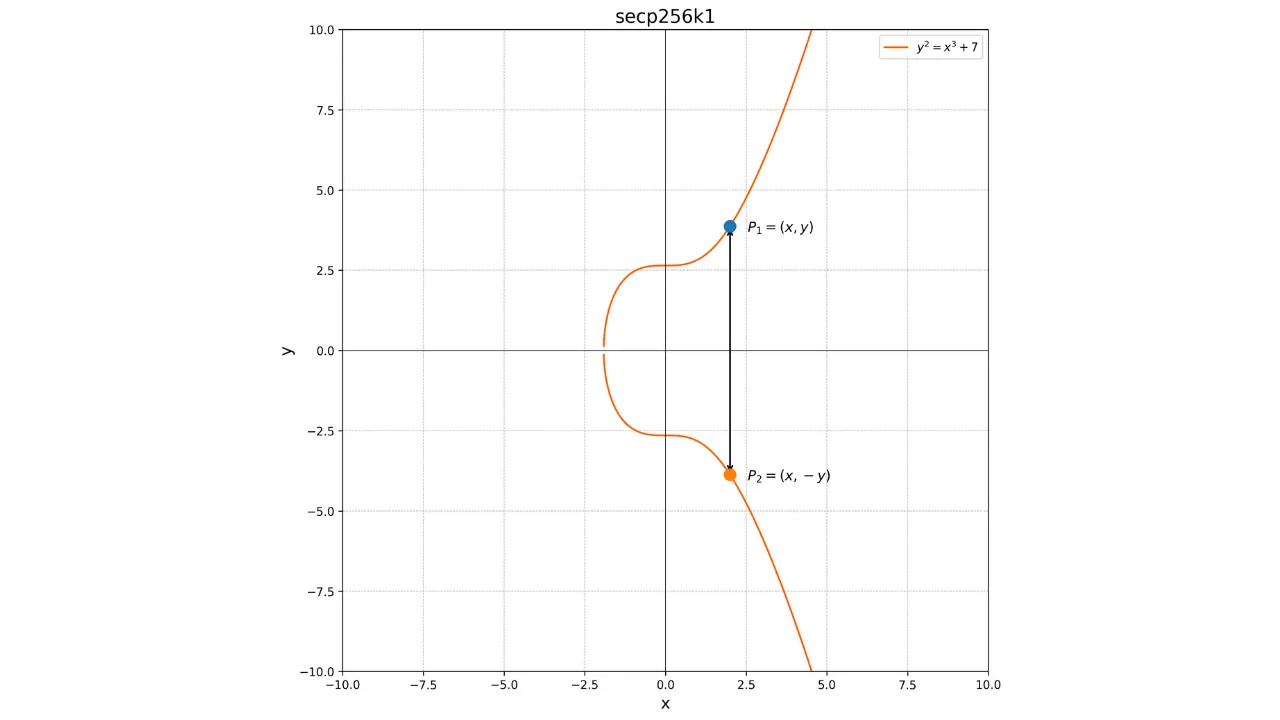
Pour compresser une clé publique, on encode uniquement x, qui occupe 256 bits, et on ajoute un préfixe pour préciser la parité de y. Cette méthode réduit la
taille de la clé publique à 264 bits au lieu des 520 initiaux. Le préfixe 0x02 indique que y est pair, et le
préfixe 0x03 indique que y est impair.
Prenons un exemple pour bien comprendre, avec une clé publique brute en représentation non compressée :
K = 04678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f
Si l'on décompose cette clé, on a :
- Le préfixe :
04; x:678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6;y:49f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f
Le dernier caractère hexadécimal de y est f. En base 10, f = 15, ce qui correspond à un
nombre impair. Par conséquent, y est impair, et le préfixe sera 0x03 pour l’indiquer.
La clé publique compressée devient :
K = 03678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6
Ce fonctionnement s’applique à tous les modèles de script reposant sur
ECDSA, c’est-à-dire tous, sauf P2TR qui utilise Schnorr. Dans le cas de
Schnorr, comme expliqué dans la partie 3, nous ne conservons que la valeur
de x, sans ajouter de préfixe
pour indiquer la parité de y,
contrairement à ECDSA. C'est rendu possible par le fait qu'une parité unique
est choisie arbitrairement pour toutes les clés. Cela permet ainsi de gagner
un peu de place dans le stockage des clés publiques.
Dérivation d'une adresse SegWit v0 (bech32)
Maintenant que nous avons obtenu notre clé publique compressée, nous pouvons dériver une adresse de réception SegWit v0 à partir de celle-ci.
La première étape consiste à appliquer la fonction de hachage HASH160 à la clé publique compressée. HASH160 est une composition de deux fonctions de hachage successives : SHA256, suivie de RIPEMD160 :
\text{HASH160}(K) = \text{RIPEMD160}(\text{SHA256}(K))On passe d'abord la clé dans SHA256 :
SHA256(K) = C489EBD66E4103B3C4B5EAFF462B92F5847CA2DCE0825F4997C7CF57DF35BF3A
Puis on passe le résultat dans RIPEMD160 :
RIPEMD160(SHA256(K)) = 9F81322CC88622CA4CCB2A52A21E2888727AA535
Nous avons obtenu un hash de 160 bits de la clé publique, qui constitue ce que l’on appelle la charge utile de l’adresse. Cette charge utile représente la partie centrale et la plus importante de l’adresse. Elle est d’ailleurs utilisée dans le scriptPubKey pour verrouiller les UTXOs.
Cependant, pour rendre cette charge utile plus facilement utilisable par les humains, on y ajoute des métadonnées. L’étape suivante consiste à encoder ce hash en groupes de 5 bits en décimal. Cette transformation en décimal nous sera utile pour la conversion en bech32, utilisée par les adresses post-SegWit. Le hash binaire de 160 bits est ainsi divisé en 32 groupes de 5 bits :
\begin{array}{|c|c|}
\hline
\text{5 bits} & \text{Decimal} \\
\hline
10011 & 19 \\
11110 & 30 \\
00000 & 0 \\
10011 & 19 \\
00100 & 4 \\
01011 & 11 \\
00110 & 6 \\
01000 & 8 \\
10000 & 16 \\
11000 & 24 \\
10001 & 17 \\
01100 & 12 \\
10100 & 20 \\
10011 & 19 \\
00110 & 6 \\
01011 & 11 \\
00101 & 5 \\
01001 & 9 \\
01001 & 9 \\
01010 & 10 \\
00100 & 4 \\
00111 & 7 \\
10001 & 17 \\
01000 & 8 \\
10001 & 17 \\
00001 & 1 \\
11001 & 25 \\
00111 & 7 \\
10101 & 21 \\
00101 & 5 \\
00101 & 5 \\
10101 & 21 \\
\hline
\end{array}On a donc :
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
Une fois le hash encodé en groupes de 5 bits, on ajoute une somme de contrôle à l’adresse. Cette checksum sert à vérifier que la charge utile de l’adresse n’a pas été altérée lors de son stockage ou de sa transmission. Par exemple, elle permet à un logiciel de portefeuille de s’assurer que vous n’avez pas commis une faute de frappe en saisissant une adresse de réception. Sans cette vérification, vous pourriez envoyer des bitcoins à une adresse incorrecte sans faire exprès, ce qui entraînerait une perte définitive des fonds, car vous ne possédez ni la clé publique ni la clé privée associées. La somme de contrôle est donc une protection contre les erreurs humaines.
Pour les anciennes adresses Bitcoin Legacy, la somme de contrôle était simplement calculée à partir du début du hash de l'adresse avec la fonction HASH256. Avec l’introduction de SegWit et du format bech32, on utilise désormais des codes BCH (Bose, Ray-Chaudhuri, et Hocquenghem). Ces codes de correction d’erreurs sont utilisés pour détecter et corriger les erreurs dans des séquences de données. Ils garantissent que les informations transmises arrivent intactes à destination, même en cas d’altérations mineures. Les codes BCH sont utilisés dans de nombreux domaines, tels que les SSD, les DVD et les QR codes. Par exemple, grâce à ces codes BCH, un QR code partiellement masqué peut encore être lu et décodé.
Dans le contexte de Bitcoin, les codes BCH offrent un meilleur compromis entre la taille et la capacité de détection d’erreurs par rapport aux simples fonctions de hachage utilisées pour les adresses Legacy. Cependant, sur Bitcoin, les codes BCH sont utilisés uniquement pour détecter les erreurs, et non pour les corriger. Ainsi, un logiciel de portefeuille signalera une adresse de réception incorrecte, mais ne la corrigera pas automatiquement. Cette limitation est délibérée : permettre la correction automatique réduirait la capacité de détection d’erreurs.
Pour calculer la somme de contrôle avec les codes BCH, nous devons préparer plusieurs éléments :
- Le HRP (Human Readable Part) : Pour le réseau
principal Bitcoin mainnet, le HRP est
bc;
Le HRP doit être étendu en séparant chaque caractère en deux parties :
On prend les caractères du HRP en ASCII :
b:01100010c:01100011
On extraie les 3 bits de poids fort et les 5 bits de poids faible :
- 3 bits de poids fort :
011(3 en décimal) - 3 bits de poids fort :
011(3 en décimal) - 5 bits de poids faible :
00010(2 en décimal) - 5 bits de poids faible :
00011(3 en décimal)
- 3 bits de poids fort :
Avec le séparateur 0 entre les deux caractères, l'extension du HRP
est donc :
03 03 00 02 03
La version du témoin : Pour SegWit version 0, c'est
00;La charge utile : Les valeurs décimales du hash de la clé publique ;
La réservation pour la checksum : Nous ajoutons 6 zéros
[0, 0, 0, 0, 0, 0]en fin de séquence.
Toutes les données combinées à transmettre en entrée du programme pour calculer la checksum sont les suivantes :
HRP = 03 03 00 02 03
SEGWIT v0 = 00
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
CHECKSUM = 00 00 00 00 00 00
INPUT = 03 03 00 02 03 00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 00 00 00 00 00 00
Le calcul de la checksum est assez complexe. Il fait appel à l’arithmétique des champs finis polynomiaux. Nous ne détaillerons pas ce calcul ici et passerons directement au résultat. Dans notre exemple, la checksum obtenue en décimal est :
10 16 11 04 13 18
Nous pouvons maintenant construire l'adresse de réception en concaténant dans l'ordre les éléments suivants :
- La version de SegWit :
00 - La charge utile : Le hash de la clé publique
- La checksum : Les valeurs obtenues à l'étape précédente (
10 16 11 04 13 18)
Cela nous donne en décimal :
00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 10 16 11 04 13 18
Puis il faut mapper chaque valeur décimale à son caractère bech32 en utilisant le tableau de conversion suivant :
\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline
& 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\
\hline
+0 & q & p & z & r & y & 9 & x & 8 \\
\hline
+8 & g & f & 2 & t & v & d & w & 0 \\
\hline
+16 & s & 3 & j & n & 5 & 4 & k & h \\
\hline
+24 & c & e & 6 & m & u & a & 7 & l \\
\hline
\end{array}Pour convertir une valeur en un caractère bech32 à l’aide de ce
tableau, il suffit de repérer les valeurs en première colonne et en première
ligne qui, une fois additionnées, donnent le résultat recherché. Ensuite, on
récupère le caractère correspondant. Par exemple, le nombre décimal 19 sera converti en la lettre n, car 19 = 16 + 3.
En mappant toutes nos valeurs, nous obtenons l'adresse suivante :
qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj
Il ne reste plus qu’à ajouter le HRP bc, qui indique qu’il
s’agit d’une adresse pour le mainnet de Bitcoin, ainsi que le séparateur 1, afin d’obtenir l’adresse de réception complète :
bc1qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj
La particularité de cet alphabet bech32 est qu’il intègre
l’ensemble des caractères alphanumériques à l’exception de 1, b, i et o pour éviter les confusions visuelles
entre des caractères semblables, notamment lors de leur saisie ou de leur lecture
par des humains.
Pour résumer, voici le processus de dérivation :
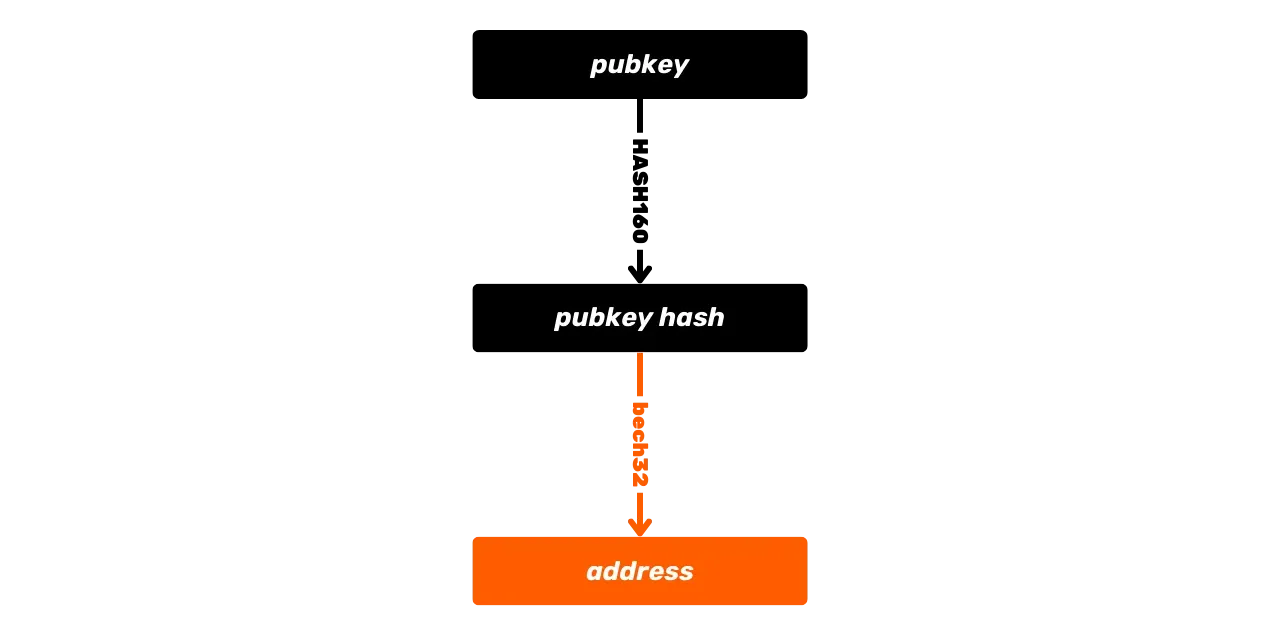
Voilà comment dériver une adresse de réception P2WPKH (SegWit v0) à partir d'une paire de clés. Passons maintenant aux adresses P2TR (SegWit v1 / Taproot) et découvrons leur processus de génération.
Dérivation d'une adresse SegWit v1 (bech32m)
Pour les adresses Taproot, le processus de génération diffère légèrement. Voyons tout cela ensemble !
Dès l’étape de compression de la clé publique, une première distinction
apparaît par rapport à ECDSA : les clés publiques utilisées pour Schnorr sur
Bitcoin sont représentées uniquement par leur abscisse (x). Il n’y a donc pas de préfixe, et la clé compressée mesure exactement 256
bits.
Comme nous l’avons vu dans le chapitre précédent, un script P2TR verrouille
des bitcoins sur une clé publique Schnorr unique, désignée par Q. Cette clé Q est un agrégat
de deux clés publiques : P,
une clé publique interne principale, et M, une clé publique dérivée
de la racine de Merkle d’une liste de scriptPubKey. Les bitcoins
verrouillés avec ce type de script peuvent être dépensés de deux manières :
- En publiant une signature pour la clé publique
P(key path) ; - En satisfaisant l’un des scripts inclus dans l’arbre de Merkle (script path).
En réalité, ces deux clés ne sont pas véritablement "agrégées". La clé P est plutôt tweakée par la clé M. En cryptographie,
"tweaker" une clé publique consiste à modifier cette clé en y appliquant une
valeur additive appelée "tweak". Cette opération permet à la clé modifiée de
rester compatible avec la clé privée d’origine et le tweak. Techniquement,
un tweak est une valeur scalaire t qui est ajoutée à la clé publique initiale. Si P est la clé publique d’origine,
la clé tweakée devient :
P' = P + tGOù G est le générateur de la courbe
elliptique utilisée. Cette opération produit une nouvelle clé publique dérivée
de la clé originale, tout en conservant des propriétés cryptographiques permettant
son utilisation.
Si vous n’avez pas besoin d’ajouter des scripts alternatifs (dépense
exclusivement via le key path), vous pouvez générer une adresse
Taproot établie uniquement sur la clé publique présente en profondeur 5 de
votre portefeuille. Dans ce cas, il est nécessaire de créer un script non
dépensable pour le script path, afin de satisfaire les exigences de
la structure. Le tweak t est
alors calculé en appliquant une fonction de hachage taguée, TapTweak, sur la clé publique interne P :
t = \text{H}_{\text{TapTweak}}(P)où :
\text{H}_{\text{TapTweak}}est une fonction de hachage SHA256 taguée avec le tagTapTweak. Si vous ne savez pas ce qu’est une fonction de hachage taguée, je vous invite à consulter le chapitre 3.3 ;Pest la clé publique interne, représentée dans son format compressé de 256 bits, utilisant uniquement l’abscissex.
La clé publique Taproot Q est
ensuite calculée en ajoutant le tweak t, multiplié par le
générateur de la courbe elliptique G, à la clé publique interne P :
Q = P + t \cdot GUne fois la clé publique Taproot Q obtenue, nous pouvons générer l’adresse de réception correspondante.
Contrairement à d’autres formats, les adresses Taproot ne sont pas établies
sur un hash de la clé publique. La clé Q est donc insérée directement
dans l’adresse, de manière brute.
Pour commencer, nous extrayons l’abscisse x du point Q afin d’obtenir une
clé publique compressée. Sur cette charge utile, une somme de contrôle est
calculée à l’aide de codes BCH, comme pour les adresses SegWit v0.
Cependant, le programme utilisé pour les adresses Taproot diffère
légèrement. En effet, après l’introduction du format bech32 avec
SegWit, un bug a été découvert : lorsque le dernier caractère d’une adresse
est un p, insérer ou supprimer des q juste avant
ce p ne rend pas la somme de contrôle invalide. Bien que ce bug
n’ait pas de conséquence sur SegWit v0 (grâce à une contrainte de taille),
il pourrait poser un problème à l’avenir. Ce bug a donc été corrigé pour les
adresses Taproot, et le nouveau format corrigé est appelé "bech32m".
L’adresse Taproot est générée en encodant la coordonnée x de Q dans le format bech32m, avec les éléments suivants :
- Le HRP (Human Readable Part) :
bc, pour indiquer le réseau principal Bitcoin ; - La version :
1pour indiquer Taproot / SegWit v1 ; - La checksum.
L'adresse finale aura donc le format :
bc1p[Qx][checksum]
En revanche, si vous souhaitez ajouter des scripts alternatifs en complément de la dépense avec la clé publique interne (script path), le calcul de l’adresse de réception sera légèrement différent. Vous devrez inclure le hash des scripts alternatifs dans le calcul du tweak. Sur Taproot, chaque script alternatif, situé au bout de l'arbre de Merkle, est appelé une "feuille".
Une fois les différents scripts alternatifs écrits, vous devez les passer
individuellement dans une fonction de hachage taguée TapLeaf,
accompagnée de quelques métadonnées :
\text{h}_{\text{leaf}} = \text{H}_{\text{TapLeaf}} (v \Vert sz \Vert S)Avec :
v: le numéro de version du script (par défaut0xC0pour Taproot) ;sz: la taille du script encodée en format CompactSize ;S: le script.
Les différents hash de script (\text{h}_{\text{leaf}}) sont d’abord triés dans l’ordre lexicographique. Ensuite, ils sont
concaténés par paires et passés dans une fonction de hachage taguée TapBranch. Ce processus est répété de manière itérative pour
construire, étape par étape, l’arbre de Merkle :
\text{h}_{\text{branch}} = \text{H}_{\text{TapBranch}}(\text{h}_{\text{leaf1}} \Vert \text{h}_{\text{leaf2}})On poursuit ensuite en concaténant les résultats deux par deux, en les
passant à chaque étape dans la fonction de hachage taguée TapBranch, jusqu’à obtenir la racine de l’arbre de Merkle :
Une fois la racine de Merkle h_{\text{root}} calculée, on va pouvoir calculer le tweak. Pour cela, on concatène la clé
publique interne du portefeuille P avec la racine h_{\text{root}}, puis on passe l’ensemble dans la fonction de hachage taguée TapTweak :
t = \text{H}_{\text{TapTweak}}(P \Vert h_{\text{root}})Enfin, comme précédemment, la clé publique Taproot Q est obtenue en ajoutant la clé publique interne P au produit du tweak t par le
point générateur G :
Q = P + t \cdot GEnsuite, la génération de l’adresse suit le même processus, en utilisant la
clé publique brute Q comme charge
utile, accompagnée de quelques métadonnées supplémentaires.
Et voilà ! Nous arrivons à la fin de cette formation CYP201. Si ce cours vous a été utile, je vous serais très reconnaissant de prendre quelques instants pour lui attribuer une bonne note dans le chapitre d’évaluation qui suit. N’hésitez pas également à le partager avec vos proches ou sur vos réseaux sociaux. Enfin, si vous souhaitez obtenir votre diplôme pour cette formation, vous pouvez passer l’examen final juste après le chapitre de l'évaluation.
Section finale
Avis & Notes
0cd71541-a7fd-53db-b66a-8611b6a28b04 true
Examen final
a53ea27d-0f84-56cd-b37c-a66210a4b31d true
Conclusion
d291428b-3cfa-5394-930e-4b514be82d5a true