name: Johdatus muodolliseen kryptografiaan goal: Syväsukellus kryptografian tieteeseen ja käytäntöön. objectives:
- Tutustutaan Beale-salauksiin ja nykyaikaisiin salausmenetelmiin, jotta ymmärretään salakirjoituksen peruskäsitteitä ja historiallisia käsitteitä.
- Syvenny lukuteoriaan, ryhmiin ja kenttiin ja hallitse salakirjoituksen taustalla olevat keskeiset matemaattiset käsitteet.
- Tutustu symmetrisiin salausalgoritmeihin tutustumalla RC4-virtasalausmenetelmään ja AES:ään 128-bittisellä avaimella.
- Tutustu RSA-kryptosysteemiin, avainten jakamiseen ja hash-funktioihin ja tutustu epäsymmetriseen kryptografiaan.
Syväsukellus kryptografiaan
On vaikea löytää monia materiaaleja, jotka tarjoaisivat hyvän keskitason kryptografian opetuksessa.
Toisaalta on olemassa pitkiä, muodollisia tutkielmia, jotka ovat oikeastaan vain niiden ulottuvilla, joilla on vahva tausta matematiikassa, logiikassa tai muussa muodollisessa tieteenalassa. Toisaalta on hyvin korkeatasoisia johdantoja, jotka todella kätkevät liian monet yksityiskohdat kaikilta, jotka ovat edes hieman uteliaita.
Tässä johdannossa kryptografiaan pyritään löytämään keskitie. Vaikka sen pitäisi olla suhteellisen haastava ja yksityiskohtainen kaikille kryptografian aloittelijoille, se ei ole tyypillisen perustavanlaatuisen tutkielman kaninkolo.
Johdanto
Kurssin yleiskatsaus
bb8a8b73-7fb2-50da-bf4e-98996d79887b Tervetuloa CYP302-kurssille!
Tämä kirja tarjoaa syvällisen johdatuksen salakirjoituksen tieteeseen ja käytäntöön. Siinä keskitytään mahdollisuuksien mukaan pikemminkin käsitteelliseen kuin muodolliseen esittelyyn.
Tämä opetussisältö on mukautettu kirjasta ja repo JWBurgers. Vaikka tekijä on ystävällisesti antanut luvan sen opetuskäyttöön, kaikki immateriaalioikeudet säilyvät alkuperäisellä tekijällä.
Motivaatio ja tavoitteet
On vaikea löytää monia materiaaleja, jotka tarjoaisivat hyvän keskitason kryptografian opetuksessa.
Toisaalta on olemassa pitkiä, muodollisia tutkielmia, jotka ovat oikeastaan vain niiden ulottuvilla, joilla on vahva tausta matematiikassa, logiikassa tai muussa muodollisessa tieteenalassa. Toisaalta on hyvin korkeatasoisia johdantoja, jotka todella kätkevät liian monet yksityiskohdat kaikilta, jotka ovat edes hieman uteliaita.
Tässä johdannossa kryptografiaan pyritään löytämään keskitie. Vaikka sen pitäisi olla suhteellisen haastava ja yksityiskohtainen kaikille kryptografian aloittelijoille, se ei ole tyypillisen perustavanlaatuisen tutkielman kaninkolo.
Kohderyhmä
Tämä kirja on hyödyllinen kaikille kehittäjistä älyllisesti uteliaisiin, jotka haluavat kryptografiasta muutakin kuin pintapuolisen ymmärryksen. Jos tavoitteenasi on hallita kryptografian alaa, tämä kirja on myös hyvä lähtökohta.
Lukemisohjeet
Kirjassa on tällä hetkellä seitsemän lukua: "(luku 1), "Kryptografian matemaattiset perusteet I" (luku 2), "Kryptografian matemaattiset perusteet II" (luku 3), "Symmetrinen kryptografia" (luku 4), "RC4 ja AES" (luku 5), "Epäsymmetrinen kryptografia" (luku 6) ja "RSA-salausjärjestelmä" (luku 7). Viimeinen luku, "Kryptografia käytännössä", lisätään vielä. Siinä keskitytään erilaisiin kryptografiasovelluksiin, kuten kuljetuskerroksen tietoturvaan, sipulireititykseen ja Bitcoinin arvonvaihtojärjestelmään.
Jos sinulla ei ole vahvaa matemaattista taustaa, numeroteoria on luultavasti tämän kirjan vaikein aihe. Annan siitä yleiskatsauksen luvussa 3, ja se esiintyy myös AES:n esittelyssä luvussa 5 ja RSA-salausjärjestelmän esittelyssä luvussa 7.
Jos sinulla on todella vaikeuksia kirjan näiden osien muodollisten yksityiskohtien kanssa, suosittelen, että tyydyt lukemaan ne korkeatasoisesti ensimmäisellä kerralla.
Kiitokset
Vaikuttavin kirja, joka on vaikuttanut tähän, on ollut Jonathan Katzin ja Yehuda Lindellin teos Introduction to Modern Cryptography, CRC Press (Boca Raton, FL), 2015. Siihen liittyvä kurssi on saatavilla Courserassa nimellä "Cryptography"
Tärkeimmät lisälähteet, joista on ollut apua tämän kirjan yleiskatsauksen luomisessa, ovat Simon Singh, The Code Book, Fourth Estate (Lontoo, 1999); Christof Paar ja Jan Pelzl, Understanding Cryptography, Springer (Heidelberg, 2010) ja Paarin kirjaan perustuva kurssi "Introduction to Cryptography"; ja Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons).
Siteeraan vain hyvin erityisiä tietoja ja tuloksia, jotka olen saanut näistä lähteistä, mutta haluan tässä yhteydessä tunnustaa yleisen kiitollisuudenvelkani niille.
Niille lukijoille, jotka haluavat tämän johdannon jälkeen etsiä syvällisempää tietoa kryptografiasta, suosittelen lämpimästi Katzin ja Lindellin kirjaa. Katzin kurssi Courserassa on hieman helpommin lähestyttävä kuin kirja.
Maksut
Tutustu arkistossa olevaan contributions-tiedostoon, josta löydät ohjeita siitä, miten projektia voi tukea.
Merkintä
Keskeiset termit:
Alkusanoissa olevat keskeiset termit esitellään lihavoimalla. Esimerkiksi Rijndael-salauksen esittely avainterminä näyttäisi seuraavalta: Rijndael-salakirjoitus.
Keskeiset termit määritellään nimenomaisesti, elleivät ne ole oikeita nimiä tai ellei niiden merkitys käy ilmi keskustelusta.
Määritelmä annetaan yleensä keskeisen termin esittelyn yhteydessä, vaikka joskus onkin kätevämpää jättää määritelmä myöhempään ajankohtaan.
Korostetut sanat ja lausekkeet:
Sanoja ja lauseita korostetaan kursiivilla. Esimerkiksi lause "Muista salasanasi" näyttäisi seuraavalta: Muista salasanasi.
Virallinen merkintätapa:
Muodollinen merkintätapa koskee pääasiassa muuttujia, satunnaismuuttujia ja joukkoja.
- Muuttujat: Muuttujat: Nämä merkitään yleensä vain pienellä kirjaimella (esim. "x" tai "y"). Joskus ne kirjoitetaan suuraakkosin selkeyden vuoksi (esim. "M" tai "K").
- Satunnaismuuttujat: Muuttujat: Nämä merkitään aina isolla kirjaimella (esim. "X" tai "Y")
- Sarjat: S)
Oletko valmis tutkimaan kryptografian kiehtovaa maailmaa? Lähdetään liikkeelle!
Mitä on kryptografia?
Bealen salakirjoitukset
Aloitetaan kryptografian alan tutkiminen yhdellä sen historian viehättävimmistä ja viihdyttävimmistä jaksoista: Bealen salakirjoitukset. [1]
Tarina Bealen salakirjoituksista on mielestäni todennäköisemmin fiktiota kuin todellisuutta. Mutta sen oletetaan tapahtuneen seuraavasti.
Sekä talvella 1820 että talvella 1822 Thomas J. Beale -niminen mies yöpyi Robert Morrissin omistamassa majatalossa Lynchburgissa (Virginia). Toisen vierailunsa päätteeksi Beale luovutti Morrissille rautaisen laatikon, jossa oli arvokkaita papereita säilytettäväksi.
Muutamaa kuukautta myöhemmin Morriss sai Bealelta kirjeen, joka oli päivätty 9. toukokuuta 1822. Siinä korostettiin rautalaatikon sisällön suurta arvoa ja kerrottiin Morrissille joitakin ohjeita: jos Beale tai kukaan hänen kumppaneistaan ei koskaan tulisi hakemaan laatikkoa, hänen tulisi avata se tasan kymmenen vuoden kuluttua kirjeen päiväyksestä (eli 9. toukokuuta 1832). Osa laatikon sisältämistä papereista olisi kirjoitettu tavallisella tekstillä. Useat muut olisivat kuitenkin "käsittämättömiä ilman avainta" Tämän "avaimen" toimitti Morrissille Bealen nimeämätön ystävä kesäkuussa 1832.
Selkeistä ohjeista huolimatta Morriss ei avannut laatikkoa toukokuussa 1832, eikä Bealen salaperäinen ystävä ilmestynyt paikalle saman vuoden kesäkuussa. Vasta vuonna 1845 majatalon isäntä päätti vihdoin avata laatikon. Morriss löysi laatikosta viestin, jossa selitettiin, kuinka Beale ja hänen kumppaninsa olivat löytäneet kultaa ja hopeaa lännestä ja haudanneet sen sekä joitakin koruja turvaan. Lisäksi laatikko sisälsi kolme kryptotekstiä eli koodilla kirjoitettuja tekstejä, joiden avaamiseen tarvitaan kryptografinen avain eli salaisuus ja siihen liittyvä algoritmi. Salatekstin lukituksen avaamista kutsutaan purkamiseksi, kun taas lukitusprosessia kutsutaan kryptaamiseksi. (Kuten luvussa 3 selitetään, termillä salakirjoitus voi olla erilaisia merkityksiä. Nimessä "Beale-salakirjoitukset" se on lyhenne sanoista salakirjoitustekstit)
Morrissin rautalaatikosta löytämät kolme salakirjoitusta koostuvat kukin sarjasta pilkulla erotettuja numeroita. Bealen muistiinpanon mukaan näissä salakirjoituksissa ilmoitetaan erikseen aarteen sijainti, aarteen sisältö ja luettelo nimistä, joissa on aarteen lailliset perilliset ja heidän osuutensa (jälkimmäinen tieto on merkityksellinen siltä varalta, että Beale ja hänen kumppaninsa eivät koskaan tulisi hakemaan laatikkoa).
Morris yritti purkaa kolmea salaustekstiä kahdenkymmenen vuoden ajan. Tämä olisi ollut helppoa avaimen avulla. Morrissilla ei kuitenkaan ollut avainta, eikä hän onnistunut palauttamaan alkuperäisiä tekstejä tai laintekstejä, kuten niitä salakirjoituksessa yleensä kutsutaan.
Elämänsä loppupuolella Morriss antoi laatikon ystävälleen vuonna 1862. Tämä ystävä julkaisi myöhemmin vuonna 1885 pamfletin salanimellä J.B. Ward. Se sisälsi kuvauksen laatikon (oletetusta) historiasta, kolme salakirjoitusta ja ratkaisun, jonka hän oli löytänyt toiselle salakirjoitukselle. (Ilmeisesti jokaiselle salakirjoitustekstille on yksi avain, eikä yksi avain, joka toimii kaikkiin kolmeen salakirjoitustekstiin, kuten Beale alun perin näyttää ehdottaneen kirjeessään Morrissille.)
Toisen salaustekstin näet alla olevasta Kuvasta 2. [2] Tämän salakirjoitustekstin avain on Yhdysvaltojen itsenäisyysjulistus. Salakirjoituksen purkaminen tapahtuu soveltamalla seuraavia kahta sääntöä:
- Etsi Yhdysvaltojen itsenäisyysjulistuksen n:s sana minkä tahansa salatun tekstin luvun n osalta
- Korvaa numero n löytämäsi sanan ensimmäisellä kirjaimella
Kuva 1: Beale-salakirjoitus nro. 2

Esimerkiksi toisen salaustekstin ensimmäinen numero on 115. Itsenäisyysjulistuksen 115. sana on "instituted", joten selvätekstin ensimmäinen kirjain on "i" Salakirjoitusteksti ei suoraan ilmoita sanaväliä ja isoja kirjaimia. Mutta kun olet purkanut ensimmäiset sanat, voit loogisesti päätellä, että selkotekstin ensimmäinen sana oli yksinkertaisesti "I" (Selkoteksti alkaa lauseella "I have deposited in the county of Bedford.")
Toisessa viestissä kerrotaan salauksen purkamisen jälkeen aarteen yksityiskohtainen sisältö (kultaa, hopeaa ja jalokiviä) ja ehdotetaan, että aarre haudattiin rautaruukkuihin ja peitettiin kivillä Bedfordin piirikunnassa (Virginia). Ihmiset rakastavat hyviä mysteerejä, joten kahden muun Bealen salakirjoituksen, erityisesti aarteen sijaintia kuvaavan salakirjoituksen, purkamiseen on panostettu paljon. Jopa useat tunnetut salakirjoittajat ovat yrittäneet selvittää niitä. Toistaiseksi kukaan ei kuitenkaan ole pystynyt purkamaan kahta muuta salakirjoitusta.
Huomautukset:
[1] Hyvä yhteenveto tarinasta on Simon Singh, The Code Book, Fourth Estate (Lontoo, 1999), s. 82-99. Andrew Allen teki tarinasta lyhyen elokuvan vuonna 2010. Elokuva, "The Thomas Beale Cipher", löytyy sen verkkosivuilta.
[2] Tämä kuva on saatavilla Wikipedian sivulla Bealen salakirjoituksista.
Nykyaikainen salaus
Useimmat meistä yhdistävät kryptografiaan värikkäitä tarinoita, kuten Bealen salakirjoituksen. Nykyaikainen salakirjoitus eroaa kuitenkin ainakin neljällä tärkeällä tavalla tällaisista historiallisista esimerkeistä.
Ensinnäkin, historiallisesti kryptografia on ollut kiinnostunut vain salassapidosta (tai luottamuksellisuudesta). [3] Salakirjoitustekstit luotiin sen varmistamiseksi, että vain tietyt osapuolet saisivat selväteksteissä olevat tiedot, kuten Bealen salakirjoitusten tapauksessa. Jotta salausjärjestelmä palvelisi tätä tarkoitusta hyvin, salaustekstin purkamisen pitäisi olla mahdollista vain, jos sinulla on avain.
Nykyaikainen salakirjoitus käsittelee muitakin aiheita kuin vain salassapitoa. Näihin aiheisiin kuuluvat ensisijaisesti (1) viestin eheys eli sen varmistaminen, että viestiä ei ole muutettu, (2) viestin aitous eli sen varmistaminen, että viesti on todella tullut tietyltä lähettäjältä, ja (3) viestin kiistämättömyys eli sen varmistaminen, että lähettäjä ei voi myöhemmin väärällä tavalla kieltää lähettäneensä viestiä. [4]
Tärkeä ero, joka on syytä pitää mielessä, on siis salausjärjestelmän ja kryptografisen järjestelmän välillä. Salausjärjestelmässä on kyse vain salassapidosta. Vaikka salausjärjestelmä on kryptografinen järjestelmä, päinvastoin. Kryptografinen järjestelmä voi palvella myös muita kryptografian pääteemoja, kuten eheyttä, aitoutta ja kiistämättömyyttä.
Rehellisyys ja aitous ovat yhtä tärkeitä teemoja kuin salassapito. Nykyaikaiset viestintäjärjestelmämme eivät voisi toimia ilman takeita viestinnän eheydestä ja aitoudesta. Kiistämättömyys on myös tärkeä huolenaihe esimerkiksi digitaalisten sopimusten yhteydessä, mutta sitä ei tarvita niinkään kaikkialla kryptografiasovelluksissa kuin salassapitoa, eheyttä ja aitoutta.
Toiseksi, klassisissa salausjärjestelmissä, kuten Beale-salauksissa, on aina yksi avain, joka jaetaan kaikkien osapuolten kesken. Monissa nykyaikaisissa salausmenetelmissä on kuitenkin yhden avaimen lisäksi kaksi avainta: yksityinen ja julkinen avain. Ensimmäisen avaimen pitäisi pysyä yksityisenä kaikissa sovelluksissa, mutta jälkimmäinen on yleensä julkista tietoa (tästä johtuvat myös niiden nimet). Salausjärjestelmässä julkista avainta voidaan käyttää viestin salaamiseen, kun taas yksityistä avainta voidaan käyttää salauksen purkamiseen.
Kryptografian haara, joka käsittelee järjestelmiä, joissa kaikki osapuolet jakavat yhden avaimen, tunnetaan nimellä symmetrinen kryptografia. Tällaisessa järjestelmässä yksittäistä avainta kutsutaan yleensä yksityiseksi avaimeksi (tai salaiseksi avaimeksi). Kryptografian haara, joka käsittelee järjestelmiä, jotka edellyttävät yksityisen ja julkisen avaimen paria, tunnetaan nimellä asymmetrinen kryptografia. Näihin haaroihin viitataan joskus myös nimillä yksityisavainten kryptografia ja julkisten avainten kryptografia (tämä voi tosin aiheuttaa sekaannusta, koska julkisten avainten kryptografiajärjestelmissä on myös yksityisiä avaimia).
Epäsymmetrisen salauksen tulo 1970-luvun lopulla on ollut yksi tärkeimmistä tapahtumista salauksen historiassa. Ilman sitä useimmat nykyaikaiset viestintäjärjestelmämme, Bitcoin mukaan lukien, eivät olisi mahdollisia tai ainakin hyvin epäkäytännöllisiä.
Tärkeää on, että nykyaikainen kryptografia ei ole yksinomaan symmetristen ja assymetristen salausjärjestelmien tutkimusta (vaikka ne kattavatkin suuren osan alasta). Kryptografia käsittelee esimerkiksi myös hash-funktioita ja pseudosatunnaislukugeneraattoreita, ja näiden primitiivien varaan voi rakentaa sovelluksia, jotka eivät liity symmetriseen tai assimetriseen avainsalakirjoitukseen.
Kolmanneksi, klassiset salausmenetelmät, kuten Bealen salakirjoituksissa käytetyt, olivat enemmän taidetta kuin tiedettä. Niiden koettu turvallisuus perustui pitkälti niiden monimutkaisuutta koskeviin intuitioihin. Niitä yleensä korjattiin, kun saatiin selville uusi hyökkäys niitä vastaan, tai niistä luovuttiin kokonaan, jos hyökkäys oli erityisen vakava. Nykyaikainen salakirjoitus on kuitenkin tiukka tiede, jossa salausjärjestelmien kehittämiseen ja analysointiin sovelletaan muodollista, matemaattista lähestymistapaa. [5]
Nykyaikaisessa salakirjoituksessa keskitytään erityisesti muodollisiin turvallisuustodistuksiin. Salausjärjestelmän turvallisuustodistus etenee kolmessa vaiheessa:
Turvallisuuden kryptografinen määritelmä eli joukko turvallisuustavoitteita ja hyökkääjän aiheuttama uhka.
Selvitys kaikista matemaattisista oletuksista, jotka liittyvät järjestelmän laskennalliseen monimutkaisuuteen. Salausjärjestelmä voi esimerkiksi sisältää pseudosatunnaislukugeneraattorin. Vaikka emme voi todistaa niiden olemassaoloa, voimme olettaa, että ne ovat olemassa.
Matemaattisen turvallisuustodistuksen esittäminen järjestelmän turvallisuudesta muodollisen turvallisuuskäsitteen ja mahdollisten matemaattisten oletusten perusteella.
Neljänneksi, vaikka salakirjoitusta käytettiin historiallisesti pääasiassa sotilaallisissa ympäristöissä, se on tullut digitaalisen aikakauden aikana läpäisemään päivittäiset toimintamme. Kryptografia on digitaalisen aikakautemme ehdoton edellytys, olipa kyse sitten verkkopankkiasioinnista, sosiaalisessa mediassa julkaistavista viesteistä, tuotteen ostamisesta Amazonista luottokortilla tai bitcoin-rahan antamisesta ystävälle.
Kun otetaan huomioon nämä neljä nykyaikaisen kryptografian näkökohtaa, nykyaikaista kryptografiaa voidaan luonnehtia tieteeksi, joka käsittelee kryptografisten järjestelmien muodollista kehittämistä ja analysointia digitaalisen tiedon suojaamiseksi vastahyökkäyksiltä. [6] Turvallisuus olisi tässä yhteydessä ymmärrettävä laajasti sellaisten hyökkäysten estämiseksi, jotka vahingoittavat viestinnän salaisuutta, eheyttä, todentamista ja/tai kiistämättömyyttä.
Kryptografia on parhaiten nähtävissä kyberturvallisuuden osa-alueena, joka käsittelee tietokonejärjestelmien varastamisen, vahingoittamisen ja väärinkäytön estämistä. Huomaa, että monilla kyberturvallisuuteen liittyvillä huolenaiheilla on vain vähän tai vain osittainen yhteys salakirjoitukseen.
Jos yritys esimerkiksi sijoittaa kalliita palvelimia paikallisesti, se voi olla huolissaan laitteiston suojaamisesta varkauksilta ja vahingoittumiselta. Vaikka tämä on kyberturvallisuuteen liittyvä huolenaihe, sillä on vain vähän tekemistä salauksen kanssa.
Toisena esimerkkinä mainittakoon phishing-hyökkäykset, jotka ovat yleinen ongelma nykyaikana. Näillä hyökkäyksillä yritetään huijata ihmisiä sähköpostin tai muun viestintävälineen välityksellä luovuttamaan arkaluonteisia tietoja, kuten salasanoja tai luottokorttinumeroita. Vaikka salaus voi auttaa tietyssä määrin phishing-hyökkäysten torjunnassa, kattava lähestymistapa edellyttää muutakin kuin vain jonkinasteista salausmenetelmää.
Huomautukset:
[3] Tarkalleen ottaen kryptografisten järjestelmien tärkeät sovellukset ovat liittyneet salassapitoon. Esimerkiksi lapset käyttävät usein yksinkertaisia kryptografisia järjestelmiä "huvikseen". Näissä tapauksissa salassapito ei ole varsinainen huolenaihe.
[4] Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons), s. 2.
[5] Katso hyvä kuvaus Jonathan Katz ja Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), erityisesti s. 16-23.
[6] Vrt. Katz ja Lindell, ibid., s. 3. Mielestäni heidän luonnehdinnassaan on joitakin ongelmia, joten esitän tässä hieman erilaisen version heidän lausunnostaan.
Avoin viestintä
Nykyaikainen salakirjoitus on suunniteltu tarjoamaan turvatakeet avoimessa viestintäympäristössä. Jos viestintäkanavamme on niin hyvin suojattu, että salakuuntelijoilla ei ole mitään mahdollisuuksia manipuloida tai edes vain tarkkailla viestejämme, salaus on tarpeeton. Suurin osa viestintäkanavistamme on kuitenkin tuskin näin hyvin suojattuja.
Nykyaikaisen maailman viestinnän selkäranka on massiivinen valokaapeliverkko. Puhelujen soittaminen, television katselu ja Internetin selaaminen nykyaikaisessa kotitaloudessa perustuu yleensä tähän valokaapeliverkkoon (pieni osa voi luottaa pelkästään satelliitteihin). On totta, että kotonasi saattaa olla erilaisia datayhteyksiä, kuten koaksiaalikaapeli, (epäsymmetrinen) digitaalinen tilaajajohto ja valokaapeli. Mutta ainakin kehittyneissä maissa nämä eri tiedonsiirtovälineet yhdistyvät nopeasti kotisi ulkopuolella koko maapallon yhdistävän valokaapeliverkon solmupisteeseen. Poikkeuksena ovat eräät kehittyneen maailman syrjäiset alueet, kuten Yhdysvallat ja Australia, joissa tietoliikenne saattaa edelleen kulkea huomattavia matkoja myös perinteisiä kuparipuhelinjohtoja pitkin.
Mahdollisia hyökkääjiä olisi mahdotonta estää pääsemästä fyysisesti käsiksi tähän kaapeliverkkoon ja sitä tukevaan infrastruktuuriin. Itse asiassa tiedämme jo nyt, että erilaiset kansalliset tiedustelupalvelut sieppaavat suurimman osan tiedoistamme Internetin tärkeissä risteyskohdissa.[7] Tämä sisältää kaiken Facebook-viesteistä verkkosivustojen osoitteisiin, joilla vierailet.
Tietojen massiivinen tarkkailu vaatii voimakkaan vastustajan, kuten kansallisen tiedustelupalvelun, mutta hyökkääjät, joilla on vain vähän resursseja, voivat helposti yrittää nuuskia tietoja paikallisemmassa mittakaavassa. Vaikka tämä voi tapahtua johtojen salakuuntelun tasolla, on paljon helpompaa vain siepata langatonta viestintää.
Suurin osa lähiverkon datasta - olipa se sitten kotona, toimistossa tai kahvilassa - kulkee nykyään fyysisten kaapeleiden sijasta radioaaltojen välityksellä langattomiin tukiasemiin monitoimireitittimissä. Hyökkääjä tarvitsee siis vain vähän resursseja siepatakseen paikallisen tietoliikenteesi. Tämä on erityisen huolestuttavaa, koska useimmat ihmiset tekevät hyvin vähän suojatakseen lähiverkoissaan liikkuvaa dataa. Mahdolliset hyökkääjät voivat lisäksi kohdistaa hyökkäyksen myös mobiililaajakaistayhteyksiimme, kuten 3G:hen, 4G:hen ja 5G:hen. Kaikki nämä langattomat tietoliikenneyhteydet ovat helppo kohde hyökkääjille.
Näin ollen ajatus viestinnän pitämisestä salassa suojaamalla viestintäkanava on toivottoman harhainen pyrkimys suurelle osalle nykymaailmaa. Kaikki mitä tiedämme, oikeuttaa vakavaan vainoharhaisuuteen: on aina oletettava, että joku kuuntelee. Kryptografia on tärkein väline, jonka avulla voimme saavuttaa minkäänlaista turvallisuutta tässä nykyaikaisessa ympäristössä.
Huomautukset:
[7] Ks. esimerkiksi Olga Khazan, "The creepy, long-standing practice of undean sea cable salakuuntelu", The Atlantic, 16. heinäkuuta 2013 (saatavilla osoitteessa The Atlantic).
Salakirjoituksen matemaattiset perusteet 1
Satunnaismuuttujat
Salaus perustuu matematiikkaan. Jos haluat ymmärtää salakirjoitusta muutenkin kuin pintapuolisesti, sinun on hallittava matematiikka.
Tässä luvussa esitellään suurin osa perusmatematiikasta, johon tulet törmäämään kryptografian opiskelussa. Aiheita ovat satunnaismuuttujat, modulo-operaatiot, XOR-operaatiot ja pseudosatunnaisuus. Sinun tulisi hallita näiden osioiden materiaali, jotta ymmärtäisit kryptografiaa muutenkin kuin pintapuolisesti.
Seuraavassa jaksossa käsitellään numeroteoriaa, joka on paljon haastavampaa.
Satunnaismuuttujat
Satunnaismuuttujaa merkitään tyypillisesti isolla kirjaimella, joka ei ole
lihavoitu. Voidaan siis esimerkiksi puhua satunnaismuuttujasta X, satunnaismuuttujasta Y tai
satunnaismuuttujasta Z. Tätä
merkintätapaa käytän myös tästä eteenpäin.
Satunnaismuuttuja voi saada kaksi tai useampia mahdollisia arvoja, joilla kullakin on tietty positiivinen todennäköisyys. Mahdolliset arvot on lueteltu tulosjoukossa.
Aina kun otat näytteen satunnaismuuttujasta, arvot tietyn arvon sen tulosjoukosta määritettyjen todennäköisyyksien mukaisesti.
Tarkastellaan yksinkertaista esimerkkiä. Oletetaan, että muuttuja X on määritelty seuraavasti:
- X:llä on tulosjoukko
\{1,2\}
Pr[X = 1] = 0.5Pr[X = 2] = 0.5On helppo nähdä, että X on
satunnaismuuttuja. Ensinnäkin on olemassa vähintään kaksi mahdollista arvoa,
jotka X voi saada, nimittäin 1 ja 2. Toiseksi kullakin
mahdollisella arvolla on positiivinen todennäköisyys esiintyä aina, kun X otetaan näytteeksi, nimittäin 0.5.
Satunnaismuuttuja tarvitsee vain tulosjoukon, jossa on kaksi tai useampia mahdollisuuksia ja jossa kullakin mahdollisuudella on positiivinen todennäköisyys esiintyä näytteenoton yhteydessä. Periaatteessa satunnaismuuttuja voidaan siis määritellä abstraktisti, ilman mitään asiayhteyttä. Tässä tapauksessa "otanta" voidaan ajatella jonkin luonnollisen kokeen suorittamiseksi satunnaismuuttujan arvon määrittämiseksi.
Yllä oleva muuttuja X määriteltiin abstraktisti. Voit siis ajatella, että edellä mainitun
muuttujan X ottaminen
näytteeksi on kuin reilun kolikon heittäminen ja "2", jos tulos on kruuna,
ja "1", jos tulos on klaava. Jokaista X:n otosta varten heitetään
kolikkoa uudelleen.
Vaihtoehtoisesti voit myös ajatella, että näytteenotto X heitetään reilulla nopalla ja annetaan "2", jos nopan tulos on 1, 3 tai 4, ja "1", jos nopan
tulos on 2, 5 tai 6. Joka kerta, kun otat
näytteen X, heität noppaa
uudelleen.
Oikeastaan mikä tahansa luonnollinen koe, jonka avulla voitaisiin määritellä
edellä mainittujen X:n
mahdollisten arvojen todennäköisyydet, voidaan kuvitella piirroksen suhteen.
Usein satunnaismuuttujia ei kuitenkaan esitellä vain abstraktisti. Sen sijaan mahdollisten lopputulosarvojen joukolla on selkeä reaalimaailman merkitys (eikä vain numeroita). Lisäksi nämä tulosarvot saatetaan määritellä jotakin tiettyä koetyyppiä vasten (sen sijaan, että ne olisivat mitä tahansa luonnollista koetta kyseisillä arvoilla).
Tarkastellaan nyt esimerkkiä muuttujasta X, jota ei ole määritelty abstraktisti. X määritellään seuraavasti, jotta
voidaan määrittää, kumpi kahdesta joukkueesta aloittaa jalkapallo-ottelun:
X:llä on tulosjoukko {punainen potkaisee pois,sininen potkaisee pois}- Heitetään kolikkoa
C: klaava = "punainen lähtee"; kruuna = "sininen lähtee"
Pr [X = \text{red kicks off}] = 0.5Pr [X = \text{blue kicks off}] = 0.5Tässä tapauksessa X:n tulosjoukolla on konkreettinen merkitys, nimittäin se,
mikä joukkue aloittaa jalkapallo-ottelussa. Lisäksi mahdolliset
lopputulokset ja niihin liittyvät todennäköisyydet määräytyvät konkreettisen
kokeen avulla, nimittäin heittämällä tiettyä kolikkoa C.
Kryptografiasta käytävissä keskusteluissa satunnaismuuttujat esitellään yleensä todellisen merkityksen omaavaa tulosjoukkoa vastaan. Se voi olla kaikkien salattavien viestien joukko, jota kutsutaan viestiavaruudeksi, tai kaikkien avainten joukko, joista salausta käyttävät osapuolet voivat valita, jota kutsutaan avainavaruudeksi.
Kryptografiakeskusteluissa satunnaismuuttujia ei kuitenkaan yleensä määritellä jotakin tiettyä luonnollista koetta vastaan, vaan mitä tahansa koetta vastaan, joka saattaisi tuottaa oikeat todennäköisyysjakaumat.
Satunnaismuuttujilla voi olla diskreetti tai jatkuva todennäköisyysjakauma.
Satunnaismuuttujilla, joilla on diskreetti todennäköisyysjakauma - eli diskreeteillä satunnaismuuttujilla - on rajallinen määrä mahdollisia
tuloksia. Satunnaismuuttuja X oli molemmissa tähän mennessä annetuissa esimerkeissä diskreetti.
Jatkuvat satunnaismuuttujat voivat sen sijaan saada arvoja yhdellä tai useammalla aikavälillä. Voit esimerkiksi sanoa, että satunnaismuuttuja ottaa näytteenoton yhteydessä minkä tahansa reaaliarvon väliltä 0 ja 1 ja että jokainen reaaliarvo tällä välillä on yhtä todennäköinen. Tämän välin sisällä on äärettömän monta mahdollista arvoa.
Kryptografiakeskusteluja varten sinun tarvitsee ymmärtää vain diskreettejä satunnaismuuttujia. Tästä eteenpäin kaikki satunnaismuuttujia koskevat keskustelut on siis ymmärrettävä siten, että niissä viitataan diskreetteihin satunnaismuuttujiin, ellei erikseen toisin mainita.
Satunnaismuuttujien kuvaajat
Satunnaismuuttujan mahdolliset arvot ja niihin liittyvät todennäköisyydet
voidaan helposti havainnollistaa kuvaajan avulla. Tarkastellaan esimerkiksi
edellisen jakson satunnaismuuttujaa X, jonka tulosjoukko on \{1, 2\} ja Pr [X = 1] = 0.5 ja Pr [X = 2] = 0.5. Tällainen
satunnaismuuttuja esitetään tyypillisesti pylväsdiagrammin muodossa, kuten Kuvassa 1.
Kuva 1: Satunnaismuuttuja X
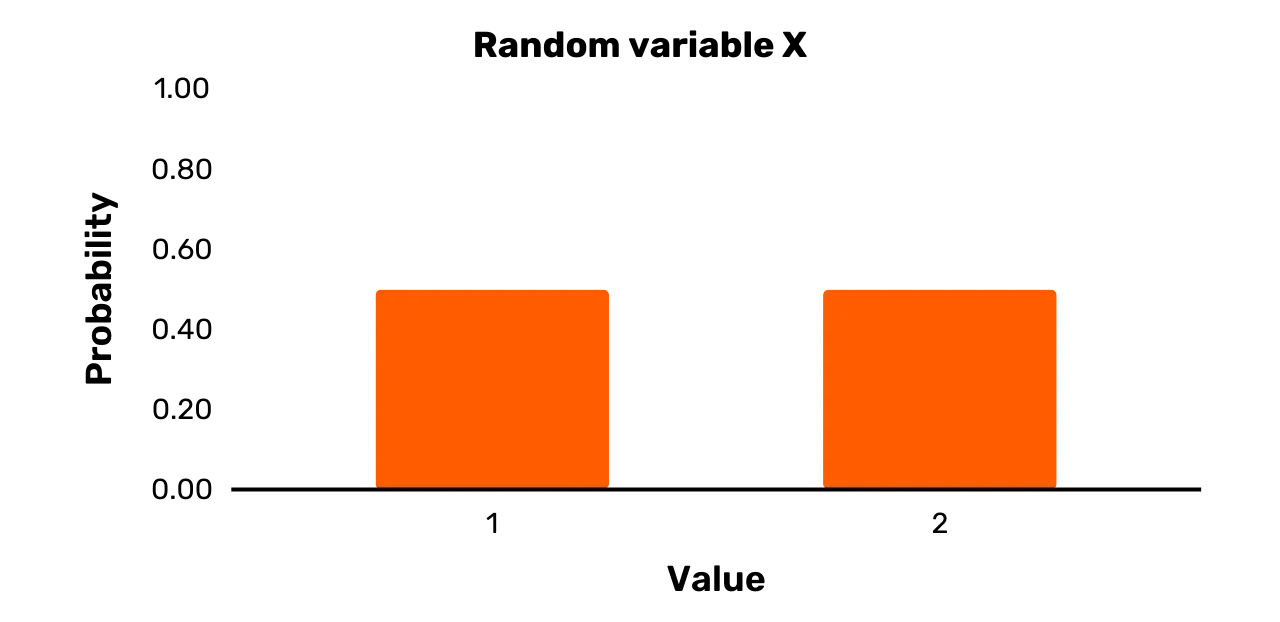
Kuvion 1 leveillä palkeilla ei tietenkään ole tarkoitus vihjata,
että satunnaismuuttuja X olisi
itse asiassa jatkuva. Sen sijaan palkit on tehty leveiksi, jotta ne olisivat
visuaalisesti miellyttävämpiä (pelkkä viiva suoraan ylöspäin on vähemmän intuitiivinen
visualisointi).
Yhtenäiset muuttujat
Ilmaisussa "satunnaismuuttuja" termi "satunnainen" tarkoittaa vain "todennäköinen". Toisin sanoen se tarkoittaa vain sitä, että muuttujan kaksi tai useampi mahdollinen lopputulos tapahtuu tietyin todennäköisyyksin. Näiden lopputulosten ei kuitenkaan välttämättä tarvitse olla yhtä todennäköisiä (vaikka termillä "satunnainen" voi toki olla tämä merkitys muissa yhteyksissä).
yhtenäinen muuttuja on satunnaismuuttujan erikoistapaus. Se
voi saada kaksi tai useampia arvoja, joilla kaikilla on sama todennäköisyys.
Kuvassa 1 esitetty satunnaismuuttuja X on selvästi tasainen muuttuja, koska molemmat mahdolliset tulokset
esiintyvät todennäköisyydellä 0.5. On kuitenkin olemassa
monia satunnaismuuttujia, jotka eivät ole yhdenmukaisia muuttujia.
Tarkastellaan esimerkiksi satunnaismuuttujaa Y. Sillä on tulosjoukko {1, 2, 3, 8, 10} ja
seuraava todennäköisyysjakauma:
\Pr[Y = 1] = 0.25\Pr[Y = 2] = 0.35\Pr[Y = 3] = 0.1\Pr[Y = 8] = 0.25\Pr[Y = 10] = 0.05Vaikka kahdella mahdollisella lopputuloksella, nimittäin 1 ja 8, on tosiaan sama
todennäköisyys, Y voi myös
ottaa tiettyjä arvoja, joiden todennäköisyys on erilainen kuin 0.25 otannan yhteydessä. Vaikka Y onkin
satunnaismuuttuja, se ei siis ole tasainen muuttuja.
Graafinen kuva Y:stä on
esitetty Kuvassa 2.
Kuva 2: Satunnaismuuttuja Y
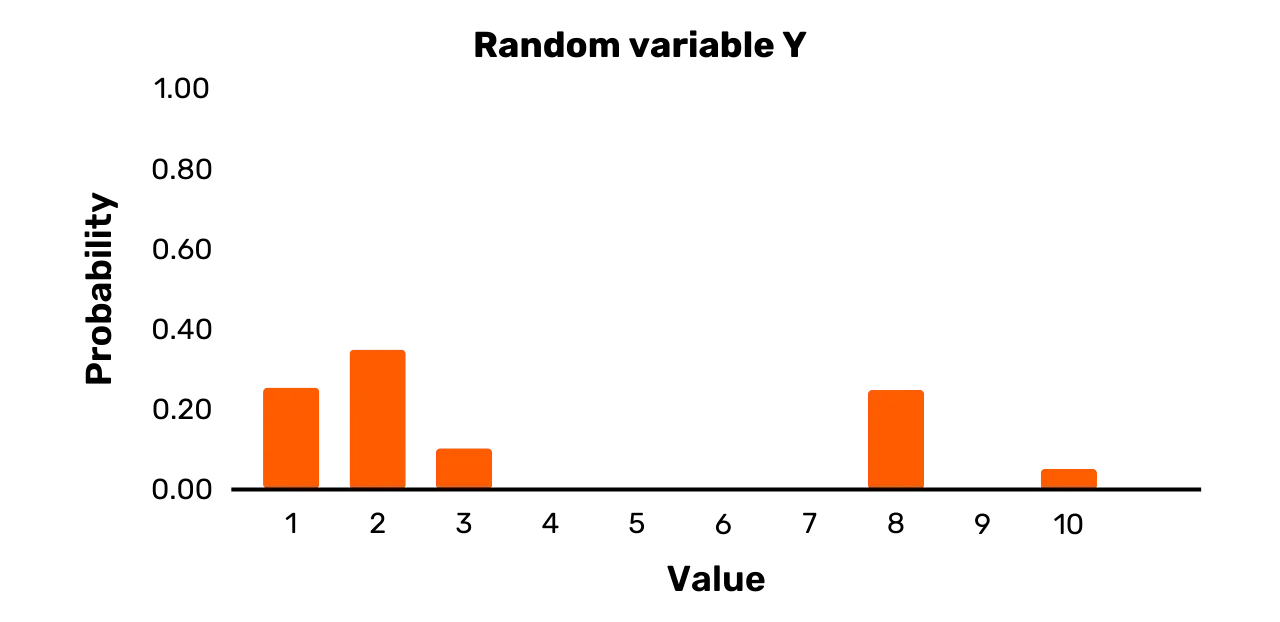
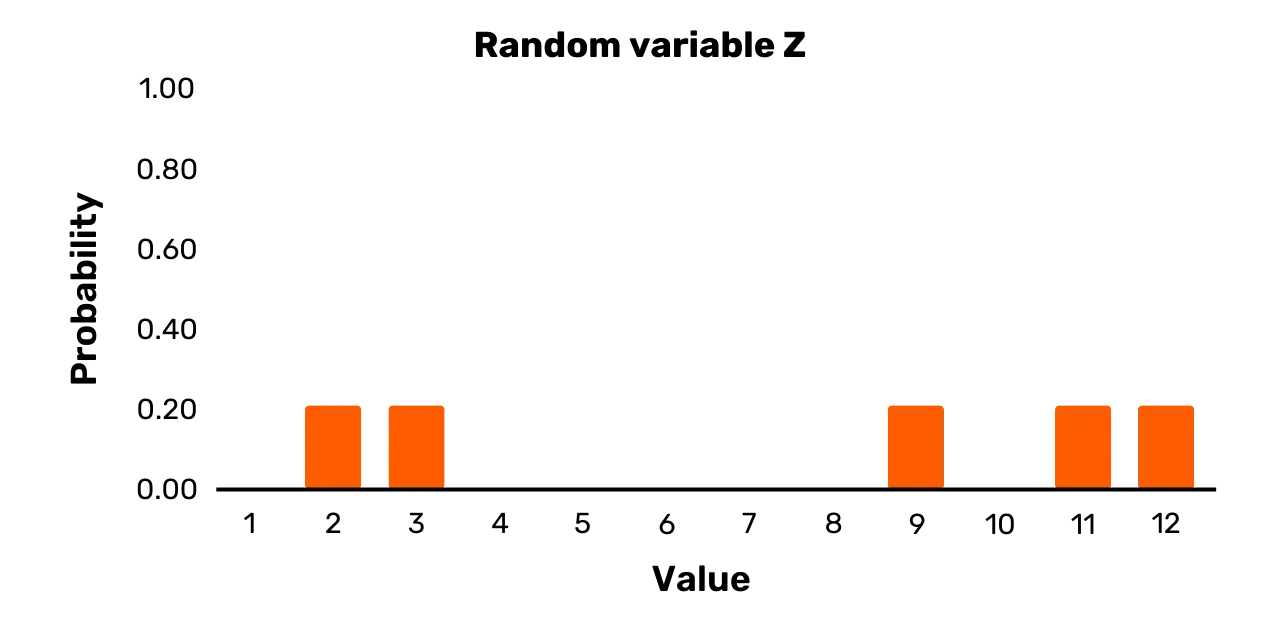
Viimeisenä esimerkkinä tarkastellaan satunnaismuuttujaa Z. Sillä on tulosjoukko {1,3,7,11,12} ja seuraava todennäköisyysjakauma:
\Pr[Z = 2] = 0.2\Pr[Z = 3] = 0.2\Pr[Z = 9] = 0.2\Pr[Z = 11] = 0.2\Pr[Z = 12] = 0.2Voit nähdä sen kuvassa Kuvassa 3. Satunnaismuuttuja Z on Y:stä poiketen tasainen muuttuja, sillä kaikki todennäköisyydet mahdollisille arvoille otannassa ovat yhtä suuret.
Kuva 3: Satunnaismuuttuja Z
Ehdollinen todennäköisyys
Oletetaan, että Bob aikoo valita yhdenmukaisesti päivän viime kalenterivuodelta. Mikä on todennäköisyys sille, että valittu päivä on kesällä?
Niin kauan kuin uskomme, että Bobin prosessi on todella yhdenmukainen, meidän on pääteltävä, että on 1/4 todennäköisyys, että Bob valitsee kesäpäivän. Tämä on ehdoton todennäköisyys sille, että satunnaisesti valittu päivä on kesällä.
Oletetaan nyt, että sen sijaan, että Bob arpoo kalenteripäivän tasaisesti, hän valitsee tasaisesti vain ne päivät, jolloin keskipäivän lämpötila Crystal Lakessa (New Jersey) oli vähintään 21 astetta Celsiusta. Kun otetaan huomioon tämä lisätieto, mitä voimme päätellä siitä todennäköisyydestä, että Bob valitsee kesäpäivän?
Meidän pitäisi todellakin tehdä eri johtopäätös kuin aiemmin, vaikka meillä ei olisi tarkempia tietoja (esim. lämpötila keskipäivällä joka päivä viime kalenterivuonna).
Kun tiedämme, että Crystal Lake sijaitsee New Jerseyssä, emme todellakaan odottaisi, että lämpötila olisi talvella keskipäivällä 21 astetta tai korkeampi. Sen sijaan on paljon todennäköisempää, että se on kevään tai syksyn lämmin päivä tai päivä jossain päin kesää. Jos siis tiedetään, että Crystal Laken keskipäivän lämpötila oli valittuna päivänä 21 astetta tai korkeampi, todennäköisyys sille, että Bobin valitsema päivä on kesällä, on paljon suurempi. Tämä on ehdollinen todennäköisyys sille, että satunnaisesti valittu päivä on kesällä, kun Crystal Laken keskipäivän lämpötila oli 21 astetta tai korkeampi.
Toisin kuin edellisessä esimerkissä, kahden tapahtuman todennäköisyydet voivat myös olla täysin riippumattomia toisistaan. Tällöin sanomme, että ne ovat riippumattomia.
Oletetaan esimerkiksi, että tietty reilu kolikko on saanut kruunaa. Mikä on sitten todennäköisyys sille, että huomenna sataa? Ehdollisen todennäköisyyden pitäisi tässä tapauksessa olla sama kuin ehdottoman todennäköisyyden, että huomenna sataa, koska kolikonheitolla ei yleensä ole vaikutusta säähän.
Käytämme "|"-symbolia ehdollisten todennäköisyyslausumien kirjoittamiseen.
Esimerkiksi tapahtuman A todennäköisyys, jos tapahtuma B on toteutunut, voidaan kirjoittaa
seuraavasti:
Pr[A|B]Kun siis kaksi tapahtumaa, A ja B, ovat riippumattomia,
niin:
Pr[A|B] = Pr[A] \text{ and } Pr[B|A] = Pr[B]Riippumattomuusehto voidaan yksinkertaistaa seuraavasti:
Pr[A, B] = Pr[A] \cdot Pr[B]Todennäköisyysteorian keskeinen tulos tunnetaan nimellä Bayesin lause. Sen mukaan Pr[A|B] voidaan
kirjoittaa uudelleen seuraavasti:
Pr[A|B] = \frac{Pr[B|A] \cdot Pr[A]}{Pr[B]}Sen sijaan, että käytämme ehdollisia todennäköisyyksiä tiettyjen tapahtumien
yhteydessä, voimme myös tarkastella kahden tai useamman satunnaismuuttujan
ehdollisia todennäköisyyksiä, jotka liittyvät useisiin mahdollisiin
tapahtumiin. Oletetaan kaksi satunnaismuuttujaa, X ja Y. Voimme merkitä X:n mitä tahansa mahdollista
arvoa x:llä ja Y:n mitä tahansa mahdollista
arvoa y:llä. Voidaan siis
sanoa, että kaksi satunnaismuuttujaa ovat riippumattomia, jos seuraava väite
pätee:
Pr[X = x, Y = y] = Pr[X = x] \cdot Pr[Y = y]kaikille x ja y.
Kerrotaanpa hieman tarkemmin, mitä tämä lausunto tarkoittaa.
Oletetaan, että X:n ja Y:n tulosjoukot määritellään
seuraavasti: X = \{x_1, x_2, \ldots, x_i, \ldots, x_n\} ja Y = \{y_1, y_2, \ldots, y_i, \ldots, y_m\}. (Tyypillistä on merkitä arvojoukkoja lihavoiduilla isoilla kirjaimilla.)
Oletetaan nyt, että otos Y otetaan ja havaitaan y_1.
Yllä oleva lauseke kertoo, että todennäköisyys saada nyt x_1 otannasta X on täsmälleen
sama kuin jos emme olisi koskaan havainneet y_1. Tämä pätee mille tahansa y_i:lle, jonka olisimme
voineet ottaa alkuperäisestä otannastamme Y. Tämä ei päde vain x_1:lle. Minkä tahansa x_i:n
esiintymistodennäköisyyteen ei vaikuta Y:n otannan tulos. Kaikki
tämä koskee myös tapausta, jossa X otetaan ensin näytteeksi.
Lopetetaan keskustelumme hieman filosofisempaan kohtaan. Missä tahansa reaalimaailman tilanteessa jonkin tapahtuman todennäköisyyttä arvioidaan aina tiettyä tietomäärää vasten. Ei ole olemassa "ehdotonta todennäköisyyttä" sanan varsinaisessa merkityksessä.
Oletetaan esimerkiksi, että kysyn sinulta todennäköisyyttä sille, että siat lentävät vuoteen 2030 mennessä. Vaikka en anna sinulle mitään lisätietoja, tiedät selvästi paljon sellaista maailmasta, joka voi vaikuttaa arvostelukykyysi. Et ole koskaan nähnyt sikojen lentävän. Tiedät, että useimmat ihmiset eivät odota niiden lentävän. Tiedät, että niitä ei oikeastaan ole rakennettu lentämään. Ja niin edelleen.
Kun siis puhumme jonkin tapahtuman "ehdottomasta todennäköisyydestä" reaalimaailman kontekstissa, termillä voi olla merkitystä vain, jos ymmärrämme sen tarkoittavan jotakin sellaista kuin "todennäköisyys ilman mitään muuta eksplisiittistä tietoa". Mikä tahansa käsitys "ehdollisesta todennäköisyydestä" olisi siis aina ymmärrettävä jotakin tiettyä tietoa vasten.
Voisin esimerkiksi kysyä, mikä on todennäköisyys sille, että siat lentävät vuoteen 2030 mennessä, sen jälkeen kun olen antanut sinulle todisteita siitä, että jotkut vuohet Uudessa-Seelannissa ovat oppineet lentämään muutaman vuoden harjoittelun jälkeen. Tällöin todennäköisesti korjaat arviotasi todennäköisyydestä, että siat lentävät vuoteen 2030 mennessä. Todennäköisyys, että siat lentävät vuoteen 2030 mennessä, riippuu siis tästä Uuden-Seelannin vuohia koskevasta todisteesta.
Modulo-operaatio
Modulo
Peruslause, jossa käytetään modulo-operaatiota, on
seuraavanlainen: x \mod y.
Muuttujaa x kutsutaan
osingoksi ja muuttujaa y jakajaksi.
Kun modulo-operaatio suoritetaan positiivisella osingolla ja positiivisella jakajalla,
määritetään vain jakojäännös.
Tarkastellaan esimerkiksi lauseketta 25 \mod 4. Luku 4 tulee lukuun 25 yhteensä 6 kertaa. Tämän jaon jäännös on 1. Näin
ollen 25 \mod 4 on 1. Vastaavalla
tavalla voimme arvioida alla olevat lausekkeet:
29 \mod 30 = 29(koska 30 menee 29:ään yhteensä 0 kertaa ja jäännös on 29)42 \mod 2 = 0(koska 2 tulee 42:een yhteensä 21 kertaa ja jäännös on 0)12 \mod 5 = 2(koska 5 tulee 12:een yhteensä 2 kertaa ja jäännös on 2)20 \mod 8 = 4(koska 8 tulee 20:een yhteensä 2 kertaa ja jäännös on 4)
Kun osingon tai jakajan arvo on negatiivinen, ohjelmointikielet voivat käsitellä modulo-operaatioita eri tavalla.
Kryptografiassa törmää varmasti tapauksiin, joissa osinko on negatiivinen. Näissä tapauksissa tyypillinen lähestymistapa on seuraava:
- Määritä ensin lähin arvo, joka on alempi tai yhtä suuri kuin
jakolasku, johon jakaja jakautuu nollan jäännöksellä. Kutsutaan tätä arvoa
nimellä
p. - Jos osinko on
x, modulo-operaation tulos on arvox - p.
Oletetaan esimerkiksi, että osinko on -20 ja jakaja 3. Lähin arvo, joka on pienempi tai yhtä suuri kuin -20 ja jolla 3 jakautuu tasan, on -21. Tällöin x - p:n arvo on -20 - (-21). Tämä on yhtä
suuri kuin 1, ja näin ollen -20 \mod 3 on yhtä suuri kuin
1. Vastaavalla tavalla voimme arvioida alla olevat lausekkeet:
-8 \mod 5 = 2-19 \mod 16 = 13-14 \mod 6 = 4
Merkintätapa on tyypillisesti seuraavanlainen: x = [y \mod z]. Suluista johtuen modulo-operaatio koskee tässä tapauksessa vain
lausekkeen oikeaa puolta. Jos y on esimerkiksi 25 ja z on 4, x on 1.
Ilman sulkuja modulo-operaatio vaikuttaa lausekkeen kummallekin puolelle. Oletetaan esimerkiksi seuraava lauseke: x = y \mod z. Jos y on 25 ja z on 4, tiedämme
vain, että x \mod 4 on 1.
Tämä sopii mihin tahansa arvoon x joukosta \\\ldots,-7, -3, 1, 5, 9,\ldots\}.
Matematiikan haaraa, joka käsittää lukuihin ja lausekkeisiin kohdistuvia modulo-operaatioita, kutsutaan modulaariseksi aritmetiikaksi. Tätä haaraa voidaan pitää aritmetiikkana tapauksissa, joissa lukujono ei ole äärettömän pitkä. Vaikka kryptografiassa törmäämme tyypillisesti (positiivisille) kokonaisluvuille tehtäviin modulo-operaatioihin, voit suorittaa modulo-operaatioita myös kaikilla reaaliluvuilla.
Siirtymäsalaus
Modulo-operaatiota käytetään usein kryptografiassa. Esimerkkinä mainittakoon yksi kuuluisimmista historiallisista salausmenetelmistä: shift cipher.
Määritellään se ensin. Oletetaan sanakirja D, joka rinnastaa kaikki
englannin aakkosten kirjaimet järjestyksessä lukujoukkoon \{0, 1, 2, \ldots, 25\}. Oletetaan viestiavaruus M. Shift cipher on siis salausjärjestelmä, joka määritellään seuraavasti:
- Valitaan tasaisesti avain
kavainavaruudesta K, jossa K =\{0, 1, 2, \ldots, 25\}[1] - Salaa viesti
m \in \mathbf{M}seuraavasti:- Erottele
msen yksittäisiin kirjaimiinm_0, m_1, \ldots, m_i, \ldots, m_l - Muunnetaan jokainen
m_iluvuksi D:n mukaisesti - Jokaisen
m_iosaltac_i = [(m_i + k) \mod 26] - Muunna jokainen
c_ikirjaimeksi D:n mukaisesti - Yhdistetään sitten
c_0, c_1, \ldots, c_l, jolloin saadaan salattu tekstic
- Erottele
- Puretaan salattu teksti
cseuraavasti:- Muunnetaan jokainen
c_iluvuksi D:n mukaisesti - Jokaisen
c_iosaltam_i = [(c_i - k) \mod 26] - Muunna jokainen
m_ikirjaimeksi D:n mukaisesti - Yhdistetään sitten
m_0, m_1, \ldots, m_l, jolloin saadaan alkuperäinen viestim
- Muunnetaan jokainen
Siirtymäsalakirjoituksen modulo-operaattori varmistaa, että kirjaimet kiertyvät ympäri, joten kaikki salatekstin kirjaimet ovat määriteltyjä. Esimerkkinä mainittakoon, että shift-salausmenetelmää sovelletaan sanaan "DOG".
Oletetaan, että valitsit yhdenmukaisesti avaimen, jonka arvo on 17. Kirjain
"O" vastaa arvoa 15. Ilman modulo-operaatiota tämän selvätekstiluvun ja
avaimen yhteenlasku antaisi salatekstiluvuksi 32. Tätä salatekstilukua ei
kuitenkaan voida muuttaa salatekstin kirjaimeksi, koska englantilaisissa
aakkosissa on vain 26 kirjainta. Modulo-operaatio varmistaa, että
salatekstin luku on itse asiassa 6 (tulos 32 \mod 26), mikä vastaa salatekstin kirjainta "G".
Koko sanan "DOG" salaus, jonka avainarvo on 17, on seuraava:
- Viesti = DOG = D,O,G = 3,15,6
c_0 = [(3 + 17) \mod 26] = [(20) \mod 26] = 20 = Uc_1 = [(15 + 17) \mod 26] = [(32) \mod 26] = 6 = Gc_2 = [(6 + 17) \mod 26] = [(23) \mod 26] = 23 = Xc = UGX
Kaikki ymmärtävät intuitiivisesti, miten shift-salaus toimii, ja todennäköisesti käyttävät sitä itse. Kryptografian tuntemuksen syventämiseksi on kuitenkin tärkeää, että alat oppia tuntemaan paremmin formalisointia, sillä skeemoista tulee paljon vaikeampia. Siksi siirtosalauksen vaiheet formalisoitiin.
Huomautukset:
[1] Voimme määritellä tämän väitteen tarkasti käyttämällä edellisen jakson
terminologiaa. Olkoon yhtenäisen muuttujan K mahdollisten tulosten joukko K. Siis:
Pr[K = 0] = \frac{1}{26}Pr[K = 1] = \frac{1}{26}...ja niin edelleen. Otetaan näytteitä yhtenäisestä muuttujasta K kerran tietyn avaimen saamiseksi.
XOR-operaatio
Kaikki tietokonedata käsitellään, tallennetaan ja lähetetään verkoissa bittien tasolla. Kaikki tietokonedataan sovellettavat salausjärjestelmät toimivat myös bittitasolla.
Oletetaan esimerkiksi, että olet kirjoittanut sähköpostiviestin sähköpostiohjelmaan. Soveltamasi salaus ei kohdistu suoraan sähköpostin ASCII-merkkeihin. Sen sijaan sitä sovelletaan sähköpostin kirjainten ja muiden symbolien bittimuotoiseen esitykseen.
Moduulioperaation lisäksi keskeinen matemaattinen operaatio, joka on
ymmärrettävä nykyaikaisessa kryptografiassa, on XOR-operaatio eli "eksklusiivinen tai" -operaatio. Tämä operaatio ottaa syötteenä kaksi
bittiä ja antaa tuloksena toisen bitin. XOR-operaatiota kutsutaan
yksinkertaisesti nimellä "XOR". Se antaa tulokseksi 0, jos kaksi bittiä ovat
samat, ja 1, jos kaksi bittiä ovat erilaiset. Alla näet neljä vaihtoehtoa.
Symboli \oplus tarkoittaa "XOR"
:
0 \oplus 0 = 00 \oplus 1 = 11 \oplus 0 = 11 \oplus 1 = 0
Kuvitellaan, että sinulla on viesti m_1 (01111001) ja viesti m_2 (01011001).
Näiden kahden viestin XOR-operaatio näkyy alla.
m_1 \oplus m_2 = 01111001 \oplus 01011001 = 00100000
Prosessi on suoraviivainen. Ensin tehdään XOR m_1:n ja m_2:n
vasemmanpuoleisimmat bitit. Tässä tapauksessa se on 0 \oplus 0 = 0. Sitten
XOR-järjestetään toinen bittipari vasemmalta. Tässä tapauksessa se on 1 \oplus 1 = 0. Tätä
jatketaan, kunnes XOR-operaatio on suoritettu oikeanpuoleisimmille biteille.
On helppo nähdä, että XOR-operaatio on kommutatiivinen, eli että m_1 \oplus m_2 = m_2 \oplus m_1. Lisäksi XOR-operaatio on myös assosiatiivinen. Toisin sanoen (m_1 \oplus m_2) \oplus m_3 = m_1 \oplus (m_2 \oplus m_3).
XOR-operaatiolla kahdelle eri pituiselle merkkijonolle voi olla erilaisia tulkintoja asiayhteydestä riippuen. Emme käsittele tässä yhteydessä eri pituisten merkkijonojen XOR-operaatioita.
XOR-operaatio vastaa erikoistapausta, jossa bittien yhteenlasku suoritetaan modulo-operaatiolla, kun jakaja on 2. Vastaavuus näkyy seuraavissa tuloksissa:
(0 + 0) \mod 2 = 0 \oplus 0 = 0(1 + 0) \mod 2 = 1 \oplus 0 = 1(0 + 1) \mod 2 = 0 \oplus 1 = 1(1 + 1) \mod 2 = 1 \oplus 1 = 0
Pseudosatunnaisuus
Satunnaisia ja yhtenäisiä muuttujia käsitellessämme erotimme toisistaan "satunnaiset" ja "yhtenäiset" muuttujat. Tämä ero säilytetään yleensä käytännössä satunnaismuuttujia kuvattaessa. Nykyisessä asiayhteydessämme tästä erottelusta on kuitenkin luovuttava ja "satunnainen" ja "yhtenäinen" käytetään synonyymeinä. Selitän miksi tämän jakson lopussa.
Aluksi voimme kutsua binäärijonoa, jonka pituus on n, sattumanvaraiseksi (tai yhtenäiseksi),
jos se on saatu otannalla yhtenäisestä muuttujasta S, joka antaa jokaiselle
tällaisen pituisen n binäärijonon
valinnan todennäköisyyden.
Oletetaan esimerkiksi, että kaikkien sellaisten binäärijonojen joukko,
joiden pituus on 8: \{0000\ 0000, 0000\ 0001, \ldots, 1111\ 1111\}. (Tyypillistä on kirjoittaa 8-bittinen merkkijono kahtena kvarttina, joita
kutakin kutsutaan nibbleksi) Kutsutaan tätä merkkijonojen
joukkoa S_8.
Yllä olevan määritelmän mukaan voimme siis kutsua tiettyä binäärijonoa,
jonka pituus on 8, satunnaiseksi (tai yhtenäiseksi), jos se on tulosta
näytteenotosta yhtenäisestä muuttujasta S, joka antaa jokaiselle merkkijonolle S_8 yhtä suuren todennäköisyyden tulla valituksi. Koska joukko S_8 sisältää 2^8 elementtiä,
otannan valinnan todennäköisyyden on oltava 1/2^8 jokaiselle joukon merkkijonolle.
Binäärijonon satunnaisuuteen liittyy olennaisesti se, että se määritellään suhteessa prosessiin, jolla se on valittu. Minkä tahansa binäärijonon muoto ei siis yksinään kerro mitään sen satunnaisuudesta valinnassa.
Esimerkiksi monet ihmiset ajattelevat intuitiivisesti, että merkkijonoa 1111\ 1111 ei ole voitu valita satunnaisesti. Tämä on kuitenkin selvästi väärin.
Määritellään yhtenäinen muuttuja S$$ kaikkien 8-pituisten binäärijonojen yli, ja todennäköisyys valita1111\ 1111joukosta **S_8** on sama kuin esimerkiksi merkkijono0111\ 0100$. Näin ollen merkkijonon satunnaisuudesta ei voi sanoa
mitään pelkästään analysoimalla itse merkkijonoa.
Voimme myös puhua satunnaisista merkkijonoista tarkoittamatta erityisesti
binäärijonoja. Voimme esimerkiksi puhua satunnaisesta heksanmerkkijonosta AF\ 02\ 82. Tällöin merkkijono olisi valittu satunnaisesti kaikkien pituudeltaan 6:n
pituisten heksalukujen joukosta. Tämä vastaa sitä, että valitaan
satunnaisesti 24:n pituinen binäärijono, koska jokainen heksaluku edustaa 4
bittiä.
Tyypillisesti ilmaus "satunnainen merkkijono" viittaa ilman tarkennuksia
merkkijonoon, joka on valittu satunnaisesti kaikkien samanpituisten
merkkijonojen joukosta. Näin olen kuvannut asian edellä. Pituudeltaan n merkkijono voidaan tietysti valita satunnaisesti myös muusta joukosta.
Esimerkiksi sellaisesta, joka muodostaa vain osajoukon kaikista
merkkijonoista, joiden pituus on n, tai ehkä joukosta, joka
sisältää eri pituisia merkkijonoja. Näissä tapauksissa emme kuitenkaan
kutsuisi sitä "satunnaiseksi merkkijonoksi" vaan "merkkijonoksi, joka on
valittu satunnaisesti joukosta S".
Pseudosatunnaisuuden käsite on keskeinen käsite kryptografiassa.
Pituudeltaan n:n pituinen pseudosatunnainen merkkijono näyttää ikään kuin se olisi tulosta näytteenotosta yhtenäisestä
muuttujasta S, joka antaa
jokaiselle merkkijonolle S_n yhtäläisen valintatodennäköisyyden. Tosiasiassa merkkijono on kuitenkin
tulosta näytteenotosta yhtenäisestä muuttujasta S', joka määrittelee vain
todennäköisyysjakauman - ei välttämättä sellaista, jossa kaikilla
mahdollisilla tuloksilla on yhtäläiset todennäköisyydet S_n:n
osajoukossa. Ratkaisevaa tässä on se, että kukaan ei voi oikeastaan erottaa
näytteitä S:sta ja S':sta, vaikka niitä
otettaisiinkin paljon.
Oletetaan esimerkiksi satunnaismuuttuja S. Sen tulosjoukko on S_{256}, joka on kaikkien niiden binäärijonojen joukko, joiden pituus on 256.
Tällä joukolla on 2^{256} alkioita. Jokaisella elementillä on otannassa yhtä suuri todennäköisyys, 1/2^{256}, tulla
valituksi.
Lisäksi oletetaan satunnaismuuttuja S'. Sen tulosjoukko sisältää vain 2^{128} binäärijonoja,
joiden pituus on 256. Sillä on jokin todennäköisyysjakauma näille merkkijonoille,
mutta tämä jakauma ei välttämättä ole tasainen.
Oletetaan, että otan nyt 1000 näytettä S:sta ja 1000 näytettä S':sta
ja annan sinulle nämä kaksi tulossarjaa. Kerron sinulle, kumpi tulosjoukko
liittyy mihinkin satunnaismuuttujaan. Seuraavaksi otan näytteen
jommastakummasta satunnaismuuttujasta. Tällä kertaa en kuitenkaan kerro,
minkä satunnaismuuttujan otoksen otan. Jos S' olisi pseudosattumanvarainen, ajatuksena on, että todennäköisyytesi arvata
oikein, mistä satunnaismuuttujasta otoksen otin, on käytännössä korkeintaan 1/2.
Tyypillisesti pseudosatunnainen merkkijono, jonka pituus on n, tuotetaan valitsemalla satunnaisesti merkkijono, jonka koko on n - x, jossa x on positiivinen kokonaisluku, ja käyttämällä sitä laajennusalgoritmin
syötteenä. Tätä satunnaista merkkijonoa, jonka koko on n - x, kutsutaan siemeneksi.
Pseudosatunnaismerkkijonot ovat avainkäsite, jonka avulla salaus voidaan tehdä käytännölliseksi. Tarkastellaan esimerkiksi virtasalakirjoituksia. Virtasalakirjoituksessa satunnaisesti valittu avain liitetään laajentavaan algoritmiin, jolloin saadaan paljon suurempi pseudosatunnainen merkkijono. Tämä pseudosattumanvarainen merkkijono yhdistetään sitten XOR-operaation avulla selkotekstiin, jolloin saadaan salattu teksti.
Jos emme pystyisi tuottamaan tällaista pseudosatunnaismerkkijonoa virran salausmenetelmää varten, tarvitsisimme avaimen, joka on yhtä pitkä kuin viesti, jotta se olisi turvallinen. Tämä ei ole kovin käytännöllinen vaihtoehto useimmissa tapauksissa.
Tässä jaksossa käsitelty pseudosatunnaisuuden käsite voidaan määritellä muodollisemmin. Se ulottuu myös muihin yhteyksiin. Meidän ei kuitenkaan tarvitse syventyä tähän keskusteluun tässä yhteydessä. Intuitiivisesti on ymmärrettävä suurimmassa osassa kryptografiaa vain satunnaisen ja pseudosatunnaisen merkkijonon välinen ero. [2]
Syy siihen, miksi "satunnaisen" ja "yhdenmukaisen" välinen ero on poistettu
keskustelustamme, pitäisi nyt myös olla selvä. Käytännössä kaikki käyttävät
termiä pseudosattumanvarainen merkitsemään merkkijonoa, joka näyttää ikään kuin se olisi tulosta yhdenmukaisen muuttujan S näytteenotosta. Tarkkaan ottaen
meidän pitäisi kutsua tällaista merkkijonoa "pseudo-epätasaiseksi", jolloin ottaisimme
käyttöön aiemmat kielenkäyttömme. Koska termi "pseudo-epätasainen" on sekä kömpelö
että epäsäännöllinen, emme ota sitä tässä käyttöön selkeyden vuoksi. Sen sijaan
jätämme vain pois eron "satunnaisen" ja "yhtenäisen" välillä tässä yhteydessä.
Huomautuksia
[2] Jos olet kiinnostunut muodollisemmasta esityksestä näistä asioista, voit tutustua Katzin ja Lindellin teokseen Introduction to Modern Cryptography, erityisesti lukuun 3.
Kryptografian matemaattiset perusteet 2
Mitä on numeroteoria?
Tässä luvussa käsitellään kryptografian matemaattisia perusteita koskevaa edistyneempää aihetta: lukuteoriaa. Vaikka numeroteoria on tärkeää symmetrisessä kryptografiassa (kuten Rijndael-salauksessa), se on erityisen tärkeää julkisen avaimen kryptografiassa.
Jos numeroteorian yksityiskohdat tuntuvat hankalilta, suosittelen, että luette sen ensimmäisellä kerralla korkeatasoisesti. Voit aina palata siihen myöhemmin.
Voit luonnehtia lukuteoriaa kokonaislukujen ominaisuuksien ja kokonaislukujen kanssa toimivien matemaattisten funktioiden tutkimukseksi.
Esimerkiksi kaksi lukua a ja N ovat kopriimejä (tai relatiivisia alkulukuja), jos niiden suurin yhteinen jakaja
on 1. Oletetaan nyt tietty kokonaisluku N. Kuinka monta N:aa pienempää kokonaislukua
on koprimia N:n kanssa?
Voimmeko tehdä yleisiä väitteitä vastauksista tähän kysymykseen? Nämä ovat
tyypillisiä kysymyksiä, joihin lukuteoria pyrkii vastaamaan.
Nykyaikainen lukuteoria perustuu abstraktin algebran työkaluihin. Abstrakti algebra** on matematiikan osa-alue, jossa analyysin pääkohteet ovat algebrallisiksi rakenteiksi kutsuttuja abstrakteja kohteita. Algebrallinen rakenne on joukko elementtejä, joihin liittyy yksi tai useampi operaatio ja jotka täyttävät tietyt aksioomat. Algebrallisten rakenteiden avulla matemaatikot voivat saada käsityksen erityisistä matemaattisista ongelmista abstrahoimalla niiden yksityiskohdista.
Abstraktin algebran alaa kutsutaan joskus myös moderniksi algebraksi. Saatat törmätä myös käsitteeseen abstrakti matematiikka (tai puhdas matematiikka). Jälkimmäinen termi ei viittaa abstraktiin algebraan, vaan tarkoittaa pikemminkin matematiikan tutkimista sen itsensä vuoksi eikä vain mahdollisia sovelluksia silmällä pitäen.
Abstraktin algebran joukot voivat käsitellä monenlaisia objekteja tasasivuisen kolmion muotoa säilyttävistä muunnoksista tapettikuvioihin. Lukuteoriassa tarkastelemme vain kokonaislukuja sisältäviä alkiojoukkoja tai kokonaislukujen kanssa toimivia funktioita.
Ryhmät
Matematiikan peruskäsite on elementtien joukko. Joukko merkitään yleensä aksenttimerkillä, jossa elementit on erotettu toisistaan pilkuilla.
Esimerkiksi kaikkien kokonaislukujen joukko on \{..., -2, -1, 0, 1, 2, ...\}. Ellipsit tarkoittavat tässä, että tietty kuvio jatkuu tiettyyn suuntaan.
Kaikkien kokonaislukujen joukkoon kuuluvat siis myös 3, 4, 5, 6 ja niin edelleen sekä -3, -4, -5, -6 ja niin edelleen. Tätä kaikkien kokonaislukujen joukkoa merkitään
tyypillisesti \mathbb{Z}.
Toinen esimerkki joukosta on \mathbb{Z} \mod 11 eli kaikkien kokonaislukujen joukko modulo 11. Toisin kuin koko joukko \mathbb{Z}, tämä
joukko sisältää vain äärellisen määrän alkioita, nimittäin \{0, 1, \ldots, 9, 10\}.
Yleinen virhe on ajatella, että joukko \mathbb{Z} \mod 11 on itse asiassa \{-10, -9, \ldots, 0, \ldots, 9, 10\}. Näin ei kuitenkaan ole, kun otetaan huomioon tapa, jolla määrittelimme
modulo-operaation aiemmin. Kaikki modulo 11:llä redusoidut negatiiviset
kokonaisluvut kietoutuvat \{0, 1, \ldots, 9, 10\}:iin. Esimerkiksi lauseke -2 \mod 11 kietoutuu 9:een, kun taas
lauseke -27 \mod 11 kietoutuu 5:een.
Toinen matematiikan peruskäsite on binäärioperaatio. Tämä on mikä tahansa operaatio, jossa kahdesta alkuaineesta saadaan kolmas alkuaine. Esimerkiksi aritmetiikan ja algebran peruslaskutoimituksista tunnet neljä binäärioperaatiota: yhteenlasku, vähennyslasku, kertolasku ja jakolasku.
Näiden kahden matemaattisen peruskäsitteen, joukkojen ja binäärioperaatioiden, avulla määritellään ryhmän käsite, joka on abstraktin algebran keskeisin rakenne.
Oletetaan, että on jokin binäärioperaatio \circ. Lisäksi oletetaan jokin elementtijoukko S, joka on
varustettu kyseisellä operaatiolla. "Varustettu" tarkoittaa tässä vain sitä,
että operaatio \circ voidaan
suorittaa minkä tahansa joukon S kahden alkion välillä.
Yhdistelmä \langle \mathbf{S}, \circ \rangle on siis ryhmä, jos se täyttää neljä erityistä ehtoa, jotka
tunnetaan ryhmäaksioomina.
Jos
ajabovat\mathbf{S}:n alkioita,a \circ bon myös\mathbf{S}:n alkio. Tätä kutsutaan sulkeisehdoksi.Kaikille
a,bjac, jotka ovat\mathbf{S}:n alkioita, pätee, että(a \circ b) \circ c = a \circ (b \circ c). Tätä kutsutaan assosiatiivisuusehdoksi.\mathbf{S}:ssa on yksikäsitteinen alkioe, joka on sellainen, että jokaiselle\mathbf{S}:n alkioilleapätee seuraava yhtälö:e \circ a = a \circ e = a. Koska tällaisia elementtejäeon vain yksi, sitä kutsutaan identiteettielementiksi. Tätä ehtoa kutsutaan identiteettiehdoksi.Jokaiselle
\mathbf{S}:naalkioille\mathbf{S}on olemassa\mathbf{S}:nbalkio, jonka suhteen pätee seuraava yhtälö:a \circ b = b \circ a = e, missäeon identtinen alkio. Elementtiäbkutsutaan tässä inversioelementiksi, ja sitä merkitään yleisestia^{-1}. Tämä ehto tunnetaan nimellä inversioehto tai inversioehto.
Tutustutaan ryhmiin hieman tarkemmin. Merkitään kaikkien kokonaislukujen
joukkoa \mathbb{Z}.
Tämä joukko yhdistettynä tavanomaiseen yhteenlaskuun eli \langle \mathbb{Z}, + \rangle vastaa selvästi ryhmän määritelmää, sillä se täyttää edellä mainitut neljä
aksioomaa.
Jos
xjayovat\mathbb{Z}:n alkioita,x + yon myös\mathbb{Z}:n alkio. Joten\langle \mathbb{Z}, + \rangletäyttää sulkemisehdon.Kaikille
x,yjaz, jotka ovat\mathbb{Z}:n alkioita, pätee(x + y) + z = x + (y + z). Joten\langle \mathbb{Z}, + \rangletäyttää assosiatiivisuusehdon.On olemassa identtinen alkio
\langle \mathbb{Z}, + \rangle, nimittäin 0. Mille tahansax:lle\mathbb{Z}:ssa pätee nimittäin, että:0 + x = x + 0 = x. Joten\langle \mathbb{Z}, + \rangletäyttää identiteettiehdon.Lopuksi, jokaiselle
\mathbb{Z}:nxalkioille\mathbb{Z}on olemassaysiten, ettäx + y = y + x = 0. Josxolisi esimerkiksi 10,yolisi-10(josxon 0, myösyon 0). Joten\langle \mathbb{Z}, + \rangletäyttää käänteisehdon.
On tärkeää, että se, että kokonaislukujen joukko yhteenlaskun kanssa
muodostaa ryhmän, ei tarkoita, että se muodostaa ryhmän kertolaskun kanssa.
Voit todentaa tämän testaamalla \langle \mathbb{Z}, \cdot \rangle neljää ryhmäaksioomaa vastaan (jossa \cdot tarkoittaa tavallista kertolaskua).
Kaksi ensimmäistä aksioomaa ovat ilmeisesti voimassa. Lisäksi kerrottuna
alkio 1 voi toimia identtisenä alkiona. Mikä tahansa kokonaisluku x kerrottuna 1:llä antaa nimittäin x. Kuitenkin \langle \mathbb{Z}, \cdot \rangle ei täytä käänteisehtoa. Toisin sanoen \mathbb{Z}:ssa ei
ole yksikäsitteistä alkua y jokaiselle x:lle \mathbb{Z}:ssa,
jotta x \cdot y = 1.
Oletetaan esimerkiksi, että x = 22. Mikä arvo y joukosta \mathbb{Z} kerrottuna x:llä antaisi
identtisen alkion 1? Arvo 1/22 toimisi, mutta se ei kuulu joukkoon \mathbb{Z}. Itse
asiassa tähän ongelmaan törmää minkä tahansa kokonaisluvun x kohdalla, lukuun ottamatta arvoja 1 ja -1 (jolloin y:n olisi oltava 1 ja -1).
Jos sallimme reaaliluvut joukossamme, ongelmamme häviävät suurelta osin.
Minkä tahansa joukkoon kuuluvan alkion x kertolasku luvulla 1/x antaa tulokseksi
1. Koska murtoluvut sisältyvät reaalilukujen joukkoon, jokaiselle reaaliluvulle
voidaan löytää käänteisluku. Poikkeuksena on nolla, sillä kertolasku nollalla
ei koskaan tuota identtistä alkiota 1. Nollasta poikkeavien reaalilukujen joukko,
joka on varustettu kertolaskulla, on siis todellakin ryhmä.
Jotkut ryhmät täyttävät viidennen yleisen ehdon, joka tunnetaan nimellä kommutatiivisuusehto. Tämä ehto on seuraava:
- Oletetaan ryhmä
G, jolla on joukko S ja binäärioperaattori\circ. Oletetaan, ettäajabovat S:n alkioita. Jos pätee, ettäa \circ b = b \circ amille tahansa kahdelle S:n elementilleajab, niinGtäyttää kommutatiivisuusehdon.
Mikä tahansa ryhmä, joka täyttää kommutatiivisuusehdon, tunnetaan kommutatiivisena ryhmänä tai Abelin ryhmänä (Niels Henrik Abelin mukaan). On helppo todentaa, että sekä reaalilukujen joukko yhteenlaskussa että kokonaislukujen joukko yhteenlaskussa ovat abelilaisia ryhmiä. Kertolaskun kokonaislukujen joukko ei ole lainkaan ryhmä, joten se ei ipso facto voi olla abelilainen ryhmä. Nollasta poikkeavien reaalilukujen joukko kertolaskun yhteydessä on sitä vastoin myös abelilainen ryhmä.
Sinun tulisi ottaa huomioon kaksi tärkeää merkintätapaa. Ensinnäkin, merkkejä "+" tai "×" käytetään usein ryhmäoperaatioiden symboleina, vaikka elementit eivät olisikaan itse asiassa numeroita. Näissä tapauksissa näitä merkkejä ei pidä tulkita tavalliseksi aritmeettiseksi yhteen- tai kertolaskuksi. Sen sijaan ne ovat operaatioita, joilla on vain abstrakti samankaltaisuus näiden aritmeettisten operaatioiden kanssa.
Jos et tarkoita erityisesti aritmeettista yhteen- tai kertolaskua, on
helpompi käyttää symboleja kuten \circ ja \diamond ryhmäoperaatioista,
koska niillä ei ole kulttuurisesti juurtuneita merkityksiä.
Toiseksi, samasta syystä kuin "+" ja "×" merkitään usein muita kuin
aritmeettisia operaatioita, ryhmien identiteettielementtejä symbolisoidaan
usein "0" ja "1", vaikka näiden ryhmien elementit eivät olisikaan numeroita.
Ellei kyseessä ole numeroita sisältävän ryhmän identtinen alkio, on helpompi
käyttää neutraalimpaa symbolia, kuten "e", identtisen alkion merkitsemiseen.
Monet erilaiset ja erittäin tärkeät matematiikan arvojoukot, jotka on varustettu tietyillä binäärioperaatioilla, ovat ryhmiä. Kryptografiset sovellukset toimivat kuitenkin vain kokonaislukujen tai ainakin kokonaisluvuilla kuvattavien elementtien joukoilla eli lukuteorian alalla. Näin ollen kryptografiasovelluksissa ei käytetä joukkoja, joissa on muita reaalilukuja kuin kokonaislukuja.
Annetaan lopuksi esimerkki alkioista, joita voidaan "kuvata kokonaisluvuilla", vaikka ne eivät ole kokonaislukuja. Hyvä esimerkki ovat elliptisten käyrien pisteet. Vaikka elliptisen käyrän mikä tahansa piste ei selvästikään ole kokonaisluku, tällainen piste kuvataan kahdella kokonaisluvulla.
Elliptiset käyrät ovat esimerkiksi ratkaisevan tärkeitä Bitcoinille. Mikä tahansa tavallinen Bitcoinin yksityisen ja julkisen avaimen pari valitaan seuraavan elliptisen käyrän määrittelemien pisteiden joukosta:
x^3 + 7 = y^2 \mod 2^{256} – 2^{32} – 29 – 28 – 27 – 26 - 24 - 1(suurin alkuluku, joka on pienempi kuin 2^{256}). x-koordinaatti on
yksityinen avain ja y-koordinaatti on julkinen
avaimesi.
Bitcoinissa tapahtuviin transaktioihin liittyy yleensä ulostulojen lukitseminen yhteen tai useampaan julkiseen avaimeen jollakin tavalla. Näiden transaktioiden arvo voidaan sitten avata tekemällä digitaalisia allekirjoituksia vastaavilla yksityisillä avaimilla.
Sykliset ryhmät
Tärkein ero, jonka voimme tehdä, on äärellisen ja äärettömän ryhmän välillä. Edellisellä on äärellinen määrä alkioita, kun taas jälkimmäisellä on ääretön määrä alkioita. Minkä tahansa äärellisen ryhmän alkioiden lukumäärä tunnetaan nimellä ryhmän järjestys. Kaikki käytännön kryptografia, jossa käytetään ryhmiä, perustuu äärellisiin (lukuteoreettisiin) ryhmiin.
Julkisen avaimen salakirjoituksessa erityisen tärkeitä ovat tietyt äärelliset abelilaiset ryhmät, joita kutsutaan syklisiksi ryhmiksi. Jotta voimme ymmärtää syklisiä ryhmiä, meidän on ensin ymmärrettävä ryhmän alkuaineiden eksponentiaalisuuden käsite.
Oletetaan, että on olemassa ryhmä G, jolla on ryhmäoperaatio \circ, ja että a on G:n alkio. Lauseke a^n on tällöin tulkittava siten, että alkio a yhdistetään itseensä yhteensä n - 1 kertaa. Esimerkiksi a^2 tarkoittaa a \circ a, a^3 tarkoittaa a \circ a \circ a ja
niin edelleen. (Huomaa, että tässä eksponentointi ei välttämättä ole eksponentointia
tavallisessa aritmeettisessa mielessä.)
Otetaanpa esimerkki. Oletetaan, että G = \langle \mathbb{Z} \mod 7, + \rangle, ja että arvomme a on 4.
Tällöin a^2 = [4 + 4 \mod 7] = [8 \mod 7] = 1 \mod 7. Vaihtoehtoisesti a^4 edustaisi [4 + 4 + 4 + 4 \mod 7] = [16 \mod 7] = 2 \mod 7.
Joillakin abelilaisilla ryhmillä on yksi tai useampi alkio, joka voi saada kaikki muut ryhmän alkiot jatkuvan potensoinnin avulla. Näitä elementtejä kutsutaan generoijiksi tai primitiivielementeiksi.
Tärkeä tällaisten ryhmien luokka on \langle \mathbb{Z}^* \mod N, \cdot \rangle, jossa N on alkuluku.
Merkintä \mathbb{Z}^* tarkoittaa tässä, että ryhmä sisältää kaikki nollasta poikkeavat
positiiviset kokonaisluvut, jotka ovat pienempiä kuin N. Tällaisella ryhmällä on
siis aina N - 1 alkioita.
Tarkastellaan esimerkiksi G = \langle \mathbb{Z}^* \mod 11, \cdot \rangle. Tällä ryhmällä on seuraavat alkiot: \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. Tämän ryhmän järjestys on 10 (joka on todellakin yhtä suuri kuin 11 - 1).
Tutkitaan tämän ryhmän alkion 2 potensointia. Alla on esitetty
laskutoimitukset 2^{12} asti. Huomaa, että yhtälön vasemmalla puolella eksponentti viittaa ryhmän alkuaineiden
eksponentointiin. Meidän esimerkissämme tämä tosiaan tarkoittaa yhtälön oikealla
puolella aritmeettista eksponentointia (mutta se olisi voinut sisältää myös esimerkiksi
yhteenlaskun). Selvyyden vuoksi olen kirjoittanut toistetun operaation, enkä
eksponenttimuotoa oikealla puolella.
- $2^1 = 2 \mod 11$$
2^2 = 2 \cdot 2 \mod 11 = 4 \mod 112^3 = 2 \cdot 2 \cdot 2 \mod 11 = 8 \mod 112^4 = 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 16 \mod 11 = 5 \mod 112^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 32 \mod 11 = 10 \mod 112^6 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 64 \mod 11 = 9 \mod 112^7 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 128 \mod 11 = 7 \mod 112^8 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 256 \mod 11 = 3 \mod 112^9 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 512 \mod 11 = 6 \mod 112^{10} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 1024 \mod 11 = 1 \mod 112^{11} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 2048 \mod 11 = 2 \mod 112^{12} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 4096 \mod 11 = 4 \mod 11
Jos katsot tarkkaan, voit nähdä, että eksponentiaalin vahvistaminen
elementille 2 kiertää kaikki \langle \mathbb{Z}^* \mod 11, \cdot \rangle:n elementit seuraavassa järjestyksessä: 2, 4, 8, 5, 10, 9, 7, 3, 6, 1. 2^{10}:n jälkeen
alkion 2 jatkettu eksponentointi kiertää kaikki alkion 2 elementit läpi taas
samassa järjestyksessä. Näin ollen alkio 2 on generaattori kohdassa \langle \mathbb{Z}^* \mod 11, \cdot \rangle.
Vaikka \langle \mathbb{Z}^* \mod 11, \cdot \rangle:llä on useita generaattoreita, kaikki tämän ryhmän alkiot eivät ole
generaattoreita. Tarkastellaan esimerkiksi elementtiä 3. Käymällä läpi
ensimmäiset 10 eksponentiaalia, näyttämättä hankalia laskutoimituksia,
saadaan seuraavat tulokset:
- $3^1 = 3 \mod 11$$
- $3^2 = 9 \mod 11$$
- $3^3 = 5 \mod 11$$
- $3^4 = 4 \mod 11$$
- $3^5 = 1 \mod 11$$
- $3^6 = 3 \mod 11$$
- $3^7 = 9 \mod 11$$
- $3^8 = 5 \mod 11$$
- $3^9 = 4 \mod 11$$
- $3^{10} = 1 \mod 11$$
Sen sijaan, että käydään läpi kaikki arvot kohdassa \langle \mathbb{Z}^* \mod 11, \cdot \rangle, elementin 3 potensointi johtaa vain osajoukkoon näistä arvoista:
viidennen potensoinnin jälkeen nämä arvot alkavat toistua.
Voimme nyt määritellä syklisen ryhmän ryhmäksi, jolla on vähintään yksi generaattori. Toisin sanoen on olemassa vähintään yksi ryhmän alkio, josta voidaan tuottaa kaikki muut ryhmän alkiot potensoimalla.
Olet ehkä huomannut yllä olevassa esimerkissä, että sekä 2^{10} että 3^{10} ovat
yhtä suuret kuin 1 \mod 11.
Itse asiassa, vaikka emme tee laskutoimituksia, minkä tahansa ryhmän \langle \mathbb{Z}^* \mod 11, \cdot \rangle alkion potensointi 10:llä antaa tulokseksi 1 \mod 11. Miksi näin on?
Tämä on tärkeä kysymys, mutta siihen vastaaminen vaatii työtä.
Aluksi oletetaan kaksi positiivista kokonaislukua a ja N. Eräs tärkeä lukuteorian
lause sanoo, että a:lla on
multiplikatiivinen käänteisluku modulo N (eli kokonaisluku b niin,
että a \cdot b = 1 \mod N),
jos ja vain jos a:n ja N:n suurin yhteinen jakaja on
yhtä suuri kuin yksi. Toisin sanoen, jos a ja N ovat yhteiskertoimia.
Näin ollen missä tahansa kokonaislukujen ryhmässä, joka on varustettu
kertolaskulla modulo N, vain
pienemmät koprimit N:n kanssa
sisältyvät joukkoon. Voimme merkitä tätä joukkoa \mathbb{Z}^c \mod N.
Oletetaan esimerkiksi, että N on 10. Ainoastaan kokonaisluvut 1, 3, 7 ja 9 ovat koprimit 10:n kanssa.
Joukkoon \mathbb{Z}^c \mod 10 kuuluu siis vain \{1, 3, 7, 9\}. Et
voi luoda ryhmää, jossa on kokonaislukukerroin modulo 10, käyttämällä muita
kokonaislukuja välillä 1-10. Tämän ryhmän käänteisluvut ovat parit 1 ja 9
sekä 3 ja 7.
Jos N itsessään on alkuluku,
kaikki kokonaisluvut 1:stä N - 1:iin ovat N:n kanssa samankaltaisia
alkulukuja. Tällaisen ryhmän järjestys on siis N - 1. Aiempaa merkintätapaa
käyttäen \mathbb{Z}^c \mod N on yhtä kuin \mathbb{Z}^* \mod N, kun N on alkuluku.
Aiempaan esimerkkiin valitsemamme ryhmä \langle \mathbb{Z}^* \mod 11, \cdot \rangle on erityinen esimerkki tästä ryhmäluokasta.
Seuraavaksi funktio \phi(N) laskee koprimien määrän tiettyyn lukuun N asti, ja se tunnetaan nimellä Eulerin Phi-funktio. [1] Eulerin lauseen mukaan aina kun kaksi kokonaislukua a ja N ovat kopriimejä, pätee seuraava:
a^{\phi(N)} \mod N = 1 \mod N
Tällä on tärkeä vaikutus ryhmäluokkaan \langle \mathbb{Z}^* \mod N, \cdot \rangle, jossa N on alkuluku.
Näissä ryhmissä ryhmäelementtien eksponentointi vastaa aritmeettista
eksponentointia. Toisin sanoen a^{\phi(N)} \mod N edustaa aritmeettista operaatiota a^{\phi(N)} \mod N.
Koska mikä tahansa alkio a näissä multiplikatiivisissa ryhmissä on koprimäinen N:n kanssa, se tarkoittaa,
että a^{\phi(N)} \mod N = a^{N - 1} \mod N = 1 \mod N.
Eulerin lause on todella tärkeä tulos. Aluksi se merkitsee, että kaikki
elementit kohdassa \langle \mathbb{Z}^* \mod N, \cdot \rangle voivat kiertää vain sellaisen määrän arvoja eksponentiaalisesti, joka
jakautuu N - 1:lla.
Tapauksessa \langle \mathbb{Z}^* \mod 11, \cdot \rangle tämä tarkoittaa, että jokainen alkio voi kiertää vain 2, 5 tai 10 alkion
läpi. Ryhmäarvoja, joiden läpi jokin alkio kiertää eksponentioinnin jälkeen,
kutsutaan alkion järjestykseksi. Elementti, jonka järjestys
vastaa ryhmän järjestystä, on generaattori.
Lisäksi Eulerin teoreema merkitsee, että voimme aina tietää tuloksen a^{N - 1} \mod N mille tahansa ryhmälle \langle \mathbb{Z}^* \mod N, \cdot \rangle, jossa N on alkuluku. Näin on
riippumatta siitä, kuinka monimutkaisia varsinaiset laskutoimitukset ovat.
Oletetaan esimerkiksi, että ryhmämme on \mathbb{Z}^* \mod 160,481,182 (jossa 160,481,182 on todellakin alkuluku). Tiedämme, että kaikkien
kokonaislukujen 1-160,481,181 on oltava tämän ryhmän alkioita ja että \phi(n) = 160,481,181. Vaikka
emme voi tehdä kaikkia laskutoimituksia, tiedämme, että sellaisten
lausekkeiden kuin 514^{160,481,181}, 2,005^{160,481,181} ja 256,212^{160,481,181} kaikkien on arvioitava arvoksi 1 \mod 160,481,182.
Huomautukset:
[1] Toiminto toimii seuraavasti. Mikä tahansa kokonaisluku N voidaan jakaa alkulukujen tuloksi. Oletetaan, että tietty N on faktoroitu seuraavasti: p_1^{e1} \cdot p_2^{e2} \cdot \ldots \cdot
p_m^{em}, jossa kaikki p:t ovat
alkulukuja ja kaikki e:t ovat
kokonaislukuja, jotka ovat suurempia tai yhtä suuria kuin 1. Tällöin:
\phi(N) = \sum_{i=1}^m \left[p_i^{e_i} - p_i^{e_i - 1}\right]Eulerin Phi-funktion kaava N:n alkulukujen kertolaskuille.
Kentät
Ryhmä on abstraktin algebran algebrallinen perusrakenne, mutta niitä on paljon muitakin. Ainoa muu algebrallinen rakenne, joka sinun on tunnettava, on kentän rakenne, erityisesti finiittisen kentän rakenne. Tämäntyyppistä algebrallista rakennetta käytetään usein kryptografiassa, kuten Advanced Encryption Standardissa. Jälkimmäinen on tärkein symmetrinen salausjärjestelmä, johon törmäät käytännössä.
Kenttä on johdettu ryhmän käsitteestä. Tarkemmin sanottuna kenttä on alkuaineiden S joukko, joka on varustettu kahdella
binäärioperaattorilla \circ ja \diamond ja joka täyttää seuraavat
ehdot:
Joukko S, joka on varustettu
\circ:llä, on abelilainen ryhmä.Joukko S, joka on varustettu
\diamond, on abelilainen ryhmä "nollasta poikkeavien" alkioiden osalta.Joukko S, joka on varustettu näillä kahdella operaattorilla, täyttää niin sanotun distributiivisen ehdon: Oletetaan, että
a,bjacovat S:n alkioita. Tällöin S, joka on varustettu kahdella operaattorilla, täyttää distributiivisen ominaisuuden, kuna \circ (b \diamond c) = (a \circ b) \diamond (a \circ c).
Huomaa, että ryhmien tapaan kentän määritelmä on hyvin abstrakti. Siinä ei
esitetä väitteitä S:n alkioiden tyypeistä tai operaatioista \circ ja \diamond. Siinä todetaan
vain, että kenttä on mikä tahansa alkioiden joukko, jolla on kaksi
operaatiota ja jolle kolme edellä mainittua ehtoa täyttyvät. (Toisen Abelin
ryhmän "nolla-alkio" voidaan tulkita abstraktisti)
Mikä voisi olla esimerkki kentästä? Hyvä esimerkki on joukko \mathbb{Z} \mod 7 eli \{0, 1, \ldots, 7\}, joka on määritelty vakiolisäyksen (edellä mainitun \circ:n sijasta) ja
vakiokertolaskun (edellä mainitun \diamond:n sijasta) avulla.
Ensinnäkin, \mathbb{Z} \mod 7 täyttää ehdon, jonka mukaan se on abelilainen ryhmä yhteenlaskussa, ja se täyttää
ehdon, jonka mukaan se on abelilainen ryhmä kertolaskussa, jos tarkastellaan
vain nollasta poikkeavia alkioita. Toiseksi joukon yhdistelmä kahdella operaattorilla
täyttää distributiivisen ehdon.
Näitä väitteitä kannattaa tutkia didaktisesti käyttämällä joitakin erityisiä
arvoja. Otetaan kokeelliset arvot 5, 2 ja 3, jotka on valittu satunnaisesti
joukosta \mathbb{Z} \mod 7, tarkastelemme kenttää \langle \mathbb{Z} \mod 7, +, \cdot \rangle. Käytämme näitä kolmea arvoa järjestyksessä tarpeen mukaan tiettyjen
ehtojen tutkimiseksi.
Tutkitaan ensin, onko \mathbb{Z} \mod 7, joka on varustettu lisäyksellä, on abelilainen ryhmä.
Sulkemisolosuhteet: Otetaan arvoiksi 5 ja 2. Tällöin
[5 + 2] \mod 7 = 7 \mod 7 = 0. Tämä on todellakin\mathbb{Z}:n alkio \mod 7, joten tulos on sopusoinnussa sulkemisehdon kanssa.Assosiatiivisuusehto: Otetaan arvoiksi 5, 2 ja 3. Tällöin
[(5 + 2) + 3] \mod 7 = [5 + (2 + 3)] \mod 7 = 10 \mod 7 = 3. Tämä on assosiatiivisuusehdon mukaista.Identiteettiehto: Otetaan arvoksi 5. Tällöin
[5 + 0] \mod 7 = [0 + 5] \mod 7 = 5. 0 näyttää siis olevan yhteenlaskun identtinen alkio.Vastakkainen tila: Tarkastellaan 5:n käänteisehtoa. On oltava niin, että
[5 + d] \mod 7 = 0, jollekind:n arvolle. Tässä tapauksessa\mathbb{Z}:n ainoa arvo on\mathbb{Z} \mod 7$, joka täyttää tämän ehdon, on 2.Kommutatiivisuusehto: Otetaan arvoiksi 5 ja 3. Tällöin
[5 + 3] \mod 7 = [3 + 5] \mod 7 = 1. Tämä on kommutatiivisuusehdon mukaista.
Joukko \mathbb{Z} \mod 7, joka on varustettu yhteenlaskulla, näyttää selvästi olevan abelilainen
ryhmä. Tutkitaan nyt, onko \mathbb{Z} \mod 7,
joka on varustettu kertolaskulla, on abelilainen ryhmä kaikkien nollasta
poikkeavien alkioiden osalta.
Sulkemisolosuhteet: Otetaan arvoiksi 5 ja 2. Tällöin
[5 \cdot 2] \mod 7 = 10 \mod 7 = 3. Tämä on myös\mathbb{Z}:n alkio \mod 7, joten tulos on sopusoinnussa sulkemisehdon kanssa.Assosiatiivisuusehto: Otetaan arvoiksi 5, 2 ja 3. Tällöin
[(5 \cdot 2) \cdot 3] \mod 7 = [5 \cdot (2 \cdot 3)] \mod 7 = 30 \mod 7 = 2. Tämä on assosiatiivisuusehdon mukaista.Identiteettiehto: Otetaan arvoksi 5. Tällöin
[5 \cdot 1] \mod 7 = [1 \cdot 5] \mod 7 = 5. 1 näyttää siis olevan kertolaskun identtinen alkio.Vastakkainen tila: Tarkastellaan 5:n käänteisehtoa. On oltava niin, että
[5 \cdot d] \mod 7 = 1, jollekind:n arvolle. Ainutkertainen arvo\mathbb{Z} \mod 7, joka täyttää tämän ehdon, on 3. Tämä on yhdenmukainen käänteisehdon kanssa.Kommutatiivisuusehto: Otetaan arvoiksi 5 ja 3. Tällöin
[5 \cdot 3] \mod 7 = [3 \cdot 5] \mod 7 = 15 \mod 7 = 1. Tämä on kommutatiivisuusehdon mukaista.
Joukko \mathbb{Z} \mod 7 näyttää selvästi täyttävän Abelin ryhmän säännöt, kun siihen liitetään joko
yhteenlasku tai kertolasku nollasta poikkeavien alkioiden kanssa.
Lopulta tämä molempien operaattoreiden kanssa yhdistetty joukko näyttää
täyttävän distributiivisen ehdon. Otetaan arvoiksi 5, 2 ja 3. Näemme, että [5 \cdot (2 + 3)] \mod 7 = [5 \cdot 2 + 5 \cdot 3] \mod 7 = 25 \mod 7 = 4.
Olemme nyt nähneet, että \mathbb{Z} \mod 7, joka on varustettu yhteen- ja kertolaskulla, täyttää äärellisen kentän
aksioomat, kun sitä testataan tietyillä arvoilla. Voimme tietysti osoittaa
tämän myös yleisesti, mutta emme tee sitä tässä.
Keskeinen ero on kahdenlaisten kenttien välillä: äärelliset ja äärettömät kentät.
Ääretön kenttä on kenttä, jonka joukko S on äärettömän suuri. Esimerkki äärettömästä kentästä on reaalilukujen joukko \mathbb{R}, joka on
varustettu yhteen- ja kertolaskulla. Päätteinen kenttä,
joka tunnetaan myös nimellä Galois'n kenttä, on kenttä,
jossa joukko S on äärellinen. Yllä oleva esimerkkimme \langle \mathbb{Z} \mod 7, +, \cdot \rangle on äärellinen kenttä.
Kryptografiassa olemme ensisijaisesti kiinnostuneita äärellisistä kentistä.
Yleisesti voidaan osoittaa, että äärellinen kenttä on olemassa jollekin
elementtijoukolle S, jos ja vain jos sillä on p^m elementtejä, missä p on
alkuluku ja m positiivinen
kokonaisluku, joka on suurempi tai yhtä suuri kuin yksi. Toisin sanoen, jos
jonkin joukon S järjestysluku on alkuluku (p^m, kun m = 1) tai jokin
alkupotentiaali (p^m, kun m > 1), voidaan löytää kaksi
operaattoria \circ ja \diamond siten, että kentän ehdot
täyttyvät.
Jos jollakin äärellisellä kentällä on alkuaineiden alkuluku, sitä kutsutaan primakentäksi. Jos äärellisen kentän alkioiden lukumäärä on alkupotentiaali, kenttää kutsutaan laajennuskentäksi. Kryptografiassa ollaan kiinnostuneita sekä primääri- että laajennuskentistä. [2]
Kryptografiassa kiinnostavia prime-kenttiä ovat lähinnä ne, joissa kaikkien
kokonaislukujen joukkoa moduloidaan jollakin alkuluvulla, ja operaattoreina
käytetään tavallisia yhteen- ja kertolaskuja. Tällaisia äärellisiä kenttiä
ovat esimerkiksi \mathbb{Z} \mod 2, \mathbb{Z} \mod 3, \mathbb{Z} \mod 5, \mathbb{Z} \mod 7, \mathbb{Z} \mod 11, \mathbb{Z} \mod 13 ja niin edelleen. Mille tahansa alkukentälle \mathbb{Z} \mod p,
kentän kokonaislukujen joukko on seuraava: \{0, 1, \ldots, p - 2, p - 1\}.
Kryptografiassa olemme kiinnostuneita myös laajennuskentistä, erityisesti
kentistä, joissa on 2^m alkioita, kun m > 1.
Tällaisia äärellisiä kenttiä käytetään esimerkiksi Rijndael-salauksessa,
joka on Advanced Encryption Standardin perusta. Vaikka prime-kentät ovatkin
suhteellisen intuitiivisia, nämä base 2 -laajennuskentät eivät luultavasti
sovi kenellekään, joka ei ole perehtynyt abstraktiin algebraan.
Aluksi on todellakin totta, että mihin tahansa kokonaislukujen joukkoon,
jossa on 2^m alkioita,
voidaan liittää kaksi operaattoria, jotka tekevät niiden yhdistelmästä
kentän (kunhan m on positiivinen
kokonaisluku). Se, että kenttä on olemassa, ei kuitenkaan välttämättä tarkoita,
että se olisi helppo löytää tai erityisen käytännöllinen tietyissä sovelluksissa.
Kuten kävi ilmi, kryptografiassa erityisen käyttökelpoisia 2^m:n laajennuskenttiä ovat ne, jotka on määritelty tiettyjen
polynomilausekkeiden joukoille, eikä jollekin kokonaislukujen joukolle.
Oletetaan esimerkiksi, että haluttaisiin laajennuskenttä, jonka joukossa on 2^3 (eli 8) alkiota. Vaikka tuon kokoisille kentille voi olla monia erilaisia
joukkoja, yksi tällainen joukko sisältää kaikki yksikäsitteiset polynomit
muodossa a_2x^2 + a_1x + a_0,
jossa jokainen kerroin a_i on
joko 0 tai 1. Tämä joukko S sisältää siis seuraavat elementit:
0: Tapaus, jossaa_2 = 0,a_1 = 0jaa_0 = 0.1: Tapaus, jossaa_2 = 0,a_1 = 0jaa_0 = 1.x: Tapaus, jossaa_2 = 0,a_1 = 1jaa_0 = 0.x + 1: Tapaus, jossaa_2 = 0,a_1 = 1jaa_0 = 1.x^2: Tapaus, jossaa_2 = 1,a_1 = 0jaa_0 = 0.x^2 + 1: Tapaus, jossaa_2 = 1,a_1 = 0jaa_0 = 1.x^2 + x: Tapaus, jossaa_2 = 1,a_1 = 1jaa_0 = 0.x^2 + x + 1: Tapaus, jossaa_2 = 1,a_1 = 1jaa_0 = 1.
Joten S olisi joukko \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x, x^2 + x + 1\}. Mitkä kaksi operaatiota voidaan määritellä tälle alkioiden joukolle,
jotta niiden yhdistelmä olisi kenttä?
Joukon S (\circ) ensimmäinen operaatio voidaan määritellä tavallisena polynomilisäyksenä
modulo 2. Sinun tarvitsee vain lisätä polynomit tavalliseen tapaan ja
soveltaa sitten modulo 2:ta tuloksena saadun polynomin kaikkiin kertoimiin.
Tässä on muutamia esimerkkejä:
[(x^2) + (x^2 + x + 1)] \mod 2 = [2x^2 + x + 1] \mod 2 = x + 1[(x^2 + x) + (x)] \mod 2 = [x^2 + 2x] \mod 2 = x^2[(x + 1) + (x^2 + x + 1)] \mod 2 = [x^2 + 2x + 2] \mod 2 = x^2 + 1
Toinen operaatio joukolle S (\diamond), jota tarvitaan kentän luomiseen, on monimutkaisempi. Se on eräänlainen
kertolasku, mutta ei tavallinen aritmeettinen kertolasku. Sen sijaan
jokainen alkio on nähtävä vektorina ja operaatio on ymmärrettävä näiden
kahden vektorin kertolaskuna redusoimattoman polynomin kanssa.
Tutustutaan ensin ajatukseen irredusoituvasta polynomista. Irreduusoituva polynomi on polynomi, jota ei voida jakaa (aivan kuten alkulukua ei voida jakaa muihin osiin kuin 1 ja alkulukuun itseensä). Tarkoituksessamme olemme kiinnostuneita polynomeista, jotka ovat redusoitumattomia kaikkien kokonaislukujen joukon suhteen. (Huomaa, että saatat pystyä faktoroimaan tiettyjä polynomeja esimerkiksi reaalilukujen tai kompleksilukujen avulla, vaikka et pystyisi faktoroimaan niitä kokonaislukujen avulla)
Tarkastellaan esimerkiksi polynomia x^2 - 3x + 2. Tämä voidaan kirjoittaa uudelleen muotoon (x - 1)(x - 2). Näin ollen se
ei ole redusoitumaton. Tarkastellaan nyt polynomia x^2 + 1. Kun käytetään vain
kokonaislukuja, tätä lauseketta ei voi enää faktoroida. Näin ollen tämä on
kokonaislukujen suhteen redusoitumaton polynomi.
Seuraavaksi käsitellään vektorikertolaskua. Emme tutki tätä aihetta syvällisesti, vaan sinun on vain ymmärrettävä perussääntö: Mikä tahansa vektorijako voi tapahtua, kunhan osingon aste on suurempi tai yhtä suuri kuin jakajan aste. Jos osingolla on pienempi aste kuin jakajalla, osingon jakaminen jakajalla ei ole enää mahdollista.
Tarkastellaan esimerkiksi lauseketta x^6 + x + 1 \mod x^5 + x^2. Tämä pienenee selvästi edelleen, koska jakajan 6 aste on suurempi kuin
jakajan 5 aste. Tarkastellaan nyt lauseketta x^5 + x + 1 \mod x^5 + x^2.
Tämäkin pienenee edelleen, koska osingon 5 ja jakajan 5 asteet ovat yhtä
suuret.
Tarkastellaan nyt kuitenkin lauseketta x^4 + x + 1 \mod x^5 + x^2. Tämä ei vähene enempää, koska osingon 4 aste on pienempi kuin jakajan 5
aste.
Näiden tietojen perusteella olemme nyt valmiita löytämään toisen operaation
joukolle \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x, x^2 + x + 1\}.
Olen jo sanonut, että toinen operaatio olisi ymmärrettävä vektorikertolaskuna modulo jonkin redusoimattoman polynomin kanssa. Tämän redusoimattoman polynomin pitäisi varmistaa, että toinen operaatio määrittelee abeliaanisen ryhmän yli S ja on yhdenmukainen distributiivisen ehdon kanssa. Mikä tämän palautumattoman polynomin pitäisi siis olla?
Koska kaikki joukon vektorit ovat astetta 2 tai pienempiä, redusoitumattoman polynomin pitäisi olla astetta 3. Jos mikä tahansa joukon kahden vektorin kertolasku tuottaa astetta 3 tai suuremman polynomin, tiedämme, että astetta 3 olevan polynomin modulointi tuottaa aina astetta 2 tai pienemmän polynomin. Tämä johtuu siitä, että mikä tahansa polynomi, jonka aste on vähintään 3, on aina jaollinen polynomilla, jonka aste on 3. Lisäksi jakajana toimivan polynomin on oltava redusoitumaton.
Osoittautuu, että on olemassa useita 3. asteen redusoitumattomia polynomeja,
joita voisimme käyttää jakajana. Kukin näistä polynomeista määrittelee eri
kentän yhdessä joukon S ja yhteenlaskun modulo 2 kanssa.
Tämä tarkoittaa, että sinulla on useita vaihtoehtoja, kun käytät
laajennuskenttiä 2^m kryptografiassa.
Oletetaan, että valitsemme esimerkissä polynomin x^3 + x + 1. Tämä on todellakin redusoitumaton, koska sitä ei voi kertoa
kokonaisluvuilla. Lisäksi se varmistaa, että mikä tahansa kahden alkion
kertolasku tuottaa enintään 2 asteen polynomin.
Käydään läpi esimerkki toisesta operaatiosta käyttäen jakajana polynomia x^3 + x + 1 ja havainnollistetaan, miten se toimii. Oletetaan, että joukossamme S kerrotaan alkioita x^2 + 1 ja x^2 + x. Meidän on tällöin
laskettava lauseke [(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1. Tämä voidaan yksinkertaistaa seuraavasti:
- $[(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1 =$$
[x^2 \cdot x^2 + x^2 \cdot x + 1 \cdot x^2 + 1 \cdot x] \mod x^3 + x + 1 =[x^4 + x^3 + x^2 + x] \mod x^3 + x + 1
Tiedämme, että [x^4 + x^3 + x^2 + x] \mod x^3 + x + 1 voidaan pienentää, koska osingonjakajalla on suurempi aste (4) kuin jakajalla
(3).
Aluksi voit nähdä, että lauseke x^3 + x + 1 muuttuu x^4 + x^3 + x^2 + x:ksi
yhteensä x kertaa. Voit
todentaa tämän kertomalla x^3 + x + 1 luvulla x, joka on x^4 + x^2 + x. Koska
jälkimmäinen termi on samaa astetta kuin osingonjako, eli 4, tiedämme, että
tämä toimii. Voit laskea tällä x:llä jaetun jäännösosan
seuraavasti:
[(x^4 + x^3 + x^2 + x) - (x^4 + x^2 + x)] \mod x^3 + x + 1 =- $[x^3] \mod x^3 + x + 1 =$$
x^3
Kun x^4 + x^3 + x^2 + x on
jaettu x^3 + x + 1:llä
yhteensä x kertaa, jäljelle
jää x^3. Voidaanko tämä jakaa
edelleen x^3 + x + 1:lla?
Intuitiivisesti saattaisi olla houkuttelevaa sanoa, että x^3 ei voi enää jakaa x^3 + x + 1:llä, koska
jälkimmäinen termi näyttää suuremmalta. Muistetaan kuitenkin aiemmin
käymämme keskustelu vektorien jakamisesta. Niin kauan kuin jakajalla on
suurempi tai yhtä suuri aste kuin jakajalla, lauseketta voidaan edelleen
pienentää. Tarkemmin sanottuna lauseke x^3 + x + 1 voi muuttua x^3:ksi tasan
kerran. Jäännös lasketaan seuraavasti:
[(x^3) - (x^3 + x + 1)] \mod x^3 + x + 1 = [x + 1] \mod x^3 + x + 1 = x + 1Saatat ihmetellä, miksi (x^3) - (x^3 + x + 1) on x + 1 eikä -x - 1. Muista, että
kenttämme ensimmäinen operaatio on määritelty modulo 2. Näin ollen kahden
vektorin vähentäminen antaa täsmälleen saman tuloksen kuin kahden vektorin
yhteenlasku.
Kertolasku x^2 + 1 ja x^2 + x: Kun nämä kaksi
termiä kerrotaan, saadaan 4. asteen polynomi x^4 + x^3 + x^2 + x, joka on
vähennettävä modulo x^3 + x + 1. Asteen 4
polynomi on jaollinen x^3 + x + 1:lla täsmälleen x + 1 kertaa. Jäännös, joka jää jäljelle, kun x^4 + x^3 + x^2 + x on jaettu x^3 + x + 1 täsmälleen x + 1 kertaa, on x + 1. Tämä on todellakin
alkio joukossamme \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.
Miksi polynomijoukkojen laajennuskentät, joiden perusta on 2, kuten yllä olevassa esimerkissä, olisivat hyödyllisiä kryptografiassa? Syynä on se, että tällaisten joukkojen polynomien kertoimia, joko 0 tai 1, voidaan tarkastella tietyn pituisten binäärijonojen alkioina. Esimerkiksi yllä olevassa esimerkissä oleva joukko S voidaan nähdä sen sijaan joukkona S, joka sisältää kaikki pituudeltaan 3 (000-111) binäärijonot. Operaatioita S:llä voidaan siis käyttää myös näiden binäärijonojen operaatioiden suorittamiseen ja saman pituisen binäärijonon tuottamiseen.
Huomautukset:
[2] Laajennuskentistä tulee hyvin intuitiivisia. Sen sijaan, että niillä olisi kokonaislukujen elementtejä, niillä on polynomien joukkoja. Lisäksi kaikki operaatiot suoritetaan modulo jonkin irreduusoituvan polynomin kanssa.
Abstrakti algebra käytännössä
Huolimatta keskustelun muodollisesta kielestä ja abstraktisuudesta ryhmän käsitteen ei pitäisi olla liian vaikea ymmärtää. Se on vain joukko elementtejä yhdessä binäärioperaation kanssa, jolloin binäärioperaation suorittaminen näille elementeille täyttää neljä yleistä ehtoa. Abeliaanisella ryhmällä on vain ylimääräinen ehto, jota kutsutaan kommutatiivisuudeksi. Syklinen ryhmä on puolestaan abelilainen ryhmä, jolla on generaattori. Kenttä on vain monimutkaisempi konstruktio perusryhmän käsitteestä.
Mutta jos olet käytännönläheinen ihminen, saatat miettiä tässä vaiheessa: Ketä kiinnostaa? Onko sillä tiedolla, että jokin joukko elementtejä, joilla on operaattori, on ryhmä, tai jopa abelilainen tai syklinen ryhmä, mitään merkitystä reaalimaailmassa? Onko sillä, että tiedämme jonkin olevan kenttä?
Menemättä liian pitkälle yksityiskohtiin, vastaus on "kyllä". Ranskalainen matemaatikko Evariste Galois loi ryhmät ensimmäisen kerran 1800-luvulla. Hän käytti niitä tehdäkseen päätelmiä yli viisiasteisten polynomiyhtälöiden ratkaisemisesta.
Sittemmin ryhmän käsite on auttanut valaisemaan monia matematiikan ja muiden alojen ongelmia. Niiden perusteella esimerkiksi fyysikko Murray-Gellman pystyi ennustamaan hiukkasen olemassaolon ennen kuin se havaittiin kokeissa. [3] Toisena esimerkkinä voidaan mainita, että kemistit käyttävät ryhmäteoriaa molekyylien muotojen luokitteluun. Matemaatikot ovat jopa käyttäneet ryhmän käsitettä vetääkseen johtopäätöksiä niinkin konkreettisesta asiasta kuin seinäpaperista!
Kun osoitetaan, että joukko elementtejä, joilla on jokin operaattori, on ryhmä, se tarkoittaa, että kuvaamallasi joukolla on tietty symmetria. Ei symmetria sanan tavallisessa merkityksessä, vaan abstraktimmassa muodossa. Ja tämä voi tarjota huomattavia oivalluksia tietyistä järjestelmistä ja ongelmista. Abstraktin algebran monimutkaisemmat käsitteet antavat meille vain lisätietoa.
Tärkeintä on, että näet lukuteoreettisten ryhmien ja kenttien merkityksen käytännössä niiden soveltamisen kautta kryptografiassa, erityisesti julkisen avaimen kryptografiassa. Olemme jo nähneet kenttiä käsitellessämme esimerkiksi sen, miten laajennuskenttiä käytetään Rijndaelin salakirjoituksessa. Selvitämme kyseisen esimerkin luvussa 5.
Jos haluat keskustella abstraktista algebrasta lisää, suosittelen Socratican erinomaista abstraktia algebraa käsittelevää videosarjaa. [4] Suosittelen erityisesti seuraavia videoita: "Mitä abstrakti algebra on?", "Ryhmän määritelmä (laajennettu)", "Renkaan määritelmä (laajennettu)" ja "Kentän määritelmä (laajennettu)" Näistä neljästä videosta saat lisäymmärrystä suureen osaan yllä olevasta keskustelusta. (Emme keskustelleet renkaista, mutta kenttä on vain erityyppinen rengas)
Jos haluat lisää keskustelua modernista numeroteoriasta, voit tutustua moniin kryptografiaa käsitteleviin syventäviin keskusteluihin. Ehdotan jatkokeskustelua varten Jonathan Katzin ja Yehuda Lindellin teosta Introduction to Modern Cryptography tai Christof Paar ja Jan Pelzlin teosta Understanding Cryptography. [5]
Huomautukset:
[3] Katso YouTube-video
[4] Socratica, Abstrakti algebra
[5] Katz ja Lindell, Introduction to Modern Cryptography, 2nd edn, 2015 (CRC Press: Boca Raton, FL). Paar ja Pelzl, Understanding Cryptography, 2010 (Springer-Verlag: Berliini).
Symmetrinen salaus
Alice ja Bob
Yksi kryptografian kahdesta päähaarasta on symmetrinen kryptografia. Siihen kuuluvat salausjärjestelmät sekä todennukseen ja eheyteen liittyvät järjestelmät. 1970-luvulle asti kaikki salakirjoitus koostui symmetrisistä salausjärjestelmistä.
Pääkeskustelun aluksi tarkastellaan symmetrisiä salausmenetelmiä ja tehdään ratkaiseva ero virtasalakirjoitusten ja lohkosalakirjoitusten välillä. Sen jälkeen siirrytään viestin todentamiskoodeihin, jotka ovat järjestelmiä viestin eheyden ja aitouden varmistamiseksi. Lopuksi tarkastelemme, miten symmetrisiä salausjärjestelmiä ja viestien todentamiskoodeja voidaan yhdistää turvallisen viestinnän varmistamiseksi.
Tässä luvussa käsitellään ohimennen erilaisia symmetrisiä kryptografisia järjestelmiä käytännöstä. Seuraavassa luvussa esitellään yksityiskohtaisesti salausta virtasalausmenetelmällä RC4 ja lohkosalausmenetelmällä AES.
Ennen kuin aloitamme keskustelun symmetrisestä salakirjoituksesta, haluan tehdä lyhyesti joitakin huomioita tässä ja seuraavissa luvuissa esitetyistä Alice- ja Bob-kuvauksista.
Kryptografian periaatteita havainnollistettaessa käytetään usein esimerkkejä, joissa Alice ja Bob ovat mukana. Niin teen myös minä.
Varsinkin jos olet uusi kryptografian alalla, on tärkeää ymmärtää, että nämä esimerkit Alicesta ja Bobista on tarkoitettu vain havainnollistamaan kryptografisia periaatteita ja rakenteita yksinkertaistetussa ympäristössä. Periaatteita ja konstruktioita voidaan kuitenkin soveltaa paljon laajempaan joukkoon tosielämän tilanteita.
Seuraavassa on viisi keskeistä seikkaa, jotka on hyvä pitää mielessä kryptografiassa esiintyvistä Alice ja Bob -esimerkeistä:
Ne voidaan helposti muuntaa esimerkkeihin, jotka koskevat muunlaisia toimijoita, kuten yrityksiä tai julkishallinnon organisaatioita.
Niitä voidaan helposti laajentaa siten, että niissä on kolme tai useampia näyttelijöitä.
Esimerkeissä Bob ja Alice ovat tyypillisesti aktiivisia osallistujia kunkin viestin luomisessa ja salausmenetelmien soveltamisessa kyseiseen viestiin. Todellisuudessa sähköinen viestintä on kuitenkin pitkälti automatisoitua. Kun esimerkiksi vierailet verkkosivustolla, jossa käytetään kuljetuskerroksen suojausta, tietokoneesi ja verkkopalvelin hoitavat tyypillisesti kaiken salauksen.
Sähköisessä viestinnässä viestintäkanavan kautta lähetettävät "viestit" ovat yleensä TCP/IP-paketteja. Ne voivat kuulua sähköpostiin, Facebook-viestiin, puhelinkeskusteluun, tiedostonsiirtoon, verkkosivustoon, ohjelmiston lataamiseen ja niin edelleen. Ne eivät ole viestejä perinteisessä mielessä. Salakirjoittajat kuitenkin usein yksinkertaistavat tätä todellisuutta toteamalla, että viesti on esimerkiksi sähköposti.
Esimerkit keskittyvät yleensä sähköiseen viestintään, mutta niitä voidaan laajentaa myös perinteisiin viestintämuotoihin, kuten kirjeisiin.
Symmetriset salausmenetelmät
Voimme vapaasti määritellä symmetrisen salausjärjestelmän kryptografiseksi järjestelmäksi, jossa on kolme algoritmia:
avainten luomisalgoritmi, joka luo yksityisen avaimen.
Salausalgoritmi, joka ottaa syötteenä yksityisen avaimen ja selkotekstin ja antaa tuloksena salatun tekstin.
Purkualgoritmi, joka ottaa syötteenä yksityisen avaimen ja salatun tekstin ja antaa tuloksena alkuperäisen selkotekstin.
Tyypillisesti salausjärjestelmä - olipa se sitten symmetrinen tai epäsymmetrinen - tarjoaa pikemminkin mallin salausta varten, joka perustuu ydinalgoritmiin, kuin tarkan määrittelyn.
Tarkastellaan esimerkiksi symmetristä Salsa20-salausjärjestelmää. Sitä voidaan käyttää sekä 128- että 256-bittisten avainten pituuksilla. Avaimen pituuden valinta vaikuttaa joihinkin algoritmin pieniin yksityiskohtiin (tarkalleen ottaen algoritmin kierrosten määrään).
Ei kuitenkaan voida sanoa, että Salsa20:n käyttäminen 128-bittisellä avaimella on eri salausjärjestelmä kuin Salsa20:n käyttäminen 256-bittisellä avaimella. Ydinalgoritmi pysyy samana. Vasta kun ydinalgoritmi muuttuu, voidaan puhua kahdesta eri salausjärjestelmästä.
Symmetriset salausjärjestelmät ovat tyypillisesti hyödyllisiä kahdenlaisissa tapauksissa: (1) tapauksissa, joissa kaksi tai useampi agentti kommunikoi etäältä ja haluaa pitää viestinsä sisällön salassa; ja (2) tapauksissa, joissa yksi agentti haluaa pitää viestin sisällön salassa ajan kuluessa.
Tilanne (1) on kuvattu alla olevassa Kuvassa 1. Bob haluaa lähettää
viestin M Alicelle etäisyyden
yli, mutta ei halua, että muut voivat lukea viestin.
Bob salaa ensin viestin M yksityisellä avaimella K. Sen
jälkeen hän lähettää salatun tekstin C Alicelle. Kun Alice on saanut salatekstin, hän voi purkaa sen avaimella K ja lukea selvätekstin. Hyvällä salausjärjestelmällä salatun tekstin C sieppaajan ei pitäisi pystyä saamaan selville mitään todella merkittävää
viestistä M.
Tilanne (2) on kuvattu alla olevassa Kuvassa 2. Bob haluaa estää muita katsomasta tiettyjä tietoja. Tyypillinen tilanne voi olla, että Bob on työntekijä, joka tallentaa tietokoneelleen arkaluonteisia tietoja, joita ulkopuoliset tai hänen kollegansa eivät saa lukea.
Bob salaa viestin M ajanhetkellä T_0 avaimella K tuottaakseen salaustekstin C.
Ajankohtana T_1 hän tarvitsee
viestin uudelleen ja purkaa salatekstin C avaimella K. Mahdollinen
hyökkääjä, joka on tällä välin törmännyt salaustekstiin C, ei olisi voinut päätellä
siitä mitään merkittävää M:stä.
Kuva 1: Salassapito koko avaruudessa

Kuva 2: Salassapito ajassa

Esimerkki: Siirtymäsalaus
Luvussa 2 tutustuimme siirtosalaukseen, joka on esimerkki hyvin yksinkertaisesta symmetrisestä salausjärjestelmästä. Tarkastellaan sitä tässä uudelleen.
Oletetaan sanakirja D, joka rinnastaa kaikki englannin aakkosten
kirjaimet järjestyksessä lukujoukkoon \{0,1,2,\dots,25\}.
Oletetaan joukko mahdollisia viestejä M. Siirtymäsalaus on
siis salausjärjestelmä, joka määritellään seuraavasti:
- Valitaan satunnaisesti avain
kmahdollisten avainten joukosta K, jossa K =\{0,1,2,\dots,25\} - Salaa viesti
m \inM seuraavasti:- Erottele
myksittäisiin kirjaimiinm_0, m_1, \dots, m_i, \dots, m_l - Muunnetaan jokainen
m_iluvuksi D:n mukaisesti - Jokaisen
m_iosaltac_i = [(m_i + k) \mod 26] - Muunna jokainen
c_ikirjaimeksi D:n mukaisesti - Yhdistetään sitten
c_0, c_1, \dots, c_l, jolloin saadaan salattu tekstic
- Erottele
- Puretaan salattu teksti
cseuraavasti:- Muunnetaan jokainen
c_iluvuksi D:n mukaisesti - Jokaisen
c_iosaltam_i = [(c_i - k) \mod 26] - Muunna jokainen
m_ikirjaimeksi D:n mukaisesti - Yhdistetään sitten
m_0, m_1, \dots, m_l, jolloin saadaan alkuperäinen viestim
- Muunnetaan jokainen
Siirtymäsalakirjoitus on symmetrinen salausjärjestelmä, koska samaa avainta käytetään sekä salauksessa että salauksen purkamisessa. Oletetaan esimerkiksi, että haluat salata viestin "DOG" käyttämällä shift-salakirjoitusta ja valitset avaimeksi satunnaisesti arvon "24". Kun viesti salataan tällä avaimella, tulokseksi saadaan "BME". Ainoa tapa saada alkuperäinen viesti takaisin on käyttää samaa avainta, "24", salauksen purkamiseen.
Tämä Shift-salaus on esimerkki monoalfaattisesta korvaussalakirjoituksesta: salausjärjestelmä, jossa salatekstin aakkoset ovat kiinteät (eli käytetään vain yhtä aakkosta). Jos oletetaan, että purkualgoritmi on deterministinen, jokainen symboli korvaavassa salakirjoitustekstissä voi liittyä korkeintaan yhteen symboliin selkotekstissä.
1700-luvulle asti monet salaussovellukset perustuivat pitkälti monoalfabeettisiin korvaaviin salakirjoituksiin, jotka olivat kuitenkin usein paljon monimutkaisempia kuin Shift-salakirjoitus. Jokaisen alkuperäisen tekstin kirjaimen tilalle voitiin esimerkiksi valita satunnaisesti kirjain aakkosista sillä edellytyksellä, että kukin kirjain esiintyy salatun tekstin aakkosissa vain kerran. Tämä tarkoittaa, että sinulla olisi 26 mahdollista yksityistä avainta, mikä oli valtava määrä tietokoneita edeltävällä aikakaudella.
Huomaa, että törmäät termiin salakirjoittaja usein kryptografiassa. Huomaa, että tällä termillä on erilaisia merkityksiä. Itse asiassa tiedän ainakin viisi erilaista merkitystä termille kryptografiassa.
Joissakin tapauksissa se viittaa salausjärjestelmään, kuten Shift cipher ja monoalfaattinen korvaussalaus. Termi voi kuitenkin viitata myös nimenomaan salausalgoritmiin, yksityiseen avaimeen tai vain salakirjoitustekstiin tällaisessa salausjärjestelmässä.
Lopuksi termi salaus voi viitata myös ydinalgoritmiin, josta voidaan rakentaa salausmenetelmiä. Näitä voivat olla erilaiset salausalgoritmit, mutta myös muun tyyppiset salausjärjestelmät. Tämä termin merkitys tulee merkitykselliseksi lohkosalakirjoitusten yhteydessä (ks. kohta "Lohkosalakirjoitukset" jäljempänä).
Saatat törmätä myös termeihin avain tai murtautua. Nämä termit ovat vain synonyymejä salaukselle ja salauksen purkamiselle.
Brute force -hyökkäykset ja Kerckhoffin periaate
Siirtymäsalaus on hyvin epävarma symmetrinen salausjärjestelmä, ainakin nykymaailmassa. [1] Hyökkääjä voisi vain yrittää purkaa minkä tahansa salaustekstin salauksen kaikilla 26 mahdollisella avaimella nähdäkseen, mikä tulos on järkevä. Tällaista hyökkäystä, jossa hyökkääjä vain käy läpi avaimia nähdäkseen, mikä toimii, kutsutaan brute force -hyökkäykseksi tai exhaustive key search.
Jotta jokin salausjärjestelmä täyttäisi vähimmäisturvallisuuden käsitteen, sillä on oltava niin suuri joukko mahdollisia avaimia eli avainavaruus, että raa'an voiman hyökkäykset ovat mahdottomia toteuttaa. Kaikki nykyaikaiset salausjärjestelmät täyttävät tämän standardin. Tämä tunnetaan nimellä riittävän avainavaruuden periaate. Samanlaista periaatetta sovelletaan yleensä erityyppisiin salausjärjestelmiin.
Jotta saisit käsityksen nykyaikaisten salausjärjestelmien massiivisesta
avainavaruuden koosta, oletetaan, että tiedosto on salattu 128-bittisellä
avaimella käyttäen kehittynyttä salausstandardia. Tämä tarkoittaa, että
hyökkääjällä on joukko 2^{128} avaimia, jotka hänen on käytävä läpi raa'an voiman hyökkäyksessä. Tämän strategian
0,78 prosentin onnistumismahdollisuus edellyttää, että hyökkääjä käy läpi noin
2,65 \ kertaa 10^{36}$ avainta.
Oletetaan optimistisesti, että hyökkääjä voi yrittää 10^{16}avainta sekunnissa (eli 10 kvadriljoonaa avainta sekunnissa). Jotta hän
voisi testata 0,78 % kaikista avainavaruuden avaimista, hänen
hyökkäyksensä pitäisi kestää 2,65 \ kertaa 10^{20} sekuntia. Tämä on noin 8,4 biljoonaa vuotta. Joten edes järjettömän voimakkaan
vastustajan tekemä raa'an voiman hyökkäys ei ole realistinen nykyaikaisessa 128-bittisessä
salausjärjestelmässä. Tässä on kyse riittävän avainavaruuden periaatteesta.
Onko siirtymäsalaus turvallisempi, jos hyökkääjä ei tunne salausalgoritmia? Ehkä, mutta ei paljon.
Nykyaikaisessa salakirjoituksessa oletetaan joka tapauksessa aina, että symmetrisen salausjärjestelmän turvallisuus perustuu ainoastaan yksityisen avaimen pitämiseen salassa. Hyökkääjän oletetaan aina tietävän kaikki muut yksityiskohdat, kuten viestiavaruuden, avainavaruuden, salatun tekstin avaruuden, avaimen valintaalgoritmin, salausalgoritmin ja salauksen purkualgoritmin.
Ajatus siitä, että symmetrisen salausjärjestelmän turvallisuus voi perustua vain yksityisen avaimen salaisuuteen, tunnetaan nimellä Kerckhoffin periaate.
Kuten Kerckhoffs alun perin tarkoitti, periaate koskee vain symmetrisiä salausjärjestelmiä. Periaatteen yleisempi versio koskee kuitenkin myös kaikkia muita nykyaikaisia salausmenetelmiä: Minkään salausjärjestelmän suunnittelun ei tarvitse olla salainen, jotta se olisi turvallinen; salaisuus voi ulottua vain joihinkin tietoihin, tyypillisesti yksityiseen avaimeen.
Kerckhoffsin periaate on keskeinen nykyaikaisessa kryptografiassa neljästä syystä. [2] Ensinnäkin on olemassa vain rajallinen määrä salausjärjestelmiä tietyntyyppisiä sovelluksia varten. Esimerkiksi useimmat nykyaikaiset symmetriset salaussovellukset käyttävät Rijndael-salausta. Siten salassapito järjestelmän suunnittelusta on vain hyvin rajallista. On kuitenkin paljon joustavampaa pitää jokin Rijndael-salauksen yksityinen avain salassa.
Toiseksi on helpompaa korvata jokin merkkijono kuin koko salausjärjestelmä. Oletetaan, että yrityksen kaikilla työntekijöillä on sama salausohjelmisto ja että jokaisella työntekijällä on yksityinen avain luottamukselliseen viestintään. Avaimen vaarantuminen on tässä skenaariossa hankalaa, mutta ainakin yritys voisi säilyttää ohjelmiston tällaisten tietoturvaloukkausten kanssa. Jos yritys luottaisi järjestelmän salassapitoon, salassapidon rikkominen edellyttäisi kaikkien ohjelmistojen vaihtamista.
Kolmanneksi Kerckhoffsin periaate mahdollistaa standardoinnin ja yhteensopivuuden salausjärjestelmien käyttäjien välillä. Tästä on valtavia hyötyjä tehokkuuden kannalta. On esimerkiksi vaikea kuvitella, miten miljoonat ihmiset voisivat muodostaa päivittäin turvallisen yhteyden Googlen verkkopalvelimiin, jos turvallisuus edellyttäisi salausmenetelmien pitämistä salassa.
Neljänneksi Kerckhoffin periaate mahdollistaa salausjärjestelmien julkisen tarkastelun. Tämäntyyppinen tarkastelu on ehdottoman välttämätöntä turvallisten salausjärjestelmien saavuttamiseksi. Esimerkkinä mainittakoon, että symmetrisen salauksen tärkein algoritmi, Rijndael-salaus, oli tulosta kilpailusta, jonka National Institute of Standards and Technology järjesti vuosina 1997-2000.
Kaikki järjestelmät, jotka pyrkivät saavuttamaan turvallisuutta hämäryyden avulla, perustuvat siihen, että niiden suunnittelun ja/tai toteutuksen yksityiskohdat pidetään salassa. Kryptografiassa tämä tarkoittaa erityisesti järjestelmää, joka perustuu salausjärjestelmän suunnittelun yksityiskohtien pitämiseen salassa. Tietoturva hämäryyden avulla on siis suorassa ristiriidassa Kerckhoffin periaatteen kanssa.
Avoimuuden kyky parantaa laatua ja turvallisuutta ulottuu digitaaliseen maailmaan myös laajemmalle kuin vain salakirjoitukseen. Esimerkiksi Debianin kaltaisilla vapaan ja avoimen lähdekoodin Linux-jakeluilla on yleensä useita etuja Windows- ja MacOS-versioihin verrattuna yksityisyyden, vakauden, turvallisuuden ja joustavuuden suhteen. Vaikka tähän voi olla useita syitä, tärkein periaate on luultavasti, kuten Eric Raymond muotoili kuuluisassa esseessään "The Cathedral and the Bazaar", että "kun tarpeeksi monta silmäparia, kaikki viat ovat pinnallisia" [3] Juuri tämä joukkojen viisaus on se periaate, joka antoi Linuxille sen merkittävimmän menestyksen.
Koskaan ei voida yksiselitteisesti todeta, että salausjärjestelmä on "turvallinen" tai "epäturvallinen" Sen sijaan kryptografisten järjestelmien turvallisuudesta on olemassa erilaisia käsitteitä. Jokaisessa kryptografisen turvallisuuden määritelmässä on määriteltävä (1) turvallisuustavoitteet sekä (2) hyökkääjän kyvyt. Analysoimalla kryptografisia järjestelmiä yhtä tai useampaa tiettyä turvallisuuskäsitystä vasten saadaan tietoa niiden sovelluksista ja rajoituksista.
Vaikka emme aio syventyä kaikkiin yksityiskohtiin kryptografisen tietoturvan eri käsitteistä, sinun on hyvä tietää, että kaksi oletusta ovat kaikkialla läsnä kaikissa nykyaikaisissa kryptografisissa tietoturvakäsitteissä, jotka liittyvät symmetrisiin ja epäsymmetrisiin järjestelmiin (ja jossakin muodossa myös muihin kryptografisiin alkutekijöihin):
- Hyökkääjän tieto järjestelmästä on Kerckhoffsin periaatteen mukainen.
- Hyökkääjä ei voi tehdä järjestelmään brute force -hyökkäystä. Kryptografisten turvallisuuskäsitysten uhkamalleissa ei yleensä edes sallita raa'an voiman hyökkäyksiä, koska niissä oletetaan, että ne eivät ole merkityksellisiä.
Huomautukset:
[1] Seutoniuksen mukaan Julius Caesar käytti sotilasviestinnässään siirtosalausta, jonka vakioavain oli 3. A:sta tulisi siis aina D, B:stä aina E, C:stä aina F ja niin edelleen. Tämä erityinen versio siirtosalauksesta tunnetaankin nimellä Caesarin salakirjoitus (vaikka se ei oikeastaan ole salakirjoitus sanan nykyisessä merkityksessä, koska avainarvo on vakio). Caesarin salakirjoitus saattoi olla turvallinen ensimmäisellä vuosisadalla eaa., jos Rooman viholliset eivät tunteneet salakirjoitusta kovinkaan hyvin. Mutta se ei selvästikään olisi kovin turvallinen järjestelmä nykyaikana.
[2] Jonathan Katz ja Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), s. 7f.
[3] Eric Raymond, "The Cathedral and the Bazaar", esitelmä esitettiin Linux-kongressissa Würzburgissa, Saksassa (27. toukokuuta 1997). Siitä on saatavilla useita myöhempiä versioita sekä kirja. Sitaattini ovat kirjan sivulta 30: Eric Raymond, The Cathedral and the Bazaar: Musings on Linux and Open Source by an Accidental Revolutionary, uudistettu painos. (2001), O'Reilly: Sebastopol, CA.
Virtaussalakirjoitukset
Symmetriset salausjärjestelmät jaetaan tavallisesti kahteen tyyppiin: virtasalakirjoitukset ja lohkosalakirjoitukset. Tämä jaottelu on kuitenkin hieman hankala, koska ihmiset käyttävät näitä termejä epäjohdonmukaisesti. Seuraavissa kappaleissa esittelen eron parhaaksi katsomallani tavalla. Kannattaa kuitenkin olla tietoinen siitä, että monet ihmiset käyttävät näitä termejä hieman eri tavalla kuin minä esitän.
Käydään ensin läpi virtaussalakirjoitukset. Virtasalaus** on symmetrinen salausjärjestelmä, jossa salaus koostuu kahdesta vaiheesta.
Ensin tuotetaan yksityisen avaimen avulla selkotekstin pituinen merkkijono. Tätä merkkijonoa kutsutaan keystreamiksi.
Seuraavaksi avainvirta yhdistetään matemaattisesti selkotekstiin salatekstin
tuottamiseksi. Tämä yhdistäminen on tyypillisesti XOR-operaatio. Salaus
voidaan purkaa kääntämällä operaatio päinvastaiseksi. (Huomaa, että A \oplus B = B \oplus A, jos A ja B ovat bittijonoja. XOR-operaation järjestyksellä ei siis ole merkitystä
tuloksen kannalta. Tämä ominaisuus tunnetaan nimellä kommutatiivisuus)
Tyypillinen XOR-virtasalaus on kuvattu Kuvassa 3. Ensin otetaan
yksityinen avain K ja luodaan
sen avulla avainvirta. Tämän jälkeen avainvirta yhdistetään XOR-operaation
avulla selkotekstiin, jolloin saadaan salattu teksti. Kuka tahansa agentti,
joka saa salatun tekstin, voi helposti purkaa sen, jos hänellä on avain K. Hänen tarvitsee vain luoda
avainvirta, joka on yhtä pitkä kuin salausteksti, järjestelmän määrittelemän
menettelyn mukaisesti ja XOR-järjestyksessä yhdistää sen salaustekstiin.
Kuva 3: XOR-virtasalaus
Muistutetaan, että salauskaavio on yleensä pikemminkin malli salaukselle, jossa käytetään samaa ydinalgoritmia, kuin tarkka määrittely. Vastaavasti virtasalaus on tyypillisesti salauksen malli, jossa voidaan käyttää eripituisia avaimia. Vaikka avaimen pituus voi vaikuttaa järjestelmän joihinkin pieniin yksityiskohtiin, se ei vaikuta sen keskeiseen muotoon.
Siirtosalaus on esimerkki hyvin yksinkertaisesta ja turvattomasta virtasalakirjoituksesta. Käyttämällä yhtä kirjainta (yksityinen avain) voidaan tuottaa viestin pituinen kirjainjono (avainvirta). Avainjono yhdistetään sitten selkotekstiin modulo-operaation avulla salakirjoituksen tuottamiseksi. (Tämä modulo-operaatio voidaan yksinkertaistaa XOR-operaatioksi, kun kirjaimet esitetään bitteinä).
Toinen kuuluisa esimerkki virtasalakirjoituksesta on Vigenere-salakirjoitus Blaise de Vigenereneren mukaan, joka kehitti sen täysin 1500-luvun lopulla (vaikka muut olivat tehneet paljon työtä sitä ennen). Se on esimerkki polyfabeettisesta korvaussalakirjoituksesta: salausjärjestelmä, jossa selkotekstin symbolin salatekstin aakkoset muuttuvat sen mukaan, mikä on sen sijainti tekstissä. Toisin kuin monoalfaattisessa korvaussalakirjoituksessa, salatekstin symboleihin voidaan liittää useampi kuin yksi selkotekstin symboli.
Kun salaus yleistyi renessanssin ajan Euroopassa, myös kryptoanalyysi eli salaustekstien murtaminen - erityisesti taajuusanalyysin avulla - yleistyi. Jälkimmäisessä käytetään kielemme tilastollisia säännönmukaisuuksia salaustekstien murtamiseen, ja arabialaiset oppineet löysivät sen jo yhdeksännellä vuosisadalla. Se on tekniikka, joka toimii erityisen hyvin pidempien tekstien kanssa. Edes kaikkein kehittyneimmät monoalfaattiset substituutiosalakirjoitukset eivät enää riittäneet taajuusanalyysia vastaan 1700-luvulla Euroopassa, erityisesti sotilas- ja turvallisuusympäristöissä. Koska Vigenere-salakirjoitus tarjosi merkittävän edistysaskeleen turvallisuudessa, siitä tuli suosittu tällä kaudella, ja se oli laajalle levinnyt 1700-luvun lopulla.
Epävirallisesti ottaen salausjärjestelmä toimii seuraavasti:
Valitse yksityiseksi avaimeksi monikirjaiminen sana.
Sovelletaan siirtymäsalausmenetelmää mihin tahansa viestiin ja käytetään viestin jokaiseen kirjaimeen käyttäen avainsanan vastaavaa kirjainta siirtymänä.
Jos olet käynyt avainsanan läpi, mutta et ole vielä täysin salannut selkotekstiä, käytä avainsanan kirjaimia uudelleen siirtymäsalakirjoituksena tekstin loppuosassa oleviin vastaaviin kirjaimiin.
Jatka tätä prosessia, kunnes koko viesti on salattu.
Kuvitellaan, että yksityinen avaimesi on "GOLD" ja haluat salata viestin "CRYPTOGRAPHY". Tällöin menetellään seuraavasti Vigenèren salakirjoituksen mukaisesti:
c_0 = [(2 + 6) \mod 26] = 8 = Ic_1 = [(17 + 14) \mod 26] = 5 = Fc_2 = [(24 + 11) \mod 26] = 9 = Jc_3 = [(15 + 3) \mod 26] = 18 = Sc_4 = [(19 + 6) \mod 26] = 25 = Zc_5 = [(14 + 14) \mod 26] = 2 = Cc_6 = [(6 + 11) \mod 26] = 17 = Rc_7 = [(17 + 3) \mod 26] = 20 = Uc_8 = [(0 + 6) \mod 26] = 6 = Gc_9 = [(15 + 14) \mod 26] = 3 = Dc_{10} = [(7 + 11) \mod 26] = 18 = Sc_{11} = [(24 + 3) \mod 26] = 1 = B
Näin ollen salattu teksti c =
"IFJSZCRUGDSB".
Toinen kuuluisa esimerkki virran salausmenetelmästä on one-time pad. Kertatäytteisessä salakirjoituksessa luodaan yksinkertaisesti merkkijono satunnaisia bittejä, jotka ovat yhtä pitkiä kuin selkotekstiviesti, ja tuotetaan salakirjoitus XOR-operaation avulla. Näin ollen yksityinen avain ja avainvirta vastaavat toisiaan one-time pad -menetelmällä.
Shift-salaus ja Vigenere-salaus ovat nykyaikana hyvin turvattomia, mutta one-time pad on erittäin turvallinen, jos sitä käytetään oikein. Todennäköisesti tunnetuin kertakäyttömuistion sovellus oli ainakin 1980-luvulle asti Washingtonin ja Moskovan välinen kuuma linja. [4]
Kuuban ohjuskriisin jälkeen käyttöön otettu kuuma linja on Washingtonin ja Moskovan välinen suora viestintäyhteys kiireellisiä asioita varten. Yhteyden tekniikka on muuttunut vuosien varrella. Nykyisin siihen kuuluu suora valokuitukaapeli sekä kaksi satelliittilinkkiä (redundanssin vuoksi), jotka mahdollistavat sähköpostin ja tekstiviestien lähettämisen. Linkki päättyy eri puolille Yhdysvaltoja. Pentagon, Valkoinen talo ja Raven Rock Mountain ovat tunnettuja päätepisteitä. Vastoin yleistä mielipidettä vihjelinjaan ei ole koskaan kuulunut puhelimia.
Pääpiirteissään kertatäyttöjärjestelmä toimi seuraavasti. Sekä Washingtonilla että Moskovalla oli kaksi satunnaislukusarjaa. Toinen satunnaislukusarja, jonka venäläiset loivat, koski kaikkien venäjänkielisten viestien salausta ja salauksen purkua. Toinen amerikkalaisten luoma satunnaislukusarja koski englanninkielisten viestien salausta ja salauksen purkua. Luotetut kuriirit toimittivat ajoittain toiselle osapuolelle lisää satunnaislukuja.
Washington ja Moskova pystyivät siis kommunikoimaan salaa käyttämällä näitä satunnaislukuja kertakäyttötunnusten luomiseen. Aina kun haluttiin viestiä, viestiin käytettiin seuraavaa satunnaislukujen osaa.
Vaikka one-time pad on erittäin turvallinen, sillä on huomattavia käytännön rajoituksia: avaimen on oltava yhtä pitkä kuin viesti, eikä mitään one-time padin osaa voi käyttää uudelleen. Tämä tarkoittaa sitä, että sinun on pidettävä kirjaa siitä, missä kohtaa one-time padia olet, tallennettava valtava määrä bittejä ja vaihdettava satunnaisia bittejä vastapuolten kanssa aika ajoin. Tämän vuoksi one-time padia ei käytetä käytännössä usein.
Sen sijaan käytännössä käytetään pääasiassa pseudosatunnaisia virtasähkösalauksia. Salsa20 ja siihen läheisesti liittyvä muunnelma ChaCha ovat esimerkkejä yleisesti käytetyistä pseudosatunnaisvirtasalaimista.
Näissä pseudosatunnaisvirtasalaimissa valitaan ensin satunnaisesti avain K, joka on lyhyempi kuin selkotekstin pituus. Tietokoneemme luo tällaisen satunnaisavaimen K yleensä ennalta arvaamattomien tietojen perusteella, joita se kerää ajan mittaan, kuten verkkoviestien, hiiren liikkeiden ja niin edelleen.
Tämä satunnaisavain K asetetaan
sitten laajennusalgoritmiin, joka luo viestin pituisen pseudosatunnaisen avainvirran.
Voit määrittää tarkasti, kuinka pitkä avainvirran on oltava (esim. 500 bittiä,
1000 bittiä, 1200 bittiä, 29 117 bittiä ja niin edelleen).
Pseudosatunnainen avainsarja näyttää * ikään kuin* se olisi valittu täysin satunnaisesti kaikkien samanpituisten merkkijonojen joukosta. Näin ollen salaus pseudosatunnaisella avainjonolla näyttää siltä, kuin se olisi tehty kertakäyttötyynyllä. Näin ei tietenkään ole.
Koska yksityinen avaimemme on lyhyempi kuin avainvirta ja laajentamisalgoritmimme on oltava deterministinen, jotta salaus- ja purkuprosessi toimisi, laajentamisoperaatiomme tuloksena ei olisi voinut olla kaikki kyseisen pituiset avainvirrat.
Oletetaan esimerkiksi, että yksityisen avaimen pituus on 128 bittiä ja että
voimme lisätä sen laajentavaan algoritmiin luodaksemme paljon pidemmän,
esimerkiksi 2 500 bitin avainvirran. Koska laajennusalgoritmimme on oltava
deterministinen, algoritmimme voi valita enintään 1/2^{128} merkkijonoja, joiden pituus on 2 500 bittiä. Tällaista avainvirtaa ei siis
voisi koskaan valita täysin satunnaisesti kaikista samanpituisista merkkijonoista.
Virtasalausmenetelmällä on kaksi ulottuvuutta: (1) avainvirta, joka on yhtä pitkä kuin selkoteksti, luodaan yksityisen avaimen avulla ja (2) tämä avainvirta yhdistetään selkotekstiin, yleensä XOR-operaation avulla, salatekstin tuottamiseksi.
Joskus määritetään ehto (1) tiukemmin ja väitetään, että avainvirran on nimenomaan oltava pseudosatunnainen. Tämä tarkoittaa sitä, että siirtosalakirjoitusta tai kertakäyttötyynyä ei pidettäisi virtasalakirjoituksena.
Mielestäni ehdon (1) laajempi määrittely tarjoaa helpomman tavan järjestää salausjärjestelmät. Lisäksi se tarkoittaa, että meidän ei tarvitse lakata kutsumasta tiettyä salausjärjestelmää virtasalakirjoitukseksi vain siksi, että saamme tietää, ettei se todellisuudessa perustu pseudosatunnaisiin avainvirtoihin.
Huomautukset:
[4] Crypto Museum, "Washington-Moskova hotline", 2013, saatavilla osoitteessa https://www.cryptomuseum.com/crypto/hotline/index.htm.
Lohkosalakirjoitukset
Ensimmäinen tapa, jolla lohkosalaus yleisesti ymmärretään, on se, että se on alkeellisempi kuin virtasalaus: Keskeinen algoritmi, joka suorittaa pituuden säilyttävän muunnoksen sopivan pituiselle merkkijonolle avaimen avulla. Tätä algoritmia voidaan käyttää salausmenetelmien ja ehkä myös muunlaisten salausmenetelmien luomiseen.
Usein lohkosalakirjoitin voi ottaa vastaan eri pituisia syöttöjonoja, kuten 64, 128 tai 256 bittiä, sekä eri pituisia avaimia, kuten 128, 192 tai 256 bittiä. Vaikka jotkut algoritmin yksityiskohdat saattavat muuttua näiden muuttujien mukaan, algoritmin ydin ei muutu. Jos se muuttuisi, puhuttaisiin kahdesta eri lohkosalauksesta. Huomaa, että tässä käytetään samaa terminologiaa kuin salausjärjestelmissä.
Lohkosalausmenetelmän toiminta on kuvattu alla olevassa Kuvassa 4.
Lohkosalakirjoituksen syötteenä on viesti M, jonka pituus on L, ja avain K. Se tuottaa viestin M', jonka pituus on L. Useimmissa lohkosalaimissa
avaimen ei välttämättä tarvitse olla yhtä pitkä kuin M ja M'.
Kuva 4: Lohkosalaus

Lohkosalaus ei yksinään ole salausjärjestelmä. Lohkosalakirjoitusta voidaan kuitenkin käyttää eri toimintatapojen kanssa erilaisten salausjärjestelmien tuottamiseksi. Toimintatapa yksinkertaisesti lisää joitakin lisäoperaatioita lohkosalakirjoituksen ulkopuolelle.
Tämän havainnollistamiseksi oletetaan lohkosalaus (BC), joka vaatii 128-bittisen syöttömerkkijonon ja 128-bittisen yksityisen avaimen. Alla olevassa kuvassa 5 esitetään, miten kyseistä lohkosalakirjoitusta voidaan käyttää elektronisen koodikirjatilan (ECB-tila) kanssa salausjärjestelmän luomiseksi. (Oikealla olevat ellipsit osoittavat, että tätä kaavaa voi toistaa niin kauan kuin on tarpeen).
Kuva 5: Lohkosalausmenetelmä, jossa on EKP-tila
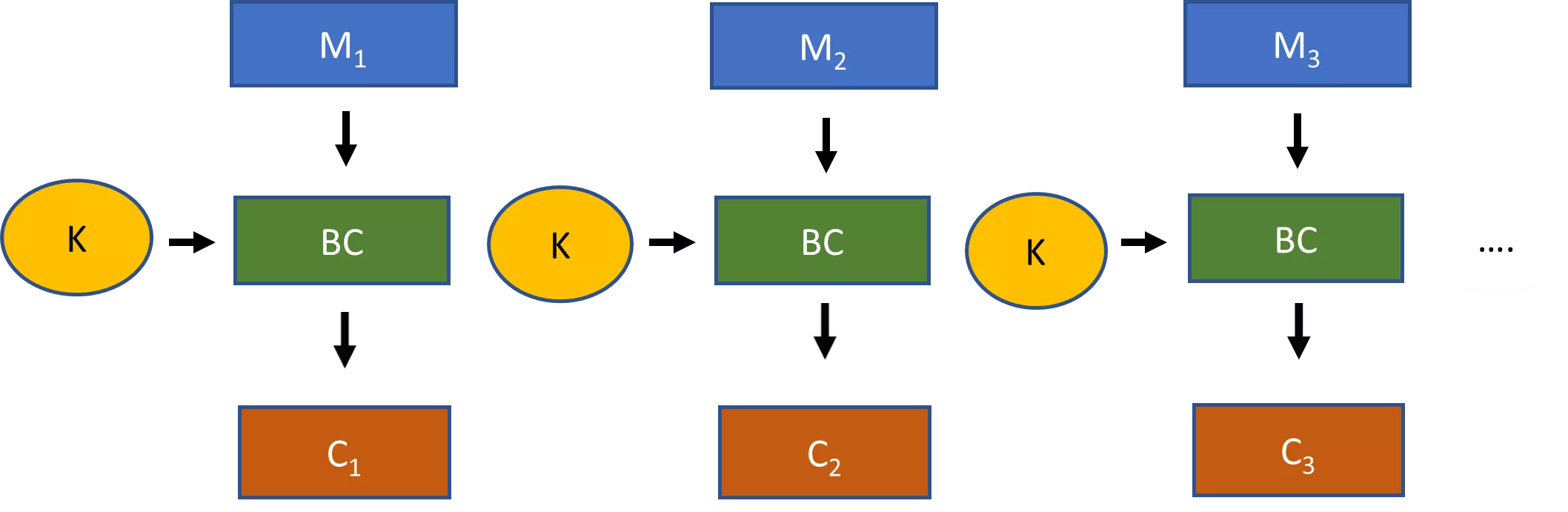
Sähköisen koodikirjan salausprosessi lohkosalakirjoituksen avulla on seuraava. Katso, voitko jakaa selvätekstiviestin 128-bittisiin lohkoihin. Jos ei, lisää viestiin padding, jotta tulos voidaan jakaa tasan 128 bitin lohkokoolla. Tätä tietoa käytetään salausprosessissa.
Jaa tiedot 128-bittisten merkkijonojen osiin (M_1, M_2, M_3 ja niin edelleen). Aja kukin 128-bittinen merkkijono lohkosalakirjoituksen
läpi 128-bittisellä avaimellasi, jolloin saat 128-bittiset salatekstipalat (C_1, C_2, C_3 jne.). Kun nämä palaset yhdistetään
uudelleen, ne muodostavat koko salatekstin.
Purkaminen on vain käänteinen prosessi, vaikka vastaanottajan on löydettävä jokin tunnistettava tapa poistaa kaikki pehmusteet puretusta datasta, jotta alkuperäisestä selväkielisestä viestistä saadaan alkuperäinen viesti.
Vaikka lohkosalaus on suhteellisen suoraviivainen, sähköisellä koodikirjatilalla varustettu lohkosalaus ei ole turvallinen. Tämä johtuu siitä, että se johtaa deterministiseen salaukseen. Kaksi identtistä 128-bittistä merkkijonoa salataan täsmälleen samalla tavalla. Tätä tietoa voidaan käyttää hyväksi.
Sen sijaan minkä tahansa lohkosalakirjoituksesta rakennetun
salausjärjestelmän pitäisi olla probabilistinen: eli minkä
tahansa viestin M tai minkä
tahansa M:n tietyn osan
salauksen pitäisi yleensä tuottaa joka kerta eri tulos. [5]
Lohkosalakirjoitustila** (CBC-tila) on luultavasti yleisin lohkosalakirjoituksen kanssa käytetty tila. Yhdistelmä tuottaa oikein tehtynä todennäköisyyspohjaisen salausjärjestelmän. Tämän toimintatavan kuvaus on kuvassa 6 alla.
Kuva 6: Lohkosalaus CBC-tilassa
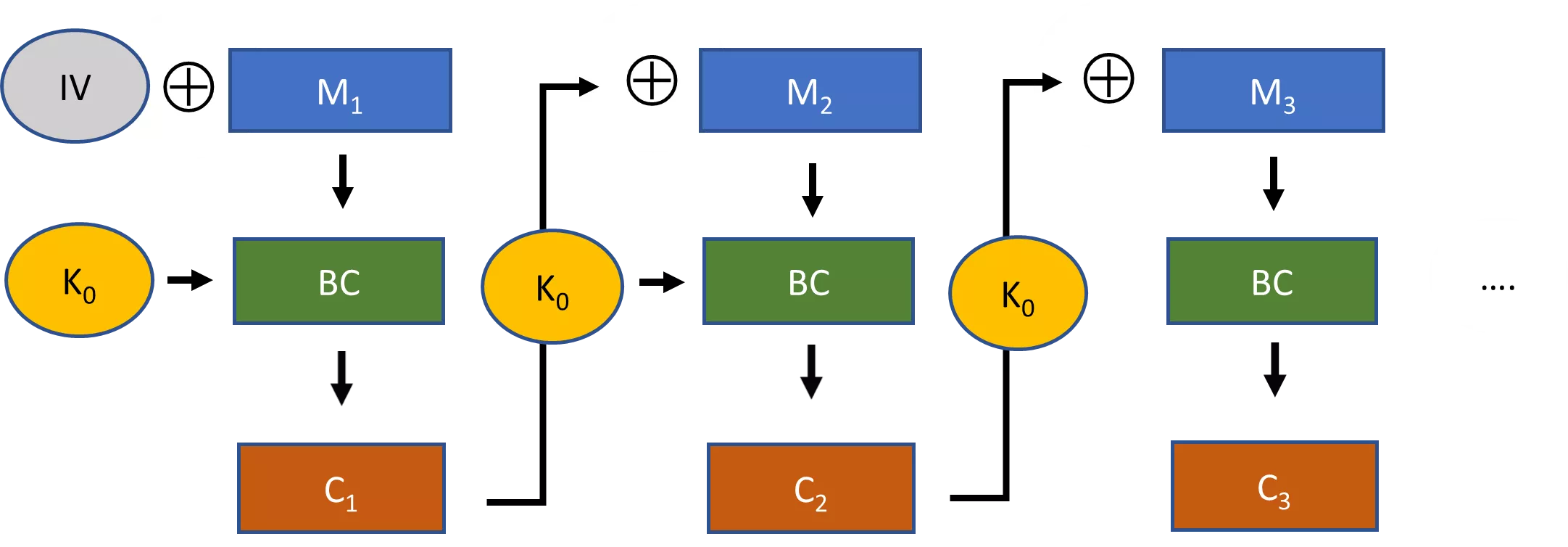
Oletetaan, että lohkokoko on taas 128 bittiä. Aluksi sinun on siis jälleen varmistettava, että alkuperäiseen selvätekstiviestiin lisätään tarvittava pehmuste.
Tämän jälkeen XOR-järjestyksessä yhdistetään 128-bittisen tekstin ensimmäinen 128-bittinen osa 128-bittiseen initialisointivektoriin. Tulos sijoitetaan lohkosalakirjoitukseen, jolloin saadaan ensimmäisen lohkon salausteksti. Toisen 128-bittisen lohkon osalta selkoteksti XOR-ratkaisu tehdään ensin ensimmäisen lohkon salakirjoitustekstin kanssa, ennen kuin se asetetaan lohkosalakirjoitukseen. Tätä prosessia jatketaan, kunnes koko selkotekstiviesti on salattu.
Kun olet valmis, lähetät salatun viestin yhdessä salaamattoman alustusvektorin kanssa vastaanottajalle. Vastaanottajan on tiedettävä alustusvektori, muuten hän ei voi purkaa salattua tekstiä.
Tämä rakenne on paljon turvallisempi kuin sähköinen koodikirja, kun sitä käytetään oikein. Ensiksi on varmistettava, että alustusvektori on satunnainen tai pseudosatunnainen merkkijono. Lisäksi sinun pitäisi käyttää eri alustusvektoria joka kerta, kun käytät tätä salausmallia.
Toisin sanoen alustusvektorisi pitäisi olla satunnainen tai pseudosatunnainen nonce, jossa nonce tarkoittaa "numeroa, jota käytetään vain kerran" Jos noudatat tätä käytäntöä, CBC-tila lohkosalakirjoituksen kanssa takaa, että kaksi identtistä selkotekstilohkoa salataan yleensä joka kerta eri tavalla.
Käännetään lopuksi huomiomme ulostulon palautetilaan (OFB-tila). Tämä tila on kuvattu Kuvassa 7.
Kuva 7: Lohkosalaus OFB-tilassa
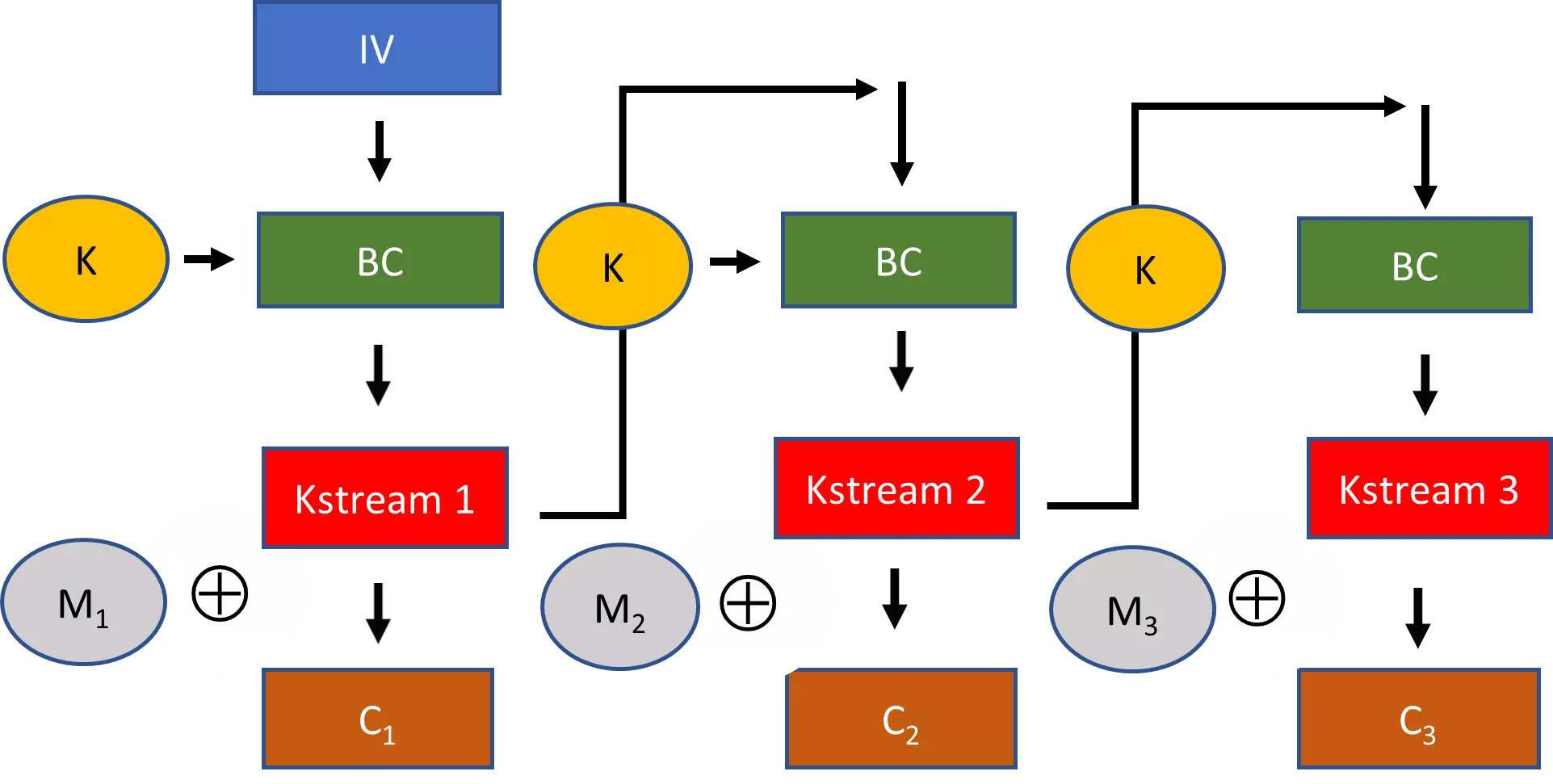
OFB-tilassa voit myös valita alustusvektorin. Mutta tässä tapauksessa ensimmäisen lohkon osalta alustusvektori lisätään suoraan lohkosalausmenetelmään avaimesi kanssa. Tuloksena syntyvää 128-bittistä koodia käsitellään sitten avainvirtana. Tämä avainvirta muunnetaan XOR-menetelmällä selkotekstin kanssa lohkon salatekstin tuottamiseksi. Seuraavissa lohkoissa käytetään edellisen lohkon avainvirtaa syötteenä lohkosalakirjoitukseen ja toistetaan vaiheet.
Jos katsot tarkkaan, tässä on itse asiassa luotu OFB-tilassa olevasta lohkosalakirjoituksesta virtasalakirjoitus. Luodaan 128-bittisiä avainvirran osia, kunnes saadaan selvätekstin pituus (hylätään viimeisestä 128-bittisestä avainvirran osasta ne bitit, joita ei tarvita). Tämän jälkeen avainvirta ja selkotekstiviesti XOR-järjestetään salatun tekstin saamiseksi.
Edellisessä virtamerkkejä käsittelevässä jaksossa totesin, että avainvirta tuotetaan yksityisen avaimen avulla. Tarkalleen ottaen sitä ei tarvitse luoda vain yksityisellä avaimella. Kuten näet OFB-tilassa, avainvirta tuotetaan sekä yksityisen avaimen että alustusvektorin avulla.
Huomaa, että kuten CBC-tilassa, on tärkeää valita pseudosatunnainen tai satunnainen nonce alustusvektoriksi joka kerta, kun käytät lohkosalausta OFB-tilassa. Muussa tapauksessa sama 128-bittinen viestiketju, joka lähetetään eri tiedonsiirroissa, salataan samalla tavalla. Tämä on yksi tapa luoda todennäköisyyteen perustuva salaus virran salausmenetelmällä.
Jotkin virta-salakirjoitukset käyttävät vain yksityistä avainta avainvirran luomiseen. Näissä virtauskoodereissa on tärkeää, että käytät satunnaista noncea yksityisen avaimen valitsemiseen jokaista viestintäkertaa varten. Muuten myös näillä virtauskoodereilla suoritetun salauksen tulokset ovat deterministisiä, mikä johtaa tietoturvaongelmiin.
Suosituin nykyaikainen lohkosalaus on Rijndael-salaus. Se voitti 15 ehdotuksen joukosta kilpailun, jonka National Institute of Standards and Technology (NIST) järjesti vuosina 1997-2000 ja jonka tarkoituksena oli korvata vanhempi salausstandardi, data encryption standard (DES).
Rijndael-salausmenetelmää voidaan käyttää erilaisilla avainten pituuksia ja lohkokokoja koskevilla eritelmillä sekä eri toimintatiloissa. NIST-kilpailun komitea hyväksyi Rijndaelin salakirjoituksen rajoitetun version, joka edellyttää 128-bittistä lohkokokoa ja joko 128, 192 tai 256 bitin pituisia avaimia, osana edistyneen salakirjoituksen standardia (AES). Tämä on symmetristen salaussovellusten tärkein standardi. Se on niin turvallinen, että jopa NSA on ilmeisesti valmis käyttämään sitä 256-bittisillä avaimilla huippusalaisiin asiakirjoihin. [6]
AES-lohkosalaus selitetään yksityiskohtaisesti luvussa 5.
Huomautukset:
[5] Todennäköisyyspohjaisen salauksen merkitystä korostivat ensimmäisen kerran Shafi Goldwasser ja Silvio Micali, "Probabilistic encryption", Journal of Computer and System Sciences, 28 (1984), 270-99.
[6] Katso NSA, "Commercial National Security Algorithm Suite", https://apps.nsa.gov/iaarchive/programs/iad-initiatives/cnsa-suite.cfm.
Sekaannuksen selvittäminen
Lohkosalakirjoitusten ja virtasalakirjoitusten erottaminen toisistaan aiheuttaa sekaannusta, koska joskus ihmiset ymmärtävät termin lohkosalakirjoitus viittaavan nimenomaan lohkosalakirjoitukseen, jossa on lohkosalakirjoitustapa.
Tarkastellaan edellisen jakson EKP- ja CBC-tiloja. Nämä vaativat erityisesti, että salattavien tietojen on oltava jaettavissa lohkokoolla (mikä tarkoittaa, että alkuperäisen viestin pehmustamista saatetaan joutua käyttämään). Lisäksi näissä tiloissa lohkosalaus käyttää dataa suoraan lohkosalausmenetelmällä (eikä vain yhdistettynä lohkosalausmenetelmän tulokseen, kuten OFB-tilassa).
Vaihtoehtoisesti voit siis määritellä lohkosalakirjoituksen millä tahansa salausjärjestelmällä, joka toimii kiinteän pituisilla viestin lohkoilla kerrallaan (missä minkä tahansa lohkon on oltava pidempi kuin tavu, muutoin se romahtaa virtasalakirjoitukseksi). Sekä salattavan datan että salatekstin on jakauduttava tasan tähän lohkokokoon. Tyypillisesti lohkokoko on 64, 128, 192 tai 256 bittiä pitkä. Virta-salausmenetelmällä sen sijaan voidaan salata mitä tahansa viestejä yhden bitin tai tavun suuruisina lohkoina kerrallaan.
Tämän tarkemman ymmärryksen perusteella voit todellakin väittää, että nykyaikaiset salausmenetelmät ovat joko virta- tai lohkosalakirjoituksia. Tästä eteenpäin käytän termiä lohkosalaus yleisemmässä merkityksessä, ellei toisin mainita.
Edellisessä jaksossa käyty keskustelu OFB-tilasta nostaa esiin myös toisen mielenkiintoisen seikan. Jotkin virtasalakirjoitukset on rakennettu lohkosalakirjoituksista, kuten Rijndael OFB:llä. Joitakin, kuten Salsa20 ja ChaCha, ei ole luotu lohkosalaimista. Jälkimmäisiä voisi kutsua alkukantaisiksi virtasalaimiksi. (Ei ole olemassa standardoitua termiä, jolla viitattaisiin tällaisiin virtapiirisalaimiin)
Kun ihmiset puhuvat virta- ja lohkosalauksen eduista ja haitoista, he yleensä vertaavat alkeellisia virta- ja lohkosalaukseen perustuvia salausjärjestelmiä.
Vaikka virran salaus voidaan aina helposti rakentaa lohkosalakirjoituksesta, on tyypillisesti hyvin vaikeaa rakentaa jonkinlainen lohkosalakirjoitustapaa käyttävä rakenne (kuten CBC-tila) alkeellisesta virran salakirjoituksesta.
Tämän keskustelun perusteella sinun pitäisi nyt ymmärtää Luku 8. Se antaa yleiskuvan symmetrisistä salausjärjestelmistä. Käytämme kolmenlaisia salausjärjestelmiä: primitiivisiä virta-salakirjoituksia, lohkosalakirjoitusvirta-salakirjoituksia ja lohkosalakirjoituksia lohkotilassa (kuvassa myös "lohkosalakirjoitukset").
Kuva 8: Yleiskatsaus symmetrisiin salausmenetelmiin
Viestin todennuskoodit
Salaus koskee salassapitoa. Kryptografia käsittelee kuitenkin myös laajempia aiheita, kuten viestin eheyttä, aitoutta ja kiistämättömyyttä. Niin sanotut viestien todentamiskoodit (MAC) ovat symmetrisen avaimen salausjärjestelmiä, jotka tukevat viestinnän aitoutta ja eheyttä.
Miksi viestinnässä tarvitaan muuta kuin salassapitoa? Oletetaan, että Bob lähettää Alicelle viestin käyttäen käytännössä murtamatonta salausta. Hyökkääjä, joka sieppaa tämän viestin, ei pysty saamaan mitään merkittävää tietoa viestin sisällöstä. Hyökkääjällä on kuitenkin edelleen käytettävissään ainakin kaksi muuta hyökkäysväylää:
Hän voisi siepata salatun tekstin, muuttaa sen sisältöä ja lähettää muutetun salatun tekstin Alicelle.
Hän voisi estää Bobin viestin kokonaan ja lähettää oman salatekstinsä.
Molemmissa tapauksissa hyökkääjä ei välttämättä saa mitään tietoa salatekstien (1) ja (2) sisällöstä. Hän voisi silti aiheuttaa merkittävää vahinkoa tällä tavoin. Tässä kohtaa viestin todentamiskoodit tulevat tärkeiksi.
Viestin todentamiskoodit määritellään väljästi symmetrisiksi salausjärjestelmiksi, joissa on kolme algoritmia: avaimen luomisalgoritmi, tunnisteen luomisalgoritmi ja todentamisalgoritmi. Turvallinen MAC varmistaa, että tunnisteet ovat olemassaolevia väärentämättömiä kenellekään hyökkääjälle - toisin sanoen hyökkääjä ei voi luoda onnistuneesti tunnistetta viestiin, joka todennetaan, ellei hänellä ole yksityistä avainta.
Bob ja Alice voivat torjua tietyn viestin manipulointia MAC:n avulla. Oletetaan toistaiseksi, että he eivät välitä salassapidosta. He haluavat vain varmistaa, että Alicen vastaanottama viesti on todellakin peräisin Bobilta eikä sitä ole muutettu millään tavalla.
Prosessi on kuvattu Kuvassa 9. Käyttääkseen MAC (Message Authentication Code) -koodia (Message Authentication Code) he
luovat ensin yksityisen avaimen K, joka jaetaan molempien
kesken. Bob luo viestille tunnisteen T käyttäen yksityistä avainta K. Sitten hän lähettää
viestin ja viestin tunnisteen Alicelle. Tämän jälkeen Alice voi tarkistaa,
että Bob todella teki tunnisteen, ajamalla yksityisen avaimen, viestin ja
tunnisteen todentamisalgoritmin läpi.
Kuva 9: Yleiskatsaus symmetrisiin salausmenetelmiin
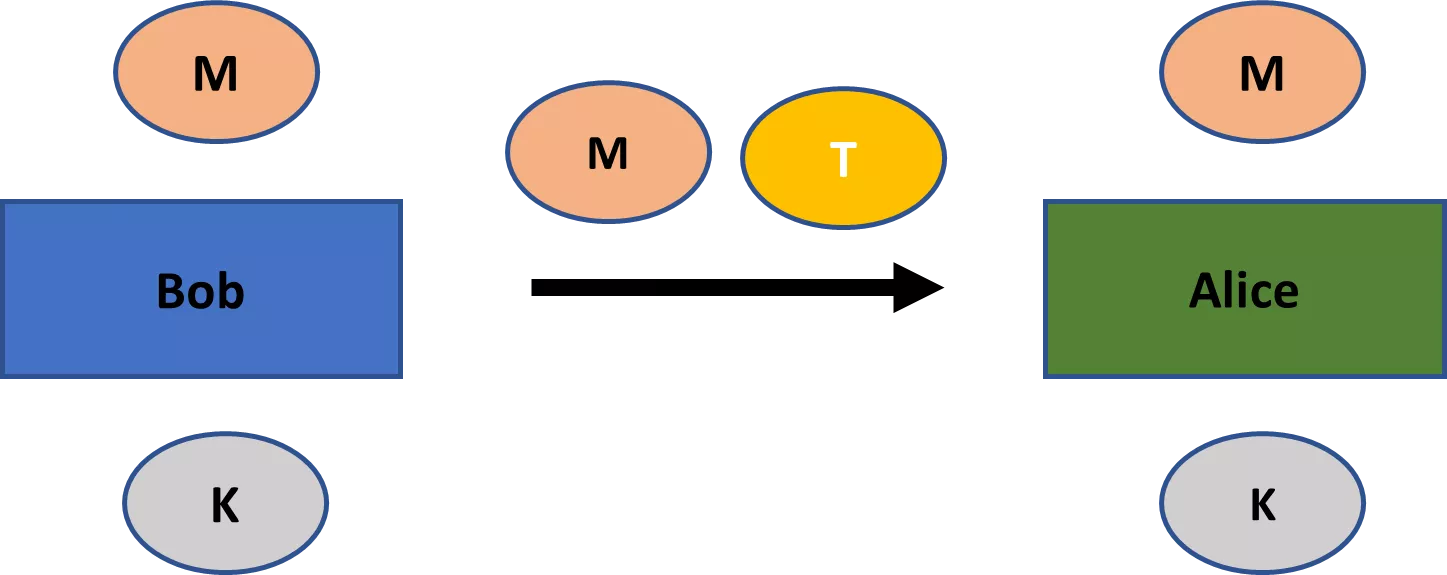
Koska viestiä ei voida väärentää**, hyökkääjä ei voi muuttaa viestiä M millään tavalla eikä luoda omaa viestiä, jolla on kelvollinen tunniste. Näin
on, vaikka hyökkääjä havaitsisi monien Bobin ja Alicen välisten, samaa
yksityistä avainta käyttävien viestien tunnisteet. Hyökkääjä voi korkeintaan
estää Alicea vastaanottamasta viestiä M (ongelma, jota kryptografia
ei voi ratkaista).
MAC takaa, että viestin on todella luonut Bob. Tämä aitous merkitsee automaattisesti viestin eheyttä - eli jos Bob on luonut jonkin viestin, hyökkääjä ei ole ipso facto muuttanut sitä millään tavalla. Tästä eteenpäin kaikki autentikointiin liittyvät huolenaiheet olisi siis automaattisesti ymmärrettävä siten, että ne merkitsevät myös huolta eheydestä.
Vaikka olen tehnyt keskustelussani eron viestin aitouden ja eheyden välille, näitä termejä käytetään usein myös synonyymeinä. Ne viittaavat siis ajatukseen viesteistä, jotka on luonut tietty lähettäjä ja joita ei ole muutettu millään tavalla. Tässä hengessä viestin todentamiskoodeja kutsutaan usein myös viestin eheyskoodeiksi.
Todennettu salaus
Tyypillisesti viestinnässä halutaan taata sekä salassapito että aitous, ja siksi salaus- ja MAC-järjestelmiä käytetään yleensä yhdessä.
Varmennettu salausjärjestelmä on järjestelmä, jossa salaus ja MAC yhdistyvät erittäin turvallisesti. Sen on erityisesti täytettävä olemassaolon väärentämättömyyttä koskevat vaatimukset sekä erittäin vahva salaisuuden käsite, nimittäin sellainen, joka on vastustuskykyinen valittuun salakirjoitustekstiin kohdistuville hyökkäyksille. [7]
Jotta salausjärjestelmä olisi vastustuskykyinen valittuun salakirjoitustekstiin kohdistuville hyökkäyksille, sen on täytettävä ei-mallinnettavuutta koskevat vaatimukset: toisin sanoen hyökkääjän tekemän salakirjoitustekstin muutoksen pitäisi tuottaa joko virheellinen salakirjoitusteksti tai sellainen salakirjoitusteksti, joka purkautuu selkokieliseksi tekstiksi, jolla ei ole mitään yhteyttä alkuperäiseen tekstiin. [8]
Koska todennettu salausjärjestelmä varmistaa, että hyökkääjän luoma salakirjoitusteksti on aina virheellinen (koska tunnistetta ei todenneta), se täyttää standardit, jotka koskevat vastustuskykyä valittuun salakirjoitustekstiin kohdistuvia hyökkäyksiä vastaan. Mielenkiintoista on, että voit todistaa, että autentikoitu salausjärjestelmä voidaan aina luoda yhdistelmästä, jossa on olemassaoleva väärentämätön MAC ja salausjärjestelmä, joka täyttää vähemmän vahvemman turvallisuuskäsitteen, joka tunnetaan nimellä valittujen salakirjoitustekstien suojaus (chosen-plaintext-attack security).
Emme aio syventyä kaikkiin todennettujen salausjärjestelmien rakentamisen yksityiskohtiin. On kuitenkin tärkeää tietää kaksi yksityiskohtaa niiden rakentamisesta.
Ensiksi todennettu salausjärjestelmä hoitaa ensin salauksen ja luo sitten salatusta tekstistä viestin tunnisteen. On käynyt ilmi, että muut lähestymistavat - kuten salatun tekstin yhdistäminen selkotekstin tunnisteeseen tai ensin tunnisteen luominen ja sitten sekä selkotekstin että tunnisteen salaaminen - eivät ole turvallisia. Lisäksi molemmilla operaatioilla on oma satunnaisesti valittu yksityinen avaimensa, muuten turvallisuus vaarantuu pahasti.
Edellä mainittua periaatetta sovelletaan yleisemmin: sinun tulisi aina käyttää erillisiä avaimia, kun yhdistät perussalausmenetelmiä.
Todennettu salausjärjestelmä on esitetty Kuvassa 10. Bob luo ensin
salatekstin C viestistä M käyttäen satunnaisesti valittua avainta K_C. Sitten hän luo viestin
tunnisteen T ajamalla
salatekstin ja toisen satunnaisesti valitun avaimen K_T tunnisteen luomisalgoritmin
läpi. Sekä salausteksti että viestin tunniste lähetetään Alicelle.
Alice tarkistaa nyt ensin, onko tunniste kelvollinen, kun otetaan huomioon
salausteksti C ja avain K_T. Jos se on voimassa, hän
voi purkaa viestin avaimella K_C. Näin hän saa varmuuden
hyvin vahvasta viestinnän salassapidosta, ja lisäksi hän tietää, että
viestin on luonut Bob.
Kuva 10: Todennettu salausjärjestelmä

Miten MACit luodaan? MAC-muistit voidaan luoda useilla eri menetelmillä, mutta yleinen ja tehokas tapa on luoda ne kryptografisten hash-funktioiden avulla.
Esittelemme kryptografiset hash-funktiot perusteellisemmin luvussa 6. Toistaiseksi riittää, että tiedät, että hash-funktio on tehokkaasti laskettavissa oleva funktio, joka ottaa mielivaltaisen kokoisia syötteitä ja tuottaa kiinteän pituisia tuotoksia. Esimerkiksi suosittu hash-funktio SHA-256 (secure hash algorithm 256) tuottaa aina 256-bittisen tulosteen syötteen koosta riippumatta. Joillakin hash-funktioilla, kuten SHA-256:lla, on hyödyllisiä sovelluksia salauksessa.
Yleisin kryptografisella hash-funktiolla tuotettu tunnistetyyppi on HMAC
(HMAC = Hash-based Message Authentication Code). Prosessi on kuvattu Kuvassa 11. Osapuoli tuottaa yksityisestä avaimesta K kaksi eri avainta, sisäisen avaimen K_1 ja ulkoisen avaimen K_2.
Selkoteksti M tai salateksti C hakkeroidaan sitten yhdessä sisäisen avaimen kanssa. Tulos T' sekoitetaan sitten ulkoisella avaimella, jolloin saadaan viestin tunniste T.
HMAC:n luomiseen voidaan käyttää useita erilaisia hash-funktioita. Yleisimmin käytetty hash-funktio on SHA-256.
Kuva 11: HMAC
Huomautukset:
[7] Tässä jaksossa käsiteltävät tulokset ovat Katzin ja Lindellin julkaisusta, s. 131-47.
[8] Teknisesti ottaen valitun salatun tekstin hyökkäyksen määritelmä on eri asia kuin ei-mallinnettavuuden käsite. Voit kuitenkin osoittaa, että nämä kaksi turvallisuuden käsitettä vastaavat toisiaan.
Turvalliset viestintäistunnot
Oletetaan, että kaksi osapuolta on viestintäistunnossa ja lähettää useita viestejä edestakaisin.
Todennetun salausjärjestelmän avulla viestin vastaanottaja voi todentaa, että viestin on luonut hänen viestintäkumppaninsa (kunhan yksityinen avain ei ole vuotanut). Tämä toimii riittävän hyvin yhden viestin osalta. Tyypillisesti kaksi osapuolta kuitenkin lähettää viestejä edestakaisin viestintäistunnossa. Tässä tilanteessa edellisessä jaksossa kuvattu pelkkä todennettu salausjärjestelmä ei tarjoa riittävää turvallisuutta.
Tärkein syy tähän on se, että todennettu salausjärjestelmä ei anna mitään takeita siitä, että viestin on todella lähettänyt myös se agentti, joka on luonut sen viestintäistunnon aikana. Tarkastellaan seuraavia kolmea hyökkäysvektoria:
Replay-hyökkäys: Hyökkääjä lähettää uudelleen salatun tekstin ja tunnisteen, jotka hän on siepannut kahden osapuolen välillä aiemmin.
Uusijärjestelyhyökkäys: Hyökkääjä sieppaa kaksi viestiä eri aikaan ja lähettää ne vastaanottajalle päinvastaisessa järjestyksessä.
Reflection-hyökkäys: Hyökkääjä tarkkailee A:sta B:hen lähetettyä viestiä ja lähettää saman viestin myös A:lle.
Vaikka hyökkääjä ei tiedä salatekstiä eikä voi luoda väärennettyjä salatekstejä, edellä mainitut hyökkäykset voivat silti aiheuttaa merkittävää vahinkoa viestinnässä.
Oletetaan esimerkiksi, että tietty viesti osapuolten välillä koskee rahavarojen siirtoa. Toistohyökkäys voisi siirtää varat toisen kerran. Vanilla autentikoidulla salausjärjestelmällä ei ole mitään suojaa tällaisia hyökkäyksiä vastaan.
Onneksi tällaisia hyökkäyksiä voidaan helposti torjua viestintäistunnossa käyttämällä tunnisteita ja suhteellisia aikaindikaattoreita.
Tunnisteet voidaan lisätä selväkieliseen viestiin ennen salausta. Tämä estää heijastushyökkäykset. Suhteellinen aikatunniste voi olla esimerkiksi järjestysnumero tietyssä viestintäistunnossa. Kukin osapuoli lisää viestiin järjestysnumeron ennen salausta, jotta vastaanottaja tietää, missä järjestyksessä viestit on lähetetty. Tämä poistaa uudelleenjärjestämishyökkäysten mahdollisuuden. Se eliminoi myös toistohyökkäykset. Hyökkääjän lähettämillä viesteillä on vanha järjestysnumero, ja vastaanottaja tietää, ettei viestiä saa käsitellä uudelleen.
Jotta voidaan havainnollistaa, miten suojatut viestintäistunnot toimivat, oletetaan jälleen Alice ja Bob. He lähettävät yhteensä neljä viestiä edestakaisin. Alla olevasta Kuvasta 11 näet, miten tunnisteiden ja järjestysnumeroiden avulla todennettu salausjärjestelmä toimisi.
Tietoliikenneistunto alkaa siten, että Bob lähettää salatun tekstin C_{0,B} Alicelle ja viestin tunnisteen T_{0,B}. Salateksti
sisältää viestin sekä tunnisteen (BOB) ja järjestysnumeron (0). Tunniste T_{0,B} tehdään koko
salatekstin päälle. Myöhemmässä viestinnässään Alice ja Bob ylläpitävät tätä
protokollaa ja päivittävät kenttiä tarpeen mukaan.
Kuva 12: Turvallinen viestintäistunto
RC4 ja AES
RC4-virtasalaus
Tässä luvussa käsitellään salausjärjestelmän yksityiskohtia, jossa käytetään nykyaikaista primitiivistä virtasalausmenetelmää, RC4:ää (tai "Rivest cipher 4"), ja nykyaikaista lohkosalausmenetelmää, AES:ää. Vaikka RC4-salaus on joutunut huonoon valoon salausmenetelmänä, AES on nykyaikaisen symmetrisen salauksen standardi. Näiden kahden esimerkin pitäisi antaa parempi käsitys siitä, miten symmetrinen salaus toimii konepellin alla.
Jotta saataisiin käsitys siitä, miten nykyaikaiset pseudosatunnaisvirtasalakirjoitukset toimivat, keskityn RC4-virtasalakirjoitukseen. Se on pseudosatunnaisvirtasalaus, jota käytettiin langattomien WEP- ja WAP-yhteyspisteiden turvallisuusprotokollissa sekä TLS:ssä. Koska RC4:llä on monia todistettuja heikkouksia, se on joutunut epäsuosioon. Itse asiassa Internet Engineering Task Force kieltää nyt RC4-sarjojen käytön asiakas- ja palvelinsovelluksissa kaikissa TLS-tapauksissa. Se toimii kuitenkin hyvin esimerkkinä, joka havainnollistaa, miten alkeellinen virtasalaus toimii.
Aluksi näytän ensin, miten salataan tavallinen viesti RC4-salauksella. Oletetaan, että selkotekstiviestimme on "SOUP" Salaus RC4-salakirjoituksella tapahtuu neljässä vaiheessa.
Vaihe 1
Määrittele ensin joukko S, jonka arvot S[0] = 0 - S[7] = 7. Joukko tarkoittaa
tässä yksinkertaisesti indeksin mukaan järjestettyä muuttuvaa arvokokoelmaa,
jota kutsutaan joissakin ohjelmointikielissä (esim. Pythonissa) myös
listaksi. Tässä tapauksessa indeksi on 0-7, ja arvot ovat myös 0-7. S on siis seuraava:
S = [0, 1, 2, 3, 4, 5, 6, 7]
Arvot eivät ole ASCII-lukuja, vaan yhden tavun merkkijonojen
desimaalilukuja. Arvo 2 olisi siis 0000 \ 0011. Joukon S pituus on siis 8 tavua.
Vaihe 2
Määritä toiseksi 8 tavun pituinen avainjoukko K valitsemalla avain 1-8 tavun väliltä (tavujen murto-osia ei sallita). Koska jokainen tavu on 8-bittinen, voit valita avaimen jokaiselle tavulle minkä tahansa luvun väliltä 0-255.
Oletetaan, että valitsemme avaimeksi k [14, 48, 9], jolloin sen
pituus on 3 tavua. Avainmatriisin jokainen indeksi asetetaan tällöin avaimen
kyseisen elementin desimaaliarvon mukaan järjestyksessä. Jos käyt läpi koko
avaimen, aloita alusta, kunnes olet täyttänyt kaikki avaintarinan 8 paikkaa.
Avainjoukkomme on siis seuraava:
K = [14, 48, 9, 14, 48, 9, 14, 48]
Vaihe 3
Kolmanneksi muunnetaan joukko S käyttämällä avainjoukkoa K, mikä tunnetaan nimellä avainten ajoitus. Prosessi on seuraava pseudokoodissa:
- Luodaan muuttujat j ja i
- Aseta muuttuja
j = 0 - Jokaisen
i:n osalta välillä 0-7:- Asetetaan
j = (j + S[i] + K[i]) \mod 8 - Vaihda
S[i]jaS[j]
- Asetetaan
Joukon S muunnos on kuvattu Taulukossa 1.
Aluksi voit nähdä S:n alkutilana [0, 1, 2, 3, 4, 5, 6, 7], kun j:n alkuarvo on 0. Tämä muunnetaan käyttämällä avainjoukkoa [14, 48, 9, 14, 48, 9, 14, 48].
For-silmukka alkaa arvolla i = 0. Edellä olevan pseudokoodin mukaan j:n uudeksi arvoksi
tulee 6 (j = (j + S[0] + K[0]) \mod 8 = (0 + 0 + 14) \mod 8 = 6 \mod 8). Kun vaihdetaan S[0] ja S[6], S:n
tilasta tulee yhden kierroksen jälkeen [6, 1, 2, 3, 4, 5, 0, 7].
Seuraavalla rivillä i = 1.
Kun for-silmukka käydään uudelleen läpi, j saa arvon 7 (j = (j + S[1] + K[1]) \mod 8 = (6 + 1 + 48) \mod 8 = 55 \mod 8 = 7 \mod 8). Vaihtamalla S[1] ja S[7] S:n
nykyisestä tilasta [6, 1, 2, 3, 4, 5, 0, 7] saadaan kierroksen 2 jälkeen [6, 7, 2, 3, 4, 5, 0, 1].
Jatketaan tätä prosessia, kunnes saadaan matriisin S viimeinen rivi alareunaan, [6, 4, 1, 0, 3, 7, 5, 2].
Taulukko 1: Keskeinen aikataulutaulukko
| Round | i | j | S[0] | S[1] | S[2] | S[3] | S[4] | S[5] | S[6] | S[7] | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 1 | 0 | 6 | 6 | 1 | 2 | 3 | 4 | 5 | 0 | 7 | |
| 2 | 1 | 7 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 3 | 2 | 2 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 4 | 3 | 3 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 5 | 4 | 3 | 6 | 7 | 2 | 0 | 3 | 5 | 4 | 1 | |
| 6 | 5 | 6 | 6 | 4 | 2 | 0 | 3 | 7 | 5 | 1 | |
| 7 | 6 | 1 | 6 | 4 | 2 | 0 | 3 | 7 | 5 | 2 | |
| 8 | 7 | 2 | 6 | 4 | 1 | 0 | 3 | 7 | 5 | 2 |
Vaihe 4
Neljäntenä vaiheena tuotetaan keystream. Tämä on pseudosatunnainen merkkijono, jonka pituus on yhtä pitkä kuin viesti, jonka haluamme lähettää. Tätä käytetään alkuperäisen viestin "SOUP" salaamiseen Koska avainjonon on oltava yhtä pitkä kuin viesti, tarvitsemme avainjonon, jossa on 4 tavua.
Avainvirta tuotetaan seuraavalla pseudokoodilla:
- Luodaan muuttujat j, i ja t.
- Asetetaan
j = 0. - Jokaisen selkotekstin
i:n kohdalla, alkaeni = 1:stä ja jatkuen ainai = 4:een asti, jokainen avainvirran tavu tuotetaan seuraavasti:j = (j + S[i]) \mod 8- Vaihda
S[i]jaS[j]. t = (S[i] + S[j]) \mod 8- Avainjonon
i^{kuudes}tavu =S[t]
Voit seurata laskelmia Taulukossa 2.
S:n alkutila on S = [6, 4, 1, 0, 3, 7, 5, 2].
Asetetaan i = 1, jolloin j:n arvoksi tulee 4 (j = (j + S[i]) \mod 8 = (0 + 4) \mod 8 = 4). Vaihdetaan sitten S[1] ja S[4], jolloin saadaan toisen
rivin S-muunnos [6, 3, 1, 0, 4, 7, 5, 2].
Tällöin t:n arvo on 7 (t = (S[i] + S[j]) \mod 8 = (3 + 4) \mod 8 = 7). Lopuksi avainvirran tavu on S[7] eli 2.
Sitten jatketaan muiden tavujen tuottamista, kunnes meillä on seuraavat neljä tavua: 2, 6, 3 ja 7. Kutakin näistä tavuista voidaan sitten käyttää salaamaan jokainen kirjain selkotekstissä "SOUP".
Aluksi ASCII-taulukon avulla voimme nähdä, että "SOUP" on koodattuna taustalla olevien tavujonojen desimaaliarvoilla "83 79 85 80". Yhdistettynä avainjonoon "2 6 3 7" saadaan "85 85 88 87", joka pysyy samana modulo 256 -operaation jälkeen. ASCII-muodossa salateksti "85 85 88 87" vastaa "UUXW".
Mitä tapahtuu, jos salattava sana olisi pidempi kuin joukko S? Tällöin joukko S vain muuttuu edellä esitetyllä tavalla jokaista tavua i kohti, kunnes avainvirrassa on tavuja, jotka vastaavat tavujen määrää tavutekstissä.
Taulukko 2: Keystream-tuotanto
| i | j | t | Keystream | S[0] | S[1] | S[2] | S[3] | S[4] | S[5] | S[6] | S[7] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 4 | 1 | 0 | 3 | 7 | 5 | 2 | |||
| 1 | 4 | 7 | 2 | 6 | 3 | 1 | 0 | 4 | 7 | 5 | 2 |
| 2 | 5 | 0 | 6 | 6 | 3 | 7 | 0 | 4 | 1 | 5 | 2 |
| 3 | 5 | 1 | 3 | 6 | 3 | 7 | 1 | 4 | 0 | 5 | 2 |
| 4 | 1 | 7 | 2 | 6 | 4 | 7 | 1 | 3 | 0 | 5 | 2 |
Äsken käsittelemämme esimerkki on vain vesitetty versio RC4-virtasalauksesta. Varsinaisessa RC4-suoritussalakirjoituksessa S-joukon pituus on 256 tavua, ei 8 tavua, ja avain voi olla 1 ja 256 tavun välillä, ei 1 ja 8 tavun välillä. Avainjoukko ja avainvirrat tuotetaan kaikki ottaen huomioon S-joukon 256 tavun pituus. Laskutoimituksista tulee huomattavasti monimutkaisempia, mutta periaatteet pysyvät samoina. Käyttämällä samaa avainta 14,48,9 tavallisella RC4-salakirjoituksella selkotekstiviesti "SOUP" salataan muodossa 67 02 ed df heksadesimaalimuodossa.
Virtasalaus, jossa avainvirta päivittyy riippumatta selväkielisestä viestistä tai salatekstistä, on synkroninen virtasalaus. Avainvirta on riippuvainen vain avaimesta. RC4 on selvästikin esimerkki synkronisesta virtasalakirjoituksesta, koska avainvirralla ei ole mitään yhteyttä selkotekstiin tai salakirjoitustekstiin. Kaikki edellisessä luvussa mainitut primitiiviset virta-salakirjoituksemme, mukaan lukien siirtosalakirjoitus, Vigenèren salakirjoitus ja kertakäyttösalakirjoitus, olivat myös synkronisia.
Sitä vastoin asynkronisessa virtasalauksessa on avainvirta, joka muodostuu sekä avaimesta että salaustekstin aiemmista elementeistä. Tämäntyyppistä salakirjoitusta kutsutaan myös itsesynkronoivaksi salakirjoitukseksi.
Tärkeää on, että RC4:llä tuotettua avainvirtaa on pidettävä kertakäyttöisenä, etkä voi tuottaa avainvirtaa täsmälleen samalla tavalla seuraavalla kerralla. Sen sijaan, että avain vaihdettaisiin joka kerta, käytännöllinen ratkaisu on yhdistää avain nonce:n kanssa bytestreamin tuottamiseksi.
AES 128-bittisellä avaimella
Kuten edellisessä luvussa mainittiin, National Institute of Standards and Technology (NIST) järjesti vuosina 1997-2000 kilpailun uuden symmetrisen salausstandardin määrittämiseksi. Voittajaksi selviytyi Rijndael-salakirjoitus. Nimi on sanaleikki belgialaisten tekijöiden Vincent Rijmenin ja Joan Daemenin nimistä.
Rijndael-salausmenetelmä on lohkosalausmenetelmä, mikä tarkoittaa, että on olemassa ydinalgoritmi, jota voidaan käyttää eri avainten pituuksien ja lohkokokojen määrityksillä. Voit siis käyttää sitä eri toimintatapojen kanssa salausjärjestelmien rakentamiseen.
NIST-kilpailun komitea hyväksyi Rijndaelin salakirjoituksen rajoitetun version, joka edellyttää 128-bittistä lohkokokoa ja joko 128, 192 tai 256 bitin pituisia avaimia, osana Advanced Encryption Standard (AES) -standardia. Tätä rajoitettua versiota Rijndael-salauksesta voidaan käyttää myös useissa eri toimintatiloissa. Standardin määrittely on niin sanottu Advanced Encryption Standard (AES).
Näytän, miten Rijndael-salaus, joka on AES:n ydin, toimii, ja havainnollistan 128-bittisellä avaimella tapahtuvaa salausta. Avaimen koko vaikuttaa kunkin salauslohkon salauskierrosten määrään. 128-bittisille avaimille tarvitaan 10 kierrosta. 192- ja 256-bittisillä avaimilla kierroksia olisi ollut 12 ja 14.
Lisäksi oletan, että AES:ää käytetään ECB-tilassa. Tämä helpottaa hieman esitystä, eikä sillä ole merkitystä Rijndael-algoritmin kannalta. EKP-tila ei tosin ole käytännössä turvallinen, koska se johtaa deterministiseen salaukseen. Yleisimmin käytetty turvallinen tila AES:n kanssa on CBC (Cipher Block Chaining).
Kutsutaan avainta K_0.
Rakenne edellä mainituilla parametreilla näyttää siis kuvassa 1 esitetyltä, jossa M_i tarkoittaa 128 bitin pituista selväkielisen viestin osaa ja C_i 128 bitin pituista salatun
tekstin osaa. Selkotekstiin lisätään täytettä viimeisen lohkon osalta, jos selkotekstiä
ei voida jakaa tasan lohkokoolla.
Kuva 1: AES-ECB 128-bittisellä avaimella
Jokainen 128-bittinen tekstilohko käy läpi kymmenen kierrosta
Rijndael-salausjärjestelmässä. Tämä edellyttää erillistä kierrosavainta
jokaista kierrosta varten (K_1 - K_{10}). Nämä
tuotetaan jokaista kierrosta varten alkuperäisestä 128-bittisestä avaimesta K_0 käyttäen avainten laajentamisalgoritmia. Jokaista
salattavaa tekstilohkoa varten käytetään siis alkuperäistä avainta K_0 sekä kymmentä erillistä kierrosavainta.
Huomaa, että näitä samoja 11 avainta käytetään jokaiseen 128-bittiseen salattavaan
tekstilohkoon.
Avaimen laajentamisalgoritmi on pitkä ja monimutkainen. Sen läpikäymisestä
on vain vähän didaktista hyötyä. Voit halutessasi käydä avaimen
laajentamisalgoritmin läpi yksin. Kun pyöreät avaimet on tuotettu,
Rijndael-salausohjelma muokkaa ensimmäistä 128-bittistä selkotekstilohkoa M_1, kuten Kuvassa 2 on esitetty. Käymme nyt läpi nämä vaiheet.
Kuva 2: M_1:n manipulointi
Rijndael-salauksella:
Kierros 0:
- XOR
M_1jaK_0tuottaaS_0
Rund n for n = {1,...,9}:
- XOR
S_{n-1}jaK_nXORS_{n-1}jaK_n - Tavun korvaaminen
- Vaihda rivejä
- Sekoita sarakkeet
- XOR
SjaK_ntuottaaS_n
Kierros 10:
- XOR
S_9jaK_{10} - Tavun korvaaminen
- Vaihda rivejä
- XOR
SjaK_{10}tuottavatS_{10} S_{10}=C_1
Kierros 0
Rijndael-salauksen 0-kierros on suoraviivainen. Joukko S_0 tuotetaan 128-bittisen selvätekstin ja yksityisen avaimen välisellä XOR-operaatiolla.
Toisin sanoen,
- $S_0 = M_1 \oplus K_0$$
Kierros 1
Kierroksella 1 yhdistetään ensin joukko S_0 ja kierroksen avain K_1 XOR-operaatiolla. Näin saadaan uusi tila S.
Toiseksi byte-korvausoperaatio suoritetaan S:n nykyiselle tilalle. Se
toimii ottamalla jokainen tavu 16 tavun S-massasta ja korvaamalla se
tavulla massasta nimeltä Rijndaelin S-laatikko. Jokaisella
tavulla on yksilöllinen muunnos, ja tuloksena saadaan S:n uusi tila. Rijndaelin
S-laatikko on esitetty Kuvassa 3.
Kuva 3: Rijndaelin S-Box
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 0A | 0B | 0C | 0D | 0E | 0F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 63 | 7C | 77 | 7B | F2 | 6B | 6F | C5 | 30 | 01 | 67 | 2B | FE | D7 | AB | 76 |
| 10 | CA | 82 | C9 | 7D | FA | 59 | 47 | F0 | AD | D4 | A2 | AF | 9C | A4 | 72 | C0 |
| 20 | B7 | FD | 93 | 26 | 36 | 3F | F7 | CC | 34 | A5 | E5 | F1 | 71 | D8 | 31 | 15 |
| 30 | 04 | C7 | 23 | C3 | 18 | 96 | 05 | 9A | 07 | 12 | 80 | E2 | EB | 27 | B2 | 75 |
| 40 | 09 | 83 | 2C | 1A | 1B | 6E | 5A | A0 | 52 | 3B | D6 | B3 | 29 | E3 | 2F | 84 |
| 50 | 53 | D1 | 00 | ED | 20 | FC | B1 | 5B | 6A | CB | BE | 39 | 4A | 4C | 58 | CF |
| 60 | D0 | EF | AA | FB | 43 | 4D | 33 | 85 | 45 | F9 | 02 | 7F | 50 | 3C | 9F | A8 |
| 70 | 51 | A3 | 40 | 8F | 92 | 9D | 38 | F5 | BC | B6 | DA | 21 | 10 | FF | F3 | D2 |
| 80 | CD | 0C | 13 | EC | 5F | 97 | 44 | 17 | C4 | A7 | 7E | 3D | 64 | 5D | 19 | 73 |
| 90 | 60 | 81 | 4F | DC | 22 | 2A | 90 | 88 | 46 | EE | B8 | 14 | DE | 5E | 0B | DB |
| A0 | E0 | 32 | 3A | 0A | 49 | 06 | 24 | 5C | C2 | D3 | AC | 62 | 91 | 95 | E4 | 79 |
| B0 | E7 | C8 | 37 | 6D | 8D | D5 | 4E | A9 | 6C | 56 | F4 | EA | 65 | 7A | AE | 08 |
| C0 | BA | 78 | 25 | 2E | 1C | A6 | B4 | C6 | E8 | DD | 74 | 1F | 4B | BD | 8B | 8A |
| D0 | 70 | 3E | B5 | 66 | 48 | 03 | F6 | 0E | 61 | 35 | 57 | B9 | 86 | C1 | 1D | 9E |
| E0 | E1 | F8 | 98 | 11 | 69 | D9 | 8E | 94 | 9B | 1E | 87 | E9 | CE | 55 | 28 | DF |
| F0 | 8C | A1 | 89 | 0D | BF | E6 | 42 | 68 | 41 | 99 | 2D | 0F | B0 | 54 | BB | 16 |
Tämä S-Box on yksi paikka, jossa abstrakti algebra tulee mukaan Rijndaelin salakirjoitukseen, erityisesti Galois-kentät.
Aluksi määritellään jokainen mahdollinen tavuelementti 00-FF 8-bittiseksi
vektoriksi. Jokainen tällainen vektori on Galois-kentän GF(2^8) alkio, jossa modulo-operaation redusoimaton polynomi on x^8 + x^4 + x^3 + x + 1.
Galois-kenttää näillä määrittelyillä kutsutaan myös Rijndaelin äärelliseksi kentäksi.
Seuraavaksi luodaan jokaiselle kentän mahdolliselle elementille niin sanottu Nybergin S-laatikko. Tässä laatikossa kukin tavu kuvataan sen kertolaskulliseen käänteislukuun (eli siten, että niiden tulo on yhtä suuri kuin 1). Tämän jälkeen nämä arvot siirretään Nybergin S-laatikosta Rijndaelin S-laatikkoon affiinimuunnoksen avulla.
Kolmas operaatio S-joukolle on operaatio rivien siirto. Se ottaa S:n tilan ja listaa kaikki kuusitoista tavua matriisiksi. Matriisin täyttäminen alkaa vasemmasta yläkulmasta ja etenee ylhäältä alaspäin ja siirtää sitten aina sarakkeen täyttyessä sarakkeen oikealle ja ylöspäin.
Kun S-matriisi on muodostettu, neljä riviä siirretään. Ensimmäinen rivi pysyy samana. Toinen rivi siirtyy yhden rivin verran vasemmalle. Kolmas rivi siirtyy kaksi riviä vasemmalle. Neljäs rivi siirtää kolme riviä vasemmalle. Esimerkki prosessista on esitetty Kuvassa 4. Ylhäällä on esitetty S:n alkuperäinen tila ja sen alapuolella on esitetty tulostila rivien siirto-operaation jälkeen.
Kuva 4: Rivien siirtäminen
| F1 | A0 | B1 | 23 |
|---|---|---|---|
| 59 | EF | 09 | 82 |
| 97 | 01 | B0 | CC |
| D4 | 72 | 04 | 21 |
| F1 | A0 | B1 | 23 |
|---|---|---|---|
| EF | 09 | 82 | 59 |
| B0 | CC | 97 | 01 |
| 21 | D4 | 72 | 04 |
Neljännessä vaiheessa Galois-kentät tulevat jälleen esiin.
Aluksi S-matriisin jokainen sarake kerrotaan Kuvassa 5 olevan 4 x 4 -matriisin sarakkeella. Mutta sen sijaan, että kyseessä olisi
tavallinen matriisikertolasku, kyseessä on vektorikertolasku modulo redusoimaton polynomi, x^8 + x^4 + x^3 + x + 1.
Tuloksena saadut vektorikertoimet edustavat tavun yksittäisiä bittejä.
Kuva 5: Sekoitussarakkeiden matriisi
| 02 | 03 | 01 | 01 |
|---|---|---|---|
| 01 | 02 | 03 | 01 |
| 01 | 01 | 02 | 03 |
| 03 | 01 | 01 | 02 |
Kun S-matriisin ensimmäinen sarake kerrotaan edellä esitetyllä 4 x 4 -matriisilla, saadaan Kuvion 6 mukainen tulos.
Kuva 6: Ensimmäisen sarakkeen kertominen:
\begin{matrix}
02 \cdot F1 + 03 \cdot EF + 01 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 02 \cdot EF + 03 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 01 \cdot EF + 02 \cdot B0 + 03 \cdot 21 \\
03 \cdot F1 + 01 \cdot EF + 01 \cdot B0 + 02 \cdot 21
\end{matrix}Seuraavassa vaiheessa kaikki matriisin termit olisi muutettava polynomeiksi.
Esimerkiksi F1 edustaa yhtä tavua, ja siitä tulisi x^7 + x^6 + x^5 + x^4 + 1, ja 03 edustaa yhtä tavua, ja siitä tulisi x + 1.
Kaikki kertolaskut suoritetaan sitten modulo x^8 + x^4 + x^3 + x + 1.
Tuloksena on neljän polynomin yhteenlasku sarakkeen jokaisessa neljässä
solussa. Kun nämä yhteenlaskut on suoritettu modulo 2,
saadaan neljä polynomia. Kukin näistä polynomeista edustaa 8-bittistä
merkkijonoa eli yhtä tavua S. Emme suorita kaikkia näitä
laskutoimituksia tässä Kuvan 6 matriisille, koska ne ovat laajoja.
Kun ensimmäinen sarake on käsitelty, S-matriisin kolme muuta saraketta käsitellään samalla tavalla. Lopulta tuloksena on kuusitoista tavua sisältävä matriisi, joka voidaan muuntaa matriisiksi.
Viimeisenä vaiheena yhdistetään joukko S ja pyöreä avain
uudelleen XOR-operaatiossa. Näin saadaan tila S_1. Toisin sanoen,
S_1 = S \oplus K_0S_1 = S \oplus K_0
Kierrokset 2-10
Kierrokset 2-9 ovat vain kierroksen 1 toistoa, mutatis mutandis. Viimeinen kierros on hyvin samanlainen kuin edelliset kierrokset, paitsi että sarakkeiden sekoittaminen on poistettu. Toisin sanoen kierros 10 suoritetaan seuraavasti:
S_9 \oplus K_{10}- Tavun korvaaminen
- Vaihda rivejä
S_{10} = S \oplus K_{10}
Tilaan S_{10} asetetaan nyt C_1, joka on
salaustekstin 128 ensimmäistä bittiä. Käymällä läpi loput 128-bittiset
selkotekstilohkot saadaan täysi salausteksti C.
Rijndael-salauksen operaatiot
Mikä on Rijndaelin salakirjoituksessa esiintyvien eri operaatioiden syy?
Menemättä yksityiskohtiin, salausjärjestelmiä arvioidaan sen perusteella, missä määrin ne aiheuttavat sekaannusta ja leviämistä. Jos salausjärjestelmässä on korkea salausaste, se tarkoittaa, että salattu teksti näyttää huomattavasti erilaiselta kuin selkoteksti. Jos salausjärjestelmässä on suuri diffuusioaste, se tarkoittaa, että mikä tahansa pieni muutos selkotekstiin tuottaa täysin erilaisen salatekstin.
Rijndael-salauksen taustalla olevat operaatiot perustuvat siihen, että ne tuottavat sekä suurta sekaannusta että hajontaa. Sekaannus syntyy tavun vaihto-operaatiosta, kun taas hajonta syntyy rivien siirto- ja sarakkeiden sekoitusoperaatioista.
Epäsymmetrinen salaus
Avainten jakelu- ja hallintaongelma
Kuten symmetrisessä salauksessa, myös epäsymmetrisillä järjestelmillä voidaan varmistaa sekä salassapito että todentaminen. Sen sijaan näissä järjestelmissä käytetään yhden sijaan kahta avainta: yksityistä ja julkista avainta.
Aloitamme tutkimuksemme epäsymmetrisen salakirjoituksen keksimisestä ja erityisesti ongelmista, jotka ovat antaneet siihen sysäyksen. Seuraavaksi keskustelemme siitä, miten epäsymmetriset salaus- ja todentamisjärjestelmät toimivat korkealla tasolla. Sen jälkeen esittelemme hash-funktiot, jotka ovat avainasemassa epäsymmetristen todennusjärjestelmien ymmärtämisessä ja joilla on merkitystä myös muissa kryptografisissa yhteyksissä, kuten luvussa 4 käsitellyissä hash-pohjaisissa viestien todennuskoodeissa.
Oletetaan, että Bob haluaa ostaa uuden sadetakin Jim's Sporting Goodsilta, urheiluvälineiden verkkokaupasta, jolla on miljoonia asiakkaita Pohjois-Amerikassa. Tämä on hänen ensimmäinen ostoksensa ja hän haluaa käyttää luottokorttiaan. Bobin on siis ensin luotava tili Jim's Sporting Goodsille, mikä edellyttää henkilökohtaisten tietojen, kuten osoitteen ja luottokorttitietojen, lähettämistä. Sen jälkeen hän voi käydä läpi sadetakin ostamiseen tarvittavat vaiheet.
Bob ja Jim's Sporting Goods haluavat varmistaa, että niiden viestintä on turvallista koko prosessin ajan, koska Internet on avoin viestintäjärjestelmä. He haluavat esimerkiksi varmistaa, ettei kukaan mahdollinen hyökkääjä saa selville Bobin luottokortti- ja osoitetietoja eikä kukaan mahdollinen hyökkääjä voi toistaa hänen ostoksiaan tai luoda väärennettyjä ostoksia hänen puolestaan.
Edellisessä luvussa käsitelty kehittynyt todennettu salausjärjestelmä voisi varmasti turvata Bobin ja Jim's Sporting Goodsin välisen viestinnän. Tällaisen järjestelmän toteuttamiselle on kuitenkin selviä käytännön esteitä.
Näiden käytännön esteiden havainnollistamiseksi oletetaan, että eläisimme maailmassa, jossa olisi olemassa vain symmetrisen salauksen välineitä. Mitä Jim's Sporting Goods ja Bob voisivat tehdä varmistaakseen turvallisen viestinnän?
Näissä olosuhteissa niille aiheutuisi huomattavia kustannuksia turvallisesta viestinnästä. Koska Internet on avoin viestintäjärjestelmä, ne eivät voi vain vaihtaa siellä avaimia. Näin ollen Bobin ja Jim's Sporting Goodsin edustajan on vaihdettava avaimet henkilökohtaisesti.
Yksi mahdollisuus on, että Jim's Sporting Goods luo erityisiä avaintenvaihtopaikkoja, joista Bob ja muut uudet asiakkaat voivat hakea avainsarjan turvallista viestintää varten. Tämä aiheuttaisi tietenkin huomattavia organisatorisia kustannuksia ja vähentäisi huomattavasti tehokkuutta, jolla uudet asiakkaat voivat tehdä ostoksia.
Vaihtoehtoisesti Jim's Sporting Goods voi lähettää Bobille avainparin erittäin luotettavan kuriirin välityksellä. Tämä on todennäköisesti tehokkaampaa kuin avaintenvaihtopaikkojen järjestäminen. Tästä aiheutuisi kuitenkin huomattavia kustannuksia, varsinkin jos monet asiakkaat tekevät vain yhden tai muutaman ostoksen.
Seuraavaksi symmetrinen järjestelmä todennettua salausta varten pakottaa myös Jim's Sporting Goodsin tallentamaan erilliset avainsarjat kaikille asiakkailleen. Tämä olisi huomattava käytännön haaste tuhansille asiakkaille, miljoonista asiakkaista puhumattakaan.
Jälkimmäisen kohdan ymmärtämiseksi oletetaan, että Jim's Sporting Goods antaa jokaiselle asiakkaalle saman avainparin. Näin jokainen asiakas - tai kuka tahansa muu, joka saisi tämän avainparin haltuunsa - voisi lukea ja jopa manipuloida kaikkea Jim's Sporting Goodsin ja sen asiakkaiden välistä viestintää. Voit siis yhtä hyvin olla käyttämättä salausta viestinnässäsi lainkaan.
Jopa avainsarjan toistaminen vain joillekin asiakkaille on kauhea turvallisuuskäytäntö. Kuka tahansa mahdollinen hyökkääjä voisi yrittää hyödyntää tätä järjestelmän ominaisuutta (muista, että hyökkääjien oletetaan Kerckhoffin periaatteen mukaisesti tietävän järjestelmästä kaiken muun paitsi avaimet)
Jim's Sporting Goods joutuisi siis tallentamaan avainparin jokaiselle asiakkaalle riippumatta siitä, miten nämä avainparit on jaettu. Tämä aiheuttaa selvästi useita käytännön ongelmia.
- Jim's Sporting Goods joutuisi varastoimaan miljoonia avainpareja, yksi sarja jokaiselle asiakkaalle.
- Nämä avaimet olisi suojattava asianmukaisesti, sillä ne olisivat varma kohde hakkereille. Turvallisuusrikkomukset edellyttäisivät kalliita avaintenvaihtoja joko erityisissä avaintenvaihtopaikoissa tai kuriiripalvelun välityksellä.
- Jokaisen Jim's Sporting Goodsin asiakkaan olisi säilytettävä avainparia turvallisesti kotona. Häviöitä ja varkauksia tapahtuu, mikä edellyttää avainten toistuvaa vaihtamista. Asiakkaat joutuisivat käymään tämän prosessin läpi myös kaikkien muiden verkkokauppojen tai muunlaisten tahojen kanssa, joiden kanssa he haluavat kommunikoida ja käydä kauppaa Internetin välityksellä.
Nämä kaksi edellä kuvattua päähaastetta olivat hyvin perustavanlaatuisia huolenaiheita 1970-luvun lopulle asti. Ne tunnettiin nimillä avainten jakeluongelma ja avainten hallintaongelma.
Nämä ongelmat ovat tietenkin aina olleet olemassa, ja ne ovat usein aiheuttaneet päänvaivaa aiemmin. Esimerkiksi sotilasjoukkojen oli jatkuvasti jaettava kenttähenkilökunnalle kirjoja, joissa oli avaimet turvalliseen viestintään, suurella riskillä ja suurilla kustannuksilla. Ongelmat olivat kuitenkin pahenemassa, kun maailma oli siirtymässä yhä enemmän digitaaliseen kaukoviestintään, erityisesti valtiosta riippumattomien tahojen osalta.
Jos näitä ongelmia ei olisi ratkaistu 1970-luvulla, tehokkaita ja turvallisia ostoksia Jim's Sporting Goodsissa ei todennäköisesti olisi ollut. Itse asiassa suurin osa nykyaikaisesta maailmastamme, jossa käytännöllinen ja turvallinen sähköpostiviestintä, verkkopankkitoiminta ja ostokset olisivat todennäköisesti vain kaukaista fantasiaa. Mitään edes Bitcoinia muistuttavaa ei olisi voinut olla olemassa lainkaan.
Mitä tapahtui 1970-luvulla? Miten on mahdollista, että voimme tehdä ostoksia välittömästi verkossa ja selata World Wide Webiä turvallisesti? Miten on mahdollista, että voimme lähettää bitcoineja ympäri maailmaa älypuhelimestamme?
Kryptografian uudet suuntaukset
1970-luvulle tultaessa avainten jakeluun ja hallintaan liittyvät ongelmat olivat kiinnittäneet amerikkalaisten akateemisten salauskirjailijoiden ryhmän huomion: Whitfield Diffie, Martin Hellman ja Ralph Merkle. Vaikka suurin osa heidän kollegoistaan suhtautui asiaan erittäin epäilevästi, he uskaltautuivat kehittämään ratkaisun.
Ainakin yksi tärkeimmistä motiiveista heidän yritykselleen oli ennakointi siitä, että avoin tietokoneviestintä vaikuttaisi syvällisesti maailmaamme. Kuten Diffie ja Helmann totesivat vuonna 1976,
Tietokoneohjattujen viestintäverkkojen kehittyminen lupaa vaivattoman ja edullisen yhteydenpidon eri puolilla maailmaa olevien ihmisten tai tietokoneiden välillä, mikä korvaa suurimman osan postista ja monet retket televiestinnällä. Monissa sovelluksissa nämä yhteydet on suojattava sekä salakuuntelulta että laittomien viestien lähettämiseltä. Tällä hetkellä tietoturvaongelmien ratkaiseminen on kuitenkin huomattavasti jäljessä muista viestintätekniikan aloista. Nykyinen kryptografia ei pysty täyttämään vaatimuksia, koska sen käyttö aiheuttaisi niin vakavia haittoja järjestelmän käyttäjille, että monet etäkäsittelyn eduista jäisivät pois. [1]
Diffien, Hellmanin ja Merklen sitkeys kannatti. Ensimmäinen julkaisu heidän tuloksistaan oli Diffien ja Helmannin vuonna 1976 julkaisema artikkeli "New Directions in Cryptography" Siinä he esittivät kaksi omaperäistä tapaa ratkaista avainjakelu- ja avainhallintaongelmat.
Ensimmäinen heidän tarjoamansa ratkaisu oli etäkäyttöön tarkoitettu avaintenvaihtoprotokolla, eli joukko sääntöjä yhden tai useamman symmetrisen avaimen vaihtamiseksi turvattomalla viestintäkanavalla. Tämä protokolla tunnetaan nykyään nimellä Diffie-Helmann-avaimenvaihto tai Diffie-Helmann-Merkle-avaimenvaihto. [2]
Diffie-Helmann-avaintenvaihdossa kaksi osapuolta vaihtaa ensin julkisesti tietoja turvattomalla kanavalla, kuten Internetissä. Näiden tietojen perusteella he luovat sitten itsenäisesti symmetrisen avaimen (tai symmetrisen avainparin) turvallista viestintää varten. Vaikka molemmat osapuolet luovat avaimensa itsenäisesti, niiden julkisesti jakamat tiedot varmistavat, että avaimen luomisprosessi tuottaa molemmille saman tuloksen.
Tärkeää on, että vaikka kaikki voivat tarkkailla tietoja, joita osapuolet vaihtavat julkisesti turvattomalla kanavalla, vain kaksi tiedonvaihtoon osallistuvaa osapuolta voi luoda niistä symmetrisiä avaimia.
Tämä kuulostaa tietysti täysin intuition vastaiselta. Miten kaksi osapuolta voisi vaihtaa julkisesti tietoja, joista vain he voisivat luoda symmetrisiä avaimia? Miksi kukaan muu tiedonvaihtoa tarkkaileva ei voisi luoda samoja avaimia?
Se perustuu tietysti kauniiseen matematiikkaan. Diffie-Helmann-avaimenvaihto toimii yksisuuntaisella funktiolla, jossa on luukku. Keskustellaan näiden kahden termin merkityksestä vuorotellen.
Oletetaan, että sinulle annetaan jokin funktio f(x) ja tulos f(a) = y, jossa a on tietty arvo x:lle.
Sanomme, että f(x) on yksisuuntainen funktio, jos arvo y on helppo laskea, kun annetaan a ja f(x), mutta arvon a laskeminen, kun annetaan y ja f(x), on laskennallisesti
mahdotonta. Nimi yksiisuuntainen funktio johtuu tietenkin siitä,
että tällainen funktio on käytännöllistä laskea vain yhteen suuntaan.
Joissakin yksisuuntaisissa funktioissa on niin sanottu loukkuovi. Vaikka a:n laskeminen on
käytännössä mahdotonta, kun tiedossa on vain y ja f(x), on olemassa tietty
tieto Z, joka tekee a:n laskemisen y:stä laskennallisesti
mahdolliseksi. Tämä tieto Z tunnetaan nimellä loukkuovi. Yksisuuntaisia funktioita,
joilla on ansaportti, kutsutaan ansaporttifunktioiksi.
Emme syvenny tässä Diffie-Helmann-avaimenvaihdon yksityiskohtiin. Mutta periaatteessa jokainen osallistuja luo tietoa, josta osa jaetaan julkisesti ja osa pysyy salassa. Kumpikin osallistuja luo sitten salaisen tietonsa ja toisen osallistujan jakaman julkisen tiedon avulla yksityisen avaimen. Ja hieman ihmeellisesti molemmilla osapuolilla on lopulta sama yksityinen avain.
Kuka tahansa osapuoli, joka tarkkailee Diffie Helmann -avaintenvaihdon kahden osapuolen välisiä julkisesti jaettuja tietoja, ei pysty jäljentämään näitä laskelmia. Se tarvitsisi siihen jommankumman osapuolen yksityiset tiedot.
Vaikka Diffie-Helmannin avaintenvaihdon perusversio, joka esiteltiin vuonna 1976 julkaistussa artikkelissa, ei ole kovin turvallinen, perusprotokollan kehittyneempiä versioita käytetään varmasti yhä nykyäänkin. Tärkeintä on, että kaikki avaintenvaihtoprotokollat siirtokerroksen tietoturvaprotokollan uusimmassa versiossa (versio 1.3) ovat olennaisesti parannettu versio Diffien ja Hellmanin vuonna 1976 esittämästä protokollasta. Kuljetuskerroksen tietoturvaprotokolla on pääasiallinen protokolla, jolla vaihdetaan turvallisesti http-protokollan (hypertext transfer protocol) mukaisesti muotoiltuja tietoja. http on web-sisällön vaihdon standardi.
On tärkeää, että Diffie-Helmann-avainten vaihto ei ole epäsymmetrinen järjestelmä. Tarkkaan ottaen se kuuluu luultavasti symmetrisen avaimen salauksen piiriin. Mutta koska sekä Diffie-Helmannin avainten vaihto että epäsymmetrinen salaus perustuvat yksisuuntaisiin numeroteoreettisiin funktioihin, joissa on luukut, niitä käsitellään yleensä yhdessä.
Toinen tapa, jolla Diffie ja Helmann tarjosivat ratkaisua avainten jakelu- ja hallintaongelmaan vuonna 1976 julkaistussa artikkelissaan, oli tietysti epäsymmetrinen salaus.
Toisin kuin Diffie-Hellmanin avaintenvaihtoa koskevassa esityksessä, he esittivät vain yleiset suuntaviivat siitä, miten epäsymmetrisiä salausjärjestelmiä voitaisiin rakentaa. He eivät tarjonneet mitään yksisuuntaista funktiota, joka voisi erityisesti täyttää ehdot, joita tarvitaan tällaisten järjestelmien kohtuulliseen turvallisuuteen.
Epäsymmetrisen järjestelmän käytännön toteutuksen löysi kuitenkin vuotta myöhemmin kolme eri akateemista salauskirjailijaa ja matemaatikkoa: Ronald Rivest, Adi Shamir ja Leonard Adleman. [3] Heidän esittämänsä salausjärjestelmä tunnettiin nimellä RSA-kryptausjärjestelmä (heidän sukunimiensä mukaan).
Epäsymmetrisessä salauksessa (ja Diffie-Helmann-avainten vaihdossa) käytetyt trapdoor-funktiot liittyvät kaikki kahteen tärkeimpään laskennallisesti vaikeaan ongelmaan: alkulukujen kertolaskuun ja diskreettien logaritmien laskemiseen.
Primitekijöihin jakaminen edellyttää, kuten nimikin kertoo, kokonaisluvun jakamista sen alkutekijöihin. RSA-ongelma on ylivoimaisesti tunnetuin esimerkki primfaktorointiin liittyvästä salausjärjestelmästä.
Diskreetin logaritmin ongelma on ongelma, joka esiintyy syklisissä ryhmissä. Kun tietyn syklisen ryhmän generaattori on annettu, on laskettava yksikäsitteinen eksponentti, joka tarvitaan, jotta generaattorista saadaan toinen ryhmän alkio.
Diskreettiin logaritmiin perustuvat järjestelmät tukeutuvat kahdenlaisiin syklisiin ryhmiin: kokonaislukujen multiplikatiivisiin ryhmiin ja ryhmiin, jotka sisältävät elliptisten käyrien pisteitä. Alkuperäinen Diffie-Helmann-avaimenvaihto, joka esiteltiin kirjassa "New Directions in Cryptography", toimii syklisellä kokonaislukujen multiplikatiivisella ryhmällä. Bitcoinin digitaalinen allekirjoitusalgoritmi ja hiljattain esitelty Schnorrin allekirjoitusjärjestelmä (2021) perustuvat molemmat diskreetin logaritmin ongelmaan tietylle elliptisen käyrän sykliselle ryhmälle.
Seuraavaksi luodaan yleiskatsaus salassapitoon ja todentamiseen epäsymmetrisessä ympäristössä. Sitä ennen meidän on kuitenkin tehtävä lyhyt historiallinen huomautus.
Nyt vaikuttaa uskottavalta, että ryhmä brittiläisiä salakirjoittajia ja matemaatikkoja, jotka työskentelivät GCHQ:n (Government Communications Headquarters) palveluksessa, oli itsenäisesti tehnyt edellä mainitut löydöt muutamaa vuotta aiemmin. Tähän ryhmään kuuluivat James Ellis, Clifford Cocks ja Malcolm Williamson.
Heidän ja GCHQ:n omien kertomusten mukaan James Ellis kehitti ensimmäisenä julkisen avaimen salauksen käsitteen vuonna 1969. Oletettavasti Clifford Cocks keksi RSA-salausjärjestelmän vuonna 1973 ja Malcolm Williamson Diffie Helmann -avaintenvaihdon vuonna 1974. [4] Heidän löytönsä paljastettiin kuitenkin tiettävästi vasta vuonna 1997, koska GCHQ:ssa tehty työ oli salaista.
Huomautukset:
[1] Whitfield Diffie ja Martin Hellman, "New directions in cryptography", IEEE Transactions on Information Theory IT-22 (1976), s. 644-654, s. 644.
[2] Ralph Merkle käsittelee avaintenvaihtoprotokollaa myös teoksessa "Secure communications over insecure channels",Communications of the Association for Computing Machinery, 21 (1978), 294-99. Merkle toimitti tämän artikkelin ennen Diffien ja Hellmanin artikkelia, mutta se julkaistiin myöhemmin. Merklen ratkaisu ei ole eksponentiaalisesti turvallinen, toisin kuin Diffie-Hellmanin ratkaisu.
[3] Ron Rivest, Adi Shamir ja Leonard Adleman, "A method for obtaining digital signatures and public-key cryptosystems", Communications of the Association for Computing Machinery, 21 (1978), s. 120-26.
[4] Simon Singh, The Code Book, Fourth Estate (Lontoo, 1999), luku 6, tarjoaa hyvän historian näistä löydöistä.
Epäsymmetrinen salaus ja todentaminen
Kuvassa 1 esitetään yleiskatsaus symmetriseen salaukseen Bobin ja Alicen avulla.
Alice luo ensin avainparin, joka koostuu yhdestä julkisesta avaimesta (K_P) ja yhdestä yksityisestä avaimesta (K_S), jossa K_P:n "P"
tarkoittaa "julkista" ja K_S:n "S" tarkoittaa
"salaista". Tämän jälkeen hän jakaa tätä julkista avainta vapaasti muille.
Palaamme tämän jakeluprosessin yksityiskohtiin hieman myöhemmin. Mutta nyt
oletetaan, että kuka tahansa, myös Bob, voi turvallisesti saada Alicen
julkisen avaimen K_P.
Jossain myöhemmässä vaiheessa Bob haluaa kirjoittaa viestin M Alicelle. Koska se sisältää arkaluonteista tietoa, hän haluaa, että sen
sisältö pysyy salassa kaikilta muilta paitsi Alicelta. Bob siis salaa ensin
viestinsä M käyttäen K_P. Sitten hän lähettää
tuloksena syntyneen salatekstin C Alicelle, joka purkaa C:n
salakirjoituksen K_S:llä ja
saa alkuperäisen viestin M.
Kuva 1: Epäsymmetrinen salaus
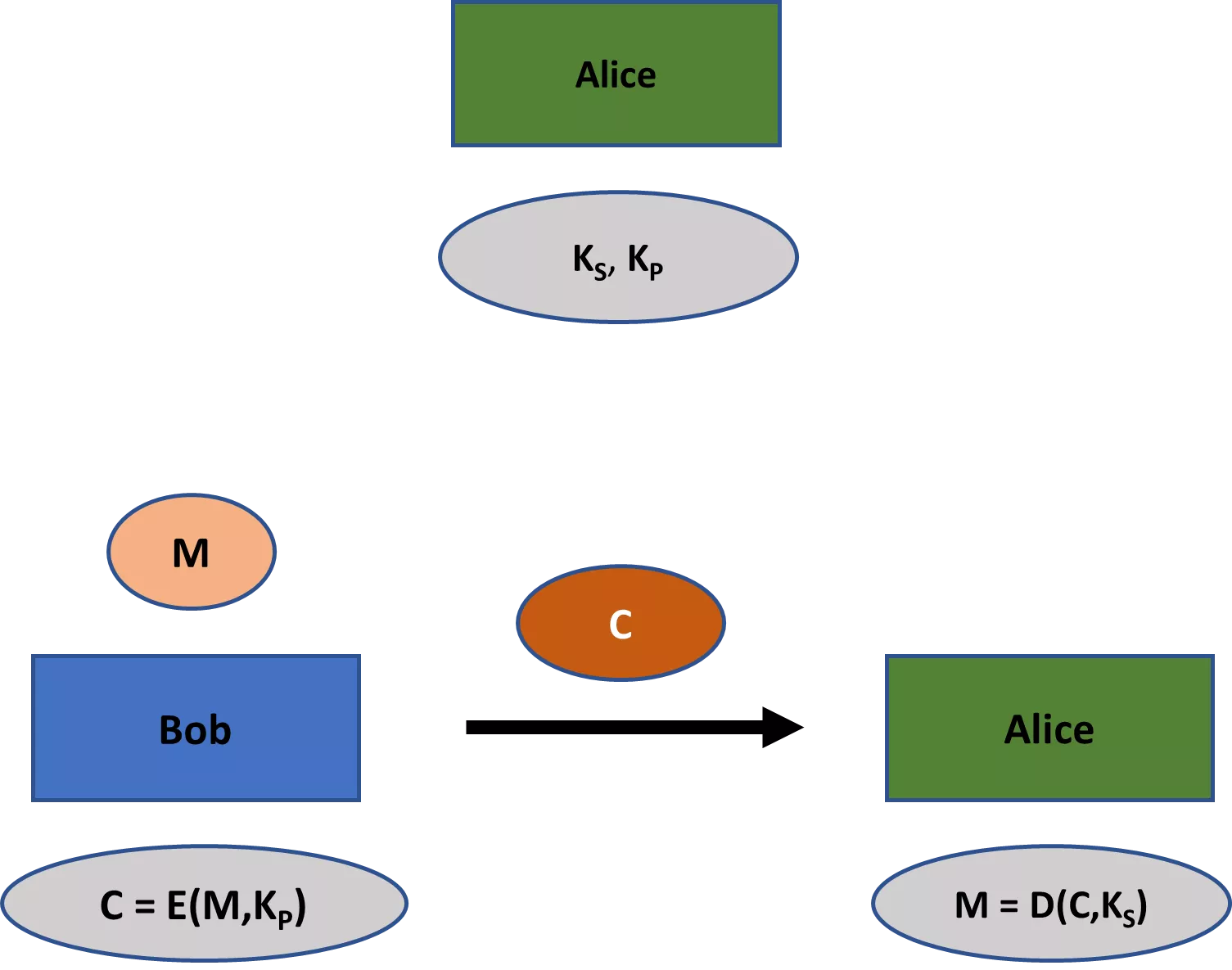
Jokainen Bobin ja Alicen viestintää kuunteleva vastustaja voi havaita C:n. Hän tietää myös K_P ja
salausalgoritmin E(\cdot).
Tärkeää on kuitenkin se, että hyökkääjä ei voi näiden tietojen avulla
helposti purkaa salatekstiä C. Salakirjoituksen
purkaminen edellyttää erityisesti K_S, jota hyökkääjällä ei
ole.
Symmetristen salausjärjestelmien on yleensä oltava turvallisia hyökkääjää vastaan, joka voi salata selkotekstiviestejä pätevästi (niin sanottu valitun salakirjoitustekstin hyökkäyksen turvallisuus). Järjestelmää ei kuitenkaan ole suunniteltu nimenomaisesti siten, että hyökkääjä tai joku muu voisi luoda tällaisia kelvollisia salaustekstejä.
Tämä on jyrkässä ristiriidassa epäsymmetrisen salausjärjestelmän kanssa, jonka tarkoituksena on antaa kenen tahansa, myös hyökkääjien, tuottaa kelvollisia salaustekstejä. Epäsymmetrisiä salausjärjestelmiä voidaan siksi kutsua monilukuisiksi salakirjoituksiksi.
Jotta ymmärtäisit paremmin, mitä tapahtuu, kuvittele, että sähköisen viestin sijaan Bob haluaisi lähettää fyysisen kirjeen salassa. Yksi tapa varmistaa salassapito olisi se, että Alice lähettäisi Bobille turvallisen riippulukon, mutta säilyttäisi avaimen, jolla lukko avataan. Kirjoitettuaan kirjeen Bob voisi laittaa kirjeen laatikkoon ja sulkea sen Alicen riippulukolla. Sitten hän voisi lähettää lukitun laatikon ja viestin Alicelle, jolla on avain lukon avaamiseen.
Vaikka Bob pystyy lukitsemaan riippulukon, hän tai kukaan muu laatikon sieppaava henkilö ei voi avata riippulukkoa, jos se on todella lukittu. Vain Alice voi avata lukon ja nähdä Bobin kirjeen sisällön, koska hänellä on avain.
Epäsymmetrinen salausjärjestelmä on karkeasti ottaen digitaalinen versio tästä prosessista. Lukko on kuin julkinen avain ja lukkoavain on kuin yksityinen avain. Koska riippulukko on kuitenkin digitaalinen, Alicen on paljon helpompi ja edullisempi jakaa se kaikille, jotka haluavat lähettää hänelle salaisia viestejä.
Epäsymmetrisessä ympäristössä käytämme todentamiseen digitaalisia allekirjoituksia. Näillä on siis sama tehtävä kuin symmetrisessä ympäristössä käytettävillä viestin todentamiskoodeilla. Yleiskuva digitaalisista allekirjoituksista on esitetty Kuvassa 2.
Bob luo ensin avainparin, joka koostuu julkisesta avaimesta (K_P) ja yksityisestä avaimesta (K_S), ja jakaa julkisen avaimensa. Kun hän haluaa lähettää todennetun viestin
Alicelle, hän luo ensin viestinsä M ja yksityisen avaimensa avulla digitaalisen allekirjoituksen D. Tämän jälkeen Bob lähettää
Alicelle viestinsä ja digitaalisen allekirjoituksen.
Alice lisää viestin, julkisen avaimen ja digitaalisen allekirjoituksen Varmennusalgoritmiin. Algoritmi tuottaa joko todellisen, jos allekirjoitus on pätevä, tai väärän, jos allekirjoitus on virheellinen.
Digitaalinen allekirjoitus on, kuten nimestä käy selvästi ilmi, kirjallinen allekirjoitus, joka vastaa kirjeitä, sopimuksia ja niin edelleen. Itse asiassa digitaalinen allekirjoitus on yleensä paljon turvallisempi. Kirjallisen allekirjoituksen voi väärentää pienellä vaivalla, ja tätä prosessia helpottaa se, että kirjallisia allekirjoituksia ei useinkaan tarkisteta tarkasti. Turvallinen digitaalinen allekirjoitus on kuitenkin, aivan kuten turvallinen viestin todentamiskoodi, olemassa oleva väärentämätön: eli turvallisessa digitaalisessa allekirjoitusjärjestelmässä kukaan ei voi luoda allekirjoitusta viestille, joka läpäisee todentamismenettelyn, ellei hänellä ole yksityistä avainta.
Kuva 2: Epäsymmetrinen todennus
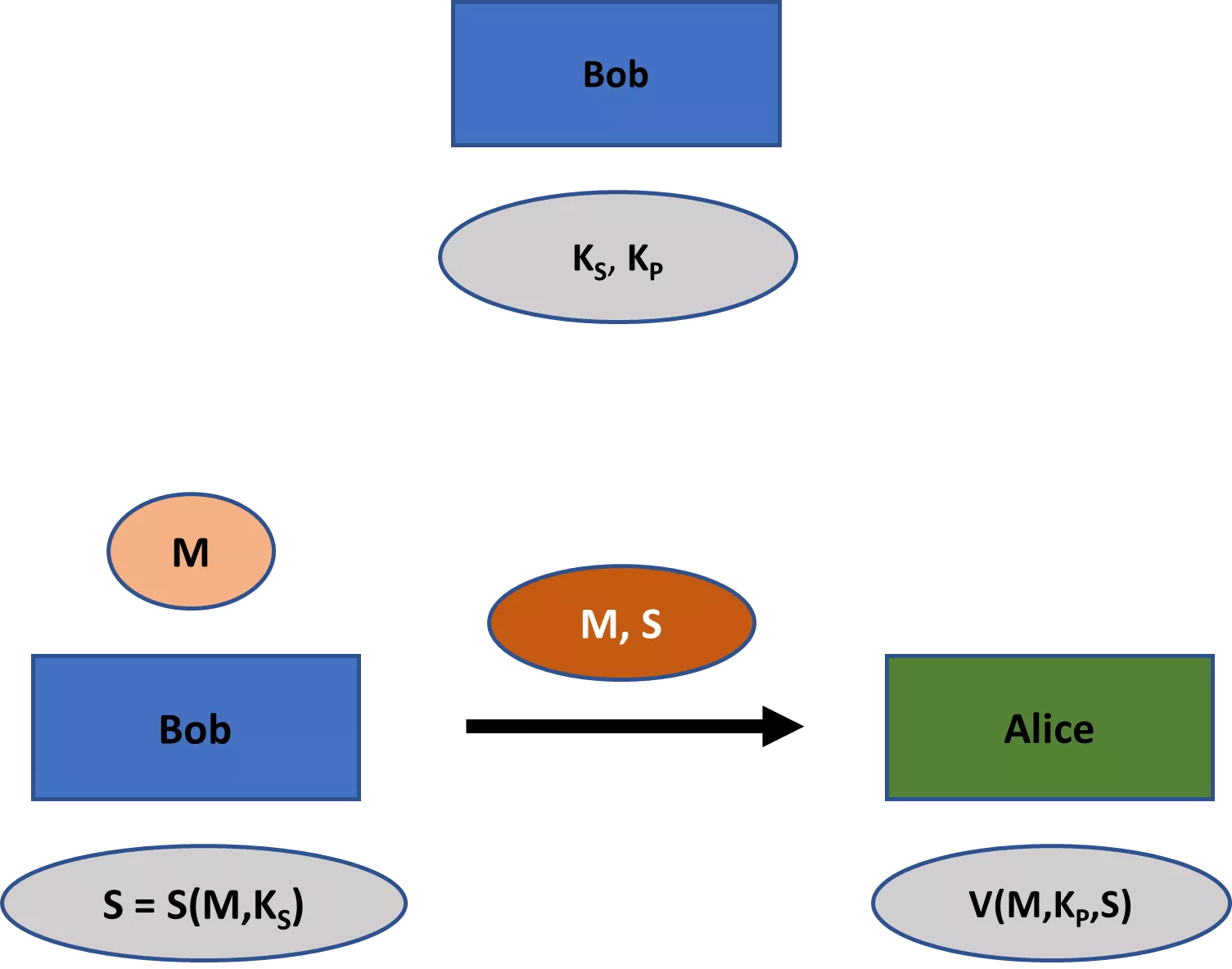
Kuten epäsymmetrisen salauksen kohdalla, myös digitaalisten allekirjoitusten
ja viestin todentamiskoodien välillä on mielenkiintoinen ero. Jälkimmäisessä
tapauksessa todentamisalgoritmia voi käyttää vain toinen suojatun viestinnän
osapuolista. Tämä johtuu siitä, että se edellyttää yksityistä avainta.
Epäsymmetrisessä ympäristössä kuka tahansa voi kuitenkin todentaa Bobin
tekemän digitaalisen allekirjoituksen S.
Kaikki tämä tekee digitaalisista allekirjoituksista erittäin tehokkaan
välineen. Sen avulla voidaan esimerkiksi luoda sopimuksiin allekirjoituksia,
jotka voidaan todentaa oikeudellisia tarkoituksia varten. Jos Bob olisi
allekirjoittanut sopimuksen edellä esitetyssä vaihdossa, Alice voi näyttää
viestin M, sopimuksen ja
allekirjoituksen S tuomioistuimelle.
Tuomioistuin voi sitten todentaa allekirjoituksen Bobin julkisen avaimen avulla.
[5]
Digitaaliset allekirjoitukset ovat esimerkiksi tärkeä osa turvallista ohjelmistojen ja ohjelmistopäivitysten jakelua. Tämäntyyppistä julkista todennettavuutta ei koskaan voitaisi luoda pelkillä viestin todennuskoodeilla.
Viimeinen esimerkki digitaalisten allekirjoitusten voimasta on Bitcoin. Yksi yleisimmistä Bitcoiniin liittyvistä väärinkäsityksistä, erityisesti tiedotusvälineissä, on se, että maksutapahtumat ovat salattuja: näin ei ole. Sen sijaan Bitcoin-tapahtumissa käytetään digitaalisia allekirjoituksia turvallisuuden varmistamiseksi.
Bitcoineja on olemassa erissä, joita kutsutaan nimellä unspent transaction outputs (tai UTXO:t). Oletetaan, että saat kolme maksua tiettyyn Bitcoin-osoitteeseen 2 bitcoinia kumpaankin. Teknisesti sinulla ei ole nyt 6 bitcoinia kyseisessä osoitteessa. Sen sijaan sinulla on kolme 2 bitcoinin erää, jotka on lukittu kyseiseen osoitteeseen liittyvän kryptografisen ongelman vuoksi. Mihin tahansa maksuun voit käyttää yhtä, kahta tai kaikkia kolmea näistä eristä riippuen siitä, kuinka paljon tarvitset maksutapahtumaan.
Käyttämättä jääneiden transaktiotulojen omistusoikeus osoitetaan yleensä yhdellä tai useammalla digitaalisella allekirjoituksella. Bitcoin toimii juuri siksi, että käyttämättömiä transaktiotuloksia koskevia kelvollisia digitaalisia allekirjoituksia on laskennallisesti mahdoton tehdä, ellei sinulla ole hallussasi niiden tekemiseen tarvittavia salaisia tietoja.
Tällä hetkellä Bitcoin-tapahtumat sisältävät läpinäkyvästi kaikki tiedot, jotka verkon osallistujien on varmennettava, kuten tapahtumassa käytettyjen käyttämättömien transaktiotulojen alkuperän. Vaikka osa näistä tiedoista on mahdollista piilottaa ja silti mahdollistaa todentaminen (kuten joissakin vaihtoehtoisissa kryptovaluutoissa, kuten Monerossa, tehdään), tämä aiheuttaa myös erityisiä turvallisuusriskejä.
Digitaaliset allekirjoitukset ja digitaalisesti tallennetut kirjalliset allekirjoitukset aiheuttavat joskus sekaannusta. Jälkimmäisessä tapauksessa otat kuvan kirjallisesta allekirjoituksestasi ja liität sen sähköiseen asiakirjaan, kuten työsopimukseen. Tämä ei kuitenkaan ole digitaalinen allekirjoitus kryptografisessa mielessä. Jälkimmäinen on vain pitkä numero, joka voidaan tuottaa vain, jos sinulla on hallussasi yksityinen avain.
Aivan kuten symmetrisen avaimen tapauksessa, voit käyttää myös epäsymmetristä salausta ja todentamismenetelmiä yhdessä. Samoja periaatteita sovelletaan. Ensinnäkin sinun pitäisi käyttää eri yksityisen ja julkisen avaimen pareja salaukseen ja digitaalisten allekirjoitusten tekemiseen. Lisäksi viesti pitäisi ensin salata ja sitten todentaa.
Tärkeää on, että monissa sovelluksissa epäsymmetristä salausta ei käytetä koko viestintäprosessin ajan. Sen sijaan sitä käytetään tyypillisesti vain symmetristen avainten vaihtamiseen osapuolten välillä, joiden avulla ne tosiasiallisesti kommunikoivat.
Näin on esimerkiksi silloin, kun ostat tavaroita verkosta. Myyjän julkisen avaimen tuntien hän voi lähettää sinulle digitaalisesti allekirjoitettuja viestejä, joiden aitouden voit tarkistaa. Tältä pohjalta voitte käyttää jotakin monista symmetristen avainten vaihtoon tarkoitetuista protokollista turvalliseen viestintään.
Tärkein syy edellä mainitun lähestymistavan yleistymiseen on se, että epäsymmetrinen kryptografia on paljon tehottomampi kuin symmetrinen kryptografia tietyn turvallisuustason saavuttamisessa. Tämä on yksi syy siihen, miksi tarvitsemme edelleen symmetrisen avaimen kryptografiaa julkisen kryptografian ohella. Lisäksi symmetrisen avaimen salaus on paljon luontevampaa tietyissä sovelluksissa, kuten tietokoneen käyttäjän salatessa omia tietojaan.
Miten digitaalisilla allekirjoituksilla ja julkisen avaimen salauksella ratkaistaan avainten jakeluun ja hallintaan liittyvät ongelmat?
Tähän ei ole yhtä vastausta. Epäsymmetrinen salaus on väline, eikä ole olemassa yhtä ainoaa tapaa käyttää sitä. Otetaan kuitenkin aiempi esimerkkimme Jim's Sporting Goodsista ja näytetään, miten ongelmat tyypillisesti ratkaistaisiin tässä esimerkissä.
Aluksi Jim's Sporting Goods lähestyisi luultavasti sertifiointiviranomaista eli organisaatiota, joka tukee julkisen avaimen jakelua. Varmentaja rekisteröisi joitakin Jim's Sporting Goodsin tietoja ja myöntäisi sille julkisen avaimen. Sitten se lähettäisi Jim's Sporting Goodsille varmenteen, joka tunnetaan nimellä TLS/SSL-varmenne ja jossa Jim's Sporting Goodsin julkinen avain on allekirjoitettu digitaalisesti käyttäen varmentajan omaa julkista avainta. Näin varmentaja vahvistaa, että tietty julkinen avain todellakin kuuluu Jim's Sporting Goodsille.
Tämän TLS/SSL-varmenteisiin liittyvän prosessin ymmärtämisen avain on se, että vaikka Jim's Sporting Goodsin julkista avainta ei yleensä ole tallennettu mihinkään tietokoneellesi, tunnustettujen varmenteiden myöntäjien julkiset avaimet on tallennettu selaimeesi tai käyttöjärjestelmääsi. Ne on tallennettu niin sanottuihin juurivarmenteisiin.
Kun Jim's Sporting Goods toimittaa sinulle TLS/SSL-varmenteensa, voit siis tarkistaa varmentajan digitaalisen allekirjoituksen selaimessasi tai käyttöjärjestelmässäsi olevan juurivarmenteen avulla. Jos allekirjoitus on voimassa, voit olla suhteellisen varma, että varmenteessa oleva julkinen avain todella kuuluu Jim's Sporting Goodsille. Tältä pohjalta on helppo luoda protokolla suojattua viestintää varten Jim's Sporting Goodsin kanssa.
Avainten jakelusta on nyt tullut huomattavasti yksinkertaisempaa Jim's Sporting Goodsille. Ei ole vaikea nähdä, että myös avainten hallinta on yksinkertaistunut huomattavasti. Sen sijaan, että Jim's Sporting Goodsin tarvitsisi säilyttää tuhansia avaimia, sen tarvitsee vain säilyttää yksityinen avain, jonka avulla se voi tehdä allekirjoituksia SSL-varmenteensa julkiselle avaimelle. Aina kun asiakas tulee Jim's Sporting Goodsin sivustolle, hän voi luoda suojatun viestintäistunnon tästä julkisesta avaimesta. Asiakkaiden ei myöskään tarvitse tallentaa mitään muita tietoja (kuin tunnustettujen varmentajien julkiset avaimet käyttöjärjestelmäänsä ja selaimeensa).
Huomautukset:
[5] Kaikkien järjestelmien, jotka pyrkivät saavuttamaan kiistämättömyyden, joka on toinen luvussa 1 käsittelemämme aihe, on perustuttava digitaalisiin allekirjoituksiin.
Hash-funktiot
Hash-funktiot ovat kaikkialla läsnä kryptografiassa. Ne eivät ole symmetrisiä eivätkä epäsymmetrisiä järjestelmiä, vaan kuuluvat omaan kryptografiseen luokkaansa.
Törmäsimme hash-funktioihin jo luvussa 4 hash-pohjaisten todennusviestien luomisen yhteydessä. Ne ovat tärkeitä myös digitaalisten allekirjoitusten yhteydessä, joskin hieman eri syystä: Digitaaliset allekirjoitukset nimittäin tehdään tyypillisesti jonkin (salatun) viestin hash-arvosta eikä varsinaisesta (salatusta) viestistä. Tässä luvussa esittelen hash-funktioita perusteellisemmin.
Aloitetaan määrittelemällä hash-funktio. Hash-funktio on mikä tahansa tehokkaasti laskettava funktio, joka ottaa mielivaltaisen kokoisia syötteitä ja tuottaa kiinteän pituisia ulostuloja.
kryptografinen hash-funktio on vain hash-funktio, joka on hyödyllinen salausohjelmissa. Kryptografisen hash-funktion tulosta kutsutaan tyypillisesti nimellä hash, hash-arvo tai viestin digesti.
Kryptografian yhteydessä "hash-funktiolla" tarkoitetaan yleensä kryptografista hash-funktiota. Tästä lähtien noudatan tätä käytäntöä.
Esimerkki suositusta hash-funktiosta on SHA-256 (secure hash algorithm 256). Riippumatta syötteen koosta (esim. 15 bittiä, 100 bittiä tai 10 000 bittiä) tämä funktio tuottaa 256-bittisen hash-arvon. Alla näet muutamia esimerkkejä SHA-256-funktion tuloksista.
"Hei": 185f8db32271fe25f561a6fc938b2e264306ec304eda518007d1764826381969
"52398": a3b14d2bf378c1bd47e7f8eaec63b445150a3d7a80465af16dd9fd319454ba90
"Kryptografia on hauskaa": 3cee2a5c7d2cc1d62db4893564c34ae553cc88623992d994e114e344359b146c
Kaikki ulostulot ovat täsmälleen 256 bittiä heksadesimaalimuodossa (jokainen heksaluku voidaan esittää neljällä binääriluvulla). Joten vaikka olisit lisännyt Tolkienin Sormusten herra -kirjan SHA-256-funktioon, tuloste olisi silti 256 bittiä.
SHA-256:n kaltaisia häivytysfunktioita käytetään salauksessa eri tarkoituksiin. Se, mitä ominaisuuksia hash-funktiolta vaaditaan, riippuu tietyn sovelluksen kontekstista. Kryptografiassa käytettäviltä hash-funktioilta halutaan yleensä kaksi pääominaisuutta: [6]
Törmäyksenkestävyys
Piilottelu
Hash-funktion H sanotaan
olevan törmäyskestävä, jos on mahdotonta löytää kahta
arvoa, x ja y, niin että x \neq y, mutta H(x) = H(y).
Törmäyksenkestävät hash-funktiot ovat tärkeitä esimerkiksi ohjelmistojen verifioinnissa. Oletetaan, että haluaisit ladata Windows-version Bitcoin Core 0.21.0:sta (palvelinsovellus Bitcoin-verkkoliikenteen käsittelyyn). Tärkeimmät vaiheet, jotka sinun pitäisi tehdä ohjelmiston laillisuuden todentamiseksi, ovat seuraavat:
Sinun on ensin ladattava ja tuotava yhden tai useamman Bitcoin Core -osallistujan julkiset avaimet ohjelmistoon, joka voi tarkistaa digitaalisia allekirjoituksia (esim. Kleopetra). Löydät nämä julkiset avaimet täältä. On suositeltavaa, että varmennat Bitcoin Core -ohjelmiston useiden avustajien julkisilla avaimilla.
Seuraavaksi sinun on tarkistettava tuodut julkiset avaimet. Ainakin yksi vaihe, joka sinun kannattaa tehdä, on tarkistaa, että löytämäsi julkiset avaimet ovat samoja kuin eri paikoissa julkaistut avaimet. Voit esimerkiksi tutustua niiden henkilöiden henkilökohtaisiin verkkosivuihin, Twitter-sivuihin tai Github-sivuihin, joiden julkiset avaimet olet tuonut. Tyypillisesti tämä julkisten avainten vertailu tehdään vertaamalla julkisen avaimen lyhyttä hash-arvoa, jota kutsutaan sormenjäljeksi.
Seuraavaksi sinun on ladattava Bitcoin Coren suoritettava ohjelma heidän verkkosivustoltaan. Tarjolla on paketteja Linux-, Windows- ja MAC-käyttöjärjestelmille.
Seuraavaksi sinun on löydettävä kaksi julkaisutiedostoa. Ensimmäinen sisältää lataamasi suoritettavan tiedoston virallisen SHA-256-hashin sekä kaikkien muiden julkaistujen pakettien hashit. Toinen julkaisutiedosto sisältää eri tekijöiden allekirjoitukset julkaisutiedoston yli pakettien hasheiden kanssa. Molempien julkaisutiedostojen pitäisi sijaita Bitcoin Core -sivustolla.
Seuraavaksi sinun on laskettava omalla tietokoneellasi Bitcoin Core -sivustolta ladatun suoritettavan tiedoston SHA-256-haaseri. Vertaat sitten tätä tulosta suoritettavan tiedoston virallisen paketin hashiin. Niiden pitäisi olla samat.
Lopuksi sinun on tarkistettava, että yksi tai useampi julkaisutiedoston digitaalinen allekirjoitus, jossa on virallisen paketin hashit, todellakin vastaa yhtä tai useampaa tuomasi julkista avainta (kaikki eivät aina allekirjoita Bitcoin Coren julkaisuja). Voit tehdä tämän Kleopetran kaltaisella sovelluksella.
Tällä ohjelmiston verifiointiprosessilla on kaksi pääasiallista etua. Ensinnäkin se varmistaa, että Bitcoin Coren verkkosivustolta ladattaessa ei ole tapahtunut lähetysvirheitä. Toiseksi se varmistaa, ettei kukaan hyökkääjä ole voinut saada sinua lataamaan muokattua, haitallista koodia joko murtautumalla Bitcoin Coren verkkosivustolle tai sieppaamalla liikennettä.
Miten edellä mainittu ohjelmiston verifiointiprosessi suojaa näiltä ongelmilta?
Jos olet huolellisesti tarkistanut tuodut julkiset avaimet, voit olla melko varma, että nämä avaimet ovat todella heidän avaimiaan eikä niitä ole vaarannettu. Koska digitaalisilla allekirjoituksilla on eksistentiaalinen väärentämättömyys, tiedät, että vain nämä tekijät ovat voineet tehdä digitaalisen allekirjoituksen julkaisutiedoston virallisten pakettien hashien päälle.
Oletetaan, että lataamasi julkaisutiedoston allekirjoitukset on tarkistettu. Voit nyt verrata paikallisesti lataamallesi Windows-ohjelmalle laskemaasi hash-arvoa oikein allekirjoitetun julkaisutiedoston sisältämään arvoon. Kuten tiedät, SHA-256-hash-funktio on kollion-kestävä, joten vastaavuus tarkoittaa, että suoritettava tiedostosi on täsmälleen sama kuin virallinen suoritettava tiedosto.
Siirrymme nyt toiseen hash-funktioiden yhteiseen ominaisuuteen: piilottaminen. Millä tahansa hash-funktiolla H sanotaan olevan kätkeytymisominaisuus, jos mille tahansa satunnaisesti
valitulle x:lle hyvin
laajasta alueesta on mahdotonta löytää x, kun annetaan vain H(x).
Alla näet kirjoittamani viestin SHA-256-tulosteen. Riittävän satunnaisuuden varmistamiseksi viestin lopussa oli satunnaisesti luotu merkkijono. Koska SHA-256:lla on piilotusominaisuus, kukaan ei pystyisi tulkitsemaan tätä viestiä.
b194221b37fa4cd1cfce15aaef90351d70de17a98ee6225088b523b586c32ded
En kuitenkaan jätä sinua odottamaan, kunnes SHA-256:sta tulee heikompi. Alkuperäinen viestini oli seuraava:
- "Tämä on hyvin sattumanvarainen viesti, tai ainakin tavallaan sattumanvarainen. Tämä alkuosa ei ole, mutta lopetan viestin muutamalla suhteellisen satunnaisella merkillä, jotta viesti olisi hyvin arvaamaton. XLWz4dVG3BxUWm7zQ9qS".
Yleinen tapa, jolla hash-funktioita, joilla on kätkemisominaisuus, käytetään salasanojen hallinnassa (törmäyskestävyys on tärkeää myös tässä sovelluksessa). Mikään kunnollinen tilipohjainen verkkopalvelu, kuten Facebook tai Google, ei tallenna salasanojasi suoraan tilisi hallintaa varten. Sen sijaan ne tallentavat vain salasanan hash-muodon. Joka kerta, kun syötät salasanasi selaimessa, ensin lasketaan hash. Vain tämä hash lähetetään palveluntarjoajan palvelimelle ja sitä verrataan taustatietokantaan tallennettuun hashiin. Piilotusominaisuuden avulla voidaan varmistaa, että hyökkääjät eivät voi palauttaa sitä hash-arvosta.
Salasanojen hallinta hashien avulla toimii tietysti vain, jos käyttäjät todella valitsevat vaikeat salasanat. Piilotusominaisuus edellyttää, että x valitaan satunnaisesti hyvin laajasta valikoimasta. Salasanojen, kuten "1234", "mypassword" tai syntymäpäiväsi valitseminen ei tarjoa todellista turvallisuutta. Yleisistä salasanoista ja niiden hasheista on olemassa pitkiä luetteloita, joita hyökkääjät voivat käyttää hyväkseen, jos he joskus saavat salasanasi hashin. Tämäntyyppisiä hyökkäyksiä kutsutaan sanakirja-hyökkäyksiksi. Jos hyökkääjät tietävät joitakin henkilökohtaisia tietojasi, he voivat myös yrittää arvailla tietoon perustuvia tietoja. Siksi tarvitset aina pitkiä ja turvallisia salasanoja (mieluiten pitkiä, satunnaisia merkkijonoja salasanahallinnasta).
Joskus sovellus saattaa tarvita hash-funktiota, jolla on sekä törmäysvarmuus että piilotettavuus. Mutta ei varmasti aina. Esimerkiksi käsittelemämme ohjelmistojen verifiointiprosessi edellyttää vain sitä, että hash-funktiolla on törmäysresistenssi, piilottaminen ei ole tärkeää.
Vaikka törmäyskestävyys ja piilottaminen ovat tärkeimmät ominaisuudet, joita hash-funktioilta haetaan kryptografiassa, tietyissä sovelluksissa myös muunlaiset ominaisuudet voivat olla toivottavia.
Huomautukset:
[6] "Piilottamisen" terminologia ei ole yleiskielistä, vaan se on otettu erityisesti Arvind Narayananin, Joseph Bonneaun, Edward Feltenin, Andrew Millerin ja Steven Goldfederin kirjasta Bitcoin and Cryptocurrency Technologies, Princeton University Press (Princeton, 2016), luku 1.
RSA-salausjärjestelmä
Faktorointiongelma
Vaikka symmetrinen salaus on useimmille ihmisille yleensä melko intuitiivista, epäsymmetrinen salaus ei yleensä ole sitä. Vaikka olet todennäköisesti tyytyväinen edellisissä kappaleissa annettuun korkean tason kuvaukseen, ihmettelet luultavasti, mitä yksisuuntaiset funktiot tarkalleen ottaen ovat ja miten niitä tarkalleen ottaen käytetään epäsymmetristen järjestelmien rakentamiseen.
Tässä luvussa poistan osan epäsymmetriseen salaukseen liittyvistä mysteereistä tarkastelemalla syvällisemmin erästä esimerkkiä, nimittäin RSA-salausjärjestelmää. Ensimmäisessä luvussa esittelen faktorointiongelman, johon RSA-ongelma perustuu. Sen jälkeen käsittelen useita keskeisiä lukuteorian tuloksia. Viimeisessä jaksossa kootaan nämä tiedot yhteen ja selitetään RSA-ongelma ja se, miten sitä voidaan käyttää epäsymmetristen salausjärjestelmien luomiseen.
Tämän syvyyden lisääminen keskusteluumme ei ole helppo tehtävä. Se edellyttää melko monen lukuteoreettisen teoreeman ja lauseen esittelyä. Mutta älä anna matematiikan lannistaa sinua. Tämän keskustelun läpikäyminen parantaa merkittävästi käsitystänne siitä, mikä on epäsymmetrisen salauksen taustalla, ja se on kannattava investointi.
Tarkastellaan nyt ensin faktorointiongelmaa.
Kun kaksi lukua, esimerkiksi a ja b, kerrotaan keskenään,
lukuja a ja b kutsutaan tekijöiksi ja tulosta tuotteeksi. Yritystä kirjoittaa luku N kahden tai useamman tekijän kertolaskuksi kutsutaan faktorisoinniksi tai faktoroinniksi. [1] Voit kutsua mitä tahansa ongelmaa,
joka vaatii tätä, faktorointiongelmaksi.
Noin 2500 vuotta sitten kreikkalainen matemaatikko Eukleideus Aleksandrialainen löysi keskeisen lauseen kokonaislukujen kertolaskuista. Sitä kutsutaan yleisesti yksikäsitteiseksi kertolaskuteoriaksi, ja siinä todetaan seuraavaa:
Teoreema 1. Jokainen kokonaisluku N, joka on suurempi kuin 1,
on joko alkuluku tai se voidaan ilmaista alkutekijöiden tulona.
Tämän lausekkeen jälkimmäinen osa tarkoittaa vain sitä, että voit ottaa
minkä tahansa kokonaisluvun N, joka ei ole alkuluku, joka on suurempi kuin 1, ja kirjoittaa sen
alkulukujen kertolaskuna. Alla on useita esimerkkejä muista kuin alkuluvun
kokonaisluvuista, jotka on kirjoitettu alkulukujen tulona.
18 = 2 \cdot 3 \cdot 3 = 2 \cdot 3^284 = 2 \cdot 2 \cdot 3 \cdot 7 = 2^2 \cdot 3 \cdot 7144 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 = 2^4 \cdot 3^2
Kaikkien kolmen edellä mainitun kokonaisluvun alkutekijöiden laskeminen on
suhteellisen helppoa, vaikka sinulle annettaisiin vain N. Aloitetaan pienimmästä alkuluvusta 2 ja katsotaan, kuinka monta kertaa
kokonaisluku N on jaollinen
sillä. Sen jälkeen testataan, onko N jaollinen luvulla 3, 5, 7 ja niin edelleen. Tätä jatketaan, kunnes
kokonaisluku N on kirjoitettu
vain alkulukujen tulona.
Otetaan esimerkiksi kokonaisluku 84. Alla näet prosessin, jolla sen alkutekijät määritetään. Jokaisessa vaiheessa otetaan pois pienin jäljellä oleva alkutekijä (vasemmalla) ja määritetään jäännöstermi, joka on faktoroitava. Jatketaan, kunnes jäännöstermi on myös alkuluku. Jokaisessa vaiheessa 84:n tämänhetkinen kertolasku näkyy oikealla.
- Primaaritekijä = 2: jäännöstermi = 42 (
84 = 2 \cdot 42) - Primaaritekijä = 2: jäännöstermi = 21 (
84 = 2 \cdot 2 \cdot 21) - Primaaritekijä = 3: jäännöstermi = 7 (
84 = 2 \cdot 2 \cdot 3 \cdot 7) - Koska 7 on alkuluku, tulos on
2 \cdot 2 \cdot 3 \cdot 7tai2^2 \cdot 3 \cdot 7.
Oletetaan nyt, että N on
hyvin suuri. Kuinka vaikeaa olisi pelkistää N alkutekijöihinsä?
Se riippuu todella N:sta.
Oletetaan esimerkiksi, että N on 50 450 400. Vaikka tämä luku näyttääkin pelottavalta, laskutoimitukset eivät
ole kovin monimutkaisia, ja ne voidaan tehdä helposti käsin. Kuten edellä, aloitetaan
vain numerosta 2 ja edetään siitä eteenpäin. Alla näet tämän prosessin tuloksen
samalla tavalla kuin edellä.
- 2:
25,225,200(50,450,400 =2 \cdot 25,225,200) - 2:
12,612,600(50,450,400 =2^2 \cdot 12,612,600) - 2:
6,306,300(50,450,400 =2^3 \cdot 6,306,300) - 2:
3,153,150(50,450,400 =2^4 \cdot 3,153,150) - 2:
1,576,575(50,450,400 =2^5 \cdot 1,576,575) - 3:
525,525(50,450,400 =2^5 \cdot 3 \cdot 525,525) - 3:
175,175(50,450,400 =2^5 \cdot 3^2 \cdot 175,175) - 5:
35,035(50,450,400 =2^5 \cdot 3^2 \cdot 5 \cdot 35,035) - 5:
7,007(50,450,400 =2^5 \cdot 3^2 \cdot 5^2 \cdot 7,007) - 7:
1,001(50,450,400 =2^5 \cdot 3^2 \cdot 5^2 \cdot 7 \cdot 1,001) - 7:
143(50,450,400 =2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 143) - 11:
13(50,450,400 =2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13) - Koska 13 on alkuluku, tulos on
2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13.
Tämän ongelman selvittäminen käsin vie jonkin aikaa. Tietokone voisi tietysti tehdä kaiken tämän sekunnin murto-osassa. Itse asiassa tietokone pystyy usein jopa kertomaan erittäin suuria kokonaislukuja sekunnin murto-osassa.
On kuitenkin olemassa tiettyjä poikkeuksia. Oletetaan, että ensin valitaan
satunnaisesti kaksi hyvin suurta alkulukua. On tyypillistä nimetä nämä luvut p ja q, ja noudatan tätä
käytäntöä tässä.
Konkreettisuuden vuoksi sanotaan, että p ja q ovat molemmat
1024-bittisiä alkulukuja ja että ne todellakin vaativat vähintään 1024
bittiä, jotta ne voidaan esittää (joten ensimmäisen bitin on oltava 1).
Joten esimerkiksi 37 ei voi olla yksi alkuluvuista. Voit toki esittää 37:n
1024 bitillä. Mutta selvästikään ei tarvita näin monta bittiä sen
esittämiseen. Voit esittää 37:n millä tahansa merkkijonolla, jossa on
vähintään 6 bittiä. (6 bitillä 37 esitetään muodossa 100101).
On tärkeää ymmärtää, kuinka suuria p ja q ovat, jos ne valitaan edellä
mainituilla ehdoilla. Esimerkkinä olen valinnut satunnaisen alkuluvun, jonka
esittämiseen tarvitaan vähintään 1024 bittiä.
- 14,752,173,874,503,595,484,930,006,383,670,759,559,764,562,721,397,166,747,289,220,945,457,932,666,751,048,198,854,920,097,085,690,793,755,254,946,188,163,753,506,778,089,706,699,671,722,089,715,624,760,049,594,106,189,662,669,156,149,028,900,805,928,183,585,427,782,974,951,355,515,394,807,209,836,870,484,558,332,897,443,152,653,214,483,870,992,618,171,825,921,582,253,023,974,514,209,142,520,026,807,636,589
Oletetaan nyt, että kun olemme valinneet satunnaisesti alkuluvut p ja q, kerromme ne ja saamme
kokonaisluvun N. Jälkimmäinen
kokonaisluku on siis 2048-bittinen luku, jonka esittämiseen tarvitaan
vähintään 2048 bittiä. Se on paljon, paljon suurempi kuin p tai q.
Oletetaan, että annat tietokoneelle vain N ja pyydät sitä etsimään kaksi 1024-bittistä N:n alkutekijää.
Todennäköisyys, että tietokone löytää p ja q, on erittäin pieni.
Voidaan sanoa, että se on käytännössä mahdotonta. Näin on, vaikka käytössä
olisi supertietokone tai jopa supertietokoneiden verkosto.
Aluksi oletetaan, että tietokone yrittää ratkaista ongelman käymällä läpi
1024-bittisiä lukuja ja testaamalla, ovatko ne primäärilukuja ja ovatko ne N:n tekijöitä. Testattavien alkulukujen joukko on tällöin noin 1.265 \cdot 10^{305}. [2]
Vaikka kaikki maailman tietokoneet yrittäisivät löytää ja testata
1024-bittisiä alkulukuja tällä tavalla, yhden miljardin todennäköisyys
löytää N:n alkuluku vaatisi
paljon maailmankaikkeuden ikää pidemmän laskenta-ajan.
Käytännössä tietokone voi tehdä paremman tuloksen kuin äsken kuvattu karkea menettely. On olemassa useita algoritmeja, joita tietokone voi soveltaa päästäkseen kertolaskuihin nopeammin. Kyse on kuitenkin siitä, että vaikka näitä tehokkaampia algoritmeja käytettäisiinkin, tietokoneen tehtävä on edelleen laskennallisesti toteuttamiskelvoton. [3]
Tärkeää on, että faktoroinnin vaikeus juuri kuvatuissa olosuhteissa perustuu oletukseen, että ei ole olemassa laskennallisesti tehokkaita algoritmeja alkutekijöiden laskemiseen. Emme voi itse asiassa todistaa, että tehokasta algoritmia ei ole olemassa. Tämä oletus on kuitenkin hyvin uskottava: satoja vuosia kestäneistä laajoista ponnisteluista huolimatta emme ole vielä löytäneet tällaista laskennallisesti tehokasta algoritmia.
Näin ollen faktorointiongelman voidaan tietyissä olosuhteissa uskottavasti
olettaa olevan vaikea ongelma. Erityisesti kun p ja q ovat hyvin suuria
alkulukuja, niiden tulo N ei
ole vaikea laskea; mutta pelkkä faktorointi N:n perusteella on
käytännössä mahdotonta.
Huomautukset:
[1] Faktorisointi voi olla tärkeää myös muiden matemaattisten objektien kuin
lukujen käsittelyssä. Esimerkiksi polynomilausekkeiden, kuten x^2 - 2x + 1, faktorointi voi olla hyödyllistä. Keskustelussamme keskitymme vain
lukujen, erityisesti kokonaislukujen, faktorointiin.
[2] Primilukuteoremin mukaan niiden alkulukujen lukumäärä,
jotka ovat pienempiä tai yhtä suuria kuin N, on noin N/\ln(N). Tämä tarkoittaa,
että voit arvioida 1024 bitin pituisten alkulukujen lukumäärän
likimääräisesti seuraavasti:
\frac{2^{1024}}{\ln(2^{1024})} -
\frac{2^{1023}}{\ln(2^{1023})}
...mikä vastaa noin 1,265 \times 10^{305}.
[3] Sama pätee myös diskreetin logaritmin ongelmiin. Tästä syystä epäsymmetriset salausrakenteet toimivat paljon suuremmilla avaimilla kuin symmetriset salausrakenteet.
Lukuteoreettiset tulokset
Valitettavasti faktorointiongelmaa ei voida käyttää suoraan epäsymmetrisiin salausjärjestelmiin. Voimme kuitenkin käyttää tähän tarkoitukseen monimutkaisempaa mutta siihen liittyvää ongelmaa: RSA-ongelmaa.
Ymmärtääksemme RSA-ongelmaa meidän on ymmärrettävä joukko lukuteorian teoreemoja ja lauseita. Ne esitellään tässä jaksossa kolmessa alajaksossa: (1) N:n järjestys, (2) käänteisyys modulo N ja (3) Eulerin lause.
Osa näiden kolmen alajakson aineistosta on jo esitelty luvussa 3. Esitän kuitenkin tässä uudelleen tuon aineiston yksinkertaisuuden vuoksi.
N
Kokonaisluku a on koprimaksi tai suhteelliseksi primaksi kokonaisluvun N kanssa, jos niiden suurin yhteinen jakaja on 1. Vaikka 1 ei sopimuksen
mukaan ole primiluku, se on kaikkien kokonaislukujen koprimaksi (kuten myös -1).
Tarkastellaan esimerkiksi tapausta, jossa a = 18 ja N = 37. Nämä ovat selvästi
kopriimeja. Suurin kokonaisluku, joka jakaa sekä 18:n että 37:n, on 1. Sitä
vastoin tarkastellaan tapausta, jossa a = 42 ja N = 16. Nämä eivät
selvästikään ole kopriimeja. Molemmat luvut ovat jaollisia luvulla 2, joka
on suurempi kuin 1.
Voimme nyt määritellä N:n
järjestyksen seuraavasti. Oletetaan, että N on kokonaisluku, joka on suurempi kuin 1. Tällöin N:n
järjestys on kaikkien niiden koprimien lukumäärä, joiden kanssa N on sellainen, että jokaiselle koprimille a pätee seuraava ehto: 1 \leq a < N.
Jos esimerkiksi N = 12, niin
1, 5, 7 ja 11 ovat ainoat koprimit, jotka täyttävät edellä mainitun
vaatimuksen. Näin ollen 12:n järjestys on 4.
Oletetaan, että N on
alkuluku. Silloin mikä tahansa kokonaisluku, joka on pienempi kuin N mutta suurempi tai yhtä suuri kuin 1, on sen kanssa samankeskinen. Tämä
sisältää kaikki seuraavan joukon alkiot: \{1,2,3,....,N - 1\}. Kun N on alkuluku, N:n järjestys on N - 1. Tämä todetaan
lauseessa 1, jossa \phi(N) tarkoittaa N:n järjestystä.
Ehdotus 1. \phi(N) = N - 1 kun N on alkuluku
Oletetaan, että N ei ole
alkuluku. Silloin voit laskea sen järjestyksen Eulerin Phi-funktion avulla. Vaikka pienen kokonaisluvun järjestyksen
laskeminen on suhteellisen yksinkertaista, Eulerin Phi-funktio on erityisen tärkeä
suuremmille kokonaisluvuille. Eulerin Phi-funktion lause on esitetty alla.
Teoreema 2. Olkoon N yhtä suuri kuin p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot
p_i^{e_i} \cdot \ldots \cdot p_n^{e_n}, jossa joukko \{p_i\} koostuu kaikista N:n eri
alkutekijöistä ja jokainen e_i osoittaa, kuinka monta kertaa alkutekijä p_i esiintyy N:n kohdalla.
Sitten,
\phi(N) = p_1^{e_1 - 1} \cdot (p_1 - 1) \cdot p_2^{e_2 -
1} \cdot (p_2 - 1) \cdot \ldots \cdot p_n^{e_n - 1} \cdot
(p_n - 1)
Teoreema 2 osoittaa, että kun jokin ei-primus N on jaettu erillisiin primustekijöihin, on helppo laskea N:n järjestys.
Oletetaan esimerkiksi, että N = 270. Tämä ei selvästikään ole alkuluku. Kun N hajotetaan alkutekijöihin, saadaan lauseke: 2 \cdot 3^3 \cdot 5. Eulerin
Phi-funktion mukaan N:n
järjestys on tällöin seuraava:
\phi(N) = 2^{1 - 1} \cdot (2 - 1) + 3^{3 - 1} \cdot
(3 - 1) + 5^{1 - 1} \cdot (5 - 1) = 1 \cdot 1 + 9 \cdot 2 + 1
\cdot 4 = 1 + 18 + 4 = 23
Oletetaan seuraavaksi, että N on kahden alkuluvun p ja q tulo. Yllä oleva lause 2 sanoo, että N:n järjestys on seuraava:
p^{1 - 1} \cdot (p - 1) \cdot q^{1 - 1} \cdot (q - 1)
= (p - 1) \cdot (q - 1)
Tämä on keskeinen tulos erityisesti RSA-ongelmaa varten, ja se esitetään jäljempänä olevassa Propositiossa 2.
Ehdotus 2. Jos N on kahden alkuluvun p ja q tulo, N:n järjestys on tulo (p - 1) \cdot (q - 1).
Kuvitellaan, että N = 119.
Tämä kokonaisluku voidaan jakaa kahteen alkulukuun, nimittäin 7:ään ja
17:ään. Näin ollen Eulerin Phi-funktion mukaan 119:n järjestys on seuraava:
\phi(119) = (7 - 1) \cdot (17 - 1) = 6 \cdot 16 = 96
Toisin sanoen kokonaisluvulla 119 on 96 koprimaa välillä 1-119. Itse asiassa tähän joukkoon kuuluvat kaikki kokonaisluvut 1-119, jotka eivät ole 7:n tai 17:n kertalukuja.
Tästä eteenpäin merkitään N:n
järjestyksen määräävää koprimien joukkoa C_N:ksi. Esimerkissämme,
jossa N = 119, joukko C_{119} on aivan liian
suuri lueteltavaksi kokonaan. Jotkin sen alkioista ovat kuitenkin seuraavat:
C_{119} = \{1, 2, \dots, 6, 8, \dots, 13, 15, 16, 18,
\dots, 33, 35, \dots, 96\}
Käänteistettävyys modulo N
Voimme sanoa, että kokonaisluku a on muunnettavissa modulo N, jos on olemassa vähintään yksi
kokonaisluku b, jonka
tapauksessa a \cdot b \mod N = 1 \mod N.
Tällaista kokonaislukua b kutsutaan a:n inversioksi (tai moninkertaiseksi inversioksi), kun se vähennetään
modulo N:n avulla.
Oletetaan esimerkiksi, että a = 5 ja N = 11. On monia
kokonaislukuja, joilla voidaan kertoa 5, niin että 5 \cdot b \mod 11 = 1 \mod 11.
Tarkastellaan esimerkiksi kokonaislukuja 20 ja 31. On helppo nähdä, että
nämä molemmat kokonaisluvut ovat 5:n käänteislukuja, kun ne vähennetään
modulo 11:een.
5 \cdot 20 \mod 11 = 100 \mod 11 = 1 \mod 115 \cdot 31 \mod 11 = 155 \mod 11 = 1 \mod 11
Vaikka 5:llä on monia käänteislukuja, jotka redusoituvat modulo 11:een, voit osoittaa, että 5:lle on olemassa vain yksi positiivinen käänteisluku, joka on pienempi kuin 11. Itse asiassa tämä ei koske vain tätä esimerkkiä, vaan on yleinen tulos.
Ehdotus 3. Jos kokonaisluku a on käänteisluku modulo N, on
oltava niin, että täsmälleen yksi positiivinen käänteisluku a on pienempi kuin N. (Tämän
ainoan käänteisluvun a on
siis tultava joukosta \{1, \dots, N - 1\}).
Merkitään a^{-1}:lla Propositiosta 3 saatavan a:n ainoaa käänteislukua a^{-1}.
Tapauksessa, jossa a = 5 ja N = 11, nähdään, että a^{-1} = 9, koska 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11.
Huomaa, että voit myös saada esimerkkimme a^{-1}:n arvon 9 yksinkertaisesti vähentämällä minkä tahansa muun a:n käänteisluvun modulo
11:llä. Esimerkiksi 20 \mod 11 = 31 \mod 11 = 9 \mod 11. Jos siis jokin kokonaisluku a > N on käänteismoduuli N, myös a \mod N on oltava käänteismoduuli N.
Ei ole välttämättä niin, että a:n käänteisluku on olemassa reduktiomoduulilla N. Oletetaan esimerkiksi,
että a = 2 ja N = 8. Ei ole olemassa
sellaista b:tä tai mitään a^{-1}:tä, että 2 \cdot b \mod 8 = 1 \mod 8.
Tämä johtuu siitä, että mikä tahansa b:n arvo tuottaa aina 2:n
kertaluvun, joten mikään jako luvulla 8 ei voi koskaan tuottaa jäännöstä,
joka on yhtä suuri kuin 1.
Mistä tarkalleen ottaen tiedämme, onko jollakin kokonaisluvulla a käänteisluku tietyllä N:llä?
Kuten olet ehkä huomannut yllä olevassa esimerkissä, suurin yhteinen jakaja
2:n ja 8:n välillä on suurempi kuin 1, nimittäin 2. Tämä havainnollistaa
itse asiassa seuraavaa yleistä tulosta:
Ehdotus 4. Kokonaisluvulle a on olemassa käänteisluku, joka on redusoitu moduuliin N, ja erityisesti ainoa
positiivinen käänteisluku, joka on pienempi kuin N, jos ja vain jos a:n ja N:n suurin yhteinen jakaja on
1 (eli jos ne ovat koprimit).
Tapauksessa, jossa a = 5 ja N = 11, päädyimme siihen,
että a^{-1} = 9,
koska 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11. On tärkeää huomata, että myös päinvastainen pätee. Toisin sanoen, kun a = 9 ja N = 11, pätee, että a^{-1} = 5.
Eulerin lause
Ennen kuin siirrymme RSA-ongelmaan, meidän on ymmärrettävä vielä yksi tärkeä lause, nimittäin Eulerin lause. Siinä todetaan seuraavaa:
Teoreema 3. Oletetaan, että kaksi kokonaislukua a ja N ovat kopriimejä. Tällöin a^{\phi(N)} \mod N = 1 \mod N.
Tämä on merkittävä tulos, mutta aluksi hieman hämmentävä. Otetaanpa esimerkki, jotta ymmärrämme sen.
Oletetaan, että a = 5 ja N = 7. Nämä ovat todellakin
kopriimeja, kuten Eulerin lause edellyttää. Tiedämme, että 7:n järjestysluku
on 6, koska 7 on alkuluku (ks. Aloite 1).
Eulerin teoreema sanoo nyt, että 5^6 \mod 7 on oltava yhtä suuri kuin 1 \mod 7. Alla on
laskutoimitukset, jotka osoittavat, että tämä on todellakin totta.
5^6 \mod 7 = 15,625 \mod 7 = 1 \mod N
Kokonaisluku 7 jakautuu 15,624:ään yhteensä 2,233 kertaa. Jäännös, joka saadaan jakamalla 16 625 luvulla 7, on siis 1.
Seuraavaksi Eulerin Phi-funktiota, Teoria 2, käyttämällä voidaan johtaa Asetus 5.
Ehdotus 5. \phi(a \cdot b) = \phi(a) \cdot \phi(b) kaikille positiivisille kokonaisluvuille a ja b.
Emme aio osoittaa, miksi näin on. Huomaa vain, että olet jo nähnyt todisteen
tälle väitteelle siitä, että \phi(p \cdot q) = \phi(p) \cdot \phi(q) = (p - 1) \cdot (q - 1), kun p ja q ovat alkulukuja, kuten Väitöskappaleessa 2 todetaan.
Eulerin lauseella yhdessä Proposition 5 kanssa on tärkeitä
vaikutuksia. Katso, mitä tapahtuu esimerkiksi alla olevissa lausekkeissa,
joissa a ja N ovat kopriimejä.
a^{2 \cdot \phi(N)} \mod N = a^{\phi(N)} \cdot a^{\phi(N)} \mod N = 1 \cdot 1 \mod N = 1 \mod Na^{\phi(N) + 1} \mod N = a^{\phi(N)} \cdot a^1 \mod N = 1 \cdot a^1 \mod N = a \mod Na^{8 \cdot \phi(N) + 3} \mod N = a^{8 \cdot \phi(N)} \cdot a^3 \mod N = 1 \cdot a^3 \mod N = a^3 \mod N
Näin ollen Eulerin lauseen ja Proposition 5 yhdistelmän avulla voimme yksinkertaisesti laskea useita lausekkeita. Yleisesti ottaen voimme tiivistää oivalluksen kuten Propositiossa 6.
Ehdotus 6. a^x \mod N = a^{x \mod \phi(N)} a^x \mod N = a^{x \mod \phi(N)}
Nyt meidän on koottava kaikki yhteen viimeisessä vaiheessa.
Aivan kuten N:llä on
järjestys \phi(N), joka
sisältää joukon C_N alkiot,
tiedämme, että kokonaisluvulla \phi(N) on puolestaan oltava myös järjestys ja joukko kopriimejä. Asetetaan \phi(N) = R. Silloin
tiedämme, että myös arvolle \phi(R) on olemassa arvo ja koprimien joukko C_R.
Oletetaan, että valitsemme nyt kokonaisluvun e joukosta C_R. Tiedämme Propositiosta 3, että tällä kokonaisluvulla e on vain yksi ainoa positiivinen käänteisluku, joka on pienempi kuin R. Toisin sanoen e:llä on yksi ainoa
käänteisluku joukosta C_R.
Kutsutaan tätä käänteislukua d. Käänteisluvun määritelmän
mukaan tämä tarkoittaa, että e \cdot d = 1 \mod R.
Voimme käyttää tätä tulosta esittääksemme väitteen alkuperäisestä
kokonaisluvusta N. Tämä on
tiivistetty Asetukseen 7.
Ehdotus 7. Oletetaan, että e \cdot d \mod \phi(N) = 1 \mod \phi(N). Tällöin mille tahansa joukon C_N alkioille a on oltava, että a^{e \cdot d \mod \phi(N)} = a^{1 \mod \phi(N)} = a
\mod N.
Meillä on nyt kaikki tarvittavat lukuteoreettiset tulokset RSA-ongelman selvittämiseksi.
RSA-salausjärjestelmä
Olemme nyt valmiita esittämään RSA-ongelman. Oletetaan, että luodaan
muuttujajoukko, joka koostuu seuraavista muuttujista: p, q, N, \phi(N), e, d ja y. Kutsutaan tätä joukkoa
nimellä \Pi. Se luodaan
seuraavasti:
Luo kaksi samankokoista satunnaista alkulukua
pjaqja laske niiden tuloN.Lasketaan
N:n järjestys\phi(N)seuraavalla tulolla:(p - 1) \cdot (q - 1).Valitse sellainen
e > 2, että se on pienempi ja samankertoiminen kuin\phi(N).Lasketaan
dasettamallae \cdot d \mod \phi(N) = 1.Valitse satunnainen arvo
y, joka on pienempi ja samankertainen kuinN.
RSA-ongelma koostuu sellaisen x:n löytämisestä, että x^e = y, kun käytettävissä on
vain osa \Pi:n tiedoista,
nimittäin muuttujat N, e ja y. Kun p ja q ovat hyvin suuria, yleensä
suositellaan, että ne ovat kooltaan 1024 bittiä, RSA-ongelman katsotaan olevan
vaikea. Ymmärrät nyt, miksi näin on, kun otetaan huomioon edellä esitetty keskustelu.
Helppo tapa laskea x, kun x^e \mod N = y \mod N, on
yksinkertaisesti laskea y^d \mod N. Tiedämme, että y^d \mod N = x \mod N seuraavien
laskutoimitusten avulla:
y^d \mod N = x^{e \cdot d} \mod N = x^{e \cdot d \mod
\phi(N)} \mod N = x^{1 \mod \phi(N)} \mod N = x \mod N.
Ongelmana on, että emme tiedä arvoa d, koska sitä ei ole annettu tehtävässä. Näin ollen emme voi suoraan laskea y^d \mod N, jotta saadaan x \mod N.
Saatamme kuitenkin pystyä laskemaan d epäsuorasti N:n järjestyksen \phi(N) perusteella, koska tiedämme, että e \cdot d \mod \phi(N) = 1 \mod \phi(N). Mutta oletuksen mukaan ongelma ei anna arvoa myöskään \phi(N):lle.
Lopuksi järjestys voidaan laskea epäsuorasti alkutekijöiden p ja q avulla, jolloin voimme
lopulta laskea d. Mutta
oletuksena on, että arvoja p ja q ei myöskään anneta meille.
Tarkkaan ottaen, vaikka RSA-ongelmaan sisältyvä faktorointiongelma olisi vaikea, emme voi todistaa, että myös RSA-ongelma on vaikea. RSA-ongelman ratkaisemiseen voi nimittäin olla muitakin tapoja kuin faktorointi. Yleisesti kuitenkin hyväksytään ja oletetaan, että jos RSA-ongelman sisällä oleva faktorointiongelma on vaikea, myös itse RSA-ongelma on vaikea.
Jos RSA-ongelma on todellakin vaikea, se tuottaa yksisuuntaisen funktion,
jossa on salaisuus. Funktio on tässä tapauksessa f(g) = g^e \mod N. Tietäen f(g), kuka tahansa
voisi helposti laskea arvon y tietylle g = x:lle. On
kuitenkin käytännössä mahdotonta laskea tiettyä arvoa x vain tuntemalla arvo y ja
funktio f(g). Poikkeuksena
on, kun sinulle annetaan tieto d, ansaportti. Tällöin voit
yksinkertaisesti laskea y^d ja saada tulokseksi x.
Käydään läpi erityinen esimerkki RSA-ongelman havainnollistamiseksi. En voi valita RSA-ongelmaa, jota pidettäisiin vaikeana edellä mainituilla ehdoilla, koska luvut olisivat liian suuret. Sen sijaan tämän esimerkin tarkoituksena on vain havainnollistaa, miten RSA-ongelma yleensä toimii.
Aluksi oletetaan, että valitset kaksi satunnaista alkulukua 13 ja 31. Siis p = 13 ja q = 31. Näiden kahden
alkuluvun tulo N on 403.
Voimme helposti laskea luvun 403 järjestyksen. Se vastaa arvoa (13 - 1) \cdot (31 - 1) = 360.
Seuraavaksi, kuten RSA-ongelman vaiheessa 3 sanotaan, meidän on valittava 360:lle coprime, joka on suurempi kuin 2 ja pienempi kuin 360. Meidän ei tarvitse valita tätä arvoa satunnaisesti. Oletetaan, että valitsemme 103. Tämä on 360:n koprimus, koska sen suurin yhteinen jakaja 103:n kanssa on 1.
Vaihe 4 edellyttää nyt, että laskemme arvon d, joka on sellainen, että 103 \cdot d \mod 360 = 1.
Tämä ei ole helppo tehtävä käsin, kun N:n arvo on suuri. Se
edellyttää, että käytämme menettelyä nimeltä laajennettu euklidinen algoritmi.
Vaikka en näytä menettelyä tässä, se antaa arvon 7, kun e = 103. Voit varmistaa, että arvopari 103 ja 7 täyttää yleisen ehdon e \cdot d \mod \phi(n) = 1 alla
olevien laskutoimitusten avulla.
103 \cdot 7 \mod 360 = 721 \mod 360 = 1 \mod 360
Tärkeää on, että Proposition 4 perusteella tiedämme, että mikään
muu kokonaisluku d välillä
1-360 ei tuota tulosta 103 \cdot d = 1 \mod 360.
Lisäksi lauseesta seuraa, että valitsemalla eri arvo arvolle e saadaan eri arvo arvolle d.
RSA-ongelman vaiheessa 5 meidän on valittava jokin positiivinen kokonaisluku y, joka on 403:n pienempi kertolasku. Oletetaan, että asetetaan y = 2^{103}. Kun 2
kerrotaan luvulla 103, saadaan alla oleva tulos.
2^{103} \mod 403 = 10,141,204,801,825,835,211,973,625,643,008 \mod 403 = 349 \mod 403
RSA-ongelma tässä esimerkissä on nyt seuraava: Annetaan seuraavat tiedot: N = 403, e = 103 ja y = 349 \mod 403. Sinun on
nyt laskettava x siten, että x^{103} = 349 \mod 403. Toisin sanoen sinun on löydettävä, että alkuperäinen arvo ennen 103:lla
potensointia oli 2.
Olisi helppoa (ainakin tietokoneelle) laskea x, jos tietäisimme, että d = 7. Siinä tapauksessa x voitaisiin määrittää alla esitetyllä
tavalla.
x = y^7 \mod 403 = 349^7 \mod 403 = 630,634,881,591,804,949 \mod 403 = 2 \mod 403
Ongelmana on se, että sinulle ei ole annettu tietoa siitä, että d = 7. Voisit tietenkin laskea d siitä, että 103 \cdot d = 1 \mod 360.
Ongelmana on, että sinulle ei myöskään ole annettu tietoa siitä, että
järjestys N = 360. Lopuksi
voisit myös laskea järjestyksen 403 laskemalla seuraavan tulon: (p - 1) \cdot (q - 1). Mutta
sinulle ei myöskään kerrota, että p = 13 ja q = 31.
Tietokone voisi tietysti silti ratkaista tämän esimerkin RSA-ongelman suhteellisen helposti, koska kyseessä olevat alkuluvut eivät ole suuria. Mutta kun alkuluvuista tulee hyvin suuria, se joutuu käytännössä mahdottoman tehtävän eteen.
Olemme nyt esitelleet RSA-ongelman, joukon ehtoja, joiden täyttyessä se on vaikea, ja sen taustalla olevan matematiikan. Miten tästä on apua epäsymmetrisessä salauksessa? Miten voimme muuttaa RSA-ongelman vaikeuden tietyissä olosuhteissa salaus- tai allekirjoitusjärjestelmäksi?
Yksi lähestymistapa on ottaa RSA-ongelma ja rakentaa järjestelmiä
suoraviivaisesti. Oletetaan esimerkiksi, että oletetaan RSA-ongelmassa
kuvattu muuttujajoukko \Pi ja
varmistetaan, että p ja q ovat riittävän suuria. Asetat julkisen avaimesi arvoksi (N, e) ja jaat tämän tiedon koko maailmalle. Kuten edellä on kuvattu, pidät arvot p, q, \phi(n) ja d salassa. Itse asiassa d on yksityinen avaimesi.
Kuka tahansa, joka haluaa lähettää sinulle viestin m, joka on C_N:n elementti,
voi yksinkertaisesti salata sen seuraavasti: voit helposti purkaa tämän
viestin laskemalla vain c^d \mod N.
Voit yrittää luoda digitaalisen allekirjoitusjärjestelmän samalla tavalla.
Oletetaan, että haluat lähettää jollekin viestin m, jossa on digitaalinen allekirjoitus S. Voisit vain asettaa S = m^d \mod N ja lähettää parin (m,S) vastaanottajalle. Kuka tahansa voi tarkistaa digitaalisen allekirjoituksen
tarkistamalla, onko S^e \mod N = m \mod N. Kenen
tahansa hyökkääjän olisi kuitenkin todella vaikea luoda viestille
kelvollinen S, koska hänellä
ei ole hallussaan d.
Valitettavasti sellaisenaan vaikean ongelman, RSA-ongelman, muuttaminen
kryptografiseksi järjestelmäksi ei ole näin suoraviivaista. Suoraviivaisessa
salausjärjestelmässä voit valita viesteiksi vain N:n kopriimejä. Näin ollen mahdollisia viestejä ei jää kovin montaa, ei
ainakaan riittävästi tavanomaiseen viestintään. Lisäksi nämä viestit on
valittava satunnaisesti. Se vaikuttaa hieman epäkäytännölliseltä. Lopuksi,
mikä tahansa kahdesti valittu viesti tuottaa täsmälleen saman salatun
tekstin. Tämä on erittäin epätoivottavaa missä tahansa salausjärjestelmässä,
eikä se vastaa mitään tiukkaa nykyaikaista standardikäsitystä salauksen
turvallisuudesta.
Ongelmat pahenevat entisestään yksinkertaisessa digitaalisessa
allekirjoitusjärjestelmässä. Nykyisessä tilanteessa kuka tahansa hyökkääjä
voi helposti väärentää digitaalisia allekirjoituksia valitsemalla ensin
allekirjoitukseksi N:n
kopriman ja laskemalla sitten vastaavan alkuperäisen viestin. Tämä rikkoo
selvästi eksistentiaalisen väärentämättömyyden vaatimuksen.
RSA-ongelmaa voidaan kuitenkin käyttää sekä turvallisen julkisen avaimen salausjärjestelmän että turvallisen digitaalisen allekirjoitusjärjestelmän luomiseen lisäämällä siihen hieman monimutkaisuutta. Emme tässä yhteydessä perehdy tällaisten rakenteiden yksityiskohtiin. [4] On kuitenkin tärkeää, että tämä lisävaikeus ei muuta sitä perustavaa laatua olevaa RSA-ongelmaa, johon nämä järjestelmät perustuvat.
Huomautukset:
[4] Katso esimerkiksi Jonathan Katz ja Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), s. 410-32 RSA-salauksesta ja s. 444-41 RSA-digitaalisista allekirjoituksista.
Johtopäätös
Arvostelu & Arviointi
366d6fd0-ceb2-4299-bf37-8c6dfcb681d5 true
Loppukoe
44882d2b-63cd-4fde-8485-f76f14d8b2fe true
Johtopäätös
f1905f78-8cf7-5031-949a-dfa8b76079b4 true