name: Sissejuhatus formaalsesse krüptograafiasse goal: Sügav sissejuhatus krüptograafia teadusesse ja praktikasse. objectives:
- Tutvuda Beale'i šifreeringute ja kaasaegsete krüptograafiliste meetoditega, et mõista krüptograafia põhilisi ja ajaloolisi mõisteid.
- Süvenege arvuteooriasse, rühmadesse ja väljadesse, et omandada krüptograafia aluseks olevad põhilised matemaatilised mõisted.
- Õppige tundma RC4 voogkrüpteerimist ja AES-i 128-bitise võtmega, et õppida tundma sümmeetrilisi krüptograafilisi algoritme.
- Uurige RSA krüptosüsteemi, võtme jaotamist ja hash-funktsioone, et uurida asümmeetrilist krüptograafiat.
Sügav sukeldumine krüptograafiasse
On raske leida palju materjale, mis pakuksid krüptograafiaõppes head keskteed.
Ühest küljest on olemas pikad formaalsed käsitlused, mis on tegelikult kättesaadavad ainult neile, kellel on tugev taust matemaatikas, loogikas või mõnes muus formaalses distsipliinis. Teisest küljest on olemas väga kõrgetasemelised sissejuhatused, mis tegelikult varjavad liiga palju üksikasju kõigile, kes on vähemalt pisutki uudishimulikud.
Käesolev sissejuhatus krüptograafiasse püüab leida kesktee. Kuigi see peaks olema suhteliselt keeruline ja üksikasjalik kõigile krüptograafia algajaile, ei ole see tüüpilise alusdokumendi küülikupea.
Sissejuhatus
Kursuse ülevaade
bb8a8b73-7fb2-50da-bf4e-98996d79887b Tere tulemast kursusele CYP302!
See raamat pakub põhjalikku sissejuhatust krüptograafia teadusse ja praktikasse. Võimaluse korral keskendutakse pigem materjali kontseptuaalsele kui formaalsele eksponeerimisele.
See õppesisu on kohandatud raamatust ja repo JWBurgers. Kuigi autor on lahkelt lubanud selle hariduslikku kasutamist, jäävad kõik intellektuaalomandi õigused algsele loojale.
Motivatsioon ja eesmärgid
On raske leida palju materjale, mis pakuksid krüptograafiaõppes head keskteed.
Ühest küljest on olemas pikad formaalsed käsitlused, mis on tegelikult kättesaadavad ainult neile, kellel on tugev taust matemaatikas, loogikas või mõnes muus formaalses distsipliinis. Teisest küljest on olemas väga kõrgetasemelised sissejuhatused, mis tegelikult varjavad liiga palju üksikasju kõigile, kes on vähemalt pisutki uudishimulikud.
Käesolev sissejuhatus krüptograafiasse püüab leida kesktee. Kuigi see peaks olema suhteliselt keeruline ja üksikasjalik kõigile krüptograafia algajaile, ei ole see tüüpilise alusdokumendi küülikupea.
Sihtrühm
Alates arendajatest kuni intellektuaalselt uudishimulike inimesteni on see raamat kasulik kõigile, kes soovivad krüptograafiast rohkem kui pealiskaudset arusaamist. Kui teie eesmärk on krüptograafia valdkonnaga tegelemine, siis on see raamat samuti hea lähtepunkt.
Lugemisjuhised
Raamatus on praegu seitse peatükki: "Mis on krüptograafia?" (1. peatükk), "Krüptograafia matemaatilised alused I" (2. peatükk), "Krüptograafia matemaatilised alused II" (3. peatükk), "Sümmeetriline krüptograafia" (4. peatükk), "RC4 ja AES" (5. peatükk), "Asümmeetriline krüptograafia" (6. peatükk) ja "RSA krüptosüsteem" (7. peatükk). Lisandub veel viimane peatükk "Krüptograafia praktikas". Selles keskendutakse erinevatele krüptograafilistele rakendustele, sealhulgas transpordikihi turvalisusele, sibulareitingule ja Bitcoini väärtusvahetussüsteemile.
Kui teil ei ole tugevat matemaatilist tausta, on arvuteooria ilmselt kõige raskem teema selles raamatus. Annan sellest ülevaate 3. peatükis ning see esineb ka AES-i ekspositsioonis 5. peatükis ja RSA krüptosüsteemi ekspositsioonis 7. peatükis.
Kui teil on tõesti raskusi raamatu nende osade formaalsete üksikasjadega, siis soovitan teil esimesel korral leppida nende kõrgetasemelise lugemisega.
Tänuavaldused
Kõige mõjukam raamat selle kujundamisel on olnud Jonathan Katzi ja Yehuda Lindelli raamat Introduction to Modern Cryptography, CRC Press (Boca Raton, FL), 2015. Coursera's on saadaval sellega kaasnev kursus "Cryptography"
Peamised täiendavad allikad, mis on olnud abiks käesolevas raamatus esitatud ülevaate loomisel, on Simon Singh, The Code Book, Fourth Estate (London, 1999); Christof Paar ja Jan Pelzl, Understanding Cryptography, Springer (Heidelberg, 2010) ja Paari raamatul põhinev kursus "Introduction to Cryptography"; ja Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons).
Tsiteerin ainult väga konkreetset teavet ja tulemusi, mida ma nendest allikatest võtan, kuid tahan siinkohal tunnistada oma üldist võlgnevust neile.
Neile lugejatele, kes soovivad pärast seda sissejuhatust otsida edasijõudnuid teadmisi krüptograafiast, soovitan väga Katzi ja Lindelli raamatut. Katzi kursus Courseras on raamatust mõnevõrra kättesaadavam.
Panused
Palun vaadake repositooriumis olevast panuste failist mõningaid juhiseid projekti toetamiseks.
Märgistus
Välisterminid:
Võtmeterminid on algtõdesid tutvustades tehtud rasvases kirjas. Näiteks Rijndaeli šifri sissejuhatus võtmeterminina näeks välja järgmiselt: Rijndaeli salastering.
Võtmeterminid on selgesõnaliselt määratletud, välja arvatud juhul, kui tegemist on pärisnimedega või kui nende tähendus on arutelust ilmne.
Mis tahes määratlus antakse tavaliselt võtmeterminite tutvustamisel, kuigi mõnikord on mugavam jätta määratlus hilisemaks.
Kõrgendatud sõnad ja fraasid:
Sõnad ja fraasid on rõhutatud kursiivis. Näiteks lause "Pea meeles oma salasõna" näeb välja järgmiselt: Pea oma salasõna meeles.
Vormiline märkimine:
Formaalne notatsioon käsitleb peamiselt muutujaid, juhuslikke muutujaid ja kogumeid.
- Muutujad: Need tähistatakse tavaliselt lihtsalt väikese tähega (nt "x" või "y"). Mõnikord kirjutatakse need selguse huvides suurtähtedega (nt "M" või "K").
- Juhuslikud muutujad: Need on alati tähistatud suure tähega (nt "X" või "Y")
- Komplektid: Need on alati tähistatud rasvaste suurtähtedega (nt S)
Kas olete valmis uurima krüptograafia põnevat maailma? Lähme!
Mis on krüptograafia?
Beale'i kodeeringud
Alustame oma uurimistööd krüptograafia valdkonnas selle ajaloo ühe võluvama ja meelelahutuslikuma episoodiga: Beale'i šifrite juhtumiga. [1]
Minu arvates on Beale'i salakirjade lugu pigem väljamõeldis kui tegelikkus. Kuid väidetavalt toimus see järgmiselt.
Nii 1820. kui ka 1822. aasta talvel viibis mees nimega Thomas J. Beale Lynchburgis (Virginia) Robert Morrissi majutusasutuses. Beale'i teise viibimise lõpus andis ta Morrissile hoiule raudkarbi, milles olid väärtuslikud paberid.
Mõni kuu hiljem sai Morriss Beale'ilt kirja, mis oli dateeritud 9. mail 1822. Selles rõhutati raudkarbi sisu suurt väärtust ja anti Morrissile mõned juhised: kui ei Beale ega keegi tema kaaslastest ei tule kunagi karbi järele, peaks ta selle avama täpselt kümne aasta pärast kirja kuupäevast (st 9. mai 1832). Mõned sees olevad paberid oleksid kirjutatud tavalise tekstiga. Mitmed teised oleksid aga "ilma võtme abita arusaamatu" Selle "võtme" annaks siis 1832. aasta juunis Morrissile üle Beale'i nimetu sõber.
Vaatamata selgetele juhistele ei avanud Morriss 1832. aasta mais kasti ja Beale'i salapärane sõber ei ilmunud sama aasta juunis. Alles 1845. aastal otsustas kõrtsiomanik lõpuks kasti avada. Morriss leidis sealt märkuse, milles selgitati, kuidas Beale ja tema kaaslased avastasid läänes kulla ja hõbeda ning matsid selle koos mõningate ehetega turvaliseks hoidmiseks maha. Lisaks sellele sisaldas kast kolm šifriteksti, st koodiga kirjutatud teksti, mille avamiseks on vaja krüptograafilist võtit ehk saladust ja sellega kaasnevat algoritmi. Krüptoteksti avamise protsessi nimetatakse dekrüpteerimiseks, samas kui lukustamise protsessi nimetatakse krüpteerimiseks. (Nagu 3. peatükis selgitatud, võib mõiste "salakirjeldus" omandada erinevaid tähendusi. Nimetuses "Beale'i šifrid" on see lühend šifritekstist)
Kolm salakirjateksti, mille Morriss leidis raudkastist, koosnesid kõik komadega eraldatud numbrite jadast. Beale'i märkuse kohaselt annavad need salakirjad eraldi teavet aarde asukoha, aarde sisu ja nimekirja nimedest koos aarde õiguspärijatega ja nende osadega (viimane teave on oluline juhul, kui Beale ja tema kaaslased ei tule kunagi kastile järele).
Morris püüdis kolme salakirjateksti dešifreerida kakskümmend aastat. See oleks olnud võtme abil lihtne. Kuid Morrissil ei olnud võtit ja tema katsed originaaltekste ehk tekste, nagu neid tavaliselt krüptograafias nimetatakse, taastada ei õnnestunud.
Oma elu lõpu poole liikudes andis Morriss 1862. aastal kasti edasi sõbrale. See sõber avaldas seejärel 1885. aastal pseudonüümi J. B. Ward all pamfleti. See sisaldas karbi (väidetava) ajaloo kirjeldust, kolme salakirja ja teise salakirja lahendust, mille ta oli leidnud. (Ilmselt on iga salakirjateksti jaoks üks võti, mitte üks võti, mis töötab kõigi kolme salakirjateksti puhul, nagu Beale oma kirjas Morrissile algselt näib olevat soovitanud)
Teist salastusteksti näete allpool oleval Kujul 2. [2] Selle šifreeritud teksti võti on Ameerika Ühendriikide iseseisvusdeklaratsioon. Dekrüpteerimise protseduur taandub kahe järgmise reegli rakendamisele:
- Leidke mis tahes arvu n puhul salakirjas tekstis n-nda sõna Ameerika Ühendriikide iseseisvusdeklaratsioonis
- Asendage number n leitud sõna esimese tähega
Joonis 1: Beale'i šifreering nr. 2

Näiteks on teise salakirja esimene number 115. Iseseisvusdeklaratsiooni 115. sõna on "asutatud", seega on lihtteksti esimene täht "i" Salatekstis ei ole otseselt märgitud sõnade vahe ja suurtähtedega kirjutamine. Kuid pärast esimeste sõnade dekrüpteerimist saab loogiliselt järeldada, et lihtteksti esimene sõna oli lihtsalt "I" (Lihttekst algab fraasiga "I have deposited in the county of Bedford.")
Pärast dekrüpteerimist esitatakse teises sõnumis aarde üksikasjalik sisu (kuld, hõbe ja juveelid) ning vihjatakse, et see oli maetud raudpottidesse ja kaetud kividega Bedfordi maakonnas (Virginia). Inimesed armastavad häid mõistatusi, mistõttu on tehtud suuri jõupingutusi kahe teise Beale'i kodeeringu, eriti selle, mis kirjeldab aarde asukohta, dekrüpteerimiseks. Isegi mitmed tuntud krüptograafid on nende kallal kätt proovinud. Kuid siiani ei ole keegi suutnud kahte ülejäänud salakirju dešifreerida.
Märkused:
[1] Hea kokkuvõte loost on esitatud Simon Singh, The Code Book, Fourth Estate (London, 1999), lk 82-99. Loo lühifilmi tegi Andrew Allen 2010. aastal. Filmi "The Thomas Beale Cipher" selle veebisaidilt leiate.
[2] See pilt on saadaval Beale'i šifrite Vikipeedia lehel.
Kaasaegne krüptograafia
Sellised värvikad lood nagu Beale'i šifrite puhul on see, mida enamik meist seostab krüptograafiaga. Ometi erineb tänapäeva krüptograafia vähemalt nelja olulise asjaolu poolest sellistest ajaloolistest näidetest.
Esiteks, ajalooliselt on krüptograafia tegelenud ainult saladuse (või konfidentsiaalsusega) säilitamisega. [3] Krüptoteegid luuakse selleks, et tagada, et ainult teatud osapooled saaksid teada salakirjas sisalduvat teavet, nagu Beale'i krüptode puhul. Selleks, et krüpteerimisskeem seda eesmärki hästi täidaks, peaks krüptoteksti dekrüpteerimine olema võimalik ainult siis, kui teil on võti olemas.
Kaasaegne krüptograafia tegeleb laiema teemaderingiga kui ainult salastamisega. Nende teemade hulka kuuluvad peamiselt 1) sõnumi terviklikkus, st selle tagamine, et sõnumit ei ole muudetud; 2) sõnumi autentsus, st selle tagamine, et sõnum on tõesti pärit konkreetselt saatjalt; ja 3) tõestamatus, st selle tagamine, et saatja ei saa hiljem valesti eitada, et ta on sõnumi saatnud. [4]
Seega on oluline vahet teha krüpteerimisskeemil ja krüptograafiaskeemil. Krüpteerimisskeem on seotud ainult salastamisega. Kuigi krüpteerimisskeem on krüptograafiline skeem, ei ole see vastupidi. Krüptograafiline skeem võib teenida ka teisi krüptograafia põhiteemasid, sealhulgas terviklikkust, autentsust ja mittevastavust.
Terviklikkuse ja autentsuse teemad on sama olulised kui salastatus. Meie tänapäevased sidesüsteemid ei saaks toimida ilma side terviklikkuse ja autentsuse garantiideta. Tagasilükkamatus on samuti oluline mure, näiteks digitaalsete lepingute puhul, kuid see on krüptograafilistes rakendustes vähem vajalik kui salastatus, terviklikkus ja autentsus.
Teiseks, klassikalised krüpteerimisskeemid, nagu Beale'i šifrid, hõlmavad alati ühte võtit, mida jagavad kõik asjaomased osapooled. Paljud kaasaegsed krüptograafilised skeemid hõlmavad aga mitte ainult ühte, vaid kahte võtit: privaatvõtit ja avalikku võtit. Kui esimene peaks igas rakenduses jääma privaatseks, siis teine on tavaliselt avalik (sellest ka vastavad nimed). Krüpteerimise puhul saab avalikku võtit kasutada sõnumi krüpteerimiseks, samas kui privaatvõtit saab kasutada dekrüpteerimiseks.
Krüptograafia haru, mis tegeleb skeemidega, kus kõik osapooled jagavad ühte võtit, on tuntud kui sümmeetriline krüptograafia. Selliste skeemide puhul nimetatakse tavaliselt ühte võtit privaatvõtmeks (või salajaks võtmeks). Krüptograafia haru, mis tegeleb skeemidega, mis nõuavad privaatse ja avaliku võtme paari, on tuntud kui asümmeetriline krüptograafia. Neid harusid nimetatakse mõnikord ka privaatvõtme krüptograafiaks ja avaliku võtme krüptograafiaks (kuigi see võib tekitada segadust, sest ka avaliku võtme krüptograafiaskeemidel on privaatvõtmed).
Asümmeetrilise krüptograafia kasutuselevõtt 1970ndate lõpus on olnud üks olulisemaid sündmusi krüptograafia ajaloos. Ilma selleta ei oleks enamik meie tänapäevaseid sidesüsteeme, sealhulgas Bitcoin, võimalik või vähemalt väga ebapraktiline.
Oluline on see, et kaasaegne krüptograafia ei ole ainult sümmeetriliste ja assümeetriliste võtmete krüptograafiliste skeemide uurimine (kuigi see hõlmab suurt osa valdkonnast). Näiteks on krüptograafia seotud ka hash-funktsioonidega ja pseudorandomnumbrite generaatoritega ning nendele algoritmidele saab ehitada rakendusi, mis ei ole seotud sümmeetrilise või assümeetrilise võtme krüptograafiaga.
Kolmandaks, klassikalised krüpteerimisskeemid, nagu Beale'i šifrites kasutatavad, olid pigem kunst kui teadus. Nende arvatav turvalisus põhines suuresti nende keerukust käsitlevatel intuitsioonidel. Tavaliselt parandati neid, kui avastati uus rünnak nende vastu, või loobuti neist täielikult, kui rünnak oli eriti tõsine. Kaasaegne krüptograafia on aga range teadus, mille puhul kasutatakse nii krüptograafiliste skeemide väljatöötamisel kui ka analüüsimisel formaalset matemaatilist lähenemist. [5]
Konkreetselt keskendub kaasaegne krüptograafia formaalsetele turvalisuse tõenditele. Krüptograafilise skeemi turvalisuse tõestamine toimub kolmes etapis:
Julgeoleku krüptograafilise määratluse, st turvalisuse eesmärkide ja ründaja poolt kujutatava ohu avaldamine.
Kõigi matemaatiliste eelduste esitamine seoses skeemi arvutusliku keerukusega. Näiteks võib krüptograafiline skeem sisaldada pseudolugude generaatorit. Kuigi me ei saa tõestada, et need on olemas, võime eeldada, et need on olemas.
Skeemi matemaatilise turvalisuse tõestuse esitamine formaalse turvamõiste ja mis tahes matemaatiliste eelduste alusel.
Neljandaks, kui ajalooliselt kasutati krüptograafiat peamiselt sõjalistes tingimustes, siis digiajastul on see jõudnud meie igapäevategevustesse. Olenemata sellest, kas te teete pangatehinguid internetis, postitate sotsiaalmeedias, ostate Amazonist krediitkaardiga toote või annate sõbrale bitcoini, on krüptograafia meie digiajastu vältimatu osa.
Võttes arvesse neid nelja aspekti, võime iseloomustada kaasaegset krüptograafiat kui teadust, mis tegeleb krüptograafiliste skeemide formaalse arendamise ja analüüsiga, et kaitsta digitaalset teavet vastaste rünnakute eest. [6] Turvalisuse all tuleks siinkohal mõista laias laastus selliste rünnakute vältimist, mis kahjustavad side salastatust, terviklikkust, autentimist ja/või mittekaitstavust.
Krüptograafia on kõige paremini käsitletav küberturbe alldistsipliinina, mis tegeleb arvutisüsteemide varguse, kahjustamise ja väärkasutuse vältimisega. Pange tähele, et paljudel küberturvalisuse probleemidel on krüptograafiaga vähe või ainult osaline seos.
Näiteks kui ettevõte hoiab kalleid servereid kohapeal, võib ta olla mures selle riistvara kaitsmise pärast varguste ja kahjustuste eest. Kuigi see on küberturvalisuse probleem, on sellel vähe pistmist krüptograafiaga.
Veel üks näide: phishing-rünnakud on tänapäeval levinud probleem. Nende rünnakutega püütakse inimesi e-posti või mõne muu sõnumi kaudu petta, et nad loovutaksid tundlikku teavet, näiteks paroole või krediitkaardi numbreid. Kuigi krüptograafia aitab teatud määral võidelda andmepüügirünnakute vastu, nõuab terviklik lähenemine enamat kui ainult krüptograafia kasutamine.
Märkused:
[3] Täpsemalt öeldes on krüptograafiliste skeemide olulised rakendused olnud seotud salastamisega. Näiteks lapsed kasutavad sageli lihtsaid krüptograafilisi skeeme "lõbuks". Salastatus ei ole neil juhtudel tegelikult probleemiks.
[4] Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons), lk 2.
[5] Vt Jonathan Katz ja Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), eriti lk 16-23, hea kirjeldus.
[6] Vrd. Katz ja Lindell, ibid., lk. 3. Arvan, et nende iseloomustuses on mõningaid probleeme, mistõttu esitan siinkohal nende väite veidi teistsuguse versiooni.
Avatud teabevahetus
Kaasaegne krüptograafia on loodud selleks, et tagada turvalisus avatud side keskkonnas. Kui meie sidekanal on nii hästi kaitstud, et pealtkuulajatel ei ole mingit võimalust meie sõnumitega manipuleerida või isegi lihtsalt jälgida, siis on krüptograafia üleliigne. Enamik meie sidekanaleid ei ole siiski nii hästi kaitstud.
Kaasaegse maailma kommunikatsiooni selgroog on tohutu kiudoptiliste kaablite võrk. Telefonikõnede tegemine, televisiooni vaatamine ja veebi sirvimine kaasaegses majapidamises tugineb üldiselt sellele fiiberoptiliste kaablite võrgule (väike osa võib tugineda üksnes satelliitidele). Tõsi, teie kodus võivad olla erinevad andmeühendused, näiteks koaksiaalkaabel, (asümmeetriline) digitaalne abonendiliin ja valguskaabel. Kuid vähemalt arenenud maailmas ühenduvad need erinevad andmesideühendused väljaspool teie maja kiiresti kogu maailma ühendava tohutu valguskaablivõrgu sõlmpunktiga. Erandiks on mõned arenenud maailma äärealad, näiteks Ameerika Ühendriigid ja Austraalia, kus andmeliiklus võib endiselt läbida märkimisväärseid vahemaid ka traditsiooniliste vasest telefonijuhtide kaudu.
Potentsiaalsete ründajate füüsilist juurdepääsu sellele kaabelvõrgule ja seda toetavale infrastruktuurile oleks võimatu takistada. Tegelikult teame juba praegu, et enamik meie andmetest on erinevate riiklike luureagentuuride poolt pealtkuulatud Interneti otsustavates ristumiskohtades.[7] See hõlmab kõike, alates Facebooki sõnumitest kuni teie poolt külastatud veebisaitide aadressideni.
Kui andmete massiline jälgimine eeldab võimsat vastast, näiteks riiklikku luureagentuuri, siis vähese ressursiga ründajad võivad hõlpsasti proovida nuhkida kohalikul tasandil. Kuigi see võib toimuda juhtmete pealtkuulamise tasandil, on palju lihtsam lihtsalt traadita side pealtkuulamine.
Enamik meie kohalikest võrguandmetest - olgu need siis meie kodus, kontoris või kohvikus - liigub nüüd raadiolainete kaudu traadita juurdepääsupunktidesse kõik-ühes ruuterites, mitte füüsiliste kaablite kaudu. Seega vajab ründaja vähe ressursse, et teie kohalikku liiklust pealtkuulata. See on eriti murettekitav, sest enamik inimesi teeb väga vähe selleks, et kaitsta andmeid, mis liiguvad nende kohalikes võrkudes. Lisaks võivad potentsiaalsed ründajad sihtida ka meie mobiilseid lairibaühendusi, näiteks 3G, 4G ja 5G. Kõik need traadita sideühendused on ründajatele kerge sihtmärk.
Seega on idee hoida side saladuses, kaitstes sidekanalit, suurele osale tänapäeva maailmast lootusetult ekslik püüdlus. Kõik, mida me teame, õigustab tõsist paranoiat: tuleb alati eeldada, et keegi kuulab pealt. Ja krüptograafia on peamine vahend, mis meil on olemas, et saavutada igasugune turvalisus selles kaasaegses keskkonnas.
Märkused:
[7] Vt näiteks Olga Khazan, "The creepy, long-standing practice of undersea cable tapping", The Atlantic, 16. juuli 2013 (kättesaadav aadressil The Atlantic).
Krüptograafia matemaatilised alused 1
Juhuslikud muutujad
Krüptograafia põhineb matemaatikal. Ja kui sa tahad krüptograafiast rohkem kui ainult pealiskaudselt aru saada, siis pead sa selle matemaatikaga hästi hakkama saama.
Selles peatükis tutvustatakse enamikku põhilistest matemaatilistest elementidest, millega puutute kokku krüptograafia õppimisel. Teemade hulka kuuluvad juhuslikud muutujad, modulooperatsioonid, XOR-operatsioonid ja pseudorandomness. Krüptograafia mitte-pealiskaudseks mõistmiseks peaksite nende peatükkide materjali omandama.
Järgmine osa käsitleb arvuteooriat, mis on palju keerulisem.
Juhuslikud muutujad
Juhuslikku muutujat tähistatakse tavaliselt mittepaksude suurtähtedega. Nii
võime näiteks rääkida juhuslikust muutujast X, juhuslikust muutujast Y või juhuslikust muutujast Z.
Seda tähistust kasutan ka mina edaspidi.
suvaline muutuja võib võtta kaks või enam võimalikku väärtust, millest igaühel on kindel positiivne tõenäosus. Võimalikud väärtused on loetletud väljundkogumis.
Iga kord, kui te võtete juhusliku muutuja, võtate selle tulemuse hulgast kindla väärtuse vastavalt määratletud tõenäosustele.
Võtame lihtsa näite. Oletame, et muutuja X on defineeritud järgmiselt:
- X-l on tulemuse hulk
\{1,2\}
Pr[X = 1] = 0.5Pr[X = 2] = 0.5On lihtne näha, et X on
juhuslik muutuja. Esiteks on kaks või enam võimalikku väärtust, mida X võib võtta, nimelt 1 ja 2. Teiseks on igal võimalikul
väärtusel positiivne tõenäosus esineda, kui te võtate proovi X, nimelt 0.5.
Kõik, mida juhuslik muutuja vajab, on kahe või enama võimalusega tulemuste kogum, kus igal võimalusel on positiivne tõenäosus esineda valimi võtmisel. Põhimõtteliselt võib juhuslikku muutujat defineerida abstraktselt, ilma igasuguse kontekstita. Sellisel juhul võiks mõelda "valimi võtmisest" kui mingi loomuliku eksperimendi läbiviimisest juhusliku muutuja väärtuse määramiseks.
Ülaltoodud muutuja X on
defineeritud abstraktselt. Seega võiks mõelda, et eespool esitatud muutuja X proovivõtmine on nagu õiglase mündi viskamine ja "2" määramine, kui tulemus
on "pea", ja "1", kui tulemus on "saba". Iga valimi X puhul viskate münti uuesti.
Alternatiivselt võib ka mõelda proovivõtust X kui õiglase täringu viskamisest ja "2" määramisest juhul, kui täringule
langeb 1, 3 või 4, ja "1" määramisest
juhul, kui täringule langeb 2, 5 või 6. Iga kord, kui te
proovi X võtate, viskate täringut
uuesti.
Tegelikult võib joonise suhtes ette kujutada mis tahes loomulikku
eksperimenti, mis võimaldaks määratleda ülaltoodud X võimalike väärtuste tõenäosusi.
Sageli ei esitata juhuslikke muutujaid siiski ainult abstraktselt. Selle asemel on võimalike tulemuste väärtuste kogumil selgesõnaline tegelik tähendus (mitte ainult numbritena). Lisaks võivad need tulemusväärtused olla määratletud mingi kindlat tüüpi eksperimendi suhtes (mitte kui mis tahes looduslik eksperiment nende väärtustega).
Vaatleme nüüd näide muutuja X kohta, mis ei ole abstraktselt defineeritud. X on defineeritud järgmiselt, et
määrata, milline kahest meeskonnast alustab jalgpallimängu:
Xon tulemuse komplekt {punane lööb välja,sinine lööb välja}- Viskame konkreetse mündi
C: saba = "punane lööb välja"; pea = "sinine lööb välja"
Pr [X = \text{red kicks off}] = 0.5Pr [X = \text{blue kicks off}] = 0.5Sellisel juhul on tulemuse X hulk varustatud konkreetse tähendusega, nimelt
sellega, milline meeskond alustab jalgpallimängus. Lisaks on võimalikud
tulemused ja nendega seotud tõenäosused määratud konkreetse eksperimendi
abil, nimelt konkreetse mündi C viskamisega.
Krüptograafiat käsitlevates aruteludes tutvustatakse tavaliselt juhuslikke muutujaid reaalse tähendusega tulemuse kogumi suhtes. See võib olla kõigi krüpteeritavate sõnumite hulk, mida tuntakse sõnumiruumina, või kõigi võtmete hulk, mille hulgast krüpteerimist kasutavad pooled saavad valida, mida tuntakse võtmeruumina.
Krüptograafiat käsitlevates aruteludes ei määratleta juhuslikke muutujaid tavaliselt siiski mitte mõne konkreetse loodusliku eksperimendi suhtes, vaid mis tahes eksperimendi suhtes, mis võib anda õigeid tõenäosusjaotusi.
Juhuslikud muutujad võivad olla diskreetse või pideva tõenäosusjaotusega. diskreetse tõenäosusjaotusega juhuslikud muutujad - st diskreetsed juhuslikud muutujad - omavad piiratud
arvu võimalikke tulemusi. Mõlemas seni toodud näites oli juhuslik muutuja X diskreetne.
Jooksvad juhuslikud muutujad võivad selle asemel võtta väärtusi ühes või mitmes intervallis. Näiteks võib öelda, et juhuslik muutuja võtab valimi võtmisel vastu mis tahes reaalväärtuse vahemikus 0 ja 1 ning et iga reaalarv selles intervallis on võrdselt tõenäoline. Selle intervalli sees on lõpmatult palju võimalikke väärtusi.
Krüptograafiliste arutelude jaoks peate mõistma ainult diskreetseid juhuslikke muutujaid. Seetõttu tuleb edaspidi kõik arutelud juhuslike muutujate üle mõista nii, et need viitavad diskreetsetele juhuslikele muutujatele, kui ei ole eraldi öeldud teisiti.
Juhuslike muutujate graafikute koostamine
Juhusliku muutuja võimalikke väärtusi ja nendega seotud tõenäosusi saab
kergesti visualiseerida graafiku abil. Näiteks vaadeldakse eelmises punktis
esitatud juhuslikku muutujat X, mille tulemuste hulk on \{1, 2\} ja Pr [X = 1] = 0.5 ning Pr [X = 2] = 0.5. Sellist
juhuslikku muutujat kujutatakse tavaliselt tulpdiagrammi kujul, nagu on
esitatud Kujul 1.
Joonis 1: Juhuslik muutuja X
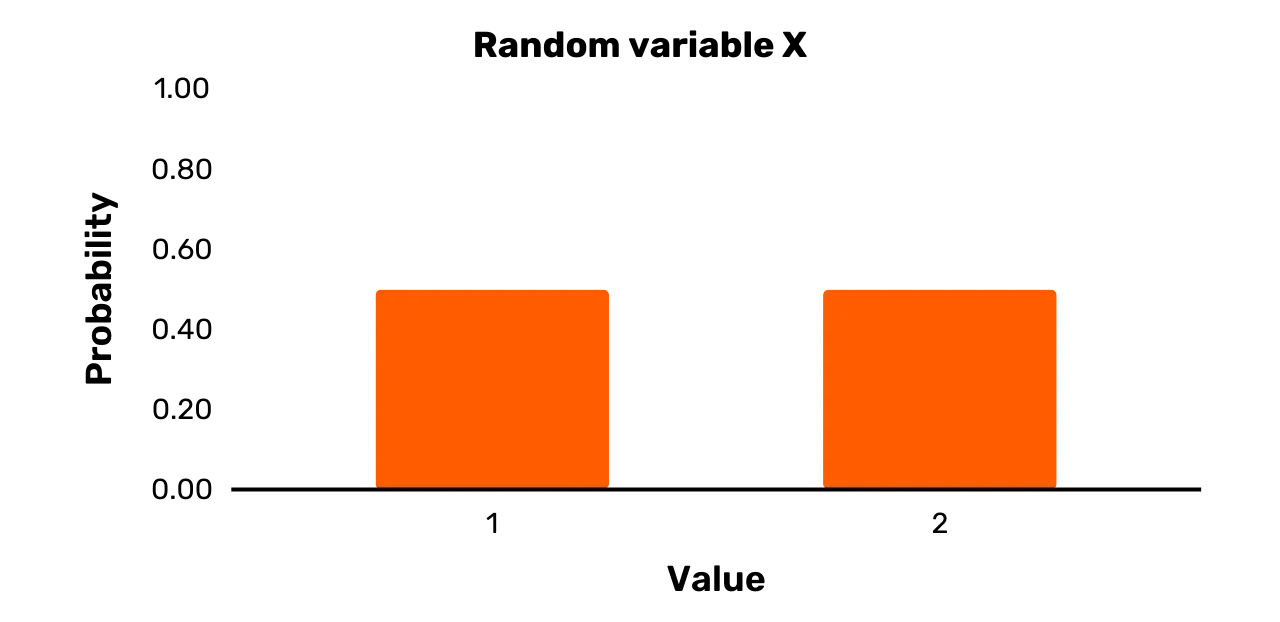
Laiad tulbad Kujul 1 ei tähenda ilmselt, et juhuslik muutuja X oleks tegelikult pidev. Selle
asemel on tulbad tehtud laiad, et need oleksid visuaalselt atraktiivsemad (lihtsalt
sirge joon annab vähem intuitiivse visualiseerimise).
Ühetaolised muutujad
Väljenduses "juhuslik muutuja" tähendab mõiste "juhuslik" lihtsalt "tõenäosuslik". Teisisõnu tähendab see lihtsalt seda, et muutuja kaks või enam võimalikku tulemust esinevad teatud tõenäosusega. Need tulemused ei pea aga vajalikult olema võrdselt tõenäolised (kuigi terminil "juhuslik" võib teistes kontekstides tõepoolest olla selline tähendus).
Ühetaoline muutuja on juhusliku muutuja erijuhtum. See võib
võtta kaks või enam väärtust, mis kõik on võrdse tõenäosusega. Joonisel 1
kujutatud juhuslik muutuja X on selgelt ühtlane muutuja, sest mõlemad võimalikud tulemused esinevad
tõenäosusega 0.5. Siiski on
palju juhuslikke muutujaid, mis ei ole ühetaolised muutujad.
Võtame näiteks juhusliku muutuja Y. Sellel on tulemuse hulk {1, 2, 3, 8, 10} ja
järgmine tõenäosusjaotus:
\Pr[Y = 1] = 0.25\Pr[Y = 2] = 0.35\Pr[Y = 3] = 0.1\Pr[Y = 8] = 0.25\Pr[Y = 10] = 0.05Kuigi kahel võimalikul tulemusel on tõepoolest võrdne tõenäosus esineda,
nimelt 1 ja 8, võib Y võtta proovivõtu korral ka teatud väärtusi, mille tõenäosus erineb 0.25-st. Seega, kuigi Y on tõepoolest juhuslik muutuja,
ei ole see ühtlane muutuja.
Graafiline kujutis Y on
esitatud Kujul 2.
Joonis 2: Juhuslik muutuja Y
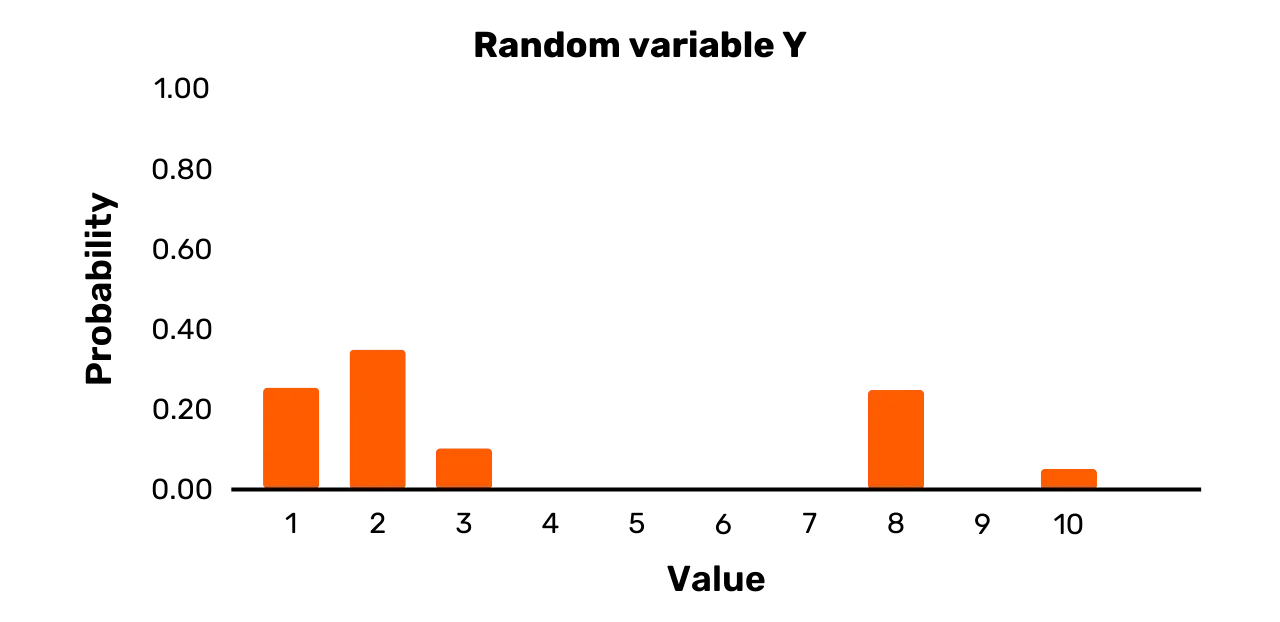
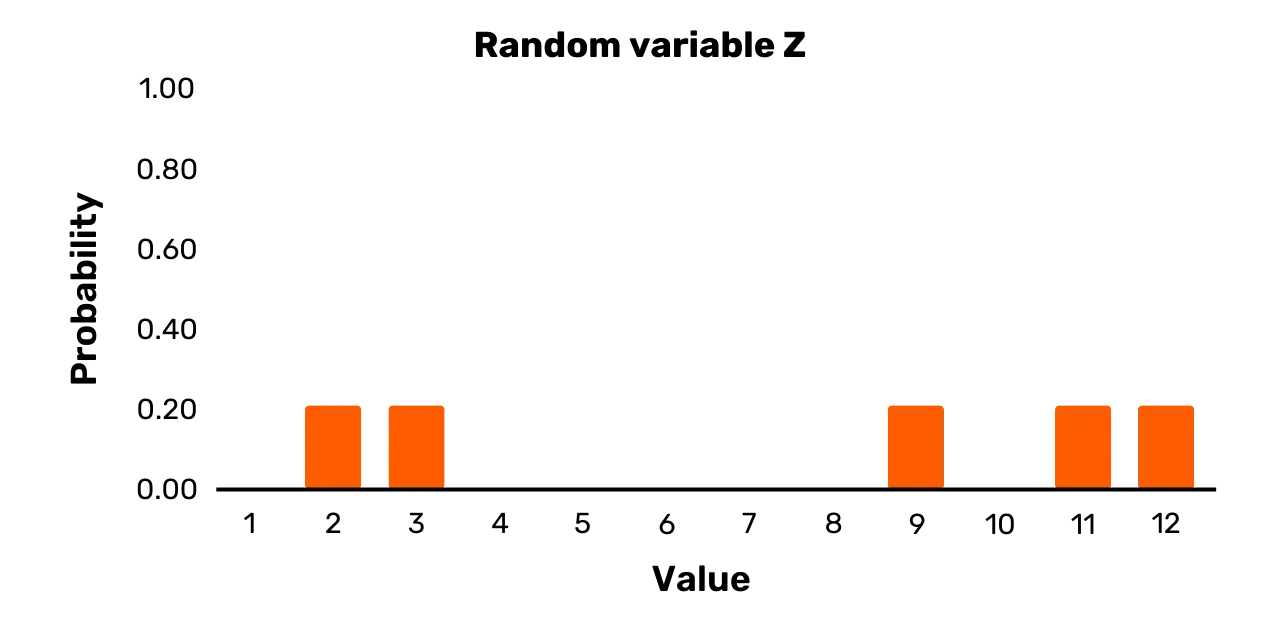
Viimase näitena vaadelgem juhuslikku muutujat Z. Sellel on tulemuse hulk {1,3,7,11,12} ja järgmine tõenäosusjaotus:
\Pr[Z = 2] = 0.2\Pr[Z = 3] = 0.2\Pr[Z = 9] = 0.2\Pr[Z = 11] = 0.2\Pr[Z = 12] = 0.2Seda on kujutatud joonisel 3*. Juhuslik muutuja Z on erinevalt Y-st ühtlane muutuja, sest kõik võimalike väärtuste tõenäosused on valimi võtmisel võrdsed.
Joonis 3: Juhuslik muutuja Z
Tingimuslik tõenäosus
Oletame, et Bob kavatseb ühtlaselt valida ühe päeva viimasest kalendriaastast. Milline on tõenäosus, et valitud päev on suvel?
Kui me arvame, et Bobi protsess on tõepoolest tõeliselt ühtlane, peaksime järeldama, et tõenäosus, et Bob valib suvise päeva, on 1/4. See on tingimuslik tõenäosus, et juhuslikult valitud päev langeb suvele.
Oletame nüüd, et Bob valib kalendripäeva ühetaolise loosimise asemel ainult ühetaoliselt nende päevade hulgast, mil keskpäevane temperatuur Crystal Lake'is (New Jersey) oli 21 kraadi Celsiuse järgi või kõrgem. Milline on selle lisateabe põhjal järeldus selle kohta, kui suure tõenäosusega valib Bob suvise päeva?
Me peaksime tõesti tegema teistsuguse järelduse kui varem, isegi ilma täiendava konkreetse teabeta (nt temperatuur iga päeva keskpäeval eelmisel kalendriaastal).
Teades, et Crystal Lake asub New Jersey's, ei ootaks me kindlasti, et temperatuur keskpäeval oleks talvel 21 kraadi või kõrgem. Selle asemel on palju tõenäolisem, et see on kevadel või sügisel või kuskil suvel soe päev. Seega, teades, et Crystal Lake'i keskpäevane temperatuur oli valitud päeval 21 kraadi Celsiuse järgi või kõrgem, on tõenäosus, et Bobi valitud päev on suvel, palju suurem. See on tingimuslik tõenäosus, et juhuslikult valitud päev on suvel, arvestades, et keskpäevane temperatuur Crystal Lake'is oli 21 kraadi Celsiuse järgi või kõrgem.
Erinevalt eelmisest näitest võivad kahe sündmuse tõenäosused olla ka täiesti sõltumatud. Sellisel juhul ütleme, et nad on sõltumatud.
Oletame näiteks, et teatud õiglane münt on langenud pähe. Arvestades seda asjaolu, milline on siis tõenäosus, et homme sajab vihma? Tingimuslik tõenäosus peaks sel juhul olema sama, mis tingimusteta tõenäosus, et homme sajab vihma, sest mündi viskamine ei mõjuta üldjuhul ilma.
Me kasutame "|" sümbolit tingimuslike tõenäosusavalduste kirjutamiseks.
Näiteks sündmuse A tõenäosus,
arvestades, et sündmus B on toimunud,
võib kirjutada järgmiselt:
Pr[A|B]Seega, kui kaks sündmust A ja B on sõltumatud, siis:
Pr[A|B] = Pr[A] \text{ and } Pr[B|A] = Pr[B]Sõltumatuse tingimust saab lihtsustada järgmiselt:
Pr[A, B] = Pr[A] \cdot Pr[B]Tõenäosusteooria võtmetulemus on tuntud kui Bayesi teoreem.
See väidab, et Pr[A|B] saab ümber
kirjutada järgmiselt:
Pr[A|B] = \frac{Pr[B|A] \cdot Pr[A]}{Pr[B]}Selle asemel, et kasutada tingimuslikke tõenäosusi konkreetsete sündmuste
puhul, võime vaadata ka kahe või enama juhusliku muutuja tingimuslikke
tõenäosusi, mis on seotud võimalike sündmuste kogumiga. Oletame, et on kaks
juhuslikku muutujat X ja Y. Me võime tähistada X-i mis tahes võimalikku
väärtust x-ga ja Y-i mis tahes võimalikku
väärtust y-ga. Võime siis
öelda, et kaks juhuslikku muutujat on sõltumatud, kui kehtib järgmine väide:
Pr[X = x, Y = y] = Pr[X = x] \cdot Pr[Y = y]kõigi x ja y puhul.
Räägime veidi selgemalt, mida see väide tähendab.
Oletame, et X ja Y tulemuste kogud on määratletud järgmiselt: X = \{x_1, x_2, \ldots, x_i, \ldots, x_n\} ja Y = \{y_1, y_2, \ldots, y_i, \ldots, y_m\}. (Tavaliselt tähistatakse väärtuste kogumeid paksult kirjutatud
suurtähtedega)
Nüüd oletame, et te võtate proovi Y ja jälgite y_1. Ülaltoodud
väide ütleb meile, et tõenäosus, et nüüd saame x_1 valimi X põhjal, on täpselt
sama, kui me poleks kunagi y_1 täheldanud. See kehtib iga y_i kohta, mille me oleksime võinud võtta meie algse valimi Y põhjal. Lõpuks kehtib see mitte ainult x_1 kohta. Mis tahes x_i puhul ei
mõjuta esinemise tõenäosust Y proovivõtu tulemus. Kõik see kehtib ka juhul, kui X võetakse esimesena proovi.
Lõpetame oma arutelu veidi filosoofilisemal teemal. Igas reaalses olukorras hinnatakse mingi sündmuse tõenäosust alati konkreetse teabe põhjal. Ei ole olemas "tingimusteta tõenäosust" selle sõna väga ranges tähenduses.
Oletame näiteks, et ma küsin teilt tõenäosust, et sead lendavad 2030. aastaks. Kuigi ma ei anna teile mingit lisateavet, teate te ilmselgelt palju maailma kohta, mis võib teie otsust mõjutada. Te ei ole kunagi näinud, et sead lendaksid. Te teate, et enamik inimesi ei oota, et nad lendavad. Te teate, et neid ei ole tegelikult ehitatud lendamiseks. Ja nii edasi.
Seega, kui me räägime mingi sündmuse "tingimusteta tõenäosusest" reaalses kontekstis, saab see termin omada tähendust ainult siis, kui me mõistame seda kui midagi sellist nagu "tõenäosus ilma igasuguse täiendava selgesõnalise informatsioonita". Igasugune arusaam "tingimuslikust tõenäosusest" peaks seega alati olema mõistetav mingi konkreetse teabe suhtes.
Ma võiksin näiteks küsida, kui suur on tõenäosus, et sead hakkavad 2030. aastaks lendama, pärast seda, kui olen andnud teile tõendeid, et mõned kitsed Uus-Meremaal on pärast mõneaastast treeningut õppinud lendama. Sellisel juhul korrigeerite tõenäoliselt oma hinnangut tõenäosusele, et sead lendavad 2030. aastaks. Seega sõltub tõenäosus, et sead lendavad 2030. aastaks, sellest tõendusmaterjalist Uus-Meremaa kitsede kohta.
Modulo operatsioon
Modulo
Kõige elementaarsem modulo-operatsiooniga seotud avaldis on
järgmises vormis: x \mod y.
Muutujat x nimetatakse
dividendiks ja muutujat y jagajaks.
Positiivse dividendi ja positiivse divisoriga modulo-operatsiooni tegemiseks
määratakse lihtsalt jagamise jääk.
Näiteks vaadelgem väljendit 25 \mod 4. Arv 4 läheb kokku 6 korda arvusse 25. Selle jagamise jääk on 1. Seega on 25 \mod 4 võrdne 1. Samamoodi
saame hinnata järgmisi väljendeid:
29 \mod 30 = 29(kuna 30 läheb kokku 0 korda 29 sisse ja jääk on 29)42 \mod 2 = 0(kuna 2 läheb kokku 21 korda 42 sisse ja jääk on 0)12 \mod 5 = 2(kuna 5 läheb kokku 2 korda 12-sse ja jääk on 2)20 \mod 8 = 4(kuna 8 läheb kokku 2 korda 20 sisse ja jääk on 4)
Kui dividend või divisor on negatiivne, võivad programmeerimiskeeled käsitleda modulooperatsioone erinevalt.
Kindlasti puutute krüptograafias kokku negatiivse dividendiga juhtumitega. Sellistel juhtudel on tüüpiline lähenemine järgmine:
- Määrake kõigepealt lähim väärtus, mis on väiksem või võrdne dividendiga, mille jagajaks on jääk null. Nimetame seda väärtust
p. - Kui dividend on
x, siis on modulo-operatsiooni tulemus väärtusx - p.
Oletame näiteks, et dividend on -20 ja jagaja 3. Lähim väärtus, mis on väiksem või võrdne -20, millega 3 jaguneb
ühtlaselt, on -21. Sellisel
juhul on x - p väärtus -20 - (-21). See on võrdne 1
ja seega on -20 \mod 3 võrdne
1. Samamoodi saame hinnata alljärgnevaid avaldisi:
-8 \mod 5 = 2-19 \mod 16 = 13-14 \mod 6 = 4
Märkimisviiside puhul näete tavaliselt järgmist tüüpi väljendeid: x = [y \mod z]. Sulgude tõttu kehtib modulo-operatsioon sel juhul ainult väljendi
paremale poolele. Kui y on
näiteks 25 ja z on 4, siis x saab väärtuseks 1.
Ilma sulgudeta mõjub modulo-operatsioon kummagi poole väljendile.
Oletame näiteks järgmist väljendit: x = y \mod z. Kui y on võrdne 25 ja z võrdne 4,
siis teame ainult, et x \mod 4 on 1. See on kooskõlas mis tahes väärtusega x hulgast \{\dots, -7, -3, 1, 5, 9, \dots\}.
Matemaatika haru, mis hõlmab arvude ja väljenditega tehtavaid modulooperatsioone, nimetatakse modulaararitmeetikaks. Seda haru võib pidada aritmeetikaks juhtudeks, mille puhul arvjoon ei ole lõpmatult pikk. Kuigi tavaliselt puutume krüptograafias kokku (positiivsete) täisarvudega tehtavate modulooperatsioonidega, saab modulooperatsioone teha ka mis tahes reaalarvudega.
Nihkešifreering
Modulo-operatsiooniga puututakse krüptograafias sageli kokku. Selle illustreerimiseks vaatleme ühte kõige kuulsamat ajaloolist krüpteerimisskeemi: nihkešifreeringut.
Määratleme selle kõigepealt. Oletame, et on olemas sõnastik D, mis
võrdsustab kõik inglise tähestiku tähed järjekorras numbrite hulgaga \{0, 1, 2, \ldots, 25\}. Oletame, et on olemas sõnumiruum M. Siis on shiftšifreering krüpteerimisskeem, mis on määratletud järgmiselt:
- Valige ühtlaselt võti
kvõtmeruumist K, kus K =\{0, 1, 2, \ldots, 25\}[1] - Krüpteerige sõnum
m \in \mathbf{M}järgmiselt:- Eraldada
müksikuteks tähtedeksm_0, m_1, \ldots, m_i, \ldots, m_l - Teisenda iga
m_inumbriks vastavalt D - Iga
m_ipuhul onc_i = [(m_i + k) \mod 26] - Teisenda iga
c_itäheks vastavalt D - Seejärel kombineeritakse
c_0, c_1, \ldots, c_l, et saada salastatud tekstc
- Eraldada
- Dekrüpteerige salastatud tekst
cjärgmiselt:- Teisenda iga
c_iarvuks vastavalt D - Iga
c_ipuhul onm_i = [(c_i - k) \mod 26] - Teisenda iga
m_itäheks vastavalt D - Seejärel kombineeritakse
m_0, m_1, \ldots, m_l, et saada algne sõnumm
- Teisenda iga
Nihkešifreeringu modulo-operaator tagab, et tähed on ümberpööratud, nii et kõik salakirjatähised on määratletud. Illustreerimiseks vaadelge nihkešifri rakendamist sõnale "DOG".
Oletame, et valisite ühtlaselt ühe võtme väärtuseks 17. Täht "O" vastab
15-le. Ilma modulo-operatsioonita annaks selle lihtkirjanumbri ja võtme
liitmine salakirjanumbrile 32. Seda salatekstinumbrit ei saa aga muuta
salatekstitäheks, sest inglise tähestikus on ainult 26 tähte.
Modulooperatsioon tagab, et salatekstinumber on tegelikult 6 (tulemus 32 \mod 26), mis vastab salatekstitähtedele "G".
Kogu sõna "DOG" krüpteerimine võtme väärtusega 17 on järgmine:
- Sõnum = DOG = D,O,G = 3,15,6
c_0 = [(3 + 17) \mod 26] = [(20) \mod 26] = 20 = Uc_1 = [(15 + 17) \mod 26] = [(32) \mod 26] = 6 = Gc_2 = [(6 + 17) \mod 26] = [(23) \mod 26] = 23 = Xc = UGX
Igaüks saab intuitiivselt aru, kuidas nihkešifreering töötab, ja tõenäoliselt kasutab seda ka ise. Krüptograafia alaste teadmiste edasiarendamiseks on aga oluline hakata end formaliseerimisega paremini kurssi viima, sest skeemid muutuvad palju keerulisemaks. Siit ka põhjus, miks nihkešifri sammud formaliseeriti.
Märkused:
[1] Selle väite võime täpselt määratleda, kasutades eelmises punktis
kasutatud terminoloogiat. Olgu ühetaolise muutuja K võimalike tulemuste hulk K.
Niisiis:
Pr[K = 0] = \frac{1}{26}Pr[K = 1] = \frac{1}{26}...ja nii edasi. Võtke üks kord ühetaolisest muutujast K proov, et saada konkreetne võti.
XOR-operatsioon
Kõiki arvutiandmeid töödeldakse, salvestatakse ja saadetakse võrkudes bittide tasandil. Kõik krüptograafilised skeemid, mida kohaldatakse arvutiandmete suhtes, toimivad samuti bittide tasandil.
Oletame näiteks, et olete kirjutanud e-kirja oma e-posti rakendusse. Krüpteerimine, mida te rakendate, ei toimu otse teie e-kirja ASCII-märkidele. Selle asemel rakendatakse seda teie e-kirjas olevate tähtede ja muude sümbolite bitide kujutamise suhtes.
Tänapäeva krüptograafias on lisaks modulo-operatsioonile oluline
matemaatiline operatsioon, mida tuleb mõista, XOR-operatsioon ehk "eksklusiivne või" operatsioon. See operatsioon võtab sisendiks kaks
bitti ja annab väljundiks teise biti. XOR-operatsiooni tähistatakse lihtsalt
kui "XOR". See annab tulemuseks 0, kui kaks bitti on samad, ja 1, kui kaks
bitti on erinevad. Allpool näete nelja võimalust. Sümbol \oplus tähistab "XOR" :
0 \oplus 0 = 00 \oplus 1 = 11 \oplus 0 = 11 \oplus 1 = 0
Illustreerimiseks oletame, et teil on sõnum m_1 (01111001) ja sõnum m_2 (01011001).
Nende kahe sõnumi XOR-operatsioon on näha allpool.
m_1 \oplus m_2 = 01111001 \oplus 01011001 = 00100000
Protsess on lihtne. Kõigepealt XOR-ida m_1 ja m_2 kõige vasakpoolsemad
bitid. Antud juhul on see 0 \oplus 0 = 0. Seejärel
XOR-ida teine paar bite vasakult. Antud juhul on see 1 \oplus 1 = 0. Seda
protsessi jätkatakse, kuni on tehtud XOR-operatsioon parempoolseima bitiga.
On lihtne näha, et XOR-operatsioon on kommutatiivne, nimelt et m_1 \oplus m_2 = m_2 \oplus m_1. Lisaks on XOR-operatsioon ka assotsiatiivne. See tähendab, et (m_1 \oplus m_2) \oplus m_3 = m_1 \oplus (m_2 \oplus m_3).
XOR-operatsioon kahele erineva pikkusega stringile võib sõltuvalt kontekstist olla erinevalt tõlgendatav. Me ei käsitle siinkohal ühtegi XOR-operatsiooni erineva pikkusega stringidega.
XOR-operatsioon on samaväärne erijuhtumiga, kui bittide liitmisel tehakse modulo-operatsioon, kui jagajaks on 2. Samaväärsust näete järgmistest tulemustest:
(0 + 0) \mod 2 = 0 \oplus 0 = 0(1 + 0) \mod 2 = 1 \oplus 0 = 1(0 + 1) \mod 2 = 0 \oplus 1 = 1(1 + 1) \mod 2 = 1 \oplus 1 = 0
Pseudorandomness
Meie arutelus juhuslike ja ühtlaste muutujate üle tegime konkreetset vahet "juhuslikel" ja "ühtlastel" muutujatel. Seda eristust säilitatakse tavaliselt praktikas juhuslike muutujate kirjeldamisel. Kuid meie praeguses kontekstis tuleb see eristamine kaotada ja "juhuslik" ja "ühtlane" kasutatakse sünonüümselt. Selgitan, miks see nii on, jao lõpus.
Alustuseks võime nimetada binaarset stringi pikkusega n juhuslikuks (või ühtlaseks), kui see on
saadud ühtlase muutuja S valimiga, mis annab igale sellise pikkusega n binaarsele stringile võrdse
valiku tõenäosuse.
Oletame näiteks, et kõigi 8 pikkusega binaarsete stringide kogum: \{0000\ 0000, 0000\ 0001, \ldots, 1111\ 1111\}. (Tüüpiliselt kirjutatakse 8-bitine string kahes kvartalis, mida
nimetatakse nibble) Nimetagem seda stringide kogumit S_8.
Vastavalt ülaltoodud definitsioonile võime me siis nimetada teatud binaarset
stringi pikkusega 8 juhuslikuks (või ühtlaseks), kui see on ühtlase muutuja S valimi tulemus, mis annab igale stringile S_8 võrdse tõenäosuse valimiseks. Arvestades, et hulk S_8 sisaldab 2^8 elemente, peaks
valiku tõenäosus valimi võtmisel olema 1/2^8 iga stringi jaoks selles
kogumis.
Binaarse stringi juhuslikkuse võtmeaspekt on see, et see on määratletud viitega protsessile, mille abil see on valitud. Seega ei ütle mis tahes konkreetse binaarse stringi vorm iseenesest midagi selle juhuslikkuse kohta valimisel.
Näiteks paljud inimesed arvavad intuitiivselt, et selline string nagu 1111\ 1111 ei saa olla juhuslikult valitud. Kuid see on selgelt vale.
Määratledes ühtlase muutuja S üle kõigi 8 pikkusega binaarsete stringide, on tõenäosus valida 1111\ 1111 hulgast S_8 sama, kui näiteks 0111\ 0100.
Seega ei saa stringi juhuslikkuse kohta midagi öelda ainult stringi enda
analüüsiga.
Me võime rääkida ka juhuslikest jadadest, ilma et mõtleksime konkreetselt
binaarsete jadade all. Võime näiteks rääkida juhuslikust
heksakombinatsioonist AF\ 02\ 82. Sellisel juhul oleks see string valitud juhuslikult kõigi
heksakombinatsioonide hulgast, mille pikkus on 6. See on samaväärne 24
pikkuse binaarkombinatsiooni juhusliku valimisega, sest iga
heksakombinatsiooniline number esindab 4 bitti.
Tavaliselt viitab väljend "juhuslik string" ilma täpsustusteta kõikide sama
pikkusega stringide hulgast juhuslikult valitud stringile. Nii olen ma seda
eespool kirjeldanud. Loomulikult võib string pikkusega n olla juhuslikult valitud ka teisest hulgast. Näiteks sellisest, mis
moodustab ainult kõigi stringide alamhulga, mille pikkus on n, või võib-olla kogumist,
mis sisaldab erineva pikkusega stringe. Sellistel juhtudel ei nimetaksime
seda aga "juhuslikuks stringiks", vaid pigem "stringiks, mis on juhuslikult
valitud mingist hulgast S".
Krüptograafia võtmekontseptsioon on pseudoristentsus. Pseudoristring pikkusega n näib kui see oleks ühtlase muutuja S proovivõtu tulemus, mis annab igale stringile S_n võrdse valiku tõenäosuse. Tegelikult on string aga ühtlase muutuja S' valimi võtmise tulemus, mis määratleb ainult tõenäosusjaotuse - mitte
tingimata kõigi võimalike tulemuste jaoks võrdse tõenäosusega - S_n alamhulga kohta. Oluline on siinkohal see, et keegi ei saa tegelikult vahet
teha proovide S ja S' vahel, isegi kui neid võtta
palju.
Oletame näiteks, et on olemas juhuslik muutuja S. Selle tulemuse hulk on S_{256}, see on kõigi 256 pikkusega binaarsete stringide hulk. Sellel hulgal on 2^{256} elemente. Igal elemendil on valimi võtmisel võrdne tõenäosus, 1/2^{256}.
Lisaks oletame, et on olemas juhuslik muutuja S'. Selle tulemuste hulk sisaldab ainult 2^{128} binaarsed stringid
pikkusega 256. Sellel on mingi tõenäosusjaotus nende stringide üle, kuid see
jaotus ei pruugi olla ühtlane.
Oletame, et ma võtsin nüüd 1000 proovi S-st ja 1000 proovi S'-st
ning andsin teile need kaks tulemuste kogumit. Ütlen teile, milline
tulemuste kogum on seotud millise juhusliku muutujaga. Järgnevalt võtan
proovi ühest neist kahest juhuslikust muutujast. Kuid seekord ei ütle ma
teile, millise juhusliku muutuja proovi ma võtan. Kui S' oleks pseudorandom, siis on mõte selles, et teie tõenäosus arvata õigesti,
millise juhusliku muutuja proovi ma võtsin, on praktiliselt mitte parem kui 1/2.
Tavaliselt toodetakse pseudorandom string pikkusega n, valides juhuslikult stringi suurusega n - x, kus x on positiivne täisarv, ja kasutades seda laiendamisalgoritmi sisendiks. Seda
juhuslikku stringi suurusega n - x nimetatakse seediks.
Pseudorandom stringid on krüptograafia praktiliseks muutmise võtmekontseptsioon. Võtame näiteks voogkoode. Voolukooderite puhul ühendatakse juhuslikult valitud võti laiendamisalgoritmiga, et saada palju suurem pseudorandom string. Seejärel kombineeritakse see pseudoristring XOR-operatsiooni abil lihtkirjaga, et saada salakirjatekst.
Kui me ei suudaks toota sellist pseudorandom stringi voošifri jaoks, siis oleks meil vaja võtit, mis oleks sama pikk kui sõnum, et tagada selle turvalisus. See ei ole enamasti väga praktiline võimalus.
Käesolevas jaotises käsitletud pseudoristentsuse mõistet võib määratleda formaalsemalt. See laieneb ka muudesse kontekstidesse. Kuid me ei pea siinkohal sellesse arutellu süvenema. Kõik, mida on vaja intuitiivselt mõista, on erinevus juhusliku ja pseudoristrandi vahel. [2]
Nüüd peaks olema selge ka põhjus, miks me loobusime "juhusliku" ja "ühtlase"
eristamisest meie arutelus. Praktikas kasutavad kõik terminit pseudorandom,
et tähistada stringi, mis ilmub kui oleks ühtlase muutuja S proovivõtu tulemus. Rangelt
võttes peaksime sellist stringi nimetama "pseudo-ühtlaseks", võttes üle meie
varasemat keelekasutust. Kuna termin "pseudo-ühtlane" on nii kohmakas kui ka
mitte kellegi poolt kasutatav, siis me seda siinkohal selguse huvides ei kasuta.
Selle asemel jätame lihtsalt praeguses kontekstis "juhusliku" ja "ühetaolise"
eristamise ära.
Märkused
[2] Kui olete huvitatud nende küsimuste ametlikumast käsitlusest, võite tutvuda Katzi ja Lindelli Introduction to Modern Cryptography, eriti peatükis 3.
Krüptograafia matemaatilised alused 2
Mis on arvuteooria?
Selles peatükis käsitletakse krüptograafia matemaatiliste aluste edasijõudnuteematikat: arvuteooriat. Kuigi arvuteooria on oluline sümmeetrilise krüptograafia jaoks (näiteks Rijndaeli šifri puhul), on see eriti oluline avaliku võtme krüptograafia puhul.
Kui arvuteooria üksikasjad tunduvad teile tülikad, siis soovitaksin esimesel korral lugeda kõrgema taseme lugemist. Te võite alati hiljem selle juurde tagasi tulla.
Lugude teooriat võiks iseloomustada kui täisarvude ja täisarvudega töötavate matemaatiliste funktsioonide omaduste uurimist.
Võtame näiteks, et mis tahes kaks arvu a ja N on kooprime (või relatiivsed priimid), kui nende suurim ühine osaleja
on võrdne 1. Oletame nüüd, et mingi kindel täisarv N. Mitu täisarvu, mis on
väiksemad kui N, on N-ga koopriimsed? Kas me
saame teha üldisi väiteid selle küsimuse vastuste kohta? Need on tüüpilised
küsimused, millele arvuteooria püüab vastata.
Kaasaegne arvuteooria tugineb abstraktse algebra vahenditele. Abstraktne algebra on matemaatika alamdistsipliin, kus analüüsi peamised objektid on abstraktsed objektid, mida nimetatakse algebralisteks struktuurideks. Algebraline struktuur on elementide hulk, mis on ühendatud ühe või mitme operatsiooniga ja vastab teatud aksioomidele. Algebraliste struktuuride abil saavad matemaatikud ülevaate konkreetsetest matemaatilistest probleemidest, abstraheerides nende üksikasjadest.
Abstraktse algebra valdkonda nimetatakse mõnikord ka kaasaegseks algebraks. Te võite kohata ka mõistet abstraktne matemaatika (või puhas matemaatika). Viimane mõiste ei viita abstraktsele algebrale, vaid tähendab pigem matemaatika uurimist selle enda pärast, mitte ainult võimalikke rakendusi silmas pidades.
Abstraktsest algebrast pärit hulkade abil saab käsitleda paljusid objekte, alates võrdkülgse kolmnurga kuju säilitavatest teisendustest kuni tapeedimustriteni. Arvuteoorias käsitleme ainult elementide kogumeid, mis sisaldavad täisarvusid või funktsioone, mis töötavad täisarvudega.
Rühmad
Matemaatika põhimõiste on elementide hulk. Kogumit tähistatakse tavaliselt akkordi märkidega, mille elemendid on eraldatud komadega.
Näiteks kõigi täisarvude hulk on \{\dots, -2, -1, 0, 1, 2, \dots\}. Ellipsid tähendavad siin, et teatud muster jätkub teatud suunas. Seega
kuulub kõikide täisarvude hulka ka 3, 4, 5, 6 jne, samuti -3, -4, -5, -6 jne. Seda kõikide täisarvude hulka tähistatakse tavaliselt \mathbb{Z}.
Teine näide kogumi kohta on \mathbb{Z} \mod 11 ehk kõigi täisarvude hulk modulo 11. Erinevalt kogu hulgast \mathbb{Z} sisaldab see hulk ainult piiratud arvu elemente, nimelt \{0, 1, \ldots, 9, 10\}.
Levinud viga on arvata, et hulk \mathbb{Z} \mod 11 on tegelikult \{-10, -9, \ldots, 0, \ldots, 9, 10\}. Kuid see ei ole nii, arvestades seda, kuidas me modulo-operatsiooni varem
defineerisime. Kõik negatiivsed täisarvud, mis on redutseeritud modulo
11-ga, jäävad \{0, 1, \ldots, 9, 10\} peale. Näiteks väljend -2 \mod 11 mähib ümber 9, samas kui
väljend -27 \mod 11 mähib
ümber 5.
Teine põhimõiste matemaatikas on binaarne operatsioon. See on mis tahes operatsioon, mis võtab kaks elementi, et saada kolmas element. Näiteks aritmeetika ja algebra põhitõdedest on teile tuttavad neli põhilist binaarset operatsiooni: liitmine, lahutamine, korrutamine ja jagamine.
Neid kahte matemaatilist põhimõistet, kogumeid ja binaaroperatsioone, kasutatakse grupi mõiste määratlemiseks, mis on abstraktse algebra kõige olulisem struktuur.
Täpsemalt, oletame, et mingi binaarne operatsioon \circ. Lisaks oletame, et mingi elementide hulk S on varustatud
selle operatsiooniga. "Varustatud" tähendab siinkohal vaid seda, et
operatsiooni \circ saab
teostada mis tahes kahe elemendi vahel kogumis S.
Kombinatsioon \langle \mathbf{S}, \circ \rangle on siis rühm, kui see vastab neljale konkreetsele
tingimusele, mida nimetatakse rühmaaksioomideks.
Mis tahes
ajab, mis on\mathbf{S}elemendid, ona \circ bsamuti\mathbf{S}element. Seda tuntakse suletud tingimusena.Mis tahes
a,bjacpuhul, mis on\mathbf{S}elemendid, kehtib, et(a \circ b) \circ c = a \circ (b \circ c). Seda nimetatakse assotsiatiivsuse tingimuseks.\mathbf{S}-s on ainuke elemente, nii et iga elemendiakohta\mathbf{S}-s kehtib järgmine võrrand:e \circ a = a \circ e = a. Kuna on ainult üks selline elemente, nimetatakse seda identiteedielemendiks. Seda tingimust nimetatakse identiteediks.Iga elemendi
ajaoks\mathbf{S}sees on olemas elementb\mathbf{S}, nii et kehtib järgmine võrrand:a \circ b = b \circ a = e, kuseon identne element. Elementbon siinkohal tuntud kui inversne element ja seda tähistatakse tavaliselt kuia^{-1}. Seda tingimust nimetatakse inversioonitingimuseks või inversioonitingimuseks.
Uurime gruppe veidi lähemalt. Tähistame kõigi täisarvude hulka \mathbb{Z}. See hulk koos standardse liitmisega ehk \langle \mathbb{Z}, + \rangle vastab selgelt grupi definitsioonile, sest see vastab eespool toodud neljale
aksioomile.
Mis tahes
xjaypuhul, mis on\mathbb{Z}elemendid, onx + ysamuti\mathbb{Z}element. Seega vastab\langle \mathbb{Z}, + \ranglesulgemistingimusele.Mis tahes
x,yjazjaoks, mis on\mathbb{Z}elemendid, kehtib(x + y) + z = x + (y + z). Seega\langle \mathbb{Z}, + \ranglevastab assotsiatiivsuse tingimusele.On olemas identne element
\langle \mathbb{Z}, + \rangle, nimelt 0. Mis tahesxjaoks\mathbb{Z}-s kehtib nimelt, et:0 + x = x + 0 = x. Seega\langle \mathbb{Z}, + \ranglevastab identsustingimusele.Lõpuks on iga elemendi
xjaoks\mathbb{Z}olemasy, nii etx + y = y + x = 0. Kuixoleks näiteks 10, oleksy-10(juhul, kuixon 0, on kay0). Seega\langle \mathbb{Z}, + \ranglevastab pöördtingimusele.
Oluline on see, et täisarvude hulk liitmisega moodustab grupi, mis ei
tähenda, et see moodustab grupi korrutamisega. Seda saab kontrollida, kui
testida \langle \mathbb{Z}, \cdot \rangle nelja rühmaaksioomi vastu (kus \cdot tähendab tavalist korrutamist).
Kaks esimest aksioomi on ilmselgelt kehtivad. Lisaks sellele võib
korrutamisel element 1 olla identne element. Mis tahes täisarv x korrutatakse 1ga, nimelt saadakse x. Kuid \langle \mathbb{Z}, \cdot \rangle ei vasta pöördtingimusele. See tähendab, et iga x jaoks \mathbb{Z} ei
ole ainuüksi elementi y \mathbb{Z}, nii et x \cdot y = 1.
Oletame näiteks, et x = 22.
Milline väärtus y hulgast \mathbb{Z} korrutatuna x annab identse
elemendi 1? Väärtus 1/22 sobiks, kuid seda ei ole kogumis \mathbb{Z}.
Tegelikult tekib see probleem iga täisarvu x puhul, välja arvatud väärtused 1 ja -1 (kus y peaks olema vastavalt 1 ja -1).
Kui me lubaksime oma kogumi jaoks reaalarvud, siis kaovad meie probleemid
suures osas ära. Iga elemendi x puhul kogumis annab 1/x korrutamine
1. Kuna murdarvud kuuluvad reaalarvude hulka, saab iga reaalarvu jaoks leida
pöördvõrrandi. Erandiks on null, sest mis tahes korrutamine nulliga ei anna kunagi
identse elemendi 1. Seega on mittenullide reaalarvude hulk, mis on varustatud
korrutamisega, tõepoolest rühm.
Mõned rühmad vastavad viiendale üldtingimusele, mida nimetatakse kommutatiivsuse tingimuseks. See tingimus on järgmine:
- Oletame rühma
Gkoos kogumi S ja binaarse operaatoriga\circ. Oletame, etajabon S elemendid. Kui kehtib, eta \circ b = b \circ amis tahes kahe elemendiajabjaoks S, siis vastabGkommutatiivsuse tingimusele.
Mis tahes rühma, mis vastab kommutatiivsuse tingimusele, nimetatakse kommutatiivseks rühmaks või Abeli rühmaks (Niels Henrik Abeli järgi). On lihtne kontrollida, et nii reaalarvude hulk liitmisel kui ka täisarvude hulk liitmisel on Abeli rühmad. Tervete arvude hulk korrutamisel ei ole üldse rühm, seega ei saa ipso facto olla Abeli rühm. Seevastu mittenullide reaalarvude hulk korrutamisel on samuti Abeli rühm.
Te peaksite järgima kahte olulist märkimisviisi. Esiteks kasutatakse sageli märke "+" või "×" grupioperatsioonide tähistamiseks, isegi kui elemendid ei ole tegelikult arvud. Sellistel juhtudel ei tohiks neid märke tõlgendada kui tavalist aritmeetilist liitmist või korrutamist. Selle asemel on tegemist operatsioonidega, millel on ainult abstraktne sarnasus nende aritmeetiliste operatsioonidega.
Kui te ei viita konkreetselt aritmeetilisele liitmisele või korrutamisele,
on lihtsam kasutada selliseid sümboleid nagu \circ ja \diamond rühmaoperatsioonide
jaoks, kuna neil ei ole kultuuriliselt väga sügavalt juurdunud tähendusi.
Teiseks, samal põhjusel, miks "+" ja "×" kasutatakse sageli mittearitmiliste
operatsioonide tähistamiseks, sümboliseeritakse rühmade identseid elemente
sageli "0" ja "1", isegi kui nende rühmade elemendid ei ole arvud. Kui te ei
viita arvudega rühma identiteedielemendile, on lihtsam kasutada
neutraalsemat sümbolit, näiteks "e", identiteedielemendi tähistamiseks.
Paljud erinevad ja väga tähtsad matemaatikas teatud binaarsete operatsioonidega varustatud väärtuste kogumid on rühmad. Krüptograafilised rakendused töötavad aga ainult täisarvude või vähemalt täisarvudega kirjeldatavate elementide hulkadega, st arvuteooria valdkonnas. Seega ei kasutata krüptograafilistes rakendustes muid reaalarvudega kogumeid kui täisarvud.
Lõpetuseks toome näite elementide kohta, mida saab "kirjeldada täisarvudega", kuigi need ei ole täisarvud. Hea näide on elliptiliste kõverate punktid. Kuigi mis tahes punkt elliptilisel kõveral ei ole ilmselgelt täisarv, on selline punkt tõepoolest kirjeldatud kahe täisarvuga.
Elliptilised kõverad on näiteks Bitcoini jaoks üliolulised. Iga standardne Bitcoini era- ja avaliku võtme paar valitakse punktide hulgast, mis on määratletud järgmise elliptilise kõveraga:
x^3 + 7 = y^2 \mod 2^{256} – 2^{32} – 29 – 28 – 27 – 26 - 24 - 1(suurim algarv, mis on väiksem kui 2^{256}). x-koordinaat on privaatne
võti ja y-koordinaat on teie
avalik võti.
Bitcoini tehingud hõlmavad tavaliselt väljundite lukustamist ühele või mitmele avalikule võtmele. Nende tehingute väärtust saab seejärel avada, tehes digitaalallkirju vastavate privaatvõtmete abil.
Tsüklilised rühmad
Peamine erinevus, mida me võime teha, on lõputu ja lõputu rühma vahel. Esimesel on piiratud arv elemente, teisel aga lõpmatu arv elemente. Mis tahes lõpliku rühma elementide arvu nimetatakse rühma järjekorranumbriks. Kogu praktiline krüptograafia, mis hõlmab rühmade kasutamist, tugineb lõplikele (arvuteoreetilistele) rühmadele.
Avaliku võtme krüptograafias on eriti oluline teatud lõplike Abeli rühmade klass, mida nimetatakse tsüklilisteks rühmadeks. Tsükliliste rühmade mõistmiseks peame kõigepealt mõistma rühmaelemendi eksponentsuse mõistet.
Oletame, et on olemas rühm G,
millel on grupioperatsioon \circ, ja et a on G element. Väljendit a^n tuleb siis tõlgendada kui element a, mis on kokku n-1 korda endaga kombineeritud. Näiteks a^2 tähendab a \circ a, a^3 tähendab a \circ a \circ a jne.
(Pange tähele, et siinkohal ei pruugi eksponentsimine olla eksponentsimine tavalises
aritmeetilises mõttes)
Võtame ühe näite. Oletame, et G = \langle \mathbb{Z} \mod 7, + \rangle ja et meie väärtus a on 4.
Sel juhul on a^2 = [4 + 4 \mod 7] = [8 \mod 7] = 1 \mod 7. Teise võimalusena oleks a^4 [4 + 4 + 4 + 4 + 4 \mod 7] = [16 \mod 7] = 2 \mod 7.
Mõnedel Abeli rühmadel on üks või mitu elementi, mis võivad läbi jätkuva korrutamise anda kõik teised rühma elemendid. Neid elemente nimetatakse generaatoriteks või primitiivseteks elementideks.
Selliste rühmade oluline klass on \langle \mathbb{Z}^* \mod N, \cdot \rangle, kus N on algarv. Tähendus \mathbb{Z}^* tähendab siin, et rühm sisaldab kõiki nullist erinevaid positiivseid
täisarvusid, mis on väiksemad kui N. Sellisel rühmal on seega
alati N - 1 elemente.
Võtame näiteks G = \langle \mathbb{Z}^* \mod 11, \cdot \rangle. Sellel rühmal on järgmised elemendid: \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. Selle grupi järjestus on 10 (mis on tõepoolest võrdne 11 - 1).
Uurime sellest rühmast elemendi 2 eksponentimist. Allpool on näidatud
arvutused kuni 2^{12}. Pange tähele, et võrrandi vasakul poolel viitab eksponent grupi elemendi
eksponentimisele. Meie konkreetses näites hõlmab see tõepoolest
aritmeetilist eksponentimist võrrandi paremal poolel (kuid see oleks võinud
hõlmata ka näiteks liitmist). Selgituseks olen välja kirjutanud
kordusoperatsiooni, mitte eksponendi vormi paremal poolel.
2^1 = 2 \mod 112^2 = 2 \cdot 2 \mod 11 = 4 \mod 112^3 = 2 \cdot 2 \cdot 2 \mod 11 = 8 \mod 112^4 = 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 16 \mod 11 = 5 \mod 112^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 32 \mod 11 = 10 \mod 112^6 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 64 \mod 11 = 9 \mod 112^7 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 128 \mod 11 = 7 \mod 112^8 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 256 \mod 11 = 3 \mod 112^9 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 512 \mod 11 = 6 \mod 112^{10} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 1024 \mod 11 = 1 \mod 112^{11} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 2048 \mod 11 = 2 \mod 112^{12} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 4096 \mod 11 = 4 \mod 11
Kui te vaatate tähelepanelikult, näete, et eksponentimine elemendile 2 läbib
kõik elemendid \langle \mathbb{Z}^* \mod 11, \cdot \rangle järgmises järjekorras: 2, 4, 8, 5, 10, 9, 7, 3, 6, 1. Pärast 2^{10} jätkub elemendi 2 eksponentimine tsükliliselt läbi kõigi elementide uuesti
ja samas järjekorras. Seega on element 2 generaator \langle \mathbb{Z}^* \mod 11, \cdot \rangle.
Kuigi \langle \mathbb{Z}^* \mod 11, \cdot \rangle on mitu generaatorit, ei ole kõik selle rühma elemendid generaatorid. Võtame
näiteks elemendi 3. Esimese 10 eksponentsi läbi jooksmine, ilma et näitaksime
tülikat arvutust, annab järgmised tulemused:
3^1 = 3 \mod 113^2 = 9 \mod 113^3 = 5 \mod 113^4 = 4 \mod 113^5 = 1 \mod 113^6 = 3 \mod 113^7 = 9 \mod 113^8 = 5 \mod 113^9 = 4 \mod 113^{10} = 1 \mod 11
Selle asemel, et käia läbi kõik väärtused dokumendis \langle \mathbb{Z}^* \mod 11, \cdot \rangle, viib elemendi 3 korrutamine ainult nende väärtuste alamhulga juurde: 3,
9, 5, 4 ja 1. Pärast viiendat korrutamist hakkavad need väärtused korduma.
Nüüd võime defineerida tsüklilist rühma kui mis tahes rühma, millel on vähemalt üks generaator. See tähendab, et on olemas vähemalt üks grupi element, millest saab kõiki teisi grupi elemente toota eksponentide abil.
Võib-olla märkasite ülaltoodud näites, et nii 2^{10} kui ka 3^{10} on
võrdsed 1 \mod 11.
Tegelikult, kuigi me ei tee arvutusi, annab mis tahes elemendi
eksponentimine 10ga grupis \langle \mathbb{Z}^* \mod 11, \cdot \rangle tulemuseks 1 \mod 11. Miks
see nii on?
See on oluline küsimus, kuid sellele vastamine nõuab tööd.
Alustuseks oletame, et on kaks positiivset täisarvu a ja N. Üks oluline arvuteooria
teoreem väidab, et a on
korrutisvõrrandi pöördväärtus modulo N (st täisarv b, nii et a \cdot b = 1 \mod N), kui ja
ainult siis, kui a ja N suurim ühine jagaja on võrdne 1. See tähendab, et a on üks ja ainult siis, kui a ja N suurim ühine jagaja on
võrdne 1. See tähendab, et kui a ja N on ühisarvud.
Seega, mis tahes täisarvude rühma puhul, mis on varustatud korrutamisega
modulo N, kuuluvad ainult
väiksemad kooprimeetrid N-ga.
Seda hulka võime tähistada \mathbb{Z}^c \mod N.
Oletame näiteks, et N on 10.
Ainult täisarvud 1, 3, 7 ja 9 on 10ga kooprimeeritud. Seega sisaldab hulk \mathbb{Z}^c \mod 10 ainult \{1, 3, 7, 9\}. Te
ei saa luua täisarvude korrutamisega modulo 10 gruppi, kasutades muid
täisarvusid vahemikus 1 ja 10. Selle konkreetse rühma puhul on
inversioonideks paarid 1 ja 9 ning 3 ja 7.
Juhul kui N ise on algarv,
siis on kõik täisarvud 1 kuni N - 1 ja N koosarvulised. Sellise
rühma suurus on seega N - 1.
Kasutades meie varasemat tähistust, on \mathbb{Z}^c \mod N võrdne \mathbb{Z}^* \mod N, kui N on primaarne. Rühm,
mille me valisime oma varasemas näites, \langle \mathbb{Z}^* \mod 11, \cdot \rangle, on selle rühmade klassi eriline näide.
Seejärel arvutab funktsioon \phi(N) koprimeetrite arvu kuni arvuni N ja on tuntud kui Euleri Phi funktsioon. [1] Vastavalt Euleri teoreemile, kui kaks täisarvu a ja N on koopriimid, kehtib järgmine:
a^{\phi(N)} \mod N = 1 \mod N
Sellel on oluline mõju rühmade \langle \mathbb{Z}^* \mod N, \cdot \rangle klassile, kus N on algarv.
Nende rühmade puhul kujutab rühmade elementide eksponentsus aritmeetilist
eksponentsust. See tähendab, et a^{\phi(N)} \mod N tähistab aritmeetilist operatsiooni a^{\phi(N)} \mod N.
Kuna iga element a nendes
korrutisgruppides on korrutisgruppi N, siis tähendab see, et a^{\phi(N)} \mod N = a^{N - 1} \mod N = 1 \mod N.
Euleri teoreem on tõesti oluline tulemus. Alustuseks tähendab see, et kõik
elemendid objektis \langle \mathbb{Z}^* \mod N, \cdot \rangle võivad ainult tsükliliselt läbida arvu väärtusi, mis jagunevad N - 1. Punkti \langle \mathbb{Z}^* \mod 11, \cdot \rangle puhul tähendab see, et iga element saab tsükliliselt läbida ainult 2, 5 või
10 elementi. Grupi väärtusi, mida iga element korrutamisel läbib,
nimetatakse elemendi järjekorraks. Element, mille järjestus
on võrdne rühma järjestusega, on generaator.
Peale selle tähendab Euleri teoreem, et me saame alati teada a^{N - 1} tulemuse \mod N mis tahes rühma \langle \mathbb{Z}^* \mod N, \cdot \rangle puhul, kus N on algarv. See on
nii olenemata sellest, kui keerulised võivad olla tegelikud arvutused.
Oletame näiteks, et meie rühm on \mathbb{Z}^* \mod 160,481,182 (kus 160,481,182 on tõepoolest algarv). Me teame, et kõik täisarvud 1 kuni
160,481,181 peavad olema selle rühma elemendid ja et \phi(n) = 160,481,181. Ehkki
me ei saa teha kõiki arvutusetappe, teame, et sellised avaldised nagu 514^{160,481,181}, 2,005^{160,481,181} ja 256,212^{160,481,181} peavad kõik saama väärtuseks 1 \mod 160,481,182.
Märkused:
[1] Funktsioon töötab järgmiselt. Iga täisarvu N saab faktoriseerida algarvude korrutiseks. Oletame, et konkreetne N on faktoriseeritud järgmiselt: p_1^{e1} \cdot p_2^{e2} \cdot \ldots \cdot
p_m^{em}, kus kõik p on algarvud ja
kõik e on täisarvud, mis on suuremad
või võrdsed 1. Siis:
\phi(N) = \sum_{i=1}^m \left[p_i^{e_i} - p_i^{e_i - 1}\right]Euleri Phi-funktsiooni valem N primaarfaktoritsiooni jaoks.
Väljad
Rühm on abstraktses algebras põhiline algebraline struktuur, kuid neid on palju rohkem. Ainus teine algebraline struktuur, mida te peate tundma, on välja, täpsemalt teraviku struktuur. Seda tüüpi algebralist struktuuri kasutatakse sageli krüptograafias, näiteks täiustatud krüpteerimisstandardis. Viimane on peamine sümmeetriline krüpteerimisskeem, millega te praktikas kokku puutute.
Väli on tuletatud grupi mõistest. Täpsemalt on väli elementide hulk S, mis on varustatud kahe binaarse
operaatoriga \circ ja \diamond, mis vastab
järgmistele tingimustele:
Kogum S, mis on varustatud
\circ-ga, on Abeli rühm.Kogum S, mis on varustatud
\diamond, on Abeli rühm "nullist erinevate" elementide jaoks.Nende kahe operaatoriga varustatud hulk S vastab nn distributiivsele tingimusele: Oletame, et
a,bjacon S elemendid. Siis vastab kahe operaatoriga varustatud S distributiivsele omadusele, kuia \circ (b \diamond c) = (a \circ b) \diamond (a \circ c).
Pange tähele, et nagu rühmade puhul, on ka valdkonna määratlus väga
abstraktne. Selles ei esitata mingeid väiteid S elementide
tüüpide või operatsioonide \circ ja \diamond kohta. Selles on lihtsalt
öeldud, et väli on mis tahes elementide hulk, millel on kaks operatsiooni, mille
puhul kehtivad kolm ülaltoodud tingimust. (Teise Abeli rühma "null" elementi
saab abstraktselt tõlgendada)
Mis võiks siis olla näide valdkonnast? Hea näide on hulk \mathbb{Z} \mod 7 ehk \{0, 1, \ldots, 7\}, mis on defineeritud standardse liitmise (ülaltoodud \circ asemel) ja standardse korrutamise (ülaltoodud \diamond asemel) kaudu.
Esiteks, \mathbb{Z} \mod 7 vastab tingimusele, et olla Abeli rühm liitmise korral, ja see vastab tingimusele,
et olla Abeli rühm korrutamise korral, kui vaadelda ainult mittenullidest elemente.
Teiseks vastab hulga kombinatsioon kahe operaatoriga distributiivsele tingimusele.
Didaktiliselt tasub neid väiteid uurida, kasutades mõningaid konkreetseid
väärtusi. Võtame eksperimentaalsed väärtused 5, 2 ja 3, mõned juhuslikult
valitud elemendid hulgast \mathbb{Z} \mod 7, et uurida välja \langle \mathbb{Z} \mod 7, +, \cdot \rangle. Kasutame neid kolme väärtust järjestikku, vastavalt vajadusele, et uurida
konkreetseid tingimusi.
Uurime kõigepealt, kas \mathbb{Z} \mod 7, mis on varustatud liitmisega, on Abeli grupp.
Sulgemistingimus: Võtame väärtusteks 5 ja 2. Sel juhul on
[5 + 2] \mod 7 = 7 \mod 7 = 0. See on tõepoolest element\mathbb{Z} \mod 7, nii et tulemus on kooskõlas sulgemistingimusega.Assotsiatiivsuse tingimus: Võtame väärtusteks 5, 2 ja 3. Sel juhul on
[(5 + 2) + 3] \mod 7 = [5 + (2 + 3)] \mod 7 = 10 \mod 7 = 3. See on kooskõlas assotsiatiivsuse tingimusega.Identsuse tingimus: Võtame väärtuseks 5. Sel juhul on
[5 + 0] \mod 7 = [0 + 5] \mod 7 = 5. Seega tundub, et 0 on liitmise identne element.Vastupidine seisund: Vaadake 5 pöördvõrdelist tingimust. Peab olema nii, et
[5 + d] \mod 7 = 0, mingidväärtuse korral. Sellisel juhul on ainuke väärtus\mathbb{Z} \mod 7, mis vastab sellele tingimusele, on 2.Kommutatiivsuse tingimus: Võtame väärtusteks 5 ja 3. Sel juhul on
[5 + 3] \mod 7 = [3 + 5] \mod 7 = 1. See on kooskõlas kommutatiivsuse tingimusega.
Kogum \mathbb{Z} \mod 7, mis on varustatud liitmisega, näib selgelt olevat Abeli rühm. Uurime
nüüd, kas \mathbb{Z} \mod 7,
mis on varustatud korrutamisega, on kõigi nullist erinevate elementide puhul
Abeli rühm.
Sulgemistingimus: Võtame väärtusteks 5 ja 2. Sel juhul on
[5 \cdot 2] \mod 7 = 10 \mod 7 = 3. See on samuti element\mathbb{Z} \mod 7, nii et tulemus on kooskõlas sulgemistingimusega.Assotsiatiivsuse tingimus: Võtame väärtusteks 5, 2 ja 3. Sel juhul on
[(5 \cdot 2) \cdot 3] \mod 7 = [5 \cdot (2 \cdot 3)] \mod 7 = 30 \mod 7 = 2. See on kooskõlas assotsiatiivsuse tingimusega.Identsuse tingimus: Võtame väärtuseks 5. Sel juhul on
[5 \cdot 1] \mod 7 = [1 \cdot 5] \mod 7 = 5. Seega näib 1 olevat identne element korrutamisel.Vastupidine seisund: Vaadake 5 pöördvõrdelist tingimust. Peab olema nii, et
[5 \cdot d] \mod 7 = 1, mingidväärtuse korral. Ainulaadne väärtus\mathbb{Z} \mod 7, mis vastab sellele tingimusele, on 3. See on kooskõlas pöördtingimusega.Kommutatiivsuse tingimus: Võtame väärtusteks 5 ja 3. Sel juhul on
[5 \cdot 3] \mod 7 = [3 \cdot 5] \mod 7 = 15 \mod 7 = 1. See on kooskõlas kommutatiivsuse tingimusega.
Kogum \mathbb{Z} \mod 7 näib selgelt vastavat Abeli rühma reeglitele, kui see on ühendatud kas liitmise
või korrutamisega nullist erinevate elementide üle.
Lõpuks tundub, et see kogum koos mõlema operaatoriga vastab
jaotustingimusele. Võtame väärtusteks 5, 2 ja 3. Näeme, et [5 \cdot (2 + 3)] \mod 7 = [5 \cdot 2 + 5 \cdot 3] \mod 7 = 25 \mod 7 = 4.
Oleme nüüd näinud, et \mathbb{Z} \mod 7, mis on varustatud liitmise ja korrutamisega, vastab lõpliku välja
aksioomidele, kui seda testitakse konkreetsete väärtustega. Loomulikult
võime seda näidata ka üldiselt, kuid ei tee seda siinkohal.
Oluline on eristada kahte tüüpi välju: lõplikud ja lõpmatud väljad.
lõputu väli on väli, mille hulk S on
lõpmatult suur. Reaalarvude hulk \mathbb{R}, mis on
varustatud liitmise ja korrutamisega, on näide lõpmatust väljast. Tahe väli, mida nimetatakse ka Galois' väljaks, on väli, mille hulk S on
piiratud. Meie ülaltoodud näide \langle \mathbb{Z} \mod 7, +, \cdot \rangle on piiratud väli.
Krüptograafias huvitavad meid eelkõige lõplikud väljad. Üldiselt võib
näidata, et mingi elementide hulga S jaoks on olemas
piiratud väli, kui ja ainult siis, kui sellel on p^m elemente, kus p on algarv ja m positiivne täisarv, mis on suurem või võrdne ühega. Teisisõnu, kui mingi
hulga S järjestus on algarv (p^m, kus m = 1) või mingi
algvõime (p^m, kus m > 1), siis võib leida kaks
operaatorit \circ ja \diamond nii, et välja tingimused
on täidetud.
Kui mõnel piiratud väljal on algarv elemente, siis nimetatakse seda põhiväljaks. Kui lõpliku välja elementide arv on primaarne potensiaal, siis nimetatakse seda välja väljaks. Krüptograafias huvitavad meid nii prima- kui ka laiendusväljad. [2]
Peamised krüptograafias huvipakkuvad primaarväljad on need, kus kõikide
täisarvude hulk on moduleeritud mingi primaarvuga ning operaatoriteks on
standardne liitmine ja korrutamine. Sellesse klassi lõplike väljade hulka
kuuluvad \mathbb{Z} \mod 2, \mathbb{Z} \mod 3, \mathbb{Z} \mod 5, \mathbb{Z} \mod 7, \mathbb{Z} \mod 11, \mathbb{Z} \mod 13 ja nii edasi. Mis tahes primaarvälja \mathbb{Z} jaoks on \mathbb{Z} \mod p on selle välja täisarvude hulk järgmine: \{0, 1, \dots, p - 2, p - 1\}.
Krüptograafias huvitavad meid ka laiendusväljad, eriti mis tahes väljad,
millel on 2^m elemente, kus m > 1. Selliseid lõplikke
välju kasutatakse näiteks Rijndaeli šifris, mis on täiustatud
krüpteerimisstandardi aluseks. Kuigi primaarväljad on suhteliselt
intuitiivsed, ei ole need baasi 2 laiendusväljad tõenäoliselt mõeldud
kõigile, kes ei ole abstraktse algebraga tuttavad.
Alustuseks on tõepoolest tõsi, et igale täisarvude hulgale, mille elemendid
on 2^m, saab määrata kaks
operaatorit, mis muudavad nende kombinatsiooni väljaks (kui m on positiivne täisarv). Kuid
see, et väli on olemas, ei tähenda tingimata, et seda on lihtne avastada või
et see on teatud rakenduste jaoks eriti praktiline.
Nagu selgub, on krüptograafias eriti kasutatavad 2^m laiendusväljad need, mis on defineeritud polünoomiavaldiste teatud hulga üle,
mitte mingi täisarvude hulga üle.
Oletame näiteks, et soovime laiendusvälja, mille hulk on 2^3 (st 8) elementi. Kuigi sellise suurusega väljadele võib olla palju erinevaid
kogumeid, sisaldab üks selline hulk kõiki unikaalseid polünoome kujul a_2x^2 + a_1x + a_0, kus iga
koefitsient a_i on kas 0 või
1. Seega sisaldab see hulk S järgmisi elemente:
0: Juhtum, kusa_2 = 0,a_1 = 0jaa_0 = 0.1: Juhtum, kusa_2 = 0,a_1 = 0jaa_0 = 1.x: Juhtum, kusa_2 = 0,a_1 = 1jaa_0 = 0.x + 1: Juhtum, kusa_2 = 0,a_1 = 1jaa_0 = 1.x^2: Juhtum, kusa_2 = 1,a_1 = 0jaa_0 = 0.x^2 + 1: Juhtum, kusa_2 = 1,a_1 = 0jaa_0 = 1.x^2 + x: Juhtum, kusa_2 = 1,a_1 = 1jaa_0 = 0.x^2 + x + 1: Juhtum, kusa_2 = 1,a_1 = 1jaa_0 = 1.
Seega S oleks hulk \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x, x^2 + x + 1\}. Milliseid kahte operatsiooni saab selle elementide hulga üle defineerida,
et nende kombinatsioon oleks väli?
Esimene operatsioon kogumi S (\circ) kohta võib olla defineeritud kui tavaline polünoomi liitmine modulo 2.
Kõik, mida te peate tegema, on polünoomide liitmine nagu tavaliselt, ja
seejärel rakendada modulo 2 igale saadud polünoomi koefitsiendile. Siin on
mõned näited:
[(x^2) + (x^2 + x + 1)] \mod 2 = [2x^2 + x + 1] \mod 2 = x + 1[(x^2 + x) + (x)] \mod 2 = [x^2 + 2x] \mod 2 = x^2[(x + 1) + (x^2 + x + 1)] \mod 2 = [x^2 + 2x + 2] \mod 2 = x^2 + 1
Teine operatsioon koguga S (\diamond), mida on vaja välja loomiseks, on keerulisem. See on mingi korrutamine,
kuid mitte tavaline aritmeetika korrutamine. Selle asemel tuleb näha iga
elementi vektorina ja mõista operatsiooni kui nende kahe vektori korrutamist
mingi taandumatu polünoomiga.
Pöördume kõigepealt taandamatu polünoomi idee juurde. Redutseeritav polünoom on selline, mida ei saa faktoreerida (nii nagu algarvu ei saa faktoreerida muudeks komponentideks peale 1 ja algarvu enda). Meie eesmärkidel huvitavad meid polünoomid, mis on kõigi täisarvude hulga suhtes taandamatud. (Pange tähele, et teatud polünoome võib olla võimalik faktoreerida näiteks reaal- või kompleksarvude abil, isegi kui neid ei saa faktoreerida täisarvude abil)
Võtame näiteks polünoomi x^2 - 3x + 2. Seda saab ümber kirjutada (x - 1)(x - 2). Seega ei ole
see taandamatu. Nüüd vaadeldakse polünoomi x^2 + 1. Kasutades ainult
täisarvusid, ei ole võimalik seda avaldist edasi korrutada. Seega on see
täisarvude suhtes taandamatu polünoom.
Järgnevalt pöördume vektorite korrutamise mõiste juurde. Me ei hakka seda teemat põhjalikult uurima, vaid te peate lihtsalt mõistma põhireeglit: Iga vektori jagamine võib toimuda seni, kuni dividendi aste on suurem või võrdne divisori astmega. Kui dividendil on madalam aste kui divisoril, siis ei saa dividendi enam jagada divisoriga.
Näiteks vaadelgem väljendit x^6 + x + 1 \mod x^5 + x^2. See väheneb selgelt edasi, sest jagaja 6 on suurem kui jagaja 5. Nüüd
vaadeldakse väljendit x^5 + x + 1 \mod x^5 + x^2.
Ka see väheneb veelgi, sest dividendi 5 ja divisori 5 aste on võrdsed.
Nüüd aga vaadelgem väljendit x^4 + x + 1 \mod x^5 + x^2. See ei taandu edasi, sest dividendi aste 4 on madalam kui jagaja aste 5.
Selle teabe põhjal oleme nüüd valmis leidma oma teise operatsiooni kogumi \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x, x^2 + x + 1\} jaoks.
Ma juba ütlesin, et teist operatsiooni tuleks mõista kui vektorite korrutamist modulo mõne taandamatu polünoomiga. See taandamatu polünoom peaks tagama, et teine operatsioon defineerib Abeli rühma üle S ja on kooskõlas distributsioonitingimusega. Milline peaks see taandamatu polünoom olema?
Kuna kõik komplektis olevad vektorid on 2. astme või madalama astmega, peaks taandamatu polünoom olema 3. astme. Kui kahe komplektis oleva vektori mis tahes korrutamisel saadakse 3. astme või kõrgema astme polünoom, siis teame, et 3. astme polünoomi modulo annab alati 2. astme või madalama astme polünoomi. See on nii, sest iga 3. või kõrgema astme polünoom on alati jagatav 3. astme polünoomiga. Lisaks peab jagajaks olev polünoom olema taandamatu.
Selgub, et on olemas mitu 3. astme taandamatut polünoomi, mida me võiksime
kasutada oma jagajaks. Iga selline polünoom määratleb koos meie kogumi S ja liitmisega modulo 2 erineva valdkonna. See tähendab, et teil on
krüptograafias 2^m laiendusväljade
kasutamisel mitu võimalust.
Oletame, et meie näite jaoks valime polünoomi x^3 + x + 1. See on tõepoolest taandamatu, sest seda ei saa korrutada täisarvude abil.
Lisaks tagab see, et iga kahe elemendi korrutamine annab tulemuseks
polünoomi, mille aste on 2 või väiksem.
Näitame teise operatsiooni näite, kasutades jagajaks polünoomi x^3 + x + 1, et illustreerida selle toimimist. Oletame, et korrutame elemente x^2 + 1 ja x^2 + x meie kogumis S. Siis peame arvutama väljendi [(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1. Seda saab lihtsustada järgmiselt:
[(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1 =[(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1 =[x^2 \cdot x^2 + x^2 \cdot x + 1 \cdot x^2 + 1 \cdot x] \mod x^3 + x + 1 =[x^4 + x^3 + x^2 + x] \mod x^3 + x + 1
Me teame, et [x^4 + x^3 + x^2 + x] \mod x^3 + x + 1 saab vähendada, kuna dividendi aste on suurem (4) kui jagajal (3).
Alustuseks näete, et väljend x^3 + x + 1 läheb kokku x^4 + x^3 + x^2 + x korda x. Seda saab
kontrollida, korrutades x^3 + x + 1 arvuga x, mis on x^4 + x^2 + x. Kuna viimane
termin on sama astmega kui dividend, nimelt 4, siis teame, et see töötab.
Selle jagamise jäägi x-ga
saab arvutada järgmiselt:
[(x^4 + x^3 + x^2 + x) - (x^4 + x^2 + x)] \mod x^3 + x + 1 =[x^3] \mod x^3 + x + 1 =x^3
Seega pärast x^4 + x^3 + x^2 + x jagamist x^3 + x + 1-ga kokku x korda, saame jäägiks x^3. Kas
seda saab veel jagada x^3 + x + 1-ga?
Intuitiivselt võib olla ahvatlev öelda, et x^3 ei saa enam jagada x^3 + x + 1, sest viimane
termin tundub suurem. Kuid meenutagem meie arutelu vektorite jagamise kohta
varem. Niikaua kui dividendi aste on suurem või võrdne jagajaga, saab
avaldist veelgi vähendada. Täpsemalt, väljend x^3 + x + 1 võib täpselt 1 kord minna sisse x^3. Jääk arvutatakse
järgmiselt:
[(x^3) - (x^3 + x + 1)] \mod x^3 + x + 1 = [x + 1] \mod x^3 + x + 1 = x + 1Te võite imestada, miks (x^3) - (x^3 + x + 1) annab tulemuseks x + 1 ja
mitte -x - 1. Pidage meeles,
et meie välja esimene operatsioon on defineeritud modulo 2. Seega annab kahe
vektori lahutamine täpselt sama tulemuse kui kahe vektori liitmine.
Summaarselt korrutatakse x^2 + 1 ja x^2 + x: Kui korrutate
need kaks terminit, saate 4. astme polünoomi x^4 + x^3 + x^2 + x, mida
tuleb redutseerida modulo x^3 + x + 1. Neljanda astme
polünoom on jagatav x^3 + x + 1-ga täpselt x + 1 korda. Jääk pärast x^4 + x^3 + x^2 + x jagamist täpselt x^3 + x + 1 korda on x + 1. See on
tõepoolest element meie kogumis \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x, x^2 + x + 1\}.
Miks peaksid laiendusväljad baasiga 2 üle polünoomide hulga, nagu ülaltoodud näites, olema kasulikud krüptograafias? Põhjus on selles, et selliste hulkade polünoomide koefitsiente, kas 0 või 1, saab vaadelda kui teatud pikkusega binaarsete stringide elemente. Näiteks meie ülaltoodud näites esitatud kogumit S võib vaadelda selle asemel kui kogumit S, mis sisaldab kõiki binaarsõnu pikkusega 3 (000 kuni 111). Operatsioone koguga S saab siis kasutada ka nende binaarsete stringidega tehtavate operatsioonide tegemiseks ja sama pikkusega binaarsete stringide saamiseks.
Märkused:
[2] Laiendusväljad muutuvad väga vastupidiseks. Selle asemel, et omada täisarvude elemente, on neil polünoomide kogumeid. Lisaks sellele tehakse kõik operatsioonid modulo mõne irreduzible polünoomi suhtes.
Abstraktne algebra praktikas
Hoolimata arutelu formaalsest keelest ja abstraktsusest ei tohiks grupi mõiste olla liiga raskesti mõistetav. See on lihtsalt elementide kogum koos binaarse operatsiooniga, kusjuures selle binaarse operatsiooni sooritamine nende elementidega vastab neljale üldisele tingimusele. Abeli grupil on lihtsalt üks lisatingimus, mida nimetatakse kommutatiivsuseks. Tsükliline rühm on omakorda Abeli rühma eriline liik, nimelt selline, millel on generaator. Väli on lihtsalt keerulisem konstruktsioon põhirühma mõistest.
Aga kui te olete praktiliselt meelestatud inimene, siis võite siinkohal küsida: Keda see huvitab? Kas teadmine, et mingi operaatoriga elementide hulk on rühm või isegi Abeli või tsükliline rühm, omab mingit reaalset tähtsust? Kas teadmine, et midagi on väli?
Laskumata liiga palju üksikasjadesse, on vastus "jah". Rühmad lõi esimest korda 19. sajandil prantsuse matemaatik Evariste Galois. Ta kasutas neid selleks, et teha järeldusi viiest suuremate astmete polünoomi võrrandite lahendamise kohta.
Sellest ajast alates on grupi mõiste aidanud valgustada mitmeid probleeme matemaatikas ja mujalgi. Nende põhjal suutis näiteks füüsik Murray-Gellman ennustada osakese olemasolu enne, kui seda tegelikult katsetes täheldati. [3] Teise näitena kasutavad keemikud rühmateooriat molekulide kuju liigitamiseks. Matemaatikud on kasutanud grupi mõistet isegi selleks, et teha järeldusi millegi nii konkreetse kui seinapaberi kohta!
Sisuliselt näitab, et mingi operaatoriga elementide hulk on rühm, mis tähendab, et see, mida te kirjeldate, on teatud sümmeetria. Mitte sümmeetria selle sõna tavatähenduses, vaid abstraktsemal kujul. Ja see võib anda olulisi teadmisi konkreetsete süsteemide ja probleemide kohta. Abstraktsema algebra keerukamad mõisted annavad meile lihtsalt lisateavet.
Kõige tähtsam on see, et näete arvuteoreetiliste rühmade ja väljade tähtsust praktikas nende rakendamise kaudu krüptograafias, eriti avalike võtmete krüptograafias. Me nägime juba väljadest rääkides näiteks, kuidas laiendusvälju kasutatakse Rijndaeli šifris. Selle näite töötame välja peatükis 5.
Abstraktse algebra edasiseks arutamiseks soovitan Socratica suurepärast videoseeriat abstraktse algebra kohta. [4] Eriti soovitaksin järgmisi videoid: "Mis on abstraktne algebra?", "Grupi definitsioon (laiendatud)", "Rõngaste definitsioon (laiendatud)" ja "Välja definitsioon (laiendatud)" Need neli videot annavad teile täiendava ülevaate suurest osast ülaltoodud arutelust. (Me ei arutanud rõngaid, kuid väli on lihtsalt rõnga eriline tüüp)
Täiendavaks aruteluks kaasaegse arvuteooria kohta võite tutvuda paljude edasijõudnute aruteludega krüptograafia kohta. Soovitan edasiseks aruteluks Jonathan Katzi ja Yehuda Lindelli raamatut "Introduction to Modern Cryptography" või Christof Paari ja Jan Pelzli raamatut "Understanding Cryptography". [5]
Märkused:
[3] Vt YouTube video
[4] Socratica, Abstraktne algebra
[5] Katz ja Lindell, Introduction to Modern Cryptography, 2nd edn, 2015 (CRC Press: Boca Raton, FL). Paar ja Pelzl, Understanding Cryptography, 2010 (Springer-Verlag: Berlin).
Sümmeetriline krüptograafia
Alice ja Bob
Üks kahest peamisest krüptograafia harust on sümmeetriline krüptograafia. See hõlmab nii krüpteerimisskeeme kui ka autentimise ja terviklikkusega seotud skeeme. Kuni 1970. aastateni koosnes kogu krüptograafia sümmeetrilistest krüpteerimisskeemidest.
Peamine arutelu algab sümmeetriliste krüpteerimisskeemide käsitlemisega ja olulise erinevuse tegemisega voogkooderite ja plokk-kooderite vahel. Seejärel pöördume sõnumi autentimiskoodide juurde, mis on sõnumite terviklikkuse ja autentsuse tagamise skeemid. Lõpuks uurime, kuidas saab sümmeetrilisi krüpteerimisskeeme ja sõnumi autentimise koode kombineerida, et tagada turvaline side.
Selles peatükis käsitletakse möödaminnes erinevaid sümmeetrilisi krüptograafilisi skeeme praktikast. Järgmises peatükis käsitletakse üksikasjalikult krüpteerimist voošifri ja plokkšifri abil, milleks on vastavalt RC4 ja AES.
Enne sümmeetrilise krüptograafia arutelu alustamist tahan teha lühidalt mõned märkused Alice'i ja Bobi illustratsioonide kohta selles ja järgmistes peatükkides.
Krüptograafia põhimõtete illustreerimisel toetutakse sageli näidetele, mis hõlmavad Alice'i ja Bobi. Seda teen ka mina.
Eriti kui te olete krüptograafia alal uus, on oluline mõista, et need Alice'i ja Bobi näited on mõeldud ainult krüptograafiliste põhimõtete ja konstruktsioonide illustreerimiseks lihtsustatud keskkonnas. Need põhimõtted ja konstruktsioonid on aga rakendatavad palju laiemalt reaalsetes olukordades.
Järgnevalt on toodud viis põhipunkti, mida tuleks silmas pidada Alice'i ja Bobi krüptograafia näidete puhul:
Neid saab hõlpsasti tõlkida näideteks teist tüüpi osalejate, näiteks ettevõtete või valitsusasutuste puhul.
Neid saab hõlpsasti laiendada, et kaasata kolm või enam näitlejat.
Näites on Bob ja Alice tavaliselt aktiivsed osalejad iga sõnumi loomisel ja krüptograafiliste skeemide rakendamisel selle sõnumi suhtes. Tegelikkuses on elektrooniline side aga suures osas automatiseeritud. Näiteks kui külastate veebilehte, mis kasutab transpordikihi turvalisust, siis tavaliselt tegelevad krüptograafiaga teie arvuti ja veebiserver.
Elektroonilise side kontekstis on sidekanali kaudu saadetavad "sõnumid" tavaliselt TCP/IP-paketid. Need võivad kuuluda e-posti, Facebooki sõnumi, telefonivestluse, failiedastuse, veebisaidi, tarkvara üleslaadimise jne juurde. Need ei ole sõnumid traditsioonilises mõttes. Sellegipoolest lihtsustavad krüptograafid sageli seda tegelikkust, öeldes, et tegemist on näiteks e-kirjaga.
Näited keskenduvad tavaliselt elektroonilisele suhtlusele, kuid neid võib laiendada ka traditsioonilistele suhtlusvormidele, näiteks kirjadele.
Sümmeetrilised krüpteerimisskeemid
Me võime vabalt defineerida sümmeetrilist krüpteerimisskeemi kui mis tahes krüptograafilist skeemi, millel on kolm algoritmi:
võtme genereerimise algoritm, mis genereerib privaatvõtme.
Krüpteerimisalgoritm, mis võtab sisendiks salajase võtme ja lihtteksti ning väljastab salakirja.
decrypteerimisalgoritm, mis võtab sisendiks salajase võtme ja salastatud teksti ning väljastab algse lihtteksti.
Tavaliselt pakub krüpteerimisskeem - olgu see siis sümmeetriline või asümmeetriline - pigem krüpteerimismalli, mis põhineb põhialgoritmil, kui täpset spetsifikatsiooni.
Võtame näiteks sümmeetrilise krüpteerimisskeemi Salsa20 . Seda saab kasutada nii 128- kui ka 256-bitise võtmepikkusega. Võtmepikkuse valik mõjutab algoritmi mõningaid väiksemaid üksikasju (täpsemalt, algoritmi voorude arvu).
Kuid ei saa öelda, et Salsa20 kasutamine 128-bitise võtmega on teistsugune krüpteerimisskeem kui Salsa20 kasutamine 256-bitise võtmega. Põhialgoritm jääb samaks. Ainult siis, kui põhialgoritm muutub, räägime tegelikult kahest erinevast krüpteerimisskeemist.
Sümmeetrilised krüpteerimisskeemid on tavaliselt kasulikud kahte tüüpi juhtudel: 1) need, kus kaks või enam agenti suhtlevad kaugelt ja soovivad hoida oma side sisu salajas; ja 2) need, kus üks agent soovib hoida sõnumi sisu ajaliselt salajas.
Olukorra (1) kujutist näete allpool oleval Kujul 1. Bob soovib
saata Alice'ile sõnumi M üle vahemaa,
kuid ei soovi, et teised saaksid seda sõnumit lugeda.
Bob krüpteerib kõigepealt sõnumi M privaatvõtmega K. Seejärel
saadab ta salastatud teksti C Alice'ile. Kui Alice on salakirjateksti kätte saanud, saab ta selle võtme K abil dekrüpteerida ja lugeda puhasteksti. Hea krüpteerimisskeemi korral ei
tohiks ükski ründaja, kes salakirju C kinni püüab, saada teada midagi olulist sõnumi M kohta.
Olukorra (2) kujutist näete allpool oleval Kujul 2. Bob soovib takistada teistel teatud teabe vaatamist. Tüüpiline olukord võib olla, et Bob on töötaja, kes salvestab oma arvutis tundlikke andmeid, mida ei tohi lugeda ei kõrvalised isikud ega kolleegid.
Bob krüpteerib sõnumi M ajal T_0 võtmega K, et saada
salastatud tekst C. Ajal T_1 vajab ta sõnumit uuesti ja dekrüpteerib salakirjateksti C võtmega K. Iga ründaja, kes
on vahepeal puutunud kokku salakirjaga C, ei tohiks sellest midagi
olulist M kohta järeldada.
Joonis 1: Salastatus kogu ruumis

Joonis 2: Salastatus ajas

Üks näide: Nihkešifreering
Peatükis 2 tutvusime nihkešifriga, mis on näide väga lihtsast sümmeetrilisest krüpteerimisskeemist. Vaatame seda siinkohal uuesti.
Oletame, et on olemas sõnastik D, mis võrdsustab kõik inglise
tähestiku tähed järjekorras numbrite hulgaga \{0,1,2,\dots,25\}.
Oletame võimalike sõnumite kogumit M. Nihkešifreering on
siis krüpteerimisskeem, mis on määratletud järgmiselt:
- Valige juhuslikult võti
kvõimalike võtmete hulgast K, kus K =\{0,1,2,\dots,25\} - Krüpteeri sõnum
m \inM järgmiselt:- Eraldada
müksikuteks tähtedeksm_0, m_1,\dots, m_i, \dots, m_l - Teisenda iga
m_inumbriks vastavalt D - Iga
m_ipuhul onc_i = [(m_i + k) \mod 26] - Teisenda iga
c_itäheks vastavalt D - Seejärel kombineeritakse
c_0, c_1,\dots, c_l, et saada salastatud tekstc
- Eraldada
- Dekrüpteerige salastatud tekst
cjärgmiselt:- Teisenda iga
c_iarvuks vastavalt D - Iga
c_ipuhul onm_i = [(c_i - k) \mod 26] - Teisenda iga
m_itäheks vastavalt D - Seejärel kombineeritakse
m_0, m_1,\dots, m_l, et saada algne sõnumm
- Teisenda iga
Nihkešifreeringu teeb sümmeetriliseks krüpteerimisskeemiks see, et nii krüpteerimiseks kui ka dekrüpteerimiseks kasutatakse sama võtit. Oletame näiteks, et te soovite krüpteerida sõnumi "DOG", kasutades nihkešifrit ja valisite võtmeks juhuslikult "24". Selle võtmega krüpteerides saadakse sõnum "BME". Ainus võimalus saada algset sõnumit tagasi on kasutada dekrüpteerimiseks sama võtit "24".
See Shift-šiffer on näide monoalfabeetilisest asendusšifferist: krüpteerimisskeem, mille puhul salakirjasõnade tähestik on fikseeritud (st kasutatakse ainult ühte tähestikku). Eeldades, et dekrüpteerimisalgoritm on deterministlik, võib iga sümbol asendussalakirjas olla maksimaalselt seotud ühe sümboliga lihtkirjas.
Kuni 1700. aastateni tuginesid paljud krüpteerimisrakendused suuresti monoalfaatilistele asendusšifritele, kuigi need olid sageli palju keerulisemad kui Shift-šifrid. Näiteks võis iga algteksti tähe jaoks juhuslikult valida tähestikust ühe tähe tingimusel, et iga täht esineb šifreeritud tekstis ainult üks kord. See tähendab, et teil oleks faktoriaalne 26 võimalikku privaatvõtit, mis oli arvutieelsel ajastul väga suur.
Pange tähele, et krüptograafias kohtate sageli mõistet šifreeri. Olge teadlik, et sellel terminil on erinevaid tähendusi. Tegelikult tean ma vähemalt viit erinevat tähendust selle termini kohta krüptograafias.
Mõnel juhul viitab see krüpteerimisskeemile, nagu näiteks Shift cipher ja monoalfaatiline asendusšiffer. Mõiste võib siiski viidata ka konkreetselt krüpteerimisalgoritmile, salajale võtmele või lihtsalt sellise krüpteerimisskeemi šifreeritud tekstile.
Lõpuks võib mõiste "šifreerimine" viidata ka põhialgoritmile, millest saab ehitada krüptograafilisi skeeme. Nende hulka võivad kuuluda mitmesugused krüpteerimisalgoritmid, aga ka muud liiki krüptograafilised skeemid. See mõiste tähendus muutub oluliseks plokkšifrite kontekstis (vt allpool jaotist "Plokkšifrid").
Te võite kohata ka mõisteid dešifreerida või dešifreerida. Need terminid on lihtsalt krüpteerimise ja dekrüpteerimise sünonüümid.
Brute force'i rünnakud ja Kerckhoffi põhimõte
Nihkešifreering on väga ebaturvaline sümmeetriline krüpteerimisskeem, vähemalt tänapäeva maailmas. [1] Ründaja võib lihtsalt proovida dekrüpteerida mis tahes salakirju kõigi 26 võimaliku võtmega, et näha, milline tulemus on mõistlik. Sellist tüüpi rünnakut, kus ründaja lihtsalt käib võtmeid läbi, et näha, mis töötab, nimetatakse brute force rünnakuks või täielikuks võtmeotsinguks.
Selleks, et mis tahes krüpteerimisskeem vastaks minimaalsele turvalisuse mõistele, peab sellel olema võimalike võtmete hulk ehk võtmeruum, mis on nii suur, et brute-force rünnakud on teostamatud. Kõik kaasaegsed krüpteerimisskeemid vastavad sellele standardile. Seda tuntakse kui piisava võtmeruumi põhimõtet. Sarnane põhimõte kehtib tavaliselt eri tüüpi krüptograafiliste skeemide puhul.
Et saada aimu kaasaegsete krüpteerimisskeemide tohutu võtmeruumi suurusest,
oletame, et fail on krüpteeritud 128-bitise võtmega, kasutades täiustatud
krüpteerimisstandardit. See tähendab, et ründajal on hulk 2^{128} võtmeid, mida ta peab brute force'i rünnakuks läbi käima. Selle strateegia
0,78%-lise edu tõenäosusega peaks ründaja läbima umbes 2,65 \times 10^{36} võtmeid.
Oletame optimistlikult, et ründaja suudab proovida 10^{16} võtmeid sekundis (st 10 kvadriljonit võtmeid sekundis). Et testida 0,78%
kõigist võtmete ruumi võtmetest, peaks tema rünnak kestma 2,65 \times 10^{20} sekundit. See on umbes 8,4 triljonit aastat. Seega ei ole isegi absurdselt võimsa
vastase poolt sooritatav brutaalrünnak kaasaegse 128-bitise krüpteerimisskeemi
puhul realistlik. See on piisava võtmeruumi põhimõte.
Kas nihkešifreering on turvalisem, kui ründaja ei tea krüpteerimisalgoritmi? Võib-olla, kuid mitte palju.
Igal juhul eeldab kaasaegne krüptograafia alati, et mis tahes sümmeetrilise krüpteerimisskeemi turvalisus sõltub ainult salajase võtme hoidmisest. Ründaja teab alati kõiki muid üksikasju, sealhulgas sõnumi ruumi, võtmeruumi, šifreeritud teksti ruumi, võtmevaliku algoritmi, krüpteerimisalgoritmi ja dekrüpteerimisalgoritmi.
Idee, et sümmeetrilise krüpteerimisskeemi turvalisus võib tugineda ainult salajase võtme salajasusele, on tuntud kui Kerckhoffi põhimõte.
Nagu Kerckhoffs algselt ette nägi, kehtib see põhimõte ainult sümmeetriliste krüpteerimisskeemide puhul. Põhimõtte üldisem versioon kehtib aga ka kõigi teiste tänapäeva krüptograafiliste skeemide puhul: Mis tahes krüptograafilise skeemi ülesehitus ei tohi olla salajane, et see oleks turvaline; salastatus võib laieneda ainult mõnele(te)le teabeahelale, tavaliselt privaatvõtmele.
Kerckhoffsi põhimõte on tänapäeva krüptograafias keskne neljal põhjusel. [2] Esiteks on olemas ainult piiratud arv krüptograafilisi skeeme teatud tüüpi rakenduste jaoks. Näiteks enamik kaasaegseid sümmeetrilisi krüpteerimisrakendusi kasutab Rijndaeli salakirja. Seega on teie salastatus seoses skeemi disainiga lihtsalt väga piiratud. Rijndaeli šifri jaoks on aga palju rohkem paindlikkust mõne privaatvõtme salajas hoidmisel.
Teiseks on kergem asendada mõnda infosarja kui tervet krüptograafilist skeemi. Oletame, et ettevõtte töötajatel on kõigil sama krüpteerimistarkvara ja et igal kahel töötajal on privaatne võti konfidentsiaalseks suhtlemiseks. Võtmete kompromiteerimine on selles stsenaariumis tülikas, kuid vähemalt võiks ettevõte selliste turvarikkumistega tarkvara säilitada. Kui ettevõte loodaks kava salajasusele, siis nõuaks selle salajasuse mis tahes rikkumine kogu tarkvara väljavahetamist.
Kolmandaks võimaldab Kerckhoffsi põhimõte krüptograafiliste skeemide kasutajate vahelist standardimist ja ühilduvust. Sellest on tohutu kasu tõhususele. Näiteks on raske ette kujutada, kuidas miljonid inimesed saaksid iga päev turvaliselt Google'i veebiserveritega ühenduda, kui see turvalisus nõuaks krüptograafiliste skeemide salajas hoidmist.
Neljandaks võimaldab Kerckhoffi põhimõte krüptograafiliste skeemide avalikku kontrollimist. Selline kontroll on hädavajalik turvaliste krüptograafiliste skeemide saavutamiseks. Näiteks sümmeetrilise krüptograafia peamine põhialgoritm, Rijndael-krüptograafia, oli aastatel 1997-2000 riikliku standardite ja tehnoloogia instituudi korraldatud konkursi tulemus.
Iga süsteem, mis üritab saavutada turvalisust teadmatuse kaudu, on süsteem, mis tugineb oma ülesehituse ja/või rakendamise üksikasjade salajas hoidmisele. Krüptograafias oleks see konkreetselt süsteem, mis põhineb krüptograafilise skeemi konstruktsiooni üksikasjade salajas hoidmisel. Seega on turvalisus varjatuse kaudu otseses vastuolus Kerckhoffi põhimõttega.
Avatuse võime tugevdada kvaliteeti ja turvalisust laieneb digitaalsele maailmale ka laiemalt kui ainult krüptograafia. Vaba ja avatud lähtekoodiga Linuxi distributsioonidel, näiteks Debianil, on üldiselt mitmeid eeliseid võrreldes Windowsi ja MacOSi vastetega privaatsuse, stabiilsuse, turvalisuse ja paindlikkuse osas. Kuigi sellel võib olla mitu põhjust, on kõige olulisem põhimõte ilmselt, nagu Eric Raymond oma kuulsas essees "The Cathedral and the Bazaar" sõnastas, et "kui piisavalt palju silmapalle anda, on kõik vead pinnapealsed" [3] Just see rahvahulkade tarkus on see põhimõte, mis andis Linuxile tema kõige suurema edu.
Kunagi ei saa üheselt väita, et krüptograafiline skeem on "turvaline" või "ebaturvaline" Selle asemel on krüptograafiliste skeemide turvalisuse kohta erinevaid mõisteid. Igas krüptograafilise turvalisuse määratluses tuleb täpsustada (1) turvalisuse eesmärke ja (2) ründaja võimeid. Krüptograafiliste skeemide analüüsimine ühe või mitme konkreetse turvamõiste suhtes annab ülevaate nende rakendustest ja piirangutest.
Kuigi me ei hakka süvenema kõikidesse krüptograafilise turvalisuse erinevate mõistete üksikasjadesse, peaksite teadma, et kaks eeldust on kõikjal olemas kõigis kaasaegsetes krüptograafilistes turvalisuse mõistetes, mis puudutavad sümmeetrilisi ja asümmeetrilisi skeeme (ja mingil kujul ka teisi krüptograafilisi primitiive):
- Ründaja teadmised skeemi kohta vastavad Kerckhoffsi põhimõttele.
- Ründaja ei saa teostada skeemi vastu brutaalrünnakut. Konkreetsemalt öeldes ei luba krüptograafiliste turvamõistete ohumudelid tavaliselt isegi toorjõu rünnakuid, kuna eeldavad, et need ei ole asjakohane kaalutlus.
Märkused:
[1] Seutoniuse sõnul kasutas Julius Caesar oma sõjalises suhtluses nihkešifrit, mille võtme konstantseks väärtuseks oli 3. Seega sai A alati D, B alati E, C alati F ja nii edasi. See konkreetne nihkešifri versioon on seega saanud tuntuks kui Caesari šifri (kuigi see ei ole tegelikult šifri tänapäevases mõttes šifri, sest võtme väärtus on konstantne). Caesari šifreering võis olla turvaline esimesel sajandil eKr, kui Rooma vaenlased ei olnud krüpteerimisega väga hästi kursis. Kuid tänapäeval ei oleks see ilmselgelt väga turvaline skeem.
[2] Jonathan Katz ja Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), lk 7f.
[3] Eric Raymond, "The Cathedral and the Bazaar", ettekanne esitati Linux Kongressil, Würzburg, Saksamaa (27. mai 1997). On olemas mitu hilisemat versiooni ja ka raamat. Minu tsitaadid pärinevad raamatu leheküljelt 30: Eric Raymond, The Cathedral and the Bazaar: Musings on Linux and Open Source by an Accidental Revolutionary, parandatud väljaanne. (2001), O'Reilly: Sebastopol, CA.
Voolukodeeringud
Sümmeetrilised krüpteerimisskeemid jaotatakse tavaliselt kahte tüüpi: voolukodeeringud ja plokk-kodeeringud. See eristamine on siiski mõnevõrra problemaatiline, kuna inimesed kasutavad neid mõisteid ebajärjekindlalt. Järgmistes punktides selgitan ma seda vahet nii, nagu ma arvan, et see on kõige parem. Te peaksite siiski teadma, et paljud inimesed kasutavad neid mõisteid mõnevõrra teisiti, kui ma neid kasutan.
Pöördume kõigepealt voogkoodide juurde. Voolukrüpteering** on sümmeetriline krüpteerimisskeem, mille puhul krüpteerimine koosneb kahest etapist.
Kõigepealt toodetakse salajase võtme abil salateksti pikkusega string. Seda stringi nimetatakse keystreamiks.
Seejärel kombineeritakse võtmevoog matemaatiliselt lihtkirjaga, et saada
šifreeritud tekst. See kombinatsioon on tavaliselt XOR-operatsioon.
Dekrüpteerimiseks saab operatsiooni lihtsalt ümber pöörata. (Pange tähele,
et A \oplus B = B \oplus A,
juhul kui A ja B on bitsõna. Seega ei ole XOR-operatsiooni järjekord voošifreeringus tulemuse
jaoks oluline. Seda omadust nimetatakse kommutatiivsuseks)
Tüüpiline XOR-voolukodeering on kujutatud kujul 3. Kõigepealt
võetakse privaatne võti K ja
genereeritakse selle abil võtmevoog. Seejärel kombineeritakse võtmevoog
XOR-operatsiooni abil lihtkirjaga, et saada salakirjatekst. Iga agent, kes
saab salateksti, saab selle hõlpsasti dekrüpteerida, kui tal on võti K. Kõik, mida ta peab tegema,
on luua võtmevoog, mis on sama pikk kui salatekst, vastavalt skeemi
täpsustatud protseduurile ja XOR-ida seda salatekstiga.
Joonis 3: XOR voogsalvesti
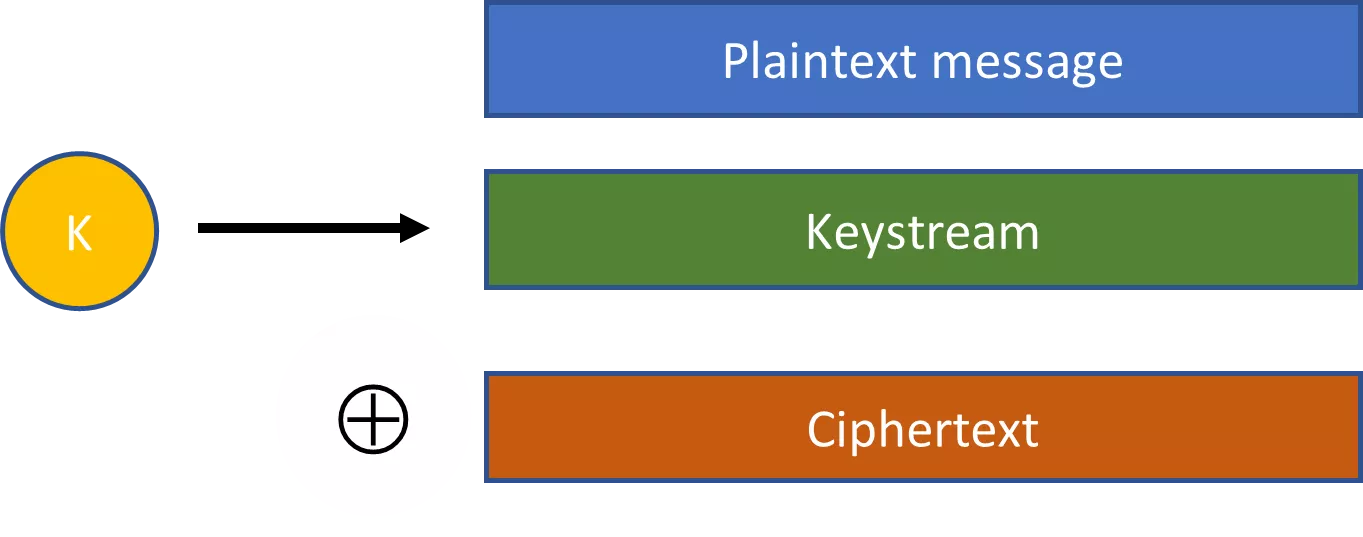
Tuletage meelde, et krüpteerimisskeem on tavaliselt sama põhialgoritmiga krüpteerimise mall, mitte täpne spetsifikatsioon. Laiendatult on voogkooder tavaliselt krüpteerimise mall, milles saab kasutada erineva pikkusega võtmeid. Kuigi võtme pikkus võib mõjutada skeemi mõningaid väiksemaid üksikasju, ei mõjuta see selle põhilist vormi.
Nihkešifreering on näide väga lihtsast ja ebaturvalisest voogšifreeringust. Kasutades ühte tähte (salajane võti), saab luua sõnumi pikkusega tähtede jada (võtmevoog). Seejärel kombineeritakse see võtmevoog lihtkirjaga modulooperatsiooni abil, et saada šifreeritud tekst. (Seda modulo-operatsiooni saab lihtsustada XOR-operatsiooniks, kui tähti esitada bittidena).
Teine kuulus näide voošifri kohta on Vigenere'i šifri, Blaise de Vigenere'i järgi, kes arendas selle täielikult välja 16. sajandi lõpus (kuigi teised olid teinud palju eelnevat tööd). See on näide polüfabeetilisest asendussalakirjastusest: krüpteerimisskeem, mille puhul salakirjasümboli salakirjasümbol muutub sõltuvalt selle positsioonist tekstis. Erinevalt monoalfabeetilisest asendussalakirjastusest võib salakirjasümboleid seostada rohkem kui ühe lihtteksti sümboliga.
Kuna krüpteerimine muutus renessansiaja Euroopas üha populaarsemaks, siis muutus ka krüptoanalüüs, s.t. krüptotekstide murdmine, eriti sagedusanalüüsi abil. Viimane kasutab meie keele statistilisi seaduspärasusi salakirjade murdmiseks ja avastati araabia õpetlaste poolt juba üheksandal sajandil. See on tehnika, mis töötab eriti hästi pikemate tekstide puhul. Ja isegi kõige keerukamad monoalfabeetilised alamsümbolikad ei olnud 1700. aastateks Euroopas enam piisavad sagedusanalüüsi vastu, eriti sõjaväe- ja julgeolekukasutuses. Kuna Vigenere'i šifreerimine pakkus märkimisväärset edasiminekut turvalisuses, muutus see sel perioodil populaarseks ja oli 1700. aastate lõpuks laialt levinud.
Mitteametlikult öeldes töötab krüpteerimisskeem järgmiselt:
Valige privaatvõtmeks mitmetäheline sõna.
Rakendage mis tahes sõnumi puhul nihkešifreerimist sõnumi iga tähe suhtes, kasutades nihkeks võtmesõna vastavat tähte.
Kui olete võtmesõna tsükliliselt läbi käinud, kuid ei ole veel täielikult krüptinud lihtteksti, rakendage võtmesõna tähti uuesti nihkešifreeringuna ülejäänud teksti vastavatele tähtedele.
Jätkake seda protsessi, kuni kogu sõnum on šifreeritud.
Oletame, et teie privaatne võti on "GOLD" ja te soovite krüpteerida sõnumi "CRYPTOGRAPHY". Sellisel juhul toimiksite Vigenère'i salakirja järgi järgmiselt:
c_0 = [(2 + 6) \mod 26] = 8 = Ic_1 = [(17 + 14) \mod 26] = 5 = Fc_2 = [(24 + 11) \mod 26] = 9 = Jc_3 = [(15 + 3) \mod 26] = 18 = Sc_4 = [(19 + 6) \mod 26] = 25 = Zc_5 = [(14 + 14) \mod 26] = 2 = Cc_6 = [(6 + 11) \mod 26] = 17 = Rc_7 = [(17 + 3) \mod 26] = 20 = Uc_8 = [(0 + 6) \mod 26] = 6 = Gc_9 = [(15 + 14) \mod 26] = 3 = Dc_{10} = [(7 + 11) \mod 26] = 18 = Sc_{11} = [(24 + 3) \mod 26] = 1 = B
Seega on salatekst c = "IFJSZCRUGDSB".
Teine kuulus näide voošifri kohta on one-time pad. Ühekordse plokkeri abil luuakse lihtsalt juhuslikest bittidest koosnev string, mis on sama pikk kui lihtteksti sõnum, ja saadakse salatekst XOR-operatsiooni abil. Seega on privaatne võti ja võtmevoog samaväärsed ühekordse padiga.
Kui Shift-kood ja Vigenere-kood on tänapäeval väga ebaturvalised, siis ühekordne salvesti on korrektsel kasutamisel väga turvaline. Tõenäoliselt oli kõige kuulsam ühekordse ploki kasutamine vähemalt 1980ndate aastate lõpuni Washingtoni-Moskva kuumaliinil. [4]
Kuumaliin on otsene sideühendus Washingtoni ja Moskva vahel kiireloomulistes küsimustes, mis loodi pärast Kuuba raketikriisi. Tehnoloogia on aastate jooksul muutunud. Praegu hõlmab see nii otsest fiiberoptilist kaablit kui ka kahte satelliitühendust (koondamise eesmärgil), mis võimaldavad e-posti ja tekstisõnumite saatmist. Ühendus lõpeb erinevates kohtades USAs. Pentagon, Valge Maja ja Raven Rock Mountain on teadaolevad lõpp-punktid. Vastupidiselt üldlevinud arvamusele ei ole vihjeliin kunagi olnud seotud telefonidega.
Sisuliselt toimis ühekordne pad-skeem järgmiselt. Nii Washingtonil kui ka Moskval oli kaks juhuslike numbrite komplekti. Üks juhuslike numbrite kogum, mille olid loonud venelased, oli mõeldud venekeelsete sõnumite krüpteerimiseks ja dekrüpteerimiseks. Üks juhuslike numbrite kogum, mille olid loonud ameeriklased, hõlmas mis tahes ingliskeelsete sõnumite krüpteerimist ja dekrüpteerimist. Aeg-ajalt edastasid usaldusväärsed kullerid teisele poolele rohkem juhuslikke numbreid.
Washington ja Moskva suutsid siis salaja suhelda, kasutades neid juhuslikke numbreid ühekordsete pattide loomiseks. Iga kord, kui oli vaja suhelda, kasutasid nad oma sõnumi jaoks järgmist osa juhuslikest numbritest.
Kuigi ühekordse turvaploki kasutamine on väga turvaline, on sellel siiski märkimisväärseid praktilisi piiranguid: võti peab olema sama pikk kui sõnum ja ühtegi ühekordse ploki osa ei saa uuesti kasutada. See tähendab, et peate jälgima, kus te olete üheaegses plokis, salvestama tohutu hulga bitte ja vahetama aeg-ajalt juhuslikke bitte oma vastaspooltega. Seetõttu ei kasutata ühekordset pad'i praktikas sageli.
Selle asemel kasutatakse praktikas valdavalt pseudorandom voogkoode. Salsa20 ja sellega tihedalt seotud variant ChaCha on näited tavaliselt kasutatavatest pseudorandom voogkoodidest.
Nende pseudorandom voogkooderite puhul valitakse kõigepealt juhuslikult võti K, mis on lühem kui lihtteksti pikkus. Sellise juhusliku võtme K loob tavaliselt meie arvuti ettearvamatute andmete põhjal, mida ta aja jooksul kogub, näiteks võrgusõnumite, hiire liigutuste jne. vaheline aeg.
See juhuslik võti K sisestatakse
seejärel laiendamisalgoritmi, mis loob sama pika pseudosagedusliku võtmevoo kui
sõnum. Saate täpselt määrata, kui pikk peab võtmevoog olema (nt 500 bitti, 1000
bitti, 1200 bitti, 29,117 bitti jne).
Pseudorandom võtmevoog näib kui see oleks valitud täiesti juhuslikult kõikide sama pikkusega stringide hulgast. Seega näib pseudorandom võtmevooga krüpteerimine olevat tehtud nagu oleks see tehtud ühekordse padiga. Kuid see ei ole muidugi nii.
Kuna meie privaatne võti on võtmevoogudest lühem ja meie laiendamisalgoritm peab olema deterministlik, et krüpteerimis- ja dekrüpteerimisprotsess toimiks, ei saanud iga konkreetse pikkusega võtmevoog meie laiendamisoperatsiooni väljundiks olla.
Oletame näiteks, et meie privaatvõtme pikkus on 128 bitti ja et me saame
selle sisestada laiendavasse algoritmi, et luua palju pikem võtmevoog,
näiteks 2500 bitti. Kuna meie laiendav algoritm peab olema deterministlik,
saab meie algoritm valida maksimaalselt 1/2^{128} pikkusega 2500 bitti. Seega ei saa sellist võtmevoogu kunagi täiesti juhuslikult
valida kõigi sama pikkuste stringide hulgast.
Meie voolukoodide definitsioonil on kaks aspekti: 1) võtmevoog, mis on sama pikk kui lihttekst, genereeritakse privaatvõtme abil; ja 2) see võtmevoog kombineeritakse lihttekstiga, tavaliselt XOR-operatsiooni abil, et saada šifreeritud tekst.
Mõnikord määratletakse tingimus (1) rangemalt, väites, et võtmevoog peab olema pseudorandom. See tähendab, et ei nihkešifreerimist ega ühekordset pad'i ei peeta voogšifreerimiseks.
Minu arvates võimaldab tingimuse (1) laiem määratlemine lihtsustada krüpteerimisskeemide korraldamist. Lisaks tähendab see, et me ei pea lõpetama konkreetse krüpteerimisskeemi nimetamist voogkrüpteerimiseks ainult seetõttu, et me saame teada, et see ei tugine tegelikult pseudorandom võtmevoogudele.
Märkused:
[4] Crypto Museum, "Washington-Moskva kuumaliin", 2013, kättesaadav aadressil https://www.cryptomuseum.com/crypto/hotline/index.htm.
Plokk-kodeeringud
Esimene viis, kuidas blokkšifrit tavaliselt mõistetakse, on midagi primitiivsemat kui voogšifri: Põhialgoritm, mis teeb võtme abil sobiva pikkusega stringil pikkust säilitava teisenduse. Seda algoritmi saab kasutada krüpteerimisskeemide ja võib-olla ka muud liiki krüptograafiliste skeemide loomiseks.
Sageli võib plokkšiffer võtta vastu erineva pikkusega sisendkettasid, näiteks 64, 128 või 256 bitti, ning erineva pikkusega võtmeid, näiteks 128, 192 või 256 bitti. Kuigi algoritmi mõned üksikasjad võivad sõltuvalt neist muutujatest muutuda, ei muutu põhialgoritm. Kui see muutuks, siis räägiksime kahest erinevast plokkšifrist. Pange tähele, et põhialgoritmi terminoloogia kasutamine on siinkohal sama, mis krüpteerimisskeemide puhul.
Plokkšifri tööpõhimõte on esitatud Ahelas 4. Plokkšifri sisendiks
on sõnum M pikkusega L ja võti K. Väljundiks on
sõnum M' pikkusega L. Enamiku plokkšifrite puhul
ei pea võti olema tingimata sama pikk kui M ja M'.
Joonis 4: Plokkšifreering

Plokkšiffer iseenesest ei ole krüpteerimisskeem. Kuid plokkšifreeringut saab kasutada erinevate töötlusviisidega, et luua erinevaid krüpteerimisskeeme. Toimimisviis lihtsalt lisab mõned täiendavad operatsioonid väljaspool plokkšifrit.
Selle toimimise näitlikustamiseks oletame, et kasutatakse plokkšifreerimist (BC), mis nõuab 128-bitist sisendkoodi ja 128-bitist privaatvõtit. Joonisel 5 on näidatud, kuidas seda plokkšiferit saab kasutada koos elektroonilise koodiraamatu režiimiga (ECB-režiim), et luua krüpteerimisskeem. (Ellipsid paremal näitavad, et seda skeemi saab korrata nii kaua, kui vaja).
Joonis 5: EKP-režiimiga plokkšifreering
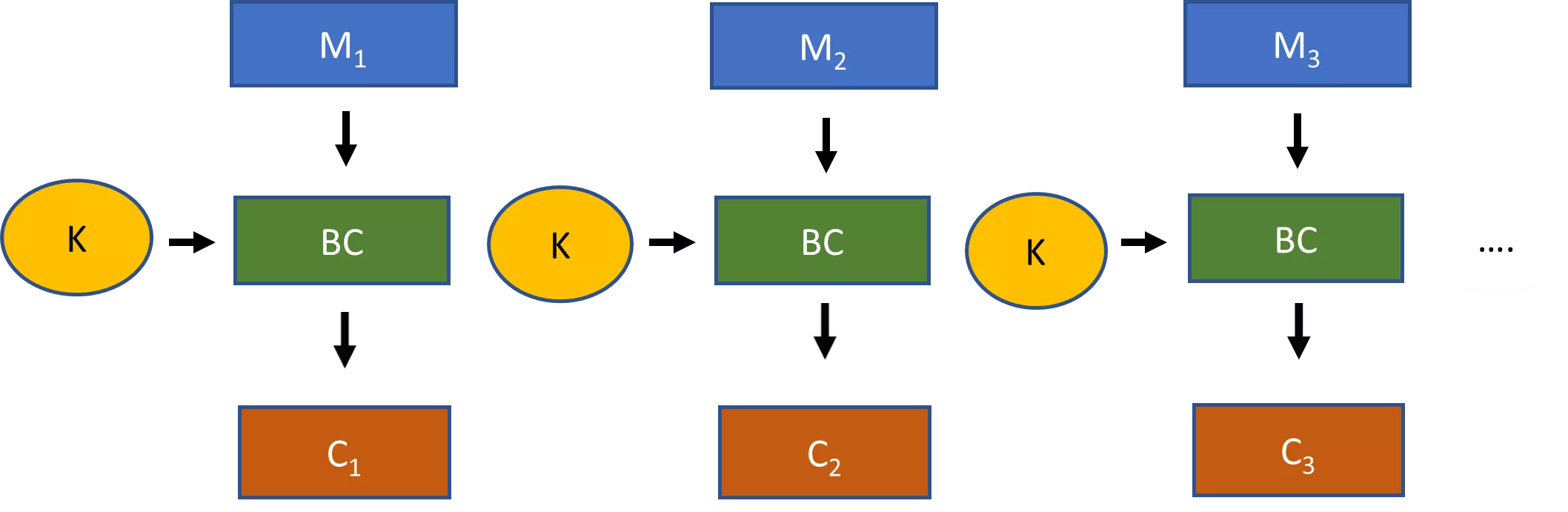
Elektroonilise koodiraamatu krüpteerimise protsess plokkšifri abil on järgmine. Vaadake, kas te saate oma lihtkirjasõnumi jagada 128-bitisteks plokkideks. Kui mitte, siis lisage sõnumile padding, nii et tulemuse saaks jagada ühtlaselt 128-bitise plokisuurusega. See on teie andmed, mida kasutatakse krüpteerimiseks.
Nüüd jagage andmed 128-bitiste stringide tükkideks (M_1, M_2, M_3 jne). Käivita iga 128-bitine string 128-bitise võtmega läbi plokkšifri, et
saada 128-bitine salakirjatekst (C_1, C_2, C_3 jne). Need tükid moodustavad
uuesti kombineerituna täieliku salastusteksti.
Dekrüpteerimine on lihtsalt vastupidine protsess, kuigi vastuvõtja vajab mingit äratuntavat viisi, et eemaldada dekrüpteeritud andmetest mis tahes täidis, et saada algne lihtkirjasõnum.
Kuigi suhteliselt lihtne, ei ole elektroonilise koodiraamatu režiimiga plokkšifreerimine piisavalt turvaline. Selle põhjuseks on see, et see viib deterministliku krüpteerimiseni. Mis tahes kaks identset 128-bitist andmerida krüpteeritakse täpselt samamoodi. Seda teavet saab ära kasutada.
Selle asemel peaks iga plokk-kodeeringust koostatud krüpteerimisskeem olema probabilistiline: see tähendab, et iga sõnumi M või M mis tahes konkreetse osa
krüpteerimine peaks üldiselt iga kord andma erineva tulemuse. [5]
Kirjutusblokkide ahelrežiim (CBC-režiim) on tõenäoliselt kõige levinum režiim, mida kasutatakse plokkšifri puhul. Õigesti tehtud kombinatsioon annab tõenäosusliku krüpteerimisskeemi. Selle töörežiimi kirjeldust näete allpool oleval kujutisel 6.
Joonis 6: CBC-režiimiga plokkšiffer
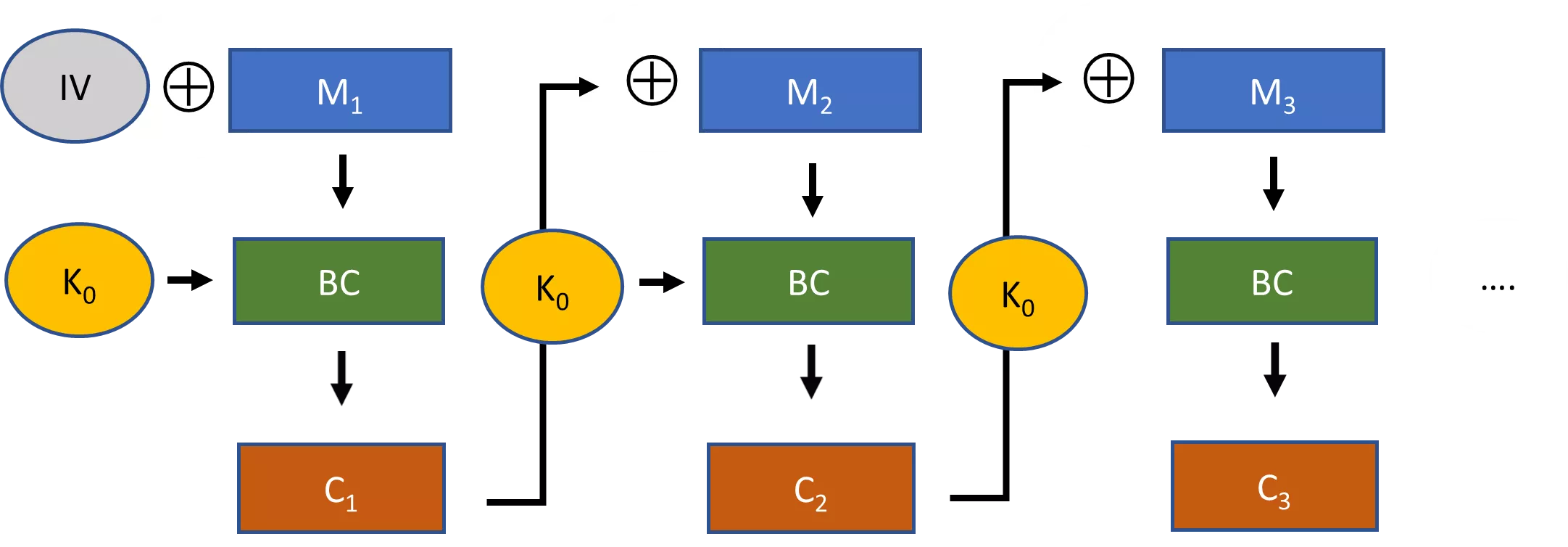
Oletame, et ploki suurus on jälle 128 bitti. Seega peaksite alustuseks jälle tagama, et teie algne lihtkirjasõnum saaks vajaliku polsterduse.
Seejärel XOR-ida esimene 128-bitine osa oma lihtkirjast 128-bitise initsialiseerimisvektoriga. Tulemus sisestatakse plokkšifrisse, et saada esimese ploki salakirjatekst. Teise 128-bitise ploki jaoks XOR-ida esmalt lihtteksti esimese ploki salakirjatekstiga, enne kui see sisestatakse plokkšifrisse. Seda protsessi jätkatakse, kuni kogu lihtkirjasõnum on krüpteeritud.
Kui olete lõpetanud, saadate krüpteeritud sõnumi koos krüpteerimata initsieerimisvektoriga vastuvõtjale. Vastuvõtja peab teadma initsialiseerimisvektorit, vastasel juhul ei saa ta salakirjateksti dekrüpteerida.
See konstruktsioon on korrektsel kasutamisel palju turvalisem kui elektrooniline koodiraamat. Kõigepealt tuleks tagada, et initsialiseerimisvektor on juhuslik või pseudorandom string. Lisaks peaksite kasutama iga kord, kui kasutate seda krüpteerimisskeemi, erinevat initsialiseerimisvektorit.
Teisisõnu, teie initsialiseerimisvektor peaks olema juhuslik või pseudorandom nonce, kus nonce tähendab "numbrit, mida kasutatakse ainult üks kord" Kui te seda praktikat järgite, siis CBC-režiim koos plokkšifriga tagab, et mis tahes kaks identset lihtteksti plokki krüpteeritakse üldiselt iga kord erinevalt.
Lõpuks pöörame tähelepanu väljundi tagasiside režiimile (OFB režiim). Selle režiimi kirjeldust näete Andmel 7.
Joonis 7: OFB-režiimiga plokkšiffer
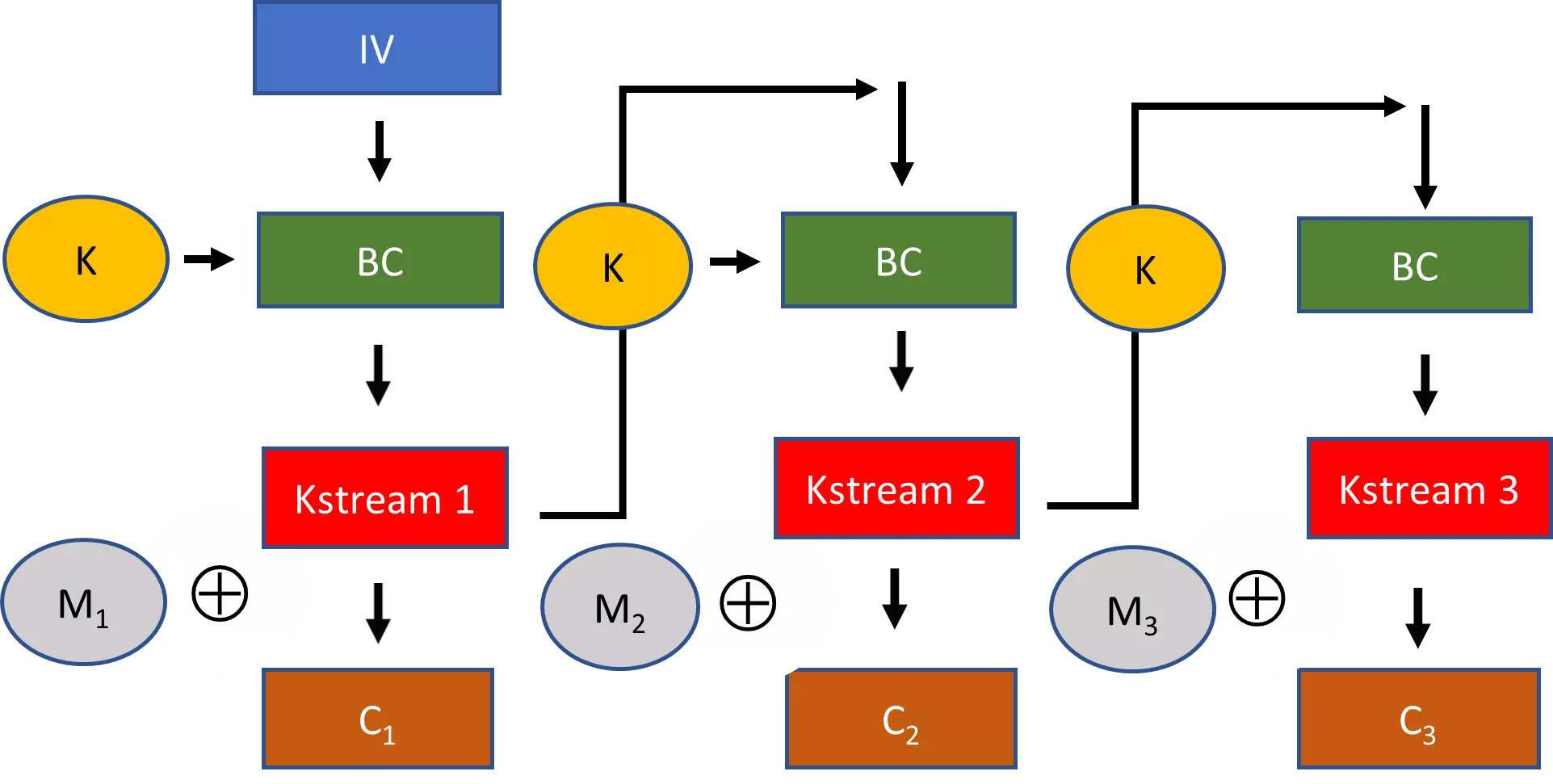
OFB-režiimi puhul valite ka initsialiseerimisvektori. Kuid siin sisestatakse initsialiseerimisvektor esimese ploki puhul otse plokkšifrile koos teie võtmega. Saadud 128 bitti käsitletakse seejärel võtmevooluna. See võtmevoog on XOR-ühendatud lihtkirjaga, et saada ploki salastustekst. Järgmiste plokkide puhul kasutatakse eelmise ploki võtmevoogu plokkšifri sisendina ja korratakse samu samme.
Kui te vaatate tähelepanelikult, siis tegelikult on siin OFB-režiimiga plokkšifreeringust loodud voogšifreering. Te genereerite 128-bitiseid võtmevoogude osi, kuni teil on selge teksti pikkus (jättes viimasest 128-bitisest võtmevoo osast ära need bitid, mida te ei vaja). Seejärel klahvivoo ja lihtteksti XOR-meetodiga, et saada šifreeritud tekst.
Eelmises voogkoode käsitlevas osas ütlesin, et võtmevooge toodetakse privaatvõtme abil. Täpsemalt öeldes ei pea see olema loodud ainult privaatvõtme abil. Nagu näete OFB-režiimis, toodetakse võtmevoog nii privaatvõtme kui ka initsialiseerimisvektori toel.
Pange tähele, et nagu CBC-režiimi puhul, on oluline valida pseudo- või juhuslik nonce initsialiseerimisvektoriks iga kord, kui kasutate OFB-režiimis plokkšifrit. Vastasel juhul krüpteeritakse sama 128-bitine sõnumijada, mis saadetakse eri andmeedastustes, samal viisil. See on üks võimalus tõenäosusliku krüpteerimise loomiseks voošifriga.
Mõni voogkooder kasutab võtmevoo loomiseks ainult privaatvõtit. Selliste voošifrite puhul on oluline, et te kasutaksite juhuslikku nonce'i, et valida privaatne võti iga suhtluse jaoks. Vastasel juhul on ka nende voošifrite abil krüpteerimise tulemused deterministlikud, mis põhjustab turvaprobleeme.
Kõige populaarsem kaasaegne plokkšifreering on Rijndaeli šifreering. See võitis viieteistkümnest võistlustöödest, mille National Institute of Standards and Technology (NIST) korraldas aastatel 1997-2000, et asendada vanem krüpteerimisstandard, data krüpteerimisstandard (DES).
Rijndaeli salastust saab kasutada erinevate võtmepikkuste ja plokisuuruste spetsifikatsioonidega, samuti erinevate töörežiimidega. NISTi konkursi komitee võttis vastu Rijndaeli šifri piiratud versiooni - nimelt sellise, mis nõuab 128-bitiseid plokke ja võtmepikkusi 128, 192 või 256 bitti -, mis on osa täiustatud krüpteerimisstandardist (AES). See on tegelikult peamine standard sümmeetriliste krüpteerimisrakenduste jaoks. See on nii turvaline, et isegi NSA on ilmselt valmis kasutama seda 256-bitiste võtmetega ülisalajaste dokumentide jaoks. [6]
AES-blokkšifreeringut selgitatakse üksikasjalikult peatükis 5.
Märkused:
[5] Tõenäosusliku krüpteerimise tähtsust rõhutasid esimest korda Shafi Goldwasser ja Silvio Micali, "Probabilistic encryption", Journal of Computer and System Sciences, 28 (1984), 270-99.
[6] Vt NSA, "Commercial National Security Algorithm Suite", https://apps.nsa.gov/iaarchive/programs/iad-initiatives/cnsa-suite.cfm.
Segaduse selgitamine
Segadus plokkšifrite ja voogšifrite eristamisel tuleneb sellest, et mõnikord mõistavad inimesed terminit plokkšifreerimise all konkreetselt plokkšifreerimist, millel on plokkšifreerimise režiim.
Võtame arvesse eelmises punktis kirjeldatud EKP ja CBC režiimi. Need nõuavad konkreetselt, et krüpteerimiseks kasutatavad andmed oleksid jagatavad plokisuurusega (mis tähendab, et te peate võib-olla kasutama algsõnumi täiendamist). Lisaks sellele toimivad andmed nendes režiimides ka otse plokkšifreeringuga (ja mitte ainult kombineerituna plokkšifreeringu tulemusega, nagu OFB-režiimis).
Seega võib alternatiivselt defineerida blokkšifreeringut kui mis tahes krüpteerimisskeemi, mis töötab korraga sõnumi fikseeritud pikkusega plokkidega (kusjuures iga plokk peab olema pikem kui üks bait, vastasel juhul langeb see kokku voogšifreeringuks). Nii krüpteeritavad andmed kui ka šifreeritud tekst peavad jagunema ühtlaselt sellesse plokisuurusesse. Tavaliselt on plokkide pikkus 64, 128, 192 või 256 bitti. Seevastu voošifreeringuga saab krüpteerida mis tahes sõnumeid ühe biti või baidi suurustes tükkides korraga.
Sellise täpsema arusaamisega plokkšifreeringust võib tõepoolest väita, et kaasaegsed krüpteerimisskeemid on kas voog- või plokkšifreeringud. Edaspidi kasutan ma terminit plokkšifreering üldisemas tähenduses, kui ei ole sätestatud teisiti.
Eelmises punktis esitatud arutelu OFB-režiimi kohta tõstatab veel ühe huvitava küsimuse. Mõned voošifreeringud on ehitatud plokkšifreeringutest, nagu Rijndael koos OFB-ga. Mõned, nagu Salsa20 ja ChaCha, ei ole loodud plokkšifritest. Viimaseid võiks nimetada primitiivseteks voogkriptoriteks. (Selliste voogkoodide tähistamiseks ei ole tegelikult standardiseeritud terminit)
Kui inimesed räägivad voošifrite ja plokkšifrite eelistest ja puudustest, siis tavaliselt võrreldakse primitiivseid voošifreid plokkšifritel põhinevate krüpteerimisskeemidega.
Kuigi voogkoode saab alati hõlpsasti konstrueerida plokk-kodeeringust, on tavaliselt väga raske ehitada mingi plokk-kodeeringuga (näiteks CBC-režiimiga) konstruktsiooni primitiivsest voogkoodist.
Sellest arutelust peaksite nüüd aru saama Kujund 8. See annab ülevaate sümmeetrilistest krüpteerimisskeemidest. Me kasutame kolme liiki krüpteerimisskeeme: primitiivseid voogkoode, plokkšifreeritud voogkoode ja plokkšifreid plokkrežiimis (joonisel ka "plokkšifrid").
Joonis 8: Ülevaade sümmeetrilistest krüpteerimisskeemidest
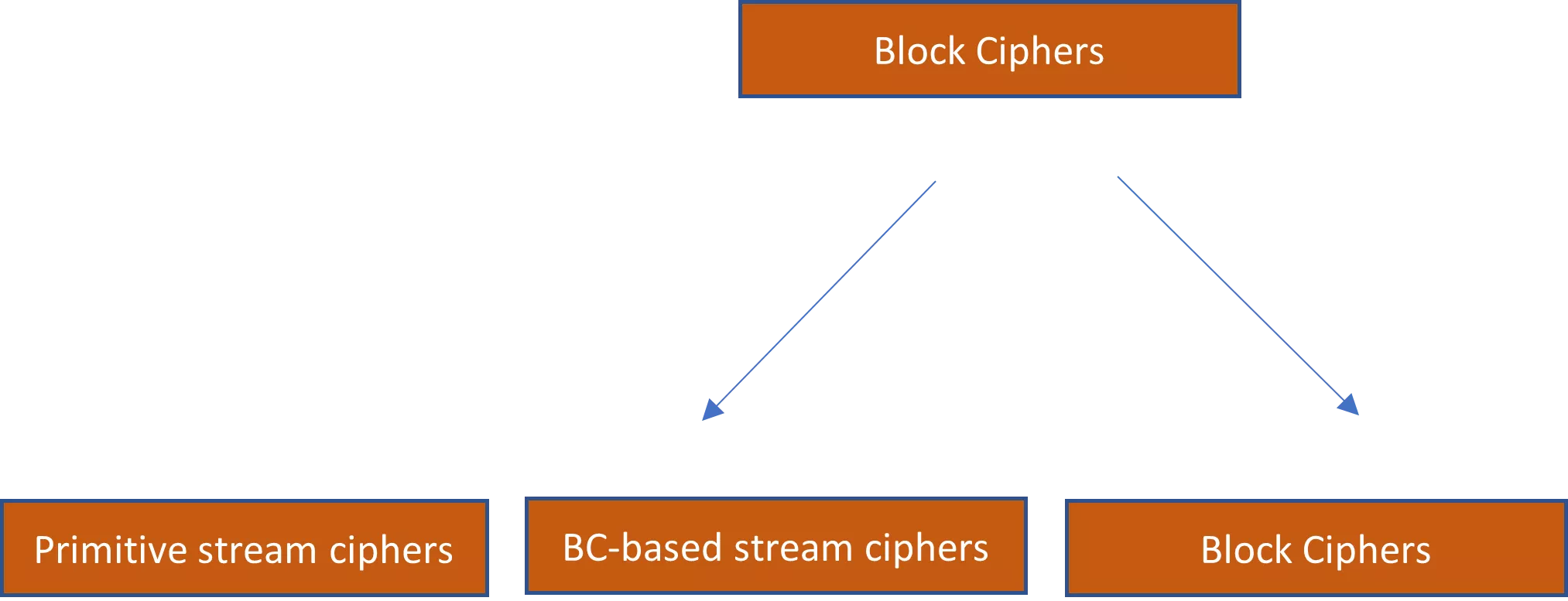
Sõnumi autentimise koodid
Krüpteerimine on seotud salastamisega. Kuid krüptograafia tegeleb ka laiemate teemadega, nagu sõnumi terviklikkus, autentsus ja mittevastavus. Niinimetatud sõnumi autentimiskoodid (MAC) on sümmeetrilise võtmega krüptograafilised skeemid, mis toetavad autentsust ja terviklikkust sidepidamises.
Miks on suhtlemisel vaja midagi muud kui salastatust? Oletame, et Bob saadab Alice'ile sõnumi, kasutades praktiliselt murdmatut krüpteerimist. Iga ründaja, kes seda sõnumit pealtkuulab, ei saa teada selle sisu kohta mingeid olulisi teadmisi. Siiski on ründajal veel vähemalt kaks muud ründevektorit:
Ta võiks salakirju pealtkuulata, selle sisu muuta ja saata muudetud salakirju Alice'ile.
Ta võiks blokeerida Bobi sõnumi täielikult ja saata oma loodud salakirju.
Mõlemal juhul ei pruugi ründaja saada teavet salakirjade (1) ja (2) sisu kohta. Kuid ta võib sel viisil siiski märkimisväärset kahju tekitada. See on koht, kus sõnumi autentimise koodid muutuvad oluliseks.
Sõnumi autentimise koodid on määratletud vabalt sümmeetriliste krüptograafiliste skeemidena, millel on kolm algoritmi: võtme genereerimise algoritm, märgistuse genereerimise algoritm ja kontrollimise algoritm. Turvaline MAC tagab, et sildid on eksistentsiaalselt võltsimatu mis tahes ründaja jaoks - see tähendab, et ta ei saa edukalt luua sildi sõnumi kohta, mida ta kontrollib, kui tal ei ole privaatvõtit.
Bob ja Alice saavad võidelda konkreetse sõnumiga manipuleerimise vastu, kasutades MACi. Oletame, et nad ei hooli salastatusest. Nad tahavad ainult tagada, et Alice'ile saabunud sõnum on tõepoolest Bobilt ja seda ei ole kuidagi muudetud.
Protsess on kujutatud joonisel 9*. MAC (Message
Authentication Code) kasutamiseks genereerivad nad kõigepealt privaatvõtme K, mida nad jagavad omavahel.
Bob loob sõnumi jaoks sildi T, kasutades privaatvõtit K. Seejärel saadab ta sõnumi
ja sõnumi sildi Alice'ile. Seejärel saab naine kontrollida, et Bob
tõepoolest tegi sildi, läbides eravõti, sõnum ja silt läbi
kontrollialgoritmi.
Joonis 9: Ülevaade sümmeetrilistest krüpteerimisskeemidest
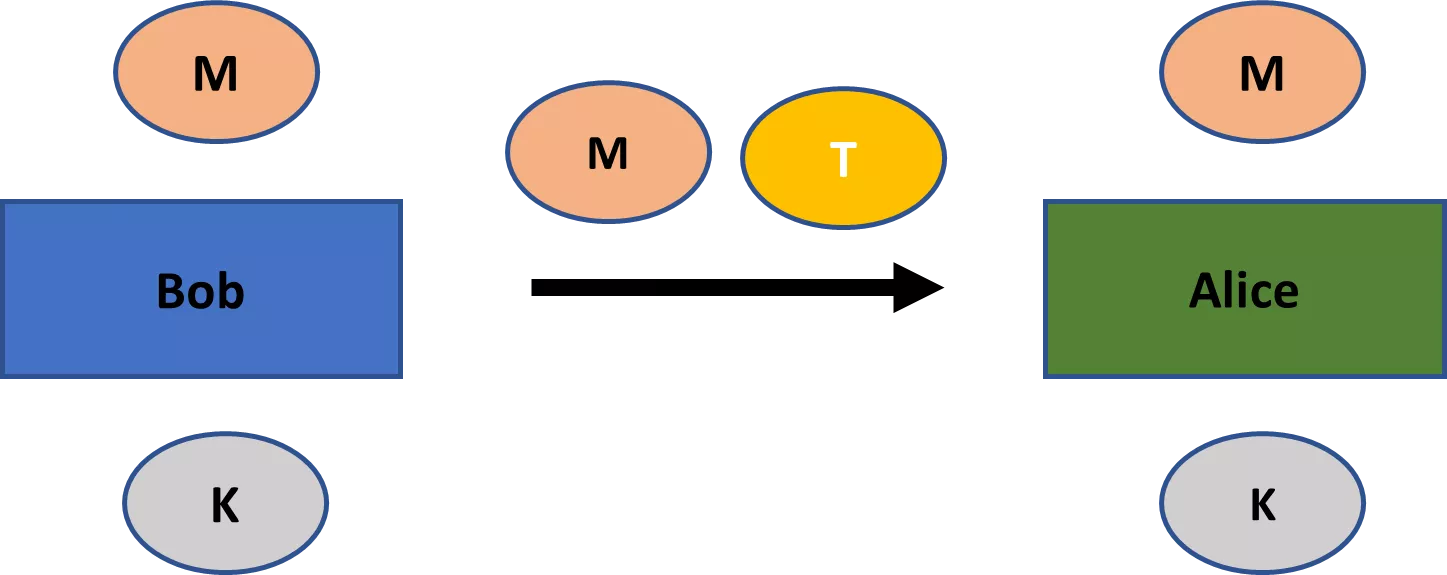
Tänu eksistentsiaalsele võltsimatusele ei saa ründaja
sõnumit M kuidagi muuta ega
luua oma sõnumit kehtiva sildiga. See on nii isegi siis, kui ründaja jälgib
paljude Bobi ja Alice'i vaheliste sõnumite silte, mis kasutavad sama
isiklikku võtit. Ründaja võib maksimaalselt takistada Alice'ile sõnumi M kättesaamist (probleem, mida
krüptograafia ei suuda lahendada).
MAC tagab, et sõnumi on tegelikult loonud Bob. See autentsus tähendab automaatselt sõnumi terviklikkust - st kui Bob on loonud mingi sõnumi, siis ipso facto ei ole seda ründaja mingil viisil muutnud. Nii et siit alates tuleks igasugune autentimise mure automaatselt mõista, et see tähendab ka mure terviklikkuse pärast.
Kuigi ma olen oma arutelus teinud vahet sõnumi autentsuse ja terviklikkuse vahel, on tavaline, et neid mõisteid kasutatakse ka sünonüümidena. Need viitavad siis ideele, et sõnumid on loodud konkreetse saatja poolt ja neid ei ole mingil viisil muudetud. Selles vaimus nimetatakse sõnumi autentimise koode sageli ka sõnumi terviklikkuse koodideks.
Autenditud krüpteerimine
Tavaliselt tahetakse tagada nii salastatus kui ka autentsus suhtluses ning seetõttu kasutatakse tavaliselt krüpteerimisskeeme ja MAC-skeeme koos.
Autentifitseeritud krüpteerimisskeem on skeem, mis kombineerib krüpteerimise ja MACi väga turvaliselt. Täpsemalt peab see vastama eksistentsiaalse võltsimatuse standarditele ning väga tugevale salastatuse mõistele, nimelt peab see olema vastupidav valiku-kirjutusteksti rünnakutele. [7]
Selleks, et krüpteerimisskeem oleks resistent valitud krüptoteksti rünnakute vastu, peab see vastama mittemalleeritavuse standarditele: see tähendab, et ründaja poolt tehtud mis tahes salateksti muudatus peaks andma kas kehtetu salateksti või sellise salateksti, mis dekrüpteeritakse selgeks tekstiks, millel ei ole mingit seost algse tekstiga. [8]
Kuna autenditud krüpteerimisskeem tagab, et ründaja poolt loodud salatekst on alati kehtetu (kuna sildi ei kontrollita), vastab see valitud salateksti ründeid käsitlevatele standarditele. Huvitaval kombel saab tõestada, et autenditud krüpteerimisskeemi saab alati luua eksistentsiaalselt võltsimata MACi ja krüpteerimisskeemi kombinatsioonist, mis vastab vähem tugevamale turvalisuse mõistele, mida tuntakse kui valik-valikteksti rünnaku turvalisust.
Me ei hakka süvenema kõikidesse autenditud krüpteerimisskeemide loomise üksikasjadesse. Kuid oluline on teada kaks nende ehitamise üksikasja.
Esiteks, autenditud krüpteerimisskeem tegeleb kõigepealt krüpteerimisega ja seejärel loob salatekstile sõnumi sildi. Selgub, et muud lähenemisviisid - näiteks salakirjateksti kombineerimine lihtteksti sildiga või esmalt sildi loomine ja seejärel nii lihtteksti kui ka sildi krüpteerimine - on ebaturvalised. Lisaks on mõlemal operatsioonil oma juhuslikult valitud privaatne võti, vastasel juhul on teie turvalisus tõsiselt ohustatud.
Eespool nimetatud põhimõte kehtib üldisemalt: põhiliste krüptograafiliste skeemide kombineerimisel tuleks alati kasutada eraldi võtmeid.
Autenditud krüpteerimisskeem on kujutatud kujul 10. Bob loob
kõigepealt sõnumist M salakirju C, kasutades
juhuslikult valitud võtit K_C. Seejärel loob ta sõnumi
sildi T, käivitades
salakirjateksti ja teise juhuslikult valitud võtme K_T abil sildi loomise algoritmi.
Nii šifreeritud tekst kui ka sõnumimärk saadetakse Alice'ile.
Alice kontrollib nüüd kõigepealt, kas silt on kehtiv, arvestades
salakirjateksti C ja võtit K_T. Kui see on kehtiv, saab
ta seejärel sõnumi dekrüpteerida, kasutades võtit K_C. Ta ei ole mitte ainult
kindel, et nende side on väga tugevalt salajane, vaid ta teab ka, et sõnumi
on loonud Bob.
Joonis 10: Autentimisele vastav krüpteerimisskeem

Kuidas luuakse MACid? Kuigi MAC-e saab luua mitmete meetoditega, on levinum ja tõhusam viis nende loomiseks krüptograafilised hash-funktsioonid.
Krüptograafilisi hash-funktsioone tutvustame põhjalikumalt peatükis 6. Praegu piisab sellest, et hash-funktsioon on tõhusalt arvutatav funktsioon, mis võtab suvalise suurusega sisendeid ja annab fikseeritud pikkusega väljundid. Näiteks populaarne hash-funktsioon SHA-256 (secure hash algorithm 256) annab alati 256-bitise väljundi, olenemata sisendi suurusest. Mõnel hash-funktsioonil, näiteks SHA-256, on kasulikud rakendused krüptograafias.
Kõige tavalisem krüptograafilise hash-funktsiooniga toodetud sildi tüüp on hash-based message authentication code (HMAC). Protsess on kujutatud kujul 11. Pool toodab privaatvõtmest K kaks erinevat võtit, sisemise võtme K_1 ja välimise võtme K_2.
Seejärel räsitakse lihttekst M või salatekst C koos sisemise
võtmega. Tulemus T' räsitakse
seejärel välise võtmega, et saada sõnumi silt T.
HMAC-i loomiseks on võimalik kasutada erinevaid hash-funktsioone. Kõige sagedamini kasutatav hash-funktsioon on SHA-256.
Joonis 11: HMAC
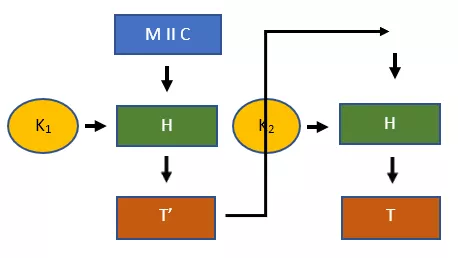
Märkused:
[7] Konkreetsed tulemused, mida käesolevas punktis käsitletakse, pärinevad Katz ja Lindell, lk 131-47.
[8] Tehniliselt on valitud salastatud teksti rünnakute määratlus erinev mittemalleeritavuse mõistest. Kuid saab näidata, et need kaks turvalisuse mõistet on samaväärsed.
Turvaline suhtlemine
Oletame, et kaks osapoolt on suhtlussessioonis, nii et nad saadavad mitu sõnumit edasi-tagasi.
Autenditud krüpteerimisskeem võimaldab sõnumi vastuvõtjal kontrollida, et sõnumi on koostanud tema suhtluspartner (tingimusel, et privaatne võti ei ole lekkinud). See toimib piisavalt hästi ühe sõnumi puhul. Tavaliselt saadavad aga kaks osapoolt sidesessioonis sõnumeid edasi-tagasi. Ja sellises olukorras ei suuda eelmises punktis kirjeldatud lihtne autentimisega krüpteerimisskeem turvalisust tagada.
Peamine põhjus on see, et autenditud krüpteerimisskeem ei anna mingit garantiid, et sõnumi saatis tegelikult ka see agent, kes selle sidesessiooni raames lõi. Mõelgem järgmistele kolmele ründevektorile:
Kordusrünnak: Ründaja saadab uuesti salakirja ja sildi, mille ta on kahe osapoole vahel varem kinni pidanud.
Kordusrünnak: Ründaja peibutab kaks eri ajal saadetud sõnumit ja saadab need vastuvõtjale vastupidises järjekorras.
Reflection rünnak: Ründaja jälgib A-st B-le saadetud sõnumit ja saadab selle sõnumi ka A-le.
Kuigi ründaja ei tea salastusteksti ja ei saa luua võltsitud salastustekste, võivad eespool kirjeldatud rünnakud siiski tekitada märkimisväärset kahju kommunikatsioonis.
Oletame näiteks, et konkreetne sõnum kahe osapoole vahel hõlmab rahaliste vahendite ülekandmist. Kordusrünnak võib raha teist korda üle kanda. Sellise rünnaku vastu ei ole autenditud krüpteerimisskeemil kaitset.
Õnneks saab selliseid rünnakuid suhtlussessioonis hõlpsasti leevendada, kasutades tunnuseid ja suhtelisi ajamõõdikuid.
Enne krüpteerimist võib lihtkirjasõnumile lisada identifikaatorid. See välistaks kõik peegeldusrünnakud. Suhteline ajaindikaator võib olla näiteks järjekorranumber konkreetses sidesessioonis. Iga osapool lisab enne krüpteerimist sõnumile järjekorranumbri, nii et vastuvõtja teab, millises järjekorras sõnumid saadeti. See välistab ümberjärjestusrünnakute võimaluse. Samuti välistab see kordusrünnakud. Iga ründaja saadetud sõnumil on vana järjekorranumber ja vastuvõtja teab, et seda sõnumit ei tohi uuesti töödelda.
Illustreerimaks, kuidas turvalised sidesessioonid toimivad, oletame taas, et Alice ja Bob. Nad saadavad kokku neli sõnumit edasi-tagasi. Allpool on näha, kuidas autenditud krüpteerimisskeem koos identifikaatorite ja järjestusnumbritega toimiks, kujutis 11.
Sidesessioon algab sellega, et Bob saadab Alice'ile salakirja C_{0,B} koos sõnumimärgiga T_{0,B}. Salatekst
sisaldab sõnumit, samuti identifikaatorit (BOB) ja järjenumbrit (0). Silt T_{0,B} on tehtud kogu
salatekstile. Järgnevas suhtluses säilitavad Alice ja Bob selle protokolli, uuendades
vajadusel välju.
Joonis 12: Turvaline sidesessioon
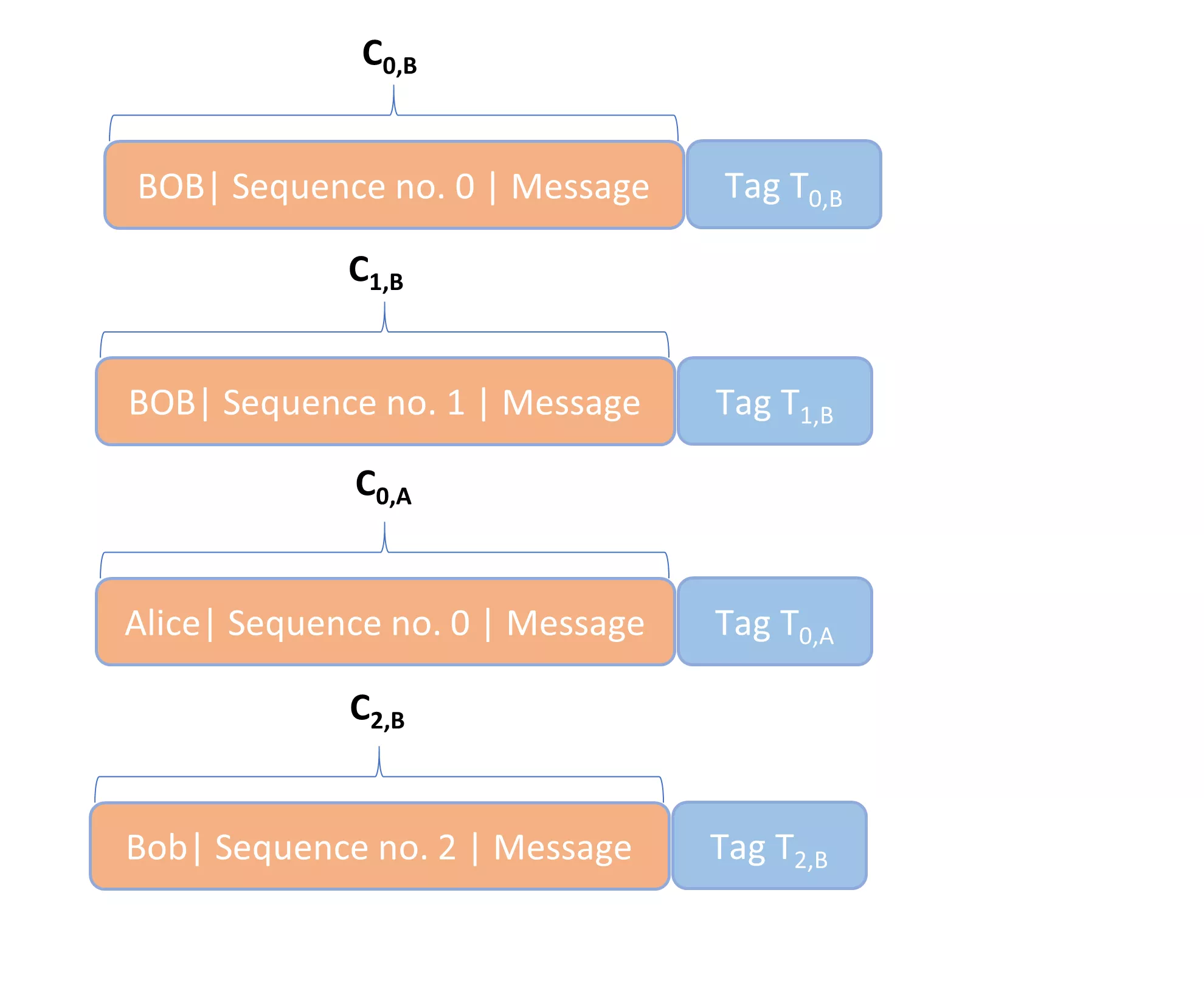
RC4 ja AES
RC4 voogkooder
Selles peatükis arutame kaasaegse primitiivse voogkoodiga RC4 (või "Rivest cipher 4") ja kaasaegse plokk-koodiga AES krüpteerimisskeemi üksikasju. Kui RC4-kood on krüpteerimismeetodina langenud ebasoosingusse, siis AES on kaasaegse sümmeetrilise krüpteerimise standard. Need kaks näidet peaksid andma parema ettekujutuse sellest, kuidas sümmeetriline krüpteerimine kapoti all töötab.
Selleks, et saada aimu, kuidas kaasaegsed pseudorandom voogkoode töötavad, keskendun ma RC4 voogkoodile. See on pseudorandom voogkood, mida kasutati traadita juurdepääsupunktide WEP ja WAP turvaprotokollides ning TLSis. Kuna RC4-l on palju tõestatud nõrkusi, on see langenud ebasoosingusse. Tegelikult keelab Internet Engineering Task Force nüüd RC4-sarjade kasutamise kliendi- ja serverirakendustes kõigis TLSi juhtudel. Sellegipoolest sobib see hästi näitena, et illustreerida, kuidas primitiivne voogkooder töötab.
Alustuseks näitan kõigepealt, kuidas krüpteerida lihtkirjasõnumit beebi RC4 salakirjaga. Oletame, et meie lihtkirjasõnum on "SOUP" Krüpteerimine meie beebi-RC4 salakirjaga toimub siis neljas etapis.
1. samm
Kõigepealt defineerime massiivi S, kus S[0] = 0 kuni S[7] = 7. Massiiv
tähendab siinkohal lihtsalt indeksi järgi korraldatud muutuvat väärtuste
kogumikku, mida mõnes programmeerimiskeeles (nt Python) nimetatakse ka
loendiks. Antud juhul ulatub indeks 0-st kuni 7-ni ja väärtused ulatuvad
samuti 0-st kuni 7-ni. Seega S on järgmine:
S = [0, 1, 2, 3, 4, 5, 6, 7]
Siin esitatud väärtused ei ole ASCII-numbrid, vaid 1 baidi pikkuste
stringide kümnendväärtused. Seega oleks väärtus 2 võrdne 0000 \ 0011. Massiivi S pikkus on seega 8 baiti.
2. samm
Teiseks, määratlege võtmemassiiv K pikkusega 8 baiti, valides võtme vahemikus 1 kuni 8 baiti (lubatud ei ole murdosa baidist). Kuna iga bait on 8-bitine, võite valida võtme iga baidi jaoks mis tahes arvu vahemikus 0-255.
Oletame, et valime võtmeks k [14, 48, 9], nii et selle
pikkus on 3 baiti. Meie võtmemassiivi iga indeks määratakse siis vastavalt
võtme selle konkreetse elemendi kümnendväärtusele, järjekorras. Kui te
jooksete kogu võtme läbi, alustage uuesti algusest, kuni olete täitnud
võtmemassiivi 8 kohta. Seega on meie võtmemassiiv järgmine:
K = [14, 48, 9, 14, 48, 9, 14, 48]
3. samm
Kolmandaks, me teisendame massiivi S, kasutades võtmemassiivi K, protsessi, mida tuntakse kui võtmete planeerimist. Protsess on pseudokoodis järgmine:
- Loo muutujad j ja i
- Määra muutuja
j = 0 - Iga
ipuhul 0 kuni 7:- Määra
j = (j + S[i] + K[i]) \mod 8 - Vahetage
S[i]jaS[j]
- Määra
Massiivi S ümberkujundamine on esitatud tabelis 1.
Alustuseks näete S algseisundit [0, 1, 2, 3, 4, 5, 6, 7],
kusjuures j algväärtus on 0. See teisendatakse, kasutades
võtmemassiivi [14, 48, 9, 14, 48, 9, 14, 48].
For-tsükkel algab algusega i = 0. Vastavalt eespool esitatud pseudokoodile saab j uueks
väärtuseks 6 (j = (j + S[0] + K[0]) \mod 8 = (0 + 0 + 14) \mod 8 = 6 \mod 8). Vahetades S[0] ja S[6], muutub S olekuks pärast 1 vooru [6, 1, 2, 3, 4, 5, 0, 7].
Järgmises reas on i = 1.
Läbides uuesti for-silmuse, saab j väärtuseks 7 (j = (j + S[1] + K[1]) \mod 8 = (6 + 1 + 48) \mod 8 = 55 \mod 8 = 7 \mod 8). Vahetades S[1] ja S[7] praegusest S olekust [6, 1, 2, 3, 4, 5, 0, 7],
saame pärast 2. vooru [6, 7, 2, 3, 4, 5, 0, 1].
Jätkame seda protsessi, kuni saame massiivi S lõpliku rea
allosas, [6, 4, 1, 0, 3, 7, 5, 2].
Tabel 1: võtmeplaanide tabel
| Round | i | j | S[0] | S[1] | S[2] | S[3] | S[4] | S[5] | S[6] | S[7] | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 1 | 0 | 6 | 6 | 1 | 2 | 3 | 4 | 5 | 0 | 7 | |
| 2 | 1 | 7 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 3 | 2 | 2 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 4 | 3 | 3 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 5 | 4 | 3 | 6 | 7 | 2 | 0 | 3 | 5 | 4 | 1 | |
| 6 | 5 | 6 | 6 | 4 | 2 | 0 | 3 | 7 | 5 | 1 | |
| 7 | 6 | 1 | 6 | 4 | 2 | 0 | 3 | 7 | 5 | 2 | |
| 8 | 7 | 2 | 6 | 4 | 1 | 0 | 3 | 7 | 5 | 2 |
4. samm
Neljanda sammuna toodame keystream. See on pseudorandom string, mille pikkus on võrdne sõnumi pikkusega, mida me tahame saata. Seda kasutatakse algse sõnumi "SOUP" krüpteerimiseks Kuna võtmevoog peab olema sama pikk kui sõnum, vajame sellist, mis on 4 baiti pikk.
Võtmevoog saadakse järgmise pseudokoodiga:
- Loo muutujad j, i ja t.
- Määra
j = 0. - Iga
ilihtteksti jaoks, alustadesi = 1ja jätkates kunii = 4, toodetakse iga baidi võtmevoog järgmiselt:j = (j + S[i]) \mod 8- Vahetage
S[i]jaS[j]. t = (S[i] + S[j]) \mod 8- Võtmevoo
i^{th}bait =S[t]
Võite jälgida arvutusi tabelis 2.
S algseisund on S = [6, 4, 1, 0, 3, 7, 5, 2].
Seades i = 1, saab j väärtuseks 4 (j = (j + S[i]) \mod 8 = (0 + 4) \mod 8 = 4). Seejärel vahetame S[1] ja S[4], et saada teises reas S teisendus [6, 3, 1, 0, 4, 7, 5, 2]. t väärtus on siis 7 (t = (S[i] + S[j]) \mod 8 = (3 + 4) \mod 8 = 7). Lõpuks on võtmevoo baidiks S[7] ehk 2.
Seejärel jätkame teiste baitide tootmist, kuni meil on järgmised neli baiti: 2, 6, 3 ja 7. Kõiki neid baite saab seejärel kasutada iga tähestiku "SOUP" iga tähe krüpteerimiseks.
ASCII-tabelit kasutades näeme, et "SOUP", mis on kodeeritud aluseks olevate baitide kümnendväärtuste järgi, on "83 79 85 80". Kombineerimine võtmevooga "2 6 3 7" annab tulemuseks "85 85 88 87", mis jääb pärast modulo 256 operatsiooni samaks. ASCII-keeles on salatekst "85 85 88 87" võrdne "UUXW".
Mis juhtub, kui krüpteeritav sõna oleks pikem kui massiiv S? Sellisel juhul jätkab massiivi S transformeerimist ülaltoodud viisil iga lihtteksti baidi i kohta, kuni meil on võtmevooga sama palju baite kui lihttekstis on tähti.
Tabel 2: Võtmevoo genereerimine
| i | j | t | Keystream | S[0] | S[1] | S[2] | S[3] | S[4] | S[5] | S[6] | S[7] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 4 | 1 | 0 | 3 | 7 | 5 | 2 | |||
| 1 | 4 | 7 | 2 | 6 | 3 | 1 | 0 | 4 | 7 | 5 | 2 |
| 2 | 5 | 0 | 6 | 6 | 3 | 7 | 0 | 4 | 1 | 5 | 2 |
| 3 | 5 | 1 | 3 | 6 | 3 | 7 | 1 | 4 | 0 | 5 | 2 |
| 4 | 1 | 7 | 2 | 6 | 4 | 7 | 1 | 3 | 0 | 5 | 2 |
Näide, mida me just arutasime, on vaid RC4 voogkooderite lahjendatud versioon. Tegelik RC4 voogsalvesti on S massiiviga, mille pikkus on 256 baiti, mitte 8 baiti, ja võti, mis võib olla vahemikus 1 kuni 256 baiti, mitte vahemikus 1 kuni 8 baiti. Võtmemassiivi ja võtmevooge toodetakse siis kõik, võttes arvesse S-massiivi 256 baidi pikkust. Arvutused muutuvad tohutult keerulisemaks, kuid põhimõtted jäävad samaks. Kasutades sama võtit [14,48,9] ja standardset RC4-krüpteerimist, krüpteeritakse selge tekst "SOUP" kuueteistkümnendsüsteemi kujul 67 02 ed df.
Voolukood, mille puhul võtmevoog uuendatakse sõltumata lihtkirjasõnumist või salatekstist, on sünkroonne voogkood. Võtmevoog sõltub ainult võtmest. On selge, et RC4 on näide sünkroonsest voošifreerimisest, kuna võtmevoog ei ole seotud liht- ega salatekstiga. Kõik meie eelmises peatükis mainitud primitiivsed voošifrid, sealhulgas nihkešifrid, Vigenère'i šifrid ja ühekordsed plokkšifrid, olid samuti sünkroonsed.
Seevastu asünkroonse voogšifri puhul on võtmevoog, mis saadakse nii võtme kui ka salakirjateksti eelnevate elementide abil. Seda tüüpi šifrit nimetatakse ka sünkroniseeruvaks šifriks.
Oluline on see, et RC4-ga toodetud võtmevooga tuleb arvestada kui ühekordse padiga ja te ei saa seda võtmevoogu järgmisel korral täpselt samamoodi toota. Selle asemel, et iga kord võtit muuta, on praktiline lahendus võtme kombineerimine nonce-ga, et toota võtmevoog.
AES 128-bitise võtmega
Nagu eelmises peatükis mainiti, korraldas riiklik standardite ja tehnoloogia instituut (NIST) aastatel 1997-2000 konkursi uue sümmeetrilise krüpteerimisstandardi kindlaksmääramiseks. Võitjaks osutus Rijndael-krüptograafia. Nimi on sõnamäng Belgia loojate Vincent Rijmeni ja Joan Daemeni nimede järgi.
Rijndael-krüptograafia on plokk-krüptograafia, mis tähendab, et on olemas põhialgoritm, mida saab kasutada erinevate võtmepikkuste ja plokisuuruste spetsifikatsioonidega. Seega saab seda kasutada erinevate töörežiimidega krüpteerimisskeemide koostamiseks.
NISTi konkursi komitee võttis vastu Rijndaeli šifri piiratud versiooni - nimelt sellise, mis nõuab 128-bitiseid plokke ja võtmepikkusi kas 128, 192 või 256 bitti - osana Advanced Encryption Standard (AES). Seda Rijndaeli salakirja piiratud versiooni saab kasutada ka mitme töörežiimi korral. Standardi spetsifikatsioon on nn Advanced Encryption Standard (AES).
Selleks, et näidata, kuidas töötab Rijndael-krüptograafia, mis on AES-i tuum, illustreerin 128-bitise võtmega krüpteerimise protsessi. Võtme suurus mõjutab iga krüpteerimisploki jaoks peetavate voorude arvu. 128-bitise võtme puhul on vaja 10 vooru. 192-bitise ja 256-bitise võtmega oleks see vastavalt 12 ja 14 vooru.
Lisaks eeldan, et AES-i kasutatakse ECB-režiimis. See teeb ekspositsiooni veidi lihtsamaks ja ei ole Rijndaeli algoritmi puhul oluline. Kindlasti ei ole EKP-režiim praktikas turvaline, sest see viib deterministliku krüpteerimiseni. Kõige sagedamini kasutatav turvaline režiim AESi puhul on CBC (Cipher Block Chaining).
Nimetame võtit K_0.
Konstruktsioon ülaltoodud parameetritega näeb siis välja nagu kujutis 1, kus M_i tähistab 128-bitise lihtteksti osa ja C_i tähistab 128-bitise šifreeritud
teksti osa. Viimase ploki puhul lisatakse lihtkirjale täiendus, kui lihtteksti
ei saa jagada ühtlaselt ploki suurusega.
Joonis 1: AES-ECB 128-bitise võtmega
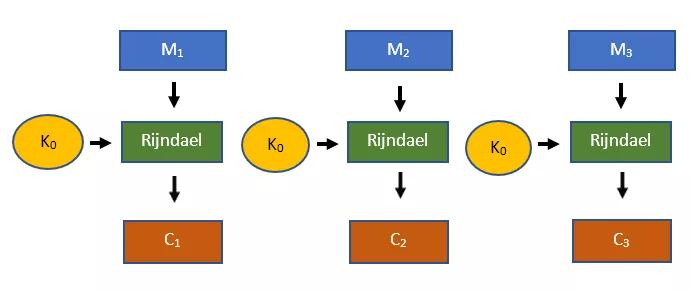
Iga 128-bitine tekstiplokk läbib Rijndaeli krüpteerimisskeemis kümme ringi.
See nõuab iga vooru jaoks eraldi võtit (K_1 kuni K_{10}). Need
luuakse iga vooru jaoks algsest 128-bitisest võtmest K_0, kasutades võtme laiendamise algoritmi. Seega kasutame iga
krüpteeritava tekstiploki jaoks nii algset võtit K_0 kui ka kümmet eraldi vooru
võtit. Pange tähele, et neid samu 11 võtit kasutatakse iga krüpteerimist vajava
128-bitise lihtteksti ploki jaoks.
Võtme laiendamise algoritm on pikk ja keeruline. Selle läbitöötamisest on
vähe didaktilist kasu. Soovi korral võite võtme laiendamise algoritmi ise
läbi vaadata. Kui ümmargused võtmed on toodetud, manipuleerib Rijndaeli
salastussüsteem esimest 128-bitist lihtteksti plokki M_1, nagu on näha Kujul 2. Käime nüüd need sammud läbi.
Joonis 2: M_1 manipuleerimine
Rijndaeli šifriga:
Round 0:
- XOR
M_1jaK_0, et saadaS_0
Round n jaoks n = {1,...,9}:
- XOR
S_{n-1}jaK_n - Baitide asendamine
- Nihkuvad read
- Veergude segamine
- XOR
SjaK_n, et saadaS_n
10. voor:
- XOR
S_9jaK_{10} - Baitide asendamine
- Nihkuvad read
- XOR
SjaK_{10}, et saadaS_{10} S_{10}=C_1
0. voor
Rijndaeli salakirja 0. voor on lihtne. Massiiv S_0 saadakse 128-bitise lihtteksti ja salajase võtme XOR-operatsiooniga. See tähendab,
S_0 = M_1 \oplus K_0
1. voor
Esimeses voorus kombineeritakse kõigepealt massiivi S_0 ümmarguse võtmega K_1,
kasutades XOR-operatsiooni. See annab uue seisundi S.
Teiseks tehakse baitide asendamise operatsioon S praeguse seisuga. See toimib nii, et võetakse iga bait 16 baidi suurusest S massiivist ja asendatakse see baidiga massiivist nimega Rijndaeli S-box. Igal baitil on unikaalne teisendus ja
selle tulemusena saadakse S uus olek. Rijndaeli S-box on kujutatud kujul 3.
Joonis 3: Rijndaeli S-Box
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 0A | 0B | 0C | 0D | 0E | 0F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 63 | 7C | 77 | 7B | F2 | 6B | 6F | C5 | 30 | 01 | 67 | 2B | FE | D7 | AB | 76 |
| 10 | CA | 82 | C9 | 7D | FA | 59 | 47 | F0 | AD | D4 | A2 | AF | 9C | A4 | 72 | C0 |
| 20 | B7 | FD | 93 | 26 | 36 | 3F | F7 | CC | 34 | A5 | E5 | F1 | 71 | D8 | 31 | 15 |
| 30 | 04 | C7 | 23 | C3 | 18 | 96 | 05 | 9A | 07 | 12 | 80 | E2 | EB | 27 | B2 | 75 |
| 40 | 09 | 83 | 2C | 1A | 1B | 6E | 5A | A0 | 52 | 3B | D6 | B3 | 29 | E3 | 2F | 84 |
| 50 | 53 | D1 | 00 | ED | 20 | FC | B1 | 5B | 6A | CB | BE | 39 | 4A | 4C | 58 | CF |
| 60 | D0 | EF | AA | FB | 43 | 4D | 33 | 85 | 45 | F9 | 02 | 7F | 50 | 3C | 9F | A8 |
| 70 | 51 | A3 | 40 | 8F | 92 | 9D | 38 | F5 | BC | B6 | DA | 21 | 10 | FF | F3 | D2 |
| 80 | CD | 0C | 13 | EC | 5F | 97 | 44 | 17 | C4 | A7 | 7E | 3D | 64 | 5D | 19 | 73 |
| 90 | 60 | 81 | 4F | DC | 22 | 2A | 90 | 88 | 46 | EE | B8 | 14 | DE | 5E | 0B | DB |
| A0 | E0 | 32 | 3A | 0A | 49 | 06 | 24 | 5C | C2 | D3 | AC | 62 | 91 | 95 | E4 | 79 |
| B0 | E7 | C8 | 37 | 6D | 8D | D5 | 4E | A9 | 6C | 56 | F4 | EA | 65 | 7A | AE | 08 |
| C0 | BA | 78 | 25 | 2E | 1C | A6 | B4 | C6 | E8 | DD | 74 | 1F | 4B | BD | 8B | 8A |
| D0 | 70 | 3E | B5 | 66 | 48 | 03 | F6 | 0E | 61 | 35 | 57 | B9 | 86 | C1 | 1D | 9E |
| E0 | E1 | F8 | 98 | 11 | 69 | D9 | 8E | 94 | 9B | 1E | 87 | E9 | CE | 55 | 28 | DF |
| F0 | 8C | A1 | 89 | 0D | BF | E6 | 42 | 68 | 41 | 99 | 2D | 0F | B0 | 54 | BB | 16 |
See S-box on üks koht, kus abstraktne algebra tuleb mängu Rijndaeli salakirjas, täpsemalt Galois' väljad.
Alustuseks defineerite iga võimaliku baidielemendi 00 kuni FF 8-bitise
vektorina. Iga selline vektor on element Galois' väljal GF(2^8), kus irreduzible polünoom modulo-operatsiooni jaoks on x^8 + x^4 + x^3 + x + 1.
Selliste spetsifikatsioonidega Galois' välja nimetatakse ka Rijndaeli lõplikuks väljaks.
Seejärel loome iga võimaliku elemendi jaoks väljal, mida nimetatakse Nybergi S-boksiks. Selles kastis on iga bait kaardistatud oma multiplikatiivsele pöördvõrrandile (st nii, et nende korrutis on võrdne 1). Seejärel kaardistame need väärtused Nybergi S-boxist Rijndaeli S-boxi, kasutades affiinset muundamist.
Kolmas operatsioon massiivi S jaoks on operatsioon riba nihutamine. See võtab S oleku ja loetleb kõik kuusteist baiti maatriksis. Maatriksi täitmine algab vasakult ülevalt ja liigub ülalt alla ning nihutab iga veeru täitmisel ühe veeru võrra paremale ja ülespoole.
Kui maatriks S on konstrueeritud, nihutatakse neli rida. Esimene rida jääb samaks. Teine rida nihkub ühe võrra vasakule. Kolmas rida nihkub kaks rida vasakule. Neljas rida nihutab kolm rida vasakule. Protsessi näide on esitatud kujul 4. Üleval on näidatud S algne olek ja all on näidatud tulemuslik olek pärast nihkerea operatsiooni.
Joonis 4: Ridade nihutamise operatsioon
| F1 | A0 | B1 | 23 |
|---|---|---|---|
| 59 | EF | 09 | 82 |
| 97 | 01 | B0 | CC |
| D4 | 72 | 04 | 21 |
| F1 | A0 | B1 | 23 |
|---|---|---|---|
| EF | 09 | 82 | 59 |
| B0 | CC | 97 | 01 |
| 21 | D4 | 72 | 04 |
Neljandas etapis ilmuvad taas Galois'i väljad. Alustuseks
korrutatakse iga S maatriksi veerg Andmel 5 vaadeldava 4 x 4 maatriksi veeruga. Kuid tavalise maatriksi korrutamise
asemel on see vektori korrutamine modulo taandamatu polünoomi, x^8 + x^4 + x^3 + x + 1.
Saadud vektorkoefitsiendid kujutavad baitide üksikuid bitte.
Joonis 5: Segu veergude maatriks
| 02 | 03 | 01 | 01 |
|---|---|---|---|
| 01 | 02 | 03 | 01 |
| 01 | 01 | 02 | 03 |
| 03 | 01 | 01 | 02 |
S maatriksi esimese veeru korrutamisel ülaltoodud 4 x 4 maatriksiga saadakse tulemus Kujul 6.
Joonis 6: Esimese veeru korrutamine:
\begin{matrix}
02 \cdot F1 + 03 \cdot EF + 01 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 02 \cdot EF + 03 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 01 \cdot EF + 02 \cdot B0 + 03 \cdot 21 \\
03 \cdot F1 + 01 \cdot EF + 01 \cdot B0 + 02 \cdot 21
\end{matrix}Järgmise sammuna tuleks kõik maatriksi terminid muuta polünoomideks. Näiteks
F1 esindab 1 baiti ja muutuks x^7 + x^6 + x^5 + x^4 + 1 ning 03 esindab 1 baiti ja muutuks x + 1.
Kõik korrutised tehakse siis moduloos x^8 + x^4 + x^3 + x + 1.
Selle tulemuseks on nelja polünoomi liitmine igas veeru neljas lahtris.
Pärast nende liitmiste modulo 2 teostamist saadakse neli
polünoomi. Iga selline polünoom esindab 8-bitist stringi ehk 1 baiti S. Me ei hakka siinkohal kõiki neid arvutusi kujutise 6 maatriksil tegema, sest need on väga ulatuslikud.
Kui esimene veerg on töödeldud, töödeldakse ülejäänud kolm S maatriksi veergu samamoodi. Lõpuks saadakse kuueteistkümne baidiga maatriks, mida saab muuta massiivi.
Viimase sammuna kombineeritakse massiiv S uuesti ümmarguse
võtmega XOR-operatsiooni käigus. Selle tulemuseks on olek S_1. See tähendab,
S_1 = S \oplus K_0
2. kuni 10. voor
Ringid 2 kuni 9 on lihtsalt 1. ringi kordus, mutatis mutandis. Viimane voor on väga sarnane eelmiste voorudega, kuid segunõudeid segav samm on välja jäetud. See tähendab, et 10. voor viiakse läbi järgmiselt:
S_9 \oplus K_{10}- Baitide asendamine
- Nihkuvad read
S_{10} = S \oplus K_{10}
Seisundile S_{10} on nüüd määratud C_1, mis on
salakirjateksti esimesed 128 bitti. Ülejäänud 128-bitiste lihttekstiplokkide
läbimine annab täieliku salakirjateksti C.
Rijndaeli salakirja operatsioonid
Mis on Rijndaeli salakirjas esinevate erinevate operatsioonide põhjendus?
Ilma üksikasjadesse laskumata hinnatakse krüpteerimisskeeme selle alusel, mil määral need tekitavad segadust ja levikut. Kui krüpteerimisskeemil on suur konfusiooni tase, tähendab see, et krüpteeritud tekst erineb oluliselt tavatekstist. Kui krüpteerimisskeemil on suur diffusiooni tase, tähendab see, et iga väike muudatus lihtsas tekstis annab oluliselt erineva salakirjelduse.
Rijndaeli šifri taga olevate operatsioonide põhjendus on see, et need tekitavad nii suurt segadust kui ka hajutatust. Segadust tekitab baitide asendamise operatsioon, samas kui hajutamist tekitavad ridade nihutamise ja veergude segamise operatsioonid.
Asümmeetriline krüptograafia
Võtmete jaotamise ja haldamise probleem
Nagu sümmeetrilise krüptograafia puhul, saab ka asümmeetrilisi skeeme kasutada nii salastatuse kui ka autentimise tagamiseks. Seevastu kasutatakse neis skeemides siiski ühe võtme asemel kahte võtit: privaatne ja avalik võti.
Alustame oma uurimist asümmeetrilise krüptograafia avastamisest, eelkõige probleemidest, mis seda käivitasid. Seejärel arutame, kuidas asümmeetrilised krüpteerimis- ja autentimisskeemid kõrgtasemel toimivad. Seejärel tutvustame hash-funktsioone, mis on võtmetähtsusega asümmeetriliste autentimisskeemide mõistmiseks ja mis on olulised ka muudes krüptograafilistes kontekstides, näiteks 4. peatükis käsitletud hash-põhiste sõnumite autentimiskoodide puhul.
Oletame, et Bob soovib osta uue vihmamantli Jim's Sporting Goodsist, spordikaupade online-müüjalt, millel on miljonid kliendid Põhja-Ameerikas. See on tema esimene ostu sealt ja ta soovib kasutada oma krediitkaarti. Seega peab Bob kõigepealt looma Jim's Sporting Goods'ile konto, milleks tuleb saata talle isiklikud andmed, näiteks tema aadress ja krediitkaardi andmed. Seejärel saab ta läbida vihmamantli ostmiseks vajalikud sammud.
Bob ja Jim's Sporting Goods soovivad tagada, et nende side on kogu selle protsessi jooksul turvaline, arvestades, et Internet on avatud sidesüsteem. Nad tahavad näiteks tagada, et ükski võimalik ründaja ei saaks teada Bobi krediitkaardi ja aadressi andmeid ning et ükski võimalik ründaja ei saaks tema ostusid korrata või tema nimel võltsinguid luua.
Eelmises peatükis käsitletud täiustatud autenditud krüpteerimisskeem võiks kindlasti muuta Bobi ja Jim's Sporting Goodsi vahelise side turvaliseks. Kuid sellise skeemi rakendamisel on selgelt praktilisi takistusi.
Nende praktiliste takistuste illustreerimiseks oletame, et me elame maailmas, kus on olemas ainult sümmeetrilise krüptograafia vahendid. Mida saaksid Jim's Sporting Goods ja Bob siis teha, et tagada turvaline side?
Sellises olukorras tuleks neil kanda märkimisväärseid kulusid turvalise teabevahetuse eest. Kuna Internet on avatud sidesüsteem, ei saa nad seal lihtsalt võtmekomplekti vahetada. Seega peavad Bob ja Jim's Sporting Goodsi esindaja vahetama võtmeid isiklikult.
Üks võimalus on, et Jim's Sporting Goods loob spetsiaalsed võtmevahetuskohad, kust Bob ja teised uued kliendid saavad turvaliseks suhtlemiseks võtmekomplekti kätte. Sellega kaasneksid ilmselt märkimisväärsed organisatsioonilised kulud ja see vähendaks oluliselt uute klientide ostude tegemise tõhusust.
Alternatiivina võib Jim's Sporting Goods saata Bobile võtmepaari usaldusväärse kulleriga. See on tõenäoliselt tõhusam kui võtmevahetuskohtade korraldamine. Kuid see tooks ikkagi kaasa märkimisväärseid kulusid, eriti kui paljud kliendid teevad ainult ühe või mõne ostu.
Järgmiseks sunnib sümmeetriline skeem autenditud krüpteerimiseks ka Jim's Sporting Goods'i säilitama kõigi oma klientide jaoks eraldi võtmekomplekte. See oleks märkimisväärne praktiline väljakutse tuhandete klientide puhul, rääkimata miljonitest klientidest.
Viimase punkti mõistmiseks oletame, et Jim's Sporting Goods annab igale kliendile ühe ja sama võtmepaari. See võimaldaks igal kliendil - või kellelgi teisel, kes saaks selle võtmepaari kätte - lugeda ja isegi manipuleerida kogu Jim's Sporting Goodsi ja tema klientide vahelist teabevahetust. Seega võiksite sama hästi jätta oma suhtluses krüptograafia üldse kasutamata.
Isegi võtmekomplekti kordamine ainult mõnele kliendile on kohutav turvapraktika. Iga potentsiaalne ründaja võib üritada seda skeemi omadust ära kasutada (pidage meeles, et Kerckhoffsi põhimõtte kohaselt eeldatakse, et ründajad teavad skeemi kohta kõike, välja arvatud võtmed)
Seega peaks Jim's Sporting Goods säilitama iga kliendi jaoks ühe võtmepaari, olenemata sellest, kuidas need võtmepaarid on jaotatud. See tekitab selgelt mitmeid praktilisi probleeme.
- Jim's Sporting Goods peaks ladustama miljoneid võtmepaare, üks komplekt iga kliendi jaoks.
- Need võtmed peaksid olema nõuetekohaselt turvatud, sest need oleksid kindel sihtmärk häkkeritele. Turvalisuse mis tahes rikkumine nõuaks kulukaid võtmevahetusi kas spetsiaalsetes võtmevahetuskohtades või kulleriga.
- Iga Jim's Sporting Goods'i klient peaks võtmepaari turvaliselt kodus hoidma. Kaotused ja vargused toimuvad, mis nõuavad korduvat võtmete vahetamist. Kliendid peaksid sama protsessi läbima ka kõigi teiste veebipoodide või muude üksuste puhul, kellega nad soovivad suhelda ja tehinguid teha Interneti kaudu.
Need kaks eelkirjeldatud põhiprobleemi olid kuni 1970. aastate lõpuni väga olulised probleemid. Neid tunti vastavalt võtmete jaotamise probleemina ja võtmete haldamise probleemina.
Need probleemid olid muidugi alati olemas ja tekitasid minevikus sageli peavalu. Näiteks pidid sõjaväeüksused pidevalt ja suure riski ja kulude hinnaga jagama välitingimustes viibivatele töötajatele turvalise side võtmetega raamatuid. Kuid need probleemid muutusid üha hullemaks, kuna maailm oli üha enam muutumas digitaalseks kaugside- ja sidesüsteemiks, eriti valitsusväliste üksuste jaoks.
Kui neid probleeme ei oleks 1970ndatel aastatel lahendatud, ei oleks tõhusaid ja turvalisi oste Jim's Sporting Goods'is tõenäoliselt olemas olnud. Tegelikult oleks suurem osa meie kaasaegsest maailmast, kus on praktiline ja turvaline e-post, internetipangandus ja sisseostud, tõenäoliselt vaid kauge fantaasia. Midagi, mis isegi sarnaneks Bitcoinile, ei oleks võinud üldse olemas olla.
Mis juhtus siis 1970ndatel? Kuidas on võimalik, et me saame koheselt internetis oste teha ja turvaliselt veebis sirvida? Kuidas on võimalik, et me saame oma nutitelefonist koheselt Bitcoine üle kogu maailma saata?
Uued suundumused krüptograafias
- aastateks olid võtmete jaotamise ja võtmehalduse probleemid äratanud Ameerika akadeemiliste krüptograafide tähelepanu: Whitfield Diffie, Martin Hellman ja Ralph Merkle. Seistes silmitsi enamiku nende kolleegide tõsise skeptitsismiga, söandasid nad välja töötada lahenduse.
Vähemalt üks nende ettevõtmise peamine ajend oli ettenägemine, et avatud arvutiside mõjutab põhjalikult meie maailma. Nagu Diffie ja Helmann 1976. aastal märkisid,
Arvutiga juhitavate sidevõrkude areng lubab vaevata ja odavat kontakti maailma eri pooltel asuvate inimeste või arvutite vahel, asendades enamiku posti ja paljud ekskursioonid telekommunikatsiooniga. Paljude rakenduste puhul tuleb need kontaktid muuta turvaliseks nii pealtkuulamise kui ka ebaseaduslike sõnumite sisestamise vastu. Praegu on aga turvaprobleemide lahendamine teistest sidetehnoloogiavaldkondadest oluliselt maha jäänud. Kaasaegne krüptograafia ei ole võimeline vastama nõuetele, sest selle kasutamine tekitaks süsteemi kasutajatele nii suuri ebamugavusi, et kaotaks paljud kaugtöötluse eelised [1]
Diffie, Hellmani ja Merkle'i visadus tasus end ära. Nende tulemused avaldati esmakordselt 1976. aastal Diffie ja Helmanni artiklis "New Directions in Cryptography" (Uued suundumused krüptograafias) Selles esitasid nad kaks originaalset viisi võtmete jaotamise ja võtmehalduse probleemide lahendamiseks.
Esimene lahendus, mida nad pakkusid, oli võtmevahetusprotokoll, st reeglite kogum ühe või mitme sümmeetrilise võtme vahetamiseks ebaturvalise sidekanali kaudu. See protokoll on nüüd tuntud kui Diffie-Helmanni võtmevahetus või Diffie-Helmanni-Merkle võtmevahetus. [2]
Diffie-Helmanni võtmevahetuse puhul vahetavad kaks osapoolt kõigepealt avalikult teavet ebaturvalises kanalis, näiteks Internetis. Seejärel loovad nad selle teabe põhjal sõltumatult sümmeetrilise võtme (või sümmeetriliste võtmete paari) turvaliseks suhtlemiseks. Kuigi mõlemad pooled loovad oma võtmed sõltumatult, tagab avalikult jagatud teave, et see võtme loomise protsess annab mõlemale poolele sama tulemuse.
Oluline on see, et kuigi kõik saavad jälgida teavet, mida pooled vahetavad avalikult ebaturvalise kanali kaudu, saavad ainult kaks teabevahetuses osalevat osapoolt luua sellest sümmeetrilisi võtmeid.
See kõlab muidugi täiesti vastupidiselt. Kuidas saaksid kaks osapoolt vahetada avalikult mingit teavet, mis võimaldaks ainult neil luua sellest sümmeetrilisi võtmeid? Miks ei saaks keegi teine, kes jälgib infovahetust, luua samu võtmeid?
See tugineb muidugi mõnele ilusale matemaatikale. Diffie-Helmanni võtmevahetus toimib ühesuunalise funktsiooni ja luugi kaudu. Arutleme nende kahe termini tähendust kordamööda.
Oletame, et teile on antud mingi funktsioon f(x) ja tulemus f(a) = y, kus a on x kindel väärtus. Ütleme,
et f(x) on ühesuunaline funktsioon, kui antud a ja f(x) korral on lihtne
arvutada väärtust y, kuid
antud y ja f(x) korral on arvutuslikult teostamatu arvutada väärtust a. Nimetus ühesuunaline funktsioon tuleneb muidugi sellest, et sellist
funktsiooni on otstarbekas arvutada ainult ühes suunas.
Mõnedel ühesuunalistel funktsioonidel on nn trapdoor. Kuigi
ainult y ja f(x) põhjal on praktiliselt võimatu arvutada a, on olemas teatud
informatsioon Z, mis muudab a arvutamise y põhjal
arvutuslikult teostatavaks. Seda informatsiooni Z nimetatakse Lõksuks. Ühepoolseid funktsioone, millel on
luuk, nimetatakse lukufunktsioonideks.
Me ei hakka siinkohal süvenema Diffie-Helmanni võtmevahetuse üksikasjadesse. Kuid sisuliselt loob iga osaleja mingi teabe, millest osa jagatakse avalikult ja osa jääb salajaseks. Iga osapool võtab siis oma salajase teabe ja teise osapoole jagatud avaliku teabe, et luua privaatne võti. Ja mõnevõrra imekombel saavad mõlemad osapooled lõpuks ühe ja sama privaatvõtme.
Iga osapool, kes jälgib vaid Diffie Helmanni võtmevahetuses kahe osapoole vahel avalikult jagatud teavet, ei saa neid arvutusi korrata. Selleks on vaja ühe poole privaatset teavet.
Kuigi 1976. aastal avaldatud Diffie-Helmanni võtmevahetuse põhiversioon ei ole väga turvaline, on selle põhiprotokolli keerukamad versioonid kindlasti tänapäevalgi kasutusel. Kõige tähtsam on see, et transpordikihi turvaprotokolli viimases versioonis (versioon 1.3) on sisuliselt Diffie ja Hellmani 1976. aastal esitatud protokolli rikastatud versioon. Transpordikihi turvaprotokoll on valdav protokoll, mille abil vahetatakse turvaliselt teavet, mis on vormindatud vastavalt veebisisu vahetamise standardile http (hypertext transfer protocol).
Oluline on, et Diffie-Helmanni võtmevahetus ei ole asümmeetriline skeem. Rangelt võttes kuulub see vaieldamatult sümmeetrilise võtme krüptograafia valdkonda. Kuid kuna nii Diffie-Helmanni võtmevahetus kui ka asümmeetriline krüptograafia tuginevad ühesuunalistele arvuteoreetilistele funktsioonidele koos luukidega, käsitletakse neid tavaliselt koos.
Teine viis, mida Diffie ja Helmann oma 1976. aasta artiklis pakkusid võtmete levitamise ja haldamise probleemi lahendamiseks, oli muidugi asümmeetriline krüptograafia.
Erinevalt nende Diffie-Hellmani võtmevahetuse esitlusest esitasid nad ainult üldised piirjooned, kuidas asümmeetrilisi krüptograafilisi skeeme võiks usutavalt konstrueerida. Nad ei pakkunud ühtegi ühesuunalist funktsiooni, mis võiks konkreetselt täita selliste skeemide mõistlikuks turvalisuseks vajalikke tingimusi.
Asümmeetrilise skeemi praktiline rakendamine leiti siiski aasta hiljem kolme erineva akadeemilise krüptograafi ja matemaatiku poolt: Ronald Rivest, Adi Shamir ja Leonard Adleman. [3] Nende poolt kasutusele võetud krüptosüsteem sai tuntuks kui RSA krüptosüsteem (nende perekonnanimede järgi).
Asümmeetrilises krüptograafias (ja Diffie Helmanni võtmevahetuses) kasutatavad trapdoor-funktsioonid on kõik seotud kahe peamise arvutuslikult raske probleemiga: primaarfaktoritega ja diskreetsete logaritmide arvutamisega.
Primifaktoriseerimine nõuab, nagu nimigi ütleb, täisarvu lahtimõtestamist selle primaarfaktoriteks. RSA-probleem on kaugelt kõige tuntum näide krüptosüsteemi kohta, mis on seotud primaarfaktoritega.
diskreetse logaritmi probleem on probleem, mis esineb tsüklilistes rühmades. Antud tsüklilise rühma generaatori korral tuleb arvutada ainuke eksponent, mis on vajalik selleks, et tekitada sellest generaatorist teine element selles rühmas.
Diskreetse logaritmi põhised skeemid tuginevad kahele peamisele tsüklilistele rühmadele: täisarvude korrutisrühmadele ja rühmadele, mis sisaldavad punkte elliptilistel kõveratel. Algne Diffie Helmanni võtmevahetus, nagu on esitatud raamatus "New Directions in Cryptography", töötab täisarvude tsüklilise multiplikatiivse grupiga. Bitcoini digitaalallkirja algoritm ja hiljuti tutvustatud Schnorri allkirja skeem (2021) põhinevad mõlemad diskreetse logaritmi probleemil konkreetse elliptilise kõvera tsüklilise rühma jaoks.
Järgnevalt anname kõrgetasemelise ülevaate salastatusest ja autentimisest asümmeetrilises keskkonnas. Enne seda peame siiski tegema lühikese ajaloolise märkuse.
Nüüd tundub usutav, et rühm Briti krüptograafide ja matemaatikute, kes töötasid valitsuse kommunikatsiooni peakorteri (GCHQ) heaks, oli paar aastat varem teinud eespool nimetatud avastused iseseisvalt. Sellesse rühma kuulusid James Ellis, Clifford Cocks ja Malcolm Williamson.
Nende enda ja GCHQ andmetel oli James Ellis see, kes 1969. aastal esimesena töötas välja avaliku võtme krüptograafia kontseptsiooni. Väidetavalt avastas Clifford Cocks seejärel 1973. aastal RSA krüptograafiasüsteemi ja Malcolm Williamson 1974. aastal Diffie Helmanni võtmevahetuse kontseptsiooni. [4] Nende avastused avalikustati aga väidetavalt alles 1997. aastal, arvestades GCHQ-s tehtud töö salajasust.
Märkused:
[1] Whitfield Diffie ja Martin Hellman, "New directions in cryptography", IEEE Transactions on Information Theory IT-22 (1976), lk 644-654, lk 644.
[2] Ralph Merkle arutab võtmevahetusprotokolli ka teoses "Secure communications over insecure channels", Communications of the Association for Computing Machinery, 21 (1978), 294-99. Kuigi Merkle esitas selle töö tegelikult enne Diffie ja Hellmani tööd, avaldati see hiljem. Merkle'i lahendus ei ole erinevalt Diffie-Hellmani omast eksponentsiaalselt turvaline.
[3] Ron Rivest, Adi Shamir ja Leonard Adleman, "A method for obtaining digital signatures and public-key cryptosystems", Communications of the Association for Computing Machinery, 21 (1978), lk 120-26.
[4] Nende avastuste hea ajalugu on esitatud Simon Singh, The Code Book, Fourth Estate (London, 1999), 6. peatükk.
Asümmeetriline krüpteerimine ja autentimine
Ülevaade asümmeetrilisest krüpteerimisest Bobi ja Alice'i abil on esitatud Kujul 1.
Alice loob kõigepealt võtmepaari, mis koosneb ühest avalikust võtmest (K_P) ja ühest salajasest võtmest (K_S), kus "P" K_P-s tähistab
"avalik" ja "S" K_S-s
"salajane". Seejärel jagab ta seda avalikku võtit vabalt teistele. Selle
levitamisprotsessi üksikasjade juurde pöördume tagasi veidi hiljem. Praegu
aga oletame, et igaüks, sealhulgas Bob, saab Alice'i avaliku võtme K_P turvaliselt kätte.
Mingil hilisemal hetkel soovib Bob kirjutada Alice'ile sõnumi M. Kuna see sisaldab tundlikku teavet, tahab ta, et selle sisu jääks
salajaseks kõigile peale Alice'i. Seega krüpteerib Bob kõigepealt oma sõnumi M, kasutades K_P. Seejärel saadab ta
saadud šifreeritud teksti C Alice'ile, kes dekrüpteerib C K_S abil, et saada algne sõnum M.
Joonis 1: Asümmeetriline krüpteerimine
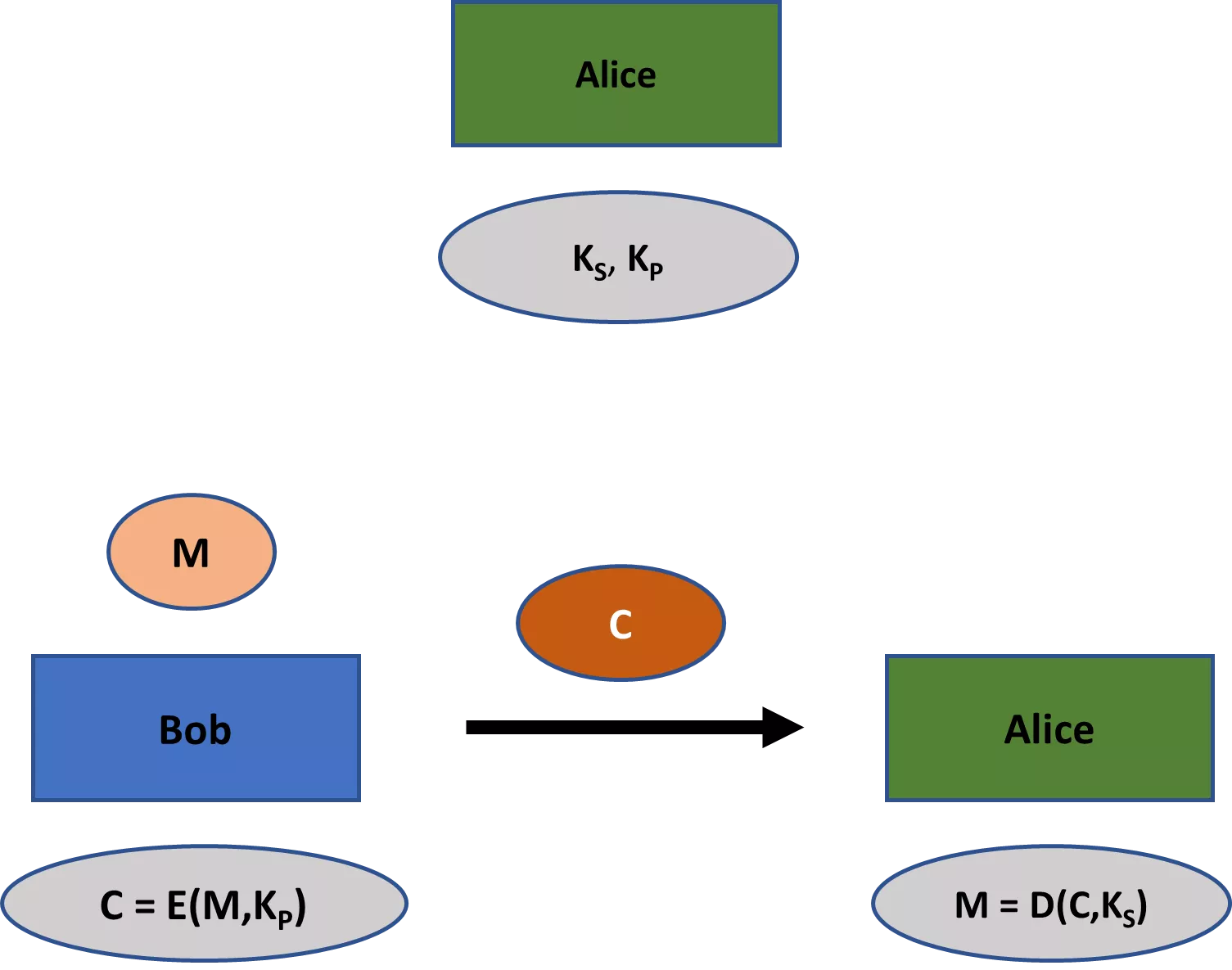
Iga vastane, kes kuulab Bobi ja Alice'i suhtlust, saab jälgida C. Ta teab ka K_P ja
krüpteerimisalgoritmi E(\cdot). Oluline on aga see,
et see teave ei võimalda ründajal tegelikkuses salakirju C dekrüpteerida. Dekrüpteerimiseks on vaja K_S, mida ründaja ei oma.
Sümmeetrilised krüpteerimisskeemid peavad üldiselt olema turvalised ründaja vastu, kes suudab õigesti krüpteerida lihtteksti sõnumeid (tuntud kui valitud šifreeritud teksti rünnaku turvalisus). See ei ole aga loodud selgesõnaliselt selleks, et võimaldada ründajal või kellelgi teisel luua selliseid kehtivaid salastustekste.
See on teravas vastuolus asümmeetrilise krüpteerimisskeemiga, mille eesmärk on võimaldada kõigil, sealhulgas ründajatel, toota kehtivaid salastustekste. Asümmeetrilisi krüpteerimisskeeme võib seetõttu nimetada mitmekordse juurdepääsuga šifriteks.
Et paremini mõista, mis toimub, kujutage ette, et elektroonilise sõnumi saatmise asemel soovib Bob saata salajase füüsilise kirja. Üks võimalus salajasuse tagamiseks oleks see, et Alice saadab Bobile turvalise tabaluku, kuid jätab endale võtme selle avamiseks. Pärast kirja kirjutamist võiks Bob panna kirja kasti ja sulgeda selle Alice'i tabalukuga. Seejärel võiks ta saata lukustatud kasti koos sõnumiga Alice'ile, kellel on selle avamise võti.
Kuigi Bob suudab tabaluku lukustada, ei saa ei tema ega ükski teine isik, kes kasti kinni paneb, tabalukku lahti teha, kui see on tõepoolest turvaline. Ainult Alice saab luku avada ja näha Bobi kirja sisu, sest tal on võti.
Asümmeetriline krüpteerimisskeem on selle protsessi digitaalne versioon. Lukk on sarnane avalikule võtmele ja lukkude võti on sarnane privaatvõtmele. Kuna tabalukk on aga digitaalne, on Alice'il palju lihtsam ja mitte nii kulukas seda levitada kõigile, kes võivad soovida talle salajasi sõnumeid saata.
Asümmeetrilises keskkonnas kasutame autentimiseks digitaalallkirju. Neil on seega sama funktsioon nagu sõnumi autentimise koodidel sümmeetrilises keskkonnas. Ülevaade digitaalallkirjadest on esitatud Ahelas 2.
Bob loob kõigepealt võtmepaari, mis koosneb avalikust võtmest (K_P) ja privaatvõtmest (K_S),
ning levitab oma avaliku võtme. Kui ta tahab saata Alice'ile autenditud
sõnumit, võtab ta kõigepealt oma sõnumi M ja oma isikliku võtme, et luua digitaalne allkiri D. Seejärel saadab Bob
Alice'ile oma sõnumi koos digitaalallkirjaga.
Alice sisestab sõnumi, avaliku võtme ja digitaalallkirja võrdlusalgoritmi. See algoritm annab kehtiva allkirja korral kas tõene või kehtetu allkirja korral vale.
Digitaalne allkiri on, nagu nimigi selgelt ütleb, kirjade, lepingute jne kirjaliku allkirja digitaalne ekvivalent. Tegelikult on digitaalallkiri tavaliselt palju turvalisem. Kirjalikku allkirja saab mõningase vaevaga võltsida; seda protsessi lihtsustab asjaolu, et kirjalikke allkirju ei kontrollita sageli hoolikalt. Turvaline digitaalallkiri on aga, nagu ka turvaline sõnumi autentimiskood, eksistentsiaalselt võltsimatu: see tähendab, et turvalise digitaalallkirjaskeemi puhul ei saa keegi luua sõnumi jaoks allkirja, mis läbib kontrollimenetluse, välja arvatud juhul, kui tal on olemas selle privaatne võti.
Joonis 2: Asümmeetriline autentimine
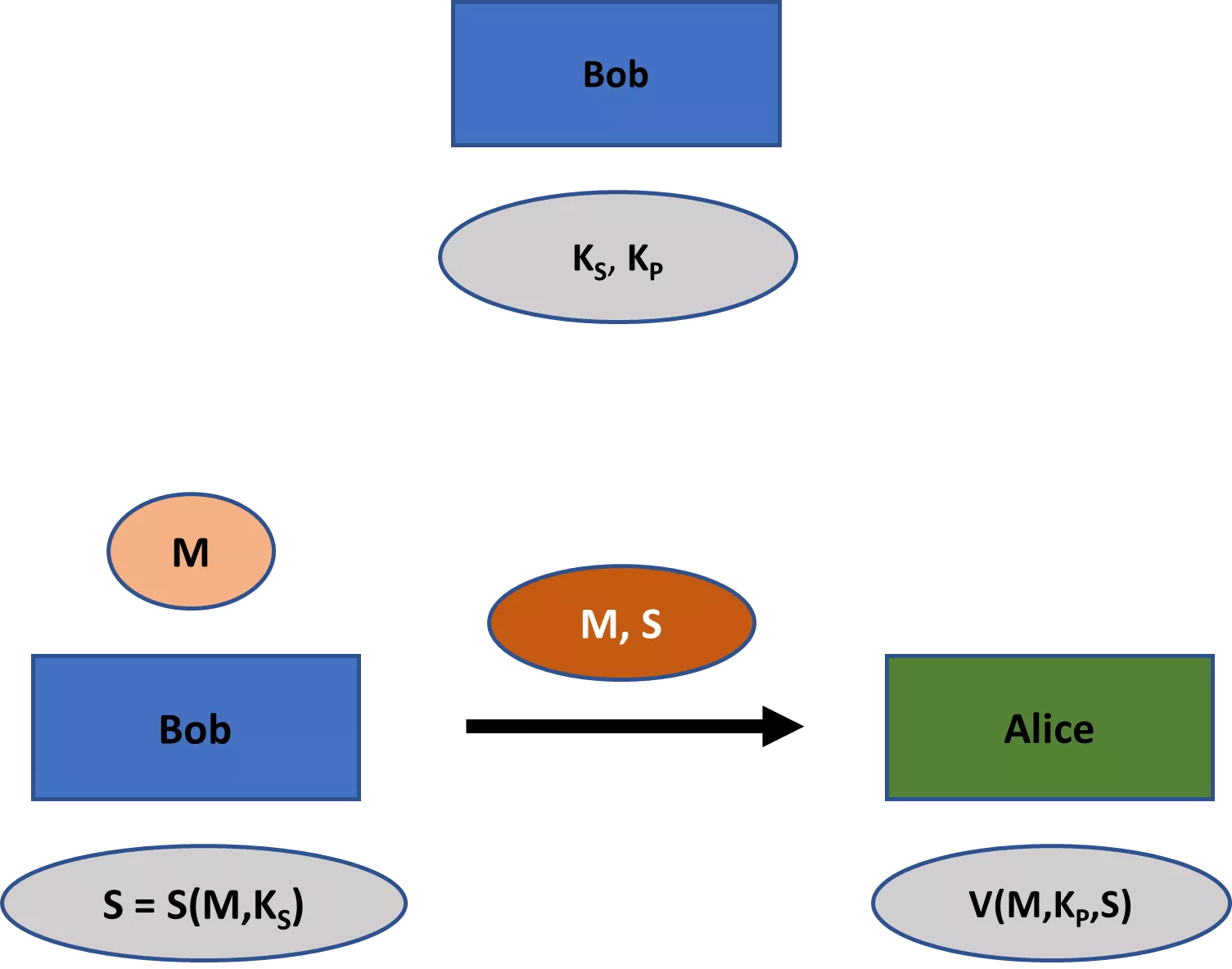
Nagu asümmeetrilise krüpteerimise puhul, näeme huvitavat kontrasti
digitaalallkirjade ja sõnumi autentimise koodide vahel. Viimase puhul saab
kontrollialgoritmi kasutada ainult üks turvalise teabevahetuse osapooltest.
Selle põhjuseks on asjaolu, et selleks on vaja isiklikku võtit.
Asümmeetrilises keskkonnas võib aga igaüks kontrollida Bobi tehtud
digitaalallkirja S.
Kõik see muudab digitaalallkirjad äärmiselt võimsaks vahendiks. See on
aluseks näiteks lepingute allkirjade loomisele, mida saab juriidilistel
eesmärkidel kontrollida. Kui Bob oleks ülalnimetatud andmevahetuse käigus
lepingu allkirjastanud, saab Alice näidata kohtule sõnumit M, lepingut ja allkirja S.
Kohus saab siis allkirja kontrollida Bobi avaliku võtme abil. [5]
Veel üks näide: digitaalallkirjad on turvalise tarkvara ja tarkvarauuenduste levitamise oluline aspekt. Seda tüüpi avalikku kontrollitavust ei saaks kunagi luua, kasutades ainult sõnumi autentimiskoode.
Viimase näitena digitaalallkirjade võimsusest võib tuua Bitcoini. Üks levinumaid väärarusaamu Bitcoini kohta, eriti meedias, on see, et tehingud on krüpteeritud: see ei ole nii. Selle asemel töötavad Bitcoini tehingud turvalisuse tagamiseks digitaalallkirjade abil.
Bitcoine on olemas partiidena, mida nimetatakse kasutamata tehinguväljunditeks (või UTXO-deks). Oletame, et saate konkreetsele Bitcoini aadressile kolm makset, millest igaühe eest saab 2 bitcoini. Tehniliselt ei ole teil nüüd sellel aadressil 6 bitcoin'i. Selle asemel on teil kolm 2 bitcoini suurust partiid, mis on lukustatud selle aadressiga seotud krüptograafilise probleemi tõttu. Mis tahes makse tegemiseks võite kasutada ühte, kahte või kõiki kolme neist partiidest, sõltuvalt sellest, kui palju te tehingu jaoks vajate.
Kasutamata tehingu väljundite omandiõigust tõendatakse tavaliselt ühe või mitme digitaalallkirjaga. Bitcoin töötab just seetõttu, et kehtivaid digitaalallkirju on kulumata tehingu väljundite kohta arvutuslikult võimatu anda, kui teil ei ole nende andmiseks vajalikku salajast teavet.
Praegu sisaldavad Bitcoini tehingud läbipaistvalt kogu teavet, mida võrgu osalejad peavad kontrollima, näiteks tehingus kasutatud kulutamata tehingu väljundite päritolu. Kuigi osa sellest teabest on võimalik varjata ja siiski kontrollida (nagu seda teevad mõned alternatiivsed krüptovaluutad, näiteks Monero), tekitab see ka erilisi turvariske.
Mõnikord tekib segadus digitaalallkirjade ja digitaalselt jäädvustatud kirjalike allkirjade osas. Viimasel juhul jäädvustate oma kirjaliku allkirja pildi ja kleebite selle elektroonilisele dokumendile, näiteks töölepingule. See ei ole aga digitaalallkiri krüptograafilises mõttes. Viimane on lihtsalt pikk number, mida saab toota ainult siis, kui on olemas privaatne võti.
Nii nagu sümmeetrilise võtme puhul, saate ka asümmeetrilise krüpteerimise ja autentimise skeeme kasutada koos. Kohaldatakse sarnaseid põhimõtteid. Kõigepealt peaksite krüpteerimiseks ja digitaalallkirjade andmiseks kasutama erinevaid privaatse ja avaliku võtme paare. Lisaks peaksite kõigepealt sõnumi krüpteerima ja seejärel autentima.
Oluline on see, et paljudes rakendustes ei kasutata asümmeetrilist krüptograafiat kogu sideprotsessi jooksul. Selle asemel kasutatakse seda tavaliselt ainult sümmeetriliste võtmete vahetamiseks osapoolte vahel, mille abil nad tegelikult suhtlevad.
Nii on see näiteks siis, kui ostate kaupu internetist. Teades müüja avalikku võtit, saab ta teile saata digitaalselt allkirjastatud sõnumeid, mille autentsust te saate kontrollida. Selle põhjal saate järgida ühte paljudest sümmeetriliste võtmete vahetamise protokollidest, et turvaliselt suhelda.
Eespool nimetatud lähenemisviisi sageduse peamine põhjus on see, et asümmeetriline krüptograafia on konkreetse turvataseme saavutamisel palju vähem tõhus kui sümmeetriline krüptograafia. See on üks põhjus, miks me vajame avaliku krüptograafia kõrval endiselt sümmeetrilise võtme krüptograafiat. Lisaks on sümmeetrilise võtme krüptograafia palju loomulikum teatud rakendustes, näiteks kui arvutikasutaja krüpteerib oma andmeid.
Kuidas täpselt lahendavad digitaalallkirjad ja avaliku võtme krüpteerimine võtme levitamise ja võtmehalduse probleeme?
Siin ei ole ühte vastust. Asümmeetriline krüptograafia on vahend ja selle kasutamiseks ei ole ainult ühte võimalust. Aga võtame meie varasema näite Jim's Sporting Goodsist, et näidata, kuidas antud näites tavaliselt probleeme lahendatakse.
Alustuseks pöörduks Jim's Sporting Goods tõenäoliselt sertifitseerimisasutuse poole, mis on organisatsioon, mis toetab avalike võtmete levitamist. Sertifitseerimisasutus registreeriks mõned andmed Jim's Sporting Goodsi kohta ja annaks talle avaliku võtme. Seejärel saadaks Jim's Sporting Goods'ile sertifikaadi, mida nimetatakse TLS/SSL sertifikaadiks, mille avalik võti on digitaalselt allkirjastatud Jim's Sporting Goods'i avaliku võtmega, kasutades sertifitseerimisasutuse enda avalikku võtit. Sel viisil kinnitab sertifitseerimisasutus, et konkreetne avalik võti kuulub tõepoolest Jim's Sporting Goods'ile.
TLS/SSL-sertifikaatide puhul on selle protsessi mõistmise võti selles, et kuigi Jim's Sporting Goodsi avalik võti ei ole tavaliselt kuskil teie arvutis salvestatud, on tunnustatud sertifitseerimisasutuste avalikud võtmed tõepoolest salvestatud teie brauseris või teie operatsioonisüsteemis. Need on salvestatud nn juurtunnistustes.
Seega, kui Jim's Sporting Goods annab teile oma TLS/SSL-sertifikaadi, saate kontrollida sertifitseerimisasutuse digitaalallkirja oma brauseris või operatsioonisüsteemis juursertifikaadi abil. Kui allkiri on kehtiv, võite olla suhteliselt kindel, et sertifikaadil olev avalik võti kuulub tõepoolest Jim's Sporting Goods'ile. Selle põhjal on lihtne luua Jim's Sporting Goodsiga turvalise suhtluse protokoll.
Võtmete levitamine on nüüd Jim's Sporting Goods'i jaoks muutunud oluliselt lihtsamaks. Pole raske näha, et ka võtmehaldus on muutunud oluliselt lihtsamaks. Selle asemel, et säilitada tuhandeid võtmeid, peab Jim's Sporting Goods säilitama vaid privaatvõtme, mis võimaldab tal teha allkirju oma SSL-sertifikaadi avaliku võtme jaoks. Iga kord, kui klient tuleb Jim's Sporting Goodsi veebisaidile, saab ta selle avaliku võtme abil luua turvalise sidesessiooni. Samuti ei pea kliendid salvestama mingit teavet (peale tunnustatud sertifitseerimisasutuste avalike võtmete oma operatsioonisüsteemis ja brauseris).
Märkused:
[5] Kõik skeemid, mis püüavad saavutada kinnitamatust, mis on teine teema, mida me arutasime 1. peatükis, peavad sisaldama digitaalallkirju.
Hash-funktsioonid
Hash-funktsioonid on krüptograafias üldlevinud. Nad ei ole ei sümmeetrilised ega asümmeetrilised skeemid, vaid kuuluvad omaette krüptograafilisse kategooriasse.
Me juba puutusime 4. peatükis kokku hash-funktsioonidega seoses hash-põhiste autentimissõnumite loomisega. Need on olulised ka digitaalallkirjade kontekstis, kuigi veidi teisel põhjusel: Digitaalallkirju tehakse nimelt tavaliselt mingi (krüpteeritud) sõnumi hash-väärtuse, mitte tegeliku (krüpteeritud) sõnumi üle. Käesolevas osas tutvustan põhjalikumalt hash-funktsioone.
Alustame hash-funktsiooni defineerimisega. Hash-funktsioon on mis tahes tõhusalt arvutatav funktsioon, mis võtab suvalise suurusega sisendeid ja annab fikseeritud pikkusega väljundeid.
Krüptograafiline hash-funktsioon on lihtsalt hash-funktsioon, mis on kasulik krüptograafia rakendustes. Kryptograafilise hash-funktsiooni väljundit nimetatakse tavaliselt hash, hash-väärtuseks või sõnumi digesti.
Krüptograafia kontekstis viitab "hash-funktsioon" tavaliselt krüptograafilisele hash-funktsioonile. Järgnevalt võtan ma selle praktika üle.
Populaarne hash-funktsioon on näiteks SHA-256 (secure hash algorithm 256). Sõltumata sisendi suurusest (nt 15 bitti, 100 bitti või 10 000 bitti) annab see funktsioon 256-bitise hash-väärtuse. Allpool näete mõned SHA-256 funktsiooni näitelahendused.
"Tere": 185f8db32271fe25f561a6fc938b2e264306ec304eda518007d1764826381969
"52398": a3b14d2bf378c1bd47e7f8eaec63b445150a3d7a80465af16dd9fd319454ba90
"Krüptograafia on lõbus": 3cee2a5c7d2cc1d62db4893564c34ae553cc88623992d994e114e344359b146c
Kõik väljundid on täpselt 256 bitti, mis on välja kirjutatud heksadekaalformaadis (iga heksakohaline number saab esitada nelja binaarkohalise numbriga). Seega isegi kui te oleksite sisestanud Tolkieni Sõrmuste isanda raamatu SHA-256 funktsiooni, oleks väljund ikkagi 256 bitti.
Krüptograafias kasutatakse erinevatel eesmärkidel selliseid šašafunktsioone nagu SHA-256. See, milliseid omadusi hash-funktsioonilt nõutakse, sõltub tegelikult konkreetse rakenduse kontekstist. Krüptograafias on kaks peamist omadust, mida krüptofunktsioonidelt üldiselt soovitakse: [6]
Kokkupõrkekindlus
Piilumine
Hash-funktsiooni H nimetatakse kokkupõrkekindlaks, kui on võimatu leida kahte
väärtust x ja y, nii et x \neq y, kuid H(x) = H(y).
Kokkupõrkekindlad hash-funktsioonid on olulised näiteks tarkvara kontrollimisel. Oletame, et soovite alla laadida Bitcoin Core 0.21.0 (serverirakendus Bitcoini võrguliikluse töötlemiseks) Windowsi versiooni. Peamised sammud, mida peaksite tarkvara õiguspärasuse kontrollimiseks tegema, on järgmised:
Esmalt tuleb alla laadida ja importida ühe või mitme toetaja avalikud võtmed Bitcoin Core'i tarkvarasse, mis suudab kontrollida digitaalallkirju (nt Kleopetra). Need avalikud võtmed leiate siit. Soovitatav on kontrollida Bitcoin Core'i tarkvara mitme toetaja avalike võtmetega.
Järgmisena peate kontrollima imporditud avalikke võtmeid. Vähemalt üks samm, mida peaksite tegema, on kontrollida, et leitud avalikud võtmed on samad, mis on avaldatud erinevates teistes kohtades. Võite näiteks tutvuda nende inimeste isiklike veebilehtede, Twitteri lehekülgede või Githubi lehekülgedega, kelle avalikud võtmed te impordisite. Tavaliselt tehakse see avalike võtmete võrdlemine avaliku võtme lühikese hash'i, mida nimetatakse sõrmejäljeks, võrdlemise teel.
Järgmisena peate Bitcoin Core'i käivitatava faili alla laadima nende veebisaidilt. Seal on saadaval paketid Linuxi, Windowsi ja MACi operatsioonisüsteemide jaoks.
Järgmisena peate leidma kaks release-faili. Esimene sisaldab allalaaditud käivitatava faili ametlikku SHA-256 hashi koos kõigi teiste avaldatud pakettide hashidega. Teine avaldamisfail sisaldab erinevate toetajate allkirju üle avaldamisfaili koos pakettide hashidega. Mõlemad vabastamisfailid peaksid asuma Bitcoin Core'i veebisaidil.
Järgmisena peate arvutama oma arvutis Bitcoin Core'i veebisaidilt alla laaditud käivitatava faili SHA-256 hashi. Seejärel võrdlete seda tulemust käivitatava faili ametliku paketi hashiga. Need peaksid olema samad.
Lõpuks peate kontrollima, et üks või mitu digitaalallkirja ametliku paketi hashiga faili üle vastab tõepoolest ühele või mitmele imporditud avalikule võtmele (Bitcoin Core'i versioonid ei ole alati kõigi poolt allkirjastatud). Seda saate teha sellise rakendusega nagu Kleopetra.
Sellisel tarkvara kontrollimise protsessil on kaks peamist kasu. Esiteks tagab see, et Bitcoin Core'i veebisaidilt allalaadimise ajal ei olnud ülekandevigu. Teiseks tagab see, et ükski ründaja ei saanud teid muudetud, pahatahtliku koodi allalaadimiseks kas Bitcoin Core'i veebisaidi häkkimise või liikluse pealtkuulamise teel.
Kuidas täpselt kaitseb eespool kirjeldatud tarkvara kontrollimise protsess nende probleemide eest?
Kui olete hoolikalt kontrollinud imporditud avalikke võtmeid, siis võite olla üsna kindel, et need võtmed on tegelikult nende omad ja neid ei ole ohustatud. Arvestades, et digitaalallkirjad on eksistentsiaalselt võltsimatult võltsimatud, teate, et ainult need toetajad võisid teha digitaalallkirja üle ametliku paketi hashi faili väljalaskefaili.
Oletame, et allalaaditud avaldamisfaili allkirjad on kontrollitud. Nüüd saate võrrelda allalaetud Windows'i käivitatava faili jaoks kohapeal arvutatud hash-väärtust nõuetekohaselt allkirjastatud avaldamisfailis sisalduva väärtusega. Nagu te teate, on SHA-256 hash-funktsioon kollioonikindel, seega tähendab vastavus, et teie käivitatav fail on täpselt sama, mis ametlik käivitatav fail.
Pöördume nüüd hash-funktsioonide teise ühise omaduse juurde: varjamine. Mis tahes hash-funktsioonil H on peitmise omadus, kui suvalise juhuslikult valitud x jaoks väga suurest vahemikust on x leidmine teostamatu, kui ainult H(x) on antud.
Allpool näete minu kirjutatud sõnumi SHA-256 väljundit. Piisava juhuslikkuse tagamiseks sisaldas sõnum lõpus juhuslikult genereeritud tähemärkide jada. Arvestades, et SHA-256-l on varjamise omadus, ei suuda keegi seda sõnumit dešifreerida.
b194221b37fa4cd1cfce15aaef90351d70de17a98ee6225088b523b586c32ded
Kuid ma ei jäta teid hätta, kuni SHA-256 muutub nõrgemaks. Algne sõnum, mille ma kirjutasin, oli järgmine:
- "See on väga juhuslik sõnum, või noh, omamoodi juhuslik. See algusosa ei ole, aga ma lõpetan mõne suhteliselt juhusliku tähemärgiga, et tagada väga ettearvamatu sõnum. XLWz4dVG3BxUWm7zQ9qS".
Levinud viis, kuidas peidutusomadusega hash-funktsioone kasutatakse paroolide haldamisel (ka selles rakenduses on oluline kokkupõrkekindlus). Ükski korralik kontopõhine veebiteenus, näiteks Facebook või Google, ei salvesta teie paroole otse, et hallata juurdepääsu teie kontole. Selle asemel salvestavad nad ainult selle salasõna hash'i. Iga kord, kui täidate oma parooli brauseris, arvutatakse kõigepealt hash. Ainult see hash saadetakse teenusepakkuja serverisse ja seda võrreldakse back-end andmebaasis salvestatud hashiga. Varjamise omadus aitab tagada, et ründajad ei saa seda hash-väärtusest taastada.
Salasõnade haldamine hashide abil toimib muidugi ainult siis, kui kasutajad valivad tegelikult keerulisi paroole. Varjamise omadus eeldab, et x valitakse juhuslikult väga suurest hulgast. Selliste paroolide nagu "1234", "mypassword" või oma sünnipäeva kuupäeva valimine ei paku mingit tõelist turvalisust. On olemas pikad nimekirjad tavalistest paroolidest ja nende hashidest, mida ründajad saavad ära kasutada, kui nad kunagi saavad teie parooli hashi kätte. Seda tüüpi rünnakuid nimetatakse sõnastikurünnakuteks. Kui ründajad teavad mõningaid teie isikuandmeid, võivad nad proovida ka mõningaid teadlikke oletusi. Seega on teil alati vaja pikki ja turvalisi paroole (eelistatavalt pikki, juhuslikke stringid paroolihaldurist).
Mõnikord võib rakendus vajada hash-funktsiooni, millel on nii kokkupõrkekindlus kui ka peitmine. Kuid kindlasti mitte alati. Näiteks tarkvara kontrollimise protsess, mida me arutasime, nõuab ainult seda, et hash-funktsioonil oleks kokkupõrkekindlus, varjamine ei ole oluline.
Kuigi kokkupõrkekindlus ja varjamine on peamised omadused, mida krüptograafias hash-funktsioonidelt taotletakse, võivad teatud rakendustes olla soovitavad ka muud tüüpi omadused.
Märkused:
[6] "Varjamise" terminoloogia ei ole üldkasutatav, vaid on võetud spetsiaalselt Arvind Narayanani, Joseph Bonneau, Edward Felten, Andrew Miller ja Steven Goldfeder, Bitcoin and Cryptocurrency Technologies, Princeton University Press (Princeton, 2016), 1. peatükk.
RSA krüptosüsteem
Faktooringuprobleem
Kui sümmeetriline krüptograafia on enamiku inimeste jaoks tavaliselt üsna intuitiivne, siis asümmeetrilise krüptograafia puhul ei ole see tavaliselt nii. Kuigi te olete tõenäoliselt rahul eelmistes peatükkides pakutud kõrgetasemelise kirjeldusega, mõtlete tõenäoliselt, mis täpselt on ühesuunalised funktsioonid ja kuidas täpselt neid kasutatakse asümmeetriliste skeemide konstrueerimiseks.
Selles peatükis eemaldan osa asümmeetrilise krüptograafia salapära, uurides põhjalikumalt ühte konkreetset näidet, nimelt RSA krüptosüsteemi. Esimeses peatükis tutvustan faktoriseerimisprobleemi, millel RSA põhineb. Seejärel käsitletakse mitmeid olulisi tulemusi arvuteooriast. Viimases osas paneme selle teabe kokku, et selgitada RSA-probleemi ja seda, kuidas seda saab kasutada asümmeetriliste krüptograafiliste skeemide loomiseks.
Sellise sügavuse lisamine meie arutelusse ei ole lihtne ülesanne. See nõuab üsna paljude arvuteoreetiliste teoreemide ja lausete tutvustamist. Kuid ärge laske matemaatikal end heidutada. Selle arutelu läbitöötamine parandab oluliselt teie arusaamist sellest, mis on asümmeetrilise krüptograafia aluseks, ja see on väärt investeering.
Pöördume nüüd kõigepealt faktooringuprobleemi juurde.
Kui te korrutate kaks arvu, näiteks a ja b, siis nimetame numbreid a ja b teguriteks ja tulemust tooteks. Katse kirjutada arv N kahe või enama faktori korrutamiseks nimetatakse faktoriteks või faktoriteks. [1] Iga probleemi, mis seda nõuab, võib
nimetada faktoorimisprobleemiks.
Umbes 2500 aastat tagasi avastas kreeka matemaatik Eukleidese Aleksandria matemaatik võtmeteoreemi täisarvude faktoriseerimise kohta. Seda nimetatakse tavaliselt Üksikordse faktoriseerimise teoreemiks ja see väidab järgmist:
Teoreem 1. Iga täisarv N, mis on suurem kui 1, on
kas algarv või on väljendatav algarvude korrutisena.
Viimane osa sellest väitest tähendab vaid seda, et võite võtta mis tahes
täisarvu N, mis ei ole
priimus, mis on suurem kui 1, ja kirjutada selle välja kui priimusarvude
korrutise. Allpool on toodud mitu näidet mittetäielike täisarvude kohta, mis
on kirjutatud algarvude korrutisena.
18 = 2 \cdot 3 \cdot 3 = 2 \cdot 3^284 = 2 \cdot 2 \cdot 3 \cdot 7 = 2^2 \cdot 3 \cdot 7144 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 = 2^4 \cdot 3^2
Kõigi kolme ülaltoodud täisarvu puhul on nende primaarfaktorite arvutamine
suhteliselt lihtne, isegi kui teile on antud ainult N. Alustate väikseimast algarvust, nimelt 2, ja vaatate, mitu korda on
täisarv N sellega jagatav.
Seejärel testite, kas N on
jagatav 3, 5, 7 jne. arvuga. Seda protsessi jätkatakse seni, kuni täisarv N on kirjutatud ainult algarvude
korrutisena.
Võtame näiteks täisarvu 84. Allpool näete, kuidas määratakse selle primaarfaktorid. Igal sammul võtame välja väikseima allesjäänud algteguri (vasakul) ja määrame faktoriseeritava jääkteguri. Jätkame seni, kuni ka jääkterm on algarv. Iga sammu juures kuvatakse paremal pool 84 praegune faktorisatsioon.
- Esmategur = 2: jääkterminus = 42 (
84 = 2 \cdot 42) - Primaarfaktor = 2: jääkterminus = 21 (
84 = 2 \cdot 2 \cdot 21) - Esmategur = 3: jääkterminus = 7 (
84 = 2 \cdot 2 \cdot 3 \cdot 7) - Kuna 7 on algarv, on tulemus
2 \cdot 2 \cdot 3 \cdot 7või2^2 \cdot 3 \cdot 7.
Oletame nüüd, et N on väga
suur. Kui raske oleks N redutseerida
algteguriteks?
See sõltub tõesti N-st.
Oletame näiteks, et N on 50 450
400. Kuigi see arv tundub hirmutav, ei ole arvutused nii keerulised ja neid saab
hõlpsasti käsitsi teha. Nagu eespool, alustate lihtsalt 2-st ja liigute edasi.
Allpool näete selle protsessi tulemust samamoodi nagu eespool.
- 2: 25 225 200 (
50 450 400 = 2 \cdot 25 225 200) - 2: 12 612 600 (
50 450 400 = 2^2 \cdot 12 612 600) - 2: 6 306 300 (
50 450 400 = 2^3 \cdot 6 306 300) - 2: 3 153 150 (
50 450 400 = 2^4 \cdot 3 153 150) - 2: 1,576,575 (
50,450,400 = 2^5 \cdot 1,576,575) - 3: 525,525 (
50 450 400 = 2^5 \cdot 3 \cdot 525,525) - 3: 175,175 (
50,450,400 = 2^5 \cdot 3^2 \cdot 175,175) - 5: 35,035 (
50,450,400 = 2^5 \cdot 3^2 \cdot 5 \cdot 35,035) - 5: 7,007 (
50,450,400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7,007) - 7: 1,001 (
50 450 400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7 \cdot 1,001) - 7: 143 (
50 450 400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 143) - 11: 13 (
50 450 400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13) - Kuna 13 on algarv, on tulemus
2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13.
Selle probleemi käsitsi välja töötamine võtab aega. Arvutiga saaks seda kõike muidugi teha sekundi murdosa jooksul. Tegelikult suudab arvuti sageli isegi väga suuri täisarvusid korrutada sekundi murdosa jooksul.
On siiski teatud erandeid. Oletame, et valime kõigepealt juhuslikult kaks
väga suurt algarvu. Tavaliselt tähistatakse neid p ja q ja ma võtan selle konventsiooni
ka siinkohal üle.
Konkreetsuse huvides ütleme, et p ja q on mõlemad 1024-bitised
priimused ja et nende esitamiseks on tõepoolest vaja vähemalt 1024 bitti
(seega peab esimene bit olema 1). Seega näiteks 37 ei saa olla üks
algarvudest. Kindlasti saab 37 esitada 1024 bitiga. Aga ilmselgelt ei ole vaja selle esitamiseks nii palju bitte. Sa võid 37 kujutada mis tahes stringiga,
millel on 6 bitti või rohkem. (6 bitiga oleks 37 esindatud kui 100101).
Oluline on hinnata, kui suured on p ja q, kui need valitakse
eespool toodud tingimustel. Näitena valisin allpool juhusliku algarvu, mille
esitamiseks on vaja vähemalt 1024 bitti.
- 14,752,173,874,503,595,484,930,006,383,670,759,559,764,562,721,397,166,747,289,220,945,457,932,666,751,048,198,854,920,097,085,690,793,755,254,946,188,163,753,506,778,089,706,699,671,722,089,715,624,760,049,594,106,189,662,669,156,149,028,900,805,928,183,585,427,782,974,951,355,515,394,807,209,836,870,484,558,332,897,443,152,653,214,483,870,992,618,171,825,921,582,253,023,974,514,209,142,520,026,807,636,589
Oletame nüüd, et pärast juhusliku algarvude p ja q valimist korrutame neid,
et saada täisarv N. Viimane
täisarv on seega 2048-bitine arv, mille esitamiseks on vaja vähemalt 2048
bitti. See on palju, palju suurem kui p või q.
Oletame, et annate arvutile ainult N ja palute tal leida kaks 1024-bitist priimafaktorit arvust N. Tõenäosus, et arvuti leiab p ja q, on äärmiselt väike.
Võib öelda, et see on praktiliselt võimatu. See on nii isegi siis, kui
kasutada superarvutit või isegi superarvutite võrgustikku.
Alustuseks oletame, et arvuti üritab probleemi lahendada, käies läbi 1024
bittilist arvu, testides igal juhul, kas need on algarvud ja kas need on N faktorid. Testitavate algarvude hulk on siis umbes 1,265 \cdot 10^{305}. [2]
Isegi kui võtta kõik arvutid planeedil ja lasta neil püüda leida ja testida
1024-bitiseid algarvusid sel viisil, siis 1 miljardist tõenäosus leida
edukalt N algarvu tegur nõuab
palju pikemat arvutamisperioodi kui Universumi vanus.
Praktikas saab arvuti paremini hakkama kui äsja kirjeldatud ligikaudne protseduur. On olemas mitu algoritmi, mida arvuti saab rakendada, et jõuda kiiremini faktoriseerimiseni. Asi on aga selles, et isegi neid tõhusamaid algoritme kasutades on arvuti ülesanne arvutuslikult ikkagi teostamatu. [3]
Oluline on see, et faktoriseerimise keerukus äsja kirjeldatud tingimustel põhineb eeldusel, et ei ole olemas arvutuslikult tõhusaid algoritme primaarfaktorite arvutamiseks. Me ei saa tegelikult tõestada, et tõhusat algoritmi ei ole olemas. Sellegipoolest on see eeldus väga usutav: vaatamata ulatuslikele, sadu aastaid kestnud jõupingutustele ei ole me veel sellist arvutuslikult tõhusat algoritmi leidnud.
Seega võib faktoriseerimisprobleemi teatud tingimustel usutavalt pidada
raskeks probleemiks. Täpsemalt, kui p ja q on väga suured algarvud,
siis nende korrutis N ei ole
raske arvutada; kuid faktoreerimine ainult antud N korral on praktiliselt võimatu.
Märkused:
[1] Faktoriseerimine võib olla oluline ka töötamisel muud tüüpi
matemaatiliste objektidega kui arvud. Näiteks võib see olla kasulik
polünoomiavaldiste, näiteks x^2 - 2x + 1, faktoriseerimiseks. Meie arutelus keskendume ainult arvude, täpsemalt
täisarvude faktoriseerimisele.
[2] Vastavalt täpsete arvude teoreemile on arvude arv, mis
on väiksem või võrdne N,
ligikaudu N/\ln(N). See
tähendab, et 1024-bitise pikkusega priimuste arvu saab ligikaudselt arvutada
järgmiselt:
\frac{2^{1024}}{\ln(2^{1024})} -
\frac{2^{1023}}{\ln(2^{1023})}
...mis võrdub umbes 1,265 \times 10^{305} dollariga.
[3] Sama kehtib ka diskreetsete logaritmiprobleemide kohta. Seetõttu töötavad asümmeetrilised konstruktsioonid palju suuremate võtmetega kui sümmeetrilised krüptograafilised konstruktsioonid.
Numbriteoreetilised tulemused
Kahjuks ei saa faktooringuprobleemi otseselt kasutada asümmeetriliste krüptograafiliste skeemide puhul. Küll aga saame selleks kasutada keerukamat, kuid sellega seotud probleemi: RSA-probleemi.
RSA-probleemi mõistmiseks peame mõistma mitmeid teoreeme ja lauseid arvuteooriast. Need on käesolevas jaotises esitatud kolmes alajaotuses: (1) N järjestus, (2) inverteeritavus modulo N ja (3) Euleri teoreem.
Osa kolme alajao materjalist on juba tutvustatud peatükis 3. Kuid ma kordan siinkohal selle materjali mugavuse huvides uuesti.
Järjestus N
Tervikarv a on kooprime või relatiivne primaarne täisarvuga N, kui nende suurim ühine
jagaja on 1. Kuigi 1 ei ole kokkuleppeliselt primaarne, on ta iga täisarvu
kooprime (nagu ka -1).
Näiteks vaadeldakse juhtumit, kus a = 18 ja N = 37. Need on selgelt
koopriimid. Suurim täisarv, mis jagab nii 18 kui ka 37, on 1. Seevastu
vaadeldakse juhtumit, kus a = 42 ja N = 16. Need ei ole
ilmselgelt kooprime. Mõlemad arvud on jagatavad 2ga, mis on suurem kui 1.
Nüüd võime defineerida N järjestuse järgmiselt. Oletame, et N on täisarv, mis on suurem kui 1. Kordaja N on siis kõigi
selliste kaasarvude arv, mille puhul iga kaasarvu a puhul kehtib järgmine tingimus: 1 \leq a < N.
Näiteks kui N = 12, siis on
1, 5, 7 ja 11 ainsad koprimeetrid, mis vastavad ülaltoodud nõudele. Seega on
12 järjekord võrdne 4.
Oletame, et N on algarv. Siis
on mis tahes täisarv, mis on väiksem kui N, kuid suurem või võrdne 1,
sellega kooprimeeritud. See hõlmab kõiki elemente järgmises kogumis: \{1,2,3,....,N - 1\}. Seega, kui N on algarv,
siis on N järjekord N - 1. See on öeldud lauses
1, kus \phi(N) tähistab N järjekorda.
Propositsioon 1. \phi(N) = N - 1, kui N on algarvud
Oletame, et N ei ole algarv.
Siis saab selle järjekorra arvutada, kasutades Euleri Phi funktsiooni. Kui väikese täisarvu järjestuse
arvutamine on suhteliselt lihtne, siis Euleri Phi funktsioon muutub eriti
oluliseks suuremate täisarvude puhul. Euleri Phi-funktsiooni lause on
esitatud allpool.
Teoreem 2. Olgu N võrdne p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot
p_i^{e_i} \cdot \ldots \cdot p_n^{e_n}, kus hulk \{p_i\} koosneb kõigist erinevatest N algteguritest ja iga e_i näitab, mitu korda esineb N jaoks algtegur p_i. Siis,
$$\phi(N) = p_1^{e_1 - 1} \cdot (p_1 - 1) \cdot p_2^{e_2 - 1} \cdot (p_2 - 1) \cdot \ldots \cdot p_n^{e_n - 1} \cdot (p_n - 1)$$$
Teoreem 2 näitab, et kui olete mis tahes mittetäieliku N jaotanud selle erinevateks primaarfaktoriteks, on lihtne arvutada N järjekorda.
Oletame näiteks, et N = 270.
See ei ole ilmselgelt algarv. Kui N jaotada oma algteguriteks, siis saadakse väljend: 2 \cdot 3^3 \cdot 5.
Vastavalt Euleri Phi funktsioonile on N järjestus siis järgmine:
$$\phi(N) = 2^{1 - 1} \cdot (2 - 1) + 3^{3 - 1} \cdot (3 - 1) + 5^{1 - 1} \cdot (5 - 1) = 1 \cdot 1 + 9 \cdot 2 + 1 \cdot 4 = 1 + 18 + 4 = 23 $$$
Oletame, et N on kahe arvu p ja q korrutis. Teoreem 2 ülalpool väidab siis, et N järjekord
on järgmine:
$$p^{1 - 1} \cdot (p - 1) \cdot q^{1 - 1} \cdot (q - 1) = (p - 1) \cdot (q - 1)$$$
See on eriti oluline tulemus RSA probleemi jaoks ja on esitatud Propositsioonis 2 allpool.
Propositsioon 2. Kui N on kahe arvu p ja q korrutis, siis on N korrutis (p - 1) \cdot (q - 1).
Illustreerimiseks oletame, et N = 119. Seda täisarvu saab jagada kaheks arvuks, nimelt 7 ja 17. Seega Euleri
Phi-funktsioonist järeldub, et 119-i järjekord on järgmine:
$$\phi(119) = (7 - 1) \cdot (17 - 1) = 6 \cdot 16 = 96$$$
Teisisõnu, täisarvul 119 on 96 koopriimi vahemikus 1 kuni 119. Tegelikult sisaldab see hulk kõiki täisarvusid alates 1 kuni 119, mis ei ole 7 või 17 kordajad.
Edaspidi tähistame N järjestuse määravat koprimeetrite kogumit C_N-ga. Meie näite puhul, kus N = 119, on hulk C_{119} liiga suur,
et seda täielikult loetleda. Kuid mõned elemendid on järgmised:
C_{119} = \{1, 2, \dots, 6, 8, \dots, 13, 15, 16, 18,
\dots, 33, 35, \dots, 96\}
Inverteeritavus modulo N
Me võime öelda, et täisarv a on inverteeritav moodul N, kui on olemas vähemalt üks
täisarv b, mille korral a \cdot b \mod N = 1 \mod N.
Iga sellist täisarvu b nimetatakse a inversiooniks (või multiplikatiivseks inversiooniks), kui taandamine
toimub modulo N järgi.
Oletame näiteks, et a = 5 ja N = 11. On palju täisarvusid,
millega saab korrutada 5, nii et 5 \cdot b \mod 11 = 1 \mod 11. Võtame näiteks täisarvud 20 ja 31. On lihtne näha, et need mõlemad
täisarvud on 5 inversioonid, kui neid vähendada modulo 11.
5 \cdot 20 \mod 11 = 100 \mod 11 = 1 \mod 115 \cdot 31 \mod 11 = 155 \mod 11 = 1 \mod 11
Kuigi 5-l on palju pöördvõrrandeid, mis vähendavad 11, saab näidata, et 5-l on ainult üks positiivne pöördvõrrand, mis on väiksem kui 11. Tegelikult ei ole see ainult meie konkreetse näite puhul, vaid üldine tulemus.
Propositsioon 3. Kui täisarv a on inverteeritav moodulitega N, siis peab olema nii, et
täpselt üks positiivne pöördväärtus a on väiksem kui N. (Seega peab
see ainuke pöördväärtus a tulema hulgast \{1, \dots, N - 1\}).
Tähistame a unikaalset
pöördväärtust Propositsioonist 3 kui a^{-1}. Juhul, kui a = 5 ja N = 11, näeme, et a^{-1} = 9,
arvestades, et 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11.
Pange tähele, et meie näites saab ka a^{-1} väärtuse 9, kui lihtsalt vähendada a mis tahes muud pöördväärtust modulo 11 abil. Näiteks 20 \mod 11 = 31 \mod 11 = 9 \mod 11. Seega, kui täisarv a > N on inverteeritav moodulitega N, siis peab ka a \mod N olema inverteeritav moodulitega N.
Ei ole tingimata nii, et a pöördväärtus on olemas reduktsioonimoodulitega N. Oletame näiteks, et a = 2 ja N = 8. Ei ole olemas b või konkreetselt mingit a^{-1}, mille puhul 2 \cdot b \mod 8 = 1 \mod 8.
See on tingitud sellest, et mis tahes b väärtus annab alati 2 kordse,
nii et ükski jagamine 8-ga ei saa kunagi anda jääki, mis on võrdne 1.
Kuidas me täpselt teame, kas mingi täisarv a omab pöördväärtust antud N jaoks?
Nagu te ehk märkasite ülaltoodud näites, on suurim ühine jagaja 2 ja 8 vahel
suurem kui 1, nimelt 2. Ja see illustreerib tegelikult järgmist üldist tulemust:
Propositsioon 4. Antud täisarvu a pöördväärtus on olemas, ja nimelt on ainuke positiivne pöördväärtus, mis on
väiksem kui N, kui ja ainult
siis, kui a ja N suurim ühine osaleja on 1 (st
kui nad on koopriimsed).
Juhul, kui a = 5 ja N = 11, jõudsime järeldusele,
et a^{-1} = 9,
arvestades, et 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11. Oluline on märkida, et kehtib ka vastupidine. See tähendab, et kui a = 9 ja N = 11, siis kehtib, et a^{-1} = 5.
Euleri teoreem
Enne RSA-probleemi käsitlemist peame mõistma veel ühte olulist teoreemi, nimelt Euleri teoreemi. See sätestab järgmist:
Teoreem 3. Oletame, et kaks täisarvu a ja N on koopriimsed. Siis on a^{\phi(N)} \mod N = 1 \mod N.
See on märkimisväärne tulemus, kuid alguses veidi segadust tekitav. Pöördume selle mõistmiseks ühe näite juurde.
Oletame, et a = 5 ja N = 7. Need on tõepoolest
koopriimid, nagu Euleri teoreem nõuab. Me teame, et 7 suurus on võrdne 6,
arvestades, et 7 on algarv (vt Propositsioon 1).
Euleri teoreem ütleb nüüd, et 5^6 \mod 7 peab olema võrdne 1 \mod 7.
Allpool on esitatud arvutused, mis näitavad, et see on tõepoolest tõsi.
5^6 \mod 7 = 15,625 \mod 7 = 1 \mod N
Tervikarv 7 jaguneb 15,624-ga kokku 2233 korda. Seega on 16,625 jagatuna 7-ga jääv osa 1.
Järgnevalt, kasutades Euleri Phi funktsiooni, Teoreem 2, saab tuletada Propositsioon 5 allpool.
Propositsioon 5. \phi(a \cdot b) = \phi(a) \cdot \phi(b) mis tahes positiivsete täisarvude a ja b korral.
Me ei näita, miks see nii on. Kuid märkige lihtsalt, et te olete juba näinud
selle väite tõestuseks asjaolu, et \phi(p \cdot q) = \phi(p) \cdot \phi(q) = (p - 1) \cdot (q - 1), kui p ja q on algarvud, nagu on öeldud Propositsioonis 2.
Euleri teoreemil koos Propositsiooniga 5 on olulised
tagajärjed. Vaadake näiteks, mis juhtub alljärgnevates avaldistes, kus a ja N on kooprimeetrilised.
a^{2 \cdot \phi(N)} \mod N = a^{\phi(N)} \cdot a^{\phi(N)} \mod N = 1 \cdot 1 \mod N = 1 \mod Na^{\phi(N) + 1} \mod N = a^{\phi(N)} \cdot a^1 \mod N = 1 \cdot a^1 \mod N = a \mod Na^{8 \cdot \phi(N) + 3} \mod N = a^{8 \cdot \phi(N)} \cdot a^3 \mod N = 1 \cdot a^3 \mod N = a^3 \mod N
Seega võimaldab Euleri teoreemi ja Propositsiooni 5 kombinatsioon meil lihtsalt arvutada mitmeid avaldisi. Üldiselt võime kokkuvõtlikult öelda, et arusaam on esitatud Positsioonis 6.
Propositsioon 6. a^x \mod N = a^{x \mod \phi(N)} a^x \mod N = a^{x \mod \phi(N)}
Nüüd peame viimase keerulise sammuna kõik kokku panema.
Nii nagu N omab järjestust \phi(N), mis sisaldab kogumi C_N elemente, teame, et täisarvul \phi(N) peab omakorda olema ka järjestus ja koopriimide hulk. Seame \phi(N) = R. Siis teame, et
ka \phi(R) on olemas väärtus
ja kopriimide hulk C_R.
Oletame, et valime nüüd hulgast C_R täisarvu e. Propositsioonist 3 teame, et sellel täisarvul e on ainult üks positiivne pöördväärtus, mis on väiksem kui R. See tähendab, et e-l on üks unikaalne
pöördväärtus hulgast C_R.
Nimetagem seda pöördväärtust d. Arvestades pöördväärtuse
definitsiooni, tähendab see, et e \cdot d = 1 \mod R.
Seda tulemust saame kasutada, et teha väide meie algse täisarvu N kohta. See on kokku võetud Propositsioonis 7.
Propositsioon 7. Oletame, et e \cdot d \mod \phi(N) = 1 \mod \phi(N). Siis peab mis tahes elemendi a jaoks kogumis C_N kehtima, et a^{e \cdot d \mod \phi(N)} = a^{1 \mod \phi(N)} = a
\mod N.
Nüüd on meil olemas kõik vajalikud arvuteoreetilised tulemused, et RSA-probleem selgelt esitada.
RSA krüptosüsteem
Nüüd oleme valmis esitama RSA probleemi. Oletame, et loome muutujate kogumi,
mis koosneb p, q, N, \phi(N), e, d ja y. Nimetage seda kogumit \Pi. See luuakse järgmiselt:
Loo kaks juhuslikku võrdse suurusega arvu
pjaqning arvuta nende korrutisN.Arvutage
Nsuurus,\phi(N), järgmise korrutise abil:(p - 1) \cdot (q - 1).Valige selline
e > 2, mis on väiksem ja korrutis\phi(N).Arvutage
d, seadese \cdot d \mod \phi(N) = 1.Valige juhuslik väärtus
y, mis on väiksem ja korrutisN-ga.
RSA-probleem seisneb sellise x leidmises, et x^e = y,
kusjuures ette on antud ainult osa informatsiooni \Pi kohta, nimelt muutujad N, e ja y. Kui p ja q on väga suured, tavaliselt
soovitatakse nende suuruseks 1024 bitti, peetakse RSA-probleemi raskeks. Nüüd
näete, miks see nii on, arvestades eelnevat arutelu.
Lihtne viis arvutada x, kui x^e \mod N = y \mod N, on
lihtsalt arvutada y^d \mod N.
Me teame y^d \mod N = x \mod N järgmiste
arvutuste abil:
y^d \mod N = x^{e \cdot d} \mod N = x^{e \cdot d \mod
\phi(N)} \mod N = x^{1 \mod \phi(N)} \mod N = x \mod N.
Probleem seisneb selles, et me ei tea väärtust d, sest see ei ole ette antud. Seega ei saa me otseselt arvutada y^d \mod N, et saada x \mod N.
Me võime siiski kaudselt arvutada d N suurusjärgu \phi(N) põhjal, sest me teame, et e \cdot d \mod \phi(N) = 1 \mod \phi(N). Kuid eelduse kohaselt ei anna ülesanne ka \phi(N) väärtust.
Lõpuks võib järjekorra arvutada kaudselt primaarfaktorite p ja q abil, nii et saame
lõpuks arvutada d. Kuid
eelduse kohaselt ei ole meile antud ka väärtusi p ja q.
Rangelt võttes, isegi kui RSA-probleemi sees olev faktooringuprobleem on raske, ei saa me tõestada, et ka RSA-probleem on raske. RSA-probleemi lahendamiseks võib nimelt olla ka muid võimalusi kui faktoorimise abil. Siiski on üldtunnustatud ja eeldatakse, et kui faktoorimisprobleem RSA-probleemi sees on raske, siis on ka RSA-probleem ise raske.
Kui RSA-probleem on tõepoolest raske, siis annab see ühepoolse funktsiooni
koos luukpäraga. Funktsioon on siin f(g) = g^e \mod N. Teades f(g), võib igaüks
hõlpsasti arvutada väärtuse y teatud g = x jaoks. Samas on
praktiliselt võimatu arvutada konkreetset väärtust x ainult väärtuse y ja
funktsiooni f(g) tundmise
põhjal. Erandiks on see, kui teile antakse informatsioon d, mis on trapdoor. Sellisel
juhul saab lihtsalt arvutada y^d, et saada x.
Käime läbi konkreetse näite, et illustreerida RSA probleemi. Ma ei saa valida RSA-probleemi, mida ülaltoodud tingimuste kohaselt peetaks raskeks, sest arvud oleksid kohmakad. Selle asemel on see näide lihtsalt selleks, et illustreerida, kuidas RSA-probleem üldiselt toimib.
Alustuseks oletame, et valite kaks juhuslikku algarvu 13 ja 31. Seega p = 13 ja q = 31. Nende kahe algarvu
korrutis N on 403. Saame
hõlpsasti välja arvutada 403 järjekorra. See on võrdne (13 - 1) \cdot (31 - 1) = 360.
Järgnevalt, nagu on ette nähtud RSA-probleemi 3. sammuga, peame valima 360 jaoks koopriimi, mis on suurem kui 2 ja väiksem kui 360. Me ei pea seda väärtust valima juhuslikult. Oletame, et valime 103. See on 360 koopriim, sest selle suurim ühine jagaja 103-ga on 1.
Samm 4 nõuab nüüd, et arvutame sellise väärtuse d, et 103 \cdot d \mod 360 = 1. See
ei ole käsitsi lihtne ülesanne, kui N väärtus on suur. Selleks on vaja kasutada protseduuri, mida nimetatakse täiendatud Eukleidese algoritmiks.
Kuigi ma ei näita siin protseduuri, annab see väärtuse 7, kui e = 103. Allpool esitatud arvutuste abil saab kontrollida, et väärtuste 103 ja 7
paar vastab tõepoolest üldisele tingimusele e \cdot d \mod \phi(n) = 1.
103 \cdot 7 \mod 360 = 721 \mod 360 = 1 \mod 360
Oluline on, et arvestades Propositsiooni 4, teame, et ükski teine
täisarv d vahemikus 1 ja 360
ei anna tulemust, et 103 \cdot d = 1 \mod 360.
Lisaks tähendab see lause, et valides e-le teistsuguse väärtuse,
saame d-le teistsuguse
unikaalse väärtuse.
RSA-probleemi 5. sammus tuleb valida mõni positiivne täisarv y, mis on 403 väiksema koopriimiga. Oletame, et seame y = 2^{103}. Kui
korrutada 2 103-ga, saame alljärgneva tulemuse.
2^{103} \mod 403 = 10,141,204,801,825,835,211,973,625,643,008 \mod 403 = 349 \mod 403
RSA-probleem selles konkreetses näites on nüüd järgmine: Teile on antud N = 403, e = 103 ja y = 349 \mod 403. Nüüd tuleb
arvutada x nii, et x^{103} = 349 \mod 403. See tähendab, et sa pead leidma, et algväärtus enne 103-ga korrutamist
oli 2. See tähendab, et sa pead leidma, et algväärtus enne 103-ga
korrutamist oli 2.
x oleks lihtne (vähemalt
arvuti jaoks) arvutada, kui me teaksime, et d = 7. Sellisel juhul võiks
lihtsalt määrata x järgmiselt.
x = y^7 \mod 403 = 349^7 \mod 403 = 630,634,881,591,804,949 \mod 403 = 2 \mod 403
Probleem on selles, et teile ei ole antud teavet, et d = 7. Sa võid muidugi arvutada d selle põhjal, et 103 \cdot d = 1 \mod 360.
Probleem on selles, et teile ei ole antud ka teavet, et N = 360. Lõpuks võiksite
arvutada ka 403 järjekorra, arvutades järgmise korrutise: (p - 1) \cdot (q - 1). Kuid
teile ei ole ka öeldud, et p = 13 ja q = 31.
Loomulikult saaks arvuti selle näite RSA-probleemi ikkagi suhteliselt lihtsalt lahendada, sest asjaomased algarvud ei ole suured. Kui aga arvud muutuvad väga suureks, on see praktiliselt võimatu ülesanne.
Oleme nüüd esitanud RSA-probleemi, tingimused, mille korral see on raske, ja selle aluseks oleva matemaatika. Kuidas aitab see kõik asümmeetrilise krüptograafia puhul? Täpsemalt, kuidas saame RSA-probleemi raskuse teatud tingimustel muuta krüpteerimisskeemiks või digitaalallkirjaskeemiks?
Üks lähenemisviis on võtta RSA-probleem ja ehitada skeemid sirgjooneliselt.
Näiteks oletame, et genereerisite muutujate kogumi \Pi, nagu on kirjeldatud RSA-probleemis, ja tagate, et p ja q on piisavalt suured. Te
määrate oma avaliku võtme võrdseks (N, e) ja jagate seda teavet kogu maailmaga. Nagu eespool kirjeldatud, hoiad sa p, q, \phi(n) ja d väärtused salajas.
Tegelikult on d teie privaatne
võti.
Igaüks, kes soovib saata teile sõnumit m, mis on C_N element, võib
selle lihtsalt krüpteerida järgmiselt: (Salatekst c on siin samaväärne RSA-probleemi väärtusega y.) Selle sõnumi saab
hõlpsasti dekrüpteerida, arvutades lihtsalt c^d \mod N.
Samamoodi võiksite proovida luua digitaalallkirja skeemi. Oletame, et
soovite saata kellelegi sõnumi m koos digitaalallkirjaga S. Sa
võid lihtsalt määrata S = m^d \mod N ja saata paar (m,S) vastuvõtjale. Igaüks saab kontrollida digitaalallkirja, kontrollides
lihtsalt, kas S^e \mod N = m \mod N.
Ründajal oleks aga väga raske luua sõnumi jaoks kehtivat S, kuna tal puudub d.
Kahjuks ei ole iseenesest raske RSA-probleemi muutmine krüptograafiliseks
skeemiks nii lihtne. Sirgjoonelise krüpteerimisskeemi puhul saab sõnumiteks
valida ainult N koprime. See ei
jäta meile palju võimalikke sõnumeid, kindlasti mitte piisavalt palju tavalise
kommunikatsiooni jaoks. Lisaks tuleb need sõnumid valida juhuslikult. See tundub
mõnevõrra ebapraktiline. Lõpuks, iga kaks korda valitud sõnum annab täpselt sama
šifreeritud teksti. See on äärmiselt ebasoovitav mis tahes krüpteerimisskeemi
puhul ja ei vasta ühelegi rangele kaasaegsele standardile, mis käsitleb krüpteerimise
turvalisust.
Meie lihtsa digitaalallkirja skeemi puhul muutuvad probleemid veelgi
hullemaks. Praeguse seisuga võib iga ründaja hõlpsasti võltsida
digitaalallkirju, valides kõigepealt allkirjaks N koefitsiendi ja arvutades seejärel vastava originaalsõnumi. See rikub selgelt
eksistentsiaalse võltsimatuse nõuet.
Sellegipoolest saab RSA-probleemi kasutades, lisades sellele veidi tarka keerukust, luua nii turvalise avaliku võtme krüpteerimisskeemi kui ka turvalise digitaalallkirjaskeemi. Me ei hakka siinkohal selliste konstruktsioonide üksikasjadesse laskuma. [4] Oluline on aga see, et see täiendav keerukus ei muuda põhilist RSA-probleemi, millel need skeemid põhinevad.
Märkused:
[4] Vt näiteks Jonathan Katz ja Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), lk 410-32 RSA krüpteerimise kohta ja lk 444-41 RSA digitaalallkirjade kohta.
Lõpusektsioon
Ülevaade & Hinnang
366d6fd0-ceb2-4299-bf37-8c6dfcb681d5 true
Lõpueksam
44882d2b-63cd-4fde-8485-f76f14d8b2fe true
Järeldus
f1905f78-8cf7-5031-949a-dfa8b76079b4 true