name: Bitcoin Rahakottide Sisemine Tööpõhimõte goal: Sukelduda krüptograafilistesse põhimõtetesse, mis toetavad Bitcoin rahakotte. objectives:
- Määratleda teoreetilised mõisted, mis on vajalikud Bitcoinis kasutatavate krüptograafiliste algoritmide mõistmiseks.
- Täielikult mõista deterministliku ja hierarhilise rahakoti ehitust.
- Teada, kuidas tuvastada ja vähendada rahakoti haldamisega seotud riske.
- Mõista hash-funktsioonide, krüptograafiliste võtmete ja digitaalallkirjade põhimõtteid.
Teekond Bitcoin Rahakottide Südamesse
Avasta deterministlike ja hierarhiliste Bitcoin rahakottide saladused meie CYP201 kursusel! Olgu sa tavaline kasutaja või entusiast, kes soovib oma teadmisi süvendada, see kursus pakub täielikku sukeldumist nende tööriistade toimimisse, mida me kõik igapäevaselt kasutame.
Õpi tundma hash-funktsioonide, digitaalallkirjade (ECDSA ja Schnorr), mnemooniliste fraaside, krüptograafiliste võtmete ja vastuvõtu aadresside loomise mehhanisme, uurides samal ajal edasijõudnute turvastrateegiaid.
See koolitus varustab sind mitte ainult teadmistega Bitcoin rahakoti struktuuri mõistmiseks, vaid valmistab sind ette ka sügavamaks sukeldumiseks krüptograafia põnevasse maailma.
Selge pedagoogiaga, üle 60 selgitava diagrammi ja konkreetsete näidetega, võimaldab CYP201 sul mõista A-st Z-ni, kuidas sinu rahakott töötab, et saaksid Bitcoin universumis kindlalt navigeerida. Võta täna kontroll oma UTXOde üle, mõistes, kuidas HD rahakotid toimivad!
Sissejuhatus
Kursuse Sissejuhatus
Tere tulemast CYP201 kursusele, kus me uurime põhjalikult HD Bitcoin rahakottide toimimist. See kursus on mõeldud kõigile, kes soovivad mõista Bitcoin'i kasutamise tehnilisi aluseid, olgu nad juhuslikud kasutajad, valgustatud entusiastid või tulevased eksperdid.
Selle koolituse eesmärk on anda sulle võtmed igapäevaselt kasutatavate tööriistade meisterlikuks kasutamiseks. HD Bitcoin rahakotid, mis on sinu kasutajakogemuse südames, põhinevad mõnikord keerulistel kontseptsioonidel, mida me püüame muuta ligipääsetavaks. Koos demüstifitseerime need!
Enne kui sukeldume Bitcoin rahakottide ehituse ja toimimise detailidesse,
alustame mõne peatükiga krüptograafilistest primitiividest, mida on vaja
järgneva jaoks teada. Alustame krüptograafilistest hash-funktsioonidest, mis
on olulised nii rahakottide kui ka Bitcoin protokolli enda jaoks. Sa avastad
nende peamised omadused, Bitcoinis kasutatavad spetsiifilised funktsioonid
ja tehnilisemas peatükis õpid detailideni tundma hash-funktsioonide
kuningannat: SHA256. 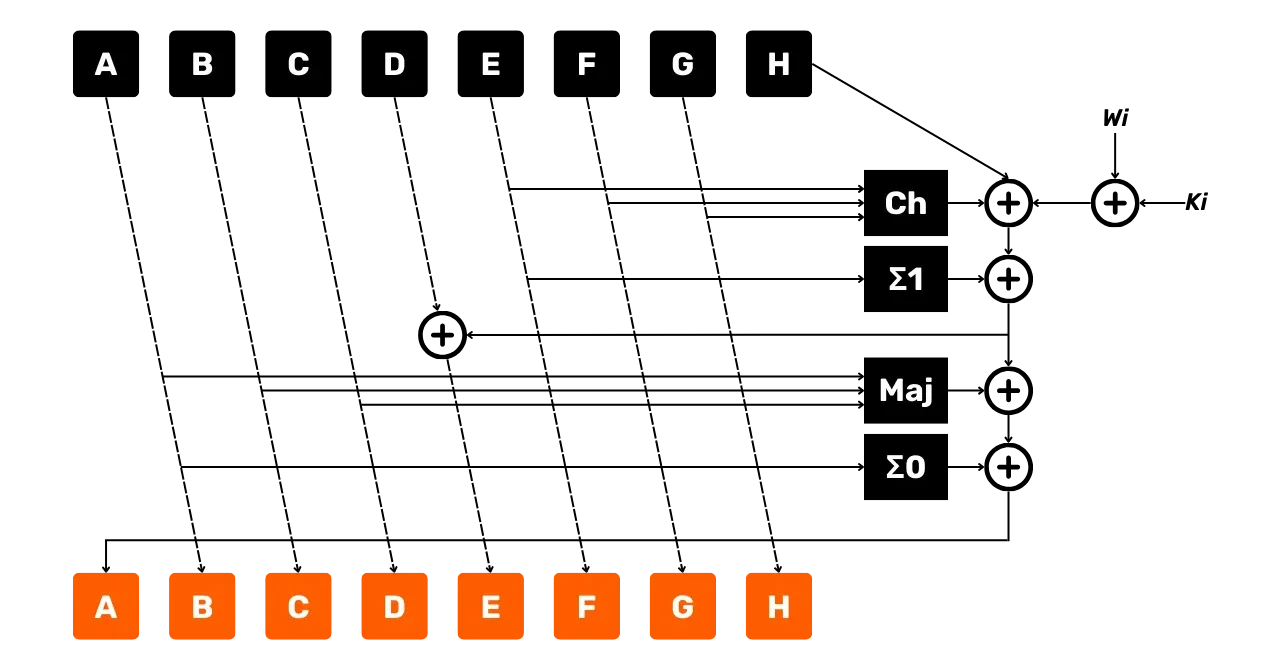
Järgnevalt arutame digitaalallkirja algoritmide toimimist, mida sa iga päev oma UTXOde turvamiseks kasutad. Bitcoin kasutab kahte: ECDSA ja Schnorri protokolli. Sa õpid, millised matemaatilised primitiivid nende algoritmide aluseks on ja kuidas need tagavad tehingute turvalisuse.
Kui meil on hea arusaam nendest krüptograafia elementidest, liigume lõpuks koolituse südamesse: deterministlikud ja hierarhilised rahakotid! Esiteks on jaotis pühendatud mnemoonilistele fraasidele, neile 12 või 24 sõna jadadele, mis võimaldavad sul luua ja taastada oma rahakotte. Sa avastad, kuidas neid sõnu genereeritakse entroopia allikast ja kuidas need lihtsustavad Bitcoin'i kasutamist.
 Koolitus jätkub BIP39 paroolifraasi, seemne (mitte segi ajada mnemoonilise fraasiga),
peamise ahelakoodi ja peamise võtme uurimisega. Vaatame üksikasjalikult, mis
need elemendid on, nende vastavad rollid ja kuidas neid arvutatakse.
Koolitus jätkub BIP39 paroolifraasi, seemne (mitte segi ajada mnemoonilise fraasiga),
peamise ahelakoodi ja peamise võtme uurimisega. Vaatame üksikasjalikult, mis
need elemendid on, nende vastavad rollid ja kuidas neid arvutatakse. 
Lõpuks, alates peamisest võtmest, avastame, kuidas krüptograafilised võtmepaarid tuletatakse deterministlikul ja hierarhilisel viisil kuni vastuvõtvate aadressideni.

See koolitus võimaldab teil oma rahakoti tarkvara usaldusväärselt kasutada, samal ajal parandades teie oskusi riskide tuvastamiseks ja leevendamiseks. Valmistuge saama tõeliseks eksperdiks Bitcoin'i rahakottides!
Hash-funktsioonid
Hash-funktsioonide tutvustus
Esimest tüüpi krüptograafilised algoritmid, mida Bitcoinis kasutatakse, hõlmavad hash-funktsioone. Need mängivad olulist rolli protokolli erinevatel tasanditel, aga ka Bitcoin'i rahakottides. Vaatame koos, mis on hash-funktsioon ja milleks seda Bitcoinis kasutatakse.
Hashimise definitsioon ja põhimõte
Hashimine on protsess, mis muundab suvalise pikkusega informatsiooni teiseks, fikseeritud pikkusega informatsiooniks läbi krüptograafilise hash-funktsiooni. Teisisõnu, hash-funktsioon võtab sisendi mis tahes suuruses ja muundab selle fikseeritud suurusega sõrmejäljeks, mida nimetatakse "hashiks". Hashi võib mõnikord nimetada ka "digestiks", "kondensaadiks", "kondenseerituks" või "hashituks".
Näiteks SHA256 hash-funktsioon toodab 256-bitise fikseeritud pikkusega hashi. Seega, kui kasutame sisendina "PlanB", suvalise pikkusega sõnumit, siis genereeritud hash on järgmine 256-bitine sõrmejälg:
24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688

Hash-funktsioonide omadused
Need krüptograafilised hash-funktsioonid omavad mitmeid olulisi omadusi, mis muudavad need eriti kasulikuks Bitcoin'i ja teiste arvutisüsteemide kontekstis:
- Pöördumatuse (või eelkujutise vastupanu)
- Muutmiskindlus (laviiniefekt)
- Kollisioonikindlus
- Teise eelkujutise vastupanu
1. Pöördumatuse (eelkujutise vastupanu):
Pöördumatus tähendab, et on lihtne arvutada räsi sisendandmetest, kuid vastupidine arvutus, st sisendi leidmine räsi põhjal, on praktiliselt võimatu. See omadus teeb räsi funktsioonid ideaalseks unikaalsete digitaalsõrmejälgede loomiseks ilma algset teavet ohustamata.
Antud näites on hashi 24f1b9… saamine teades sisendit "PlanB" lihtne ja kiire. Kuid sõnumi "PlanB" leidmine teades ainult 24f1b9… on võimatu.

Seega on võimatu leida eelkujutist m hashi h jaoks nii, et h = \text{HASH}(m),
kus \text{HASH} on krüptograafiline
hash-funktsioon.
2. Muutmiskindlus (laviiniefekt)
Teine omadus on rikkumiskindlus, mida tuntakse ka kui laviiniefekti. Seda omadust täheldatakse räsifunktsioonis, kui sisendsõnumis tehtud väike muudatus põhjustab radikaalse muutuse väljundräsis. Kui me pöördume tagasi meie näite juurde sisendiga "PlanB" ja SHA256 funktsiooni kasutades, oleme näinud, et genereeritud räsi on järgmine:
24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688
Kui me teeme sisendis väga väikese muudatuse, kasutades seekord "Planb", siis lihtsalt muutes suurtähte "B" väiketäheks "b", muudab see täielikult SHA256 väljundräsi:
bb038b4503ac5d90e1205788b00f8f314583c5e22f72bec84b8735ba5a36df3f

See omadus tagab, et isegi algse sõnumi väike muutmine on kohe tuvastatav, kuna see ei muuda ainult räsi väikest osa, vaid kogu räsi. See võib olla huvipakkuv erinevates valdkondades, et kontrollida sõnumite, tarkvara või isegi Bitcoin'i tehingute terviklikkust.
3. Kokkupõrkekindlus
Kolmas omadus on kokkupõrkekindlus. Räsifunktsioon on kokkupõrkekindel, kui
on arvutuslikult võimatu leida kahte erinevat sõnumit, mis annavad
funktsioonist sama räsi väljundi. Formaalselt on raske leida kahte eristuvat
sõnumit m_1 ja m_2 nii, et:
\text{HASH}(m_1) = \text{HASH}(m_2)
Tegelikkuses on matemaatiliselt paratamatu, et räsifunktsioonide jaoks
eksisteerivad kokkupõrked, kuna sisendite suurus võib olla suurem kui
väljundite suurus. Seda tuntakse Dirichlet'i sahtli põhimõttena: kui n objekti jaotatakse m sahtlisse, kusjuures m < n, siis vähemalt
ühes sahtlis peab tingimata olema kaks või enam objekti. Räsifunktsiooni
puhul kehtib see põhimõte, kuna võimalike sõnumite arv on (peaaegu) lõpmatu,
samas kui võimalike räside arv on piiratud (2^{256} SHA256 puhul).
Seega ei tähenda see omadus, et räsifunktsioonidel poleks kokkupõrkeid, vaid
pigem seda, et hea räsifunktsioon muudab kokkupõrke leidmise tõenäosuse
tühiseks. Näiteks SHA-0 ja SHA-1 algoritmid, SHA-2 eelkäijad, mille puhul on
leitud kokkupõrkeid, ei vasta enam sellele omadusele. Neid funktsioone
peetakse seetõttu nüüdseks aegunuks ja soovitatakse vältida. n biti räsifunktsiooni puhul
on kokkupõrkekindlus järjekorras 2^{\frac{n}{2}}, vastavalt sünnipäevarünnakule. Näiteks SHA256 (n = 256) puhul on kokkupõrke leidmise keerukus järjekorras 2^{128} katset. Praktiliselt tähendab see, et kui funktsioonist läbib 2^{128} erinevat sõnumit,
on tõenäoline, et leitakse kokkupõrge.
4. Teise Eelkujutise Kindlus
Teise eelkujutise kindlus on veel üks oluline räsifunktsioonide omadus. See
tähendab, et antud sõnumi m_1 ja selle räsi h korral on
arvutuslikult teostamatu leida teist sõnumit m_2 \neq m_1, nii et:
\text{HASH}(m_1) = \text{HASH}(m_2)Seega on teise eelkujutise kindlus mõnevõrra sarnane kokkupõrkekindlusega,
välja arvatud see, et siin on rünnak raskem, kuna ründaja ei saa vabalt
valida m_1. 
Hash-funktsioonide rakendused Bitcoinis
Bitcoinis kõige enam kasutatav hash-funktsioon on SHA256 ("Secure Hash Algorithm 256 bits"). Selle on NSA poolt 2000ndate alguses välja töötatud ja NIST standardiseerinud, see toodab 256-bitise hash-väljundi.
See funktsioon on kasutusel paljudes Bitcoiniga seotud aspektides. Protokolli tasandil on see kaasatud Proof-of-Work mehhanismi, kus seda rakendatakse kahekordses hashimises, et otsida osalist kokkulangevust kaevandaja loodud kandidaatbloki päise ja raskusastme sihtmärgi vahel. Kui see osaline kokkulangevus leitakse, muutub kandidaatblokk kehtivaks ja seda saab lisada plokiahelasse.
SHA256 on kasutusel ka Merkle puu konstrueerimisel, mis on märkimisväärne akumulaator tehingute salvestamiseks plokkides. See struktuur on leitav ka Utreexo protokollis, mis võimaldab vähendada UTXO Seti suurust. Lisaks, Taprooti tutvustamisega 2021. aastal, kasutatakse SHA256 MASTis (Merkelised Alternative Script Tree), mis võimaldab paljastada ainult skriptis tegelikult kasutatud kulutamistingimused, ilma teisi võimalikke valikuid avaldamata. Seda kasutatakse ka tehingute identifikaatorite arvutamisel, pakettide edastamisel P2P võrgus, elektroonilistes allkirjades... Lõpuks, ja see on eriti huvipakkuv selles koolituses, kasutatakse SHA256 rakendustasandil Bitcoin rahakottide konstrueerimisel ja aadresside tuletamisel.
Enamasti, kui kohtate Bitcoinis SHA256 kasutamist, on tegemist tegelikult kahekordse hashiga SHA256, mida tähistatakse "HASH256", mis lihtsalt seisneb SHA256 kaks korda järjest rakendamises: HASH256(m) = SHA256(SHA256(m))
See kahekordse hashimise praktika lisab lisakaitsekihi teatud potentsiaalsete rünnakute vastu, kuigi tänapäeval peetakse üksikut SHA256 krüptograafiliselt turvaliseks.
Teine Script keeles saadaolev hashimisfunktsioon, mida kasutatakse vastuvõtvate aadresside tuletamiseks, on RIPEMD160 funktsioon. See funktsioon toodab 160-bitise hashi (seega lühema kui SHA256). See ühendatakse tavaliselt SHA256-ga, et moodustada HASH160 funktsioon:
\text{HASH160}(m) = \text{RIPEMD160}(\text{SHA256}(m))Seda kombinatsiooni kasutatakse lühemate hashide genereerimiseks, eriti teatud Bitcoin aadresside loomisel, mis esindavad võtmete või skripti hashisid, samuti võtme sõrmejälgede tootmiseks.
Lõpuks, ainult rakendustasandil, kasutatakse mõnikord ka SHA512 funktsiooni, mis mängib kaudselt rolli rahakottide võtmete tuletamisel. See funktsioon on oma toimimiselt väga sarnane SHA256-ga; mõlemad kuuluvad samasse SHA2 perekonda, kuid SHA512 toodab, nagu nimigi ütleb, 512-bitise hashi, võrreldes 256 bitiga SHA256 puhul. Selle kasutust käsitleme järgmistes peatükkides.
Nüüd teate hashimisfunktsioonide olulisi põhitõdesid edasiseks. Järgmises peatükis pakun avastada üksikasjalikumalt funktsiooni, mis on Bitcoin'i südames: SHA256. Me lahkame seda, et mõista, kuidas see saavutab siin kirjeldatud omadused. Järgmine peatükk on üsna pikk ja tehniline, kuid ei ole oluline järgneva koolituse jälgimiseks. Seega, kui teil on selle mõistmisega raskusi, ärge muretsege ja liikuge otse järgmisse peatükki, mis on palju ligipääsetavam.
SHA256 sisemine toimimine
905eb320-f15b-5fb6-8d2d-5bb447337deb Oleme varem näinud, et räsifunktsioonidel on olulised omadused, mis õigustavad nende kasutamist Bitcoinis. Vaatame nüüd nende räsifunktsioonide sisemisi mehhanisme, mis annavad neile need omadused, ja selleks pakun ma lahti võtta SHA256 toimimise. SHA256 ja SHA512 funktsioonid kuuluvad samasse SHA2 perekonda. Nende mehhanism põhineb spetsiifilisel konstruktsioonil, mida nimetatakse Merkle-Damgårdi konstruktsiooniks. RIPEMD160 kasutab samuti seda tüüpi konstruktsiooni.
Meenutuseks, SHA256 sisendiks on suvalise suurusega sõnum ja me läbime selle funktsiooni, et saada väljundiks 256-bitine räsi.
Sisendi eeltöötlus
Alustuseks peame valmistama ette meie sisendsõnumi m, nii et sellel oleks standardpikkus, mis on 512 biti kordne. See samm on
algoritmi nõuetekohaseks toimimiseks hädavajalik. Selleks alustame
täitebittide lisamise sammuga. Lisame esmalt sõnumile eraldaja biti 1, millele järgneb teatud arv 0 bitte. Lisatavate 0 bittide arv arvutatakse nii, et sõnumi kogupikkus pärast seda lisamist on
kongruentne 448 modulo 512-ga. Seega on sõnumi pikkus L koos täitebittidega võrdne:
L \equiv 448 \mod 512\text{mod}, modulo
jaoks, on matemaatiline operatsioon, mis kahe täisarvu vahel tagastab
esimese Euroopa jagamise jäägi teise poolt. Näiteks: 16 \mod 5 = 1. See on
krüptograafias laialdaselt kasutatav operatsioon.
Siin tagab täitesamm, et pärast järgmises etapis 64 biti lisamist on
võrdsustatud sõnumi kogupikkus 512 biti kordne. Kui algse sõnumi pikkus on M bitti, siis lisatavate 0 bittide arv (N) on:
N = (448 - (M + 1) \mod 512) \mod 512Näiteks, kui algne sõnum on 950 bitti, oleks arvutus järgmine:
\begin{align*}
M & = 950 \\
M + 1 & = 951 \\
(M + 1) \mod 512 & = 951 \mod 512 \\
& = 951 - 512 \cdot \left\lfloor \frac{951}{512} \right\rfloor \\
& = 951 - 512 \cdot 1 \\
& = 951 - 512 \\
& = 439 \\
\\
448 - (M + 1) \mod 512 & = 448 - 439 \\
& = 9 \\
\\
N & = (448 - (M + 1) \mod 512) \mod 512 \\
N & = 9 \mod 512 \\
& = 9
\end{align*}Seega, meil oleks lisaks eraldajale 1 veel 9 0.
Meie sõnumile M otse lisatavad
täitebitid oleksid seega:
1000 0000 00
Pärast täitebittide lisamist meie sõnumile M, lisame ka 64-bitise esituse sõnumi M algsest pikkusest, väljendatuna binaarselt. See võimaldab räsifunktsioonil
olla tundlik bittide järjekorra ja sõnumi pikkuse suhtes. Kui me pöördume
tagasi meie näite juurde algse sõnumiga 950 bitti, teisendame kümnendarvu 950 binaararvuks, mis annab meile 1110 1101 10. Täidame selle arvu
alusel nullidega, et saada kokku 64 bitti. Meie näites annab see:
0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0011 1011 0110
Seda täite suurust lisatakse järgides bittäidet. Seega koosneb sõnum pärast meie eeltöötlust kolmest osast:
- Algne sõnum
M; - Bitt
1järgneb mitmele bitile0, et moodustada bittäide; - 64-bitine esitus
Mpikkusest, et moodustada suurusega täide.

Muutujate Algväärtustamine
SHA256 kasutab kaheksat algset olekumuutujat, tähistatud A kuni H, igaüks 32 bitti. Need
muutujad on algväärtustatud spetsiifiliste konstantidega, mis on esimese
kaheksa algarvu ruutjuurte murdosad. Me kasutame neid väärtusi järgnevalt
räsiprotsessi jooksul:
A = 0x6a09e667B = 0xbb67ae85C = 0x3c6ef372D = 0xa54ff53aE = 0x510e527fF = 0x9b05688cG = 0x1f83d9abH = 0x5be0cd19
SHA256 kasutab ka 64 muud konstanti, tähistatud K_0 kuni K_{63}, mis on
esimese 64 algarvu kuupjuurte murdosad:
K[0 \ldots 63] = \begin{pmatrix}
0x428a2f98, & 0x71374491, & 0xb5c0fbcf, & 0xe9b5dba5, \\
0x3956c25b, & 0x59f111f1, & 0x923f82a4, & 0xab1c5ed5, \\
0xd807aa98, & 0x12835b01, & 0x243185be, & 0x550c7dc3, \\
0x72be5d74, & 0x80deb1fe, & 0x9bdc06a7, & 0xc19bf174, \\
0xe49b69c1, & 0xefbe4786, & 0x0fc19dc6, & 0x240ca1cc, \\
0x2de92c6f, & 0x4a7484aa, & 0x5cb0a9dc, & 0x76f988da, \\
0x983e5152, & 0xa831c66d, & 0xb00327c8, & 0xbf597fc7, \\
0xc6e00bf3, & 0xd5a79147, & 0x06ca6351, & 0x14292967, \\
0x27b70a85, & 0x2e1b2138, & 0x4d2c6dfc, & 0x53380d13, \\
0x650a7354, & 0x766a0abb, & 0x81c2c92e, & 0x92722c85, \\
0xa2bfe8a1, & 0xa81a664b, & 0xc24b8b70, & 0xc76c51a3, \\
0xd192e819, & 0xd6990624, & 0xf40e3585, & 0x106aa070, \\
0x19a4c116, & 0x1e376c08, & 0x2748774c, & 0x34b0bcb5, \\
0x391c0cb3, & 0x4ed8aa4a, & 0x5b9cca4f, & 0x682e6ff3, \\
0x748f82ee, & 0x78a5636f, & 0x84c87814, & 0x8cc70208, \\
0x90befffa, & 0xa4506ceb, & 0xbef9a3f7, & 0xc67178f2
\end{pmatrix}Sisendi Jaotamine
Nüüd, kui meil on võrdsustatud sisend, liigume edasi SHA256 algoritmi peamise töötlemisfaasi juurde: kompressioonifunktsioon. See samm on väga oluline, kuna just see annab räsi funktsioonile selle krüptograafilised omadused, mida me eelmises peatükis uurisime.
Esmalt jaotame meie võrdsustatud sõnumi (eeltöötlusetappide tulemus) mitmeks
512-bitiseks plokiks P. Kui
meie võrdsustatud sõnumil on kokku suurus n \times 512 bitti, siis meil on seega n plokki, igaüks 512 bitti. Iga 512-bitine plokk töödeldakse individuaalselt
kompressioonifunktsiooni poolt, mis koosneb 64 järjestikusest
operatsioonist. Nimetame neid plokke P_1, P_2, P_3...
Loogilised Operatsioonid
Enne kompressioonifunktsiooni detailide uurimist on oluline mõista selles kasutatavaid põhilisi loogilisi operatsioone. Need operatsioonid, mis põhinevad Boole'i algebral, toimivad bittide tasemel. Kasutatavad põhilised loogilised operatsioonid on:
- Konjunktsioon (JA): tähistatud
\land, vastab loogilisele "JA". - Disjunktsioon (VÕI): tähistatud
\lor, vastab loogilisele "VÕI". - Negatsioon (EI): tähistatud
\lnot, vastab loogilisele "EI".
Nendest põhioperatsioonidest saame defineerida keerukamaid operatsioone,
nagu "Eksklusiivne VÕI" (XOR) tähistatud \oplus, mida laialdaselt kasutatakse krüptograafias. Iga loogiline operatsioon
saab esitada tõeväärtustabeliga, mis näitab tulemust kõigi võimalike
binaarsete sisendväärtuste kombinatsioonide korral (kaks operandi p ja q). XOR-i (\oplus) puhul:
p | q | p \oplus q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
AND (\land) puhul:
p | q | p \land q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Eituse (NOT) (\lnot p) jaoks:
p | \lnot p |
|---|---|
| 0 | 1 |
| 1 | 0 |
Vaatame näidet, et mõista XOR operatsiooni biti tasemel. Kui meil on kaks binaararvu kuuel bitil:
a = 101100b = 001000
Siis:
a \oplus b = 101100 \oplus 001000 = 100100Rakendades XOR operatsiooni biti haaval:
| Biti Positsioon | a | b | a \oplus b |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 1 | 0 | 1 |
| 5 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 |
Tulemus on seega 100100.
Lisaks loogilistele operatsioonidele kasutab kompressioonifunktsioon biti-nihutamise operatsioone, mis mängivad olulist rolli bitide difusioonis algoritmis.
Esiteks on loogiline paremale nihutamise operatsioon, tähistatud ShR_n(x), mis nihutab kõik x bitid
paremale n positsiooni võrra,
täites vasakul pool olevad tühjad bitid nullidega.
Näiteks, x = 101100001 (9
bitil) ja n = 4 puhul:
ShR_4(101100001) = 000010110Skeemiliselt võib paremale nihutamise operatsiooni näha nii:
 Teine SHA256-s biti manipuleerimiseks kasutatav operatsioon on paremale ringikujuline
rotatsioon, tähistatud
Teine SHA256-s biti manipuleerimiseks kasutatav operatsioon on paremale ringikujuline
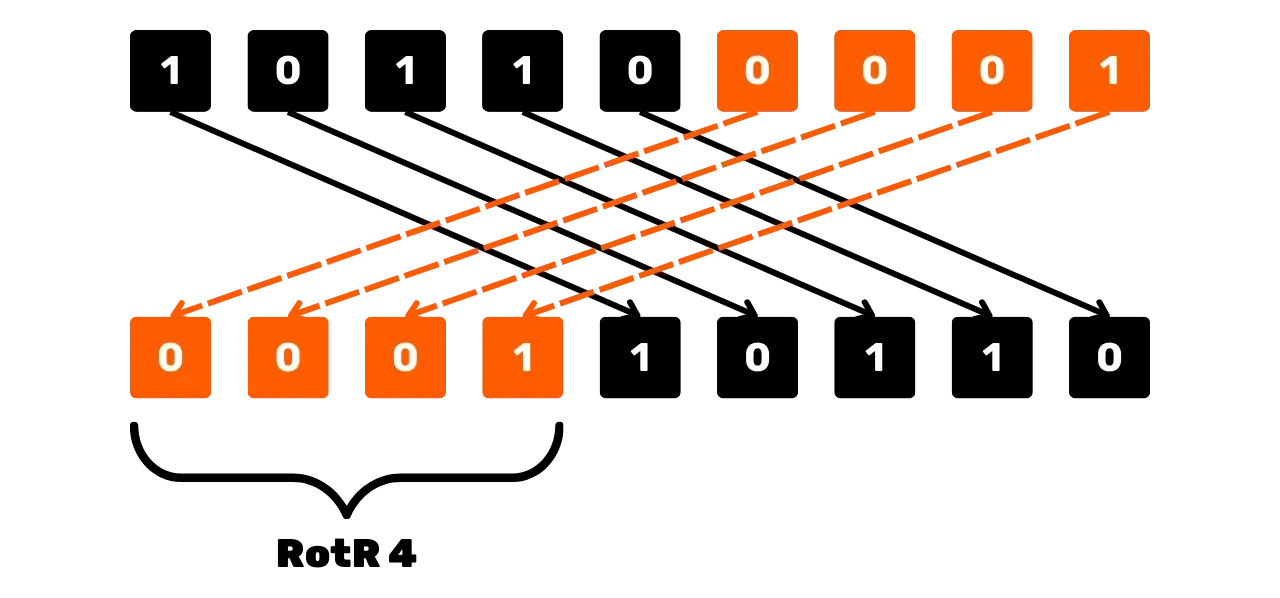
rotatsioon, tähistatud RotR_n(x), mis nihutab x bitid paremale n positsiooni
võrra, sisestades nihutatud bitid stringi algusesse tagasi. Näiteks, x = 101100001 (üle 9 biti) ja n = 4 puhul:
RotR_4(101100001) = 000110110Skeemiliselt võib paremale ringikujulise nihutamise operatsiooni näha nii:
Kompressioonifunktsioon
Nüüd, kui oleme mõistnud põhioperatsioone, vaatame lähemalt SHA256 kompressioonifunktsiooni.
Eelmises sammus jagasime sisendi mitmeks 512-bitiseks tükiks P. Iga 512-bitise bloki P jaoks
on meil:
- Sõnumi sõnad
W_i:iväärtustele 0 kuni 63. - Konstandid
K_i:iväärtustele 0 kuni 63, määratletud eelmises sammus. - Olekumuutujad
A, B, C, D, E, F, G, H: alustatud väärtustega eelmisest sammust. Esimesed 16 sõna,W_0kuniW_{15}, ekstraheeritakse otse töödeldud 512-bitisest plokistP. Iga sõnaW_ikoosneb 32 järjestikusest bitist plokist. Näiteks võtame meie esimese sisendi tükiP_1ja jagame selle edasi väiksemateks 32-bitisteks tükkideks, mida nimetame sõnadeks. Järgmised 48 sõna (W_{16}kuniW_{63}) genereeritakse järgneva valemi abil:
W_i = W_{i-16} + \sigma_0(W_{i-15}) + W_{i-7} + \sigma_1(W_{i-2}) \mod 2^{32}Kusjuures:
\sigma_0(x) = RotR_7(x) \oplus RotR_{18}(x) \oplus ShR_3(x)\sigma_1(x) = RotR_{17}(x) \oplus RotR_{19}(x) \oplus ShR_{10}(x)
Sel juhul x võrdub W_{i-15} jaoks \sigma_0(x) ja W_{i-2} jaoks \sigma_1(x).
Kui oleme kõik sõnad W_i meie
512-bitise tüki jaoks kindlaks määranud, võime liikuda edasi kompressioonifunktsiooni
juurde, mis koosneb 64 vooru sooritamisest.
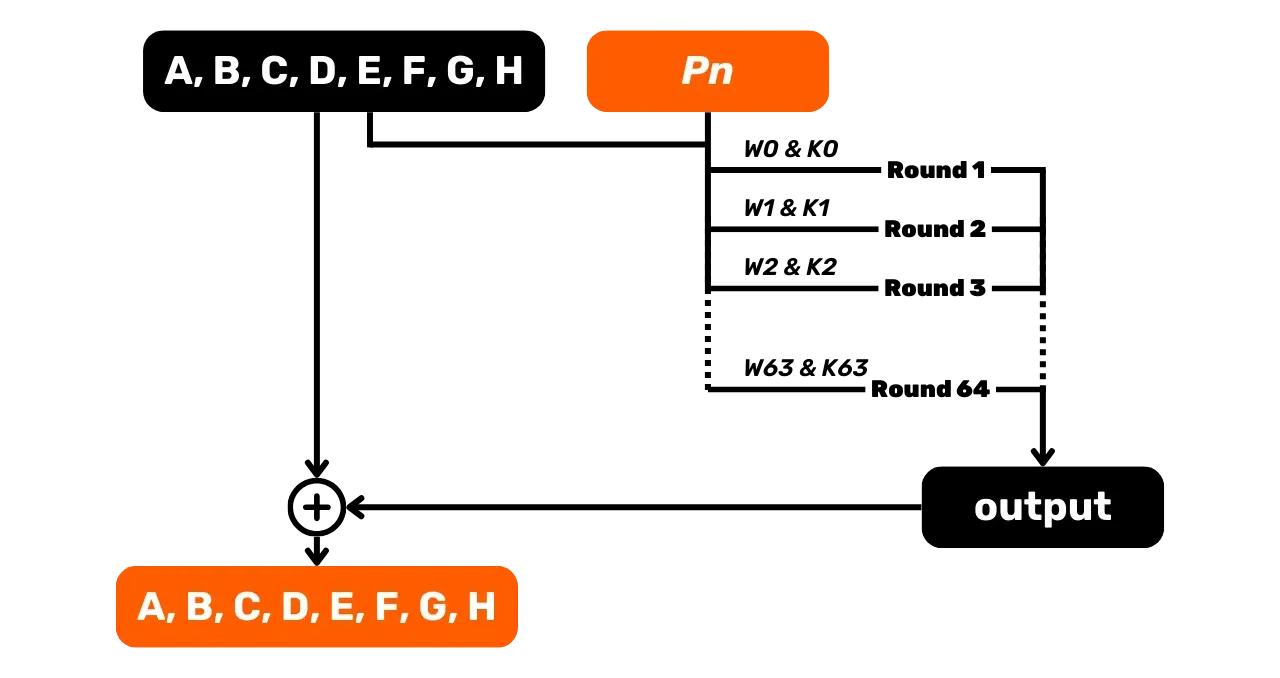 Iga vooru
Iga vooru i jaoks vahemikus 0
kuni 63 on meil kolm erinevat tüüpi sisendeid. Esiteks, W_i, mille oleme just
kindlaks määranud, osaliselt koosnedes meie sõnumitükist P_n. Järgmiseks, 64 konstanti K_i. Lõpuks kasutame
olekumuutujaid A, B, C, D, E, F, G ja H, mis arenevad läbi
räsiprotsessi ja muudetakse iga kompressioonifunktsiooni käigus. Siiski,
esimese tüki P_1 jaoks kasutame
eelnevalt antud algkonstante. Seejärel teostame oma sisenditega järgmised toimingud:
- Funktsioon
\Sigma_0:
\Sigma_0(A) = RotR_2(A) \oplus RotR_{13}(A) \oplus RotR_{22}(A)- Funktsioon
\Sigma_1:
\Sigma_1(E) = RotR_6(E) \oplus RotR_{11}(E) \oplus RotR_{25}(E)- Funktsioon
Ch("Vali"):
Ch(E, F, G) = (E \land F) \oplus (\lnot E \land G)- Funktsioon
Maj("Enamus"):
Maj(A, B, C) = (A \land B) \oplus (A \land C) \oplus (B \land C)Seejärel arvutame 2 ajutist muutujat:
temp1:
temp1 = H + \Sigma_1(E) + Ch(E, F, G) + K_i + W_i \mod 2^{32}temp2:
temp2 = \Sigma_0(A) + Maj(A, B, C) \mod 2^{32}Järgmisena uuendame olekumuutujaid järgnevalt:
\begin{cases}
H = G \\
G = F \\
F = E \\
E = D + temp1 \mod 2^{32} \\
D = C \\
C = B \\
B = A \\
A = temp1 + temp2 \mod 2^{32}
\end{cases}Järgnev diagramm esindab ühte vooru SHA256 tihendusfunktsioonis, nagu me just kirjeldasime:

- Nooled näitavad andmevoo suunda;
- Kastid esindavad teostatud operatsioone;
+ümbritsetud esindavad modulo2^{32}lisamist.
Me võime juba märgata, et see voor annab välja uued olekumuutujad A, B, C, D, E, F, G ja H. Need uued muutujad
toimivad sisendina järgmisele voorule, mis omakorda toodab uued muutujad A, B, C, D, E, F, G ja H, mida kasutatakse
järgnevas voorus. See protsess jätkub kuni 64. vooruni. Pärast 64 vooru
uuendame olekumuutujate algväärtusi, lisades need lõppväärtustele pärast 64.
vooru lõppu:
\begin{cases}
A = A_{\text{initial}} + A \mod 2^{32} \\
B = B_{\text{initial}} + B \mod 2^{32} \\
C = C_{\text{initial}} + C \mod 2^{32} \\
D = D_{\text{initial}} + D \mod 2^{32} \\
E = E_{\text{initial}} + E \mod 2^{32} \\
F = F_{\text{initial}} + F \mod 2^{32} \\
G = G_{\text{initial}} + G \mod 2^{32} \\
H = H_{\text{initial}} + H \mod 2^{32}
\end{cases}
Need uued väärtused A, B, C, D, E, F, G ja H toimivad algväärtustena
järgmisele plokile, P_2.
Selle ploki P_2 jaoks kordame
sama tihendusprotsessi 64 vooruga, seejärel uuendame muutujaid ploki P_3 jaoks, ja nii edasi kuni meie
võrdsustatud sisendi viimase plokini.
Pärast kõikide sõnumiplokkide töötlemist ühendame muutujate A, B, C, D, E, F, G ja H lõppväärtused, et moodustada
meie räsifunktsiooni lõplik 256-bitine räsi:
\text{Räsi} = A \Vert B \Vert C \Vert D \Vert E \Vert F \Vert G \Vert H
Iga muutuja on 32-bitine täisarv, seega nende ühendamine annab alati 256-bitise tulemuse, sõltumata meie sõnumi sisendi suurusest räsifunktsioonile.
Krüptograafiliste Omaduste Põhjendus
Aga kuidas on see funktsioon pöördumatu, kokkupõrkekindel ja muutmiskindel?
Muutmiskindluse mõistmine on üsna lihtne. Kaskaadselt teostatakse nii palju
arvutusi, mis sõltuvad nii sisendist kui ka konstantidest, et algse sõnumi
vähimgi muutmine muudab täielikult võetud rada ja seega muudab täielikult
väljundräsi. Seda nimetatakse laviiniefektiks. See omadus on osaliselt
tagatud vaheolekute segamisega algolekutega iga tüki jaoks. Järgnevalt, kui
arutame krüptograafilise räsifunktsiooni üle, ei kasutata üldiselt terminit
"pöördumatus". Selle asemel räägime me "eelkujutise vastupanust", mis
täpsustab, et mis tahes antud y korral on raske leida sellist x, et h(x) = y. Seda eelkujutise
vastupanu tagavad operatsioonide algebraline keerukus ja tugev
mittelineaarsus kompressioonifunktsioonis, samuti teatud informatsiooni kadu
protsessis. Näiteks, antud modulo liitmise tulemuse korral on mitu
võimalikku operandi:$$ 3+2 \mod 10 = 5 \ 7+8 \mod 10 = 5 \ 5+10 \mod 10 = 5
Selles näites, teades ainult kasutatud modulo (10) ja tulemust (5), ei saa kindlalt öelda, millised on õiged operandid liitmisel. Öeldakse, et on mitu kongruentsi modulo 10 suhtes.
XOR-operatsiooni puhul seisame silmitsi sama probleemiga. Meenutagem selle operatsiooni tõeväärtustabelit: iga 1-bitise väljundi võib määrata kahe erineva sisendkonfiguratsiooniga, millel on täpselt sama tõenäosus olla õiged väärtused. Seega ei saa teades ainult selle tulemust kindlalt öelda XOR-i operandid. Kui suurendame XOR operandide suurust, suureneb eksponentsiaalselt võimalike sisendite arv, teades ainult tulemust. Lisaks kasutatakse XOR-i sageli koos teiste bittasandi operatsioonidega, nagu $\text{RotR}$ operatsioon, mis lisab tulemusele veelgi võimalikke tõlgendusi.
Kompressioonifunktsioon kasutab ka $\text{ShR}$ operatsiooni. See operatsioon eemaldab osa põhiinformatsioonist, mida hiljem on võimatu taastada. Taaskord ei ole algebralist meetodit selle operatsiooni pööramiseks. Kõiki neid ühesuunalisi ja informatsioonikaoga operatsioone kasutatakse kompressioonifunktsioonides väga sageli. Antud väljundi jaoks võimalike sisendite arv on seega peaaegu lõpmatu ja iga katse arvutust pöörata viiks võrranditeni, millel on väga suur arv tundmatuid, mis iga sammuga eksponentsiaalselt suureneks.
Lõpuks, kokkupõrkekindluse omaduse puhul tulevad mängu mitmed parameetrid. Algse sõnumi eeltöötlusel on oluline roll. Ilma selle eeltöötluseta võiks olla lihtsam leida funktsioonil kokkupõrkeid. Kuigi teoreetiliselt kokkupõrked eksisteerivad (tänu tuvipuuripõhimõttele), muudab räsifunktsiooni struktuur, kombineerituna eelpool mainitud omadustega, kokkupõrke leidmise tõenäosuse äärmiselt madalaks.
Selleks, et räsifunktsioon oleks kokkupõrkekindel, on oluline, et:
- Väljund oleks ettearvamatu: Iga ettearvatavus võib olla ära kasutatud kokkupõrgete leidmiseks kiiremini kui pimejõu rünnakuga. Funktsioon tagab, et iga väljundi bitt sõltub sisendist mitte-triviaalsel viisil. Teisisõnu, funktsioon on kavandatud nii, et iga lõpptulemuse bitt omab sõltumatut tõenäosust olla 0 või 1, isegi kui see sõltumatus praktikas absoluutne ei ole.
- Räside jaotus on pseudojuhuslik: See tagab, et räsid on ühtlaselt jaotatud.
- Räsi suurus on märkimisväärne: mida suurem on võimalike tulemuste ruum, seda raskem on leida kokkupõrget.
Krüptograafid kavandavad neid funktsioone, hinnates parimaid võimalikke rünnakuid kokkupõrgete leidmiseks, seejärel kohandades parameetreid, et muuta need rünnakud ebaefektiivseks.
### Merkle-Damgårdi konstruktsioon
SHA256 struktuur põhineb Merkle-Damgårdi konstruktsioonil, mis võimaldab muuta kompressioonifunktsiooni räsifunktsiooniks, mis suudab töödelda suvalise pikkusega sõnumeid. Just seda oleme selles peatükis näinud.
Siiski on mõned vanad räsifunktsioonid nagu SHA1 või MD5, mis kasutavad seda konkreetset konstruktsiooni, haavatavad pikkuse laiendamise rünnakute suhtes. See on tehnika, mis võimaldab ründajal, kes teab sõnumi $M$ räsi ja $M$ pikkust (ilma, et ta teaks sõnumit ennast), arvutada räsi sõnumile $M'$, mis on moodustatud $M$-le lisasisu lisamisega.
SHA256, kuigi kasutab sama tüüpi konstruktsiooni, on teoreetiliselt vastupidav sellist tüüpi rünnakule, erinevalt SHA1-st ja MD5-st. See võib selgitada Satoshi Nakamoto poolt Bitcoinis rakendatud topelträsimise saladust. Sellist tüüpi rünnaku vältimiseks võis Satoshi eelistada kasutada topelt SHA256:
\text{HASH256}(m) = \text{SHA256}(\text{SHA256}(m))
See suurendab turvalisust potentsiaalsete rünnakute vastu, mis on seotud Merkle-Damgårdi konstruktsiooniga, kuid see ei suurenda räsimisprotsessi turvalisust kokkupõrkekindluse osas. Pealegi, isegi kui SHA256 oleks olnud sellist tüüpi rünnakule haavatav, ei oleks see tõenäoliselt avaldanud tõsist mõju, kuna kõik räsifunktsioonide kasutusjuhud Bitcoinis hõlmavad avalikke andmeid. Siiski võib pikkuse laiendamise rünnak olla kasulik ründajale ainult juhul, kui räsitavad andmed on privaatsed ja kasutaja on kasutanud räsifunktsiooni nende andmete autentimismehhanismina, sarnaselt MAC-iga. Seega jääb Bitcoinis topelträsimise rakendamine disaini saladuseks.
Nüüd, kui oleme üksikasjalikult vaadelnud räsifunktsioonide toimimist, eriti SHA256, mida Bitcoinis laialdaselt kasutatakse, keskendume spetsiifilisemalt rakendustasandi krüptograafilistele tuletusalgoritmidele, eriti võtmete tuletamiseks teie rahakotis.
## Tuletusalgoritmid
<chapterId>cc668121-7789-5e99-bf5e-1ba085f4f5f2</chapterId>
Bitcoinis rakendustasandil kasutatakse räsifunktsioonide kõrval krüptograafilisi tuletusalgoritme, et genereerida turvalisi andmeid algsetest sisenditest. Kuigi need algoritmid toetuvad räsifunktsioonidele, teenivad nad erinevaid eesmärke, eriti autentimise ja võtmegeneratsiooni osas. Need algoritmid säilitavad mõningaid räsifunktsioonide omadusi, nagu pöördumatuse, võltsimiskindluse ja kokkupõrkekindluse.
Bitcoin rahakottides kasutatakse peamiselt kahte tuletusalgoritmi:
- **HMAC (_Hash-based Message Authentication Code_)**
- **PBKDF2 (_Password-Based Key Derivation Function 2_)**
Uurime koos igaühe toimimist ja rolli.
### HMAC-SHA512
HMAC on krüptograafiline algoritm, mis arvutab autentimiskoodi, põhinedes räsifunktsiooni ja salajase võtme kombinatsioonil. Bitcoin kasutab HMAC-SHA512 varianti, mis kasutab SHA512 räsifunktsiooni. Oleme juba eelmises peatükis näinud, et SHA512 kuulub samasse räsifunktsioonide perekonda nagu SHA256, kuid see toodab 512-bitist väljundit.
Siin on selle üldine tööpõhimõte, kus $m$ on sisendsõnum ja $K$ salajane võti:
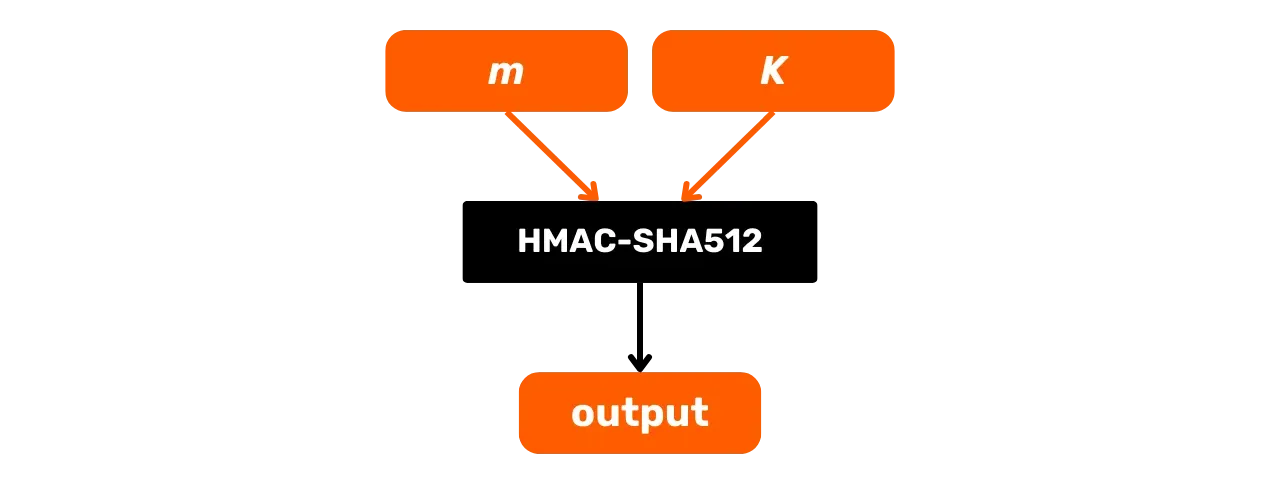
Uurime üksikasjalikumalt, mis toimub selles HMAC-SHA512 mustas kastis. HMAC-SHA512 funktsioon koos:
- $m$: kasutaja poolt valitud suvalise suurusega sõnum (esimene sisend);
- $K$: kasutaja poolt valitud suvaline salajane võti (teine sisend);
- $K'$: võti $K$, mis on kohandatud räsifunktsiooni plokkide suurusele $B$ (1024 bitti SHA512 jaoks, ehk 128 baiti);
- $\text{SHA512}$: SHA512 räsifunktsioon;
- $\oplus$: XOR (eksklusiivne või) operatsioon;
- $\Vert$: jadamisoperaator, mis ühendab bitijadasid otsast lõpuni;
- $\text{opad}$: konstant, mis koosneb korduvast baidist $0x5c$ 128 korda
- $\text{ipad}$: konstant, mis koosneb korduvast baidist $0x36$ 128 korda
Enne HMAC-i arvutamist on vajalik võtme ja konstantide võrdsustamine bloki suurusega $B$. Näiteks, kui võti $K$ on lühem kui 128 baiti, täidetakse see nullidega, et jõuda suuruseni $B$. Kui $K$ on pikem kui 128 baiti, kompresseeritakse see kasutades SHA512 ja seejärel lisatakse nulle, kuni jõutakse 128 baidini. Sel viisil saadakse võrdsustatud võti nimega $K'$.
Väärtused $\text{opad}$ ja $\text{ipad}$ saadakse nende baasbaidi ($0x5c$ $\text{opad}$ jaoks, $0x36$ $\text{ipad}$ jaoks) kordamisega, kuni suurus $B$ on saavutatud. Seega, $B = 128$ baiti korral, meil on:
\text{opad} = \underbrace{0x5c5c\ldots5c}_{128 , \text{baiti}}
Kui eeltöötlus on tehtud, on HMAC-SHA512 algoritm defineeritud järgneva võrrandiga:
\text {HMAC-SHA512}_K(m) = \text{SHA512} \left( (K' \oplus \text{opad}) \parallel \text{SHA512} \left( (K' \oplus \text{ipad}) \parallel m \right) \right)
See võrrand jaguneb järgmisteks sammudeks:
- Võtme $K'$ ja $\text{ipad}$ XOR, et saada $\text{iKpad}$;
- Võtme $K'$ ja $\text{opad}$ XOR, et saada $\text{oKpad}$;
- Ühenda $\text{iKpad}$ sõnumiga $m$.
- Hashi see tulemus SHA512-ga, et saada vahehash $H_1$.
- Ühenda $\text{oKpad}$ $H_1$-ga.
- Hashi see tulemus SHA512-ga, et saada lõplik tulemus $H_2$.
Need sammud võib kokku võtta skeemiliselt järgmiselt:
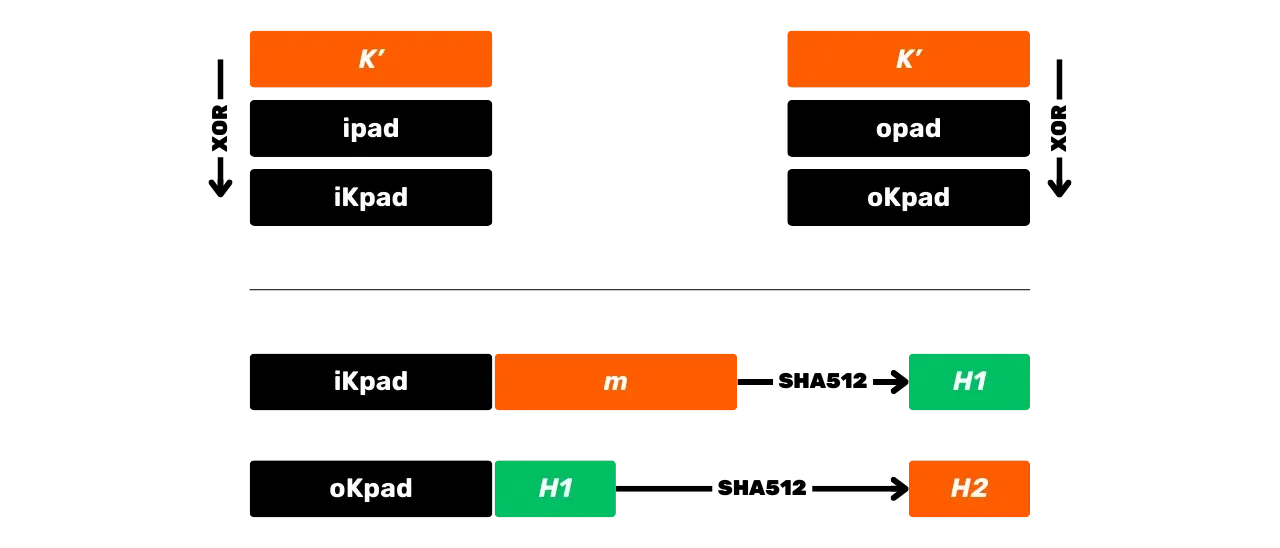
HMAC-i kasutatakse Bitcoinis märkimisväärselt võtmete tuletamiseks HD (Hierarhiliselt Deterministlikes) rahakottides (räägime sellest üksikasjalikumalt tulevates peatükkides) ja kui PBKDF2 komponenti.
### PBKDF2
PBKDF2 (_Password-Based Key Derivation Function 2_) on võtmetuletusalgoritm, mis on loodud paroolide turvalisuse suurendamiseks. Algoritm rakendab pseudojuhuslikku funktsiooni (siin HMAC-SHA512) paroolile ja krüptograafilisele soolale ning kordab seda toimingut teatud arv kordi, et toota väljundvõti.
Bitcoinis kasutatakse PBKDF2-t, et genereerida HD rahakoti seeme mnemoonilisest fraasist ja paroolist (kuid räägime sellest üksikasjalikumalt tulevates peatükkides).
PBKDF2 protsess on järgmine, kus:
- $m$: kasutaja mnemooniline fraas;
- $s$: valikuline parool turvalisuse suurendamiseks (tühi väli, kui parooli pole);
- $n$: funktsiooni iteratsioonide arv, meie juhul on see 2048.
PBKDF2 funktsioon on defineeritud iteratiivselt. Iga iteratsioon võtab eelmise tulemuse, läbib selle HMAC-SHA512 kaudu ja ühendab järjestikused tulemused, et toota lõplik võti:\text{PBKDF2}(m, s) = \text{HMAC-SHA512}^{2048}(m, s)
Skeemiliselt saab PBKDF2 esitada järgmiselt:
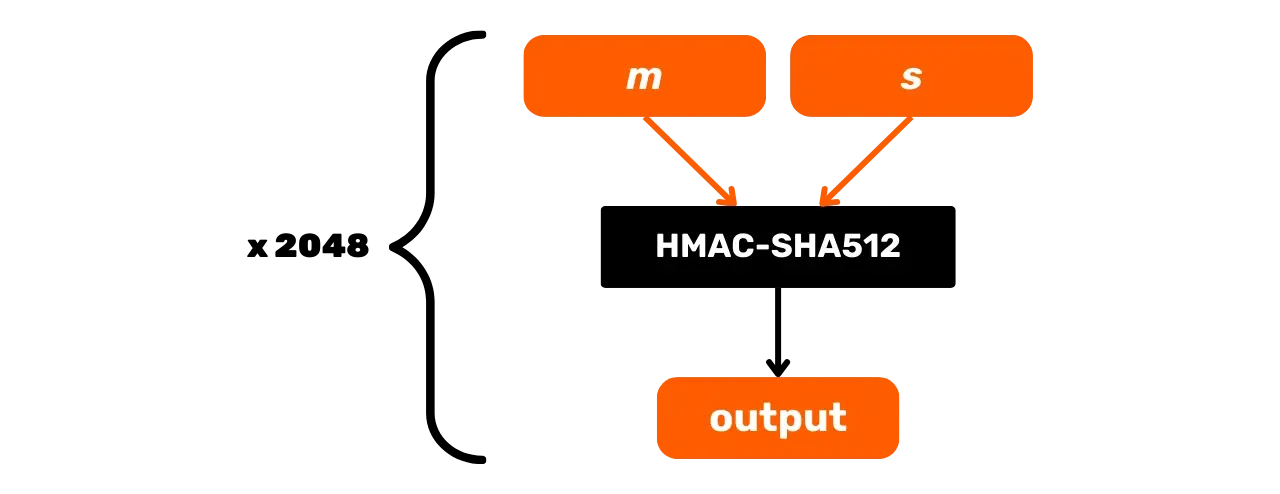
Sel peatükis oleme uurinud HMAC-SHA512 ja PBKDF2 funktsioone, mis kasutavad räsifunktsioone, et tagada võtmete tuletamise terviklikkus ja turvalisus Bitcoin protokollis. Järgmises osas vaatleme digitaalseid allkirju, teist krüptograafilist meetodit, mida Bitcoinis laialdaselt kasutatakse.
# Digitaalsed Allkirjad
<partId>76b58a00-0c18-54b9-870d-6b7e34029db8</partId>
## Digitaalsed Allkirjad ja Elliptilised Kõverad
<chapterId>c9dd9672-6da1-57f8-9871-8b28994d4c1a</chapterId>
Teine krüptograafiline meetod, mida Bitcoinis kasutatakse, hõlmab digitaalse allkirja algoritme. Vaatleme, mida see endast kujutab ja kuidas see töötab.
### Bitcoinid, UTXOd ja Kulutamistingimused
Termin "_rahakott_" Bitcoinis võib algajatele olla üsna segadusttekitav. Tõepoolest, see, mida nimetatakse Bitcoin rahakotiks, on tarkvara, mis ei hoia otseselt teie bitcoine, erinevalt füüsilisest rahakotist, mis võib hoida münte või rahatähti. Bitcoinid on lihtsalt arvestusühikud. See arvestusühik on esindatud **UTXO** (_Unspent Transaction Outputs_, kulutamata tehinguväljundid) kaudu, mis on kulutamata tehinguväljundid. Kui need väljundid on kulutamata, tähendab see, et need kuuluvad kasutajale. UTXOd on omamoodi bitcoini tükid, erineva suurusega, mis kuuluvad kasutajale.
Bitcoin protokoll on jaotatud ja toimib ilma keskse autoriteedita. Seetõttu ei ole see nagu traditsioonilised pangarekordid, kus teile kuuluvad eurod on lihtsalt seotud teie isikliku identiteediga. Bitcoinis kuuluvad teie UTXOd teile, sest need on kaitstud kulutamistingimustega, mis on määratletud Script keeles. Lihtsustatult on olemas kahte tüüpi skripte: lukustav skript (_scriptPubKey_), mis kaitseb UTXOt, ja avav skript (_scriptSig_), mis võimaldab UTXO avada ja seega kulutada bitcoini ühikuid, mida see esindab.
Bitcoiniga algne toimimine P2PK skriptidega hõlmab avaliku võtme kasutamist vahendite lukustamiseks, määrates *scriptPubKey*s, et see isik, kes soovib seda UTXOt kulutada, peab esitama kehtiva allkirja privaatvõtmega, mis vastab sellele avalikule võtmele. Selle UTXO avamiseks on seega vajalik esitada kehtiv allkiri *scriptSig*s. Nagu nende nimed viitavad, on avalik võti kõigile teada, kuna see on edastatud blockchainis, samas kui privaatvõti on teada ainult vahendite legitiimsele omanikule.
See on Bitcoin'i põhitoimimine, kuid aja jooksul on see toiming muutunud keerukamaks. Esiteks tutvustas Satoshi ka P2PKH skripte, mis kasutavad *scriptPubKey*s vastuvõtu aadressi, mis esindab avaliku võtme räsi. Seejärel muutus süsteem veelgi keerukamaks SegWiti ja seejärel Taprooti saabumisega. Siiski jääb üldpõhimõte põhimõtteliselt samaks: avalik võti või selle võtme esindus kasutatakse UTXOde lukustamiseks ja vastav privaatvõti on vajalik nende avamiseks ja seega kulutamiseks.
Kasutaja, kes soovib teha Bitcoin'i tehingu, peab looma digitaalse allkirja kasutades oma privaatvõtit küsimuses oleva tehingu jaoks. Allkirja saavad kontrollida teised võrgu osalejad. Kui see on kehtiv, tähendab see, et tehingut alustav kasutaja on tõepoolest privaatvõtme omanik ja seega ka bitcoinide omanik, mida ta soovib kulutada. Teised kasutajad saavad seejärel tehingu aktsepteerida ja edasi levitada.
Selle tulemusena peab kasutaja, kes omab bitcoine, mis on lukustatud avaliku võtmega, leidma viisi, kuidas turvaliselt hoida seda, mis võimaldab nende vahendite lukust avada: privaatvõti. Bitcoin'i rahakott on täpselt seade, mis võimaldab teil kõiki oma võtmeid hõlpsalt hoida ilma, et teised inimesed neile juurde pääseksid. Seega on see pigem võtmehoidja kui rahakott.
Matemaatiline seos avaliku võtme ja privaatvõtme vahel, samuti võime teostada allkirja, et tõestada privaatvõtme omamist ilma seda paljastamata, on võimalik digitaalse allkirja algoritmi abil. Bitcoin'i protokollis kasutatakse 2 allkirja algoritmi: **ECDSA** (_Elliptic Curve Digital Signature Algorithm_) ja **Schnorri allkirja skeem**. ECDSA on digitaalse allkirja protokoll, mida on Bitcoin'is kasutatud selle algusest peale. Schnorr on Bitcoin'is uuem, kuna see tutvustati novembris 2021 Taprooti uuendusega.
Need kaks algoritmi on oma mehhanismides üsna sarnased. Mõlemad põhinevad elliptilise kõvera krüptograafial. Peamine erinevus nende kahe protokolli vahel seisneb allkirja struktuuris ja mõnedes spetsiifilistes matemaatilistes omadustes. Seega uurime nende algoritmide toimimist, alustades vanimast: ECDSA.
### Elliptilise Kõvera Krüptograafia
Elliptilise Kõvera Krüptograafia (ECC) on algoritmide kogum, mis kasutab krüptograafilistel eesmärkidel elliptilist kõverat selle mitmesuguste matemaatiliste ja geomeetriliste omaduste tõttu. Nende algoritmide turvalisus põhineb elliptilistel kõveratel diskreetse logaritmi probleemi raskusel. Elliptilisi kõveraid kasutatakse eriti võtmevahetusteks, asümmeetriliseks krüpteerimiseks või digitaalsete allkirjade loomiseks.
Üks oluline omadus nendest kõveratest on, et need on sümmeetrilised x-telje suhtes. Seega, iga mittevertikaalne joon, mis lõikab kõverat kahes erinevas punktis, lõikub alati kõveraga kolmandas punktis. Lisaks, iga kõvera puutuja mitte-singulaarses punktis lõikub kõveraga teises punktis. Neid omadusi kasutatakse kõveral toimingute määratlemiseks.
Siin on esitus elliptilisest kõverast reaalarvude väljal:
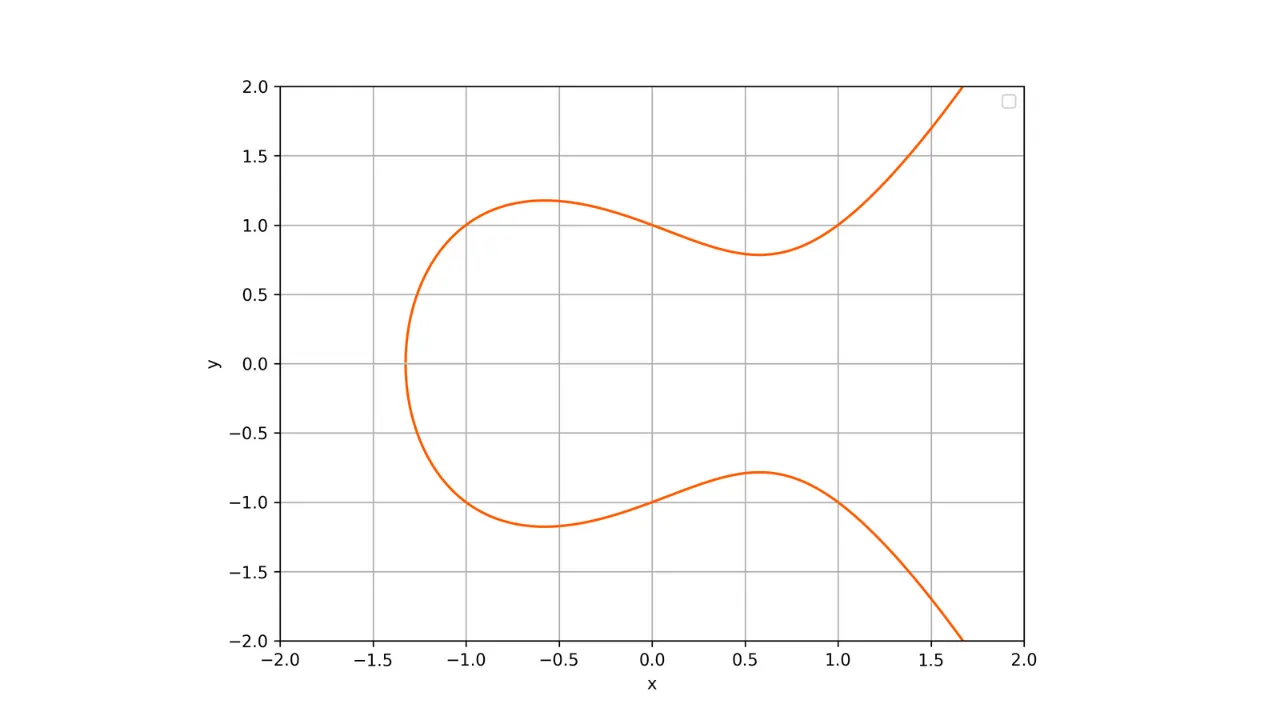
Iga elliptiline kõver on määratletud võrrandiga kujul:
y^2 = x^3 + ax + b
### secp256k1
ECDSA või Schnorri kasutamiseks tuleb valida elliptilise kõvera parameetrid, st $a$ ja $b$ väärtused kõvera võrrandis. On erinevaid elliptiliste kõverate standardeid, mis on tuntud kui krüptograafiliselt turvalised. Kõige tuntum on _secp256r1_ kõver, mille on määratlenud ja soovitanud NIST (_National Institute of Standards and Technology_).
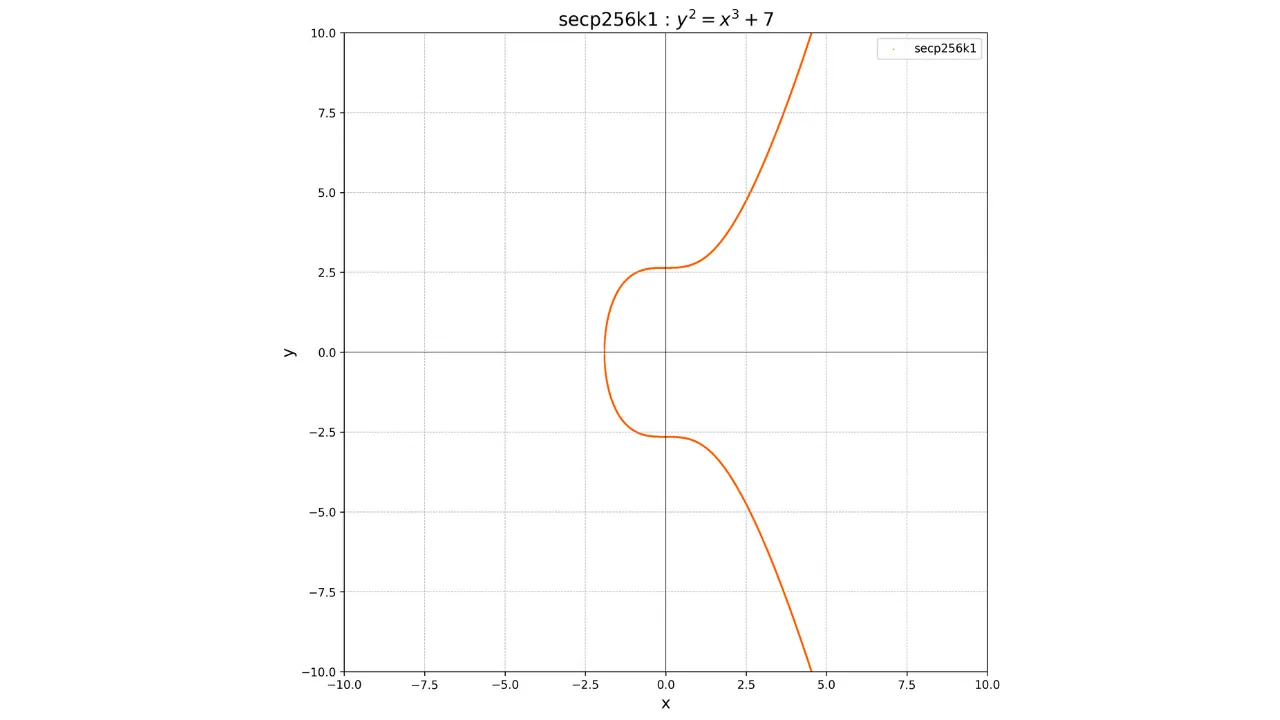
Sellest hoolimata valis Satoshi Nakamoto, Bitcoin'i leiutaja, mitte kasutada seda kõverat. Selle valiku põhjus on teadmata, kuid mõned usuvad, et ta eelistas leida alternatiivi, kuna selle kõvera parameetrid võivad potentsiaalselt sisaldada tagaust. Selle asemel kasutab Bitcoin'i protokoll standardit **_secp256k1_**. See kõver on määratletud parameetritega $a = 0$ ja $b = 7$. Selle võrrand on seega:
y^2 = x^3 + 7
Selle graafiline esitus reaalarvude väljal näeb välja selline:
Kuid krüptograafias töötame me lõplike arvude hulkadega. Täpsemalt töötame lõplikul väljal $\mathbb{F}_p$, mis on täisarvude välja modulo algarv $p$.
**Definitsioon**: Algarv on loomulik täisarv, mis on suurem või võrdne 2-ga ja millel on ainult kaks erinevat positiivset täisarvu jagajat: 1 ja iseennast. Näiteks number 7 on algarv, kuna seda saab jagada ainult 1 ja 7-ga. Teisest küljest, number 8 ei ole algarv, kuna seda saab jagada 1, 2, 4 ja 8-ga.
Bitcoini puhul kasutatav algarv $p$ lõpliku välja määratlemiseks on väga suur. See on valitud nii, et välja järk (st elementide arv $\mathbb{F}_p$-s) on piisavalt suur, et tagada krüptograafiline turvalisus.
Kasutatav algarv $p$ on:
```text
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
```
Kümnendkohasüsteemis vastab see:
p = 2^{256} - 2^{32} - 977
Seega on meie elliptilise kõvera võrrand tegelikult:
y^2 \equiv x^3 + 7 \mod p
Arvestades, et see kõver on määratletud lõplikul väljal $\mathbb{F}_p$, ei meenuta see enam pidevat kõverat, vaid pigem diskreetsete punktide hulka. Näiteks siin on, milline näeb välja Bitcoini kasutatav kõver väga väikese $p = 17$ korral:
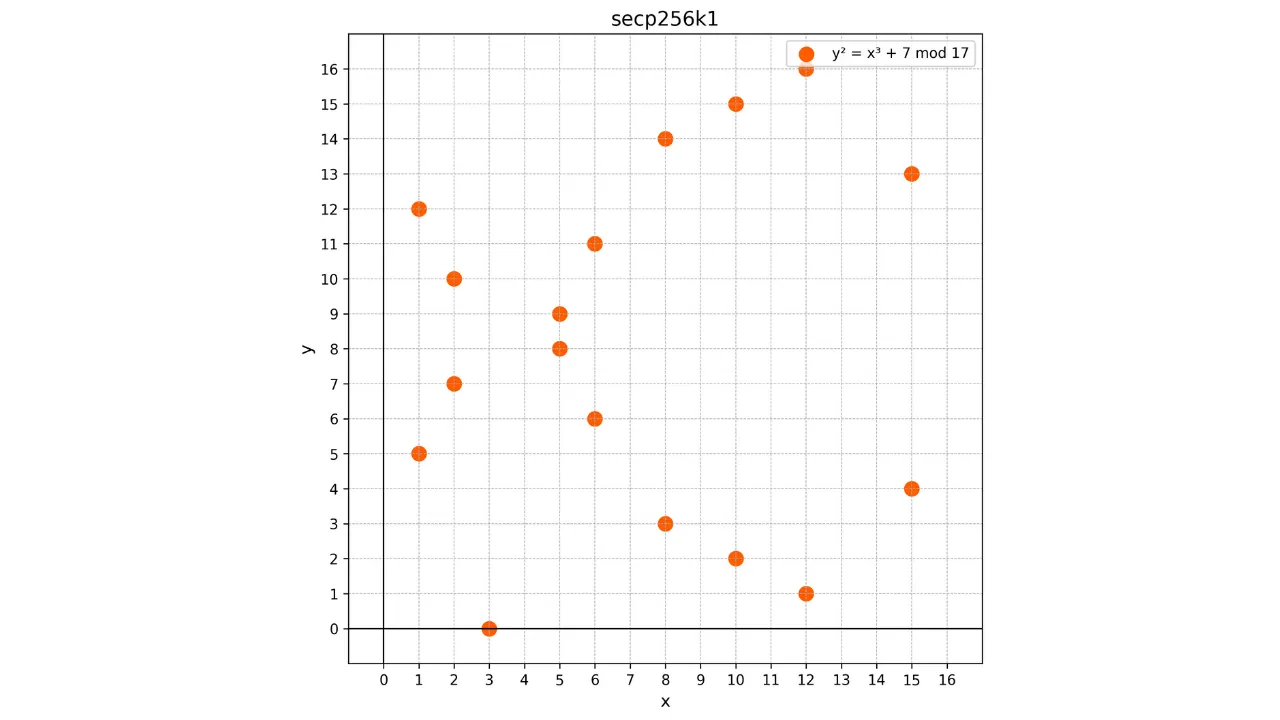
Selles näites olen tahtlikult piiranud lõpliku välja $p = 17$-ga hariduslikel eesmärkidel, kuid tuleb ette kujutada, et Bitcoini kasutatav on tohutult suurem, peaaegu $2^{256}$.
Kasutame lõplikku välja täisarvude modulo $p$ täpsuse tagamiseks kõvera operatsioonidel. Tõepoolest, reaalarvude väljal määratletud elliptilised kõverad on arvutuslike arvutuste ajal ümardamisvigade tõttu ebatäpsed. Kui kõveral tehakse arvukalt operatsioone, kuhjuvad need vead ja lõpptulemus võib olla ebatäpne või raskesti taasloomatav. Positiivsete täisarvude eksklusiivne kasutamine tagab arvutuste täpse täpsuse ja seega tulemuse taasloomise.
Elliptiliste kõverate matemaatika lõplikel väljadel on analoogne reaalarvude väljal olevaga, kohandusega, et kõik operatsioonid tehakse modulo $p$ järgi. Selgituste lihtsustamiseks jätkame järgmistes peatükkides kontseptsioonide illustreerimist kõvera abil, mis on määratletud reaalarvude üle, hoides meeles, et praktikas on kõver määratletud lõplikul väljal.
Kui soovite rohkem teada saada kaasaegse krüptograafia matemaatilistest alustest, soovitan samuti konsulteerida selle teise kursusega Plan ₿ võrgustikus:
https://planb.network/courses/d2fd9fc0-d9ed-4a87-9fa3-0fdbb3937e28
## Avaliku võtme arvutamine privaatvõtmest
<chapterId>fcb2bd58-5dda-5ecf-bb8f-ad1a0561ab4a</chapterId>
Nagu varem nähtud, põhinevad Bitcoini digitaalsed allkirja algoritmid privaat- ja avalike võtmete paaril, mis on matemaatiliselt seotud. Vaatame koos, mis see matemaatiline seos on ja kuidas neid genereeritakse.
### Privaatvõti
Privaatvõti on lihtsalt juhuslik või pseudojuhuslik number. Bitcoini puhul on see number 256 bitti suur. Seega on Bitcoini privaatvõtme võimalike variantide teoreetiline arv $2^{256}$.
**Märkus**: "Pseudojuhuslik number" on number, millel on omadused, mis on lähedased tõeliselt juhusliku numbri omadustele, kuid mis on genereeritud deterministliku algoritmi abil.
Siiski praktikas on meie elliptilisel kõveral secp256k1 ainult $n$ eristatavat punkti, kus $n$ on kõvera generaatorpunkti $G$ järk. Hiljem näeme, millele see number vastab, kuid lihtsalt pidage meeles, et kehtiv privaatvõti on täisarv vahemikus $1$ kuni $n-1$, teades, et $n$ on number, mis on lähedane, kuid veidi väiksem kui $2^{256}$. Seega on mõned 256-bitised numbrid, mis ei sobi Bitcoin'i privaatvõtmeks, eriti kõik numbrid vahemikus $n$ kuni $2^{256}$. Kui juhusliku numbri (privaatvõtme) genereerimine annab väärtuse $k$ nii, et $k \geq n$, peetakse seda kehtetuks ja tuleb genereerida uus juhuslik väärtus.
Bitcoin'i privaatvõtme võimaluste arv on seega umbes $n$, mis on number lähedane $1.158 \times 10^{77}$. See number on nii suur, et kui valite privaatvõtme juhuslikult, on statistiliselt peaaegu võimatu sattuda teise kasutaja privaatvõtmele. Et anda teile ettekujutus mastaabist, on Bitcoin'i võimalike privaatvõtmete arv suurusjärgus lähedane hinnangulisele aatomite arvule vaadeldavas universumis.
Nagu me tulevates peatükkides näeme, ei genereerita tänapäeval enamikku Bitcoin'is kasutatavatest privaatvõtmetest juhuslikult, vaid need on deterministliku tuletise tulemus mnemoonilisest fraasist, mis on iseenesest pseudojuhuslik (see on kuulus 12 või 24 sõna fraas). See teave ei muuda midagi allkirja algoritmide, nagu ECDSA, kasutamise kohta, kuid aitab meil Bitcoin'i populariseerimisele uuesti keskenduda.
Edasise selgituse jätkamiseks tähistatakse privaatvõtit väikese tähega $k$.
### Avalik Võti
Avalik võti on punkt elliptilisel kõveral, mida tähistatakse suurtähega $K$, ja see arvutatakse privaatvõtmest $k$. See punkt $K$ on esindatud koordinaatide paariga $(x, y)$ elliptilisel kõveral, iga koordinaat on täisarv modulo $p$, algarv, mis määratleb lõpliku välja $\mathbb{F}_p$.
Praktikas esindatakse lahtipakitud avalikku võtit 512 bitiga (või 64 baiti), mis vastab kahele 256-bitisele numbrile ($x$ ja $y$), mis on asetatud üksteise järel. Need numbrid on meie punkti abskiss ($x$) ja ordinaat ($y$) secp256k1-l. Kui lisame prefiksi, on avaliku võtme kogusumma 520 bitti.
Siiski on võimalik esindada avalikku võtit ka kompresseeritud kujul, kasutades ainult 33 baiti (264 bitti), hoides alles ainult meie punkti abskissi $x$ kõveral ja baiti, mis näitab $y$ pariteeti. See on tuntud kui kompresseeritud avalik võti. Räägin sellest rohkem koolituse viimastes peatükkides. Kuid mida peate meeles pidama, on see, et avalik võti $K$ on punkt, mida kirjeldatakse $x$ ja $y$ abil.
Punkti $K$, mis vastab meie avalikule võtmele, arvutamiseks kasutame elliptilistel kõveratel skalaarset korrutamist, mis on määratletud kui korduv lisamine ($k$ korda) generaatorpunktist $G$:
K = k \cdot G
kus:
- $k$ on privaatvõti (juhuslik täisarv vahemikus $1$ kuni $n-1$);
- $G$ on elliptilise kõvera generaatorpunkt, mida kasutavad kõik Bitcoin võrgu osalejad;
- $\cdot$ tähistab skalaarset korrutamist elliptilisel kõveral, mis on ekvivalentne punkti $G$ iseendale $k$ korda lisamisega.
Asjaolu, et see punkt $G$ on kõigile Bitcoin'i avalikele võtmetele ühine, võimaldab meil olla kindlad, et sama privaatvõti $k$ annab meile alati sama avaliku võtme $K$:
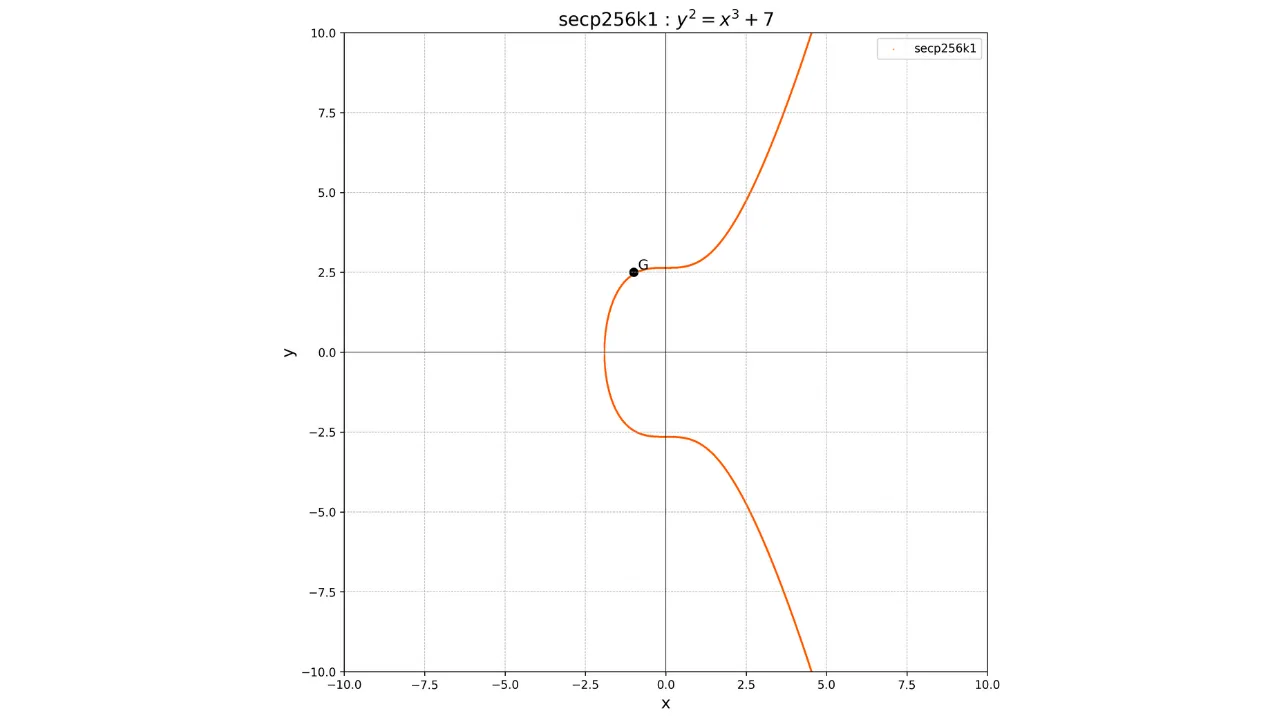
Selle operatsiooni peamine omadus on see, et see on ühesuunaline funktsioon. Avaliku võtme $K$ arvutamine on lihtne, teades privaatvõtit $k$ ja generaatorpunkti $G$, kuid privaatvõtme $k$ arvutamine, teades ainult avalikku võtit $K$ ja generaatorpunkti $G$, on praktiliselt võimatu. $k$ leidmine $K$ ja $G$ põhjal tähendab diskreetse logaritmi probleemi lahendamist elliptilistel kõveratel, mis on matemaatiliselt keeruline probleem, mille jaoks ei ole teada ühtegi efektiivset algoritmi. Isegi kõige võimsamad praegused arvutid ei suuda seda probleemi mõistliku aja jooksul lahendada.

### Punkti Lisamine ja Kahekordistamine Elliptilistel Kõveratel
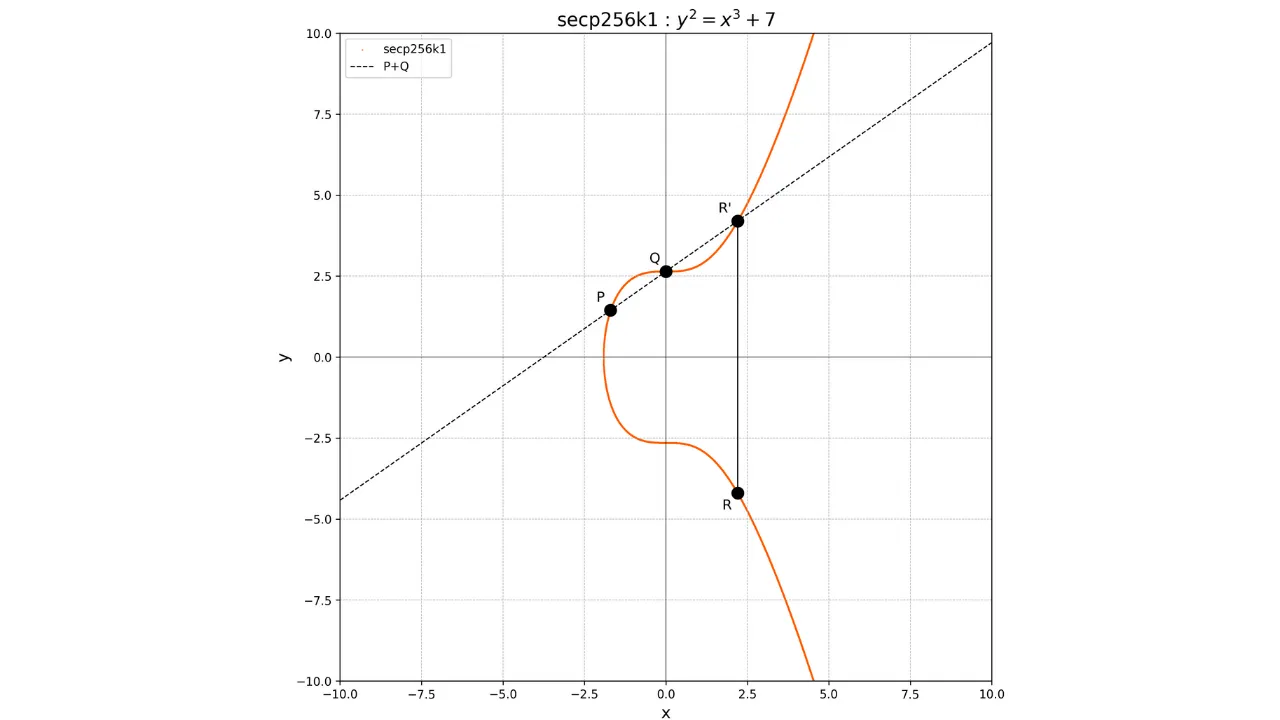
Lisamine elliptilistel kõveratel on määratletud geomeetriliselt. Kui meil on kõveral kaks punkti $P$ ja $Q$, siis operatsiooni $P + Q$ arvutatakse joonestades joon, mis läbib punkte $P$ ja $Q$. See joon lõikub kõveraga kindlasti kolmandas punktis $R'$. Seejärel võtame selle punkti peegelpildi x-telje suhtes, et saada punkt $R$, mis on lisamise tulemus:
P + Q = R
Graafiliselt saab seda esitada järgmiselt:
Punkti kahekordistamiseks, ehk operatsiooni $P + P$ jaoks, joonestame kõvera punktis $P$ puudutaja. See puudutaja lõikub kõveraga teises punktis $S'$. Seejärel võtame selle punkti peegelpildi x-telje suhtes, et saada punkt $S$, mis on kahekordistamise tulemus:
2P = S
Graafiliselt on see näidatud järgmiselt:
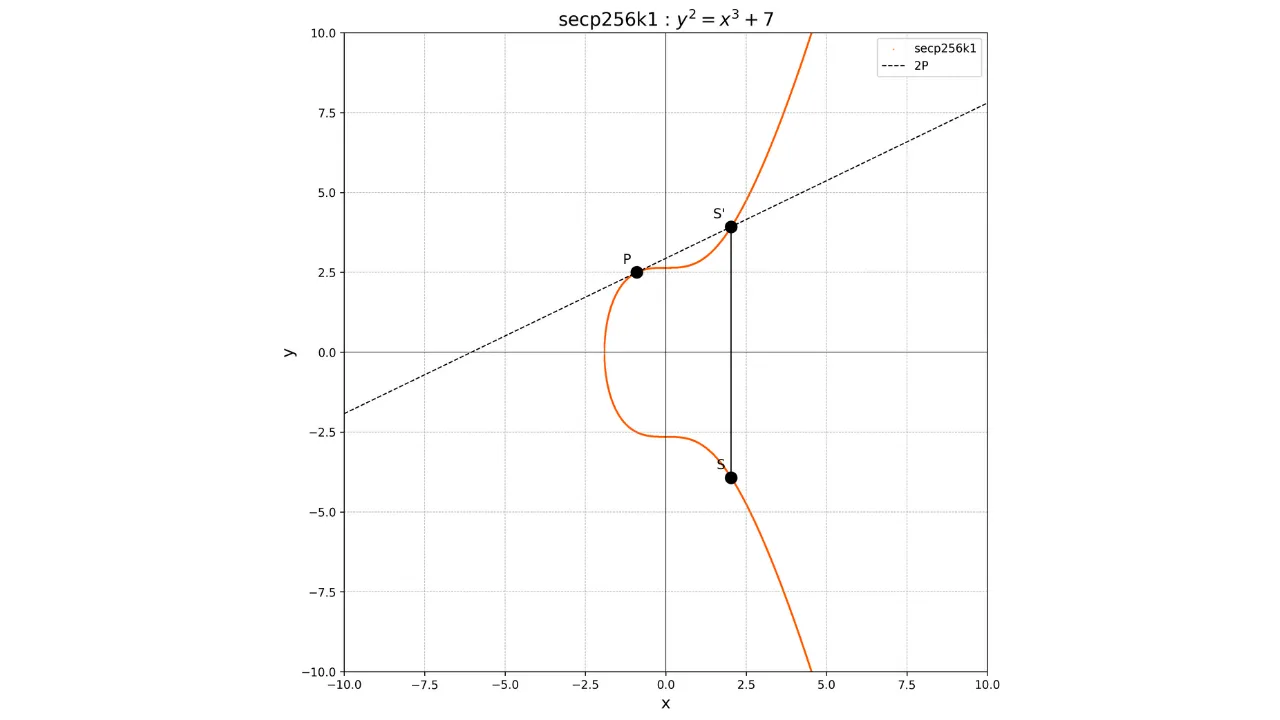
Kasutades neid lisamise ja kahekordistamise operatsioone, saame teostada punkti skalaarset korrutamist täisarvuga $k$, tähistatuna $kP$, teostades korduvaid kahekordistamisi ja lisamisi.
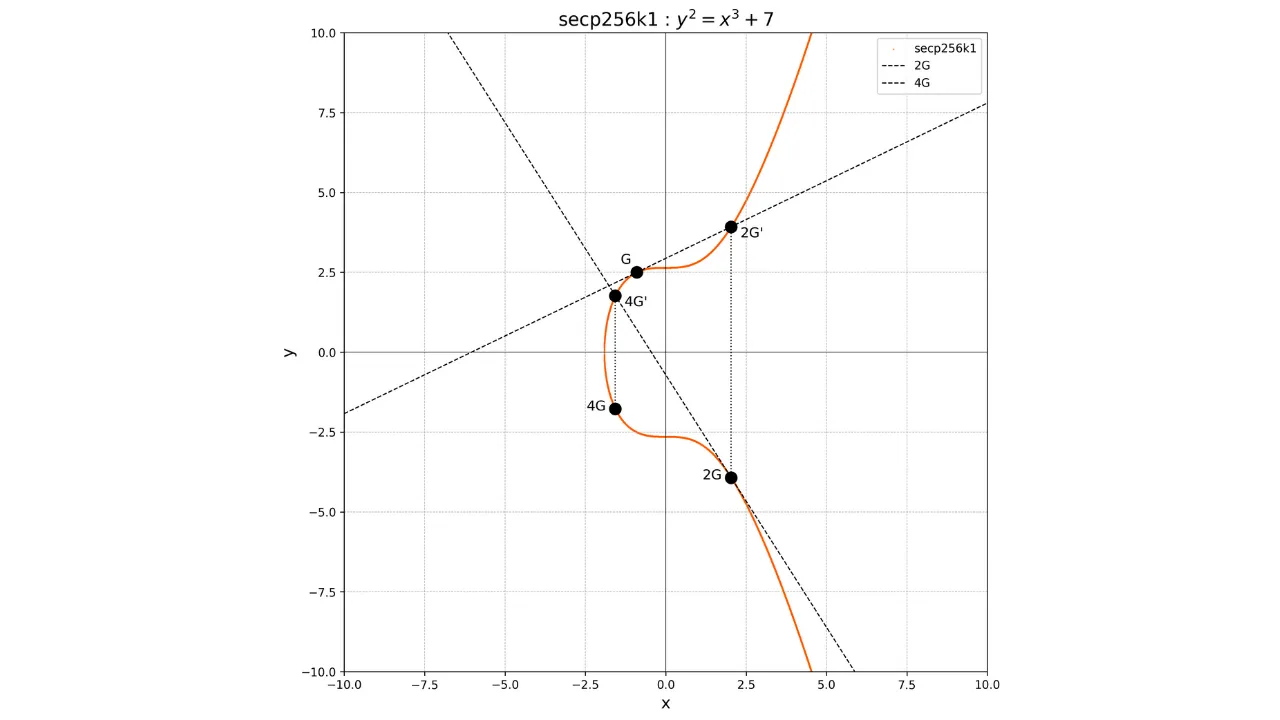
Näiteks, kui oleme valinud privaatvõtme $k = 4$. Avaliku võtme arvutamiseks teostame:
K = k \cdot G = 4G
Graafiliselt vastab see jada lisamistele ja kahekordistamistele:
- Arvuta $2G$, kahekordistades $G$.
- Arvuta $4G$, kahekordistades $2G$.

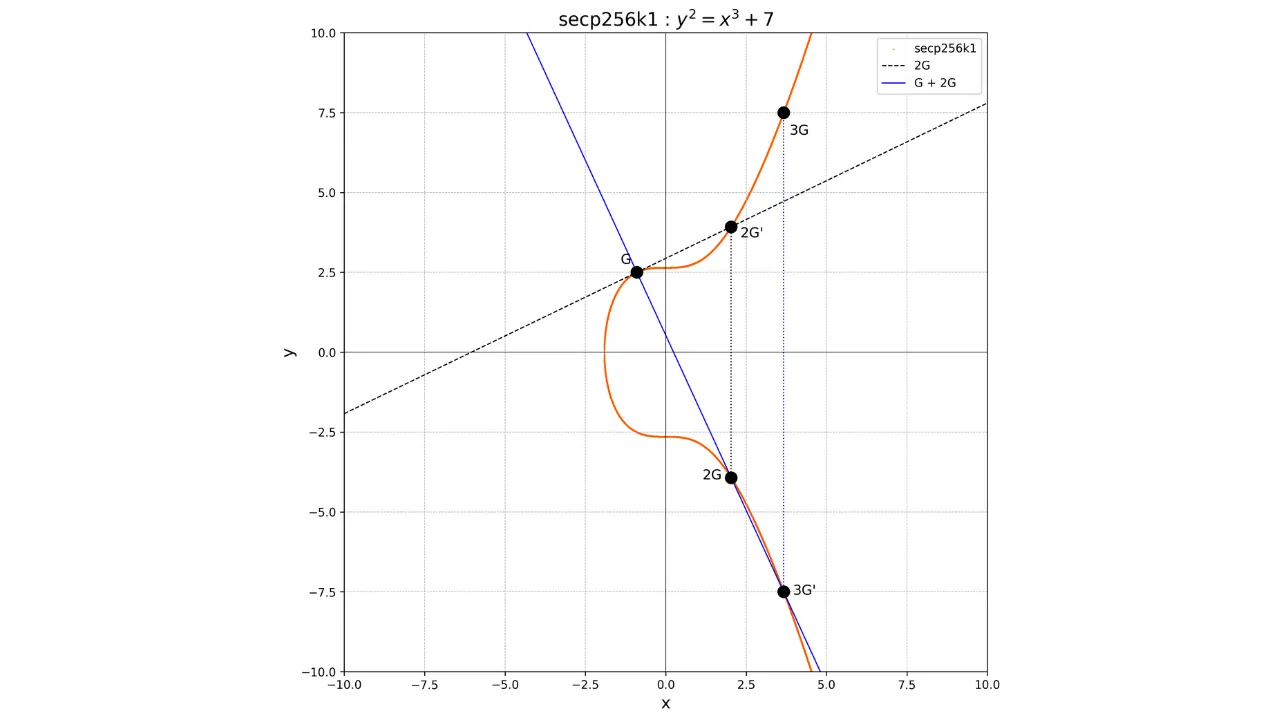
Kui soovime näiteks arvutada punkti $3G$, peame esmalt arvutama punkti $2G$, kahekordistades punkti $G$, seejärel lisame $G$ ja $2G$. $G$ ja $2G$ lisamiseks joonistame lihtsalt joone, mis ühendab neid kahte punkti, leiame elliptilise kõvera ja selle joone lõikepunktis unikaalse punkti $-3G$ ja seejärel määrame $3G$ kui $-3G$ vastandi.
Meil on:
G + G = 2G
2G + G = 3G
Graafiliselt kujutataks seda järgmiselt:
### Ühesuunaline Funktsioon
Tänu nendele toimingutele saame mõista, miks on lihtne tuletada avalik võti privaatvõtmest, kuid vastupidine on praktiliselt võimatu.
Tagasi minnes meie lihtsustatud näite juurde. Privaatvõtmega $k = 4$. Avaliku võtme arvutamiseks teostame:
K = k \cdot G = 4G
Oleme seega suutnud kergesti arvutada avaliku võtme $K$, teades $k$ ja $G$.
Nüüd, kui keegi teab ainult avalikku võtit $K$, seisab ta silmitsi diskreetse logaritmi probleemiga: leida $k$ nii, et $K = k \cdot G$. See probleem on peetud keeruliseks, kuna elliptilistel kõveratel ei ole efektiivset algoritmi selle lahendamiseks. See tagab ECDSA ja Schnorri algoritmide turvalisuse.
Muidugi, selles lihtsustatud näites, kus $k = 4$, oleks võimalik leida $k$ katse-eksituse meetodil, kuna võimaluste arv on madal. Kuid praktikas Bitcoinis on $k$ 256-bitine täisarv, muutes võimaluste arvu astronoomiliselt suureks (umbes $1.158 \times 10^{77}$). Seega on $k$ leidmine jõuga läbimurdmise teel teostamatu.
## Allkirjastamine Privaatvõtmega
<chapterId>bb07826f-826e-5905-b307-3d82001fb778</chapterId>
Nüüd, kui te teate, kuidas tuletada avalik võti privaatvõtmest, võite juba bitcoine vastu võtta, kasutades seda võtmepaari kulutamise tingimusena. Kuid kuidas neid kulutada? Bitcoinide kulutamiseks peate avama oma UTXO külge kinnitatud _scriptPubKey_, et tõestada, et olete selle legitiimne omanik. Selleks peate tootma allkirja $s$, mis vastab _scriptPubKey_-s olevale avalikule võtmele $K$, kasutades privaatvõtit $k$, mida algselt kasutati $K$ arvutamiseks. Digitaalne allkiri on seega vaieldamatu tõend, et olete privaatvõtme omanik, mis on seotud väidetava avaliku võtmega.
### Elliptilise Kõvera Parameetrid
Digitaalse allkirja sooritamiseks peavad kõik osalejad esmalt kokku leppima kasutatava elliptilise kõvera parameetrites. Bitcoin'i puhul on **secp256k1** parameetrid järgmised:
Lõplik väli $\mathbb{Z}_p$ on määratletud:
p = 2^{256} - 2^{32} - 977
```text
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
```
$p$ on väga suur algarv, mis on veidi väiksem kui $2^{256}$.
Elliptiline kõver $y^2 = x^3 + ax + b$ üle $\mathbb{Z}_p$ on määratletud:
a = 0, \quad b = 7
Generaatorpunkt ehk alguspunkt $G$:
```text
G = 0x0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
```
See number on kompresseeritud vorm, mis annab ainult punkti $G$ abskissa. Alguses olev eesliide `02` määrab, kumb kahest selle abskissaga $x$ väärtusest tuleb kasutada generaatorpunktina.
$G$ järjekord $n$ (olemasolevate punktide arv) ja kofaktor $h$:
```text
n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
```
$n$ on väga suur arv, mis on veidi väiksem kui $p$.
h=1
$h$ on kofaktor ehk alamgruppide arv. Ma ei hakka siin detailidesse laskuma, mis see täpselt tähendab, kuna see on üsna keeruline ja Bitcoini puhul ei pea me seda arvesse võtma, kuna see on võrdne $1$-ga.
Kõik see informatsioon on avalik ja kõigile osalejatele teada. Tänu sellele saavad kasutajad luua digitaalse allkirja ja seda kontrollida.
### Allkirjastamine ECDSA abil
ECDSA algoritm võimaldab kasutajal allkirjastada sõnumit oma privaatvõtmega nii, et igaüks, kes teab vastavat avalikku võtit, saab allkirja kehtivust kontrollida, ilma et privaatvõti oleks kunagi avalikustatud. Bitcoini kontekstis sõltub allkirjastatava sõnumi sisu kasutaja poolt valitud _sighash_'ist. Just see _sighash_ määrab, millised tehingu osad on allkirjaga kaetud. Sellest räägin lähemalt järgmises peatükis.
Siin on sammud ECDSA allkirja genereerimiseks:
Esmalt arvutame sõnumi, mida tuleb allkirjastada, räsi ($e$). Sõnum $m$ läbib seega krüptograafilise räsi funktsiooni, üldiselt SHA256 või topelt SHA256 Bitcoini puhul:
e = \text{HASH}(m)
Järgmisena arvutame nonce. Krüptograafias on nonce lihtsalt juhuslikul või pseudojuhuslikul viisil genereeritud number, mida kasutatakse ainult üks kord. See tähendab, et iga kord, kui uus digitaalne allkiri tehakse selle võtmepaariga, on väga oluline kasutada erinevat nonce'i, vastasel juhul kompromiteeritakse privaatvõtme turvalisust. Seega piisab juhusliku ja unikaalse täisarvu $r$ määramisest nii, et $1 \leq r \leq n-1$, kus $n$ on elliptilise kõvera genereeriva punkti $G$ järjekord.
Seejärel arvutame elliptilisel kõveral punkti $R$ koordinaatidega $(x_R, y_R)$ nii, et:
R = r \cdot G
Eraldame punkti $R$ abskissa väärtuse ($x_R$). See väärtus esindab allkirja esimest osa. Ja lõpuks arvutame allkirja teise osa $s$ järgmiselt:
s = r^{-1} \left( e + k \cdot x_R \right) \mod n
kus:
- $r^{-1}$ on $r$ modulaarne pöördväärtus modulo $n$, st täisarv, mille korral $r \cdot r^{-1} \equiv 1 \mod n$;
- $k$ on kasutaja privaatvõti;
- $e$ on sõnumi räsi;
- $n$ on elliptilise kõvera genereeriva punkti $G$ järjekord.
Allkiri on siis lihtsalt $x_R$ ja $s$ konkatenatsioon:
\text{SIG} = x_R \Vert s
### ECDSA Allkirja Kontrollimine
Allkirja $(x_R, s)$ kontrollimiseks, kui keegi teab avalikku võtit $K$ ja elliptilise kõvera parameetreid, saab protsessi järgmiselt läbi viia:
Esmalt kontrollige, et $x_R$ ja $s$ on vahemikus $[1, n-1]$. See tagab, et allkiri järgib elliptilise grupi matemaatilisi piiranguid. Kui see pole nii, lükkab kontrollija allkirja kohe tagasi kui kehtetu.
Seejärel arvutage sõnumi räsi:
e = \text{HASH}(m)
Arvutage $s$ modulaarne pöördväärtus modulo $n$:
s^{-1} \mod n
Arvutage kaks skalaarväärtust $u_1$ ja $u_2$ järgmiselt:
\begin{align*} u_1 &= e \cdot s^{-1} \mod n \ u_2 &= x_R \cdot s^{-1} \mod n \end{align*}
Ja lõpuks arvutage punkt $V$ elliptilisel kõveral nii, et:
V = u_1 \cdot G + u_2 \cdot K
Allkiri on kehtiv ainult juhul, kui $x_V \equiv x_R \mod n$, kus $x_V$ on punkti $V$ $x$ koordinaat. Tõepoolest, kombineerides $u_1 \cdot G$ ja $u_2 \cdot K$, saadakse punkt $V$, mis, kui allkiri on kehtiv, peab vastama allkirjastamisel kasutatud punktile $R$ (modulo $n$).
### Allkirjastamine Schnorri protokolliga
Schnorri allkirjastamise skeem on alternatiiv ECDSA-le, mis pakub palju eeliseid. Seda on võimalik kasutada Bitcoinis alates 2021. aastast ja Taprooti tutvustamisest, P2TR skriptimustritega. Nagu ECDSA puhul, võimaldab Schnorri skeem sõnumit allkirjastada privaatvõtmega nii, et allkirja saab kontrollida igaüks, kes teab vastavat avalikku võtit.
Schnorri puhul kasutatakse täpselt sama kõverat kui ECDSA puhul, samade parameetritega. Siiski esitatakse avalikud võtmed veidi erinevalt võrreldes ECDSA-ga. Tõepoolest, neid tähistatakse ainult punkti $x$ koordinaadiga elliptilisel kõveral. Erinevalt ECDSA-st, kus komprimeeritud avalikud võtmed on esitatud 33 baiti suuruses (eessõnaga, mis näitab $y$ pariteeti), kasutab Schnorr 32-baidiseid avalikke võtmeid, mis vastavad ainult punkti $K$ $x$ koordinaadile, ja eeldatakse, et $y$ on vaikimisi paaris. See lihtsustatud esitus vähendab allkirjade suurust ja hõlbustab teatud optimeerimisi kontrollimisalgoritmides.
Avalik võti on siis punkti $K$ $x$ koordinaat:
\text{pk} = K_x
Allkirja genereerimise esimene samm on sõnumi räsimine. Kuid erinevalt ECDSA-st tehakse seda teiste väärtustega ja kasutatakse märgistatud räsi funktsiooni, et vältida kokkupõrkeid erinevates kontekstides. Märgistatud räsi funktsioon hõlmab lihtsalt suvalise sildi lisamist räsi funktsiooni sisenditele koos sõnumi andmetega.
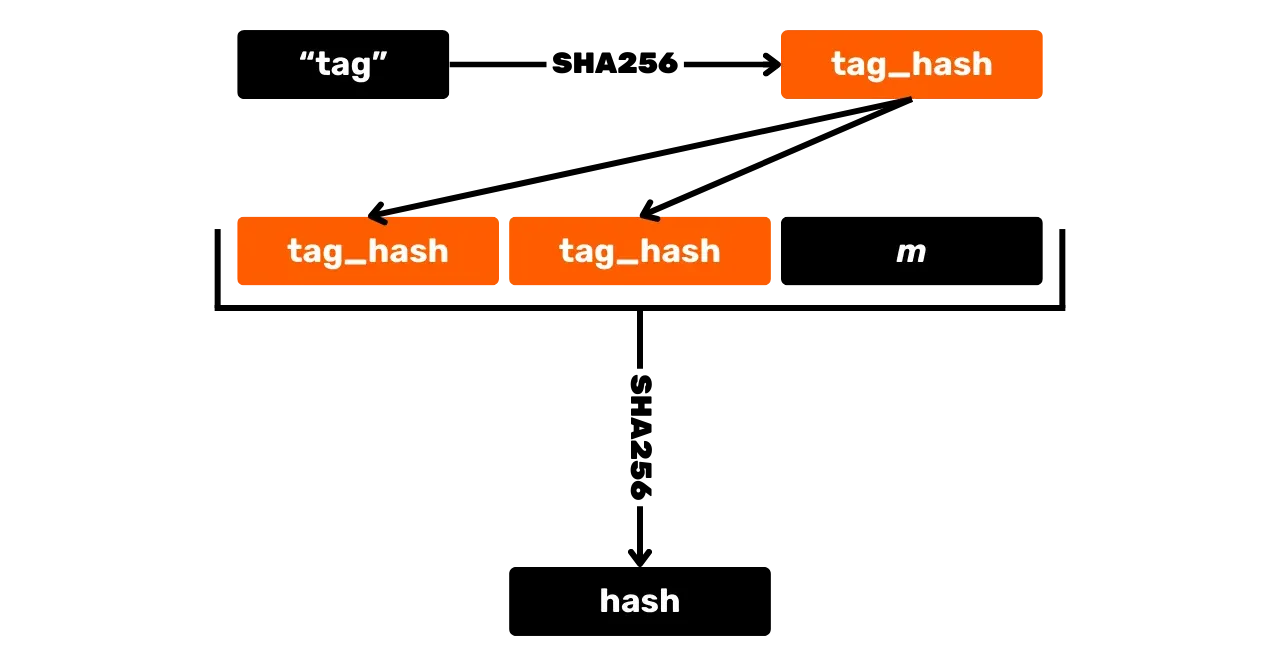
Lisaks sõnumile edastatakse märgistatud funktsiooni ka avaliku võtme $K_x$ $x$ koordinaat, samuti punkt $R$, mis on arvutatud nontsist $r$ ($R=r \cdot G$), mis on ise iga allkirja jaoks unikaalne täisarv, arvutatud deterministlikult privaatvõtmest ja sõnumist, et vältida haavatavusi, mis on seotud nontsi korduvkasutusega. Nagu avaliku võtme puhul, säilitatakse kirjeldamiseks ainult nontsipunkti $R_x$ $x$ koordinaat.
Selle räsimise tulemust, mida nimetatakse "väljakutseks":
e = \text{HASH}(\text{``BIP0340/väljakutse''}, R_x \Vert K_x \Vert m) \mod n
Siin $\text{HASH}$ on SHA256 räsifunktsioon ja $\text{``BIP0340/väljakutse''}$ on spetsiifiline silt räsimiseks.
Lõpuks arvutatakse parameeter $s$ järgmiselt privaatvõtmest $k$, nönsist $r$ ja väljakutsest $e$:
s = (r + e \cdot k) \mod n
Allkiri on lihtsalt paar $Rx$ ja $s$.
\text{SIG} = R_x \Vert s
### Schnorri allkirja kontrollimine
Schnorri allkirja kontrollimine on lihtsam kui ECDSA allkirja kontrollimine. Siin on sammud allkirja $(R_x, s)$ kontrollimiseks avaliku võtmega $K_x$ ja sõnumiga $m$:
Esmalt kontrollime, et $K_x$ on kehtiv täisarv ja väiksem kui $p$. Kui see nii on, taastame vastava punkti kõveral, kus $K_y$ on paaris. Samuti eraldame $R_x$ ja $s$, eraldades allkirja $\text{SIG}$. Seejärel kontrollime, et $R_x < p$ ja $s < n$ (kõvera järjekord).
Järgmisena arvutame väljakutse $e$ samal viisil nagu allkirja väljastaja:
e = \text{HASH}(\text{``BIP0340/väljakutse''}, R_x \Vert K_x \Vert m) \mod n
Seejärel arvutame kõveral viitepunkti järgmiselt:
R' = s \cdot G - e \cdot K
Lõpuks kontrollime, et $R'_x = R_x$. Kui kaks x-koordinaati ühtivad, siis on allkiri $(R_x, s)$ tõepoolest kehtiv avaliku võtmega $K_x$.
### Miks see toimib?
Allkirjastaja on arvutanud $s = r + e \cdot k \mod n$, nii et $R' = s \cdot G - e \cdot K$ peaks olema võrdne algse punktiga $R$, sest:
s \cdot G = (r + e \cdot k) \cdot G = r \cdot G + e \cdot k \cdot G
Kuna $K = k \cdot G$, siis meil on $e \cdot k \cdot G = e \cdot K$. Seega:
R' = r \cdot G = R
Seetõttu meil on:
R'_x = R_x
### Schnorri allkirjade eelised
Schnorri allkirjade skeem pakub Bitcoinile mitmeid eeliseid võrreldes algse ECDSA algoritmiga. Esiteks võimaldab Schnorr võtmete ja allkirjade agregatsiooni. See tähendab, et mitu avalikku võtit saab ühendada üheks võtmeks.
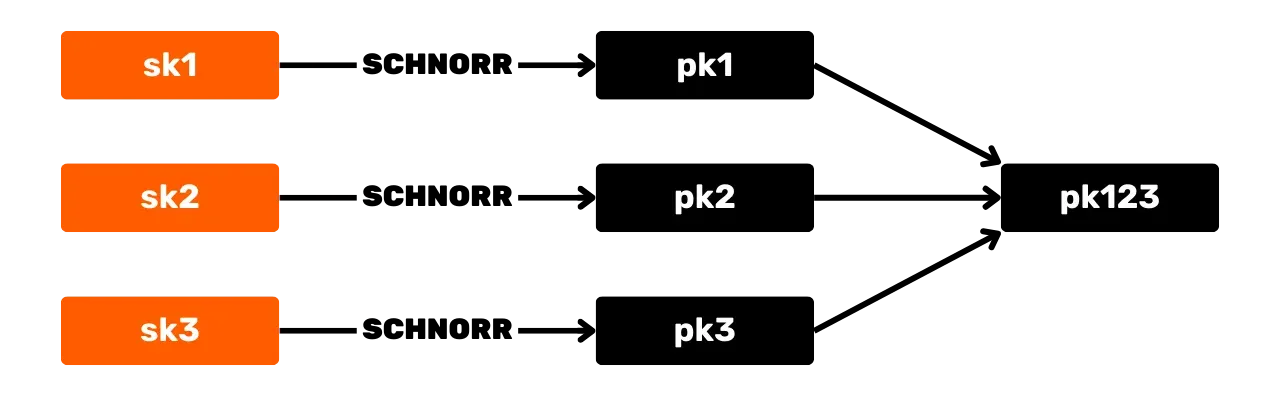
Samamoodi saab mitu allkirja agregatsioonida üheks kehtivaks allkirjaks. Seega, multisignatuuri tehingu puhul saab osalejate rühm allkirjastada ühe allkirja ja ühe agregatud avaliku võtmega. See vähendab oluliselt võrgu salvestus- ja arvutuskulusid, kuna iga sõlm peab kontrollima ainult ühte allkirja.

Lisaks parandab allkirjade agregatsioon privaatsust. Schnorriga muutub võimatuks eristada multisignatuuri tehingut standardsest ühe allkirjaga tehingust. See homogeensus muudab ahela analüüsi raskemaks, kuna see piirab võimalust tuvastada rahakoti jälgi.
Lõpuks pakub Schnorr ka partii kinnitamise võimalust. Mitme allkirja samaaegse kinnitamisega saavad sõlmed tõhusust, eriti plokkide puhul, mis sisaldavad palju tehinguid. See optimeerimine vähendab aega ja ressursse, mis on vajalikud ploki valideerimiseks. Lisaks ei ole Schnorri allkirjad muudetavad, erinevalt ECDSA abil loodud allkirjadest. See tähendab, et ründaja ei saa muuta kehtivat allkirja, et luua teine kehtiv allkirja sama sõnumi ja sama avaliku võtme jaoks. See haavatavus oli varem Bitcoinis olemas ja takistas Lightning Networki turvalist rakendamist. See probleem lahendati ECDSA jaoks SegWiti pehme kahvliga 2017. aastal, mis hõlmas allkirjade liigutamist tehingutest eraldi andmebaasi, et vältida nende muudetavust.
### Miks valis Satoshi ECDSA?
Nagu oleme näinud, valis Satoshi alguses Bitcoinile digitaalsete allkirjade jaoks ECDSA rakendamise. Ometi oleme näinud ka, et Schnorr on paljudes aspektides ECDSA-st üle ja selle protokolli lõi Claus-Peter Schnorr 1989. aastal, 20 aastat enne Bitcoini leiutamist.
Tegelikult me ei tea, miks Satoshi seda ei valinud, kuid tõenäoline hüpotees on, et see protokoll oli patendi all kuni 2008. aastani. Kuigi Bitcoin loodi aasta hiljem, jaanuaris 2009, ei olnud sel ajal saadaval Schnorri allkirjade avatud lähtekoodiga standardiseerimist. Võib-olla pidas Satoshi turvalisemaks kasutada ECDSA-d, mis oli juba laialdaselt kasutusel ja testitud avatud lähtekoodiga tarkvaras ning millel oli mitu tunnustatud rakendust (eriti OpenSSL teek, mida kasutati Bitcoini tuumas kuni 2015. aastani, seejärel asendati libsecp256k1-ga versioonis 0.10.0). Või võib-olla ei olnud ta teadlik, et see patent aegub 2008. aastal. Igatahes tundub kõige tõenäolisem hüpotees seotud olevat selle patendi ja asjaoluga, et ECDSA-l oli tõestatud ajalugu ja see oli lihtsamini rakendatav.
## Sighash lipud
<chapterId>231c41a2-aff2-4655-9048-47b6d2d83d64</chapterId>
Nagu eelmistes peatükkides oleme näinud, kasutatakse digitaalseid allkirju sageli sisendi skripti avamiseks. Allkirjastamisprotsessis on vajalik kaasata allkirjastatud andmed arvutusse, mida meie näidetes tähistatakse sõnumiga $m$. Kord allkirjastatud, ei saa neid andmeid muuta ilma allkirja kehtetuks muutmata. Tõepoolest, olgu tegemist ECDSA või Schnorriga, peab allkirja kontrollija oma arvutusse kaasama sama sõnumi $m$. Kui see erineb algsest sõnumist $m$, mida allkirjastaja kasutas, on tulemus vale ja allkirja peetakse kehtetuks. Öeldakse, et allkiri katab teatud andmed ja kaitseb neid omamoodi volitamata muudatuste eest.
### Mis on sighash lipp?
Bitcoin'i konkreetse juhtumi puhul oleme näinud, et sõnum $m$ vastab tehingule. Tegelikkuses on see veidi keerulisem. Tänu sighash lippudele on võimalik valida tehingu konkreetseid andmeid, mida allkiri katab või ei kata.
"Sighash lipp" on seega parameeter, mis lisatakse igale sisendile, võimaldades määrata tehingu komponente, mida seostatud allkiri katab. Need komponendid on sisendid ja väljundid. Sighash lipu valik määrab, millised sisendid ja millised väljundid tehingust on allkirja poolt fikseeritud ja milliseid saab veel muuta ilma seda kehtetuks muutmata. See mehhanism võimaldab allkirjadel pühenduda tehinguandmetele vastavalt allkirjastaja kavatsustele.
Ilmselgelt, kui tehing on blockchainis kinnitatud, muutub see muutumatuks, olenemata kasutatud sighash lipudest. Sighash lippude kaudu muutmise võimalus on piiratud ajaga allkirjastamise ja kinnitamise vahel.
Üldiselt ei paku rahakottide tarkvara teile võimalust käsitsi muuta oma sisendite sighash lippu, kui koostate tehingu. Vaikimisi on määratud `SIGHASH_ALL`. Isiklikult tean ainult Sparrow Wallet'it, mis võimaldab seda muudatust kasutajaliidesest.
### Millised on olemasolevad sighash lipud Bitcoinis?
Bitcoinis on esmajoones kolm põhilist sighash lippu:
- `SIGHASH_ALL` (`0x01`): Allkiri kehtib kõigi tehingu sisendite ja väljundite kohta. Tehing on seega täielikult allkirja poolt kaetud ja seda ei saa enam muuta. `SIGHASH_ALL` on kõige sagedamini kasutatav sighash igapäevastes tehingutes, kui soovitakse lihtsalt tehingut teha, ilma et seda saaks muuta.

Kõigis selle peatüki diagrammides tähistab oranž värv allkirja poolt kaetud elemente, samas kui must värv näitab neid, mis ei ole kaetud.
- `SIGHASH_NONE` (`0x02`): Allkiri hõlmab kõiki sisendeid, kuid ühtegi väljundit, võimaldades seega väljundite muutmist pärast allkirjastamist. Konkreetselt on see sarnane tühjale tšekile. Allkirjastaja avab sisendites UTXO-d, kuid jätab väljundite välja täielikult muudetavaks. Igaüks, kes teab seda tehingut, saab seega lisada oma valitud väljundi, näiteks määrates vastuvõtva aadressi sisendite poolt tarbitud vahendite kogumiseks, ja seejärel edastada tehingu bitcoinide taastamiseks. Sisendite omaniku allkiri ei muutu kehtetuks, kuna see hõlmab ainult sisendeid.

- `SIGHASH_SINGLE` (`0x03`): Allkiri hõlmab kõiki sisendeid ning ühte väljundit, mis vastab allkirjastatud sisendi indeksile. Näiteks, kui allkiri avab sisendi #0 _scriptPubKey_, siis hõlmab see ka väljundit #0. Allkiri kaitseb ka kõiki teisi sisendeid, mida ei saa enam muuta. Siiski võib igaüks lisada täiendava väljundi ilma allkirja kehtetuks muutmata, tingimusel, et väljundit #0, mis on ainus, mida see hõlmab, ei muudeta.

Lisaks nendele kolmele sighash lipule on olemas ka modifikaator `SIGHASH_ANYONECANPAY` (`0x80`). Seda modifikaatorit saab kombineerida põhilise sighash lipuga, et luua kolm uut sighash lippu:
- `SIGHASH_ALL | SIGHASH_ANYONECANPAY` (`0x81`): Allkiri hõlmab ühte sisendit, kaasates kõik tehingu väljundid. See kombineeritud sighash lipp võimaldab näiteks korraldada ühisrahastuse tehingut. Korraldaja valmistab väljundi oma aadressi ja sihtsummaga ning iga investor saab seejärel lisada sisendeid selle väljundi rahastamiseks. Kui sisendites on kogutud piisavalt vahendeid väljundi rahuldamiseks, saab tehingu edastada.

- `SIGHASH_NONE | SIGHASH_ANYONECANPAY` (`0x82`): Allkiri hõlmab ühte sisendit, ilma et see oleks seotud ühegi väljundiga;

- `SIGHASH_SINGLE | SIGHASH_ANYONECANPAY` (`0x83`): Allkiri katab ühe sisendi ning väljundi, mille indeks on sama kui sellel sisendil. Näiteks, kui allkiri avab sisendi #3 _scriptPubKey_, katab see samuti väljundi #3. Ülejäänud tehingu saab muuta, nii teiste sisendite kui ka teiste väljundite osas.

### Projektid uute Sighash-lippude lisamiseks
Praegu (2024) on Bitcoinis kasutatavad ainult eelmises jaotises tutvustatud sighash-lipud. Siiski kaaluvad mõned projektid uute sighash-lippude lisamist. Näiteks BIP118, mille pakkusid välja Christian Decker ja Anthony Towns, tutvustab kahte uut sighash-lippu: `SIGHASH_ANYPREVOUT` ja `SIGHASH_ANYPREVOUTANYSCRIPT` (_AnyPrevOut = "Ükskõik milline eelmine väljund"_).
Need kaks sighash-lippu pakuksid Bitcoinile lisavõimalust: luua allkirju, mis ei kata ühtegi konkreetset tehingu sisendit.

See idee formuleeriti esialgu Joseph Pooni ja Thaddeus Dryja poolt Lightningi Valge Raamatus. Enne ümbernimetamist oli selle sighash-lipu nimi `SIGHASH_NOINPUT`.
Kui see sighash-lipp integreeritakse Bitcoini, võimaldab see kasutada kovenantide, kuid see on ka kohustuslik eeltingimus Eltoo implementeerimiseks, mis on üldine protokoll teise kihi jaoks, mis määratleb, kuidas ühiselt hallata UTXO omandiõigust. Eltoo oli spetsiaalselt välja töötatud probleemide lahendamiseks, mis on seotud Lightningi kanalite oleku läbirääkimise mehhanismidega, st avamise ja sulgemise vahel.
Et süvendada oma teadmisi Lightningi Võrgust, pärast CYP201 kursust, soovitan väga LNP201 kursust Fanis Michalakise poolt, mis katab teema üksikasjalikult:
https://planb.network/courses/34bd43ef-6683-4a5c-b239-7cb1e40a4aeb
Järgmises osas pakun avastada, kuidas töötab teie Bitcoin rahakoti aluseks olev mnemooniline fraas.
# Mnemooniline fraas
<partId>4070af16-c8a2-58b5-9871-a22c86c07458</partId>
## Bitcoini rahakottide areng
<chapterId>9d9acd5d-a0e5-5dfd-b544-f043fae8840f</chapterId>
Nüüd, kui oleme uurinud räsifunktsioonide ja digitaalsete allkirjade toimimist, saame uurida, kuidas Bitcoini rahakotid toimivad. Eesmärk on ette kujutada, kuidas Bitcoini rahakott on üles ehitatud, kuidas see on jaotatud ja milliseid erinevaid teabeosi see kasutab. Rahakoti mehhanismide mõistmine võimaldab teil parandada oma Bitcoini kasutamist turvalisuse ja privaatsuse osas.
Enne tehnilistesse üksikasjadesse sukeldumist on oluline selgitada, mida mõeldakse "Bitcoini rahakoti" all ja mõista selle kasulikkust.
### Mis on Bitcoini rahakott?
Erinevalt traditsioonilistest rahakottidest, mis võimaldavad teil hoida füüsilisi rahatähti ja münte, ei "sisalda" Bitcoini rahakott per se bitcoine. Tegelikult ei eksisteeri bitcoine füüsilisel ega digitaalsel kujul, mida saaks hoida, vaid need on esindatud kontode ühikutena süsteemis **UTXOde** (_Kulutamata Tehingu Väljund_) kujul.
UTXO-d esindavad seega bitcoini fragmente erinevates suurustes, mida saab kulutada, eeldusel, et nende _scriptPubKey_ on rahuldatud. Oma bitcoinide kulutamiseks peab kasutaja esitama _scriptSig_, mis avab tema UTXO-ga seotud _scriptPubKey_. See tõestus tehakse tavaliselt digitaalse allkirja kaudu, mis on genereeritud privaatvõtmest, mis vastab _scriptPubKey_'s esinevale avalikule võtmele. Seega on kasutaja jaoks kriitilise tähtsusega element privaatvõtme turvalisus. Bitcoini rahakoti ülesanne on just nende privaatvõtmete turvaline haldamine. Tegelikkuses on selle roll pigem võtmehoidja kui traditsioonilises mõttes rahakoti oma.
### JBOK Rahakotid (_Just a Bunch Of Keys_)
Bitcoinis esialgu kasutatud rahakotid olid JBOK (_Just a Bunch Of Keys_) rahakotid, mis grupeerisid koos eraldi ja omavahel seostamata privaatselt genereeritud võtmed. Need rahakotid töötasid lihtsal mudelil, kus iga privaatvõti võis avada unikaalse Bitcoini vastuvõtu aadressi.
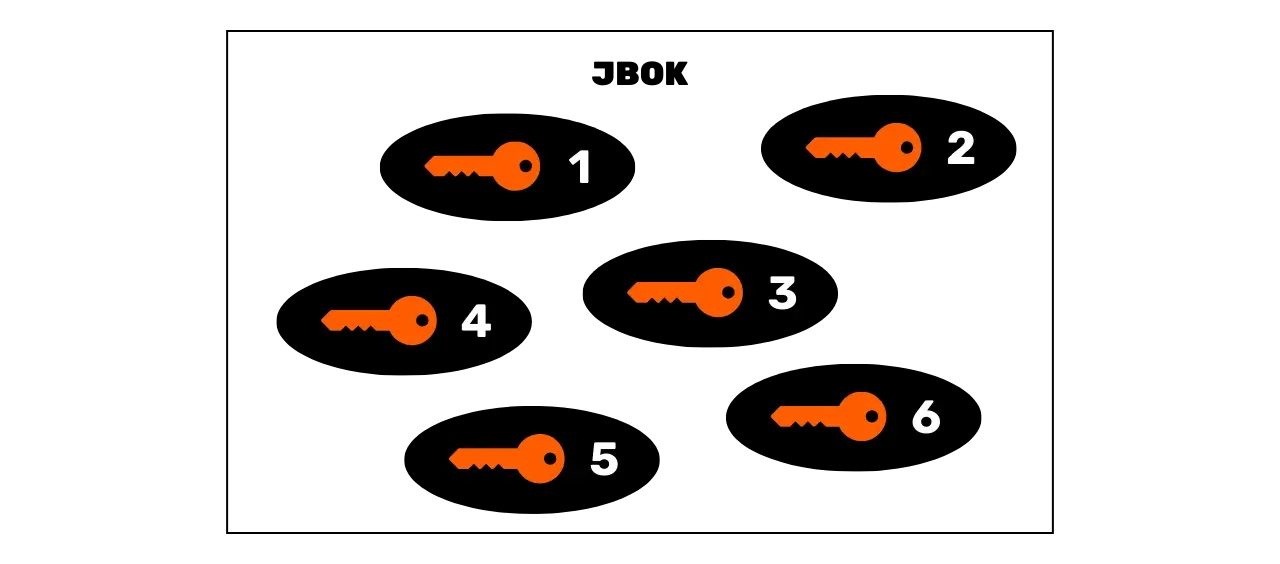
Kui sooviti kasutada mitut privaatvõtit, oli vajalik teha sama palju varukoopiaid, et tagada fondidele juurdepääs probleemide korral seadmega, kus rahakott asub. Ühe privaatvõtme kasutamisel võib see rahakoti struktuur piisav, kuna piisab ühest varukoopiast. Siiski tekib probleem: Bitcoinis on tungivalt soovitatav mitte alati kasutada sama privaatvõtit. Tõepoolest, privaatvõti on seotud unikaalse aadressiga ja Bitcoini vastuvõtu aadressid on tavaliselt mõeldud ühekordseks kasutamiseks. Iga kord, kui saate vahendeid, peaksite genereerima uue tühja aadressi.
See piirang tuleneb Bitcoini privaatsusmudelist. Sama aadressi korduva kasutamisega muudetakse välisvaatlejate jaoks lihtsamaks kõigi minu Bitcoini tehingute jälgimine. Seetõttu on vastuvõtu aadressi korduvkasutamine tungivalt soovitatav. Siiski, et omada mitut aadressi ja avalikult eraldada meie tehinguid, on vajalik hallata mitut privaatvõtit. JBOK rahakottide puhul tähendab see nii paljude varukoopiaid loomist, kui on uusi võtmepaare, ülesanne, mis võib kasutajate jaoks kiiresti muutuda keerukaks ja raskesti hooldatavaks.
Bitcoini privaatsusmudeli kohta lisateabe saamiseks ja oma privaatsuse kaitsmise meetodite avastamiseks soovitan samuti jälgida minu BTC204 kursust Plan ₿ võrgustikus:
https://planb.network/courses/65c138b0-4161-4958-bbe3-c12916bc959c
### HD Rahakotid (_Hierarchical Deterministic_)
JBOK rahakottide piirangute lahendamiseks kasutati hiljem uut rahakoti struktuuri. 2012. aastal tutvustas Pieter Wuille täiustust BIP32-ga, mis tutvustab hierarhilisi deterministlikke rahakotte. HD rahakoti põhimõte on tuletada kõik privaatvõtmed ühest teabeallikast, mida nimetatakse seemneks, deterministlikul ja hierarhilisel viisil. See seeme genereeritakse juhuslikult rahakoti loomisel ja moodustab unikaalse varukoopia, mis võimaldab kõigi rahakoti privaatvõtmete taasloomist. Seega saab kasutaja genereerida väga suure hulga privaatvõtmeid, et vältida aadressi korduvkasutust ja säilitada oma privaatsust, vajades samal ajal teha ainult ühe varukoopia oma rahakotist seemne kaudu.
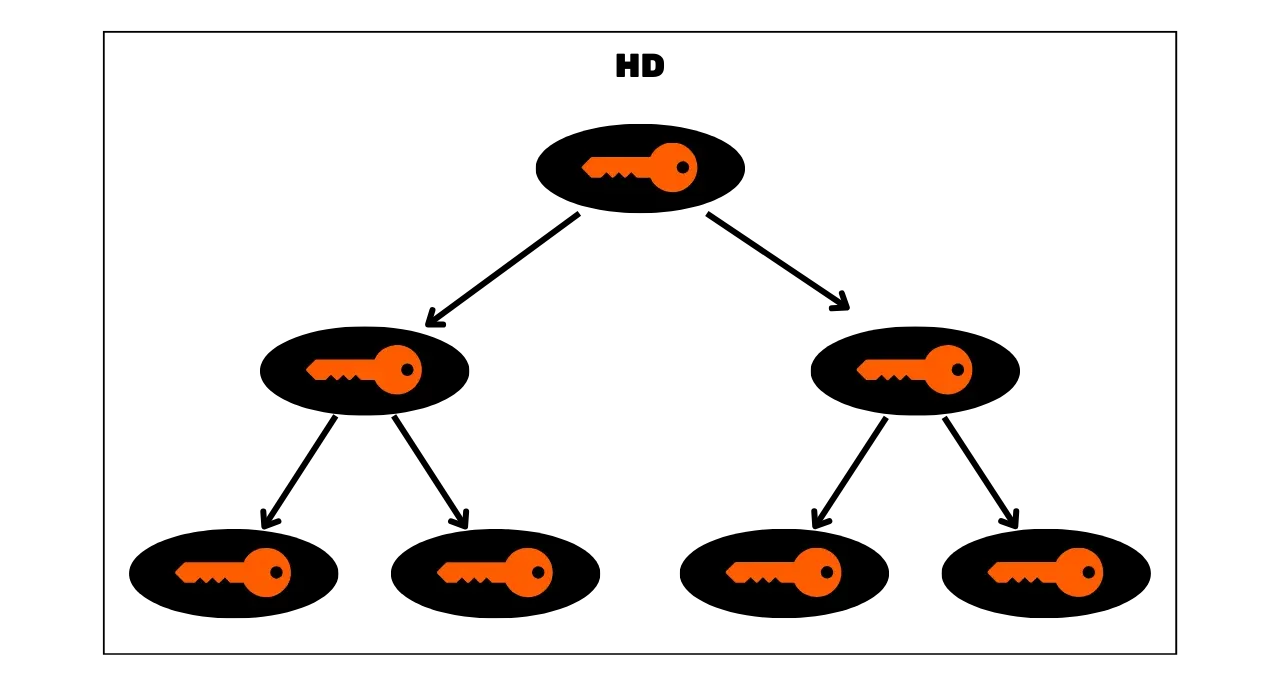
HD rahakottides toimub võtmete tuletamine vastavalt hierarhilisele struktuurile, mis võimaldab võtmeid korraldada tuletusalampiirkondadesse, iga alampiirkond omakorda edasi jaotatav, et hõlbustada fondide haldamist ja erinevate rahakottide tarkvara vahelist koostalitlusvõimet. Tänapäeval on see standard vastu võetud enamiku Bitcoini kasutajate poolt. Sel põhjusel uurime seda järgnevates peatükkides üksikasjalikult.
### BIP39 Standard: Mnemooniline Fraas
Lisaks BIP32-le standardiseerib BIP39 seemne formaadi mnemoonilise fraasina, et hõlbustada varundamist ja kasutajate poolt loetavust. Mnemooniline fraas, mida nimetatakse ka taastefraasiks või 24-sõnaliseks fraasiks, on sõnade jada, mis on tõmmatud eelnevalt määratletud loendist ja mis turvaliselt kodeerib rahakoti seemne.
Mnemooniline fraas lihtsustab oluliselt kasutaja jaoks varundamist. Seadme kaotuse, kahjustumise või varguse korral, mis majutab rahakotti, võimaldab lihtsalt selle mnemoonilise fraasi teadmine taastada rahakoti ja taastada juurdepääsu kõigile sellega turvatud vahenditele.
Järgnevates peatükkides uurime HD rahakottide sisemist tööd, sealhulgas võtmete tuletamise mehhanisme ja erinevaid võimalikke hierarhilisi struktuure. See võimaldab teil paremini mõista krüptograafilisi aluseid, millele Bitcoinis vahendite turvalisus põhineb. Ja alustuseks, järgmises peatükis, pakun et avastame entroopia rolli teie rahakoti alusel.
## Entroopia ja Juhuarv
<chapterId>b43c715d-affb-56d8-a697-ad5bc2fffd63</chapterId>
Kaasaegsed HD rahakotid (deterministlikud ja hierarhilised) tuginevad ühele algsele informatsioonitükile, mida nimetatakse "entroopiaks", et deterministlikult genereerida kogu rahakoti võtmete komplekt. See entroopia on pseudojuhuarv, mille kaose tase osaliselt määrab rahakoti turvalisuse.
### Entroopia Definitsioon
Entroopia, krüptograafia ja informatsiooni kontekstis, on kvantitatiivne mõõt ebakindluse või ettearvamatuse kohta, mis on seotud andmeallika või juhusliku protsessiga. See mängib olulist rolli krüptograafiliste süsteemide turvalisuses, eriti võtmete ja juhuarvude genereerimisel. Kõrge entroopia tagab, et genereeritud võtmed on piisavalt ettearvamatud ja vastupidavad jõuga ründamisele, kus ründaja proovib kõiki võimalikke kombinatsioone võtme ära arvamiseks.
Bitcoin'i kontekstis kasutatakse entroopiat seemne genereerimiseks. Deterministliku ja hierarhilise rahakoti loomisel tehakse mnemooniline fraas juhuarvust, mis omakorda on tuletatud entroopia allikast. Seejärel kasutatakse fraasi mitme privaatvõtme genereerimiseks deterministlikul ja hierarhilisel viisil, et luua kulutamistingimused UTXO-dele.
### Entroopia Genereerimise Meetodid
HD rahakoti jaoks kasutatav algne entroopia on üldjuhul 128 bitti või 256 bitti, kus:
- **128 biti entroopia** vastab **12 sõna** mnemoonilisele fraasile;
- **256 biti entroopia** vastab **24 sõna** mnemoonilisele fraasile.
Enamikul juhtudel genereeritakse see juhuarv automaatselt rahakoti tarkvara poolt, kasutades PRNG-d (_Pseudo-Random Number Generator_). PRNG-d on algoritmide kategooria, mida kasutatakse numbrijadade genereerimiseks algseisundist, millel on omadused, mis lähenemiselt sarnanevad juhuarvuga, ilma et see tegelikult oleks. Hea PRNG peab omama omadusi nagu väljundi ühtlus, ettearvamatus ja vastupidavus ennustatavatele rünnakutele. Erinevalt tõelistest juhuarvugeneraatoritest (TRNG), on PRNG-d deterministlikud ja reprodutseeritavad.
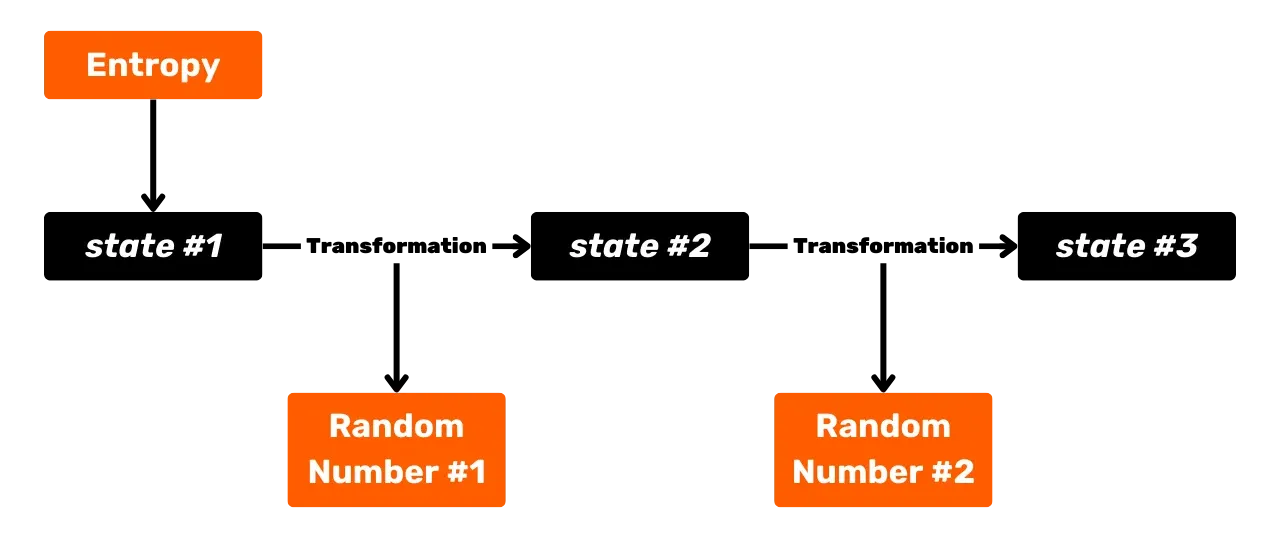
Alternatiiviks on entroopia käsitsi genereerimine, mis pakub paremat kontrolli, kuid on ka palju riskantsem. Ma soovitan tungivalt mitte genereerida entroopiat oma HD rahakoti jaoks ise.
Järgmises peatükis näeme, kuidas me liigume juhuarvust 12 või 24 sõna mnemoonilise fraasini.
## Mnemooniline Fraas
<chapterId>8f9340c1-e6dc-5557-a2f2-26c9669987d5</chapterId>
Mnemooniline fraas, mida nimetatakse ka "seemnefraasiks", "taastefraasiks", "salafraasiks" või "24-sõnaliseks fraasiks", on tavaliselt 12 või 24 sõnast koosnev jada, mis on genereeritud entroopiast. Seda kasutatakse HD rahakoti kõikide võtmete deterministlikuks tuletamiseks. See tähendab, et sellest fraasist on võimalik deterministlikult genereerida ja taasluua kõik Bitcoin rahakoti privaatsed ja avalikud võtmed ning seeläbi pääseda ligi sellega kaitstud vahenditele. Mnemoonilise fraasi eesmärk on pakkuda bitcoini varundamise ja taastamise vahendit, mis on nii turvaline kui ka lihtne kasutada. See viidi standarditesse sisse 2013. aastal BIP39-ga.
Avastame koos, kuidas minna entroopiast mnemoonilise fraasini.
### Kontrollsumma
Entroopia muutmiseks mnemooniliseks fraasiks tuleb kõigepealt entroopia lõppu lisada kontrollsumma (või "kontrollsumma"). See kontrollsumma on lühike bittide jada, mis tagab andmete terviklikkuse, kontrollides, et ei ole toimunud juhuslikke muudatusi.
Kontrollsumma arvutamiseks rakendatakse entroopiale SHA256 räsifunktsiooni (ainult üks kord; see on üks harvadest juhtudest Bitcoinis, kus kasutatakse ühekordset SHA256 räsi asemel kahekordset räsi). See toiming toodab 256-bitise räsi. Kontrollsumma koosneb selle räsi esimestest bittidest ja selle pikkus sõltub entroopia pikkusest järgmise valemi kohaselt:
\text{CS} = \frac{\text{ENT}}{32}
kus $\text{ENT}$ tähistab entroopia pikkust bittides ja $\text{CS}$ kontrollsumma pikkust bittides.
Näiteks 256-bitise entroopia puhul võetakse räsi esimesed 8 bitti, et moodustada kontrollsumma:
\text{CS} = \frac{256}{32} = 8 \text{ bitti}
Kui kontrollsumma on arvutatud, liidetakse see entroopiaga, et saada pikendatud bittide jada, mida tähistatakse $\text{ENT} \Vert \text{CS}$ ("liitmine" tähendab järjestikku panemist).

### Vastavus Entroopia ja Mnemoonilise Fraasi Vahel
Mnemoonilise fraasi sõnade arv sõltub algse entroopia suurusest, nagu on illustreeritud järgnevas tabelis:
- $\text{ENT}$: entroopia suurus bittides;
- $\text{CS}$: kontrollsumma suurus bittides;
- $w$: sõnade arv lõplikus mnemoonilises fraasis.
\begin{array}{|c|c|c|c|} \hline \text{ENT} & \text{CS} & \text{ENT} \Vert \text{CS} & w \ \hline 128 & 4 & 132 & 12 \ 160 & 5 & 165 & 15 \ 192 & 6 & 198 & 18 \ 224 & 7 & 231 & 21 \ 256 & 8 & 264 & 24 \ \hline \end{array}
### Binaarjada Muundamine Mnemooniliseks Fraasiks
Bittide jada $\text{ENT} \Vert \text{CS}$ jagatakse seejärel 11-bitisteks segmentideks. Iga 11-bitine segment, kui see on muundatud kümnendkohaks, vastab numbrile vahemikus 0 kuni 2047, mis määrab sõna positsiooni [2048 sõna standardiseeritud nimekirjas BIP39 poolt](https://github.com/Planb-Network/bitcoin-educational-content/blob/dev/resources/bet/bip39-wordlist//courses/cyp201/assets/BIP39-WORDLIST.pdf).
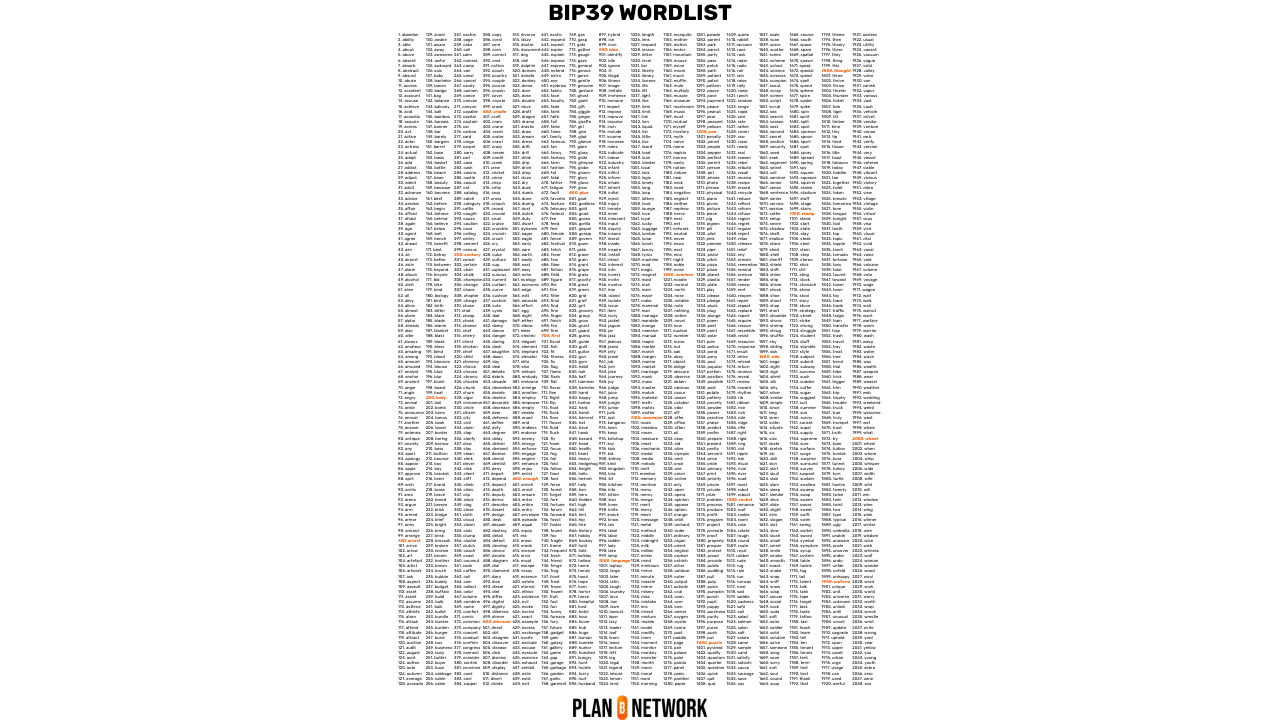
Näiteks 128-bitise entroopia korral on kontrollsumma 4 bitti, seega kogu jada mõõdab 132 bitti. See jagatakse 12 segmendiks, millest igaüks on 11 bitti (oranžid bitid tähistavad kontrollsummat):

Iga segment teisendatakse seejärel kümnendarvuks, mis esindab sõna nimekirjas. Näiteks binaarne segment `01011010001` on kümnendsüsteemis võrdne arvuga `721`. Lisades 1, et viia see kooskõlla nimekirja indekseerimisega (mis algab 1-st, mitte 0-st), annab see sõna järjekorranumbri `722`, mis nimekirjas on "*focus*".

See vastavus korratakse iga 12 segmendi jaoks, et saada 12-sõnaline fraas.

### BIP39 Sõnaloendi Omadused
BIP39 sõnaloendi eripära on see, et ükski sõna ei jaga samu esimesi nelja tähte samas järjekorras teise sõnaga. See tähendab, et iga sõna esimese nelja tähe märkimine on piisav, et salvestada mnemooniline fraas. See võib olla huvitav ruumi säästmiseks, eriti neile, kes soovivad selle metallkandjale graveerida.
See 2048 sõna nimekiri eksisteerib mitmes keeles. Need ei ole lihtsad tõlked, vaid iga keele jaoks erinevad sõnad. Siiski on tungivalt soovitatav kinni pidada inglise versioonist, kuna teistes keeltes versioone ei toetata üldiselt rahakottide tarkvaras.
### Millist Pikkust Valida Oma Mnemoonilise Fraasi Jaoks?
Optimaalse mnemoonilise fraasi pikkuse määramiseks tuleb arvestada tegelikku turvalisust, mida see pakub. 12-sõnaline fraas tagab 128 biti turvalisuse, samas kui 24-sõnaline fraas pakub 256 biti turvalisust.
Siiski ei paranda see fraasi tasemel turvalisuse erinevus Bitcoin'i rahakoti üldist turvalisust, kuna sellest fraasist tuletatud privaatvõtmed saavad kasu ainult 128 biti turvalisusest. Tõepoolest, nagu me varem nägime, genereeritakse Bitcoin'i privaatvõtmed juhuslikest arvudest (või tuletatakse juhuslikust allikast) vahemikus $1$ kuni $n-1$, kus $n$ esindab secp256k1 kõvera generaatori punkti $G$ järjekorda, number, mis on veidi väiksem kui $2^{256}$. Seega võiks arvata, et need privaatvõtmed pakuvad 256 biti turvalisust. Siiski põhineb nende turvalisus raskusel leida privaatvõti selle seotud avalikust võtmest, raskus, mis on kehtestatud elliptiliste kõverate diskreetse logaritmi matemaatilise probleemi (*ECDLP*) abil. Praeguse seisuga on selle probleemi lahendamiseks tuntud parim algoritm Pollard'i rho algoritm, mis vähendab vajalike operatsioonide arvu võtme murdmiseks selle suuruse ruutjuureni.
256-bitiste võtmete puhul, nagu neid kasutatakse Bitcoin'is, vähendab Pollard'i rho algoritm seega keerukust $2^{128}$ operatsioonini:
O(\sqrt{2^{256}}) = O(2^{128})
Seetõttu peetakse, et Bitcoin'is kasutatav privaatvõti pakub 128 biti turvalisust.
Selle tulemusena ei paku 24-sõnalise fraasi valimine rahakotile lisakaitset, kuna fraasi 256 biti turvalisus on mõttetu, kui tuletatud võtmed pakuvad ainult 128 biti turvalisust. Selle põhimõtte illustreerimiseks on see nagu majal, millel on kaks ust: vana puidust uks ja tugevdatud uks. Murdvarguse korral ei oleks tugevdatud uksel mingit kasu, kuna sissetungija läheks läbi puidust ukse. Siin on analoogne olukord.
12-sõnaline fraas, mis pakub samuti 128-bitist turvalisust, on seega praegu piisav, et kaitsta teie bitcoine igasuguse varguskatse eest. Niikaua kui digitaalse allkirja algoritm ei muutu suuremate võtmete kasutamiseks või ei hakka sõltuma mõnest muust matemaatilisest probleemist peale ECDLP, jääb 24-sõnaline fraas üleliigseks. Pealegi suurendab pikem fraas kaotamise riski varundamise ajal: varukoopia, mis on kaks korda lühem, on alati lihtsamini hallatav.
Et minna kaugemale ja õppida konkreetsemalt, kuidas käsitsi genereerida test-mnemoonilist fraasi, soovitan teil avastada seda õpetust:
https://planb.network/tutorials/wallet/backup/generate-mnemonic-phrase-47507d90-e6af-4cac-b01b-01a14d7a8228
Enne kui jätkame rahakoti tuletamist sellest mnemoonilisest fraasist, tutvustan teile järgmises peatükis BIP39 paroolilauset, kuna see mängib tuletamisprotsessis rolli ja on mnemoonilise fraasiga samal tasemel.
## Paroolilause
<chapterId>6a51b397-f3b5-5084-b151-cef94bc9b93f</chapterId>
Nagu me just nägime, genereeritakse HD rahakotid tavaliselt 12 või 24 sõnast koosnevast mnemoonilisest fraasist. See fraas on väga oluline, kuna see võimaldab taastada kõik rahakoti võtmed juhul, kui selle füüsiline seade (näiteks riistvaraline rahakott) kaob. Siiski kujutab see endast ühtset rikkepunkti, sest kui see on kompromiteeritud, võib ründaja varastada kõik bitcoinid. Siin tulebki mängu BIP39 paroolilause.
### Mis on BIP39 paroolilause?
Paroolilause on valikuline salasõna, mida saate vabalt valida, mis lisatakse mnemoonilisele fraasile võtmete tuletamise protsessis, et suurendada rahakoti turvalisust.
Olge ettevaatlik, paroolilauset ei tohiks segi ajada teie riistvaralise rahakoti PIN-koodiga või parooliga, mida kasutate oma rahakotile arvutis juurdepääsu avamiseks. Erinevalt kõigist nendest elementidest mängib paroolilause rolli teie rahakoti võtmete tuletamisel. **See tähendab, et ilma selleta ei saa te kunagi oma bitcoine taastada.**
Paroolilause töötab koos mnemoonilise fraasiga, muutes seemne, millest võtmed genereeritakse. Seega, isegi kui keegi saab kätte teie 12 või 24-sõnalise fraasi, ei pääse nad ilma paroolilauseita teie vahenditele ligi. Paroolilause kasutamine loob sisuliselt uue rahakoti eristuvate võtmetega. Paroolilause muutmine (isegi veidi) genereerib erineva rahakoti.

### Miks peaksite kasutama paroolilauset?
Paroolilause on suvaline ja võib olla kasutaja poolt valitud mis tahes tähemärkide kombinatsioon. Paroolilause kasutamine pakub seega mitmeid eeliseid. Esiteks vähendab see kõiki riske, mis on seotud mnemoonilise fraasi kompromiteerimisega, nõudes fondidele juurdepääsuks teist faktorit (sissemurdmine, juurdepääs teie koju jne).
Järgmisena saab seda strateegiliselt kasutada petterahakoti loomiseks, et tulla toime füüsiliste piirangutega teie vahendite varastamisel, nagu kurikuulus "_5 dollari mutrivõtme rünnak_". Selles stsenaariumis on idee omada rahakotti ilma paroolilauseita, mis sisaldab ainult väikest kogust bitcoine, piisavalt, et rahuldada potentsiaalset ründajat, samal ajal omades peidetud rahakotti. Viimane kasutab sama mnemoonilist fraasi, kuid on kaitstud lisaparoolilausega.
Lõpuks on paroolilause kasutamine huvitav, kui soovitakse kontrollida HD rahakoti seemne genereerimise juhuslikkust.
### Kuidas valida hea paroolilause?
Et paroolilause oleks tõhus, peab see olema piisavalt pikk ja juhuslik. Nagu tugeva parooli puhul, soovitan valida paroolilause, mis on võimalikult pikk ja juhuslik, sisaldades tähtede, numbrite ja sümbolite mitmekesisust, et muuta mis tahes jõuga ründamine võimatuks.
On oluline ka see salafraas korralikult salvestada, samamoodi nagu mnemooniline fraas. **Selle kaotamine tähendab juurdepääsu kaotamist oma bitcoinidele**. Ma soovitan tungivalt mitte jätta seda ainult meelde, kuna see suurendab mõttetult kaotuse riski. Ideaalne on see üles kirjutada füüsilisele kandjale (paberile või metallile) eraldi mnemoonilisest fraasist. See varukoopia peab ilmselgelt olema hoitud erinevas kohas, kus teie mnemooniline fraas, et vältida mõlema samaaegset kompromiteerimist.
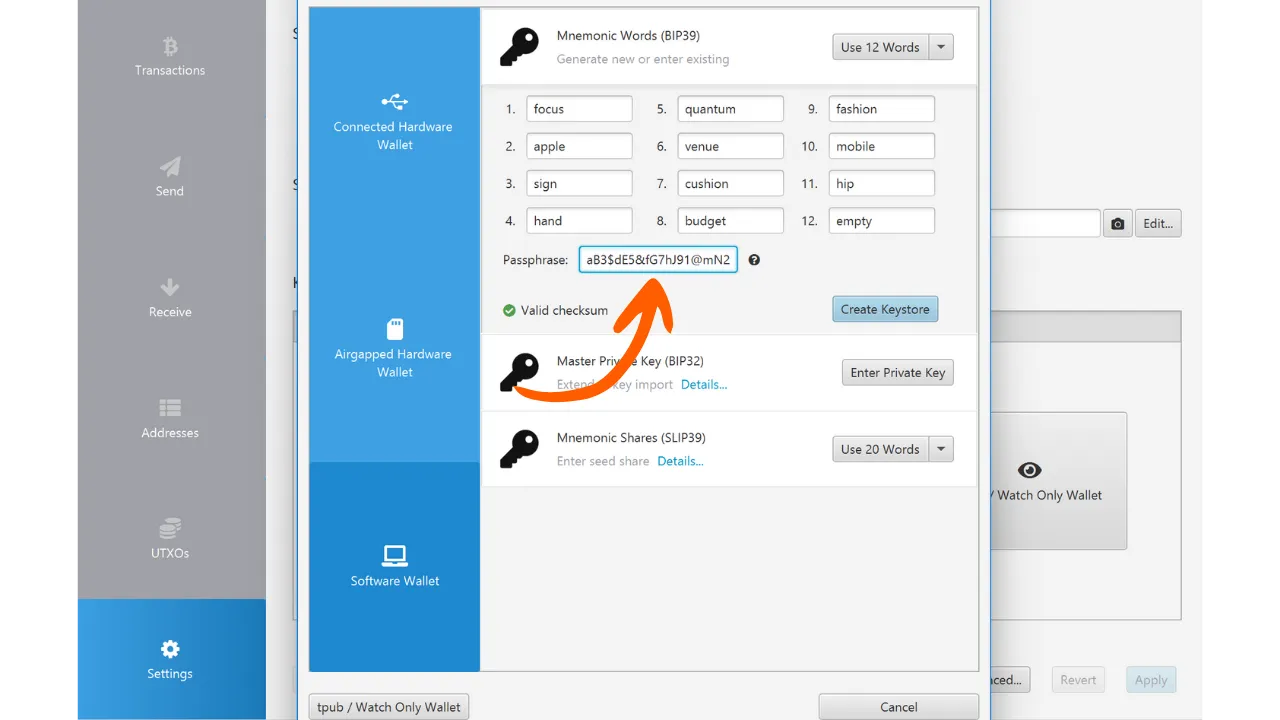
Järgmises jaotises avastame, kuidas neid kahte teie rahakoti aluseks olevat elementi — mnemoonilist fraasi ja salafraasi — kasutatakse võtmepaaride tuletamiseks, mida kasutatakse *scriptPubKey*'s, mis lukustavad teie UTXOsid.
# Bitcoinide Rahakottide Loomine
<partId>9c25e767-7eae-50b8-8c5f-679d8fc83bab</partId>
## Seemne ja Peavõtme Loomine
<chapterId>63093760-2010-5691-8d0e-9a04732ae557</chapterId>
Kui mnemooniline fraas ja valikuline salafraas on genereeritud, võib alata Bitcoin HD rahakoti tuletamise protsess. Mnemooniline fraas teisendatakse esmalt seemneks, mis on kõigi rahakoti võtmete aluseks.
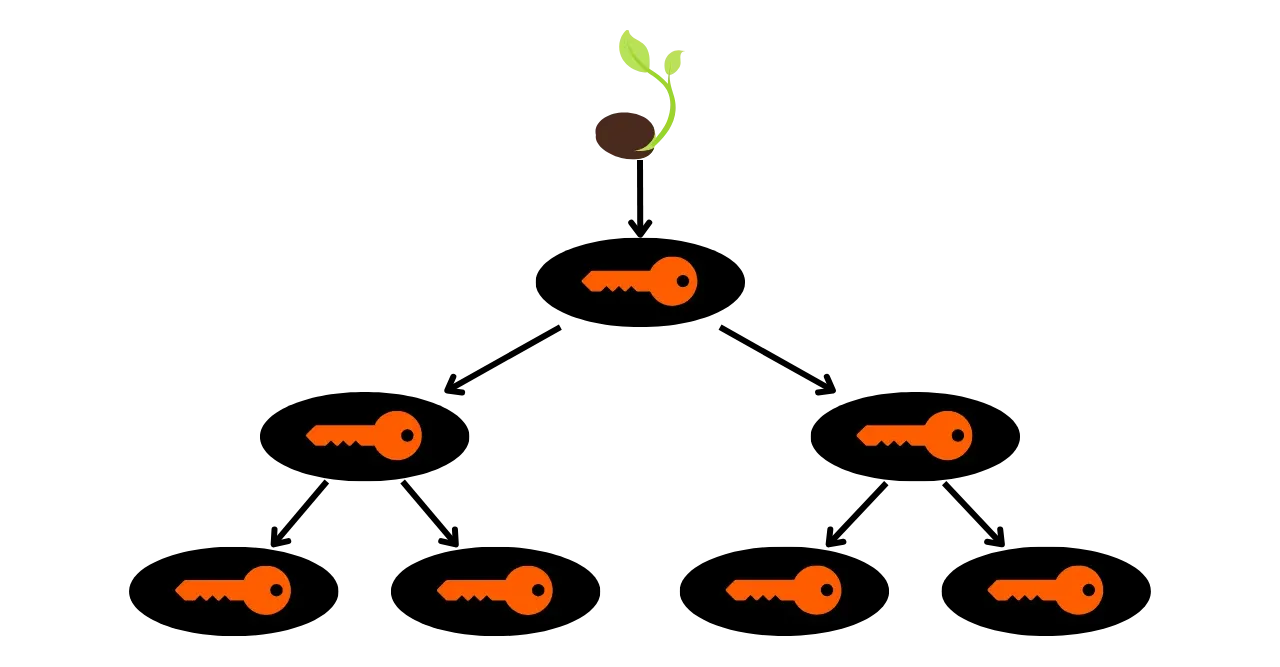
### HD Rahakoti Seeme
BIP39 standard määratleb seemne kui 512-bitise jada, mis toimib kõigi HD rahakoti võtmete tuletamise lähtepunktina. Seeme tuletatakse mnemoonilisest fraasist ja võimalikust salafraasist kasutades **PBKDF2** algoritmi (*Password-Based Key Derivation Function 2*), millest oleme juba rääkinud peatükis 3.3. Selles tuletamisfunktsioonis kasutame järgmisi parameetreid:
- $m$ : mnemooniline fraas;
- $p$ : kasutaja poolt valitud valikuline salafraas, et suurendada seemne turvalisust. Kui salafraasi ei ole, jäetakse see väli tühjaks;
- $\text{PBKDF2}$ : tuletamisfunktsioon koos $\text{HMAC-SHA512}$ ja $2048$ iteratsiooniga;
- $s$: 512-bitine rahakoti seeme.
Sõltumata valitud mnemoonilise fraasi pikkusest (132 bitti või 264 bitti), toodab PBKDF2 funktsioon alati 512-bitise väljundi ja seega on seeme alati selle suurusega.
### Seemne Tuletamise Skeem PBKDF2 abil
Järgmine võrrand illustreerib seemne tuletamist mnemoonilisest fraasist ja salafraasist:
s = \text{PBKDF2}_{\text{HMAC-SHA512}}(m, p, 2048)

Seega mõjutab seemne väärtust mnemoonilise fraasi ja salafraasi väärtus. Salafraasi muutmisel saadakse erinev seeme. Siiski, sama mnemoonilise fraasi ja salafraasiga, genereeritakse alati sama seeme, kuna PBKDF2 on deterministlik funktsioon. See tagab, et samu võtmepaare saab meie varukoopiate kaudu taastada.
**Märkus:** Tavakeeles viitab termin "seeme" sageli, keelekasutuse väärkasutuse tõttu, mnemoonilisele fraasile. Tõepoolest, salafraasi puudumisel on üks lihtsalt teise kodeering. Siiski, nagu oleme näinud, on rahakottide tehnilises reaalsuses seeme ja mnemooniline fraas tõepoolest kaks eristatavat elementi.
Nüüd, kui meil on meie seeme, võime jätkata meie Bitcoin rahakoti tuletamisega.
### Meistervõti ja Meisterahelakood
Kui seeme on saadud, on järgmine samm HD rahakoti tuletamisel meistri privaatvõtme ja meisterahelakoodi arvutamine, mis esindavad meie rahakoti sügavust 0.
Meistri privaatvõtme ja meisterahelakoodi saamiseks rakendatakse seemnele HMAC-SHA512 funktsiooni, kasutades fikseeritud võtit "*Bitcoin Seed*", mis on identne kõigi Bitcoin'i kasutajate jaoks. See konstant on valitud tagamaks, et võtmete tuletused on spetsiifilised Bitcoin'ile. Siin on elemendid:
- $\text{HMAC-SHA512}$: tuletusfunktsioon;
- $s$: 512-bitine rahakoti seeme;
- $\text{"Bitcoin Seed"}$: kõigi Bitcoin'i rahakottide ühine tuletuskonstant.
\text{väljund} = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)
Selle funktsiooni väljund on seega 512 bitti. See jagatakse seejärel kaheks osaks:
- Vasak 256 bitti moodustavad **meistri privaatvõtme**;
- Paremal 256 bitti moodustavad **meisterahelakoodi**.
Matemaatiliselt võib neid kahte väärtust märkida järgmiselt, $k_M$ olles meistri privaatvõti ja $C_M$ meisterahelakood:k_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[:256]}
C_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[256:]}

### Meistervõtme ja Ahelakoodi Roll
Meistri privaatvõtit peetakse vanemvõtmeks, millest kõik tuletatud privaatvõtmed — lapsed, lapselapsed, lapselapselapsed jne — genereeritakse. See esindab tuletushierarhia nulltaset.
Meisterahelakood seevastu toob võtmete tuletusprotsessi lastele lisaks entroopia allika, et vastu seista teatud potentsiaalsetele rünnakutele. Lisaks, HD rahakotis, on igal võtmepaaril unikaalne ahelakood, mida kasutatakse ka laste võtmete tuletamiseks sellest paarist, kuid me arutame seda üksikasjalikumalt tulevates peatükkides.
Enne HD rahakoti tuletamise jätkamist järgmiste elementidega soovin ma järgmises peatükis tutvustada teile laiendatud võtmeid, mida sageli ajatakse segamini meistervõtmega. Me näeme, kuidas neid konstrueeritakse ja millist rolli nad mängivad Bitcoin'i rahakotis.
## Laiendatud Võtmed
<chapterId>8dcffce1-31bd-5e0b-965b-735f5f9e4602</chapterId>
Laiendatud võti on lihtsalt võtme (olgu see siis privaatne või avalik) ja selle seotud ahelakoodi ühendus. See ahelakood on lastevõtmete tuletamiseks hädavajalik, sest ilma selleta on võimatu tuletada lastevõtmeid vanemvõtmest, kuid me uurime seda protsessi täpsemalt järgmises peatükis. Need laiendatud võtmed võimaldavad seega koondada kõik vajaliku teabe lastevõtmete tuletamiseks, lihtsustades seeläbi konto haldamist HD rahakotis.
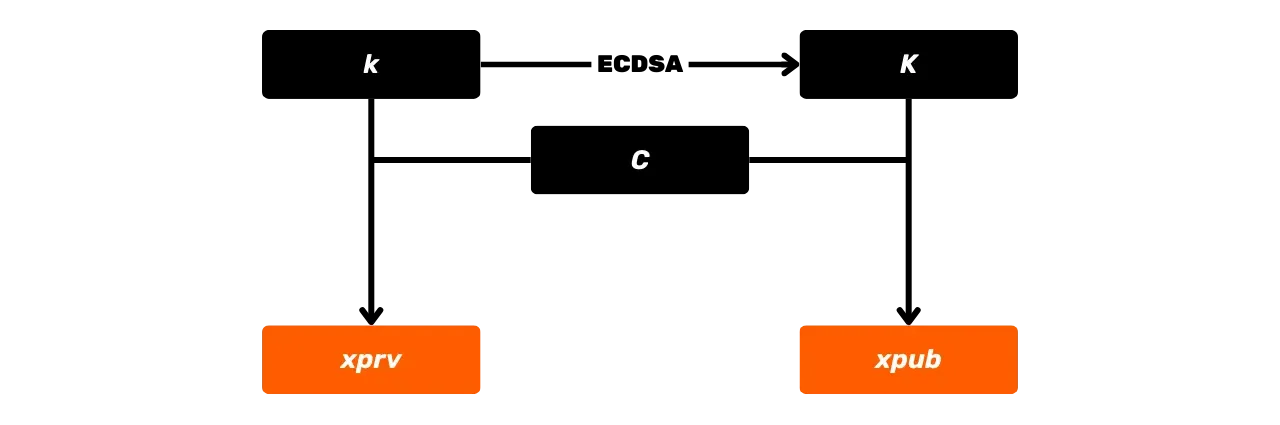
Laiendatud võti koosneb kahest osast:
- Koormus, mis sisaldab privaatset või avalikku võtit ning seotud ahelakoodi;
- Metaandmed, mis on erinevad teabeosad, et hõlbustada tarkvara vahelist koostalitlusvõimet ja parandada kasutaja mõistmist.
### Kuidas Laiendatud Võtmed Töötavad
Kui laiendatud võti sisaldab privaatvõtit, nimetatakse seda laiendatud privaatvõtmeks. Seda tunnustatakse selle prefiksi järgi, mis sisaldab märget `prv`. Lisaks privaatvõtmele sisaldab laiendatud privaatvõti ka seotud ahelakoodi. Sellise tüüpi laiendatud võtmega on võimalik tuletada kõiki tüüpi lapsprivaatvõtmeid ja seega, lisades ja kahekordistades punkte elliptilistel kõveratel, võimaldab see ka kõigi lapsavalikvõtmete tuletamist.
Kui laiendatud võti ei sisalda privaatvõtit, vaid avaliku võtme, nimetatakse seda laiendatud avalikuks võtmeks. Seda tunnustatakse selle prefiksi järgi, mis sisaldab märget `pub`. Ilmselgelt sisaldab see lisaks võtmele ka seotud ahelakoodi. Erinevalt laiendatud privaatvõtmest võimaldab laiendatud avalik võti tuletada ainult "tavalisi" lapsavalikvõtmeid (see tähendab, et see ei saa tuletada "kõvastunud" lapsvõtmeid). Järgmises peatükis vaatame, mida need "tavalised" ja "kõvastunud" kvalifikaatorid tähendavad.
Igal juhul ei võimalda laiendatud avalik võti lapsprivaatvõtmete tuletamist. Seega, isegi kui keegi pääseb ligi `xpub`-ile, ei saa nad seotud vahendeid kulutada, kuna neil ei ole juurdepääsu vastavatele privaatvõtmetele. Nad saavad tuletada ainult lapsavalikvõtmeid, et jälgida seotud tehinguid.
Edaspidi kasutame järgmist notatsiooni:
- $K_{\text{PAR}}$: vanema avalik võti;
- $k_{\text{PAR}}$: vanema privaatvõti;
- $C_{\text{PAR}}$: vanema ahelakood;
- $C_{\text{CHD}}$: lapse ahelakood;
- $K_{\text{CHD}}^n$: tavaline lapsavalik võti;
- $k_{\text{CHD}}^n$: tavaline lapsprivaatvõti;
- $K_{\text{CHD}}^h$: kõvastunud lapsavalik võti;
- $k_{\text{CHD}}^h$: kõvastunud lapsprivaatvõti.

### Laiendatud Võtme Konstruktsioon
Laiendatud võti on struktureeritud järgnevalt:
- **Versioon**: Versioonikood võtme olemuse tuvastamiseks (`xprv`, `xpub`, `yprv`, `ypub`...). Peatüki lõpus vaatame, mida tähendavad tähed `x`, `y` ja `z`.
- **Sügavus**: Hierarhilisel tasemel HD rahakotis suhtes meistervõtmega (0 meistervõtme puhul).
- **Vanema Sõrmejälg**: Vanema avaliku võtme HASH160 räsi esimesed 4 baiti, mida kasutatakse võtme tuletamiseks, mis on esitatud koormas.
- **Indeksi Number**: Lapse identifikaator õdede-vendade võtmete seas, st samal tuletustasemel olevate võtmete seas, millel on samad vanemvõtmed.
- **Ahelakood**: Unikaalne 32-baidine kood lastevõtmete tuletamiseks.
- **Võti**: Privaatvõti (prefikseeritud 1 baidiga suuruse jaoks) või avalik võti.
- **Kontrollsumma**: Kontrollsumma, mis on arvutatud HASH256 funktsiooniga (topelt SHA256), lisatakse samuti, mis võimaldab laiendatud võtme terviklikkuse kontrollimist selle edastamisel või salvestamisel.
Laiendatud võtme täielik formaat on seega 78 baiti ilma kontrollsummateta ja 82 baiti kontrollsummaga. Seejärel konverteeritakse see Base58 formaati, et toota kasutajatele hõlpsasti loetav esitus. Base58 formaat on sama, mis kasutatakse *Legacy* vastuvõtu aadresside jaoks (enne *SegWit*'i).
| Element | Kirjeldus | Suurus |
| ----------------- | ------------------------------------------------------------------------------------------------------------------ | --------- |
| Versioon | Näitab, kas võti on avalik (`xpub`, `ypub`) või privaatne (`xprv`, `zprv`), samuti laiendatud võtme versiooni | 4 baiti |
| Sügavus | Tase hierarhias võrreldes peamise võtmega | 1 bait |
| Vanema Sõrmejälg| Vanema avaliku võtme HASH160 esimesed 4 baiti | 4 baiti |
| Indeksi Number | Võtme positsioon laste järjekorras | 4 baiti |
| Ahelakood | Kasutatakse lastevõtmete tuletamiseks | 32 baiti |
| Võti | Privaatvõti (1-baidise prefiksiga) või avalik võti | 33 baiti |
| Kontrollsumma | Kontrollsumma terviklikkuse kontrollimiseks | 4 baiti |
Kui privaatvõtmele lisatakse ainult üks bait, on see seetõttu, et komprimeeritud avalik võti on privaatvõtmest ühe baiti võrra pikem. See lisabait, mis on lisatud privaatvõtme algusesse kui `0x00`, võrdsustab nende suuruse, tagades, et laiendatud võtme sisu on sama pikk, olenemata sellest, kas tegemist on avaliku või privaatvõtmega.
### Laiendatud Võtmete Prefiksid
Nagu me just nägime, sisaldavad laiendatud võtmed prefiksi, mis näitab nii laiendatud võtme versiooni kui ka selle olemust. Notatsioon `pub` näitab, et see viitab laiendatud avalikule võtmele, ja notatsioon `prv` näitab laiendatud privaatvõtit. Lisatäht laiendatud võtme aluses aitab näidata, kas järgitakse standardit Legacy, SegWit v0, SegWit v1 jne.
Siin on kokkuvõte kasutatud prefiksidest ja nende tähendustest:
| Base 58 Prefix | Base 16 Prefix | Network | Purpose | Associated Scripts | Derivation | Key Type |
| --------------- | --------------- | ------- | ------------------- | ------------------- | --------------------- | ------------ |
| `xpub` | `0488b21e` | Mainnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/0'`, `m/86'/0'` | public |
| `xprv` | `0488ade4` | Mainnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/0'`, `m/86'/0'` | private |
| `tpub` | `043587cf` | Testnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/1'`, `m/86'/1'` | public |
| `tprv` | `04358394` | Testnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/1'`, `m/86'/1'` | private |
| `ypub` | `049d7cb2` | Mainnet | Nested SegWit | P2WPKH in P2SH | `m/49'/0'` | public |
| `yprv` | `049d7878` | Mainnet | Nested SegWit | P2WPKH in P2SH | `m/49'/0'` | private |
| `upub` | `049d7cb2` | Testnet | Nested SegWit | P2WPKH in P2SH | `m/49'/1'` | public |
| `uprv` | `044a4e28` | Testnet | Nested SegWit | P2WPKH in P2SH | `m/49'/1'` | private |
| `zpub` | `04b24746` | Mainnet | SegWit V0 | P2WPKH | `m/84'/0'` | public |
| `zprv` | `04b2430c` | Mainnet | SegWit V0 | P2WPKH | `m/84'/0'` | private |
| `vpub` | `045f1cf6` | Testnet | SegWit V0 | P2WPKH | `m/84'/1'` | public |
| `vprv` | `045f18bc` | Testnet | SegWit V0 | P2WPKH | `m/84'/1'` | private |
### Laiendatud võtme elementide detailid
Laiendatud võtme sisemise struktuuri paremaks mõistmiseks vaatame ühte näidet ja jaotame selle. Siin on laiendatud võti:
- **Base58-s**:
```text
xpub6CTNzMUkzpurBWaT4HQoYzLP4uBbGJuWY358Rj7rauiw4rMHCyq3Rfy9w4kyJXJzeFfyrKLUar2rUCukSiDQFa7roTwzjiAhyQAdPLEjqHT
```
- **Heksadetsimaalselt**:
```text
0488B21E036D5601AD80000000C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A89303772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF50658051F067C3A
```
See laiendatud võti jaotub mitmeks eristuvaks elemendiks:
- **Versioon**: `0488B21E`
Esimesed 4 baiti on versioon. Siin vastab see laiendatud avalikule võtmele Mainnetis tuletuse eesmärgiga kas _Legacy_ või _SegWit v1_.
- **Sügavus**: `03`
See väli näitab võtme hierarhilist taset HD rahakotis. Sel juhul tähendab sügavus `03`, et see võti on kolm tuletustaset peavõtmest allpool.
- **Vanema sõrmejälg**: `6D5601AD`
Need on vanema avaliku võtme HASH160 räsi esimesed 4 baiti, millest tuletati see `xpub`.
- **Indeksi number**: `80000000`
See indeks näitab võtme positsiooni oma vanema laste seas. `0x80` eesliide näitab, et võti on tuletatud kõvastunud (hardened) viisil ja kuna ülejäänud osa on täidetud nullidega, näitab see, et see võti on esimene oma võimalike õdede-vendade seas.
- **Ahela kood**: `C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A893`
- **Avalik võti**: `03772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF5065805`
- **Kontrollsumma**: `1F067C3A`
Kontrollsumma vastab kõige muu topelt SHA256 räsi esimesele 4 baidile.
Sel peatükis avastasime, et on olemas kahte tüüpi alamvõtmeid. Samuti õppisime, et nende alamvõtmete tuletamine nõuab võtit (kas privaatset või avalikku) ja selle ahela koodi. Järgmises peatükis uurime üksikasjalikult nende erinevate võtmetüüpide olemust ja kuidas neid tuletada nende vanemvõtmest ja ahela koodist.
## Alamvõtmepaaride Tuletamine
<chapterId>61c0807c-845b-5076-ad06-7f395b36adfd</chapterId>
Bitcoin HD rahakottide alamvõtmepaaride tuletamine toetub hierarhilisele struktuurile, mis võimaldab genereerida suure hulga võtmeid, samal ajal korraldades neid paare erinevatesse rühmadesse harude kaudu. Iga vanemapaarist tuletatud alampaari saab kasutada otse _scriptPubKey_'s, et lukustada bitcoine, või kui lähtepunkti rohkemate alamvõtmete genereerimiseks, ja nii edasi, luues võtmete puu.
Kõik need tuletised algavad peamise võtme ja peamise ahela koodiga, mis on esimesed vanemad sügavuse tasemel 0. Nad on omamoodi teie rahakoti võtmete Aadam ja Eeva, kõigi tuletatud võtmete ühised esivanemad.
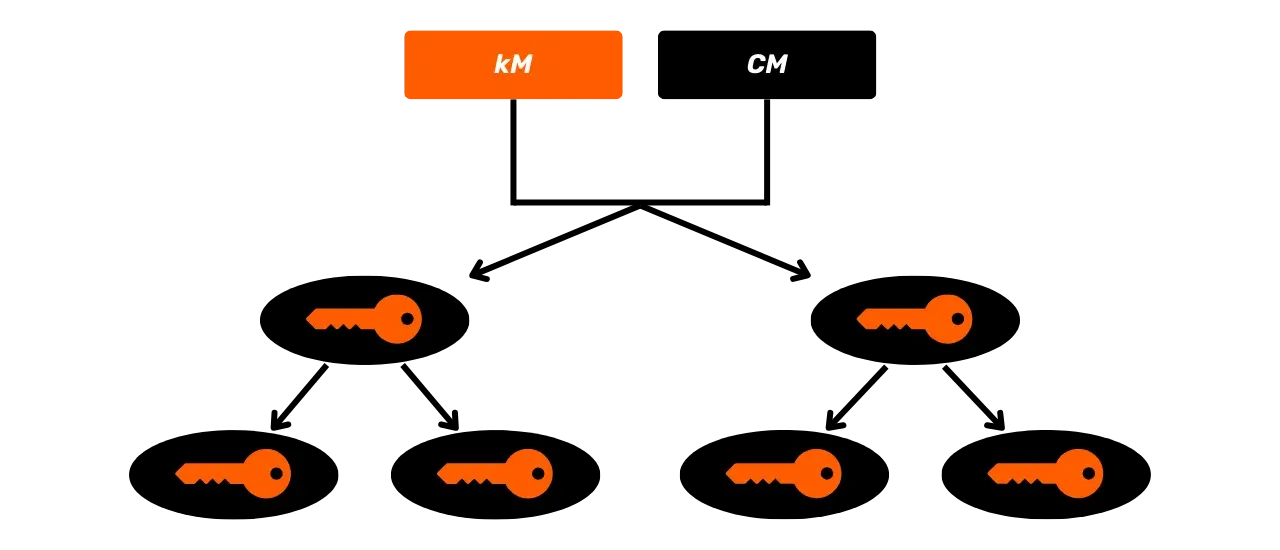
Uurime, kuidas see deterministlik tuletamine töötab.
### Erinevat Tüüpi Alamvõtmete Tuletamine
Nagu me eelmises peatükis lühidalt mainisime: alamvõtmed jagunevad kahte peamisse tüüpi:
- **Tavalised alamvõtmed** ($k_{\text{CHD}}^n, K_{\text{CHD}}^n$): Need on tuletatud laiendatud avalikust võtmest ($K_{\text{PAR}}$) või laiendatud privaatvõtmest ($k_{\text{PAR}}$), kõigepealt tuletades avaliku võtme.
- **Kõvastunud alamvõtmed** ($k_{\text{CHD}}^h, K_{\text{CHD}}^h$): Neid saab tuletada ainult laiendatud privaatvõtmest ($k_{\text{PAR}}$) ja seetõttu on need peidetud vaatlejate eest, kellel on ainult laiendatud avalik võti.
Iga lapse võtmepaari identifitseerib 32-bitine **indeks** (meie arvutustes nimetatud $i$). Tavaliste võtmete indeksid jäävad vahemikku $0$ kuni $2^{31}-1$, samas kui kõvendatud võtmete indeksid jäävad vahemikku $2^{31}$ kuni $2^{32}-1$. Neid numbreid kasutatakse tuletamisel õdede-vendade võtmepaaride eristamiseks. Tõepoolest, iga vanemvõtmepaar peab olema võimeline tuletama mitu lapse võtmepaari. Kui me rakendaksime vanemvõtmetele süstemaatiliselt sama arvutust, oleksid kõik saadud õdede-vendade võtmed identsed, mis ei ole soovitav. Indeks toob seega sisse muutuja, mis muudab tuletusarvutust, võimaldades iga õdede-vendade paari eristada. Välja arvatud spetsiifiline kasutamine teatud protokollides ja tuletusstandardites, alustame me üldiselt esimese lapse võtme tuletamist indeksiga `0`, teise indeksiga `1` ja nii edasi.
### Tuletusprotsess HMAC-SHA512 abil
Iga lapse võtme tuletamine põhineb HMAC-SHA512 funktsioonil, millest rääkisime 2. jaotises rääkides räsifunktsioonidest. See võtab kaks sisendit: vanema ahelakoodi $C_{\text{PAR}}$ ja vanemvõtme (kas avaliku võtme $K_{\text{PAR}}$ või privaatvõtme $k_{\text{PAR}}$, sõltuvalt soovitud lapse võtme tüübist) ning indeksi konkatenatsiooni. HMAC-SHA512 väljund on 512-bitine jada, mis jaguneb kaheks osaks:
- **Esimesed 32 baiti** (või $h_1$) kasutatakse uue lapse paari arvutamiseks.
- **Viimased 32 baiti** (või $h_2$) toimivad uue ahelakoodina $C_{\text{CHD}}$ lapse paarile.
Kõigis meie arvutustes tähistab $\text{hash}$ HMAC-SHA512 funktsiooni väljundit.
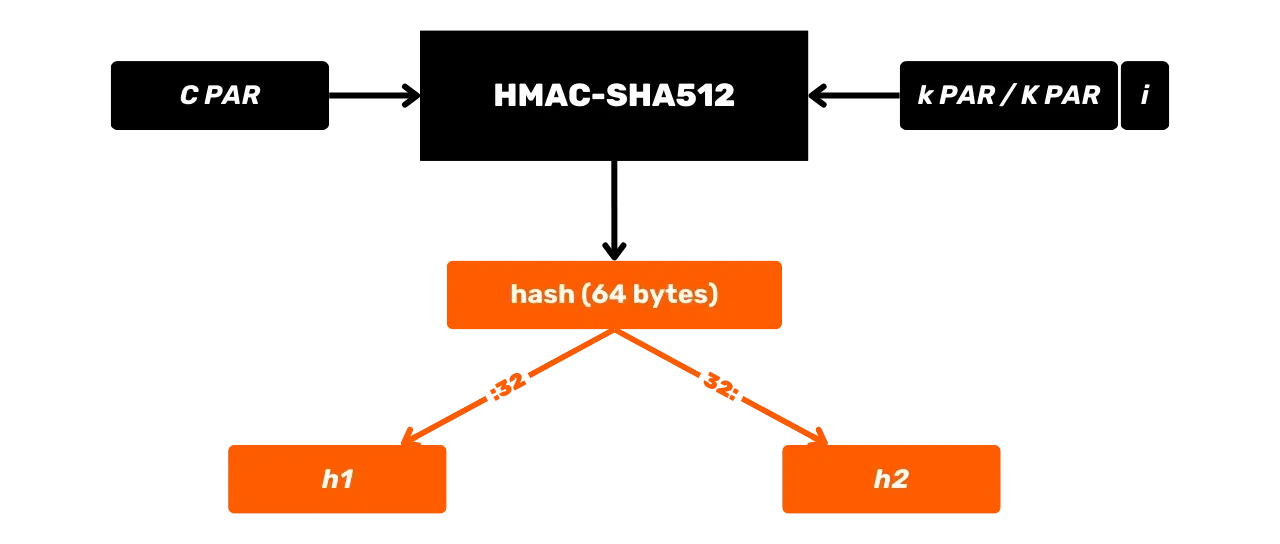
#### Lapse privaatvõtme tuletamine vanema privaatvõtmest
Lapse privaatvõtme $k_{\text{CHD}}$ tuletamiseks vanema privaatvõtmest $k_{\text{PAR}}$ on võimalik kaks stsenaariumi, sõltuvalt sellest, kas soovitakse kõvendatud või tavalist võtit.
**Tavalise lapse võtme** ($i < 2^{31}$) puhul on $\text{hash}$ arvutus järgmine:
\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, G \cdot k_{\text{PAR}} \Vert i)
Selles arvutuses märkame, et meie HMAC funktsioon võtab kaks sisendit: esiteks vanema ahelakoodi ja seejärel indeksi konkatenatsiooni vanema privaatvõtmega seotud avaliku võtmega. Vanema avalikku võtit kasutatakse siin, kuna me soovime tuletada tavalist lapse võtit, mitte kõvendatud võtit.
Nüüd on meil 64-baidine $\text{hash}$, mille jagame kaheks 32-baidiseks osaks: $h_1$ ja $h_2$:
\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}{[:32]} \quad, \quad h_2 = \text{hash}{[32:]}
Lapse privaatvõti $k_{\text{CHD}}^n$ arvutatakse seejärel järgmiselt:
k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n
Selles arvutuses koosneb toiming $\text{parse256}(h_1)$ esimese 32 baidi tõlgendamisest $\text{hash}$'is kui 256-bitisest täisarvust. See number liidetakse seejärel vanema privaatvõtmega, kõik võetakse modulo $n$, et jääda elliptilise kõvera järjekorra piiresse, nagu nägime jaotises 3 digitaalallkirjade kohta. Seega, tavalise lapse privaatvõtme tuletamiseks, kuigi vanema avalik võti kasutatakse arvutuse alusena HMAC-SHA512 funktsiooni sisendites, on alati vajalik vanema privaatvõtme olemasolu, et arvutus lõpule viia.
Sellest lapse privaatvõtmest on võimalik tuletada vastav avalik võti, rakendades ECDSA-d või Schnorri. Sel viisil saame täieliku võtmepaari.
Seejärel tõlgendatakse $\text{hash}$'i teist osa lihtsalt kui ahelakoodi äsja tuletatud lapse võtmepaarile:
C_{\text{CHD}} = h_2
Siin on skeemiline esitus kogu tuletusprotsessist:
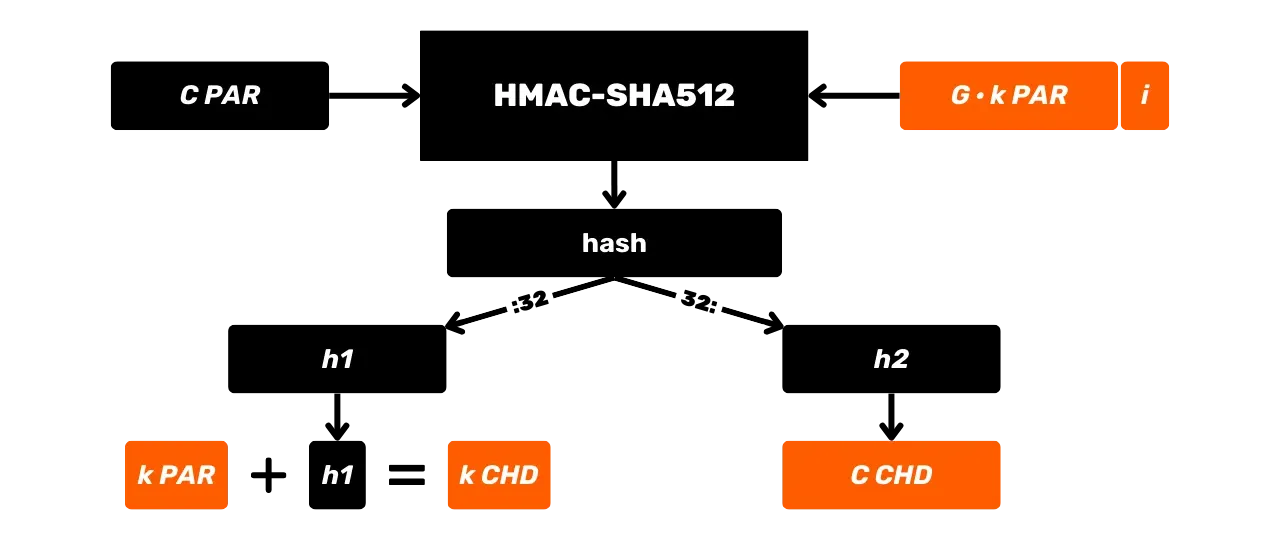
**Tugevdatud lapse võtme** ($i \geq 2^{31}$) puhul on $\text{hash}$ arvutamine järgmine:
hash = \text{HMAC-SHA512}(C_{\text{PAR}}, 0x00 \Vert k_{\text{PAR}} \Vert i)
Selles arvutuses märkame, et meie HMAC funktsioon võtab kaks sisendit: esiteks vanema ahelakoodi ja seejärel indeksi konkatenatsiooni vanema privaatvõtmega. Vanema privaatvõtit kasutatakse siin, kuna me soovime tuletada tugevdatud lapse võtit. Lisaks lisatakse võtme algusesse bait, mis on võrdne `0x00`-ga. See toiming võrdsustab selle pikkuse kokkusurutud avaliku võtmega.
Nii on meil nüüd 64-baidine $\text{hash}$, mille jaotame kaheks 32-baidiseks osaks: $h_1$ ja $h_2$:
\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}[:32] \quad, \quad h_2 = \text{hash}[32:]
Lapse privaatvõti $k_{\text{CHD}}^h$ arvutatakse seejärel järgmiselt:
k_{\text{CHD}}^h = \text{parse256}(h_1) + k_{\text{PAR}} \mod n
Järgmisena tõlgendame lihtsalt $\text{hash}$'i teist osa kui ahelakoodi äsja tuletatud lapse võtmepaarile:
C_{\text{CHD}} = h_2
Siin on skeemiline esitus kogu tuletusprotsessist:

Näeme, et tavaline tuletamine ja tugevdatud tuletamine toimivad samal viisil, selle erinevusega: tavaline tuletamine kasutab HMAC funktsiooni sisendina vanema avalikku võtit, samal ajal kui tugevdatud tuletamine kasutab vanema privaatvõtit.
#### Lapse avaliku võtme tuletamine vanema avalikust võtmest
Kui me teame ainult vanema avalikku võtit $K_{\text{PAR}}$ ja sellega seotud ahelakoodi $C_{\text{PAR}}$, ehk laiendatud avalikku võtit, on võimalik tuletada laste avalikke võtmeid $K_{\text{CHD}}^n$, kuid ainult tavaliste (mitte-kõvastatud) laste võtmete puhul. See põhimõte võimaldab eriti jälgida konto liikumisi Bitcoin'i rahakotis `xpub` (_ainult-vaatamiseks_) kaudu.
Selle arvutuse sooritamiseks arvutame $\text{hash}$ indeksiga $i < 2^{31}$ (tavaline tuletamine):
\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, K_{\text{PAR}} \Vert i)
Selles arvutuses märkame, et meie HMAC funktsioon võtab kaks sisendit: esmalt vanema ahelakoodi, seejärel indeksi ja vanema avaliku võtme konkatenatsiooni.
Nii on meil nüüd 64-baidine $hash$, mille jaotame kaheks 32-baidiseks osaks: $h_1$ ja $h_2$:
\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}[:32] \quad, \quad h_2 = \text{hash}[32:]
Lapse avalik võti $K_{\text{CHD}}^n$ arvutatakse seejärel järgmiselt:
K_{\text{CHD}}^n = G \cdot \text{parse256}(h_1) + K_{\text{PAR}}
Kui $\text{parse256}(h_1) \geq n$ (elliptilise kõvera järk) või kui $K_{\text{CHD}}^n$ on lõpmatuspunkt, on tuletamine kehtetu ja tuleb valida teine indeks.
Selles arvutuses hõlmab toiming $\text{parse256}(h_1)$ esimese 32 baidi tõlgendamist $\text{hash}$-ist kui 256-bitist täisarvu. Seda numbrit kasutatakse punkti arvutamiseks elliptilisel kõveral läbi liitmise ja kahekordistamise generaatorpunktist $G$. See punkt liidetakse seejärel vanema avaliku võtmega, et saada tavaline lapse avalik võti. Seega, tavalise lapse avaliku võtme tuletamiseks on vajalik ainult vanema avalik võti ja vanema ahelakood; vanema privaatvõti ei tule sellesse protsessi, erinevalt lapse privaatvõtme arvutusest, mida me varem nägime.
Järgmisena on lapse ahelakood lihtsalt:
C_{\text{CHD}} = h_2
Siin on üldise tuletamise skeemiline esitus:
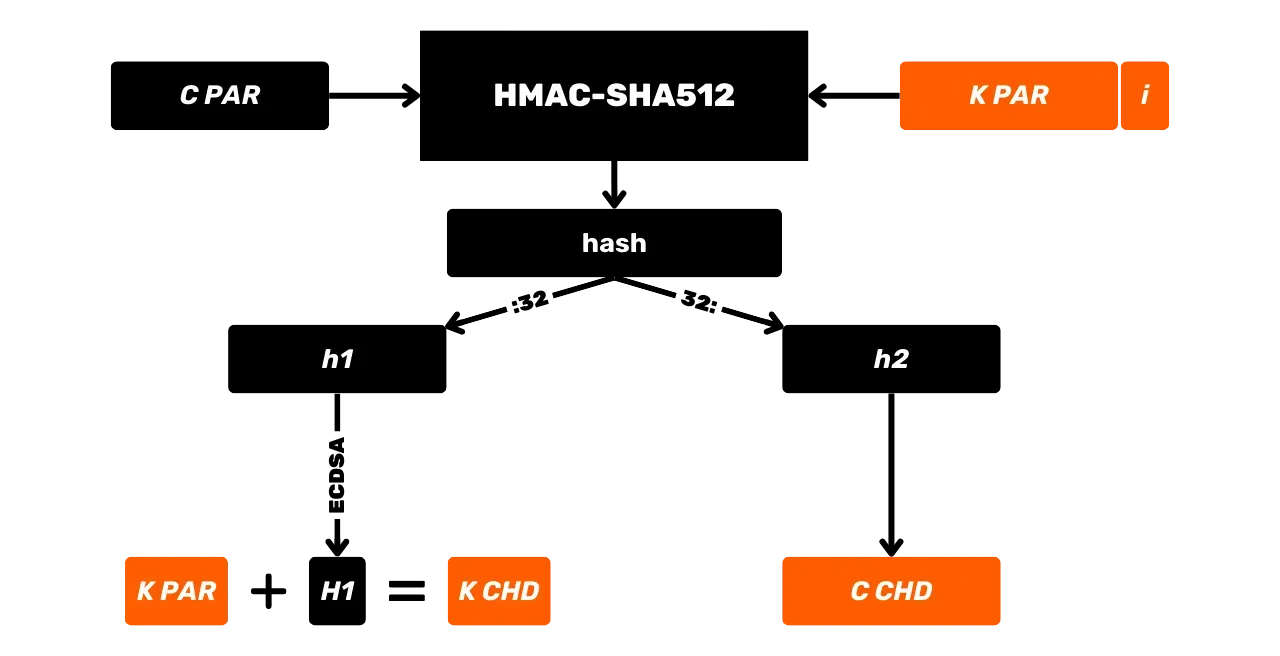
### Vastavus lapse avalike ja privaatvõtmete vahel
Küsimus, mis võib tekkida, on see, kuidas tavaline lapse avalik võti, mis on tuletatud vanema avalikust võtmest, vastab tavalisele lapse privaatvõtmele, mis on tuletatud vastavast vanema privaatvõtmest. See seos on täpselt tagatud elliptiliste kõverate omadustega. Tõepoolest, tavalise lapse avaliku võtme tuletamiseks rakendatakse HMAC-SHA512 samal viisil, kuid selle väljundit kasutatakse erinevalt:
- **Tavaline lapse privaatvõti**: $k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n$
- **Tavaline lapse avalik võti**: $K_{\text{CHD}}^n = G \cdot \text{parse256}(h_1) + K_{\text{PAR}}$
Tänu elliptilisel kõveral toimuvatele liitmise ja kahekordistamise operatsioonidele annavad mõlemad meetodid järjepidevaid tulemusi: lapse privaatvõtmest tuletatud avalik võti on identne lapse avaliku võtmega, mis on otseselt tuletatud vanema avalikust võtmest.
### Tuletamistüüpide kokkuvõte
Kokkuvõtteks, siin on erinevad võimalikud tuletamistüübid:
\begin{array}{|c|c|c|c|} \hline \rightarrow & \text{PAR} & \text{CHD} & \text{n/h} \ \hline k_{\text{PAR}} \rightarrow k_{\text{CHD}} & k_{\text{PAR}} & { k_{\text{CHD}}^n, k_{\text{CHD}}^h } & { n, h } \ k_{\text{PAR}} \rightarrow K_{\text{CHD}} & k_{\text{PAR}} & { K_{\text{CHD}}^n, K_{\text{CHD}}^h } & { n, h } \ K_{\text{PAR}} \rightarrow k_{\text{CHD}} & K_{\text{PAR}} & \times & \times \ K_{\text{PAR}} \rightarrow K_{\text{CHD}} & K_{\text{PAR}} & K_{\text{CHD}}^n & n \ \hline \end{array}
Kokkuvõtteks, seni olete õppinud looma HD rahakoti põhielemente: mnemoonilist fraasi, seemet ja seejärel peavõtit ning peamist ahelakoodi. Olete samuti avastanud, kuidas tuletada lapse võtmepaare selles peatükis. Järgmises peatükis uurime, kuidas neid tuletusi on organiseeritud Bitcoin'i rahakottides ja millist struktuuri järgida, et konkreetselt saada vastuvõtu aadresse ning võtmepaare, mida kasutatakse _scriptPubKey_ ja _scriptSig_ jaoks.
## Rahakoti Struktuur ja Tuletamisteed
<chapterId>34e1bbda-67de-5493-b268-1fded8d67689</chapterId>
HD rahakottide hierarhiline struktuur Bitcoinis võimaldab võtmepaaride organiseerimist mitmel viisil. Idee on tuletada peamisest privaatvõtmest ja peamisest ahelakoodist mitu sügavuse taset. Iga lisatud tase vastab lapse võtmepaari tuletamisele vanema võtmepaarist.
Aja jooksul on erinevad BIP-id (_Bitcoin Improvement Proposals_) tutvustanud standardeid nende tuletamisteede jaoks, eesmärgiga standardiseerida nende kasutust erinevas tarkvaras. Seega selles peatükis avastame iga HD rahakottide tuletamistaseme tähendust, vastavalt nendele standarditele.
### HD Rahakoti Tuletamissügavused
Tuletamisteed on organiseeritud sügavuse kihtidesse, alates sügavusest 0, mis esindab peavõtit ja peamist ahelakoodi, kuni alamtasemeteni aadresside tuletamiseks, mida kasutatakse UTXO-de lukustamiseks. BIP-id (_Bitcoin Improvement Proposals_) määratlevad iga kihi standardid, mis aitavad harmoneerida praktikaid erinevate rahakoti haldustarkvarade vahel.
Tuletamistee viitab seega indeksite jadale, mida kasutatakse lapse võtmete tuletamiseks peavõtmest.
**Sügavus 0: Peavõti (BIP32)**
See sügavus vastab rahakoti peamisele privaatvõtmele ja peamisele ahelakoodile. See on esindatud notatsiooniga $m/$.
**Sügavus 1: Eesmärk (BIP43)**
Eesmärk määrab tuletuse loogilise struktuuri. Näiteks P2WPKH aadressil on sügavusel 1 $/84'/$ (vastavalt BIP84), samas kui P2TR aadressil on $/86'/$ (vastavalt BIP86). See kiht hõlbustab rahakottide vahelist ühilduvust, näidates indeksinumbreid, mis vastavad BIP numbritele.
Teisisõnu, kui teil on peamine võti ja peamine ahelakood, siis need toimivad vanemvõtmepaarina, et tuletada lapse võtmepaar. Kasutatav indeks selles tuletuses võib olla näiteks $/84'/$, kui rahakott on mõeldud kasutama SegWit v0 tüüpi skripte. See võtmepaar asub siis sügavusel 1. Selle roll ei ole bitcoine lukustada, vaid lihtsalt toimida vahepunktina tuletushierarhias.
**Sügavus 2: Valuuta Tüüp (BIP44)**
Sügavuselt 1 saadud võtmepaarist tehakse uus tuletus, et saada võtmepaar sügavusel 2. See sügavus võimaldab eristada Bitcoin'i kontosid teistest krüptovaluutadest samas rahakotis.
Igal valuutal on unikaalne indeks, et tagada ühilduvus mitme valuutaga rahakottide vahel. Näiteks Bitcoin'i puhul on indeks $/0'/$ (või `0x80000000` heksadesimaalnotatsioonis). Valuutaindeksid on valitud vahemikus $2^{31}$ kuni $2^{32}-1$, et tagada kõvastatud tuletus.
Teiste näidetena, siin on mõnede valuutade indeksid:
- $1'$ (`0x80000001`) testnet bitcoinide jaoks;
- $2'$ (`0x80000002`) Litecoin'i jaoks;
- $60'$ (`0x8000003c`) Ethereum'i jaoks...
**Sügavus 3: Konto (BIP32)**
Iga rahakott võib olla jaotatud mitmeks kontoks, nummerdatud alates $2^{31}$, ja esindatud sügavusel 3 $/0'/$ esimese konto jaoks, $/1'/$ teise ja nii edasi. Üldiselt, kui viidatakse laiendatud võtmele `xpub`, siis see viitab võtmetele selle tuletussügavuse juures.
See eraldamine erinevateks kontodeks on valikuline. Selle eesmärk on lihtsustada kasutajate jaoks rahakoti korraldamist. Praktikas kasutatakse sageli ainult ühte kontot, tavaliselt vaikimisi esimest. Siiski, mõnel juhul, kui soovitakse selgelt eristada võtmepaare erinevateks otstarveteks, võib see olla kasulik. Näiteks on võimalik luua isiklik ja professionaalne konto samast seemnest, täiesti eristuvate võtmegruppidega sellest tuletussügavusest.
**Sügavus 4: Ahel (BIP32)**
Sügavusel 3 määratletud iga konto struktureeritakse seejärel kahte ahelasse:
- **Väline ahel**: Selles ahelas tuletatakse nn "avalikud" aadressid. Need vastuvõtu aadressid on mõeldud UTXO-de lukustamiseks, mis pärinevad välistest tehingutest (st UTXO-de tarbimisest, mis ei kuulu teile). Lihtsalt öeldes kasutatakse seda välist ahelat alati, kui soovitakse bitcoine vastu võtta. Kui klõpsate oma rahakotitarkvaras "_vasta_", pakutakse teile alati aadressi välisest ahelast. See ahel on esindatud indeksiga $/0/$ tuletatud võtmepaariga.
- **Sisemine ahel (vahetus)**: See ahel on reserveeritud vastuvõtu aadressidele, mis lukustavad bitcoine, mis pärinevad teile kuuluvate UTXO-de tarbimisest, teisisõnu vahetusaadressid. See on tuvastatud indeksiga $/1/$.
**Sügavus 5: Aadressi Indeks (BIP32)**
Lõpuks, sügavus 5 esindab rahakoti tuletamise viimast sammu. Kuigi tehniliselt on võimalik jätkata lõputult, peatuvad praegused standardid siin. Selles viimases sügavuses tuletatakse võtmepaarid, mida tegelikult kasutatakse UTXO-de lukustamiseks ja avamiseks. Iga indeks võimaldab eristada üksteisest võtmepaare: seega esimene vastuvõttev aadress kasutab indeksit $/0/$, teine indeksit $/1/$ ja nii edasi.
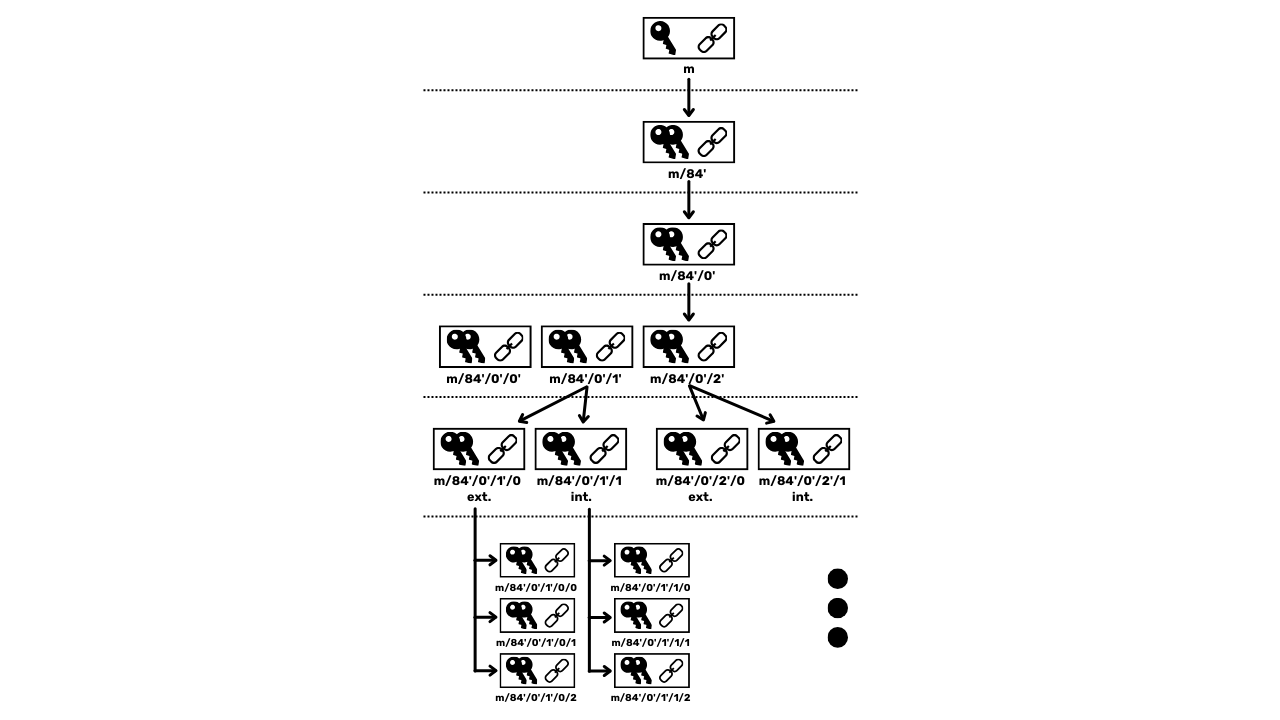
### Tuletamisteede Notatsioon
Tuletamistee on kirjutatud iga taseme eraldamisega kaldkriipsuga ($/$). Iga kaldkriips näitab seega vanema võtmepaari ($k_{\text{PAR}}$, $K_{\text{PAR}}$, $C_{\text{PAR}}$) tuletamist lapse võtmepaariks ($k_{\text{CHD}}$, $K_{\text{CHD}}$, $C_{\text{CHD}}$). Igal sügavusel märgitud number vastab indeksile, mida kasutatakse selle võtme tuletamiseks vanematelt. Apostroof ($'$), mis mõnikord asetatakse indeksi paremale küljele, näitab kõvendatud tuletamist ($k_{\text{CHD}}^h$, $K_{\text{CHD}}^h$). Mõnikord asendatakse see apostroof $h$-ga. Apostroofi või $h$ puudumisel on tegemist seega tavalise tuletamisega ($k_{\text{CHD}}^n$, $K_{\text{CHD}}^n$).
Nagu oleme eelmistes peatükkides näinud, algavad kõvendatud võtmeindeksid alates $2^{31}$ ehk `0x80000000` heksadesimaalselt. Seega, kui tuletamistee märgib indeksi järel apostroofi, tuleb näidatud numbrile lisada $2^{31}$, et saada HMAC-SHA512 funktsioonis kasutatav tegelik väärtus. Näiteks, kui tuletamistee määrab $/44'/$, on tegelik indeks:
i = 44 + 2^{31} = 2,147,483,692
Heksadesimaalselt on see `0x8000002C`.
Nüüd, kui oleme mõistnud tuletamisteede peamisi põhimõtteid, vaatame näidet! Siin on tuletamistee Bitcoin'i vastuvõtva aadressi jaoks:
m / 84' / 0' / 1' / 0 / 7
Selles näites:
- $84'$ näitab P2WPKH (SegWit v0) standardit;
- $0'$ näitab Bitcoin'i valuutat peavõrgus;
- $1'$ vastab rahakoti teisele kontole;
- $0$ näitab, et aadress asub välisel ketil;
- $7$ näitab selle konto 8. välist aadressi.
### Tuletamisstruktuuri Kokkuvõte
| Sügavus | Kirjeldus | Standardnäide |
| ------- | --------------- | --------------------------------- |
| 0 | Peavõti | $m/$ |
| 1 | Eesmärk | $/86'/$ (P2TR) |
| 2 | Valuuta | $/0'/$ (Bitcoin) |
| 3 | Konto | $/0'/$ (Esimene konto) |
| 4 | Kett | $/0/$ (väline) või $/1/$ (muutus) |
| 5 | Aadressi Indeks | $/0/$ (esimene aadress) |
Järgmises peatükis avastame, mis on "_väljundskripti kirjeldajad_" (output script descriptors), mis on hiljuti tutvustatud uuendus Bitcoin Core'is, mis lihtsustab Bitcoin'i rahakoti varundamist.
## Väljundskripti kirjeldajad
<chapterId>e4f1c2d3-9b8a-4d3e-8f2a-7b6c5d4e3f2a</chapterId>
Teile on sageli öeldud, et mnemooniline fraas üksi on piisav, et taastada juurdepääs rahakotile. Tegelikkuses on asjad natuke keerulisemad. Eelmises peatükis vaatasime HD rahakoti tuletusstruktuuri ja võisite märgata, et see protsess on üsna keeruline. Tuletusteed ütlevad tarkvarale, millist suunda järgida kasutaja võtmete tuletamiseks. Kuid Bitcoin'i rahakoti taastamisel, kui neid teid ei teata, ei piisa ainult mnemoonilisest fraasist. See võimaldab saada peavõtme ja peamise ahelakoodi, kuid siis on vajalik teada indekseid, et jõuda lastevõtmeteni.
Teoreetiliselt oleks vajalik salvestada mitte ainult meie rahakoti mnemooniline fraas, vaid ka kontodele, mida kasutame, viivad teed. Praktikas on sageli võimalik lastevõtmetele juurdepääs taastada ilma selle teabeta, eeldusel, et on järgitud standardeid. Testides iga standardit ükshaaval, on üldiselt võimalik bitcoine'idele juurdepääs taastada. Siiski ei ole see garanteeritud ja eriti keeruline algajatele. Lisaks, skriptitüüpide mitmekesistumise ja keerukamate konfiguratsioonide ilmnemisega võib see teave muutuda raskesti ekstrapoleeritavaks, muutes selle andmed privaatseks teabeks ja raskesti taastatavaks jõuga. Seetõttu on hiljuti tutvustatud uuendust, mis hakkab olema integreeritud teie lemmik rahakott tarkvarasse: _väljundskripti kirjeldajad_.
### Mis on "kirjeldaja"?
"_Väljundskripti kirjeldajad_", või lihtsalt "_kirjeldajad_", on struktureeritud väljendid, mis kirjeldavad täielikult väljundskripti (_scriptPubKey_) ja annavad kõik vajaliku teabe, et jälgida tehinguid, mis on seotud konkreetse skriptiga. Need hõlbustavad võtmete haldamist HD rahakottides, pakkudes standardiseeritud ja täielikku kirjeldust rahakoti struktuurist ja kasutatud aadressitüüpidest.
Kirjeldajate peamine eelis seisneb nende võimes kapseldada kõik oluline teave rahakoti taastamiseks ühte stringi (lisaks taastefraasile). Salvestades kirjeldaja koos seotud mnemooniliste fraasidega, muutub võimalikuks taastada privaatvõtmed, teades täpselt nende asukohta hierarhias. Multisig rahakottide jaoks, mille varundamine oli algselt keerulisem, sisaldab kirjeldaja iga faktori `xpub`, tagades seeläbi aadresside regenereerimise võimaluse probleemi korral.
### Kirjeldaja konstruktsioon
Kirjeldaja koosneb mitmest elemendist:
- Skriptifunktsioonid nagu `pk` (_Pay-to-PubKey_), `pkh` (_Pay-to-PubKey-Hash_), `wpkh` (_Pay-to-Witness-PubKey-Hash_), `sh` (_Pay-to-Script-Hash_), `wsh` (_Pay-to-Witness-Script-Hash_), `tr` (_Pay-to-Taproot_), `multi` (_Mitmeallkirjaga_), ja `sortedmulti` (_Sorteeritud võtmetega mitmeallkirjaga_);
- Tuletusteed, näiteks `[d34db33f/44h/0h/0h]`, mis näitab tuletatud konto teed ja konkreetse peavõtme sõrmejälge;
- Võtmed erinevates formaatides nagu heksadetsimaalsed avalikud võtmed või laiendatud avalikud võtmed (`xpub`);
- Kontrollsumma, mida eelneb räsimärk, et kontrollida kirjeldaja terviklikkust.
Näiteks P2WPKH (SegWit v0) rahakoti kirjeldus võib välja näha selline:
```text
wpkh([cdeab12f/84h/0h/0h]xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U/<0;1>/*)#jy0l7nr4
```
Selles kirjelduses tähistab tuletusfunktsioon `wpkh` skripti tüüpi _Maksa tunnistaja avaliku võtme räsi_. Sellele järgneb tuletustee, mis sisaldab:
- `cdeab12f`: peamise võtme sõrmejälge;
- `84h`: mis tähistab BIP84 eesmärgi kasutamist, mis on mõeldud SegWit v0 aadresside jaoks;
- `0h`: mis näitab, et tegemist on BTC valuutaga peavõrgus;
- `0h`: mis viitab rahakotis kasutatavale konkreetsele kontonumbrile.
Kirjeldus sisaldab ka selles rahakotis kasutatavat laiendatud avalikku võtit:
```text
xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U
```
Järgmine märge `/<0;1>/*` täpsustab, et kirjeldus võib genereerida aadresse väliselt ketilt (`0`) ja sisemiselt ketilt (`1`), kasutades metamärki (`*`), mis võimaldab mitme aadressi järjestikust tuletamist konfigureeritaval viisil, sarnaselt traditsioonilise rahakotitarkvara "gap limit" haldamisega.
Lõpuks tähistab `#jy0l7nr4` kontrollsummat, mis kinnitab kirjelduse terviklikkust.
Nüüd teate kõike HD rahakoti toimimisest Bitcoinis ja võtmepaaride tuletamise protsessist. Siiski viimastes peatükkides piirdusime privaat- ja avalike võtmete genereerimisega, jättes käsitlemata vastuvõtu aadresside konstrueerimise. Just see saab olema järgmise peatüki teema!
## Vastuvõtu Aadressid
<chapterId>ca80a89d-f8da-4e09-8c35-43179b65bced</chapterId>
Vastuvõtu aadressid on teabe killud, mis on sisestatud _scriptPubKey_'sse, et lukustada äsja loodud UTXOsid. Lihtsalt öeldes on aadress mõeldud bitcoinide vastuvõtmiseks. Uurime nende toimimist seoses sellega, mida oleme eelmistes peatükkides õppinud.
### Bitcoinide Aadresside Roll Skriptides
Nagu varem selgitatud, on tehingu eesmärk üle kanda bitcoinide omandiõigus sisenditest väljunditesse. See protsess hõlmab UTXOde tarbimist sisenditena, luues samal ajal uusi UTXOsid väljunditena. Neid UTXOsid kaitsevad skriptid, mis määratlevad vajalikud tingimused vahendite vabastamiseks.
Kui kasutaja saab bitcoine, loob saatja väljundi UTXO ja lukustab selle _scriptPubKey_ abil. See skript sisaldab tavaliselt reegleid, mis täpsustavad allkirju ja avalikke võtmeid, mis on vajalikud selle UTXO avamiseks. Selle UTXO kulutamiseks uues tehingus peab kasutaja esitama nõutud teabe _scriptSig_ kaudu. _scriptSig_ täitmine koos _scriptPubKey_-ga peab tagastama "true" või `1`. Kui see tingimus on täidetud, saab UTXO kulutada uue UTXO loomiseks, mis omakorda lukustatakse uue _scriptPubKey_-ga, ja nii edasi.

Täpselt _scriptPubKey_-s leitakse vastuvõtvad aadressid. Siiski, nende kasutamine varieerub sõltuvalt kasutatavast skripti standardist. Siin on kokkuvõttev tabel teabest, mis sisaldub _scriptPubKey_-s vastavalt kasutatud standardile, samuti teabest, mida oodatakse _scriptSig_-s, et avada _scriptPubKey_.
| Standard | _scriptPubKey_ | _scriptSig_ | _redeem script_ | _witness_ |
| ------------------ | ----------------------------------------------------------- | ------------------------------- | ---------------- | ---------------------------------------- |
| P2PK | `<pubkey> OP_CHECKSIG` | `<signature>` | | |
| P2PKH | `OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG` | `<signature> <public key>` | | |
| P2SH | `OP_HASH160 <scriptHash> OP_EQUAL` | `<data pushes> <redeem script>` | Suvalised andmed | |
| P2WPKH | `0 <pubKeyHash>` | | | `<signature> <public key>` |
| P2WSH | `0 <witnessScriptHash>` | | | `<data pushes> <witness script>` |
| P2SH-P2WPKH | `OP_HASH160 <redeemScriptHash> OP_EQUAL` | `<redeem script>` | `0 <pubKeyHash>` | `<signature> <public key>` |
| P2SH-P2WSH | `OP_HASH160 <redeemScriptHash> OP_EQUAL` | `<redeem script>` | `0 <scriptHash>` | `<data pushes> <witness script>` |
| P2TR (key path) | `1 <public key>` | | | `<signature>` |
| P2TR (script path) | `1 <public key>` | | | `<data pushes> <script> <control block>` |
_Allikas: Bitcoin Core PR review club, 7. juuli 2021 - Gloria Zhao_
Skriptis kasutatavad operaatorid on mõeldud teabe manipuleerimiseks ja vajadusel selle võrdlemiseks või testimiseks. Võtame näiteks P2PKH skripti, mis on järgmine:
```text
OP_DUP OP_HASH160 OP_PUSHBYTES_20 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG
```
Nagu me selles peatükis näeme, esindab `<pubKeyHash>` tegelikult vastuvõtva aadressi koormust, mida kasutatakse UTXO lukustamiseks. Selle _scriptPubKey_ avamiseks on vajalik esitada _scriptSig_, mis sisaldab:
```text
<signature> <public key>
```
Skriptikeeles on "stack" (lükkamisega ja võtmisega andmestruktuur) "_LIFO_" ("_Last In, First Out_") andmestruktuur, mida kasutatakse elementide ajutiseks salvestamiseks skripti täitmise ajal. Iga skripti toiming manipuleerib seda stacki, kus elemente saab lisada (_push_) või eemaldada (_pop_). Skriptid kasutavad neid stacke avaldiste hindamiseks, ajutiste muutujate salvestamiseks ja tingimuste haldamiseks.
Antud näite skripti täitmine järgib seda protsessi:
- Meil on _scriptSig_, _ScriptPubKey_ ja stack:

- _scriptSig_ lükatakse stackile:

- `OP_DUP` dubleerib stackil oleva _scriptSig_-is esitatud avaliku võtme:

- `OP_HASH160` tagastab just dubleeritud avaliku võtme räsi:
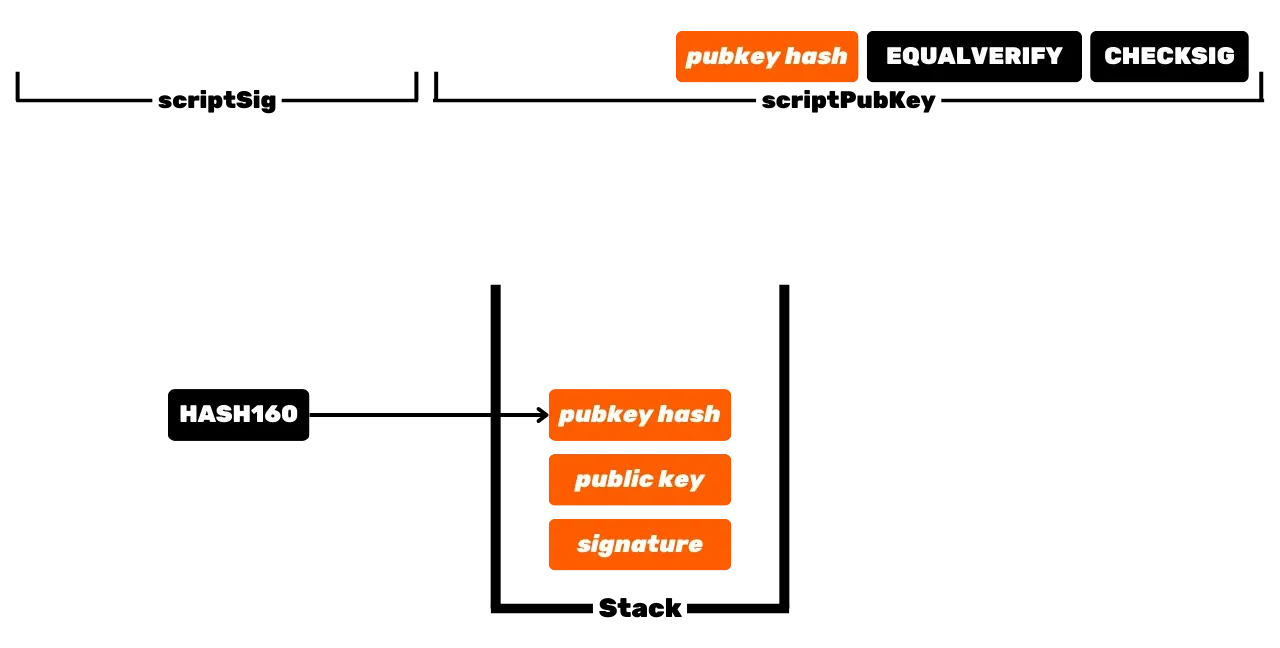
- `OP_PUSHBYTES_20 <pubKeyHash>` lükkab _scriptPubKey_-is sisalduva Bitcoini aadressi stackile:

- `OP_EQUALVERIFY` kontrollib, kas räsitud avalik võti vastab esitatud saaja aadressile:

`OP_CHECKSIG` kontrollib _scriptSig_-is sisalduvat allkirja kasutades avalikku võtit. See operatsioonikood teostab põhimõtteliselt allkirja kontrollimist, nagu kirjeldasime selle koolituse 3. osas:

- Kui stackil jääb alles `1`, siis on skript kehtiv:
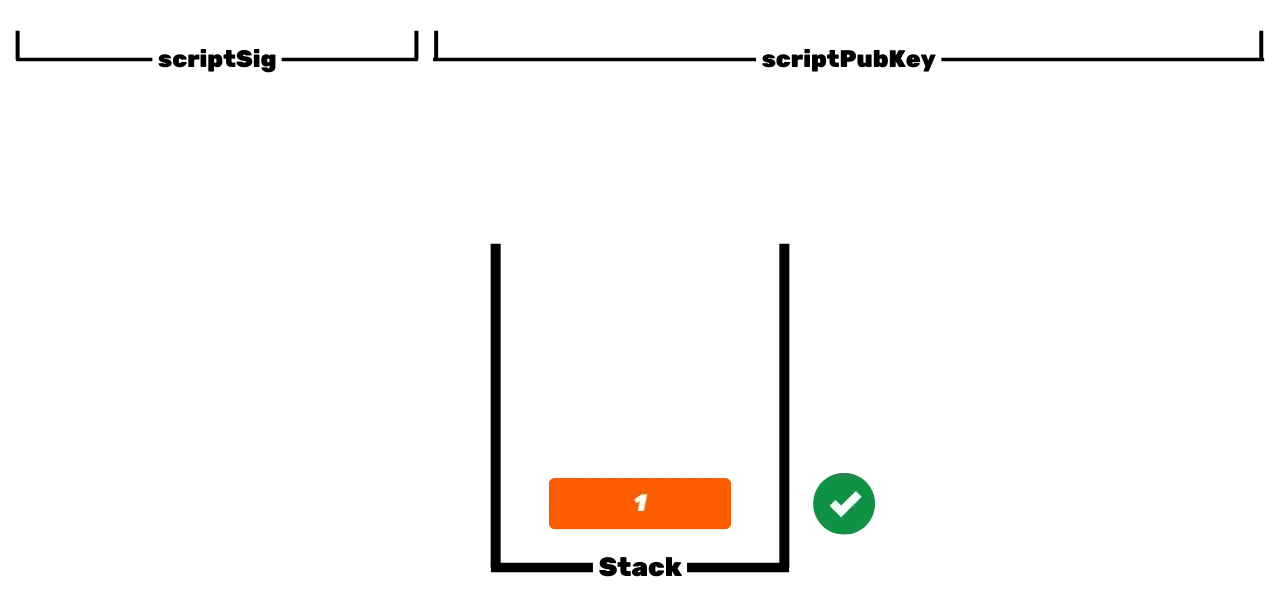
Kokkuvõtteks, see skript võimaldab digitaalse allkirja abil kontrollida, et kasutaja, kes väidab end olevat selle UTXO omanik ja soovib seda kulutada, tõepoolest omab saaja aadressiga seotud privaatvõtit, mida kasutati selle UTXO loomisel.
### Erinevad Bitcoini aadresside tüübid
Bitcoini arengu käigus on lisatud mitu standardset skriptimudelit. Igaüks neist kasutab erinevat tüüpi saaja aadressi. Siin on ülevaade peamistest praegu saadaolevatest skriptimudelitest:
**P2PK (_Pay-to-PubKey_)**:
See skriptimudel tutvustati Bitcoini esimeses versioonis Satoshi Nakamoto poolt. P2PK skript lukustab bitcoinid otse kasutades toorest avalikku võtit (seega, selle mudeliga ei kasutata saaja aadressi). Selle struktuur on lihtne: see sisaldab avalikku võtit ja nõuab vastavat digitaalset allkirja vahendite vabastamiseks. See skript kuulub "_Legacy_" standardi hulka.
**P2PKH (_Pay-to-PubKey-Hash_)**:
Nagu P2PK, tutvustati P2PKH skripti Bitcoini käivitamisel. Erinevalt eelkäijast lukustab see bitcoinid kasutades avaliku võtme räsi, mitte otse toorest avalikku võtit. _scriptSig_ peab seejärel esitama saaja aadressiga seotud avaliku võtme, samuti kehtiva allkirja. Selle mudeli aadressid algavad `1`-ga ja on kodeeritud _base58check_-is. See skript kuulub samuti "_Legacy_" standardi hulka.
**P2SH (_Pay-to-Script-Hash_)**:
2012.aastal BIP16-ga tutvustatud P2SH mudel võimaldab kasutada suvalise skripti räsi _scriptPubKey_-s. Seda räsitud skripti, mida nimetatakse "_redeemScript_-iks", sisaldavad tingimused vahendite vabastamiseks. UTXO kulutamiseks, mis on lukustatud P2SH-ga, on vajalik esitada _scriptSig_, mis sisaldab algset _redeemScript_-i ning vajalikke andmeid selle valideerimiseks. Seda mudelit kasutatakse märkimisväärselt vanade multisigide jaoks. P2SH-ga seotud aadressid algavad `3`-ga ja on kodeeritud _base58check_-is. See skript kuulub ka "_Legacy_" standardi alla.
**P2WPKH (_Pay-to-Witness-PubKey-Hash_)**:
See skript on sarnane P2PKH-ga, kuna see samuti lukustab bitcoine avaliku võtme räsi kasutades. Siiski, erinevalt P2PKH-st, on _scriptSig_ viidud eraldi sektsiooni nimega "_Witness_". Seda nimetatakse mõnikord "_scriptWitness_-iks", et tähistada allkirja ja avaliku võtme komplekti. Igal SegWit sisendil on oma _scriptWitness_, ja _scriptWitness_-ide kogum moodustab tehingu _Witness_ välja. Allkirjaandmete selline liigutamine on uuendus, mida tutvustati SegWit uuendusega, eesmärgiga eriti vältida tehingute muudetavust ECDSA allkirjade tõttu.
P2WPKH aadressid kasutavad _bech32_ kodeeringut ja algavad alati `bc1q`. See skripti tüüp vastab versioon 0 SegWit väljunditele.
**P2WSH (_Pay-to-Witness-Script-Hash_)**:
P2WSH mudel tutvustati samuti SegWit uuendusega augustis 2017. Sarnaselt P2SH mudelile, lukustab see bitcoine skripti räsi kasutades. Peamine erinevus seisneb selles, kuidas allkirjad ja skriptid on tehingusse lisatud. Bitcoine, mis on lukustatud sellise skriptiga, kulutamiseks peab saaja esitama algse skripti, mida nimetatakse _witnessScript_-iks (võrdne _redeemScript_-iga P2SH-s), koos vajalike andmetega selle _witnessScript_-i valideerimiseks. See mehhanism võimaldab keerukamate kulutamistingimuste rakendamist, nagu multisigid.
P2WSH aadressid kasutavad _bech32_ kodeeringut ja algavad alati `bc1q`. See skript vastab samuti versioon 0 SegWit väljunditele.
**P2TR (_Pay-to-Taproot_)**:
P2TR mudel tutvustati Taprooti rakendamisega novembris 2021. See põhineb Schnorri protokollil krüptograafilise võtme agregatsiooni jaoks, samuti MAST-il (_Merkelized Alternative Script Tree_) alternatiivsete skriptide jaoks. Erinevalt teistest skripti tüüpidest, kus kulutamistingimused on avalikult nähtavad (kas vastuvõtmisel või kulutamisel), võimaldab P2TR keerukate skriptide peitmist ühe näilise avaliku võtme taha.
Tehniliselt lukustab P2TR skript bitcoine unikaalse Schnorri avaliku võtmega, mida tähistatakse kui $Q$. See võti $Q$ on tegelikult avaliku võtme $P$ ja avaliku võtme $M$ agregaat, viimane arvutatakse _scriptPubKey_-de Merkle juurest. Bitcoine, mis on lukustatud sellise skriptiga, saab kulutada kahel viisil:
- Avaldades allkirja avaliku võtme $P$ jaoks (_key path_).
- Täites ühe skriptidest, mis sisalduvad Merkle puus (_script path_).
P2TR pakub suurt paindlikkust, kuna see võimaldab bitcoine lukustada kas unikaalse avaliku võtmega, mitme valitud skriptiga või mõlemaga korraga. Selle Merkle puu struktuuri eelis on see, et tehingu ajal paljastatakse ainult kasutatud kulutamise skript, kuid kõik teised alternatiivsed skriptid jäävad saladuseks.
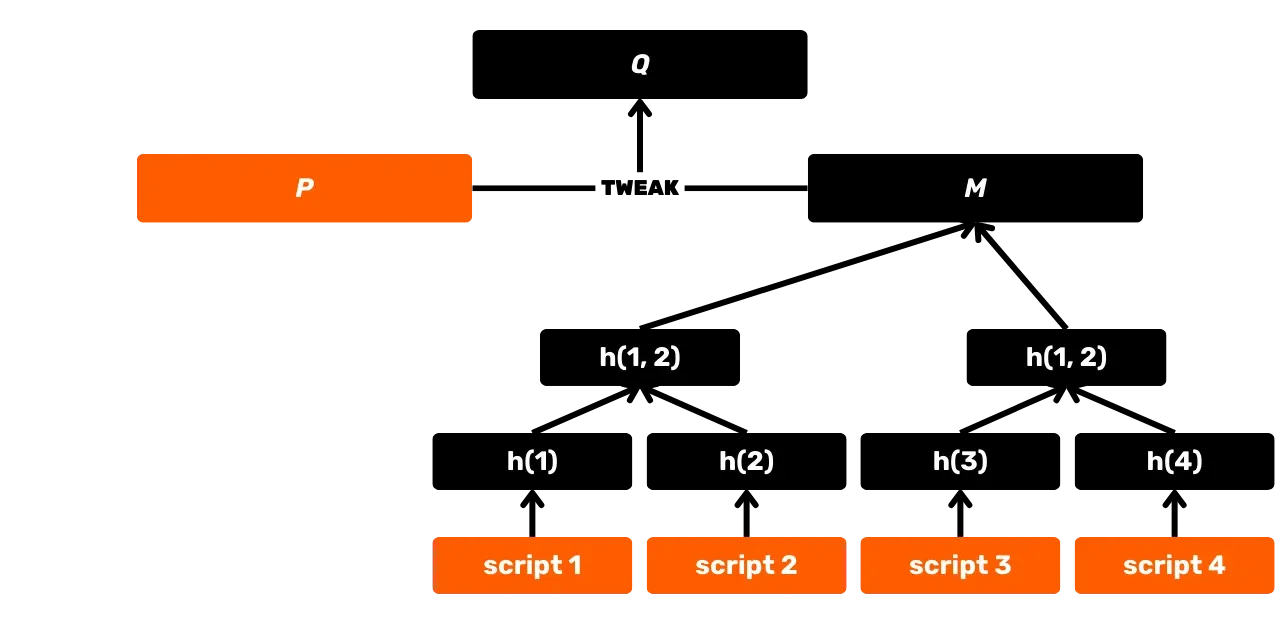
P2TR vastab versiooni 1 SegWit väljunditele, mis tähendab, et P2TR sisendite allkirjad salvestatakse tehingu _Witness_ sektsiooni, mitte _scriptSig_-i. P2TR aadressid kasutavad _bech32m_ kodeeringut ja algavad `bc1p`-ga, kuid need on üsna unikaalsed, kuna nende konstrueerimiseks ei kasutata räsi funktsiooni. Tegelikult esindavad nad otse avalikku võtit $Q$, mis on lihtsalt vormindatud metateabega. Seega on see skripti mudel lähedane P2PK-le.
Nüüd, kui oleme teooria läbi käinud, liigume praktika juurde! Järgmises peatükis pakun välja nii SegWit v0 aadressi kui ka SegWit v1 aadressi tuletamise võtmepaarist.
## Aadressi Tuletamine
<chapterId>3ebdc750-4135-4881-b07e-08965941b93e</chapterId>
Uurime koos, kuidas genereerida vastuvõtu aadress võtmepaarist, mis asub näiteks HD rahakoti sügavusel 5. Seda aadressi saab seejärel kasutada rahakotitarkvaras UTXO lukustamiseks.
Kuna aadressi genereerimise protsess sõltub vastuvõetud skripti mudelist, keskendume kahele konkreetsele juhtumile: SegWit v0 aadressi genereerimine P2WPKH-s ja SegWit v1 aadressi genereerimine P2TR-s. Need kaks aadressitüüpi hõlmavad tänapäeval valdavat enamust kasutusjuhtudest.
### Avaliku Võtme Kompressioon
Pärast kõigi tuletamisetappide sooritamist meistervõtmest sügavusele 5, kasutades sobivaid indekseid, saame võtmepaari ($k$, $K$), kus $K = k \cdot G$. Kuigi on võimalik kasutada seda avalikku võtit sellisena, nagu see on, vahendite lukustamiseks P2PK standardi järgi, ei ole see meie siin eesmärk. Selle asemel on meie eesmärk esmalt luua aadress P2WPKH-s ja seejärel P2TR-s teise näitena.
Esimene samm on avaliku võtme $K$ kompressioon. Selle protsessi mõistmiseks meenutagem kõigepealt mõningaid põhitõdesid, mida käsitleti osas 3.
Bitcoinis on avalik võti punkt $K$, mis asub elliptilisel kõveral. See on esitatud kujul $(x, y)$, kus $x$ ja $y$ on punkti koordinaadid. Oma lahtipakitud kujul mõõdab see avalik võti 520 bitti: 8 bitti prefiksi jaoks (algväärtus `0x04`), 256 bitti $x$ koordinaadi jaoks ja 256 bitti $y$ koordinaadi jaoks.
Siiski, elliptilistel kõveratel on sümmeetriaomadus x-telje suhtes: antud $x$ koordinaadi jaoks on $y$ jaoks võimalikud ainult kaks väärtust: $y$ ja $-y$. Need kaks punkti asuvad x-telje mõlemal küljel. Teisisõnu, kui me teame $x$, piisab sellest, kui määrata, kas $y$ on paaris või paaritu, et tuvastada täpne punkt kõveral.
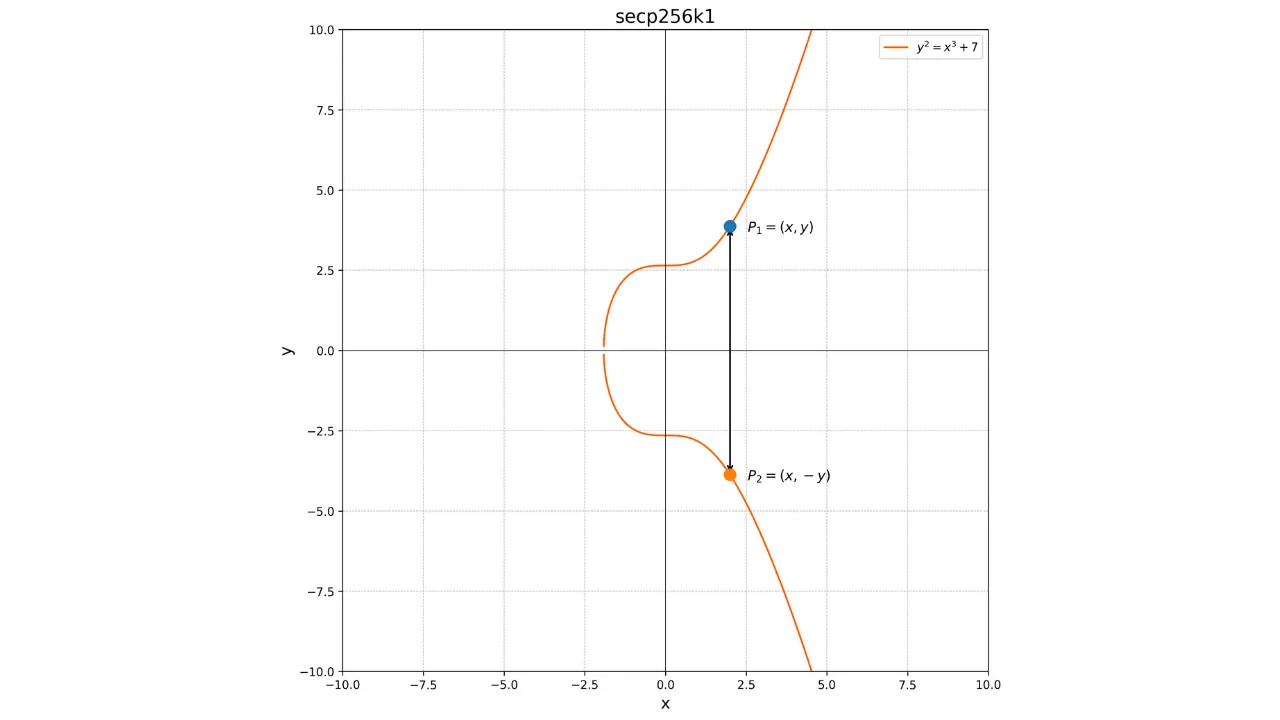
Avaliku võtme kokkusurumiseks kodeeritakse ainult $x$, mis hõivab 256 bitti, ja lisatakse prefiks, et määrata $y$ paarsus. See meetod vähendab avaliku võtme suurust 264 bitini algse 520 asemel. Prefiks `0x02` näitab, et $y$ on paaris, ja prefiks `0x03` näitab, et $y$ on paaritu.
Vaatame näidet, et paremini aru saada, kasutades toorest avalikku võtit kokkusurumata esituses:
```text
K = 04678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f
```
Kui me selle võtme lahti võtame, on meil:
- Prefiks: `04`;
- $x$: `678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6`;
- $y$: `49f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f`
$y$ viimane heksadesimaalne tähemärk on `f`. Kümnendsüsteemis `f = 15`, mis vastab paaritule numbrile. Seega on $y$ paaritu ja prefiksiks saab `0x03`, et seda näidata.
Kokkusurutud avalik võti saab olema:
```text
K = 03678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6
```
See toiming kehtib kõigi ECDSA-l põhinevate skriptimudelite kohta, välja arvatud P2TR, mis kasutab Schnorri. Schnorri puhul, nagu selgitati osas 3, säilitame ainult $x$ väärtuse, lisamata prefiksit, et näidata $y$ paarsust, erinevalt ECDSA-st. See on võimalik, kuna kõigi võtmete jaoks on suvaliselt valitud ainulaadne paarsus. See võimaldab avalike võtmete salvestusruumi veidi vähendada.
### SegWit v0 (bech32) aadressi tuletamine
Nüüd, kui oleme saanud oma kokkusurutud avaliku võtme, saame sellest tuletada SegWit v0 vastuvõtu aadressi.
Esimene samm on rakendada kokkusurutud avalikule võtmele HASH160 räsifunktsiooni. HASH160 on kahe järjestikuse räsifunktsiooni kompositsioon: SHA256, millele järgneb RIPEMD160:
\text{HASH160}(K) = \text{RIPEMD160}(\text{SHA256}(K))
Esmalt läbib võti SHA256:
```text
SHA256(K) = C489EBD66E4103B3C4B5EAFF462B92F5847CA2DCE0825F4997C7CF57DF35BF3A
```
Seejärel läbib tulemus RIPEMD160:
```text
RIPEMD160(SHA256(K)) = 9F81322CC88622CA4CCB2A52A21E2888727AA535
```
Me oleme saanud 160-bitise räsi avalikust võtmest, mis moodustab nn aadressi sisu (payload). See sisu esindab aadressi keskset ja kõige olulisemat osa. Samuti kasutatakse seda _scriptPubKey_'s, et lukustada UTXOd.
Siiski, et muuta see sisu inimestele kergemini kasutatavaks, lisatakse sellele metaandmed. Järgmine samm hõlmab selle räsi kodeerimist 5-bitisteks rühmadeks kümnendsüsteemis. See kümnendkood muutub kasulikuks muundamisel _bech32_-ks, mida kasutatakse post-SegWit aadressidel. 160-bitine binaarne räsi jagatakse seega 32 rühmaks, millest igaüks on 5 bitti:
\begin{array}{|c|c|} \hline \text{5 bits} & \text{Decimal} \ \hline 10011 & 19 \ 11110 & 30 \ 00000 & 0 \ 10011 & 19 \ 00100 & 4 \ 01011 & 11 \ 00110 & 6 \ 01000 & 8 \ 10000 & 16 \ 11000 & 24 \ 10001 & 17 \ 01100 & 12 \ 10100 & 20 \ 10011 & 19 \ 00110 & 6 \ 01011 & 11 \ 00101 & 5 \ 01001 & 9 \ 01001 & 9 \ 01010 & 10 \ 00100 & 4 \ 00111 & 7 \ 10001 & 17 \ 01000 & 8 \ 10001 & 17 \ 00001 & 1 \ 11001 & 25 \ 00111 & 7 \ 10101 & 21 \ 00101 & 5 \ 00101 & 5 \ 10101 & 21 \ \hline \end{array}
Niisiis, meil on:
```text
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
```
Kui räsi on kodeeritud 5-bitisteks rühmadeks, lisatakse aadressile kontrollsumma. Seda kontrollsummat kasutatakse selleks, et kinnitada, et aadressi sisu ei ole selle salvestamise või edastamise ajal muudetud. Näiteks võimaldab see rahakottide tarkvaral veenduda, et te ei ole sisestades saaja aadressi trükiviga teinud. Ilma selle kontrollita võiksite kogemata saata bitcoine valele aadressile, põhjustades vahendite pöördumatu kaotuse, kuna te ei oma seotud avalikku ega privaatvõtit. Seega on kontrollsumma kaitse inimlike eksimuste vastu.
Vanade Bitcoin _Legacy_ aadresside puhul arvutati kontrollsumma lihtsalt aadressi räsi algusest HASH256 funktsiooni abil. SegWit'i ja _bech32_ formaadi tutvustamisega kasutatakse nüüd BCH koode (_Bose, Ray-Chaudhuri ja Hocquenghem_). Neid veaparanduskoode kasutatakse andmejärjestuste vigade tuvastamiseks ja parandamiseks. Need tagavad, et edastatud teave jõuab sihtkohta terviklikult, isegi väikeste muudatuste korral. BCH koode kasutatakse paljudes valdkondades, nagu SSD-d, DVD-d ja QR-koodid. Näiteks tänu nendele BCH koodidele saab osaliselt varjatud QR-koodi siiski lugeda ja dekodeerida.
Bitcoin'i kontekstis pakuvad BCH koodid paremat kompromissi suuruse ja veatuvastusvõime vahel võrreldes lihtsate räsi funktsioonidega, mida kasutatakse _Legacy_ aadresside jaoks. Siiski, Bitcoin'is kasutatakse BCH koode ainult veatuvastuseks, mitte parandamiseks. Seega rahakottide tarkvara annab märku valest saaja aadressist, kuid ei paranda seda automaatselt. See piirang on tahtlik: automaatse parandamise lubamine vähendaks veatuvastusvõimet.
Kontrollsumma arvutamiseks BCH koodidega peame ette valmistama mitu elementi:
- **Inimloetav osa (HRP)**: Bitcoin'i peamise võrgu jaoks on HRP `bc`;
HRP tuleb laiendada, eraldades iga tähemärgi kaheks osaks:
- Võttes HRP tähemärgid ASCII kujul:
- `b`: `01100010`
- `c`: `01100011`
- Eraldades 3 kõige olulisemat bitti ja 5 vähem olulist bitti:
- 3 kõige olulisemat bitti: `011` (3 kümnendsüsteemis)
- 3 kõige olulisemat bitti: `011` (3 kümnendsüsteemis)
- 5 vähem olulist bitti: `00010` (2 kümnendsüsteemis)
- 5 vähem olulist bitti: `00011` (3 kümnendsüsteemis)
Kahe tähemärgi vahelise eraldajaga `0` on HRP laiendus seega:
```text
03 03 00 02 03
```
- **Tunnistaja versioon**: SegWit versiooni 0 jaoks on see `00`;
- **Koormus (payload)**: Avaliku võtme räsi kümnendarvud;
- **Kontrollsumma reserveerimine**: Lisame jada lõppu kuus nulli `[0, 0, 0, 0, 0, 0]`.
Kõik programmi sisestamiseks kombineeritud andmed kontrollsumma arvutamiseks on järgmised:
```text
HRP = 03 03 00 02 03
SEGWIT v0 = 00
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
CHECKSUM = 00 00 00 00 00 00
INPUT = 03 03 00 02 03 00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 00 00 00 00 00 00
```
Kontrollsumma arvutamine on üsna keeruline. See hõlmab polünoomide lõpliku välja aritmeetikat. Me ei kirjelda seda arvutust siin detailsemalt ja liigume otse tulemuse juurde. Meie näites saadud kontrollsumma kümnendsüsteemis on:
```text
10 16 11 04 13 18
```
Nüüd saame konstrueerida vastuvõtu aadressi, järjestades järgmised elemendid:
- **SegWit versioon**: `00`
- **Koormus (payload)**: Avaliku võtme räsi
- **Kontrollsumma**: Eelmises etapis saadud väärtused (`10 16 11 04 13 18`)
See annab meile kümnendsüsteemis:
```text
00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 10 16 11 04 13 18
```
Seejärel tuleb iga kümnendarv kaardistada vastavale _bech32_ tähemärgile, kasutades järgmist konversioonitabelit:
\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \ \hline +0 & q & p & z & r & y & 9 & x & 8 \ \hline +8 & g & f & 2 & t & v & d & w & 0 \ \hline +16 & s & 3 & j & n & 5 & 4 & k & h \ \hline +24 & c & e & 6 & m & u & a & 7 & l \ \hline \end{array}
Väärtuse teisendamiseks _bech32_ tähemärgiks kasutades seda tabelit, tuleb lihtsalt leida väärtused esimeses veerus ja esimeses reas, mis kokku liidetuna annavad soovitud tulemuse. Seejärel tuleb leida vastav tähemärk. Näiteks kümnendarv `19` teisendatakse täheks `n`, sest $19 = 16 + 3$.
Kõigi meie väärtuste kaardistamisel saame järgmise aadressi:
```
qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj
```
Jääb üle lisada HRP `bc`, mis näitab, et tegemist on Bitcoin'i peamise võrgu aadressiga, samuti eraldaja `1`, et saada täielik vastuvõtu aadress:
```
bc1qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj
```
Selle _bech32_ tähestiku eripära on see, et see sisaldab kõiki tähestiku ja numbrite tähemärke, välja arvatud `1`, `b`, `i` ja `o`, et vältida visuaalset segadust sarnaste tähemärkide vahel, eriti nende sisestamisel või inimeste poolt lugemisel.
Kokkuvõtteks, siin on tuletusprotsess:
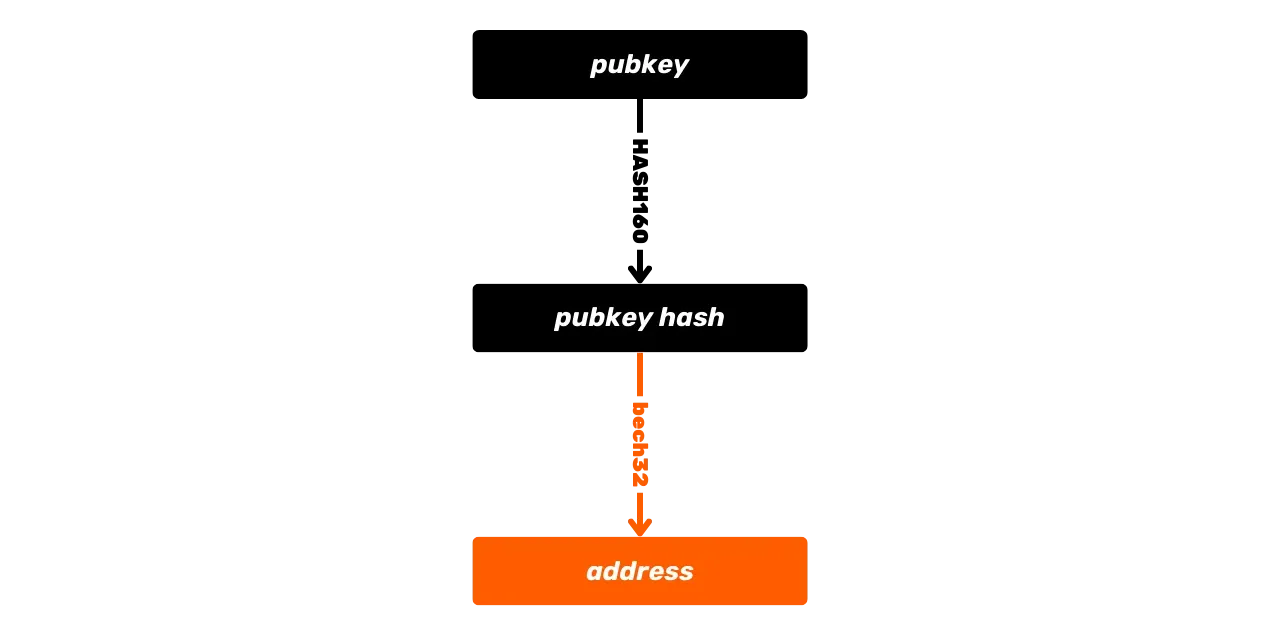
Nii tuletatakse P2WPKH (SegWit v0) vastuvõtu aadress võtmepaarist. Liikugem nüüd edasi P2TR (SegWit v1 / Taproot) aadresside juurde ja uurigem nende genereerimise protsessi.
### SegWit v1 (bech32m) aadressi tuletamine
Taproot aadresside puhul erineb genereerimise protsess veidi. Vaatame seda koos!
Avaliku võtme kompressiooni sammust alates ilmneb esimene erinevus võrreldes ECDSA-ga: Bitcoinis Schnorri jaoks kasutatavad avalikud võtmed on esindatud ainult nende abskissiga ($x$). Seega pole eesliidet ja kompressitud võti on täpselt 256 bitti.
Nagu eelmises peatükis nägime, lukustab P2TR skript bitcoine unikaalse Schnorri avaliku võtmega, mida tähistatakse $Q$-ga. See võti $Q$ on kahe avaliku võtme agregaat: $P$, peamine sisemine avalik võti, ja $M$, avalik võti, mis on tuletatud Merkle'i juurest _scriptPubKey_ nimekirjast. Sellise skriptiga lukustatud bitcoinid saab kulutada kahel viisil:
- Avaldades allkirja avaliku võtme $P$ jaoks (_võtmee tee_);
- Rahuldades ühe Merkle'i puus sisalduva skripti (_skripti tee_).
Tegelikkuses neid kahte võtit päriselt "agregeeritud" ei ole. Võtit $P$ muudetakse selle asemel võtmega $M$. Krüptograafias tähendab avaliku võtme "tweakimine" selle võtme muutmist, rakendades lisaväärtust, mida nimetatakse "tweakiks". See toiming võimaldab muudetud võtit jääda ühilduvaks algse privaatvõtme ja tweakiga. Tehniliselt on tweak skalaarväärtus $t$, mis lisatakse algsele avalikule võtmele. Kui $P$ on algne avalik võti, siis muudetud võti saab olema:
P' = P + tG
Kus $G$ on kasutatava elliptilise kõvera generaator. See toiming toodab uue avaliku võtme, mis on tuletatud algsest võtmest, säilitades samal ajal krüptograafilised omadused, mis võimaldavad selle kasutamist.
Kui te ei pea lisama alternatiivseid skripte (kulutades ainult _võtmeele_), saate genereerida Taproot aadressi, mis põhineb ainult avalikul võtmel, mis asub teie rahakoti sügavusel 5. Sellisel juhul on vajalik luua mittekulutatav skript _skriptiteele_, et rahuldada struktuuri nõudeid. Korrigeerimine $t$ arvutatakse rakendades märgistatud räsifunktsiooni, **`TapTweak`**, sisemisele avalikule võtmele $P$:
t = \text{H}_{\text{TapTweak}}(P)
kus:
- **$\text{H}_{\text{TapTweak}}$** on SHA256 räsifunktsioon, mis on märgistatud sildiga `TapTweak`. Kui te ei ole tuttav, mis on märgistatud räsifunktsioon, siis soovitan teil tutvuda peatükiga 3.3;
- $P$ on sisemine avalik võti, esitatud oma komprimeeritud 256-bitises formaadis, kasutades ainult $x$ koordinaati.
Taproot avalik võti $Q$ arvutatakse seejärel lisades korrigeerimise $t$, korrutatuna elliptilise kõvera generaatoriga $G$, sisemisele avalikule võtmele $P$:
Q = P + t \cdot G
Kui Taproot avalik võti $Q$ on saadud, saame genereerida vastava vastuvõtu aadressi. Erinevalt teistest formaatidest, Taproot aadresse ei looda avaliku võtme räsi põhjal. Seetõttu sisestatakse võti $Q$ otse aadressile, toores viisil.
Alustuseks ekstraheerime punkti $Q$ $x$ koordinaadi, et saada komprimeeritud avalik võti. Sellele koormusele arvutatakse kontrollsumma kasutades BCH koode, nagu SegWit v0 aadresside puhul. Siiski, Taproot aadressidele kasutatav programm erineb veidi. Tõepoolest, pärast _bech32_ formaadi tutvustamist SegWit'iga, avastati viga: kui aadressi viimane tähemärk on `p`, siis `q`-de lisamine või eemaldamine just enne seda `p`-d ei muuda kontrollsummat kehtetuks. Kuigi see viga ei mõjuta SegWit v0 (tänu suuruse piirangule), võib see tulevikus probleemi tekitada. See viga on seetõttu Taproot aadresside jaoks parandatud ja uut parandatud formaati nimetatakse "_bech32m_".
Taproot aadress genereeritakse kodeerides $x$ koordinaadi $Q$ _bech32m_ formaadis, järgmiste elementidega:
- **HRP (_Human Readable Part_)**: `bc`, et näidata peamist Bitcoin võrku;
- **Versioon**: `1` et näidata Taproot / SegWit v1;
- **Kontrollsumma**.
Lõplik aadress on seega formaadis:
```
bc1p[Qx][kontrollsumma]
```
Teisest küljest, kui soovite lisada alternatiivseid skripte lisaks kulutamisele sisemise avaliku võtmega (_skriptitee_), on vastuvõtu aadressi arvutamine veidi erinev. Peate kaasama alternatiivsete skriptide räsi korrigeerimise arvutamisse. Taproot'is nimetatakse iga alternatiivset skripti, mis asub Merkle puu lõpus, "leheks".
Kui erinevad alternatiivsed skriptid on kirjutatud, peate need individuaalselt läbi viima märgistatud räsifunktsiooni `TapLeaf`, koos mõningate metaandmetega:
\text{h}{\text{leaf}} = \text{H}{\text{TapLeaf}} (v \Vert sz \Vert S)
Kus:
- $v$: skripti versiooni number (vaikimisi `0xC0` Taproot'i jaoks);
- $sz$: skripti suurus kodeeritud _CompactSize_ formaadis; - $S$: skript.
Erinevad skripti räsid ($\text{h}_{\text{leaf}}$) sorteeritakse esmalt leksikograafilises järjekorras. Seejärel ühendatakse need paarikaupa ja lastakse läbi märgistatud räsi funktsiooni `TapBranch`. See protsess korratakse iteratiivselt, et ehitada samm-sammult Merkle'i puu:
Haru räsi \(\text{h}_{\text{branch}}\) arvutatakse kui märgistatud räsi funktsiooni `TapBranch` rakendamine leheräside \(\text{h}_{\text{leaf1}} \Vert \text{h}\_{\text{leaf2}}\) ühendamisele:
Seejärel jätkame tulemuste kaupa kaupa ühendamist, lastes need igal sammul läbi märgistatud räsi funktsiooni `TapBranch`, kuni saame Merkle'i puu juure:
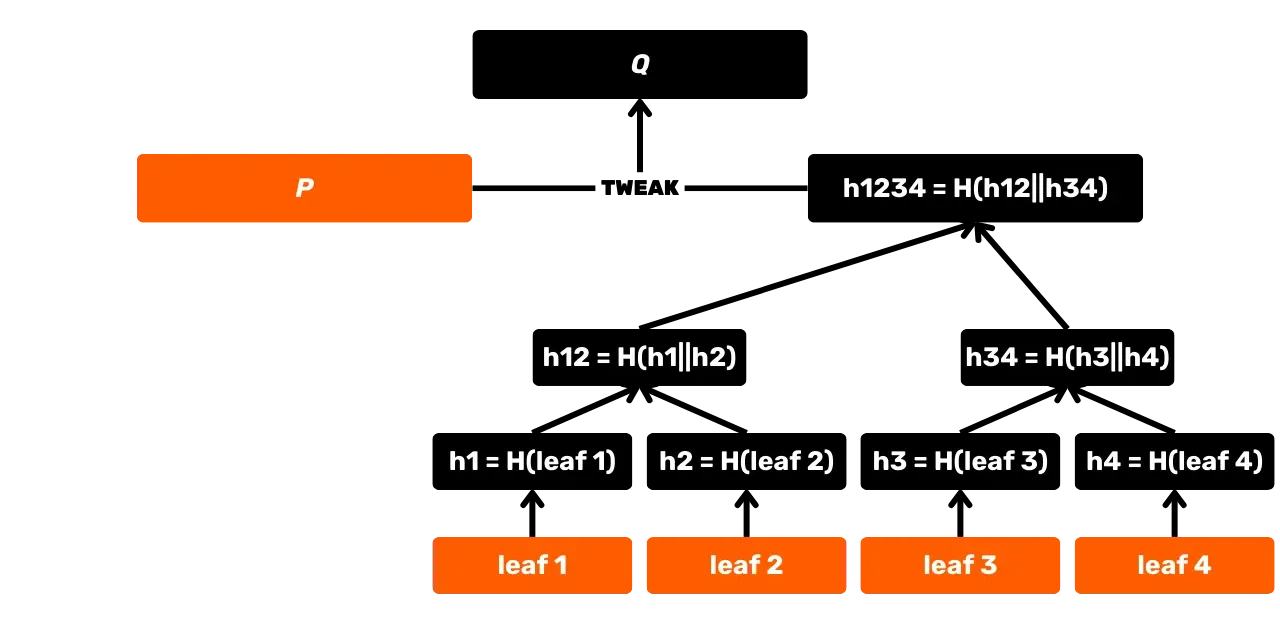
Kui Merkle'i juur $h_{\text{root}}$ on arvutatud, saame arvutada tweak'i. Selleks ühendame rahakoti sisemise avaliku võtme $P$ juurega $h_{\text{root}}$ ja viime tulemuse läbi märgistatud räsifunktsiooni `TapTweak`:
t = \text{H}{\text{TapTweak}}(P \Vert h{\text{root}})
Lõpuks saadakse Taprooti avalik võti $Q$ samamoodi nagu varem, lisades sisemise avaliku võtme $P$ tweak'i $t$ ja generaatori punkti $G$ korrutisele:
Q = P + t \cdot G
Seejärel jätkub aadressi genereerimine sama protsessiga, kasutades toorandmetena avalikku võtit $Q$ koos mõne lisametainfoga.
Ja nii me jõudsimegi CYP201 kursuse lõppu. Kui leidsite selle kursuse kasuliku olevat, oleksin väga tänulik, kui võtaksite hetke, et anda sellele järgnevas hinnangupeatükis hea hinnang. Julgustan teid jagama seda ka oma lähedastega või sotsiaalvõrgustikes. Lõpuks, kui soovite saada selle kursuse diplomit, saate lõpueksamit teha kohe pärast hinnangupeatükki.
# Lõpusektsioon
<partId>58111408-b734-54db-9ea7-0d5b67f99f99</partId>
## Hinnangud & Reitingud
<chapterId>0cd71541-a7fd-53db-b66a-8611b6a28b04</chapterId>
<isCourseReview>true</isCourseReview>
## Lõpueksam
<chapterId>a53ea27d-0f84-56cd-b37c-a66210a4b31d</chapterId>
<isCourseExam>true</isCourseExam>
## Kokkuvõte
<chapterId>d291428b-3cfa-5394-930e-4b514be82d5a</chapterId>
<isCourseConclusion>true</isCourseConclusion>