name: Introducción a la criptografía formal goal: Una introducción en profundidad a la ciencia y la práctica de la criptografía. objectives:
- Explore los cifrados Beale y los métodos criptográficos modernos para comprender los conceptos básicos e históricos de la criptografía.
- Profundice en la teoría de números, grupos y campos para dominar los conceptos matemáticos clave que subyacen a la criptografía.
- Estudia el cifrado de flujo RC4 y AES con una clave de 128 bits para conocer los algoritmos criptográficos simétricos.
- Investigar el criptosistema RSA, la distribución de claves y las funciones hash para explorar la criptografía asimétrica.
Profundizar en la criptografía
Es difícil encontrar muchos materiales que ofrezcan un buen término medio en la enseñanza de la criptografía.
Por un lado, hay tratados largos y formales, sólo accesibles para quienes tengan una sólida formación en matemáticas, lógica u otra disciplina formal. Por otro lado, hay introducciones de muy alto nivel que ocultan demasiados detalles para cualquiera que tenga al menos un poco de curiosidad.
Esta introducción a la criptografía pretende situarse en un término medio. Aunque debería ser relativamente desafiante y detallada para cualquier persona nueva en criptografía, no es la madriguera de conejo de un típico tratado fundacional.
Introducción
Descripción del curso
bb8a8b73-7fb2-50da-bf4e-98996d79887b ¡Bienvenido al curso CYP302!
Este libro ofrece una introducción en profundidad a la ciencia y la práctica de la criptografía. En la medida de lo posible, se centra en la exposición conceptual, más que formal, del material.
Este contenido educativo está adaptado del libro y repo JWBurgers. Si bien el autor ha permitido generosamente su uso educativo, todos los derechos de propiedad intelectual permanecen con el creador original.
Motivación y objetivos
Es difícil encontrar muchos materiales que ofrezcan un buen término medio en la enseñanza de la criptografía.
Por un lado, hay tratados largos y formales, sólo accesibles para quienes tengan una sólida formación en matemáticas, lógica u otra disciplina formal. Por otro lado, hay introducciones de muy alto nivel que ocultan demasiados detalles para cualquiera que tenga al menos un poco de curiosidad.
Esta introducción a la criptografía pretende situarse en un término medio. Aunque debería ser relativamente desafiante y detallada para cualquier persona nueva en criptografía, no es la madriguera de conejo de un típico tratado fundacional.
Destinatarios
Desde desarrolladores hasta curiosos intelectuales, este libro es útil para cualquiera que desee algo más que una comprensión superficial de la criptografía. Si su objetivo es dominar el campo de la criptografía, este libro es también un buen punto de partida.
Pautas de lectura
Actualmente, el libro contiene siete capítulos: "¿Qué es la criptografía?" (capítulo 1), "Fundamentos matemáticos de la criptografía I" (capítulo 2), "Fundamentos matemáticos de la criptografía II" (capítulo 3), "Criptografía simétrica" (capítulo 4), "RC4 y AES" (capítulo 5), "Criptografía asimétrica" (capítulo 6) y "El criptosistema RSA" (capítulo 7). Todavía se añadirá un último capítulo, "La criptografía en la práctica". Se centra en varias aplicaciones criptográficas, como la seguridad de la capa de transporte, el enrutamiento cebolla y el sistema de intercambio de valores de Bitcoin.
A menos que tengas una sólida formación en matemáticas, la teoría de números es probablemente el tema más difícil de este libro. Ofrezco una visión general de ella en el Capítulo 3, y también aparece en la exposición de AES en el Capítulo 5 y del criptosistema RSA en el Capítulo 7.
Si realmente tiene dificultades con los detalles formales de estas partes del libro, le recomiendo que se conforme con una lectura de alto nivel de las mismas la primera vez.
Agradecimientos
El libro que más ha influido en la configuración de esta ha sido Introduction to Modern Cryptography, de Jonathan Katz y Yehuda Lindell, CRC Press (Boca Ratón, FL), 2015. Hay un curso complementario disponible en Coursera llamado "Cryptography"
Las principales fuentes adicionales que han sido útiles para crear la visión general de este libro son Simon Singh, The Code Book, Fourth Estate (Londres, 1999); Christof Paar y Jan Pelzl, Understanding Cryptography, Springer (Heidelberg, 2010) y un curso basado en el libro de Paar llamado "Introduction to Cryptography"; y Bruce Schneier, Applied Cryptography, 2ª edn, 2015 (Indianapolis, IN: John Wiley & Sons).
Sólo citaré información y resultados muy concretos que extraigo de estas fuentes, pero quiero reconocer aquí mi deuda general con ellas.
Para aquellos lectores que deseen buscar conocimientos más avanzados sobre criptografía después de esta introducción, recomiendo encarecidamente el libro de Katz y Lindell. El curso de Katz en Coursera es algo más accesible que el libro.
Contribuciones
Por favor, eche un vistazo a el archivo de contribuciones en el repositorio para ver algunas directrices sobre cómo apoyar el proyecto.
Notación
Términos clave:
Los términos clave de las cartillas se introducen en negrita. Por ejemplo, la introducción del cifrado Rijndael como término clave tendría el siguiente aspecto: Cifrado Rijndael.
Los términos clave se definen explícitamente, a menos que sean nombres propios o su significado resulte obvio a partir de la discusión.
La definición suele darse al introducir un término clave, aunque a veces es más conveniente dejarla para más adelante.
Palabras y frases destacadas:
Las palabras y frases se resaltan mediante cursiva. Por ejemplo, la frase "Recuerde su contraseña" tendría el siguiente aspecto: Recuerde su contraseña.
Notación formal:
La notación formal se refiere principalmente a variables, variables aleatorias y conjuntos.
- Variables: Normalmente se indican con una letra minúscula (por ejemplo, "x" o "y"). A veces se escriben en mayúsculas para mayor claridad (por ejemplo, "M" o "K").
- Variables aleatorias: Se indican siempre con una letra mayúscula (por ejemplo, "X" o "Y")
- Conjuntos: Se indican siempre con letras mayúsculas y en negrita (por ejemplo, S)
¿Listo para explorar el fascinante universo de la criptografía? ¡Vamos allá!
¿Qué es la criptografía?
Las cifras de Beale
Comencemos nuestra indagación en el campo de la criptografía con uno de los episodios más entrañables y divertidos de su historia: el de los cifrados Beale. [1]
La historia de las claves Beale tiene, en mi opinión, más visos de ficción que de realidad. Pero supuestamente ocurrió lo siguiente.
Tanto en el invierno de 1820 como en el de 1822, un hombre llamado Thomas J. Beale se alojó en una posada propiedad de Robert Morriss en Lynchburg (Virginia). Al final de su segunda estancia, Beale entregó a Morriss una caja de hierro con documentos valiosos para su custodia.
Unos meses más tarde, Morriss recibió una carta de Beale fechada el 9 de mayo de 1822. En ella se destacaba el gran valor del contenido de la caja de hierro y se daban algunas instrucciones a Morriss: si ni Beale ni ninguno de sus socios venían nunca a reclamar la caja, debería abrirla precisamente diez años después de la fecha de la carta (es decir, el 9 de mayo de 1832). Algunos de los papeles del interior estarían escritos en texto normal. Otros, sin embargo, serían "ininteligibles sin la ayuda de una llave" Esta "llave" sería, pues, entregada a Morriss por un amigo anónimo de Beale en junio de 1832.
A pesar de las claras instrucciones, Morriss no abrió la caja en mayo de 1832 y el misterioso amigo de Beale nunca apareció en junio de ese año. No fue hasta 1845 cuando el posadero se decidió por fin a abrir la caja. En ella, Morriss encontró una nota en la que se explicaba cómo Beale y sus socios habían descubierto oro y plata en el Oeste y los habían enterrado, junto con algunas joyas, para ponerlos a buen recaudo. Además, la caja contenía tres textos cifrados, es decir, textos escritos en código que requieren una clave criptográfica, o un secreto, y un algoritmo para descifrarlos. Este proceso de desbloqueo de un texto cifrado se conoce como descifrado, mientras que el proceso de bloqueo se conoce como cifrado. (Como se explica en el capítulo 3, el término cifrado puede tener varios significados. En el nombre "cifrados Beale", es la abreviatura de ciphertexts)
Los tres textos cifrados que Morriss encontró en la caja de hierro consisten cada uno en una serie de números separados por comas. Según la nota de Beale, estos textos cifrados proporcionan por separado la ubicación del tesoro, su contenido y una lista de nombres con los herederos legítimos del tesoro y sus participaciones (esta última información sería relevante en caso de que Beale y sus socios nunca llegaran a reclamar la caja).
Morris intentó descifrar los tres textos cifrados durante veinte años. Esto habría sido fácil con la clave. Pero Morriss no tenía la clave y fracasó en sus intentos de recuperar los textos originales, o textos planos, como se les suele llamar en criptografía.
Al final de su vida, Morriss cedió la caja a un amigo en 1862. Este amigo publicó posteriormente un panfleto en 1885, bajo el seudónimo de J.B. Ward. Incluía una descripción de la (supuesta) historia de la caja, los tres textos cifrados y una solución que había encontrado para el segundo texto cifrado. (Aparentemente, hay una clave para cada texto cifrado, y no una clave que funcione con los tres textos cifrados, como Beale parece haber sugerido originalmente en su carta a Morriss)
Puedes ver el segundo texto cifrado en la Figura 2 de abajo. La clave de este texto cifrado es la Declaración de Independencia de los Estados Unidos. El procedimiento de descifrado se reduce a la aplicación de las dos reglas siguientes:
- Para cualquier número n en el texto cifrado, localice la enésima palabra en la Declaración de Independencia de los Estados Unidos
- Sustituye el número n por la primera letra de la palabra encontrada
Figura 1: Cifrado Beale no. 2

Por ejemplo, el primer número del segundo texto cifrado es 115. La palabra 115 de la Declaración de Independencia es "instituido". La palabra 115 de la Declaración de Independencia es "instituyó", por lo que la primera letra del texto plano es "i" El texto cifrado no indica directamente el espaciado entre palabras ni las mayúsculas. Pero tras descifrar las primeras palabras, se puede deducir lógicamente que la primera palabra del texto plano era simplemente "I" (El texto plano comienza con la frase "He depositado en el condado de Bedford")
Una vez descifrado, el segundo mensaje proporciona el contenido detallado del tesoro (oro, plata y joyas) y sugiere que fue enterrado en vasijas de hierro y cubierto de rocas en el condado de Bedford (Virginia). A la gente le encantan los buenos misterios, por lo que se han dedicado grandes esfuerzos a descifrar las otras dos claves de Beale, en particular la que describe la ubicación del tesoro. Incluso varios destacados criptógrafos han intentado descifrarlas. Sin embargo, hasta ahora nadie ha sido capaz de descifrar los otros dos textos cifrados.
Notas:
[1] Para un buen resumen de la historia, véase Simon Singh, The Code Book, Fourth Estate (Londres, 1999), pp. 82-99. Andrew Allen realizó un cortometraje de la historia en 2010. Puede encontrar la película, "The Thomas Beale Cipher", en su sitio web.
[2] Esta imagen está disponible en la página de Wikipedia sobre los cifrados Beale.
Criptografía moderna
Historias pintorescas como la de los cifradores Beale son las que la mayoría de nosotros asociamos con la criptografía. Sin embargo, la criptografía moderna difiere al menos en cuatro aspectos importantes de este tipo de ejemplos históricos.
En primer lugar, históricamente la criptografía sólo se ha ocupado del secreto (o confidencialidad). Los textos cifrados se creaban para garantizar que sólo determinadas partes pudieran conocer la información de los textos sin cifrar, como en el caso de los cifrados Beale. Para que un sistema de cifrado cumpla bien este propósito, sólo se puede descifrar el texto cifrado si se tiene la clave.
La criptografía moderna se ocupa de una gama de temas más amplia que el secreto. Estos temas incluyen principalmente (1) la integridad del mensaje, es decir, garantizar que un mensaje no ha sido modificado; (2) la autenticidad del mensaje, es decir, garantizar que un mensaje procede realmente de un remitente concreto; y (3) el no repudio, es decir, garantizar que un remitente no puede negar falsamente más tarde que ha enviado un mensaje. [4]
Por tanto, es importante distinguir entre un esquema de cifrado y un esquema criptográfico. Un esquema de cifrado sólo se ocupa del secreto. Mientras que un esquema de cifrado es un esquema criptográfico, lo contrario no es cierto. Un esquema criptográfico también puede servir para los otros temas principales de la criptografía, como la integridad, la autenticidad y el no repudio.
Los temas de la integridad y la autenticidad son tan importantes como el secreto. Nuestros modernos sistemas de comunicación no podrían funcionar sin garantías de integridad y autenticidad de las comunicaciones. El no repudio también es una preocupación importante, como en el caso de los contratos digitales, pero es menos necesario en las aplicaciones criptográficas que el secreto, la integridad y la autenticidad.
En segundo lugar, los esquemas de cifrado clásicos, como los cifrados Beale, siempre implican una clave que se comparte entre todas las partes implicadas. Sin embargo, muchos esquemas criptográficos modernos implican no sólo una, sino dos claves: una privada y una pública. Mientras que la primera debe permanecer privada en cualquier aplicación, la segunda suele ser de dominio público (de ahí sus respectivos nombres). En el ámbito del cifrado, la clave pública puede utilizarse para cifrar el mensaje, mientras que la privada puede utilizarse para descifrarlo.
La rama de la criptografía que se ocupa de los esquemas en los que todas las partes comparten una clave se conoce como criptografía simétrica. La clave única en un esquema de este tipo suele denominarse clave privada (o clave secreta). La rama de la criptografía que se ocupa de los esquemas que requieren un par de claves privada-pública se conoce como criptografía asimétrica. A veces también se hace referencia a estas ramas como criptografía de clave privada y criptografía de clave pública, respectivamente (aunque esto puede crear confusión, ya que los esquemas criptográficos de clave pública también tienen claves privadas).
La aparición de la criptografía asimétrica a finales de los años 70 ha sido uno de los acontecimientos más importantes de la historia de la criptografía. Sin ella, la mayoría de nuestros sistemas de comunicación modernos, incluido Bitcoin, no serían posibles, o al menos serían muy poco prácticos.
Es importante destacar que la criptografía moderna no consiste exclusivamente en el estudio de esquemas criptográficos de clave simétrica y asimétrica (aunque esto abarca gran parte del campo). Por ejemplo, la criptografía también se ocupa de las funciones hash y los generadores de números pseudoaleatorios, y se pueden crear aplicaciones basadas en estas primitivas que no están relacionadas con la criptografía de clave simétrica o asimétrica.
En tercer lugar, los esquemas de cifrado clásicos, como los utilizados en los cifradores Beale, eran más arte que ciencia. Su seguridad se basaba en gran medida en intuiciones sobre su complejidad. Normalmente se parcheaban cuando se descubría un nuevo ataque contra ellos, o se abandonaban por completo si el ataque era especialmente grave. Sin embargo, la criptografía moderna es una ciencia rigurosa con un enfoque formal y matemático para desarrollar y analizar esquemas criptográficos. [5]
En concreto, la criptografía moderna se centra en pruebas formales de seguridad. Cualquier prueba de seguridad de un esquema criptográfico consta de tres pasos:
La declaración de una definición criptográfica de seguridad, es decir, un conjunto de objetivos de seguridad y la amenaza que supone el atacante.
La declaración de cualquier suposición matemática con respecto a la complejidad computacional del esquema. Por ejemplo, un esquema criptográfico puede contener un generador de números pseudoaleatorios. Aunque no podemos demostrar que existan, podemos suponer que sí.
La exposición de una prueba matemática de seguridad del esquema sobre la base de la noción formal de seguridad y de cualquier supuesto matemático.
En cuarto lugar, mientras que históricamente la criptografía se utilizaba sobre todo en entornos militares, en la era digital ha llegado a impregnar nuestras actividades cotidianas. La criptografía es la condición sine qua non de nuestra era digital, ya sea para realizar operaciones bancarias en línea, publicar en las redes sociales, comprar un producto en Amazon con tarjeta de crédito o dar una propina en bitcoin a un amigo.
Teniendo en cuenta estos cuatro aspectos de la criptografía moderna, podríamos caracterizar la criptografía moderna como la ciencia que se ocupa del desarrollo formal y el análisis de esquemas criptográficos para asegurar la información digital contra ataques adversarios[6]. La seguridad debe entenderse en sentido amplio como la prevención de ataques que dañan el secreto, la integridad, la autenticación y/o el no repudio en las comunicaciones.
La criptografía se considera una subdisciplina de la ciberseguridad, que se ocupa de prevenir el robo, el daño y el uso indebido de los sistemas informáticos. Hay que tener en cuenta que muchos problemas de ciberseguridad están poco o nada relacionados con la criptografía.
Por ejemplo, si una empresa aloja costosos servidores a nivel local, puede que le preocupe proteger este hardware de robos y daños. Aunque se trata de un problema de ciberseguridad, tiene poco que ver con la criptografía.
Por ejemplo, los ataques de suplantación de identidad (phishing)** son un problema común en nuestra era moderna. Estos ataques intentan engañar a la gente a través de un correo electrónico o algún otro medio de mensaje para que renuncie a información sensible como contraseñas o números de tarjetas de crédito. Aunque la criptografía puede ayudar a hacer frente a los ataques de phishing hasta cierto punto, un enfoque integral requiere algo más que el uso de algo de criptografía.
Notas:
Para ser exactos, las aplicaciones importantes de los esquemas criptográficos han estado relacionadas con el secreto. Los niños, por ejemplo, suelen utilizar esquemas criptográficos sencillos para "divertirse". El secreto no es realmente una preocupación en esos casos.
[4] Bruce Schneier, Applied Cryptography, 2ª edn, 2015 (Indianápolis, IN: John Wiley & Sons), p. 2.
[5] Véase Jonathan Katz y Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), esp. pp. 16-23, para una buena descripción.
[6] Véase Katz y Lindell, ibíd., p. 3. Creo que su caracterización tiene algunos problemas, por lo que presento aquí una versión ligeramente diferente de su afirmación.
Comunicaciones abiertas
La criptografía moderna está diseñada para ofrecer garantías de seguridad en un entorno de comunicaciones abiertas. Si nuestro canal de comunicación está tan bien protegido que los fisgones no tienen ninguna posibilidad de manipular o simplemente observar nuestros mensajes, entonces la criptografía es superflua. Sin embargo, la mayoría de nuestros canales de comunicación no están tan bien protegidos.
La columna vertebral de las comunicaciones en el mundo moderno es una enorme red de cables de fibra óptica. Hacer llamadas telefónicas, ver la televisión y navegar por Internet en un hogar moderno depende generalmente de esta red de cables de fibra óptica (un pequeño porcentaje puede depender exclusivamente de los satélites). Es cierto que puedes tener diferentes conexiones de datos en tu casa, como cable coaxial, línea de abonado digital (asimétrica) y cable de fibra óptica. Pero, al menos en el mundo desarrollado, estos diferentes medios de datos se unen rápidamente fuera de tu casa a un nodo de una red masiva de cables de fibra óptica que conecta todo el globo. Las excepciones son algunas zonas remotas del mundo desarrollado, como Estados Unidos y Australia, donde el tráfico de datos todavía puede recorrer distancias considerables a través de los tradicionales cables telefónicos de cobre.
Sería imposible impedir que los posibles atacantes accedieran físicamente a esta red de cables y a su infraestructura de apoyo. De hecho, ya sabemos que la mayoría de nuestros datos son interceptados por diversas agencias nacionales de inteligencia en intersecciones cruciales de Internet[7], lo que incluye desde los mensajes de Facebook hasta las direcciones de los sitios web que visitas.
Mientras que la vigilancia de datos a escala masiva requiere un adversario poderoso, como una agencia nacional de inteligencia, los atacantes con pocos recursos pueden intentar fácilmente fisgonear a una escala más local. Aunque esto puede ocurrir a nivel de intervención de cables, es mucho más fácil interceptar las comunicaciones inalámbricas.
La mayoría de nuestros datos de red local -ya sea en nuestros hogares, en la oficina o en una cafetería- viajan ahora a través de ondas de radio a puntos de acceso inalámbricos en routers todo en uno, en lugar de a través de cables físicos. Por tanto, un atacante necesita pocos recursos para interceptar el tráfico local. Esto es especialmente preocupante, ya que la mayoría de la gente hace muy poco para proteger los datos que viajan a través de sus redes locales. Además, los atacantes potenciales también pueden apuntar a nuestras conexiones de banda ancha móvil, como 3G, 4G y 5G. Todas estas comunicaciones inalámbricas son un blanco fácil para los atacantes.
De ahí que la idea de mantener en secreto las comunicaciones protegiendo el canal de comunicación sea una aspiración irremediablemente delirante para gran parte del mundo moderno. Todo lo que sabemos justifica una paranoia severa: siempre hay que suponer que alguien está escuchando. Y la criptografía es la principal herramienta de que disponemos para obtener cualquier tipo de seguridad en este entorno moderno.
Notas:
[7] Véase, por ejemplo, Olga Khazan, "The creepy, long-standing practice of undersea cable tapping", The Atlantic, 16 de julio de 2013 (disponible en The Atlantic).
Fundamentos matemáticos de la criptografía 1
Variables aleatorias
La criptografía se basa en las matemáticas. Y si quieres construir algo más que una comprensión superficial de la criptografía, necesitas sentirte cómodo con esas matemáticas.
Este capítulo presenta la mayoría de las matemáticas básicas que encontrarás en el aprendizaje de la criptografía. Los temas incluyen variables aleatorias, operaciones módulo, operaciones XOR y pseudoaleatoriedad. Deberías dominar el material de estas secciones para cualquier comprensión no superficial de la criptografía.
La siguiente sección trata de la teoría de números, que supone un reto mucho mayor.
Variables aleatorias
Una variable aleatoria se denota normalmente con una letra mayúscula no
negrita. Así, por ejemplo, podríamos hablar de una variable aleatoria X, una variable aleatoria Y o
una variable aleatoria Z.
Esta es la notación que emplearé de ahora en adelante.
Una variable aleatoria puede tomar dos o más valores posibles, cada uno con una cierta probabilidad positiva. Los valores posibles se enumeran en el conjunto de resultados.
Cada vez que se muestrea una variable aleatoria, se extrae un valor concreto de su conjunto de resultados según las probabilidades definidas.
Veamos un ejemplo sencillo. Supongamos una variable X que se define de la siguiente manera:
- X tiene el conjunto de resultados
\{1,2\}
Pr[X = 1] = 0.5Pr[X = 2] = 0.5Es fácil ver que X es una
variable aleatoria. En primer lugar, hay dos o más valores posibles que
puede tomar X, a saber, 1 y 2. En segundo lugar, cada
valor posible tiene una probabilidad positiva de ocurrir siempre que se
muestrea X, a saber, 0,5.
Lo único que necesita una variable aleatoria es un conjunto de resultados con dos o más posibilidades, en el que cada posibilidad tenga una probabilidad positiva de ocurrir en el momento del muestreo. En principio, una variable aleatoria puede definirse de forma abstracta, sin contexto. En este caso, el "muestreo" puede entenderse como la realización de un experimento natural para determinar el valor de la variable aleatoria.
La variable X anterior se
definió de forma abstracta. Por lo tanto, se puede pensar en el muestreo de
la variable X como lanzar una
moneda al aire y asignar "2" en el caso de cara y "1" en el caso de cruz.
Para cada muestra de X, se
vuelve a lanzar la moneda.
Alternativamente, también se puede pensar en el muestreo X, como lanzar un dado justo y asignar "2" en caso de que el dado caiga 1, 3, o 4, y asignar "1" en caso de
que el dado caiga 2, 5, o 6. Cada vez que muestres X, vuelve a lanzar el dado.
Realmente, cualquier experimento natural que permita definir las
probabilidades de los posibles valores de X anteriores se puede imaginar con respecto al dibujo.
Con frecuencia, sin embargo, las variables aleatorias no se introducen simplemente de forma abstracta. Por el contrario, el conjunto de posibles valores de resultado tiene un significado explícito en el mundo real (en lugar de ser sólo números). Además, estos valores de resultado pueden definirse con respecto a algún tipo específico de experimento (en lugar de como cualquier experimento natural con esos valores).
Consideremos ahora un ejemplo de variable X que no está definida de forma abstracta. X se define de la siguiente manera
para determinar cuál de los dos equipos empieza un partido de fútbol:
Xtiene el conjunto de resultados {rojo arranca,azul arranca}- Lanza una moneda
C: cruz = "sale rojo"; cara = "sale azul"
Pr [X = \text{red kicks off}] = 0.5Pr [X = \text{blue kicks off}] = 0.5En este caso, el conjunto de resultados de X tiene un significado concreto,
a saber, qué equipo empieza en un partido de fútbol. Además, los posibles
resultados y sus probabilidades asociadas se determinan mediante un
experimento concreto, a saber, lanzar una moneda C.
En los debates sobre criptografía, las variables aleatorias suelen introducirse en relación con un conjunto de resultados con significado en el mundo real. Puede ser el conjunto de todos los mensajes que pueden cifrarse, conocido como el espacio de mensajes, o el conjunto de todas las claves que las partes que utilizan el cifrado pueden elegir, conocido como el espacio de claves.
Sin embargo, en los debates sobre criptografía, las variables aleatorias no suelen definirse frente a un experimento natural concreto, sino frente a cualquier experimento que pueda arrojar las distribuciones de probabilidad adecuadas.
Las variables aleatorias pueden tener distribuciones de probabilidad
discretas o continuas. Las variables aleatorias con una distribución de probabilidad discreta -es decir, variables aleatorias discretas- tienen un número finito de
resultados posibles. La variable aleatoria X en los dos ejemplos dados hasta
ahora era discreta.
En cambio, las variables aleatorias continuas pueden tomar valores en uno o más intervalos. Se podría decir, por ejemplo, que una variable aleatoria, en el muestreo, tomará cualquier valor real entre 0 y 1, y que cada número real en este intervalo es igualmente probable. Dentro de este intervalo, hay infinitos valores posibles.
Para las discusiones criptográficas, sólo necesitarás entender las variables aleatorias discretas. Cualquier discusión sobre variables aleatorias de aquí en adelante debe, por lo tanto, entenderse como referida a variables aleatorias discretas, a menos que se especifique lo contrario.
Graficación de variables aleatorias
Los valores posibles y las probabilidades asociadas de una variable
aleatoria pueden visualizarse fácilmente mediante un gráfico. Por ejemplo,
consideremos la variable aleatoria X de la sección anterior con un conjunto de resultados de \{1, 2\}, y Pr [X = 1] = 0,5 y Pr [X = 2] = 0,5.
Normalmente mostraríamos una variable aleatoria de este tipo en forma de
gráfico de barras como en la Figura 1.
Figura 1: Variable aleatoria X
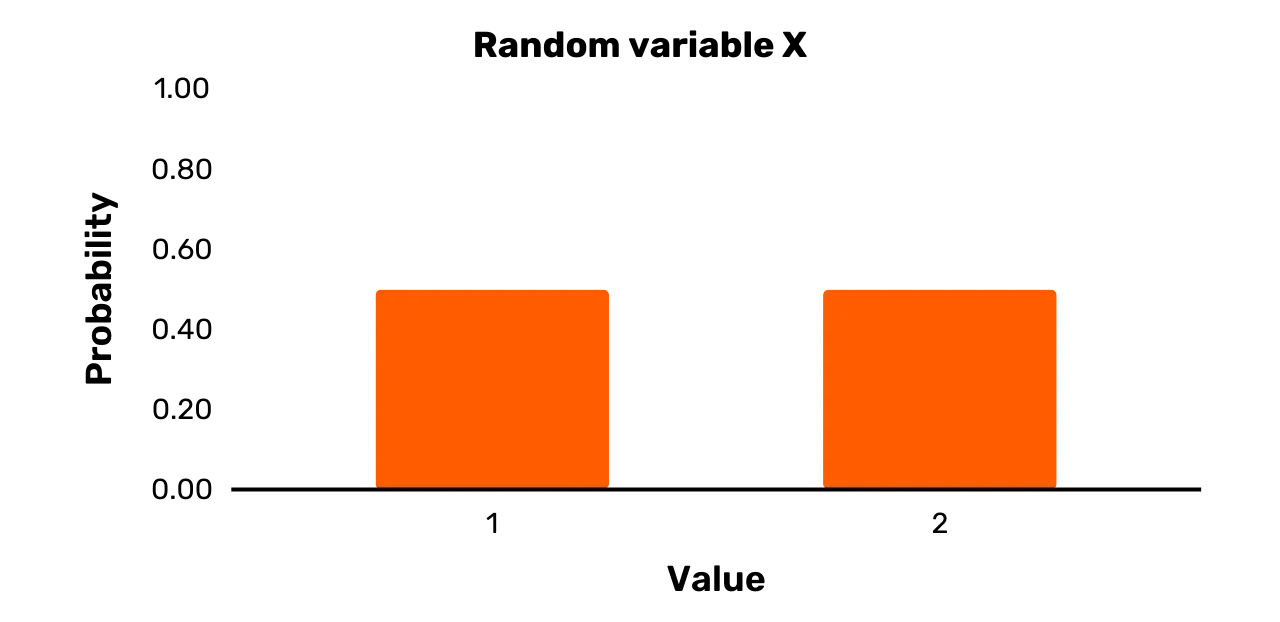
Las barras anchas de la Figura 1 obviamente no pretenden sugerir
que la variable aleatoria X sea
realmente continua. En cambio, las barras son anchas para que resulten más atractivas
visualmente (una simple línea recta hacia arriba proporciona una visualización
menos intuitiva).
Variables uniformes
En la expresión "variable aleatoria", el término "aleatorio" sólo significa "probabilístico". En otras palabras, sólo significa que dos o más resultados posibles de la variable ocurren con ciertas probabilidades. Sin embargo, estos resultados no tienen por qué ser igual de probables (aunque el término "aleatorio" puede tener ese significado en otros contextos).
Una variable uniforme es un caso especial de variable
aleatoria. Puede tomar dos o más valores, todos con la misma probabilidad.
La variable aleatoria X representada en la Figura 1 es claramente una variable uniforme, ya
que ambos resultados posibles se producen con una probabilidad de 0,5. Sin embargo, hay muchas
variables aleatorias que no son casos de variables uniformes.
Consideremos, por ejemplo, la variable aleatoria Y. Tiene un conjunto de resultados {1, 2, 3, 8, 10} y la
siguiente distribución de probabilidad:
\Pr[Y = 1] = 0.25\Pr[Y = 2] = 0.35\Pr[Y = 3] = 0.1\Pr[Y = 8] = 0.25\Pr[Y = 10] = 0.05Aunque hay dos resultados posibles que tienen la misma probabilidad de
ocurrir, a saber, 1 y 8, Y también puede tomar ciertos valores con probabilidades diferentes de 0,25 en el muestreo. Por lo tanto, aunque Y es una variable aleatoria, no
es una variable uniforme.
En la Figura 2 se ofrece una representación gráfica de Y.
Figura 2: Variable aleatoria Y
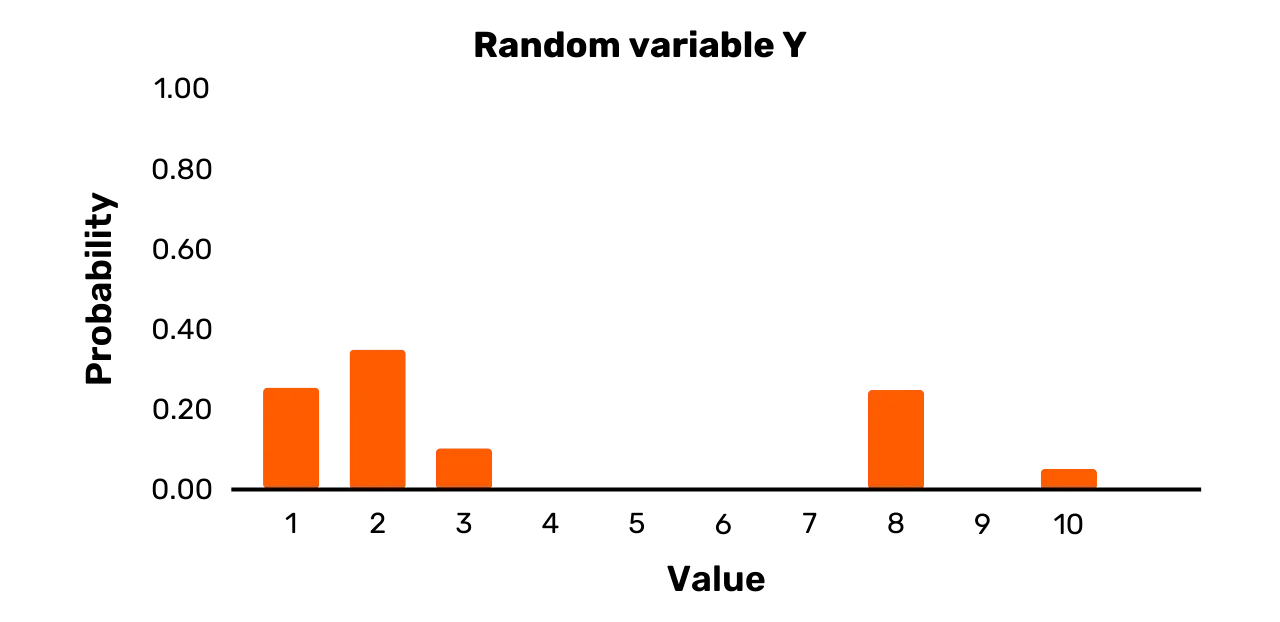
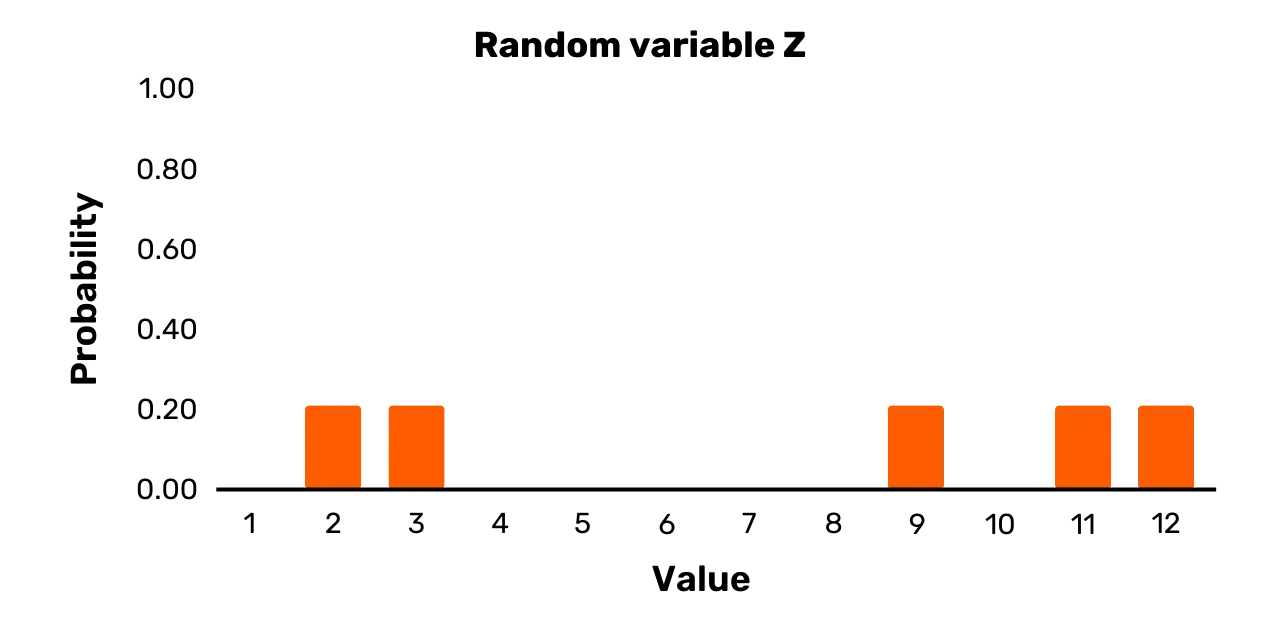
Como último ejemplo, consideremos la variable aleatoria Z. Tiene el conjunto
de resultados {1,3,7,11,12} y la siguiente distribución de probabilidad:
\Pr[Z = 2] = 0.2\Pr[Z = 3] = 0.2\Pr[Z = 9] = 0.2\Pr[Z = 11] = 0.2\Pr[Z = 12] = 0.2Puedes verlo representado en la Figura 3. La variable aleatoria Z es, a diferencia de Y, una variable uniforme, ya que todas las probabilidades de los valores posibles en el muestreo son iguales.
Figura 3: Variable aleatoria Z
Probabilidad condicional
Supongamos que Bob pretende seleccionar uniformemente un día del último año natural. ¿Cuál es la probabilidad de que el día elegido sea verano?
Siempre que pensemos que el proceso de Bob será realmente uniforme, deberíamos concluir que existe 1/4 de probabilidad de que Bob seleccione un día en Verano. Esta es la probabilidad incondicional de que el día elegido al azar esté en Verano.
Supongamos ahora que, en lugar de extraer uniformemente un día del calendario, Bob sólo selecciona uniformemente entre aquellos días en los que la temperatura al mediodía en Crystal Lake (Nueva Jersey) fue de 21 grados Celsius o superior. Dada esta información adicional, ¿qué podemos concluir sobre la probabilidad de que Bob seleccione un día de verano?
En realidad, deberíamos sacar una conclusión diferente a la anterior, incluso sin disponer de más información específica (por ejemplo, la temperatura al mediodía de cada día del último año natural).
Sabiendo que Crystal Lake está en Nueva Jersey, no cabe esperar que la temperatura al mediodía sea de 21 grados centígrados o más en invierno. En cambio, es mucho más probable que sea un día cálido de primavera u otoño, o un día en algún lugar del verano. Por lo tanto, sabiendo que la temperatura al mediodía en Crystal Lake en el día seleccionado fue de 21 grados Celsius o superior, la probabilidad de que el día seleccionado por Bob sea en Verano es mucho mayor. Esta es la probabilidad condicional de que el día seleccionado al azar esté en Verano, dado que la temperatura al mediodía en Crystal Lake era de 21 grados Celsius o superior.
A diferencia del ejemplo anterior, las probabilidades de dos sucesos también pueden no estar relacionadas en absoluto. En ese caso, decimos que son independientes.
Supongamos, por ejemplo, que una moneda ha salido cara. Dada esta circunstancia, ¿cuál es la probabilidad de que llueva mañana? En este caso, la probabilidad condicional debería ser la misma que la probabilidad incondicional de que llueva mañana, ya que el lanzamiento de una moneda no suele influir en el tiempo.
Utilizamos el símbolo "|" para escribir enunciados de probabilidad
condicional. Por ejemplo, la probabilidad del suceso A dado que ha ocurrido el suceso B se puede escribir de la siguiente
manera:
Pr[A|B]Así, cuando dos eventos, A y B, son independientes,
entonces:
Pr[A|B] = Pr[A] \text{ and } Pr[B|A] = Pr[B]La condición de independencia puede simplificarse del siguiente modo:
Pr[A, B] = Pr[A] \cdot Pr[B]Un resultado clave en la teoría de la probabilidad se conoce como Teorema de Bayes. Básicamente afirma que Pr[A|B] se puede reescribir de
la siguiente manera:
Pr[A|B] = \frac{Pr[B|A] \cdot Pr[A]}{Pr[B]}En lugar de utilizar probabilidades condicionales con sucesos específicos,
también podemos considerar las probabilidades condicionales implicadas con
dos o más variables aleatorias sobre un conjunto de sucesos posibles.
Supongamos dos variables aleatorias, X y Y. Podemos denotar
cualquier valor posible de X por x, y cualquier valor
posible de Y por y. Podríamos decir, entonces,
que dos variables aleatorias son independientes si se cumple la siguiente
afirmación:
Pr[X = x, Y = y] = Pr[X = x] \cdot Pr[Y = y]para todo x y y.
Seamos un poco más explícitos sobre lo que significa esta afirmación.
Supongamos que los conjuntos de resultados para X y Y se definen como sigue: X = \{x_1, x_2, \ldots, x_i, \ldots, x_n\} y Y = \{y_1, y_2, \ldots, y_i, \ldots, y_m\}. (Es típico indicar conjuntos de valores mediante letras mayúsculas en
negrita)
Supongamos ahora que se muestrea Y y se observa y_1. La
afirmación anterior nos dice que la probabilidad de obtener ahora x_1 a partir del muestreo X es
exactamente la misma que si nunca hubiéramos observado y_1. Esto es cierto para
cualquier y_i que pudiéramos
haber obtenido de nuestro muestreo inicial de Y. Por último, esto es cierto
no sólo para x_1. Para
cualquier x_i, la
probabilidad de que ocurra no está influida por el resultado de un muestreo
de Y. Todo esto también se
aplica al caso en el que X se
muestrea primero.
Terminemos nuestra discusión con un punto un poco más filosófico. En cualquier situación del mundo real, la probabilidad de un acontecimiento siempre se evalúa en función de un conjunto concreto de información. No existe una "probabilidad incondicional" en el sentido estricto de la palabra.
Por ejemplo, supongamos que le pregunto por la probabilidad de que los cerdos vuelen en 2030. Aunque no le doy más información, es evidente que usted sabe muchas cosas sobre el mundo que pueden influir en su juicio. Nunca ha visto volar cerdos. Sabe que la mayoría de la gente no espera que vuelen. Sabe que no están hechos para volar. Y así sucesivamente.
Por lo tanto, cuando hablamos de "probabilidad incondicional" de un acontecimiento en un contexto real, ese término sólo puede tener sentido si lo entendemos como "la probabilidad sin ninguna información explícita adicional". Por tanto, cualquier concepto de "probabilidad condicional" debe entenderse siempre en relación con algún dato concreto.
Yo podría, por ejemplo, preguntarle la probabilidad de que los cerdos vuelen en 2030, después de darle pruebas de que algunas cabras de Nueva Zelanda han aprendido a volar tras unos años de entrenamiento. En este caso, probablemente ajustará su juicio sobre la probabilidad de que los cerdos vuelen en 2030. Así pues, la probabilidad de que los cerdos vuelen en 2030 está condicionada a esta prueba sobre las cabras de Nueva Zelanda.
La operación módulo
Módulo
La expresión más básica con la operación módulo es de la
siguiente forma: x \mod y.
La variable x se llama
dividendo y la variable y divisor.
Para realizar una operación de módulo con un dividendo positivo y un divisor
positivo, basta con determinar el resto de la división.
Por ejemplo, consideremos la expresión 25 \mod 4. El número 4 entra en el número 25 un total de 6 veces. El resto de esa
división es 1. Por lo tanto, 25 \mod 4 es igual a 1. De forma
similar, podemos evaluar las expresiones siguientes:
29 \mod 30 = 29(ya que 30 entra en 29 un total de 0 veces y el resto es 29)42 \mod 2 = 0(como 2 entra en 42 un total de 21 veces y el resto es 0)12 \mod 5 = 2(ya que 5 entra en 12 un total de 2 veces y el resto es 2)20 \mod 8 = 4(ya que 8 entra en 20 un total de 2 veces y el resto es 4)
Cuando el dividendo o divisor es negativo, las operaciones de módulo pueden ser tratadas de forma diferente por los lenguajes de programación.
Seguro que te encuentras con casos de dividendo negativo en criptografía. En estos casos, el enfoque típico es el siguiente:
- Primero determina el valor más cercano inferior o igual al
dividendo en el que el divisor divide con resto cero. Llamamos a ese valor
p. - Si el dividendo es
x, entonces el resultado de la operación módulo es el valor dex - p.
Por ejemplo, supongamos que el dividendo es -20 y el divisor 3. El valor más próximo menor o igual que -20 en el que 3 divide a partes iguales es -21. El valor de x - p en este caso es -20 - (-21).
Esto es igual a 1 y, por tanto, -20 \mod 3 es igual a 1. De manera
similar, podemos evaluar las expresiones siguientes:
-8 \mod 5 = 2-19 \mod 16 = 13-14 \mod 6 = 4
En cuanto a la notación, normalmente verás los siguientes tipos de
expresiones: x = [y \mod z].
Debido a los paréntesis, la operación módulo en este caso sólo se aplica al
lado derecho de la expresión. Si y es igual a 25 y z es igual a
4, por ejemplo, entonces x se
evalúa como 1.
Sin paréntesis, la operación módulo actúa sobre ambos lados de una
expresión. Supongamos, por ejemplo, la siguiente expresión: x = y \mod z. Si y es igual a 25 y z es igual a
4, entonces todo lo que sabemos es que x \mod 4 se evalúa a 1. Esto es consistente con cualquier valor de x del conjunto \{\ldots, -7, -3, 1, 5, 9, \ldots\}.
La rama de las matemáticas que incluye operaciones modulares con números y expresiones se denomina aritmética modular. Se puede considerar esta rama como aritmética para casos en los que la recta numérica no es infinitamente larga. Aunque normalmente nos encontramos con operaciones modulares para números enteros (positivos) dentro de la criptografía, también se pueden realizar operaciones modulares utilizando cualquier número real.
El cifrado por turnos
La operación módulo es frecuente en criptografía. Para ilustrarlo, consideremos uno de los esquemas de cifrado históricos más famosos: el cifrado por turnos.
Definámoslo primero. Supongamos un diccionario D que equipara todas
las letras del alfabeto inglés, en orden, con el conjunto de números \{0, 1, 2, \ldots, 25\}. Supongamos un espacio de mensajes M. El cifrado por desplazamiento es, entonces, un esquema de cifrado
definido como sigue:
- Seleccionar uniformemente una clave
kdel espacio de claves K, donde K =\{0, 1, 2, \ldots, 25\}[1] - Cifrar un mensaje
m \in \mathbf{M}, de la siguiente manera:- Separar
men sus letras individualesm_0, m_1, \ldots, m_i, \ldots, m_l - Convertir cada
m_ien un número según D - Para cada
m_i,c_i = [(m_i + k) \mod 26] - Convierte cada
c_ien una letra según D - Luego combina
c_0, c_1, \ldots, c_lpara obtener el texto cifradoc
- Separar
- Descifrar un texto cifrado
cde la siguiente manera:- Convierte cada
c_ien un número según D - Para cada
c_i,m_i = [(c_i - k) \mod 26] - Convierte cada
m_ien una letra según D - Luego combina
m_0, m_1, \ldots, m_lpara obtener el mensaje originalm
- Convierte cada
El operador módulo del cifrado por turnos garantiza que las letras se envuelvan, de modo que todas las letras del texto cifrado queden definidas. Para ilustrarlo, consideremos la aplicación del cifrado por turnos a la palabra "DOG".
Supongamos que ha seleccionado uniformemente una tecla para que tenga el
valor 17. La letra "O" equivale a 15. Sin la operación de módulo, la suma de
este número de texto plano con la clave daría como resultado un número de
texto cifrado de 32. Sin embargo, ese número de texto cifrado no puede
convertirse en una letra de texto cifrado, ya que el alfabeto inglés sólo
tiene 26 letras. La operación de módulo garantiza que el número del texto
cifrado sea en realidad 6 (el resultado de 32 \mod 26), lo que equivale a la letra "G" del texto cifrado.
El cifrado completo de la palabra "DOG" con un valor de clave de 17 es el siguiente:
- Mensaje = DOG = D,O,G = 3,15,6
c_0 = [(3 + 17) \mod 26] = [(20) \mod 26] = 20 = Uc_1 = [(15 + 17) \mod 26] = [(32) \mod 26] = 6 = Gc_2 = [(6 + 17) \mod 26] = [(23) \mod 26] = 23 = Xc = UGX
Todo el mundo puede entender intuitivamente cómo funciona el cifrado por turnos y probablemente utilizarlo por sí mismo. Sin embargo, para avanzar en el conocimiento de la criptografía, es importante empezar a sentirse más cómodo con la formalización, ya que los esquemas se volverán mucho más difíciles. De ahí que se hayan formalizado los pasos del cifrado por turnos.
Notas:
[1] Podemos definir esta afirmación exactamente, utilizando la terminología
de la sección anterior. Sea una variable uniforme K su conjunto de resultados posibles. Entonces
Pr[K = 0] = \frac{1}{26}Pr[K = 1] = \frac{1}{26}...y así sucesivamente. Muestrear la variable uniforme K una vez para obtener una clave concreta.
La operación XOR
Todos los datos informáticos se procesan, almacenan y envían a través de redes a nivel de bits. Todos los esquemas criptográficos que se aplican a los datos informáticos funcionan también a nivel de bits.
Por ejemplo, supongamos que has escrito un correo electrónico en tu aplicación de correo electrónico. El cifrado no se aplica directamente a los caracteres ASCII del mensaje. Se aplica a la representación en bits de las letras y otros símbolos del mensaje.
Una operación matemática clave que hay que entender para la criptografía
moderna, además de la operación módulo, es la operación XOR, u "or exclusivo". Esta operación toma como entrada dos bits y da como
salida otro bit. La operación XOR se denominará simplemente "XOR". Da 0 si
los dos bits son iguales y 1 si los dos bits son diferentes. A continuación
puede ver las cuatro posibilidades. El símbolo \oplus representa "XOR" :
0 \oplus 0 = 0- 0
\oplus 1 = 1 1 \oplus 0 = 11 \oplus 1 = 0
Para ilustrarlo, supongamos que tenemos un mensaje m_1 (01111001) y un mensaje m_2 (01011001).
La operación XOR de estos dos mensajes se puede ver a continuación.
m_1 \oplus m_2 = 01111001 \oplus 01011001 = 00100000
El proceso es sencillo. Primero XOR los bits más a la izquierda de m_1 y m_2. En este caso es 0 \oplus 0 = 0. A
continuación, XOR el segundo par de bits de la izquierda. En este caso es 1 \oplus 1 = 0. Continúe este
proceso hasta que haya realizado la operación XOR en los bits más a la
derecha.
Es fácil ver que la operación XOR es conmutativa, es decir, que m_1 \oplus m_2 = m_2 \oplus m_1. Además, la operación XOR también es asociativa. Es decir, (m_1 \oplus m_2) \oplus m_3 = m_1 \oplus (m_2 \oplus m_3).
Una operación XOR sobre dos cadenas de longitudes alternativas puede tener diferentes interpretaciones, dependiendo del contexto. No nos ocuparemos aquí de ninguna operación XOR sobre cadenas de longitudes diferentes.
Una operación XOR es equivalente al caso especial de realizar una operación módulo sobre la suma de bits cuando el divisor es 2. Puedes ver la equivalencia en los siguientes resultados:
(0 + 0) \mod 2 = 0 \oplus 0 = 0(1 + 0) \mod 2 = 1 \oplus 0 = 1(0 + 1) \mod 2 = 0 \oplus 1 = 1(1 + 1) \mod 2 = 1 \oplus 1 = 0
Pseudoaleatoriedad
En nuestra discusión sobre variables aleatorias y uniformes, establecimos una distinción específica entre "aleatoria" y "uniforme". Esta distinción suele mantenerse en la práctica cuando se describen variables aleatorias. Sin embargo, en nuestro contexto actual, es necesario eliminar esta distinción y utilizar "aleatoria" y "uniforme" como sinónimos. Al final de esta sección explicaré por qué.
Para empezar, podemos llamar a una cadena binaria de longitud n aleatoria (o uniforme), si fuera el
resultado del muestreo de una variable uniforme S que da a cada cadena binaria de dicha longitud n una probabilidad igual de selección.
Supongamos, por ejemplo, el conjunto de todas las cadenas binarias de
longitud 8: \{0000\ 0000, 0000\ 0001, \ldots , 1111\ 1111\}. (Es típico escribir una cadena de 8 bits en dos cuartetos, cada uno
llamado nibble) Llamemos a este conjunto de cadenas S_8.
Según la definición anterior, podemos llamar aleatoria (o uniforme) a una
cadena binaria concreta de longitud 8, si es el resultado del muestreo de
una variable uniforme S que
da a cada cadena de S_8 la misma probabilidad de selección. Dado que el conjunto S_8 incluye 2^8 elementos, la
probabilidad de selección en el muestreo tendría que ser 1/2^8 para cada cadena del conjunto.
Un aspecto clave de la aleatoriedad de una cadena binaria es que se define con referencia al proceso por el que fue seleccionada. Por lo tanto, la forma de una cadena binaria no revela nada sobre su aleatoriedad en la selección.
Por ejemplo, mucha gente tiene la idea intuitiva de que una cadena como 1111\ 1111 no puede haber sido seleccionada al azar. Pero esto es claramente falso.
Definiendo una variable uniforme S sobre todas las cadenas binarias de longitud 8, la probabilidad de
seleccionar 1111\ 1111 del
conjunto S_8 es la misma que la de una cadena como 0111\ 0100. Por lo tanto, no
se puede decir nada acerca de la aleatoriedad de una cadena, simplemente
analizando la propia cadena.
También podemos hablar de cadenas aleatorias sin referirnos específicamente
a cadenas binarias. Por ejemplo, podríamos hablar de una cadena hexadecimal
aleatoria AF\ 02\ 82. En este
caso, la cadena se habría seleccionado al azar del conjunto de todas las
cadenas hexadecimales de longitud 6. Esto equivale a seleccionar al azar una
cadena binaria de longitud 24, ya que cada dígito hexadecimal representa 4
bits.
Normalmente, la expresión "una cadena aleatoria", sin calificarla, se
refiere a una cadena seleccionada al azar del conjunto de todas las cadenas
con la misma longitud. Así es como lo he descrito anteriormente. Por
supuesto, una cadena de longitud n también puede seleccionarse al azar de un conjunto diferente. Uno, por
ejemplo, que sólo constituya un subconjunto de todas las cadenas de longitud n, o quizás un conjunto que
incluya cadenas de longitud variable. En esos casos, sin embargo, no nos
referiríamos a ella como una "cadena aleatoria", sino como "una cadena
seleccionada aleatoriamente de un conjunto S".
Un concepto clave en criptografía es el de pseudoaleatoriedad. Una cadena pseudoaleatoria de longitud n aparece como si fuera el resultado del muestreo de una variable uniforme S que da a cada cadena en S_n una probabilidad igual de selección. De hecho, sin embargo, la cadena es el
resultado del muestreo de una variable uniforme S' que sólo define una distribución de probabilidad -no necesariamente una con
probabilidades iguales para todos los resultados posibles- en un subconjunto
de S_n. El
punto crucial aquí es que nadie puede distinguir realmente entre muestras de S y S', aunque se tomen muchas.
Supongamos, por ejemplo, una variable aleatoria S. Su conjunto de resultados es S_{256}, es decir, el conjunto de todas las cadenas binarias de longitud 256. Este
conjunto tiene 2^{256} elementos. Este conjunto tiene 2^{256} elementos. Cada elemento tiene la misma probabilidad de selección, 1/2^{256}, en el
muestreo.
Además, supongamos una variable aleatoria S'. Su conjunto de resultados sólo incluye 2^{128} cadenas binarias
de longitud 256. Tiene alguna distribución de probabilidad sobre esas cadenas,
pero esta distribución no es necesariamente uniforme.
Supongamos que ahora tomo 1000 muestras de S y 1000 muestras de S' y te
doy los dos conjuntos de resultados. Te digo qué conjunto de resultados está
asociado a qué variable aleatoria. A continuación, tomo una muestra de una
de las dos variables aleatorias. Pero esta vez no te digo de qué variable
aleatoria tomo la muestra. Si S' fuera pseudoaleatoria, entonces la idea es que tu probabilidad de acertar
qué variable aleatoria he muestreado no es prácticamente mejor que 1/2.
Normalmente, una cadena pseudoaleatoria de longitud n se produce seleccionando aleatoriamente una cadena de tamaño n - x, donde x es un número entero positivo, y utilizándola como entrada para un algoritmo
expansivo. Esta cadena aleatoria de tamaño n - x se conoce como semilla.
Las cadenas pseudoaleatorias son un concepto clave para que la criptografía sea práctica. Pensemos, por ejemplo, en los cifradores de flujo. Con un cifrado de flujo, una clave seleccionada al azar se introduce en un algoritmo expansivo para producir una cadena pseudoaleatoria mucho mayor. A continuación, esta cadena pseudoaleatoria se combina con el texto plano mediante una operación XOR para producir un texto cifrado.
Si no pudiéramos producir este tipo de cadena pseudoaleatoria para un cifrado de flujo, necesitaríamos una clave tan larga como el mensaje para su seguridad. Esta no es una opción muy práctica en la mayoría de los casos.
La noción de pseudoaleatoriedad analizada en esta sección puede definirse de manera más formal. También se extiende a otros contextos. Pero no es necesario que nos adentremos en este debate. Todo lo que necesitas entender intuitivamente para gran parte de la criptografía es la diferencia entre una cadena aleatoria y una pseudoaleatoria. [2]
Ahora también debería quedar clara la razón por la que dejamos de distinguir
entre "aleatorio" y "uniforme". En la práctica, todo el mundo utiliza el
término pseudoaleatorio para indicar una cadena que aparece como si fuera el resultado del muestreo de una variable uniforme S. Estrictamente hablando,
deberíamos llamar a una cadena de este tipo "pseudo-uniforme", adoptando
nuestro lenguaje de antes. Como el término "pseudo-uniforme" es un poco
anticuado y nadie lo utiliza, no lo introduciremos aquí para mayor claridad.
En su lugar, nos limitaremos a eliminar la distinción entre "aleatorio" y
"uniforme" en el contexto actual.
Notas
[2] Si está interesado en una exposición más formal sobre estas cuestiones, puede consultar Introduction to Modern Cryptography de Katz y Lindell, especialmente el capítulo 3.
Fundamentos matemáticos de la criptografía 2
¿Qué es la teoría de números?
Este capítulo trata un tema más avanzado de los fundamentos matemáticos de la criptografía: la teoría de números. Aunque la teoría de números es importante para la criptografía simétrica (como en el Cifrado Rijndael), es particularmente importante en el entorno criptográfico de clave pública.
Si los detalles de la teoría de números le resultan engorrosos, le recomendaría una lectura de alto nivel la primera vez. Siempre puedes volver a ella más adelante.
Se podría caracterizar la teoría de números como el estudio de las propiedades de los números enteros y las funciones matemáticas que trabajan con números enteros.
Consideremos, por ejemplo, que dos números cualesquiera a y N son coprimos (o primos relativos) si su máximo común divisor es igual a
1. Supongamos ahora un número entero N. ¿Cuántos números enteros
menores que N son coprimos de N? ¿Podemos hacer
afirmaciones generales sobre las respuestas a esta pregunta? Estos son los
tipos típicos de preguntas que la teoría de números trata de responder.
La teoría moderna de números se basa en las herramientas del álgebra abstracta. El campo del álgebra abstracta es una subdisciplina de las matemáticas en la que los principales objetos de análisis son objetos abstractos conocidos como estructuras algebraicas. Una estructura algebraica es un conjunto de elementos unido a una o más operaciones, que cumple ciertos axiomas. A través de las estructuras algebraicas, los matemáticos pueden comprender problemas matemáticos concretos abstrayéndose de sus detalles.
El campo del álgebra abstracta a veces también se denomina álgebra moderna. También se puede encontrar el concepto de matemáticas abstractas (o matemáticas puras). Este último término no se refiere al álgebra abstracta, sino al estudio de las matemáticas por sí mismas, y no sólo con vistas a sus posibles aplicaciones.
Los conjuntos del álgebra abstracta pueden tratar muchos tipos de objetos, desde las transformaciones que preservan la forma de un triángulo equilátero hasta los patrones del papel pintado. Para la teoría de números, sólo consideramos conjuntos de elementos que contienen números enteros o funciones que trabajan con números enteros.
Grupos
Un concepto básico en matemáticas es el de conjunto de elementos. Un conjunto suele denotarse mediante signos de acolación con los elementos separados por comas.
Por ejemplo, el conjunto de todos los números enteros es \{..., -2, -1, 0, 1, 2, ...\}. Las elipses aquí significa que un cierto patrón continúa en una dirección
particular. Así que el conjunto de todos los números enteros también incluye 3, 4, 5, 6 y así sucesivamente, así como -3, -4, -5, -6 y así sucesivamente. Este conjunto de todos los números enteros se suele
denotar por \mathbb{Z}.
Otro ejemplo de conjunto es \mathbb{Z} \mod 11, o el conjunto de todos los números enteros módulo 11. A diferencia del
conjunto entero \mathbb{Z}, este
conjunto sólo contiene un número finito de elementos, a saber \{0, 1, \ldots, 9, 10\}.
Un error común es pensar que el conjunto \mathbb{Z} \mod 11 es en realidad \{-10, -9, \ldots, 0, \ldots, 9, 10\}. Pero este no es el caso, dada la forma en que definimos la operación
módulo antes. Cualquier entero negativo reducido por el módulo 11 se
envuelve en \{0, 1, \ldots, 9, 10\}. Por ejemplo, la expresión -2 \mod 11 envuelve a 9, mientras que la
expresión -27 \mod 11 envuelve a 5.
Otro concepto básico en matemáticas es el de operación binaria. Se trata de cualquier operación que toma dos elementos para producir un tercero. Por ejemplo, a partir de la aritmética y el álgebra básicas, estarás familiarizado con cuatro operaciones binarias fundamentales: suma, resta, multiplicación y división.
Estos dos conceptos matemáticos básicos, conjuntos y operaciones binarias, se utilizan para definir la noción de grupo, la estructura más esencial del álgebra abstracta.
En concreto, supongamos alguna operación binaria \circ. Además, supongamos un conjunto de elementos S equipado
con esa operación. Todo lo que "equipado" significa aquí es que la operación \circ se puede realizar entre dos elementos cualesquiera del conjunto S.
La combinación \langle \mathbf{S}, \circ \rangle es, entonces, un grupo si cumple cuatro condiciones específicas,
conocidas como axiomas de grupo.
Para cualquier
aybque sean elementos de\mathbf{S},a \circ bes también un elemento de\mathbf{S}. Esto se conoce como condición de cierre.Para cualesquiera
a,bycque sean elementos de\mathbf{S}, se da el caso de que(a \circ b) \circ c = a \circ (b \circ c). Esto se conoce como condición de asociatividad.Existe un único elemento
een\mathbf{S}, tal que para cada elementoaen\mathbf{S}, se cumple la siguiente ecuación:e \circ a = a \circ e = a. Como sólo hay un elementoe, se llama elemento de identidad. Esta condición se conoce como condición de identidad.Para cada elemento
aen\mathbf{S}, existe un elementoben\mathbf{S}, tal que se cumple la siguiente ecuación:a \circ b = b \circ a = e, dondeees el elemento identidad. El elementobaquí se conoce como el elemento inverso, y se denota comúnmente comoa^{-1}. Esta condición se conoce como condición inversa o condición de invertibilidad.
Exploremos un poco más los grupos. Denotemos el conjunto de todos los
números enteros por \mathbb{Z}. Este conjunto combinado con la suma estándar, o \langle \mathbb{Z}, + \rangle, se ajusta claramente a la definición de grupo, ya que cumple los cuatro
axiomas anteriores.
Para cualesquiera
xeyque sean elementos de\mathbb{Z},x + yes también un elemento de\mathbb{Z}. Así que\langle \mathbb{Z}, + \ranglecumple la condición de cierre.Para cualesquiera
x,yyzque sean elementos de\mathbb{Z},(x + y) + z = x + (y + z). Así que\langle \mathbb{Z}, + \ranglecumple la condición de asociatividad.Hay un elemento de identidad en
\langle \mathbb{Z}, + \rangle, a saber, 0. Para cualquierxen\mathbb{Z}, a saber, sostiene que:0 + x = x + 0 = x. Por tanto\langle \mathbb{Z}, + \ranglecumple la condición de identidad.Por último, para cada elemento
xen\mathbb{Z}, existe unytal quex + y = y + x = 0. Sixfuera 10, por ejemplo,ysería-10(en el caso de quexsea 0,ytambién es 0). Por tanto\langle \mathbb{Z}, + \ranglecumple la condición inversa.
Es importante destacar que el hecho de que el conjunto de enteros con
adición constituya un grupo no significa que constituya un grupo con
multiplicación. Se puede verificar esto probando \langle \mathbb{Z}, \cdot \rangle contra los cuatro axiomas de grupo (donde \cdot significa multiplicación
estándar).
Es evidente que los dos primeros axiomas se cumplen. Además, bajo
multiplicación el elemento 1 puede servir como elemento identidad. Cualquier
entero x multiplicado por 1,
a saber, da x. Sin embargo, \langle \mathbb{Z}, \cdot \rangle no cumple la condición inversa. Es decir, no hay un único elemento y en \mathbb{Z} para
cada x en \mathbb{Z}, de modo
que x \cdot y = 1.
Por ejemplo, supongamos que x = 22. ¿Qué valor y del conjunto \mathbb{Z} multiplicado por x daría el
elemento identidad 1? El valor de 1/22 funcionaría, pero no está en el conjunto \mathbb{Z}. De
hecho, te encuentras con este problema para cualquier entero x, distintos de los valores
de 1 y -1 (donde y tendría que
ser 1 y -1, respectivamente).
Si permitimos números reales para nuestro conjunto, entonces nuestros
problemas desaparecen en gran medida. Para cualquier elemento x del conjunto, la multiplicación por 1/x da 1. Como las fracciones
están incluidas en el conjunto de los números reales, se puede encontrar un inverso
para cada número real. La excepción es el cero, ya que cualquier multiplicación
por cero nunca dará como resultado el elemento de identidad 1. Por lo tanto,
el conjunto de los números reales distintos de cero dotados de multiplicación
es efectivamente un grupo.
Algunos grupos cumplen una quinta condición general, conocida como condición de conmutatividad. Esta condición es la siguiente:
- Supongamos un grupo
Gcon un conjunto S y un operador binario\circ. Supongamos queaybson elementos de S. Si se da el caso de quea \circ b = b \circ apara cualesquiera dos elementosayben S, entoncesGcumple la condición de conmutatividad.
Cualquier grupo que cumpla la condición de conmutatividad se conoce como grupo conmutativo, o grupo abeliano (en honor a Niels Henrik Abel). Es fácil comprobar que tanto el conjunto de los números reales sobre la suma como el conjunto de los números enteros sobre la suma son grupos abelianos. El conjunto de los números enteros sobre la multiplicación no es un grupo en absoluto, por lo que ipso facto no puede ser un grupo abeliano. En cambio, el conjunto de los números reales distintos de cero sobre la multiplicación también es un grupo abeliano.
Debe tener en cuenta dos convenciones importantes sobre notación. En primer lugar, los signos "+" o "×" se emplearán con frecuencia para simbolizar operaciones de grupo, incluso cuando los elementos no sean, de hecho, números. En estos casos, no debe interpretar estos signos como sumas o multiplicaciones aritméticas estándar. En su lugar, son operaciones que sólo tienen una similitud abstracta con estas operaciones aritméticas.
A menos que nos refiramos específicamente a sumas o multiplicaciones
aritméticas, es más fácil utilizar símbolos como \circ y \diamond para las operaciones
de grupo, ya que no tienen connotaciones muy arraigadas culturalmente.
En segundo lugar, por la misma razón que "+" y "×" se utilizan a menudo para
indicar operaciones no aritméticas, los elementos de identidad de los grupos
se simbolizan frecuentemente con "0" y "1", incluso cuando los elementos de
estos grupos no son números. A menos que se refiera al elemento de identidad
de un grupo con números, es más fácil utilizar un símbolo más neutro como "e" para indicar el elemento de identidad.
Muchos conjuntos de valores diferentes y muy importantes en matemáticas dotados de ciertas operaciones binarias son grupos. Sin embargo, las aplicaciones criptográficas sólo trabajan con conjuntos de números enteros o, al menos, con elementos que se describen mediante números enteros, es decir, dentro del dominio de la teoría de números. Por lo tanto, los conjuntos con números reales distintos de los enteros no se emplean en aplicaciones criptográficas.
Terminemos con un ejemplo de elementos que pueden "describirse mediante enteros", aunque no sean enteros. Un buen ejemplo son los puntos de las curvas elípticas. Aunque cualquier punto de una curva elíptica no es claramente un número entero, dicho punto está descrito por dos números enteros.
Las curvas elípticas son, por ejemplo, cruciales para Bitcoin. Cualquier par de claves pública y privada estándar de Bitcoin se selecciona a partir del conjunto de puntos definido por la siguiente curva elíptica:
x^3 + 7 = y^2 \mod 2^{256} – 2^{32} – 29 – 28 – 27 – 26 - 24 - 1(el mayor número primo menor que 2^{256}). La coordenada x es la
clave privada y la coordenada y es tu clave pública.
Las transacciones en Bitcoin normalmente implican bloquear las salidas a una o más claves públicas de alguna manera. El valor de estas transacciones puede, entonces, ser desbloqueado haciendo firmas digitales con las correspondientes claves privadas.
Grupos cíclicos
Podemos distinguir entre un grupo finito y un grupo infinito. El primero tiene un número finito de elementos, mientras que el segundo tiene un número infinito. El número de elementos de cualquier grupo finito se conoce como orden del grupo. Toda la criptografía práctica que implica el uso de grupos se basa en grupos finitos (teóricos numéricos).
Dentro de la criptografía de clave pública, cierta clase de grupos abelianos finitos conocidos como grupos cíclicos son especialmente importantes. Para entender los grupos cíclicos, primero tenemos que entender el concepto de exponenciación de elementos de grupo.
Supongamos un grupo G con una
operación de grupo \circ, y
que a es un elemento de G. La expresión a^n debe, entonces, interpretarse como el elemento a combinado consigo mismo un total de n - 1 veces. Por ejemplo, a^2 significa a \circ a, a^3 significa a \circ a \circ a,
y así sucesivamente. (Nótese que la exponenciación aquí no es necesariamente
exponenciación en el sentido aritmético estándar)
Veamos un ejemplo. Supongamos que G = \langle \mathbb{Z} \mod 7, + \rangle, y que nuestro valor para a es igual a 4. En este caso, a^2 = [4 + 4 \mod 7] = [8 \mod 7] = 1 \mod 7. Alternativamente, a^4 representaría [4 + 4 + 4 + 4 \mod 7] = [16 \mod 7] = 2 \mod 7.
Algunos grupos abelianos tienen uno o más elementos que pueden dar lugar a todos los demás elementos del grupo mediante exponenciación continua. Estos elementos se denominan generadores o elementos primitivos.
Una clase importante de tales grupos es \langle \mathbb{Z}^* \mod N, \cdot \rangle, donde N es un número
primo. La notación \mathbb{Z}^* significa aquí que el grupo contiene todos los enteros positivos distintos
de cero menores que N. Por lo
tanto, un grupo de este tipo siempre tiene N - 1 elementos.
Consideremos, por ejemplo, G = \langle \mathbb{Z}^* \mod 11, \cdot \rangle. Este grupo tiene los siguientes elementos: \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. El orden de este grupo es 10 (que es igual a 11 - 1).
Vamos a explorar exponenciando el elemento 2 de este grupo. Los cálculos
hasta 2^{12} se muestran
a continuación. Nótese que en el lado izquierdo de la ecuación, el exponente
se refiere a la exponenciación del elemento del grupo. En nuestro ejemplo particular,
esto implica de hecho la exponenciación aritmética en el lado derecho de la ecuación
(pero también podría haber implicado, por ejemplo, la adición). Para aclarar,
he escrito la operación repetida, en lugar de la forma del exponente en el lado
derecho.
2^1 = 2 \mod 112^2 = 2 \cdot 2 \mod 11 = 4 \mod 112^3 = 2 \cdot 2 \cdot 2 \cdot 11 = 8 \cdot 112^4 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 16 \mod 11 = 5 \mod 112^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 32 \cdot 11 = 10 \cdot 112^6 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 64 \cdot 11 = 9 \cdot 112^7 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 11 = 128 \cdot 11 = 7 \cdot 112^8 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 11 = 256 \cdot 11 = 3 \cdot 112^9 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 11 = 512 \cdot 11 = 6 \mod 112^{10} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 11 = 1024 \cdot 11 = 1 \cdot 112^{11} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 2048 \cdot 11 = 2 \cdot 112^{12} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 11 = 4096 \cdot 11 = 4 \cdot 11
Si nos fijamos bien, podemos ver que la exponenciación del elemento 2
recorre todos los elementos de \langle \mathbb{Z}^* \mod 11, \cdot \rangle en el siguiente orden: 2, 4, 8, 5, 10, 9, 7, 3, 6, 1. Después de 2^{10}, la
exponenciación continuada del elemento 2 recorre todos los elementos de
nuevo y en el mismo orden. Por lo tanto, el elemento 2 es un generador en \langle \mathbb{Z}^* \mod 11, \cdot \rangle.
Aunque \langle \mathbb{Z}^* \mod 11, \cdot \rangle tiene múltiples generadores, no todos los elementos de este grupo son generadores.
Consideremos, por ejemplo, el elemento 3. Corriendo a través de los primeros
10 exponentiations, sin mostrar los cálculos engorrosos, produce los siguientes
resultados:
3^1 = 3 \mod 113^2 = 9 \mod 113^3 = 5 \mod 113^4 = 4 \mod 113^5 = 1 \mod 113^6 = 3 \mod 113^7 = 9 \mod 113^8 = 5 \mod 113^9 = 4 \mod 113^{10} = 1 \mod 11
En lugar de recorrer todos los valores en \langle \mathbb{Z}^* \mod 11, \cdot \rangle, la exponenciación del elemento 3 sólo conduce a un subconjunto de esos
valores: 3, 9, 5, 4, y 1. Después de la quinta exponenciación, estos valores
comienzan a repetirse.
Ahora podemos definir un grupo cíclico como cualquier grupo con al menos un generador. Es decir, hay al menos un elemento del grupo a partir del cual se pueden producir todos los demás elementos del grupo mediante exponenciación.
Habrás observado en nuestro ejemplo anterior que tanto 2^{10} como 3^{10} son
iguales a 1 \mod 11. De
hecho, aunque no vamos a realizar los cálculos, la exponenciación por 10 de
cualquier elemento del grupo \langle \mathbb{Z}^* \mod 11, \cdot \rangle dará como resultado 1 \mod 11. ¿Por qué ocurre
esto?
Es una pregunta importante, pero hay que trabajar un poco para responderla.
Para empezar, supongamos dos enteros positivos a y N. Un teorema importante en
la teoría de números afirma que a tiene un inverso multiplicativo módulo N (es decir, un entero b de
modo que a \cdot b = 1 \mod N) si y
sólo si el máximo común divisor entre a y N es igual a 1. Es decir,
si a y N son coprimos. Es decir, si a y N son coprimos.
Así, para cualquier grupo de enteros dotado de multiplicación módulo N, sólo los coprimas más pequeños con N están incluidos en el conjunto. Podemos denotar este conjunto por \mathbb{Z}^c \mod N.
Por ejemplo, supongamos que N es 10. Sólo los números enteros 1, 3, 7 y 9 son coprimas con 10. Así que el conjunto\mathbb{Z}^c \mod 10sólo incluye{1, 3, 7, 9}$. No se puede crear un grupo con multiplicación
entera módulo 10 utilizando cualquier otro número entero entre 1 y 10. Para
este grupo en particular, los inversos son los pares 1 y 9, y 3 y 7.
En el caso de que N sea
primo, todos los números enteros de 1 a N - 1 son coprimas de N. Tal grupo,
por lo tanto, tiene un orden de N - 1. Utilizando nuestra
notación anterior, \mathbb{Z}^c \mod N es igual a \mathbb{Z}^* \mod N cuando N es primo. El grupo
que seleccionamos para nuestro ejemplo anterior, \langle \mathbb{Z}^* \mod 11, \cdot \rangle, es un caso particular de esta clase de grupos.
A continuación, la función \phi(N) calcula el número de coprimos hasta un número N, y se conoce como función Phi de Euler. [1] Según el teorema de Euler, siempre que dos números enteros a y N sean coprimos, se cumple lo
siguiente:
a^{\phi(N)} \mod N = 1 \mod N
Esto tiene una implicación importante para la clase de grupos \langle \mathbb{Z}^* \mod N, \cdot \rangle donde N es primo. Para estos
grupos, la exponenciación de elementos de grupo representa la exponenciación
aritmética. Es decir, a^{\phi(N)} \mod N representa la operación aritmética a^{\phi(N)} \mod N.
Como cualquier elemento a en
estos grupos multiplicativos es coprimo con N, significa que a^{\phi(N)} \mod N = a^{N - 1} \mod N = 1 \mod N.
El teorema de Euler es un resultado realmente importante. Para empezar,
implica que todos los elementos en \langle \mathbb{Z}^* \mod N, \cdot \rangle sólo puede ciclo a través de un número de valores por exponenciación que se
divide en N - 1. En el caso
de \langle \mathbb{Z}^* \mod 11, \cdot \rangle, esto significa que cada elemento sólo puede ciclo a través de 2, 5, o 10
elementos. Los valores del grupo que los ciclos de cualquier elemento a
través de la exponenciación se conoce como el orden del elemento. Un elemento con un orden equivalente al
orden de un grupo es un generador.
Además, el teorema de Euler implica que siempre podemos conocer el resultado
de a^{N - 1} \mod N para cualquier grupo \langle \mathbb{Z}^* \mod N, \cdot \rangle donde N es primo. Esto es así
independientemente de lo complicados que puedan ser los cálculos reales.
Por ejemplo, supongamos que nuestro grupo es \mathbb{Z}^* \mod 160.481.182 (donde 160.481.182 es efectivamente un número primo). Sabemos que todos los
números enteros 1 a 160.481.181 deben ser elementos de este grupo, y que \phi(n) = 160.481.181. Aunque
no podemos hacer todos los pasos de los cálculos, sabemos que expresiones
como 514^{160,481,181}, 2,005^{160,481,181}, y 256,212^{160,481,181} deben evaluarse todas a 1 \mod 160,481,182.
Notas:
[1] La función funciona de la siguiente manera. Cualquier número entero N se puede factorizar en un producto de números primos. Supongamos que un
determinado N se factoriza de
la siguiente manera: p_1^{e1} \cdot p_2^{e2} \cdot \ldots \cdot
p_m^{em} donde todos los p son números
primos y todos los e son enteros
mayores o iguales que 1. Entonces:
\phi(N) = \sum_{i=1}^m \left[p_i^{e_i} - p_i^{e_i - 1}\right]Fórmula de la función Phi de Euler para la factorización en primos de N.
Campos
Un grupo es la estructura algebraica básica del álgebra abstracta, pero hay muchas más. La única otra estructura algebraica con la que debes estar familiarizado es la de un campo, concretamente la de un campo finito. Este tipo de estructura algebraica se utiliza con frecuencia en criptografía, como en el Advanced Encryption Standard. Este último es el principal esquema de cifrado simétrico que encontrarás en la práctica.
Un campo se deriva de la noción de grupo. En concreto, un campo es un conjunto de elementos S dotado de dos operadores
binarios \circ y \diamond, que cumple las
siguientes condiciones:
El conjunto S dotado de
\circes un grupo abeliano.El conjunto S equipado con
\diamondes un grupo abeliano para los elementos "no nulos".El conjunto S dotado de los dos operadores cumple lo que se conoce como condición distributiva: Supongamos que
a,bycson elementos de S. Entonces S equipado con los dos operadores cumple la propiedad distributiva cuandoa \circ (b \diamond c) = (a \circ b) \diamond (a \circ c).
Obsérvese que, como en el caso de los grupos, la definición de campo es muy
abstracta. No hace ninguna afirmación sobre los tipos de elementos de S, ni sobre las operaciones \circ y \diamond. Sólo afirma que
un campo es cualquier conjunto de elementos con dos operaciones para las que
se cumplen las tres condiciones anteriores. (El elemento "cero" en el
segundo grupo abeliano puede interpretarse de forma abstracta)
Entonces, ¿cuál podría ser un ejemplo de un campo? Un buen ejemplo es el
conjunto \mathbb{Z} \mod 7, o \{0, 1, \ldots, 7\} definido sobre la suma estándar (en lugar de \circ más arriba) y la multiplicación estándar (en lugar de \diamond más arriba).
En primer lugar, \mathbb{Z} \mod 7 cumple la condición de ser un grupo abeliano sobre la suma, y cumple la condición
de ser un grupo abeliano sobre la multiplicación si sólo se consideran los elementos
distintos de cero. En segundo lugar, la combinación del conjunto con los dos
operadores cumple la condición distributiva.
Desde el punto de vista didáctico, merece la pena explorar estas
afirmaciones utilizando algunos valores concretos. Tomemos los valores
experimentales 5, 2 y 3, algunos elementos elegidos al azar del conjunto \mathbb{Z} \mod 7, para inspeccionar el campo \langle \mathbb{Z} \mod 7, +, \cdot \rangle. Utilizaremos estos tres valores en orden, según sea necesario para
explorar condiciones particulares.
Exploremos primero si \mathbb{Z} \mod 7 equipado con la adición es un grupo abeliano.
Condición de cierre: Tomemos 5 y 2 como valores. En ese caso,
[5 + 2] \mod 7 = 7 \mod 7 = 0. Este es de hecho un elemento de\mathbb{Z} \mod 7, por lo que el resultado es consistente con la condición de cierre.Condición de asociatividad: Tomemos como valores 5, 2 y 3. En ese caso,
[(5 + 2) + 3] \mod 7 = [5 + (2 + 3)] \mod 7 = 10 \mod 7 = 3. Esto es consistente con la condición de asociatividad.Condición de identidad: Tomemos 5 como valor. En ese caso,
[5 + 0] \mod 7 = [0 + 5] \mod 7 = 5. Así que 0 parece ser el elemento de identidad para la suma.Condición inversa: Consideremos la inversa de 5. Tiene que darse el caso de que
[5 + d] \mod 7 = 0, para algún valor ded. En este caso, el único valor de\mathbb{Z} \mod 7que cumple esta condición es 2.Condición de conmutatividad: Tomemos como valores 5 y 3. En ese caso,
[5 + 3] \mod 7 = [3 + 5] \mod 7 = 1. Esto es consistente con la condición de conmutatividad.
El conjunto \mathbb{Z} \mod 7 dotado de adición parece claramente ser un grupo abeliano. Exploremos ahora
si \mathbb{Z} \mod 7 equipado
con la multiplicación es un grupo abeliano para todos los elementos distintos
de cero.
Condición de cierre: Tomemos 5 y 2 como valores. En ese caso,
[5 \cdot 2] \mod 7 = 10 \mod 7 = 3. Este es también un elemento de\mathbb{Z} \mod 7, por lo que el resultado es consistente con la condición de cierre.Condición de asociatividad: Tomemos 5, 2 y 3 como nuestros valores. En ese caso,
[(5 \cdot 2) \cdot 3] \mod 7 = [5 \cdot (2 \cdot 3)] \mod 7 = 30 \cdot 7 = 2. Esto es consistente con la condición de asociatividad.Condición de identidad: Tomemos 5 como valor. En ese caso,
[5 \cdot 1] \mod 7 = [1 \cdot 5] \mod 7 = 5. Así que 1 parece ser el elemento de identidad para la multiplicación.Condición inversa: Consideremos la inversa de 5. Tiene que ser el caso de que
[5 \cdot d] \mod 7 = 1, para algún valor ded. El único valor de\mathbb{Z} \mod 7que cumple esta condición es 3. Esto es consistente con la condición inversa.Condición de conmutatividad: Tomemos 5 y 3 como valores. En ese caso,
[5 \cdot 3] \mod 7 = [3 \cdot 5] \mod 7 = 15 \cdot 7 = 1. Esto es consistente con la condición de conmutatividad.
El conjunto \mathbb{Z} \mod 7 parece cumplir claramente las reglas para ser un grupo abeliano cuando se combina
con la suma o la multiplicación sobre los elementos distintos de cero.
Por último, este conjunto combinado con ambos operadores parece cumplir la
condición distributiva. Tomemos 5, 2 y 3 como valores. Podemos ver que [5 \cdot (2 + 3)] \cdot 7 = [5 \cdot 2 + 5 \cdot 3] \cdot 7 = 25 \cdot 7
= 4.
Ahora hemos visto que \mathbb{Z} \mod 7 equipado con adición y multiplicación cumple los axiomas para un campo finito
cuando se prueba con valores particulares. Por supuesto, también podemos demostrar
que en general, pero no lo hará aquí.
Hay que distinguir entre dos tipos de campos: finitos e infinitos.
Un campo infinito implica un campo donde el conjunto S es infinitamente grande. El conjunto de números reales \mathbb{R} dotado de suma y multiplicación es un ejemplo de campo infinito. Un campo finito, también conocido como campo de Galois, es un campo donde el conjunto S es finito. Nuestro ejemplo anterior de \langle \mathbb{Z} \mod 7, +, \cdot \rangle es un campo finito.
En criptografía, nos interesan principalmente los campos finitos. En
general, se puede demostrar que existe un campo finito para un conjunto de
elementos S si y sólo si tiene p^m elementos, donde p es un
número primo y m un número
entero positivo mayor o igual que uno. En otras palabras, si el orden de
algún conjunto S es un número primo (p^m donde m = 1) o alguna
potencia prima (p^m donde m > 1), entonces se pueden
encontrar dos operadores \circ y \diamond tales que se cumplan
las condiciones para un campo.
Si un campo finito tiene un número primo de elementos, se denomina campo primo. Si el número de elementos del campo finito es una potencia prima, el campo se denomina campo de extensión. En criptografía, nos interesan tanto los campos primos como los campos de extensión. [2]
Los principales campos primos de interés en criptografía son aquellos en los
que el conjunto de todos los números enteros está modulado por algún número
primo, y los operadores son la suma y la multiplicación estándar. Esta clase
de campos finitos incluiría \mathbb{Z} \mod 2, \mathbb{Z} \mod 3, \mathbb{Z} \mod 5, \mathbb{Z} \mod 7, \mathbb{Z} \mod 11, \mathbb{Z} \mod 13,
y así sucesivamente. Para cualquier campo primo \mathbb{Z} \mod p,
el conjunto de enteros del campo es el siguiente: \{0, 1, \ldots, p - 2, p - 1\}.
En criptografía, también nos interesan los campos de extensión, en
particular cualquier campo con 2^m elementos donde m > 1. Estos
campos finitos se utilizan, por ejemplo, en el cifrado Rijndael, que
constituye la base del estándar de cifrado avanzado. Mientras que los campos
primos son relativamente intuitivos, estos campos de extensión de base 2
probablemente no sean para nadie que no esté familiarizado con el álgebra
abstracta.
Para empezar, es cierto que a cualquier conjunto de enteros con 2^m elementos se le pueden asignar dos operadores que harían de su combinación
un campo (siempre que m sea un
entero positivo). Sin embargo, que exista un campo no significa necesariamente
que sea fácil de descubrir o especialmente práctico para determinadas aplicaciones.
Resulta que los campos de extensión de 2^m particularmente aplicables en criptografía son los definidos sobre conjuntos
particulares de expresiones polinómicas, en lugar de algún conjunto de números
enteros.
Por ejemplo, supongamos que queremos un campo de extensión con 2^3 (es decir, 8) elementos en el conjunto. Aunque podría haber muchos conjuntos
diferentes que se pueden utilizar para campos de ese tamaño, uno de esos
conjuntos incluye todos los polinomios únicos de la forma a_2x^2 + a_1x + a_0, donde
cada coeficiente a_i es 0 ó
1. Por lo tanto, este conjunto S incluye los siguientes
elementos: a_2x^2 + a_1x + a_0$. Por lo tanto, este conjunto S incluye los siguientes elementos:
0: El caso en quea_2 = 0,a_1 = 0, ya_0 = 0.1: El caso en quea_2 = 0,a_1 = 0, ya_0 = 1.x: El caso en quea_2 = 0,a_1 = 1, ya_0 = 0.x + 1: El caso en quea_2 = 0,a_1 = 1, ya_0 = 1.x^2: El caso en quea_2 = 1,a_1 = 0, ya_0 = 0.x^2 + 1: El caso en quea_2 = 1,a_1 = 0, ya_0 = 1.x^2 + x: El caso en quea_2 = 1,a_1 = 1, ya_0 = 0.x^2 + x + 1: El caso en quea_2 = 1,a_1 = 1, ya_0 = 1.
Así S sería el conjunto \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}. ¿Qué dos operaciones se pueden definir sobre este conjunto de elementos
para asegurar que su combinación es un campo?
La primera operación sobre el conjunto S (\circ) se puede definir como una suma de polinomios estándar módulo 2. Todo lo
que tienes que hacer es sumar los polinomios como lo harías normalmente, y
luego aplicar el módulo 2 a cada uno de los coeficientes del polinomio
resultante. He aquí algunos ejemplos:
[(x^2) + (x^2 + x + 1)] \mod 2 = [2x^2 + x + 1] \mod 2 = x + 1[(x^2 + x) + (x)] \mod 2 = [x^2 + 2x] \mod 2 = x^2[(x + 1) + (x^2 + x + 1)] \mod 2 = [x^2 + 2x + 2] \mod 2 = x^2 + 1
La segunda operación sobre el conjunto S (\diamond) que se necesita para crear el campo es más complicada. Es un tipo de
multiplicación, pero no la multiplicación estándar de la aritmética. En su
lugar, hay que ver cada elemento como un vector y entender la operación como
la multiplicación de esos dos vectores módulo de un polinomio irreducible.
Veamos primero la idea de polinomio irreducible. Un polinomio irreducible es aquel que no se puede factorizar (igual que un número primo no se puede factorizar en componentes distintos de 1 y el propio número primo). Para nuestros propósitos, estamos interesados en polinomios que son irreducibles con respecto al conjunto de todos los números enteros. (Tenga en cuenta que puede ser capaz de factorizar ciertos polinomios mediante, por ejemplo, los números reales o complejos, aunque no pueda factorizarlos utilizando números enteros)
Por ejemplo, consideremos el polinomio x^2 - 3x + 2. Esto puede ser reescrito como (x - 1)(x - 2). Por lo tanto,
esto no es irreducible. Consideremos ahora el polinomio x^2 + 1. Utilizando sólo
números enteros, no hay manera de factorizar aún más esta expresión. Por lo
tanto, este es un polinomio irreducible con respecto a los números enteros.
A continuación, pasemos al concepto de multiplicación vectorial. No exploraremos este tema en profundidad, pero basta con que entiendas una regla básica: Cualquier división vectorial puede tener lugar siempre que el dividendo tenga un grado mayor o igual que el del divisor. Si el dividendo tiene un grado menor que el divisor, entonces el dividendo ya no puede ser dividido por el divisor.
Por ejemplo, consideremos la expresión x^6 + x + 1 \mod x^5 + x^2. Esto claramente reduce aún más como el grado del dividendo, 6, es mayor
que el grado del divisor, 5. Ahora considere la expresión x^5 + x + 1 \mod x^5 + x^2.
Esto también reduce aún más, como el grado del dividendo, 5, y el divisor,
5, son iguales.
Sin embargo, consideremos ahora la expresión x^4 + x + 1 \mod x^5 + x^2. Esto no se reduce más, ya que el grado del dividendo, 4, es menor que el
grado del divisor, 5.
Sobre la base de esta información, ahora estamos listos para encontrar
nuestra segunda operación para el conjunto \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.
Ya he dicho que la segunda operación debe entenderse como multiplicación vectorial módulo a algún polinomio irreducible. Este polinomio irreducible debe asegurar que la segunda operación define un grupo abeliano sobre S y es consistente con la condición distributiva. ¿Cuál debería ser ese polinomio irreducible?
Como todos los vectores del conjunto son de grado 2 o inferior, el polinomio irreducible debe ser de grado 3. Si cualquier multiplicación de dos vectores del conjunto da un polinomio de grado 3 o superior, sabemos que el módulo de un polinomio de grado 3 siempre da un polinomio de grado 2 o inferior. Esto es así porque cualquier polinomio de grado 3 o superior es siempre divisible por un polinomio de grado 3. Además, el polinomio que funciona como divisor tiene que ser irreducible.
Resulta que hay varios polinomios irreducibles de grado 3 que podríamos
utilizar como divisor. Cada uno de estos polinomios define un campo
diferente en conjunción con nuestro conjunto S y la suma
módulo 2. Esto significa que tenemos múltiples opciones a la hora de
utilizar campos de extensión 2^m en criptografía.
Para nuestro ejemplo, supongamos que seleccionamos el polinomio x^3 + x + 1. Éste sí que es irreducible, porque no se puede factorizar con enteros.
Además, se asegurará de que cualquier multiplicación de dos elementos dará
lugar a un polinomio de grado 2 o menos.
Veamos un ejemplo de la segunda operación utilizando el polinomio x^3 + x + 1 como divisor para ilustrar su funcionamiento. Supongamos que multiplicamos
los elementos x^2 + 1 por x^2 + x en nuestro conjunto S. Nosotros, entonces, necesitamos
calcular la expresión [(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1. Esto se puede simplificar de la siguiente manera:
[(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1 =[x^2 \cdot x^2 + x^2 \cdot x + 1 \cdot x^2 + 1 \cdot x] \mod x^3 + x + 1 =[x^4 + x^3 + x^2 + x] \mod x^3 + x + 1
Sabemos que [x^4 + x^3 + x^2 + x] \mod x^3 + x + 1 se puede reducir ya que el dividendo tiene mayor grado (4) que el divisor (3).
Para empezar, puedes ver que la expresión x^3 + x + 1 entra en x^4 + x^3 + x^2 + x un total de x veces. Puedes
comprobarlo multiplicando x^3 + x + 1 por x, que es x^4 + x^2 + x. Como este
último término es del mismo grado que el dividendo, es decir, 4, sabemos que
funciona. Se puede calcular el resto de esta división por x de la siguiente manera:
[(x^4 + x^3 + x^2 + x) - (x^4 + x^2 + x)] \mod x^3 + x + 1 =[x^3] \mod x^3 + x + 1 =x^3
Así que después de dividir x^4 + x^3 + x^2 + x entre x^3 + x + 1 un total de x veces, tenemos un resto de x^3. ¿Se puede volver a
dividir entre x^3 + x + 1?
Intuitivamente, podría ser atractivo decir que x^3 ya no se puede dividir por x^3 + x + 1, porque este
último término parece más grande. Sin embargo, recordemos nuestra discusión
anterior sobre la división vectorial. Siempre que el dividendo tenga un
grado mayor o igual que el divisor, la expresión puede seguir reduciéndose.
En concreto, la expresión x^3 + x + 1 puede entrar en x^3 exactamente
1 vez. El resto se calcula de la siguiente manera:
[(x^3) - (x^3 + x + 1)] \mod x^3 + x + 1 = [x + 1] \mod x^3 + x + 1 = x + 1Quizás te preguntes por qué (x^3) - (x^3 + x + 1) equivale a x + 1 y no a -x - 1. Recuerda que la
primera operación de nuestro campo está definida en módulo 2. Por tanto, la
resta de dos vectores es x + 1. Por lo tanto, la resta
de dos vectores da exactamente el mismo resultado que la suma de dos
vectores.
Para resumir la multiplicación de x^2 + 1 y x^2 + x: Al multiplicar
esos dos términos, se obtiene un polinomio de grado 4, x^4 + x^3 + x^2 + x, que hay
que reducir módulo x^3 + x + 1. El polinomio de
grado 4 es divisible por x^3 + x + 1 exactamente x + 1 veces. El
resto después de dividir x^4 + x^3 + x^2 + x por x^3 + x + 1 exactamente x + 1 veces es x + 1. Se trata,
efectivamente, de un elemento de nuestro conjunto \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.
¿Por qué los campos de extensión de base 2 sobre conjuntos de polinomios, como en el ejemplo anterior, pueden ser útiles para la criptografía? La razón es que se pueden ver los coeficientes en los polinomios de dichos conjuntos, ya sean 0 ó 1, como elementos de cadenas binarias con una longitud determinada. El conjunto S de nuestro ejemplo anterior, por ejemplo, podría verse como un conjunto S que incluye todas las cadenas binarias de longitud 3 (de 000 a 111). Las operaciones en S, entonces, también se pueden utilizar para realizar operaciones en estas cadenas binarias y producir una cadena binaria de la misma longitud.
Notas:
[2] Los campos de extensión se vuelven muy contraintuitivos. En lugar de tener elementos enteros, tienen conjuntos de polinomios. Además, cualquier operación se realiza modulo algún polinomio irreducible.
El álgebra abstracta en la práctica
A pesar del lenguaje formal y lo abstracto de la discusión, el concepto de grupo no debería ser demasiado difícil de entender. No es más que un conjunto de elementos junto con una operación binaria, donde la realización de esa operación binaria sobre esos elementos cumple cuatro condiciones generales. Un grupo abeliano sólo tiene una condición adicional conocida como conmutatividad. Un grupo cíclico, a su vez, es un tipo especial de grupo abeliano, es decir, uno que tiene un generador. Un campo no es más que una construcción más compleja a partir de la noción básica de grupo.
Pero si eres una persona con inclinaciones prácticas, puede que en este punto te preguntes: ¿A quién le importa? ¿Saber que un conjunto de elementos con un operador es un grupo, o incluso un grupo abeliano o cíclico, tiene alguna relevancia en el mundo real? ¿Saber que algo es un campo?
Sin entrar en demasiados detalles, la respuesta es "sí". Los grupos fueron creados por primera vez en el siglo XIX por el matemático francés Evariste Galois. Los utilizó para sacar conclusiones sobre la resolución de ecuaciones polinómicas de grado superior a cinco.
Desde entonces, el concepto de grupo ha contribuido a arrojar luz sobre numerosos problemas matemáticos y de otros ámbitos. Basándose en ellos, por ejemplo, el físico Murray-Gellman pudo predecir la existencia de una partícula antes de que se observara realmente en experimentos[3]. Otro ejemplo: los químicos utilizan la teoría de grupos para clasificar las formas de las moléculas. Los matemáticos incluso han utilizado el concepto de grupo para sacar conclusiones sobre algo tan concreto como el papel pintado
Esencialmente, demostrar que un conjunto de elementos con algún operador es un grupo, significa que lo que estás describiendo tiene una simetría particular. No una simetría en el sentido común de la palabra, sino en una forma más abstracta. Y esto puede aportar información sustancial sobre sistemas y problemas concretos. Las nociones más complejas del álgebra abstracta sólo nos dan información adicional.
Y lo que es más importante, verás la importancia de los grupos y campos de la teoría de números en la práctica a través de su aplicación en criptografía, en particular en la criptografía de clave pública. Ya hemos visto en nuestra discusión de campos, por ejemplo, cómo se emplean los campos de extensión en el Cifrado Rijndael. Resolveremos ese ejemplo en el Capítulo 5.
Para profundizar en el álgebra abstracta, recomiendo la excelente serie de vídeos sobre álgebra abstracta de Socratica. [4] Recomiendo especialmente los siguientes vídeos: "¿Qué es el álgebra abstracta?", "Definición de grupo (ampliada)", "Definición de anillo (ampliada)" y "Definición de campo (ampliada)" Estos cuatro vídeos te proporcionarán información adicional sobre gran parte de lo tratado anteriormente. (No hemos hablado de anillos, pero un campo no es más que un tipo especial de anillo)
Para profundizar en la teoría moderna de números, puede consultar muchos debates avanzados sobre criptografía. Para profundizar en el tema, le sugiero los libros Introduction to Modern Cryptography, de Jonathan Katz y Yehuda Lindell, o Understanding Cryptography, de Christof Paar y Jan Pelzl. [5]
Notas:
[3] Ver YouTube Video
[4] Socratica, Álgebra Abstracta
[5] Katz y Lindell, Introduction to Modern Cryptography, 2ª edn, 2015 (CRC Press: Boca Ratón, FL). Paar y Pelzl, Understanding Cryptography, 2010 (Springer-Verlag: Berlín).
Criptografía simétrica
Alice y Bob
Una de las dos ramas principales de la criptografía es la criptografía simétrica. Incluye tanto los esquemas de cifrado como los de autenticación e integridad. Hasta los años 70, toda la criptografía consistía en esquemas de cifrado simétrico.
El debate principal comienza con el examen de los esquemas de cifrado simétrico y la distinción crucial entre cifradores de flujo y cifradores de bloque. A continuación pasamos a los códigos de autenticación de mensajes, que son sistemas para garantizar la integridad y autenticidad de los mensajes. Por último, se estudia cómo combinar los sistemas de cifrado simétrico y los códigos de autenticación de mensajes para garantizar la seguridad de las comunicaciones.
En este capítulo se examinan de pasada varios esquemas criptográficos simétricos de la práctica. El capítulo siguiente ofrece una exposición detallada del cifrado con un cifrado de flujo y un cifrado de bloque a partir de la práctica, a saber, RC4 y AES respectivamente.
Antes de comenzar nuestra discusión sobre la criptografía simétrica, quiero hacer brevemente algunas observaciones sobre las ilustraciones de Alicia y Bob en este capítulo y en los siguientes.
Para ilustrar los principios de la criptografía, a menudo se recurre a ejemplos en los que intervienen Alicia y Bob. Yo también lo haré.
Especialmente si eres nuevo en criptografía, es importante que te des cuenta de que estos ejemplos de Alice y Bob sólo pretenden servir como ilustración de los principios y construcciones criptográficas en un entorno simplificado. Sin embargo, los principios y las construcciones son aplicables a una gama mucho más amplia de contextos de la vida real.
A continuación se presentan cinco puntos clave a tener en cuenta sobre los ejemplos que implican a Alice y Bob en criptografía:
Pueden traducirse fácilmente en ejemplos con otros tipos de actores, como empresas u organizaciones gubernamentales.
Pueden ampliarse fácilmente para incluir a tres o más actores.
En los ejemplos, Bob y Alice suelen participar activamente en la creación de cada mensaje y en la aplicación de esquemas criptográficos sobre ese mensaje. Pero en la realidad, las comunicaciones electrónicas están en gran medida automatizadas. Por ejemplo, cuando visitas un sitio web que utiliza seguridad de la capa de transporte, la criptografía suele estar gestionada por tu ordenador y el servidor web.
En el contexto de la comunicación electrónica, los "mensajes" que se envían a través de un canal de comunicación suelen ser paquetes TCP/IP. Pueden pertenecer a un correo electrónico, un mensaje de Facebook, una conversación telefónica, una transferencia de archivos, una página web, una carga de software, etcétera. No son mensajes en el sentido tradicional. No obstante, los criptógrafos suelen simplificar esta realidad afirmando que el mensaje es, por ejemplo, un correo electrónico.
Los ejemplos suelen centrarse en la comunicación electrónica, pero también pueden extenderse a formas tradicionales de comunicación como las cartas.
Esquemas de cifrado simétrico
Podemos definir un esquema de cifrado simétrico como cualquier esquema criptográfico con tres algoritmos:
Un algoritmo de generación de claves, que genera una clave privada.
Un algoritmo de cifrado, que toma la clave privada y un texto plano como entradas y produce un texto cifrado.
Un algoritmo de descifrado, que toma la clave privada y el texto cifrado como entradas y produce el texto plano original.
Normalmente, un esquema de cifrado -ya sea simétrico o asimétrico- ofrece una plantilla para el cifrado basada en un algoritmo central, en lugar de una especificación exacta.
Por ejemplo, consideremos Salsa20, un esquema de cifrado simétrico. Puede utilizarse con claves de 128 y 256 bits. La elección de la longitud de la clave afecta a algunos detalles menores del algoritmo (el número de rondas del algoritmo, para ser exactos).
Pero no se puede decir que utilizar Salsa20 con una clave de 128 bits sea un esquema de cifrado diferente de Salsa20 con una clave de 256 bits. El algoritmo central sigue siendo el mismo. Sólo cuando cambia el algoritmo central se puede hablar realmente de dos esquemas de cifrado diferentes.
Los esquemas de cifrado simétrico suelen ser útiles en dos tipos de casos: (1) Aquellos en los que dos o más agentes se comunican a distancia y quieren mantener en secreto el contenido de sus comunicaciones; y (2) aquellos en los que un agente quiere mantener en secreto el contenido de un mensaje a lo largo del tiempo.
Puede ver una representación de la situación (1) en la Figura 1 a
continuación. Bob quiere enviar un mensaje M a Alice a distancia, pero no
quiere que otros puedan leer ese mensaje.
Bob cifra primero el mensaje M con la clave privada K. A
continuación, envía el texto cifrado C a Alice. Una vez que Alice ha recibido el texto cifrado, puede descifrarlo
utilizando la clave K y leer
el texto sin formato. Con un buen esquema de cifrado, cualquier atacante que
intercepte el texto cifrado C no debería ser capaz de averiguar nada realmente significativo sobre el
mensaje M.
Puede ver una representación de la situación (2) en la Figura 2 a continuación. Bob quiere evitar que otros vean cierta información. Una situación típica podría ser que Bob es un empleado que almacena datos sensibles en su ordenador, que se supone que ni las personas ajenas ni sus compañeros pueden leer.
Bob cifra el mensaje M en el
tiempo T_0 con la clave K para producir el texto cifrado C. En el momento T_1 vuelve a necesitar el mensaje y descifra el texto cifrado C con la clave K. Cualquier
atacante que pudiera haber encontrado el texto cifrado C entretanto no debería haber sido capaz de deducir nada significativo sobre M a partir de él.
Figura 1: Secreto a través del espacio

Figura 2: Secretismo a lo largo del tiempo

Un ejemplo: El cifrado por turnos
En el capítulo 2 vimos el cifrado por turnos, que es un ejemplo de esquema de cifrado simétrico muy sencillo. Veámoslo de nuevo aquí.
Supongamos un diccionario D que equipara todas las letras del
alfabeto inglés, en orden, con el conjunto de números \{0,1,2,\dots,25\}.
Supongamos un conjunto de mensajes posibles M. El cifrado
por turnos es, entonces, un esquema de cifrado definido como sigue:
- Seleccionar aleatoriamente una clave
kdel conjunto de posibles claves K, donde K =\{0,1,2,\dots,25\} - Cifrar un mensaje
m \inM, de la siguiente manera:- Separar
men sus letras individualesm_0, m_1,\dots, m_i, \dots, m_l - Convertir cada
m_ien un número según D - Para cada
m_i,c_i = [(m_i + k) \mod 26] - Convierte cada
c_ien una letra según D - Luego combina
c_0, c_1,\dots, c_lpara obtener el texto cifradoc
- Separar
- Descifrar un texto cifrado
cde la siguiente manera:- Convierte cada
c_ien un número según D - Para cada
c_i,m_i = [(c_i - k) \mod 26] - Convierte cada
m_ien una letra según D - Entonces combina
m_0, m_1,\dots, m_lpara obtener el mensaje originalm
- Convierte cada
Lo que hace que el cifrado por turnos sea un esquema de cifrado simétrico es que se utiliza la misma clave tanto para el proceso de cifrado como para el de descifrado. Por ejemplo, supongamos que queremos cifrar el mensaje "DOG" utilizando el cifrado por turnos y que hemos elegido aleatoriamente "24" como clave. Al cifrar el mensaje con esta clave se obtendría "BME". La única forma de recuperar el mensaje original es utilizar la misma clave, "24", para el proceso de descifrado.
Este cifrado por turnos es un ejemplo de cifrado de sustitución monoalfabético: un esquema de cifrado en el que el alfabeto del texto cifrado es fijo (es decir, sólo se utiliza un alfabeto). Suponiendo que el algoritmo de descifrado sea determinista, cada símbolo del texto cifrado por sustitución puede corresponder como máximo a un símbolo del texto sin cifrar.
Hasta el siglo XVIII, muchas aplicaciones del cifrado se basaban en cifrados de sustitución monoalfabéticos, aunque a menudo eran mucho más complejos que el cifrado Shift. Se podía, por ejemplo, seleccionar aleatoriamente una letra del alfabeto para cada letra del texto original con la restricción de que cada letra sólo apareciera una vez en el alfabeto del texto cifrado. Eso significa que tendrías un factorial de 26 posibles claves privadas, lo que era enorme en la era preinformática.
Ten en cuenta que te encontrarás con el término cifrar muchas veces en criptografía. Ten en cuenta que este término tiene varios significados. De hecho, conozco al menos cinco significados distintos del término dentro de la criptografía.
En algunos casos, se refiere a un esquema de cifrado, como ocurre con el cifrado por turnos y el cifrado por sustitución monoalfabética. Sin embargo, el término también puede referirse específicamente al algoritmo de cifrado, a la clave privada o simplemente al texto cifrado de cualquier esquema de cifrado de este tipo.
Por último, el término cifra también puede referirse a un algoritmo central a partir del cual se pueden construir esquemas criptográficos. Estos pueden incluir varios algoritmos de cifrado, pero también otros tipos de esquemas criptográficos. Este sentido del término cobra relevancia en el contexto de los cifradores de bloques (véase la sección "Cifradores de bloques" más adelante).
Puede que también te encuentres con los términos encriptar o descifrar. Estos términos no son más que sinónimos de cifrar y descifrar.
Ataques de fuerza bruta y principio de Kerckhoff
El cifrado por turnos es un esquema de cifrado simétrico muy inseguro, al menos en el mundo moderno. [1] Un atacante podría intentar descifrar cualquier texto cifrado con las 26 claves posibles para ver qué resultado tiene sentido. Este tipo de ataque, en el que el atacante simplemente recorre las claves para ver cuál funciona, se conoce como ataque de fuerza bruta o búsqueda exhaustiva de claves.
Para que un sistema de cifrado cumpla una noción mínima de seguridad, debe tener un conjunto de claves posibles, o espacio de claves, tan amplio que los ataques de fuerza bruta sean inviables. Todos los sistemas de cifrado modernos cumplen esta norma. Es lo que se conoce como el principio del espacio de claves suficiente. Un principio similar se aplica normalmente en diferentes tipos de esquemas criptográficos.
Para hacernos una idea del enorme tamaño del espacio de claves de los
sistemas de cifrado modernos, supongamos que un archivo se ha cifrado con
una clave de 128 bits utilizando el estándar de cifrado avanzado. Esto
significa que un atacante dispone de un conjunto de claves de 2^{128} que necesita recorrer para realizar un ataque de fuerza bruta. Una
probabilidad de éxito del 0,78% con esta estrategia requeriría que el
atacante recorriera aproximadamente 2,65 \times 10^{36} claves.
Supongamos que un atacante puede probar 10^{16} claves por segundo (es decir, 10 cuatrillones de claves por segundo). Para
probar el 0,78% de todas las claves del espacio de claves, su ataque tendría
que durar 2,65 \times 10^{20} segundos. Esto equivale a unos 8,4 billones de años. Así que ni siquiera un ataque
de fuerza bruta por parte de un adversario absurdamente poderoso es realista
con un esquema de cifrado moderno de 128 bits. Este es el principio de espacio
de claves suficiente en juego.
¿Es el cifrado por turnos más seguro si el atacante no conoce el algoritmo de cifrado? Tal vez, pero no mucho.
En cualquier caso, la criptografía moderna siempre asume que la seguridad de cualquier esquema de cifrado simétrico sólo se basa en mantener en secreto la clave privada. Siempre se supone que el atacante conoce todos los demás detalles, incluido el espacio de mensajes, el espacio de claves, el espacio de textos cifrados, el algoritmo de selección de claves, el algoritmo de cifrado y el algoritmo de descifrado.
La idea de que la seguridad de un esquema de cifrado simétrico sólo puede basarse en el secreto de la clave privada se conoce como principio de Kerckhoffs.
Tal como lo concibió Kerckhoffs, este principio sólo se aplica a los sistemas de cifrado simétricos. Sin embargo, una versión más general del principio se aplica también a todos los demás tipos de esquemas criptográficos actuales: No se debe exigir que el diseño de cualquier esquema criptográfico sea secreto para que sea seguro; el secreto sólo puede extenderse a algunas cadenas de información, normalmente una clave privada.
El principio de Kerckhoffs es fundamental para la criptografía moderna por cuatro razones. En primer lugar, sólo existe un número limitado de esquemas criptográficos para determinados tipos de aplicaciones. Por ejemplo, la mayoría de las aplicaciones modernas de cifrado simétrico utilizan el cifrado Rijndael. Por tanto, el secreto sobre el diseño de un esquema es muy limitado. Sin embargo, hay mucha más flexibilidad en mantener en secreto alguna clave privada para el cifrado Rijndael.
En segundo lugar, es más fácil sustituir una cadena de información que todo un esquema criptográfico. Supongamos que todos los empleados de una empresa disponen del mismo software de cifrado y que cada dos empleados tienen una clave privada para comunicarse confidencialmente. En este escenario, las claves comprometidas son una molestia, pero al menos la empresa podría conservar el software con tales fallos de seguridad. Si la empresa confiara en el secreto del esquema, cualquier violación de ese secreto exigiría sustituir todo el software.
En tercer lugar, el principio de Kerckhoffs permite la normalización y compatibilidad entre usuarios de esquemas criptográficos. Esto tiene enormes ventajas para la eficiencia. Por ejemplo, es difícil imaginar cómo millones de personas podrían conectarse de forma segura a los servidores web de Google cada día, si esa seguridad exigiera mantener en secreto los esquemas criptográficos.
En cuarto lugar, el principio de Kerckhoff permite el escrutinio público de los esquemas criptográficos. Este tipo de escrutinio es absolutamente necesario para lograr esquemas criptográficos seguros. A título ilustrativo, el principal algoritmo básico de la criptografía simétrica, el cifrado Rijndael, fue el resultado de un concurso organizado por el Instituto Nacional de Normas y Tecnología entre 1997 y 2000.
Cualquier sistema que intente conseguir seguridad por oscuridad es aquel que se basa en mantener en secreto los detalles de su diseño y/o implementación. En criptografía, esto sería específicamente un sistema que se basa en mantener en secreto los detalles de diseño del esquema criptográfico. Por tanto, la seguridad por oscuridad contrasta directamente con el principio de Kerckhoffs.
La capacidad de la apertura para reforzar la calidad y la seguridad también se extiende al mundo digital más allá de la criptografía. Las distribuciones de Linux libres y de código abierto como Debian, por ejemplo, suelen tener varias ventajas sobre sus homólogas de Windows y MacOS en términos de privacidad, estabilidad, seguridad y flexibilidad. Aunque eso puede tener múltiples causas, el principio más importante es probablemente, como Eric Raymond lo expresó en su famoso ensayo "La catedral y el bazar", que "dados suficientes globos oculares, todos los bugs son superficiales" [3] Es este principio del tipo de la sabiduría de las multitudes el que dio a Linux su éxito más significativo.
Nunca se puede afirmar sin ambigüedades que un esquema criptográfico sea "seguro" o "inseguro" En su lugar, existen varias nociones de seguridad para los esquemas criptográficos. Cada definición de seguridad criptográfica debe especificar (1) los objetivos de seguridad, así como (2) las capacidades de un atacante. El análisis de los esquemas criptográficos con respecto a uno o varios conceptos de seguridad específicos permite comprender mejor sus aplicaciones y limitaciones.
Aunque no profundizaremos en todos los detalles de las distintas nociones de seguridad criptográfica, debes saber que hay dos supuestos omnipresentes en todas las nociones criptográficas modernas de seguridad relativas a los esquemas simétricos y asimétricos (y de alguna forma a otras primitivas criptográficas):
- El conocimiento del atacante sobre el esquema se ajusta al principio de Kerckhoffs.
- No es factible que el atacante realice un ataque de fuerza bruta contra el esquema. En concreto, los modelos de amenazas de las nociones criptográficas de seguridad no suelen permitir siquiera los ataques de fuerza bruta, ya que asumen que no son una consideración relevante.
Notas:
[1] Según Seutonius, Julio César utilizaba en sus comunicaciones militares un cifrado por desplazamiento con un valor de clave constante de 3. Así, A se convertía siempre en D, B siempre en E, C siempre en F, y así sucesivamente. Así, A se convertía siempre en D, B siempre en E, C siempre en F, y así sucesivamente. Esta versión concreta del cifrado por turnos se conoce como el Cifrado César (aunque en realidad no es un cifrado en el sentido moderno de la palabra, ya que el valor de la clave es constante). El cifrado César podría haber sido seguro en el siglo I a.C., si los enemigos de Roma no estaban muy familiarizados con el cifrado. Pero está claro que no sería un esquema muy seguro en los tiempos modernos.
[2] Jonathan Katz y Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Ratón, FL: 2015), p. 7f.
[3] Eric Raymond, "The Cathedral and the Bazaar", ponencia presentada en el Linux Kongress, Würzburg, Alemania (27 de mayo de 1997). Existen varias versiones posteriores, así como un libro. Mis citas proceden de la página 30 del libro: Eric Raymond, The Cathedral and the Bazaar: Musings on Linux and Open Source by an Accidental Revolutionary, edn. revisada. (2001), O'Reilly: Sebastopol, CA.
Cifrado de flujos
Los sistemas de cifrado simétrico se dividen normalmente en dos tipos: cifradores de flujo y cifradores de bloque. Sin embargo, esta distinción es algo problemática, ya que la gente utiliza estos términos de forma incoherente. En las próximas secciones expondré la distinción de la forma que considero más adecuada. Sin embargo, debes tener en cuenta que mucha gente utilizará estos términos de forma algo diferente a la que yo expongo.
Hablemos primero de los cifradores de flujo. Un cifrador de flujo es un esquema de cifrado simétrico en el que el cifrado consta de dos pasos.
En primer lugar, se produce una cadena de la longitud del texto plano mediante una clave privada. Esta cadena se denomina keystream.
A continuación, el flujo de claves se combina matemáticamente con el texto
plano para producir un texto cifrado. Esta combinación suele ser una
operación XOR. Para descifrar, basta con invertir la operación. (Tenga en
cuenta que A \oplus B = B \oplus A, en el caso de que A y B sean cadenas de bits. Así que el orden de una operación XOR en un cifrado de
flujo no importa para el resultado. Esta propiedad se conoce como comutatividad)
En la Figura 3 se muestra un cifrado de flujo XOR típico. Primero
se toma una clave privada K y
se utiliza para generar un flujo de claves. A continuación, el flujo clave
se combina con el texto plano mediante una operación XOR para producir el
texto cifrado. Cualquier agente que reciba el texto cifrado puede
descifrarlo fácilmente si dispone de la clave K. Todo lo que tiene que
hacer es crear un flujo de claves tan largo como el texto cifrado de acuerdo
con el procedimiento especificado del esquema y XOR con el texto cifrado.
Figura 3: Cifrado de flujo XOR
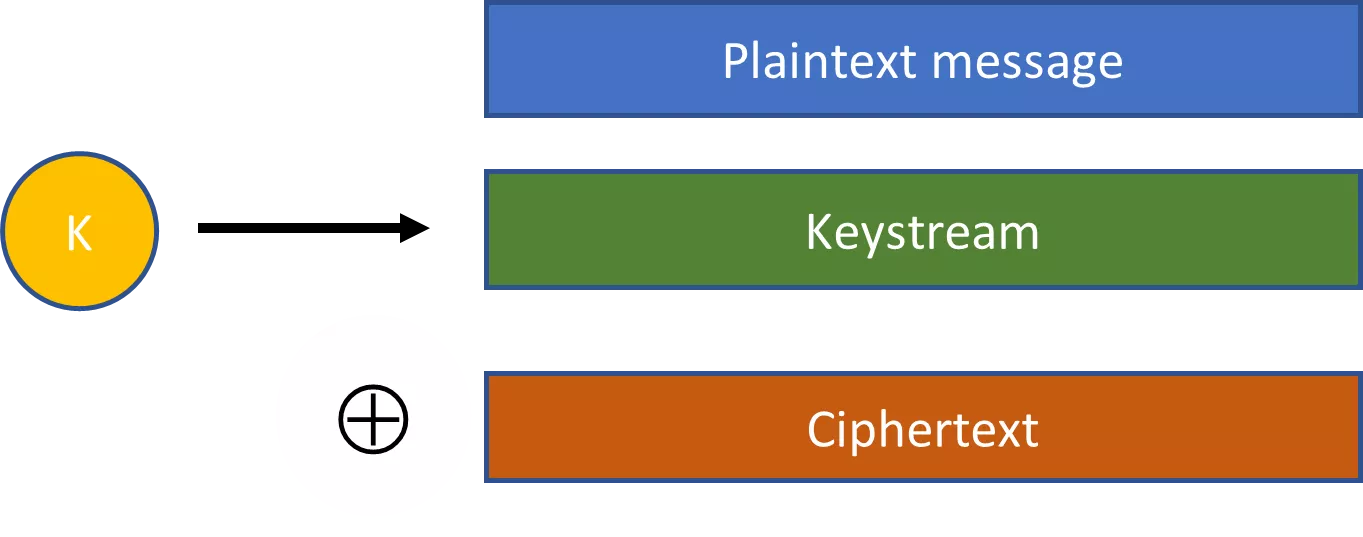
Recuerda que un esquema de cifrado suele ser una plantilla de cifrado con el mismo algoritmo central, y no una especificación exacta. Por extensión, un cifrado de flujo es normalmente una plantilla de cifrado en la que se pueden utilizar claves de diferentes longitudes. Aunque la longitud de la clave puede afectar a algunos detalles menores del esquema, no afectará a su forma esencial.
El cifrado por turnos es un ejemplo de cifrado de flujo muy sencillo e inseguro. Utilizando una sola letra (la clave privada), se puede producir una cadena de letras de la longitud del mensaje (el flujo de claves). Este flujo de claves se combina con el texto plano mediante una operación de módulo para producir un texto cifrado. (Esta operación de módulo puede simplificarse a una operación XOR si se representan las letras en bits).
Otro ejemplo famoso de cifrado de flujo es el cifrado de Vigenere, en honor a Blaise de Vigenere, que lo desarrolló completamente a finales del siglo XVI (aunque otros habían hecho mucho trabajo antes). Es un ejemplo de cifrado de sustitución polialfabética: un sistema de cifrado en el que el alfabeto del texto cifrado para un símbolo del texto plano cambia en función de su posición en el texto. A diferencia de un cifrado por sustitución monoalfabético, los símbolos del texto cifrado pueden asociarse a más de un símbolo del texto plano.
A medida que la encriptación ganaba popularidad en la Europa del Renacimiento, también lo hacía el criptoanálisis, es decir, el descifrado de textos cifrados, especialmente mediante el análisis de frecuencias. Este último emplea regularidades estadísticas de nuestro lenguaje para descifrar textos cifrados, y fue descubierto por eruditos árabes ya en el siglo IX. Es una técnica que funciona especialmente bien con textos largos. En Europa, incluso los cifrados por sustitución monoalfabética más sofisticados dejaron de ser suficientes contra el análisis de frecuencias en el siglo XVIII, sobre todo en entornos militares y de seguridad. El cifrado Vigenere supuso un importante avance en materia de seguridad, por lo que se popularizó en esta época y se generalizó a finales del siglo XVIII.
De manera informal, el esquema de cifrado funciona como sigue:
Seleccione una palabra de varias letras como clave privada.
Para cualquier mensaje, aplica el cifrado por desplazamiento a cada letra del mensaje utilizando la letra correspondiente de la palabra clave como desplazamiento.
Si ha recorrido la palabra clave pero aún no ha cifrado totalmente el texto sin cifrar, aplique de nuevo las letras de la palabra clave como cifrado por desplazamiento a las letras correspondientes del resto del texto.
Continúa este proceso hasta que todo el mensaje haya sido cifrado.
Para ilustrarlo, supongamos que su clave privada es "ORO" y desea cifrar el mensaje "CRYPTOGRAPHY". En ese caso, procedería del siguiente modo según el cifrado de Vigenère:
c_0 = [(2 + 6) \mod 26] = 8 = Ic_1 = [(17 + 14) \mod 26] = 5 = Fc_2 = [(24 + 11) \mod 26] = 9 = Jc_3 = [(15 + 3) \mod 26] = 18 = Sc_4 = [(19 + 6) \mod 26] = 25 = Zc_5 = [(14 + 14) \mod 26] = 2 = Cc_6 = [(6 + 11) \mod 26] = 17 = Rc_7 = [(17 + 3) \mod 26] = 20 = Uc_8 = [(0 + 6) \mod 26] = 6 = Gc_9 = [(15 + 14) \mod 26] = 3 = Dc_{10} = [(7 + 11) \mod 26] = 18 = Sc_{11} = [(24 + 3) \mod 26] = 1 = B
Así, el texto cifrado c = "IFJSZCRUGDSB".
Otro ejemplo famoso de cifrado de flujo es la "almohadilla de un solo uso". Con la almohadilla de un solo uso, basta con crear una cadena de bits aleatorios tan larga como el mensaje en texto plano y producir el texto cifrado mediante la operación XOR. Por lo tanto, la clave privada y el flujo de claves son equivalentes con una almohadilla de un solo uso.
Mientras que el cifrado Shift y los cifrados Vigenere son muy inseguros en la era moderna, la almohadilla de un solo uso es muy segura si se utiliza correctamente. Probablemente, la aplicación más famosa de la almohadilla de un solo uso fue, al menos hasta la década de 1980, para la línea directa Washington-Moscú. [4]
La línea directa es un enlace de comunicaciones directas entre Washington y Moscú para asuntos urgentes que se instaló tras la Crisis de los Misiles de Cuba. La tecnología de la línea se ha ido transformando con los años. Actualmente, incluye un cable directo de fibra óptica, así como dos enlaces por satélite (para redundancia), que permiten el correo electrónico y los mensajes de texto. El enlace termina en varios lugares de Estados Unidos. El Pentágono, la Casa Blanca y Raven Rock Mountain son puntos finales conocidos. Contrariamente a la opinión popular, la línea directa nunca ha utilizado teléfonos.
En esencia, el esquema de la almohadilla de un solo uso funcionaba de la siguiente manera. Tanto Washington como Moscú dispondrían de dos conjuntos de números aleatorios. Un conjunto de números aleatorios, creado por los rusos, se utilizaba para cifrar y descifrar cualquier mensaje en ruso. Un conjunto de números aleatorios, creados por los estadounidenses, correspondía al cifrado y descifrado de cualquier mensaje en inglés. De vez en cuando se enviaban más números aleatorios a la otra parte a través de mensajeros de confianza.
Washington y Moscú pudieron, entonces, comunicarse en secreto utilizando estos números aleatorios para crear almohadillas de un solo uso. Cada vez que necesitaban comunicarse, utilizaban la siguiente porción de números aleatorios para su mensaje.
Aunque muy segura, la almohadilla de un solo uso se enfrenta a importantes limitaciones prácticas: la clave tiene que ser tan larga como el mensaje y ninguna parte de una almohadilla de un solo uso puede reutilizarse. Esto significa que hay que llevar un registro de dónde se encuentra en la almohadilla de un solo uso, almacenar un número masivo de bits e intercambiar bits aleatorios con las contrapartes de vez en cuando. Como consecuencia, la almohadilla de un solo uso no se utiliza con frecuencia en la práctica.
En su lugar, los cifradores de flujo predominantes en la práctica son los cifradores de flujo pseudoaleatorios. Salsa20 y una variante estrechamente relacionada llamada ChaCha son ejemplos de cifradores de flujo pseudoaleatorios de uso común.
Con estos cifradores de flujo pseudoaleatorios, primero se selecciona aleatoriamente una clave K que sea más corta que la longitud del texto plano. Dicha clave aleatoria K suele ser creada por nuestro ordenador a partir de datos impredecibles que recopila a lo largo del tiempo, como el tiempo entre mensajes de red, los movimientos del ratón, etc.
A continuación, esta clave aleatoria K se inserta en un algoritmo de expansión que crea un flujo de claves pseudoaleatorias
tan largo como el mensaje. Puedes especificar con precisión la longitud que debe
tener el flujo de claves (por ejemplo, 500 bits, 1.000 bits, 1.200 bits, 29.117
bits, etc.).
Un flujo de claves pseudoaleatorio aparece como si se hubiera elegido de forma completamente aleatoria del conjunto de todas las cadenas con la misma longitud. Por lo tanto, el cifrado con un flujo de claves pseudoaleatorio parece como si se hubiera realizado con una almohadilla de un solo uso. Pero, por supuesto, no es así.
Como nuestra clave privada es más corta que el flujo de claves y nuestro algoritmo de expansión tiene que ser determinista para que el proceso de cifrado/descifrado funcione, no todos los flujos de claves de esa longitud concreta podrían haber resultado como salida de nuestra operación de expansión.
Supongamos, por ejemplo, que nuestra clave privada tiene una longitud de 128
bits y que podemos insertarla en un algoritmo expansivo para crear una
cadena de claves mucho más larga, digamos de 2.500 bits. Como nuestro
algoritmo expansivo tiene que ser determinista, como mucho puede seleccionar
cadenas de 1/2^{128} con una longitud de 2.500 bits. Por lo tanto, un flujo de claves de este tipo
nunca podría seleccionarse de forma totalmente aleatoria entre todas las cadenas
de la misma longitud.
Nuestra definición de un cifrado de flujo tiene dos aspectos: (1) un flujo de claves tan largo como el texto plano se genera con la ayuda de una clave privada; y (2) este flujo de claves se combina con el texto plano, normalmente mediante una operación XOR, para producir el texto cifrado.
A veces se define la condición (1) de forma más estricta, afirmando que el flujo de claves debe ser específicamente pseudoaleatorio. Esto significa que ni el cifrado por turnos ni la almohadilla de un solo uso se considerarían cifrados de flujo.
En mi opinión, una definición más amplia de la condición (1) facilita la organización de los esquemas de cifrado. Además, significa que no tenemos que dejar de llamar cifrado de flujo a un esquema de cifrado concreto sólo porque nos enteremos de que en realidad no se basa en flujos de claves pseudoaleatorios.
Notas:
[4] Cripto Museo, "Línea directa Washington-Moscú", 2013, disponible en https://www.cryptomuseum.com/crypto/hotline/index.htm.
Cifrado por bloques
La primera forma en que se entiende comúnmente un cifrado de bloques es como algo más primitivo que un cifrado de flujo: Un algoritmo central que realiza una transformación que preserva la longitud en una cadena de una longitud adecuada con la ayuda de una clave. Este algoritmo puede utilizarse para crear esquemas de cifrado y quizás otros tipos de esquemas criptográficos.
Con frecuencia, un cifrado por bloques puede aceptar cadenas de entrada de longitudes variables, como 64, 128 o 256 bits, así como claves de longitudes variables, como 128, 192 o 256 bits. Aunque algunos detalles del algoritmo pueden cambiar en función de estas variables, el núcleo del algoritmo no cambia. Si lo hiciera, hablaríamos de dos cifrados de bloques diferentes. Tenga en cuenta que el uso de la terminología del algoritmo central es el mismo que para los esquemas de cifrado.
La Figura 4 muestra cómo funciona un cifrado por bloques. Un
mensaje M de longitud L y una clave K sirven de
entrada al cifrado por bloques. Éste produce un mensaje M' de longitud L. La clave no
tiene por qué tener la misma longitud que M y M' en la mayoría de los cifrados
por bloques.
Figura 4: Cifrado por bloques

Un cifrado por bloques en sí mismo no es un esquema de cifrado. Pero un cifrado por bloques puede utilizarse con varios modos de operación para producir diferentes esquemas de cifrado. Un modo de operación simplemente añade algunas operaciones adicionales fuera del cifrado por bloques.
Para ilustrar cómo funciona, supongamos un cifrado por bloques (BC) que requiere una cadena de entrada de 128 bits y una clave privada de 128 bits. La figura 5 muestra cómo puede utilizarse ese cifrado por bloques con el modo de libro de códigos electrónicos (modo ECB) para crear un esquema de cifrado. (Las elipses de la derecha indican que se puede repetir este esquema tanto como sea necesario).
Figura 5: Cifrado por bloques con modo BCE
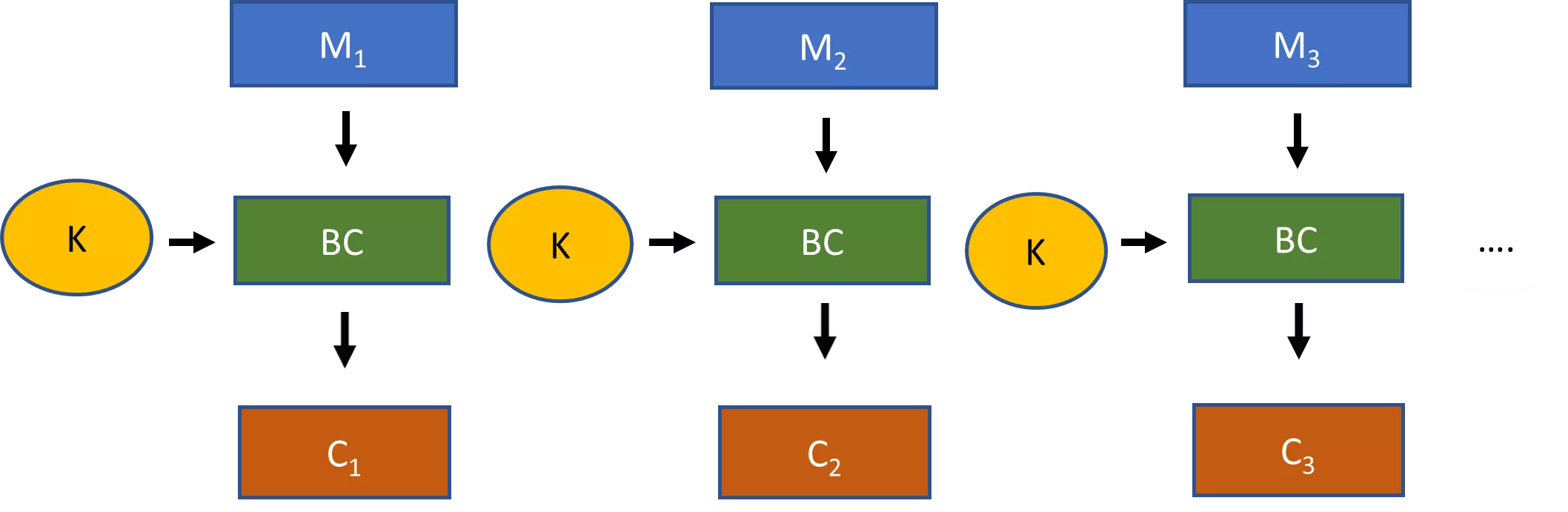
El proceso de cifrado de libros de códigos electrónicos con el cifrado por bloques es el siguiente. Comprueba si puedes dividir tu mensaje de texto plano en bloques de 128 bits. Si no es así, añada acolchado al mensaje, de modo que el resultado pueda dividirse uniformemente por el tamaño de bloque de 128 bits. Estos son los datos utilizados para el proceso de cifrado.
Ahora divide los datos en trozos de cadenas de 128 bits (M_1, M_2, M_3, etc.). Pasa cada cadena
de 128 bits por el cifrado por bloques con tu clave de 128 bits para
producir trozos de texto cifrado de 128 bits (C_1, C_2, C_3, etc.). Estos trozos,
cuando se vuelven a combinar, forman el texto cifrado completo.
El descifrado no es más que el proceso inverso, aunque el destinatario necesita alguna forma reconocible de eliminar cualquier relleno de los datos descifrados para obtener el mensaje original en texto plano.
Aunque relativamente sencillo, un cifrado por bloques con modo de libro de códigos electrónico carece de seguridad. Esto se debe a que conduce a un cifrado determinista. Dos cadenas de datos idénticas de 128 bits se cifran exactamente igual. Esa información puede ser explotada.
En cambio, cualquier esquema de cifrado construido a partir de un cifrado
por bloques debería ser probabilístico: es decir, el
cifrado de cualquier mensaje M, o de cualquier fragmento
específico de M, debería
producir generalmente un resultado diferente cada vez. [5]
El modo de encadenamiento de cifrado por bloques (modo CBC) es probablemente el modo más común utilizado con un cifrado por bloques. La combinación, si se hace bien, produce un esquema de cifrado probabilístico. Puedes ver una representación de este modo de funcionamiento en la Figura 6 a continuación.
Figura 6: Cifrado por bloques en modo CBC
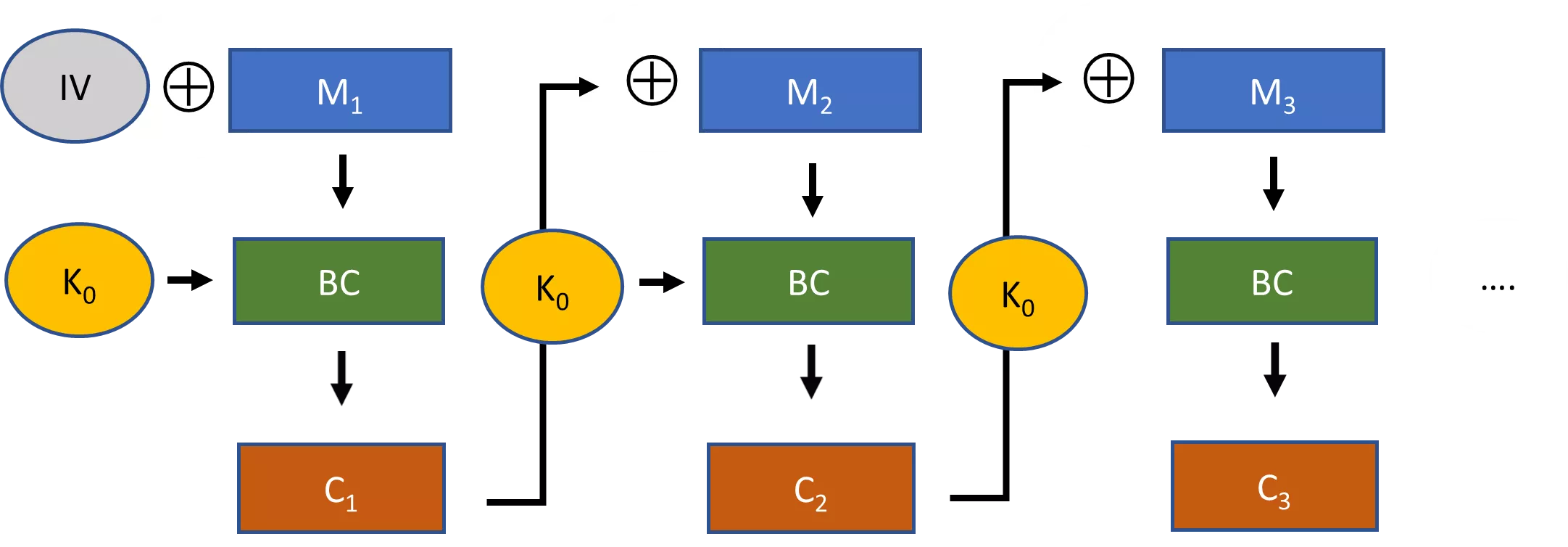
Supongamos que el tamaño del bloque vuelve a ser de 128 bits. Para empezar, tendrías que asegurarte de que tu mensaje de texto plano original recibe el relleno necesario.
A continuación, XOR la primera porción de 128 bits de su texto plano con un vector de inicialización de 128 bits. El resultado se introduce en el cifrado por bloques para obtener el texto cifrado del primer bloque. Para el segundo bloque de 128 bits, primero XOR el texto plano con el texto cifrado del primer bloque, antes de insertarlo en el cifrado por bloques. Continúa este proceso hasta que hayas cifrado todo el mensaje en texto plano.
Cuando haya terminado, envía el mensaje cifrado junto con el vector de inicialización sin cifrar al destinatario. El destinatario necesita conocer el vector de inicialización, de lo contrario no podrá descifrar el texto cifrado.
Esta construcción es mucho más segura que el modo de libro de códigos electrónico cuando se utiliza correctamente. En primer lugar, debes asegurarte de que el vector de inicialización es una cadena aleatoria o pseudoaleatoria. Además, debes utilizar un vector de inicialización diferente cada vez que utilices este esquema de cifrado.
En otras palabras, tu vector de inicialización debería ser un nonce aleatorio o pseudoaleatorio, donde un nonce significa "un número que sólo se usa una vez" Si mantienes esta práctica, entonces el modo CBC con un cifrado por bloques asegura que dos bloques de texto plano idénticos serán generalmente cifrados de forma diferente cada vez.
Por último, vamos a centrarnos en el modo de realimentación de salida (modo OFB). Puedes ver una representación de este modo en la Figura 7.
Figura 7: Cifrado por bloques en modo OFB
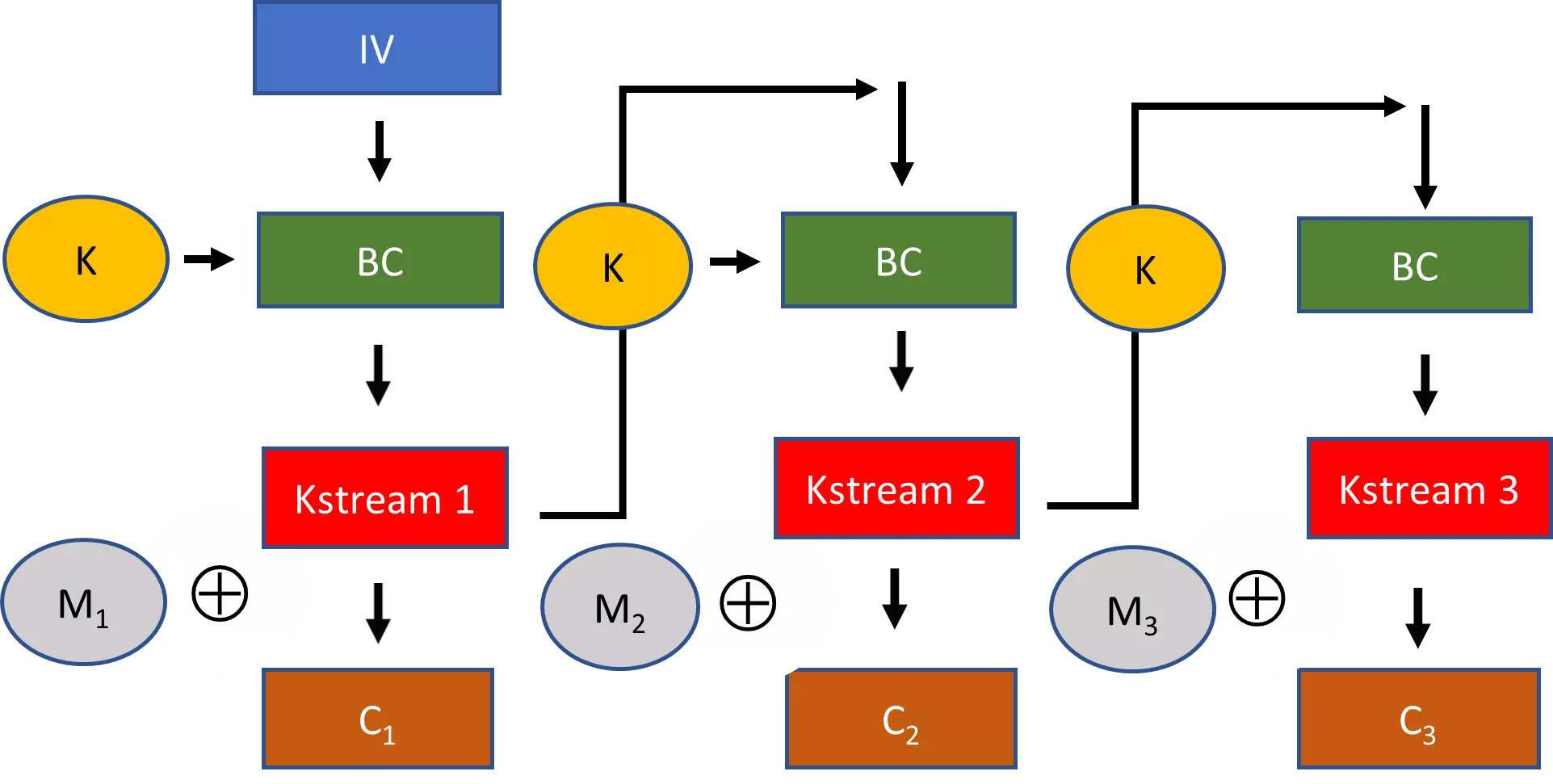
Con el modo OFB también se selecciona un vector de inicialización. Pero aquí, para el primer bloque, el vector de inicialización se inserta directamente en el cifrado por bloques con su clave. Los 128 bits resultantes se tratan como un flujo de claves. Este flujo de claves se combina con el texto plano para obtener el texto cifrado del bloque. Para los bloques siguientes, se utiliza el flujo de claves del bloque anterior como entrada en el cifrado por bloques y se repiten los pasos.
Si te fijas bien, lo que en realidad se ha creado aquí a partir del cifrado por bloques con el modo OFB es un cifrado de flujo. Generas porciones de flujo de claves de 128 bits hasta que tienes la longitud del texto plano (descartando los bits que no necesitas de la última porción de flujo de claves de 128 bits). A continuación, XOR el flujo de claves con su mensaje de texto sin formato para obtener el texto cifrado.
En la sección anterior sobre cifrados de flujo, he dicho que se produce un flujo de claves con la ayuda de una clave privada. Para ser exactos, no sólo tiene que crearse con una clave privada. Como puedes ver en el modo OFB, el flujo de claves se produce con la ayuda tanto de una clave privada como de un vector de inicialización.
Tenga en cuenta que, al igual que con el modo CBC, es importante seleccionar un nonce pseudoaleatorio o aleatorio para el vector de inicialización cada vez que utilice un cifrado por bloques en modo OFB. De lo contrario, la misma cadena de mensajes de 128 bits enviada en diferentes comunicaciones se cifrará de la misma manera. Esta es una forma de crear cifrado probabilístico con un cifrado de flujo.
Algunos cifradores de flujo sólo utilizan una clave privada para crear un flujo de claves. Para estos cifradores de flujo, es importante que utilices un nonce aleatorio para seleccionar la clave privada para cada instancia de comunicación. De lo contrario, los resultados del cifrado con esos cifradores de flujo también serán deterministas, lo que provocará problemas de seguridad.
El cifrado por bloques moderno más popular es el cifrado Rijndael. Fue el ganador de un concurso convocado por el Instituto Nacional de Estándares y Tecnología (NIST) entre 1997 y 2000 para sustituir a un estándar de cifrado más antiguo, el estándar de cifrado de datos (DES).
El cifrado Rijndael puede utilizarse con distintas especificaciones de longitud de clave y tamaño de bloque, así como en distintos modos de funcionamiento. El comité del concurso del NIST adoptó una versión restringida del cifrado Rijndael, que requiere bloques de 128 bits y longitudes de clave de 128, 192 o 256 bits, como parte del estándar de cifrado avanzado (AES). Se trata del principal estándar para aplicaciones de cifrado simétrico. Es tan seguro que incluso la NSA parece estar dispuesta a utilizarlo con claves de 256 bits para documentos de alto secreto. [6]
El cifrado por bloques AES se explicará en detalle en el Capítulo 5.
Notas:
[5] La importancia del cifrado probabilístico fue destacada por primera vez por Shafi Goldwasser y Silvio Micali, "Probabilistic encryption", Journal of Computer and System Sciences, 28 (1984), 270-99.
[6] Véase NSA, "Commercial National Security Algorithm Suite", https://apps.nsa.gov/iaarchive/programs/iad-initiatives/cnsa-suite.cfm.
Aclarar la confusión
La confusión sobre la distinción entre cifrado por bloques y cifrado por flujos se debe a que a veces la gente entiende que el término cifrado por bloques se refiere específicamente a un cifrado por bloques con un modo de cifrado por bloques.
Considera los modos ECB y CBC de la sección anterior. Estos requieren específicamente que los datos para el cifrado sean divisibles por el tamaño del bloque (lo que significa que podrías tener que usar relleno para el mensaje original). Además, en estos modos los datos también son operados directamente por el cifrado por bloques (y no sólo combinados con el resultado de una operación de cifrado por bloques como en el modo OFB).
Por lo tanto, se puede definir un cifrado por bloques como cualquier esquema de cifrado que funcione con bloques de longitud fija del mensaje cada vez (donde cualquier bloque debe ser mayor que un byte, de lo contrario se convierte en un cifrado de flujo). Tanto los datos para cifrar como el texto cifrado deben dividirse uniformemente en este tamaño de bloque. Normalmente, el tamaño del bloque es de 64, 128, 192 o 256 bits de longitud. En cambio, un cifrado de flujo puede cifrar cualquier mensaje en trozos de un bit o byte cada vez.
Con este concepto más específico de cifrado por bloques, se puede afirmar que los esquemas de cifrado modernos son cifrados de flujo o de bloques. A partir de ahora, utilizaré el término cifrado por bloques en su sentido más general, a menos que se especifique lo contrario.
La discusión sobre el modo OFB en la sección anterior también plantea otro punto interesante. Algunos cifradores de flujo se crean a partir de cifradores de bloques, como Rijndael con OFB. Otros, como Salsa20 y ChaCha, no se crean a partir de cifradores de bloques. A estos últimos se les podría llamar cifradores de flujo primitivos. (En realidad no existe un término estandarizado para referirse a este tipo de cifradores de flujo)
Cuando se habla de las ventajas y desventajas de los cifradores de flujo y los cifradores de bloque, normalmente se comparan los cifradores de flujo primitivos con los esquemas de cifrado basados en cifradores de bloque.
Mientras que siempre se puede construir fácilmente un cifrado de flujo a partir de un cifrado de bloque, normalmente es muy difícil construir algún tipo de construcción con un modo de cifrado de bloque (como con el modo CBC) a partir de un cifrado de flujo primitivo.
A partir de esta discusión, ahora deberías entender la Figura 8. Proporciona una visión general de los esquemas de cifrado simétrico. Utilizamos tres tipos de esquemas de cifrado: cifradores de flujo primitivos, cifradores de flujo de cifrado por bloques y cifradores de bloques en modo bloque (también llamados "cifradores de bloques" en el diagrama).
Figura 8: Visión general de los esquemas de cifrado simétrico
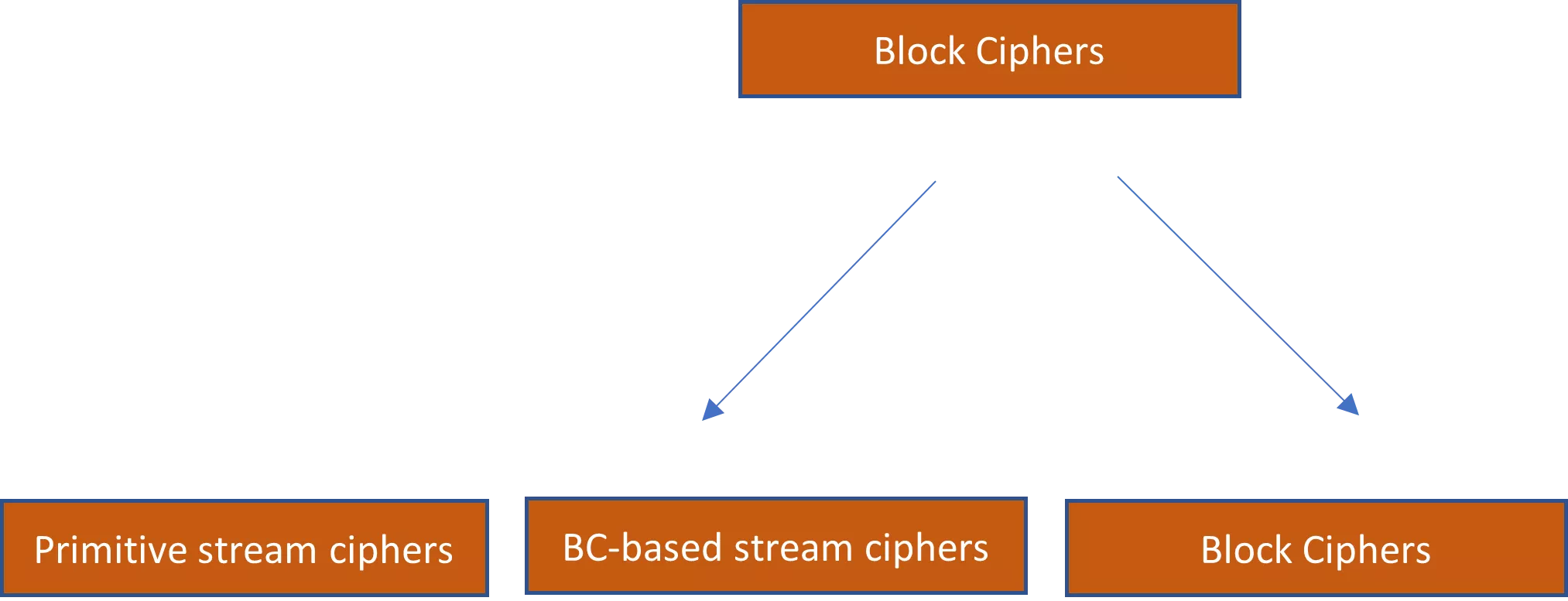
Códigos de autenticación de mensajes
El cifrado tiene que ver con el secreto. Pero la criptografía también se ocupa de temas más amplios, como la integridad de los mensajes, la autenticidad y el no repudio. Los llamados códigos de autenticación de mensajes (MAC) son esquemas criptográficos de clave simétrica que soportan la autenticidad y la integridad en las comunicaciones.
¿Por qué se necesita algo más que el secreto en la comunicación? Supongamos que Bob envía un mensaje a Alice utilizando un cifrado prácticamente indescifrable. Cualquier atacante que intercepte este mensaje no podrá averiguar nada significativo sobre su contenido. Sin embargo, el atacante todavía tiene al menos otros dos vectores de ataque a su disposición:
Ella podría interceptar el texto cifrado, alterar su contenido, y enviar el texto cifrado alterado a Alice.
Podría bloquear por completo el mensaje de Bob y enviar su propio texto cifrado.
En ambos casos, el atacante podría no tener ninguna idea del contenido de los textos cifrados (1) y (2). Pero aún así podría causar daños significativos de esta manera. Aquí es donde cobran importancia los códigos de autenticación de mensajes.
Los códigos de autenticación de mensajes se definen vagamente como esquemas criptográficos simétricos con tres algoritmos: un algoritmo de generación de claves, un algoritmo de generación de etiquetas y un algoritmo de verificación. Un MAC seguro garantiza que las etiquetas sean inexistentemente infalsificables para cualquier atacante, es decir, que no puedan crear con éxito una etiqueta en el mensaje que verifica, a menos que tengan la clave privada.
Bob y Alice pueden combatir la manipulación de un mensaje concreto utilizando una MAC. Supongamos por el momento que no les importa el secreto. Sólo quieren asegurarse de que el mensaje recibido por Alice procede realmente de Bob y no ha sido modificado en modo alguno.
El proceso se muestra en la Figura 9. Para utilizar un MAC (Código de Autenticación de Mensaje), primero generarían una clave privada K que se comparte entre los dos. Bob crea una etiqueta T para el mensaje utilizando la clave privada K. A continuación, envía el
mensaje y la etiqueta a Alice. Ésta puede verificar que Bob ha creado la
etiqueta, pasando la clave privada, el mensaje y la etiqueta por un
algoritmo de verificación.
Figura 9: Visión general de los esquemas de cifrado simétrico
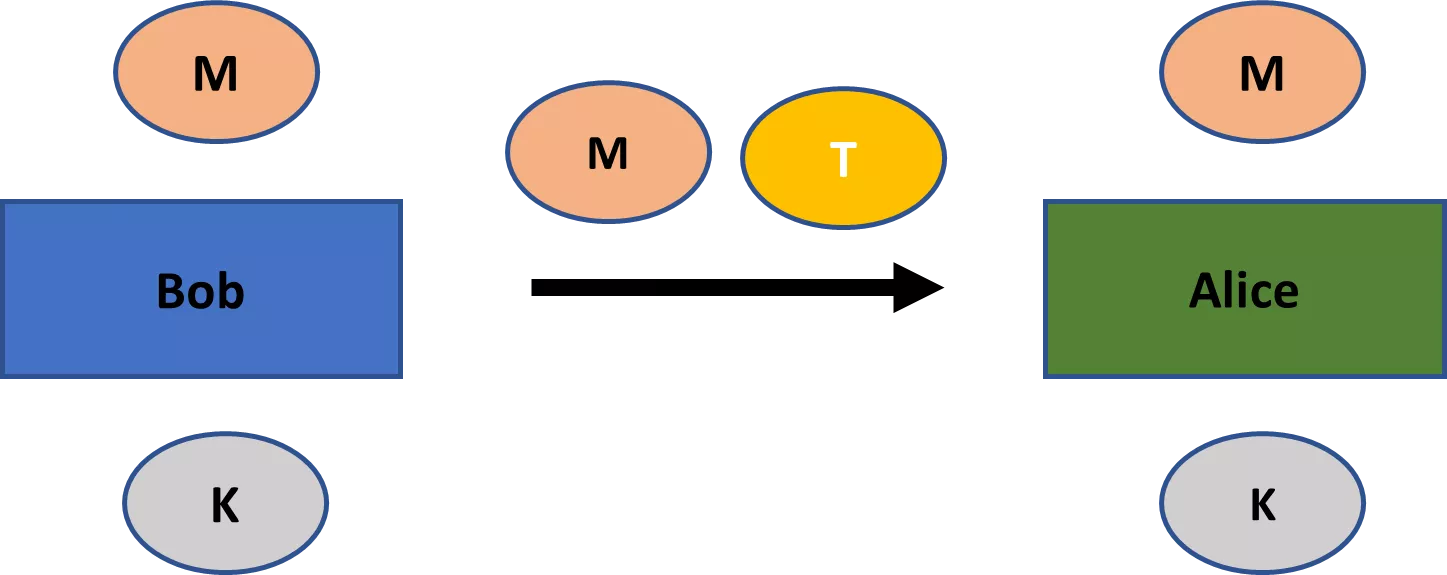
Debido a la imposibilidad de falsificación existencial, un
atacante no puede alterar el mensaje M de ninguna manera ni crear un mensaje propio con una etiqueta válida. Esto
es así, incluso si el atacante observa las etiquetas de muchos mensajes
entre Bob y Alice que utilizan la misma clave privada. Como mucho, un
atacante podría impedir que Alice recibiera el mensaje M (un problema que la criptografía
no puede resolver).
Una MAC garantiza que un mensaje ha sido realmente creado por Bob. Esta autenticidad implica automáticamente la integridad del mensaje, es decir, si Bob ha creado un mensaje, entonces, ipso facto, no ha sido alterado de ninguna manera por un atacante. De aquí en adelante, cualquier preocupación por la autenticación debe entenderse automáticamente como una preocupación por la integridad.
Aunque he distinguido entre autenticidad e integridad de los mensajes, también es habitual utilizar estos términos como sinónimos. Así, se refieren a la idea de mensajes que fueron creados por un remitente en particular y que no fueron alterados de ninguna manera. En este sentido, los códigos de autenticación de mensajes suelen denominarse también códigos de integridad de mensajes.
Cifrado autenticado
Normalmente, se desea garantizar tanto el secreto como la autenticidad en la comunicación y, por ello, los esquemas de cifrado y los esquemas MAC suelen utilizarse conjuntamente.
Un esquema de cifrado autenticado es un esquema que combina el cifrado con una MAC de forma altamente segura. En concreto, tiene que cumplir las normas de infalsificabilidad existencial, así como una noción muy fuerte de secreto, es decir, que sea resistente a ataques de elección de texto cifrado. [7]
Para que un esquema de cifrado sea resistente a los ataques de elección de texto cifrado, debe cumplir las normas de no maleabilidad: es decir, cualquier modificación de un texto cifrado por parte de un atacante debe dar lugar a un texto cifrado no válido o a un texto plano que no tenga ninguna relación con el original. [8]
Como un esquema de cifrado autenticado garantiza que un texto cifrado creado por un atacante siempre es inválido (ya que la etiqueta no se verificará), cumple las normas de resistencia a los ataques de texto cifrado elegido. Curiosamente, se puede demostrar que siempre se puede crear un esquema de cifrado autenticado a partir de la combinación de un MAC existencialmente infalsificable y un esquema de cifrado que cumpla una noción de seguridad menos fuerte, conocida como seguridad contra ataques de texto plano elegido.
No vamos a entrar en todos los detalles de la construcción de esquemas de cifrado autentificados. Pero es importante conocer dos detalles de su construcción.
En primer lugar, un esquema de cifrado autenticado se encarga primero del cifrado y luego crea una etiqueta de mensaje en el texto cifrado. Resulta que otros enfoques -como combinar el texto cifrado con una etiqueta en el texto sin cifrar, o crear primero una etiqueta y luego cifrar tanto el texto sin cifrar como la etiqueta- son inseguros. Además, ambas operaciones tienen su propia clave privada seleccionada aleatoriamente, de lo contrario su seguridad se ve gravemente comprometida.
El principio antes mencionado se aplica de forma más general: siempre debes usar claves distintas cuando combines esquemas criptográficos básicos.
En la Figura 10 se muestra un esquema de cifrado autenticado. Bob
crea primero un texto cifrado C a partir del mensaje M utilizando una clave seleccionada aleatoriamente K_C. A continuación, crea una
etiqueta de mensaje T ejecutando el texto cifrado y una clave diferente seleccionada
aleatoriamente K_T a través del
algoritmo de generación de etiquetas. Tanto el texto cifrado como la etiqueta
del mensaje se envían a Alice.
Alice comprueba primero si la etiqueta es válida dado el texto cifrado C y la clave K_T. Si es válida,
puede descifrar el mensaje utilizando la clave K_C. No sólo se asegura una
noción muy fuerte de secreto en sus comunicaciones, sino que también sabe
que el mensaje fue creado por Bob.
Figura 10: Esquema de encriptación autenticada

¿Cómo se crean las MAC? Aunque las MAC pueden crearse mediante múltiples métodos, una forma común y eficiente de crearlas es mediante funciones hash criptográficas.
Introduciremos las funciones hash criptográficas más a fondo en el Capítulo 6. Por ahora, basta con saber que una función hash es una función eficientemente computable que toma entradas de tamaño arbitrario y produce salidas de longitud fija. Por ejemplo, la popular función hash SHA-256 (algoritmo hash seguro 256) siempre genera una salida de 256 bits independientemente del tamaño de la entrada. Algunas funciones hash, como SHA-256, tienen aplicaciones útiles en criptografía.
El tipo más común de etiqueta producida con una función hash criptográfica
es el código de autenticación de mensajes basado en hash (HMAC). El proceso se representa en la Figura 11. Una parte produce
dos claves distintas a partir de una clave privada K, la clave interna K_1 y la clave externa K_2. El
texto plano M o el texto
cifrado C se combina con la
clave interna. El resultado T' se combina con la clave externa para producir la etiqueta de mensaje T.
Existe una paleta de funciones hash que pueden utilizarse para crear un HMAC. La función hash más utilizada es SHA-256.
Figura 11: HMAC
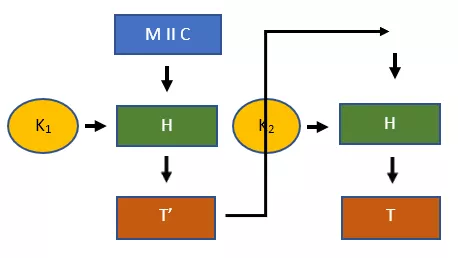
Notas:
[7] Los resultados específicos analizados en esta sección proceden de Katz y Lindell, pp. 131-47.
[8] Técnicamente, la definición de ataques de texto cifrado elegido es diferente de la noción de no maleabilidad. Pero se puede demostrar que esas dos nociones de seguridad son equivalentes.
Sesiones de comunicación seguras
Supongamos que dos partes están en una sesión de comunicación, por lo que envían múltiples mensajes de ida y vuelta.
Un esquema de cifrado autenticado permite al destinatario de un mensaje verificar que ha sido creado por su interlocutor en la sesión de comunicación (siempre que la clave privada no se haya filtrado). Esto funciona bien para un solo mensaje. Sin embargo, lo habitual es que dos partes se envíen mensajes en una sesión de comunicación. Y en ese caso, un esquema de cifrado autenticado simple como el descrito en la sección anterior se queda corto a la hora de proporcionar seguridad.
La razón principal es que un esquema de cifrado autenticado no ofrece ninguna garantía de que el mensaje haya sido realmente enviado también por el agente que lo creó dentro de una sesión de comunicación. Consideremos los tres vectores de ataque siguientes:
Ataque de repetición: Un atacante reenvía un texto cifrado y una etiqueta que interceptó entre dos partes en un momento anterior.
Ataque de reordenación: Un atacante intercepta dos mensajes en momentos diferentes y los envía al destinatario en el orden inverso.
Ataque por reflexión: Un atacante observa un mensaje enviado de A a B, y también envía ese mensaje a A.
Aunque el atacante no tiene conocimiento del texto cifrado y no puede crear textos cifrados falsos, los ataques anteriores pueden causar daños significativos en las comunicaciones.
Supongamos, por ejemplo, que un mensaje concreto entre las dos partes implica la transferencia de fondos financieros. Un ataque de repetición podría transferir los fondos por segunda vez. Un esquema de cifrado autenticado no tiene defensa contra este tipo de ataques.
Afortunadamente, este tipo de ataques pueden mitigarse fácilmente en una sesión de comunicación utilizando identificadores e indicadores de tiempo relativo.
Se pueden añadir identificadores al mensaje en texto plano antes de cifrarlo. Esto impediría cualquier ataque por reflexión. Un indicador de tiempo relativo puede ser, por ejemplo, un número de secuencia en una sesión de comunicación concreta. Cada parte añade un número de secuencia a un mensaje antes del cifrado, de modo que el destinatario sepa en qué orden se enviaron los mensajes. Esto elimina la posibilidad de ataques de reordenación. También elimina los ataques de repetición. Cualquier mensaje que envíe un atacante tendrá un número de secuencia antiguo y el destinatario sabrá que no debe volver a procesarlo.
Para ilustrar cómo funcionan las sesiones de comunicación seguras, supongamos de nuevo que Alice y Bob. Se envían un total de cuatro mensajes. En la Figura 11 puedes ver cómo funcionaría un esquema de cifrado autenticado con identificadores y números de secuencia.
La sesión de comunicación comienza con Bob enviando un texto cifrado C_{0,B} a Alice con una etiqueta de mensaje T_{0,B}. El texto
cifrado contiene el mensaje, así como un identificador (BOB) y un número de
secuencia (0). La etiqueta T_{0,B} se realiza sobre
todo el texto cifrado. En sus comunicaciones posteriores, Alice y Bob mantienen
este protocolo, actualizando los campos según sea necesario.
Figura 12: Una sesión de comunicación segura
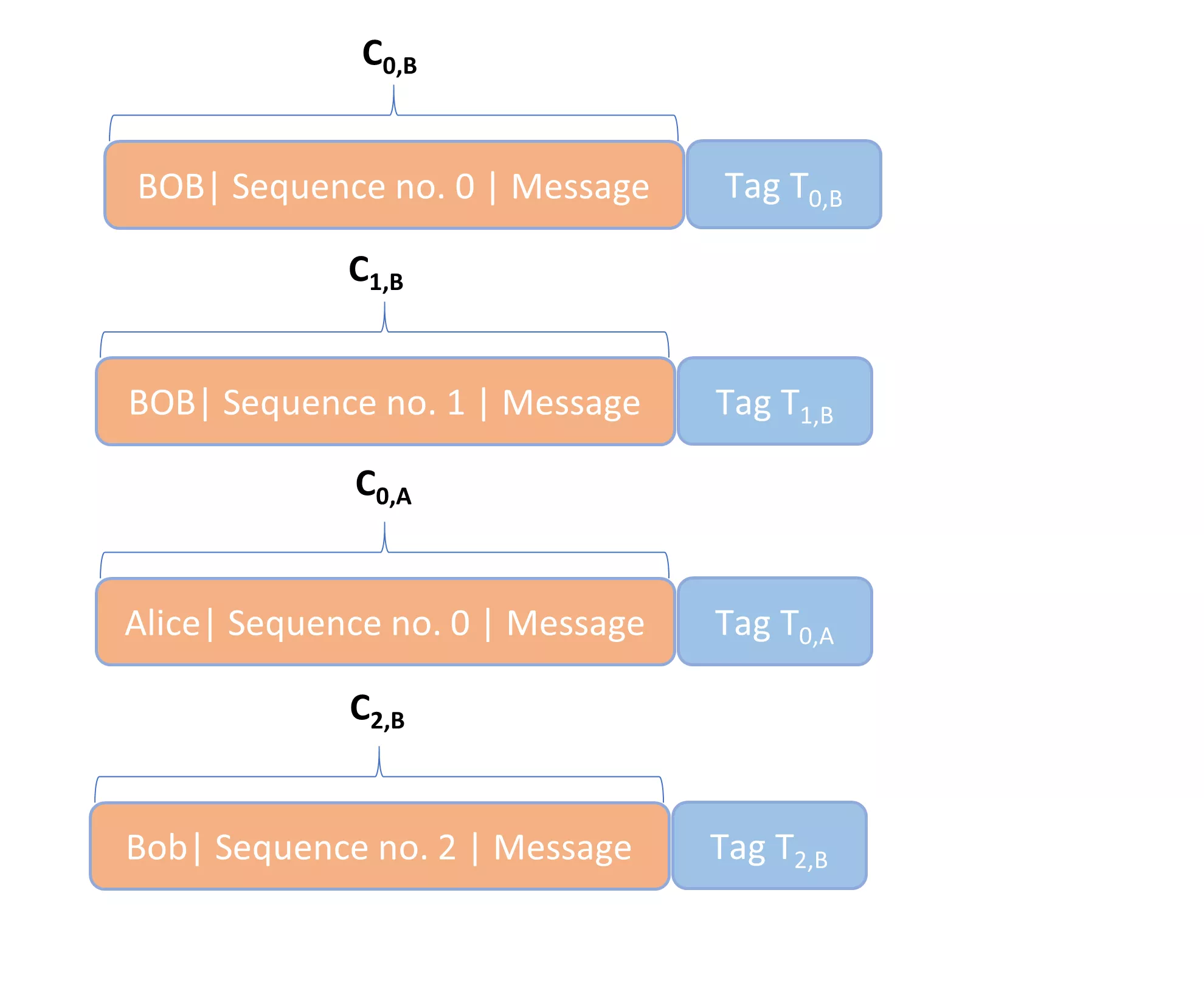
RC4 y AES
Cifrado de flujo RC4
En este capítulo, discutiremos los detalles de un esquema de cifrado con un moderno cifrado de flujo primitivo, RC4 (o "Rivest cipher 4"), y un moderno cifrado de bloque, AES. Mientras que el cifrado RC4 ha caído en desgracia como método de cifrado, AES es el estándar para el cifrado simétrico moderno. Estos dos ejemplos te darán una mejor idea de cómo funciona el cifrado simétrico.
Para tener una idea de cómo funcionan los cifrados de flujo pseudoaleatorios modernos, me centraré en el cifrado de flujo RC4. Se trata de un cifrado de flujo pseudoaleatorio que se utilizaba en los protocolos de seguridad de puntos de acceso inalámbricos WEP y WAP, así como en TLS. Como se ha demostrado que RC4 tiene muchos puntos débiles, ha caído en desgracia. De hecho, la Internet Engineering Task Force prohíbe ahora el uso de suites RC4 por parte de aplicaciones cliente y servidor en todas las instancias de TLS. Sin embargo, funciona bien como ejemplo para ilustrar cómo funciona un cifrado de flujo primitivo.
Para empezar, primero mostraré cómo cifrar un mensaje de texto plano con un cifrado RC4 para bebés. Supongamos que nuestro mensaje en texto plano es "SOUP" El cifrado con nuestro cifrado RC4 bebé, entonces, procede en cuatro pasos.
Primer paso
En primer lugar, defina una matriz S con S[0] = 0 a S[7] = 7. Una matriz aquí
significa simplemente una colección mutable de valores organizados por un
índice, también llamado una lista en algunos lenguajes de programación (por
ejemplo, Python). En este caso, el índice va de 0 a 7, y los valores también
van de 0 a 7. Así que S es como sigue:
S = [0, 1, 2, 3, 4, 5, 6, 7]
Los valores aquí no son números ASCII, sino las representaciones en valor
decimal de cadenas de 1 byte. Así, el valor 2 sería igual a 0000 \ 0011. La longitud de la matriz S es, por tanto, de 8 bytes.
Paso 2
En segundo lugar, defina una matriz de claves K de 8 bytes de longitud eligiendo una clave entre 1 y 8 bytes (sin permitir fracciones de bytes). Como cada byte tiene 8 bits, puedes seleccionar cualquier número entre 0 y 255 para cada byte de tu clave.
Supongamos que elegimos nuestra clave k como [14, 48, 9], para que tenga
una longitud de 3 bytes. Cada índice de nuestra matriz de claves se
establece de acuerdo con el valor decimal para ese elemento particular de la
clave, en orden. Si recorre toda la clave, empiece de nuevo por el
principio, hasta que haya llenado las 8 ranuras de la matriz de claves. Por
lo tanto, nuestra matriz de claves es la siguiente:
K = [14, 48, 9, 14, 48, 9, 14, 48]
Paso 3
En tercer lugar, transformaremos la matriz S utilizando la matriz de claves K, en un proceso conocido como programación de claves. El proceso es el siguiente en pseudocódigo:
- Crear variables j y i
- Establecer la variable
j = 0 - Para cada
ide 0 a 7:- Establece
j = (j + S[i] + K[i]) \mod 8 - Intercambia
S[i]yS[j]
- Establece
La transformación de la matriz S se recoge en la Tabla 1.
Para empezar, puedes ver el estado inicial de S como [0, 1, 2, 3, 4, 5, 6, 7] con un valor inicial de 0 para j. Esto se transformará
utilizando la matriz de claves [14, 48, 9, 14, 48, 9, 14, 48].
El bucle for comienza con i = 0. Según nuestro pseudocódigo anterior, el nuevo valor de j pasa a ser 6 (j = (j + S[0] + K[0]) \mod 8 = (0 + 0 + 14) \mod 8 = 6 \mod 8). Intercambiando S[0] y S[6], el estado de S después de 1 ronda pasa a ser [6, 1, 2, 3, 4, 5, 0, 7].
En la siguiente fila, i = 1.
Recorriendo de nuevo el bucle for, j obtiene un valor de 7
(j = (j + S[1] + K[1]) \mod 8 = (6 + 1 + 48) \mod 8 = 55 \mod 8 = 7 \mod 8). Intercambiando S[1] y S[7] desde el estado actual de S, [6, 1, 2, 3, 4, 5, 0, 7], se
obtiene [6, 7, 2, 3, 4, 5, 0, 1] después
de la ronda 2.
Continuamos con este proceso hasta que producimos la fila final en la parte
inferior para la matriz S, [6, 4, 1, 0, 3, 7, 5, 2].
Cuadro 1: Tabla de programación
| Round | i | j | S[0] | S[1] | S[2] | S[3] | S[4] | S[5] | S[6] | S[7] | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 1 | 0 | 6 | 6 | 1 | 2 | 3 | 4 | 5 | 0 | 7 | |
| 2 | 1 | 7 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 3 | 2 | 2 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 4 | 3 | 3 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 5 | 4 | 3 | 6 | 7 | 2 | 0 | 3 | 5 | 4 | 1 | |
| 6 | 5 | 6 | 6 | 4 | 2 | 0 | 3 | 7 | 5 | 1 | |
| 7 | 6 | 1 | 6 | 4 | 2 | 0 | 3 | 7 | 5 | 2 | |
| 8 | 7 | 2 | 6 | 4 | 1 | 0 | 3 | 7 | 5 | 2 |
Paso 4
Como cuarto paso, producimos el keystream. Se trata de la cadena pseudoaleatoria de longitud igual al mensaje que queremos enviar. Se utilizará para cifrar el mensaje original "SOUP" Como el keystream tiene que ser tan largo como el mensaje, necesitamos uno que tenga 4 bytes.
El flujo de claves se produce mediante el siguiente pseudocódigo:
- Crea las variables j, i y t.
- Fijar
j = 0. - Para cada
idel texto sin formato, empezando pori = 1y siguiendo hastai = 4, cada byte del flujo de claves se produce de la siguiente manera:j = (j + S[i]) \mod 8- Intercambia
S[i]yS[j]. t = (S[i] + S[j]) \mod 8- El
i^{th}byte de la secuencia de claves =S[t]
Puede seguir los cálculos en la Tabla 2.
El estado inicial de S es S = [6, 4, 1, 0, 3, 7, 5, 2].
Fijando i = 1, el valor de j pasa a ser 4 (j = (j + S[i]) \mod 8 = (0 + 4) \mod 8 = 4). A continuación, intercambiamos S[1] y S[4] para producir la
transformación de S en la segunda fila, [6, 3, 1, 0, 4, 7, 5, 2]. El
valor de t es entonces 7 (t = (S[i] + S[j]) \mod 8 = (3 + 4) \mod 8 = 7). Por último, el byte para el flujo de claves es S[7], o 2.
A continuación, seguimos produciendo los demás bytes hasta que tengamos los cuatro bytes siguientes: 2, 6, 3 y 7. Cada uno de estos bytes se puede utilizar para cifrar cada letra del texto plano, "SOUP".
Para empezar, utilizando una tabla ASCII, podemos ver que "SOUP" codificado por los valores decimales de las cadenas de bytes subyacentes es "83 79 85 80". Combinado con la cadena de claves "2 6 3 7" se obtiene "85 85 88 87", que se mantiene igual tras una operación de módulo 256. En ASCII, el texto cifrado "85 85 88 87" equivale a "UUXW".
¿Qué pasaría si la palabra a cifrar fuera más larga que la matriz S? En ese caso, la matriz S sigue transformándose de la manera mostrada arriba para cada byte i del texto plano, hasta que tengamos un número de bytes en el flujo de claves igual al número de letras en el texto plano.
Cuadro 2: Generación de flujos clave
| i | j | t | Keystream | S[0] | S[1] | S[2] | S[3] | S[4] | S[5] | S[6] | S[7] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 4 | 1 | 0 | 3 | 7 | 5 | 2 | |||
| 1 | 4 | 7 | 2 | 6 | 3 | 1 | 0 | 4 | 7 | 5 | 2 |
| 2 | 5 | 0 | 6 | 6 | 3 | 7 | 0 | 4 | 1 | 5 | 2 |
| 3 | 5 | 1 | 3 | 6 | 3 | 7 | 1 | 4 | 0 | 5 | 2 |
| 4 | 1 | 7 | 2 | 6 | 4 | 7 | 1 | 3 | 0 | 5 | 2 |
El ejemplo que acabamos de discutir es sólo una versión diluida del cifrado de flujo RC4. El cifrado de flujo RC4 real tiene una matriz S de 256 bytes de longitud, no 8 bytes, y una clave que puede estar entre 1 y 256 bytes, no entre 1 y 8 bytes. La matriz de claves y los flujos de claves se producen teniendo en cuenta la longitud de 256 bytes de la matriz S. Los cálculos se vuelven inmensamente más complejos, pero los principios siguen siendo los mismos. Utilizando la misma clave, 14,48,9, con el cifrado estándar RC4, el mensaje en texto plano "SOUP" se cifra como 67 02 ed df en formato hexadecimal.
Un cifrado de flujo en el que el flujo de claves se actualiza independientemente del mensaje en claro o del texto cifrado es un cifrado de flujo síncrono. El flujo de claves sólo depende de la clave. Claramente, RC4 es un ejemplo de cifrado de flujo síncrono, ya que el flujo de claves no tiene relación con el texto plano o el texto cifrado. Todos nuestros cifradores de flujo primitivos mencionados en el capítulo anterior, incluidos el cifrado por desplazamiento, el cifrado de Vigenère y la almohadilla de un solo uso, también eran de la variedad síncrona.
Por el contrario, un cifrado de flujo asíncrono tiene un flujo clave que es producido tanto por la clave como por los elementos previos del texto cifrado. Este tipo de cifrado también se denomina cifrado autosincrónico.
Es importante destacar que el flujo de claves producido con RC4 debe tratarse como una almohadilla de un solo uso, y no se puede producir el flujo de claves exactamente de la misma manera la próxima vez. En lugar de cambiar la clave cada vez, la solución práctica es combinar la clave con un nonce para producir el flujo de bytes.
AES con una clave de 128 bits
Como se mencionó en el capítulo anterior, el Instituto Nacional de Estándares y Tecnología (NIST) convocó un concurso entre 1997 y 2000 para determinar un nuevo estándar de cifrado simétrico. El cifrado Rijndael resultó ser la propuesta ganadora. El nombre es un juego de palabras con los nombres de los creadores belgas, Vincent Rijmen y Joan Daemen.
El cifrado Rijndael es un cifrado por bloques, lo que significa que existe un algoritmo central que puede utilizarse con diferentes especificaciones de longitud de clave y tamaño de bloque. Así, puedes utilizarlo con diferentes modos de funcionamiento para construir esquemas de cifrado.
El comité del concurso del NIST adoptó una versión restringida del cifrado Rijndael, que requiere bloques de 128 bits y longitudes de clave de 128, 192 o 256 bits, como parte del estándar de cifrado avanzado (AES). Esta versión restringida del cifrado Rijndael también puede utilizarse en varios modos de funcionamiento. La especificación del estándar es lo que se conoce como estándar de cifrado avanzado (AES).
Para mostrar cómo funciona el cifrado Rijndael, el núcleo de AES, ilustraré el proceso de cifrado con una clave de 128 bits. El tamaño de la clave influye en el número de rondas que se realizan para cada bloque de cifrado. Para claves de 128 bits, se necesitan 10 rondas. Con 192 bits y 256 bits, serían 12 y 14 rondas, respectivamente.
Además, supondré que AES se utiliza en modo ECB. Esto facilita ligeramente la exposición y no tiene importancia para el algoritmo Rijndael. Sin duda, el modo ECB no es seguro en la práctica porque conduce a un cifrado determinista. El modo seguro más utilizado con AES es CBC (encadenamiento de bloques cifrados).
Llamemos a la clave K_0. La
construcción con los parámetros anteriores tiene el aspecto que se muestra
en la Figura 1, donde M_i representa una parte del mensaje en texto plano de 128 bits y C_i una parte del texto cifrado
de 128 bits. Se añade relleno al texto sin formato para el último bloque, si
el texto sin formato no puede dividirse uniformemente por el tamaño del bloque.
Figura 1: AES-ECB con una clave de 128 bits
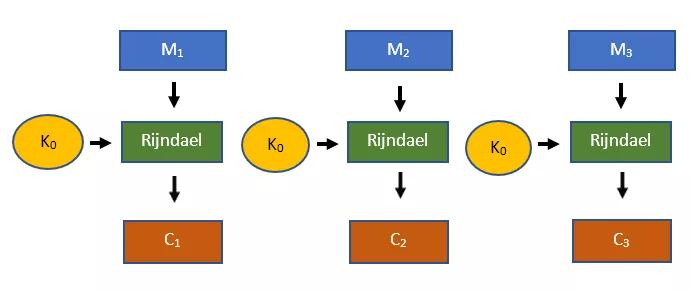
Cada bloque de texto de 128 bits pasa por diez rondas en el esquema de
cifrado Rijndael. Esto requiere una clave distinta para cada ronda (de K_1 a K_{10}). Éstas se
producen para cada ronda a partir de la clave original de 128 bits K_0 utilizando un algoritmo de expansión de claves. Por lo
tanto, para cada bloque de texto a cifrar, utilizaremos la clave original K_0 y diez claves de ronda distintas.
Tenga en cuenta que estas mismas 11 claves se utilizan para cada bloque de texto
plano de 128 bits que requiera cifrado.
El algoritmo de expansión de claves es largo y complejo. Trabajar a través
de él tiene poco beneficio didáctico. Si lo desea, puede revisar el
algoritmo de expansión de claves por su cuenta. Una vez obtenidas las claves
redondas, el cifrado Rijndael manipulará el primer bloque de 128 bits de
texto plano, M_1, como se ve
en la Figura 2. Ahora repasaremos estos pasos.
Figura 2: Manipulación de M_1 con el cifrado Rijndael:
Ronda 0:
- XOR
M_1yK_0para producirS_0
Ronda n para n = {1,...,9}:
- XOR
S_{n-1}yK_n - Sustitución de bytes
- Desplazar filas
- Columnas de mezcla
- XOR
SyK_npara producirS_n
Ronda 10:
- XOR
S_9yK_{10} - Sustitución de bytes
- Desplazar filas
- XOR
SyK_{10}para producirS_{10} S_{10}=C_1
Ronda 0
La ronda 0 del cifrado Rijndael es sencilla. Se genera una matriz S_0 mediante una operación XOR entre el texto plano de 128 bits y la clave privada.
Es decir,
S_0 = M_1 \oplus K_0
Ronda 1
En la ronda 1, la matriz S_0 se combina primero con la clave de ronda K_1 mediante una operación XOR. Esto produce un nuevo estado de S.
En segundo lugar, la operación de sustitución de bytes se
realiza en el estado actual de S. Funciona tomando cada byte
de la matriz S de 16 bytes y
sustituyéndolo por un byte de una matriz llamada caja S de Rijndael. Cada byte tiene una transformación
única, y como resultado se produce un nuevo estado de S. La S-box de Rijndael se
muestra en la Figura 3.
Figura 3: S-Box de Rijndael
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 0A | 0B | 0C | 0D | 0E | 0F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 63 | 7C | 77 | 7B | F2 | 6B | 6F | C5 | 30 | 01 | 67 | 2B | FE | D7 | AB | 76 |
| 10 | CA | 82 | C9 | 7D | FA | 59 | 47 | F0 | AD | D4 | A2 | AF | 9C | A4 | 72 | C0 |
| 20 | B7 | FD | 93 | 26 | 36 | 3F | F7 | CC | 34 | A5 | E5 | F1 | 71 | D8 | 31 | 15 |
| 30 | 04 | C7 | 23 | C3 | 18 | 96 | 05 | 9A | 07 | 12 | 80 | E2 | EB | 27 | B2 | 75 |
| 40 | 09 | 83 | 2C | 1A | 1B | 6E | 5A | A0 | 52 | 3B | D6 | B3 | 29 | E3 | 2F | 84 |
| 50 | 53 | D1 | 00 | ED | 20 | FC | B1 | 5B | 6A | CB | BE | 39 | 4A | 4C | 58 | CF |
| 60 | D0 | EF | AA | FB | 43 | 4D | 33 | 85 | 45 | F9 | 02 | 7F | 50 | 3C | 9F | A8 |
| 70 | 51 | A3 | 40 | 8F | 92 | 9D | 38 | F5 | BC | B6 | DA | 21 | 10 | FF | F3 | D2 |
| 80 | CD | 0C | 13 | EC | 5F | 97 | 44 | 17 | C4 | A7 | 7E | 3D | 64 | 5D | 19 | 73 |
| 90 | 60 | 81 | 4F | DC | 22 | 2A | 90 | 88 | 46 | EE | B8 | 14 | DE | 5E | 0B | DB |
| A0 | E0 | 32 | 3A | 0A | 49 | 06 | 24 | 5C | C2 | D3 | AC | 62 | 91 | 95 | E4 | 79 |
| B0 | E7 | C8 | 37 | 6D | 8D | D5 | 4E | A9 | 6C | 56 | F4 | EA | 65 | 7A | AE | 08 |
| C0 | BA | 78 | 25 | 2E | 1C | A6 | B4 | C6 | E8 | DD | 74 | 1F | 4B | BD | 8B | 8A |
| D0 | 70 | 3E | B5 | 66 | 48 | 03 | F6 | 0E | 61 | 35 | 57 | B9 | 86 | C1 | 1D | 9E |
| E0 | E1 | F8 | 98 | 11 | 69 | D9 | 8E | 94 | 9B | 1E | 87 | E9 | CE | 55 | 28 | DF |
| F0 | 8C | A1 | 89 | 0D | BF | E6 | 42 | 68 | 41 | 99 | 2D | 0F | B0 | 54 | BB | 16 |
Esta S-Box es uno de los lugares donde el álgebra abstracta entra en juego en el cifrado Rijndael, concretamente en los campos de Galois.
Para empezar, se define cada posible elemento de byte 00 a FF como un vector
de 8 bits. Cada uno de estos vectores es un elemento del campo de Galois GF(2^8) donde el polinomio irreducible para la operación módulo es x^8 + x^4 + x^3 + x + 1. El
campo de Galois con estas especificaciones también se denomina campo finito de Rijndael.
A continuación, para cada elemento posible del campo, creamos lo que se denomina la Caja S de Nyberg. En esta caja, cada byte se mapea en su inverso multiplicativo (es decir, de modo que su producto sea igual a 1). A continuación mapeamos esos valores de la caja S de Nyberg a la caja S de Rijndael utilizando la transformación afín.
La tercera operación sobre la matriz S es la operación desplazar filas. Toma el estado de S y lista los dieciséis bytes en una matriz. El llenado de la matriz comienza en la parte superior izquierda y va de arriba a abajo y luego, cada vez que se llena una columna, se desplaza una columna a la derecha y hacia arriba.
Una vez construida la matriz de S, se desplazan las cuatro filas. La primera fila permanece igual. La segunda fila se desplaza una a la izquierda. La tercera desplaza dos a la izquierda. La cuarta desplaza tres a la izquierda. En la Figura 4 se muestra un ejemplo del proceso. El estado original de S se muestra en la parte superior, y el estado resultante después de la operación de desplazamiento de filas se muestra debajo.
Figura 4: Operación de desplazamiento de filas
| F1 | A0 | B1 | 23 |
|---|---|---|---|
| 59 | EF | 09 | 82 |
| 97 | 01 | B0 | CC |
| D4 | 72 | 04 | 21 |
| F1 | A0 | B1 | 23 |
|---|---|---|---|
| EF | 09 | 82 | 59 |
| B0 | CC | 97 | 01 |
| 21 | D4 | 72 | 04 |
En el cuarto paso, los campos de Galois vuelven a hacer
acto de presencia. Para empezar, cada columna de la matriz S se multiplica por la columna de la matriz 4 x 4 que se ve en la Figura 5. Pero en lugar de ser una multiplicación matricial normal,
es una multiplicación vectorial módulo de un polinomio irreducible, x^8 + x^4 + x^3 + x + 1. Los
coeficientes vectoriales resultantes representan los bits individuales de un
byte.
Figura 5: Matriz de columnas de la mezcla
| 02 | 03 | 01 | 01 |
|---|---|---|---|
| 01 | 02 | 03 | 01 |
| 01 | 01 | 02 | 03 |
| 03 | 01 | 01 | 02 |
La multiplicación de la primera columna de la matriz S por la matriz 4 x 4 anterior da el resultado de la Figura 6.
Figura 6: Multiplicación de la primera columna:
\begin{matrix}
02 \cdot F1 + 03 \cdot EF + 01 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 02 \cdot EF + 03 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 01 \cdot EF + 02 \cdot B0 + 03 \cdot 21 \\
03 \cdot F1 + 01 \cdot EF + 01 \cdot B0 + 02 \cdot 21
\end{matrix}Como siguiente paso, habría que convertir todos los términos de la matriz en
polinomios. Por ejemplo, F1 representa 1 byte y se convertiría en x^7 + x^6 + x^5 + x^4 + 1, y 03 representa 1 byte y se convertiría en x + 1.
Todas las multiplicaciones se realizan entonces módulo x^8 + x^4 + x^3 + x + 1. El
resultado es la suma de cuatro polinomios en cada una de las cuatro celdas
de la columna. Después de realizar esas sumas módulo 2,
obtendremos cuatro polinomios. Cada uno de estos polinomios representa una
cadena de 8 bits, o 1 byte, de S. No realizaremos aquí
todos estos cálculos en la matriz de la Figura 6 porque son extensos.
Una vez procesada la primera columna, se procesan del mismo modo las otras tres columnas de la matriz S. Finalmente, se obtendrá una matriz con dieciséis bytes que puede transformarse en una matriz.
Como paso final, la matriz S se combina de nuevo con la
clave redonda en una operación XOR. Esto produce el estado S_1. Es decir,
S_1 = S \oplus K_0
Rondas 2 a 10
Las rondas 2 a 9 no son más que una repetición de la ronda 1, mutatis mutandis. La ronda final es muy similar a las anteriores, salvo que se elimina el paso de mezclar columnas. Es decir, la ronda 10 se ejecuta de la siguiente manera:
S_9 \oplus K_{10}- Sustitución de bytes
- Desplazar filas
S_{10} = S \oplus K_{10}
El estado S_{10} se
establece ahora en C_1, los
primeros 128 bits del texto cifrado. Procediendo a través de los restantes
bloques de texto plano de 128 bits se obtiene el texto cifrado completo C.
Las operaciones del cifrado Rijndael
¿Cuál es el razonamiento que hay detrás de las diferentes operaciones que se ven en el cifrado Rijndael?
Sin entrar en detalles, los esquemas de cifrado se evalúan en función del grado en que crean confusión y difusión. Si el esquema de cifrado tiene un alto grado de confusión, significa que el texto cifrado parece drásticamente diferente del texto sin cifrar. Si el esquema de cifrado tiene un alto grado de difusión, significa que cualquier pequeño cambio en el texto plano produce un texto cifrado drásticamente diferente.
El razonamiento para las operaciones detrás del cifrado Rijndael es que producen tanto un alto grado de confusión como de difusión. La confusión la produce la operación de sustitución de bytes, mientras que la difusión la producen las operaciones de desplazamiento de filas y mezcla de columnas.
Criptografía asimétrica
El problema de la distribución y gestión de claves
Al igual que la criptografía simétrica, los esquemas asimétricos pueden utilizarse para garantizar tanto el secreto como la autenticación. Sin embargo, estos esquemas emplean dos claves en lugar de una: una privada y otra pública.
Comenzamos nuestra investigación con el descubrimiento de la criptografía asimétrica y, en particular, con los problemas que la impulsaron. A continuación, analizaremos cómo funcionan a alto nivel los esquemas asimétricos de cifrado y autenticación. A continuación, introducimos las funciones hash, que son clave para entender los esquemas de autenticación asimétrica y también tienen relevancia en otros contextos criptográficos, como los códigos de autenticación de mensajes basados en hash que analizamos en el capítulo 4.
Supongamos que Bob quiere comprar un chubasquero nuevo en Jim's Sporting Goods, una tienda online de artículos deportivos con millones de clientes en Norteamérica. Será su primera compra y quiere utilizar su tarjeta de crédito. Así que Bob tendrá que crear una cuenta en Jim's Sporting Goods, para lo que tendrá que enviar datos personales como su dirección y la información de su tarjeta de crédito. A continuación, puede seguir los pasos necesarios para comprar el chubasquero.
Bob y Jim's Sporting Goods querrán asegurarse de que sus comunicaciones son seguras durante todo este proceso, teniendo en cuenta que Internet es un sistema de comunicaciones abierto. Querrán asegurarse, por ejemplo, de que ningún atacante potencial pueda averiguar los datos de la tarjeta de crédito y la dirección de Bob, y de que ningún atacante potencial pueda repetir sus compras o crear otras falsas en su nombre.
Un esquema avanzado de encriptación autenticada como el discutido en el capítulo anterior podría ciertamente hacer seguras las comunicaciones entre Bob y Jim's Sporting Goods. Pero es evidente que existen obstáculos prácticos a la hora de aplicar un esquema de este tipo.
Para ilustrar estos obstáculos prácticos, supongamos que viviéramos en un mundo en el que sólo existieran las herramientas de la criptografía simétrica. ¿Qué podrían hacer entonces Jim's Sporting Goods y Bob para garantizar una comunicación segura?
En esas circunstancias, se enfrentarían a costes sustanciales para comunicarse de forma segura. Como Internet es un sistema de comunicaciones abierto, no pueden intercambiar un juego de claves a través de él. Por lo tanto, Bob y un representante de Jim's Sporting Goods tendrán que realizar un intercambio de claves en persona.
Una posibilidad es que Jim's Sporting Goods cree lugares especiales de intercambio de claves, donde Bob y otros nuevos clientes puedan recuperar un juego de claves para una comunicación segura. Obviamente, esto supondría un coste organizativo considerable y reduciría en gran medida la eficacia con la que los nuevos clientes pueden realizar sus compras.
Como alternativa, Jim's Sporting Goods puede enviar a Bob un par de llaves con un mensajero de confianza. Esto es probablemente más eficaz que organizar lugares de intercambio de llaves. Pero esto seguiría teniendo un coste considerable, sobre todo si muchos clientes sólo hacen una o pocas compras.
Además, un esquema simétrico para el cifrado autenticado también obliga a Jim's Sporting Goods a almacenar conjuntos separados de claves para todos sus clientes. Esto supondría un reto práctico importante para miles de clientes, por no hablar de millones.
Para entender este último punto, supongamos que Jim's Sporting Goods proporciona a cada cliente el mismo par de claves. Esto permitiría a cada cliente -o a cualquier otra persona que pudiera obtener este par de claves- leer e incluso manipular todas las comunicaciones entre Jim's Sporting Goods y sus clientes. Por tanto, sería mejor que no utilizara criptografía en sus comunicaciones.
Incluso repetir un conjunto de claves sólo para algunos clientes es una práctica de seguridad terrible. Cualquier atacante potencial podría intentar explotar esa característica del esquema (recuerde que se supone que los atacantes lo saben todo sobre un esquema excepto las claves, de acuerdo con el principio de Kerckhoffs)
Así, Jim's Sporting Goods tendría que almacenar un par de claves para cada cliente, independientemente de cómo se distribuyan estos pares de claves. Esto plantea claramente varios problemas prácticos.
- Jim's Sporting Goods tendría que almacenar millones de pares de llaves, un juego para cada cliente.
- Estas claves tendrían que estar debidamente protegidas, ya que serían un blanco seguro para los piratas informáticos. Cualquier violación de la seguridad requeriría la repetición de costosos intercambios de claves, ya sea en lugares especiales de intercambio de claves o por mensajería.
- Cualquier cliente de Jim's Sporting Goods tendría que guardar un par de llaves en su casa. Se producirían pérdidas y robos, lo que obligaría a repetir los intercambios de claves. Los clientes también tendrían que pasar por este proceso para cualquier otra tienda en línea u otro tipo de entidad con la que deseen comunicarse y realizar transacciones a través de Internet.
Estos dos retos principales que acabamos de describir fueron preocupaciones muy fundamentales hasta finales de los años setenta. Se conocían como el problema de la distribución de claves y el problema de la gestión de claves, respectivamente.
Estos problemas siempre han existido, por supuesto, y a menudo han creado quebraderos de cabeza en el pasado. Las fuerzas militares, por ejemplo, tenían que distribuir constantemente libros con claves para una comunicación segura al personal sobre el terreno, con grandes riesgos y costes. Pero estos problemas se estaban agravando a medida que el mundo se adentraba cada vez más en la comunicación digital a larga distancia, sobre todo para las entidades no gubernamentales.
Si estos problemas no se hubieran resuelto en la década de 1970, probablemente no habría existido una compra eficaz y segura en Jim's Sporting Goods. De hecho, la mayor parte de nuestro mundo moderno, con el correo electrónico práctico y seguro, la banca en línea y las compras, probablemente no serían más que una fantasía lejana. Algo parecido al Bitcoin no habría existido.
¿Qué ocurrió en los años setenta? ¿Cómo es posible que podamos hacer compras en línea al instante y navegar de forma segura por la World Wide Web? ¿Cómo es posible que podamos enviar instantáneamente Bitcoins a todo el mundo desde nuestros teléfonos inteligentes?
Nuevas orientaciones en criptografía
En los años 70, los problemas de distribución y gestión de claves habían captado la atención de un grupo de criptógrafos académicos estadounidenses: Whitfield Diffie, Martin Hellman y Ralph Merkle. Ante el gran escepticismo de la mayoría de sus colegas, se aventuraron a idear una solución.
Al menos una de las principales motivaciones de su aventura fue la previsión de que las comunicaciones informáticas abiertas afectarían profundamente a nuestro mundo. Como señalaron Diffie y Helmann en 1976,
El desarrollo de redes de comunicación controladas por ordenador promete un contacto sin esfuerzo y barato entre personas u ordenadores situados en puntos opuestos del planeta, sustituyendo la mayor parte del correo y muchas excursiones por las telecomunicaciones. Para muchas aplicaciones, estos contactos deben ser seguros tanto contra las escuchas como contra la inyección de mensajes ilegítimos. En la actualidad, sin embargo, la solución de los problemas de seguridad va muy a la zaga de otras áreas de la tecnología de las comunicaciones. La criptografía contemporánea es incapaz de cumplir los requisitos, en el sentido de que su uso impondría inconvenientes tan graves a los usuarios del sistema, como para eliminar muchos de los beneficios del teleproceso. [1]
La tenacidad de Diffie, Hellman y Merkle dio sus frutos. La primera publicación de sus resultados fue un artículo de Diffie y Helmann en 1976 titulado "New Directions in Cryptography" En él, presentaban dos formas originales de abordar los problemas de distribución y gestión de claves.
La primera solución que ofrecieron fue un protocolo de intercambio de claves remoto, es decir, un conjunto de reglas para el intercambio de una o más claves simétricas a través de un canal de comunicación inseguro. Este protocolo se conoce ahora como intercambio de claves Diffie-Helmann o intercambio de claves Diffie-Helmann-Merkle. [2]
Con el intercambio de claves Diffie-Helmann, dos partes intercambian primero cierta información públicamente en un canal inseguro como Internet. A partir de esa información, crean independientemente una clave simétrica (o un par de claves simétricas) para una comunicación segura. Aunque ambas partes crean sus claves de forma independiente, la información que comparten públicamente garantiza que este proceso de creación de claves produce el mismo resultado para ambas.
Es importante destacar que, aunque todo el mundo puede observar la información que intercambian públicamente las partes a través del canal inseguro, sólo las dos partes que participan en el intercambio de información pueden crear claves simétricas a partir de ella.
Esto, por supuesto, suena completamente contraintuitivo. ¿Cómo podrían dos partes intercambiar públicamente una información que sólo les permitiera crear claves simétricas a partir de ella? ¿Por qué nadie más que observe el intercambio de información podría crear las mismas claves?
Por supuesto, se basa en unas bellas matemáticas. El intercambio de claves Diffie-Helmann funciona mediante una función unidireccional con una trampilla. Veamos el significado de estos dos términos.
Supongamos que nos dan una función f(x) y el resultado f(a) = y,
donde a es un valor
particular de x. Decimos que f(x) es una función unidireccional si es fácil calcular el valor y cuando se dan a y f(x), pero es
computacionalmente inviable calcular el valor a cuando se dan y y f(x). El nombre función unidireccional, por supuesto, proviene del hecho de
que tal función sólo es práctica para calcular en una dirección.
Algunas funciones unidireccionales tienen lo que se conoce como puerta trampa. Mientras que es prácticamente imposible calcular a a partir de y y f(x), existe una cierta
información Z que hace que
calcular a a partir de y sea computacionalmente factible. Este dato Z se conoce como puerta trampa. Las funciones
unidireccionales que tienen una trampilla se conocen como funciones de trampilla.
No vamos a entrar aquí en los detalles del intercambio de claves Diffie-Helmann. Pero, en esencia, cada participante crea cierta información, de la que una parte se comparte públicamente y otra permanece secreta. Cada parte, entonces, toma su parte secreta de información y la información pública compartida por la otra parte para crear una clave privada. Y, milagrosamente, ambas partes acabarán teniendo la misma clave privada.
Cualquiera que observe sólo la información compartida públicamente entre las dos partes en un intercambio de claves Diffie Helmann es incapaz de replicar estos cálculos. Para ello necesitaría la información privada de una de las dos partes.
Aunque la versión básica del intercambio de claves Diffie-Helmann presentada en el artículo de 1976 no es muy segura, hoy en día se siguen utilizando versiones sofisticadas del protocolo básico. Y lo que es más importante, cada protocolo de intercambio de claves de la última versión del protocolo de seguridad de la capa de transporte (versión 1.3) es esencialmente una versión enriquecida del protocolo presentado por Diffie y Hellman en 1976. El protocolo de seguridad de la capa de transporte es el protocolo predominante para el intercambio seguro de información formateada según el protocolo de transferencia de hipertexto (http), el estándar para el intercambio de contenidos Web.
Es importante destacar que el intercambio de claves Diffie-Helmann no es un esquema asimétrico. En sentido estricto, podría decirse que pertenece al ámbito de la criptografía de clave simétrica. Pero como tanto el intercambio de claves de Diffie-Helmann como la criptografía asimétrica se basan en funciones numéricas teóricas unidireccionales con trampillas, normalmente se tratan juntos.
La segunda forma que Diffie y Helmann ofrecieron para abordar el problema de la distribución y gestión de claves en su artículo de 1976 fue, por supuesto, la criptografía asimétrica.
En contraste con su presentación del intercambio de claves Diffie-Hellman, sólo proporcionaron los contornos generales de cómo podrían construirse esquemas criptográficos asimétricos. No ofrecían ninguna función unidireccional que pudiera cumplir específicamente las condiciones necesarias para una seguridad razonable en dichos esquemas.
Sin embargo, un año más tarde, tres criptógrafos y matemáticos académicos encontraron una aplicación práctica de un esquema asimétrico: Ronald Rivest, Adi Shamir y Leonard Adleman [3]. El criptosistema que introdujeron se conoció como el criptosistema RSA (por sus apellidos).
Las funciones de trampilla utilizadas en la criptografía asimétrica (y en el intercambio de claves Diffie Helmann) están relacionadas con dos problemas informáticos principales: la factorización de números primos y el cálculo de logaritmos discretos.
La factorización de números primos requiere, como su nombre indica, descomponer un número entero en sus factores primos. El problema RSA es, con diferencia, el ejemplo más conocido de criptosistema relacionado con la factorización de números primos.
El problema del logaritmo discreto es un problema que se plantea en los grupos cíclicos. Dado un generador en un grupo cíclico particular, requiere el cálculo del exponente único necesario para producir otro elemento en el grupo a partir del generador.
Los esquemas basados en logaritmos discretos se basan en dos tipos principales de grupos cíclicos: grupos multiplicativos de enteros y grupos que incluyen los puntos de las curvas elípticas. El intercambio de claves original de Diffie Helmann presentado en "New Directions in Cryptography" funciona con un grupo cíclico multiplicativo de enteros. El algoritmo de firma digital de Bitcoin y el recientemente introducido esquema de firma Schnorr (2021) se basan ambos en el problema del logaritmo discreto para un grupo cíclico de curvas elípticas concreto.
A continuación, pasaremos a una visión general de alto nivel del secreto y la autenticación en el entorno asimétrico. Antes de hacerlo, sin embargo, debemos hacer un breve apunte histórico.
Ahora parece verosímil que un grupo de criptógrafos y matemáticos británicos que trabajaban para el Cuartel General de Comunicaciones del Gobierno (GCHQ) hubiera realizado de forma independiente los descubrimientos mencionados unos años antes. Este grupo estaba formado por James Ellis, Clifford Cocks y Malcolm Williamson.
Según sus propios relatos y los del GCHQ, fue James Ellis quien ideó por primera vez el concepto de criptografía de clave pública en 1969. Supuestamente, Clifford Cocks descubrió después el sistema criptográfico RSA en 1973, y Malcolm Williamson el concepto de intercambio de claves Diffie Helmann en 1974[4]. Sin embargo, sus descubrimientos no se revelaron hasta 1997, dada la naturaleza secreta del trabajo realizado en el GCHQ.
Notas:
[1] Whitfield Diffie y Martin Hellman, "New directions in cryptography," IEEE Transactions on Information Theory IT-22 (1976), pp. 644-654, en p. 644.
[2] Ralph Merkle también analiza un protocolo de intercambio de claves en "Secure communications over insecure channels", Communications of the Association for Computing Machinery, 21 (1978), 294-99. Aunque Merkle presentó este artículo antes que el de Diffie y Hellman, se publicó más tarde. La solución de Merkle no es exponencialmente segura, a diferencia de la de Diffie-Hellman.
[3] Ron Rivest, Adi Shamir y Leonard Adleman, "A method for obtaining digital signatures and public-key cryptosystems", Communications of the Association for Computing Machinery, 21 (1978), pp. 120-26.
[4] Simon Singh, The Code Book, Fourth Estate (Londres, 1999), capítulo 6, ofrece una buena historia de estos descubrimientos.
Cifrado asimétrico y autenticación
En la Figura 1 se ofrece una visión general del cifrado asimétrico con la ayuda de Bob y Alice.
En primer lugar, Alice crea un par de claves, consistentes en una clave
pública (K_P) y una clave
privada (K_S), donde la "P"
de K_P significa "pública" y
la "S" de K_S significa
"secreta". A continuación, distribuye esta clave pública libremente a otras
personas. Volveremos a los detalles de este proceso de distribución más
adelante. Pero por ahora, supongamos que cualquiera, incluido Bob, puede
obtener de forma segura la clave pública K_P de Alice.
Más adelante, Bob quiere escribir un mensaje M a Alice. Como incluye información sensible, quiere que su contenido
permanezca secreto para todos excepto para Alice. Por lo tanto, Bob primero
encripta su mensaje M utilizando K_P. A
continuación, envía el texto cifrado resultante C a Alice, que descifra C con K_S para obtener el mensaje original M.
Figura 1: Cifrado asimétrico
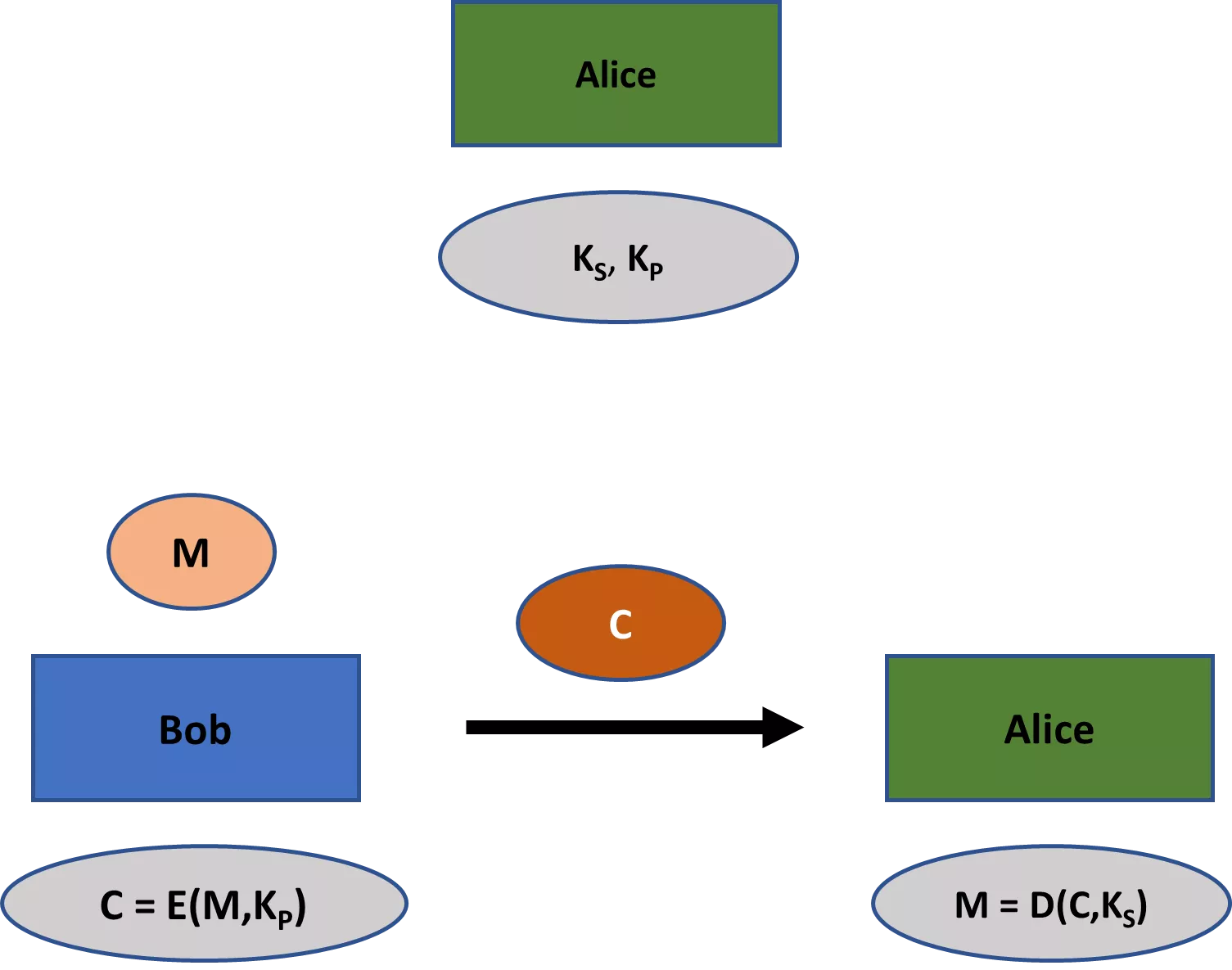
Cualquier adversario que escuche la comunicación entre Bob y Alice puede
observar C. También conoce K_P y el algoritmo de cifrado E(\cdot). Sin embargo, es
importante destacar que esta información no permite al atacante descifrar el
texto cifrado C. El
descifrado requiere específicamente K_S, que el atacante no
posee.
Por lo general, los esquemas de cifrado simétrico deben ser seguros frente a un atacante que pueda cifrar válidamente mensajes de texto plano (lo que se conoce como seguridad frente a ataques de texto cifrado elegido). Sin embargo, no se ha diseñado con el propósito explícito de permitir la creación de dichos textos cifrados válidos por parte de un atacante o de cualquier otra persona.
Esto contrasta fuertemente con un esquema de cifrado asimétrico, en el que todo su propósito es permitir que cualquiera, incluidos los atacantes, produzca textos cifrados válidos. Los esquemas de cifrado asimétrico pueden, por tanto, denominarse cifradores de acceso múltiple.
Para entender mejor lo que ocurre, imagina que en lugar de enviar un mensaje electrónicamente, Bob quisiera enviar una carta física en secreto. Una forma de garantizar el secreto sería que Alice enviara un candado seguro a Bob, pero se quedara con la llave para abrirlo. Después de escribir su carta, Bob podría meterla en una caja y cerrarla con el candado de Alice. A continuación, podría enviar la caja cerrada con el mensaje a Alice, que tiene la llave para abrirla.
Aunque Bob es capaz de cerrar el candado, ni él ni ninguna otra persona que intercepte la caja puede deshacer el candado si es que es seguro. Sólo Alice puede abrirlo y ver el contenido de la carta de Bob porque tiene la llave.
Un esquema de cifrado asimétrico es, a grandes rasgos, una versión digital de este proceso. El candado es similar a la clave pública y la clave del candado es similar a la clave privada. Sin embargo, como el candado es digital, es mucho más fácil y no tan costoso para Alicia distribuirlo a cualquiera que quiera enviarle mensajes secretos.
Para la autenticación en el entorno asimétrico, utilizamos firmas digitales. Éstas tienen la misma función que los códigos de autenticación de mensajes en el entorno simétrico. En la Figura 2 se ofrece una visión general de las firmas digitales.
Bob crea primero un par de claves, formado por la clave pública (K_P) y la clave privada (K_S),
y distribuye su clave pública. Cuando quiere enviar un mensaje autenticado a
Alice, primero toma su mensaje M y su clave privada para crear una firma digital D. A continuación, Bob envía
a Alice su mensaje junto con la firma digital.
Alice inserta el mensaje, la clave pública y la firma digital en un algoritmo de verificación. Este algoritmo produce verdadero para una firma válida, o falso para una firma inválida.
Una firma digital es, como su nombre indica claramente, el equivalente digital de una firma escrita en cartas, contratos, etcétera. De hecho, una firma digital suele ser mucho más segura. Con un poco de esfuerzo, se puede falsificar una firma escrita; un proceso facilitado por el hecho de que las firmas escritas a menudo no se verifican minuciosamente. Sin embargo, una firma digital segura es, al igual que un código seguro de autenticación de mensajes, imposible de falsificar: es decir, con un esquema de firma digital segura, nadie puede crear una firma para un mensaje que supere el procedimiento de verificación, a menos que disponga de la clave privada.
Figura 2: Autenticación asimétrica
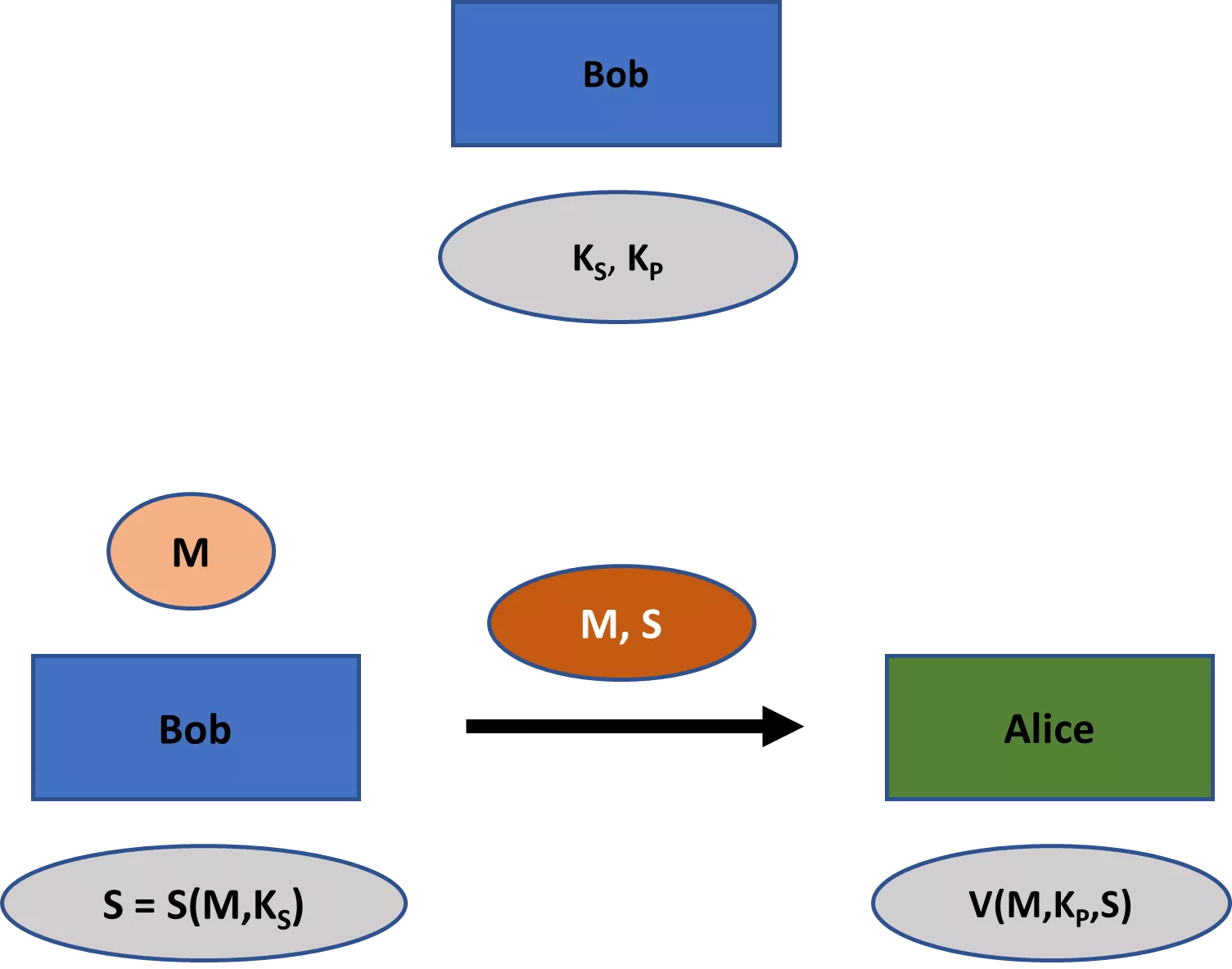
Al igual que ocurre con el cifrado asimétrico, observamos un interesante
contraste entre las firmas digitales y los códigos de autenticación de
mensajes. En el caso de estos últimos, el algoritmo de verificación sólo
puede ser empleado por una de las partes conocedoras de la comunicación
segura. Esto se debe a que requiere una clave privada. Sin embargo, en la
configuración asimétrica, cualquiera puede verificar una firma digital S realizada por Bob.
Todo esto convierte a la firma digital en una herramienta extremadamente
poderosa. Constituye la base, por ejemplo, de la creación de firmas en
contratos que pueden verificarse con fines legales. Si Bob ha firmado un
contrato en el intercambio anterior, Alice puede mostrar el mensaje M, el contrato y la firma S a
un tribunal. El tribunal puede, entonces, verificar la firma utilizando la clave
pública de Bob. [5]
Por ejemplo, las firmas digitales son un aspecto importante de la distribución segura de software y de sus actualizaciones. Este tipo de verificabilidad pública nunca podría crearse utilizando únicamente códigos de autenticación de mensajes.
Un último ejemplo del poder de las firmas digitales es Bitcoin. Uno de los errores más comunes sobre Bitcoin, sobre todo en los medios de comunicación, es que las transacciones están encriptadas: no es así. En cambio, las transacciones de Bitcoin funcionan con firmas digitales para garantizar la seguridad.
Los bitcoins existen en lotes llamados salidas de transacciones no gastadas (o UTXO's). Supongamos que recibe tres pagos en una dirección Bitcoin concreta por 2 bitcoins cada uno. Técnicamente, ahora no tiene 6 bitcoins en esa dirección. En su lugar, tienes tres lotes de 2 bitcoins que están bloqueados por un problema criptográfico asociado a esa dirección. Para cualquier pago que hagas, puedes usar uno, dos o los tres lotes, dependiendo de cuánto necesites para la transacción.
La prueba de propiedad sobre los resultados de transacciones no gastadas se muestra normalmente a través de una o más firmas digitales. Bitcoin funciona precisamente porque las firmas digitales válidas sobre los resultados de transacciones no gastadas son computacionalmente inviables de hacer, a menos que se esté en posesión de la información secreta necesaria para hacerlas.
Actualmente, las transacciones de Bitcoin incluyen de forma transparente toda la información que debe ser verificada por los participantes en la red, como el origen de los productos de transacción no gastados utilizados en la transacción. Aunque es posible ocultar parte de esa información y seguir permitiendo la verificación (como hacen algunas criptodivisas alternativas como Monero), esto también genera riesgos de seguridad particulares.
A veces se produce confusión entre las firmas digitales y las firmas escritas capturadas digitalmente. En este último caso, usted captura una imagen de su firma escrita y la pega en un documento electrónico como un contrato de trabajo. Sin embargo, esto no es una firma digital en el sentido criptográfico. Esta última es sólo un número largo que sólo puede producirse estando en posesión de una clave privada.
Al igual que en la configuración de clave simétrica, también puedes utilizar conjuntamente esquemas de cifrado y autenticación asimétricos. Se aplican principios similares. En primer lugar, debes utilizar diferentes pares de claves públicas y privadas para el cifrado y la firma digital. Además, primero debes cifrar un mensaje y luego autenticarlo.
Es importante destacar que, en muchas aplicaciones, la criptografía asimétrica no se utiliza durante todo el proceso de comunicación. En su lugar, normalmente sólo se utilizará para intercambiar claves simétricas entre las partes por las que realmente se comunicarán.
Es el caso, por ejemplo, de las compras en línea. Conociendo la clave pública del vendedor, éste puede enviarle mensajes firmados digitalmente cuya autenticidad usted puede verificar. Sobre esta base, puede seguir uno de los múltiples protocolos de intercambio de claves simétricas para comunicarse de forma segura.
La razón principal de la frecuencia del enfoque mencionado es que la criptografía asimétrica es mucho menos eficaz que la simétrica a la hora de producir un determinado nivel de seguridad. Esta es una de las razones por las que seguimos necesitando la criptografía de clave simétrica junto a la criptografía pública. Además, la criptografía de clave simétrica es mucho más natural en aplicaciones concretas como, por ejemplo, que un usuario de ordenador cifre sus propios datos.
Entonces, ¿cómo resuelven exactamente la firma digital y el cifrado de clave pública los problemas de distribución y gestión de claves?
No hay una única respuesta. La criptografía asimétrica es una herramienta y no hay una única forma de emplearla. Pero tomemos nuestro ejemplo anterior de Jim's Sporting Goods para mostrar cómo se abordarían normalmente los problemas en este ejemplo.
Para empezar, Jim's Sporting Goods probablemente se dirigiría a una autoridad de certificación, una organización que se dedica a la distribución de claves públicas. La autoridad de certificación registraría algunos datos sobre Jim's Sporting Goods y le otorgaría una clave pública. A continuación, enviaría a Jim's Sporting Goods un certificado, conocido como certificado TLS/SSL, con la clave pública de Jim's Sporting Goods firmada digitalmente utilizando la propia clave pública de la autoridad de certificación. De este modo, la autoridad de certificación confirma que una determinada clave pública pertenece efectivamente a Jim's Sporting Goods.
La clave para entender este proceso con los certificados TLS/SSL es que, aunque generalmente no tendrá la clave pública de Jim's Sporting Goods almacenada en ningún lugar de su ordenador, las claves públicas de las autoridades de certificación reconocidas sí están almacenadas en su navegador o en su sistema operativo. Se almacenan en lo que se denominan certificados raíz.
Por lo tanto, cuando Jim's Sporting Goods le proporcione su certificado TLS/SSL, puede verificar la firma digital de la autoridad de certificación mediante un certificado raíz en su navegador o sistema operativo. Si la firma es válida, puede estar relativamente seguro de que la clave pública del certificado pertenece realmente a Jim's Sporting Goods. Sobre esta base, es fácil establecer un protocolo de comunicación segura con Jim's Sporting Goods.
La distribución de llaves se ha simplificado enormemente para Jim's Sporting Goods. No es difícil ver que la gestión de claves también se ha simplificado enormemente. En lugar de tener que almacenar miles de claves, Jim's Sporting Goods sólo necesita almacenar una clave privada que le permita firmar la clave pública de su certificado SSL. Cada vez que un cliente entra en el sitio de Jim's Sporting Goods, puede establecer una sesión de comunicación segura a partir de esta clave pública. Los clientes tampoco necesitan almacenar ninguna información (aparte de las claves públicas de las autoridades de certificación reconocidas en su sistema operativo y navegador).
Notas:
[5] Cualquier esquema que intente conseguir el no repudio, el otro tema que tratamos en el capítulo 1, necesitará en su base implicar firmas digitales.
Funciones hash
Las funciones hash son omnipresentes en criptografía. No son esquemas simétricos ni asimétricos, sino que constituyen una categoría criptográfica por derecho propio.
Ya vimos las funciones hash en el capítulo 4 con la creación de mensajes de autenticación basados en hash. También son importantes en el contexto de las firmas digitales, aunque por una razón ligeramente distinta: Las firmas digitales se realizan normalmente sobre el valor hash de algún mensaje (cifrado), en lugar del mensaje (cifrado) real. En esta sección, ofreceré una introducción más completa de las funciones hash.
Empecemos definiendo una función hash. Una función hash es cualquier función eficientemente computable que toma entradas de tamaño arbitrario y produce salidas de longitud fija.
Una función hash criptográfica es simplemente una función hash que es útil para aplicaciones en criptografía. El resultado de una función hash criptográfica se denomina normalmente hash, hash-value o resumen del mensaje.
En el contexto de la criptografía, una "función hash" suele referirse a una función hash criptográfica. Adoptaré esa práctica de aquí en adelante.
Un ejemplo de función hash popular es SHA-256 (algoritmo hash seguro 256). Independientemente del tamaño de la entrada (por ejemplo, 15 bits, 100 bits o 10.000 bits), esta función producirá un valor hash de 256 bits. A continuación puedes ver algunos ejemplos de resultados de la función SHA-256.
"Hola": 185f8db32271fe25f561a6fc938b2e264306ec304eda518007d1764826381969
"52398": a3b14d2bf378c1bd47e7f8eaec63b445150a3d7a80465af16dd9fd319454ba90
"La criptografía es divertida": 3cee2a5c7d2cc1d62db4893564c34ae553cc88623992d994e114e344359b146c
Todas las salidas son exactamente 256 bits escritos en formato hexadecimal (cada dígito hexadecimal puede representarse con cuatro dígitos binarios). Por tanto, aunque hubieras insertado el libro de Tolkien El Señor de los Anillos en la función SHA-256, la salida seguiría siendo de 256 bits.
Las funciones hash como SHA-256 se emplean con diversos fines en criptografía. Las propiedades que se exigen a una función hash dependen realmente del contexto de una aplicación concreta. Hay dos propiedades principales generalmente deseadas de las funciones hash en criptografía: [6]
Resistencia a las colisiones
Ocultar
Se dice que una función hash H es resistente a colisiones si no es factible encontrar dos
valores, x e y, tales que x \neq y, y sin embargo H(x) = H(y).
Las funciones hash resistentes a colisiones son importantes, por ejemplo, en la verificación de software. Supongamos que quiere descargar la versión para Windows de Bitcoin Core 0.21.0 (una aplicación de servidor para procesar el tráfico de red de Bitcoin). Los principales pasos que tendría que dar, para verificar la legitimidad del software, son los siguientes:
Primero debe descargar e importar las claves públicas de uno o más colaboradores Bitcoin Core en un software que pueda verificar firmas digitales (por ejemplo, Kleopetra). Puede encontrar estas claves públicas aquí. Se recomienda verificar el software Bitcoin Core con las claves públicas de múltiples contribuidores.
A continuación, tienes que verificar las claves públicas que has importado. Al menos un paso que deberías dar es verificar que las claves públicas que has encontrado son las mismas que se han publicado en otros lugares. Por ejemplo, puedes consultar las páginas web personales, las páginas de Twitter o las páginas de Github de las personas cuyas claves públicas importaste. Normalmente, esta comparación de claves públicas se realiza comparando un hash corto de la clave pública conocido como huella digital.
A continuación, debe descargar el ejecutable para Bitcoin Core desde su sitio web. Habrá paquetes disponibles para los sistemas operativos Linux, Windows y MAC.
A continuación, tienes que localizar dos archivos de liberación. El primero contiene el hash SHA-256 oficial del ejecutable que ha descargado junto con los hashes de todos los demás paquetes que se han publicado. Otro archivo de publicación contendrá las firmas de varios colaboradores sobre el archivo de publicación con los hashes de los paquetes. Ambos archivos deberían estar localizados en el sitio web de Bitcoin Core.
A continuación, tendrá que calcular el hash SHA-256 del ejecutable que descargó del sitio web de Bitcoin Core en su propio ordenador. A continuación, compare este resultado con el hash del paquete oficial del ejecutable. Deberían ser iguales.
Finalmente, tendrías que verificar que una o más de las firmas digitales sobre el archivo de lanzamiento con los hashes oficiales del paquete corresponden efectivamente a una o más claves públicas que importaste (los lanzamientos de Bitcoin Core no siempre están firmados por todos). Puedes hacer esto con una aplicación como Kleopetra.
Este proceso de verificación del software tiene dos beneficios principales. En primer lugar, garantiza que no se han producido errores en la transmisión durante la descarga desde el sitio web de Bitcoin Core. En segundo lugar, garantiza que ningún atacante haya podido hacer que descargara código malicioso modificado, ya sea pirateando el sitio web de Bitcoin Core o interceptando el tráfico.
¿Cómo protege exactamente de estos problemas el proceso de verificación de software descrito anteriormente?
Si verificaste diligentemente las claves públicas que importaste, entonces puedes estar bastante seguro de que estas claves son realmente suyas y no han sido comprometidas. Dado que las firmas digitales tienen infalsificabilidad existencial, usted sabe que sólo estos contribuyentes podrían haber hecho una firma digital sobre los hashes del paquete oficial en el archivo de lanzamiento.
Supongamos que las firmas del archivo de lanzamiento que ha descargado son correctas. Ahora puede comparar el valor hash que calculó localmente para el ejecutable de Windows que descargó con el incluido en el archivo de lanzamiento correctamente firmado. Como sabes, la función hash SHA-256 es resistente a la colisión, una coincidencia significa que tu ejecutable es exactamente igual al ejecutable oficial.
Pasemos ahora a la segunda propiedad común de las funciones hash: ocultamiento. Se dice que cualquier función hash H tiene la propiedad de ocultación si, para cualquier x seleccionada aleatoriamente de un rango muy grande, es inviable encontrar x cuando sólo se da H(x).
A continuación, puedes ver la salida SHA-256 de un mensaje que escribí. Para garantizar una aleatoriedad suficiente, el mensaje incluía al final una cadena de caracteres generada aleatoriamente. Dado que SHA-256 tiene la propiedad de ocultación, nadie sería capaz de descifrar este mensaje.
b194221b37fa4cd1cfce15aaef90351d70de17a98ee6225088b523b586c32ded
Pero no te dejaré en suspenso hasta que SHA-256 se debilite. El mensaje original que escribí era el siguiente:
- "Este es un mensaje muy aleatorio, o bueno, algo aleatorio. Esta parte inicial no lo es, pero terminaré con algunos caracteres relativamente aleatorios para asegurar un mensaje muy impredecible. XLWz4dVG3BxUWm7zQ9qS".
Una forma habitual de utilizar funciones hash con la propiedad de ocultación es en la gestión de contraseñas (la resistencia a las colisiones también es importante para esta aplicación). Cualquier servicio online decente basado en cuentas, como Facebook o Google, no almacenará tus contraseñas directamente para gestionar el acceso a tu cuenta. En su lugar, sólo almacenarán un hash de esa contraseña. Cada vez que introduces tu contraseña en un navegador, primero se calcula un hash. Sólo ese hash se envía al servidor del proveedor de servicios y se compara con el hash almacenado en la base de datos back-end. La propiedad de ocultación puede ayudar a garantizar que los atacantes no puedan recuperarla a partir del valor hash.
La gestión de contraseñas mediante hashes, por supuesto, sólo funciona si los usuarios eligen realmente contraseñas difíciles. La propiedad de ocultar supone que x se elige aleatoriamente entre un rango muy amplio. Elegir contraseñas como "1234", "mypassword" o la fecha de tu cumpleaños no proporcionará ninguna seguridad real. Existen largas listas de contraseñas comunes y sus hashes que los atacantes pueden aprovechar si alguna vez obtienen el hash de tu contraseña. Este tipo de ataques se conocen como ataques de diccionario. Si los atacantes conocen algunos de tus datos personales, también pueden intentar adivinarlos con conocimiento de causa. Por lo tanto, siempre necesitas contraseñas largas y seguras (preferiblemente cadenas largas y aleatorias de un gestor de contraseñas).
A veces una aplicación puede necesitar una función hash que tenga tanto resistencia a las colisiones como ocultación. Pero no siempre. El proceso de verificación de software del que hablamos, por ejemplo, sólo requiere que la función hash muestre resistencia a las colisiones, la ocultación no es importante.
Aunque la resistencia a las colisiones y la ocultación son las principales propiedades que se buscan de las funciones hash en criptografía, en determinadas aplicaciones también pueden ser deseables otro tipo de propiedades.
Notas:
[6] La terminología "ocultación" no es lenguaje común, sino tomada específicamente de Arvind Narayanan, Joseph Bonneau, Edward Felten, Andrew Miller y Steven Goldfeder, Bitcoin and Cryptocurrency Technologies, Princeton University Press (Princeton, 2016), capítulo 1.
El criptosistema RSA
El problema de la factorización
Mientras que la criptografía simétrica suele ser bastante intuitiva para la mayoría de la gente, no ocurre lo mismo con la criptografía asimétrica. Aunque probablemente te sientas cómodo con la descripción de alto nivel ofrecida en las secciones anteriores, probablemente te preguntes qué son exactamente las funciones unidireccionales y cómo se utilizan exactamente para construir esquemas asimétricos.
En este capítulo, eliminaré parte del misterio que rodea a la criptografía asimétrica, profundizando en un ejemplo concreto, a saber, el criptosistema RSA. En la primera sección, presentaré el problema de factorización en el que se basa el problema RSA. A continuación, abordaré una serie de resultados clave de la teoría de números. En la última sección, uniremos esta información para explicar el problema RSA y cómo puede utilizarse para crear esquemas criptográficos asimétricos.
Añadir esta profundidad a nuestra discusión no es tarea fácil. Requiere introducir bastantes teoremas y proposiciones de teoría numérica. Pero no dejes que las matemáticas te disuadan. Trabajar en esta discusión mejorará significativamente tu comprensión de lo que subyace en la criptografía asimétrica y es una inversión que merece la pena.
Pasemos ahora al problema de la factorización.
Siempre que se multiplican dos números, digamos a y b, nos referimos a los
números a y b como factores, y al resultado como el producto. Intentar escribir un número N en la multiplicación de dos o más factores se llama factorización o factorización. [1] Se puede llamar problema de factorización a cualquier problema que lo requiera.
Hace unos 2.500 años, el matemático griego Euclides de Alejandría descubrió un teorema clave sobre la factorización de los números enteros. Se conoce comúnmente como el teorema de la factorización única y afirma lo siguiente:
Teorema 1. Todo número entero N mayor que 1 es o bien un número
primo, o bien puede expresarse como producto de factores primos.
Todo lo que la última parte de esta afirmación significa es que se puede
tomar cualquier entero no primo N mayor que 1, y escribirlo como una multiplicación de números primos. A continuación
se muestran varios ejemplos de números enteros no primos escritos como el producto
de factores primos.
18 = 2 \cdot 3 \cdot 3 = 2 \cdot 3^284 = 2 \cdot 2 \cdot 3 \cdot 7 = 2^2 \cdot 3 \cdot 7144 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 = 2^4 \cdot 3^2
Para los tres números enteros anteriores, calcular sus factores primos es
relativamente fácil, incluso si sólo se dan N. Se empieza con el número primo más pequeño, el 2, y se comprueba cuántas
veces el entero N es
divisible por él. A continuación, se comprueba la divisibilidad de N por 3, 5, 7, etc. Se continúa este proceso hasta que el número entero N es divisible por N. Se
continúa este proceso hasta que el entero N se escribe como el producto
de sólo números primos.
Tomemos, por ejemplo, el número entero 84. A continuación puedes ver el proceso para determinar sus factores primos. En cada paso, sacamos el factor primo más pequeño que queda (a la izquierda) y determinamos el término restante que hay que factorizar. Continuamos hasta que el término restante es también un número primo. En cada paso, la factorización actual de 84 se muestra en el extremo derecho.
- Factor primo = 2: término resto = 42 (
84 = 2 \cdot 42) - Factor primo = 2: término resto = 21 (
84 = 2 \cdot 2 \cdot 21) - Factor primo = 3: término resto = 7 (
84 = 2 \cdot 2 \cdot 3 \cdot 7) - Como 7 es un número primo, el resultado es
2 \cdot 2 \cdot 3 \cdot 7, o2^2 \cdot 3 \cdot 7.
Supongamos ahora que N es muy
grande. Sería muy difícil reducir N a sus factores primos?
Eso depende realmente de N.
Supongamos, por ejemplo, que N es 50.450.400. Aunque este número
parece intimidante, los cálculos no son tan complicados y se pueden hacer fácilmente
a mano. Como en el caso anterior, basta con empezar por 2 e ir avanzando. A continuación,
puedes ver el resultado de este proceso de forma similar al anterior.
- 2: 25.225.200 (
50.450.400 = 2 \cdot 25.225.200) - 2: 12.612.600 (
50.450.400 = 2^2 \cdot 12.612.600) - 2: 6.306.300 (
50.450.400 = 2^3 \cdot 6.306.300) - 2: 3.153.150 (
50.450.400 = 2^4 \cdot 3.153.150) - 2: 1.576.575 (
50.450.400 = 2^5 \cdot 1.576.575) - 3: 525,525 (
50,450,400 = 2^5 \cdot 3 \cdot 525,525) - 3: 175,175 (
50,450,400 = 2^5 \cdot 3^2 \cdot 175,175) - 5: 35,035 (
50,450,400 = 2^5 \cdot 3^2 \cdot 5 \cdot 35,035) - 5: 7,007 (
50,450,400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7,007) - 7: 1,001 (
50,450,400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7 \cdot 1,001) - 7: 143 (
50.450.400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 143) - 11: 13 (
50,450,400 = 2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13) - Como 13 es un número primo, el resultado es
2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13.
Resolver este problema a mano lleva su tiempo. Un ordenador, por supuesto, podría hacer todo esto en una pequeña fracción de segundo. De hecho, un ordenador puede incluso factorizar números enteros extremadamente grandes en una fracción de segundo.
Sin embargo, hay ciertas excepciones. Supongamos que primero elegimos al
azar dos números primos muy grandes. Es típico etiquetarlos como p y q, y adoptaré esa
convención aquí.
Para concretar, digamos que p y q son ambos primos de 1024
bits, y que efectivamente requieren al menos 1024 bits para ser
representados (por lo que el primer bit debe ser 1). Así, por ejemplo, 37 no
podría ser uno de los números primos. Sin duda se puede representar 37 con
1024 bits. Pero está claro que no se necesitan tantos bits para
representarlo. Puedes representar 37 con cualquier cadena que tenga 6 bits o
más. (En 6 bits, 37 se representaría como 100101).
Es importante apreciar lo grandes que son p y q si se seleccionan en las condiciones
anteriores. Como ejemplo, a continuación he seleccionado un número primo aleatorio
que necesita al menos 1024 bits para su representación.
- 14,752,173,874,503,595,484,930,006,383,670,759,559,764,562,721,397,166,747,289,220,945,457,932,666,751,048,198,854,920,097,085,690,793,755,254,946,188,163,753,506,778,089,706,699,671,722,089,715,624,760,049,594,106,189,662,669,156,149,028,900,805,928,183,585,427,782,974,951,355,515,394,807,209,836,870,484,558,332,897,443,152,653,214,483,870,992,618,171,825,921,582,253,023,974,514,209,142,520,026,807,636,589
Supongamos ahora que tras seleccionar aleatoriamente los números primos p y q, los multiplicamos para
obtener un número entero N.
Este último entero, por tanto, es un número de 2048 bits que requiere al
menos 2048 bits para su representación. Es muchísimo mayor que p o q.
Supongamos que sólo le damos a un ordenador N, y le pedimos que encuentre los dos factores primos de 1024 bits de N. La probabilidad de que el
ordenador descubra p y q es extremadamente pequeña. Se
puede decir que es imposible a efectos prácticos. Esto es así, incluso si se
empleara un superordenador o incluso una red de superordenadores.
Para empezar, supongamos que el ordenador intenta resolver el problema
recorriendo 1024 números de bits, probando en cada caso si son primos y si
son factores de N. El
conjunto de números primos a probar es entonces aproximadamente 1.265 \cdot 10^{305}. [2]
Incluso si se toman todos los ordenadores del planeta y se les hace intentar
encontrar y probar números primos de 1024 bits de esta manera, una
probabilidad de 1 entre mil millones de encontrar con éxito un factor primo
de N requeriría un período de
cálculo mucho más largo que la edad del Universo.
Ahora bien, en la práctica, un ordenador puede hacerlo mejor que el procedimiento aproximado que acabamos de describir. Existen varios algoritmos que el ordenador puede aplicar para llegar a una factorización más rápidamente. La cuestión, sin embargo, es que incluso utilizando estos algoritmos más eficientes, la tarea del ordenador sigue siendo computacionalmente inviable. [3]
Es importante destacar que la dificultad de la factorización en las condiciones que acabamos de describir se basa en la suposición de que no existen algoritmos computacionalmente eficientes para calcular los factores primos. En realidad, no podemos demostrar que no exista un algoritmo eficiente. Sin embargo, esta suposición es muy plausible: a pesar de los grandes esfuerzos realizados durante cientos de años, todavía no hemos encontrado un algoritmo computacionalmente eficiente.
Por lo tanto, el problema de factorización, bajo ciertas circunstancias,
puede suponerse plausiblemente que es un problema difícil. En concreto,
cuando p y q son números primos muy grandes, su producto N no es difícil de calcular; pero la factorización sólo dado N es prácticamente imposible.
Notas:
[1] La factorización también puede ser importante para trabajar con otros
tipos de objetos matemáticos distintos de los números. Por ejemplo, puede
ser útil para factorizar expresiones polinómicas como x^2 - 2x + 1. En nuestra discusión, sólo nos centraremos en la factorización de
números, específicamente enteros.
[2] Según el teorema del número primo, el número de primos
menores o iguales que N es
aproximadamente N/\ln(N).
Esto significa que se puede aproximar el número de primos de longitud 1024
bits por:
\frac{2^{1024}}{\ln(2^{1024})} -
\frac{2^{1023}}{\ln(2^{1023})}
...que equivale aproximadamente a 1,265 \N veces 10^{305}$.
[3] Lo mismo ocurre con los problemas de logaritmos discretos. De ahí que las construcciones asimétricas funcionen con claves mucho mayores que las construcciones criptográficas simétricas.
Resultados de la teoría de números
Por desgracia, el problema de la factorización no puede utilizarse directamente para esquemas criptográficos asimétricos. Sin embargo, podemos utilizar para ello un problema más complejo pero relacionado: el problema RSA.
Para entender el problema RSA, necesitaremos comprender una serie de teoremas y proposiciones de la teoría de números. Estos se presentan en esta sección en tres subsecciones: (1) el orden de N, (2) la invertibilidad módulo N y (3) el teorema de Euler.
Parte del material de las tres subsecciones ya se ha presentado en el Capítulo 3. Pero, por comodidad, volveré a exponerlo aquí.
El orden de N
Un número entero a es coprimo o primo relativo de un número entero N, si el máximo común divisor
entre ellos es 1. Aunque por convención 1 no es un número primo, es coprimo
de todo número entero (al igual que -1).
Por ejemplo, consideremos el caso en que a = 18 y N = 37. Se trata claramente
de coprimos. El mayor número entero que divide a 18 y 37 es 1. Por el
contrario, consideremos el caso en que a = 42 y N = 16. Está claro que no
son coprimos. Ambos números son divisibles por 2, que es mayor que 1.
Ahora podemos definir el orden de N como sigue. Supongamos que N es un entero mayor que 1. El orden de N es, entonces, el
número de todos los coprimos con N tales que para cada coprimo a se cumple la siguiente condición: 1 \leq a < N.
Por ejemplo, si N = 12,
entonces 1, 5, 7 y 11 son los únicos coprimos que cumplen el requisito
anterior. Por lo tanto, el orden de 12 es igual a 4.
Supongamos que N es un número
primo. Entonces cualquier número entero menor que N pero mayor o igual que 1 es coprimo con él. Esto incluye todos los elementos
del siguiente conjunto: \{1,2,3,....,N - 1\}. Por tanto, cuando N es
primo, el orden de N es N - 1. Esto se afirma en la
proposición 1, donde \phi(N) denota el orden de N.
Proposición 1. \phi(N) = N - 1 cuando N es primo
Supongamos que N no es primo.
En ese caso, se puede calcular su orden mediante la función Phi de Euler. Aunque calcular el orden de un número
entero pequeño es relativamente sencillo, la función Phi de Euler adquiere
especial importancia para los números enteros más grandes. A continuación se
expone la proposición de la función Phi de Euler.
Teorema 2. Sea N igual a p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot
p_i^{e_i} \cdot \ldots \cdot p_n^{e_n}, donde el conjunto \{p_i\} está formado por todos los factores primos distintos de N y cada e_i indica cuántas
veces se da el factor primo p_i para N. Entonces,
\phi(N) = p_1^{e_1 - 1} \cdot (p_1 - 1) \cdot p_2^{e_2 -
1} \cdot (p_2 - 1) \cdot \ldots \cdot p_n^{e_n - 1} \cdot
(p_n - 1)
El teorema 2 muestra que una vez descompuesto cualquier N no primo en sus distintos factores primos, es fácil calcular el orden de N.
Por ejemplo, supongamos que N = 270. Está claro que no es un número primo. Desglosando N en sus factores primos se obtiene la expresión: 2 \cdot 3^3 \cdot 5. Según la
función Phi de Euler, el orden de N es entonces el siguiente:
\phi(N) = 2^{1 - 1} \cdot (2 - 1) + 3^{3 - 1} \cdot
(3 - 1) + 5^{1 - 1} \cdot (5 - 1) = 1 \cdot 1 + 9 \cdot 2 + 1
\cdot 4 = 1 + 18 + 4 = 23
Supongamos a continuación que N es un producto de dos primos, p y q. entonces, el teorema 2 anterior establece que el orden de N es el siguiente:
p^{1 - 1} \cdot (p - 1) \cdot q^{1 - 1} \cdot (q - 1)
= (p - 1) \cdot (q - 1)
Este es un resultado clave para el problema RSA en particular, y se establece en la Proposición 2 a continuación.
Proposición 2. Si N es el producto de dos primos, p y q, el orden de N es el producto (p - 1) \cdot (q - 1).
Para ilustrarlo, supongamos que N = 119. Este número entero se puede descomponer en dos primos, a saber, 7 y 17.
Por lo tanto, la función Phi de Euler sugiere que el orden de 119 es el
siguiente:
\phi(119) = (7 - 1) \cdot (17 - 1) = 6 \cdot 16 = 96
En otras palabras, el número entero 119 tiene 96 coprimos en el intervalo de 1 a 119. De hecho, este conjunto incluye todos los números enteros de 1 a 119 que no son múltiplos ni de 7 ni de 17. De hecho, este conjunto incluye todos los números enteros de 1 a 119 que no son múltiplos de 7 ni de 17.
De aquí en adelante, vamos a denotar el conjunto de coprimas que determina
el orden de N como C_N. Para nuestro ejemplo en
el que N = 119, el conjunto C_{119} es demasiado
grande para enumerarlo completamente. Pero algunos de los elementos son los siguientes:
C_{119} = \{1, 2, \dots, 6, 8, \dots, 13, 15, 16, 18,
\dots, 33, 35, \dots, 96\}
Invertibilidad módulo N
Podemos decir que un entero a es invertible módulo N, si existe al menos un entero b tal que a \cdot b \mod N = 1 \mod N.
Cualquier número entero b se
denomina inverso (o inverso multiplicativo) de a dada la reducción en módulo N.
Supongamos, por ejemplo, que a = 5 y N = 11. Hay muchos enteros
por los que se puede multiplicar 5, de modo que a = 5 y N = 11. Consideremos, por
ejemplo, los enteros 20 y 31$. Es fácil ver que estos dos enteros son
inversos de 5 por reducción módulo 11.
5 \cdot 20 \mod 11 = 100 \mod 11 = 1 \mod 115 \cdot 31 \mod 11 = 155 \mod 11 = 1 \mod 11
Mientras que 5 tiene muchos inversos de reducción módulo 11, se puede demostrar que sólo existe un único inverso positivo de 5 que es menor que 11. De hecho, esto no es exclusivo de nuestro ejemplo particular, sino un resultado general.
Proposición 3. Si el entero a es invertible módulo N, debe
darse el caso de que exactamente un inverso positivo de a sea menor que N. (Así, este
único inverso de a debe
proceder del conjunto \{1, \dots, N - 1\}).
Vamos a denotar el inverso único de a de la Proposición 3 como a^{-1}. Para el
caso en que a = 5 y N = 11, se puede ver que a^{-1} = 9, dado
que 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11.
Observe que también puede obtener el valor 9 para a^{-1} en nuestro ejemplo simplemente reduciendo cualquier otro inverso de a por el módulo 11. Por ejemplo, 20 \mod 11 = 31 \mod 11 = 9 \mod 11. Así que siempre que un número entero a > N es invertible módulo N,
entonces a \mod N también
debe ser invertible módulo N.
No es necesariamente el caso de que exista una reducción inversa de a módulo N. Supongamos, por
ejemplo, que a = 2 y N = 8. No hay b, o cualquier a^{-1} específicamente, tal que 2 \cdot b \mod 8 = 1 \mod 8.
Esto se debe a que cualquier valor de b siempre producirá un múltiplo
de 2, por lo que ninguna división por 8 puede producir nunca un resto igual a
1.
¿Cómo sabemos exactamente si un número entero a tiene inverso para un N dado?
Como habrás observado en el ejemplo anterior, el máximo común divisor entre 2
y 8 es mayor que 1, es decir, 2. Y esto es en realidad ilustrativo del siguiente
resultado general:
Proposición 4. Existe un inverso de un entero a dada la reducción módulo N, y
en concreto un único inverso positivo menor que N, si y sólo si el máximo
común divisor entre a y N es 1 (es decir, si son coprimos).
Para el caso en que a = 5 y N = 11, concluimos que a^{-1} = 9, dado
que 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11. Es importante señalar que lo contrario también es cierto. Es decir,
cuando a = 9 y N = 11, se da el caso de que a^{-1} = 5.
Teorema de Euler
Antes de pasar al problema RSA, necesitamos entender otro teorema crucial, el teorema de Euler. Establece lo siguiente:
Teorema 3. Supongamos que dos enteros a y N son coprimas. Entonces, a^{\phi(N)} \mod N = 1 \mod N.
Es un resultado notable, pero un poco confuso al principio. Recurramos a un ejemplo para entenderlo.
Supongamos que a = 5 y N = 7. Efectivamente, son
coprimas, como exige el teorema de Euler. Sabemos que el orden de 7 es igual
a 6, dado que 7 es un número primo (ver Proposición 1).
Lo que el teorema de Euler afirma ahora es que 5^6 \mod 7 debe ser igual a 1 \mod 7. A
continuación se presentan los cálculos para demostrar que esto es cierto.
5^6 \mod 7 = 15,625 \mod 7 = 1 \mod N
El entero 7 se divide entre 15.624 un total de 2.233 veces. Por lo tanto, el resto de dividir 16.625 entre 7 es 1.
A continuación, utilizando la función Phi de Euler, Teorema 2, se puede derivar la Proposición 5 siguiente.
Proposición 5. \phi(a \cdot b) = \phi(a) \cdot \phi(b) para cualesquiera enteros positivos a y b.
No vamos a demostrar por qué es así. Pero simplemente tenga en cuenta que ya
ha visto la evidencia de esta proposición por el hecho de que \phi(p \cdot q) = \phi(p) \cdot \phi(q) = (p - 1) \cdot (q - 1) cuando p y q son primos, como se indica en Proposición 2.
El teorema de Euler junto con la Proposición 5 tiene
implicaciones importantes. Véase lo que ocurre, por ejemplo, en las
expresiones siguientes, donde a y N son coprimas.
a^{2 \cdot \phi(N)} \mod N = a^{\phi(N)} \cdot a^{\phi(N)} \mod N = 1 \cdot 1 \mod N = 1 \mod Na^{\phi(N) + 1} \mod N = a^{\phi(N)} \cdot a^1 \mod N = 1 \cdot a^1 \mod N = a \mod Na^{8 \cdot \phi(N) + 3} \mod N = a^{8 \cdot \phi(N)} \cdot a^3 \mod N = 1 \cdot a^3 \mod N = a^3 \mod N
Por tanto, la combinación del teorema de Euler y la Proposición 5 nos permite calcular de forma sencilla una serie de expresiones. En general, podemos resumir la idea como en la Proposición 6.
Proposición 6. a^x \mod N = a^{x \mod \phi(N)}
Ahora tenemos que unirlo todo en un último paso complicado.
Igual que N tiene un orden \phi(N) que incluye los elementos del conjunto C_N, sabemos que el entero \phi(N) debe tener a su vez también un orden y un conjunto de coprimas. Pongamos que \phi(N) = R. Entonces sabemos
que también hay un valor para \phi(R) y un conjunto de coprimas C_R.
Supongamos que ahora seleccionamos un entero e del conjunto C_R. Sabemos por
la Proposición 3 que este entero e sólo tiene un único inverso positivo menor que R. Es decir, e tiene un único inverso del conjunto C_R. Llamemos a este inverso d. Dada la definición de
inverso, esto significa que e \cdot d = 1 \mod R.
Podemos usar este resultado para hacer una afirmación sobre nuestro entero
original N. Esto se resume en
la Proposición 7.
Proposición 7. Supongamos que e \cdot d \mod \phi(N) = 1 \mod \phi(N). Entonces para cualquier elemento a del conjunto C_N debe darse
el caso de que a^{e \cdot d \mod \phi(N)} = a^{1 \mod \phi(N)} = a
\mod N.
Ahora tenemos todos los resultados de teoría de números necesarios para plantear claramente el problema RSA.
El criptosistema RSA
Ahora estamos listos para plantear el problema RSA. Supongamos que creamos
un conjunto de variables formado por p, q, N, \phi(N), e, d e y. Llamemos a este conjunto \Pi. Se crea de la siguiente
manera:
Genera dos primos aleatorios
pyqde igual tamaño y calcula su productoN.Calcular el orden de
N,\phi(N), mediante el siguiente producto:(p - 1) \cdot (q - 1).Seleccionar una
e > 2tal que sea menor y coprima a\phi(N).Calcular
destableciendoe \cdot d \mod \phi(N) = 1.Selecciona un valor aleatorio
yque sea menor y coprimo aN.
El problema RSA consiste en encontrar una x tal que x^e = y, con sólo un
subconjunto de información sobre \Pi, a saber, las variables N, e e y. Cuando p y q son muy grandes, normalmente
se recomienda que tengan un tamaño de 1024 bits, se considera que el problema
RSA es difícil. Ahora puede ver por qué es así, dada la discusión anterior.
Una forma fácil de calcular x cuando x^e \mod N = y \mod N es simplemente calculando y^d \mod N. Sabemos y^d \mod N = x \mod N por los
siguientes cálculos:
y^d \mod N = x^{e \cdot d} \mod N = x^{e \cdot d \mod
\phi(N)} \mod N = x^{1 \mod \phi(N)} \mod N = x \mod N.
El problema es que no conocemos el valor d, ya que no se da en el problema. Por lo tanto, no podemos calcular
directamente y^d \mod N para
producir x \mod N.
Sin embargo, podríamos calcular d indirectamente a partir del orden de N, \phi(N), ya que sabemos que e \cdot d \mod \phi(N) = 1 \mod \phi(N). Pero por suposición el problema tampoco da un valor para \phi(N).
Por último, el orden podría calcularse indirectamente con los factores
primos p y q, de modo que al final
podamos calcular d. Pero, por
suposición, los valores p y q tampoco se nos han proporcionado.
En sentido estricto, aunque el problema de factorización dentro de un problema RSA sea difícil, no podemos demostrar que el problema RSA también lo sea. Es posible que haya otras formas de resolver el problema RSA que no sean la factorización. Sin embargo, en general se acepta y se asume que si el problema de factorización dentro del problema RSA es difícil, el problema RSA en sí también lo es.
Si el problema RSA es realmente difícil, entonces produce una función
unidireccional con una puerta trampa. La función aquí es f(g) = g^e \mod N. Conociendo f(g),
cualquiera podría calcular fácilmente un valor y para un g = x concreto. Sin
embargo, es prácticamente imposible calcular un valor concreto x sólo conociendo el valor y y
la función f(g). La excepción
es cuando te dan un dato d,
la trampilla. En ese caso, basta con calcular y^d para obtener x.
Veamos un ejemplo concreto para ilustrar el problema RSA. No puedo seleccionar un problema RSA que se consideraría difícil en las condiciones anteriores, ya que los números serían difíciles de manejar. En su lugar, este ejemplo es sólo para ilustrar cómo funciona en general el problema RSA.
Para empezar, supongamos que seleccionamos dos números primos aleatorios 13
y 31. Entoncesp = 13yq = 31. El productoNde estos dos primos es igual a 403. Podemos calcular fácilmente el orden
de 403. Equivale a(13 - 1) \cdot (31 - 1) = 360$.
A continuación, como dicta el paso 3 del problema RSA, tenemos que seleccionar un coprimo para 360 que sea mayor que 2 y menor que 360. No tenemos que seleccionar este valor al azar. No tenemos que seleccionar este valor al azar. Supongamos que seleccionamos 103. Este es un coprimo de 360 ya que su máximo común divisor con 103 es 1.
El paso 4 requiere ahora que calculemos un valor d tal que 103 \cdot d \mod 360 = 1.
Esto no es una tarea fácil a mano cuando el valor de N es grande. Requiere que utilicemos un procedimiento llamado algoritmo euclídeo ampliado.
Aunque no muestro aquí el procedimiento, se obtiene el valor 7 cuando e = 103. Se puede comprobar que el par de valores 103 y 7 cumple efectivamente la
condición general e \cdot d \mod \phi(n) = 1 mediante
los cálculos siguientes.
103 \cdot 7 \mod 360 = 721 \mod 360 = 1 \mod 360
Es importante destacar que, dada la Proposición 4, sabemos que
ningún otro número entero entre 1 y 360 para d producirá el resultado de que 103 \cdot d = 1 \cdot 360.
Además, la proposición implica que la selección de un valor diferente para e, producirá un valor único
diferente para d.
En el paso 5 del problema RSA, tenemos que seleccionar algún entero positivo y que sea un coprimo menor de 403. Supongamos que fijamos y = 2^{103}.
Exponenciación de 2 por 103 produce el resultado a continuación.
2^{103} \mod 403 = 10,141,204,801,825,835,211,973,625,643,008 \mod 403 = 349 \mod 403
El problema RSA en este ejemplo concreto es ahora el siguiente: Se le
proporciona N = 403, e = 103, y y = 349 \mod 403. Ahora hay
que calcular x de modo que x^{103} = 349 \mod 403. Es decir, debe encontrar que el valor original antes de la exponenciación
por 103 fue 2.
Sería fácil (al menos para un ordenador) calcular x si supiéramos que d = 7. En
ese caso, bastaría con determinar x como se indica a continuación.
x = y^7 \mod 403 = 349^7 \mod 403 = 630,634,881,591,804,949 \mod 403 = 2 \mod 403
El problema es que no se te ha proporcionado la información de que d = 7. Podrías, por supuesto, calcular d a partir del hecho de que 103 \cdot d = 1 \mod 360. El
problema es que tampoco se te da la información de que el orden de N = 360. Por último, también
se podría calcular el orden de 403 calculando el siguiente producto: (p - 1) \cdot (q - 1). Pero
tampoco se te dice que p = 13 y q = 31.
Por supuesto, un ordenador podría resolver el problema RSA de este ejemplo con relativa facilidad, porque los números primos implicados no son grandes. Pero cuando los números primos son muy grandes, se enfrenta a una tarea prácticamente imposible.
Ya hemos presentado el problema RSA, un conjunto de condiciones bajo las cuales es difícil y las matemáticas subyacentes. ¿En qué ayuda todo esto a la criptografía asimétrica? Concretamente, ¿cómo podemos convertir la dureza del problema RSA bajo ciertas condiciones en un esquema de cifrado o de firma digital?
Un enfoque consiste en tomar el problema RSA y construir esquemas de forma
directa. Por ejemplo, supongamos que hemos generado un conjunto de variables \Pi como se describe en el problema RSA, y nos aseguramos de que p y q son suficientemente
grandes. Establece su clave pública igual a (N, e) y comparte esta información con el mundo. Como se ha descrito anteriormente,
se mantienen en secreto los valores de p, q, \phi(n) y d. De hecho, d es tu clave privada.
Cualquiera que quiera enviarte un mensaje m que sea un elemento de C_N podría simplemente cifrarlo de la siguiente manera: c = m^e \mod N. (El texto
cifrado c aquí es equivalente
al valor y en el problema
RSA.) Se puede descifrar fácilmente este mensaje con sólo calcular c^d \mod N.
Puedes intentar crear un esquema de firma digital de la misma manera.
Supongamos que queremos enviar a alguien un mensaje m con una firma digital S.
Podría simplemente establecer S = m^d \mod N y enviar el par (m,S) al
destinatario. Cualquiera puede verificar la firma digital simplemente
comprobando si S^e \mod N = m \mod N.
Cualquier atacante, sin embargo, lo tendría realmente difícil para crear una S válida para un mensaje, dado que no posee d.
Desgraciadamente, convertir lo que de por sí es un problema difícil, el
problema RSA, en un esquema criptográfico no es tan sencillo. Para el
esquema de cifrado directo, sólo se pueden seleccionar coprimos de N como mensajes. Eso no nos deja con muchos mensajes posibles, desde luego no
los suficientes para una comunicación estándar. Además, estos mensajes tienen
que seleccionarse aleatoriamente. Parece poco práctico. Por último, cualquier
mensaje que se seleccione dos veces producirá exactamente el mismo texto cifrado.
Esto es extremadamente indeseable en cualquier esquema de cifrado y no cumple
ninguna noción estándar moderna rigurosa de seguridad en el cifrado.
Los problemas se agravan aún más para nuestro sencillo esquema de firma
digital. Tal y como está, cualquier atacante puede falsificar fácilmente
firmas digitales simplemente seleccionando primero un coprimo de N como firma y calculando después el mensaje original correspondiente. Esto incumple
claramente el requisito de infalsificabilidad existencial.
No obstante, añadiendo un poco de complejidad inteligente, el problema RSA puede utilizarse para crear un esquema seguro de cifrado de clave pública, así como un esquema seguro de firma digital. No entraremos aquí en los detalles de tales construcciones. Sin embargo, es importante destacar que esta complejidad adicional no cambia el problema fundamental subyacente de RSA en el que se basan estos esquemas.
Notas:
[4] Véase, por ejemplo, Jonathan Katz y Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Ratón, FL: 2015), pp. 410-32 sobre cifrado RSA y pp. 444-41 para firmas digitales RSA.
Sección final
Reseñas & Valoraciones
366d6fd0-ceb2-4299-bf37-8c6dfcb681d5 true
Examen Final
44882d2b-63cd-4fde-8485-f76f14d8b2fe true
Conclusión
f1905f78-8cf7-5031-949a-dfa8b76079b4 true