name: El Funcionamiento Interno de las Carteras de Bitcoin goal: Sumergirse en los principios criptográficos que impulsan las carteras de Bitcoin. objectives:
- Definir las nociones teóricas necesarias para entender los algoritmos criptográficos usados en Bitcoin.
- Comprender completamente la construcción de una cartera determinista y jerárquica.
- Saber cómo identificar y reducir los riesgos asociados con la gestión de una cartera.
- Entender los principios de las funciones hash, las claves criptográficas y las firmas digitales.
Un Viaje al Corazón de las Carteras de Bitcoin
¡Descubre los secretos de las carteras de Bitcoin deterministas y jerárquicas con nuestro curso CYP201! Ya seas un usuario regular o un entusiasta que busca profundizar su conocimiento, este curso ofrece una inmersión completa en el funcionamiento de estas herramientas que todos usamos a diario.
Aprende sobre los mecanismos de las funciones hash, firmas digitales (ECDSA y Schnorr), frases mnemotécnicas, claves criptográficas y la creación de direcciones de recepción, todo mientras exploras estrategias de seguridad avanzadas.
Este entrenamiento no solo te equipará con el conocimiento para entender la estructura de una cartera de Bitcoin, sino que también te preparará para sumergirte más profundamente en el emocionante mundo de la criptografía.
Con una pedagogía clara, más de 60 diagramas explicativos y ejemplos concretos, CYP201 te permitirá entender de la A a la Z cómo funciona tu cartera, para que puedas navegar el universo de Bitcoin con confianza. ¡Toma control de tus UTXOs hoy entendiendo cómo funcionan las carteras deterministas y jerárquicas (HD)!
Introducción
Introducción al Curso
Bienvenido al curso CYP201, donde exploraremos en profundidad el funcionamiento de las carteras de Bitcoin HD (del inglès deterministic and hierarchical). Este curso está diseñado para cualquier persona que quiera entender los fundamentos técnicos del uso de Bitcoin, ya sean usuarios casuales, entusiastas que han visto la luz o futuros expertos.
El objetivo de esta formación es darte las claves para dominar las herramientas que usas a diario. Las carteras de Bitcoin HD, que están en el corazón de tu experiencia de usuario, se basan en conceptos a veces complejos, los cuales intentaremos hacer accesibles. ¡Eliminemos esos mitos!
Antes de sumergirnos en los detalles de la construcción y operación de las
carteras de Bitcoin, comenzaremos con algunos capítulos sobre los
fundamentos de la criptografía que hay que conocer para lo que sigue.
Comenzaremos con las funciones hash criptográficas, fundamentales tanto para
las carteras como para el propio protocolo de Bitcoin. Descubrirás sus
principales características, las funciones específicas usadas en Bitcoin y,
en un capítulo más técnico, aprenderás en detalle sobre el funcionamiento de
la reina de las funciones hash: SHA256. 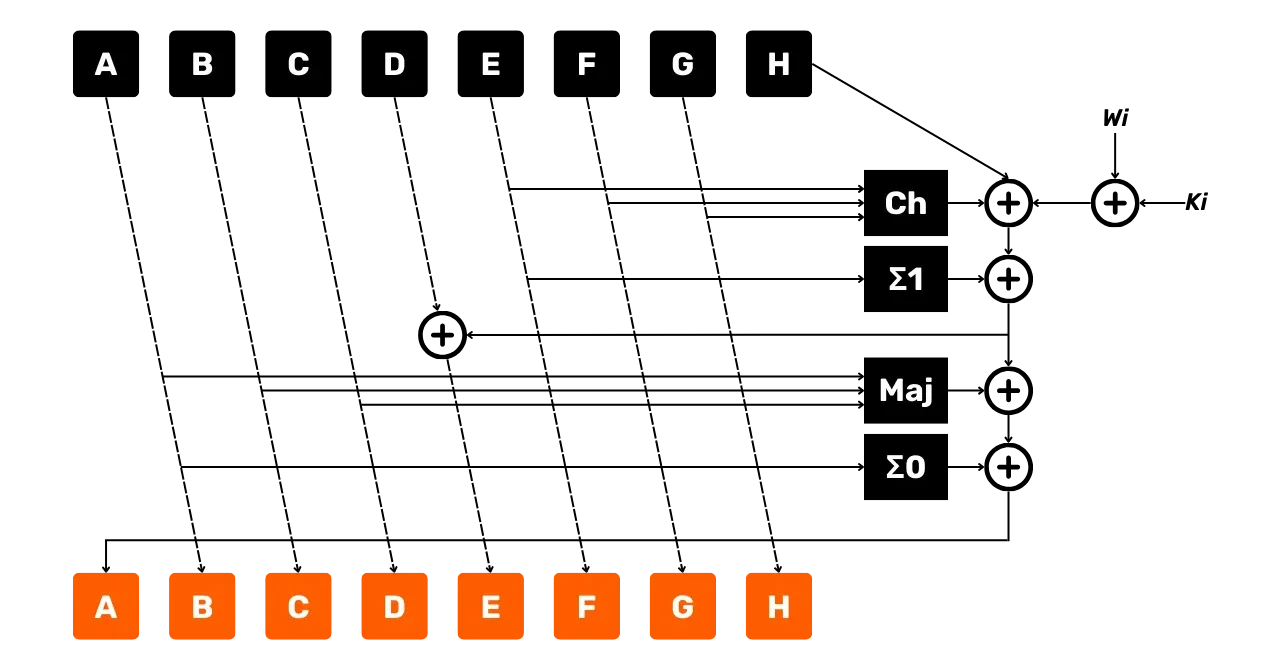
A continuación, discutiremos el funcionamiento de los algoritmos de firma digital que usas todos los días para asegurar tus UTXOs. Bitcoin utiliza dos: ECDSA y el protocolo Schnorr. Aprenderás qué fundamentos matemátioas subyacen a estos algoritmos y cómo aseguran las transacciones.
Una vez que tengamos una buena comprensión de estos elementos de criptografía, finalmente pasaremos al corazón de la formación: ¡las carteras deterministas y jerárquicas! Primero, hay una sección dedicada a las frases mnemotécnicas, estas secuencias de 12 o 24 palabras que te permiten crear y restaurar tus carteras. Descubrirás cómo se generan estas palabras a partir de una fuente de entropía y cómo facilitan el uso de Bitcoin.
 La formación continuará con el estudio de la passphrase BIP39, la semilla (no
confundir con la frase mnemotécnica), el código de cadena maestro y la llave
maestra. Veremos en detalle qué son estos elementos, sus respectivos roles y
cómo se calculan.
La formación continuará con el estudio de la passphrase BIP39, la semilla (no
confundir con la frase mnemotécnica), el código de cadena maestro y la llave
maestra. Veremos en detalle qué son estos elementos, sus respectivos roles y
cómo se calculan. 
Finalmente, a partir de la llave maestra, descubriremos cómo se derivan los pares de claves criptográficas de manera determinista y jerárquica hasta las direcciones de recepción.

Esta formación te permitirá usar tu software de billetera con confianza, al mismo tiempo que mejora tus habilidades para identificar y mitigar riesgos. ¡Prepárate para convertirte en un verdadero experto en billeteras de Bitcoin!
Funciones Hash
Introducción a las Funciones Hash
El primer tipo de algoritmos criptográficos utilizados en Bitcoin abarca las funciones hash. Juegan un papel esencial en diferentes niveles del protocolo, pero también dentro de las billeteras de Bitcoin. Descubramos juntos qué es una función hash y para qué se utiliza en Bitcoin.
Definición y Principio del Hashing
El hashing es un proceso que transforma información de longitud arbitraria en otra pieza de información de longitud fija a través de una función hash criptográfica. En otras palabras, una función hash toma una entrada de cualquier tamaño y la convierte en una huella digital de tamaño fijo, llamada "hash". El hash también puede ser referido a veces como "digest", "condensado", o "hasheado".
Por ejemplo, la función hash SHA256 produce un hash de una longitud fija de 256 bits. Así, si usamos el input "PlanB", un mensaje de longitud arbitraria, el hash generado será la siguiente huella digital de 256 bits:
24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688

Características de las Funciones Hash
Estas funciones hash criptográficas tienen varias características esenciales que las hacen particularmente útiles en el contexto de Bitcoin y otros sistemas informáticos:
- Irreversibilidad (o resistencia a la preimagen)
- Resistencia a la manipulación (efecto avalancha)
- Resistencia a colisiones
- Resistencia a la segunda preimagen
1. Irreversibilidad (resistencia a la preimagen):
La irreversibilidad significa que es fácil calcular el hash a partir de la información dada como input, pero que el cálculo inverso, es decir, encontrar el input a partir del hash, es prácticamente imposible. Esta propiedad hace que las funciones hash sean perfectas para crear huellas digitales únicas sin comprometer la información original.
En el ejemplo dado, obtener el hash 24f1b9… sabiendo el input "PlanB" es simple y rápido. Sin embargo, encontrar el mensaje "PlanB"
solo sabiendo 24f1b9… es imposible.

Por lo tanto, es imposible encontrar una preimagen m para un hash h tal que h = \text{HASH}(m),
donde \text{HASH} es
una función hash criptográfica.
2. Resistencia a la manipulación (efecto avalancha)
La segunda característica es la resistencia a la manipulación, también conocida como el efecto avalancha. Esta característica se observa en una función hash si un pequeño cambio en el mensaje de entrada resulta en un cambio radical en el hash de salida. Si volvemos a nuestro ejemplo con el input "PlanB" y la función SHA256, hemos visto que el hash generado es el siguiente:
24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688
Si hacemos un cambio muy leve en el input usando "Planb" esta vez, entonces simplemente cambiando de una "B" mayúscula a una "b" minúscula altera completamente el hash de salida SHA256:
bb038b4503ac5d90e1205788b00f8f314583c5e22f72bec84b8735ba5a36df3f

Esta propiedad asegura que incluso una alteración menor del mensaje original es inmediatamente detectable, ya que no solo cambia una pequeña parte del hash, sino el hash completo. Esto puede ser de interés en varios campos para verificar la integridad de mensajes, software o incluso transacciones de Bitcoin.
3. Resistencia a Colisiones
La tercera característica es la resistencia a colisiones. Una función hash
es resistente a colisiones si es computacionalmente imposible encontrar 2
mensajes diferentes que produzcan el mismo hash de salida de la función.
Formalmente, es difícil encontrar dos mensajes distintos m_1 y m_2 tales que:
\text{HASH}(m_1) = \text{HASH}(m_2)
En realidad, es matemáticamente inevitable que existan colisiones para las
funciones hash, porque el tamaño de las entradas puede ser mayor que el
tamaño de las salidas. Esto se conoce como el principio del cajón de
Dirichlet: si n objetos se
distribuyen en m cajones, con m < n, entonces al menos
un cajón necesariamente contendrá dos o más objetos. Para una función hash,
este principio se aplica porque el número de mensajes posibles es (casi)
infinito, mientras que el número de hashes posibles es finito (2^{256} en el caso de SHA256).
Por lo tanto, esta característica no significa que no haya colisiones para las funciones hash, sino más bien que una buena función hash hace que la probabilidad de encontrar una colisión sea despreciable. Esta característica, por ejemplo, ya no se verifica en los algoritmos SHA-0 y SHA-1, predecesores de SHA-2, para los cuales se han encontrado colisiones. Estas funciones, por lo tanto, ahora se desaconsejan y a menudo se consideran obsoletas.
Para una función hash de n bits, la resistencia a colisiones es del orden de 2^{\frac{n}{2}}, de acuerdo con el ataque de cumpleaños. Por ejemplo, para SHA256 (n = 256), la complejidad de encontrar una colisión es del orden de 2^{128} intentos. En términos prácticos, esto significa que si uno pasa 2^{128} mensajes diferentes
a través de la función, es probable que encuentre una colisión.
4. Resistencia a la Segunda Preimagen
La resistencia a la segunda preimagen es otra característica importante de
las funciones hash. Declara que dado un mensaje m_1 y su hash h, es
computacionalmente inviable encontrar otro mensaje m_2 \neq m_1 tal que:
\text{HASH}(m_1) = \text{HASH}(m_2)Por lo tanto, la resistencia a la segunda preimagen es algo similar a la
resistencia a colisiones, excepto que aquí, el ataque es más difícil porque
el atacante no puede elegir libremente m_1.

Aplicaciones de las Funciones Hash en Bitcoin
La función hash más utilizada en Bitcoin es SHA256 ("Secure Hash Algorithm 256 bits"). Diseñada a principios de los años 2000 por la NSA y estandarizada por el NIST, produce un output hash de 256 bits.
Esta función se utiliza en muchos aspectos de Bitcoin. A nivel de protocolo, está involucrada en el mecanismo de Prueba de Trabajo, donde se aplica un doble hash para buscar una colisión parcial entre el encabezado de un bloque candidato, creado por un minero, y el objetivo de dificultad. Si se encuentra esta colisión parcial, el bloque candidato se valida y puede añadirse a la blockchain.
SHA256 también se utiliza en la construcción de un árbol de Merkle, que es notablemente el acumulador utilizado para registrar transacciones en bloques. Esta estructura también se encuentra en el protocolo Utreexo, que permite reducir el tamaño del Conjunto UTXO. Además, con la introducción de Taproot en 2021, SHA256 se explota en MAST (Merkelised Alternative Script Tree), que permite revelar solo las condiciones de gasto realmente utilizadas en un script, sin divulgar las otras opciones posibles. También se utiliza en el cálculo de identificadores de transacción, en la transmisión de paquetes a través de la red P2P, en firmas electrónicas... Finalmente, y esto es de particular interés en esta formación, SHA256 se utiliza a nivel de aplicación para la construcción de carteras de Bitcoin y la derivación de direcciones.
La mayoría de las veces, cuando te encuentres con el uso de SHA256 en Bitcoin, en realidad será un doble hash SHA256, denominado "HASH256", que simplemente consiste en aplicar SHA256 dos veces sucesivamente: HASH256(m) = SHA256(SHA256(m))
Esta práctica de doble hash añade una capa extra de seguridad contra ciertos ataques potenciales, aunque un solo SHA256 se considera hoy en día criptográficamente seguro.
Otra función de hash disponible en el lenguaje Script y utilizada para derivar direcciones de recepción es la función RIPEMD160. Esta función produce un hash de 160 bits (por lo tanto, más corto que SHA256). Generalmente se combina con SHA256 para formar la función HASH160:
\text{HASH160}(m) = \text{RIPEMD160}(\text{SHA256}(m))Esta combinación se utiliza para generar hashes más cortos, notablemente en la creación de ciertas direcciones de Bitcoin que representan hashes de claves o hashes de script, así como para producir huellas digitales de claves.
Finalmente, solo a nivel de aplicación, la función SHA512 también se utiliza a veces, que juega indirectamente un papel en la derivación de claves para carteras. Esta función es muy similar a SHA256 en su operación; ambos pertenecen a la misma familia SHA2, pero SHA512 produce, como indica su nombre, un hash de 512 bits, en comparación con 256 bits para SHA256. Detallaremos su uso en los siguientes capítulos.
Ahora conoces los conceptos básicos esenciales sobre las funciones hash para lo que sigue. En el próximo capítulo, propongo descubrir con más detalle el funcionamiento de la función que está en el corazón de Bitcoin: SHA256. Lo diseccionaremos para entender cómo logra las características que hemos descrito aquí. Este próximo capítulo es bastante largo y técnico, pero no es esencial para seguir el resto de la formación. Así que, si tienes dificultades para entenderlo, no te preocupes y pasa directamente al siguiente capítulo, que será mucho más accesible.
El Funcionamiento Interno de SHA256
905eb320-f15b-5fb6-8d2d-5bb447337deb Hemos visto anteriormente que las funciones de hashing poseen características importantes que justifican su uso en Bitcoin. Ahora examinemos los mecanismos internos de estas funciones de hashing que les otorgan estas propiedades, y para hacer esto, propongo diseccionar el funcionamiento de SHA256.
Las funciones SHA256 y SHA512 pertenecen a la misma familia SHA2. Su mecanismo se basa en una construcción específica llamada construcción de Merkle-Damgård. RIPEMD160 también utiliza este mismo tipo de construcción.
Como recordatorio, tenemos un mensaje de tamaño arbitrario como entrada a SHA256, y lo pasaremos a través de la función para obtener un hash de 256 bits como salida.
Pre-procesamiento del input
Para comenzar, necesitamos preparar nuestro mensaje de entrada m para que tenga una longitud estándar que sea múltiplo de 512 bits. Este paso
es crucial para el correcto funcionamiento del algoritmo posteriormente.
Para hacer esto, comenzamos con el paso de bits de relleno. Primero
agregamos un bit separador 1 al mensaje, seguido de cierto
número de bits 0. El número de bits 0 agregados se
calcula de modo que la longitud total del mensaje después de esta adición
sea congruente con 448 módulo 512. Así, la longitud L del mensaje con los bits de
relleno es igual a:
L \equiv 448 \mod 512\text{mod}, por
módulo, es una operación matemática que, entre dos enteros, devuelve el
resto de la división euclidiana del primero por el segundo. Por ejemplo: 16 \mod 5 = 1. Es una
operación ampliamente utilizada en criptografía.
Aquí, el paso de relleno asegura que, después de agregar los 64 bits en el
siguiente paso, la longitud total del mensaje igualado será un múltiplo de
512 bits. Si el mensaje inicial tiene una longitud de M bits, el número (N) de bits 0 a agregar es entonces:
N = (448 - (M + 1) \mod 512) \mod 512Por ejemplo, si el mensaje inicial es de 950 bits, el cálculo sería el siguiente:
\begin{align*}
M & = 950 \\
M + 1 & = 951 \\
(M + 1) \mod 512 & = 951 \mod 512 \\
& = 951 - 512 \cdot \left\lfloor \frac{951}{512} \right\rfloor \\
& = 951 - 512 \\
& = 951 - 512 \\
& = 439 \\
\\
448 - (M + 1) \mod 512 & = 448 - 439 \\
& = 9 \\
\\
N & = (448 - (M + 1) \mod 512) \mod 512 \\
N & = 9 \mod 512 \\
& = 9
\end{align*}Así, tendríamos 9 0s además del separador 1.
Nuestros bits de relleno a agregar directamente después de nuestro mensaje M serían así:
1000 0000 00
Después de agregar los bits de relleno a nuestro mensaje M, también agregamos una representación de 64 bits de la longitud original
del mensaje M, expresada en
binario. Esto permite que la función hash sea sensible al orden de bits y a
la longitud del mensaje. Si volvemos a nuestro ejemplo con un mensaje
inicial de 950 bits, convertimos el número decimal 950 a
binario, lo que nos da 1110 1101 10. Completamos este número
con ceros en la base para hacer un total de 64 bits. En nuestro ejemplo,
esto da:
0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0011 1011 0110
Este tamaño de relleno se añade siguiendo el relleno de bits. Por lo tanto, el mensaje después de nuestro preprocesamiento consiste en tres partes:
- El mensaje original
M; - Un bit
1seguido por varios bits0para formar el relleno de bits; - Una representación de 64 bits de la longitud de
Mpara formar el relleno con el tamaño.

Inicialización de Variables
SHA256 utiliza ocho variables de estado inicial, denotadas de A a H, cada una de 32 bits.
Estas variables se inicializan con constantes específicas, que son las
partes fraccionarias de las raíces cuadradas de los primeros ocho números
primos. Utilizaremos estos valores posteriormente durante el proceso de
hashing:
A = 0x6a09e667B = 0xbb67ae85C = 0x3c6ef372D = 0xa54ff53aE = 0x510e527fF = 0x9b05688cG = 0x1f83d9abH = 0x5be0cd19
SHA256 también utiliza otras 64 constantes, denotadas de K_0 a K_{63}, que son
las partes fraccionarias de las raíces cúbicas de los primeros 64 números
primos:
K[0 \ldots 63] = \begin{pmatrix}
0x428a2f98, & 0x71374491, & 0xb5c0fbcf, & 0xe9b5dba5, \\
0x3956c25b, & 0x59f111f1, & 0x923f82a4, & 0xab1c5ed5, \\
0xd807aa98, & 0x12835b01, & 0x243185be, & 0x550c7dc3, \\
0x72be5d74, & 0x80deb1fe, & 0x9bdc06a7, & 0xc19bf174, \\
0xe49b69c1, & 0xefbe4786, & 0x0fc19dc6, & 0x240ca1cc, \\
0x2de92c6f, & 0x4a7484aa, & 0x5cb0a9dc, & 0x76f988da, \\
0x983e5152, & 0xa831c66d, & 0xb00327c8, & 0xbf597fc7, \\
0xc6e00bf3, & 0xd5a79147, & 0x06ca6351, & 0x14292967, \\
0x27b70a85, & 0x2e1b2138, & 0x4d2c6dfc, & 0x53380d13, \\
0x650a7354, & 0x766a0abb, & 0x81c2c92e, & 0x92722c85, \\
0xa2bfe8a1, & 0xa81a664b, & 0xc24b8b70, & 0xc76c51a3, \\
0xd192e819, & 0xd6990624, & 0xf40e3585, & 0x106aa070, \\
0x19a4c116, & 0x1e376c08, & 0x2748774c, & 0x34b0bcb5, \\
0x391c0cb3, & 0x4ed8aa4a, & 0x5b9cca4f, & 0x682e6ff3, \\
0x748f82ee, & 0x78a5636f, & 0x84c87814, & 0x8cc70208, \\
0x90befffa, & 0xa4506ceb, & 0xbef9a3f7, & 0xc67178f2
\end{pmatrix}División del input
Ahora que tenemos una entrada igualada, pasaremos a la fase principal de procesamiento del algoritmo SHA256: la función de compresión. Este paso es muy importante, ya que es principalmente lo que le da a la función hash sus propiedades criptográficas que estudiamos en el capítulo anterior.
Primero, comenzamos dividiendo nuestro mensaje igualado (resultado de los
pasos de preprocesamiento) en varios bloques P de 512 bits cada uno. Si nuestro mensaje igualado tiene un tamaño total de n \times 512 bits, por lo tanto, tendremos n bloques, cada uno de 512 bits. Cada bloque de 512 bits será procesado
individualmente por la función de compresión, que consiste en 64 rondas de
operaciones sucesivas. Nombraremos estos bloques P_1, P_2, P_3...
Operaciones Lógicas
Antes de explorar la función de compresión en detalle, es importante entender las operaciones lógicas básicas utilizadas en ella. Estas operaciones, basadas en el álgebra booleana, operan a nivel de bit. Las operaciones lógicas básicas utilizadas son:
- Conjunción (AND): denotada
\land, corresponde a un "Y" lógico. - Disyunción (OR): denotada
\lor, corresponde a un "O" lógico. - Negación (NOT): denotada
\lnot, corresponde a un "NO" lógico.
A partir de estas operaciones básicas, podemos definir operaciones más
complejas, como el "O exclusivo" (XOR) denotado \oplus, que es ampliamente utilizado en criptografía. Cada operación lógica puede
ser representada por una tabla de verdad, que indica el resultado para todas
las combinaciones posibles de valores de entrada binarios (dos operandos p y q). Para XOR (\oplus):
p | q | p \oplus q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Para AND (\land):
p | q | p \land q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Para NOT (\lnot p):
p | \lnot p |
|---|---|
| 0 | 1 |
| 1 | 0 |
Tomemos un ejemplo para entender la operación de XOR a nivel de bit. Si tenemos dos números binarios de 6 bits:
a = 101100b = 001000
Entonces:
a \oplus b = 101100 \oplus 001000 = 100100
Aplicando XOR bit a bit:
| Posición del Bit | a | b | a \oplus b |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 1 | 0 | 1 |
| 5 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 |
El resultado es, por lo tanto, 100100.
Además de las operaciones lógicas, la función de compresión utiliza operaciones de desplazamiento de bits, que jugarán un papel esencial en la difusión de bits en el algoritmo.
Primero, está la operación de desplazamiento lógico hacia la derecha,
denotada ShR_n(x), que
desplaza todos los bits de x hacia la derecha por n posiciones,
llenando los bits vacantes a la izquierda con ceros.
Por ejemplo, para x = 101100001 (en 9 bits) y n = 4:
ShR_4(101100001) = 000010110
Esquemáticamente, la operación de desplazamiento hacia la derecha podría verse así:
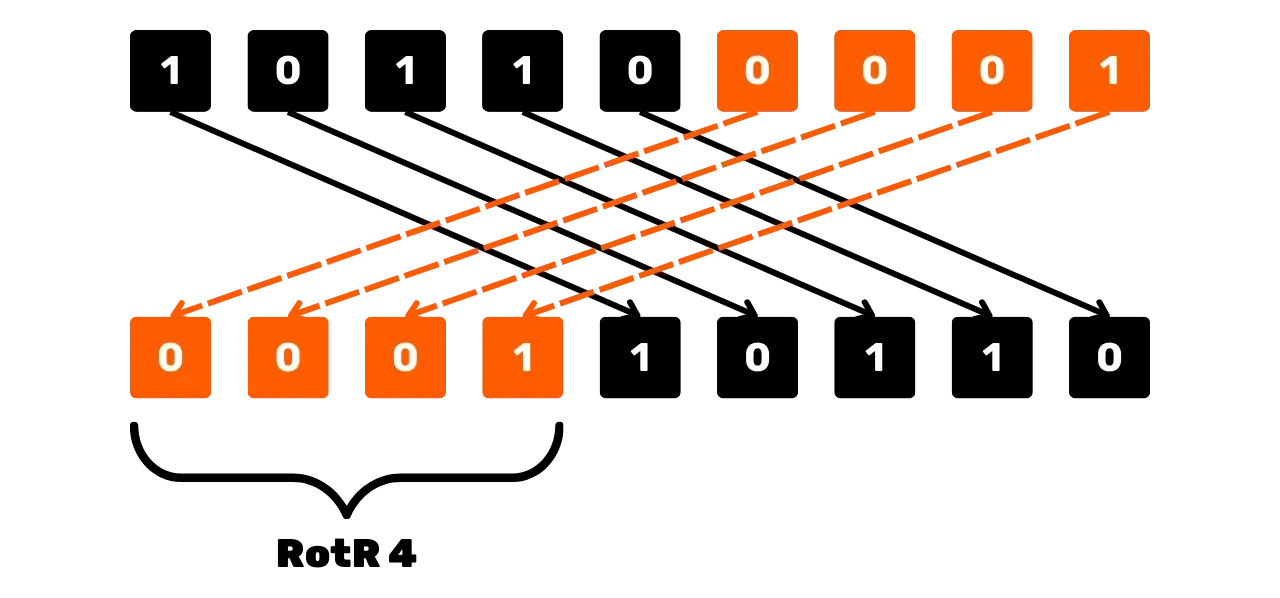
 Otra operación utilizada en SHA256 para la manipulación de bits es la rotación
circular hacia la derecha, denotada
Otra operación utilizada en SHA256 para la manipulación de bits es la rotación
circular hacia la derecha, denotada RotR_n(x), que desplaza los
bits de x hacia la derecha
por n posiciones,
reinsertando los bits desplazados al principio de la cadena. Por ejemplo,
para x = 101100001 (sobre 9
bits) y n = 4:
RotR_4(101100001) = 000110110
Esquemáticamente, la operación de desplazamiento circular hacia la derecha podría verse así:
Función de Compresión
Ahora que hemos entendido las operaciones básicas, examinemos en detalle la función de compresión SHA256.
En el paso anterior, dividimos nuestra entrada en varias piezas de 512 bits P. Para cada bloque de 512 bits P, tenemos:
- Las palabras del mensaje
W_i: paraide 0 a 63. - Las constantes
K_i: paraide 0 a 63, definidas en el paso anterior. - Las variables de estado
A, B, C, D, E, F, G, H: inicializadas con los valores del paso anterior.
Las primeras 16 palabras, W_0 hasta W_{15}, se
extraen directamente del bloque procesado de 512 bits P. Cada palabra W_i consta de 32 bits consecutivos del bloque. Así, por ejemplo, tomamos nuestra
primera pieza de entrada P_1,
y la dividimos aún más en piezas más pequeñas de 32 bits que llamamos
palabras. Las siguientes 48 palabras (W_{16} hasta W_{63}) se
generan utilizando la siguiente fórmula:
W_i = W_{i-16} + \sigma_0(W_{i-15}) + W_{i-7} + \sigma_1(W_{i-2}) \mod 2^{32}Con:
\sigma_0(x) = RotR_7(x) \oplus RotR_{18}(x) \oplus ShR_3(x)\sigma_1(x) = RotR_{17}(x) \oplus RotR_{19}(x) \oplus ShR_{10}(x)
En este caso, x es igual a W_{i-15} para \sigma_0(x) y W_{i-2} para \sigma_1(x).
Una vez que hemos determinado todas las palabras W_i para nuestra pieza de 512 bits, podemos pasar a la función de compresión, que
consiste en realizar 64 rondas.
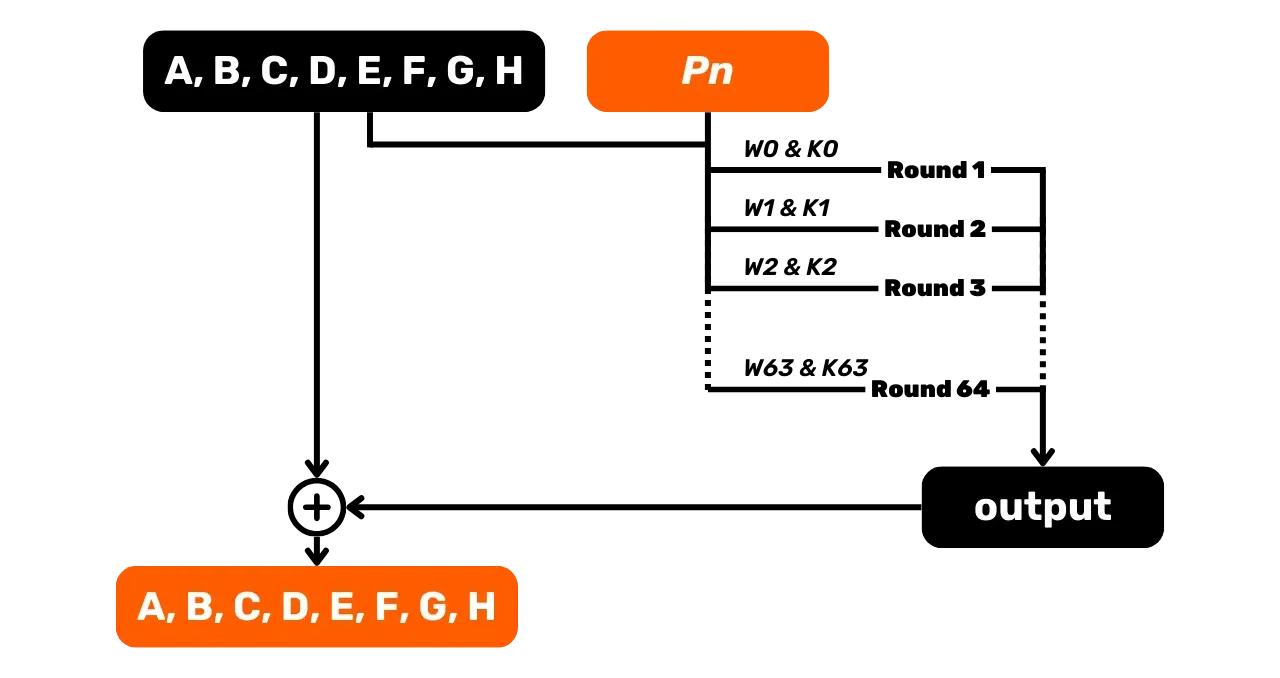 Para cada ronda
Para cada ronda i de 0 a 63,
tenemos tres tipos diferentes de entradas. Primero, el W_i que acabamos de determinar, que consiste parcialmente en nuestra pieza de
mensaje P_n. A continuación,
las 64 constantes K_i.
Finalmente, usamos las variables de estado A, B, C, D, E, F, G y H, que evolucionarán a lo
largo del proceso de hash y se modificarán con cada función de compresión.
Sin embargo, para la primera pieza P_1, usamos las constantes
iniciales dadas anteriormente. Luego realizamos las siguientes operaciones
en nuestras entradas:
- Función
\Sigma_0:
\Sigma_0(A) = RotR_2(A) \oplus RotR_{13}(A) \oplus RotR_{22}(A)- Función
\Sigma_1:
\Sigma_1(E) = RotR_6(E) \oplus RotR_{11}(E) \oplus RotR_{25}(E)
- Función
Ch("Elegir"):
Ch(E, F, G) = (E \land F) \oplus (\lnot E \land G)
- Función
Maj("Mayoría"):
Maj(A, B, C) = (A \land B) \oplus (A \land C) \oplus (B \land C)
Luego calculamos 2 variables temporales:
temp1:
temp1 = H + \Sigma_1(E) + Ch(E, F, G) + K_i + W_i \mod 2^{32}
temp2:
temp2 = \Sigma_0(A) + Maj(A, B, C) \mod 2^{32}
A continuación, actualizamos las variables de estado de la siguiente manera:
\begin{cases}
H = G \\
G = F \\
F = E \\
E = D + temp1 \mod 2^{32} \\
D = C \\
C = B \\
B = A \\
A = temp1 + temp2 \mod 2^{32}
\end{cases}El siguiente diagrama representa una ronda de la función de compresión SHA256 tal como acabamos de describir:

- Las flechas indican el flujo de datos;
- Los cuadros representan las operaciones realizadas;
- Los
+rodeados representan la adición módulo2^{32}.
Ya podemos observar que esta ronda produce nuevas variables de estado A, B, C, D, E, F, G y H. Estas nuevas variables
servirán como entrada para la siguiente ronda, la cual a su vez producirá
nuevas variables A, B, C, D, E, F, G y H, para ser utilizadas en
la ronda siguiente. Este proceso continúa hasta la ronda 64.
Después de las 64 rondas, actualizamos los valores iniciales de las variables de estado sumándolos a los valores finales al final de la ronda 64:
\begin{cases}
A = A_{\text{inicial}} + A \mod 2^{32} \\
B = B_{\text{inicial}} + B \mod 2^{32} \\
C = C_{\text{inicial}} + C \mod 2^{32} \\
D = D_{\text{inicial}} + D \mod 2^{32} \\
E = E_{\text{inicial}} + E \mod 2^{32} \\
F = F_{\text{inicial}} + F \mod 2^{32} \\
G = G_{\text{inicial}} + G \mod 2^{32} \\
H = H_{\text{inicial}} + H \mod 2^{32}
\end{cases}Estos nuevos valores de A, B, C, D, E, F, G y H servirán como los valores
iniciales para el siguiente bloque, P_2. Para este bloque P_2, replicamos el mismo
proceso de compresión con 64 rondas, luego actualizamos las variables para
el bloque P_3, y así
sucesivamente hasta el último bloque de nuestra entrada igualada.
Después de procesar todos los bloques del mensaje, concatenamos los valores
finales de las variables A, B, C, D, E, F, G y H para formar el hash final
de 256 bits de nuestra función de hashing:
\text{Hash} = A \Vert B \Vert C \Vert D \Vert E \Vert F \Vert G \Vert HCada variable es un entero de 32 bits, por lo que su concatenación siempre produce un resultado de 256 bits, independientemente del tamaño de nuestro mensaje de entrada a la función de hashing.
Justificación de Propiedades Criptográficas
Pero entonces, ¿cómo es esta función irreversible, resistente a colisiones y resistente a manipulaciones?
Para la resistencia a manipulaciones, es bastante simple de entender. Se realizan tantos cálculos en cascada, que dependen tanto del input como de las constantes, que la modificación más mínima del mensaje inicial cambia completamente el camino tomado, y por lo tanto, cambia completamente el hash de salida. Esto es lo que se llama el efecto avalancha. Esta propiedad se asegura en parte por la mezcla de los estados intermedios con los estados iniciales para cada pieza.
A continuación, al discutir una función hash criptográfica, el término
"irreversibilidad" generalmente no se utiliza. En su lugar, hablamos de
"resistencia a la preimagen", que especifica que para cualquier y dado, es difícil encontrar un x tal que h(x) = y. Esta
resistencia a la preimagen está garantizada por la complejidad algebraica y
la fuerte no linealidad de las operaciones realizadas en la función de
compresión, así como por la pérdida de cierta información en el proceso. Por
ejemplo, para un resultado dado de una adición módulo, hay varios operandos
posibles:
3+2 \mod 10 = 5 \\
7+8 \mod 10 = 5 \\
5+10 \mod 10 = 5En este ejemplo, sabiendo solo el módulo utilizado (10) y el resultado (5), no se puede determinar con certeza cuáles son los operandos correctos utilizados en la adición. Se dice que hay múltiples congruencias módulo 10.
Para la operación XOR, nos enfrentamos al mismo problema. Recuerda la tabla
de verdad para esta operación: cualquier salida de 1 bit puede ser
determinada por dos configuraciones de entrada diferentes que tienen
exactamente la misma probabilidad de ser los valores correctos. Por lo
tanto, no se puede determinar con certeza los operandos de un XOR sabiendo
solo su resultado. Si aumentamos el tamaño de los operandos de XOR, el
número de entradas posibles sabiendo solo el resultado aumenta
exponencialmente. Además, el XOR se usa a menudo junto con otras operaciones
a nivel de bit, como la operación \text{RotR}, que añade aún más interpretaciones posibles al resultado.
La función de compresión también utiliza la operación \text{ShR}. Esta operación elimina una parte de la información básica, que luego es
imposible recuperar más tarde. Una vez más, no hay medios algebraicos para
revertir esta operación. Todas estas operaciones unidireccionales y de
pérdida de información se utilizan muy frecuentemente en funciones de
compresión. El número de entradas posibles para un output dado es casi
infinito, y cada intento de cálculo inverso conduciría a ecuaciones con un
número muy alto de incógnitas, que aumentaría exponencialmente en cada paso.
Finalmente, para la característica de resistencia a colisiones, entran en juego varios parámetros. El preprocesamiento del mensaje original juega un papel esencial. Sin este preprocesamiento, podría ser más fácil encontrar colisiones en la función. Aunque, teóricamente, existen colisiones (debido al principio del palomar), la estructura de la función hash, combinada con las propiedades mencionadas anteriormente, hace que la probabilidad de encontrar una colisión sea extremadamente baja.
Para que una función hash sea resistente a colisiones, es esencial que:
- El output sea impredecible: Cualquier previsibilidad puede ser explotada para encontrar colisiones más rápido que con un ataque de fuerza bruta. La función asegura que cada bit de el output dependa de una manera no trivial del input. En otras palabras, la función está diseñada de tal manera que cada bit del resultado final tiene una probabilidad independiente de ser 0 o 1, incluso si esta independencia no es absoluta en la práctica.
- La distribución de los hashes sea pseudoaleatoria: Esto asegura que los hashes estén uniformemente distribuidos.
- El tamaño del hash sea sustancial: cuanto mayor sea el espacio posible para los resultados, más difícil es encontrar una colisión.
Los criptógrafos diseñan estas funciones evaluando los mejores ataques posibles para encontrar colisiones, luego ajustando los parámetros para hacer estos ataques ineficaces.
Construcción de Merkle-Damgård
La estructura de SHA256 se basa en la construcción de Merkle-Damgård, que
permite transformar una función de compresión en una función hash que puede
procesar mensajes de longitud arbitraria. Esto es precisamente lo que hemos
visto en este capítulo. Sin embargo, algunas funciones hash antiguas como
SHA1 o MD5, que utilizan esta construcción específica, son vulnerables a
ataques de extensión de longitud. Esta es una técnica que permite a un
atacante que conoce el hash de un mensaje M y la longitud de M (sin
conocer el mensaje en sí) calcular el hash de un mensaje M' formado por la concatenación de M con contenido adicional. SHA256,
aunque utiliza el mismo tipo de construcción, es teóricamente resistente a este
tipo de ataque, a diferencia de SHA1 y MD5. Esto podría explicar el misterio
de la doble hash implementada en todo Bitcoin por Satoshi Nakamoto. Para evitar
este tipo de ataque, Satoshi podría haber preferido usar un doble SHA256:
\text{HASH256}(m) = \text{SHA256}(\text{SHA256}(m))
Esto mejora la seguridad contra ataques potenciales relacionados con la construcción de Merkle-Damgård, pero no aumenta la seguridad del proceso de hashing en términos de resistencia a colisiones. Además, incluso si SHA256 hubiera sido vulnerable a este tipo de ataque, no habría tenido un impacto grave, ya que todos los casos de uso de funciones hash en Bitcoin involucran datos públicos. Sin embargo, el ataque de extensión de longitud solo sería útil para un atacante si los datos hasheados son privados y el usuario ha utilizado la función hash como un mecanismo de autenticación para estos datos, similar a un MAC. Por lo tanto, la implementación de doble hashing sigue siendo un misterio en el diseño de Bitcoin. Ahora que hemos examinado en detalle el funcionamiento de las funciones hash, particularmente SHA256, que se utiliza extensivamente en Bitcoin, nos centraremos más específicamente en los algoritmos de derivación criptográfica utilizados a nivel de aplicación, especialmente para derivar las claves para tu billetera.
Los algoritmos utilizados para la derivación
En Bitcoin a nivel de aplicación, además de las funciones hash, se utilizan algoritmos de derivación criptográfica para generar datos seguros a partir de entradas iniciales. Aunque estos algoritmos dependen de las funciones hash, sirven para diferentes propósitos, especialmente en términos de autenticación y generación de claves. Estos algoritmos retienen algunas de las características de las funciones hash, como la irreversibilidad, resistencia a la manipulación y resistencia a colisiones.
En las billeteras de Bitcoin, principalmente se utilizan 2 algoritmos de derivación:
- HMAC (Código de Autenticación de Mensaje Basado en Hash)
- PBKDF2 (Función de Derivación de Clave Basada en Contraseña 2)
Exploraremos juntos el funcionamiento y el papel de cada uno de ellos.
HMAC-SHA512
HMAC (Hash-based Message Authentication Code) es un algoritmo criptográfico que calcula un código de autenticación basado en una combinación de una función hash y una clave secreta. Bitcoin utiliza HMAC-SHA512, la variante de HMAC que usa la función hash SHA512. Ya hemos visto en el capítulo anterior que SHA512 es parte de la misma familia de funciones hash que SHA256, pero produce un output de 512 bits.
Aquí está su esquema de funcionamiento general con m siendo el mensaje de entrada y K una clave secreta:
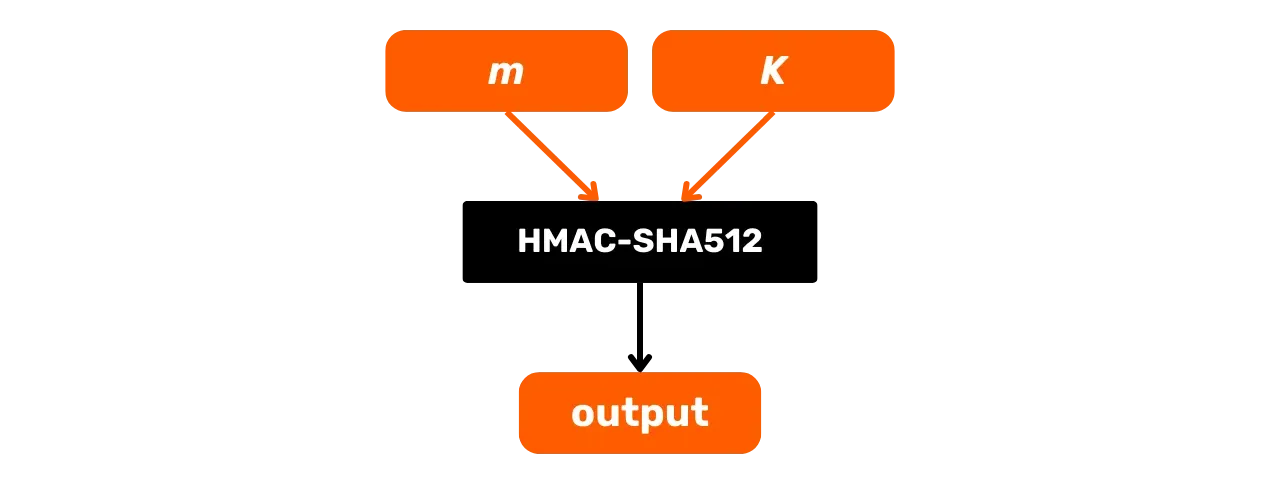
Estudiemos con más detalle lo que sucede en esta caja negra de HMAC-SHA512. La función HMAC-SHA512 con:
m: el mensaje de tamaño arbitrario elegido por el usuario (primera entrada);K: la clave secreta arbitraria elegida por el usuario (segunda entrada);K': la claveKajustada al tamañoBde los bloques de la función hash (1024 bits para SHA512, o 128 bytes);\text{SHA512}: la función hash SHA512;\oplus: la operación XOR (o exclusivo);\Vert: el operador de concatenación, que enlaza cadenas de bits de extremo a extremo;\text{opad}: constante compuesta por el byte0x5crepetido 128 veces\text{ipad}: constante compuesta por el byte0x36repetido 128 veces
Antes de calcular el HMAC, es necesario igualar la clave y las constantes de
acuerdo con el tamaño de bloque B. Por ejemplo, si la clave K es más corta que 128 bytes, se rellena con ceros hasta alcanzar el tamaño B. Si K es más larga que 128 bytes, se comprime usando SHA512, y luego se añaden
ceros hasta que alcanza 128 bytes. De esta manera, se obtiene una clave
igualada denominada K'.
Los valores de \text{opad} y \text{ipad} se
obtienen repitiendo su byte base (0x5c para \text{opad}, 0x36 para \text{ipad})
hasta que se alcanza el tamaño B. Así, con B = 128 bytes, tenemos:
\text{opad} = \underbrace{0x5c5c\ldots5c}_{128 \, \text{bytes}}
Una vez hecho el preprocesamiento, el algoritmo HMAC-SHA512 se define por la siguiente ecuación:
\text {HMAC-SHA512}\_K(m) = \text{SHA512} \left( (K' \oplus \text{opad}) \parallel \text{SHA512} \left( (K' \oplus \text{ipad}) \parallel m \right) \right)
Esta ecuación se desglosa en los siguientes pasos:
- XOR la clave ajustada
K'con\text{ipad}para obtener\text{iKpad}; - XOR la clave ajustada
K'con\text{opad}para obtener\text{oKpad}; - Concatenar
\text{iKpad}con el mensajem. - Hashear este resultado con SHA512 para obtener un hash intermedio
H_1. - Concatenar
\text{oKpad}conH_1. - Hashear este resultado con SHA512 para obtener el resultado final
H_2.
Estos pasos se pueden resumir esquemáticamente de la siguiente manera:
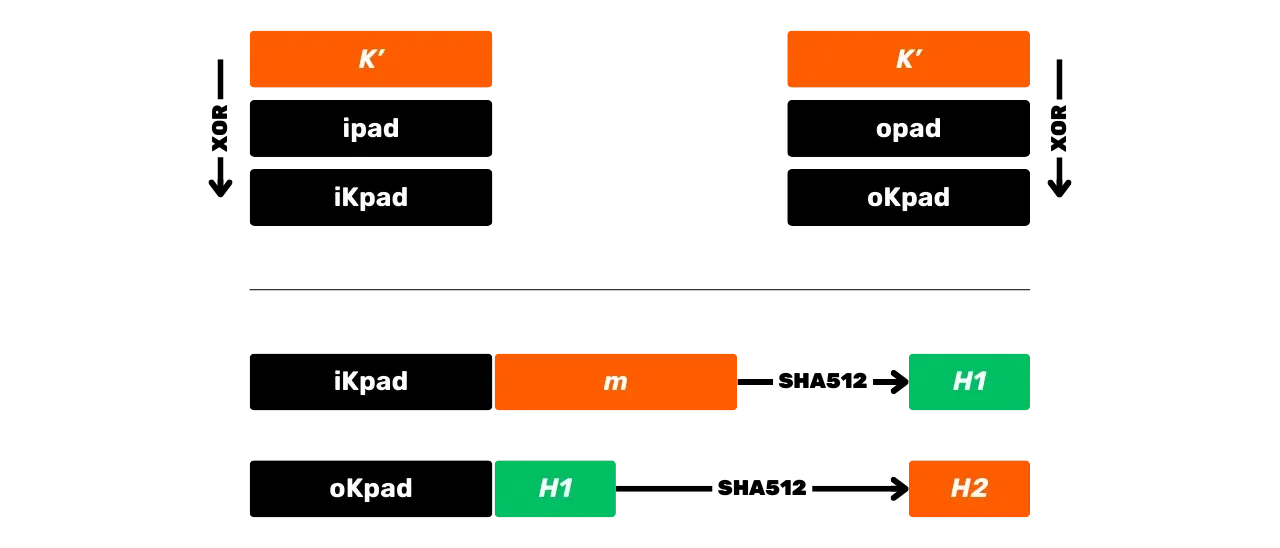
HMAC se utiliza en Bitcoin notablemente para la derivación de claves en carteras HD (Hierarchical Deterministic) (hablaremos de esto con más detalle en los próximos capítulos) y como componente de PBKDF2.
PBKDF2
PBKDF2 (Password-Based Key Derivation Function 2) es un algoritmo de derivación de claves diseñado para mejorar la seguridad de las contraseñas. El algoritmo aplica una función pseudoaleatoria (en este caso, HMAC-SHA512) sobre una contraseña y una sal criptográfica, y luego repite esta operación un cierto número de veces para producir una clave de salida.
En Bitcoin, PBKDF2 se utiliza para generar la semilla de una cartera HD a partir de una frase mnemotécnica y una passphrase (pero hablaremos de esto con más detalle en los próximos capítulos).
El proceso PBKDF2 es el siguiente, con:
m: la frase mnemotécnica del usuario;s: la passphrase opcional para aumentar la seguridad (campo vacío si no hay passphrase);n: el número de iteraciones de la función, en nuestro caso, es 2048.
La función PBKDF2 se define de manera iterativa. Cada iteración toma el resultado de la anterior, lo pasa a través de HMAC-SHA512 y combina los resultados sucesivos para producir la clave final:
\text{PBKDF2}(m, s) = \text{HMAC-SHA512}^{2048}(m, s)
Esquemáticamente, PBKDF2 se puede representar de la siguiente manera:
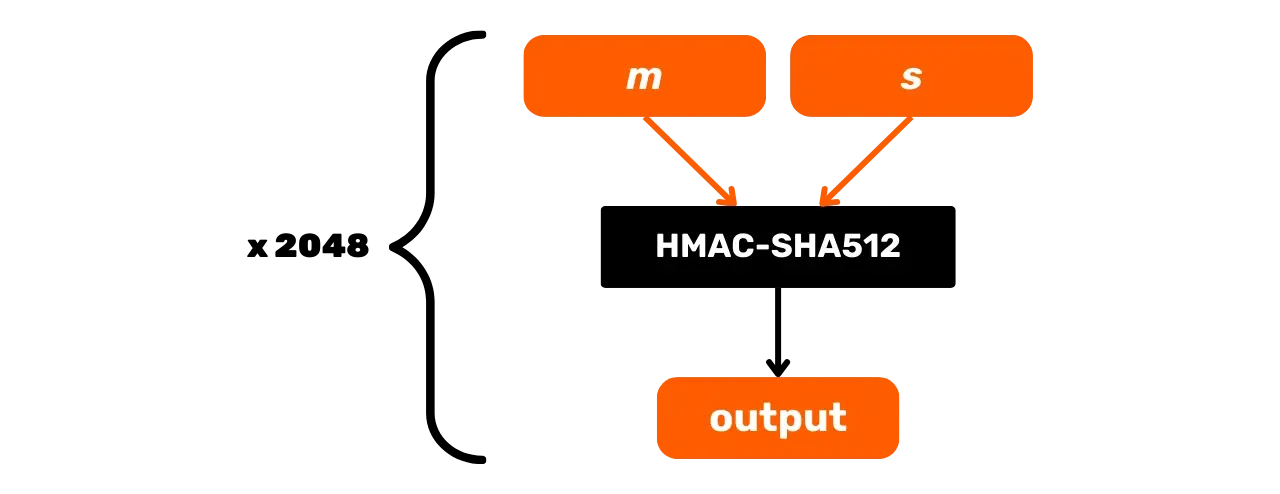
En este capítulo, hemos explorado las funciones HMAC-SHA512 y PBKDF2, que utilizan funciones de hash para asegurar la integridad y seguridad de las derivaciones de claves en el protocolo de Bitcoin. En la próxima parte, veremos las firmas digitales, otro método criptográfico ampliamente utilizado en Bitcoin.
Firmas Digitales
Firmas Digitales y Curvas Elípticas
El segundo método criptográfico utilizado en Bitcoin involucra algoritmos de firma digital. Veamos de qué se trata y cómo funciona.
Bitcoins, UTXOs y Condiciones de Gasto
El término "wallet" (cartera) en Bitcoin puede ser bastante confuso para los principiantes. De hecho, lo que se llama una cartera de Bitcoin es software que no contiene directamente tus bitcoins, a diferencia de una cartera física que puede contener monedas o billetes. Los bitcoins son simplemente unidades de cuenta. Esta unidad de cuenta está representada por UTXO (Unspent Transaction Outputs o Salidas de Transacción No Gastadas), que son salidas de transacciones no gastadas. Si estas salidas no se han gastado, significa que pertenecen a un usuario. Los UTXOs son, de cierta manera, piezas de bitcoins, de tamaño variable, que pertenecen a un usuario.
El protocolo de Bitcoin es distribuido y opera sin una autoridad central. Por lo tanto, no es como los registros bancarios tradicionales, donde los euros que te pertenecen están simplemente asociados con tu identidad personal. En Bitcoin, tus UTXOs te pertenecen porque están protegidos por condiciones de gasto especificadas en el lenguaje Script. Para simplificar, hay dos tipos de scripts: el script de bloqueo (scriptPubKey), que protege un UTXO, y el script de desbloqueo (scriptSig), que permite desbloquear un UTXO y así gastar las unidades de bitcoin que representa. La operación inicial de Bitcoin con scripts P2PK implica usar una clave pública para bloquear fondos, especificando en un scriptPubKey que la persona que desee gastar este UTXO debe proporcionar una firma válida con la clave privada correspondiente a esta clave pública. Para desbloquear este UTXO, por lo tanto, es necesario proporcionar una firma válida en el scriptSig. Como sugieren sus nombres, la clave pública es conocida por todos ya que se transmite en la blockchain, mientras que la clave privada solo es conocida por el legítimo propietario de los fondos.
Esta es la operación básica de Bitcoin, pero con el tiempo, esta operación se ha vuelto más compleja. Primero, Satoshi también introdujo scripts P2PKH, que usan una dirección de recepción en el scriptPubKey, que representa el hash de la clave pública. Luego, el sistema se volvió aún más complejo con la llegada de SegWit y luego Taproot. Sin embargo, el principio general sigue siendo fundamentalmente el mismo: una clave pública o una representación de esta clave se usa para bloquear UTXOs, y se requiere una clave privada correspondiente para desbloquearlos y así gastarlos.
Un usuario que desee realizar una transacción de Bitcoin debe, por lo tanto, crear una firma digital usando su clave privada en la transacción en cuestión. La firma puede ser verificada por otros participantes de la red. Si es válida, esto significa que el usuario que inicia la transacción es de hecho el propietario de la clave privada, y por lo tanto, el propietario de los bitcoins que desea gastar. Otros usuarios pueden entonces aceptar y propagar la transacción.
Como resultado, un usuario que posee bitcoins asegurados con una clave pública debe encontrar una manera de almacenar de forma segura lo que permite desbloquear sus fondos: la clave privada. Una cartera de Bitcoin es precisamente un dispositivo que te permitirá mantener todas tus claves sin que otras personas tengan acceso a ellas. Por lo tanto, es más como un llavero que como una cartera.
El vínculo matemático entre una clave pública y una clave privada, así como la capacidad de realizar una firma para probar la posesión de una clave privada sin revelarla, son posibles gracias a un algoritmo de firma digital. En el protocolo de Bitcoin, se utilizan 2 algoritmos de firma: ECDSA (Elliptic Curve Digital Signature Algorithm) y el esquema de firma Schnorr. ECDSA es el protocolo de firma digital utilizado en Bitcoin desde sus inicios. Schnorr es más reciente en Bitcoin, ya que fue introducido en noviembre de 2021 con la actualización de Taproot.
Estos dos algoritmos son bastante similares en sus mecanismos. Ambos se basan en la criptografía de curva elíptica. La principal diferencia entre estos dos protocolos radica en la estructura de la firma y algunas propiedades matemáticas específicas. Por lo tanto, estudiaremos el funcionamiento de estos algoritmos, comenzando con el más antiguo: ECDSA.
Criptografía de Curva Elíptica
La Criptografía de Curva Elíptica (ECC) es un conjunto de algoritmos que utilizan una curva elíptica por sus diversas propiedades matemáticas y geométricas para fines criptográficos. La seguridad de estos algoritmos se basa en la dificultad del problema del logaritmo discreto en curvas elípticas. Las curvas elípticas se utilizan notablemente para intercambios de claves, cifrado asimétrico o para crear firmas digitales.
Una propiedad importante de estas curvas es que son simétricas con respecto al eje x. Así, cualquier línea no vertical que corte la curva en dos puntos distintos siempre intersectará la curva en un tercer punto. Además, cualquier tangente a la curva en un punto no singular intersectará la curva en otro punto. Estas propiedades serán útiles para definir operaciones en la curva.
Aquí hay una representación de una curva elíptica sobre el campo de los números reales:
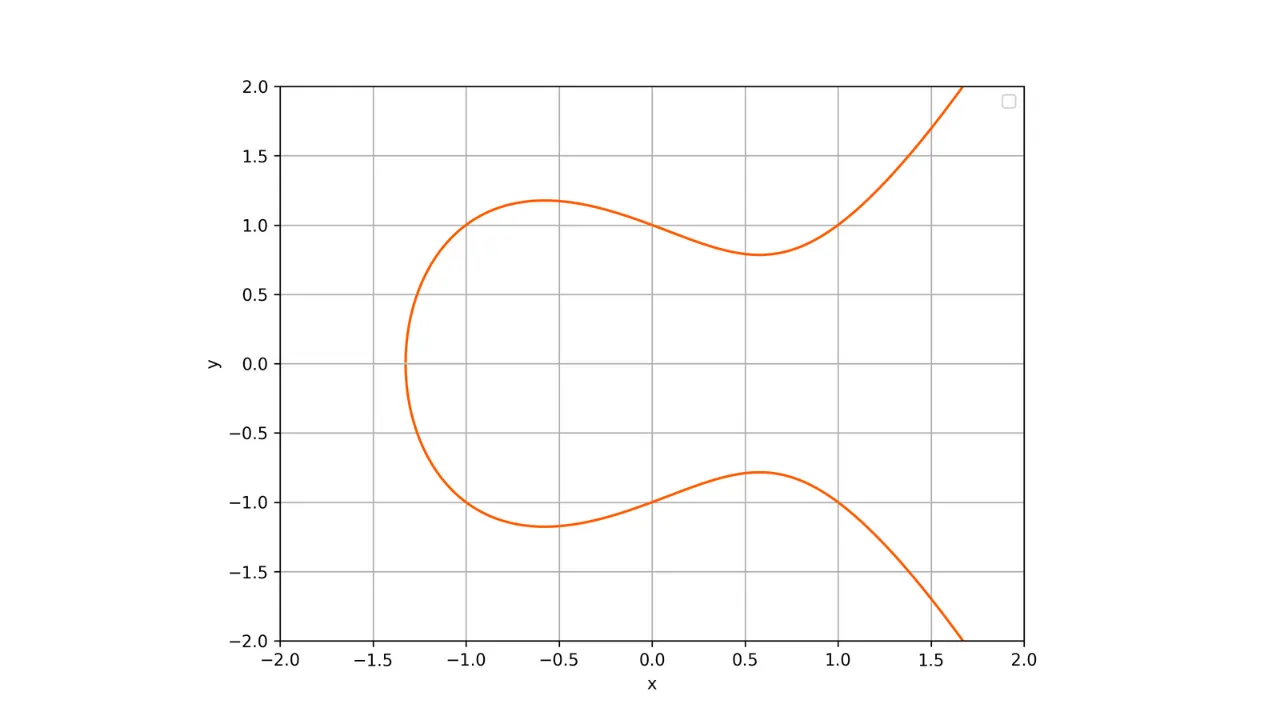
Cada curva elíptica se define por una ecuación de la forma:
y^2 = x^3 + ax + b
secp256k1
Para usar ECDSA o Schnorr, uno debe elegir los parámetros de la curva
elíptica, es decir, los valores de a y b en la ecuación de la
curva. Hay diferentes estándares de curvas elípticas que se reputan como
seguras criptográficamente. La más conocida es la curva secp256r1,
definida y recomendada por el NIST (Instituto Nacional de Estándares y Tecnología).
A pesar de esto, Satoshi Nakamoto, el inventor de Bitcoin, eligió no usar
esta curva. La razón de esta elección es desconocida, pero algunos creen que
prefirió encontrar una alternativa porque los parámetros de esta curva
podrían contener potencialmente una puerta trasera. En su lugar, el
protocolo de Bitcoin utiliza la curva estándar secp256k1. Esta curva está definida por los parámetros a = 0 y b = 7. Su ecuación es, por
lo tanto:
y^2 = x^3 + 7
Su representación gráfica sobre el campo de los números reales se ve así: 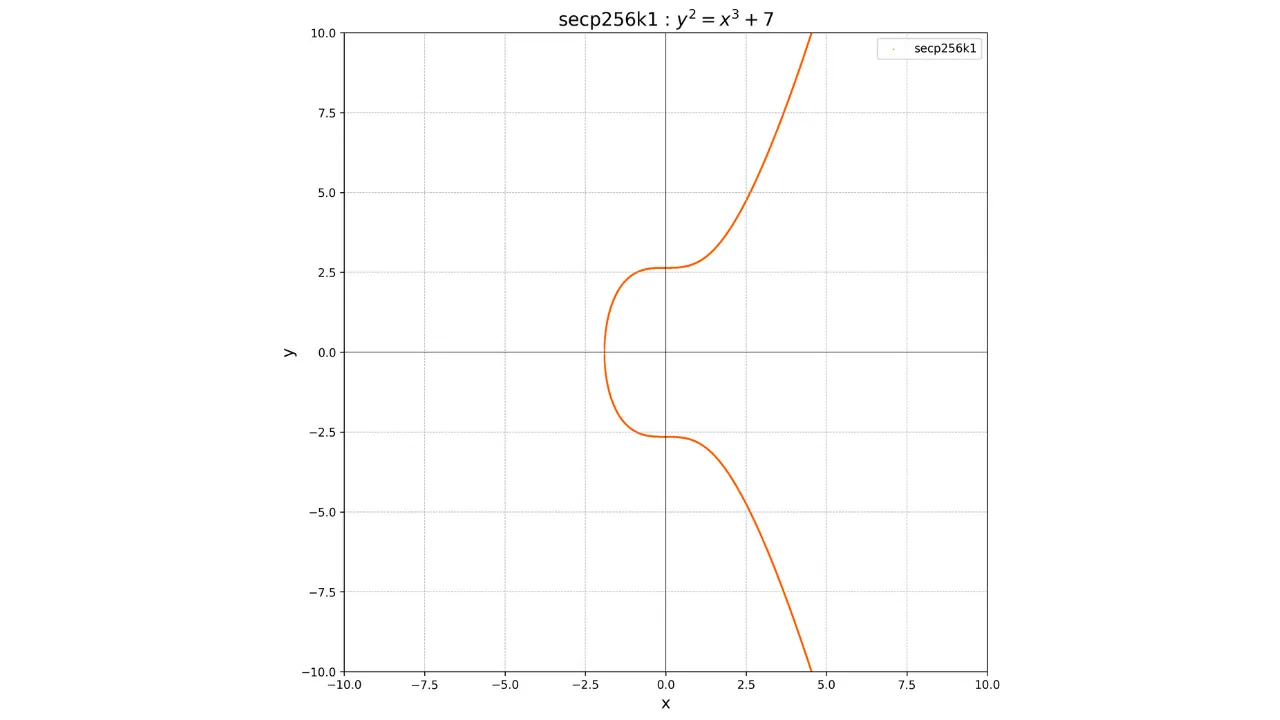 Sin embargo, en criptografía, trabajamos con conjuntos finitos de números. Más
específicamente, trabajamos en el campo finito
Sin embargo, en criptografía, trabajamos con conjuntos finitos de números. Más
específicamente, trabajamos en el campo finito \mathbb{F}_p, que
es el campo de los enteros módulo un número primo p. Definición: Un número primo es un entero natural mayor o
igual a 2 que solo tiene dos divisores enteros positivos distintos: 1 y él
mismo. Por ejemplo, el número 7 es un número primo ya que solo puede ser
dividido por 1 y 7. Por otro lado, el número 8 no es primo porque puede ser
dividido por 1, 2, 4 y 8.
En Bitcoin, el número primo p utilizado para definir el campo finito es muy grande. Se elige de tal manera
que el orden del campo (es decir, el número de elementos en \mathbb{F}_p) sea
suficientemente grande para asegurar la seguridad criptográfica.
El número primo p utilizado es:
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
En notación decimal, esto corresponde a:
p = 2^{256} - 2^{32} - 977
Por lo tanto, la ecuación de nuestra curva elíptica es en realidad:
y^2 \equiv x^3 + 7 \mod p
Dado que esta curva está definida sobre el campo finito \mathbb{F}_p, ya no se asemeja a una curva continua sino más bien a un conjunto
discreto de puntos. Por ejemplo, aquí está cómo se ve la curva utilizada en
Bitcoin para un p muy
pequeño, p = 17:
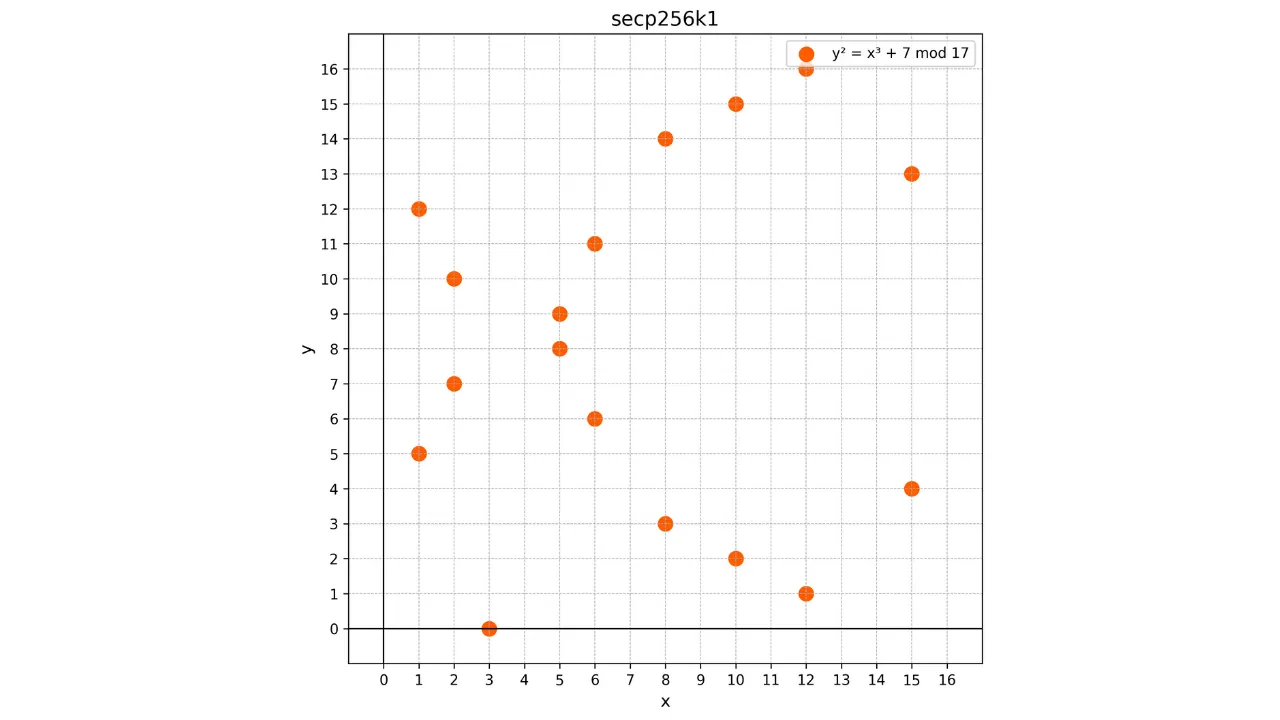
En este ejemplo, he limitado intencionalmente el campo finito a p = 17 por razones educativas, pero uno debe imaginar que el utilizado en Bitcoin
es inmensamente mayor, casi 2^{256}.
Usamos un campo finito de enteros módulo p para asegurar la precisión de las operaciones en la curva. De hecho, las curvas
elípticas sobre el campo de los números reales están sujetas a inexactitudes
debido a errores de redondeo durante los cálculos computacionales. Si se realizan
numerosas operaciones en la curva, estos errores se acumulan y el resultado final
puede ser incorrecto o difícil de reproducir. El uso exclusivo de enteros positivos
asegura una precisión perfecta de los cálculos y, por lo tanto, la reproducibilidad
del resultado.
La matemática de las curvas elípticas sobre campos finitos es análoga a la
de los campos de números reales, con la adaptación de que todas las
operaciones se realizan módulo p. Para simplificar las explicaciones, continuaremos en los siguientes
capítulos ilustrando conceptos usando una curva definida sobre números
reales, mientras mantenemos en mente que, en la práctica, la curva está
definida sobre un campo finito.
Si deseas aprender más sobre los fundamentos matemáticos de la criptografía moderna, también recomiendo consultar este otro curso en Plan ₿ Network:
https://planb.network/courses/d2fd9fc0-d9ed-4a87-9fa3-0fdbb3937e28
Calculando la Clave Pública a partir de la Clave Privada
fcb2bd58-5dda-5ecf-bb8f-ad1a0561ab4a Como se vio anteriormente, los algoritmos de firma digital en Bitcoin se basan en un par de claves privadas y públicas que están matemáticamente vinculadas. Vamos a explorar juntos cuál es este vínculo matemático y cómo se generan.
La Clave Privada
La clave privada es simplemente un número aleatorio o pseudoaleatorio. En el
caso de Bitcoin, este número tiene un tamaño de 256 bits. El número de
posibilidades para una clave privada de Bitcoin es, por lo tanto,
teóricamente 2^{256}.
Nota: Un "número pseudoaleatorio" es un número que tiene
propiedades cercanas a las de un número verdaderamente aleatorio pero es
generado por un algoritmo determinista. Sin embargo, en la práctica, solo
hay n puntos distintos en
nuestra curva elíptica secp256k1, donde n es el orden del punto generador G de la curva. Veremos más adelante a qué corresponde este número, pero
simplemente recuerda que una clave privada válida es un entero entre 1 y n-1, sabiendo que n es un número cercano a, pero ligeramente menor que 2^{256}. Por lo
tanto, hay algunos números de 256 bits que no son válidos para convertirse
en una clave privada en Bitcoin, específicamente, todos los números entre n y 2^{256}. Si la
generación del número aleatorio (la clave privada) produce un valor k tal que k \geq n, se
considera inválido, y debe generarse un nuevo valor aleatorio.
El número de posibilidades para una clave privada de Bitcoin es, por lo
tanto, de aproximadamente n,
que es un número cercano a 1.158 \times 10^{77}. Este número es tan grande que si eliges una clave privada al azar, es
estadísticamente casi imposible caer en la clave privada de otro usuario.
Para darte una idea de la escala, el número de claves privadas posibles en
Bitcoin es de un orden de magnitud cercano al de los átomos estimados en el
universo observable.
Como veremos en los próximos capítulos, hoy en día, la mayoría de las claves privadas utilizadas en Bitcoin no se generan aleatoriamente sino que son el resultado de una derivación determinista de una frase mnemónica, ella misma pseudoaleatoria (esta es la famosa frase de 12 o 24 palabras). Esta información no cambia nada para el uso de algoritmos de firma como ECDSA, pero ayuda a reenfocar nuestra divulgación sobre Bitcoin.
Para la continuación de la explicación, la clave privada se denotará con la
letra minúscula k.
La Clave Pública
La clave pública es un punto en la curva elíptica, denotado por la letra
mayúscula K, y se calcula a
partir de la clave privada k.
Este punto K está
representado por un par de coordenadas (x, y) en la curva elíptica, siendo cada coordenada un entero módulo p, el número primo que define
el campo finito \mathbb{F}_p.
En la práctica, una clave pública no comprimida se representa por 512 bits
(o 64 bytes), correspondientes a dos números de 256 bits (x y y) colocados uno tras otro.
Estos números son la abscisa (x) y la ordenada (y) de
nuestro punto en secp256k1. Si añadimos el prefijo, la clave pública
totaliza 520 bits.
Sin embargo, también es posible representar la clave pública en una forma
comprimida usando solo 33 bytes (264 bits) manteniendo solo la abscisa x de nuestro punto en la curva y un byte indicando la paridad de y. Esto es lo que se conoce
como una clave pública comprimida. Hablaré más sobre esto en los últimos
capítulos de esta formación. Pero lo que necesitas recordar es que una clave
pública K es un punto
descrito por x y y.
Para calcular el punto K que
corresponde a nuestra clave pública, usamos la operación de multiplicación
escalar en curvas elípticas, definida como una adición repetida (k veces) del punto generador G:
K = k \cdot G
donde:
kes la clave privada (un entero aleatorio entre1yn-1);Ges el punto generador de la curva elíptica utilizado por todos los participantes de la red Bitcoin; -\cdotrepresenta la multiplicación escalar en la curva elíptica, lo cual es equivalente a sumar el puntoGconsigo mismokveces.
El hecho de que este punto G sea común a todas las claves públicas en Bitcoin nos permite estar seguros
de que la misma clave privada k siempre nos dará la misma clave pública K:
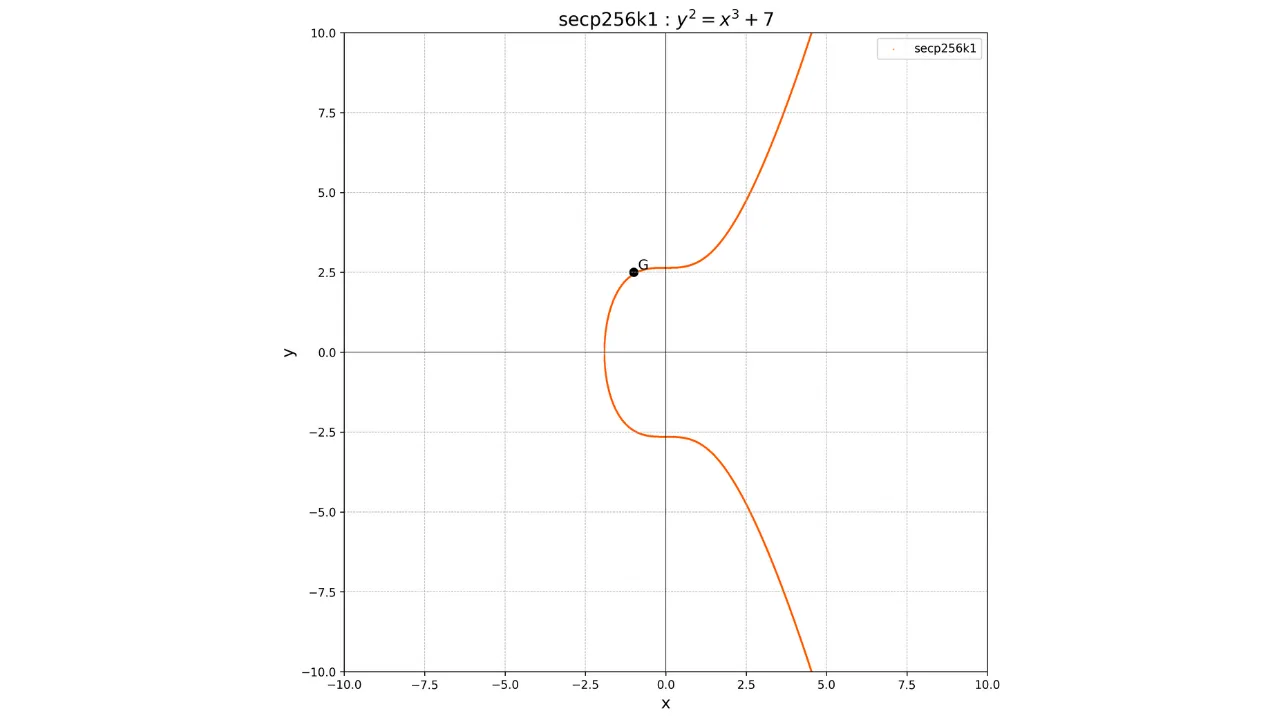
La principal característica de esta operación es que es una función
unidireccional. Es fácil calcular la clave pública K conociendo la clave privada k y el punto generador G, pero
es prácticamente imposible calcular la clave privada k conociendo solo la clave pública K y el punto generador G.
Encontrar k a partir de K y G equivale a resolver el problema
del logaritmo discreto en curvas elípticas, un problema matemáticamente difícil
para el cual no se conoce ningún algoritmo eficiente. Incluso los calculadores
más potentes actuales son incapaces de resolver este problema en un tiempo razonable.

Adición y Duplicación de Puntos en Curvas Elípticas
El concepto de adición en curvas elípticas se define geométricamente. Si
tenemos dos puntos P y Q en la curva, la operación P + Q se calcula trazando una línea que pase por P y Q. Esta línea
necesariamente intersectará la curva en un tercer punto R'. Luego tomamos la imagen
espejo de este punto con respecto al eje x para obtener el punto R, que es el resultado de la
adición:
P + Q = R
Gráficamente, esto se puede representar de la siguiente manera:
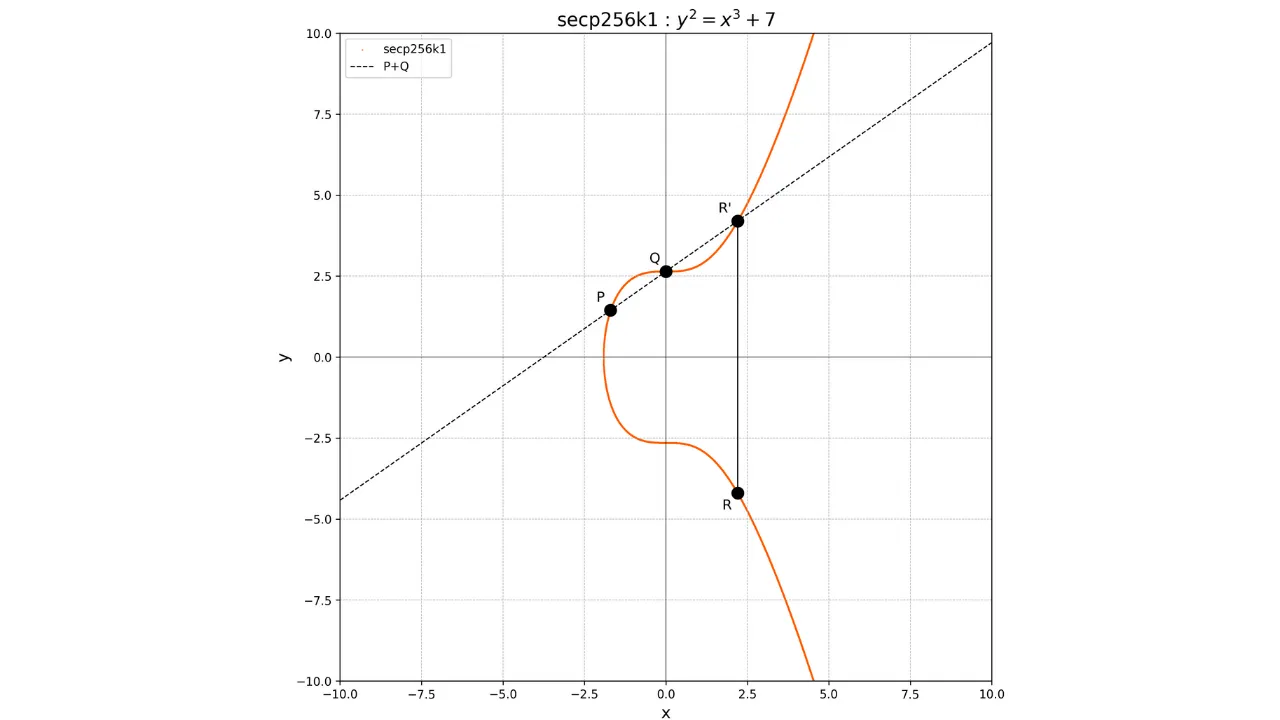
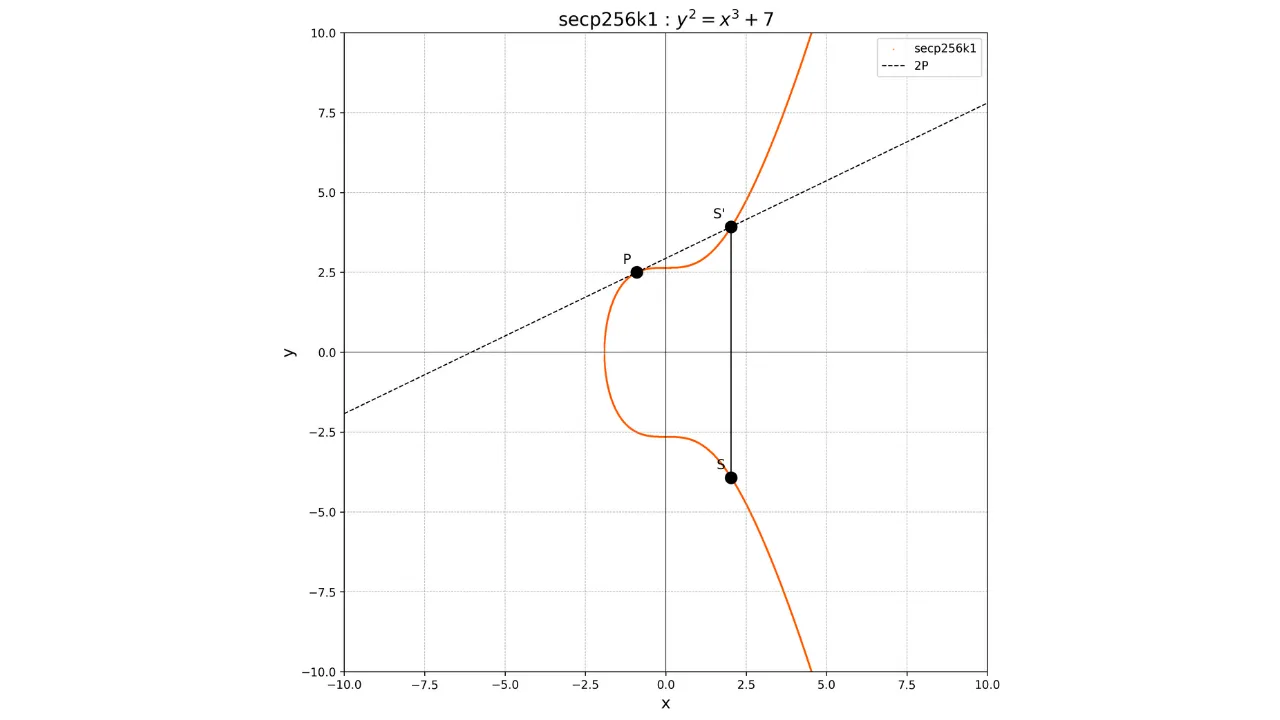
Para la duplicación de un punto, es decir, la operación P + P, trazamos la tangente a la curva en el punto P. Esta tangente intersecta
la curva en otro punto S'.
Luego tomamos la imagen espejo de este punto con respecto al eje x para
obtener el punto S, que es el
resultado de la duplicación:
2P = S
Gráficamente, se muestra así:
Utilizando estas operaciones de adición y duplicación, podemos realizar la
multiplicación escalar de un punto por un entero k, denotado kP, realizando
duplicaciones y adiciones repetidas.
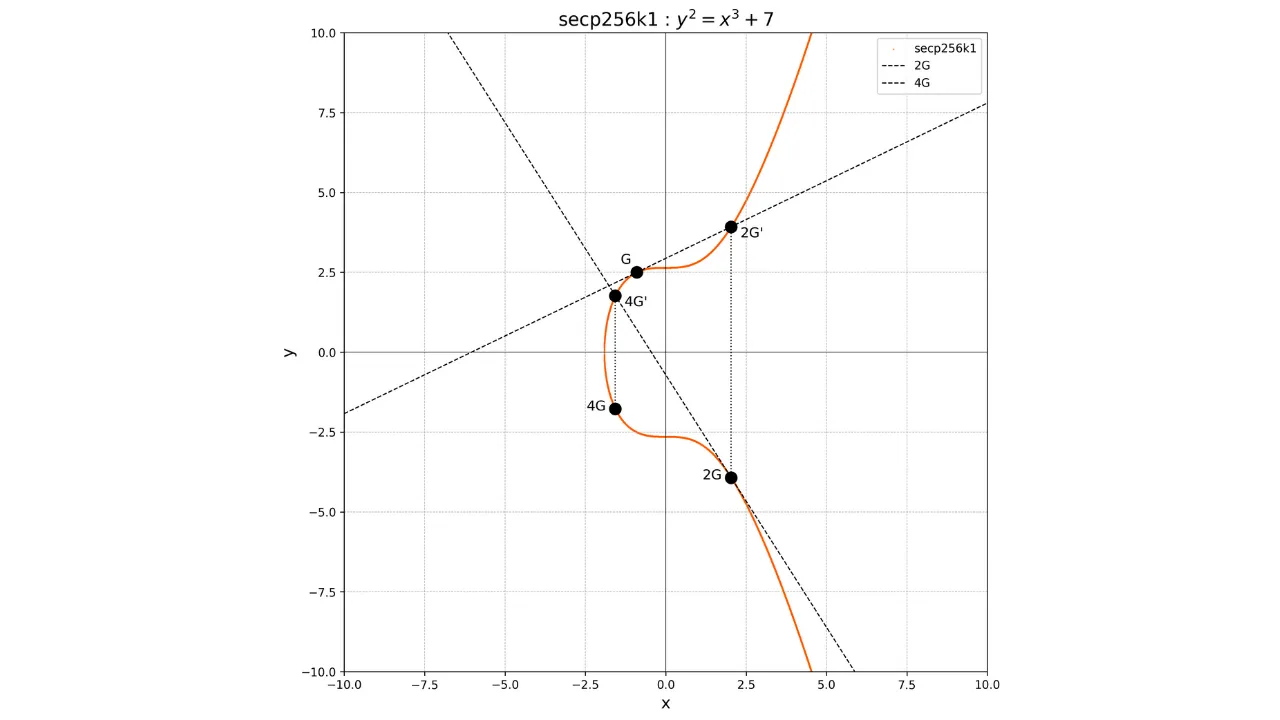
Por ejemplo, supongamos que hemos elegido una clave privada k = 4. Para calcular la clave pública asociada, realizamos:
K = k \cdot G = 4G
Gráficamente, esto corresponde a realizar una serie de adiciones y duplicaciones:
- Calcular
2GduplicandoG. - Calcular
4Gduplicando2G.

Si deseamos, por ejemplo, calcular el punto 3G, primero debemos calcular el punto 2G duplicando el punto G, luego
sumar G y 2G. Para sumar G y 2G, simplemente trazamos la
línea que conecta estos dos puntos, recuperamos el único punto -3G en la intersección entre esta línea y la curva elíptica, y luego
determinamos 3G como el
opuesto de -3G.
Tendremos:
G + G = 2G
2G + G = 3G
Gráficamente, esto se representaría de la siguiente manera: 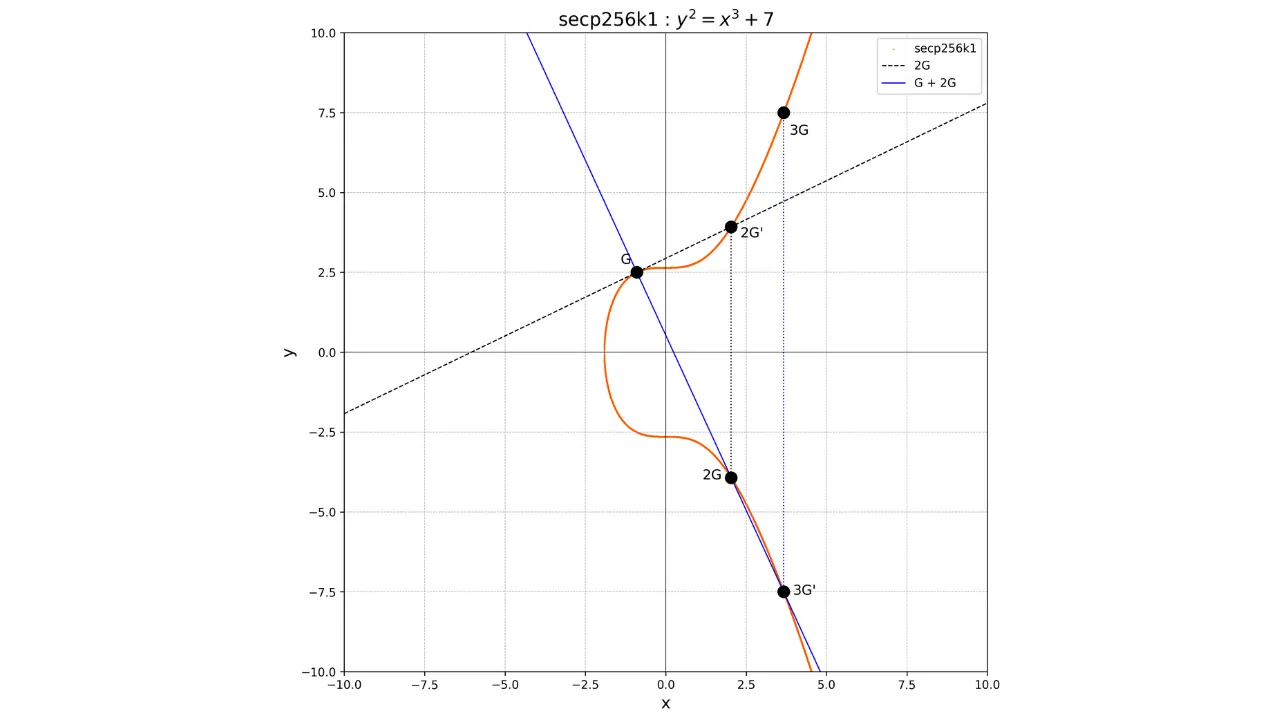
Función Unidireccional
Gracias a estas operaciones, podemos entender por qué es fácil derivar una clave pública a partir de una clave privada, pero lo contrario es prácticamente imposible.
Volvamos a nuestro ejemplo simplificado. Con una clave privada k = 4. Para calcular la clave pública asociada, realizamos:
K = k \cdot G = 4GAsí hemos podido calcular fácilmente la clave pública K conociendo k y G.
Ahora, si alguien solo conoce la clave pública K, se enfrenta al problema del logaritmo discreto: encontrar k tal que K = k \cdot G. Este
problema se considera difícil porque no existe un algoritmo eficiente para
resolverlo en curvas elípticas. Esto asegura la seguridad de los algoritmos
ECDSA y Schnorr.
Por supuesto, en este ejemplo simplificado con k = 4, sería posible encontrar k mediante prueba y error, ya que el número de posibilidades es bajo. Sin
embargo, en la práctica en Bitcoin, k es un entero de 256 bits, lo que hace que el número de posibilidades sea
astronómicamente grande (alrededor de 1.158 \times 10^{77}). Por lo tanto, es inviable encontrar k por fuerza bruta.
Firmando con la Clave Privada
Ahora que sabes cómo derivar una clave pública a partir de una clave
privada, ya puedes recibir bitcoins utilizando este par de claves como
condición de gasto. Pero, ¿cómo gastarlos? Para gastar bitcoins, necesitarás
desbloquear el scriptPubKey adjunto a tu UTXO para probar que eres
de hecho su legítimo propietario. Para hacer esto, debes producir una firma s que coincida con la clave pública K presente en el scriptPubKey utilizando la clave privada k que se utilizó inicialmente para calcular K. La firma digital es así
una prueba irrefutable de que estás en posesión de la clave privada asociada
con la clave pública que reclamas.
Parámetros de la Curva Elíptica
Para realizar una firma digital, todos los participantes deben primero acordar los parámetros de la curva elíptica utilizada. En el caso de Bitcoin, los parámetros de secp256k1 son los siguientes:
El campo finito \mathbb{Z}_p definido por:
p = 2^{256} - 2^{32} - 977p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
p es un número primo muy
grande ligeramente menor que 2^{256}.
La curva elíptica y^2 = x^3 + ax + b sobre \mathbb{Z}_p definida
por:
a = 0, \quad b = 7El punto generador o punto de origen G:
G = 0x0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
Este número es la forma comprimida que solo da la abscisa del punto G. El prefijo 02 al principio determina cuál de los dos valores
que tienen esta abscisa x se
debe usar como punto generador. El orden n de G (el número de puntos
existentes) y el cofactor h:
$n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
n es un número muy grande
ligeramente menor que p.
h=1h es el cofactor o el número
de subgrupos. No me extenderé sobre lo que esto representa aquí, ya que es
bastante complejo, y en el caso de Bitcoin, no necesitamos tenerlo en cuenta
ya que es igual a 1.
Toda esta información es pública y conocida por todos los participantes. Gracias a ella, los usuarios pueden realizar una firma digital y verificarla.
Firma con ECDSA
El algoritmo ECDSA permite a un usuario firmar un mensaje usando su clave privada, de tal manera que cualquiera que conozca la clave pública correspondiente puede verificar la validez de la firma, sin que la clave privada sea revelada. En el contexto de Bitcoin, el mensaje a firmar depende del sighash elegido por el usuario. Es este sighash el que determinará qué partes de la transacción están cubiertas por la firma. Hablaré más sobre esto en el próximo capítulo.
Aquí están los pasos para generar una firma ECDSA:
Primero, calculamos el hash (e) del mensaje que necesita ser firmado. El mensaje m es pasado a través de una función
hash criptográfica, generalmente SHA256 o doble SHA256 en el caso de Bitcoin:
e = \text{HASH}(m)A continuación, calculamos un nonce. En criptografía, un nonce es
simplemente un número generado de manera aleatoria o pseudo-aleatoria que se
usa solo una vez. Es decir, cada vez que se hace una nueva firma digital con
este par de claves, será muy importante usar un nonce diferente, de lo
contrario, comprometerá la seguridad de la clave privada. Por lo tanto, es
suficiente determinar un entero aleatorio y único r tal que 1 \leq r \leq n-1,
donde n es el orden del punto
generador G de la curva elíptica.
Luego, calcularemos el punto R en la curva elíptica con las coordenadas (x_R, y_R) tal que:
R = r \cdot GExtraemos el valor de la abscisa del punto R (x_R). Este valor representa
la primera parte de la firma. Y finalmente, calculamos la segunda parte de
la firma s de esta manera:
s = r^{-1} \left( e + k \cdot x_R \right) \mod ndonde:
r^{-1}es el inverso modular dermódulon, es decir, un entero tal quer \cdot r^{-1} \equiv 1 \mod n;kes la clave privada del usuario;ees el hash del mensaje;nes el orden del punto generadorGde la curva elíptica.
La firma es entonces simplemente la concatenación de x_R y s:
\text{SIG} = x_R \Vert sVerificación de la Firma ECDSA
Para verificar una firma (x_R, s), cualquiera que conozca la clave pública K y los parámetros de la curva elíptica puede proceder de esta manera:
Primero, verifica que x_R y s estén dentro del intervalo [1, n-1]. Esto asegura que la
firma respeta las restricciones matemáticas del grupo elíptico. Si este no
es el caso, el verificador rechaza inmediatamente la firma como inválida.
Luego, calcula el hash del mensaje:
e = \text{HASH}(m)Calcula el inverso modular de s módulo n:
s^{-1} \mod nCalcula dos valores escalares u_1 y u_2 de esta manera:
\begin{align*}
u_1 &= e \cdot s^{-1} \mod n \\
u_2 &= x_R \cdot s^{-1} \mod n
\end{align*}Y finalmente, calcula el punto V en la curva elíptica tal que:
V = u_1 \cdot G + u_2 \cdot KLa firma es válida solo si x_V \equiv x_R \mod n, donde x_V es la coordenada x del punto V. De hecho,
combinando u_1 \cdot G y u_2 \cdot K, se obtiene un
punto V que, si la firma es
válida, debe corresponder al punto R utilizado durante la firma (módulo n).
Firma con el Protocolo Schnorr
El esquema de firma Schnorr es una alternativa a ECDSA que ofrece muchas
ventajas. Ha sido posible usarlo en Bitcoin desde 2021 y la introducción de
Taproot, con los patrones de script P2TR. Al igual que ECDSA, el esquema
Schnorr permite firmar un mensaje usando una clave privada, de tal manera
que la firma puede ser verificada por cualquiera que conozca la clave
pública correspondiente. En el caso de Schnorr, se utiliza la misma curva
exacta que ECDSA con los mismos parámetros. Sin embargo, las claves públicas
se representan de manera ligeramente diferente en comparación con ECDSA. De
hecho, solo se designan por la coordenada x del punto en la curva elíptica. A diferencia de ECDSA, donde las claves
públicas comprimidas se representan por 33 bytes (con el byte de prefijo
indicando la paridad de y),
Schnorr utiliza claves públicas de 32 bytes, correspondientes solo a la
coordenada x del punto K, y se asume por defecto que y es par. Esta representación simplificada reduce el tamaño de las firmas y
facilita ciertas optimizaciones en los algoritmos de verificación. La clave
pública es entonces la coordenada x del punto K:
\text{pk} = K_xEl primer paso para generar una firma es hacer hash del mensaje. Pero a diferencia de ECDSA, se hace con otros valores y se utiliza una función de hash etiquetada para evitar colisiones en diferentes contextos. Una función de hash etiquetada simplemente implica agregar una etiqueta arbitraria a las entradas de la función de hash junto con los datos del mensaje.
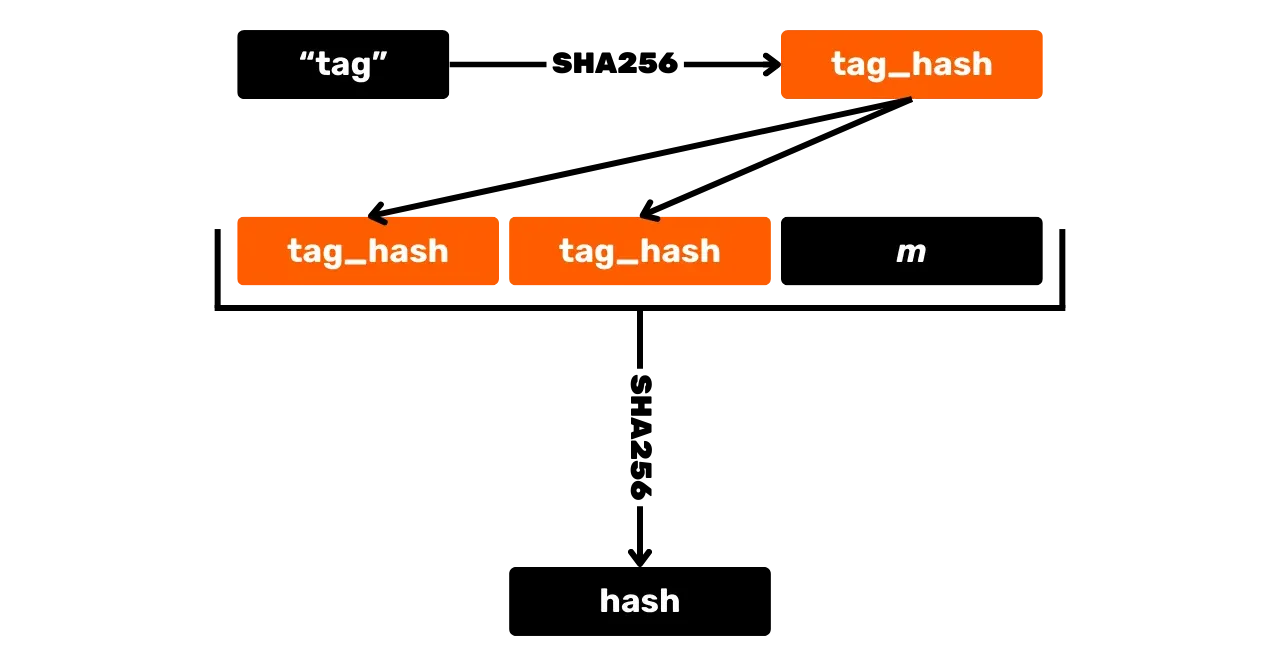
Además del mensaje, la coordenada x de la clave pública K_x, así
como un punto R calculado a
partir del nonce r (R=r \cdot G) que es en sí mismo un entero único para cada firma, calculado de manera
determinista a partir de la clave privada y el mensaje para evitar
vulnerabilidades relacionadas con la reutilización del nonce, también se
pasan a la función etiquetada. Al igual que para la clave pública, solo se
retiene la coordenada x del
punto nonce R_x para describir
el punto.
El resultado de este hash, notado e, se llama "the challenge" (el desafio):
e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod nAquí, \text{HASH} es la función de hash SHA256, y \text{``BIP0340/challenge''} es la etiqueta específica para el hashing.
Finalmente, el parámetro s se
calcula de esta manera a partir de la clave privada k, el nonce r, y el desafío e:
s = (r + e \cdot k) \mod nLa firma es entonces simplemente el par Rx y s.
\text{SIG} = R_x \Vert sVerificación de la Firma Schnorr
La verificación de una firma Schnorr es más simple que la de una firma
ECDSA. Aquí están los pasos para verificar la firma (R_x, s) con la clave pública K_x y el
mensaje m: Primero,
verificamos que K_x sea un
entero válido y menor que p.
Si este es el caso, recuperamos el punto correspondiente en la curva con K_y siendo par. También extraemos R_x y s separando la firma \text{SIG}. Luego,
comprobamos que R_x < p y s < n (el orden de la
curva). A continuación, calculamos el desafío e de la misma manera que el emisor
de la firma:
e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod nLuego, calculamos un punto de referencia en la curva de esta manera:
R' = s \cdot G - e \cdot KFinalmente, verificamos que R'_x = R_x. Si las dos coordenadas x coinciden, entonces la firma (R_x, s) es de hecho válida con la clave pública K_x.
¿Por qué funciona esto?
El firmante ha calculado s = r + e \cdot k \mod n, así que R' = s \cdot G - e \cdot K debería ser igual al punto original R, porque:
s \cdot G = (r + e \cdot k) \cdot G = r \cdot G + e \cdot k \cdot GDado que K = k \cdot G,
tenemos e \cdot k \cdot G = e \cdot K. Así:
R' = r \cdot G = RPor lo tanto, tenemos:
R'_x = R_xLas ventajas de las firmas Schnorr
El esquema de firma Schnorr ofrece varias ventajas para Bitcoin sobre el algoritmo ECDSA original. Primero, Schnorr permite la agregación de claves y firmas. Esto significa que múltiples claves públicas pueden combinarse en una sola clave.
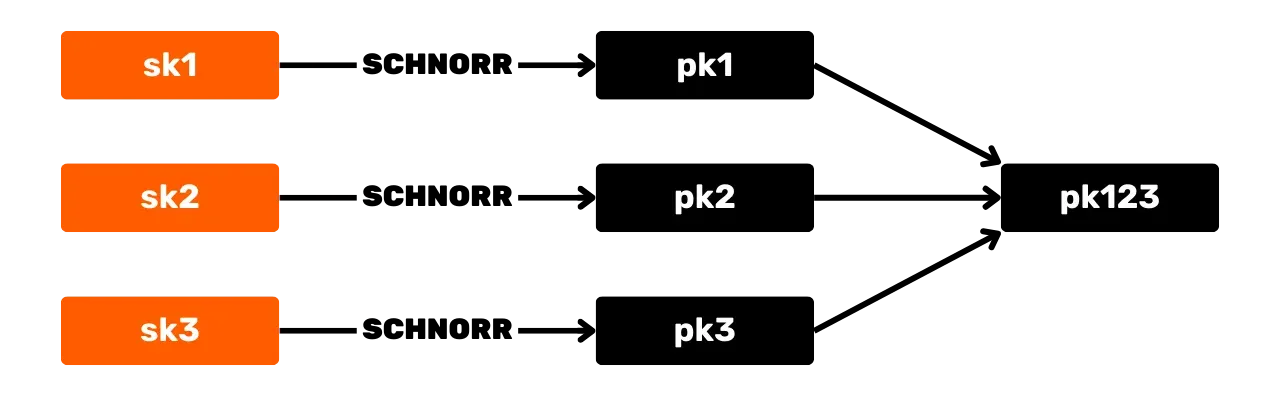
Y de manera similar, múltiples firmas pueden ser agregadas en una única firma válida. Así, en el caso de una transacción de multifirma, un conjunto de participantes puede firmar con una única firma y una única clave pública agregada. Esto reduce significativamente los costos de almacenamiento y computación para la red, ya que cada nodo solo necesita verificar una única firma.

Además, la agregación de firmas mejora la privacidad. Con Schnorr, se vuelve imposible distinguir una transacción multifirma de una transacción de firma única estándar. Esta homogeneidad hace que el análisis de la cadena sea más difícil, ya que limita la capacidad de identificar huellas de billeteras. Finalmente, Schnorr también ofrece la posibilidad de verificación por lotes. Al verificar múltiples firmas simultáneamente, los nodos pueden ganar eficiencia, especialmente para bloques que contienen muchas transacciones. Esta optimización reduce el tiempo y los recursos necesarios para validar un bloque. Además, las firmas Schnorr no son maleables, a diferencia de las firmas producidas con ECDSA. Esto significa que un atacante no puede modificar una firma válida para crear otra firma válida para el mismo mensaje y la misma clave pública. Esta vulnerabilidad estaba previamente presente en Bitcoin y evitaba notablemente la implementación segura de la Lightning Network. Se resolvió para ECDSA con el softfork SegWit en 2017, que implica mover las firmas a una base de datos separada de las transacciones para prevenir su maleabilidad.
¿Por qué Satoshi eligió ECDSA?
Como hemos visto, Satoshi inicialmente eligió implementar ECDSA para firmas digitales en Bitcoin. Sin embargo, también hemos visto que Schnorr es superior a ECDSA en muchos aspectos, y este protocolo fue creado por Claus-Peter Schnorr en 1989, 20 años antes de la invención de Bitcoin.
Bueno, realmente no sabemos por qué Satoshi no lo eligió, pero una hipótesis probable es que este protocolo estaba bajo patente hasta 2008. Aunque Bitcoin fue creado un año después, en enero de 2009, no había una estandarización de código abierto para las firmas Schnorr disponible en ese momento. Quizás Satoshi consideró más seguro usar ECDSA, que ya estaba ampliamente utilizado y probado en software de código abierto y tenía varias implementaciones reconocidas (notablemente la biblioteca OpenSSL utilizada hasta 2015 en Bitcoin Core, luego reemplazada por libsecp256k1 en la versión 0.10.0). O tal vez simplemente no estaba al tanto de que esta patente iba a expirar en 2008. En cualquier caso, la hipótesis más probable parece estar relacionada con esta patente y el hecho de que ECDSA tenía un historial probado y era más fácil de implementar.
Los sighash flags
Como hemos visto en capítulos anteriores, las firmas digitales se utilizan a
menudo para desbloquear el script de una entrada. En el proceso de firma, es
necesario incluir los datos firmados en el cálculo, designados en nuestros
ejemplos por el mensaje m.
Estos datos, una vez firmados, no pueden ser modificados sin invalidar la
firma. De hecho, ya sea para ECDSA o Schnorr, el verificador de la firma
debe incluir en su cálculo el mismo mensaje m. Si difiere del mensaje m inicialmente utilizado por el
firmante, el resultado será incorrecto y la firma se considerará inválida. Entonces
se dice que una firma cubre ciertos datos y los protege, de cierta manera, contra
modificaciones no autorizadas.
¿Qué es un sighash flash?
En el caso específico de Bitcoin, hemos visto que el mensaje m corresponde a la transacción. Sin embargo, en realidad, es un poco más complejo.
De hecho, gracias a los flags de sighash, es posible seleccionar datos específicos
dentro de la transacción que estarán cubiertos o no por la firma.
El "flag de sighash" es, por lo tanto, un parámetro agregado a cada entrada, permitiendo la determinación de los componentes de una transacción que están cubiertos por la firma asociada. Estos componentes son las entradas y las salidas. La elección del flag de sighash determina así cuáles entradas y cuáles salidas de la transacción son fijadas por la firma y cuáles pueden aún ser modificadas sin invalidarla. Este mecanismo permite que las firmas comprometan datos de la transacción de acuerdo con las intenciones del firmante.
Obviamente, una vez que la transacción es confirmada en la blockchain, se vuelve inmutable, independientemente de los flags de sighash utilizados. La posibilidad de modificación a través de los flags de sighash está limitada al período entre la firma y la confirmación.
Generalmente, el software de billetera no te ofrece la opción de modificar
manualmente el flag de sighash de tus entradas cuando construyes una
transacción. Por defecto, se establece SIGHASH_ALL.
Personalmente, solo conozco Sparrow Wallet que permite esta modificación
desde la interfaz de usuario.
¿Cuáles son los flags de sighash existentes en Bitcoin?
En Bitcoin, hay 3 flags de sighash básicos:
SIGHASH_ALL(0x01): La firma se aplica a todas las entradas y todas las salidas de la transacción. La transacción está así completamente cubierta por la firma y ya no puede ser modificada.SIGHASH_ALLes el sighash más comúnmente usado en transacciones cotidianas cuando uno simplemente quiere realizar una transacción sin que pueda ser modificada.

En todos los diagramas de este capítulo, el color naranja representa los elementos cubiertos por la firma, mientras que el color negro indica aquellos que no lo están.
SIGHASH_NONE(0x02): La firma cubre todas las entradas pero ninguna de las salidas, permitiendo así la modificación de las salidas después de la firma. En términos concretos, esto es similar a un cheque en blanco. El firmante desbloquea los UTXOs en las entradas pero deja el campo de las salidas completamente modificable. Cualquiera que conozca esta transacción puede así agregar el output de su elección, por ejemplo especificando una dirección de recepción para recoger los fondos consumidos por las entradas, y luego transmitir la transacción para recuperar los bitcoins. La firma del propietario de las entradas no será invalidada, ya que solo cubre las entradas.

SIGHASH_SINGLE(0x03): La firma cubre todas las entradas así como una único output, correspondiente al índice del input firmado. Por ejemplo, si la firma desbloquea el scriptPubKey del input #0, entonces también cubre el output #0. La firma también protege todas las otras entradas, las cuales ya no pueden ser modificadas. Sin embargo, cualquiera puede agregar un output adicional sin invalidar la firma, siempre que el output #0, que es la única cubierta por ella, no sea modificada.
Además de estos tres flags de sighash, también existe el modificador SIGHASH_ANYONECANPAY (0x80). Este modificador puede combinarse con un flag de
sighash básico para crear tres nuevos flags de sighash:
SIGHASH_ALL | SIGHASH_ANYONECANPAY(0x81): La firma cubre una única entrada mientras incluye todas las salidas de la transacción. Este flag de sighash combinado permite, por ejemplo, la creación de una transacción de crowdfunding. El organizador prepara el output con su dirección y el monto objetivo, y cada inversor puede entonces agregar entradas para financiar este output. Una vez que se reúnen fondos suficientes en las entradas para satisfacer el output, la transacción puede ser transmitida.

SIGHASH_NONE | SIGHASH_ANYONECANPAY(0x82): La firma cubre una única entrada, sin comprometerse con ningun output;

SIGHASH_SINGLE | SIGHASH_ANYONECANPAY(0x83): La firma cubre una sola entrada así como el output que tiene el mismo índice que esta entrada. Por ejemplo, si la firma desbloquea el scriptPubKey del input #3, también cubrirá el output #3. El resto de la transacción permanece modificable, tanto en términos de otras entradas como de otras salidas.
Proyectos para Agregar Nuevos sighash flags
Actualmente (2024), solo los sighash flags presentados en la sección
anterior son utilizables en Bitcoin. Sin embargo, algunos proyectos están
considerando la adición de nuevas banderas de sighash. Por ejemplo, el
BIP118, propuesto por Christian Decker y Anthony Towns, introduce dos nuevos
sighash flags: SIGHASH_ANYPREVOUT y SIGHASH_ANYPREVOUTANYSCRIPT (AnyPrevOut = "Cualquier Salida Anterior").
Estas dos banderas de sighash ofrecerían una posibilidad adicional en Bitcoin: crear firmas que no cubren ninguna entrada específica de la transacción.

Esta idea fue inicialmente formulada por Joseph Poon y Thaddeus Dryja en el
White Paper de Lightning. Antes de su renombramiento, esta bandera de
sighash se llamaba SIGHASH_NOINPUT. Si esta bandera de sighash
se integra en Bitcoin, permitirá el uso de covenants, pero también es un
prerrequisito obligatorio para implementar Eltoo, un protocolo general para
segundas capas que define cómo gestionar conjuntamente la propiedad de un
UTXO. Eltoo fue diseñado específicamente para resolver los problemas
asociados con los mecanismos para negociar el estado de los canales de
Lightning, es decir, entre la apertura y el cierre.
Para profundizar tu conocimiento sobre la Red Lightning, después del curso CYP201, te recomiendo altamente el curso LNP201 por Fanis Michalakis, que cubre el tema en detalle:
https://planb.network/courses/34bd43ef-6683-4a5c-b239-7cb1e40a4aeb
En la siguiente parte, propongo descubrir el funcionamiento de la frase mnemónica en tu billetera Bitcoin.
La frase mnemónica
Evolución de las billeteras Bitcoin
Ahora que hemos explorado el funcionamiento de las funciones hash y las firmas digitales, podemos estudiar cómo funcionan las billeteras Bitcoin. El objetivo será imaginar cómo se construye una billetera en Bitcoin, cómo se descompone y cuáles son las diferentes piezas de información que la constituyen y para qué se utilizan. Este entendimiento de los mecanismos de la billetera te permitirá mejorar tu uso de Bitcoin en términos de seguridad y privacidad.
Antes de sumergirnos en los detalles técnicos, es esencial aclarar qué se entiende por "billetera Bitcoin" y comprender su utilidad.
¿Qué es una billetera Bitcoin?
A diferencia de las billeteras tradicionales, que te permiten almacenar billetes y monedas físicas, una billetera Bitcoin no "contiene" bitcoins per se. De hecho, los bitcoins no existen en una forma física o digital que pueda ser almacenada, sino que están representados por unidades de cuenta descritas en el sistema en forma de UTXOs (Unspent Transaction Outputs - Salida de Transacción No Gastada).
Los UTXOs representan fragmentos de bitcoins, de diversos tamaños, que pueden ser gastados siempre que su scriptPubKey sea satisfecho. Para gastar sus bitcoins, un usuario debe proporcionar un scriptSig que desbloquee el scriptPubKey asociado con su UTXO. Esta prueba generalmente se realiza a través de una firma digital, generada desde la clave privada correspondiente a la clave pública presente en el scriptPubKey. Por lo tanto, el elemento crucial que el usuario debe asegurar es la clave privada. El papel de una billetera de Bitcoin es precisamente gestionar estas claves privadas de manera segura. En realidad, su papel es más similar al de un llavero que al de una billetera en el sentido tradicional.
JBOK Wallets (Just a Bunch Of Keys)
Las primeras billeteras utilizadas en Bitcoin fueron las billeteras JBOK (Just a Bunch Of Keys), que agrupaban claves privadas generadas de manera independiente y sin ningún vínculo entre ellas. Estas billeteras operaban en un modelo simple donde cada clave privada podía desbloquear una dirección de recepción de Bitcoin única.
Si se deseaba utilizar múltiples claves privadas, entonces era necesario hacer tantas copias de seguridad para asegurar el acceso a los fondos en caso de problemas con el dispositivo que aloja la billetera. Si se usa una única clave privada, esta estructura de billetera puede ser suficiente, ya que una sola copia de seguridad es suficiente. Sin embargo, esto plantea un problema: en Bitcoin, se desaconseja fuertemente usar siempre la misma clave privada. De hecho, una clave privada está asociada con una dirección única, y las direcciones de recepción de Bitcoin están diseñadas normalmente para un solo uso. Cada vez que recibes fondos, deberías generar una nueva dirección en blanco.
Esta restricción proviene del modelo de privacidad de Bitcoin. Al reutilizar la misma dirección, facilita a los observadores externos rastrear todas mis transacciones de Bitcoin. Es por eso que se desaconseja fuertemente reutilizar una dirección de recepción. Sin embargo, para tener múltiples direcciones y separar públicamente nuestras transacciones, es necesario gestionar múltiples claves privadas. En el caso de las billeteras JBOK, esto implica crear tantas copias de seguridad como nuevos pares de claves, una tarea que rápidamente puede volverse compleja y difícil de mantener para los usuarios.
Para aprender más sobre el modelo de privacidad de Bitcoin y descubrir métodos para proteger tu privacidad, también recomiendo seguir mi curso BTC204 en Plan ₿ Network:
https://planb.network/courses/65c138b0-4161-4958-bbe3-c12916bc959c
HD Wallets (Hierarchical Deterministic)
Para abordar la limitación de las billeteras JBOK, posteriormente se utilizó
una nueva estructura de billetera. En 2012, Pieter Wuille introdujo una
mejora con BIP32, que introduce billeteras deterministas jerárquicas. El
principio de una billetera HD es derivar todas las claves privadas de una
única fuente de información, llamada semilla, de manera determinista y
jerárquica. Esta semilla se genera aleatoriamente cuando se crea la
billetera y constituye una copia de seguridad única que permite la
recreación de todas las claves privadas de la billetera. Así, el usuario
puede generar un número muy grande de claves privadas para evitar la
reutilización de direcciones y preservar su privacidad, mientras que solo
necesita hacer una única copia de seguridad de su billetera a través de la
semilla. 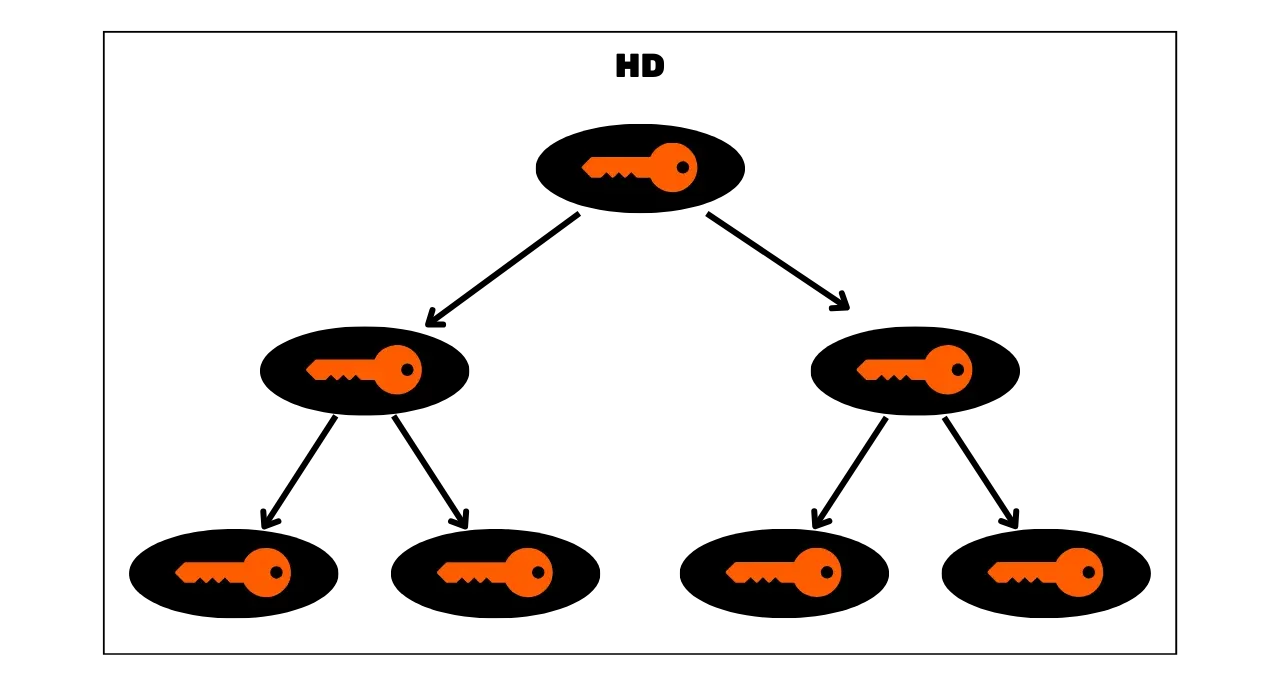
En las billeteras HD, la derivación de claves se realiza de acuerdo con una estructura jerárquica que permite organizar las claves en subespacios de derivación, cada subespacio siendo aún más subdivisible, para facilitar la gestión de fondos y la interoperabilidad entre diferentes software de billetera. Hoy en día, este estándar es adoptado por la gran mayoría de los usuarios de Bitcoin. Por esta razón, lo examinaremos en detalle en los siguientes capítulos.
El Estándar BIP39: La Frase Mnemotécnica
Además de BIP32, BIP39 estandariza el formato de la semilla como una frase mnemotécnica, para facilitar la copia de seguridad y la legibilidad por parte de los usuarios. La frase mnemotécnica, también llamada frase de recuperación o frase de 24 palabras, es una secuencia de palabras extraídas de una lista predefinida que codifica de manera segura la semilla de la cartera.
La frase mnemotécnica simplifica enormemente la copia de seguridad para el usuario. En caso de pérdida, daño o robo del dispositivo que aloja la cartera, simplemente con conocer esta frase mnemotécnica permite la recreación de la cartera y la recuperación del acceso a todos los fondos asegurados por ella.
En los próximos capítulos, exploraremos el funcionamiento interno de las carteras HD, incluyendo los mecanismos de derivación de claves y las diferentes estructuras jerárquicas posibles. Esto te permitirá entender mejor los fundamentos criptográficos sobre los cuales se basa la seguridad de los fondos en Bitcoin. Y para comenzar, en el próximo capítulo, propongo que descubramos el papel de la entropía en la base de tu cartera.
Entropía y Número Aleatorio
b43c715d-affb-56d8-a697-ad5bc2fffd63 Las carteras HD modernas (deterministas y jerárquicas) dependen de una única pieza inicial de información llamada "entropía" para generar de manera determinista el conjunto completo de claves de la cartera. Esta entropía es un número pseudoaleatorio cuyo nivel de caos determina en parte la seguridad de la cartera.
Definición de Entropía
La entropía, en el contexto de la criptografía y la información, es una medida cuantitativa de la incertidumbre o imprevisibilidad asociada con una fuente de datos o un proceso aleatorio. Juega un papel importante en la seguridad de los sistemas criptográficos, especialmente en la generación de claves y números aleatorios. Una alta entropía asegura que las claves generadas sean suficientemente impredecibles y resistentes a ataques de fuerza bruta, donde un atacante intenta todas las combinaciones posibles para adivinar la clave.
En el contexto de Bitcoin, la entropía se utiliza para generar la semilla. Al crear una cartera determinista y jerárquica, la construcción de la frase mnemotécnica se realiza a partir de un número aleatorio, derivado a su vez de una fuente de entropía. La frase se utiliza entonces para generar múltiples claves privadas, de manera determinista y jerárquica, para crear condiciones de gasto en UTXOs.
Métodos de Generación de Entropía
La entropía inicial utilizada para una cartera HD es generalmente de 128 bits o 256 bits, donde:
- 128 bits de entropía corresponden a una frase mnemotécnica de 12 palabras;
- 256 bits de entropía corresponden a una frase mnemotécnica de 24 palabras.
En la mayoría de los casos, este número aleatorio se genera automáticamente por el software de la cartera utilizando un PRNG (Pseudo-Random Number Generator). Los PRNG son una categoría de algoritmos utilizados para generar secuencias de números a partir de un estado inicial, que tienen características que se acercan a las de un número aleatorio, sin serlo realmente. Un buen PRNG debe tener propiedades como uniformidad de salida, imprevisibilidad y resistencia a ataques predictivos. A diferencia de los generadores de números aleatorios verdaderos (TRNG), los PRNG son deterministas y reproducibles.
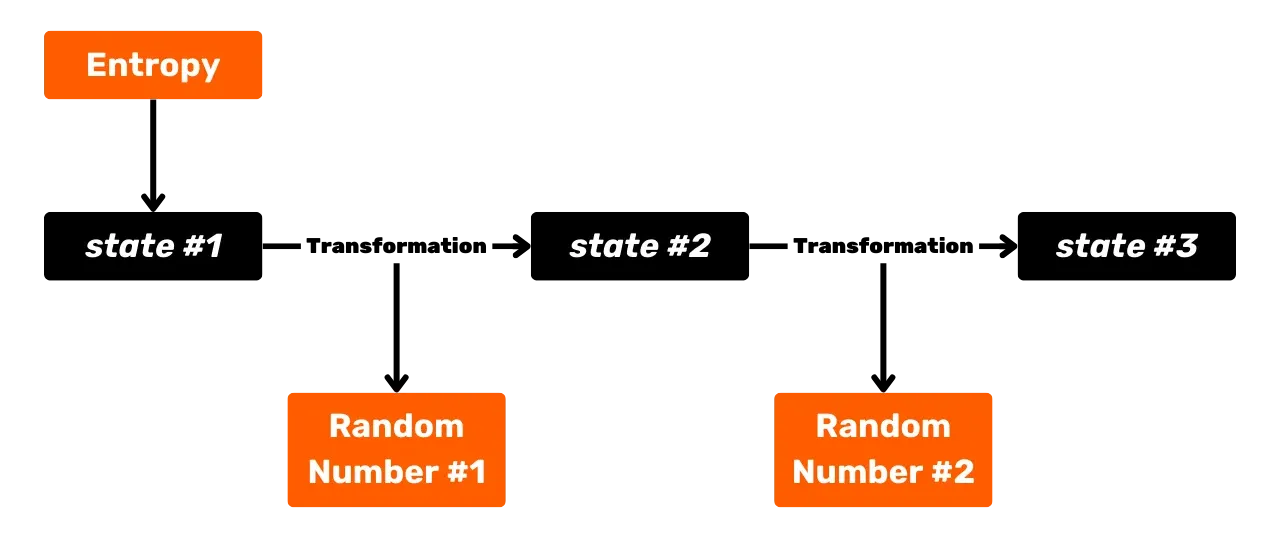
Una alternativa es generar manualmente la entropía, lo que ofrece un mejor control pero también es mucho más arriesgado. Desaconsejo fuertemente de generar la entropía para tu cartera HD tú mismo.
En el próximo capítulo, veremos cómo pasamos de un número aleatorio a una frase mnemotécnica de 12 o 24 palabras.
La Frase Mnemotécnica
La frase mnemotécnica, también llamada "frase semilla", "frase de recuperación", "frase secreta" o "frase de 24 palabras", es una secuencia compuesta usualmente de 12 o 24 palabras, que se genera a partir de la entropía. Se utiliza para derivar de manera determinista todas las claves de una cartera HD (Hierarchical Deterministic Wallet). Esto significa que a partir de esta frase, es posible generar y recrear de manera determinista todas las claves privadas y públicas de la cartera de Bitcoin, y consecuentemente acceder a los fondos que están protegidos con ella. El propósito de la frase mnemotécnica es proporcionar un medio de respaldo y recuperación de bitcoins que sea seguro y fácil de usar. Fue introducida en los estándares en 2013 con el BIP39. Descubramos juntos cómo pasar de la entropía a la frase mnemotécnica.
La Suma de Verificación
Para transformar la entropía en una frase mnemotécnica, primero se debe agregar una suma de verificación (o "checksum") al final de la entropía. Esta suma de verificación es una corta secuencia de bits que asegura la integridad de los datos verificando que no se haya introducido ninguna modificación accidental.
Para calcular la suma de verificación, se aplica la función hash SHA256 a la entropía (solo una vez; este es uno de los casos raros en Bitcoin donde se usa un único hash SHA256 en lugar de un doble hash). Esta operación produce un hash de 256 bits. La suma de verificación consiste en los primeros bits de este hash, y su longitud depende de la de la entropía, según la siguiente fórmula:
\text{CS} = \frac{\text{ENT}}{32}donde \text{ENT} representa la longitud de la entropía en bits, y \text{CS} la longitud
de la suma de verificación en bits.
Por ejemplo, para una entropía de 256 bits, se toman los primeros 8 bits del hash para formar la suma de verificación:
\text{CS} = \frac{256}{32} = 8 \text{ bits}Una vez calculada la suma de verificación, se concatena con la entropía para
obtener una secuencia de bits extendida notada \text{ENT} \Vert \text{CS} ("concatenar" significa poner uno al final del otro).

Correspondencia entre la Entropía y la Frase Mnemotécnica
El número de palabras en la frase mnemotécnica depende del tamaño de la entropía inicial, como se ilustra en la siguiente tabla con:
\text{ENT}: el tamaño en bits de la entropía;\text{CS}: el tamaño en bits de la suma de verificación;w: el número de palabras en la frase mnemotécnica final.
\begin{array}{|c|c|c|c|}
\hline
\text{ENT} & \text{CS} & \text{ENT} \Vert \text{CS} & w \\
\hline
128 & 4 & 132 & 12 \\
160 & 5 & 165 & 15 \\
192 & 6 & 198 & 18 \\
224 & 7 & 231 & 21 \\
256 & 8 & 264 & 24 \\
\hline
\end{array}Conversión de la Secuencia Binaria en una Frase Mnemotécnica
La secuencia de bits \text{ENT} \Vert \text{CS} se divide entonces en segmentos de 11 bits. Cada segmento de 11 bits, una
vez convertido a decimal, corresponde a un número entre 0 y 2047, que
designa la posición de una palabra en una lista de 2048 palabras estandarizadas por el BIP39.
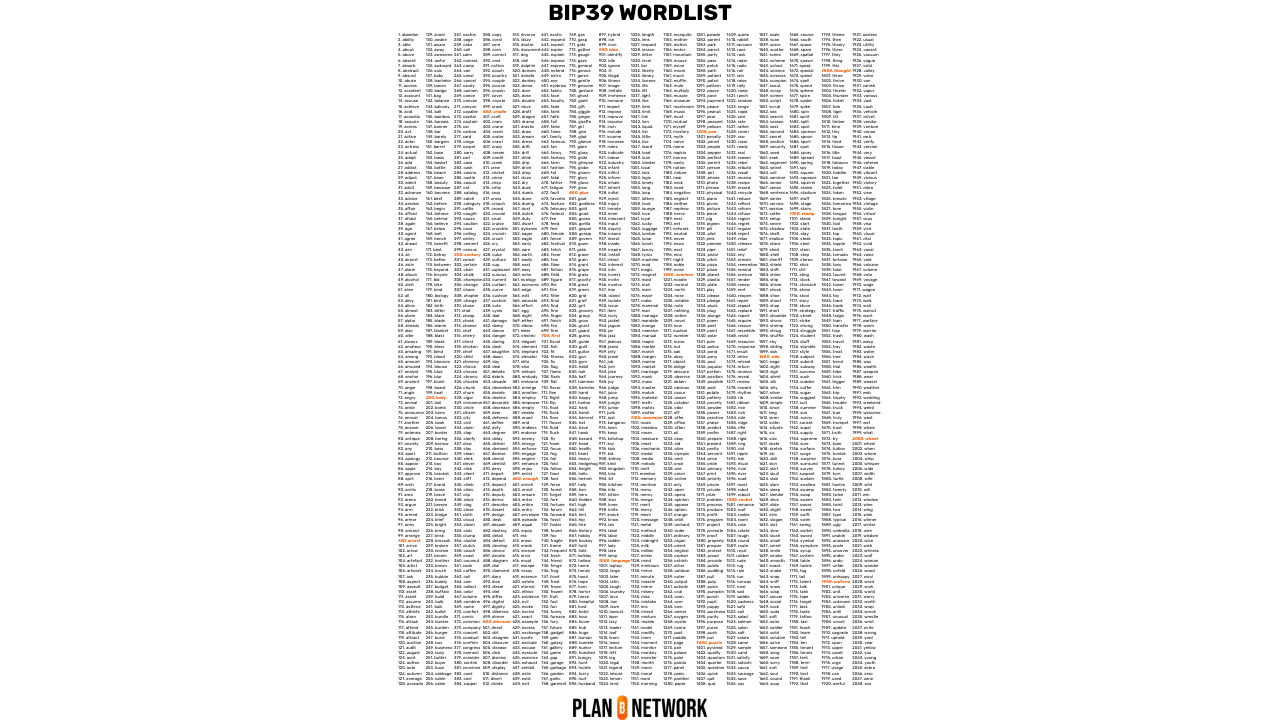
Por ejemplo, para una entropía de 128 bits, la suma de verificación es de 4 bits, y así la secuencia total mide 132 bits. Se divide en 12 segmentos de 11 bits (los bits naranjas designan la suma de verificación):

Cada segmento se convierte entonces en un número decimal que representa una
palabra en la lista. Por ejemplo, el segmento binario 01011010001 es equivalente en decimal a 721. Al sumar 1 para alinearse con
la indexación de la lista (que comienza en 1 y no en 0), esto da el rango de
la palabra 722, que es "focus" en la lista.

Esta correspondencia se repite para cada uno de los 12 segmentos, con el fin de obtener una frase de 12 palabras.

Características de la Lista de Palabras BIP39
Una particularidad de la lista de palabras BIP39 es que ninguna palabra comparte las mismas primeras cuatro letras en el mismo orden con otra palabra. Esto significa que anotar solo las primeras cuatro letras de cada palabra es suficiente para guardar la frase mnemotécnica. Esto puede ser interesante para ahorrar espacio, especialmente para aquellos que desean grabarla en un soporte metálico.
Esta lista de 2048 palabras existe en varios idiomas. Estas no son simples traducciones, sino palabras distintas para cada idioma. Sin embargo, se recomienda encarecidamente apegarse a la versión en inglés, ya que las versiones en otros idiomas generalmente no son compatibles con el software de billetera.
¿Qué longitud elegir para tu frase mnemotécnica?
Para determinar la longitud óptima de tu frase mnemotécnica, se debe considerar la seguridad real que proporciona. Una frase de 12 palabras asegura 128 bits de seguridad, mientras que una frase de 24 palabras ofrece 256 bits.
Sin embargo, esta diferencia en la seguridad a nivel de frase no mejora la
seguridad general de una billetera de Bitcoin, ya que las claves privadas
derivadas de esta frase solo se benefician de 128 bits de seguridad. De
hecho, como hemos visto anteriormente, las claves privadas de Bitcoin se
generan a partir de números aleatorios (o derivados de una fuente aleatoria)
que van desde 1 hasta n-1, donde n representa el orden del punto generador G de la curva secp256k1, un número ligeramente menor que 2^{256}. Uno podría
pensar, por lo tanto, que estas claves privadas ofrecen 256 bits de
seguridad. Sin embargo, su seguridad radica en la dificultad de encontrar
una clave privada a partir de su clave pública asociada, una dificultad
establecida por el problema matemático del logaritmo discreto en curvas
elípticas (ECDLP). Hasta la fecha, el algoritmo más conocido para
resolver este problema es el algoritmo rho de Pollard, que reduce el número
de operaciones necesarias para romper una clave a la raíz cuadrada de su
tamaño.
Para claves de 256 bits, como las utilizadas en Bitcoin, el algoritmo rho de
Pollard reduce así la complejidad a 2^{128} operaciones:
O(\sqrt{2^{256}}) = O(2^{128})
Por lo tanto, se considera que una clave privada utilizada en Bitcoin ofrece 128 bits de seguridad.
Como resultado, elegir una frase de 24 palabras no proporciona protección adicional para la billetera, ya que 256 bits de seguridad en la frase son inútiles si las claves derivadas solo ofrecen 128 bits de seguridad. Para ilustrar este principio, es como tener una casa con dos puertas: una puerta de madera vieja y una puerta reforzada. En caso de un robo, la puerta reforzada no serviría de nada, ya que el intruso pasaría por la puerta de madera. Esta es una situación análoga aquí. Una frase de 12 palabras, que además ofrece 128 bits de seguridad, es por lo tanto actualmente suficiente para proteger tus bitcoins contra cualquier intento de robo. Mientras el algoritmo de firma digital no cambie para usar claves más grandes o para depender de un problema matemático distinto al ECDLP, una frase de 24 palabras sigue siendo superflua. Además, una frase más larga aumenta el riesgo de pérdida durante la copia de seguridad: una copia de seguridad que es la mitad de corta siempre es más fácil de manejar.
Para ir más allá y aprender concretamente cómo generar manualmente una frase mnemotécnica de prueba, te aconsejo descubrir este tutorial:
Antes de continuar con la derivación de la billetera a partir de esta frase mnemotécnica, te presentaré, en el siguiente capítulo, la passphrase BIP39, ya que juega un papel en el proceso de derivación, y está al mismo nivel que la frase mnemotécnica.
La passphrase
Como acabamos de ver, las billeteras HD se generan a partir de una frase mnemotécnica que típicamente consiste en 12 o 24 palabras. Esta frase es muy importante porque permite la restauración de todas las claves de una billetera en caso de que su dispositivo físico (como una billetera de hardware, por ejemplo) se pierda. Sin embargo, constituye un único punto de fallo, porque si se ve comprometida, un atacante podría robar todos los bitcoins. Aquí es donde entra en juego la passphrase BIP39.
¿Qué es una passphrase BIP39?
La passphrase es una contraseña opcional, que puedes elegir libremente, que se añade a la frase mnemotécnica en el proceso de derivación de claves para mejorar la seguridad de la billetera.
Ten cuidado, la passphrase no debe confundirse con el código PIN de tu billetera de hardware o la contraseña utilizada para desbloquear el acceso a tu billetera en tu computadora. A diferencia de todos estos elementos, la passphrase juega un papel en la derivación de las claves de tu billetera. Esto significa que sin ella, nunca podrás recuperar tus bitcoins.
La passphrase trabaja en conjunto con la frase mnemotécnica, modificando la semilla de la cual se generan las claves. Así, incluso si alguien obtiene tu frase de 12 o 24 palabras, sin la passphrase, no pueden acceder a tus fondos. Usar una passphrase crea esencialmente una nueva billetera con claves distintas. Modificar (incluso ligeramente) la passphrase generará una billetera diferente.

¿Por qué deberías usar una passphrase?
La passphrase es arbitraria y puede ser cualquier combinación de caracteres elegida por el usuario. Usar una passphrase ofrece varias ventajas. En primer lugar, reduce todos los riesgos asociados con el compromiso de la frase mnemotécnica al requerir un segundo factor para acceder a los fondos (robo, acceso a tu hogar, etc.).
Luego, puede usarse estratégicamente para crear una billetera señuelo, para enfrentar restricciones físicas para robar tus fondos como el infame "ataque de la llave inglesa de 5 dólares". En este escenario, la idea es tener una billetera sin passphrase que contenga solo una pequeña cantidad de bitcoins, suficiente para satisfacer a un posible agresor, mientras se tiene una billetera oculta. Esta última utiliza la misma frase mnemotécnica pero está asegurada con una passphrase adicional.
Finalmente, el uso de una passphrase es interesante cuando se desea controlar la aleatoriedad de la generación de la semilla de la billetera HD.
¿Cómo elegir una buena passphrase?
Para que la passphrase sea efectiva, debe ser suficientemente larga y aleatoria. Al igual que con una contraseña fuerte, recomiendo elegir una passphrase que sea lo más larga y aleatoria posible, con una diversidad de letras, números y símbolos para hacer cualquier ataque de fuerza bruta imposible.
También es importante guardar adecuadamente esta frase de contraseña, de la misma manera que la frase mnemotécnica. Perderla significa perder el acceso a tus bitcoins. Aconsejo encarecidamente no recordarla solo de memoria, ya que esto aumenta de manera irrazonable el riesgo de pérdida. Lo ideal es anotarla en un medio físico (papel o metal) separado de la frase mnemotécnica. Esta copia de seguridad debe, obviamente, almacenarse en un lugar diferente de donde se guarda tu frase mnemotécnica para evitar que ambos se vean comprometidos simultáneamente.
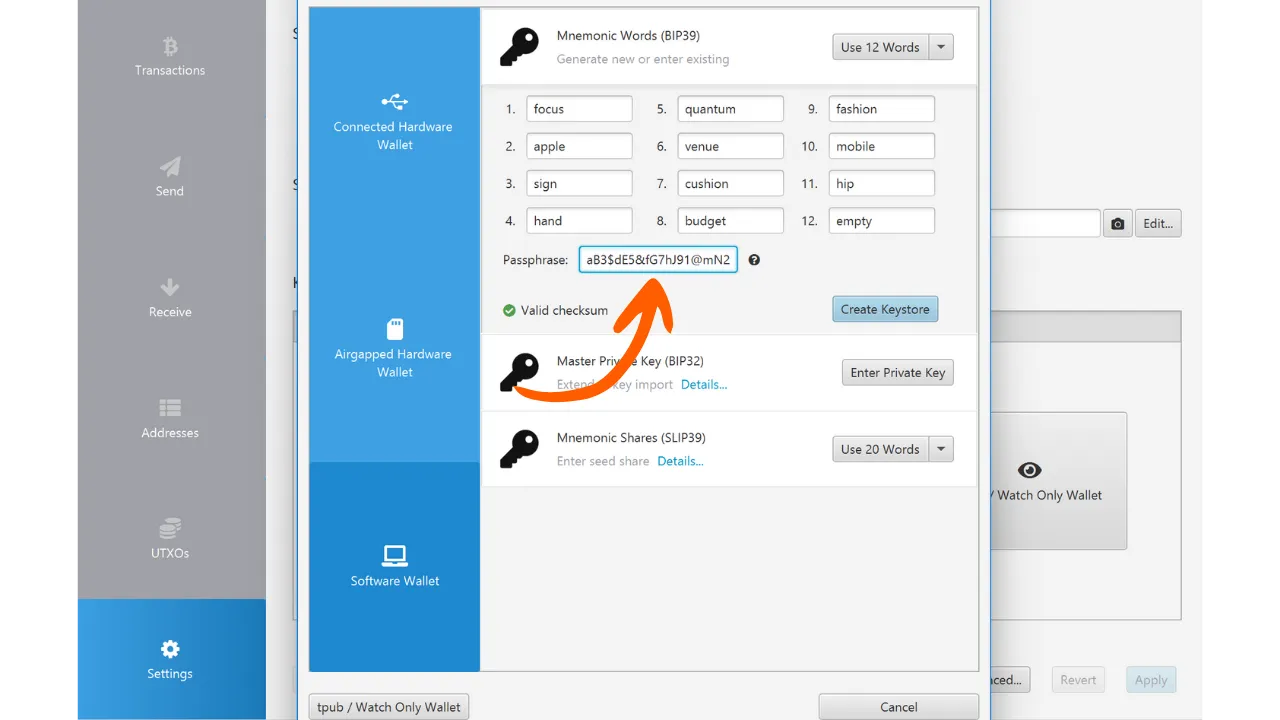
En la siguiente sección, descubriremos cómo estos dos elementos en la base de tu billetera — la frase mnemotécnica y la frase de contraseña — se utilizan para derivar los pares de claves usados en el scriptPubKey que bloquea tus UTXOs.
Creación de Carteras de Bitcoin
Creación de la Semilla y la Clave Maestra
Una vez generada la frase mnemotécnica y la frase de contraseña opcional, puede comenzar el proceso de derivación de una cartera HD de Bitcoin. La frase mnemotécnica se convierte primero en una semilla que constituye la base de todas las claves de la cartera.
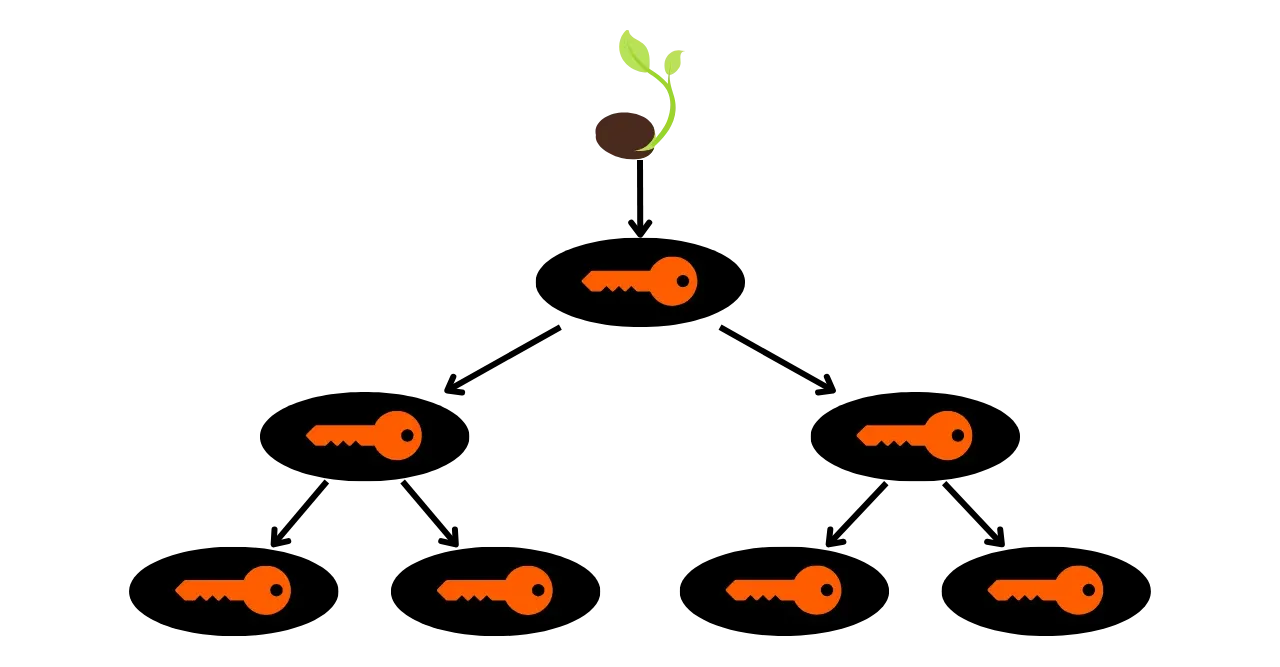
La Semilla de una Cartera HD
El estándar BIP39 define la semilla como una secuencia de 512 bits, que sirve como punto de partida para la derivación de todas las claves de una cartera HD. La semilla se deriva de la frase mnemotécnica y la posible frase de contraseña utilizando el algoritmo PBKDF2 (Password-Based Key Derivation Function 2) del cual ya hemos hablado en el capítulo 3.3. En esta función de derivación, utilizaremos los siguientes parámetros:
m: la frase mnemotécnica;p: una frase de contraseña (passphrase) opcional elegida por el usuario para aumentar la seguridad de la semilla. Si no hay frase de contraseña, este campo se deja vacío;\text{PBKDF2}: la función de derivación con\text{HMAC-SHA512}y2048iteraciones;s: la semilla de la cartera de 512 bits.
Independientemente de la longitud de la frase mnemotécnica elegida (132 bits o 264 bits), la función PBKDF2 siempre producirá un output de 512 bits, y la semilla por lo tanto siempre será de este tamaño.
Esquema de Derivación de la Semilla con PBKDF2
La siguiente ecuación ilustra la derivación de la semilla a partir de la frase mnemotécnica y la frase de contraseña:
s = \text{PBKDF2}_{\text{HMAC-SHA512}}(m, p, 2048)

El valor de la semilla está así influenciado por el valor de la frase mnemotécnica y la frase de contraseña. Al cambiar la frase de contraseña, se obtiene una semilla diferente. Sin embargo, con la misma frase mnemotécnica y frase de contraseña, siempre se genera la misma semilla, ya que PBKDF2 es una función determinista. Esto asegura que los mismos pares de claves pueden ser recuperados a través de nuestras copias de seguridad.
Nota: En el lenguaje común, el término "semilla" a menudo se refiere, por mal uso del lenguaje, a la frase mnemotécnica. De hecho, en ausencia de una passphrase, una es simplemente la codificación de la otra. Sin embargo, como hemos visto, en la realidad técnica de las carteras, la semilla y la frase mnemotécnica son de hecho dos elementos distintos.
Ahora que tenemos nuestra semilla, podemos continuar con la derivación de nuestra cartera de Bitcoin.
La Llave Maestra y el Código de Cadena Maestro
Una vez obtenida la semilla, el siguiente paso en la derivación de una cartera HD implica calcular la llave privada maestra y el código de cadena maestro, que representarán la profundidad 0 de nuestra cartera.
Para obtener la llave privada maestra y el código de cadena maestro, se aplica la función HMAC-SHA512 a la semilla, utilizando una clave fija "Bitcoin Seed" idéntica para todos los usuarios de Bitcoin. Esta constante se elige para asegurar que las derivaciones de clave sean específicas para Bitcoin. Aquí están los elementos:
\text{HMAC-SHA512}: la función de derivación;s: la semilla de la cartera de 512 bits;\text{"Bitcoin Seed"}: la constante de derivación común para todas las carteras Bitcoin.
\text{output} = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)El output de esta función es, por lo tanto, de 512 bits. Luego se divide en 2 partes:
- Los 256 bits izquierdos forman la llave privada maestra;
- Los 256 bits derechos forman el código de cadena maestro.
Matemáticamente, estos dos valores se pueden notar de la siguiente manera
con k_M siendo la llave
privada maestra y C_M el código
de cadena maestro:
k_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[:256]}C_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[256:]}
Rol de la Llave Maestra y el Código de Cadena
La llave privada maestra se considera la llave padre, de la cual se generarán todas las llaves privadas derivadas — hijos, nietos, bisnietos, etc. —. Representa el nivel cero en la jerarquía de derivación.
El código de cadena maestro, por otro lado, introduce una fuente adicional de entropía en el proceso de derivación de llaves para los hijos, con el fin de contrarrestar ciertos ataques potenciales. Además, en la cartera HD, cada par de llaves tiene un código de cadena único asociado con él, que también se utiliza para derivar llaves hijo de este par, pero discutiremos esto con más detalle en los próximos capítulos.
Antes de continuar con la derivación de la cartera HD con los siguientes elementos, deseo, en el próximo capítulo, presentarles las llaves extendidas, que a menudo se confunden con la llave maestra. Veremos cómo se construyen y qué papel juegan en la cartera Bitcoin.
Llaves Extendidas
Una llave extendida es simplemente la concatenación de una llave (ya sea privada o pública) y su código de cadena asociado. Este código de cadena es esencial para la derivación de llaves hijo porque, sin él, es imposible derivar llaves hijo de una llave padre, pero descubriremos este proceso más precisamente en el próximo capítulo. Estas llaves extendidas permiten así agregar toda la información necesaria para derivar llaves hijo, simplificando así la gestión de cuentas dentro de una cartera HD.
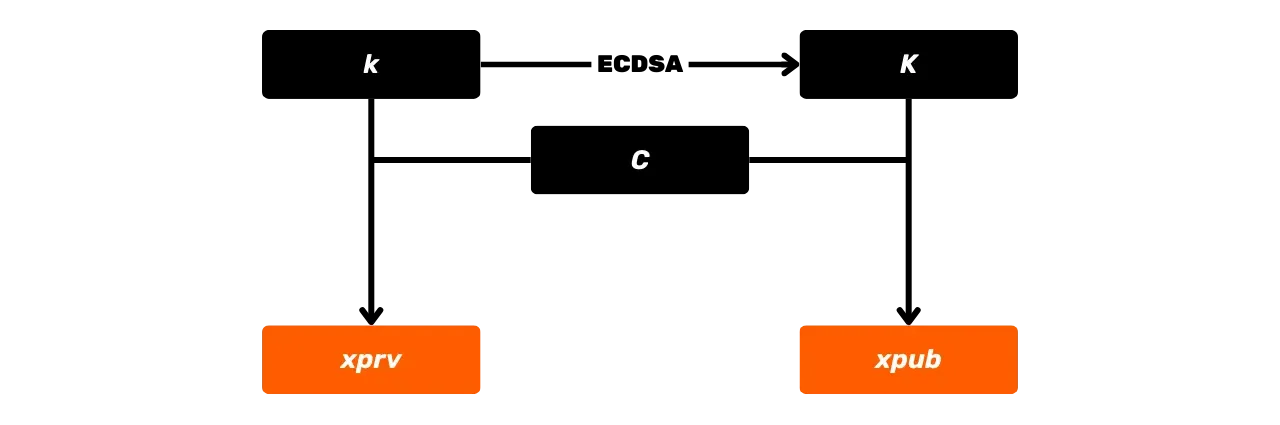
La llave extendida consta de dos partes:
- El payload, que contiene la llave privada o pública así como el código de cadena asociado;
- Los metadatos, que son diversas piezas de información para facilitar la interoperabilidad entre software y mejorar la comprensión para el usuario.
Cómo Funcionan las Llaves Extendidas
Cuando la clave extendida contiene una clave privada, se le denomina clave
privada extendida. Se reconoce por su prefijo que contiene la mención prv. Además de la clave privada, la clave privada extendida también contiene
el código de cadena asociado. Con este tipo de clave extendida, es posible
derivar todos los tipos de claves privadas hijas, y por lo tanto, mediante
la adición y duplicación de puntos en curvas elípticas, también permite la
derivación de la totalidad de claves públicas hijas.
Cuando la clave extendida no contiene una clave privada, sino en cambio, una
clave pública, se le denomina clave pública extendida. Se reconoce por su
prefijo que contiene la mención pub. Obviamente, además de la
clave, también contiene el código de cadena asociado. A diferencia de la
clave privada extendida, la clave pública extendida permite la derivación
solo de claves públicas hijas "normales" (lo que significa que no puede
derivar claves hijas "endurecidas"). Veremos en el siguiente capítulo qué
significan estos calificativos de "normal" y "endurecido".
Pero en cualquier caso, la clave pública extendida no permite la derivación
de claves privadas hijas. Por lo tanto, incluso si alguien tiene acceso a un xpub, no podrá gastar los fondos asociados, ya que no tendrá acceso a las
claves privadas correspondientes. Solo pueden derivar claves públicas hijas
para observar las transacciones asociadas.
Para lo siguiente, adoptaremos la siguiente notación:
K_{\text{PAR}}: una clave pública padre;k_{\text{PAR}}: una clave privada padre;C_{\text{PAR}}: un código de cadena padre;C_{\text{CHD}}: un código de cadena hijo;K_{\text{CHD}}^n: una clave pública hija normal;k_{\text{CHD}}^n: una clave privada hija normal;K_{\text{CHD}}^h: una clave pública hija endurecida;k_{\text{CHD}}^h: una clave privada hija endurecida.

Construcción de una Clave Extendida
Una clave extendida se estructura de la siguiente manera:
- Version: Código de versión para identificar la naturaleza
de la clave (
xprv,xpub,yprv,ypub...). Veremos al final de este capítulo a qué corresponden las letrasx,yyz. - Depth: Nivel jerárquico en la billetera HD relativo a la clave maestra (0 para la clave maestra).
- Parent Fingerprint: Los primeros 4 bytes del hash HASH160 de la clave pública padre utilizada para derivar la clave presente en el payload.
- Index Number: Identificador del hijo entre claves hermanas, es decir, entre todas las claves en el mismo nivel de derivación que tienen las mismas claves padres.
- Chain Code: Un código único de 32 bytes para derivar claves hijas.
- Key: La clave privada (prefijada por 1 byte por tamaño) o la clave pública.
- Checksum: Un checksum calculado con la función HASH256 (doble SHA256) también se agrega, lo que permite la verificación de la integridad de la clave extendida durante su transmisión o almacenamiento.
El formato completo de una clave extendida es, por lo tanto, de 78 bytes sin el checksum, y de 82 bytes con el checksum. Luego se convierte a Base58 para producir una representación que es fácilmente legible por los usuarios. El formato Base58 es el mismo que se utiliza para direcciones de recepción Legacy (antes de SegWit).
| Elemento | Descripción | Tamaño |
|---|---|---|
| Versión | Indica si la clave es pública (xpub, ypub)
o privada (xprv, zprv), así como la versión
de la clave extendida | 4 bytes |
| Profundidad | Nivel en la jerarquía relativo a la clave maestra | 1 byte |
| Huella del Padre | Los primeros 4 bytes del HASH160 de la clave pública del padre | 4 bytes |
| Número de Índice | Posición de la clave en el orden de los hijos | 4 bytes |
| Código de Cadena | Utilizado para derivar claves hijas | 32 bytes |
| Clave | La clave privada (con un prefijo de 1 byte) o la clave pública | 33 bytes |
| Suma de Verificación | Suma de verificación para verificar la integridad | 4 bytes |
Si se añade un byte a la clave privada solamente, es porque la clave pública
comprimida es más larga que la clave privada por un byte. Este byte
adicional, añadido al principio de la clave privada como 0x00,
iguala su tamaño, asegurando que la carga útil de la clave extendida tenga
la misma longitud, ya sea una clave pública o privada.
Prefijos de Clave Extendida
Como acabamos de ver, las claves extendidas incluyen un prefijo que indica
tanto la versión de la clave extendida como su naturaleza. La notación pub indica que se refiere a una clave pública extendida, y la notación prv indica una clave privada extendida. La letra adicional en la
base de la clave extendida ayuda a indicar si el estándar seguido es Legacy,
SegWit v0, SegWit v1, etc. Aquí hay un resumen de los prefijos utilizados y sus
significados:
| Base 58 Prefix | Base 16 Prefix | Network | Purpose | Associated Scripts | Derivation | Key Type |
|---|---|---|---|---|---|---|
xpub | 0488b21e | Mainnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | m/44'/0', m/86'/0' | public |
xprv | 0488ade4 | Mainnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | m/44'/0', m/86'/0' | private |
tpub | 043587cf | Testnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | m/44'/1', m/86'/1' | public |
tprv | 04358394 | Testnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | m/44'/1', m/86'/1' | private |
ypub | 049d7cb2 | Mainnet | Nested SegWit | P2WPKH in P2SH | m/49'/0' | public |
yprv | 049d7878 | Mainnet | Nested SegWit | P2WPKH in P2SH | m/49'/0' | private |
upub | 049d7cb2 | Testnet | Nested SegWit | P2WPKH in P2SH | m/49'/1' | public |
uprv | 044a4e28 | Testnet | Nested SegWit | P2WPKH in P2SH | m/49'/1' | private |
zpub | 04b24746 | Mainnet | SegWit V0 | P2WPKH | m/84'/0' | public |
zprv | 04b2430c | Mainnet | SegWit V0 | P2WPKH | m/84'/0' | private |
vpub | 045f1cf6 | Testnet | SegWit V0 | P2WPKH | m/84'/1' | public |
vprv | 045f18bc | Testnet | SegWit V0 | P2WPKH | m/84'/1' | private |
Detalles de los Elementos de una Clave Extendida
Para entender mejor la estructura interna de una clave extendida, tomemos una como ejemplo y desglosémosla. Aquí hay una clave extendida:
- En Base58:
xpub6CTNzMUkzpurBWaT4HQoYzLP4uBbGJuWY358Rj7rauiw4rMHCyq3Rfy9w4kyJXJzeFfyrKLUar2rUCukSiDQFa7roTwzjiAhyQAdPLEjqHT
- En hexadecimal:
0488B21E036D5601AD80000000C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A89303772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF50658051F067C3A
Esta clave extendida se desglosa en varios elementos distintos:
- Versión:
0488B21E
Los primeros 4 bytes son la versión. Aquí, corresponde a una clave pública extendida en el Mainnet con un propósito de derivación de Legacy o SegWit v1.
- Profundidad:
03
Este campo indica el nivel jerárquico de la clave dentro de la cartera HD.
En este caso, una profundidad de 03 significa que esta clave es
tres niveles de derivación por debajo de la clave maestra.
- Huella digital del padre:
6D5601ADEstos son los primeros 4 bytes del hash HASH160 de la clave pública padre que se utilizó para derivar estexpub. - Número de índice:
80000000
Este índice indica la posición de la clave entre los hijos de su padre. El
prefijo 0x80 indica que la clave se deriva de manera endurecida,
y dado que el resto está lleno de ceros, indica que esta clave es la primera
entre sus posibles hermanos.
- Código de cadena:
C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A893 - Clave Pública:
03772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF5065805 - Checksum:
1F067C3A
El checksum corresponde a los primeros 4 bytes del hash (doble SHA256) de todo lo demás.
En este capítulo, descubrimos que existen dos tipos diferentes de claves hijas. También aprendimos que la derivación de estas claves hijas requiere una clave (ya sea privada o pública) y su código de cadena. En el próximo capítulo, examinaremos en detalle la naturaleza de estos diferentes tipos de claves y cómo derivarlas de su clave padre y código de cadena.
Derivación de Pares de Claves Hijas
La derivación de pares de claves hijas en las carteras HD de Bitcoin se basa en una estructura jerárquica que permite generar un gran número de claves, mientras organiza estos pares en diferentes grupos a través de ramas. Cada par hijo derivado de un par padre puede usarse directamente en un scriptPubKey para bloquear bitcoins, o como punto de partida para generar más claves hijas, y así sucesivamente, para crear un árbol de claves.
Todas estas derivaciones comienzan con la clave maestra y el código de cadena maestro, que son los primeros padres en el nivel de profundidad 0. Son, de cierta manera, el Adán y Eva de las claves de tu cartera, ancestros comunes de todas las claves derivadas.
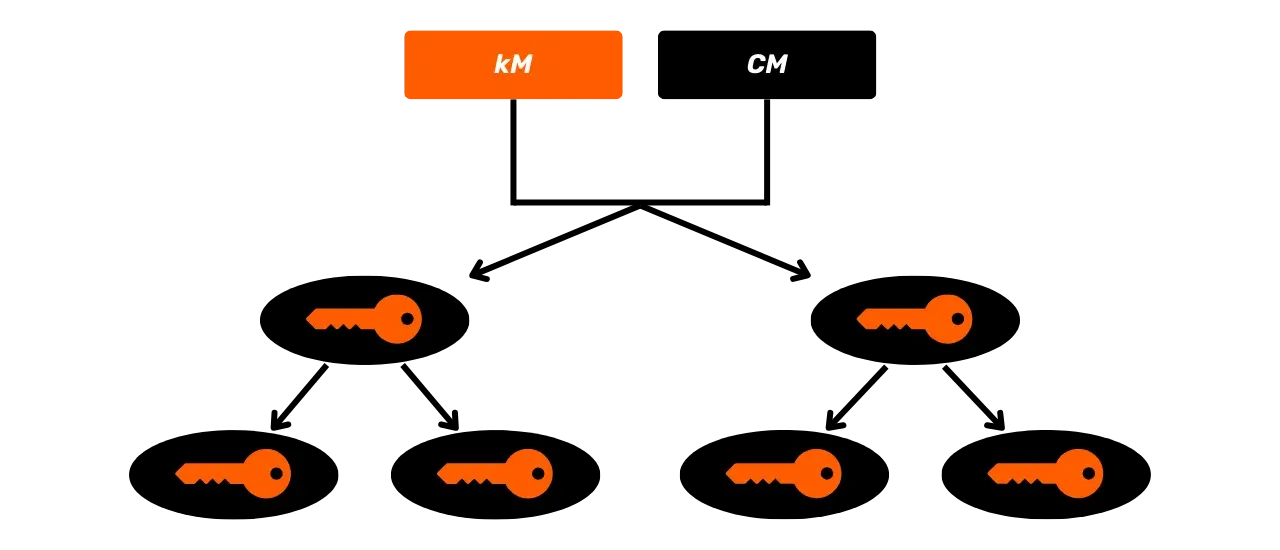
Exploraremos cómo funciona esta derivación determinista.
Los Diferentes Tipos de Derivaciones de Claves Hijas
Como mencionamos brevemente en el capítulo anterior: las claves hijas se dividen en dos tipos principales:
- Claves hijas normales (
k_{\text{CHD}}^n, K_{\text{CHD}}^n): Estas se derivan de la clave pública extendida (K_{\text{PAR}}), o de la clave privada extendida (k_{\text{PAR}}), derivando primero la clave pública. - Claves hijas endurecidas (
k_{\text{CHD}}^h, K_{\text{CHD}}^h): Estas solo pueden derivarse de la clave privada extendida (k_{\text{PAR}}) y, por lo tanto, son invisibles para los observadores que solo tienen la clave pública extendida.
Cada par de claves hijo se identifica por un índice de 32
bits (denominado i en
nuestros cálculos). Los índices para las claves normales van de 0 a 2^{31}-1,
mientras que los de las claves endurecidas van de 2^{31} a 2^{32}-1. Estos
números se utilizan para distinguir entre pares de claves hermanas durante
la derivación. De hecho, cada par de claves padre debe ser capaz de derivar
múltiples pares de claves hijo. Si aplicáramos el mismo cálculo
sistemáticamente desde las claves padre, todas las claves hermanas obtenidas
serían idénticas, lo cual no es deseable. El índice introduce así una
variable que modifica el cálculo de derivación, permitiendo diferenciar cada
par de hermanos. Excepto por el uso específico en ciertos protocolos y
estándares de derivación, generalmente comenzamos derivando la primera clave
hijo con el índice 0, la segunda con el índice 1,
y así sucesivamente.
Proceso de Derivación con HMAC-SHA512
La derivación de cada clave hijo se basa en la función HMAC-SHA512, la cual
discutimos en la Sección 2 sobre funciones hash. Toma dos entradas: el
código de cadena padre C_{\text{PAR}} y la concatenación de la clave padre (ya sea la clave pública K_{\text{PAR}} o la clave privada k_{\text{PAR}}, dependiendo del tipo de clave hijo deseada) y el índice. El output del
HMAC-SHA512 es una secuencia de 512 bits, dividida en dos partes:
- Los primeros 32 bytes (o
h_1) se utilizan para calcular el nuevo par hijo. - Los últimos 32 bytes (o
h_2) sirven como el nuevo código de cadenaC_{\text{CHD}}para el par hijo.
En todos nuestros cálculos, denotaré \text{hash} El output de la función HMAC-SHA512.
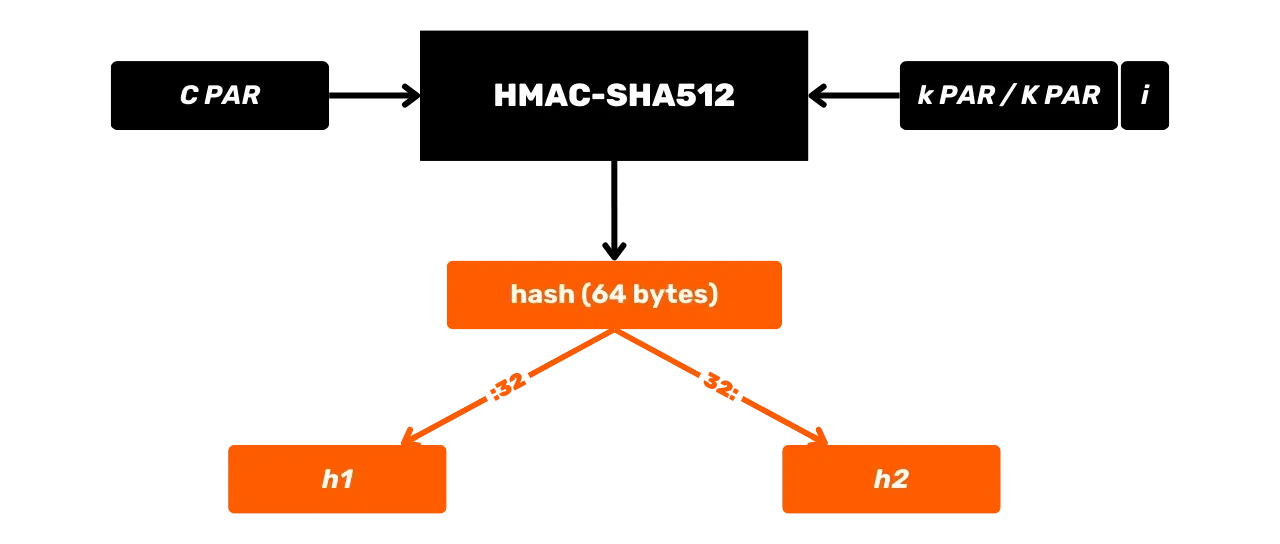
Derivación de una Clave Privada Hijo de una Clave Privada Padre
Para derivar una clave privada hijo k_{\text{CHD}} de una clave privada padre k_{\text{PAR}}, hay dos escenarios posibles dependiendo de si se desea una clave
endurecida o normal.
Para una clave hijo normal (i < 2^{31}), el cálculo de \text{hash} es el siguiente:
\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, G \cdot k_{\text{PAR}} \Vert i)En este cálculo, observamos que nuestra función HMAC toma dos entradas: primero, el código de cadena padre, y luego la concatenación del índice con la clave pública asociada a la clave privada padre. La clave pública padre se utiliza aquí porque estamos buscando derivar una clave hijo normal, no una endurecida.
Ahora tenemos un \text{hash} de 64 bytes que dividiremos en 2 partes de 32 bytes cada una: h_1 y h_2:
\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}_{[:32]} \quad, \quad h_2 = \text{hash}_{[32:]}
La clave privada hijo k_{\text{CHD}}^n se calcula entonces de la siguiente manera:
k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod nEn este cálculo, la operación \text{parse256}(h_1) consiste en interpretar los primeros 32 bytes del \text{hash} como un entero de 256 bits. Este número se suma luego a la clave privada
padre, todo tomado módulo n para
permanecer dentro del orden de la curva elíptica, como vimos en la sección 3
sobre firmas digitales. Así, para derivar una clave privada de hijo normal, aunque
la clave pública padre se usa como base para el cálculo en las entradas de la
función HMAC-SHA512, siempre es necesario tener la clave privada padre para finalizar
el cálculo. A partir de esta clave privada de hijo, es posible derivar la clave
pública correspondiente aplicando ECDSA o Schnorr. De esta manera, obtenemos
un par completo de claves.
Luego, la segunda parte del \text{hash} se interpreta simplemente como el código de cadena para el par de claves de
hijo que acabamos de derivar:
C_{\text{CHD}} = h_2
Aquí hay una representación esquemática de la derivación general:
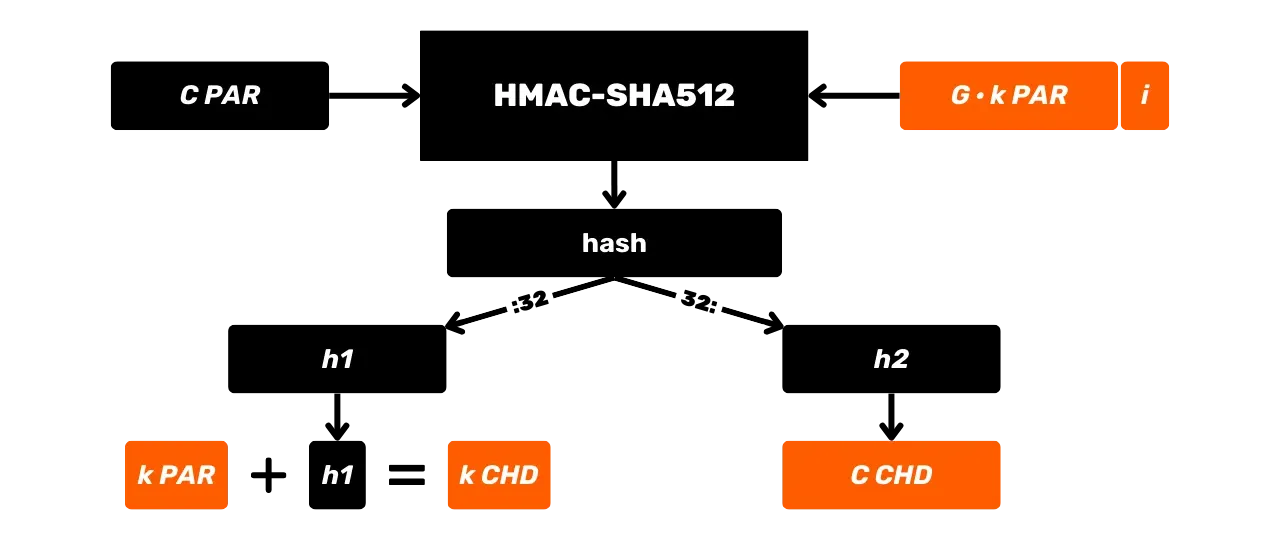
Para una clave de hijo endurecida (i \geq 2^{31}), el cálculo del \text{hash} es como
sigue:
hash = \text{HMAC-SHA512}(C_{\text{PAR}}, 0x00 \Vert k_{\text{PAR}} \Vert i)
En este cálculo, observamos que nuestra función HMAC toma dos entradas:
primero, el código de cadena padre, y luego la concatenación del índice con
la clave privada padre. La clave privada padre se usa aquí porque estamos
buscando derivar una clave de hijo endurecida. Además, un byte igual a 0x00 se añade al principio de la clave. Esta operación iguala su longitud para
que coincida con la de una clave pública comprimida. Así que ahora tenemos
un \text{hash} de
64 bytes que dividiremos en 2 partes de 32 bytes cada una: h_1 y h_2:
\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}_{[:32]} \quad, \quad h_2 = \text{hash}_{[32:]}
La clave privada de hijo k_{\text{CHD}}^h se calcula entonces de la siguiente manera:
k_{\text{CHD}}^h = \text{parse256}(h_1) + k_{\text{PAR}} \mod nA continuación, simplemente interpretamos la segunda parte del \text{hash} como el código de cadena para el par de claves de hijo que acabamos de derivar:
C_{\text{CHD}} = h_2Aquí hay una representación esquemática de la derivación general:

Podemos ver que la derivación normal y la derivación endurecida funcionan de la misma manera, con esta diferencia: la derivación normal usa la clave pública padre como entrada a la función HMAC, mientras que la derivación endurecida usa la clave privada padre.
Derivando una clave pública de hijo a partir de una clave pública padre
Si solo conocemos la clave pública del padre K_{\text{PAR}} y el código de cadena asociado C_{\text{PAR}}, es decir, una clave pública extendida, es posible derivar claves públicas
hijas K_{\text{CHD}}^n, pero solo para claves hijas normales (no endurecidas). Este principio
permite notablemente monitorear los movimientos de una cuenta en una
billetera de Bitcoin desde el xpub (solo visualización, watchonly). Para realizar este cálculo, computaremos el \text{hash} con un índice i < 2^{31} (derivación
normal):
\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, K_{\text{PAR}} \Vert i)En este cálculo, observamos que nuestra función HMAC toma dos entradas: primero el código de cadena del padre, luego la concatenación del índice con la clave pública del padre.
Así, ahora tenemos un hash de
64 bytes que dividiremos en 2 partes de 32 bytes cada una: h_1 y h_2:
\text{hash} = h_1 \Vert h_2h_1 = \text{hash}_{[:32]} \quad, \quad h_2 = \text{hash}_{[32:]}La clave pública hija K_{\text{CHD}}^n se calcula entonces de la siguiente manera:
K_{\text{CHD}}^n = G \cdot \text{parse256}(h_1) + K_{\text{PAR}}Si \text{parse256}(h_1) \geq n (orden de la curva elíptica) o si K_{\text{CHD}}^n es el punto en el infinito, la derivación es inválida y se debe elegir otro
índice.
En este cálculo, la operación \text{parse256}(h_1) implica interpretar los primeros 32 bytes del \text{hash} como un entero de 256 bits. Este número se utiliza para calcular un punto en
la curva elíptica a través de la adición y duplicación desde el punto
generador G. Este punto se
suma entonces a la clave pública del padre para obtener la clave pública
hija normal. Así, para derivar una clave pública hija normal, solo se
necesitan la clave pública del padre y el código de cadena del padre; la
clave privada del padre nunca entra en este proceso, a diferencia del
cálculo de la clave privada hija que vimos anteriormente.
A continuación, el código de cadena hijo es simplemente:
C_{\text{CHD}} = h_2
Aquí hay una representación esquemática de la derivación general:
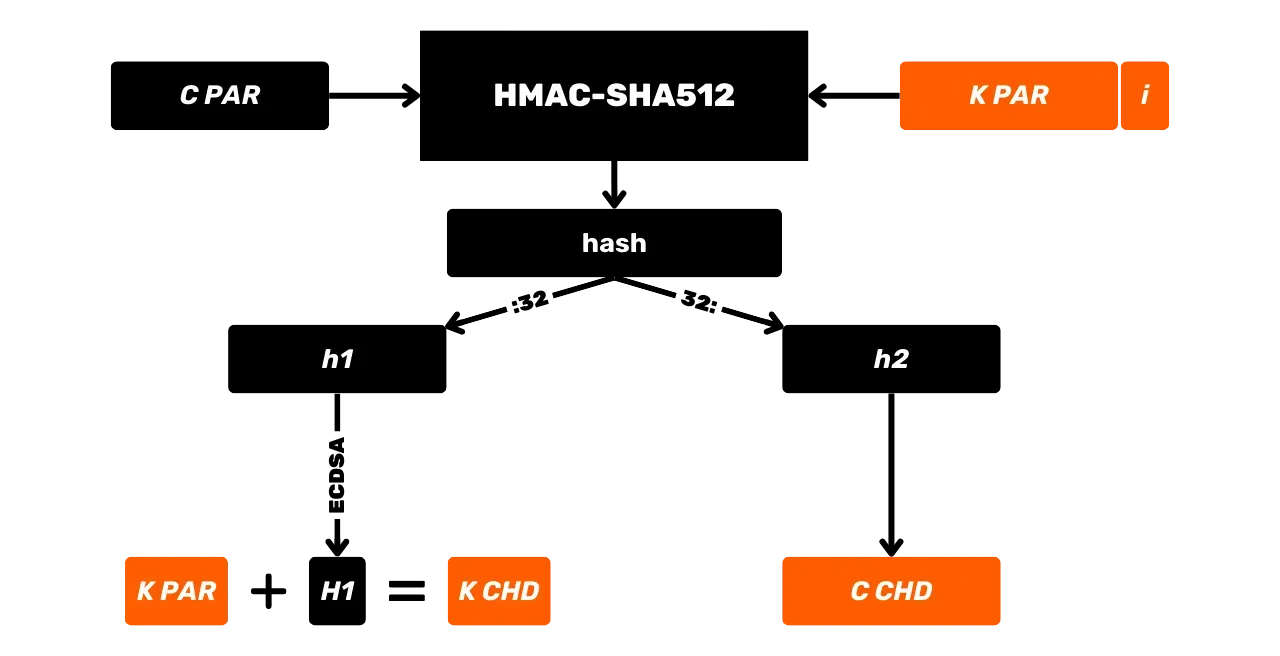
Correspondencia entre claves públicas y privadas hijas
Una pregunta que puede surgir es cómo una clave pública hija normal derivada de una clave pública padre puede corresponder a una clave privada hija normal derivada de la clave privada padre correspondiente. Este enlace está precisamente asegurado por las propiedades de las curvas elípticas. De hecho, para derivar una clave pública hija normal, se aplica HMAC-SHA512 de la misma manera, pero su salida se utiliza de manera diferente:
- Clave privada hija normal:
k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n - Clave pública hija normal:
K_{\text{CHD}}^n = G \cdot \text{parse256}(h_1) + K_{\text{PAR}}
Gracias a las operaciones de adición y duplicación en la curva elíptica, ambos métodos producen resultados consistentes: la clave pública derivada de la clave privada hija es idéntica a la clave pública hija derivada directamente de la clave pública padre.
Resumen de los tipos de derivación
Para resumir, aquí están los diferentes tipos posibles de derivaciones:
\begin{array}{|c|c|c|c|}
\hline
\rightarrow & \text{PAR} & \text{CHD} & \text{n/h} \\
\hline
k_{\text{PAR}} \rightarrow k_{\text{CHD}} & k_{\text{PAR}} & \{ k_{\text{CHD}}^n, k_{\text{CHD}}^h \} & \{ n, h \} \\
k_{\text{PAR}} \rightarrow K_{\text{CHD}} & k_{\text{PAR}} & \{ K_{\text{CHD}}^n, K_{\text{CHD}}^h \} & \{ n, h \} \\
K_{\text{PAR}} \rightarrow k_{\text{CHD}} & K_{\text{PAR}} & \times & \times \\
K_{\text{PAR}} \rightarrow K_{\text{CHD}} & K_{\text{PAR}} & K_{\text{CHD}}^n & n \\
\hline
\end{array}Para resumir, hasta ahora has aprendido a crear los elementos básicos de la billetera HD: la frase mnemotécnica, la semilla y luego la clave maestra y el código de cadena maestro. También has descubierto cómo derivar pares de claves hijas en este capítulo. En el próximo capítulo, exploraremos cómo se organizan estas derivaciones en las billeteras de Bitcoin y qué estructura seguir para obtener concretamente las direcciones de recepción así como los pares de claves utilizados en el scriptPubKey y scriptSig.
Estructura de la Billetera y Caminos de Derivación
La estructura jerárquica de las billeteras HD en Bitcoin permite la organización de pares de claves de varias maneras. La idea es derivar, desde la clave privada maestra y el código de cadena maestro, varios niveles de profundidad. Cada nivel agregado corresponde a la derivación de un par de claves hija de un par de claves padre.
Con el tiempo, diferentes BIPs han introducido estándares para estos caminos de derivación, con el objetivo de estandarizar su uso en diferentes software. Así que, en este capítulo, descubriremos el significado de cada nivel de derivación en las billeteras HD, de acuerdo con estos estándares.
Las Profundidades de Derivación de una Billetera HD
Los caminos de derivación se organizan en capas de profundidad, que van desde la profundidad 0, que representa la clave maestra y el código de cadena maestro, hasta capas de subniveles para derivar direcciones utilizadas para bloquear UTXOs. Los BIPs (Propuestas de Mejora de Bitcoin, Bitcoin Improvement Proposal) definen los estándares para cada capa, lo que ayuda a armonizar las prácticas en diferentes software de gestión de billeteras.
Un camino de derivación, por lo tanto, se refiere a la secuencia de índices utilizados para derivar claves hijas de una clave maestra.
Profundidad 0: Clave Maestra (BIP32)
Esta profundidad corresponde a la clave privada maestra de la billetera y al
código de cadena maestro. Está representada por la notación m/.
Profundidad 1: Propósito (BIP43)
El objetivo determina la estructura lógica de derivación. Por ejemplo, una
dirección P2WPKH tendrá /84'/ en profundidad 1 (según BIP84), mientras que una dirección P2TR tendrá /86'/ (según BIP86). Esta capa
facilita la compatibilidad entre billeteras al indicar números de índice correspondientes
a los números de BIP.
En otras palabras, una vez que tienes la llave maestra y el código de cadena
maestro, estos sirven como un par de llaves padre para derivar un par de
llaves hijo. El índice utilizado en esta derivación puede ser, por ejemplo, /84'/ si la billetera está destinada a usar scripts de tipo SegWit v0. Este par de
llaves está entonces en profundidad 1. Su rol no es bloquear bitcoins, sino simplemente
servir como un punto de referencia en la jerarquía de derivación.
Profundidad 2: Tipo de Moneda (BIP44)
Desde el par de llaves en profundidad 1, se realiza una nueva derivación para obtener el par de llaves en profundidad 2. Esta profundidad permite diferenciar cuentas de Bitcoin de otras criptomonedas dentro de la misma billetera.
Cada moneda tiene un índice único para asegurar la compatibilidad a través
de billeteras multicriptomoneda. Por ejemplo, para Bitcoin, el índice es /0'/ (o 0x80000000 en notación hexadecimal). Los índices de las
monedas se eligen en el rango de 2^{31} a 2^{32}-1 para asegurar
una derivación reforzada.
Para darte otros ejemplos, aquí están los índices de algunas monedas:
1'(0x80000001) para bitcoins de testnet;2'(0x80000002) para Litecoin;60'(0x8000003c) para Ethereum...
Profundidad 3: Cuenta (BIP32)
Cada billetera puede dividirse en varias cuentas, numeradas desde 2^{31}, y representadas en profundidad 3 por /0'/ para la primera cuenta, /1'/ para la segunda, y así sucesivamente. Generalmente, cuando se refiere a una
llave extendida xpub, se refiere a llaves en esta profundidad
de derivación.
Esta separación en diferentes cuentas es opcional. Su objetivo es simplificar la organización de la billetera para los usuarios. En la práctica, a menudo solo se usa una cuenta, generalmente la primera por defecto. Sin embargo, en algunos casos, si se desea distinguir claramente pares de llaves para diferentes usos, esto puede ser útil. Por ejemplo, es posible crear una cuenta personal y una cuenta profesional a partir de la misma semilla, con grupos completamente distintos de llaves desde esta profundidad de derivación.
Profundidad 4: Cadena (BIP32)
Cada cuenta definida en profundidad 3 se estructura entonces en dos cadenas:
La cadena externa: En esta cadena, lo que se conocen como direcciones "públicas" son derivadas. Estas direcciones de recepción están destinadas a bloquear UTXOs provenientes de transacciones externas (es decir, originadas del consumo de UTXOs que no te pertenecen). Para ponerlo simplemente, esta cadena externa se utiliza siempre que se desea recibir bitcoins. Cuando haces clic en "recibir" en tu software de billetera, siempre es una dirección de la cadena externa la que se te ofrece. Esta cadena está representada por un par de llaves derivadas con el índice
/0/.La cadena interna (cambio): Esta cadena está reservada para direcciones de recepción que bloquean bitcoins provenientes del consumo de UTXOs que te pertenecen, en otras palabras, direcciones de cambio. Se identifica por el índice
/1/.
Profundidad 5: Índice de Dirección (BIP32)
Finalmente, la profundidad 5 representa el último paso de derivación en la
billetera. Aunque técnicamente es posible continuar indefinidamente, los
estándares actuales se detienen aquí. En esta profundidad final, se derivan
los pares de claves que realmente se utilizarán para bloquear y desbloquear
los UTXOs. Cada índice permite distinguir entre pares de claves hermanos:
así, la primera dirección de recepción utilizará el índice /0/, la segunda el índice /1/,
y así sucesivamente. 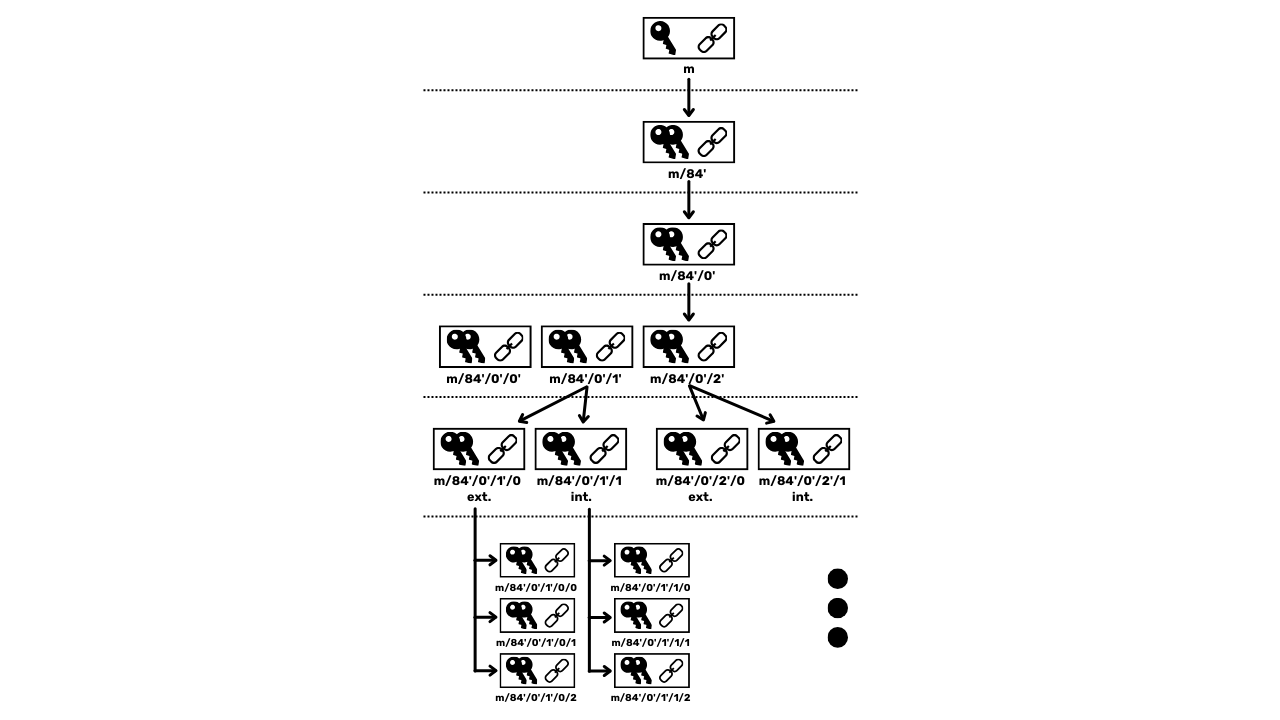
Notación de las Rutas de Derivación
La ruta de derivación se escribe separando cada nivel con una barra (/). Cada barra indica así una derivación de un par de claves padre (k_{\text{PAR}}, K_{\text{PAR}}, C_{\text{PAR}}) a un par de claves hijo (k_{\text{CHD}}, K_{\text{CHD}}, C_{\text{CHD}}). El número anotado en cada profundidad corresponde al índice utilizado
para derivar esta clave de sus padres. El apóstrofo (') a veces colocado a la derecha del índice indica una derivación endurecida
(k_{\text{CHD}}^h, K_{\text{CHD}}^h). A veces, este apóstrofo es reemplazado por una h. En ausencia de un
apóstrofo o h, se trata por
lo tanto de una derivación normal (k_{\text{CHD}}^n, K_{\text{CHD}}^n).
Como hemos visto en los capítulos anteriores, los índices de claves
endurecidas comienzan desde 2^{31}, o 0x80000000 en hexadecimal. Por lo tanto, cuando un índice
es seguido por un apóstrofo en una ruta de derivación, se debe agregar 2^{31} al número indicado para obtener el valor real utilizado en la función
HMAC-SHA512. Por ejemplo, si la ruta de derivación especifica /44'/, el índice real será:
i = 44 + 2^{31} = 2\,147\,483\,692
En hexadecimal, esto es 0x8000002C.
Ahora que hemos entendido los principios principales de las rutas de derivación, ¡tomemos un ejemplo! Aquí está la ruta de derivación para una dirección de recepción de Bitcoin:
m / 84' / 0' / 1' / 0 / 7
En este ejemplo:
84'indica el estándar P2WPKH (SegWit v0);0'indica la moneda Bitcoin en la red principal;1'corresponde a la segunda cuenta en la billetera;0indica que la dirección está en la cadena externa;7indica la 8va dirección externa de esta cuenta.
Resumen de la estructura de derivación
| Profundidad | Descripción | Ejemplo Estándar |
|---|---|---|
| 0 | Clave Maestra | m/ |
| 1 | Propósito | /86'/ (P2TR) |
| 2 | Moneda | /0'/ (Bitcoin) |
| 3 | Cuenta | /0'/ (Primera cuenta) |
| 4 | Cadena | /0/ (externa) o /1/ (cambio) |
| 5 | Índice de Dirección | /0/ (primera dirección) |
En el próximo capítulo, descubriremos qué son los "output script descriptors", una innovación recientemente introducida en Bitcoin Core que simplifica la copia de seguridad de una cartera de Bitcoin.
Descriptores de script de salida
e4f1c2d3-9b8a-4d3e-8f2a-7b6c5d4e3f2a A menudo se dice que la frase mnemotécnica por sí sola es suficiente para recuperar el acceso a una cartera. En realidad, las cosas son un poco más complejas. En el capítulo anterior, examinamos la estructura de derivación de la cartera HD, y podrías haber notado que este proceso es bastante complejo. Los caminos de derivación le dicen al software qué dirección seguir para derivar las claves del usuario. Sin embargo, al recuperar una cartera de Bitcoin, si uno no conoce estos caminos, la frase mnemotécnica por sí sola no es suficiente. Permite obtener la clave maestra y el código de cadena maestro, pero luego es necesario conocer los índices utilizados para alcanzar las claves secundarias.
Teóricamente, sería necesario guardar no solo la frase mnemotécnica de nuestra cartera, sino también los caminos hacia las cuentas que usamos. En la práctica, a menudo es posible recuperar el acceso a las claves secundarias sin esta información, siempre que se hayan seguido los estándares. Probando cada estándar uno por uno, generalmente es posible recuperar el acceso a los bitcoins. Sin embargo, esto no está garantizado y es especialmente complicado para los principiantes. Además, con la diversificación de los tipos de script y la aparición de configuraciones más complejas, esta información podría volverse difícil de extrapolar, convirtiendo así estos datos en información privada y difícil de recuperar por fuerza bruta. Es por esto que recientemente se ha introducido una innovación y está comenzando a integrarse en tu wallet favorito: los output script descriptors.
¿Qué es un "descriptor"?
Los "output script descriptors", o simplemente "descriptors", son expresiones estructuradas que describen completamente un script de salida (scriptPubKey) y proporcionan toda la información necesaria para seguir las transacciones asociadas con un script particular. Facilitan la gestión de claves en carteras HD al ofrecer una descripción estandarizada y completa de la estructura de la cartera y los tipos de direcciones utilizadas.
La principal ventaja de los descriptores radica en su capacidad para
encapsular toda la información esencial para restaurar una cartera en una
sola cadena (además de la frase de recuperación). Al guardar un descriptor
con las frases mnemotécnicas asociadas, se hace posible restaurar las claves
privadas conociendo precisamente su posición en la jerarquía. Para las
carteras multisig, cuya copia de seguridad inicialmente era más compleja, el
descriptor incluye el xpub de cada factor, asegurando así la posibilidad
de regenerar las direcciones en caso de un problema.
Construcción de un descriptor
Un descriptor consiste en varios elementos:
- Funciones de script como
pk(Pay-to-PubKey),pkh(Pay-to-PubKey-Hash),wpkh(Pay-to-Witness-PubKey-Hash),sh(Pay-to-Script-Hash),wsh(Pay-to-Witness-Script-Hash),tr(Pay-to-Taproot),multi(Multifirma), ysortedmulti(Multifirma con claves ordenadas); - Caminos de derivación, por ejemplo,
[d34db33f/44h/0h/0h]que indica un camino de cuenta derivada y una huella digital de clave maestra específica; - Claves en varios formatos como claves públicas hexadecimales o claves
públicas extendidas (
xpub); - Un checksum, precedido por un hash sign, para verificar la integridad del descriptor. Por ejemplo, un descriptor para una cartera P2WPKH (SegWit v0) podría verse así:
wpkh([cdeab12f/84h/0h/0h]xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U/<0;1>/*)#jy0l7nr4
En este descriptor, la función de derivación wpkh indica un
tipo de script Pay-to-Witness-Public-Key-Hash. Le sigue la ruta de
derivación que contiene:
cdeab12f: la huella de la clave maestra;84h: que significa el uso de un propósito BIP84, destinado para direcciones SegWit v0;0h: que indica que es una moneda BTC en la red principal;0h: que se refiere al número de cuenta específico utilizado en la cartera.
El descriptor también incluye la clave pública extendida utilizada en esta cartera:
xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U
A continuación, la notación /<0;1>/* especifica que el
descriptor puede generar direcciones de la cadena externa (0) y
de la cadena interna (1), con un asterisco (*) que
permite la derivación secuencial de múltiples direcciones de manera
configurable, similar a la gestión de un "límite de brecha" en el software
de cartera tradicional.
Finalmente, #jy0l7nr4 representa la suma de comprobación para verificar
la integridad del descriptor.
Ahora sabes todo sobre el funcionamiento de la cartera HD en Bitcoin y el proceso de derivación de pares de claves. Sin embargo, en los últimos capítulos, nos limitamos a la generación de claves privadas y públicas, sin abordar la construcción de direcciones de recepción. ¡Este será precisamente el tema del próximo capítulo!
Direcciones de Recepción
Las direcciones de recepción son piezas de información incrustadas en scriptPubKey para bloquear los UTXOs recién creados. En pocas palabras, una dirección sirve para recibir bitcoins. Vamos a explorar su funcionamiento en conexión con lo que hemos estudiado en los capítulos anteriores.
El Papel de las Direcciones de Bitcoin en los Scripts
Como se explicó anteriormente, el papel de una transacción es transferir la propiedad de bitcoins de entradas a salidas. Este proceso implica consumir UTXOs como entradas mientras se crean nuevos UTXOs como salidas. Estos UTXOs están asegurados por scripts, que definen las condiciones necesarias para desbloquear los fondos.
Cuando un usuario recibe bitcoins, el emisor crea un output UTXO y la
bloquea con un scriptPubKey. Este script contiene las reglas que
especifican típicamente las firmas y claves públicas requeridas para
desbloquear este UTXO. Para gastar este UTXO en una nueva transacción, el
usuario debe proporcionar la información solicitada a través de un scriptSig. La ejecución de scriptSig en combinación con scriptPubKey debe retornar "verdadero" o 1. Si se cumple esta condición, el
UTXO puede gastarse para crear un nuevo UTXO, a su vez bloqueado por un
nuevo scriptPubKey, y así sucesivamente.

Es precisamente en el scriptPubKey donde se encuentran las direcciones de recepción. Sin embargo, su uso varía dependiendo del estándar de script adoptado. Aquí hay una tabla resumen de la información contenida en el scriptPubKey según el estándar utilizado, así como la información esperada en el scriptSig para desbloquear el scriptPubKey.
| Estándar | scriptPubKey | scriptSig | script de redención | testigo |
|---|---|---|---|---|
| P2PK | <pubkey> OP_CHECKSIG | <firma> | ||
| P2PKH | OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG | <firma> <clave pública> | ||
| P2SH | OP_HASH160 <scriptHash> OP_EQUAL | <empujes de datos> <script de redención> | Datos arbitrarios | |
| P2WPKH | 0 <pubKeyHash> | <firma> <clave pública> | ||
| P2WSH | 0 <witnessScriptHash> | <empujes de datos> <script de testigo> | ||
| P2SH-P2WPKH | OP_HASH160 <redeemScriptHash> OP_EQUAL | <script de redención> | 0 <pubKeyHash> | <firma> <clave pública> |
| P2SH-P2WSH | OP_HASH160 <redeemScriptHash> OP_EQUAL | <script de redención> | 0 <scriptHash> | <empujes de datos> <script de testigo> |
| P2TR (ruta de clave) | 1 <clave pública> | <firma> | ||
| P2TR (ruta de script) | 1 <clave pública> | <empujes de datos> <script> <bloque de control> |
Fuente: Bitcoin Core PR review club, 7 de julio de 2021 - Gloria Zhao
Los opcodes utilizados en un script están diseñados para manipular información y, si es necesario, para compararla o probarla. Tomemos el ejemplo de un script P2PKH, que es como sigue:
OP_DUP OP_HASH160 OP_PUSHBYTES_20 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG
Como veremos en este capítulo, <pubKeyHash> representa en
realidad el payload de la dirección de recepción utilizada para bloquear el
UTXO. Para desbloquear este scriptPubKey, es necesario proporcionar
un scriptSig que contenga:
<signature> <public key>
En el lenguaje de script, la "pila" es una estructura de datos "LIFO" ("Last In, First Out" o "Último en Entrar, Primero en Salir") utilizada para almacenar temporalmente elementos durante la ejecución del script. Cada operación del script manipula esta pila, donde los elementos pueden ser añadidos (push) o eliminados (pop). Los scripts utilizan estas pilas para evaluar expresiones, almacenar variables temporales y gestionar condiciones.
La ejecución del script que acabo de dar como ejemplo sigue este proceso:
- Tenemos el scriptSig, el ScriptPubKey, y la pila:

- El scriptSig se introduce en la pila:

OP_DUPduplica la clave pública proporcionada en el scriptSig en la pila:

OP_HASH160devuelve el hash de la clave pública que acaba de ser duplicada:
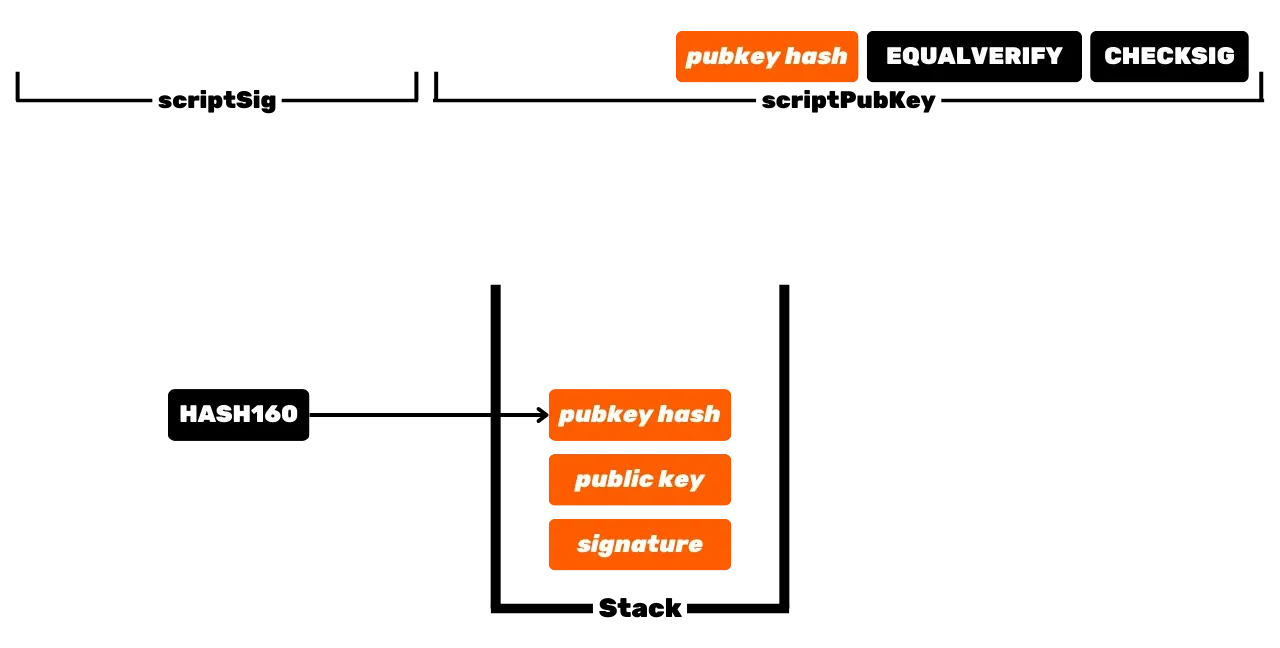
OP_PUSHBYTES_20 <pubKeyHash>introduce la dirección de Bitcoin contenida en el scriptPubKey en la pila:

OP_EQUALVERIFYverifica que la clave pública hasheada coincida con la dirección de recepción proporcionada:

OP_CHECKSIGverifica la firma contenida en el scriptSig usando la clave pública. Este opcode esencialmente realiza una verificación de firma como describimos en la parte 3 de esta formación:
Si
1permanece en la pila, entonces el script es válido:
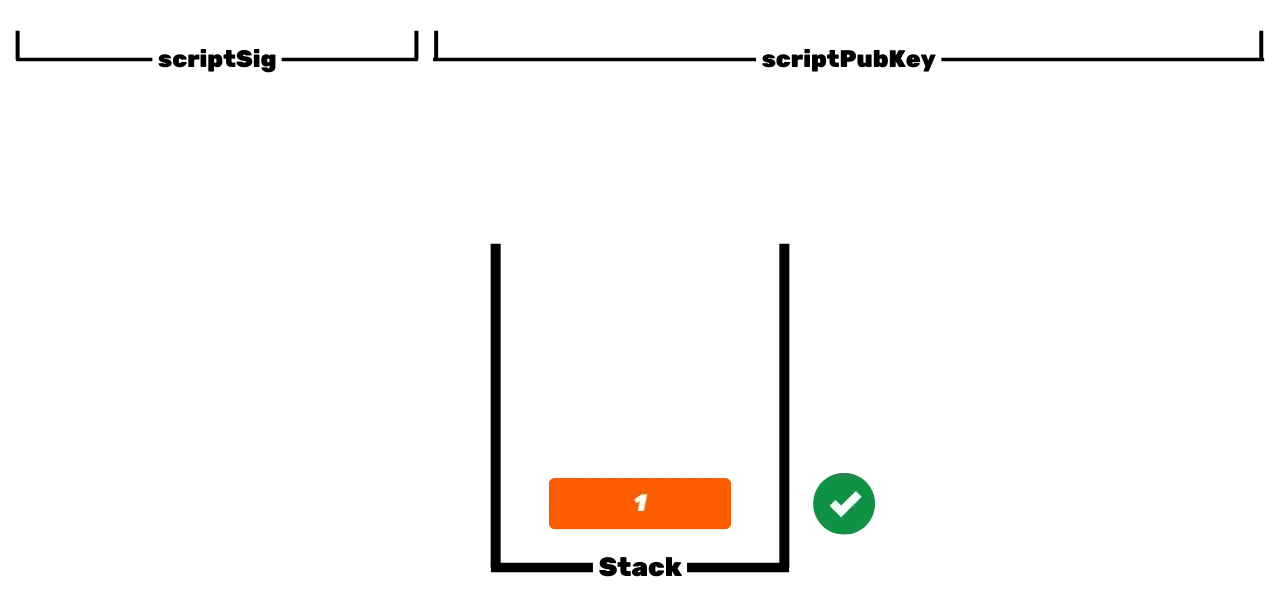
Por lo tanto, para resumir, este script permite verificar, con la ayuda de la firma digital, que el usuario que reclama la propiedad de este UTXO y desea gastarlo posee de hecho la clave privada asociada con la dirección de recepción utilizada durante la creación de este UTXO.
Los diferentes tipos de direcciones de Bitcoin
A lo largo de la evolución de Bitcoin, se han añadido varios modelos de script estándar. Cada uno de ellos utiliza un tipo distinto de dirección de recepción. Aquí hay una visión general de los principales modelos de script disponibles hasta la fecha:
P2PK (Pay-to-PubKey):
Este modelo de script fue introducido en la primera versión de Bitcoin por Satoshi Nakamoto. El script P2PK bloquea los bitcoins directamente usando una clave pública raw (por lo tanto, no se utiliza ninguna dirección de recepción con este modelo). Su estructura es simple: contiene una clave pública y requiere una firma digital correspondiente para desbloquear los fondos. Este script es parte del estándar "Legacy".
P2PKH (Pay-to-PubKey-Hash):
Al igual que P2PK, el script P2PKH fue introducido en el lanzamiento de
Bitcoin. A diferencia de su predecesor, bloquea los bitcoins usando el hash
de la clave pública, en lugar de usar directamente la clave pública sin
procesar. El scriptSig debe entonces proporcionar la clave pública
asociada con la dirección de recepción, así como una firma válida. Las
direcciones correspondientes a este modelo comienzan con 1 y
están codificadas en base58check. Este script también pertenece al
estándar "Legacy".
P2SH (Pay-to-Script-Hash):
Introducido en 2012 con el BIP16, el modelo P2SH permite usar el hash de un
script arbitrario en el scriptPubKey. Este script hasheado, llamado
"redeemScript", contiene las condiciones para desbloquear los
fondos. Para gastar un UTXO bloqueado con P2SH, es necesario proporcionar un scriptSig que contenga el redeemScript original así como los datos necesarios
para validar dicho script. Este modelo es notablemente utilizado para
multisigs antiguos. Las direcciones asociadas con P2SH comienzan con 3 y están codificadas en base58check. Este script también pertenece
al estándar "Legacy".
P2WPKH (Pay-to-Witness-PubKey-Hash):
Este script es similar a P2PKH, ya que también bloquea bitcoins usando el hash de una clave pública. Sin embargo, a diferencia de P2PKH, el scriptSig se traslada a una sección separada llamada "Witness". Esto a veces se refiere como "scriptWitness" para denotar el conjunto que comprende la firma y la clave pública. Cada entrada SegWit tiene su propio scriptWitness, y la colección de scriptWitnesses constituye el campo Witness de la transacción. Este movimiento de datos de firma es una innovación introducida por la actualización SegWit, dirigida particularmente a prevenir la maleabilidad de las transacciones debido a las firmas ECDSA.
Las direcciones P2WPKH usan codificación bech32 y siempre comienzan
con bc1q. Este tipo de script corresponde a las salidas SegWit
versión 0.
P2WSH (Pay-to-Witness-Script-Hash):
El modelo P2WSH también fue introducido con la actualización SegWit en agosto de 2017. Similar al modelo P2SH, bloquea bitcoins usando el hash de un script. La principal diferencia radica en cómo se incorporan las firmas y los scripts en la transacción. Para gastar bitcoins bloqueados con este tipo de script, el destinatario debe proporcionar el script original, llamado witnessScript (equivalente a redeemScript en P2SH), junto con los datos necesarios para validar este witnessScript. Este mecanismo permite la implementación de condiciones de gasto más complejas, como multisigs.
Las direcciones P2WSH usan codificación bech32 y siempre comienzan
con bc1q. Este script también corresponde a las salidas SegWit
versión 0.
P2TR (Pay-to-Taproot):
El modelo P2TR fue introducido con la implementación de Taproot en noviembre de 2021. Se basa en el protocolo Schnorr para la agregación de claves criptográficas, así como en un árbol de Merkle para scripts alternativos, llamado MAST (Merkelized Alternative Script Tree). A diferencia de otros tipos de scripts, donde las condiciones de gasto se exponen públicamente (ya sea al recibir o al gastar), P2TR permite ocultar scripts complejos detrás de una única clave pública aparente.
Técnicamente, un script P2TR bloquea bitcoins en una clave pública Schnorr
única, denotada como Q. Esta
clave Q es en realidad un
agregado de una clave pública P y una clave pública M, siendo
esta última calculada a partir de la raíz de Merkle de una lista de scriptPubKey. Los bitcoins bloqueados con este tipo de script
pueden gastarse de dos maneras:
- Publicando una firma para la clave pública
P(key path). - Satisfaciendo uno de los scripts contenidos en el árbol de Merkle (script path).
P2TR ofrece así una gran flexibilidad, ya que permite bloquear bitcoins ya
sea con una clave pública única, con varios scripts de elección, o ambos
simultáneamente. La ventaja de esta estructura de árbol de Merkle es que
solo se revela el script de gasto utilizado durante la transacción, pero
todos los demás scripts alternativos permanecen en secreto. 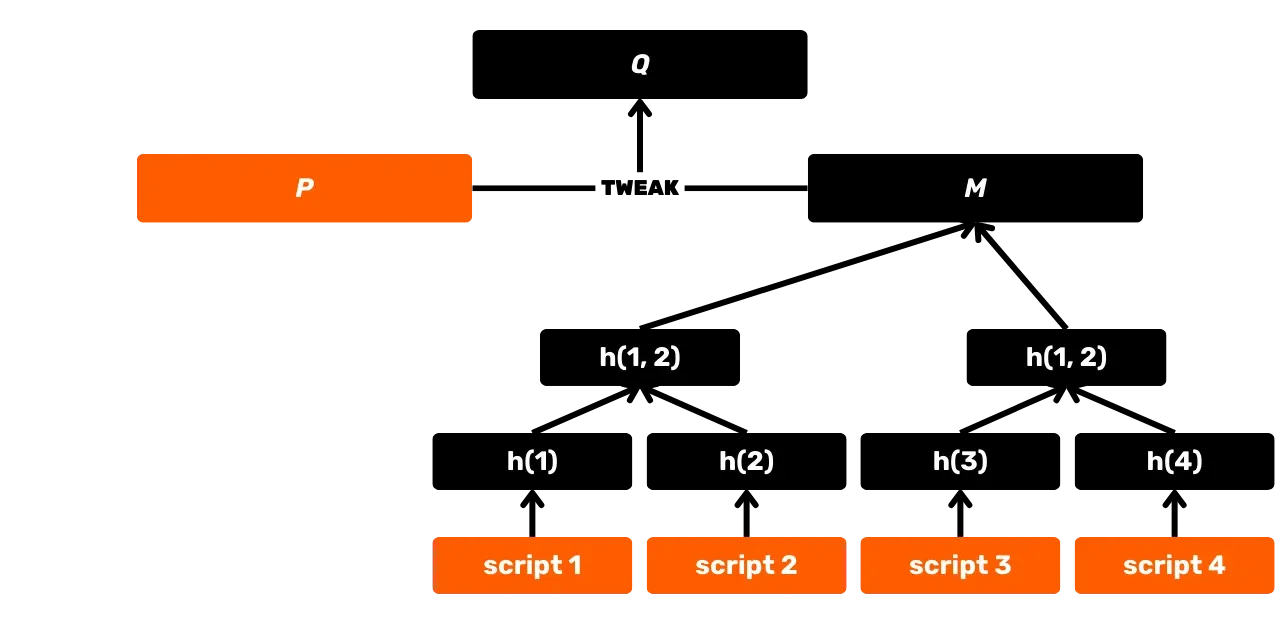
P2TR corresponde a las salidas de versión 1 de SegWit, lo que significa que
las firmas para las entradas P2TR se almacenan en la sección Witness de la transacción, y no en el scriptSig. Las direcciones P2TR
utilizan la codificación bech32m y comienzan con bc1p,
pero son bastante únicas porque no utilizan una función hash para su
construcción. De hecho, representan directamente la clave pública Q que simplemente está formateada
con metadatos. Por lo tanto, es un modelo de script cercano a P2PK.
Ahora que hemos cubierto la teoría, ¡pasemos a la práctica! En el siguiente capítulo, propongo derivar tanto una dirección SegWit v0 como una dirección SegWit v1 a partir de un par de claves.
Derivación de Direcciones
Exploremos juntos cómo generar una dirección de recepción a partir de un par de claves ubicadas, por ejemplo, en la profundidad 5 de una cartera HD. Esta dirección puede entonces utilizarse en un software de cartera para bloquear un UTXO.
Dado que el proceso de generación de una dirección depende del modelo de script adoptado, centrémonos en dos casos específicos: generar una dirección SegWit v0 en P2WPKH y una dirección SegWit v1 en P2TR. Estos dos tipos de direcciones cubren la gran mayoría de los usos hoy en día.
Compresión de la Clave Pública
Después de realizar todos los pasos de derivación desde la clave maestra
hasta la profundidad 5 utilizando los índices apropiados, obtenemos un par
de claves (k, K) con K = k \cdot G. Aunque es
posible usar esta clave pública tal cual para bloquear fondos con el
estándar P2PK, ese no es nuestro objetivo aquí. En cambio, nuestro objetivo
es crear una dirección en P2WPKH en primera instancia, y luego en P2TR para
otro ejemplo.
El primer paso es comprimir la clave pública K. Para entender bien este proceso, primero recordemos algunos fundamentos
cubiertos en la parte 3.
Una clave pública en Bitcoin es un punto K ubicado en una curva elíptica. Se representa en la forma (x, y), donde x y y son las coordenadas del
punto. En su forma no comprimida, esta clave pública mide 520 bits: 8 bits
para un prefijo (valor inicial de 0x04), 256 bits para la
coordenada x, y 256 bits para
la coordenada y.
Sin embargo, las curvas elípticas tienen una propiedad de simetría con
respecto al eje x: para una coordenada x dada, solo hay dos valores posibles para y: y y -y. Estos dos puntos están
ubicados a cada lado del eje x. En otras palabras, si conocemos x, es suficiente especificar
si y es par o impar para identificar
el punto exacto en la curva.
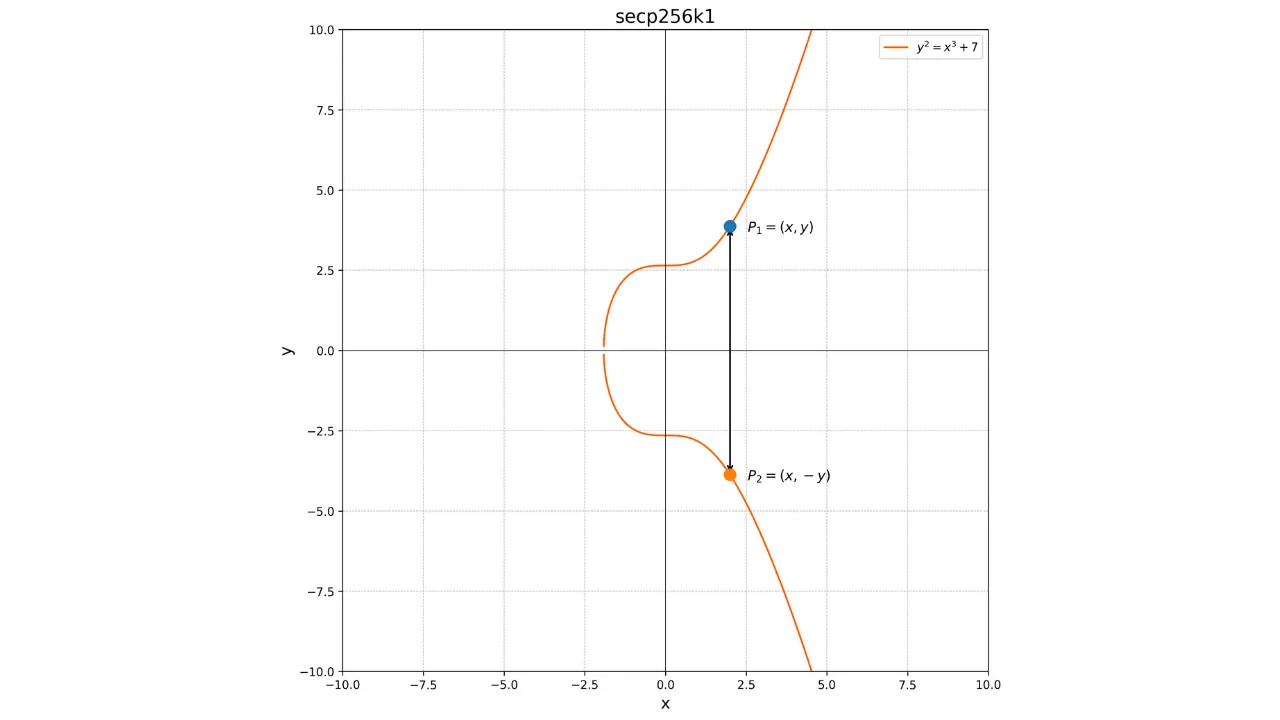 Para comprimir una clave pública, solo se codifica
Para comprimir una clave pública, solo se codifica x, que ocupa 256 bits, y se
añade un prefijo para especificar la paridad de y. Este método reduce el
tamaño de la clave pública a 264 bits en lugar de los 520 iniciales. El
prefijo 0x02 indica que y es par, y el prefijo 0x03 indica que y es impar. Tomemos un ejemplo para entender bien, con una clave pública sin
procesar (raw public key) en representación no comprimida:
K = 04678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f
Si descomponemos esta clave, tenemos:
- El prefijo:
04; x:678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6;y:49f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f
El último carácter hexadecimal de y es f. En base 10, f = 15, lo que corresponde a un
número impar. Por lo tanto, y es impar, y el prefijo será 0x03 para indicar esto.
La clave pública comprimida se convierte en:
K = 03678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6
Esta operación se aplica a todos los modelos de script basados en ECDSA, es
decir, todos excepto P2TR que utiliza Schnorr. En el caso de Schnorr, como
se explicó en la parte 3, solo retenemos el valor de x, sin añadir un prefijo para indicar la paridad de y, a diferencia de ECDSA.
Esto es posible por el hecho de que se elige arbitrariamente una paridad
única para todas las claves. Esto permite una ligera reducción en el espacio
de almacenamiento requerido para las claves públicas.
Derivación de una dirección SegWit v0 (bech32)
Ahora que hemos obtenido nuestra clave pública comprimida, podemos derivar de ella una dirección de recepción SegWit v0.
El primer paso es aplicar la función de hash HASH160 a la clave pública comprimida. HASH160 es una composición de dos funciones de hash sucesivas: SHA256, seguido por RIPEMD160:
\text{HASH160}(K) = \text{RIPEMD160}(\text{SHA256}(K))
Primero, pasamos la clave por SHA256:
SHA256(K) = C489EBD66E4103B3C4B5EAFF462B92F5847CA2DCE0825F4997C7CF57DF35BF3A
Luego pasamos el resultado por RIPEMD160:
RIPEMD160(SHA256(K)) = 9F81322CC88622CA4CCB2A52A21E2888727AA535
Hemos obtenido un hash de 160 bits de la clave pública, lo que constituye lo que se llama el payload de la dirección. Este payload representa la parte central y más importante de la dirección. También se utiliza en el scriptPubKey para bloquear los UTXOs. Sin embargo, para hacer este payload más fácilmente utilizable por humanos, se le añade metadatos. El siguiente paso implica codificar este hash en grupos de 5 bits en decimal. Esta transformación decimal será útil para la conversión a bech32, utilizado por direcciones post-SegWit. El hash binario de 160 bits se divide así en 32 grupos de 5 bits:
\begin{array}{|c|c|}
\hline
\text{5 bits} & \text{Decimal} \\
\hline
10011 & 19 \\
11110 & 30 \\
00000 & 0 \\
10011 & 19 \\
00100 & 4 \\
01011 & 11 \\
00110 & 6 \\
01000 & 8 \\
10000 & 16 \\
11000 & 24 \\
10001 & 17 \\
01100 & 12 \\
10100 & 20 \\
10011 & 19 \\
00110 & 6 \\
01011 & 11 \\
00101 & 5 \\
01001 & 9 \\
01001 & 9 \\
01010 & 10 \\
00100 & 4 \\
00111 & 7 \\
10001 & 17 \\
01000 & 8 \\
10001 & 17 \\
00001 & 1 \\
11001 & 25 \\
00111 & 7 \\
10101 & 21 \\
00101 & 5 \\
00101 & 5 \\
10101 & 21 \\
\hline
\end{array}Entonces, tenemos:
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
Una vez que el hash está codificado en grupos de 5 bits, se añade un checksum a la dirección. Este checksum se utiliza para verificar que el payload de la dirección no ha sido alterado durante su almacenamiento o transmisión. Por ejemplo, permite a un software de billetera asegurarse de que no has cometido un error al ingresar una dirección de recepción. Sin esta verificación, podrías enviar accidentalmente bitcoins a una dirección incorrecta, resultando en una pérdida permanente de fondos, ya que no posees la clave pública o privada asociada. Por lo tanto, el checksum es una protección contra errores humanos.
Para las antiguas direcciones de Bitcoin Legacy, el checksum se calculaba simplemente desde el principio del hash de la dirección con la función HASH256. Con la introducción de SegWit y el formato bech32, ahora se utilizan los códigos BCH (Bose, Ray-Chaudhuri y Hocquenghem). Estos códigos de corrección de errores se utilizan para detectar y corregir errores en secuencias de datos. Aseguran que la información transmitida llegue intacta a su destino, incluso en caso de alteraciones menores. Los códigos BCH se utilizan en muchos campos, como SSDs, DVDs y códigos QR. Por ejemplo, gracias a estos códigos BCH, un código QR parcialmente oscurecido aún puede ser leído y decodificado.
En el contexto de Bitcoin, los códigos BCH ofrecen un mejor compromiso entre tamaño y capacidad de detección de errores en comparación con las simples funciones hash utilizadas para direcciones Legacy. Sin embargo, en Bitcoin, los códigos BCH se utilizan solo para la detección de errores, no para la corrección. Así, el software de billetera señalará una dirección de recepción incorrecta pero no la corregirá automáticamente. Esta limitación es deliberada: permitir la corrección automática reduciría la capacidad de detección de errores.
Para calcular el checksum con códigos BCH, necesitamos preparar varios elementos:
- La Parte Legible por Humanos (HRP): Para la red principal
de Bitcoin, el HRP es
bc; El HRP debe expandirse separando cada carácter en dos partes: - Tomando los caracteres del HRP en ASCII:
b:01100010c:01100011
- Extrayendo los 3 bits más significativos y los 5 bits menos
significativos:
- 3 bits más significativos:
011(3 en decimal) - 3 bits más significativos:
011(3 en decimal) - 5 bits menos significativos:
00010(2 en decimal) - 5 bits menos significativos:
00011(3 en decimal)
- 3 bits más significativos:
Con el separador 0 entre los dos caracteres, la extensión del HRP
es, por lo tanto:
03 03 00 02 03
La versión witness: Para la versión 0 de SegWit, es
00;El payload: Los valores decimales del hash de la clave pública;
La reserva para el checksum: Añadimos 6 ceros
[0, 0, 0, 0, 0, 0]al final de la secuencia.
Todos los datos combinados para introducir en el programa para calcular el checksum son los siguientes:
HRP = 03 03 00 02 03
SEGWIT v0 = 00
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
CHECKSUM = 00 00 00 00 00 00
INPUT = 03 03 00 02 03 00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 00 00 00 00 00 00
El cálculo del checksum es bastante complejo. Involucra aritmética de campos finitos polinomiales. No detallaremos este cálculo aquí y pasaremos directamente al resultado. En nuestro ejemplo, el checksum obtenido en decimal es:
10 16 11 04 13 18
Ahora podemos construir la dirección de recepción concatenando en orden los siguientes elementos:
- La versión de SegWit:
00 - El payload: El hash de la clave pública
- El checksum: Los valores obtenidos en el paso anterior (
10 16 11 04 13 18)
Esto nos da en decimal:
00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 10 16 11 04 13 18
Luego, cada valor decimal debe mapearse a su carácter bech32 usando la siguiente tabla de conversión:
\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline
& 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\
\hline
+0 & q & p & z & r & y & 9 & x & 8 \\
\hline
+8 & g & f & 2 & t & v & d & w & 0 \\
\hline
+16 & s & 3 & j & n & 5 & 4 & k & h \\
\hline
+24 & c & e & 6 & m & u & a & 7 & l \\
\hline
\end{array}Para convertir un valor en un carácter bech32 usando esta tabla,
simplemente localiza los valores en la primera columna y la primera fila
que, al sumarlos, produzcan el resultado deseado. Luego, recupera el
carácter correspondiente. Por ejemplo, el número decimal 19 se
convertirá en la letra n, porque 19 = 16 + 3.
Al mapear todos nuestros valores, obtenemos la siguiente dirección:
qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj
Todo lo que queda es añadir el HRP bc, que indica que es una
dirección para la red principal de Bitcoin, así como el separador 1, para obtener la dirección de recepción completa:
bc1qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj
La particularidad de este alfabeto bech32 es que incluye todos los
caracteres alfanuméricos excepto 1, b, i y o para evitar la confusión visual entre caracteres similares,
especialmente durante su entrada o lectura por humanos.
Para resumir, aquí está el proceso de derivación:
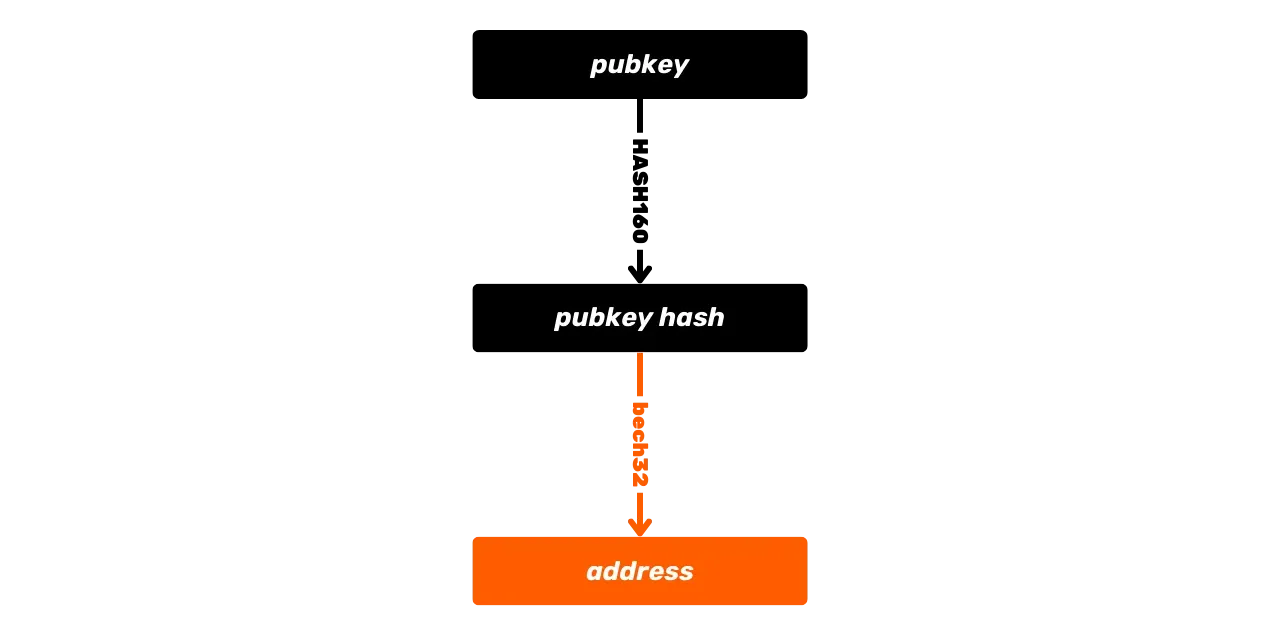
Así es como se deriva una dirección de recepción P2WPKH (SegWit v0) a partir de un par de claves. Ahora pasemos a las direcciones P2TR (SegWit v1 / Taproot) y descubramos su proceso de generación.
Derivación de una Dirección SegWit v1 (bech32m)
Para las direcciones Taproot, el proceso de generación difiere ligeramente. ¡Veámoslo juntos!
Desde el paso de la compresión de la clave pública, aparece una primera
distinción en comparación con ECDSA: las claves públicas utilizadas para
Schnorr en Bitcoin están representadas solo por su abscisa (x). Por lo tanto, no hay prefijo, y la clave comprimida mide exactamente 256
bits.
Como vimos en el capítulo anterior, un script P2TR bloquea bitcoins en una
única clave pública Schnorr, designada por Q. Esta clave Q es un
agregado de dos claves públicas: P, una clave pública interna
principal, y M, una clave
pública derivada de la raíz de Merkle de una lista de scriptPubKey.
Los bitcoins bloqueados con este tipo de script pueden gastarse de dos
maneras:
- Publicando una firma para la clave pública
P(key path); - Satisfaciendo uno de los scripts incluidos en el árbol de Merkle (script path).
En realidad, estas dos claves no están verdaderamente "agregadas". La clave P en cambio es modificada por la clave M. En criptografía,
"modificar" una clave pública significa modificar esta clave aplicando un
valor aditivo llamado "modificación". Esta operación permite que la clave
modificada siga siendo compatible con la clave privada original y la
modificación. Técnicamente, una modificación es un valor escalar t que se suma a la clave pública inicial. Si P es la clave pública original,
la clave modificada se convierte en:
P' = P + tG
Donde G es el generador de la
curva elíptica utilizada. Esta operación produce una nueva clave pública derivada
de la clave original, mientras retiene propiedades criptográficas que permiten
su uso.
Si no necesitas agregar scripts alternativos (gastando exclusivamente a
través del key path), puedes generar una dirección Taproot basada
únicamente en la clave pública presente en el nivel 5 de tu billetera. En
este caso, es necesario crear un script no gastable para el script path, con el fin de satisfacer los requisitos de la
estructura. El ajuste t se
calcula entonces aplicando una función de hash etiquetada, TapTweak, sobre la clave pública interna P:
t = \text{H}_{\text{TapTweak}}(P)donde:
\text{H}_{\text{TapTweak}}es una función de hash SHA256 etiquetada con la etiquetaTapTweak. Si no estás familiarizado con lo que es una función de hash etiquetada, te invito a consultar el capítulo 3.3;Pes la clave pública interna, representada en su formato comprimido de 256 bits, utilizando solo la coordenadax.
La clave pública Taproot Q se
calcula entonces sumando el ajuste t, multiplicado por el
generador de curva elíptica G, a la clave pública interna P:
Q = P + t \cdot G
Una vez que se obtiene la clave pública Taproot Q, podemos generar la dirección de recepción correspondiente. A diferencia
de otros formatos, las direcciones Taproot no se establecen en un hash de la
clave pública. Por lo tanto, la clave Q se inserta directamente en la
dirección, de manera cruda.
Para comenzar, extraemos la coordenada x del punto Q para obtener una
clave pública comprimida. Sobre este payload, se calcula un checksum usando
códigos BCH, como con las direcciones SegWit v0. Sin embargo, el programa
utilizado para las direcciones Taproot difiere ligeramente. De hecho,
después de la introducción del formato bech32 con SegWit, se
descubrió un bug: cuando el último carácter de una dirección es una p, insertar o quitar qs justo antes de esta p no hace que el checksum sea inválido. Aunque este bug no tiene consecuencias
en SegWit v0 (gracias a una restricción de tamaño), podría plantear un
problema en el futuro. Este bug ha sido corregido para las direcciones
Taproot, y el nuevo formato corregido se llama "bech32m".
La dirección Taproot se genera codificando la coordenada x de Q en el formato bech32m, con los siguientes elementos:
- La HRP (Human Readable Part):
bc, para indicar la red principal de Bitcoin; - La versión:
1para indicar Taproot / SegWit v1; - El checksum.
La dirección final tendrá por lo tanto el formato:
bc1p[Qx][checksum]
Por otro lado, si deseas agregar scripts alternativos además de gastar con la clave pública interna (script path), el cálculo de la dirección de recepción será ligeramente diferente. Necesitarás incluir el hash de los scripts alternativos en el cálculo del ajuste. En Taproot, cada script alternativo, ubicado al final del árbol de Merkle, se llama "hoja".
Una vez que se escriben los diferentes scripts alternativos, debes pasarlos
individualmente a través de una función de hash etiquetada TapLeaf, acompañada de algunos metadatos:
\text{h}_{\text{leaf}} = \text{H}_{\text{TapLeaf}} (v \Vert sz \Vert S)
Con:
v: el número de versión del script (por defecto0xC0para Taproot);sz: el tamaño del script codificado en formato CompactSize;S: el script.
Los diferentes hashes de script (\text{h}_{\text{leaf}}) se ordenan primero en orden lexicográfico. Luego, se concatenan en pares
y se pasan a través de una función hash etiquetada TapBranch.
Este proceso se repite iterativamente para construir, paso a paso, el árbol
de Merkle:
\text{h}_{\text{branch}} = \text{H}_{\text{TapBranch}}(\text{h}_{\text{leaf1}} \Vert \text{h}_{\text{leaf2}})Luego continuamos concatenando los resultados de dos en dos, pasándolos en
cada paso a través de la función hash etiquetada TapBranch,
hasta obtener la raíz del árbol de Merkle:
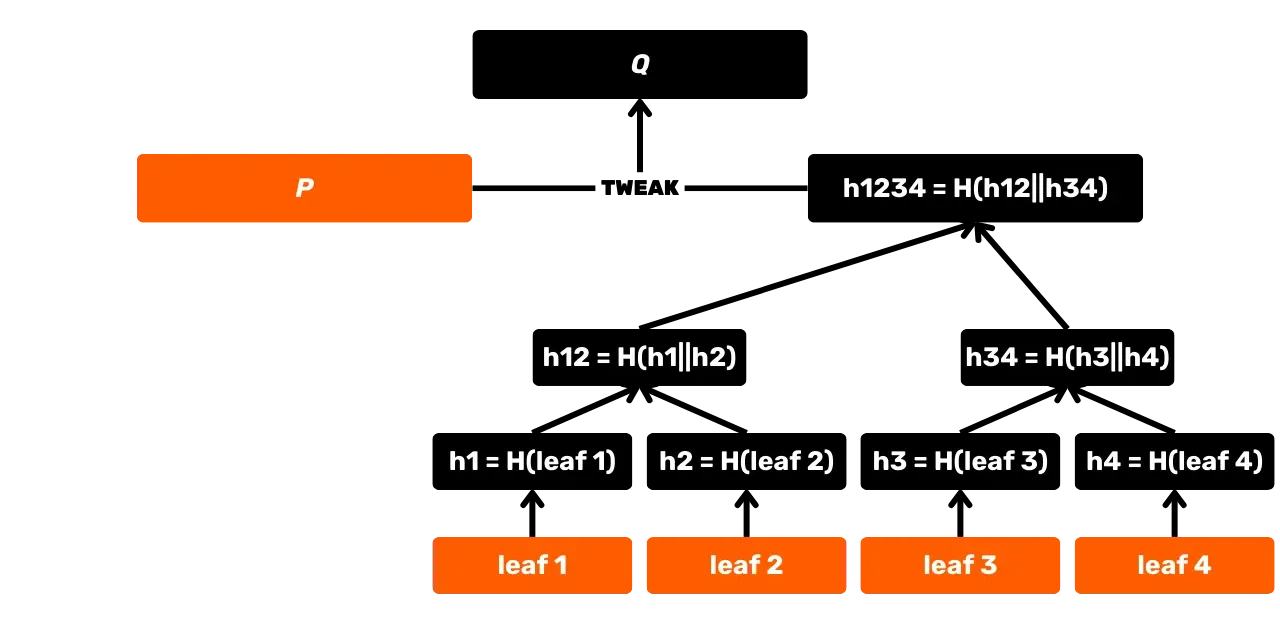
Una vez calculada la raíz de Merkle h_{\text{root}}, se puede calcular el tweak. Para ello, se concatena la clave pública
interna de la billetera P con
la raíz h_{\text{root}}, y el resultado se pasa por la función de hash etiquetada TapTweak:
t = \text{H}_{\text{TapTweak}}(P \Vert h_{\text{root}})Finalmente, como antes, la clave pública Taproot Q se obtiene sumando la clave pública interna P al producto del tweak t y el
punto generador G:
Q = P + t \cdot GLuego, la generación de la dirección sigue el mismo proceso, utilizando la
clave pública Q como carga útil,
junto con algunos metadatos adicionales.
¡Y ahí lo tienes! Hemos llegado al final de este curso CYP201. Si encontraste este curso útil, estaría muy agradecido si pudieras tomar unos momentos para darle una buena calificación en el siguiente capítulo de evaluación. Siéntete libre de compartirlo también con tus seres queridos o en tus redes sociales. Finalmente, si deseas obtener tu diploma para este curso, puedes tomar el examen final justo después del capítulo de evaluación.
Sección final
Reseñas & Valoraciones
0cd71541-a7fd-53db-b66a-8611b6a28b04 true
Examen final
a53ea27d-0f84-56cd-b37c-a66210a4b31d true
Conclusión
d291428b-3cfa-5394-930e-4b514be82d5a true