name: The Inner Workings of Bitcoin Wallets goal: Dive into the cryptographic principles that power Bitcoin wallets. objectives:

A Journey into the Heart of Bitcoin Wallets

Discover the secrets of deterministic and hierarchical Bitcoin wallets with our CYP201 course! Whether you're a regular user or an enthusiast looking to deepen your knowledge, this course offers a complete immersion into the workings of these tools that we all use daily.

Learn about the mechanisms of hash functions, digital signatures (ECDSA and Schnorr), mnemonic phrases, cryptographic keys, and the creation of receiving addresses, all while exploring advanced security strategies.

This training will not only equip you with the knowledge to understand the structure of a Bitcoin wallet but will also prepare you to dive deeper into the exciting world of cryptography.

With clear pedagogy, over 60 explanatory diagrams, and concrete examples, CYP201 will enable you to understand from A to Z how your wallet works, so you can navigate the Bitcoin universe with confidence. Take control of your UTXOs today by understanding how HD wallets function!

Introduction

Course Introduction

Welcome to the CYP201 course, where we will explore in depth the workings of HD Bitcoin wallets. This course is designed for anyone who wants to understand the technical basics of using Bitcoin, whether they are casual users, enlightened enthusiasts, or future experts.

The goal of this training is to give you the keys to master the tools you use daily. HD Bitcoin wallets, which are at the heart of your user experience, are based on sometimes complex concepts, which we will try to make accessible. Together, we will demystify them!

Before diving into the details of the construction and operation of Bitcoin wallets, we will start with a few chapters on the cryptographic primitives to know for what follows. We will start with cryptographic hash functions, fundamental for both wallets and the Bitcoin protocol itself. You will discover their main characteristics, the specific functions used in Bitcoin, and in a more technical chapter, you will learn in detail about the workings of the queen of hash functions: SHA256.

CYP201

Next, we will discuss the operation of digital signature algorithms that you use every day to secure your UTXOs. Bitcoin uses two: ECDSA and the Schnorr protocol. You will learn which mathematical primitives underlie these algorithms and how they ensure the security of transactions.

CYP201

Once we have a good understanding of these elements of cryptography, we will finally move on to the heart of the training: deterministic and hierarchical wallets! First, there is a section dedicated to mnemonic phrases, these sequences of 12 or 24 words that allow you to create and restore your wallets. You will discover how these words are generated from a source of entropy and how they facilitate the use of Bitcoin.

CYP201

The training will continue with the study of the BIP39 passphrase, the seed (not to be confused with the mnemonic phrase), the master chain code, and the master key. We will see in detail what these elements are, their respective roles, and how they are calculated.

CYP201

Finally, from the master key, we will discover how cryptographic key pairs are derived in a deterministic and hierarchical manner up to the receiving addresses.

CYP201

This training will enable you to use your wallet software with confidence, while enhancing your skills to identify and mitigate risks. Prepare to become a true expert in Bitcoin wallets!

Hash Functions

Introduction to Hash Functions

The first type of cryptographic algorithms used in Bitcoin encompasses hash functions. They play an essential role at different levels of the protocol, but also within Bitcoin wallets. Let's discover together what a hash function is and what it's used for in Bitcoin.

Definition and Principle of Hashing

Hashing is a process that transforms information of arbitrary length into another piece of information of fixed length through a cryptographic hash function. In other words, a hash function takes an input of any size and converts it into a fixed-size fingerprint, called a "hash". The hash can also sometimes be referred to as "digest", "condensate", "condensed", or "hashed".

For example, the SHA256 hash function produces a hash of a fixed length of 256 bits. Thus, if we use the input "PlanB", a message of arbitrary length, the generated hash will be the following 256-bit fingerprint:

24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688
CYP201

Characteristics of Hash Functions

These cryptographic hash functions have several essential characteristics that make them particularly useful in the context of Bitcoin and other computer systems:

1. Irreversibility (preimage resistance):

Irreversibility means that it is easy to calculate the hash from the input information, but the inverse calculation, that is, finding the input from the hash, is practically impossible. This property makes hash functions perfect for creating unique digital fingerprints without compromising the original information. This characteristic is often referred to as a one-way function.

In the given example, obtaining the hash 24f1b9… by knowing the input "PlanB" is simple and quick. However, finding the message "PlanB" by only knowing 24f1b9… is impossible.

CYP201

Therefore, it is impossible to find a preimage m for a hash h such that h = \text{HASH}(m), where \text{HASH} is a cryptographic hash function.

2. Tamper resistance (avalanche effect)

The second characteristic is tamper resistance, also known as the avalanche effect. This characteristic is observed in a hash function if a small change in the input message results in a radical change in the output hash.

If we go back to our example with the input "PlanB" and the SHA256 function, we have seen that the generated hash is as follows:

24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688

If we make a very slight change to the input by using "Planb" this time, then simply changing from an uppercase "B" to a lowercase "b" completely alters the SHA256 output hash:

bb038b4503ac5d90e1205788b00f8f314583c5e22f72bec84b8735ba5a36df3f
CYP201

This property ensures that even a minor alteration of the original message is immediately detectable, as it does not just change a small part of the hash, but the entire hash. This can be of interest in various fields to verify the integrity of messages, software, or even Bitcoin transactions.

3. Collision Resistance

The third characteristic is collision resistance. A hash function is collision-resistant if it is computationally impossible to find 2 different messages that produce the same hash output from the function. Formally, it is difficult to find two distinct messages m_1 and m_2 such that:

\text{HASH}(m_1) = \text{HASH}(m_2)
CYP201

In reality, it is mathematically inevitable that collisions exist for hash functions, because the size of the inputs can be larger than the size of the outputs. This is known as the Dirichlet drawer principle: if n objects are distributed into m drawers, with m < n, then at least one drawer will necessarily contain two or more objects. For a hash function, this principle applies because the number of possible messages is (almost) infinite, while the number of possible hashes is finite (2^{256} in the case of SHA256).

Thus, this characteristic does not mean that there are no collisions for hash functions, but rather that a good hash function makes the probability of finding a collision negligible. This characteristic, for example, is no longer verified on the SHA-0 and SHA-1 algorithms, predecessors of SHA-2, for which collisions have been found. These functions are therefore now advised against and often considered obsolete. For a hash function of n bits, the collision resistance is of the order of 2^{\frac{n}{2}}, in accordance with the birthday attack. For example, for SHA256 (n = 256), the complexity of finding a collision is of the order of 2^{128} attempts. In practical terms, this means that if one passes 2^{128} different messages through the function, one is likely to find a collision.

4. Resistance to Second Preimage

Resistance to second preimage is another important characteristic of hash functions. It states that given a message m_1 and its hash h, it is computationally infeasible to find another message m_2 \neq m_1 such that:

\text{HASH}(m_1) = \text{HASH}(m_2)

Therefore, resistance to second preimage is somewhat similar to collision resistance, except here, the attack is more difficult because the attacker cannot freely choose m_1.

CYP201

Applications of Hash Functions in Bitcoin

The most used hash function in Bitcoin is SHA256 ("Secure Hash Algorithm 256 bits"). Designed in the early 2000s by the NSA and standardized by the NIST, it produces a 256-bit hash output.

This function is used in many aspects of Bitcoin. At the protocol level, it is involved in the Proof-of-Work mechanism, where it is applied in double hashing to search for a partial collision between the header of a candidate block, created by a miner, and the difficulty target. If this partial collision is found, the candidate block becomes valid and can be added to the blockchain.

SHA256 is also used in the construction of a Merkle tree, which is notably the accumulator used for recording transactions in blocks. This structure is also found in the Utreexo protocol, which allows for reducing the size of the UTXO Set. Additionally, with the introduction of Taproot in 2021, SHA256 is exploited in MAST (Merkelised Alternative Script Tree), which allows revealing only the spending conditions actually used in a script, without disclosing the other possible options. It is also used in the calculation of transaction identifiers, in the transmission of packets over the P2P network, in electronic signatures... Finally, and this is of particular interest in this training, SHA256 is used at the application level for the construction of Bitcoin wallets and the derivation of addresses.

Most of the time, when you come across the use of SHA256 in Bitcoin, it will actually be a double hash SHA256, noted "HASH256", which simply consists of applying SHA256 twice successively:

\text{HASH256}(m) = \text{SHA256}(\text{SHA256}(m))

This practice of double hashing adds an extra layer of security against certain potential attacks, even though a single SHA256 is today considered cryptographically secure.

Another hashing function available in the Script language and used for deriving receiving addresses is the RIPEMD160 function. This function produces a 160-bit hash (thus shorter than SHA256). It is generally combined with SHA256 to form the HASH160 function:

\text{HASH160}(m) = \text{RIPEMD160}(\text{SHA256}(m))

This combination is used to generate shorter hashes, notably in the creation of certain Bitcoin addresses which represent hashes of keys or script hashes, as well as to produce key fingerprints.

Finally, at the application level only, the SHA512 function is sometimes also used, which indirectly plays a role in key derivation for wallets. This function is very similar to SHA256 in its operation; both belong to the same SHA2 family, but SHA512 produces, as its name indicates, a 512-bit hash, compared to 256 bits for SHA256. We will detail its use in the following chapters.

You now know the essential basics about hashing functions for what follows. In the next chapter, I propose to discover in more detail the workings of the function that is at the heart of Bitcoin: SHA256. We will dissect it to understand how it achieves the characteristics we have described here. This next chapter is quite long and technical, but it is not essential to follow the rest of the training. So, if you have difficulty understanding it, do not worry and move directly to the following chapter, which will be much more accessible.

The Inner Workings of SHA256

We have previously seen that hashing functions possess important characteristics that justify their use in Bitcoin. Let's now examine the internal mechanisms of these hashing functions that give them these properties, and to do this, I propose to dissect the operation of SHA256.

The SHA256 and SHA512 functions belong to the same SHA2 family. Their mechanism is based on a specific construction called Merkle-Damgård construction. RIPEMD160 also uses this same type of construction.

As a reminder, we have a message of arbitrary size as input to SHA256, and we will pass it through the function to obtain a 256-bit hash as output.

Pre-processing of the input

To begin, we need to prepare our input message m so that it has a standard length that is a multiple of 512 bits. This step is crucial for the proper functioning of the algorithm subsequently. To do this, we start with the padding bits step. We first add a separator bit 1 to the message, followed by a certain number of 0 bits. The number of 0 bits added is calculated so that the total length of the message after this addition is congruent to 448 modulo 512. Thus, the length L of the message with the padding bits is equal to:

L \equiv 448 \mod 512

\text{mod}, for modulo, is a mathematical operation that, between two integers, returns the remainder of the Euclidean division of the first by the second. For example: 16 \mod 5 = 1. It is an operation widely used in cryptography.

Here, the padding step ensures that, after adding the 64 bits in the next step, the total length of the equalized message will be a multiple of 512 bits. If the initial message has a length of M bits, the number (N) of 0 bits to be added is thus:

N = (448 - (M + 1) \mod 512) \mod 512

For example, if the initial message is 950 bits, the calculation would be as follows:

\begin{align*}
M & = 950 \\
M + 1 & = 951 \\
(M + 1) \mod 512 & = 951 \mod 512 \\
& = 951 - 512 \cdot \left\lfloor \frac{951}{512} \right\rfloor \\
& = 951 - 512 \cdot 1 \\
& = 951 - 512 \\
& = 439 \\
\\
448 - (M + 1) \mod 512 & = 448 - 439 \\
& = 9 \\
\\
N & = (448 - (M + 1) \mod 512) \mod 512 \\
N & = 9 \mod 512 \\
& = 9
\end{align*}

Thus, we would have 9 0s in addition to the separator 1. Our padding bits to be added directly after our message M would thus be:

1000 0000 00

After adding the padding bits to our message M, we also add a 64-bit representation of the original length of the message M, expressed in binary. This allows the hash function to be sensitive to the order of bits and the length of the message.

If we go back to our example with an initial message of 950 bits, we convert the decimal number 950 into binary, which gives us 1110 1101 10. We complete this number with zeros at the base to make a total of 64 bits. In our example, this gives:

0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0011 1011 0110

This padding size is added following the bit padding. Therefore, the message after our preprocessing consists of three parts:

CYP201

Initialization of Variables

SHA256 uses eight initial state variables, denoted A to H, each of 32 bits. These variables are initialized with specific constants, which are the fractional parts of the square roots of the first eight prime numbers. We will use these values subsequently during the hashing process:

SHA256 also uses 64 other constants, denoted K_0 to K_{63}, which are the fractional parts of the cube roots of the first 64 prime numbers:

K[0 \ldots 63] = \begin{pmatrix}
0x428a2f98, & 0x71374491, & 0xb5c0fbcf, & 0xe9b5dba5, \\
0x3956c25b, & 0x59f111f1, & 0x923f82a4, & 0xab1c5ed5, \\
0xd807aa98, & 0x12835b01, & 0x243185be, & 0x550c7dc3, \\
0x72be5d74, & 0x80deb1fe, & 0x9bdc06a7, & 0xc19bf174, \\
0xe49b69c1, & 0xefbe4786, & 0x0fc19dc6, & 0x240ca1cc, \\
0x2de92c6f, & 0x4a7484aa, & 0x5cb0a9dc, & 0x76f988da, \\
0x983e5152, & 0xa831c66d, & 0xb00327c8, & 0xbf597fc7, \\
0xc6e00bf3, & 0xd5a79147, & 0x06ca6351, & 0x14292967, \\
0x27b70a85, & 0x2e1b2138, & 0x4d2c6dfc, & 0x53380d13, \\
0x650a7354, & 0x766a0abb, & 0x81c2c92e, & 0x92722c85, \\
0xa2bfe8a1, & 0xa81a664b, & 0xc24b8b70, & 0xc76c51a3, \\
0xd192e819, & 0xd6990624, & 0xf40e3585, & 0x106aa070, \\
0x19a4c116, & 0x1e376c08, & 0x2748774c, & 0x34b0bcb5, \\
0x391c0cb3, & 0x4ed8aa4a, & 0x5b9cca4f, & 0x682e6ff3, \\
0x748f82ee, & 0x78a5636f, & 0x84c87814, & 0x8cc70208, \\
0x90befffa, & 0xa4506ceb, & 0xbef9a3f7, & 0xc67178f2
\end{pmatrix}

Division of the Input

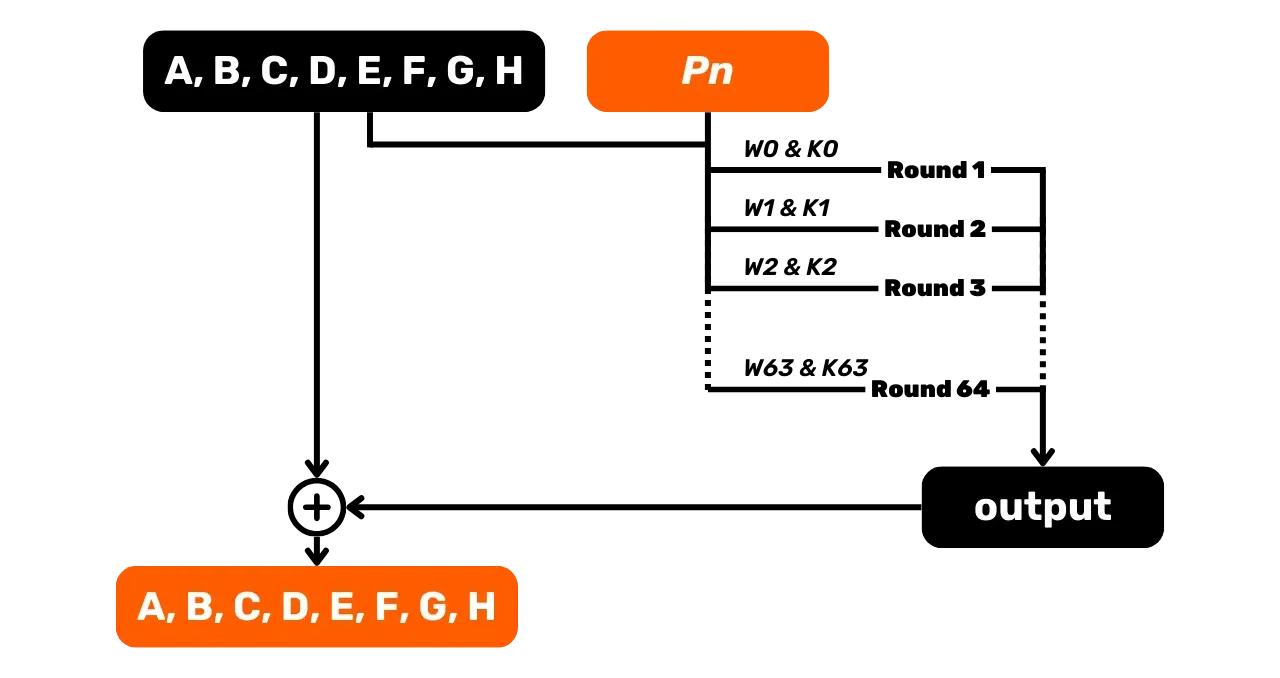
Now that we have an equalized input, we will now move on to the main processing phase of the SHA256 algorithm: the compression function. This step is very important, as it is primarily what gives the hash function its cryptographic properties that we studied in the previous chapter.

First, we start by dividing our equalized message (result of the preprocessing steps) into several blocks P of 512 bits each. If our equalized message has a total size of n \times 512 bits, we will therefore have n blocks, each of 512 bits. Each 512-bit block will be processed individually by the compression function, which consists of 64 rounds of successive operations. Let's name these blocks P_1, P_2, P_3...

Logical Operations

Before exploring the compression function in detail, it is important to understand the basic logical operations used in it. These operations, based on Boolean algebra, operate at the bit level. The basic logical operations used are:

From these basic operations, we can define more complex operations, such as the "Exclusive OR" (XOR) denoted \oplus, which is widely used in cryptography. Every logical operation can be represented by a truth table, which indicates the result for all possible combinations of binary input values (two operands p and q). For XOR (\oplus):

pqp \oplus q
000
011
101
110

For AND (\land):

pqp \land q
000
010
100
111

For NOT (\lnot p):

p\lnot p
01
10

Let's take an example to understand the operation of XOR at the bit level. If we have two binary numbers on 6 bits:

Then:


a \oplus b = 101100 \oplus 001000 = 100100

By applying XOR bit by bit:

Bit Positionaba \oplus b
1101
2000
3110
4101
5000
6000

The result is therefore 100100.

In addition to logical operations, the compression function uses bit-shifting operations, which will play an essential role in the diffusion of bits in the algorithm.

First, there is the logical right shift operation, denoted ShR_n(x), which shifts all the bits of x to the right by n positions, filling the vacant bits on the left with zeros.

For example, for x = 101100001 (on 9 bits) and n = 4:


ShR_4(101100001) = 000010110

Schematically, the right shift operation could be seen like this:

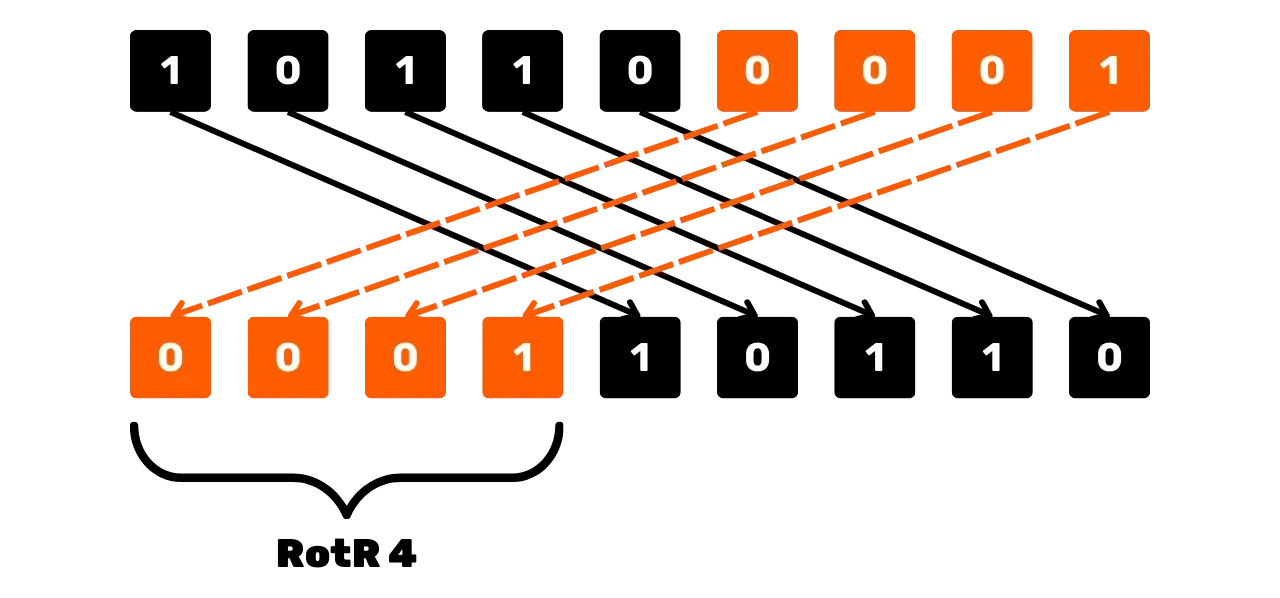
CYP201

Another operation used in SHA256 for bit manipulation is the right circular rotation, denoted RotR_n(x), which shifts the bits of x to the right by n positions, reinserting the shifted bits at the beginning of the string. For example, for x = 101100001 (over 9 bits) and n = 4:


RotR_4(101100001) = 000110110

Schematically, the right circular shift operation could be seen like this:

CYP201

Compression Function

Now that we have understood the basic operations, let's examine the SHA256 compression function in detail.

In the previous step, we divided our input into several 512-bit pieces P. For each 512-bit block P, we have:

The first 16 words, W_0 to W_{15}, are directly extracted from the processed 512-bit block P. Each word W_i consists of 32 consecutive bits from the block. So, for example, we take our first piece of input P_1, and we further divide it into smaller 32-bit pieces that we call words.

The next 48 words (W_{16} to W_{63}) are generated using the following formula:

W_i = W_{i-16} + \sigma_0(W_{i-15}) + W_{i-7} + \sigma_1(W_{i-2}) \mod 2^{32}

With:

In this case, x equals W_{i-15} for \sigma_0(x) and W_{i-2} for \sigma_1(x).

Once we have determined all the words W_i for our 512-bit piece, we can move on to the compression function, which consists of performing 64 rounds.

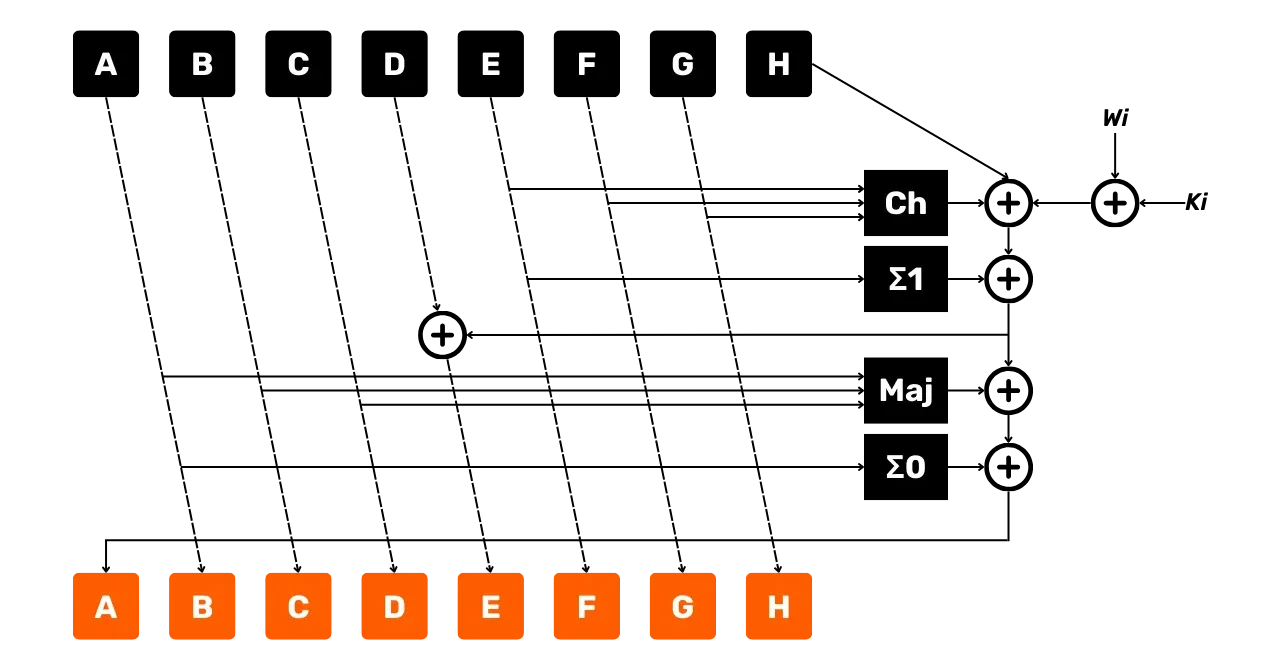
CYP201 For each round i from 0 to 63, we have three different types of inputs. First, the W_i that we have just determined, partly consisting of our message piece P_n. Next, the 64 constants K_i. Finally, we use the state variables A, B, C, D, E, F, G, and H, which will evolve throughout the hashing process and be modified with each compression function. However, for the first piece P_1, we use the initial constants given previously.

We then perform the following operations on our inputs:

\Sigma_0(A) = RotR_2(A) \oplus RotR_{13}(A) \oplus RotR_{22}(A)
\Sigma_1(E) = RotR_6(E) \oplus RotR_{11}(E) \oplus RotR_{25}(E)
Ch(E, F, G) = (E \land F) \oplus (\lnot E \land G)
Maj(A, B, C) = (A \land B) \oplus (A \land C) \oplus (B \land C)

We then calculate 2 temporary variables:

temp1 = H + \Sigma_1(E) + Ch(E, F, G) + K_i + W_i \mod 2^{32}
temp2 = \Sigma_0(A) + Maj(A, B, C) \mod 2^{32}

Next, we update the state variables as follows:

\begin{cases}
H = G \\
G = F \\
F = E \\
E = D + temp1 \mod 2^{32} \\
D = C \\
C = B \\
B = A \\
A = temp1 + temp2 \mod 2^{32}
\end{cases}

The following diagram represents a round of the SHA256 compression function as we have just described:

CYP201

We can already observe that this round outputs new state variables A, B, C, D, E, F, G, and H. These new variables will serve as input for the next round, which will in turn produce new variables A, B, C, D, E, F, G, and H, to be used for the following round. This process continues up to the 64th round. After the 64 rounds, we update the initial values of the state variables by adding them to the final values at the end of round 64:

\begin{cases}
A = A_{\text{initial}} + A \mod 2^{32} \\
B = B_{\text{initial}} + B \mod 2^{32} \\
C = C_{\text{initial}} + C \mod 2^{32} \\
D = D_{\text{initial}} + D \mod 2^{32} \\
E = E_{\text{initial}} + E \mod 2^{32} \\
F = F_{\text{initial}} + F \mod 2^{32} \\
G = G_{\text{initial}} + G \mod 2^{32} \\
H = H_{\text{initial}} + H \mod 2^{32}
\end{cases}

These new values of A, B, C, D, E, F, G, and H will serve as the initial values for the next block, P_2. For this block P_2, we replicate the same compression process with 64 rounds, then we update the variables for block P_3, and so on until the last block of our equalized input.

After processing all the message blocks, we concatenate the final values of the variables A, B, C, D, E, F, G, and H to form the final 256-bit hash of our hashing function:


\text{Hash} = A \Vert B \Vert C \Vert D \Vert E \Vert F \Vert G \Vert H

Each variable is a 32-bit integer, so their concatenation always yields a 256-bit result, regardless of the size of our message input to the hashing function.

Justification of Cryptographic Properties

But then, how is this function irreversible, collision-resistant, and tamper-resistant?

For tamper resistance, it's quite simple to understand. There are so many calculations performed in cascade, which depend both on the input and the constants, that the slightest modification of the initial message completely changes the path taken, and thus completely changes the output hash. This is what is called the avalanche effect. This property is partly ensured by the mixing of the intermediate states with the initial states for each piece. Next, when discussing a cryptographic hash function, the term "irreversibility" is not generally used. Instead, we talk about "preimage resistance," which specifies that for any given y, it is difficult to find an x such that h(x) = y. This preimage resistance is guaranteed by the algebraic complexity and the strong non-linearity of the operations performed in the compression function, as well as by the loss of certain information in the process. For example, for a given result of an addition modulo, there are several possible operands:


3+2 \mod 10 = 5 \\
7+8 \mod 10 = 5 \\
5+10 \mod 10 = 5

In this example, knowing only the modulo used (10) and the result (5), one cannot determine with certainty which are the correct operands used in the addition. It is said that there are multiple congruences modulo 10.

For the XOR operation, we are faced with the same problem. Remember the truth table for this operation: any 1-bit output can be determined by two different input configurations that have exactly the same probability of being the correct values. Therefore, one cannot determine with certainty the operands of an XOR by knowing only its result. If we increase the size of the XOR operands, the number of possible inputs knowing only the result increases exponentially. Moreover, XOR is often used alongside other bit-level operations, such as the \text{RotR} operation, which add even more possible interpretations to the result.

The compression function also uses the \text{ShR} operation. This operation removes a part of the basic information, which is then impossible to retrieve later. Once again, there is no algebraic means to reverse this operation. All these one-way and information-loss operations are used very frequently in compression functions. The number of possible inputs for a given output is thus almost infinite, and each attempt at reverse calculation would lead to equations with a very high number of unknowns, which would increase exponentially at each step.

Finally, for the characteristic of collision resistance, several parameters come into play. The pre-processing of the original message plays an essential role. Without this pre-processing, it might be easier to find collisions on the function. Although, theoretically, collisions exist (due to the pigeonhole principle), the structure of the hash function, combined with the aforementioned properties, makes the probability of finding a collision extremely low. For a hash function to be collision-resistant, it is essential that:

Cryptographers design these functions by evaluating the best possible attacks to find collisions, then adjusting the parameters to render these attacks ineffective.

Merkle-Damgård Construction

The structure of SHA256 is based on the Merkle-Damgård construction, which allows transforming a compression function into a hash function that can process messages of arbitrary length. This is precisely what we have seen in this chapter.

However, some old hash functions like SHA1 or MD5, which use this specific construction, are vulnerable to length extension attacks. This is a technique that allows an attacker who knows the hash of a message M and the length of M (without knowing the message itself) to calculate the hash of a message M' formed by concatenating M with additional content.

SHA256, even though it uses the same type of construction, is theoretically resistant to this type of attack, unlike SHA1 and MD5. This might explain the mystery of the double hashing implemented throughout Bitcoin by Satoshi Nakamoto. To avoid this type of attack, Satoshi might have preferred to use a double SHA256:


\text{HASH256}(m) = \text{SHA256}(\text{SHA256}(m))

This enhances security against potential attacks related to the Merkle-Damgård construction, but it does not increase the hashing process's security in terms of collision resistance. Moreover, even if SHA256 had been vulnerable to this type of attack, it would not have had a serious impact, as all use cases of hash functions in Bitcoin involve public data. However, the length extension attack might only be useful for an attacker if the hashed data are private and the user has used the hash function as an authentication mechanism for these data, similar to a MAC. Thus, the implementation of double hashing remains a mystery in the design of Bitcoin. Now that we have looked in detail at the workings of hash functions, particularly SHA256, which is used extensively in Bitcoin, we will focus more specifically on the cryptographic derivation algorithms used at the application level, especially for deriving the keys for your wallet.

The algorithms used for derivation

In Bitcoin at the application level, in addition to hash functions, cryptographic derivation algorithms are used to generate secure data from initial inputs. Although these algorithms rely on hash functions, they serve different purposes, especially in terms of authentication and key generation. These algorithms retain some of the characteristics of hash functions, such as irreversibility, tamper resistance, and collision resistance.

In Bitcoin wallets, mainly 2 derivation algorithms are used:

We will explore together the functioning and role of each of them.

HMAC-SHA512

HMAC is a cryptographic algorithm that calculates an authentication code based on a combination of a hash function and a secret key. Bitcoin uses HMAC-SHA512, the variant of HMAC that uses the SHA512 hash function. We have already seen in the previous chapter that SHA512 is part of the same family of hash functions as SHA256, but it produces a 512-bit output.

Here is its general operating scheme with m being the input message and K a secret key:

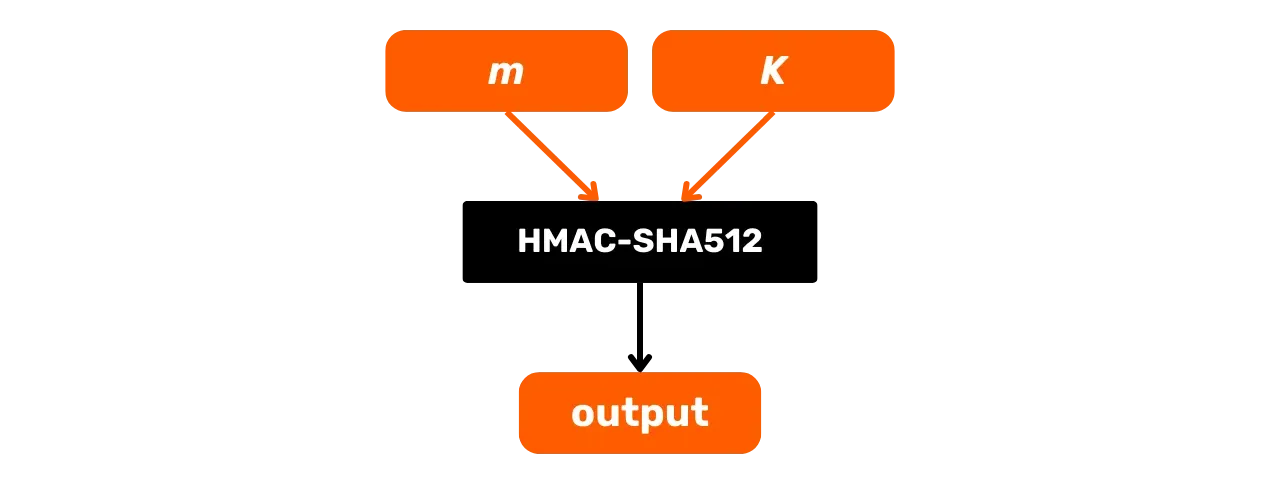
CYP201

Let's study in more detail what happens in this HMAC-SHA512 black box. The HMAC-SHA512 function with:

Before calculating the HMAC, it is necessary to equalize the key and constants according to the block size B. For example, if the key K is shorter than 128 bytes, it is padded with zeros to reach the size B. If K is longer than 128 bytes, it is compressed using SHA512, and then zeros are added until it reaches 128 bytes. In this way, an equalized key named K' is obtained. The values of \text{opad} and \text{ipad} are obtained by repeating their base byte (0x5c for \text{opad}, 0x36 for \text{ipad}) until the size B is reached. Thus, with B = 128 bytes, we have:


\text{opad} = \underbrace{0x5c5c\ldots5c}\_{128 \  \text{bytes}}

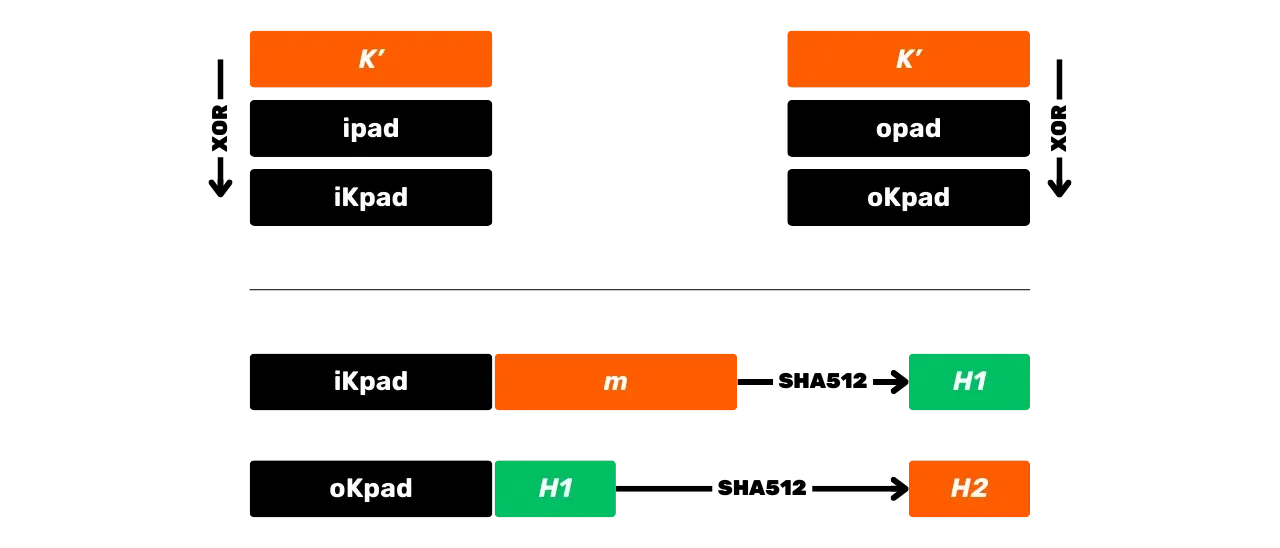
Once the preprocessing is done, the HMAC-SHA512 algorithm is defined by the following equation:


\text{HMAC-SHA512}(K,m) = \text{SHA512} \left( (K' \oplus \text{opad}) \parallel \text{SHA512} \left( (K' \oplus \text{ipad}) \parallel m \right) \right)

This equation is broken down into the following steps:

These steps can be summarized schematically as follows:

CYP201

HMAC is used in Bitcoin notably for key derivation in HD (Hierarchical Deterministic) wallets (we will talk about this in more detail in the coming chapters) and as a component of PBKDF2.

PBKDF2

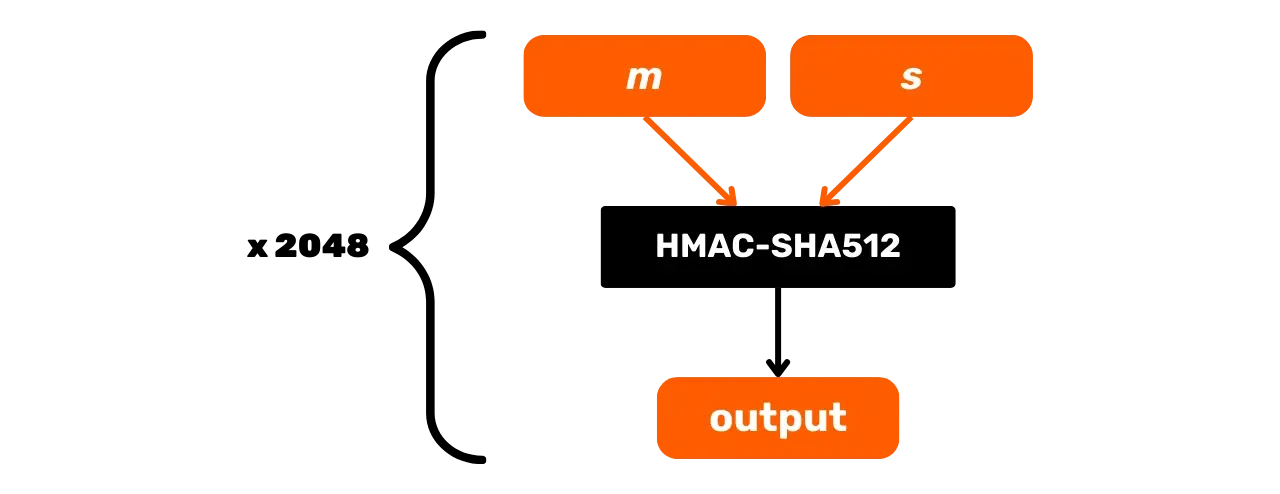
PBKDF2 (Password-Based Key Derivation Function 2) is a key derivation algorithm designed to enhance the security of passwords. The algorithm applies a pseudo-random function (here HMAC-SHA512) on a password and a cryptographic salt, and then repeats this operation a certain number of times to produce an output key.

In Bitcoin, PBKDF2 is used to generate the seed of an HD wallet from a mnemonic phrase and a passphrase (but we will talk about this in more detail in the coming chapters).

The PBKDF2 process is as follows, with:

The PBKDF2 function is defined iteratively. Each iteration takes the result of the previous one, passes it through HMAC-SHA512, and combines the successive results to produce the final key:


\text{PBKDF2}(m, s) = \text{HMAC-SHA512}^{2048}(m, s)

Schematically, PBKDF2 can be represented as follows:

CYP201

In this chapter, we have explored the HMAC-SHA512 and PBKDF2 functions, which use hashing functions to ensure the integrity and security of key derivations in the Bitcoin protocol. In the next part, we will look into digital signatures, another cryptographic method widely used in Bitcoin.

Digital Signatures

Digital Signatures and Elliptic Curves

The second cryptographic method used in Bitcoin involves digital signature algorithms. Let's explore what this entails and how it works.

Bitcoins, UTXOs, and Spending Conditions

The term "wallet" in Bitcoin can be quite confusing for beginners. Indeed, what is called a Bitcoin wallet is software that does not directly hold your bitcoins, unlike a physical wallet that can hold coins or bills. Bitcoins are simply units of account. This unit of account is represented by UTXO (Unspent Transaction Outputs), which are unspent transaction outputs. If these outputs are unspent, it means they belong to a user. UTXOs are, in a way, pieces of bitcoins, of variable size, belonging to a user.

The Bitcoin protocol is distributed and operates without a central authority. Therefore, it is not like traditional banking records, where the euros that belong to you are simply associated with your personal identity. In Bitcoin, your UTXOs belong to you because they are protected by spending conditions specified in the Script language. To simplify, there are two types of scripts: the locking script (scriptPubKey), which protects a UTXO, and the unlocking script (scriptSig), which allows unlocking a UTXO and thus spending the bitcoin units it represents. The initial operation of Bitcoin with P2PK scripts involves using a public key to lock funds, specifying in a scriptPubKey that the person wishing to spend this UTXO must provide a valid signature with the private key corresponding to this public key. To unlock this UTXO, it is therefore necessary to provide a valid signature in the scriptSig. As their names suggest, the public key is known to all since it is broadcast on the blockchain, while the private key is only known to the legitimate owner of the funds. This is the basic operation of Bitcoin, but over time, this operation has become more complex. First, Satoshi also introduced P2PKH scripts, which use a receiving address in the scriptPubKey, which represents the hash of the public key. Then, the system became even more complex with the arrival of SegWit and then Taproot. However, the general principle remains fundamentally the same: a public key or a representation of this key is used to lock UTXOs, and a corresponding private key is required to unlock them and thus spend them.

A user who wishes to make a Bitcoin transaction must therefore create a digital signature using their private key on the transaction. The signature can be verified by other network participants. If it is valid, this means that the user initiating the transaction is indeed the owner of the private key, and therefore the owner of the bitcoins they wish to spend. Other users can then accept and propagate the transaction.

As a result, a user who owns bitcoins locked with a public key must find a way to securely store what allows unlocking their funds: the private key. A Bitcoin wallet is precisely a device that will allow you to easily keep all your keys without other people having access to them. It is therefore more like a keychain than a wallet.

The mathematical link between a public key and a private key, as well as the ability to perform a signature to prove the possession of a private key without revealing it, are made possible by a digital signature algorithm. In the Bitcoin protocol, two signature algorithms are used: ECDSA (Elliptic Curve Digital Signature Algorithm) and the Schnorr signature scheme. ECDSA is the digital signature protocol used in Bitcoin from its beginnings. Schnorr is more recent in Bitcoin, as it was introduced in November 2021 with the Taproot update. These two algorithms are quite similar in their mechanisms. They are both based on elliptic curve cryptography. The major difference between these two protocols lies in the structure of the signature and some specific mathematical properties. We will therefore study the functioning of these algorithms, starting with the oldest: ECDSA.

Elliptic Curve Cryptography

Elliptic Curve Cryptography (ECC) is a set of algorithms that use an elliptic curve for its various mathematical and geometric properties for cryptographic purposes. The security of these algorithms relies on the difficulty of the discrete logarithm problem on elliptic curves. Elliptic curves are notably used for key exchanges, asymmetric encryption, or for creating digital signatures.

An important property of these curves is that they are symmetric with respect to the x-axis. Thus, any non-vertical line cutting the curve at two distinct points will always intersect the curve at a third point. Moreover, any tangent to the curve at a non-singular point will intersect the curve at another point. These properties will be useful for defining operations on the curve.

Here is a representation of an elliptic curve over the field of real numbers:

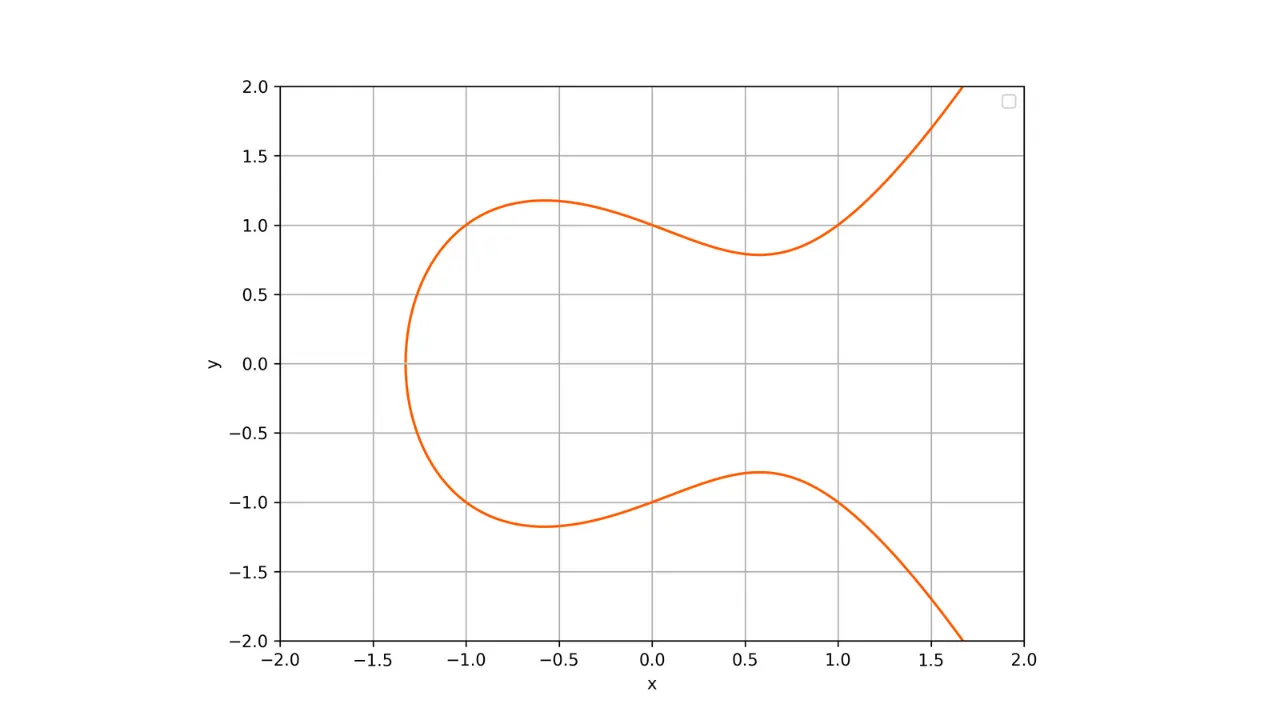
CYP201

Every elliptic curve is defined by an equation of the form:


y^2 = x^3 + ax + b

secp256k1

To use ECDSA or Schnorr, one must choose the parameters of the elliptic curve, that is, the values of a and b in the curve equation. There are different standards of elliptic curves that are reputed to be cryptographically secure. The most well-known is the secp256r1 curve, defined and recommended by the NIST (National Institute of Standards and Technology).

Despite this, Satoshi Nakamoto, the inventor of Bitcoin, chose not to use this curve. The reason for this choice is unknown, but some believe he preferred to find an alternative because the parameters of this curve could potentially contain a backdoor. Instead, the Bitcoin protocol uses the standard secp256k1 curve. This curve is defined by the parameters a = 0 and b = 7. Its equation is therefore:


y^2 = x^3 + 7

Its graphical representation over the field of real numbers looks like this:

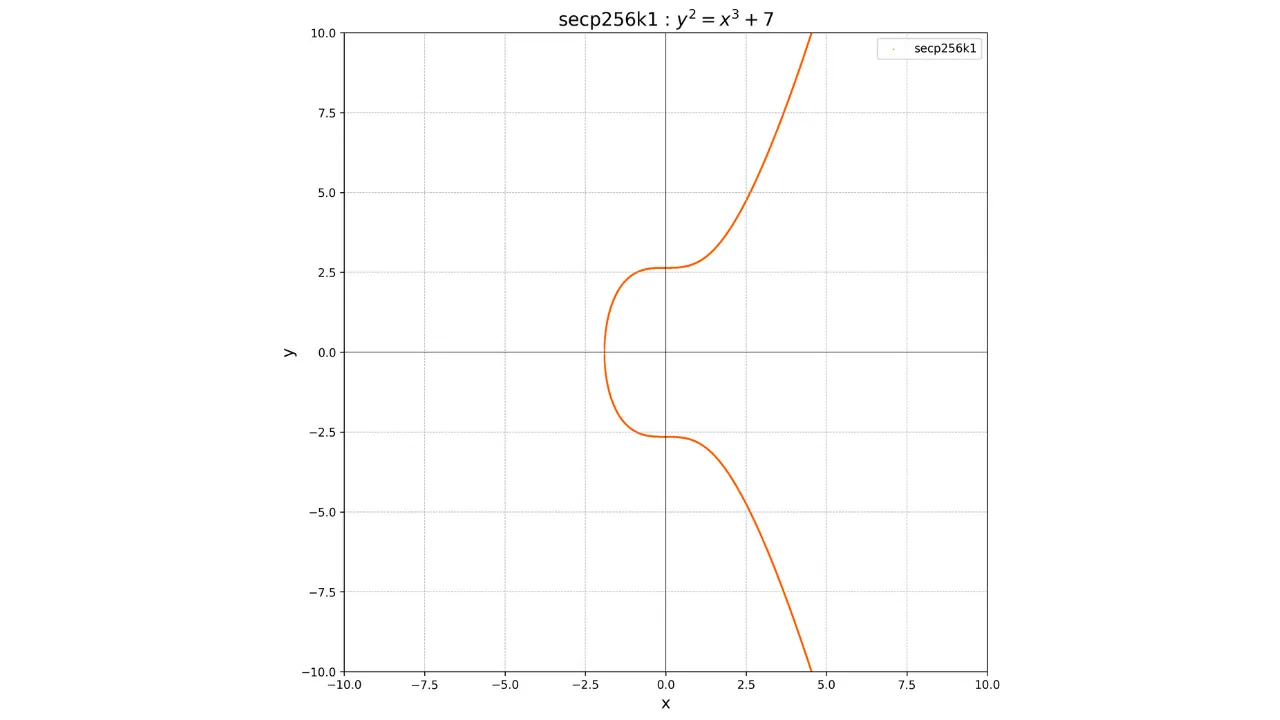
CYP201

However, in cryptography, we work with finite sets of numbers. More specifically, we work on the finite field \mathbb{F}_p, which is the field of integers modulo a prime number p. Definition: A prime number is a natural integer greater than or equal to 2 that has only two distinct positive integer divisors: 1 and itself. For example, the number 7 is a prime number since it can only be divided by 1 and 7. On the other hand, the number 8 is not prime because it can be divided by 1, 2, 4, and 8. In Bitcoin, the prime number p used to define the finite field is very large. It is chosen in such a way that the order of the field (i.e., the number of elements in \mathbb{F}_p) is sufficiently large to ensure cryptographic security.

The prime number p used is:

p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F

In decimal notation, this corresponds to:


p = 2^{256} - 2^{32} - 977

Thus, the equation of our elliptic curve is actually:


y^2 \equiv x^3 + 7 \mod p

Given that this curve is defined over the finite field \mathbb{F}_p, it no longer resembles a continuous curve but rather a discrete set of points. For example, here is what the curve used in Bitcoin looks like for a very small p = 17:

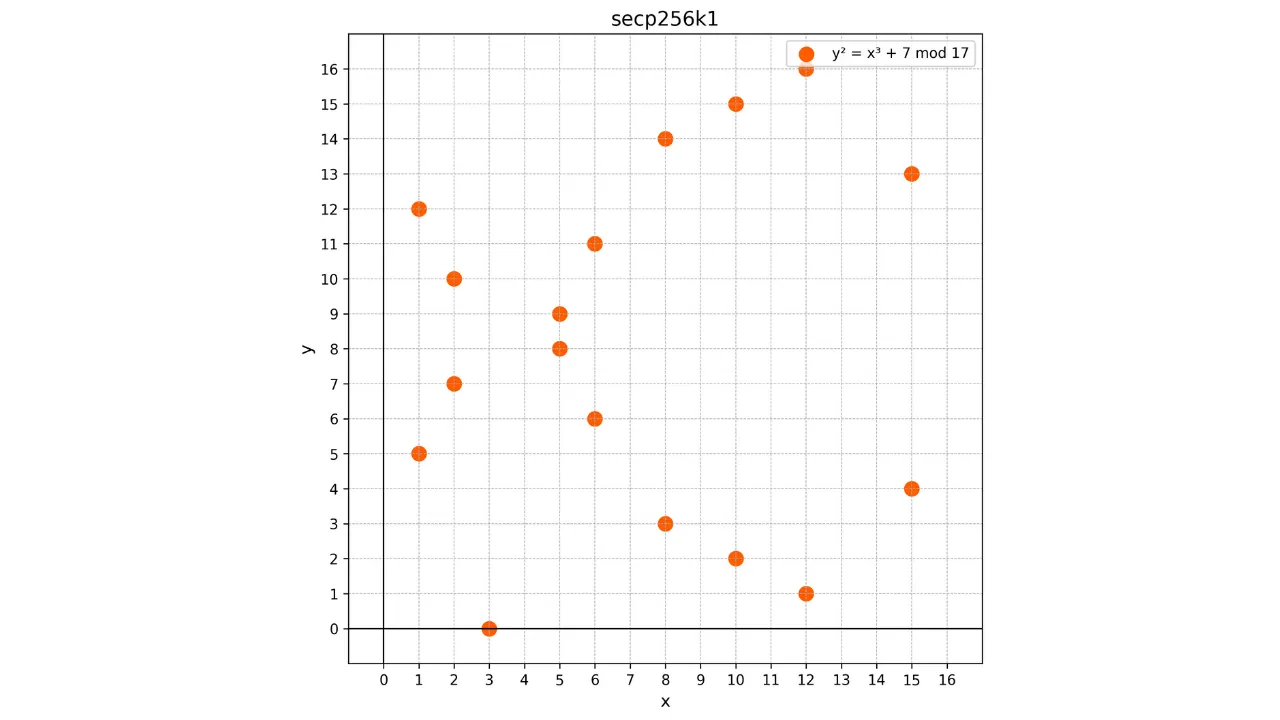
CYP201

In this example, I have intentionally limited the finite field to p = 17 for educational reasons, but one must imagine that the one used in Bitcoin is immensely larger, almost 2^{256}.

We use a finite field of integers modulo p to ensure the accuracy of operations on the curve. Indeed, elliptic curves over the field of real numbers are subject to inaccuracies due to rounding errors during computational calculations. If numerous operations are performed on the curve, these errors accumulate and the final result can be incorrect or difficult to reproduce. The exclusive use of positive integers ensures perfect accuracy of calculations and thus reproducibility of the result.

The mathematics of elliptic curves over finite fields are analogous to those over the field of real numbers, with the adaptation that all operations are performed modulo p. To simplify explanations, we will continue in the following chapters to illustrate concepts using a curve defined over real numbers, while keeping in mind that, in practice, the curve is defined over a finite field.

If you wish to learn more about the mathematical foundations of modern cryptography, I also recommend consulting this other course on Plan ₿ Network:

https://planb.network/courses/d2fd9fc0-d9ed-4a87-9fa3-0fdbb3937e28

Calculating the Public Key from the Private Key

fcb2bd58-5dda-5ecf-bb8f-ad1a0561ab4a As previously seen, the digital signature algorithms in Bitcoin are based on a pair of private and public keys that are mathematically linked. Let's explore together what this mathematical link is and how they are generated.

The Private Key

The private key is simply a random or pseudo-random number. In the case of Bitcoin, this number is 256 bits in size. The number of possibilities for a Bitcoin private key is therefore theoretically 2^{256}.

Note: A "pseudo-random number" is a number that has properties close to those of a truly random number but is generated by a deterministic algorithm.

However, in practice, there are only n distinct points on our elliptic curve secp256k1, where n is the order of the generator point G of the curve. We will see later what this number corresponds to, but simply remember that a valid private key is an integer between 1 and n-1, knowing that n is a number close to but slightly less than 2^{256}. Therefore, there are some 256-bit numbers that are not valid for becoming a private key in Bitcoin, specifically, all the numbers between n and 2^{256}. If the generation of the random number (the private key) produces a value k such that k \geq n, it is considered invalid, and a new random value must be generated.

The number of possibilities for a Bitcoin private key is therefore about n, which is a number close to 1.158 \times 10^{77}. This number is so large that if you choose a private key at random, it is statistically almost impossible to land on another user's private key. To give you an idea of scale, the number of possible private keys in Bitcoin is of an order of magnitude close to that of the estimated atoms in the observable universe.

As we will see in the coming chapters, today, the majority of private keys used in Bitcoin are not generated randomly but are the result of deterministic derivation from a mnemonic phrase, itself pseudo-random (this is the famous phrase of 12 or 24 words). This information does not change anything for the use of signature algorithms like ECDSA, but it helps to refocus our popularization in Bitcoin.

For the rest of the explanation, the private key will be denoted by the lowercase letter k.

The Public Key

The public key is a point on the elliptic curve, denoted by the capital letter K, and is calculated from the private key k. This point K is represented by a pair of coordinates (x, y) on the elliptic curve, each coordinate being an integer modulo p, the prime number defining the finite field \mathbb{F}_p. In practice, an uncompressed public key is represented by 520 bits (or 65 bytes), corresponding to two 256-bit numbers (x and y) placed end-to-end, preceded by the 8-bit prefix 0x04.

However, it is also possible to represent the public key in a compressed form using only 33 bytes (264 bits) by keeping only the abscissa x of our point on the curve and a byte indicating the parity of y. This is what is known as a compressed public key. I will talk more about this in the last chapters of this training. But what you need to remember is that a public key K is a point described by x and y.

To calculate the point K that corresponds to our public key, we use the operation of scalar multiplication on elliptic curves, defined as a repeated addition (k times) of the generator point G:


K = k \cdot G

where:

The fact that this point G is common to all public keys in Bitcoin allows us to be sure that the same private key k will always give us the same public key K:

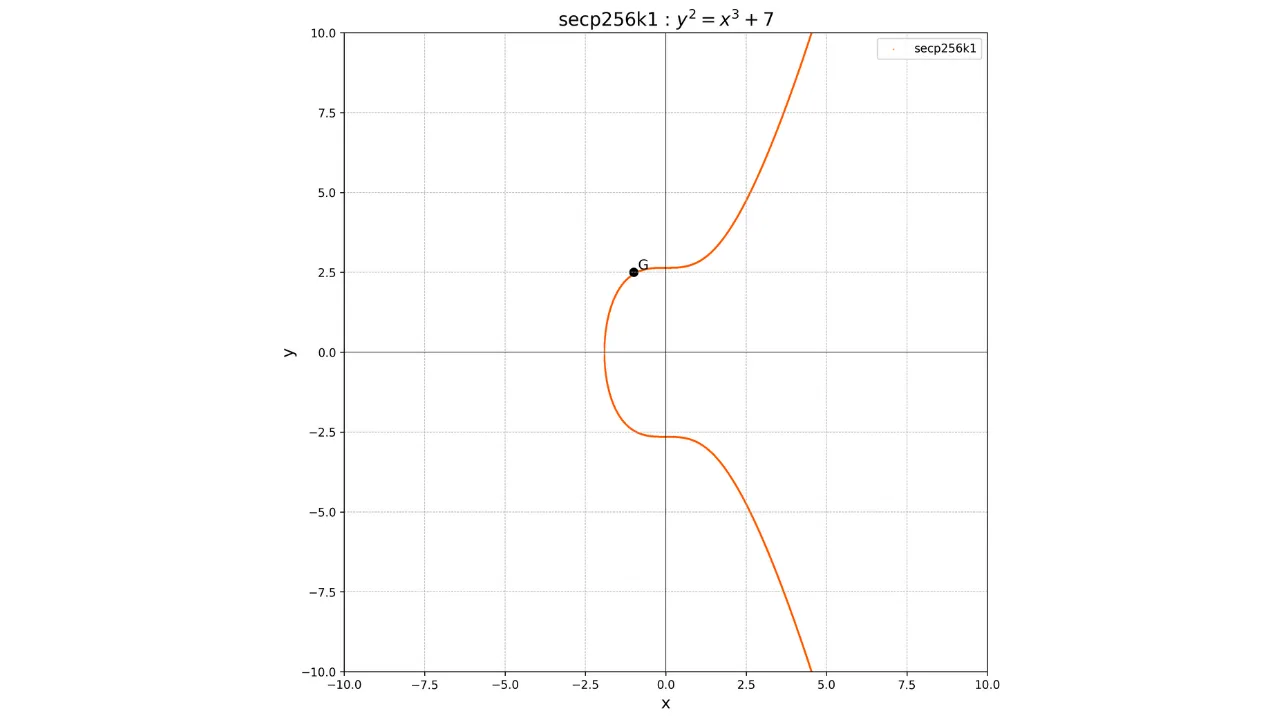
CYP201

The main characteristic of this operation is that it is a one-way function. It is easy to calculate the public key K knowing the private key k and the generator point G, but it is practically impossible to calculate the private key k knowing only the public key K and the generator point G. Finding k from K and G amounts to solving the discrete logarithm problem on elliptic curves, a mathematically difficult problem for which no efficient algorithm is known. Even the most powerful current calculators are unable to solve this problem in a reasonable time.

CYP201

Addition and Doubling of Points on Elliptic Curves

The concept of addition on elliptic curves is defined geometrically. If we have two points P and Q on the curve, the operation P + Q is calculated by drawing a line passing through P and Q. This line will necessarily intersect the curve at a third point R'. We then take the mirror image of this point with respect to the x-axis to obtain the point R, which is the result of the addition:


P + Q = R

Graphically, this can be represented as follows:

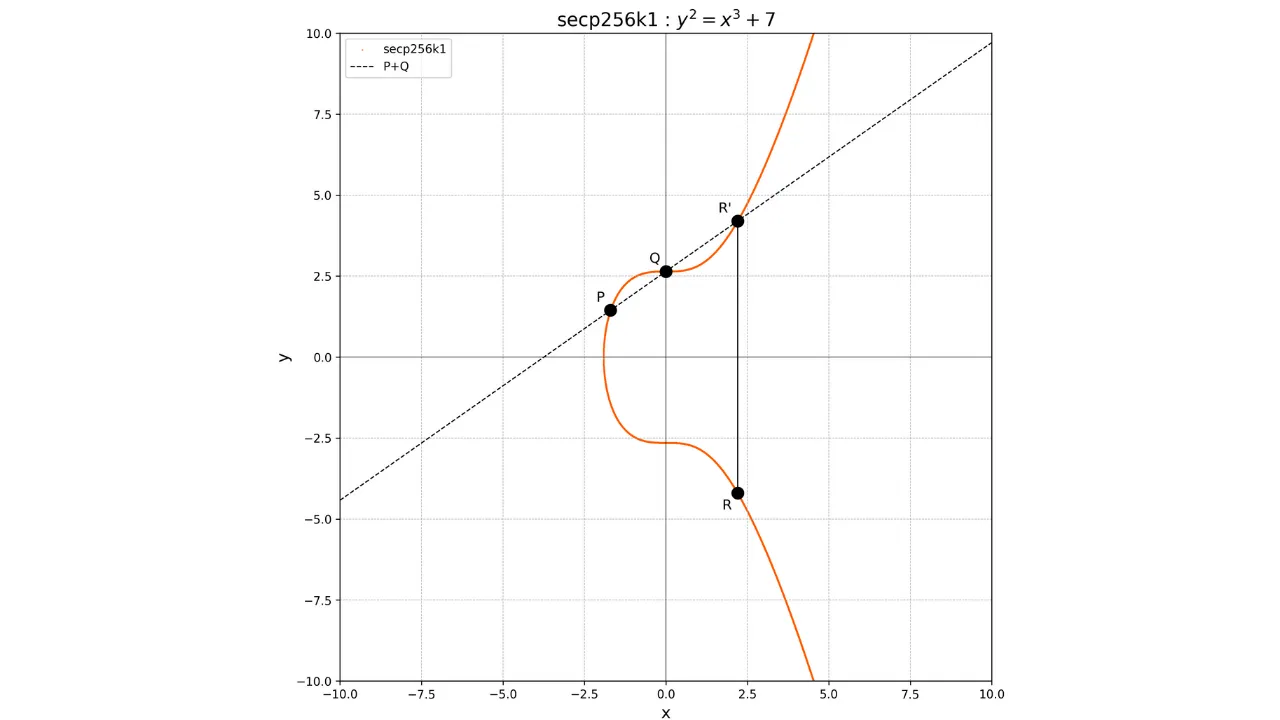
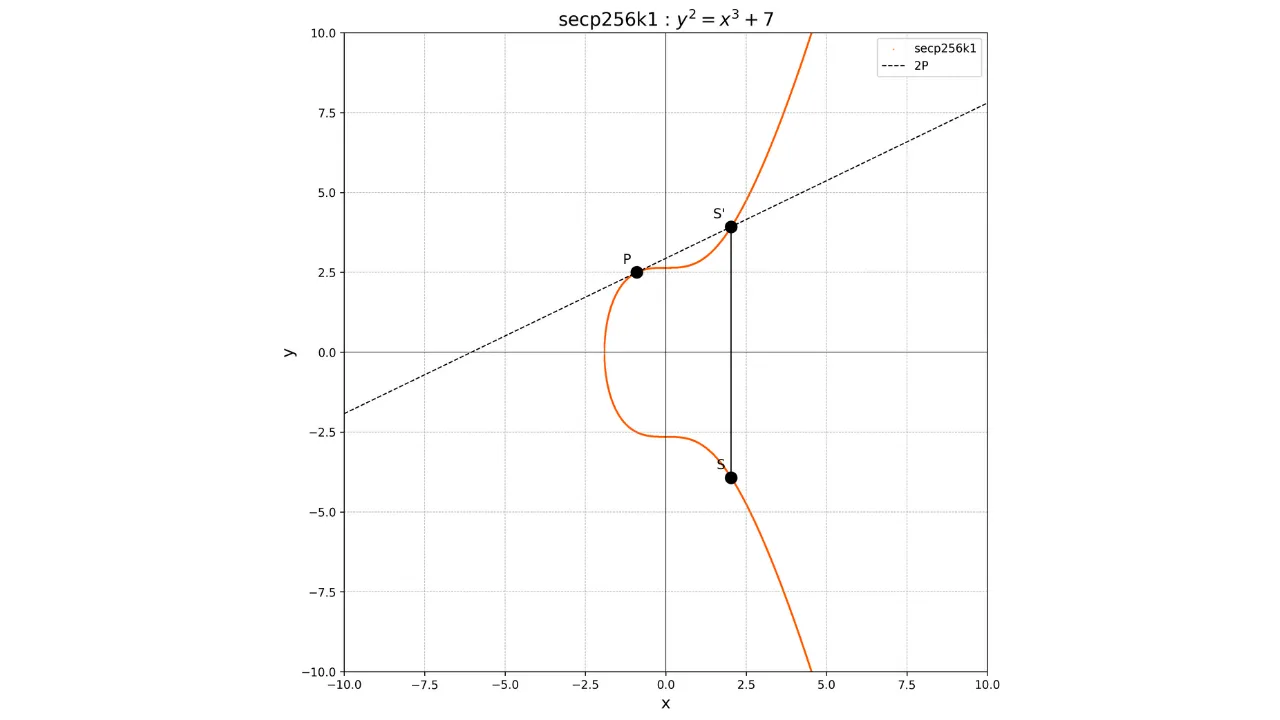
CYP201

For the doubling of a point, that is the operation P + P, we draw the tangent to the curve at point P. This tangent intersects the curve at another point S'. We then take the mirror image of this point with respect to the x-axis to obtain the point S, which is the result of the doubling:


2P = S

Graphically, this is shown as:

CYP201

By using these operations of addition and doubling, we can perform the scalar multiplication of a point by an integer k, denoted kP, by performing repeated doublings and additions.

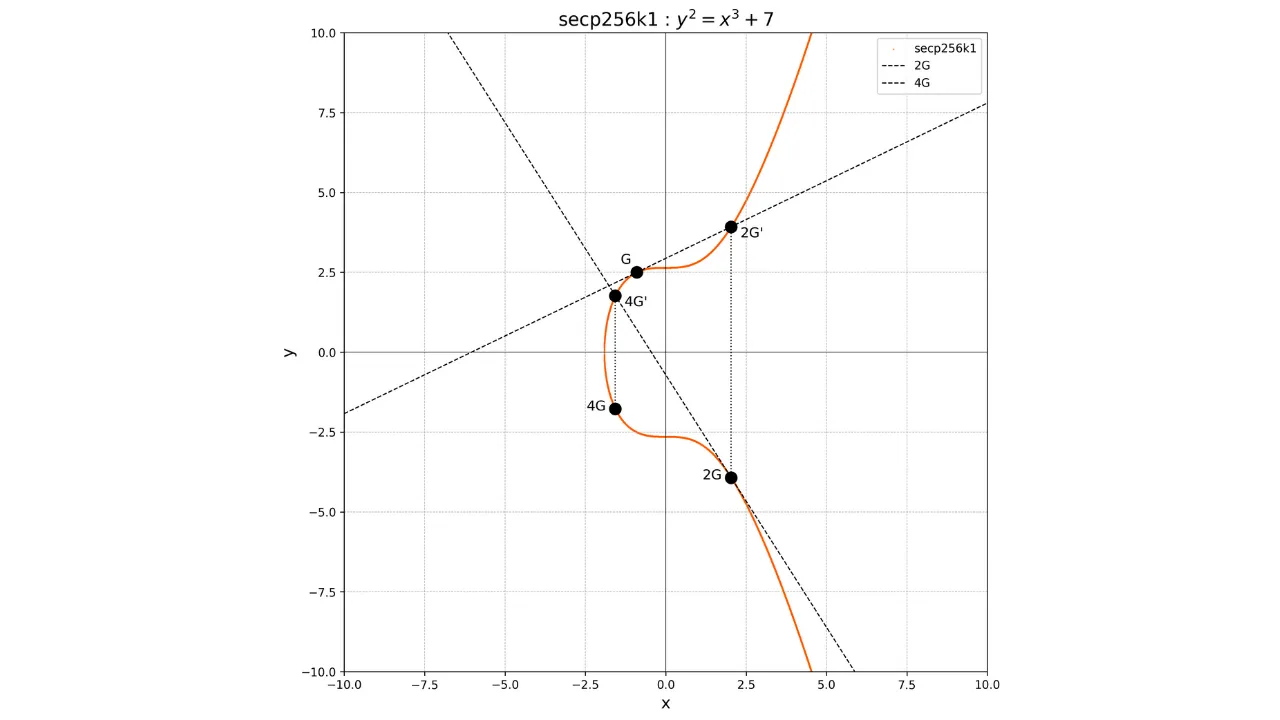
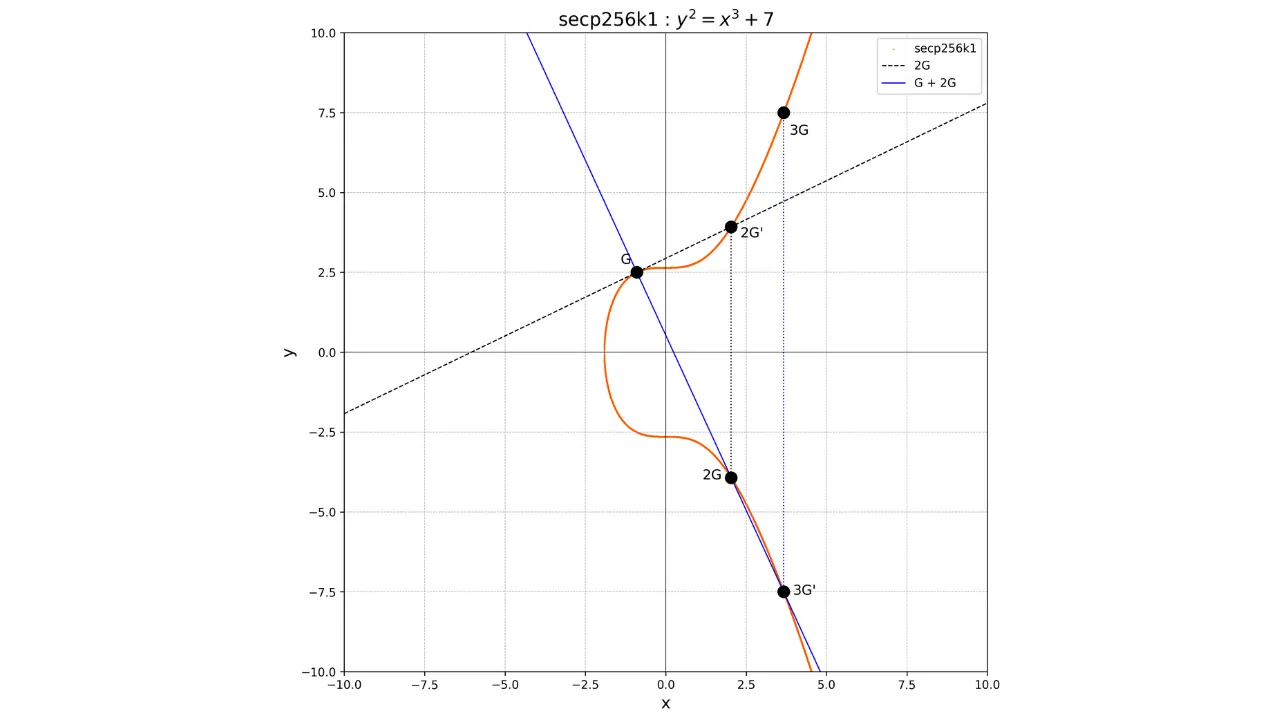
For example, suppose we have chosen a private key k = 4. To compute the associated public key, we perform:


K = k \cdot G = 4G

Graphically, this corresponds to performing a series of additions and doublings:

CYP201

If we wish, for example, to calculate the point 3G, we must first calculate the point 2G by doubling the point G, then add G and 2G. To add G and 2G, simply draw the line connecting these two points, retrieve the unique point -3G at the intersection between this line and the elliptic curve, and then determine 3G as the opposite of -3G.

We will have:


G + G = 2G



2G + G = 3G

Graphically, this would be represented as follows:

CYP201

One-Way Function

Thanks to these operations, we can understand why it is easy to derive a public key from a private key, but the reverse is practically impossible.

Let's go back to our simplified example. With a private key k = 4. To calculate the associated public key, we perform:

K = k \cdot G = 4G

We have thus been able to easily calculate the public key K by knowing k and G.

Now, if someone only knows the public key K, they are faced with the discrete logarithm problem: finding k such that K = k \cdot G. This problem is considered difficult because there is no efficient algorithm to solve it on elliptic curves. This ensures the security of the ECDSA and Schnorr algorithms.

Of course, in this simplified example with k = 4, it would be possible to find k through trial and error, as the number of possibilities is low. However, in practice, k is a 256-bit integer, making the number of possibilities astronomically large (about 1.158 \times 10^{77}). Therefore, it is infeasible to find k by brute force.

Signing with the Private Key

Now that you know how to derive a public key from a private key, you can already receive bitcoins by using this pair of keys as a spending condition. But how to spend them? To spend bitcoins, you will need to unlock the scriptPubKey attached to your UTXO to prove that you are indeed its legitimate owner. To do this, you must produce a signature s that matches the public key K present in the scriptPubKey using the private key k that was initially used to calculate K. The digital signature is thus irrefutable proof that you are in possession of the private key associated with the public key you claim.

Elliptic Curve Parameters

To perform a digital signature, all participants must first agree on the parameters of the elliptic curve used. In the case of Bitcoin, the parameters of secp256k1 are as follows:

The finite field \mathbb{Z}_p defined by:

p = 2^{256} - 2^{32} - 977
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F

p is a very large prime number slightly less than 2^{256}.

The elliptic curve y^2 = x^3 + ax + b over \mathbb{Z}_p defined by:

a = 0, \quad b = 7

The generator point or origin point G:

G = 0x0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798

This number is the compressed form that only gives the abscissa of point G. The prefix 02 at the beginning determines which of the two values having this abscissa x is to be used as the generating point. The order n of G (the number of existing points) and the cofactor h:

n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141

n is a very large number slightly less than p.

h=1

h is the cofactor or the number of subgroups. I will not elaborate on what this represents here, as it’s quite complex, and in the case of Bitcoin, we do not need to take it into account since it is equal to 1.

All this information is public and known to all participants. Thanks to them, users are able to make a digital signature and verify it.

Signature with ECDSA

The ECDSA algorithm allows a user to sign a message using their private key, in such a way that anyone knowing the corresponding public key can verify the validity of the signature, without the private key ever being revealed. In the context of Bitcoin, the message to be signed depends on the sighash chosen by the user. It is this sighash that will determine which parts of the transaction are covered by the signature. I will talk more about this in the next chapter.

Here are the steps to generate an ECDSA signature:

First, we calculate the hash (e) of the message that needs to be signed. The message m is thus passed through a cryptographic hash function, generally SHA256 or double SHA256 in the case of Bitcoin:

e = \text{HASH}(m)

Next, we calculate a nonce. In cryptography, a nonce is simply a number generated in a random or pseudo-random manner that is used only once. That is to say, each time a new digital signature is made with this pair of keys, it will be very important to use a different nonce, otherwise, it will compromise the security of the private key. It is therefore sufficient to determine a random and unique integer r such that 1 \leq r \leq n-1, where n is the order of the generating point G of the elliptic curve.

Then, we will calculate the point R on the elliptic curve with the coordinates (x_R, y_R) such that:

R = r \cdot G

We extract the value of the abscissa of the point R (x_R). This value represents the first part of the signature. And finally, we calculate the second part of the signature s in this manner:

s = r^{-1} \left( e + k \cdot x_R \right) \mod n

where:

The signature is then simply the concatenation of x_R and s:

\text{SIG} = x_R \Vert s

Verification of the ECDSA Signature

To verify a signature (x_R, s), anyone knowing the public key K and the parameters of the elliptic curve can proceed in this way:

First, verify that x_R and s are within the interval [1, n-1]. This ensures that the signature respects the mathematical constraints of the elliptic group. If this is not the case, the verifier immediately rejects the signature as invalid.

Then, calculate the hash of the message:

e = \text{HASH}(m)

Calculate the modular inverse of s modulo n:

s^{-1} \mod n

Calculate two scalar values u_1 and u_2 in this way:

\begin{align*}
u_1 &= e \cdot s^{-1} \mod n \\
u_2 &= x_R \cdot s^{-1} \mod n
\end{align*}

And finally, calculate the point V on the elliptic curve such that:

V = u_1 \cdot G + u_2 \cdot K

The signature is valid only if x_V \equiv x_R \mod n, where x_V is the x coordinate of the point V. Indeed, by combining u_1 \cdot G and u_2 \cdot K, one obtains a point V which, if the signature is valid, must correspond to the point R used during the signature (modulo n).

Signature with the Schnorr Protocol

The Schnorr signature scheme is an alternative to ECDSA that offers many advantages. It has been possible to use it in Bitcoin since 2021 and the introduction of Taproot, with the P2TR script patterns. Like ECDSA, the Schnorr scheme allows signing a message using a private key, in such a way that the signature can be verified by anyone knowing the corresponding public key. In the case of Schnorr, the exact same curve as ECDSA is used with the same parameters. However, public keys are represented slightly differently compared to ECDSA. Indeed, they are designated only by the x coordinate of the point on the elliptic curve. Unlike ECDSA, where compressed public keys are represented by 33 bytes (with the prefix byte indicating the parity of y), Schnorr uses 32-byte public keys, corresponding only to the x coordinate of the point K, and it is assumed that y is even by default. This simplified representation reduces the size of the signatures and facilitates certain optimizations in the verification algorithms. The public key is then the x coordinate of the point K:

\text{pk} = K_x

The first step to generate a signature is to hash the message. But unlike ECDSA, it is done with other values and a labeled hash function is used to avoid collisions in different contexts. A labeled hash function simply involves adding an arbitrary label to the hash function's inputs alongside the message data.

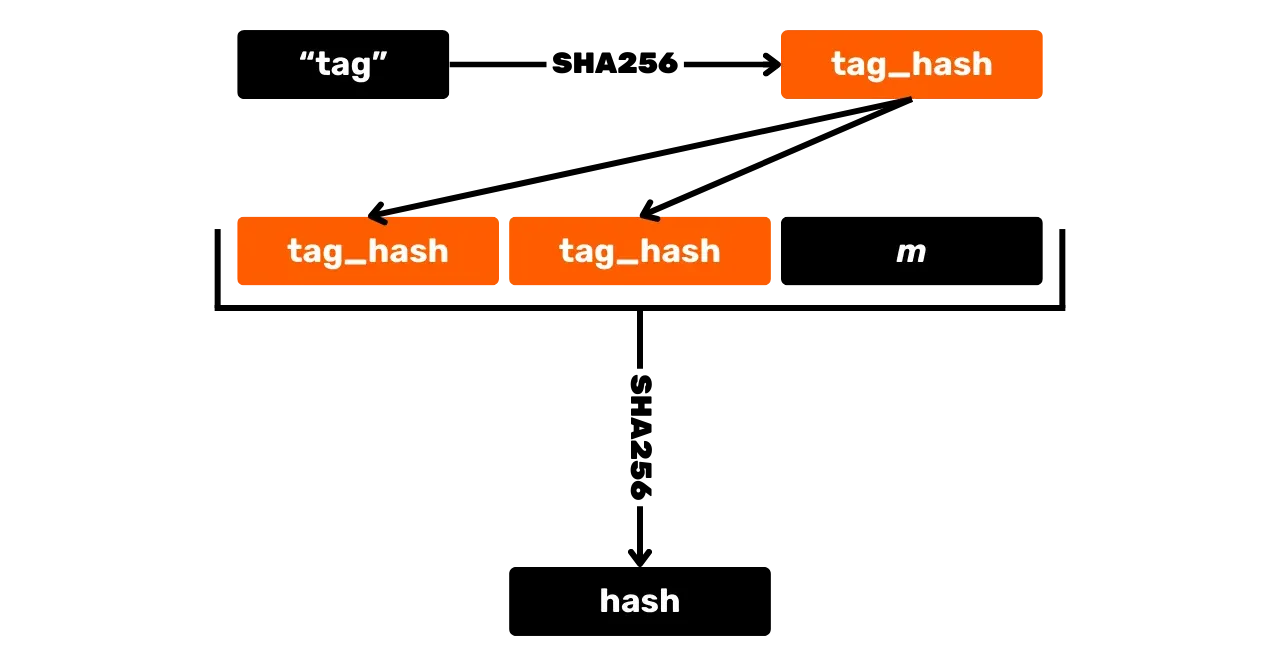
CYP201

In addition to the message, the x coordinate of the public key K_x, as well as the point R = r \cdot G, calculated from the nonce r (which is itself a unique integer for each signature, calculated deterministically from the private key and the message to avoid vulnerabilities related to nonce reuse), are also passed into the labeled function. Just like for the public key, only the x coordinate of the nonce point R_x is retained to describe the point.

The result of this hashing noted e is called the "challenge":

e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod n

Here, \text{HASH} is the SHA256 hash function, and \text{``BIP0340/challenge''} is the specific tag for the hashing.

Finally, the parameter s is calculated from the private key k, the nonce r, and the challenge e as follows:

s = (r + e \cdot k) \mod n

The signature is then simply the pair R_x and s.

\text{SIG} = R_x \Vert s

Verification of the Schnorr Signature

The verification of a Schnorr signature is simpler than that of an ECDSA signature. Here are the steps to verify the signature (R_x, s) with the public key K_x and the message m. First, we verify that K_x is a valid integer less than p. If this is the case, we retrieve the corresponding point on the curve with K_y being even. We also extract R_x and s by splitting the signature \text{SIG}. Then, we check that R_x < p and s < n (the order of the curve). Next, we calculate the challenge e in the same way as the issuer of the signature:

e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod n

Then, we calculate a reference point on the curve in this way:

R' = s \cdot G - e \cdot K

Finally, we verify that R'_x = R_x. If the two x-coordinates match, then the signature (R_x, s) is indeed valid with the public key K_x.

Why does this work?

The signer has calculated s = r + e \cdot k \mod n, so R' = s \cdot G - e \cdot K should be equal to the original point R, because:

s \cdot G = (r + e \cdot k) \cdot G = r \cdot G + e \cdot k \cdot G

Since K = k \cdot G, we have e \cdot k \cdot G = e \cdot K. Thus:

R' = r \cdot G = R

Therefore, we have:

R'_x = R_x

The advantages of Schnorr signatures

The Schnorr signature scheme offers several advantages for Bitcoin over the original ECDSA algorithm. First, Schnorr allows for the aggregation of keys and signatures. This means that multiple public keys can be combined into a single key.

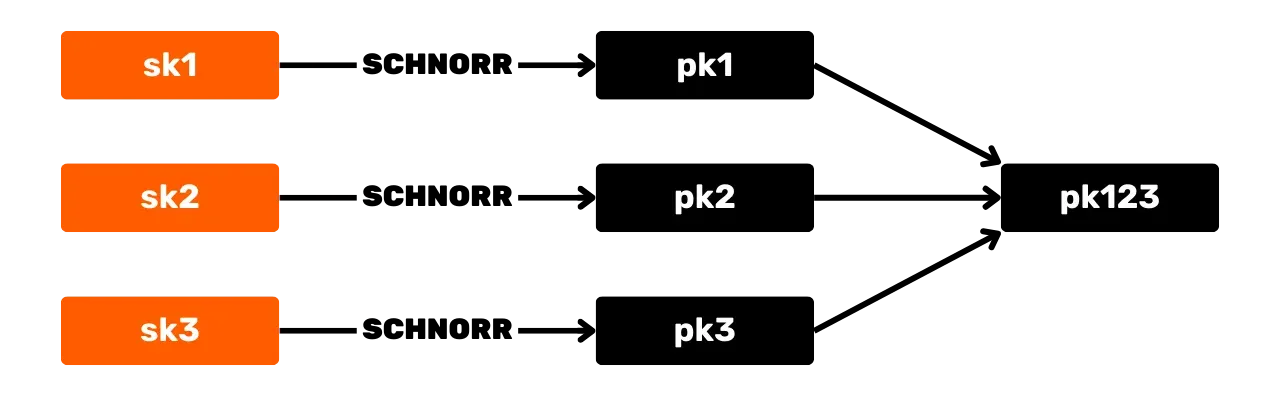
CYP201

And similarly, multiple signatures can be aggregated into a single valid signature. Thus, in the case of a multisignature transaction, a set of participants can sign with a single signature and a single aggregated public key. This significantly reduces storage and computation costs for the network, as each node only needs to verify a single signature.

CYP201

Moreover, signature aggregation improves privacy. With Schnorr, it becomes impossible to distinguish a multisignature transaction from a standard single-signature transaction. This homogeneity makes chain analysis more difficult, as it limits the ability to identify wallet fingerprints.

Finally, Schnorr also offers the possibility of batch verification. By verifying multiple signatures simultaneously, nodes can gain efficiency, especially for blocks containing many transactions. This optimization reduces the time and resources needed to validate a block. Also, Schnorr signatures are not malleable, unlike signatures produced with ECDSA. This means that an attacker cannot modify a valid signature to create another valid signature for the same message and the same public key. This vulnerability was previously present in Bitcoin and notably prevented the secure implementation of the Lightning Network. It was resolved for ECDSA with the SegWit softfork in 2017, which involves moving the signatures to a separate database from the transactions to prevent their malleability.

Why did Satoshi choose ECDSA?

As we have seen, Satoshi initially chose to implement ECDSA for digital signatures in Bitcoin. Yet, we have also seen that Schnorr is superior to ECDSA in many aspects, and this protocol was created by Claus-Peter Schnorr in 1989, 20 years before the invention of Bitcoin.

Well, we don't really know why Satoshi didn't choose it, but a likely hypothesis is that this protocol was under patent until 2008. Although Bitcoin was created a year later, in January 2009, no open-source standardization for Schnorr signatures was available at that time. Perhaps Satoshi deemed it safer to use ECDSA, which was already widely used and tested in open-source software and had several recognized implementations (notably the OpenSSL library used until 2015 in Bitcoin Core, then replaced by libsecp256k1 in version 0.10.0). Or maybe he simply wasn't aware that this patent was going to expire in 2008. In any case, the most probable hypothesis seems related to this patent and the fact that ECDSA had a proven history and was easier to implement.

The sighash flags

As we have seen in previous chapters, digital signatures are often used to unlock the script of an input. In the signing process, it is necessary to include the signed data in the calculation, designated in our examples by the message m. This data, once signed, cannot be modified without rendering the signature invalid. Indeed, whether for ECDSA or Schnorr, the signature verifier must include in their calculation the same message m. If it differs from the message m initially used by the signer, the result will be incorrect and the signature will be deemed invalid. It is then said that a signature covers certain data and protects it, in a way, against unauthorized modifications.

What is a sighash flag?

In the specific case of Bitcoin, we've seen that the message m corresponds to the transaction. However, in reality, it's a bit more complex. Indeed, thanks to sighash flags, it's possible to select specific data within the transaction that will be covered or not by the signature. The "sighash flag" is thus a parameter added to each input, allowing the determination of the components of a transaction that are covered by the associated signature. These components are the inputs and the outputs. The choice of the sighash flag thus determines which inputs and which outputs of the transaction are fixed by the signature and which can still be modified without invalidating it. This mechanism allows signatures to commit transaction data according to the signer's intentions.

Obviously, once the transaction is confirmed on the blockchain, it becomes immutable, regardless of the sighash flags used. The possibility of modification via the sighash flags is limited to the period between the signing and the confirmation.

Generally, wallet software does not offer you the option to manually modify the sighash flag of your inputs when you construct a transaction. By default, SIGHASH_ALL is set. Personally, I only know of Sparrow Wallet that allows this modification from the user interface.

What are the existing sighash flags in Bitcoin?

In Bitcoin, there are first and foremost 3 basic sighash flags:

CYP201

In all the diagrams of this chapter, the orange color represents the elements covered by the signature, while the black color indicates those that are not.

CYP201 CYP201

In addition to these three sighash flags, there is also the modifier SIGHASH_ANYONECANPAY (0x80). This modifier can be combined with a basic sighash flag to create three new sighash flags:

CYP201 CYP201 CYP201

Projects to Add New Sighash Flags

Currently (2024), only the sighash flags presented in the previous section are usable in Bitcoin. However, some projects are considering the addition of new sighash flags. For example, BIP118, proposed by Christian Decker and Anthony Towns, introduces two new sighash flags: SIGHASH_ANYPREVOUT and SIGHASH_ANYPREVOUTANYSCRIPT (AnyPrevOut = "Any Previous Output").

These two sighash flags would offer an additional possibility in Bitcoin: creating signatures that do not cover any specific input of the transaction.

CYP201

This idea was initially formulated by Joseph Poon and Thaddeus Dryja in the Lightning White Paper. Before its renaming, this sighash flag was named SIGHASH_NOINPUT. If this sighash flag is integrated into Bitcoin, it will enable the use of covenants, but it is also a mandatory prerequisite for implementing Eltoo, a general protocol for second layers that defines how to jointly manage the ownership of a UTXO. Eltoo was specifically designed to solve the problems associated with the mechanisms for negotiating the state of Lightning channels, that is, between opening and closing.

To deepen your knowledge of the Lightning Network, after the CYP201 course, I highly recommend the LNP201 course by Fanis Michalakis, which covers the topic in detail:

https://planb.network/courses/34bd43ef-6683-4a5c-b239-7cb1e40a4aeb

In the next part, I propose to discover how the mnemonic phrase at the base of your Bitcoin wallet works.

The mnemonic phrase

Evolution of Bitcoin wallets

Now that we have explored the workings of hash functions and digital signatures, we can study how Bitcoin wallets function. The goal will be to describe how a wallet in Bitcoin is constructed, how it is decomposed, and what the different pieces of information that constitute it are used for. This understanding of the wallet mechanisms will allow you to improve your use of Bitcoin in terms of security and privacy.

Before diving into the technical details, it is essential to clarify what is meant by "Bitcoin wallet" and to understand its utility.

What is a Bitcoin wallet?

Unlike traditional wallets, which allow you to store physical bills and coins, a Bitcoin wallet does not "contain" bitcoins per se. Indeed, bitcoins do not exist in a physical or digital form that can be stored, but are represented by units of account depicted in the Bitcoin system in the form of UTXOs (Unspent Transaction Outputs).

UTXOs thus represent fragments of bitcoins, of varying sizes, that can be spent provided that their scriptPubKey is satisfied. To spend his bitcoins, a user must provide a scriptSig that unlocks the scriptPubKey associated with his UTXO. This proof is generally made through a digital signature, generated from the private key corresponding to the public key present in the scriptPubKey. Thus, the crucial element that the user must secure is the private key. The role of a Bitcoin wallet is precisely to manage these private keys securely. In reality, its role is more akin to that of a keychain than a wallet in the traditional sense.

JBOK Wallets

The first wallets used in Bitcoin were JBOK (Just a Bunch Of Keys) wallets, which grouped together private keys generated independently and without any link between them. These wallets operated on a simple model where each private key could unlock a unique Bitcoin receiving address.

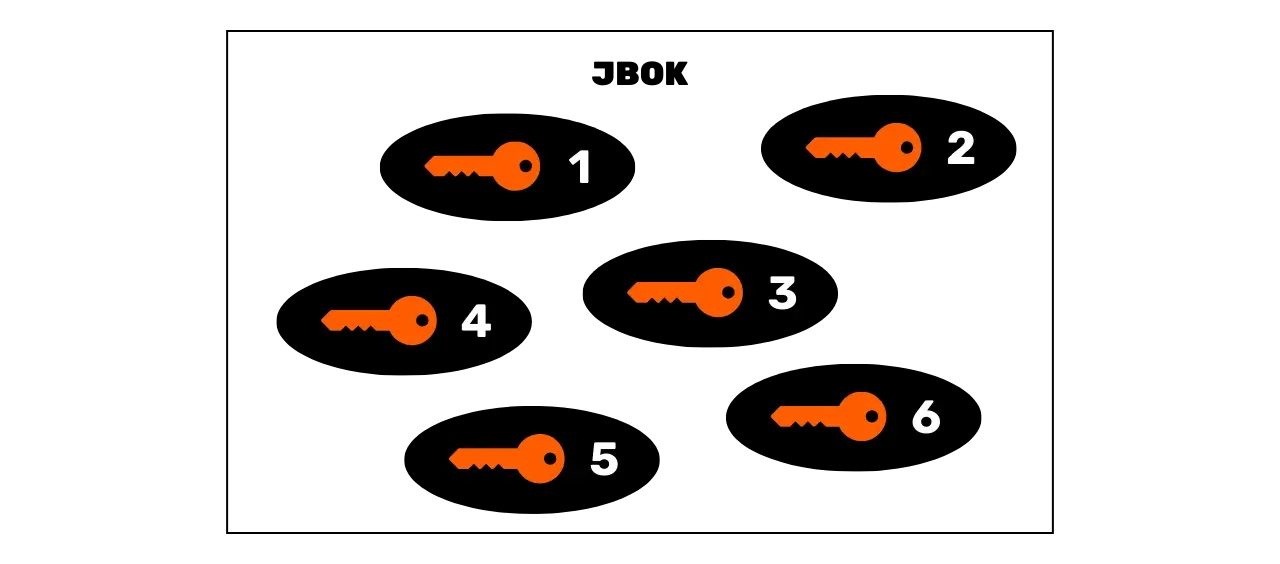
CYP201

If one wished to use multiple private keys, it was then necessary to make as many backups to ensure access to funds in case of problems with the device hosting the wallet. If using a single private key, this wallet structure may suffice, since a single backup is enough. However, this poses a problem: in Bitcoin, it is strongly advised against using always the same private key. Indeed, a private key is associated with a unique address, and Bitcoin receiving addresses are normally designed for one-time use. Each time you receive funds, you should generate a new blank address.

This constraint stems from Bitcoin's privacy model. By reusing the same address, it makes it easier for external observers to trace Bitcoin transactions. That's why reusing a receiving address is strongly discouraged. However, to have multiple addresses and publicly separate our transactions, it is necessary to manage multiple private keys. In the case of JBOK wallets, this implies creating as many backups as there are new pairs of keys, a task that can quickly become complex and difficult to maintain for users.

To learn more about Bitcoin's privacy model and discover methods to protect your privacy, I also recommend following my BTC204 course on Plan ₿ Network:

https://planb.network/courses/65c138b0-4161-4958-bbe3-c12916bc959c

HD Wallets

To address the limitation of JBOK wallets, a new wallet structure was subsequently utilized. In 2012, Pieter Wuille proposed an improvement with BIP32, which introduces HD (Hierarchical Deterministic) wallets. The principle of an HD wallet is to derive all private keys from a single source of information, called a seed, in a deterministic and hierarchical manner. This seed is generated randomly when the wallet is created and constitutes a unique backup that allows for the recreation of all the wallet's private keys. Thus, the user can generate a very large number of private keys to avoid address reuse and preserve their privacy, while only needing to make a single backup of their wallet via the seed.

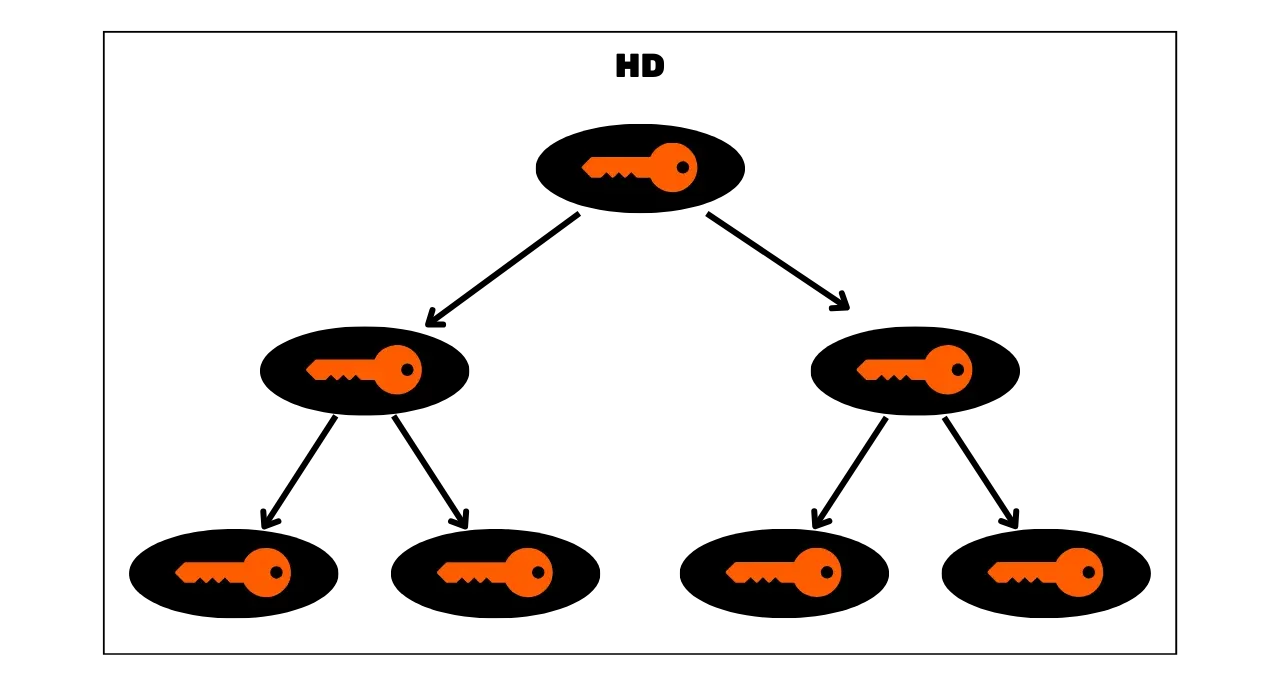
CYP201

In HD wallets, key derivation is performed according to a hierarchical structure that allows keys to be organized into derivation subspaces, each subspace being further subdividable, to facilitate fund management and interoperability between different wallet software. Nowadays, this standard is adopted by the vast majority of Bitcoin users. For this reason, we will examine it in detail in the following chapters.

The BIP39 Standard: The Mnemonic Phrase

In addition to BIP32, BIP39 standardizes the seed format as a mnemonic phrase, to facilitate backup and readability by users. The mnemonic phrase, also called a recovery phrase or 24-word phrase, is a sequence of words drawn from a predefined list that securely encodes the wallet's seed.

The mnemonic phrase greatly simplifies backup for the user. In case of loss, damage, or theft of the device hosting the wallet, simply knowing this mnemonic phrase allows for the recreation of the wallet and recovery of access to all the funds secured by it.

In the upcoming chapters, we will explore the internal workings of HD wallets, including key derivation mechanisms and the different possible hierarchical structures. This will allow you to better understand the cryptographic foundations upon which the security of funds in Bitcoin is based. And to start, in the next chapter, I propose we discover the role of entropy at the base of your wallet.

Entropy and Random Numbers

b43c715d-affb-56d8-a697-ad5bc2fffd63 Modern HD wallets rely on a single initial piece of information called "entropy" to deterministically generate the entire set of wallet keys. This entropy is a pseudo-random number that partly determines the security of the wallet.

Definition of Entropy

Entropy, in the context of cryptography and information, is a quantitative measure of the uncertainty or unpredictability associated with a data source or a random process. It plays an important role in the security of cryptographic systems, especially in the generation of keys and random numbers. High entropy ensures that the generated keys are sufficiently unpredictable and resistant to brute force attacks, where an attacker tries all possible combinations to guess the key.

In the context of Bitcoin, entropy is used to generate the seed. When creating an HD wallet, the construction of the mnemonic phrase is done from a random number, itself derived from a source of entropy. The phrase is then used to generate multiple private keys, in a deterministic and hierarchical manner, to create spending conditions on UTXOs.

Methods of Generating Entropy

The initial entropy used for an HD wallet is generally 128 bits or 256 bits, where:

In most cases, this random number is generated automatically by the wallet software using a PRNG (Pseudo-Random Number Generator). PRNGs are a category of algorithms used to generate sequences of numbers from an initial state, which have characteristics approaching that of a random number, without actually being one. A good PRNG must have properties such as output uniformity, unpredictability, and resistance to predictive attacks. Unlike true random number generators (TRNGs), PRNGs are deterministic and reproducible.

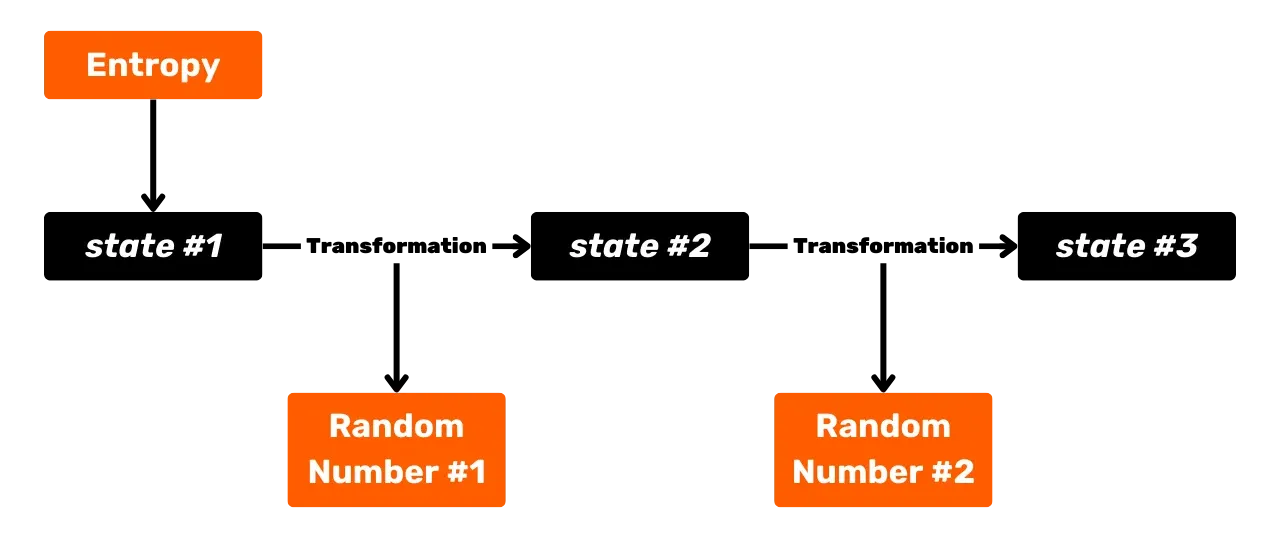
CYP201

An alternative is to manually generate the entropy, which offers better control but is also much riskier. I strongly advise against generating the entropy for your HD wallet yourself.

In the next chapter, we will see how we go from a random number to a mnemonic phrase of 12 or 24 words.

The Mnemonic Phrase

8f9340c1-e6dc-5557-a2f2-26c9669987d5 The mnemonic phrase, also called "seed phrase", "recovery phrase", "secret phrase", or "24-word phrase", is a sequence usually composed of 12 or 24 words, which is generated from entropy. It is used to deterministically derive all the keys of an HD wallet. This means that from this phrase, it is possible to deterministically generate and recreate all the private and public keys of the Bitcoin wallet, and consequently access the funds that are protected with it. The purpose of the mnemonic phrase is to provide a means of backup and recovery of bitcoins that is both secure and easy to use. It was introduced in 2013 with the BIP39 standard.

Let's discover together how to go from entropy to a mnemonic phrase.

The Checksum

To transform entropy into a mnemonic phrase, one must first add a checksum (or "control sum") at the end of the entropy. This checksum is a short sequence of bits that ensures the integrity of the data by verifying that no accidental modification has been introduced.

To calculate the checksum, the SHA256 hash function is applied to the entropy (just once; this is one of the rare cases in Bitcoin where a single SHA256 hash is used instead of a double hash). This operation produces a 256-bit hash. The checksum consists of the first bits of this hash, and its length depends on that of the entropy, according to the following formula:

\text{CS} = \frac{\text{ENT}}{32}

where \text{ENT} represents the length of the entropy in bits, and \text{CS} the length of the checksum in bits.

For example, for an entropy of 256 bits, the first 8 bits of the hash are taken to form the checksum:

\text{CS} = \frac{256}{32} = 8 \text{ bits}

Once the checksum is calculated, it is concatenated with the entropy to obtain an extended bit sequence noted \text{ENT} \Vert \text{CS} ("concatenate" means to put end-to-end).

CYP201

Correspondence between the Entropy and the Mnemonic Phrase

The number of words in the mnemonic phrase depends on the size of the initial entropy, as illustrated in the following table with:

\begin{array}{|c|c|c|c|}
\hline
\text{ENT} & \text{CS} & \text{ENT} \Vert \text{CS} & w \\
\hline
128 & 4 & 132 & 12 \\
160 & 5 & 165 & 15 \\
192 & 6 & 198 & 18 \\
224 & 7 & 231 & 21 \\
256 & 8 & 264 & 24 \\
\hline
\end{array}

For example, for a 256-bit entropy, the result \text{ENT} \Vert \text{CS} is 264 bits and yields a mnemonic phrase of 24 words.

Conversion of the Binary Sequence into a Mnemonic Phrase

The bit sequence \text{ENT} \Vert \text{CS} is then divided into segments of 11 bits. Each 11-bit segment, once converted to decimal, corresponds to a number between 0 and 2047, which designates the position of a word in a list of 2048 words standardized by BIP39.

CYP201

For example, for a 128-bit entropy, the checksum is 4 bits, and thus the total sequence measures 132 bits. It is divided into 12 segments of 11 bits (the orange bits designate the checksum):

CYP201

Each segment is then converted into a decimal number that represents a word in the list. For example, the binary segment 01011010001 is equivalent in decimal to 721. By adding 1 to align with the list's indexing (which starts at 1 and not 0), this gives the word rank 722, which is "focus" in the list.

CYP201

This correspondence is repeated for each of the 12 segments, in order to obtain a 12-word phrase.

CYP201

Characteristics of the BIP39 Word List

A particularity of the BIP39 word list is that no word shares the same first four letters in the same order with another word. This means that writing down only the first four letters of each word is sufficient to save the mnemonic phrase. This can be interesting for saving space, especially for those who wish to engrave it on a metal support.

This list of 2048 words exists in several languages. These are not simple translations, but distinct words for each language. However, it is strongly recommended to stick to the English version, as versions in other languages are generally not supported by wallet software.

Which Length to Choose for Your Mnemonic Phrase?

To determine the optimal length of your mnemonic phrase, one must consider the actual security it provides. A 12-word phrase ensures 128 bits of security, while a 24-word phrase offers 256 bits.

However, this difference in phrase-level security does not improve the overall security of a Bitcoin wallet, as the private keys derived from this phrase only benefit from 128 bits of security. Indeed, as we have seen previously, Bitcoin private keys are generated from random numbers (or derived from a random source) ranging between 1 and n-1, where n represents the order of the generator point G of the secp256k1 curve, a number slightly less than 2^{256}. One might therefore think that these private keys offer 256 bits of security. However, their security lies in the difficulty of finding a private key from its associated public key, a difficulty established by the mathematical problem of the discrete logarithm on elliptic curves (ECDLP). To date, the best-known algorithm for solving this problem is Pollard's rho algorithm, which reduces the number of operations needed to break a key to the square root of its size.

For 256-bit keys, such as those used in Bitcoin, Pollard's rho algorithm thus reduces the complexity to 2^{128} operations:


O(\sqrt{2^{256}}) = O(2^{128})

Therefore, it is considered that a private key used in Bitcoin offers 128 bits of security.

As a result, choosing a 24-word phrase does not provide additional protection for the wallet, as 256 bits of security on the phrase is pointless if the derived keys only offer 128 bits of security. To illustrate this principle, it's like having a house with two doors: an old wooden door and a reinforced door. In the event of a burglary, the reinforced door would be of no use, since the intruder would go through the wooden door. This is an analogous situation here.

A 12-word phrase, which also offers 128 bits of security, is therefore currently sufficient to protect your bitcoins against any theft attempt. As long as the digital signature algorithm does not change to use larger keys or to rely on a mathematical problem other than the ECDLP, a 24-word phrase remains superfluous. Moreover, a longer phrase increases the risk of loss during backup: a backup that is twice as short is always easier to manage.

To go further and learn concretely how to manually generate a test mnemonic phrase, I advise you to discover this tutorial:

https://planb.network/tutorials/wallet/backup/generate-mnemonic-phrase-47507d90-e6af-4cac-b01b-01a14d7a8228

Before continuing with the derivation of the wallet from this mnemonic phrase, I will introduce you, in the following chapter, to the BIP39 passphrase, as it plays a role in the derivation process, and it is at the same level as the mnemonic phrase.

The passphrase

As we have just seen, HD wallets are generated from a mnemonic phrase typically consisting of 12 or 24 words. This phrase is very important because it allows for the restoration of all the keys of a wallet in case its physical device (like a hardware wallet, for example) is lost. However, it constitutes a single point of failure, because if it is compromised, an attacker could steal all the bitcoins. This is where the BIP39 passphrase comes into play.

What is a BIP39 passphrase?

The passphrase is an optional password, which you can freely choose, that is added to the mnemonic phrase in the key derivation process to enhance the wallet's security.

Be careful, the passphrase should not be confused with the PIN code of your hardware wallet or the password used to unlock access to your wallet on your computer. Unlike all these elements, the passphrase plays a role in the derivation of your wallet's keys. This means that without it, you will never be able to recover your bitcoins.

The passphrase works in tandem with the mnemonic phrase, modifying the seed from which the keys are generated. Thus, even if someone obtains your 12 or 24-word phrase, without the passphrase, they cannot access your funds. Using a passphrase essentially creates a new wallet with distinct keys. Modifying (even slightly) the passphrase will generate a different wallet.

CYP201

Why should you use a passphrase?

The passphrase is arbitrary and can be any combination of characters chosen by the user. Using a passphrase thus offers several advantages. First of all, it reduces all risks associated with the compromise of the mnemonic phrase by requiring a second factor to access the funds (burglary, access to your home, etc.).

Next, it can be used strategically to create a decoy wallet, to face physical constraints to steal your funds like the infamous "$5 wrench attack". In this scenario, the idea is to have a wallet without a passphrase containing only a small amount of bitcoins, enough to satisfy a potential aggressor, while having a hidden wallet. This latter uses the same mnemonic phrase but is secured with an additional passphrase. Finally, the use of a passphrase is interesting when one wishes to control the randomness of the generation of the seed of the HD wallet.

How to choose a good passphrase?

For the passphrase to be effective, it must be sufficiently long and random. As with a strong password, I recommend choosing a passphrase that is as long and random as possible, with a diversity of letters, numbers, and symbols to make any brute force attack impossible.

It is also important to properly save this passphrase, in the same way as the mnemonic phrase. Losing it means losing access to your bitcoins. I strongly advise against remembering it only by heart, as this unreasonably increases the risk of loss. The ideal is to write it down on a physical medium (paper or metal) separate from the mnemonic phrase. This backup must obviously be stored in a different place from where your mnemonic phrase is stored to prevent both from being compromised simultaneously.

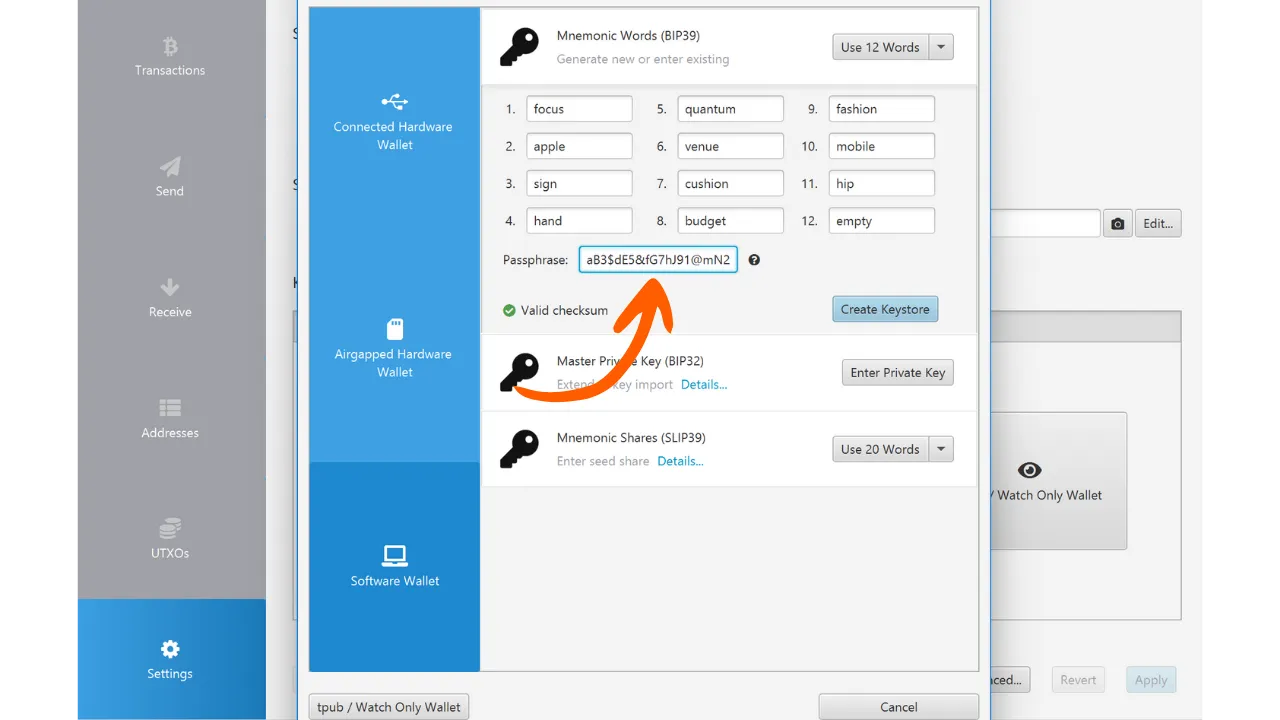
CYP201

In the following section, we will discover how these two elements at the base of your wallet — the mnemonic phrase and the passphrase — are used to derive the key pairs used in the scriptPubKey that lock your UTXOs.

Creation of Bitcoin Wallets

Creation of the Seed and Master Key

Once the mnemonic phrase and the optional passphrase are generated, the process of deriving a Bitcoin HD wallet can begin. The mnemonic phrase is first converted into a seed which constitutes the base of all the keys of the wallet.

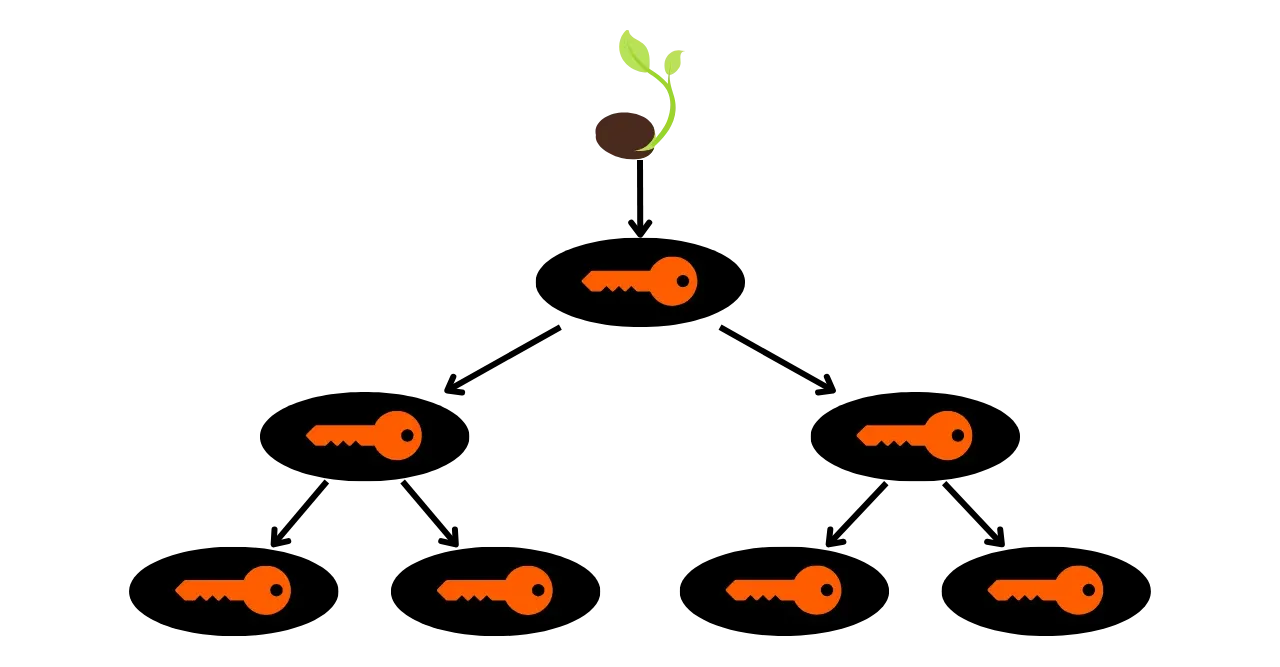
CYP201

The Seed of an HD Wallet

The BIP39 standard defines the seed as a 512-bit sequence, which serves as the starting point for the derivation of all the keys of an HD wallet. The seed is derived from the mnemonic phrase and the possible passphrase using the PBKDF2 algorithm (Password-Based Key Derivation Function 2) which we have already discussed in chapter 3.3. In this derivation function, we will use the following parameters:

Seed Derivation Scheme with PBKDF2

The following equation illustrates the derivation of the seed from the mnemonic phrase and the passphrase:

s = \text{PBKDF2}_{\text{HMAC-SHA512}}(m, p, 2048)
CYP201

The value of the seed is thus influenced by the value of the mnemonic phrase and the passphrase. By changing the passphrase, a different seed is obtained. However, with the same mnemonic phrase and passphrase, the same seed is always generated, since PBKDF2 is a deterministic function. This ensures that the same pairs of keys can be retrieved through our backups.

Note: In common language, the term "seed" often refers, by misuse of language, to the mnemonic phrase. Indeed, in the absence of a passphrase, one is simply the encoding of the other. However, as we have seen, in the technical reality of wallets, the seed and the mnemonic phrase are indeed two distinct elements.

Now that we have our seed, we can continue with the derivation of our Bitcoin wallet.

The Master Key and the Master Chain Code

Once the seed is obtained, the next step in deriving an HD wallet involves calculating the master private key and the master chain code, which will represent depth 0 of our wallet.

To obtain the master private key and the master chain code, the HMAC-SHA512 function is applied to the seed, using a fixed key "Bitcoin Seed" identical for all Bitcoin users. This constant is chosen to ensure that the key derivations are specific to Bitcoin. Here are the elements:


\text{output} = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)

The output of this function is therefore 512 bits. It is then divided into 2 parts:

Mathematically, these two values can be written as follows with k_M being the master private key and C_M the master chain code:

k_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[:256]}
C_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[256:]}
CYP201

Role of the Master Key and the Chain Code

The master private key is considered the parent key, from which all derived private keys — children, grandchildren, great-grandchildren, etc. — will be generated. It represents the zero level in the hierarchy of derivation.

The master chain code, on the other hand, introduces an additional source of entropy into the key derivation process for children, in order to counter certain potential attacks. Moreover, in the HD wallet, each pair of keys has a unique chain code associated with it, which is also used to derive child keys from this pair, but we will discuss this in more detail in the coming chapters.

Before continuing with the derivation of the HD wallet with the following elements, I wish, in the next chapter, to introduce you to extended keys, which are often confused with the master key. We will see how they are constructed and what role they play in the Bitcoin wallet.

Extended Keys

An extended key is simply the concatenation of a key (whether private or public) and its associated chain code. This chain code is essential for the derivation of child keys because, without it, it is impossible to derive child keys from a parent key, but we will discover this process more precisely in the next chapter. These extended keys thus allow aggregating all the necessary information to derive child keys, thereby simplifying account management within an HD wallet.

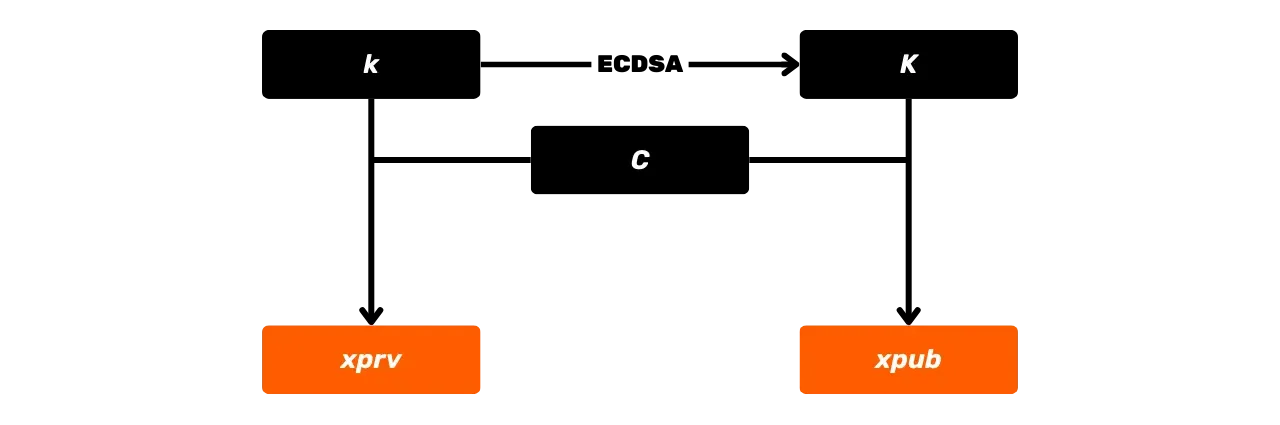
CYP201

The extended key consists of two parts:

How Extended Keys Work

When the extended key contains a private key, it is referred to as an extended private key. It is recognized by its prefix which contains the identifier prv. In addition to the private key, the extended private key also contains the associated chain code. With this type of extended key, it is possible to derive all types of child private keys. Therefore, by addition and doubling of points on elliptic curves, it also allows for the derivation of child public keys.

When the extended key does not contain a private key, but instead a public key, it is referred to as an extended public key. It is recognized by its prefix which contains the identifier pub. Obviously, in addition to the key, it also contains the associated chain code. Unlike the extended private key, the extended public key allows for the derivation of only "normal" child public keys (meaning it cannot derive "hardened" child keys). We will see in the following chapter what these "normal" and "hardened" qualifiers mean.

In any case, the extended public key does not allow for the derivation of child private keys. Therefore, even if someone has access to an xpub, they will not be able to spend the associated funds, as they will not have access to the corresponding private keys. They can only derive child public keys to observe the associated transactions.

For the following, we will adopt the following notation:

CYP201

Construction of an Extended Key

An extended key is structured as follows:

The complete format of an extended key is therefore 78 bytes without the checksum, and 82 bytes with the checksum. It is then converted to Base58 to produce a representation that is easily readable by users. The Base58 format is the same as that used for Legacy receiving addresses (before SegWit).

ElementDescriptionSize
VersionIndicates whether the key is public (xpub, ypub) or private (xprv, zprv), as well as the version of the extended key4 bytes
DepthLevel in the hierarchy relative to the master key1 byte
Parent FingerprintThe first 4 bytes of HASH160 of the parent public key4 bytes
Index NumberPosition of the key in the order of children4 bytes
Chain CodeUsed to derive child keys32 bytes
KeyThe private key (with a 1-byte prefix) or the public key33 bytes
ChecksumChecksum to verify integrity4 bytes

If one byte is added to the private key only, it's because the compressed public key is longer than the private key by one byte. This additional byte, added at the beginning of the private key as 0x00, equalizes their size, ensuring that the payload of the extended key is of the same length, whether it's a public or a private key.

Extended Key Prefixes

As we have just seen, extended keys include a prefix that indicates both the version of the extended key and its nature. The notation pub indicates that it refers to an extended public key, and the notation prv indicates an extended private key. The additional letter at the base of the extended key helps to indicate whether the standard followed is Legacy, SegWit v0, SegWit v1, etc. Here is a summary of the prefixes used and their meanings:

Base 58 PrefixBase 16 PrefixNetworkPurposeAssociated ScriptsDerivationKey Type
xpub0488b21eMainnetLegacy and SegWit V1P2PK / P2PKH / P2TRm/44'/0', m/86'/0'public
xprv0488ade4MainnetLegacy and SegWit V1P2PK / P2PKH / P2TRm/44'/0', m/86'/0'private
tpub043587cfTestnetLegacy and SegWit V1P2PK / P2PKH / P2TRm/44'/1', m/86'/1'public
tprv04358394TestnetLegacy and SegWit V1P2PK / P2PKH / P2TRm/44'/1', m/86'/1'private
ypub049d7cb2MainnetNested SegWitP2WPKH in P2SHm/49'/0'public
yprv049d7878MainnetNested SegWitP2WPKH in P2SHm/49'/0'private
upub049d7cb2TestnetNested SegWitP2WPKH in P2SHm/49'/1'public
uprv044a4e28TestnetNested SegWitP2WPKH in P2SHm/49'/1'private
zpub04b24746MainnetSegWit V0P2WPKHm/84'/0'public
zprv04b2430cMainnetSegWit V0P2WPKHm/84'/0'private
vpub045f1cf6TestnetSegWit V0P2WPKHm/84'/1'public
vprv045f18bcTestnetSegWit V0P2WPKHm/84'/1'private

Details of an Extended Key's Elements

To better understand the internal structure of an extended key, let's take one as an example and break it down. Here is an extended key:

xpub6CTNzMUkzpurBWaT4HQoYzLP4uBbGJuWY358Rj7rauiw4rMHCyq3Rfy9w4kyJXJzeFfyrKLUar2rUCukSiDQFa7roTwzjiAhyQAdPLEjqHT

0488B21E036D5601AD80000000C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A89303772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF50658051F067C3A

This extended key breaks down into several distinct elements:

1.Version: 0488B21E

The first 4 bytes are the version. Here, it corresponds to an extended public key on the Mainnet with a derivation purpose of either Legacy or SegWit v1.

2.Depth: 03

This field indicates the hierarchical level of the key within the HD wallet. In this case, a depth of 03 means that this key is three levels of derivation below the master key.

3.Parent fingerprint: 6D5601AD

These are the first 4 bytes of the HASH160 hash of the parent public key that was used to derive this xpub.

4.Index number: 80000000

This index indicates the key's position among its parent's children. The 0x80 prefix indicates that the key is derived in a hardened manner, and since the rest is filled with zeros, it indicates that this key is the first among its possible siblings.

5.Chain code: C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A893

6.Public Key: 03772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF5065805

7.Checksum: 1F067C3A

The checksum corresponds to the first 4 bytes of the hash (double SHA256) of everything else.

In this chapter, we discovered that there are two different types of child keys. We also learned that the derivation of these child keys requires a key (either private or public) and its chain code. In the next chapter, we will examine in detail the nature of these different types of keys and how to derive them from their parent key and chain code.

Derivation of Child Key Pairs

The derivation of child key pairs in Bitcoin HD wallets relies on a hierarchical structure that allows generating a large number of keys, while organizing these pairs into different groups through branches. Each child pair derived from a parent pair can be used either directly in a scriptPubKey to lock bitcoins, or as a starting point to generate more child keys, and so on, to create a tree of keys.

All these derivations start with the master key and the master chain code, which are the first parents at depth level 0. They are, in a way, the Adam and Eve of your wallet's keys, common ancestors of all derived keys.

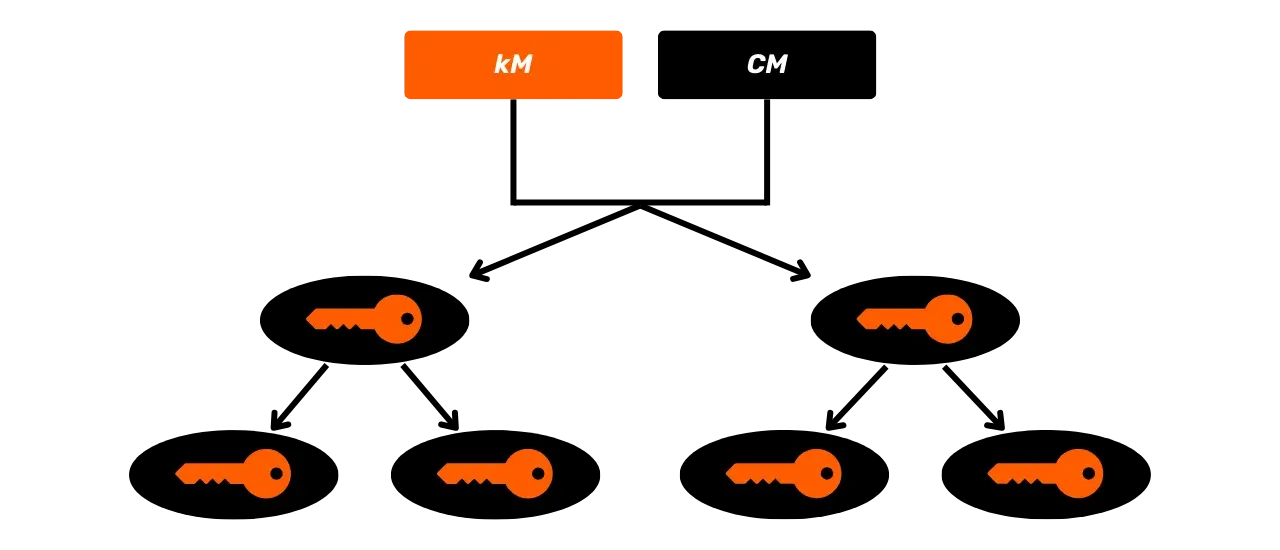
CYP201

Let's explore how this deterministic derivation works.

The Different Types of Child Key Derivations

As we briefly touched upon in the previous chapter, child keys are divided into two main types.

Every child key pair is identified by a 32-bit index (named i in our calculations). The indexes for normal keys range from 0 to 2^{31}-1, while those for hardened keys range from 2^{31} to 2^{32}-1. These numbers are used to distinguish sibling key pairs during derivation. Indeed, each parent key pair must be capable of deriving multiple child key pairs. If we were to apply the same calculation systematically from the parent keys, all the sibling keys obtained would be identical, which is not desirable. The index thus introduces a variable that modifies the derivation calculation, allowing each sibling pair to be differentiated. Except for specific use in certain protocols and derivation standards, we generally start by deriving the first child key with the index 0, the second with the index 1, and so on.

Derivation Process with HMAC-SHA512

The derivation of each child key is based on the HMAC-SHA512 function, which we discussed in Section 2 on hash functions. It takes two inputs: the parent chain code C_{\text{PAR}}, and the concatenation of the parent key (either the public key K_{\text{PAR}} or the private key k_{\text{PAR}}, depending on the type of child key desired) with the index. The output of the HMAC-SHA512 is a 512-bit sequence, divided into two parts:

In all our calculations, I will denote \text{hash} the output of the HMAC-SHA512 function.

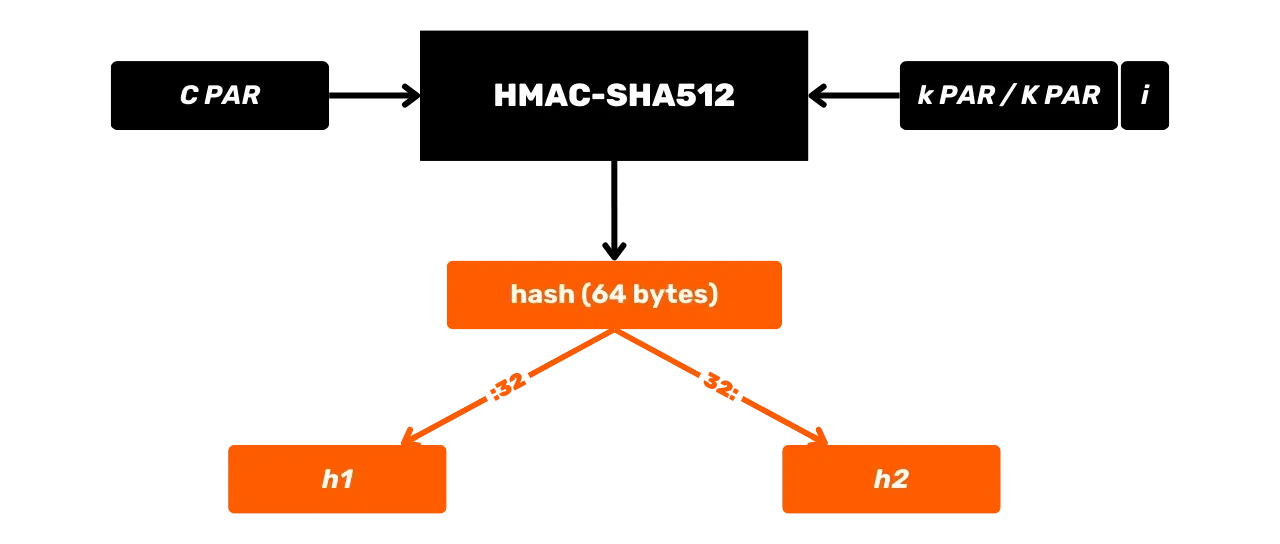
CYP201

Derivation of a Child Private Key from a Parent Private Key

To derive a child private key k_{\text{CHD}} from a parent private key k_{\text{PAR}}, two scenarios are possible depending on whether a hardened or normal key is desired.

For a normal child key (i < 2^{31}), the calculation of \text{hash} is as follows:

\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}},  k_{\text{PAR}} \cdot G \Vert i)

In this calculation, we observe that our HMAC function takes two inputs: first, the parent chain code, and then the concatenation of the index with the public key associated with the parent private key. The parent public key is used here because we are looking to derive a normal child key, not a hardened one. We now have a 64-byte \text{hash} that we will split into 2 parts of 32 bytes each, h_1 and h_2:


\text{hash} = h_1 \Vert h_2

h_1 = \text{hash}_{[:32]} \quad, \quad h_2 = \text{hash}_{[32:]}

The child private key k_{\text{CHD}}^n is then calculated as follows:

k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n

In this calculation, the operation \text{parse256}(h_1) consists of interpreting the first 32 bytes of the \text{hash} as a 256-bit integer. This number is then added to the parent private key, all taken modulo n to stay within the order of the elliptic curve, as we saw in section 3 on digital signatures. Thus, to derive a normal child private key, although the parent public key is used as the basis for calculation in the inputs of the HMAC-SHA512 function, it is always necessary to have the parent private key to finalize the calculation.

From this child private key, it is possible to derive the corresponding public key by applying ECDSA or Schnorr. This way, we obtain a complete pair of keys.

Then, the second part of the \text{hash} is simply interpreted as being the chain code for the child key pair that we have just derived:

C_{\text{CHD}} = h_2

Here is a schematic representation of the overall derivation:

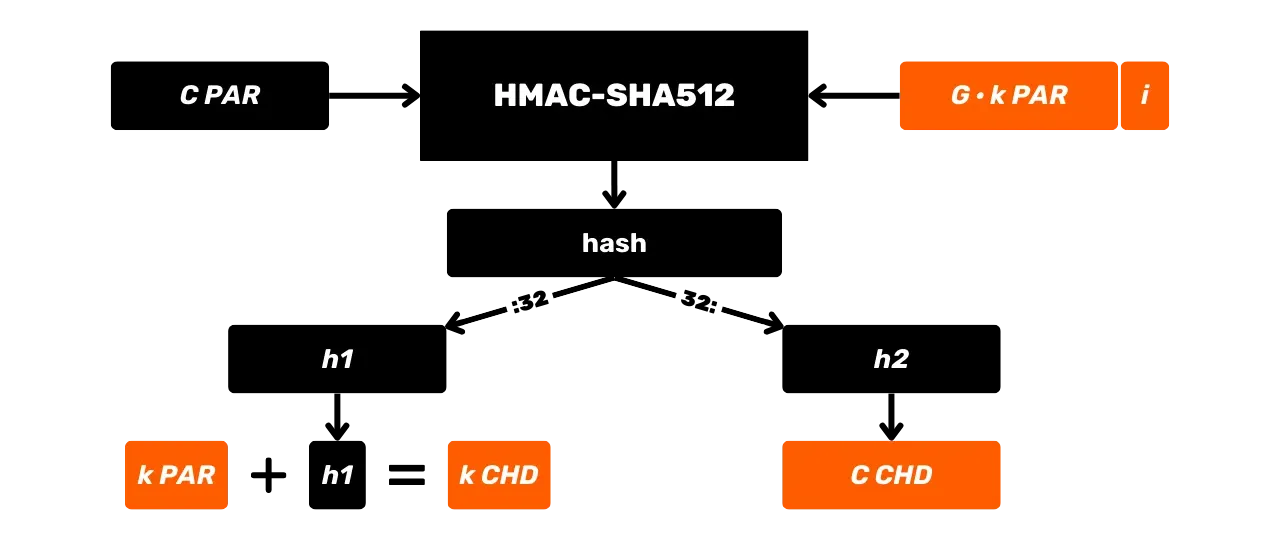
CYP201

For a hardened child key (i \geq 2^{31}), the calculation of the \text{hash} is as follows:

\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, 0x00 \Vert k_{\text{PAR}} \Vert i)

In this calculation, we observe that our HMAC function takes two inputs: first, the parent chain code, and then the concatenation of the index with the parent private key. The parent private key is used here because we are looking to derive a hardened child key. Moreover, a byte equal to 0x00 is added at the beginning of the key. This operation equalizes its length to match that of a compressed public key. So, we now have a 64-byte \text{hash} that we will split into 2 parts of 32 bytes each, h_1 and h_2:


\text{hash} = h_1 \Vert h_2

h_1 = \text{hash}[:32] \quad, \quad h_2 = \text{hash}[32:]

The child private key k_{\text{CHD}}^h is then calculated as follows:

k_{\text{CHD}}^h = \text{parse256}(h_1) + k_{\text{PAR}} \mod n

Next, we simply interpret the second part of the \text{hash} as being the chain code for the pair of child keys that we have just derived:

C_{\text{CHD}} = h_2

Here is a schematic representation of the overall derivation:

CYP201

We can see that normal derivation and hardened derivation function in the same way, with this difference: normal derivation uses the parent public key as input to the HMAC function, while hardened derivation uses the parent private key.

Deriving a child public key from a parent public key

If we only know the parent public key K_{\text{PAR}} and the associated chain code C_{\text{PAR}}, that is, an extended public key, it is possible to derive child public keys K_{\text{CHD}}^n, but only for normal (non-hardened) child keys. This principle notably allows for monitoring the movements of an account in a Bitcoin wallet from the xpub (watch-only).

To perform this calculation, we will compute the \text{hash} with an index i < 2^{31} (normal derivation):

\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, K_{\text{PAR}} \Vert i)

In this calculation, we observe that our HMAC function takes two inputs: first the parent chain code, then the concatenation of the index with the parent public key.

So, we now have a \text{hash} of 64 bytes that we will split into 2 parts of 32 bytes each, h_1 and h_2:


\text{hash} = h_1 \Vert h_2


h_1 = \text{hash}[:32] \quad, \quad h_2 = \text{hash}[32:]

The child public key K_{\text{CHD}}^n is then calculated as follows:

K_{\text{CHD}}^n = \text{parse256}(h_1) \cdot G + K_{\text{PAR}}

If \text{parse256}(h_1) \geq n (order of the elliptic curve) or if K_{\text{CHD}}^n is the point at infinity, the derivation is invalid, and another index must be chosen.

In this calculation, the operation \text{parse256}(h_1) involves interpreting the first 32 bytes of the \text{hash} as a 256-bit integer. This number is used to calculate a point on the elliptic curve through addition and doubling from the generator point G. This point is then added to the parent public key to obtain the normal child public key. Thus, to derive a normal child public key, only the parent public key and the parent chain code are necessary; the parent private key never comes into this process, unlike the calculation of the child private key we saw earlier.

Next, the child chain code is simply:

C_{\text{CHD}} = h_2

Here is a schematic representation of the overall derivation:

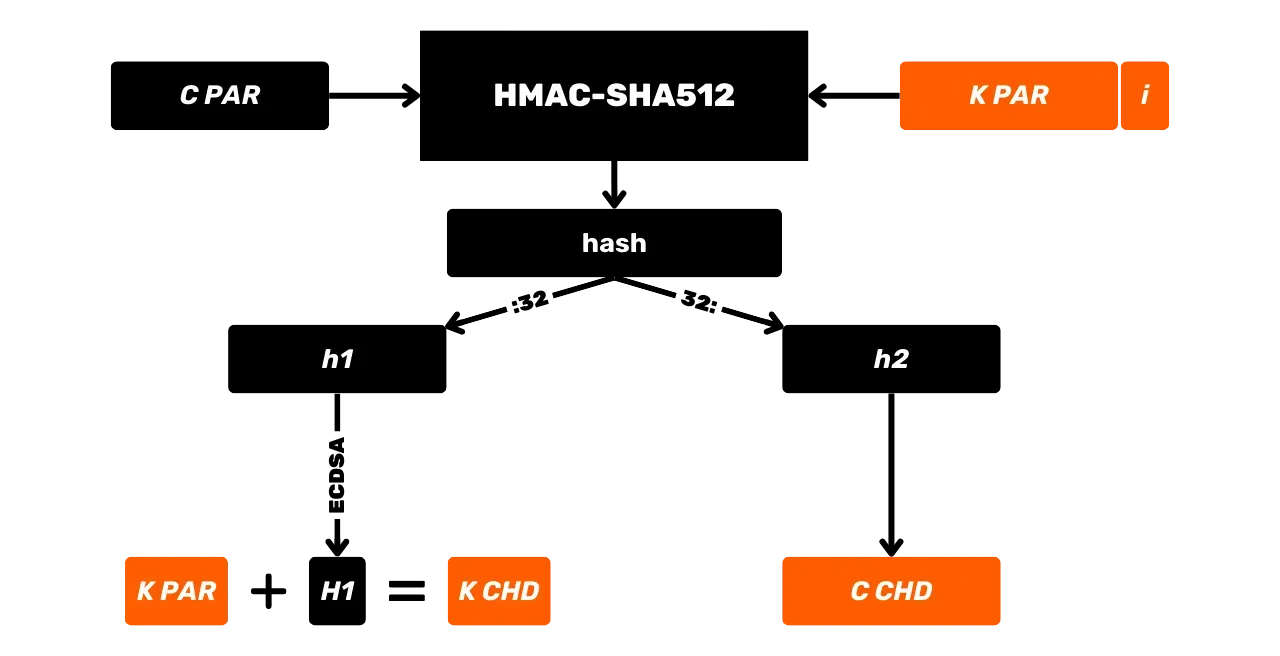
CYP201

Correspondence between child public and private keys

A question that may arise is how a normal child public key derived from a parent public key can correspond to a normal child private key derived from the corresponding parent private key. This link is precisely ensured by the properties of elliptic curves. Indeed, to derive a normal child public key, HMAC-SHA512 is applied in the same way, but its output is used differently:

Thanks to the addition and doubling operations on the elliptic curve, both methods produce consistent results: the public key derived from the child private key is identical to the child public key derived directly from the parent public key.

Summary of derivation types

To summarize, here are the different possible types of derivations:

\begin{array}{|c|c|c|c|}
\hline
\rightarrow & \text{PAR} & \text{CHD} & \text{n/h} \\
\hline
k_{\text{PAR}} \rightarrow k_{\text{CHD}} & k_{\text{PAR}} & \{ k_{\text{CHD}}^n, k_{\text{CHD}}^h \} & \{ n, h \} \\
k_{\text{PAR}} \rightarrow K_{\text{CHD}} & k_{\text{PAR}} & \{ K_{\text{CHD}}^n, K_{\text{CHD}}^h \} & \{ n, h \} \\
K_{\text{PAR}} \rightarrow k_{\text{CHD}} & K_{\text{PAR}} & \times & \times \\
K_{\text{PAR}} \rightarrow K_{\text{CHD}} & K_{\text{PAR}} & K_{\text{CHD}}^n & n \\
\hline
\end{array}

So far you have learned to create the basic elements of an HD wallet: the mnemonic phrase, the seed, and then the master key and master chain code. You have also discovered how to derive child key pairs in this chapter. In the next chapter, we will explore how these derivations are organized in Bitcoin wallets and what structure to follow to concretely obtain the receiving addresses as well as the key pairs used in the scriptPubKey and scriptSig.

Wallet Structure and Derivation Paths

The hierarchical structure of HD wallets in Bitcoin allows for the organization of key pairs in various ways. The idea is to derive, from the master private key and master chain code, several levels of depth. Each added level corresponds to the derivation of a child key pair from a parent key pair.

Over time, different BIPs have introduced standards for these derivation paths, aiming to standardize their use across different software. So, in this chapter, we will discover the meaning of each level of derivation in HD wallets, according to these standards.

The Depths of Derivation of an HD Wallet

Derivation paths are organized into layers of depth, ranging from depth 0, which represents the master key and master chain code, to layers of sub-levels for deriving addresses used to lock UTXOs. The BIPs (Bitcoin Improvement Proposals) define the standards for each layer, which helps to harmonize practices across different wallet management software.

A derivation path, therefore, refers to the sequence of indices used to derive child keys from a master key.

Depth 0: Master Key (BIP32)

This depth corresponds to the wallet's master private key and master chain code. It is represented by the notation m/.

Depth 1: Purpose (BIP43)

The purpose determines the logical structure of derivation. For example, a P2WPKH address will have /84'/ at depth 1 (according to BIP84), while a P2TR address will have /86'/ (according to BIP86). This layer facilitates compatibility between wallets by indicating index numbers corresponding to the BIP numbers.

In other words, once you have the master key and the master chain code, these serve as a parent key pair to derive a child key pair. The index used in this derivation can be, for example, /84'/ if the wallet is intended to use SegWit v0 type scripts. This key pair is then at depth 1. Its role is not to lock bitcoins, but simply to serve as a waypoint in the derivation hierarchy.

Depth 2: Currency Type (BIP44)

From the key pair at depth 1, a new derivation is performed to obtain the key pair at depth 2. This depth allows differentiating Bitcoin accounts from other cryptocurrencies within the same wallet.

Each currency has a unique index to ensure compatibility across multi-currency wallets. For example, for Bitcoin, the index is /0'/ (or 0x80000000 in hexadecimal notation). Currency indexes are chosen in the range from 2^{31} to 2^{32}-1 to ensure hardened derivation.

To give you other examples, here are the indexes of some currencies:

Depth 3: Account (BIP32)

Each wallet can be divided into several accounts, numbered from 2^{31}, and represented at depth 3 by /0'/ for the first account, /1'/ for the second, and so on. Generally, when referring to an extended key xpub, it refers to keys at this depth of derivation.

This separation into different accounts is optional. It aims to simplify the organization of the wallet for users. In practice, often only one account is used, usually the first by default. However, in some cases, if one wishes to clearly distinguish key pairs for different uses, this can be useful. For example, it is possible to create a personal account and a professional account from the same seed, with completely distinct groups of keys from this depth of derivation.

Depth 4: Chain (BIP32)

Each account defined at depth 3 is then structured into two chains:

Depth 5: Address Index (BIP32)

Finally, depth 5 represents the last step of derivation in the wallet. Although it is technically possible to continue indefinitely, current standards stop here. At this final depth, the pairs of keys that will actually be used to lock and unlock the UTXOs are derived. Each index allows distinguishing between sibling key pairs: thus, the first receiving address will use the index /0/, the second the index /1/, and so on.

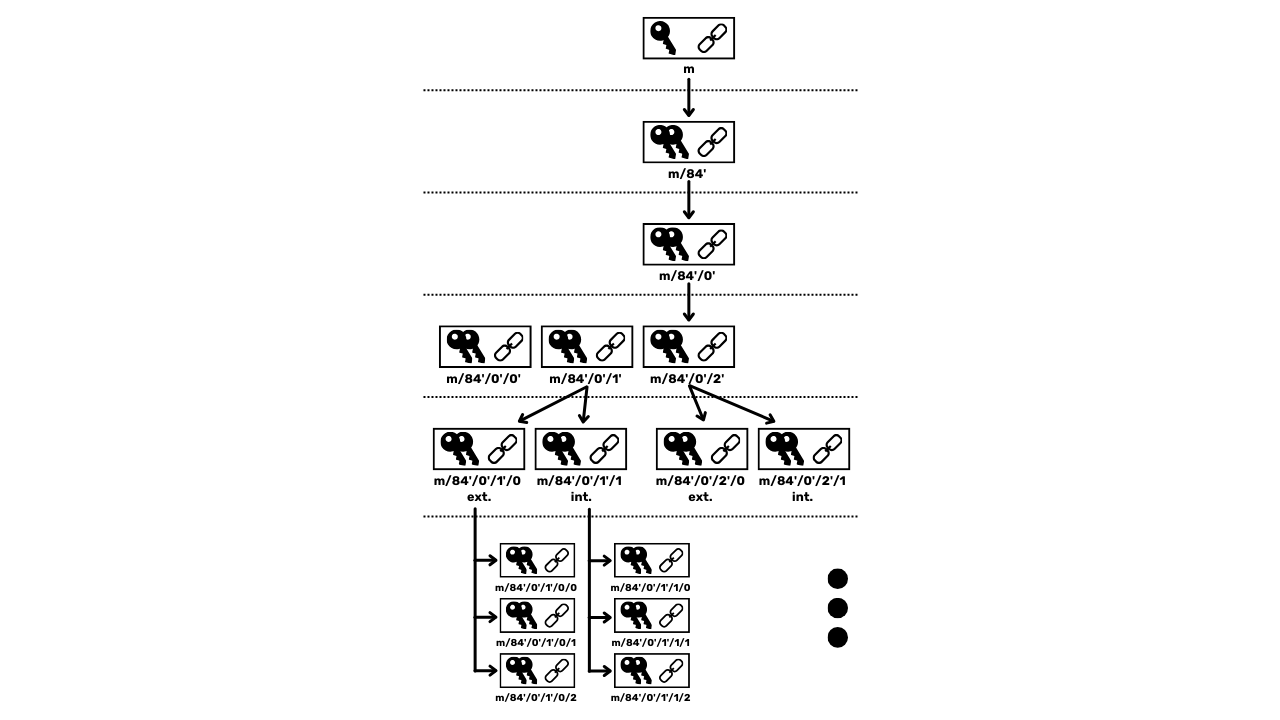
CYP201

Notation of Derivation Paths

The derivation path is written by separating each level with a slash (/). Each slash thus indicates a derivation of a parent key pair (k_{\text{PAR}}, K_{\text{PAR}}, C_{\text{PAR}}) to a child key pair (k_{\text{CHD}}, K_{\text{CHD}}, C_{\text{CHD}}). The number noted at each depth corresponds to the index used to derive this key from its parents. The apostrophe (') sometimes placed to the right of the index indicates a hardened derivation (k_{\text{CHD}}^h, K_{\text{CHD}}^h). Sometimes, this apostrophe is replaced by an h. In the absence of an apostrophe or h, it is therefore a normal derivation (k_{\text{CHD}}^n, K_{\text{CHD}}^n). As we have seen in the previous chapters, hardened key indexes start from 2^{31}, or 0x80000000 in hexadecimal. Therefore, when an index is followed by an apostrophe in a derivation path, 2^{31} must be added to the indicated number to obtain the actual value used in the HMAC-SHA512 function. For example, if the derivation path specifies /44'/, the actual index will be:


i = 44 + 2^{31} = 2\,147\,483\,692

In hexadecimal, this is 0x8000002C.

Now that we have understood the main principles of derivation paths, let's take an example! Here is the derivation path for a Bitcoin receiving address:


m / 84' / 0' / 1' / 0 / 7

In this example:

Summary of the derivation structure

DepthDescriptionStandard Example
0Master Keym/
1Purpose/86'/ (P2TR)
2Currency/0'/ (Bitcoin)
3Account/0'/ (First account)
4Chain/0/ (external) or /1/ (change)
5Address Index/0/ (first address)

In the next chapter, we will discover what "output script descriptors" are, a recently introduced innovation in Bitcoin Core that simplifies the backup of a Bitcoin wallet.

Output script descriptors

e4f1c2d3-9b8a-4d3e-8f2a-7b6c5d4e3f2a You are often told that the mnemonic phrase alone is sufficient to recover access to a wallet. In reality, things are a bit more complex. In the previous chapter, we looked at the derivation structure of the HD wallet, and you may have noticed that this process is quite complex. Derivation paths tell software which direction to follow to derive the user's keys. However, when recovering a Bitcoin wallet, if one does not know these paths, the mnemonic phrase alone is not enough. It allows obtaining the master key and the master chain code, but it is then necessary to know the indexes used to reach the child keys.

Theoretically, it would be necessary to save not only the mnemonic phrase of our wallet but also the paths to the accounts we use. In practice, it is often possible to regain access to the child keys without this information, provided that the standards have been followed. By testing each standard one by one, it is generally possible to regain access to the bitcoins. However, this is not guaranteed and it's especially complicated for beginners. Also, with the diversification of script types and the emergence of more complex configurations, this information could become difficult to extrapolate, thus turning this data into private information and difficult to recover by brute force. This is why an innovation has recently been introduced and is starting to be integrated into your favorite wallet software: the output script descriptors.

What is a "descriptor"?

The "output script descriptors", or simply "descriptors", are structured expressions that fully describe an output script (scriptPubKey) and provide all the necessary information to follow the transactions associated with a particular script. They facilitate the management of keys in HD wallets by offering a standardized and complete description of the wallet structure and the types of addresses used.

The main advantage of descriptors lies in their ability to encapsulate all the essential information to restore a wallet in a single string (in addition to the recovery phrase). By saving a descriptor with the associated mnemonic phrases, it becomes possible to restore the private keys by knowing precisely their position in the hierarchy. For multisig wallets, whose backup was initially more complex, the descriptor includes the xpub of each factor, thus ensuring the possibility of regenerating the addresses in case of a problem.

Construction of a descriptor

A descriptor consists of several elements:

For example, a descriptor for a P2WPKH (SegWit v0) wallet could look like:

wpkh([cdeab12f/84h/0h/0h]xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U/<0;1>/*)#jy0l7nr4

In this descriptor, the derivation function wpkh indicates a script type Pay-to-Witness-Public-Key-Hash. It is followed by the derivation path that contains:

The descriptor also includes the extended public key used in this wallet:

xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U

Next, the notation /<0;1>/* specifies that the descriptor can generate addresses from the external chain (0) and internal chain (1), with a wildcard (*) allowing for the sequential derivation of multiple addresses in a configurable manner, similar to managing a "gap limit" on traditional wallet software.

Finally, #jy0l7nr4 represents the checksum to verify the integrity of the descriptor.

You now know everything about the operation of HD wallets in Bitcoin and the process of deriving key pairs. However, in the last chapters, we limited ourselves to the generation of private and public keys, without addressing the construction of receiving addresses. This will precisely be the subject of the next chapter!

Receiving Addresses

Receiving addresses are pieces of information embedded in scriptPubKey to lock newly created UTXOs. Simply put, an address serves to receive bitcoins. Let's explore their operation in connection with what we have studied in the previous chapters.

The Role of Bitcoin Addresses in Scripts

As explained earlier, a transaction's role is to transfer the ownership of bitcoins from inputs to outputs. This process involves consuming UTXOs as inputs while creating new UTXOs as outputs. These UTXOs are secured by scripts, which define the necessary conditions to unlock the funds.

When a user receives bitcoins, the sender creates a UTXO and locks it with a scriptPubKey. This script contains the rules to unlock the UTXO, typically specifying the signatures and public keys required. To spend this UTXO in a new transaction, the user must provide the requested information via a scriptSig. The execution of scriptSig in combination with scriptPubKey must return "true" or 1. If this condition is met, the UTXO can be spent to create a new UTXO, itself locked by a new scriptPubKey, and so on.

CYP201

It is precisely in the scriptPubKey that the receiving addresses are found. However, their use varies depending on the script standard adopted. Here is a summary table of the information contained in the scriptPubKey according to the standard used, as well as the information expected in the scriptSig to unlock the scriptPubKey.

StandardscriptPubKeyscriptSigredeem scriptwitness
P2PK<pubkey> OP_CHECKSIG<signature>
P2PKHOP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG<signature> <public key>
P2SHOP_HASH160 <scriptHash> OP_EQUAL<data pushes> <redeem script>Arbitrary data
P2WPKH0 <pubKeyHash><signature> <public key>
P2WSH0 <witnessScriptHash><data pushes> <witness script>
P2SH-P2WPKHOP_HASH160 <redeemScriptHash> OP_EQUAL<redeem script>0 <pubKeyHash><signature> <public key>
P2SH-P2WSHOP_HASH160 <redeemScriptHash> OP_EQUAL<redeem script>0 <scriptHash><data pushes> <witness script>
P2TR (key path)1 <public key><signature>
P2TR (script path)1 <public key><data pushes> <script> <control block>

Source: Bitcoin Core PR review club, July 7, 2021 - Gloria Zhao

The opcodes used in a script are designed to manipulate information, and, if necessary, to compare or test it. Let's take the example of a P2PKH script, which is as follows:

OP_DUP OP_HASH160 OP_PUSHBYTES_20 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG

As we will see in this chapter, <pubKeyHash> actually represents the payload of the receiving address used to lock the UTXO. To unlock this scriptPubKey, it is necessary to provide a scriptSig containing:

<signature> <public key>

In script language, the stack is a LIFO ("Last In, First Out") data structure used to temporarily store elements during script execution. Each script operation manipulates this stack, where elements can be added (push) or removed (pop). Scripts use the stack to evaluate expressions, store temporary variables, and manage conditions.

The execution of the script I just gave as an example follows this process:

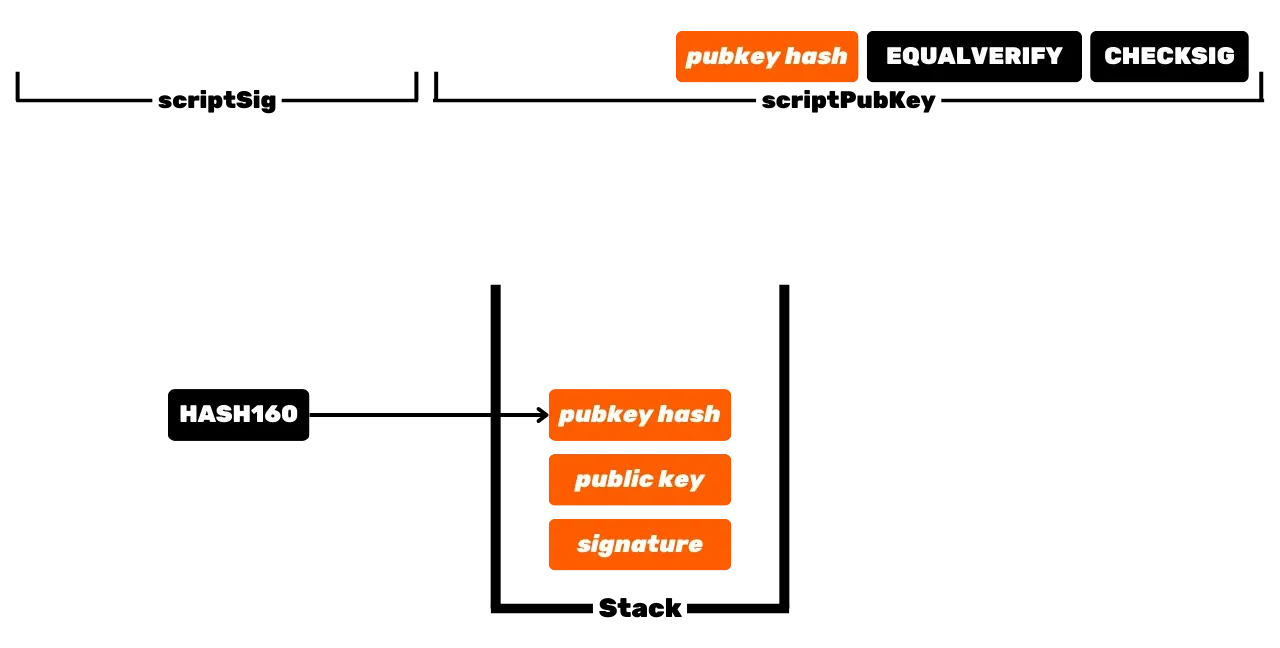
CYP201 CYP201 CYP201 CYP201 CYP201 CYP201

OP_CHECKSIG checks the signature contained in the scriptSig using the public key. This opcode essentially performs a signature verification as we described in part 3 of this training:

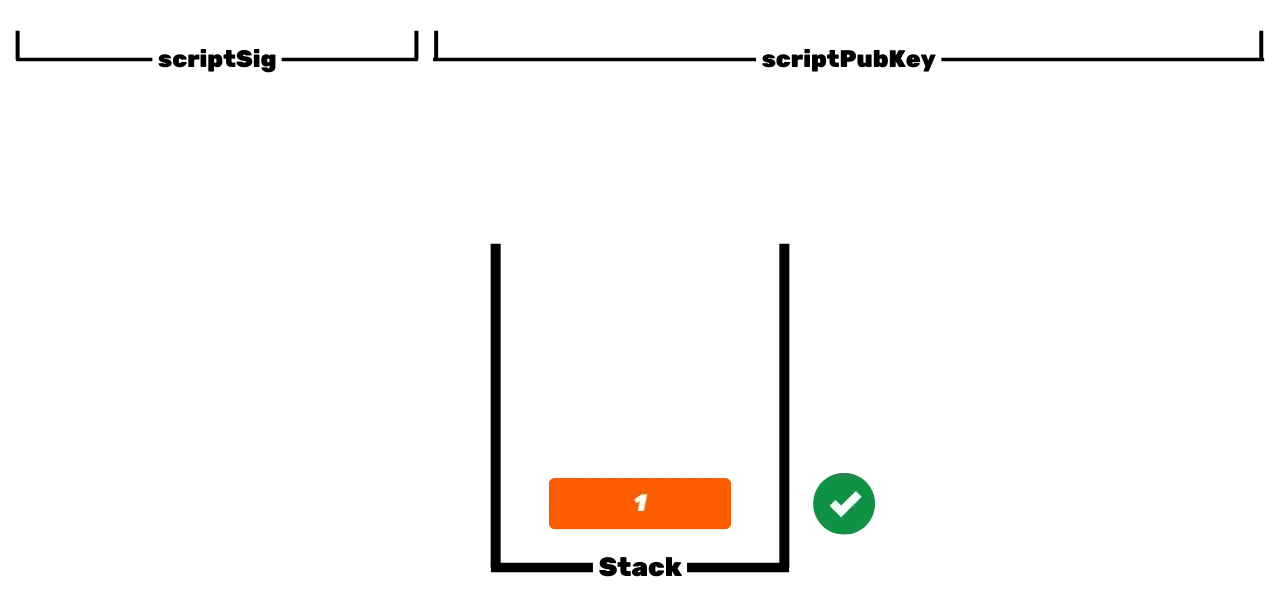
CYP201 CYP201

Therefore, to summarize, this script allows verifying, with the help of the digital signature, that the user claiming ownership of this UTXO and wishing to spend it indeed possesses the private key associated with the receiving address used during the creation of this UTXO.

The different types of Bitcoin addresses

Over the evolution of Bitcoin, several standard script models have been added. Each of them uses a distinct type of receiving address. Here is an overview of the main script models available to date:

P2PK (Pay-to-PubKey):

This script model was introduced in the first version of Bitcoin by Satoshi Nakamoto. The P2PK script locks bitcoins directly using a raw public key (thus, no receiving address is used with this model). Its structure is simple: it contains a public key and requires a corresponding digital signature to unlock the funds. This script is part of the "Legacy" standard.

P2PKH (Pay-to-PubKey-Hash):

Like P2PK, the P2PKH script was introduced at the launch of Bitcoin. Unlike its predecessor, it locks the bitcoins using the hash of the public key, rather than directly using the raw public key. The scriptSig must then provide the public key associated with the receiving address, as well as a valid signature. The addresses corresponding to this model start with 1 and are encoded in base58check. This script also belongs to the "Legacy" standard.

P2SH (Pay-to-Script-Hash):

Introduced in 2012 with BIP16, the P2SH model allows using the hash of an arbitrary script in the scriptPubKey. This hashed script, called "redeemScript", contains the conditions for unlocking the funds. To spend a UTXO locked with P2SH, it is necessary to provide a scriptSig containing the original redeemScript as well as the necessary data to validate it. This model is notably used for old multisigs. The addresses associated with P2SH start with 3 and are encoded in base58check. This script also belongs to the "Legacy" standard.

P2WPKH (Pay-to-Witness-PubKey-Hash):

This script is similar to P2PKH, as it also locks bitcoins using the hash of a public key. However, unlike P2PKH, the scriptSig is moved to a separate section called "Witness". This is sometimes referred to as "scriptWitness" to denote the set comprising the signature and the public key. Each SegWit input has its own scriptWitness, and the collection of scriptWitnesses constitutes the Witness field of the transaction. This movement of signature data is an innovation introduced by the SegWit update, aimed particularly at preventing the malleability of transactions due to ECDSA signatures. P2WPKH addresses use bech32 encoding and always start with bc1q. This type of script corresponds to version 0 SegWit outputs.

P2WSH (Pay-to-Witness-Script-Hash):

The P2WSH model was also introduced with the SegWit update in August 2017. Similar to the P2SH model, it locks bitcoins using the hash of a script. The main difference lies in how signatures and scripts are incorporated into the transaction. To spend bitcoins locked with this type of script, the recipient must provide the original script, called witnessScript (equivalent to redeemScript in P2SH), along with the necessary data to validate this witnessScript. This mechanism allows for the implementation of more complex spending conditions, such as multisigs.

P2WSH addresses use bech32 encoding and always start with bc1q. This script also corresponds to version 0 SegWit outputs.

P2TR (Pay-to-Taproot):

The P2TR model was introduced with the implementation of Taproot in November 2021. It is based on the Schnorr protocol for cryptographic key aggregation, as well as on a Merkle tree for alternative scripts, called MAST (Merkelized Alternative Script Tree). Unlike other types of scripts, where spending conditions are publicly exposed (either at receipt or at spending), P2TR allows for the hiding of complex scripts behind a single, apparent public key.

Technically, a P2TR script locks bitcoins on a unique Schnorr public key, denoted as Q. This key Q is actually an aggregate of a public key P and a public key M, the latter being calculated from the Merkle root of a list of scriptPubKey. Bitcoins locked with this type of script can be spent in two ways:

P2TR thus offers great flexibility, as it allows locking bitcoins either with a unique public key, with several scripts of choice, or both simultaneously. The advantage of this Merkle tree structure is that only the spending script used is revealed during the transaction, but all other alternative scripts remain secret.

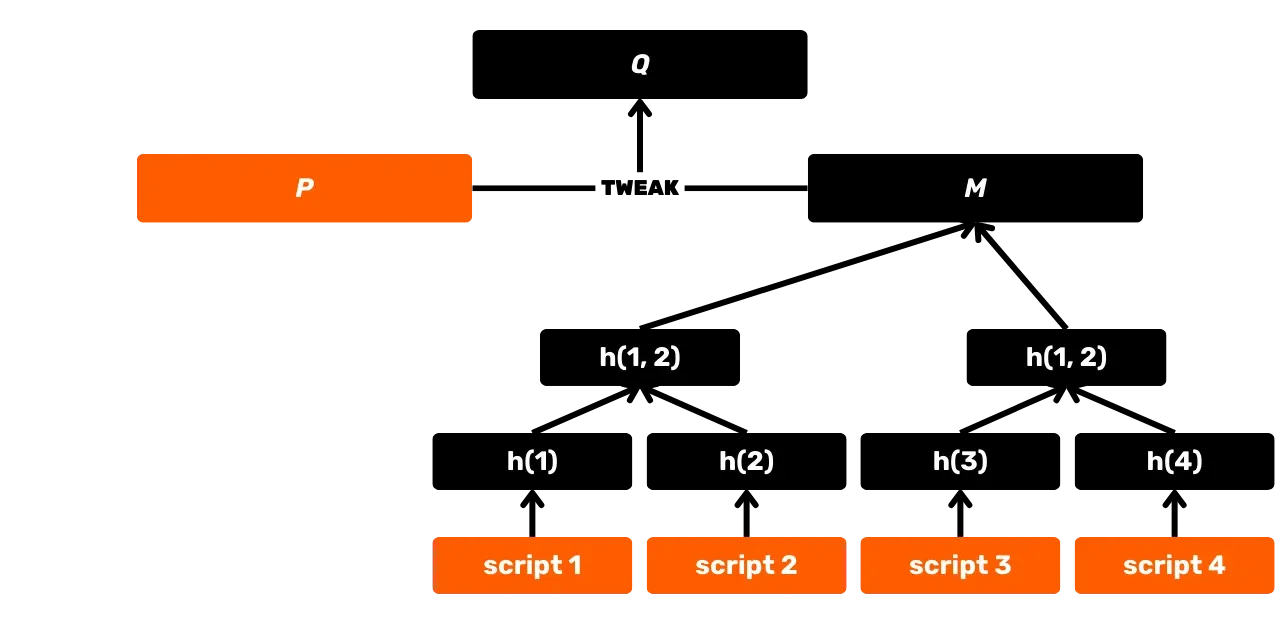
CYP201

P2TR corresponds to version 1 SegWit outputs, which means that the signatures for P2TR inputs are stored in the transaction's Witness section, and not in the scriptSig. P2TR addresses use the bech32m encoding and start with bc1p, but they are quite unique because they do not use a hash function for their construction. Indeed, they directly represent the public key Q which is simply formatted with metadata. It is, therefore, a script model close to P2PK.

Now that we have covered the theory, let's move on to practice! In the following chapter, I propose deriving both a SegWit v0 address and a SegWit v1 address from a pair of keys.

Address Derivation

Let's explore together how to generate a receiving address from a pair of keys located, for example, at depth 5 of an HD wallet. This address can then be used in a wallet software to lock a UTXO.

Since the process of generating an address depends on the script model adopted, let's focus on two specific cases: generating a SegWit v0 address in P2WPKH and a SegWit v1 address in P2TR. These two types of addresses cover the vast majority of uses today.

Public Key Compression

After performing all the derivation steps from the master key to depth 5 using the appropriate indexes, we obtain a pair of keys (k, K) with K = k \cdot G. Although it is possible to use this public key as is to lock funds with the P2PK standard, that is not our goal here. Instead, we aim to create an address in P2WPKH in the first instance, and then in P2TR for another example.

The first step is to compress the public key K. To understand this process well, let's first recall some fundamentals covered in part 3. A public key in Bitcoin is a point K located on an elliptic curve. It is represented in the form (x, y), where x and y are the coordinates of the point. In its uncompressed form, this public key measures 520 bits: 8 bits for a prefix (initial value of 0x04), 256 bits for the x coordinate, and 256 bits for the y coordinate. However, elliptic curves have a symmetry property with respect to the x-axis: for a given x coordinate, there are only two possible values for y: y and -y. These two points are located on either side of the x-axis. In other words, if we know x, it is sufficient to specify whether y is even or odd to identify the exact point on the curve.

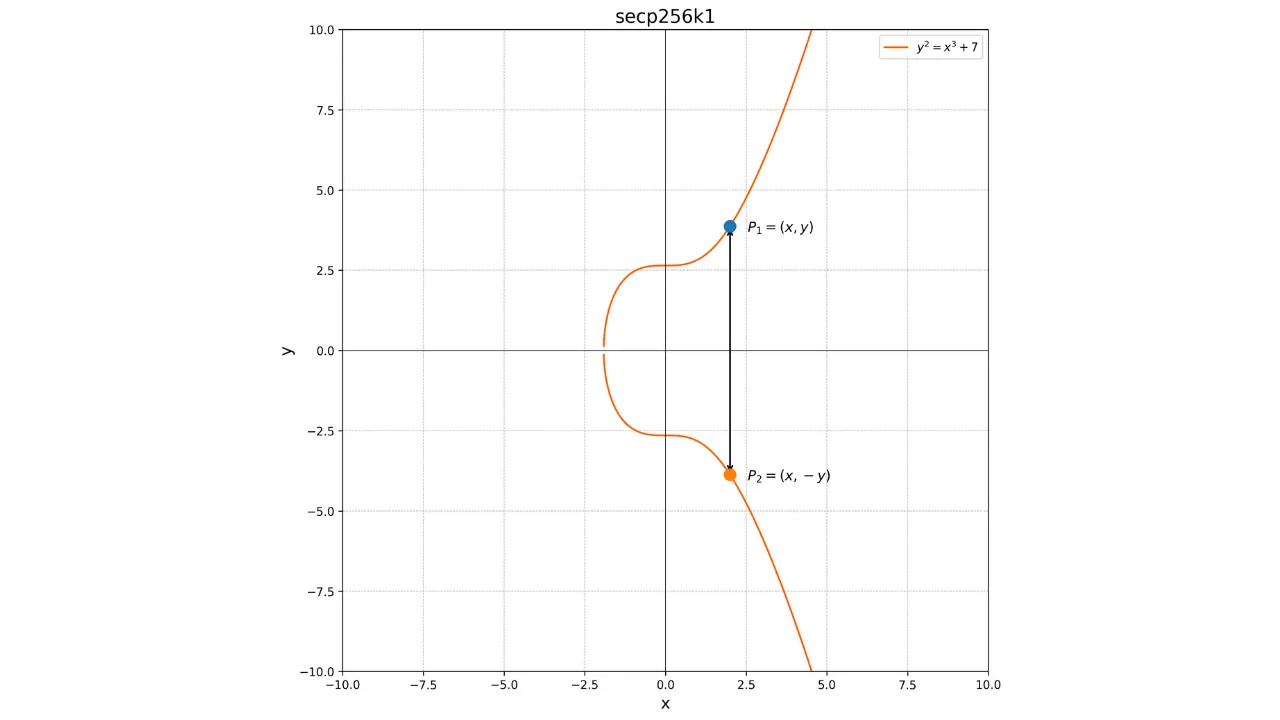
CYP201

To compress a public key, only x is encoded, which occupies 256 bits, and a prefix is added to specify the parity of y. This method reduces the size of the public key to 264 bits instead of the initial 520. The prefix 0x02 indicates that y is even, and the prefix 0x03 indicates that y is odd.

Let's take an example to understand well, with a raw public key in uncompressed representation:

K = 04678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f

If we decompose this key, we have:

The last hexadecimal character of y is f. In base 10, f = 15, which corresponds to an odd number. Therefore, y is odd, and the prefix will be 0x03 to indicate this.

The compressed public key becomes:

K = 03678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6

This operation applies to all script models based on ECDSA, that is, all except P2TR which uses Schnorr. In the case of Schnorr, as explained in part 3, we only retain the value of x, without adding a prefix to indicate the parity of y, unlike ECDSA. This is made possible by the fact that a unique parity is arbitrarily chosen for all keys. This allows for a slight reduction in the storage space required for public keys.

Derivation of a SegWit v0 (bech32) address

Now that we have obtained our compressed public key, we can derive a SegWit v0 receiving address from it.

The first step is to apply the HASH160 hash function to the compressed public key. HASH160 is a composition of two successive hash functions: SHA256, followed by RIPEMD160:


\text{HASH160}(K) = \text{RIPEMD160}(\text{SHA256}(K))

First, we pass the key through SHA256:

SHA256(K) = C489EBD66E4103B3C4B5EAFF462B92F5847CA2DCE0825F4997C7CF57DF35BF3A

Then we pass the result through RIPEMD160:

RIPEMD160(SHA256(K)) = 9F81322CC88622CA4CCB2A52A21E2888727AA535

We have obtained a 160-bit hash of the public key, which constitutes what is called the payload of the address. This payload represents the central and most important part of the address. It is also used in the scriptPubKey to lock the UTXOs.

However, to make this payload more easily usable by humans, metadata is added to it. The next step involves encoding this hash into groups of 5 bits in decimal. This decimal transformation will be useful for conversion into bech32, used by post-SegWit addresses. The 160-bit binary hash is thus divided into 32 groups of 5 bits:


\begin{array}{|c|c|}
\hline
\text{5 bits} & \text{Decimal} \\
\hline
10011 & 19 \\
11110 & 30 \\
00000 & 0 \\
10011 & 19 \\
00100 & 4 \\
01011 & 11 \\
00110 & 6 \\
01000 & 8 \\
10000 & 16 \\
11000 & 24 \\
10001 & 17 \\
01100 & 12 \\
10100 & 20 \\
10011 & 19 \\
00110 & 6 \\
01011 & 11 \\
00101 & 5 \\
01001 & 9 \\
01001 & 9 \\
01010 & 10 \\
00100 & 4 \\
00111 & 7 \\
10001 & 17 \\
01000 & 8 \\
10001 & 17 \\
00001 & 1 \\
11001 & 25 \\
00111 & 7 \\
10101 & 21 \\
00101 & 5 \\
00101 & 5 \\
10101 & 21 \\
\hline
\end{array}

So, we have:

HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21

Once the hash is encoded into groups of 5 bits, a checksum is added to the address. This checksum is used to verify that the payload of the address has not been altered during its storage or transmission. For example, it allows a wallet software to ensure that you have not made a typo when entering a receiving address. Without this verification, you could accidentally send bitcoins to an incorrect address, resulting in a permanent loss of funds, as you do not own the associated public or private key. Therefore, the checksum is a protection against human errors.

For the old Bitcoin Legacy addresses, the checksum was simply calculated from the beginning of the address hash with the HASH256 function. With the introduction of SegWit and the bech32 format, BCH codes (Bose, Ray-Chaudhuri, and Hocquenghem) are now used. These error-correcting codes are used to detect and correct errors in data sequences. They ensure that the transmitted information arrives intact at its destination, even in the case of minor alterations. BCH codes are used in many fields, such as SSDs, DVDs, and QR codes. For example, thanks to these BCH codes, a partially obscured QR code can still be read and decoded.

In the context of Bitcoin, BCH codes offer a better compromise between size and error detection capability compared to the simple hash functions used for Legacy addresses. However, in Bitcoin, BCH codes are used only for error detection, not correction. Thus, wallet software will signal an incorrect receiving address but will not automatically correct it. This limitation is deliberate: allowing automatic correction would reduce the error detection capability.

To calculate the checksum with BCH codes, we need to prepare several elements.

The HRP must be expanded by separating each character into two parts:

With the separator 0 between the two characters, the HRP extension is therefore:

03 03 00 02 03

All the data combined to input into the program to calculate the checksum are as follows:

HRP = 03 03 00 02 03
SEGWIT v0 = 00
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
CHECKSUM = 00 00 00 00 00 00

INPUT = 03 03 00 02 03 00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 00 00 00 00 00 00

The calculation of the checksum is quite complex. It involves polynomial finite field arithmetic. We will not detail this calculation here and will move directly to the result. In our example, the checksum obtained in decimal is:

10 16 11 04 13 18

We can now construct the receiving address by concatenating in order the following elements:

This gives us in decimal:

00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 10 16 11 04 13 18

Then, each decimal value must be mapped to its bech32 character using the following conversion table:


\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline
& 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\
\hline
+0 & q & p & z & r & y & 9 & x & 8 \\
\hline
+8 & g & f & 2 & t & v & d & w & 0 \\
\hline
+16 & s & 3 & j & n & 5 & 4 & k & h \\
\hline
+24 & c & e & 6 & m & u & a & 7 & l \\
\hline
\end{array}

To convert a value into a bech32 character using this table, simply locate the values in the first column and the first row which, when added together, yield the desired result. Then, retrieve the corresponding character. For example, the decimal number 19 will be converted into the letter n, because 19 = 16 + 3.

By mapping all our values, we obtain the following address:

qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj

All that remains is to add the HRP bc, which indicates that it is an address for the Bitcoin mainnet, as well as the separator 1, to obtain the complete receiving address:

bc1qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj

The particularity of this bech32 alphabet is that it includes all alphanumeric characters except for 1, b, i, and o to avoid visual confusion between similar characters, especially during their entry or reading by humans.

To summarize, here is the derivation process:

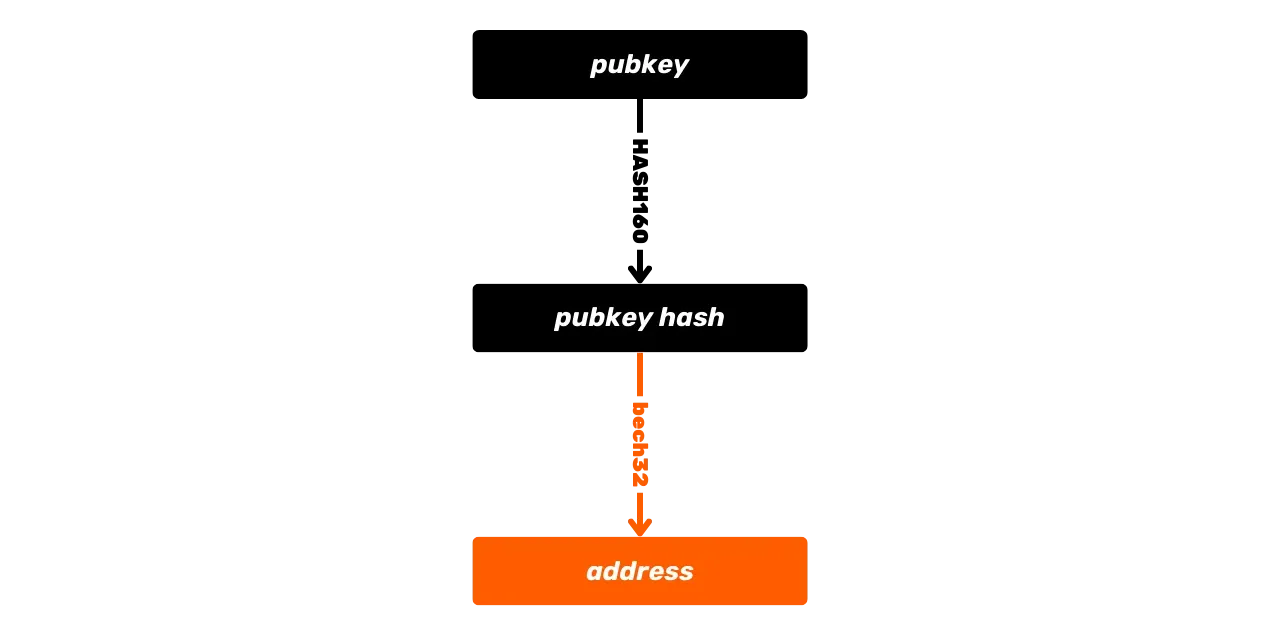
CYP201

This is how to derive a P2WPKH (SegWit v0) receiving address from a pair of keys. Let's now move on to P2TR (SegWit v1 / Taproot) addresses and discover their generation process.

Derivation of a SegWit v1 (bech32m) Address

For Taproot addresses, the generation process differs slightly. Let's look at this together!

From the step of public key compression, a first distinction appears compared to ECDSA: the public keys used for Schnorr in Bitcoin are represented only by their abscissa (x). Therefore, there is no prefix, and the compressed key measures exactly 256 bits. As we saw in the previous chapter, a P2TR script locks bitcoins on a unique Schnorr public key, designated by Q. This key Q is an aggregate of two public keys: P, a main internal public key, and M, a public key derived from the Merkle root of a list of scriptPubKey. The bitcoins locked with this type of script can be spent in two ways:

In reality, these two keys are not truly "aggregated." The key P is instead tweaked by the key M. In cryptography, to "tweak" a public key means to modify this key by applying an additive value called a "tweak." This operation allows the modified key to remain compatible with the original private key and the tweak. Technically, a tweak is a scalar value t that is added to the initial public key. If P is the original public key, the tweaked key becomes:


P' = P + t \cdot G

Where G is the generator of the elliptic curve used. This operation produces a new public key derived from the original key, while retaining cryptographic properties allowing its use.

If you do not need to add alternative scripts (spending exclusively via the key path), you can generate a Taproot address established solely on the public key present at depth 5 of your wallet. In this case, it is necessary to create a non-spendable script for the script path, in order to satisfy the requirements of the structure. The tweak t is then calculated by applying a tagged hash function, TapTweak, on the internal public key P:


t = \text{H}_{\text{TapTweak}}(P)

where:

The Taproot public key Q is then calculated by adding the tweak t, multiplied by the elliptic curve generator G, to the internal public key P:


Q = P + t \cdot G

Once the Taproot public key Q is obtained, we can generate the corresponding receiving address. Unlike other formats, Taproot addresses are not established on a hash of the public key. Therefore, the key Q is inserted directly into the address, in a raw manner.

To begin, we extract the x coordinate of the point Q to obtain a compressed public key. On this payload, a checksum is calculated using BCH codes, as with SegWit v0 addresses. However, the program used for Taproot addresses differs slightly. Indeed, after the introduction of the bech32 format with SegWit, a bug was discovered: when the last character of an address is a p, inserting or removing qs just before this p does not make the checksum invalid. Although this bug does not have consequences on SegWit v0 (thanks to a size constraint), it could pose a problem in the future. This bug has therefore been corrected for Taproot addresses, and the new corrected format is called "bech32m".

The Taproot address is generated by encoding the x coordinate of Q in the bech32m format, with the following elements:

The final address will therefore have the format:

bc1p[Qx][checksum]

On the other hand, if you wish to add alternative scripts in addition to spending with the internal public key (script path), the calculation of the receiving address will be slightly different. You will need to include the hash of the alternative scripts in the calculation of the tweak. In Taproot, each alternative script, located at the end of the Merkle tree, is called a "leaf".

Once the different alternative scripts are written, you must pass them individually through a tagged hash function TapLeaf, accompanied by some metadata:


\text{h}_{\text{leaf}} = \text{H}_{\text{TapLeaf}} (v \Vert sz \Vert S)

With:

The different script hashes (\text{h}_{\text{leaf}}) are first sorted in lexicographical order. Then, they are concatenated in pairs and passed through a tagged hash function TapBranch. This process is repeated iteratively to build, step by step, the Merkle tree:


\text{h}_{\text{branch}} = \text{H}_{\text{TapBranch}}(\text{h}_{\text{leaf1}} \Vert \text{h}_{\text{leaf2}})

We then continue by concatenating the results two by two, passing them at each step through the tagged hash function TapBranch, until we obtain the Merkle tree root:

CYP201

Once the Merkle root h_{\text{root}} is calculated, we can calculate the tweak. For this, we concatenate the internal public key of the wallet P with the root h_{\text{root}}, and then pass the whole through the tagged hash function TapTweak:


t = \text{H}_{\text{TapTweak}}(P \Vert h_{\text{root}})

Finally, as before, the Taproot public key Q is obtained by adding the internal public key P to the product of the tweak t by the generator point G:


Q = P + t \cdot G

Then, the generation of the address follows the same process, using the raw public key Q as the payload, accompanied by some additional metadata.

And there you have it! We have reached the end of this CYP201 course. If you found this course helpful, I would be very grateful if you could take a few moments to give it a good rating in the following evaluation chapter. Feel free to also share it with your loved ones or on your social networks. Finally, if you wish to obtain your diploma for this course, you can take the final exam right after the evaluation chapter.

Final Section

Reviews & Ratings

0cd71541-a7fd-53db-b66a-8611b6a28b04 true

Final Exam

a53ea27d-0f84-56cd-b37c-a66210a4b31d true

Conclusion

d291428b-3cfa-5394-930e-4b514be82d5a true