name: Privacy on Bitcoin goal: Understand and master the principles of privacy protection when using Bitcoin objectives:

Define the theoretical concepts needed to understand privacy issues
Identify and mitigate the risks associated with loss of confidentiality for Bitcoin users
Using methods and tools to protect your privacy on Bitcoin
Understand chain analysis methods and develop defense strategies

Protect your privacy on Bitcoin

In a world where the confidentiality of financial transactions is gradually becoming a luxury, understanding and mastering the principles of privacy protection when using Bitcoin is essential. This training course gives you all the keys, both theoretical and practical, to achieve this autonomously.

Today, on Bitcoin, companies specialize in blockchain analysis. Their core business consists precisely in intruding into your private sphere, in order to compromise the confidentiality of your transactions. In reality, there is no such thing as a "right to privacy" in Bitcoin. So it's up to you, the user, to assert your natural rights and protect the confidentiality of your transactions, because nobody else is going to do it for you.

The course is designed to be comprehensive and general. Each technical concept is covered in detail and supported by explanatory diagrams. The aim is to make the knowledge accessible to all. BTC204 is therefore affordable for beginners and intermediate users. The course also offers added value for more experienced bitcoiners, as we delve deeper into certain technical concepts that are often misunderstood.

Join us to transform your use of Bitcoin and become an informed user, capable of understanding the issues around confidentiality and protecting your privacy.

Introduction

Course overview

Welcome to the BTC204 course!

Bitcoin isn't just about "Number Go Up" and preserving the value of savings. With its unique characteristics and history, it is first and foremost the tool of the counter-economy. Thanks to this formidable invention, you can freely dispose of your money, spend it and accumulate it, without anyone being able to stop you.

Bitcoin offers a peaceful escape from the yoke of the state, allowing you to fully enjoy your natural rights, which cannot be challenged by established laws. Thanks to Satoshi Nakamoto's invention, you have the power to enforce respect for your private property and regain the freedom to contract.

However, Bitcoin is not anonymous by default, which can represent a risk for individuals engaged in the counter-economy, particularly in regions under despotic rule. But this is not the only danger. Since bitcoin is a valuable and incensurable asset, it can be a target for thieves. So protecting your privacy becomes a matter of security too: it can help you prevent hacking and physical assault.

As we'll see, although the protocol offers certain confidentiality protections in its own right, it's crucial to use additional tools to optimize and defend this confidentiality.

This training course is designed to provide a comprehensive, general overview of the issues involved in Bitcoin confidentiality. Each technical concept is covered in detail, supported by explanatory diagrams. The aim is to make this knowledge accessible to everyone, even beginners and intermediate users. For the more seasoned Bitcoiners, we also cover highly technical and sometimes little-known concepts throughout the course, to deepen understanding of each subject.

The aim of this training course is not to make you totally anonymous in your use of Bitcoin, but rather to provide you with the essential tools to know how to protect your confidentiality according to your personal objectives. You'll have the freedom to choose from the concepts and tools presented to develop your own strategies, tailored to your specific goals and needs.

Section 1: Definitions and key concepts

To begin with, we're going to review the fundamental principles governing the operation of Bitcoin, so that we can then calmly tackle the notions relating to confidentiality. It's essential to master a few basic concepts, such as UTXO, receiving addresses and scripting, before you can fully understand the concepts we'll cover in the following sections. We will also introduce Bitcoin's general confidentiality model, as imagined by Satoshi Nakamoto, which will enable us to grasp the associated stakes and risks.

Section 2: Understanding and protecting against chain analysis

In the second section, we look at the techniques used by blockchain analysis companies to track your activity on Bitcoin. Understanding these methods is crucial to strengthening your privacy protection. The aim of this section is to examine attackers' strategies in order to better understand the risks and prepare the ground for the techniques we will study in the following sections. We will analyze transaction patterns, internal and external heuristics, and likely interpretations of these patterns. In addition to theory, we'll learn how to use a block explorer for chain analysis, through practical examples and exercises.

Section 3: Mastering best practices to protect your privacy

In the third section of our training course, we get down to the nitty-gritty: practice! The aim is to master all the essential best practices that should become natural reflexes for any Bitcoin user. We'll be covering the use of blank addresses, tagging, consolidation, the use of complete nodes, as well as KYC and acquisition methods. The aim is to provide you with a comprehensive overview of the pitfalls to avoid in order to establish a solid foundation in our quest to protect privacy. For some of these practices, you will be guided to a specific tutorial on how to implement them.

Section 4: Understanding coinjoin transactions

How can we talk about privacy on Bitcoin without mentioning coinjoins? In section 4, you'll find out all you need to know about this mixing method. You'll learn what coinjoins are, their history and objectives, as well as the different types of coinjoin that exist. Finally, for the more experienced user, we'll take a look at what anonsets and entropy are, and how to calculate them.

Section 5: Understanding the challenges of other advanced confidentiality techniques

In the fifth section, we'll take a look at all the other techniques available to protect your privacy on Bitcoin, apart from coinjoin. Over the years, developers have shown remarkable creativity in designing tools dedicated to privacy. We'll look at all these methods, such as payjoin, collaborative transactions, Coin Swap and Atomic Swap, detailing how they work, their objectives and any weaknesses.

We'll also look at privacy at the level of the network of nodes and transaction dissemination. We'll also discuss the various protocols that have been proposed over the years to enhance user privacy on Bitcoin, including static address protocols.

BTC204 Ready to explore the intricacies of privacy on Bitcoin? Let's go!

Definitions and key concepts

Bitcoin's UTXO model

Bitcoin is first and foremost a currency, but do you actually know how BTC are represented on the protocol?

UTXOs on Bitcoin: what are they?

The Bitcoin protocol is based on the UTXO model, which stands for "Unspent Transaction Output".

This model differs profoundly from traditional banking systems, which rely on a mechanism of accounts and balances to track financial flows. Indeed, in the banking system, individual balances are maintained in accounts attached to an identity. For example, when you buy a baguette from a baker, your bank simply debits the purchase amount from your account, reducing your balance, while the baker's account is credited with the same amount, increasing its balance. In this system, there is no notion of a link between the money entering your account and the money leaving it, apart from transaction records.

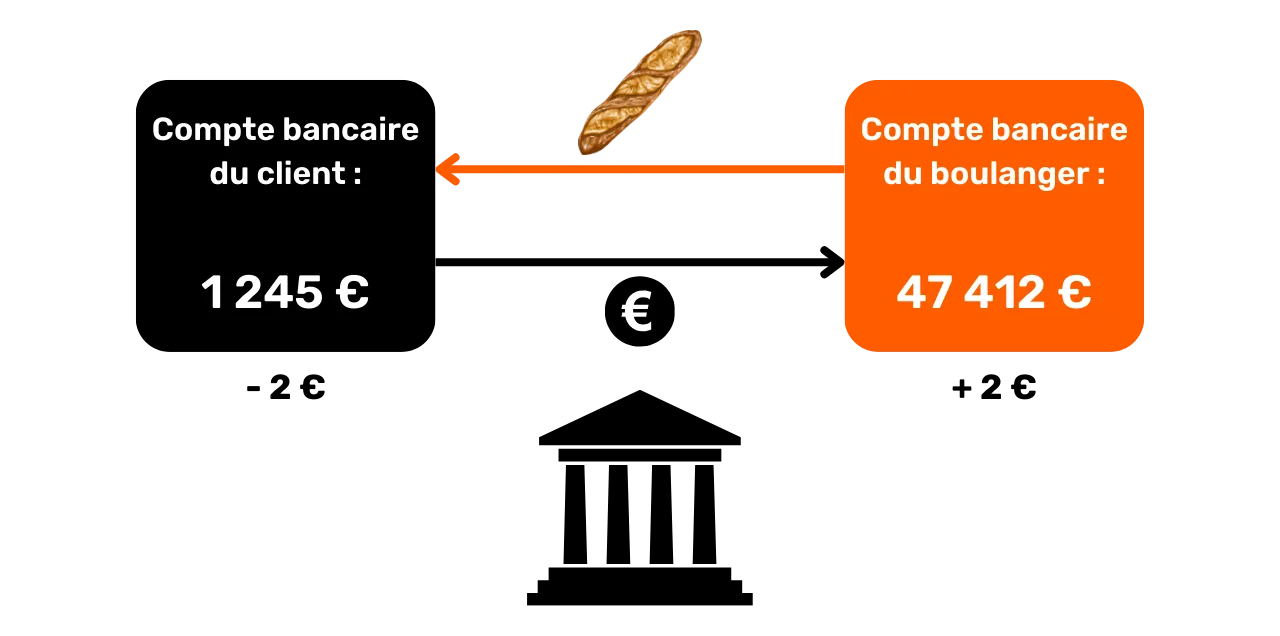
Bitcoin works differently. The concept of an account does not exist, and monetary units are not managed via balances, but through UTXOs. A UTXO represents a specific quantity of bitcoins that has not yet been spent, thus forming a "piece of bitcoin", which can be large or small. For example, one UTXO could be worth 500 BTC or simply 700 SATS.

**> The satoshi, often abbreviated to sat, is Bitcoin's smallest unit, comparable to the centime in fiat currencies.

1 BTC = 100 000 000 SATS

Theoretically, one UTXO can represent any value in bitcoins, ranging from a sat to a theoretical maximum of around 21 million BTC. However, it is logically impossible to own all 21 million bitcoins, and there is a lower economic threshold called "dust", below which a UTXO is considered economically unprofitable to spend.

**> The largest UTXO ever created on Bitcoin had a value of 500,000 BTC. It was created by the MtGox platform during a consolidation operation in November 2011: 29a3efd3ef04f9153d47a990bd7b048a4b2d213daaa5fb8ed670fb85f13bdbcf

UTXOs and spending conditions

UTXOs are the instruments of exchange on Bitcoin. Each transaction results in the consumption of UTXOs as inputs and the creation of new UTXOs as outputs. When a transaction is completed, the UTXOs used as inputs are considered "spent", and new UTXOs are generated and allocated to the recipients indicated in the transaction outputs. Thus, a UTXO simply represents an unspent transaction output, and therefore a quantity of bitcoins belonging to a user at a given time.

All UTXOs are secured by scripts that define the conditions under which they can be spent. To consume a UTXO, a user must demonstrate to the network that he or she satisfies the conditions stipulated by the script securing that UTXO. Typically, UTXOs are protected by a public key (or a receiving address that represents this public key). To spend a UTXO associated with this public key, the user must prove that he holds the corresponding private key, by providing a digital signature made with this key. This is why we say that your Bitcoin wallet doesn't actually contain bitcoins, but stores your private keys, which in turn give you access to your UTXOs and, by extension, to the bitcoins they represent.

Since there's no concept of an account in Bitcoin, a wallet's balance is simply the sum of the values of all the UTXOs it can spend. For example, if your Bitcoin wallet can spend the following 4 UTXOs:

- 2 BTC
- 8 BTC
- 5 BTC
- 2 BTC

The total balance of your portfolio would be 17 BTC.

The structure of Bitcoin transactions

Transaction inputs and outputs

A Bitcoin transaction is an operation recorded on the blockchain that transfers ownership of bitcoins from one person to another. More precisely, since we're on a UTXO model and there are no accounts, the transaction satisfies the spending conditions that secured one or more UTXOs, consumes them and equivalently creates new UTXOs with new spending conditions. In short, a transaction moves bitcoins from a satisfied script to a new script designed to secure them.

Each Bitcoin transaction therefore consists of one or more inputs and one or more outputs. Inputs are UTXOs consumed by the transaction to generate outputs. Outputs are new UTXOs that can be used as inputs for future transactions.

**> Theoretically, a bitcoin transaction could have an infinite number of inputs and outputs. The only limit is the maximum block size.

Each input in a Bitcoin transaction refers to a previous unspent UTXO. To use a UTXO as an input, its holder must demonstrate that he/she is the rightful owner by validating the associated script, i.e. by satisfying the spending condition imposed. Generally speaking, this means providing a digital signature produced with the private key corresponding to the public key that initially secured this UTXO. The script therefore consists in verifying that the signature corresponds to the public key used when the funds were received.

Each output, in turn, specifies the amount of bitcoins to be transferred, as well as the recipient. The latter is defined by a new script, which usually blocks the newly created UTXO with a receiving address or a new public key.

For a transaction to be considered valid according to the consensus rules, total outputs must be less than or equal to total inputs. In other words, the sum of new UTXOs generated by the transaction must not exceed the sum of UTXOs consumed as inputs. This principle is logical: if you only have 500,000 SATS, you can't make a purchase of 700,000 SATS.

Exchange and merging in a Bitcoin transaction

The action of a Bitcoin transaction on UTXO can thus be compared to recasting a gold coin. Indeed, a UTXO is not divisible, but only fusible. This means that a user cannot simply divide a UTXO representing a certain amount in bitcoins into several smaller UTXOs. He must consume it entirely in a transaction to create one or more new UTXOs of arbitrary values in outputs, which must be less than or equal to the initial value.

This mechanism is similar to that of a gold coin. Let's say you own a 2-ounce coin and want to make a payment of 1 ounce, assuming the seller can't give you change. You would have to melt your coin and cast 2 new ones of 1 ounce each.

Bitcoin works in a similar way. Let's imagine that Alice has a UTXO of 10,000 SATS and wishes to buy a baguette costing 4,000 SATS. Alice will make a transaction with 1 UTXO of 10,000 SATS as input, which she will consume in full, and 2 UTXOs of 4,000 SATS and 6,000 SATS as output. The UTXO of 4,000 SATS will be sent to the baker in payment for the baguette, while the UTXO of 6,000 SATS will return to Alice in the form of change. This UTXO, which returns to the original issuer of the transaction, is known as "exchange" in Bitcoin jargon.

Now let's imagine that Alice doesn't have a single UTXO of 10,000 SATS, but rather two UTXOs of 3,000 SATS each. In this situation, neither of the UTXOs individually is sufficient to set the wand's 4,000 SATS. Alice must therefore simultaneously use the 2 UTXOs of 3,000 SATS as inputs to her transaction. In this way, the total amount of inputs will reach 6,000 SATS, enabling her to satisfy the 4,000 SATS payment to the baker. This method, in which several UTXOs are grouped together as inputs to a transaction, is often referred to as "merging".

Transaction fees

Intuitively, one might think that transaction costs also represent the output of a transaction. But in reality, this is not the case. Transaction costs represent the difference between total inputs and total outputs. This means that, after using part of the value of the inputs to cover the desired outputs in a transaction, a certain sum of the inputs remains unused. This residual sum constitutes the transaction costs.

Frais = total inputs - total outputs

Let's take the example of Alice, who has a UTXO of 10,000 SATS and wants to buy a baguette at 4,000 SATS. Alice creates a transaction with her UTXO of 10,000 SATS as input. She then generates an output of 4,000 SATS for the baker to pay for the baguette. To encourage miners to integrate her transaction into a block, Alice allocates 200 SATS in fees. She then creates a second output, the exchange, which will be returned to her, amounting to 5,800 SATS.

Applying the fee formula, we see that there are indeed 200 SATS left for minors:

Frais = total inputs - total outputs
Frais = 10 000 - (4 000 + 5 800)
Frais = 10 000 - 9 800
Frais = 200

When a miner succeeds in validating a block, he is authorized to collect these fees for all the transactions included in his block, via the so-called "coinbase" transaction.

Creating UTXOs on Bitcoin

If you've followed the previous paragraphs carefully, you'll now know that UTXOs can only be created by consuming other existing UTXOs. In this way, Bitcoin coins form a continuous chain. However, you may be wondering how the first UTXOs in this chain came about. This raises a problem similar to that of the chicken and the egg: where did these original UTXOs come from?

The answer is in the transaction coinbase.

The coinbase is a specific type of Bitcoin transaction, which is unique for each block and is always the first of these. It allows the miner who has found a valid proof of work to receive his block reward. This reward is made up of two elements: block grant and transaction fee, discussed in the previous section.

The coinbase transaction is unique in that it is the only one capable of creating bitcoins ex nihilo, without the need to consume inputs to generate outputs. These newly-created bitcoins are what we might call "original UTXOs".

Block-subsidized bitcoins are new BTC created from scratch, according to a pre-established issuance schedule in the consensus rules. The block grant is halved every 210,000 blocks, i.e. approximately every four years, in a process known as "halving". Originally, 50 bitcoins were created with each subsidy, but this amount has gradually decreased; currently, it is 3.125 bitcoins per block.

As for transaction fees, although they also represent newly created BTC, they must not exceed the difference between the total inputs and outputs of all transactions in a block. We saw earlier that these fees represent the portion of inputs that is not used in transaction outputs. This portion is technically "lost" during the transaction, and the miner has the right to recreate this value in the form of one or more new UTXOs. This is a transfer of value between the issuer of the transaction and the miner who adds it to the blockchain.

**> Bitcoins generated by a coinbase transaction are subject to a maturity period of 100 blocks, during which they cannot be spent by the miner. This rule is designed to avoid complications linked to the use of newly created bitcoins on a chain that could later be rendered obsolete.

The implications of the UTXO model

First of all, the UTXO model directly influences Bitcoin's transaction fees. Since the capacity of each block is limited, miners favor transactions that offer the best fees in relation to the space they will take up in the block. Indeed, the more UTXOs a transaction includes in its inputs and outputs, the heavier it is, and therefore requires higher fees. This is one of the reasons why we often try to reduce the number of UTXOs in our portfolio, which can also affect confidentiality, a subject we'll be tackling in detail in the third part of this course.

Secondly, as mentioned in the previous sections, Bitcoin coins are essentially a chain of UTXOs. Each transaction thus creates a link between a past UTXO and a future UTXO. UTXOs therefore make it possible to explicitly follow the path of Bitcoins from their creation to their current expenditure. This transparency can be viewed positively, as it enables each user to ascertain the authenticity of the bitcoins received. However, it is also on this principle of traceability and auditability that blockchain analysis is based, a practice designed to compromise your confidentiality. We'll be taking an in-depth look at this practice in the second part of the course.

Bitcoin's privacy model

Money: authenticity, integrity and double spending

One of the functions of money is to solve the problem of the double coincidence of needs. In a system based on bartering, the completion of an exchange requires not only finding an individual who is giving away a good corresponding to my need, but also providing him with a good of equivalent value that satisfies his own need. Striking this balance is a complex matter.

That's why we use money to move value in both space and time.

For coinage to solve this problem, it is essential that the party providing a good or service is convinced of its ability to spend that sum at a later date. Thus, any rational individual wishing to accept a coin, whether digital or physical, will ensure that it meets two fundamental criteria:

The piece must have integrity and authenticity ;**
and must not be double-spent.**

If you're using physical currency, it's the first characteristic that's the most complex to assert. At different periods in history, the integrity of metal coins has often been affected by practices such as trimming or piercing. In ancient Rome, for example, it was common practice for citizens to scrape the edges of gold coins to collect a little precious metal, while saving them for future transactions. The intrinsic value of the coin was thus reduced, but its face value remained the same. This is one of the reasons why the edge of the coin was later fluted.

Authenticity is also a difficult characteristic to verify on a physical monetary medium. Today's techniques for combating counterfeit currency are increasingly complex, forcing retailers to invest in costly verification systems.

On the other hand, because of their nature, double spending is not a problem for physical currencies. If I give you a €10 bill, it irrevocably leaves my possession and enters yours, which naturally rules out any possibility of multiple spending of the monetary units it embodies. In short, I won't be able to spend this €10 bill again.

For digital currency, the difficulty is different. Ensuring the authenticity and integrity of a coin is often simpler. As we saw in the previous section, Bitcoin's UTXO model makes it possible to trace a coin back to its origin, and thus verify that it was indeed created by a miner in compliance with consensus rules.

On the other hand, ensuring that there is no double-spending is more complex, since all digital goods are in essence information. Unlike physical goods, information is not divided up when it is exchanged, but spreads by multiplying. For example, if I send you a document by e-mail, it will be duplicated. You can't be sure that I've deleted the original document.

Preventing double spending on Bitcoin

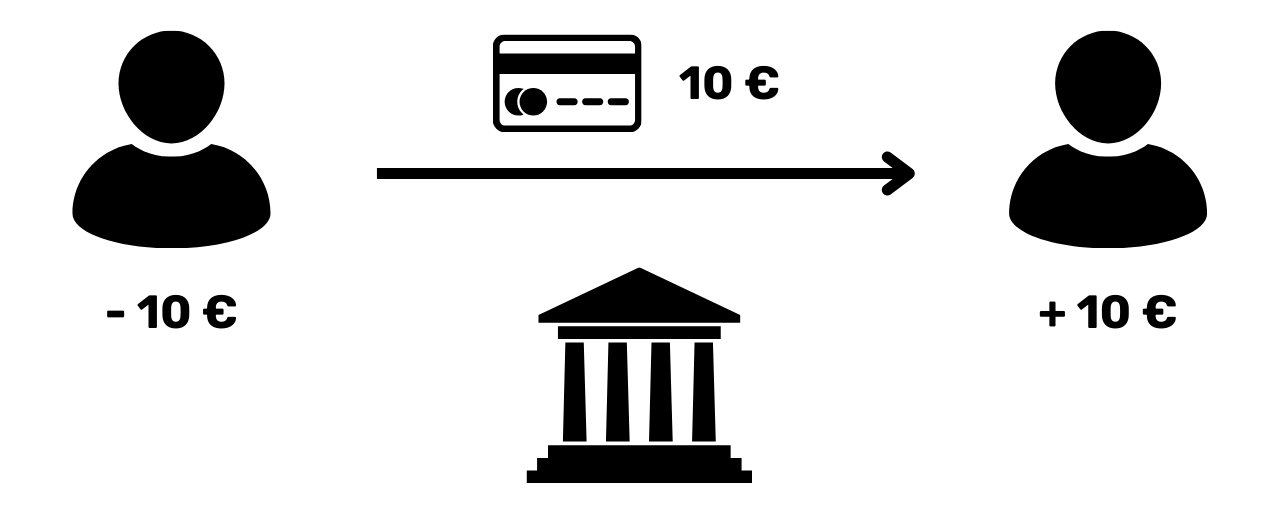
The only way to avoid this duplication of a digital asset is to be aware of all exchanges on the system. In this way, we can know who owns what and update each person's holdings according to the transactions carried out. This is what happens, for example, with scriptural money in the banking system. When you pay €10 to a merchant by credit card, the bank records the exchange and updates the account book.

On Bitcoin, double-spending is prevented in the same way. We seek to confirm the absence of a transaction that has already spent the coins in question. If the coins have never been used, then we can be sure that no double spending will occur. This principle was described by Satoshi Nakamoto in the White Paper with the famous phrase:

**The only way to confirm the absence of a transaction is to be aware of all transactions

But unlike the banking model, we don't want to have to trust a central entity on Bitcoin. So all users need to be able to confirm this absence of double spending, without relying on a third party. So everyone needs to be aware of all Bitcoin transactions. This is why Bitcoin transactions are publicly broadcast on all network nodes and recorded in clear text on the blockchain.

It is precisely this public dissemination of information that complicates the protection of privacy in Bitcoin. In the traditional banking system, in theory, only the financial institution is aware of the transactions carried out. With Bitcoin, on the other hand, all users are informed of all transactions, via their respective nodes.

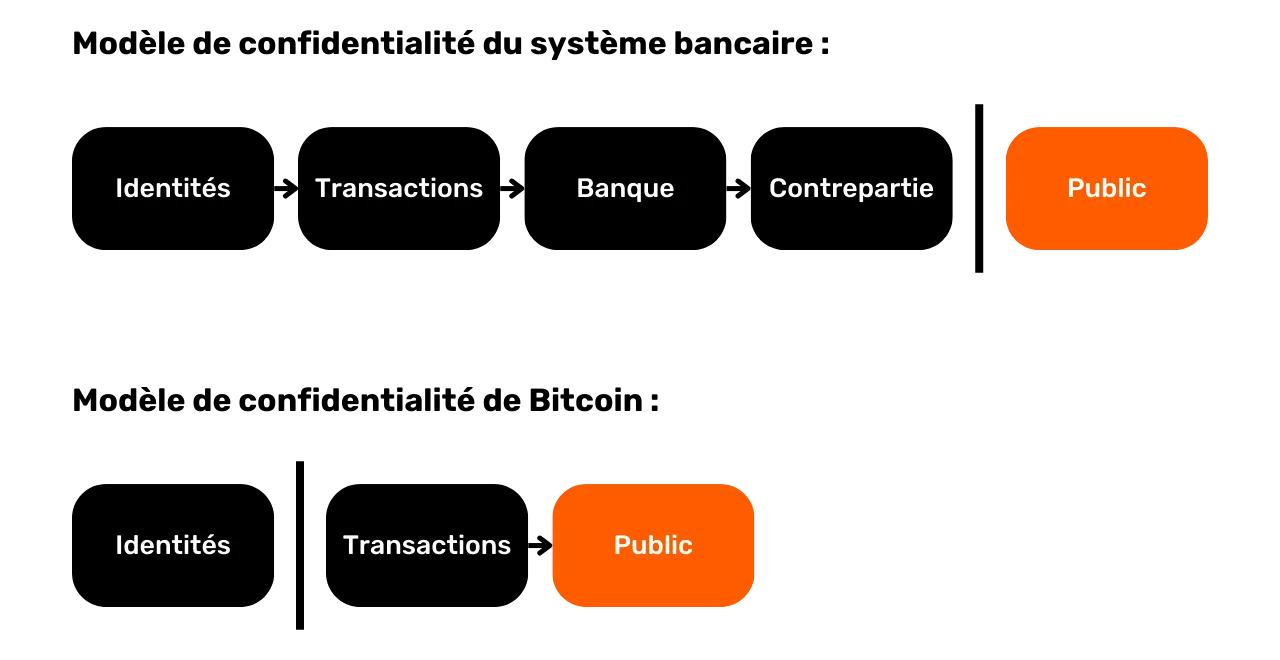
The confidentiality model: banking system vs. Bitcoin

In the traditional system, your bank account is linked to your identity. The banker is able to know which bank account belongs to which customer, and which transactions are associated with it. However, this flow of information is cut off between the bank and the public domain. In other words, it is impossible to know the balance and transactions of a bank account belonging to another individual. Only the bank has access to this information.

For example, your banker knows that you buy your baguette every morning from the local baker, but your neighbor has no knowledge of this transaction. In this way, the flow of information is accessible to the parties concerned, notably the bank, but remains inaccessible to outsiders.

Because of the constraint of public dissemination of transactions that we saw in the previous section, Bitcoin's confidentiality model cannot follow the model of the banking system. In Bitcoin's case, since the flow of information cannot be broken between the transactions and the public domain, the privacy model relies on the separation between the user's identity and the transactions themselves.

For example, if you buy a baguette from the baker, paying in BTC, your neighbor, who has his own complete node, can see your transaction go through, just as he can see all the other transactions in the system. However, if confidentiality principles are respected, he should not be able to link this specific transaction to your identity.

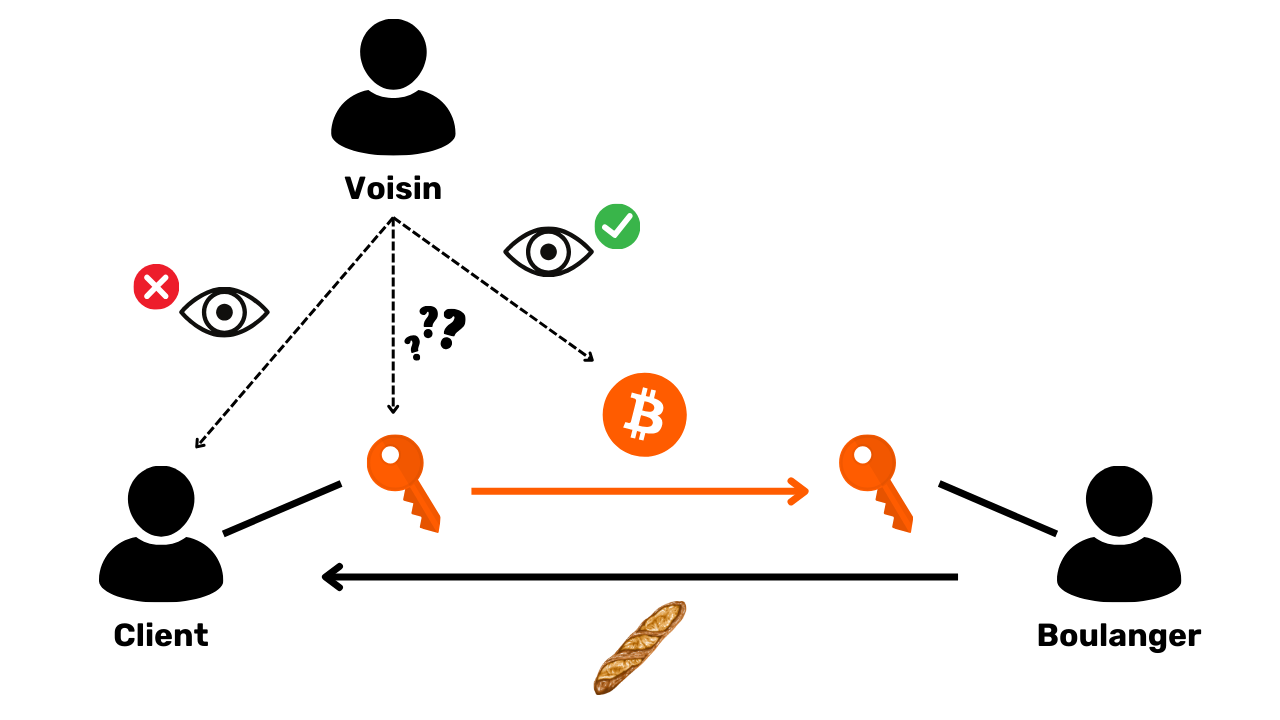
But since Bitcoin transactions are made public, it is still possible to establish links between them to deduce information about the parties involved. This activity even constitutes a specialty in its own right, known as "blockchain analysis". In the next part of the course, I invite you to explore the fundamentals of blockchain analysis, so that you can understand how your bitcoins are traced and better defend yourself against them.

Understanding and protecting against chain analysis

What is Bitcoin chain analysis?

Definition and operation

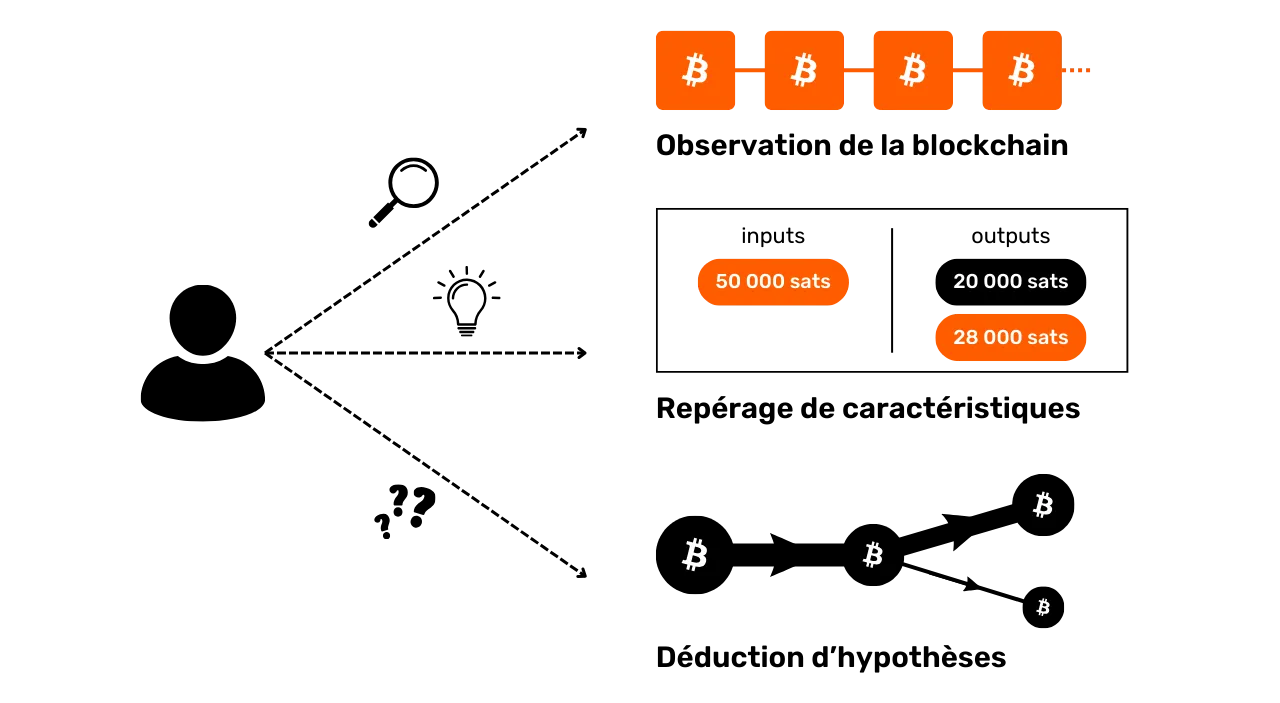
Blockchain analysis is the practice of tracing the flow of bitcoins on the blockchain. Generally speaking, chain analysis is based on the observation of characteristics in samples of previous transactions. It then consists of identifying these same characteristics on a transaction that we wish to analyze, and deducing plausible interpretations from them. This problem-solving method, based on a practical approach to finding a good enough solution, is known as a "heuristic".

In layman's terms, there are three main stages in chain analysis:

Observing the blockchain ;
The identification of known features ;
**The deduction of assumptions **

Blockchain analysis can be performed by anyone. All you need is access to the blockchain's public information via a complete node to observe transaction movements and make hypotheses. There are also free tools that facilitate this analysis, such as OXT.me, which we'll explore in detail in the last two chapters of this section. However, the main risk to confidentiality comes from companies specializing in string analysis. These companies have taken blockchain analysis to an industrial scale and sell their services to financial institutions and governments. Among these companies, Chainalysis is surely the best known.

Chain analysis objectives

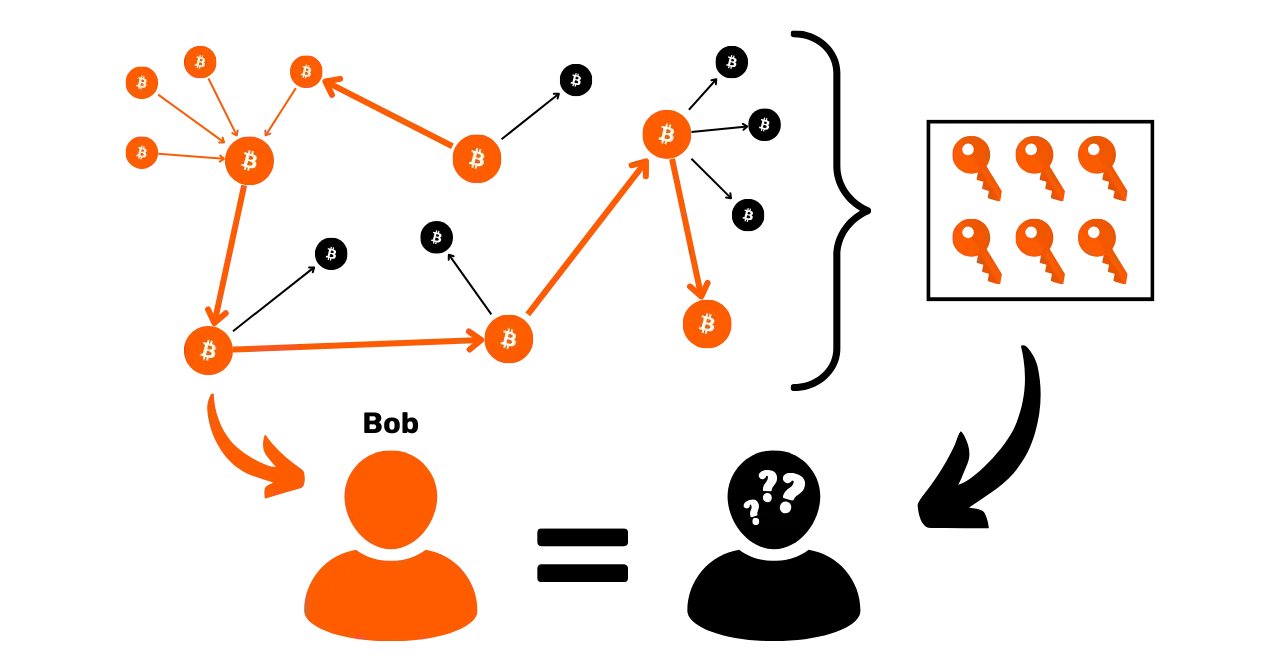
One of the aims of blockchain analysis is to group together various activities on Bitcoin in order to determine the uniqueness of the user who carried them out. Subsequently, it will be possible to attempt to link this cluster of activities to a real identity.

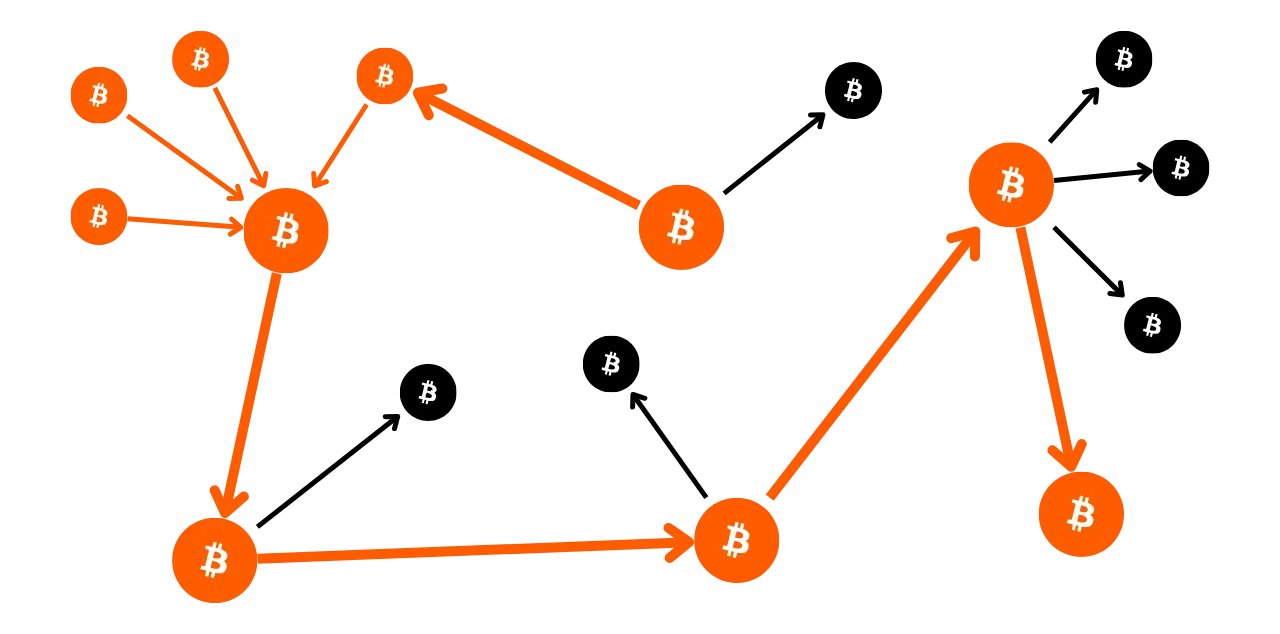
Think back to the previous chapter. I explained why Bitcoin's privacy model was originally based on the separation of user identity from transactions. It would therefore be tempting to think that blockchain analysis is useless, since even if we manage to aggregate onchain activities, we can't associate them with a real identity.

Theoretically, this statement is correct. In the first part of this course, we saw that cryptographic key pairs are used to establish conditions on UTXO. In essence, these key pairs divulge no information about the identity of their holders. So, even if we manage to group together the activities associated with different key pairs, this tells us nothing about the entity behind these activities.

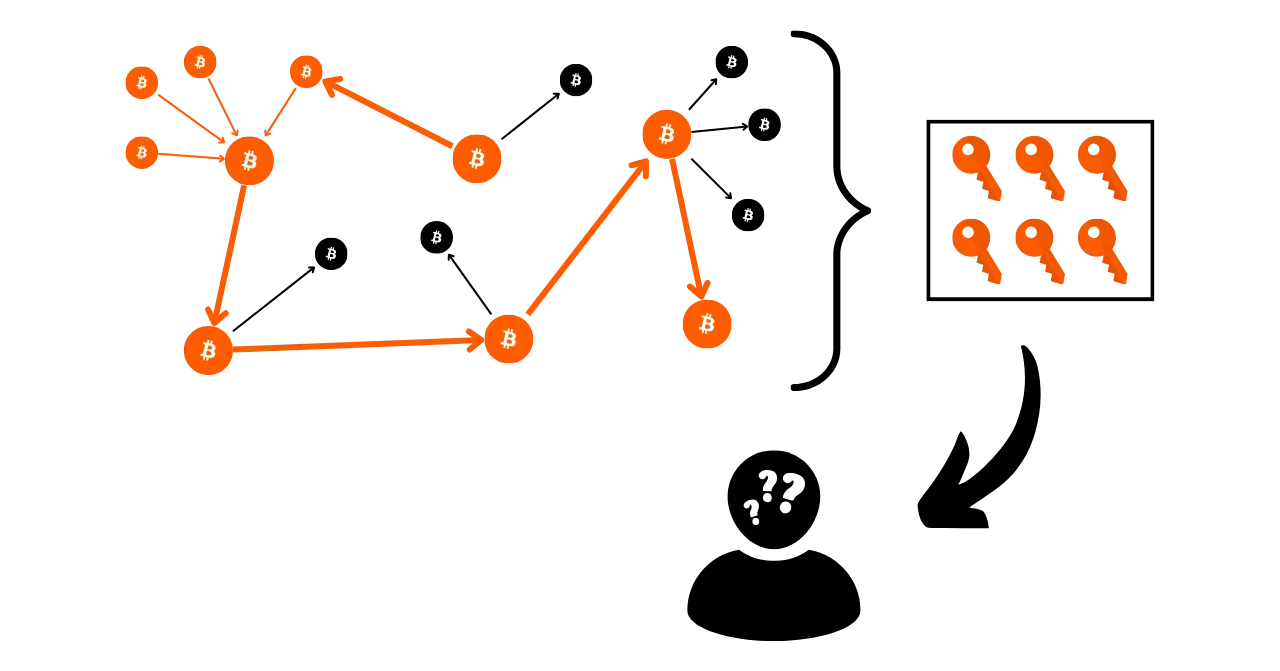
However, the practical reality is far more complex. There are a multitude of behaviors that can link a real identity to onchain activity. In analysis, this is called an entry point, and there are a multitude of them.

The most common is KYC (Know Your Customer). If you withdraw your Bitcoins from a regulated platform to one of your personal receiving addresses, then some people are able to link your identity to that address. More broadly, an entry point can be any form of interaction between your real life and a Bitcoin transaction. For example, if you publish a receiving address on your social networks, this could be an entry point for analysis. If you make a payment in Bitcoins to your baker, he will be able to associate your face (part of your identity) with a Bitcoin address.

These entry points are virtually unavoidable when using Bitcoin. Although we may seek to restrict their scope, they will always be present. That's why it's crucial to combine methods aimed at preserving your privacy. While maintaining a separation between your real identity and your transactions is an interesting approach, it remains insufficient today. Indeed, if all your onchain activities can be grouped together, then even the smallest entry point is likely to compromise the single layer of confidentiality you've established.

Defending yourself against chain analysis

So we also need to be able to cope with blockchain analysis in our use of Bitcoin. By doing so, we can minimize the aggregation of our activities and limit the impact of an entry point on our privacy.

What better way to counter blockchain analysis than to learn about the methods used in it? If you want to know how to improve your privacy on Bitcoin, you need to understand these methods. This will give you a better grasp of techniques such as coinjoin or payjoin (techniques we'll look at in the final parts of the course), and reduce the mistakes you might make.

https://planb.network/tutorials/privacy/on-chain/coinjoin-samourai-wallet-e566803d-ab3f-4d98-9136-5462009262ef

https://planb.network/tutorials/privacy/on-chain/payjoin-848b6a23-deb2-4c5f-a27e-93e2f842140f

In this, we can draw an analogy with cryptography and cryptanalysis. A good cryptographer is first and foremost a good cryptanalyst. To devise a new encryption algorithm, you need to know what attacks it will face, and also study why previous algorithms have been broken. The same principle applies to Bitcoin privacy. Understanding blockchain analysis methods is the key to protecting against them. That's why I've included a whole section on chain analysis in this training course.

Chain analysis methods

It's important to understand that string analysis is not an exact science. It relies on heuristics derived from previous observations or logical interpretations. These rules allow us to obtain fairly reliable results, but never with absolute precision. In other words, chain analysis always involves a dimension of probability in the conclusions reached. For example, it may be possible to estimate with varying degrees of certainty that two addresses belong to the same entity, but total certainty will always be out of reach.

The whole point of chain analysis lies precisely in the aggregation of various heuristics to minimize the risk of error. In a way, it's an accumulation of evidence that brings us closer to reality.

These famous heuristics can be grouped into different categories, which we will describe in detail below:

Transaction patterns ;**
Transaction-internal heuristics ;**
Heuristics external to the transaction.**

Satoshi Nakamoto and chain analysis

The first two chain analysis heuristics were discovered by Satoshi Nakamoto himself. He talks about them in Part 10 of Bitcoin's White Paper. They are :

cIOH (Common Input Ownership Heuristic);
and address reuse.

Source: S. Nakamoto, "Bitcoin: A Peer-to-Peer Electronic Cash System", https://bitcoin.org/bitcoin.pdf, 2009.

We'll see what they are in the following chapters, but it's already interesting to note that these two heuristics still retain a pre-eminence in chain analysis today.

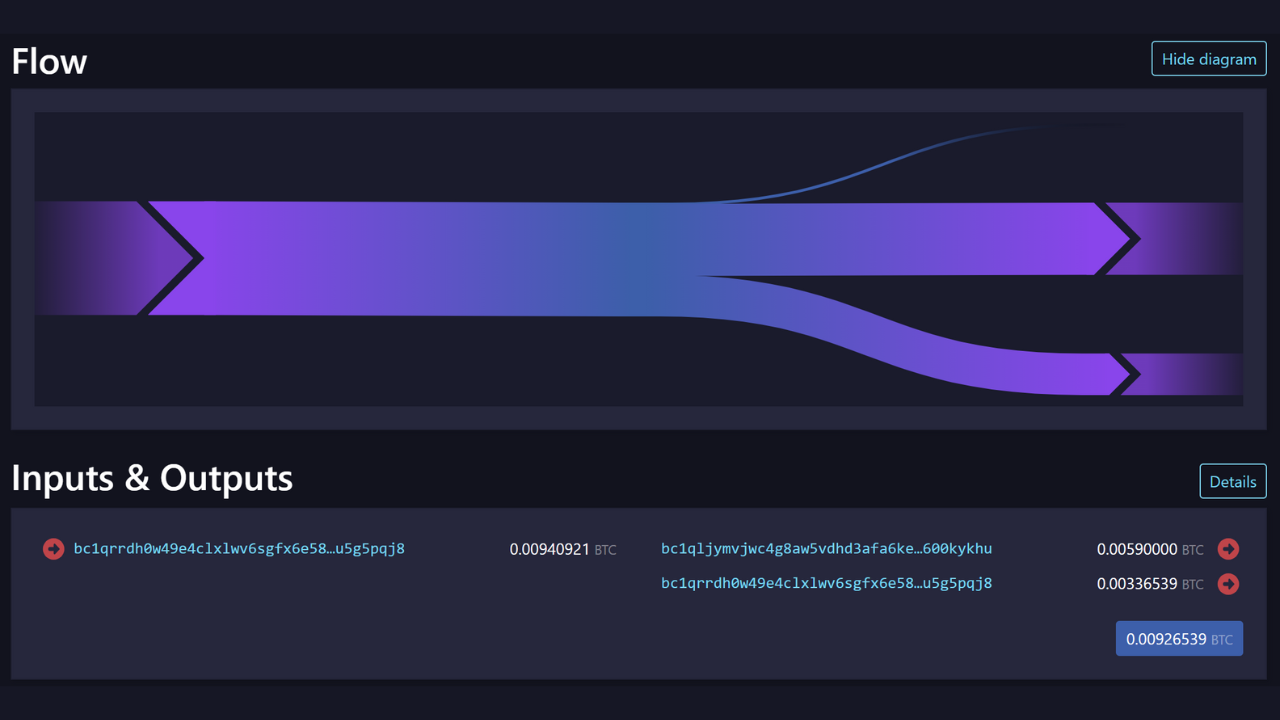
Transaction patterns

A transaction pattern is simply an overall model or structure of a typical transaction, which can be found on the blockchain, and whose likely interpretation is known. When studying patterns, we focus on a single transaction and analyze it at a high level.

In other words, we're only going to look at the number of UTXO in inputs and the number of UTXO in outputs, without dwelling on the more specific details or environment of the transaction. Based on the observed pattern, we can interpret the nature of the transaction. We will then look for characteristics of its structure and deduce an interpretation.

In this section, we'll look together at the main transaction models encountered in chain analysis, and for each model, I'll give you the likely interpretation of this structure, as well as a concrete example.

Single shipment (or single payment)

Let's start with a very common pattern, since it's the one that emerges on most bitcoin payments. The simple payment model is characterized by the consumption of one or more UTXOs as inputs and the production of 2 UTXOs as outputs. This model therefore looks like this:

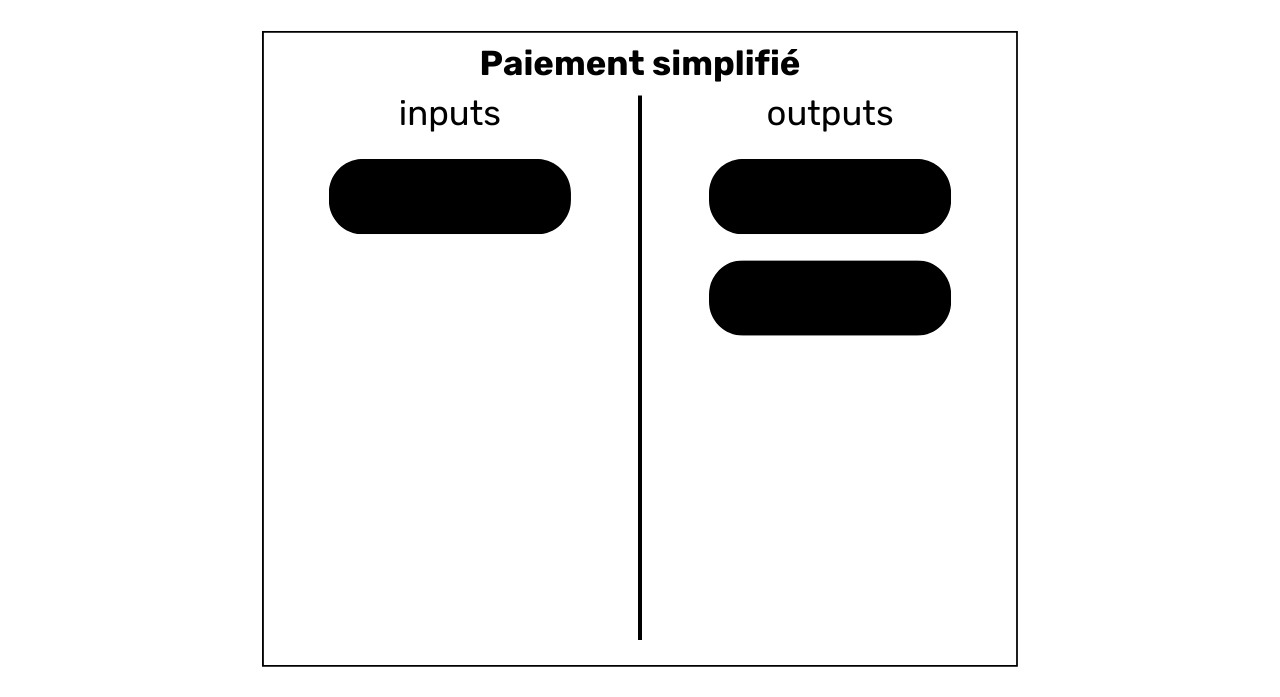
When we spot this transaction structure on the blockchain, we can already draw an interpretation. As its name suggests, this model indicates that we are in the presence of a sending or payment transaction. The user has consumed his own UTXO in inputs to satisfy in outputs a payment UTXO and an exchange UTXO (money returned to the same user).

We therefore know that the observed user is probably no longer in possession of one of the two output UTXOs (the payment UTXO), but is still in possession of the other UTXO (the exchange UTXO).

For the moment, we can't specify which output represents which UTXO, as this is not the purpose of the pattern study. We'll get there by relying on the heuristics we'll study in the following sections. At this stage, our objective is limited to identifying the nature of the transaction in question, which in this case is a simple send.

For example, here is a Bitcoin transaction that adopts the simple send pattern:

b6cc79f45fd2d7669ff94db5cb14c45f1f879ea0ba4c6e3d16ad53a18c34b769

Source : Mempool.space

After this first example, you should have a better understanding of what it means to study a "transaction model". We examine a transaction by focusing solely on its structure, without taking into account its environment or the specific details of the transaction. In this first step, we're only looking at the big picture.

Now that you understand what a pattern is, let's move on to the other existing models.

Sweeping

This second model is characterized by the consumption of a single UTXO as input and the production of a single UTXO as output.

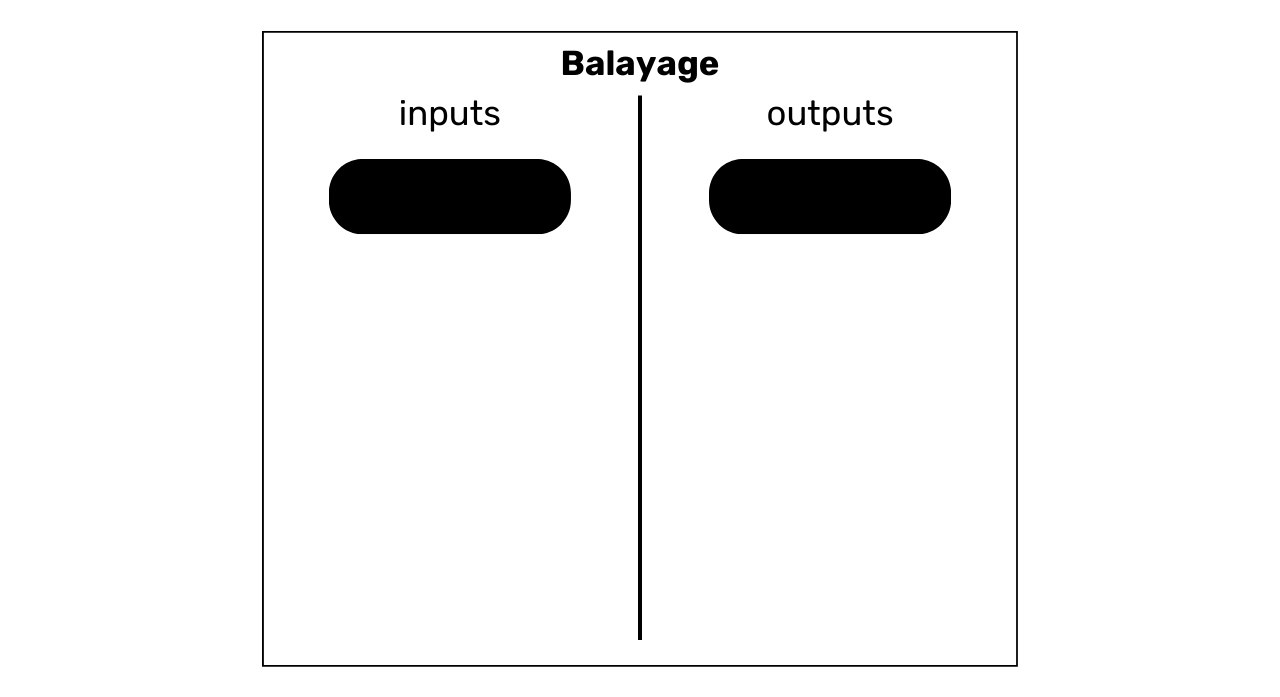
The interpretation of this model is that we are in the presence of a self-transfer. The user has transferred his bitcoins to himself, to another address belonging to him. Since there is no exchange on the transaction, it's highly unlikely that we're in the presence of a payment. Indeed, when a payment is made, it is almost impossible for the payer to have a UTXO corresponding exactly to the amount required by the seller, plus the transaction fee. In general, the payer is therefore obliged to produce an exchange output.

We then know that the observed user is probably still in possession of this UTXO. In the context of a chain analysis, if we know that the UTXO used as input to the transaction belongs to Alice, we can assume that the UTXO used as output also belongs to her. What will become interesting later on is to find transaction-internal heuristics that could reinforce this assumption (we'll look at these heuristics in chapter 3.3).

For example, here is a Bitcoin transaction that adopts the sweep pattern:

35f1072a0fda5ae106efb4fda871ab40e1f8023c6c47f396441ad4b995ea693d

Source : Mempool.space

Beware, however, that this type of pattern can also reveal a self-transfer to the account of a cryptocurrency exchange platform. It will be the study of known addresses and the context of the transaction that will tell us whether it's a swipe to a self-custody wallet or a withdrawal to a platform. Indeed, the addresses of exchange platforms are often easily identifiable.

Let's take Alice's example again: if the scan leads to an address known to a platform (such as Binance, for example), this may mean that the bitcoins have been transferred out of Alice's direct possession, probably with the intention of selling them or storing them on this platform. On the other hand, if the destination address is unknown, it's reasonable to assume that it's simply another wallet still belonging to Alice. But this type of study is more in the category of heuristics than patterns.

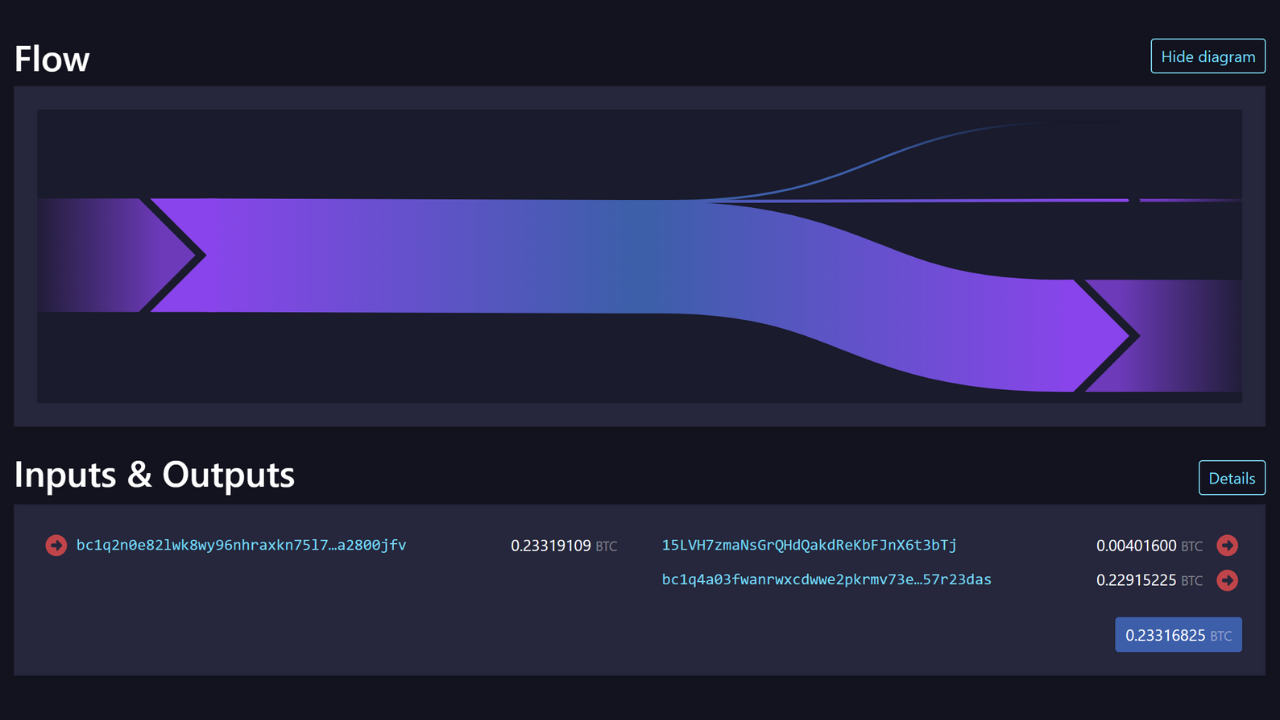
Consolidation

This model is characterized by the consumption of several UTXOs at the input and the production of a single UTXO at the output.

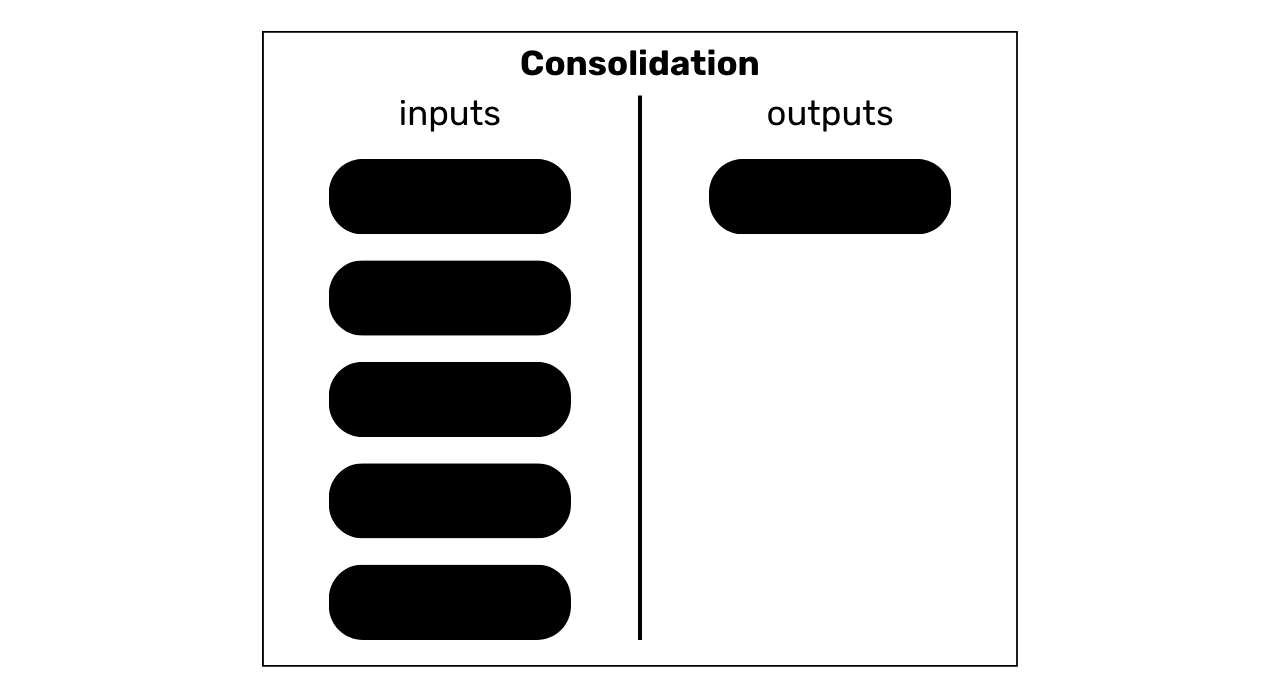
The interpretation of this pattern is that we are in the presence of consolidation. This is a common practice among Bitcoin users, aimed at merging several UTXOs in anticipation of a possible increase in transaction fees. By performing this operation during a period when fees are low, it is possible to save on future fees. We'll talk more about this practice in chapter 4.3.

We can deduce that the user behind this transaction model was probably in possession of all the UTXOs in input and is still in possession of the UTXO in output. So it's probably an auto-transfer.

Like the sweep, this type of pattern can also reveal a self-transfer to the account of an exchange platform. It will be the study of known addresses and the context of the transaction that will tell us whether it's a consolidation to a self-custody portfolio or a withdrawal to a platform.

For example, here is a Bitcoin transaction that adopts the consolidation pattern:

77c16914211e237a9bd51a7ce0b1a7368631caed515fe51b081d220590589e94

Source : Mempool.space

In a chain analysis, this model can reveal a great deal of information. For example, if we know that one of the inputs belongs to Alice, we can assume that all the other inputs and the output of this transaction also belong to her. This assumption would then make it possible to go back up the chain of previous transactions to discover and analyze other transactions likely to be associated with Alice.

Grouped expenditure

This model is characterized by the consumption of a few UTXOs as inputs (often just one) and the production of many UTXOs as outputs.

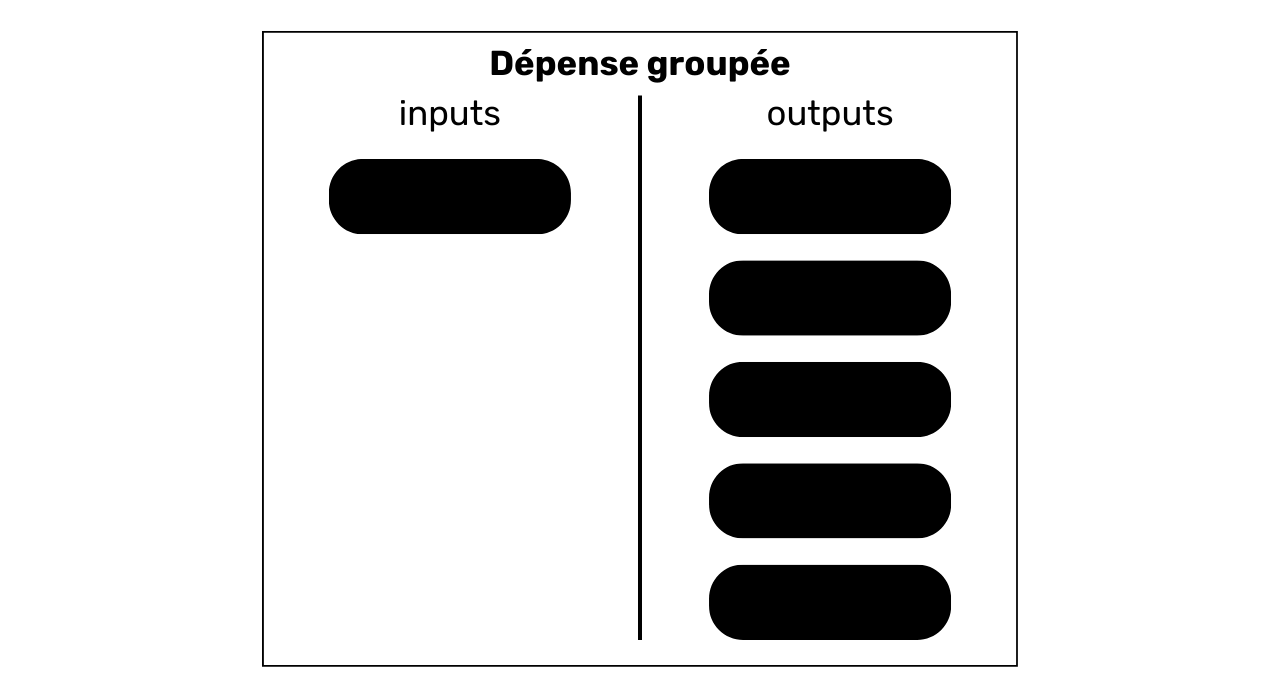
The interpretation of this model is that we are in the presence of grouped spending. It's a practice that probably reveals a very large economic activity, such as an exchange platform. Grouped spending enables these entities to save costs by combining their expenses in a single transaction.

We can deduce from this model that the UTXO in input comes from a company with a high level of economic activity, and that the UTXOs in output will disperse. Many will belong to the company's customers who have withdrawn bitcoins from the platform. Others may go to partner companies. Finally, there will certainly be one or more exchanges going back to the issuing company.

For example, here's a Bitcoin transaction that adopts the bundled spend pattern (presumably, it's a transaction issued by the Bybit platform):

8a7288758b6e5d550897beedd13c70bcbaba8709af01a7dbcc1f574b89176b43

Source : Mempool.space

Protocol-specific transactions

Among transaction patterns, we can also identify those that reveal the use of a specific protocol. For example, Whirlpool coinjoins (discussed in part 5) will have an easily identifiable structure that differentiates them from other, more conventional transactions.

Analysis of this pattern suggests that we are likely to be in the presence of a collaborative transaction. It is also possible to observe a coinjoin. If this latter hypothesis proves correct, then the number of exits could provide us with a rough estimate of the number of participants in the coinjoin.

For example, here is a Bitcoin transaction that adopts the coinjoin collaborative transaction pattern:

00601af905bede31086d9b1b79ee8399bd60c97e9c5bba197bdebeee028b9bea

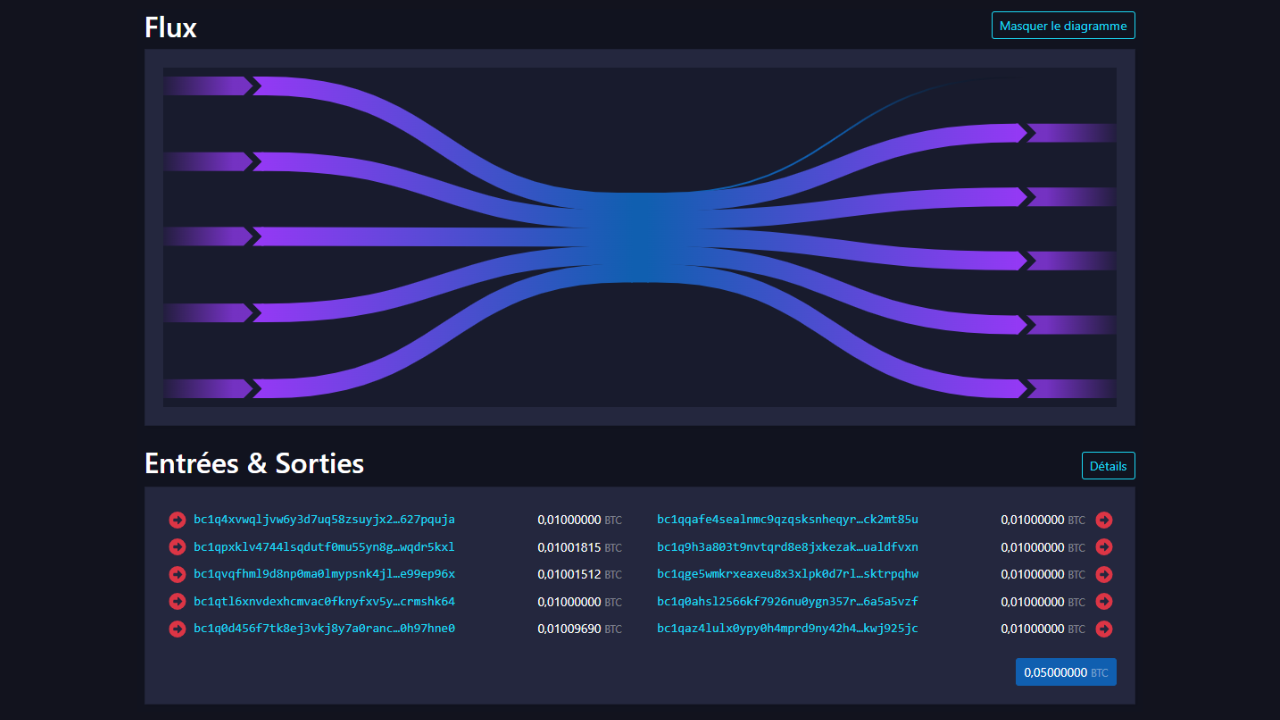
Source : Mempool.space

There are many other protocols with their own specific structures. For example, there are Wabisabi transactions, Stamps transactions and Runes transactions.

Thanks to these transaction patterns, we can already interpret a certain amount of information about a given transaction. But transaction structure is not the only source of information for analysis. We can also study its details. These internal details are what I like to call "internal heuristics", and we'll be looking at them in the next chapter.

Internal heuristics

An internal heuristic is a specific characteristic that we identify within a transaction itself, without needing to examine its environment, and which enables us to make deductions. Unlike patterns, which focus on the overall structure of the transaction at a high level, internal heuristics are based on the set of extractable data. This includes:

The amounts of the various UTXOs in and out;
Everything to do with scripts: reception addresses, versioning, locktimes..

Generally speaking, this type of heuristic will enable us to identify the exchange in a specific transaction. By doing so, we can then perpetuate the tracing of an entity over several different transactions. Indeed, if we identify a UTXO belonging to a user we wish to track, it's crucial to determine, when he carries out a transaction, which output has been transferred to another user and which output represents the exchange, which thus remains in his possession.

Once again, let me remind you that these heuristics are not absolutely precise. Taken individually, they only enable us to identify likely scenarios. It's the accumulation of several heuristics that helps to reduce uncertainty, without ever being able to eliminate it completely.

Internal similarities

This heuristic involves the study of similarities between the inputs and outputs of the same transaction. If the same characteristic is observed on the inputs and on just one of the transaction's outputs, then it is likely that this output constitutes the exchange.

The most obvious feature is the reuse of a receiving address in the same transaction.

This heuristic leaves little room for doubt. Unless he's had his private key hacked, the same receiving address necessarily reveals the activity of a single user. The resulting interpretation is that the transaction exchange is the output with the same address as the input. We can then continue to trace the individual from this exchange.

For example, here is a transaction on which this heuristic can probably be applied:

54364146665bfc453a55eae4bfb8fdf7c721d02cb96aadc480c8b16bdeb8d6d0

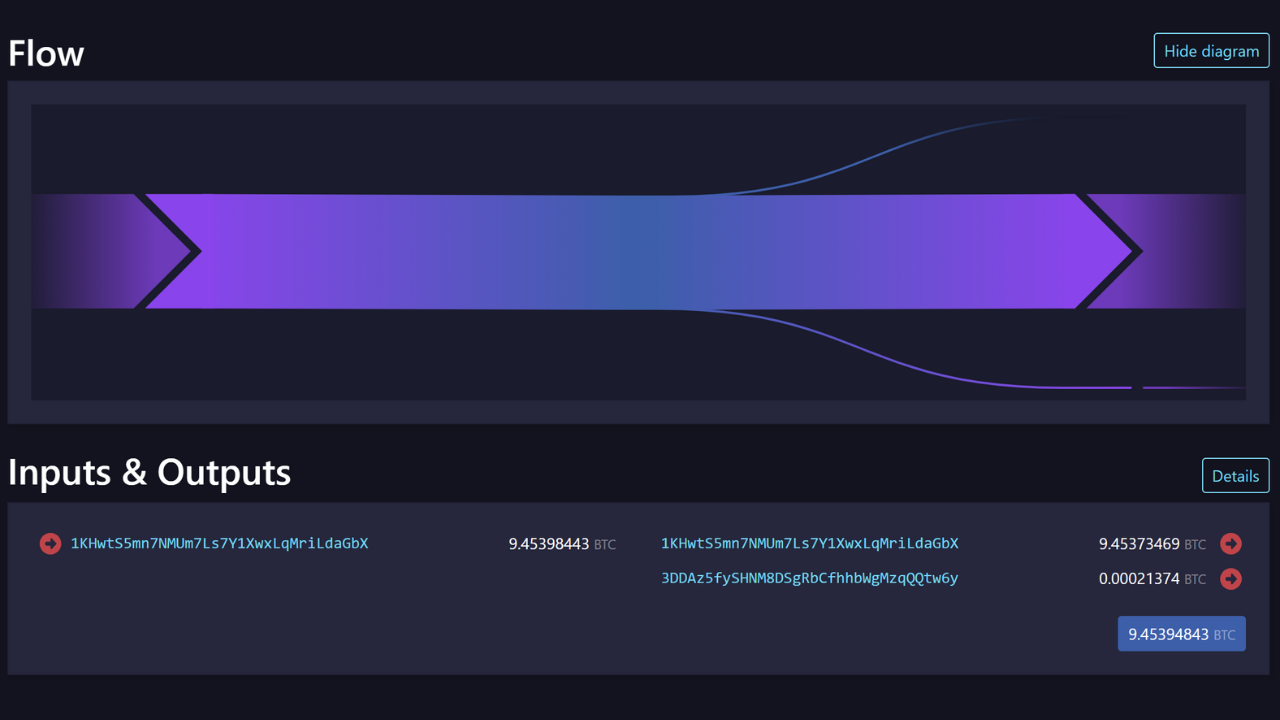
Source : Mempool.space

These similarities between inputs and outputs don't stop at address reuse. Any similarity in the use of scripts can be used to apply a heuristic. For example, we can sometimes observe the same versioning between the input and one of the transaction outputs.

On this diagram, we can see that input n° 0 unlocks a P2WPKH script (SegWit V0 starting with bc1q). Output n° 0 uses the same type of script. Output n° 1, on the other hand, uses a P2TR script (SegWit V1 beginning with bc1p). The interpretation of this feature is that it is likely that the address with the same versioning as the input is the exchange address. It would therefore always belong to the same user.

Here is a transaction on which this heuristic can probably be applied:

db07516288771ce5d0a06b275962ec4af1b74500739f168e5800cbcb0e9dd578

Source : Mempool.space

On the latter, we can see that input no. 0 and output no. 1 use P2WPKH scripts (SegWit V0), while output no. 0 uses a different P2PKH script (Legacy).

In the early 2010s, this heuristic based on script versioning was relatively unhelpful due to the limited types of scripts available. However, over time and with successive Bitcoin updates, an increasing diversity of script types has been introduced. This heuristic is therefore becoming increasingly relevant, as with a wider range of script types, users divide into smaller groups, thus increasing the chances of applying this internal versioning reuse heuristic. For this reason, from a confidentiality perspective only, it's advisable to opt for the most common type of script. For example, as I write these lines, Taproot scripts (bc1p) are less frequently used than SegWit V0 scripts (bc1q). Although the former offer economic and confidentiality benefits in certain specific contexts, for more traditional single-signature uses, it may make sense to stick with an older standard for confidentiality reasons, until the new standard is more widely adopted.

Round number payments

Another internal heuristic that can help us identify the exchange is the round number heuristic. Generally speaking, when faced with a simple payment pattern (1 input and 2 outputs), if one of the outputs spends a round amount, then this represents the payment.

By elimination, if one output represents payment, the other represents exchange. It can therefore be interpreted as likely that the input user is always in possession of the output identified as the exchange.

It should be stressed that this heuristic is not always applicable, since the majority of payments are still made in fiduciary units of account. Indeed, when a retailer in France accepts bitcoin, he will generally not display stable prices in sats. Instead, he will opt for a conversion between the price in euros and the amount in bitcoins to be paid. There should therefore be no round numbers at the end of the transaction.

Nevertheless, an analyst could try to make this conversion taking into account the exchange rate in effect when the transaction was broadcast on the network. Let's take the example of a transaction with an input of 97,552 sats and two outputs, one of 31,085 sats and the other of 64,152 sats. At first glance, this transaction does not appear to involve round amounts. However, by applying the exchange rate of €64,339 at the time of the transaction, we obtain a conversion into euros as follows:

An input of €62.76;
An output of €20;
An output of €41.27.

Once converted into fiat currency, this transaction can be used to apply the round amount payment heuristic. The €20 output probably went to a merchant, or at least changed ownership. By deduction, the €41.27 output is likely to have remained in the possession of the original user.

If, one day, bitcoin becomes the preferred unit of account in our exchanges, this heuristic could become even more useful for analysis.

For example, here is a transaction on which this heuristic can probably be applied:

2bcb42fab7fba17ac1b176060e7d7d7730a7b807d470815f5034d52e96d2828a

Source : Mempool.space

The largest output

When we identify a sufficiently large gap between 2 transaction outputs on a simple payment model, we can estimate that the largest output is likely to be foreign exchange.

This largest output heuristic is surely the most imprecise of all. On its own, it's pretty weak. However, this feature can be combined with other heuristics to reduce the uncertainty of our interpretation.

For example, if we're looking at a transaction with a round payment and a larger payment, applying the round payment heuristic and the larger payment heuristic together reduces our level of uncertainty.

For example, here is a transaction on which this heuristic can probably be applied:

b79d8f8e4756d34bbb26c659ab88314c220834c7a8b781c047a3916b56d14dcf

Source : Mempool.space

External heuristics

The study of external heuristics means analyzing the similarities, patterns and characteristics of certain elements that are not specific to the transaction itself. In other words, while we previously limited ourselves to exploiting elements intrinsic to the transaction with internal heuristics, we are now broadening our field of analysis to include the transaction's environment, thanks to external heuristics.

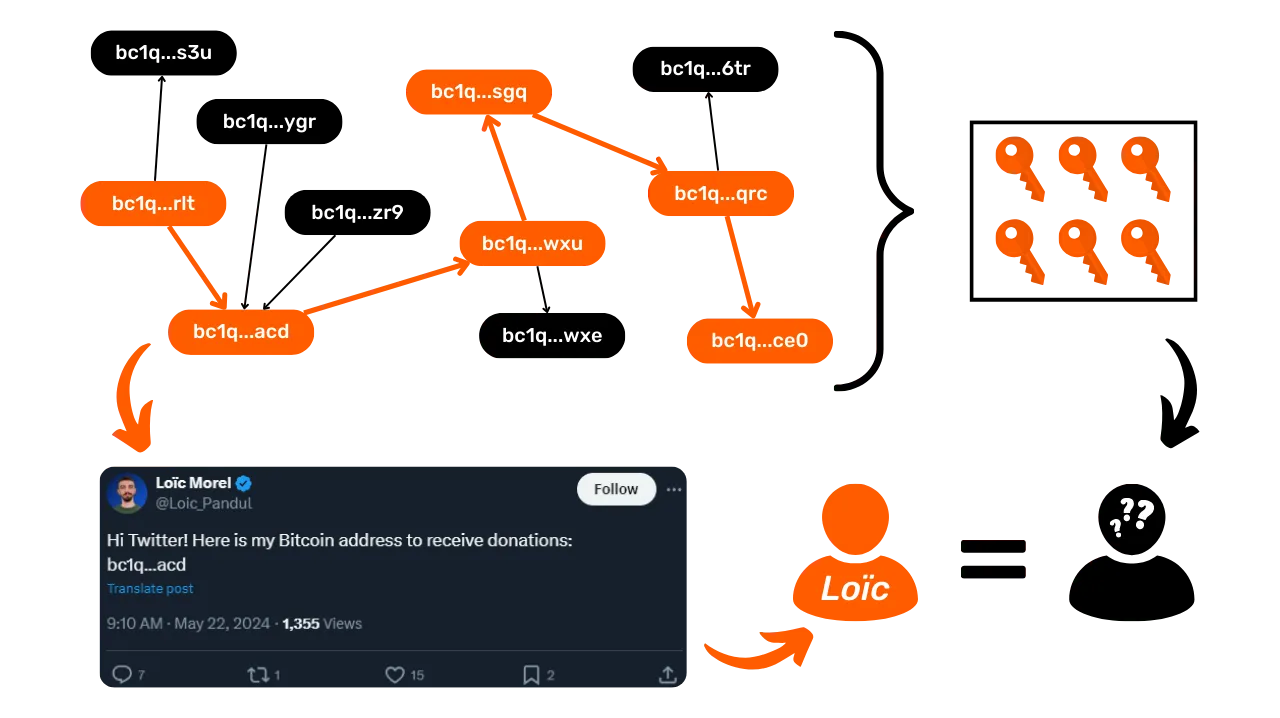
Address reuse

This is one of bitcoiners' best-known heuristics. Address reuse makes it possible to establish a link between different transactions and different UTXOs. It occurs when a Bitcoin receiving address is used several times.

Thus, it is possible to exploit address reuse within the same transaction as an internal heuristic to identify the exchange (as we saw in the previous chapter). But address reuse can also be used as an external heuristic to recognize the uniqueness of an entity behind several transactions.

The interpretation of the reuse of an address is that all UTXOs blocked on that address belong (or have belonged) to the same entity. This heuristic leaves little room for uncertainty. Once identified, the resulting interpretation is likely to correspond to reality. It therefore enables the grouping of different onchain activities.

As explained in the introduction to Part 3, this heuristic was discovered by Satoshi Nakamoto himself. In the White Paper, he mentions a solution to help users avoid generating it, which is simply to use a blank address for each new transaction:

"As an additional firewall, a new key pair could be used for each transaction to keep them unlinked to a common owner."

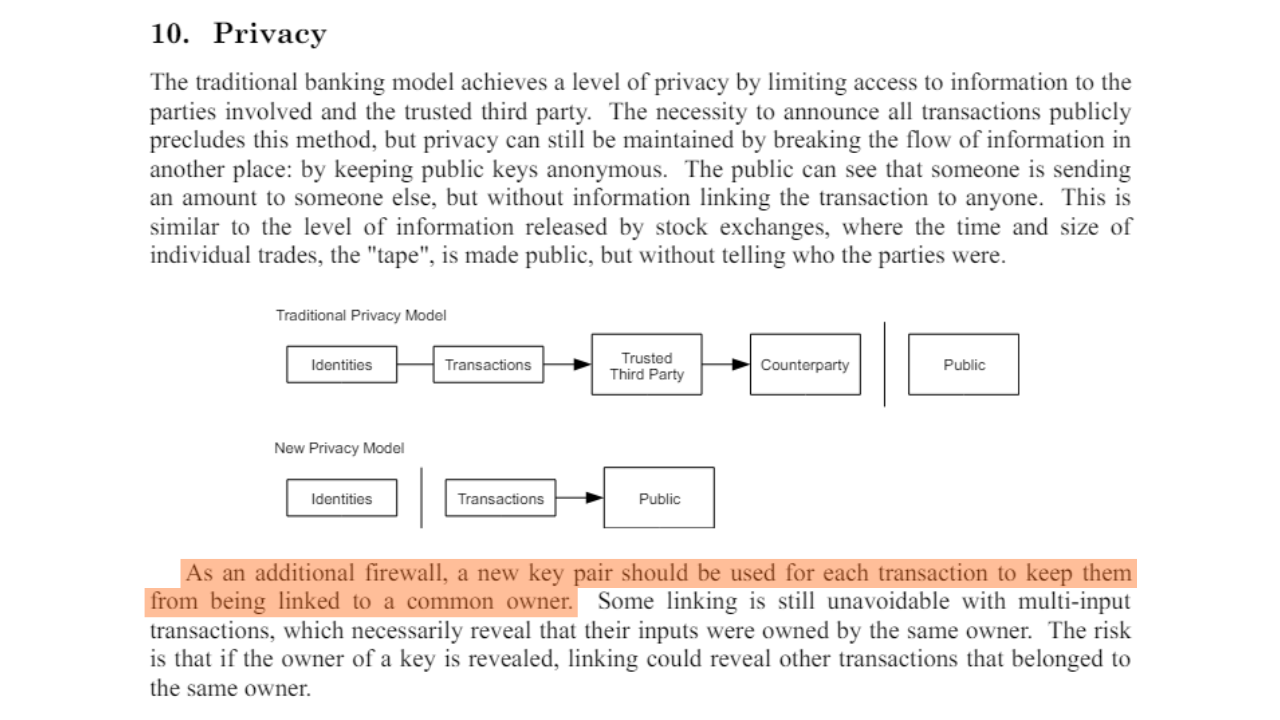
Source: S. Nakamoto, "Bitcoin: A Peer-to-Peer Electronic Cash System", https://bitcoin.org/bitcoin.pdf, 2009.

For example, here is an address that is reused in several transactions:

bc1qqtmeu0eyvem9a85l3sghuhral8tk0ar7m4a0a0

Source : Mempool.space

Script similarity and wallet imprints

In addition to address reuse, there are many other heuristics that allow you to link actions to the same portfolio or address cluster.

Firstly, an analyst can look for similarities in script usage. For example, certain minority scripts such as multisig may be easier to spot than SegWit V0 scripts. The larger the group we're hiding in, the harder it is to spot us. This is one of the reasons why, on good Coinjoin protocols, all participants use exactly the same type of script.

More generally, an analyst can also focus on the characteristic fingerprints of a portfolio. These are use-specific processes that can be identified with a view to exploiting them as tracing heuristics. In other words, if we observe an accumulation of the same internal characteristics on transactions attributed to the traced entity, we can attempt to identify these same characteristics on other transactions.

For example, we'll be able to identify that the traced user systematically sends his change to P2TR addresses (bc1p...). If this process is repeated, we can use it as a heuristic for the rest of our analysis. We can also use other fingerprints, such as the order of UTXOs, the place of the change in the outputs, RBF (Replace-by-Fee) signaling, or the version number, the nSequence field and the nLockTime field.

As @LaurentMT points out in Space Kek #19 (a French-language podcast), the usefulness of portfolio fingerprints in chain analysis is increasing significantly over time. Indeed, the growing number of script types and the increasingly progressive deployment of these new features by portfolio software accentuate the differences. In some cases, it is even possible to identify the exact software used by the entity being tracked. It is therefore important to understand that the study of portfolio footprints is particularly relevant for recent transactions, rather than those initiated in the early 2010s.

To sum up, a footprint can be any specific practice, performed automatically by the wallet or manually by the user, that we can find on other transactions to help us in our analysis.

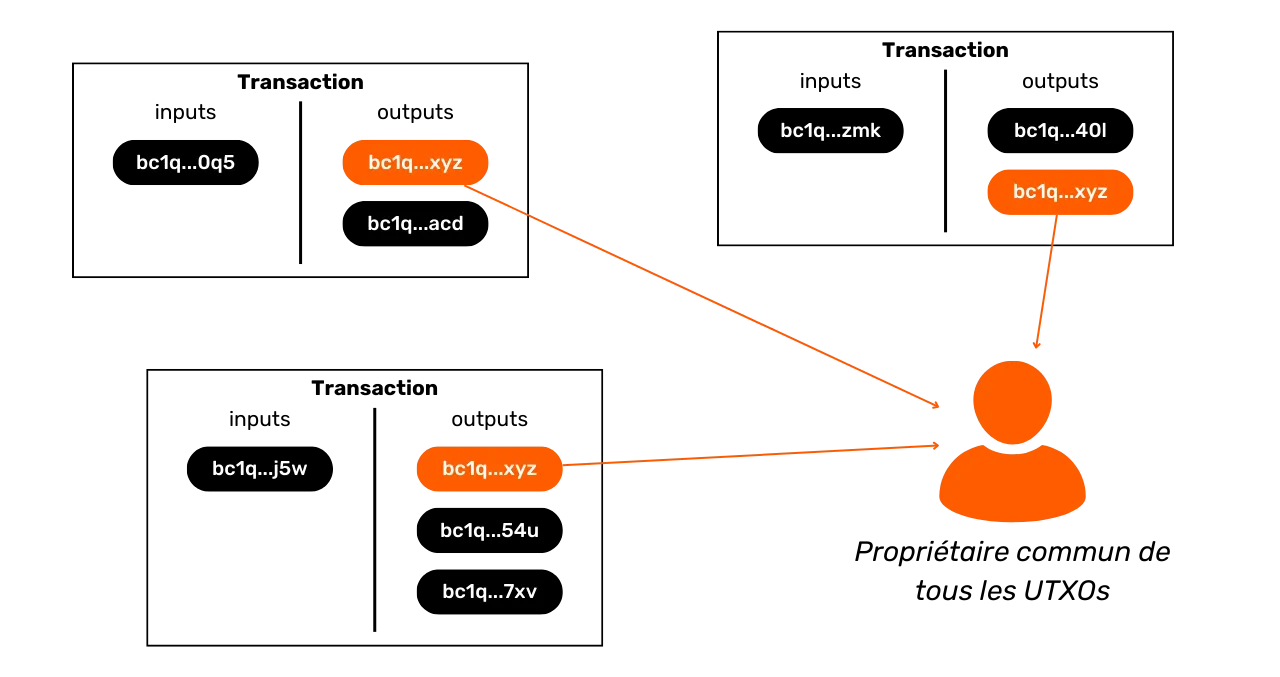
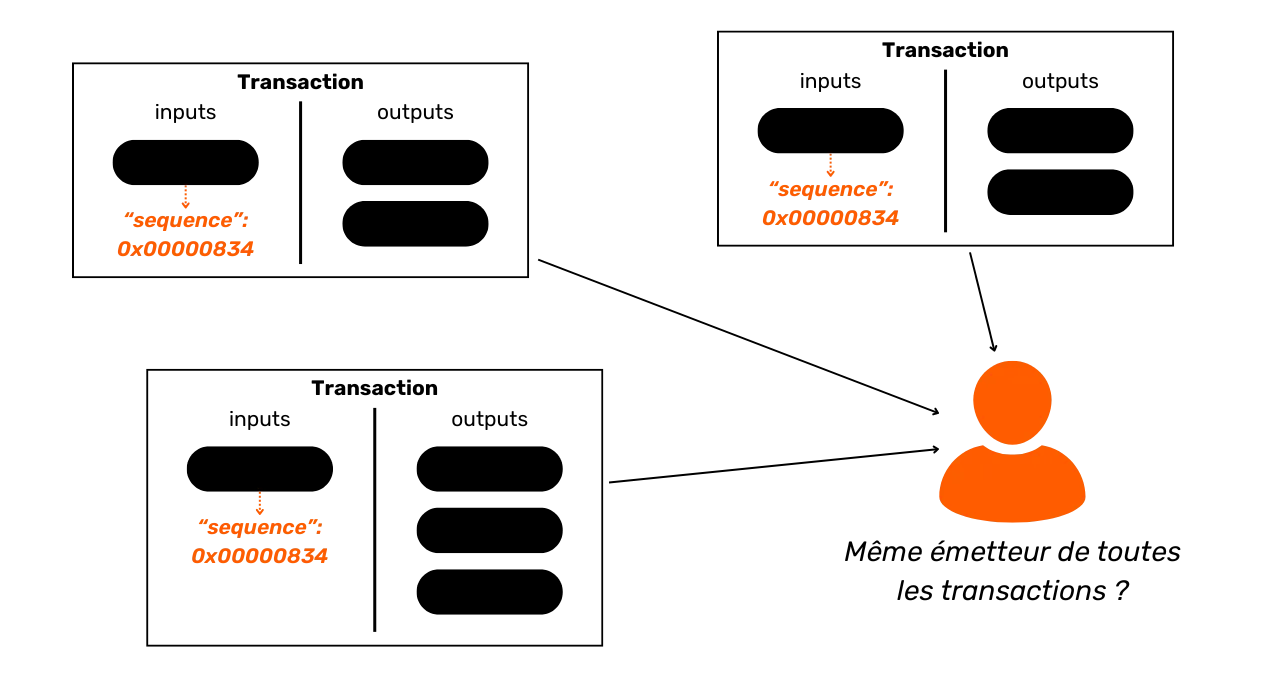
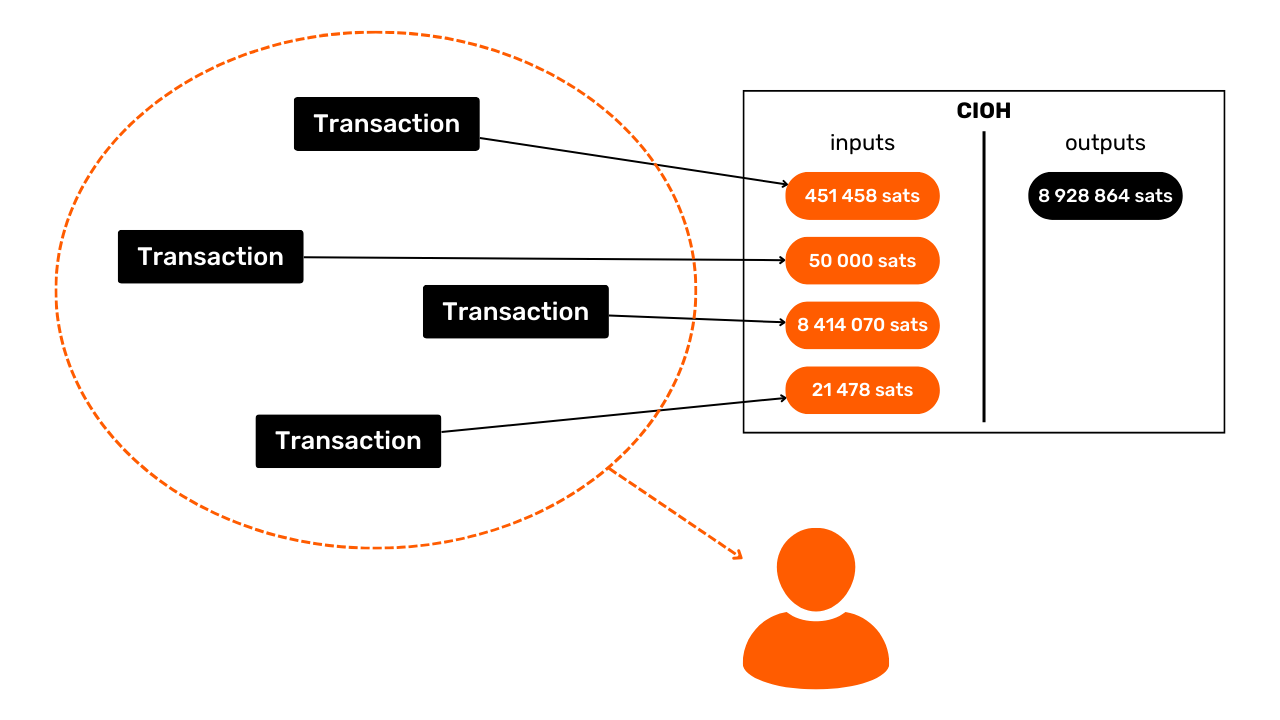
The Common Input Ownership Heuristic (CIOH)

The Common Input Ownership Heuristic (CIOH) is a heuristic that states that when a transaction has multiple inputs, they are all likely to emanate from a single entity. Consequently, their ownership is common.

To apply the CIOH, we first observe a transaction with several inputs. This could be 2 inputs, or 30 inputs. Once this characteristic has been identified, we check whether the transaction fits into a known transaction model. For example, if there are 5 inputs with roughly the same amount and 5 outputs with exactly the same amount, we'll know that this is the structure of a coinjoin. We won't be able to apply the CIOH.

On the other hand, if the transaction doesn't fit into any known collaborative transaction model, then we can interpret that all inputs are likely to come from the same entity. This can be very useful for extending an already known cluster or continuing a trace.

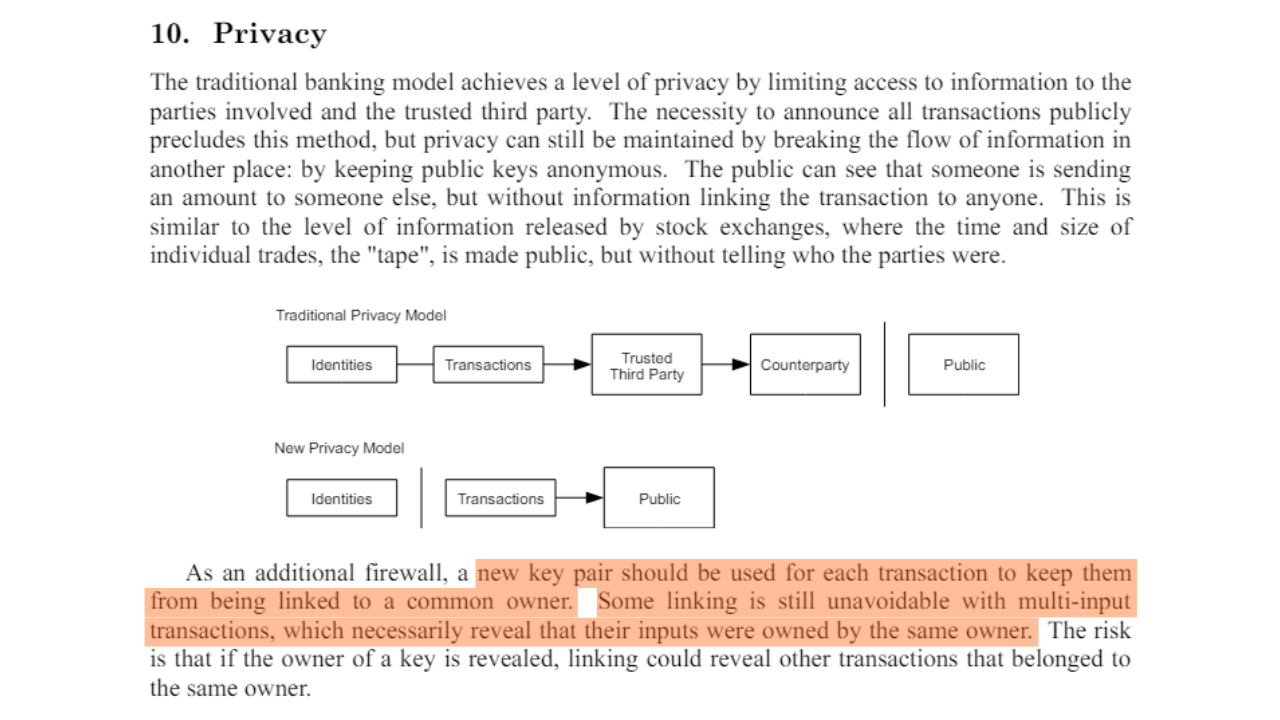
CIOH was discovered by Satoshi Nakamoto. He talks about it in part 10 of the White Paper:

"[...] linking is inevitable with multi-entry transactions, which necessarily reveal that their entries were held by the same owner. The risk is that if the owner of a key is revealed, the links may reveal other transactions that belonged to the same owner."

It's particularly fascinating to note that Satoshi Nakamoto, even before the official launch of Bitcoin, had already identified the two main privacy vulnerabilities for users, namely CIOH and address reuse. Such foresight is quite remarkable, as these two heuristics remain, even today, the most useful in blockchain analysis.

To give you an example, here is a transaction on which we can probably apply CIOH:

20618e63b6eed056263fa52a2282c8897ab2ee71604c7faccfe748e1a202d712

Source : Mempool.space

Off-chain data

Of course, chain analysis is not limited exclusively to onchain data. Any data from a previous analysis or available on the Internet can also be used to refine an analysis.

For example, if we observe that traced transactions are systematically broadcast from the same Bitcoin node, and we manage to identify its IP address, we may be able to identify other transactions from the same entity, as well as determining part of the issuer's identity. Although this practice is not easily achievable, as it requires the operation of numerous nodes, it may be employed by some companies specializing in blockchain analysis.

The analyst also has the option of relying on analyses previously made open-source, or on his own previous analyses. Perhaps we'll be able to find an output that points to a cluster of addresses we've already identified. Sometimes, it's also possible to rely on outputs that point to an exchange platform, as the addresses of these companies are generally known.

In the same way, you can perform an analysis by elimination. For example, if when analyzing a transaction with two outputs, one of them relates to an address cluster already known, but distinct from the entity we're tracing, then we can interpret that the other output probably represents the exchange.

Channel analysis also includes a slightly more general OSINT (Open Source Intelligence) component, involving internet searches. It is for this reason that we advise against publishing addresses directly on social networks or on a website, whether pseudonymous or not.

Temporal models

We think about it less, but certain human behaviors are recognizable onchain. Perhaps the most useful in an analysis is your sleep pattern! Yes, when you sleep, you don't broadcast Bitcoin transactions. But you generally sleep at roughly the same time. This is why it's common practice to use temporal analysis in blockchain analysis. Quite simply, this is a census of the times at which a given entity's transactions are broadcast to the Bitcoin network. By analyzing these temporal patterns, we can deduce a wealth of information.

First of all, a temporal analysis can sometimes identify the nature of the traced entity. If we observe that the transactions are broadcast consistently over 24 hours, then this will betray a high level of economic activity. The entity behind these transactions is likely to be a company, potentially international and perhaps with automated in-house procedures.

For example, I recognized this pattern a few months ago when analyzing the transaction that had mistakenly allocated 19 bitcoins in fees. A simple temporal analysis allowed me to hypothesize that we were dealing with an automated service, and therefore probably with a large entity such as an exchange platform.

Indeed, a few days later, it was discovered that the funds belonged to PayPal, via the Paxos exchange platform.

On the contrary, if we can see that the temporal pattern is rather spread over 16 specific hours, then we can estimate that we're dealing with an individual user, or perhaps a local company depending on the volumes exchanged.

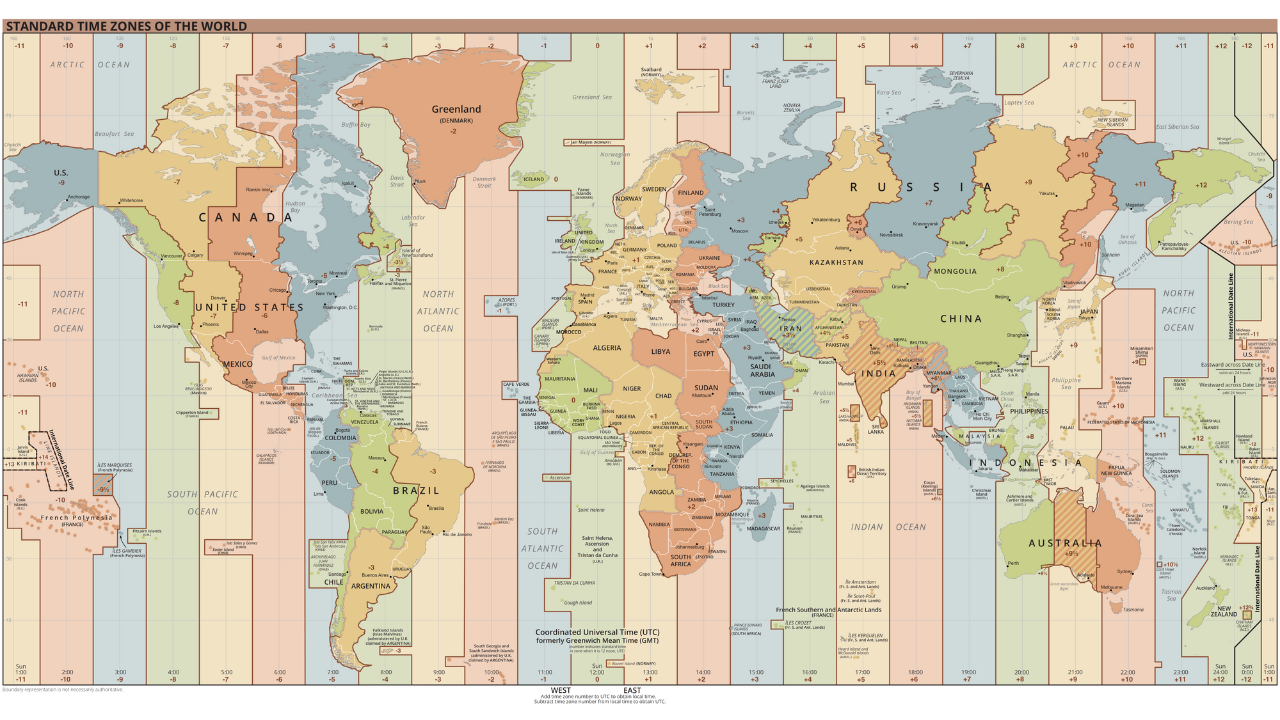
Beyond the nature of the entity observed, the temporal pattern can also tell us approximately where the user is located, thanks to time zones. In this way, we can match other transactions, and use their timestamps as an additional heuristic that can be added to our analysis.

For example, on the multi-used address I mentioned earlier, we can see that transactions, both incoming and outgoing, are concentrated on a 13-hour interval.

bc1qqtmeu0eyvem9a85l3sghuhral8tk0ar7m4a0a0

Source : OXT.me

This range probably corresponds to Europe, Africa or the Middle East. We can therefore assume that the user behind these transactions lives in these areas.

In a different vein, a time analysis of this type also led to the hypothesis that Satoshi Nakamoto was not operating from Japan, but from the USA: The Time Zones of Satoshi Nakamoto

Putting it into practice with a block explorer

In this final chapter, we're going to put the concepts we've studied so far into practice. I'm going to show you examples of real Bitcoin transactions, and you'll have to extract the information I'm asking you for.

Ideally, to perform these exercises, the use of a professional chain analysis tool would be preferable. However, since the arrest of the creators of Samourai Wallet, the only free analysis tool OXT.me is no longer available. We'll therefore opt for a classic block explorer for these exercises. I recommend using Mempool.space for its many features and range of chain analysis tools, but you can also opt for another explorer such as Bitcoin Explorer.

To begin with, I'll introduce you to the exercises. Use your block explorer to complete them, and write down your answers on a sheet of paper. Then, at the end of this chapter, I'll provide you with the answers so you can check and correct your results.

The transactions selected for these exercises have been chosen purely for their characteristics in a somewhat random fashion. This chapter is intended for educational and informative purposes only. I would like to make it clear that I neither support nor encourage the use of these tools for malicious purposes. The aim is to teach you how to protect yourself against string analysis, not to conduct analysis to expose other people's private information.

Exercise 1

Identifier of the transaction to be analyzed :

3769d3b124e47ef4ffb5b52d11df64b0a3f0b82bb10fd6b98c0fd5111789bef7

What is the name of this transaction's model, and what plausible interpretations can be drawn by examining only its model, i.e. the structure of the transaction?

Exercise 2

Identifier of the transaction to be analyzed :

baa228f6859ca63e6b8eea24ffad7e871713749d693ebd85343859173b8d5c20

What is the name of this transaction's model, and what plausible interpretations can be drawn by examining only its model, i.e. the structure of the transaction?

Exercise 3

Identifier of the transaction to be analyzed :

3a9eb9ccc3517cc25d1860924c66109262a4b68f4ed2d847f079b084da0cd32b

What is the model for this transaction?

Having identified its model, using the transaction's internal heuristics, what output is the exchange likely to represent?

Exercise 4

Identifier of the transaction to be analyzed :

35f0b31c05503ebfdf7311df47f68a048e992e5cf4c97ec34aa2833cc0122a12

What is the model for this transaction?

Having identified its model, using the transaction's internal heuristics, what output is the exchange likely to represent?

Exercise 5

Let's imagine that Loïc has posted one of his Bitcoin receiving addresses on the social network Twitter :

bc1qja0hycrv7g9ww00jcqanhfpqmzx7luqalum3vu

Based on this information and using only the address reuse heuristic, which Bitcoin transactions can be linked to Loïc's identity?

Obviously, I'm not the real owner of this reception address and I didn't post it on social networks. It's an address I took randomly from the blockchain

Exercise 6

Following exercise 5, thanks to the address reuse heuristic, you were able to identify several Bitcoin transactions in which Loïc seems to be involved. Normally, among the transactions identified, you should have spotted this one:

2d9575553c99578268ffba49a1b2adc3b85a29926728bd0280703a04d051eace

This transaction is the very first to send funds to Loïc's address. Where do you think the bitcoins received by Loïc via this transaction came from?

Exercise 7

Following exercise 5, thanks to the address reuse heuristic, you've been able to identify several Bitcoin transactions in which Loïc seems to be involved. Now you want to find out where Loïc came from. Based on the transactions found, perform a time analysis to find the time zone most likely used by Loïc. From this time zone, determine a location where Loïc seems to live (country, state/region, city...).

Exercise 8

Here is the Bitcoin transaction to study:

bb346dae645d09d32ed6eca1391d2ee97c57e11b4c31ae4325bcffdec40afd4f

Looking at this transaction alone, what information can we interpret?

Exercise solutions

Exercise 1:

The model for this transaction is the simple payment model. If we study only its structure, we can interpret that one output represents the exchange and the other output represents an actual payment. We therefore know that the observed user is probably no longer in possession of one of the two UTXOs in output (that of payment), but is still in possession of the other UTXO (that of exchange).

Exercise 2:

The model for this transaction is that of grouped spending. This model probably reveals a large-scale economic activity, such as an exchange platform. We can deduce that the input UTXO comes from a company with a high level of economic activity, and that the output UTXOs will be scattered. Some will belong to company customers who have withdrawn their bitcoins to self-custody wallets. Others may go to partner companies. Finally, there will undoubtedly be some exchange that will go back to the issuing company.

Exercise 3:

The model for this transaction is simple payment. We can therefore apply internal heuristics to the transaction to try to identify the exchange.

I have personally identified at least two internal heuristics that support the same hypothesis:

The reuse of the same type of script ;
The largest output.

The most obvious heuristic is that of reusing the same type of script. Indeed, output 0 is a P2SH, recognizable by its reception address starting with 3 :

3Lcdauq6eqCWwQ3UzgNb4cu9bs88sz3mKD

While output 1 is a P2WPKH, identifiable by its address starting with bc1q :

bc1qya6sw6sta0mfr698n9jpd3j3nrkltdtwvelywa

The UTXO used as input for this transaction also uses a P2WPKH script:

bc1qyfuytw8pcvg5vx37kkgwjspg73rpt56l5mx89k

Thus, we can assume that output 0 corresponds to a payment and output 1 is the transaction exchange, which would mean that the input user always owns output 1.

To support or refute this hypothesis, we can look for other heuristics that either confirm our thinking, or decrease the probability that our hypothesis is correct.

I've identified at least one other heuristic. It's the largest output heuristic. Output 0 measures 123,689 sats, while output 1 measures 505,839 sats. There is therefore a significant difference between these two outputs. The largest output heuristic suggests that the largest output is likely to be foreign exchange. This heuristic further strengthens our initial hypothesis.

It therefore seems likely that the user who supplied the UTXO as input still holds the 1 output, which seems to embody the transaction's exchange.

Exercise 4:

The model for this transaction is simple payment. We can therefore apply internal heuristics to the transaction to try to identify the exchange.

I have personally identified at least two internal heuristics that support the same hypothesis:

The reuse of the same type of script ;
The round post output.

The most obvious heuristic is that of reusing the same type of script. Indeed, output 0 is a P2SH, recognizable by its reception address starting with 3 :

3FSH5Mnq6S5FyQoKR9Yjakk3X4KCGxeaD4

While output 1 is a P2WPKH, identifiable by its address starting with bc1q :

bc1qvdywdcfsyavt4v8uxmmrdt6meu4vgeg439n7sg

The UTXO used as input for this transaction also uses a P2WPKH script:

bc1qku3f2y294h3ks5eusv63dslcua2xnlzxx0k6kp

Thus, we can assume that output 0 corresponds to a payment and output 1 is the transaction exchange, which would mean that the input user always owns output 1.

To support or refute this hypothesis, we can look for other heuristics that either confirm our thinking, or decrease the probability that our hypothesis is correct.

I've identified at least one other heuristic. It's the round amount output. Output 0 measures 70,000 sats, while output 1 measures 22,962 sats. We therefore have a perfectly round output in the BTC unit of account. The round output heuristic suggests that the UTXO with a round amount is most likely that of payment, and that by elimination, the other represents exchange. This heuristic further strengthens our initial hypothesis.

However, in this example, another heuristic could challenge our initial hypothesis. Indeed, output 0 is greater than output 1. Based on the heuristic that the largest output is generally foreign exchange, we could deduce that output 0 is foreign exchange. However, this counter-hypothesis seems implausible, as the other two heuristics appear substantially more convincing than the largest output heuristic. Consequently, it seems reasonable to maintain our initial hypothesis despite this apparent contradiction.

It therefore seems likely that the user who supplied the UTXO as input still holds the 1 output, which seems to embody the transaction's exchange.

Exercise 5:

We can see that 8 transactions can be associated with Loïc's identity. Of these, 4 involve the receipt of bitcoins:

2d9575553c99578268ffba49a1b2adc3b85a29926728bd0280703a04d051eace
8b70bd322e6118b8a002dbdb731d16b59c4a729c2379af376ae230cf8cdde0dd
d5864ea93e7a8db9d3fb113651d2131567e284e868021e114a67c3f5fb616ac4
bc4dcf2200c88ac1f976b8c9018ce70f9007e949435841fc5681fd33308dd762

The other 4 concern bitcoin shipments:

8b52fe3c2cf8bef60828399d1c776c0e9e99e7aaeeff721fff70f4b68145d540
c12499e9a865b9e920012e39b4b9867ea821e44c047d022ebb5c9113f2910ed6
a6dbebebca119af3d05c0196b76f80fdbf78f20368ebef1b7fd3476d0814517d
3aeb7ce02c35eaecccc0a97a771d92c3e65e86bedff42a8185edd12ce89d89cc

Exercise 6:

If we look at the model of this transaction, it's clear that it's a bundled expenditure. Indeed, the transaction has a single input and 51 outputs, indicating a high level of economic activity. We can therefore hypothesize that Loïc has withdrawn bitcoins from an exchange platform.

Several factors reinforce this hypothesis. Firstly, the type of script used to secure the UTXO input is a P2SH 2/3 multisig script, which indicates an advanced level of security typical of exchange platforms:

OP_PUSHNUM_2
OP_PUSHBYTES_33 03eae02975918af86577e1d8a257773118fd6ceaf43f1a543a4a04a410e9af4a59
OP_PUSHBYTES_33 03ba37b6c04aaf7099edc389e22eeb5eae643ce0ab89ac5afa4fb934f575f24b4e
OP_PUSHBYTES_33 03d95ef2dc0749859929f3ed4aa5668c7a95baa47133d3abec25896411321d2d2d
OP_PUSHNUM_3
OP_CHECKMULTISIG

What's more, the address studied 3PUv9tQMSDCEPSMsYSopA5wDW86pwRFbNF is reused in over 220,000 different transactions, which is often characteristic of exchange platforms, generally unconcerned about their confidentiality.

The temporal heuristic applied to this address also shows a regular broadcast of transactions almost daily over a 3-month period, with extended hours over 24 hours, suggesting the continuous activity of an exchange platform.

Finally, the volumes handled by this entity are colossal. The address received and sent 44 BTC in 222,262 transactions between December 2022 and March 2023. These large volumes further confirm the likely nature of an exchange platform's activity.

Exercise 7:

By analyzing the transaction confirmation times, the following UTC times can be identified:

An analysis of these schedules shows that UTC-7 and UTC-8 are consistent with a range of current human activity (between 08:00 and 23:00) for the majority of schedules:

05:43 UTC > 22:43 UTC-7
20:51 UTC > 13:51 UTC-7
18:12 UTC > 11:12 UTC-7
17:16 UTC > 10:16 UTC-7
04:28 UTC > 21:28 UTC-7
23:38 UTC > 16:38 UTC-7
07:45 UTC > 00:45 UTC-7
21:55 UTC > 14:55 UTC-7
05:43 UTC > 21:43 UTC-8
20:51 UTC > 12:51 UTC-8
18:12 UTC > 10:12 UTC-8
17:16 UTC > 09:16 UTC-8
04:28 UTC > 20:28 UTC-8
23:38 UTC > 15:38 UTC-8
07:45 UTC > 23:45 UTC-8
21:55 UTC > 13:55 UTC-8

The UTC-7 time zone is particularly relevant in summer, as it includes states and regions such as :

California (with cities such as Los Angeles, San Francisco, and San Diego);
Nevada (with Las Vegas) ;
Oregon (with Portland) ;
Washington (with Seattle) ;
The Canadian region of British Columbia (with cities like Vancouver and Victoria).

This information suggests that Loïc is likely to reside on the west coast of the United States or Canada.

Exercise 8:

Analysis of this transaction reveals 5 inputs and a single output, suggesting consolidation. Applying the CIOH heuristic, we can assume that all the input UTXOs are owned by a single entity, and that the output UTXO also belongs to this entity. It seems that the user chose to group together several UTXOs he owned, to form a single UTXO in output, with the aim of consolidating his parts. This move was probably motivated by a desire to take advantage of the low transaction costs of the time, in order to reduce future costs.

To write this part 3 on chain analysis, I drew on the following resources:

The series of four articles entitled: Understanding Bitcoin Privacy with OXT, produced by Samourai Wallet in 2021 ;*
The various reports from OXT Research, as well as their free blockchain analysis tool (no longer available for the moment following the arrest of the founders of Samourai Wallet) ;*
More broadly, my knowledge comes from various tweets and content from @LaurentMT and @ErgoBTC ;*
The Space Kek #19 in which I participated in the company of @louneskmt, @TheoPantamis, @Sosthene___ and @LaurentMT.*

I'd like to thank their authors, developers and producers. Thanks also to the proofreaders who meticulously corrected the article on which this part 3 is based, and gave me their expert advice :

Gilles Cadignan ;*
Ludovic Lars

Mastering best practices to protect your privacy

Address reuse

Having studied the techniques that can break your confidentiality on Bitcoin, in this third part we'll now look at the best practices to adopt to protect yourself. The aim of this part is not to explore methods of improving confidentiality, a subject which will be dealt with later, but rather to understand how to interact correctly with Bitcoin to retain the confidentiality it naturally offers, without resorting to additional techniques.

Obviously, to begin this third part, we're going to talk about address reuse. This phenomenon is the main threat to user confidentiality. This chapter is surely the most important of the entire course.

What's a receiving address?

A Bitcoin receiving address is a string or identifier used to receive bitcoins on a wallet.

Technically, a Bitcoin receiving address does not "receive" bitcoins in the literal sense, but rather serves to define the conditions under which bitcoins can be spent. In concrete terms, when a payment is sent to you, the sender's transaction creates a new UTXO for you as an output from the UTXOs it has consumed as inputs. On this output, it affixes a script defining how this UTXO can be spent at a later date. This script is known as "ScriptPubKey" or "Locking Script". Your receiving address, or more precisely its payload, is integrated into this script. In layman's terms, this script basically states:

"To spend this new UTXO, you must provide a digital signature using the private key associated with this receiving address."

Bitcoin addresses come in different types, depending on the scripting model used. The first models, known as "Legacy*", include the P2PKH (Pay-to-PubKey-Hash) and P2SH (Pay-to-Script-Hash) addresses. P2PKH addresses always begin with 1, and P2SH with 3. Although still secure, these formats are now obsolete, as they entail higher transaction costs and offer less confidentiality than the new standards.

SegWit V0 (P2WPKH and P2WSH) and Taproot / SegWit V1 (P2TR) addresses represent modern formats. SegWit addresses start with bc1q and Taproot addresses, introduced in 2021, start with bc1p.

For example, here is a Taproot reception address:

bc1ps5gd2ys8kllz9alpmcwxqegn7kl3elrpnnlegwkm3xpq2h8da07spxwtf5

How the ScriptPubKey is constructed will depend on the standard you are using:

| ScriptPubKey | Script template

| ---------------- | ----------------------------------------------------------- |

| P2PKH | OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG |

| P2SH | OP_HASH160 <scriptHash> OP_EQUAL |

| P2WPKH | 0 <pubKeyHash> |

| P2WSH | 0 <witnessScriptHash> |

| P2SH - P2WPKH | OP_HASH160 <redeemScriptHash> OP_EQUAL |

| P2SH - P2WSH | OP_HASH160 <redeemScriptHash> OP_EQUAL |

| P2TR | 1 <pubKey> |

The construction of reception addresses also depends on the script model chosen:

For P2PKH and P2WPKH addresses, the payload, i.e. the core of the address, represents the hash of the public key;
For P2SH and P2WSH addresses, the payload represents the hash of a ;
As for P2TR addresses, the payload is a tweaked public key. P2TR outputs combine aspects of Pay-to-PubKey and Pay-to-Script. The tweaked public key is the result of adding a classic spending public key with a "tweak", derived from the Merkle root of a set of scripts that can also be used to spend bitcoins.

Addresses displayed on your portfolio software also include an HRP (Human-Readable Part), typically bc for post-SegWit addresses, a 1 separator, and a version number q for SegWit V0 and p for Taproot/SegWit V1. A checksum is also added to guarantee the integrity and validity of the address during transmission.

Finally, the addresses are put into a standard format:

Base58check for old Legacy addresses ;
Bech32 for SegWit addresses ;
Bech32m for Taproot addresses.

Here is the addition matrix for bech32 and bech32m formats (SegWit and Taproot) from base 10:

| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

| --- | --- | --- | --- | --- | --- | --- | --- | --- |

| 0 | q | p | z | r | y | 9 | x | 8 |

| 8 | g | f | 2 | t | v | d | w | 0 |

| 16 | s | 3 | j | n | 5 | 4 | k | h |

| 24 | c | e | 6 | m | u | a | 7 | l |

What is address reuse?

Address reuse is the use of the same receiving address to block several different UTXOs.

As we saw in the previous section, each UTXO has its own ScriptPubKey, which locks it and must be satisfied for the UTXO to be consumed as input in a new transaction. It is within this ScriptPubKey that payload addresses are integrated.

When different ScriptPubKeys contain the same receiving address, this is called address reuse. In practice, this means that a user has repeatedly provided the same address to senders in order to receive bitcoins via multiple payments. And it's precisely this practice that is disastrous for your privacy.

Why is address reuse a problem?

Since the blockchain is public, it's easy to see which addresses lock which UTXO and how many bitcoins. If the same address is used for several transactions, it becomes possible to deduce that all the bitcoins associated with that address belong to the same person. This practice compromises user privacy by enabling deterministic links to be established between different transactions and bitcoins to be traced on the blockchain. Satoshi Nakamoto himself already highlighted this problem in Bitcoin's White Paper:

As an additional firewall, a new pair of keys could be used for each transaction to keep them unlinked to a common owner

Source: S. Nakamoto, "Bitcoin: A Peer-to-Peer Electronic Cash System", https://bitcoin.org/bitcoin.pdf, 2009.

Satoshi's intention in this sentence was to create an additional firewall in the event of an association between a user's identity and a key pair on Bitcoin, to prevent his entire activity from being publicly linked to his identity. Today, with the proliferation of blockchain analysis companies and KYC regulations, the use of unique addresses is no longer an "additional firewall", but an indispensable practice for anyone wishing to preserve a minimum of privacy.

When you reuse an address, you make an almost undeniable link between all the transactions associated with that address. Although this doesn't directly jeopardize your funds, as elliptic curve cryptography guarantees the security of your private keys, it does make it easier to monitor your activities. Indeed, anyone with a node can observe the transactions and balances of the addresses, totally compromising your anonymity.

To illustrate this point, let's take the example of Bob, a user who regularly buys bitcoins in small amounts in DCA and always sends them to the same address. After two years, this address contains a substantial quantity of bitcoins. If Bob uses this address to make a payment to a local merchant, the latter will be able to see all the associated funds and deduce Bob's wealth. This can lead to personal security risks, such as attempted theft or extortion. If Bob had used a blank address to receive each periodic purchase, he would have revealed infinitely less information to his merchant.

In string analysis, there are 2 types of address reuse:

External reuse ;
Internal reuse within a transaction.

The first is when an address is reused in several different Bitcoin transactions. This is what we talked about earlier: this heuristic deduces that all UTXOs passed through this address belong to a single entity.

Internal address reuse does not occur when reuse occurs across several transactions, but when it occurs within a single transaction. Indeed, if the same address used to lock an input is used as the output of a transaction, then we can deduce that this output still belongs to the same user (exchange), and that the second output represents the actual payment. This other heuristic makes it possible to perpetuate a funds trace over several transactions.

Address reuse is a real scourge on Bitcoin. According to the OXT.me website (currently inaccessible), the overall rate of address reuse on Bitcoin was around 52% in 2022:

This rate is enormous, but it comes overwhelmingly from exchange platforms rather than individual users.

How to avoid address reuse?

Avoiding address reuse is quite simple: simply use a new, blank address for all new payments to your wallet.

Thanks to BIP32, modern portfolios are now deterministic and hierarchical. This means that a user can generate a large number of addresses from a single initial piece of information: the seed. By saving this single piece of information, it is possible to restore all the private keys in the portfolio, enabling access to the funds secured by the corresponding addresses.

This is why, when you press the "receive" button in your wallet software, an unused receiving address is suggested every time. After receiving bitcoins at this address, the software automatically suggests a new one.

PS: Recently, some wallet software programs have announced their intention to stop generating blank addresses, fearing that this will be perceived as a form of money laundering by the authorities. If your software is one of these, I strongly advise you to replace it immediately, as this is not acceptable to the user. If you need a static identifier to receive payments, such as donations, it's not advisable to use a classic Bitcoin address because of the risk of reuse. Instead, use a Lightning address, or opt for a static onchain payment identifier, such as BIP47 or Silent Payments. These protocols are explained in detail in Part 6 of this training course.

Labeling and checking parts

As we discovered in the section on string analysis, there are a multitude of heuristics and patterns that can be used to deduce information about a transaction. As a user, it's important to be aware of these techniques in order to better protect yourself against them.

This involves rigorous management of your wallet in self-custody, which means knowing the origin of your UTXOs, as well as carefully selecting which UTXOs to consume when making payments. This efficient wallet management relies on two important features of good Bitcoin wallets: tagging and coin control.

In this chapter, we'll look at these features and see how you can use them intelligently, without adding too much workload, to greatly optimize your privacy on Bitcoin.

What is labeling?

Labeling is the practice of assigning an annotation or label to a specific UTXO in a Bitcoin wallet. These annotations are stored locally by the wallet software and are never transmitted over the Bitcoin network. Labelling is therefore a personal management tool.

For example, if I have a UTXO from a P2P purchase on Bisq with Charles, I could label it "Non-KYC Bisq Charles".

Tagging is a good practice that helps to remember the origin or intended destination of a UTXO, which therefore facilitates the management of funds and the optimization of privacy. Indeed, your Bitcoin wallet surely secures several UTXOs. If the sources of these UTXOs are different, you may not want to merge these UTXOs in the future, otherwise you could reveal their common ownership. By properly labeling all your parts, you can be sure that you'll remember where they came from when you need to use them, even if that's years from now.

What's corner control?

The active use of labelling becomes even more interesting when coupled with a coin control option on your portfolio software.

Coin control is a feature found in good Bitcoin wallet software, giving you the ability to manually select specific UTXOs to use as inputs to complete a transaction. In fact, in order to satisfy an output payment, you need to consume an input UTXO in return. For a number of reasons, which we'll look at later, you may want to choose precisely which parts to consume as inputs to satisfy a given payment. This is exactly what coin control allows you to do. To give you an analogy, this feature is similar to choosing a specific coin from your wallet when you pay for your baguette.

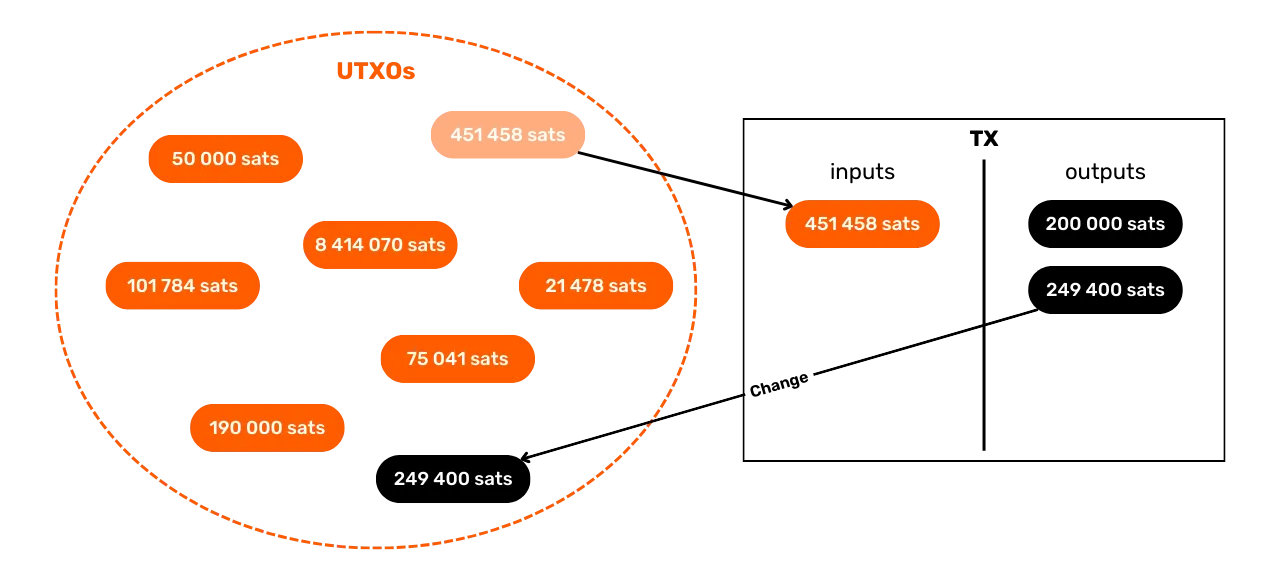
The use of portfolio software with coin control, coupled with UTXO labeling, enables users to both distinguish and accurately select UTXOs for their transactions.

How do you label your UTXOs?

There's no one-size-fits-all method of labeling UTXOs. It's up to you to define a labeling system that's easy to understand for your portfolio. In any case, keep in mind that good labeling is labeling you can understand when you need it. If your Bitcoin wallet is primarily intended for savings, the labels may not be useful to you for decades to come. So make sure they're clear, precise and comprehensive.

It's important that your loved ones can easily identify the origin of the funds if, one day, they need access to your portfolio. This will help them both for reasons of confidentiality and for legal purposes, should they need to justify the origin of the funds to an authority.

The most important thing to note on the label is the source of the UTXO. You should simply indicate how the coin came to be in your wallet. Is it the result of a purchase on an exchange platform? An invoice payment from a customer? A peer-to-peer exchange? Or does it represent the exchange of an expense? For example, you could specify:

remove Exchange.com` ;
customer payment David` ;
buy P2P Charles` ;
Change sofa purchase

To fine-tune your UTXO management and respect your fund segregation strategies within your portfolio, you could enrich your labels with an additional indicator that reflects these separations. If your portfolio contains two categories of UTXO that you are keen not to mix, you could incorporate a marker into your labels to clearly distinguish these groups. These separation markers will depend on your own criteria, such as distinguishing between UTXOs resulting from an acquisition process that involves KYC, or between professional and personal funds. Taking the label examples mentioned above, this could translate into:

KYC - Withdrawal Exchange.com ;
KYC - Customer Payment David ;
NO KYC - Buy P2P Charles ;
NO KYC - Change sofa purchase

It is also advisable to perpetuate the labeling of a part over the course of transactions. For example, when consolidating UTXO no-KYC, be sure to mark the resulting UTXO not just as consolidation, but specifically as consolidation no-KYC to keep a clear record of where the coins came from.

Finally, it's not mandatory to put a date on a label. Most wallet software already displays the transaction date, and it's always possible to find this information on a block explorer thanks to its TXID.

How to choose the right parts?

When you perform a transaction, the coin control lets you specifically choose which UTXOs to consume as inputs to satisfy the payment output. There are two aspects to this choice:

The possibility for the recipient of the payment to link part of your identity to the UTXOs used in inputs;
The ability of an external observer to establish links between all the UTXOs consumed as inputs.

To illustrate the first point, let's take a concrete example. Suppose you buy a baguette in bitcoins from your baker. You use one or more UTXOs that you hold as inputs to meet at least the price of the baguette in outputs, as well as the transaction fees. Your baker could then potentially associate your face, or any other part of your identity that he knows, with the coins used as inputs. Knowing the existence of this link, you might prefer to choose a specific UTXO rather than another when paying.

For example, if one of your UTXOs comes from an exchange platform and you'd rather the baker didn't know about your account on that platform, you'll avoid using that UTXO for payment. If you have a high-value UTXO that reveals a significant amount of bitcoins, you might also choose not to use it to avoid the baker becoming aware of your BTC fortune.

Choosing which UTXOs to use for this first point is therefore a personal decision, influenced by what you are willing to reveal or not. The labels you assign to your UTXOs when you receive them will help you select those which, once spent, only expose information you're comfortable revealing to the recipient.

Beyond the information potentially revealed to the recipient, the choice of inputs also influences what you reveal to all observers of the blockchain. Indeed, by using several UTXOs as inputs to your transaction, you reveal that they are owned by the same entity, according to the CIOH heuristic (Common Input Ownership Heuristic).

When selecting your parts, therefore, you need to be aware that the transaction you're about to broadcast will create a link between all the UTXOs used. This link can be problematic for your personal privacy, especially if the UTXOs come from different sources.

Let's take the example of my no-KYC UTXO from Bisq; I want to avoid combining it with a UTXO from, say, a regulated exchange platform that knows my identity. Indeed, if I ever use these 2 UTXOs as inputs to the same transaction, the regulated platform will be able to link my identity with the UTXO I bought on Bisq, which was not previously linked to my identity.

Finally, when choosing which UTXOs to use as inputs to a transaction, the most important thing is to avoid using multiple UTXOs. At most, when you can, select a single coin large enough to satisfy your payment. In this way, you completely avoid the risks associated with CIOH. However, if no single UTXO is sufficient for payment and you need to consume several, make sure they come from similar sources to minimize the risk of unwanted links. Also bear in mind that the recipient could associate the information they hold on you with the history of coins used in inputs.

Understanding automatic part selection

In the previous sections, we discussed the manual selection of UTXOs to be used for a transaction. But what happens when the wallet software performs this selection automatically? Several methods exist for determining which coins to consume, and the selection of UTXOs constitutes a veritable field of research on Bitcoin. The main aim of this automatic process is often to minimize transaction costs for the user.

UTXO selection methods such as FIFO (First In First Out) and LIFO (Last In First Out) are among the simplest, but also the least efficient. With FIFO, the oldest parts in the portfolio are used first. This approach is generally inefficient both for minimizing transaction costs and for preserving confidentiality, except in cases where relative timelocks are used and need to be renewed regularly. Conversely, LIFO prioritizes the use of the most recent UTXOs. Both methods, though simple, often prove ineffective.

A more advanced method is the Knapsack Solver. This was used on the Bitcoin Core wallet until version 0.17. It consists of iteratively and randomly selecting UTXOs from the wallet, adding them up in subsets, and keeping the solution that reduces the transaction weight as much as possible, in order to reduce the cost to the user.

The Branch-and-Bound (BNB), often nicknamed the "Murch algorithm" after its inventor, has replaced the Knapsack Solver in Bitcoin Core as of version 0.17. This more advanced method aims to find a set of UTXOs that corresponds exactly to the amount needed to satisfy the outputs of a transaction. The objective of BNB is to minimize the exchange amount as well as the fees, by reducing the so-called waste criterion, which takes into account both the immediate costs and the expected future costs of the exchange. This method is derived from the original concept of Branch-and-Bound, conceived in 1960 by Ailsa Land and Alison Harcourt, and offers a more precise optimization of fees than the Knapsack Solver.

All these automatic UTXO selection methods may be effective in reducing transaction costs, but they are often ineffective in preserving user confidentiality. Indeed, these algorithms can merge several UTXOs into inputs, thus revealing a common property of these UTXOs due to CIOH. Obviously, these methods cannot take into account the labels affixed to the UTXOs, which are nonetheless crucial for consciously choosing which parts to reveal to the transaction recipient. At present, the only way to optimize confidentiality when selecting coins is to do so manually.

Tutorial on UTXO labeling

If you'd like to find out how to tag your UTXOs, we've done a comprehensive tutorial on the main Bitcoin wallet software out there:

https://planb.network/tutorials/privacy/on-chain/utxo-labelling-d997f80f-8a96-45b5-8a4e-a3e1b7788c52

KYC and key identification

KYC stands for "Know Your Customer". It's a regulatory procedure implemented by certain companies operating in the Bitcoin sector. The aim of this procedure is to verify and register the identity of their customers, with the stated aim of combating money laundering and the financing of terrorism.

In practical terms, KYC involves the collection of various personal data from the customer, which may vary according to jurisdiction, but generally include ID, photograph and proof of address. This information is then verified and stored for future use.

This procedure has become mandatory for all regulated exchange platforms in the majority of Western countries. This means that anyone wishing to exchange state currencies for bitcoin via these platforms must comply with KYC requirements.

This procedure is not without risks for the privacy and security of users. In this chapter, we will examine these risks in detail and analyze the specific impacts of KYC and identification processes on the privacy of Bitcoin users.

Facilitating onchain tracing

The first risk associated with KYC is that it offers a privileged entry point for blockchain analysis. As we saw in the previous section, analysts can cluster and track activity on the blockchain using transaction patterns and heuristics. Once they have succeeded in clustering a user's onchain activity, all they need to do is find a single entry point among all his transactions and keys to fully compromise his confidentiality.

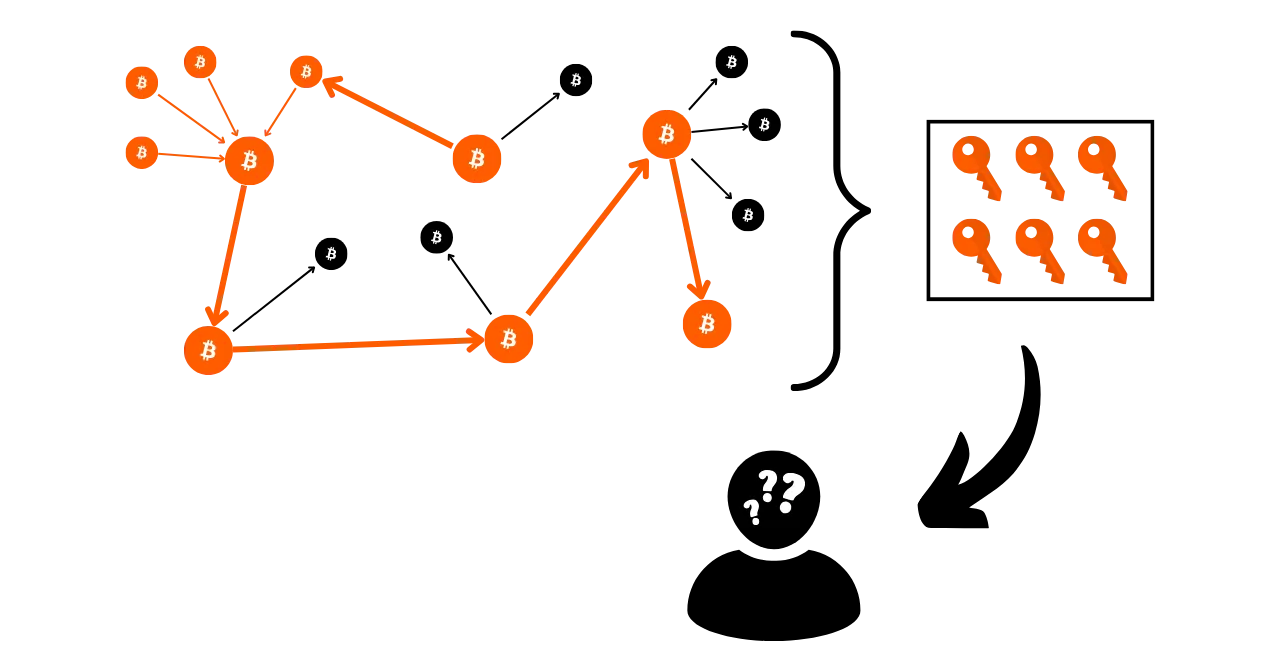
When you perform a KYC, you provide a high-quality entry point for blockchain analysis, as you associate your receiving addresses used when withdrawing your bitcoins from an exchange platform with your full, verified identity. In theory, this information is known only to the company to which you provided it, but, as we'll see below, the risk of data leakage is real. What's more, the mere fact that a company holds this information can be problematic, even if they don't share it.

So, if you don't take other steps to limit the aggregation of your activities on the blockchain, anyone with knowledge of this KYC entry point can potentially link all your activity on Bitcoin to your identity. From that company's point of view, your use of Bitcoin loses all confidentiality.

To illustrate this with a comparison, it's as if your banker at Bank X not only had access to all your transactions with Bank X, but could also observe your transactions with Bank Y and all your cash transactions.

Remember from the first part of this training course: Bitcoin's confidentiality model, as conceived by Satoshi Nakamoto, is based on the separation between the user's identity and his key pairs. Although this layer of confidentiality is no longer sufficient today, it is still prudent to limit its degradation as much as possible.

Exposure to state surveillance

The second major problem with KYC is that it reveals to the state that you have owned bitcoin at some point in time. When you buy bitcoins via a regulated actor, it becomes possible for the state to know about this possession. At the moment, this may seem trivial, but it's important to remember that your country's political and economic future is not in your hands.

Firstly, the state can quickly adopt an authoritarian stance. History is full of examples where policies have changed abruptly. Today, in Europe, Bitcoiners can write articles about Bitcoin, take part in conferences, and manage their wallets in self-custody. But who can say what tomorrow holds? If Bitcoin suddenly becomes public enemy number one, being associated with it in government files could prove problematic.

Then, in the face of severe economic crises, the state might consider seizing bitcoins held by citizens. Perhaps tomorrow, bitcoiners will be perceived as crisis profiteers, and will be taxed excessively for their capital gains in the face of fiat currency devaluation.

You might think this isn't a problem, as your bitcoins are mixed, and therefore untraceable. However, tracing is not the issue here. The real issue is that the state knows you've owned bitcoin. This information alone could be enough to incriminate you or hold you to account. You could try to claim that you've spent your bitcoins, but that would have to be reflected in your tax return, and you'd get caught. You could also say you lost your keys in a boating accident, but beyond the Twitter joke, do you really think that would be enough to exonerate you?

So it's important to take into account the risk of the state knowing that you've owned BTC, however remote that risk may seem today.

Another problem posed by KYC in terms of state supervision is the mandatory reporting by regulated platforms. Although I'm not familiar with regulations in other jurisdictions, in France, Prestataires de Services sur Actifs Numériques (PSAN) are obliged to report to the financial supervisory authorities any movement of funds they consider suspicious.

In France in 2023, 1,449 suspicious acts were reported by PSANs. For the time being, the majority of these acts are crime-related. However, the authorities are also asking regulated platforms to report any suspicious Bitcoin transactions solely on the basis of their structure. If you carry out a collaborative transaction, or even just a transaction with a slightly atypical pattern, and this transaction occurs not far from the withdrawal of your Bitcoins from these platforms, you could find yourself reported to the authorities. Even in the absence of malfeasance and in the legitimate exercise of your rights, such reporting could lead to increased checks and surveillance, inconveniences you would have avoided without KYC.

The risk of personal data leakage

Another problem with KYC is that it requires all your personal data to be stored on the servers of a private company.

Recent events have reminded us that no one is immune to financial or IT failures. In 2022, Celsius customers suffered the consequences. Following the company's bankruptcy, the names of the creditors and the amount of their assets were made public by the American courts during the administrative proceedings.

Just over two years ago, it was a flagship in cryptocurrency cybersecurity that saw its customers' personal data stolen. Although this incident was not directly linked to the purchase of bitcoins, such a risk also remains for exchange platforms. There is therefore a definite risk associated with personal data.

It's true that we already entrust many of our personal data to private companies. However, the risk here is twofold, since this data not only identifies you, but is also linked to activity on Bitcoin. Indeed, when a hacker gains access to the customer data of an exchange platform, he can reasonably assume that these customers possess Bitcoins. This risk is heightened by the fact that Bitcoin, like any other valuable asset, attracts the attention of thieves.

In the event of a data leak, at best you could be the target of targeted phishing attempts. In the worst case, you could find yourself at the center of physical threats to your home.

In addition to the specific risks associated with Bitcoin, there are also the dangers associated with the transmission of identity documents. Indeed, in the event of a data leak, it is possible to become a victim of identity theft. So the stakes are not just limited to protecting the confidentiality of transactions, but also concern the personal security of each individual.

Some preconceived ideas about KYC

It's important to deconstruct some of the preconceived ideas about KYC that we frequently come across on Twitter or in our exchanges between bitcoiners.

First of all, it's inaccurate to think that protecting your privacy for Bitcoins acquired via KYC is pointless. Privacy tools and methods on Bitcoin are varied and serve different purposes. Using coinjoin transactions on Bitcoins acquired via KYC, for example, is not a bad idea. Of course, you need to be careful with regulated exchange platforms to avoid having your account frozen or banned, but from a strictly technical point of view, these practices are not incompatible. Coinjoin has the effect of breaking a coin's history, thus helping you to thwart certain chain analysis risks associated with KYC. Although it doesn't eliminate all risks, it does represent a significant benefit.

Confidentiality on Bitcoin should not be viewed in a binary way, as a distinction between "anonymous" bitcoins and others that are not. Owning Bitcoins acquired via KYC does not mean that all is lost; on the contrary, the use of confidentiality tools can prove even more beneficial.

Conversely, acquiring bitcoin via a non-KYC method does not guarantee perfect confidentiality, nor does it exempt you from the need to take other protective measures. If you hold non-KYC bitcoin but re-use receiving addresses several times, your transactions may be traced and aggregated. The slightest link to the world outside Bitcoin could compromise the only layer of confidentiality you have. So it's important to consider all the privacy-enhancing tools and methods on Bitcoin as complementary. Each technique addresses a specific risk and can add an extra layer of protection. So owning non-KYC Bitcoin doesn't mean you don't need to take other precautions.

Can KYC be cancelled?

I'm sometimes asked whether it's possible to "go back" after performing a KYC, and as you can imagine from the preceding paragraphs, the answer is nuanced. The simplest way to avoid the risks associated with KYC is not to use it when acquiring bitcoins. We'll look at this subject in greater depth in the next chapter. However, if KYC has already been carried out and bitcoins purchased, are there ways of mitigating the risks involved?

When it comes to the risk of tracing your transactions, the use of coinjoin is a solution. We'll look at this method in detail later in the course, but you should know that coinjoin enables you to break the history of a coin and prevent it from being traced past-present and present-past. Even for BTC obtained via a regulated platform, this technique can prevent their traceability.

However, coinjoin does not erase the second risk associated with KYC: the fact that the state may be informed of your possession of bitcoins. Indeed, even if your coins are no longer traceable, the State, depending on the jurisdiction, may have access to your crypto-asset transfer declarations. As this risk is not technical, but administrative, there are no Bitcoin-specific solutions to eliminate it, apart from not exposing yourself to KYC in the first place. The only legal approach to mitigating this risk is to sell on regulated platforms your Bitcoins acquired via regulated platforms, then repurchase them via KYC-free means. By selling and declaring the transfer, the authorities should see that you no longer own them.

As for the risk of leaking your personal data and identity documents, this is a danger external to Bitcoin, and there is no technical solution to avoid it. Once your data has been revealed, it's difficult to undo the operation. You can try to close your account on the platform, but this does not guarantee the deletion of your KYC data, especially when identity verification is outsourced. Verification of complete deletion of your information is impossible. There is therefore no solution to completely prevent this risk and ensure that it no longer exists.

The difference between KYC and key identification

Sometimes, some bitcoiners tend to extend the term "KYC" to any BTC exchange involving a wire transfer or credit card payment, as these means can also reveal the origin of the payment, just as a KYC would. However, KYC should not be confused with key identification. On a personal note, I must admit that my perception of this subject has evolved over time.

KYC refers specifically to a regulatory procedure implemented by certain companies to verify and register the identity of their customers. It's a binary thing: when acquiring your bitcoins, either you do KYC, or you don't. However, key identification, which concerns the link between a facet of a user's identity and onchain activity, is not as binary, but rather represents a continuum. Indeed, in the context of bitcoin acquisition or transfer, such identification is always possible to varying degrees.

For example, if you buy bitcoins on a regulated platform in Switzerland, KYC is not required. However, your keys may be identified, as the purchase was made via your bank account. This is where the first two risks associated with KYC - facilitation of onchain tracing and exposure to state surveillance - can also manifest themselves in an exchange without KYC. If the Swiss entity reports suspicious transactions to the authorities in your country, they can simply check the bank account used for the purchase to discover your identity. So, buying without KYC on regulated platforms is rather high on the risk scale for key identification.

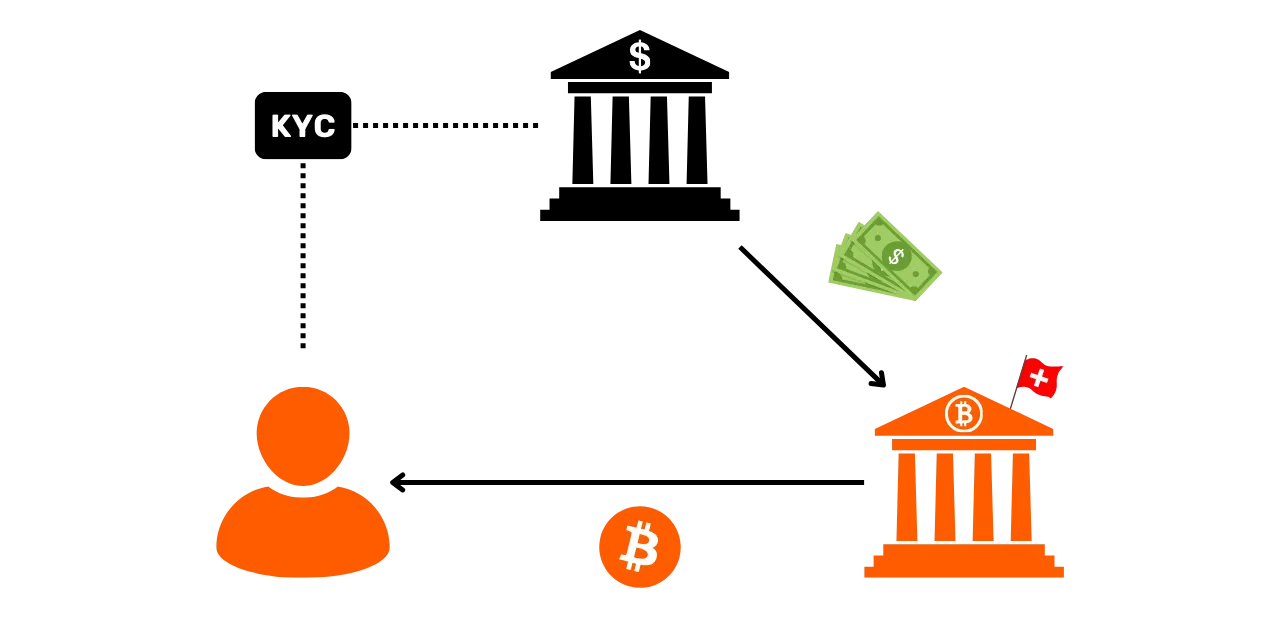
However, avoiding regulated platforms and opting for P2P acquisition methods does not totally eliminate the risk of key identification, but merely reduces it. Let's take the example of a purchase on Bisq or another P2P platform. To pay your counterparty, you'll probably use your bank account. If the authorities question the person you've traded with and ask for your name, we're back to risks 1 and 2. Although these risks are much lower than when buying on a platform without KYC, and even lower than when buying with KYC, they are still present to a lesser extent.

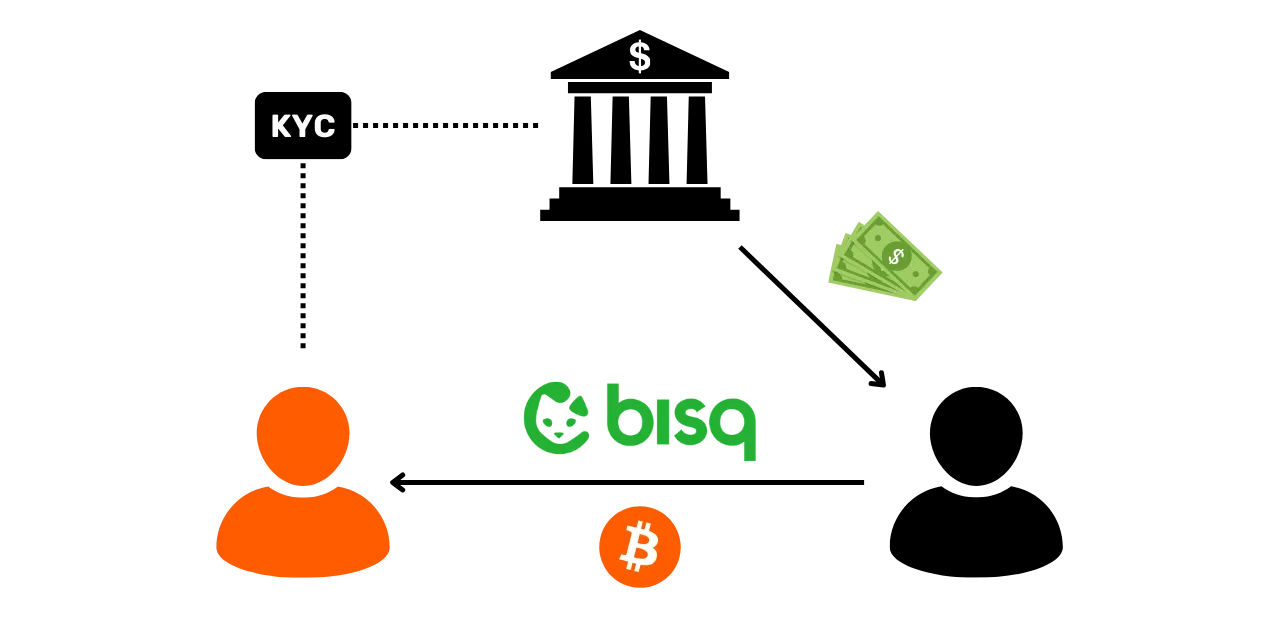
Finally, even if you acquire your bitcoins through a physical exchange for cash, you're not totally anonymous. The person you exchanged with has seen your face, which is part of your identity. Although minimal in this example, there is still a possibility of key identification.

In conclusion, when bitcoins are exchanged for other assets, be it a purchase in state currency or a sale against a real good, there is always some form of key identification. Depending on the exchange method chosen, this identification may vary in intensity. It is important not to confuse this identification with KYC, which is a well-defined regulatory process. However, there is a link between KYC and the identification spectrum, since KYC is at the higher end of the spectrum, as it systematically facilitates the identification of user keys by the authorities.

Sales and acquisition methods

After reading the previous chapter, you may be wondering how you can buy or sell bitcoin without having to undergo an identity verification procedure, in order to avoid the risks associated with KYC. There are several ways to trade bitcoin.

P2P cash exchanges

As we have seen, the best method in terms of confidentiality remains P2P (person-to-person) exchange with cash settlement. This method allows you to minimize the traces left behind, and considerably reduces the possibility of key identification, whether you're buying or selling.

Nevertheless, there are risks to personal security. The main danger lies in the fact that, during the exchange, the counterparty will know that you are holding a large sum of money, either in cash or in bitcoins. This information can attract the attention of malicious persons. Indeed, it's generally advisable to be discreet about your bitcoin holdings. This advice could also be applied to cash. However, when exchanging in person, it's inevitable to reveal that you own bitcoins, and this may attract unwelcome attention.

To limit this risk, I'd advise you to favor cash transactions with trusted individuals, such as family members or close friends. Alternatively, you could also consider trading at local Bitcoin meetups, after attending a few times. This will allow you to get to know the other participants better and not be alone when physically exchanging. However, it's important to recognize that P2P cash exchanges inherently carry risks to your personal security that don't exist when buying via a regulated platform and your bank account.

What's more, depending on where you live, transporting and storing large sums of money can be risky, whether it's bitcoin or cash.

Exchanging cash can also pose legal risks in the event of police or other checks. Although in most countries there are no restrictions on the amount of cash you can carry with you, excessive amounts can arouse suspicion. So be careful, especially if you have to travel long distances, and avoid making too many large transactions at once, so as not to have to justify possession of large sums.

Finally, another disadvantage of P2P purchases is that the price is often higher than on regulated platforms. Sellers often charge a mark-up ranging from 1% to sometimes more than 10%. There are several reasons for this price difference. Firstly, this is a common practice among P2P sellers that has become established over time. Secondly, sellers have fees associated with the transaction to send the funds to the buyer. There is also an increased risk of theft in P2P sales compared to platform transactions, which justifies compensation for the risk taken. Finally, the extra cost may be linked to the demand and quality of the exchange in terms of confidentiality. As a buyer, the gain in confidentiality has a price which is reflected in the mark-up applied by the seller. Some bitcoiners also believe that the mark-up price of BTC bought on P2P reflects its true price, and argue that the lower prices on regulated platforms are the result of a compromise on the confidentiality of your personal data.

P2P exchanges via a matchmaking platform

A less risky alternative in terms of personal security is to carry out P2P exchanges exclusively online, via electronic payment methods such as PayPal, bank transfers or Revolut.

This approach avoids many of the risks associated with cash transactions. However, the risk of the counterparty defaulting on an online exchange is greater. Indeed, in a physical exchange, if you hand over money to the seller who doesn't send you the bitcoins in return, you can immediately call him to account, since he's standing in front of you. Online, on the other hand, it's often impossible to track down someone who has stolen from you.

To mitigate this risk, it is possible to use specialized platforms for P2P exchanges. These platforms use conflict resolution mechanisms to protect aggrieved users. Typically, they offer an escrow system, where bitcoins are held until payment in fiat currency is confirmed by the seller.

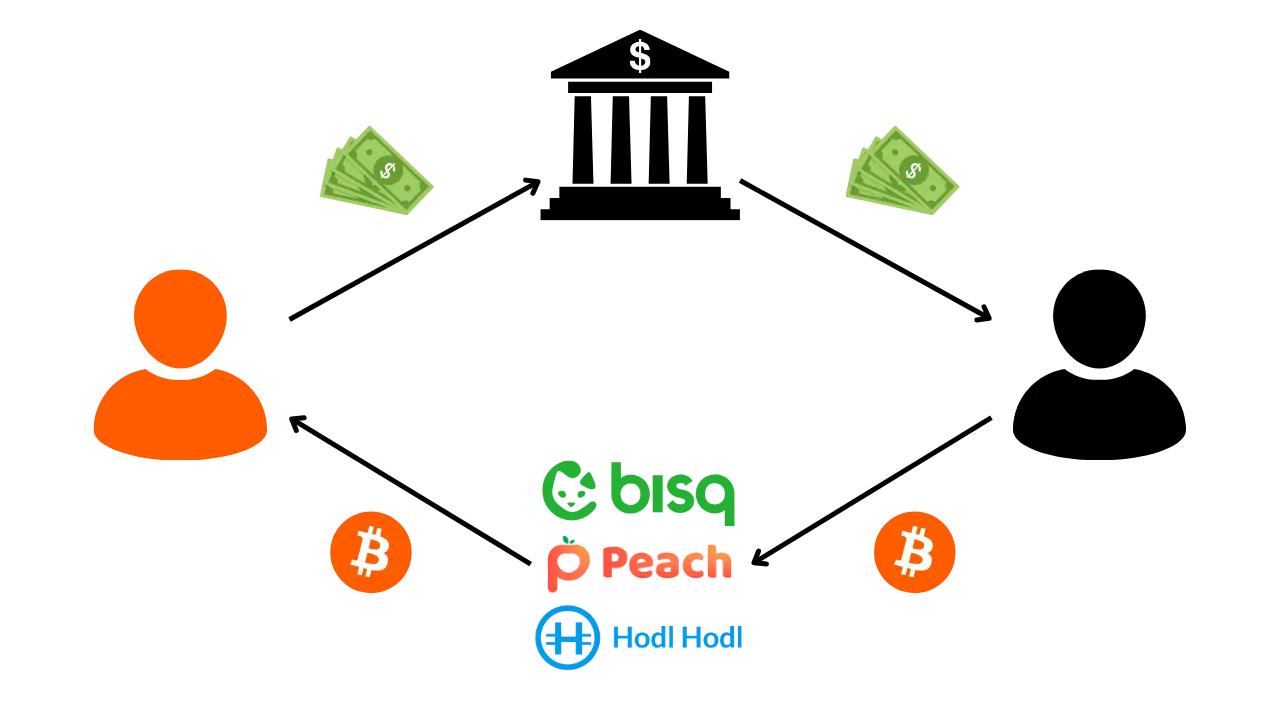
In terms of personal security, this method of purchase is considerably safer than a physical cash exchange. However, as mentioned above, online P2P exchanges leave more traces than a physical exchange, which can be detrimental to privacy on Bitcoin. By using an online fiat payment method such as a bank, you expose more information that could facilitate key identification.

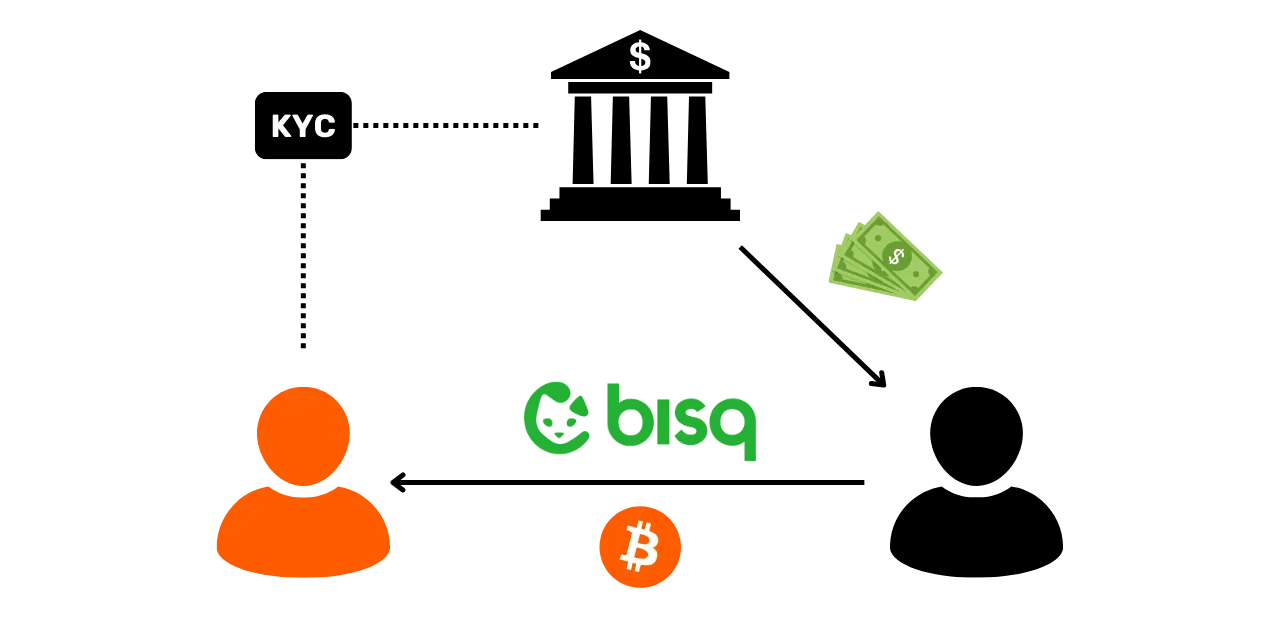
Once again, I wouldn't recommend making too many large trades in a single transaction on these platforms. By splitting up your transactions, you spread the risk of counterparty theft.

Once again, another disadvantage of P2P purchases is that the price is often higher than that observed on regulated platforms. Sellers often charge a mark-up ranging from 1% to sometimes more than 10%. There are several reasons for this price difference. Firstly, this is a common practice among P2P sellers that has become established over time. Secondly, sellers have fees associated with the transaction to send the funds to the buyer. There is also an increased risk of theft in P2P sales compared to platform transactions, which justifies compensation for the risk taken. Finally, the extra cost may be linked to the demand and quality of the exchange in terms of confidentiality. As a buyer, the gain in confidentiality has a price which is reflected in the mark-up applied by the seller. Some bitcoiners also believe that the mark-up price of BTC bought on P2P reflects its true price, and argue that the lower prices on regulated platforms are the result of a compromise on the confidentiality of your personal data.

As far as solutions are concerned, I've personally always used Bisq and I'm very happy with it. Their system is tried and tested and seems reliable. However, Bisq is only available on PC and its interface may be too complex for beginners. Another drawback is that Bisq only operates with onchain transactions, which can become costly during periods of high Bitcoin transaction fees.

-> See our Bisq tutorial.

https://planb.network/tutorials/exchange/peer-to-peer/bisq-fe244bfa-dcc4-4522-8ec7-92223373ed04

For a simpler option, you can try Peach, a mobile app that connects buyers and sellers with a built-in conflict resolution system. The process is more intuitive than Bisq's.

-> See our Peach tutorial.

https://planb.network/tutorials/exchange/peer-to-peer/peach-c6143241-d900-4047-9b73-1caba5e1f874

Another online option is HodlHodl, a well-established platform that offers good liquidity, although I haven't personally tested it.

-> See our HodlHodl tutorial.

https://planb.network/tutorials/exchange/peer-to-peer/hodlhodl-d7344cd5-6b18-40f5-8e78-2574a93a3879

For Lightning Network-based solutions, try RoboSats and LNP2PBot. RoboSats is accessible via a website and is relatively simple to use. LNP2PBot is more atypical, as it works via an exchange system on the Telegram messaging application.

-> See our RoboSats tutorial.

-> See our LNP2PBot tutorial.

https://planb.network/tutorials/exchange/peer-to-peer/robosats-b60e4f7c-533a-4295-9f6d-5368152e8c06

https://planb.network/tutorials/exchange/peer-to-peer/lnp2pbot-v2-e6bcb210-610b-487d-970c-7cce85273e3c

Regulated platforms without KYC

Depending on the country you live in, you may have access to regulated platforms that don't require KYC procedures to buy or sell bitcoins. In Switzerland, for example, you can use platforms such as Relai and MtPelerin.

-> See our tutorial on Relai.

https://planb.network/tutorials/exchange/centralized/relai-v2-30a9671d-e407-459d-9203-4c3eae15b30e

As we saw in the previous chapter, this type of platform saves you from the risks associated with KYC procedures, but they do present a higher level of risk for key identification. In terms of Bitcoin confidentiality, then, these platforms offer better protection than buying methods with KYC, but they remain less attractive than P2P exchanges.

However, in terms of personal security, using these platforms is far less risky than P2P exchanges. They are also often simpler to use than P2P platforms.

ATMs

Another option for buying or selling bitcoins without KYC are cryptocurrency ATMs. Personally, I've never had the opportunity to test this solution, as there aren't any in my country. But this method can be very interesting, depending on where you live.

The problem with ATMs is that they are either prohibited in some countries, or highly regulated in others. If an ATM requires an identity verification procedure, then it is exposed to the same risks as those inherent in KYC-regulated platforms. On the other hand, if the ATM allows transactions without identity verification for small amounts, then its use can offer a level of confidentiality comparable to that of a P2P cash exchange, while avoiding most of the risks associated with this type of exchange.

The main disadvantage of ATMs is their often high exchange fees, ranging from a few percent up to sometimes 15% of the amount exchanged.

Gift cards

Finally, I also wanted to introduce you to a solution that works well for those who want to use their bitcoins on a daily basis to make purchases rather than sell them against fiat currencies.

The best way to spend BTC is, of course, to use Bitcoin or the Lightning Network directly to purchase a good or service. However, in many countries, the number of merchants accepting Bitcoin is still limited. A practical alternative is to use gift cards.

Several platforms that do not require KYC procedures offer the possibility of exchanging bitcoins for gift cards that can be used at major retailers. These include CoinsBee, The Bitcoin Company and Bitrefill. These platforms make it much easier to use your bitcoins on a daily basis, giving you access to a wide range of products and services without having to convert them into fiat currency.

https://planb.network/tutorials/exchange/centralized/bitrefill-8c588412-1bfc-465b-9bca-e647a647fbc1

Other acquisition methods

Other ways of acquiring bitcoins while protecting your privacy include, of course, mining. To start mining sats, you don't need to reveal your identity; simply find a valid proof of work and submit it to the network. If you opt for pool mining, some pools require some form of identification, such as a KYC, while others do not.

Another method is to work in exchange for bitcoins. This method of acquisition can be interesting, but the degree of identification required varies considerably depending on the circumstances.

*To write this chapter, I used the BTC205 training course given by @pivi___ on the Plan ₿ Network (available only in French for the moment)

Consolidation, UTXO management and CIOH

One of the most complicated aspects of running a self-custody portfolio is consolidation. Should you consolidate? What's the point? What size of UTXO should be respected? What are the compromises in terms of confidentiality? That's what we're going to look at in this section.

What is consolidation?

Bitcoin operates like an auction market, with miners giving preference to transactions offering the lowest fees. However, each block has a maximum weight, which limits the number of transactions that can be included. As a block is produced on average every 10 minutes, the space available in each block is a scarce resource.

Miners, whose activities generate significant costs in terms of electricity, fixed assets and maintenance, naturally seek to maximize their profitability. They therefore tend to favour transactions that generate the highest fees relative to their weight.

Not all Bitcoin transactions carry the same weight. Those with more inputs and outputs will weigh more. For example, let's imagine 2 transactions:

Transaction A comprises 1 input and 1 output. It allocates 1,994 sats of fees and has a weight of 141 vB ;
Transaction B, a more complex transaction with 2 inputs and 2 outputs, allocates 2,640 sats in fees for a weight of 220 vB.

In this example, although transaction B offers a higher total fee, miners will prefer transaction A, as it offers a better ratio between fee and weight. Here's the calculation for each transaction, expressed in sats per virtual byte (sat/vB):

TXA : 1994 / 141 = 14 sats/vB
TXB : 2640 / 220 = 12 sats / vB

This means that for each unit of weight, transaction A offers more costs than transaction B, even though transaction B offers more costs in absolute terms.

It is therefore always more interesting for the user to consume as little input as possible in his transactions. However, you need to consume sufficient amounts to be able to satisfy the output payment. When managing your portfolio, you need to have sufficiently large UTXOs.

The principle of consolidation is precisely to take advantage of periods when fees are low on Bitcoin to merge its smaller UTXOs into a single larger one. This way, when fees rise on Bitcoin, you'll be able to make transactions with a minimum of inputs, and therefore spend less on fees in absolute terms. The aim is therefore to anticipate the compulsory transactions to be carried out during periods of high fees.

In addition to saving on transaction costs, consolidating UTXOs helps prevent the formation of "dust". Dust" refers to UTXOs whose value in sats is so low that it is insufficient to cover the transaction costs required to spend them. This makes these UTXOs economically irrational to use for as long as the transaction costs remain high. By proactively pooling your UTXOs, you prevent them from turning to dust, ensuring that all your funds remain usable.

What's the minimum size for your UTXOs?

I'm sometimes asked what the recommended minimum value for a UTXO is. Unfortunately, there's no universal answer, as it depends on your preferences and the conditions of the fee market. However, here's a formula that may help you determine a threshold suited to your needs:

 $\frac {P \times F}T = M$

Where:

p$ is the transaction weight;
$F$ represents the maximum charge rate in satoshis per vbyte (sats/vB) against which you hedge;
t$ is the percentage of the transaction fee you are willing to pay in relation to the total value of the UTXO ;
m$ is the minimum amount in satoshis for each UTXO.

Let's assume that you plan to cover the fees for a standard SegWit transaction with 1 input and 2 outputs, weighing 141 vB. If you're hedging up to 800 sats/vB, and you're willing to spend up to 12% of the UTXO value in fees at most, then the calculation would be:

 $\frac{141 \times 800}{0.12} = 940\ 000$

In this example, it would therefore be wise to keep a minimum value of 940,000 sats for UTXOs in your portfolio.

Consolidation and CIOH

One of the most widely used heuristics in blockchain analysis is the CIOH (Common Input Ownership Heuristic), which assumes that all inputs to a Bitcoin transaction belong to the same entity. The very principle of consolidation is to consume several UTXOs as inputs and create a single UTXO as an output. Consolidation thus enables the ICOH to be applied.

In practice, this means that an outside observer can deduce that all the consolidated UTXOs probably belong to the same person, and that the unique output generated also belongs to him or her. This situation can jeopardize your confidentiality by associating different transaction histories. For example, let's say I consolidate 3 UTXOs acquired via P2P with one UTXO obtained via a platform that requires KYC :

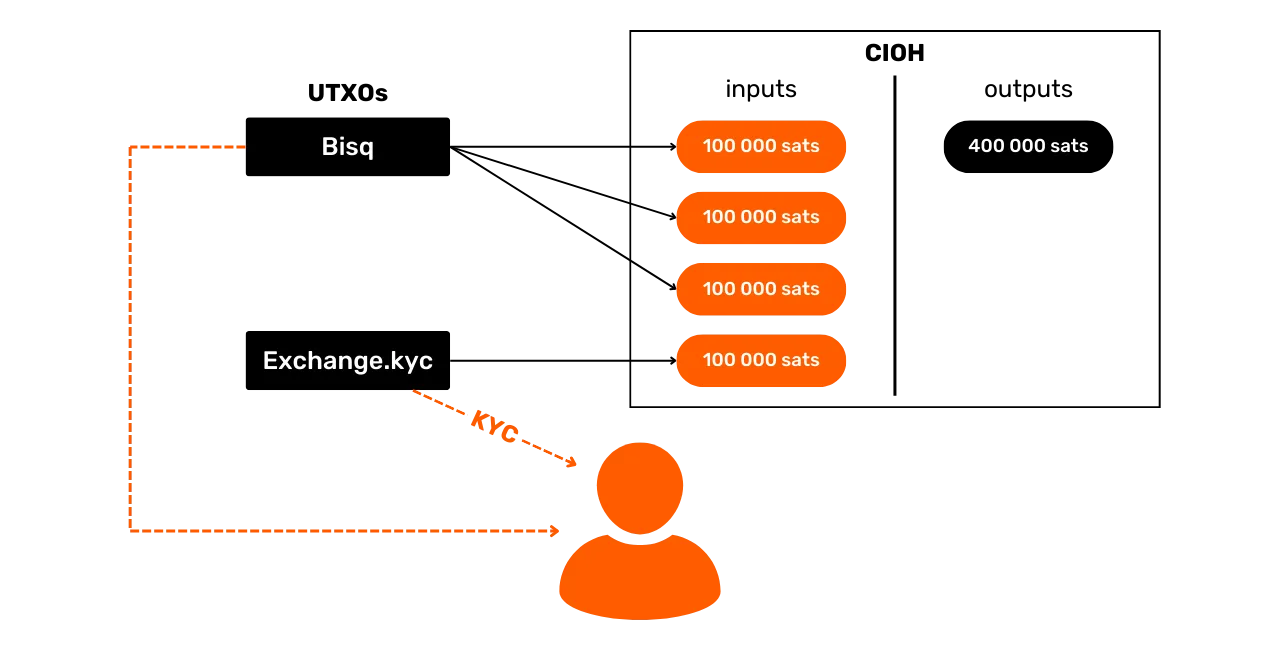
By doing so, any entity with access to the exchange platform's data, potentially including government agencies, will be able to identify that I own other amounts of BTC. Previously, these UTXOs were not directly linked to my identity; now they are. What's more, it reveals to all sources that I'm in possession of a certain amount of bitcoins.

When it comes to managing UTXOs, economic considerations, which drive consolidation to reduce costs, come into conflict with good privacy practice, which would recommend never merging UTXOs. The choice between economy and confidentiality therefore depends on the priorities of each user.

If you can avoid consolidation while maintaining substantial UTXOs, that's ideal. To do this, optimize your acquisition methods. If you buy your bitcoins in DCA, try to space out your one-off purchases as much as possible to consolidate value over fewer UTXOs. It will be easier to manage a one-off purchase of €1,000 every 2 months, rather than a purchase of €120 every week. This minimizes the number of UTXOs generated and simplifies the management of your portfolio while preserving your confidentiality.

If you find yourself having to consolidate your bitcoins, give preference first to consolidating UTXOs from the same source. For example, merging 10 UTXOs from a single platform will affect your confidentiality less than mixing 5 UTXOs from platform A with 5 UTXOs from platform B. If consolidation of various sources is unavoidable, try to separate them according to their characteristics. For example, group together UTXOs acquired via KYC in one transaction, and those obtained via P2P in another.

In any case, don't forget that any consolidation inevitably entails a loss of confidentiality. So carefully assess the need for this operation and the potential impact on your privacy, taking into account the CIOH.

Other best practices

Let's take a look at a few other best practices for optimizing your privacy on Bitcoin.

The complete knot

Owning your bitcoins in self-custody is great, but using your own complete node is even better! Here's why having your own node is crucial for fully sovereign use of Bitcoin:

Resistance to censorship**: Your transactions cannot be blocked by anyone;
Independence from third parties**: You no longer depend on any external service to verify blockchain data;
Active participation**: You can define your own validation rules and take part directly in the consensus;
Network contribution**: By running a node, you help strengthen and distribute the Bitcoin network;
Technical education**: Managing a complete node is a great way to deepen your technical knowledge of Bitcoin.

In addition to these benefits, using a complete node also improves your confidentiality when broadcasting your transactions. When you issue a transaction, it is first created and signed via your wallet. To broadcast it on the Bitcoin network, it must be known by at least one node. By using your own node, you have direct control over this distribution, thereby reinforcing your confidentiality and limiting the risk of data leakage.

If you don't have your own Bitcoin node, you'll be forced to use a third-party one, such as the one offered by your wallet software provider. In addition to broadcasting transactions, your wallet requires access to various information such as pending transactions, balances associated with your addresses and the number of confirmations for your transactions. To access all this data, you need to query a node.

The main risk when you're not using your own Bitcoin node is that the operator of the third-party node could observe your activities on the blockchain, or even share this information with other entities. To limit this risk, an intermediate solution is to use wallet software that masks your connections via Tor. This can reduce the exposure of your data. However, the optimal solution is to have your own Bitcoin node and use it to broadcast your transactions. Of course, you'll also need to be careful not to leak any information through your node, but that's another subject we'll look at in later sections.

Beyond the obvious advantage for your privacy, having your own complete node also assures you of the veracity of data on the blockchain, protects you against censorship and allows you to actively participate in Bitcoin's governance. By using your own node, you contribute your economic weight to the chain of your choice, which is important during conflicts within the community, such as during the Blocksize War from 2015 to 2017 for example. In the event of a fork, using a third-party node could lead you to support a chain you don't want to favor, as the node operator makes the choice for you.

As you can see, in the interests of confidentiality and individual sovereignty, it's essential to run and use your own complete node!

Deceiving analysis heuristics

More broadly, it's important to understand the heuristics we talked about in the previous section, so as to better avoid or deceive them. Adopting a series of best practices can be beneficial, even if they are not essential. They offer an extra layer of protection that can be important in maintaining confidentiality when using Bitcoin.

The first piece of advice I could give is to blend in with the densest crowd. On Bitcoin, this means using the most widely adopted script templates. For example, P2WSH scripts, often used for SegWit V0 multisig configurations, are very uncommon. They don't allow you to hide in a large anonymity set. The same goes for older models such as P2PKH or P2SH. Although they are widely present in the UTXO set, they are used less and less for new transactions.

Generally speaking, it's wiser to opt for the most recent scripting standard, provided that it has been sufficiently adopted. So, if in 2022, I would have advised against using P2TR (Taproot) due to its low adoption, in 2024, I would recommend opting for this type of script instead, or failing that, for SegWit V0 script, as the number of transactions using P2TR is starting to represent a very significant proportion.

Source : txstats.com

Another tip for preserving your confidentiality is to try to bypass internal transaction heuristics. For example, when making a payment, you can try to avoid creating an output with a round amount, as this could signal that the other output represents foreign exchange. If you need to send 100 k sats to a friend, consider transferring a slightly higher amount to escape this heuristic. Similarly, try not to create foreign exchange outputs that are disproportionately high in relation to the payment made, as this could also reveal which of the outputs represents foreign exchange.

Finally, if you carry out Bitcoin transactions on a regular basis, make sure you don't always broadcast them at the same times. By spreading the broadcast of your transactions throughout the day and week, you avoid giving outside observers the opportunity to detect a time-zone-based temporal pattern that could reinforce their analysis.

In addition to all these good practices to be adopted on a daily basis, there are even more effective methods for completely breaking the traceability of your bitcoins. These include, of course, coinjoin transactions, which we'll look at in depth in the next section.

Understanding coinjoin transactions

What's a coinjoin transaction?

Having studied the fundamentals of privacy protection, we're now going to look at more sophisticated techniques aimed at actively defending your confidentiality, in particular by unbundling your bitcoin history. In the next part, we'll be looking at a whole host of little techniques, but first, I'd like to tell you about coinjoin.

Coinjoin is often considered the most effective method of protecting Bitcoin users' privacy. But what exactly is a coinjoin transaction? Let's find out.

The basic principles of coinjoin

Coinjoin is a technique for breaking bitcoin tracking on the blockchain. It is based on a collaborative transaction with a specific structure of the same name: the coinjoin transaction.

As we saw in the first parts of this course, Bitcoin transactions are known to all users via their node. It is therefore easy to check the electronic signature chain of each coin and observe its history. This means that all users can attempt to analyze the transactions of other users. As a result, anonymity at transaction level is impossible. However, anonymity is preserved at the level of individual identification. Unlike the conventional banking system, where each account is linked to a personal identity, on Bitcoin, funds are associated with cryptographic key pairs (or scripts), offering users a form of pseudonymity behind cryptographic identifiers.

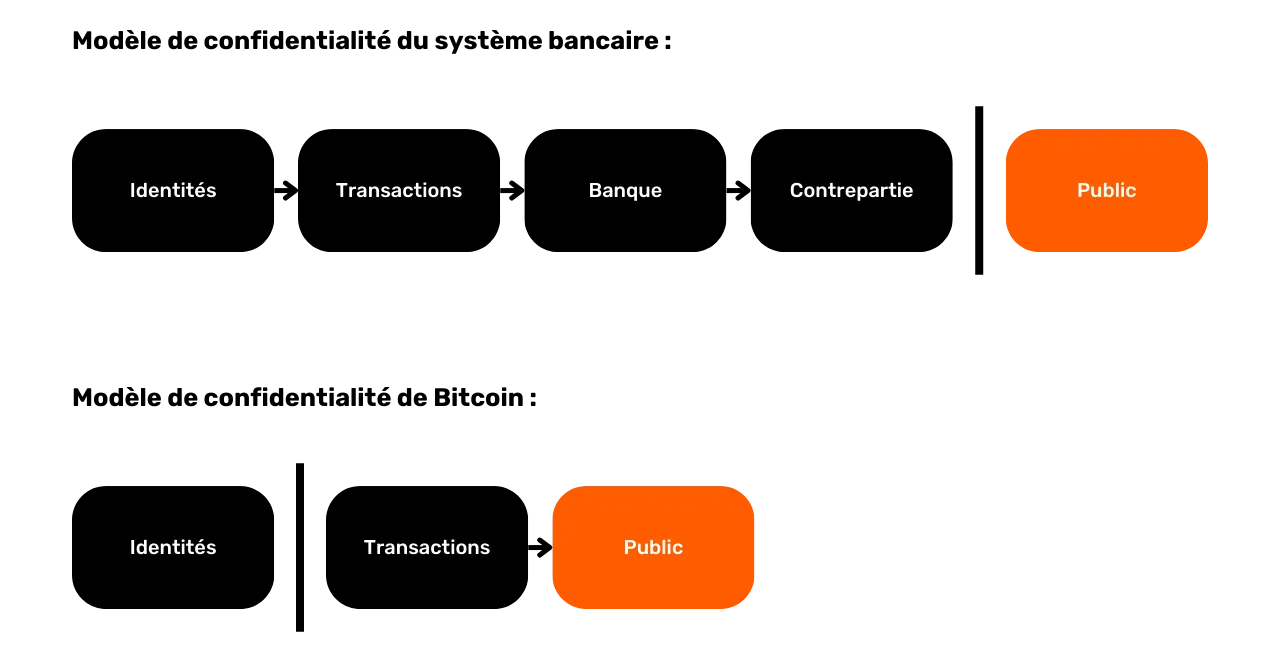
Bitcoin's confidentiality is undermined when outside observers are able to associate specific UTXOs with identified users. Once this association has been established, it becomes possible to trace their transactions and analyze their Bitcoin history. Coinjoin is precisely a technique developed to break the traceability of UTXOs, in order to offer Bitcoin users a certain layer of confidentiality at transaction level.

Coinjoins reinforce the confidentiality of Bitcoin users by making chain analysis more complex for external observers. Their structure allows multiple coins from different users to be merged into a single transaction, blurring the lines and making it difficult to determine the links between input and output addresses.

It's important to understand that the aim of a coinjoin transaction is to break the history of a coin. This technique does not confer permanent anonymity or definitively block bitcoin tracking, contrary to what you might think. Coinjoin only aims to break the history at the point where the coinjoin transaction is carried out. However, before and after this operation, the coin remains subject to the same risks in terms of confidentiality.

How do coinjoins work?

The coinjoin principle is based on a collaborative approach: several users wishing to mix their bitcoins deposit identical amounts as inputs to the same transaction. These amounts are then redistributed in outputs of equal value to each user.

At the end of the transaction, it becomes impossible to associate a specific output with a user known as an input. There is no direct link between inputs and outputs, which breaks the association between users and their UTXOs, as well as the history of each part.

Let's take Alice's example. She wants to send around 100,000 sats to her sister Eve for her birthday. However, Alice doesn't want Eve to be able to trace her transaction history, as she doesn't want to reveal how many bitcoins she has or how she got them. To this end, Alice decides to break her UTXO history with a coinjoin transaction. She organizes with Bob, Charles, David and Frank to carry out a collaborative transaction:

Alice, Bob, Charles, David and Frank each commit a UTXO of 105,000 sats (with 5,000 sats for mining fees) as inputs to the transaction:

In return for consuming these inputs, each generates a blank address to create five identical outputs of 100,000 sats each. Each retrieves one output:

Alice finds herself with an UTXO of 100,000 sats whose history is mixed up. She uses this UTXO in a new transaction to send the amount to Eve for her birthday:

If Eve tries to analyze this transaction to extract information, she will be confronted with the coinjoin transaction involving Alice, Bob, Charles, David and Frank. Unable to distinguish which input belongs to whom due to the uniformity of the amounts, Eve cannot trace Alice's UTXO history, nor determine how many bitcoins her sister owns or how she acquired them:

In this case, Alice has used the coinjoin technique to increase confidentiality with regard to retrospective analysis. In effect, Alice is protecting herself against a possible analysis by Eve, who would start from a specific transaction and work backwards through the history of the UTXO. This protection against analysis from the present to the past is known as retrospective anonset. We'll look at this concept in more detail in the final chapters of this section.

However, coinjoin also offers the possibility of reinforcing confidentiality in the face of an analysis from the past to the present, known as prospective anonset. Let's go back to our example where Alice sent Eve 98,000 sats for her birthday, but with the roles reversed. Now let's imagine that it's Eve who's worried about her privacy. Indeed, Alice might be tempted to track the coin she sent Eve in order to extract information from it. Eve could well consolidate this UTXO she has just received with all her other UTXOs, which could reveal to Alice the amount of bitcoins she has in her wallet. To avoid this, Eve can also break the history of the coin she has just received:

Eve, Grace, Mallory, Oscar and Victor each put in a UTXO of 98,000 sats as input to a Bitcoin transaction:

In return for consuming these inputs, each user provides a blank address to be used to create 5 outputs of 97,500 perfectly equal sats. Each user gets one output:

Eve now holds a UTXO of 97,500 sats whose history has been broken. She can use it without fear to carry out future transactions. Indeed, if Alice tries to track the bitcoins she has sent to Eve, she will be confronted with a coinjoin transaction. She will be unable to determine which outgoing UTXO belongs to Eve. Analysis becomes impossible:

In the first example, we saw how the coinjoin can protect a room's privacy in relation to its past, and in the second example, how it can also secure a room's history in relation to its future. That's why I mentioned that the coinjoin should be seen as a one-off event that segments a part history in both directions:

Mixer, coinjoin, mixer... What's the difference?

Coinjoins are sometimes described as "mixers", a term that some bitcoiners reject, fearing that it could be confused with custodial mixers. I believe, however, that this apprehension is ill-founded, since, in a mathematical context, the coinjoin embodies precisely the concept of mixing.

In the general field of mathematics, mixing refers to the property of a dynamical system where, after a certain period of time, all portions of the initial space can theoretically become mixed with any other portion. Mixing implies that the position of a particle or the state of a system evolves in such a way that its future distribution is independent of its initial distribution, thus reaching a state where the characteristics of the initial state are uniformly distributed throughout the system's space. This is exactly what happens in a coinjoin with bitcoins. So, in my opinion, coinjoin is truly a coin mixing method.

On the other hand, it's important to distinguish coinjoin from shufflers. A shuffler is a service where users send their bitcoins to be shuffled. These services were popular during the 2010s, but their use has declined due to two major drawbacks compared to coinjoin:

They require users to relinquish custody of their funds during the blending process, which exposes them to the risk of theft;
There's no guarantee that the mixer won't record transaction details, or even sell this information to chain analysis companies.

Today's users therefore prefer coinjoin, as it allows them to retain total control over their funds throughout the process. Coinjoin participants run no risk of having their bitcoins stolen by the other parties involved. Let's take a look at how all this is possible in the next chapter.

Zerolink and chaumian coinjoins

The privacy provided by a coinjoin is earned by the size of the group in which our piece is hidden. This means finding as many participants as possible. It's perfectly possible to create a coinjoin manually, with users we've found ourselves, but this is a complex process, and won't win you any big anonsets.

This is why coinjoin coordinators have developed on Bitcoin. Their role is to put the various users in touch with each other and transmit the information needed to complete the collaborative transaction.

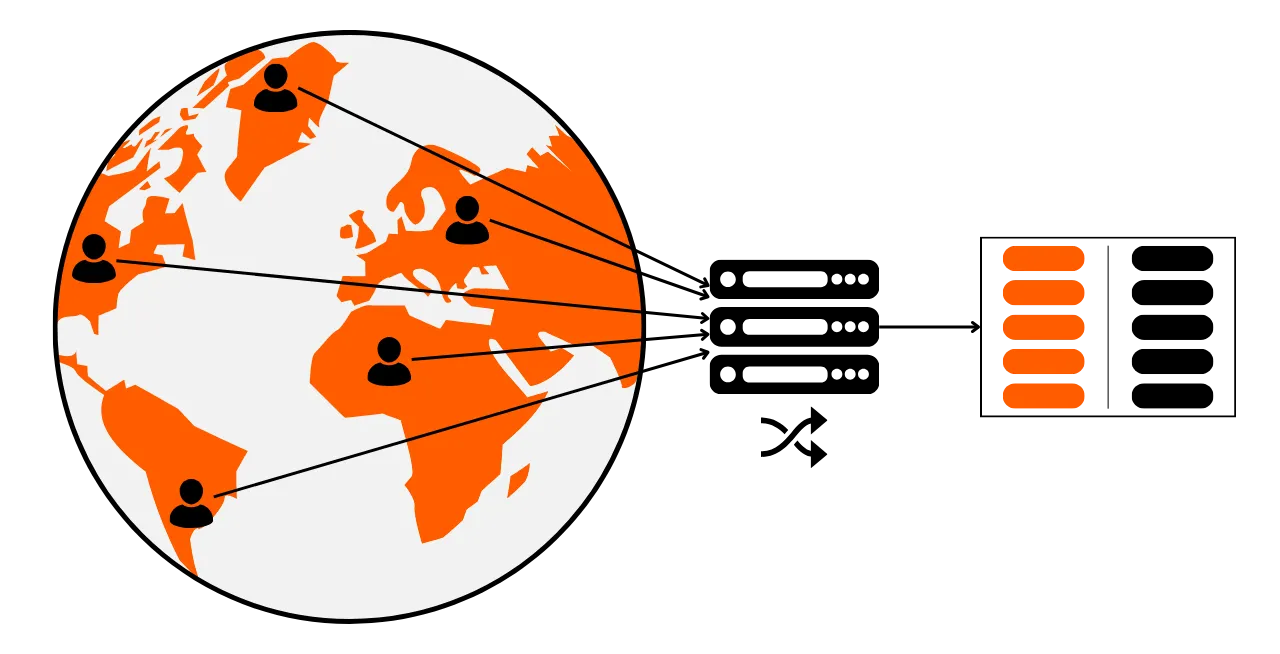
But how can we ensure that the coordinator never has his hands on users' bitcoins, and despite the fact that he's the person building the coinjoin transaction, how can we ensure that he can't link users' inputs and outputs, which could constitute a confidentiality leak?

Chaum's blind signatures

Modern coinjoin implementations use David Chaum's blind signatures to avoid leaking information. Let's take a quick look at how these blind signatures work.

Chaum's blind signatures are a form of digital signature in which the issuer of a signature does not know the content of the message he is signing. But the signature can then be verified against the original message. This technique was developed by cryptographer David Chaum in 1983.

Let's take the example of a company wishing to authenticate a confidential document, such as a contract, without revealing its content. The company applies a masking process that cryptographically transforms the original document in a reversible way. This modified document is sent to a certification authority, which affixes a blind signature without knowing the underlying content. After receiving the signed document, the company unmasks the signature. The result is an original document authenticated by the authority's signature, without the authority ever having seen the original content.

Chaum's blind signatures can therefore certify the authenticity of a document without knowing its content, thus guaranteeing both the confidentiality of the user's data and the integrity of the signed document.

Chaumian coinjoins

So-called "Chaumian" coinjoins combine the use of Tor and David Chaum's blind signatures to ensure that the coordinator can't know which output belongs to which user.

The coinjoin transaction construction process involves 3 main stages: input registration, output registration and transaction signature. Let's look at this process through the example of Alice, one of the coinjoin participants. All the other participants follow the same steps as Alice, each on their own.

**Step 1: Input registration

Alice transmits to the coordinator the UTXO she wishes to use as input to the transaction, as well as the masked receive address she wishes to use as output to receive her bitcoins. The coordinator therefore has no way of knowing Alice's address. It only sees her masked version:

The coordinator checks the validity of the inputs, then signs Alice's masked address with his private key. He returns the blind signature to Alice:

Step 2: Outputs registration

Alice can unmask her address, now signed by the coordinator's private key. She will establish a new connection under a different Tor identity. The coordinator can't identify that it's Alice who's connecting under this new identity:

Alice sends the unmasked address and signature to the coordinator (who still doesn't know it's Alice):

Step 3: Signing the transaction

In the same way, the coordinator retrieves unmasked outputs from all participants. Thanks to the associated signatures, he can check that each anonymously submitted output has been signed by his private key beforehand, thus guaranteeing their legitimacy. He is then ready to build the coinjoin transaction and sends it to the participants for signature:

Alice, like the other participants, checks that her input and output are correctly included in the transaction constructed by the coordinator. If everything is satisfactory, she sends the signature that unlocks her input script to the coordinator:

After collecting signatures from all coinjoin participants, the coordinator can broadcast the transaction on the Bitcoin network, so that it can be added to a block.

In this system, the coordinator is unable to link an input to a specific output. What's more, he can't appropriate participants' funds, as he never has access to the private keys needed to unlock their UTXOs. Throughout the process, until the end of step 3, he also has no access to the signatures. When Alice and the other participants sign the global transaction, after checking that everything is correct, the coordinator can no longer modify the transaction, including the outputs, without invalidating it. This prevents the coordinator from stealing bitcoins.

Finally, when registering his output in the transaction, the coinjoin user wishes to have guarantees similar to those of a citizen voting in an election. There is a duality between the public and private aspects of these actions. On the one hand, there's what you want to keep private: for the voter, he doesn't want his ballot to be linked to his identity; for the coinjoin user, he doesn't want his output to be associated with his input. Indeed, if the coordinator, or any other party, manages to establish a link between an input and an output, the coinjoin loses all interest. As explained above, the coinjoin must function as a break in the history of a coin. This stop occurs precisely because of the impossibility of associating a specific input with a specific output in the coinjoin transaction (prospective anonset) and vice versa (retrospective anonset).

On the other hand, there's the public aspect: the voter wants to be sure that his ballot is included in the ballot box; similarly, the coinjoin user wants to be sure that his output is included in the coinjoin transaction. Indeed, coinjoin participants absolutely must be able to verify the presence of their output before signing the transaction, otherwise the coordinator could steal the funds.

It is precisely these 2 public and private aspects, enabled by the use of David Chaum's blind signatures, that guarantee participants in Chaumian coinjoins that their bitcoins will not be stolen, and that their funds cannot be traced.

Who invented the coinjoin concept?

It's hard to say for sure who first introduced the coinjoin idea to Bitcoin, and who came up with the idea of using David Chaum's blind signatures in this context. It's often thought that it was Gregory Maxwell who first mentioned it in a message on BitcoinTalk in 2013 :

*"Using Chaum's blind signatures: Users log in and provide inputs (and exchange addresses) as well as a cryptographically blinded version of the address to which they wish to send their private parts; the server signs the tokens and sends them back. Users reconnect anonymously, unmask their output addresses and send them back to the server. The server can see that all outputs have been signed by it and that, consequently, all outputs come from valid participants. Later, people reconnect and sign in Maxwell, G. (2013, August 22). CoinJoin: Bitcoin privacy for the real world. BitcoinTalk Forum. https://bitcointalk.org/index.php?topic=279249.0

However, there are other earlier mentions, both for Chaum signatures as part of mixing, but also for coinjoins. In June 2011, Duncan Townsend presented on BitcoinTalk a mixer that uses Chaum signatures in a manner quite similar to modern Chaumian coinjoins.

In the same thread, we can find a message from hashcoin in response to Duncan Townsend to improve his mixer. The process described in this message is exactly what coinjoins are all about. Mention of a similar system can also be found in a message from Alex Mizrahi in 2012, when he was advising the creators of Tenebrix, one of the first altcoins that served as the basis for later creating Litecoin. Even the term "coinjoin" itself is said not to have been coined by Greg Maxwell, but to have come from an idea by Peter Todd.

Zerolink

Zerolink is a comprehensive mixing protocol that incorporates Chaumian coinjoins and various strategies to protect users' anonymity against several forms of chain analysis, in particular by minimizing errors associated with portfolio management. This protocol was introduced by nopara73 and TDevD in 2017.

As its name suggests, the principle behind Zerolink is to create coinjoin transactions which ensure that the links between inputs and outputs cannot be traced. This is achieved by ensuring that all outputs have perfectly identical amounts.

An important preventive measure taken by Zerolink is to keep unmixed UTXOs completely separate from mixed UTXOs by using separate cryptographic key sets, or even separate portfolios. This differentiates the "pre-mix" wallet, intended for parts before mixing, from the "post-mix" wallet, reserved for parts that have been mixed.

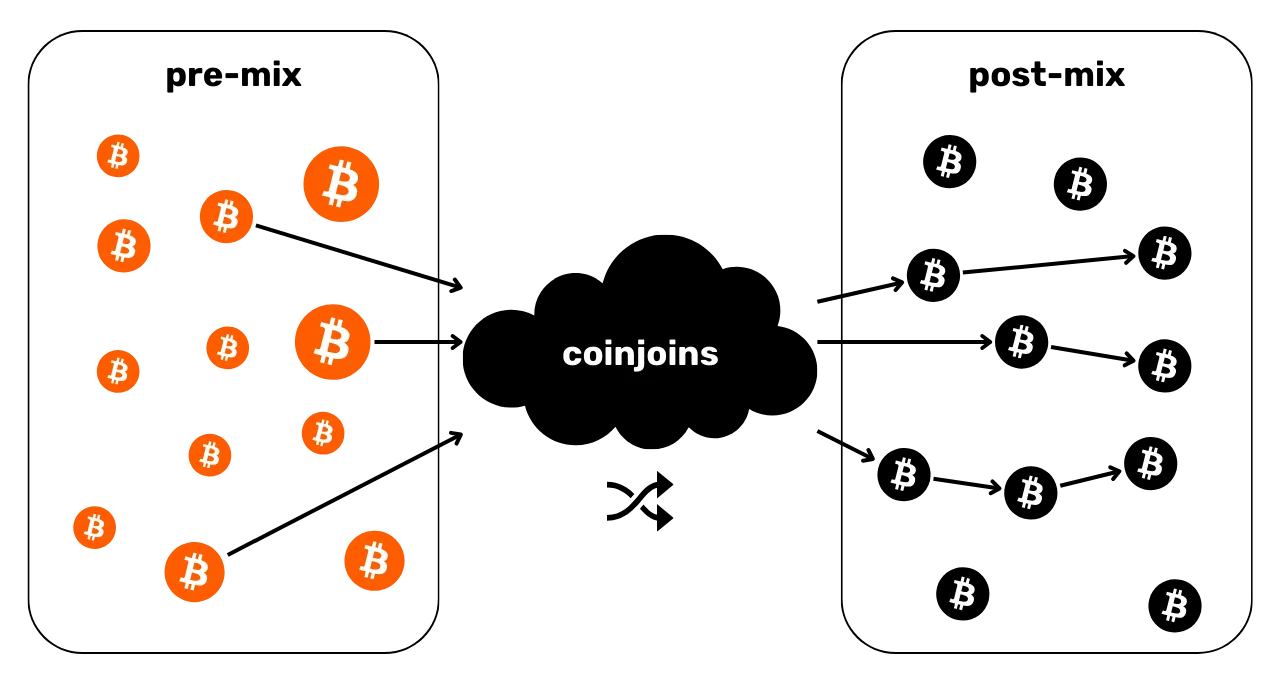
This rigorous separation of UTXOs serves above all to prevent accidental associations between a mixed UTXO and an unmixed UTXO. Indeed, if such links occur, the effectiveness of the coinjoin on the mixed UTXO is cancelled without the user being aware of it, thus compromising the confidentiality of a UTXO whose history he thought he had broken. These links can occur either through address reuse on the securing of a mixed UTXO with an unmixed one, or through the application of CIOH (Common-Input-Ownership Heuristic), if the user consumes mixed and unmixed UTXOs as inputs to the same transaction. By separating the pre-mix and post-mix portfolios, we avoid such accidental associations and protect the user against unintentional errors.

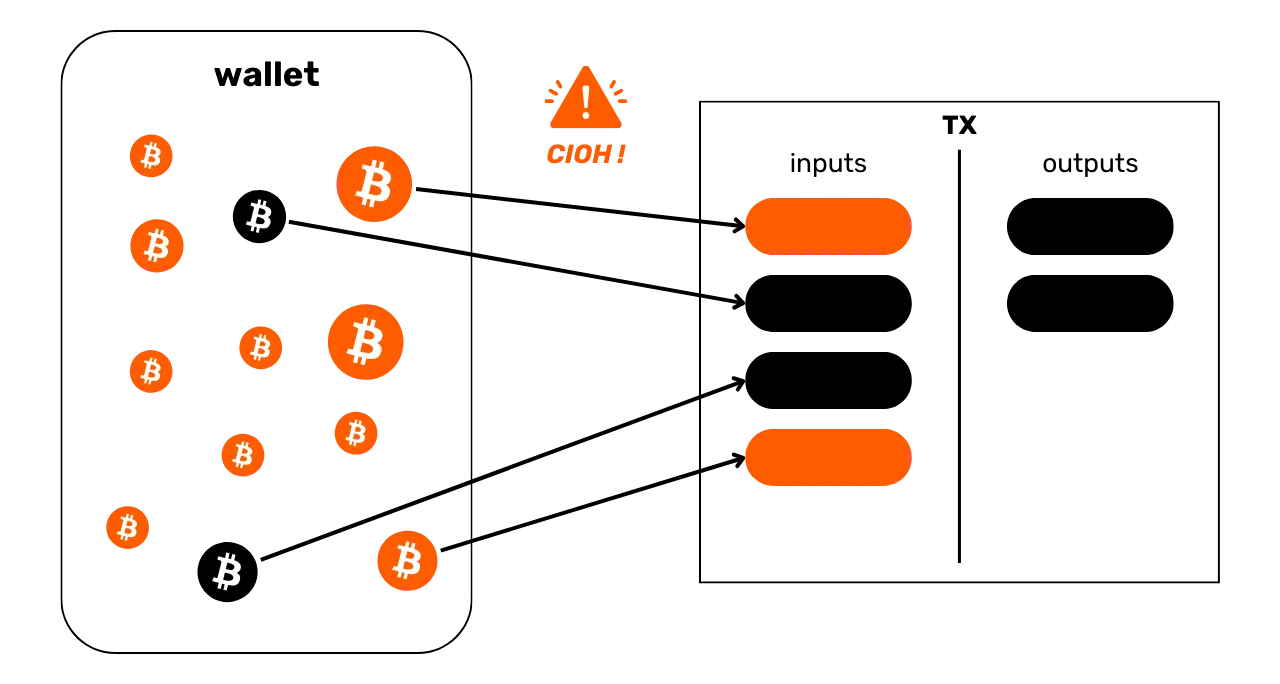
This separation also offers the possibility of applying distinct rules between pre-mix and post-mix portfolios at the portfolio software level. For example, in the post-mixing portfolio, the software can prohibit the merging of UTXOs into inputs to prevent the application of CIOH, which would compromise the user's anonset. It is also possible to standardize the use of scripts and transaction options (such as RBF reporting, for example) to prevent identification by wallet fingerprints.

Currently, Whirlpool is the only coinjoin implementation that rigorously applies the Zerolink protocol. In the next chapter, we'll take a look at the various coinjoin implementations that exist, and the advantages and disadvantages of each.

Coinjoin implementations

*In 2024, we are witnessing major changes in the tools available to users wishing to make coinjoins on Bitcoin. We're currently at a turning point, and the coinjoin market is undergoing major restructuring. This chapter is sure to be updated over time

For the moment there are mainly 3 different coinjoin implementations on Bitcoin:

Whirlpool;
Wabisabi;
JoinMarket.

Each of these implementations aims to break the history of UTXOs via coinjoin transactions. However, their mechanisms vary considerably. It is therefore essential to understand how each works, so you can choose the option best suited to your needs.

JoinMarket

JoinMarket, founded in 2015 by Adam Gibson and Chris Belcher, stands out clearly from other coinjoin implementations thanks to its unique model for connecting users. The system is based on a P2P exchange market where some users, the "makers", make their bitcoins available for mixing, while others, the "takers", use this cash to make coinjoins in return for a fee.

In this model, "makers" make their bitcoins available to "takers" and receive a fee for their service. The takers, in turn, pay to use the makers' bitcoins to carry out their own coinjoin transactions. Service fees vary according to the role occupied: "makers" accumulate fees for offering liquidity, while "takers" pay the fees. The market operates freely, with no conditions of use.

One of JoinMarket's main drawbacks is its complexity of use, which requires a certain degree of comfort with terminals to operate it effectively. While this complexity is not an obstacle for the experienced user, it may limit access to the general public. However, the recent introduction of a web interface called JAM has made it a little easier to use.

Source : JAM

However, the technical barrier remains a major obstacle. In the coinjoin ecosystem, where confidentiality is reinforced by the number of participants, any limitation reducing accessibility directly affects the available liquidity, which is a crucial factor in the efficiency of the mix. Bitcoin, being already a niche in financial transactions, sees its use of coinjoins as a sub-niche, and JoinMarket represents an even more specialized fraction of it, which therefore restricts its potential to increase its users' anonsets.

Despite its innovative P2P linking model for coinjoiners, JoinMarket has some significant disadvantages, particularly in terms of transactional structure. Unlike other implementations such as Whirlpool, JoinMarket does not guarantee perfect equality between outputs, and it is possible to trace deterministic links between inputs and outputs. Moreover, it has no tools to prevent parts already mixed together from being mixed again, which could compromise the confidentiality sought by users.

Finally, while the JoinMarket concept is interesting, especially for those interested in a dynamic liquidity market, its structural weaknesses and technical complexity make it, in my opinion, less interesting for both novices and experts looking for a coinjoin implementation.

Wabisabi

Wabisabi is another coinjoin implementation, with an approach that centralizes transaction coordination. This model was conceived Ádám Ficsór (nopara73), Yuval Kogman, Lucas Ontivero, and István András Seres in 2021, and was integrated into Wasabi 2.0 software the following year. Wabisabi is precisely an evolution of the Wasabi software coinjoin model launched in 2018.

Towards the end of the 2010s, Wasabi adopted a radically different coinjoin transaction structure to Whirlpool. Wasabi used very large coinjoin transactions involving dozens of participants to increase the anonsets of its participants. In contrast, Whirlpool opted for multiple small transactions, enabling anonsets to grow exponentially with each cycle.

Exchange management methods also distinguished the two implementations. With Whirlpool, foreign exchange was excluded and isolated from UTXOs prior to coinjoin cycles thanks to TX0, a concept I'll explain further in the next chapter. With Wasabi, on the other hand, foreign exchange formed one of the outputs of the coinjoin transaction, maintaining deterministic links between certain inputs and outputs.

With Wabisabi, Wasabi version 2.0 has adapted its approach to coinjoins to match that of Whirlpool. Although coinjoin transactions remain very large, it is now possible to chain several successive cycles, following the Whirlpool model. Particular attention has also been paid to exchange rate management: unlike Wasabi 1.0, where the exchange rate was directly linked to user inputs, Wabisabi seeks to subdivide the exchange rate into several small sums, divided into equal denominations for all participants.

Let's illustrate this with a simplified example involving just 2 users: Alice wishes to mix 115,000 sats and Bob, 210,000 sats. Ignoring fees, with Wasabi 1.0, a coinjoin transaction would have generated 3 outputs of 100,000 sats, plus 1 exchange of 15,000 sats for Alice and 1 exchange of 10,000 sats for Bob. The exchange outputs would still be linked to the inputs:

Under Wabisabi, the same transaction would have produced 3 outputs of 100,000 sats and 5 outputs of 5,000 sats, thus dispersing the exchange so that it could not be directly linked to a specific input:

Personally, I find that Wabisabi's foreign exchange management presents several risks that could compromise its effectiveness in terms of confidentiality:

When a user contributes a UTXO that is significantly larger than those of other participants, he inevitably ends up with an exchange amount that will be linked to his input. This runs counter to the original aim of the protocol, which is to eliminate all identifiable exchanges;
The multiplication of denominations with the aim of fragmenting the exchange can paradoxically be detrimental to mixing efficiency. This process can lead to a reduction in anonsets for certain outputs, as they become more easily identifiable;
This method also generates low-value UTXOs which pose a management problem for the user. These small UTXOs, if they become too costly to spend in relation to their value, can become "dust". This phenomenon leads the user to merge several UTXOs into inputs for future transactions, or to consolidate them. In both cases, because of the CIOH, this can either reduce the anonsets obtained, or completely cancel out the confidentiality benefits acquired by the initial coinjoin.

Unlike Whirlpool, which implements the ZeroLink protocol ensuring rigorous separation between pre-mix and post-mix UTXOs, Wabisabi does not maintain this strict segregation. There have also been problems of address reuse by some Wasabi customers, which are obviously very detrimental to the user.

In Wasabi version 2.0, a new coinjoin fee policy has been implemented. From now on, coordinator fees are set at 0.3% for UTXOs above 0.01 bitcoin, while for smaller UTXOs, these fees are offered in full. In addition, remixes for these smaller UTXOs are free of charge, although mining fees remain payable by the user for all transactions, including remixes.

This contrasts with Whirlpool's policy, where fees remain fixed, regardless of the size of the anonsets obtained. With Wasabi 2.0, although coordinator fees are waived for small UTXOs, the user still has to pay mining fees on all transactions, including remixes.

As I write these lines, the use of Wabisabi has become significantly more complex as a result of recent events. Following the arrest of Samourai Wallet's founders, zkSNACKs, the company that finances and manages Wasabi's development, announced that its coinjoin coordinator service would be discontinued on June 1, 2024. This coordinator, which was set up by default on Wasabi, was responsible for the vast majority of liquidity.

With the discontinuation of this main coordinator, users must now connect to new, independent coordinators. This change raises a number of concerns: on the one hand, new coordinators may not have sufficient liquidity, reducing the effectiveness of coinjoins in terms of confidentiality. On the other hand, there is the risk of running into a malicious coordinator. This situation adds significant new risks for those seeking to use Wabisabi.

Beyond the technical issues, the decision by zkSNACKs, the company behind Wasabi, to use the services of a string analysis company to filter coinjoin participants raises serious ethical and strategic questions. The initial idea was to prevent the use of coinjoins on Wasabi by criminals, a move that may seem legitimate. However, it raises a paradox: paying fees to a coordinator whose primary mission is to reinforce user confidentiality, only to have him fund a company whose aim is to compromise that same confidentiality.

Even more worrying is the principle of filtering, which contrasts radically with Bitcoin's philosophy of offering an open, uncensored financial system. While it may seem justified to want to exclude criminal activities, this filtering could also affect individuals whose actions, although classified as illegal in certain contexts, could be morally justifiable or socially beneficial. The example of Edward Snowden perfectly illustrates this dichotomy: considered a criminal by some governments for his revelations, he is seen by others as a whistleblower who acted in the public interest. This complexity underlines the potential danger of filtering which, although well-intentioned, can ultimately undermine the rights and security of legitimate users. I could also have mentioned activists and journalists who are persecuted under certain authoritarian regimes.

As you'll have gathered by now, my preference is definitely for the Whirlpool model for coinjoins on Bitcoin. This system stands out for its rigor and offers superior guarantees of confidentiality. It is also the only one to offer a mix considered perfect in a mathematical context. In my opinion, this model represents the future of coinjoins on Bitcoin. I invite you to explore this model in greater depth in the next chapter.

How Whirlpool works

What sets Whirlpool apart from other coinjoin methods is the use of "ZeroLink" transactions, which ensure that there is strictly no possible technical link between all inputs and outputs. This perfect mix is achieved through a structure in which each participant contributes an identical amount of input (with the exception of mining fees), generating outputs of perfectly equal amounts.

This restrictive approach to inputs gives Whirlpool's coinjoin transactions a unique feature: the total absence of deterministic links between inputs and outputs. In other words, each output has an equal probability of being attributed to any participant, relative to all other outputs in the transaction.

How Whirlpool works

Initially, the number of participants in each Whirlpool coinjoin was limited to 5, with 2 new entrants and 3 remixers (we'll explain these concepts later). However, the increase in on-chain transaction fees observed in 2023 prompted Samourai's teams to rethink their model to improve confidentiality while reducing costs. Thus, taking into account the fee market situation and the number of participants, the coordinator can now organize coinjoins including 6, 7 or 8 participants. These enhanced sessions are known as "Surge Cycles". It's important to note that, whatever the configuration, there are always only 2 new entrants to Whirlpool coinjoins.

Thus, Whirlpool transactions are characterized by an identical number of inputs and outputs, which can be :

5 inputs and 5 outputs ;

6 inputs and 6 outputs ;

7 inputs and 7 outputs ;

8 inputs and 8 outputs.

Whirlpool's model is based on small coinjoin transactions. Unlike Wabisabi and JoinMarket, where the robustness of anonsets is based on the volume of participants in a single cycle (or on a few cycles), Whirlpool relies on the sequence of several small cycles.

In this model, users pay fees only when they first join a pool, enabling them to participate in a multitude of remixes at no extra cost. New entrants pay the mining fees for remixers.

With each additional coinjoin in which a piece participates, as well as its peers encountered in the past, the anonsets will grow exponentially. The aim is to take advantage of these free remixes, which, each time they occur, contribute to reinforcing the density of the anonsets associated with each piece mixed.

Whirlpool has been designed with two important requirements in mind:

The accessibility of the implementation on mobile devices, given that Samourai Wallet is first and foremost a smartphone application;
Fast remixing cycles to promote a significant increase in anonsets.

These imperatives guided the choices made by Samourai Wallet's developers in designing Whirlpool, leading them to restrict participants to a limited number per cycle. Too few would have compromised coinjoin efficiency, drastically reducing the anonsets generated per cycle, while too many would have posed management problems on mobile applications and hampered cycle flow.

Finally, there's no need to have a high number of participants per coinjoin on Whirlpool, since anonsets are made on the accumulation of several coinjoin cycles. The most important principle here is the homogeneity of the UTXOs of all participants, as this ensures perfect mixing, and therefore full benefit from the mixing and remixing cycles.

Coinjoin pools and fees

For these multiple cycles to increase the anonsets of the mixed parts, a certain framework is needed to restrict the amounts of UTXOs used. Whirlpool defines different pools.

A pool represents a group of users wishing to mix together, who agree on the amount of UTXOs to be used to optimize the coinjoin process while maintaining perfect part homogeneity. Each pool specifies a fixed UTXO amount, which the user must adhere to in order to participate. So, to make coinjoins with Whirlpool, you need to select a pool. The following pools are currently available:

0.5 bitcoins ;
0.05 bitcoin ;
0.01 bitcoin ;
0.001 bitcoin (= 100,000 sats).

When you enter a pool with your bitcoins, they will be divided up to generate UTXOs that are perfectly homogenous with those of the other participants in the pool. Each pool has a maximum limit, so for amounts exceeding this limit, you will either have to make two separate entries into the same pool, or move to another pool with a higher amount:

| Pool (bitcoin) | Maximum amount per entry (bitcoin) |

|----------------|--------------------------------------|

| 0,5 | 35 |

| 0,05 | 3,5 |

| 0,01 | 0,7 |

| 0,001 | 0,025 |

A UTXO is considered to belong to a pool when it is ready to be integrated into a coinjoin. However, this does not mean that the user loses possession of it. As we saw in the first chapters of this section, through the various mixing cycles, you retain full control of your keys and, consequently, of your bitcoins. This is what differentiates the coinjoin technique from other centralized mixing techniques.

To join a coinjoin pool, you need to pay a service fee and a mining fee. Service fees are fixed for each pool and are intended to remunerate the teams responsible for Whirlpool's development and maintenance.

The service fee for the use of Whirlpool is payable only once when you join the pool. Once you've joined, you can participate in an unlimited number of remixes at no extra charge. Here are the current fixed fees for each pool:

| Pool (bitcoin) | Entry fee (bitcoin) |

|----------------|---------------------------------|

| 0,5 | 0,0175 |

| 0,05 | 0,00175 |

| 0.01 | 0.0005 (50,000 sats) |

| 0.001 | 0.00005 (5,000 sats) |

These fees essentially function as an entry ticket to the chosen pool, regardless of the amount you put in coinjoin. So, whether you enter the 0.01 pool with exactly 0.01 BTC or 0.5 BTC, the fees will remain the same in absolute terms.

Before proceeding with Whirlpool coinjoins, the user can choose between 2 strategies:

Opt for a smaller pool to minimize service costs, knowing that he'll get several smaller UTXOs in return;
Or opt for a larger pool, willing to pay higher fees, only to end up with a smaller number of higher-value UTXOs.

It's generally not advisable to merge several mixed UTXOs after coinjoin cycles, as this could compromise acquired confidentiality, particularly due to the common input ownership heuristic (CIOH: Common-Input-Ownership-Heuristic). Consequently, it may make sense to choose a larger pool, even if this means paying more, to avoid having too many small-value UTXOs in output. The user must evaluate these trade-offs to choose the pool he prefers.

In addition to the service fee, the mining fee specific to any Bitcoin transaction must also be taken into account. As a Whirlpool user, you will be required to pay the mining fee for the preparation transaction (Tx0) as well as for the first coinjoin. All subsequent remixes will be free of charge, thanks to Whirlpool's model based on paying new entrants.

In fact, in each Whirlpool coinjoin, 2 users among the inputs are new entrants. The other inputs come from remixers. As a result, the mining costs for all participants in the transaction are borne by these 2 new entrants, who can then also benefit from free remixes:

Thanks to this fee system, Whirlpool really stands out from other coinjoin implementations, since the UTXOs' anonsets are not proportional to the price paid by the user. As a result, it is possible to achieve considerably higher levels of anonymity by paying only the pool entry fee and the mining fee for 2 transactions (the Tx0 and the initial mix).

It's important to note that the user will also have to pay the mining fees to withdraw his UTXOs from the pool after completing his multiple coinjoins, unless he has selected the mix to option, which provides an external address that will receive the funds directly out of coinjoin, without any additional transaction.

HD portfolio accounts

To create a coinjoin via Whirlpool, the wallet must generate several separate accounts. This is the principle behind the ZeroLink protocol. An account, in the context of an HD (Hierarchical Deterministic) portfolio, constitutes a section entirely isolated from the others, this separation occurring at the level of the third depth of the portfolio hierarchy, i.e. at the xpub level.

An HD wallet can theoretically derive up to 2^(31) different accounts. The initial account, used by default on all Bitcoin wallets, corresponds to the 0' index.

For portfolios adapted to Whirlpool, 4 accounts are used to meet the needs of the ZeroLink process:

The deposit account, identified by index 0' ;
The bad bank (or "doxxic change") account, identified by the index 2,147,483,644' ;
The premix account, identified by the index 2 147 483 645' ;
The postmix account, identified by the index 2 147 483 646'.

Each of these accounts fulfills a particular function in the coinjoin process, which we'll explore in the following sections.

All these accounts are linked to a single seed, enabling the user to recover access to all his bitcoins using his recovery phrase and, where applicable, his passphrase. During the recovery operation, however, the software must be informed of the various account indexes used.

Let's take a look at the different stages of a Whirlpool coinjoin within these accounts.

The TX0

The starting point of any Whirlpool coinjoin is the deposit account. This is the account you automatically use when you create a new Bitcoin wallet. This account will need to be credited with the bitcoins you wish to mix.

Tx0" is the first step in Whirlpool's mixing process. Its purpose is to prepare and equalize the UTXOs for the coinjoin, dividing them into units corresponding to the amount of the selected pool, to ensure homogeneous mixing. The UTXOs thus equalized are then sent to the premix account. As for the difference that cannot enter the pool, it is separated into a specific account: the bad bank (or "doxxic change").

This initial Tx0 transaction is also used to pay the service fee due to the coinjoin coordinator. Unlike the following steps, this transaction is not collaborative, so the user must bear the full cost of mining:

In this example of a Tx0 transaction, an input of 372,000 sats from our deposit account is split into several output UTXOs, which break down as follows:

An amount of 5,000 sats for the coordinator for service fees, corresponding to the pool entry of 100,000 sats;
3 UTXOs prepared for mixing, redirected to our premix account and registered with the coordinator. These UTXOs are equalized at 108,000 sats each, to cover the mining costs for their future initial mix;
The surplus, which cannot enter the pool because it is too small, is considered as toxic foreign exchange. It is sent to its specific account. Here, this exchange amounts to 40,000 sats ;
Finally, there are 3,000 sats left, which do not constitute an output, but are the mining costs required to confirm Tx0.

For example, here's a real Whirlpool Tx0 (not mine): edef60744f539483d868caff49d4848e5cc6e805d6cdc8d0f9bdbbaedcb5fc46

The doxxic changes

The surplus that could not be integrated into the pool, here equivalent to 40,000 sats, is redirected to the bad bank account, also known as "doxxic exchange", to ensure strict separation from the other UTXOs in the portfolio.

This UTXO is dangerous for the user's confidentiality, because not only is it still attached to its past, and therefore possibly to the identity of its owner, but it is also noted as belonging to a user who has made a coinjoin.

If this UTXO is merged with mixed outputs, the latter will lose all the confidentiality gained during coinjoin cycles, notably due to CIOH (Common-Input-Ownership-Heuristic). If it is merged with other doxxic changes, the user risks losing confidentiality, since it will link the various coinjoin cycle entries. It should therefore be treated with caution. We'll go into more detail on the management of these UTXOs doxxic in the last section of this chapter.

The initial mix

After Tx0, the equalized UTXOs are sent to our portfolio's premix account, ready to be introduced into their first coinjoin cycle, also known as the "initial mix". If, as in our example, the Tx0 generates several UTXOs for mixing, each of them will be integrated into a separate initial mix.

At the end of these first mixes, the premix account will be empty, while our coins, having paid the mining fees for this first coinjoin, will be adjusted exactly to the amount defined by the chosen pool. In our example, our initial UTXOs of 108,000 sats will have been reduced to exactly 100,000 sats.

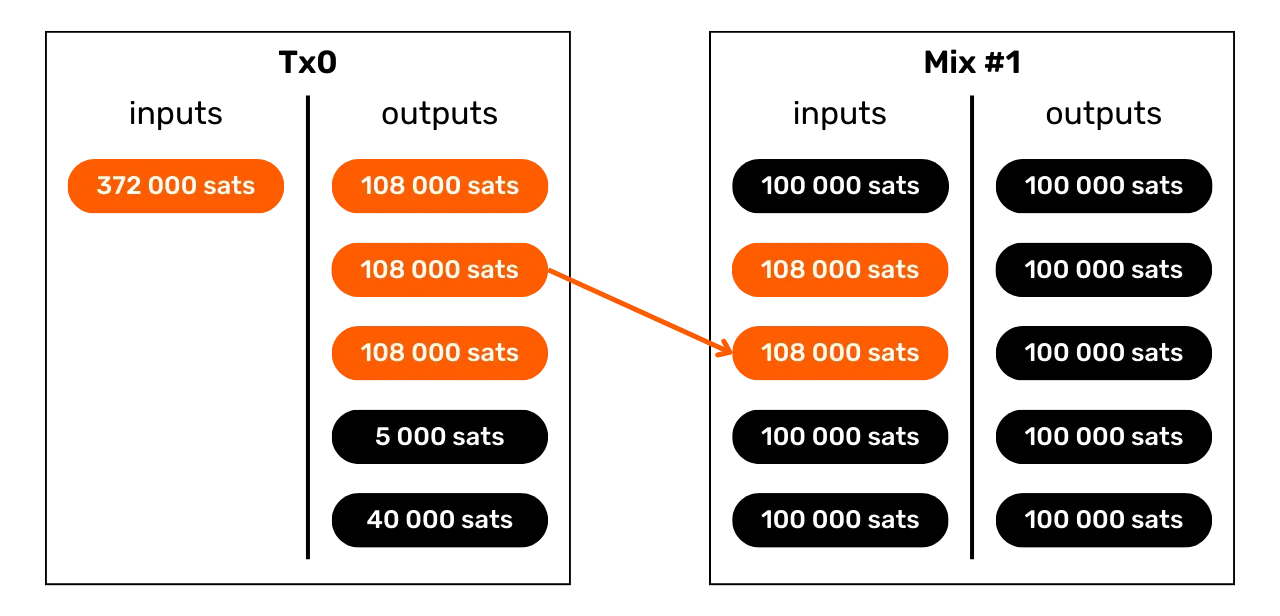
Remixes

After the initial mix, the UTXOs are transferred to the postmix account. This account collects UTXOs already mixed and those awaiting remixing. When the Whirlpool customer is active, UTXOs located in the postmix account are automatically available for remixes and will be randomly selected to participate in these new cycles.

As a reminder, remixes are then 100% free: no additional service charges or mining fees are required. Keeping UTXOs in the postmix account therefore keeps their value intact, and improves their anonsets at the same time. That's why it's important to allow these coins to participate in several coinjoin cycles. It costs you absolutely nothing, and increases their anonymity levels.

When you decide to spend mixed UTXOs, you can do so directly from this postmix account. We advise you to keep mixed UTXOs in this account to benefit from free remixes and to prevent them from leaving the Whirlpool circuit, which could reduce their confidentiality.

How do you manage your postmixes?

After running coinjoin cycles, the best strategy is to keep your UTXOs in the postmix account, awaiting future use. It's even advisable to let them remix indefinitely until you need to spend them.

Some users might consider transferring their mixed bitcoins to a wallet secured by a hardware wallet. This is possible, but it's important to follow Samourai Wallet's recommendations scrupulously so as not to compromise the confidentiality acquired.

Merging UTXOs is the most common mistake. To avoid CIOH (Common-Input-Ownership-Heuristic), you must avoid combining mixed UTXOs with unmixed UTXOs in the same transaction. This requires careful management of your UTXOs within your portfolio, particularly in terms of labeling.

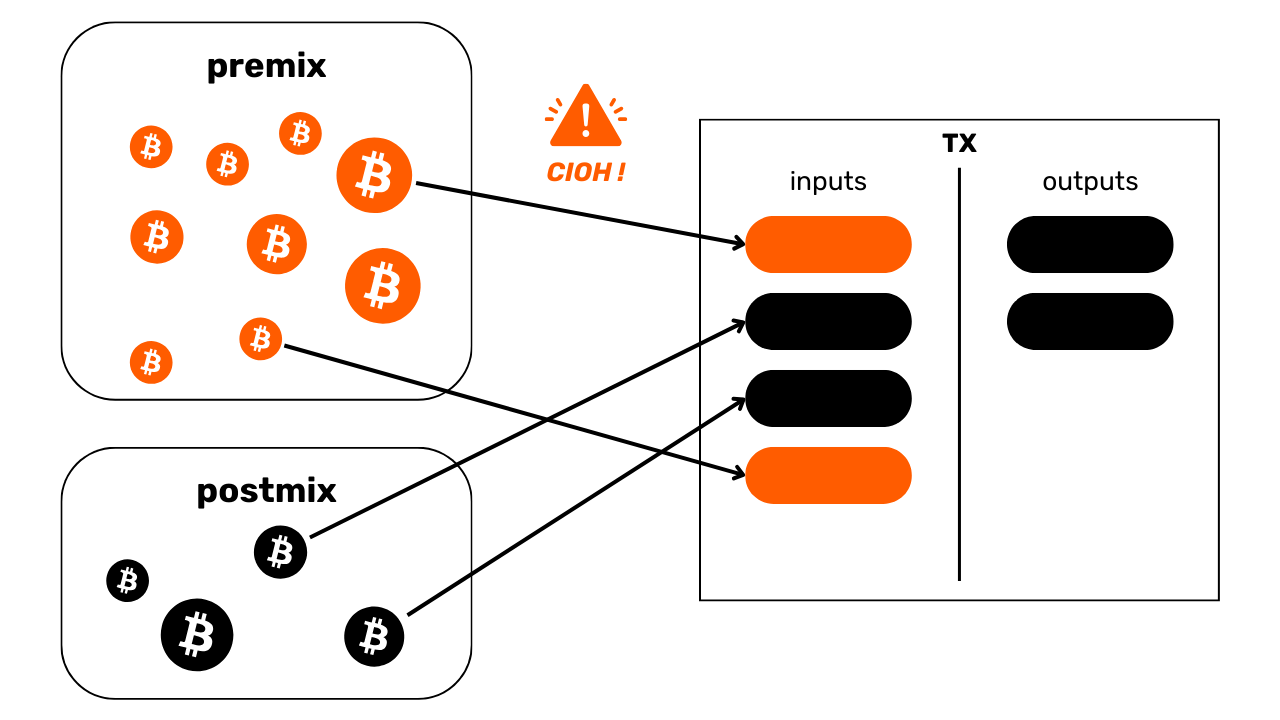
Care must also be taken when consolidating mixed UTXOs. Moderate consolidation is possible if your mixed UTXOs have significant anonsets, but this will inevitably reduce the confidentiality of your parts. Make sure that consolidations are neither too extensive, nor carried out after an insufficient number of remixes, at the risk of establishing deducible links between your UTXOs before and after coinjoin cycles. When in doubt about these manipulations, the best practice is not to consolidate postmix UTXOs, but to transfer them one by one to your hardware wallet, generating a new blank address each time. Once again, remember to label each UTXO you receive.

It's also not advisable to transfer your postmix UTXOs to a wallet using scripts that are not widely used. For example, if you enter Whirlpool from a multisig wallet using P2WSH scripts, there's little chance that you'll be mixed with other users who originally had the same type of wallet. If you re-mix your postmixes to this same multisig wallet, the level of confidentiality of your mixed bitcoins will be greatly reduced. Beyond scripts, there are many other wallet fingerprints that can play tricks on you.

As with any Bitcoin transaction, it is also important not to reuse the receiving address. Each new transaction must be received on a new, blank address.

The simplest and safest solution is to leave your mixed UTXOs at rest in their postmix account, letting them remix and only touching them to spend. Samurai and Sparrow wallets feature additional protections against all these chain analysis risks. These protections help you avoid making mistakes.

How do you manage toxic exchanges?

Next, you'll need to be careful about your management of doxxic exchange, the exchange that didn't make it into the coinjoin pool. These toxic UTXOs, resulting from the use of Whirlpool, pose a risk to your privacy, since they establish a link between you and the coinjoin user. It is therefore imperative to manage them with care and not to combine them with other UTXOs, especially mixed UTXOs.

Here are some strategies for using them:

Mix them into smaller pools:** If your toxic UTXO is large enough to fit into a smaller pool on its own, consider mixing it. This is often the best option. However, it's not advisable to merge several toxic UTXOs to access a pool, as this could link your different entries;
Mark them as "non-spendable":** Another approach is to stop using them, mark them as "non-spendable" in their dedicated account, and just hodl. This ensures that you don't accidentally spend them. If the value of bitcoin rises, new pools more suited to your toxic UTXOs may emerge;
Make donations:** Consider making donations, however modest, to developers working on Bitcoin and related software. You can also donate to associations that accept BTC. If managing your toxic UTXOs seems too complicated, you can simply get rid of them and make a donation;
Buy gift cards:** Platforms such as Bitrefill allow you to exchange bitcoins for gift cards that can be used at various merchants. This can be a way of parting with your toxic UTXOs without losing the associated value;
Consolidate them on Monero:** Samourai Wallet offers an atomic swap service between BTC and XMR. This is ideal for managing toxic UTXOs by consolidating them on Monero, without compromising your confidentiality via CIOH, before sending them back to Bitcoin. However, this option can be costly in terms of mining fees and premium due to liquidity constraints;
Send them to the Lightning Network:** Transferring these UTXOs to the Lightning Network to benefit from reduced transaction fees can be an attractive option. However, this method may reveal certain information depending on how you use Lightning, and should therefore be used with caution.

How do I use Whirlpool?

Following the arrest of Samourai Wallet's founders and the seizure of their servers on April 24, 2024, the Whirlpool tool no longer works, even for those with their own Dojo. Previously, it was available on Samourai Wallet and Sparrow Wallet.

It remains possible, however, that this tool will be reactivated in the coming weeks, depending on the outcome of the trials, or relaunched in a different way. In any case, I don't think the Bitcoin coinjoin market will be without supply for long, as demand is there. What's more, as Whirlpool's model is the most advanced in terms of confidentiality, it will surely be the model of choice for other implementations in the future.

We're keeping a close eye on this case and developments in the associated tools. Rest assured that we will be updating this training course as new information becomes available.

In the next chapter, we'll find out what "anonsets" are, how these indicators are calculated, and how they can help us estimate the efficiency of coinjoin cycles.

https://planb.network/tutorials/privacy/on-chain/coinjoin-sparrow-wallet-84def86d-faf5-4589-807a-83be60720c8b

https://planb.network/tutorials/privacy/on-chain/coinjoin-samourai-wallet-e566803d-ab3f-4d98-9136-5462009262ef

https://planb.network/tutorials/privacy/on-chain/coinjoin-dojo-c4b20263-5b30-4c74-ae59-dc8d0f8715c2

Anonymity sets

Having studied how coinjoins work and the issues involved in effective mixing, we're now going to find out how to measure their effectiveness. How can we determine whether a coinjoining process has been effective, and what degree of anonymity a part has acquired? That's what we're going to find out in this chapter with anonymity sets or "anonsets".

A reminder of the usefulness of coinjoin

The usefulness of coinjoin lies in its ability to produce plausible deniability, by embedding your part within a group of indistinguishable parts. The aim of this action is to break the links of traceability, both from the past to the present and from the present to the past.

In other words, an analyst who knows your initial transaction (Tx0) at the entry of coinjoin cycles should not be able to identify with certainty your UTXO at the exit of remix cycles (cycle entry to cycle exit analysis).

Conversely, an analyst who knows your UTXO at the exit of coinjoin cycles must be unable to determine the original transaction at the entry of the cycles (cycle exit to cycle entry analysis).

To assess how difficult it is for an analyst to link the past to the present and vice-versa, we need to quantify the size of the groups of homogeneous parts within which your part is hidden. This measure tells us how many analyses have the same probability. So, if the correct analysis is drowned among 3 other analyses of equal probability, your level of concealment is very low. On the other hand, if the correct analysis is found within a set of 20,000 equally probable analyses, your part is very well hidden. The size of these groups represents indicators known as "anonsets".

Understanding anonsets

Anonsets are used as indicators to assess the degree of confidentiality of a particular UTXO. More specifically, they measure the number of indistinguishable UTXOs within the set that includes the part under study. The requirement for a homogeneous set of UTXOs means that anonsets are usually calculated on coinjoin cycles. The use of these indicators is particularly relevant for Whirlpool coinjoints, due to their uniformity.

If necessary, anonsets can be used to judge the quality of coinjoins. A large anonset means a high level of anonymity, as it becomes difficult to distinguish a specific UTXO within the homogeneous set.

2 types of anonsets exist:

The prospective anonset ;**
Retrospective anonset.**

The prospective anonset

The forward-looking anonset indicates the size of the group among which the UTXO studied at the end of the cycle is hidden, given the UTXO at the start, i.e. the number of indistinguishable parts present within this group. The name of this indicator is "forward-looking metrics".

This indicator measures the resistance of the room's confidentiality to a past-to-present (input-to-output) analysis.

This metric is used to estimate the extent to which your UTXO is protected against attempts to reconstruct its history from its point of entry to its point of exit in the coinjoin process.

For example, if your transaction has participated in its first coinjoin cycle and two further descending cycles have been completed, your coin's prospective anonset would be 13 :

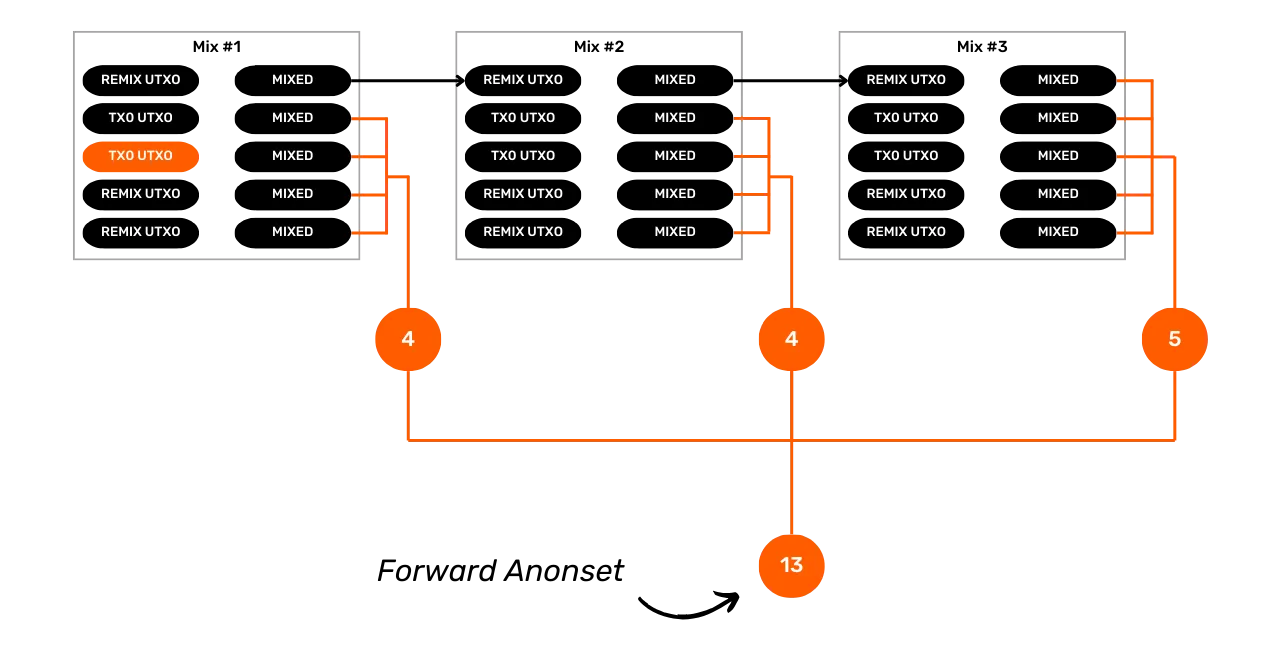
For example, let's imagine that our coin at the start of the coinjoin cycle has a prospective anonset of 86,871. In practical terms, this means that it is hidden among 86,871 indistinguishable parts. For an outside observer who knows this coin at the start of the coinjoin cycles and tries to trace its exit, he will be confronted with 86,871 possible UTXOs, each with an identical probability of being the coin he is looking for.

The retrospective anonset

The retrospective anonset indicates the number of possible sources for a given part, knowing the UTXO at the end of the cycle. This indicator measures the resistance of the part's confidentiality to a present-to-past (output-to-input) analysis, i.e. how difficult it is for an analyst to trace your part back to its origin, before the coinjoin cycles. The name of this indicator is "backward anonset", or "backward-looking metrics".

By knowing your UTXO at the exit of the cycles, the retrospective anonset determines the number of potential Tx0 transactions that could have constituted your entry into the coinjoin cycles. In the diagram below, this corresponds to the sum of all the orange bubbles.

For example, let's imagine that our coinjoin part has a retrospective anonset of 42,185. In practical terms, this means that there are 42,185 potential sources for this UTXO. If an external observer identifies this coin at the end of the cycles and seeks to trace its origin, he or she will be faced with 42,185 possible sources, all with equal probability of being the origin sought.

How do you calculate anonsets?

It's possible to calculate anonsets manually using a block explorer for small ensembles. However, for larger anonsets, the use of a specialized tool becomes imperative. As far as I know, the only software capable of performing this task is Whirlpool Stats Tool, a Python tool developed by the Samourai and OXT teams. Unfortunately, this tool is currently out of service following the arrest of Samourai's founders and the interruption of OXT, which was used to extract data from the blockchain.

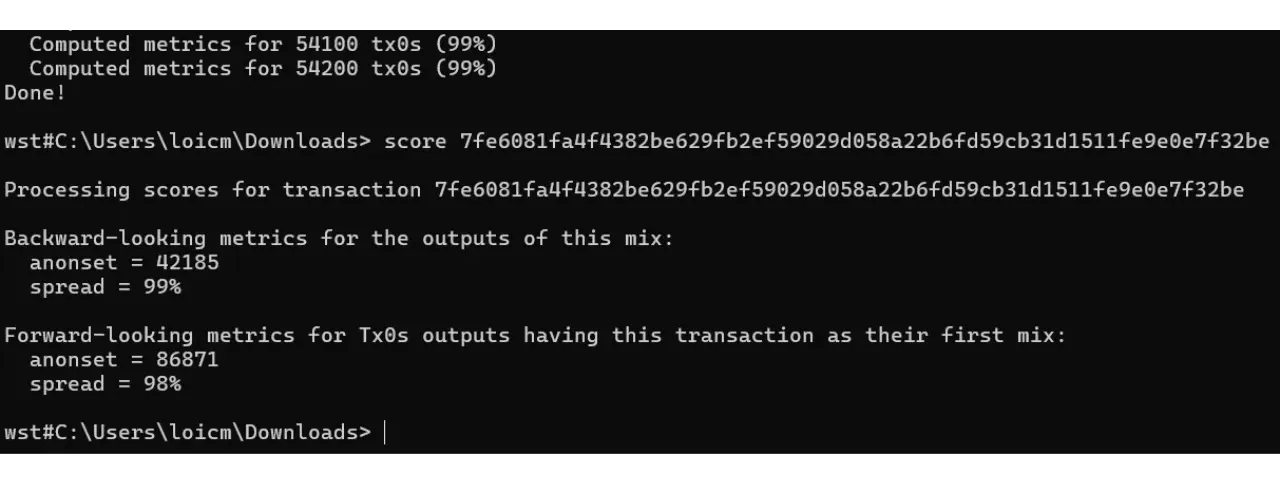
As we have seen in this chapter, anonsets can only be calculated if there is a certain homogeneity in the coinjoin structure. In the next chapter, we'll find out how to quantify this homogeneity on a Bitcoin transaction, whether it's a coinjoin or a more traditional transaction.

https://planb.network/tutorials/privacy/analysis/wst-anonsets-0354b793-c301-48af-af75-f87569756375

Entropy

As we have seen in this section on coinjoins, the homogeneity of UTXOs in input and output plays an important role in improving the confidentiality of a Bitcoin transaction. This parameter creates a plausible deniability in the face of blockchain analysis. Several methods can be used to measure this homogeneity, but one of the most effective, in my opinion, is the use of the indicators provided by the Boltzmann tool, developed by the OXT and Samourai Wallet teams, and in particular the entropy of the transaction. This is what we'll be looking at in detail in this chapter.

Unlike anonsets, which are calculated on a set of transactions, the indicators presented here focus on a single transaction, be it a coinjoin or a more traditional transaction.

The number of interpretations

The first indicator that can be observed on a Bitcoin transaction is the total number of possible interpretations faced with an analysis from an outside observer. Taking into account the values of the UTXOs involved in the transaction, this indicator shows the number of ways in which inputs can be associated with outputs. In other words, it determines the number of possible interpretations a transaction can elicit in bitcoin flows from the point of view of an outside observer analyzing it.

For example, a simple payment transaction with 1 input and 2 outputs will have only one interpretation, namely that input #0 financed output #0 and output #1. There is no other possible interpretation:

On the other hand, a Whirlpool 5x5 corner has $1\,496$ possible combinations:

A Whirlpool Surge Cycle 8x8 coinjoin has $9\,934\,563$ possible interpretations:

Entropy

From the number of interpretations of a Bitcoin transaction, we can calculate its entropy.

In the general context of cryptography and information, entropy is a quantitative measure of the uncertainty or unpredictability associated with a data source or random process. In other words, entropy is a way of measuring how difficult a piece of information is to predict or guess.

In the specific context of blockchain analysis, entropy is also the name of an indicator, derived from Shannon's entropy and invented by LaurentMT, that can be calculated on a Bitcoin transaction.

When a transaction presents a large number of possible interpretations, it is often more relevant to refer to its entropy. This indicator measures the analysts' lack of knowledge about the exact configuration of the transaction. In other words, the higher the entropy, the more difficult it becomes for analysts to identify the flow of bitcoins between inputs and outputs.

In practice, entropy reveals whether, from an external observer's point of view, a transaction presents multiple possible interpretations, based solely on input and output amounts, without taking into account other external or internal patterns and heuristics. A high entropy is therefore synonymous with greater confidentiality for the transaction.

Entropy is defined as the binary logarithm of the number of possible combinations. Here's the formula used with $E$ the entropy of the transaction and $C$ the number of possible interpretations:

 $E = \log_2(C)$

In mathematics, the binary logarithm (base-2 logarithm) is the inverse operation of the exponentiation of 2. In other words, the binary logarithm of $x$ is the exponent to which $2$ must be raised to obtain $x$ . This indicator is therefore expressed in bits.

Let's take the example of entropy calculation for a coinjoin transaction structured according to the Whirlpool 5x5 model, which, as mentioned in the previous section, has a number of possible interpretations of $1\,496$ :

 $\begin{align*} C &= 1\,496 \\ E &= \log_2(1\,496) \\ E &= 10.5469 \text{ bits} \end{align*}$

Thus, this coinjoin transaction has an entropy of $10.5469$ bits, which is considered very satisfactory. The higher this value, the more different interpretations the transaction admits, thus reinforcing its level of confidentiality.

For a coinjoin 8x8 transaction with $9\,934\,563$ interpretations, the entropy would be :

 $\begin{align*} C &= 9\,934\,563 \\ E &= \log_2(9\,934\,563) \\ E &= 23.244 \text{ bits} \end{align*}$

Let's take another example with a classic payment transaction, with 1 input and 2 outputs: 1b1b0c3f0883a99f1161c64da19471841ed12a1f78e77fab128c69a5f578ccce

In the case of this transaction, the only possible interpretation is: (In.0) > (Out.0 ; Out.1). Consequently, its entropy is $0$ :

 $\begin{align*} C &= 1 \\ E &= \log_2(1) \\ E &= 0 \text{ bits} \end{align*}$

Efficiency

Based on the transaction's entropy, we can also calculate its efficiency in terms of confidentiality. This indicator evaluates the efficiency of the transaction by comparing it with the optimal transaction that could be envisaged in an identical configuration.

This brings us to the concept of maximum entropy, which corresponds to the highest entropy that a specific transaction structure can theoretically achieve. Transaction efficiency is then calculated by comparing this maximum entropy with the actual entropy of the transaction under analysis.

The formula used is as follows with :

e_R$: the actual entropy of the transaction expressed in bits;
e_M$: the maximum possible entropy for a transaction structure, also expressed in bits;
$Ef$ : transaction efficiency in bits :

 $Ef = E_R - E_M$

For example, for a Whirlpool 5x5 coinjoin structure, the maximum entropy is $10.5469$ :

 $\begin{align*} E_R &= 10.5469 \\ E_M &= 10.5469 \\ Ef &= E_R - E_M \\ Ef &= 10.5469 - 10.5469 \\ Ef &= 0 \text{ bits} \end{align*}$

This indicator is also expressed as a percentage. The formula used is as follows: :

c_R$ : the number of possible real interpretations ;
c_M$: the maximum number of possible interpretations of the same structure;
$Ef$ : efficiency expressed as a percentage:

 $\begin{align*} E_f &= \frac{C_R}{C_M} \\ E_f &= \frac{1\,496}{1\,496} \\ E_f &= 100 \% \end{align*}$

An efficiency of $100$ indicates that the transaction is making the most of its confidentiality potential, depending on its structure.

Entropy density

Entropy is a good indicator for measuring the confidentiality of a transaction, but it depends in part on the number of inputs and outputs in the transaction. To compare the entropy of 2 different transactions with different numbers of inputs and outputs, we can calculate the entropy density. This indicator provides a perspective on the entropy relative to each input or output of the transaction. Density is useful for evaluating and comparing the efficiency of transactions of different sizes.

To calculate it, we simply divide the total entropy of the transaction by the total number of inputs and outputs involved in the transaction:

e_D$: entropy density expressed in bits;
e$: the entropy of the transaction expressed in bits;
t$: total number of inputs and outputs in the transaction:

 $E_D = \frac{E}{T}$

Let's take the example of a Whirlpool 5x5 coinjoin:

 $\begin{align*} T &= 5 + 5 = 10 \\ E &= 10.5469 \\ E_D &= \frac{E}{T} \\ E_D &= \frac{10.5469}{10} \\ E_D &= 1.054 \text{ bits} \end{align*}$

Let's also calculate the entropy density of an 8x8 Whirlpool coinjoin:

 $\begin{align*} T &= 8 + 8 = 16 \\ E &= 23.244 \\ E_D &= \frac{E}{T} \\ E_D &= \frac{23.244}{16} \\ E_D &= 1.453 \text{ bits} \end{align*}$

By analyzing the entropy density of these two types of coinjoin, it becomes clear that, even when normalizing entropy by the number of elements, the "Surge Cycle 8x8" coinjoin generates more uncertainty for the analysis.

The Boltzmann score

Another piece of information analyzed in a transaction is the Boltzmann score of each element relative to another. This is the table of matching probabilities between inputs and outputs. This table indicates, through the Boltzmann score, the conditional probability that a specific input is linked to a given output. It is therefore a quantitative measure of the conditional probability that an association between an input and an output in a transaction will occur, based on the ratio of the number of favorable occurrences of this event to the total number of possible occurrences, in a set of interpretations.

Using the example of a Whirlpool coinjoin, the conditional probability table would highlight the chances of a link between each input and output, offering a quantitative measure of the ambiguity of associations in the transaction:

| ------- | -------- | -------- | -------- | -------- | -------- |

| Input 0 | 34% | 34% | 34% | 34% | 34% |

| Input 1 | 34% | 34% | 34% | 34% | 34% | 34% | Input 1

| Input 2 | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34

| Input 3 | 34% | 34% | 34% | 34% | 34% | 34% | Input 3

| Input 4 | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34% | 34

Clearly, each input has an equal chance of being associated with any output, which reinforces the confidentiality of the transaction.

The Boltzmann score is calculated by dividing the number of interpretations in which a certain event occurs by the total number of interpretations available. Thus, to determine the score associating input #0 with output #3 (event present in $512$ interpretations), we proceed as follows:

 $\begin{align*} \text{Interpretations (IN.0 > OUT.3)} &= 512 \\ \text{Interpretations totales} &= 1496 \\ \text{Score} &= \frac{512}{1496} \\ \text{Score} &= 34 \% \end{align*}$

If we take the example of a Whirlpool 8x8 Surge Cycle coinjoin, the Boltzmann table would look like this:

| OUT.0 | OUT.1 | OUT.2 | OUT.3 | OUT.4 | OUT.5 | OUT.6 | OUT.7 |

|-------|-------|-------|-------|-------|-------|-------|-------|-------|

| IN.0 | 23% | 23% | 23% | 23% | 23% | 23% | 23% | 23% |

| IN.1 | 23% | 23% | 23% | 23% | 23% | 23% | 23% | 23% |

| IN.2 | 23% | 23% | 23% | 23% | 23% | 23% | 23% | 23% |

| IN.3 | 23% | 23% | 23% | 23% | 23% | 23% | 23% | 23% |

| IN.4 | 23% | 23% | 23% | 23% | 23% | 23% | 23% | 23% |

| IN.5 | 23% | 23% | 23% | 23% | 23% | 23% | 23% | 23% |

| IN.6 | 23% | 23% | 23% | 23% | 23% | 23% | 23% | 23% |

| IN.7 | 23% | 23% | 23% | 23% | 23% | 23% | 23% | 23% |

However, in the case of a simple transaction with a single input and 2 outputs, the situation is different:

| Output 0 | Output 1 |

|---------|----------|----------|

| Input 0 | 100% | 100% |

Here, we see that the probability of each output originating from input #0 is 100%. A lower probability thus reflects greater confidentiality, diluting the direct links between inputs and outputs.

Deterministic links

We can also calculate the number of deterministic links in a transaction. This indicator reveals how many of the connections between inputs and outputs in the analyzed transaction are unquestionable, with a probability of 100%. This indicator can then be completed by calculating the ratio of deterministic links. The ratio provides a perspective on the weight of these deterministic links within the transaction's total links.

For example, a Whirlpool coinjoin transaction has no deterministic links between inputs and outputs, and therefore displays an indicator of 0 links and a ratio of 0%. Conversely, in our second simple payment transaction examined (with one input and 2 outputs), the indicator tells us that there are 2 deterministic links, and the ratio reaches 100%. In other words, a zero indicator indicates excellent confidentiality, thanks to the absence of direct and indisputable links between inputs and outputs.

How do you calculate these indicators?

Calculating these indicators manually using the equations I've provided is relatively straightforward. The difficulty lies mainly in determining the number of possible interpretations of a transaction. For a classic transaction, this calculation can be done by hand. For a coinjoin, however, the task is far more complex.

Previously, there was a Python tool called Boltzmann Calculator, developed by the OXT and Samourai teams, which automatically calculated all these indicators for a Bitcoin transaction :

It was also possible to use the KYCP.org website for these analyses:

Unfortunately, following the arrest of Samourai's founders, these tools are no longer operational.

Now that we've covered coinjoins in detail, we'll look at the other privacy techniques available on Bitcoin in the final section of our course. We'll be looking at payjoins, specific pseudo-coinjoin transaction types, static address protocols, as well as measures to reinforce confidentiality not at the level of the transactions themselves, but at the level of the network of nodes.

https://planb.network/tutorials/privacy/analysis/boltzmann-entropy-738e45af-18a6-4ce6-af1a-1bf58e15f1fe

Understanding the challenges of other advanced confidentiality techniques

Payjoin transactions

Coinjoin is currently the most effective method of introducing uncertainty into the tracing of parts in a chain analysis. As we have seen in previous chapters, to obtain a high-performance mix, inputs and outputs must be as homogeneous as possible. In addition, it's important that parts are integrated into as large a group as possible to maximize anonsets. So, for coinjoins to be effective, they must involve a large number of uniform parts. This multitude of requirements means that coinjoin transactions have a very rigid structure: the amounts are fixed in advance, and all participants must adhere to them to guarantee the uniformity of the process. In addition, coinjoins require synchronization between all participants and the coordinator during transaction construction.

These requirements make coinjoin unsuitable for direct payments. For example, if you have a 1M sats coin in a coinjoin pool, using it directly as a payment would be complex. It would require synchronization with the other participants and the coordinator to build the collaborative transaction precisely at the moment you need to make a payment, and the purchase amount would have to correspond exactly to the value of your coin, which is virtually unfeasible. The coinjoin transaction is therefore by its very nature a collaborative sweep transaction, i.e. it's usually the same owners of the inputs that we find in the outputs.

However, it would be interesting to have transaction structures that allow payments to be made in a practical way, while at the same time introducing doubt into chain analysis. This is precisely what we'll be looking at in this chapter and the next.

What's a payjoin transaction?

The payjoin is a specific Bitcoin transaction structure that enhances user privacy when spending by collaborating with the payment recipient.

It was in 2015 that LaurentMT first discussed this method under the name "steganographic transactions", according to a document available here. This technique was later adopted by the Samourai Wallet, which in 2018 became the first client to implement it using the Stowaway tool. The concept of payjoin is also found in BIP79, BIP78, and BIP77. Several terms are thus used to refer to a payjoin:

Payjoin ;
Stowaway;
P2EP (Pay-to-End-Point) ;
Steganographic transaction.

The special feature of payjoin lies in its ability to generate a transaction that appears ordinary at first glance, but is in fact a mini Coinjoin between two people. To achieve this, the transaction structure involves the payment recipient in the inputs alongside the actual sender. The recipient thus includes a payment to himself in the middle of the transaction which itself enables him to be paid.

Let's take an example to better understand this process. Alice buys a baguette for 4,000 sats using a UTXO of 10,000 sats and opts for a payjoin. Her baker, Bob, adds a UTXO of 15,000 sats belonging to him as input, which he recovers in full as output, in addition to Alice's 4,000 sats.

In this example, Bob the baker enters 15,000 sats in input and exits with 19,000 sats, the difference being exactly 4,000 sats, i.e. the price of the baguette. On Alice's side, she enters 10,000 sats and ends up with 6,000 sats in output, which represents a balance of -4,000 sats, i.e. the price of the baguette. To simplify the example, I've deliberately omitted the mining costs in this transaction.

What's the payjoin for?

The payjoin transaction fulfils two objectives, enabling users to enhance the confidentiality of their payment.

Firstly, payjoin aims to mislead an outside observer by creating a lure in the chain analysis. This is made possible by the CIOH heuristic (Common Input Ownership Heuristic). As we saw in part 3, usually, when a transaction on the blockchain has several inputs, it is assumed that all these inputs belong to the same entity or user.

So, when an analyst examines a payjoin transaction, he or she is led to believe that all inputs come from the same person. However, this perception is wrong, because the payee also contributes to the inputs alongside the actual payer. The chain analysis is therefore diverted towards an interpretation that turns out to be wrong.

Let's take our example of a payjoin transaction for the payment of a baguette:

Seeing this transaction on the blockchain, an outside observer following the usual heuristics of blockchain analysis would make the following interpretation: "Alice merged 2 UTXOs as inputs to the transaction in order to pay 19,000 sats to Bob".

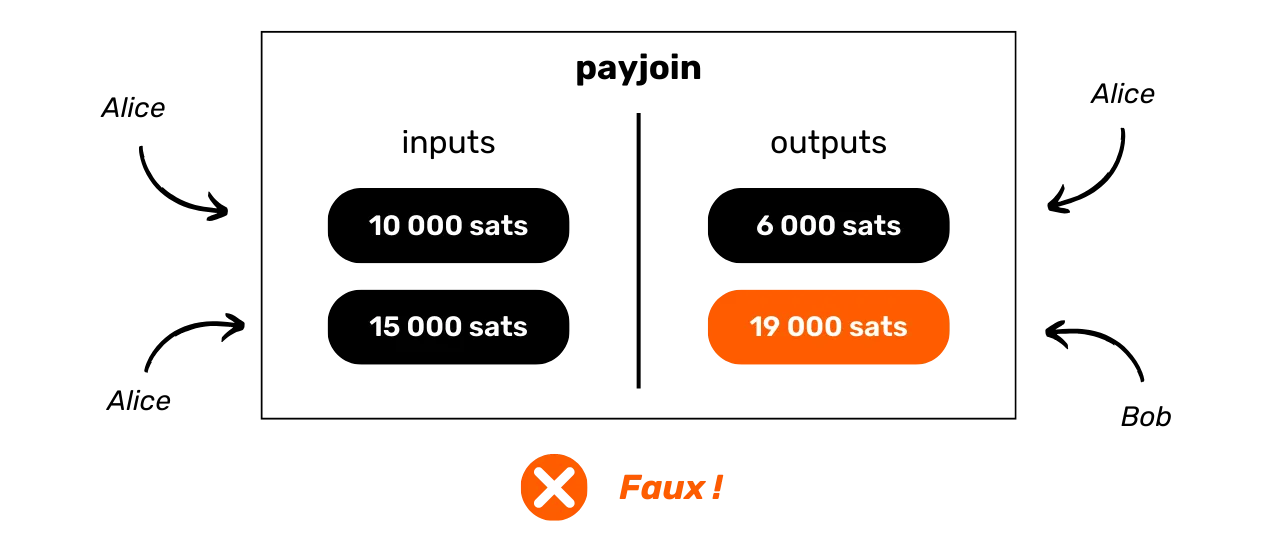
This interpretation is obviously incorrect, because as you already know, the two UTXOs in inputs don't belong to the same person. One comes from Alice, the baguette buyer, and the other from Bob, the baker.

In this way, the external observer's analysis is steered towards an erroneous conclusion, ensuring that the confidentiality of stakeholders is preserved.

The steganographic transaction

The second purpose of payjoin is to mislead an outside observer about the actual amount of the payment that has been made. By examining the structure of the transaction, the analyst might believe that the payment is equivalent to the amount of one of the outputs.

If we go back to our example of the purchase of a baguette, the analyst will think that the payment amount corresponds either to the UTXO of 6,000 sats, or to the UTXO of 19,000 sats. In this case, the analyst will rather think that the payment amount is 19,000 sats, because there are 2 UTXOs in outputs, at least one of which is greater than 6,000 sats (there is no logical reason to use 2 UTXOs to pay 6,000 sats when a single UTXO would have been sufficient to satisfy this payment).

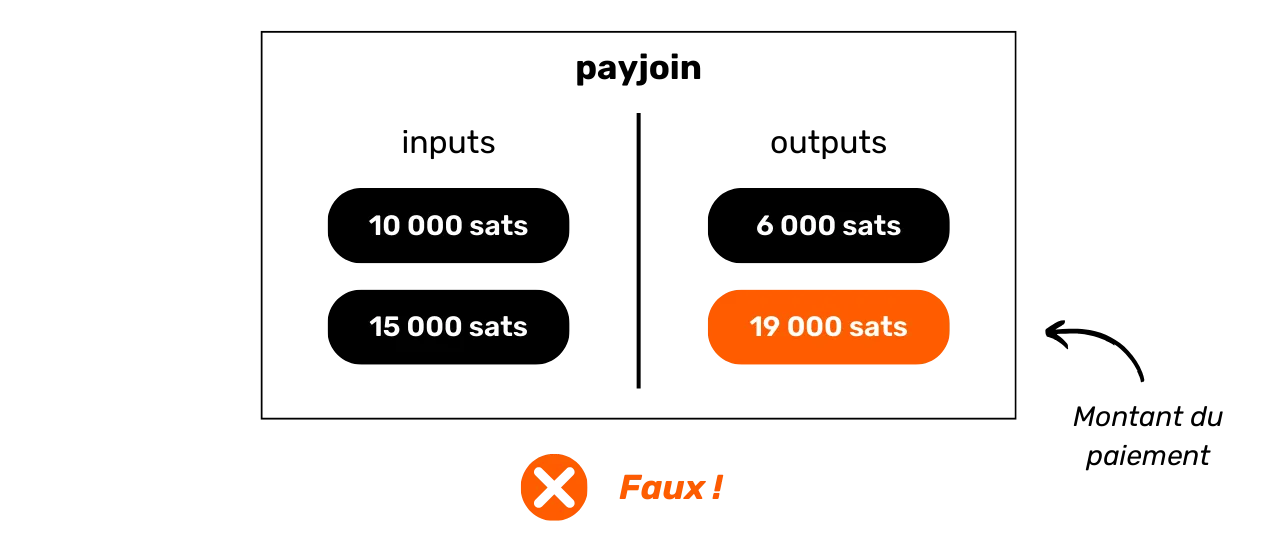
But in reality, this analysis is flawed. The payment amount does not correspond to any of the outputs. It is in fact the difference between the recipient's UTXO in output and the recipient's UTXO in input.

In this respect, the payjoin transaction falls into the realm of steganography. It allows the real amount of a transaction to be hidden within a fake transaction that acts as a decoy.

Steganography is a technique for concealing information within other data or objects, so that the presence of the hidden information is not perceptible. For example, a secret message can be concealed within a dot in unrelated text, making it undetectable to the naked eye (this is the microdot technique).

Unlike encryption, which renders information incomprehensible without the decryption key, steganography does not modify information. It remains displayed in clear text. Rather, its aim is to conceal the very existence of the secret message, whereas encryption clearly reveals the presence of hidden information, albeit inaccessible without the key. This is why the original name of payjoin was "steganographic transactions".

An analogy can be drawn between cryptography and coinjoin, and between steganography and payjoin. Coinjoin has similar attributes to encryption: the method is recognizable, but the information is indecipherable. Conversely, payjoin is similar to steganography: the information is theoretically accessible, but since the method of concealment is not recognizable, it becomes inaccessible.

How do I use payjoin?

Well-known software programs that support payjoin include Sparrow Wallet, Wasabi Wallet, Mutiny, BitMask, BlueWallet and JoinMarket, as well as payment processor BTCPay.

The most advanced payjoin implementation was only Stowaway on Samourai Wallet. However, since the arrest of the software's founders, this tool is now only partially functional. The advantage of Stowaway is that it's a comprehensive, easy-to-use protocol, which supports both receiving and sending payjoins. Partially signed transactions can be exchanged manually by scanning several QR codes, or automatically by Tor via Soroban. The latter communication option is currently out of service.

The difficulty in using payjoin lies in its dependence on the merchant's participation. As a customer, you can't use a payjoin if the merchant doesn't support it. This adds a further difficulty to the purchase process: not only is it difficult to find merchants who accept bitcoin, but if you also look for those who support payjoins, it becomes even more complicated.

One solution would be to use transaction structures that introduce ambiguity into the chain analysis without requiring the cooperation of the recipient. This would enable us to improve the confidentiality of our payments without relying on the active participation of merchants. This is precisely what we'll be looking at in the next chapter.

https://planb.network/tutorials/privacy/on-chain/payjoin-sparrow-wallet-087a0e49-61cd-41f5-8440-ac7b157bdd62

https://planb.network/tutorials/privacy/on-chain/payjoin-samourai-wallet-48a5c711-ee3d-44db-b812-c55913080eab

Payment mini-coinjoin

When you want to carry out a payment transaction while maintaining a certain degree of confidentiality, payjoin is a good option. But as we've just seen, payjoin requires the involvement of the recipient. So what do you do if the recipient refuses to participate in a payjoin, or if you simply prefer not to involve them? One alternative is to use a Stonewall or Stonewall x2 transaction. Let's take a closer look at these two types of transaction.

The Stonewall transaction

Stonewall is a specific form of Bitcoin transaction designed to increase user confidentiality when spending by imitating a pseudo-coinjoin between two people, without actually being one. In fact, this transaction is not collaborative. A user can build it on his or her own, using only the UTXOs he or she owns as inputs. So you can create a Stonewall transaction for any occasion, without needing to synchronize with another user or the recipient.

The Stonewall transaction works as follows: as input to the transaction, the issuer uses 2 UTXOs that belong to him. On output, the transaction produces 4 UTXOs, 2 of which are exactly the same amount. The other 2 UTXOs will constitute foreign exchange. Of the 2 outputs of the same amount, only one will actually go to the payee.

So there are only 2 roles in a Stonewall transaction:

The issuer, who makes the payment ;
The recipient, who may be unaware of the specific nature of the transaction and simply expects payment from the sender.

Let's take an example to understand this transaction structure. Alice goes to Bob the baker to buy her baguette, which costs 4,000 sats. She wants to pay in bitcoins, while maintaining some form of confidentiality regarding her payment. So she decides to build a Stonewall transaction for the payment.

By analyzing this transaction, we can see that Bob the baker actually received 4,000 sats in payment for the baguette. Alice used 2 UTXOs as inputs: one for 10,000 sats and one for 15,000 sats. In outputs, she has recovered 3 UTXOs: one for 4,000 sats, one for 6,000 sats and one for 11,000 sats. Alice therefore has a net balance of -4,000 sats on this transaction, which corresponds to the price of the baguette.

In this example, I have intentionally neglected the mining fees to make it easier to understand. In reality, transaction costs are borne entirely by the issuer.

What are the objectives of a Stonewall transaction?

The Stonewall structure adds an enormous amount of entropy to the transaction, blurring the lines of chain analysis. Seen from the outside, such a transaction might be interpreted as a mini-coinjoin between two people. But in reality, it's a payment. This method therefore creates uncertainties in chain analysis, or even leads to false leads.

Let's take the example of Alice at Bob the baker's. The transaction on the blockchain would look like this:

An outside observer relying on common chain analysis heuristics might wrongly conclude that "two people have made a small coinjoin, with one UTXO each in input and two UTXOs each in output". Analyzing this transaction from the outside does not lead to the application of the CIOH, as the presence of two outputs of the same amount suggests a coinjoin pattern. From an external point of view, the CIOH is therefore not applicable in this specific case.

This interpretation is inaccurate, because, as you know, one UTXO was sent to Bob the baker, the 2 UTXO inputs came from Alice, and she recovered 3 exchange outputs.

And what's particularly interesting about the structure of the Stonewall transaction is that, from the point of view of an outside observer, it resembles that of a Stonewall x2 transaction in every way.

The Stonewall transaction x2

Stonewall x2 is another specific form of Bitcoin transaction that also aims to increase user confidentiality when making a spend, but this time by collaborating with a third person not involved in that spend. This method works like a pseudo-coinjoin between two participants, while simultaneously making a payment to a third person.

The operation of the Stonewall x2 transaction is relatively simple: we use a UTXO in our possession to make the payment, and enlist the help of a third party who also contributes with a UTXO belonging to him or her. The transaction ends up with four outputs: two of them in equal amounts, one destined for the payee's address, the other for an address belonging to the collaborator. A third UTXO is returned to another address belonging to the collaborator, enabling him to recover the initial amount (a neutral action for him, modulo the mining costs), and a final UTXO returns to an address belonging to us, which constitutes the payment exchange.

Three different roles are thus defined in Stonewall x2 transactions:

The issuer, who makes the actual payment ;
The recipient, who may be unaware of the specific nature of the transaction and simply expects payment from the sender;
The collaborator, who makes bitcoins available in order to cast doubt on the analysis of the transaction, while recovering his funds in full at the end (a neutral action for him, modulo the mining costs).

Let's go back to our example with Alice, who is at Bob the baker's to buy her baguette, which costs 4,000 sats. She wants to pay in bitcoins, while maintaining a certain level of confidentiality regarding her payment. So she calls on her friend Charles, who will help her in this process.

Analyzing this transaction, we can see that Bob the baker actually received 4,000 sats in payment for the baguette. Alice used 10,000 sats in input and recovered 6,000 sats in output, i.e. a net balance of -4,000 sats, which corresponds to the price of the baguette. As for Charles, he provided 15,000 sats in input and received two outputs: one of 4,000 sats and the other of 11,000 sats, giving a balance of 0.

In this example, I've intentionally left out the fees to make it easier to understand. In reality, mining fees are generally shared equally between the issuer of the payment and the contributor.

What are the objectives of a Stonewall x2 transaction?

Like the Stonewall structure, the Stonewall x2 structure adds a great deal of entropy to the transaction and confuses the chain analysis. Seen from the outside, such a transaction can be interpreted as a little coinjoin between two people. But in reality, it's a payment. This method therefore creates uncertainties in chain analysis, or even leads to false leads.

Let's take the example of Alice, Bob the Baker and Charles. The transaction on the blockchain would look like this:

An outside observer relying on common chain analysis heuristics might wrongly conclude that "Alice and Charles have performed a small coinjoin, with one UTXO each in input and two UTXOs each in output". Again, analyzing this transaction from the outside does not lead to the application of the ICOH, as the presence of two outputs of the same amount suggests a coinjoin pattern. From an external point of view, the CIOH is therefore not applicable in this specific case.

This interpretation is incorrect, because, as you know, one UTXO has been sent to Bob the baker, Alice has only one exchange output, and Charles has two.

And once again, what's particularly interesting about the structure of the Stonewall x2 transaction is that, from the point of view of an outside observer, it resembles that of a Stonewall transaction in every way.

What's the difference between Stonewall and Stonewall x2?

A StonewallX2 transaction works exactly like a Stonewall transaction, except that the former is collaborative, whereas the latter is not. As we have seen, a Stonewall x2 transaction involves the participation of a third party (Charles), who is external to the payment, and who will make his bitcoins available to enhance the confidentiality of the transaction. In a classic Stonewall transaction, the role of the collaborator is taken on by the sender.

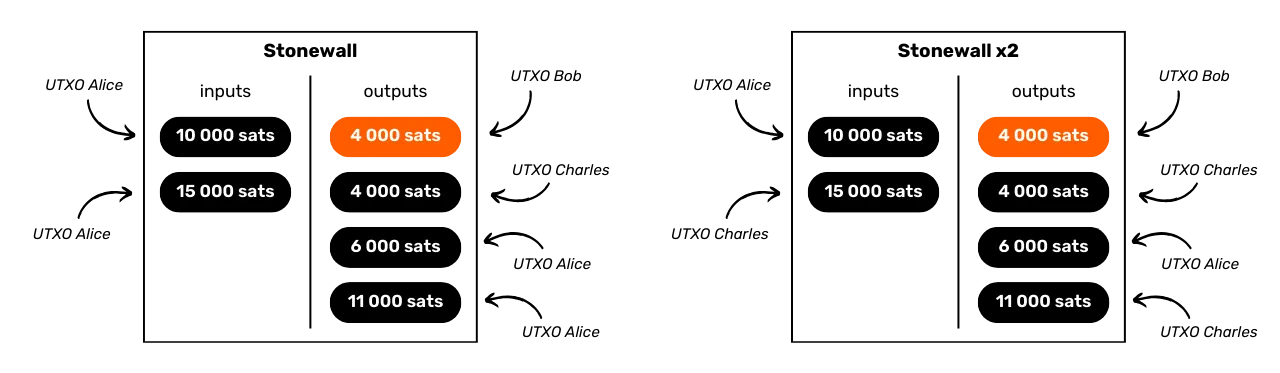
From an external point of view, the transaction pattern is exactly the same.

The fact that these two transaction structures share exactly the same pattern means that even if an outside observer manages to identify a "Stonewall(x2)" pattern, he won't have all the information. He won't be able to determine which of the two UTXOs of the same amounts corresponds to the payment. Furthermore, he won't be able to determine whether the two UTXOs with inputs come from two different people (Stonewall x2) or whether they belong to a single person who has merged them (Stonewall).

This last point is due to the fact that Stonewall x2 transactions follow exactly the same pattern as Stonewall transactions. Seen from the outside, and without additional contextual information, it's impossible to differentiate a Stonewall transaction from a Stonewall x2 transaction. The former are not collaborative transactions, whereas the latter are. This adds even more doubt to the analysis of one of these transactions.

When should Stonewall and Stonewall x2 transactions be used?

The logic should be as follows when you want to use a confidentiality tool for an expense:

As a priority, we can choose to make a payjoin;
If the merchant does not support payjoins, a collaborative transaction can be made with another person outside the payment using the Stonewall x2 structure;
If you can't find anyone to make a Stonewall x2 transaction, you can make a Stonewall only transaction, which will mimic the behavior of a Stonewall x2 transaction.

How do I use Stonewall and Stonewall x2 transactions?

Stonewall and Stonewall x2 transactions are available on both the Samourai Wallet application and the Sparrow Wallet software.

However, as with payjoins, following the arrest of Samourai's founders, Stonewall x2 transactions now only work by manually exchanging PSBTs between the parties concerned. Unfortunately, automatic exchange via Soroban is no longer available.

It is also possible to carry out this type of transaction manually from any Bitcoin wallet software.

In the next chapter, we'll take a look at another confidentiality technique that's relatively unknown, but which is very useful as a complement to what we've already studied.

https://planb.network/tutorials/privacy/on-chain/stonewall-033daa45-d42c-40e1-9511-cea89751c3d4

https://planb.network/tutorials/privacy/on-chain/stonewall-x2-05120280-f6f9-4e14-9fb8-c9e603f73e5b

The ricochets

The use of Bitcoin transaction structures that add ambiguity to chain analysis, such as coinjoin, is particularly beneficial for privacy protection. However, as we discussed in the chapter on payjoins, coinjoin transactions are naturally identifiable on the chain. Remember the analogy we drew between encryption and coinjoins: when a file is encrypted, a third party who discovers the encrypted file cannot access its contents, but can clearly identify that the file has been modified to hide its contents. The same applies to coinjoin: when an analyst examines a coinjoin transaction, although he or she cannot establish direct links between inputs and outputs (and vice versa), he or she can nevertheless recognize that the observed transaction is a coinjoin.

Depending on how you intend to use your part after coinjoin cycles, the fact that it has undergone this process can be problematic. For example, if you plan to sell your coin on a regulated exchange platform, but it has recently undergone a coinjoin, the platform's chain analysis tool will detect this fact. The platform may then refuse to accept your coinjoined UTXO, or even demand an explanation from you, with the risk of your account being suspended or your funds frozen. In some cases, the platform may also report your behavior to state authorities (this is, for example, what TRACFIN requires of PSANs in France).

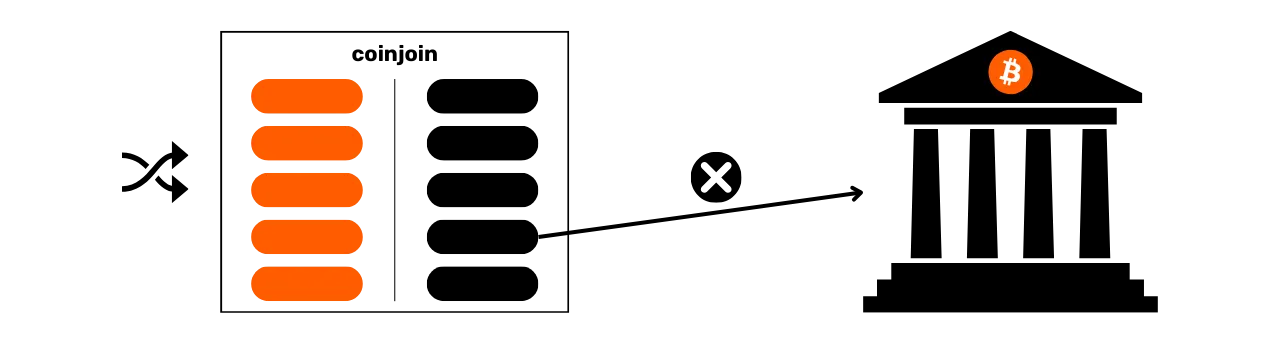
What we need to avoid this is a tool capable of blurring the traces of a Bitcoin coin's past, in order to restore some form of fungibility. This is precisely the purpose of ricochet.

What's a ricochet?

The ricochet is a technique consisting of performing several fictitious transactions towards oneself (sweep) to simulate a transfer of bitcoin ownership. This tool differs from the other transaction structures we've discussed, in that it doesn't gain prospective anonymity, but rather a form of retrospective anonymity. In effect, ricochet blurs the specificities that can compromise the fungibility of a Bitcoin coin due to its past.

To smooth out the imprint left by a past event on a coin, such as coinjoin cycles, ricochet executes four successive transactions in which the user transfers funds to himself at different addresses.

After this sequence of transactions, the ricochet tool finally routes the bitcoins to their final destination, such as an exchange platform.

The aim is to create distance affecting the fungibility of the coin, such as a coinjoin transaction, and the final act of expenditure, which could reject this coin because of its past. Thus, chain analysis tools might conclude that there was probably a change of ownership after the event, and consider this coin to be fungible. In the case of a coinjoin, blockchain analysis tools could then assume that it was not the same person who sent the bitcoins and carried out the coinjoin, and that there is therefore no point in taking action against the sender.

Why does it work?

Faced with this ricochet method, one might imagine that chain analysis software would deepen its examination beyond four bounces. However, these platforms face a dilemma in optimizing the detection threshold. They have to set a limit on the number of hops after which they accept that a property change has probably taken place, and that the link with a previous event (such as a coinjoin) should be ignored.

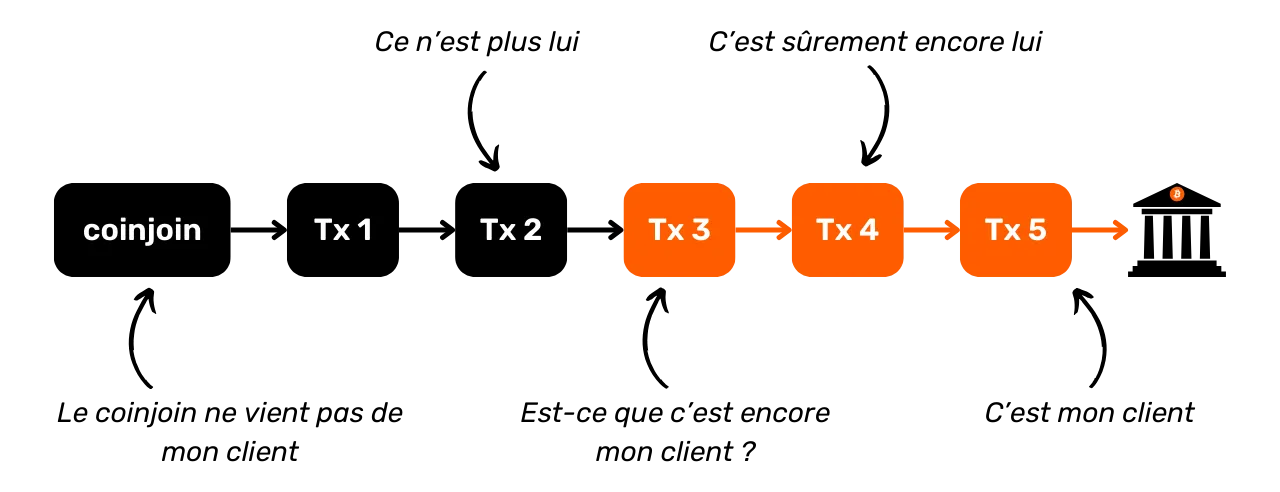
However, setting this threshold is risky: each extension in the number of observed jumps exponentially increases the volume of false positives, i.e. individuals erroneously marked as participants in an event, when in fact the operation was carried out by someone else. This scenario poses a major risk for these companies, as false positives lead to dissatisfaction, which can drive affected customers to the competition. In the long term, too high a detection threshold leads a platform to lose more customers than its competitors, which could threaten its viability. It is therefore complicated for these platforms to increase the number of bounces observed, and 4 is often a sufficient number to counter their analyses.

The phenomenon observed here is somewhat analogous to the theory of the six degrees of separation.

The theory of the six degrees of separation suggests that every person on Earth is connected to any other by a chain of relationships comprising at most six intermediaries. It would therefore be enough to pass through a series of six people, each personally knowing the next, to reach any individual in the world.

In the case of Bitcoin transactions, we find a similar phenomenon. By tracing a sufficient number of Bitcoin transactions, we inevitably come across a coinjoin. The ricochet method takes advantage of this principle by using a greater number of hops than the exchange platforms can reasonably track. If the platforms decide to track more transactions, it is then possible to simply add an extra hop to circumvent this measure.

When and how to use ricochet?

The most common use case for ricochet occurs when it's necessary to conceal a previous participation in a coinjoin on a UTXO you own. Ideally, it's best to avoid transferring bitcoins that have undergone a coinjoin to regulated entities. Nevertheless, in the event that you find yourself with no other option, particularly in the urgent need to liquidate bitcoins in state currency, ricochet offers an effective solution.

This method is effective not only for coinjoins, but also for any other mark that could compromise a part's fungibility.

The idea for this ricochet method originally came from the Samourai Wallet teams, who integrated it into their application to automate the process. The service is not free on Samourai, since a ricochet involves a service fee of 100,000 sats, plus mining costs. Its use is therefore recommended for transfers of significant amounts.

The Samurai application offers two ricochet variants:

Reinforced ricochet, or "staggered delivery", which offers the advantage of spreading the Samurai service charge over the five successive transactions. This option also ensures that each transaction is broadcast at a separate time and recorded in a different block, mimicking as closely as possible the behavior of an owner change. Although slower, this method is preferable for those who are not in a hurry, as it maximizes the efficiency of the ricochet by reinforcing its resistance to chain analysis;

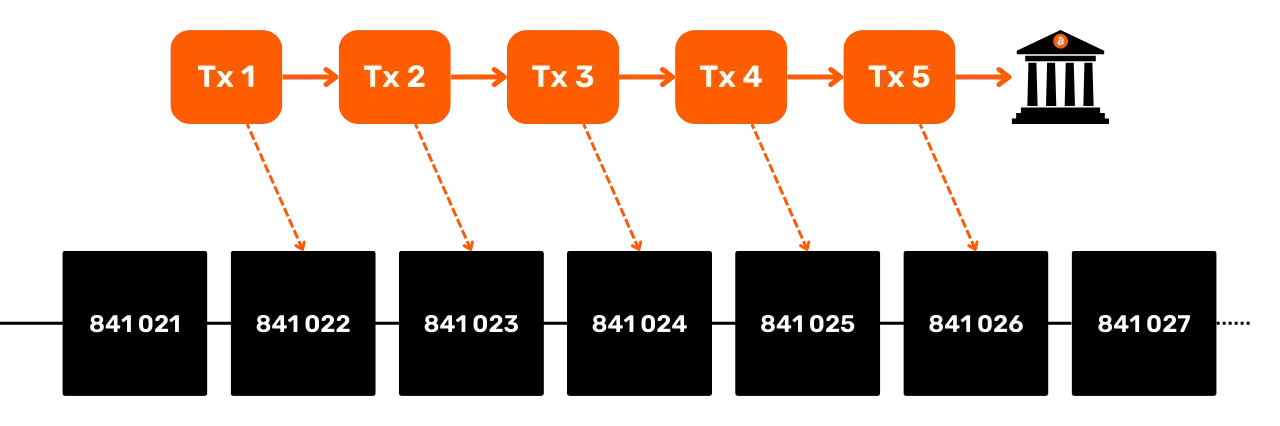
The classic ricochet, which is designed to execute the operation with speed, broadcasting all transactions in a reduced time interval. This method, therefore, offers less confidentiality and less resistance to analysis than the reinforced method. It should only be used for urgent shipments.

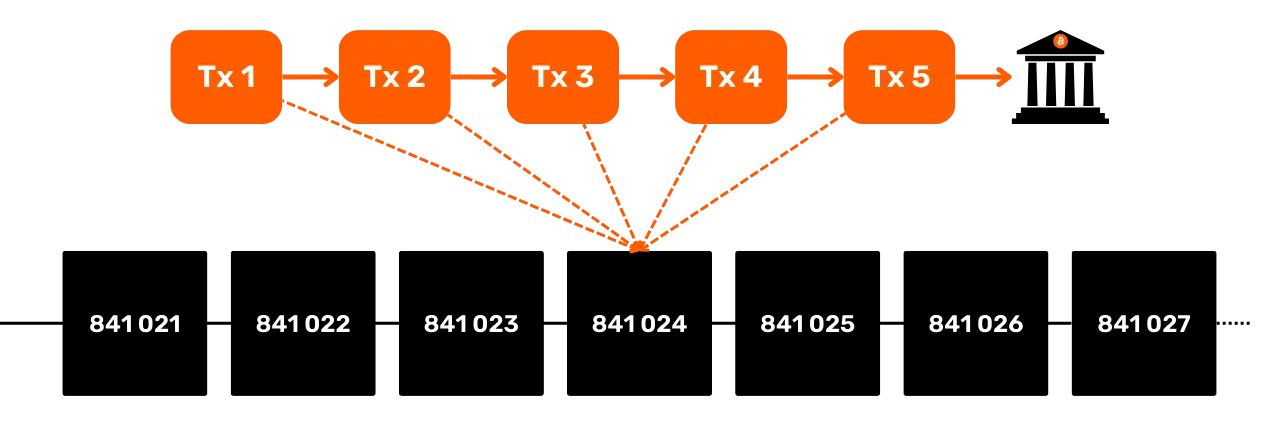
Ricocheting simply means sending bitcoins to yourself. It's perfectly possible to ricochet bitcoins manually on any wallet software, without using a specialized tool. All you have to do is successively transfer the same coin to yourself, using a new, blank address each time.

In the next chapter, we look at different techniques for secret transfers of ownership. These methods differ radically from those we have examined so far, both in terms of operation and results.

https://planb.network/tutorials/privacy/on-chain/ricochet-e0bb1afe-becd-44a6-a940-88a463756589

Secret transfers of ownership

Another of Bitcoin's confidentiality techniques is the secret transfer of ownership. This method aims to transfer ownership of Bitcoins from one person to another, and vice versa, without the transaction being explicitly visible on the blockchain. Let's take a look at the different techniques available, along with their advantages and disadvantages.

The coinswap

Coinwap is based on a relatively simple concept: it uses smart contracts to facilitate a transfer of bitcoin ownership between two users, without the need for trust and without this transfer being explicitly visible on the blockchain.

Let's imagine a naive example with Alice and Bob. Alice holds 1 BTC secured with private key $A$ , and Bob also holds 1 BTC secured with private key $B$ . They could theoretically exchange their private keys via an external communication channel to carry out a secret transfer.

However, this naive method presents a high risk in terms of trust. There's nothing to stop Alice keeping a copy of the $A$ private key after the exchange and using it later to steal the bitcoins, once the key is in Bob's hands.

Furthermore, there is no guarantee that Alice will not receive Bob's private key $B$ and never pass on her private key $A$ in exchange. This exchange therefore relies on excessive trust between the parties, and is ineffective in ensuring a secure secret transfer of ownership.

To solve these problems and enable exchanges between parties who don't trust each other, we're going to use smart contract systems instead. A smart contract is a program that executes automatically when predefined conditions are met. In our case, this ensures that the exchange of property takes place automatically, without the need for mutual trust.

This can be achieved using HTLC (Hash Time-Locked Contracts) or PTLC (Point Time-Locked Contracts). These two protocols operate in a similar way, using a time-locking system which ensures that the exchange is either completed successfully or cancelled entirely, thus protecting the integrity of both parties' funds. The main difference between HTLC and PTLC is that HTLC uses hashes and preimages to secure the transaction, while PTLC uses Adaptor Signatures.

In a coinswap scenario using HTLC or PTLC between Alice and Bob, the exchange takes place securely: either it succeeds and each receives the other's BTC, or it fails and each keeps their own BTC. This makes it impossible for either party to cheat or steal the other's BTC.

HTLC is also the mechanism used to securely route payments through the Lightning Network's bidirectional channels The use of Adaptor Signatures is particularly interesting in this context, as it makes it possible to dispense with traditional scripts (a mechanism sometimes referred to as "scriptless scripts"). This feature reduces the costs associated with exchange. Another major advantage of Adaptor Signatures is that they do not require the use of a common hash for both parties to the transaction, thus avoiding the need to reveal a direct link between them in certain types of exchange.

Adaptor Signatures

Adaptor Signatures are a cryptographic method that integrates a valid signature with an additional signature, called the "adaptor signature", to reveal secret data. This mechanism is designed in such a way that knowledge of 2 of the 3 following elements: the valid signature, the adaptor signature and the secret, allows us to deduce the missing third element. An interesting property of this method is that, if we know our peer's adaptor signature and the specific point on the elliptic curve associated with the secret used to calculate that adaptor signature, we can derive our own adaptor signature that will be compatible with that same secret, without ever having direct access to the secret itself.

In a coinswap, the use of Adaptor Signatures enables the simultaneous disclosure of two pieces of sensitive information between participants, thus avoiding the need for mutual trust. Let's take an example to illustrate this process with Alice and Bob, who wish to exchange possession of 1 BTC each, but don't trust each other. They use Adaptor Signatures to eliminate the need to trust each other in this exchange. Here's how they do it:

Alice initiates the exchange by creating a $m_A$ transaction that sends 1 BTC to Bob. She generates a signature $s_A$ , which validates this transaction, using her private key $p_A$ ( $P_A = p_A \cdot G$ ), a nonce $n_A$ ( $N_A = n_A \cdot G$ ) and a secret $t$ ( $T = t \cdot G$ ) :

$s_A = n_A + t + H(N_A + T \parallel P_A \parallel m_A) \cdot p_A$

Alice calculates the adaptor signature $s_A'$ by subtracting the secret $t$ from its true signature $s_A$ :

$s_A' = s_A - t$

Alice sends Bob her signature adaptor $s'_A$ , her unsigned transaction $m_A$ , the point corresponding to the secret ( $T$ ), and the point corresponding to the nonce ( $N_A$ ). These elements constitute what is known as an "adaptor". It's important to note that, with only this information, Bob can't recover Alice's BTC.
However, Bob can check that Alice is not trying to steal from him. To do this, he checks whether Alice's adaptor signature $s_A'$ actually corresponds to the proposed transaction $m_A$ . If the following equation is correct, then he can be sure that Alice's signature adaptor is valid:

$s_A' \cdot G = N_A + H(N_A + T \parallel P_A \parallel m_A) \cdot P_A$

This verification provides Bob with sufficient guarantees that he can continue the exchange in complete confidence. He then creates his own transaction $m_B$ , intended to send 1 BTC to Alice, and generates his adaptor signature $s_B'$ , which will also be linked to the same secret $t$ . At this stage, only Alice knows the value of $t$ ; Bob only knows the corresponding point $T$ that Alice has transmitted to him:

$s_B' = n_B + H(N_B + T \parallel P_B \parallel m_B) \cdot p_B$

Bob sends Alice his adaptor signature $s_B'$ , his unsigned transaction $m_B$ , as well as the point corresponding to the secret ( $T$ ) and the point corresponding to the nonce ( $N_B$ ). Alice, who knows the secret $t$ , can now combine Bob's adaptor signature $s_B'$ with this secret to generate a valid signature $s_B$ for the transaction $m_B$ that will transfer Bob's BTC to her:

$s_B = s_B' + t$

$(s_B' + t) \cdot G = N_B + T + H(N_B + T \parallel P_B \parallel m_B) \cdot P_B$

Alice broadcasts this signed $m_B$ transaction on the Bitcoin blockchain to retrieve the BTC promised by Bob. When Bob sees this transaction on the blockchain, he can extract the signature $s_B = s_B' + t$ . With this information, Bob is then able to isolate the famous secret $t$ he needed:

$t = (s_B' + t) - s_B' = s_B - s_B'$

And this secret $t$ was the only element missing for Bob to generate the valid signature $s_A$ from Alice's adaptor signature $s_A'$ . This signature validates the $m_A$ transaction, which sends a BTC from Alice to Bob. Bob then calculates $s_A$ and broadcasts the $m_A$ transaction on the blockchain:

$s_A = s_A' + t$

$(s_A' + t) \cdot G = N_A + T + H(N_A + T \parallel P_A \parallel m_A) \cdot P_A$

Let's summarize how an Adaptor Signature works in a coinswap. Initially, Alice sends Bob an unsigned transaction accompanied by an adaptor, enabling Bob to verify that the secret revealed later will give him access to bitcoins. In return, Bob sends Alice his own unsigned transaction and adaptor. Alice can then finalize Bob's transaction and retrieve the bitcoins by broadcasting a valid transaction thanks to the secret. When this transaction is published on the blockchain, Bob has the ability to extract the secret and thus unlock Alice's transaction. Consequently, if Alice initiates a transfer of Bob's bitcoin, Bob can, in turn, access Alice's bitcoin without the need for mutual trust.

Note that coinswaps were first proposed by Gregory Maxwell in October 2013 on BitcoinTalk.

Atomic swap

In a similar way to coinswap, and using the same types of smart contracts, it is also possible to carry out atomic swaps. An atomic swap enables a direct exchange of different cryptocurrencies, such as BTC and XMR, between two users without the need for trust or the intervention of an intermediary. These exchanges are termed "atomic" because they have only two possible outcomes: either the swap is successful and both parties are satisfied, or it fails and each retains their original cryptocurrencies, eliminating the need to trust the other party.

Atomic swap and coinswap share a similar method of operation and offer the same advantages and disadvantages in terms of confidentiality. Indeed, from Bitcoin's point of view, an atomic swap is comparable to a coinswap carried out in two stages. First, we exchange our BTC for another cryptocurrency, then this cryptocurrency can be exchanged for other BTC. In the end, we recover another user's BTC. This is why, in the analysis of confidentiality issues, I group these two protocols under the category of proprietary secret exchanges.

Beware, however, that unlike coinswap, atomic swap can have imbalances in terms of available liquidity, particularly in BTC/XMR exchanges. It's generally easier to swap bitcoins for altcoins, as there's strong demand for bitcoins, which keeps premiums low for this conversion direction. However, exchanging altcoins for BTC can be more complex due to lower demand, often resulting in very high premiums.

Finally, when an atomic swap involves onchain bitcoins and bitcoins on the Lightning network, we speak of a "submarine swap".

Is it really useful?

Secret transfers of ownership, such as coinswaps and atomic swaps, have the advantage of fooling chain analysis heuristics. These methods can suggest that the transactions involve the same user, whereas the actual ownership has changed hands. However, the main drawback of these methods is that they are very risky without the use of an additional technique to break the coin's history.

Indeed, when Alice performs a coinswap or atomic swap with Bob, she exchanges possession of her bitcoins with those of Bob. In the case of an atomic swap, the exchange includes an altcoin, but the principle remains the same. Thus, Alice ends up with the $B$ coin and Bob with the $A$ coin. This adds doubt to the chain analysis, but the history of the coins remains traceable. If an analyst examines part $A$ , he or she can trace Alice's previous activities, and vice versa for part $B$ .

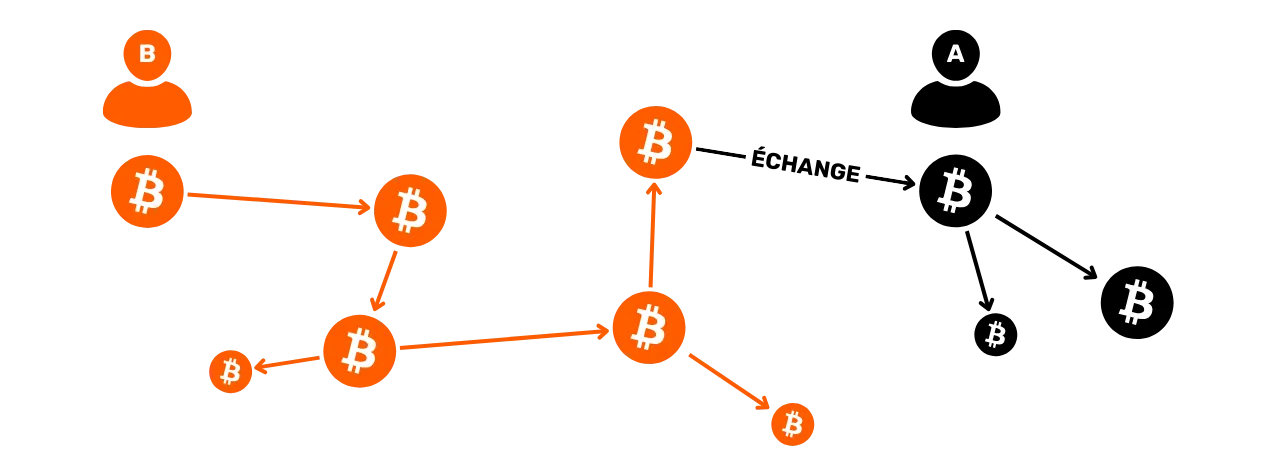
From Alice's point of view, the risk is that the history of the $B$ coin could be considered suspicious by certain entities. If, for example, Bob had acquired the $B$ coin through a criminal act such as hacking, the coin would remain linked to his illegal activities. Alice could then find herself in possession of a coin that she could not transfer to regulated exchange platforms without risking having her funds frozen, or even being accused of Bob's crimes, even though she had nothing to do with them.

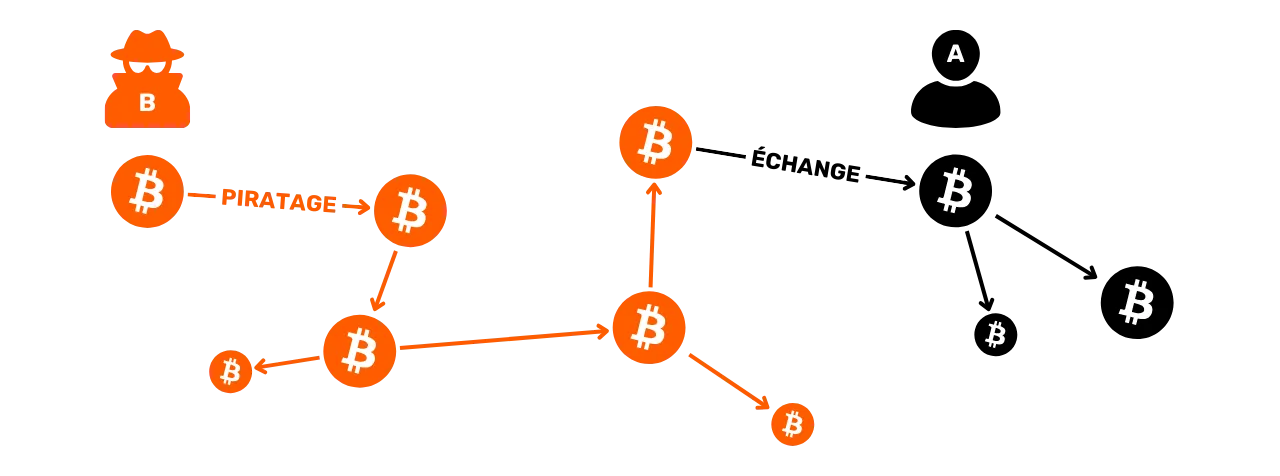
Inevitably, confidentiality methods such as coinswap or atomic swap are favoured by criminals whose funds are under surveillance by the authorities. These protocols enable them to dispose of their bitcoins under surveillance in exchange for perfectly fungible bitcoins. It also enables them to create a diversion, by directing the authorities towards other users. So there's a double purpose for these people.

With coinjoin, even if your coin is mixed with monitored bitcoins, the coin's history is broken, providing a form of plausible deniability that is non-existent in secret ownership transfer protocols like coinswap or atomic swap.

If Alice wishes to avoid any risk, she must necessarily use a method to break the history of the $B$ coin, such as passing it through coinjoins. This raises a question about the usefulness of combining the secret transfer of ownership and the coinjoin. The coinjoin, by breaking a coin's history, already offers a sufficient level of confidentiality for Alice. Thus, my opinion is that if Alice is looking to protect her privacy, it would be wiser to proceed directly to a coinjoin rather than engage a coinswap followed by a coinjoin.

For secret ownership transfer methods to be truly effective, and avoid the risk of linking the history of an $A$ user to a $B$ user, it would paradoxically be necessary for their use to be widely known. If coinswap is used massively and the authorities are aware of this common practice, then a plausible form of denial could be established. However, as long as the use of these transfers remains marginal, I think these methods will remain too risky for users.

Up to now, we have mainly studied confidentiality methods at the level of the transactions themselves. In the next chapter, we'll be looking at issues at the network level and at transaction dissemination.

Privacy on the P2P network

In Part 4, we discussed the importance of using a complete node to protect the confidentiality of your transactions. However, it's important to understand that your node may itself be subject to attacks seeking to extract information about your activities. In this chapter, therefore, we'll look at the various measures you can take to protect your privacy, not at the level of the transactions themselves or the bitcoin flows, but at the level of the network.

Dandelion

One way of avoiding the various de-anonymization attacks is to use the Dandelion proposal. This broadcast protocol was formalized in BIP156, but has never been implemented on Bitcoin.

The idea behind Dandelion is to improve the confidentiality of transaction routing in the Bitcoin network to counter various forms of attack. Its main objective is to hide the source node that initially broadcast a transaction on the network. Disclosure of this node could make it possible to link a Bitcoin transaction to a specific IP address (if the node operates on the clearnet), which could provide an entry point for chain analysis.

This association between activity on Bitcoin and an IP address represents a considerable risk to user confidentiality. Indeed, many entities are in a position to easily link an IP address to a personal identity. This includes governments and Internet service providers. What's more, this information can become publicly accessible, for example, if your IP address and personal data are leaked when a website's database is hacked.

In classic Bitcoin operation, transactions built by a user on his wallet software are transmitted to his personal node. This node will immediately broadcast the new transaction to all the peers to which it is connected.

These peers then check the transaction to ensure that it complies with consensus and local standardization rules. Once validated, each peer in turn forwards the transaction to his or her peers, and so on.

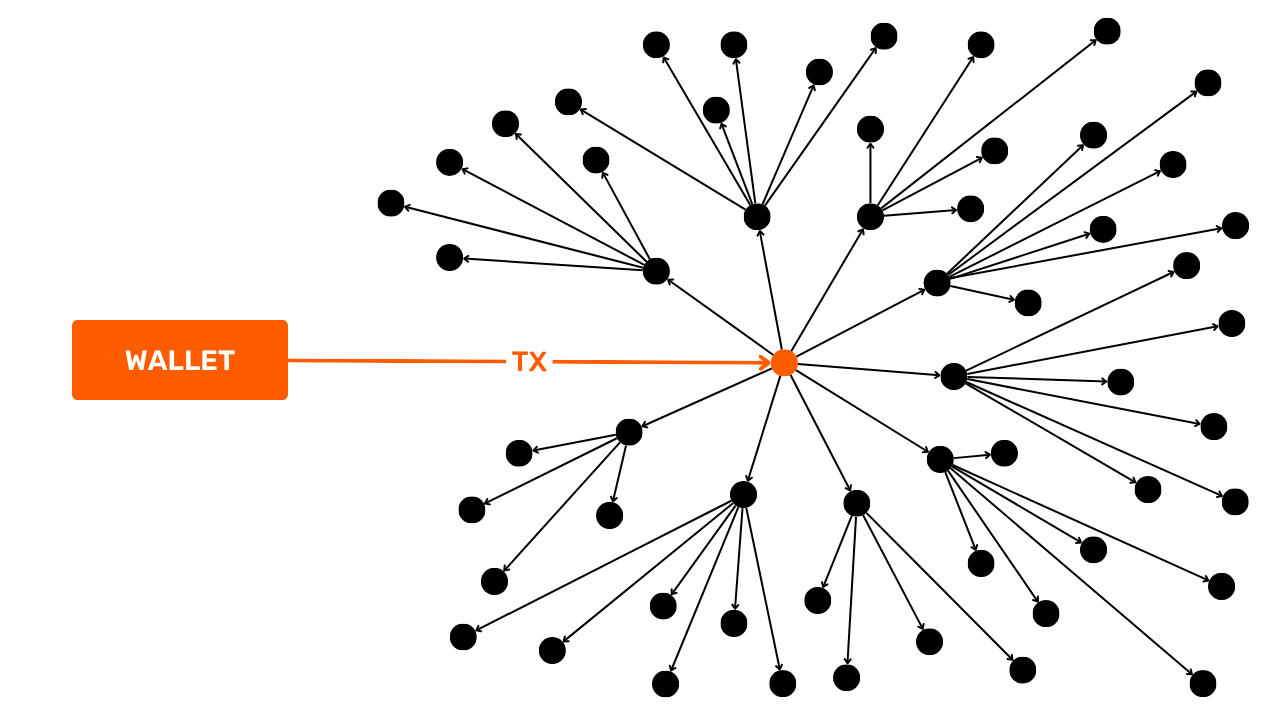
This distribution of transactions awaiting integration into a block is fairly balanced and statistically predictable. This weakness can be exploited by complicit spy nodes, who collaborate to monitor and analyze the network, in order to identify the first node to have broadcast a transaction. If an observer succeeds in locating the source node, he or she can assume that the transaction originated from that node's operator. This type of observation can be used to link normally anonymous transactions to specific IP addresses.

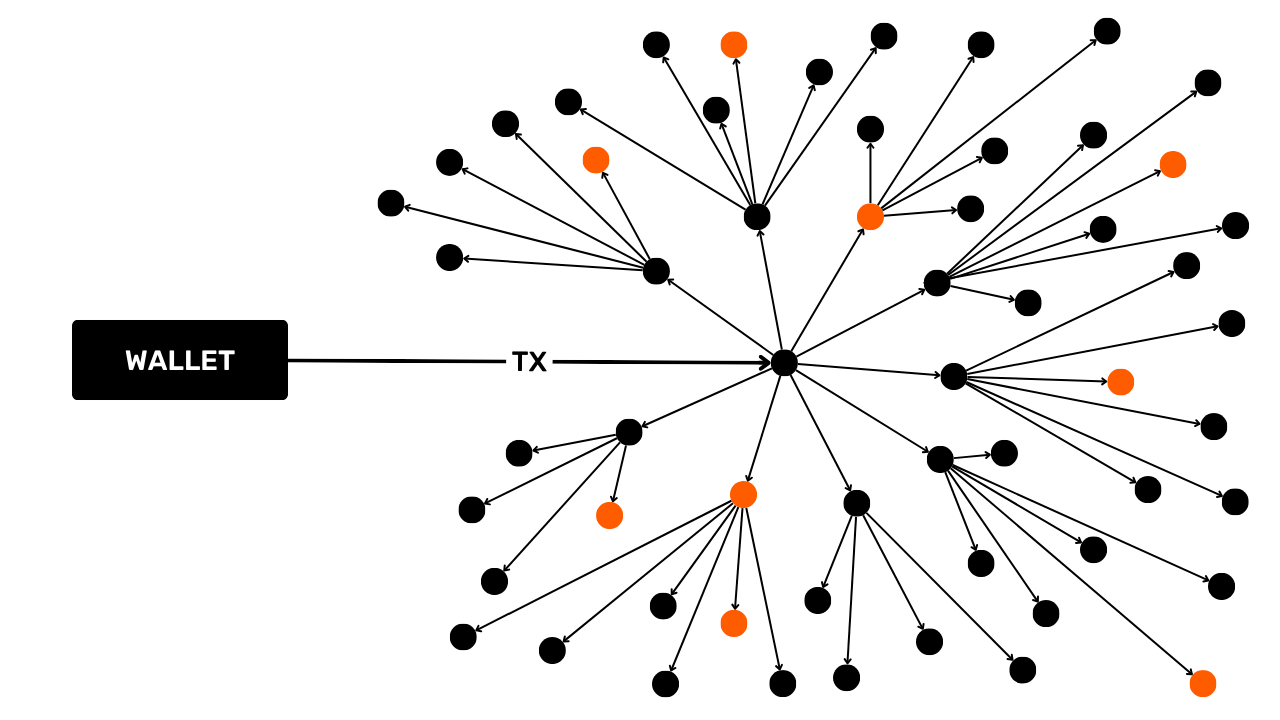
The aim of BIP156 is to address this problem. To do this, it introduces an additional phase in the dissemination of a new transaction to preserve anonymity before wide public propagation. Dandelion first uses a "stem" phase where the transaction is sent through a random path of nodes.

The transaction is then broadcast to the entire network during the "Fluff" phase.

The stem and the "Fluff" are references to the behavior of transaction propagation through the network, which resembles the shape and evolution of a dandelion.

Thus, spy nodes can potentially trace the transaction back to the node that initiated the "Fluff" phase (the mass broadcast), but that node is not the one that first broadcast the transaction, as it received it from the last node of the stem. If the spy nodes cannot trace the stem, they also cannot identify the source node.

Even in the presence of spy nodes during the stem phase, a doubt always remains, because as soon as they encounter an honest node in the diffusion graph, the spies can't determine whether this node is the original source or simply an intermediary.

This routing method blurs the trail leading back to the source node, making it difficult to trace a transaction back through the network to its origin. Dandelion thus improves confidentiality by limiting the ability of adversaries to de-anonymize the network. This method is all the more effective when, during the "stemming" phase, the transaction crosses a node that encrypts its network communications, as with Tor or P2P Transport V2.

BIP156 has not been integrated into Bitcoin Core and is currently classified as "rejected". One of the main concerns with this protocol is that, during the stem phase, transactions must be relayed through intermediate nodes before being verified. As we have seen, in the normal Bitcoin model, each node first verifies the transaction before broadcasting it to its peers. If a transaction does not comply with the node's consensus rules or local standardization rules, the node ignores it and does not distribute it. This process is important to counter DoS attacks, as only valid transactions are broadcast to the entire network. Invalid transactions, potentially generated en masse to overload the network, are stopped at the first node encountered and do not propagate. The main risk with Dandelion is that this new protocol could introduce new vectors for DoS attacks by allowing invalid transactions to be broadcast across part of the network.

P2P transport V2

P2P transport V2 is another network protocol presented in BIP324. It's a new version of the Bitcoin P2P transport protocol that incorporates opportunistic encryption to improve the confidentiality and security of communications between nodes.

This enhancement is designed to solve several problems with the basic version of the P2P protocol. On the one hand, it makes the data exchanged indistinguishable from other types of data circulating on the Internet for a passive observer. The main aim is to prevent governments, ISPs and VPN providers from massively monitoring Bitcoin users. This also makes it more difficult for these entities to determine whether an Internet user is also a Bitcoin user, i.e. whether he or she is operating a complete node.

P2P V2 also helps reduce the risk of censorship and attacks by detecting specific patterns in data packets. It complicates and makes more costly the execution of various types of Sybil attacks at network level. A Sybil attack occurs when an actor creates multiple false identities in order to gain an unfair advantage. In the context of the Bitcoin network, this often manifests itself as an actor controlling a large number of complete nodes and aggressively using them to multiply connections. Sybil attacks can be passive, to gather information and compromise user confidentiality, or active, in the form of Eclipse attacks. The latter isolate a specific node from the rest of the network, either censoring the user or altering the data it receives. Finally, P2P V2 also makes Man-In-The-Middle (MITM) attacks more costly and easier to detect.

The encryption implemented by P2P V2 does not include authentication, so as not to add unnecessary complexity, or compromise the fact that connection to the network remains permissionless. Nevertheless, this new P2P transport protocol offers better security against passive attacks, and makes active attacks considerably more costly and detectable. The introduction of a pseudo-random data stream in network messages makes it more difficult for attackers to censor or manipulate communications.

P2P V2 transport was included as an option (disabled by default) in Bitcoin Core version 26.0, deployed in December 2023. It was then enabled by default in version 27.0 of April 2024. It can be modified with the v2transport= option in the configuration file.

Tor

Another simple solution to avoid the risk of loss of confidentiality for a network node is to run it entirely under Tor.

Tor is a network of relay servers (nodes) that anonymizes the origin of TCP connections on the Internet. It works by encapsulating data in several layers of encryption. Each relay node removes a layer to reveal the address of the next node, until the final destination is reached. The Tor network ensures anonymity by preventing intermediary nodes from knowing both the origin and destination of data, making it very difficult for an observer to trace a user's activity.

Tor not only encrypts data, but also masks the origin and destination of communications. By using Tor for communications from your personal node, you reinforce the confidentiality of your transactions: your ISP can't decrypt communications, and other nodes in the Bitcoin network can't identify the source node's IP address. What's more, Tor also hides your very use of Bitcoin from your ISP.

The main risk with this method is that Tor is a protocol independent of Bitcoin. If you have a Bitcoin node running under Tor and Tor stops working, then your Bitcoin node will no longer be able to communicate.

Also, it's important to note that communications on Tor are slower. This latency is particularly annoying during the initial launch of a node, as IBD (Initial Block Download) requires a lot of communication. As a result, your initial synchronization with the Bitcoin network could take significantly longer using Tor. It's also possible to perform IBD on the clearnet, then activate Tor as a second step. Although this method discloses the existence of your Bitcoin node to your ISP, it protects your personal transaction information once you switch to Tor.

Having explored the various methods of confidentiality at network level, in the next few chapters I'd also like to introduce you to two elegant solutions for avoiding address reuse: BIP47 and Silent Payments.

BIP47 and reusable payment codes

As we saw in part 3, address reuse is a serious obstacle to user confidentiality on the Bitcoin protocol. To mitigate these risks, it is strongly recommended to generate a blank receiving address for each new payment received in a wallet. Although generating a new address is now simplified by the use of modern software and hierarchical deterministic wallets, this practice may seem counter-intuitive.

In the traditional banking system, for example, we are used to sharing our IBAN, which always remains the same. Once we've given it to someone, they can send us multiple payments without having to interact with us again. Neo-banks also offer more modern possibilities, such as the use of unique email addresses on PayPal or RevTags on Revolut. Even outside the financial sphere, our everyday identifiers such as our postal address, telephone number and email address are also unique and permanent. We don't have to renew them for each new interaction.

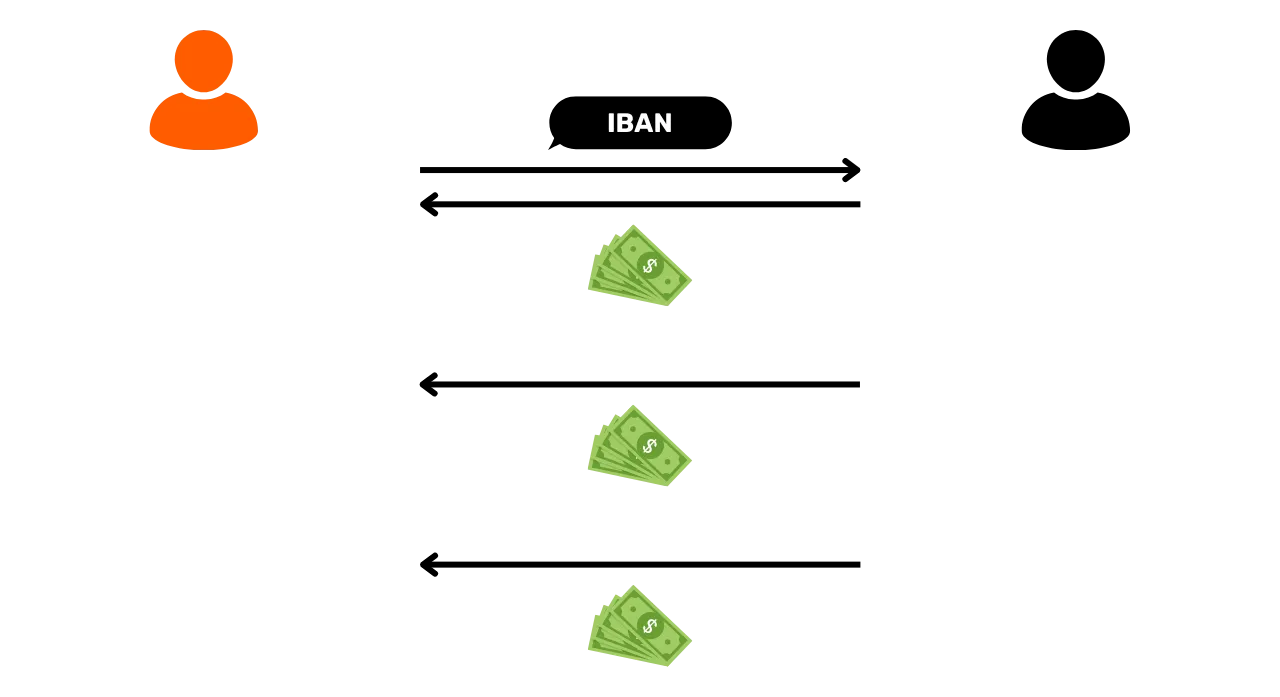
However, Bitcoin works differently: a new receiving address must be generated for each incoming transaction. This compromise between ease of use and confidentiality goes back to the very origins of Bitcoin's White Paper. As early as the publication of the first version of his document at the end of 2008, Satoshi Nakamoto was already alerting us to this risk:

**As an additional firewall, a new key pair could be used for each transaction to keep them unlinked to a common owner

There are many ways to receive multiple payments on a single identifier without having to re-use an address. Each has its own trade-offs and drawbacks. Among these methods is BIP47, a proposal developed by Justus Ranvier and published in 2015. This proposal aims to create reusable payment codes that enable multiple transactions to be carried out against the same person, while avoiding address reuse. In short, BIP47 aims to offer a payment system as intuitive as a unique identifier, while preserving the confidentiality of transactions.

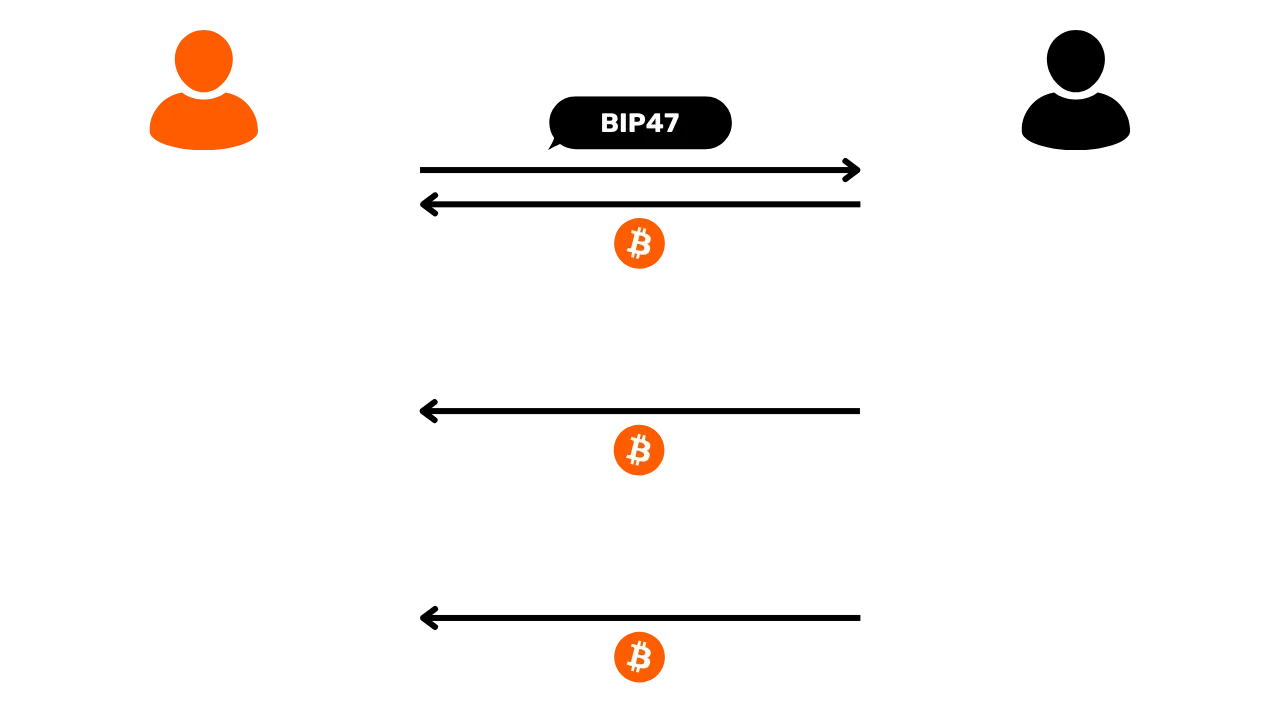
BIP47 does not directly improve user confidentiality, as a BIP47 payment offers the same level of confidentiality as a classic Bitcoin transaction using blank addresses. However, it does make using Bitcoin more convenient and intuitive, an ease that would normally compromise confidentiality. Thanks to BIP47, this ease of use achieves the same level of confidentiality as a classic transaction. That's why BIP47 is such a valuable tool for preserving privacy.

Initially, BIP47 was proposed for integration into Bitcoin Core, but was never actually implemented. However, some software applications chose to implement it on their own. For example, the Samourai Wallet teams have developed their own implementation of BIP47 called "PayNym".

General principle of BIP47 and PayNym

The aim of BIP47 is to make it possible to receive a large number of payments without reusing addresses. It is based on the use of a reusable payment code, which enables different issuers to send several payments to a single code belonging to another user. As a result, the recipient does not have to provide a new, blank address for each transaction, which greatly facilitates exchanges while preserving confidentiality.

A user can therefore share his or her payment code in complete freedom, whether on social networks or on his or her website, without risking any loss of confidentiality, unlike with a conventional recipient address or public key.

To carry out a transaction, both parties need a Bitcoin wallet with a BIP47 implementation, such as PayNym on Samurai Wallet or Sparrow Wallet. The joint use of their payment codes creates a secret channel between them. To establish this channel effectively, the issuer must carry out a specific transaction on the Bitcoin blockchain, known as a "notification transaction" (more on this later).

Combining the payment codes of the two users generates shared secrets, which in turn create a large number of unique Bitcoin receiving addresses (exactly 2^32, or around 4 billion). In this way, payments made via BIP47 are not actually addressed to the payment code itself, but rather to classic receipt addresses derived from the payment codes of the users involved.

The payment code thus serves as a virtual identifier derived from the portfolio seed. In the portfolio's hierarchical derivation structure, the payment code is positioned at level 3, i.e. at account level.

The derivation target for BIP47 is identified by the index 47' (0x8000002F), referring to BIP47. An example of a derivation path for a reusable payment code would be as follows:

m/47'/0'/0'/

To give you an idea of what a payment code looks like, here's mine:

PM8TJSBiQmNQDwTogMAbyqJe2PE2kQXjtgh88MRTxsrnHC8zpEtJ8j7Aj628oUFk8X6P5rJ7P5qDudE4Hwq9JXSRzGcZJbdJAjM9oVQ1UKU5j2nr7VR5

This code can also be encoded as a QR code, to make it easier to communicate, just like a conventional reception address.

As for PayNym Bots, the robots sometimes seen on Twitter, these are visual representations of the payment code, created by Samourai Wallet. They are generated using a hash function, giving them near-uniqueness. They take the form of a small string of characters beginning with + :

+throbbingpond8B1
+twilightresonance487
+billowingfire340

These avatars can also be represented as images:

Although these robots have no specific technical functionality within the BIP47 framework, they do play a role in facilitating user interaction by offering an easily recognizable visual identity.

In the following sections of this chapter dedicated to BIP47, we'll take a detailed look at how it works, with particular emphasis on the cryptographic methods used. To fully grasp these somewhat technical explanations, it's essential to first understand the structure of HD wallets, key derivation procedures and the fundamentals of elliptic curve cryptography. If you'd like to delve deeper into these concepts, another free training course is available on Plan ₿ Network :

https://planb.network/courses/46b0ced2-9028-4a61-8fbc-3b005ee8d70f

I'd still advise you to follow them, because understanding the technical operation of BIP47 will make it much easier for you to understand other, similar proposals, which we'll discuss in the following chapters

The reusable payment code

As mentioned earlier, the reusable payment code is located at depth 3 of the HD wallet, making it comparable to an xpub, both in terms of its position in the wallet structure and its role.

The 80-byte payment code breaks down as follows:

Byte 0: The version**. For the first version of BIP47, this byte is set to 0x01 ;
Byte 1: The bit field**. This space is reserved for integrating additional indications for specific uses. For classic PayNym use, this byte is set to 0x00 ;
The 2 byte: The parity of y**. This byte is 0x02 or 0x03, indicating whether the ordinate of the public key is even or odd, as a compressed public key is used;
From byte 3 to byte 34: The value of x**. These bytes represent the abscissa of the public key. The concatenation of x and the parity of y forms the complete compressed public key;
From byte 35 to byte 66: The string code**. This space contains the string code associated with the public key;
From byte 67 to byte 79: The padding**. This space is intended for possible future evolutions. For the current version, we simply place zeros here to reach the 80-byte size required for OP_RETURN output.

Here is the hexadecimal representation of my reusable payment code already presented in the previous section:

0x010002a0716529bae6b36c5c9aa518a52f9c828b46ad8d907747f0d09dcd4d9a39e97c3c5f37c470c390d842f364086362f6122f412e2b0c7e7fc6e32287e364a7a36a00000000000000000000000000

Next, the P prefix byte must be added at the beginning to clearly indicate that this is a payment code. This byte is represented by 0x47 :

0x47010002a0716529bae6b36c5c9aa518a52f9c828b46ad8d907747f0d09dcd4d9a39e97c3c5f37c470c390d842f364086362f6122f412e2b0c7e7fc6e32287e364a7a36a00000000000000000000000000

Finally, to ensure the integrity of the payment code, a checksum calculation is performed using HASH256, which consists of a double hash using the SHA256 function. The first four bytes of this hash are then concatenated at the end of the payment code:

0x47010002a0716529bae6b36c5c9aa518a52f9c828b46ad8d907747f0d09dcd4d9a39e97c3c5f37c470c390d842f364086362f6122f412e2b0c7e7fc6e32287e364a7a36a00000000000000000000000000567080c4

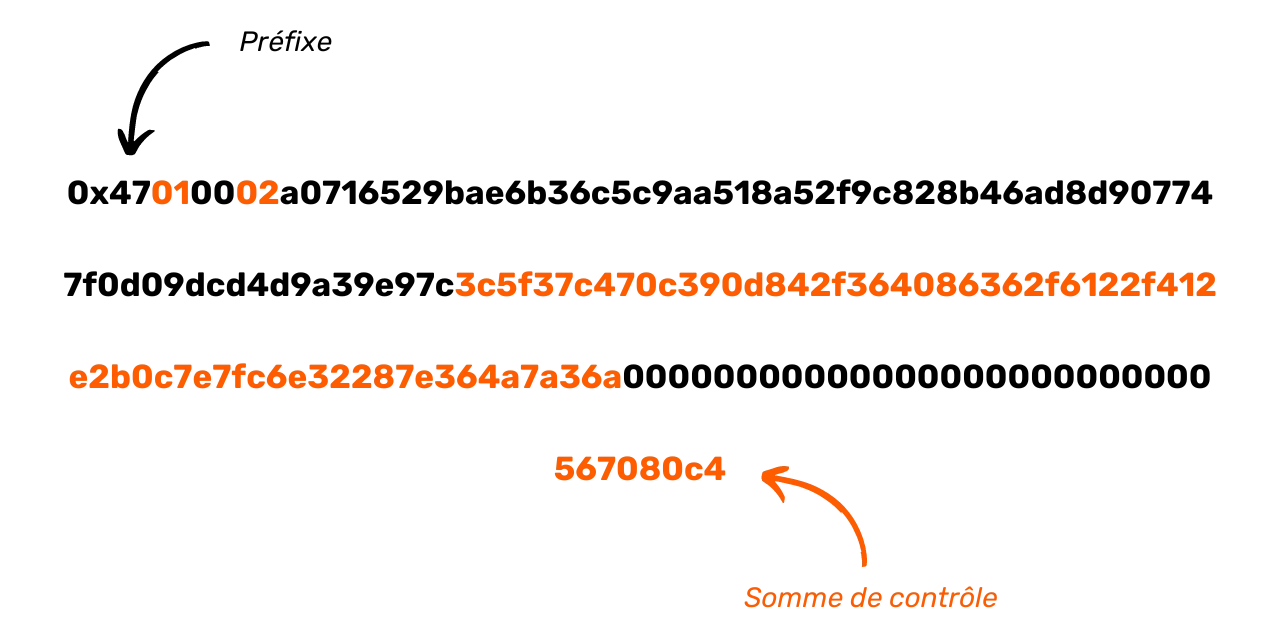
Once these steps have been completed, the payment code is ready. All that remains is to convert it to base 58 to obtain the final version:

PM8TJSBiQmNQDwTogMAbyqJe2PE2kQXjtgh88MRTxsrnHC8zpEtJ8j7Aj628oUFk8X6P5rJ7P5qDudE4Hwq9JXSRzGcZJbdJAjM9oVQ1UKU5j2nr7VR5

In the process of creating the payment code, we use a compressed public key and a string code. Both are derived deterministically and hierarchically from the wallet seed. The derivation path used to achieve this is :

m/47'/0'/0'/

In concrete terms, to generate the compressed public key and string code associated with the reusable payment code, we start by calculating the master private key from the wallet seed. We then proceed to derive a pair of daughter keys using the index 47 + 2^31 (strengthened derivation). This is followed by two further successive derivations of daughter pairs, each using the index 2^31 (strengthened derivation).

Diffie-Hellman key exchange on elliptic curves (ECDH)

The cryptographic protocol at the heart of BIP47 is known by the acronym ECDH, for Elliptic-Curve Diffie-Hellman. This method is a variant of the original Diffie-Hellman key exchange.

Introduced in 1976, Diffie-Hellman is a key agreement protocol that enables two parties, each equipped with a key pair (public and private), to agree on a common secret, even when communicating only via a public, unsecured channel.

This shared secret (in this case, the blue key) can then be used for other operations. Typically, this shared secret can be used to encrypt and decrypt a communication on an unsecured network:

To achieve this, Diffie-Hellman uses modular arithmetic to calculate the shared secret. Here's how it works in layman's terms:

Alice and Bob agree on a common color, in this case yellow, which is public data (the attackers know this color);
Alice selects a secret color, in this case red, and mixes the two to obtain orange;
Bob also chooses a secret color, in this case blue, and mixes it with yellow to obtain green;
They then exchange the resulting colors, orange and green. This exchange can take place on an insecure network and be observed by attackers;
By mixing Bob's green with her own secret color, Alice produces brown;
Bob, doing the same with Alice's orange and secret blue, also obtains brown.

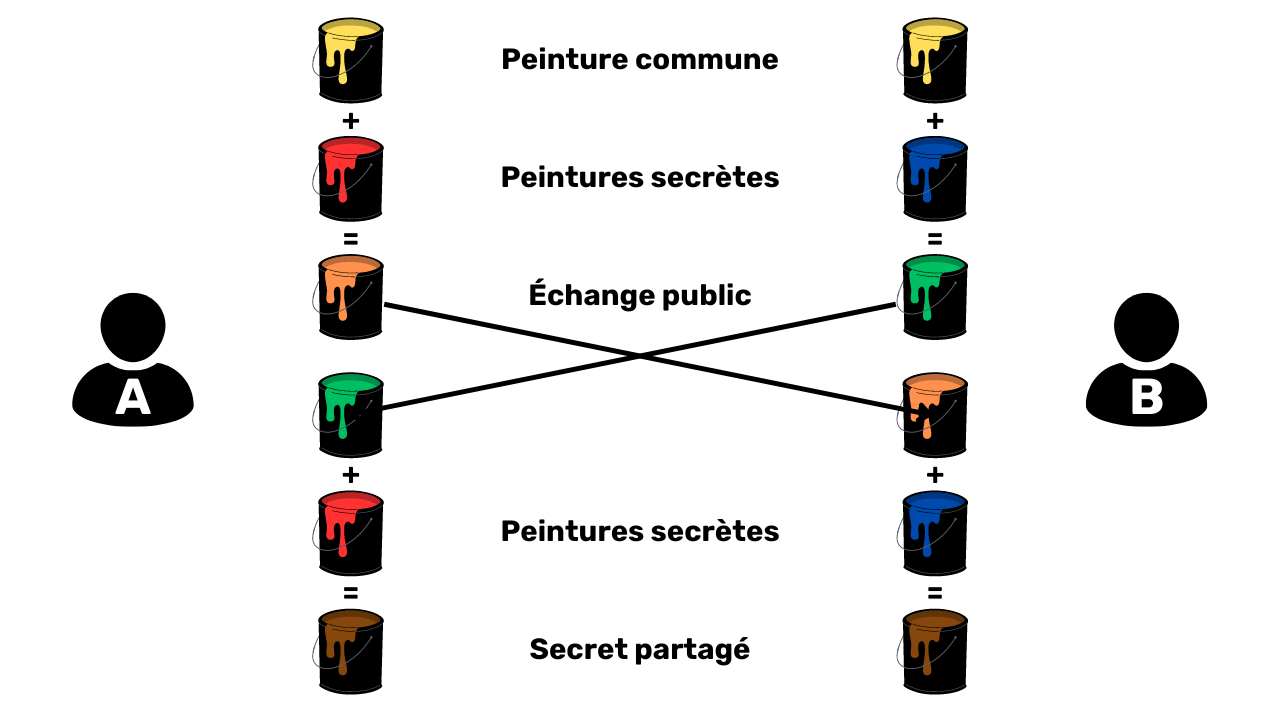
In this popularization, the color brown represents the secret shared by Alice and Bob. Imagine that, in reality, it's impossible for the attacker to separate the colors orange and green, in order to find Alice's or Bob's secret colors.

Now let's take a look at how this protocol actually works, not with color analogies, but using real numbers and modular arithmetic!

Before we get into the Diffie-Hellman mechanisms, let me briefly remind you of two essential mathematical concepts we'll need:

A prime number is a natural number that has only two divisors: $1$ and itself. For example, $7$ is a prime number because it can only be divided by $1$ and $7$ . On the other hand, $8$ is not a prime number, since it is divisible by $1$ , $2$ , $4$ and $8$ . It therefore has four positive integer divisors instead of two;
The modulo (noted $mod$ or $\%$ ) is a mathematical operation which, between two integers, returns the remainder of the Euclidean division of the first by the second. For example, $16\bmod 5 =$ 1$.

The Diffie-Hellman key exchange between Alice and Bob takes place as follows:

Alice and Bob agree on two common numbers: $p$ and $g$ . $p$ is a prime number, and the larger the number, the more secure Diffie-Hellman will be. $g$ is a primitive root of $p$ . These two numbers can be communicated in the clear on an unsecured network. They represent the equivalent of the color yellow in the previous popularization. It is therefore important that Alice and Bob use exactly the same values for $p$ and $g$ .
Once these parameters have been defined, Alice and Bob each choose a secret random number. Alice names her secret random number $a$ (equivalent to the color red) and Bob names his $b$ (equivalent to the color blue). These numbers must remain secret.
Instead of directly exchanging the numbers $a$ and $b$ , each party calculates $A$ and $B$ as follows:

$A$ is equal to $g$ raised to the power $a$ modulo $p$ :

 $A = g^a \bmod p$

$B$ is equal to $g$ raised to the power $b$ modulo $p$ :

 $B = g^b \bmod p$

The values $A$ (equivalent to the color orange) and $B$ (equivalent to the color green) are exchanged between the two parties. This exchange can take place in clear text on an unsecured network;
Alice, having received $B$ , calculates the value of $z$ as follows:

$z$ is equal to $B$ raised to the power $a$ modulo $p$ :

 $z = B^a \bmod p$

A reminder:

 $B = g^b \bmod p$

The result is :

 $z = B^a \bmod p$

 $z = (g^b)^a \bmod p$

By applying the power rules :

 $(x^n)^m = x^{nm}$

The result is :

 $z = g^{ba} \bmod p$

For his part, Bob, having received $A$ , also calculates the value of $z$ as follows:

$z$ is equal to $A$ raised to the power $b$ modulo $p$ :

 $z = A^b \bmod p$

The result is :

 $z = (g^a)^b \bmod p$

 $z = g^{ab} \bmod p$

 $z = g^{ba} \bmod p$

Thanks to the distributivity of the modulo operator, Alice and Bob obtain exactly the same value $z$ . This number represents their common secret, equivalent to the color brown in the previous popularization with paint cans. They can now use this common secret to symmetrically encrypt their communications over an unsecured network.

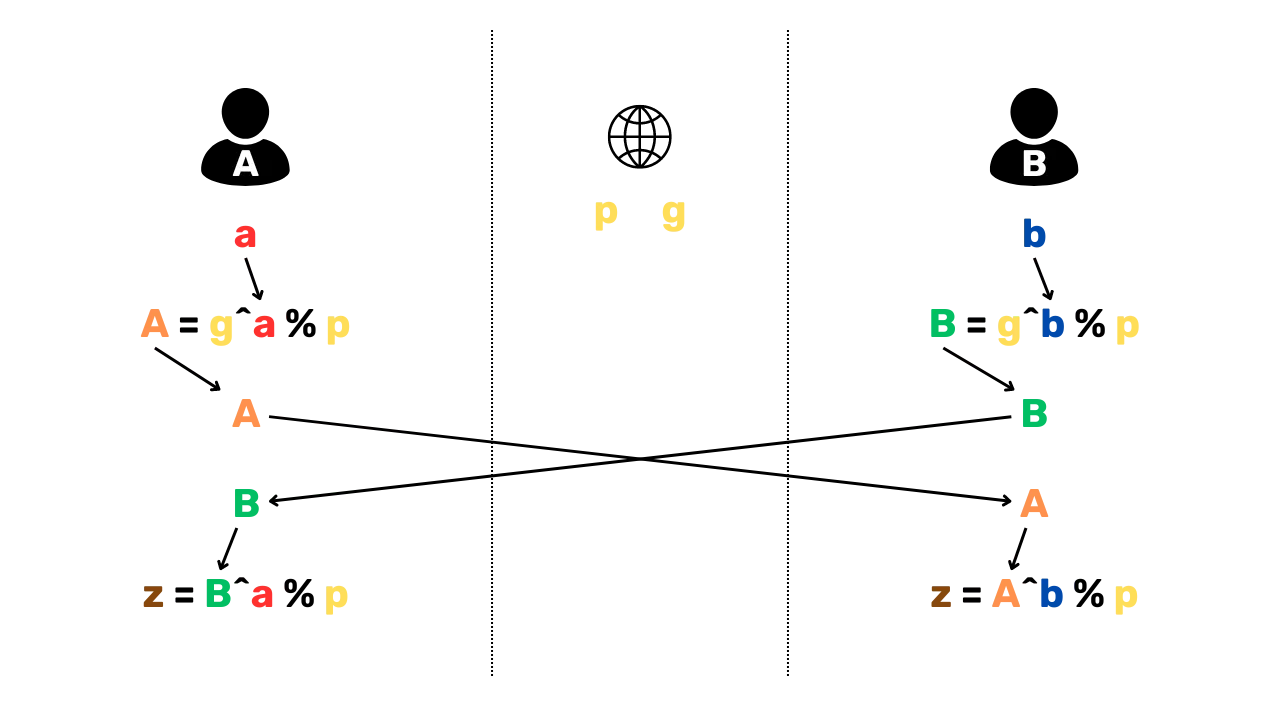
An attacker, even in possession of $p$ , $g$ , $A$ and $B$ (the public values), won't be able to calculate $a$ , $b$ or $z$ (the private values). To achieve this, the exponentiation would have to be reversed, an operation that is impossible without trying all the possibilities one by one, as it amounts to calculating the discrete logarithm, i.e. the reciprocal of the exponential in a finite cyclic group.

So, as long as the values of $a$ , $b$ and $p$ are large enough, the Diffie-Hellman protocol is secure. Typically, with parameters of 2048 bits (a 600-digit decimal number), testing all possibilities for $a$ and $b$ would be impractical. To date, with such numbers, this algorithm is considered secure.

Herein lies the main drawback of the Diffie-Hellman protocol. To be secure, the algorithm must use large numbers. That's why, these days, we prefer to use the ECDH (Elliptic Curve Diffie-Hellman) algorithm, a variant of Diffie-Hellman based on an algebraic curve, more precisely an elliptic curve. This approach makes it possible to work with much smaller numbers while maintaining equivalent security, thus reducing the resources required for calculation and storage.

The general principle of the algorithm remains the same. However, instead of using a random number $a$ and a number $A$ calculated from $a$ by modular exponentiation, we use a pair of keys established on an elliptic curve. Instead of relying on the distributivity of the modulo operator, we use the group law on elliptic curves, and more precisely the associativity of this law.

To briefly explain the principle of cryptography on elliptic curves, a private key is represented by a random number between $1$ and $n-1$ , where $n$ represents the order of the curve. The public key, on the other hand, is a specific point on this curve, obtained from the private key by adding and doubling points from the generating point, according to the equation :

 $K = k \cdot G$

In this formula, $K$ designates the public key, $k$ the private key, and $G$ the generator point.

An essential feature of these keys is the ease with which $K$ can be calculated from $k$ and $G$ , while it is virtually impossible to find $k$ from $K$ and $G$ . This asymmetry creates a one-way function. In other words, it's easy to calculate the public key if you know the private key, but retrieving the private key from the public key is impossible. This security is further underpinned by the computational difficulty of the discrete logarithm.

We'll use this property to adapt our Diffie-Hellman algorithm. The ECDH operating principle is as follows:

Alice and Bob agree on a cryptographically secure elliptic curve and its parameters. This information is public;
Alice generates a random number $ka$ which will be her private key. This private key must remain secret. She determines her public key $Ka$ by adding and doubling points on the chosen elliptic curve:

 $K_a = k_a \cdot G$

Bob also generates a random number $kb$ , which will be his private key. He calculates the associated public key $Kb$ :

 $K_b = k_b \cdot G$

Alice and Bob exchange their public keys $Ka$ and $Kb$ on an unsecured public network.
Alice calculates a point $(x,y)$ on the curve by applying her private key $ka$ to Bob's public key $Kb$ :

 $(x,y) = k_a \cdot K_b$

Bob calculates a point $(x,y)$ on the curve by applying his private key $kb$ to Alice's public key $Ka$ :

 $(x,y) = k_b \cdot K_a$

Alice and Bob obtain the same point on the elliptic curve. The shared secret will be the abscissa $x$ of this point.

They get the same shared secret because :

 $(x,y) = k_a \cdot K_b = k_a \cdot (k_b \cdot G) = (k_a \cdot k_b) \cdot G = (k_b \cdot k_a) \cdot G = k_b \cdot (k_a \cdot G) = k_b \cdot K_a$

A potential attacker observing the unsecured public network will only be able to obtain the public keys of each individual and the parameters of the chosen elliptic curve. As explained above, this information alone is not sufficient to determine the private keys. Consequently, the attacker cannot find the secret shared between Alice and Bob.

ECDH is therefore a key exchange algorithm. It is often used in conjunction with other cryptographic methods to establish a complete protocol. For example, ECDH is at the heart of TLS (Transport Layer Security), an encryption and authentication protocol used for the Internet transport layer. TLS uses ECDHE for key exchange, a variant of ECDH where keys are ephemeral, to provide persistent confidentiality. In addition, TLS uses authentication algorithms such as ECDSA, encryption algorithms such as AES, and hash functions such as SHA256.

TLS is responsible for the s in https and the padlock in your browser's address bar - symbols of encrypted communications. By taking this course, you'll be using ECDH, and it's highly likely that you'll be using it on a daily basis without even knowing it.

The notification transaction

As we saw in the previous section, ECDH is a variant of the Diffie-Hellman exchange using key pairs established on an elliptic curve. It's a good thing we already have many key pairs respecting this standard in our Bitcoin wallets! The idea of BIP47 is to use the key pairs of both parties' hierarchical deterministic Bitcoin wallets to establish shared, ephemeral secrets between them. BIP47 uses ECDHE (Elliptic Curve Diffie-Hellman Ephemeral) instead.

ECDHE is first used in BIP47 to transmit the payment code from the sender to the recipient. This is the famous notification transaction. This step is essential, because for BIP47 to work effectively, both parties involved (sender and receiver) need to know each other's payment codes. This knowledge enables the derivation of ephemeral public keys and, consequently, the associated blank receiving addresses.

Prior to this exchange, the sender is logically already aware of the recipient's payment code, having retrieved it off-chain, for example from his or her website, invoice or social networks. However, the recipient is not necessarily aware of the sender's payment code. However, the code must be transmitted to him; otherwise, he won't be able to derive the ephemeral keys needed to identify the addresses where his bitcoins are stored, or access his funds. Although this transmission of the sender's code can technically be carried out off-chain by other means of communication, this poses a problem if the wallet is to be retrieved from the seed only.

This is because, unlike conventional addresses, BIP47 addresses are not derived directly from the recipient's seed - using an xpub would be simpler in this case - but result from a calculation combining the two payment codes: that of the sender and that of the recipient. So, if the recipient loses his wallet and tries to restore it from his seed, he will recover his own payment code, which is directly derived from his seed. However, to recover ephemeral addresses, he will also need the payment codes of all those who have sent him bitcoins via BIP47. Hence the importance of the notification transaction, which enables this information to be saved on the Bitcoin blockchain, while still being able to find it very easily without having to search through the billion transactions executed since its launch in 2009.

It would therefore be possible to implement BIP47 without using the notification transaction, provided that each user keeps a backup of his peers' payment codes. However, this method proves complex to manage until a simple, robust and efficient solution for making, storing and updating these backups is developed. As things stand, the notification transaction is almost unavoidable.

In the following chapters, however, we will look at other protocols with similar objectives to BIP47, but which do not require a notification transaction. These alternatives do, however, introduce their own trade-offs.

In addition to its role of saving payment codes, the notification transaction also has a notification function for the recipient, as its name suggests. It alerts the recipient's customer to the fact that a new payment tunnel has been established, and suggests that he or she keep an eye on the resulting ephemeral addresses.

The BIP47 confidentiality model

Before detailing the technical operation of the notification transaction, it is important to discuss the confidentiality model associated with BIP47, which justifies certain measures taken when creating this initial transaction.

The payment code itself does not present a direct risk to confidentiality. Unlike the traditional Bitcoin model, which aims to break the link between the user's identity and his transactions (which are public) by preserving the anonymity of keys and addresses, the payment code can be openly associated with an identity without posing a threat.

This is because the payment code is not used to directly derive the addresses receiving BIP47 payments. Instead, these addresses are generated via the ECDH application between the keys derived from the payment codes of the two parties involved.

Thus, a payment code in itself does not directly lead to a loss of confidentiality, since only the notification address is derived from it. Although this address can reveal certain information, it does not normally reveal the parties with whom you are transacting, unless a thorough chain analysis is carried out. Indeed, if the sender uses UTXOs that can be linked to his identity to carry out the notification transaction, then it becomes possible to deduce that his identity is probably linked to BIP47 payments to your payment code. This will not reveal the underlying transactions, but will indicate their likely existence.

It is therefore essential to maintain this strict separation between users' payment codes. With this in mind, the initial communication of the code is a critical moment for payment confidentiality, yet one that is essential for the protocol to function correctly. If one of the payment codes can be obtained publicly (as on a website), the second code, that of the sender, must under no circumstances be linked to the first.

Let's take a concrete example: I want to make a donation to a political movement via BIP47 :

The organization has made its payment code public on its website or via its social networks;
This code is therefore linked to the political movement;
I get this payment code ;
Before sending, I have to make sure they know my own payment code, which is also linked to my identity since I use it to receive transactions on my social networks.

How can I pass on my code without risk? Using conventional means of communication could lead to information leakage, and thus associate me with this political movement. The notification transaction offers a solution, thanks to a layer of encryption that prevents just such an association between two codes. Although it's not the only method of secretly transmitting the sender's payment code, it's a very effective one.

In the diagram below, the orange lines indicate the points where the flow of information must be interrupted, and the black arrows show the connections potentially observable by third parties:

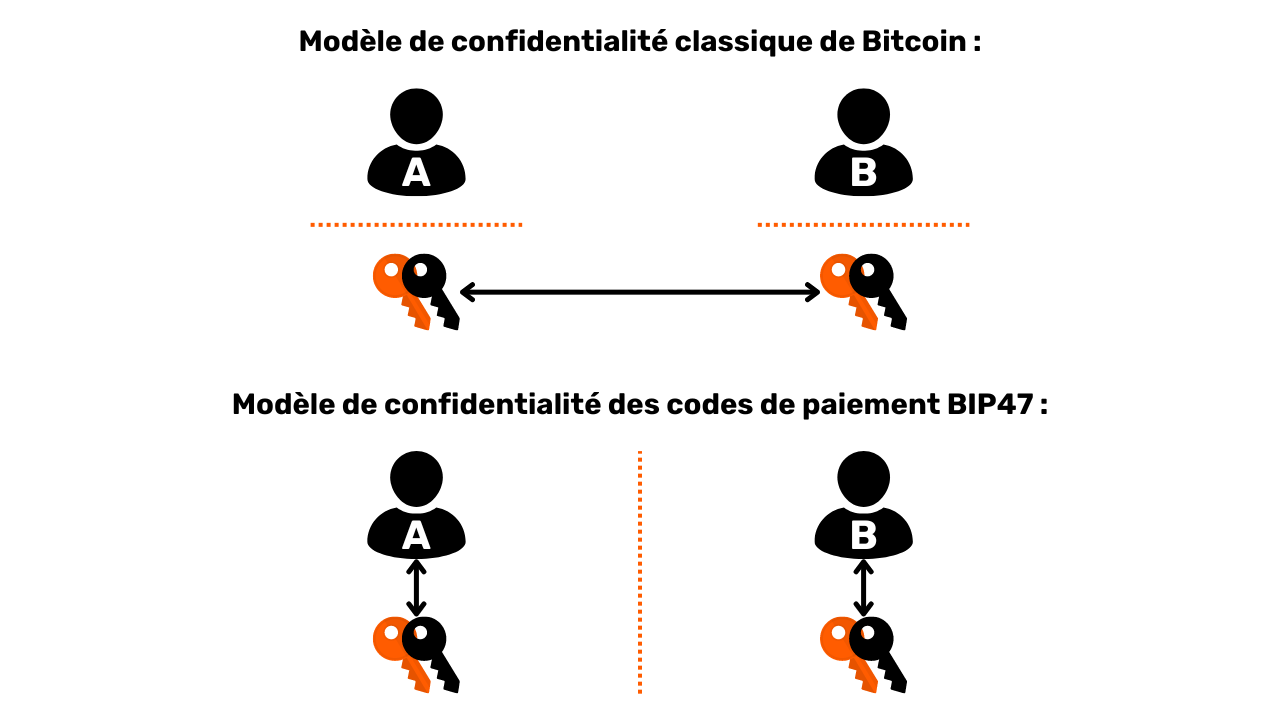
In reality, in Bitcoin's traditional confidentiality model, it is often complex to completely dissociate the flow of information between the key pair and the user, especially in remote transactions. For example, in the context of a donation campaign, the recipient must inevitably disclose an address or public key via his or her website or social networks. The correct use of BIP47, particularly with the notification transaction, makes it possible to get around this problem thanks to ECDHE and the encryption layer we'll be looking at later.

Of course, Bitcoin's classic confidentiality model still applies to ephemeral public keys, which are derived from the combination of the two payment codes. The two models are in fact complementary. What I want to emphasize here is that, unlike the usual use of a public key to receive Bitcoins, the payment code can be linked to a specific identity, as the information "Alice is transacting with Bob" is broken at another stage. The payment code is used to generate payment addresses, but based solely on observation of the blockchain, it is impossible to link a BIP47 payment transaction to the payment codes used to execute it, unless the UTXOs involved were already linked to an identity previously and the users associated their payment codes with their respective identities.

To sum up, the confidentiality model offered by BIP47 payments could be considered superior to Bitcoin's basic model, although this doesn't mean it's magic.

Building the notification transaction

Now let's see how this notification transaction works. Let's imagine that Alice wishes to send funds to Bob using BIP47. In my example, Alice acts as the sender and Bob as the receiver. Bob has published his payment code on his website. Alice therefore already knows Bob's payment code.

1- Alice calculates a shared secret with ECDH :

She selects a key pair from her HD wallet on a different branch from her payment code. Note that this pair must not be easily associated with Alice's notification address, nor with Alice's identity (see previous section);
Alice selects the private key for this pair. We call it $a$ (lowercase);

$a$

Alice retrieves the public key associated with Bob's notification address. This key is the first child derived from Bob's payment code (index $/0$ ). We call this public key $B$ (uppercase). The private key associated with this public key is named $b$ (lower case). $B$ is determined by adding and doubling points on the elliptic curve from $G$ (the generating point) with $b$ (the private key):

$B = b \cdot G$

Alice calculates a secret point $S$ (uppercase) on the elliptic curve by adding and doubling points, applying her private key $a$ from Bob's public key $B$ .

$S = a \cdot B$

Alice calculates the blinding factor $f$ that will be used to encrypt her payment code. To do this, she uses the HMAC-SHA512 function to determine a pseudo-random number. The second input to this function is a value that only Bob will be able to find: $x$ , which is the abscissa of the secret point calculated above. The first input is $o$ , which is the UTXO consumed as input to this transaction (outpoint).

$f = \text{HMAC-SHA512}(o, x)$

**2 - Alice converts her personal payment code to base 2 (binary) **

3- It uses this blinding factor as a key to perform symmetrical encryption on the payload of its payment code. The encryption algorithm used is simply an XOR. The operation performed is comparable to the Vernam cipher, also known as "One-Time Pad".

Alice first splits her blinding factor in two: the first 32 bytes are named $f1$ and the last 32 bytes are named $f2$ . This gives us :

$f = f1 || f2$

Alice calculates the cipher $x'$ of the abscissa of the public key $x$ of her payment code, and the cipher $c'$ of her string code $c$ separately. $f1$ and $f2$ act as cipher keys respectively. The operation used is XOR (or exclusive).

$x' = x \oplus f1$

$c' = c \oplus f2$

Alice replaces the real values of the public key abscissa $x$ and the string code $c$ in her payment code with the encrypted values $x'$ and $c'$ .

4- Alice therefore currently has her payment code with an encrypted payload. She will construct and broadcast a transaction involving her public key $A$ as input, an output to Bob's notification address, and an output OP_RETURN consisting of her payment code with the encrypted payload. This transaction is the notification transaction.

An OP_RETURN is an opcode that marks the output of a Bitcoin transaction as invalid. Today, it is used to broadcast or anchor information on the Bitcoin blockchain. It can store up to 80 bytes of data, which is then written to the chain and visible to all other users.

As we have seen in previous sections, ECDH is used to generate a shared secret between two users communicating over an insecure network, and potentially observed by attackers. In BIP47, ECDH is used to communicate on the Bitcoin network, which by its very nature is a transparent communication network, and is observed by many attackers. The shared secret calculated through ECDH key exchange is then used to encrypt the secret information to be transmitted: the sender's payment code (Alice).

I'll summarize the steps we've just seen together to carry out a notification transaction:

Alice retrieves Bob's payment code and notification address;
Alice selects a UTXO from her HD portfolio with the corresponding key pair;
It calculates a secret point on the elliptic curve using ECDH ;
It uses this secret point to calculate an HMAC, which is the blinding factor;
She uses this blinding factor to encrypt the payload of her personal payment code;
It uses a OP_RETURN transaction output to communicate the hidden payment code to Bob.

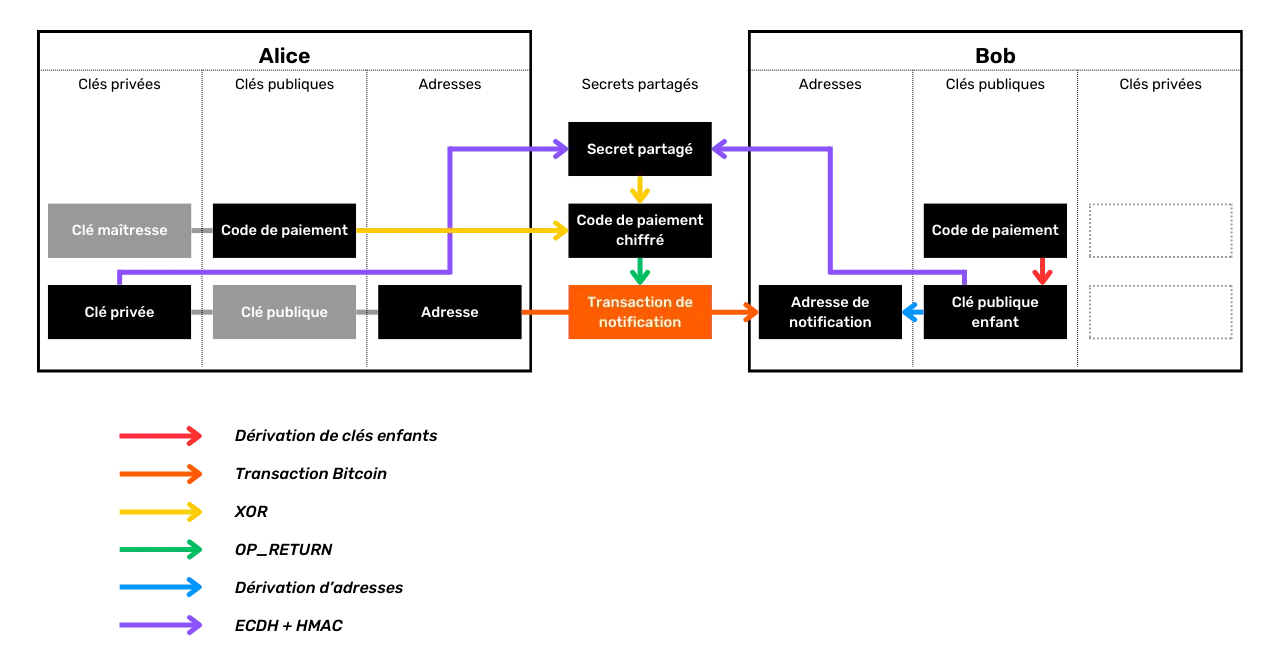
Transaction notification: a practical study

To understand how it works in more detail, and in particular the use of OP_RETURN, let's take a look at a real notification transaction. I carried out such a transaction on the testnet, which you can find by clicking here.

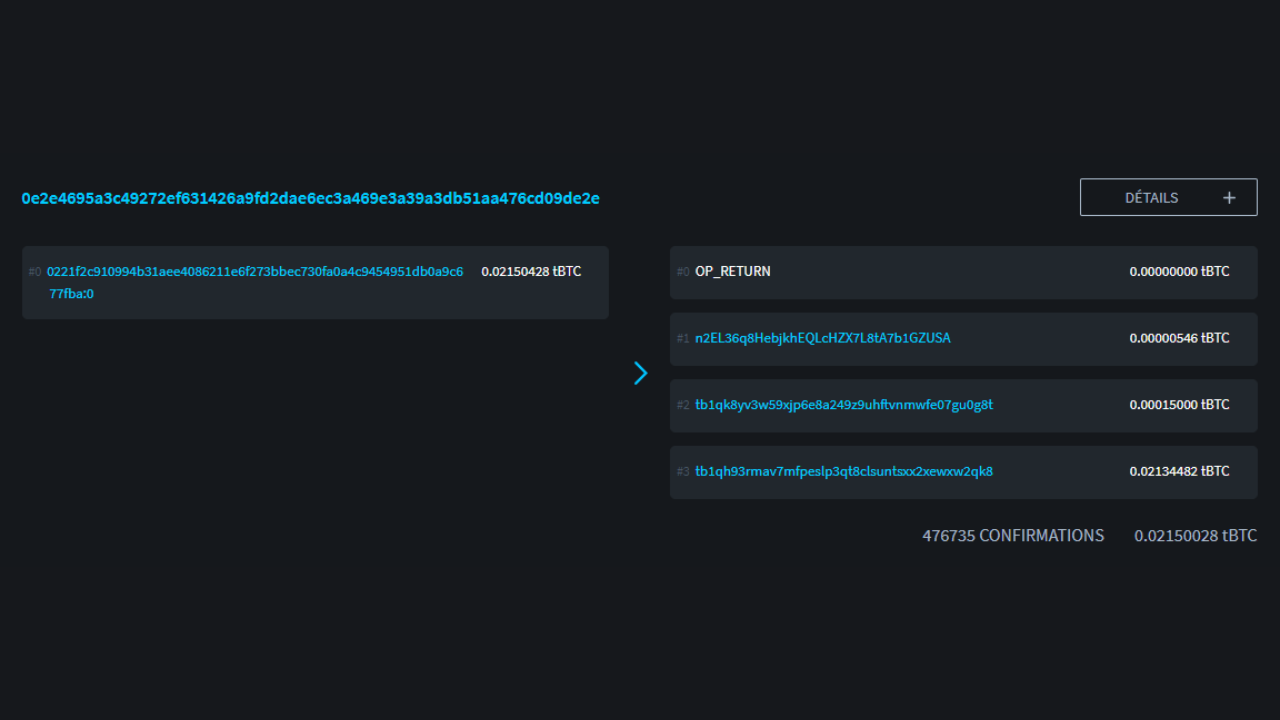
Looking at this transaction, we can already see that it has a single input and 4 outputs:

The first output is the OP_RETURN which contains my hidden payment code;
The second output of 546 sats points to my recipient's notification address;
The third output of 15,000 sats represents the service fee, as I used Samourai Wallet to build this transaction;
The fourth output of 2 million sats represents the exchange rate, i.e. the remaining difference in my input which returns to another address belonging to me.

The most interesting to study is obviously output 0 using OP_RETURN. Let's take a closer look at what it contains. Here's the scriptPubKey in hexadecimal :

6a4c50010002b13b2911719409d704ecc69f74fa315a6cb20fdd6ee39bc9874667703d67b164927b0e88f89f3f8b963549eab2533b5d7ed481a3bea7e953b546b4e91b6f50d800000000000000000000000000

There are several parts to this script. Firstly, the :

6a4c

Among the opcodes, we can recognize 0x6a which designates the OP_RETURN and 0x4c which designates the OP_PUSHDATA1.

The byte following this last opcode indicates the size of the subsequent payload. It indicates 0x50, or 80 bytes:

6a4c50

Next, we have the metadata of my payment code in clear text:

The encrypted abscissa of the public key of my payment code :

b13b2911719409d704ecc69f74fa315a6cb20fdd6ee39bc9874667703d67b164

The encrypted string code of my payment code :

927b0e88f89f3f8b963549eab2533b5d7ed481a3bea7e953b546b4e91b6f50d8

And finally, padding to 80 bytes, the standard size of an OP_RETURN :

00000000000000000000000000

To help you understand, here is my payment code in plain text in base 58 :

PM8TJQCyt6ovbozreUCBrfKqmSVmTzJ5vjqse58LnBzKFFZTwny3KfCDdwTqAEYVasn11tTMPc2FJsFygFd3YzsHvwNXLEQNADgxeGnMK8Ugmin62TZU

And in base 16 :

4701000277507c9c17a89cfca2d3af554745d6c2db0e7f6b2721a3941a504933103cc42add94881210d6e752a9abc8a9fa0070e85184993c4f643f1121dd807dd556d1dc000000000000000000000000008604e4db

If we compare my plaintext payment code with the OP_RETURN, we can see that the HRP (0x47) and the checksum (0x8604e4db) are not transmitted. This is normal, as this information is intended for humans.

Next, we can recognize the version (0x01), the bit field (0x00) and the parity of the public key (0x02). And, at the end of the payment code, the empty bytes (0x000000000000000000000000000000) that allow padding to reach a total of 80 bytes. All this metadata is transmitted unencrypted.

Finally, we can observe that the public key abscissa (0x77507c9c17a89cfca2d3af554745d6c2db0e7f6b2721a3941a504933103cc42a) and the string code (0xdd94881210d6e752a9abc8a9fa0070e85184993c4f643f1121dd807dd556d1dc) have been encrypted. This is the payload of the payment code.

What is XOR?

We have seen in previous sections that the payment code is transmitted encrypted using the XOR operation. Let's take a closer look at how this operator works, as it is widely used in cryptography.

XOR is a bitwise logical operator based on Boolean algebra. Given two operands in bits, it returns 1 if the bits of the same rank are different, and it returns 0 if the bits of the same rank are equal. Here's the XOR truth table according to the values of the operands D and E :

| D | E | D XOR E |

| --- | --- | ------- |

| 0 | 0 | 0 |

| 0 | 1 | 1 |

| 1 | 0 | 1 |

| 1 | 1 | 0 |

For example:

 $0110 \oplus 1110 = 1000$

Or :

 $010011 \oplus 110110 = 100101$

With ECDH, the use of XOR as an encryption layer is particularly consistent. Firstly, thanks to this operator, encryption is symmetrical. This means that the recipient can decrypt the payment code with the same key used for encryption. The encryption and decryption keys are calculated from the shared secret using ECDH. This symmetry is made possible by the commutativity and associativity properties of the XOR operator:

Other properties :

 $D \oplus D = 0$

 $D \oplus 0 = D$

Commutativity :

 $D \oplus E = E \oplus D$

Associativity :

 $D \oplus (E \oplus Z) = (D \oplus E) \oplus Z = D \oplus E \oplus Z$

If :

 $D \oplus E = L$

Then :

 $D \oplus L = D \oplus (D \oplus E) = D \oplus D \oplus E = 0 \oplus E = E \\ \therefore D \oplus L = E$

Secondly, this encryption method is very similar to the Vernam (One-Time Pad) cipher, the only encryption algorithm known to date that has unconditional (or absolute) security. For Vernam's cipher to have this feature, the encryption key must be perfectly random, of the same size as the message and used only once. In the encryption method used here for BIP47, the key is indeed the same size as the message, and the blinding factor is exactly the same size as the concatenation of the abscissa of the public key with the string code of the payment code. This encryption key is used only once. On the other hand, this key is not derived from a perfect randomness, since it is an HMAC. Rather, it is pseudo-random. So it's not a Vernam cipher, but the method comes close.

Receipt of notification transaction

Now that Alice has sent the notification transaction to Bob, let's see how Bob interprets it. As a reminder, Bob must have access to Alice's payment code. Without this information, as we'll see in the next section, he won't be able to derive the key pairs created by Alice, and therefore won't be able to access his bitcoins received via BIP47. For the moment, Alice's payment code payload is encrypted. Let's see how Bob decrypts it.

1- Bob monitors transactions that create outputs with his notification address.

2- When a transaction has an output on its notification address, Bob analyzes it to see if it contains an OP_RETURN output that complies with the BIP47 standard.

3- If the first byte of the OP_RETURN payload is 0x01, Bob begins his search for a possible secret shared with ECDH :

Bob selects the input public key for the transaction. That is, Alice's public key named $A$ with :

$A = a \cdot G$

Bob selects the private key $b$ associated with his personal notification address :

$b$

Bob calculates the secret point $S$ (shared secret ECDH) on the elliptic curve by adding and doubling points, applying his private key $b$ to Alice's public key $A$ :

$S = b \cdot A$

Bob determines the blinding factor $f$ that will enable the payload of Alice's payment code to be decrypted. In the same way as Alice had calculated it previously, Bob will find $f$ by applying HMAC-SHA512 to $x$ , the abscissa value of the secret point $S$ , and to $o$ , the UTXO consumed as input to this notification transaction:

$f = \text{HMAC-SHA512}(o, x)$

4- Bob interprets the OP_RETURN data in the notification transaction as a payment code. He will simply decrypt the payload of this potential payment code using the $f$ blinding factor:

Bob splits the blinding factor $f$ into 2 parts: the first 32 bytes of $f$ will be $f1$ and the last 32 bytes will be $f2$ ;
Bob decrypts the value of the encrypted abscissa $x'$ from the public key of Alice's payment code:

$x = x' \oplus f1$

Bob decrypts the value of the encrypted string code $c'$ from Alice's payment code:

$c = c' \oplus f2$

5- Bob checks whether the public key value of Alice's payment code is part of the secp256k1 group. If so, he interprets this as a valid payment code. If not, he ignores the transaction.

Now that Bob knows Alice's payment code, Alice can send him up to 2^32 payments, without ever having to repeat a notification transaction of this type.

Why does it work? How can Bob determine the same blinding factor as Alice, and thus decipher her payment code? Let's take a closer look at ECDH's action in what we've just described.

First of all, we're dealing with symmetrical encryption. This means that the encryption key and the decryption key are the same value. This key in the notification transaction is the blinding factor:

$f = f1 || f2$

Alice and Bob must therefore obtain the same value for $f$ , without transmitting it directly, since an attacker could steal it and decrypt the secret information. This blinding factor is obtained by applying HMAC-SHA512 to 2 values:

the abscissa of a secret point ;
and the UTXO consumed at the transaction input.

Bob therefore needs both these pieces of information to decrypt Alice's payment code payload. For the input UTXO, Bob can simply retrieve it by observing the notification transaction. For the secret point, Bob will need to use ECDH. As seen in the previous section on Diffie-Hellman, simply by exchanging their respective public keys and secretly applying their private keys to each other's public key, Alice and Bob can find a precise secret point on the elliptic curve. The notification transaction is based on this mechanism:

Bob's pair of keys :

$B = b \cdot G$

Alice's key pair :

$A = a \cdot G$

For a secret $S (x, y)$ :

$S = a \cdot B = a \cdot (b \cdot G) = (b \cdot a) \cdot G = b \cdot A$

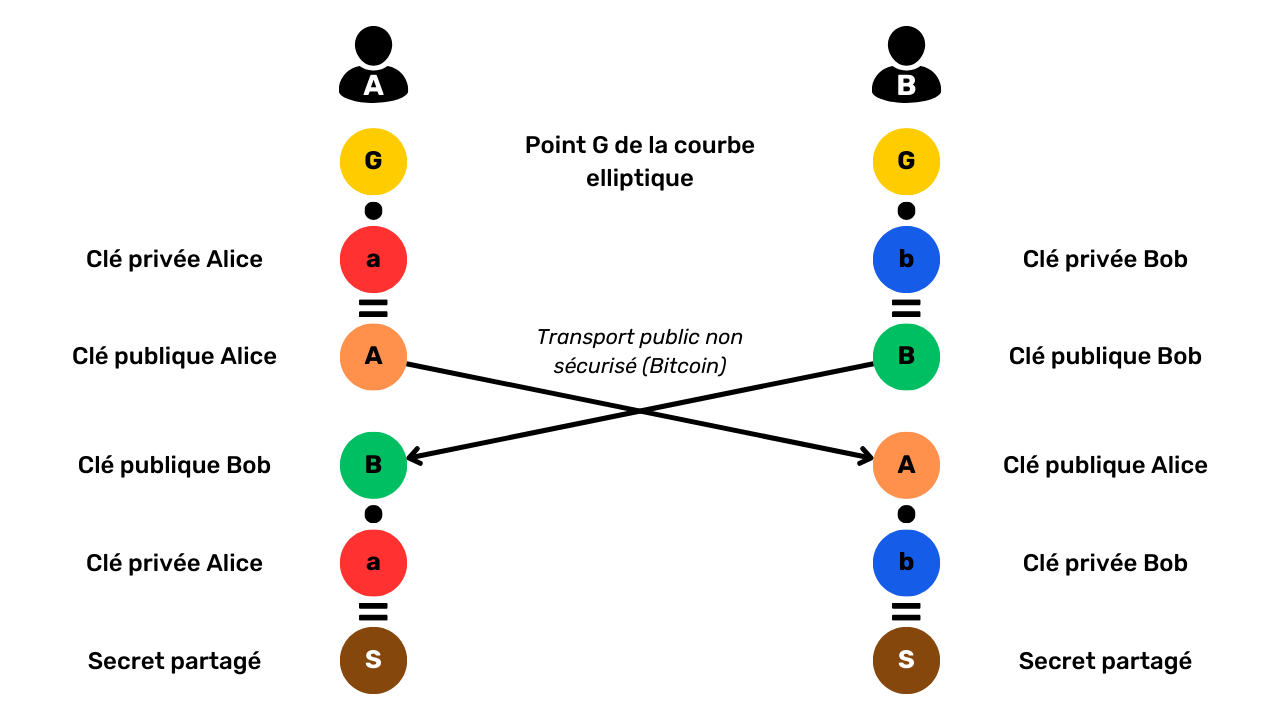
Now that Bob knows Alice's payment code, he'll be able to detect her BIP47 payments, and he'll be able to derive the private keys blocking the bitcoins received.

I'll summarize the steps we've just seen together to receive and interpret a notification transaction:

Bob monitors transaction output to his notification address;
When it detects one, it retrieves the information contained in the OP_RETURN ;
Bob selects the public key as input and calculates a secret point using ECDH ;
It uses this secret point to calculate a HMAC, which is the blinding factor;
It uses this blinding factor to decrypt Alice's payment code payload contained in the OP_RETURN.

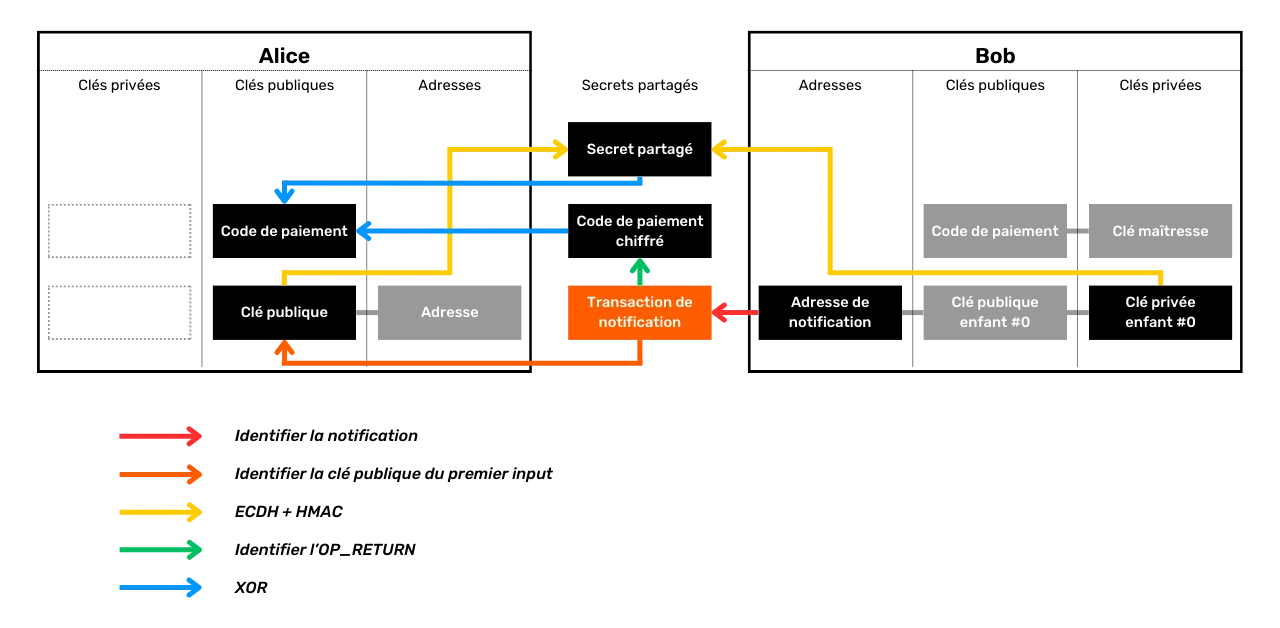
The BIP47 payment transaction

Let's take a look at the payment process with BIP47. To remind you of the current situation :

Alice knows Bob's payment code, which she simply retrieved from his website;
Bob knows Alice's payment code from the notification transaction;
Alice will make her first payment to Bob. She can make many more in the same way.

Before explaining this process, I think it's important to remember which indexes we're currently working on. The derivation path for a payment code is described as follows: m/47'/0'/0'. The following depth divides the indexes as follows:

The first normal (non-reinforced) daughter pair is the one used to generate the notification address discussed in the previous section: m/47'/0'/0'/0 ;
Normal daughter key pairs are used within ECDH to generate BIP47 payment receipt addresses, as we will see in this section: from m/47'/0'/0'/0 to m/47'/0'/0'/2,147,483,647 ;
Reinforced daughter key pairs are ephemeral payment codes: from m/47'/0'/0'/0' to m/47'/0'/0'/2,147,483,647'.

Each time Alice wants to send a payment to Bob, she derives a new, unique, blank address, once again using the ECDH protocol:

Alice selects the first private key derived from her personal reusable payment code :

$a$

Alice selects the first unused public key derived from Bob's payment code. We'll call this public key $B$ . It is associated with the private key $b$ known only to Bob:

$B = b \cdot G$

Alice calculates a secret point $S$ on the elliptic curve by adding and doubling points by applying her private key $a$ from Bob's public key $B$ :

$S = a \cdot B$

From this secret point, Alice calculates the shared secret $s$ (lowercase). To do this, she selects the abscissa of the secret point $S$ named $Sx$ , and passes this value to the SHA256 hash function:

$S = (Sx, Sy)$

$s = \text{SHA256}(Sx)$

Alice uses this shared secret $s$ to calculate a Bitcoin payment reception address. First, she checks that $s$ is contained in the order of the secp256k1 curve. If this is not the case, she increments Bob's public key index to derive another shared secret ;
In a second step, she calculates a public key $K0$ by adding the points $B$ and $s-G$ on the elliptic curve. In other words, Alice adds the public key derived from Bob's payment code $B$ to another point calculated on the elliptic curve by adding and doubling points with the shared secret $s$ from the secp256k1 curve generator point $G$ . This new point represents a public key, and we call it $K0$ :

$K0 = B + s \cdot G$

With this public key $K0$ , Alice can derive a blank receive address in the standard way (e.g. SegWit V0 in bech32).

Once Alice has obtained Bob's $K0$ receiving address, she can carry out a Bitcoin transaction in the standard way. To do this, she chooses a UTXO she owns, secured by a key pair from a different branch of her HD wallet, and consumes it to satisfy an output to Bob's $K0$ address. It's important to note that this payment, once the address has been derived, follows a classic process and no longer depends on the keys associated with the BIP47.

I'll summarize the steps we've just seen together to send a BIP47 payment:

Alice selects the first daughter private key derived from her personal payment code ;
It calculates a secret point on the elliptic curve using ECDH from the first unused daughter public key derived from Bob's payment code;
It uses this secret point to calculate a shared secret with SHA256 ;
She uses this shared secret to calculate a new secret point on the elliptic curve;
She adds this new secret point to Bob's public key;
She obtains a new ephemeral public key for which only Bob has the associated private key;
Alice can make a classic transaction to Bob with the derived ephemeral receive address.

If Alice wants to make a second payment, she'll follow the same steps as before, except that this time she'll select the second public key derived from Bob's payment code. Specifically, she will use the next unused key. She will thus obtain a new receiving address belonging to Bob, designated $K1$ :

It can continue in this way and derive up to 2^32 blank addresses belonging to Bob.

From an outside perspective, looking at the blockchain, it is theoretically impossible to differentiate a BIP47 payment from a conventional payment. Here's an example of a BIP47 payment transaction on Testnet:

94b2e59510f2e1fa78411634c98a77bbb638e28fb2da00c9f359cd5fc8f87254

It looks like a classic transaction with a consumed input, a payment output and an exchange rate:

Receipt of BIP47 payment and derivation of private key

Alice has just made her first payment to a blank BIP47 address belonging to Bob. Now let's see how Bob receives this payment. We'll also see why Alice doesn't have access to the private key of the address she's just generated herself, and how Bob finds this key to spend the bitcoins he's just received.

As soon as Bob receives the notification transaction from Alice, he derives the public key BIP47 $K0$ even before his correspondent has sent a payment. He therefore observes any payment to the associated address. In fact, he immediately derives several addresses that he observes ( $K0$ , $K1$ , $K2$ , $K3$ ...). Here's how it derives this public key $K0$ :

Bob selects the first daughter private key derived from his payment code. This private key is named $b$ . It is associated with the public key $B$ with which Alice made her calculations in the previous step:

$b$

Bob selects Alice's first public key derived from her payment code. This key is named $A$ . It is associated with the private key $a$ with which Alice made her calculations, and which is known only to Alice. Bob can carry out this process, since he knows Alice's payment code, which was sent to him with the notification transaction:

$A = a \cdot G$

Bob calculates the secret point $S$ , by adding and doubling points on the elliptic curve, by applying his private key $b$ to Alice's public key $A$ . Here again, ECDH is used to guarantee that this point $S$ will be the same for both Bob and Alice:

$S = b \cdot A$

In the same way as Alice, Bob isolates the abscissa of this point $S$ . We've named this value $Sx$ . He passes this value to the SHA256 function to find the shared secret $s$ (lowercase):

$s = \text{SHA256}(Sx)$

In the same way as Alice, Bob calculates the $s-G$ point on the elliptic curve. He then adds this secret point to his public key $B$ . He then obtains a new point on the elliptic curve, which he interprets as a public key $K0$ :

$K0 = B + s \cdot G$

Once Bob has this public key $K0$ , he can derive the associated private key to spend his bitcoins. Only he can generate this private key:

Bob adds up his daughter's private key $b$ derived from his personal payment code. Only he can obtain the value of $b$ . He then adds $b$ to the shared secret $s$ to obtain $k0$ , $K0$ 's private key:

$k0 = b + s$

Thanks to the group law of the elliptic curve, Bob obtains exactly the private key corresponding to the public key used by Alice. We therefore have :

$K0 = k0 \cdot G$

I'll summarize the steps we've just seen together to receive a BIP47 payment and calculate the corresponding private key:

Bob selects the first daughter private key derived from his personal payment code ;
It calculates a secret point on the elliptic curve using ECDH from the first daughter public key derived from Alice's string code;
It uses this secret point to calculate a shared secret with SHA256 ;
He uses this shared secret to calculate a new secret point on the elliptic curve;
He adds this new secret point to his personal public key;
He obtains a new ephemeral public key, the one to which Alice will send her first payment;
Bob calculates the private key associated with this ephemeral public key by adding his daughter private key derived from his payment code and the shared secret.

Since Alice cannot obtain $b$ (Bob's private key), she is unable to determine $k0$ (the private key associated with Bob's BIP47 reception address). Schematically, we can represent the calculation of the shared secret $S$ as follows:

Once the shared secret is found with ECDH, Alice and Bob calculate the BIP47 payment public key $K0$ , and Bob also calculates the associated private key $k0$ :

Refund of BIP47 payment

Since Bob knows Alice's reusable payment code, he already has all the information he needs to send her a refund. He won't need to contact Alice again to ask for any information. He simply needs to notify her with a notification transaction, so that she can retrieve her BIP47 addresses with her seed, and then he can also send her up to 2^32 payments.

The refund feature is specific to BIP47 and is one of its advantages over other methods, such as Silent Payments, which we'll look at in later chapters.

Bob can then reimburse Alice in the same way she sent him payments. The roles are reversed:

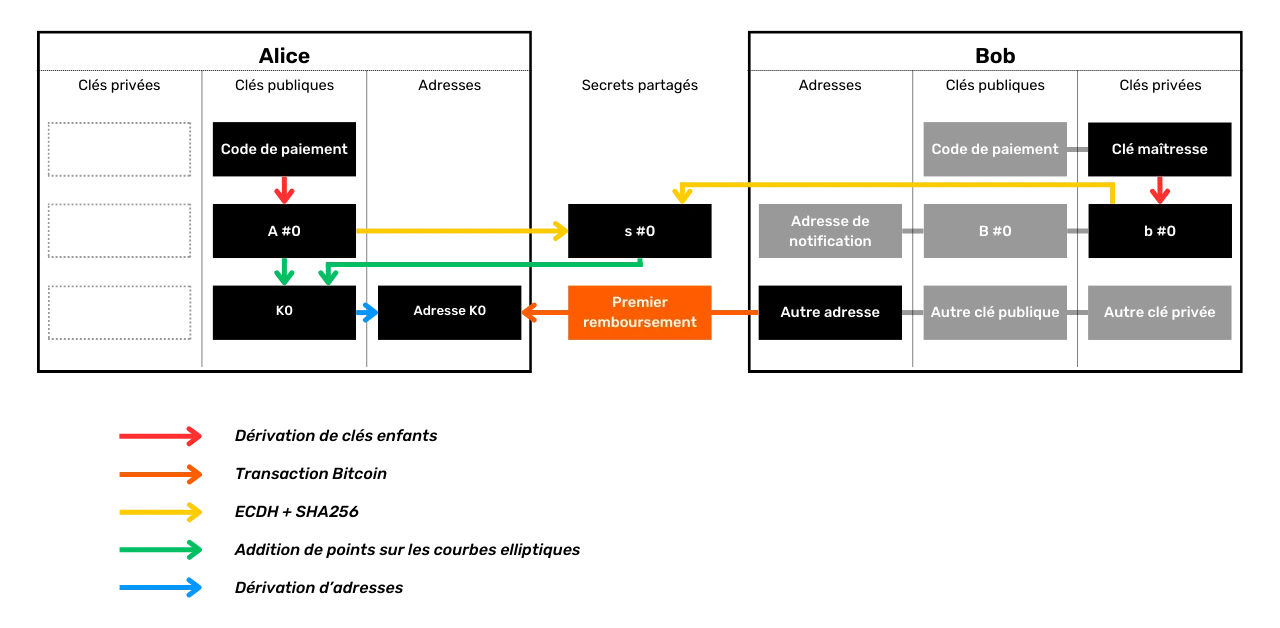
*Many thanks to Fanis Michalakis for his proofreading and expert advice on the article that inspired the writing of this chapter!

https://planb.network/tutorials/privacy/on-chain/paynym-bip47-a492a70b-50eb-4f95-a766-bae2c5535093

Silent Payments

BIP47 has been widely criticized for its onchain inefficiency. As explained in the previous chapter, it requires a notification transaction to be carried out for each new recipient. This constraint becomes negligible if we plan to establish a sustainable payment channel with this recipient. Indeed, a single notification transaction paves the way for an almost infinite number of subsequent BIP47 payments.

However, in certain situations, the notification transaction can be an obstacle for the user. Let's take the example of a one-off donation to a recipient: with a classic Bitcoin address, a single transaction is enough to complete the donation. But with BIP47, two transactions are required: one for the notification and another for the actual payment. When demand for block space is low and transaction fees are low, this extra step is not usually a problem. However, in times of congestion, transaction fees can become exorbitant for a single payment, potentially doubling the cost to the user compared to a standard Bitcoin transaction, which may prove unacceptable to the user.

For situations where the user plans to make only a few payments to a static identifier, other solutions have been developed. These include Silent Payments, described in BIP352. This protocol makes it possible to use a static identifier to receive payments without producing address reuses, and without requiring the use of notification transactions. Let's take a look at how this protocol works.

To fully understand this chapter, it is essential to master the workings of ECDH (Elliptic Curve Diffie-Hellman) and cryptographic key derivation in an HD wallet. These concepts were covered in detail in the previous chapter on BIP47. I won't repeat them here. If you are not yet familiar with these concepts, I recommend that you consult the previous chapter before continuing with this one. I won't go back over the risks associated with the reuse of receiving addresses, nor the importance of having a unique identifier for receiving payments. I'll just mention a few points that I'd like to make here

Why not move the notification?

As discussed in the BIP47 chapter, the notification transaction has two main functions:

It notifies the recipient ;
It transmits the sender's payment code.

One might naively think that this notification process could be carried out off-chain. In theory, it's perfectly feasible: all the recipient would have to do is indicate a means of communication to receive the BIP47 payment codes from the senders. However, there are two major problems with this approach:

Firstly, it would move the code transmission process to another communication protocol. Problems relating to the cost and confidentiality of the exchange would remain, but would simply be transferred to this new protocol. In terms of confidentiality, this could also create a link between a user's identity and onchain activity, which is what we seek to avoid by performing the notification directly on the blockchain. Furthermore, making the notification outside the blockchain would introduce risks of censorship (such as blocking funds) that do not exist on Bitcoin;
Secondly, this would pose a recovery problem. With BIP47, the recipient must know the payment codes of the senders in order to access the funds. This is true on receipt, but also in the event of funds being recovered via the seed if the wallet is lost. With onchain notifications, this risk is avoided, as the user can retrieve and decrypt notification transactions simply by knowing his seed. However, if the notification is made outside the blockchain, the user would have to maintain a dynamic backup of all payment codes received, which is impractical for the average user.

All these constraints make the use of onchain notification essential for BIP47. However, Silent Payments seek to avoid this onchain notification step precisely because of its cost. The solution adopted is therefore not to move notification, but to eliminate it entirely. To achieve this, a compromise has to be accepted: scanning. Unlike BIP47, where the user knows exactly where to find his funds thanks to notification transactions, with Silent Payments, the user has to examine all existing Bitcoin transactions to detect any payments intended for him. To reduce this operational burden, the Silent Payments search is limited only to transactions likely to contain such payments, i.e. those with at least one Taproot P2TR output. The scan also focuses exclusively on transactions from the wallet creation date (there's no need to scan transactions dating back to 2009 if the wallet was created in 2024).

So you can see why BIP47 and Silent Payments, although aimed at a similar objective, involve different trade-offs and therefore actually meet distinct use cases. For one-off payments, such as one-off donations, Silent Payments are more appropriate because of their lower cost. On the other hand, for regular transactions to the same recipient, as in the case of exchange platforms or mining pools, BIP47 may be preferred.

Let's take a look at the technical operation of Silent Payments to better understand what's at stake. To do this, I suggest we take the same approach as the BIP352 explanatory document. We'll gradually break down the calculations to be carried out, element by element, justifying each new addition.

A few concepts to understand

Before getting started, it's important to point out that Silent Payments rely on the use of P2TR (Pay to Taproot) script types exclusively. Unlike BIP47, it is not necessary to derive receiving addresses from child public keys by hashing. In the P2TR standard, the tweaked public key is used directly and unencrypted in the address. So a Taproot receive address is essentially a public key with some metadata. This tweaked public key is the aggregation of two other public keys: one enabling direct, traditional spending via a simple signature, and the other representing the Merkle root of the MAST, which authorizes spending subject to the satisfaction of one of the conditions potentially inscribed in the Merkle tree.

There are two main reasons for the decision to limit Silent Payments exclusively to Taproot:

Firstly, it considerably facilitates implementation and future upgrades in portfolio software, since only one standard needs to be respected;
Secondly, this approach helps to improve users' anonset by encouraging them not to divide themselves between different types of scripts, which generate distinct portfolio fingerprints in chain analysis (for more information on this concept, please refer to chapter 4 of part 2).

Naive derivation of a Silent Payments public key

Let's start with a simple example to get to the heart of how SPs (Silent Payments) work. Let's take Alice and Bob, two Bitcoin users. Alice wishes to send Bitcoins to Bob on a blank receiving address. There are three objectives to this process:

Alice must be able to generate a blank address;
Bob must be able to identify a payment sent to this specific address;
Bob needs to be able to obtain the private key associated with this address in order to spend his funds.

Alice has a UTXO in her secure Bitcoin wallet with the following key pair:

$a$ : the private key ;
$A$ : the public key ( $A = a \cdot G$ )

Bob has an SP address which he has published on the Internet with :

$b$ : the private key ;
$B$ : the public key ( $B = b \cdot G$ )

By retrieving Bob's address, Alice is able to calculate a new blank address that belongs to Bob using ECDH. Let's call this address $P$ :

$P = B + \text{hash}(a \cdot B) \cdot G$

In this equation, Alice has simply calculated the scalar product of her private key $a$ and Bob's public key $B$ . She has passed this result into a hash function known to everyone. The resulting value is then multiplied scalarly by the generating point $G$ of the elliptic curve secp256k1. Finally, Alice adds the resulting point to Bob's public key $B$ . Once Alice has this address $P$ , she uses it as an output in a transaction, i.e. she sends bitcoins to it.

In the context of Silent Payments, the "hash" function corresponds to a SHA256 hash function specifically tagged with BIP0352/SharedSecret, which ensures that the hashes generated are unique to this protocol and cannot be reused in other contexts, while offering additional protection against the reuse of nonces in signatures. This standard corresponds to that specified in BIP340 for Schnorr signatures on secp256k1. Thanks to the properties of the elliptic curve on which ECDH is based, we know that :

$a \cdot B = b \cdot A$

Bob will therefore be able to calculate the receiving address to which Alice has sent the bitcoins. To do this, he monitors all Bitcoin transactions that meet the Silent Payments criteria and applies the following calculation to each of them to see if the payment is addressed to him (scanning):

$P' = B + \text{hash}(b \cdot A) \cdot G$

When he scans Alice's transaction, he realizes that $P'$ is equal to $P$ . He therefore knows that the payment is addressed to her:

$P' = B + \text{hash}(b \cdot A) \cdot G = B + \text{hash}(a \cdot B) \cdot G = P$

From here, Bob will be able to calculate the private key $p$ which allows the address $P$ to be spent:

$p = (b + \text{hash}(b \cdot A)) \bmod n$

As you can see, to calculate this private key $p$ , you must have the private key $b$ . Only Bob has this private key $b$ . He will therefore be the only one able to spend the bitcoins sent to his Silent Payments address.

Legend:

$B$ : The public key/static address published by Bob
$b$ : Bob's private key
$A$ : Alice's UTXO public key used as transaction input
$a$ : Alice's private key
$G$ : The generating point of the elliptic curve secp256k1
$\text{SHA256}$ : The SHA256 hash function tagged with BIP0352/SharedSecret
$s$ : The ECDH common secret
$P$ : The public key/unique address for payment to Bob

Here's a rather naive initial approach to using Bob's static address, noted $B$ , to derive a unique address $P$ to send bitcoins to. However, this method is too simplistic and has several flaws that need to be corrected. The first problem is that, in this scheme, Alice cannot create multiple outputs to Bob within the same transaction.

How do I create multiple outputs?

In the example in the previous section, Alice creates a single output that will go to Bob at his unique address $P$ . With the same input selected, it is impossible for Alice to create two separate blank addresses for Bob, as the method used would always lead to the same result for $P$ , i.e. the same address. However, there may be many situations where Alice wishes to divide her payment to Bob into several smaller amounts, thus creating several UTXOs. It is therefore necessary to find a method of achieving this.

To achieve this, we're going to slightly modify the calculation Alice performs to derive $P$ , so that she can generate two distinct addresses for Bob, namely $P_0$ and $P_1$ .

To modify the calculation and obtain 2 different addresses, simply add an integer that modifies the result. Thus, Alice will add $0$ to her calculation to obtain the address $P_0$ and $1$ to obtain the address $P_1$ . Let's call this integer $i$ :

$P_i = B + \text{hash}(a \cdot B \text{ ‖ } i) \cdot G$

The calculation process remains unchanged from the previous method, except that this time Alice will concatenate $a \cdot B$ with $i$ before proceeding with the hash. You then simply modify $i$ to obtain a new address belonging to Bob. For example:

$P_0 = B + \text{hash}(a \cdot B \text{ ‖ } 0) \cdot G$

$P_1 = B + \text{hash}(a \cdot B \text{ ‖ } 1) \cdot G$

When Bob scans the blockchain for Silent Payments intended for him, he starts by using $i = 0$ for address $P_0$ . If he doesn't find any payments on $P_0$ , he concludes that this transaction contains no Silent Payments intended for him, and abandons the scan. However, if $P_0$ is valid and contains a payment for him, he continues with $P_1$ in the same transaction to check whether Alice has made a second payment. If $P_1$ turns out to be invalid, it stops searching for this transaction; otherwise, it continues testing successive $i$ values:

$P_0 = B + \text{hash}(b \cdot A \text{ ‖ } 0) \cdot G$

$P_1 = B + \text{hash}(b \cdot A \text{ ‖ } 1) \cdot G$

Since Bob stops immediately at $i = 0$ if $P_0$ doesn't work, using this integer adds almost no additional operational load on Bob for the transaction scanning stage.

Bob can then calculate the private keys in the same way:

 $p_0 = (b + \text{hash}(b \cdot A \text{ ‖ } 0)) \bmod n$

 $p_1 = (b + \text{hash}(b \cdot A \text{ ‖ } 1)) \bmod n$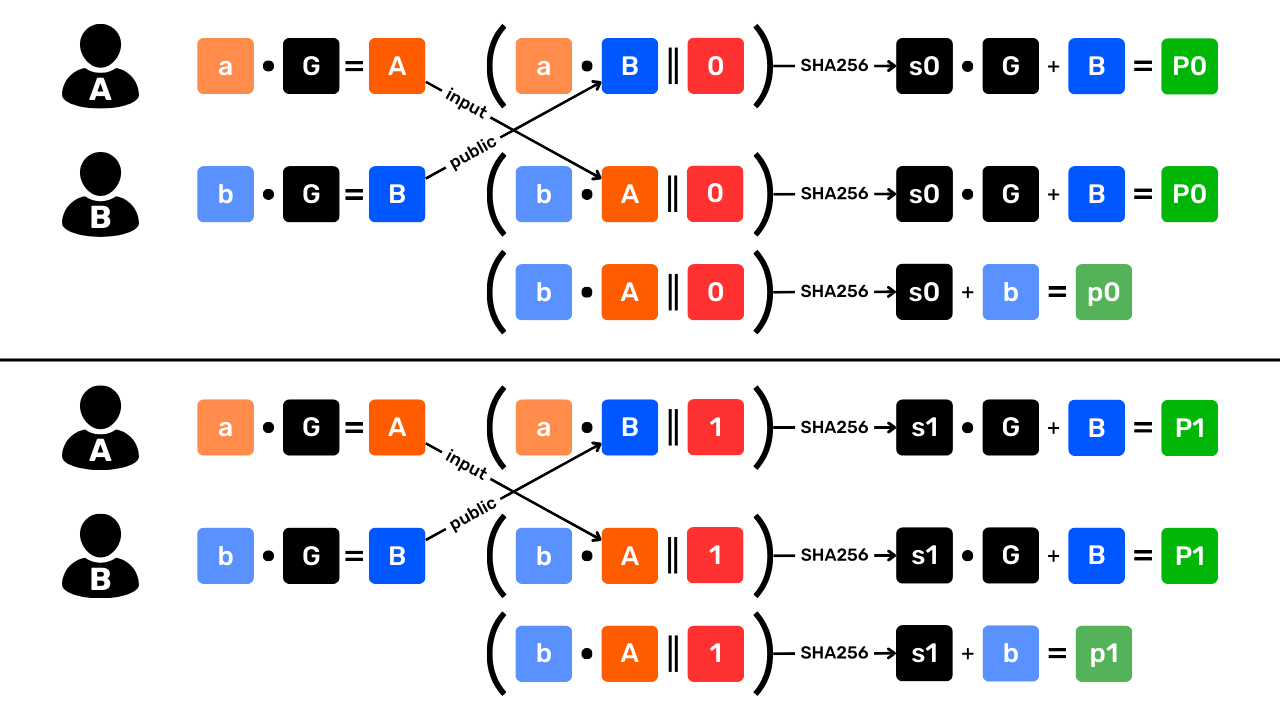

Legend:

$B$ : The public key/static address published by Bob
$b$ : Bob's private key
$A$ : Alice's UTXO public key used as transaction input
$a$ : Alice's private key
$G$ : The generating point of the elliptic curve secp256k1
$\text{SHA256}$ : The SHA256 hash function tagged with BIP0352/SharedSecret
$s_0$ : The first common secret ECDH
$s_1$ : The second ECDH common secret
$P_0$ : The first public key / unique address for payment to Bob
$P_1$ : The second public key / unique address for payment to Bob

With this method, we're starting to get a nice protocol, but there are still a few challenges to overcome, not least the prevention of address reuse.

How to avoid address reuse?

As we saw in the previous sections, Alice uses the key pair that secures her UTXO, which she will spend to calculate the ECDH shared secret with Bob. This secret enables her to derive the unique address $P_0$ . However, the key pair ( $a$ , $A$ ) used by Alice can secure several UTXOs if she has reused this address several times. In the event that Alice makes two payments to Bob's static address $B$ using two UTXOs secured by the same key $A$ , this would result in address reuse for Bob.

Address reuse is a very bad practice in terms of user confidentiality. To find out why, I advise you to review the first parts of this training course. Indeed, since the unique address $P_0$ is derived from $A$ and $B$ , well if Alice derives a second address for a second payment to $B$ , with the same key $A$ , she'll end up on exactly the same address $P_0$ . To avoid this risk and prevent address reuse within Silent Payments, we'll need to modify our calculations a little.

What we want is for each UTXO consumed by Alice as input to a payment to give a unique address on Bob's side, even if several UTXOs are secured by the same key pair. So all we need to do is add a reference to the UTXO when calculating the unique address $P_0$ . This reference will simply be the hash of the UTXO consumed as input:

$\text{inputHash} = \text{hash}(\text{outpoint} \text{ ‖ } A)$

And Alice will add this reference to the input to her calculation of the unique address $P_0$ :

$P_0 = B + \text{hash}(\text{inputHash} \cdot a \cdot B \text{ ‖ } 0) \cdot G$

When scanning, Bob can also add $\text{inputHash}$ , since all he has to do is observe the transaction to deduce $\text{outpoint}$ :

$P_0 = B + \text{hash}(\text{inputHash} \cdot b \cdot A \text{ ‖ } 0) \cdot G$

When it finds a valid $P_0$ , it can calculate the corresponding $p_0$ private key:

 $p_0 = (b + \text{hash}(\text{inputHash} \cdot b \cdot A \text{ ‖ } 0)) \bmod n$

Legend:

$B$ : The public key/static address published by Bob
$b$ : Bob's private key
$A$ : Alice's UTXO public key used as transaction input
$a$ : Alice's private key
$H$ : UTXO hash used as input
$G$ : The generating point of the elliptic curve secp256k1
$\text{SHA256}$ : The SHA256 hash function tagged with BIP0352/SharedSecret
$s_0$ : The first ECDH common secret
$P_0$ : The first public key / unique address for payment to Bob

For the moment, our calculations assume that Alice uses a single input for her transaction. However, she should be able to use several inputs. Consequently, on Bob's side, for each transaction involving several inputs, he should theoretically calculate the ECDH for each input to determine whether a payment is intended for him. This method is not satisfactory, so we need to find a solution to reduce the workload!

Tweaking public keys into inputs

To solve this problem, instead of using the key pair securing a specific input on Alice's side, we'll use the sum of all the key pairs used in the transaction's inputs. This sum will then be considered as a new key pair. This technique is known as "tweaking".

For example, let's imagine that Alice's transaction has 3 inputs, each secured with a different key pair:

$a_0$ is used to secure input #0 ;
$a_1$ is used to secure input #1;
$a_2$ secures input #2.

Following the method previously described, Alice would have to choose a single key pair from among $a_0$ , $a_1$ , and $a_2$ to calculate the ECDH secret and generate the single payment address $P$ from Bob's static address $B$ . However, this approach requires Bob to test each possibility sequentially, starting with $a_0$ , then $a_1$ , and so on, until he identifies a pair that generates a valid $P$ address. This process requires Bob to run the ECDH calculation on all inputs to all transactions, which considerably increases the operational load of scanning.

To avoid this, we'll ask Alice to calculate $P$ using the sum of all input keys. Using our example, the tweaked private key $a$ would be calculated as follows:

$a = a_0 + a_1 + a_2$

In the same way, Alice and Bob can calculate the tweaked public key:

$A = A_0 + A_1 + A_2$

With this method, Bob only needs to calculate the sum of the transaction's public keys, then calculate the ECDH secret from $A$ alone, which greatly reduces the number of calculations required for the scanning stage.

However, remember the previous section. We had added the $\text{inputHash}$ hash to our calculation, which is used as a nonce to avoid address reuse:

$\text{inputHash} = \text{hash}(\text{outpoint} \text{ ‖ } A)$

But if you have several inputs in a transaction, you need to be able to determine which $\text{outpoint}$ is chosen in this calculation. According to BIP352, the $\text{outpoint}$ selection criterion to be used is to choose the smallest lexicographically, which means selecting the UTXO that appears first in alphabetical order. This method standardizes the UTXO to be chosen in each transaction. For example, if this lexicographically smallest $\text{outpoint}$ is $\text{outpoint}_L$ , the calculation of $\text{inputHash}$ will be :

$\text{inputHash} = \text{hash}(\text{outpoint}_L \text{ ‖ } A)$

The calculations then remain identical to those presented in the previous section, except that the private key $a$ and its corresponding public key $A$ are no longer a pair used to secure a single input, but now represent the tweak for all key pairs in inputs.

Separate expense and scan keys

For the moment, we've referred to the Silent Payment static address $B$ as a unique public key. Remember, it's this public key $B$ that Alice uses to create the shared secret ECDH, which in turn calculates the unique payment address $P$ . Bob uses this public key $B$ and the corresponding private key $b$ for the scanning stage. But he will also use the private key $b$ to calculate the private key $p$ that enables spending from the address $P$ .

The disadvantage of this method is that the $b$ private key, which is used to calculate all the private keys of addresses that have received Silent Payments, is also used by Bob to scan the transactions. This step requires the $b$ key to be available on internet-connected wallet software, which exposes it more to the risk of theft than keeping it on a cold wallet. Ideally, it would be beneficial to be able to take advantage of Silent Payments while keeping the $b$ private key, which controls access to all other private keys, secure on a hardware wallet. Fortunately, the protocol has been adapted to allow just that.

To do this, BIP352 requires the receiver to use 2 different pairs of keys:

b_{\text{spend}}$: to calculate the private keys of unique payment addresses;
b_{\text{scan}}$: to find unique payment addresses.

In this way, Bob can keep the private key $b_{\text{spend}}$ on a hardware wallet and use the private key $b_{\text{scan}}$ on online software to find his Silent Payments, without revealing $b_{\text{spend}}$ . On the other hand, the public keys $B_{\text{scan}}$ and $B_{\text{spend}}$ are both publicly revealed, since they are located in Bob's static address $B$ :

$B = B_{\text{scan}} \text{ ‖ } B_{\text{spend}}$

To calculate a unique payment address $P_0$ belonging to Bob, Alice will now perform the following calculation:

$P_0 = B_{\text{spend}} + \text{hash}(\text{inputHash} \cdot a \cdot B_{\text{scan}} \text{ ‖ } 0) \cdot G$

To find the payments addressed to him, Bob will perform the following calculation:

$P_0 = B_{\text{spend}} + \text{hash}(\text{inputHash} \cdot b_{\text{scan}} \cdot A \text{ ‖ } 0) \cdot G$

As you can see, so far Bob hasn't needed to use $b_{\text{spend}}$ , which is on his hardware wallet. When he wants to spend $P_0$ , he can do the following calculation to find the private key $p_0$ :

$p_0 = (b_{\text{spend}} + \text{hash}(\text{inputHash} \cdot b_{\text{scan}} \cdot A \text{ ‖ } 0)) \bmod n$

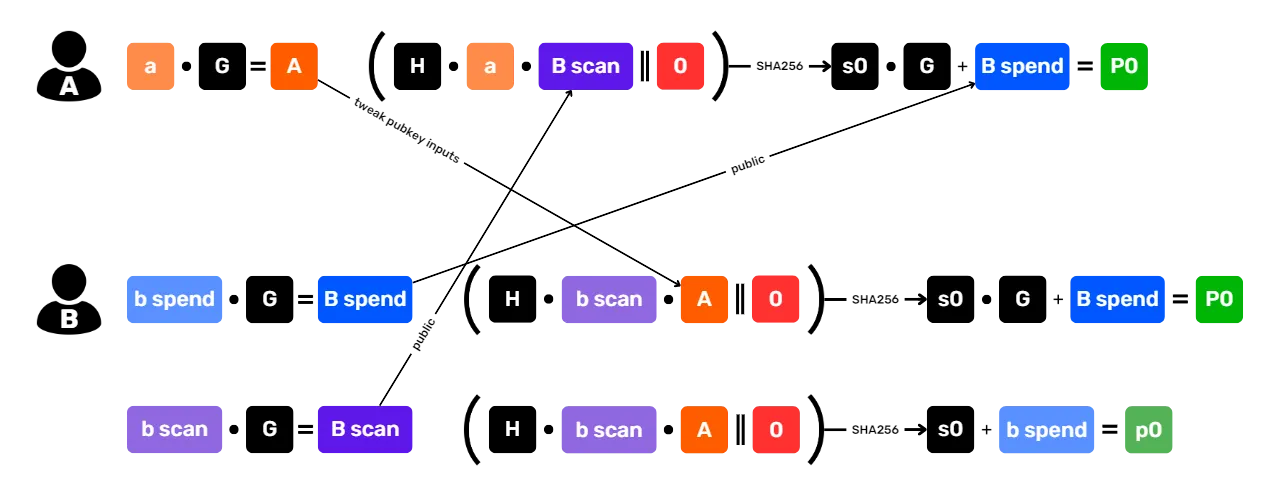
Legend:

$B_{\text{scan}}$ : Bob's public scan key (static address)
$b_{\text{scan}}$ : Bob's private scan key
$B_{\text{spend}}$ : Bob's public spending key (static address)
$b_{\text{spend}}$ : Bob's private spending key
$A$ : Sum of public key inputs (tweak)
$a$ : The private key corresponding to the tweaked public key
$H$ : The hash of the smallest UTXO (lexicographically) used as input
$G$ : The generating point of the elliptic curve secp256k1
$\text{SHA256}$ : The SHA256 hash function tagged with BIP0352/SharedSecret
$s_0$ : The first common secret ECDH
$P_0$ : The first public key / unique address for payment to Bob

Using SP addresses with a label

Bob therefore has a static address $B$ for Silent Payments such as :

$B = B_{\text{scan}} \text{ ‖ } B_{\text{spend}}$

The problem with this method is that it doesn't allow you to segregate the different payments sent to this address. For example, if Bob has 2 different customers for his business, and he wants to differentiate payments to each, he'll need 2 different static addresses. A naive solution, with the current approach, would be for Bob to create two separate wallets, each with its own static address, or even to establish two different static addresses within the same wallet. However, this solution requires scanning the entire blockchain twice (once for each address) in order to detect payments destined for each address respectively. This double scanning unreasonably increases Bob's operational load.

To solve this problem, BIP352 uses a label system that allows different static addresses, without unreasonably increasing the workload of finding Silent Payments on the blockchain. To do this, we add an integer $m$ to the public spending key $B_{\text{spend}}$ . This integer can take the value of $1$ for the first static address, then $2$ for the second, and so on. The spending keys $B_{\text{spend}}$ will now be called $B_m$ and will be constructed in this way:

$B_m = B_{\text{spend}} + \text{hash}(b_{\text{scan}} \text{ ‖ } m) \cdot G$

For example, for the first expense key with the label $1$ :

$B_1 = B_{\text{spend}} + \text{hash}(b_{\text{scan}} \text{ ‖ } 1) \cdot G$

The static address published by Bob will now consist of $B_{\text{scan}}$ and $B_m$ . For example, the first static address with the label $1$ will be :

$B = B_{\text{scan}} \text{ ‖ } B_1$

We only start from label 1 because label 0 is reserved for the change. Alice, for her part, will derive the single payment address $P$ in the same way as before, but using the new $B_1$ instead of $B_{\text{spend}}$ :

$P_0 = B_1 + \text{hash}(\text{inputHash} \cdot a \cdot B_{\text{scan}} \text{ ‖ } 0) \cdot G$

In reality, Alice doesn't even necessarily know that Bob has a labeled address, as she's simply using the second part of the static address he provided, and in this case, it's the value $B_1$ rather than $B_{text{spend}}$ .

To scan payments, Bob will always use the value of his initial static address with $B_{\text{spend}}$ in this way:

$P_0 = B_{\text{spend}} + \text{hash}(\text{inputHash} \cdot b_{\text{scan}} \cdot A \text{ ‖ } 0) \cdot G$

Then, he simply subtracts the value he finds for $P_0$ from each output one by one. He then checks whether one of the results of these subtractions matches the value of one of the labels he's using on his portfolio. If, for example, output #4 matches the $1$ label, this means that this output is a Silent Payment associated with its statically labeled address $B_1$ :

$Out_4 - P_0 = \text{hash}(b_{\text{scan}} \text{ ‖ } 1) \cdot G$

It works because :

$B_1 = B_{\text{spend}} + \text{hash}(b_{\text{scan}} \text{ ‖ } 1) \cdot G$

Thanks to this method, Bob can use a multitude of static addresses ( $B_1$ , $B_2$ , $B_3$ ...), all derived from his basic static address ( $B = B_{\text{scan}} \text{ ‖ } B_{\text{spend}}$ ), in order to keep usage separate.

Please note, however, that this separation of static addresses is only valid from a personal portfolio management point of view, but does not separate identities. Since they all have the same $B_{\text{scan}}$ , it's very easy to associate all static addresses together and deduce that they belong to a single entity.

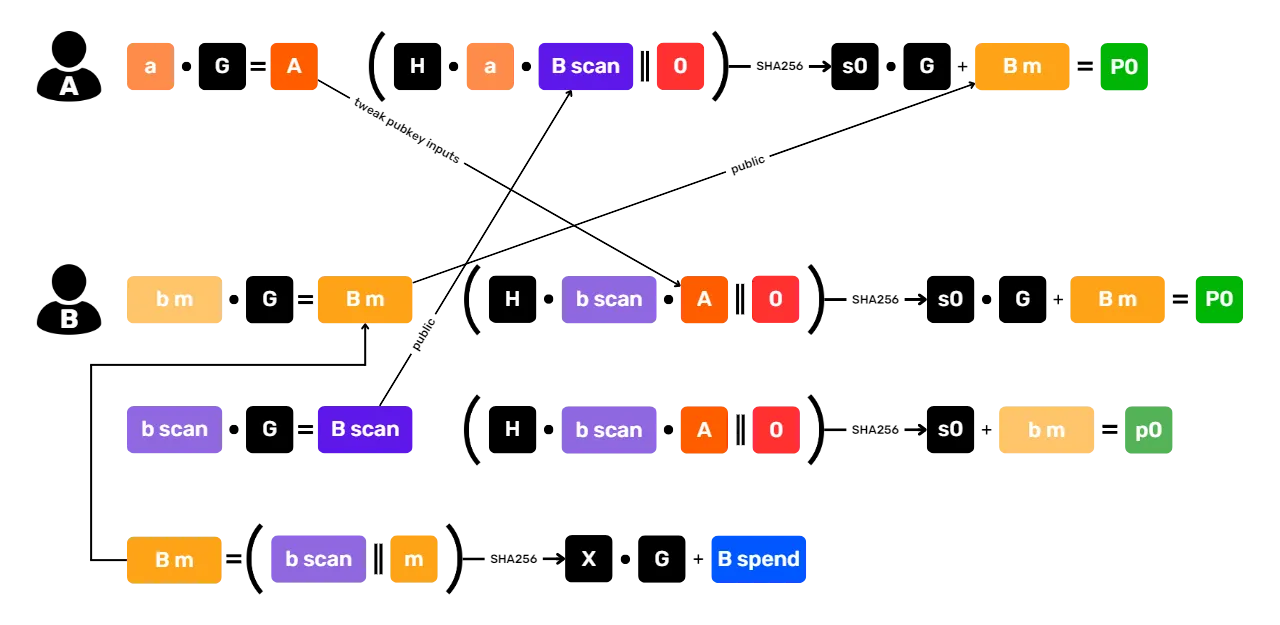
Legend:

$B_{\text{scan}}$ : Bob's public scan key (static address)
$b_{\text{scan}}$ : Bob's private scan key
$B_{\text{spend}}$ : Bob's public spending key (initial address)
$B_m$ : Bob's public spending key labeled (static address)
$b_m$ : Bob's private spending key labelled
$A$ : Sum of public key inputs (tweak)
$a$ : The private key corresponding to the tweaked public key
$H$ : The hash of the smallest UTXO (lexicographically) used as input
$G$ : The generating point of the elliptic curve secp256k1
$\text{SHA256}$ : The SHA256 hash function tagged with BIP0352/SharedSecret
$s_0$ : The first ECDH common secret
$P_0$ : The first public key / unique address for payment to Bob
$p_0$ : The private key of the first unique payment address to Bob
$X$ : The hash of the scan private key with the label

How do I build a Silent Payments address?

To build an address dedicated to Silent Payments, you first need to derive 2 key pairs from your Bitcoin HD wallet:

The pair $b_{\text{scan}}$ , $B_{\text{scan}}$ to search for payments addressed to us;
The pair $b_{\text{spend}}$ , $B_{\text{spend}}$ to think of the bitcoins we've received.

These pairs are derived using the following paths (Bitcoin Mainnet):

scan : m / 352' / 0' / 0' / 1' / 0
spend : m / 352' / 0' / 0' / 0' / 0

Once we have these 2 pairs of keys, we simply concatenate them (end-to-end) to create the static address payload:

$B = B_{\text{scan}} \text{ ‖ } B_{\text{spend}}$

If we want to use labels, we'll replace $B_{\text{spend}}$ with $B_m$ :

$B = B_{\text{scan}} \text{ ‖ } B_m$

With label $m$ :

$B_m = B_{\text{spend}} + \text{hash}(b_{\text{scan}} \text{ ‖ } m) \cdot G$

Once we have this payload, we add the HRP (Human-Readable Part) sp and the version q (= version 0). We also add a checksum and format the address as bech32m.

For example, here is my Silent Payments static address:

sp1qqvhjvsq2vz8zwrw372vuzle7472zup2ql3pz64yn5cpkw5ngv2n6jq4nl8cgm6zmu48yk3eq33ryc7aam6jrvrg0d0uuyzecfhx2wgsumcurv77e

An important point concerning static addresses, which you may have grasped in the previous sections, is that these addresses are not visible in Bitcoin transactions. Only the $P$ payment addresses used in outputs appear on the blockchain in the standard Taproot format. So, from the outside, it's impossible to distinguish a transaction involving Silent Payment from an ordinary transaction using P2TR outputs.

As with BIP47, it is impossible to establish a connection between a static address $B$ and a payment address $P$ derived from $B$ . Indeed, even if Eve, a potential attacker, attempts to scan the blockchain with Bob's static $B$ address, she won't be able to perform the calculations required to determine $P$ . To do so, she would need either Bob's private key $b_{\text{scan}}$ , or the sender's private keys $a$ , but both are of course private. It is therefore possible to explicitly link one's static address with a form of personal identity.

How do I use Silent Payments?

The Silent Payments proposal is relatively recent and has only been implemented by a very limited number of wallets at the moment. To my knowledge, there are only 3 software products that support them:

We'll soon be giving you a detailed tutorial on how to set up your own Silent Payments static address.

Since this feature is new, we advise you to exercise caution and avoid using Silent Payments for large amounts on mainnet.

To create this chapter on Silent Payments, I used the Silent Payments explanation site and the BIP352 explanation document.

Final Section

Reviews & Ratings

true

Final examination

true

Conclusion

true