name: Einführung in die formale Kryptographie goal: Eine tiefgehende Einführung in die Wissenschaft und Praxis der Kryptographie. objectives:

Tiefes Eintauchen in die Kryptographie

Es ist schwierig, viele Materialien zu finden, die einen guten Mittelweg im Kryptographieunterricht bieten.

Auf der einen Seite gibt es lange, formale Abhandlungen, die wirklich nur für diejenigen zugänglich sind, die einen starken Hintergrund in Mathematik, Logik oder einer anderen formalen Disziplin haben. Andererseits gibt es sehr anspruchsvolle Einführungen, die wirklich zu viele Details für jeden verbergen, der auch nur ein bisschen neugierig ist.

Diese Einführung in die Kryptographie versucht, einen Mittelweg zu finden. Während sie für jeden, der neu in die Kryptographie einsteigt, relativ anspruchsvoll und detailliert sein sollte, ist sie nicht das Kaninchenloch einer typischen grundlegenden Abhandlung.

Einführung

Kursübersicht

bb8a8b73-7fb2-50da-bf4e-98996d79887b Willkommen im Kurs CYP302!

Dieses Buch bietet eine tiefgehende Einführung in die Wissenschaft und Praxis der Kryptographie. Wo immer möglich, konzentriert es sich auf die konzeptionelle und nicht auf die formale Darstellung des Materials.

Dieser Bildungsinhalt ist eine Adaption des Buches und repo JWBurgers. Während der Autor die pädagogische Nutzung freundlicherweise gestattet hat, verbleiben alle geistigen Eigentumsrechte beim ursprünglichen Ersteller.

Motivation und Ziele

Es ist schwierig, viele Materialien zu finden, die einen guten Mittelweg im Kryptographieunterricht bieten.

Auf der einen Seite gibt es lange, formale Abhandlungen, die wirklich nur für diejenigen zugänglich sind, die einen starken Hintergrund in Mathematik, Logik oder einer anderen formalen Disziplin haben. Andererseits gibt es sehr anspruchsvolle Einführungen, die wirklich zu viele Details für jeden verbergen, der auch nur ein bisschen neugierig ist.

Diese Einführung in die Kryptographie versucht, einen Mittelweg zu finden. Während sie für jeden, der neu in die Kryptographie einsteigt, relativ anspruchsvoll und detailliert sein sollte, ist sie nicht das Kaninchenloch einer typischen Grundlagenabhandlung.

Zielpublikum

Vom Entwickler bis zum intellektuell Neugierigen ist dieses Buch für jeden nützlich, der mehr als nur ein oberflächliches Verständnis der Kryptographie haben möchte. Wenn Sie das Ziel haben, das Gebiet der Kryptographie zu beherrschen, ist dieses Buch ebenfalls ein guter Ausgangspunkt.

Leitlinien zum Lesen

Das Buch besteht derzeit aus sieben Kapiteln: "Was ist Kryptographie?" (Kapitel 1), "Mathematische Grundlagen der Kryptographie I" (Kapitel 2), "Mathematische Grundlagen der Kryptographie II" (Kapitel 3), "Symmetrische Kryptographie" (Kapitel 4), "RC4 und AES" (Kapitel 5), "Asymmetrische Kryptographie" (Kapitel 6) und "Das RSA-Kryptosystem" (Kapitel 7). Ein letztes Kapitel, "Kryptographie in der Praxis", wird noch hinzugefügt werden. Es befasst sich mit verschiedenen kryptografischen Anwendungen, darunter Sicherheit auf der Transportschicht, Onion-Routing und das Bitcoin-Wertesystem.

Die Zahlentheorie ist wahrscheinlich das schwierigste Thema in diesem Buch, es sei denn, Sie verfügen über fundierte Kenntnisse in Mathematik. Ich biete einen Überblick darüber in Kapitel 3, und sie erscheint auch in der Erklärung von AES in Kapitel 5 und dem RSA-Kryptosystem in Kapitel 7.

Wenn Sie sich mit den formalen Details in diesen Teilen des Buches wirklich schwer tun, empfehle ich Ihnen, sich beim ersten Mal mit dem Lesen auf hohem Niveau zu begnügen.

Danksagung

Das einflussreichste Buch bei der Entwicklung dieses Themas war Jonathan Katz und Yehuda Lindell's Introduction to Modern Cryptography, CRC Press (Boca Raton, FL), 2015. Ein begleitender Kurs mit dem Titel "Kryptografie" ist auf Coursera verfügbar

Die wichtigsten zusätzlichen Quellen, die bei der Erstellung des Überblicks in diesem Buch hilfreich waren, sind Simon Singh, The Code Book, Fourth Estate (London, 1999); Christof Paar und Jan Pelzl, Understanding Cryptography, Springer (Heidelberg, 2010) und ein auf dem Buch von Paar basierender Kurs namens "Introduction to Cryptography"; und Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons).

Ich werde nur ganz bestimmte Informationen und Ergebnisse zitieren, die ich aus diesen Quellen entnommen habe, möchte aber an dieser Stelle meine allgemeine Dankbarkeit gegenüber diesen Quellen zum Ausdruck bringen.

Denjenigen Lesern, die nach dieser Einführung fortgeschrittenere Kenntnisse über Kryptografie erwerben möchten, empfehle ich das Buch von Katz und Lindell sehr. Der Kurs von Katz auf Coursera ist etwas zugänglicher als das Buch.

Beiträge

Bitte werfen Sie einen Blick auf die Beitragsdatei im Repository für einige Richtlinien, wie Sie das Projekt unterstützen können.

Notation

Schlüsselbegriffe:

Schlüsselbegriffe in den Fibeln werden durch Fettdruck eingeleitet. Zum Beispiel würde die Einführung der Rijndael-Chiffre als Schlüsselbegriff wie folgt aussehen: Rijndael-Chiffre.

Wichtige Begriffe werden ausdrücklich definiert, es sei denn, es handelt sich um Eigennamen oder ihre Bedeutung ergibt sich aus der Diskussion.

Eine Definition wird in der Regel bei der Einführung eines Schlüsselbegriffs gegeben, obwohl es manchmal günstiger ist, die Definition auf einen späteren Zeitpunkt zu verschieben.

Hervorgehobene Wörter und Ausdrücke:

Wörter und Ausdrücke werden durch Kursivschrift hervorgehoben. Der Satz "Merken Sie sich Ihr Passwort" würde zum Beispiel wie folgt aussehen: Merken Sie sich Ihr Passwort.

Formale Notation:

Die formale Notation betrifft hauptsächlich Variablen, Zufallsvariablen und Mengen.

Bereit, die faszinierende Welt der Kryptographie zu erkunden? Los geht's!

Was ist Kryptographie?

Die Beale-Chiffren

Beginnen wir unsere Untersuchung auf dem Gebiet der Kryptographie mit einer der charmantesten und unterhaltsamsten Episoden ihrer Geschichte: der Beale-Chiffre. [1]

Die Geschichte der Beale-Chiffren ist meiner Meinung nach eher Fiktion als Realität. Aber sie soll sich wie folgt zugetragen haben.

Sowohl im Winter 1820 als auch im Winter 1822 übernachtete ein Mann namens Thomas J. Beale in einem Gasthaus von Robert Morriss in Lynchburg (Virginia). Am Ende seines zweiten Aufenthalts übergab Beale Morriss eine Eisenkiste mit wertvollen Papieren zur sicheren Aufbewahrung.

Einige Monate später erhielt Morriss einen Brief von Beale vom 9. Mai 1822. Darin betonte er den großen Wert des Inhalts der eisernen Kiste und gab Morriss einige Anweisungen: Wenn weder Beale noch einer seiner Mitarbeiter die Kiste jemals abholen würde, sollte er sie genau zehn Jahre nach dem Datum des Briefs (also am 9. Mai 1832) öffnen. Einige der darin enthaltenen Papiere wären in normaler Schrift verfasst. Einige andere jedoch wären "ohne die Hilfe eines Schlüssels unverständlich" Dieser "Schlüssel" würde Morriss im Juni 1832 von einem ungenannten Freund von Beale übergeben werden.

Trotz der klaren Anweisungen öffnete Morriss das Kästchen im Mai 1832 nicht, und Beales geheimnisvoller Freund tauchte im Juni desselben Jahres nicht auf. Erst 1845 beschloss der Gastwirt schließlich, die Kiste zu öffnen. Darin fand Morriss eine Notiz, in der erklärt wurde, wie Beale und seine Gefährten im Westen Gold und Silber entdeckten und es zusammen mit einigen Schmuckstücken vergruben, um es sicher aufzubewahren. Außerdem enthielt die Kiste drei Chiffretexte, d. h. kodierte Texte, für deren Entschlüsselung ein kryptografischer Schlüssel, d. h. ein Geheimnis, und ein dazugehöriger Algorithmus erforderlich sind. Der Vorgang des Entschlüsselns eines Chiffretextes wird als Entschlüsselung bezeichnet, während der Vorgang des Verschließens als Verschlüsselung bezeichnet wird. (Wie in Kapitel 3 erläutert, kann der Begriff Chiffre verschiedene Bedeutungen annehmen. In der Bezeichnung "Beale-Chiffren" ist er die Abkürzung für Chiffretexte)

Die drei Chiffretexte, die Morriss in der Eisenkiste fand, bestehen jeweils aus einer Reihe von durch Kommata getrennten Zahlen. Laut der Notiz von Beale geben diese Chiffretexte getrennt voneinander den Standort des Schatzes, den Inhalt des Schatzes und eine Liste von Namen mit rechtmäßigen Erben des Schatzes und deren Anteilen an (letztere Informationen sind für den Fall relevant, dass Beale und seine Partner die Kiste nie abholen).

Morris hat zwanzig Jahre lang versucht, die drei Chiffretexte zu entschlüsseln. Mit dem Schlüssel wäre dies ein Leichtes gewesen. Aber Morriss hatte den Schlüssel nicht und war bei seinen Versuchen, die Originaltexte oder Klartexte, wie sie in der Kryptografie üblicherweise genannt werden, wiederherzustellen, erfolglos.

Gegen Ende seines Lebens gab Morriss die Schachtel 1862 an einen Freund weiter. Dieser Freund veröffentlichte daraufhin 1885 unter dem Pseudonym J.B. Ward eine Flugschrift. Darin beschrieb er die (angebliche) Geschichte des Kästchens, die drei Chiffretexte und eine Lösung, die er für den zweiten Chiffretext gefunden hatte. (Offenbar gibt es einen Schlüssel für jeden Chiffretext und nicht einen Schlüssel, der für alle drei Chiffretexte funktioniert, wie Beale in seinem Brief an Morriss ursprünglich angedeutet zu haben scheint.)

Der zweite Chiffretext ist in Abbildung 2 unten zu sehen. [2] Der Schlüssel zu diesem Chiffriertext ist die Unabhängigkeitserklärung der Vereinigten Staaten. Das Entschlüsselungsverfahren läuft auf die Anwendung der folgenden zwei Regeln hinaus:

Abbildung 1: Beale-Chiffre Nr. 2

Figure 1: Beale cipher no 2.

Die erste Zahl des zweiten Chiffretextes ist zum Beispiel 115. Das 115. Wort der Unabhängigkeitserklärung lautet "instituted", also ist der erste Buchstabe des Klartextes "i" Der Chiffretext gibt keine direkten Hinweise auf Wortabstände und Großschreibung. Aber nach der Entschlüsselung der ersten paar Wörter kann man logisch ableiten, dass das erste Wort des Klartextes einfach "I" war (Der Klartext beginnt mit der Phrase "I have deposited in the county of Bedford.")

Nach der Entschlüsselung liefert die zweite Nachricht den genauen Inhalt des Schatzes (Gold, Silber und Juwelen) und deutet darauf hin, dass er in Eisentöpfen vergraben und mit Steinen in Bedford County (Virginia) bedeckt war. Die Menschen lieben ein gutes Rätsel, und so wurden große Anstrengungen unternommen, um die beiden anderen Beale-Chiffren zu entschlüsseln, insbesondere diejenige, die den Ort des Schatzes beschreibt. Sogar verschiedene prominente Kryptographen haben sich an ihnen versucht. Bisher ist es jedoch niemandem gelungen, die beiden anderen Chiffriertexte zu entschlüsseln.

Anmerkungen:

[1] Für eine gute Zusammenfassung der Geschichte siehe Simon Singh, The Code Book, Fourth Estate (London, 1999), S. 82-99. Ein kurzer Film über die Geschichte wurde 2010 von Andrew Allen gedreht. Sie finden den Film, "The Thomas Beale Cipher", auf seiner Website.

[2] Dieses Bild ist auf der Wikipedia-Seite für die Beale-Chiffren verfügbar.

Moderne Kryptographie

Bunte Geschichten wie die der Beale-Chiffren sind das, was die meisten von uns mit Kryptografie verbinden. Die moderne Kryptografie unterscheidet sich jedoch in mindestens vier wichtigen Punkten von diesen historischen Beispielen.

Erstens hat sich die Kryptographie in der Vergangenheit nur mit Geheimhaltung (oder Vertraulichkeit) befasst. [3] Chiffriertexte werden erstellt, um sicherzustellen, dass nur bestimmte Parteien in die Informationen in den Klartexten eingeweiht werden können, wie im Fall der Beale-Chiffren. Damit ein Verschlüsselungsverfahren diesen Zweck erfüllen kann, sollte die Entschlüsselung des Chiffriertextes nur möglich sein, wenn man den Schlüssel hat.

Die moderne Kryptographie befasst sich mit einer größeren Bandbreite von Themen als nur der Geheimhaltung. Zu diesen Themen gehören in erster Linie (1) Integrität von Nachrichten, d. h. die Sicherstellung, dass eine Nachricht nicht verändert wurde; (2) Authentizität von Nachrichten, d. h. die Sicherstellung, dass eine Nachricht wirklich von einem bestimmten Absender stammt; und (3) Nichtabstreitbarkeit, d. h. die Sicherstellung, dass ein Absender später nicht fälschlicherweise leugnen kann, dass er eine Nachricht gesendet hat. [4]

Eine wichtige Unterscheidung, die es zu beachten gilt, ist daher die zwischen einem Verschlüsselungsverfahren und einem Kryptographieverfahren. Bei einem Verschlüsselungsverfahren geht es nur um die Geheimhaltung. Ein Verschlüsselungsschema ist zwar ein kryptographisches Schema, aber das Gegenteil ist nicht der Fall. Ein kryptografisches Schema kann auch den anderen Hauptthemen der Kryptografie dienen, einschließlich Integrität, Authentizität und Nichtabstreitbarkeit.

Genauso wichtig wie die Geheimhaltung sind die Themen Integrität und Authentizität. Unsere modernen Kommunikationssysteme wären ohne Garantien für die Integrität und Authentizität der Kommunikation nicht funktionsfähig. Die Nichtabstreitbarkeit ist ebenfalls ein wichtiges Anliegen, z. B. bei digitalen Verträgen, wird aber in kryptografischen Anwendungen weniger häufig benötigt als Geheimhaltung, Integrität und Authentizität.

Zweitens beinhalten klassische Verschlüsselungssysteme wie die Beale-Chiffren immer einen Schlüssel, der von allen beteiligten Parteien gemeinsam genutzt wird. Viele moderne kryptografische Verfahren verwenden jedoch nicht nur einen, sondern zwei Schlüssel: einen privaten und einen öffentlichen Schlüssel. Während der erste in allen Anwendungen privat bleiben sollte, ist der zweite in der Regel öffentlich bekannt (daher auch die jeweiligen Namen). Im Bereich der Verschlüsselung kann der öffentliche Schlüssel zur Verschlüsselung der Nachricht verwendet werden, während der private Schlüssel für die Entschlüsselung verwendet werden kann.

Der Zweig der Kryptografie, der sich mit Verfahren befasst, bei denen alle Parteien einen Schlüssel gemeinsam nutzen, wird als symmetrische Kryptografie bezeichnet. Der einzige Schlüssel in einem solchen System wird gewöhnlich privater Schlüssel (oder geheimer Schlüssel) genannt. Der Zweig der Kryptografie, der sich mit Verfahren befasst, die ein Paar aus privatem und öffentlichem Schlüssel erfordern, wird als asymmetrische Kryptografie bezeichnet. Diese Zweige werden manchmal auch als Privatschlüsselkryptografie bzw. Öffentlichkeitsschlüsselkryptografie bezeichnet (dies kann jedoch zu Verwirrung führen, da es bei Kryptografiesystemen mit öffentlichem Schlüssel auch private Schlüssel gibt).

Das Aufkommen der asymmetrischen Kryptographie in den späten 1970er Jahren war eines der wichtigsten Ereignisse in der Geschichte der Kryptographie. Ohne sie wären die meisten unserer modernen Kommunikationssysteme, einschließlich Bitcoin, nicht möglich, oder zumindest sehr unpraktisch.

Wichtig ist, dass sich die moderne Kryptografie nicht ausschließlich mit symmetrischen und assymetrischen Verschlüsselungsverfahren befasst (obwohl dies einen Großteil des Fachgebiets ausmacht). So befasst sich die Kryptografie beispielsweise auch mit Hash-Funktionen und Pseudozufallszahlengeneratoren, und man kann auf diesen Primitiven Anwendungen aufbauen, die nicht mit der symmetrischen oder assymetrischen Schlüsselkryptografie zusammenhängen.

Drittens waren die klassischen Verschlüsselungssysteme, wie sie in den Beale-Chiffren verwendet wurden, mehr Kunst als Wissenschaft. Ihre vermeintliche Sicherheit basierte weitgehend auf Intuitionen bezüglich ihrer Komplexität. Sie wurden in der Regel gepatcht, wenn ein neuer Angriff auf sie bekannt wurde, oder ganz fallen gelassen, wenn der Angriff besonders schwerwiegend war. Die moderne Kryptografie ist jedoch eine strenge Wissenschaft mit einem formalen, mathematischen Ansatz zur Entwicklung und Analyse kryptografischer Verfahren. [5]

Im Mittelpunkt der modernen Kryptographie stehen formale Sicherheitsbeweise. Jeder Sicherheitsnachweis für ein kryptographisches Verfahren erfolgt in drei Schritten:

  1. Die Angabe einer kryptographischen Definition von Sicherheit, d. h. einer Reihe von Sicherheitszielen und der vom Angreifer ausgehenden Bedrohung.

  2. Die Angabe etwaiger mathematischer Annahmen in Bezug auf die Rechenkomplexität des Systems. So kann ein kryptographisches Verfahren beispielsweise einen Pseudozufallszahlengenerator enthalten. Wir können zwar nicht beweisen, dass diese existieren, aber wir können annehmen, dass sie existieren.

  3. Die Darlegung eines mathematischen Sicherheitsnachweises des Systems auf der Grundlage des formalen Sicherheitsbegriffs und etwaiger mathematischer Annahmen.

Viertens: Während die Kryptografie in der Vergangenheit vor allem im militärischen Bereich eingesetzt wurde, hat sie im digitalen Zeitalter Einzug in unsere täglichen Aktivitäten gehalten. Ganz gleich, ob Sie Online-Banking betreiben, in den sozialen Medien posten, mit Ihrer Kreditkarte ein Produkt bei Amazon kaufen oder einem Freund ein Trinkgeld in Bitcoin geben - Kryptografie ist die unabdingbare Voraussetzung für unser digitales Zeitalter.

Angesichts dieser vier Aspekte der modernen Kryptographie können wir die moderne Kryptographie als die Wissenschaft bezeichnen, die sich mit der formalen Entwicklung und Analyse kryptographischer Verfahren zur Sicherung digitaler Informationen gegen gegnerische Angriffe beschäftigt. [6] Sicherheit sollte hier im weitesten Sinne als Verhinderung von Angriffen verstanden werden, die die Geheimhaltung, Integrität, Authentifizierung und/oder Nichtabstreitbarkeit der Kommunikation beeinträchtigen.

Kryptografie ist am besten als Unterdisziplin der Cybersicherheit zu verstehen, die sich mit der Verhinderung von Diebstahl, Beschädigung und Missbrauch von Computersystemen befasst. Es ist zu beachten, dass viele Belange der Cybersicherheit wenig oder nur teilweise mit der Kryptografie zu tun haben.

Wenn ein Unternehmen z. B. teure Server vor Ort unterbringt, ist es vielleicht wichtig, diese Hardware vor Diebstahl und Beschädigung zu schützen. Dies ist zwar ein Problem der Cybersicherheit, hat aber wenig mit Kryptografie zu tun.

Ein weiteres Beispiel: Phishing-Angriffe sind ein häufiges Problem in unserer modernen Zeit. Bei diesen Angriffen wird versucht, Menschen über eine E-Mail oder ein anderes Nachrichtenmedium dazu zu verleiten, sensible Informationen wie Passwörter oder Kreditkartennummern preiszugeben. Zwar kann die Kryptografie bis zu einem gewissen Grad dazu beitragen, Phishing-Angriffe zu bekämpfen, doch erfordert ein umfassender Ansatz mehr als nur den Einsatz einiger Kryptografieverfahren.

Anmerkungen:

[3] Um genau zu sein, ging es bei den wichtigsten Anwendungen kryptografischer Verfahren um die Geheimhaltung. Kinder verwenden beispielsweise häufig einfache kryptografische Verfahren zum "Spaß". In diesen Fällen ist die Geheimhaltung nicht wirklich ein Problem.

[4] Bruce Schneier, Applied Cryptography, 2. Aufl., 2015 (Indianapolis, IN: John Wiley & Sons), S. 2.

[5] Siehe Jonathan Katz und Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), insbesondere S. 16-23, für eine gute Beschreibung.

[6] Vgl. Katz und Lindell, ebd., S. 3. Ich denke, dass ihre Charakterisierung einige Probleme aufweist und präsentiere daher hier eine leicht veränderte Version ihrer Aussage.

Offene Kommunikation

Die moderne Kryptografie ist so konzipiert, dass sie in einer offenen Kommunikationsumgebung Sicherheit bietet. Wenn unser Kommunikationskanal so gut geschützt ist, dass Lauscher keine Chance haben, unsere Nachrichten zu manipulieren oder auch nur zu beobachten, dann ist Kryptographie überflüssig. Die meisten unserer Kommunikationskanäle sind jedoch kaum so gut bewacht.

Das Rückgrat der Kommunikation in der modernen Welt ist ein riesiges Netz von Glasfaserkabeln. Das Telefonieren, Fernsehen und Surfen im Internet in einem modernen Haushalt stützt sich im Allgemeinen auf dieses Netz von Glasfaserkabeln (ein kleiner Prozentsatz stützt sich vielleicht nur auf Satelliten). Es stimmt, dass Sie in Ihrem Haus verschiedene Datenverbindungen haben können, z. B. Koaxialkabel, (asymmetrische) digitale Teilnehmerleitungen und Glasfaserkabel. Aber zumindest in den Industrieländern verbinden sich diese verschiedenen Datenträger außerhalb Ihres Hauses schnell zu einem Knotenpunkt in einem riesigen Netz von Glasfaserkabeln, das den gesamten Globus miteinander verbindet. Ausnahmen sind einige abgelegene Gebiete in den Industrieländern, z. B. in den Vereinigten Staaten und Australien, wo der Datenverkehr noch über große Entfernungen über herkömmliche Kupfertelefonleitungen läuft.

Es wäre unmöglich, potenzielle Angreifer daran zu hindern, physisch auf dieses Kabelnetz und seine unterstützende Infrastruktur zuzugreifen. Tatsächlich wissen wir bereits, dass die meisten unserer Daten von verschiedenen nationalen Nachrichtendiensten an wichtigen Knotenpunkten des Internets abgefangen werden[7] - von Facebook-Nachrichten bis hin zu den Adressen der von Ihnen besuchten Websites ist alles dabei.

Während für die Überwachung von Daten in großem Maßstab ein mächtiger Gegner, z. B. ein nationaler Geheimdienst, erforderlich ist, können Angreifer, die nur über geringe Ressourcen verfügen, leicht versuchen, auf lokaler Ebene zu schnüffeln. Obwohl dies auf der Ebene des Anzapfens von Kabeln geschehen kann, ist es viel einfacher, nur die drahtlose Kommunikation abzuhören.

Die meisten unserer lokalen Netzwerkdaten - ob zu Hause, im Büro oder in einem Café - werden heute über Funkwellen zu drahtlosen Zugangspunkten auf All-in-One-Routern und nicht mehr über physische Kabel übertragen. Ein Angreifer braucht also nur wenige Ressourcen, um Ihren lokalen Datenverkehr abzufangen. Dies ist besonders besorgniserregend, da die meisten Menschen sehr wenig tun, um die Daten zu schützen, die über ihre lokalen Netzwerke übertragen werden. Darüber hinaus können potenzielle Angreifer auch unsere mobilen Breitbandverbindungen wie 3G, 4G und 5G ins Visier nehmen. Alle diese drahtlosen Kommunikationsverbindungen sind ein leichtes Ziel für Angreifer.

Daher ist die Idee, Kommunikation durch den Schutz des Kommunikationskanals geheim zu halten, für einen Großteil der modernen Welt ein hoffnungslos wahnhaftes Ziel. Alles, was wir wissen, rechtfertigt eine starke Paranoia: Man sollte immer davon ausgehen, dass jemand zuhört. Und die Kryptographie ist das wichtigste Instrument, das uns zur Verfügung steht, um in diesem modernen Umfeld irgendeine Art von Sicherheit zu erreichen.

Anmerkungen:

[7] Siehe z. B. Olga Khazan, "The creepy, long-standing practice of undersea cable tapping", The Atlantic, 16. Juli 2013 (abrufbar unter The Atlantic).

Mathematische Grundlagen der Kryptographie 1

Zufallsvariablen

Kryptografie beruht auf Mathematik. Und wenn Sie mehr als nur ein oberflächliches Verständnis der Kryptografie entwickeln wollen, müssen Sie mit dieser Mathematik vertraut sein.

In diesem Kapitel werden die meisten mathematischen Grundlagen vorgestellt, auf die Sie beim Erlernen der Kryptografie stoßen werden. Zu den Themen gehören Zufallsvariablen, Modulo-Operationen, XOR-Operationen und Pseudozufälligkeit. Sie sollten das Material in diesen Abschnitten beherrschen, um ein nicht nur oberflächliches Verständnis der Kryptographie zu erlangen.

Der nächste Abschnitt befasst sich mit der Zahlentheorie, die sehr viel anspruchsvoller ist.

Zufallsvariablen

Eine Zufallsvariable wird in der Regel durch einen nicht fettgedruckten Großbuchstaben bezeichnet. So kann man z.B. von einer Zufallsvariablen X, einer Zufallsvariablen Y oder einer Zufallsvariablen Z sprechen. Diese Schreibweise werde ich im Folgenden auch verwenden.

Eine Zufallsvariable kann zwei oder mehr mögliche Werte annehmen, jeder mit einer bestimmten positiven Wahrscheinlichkeit. Die möglichen Werte sind in der Ergebnismenge aufgeführt.

Jedes Mal, wenn Sie eine Zufallsvariable stichprobenartig auswählen, ziehen Sie einen bestimmten Wert aus der Ergebnismenge entsprechend den festgelegten Wahrscheinlichkeiten.

Wenden wir uns einem einfachen Beispiel zu. Nehmen wir eine Variable X an, die wie folgt definiert ist:

Pr[X = 1] = 0.5
Pr[X = 2] = 0.5

Es ist leicht zu erkennen, dass X eine Zufallsvariable ist. Erstens gibt es zwei oder mehr mögliche Werte, die X annehmen kann, nämlich 1 und 2. Zweitens hat jeder mögliche Wert eine positive Eintrittswahrscheinlichkeit, nämlich 0,5, wenn man X abfragt.

Alles, was eine Zufallsvariable benötigt, ist eine Ergebnismenge mit zwei oder mehr Möglichkeiten, wobei jede Möglichkeit eine positive Eintrittswahrscheinlichkeit bei der Stichprobe hat. Im Prinzip kann eine Zufallsvariable also abstrakt definiert werden, ohne jeglichen Kontext. In diesem Fall könnte man sich die "Stichprobe" als ein natürliches Experiment vorstellen, bei dem der Wert der Zufallsvariablen ermittelt wird.

Die obige Variable X wurde abstrakt definiert. Man kann sich die Stichprobe der obigen Variable X also so vorstellen, als würde man eine faire Münze werfen und bei Kopf eine "2" und bei Zahl eine "1" zuordnen. Für jede Stichprobe von X wirft man die Münze erneut.

Alternativ kann man sich die Stichprobe X auch so vorstellen, dass man einen fairen Würfel wirft und eine "2" zuweist, wenn der Würfel 1, 3 oder 4 fällt, und eine "1" zuweist, wenn der Würfel 2, 5 oder 6 fällt. Jedes Mal, wenn Sie X probieren, würfeln Sie erneut.

Man kann sich wirklich jedes natürliche Experiment vorstellen, das es erlaubt, die Wahrscheinlichkeiten der oben genannten möglichen Werte von X zu definieren.

Häufig werden Zufallsvariablen jedoch nicht nur abstrakt eingeführt. Stattdessen hat die Menge der möglichen Ergebniswerte eine ausdrückliche Bedeutung in der realen Welt (und nicht nur als Zahlen). Darüber hinaus können diese Ergebniswerte für eine bestimmte Art von Experiment definiert werden (und nicht für ein beliebiges natürliches Experiment mit diesen Werten).

Betrachten wir nun ein Beispiel für eine Variable X, die nicht abstrakt definiert ist. X wird wie folgt definiert, um zu bestimmen, welche von zwei Mannschaften ein Fußballspiel beginnt:

Pr [X = \text{red kicks off}] = 0.5
Pr [X = \text{blue kicks off}] = 0.5

In diesem Fall ist die Ergebnismenge von X mit einer konkreten Bedeutung versehen, nämlich welche Mannschaft bei einem Fußballspiel beginnt. Außerdem werden die möglichen Ergebnisse und die damit verbundenen Wahrscheinlichkeiten durch ein konkretes Experiment, nämlich das Werfen einer bestimmten Münze C, bestimmt.

In Diskussionen über Kryptografie werden Zufallsvariablen in der Regel gegen eine Ergebnismenge mit realer Bedeutung eingeführt. Dabei kann es sich um die Menge aller Nachrichten handeln, die verschlüsselt werden können, bekannt als Nachrichtenraum, oder um die Menge aller Schlüssel, aus denen die an der Verschlüsselung beteiligten Parteien wählen können, bekannt als Schlüsselraum.

In Diskussionen über Kryptographie werden Zufallsvariablen jedoch in der Regel nicht gegen ein bestimmtes natürliches Experiment definiert, sondern gegen jedes Experiment, das die richtigen Wahrscheinlichkeitsverteilungen ergeben könnte.

Zufallsvariablen können diskrete oder kontinuierliche Wahrscheinlichkeitsverteilungen haben. Zufallsvariablen mit einer diskreten Wahrscheinlichkeitsverteilung - also diskrete Zufallsvariablen - haben eine endliche Anzahl von möglichen Ergebnissen. Die Zufallsvariable X in den beiden bisher genannten Beispielen war diskret.

Kontinuierliche Zufallsvariablen können stattdessen Werte in einem oder mehreren Intervallen annehmen. Man könnte zum Beispiel sagen, dass eine Zufallsvariable bei einer Stichprobe jeden reellen Wert zwischen 0 und 1 annimmt und dass jede reelle Zahl in diesem Intervall gleich wahrscheinlich ist. Innerhalb dieses Intervalls gibt es unendlich viele mögliche Werte.

Für kryptografische Diskussionen müssen Sie nur diskrete Zufallsvariablen verstehen. Jede Diskussion über Zufallsvariablen sollte sich daher auf diskrete Zufallsvariablen beziehen, sofern nicht ausdrücklich anders angegeben.

Graphische Darstellung von Zufallsvariablen

Die möglichen Werte und zugehörigen Wahrscheinlichkeiten für eine Zufallsvariable lassen sich leicht durch einen Graphen veranschaulichen. Betrachten wir zum Beispiel die Zufallsvariable X aus dem vorherigen Abschnitt mit einer Ergebnismenge von \{1, 2\} und Pr [X = 1] = 0,5 und Pr [X = 2] = 0,5. Wir würden eine solche Zufallsvariable typischerweise in Form eines Balkendiagramms wie in Abbildung 1 darstellen.

Abbildung 1: Zufallsvariable X

Figure 1: Random variable X.

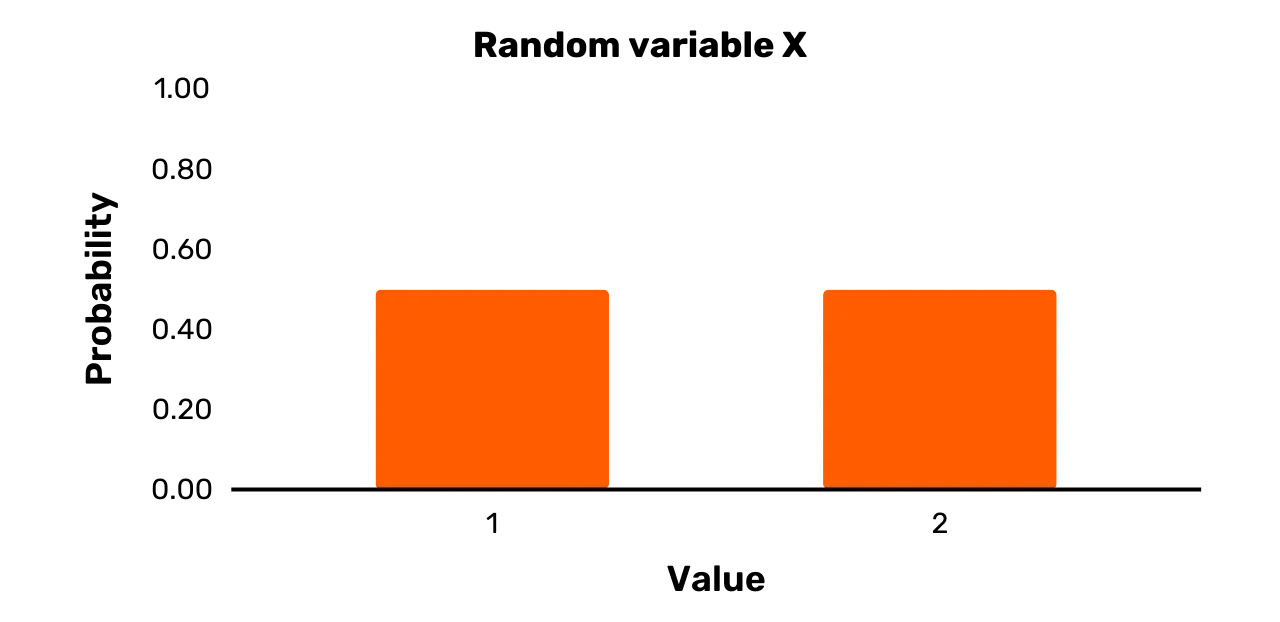
Die breiten Balken in Abbildung 1 sollen natürlich nicht suggerieren, dass die Zufallsvariable X tatsächlich kontinuierlich ist. Stattdessen werden die Balken breit gemacht, um sie optisch ansprechender zu gestalten (eine gerade Linie nach oben ist weniger intuitiv).

Einheitliche Variablen

Im Ausdruck "Zufallsvariable" bedeutet der Begriff "zufällig" einfach "probabilistisch". Mit anderen Worten, es bedeutet, dass zwei oder mehr mögliche Ergebnisse der Variablen mit bestimmten Wahrscheinlichkeiten auftreten. Diese Ergebnisse müssen jedoch nicht unbedingt gleich wahrscheinlich sein (obwohl der Begriff "zufällig" in anderen Zusammenhängen durchaus diese Bedeutung haben kann).

Eine uniforme Variable ist ein Spezialfall einer Zufallsvariablen. Sie kann zwei oder mehr Werte annehmen, die alle die gleiche Wahrscheinlichkeit haben. Die in Abbildung 1 dargestellte Zufallsvariable X ist eindeutig eine gleichförmige Variable, da beide möglichen Ergebnisse mit einer Wahrscheinlichkeit von 0,5 auftreten. Es gibt jedoch viele Zufallsvariablen, die nicht zu den gleichförmigen Variablen gehören.

Betrachten wir zum Beispiel die Zufallsvariable Y. Sie hat eine Ergebnismenge {1, 2, 3, 8, 10} und die folgende Wahrscheinlichkeitsverteilung:

\Pr[Y = 1] = 0.25
\Pr[Y = 2] = 0.35
\Pr[Y = 3] = 0.1
\Pr[Y = 8] = 0.25
\Pr[Y = 10] = 0.05

Während zwei mögliche Ergebnisse tatsächlich die gleiche Eintrittswahrscheinlichkeit haben, nämlich 1 und 8, kann Y bei der Stichprobe auch bestimmte Werte mit anderen Wahrscheinlichkeiten als 0,25 annehmen. Daher ist Y zwar eine Zufallsvariable, aber keine einheitliche Variable.

Eine grafische Darstellung von Y findet sich in Abbildung 2.

Abbildung 2: Zufallsvariable Y

Figure 2: Random variable Y.

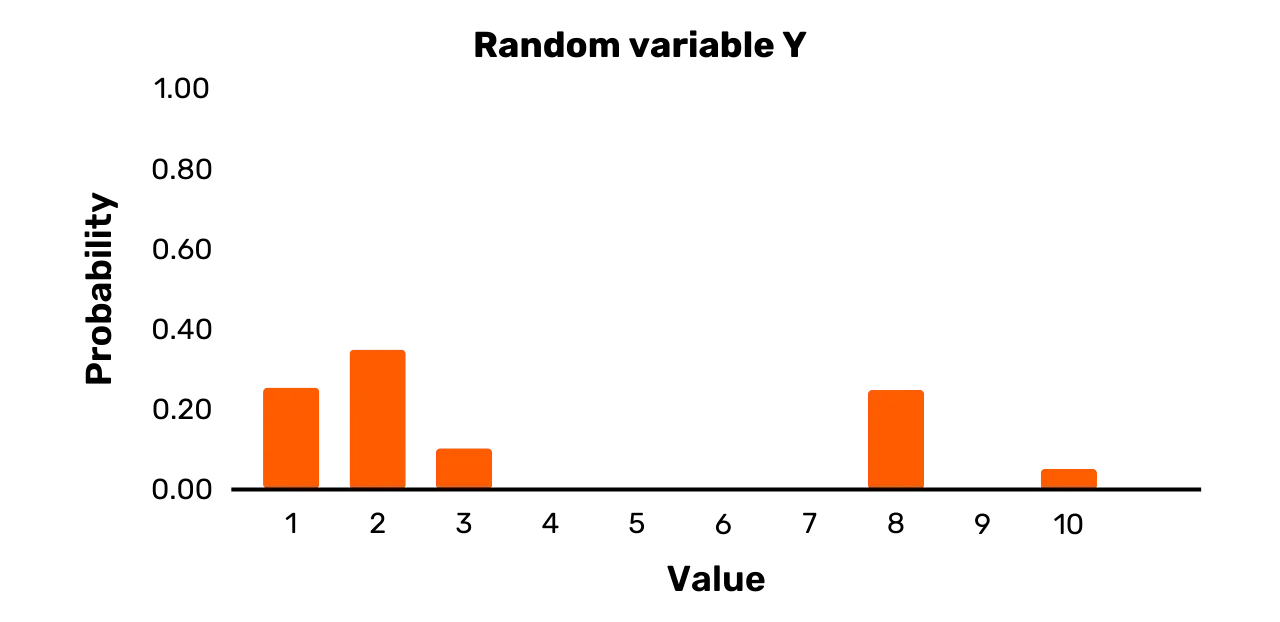
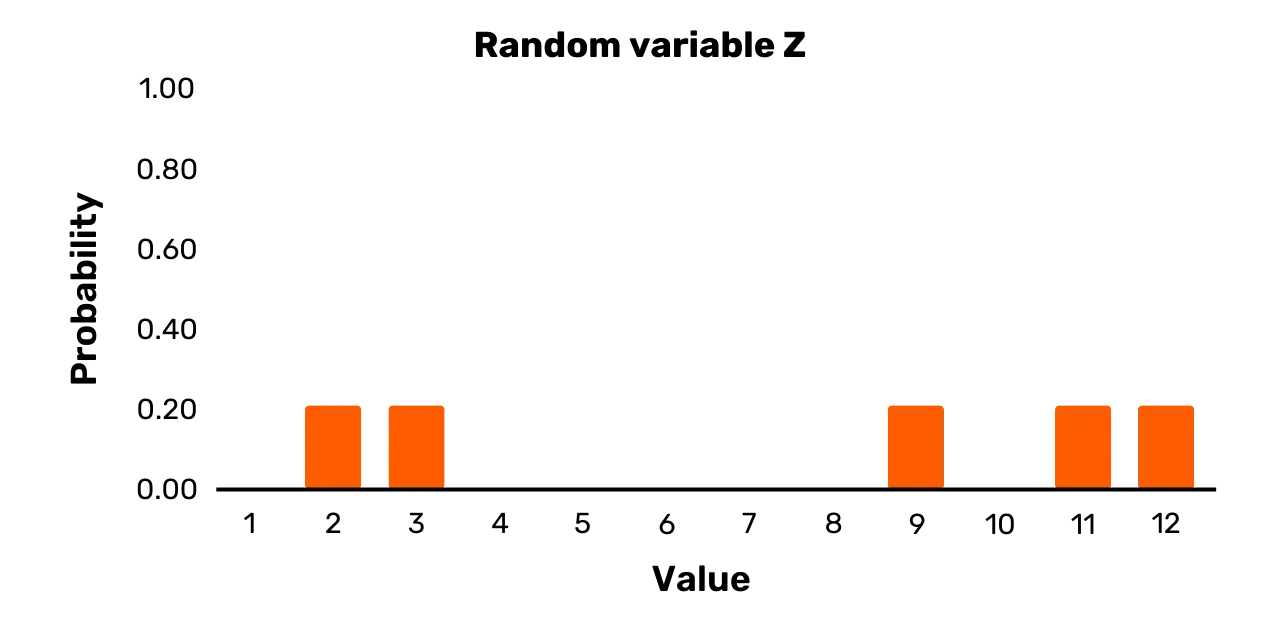
Als letztes Beispiel betrachten wir die Zufallsvariable Z. Sie hat die Ergebnismenge {1,3,7,11,12} und die folgende Wahrscheinlichkeitsverteilung:

\Pr[Z = 2] = 0.2
\Pr[Z = 3] = 0.2
\Pr[Z = 9] = 0.2
\Pr[Z = 11] = 0.2
\Pr[Z = 12] = 0.2

Sie können es in Abbildung 3 sehen. Die Zufallsvariable Z ist im Gegensatz zu Y eine einheitliche Variable, da alle Wahrscheinlichkeiten für die möglichen Werte bei der Stichprobe gleich sind.

Abbildung 3: Zufallsvariable Z

Figure 3: Random variable Z.

Bedingte Wahrscheinlichkeit

Angenommen, Bob will einen Tag aus dem letzten Kalenderjahr einheitlich auswählen. Wie hoch ist die Wahrscheinlichkeit, dass der ausgewählte Tag im Sommer liegt?

Solange wir davon ausgehen, dass Bobs Prozess wirklich gleichförmig ist, sollten wir zu dem Schluss kommen, dass die Wahrscheinlichkeit, dass Bob einen Tag im Sommer auswählt, bei 1/4 liegt. Dies ist die unbedingte Wahrscheinlichkeit, dass der zufällig ausgewählte Tag im Sommer liegt.

Nehmen wir nun an, dass Bob nicht gleichmäßig einen Kalendertag zieht, sondern nur gleichmäßig aus den Tagen auswählt, an denen die Mittagstemperatur am Crystal Lake (New Jersey) 21 Grad Celsius oder mehr betrug. Was lässt sich aus dieser zusätzlichen Information über die Wahrscheinlichkeit schließen, dass Bob einen Tag im Sommer auswählt?

Auch ohne weitere spezifische Informationen (z. B. die Temperatur zur Mittagszeit an jedem Tag des letzten Kalenderjahres) sollten wir eigentlich eine andere Schlussfolgerung ziehen als bisher.

Wenn man weiß, dass Crystal Lake in New Jersey liegt, würde man nicht erwarten, dass die Temperatur am Mittag im Winter 21 Grad Celsius oder mehr beträgt. Stattdessen ist es viel wahrscheinlicher, dass es sich um einen warmen Tag im Frühling oder Herbst oder um einen Tag irgendwo im Sommer handelt. Wenn man also weiß, dass die Mittagstemperatur am Crystal Lake an dem gewählten Tag 21 Grad Celsius oder mehr beträgt, ist die Wahrscheinlichkeit, dass der von Bob gewählte Tag im Sommer liegt, sehr viel höher. Dies ist die bedingte Wahrscheinlichkeit, dass der zufällig ausgewählte Tag im Sommer liegt, wenn die Mittagstemperatur am Crystal Lake 21 Grad Celsius oder mehr beträgt.

Anders als im vorherigen Beispiel können die Wahrscheinlichkeiten zweier Ereignisse auch völlig unabhängig voneinander sein. In diesem Fall sagen wir, dass sie unabhängig sind.

Nehmen wir zum Beispiel an, dass eine bestimmte, gerechte Münze Kopf zeigt. Wie hoch ist dann die Wahrscheinlichkeit, dass es morgen regnen wird? Die bedingte Wahrscheinlichkeit sollte in diesem Fall dieselbe sein wie die unbedingte Wahrscheinlichkeit, dass es morgen regnen wird, da ein Münzwurf im Allgemeinen keinen Einfluss auf das Wetter hat.

Wir verwenden ein "|"-Symbol, um bedingte Wahrscheinlichkeitsaussagen zu formulieren. Zum Beispiel kann die Wahrscheinlichkeit des Ereignisses A unter der Voraussetzung, dass das Ereignis B eingetreten ist, wie folgt geschrieben werden:

Pr[A|B]

Wenn also zwei Ereignisse, A und B, unabhängig sind, dann:

Pr[A|B] = Pr[A] \text{ and } Pr[B|A] = Pr[B]

Die Bedingung für die Unabhängigkeit kann wie folgt vereinfacht werden:

Pr[A, B] = Pr[A] \cdot Pr[B]

Ein Schlüsselergebnis der Wahrscheinlichkeitstheorie ist als Bayes Theorem bekannt. Es besagt im Wesentlichen, dass Pr[A|B] wie folgt umgeschrieben werden kann:

Pr[A|B] = \frac{Pr[B|A] \cdot Pr[A]}{Pr[B]}

Anstatt bedingte Wahrscheinlichkeiten für bestimmte Ereignisse zu verwenden, können wir auch die bedingten Wahrscheinlichkeiten für zwei oder mehr Zufallsvariablen über eine Reihe möglicher Ereignisse betrachten. Nehmen wir zwei Zufallsvariablen an, X und Y. Wir können jeden möglichen Wert für X mit x und jeden möglichen Wert für Y mit y bezeichnen. Man kann also sagen, dass zwei Zufallsvariablen unabhängig sind, wenn die folgende Aussage zutrifft:

Pr[X = x, Y = y] = Pr[X = x] \cdot Pr[Y = y]

für alle x und y.

Lassen Sie uns etwas deutlicher sagen, was diese Aussage bedeutet.

Angenommen, die Ergebnismengen für X und Y sind wie folgt definiert: X = \{x_1, x_2, \ldots, x_i, \ldots, x_n\} und Y = \{y_1, y_2, \ldots, y_i, \ldots, y_m\}. (Es ist üblich, Wertemengen durch fettgedruckte Großbuchstaben zu kennzeichnen.)

Nehmen wir nun an, Sie nehmen eine Stichprobe Y und beobachten y_1. Die obige Aussage besagt, dass die Wahrscheinlichkeit, nun x_1 aus der Stichprobe X zu erhalten, genau die gleiche ist, als wenn wir y_1 nie beobachtet hätten. Dies gilt für jedes y_i, das wir aus unserer anfänglichen Stichprobe von Y hätten ziehen können. Schließlich gilt dies nicht nur für x_1. Für jedes x_i wird die Wahrscheinlichkeit des Auftretens nicht durch das Ergebnis einer Stichprobe von Y beeinflusst. All dies gilt auch für den Fall, dass X zuerst abgetastet wird.

Lassen Sie uns unsere Diskussion mit einem etwas philosophischeren Punkt beenden. In jeder realen Situation wird die Wahrscheinlichkeit eines Ereignisses immer vor dem Hintergrund einer bestimmten Menge von Informationen bewertet. Es gibt keine "unbedingte Wahrscheinlichkeit" im strengen Sinne des Wortes.

Nehmen wir zum Beispiel an, ich frage Sie nach der Wahrscheinlichkeit, dass im Jahr 2030 Schweine fliegen werden. Obwohl ich Ihnen keine weiteren Informationen gebe, wissen Sie offensichtlich eine Menge über die Welt, was Ihr Urteil beeinflussen kann. Sie haben noch nie Schweine fliegen sehen. Sie wissen, dass die meisten Menschen nicht erwarten, dass sie fliegen können. Sie wissen, dass sie nicht wirklich zum Fliegen gebaut sind. Und so weiter.

Wenn wir also von einer "unbedingten Wahrscheinlichkeit" eines Ereignisses in einem realen Kontext sprechen, kann dieser Begriff nur dann Bedeutung haben, wenn wir darunter so etwas wie "die Wahrscheinlichkeit ohne weitere explizite Informationen" verstehen. Eine "bedingte Wahrscheinlichkeit" sollte also immer im Zusammenhang mit einer bestimmten Information verstanden werden.

Ich könnte Sie zum Beispiel fragen, wie wahrscheinlich es ist, dass Schweine bis 2030 fliegen werden, nachdem ich Ihnen den Beweis geliefert habe, dass einige Ziegen in Neuseeland nach einigen Jahren Training fliegen gelernt haben. In diesem Fall werden Sie wahrscheinlich Ihre Einschätzung der Wahrscheinlichkeit, dass Schweine bis 2030 fliegen werden, anpassen. Die Wahrscheinlichkeit, dass Schweine bis 2030 fliegen werden, hängt also von diesem Beweis über Ziegen in Neuseeland ab.

Die Modulo-Operation

Modulo

Der einfachste Ausdruck mit der Modulo-Operation hat die folgende Form: x \mod y.

Die Variable x wird als Dividend und die Variable y als Divisor bezeichnet. Um eine Modulo-Operation mit einem positiven Dividend und einem positiven Divisor durchzuführen, bestimmt man einfach den Rest der Division.

Betrachten wir zum Beispiel den Ausdruck 25 \mod 4. Die Zahl 4 wird insgesamt 6 Mal durch die Zahl 25 geteilt. Der Rest dieser Division ist 1. 25 \mod 4 ist also gleich 1. Auf ähnliche Weise können wir die folgenden Ausdrücke auswerten:

Wenn der Dividend oder Divisor negativ ist, können Modulo-Operationen von Programmiersprachen unterschiedlich gehandhabt werden.

In der Kryptographie werden Sie mit Sicherheit auf Fälle mit einer negativen Dividende stoßen. In diesen Fällen ist die typische Vorgehensweise wie folgt:

Nehmen wir zum Beispiel an, dass der Dividend -20 und der Divisor 3 ist. Der nächstgelegene Wert, der kleiner oder gleich -20 ist und durch den 3 gleichmäßig geteilt wird, ist -21. Der Wert von x - p ist in diesem Fall -20 - (-21). Dies ist gleich 1 und somit ist -20 \mod 3 gleich 1. Auf ähnliche Weise können wir die folgenden Ausdrücke auswerten:

Was die Notation betrifft, so werden Sie typischerweise die folgenden Ausdrücke sehen: x = [y \mod z]. Aufgrund der Klammern gilt die Modulo-Operation in diesem Fall nur für die rechte Seite des Ausdrucks. Ist y beispielsweise gleich 25 und z gleich 4, so ergibt x den Wert 1.

Ohne Klammern wirkt die Modulo-Operation auf beide Seiten eines Ausdrucks. Nehmen wir zum Beispiel den folgenden Ausdruck an: x = y \mod z. Wenn y gleich 25 und z gleich 4 ist, dann wissen wir nur, dass x \mod 4 den Wert 1 hat. Dies ist mit jedem Wert für x aus der Menge \{\ldots,-7, -3, 1, 5, 9,\ldots\} vereinbar.

Der Zweig der Mathematik, der sich mit Modulo-Operationen an Zahlen und Ausdrücken befasst, wird als modulare Arithmetik bezeichnet. Man kann sich diesen Zweig als Arithmetik für Fälle vorstellen, in denen die Zahlenreihe nicht unendlich lang ist. Obwohl wir in der Kryptographie typischerweise mit Modulo-Operationen für (positive) ganze Zahlen zu tun haben, können Sie Modulo-Operationen auch mit beliebigen reellen Zahlen durchführen.

Die Shift-Chiffre

Die Modulo-Operation ist in der Kryptographie häufig anzutreffen. Betrachten wir zur Veranschaulichung eines der berühmtesten historischen Verschlüsselungsverfahren: die Shift-Chiffre.

Definieren wir sie zunächst. Nehmen wir ein Wörterbuch D an, das alle Buchstaben des englischen Alphabets der Reihe nach mit der Menge der Zahlen \{0, 1, 2, \ldots, 25\} gleichsetzt. Nehmen wir einen Nachrichtenraum M an. Die Shift-Chiffre ist dann ein Verschlüsselungsverfahren, das wie folgt definiert ist:

Der Modulo-Operator in der Shift-Chiffre sorgt dafür, dass die Buchstaben umlaufen, so dass alle Buchstaben des Chiffretextes definiert sind. Zur Veranschaulichung betrachten wir die Anwendung der Shift-Chiffre auf das Wort "DOG".

Nehmen wir an, Sie haben einheitlich einen Schlüssel ausgewählt, der den Wert 17 hat. Der Buchstabe "O" entspricht der Zahl 15. Ohne die Modulo-Operation würde die Addition dieser Klartextnummer mit dem Schlüssel eine Chiffretextnummer von 32 ergeben. Diese Geheimtextnummer kann jedoch nicht in einen Geheimtextbuchstaben umgewandelt werden, da das englische Alphabet nur 26 Buchstaben hat. Die Modulo-Operation stellt sicher, dass die Chiffretext-Zahl tatsächlich 6 ist (das Ergebnis von 32 \mod 26), was dem Chiffretext-Buchstaben "G" entspricht.

Die gesamte Verschlüsselung des Wortes "DOG" mit einem Schlüsselwert von 17 sieht wie folgt aus:

Jeder kann intuitiv verstehen, wie die Shift-Chiffre funktioniert, und sie wahrscheinlich auch selbst anwenden. Für das Vorankommen in der Kryptographie ist es jedoch wichtig, sich mit der Formalisierung vertraut zu machen, da die Schemata dann viel schwieriger werden. Aus diesem Grund wurden die Schritte für die Shift-Chiffre formalisiert.

Anmerkungen:

[1] Wir können diese Aussage genau definieren, indem wir die Terminologie aus dem vorherigen Abschnitt verwenden. Eine gleichförmige Variable K habe K als Menge der möglichen Ergebnisse. So:

Pr[K = 0] = \frac{1}{26}
Pr[K = 1] = \frac{1}{26}

...und so weiter. Die einheitliche Variable K einmal abtasten, um einen bestimmten Schlüssel zu erhalten.

Die XOR-Operation

Alle Computerdaten werden auf Bitebene verarbeitet, gespeichert und über Netze gesendet. Alle kryptografischen Verfahren, die auf Computerdaten angewendet werden, arbeiten ebenfalls auf Bitebene.

Nehmen wir zum Beispiel an, Sie haben eine E-Mail in Ihr E-Mail-Programm eingegeben. Die Verschlüsselung erfolgt nicht direkt an den ASCII-Zeichen Ihrer E-Mail. Stattdessen wird sie auf die Bit-Repräsentation der Buchstaben und anderer Symbole in Ihrer E-Mail angewendet.

Eine für die moderne Kryptographie wichtige mathematische Operation ist neben der Modulo-Operation die XOR-Operation, die "Exklusiv-Oder"-Operation. Bei dieser Operation werden zwei Bits eingegeben und es wird ein weiteres Bit ausgegeben. Die XOR-Operation wird einfach als "XOR" bezeichnet. Sie ergibt 0, wenn die beiden Bits gleich sind, und 1, wenn die beiden Bits unterschiedlich sind. Die vier Möglichkeiten sind unten zu sehen. Das Symbol \oplus steht für "XOR":

Zur Veranschaulichung: Nehmen wir an, Sie haben eine Nachricht m_1 (01111001) und eine Nachricht m_2 (01011001). Die XOR-Verknüpfung dieser beiden Nachrichten ist unten zu sehen.

Das Verfahren ist einfach. Zuerst werden die äußersten linken Bits von m_1 und m_2 XOR-verknüpft. In diesem Fall ist das 0 \oplus 0 = 0. Dann wird das zweite Bitpaar von links XOR-verknüpft. In diesem Fall ist das 1 \oplus 1 = 0. Dieser Vorgang wird so lange fortgesetzt, bis die XOR-Operation für die ganz rechts liegenden Bits durchgeführt wurde.

Es ist leicht zu sehen, dass die XOR-Operation kommutativ ist, nämlich m_1 \oplus m_2 = m_2 \oplus m_1. Außerdem ist die XOR-Operation auch assoziativ. Das heißt, (m_1 \oplus m_2) \oplus m_3 = m_1 \oplus (m_2 \oplus m_3).

Eine XOR-Verknüpfung von zwei Zeichenfolgen unterschiedlicher Länge kann je nach Kontext unterschiedlich interpretiert werden. Wir befassen uns hier nicht mit XOR-Verknüpfungen von Zeichenketten unterschiedlicher Länge.

Eine XOR-Verknüpfung ist äquivalent zum Spezialfall der Durchführung einer Modulo-Operation bei der Addition von Bits, wenn der Divisor 2 ist. Die Äquivalenz ist in den folgenden Ergebnissen ersichtlich:

Pseudozufälligkeit

In unserer Diskussion über Zufalls- und Gleichheitsvariablen haben wir eine spezifische Unterscheidung zwischen "zufällig" und "gleichmäßig" getroffen. Diese Unterscheidung wird in der Praxis bei der Beschreibung von Zufallsvariablen in der Regel beibehalten. In unserem aktuellen Kontext muss diese Unterscheidung jedoch fallen gelassen werden, und "zufällig" und "gleichförmig" werden synonym verwendet. Warum, werde ich am Ende des Abschnitts erläutern.

Zunächst können wir eine binäre Zeichenkette der Länge n zufällig (oder gleichförmig) nennen, wenn sie das Ergebnis einer Stichprobe einer gleichförmigen Variablen S ist, die jeder binären Zeichenkette dieser Länge n die gleiche Wahrscheinlichkeit der Auswahl gibt.

Nehmen wir zum Beispiel die Menge aller binären Zeichenketten mit der Länge 8: \{0000\ 0000, 0000\ 0001, \ldots, 1111\ 1111\}. (Es ist üblich, eine 8-Bit-Zeichenkette in zwei Quartetten zu schreiben, die jeweils als Nibble bezeichnet werden.) Nennen wir diese Menge von Zeichenketten S_8.

Gemäß der obigen Definition können wir eine bestimmte binäre Zeichenkette der Länge 8 als zufällig (oder gleichförmig) bezeichnen, wenn sie das Ergebnis einer Stichprobe einer gleichförmigen Variablen S ist, die jeder Zeichenkette in S_8 eine gleiche Auswahlwahrscheinlichkeit gibt. Da die Menge S_8 2^8 Elemente enthält, müsste die Auswahlwahrscheinlichkeit bei der Stichprobe für jede Zeichenkette in der Menge 1/2^8 betragen.

Ein wichtiger Aspekt der Zufälligkeit einer binären Zeichenfolge ist, dass sie in Bezug auf den Prozess definiert ist, durch den sie ausgewählt wurde. Die Form einer bestimmten binären Zeichenfolge allein sagt daher nichts über ihre Zufälligkeit bei der Auswahl aus.

Viele Menschen haben zum Beispiel intuitiv die Vorstellung, dass eine Zeichenfolge wie 1111\ 1111 nicht zufällig ausgewählt worden sein kann. Aber das ist eindeutig falsch.

Definiert man eine einheitliche Variable S über alle binären Zeichenketten der Länge 8, so ist die Wahrscheinlichkeit, 1111\ 1111 aus der Menge S_8 auszuwählen, die gleiche wie die einer Zeichenkette wie 0111\ 0100. Man kann also nichts über die Zufälligkeit einer Zeichenkette aussagen, wenn man nur die Zeichenkette selbst analysiert.

Wir können auch von zufälligen Zeichenketten sprechen, ohne damit speziell binäre Zeichenketten zu meinen. Wir könnten zum Beispiel von einer zufälligen Hex-Zeichenkette AF\ 02\ 82 sprechen. In diesem Fall wäre die Zeichenkette zufällig aus der Menge aller Hex-Zeichenketten der Länge 6 ausgewählt worden. Dies entspricht der zufälligen Auswahl einer binären Zeichenkette der Länge 24, da jede Hex-Ziffer 4 Bits darstellt.

Normalerweise bezieht sich der Ausdruck "eine zufällige Zeichenkette" ohne Einschränkung auf eine Zeichenkette, die nach dem Zufallsprinzip aus der Menge aller Zeichenketten mit der gleichen Länge ausgewählt wird. So habe ich es oben beschrieben. Eine Zeichenkette der Länge n kann natürlich auch zufällig aus einer anderen Menge ausgewählt werden. Zum Beispiel aus einer Menge, die nur eine Teilmenge aller Zeichenketten der Länge n darstellt, oder vielleicht aus einer Menge, die Zeichenketten unterschiedlicher Länge enthält. In diesen Fällen würde man jedoch nicht von einer "zufälligen Zeichenkette" sprechen, sondern von einer "Zeichenkette, die zufällig aus einer Menge S ausgewählt wurde".

Ein Schlüsselbegriff in der Kryptographie ist der der Pseudozufälligkeit. Eine pseudozufällige Zeichenkette der Länge n sieht so aus, als ob sie das Ergebnis einer Stichprobe einer gleichförmigen Variablen S wäre, die jeder Zeichenkette in S_n eine gleiche Auswahlwahrscheinlichkeit gibt. Tatsächlich ist die Zeichenkette jedoch das Ergebnis einer Stichprobe einer gleichförmigen Variablen S', die nur eine Wahrscheinlichkeitsverteilung - nicht unbedingt eine mit gleichen Wahrscheinlichkeiten für alle möglichen Ergebnisse - auf einer Teilmenge von S_n definiert. Der entscheidende Punkt dabei ist, dass niemand wirklich zwischen Stichproben aus S und S' unterscheiden kann, selbst wenn man viele davon nimmt.

Nehmen wir an, es handelt sich um eine Zufallsvariable S. Ihre Ergebnismenge ist S_{256}, das ist die Menge aller binären Zeichenketten der Länge 256. Diese Menge hat 2^{256} Elemente. Jedes Element hat eine gleiche Auswahlwahrscheinlichkeit von 1/2^{256} bei der Stichprobenziehung.

Nehmen wir außerdem eine Zufallsvariable S' an. Ihre Ergebnismenge enthält nur 2^{128} binäre Zeichenketten der Länge 256. Sie hat eine Wahrscheinlichkeitsverteilung über diese Zeichenketten, die aber nicht unbedingt gleichmäßig ist.

Nehmen wir an, ich habe 1000 Stichproben aus S und 1000 Stichproben aus S' genommen und gebe Ihnen die beiden Ergebnismengen. Ich sage Ihnen, welcher Satz von Ergebnissen mit welcher Zufallsvariablen verbunden ist. Als nächstes entnehme ich eine Stichprobe aus einer der beiden Zufallsvariablen. Diesmal sage ich Ihnen aber nicht, welche Zufallsvariable ich nehme. Wenn S' ein Pseudozufall wäre, dann wäre die Wahrscheinlichkeit, dass Sie richtig erraten, welche Zufallsvariable ich genommen habe, praktisch nicht besser als 1/2.

Eine pseudozufällige Zeichenkette der Länge n wird in der Regel durch zufällige Auswahl einer Zeichenkette der Größe n - x erzeugt, wobei x eine positive ganze Zahl ist, und als Eingabe für einen Expansionsalgorithmus verwendet. Diese Zufallsfolge der Größe n - x wird als Saatgut bezeichnet.

Pseudozufallszeichenfolgen sind ein Schlüsselkonzept, das die Kryptographie praktikabel macht. Nehmen wir zum Beispiel die Stromchiffren. Bei einer Stromchiffre wird ein zufällig ausgewählter Schlüssel in einen Expansionsalgorithmus eingefügt, um eine viel größere Pseudozufallsfolge zu erzeugen. Diese pseudozufällige Zeichenfolge wird dann mit dem Klartext durch eine XOR-Operation kombiniert, um einen Geheimtext zu erzeugen.

Wenn wir nicht in der Lage wären, diese Art von Pseudozufallszeichenfolge für eine Stromchiffre zu erzeugen, dann bräuchten wir einen Schlüssel, der so lang wie die Nachricht ist, um sie zu sichern. Dies ist in den meisten Fällen keine sehr praktische Option.

Der in diesem Abschnitt behandelte Begriff der Pseudozufälligkeit kann formaler definiert werden. Er lässt sich auch auf andere Kontexte übertragen. Aber wir müssen uns hier nicht mit dieser Diskussion befassen. Alles, was Sie für einen Großteil der Kryptografie intuitiv verstehen müssen, ist der Unterschied zwischen einer zufälligen und einer pseudozufälligen Zeichenfolge. [2]

Der Grund für den Wegfall der Unterscheidung zwischen "zufällig" und "gleichförmig" in unserer Diskussion sollte nun ebenfalls klar sein. In der Praxis verwendet jeder den Begriff "pseudozufällig", um eine Zeichenkette zu bezeichnen, die so aussieht, als wäre sie das Ergebnis einer Stichprobe einer gleichförmigen Variablen S. Streng genommen sollten wir eine solche Zeichenkette "pseudo-uniform" nennen, um unsere Sprache von vorhin zu übernehmen. Da der Begriff "pseudo-uniform" sowohl klobig als auch ungebräuchlich ist, werden wir ihn hier der Klarheit halber nicht einführen. Stattdessen lassen wir die Unterscheidung zwischen "zufällig" und "gleichförmig" im aktuellen Kontext einfach weg.

Anmerkungen

[2] Wenn Sie an einer formaleren Darstellung dieser Fragen interessiert sind, können Sie Katz und Lindells Introduction to Modern Cryptography, insbesondere Kapitel 3, zu Rate ziehen.

Mathematische Grundlagen der Kryptographie 2

Was ist Zahlentheorie?

Dieses Kapitel behandelt ein fortgeschritteneres Thema der mathematischen Grundlagen der Kryptographie: die Zahlentheorie. Die Zahlentheorie ist zwar für die symmetrische Kryptographie wichtig (z. B. für die Rijndael-Chiffre), aber besonders wichtig ist sie für die Kryptographie mit öffentlichem Schlüssel.

Wenn Sie die Details der Zahlentheorie als mühsam empfinden, würde ich Ihnen empfehlen, beim ersten Mal nur die Grundlagen zu lesen. Sie können zu einem späteren Zeitpunkt immer wieder darauf zurückkommen.

Man könnte Zahlentheorie als das Studium der Eigenschaften von ganzen Zahlen und mathematischen Funktionen, die mit ganzen Zahlen arbeiten, bezeichnen.

Nehmen wir zum Beispiel an, dass zwei beliebige Zahlen a und N Koprimzahlen (oder relative Primzahlen) sind, wenn ihr größter gemeinsamer Teiler gleich 1 ist. Nehmen wir nun eine bestimmte ganze Zahl N an. Wie viele ganze Zahlen kleiner als N sind Koprimzahlen mit N? Können wir allgemeine Aussagen über die Antworten auf diese Frage machen? Dies sind die typischen Fragen, die die Zahlentheorie zu beantworten versucht.

Die moderne Zahlentheorie stützt sich auf die Werkzeuge der abstrakten Algebra. Das Gebiet der abstrakten Algebra ist eine Teildisziplin der Mathematik, in der die Hauptobjekte der Analyse abstrakte Objekte sind, die als algebraische Strukturen bekannt sind. Eine algebraische Struktur ist eine Menge von Elementen, die mit einer oder mehreren Operationen verknüpft sind und bestimmten Axiomen entsprechen. Durch algebraische Strukturen können Mathematiker Einblicke in spezifische mathematische Probleme gewinnen, indem sie von deren Details abstrahieren.

Das Gebiet der abstrakten Algebra wird manchmal auch als moderne Algebra bezeichnet. Vielleicht stoßen Sie auch auf den Begriff der abstrakten Mathematik (oder reinen Mathematik). Der letztgenannte Begriff bezieht sich nicht auf die abstrakte Algebra, sondern bezeichnet vielmehr das Studium der Mathematik um ihrer selbst willen und nicht nur mit Blick auf mögliche Anwendungen.

Die Mengen der abstrakten Algebra können mit vielen Arten von Objekten umgehen, von den formbeständigen Transformationen eines gleichseitigen Dreiecks bis zu Tapetenmustern. In der Zahlentheorie betrachten wir nur Mengen von Elementen, die ganze Zahlen enthalten, oder Funktionen, die mit ganzen Zahlen arbeiten.

Gruppen

Ein grundlegendes Konzept in der Mathematik ist das einer Menge von Elementen. Eine Menge wird in der Regel durch Akkoladenzeichen bezeichnet, wobei die Elemente durch Kommata getrennt sind.

Zum Beispiel ist die Menge aller ganzen Zahlen \{..., -2, -1, 0, 1, 2, ...\}. Die Ellipsen bedeuten hier, dass sich ein bestimmtes Muster in eine bestimmte Richtung fortsetzt. Die Menge aller ganzen Zahlen umfasst also auch 3, 4, 5, 6 und so weiter, sowie -3, -4, -5, -6 und so weiter. Diese Menge aller ganzen Zahlen wird üblicherweise mit \mathbb{Z} bezeichnet.

Ein weiteres Beispiel für eine Menge ist \mathbb{Z} \mod 11, also die Menge aller ganzen Zahlen modulo 11. Im Gegensatz zur gesamten Menge \mathbb{Z} enthält diese Menge nur eine endliche Anzahl von Elementen, nämlich \{0, 1, \ldots, 9, 10\}.

Ein häufiger Fehler ist die Annahme, dass die Menge \mathbb{Z} \mod 11 tatsächlich \{-10, -9, \ldots, 0, \ldots, 9, 10\} ist. Aber das ist nicht der Fall, wenn man bedenkt, wie wir die Modulo-Operation zuvor definiert haben. Alle negativen ganzen Zahlen, die durch Modulo 11 reduziert werden, werden auf \{0, 1, \ldots, 9, 10\} übertragen. Zum Beispiel wird der Ausdruck -2 \mod 11 auf 9 umgeschlagen, während der Ausdruck -27 \mod 11 auf 5 umgeschlagen wird.

Ein weiteres grundlegendes Konzept in der Mathematik ist das der binären Operation. Dabei handelt es sich um jede Operation, bei der aus zwei Elementen ein drittes entsteht. Aus den Grundrechenarten und der Algebra kennen Sie beispielsweise die vier grundlegenden binären Operationen: Addition, Subtraktion, Multiplikation und Division.

Diese beiden grundlegenden mathematischen Konzepte, Mengen und binäre Operationen, werden verwendet, um den Begriff der Gruppe zu definieren, die wichtigste Struktur in der abstrakten Algebra.

Genauer gesagt, nehmen wir eine binäre Operation \circ an. Außerdem nehmen wir an, dass eine Menge von Elementen S mit dieser Operation ausgestattet ist. Ausgestattet" bedeutet hier nur, dass die Operation \circ zwischen zwei beliebigen Elementen der Menge S durchgeführt werden kann.

Die Kombination \langle \mathbf{S}, \circ \rangle ist dann eine Gruppe, wenn sie vier bestimmte Bedingungen erfüllt, die als Gruppenaxiome bekannt sind.

  1. Für jedes a und b, die Elemente von \mathbf{S} sind, ist a \circ b ebenfalls ein Element von \mathbf{S}. Dies wird als Schlussbedingung bezeichnet.

  2. Für beliebige a, b und c, die Elemente von \mathbf{S} sind, ist es der Fall, dass (a \circ b) \circ c = a \circ (b \circ c). Dies wird als Assoziativitätsbedingung bezeichnet.

  3. Es gibt ein einziges Element e in \mathbf{S}, so dass für jedes Element a in \mathbf{S} die folgende Gleichung gilt: e \circ a = a \circ e = a. Da es nur ein solches Element e gibt, nennt man es das Identitätselement. Diese Bedingung ist als Identitätsbedingung bekannt.

  4. Für jedes Element a in \mathbf{S} gibt es ein Element b in \mathbf{S}, so dass die folgende Gleichung gilt: a \circ b = b \circ a = e, wobei e das Identitätselement ist. Das Element b wird hier als inverses Element bezeichnet, und es wird üblicherweise als a^{-1} bezeichnet. Diese Bedingung wird als Inversitätsbedingung oder Invertierbarkeitsbedingung bezeichnet.

Erforschen wir die Gruppen ein wenig weiter. Bezeichnen Sie die Menge aller ganzen Zahlen mit \mathbb{Z}. Diese Menge in Verbindung mit der Standardaddition, oder \langle \mathbb{Z}, + \rangle, entspricht eindeutig der Definition einer Gruppe, da sie die vier obigen Axiome erfüllt.

  1. Für jedes x und y, die Elemente von \mathbb{Z} sind, ist x + y auch ein Element von \mathbb{Z}. Also erfüllt \langle \mathbb{Z}, + \rangle die Schließungsbedingung.

  2. Für beliebige x, y und z, die Elemente von \mathbb{Z} sind, ist (x + y) + z = x + (y + z). Also erfüllt \langle \mathbb{Z}, + \rangle die Assoziativitätsbedingung.

  3. Es gibt ein Identitätselement in \langle \mathbb{Z}, + \rangle, nämlich 0. Für jedes x in \mathbb{Z} gilt nämlich, dass: 0 + x = x + 0 = x. Also erfüllt \langle \mathbb{Z}, + \rangle die Identitätsbedingung.

  4. Schließlich gibt es für jedes Element x in \mathbb{Z} ein y, so dass x + y = y + x = 0. Wäre x beispielsweise 10, so wäre y -10 (wenn x 0 ist, ist auch y 0). Also erfüllt \langle \mathbb{Z}, + \rangle die inverse Bedingung.

Wichtig ist, dass die Menge der ganzen Zahlen mit Addition eine Gruppe darstellt, was nicht bedeutet, dass sie eine Gruppe mit Multiplikation darstellt. Das kann man überprüfen, indem man \langle \mathbb{Z}, \cdot \rangle gegen die vier Gruppenaxiome prüft (wobei \cdot die Standardmultiplikation bedeutet).

Die ersten beiden Axiome sind offensichtlich gültig. Darüber hinaus kann das Element 1 bei der Multiplikation als Identitätselement dienen. Jede ganze Zahl x, die mit 1 multipliziert wird, ergibt nämlich x. Allerdings erfüllt \langle \mathbb{Z}, \cdot \rangle nicht die inverse Bedingung. Das heißt, es gibt nicht für jedes x in \mathbb{Z} ein eindeutiges Element y in \mathbb{Z}, so dass x \cdot y = 1 ist.

Nehmen wir zum Beispiel an, dass x = 22 ist. Welcher Wert y aus der Menge \mathbb{Z} multipliziert mit x würde das Identitätselement 1 ergeben? Der Wert 1/22 würde funktionieren, aber dieser ist nicht in der Menge \mathbb{Z} enthalten. In der Tat stößt man bei jeder ganzen Zahl x auf dieses Problem, außer bei den Werten 1 und -1 (wobei y 1 bzw. -1 sein müsste).

Wenn wir reelle Zahlen für unsere Menge zulassen, dann verschwinden unsere Probleme weitgehend. Für jedes Element x in der Menge ergibt die Multiplikation mit 1/x den Wert 1. Da Brüche in der Menge der reellen Zahlen enthalten sind, kann für jede reelle Zahl eine Umkehrung gefunden werden. Die Ausnahme ist die Null, da jede Multiplikation mit der Null niemals das Identitätselement 1 ergibt. Daher ist die Menge der reellen Zahlen ungleich Null, die mit einer Multiplikation versehen sind, tatsächlich eine Gruppe.

Einige Gruppen erfüllen eine fünfte allgemeine Bedingung, die so genannte Kommutativitätsbedingung. Diese Bedingung lautet wie folgt:

Jede Gruppe, die die Kommutativitätsbedingung erfüllt, wird als kommutative Gruppe oder Abelsche Gruppe (nach Niels Henrik Abel) bezeichnet. Es ist leicht zu überprüfen, dass sowohl die Menge der reellen Zahlen über der Addition als auch die Menge der ganzen Zahlen über der Addition abelsche Gruppen sind. Die Menge der ganzen Zahlen über der Multiplikation ist überhaupt keine Gruppe, kann also ipso facto keine abelsche Gruppe sein. Die Menge der reellen Zahlen ungleich Null über der Multiplikation ist dagegen ebenfalls eine abelsche Gruppe.

Sie sollten zwei wichtige Konventionen zur Notation beachten. Erstens werden die Zeichen "+" oder "×" häufig verwendet, um Gruppenoperationen zu symbolisieren, auch wenn die Elemente in Wirklichkeit keine Zahlen sind. In diesen Fällen sollten Sie diese Zeichen nicht als normale arithmetische Addition oder Multiplikation interpretieren. Stattdessen handelt es sich um Operationen, die nur eine abstrakte Ähnlichkeit mit diesen arithmetischen Operationen haben.

Sofern Sie sich nicht speziell auf die arithmetische Addition oder Multiplikation beziehen, ist es einfacher, Symbole wie \circ und \diamond für Gruppenoperationen zu verwenden, da diese kulturell nicht sehr tief verwurzelt sind.

Zweitens werden aus demselben Grund, aus dem "+" und "×" häufig zur Angabe von nicht-arithmetischen Operationen verwendet werden, die Identitätselemente von Gruppen häufig durch "0" und "1" symbolisiert, auch wenn die Elemente in diesen Gruppen keine Zahlen sind. Sofern man sich nicht auf das Identitätselement einer Gruppe mit Zahlen bezieht, ist es einfacher, ein neutraleres Symbol wie "e" zu verwenden, um das Identitätselement anzugeben.

Viele verschiedene und sehr wichtige Wertemengen in der Mathematik, die mit bestimmten binären Operationen ausgestattet sind, sind Gruppen. Kryptographische Anwendungen arbeiten jedoch nur mit Mengen ganzer Zahlen oder zumindest mit Elementen, die durch ganze Zahlen beschrieben werden, d. h. im Bereich der Zahlentheorie. Daher werden Mengen mit anderen reellen Zahlen als ganzen Zahlen in kryptografischen Anwendungen nicht verwendet.

Abschließend noch ein Beispiel für Elemente, die "durch ganze Zahlen beschrieben" werden können, obwohl sie keine ganzen Zahlen sind. Ein gutes Beispiel sind die Punkte von elliptischen Kurven. Obwohl jeder Punkt auf einer elliptischen Kurve eindeutig keine ganze Zahl ist, wird ein solcher Punkt tatsächlich durch zwei ganze Zahlen beschrieben.

Elliptische Kurven sind z. B. für Bitcoin von entscheidender Bedeutung. Jedes standardmäßige Bitcoin-Schlüsselpaar aus privatem und öffentlichem Schlüssel wird aus der Menge der Punkte ausgewählt, die durch die folgende elliptische Kurve definiert ist:

x^3 + 7 = y^2 \mod 2^{256} – 2^{32} – 29 – 28 – 27 – 26 - 24 - 1

(die größte Primzahl kleiner als 2^{256}). Die x-Koordinate ist der private Schlüssel und die y-Koordinate ist Ihr öffentlicher Schlüssel.

Bei Bitcoin-Transaktionen werden die Ausgaben in der Regel auf irgendeine Weise an einen oder mehrere öffentliche Schlüssel gebunden. Der Wert dieser Transaktionen kann dann durch digitale Signaturen mit den entsprechenden privaten Schlüsseln entriegelt werden.

Zyklische Gruppen

Eine wichtige Unterscheidung, die wir treffen können, ist die zwischen einer endlichen und einer unendlichen Gruppe. Erstere hat eine endliche Anzahl von Elementen, während letztere eine unendliche Anzahl von Elementen hat. Die Anzahl der Elemente in jeder endlichen Gruppe wird als Ordnung der Gruppe bezeichnet. Die gesamte praktische Kryptografie, bei der Gruppen verwendet werden, beruht auf endlichen (zahlentheoretischen) Gruppen.

In der Kryptographie mit öffentlichem Schlüssel ist eine bestimmte Klasse endlicher abelscher Gruppen, die sogenannten zyklischen Gruppen, besonders wichtig. Um zyklische Gruppen zu verstehen, müssen wir zunächst das Konzept der Potenzierung von Gruppenelementen verstehen.

Nehmen wir an, dass eine Gruppe G mit einer Gruppenoperation \circ existiert und dass a ein Element von G ist. Der Ausdruck a^n ist dann so zu interpretieren, dass das Element a insgesamt n - 1 mal mit sich selbst kombiniert ist. Zum Beispiel bedeutet a^2: a \circ a, a^3: a \circ a \circ a, und so weiter. (Man beachte, dass die Potenzierung hier nicht notwendigerweise eine Potenzierung im Sinne der Standardarithmetik ist)

Wenden wir uns einem Beispiel zu. Nehmen wir an, dass G = \langle \mathbb{Z} \mod 7, + \rangle, und dass unser Wert für a gleich 4 ist. In diesem Fall ist a^2 = [4 + 4 \mod 7] = [8 \mod 7] = 1 \mod 7. Alternativ dazu würde a^4 [4 + 4 + 4 + 4 \mod 7] = [16 \mod 7] = 2 \mod 7 darstellen.

Einige abelsche Gruppen haben ein oder mehrere Elemente, die durch fortgesetzte Potenzierung alle anderen Gruppenelemente ergeben können. Diese Elemente werden Generatoren oder Primitivelemente genannt.

Eine wichtige Klasse solcher Gruppen ist \langle \mathbb{Z}^* \mod N, \cdot \rangle, wobei N eine Primzahl ist. Die Schreibweise \mathbb{Z}^* bedeutet hier, dass die Gruppe alle von Null verschiedenen, positiven ganzen Zahlen kleiner als N enthält. Eine solche Gruppe hat also immer N - 1 Elemente.

Betrachten wir zum Beispiel G = \langle \mathbb{Z}^* \mod 11, \cdot \rangle. Diese Gruppe hat die folgenden Elemente: \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. Die Ordnung dieser Gruppe ist 10 (was tatsächlich gleich 11 - 1 ist).

Untersuchen wir die Potenzierung des Elements 2 aus dieser Gruppe. Die Berechnungen bis zu 2^{12} sind unten dargestellt. Beachten Sie, dass sich der Exponent auf der linken Seite der Gleichung auf die Potenzierung von Gruppenelementen bezieht. In unserem Beispiel handelt es sich tatsächlich um arithmetische Potenzierung auf der rechten Seite der Gleichung (es hätte aber auch z. B. um Addition gehen können). Zur Verdeutlichung habe ich die wiederholte Operation und nicht die Exponentenform auf der rechten Seite ausgeschrieben.

Wenn man genau hinsieht, kann man sehen, dass die Potenzierung des Elements 2 alle Elemente von \langle \mathbb{Z}^* \mod 11, \cdot \rangle in der folgenden Reihenfolge durchläuft: 2, 4, 8, 5, 10, 9, 7, 3, 6, 1. Nach 2^{10} durchläuft die fortgesetzte Potenzierung des Elements 2 wieder alle Elemente in der gleichen Reihenfolge. Folglich ist das Element 2 ein Generator in \langle \mathbb{Z}^* \mod 11, \cdot \rangle.

Obwohl \langle \mathbb{Z}^* \mod 11, \cdot \rangle mehrere Generatoren hat, sind nicht alle Elemente dieser Gruppe Generatoren. Betrachten wir zum Beispiel das Element 3. Wenn man die ersten 10 Potenzierungen durchgeht, ohne die umständlichen Berechnungen zu zeigen, erhält man die folgenden Ergebnisse:

Anstatt alle Werte in \langle \mathbb{Z}^* \mod 11, \cdot \rangle zu durchlaufen, führt die Potenzierung des Elements 3 nur zu einer Teilmenge dieser Werte: 3, 9, 5, 4 und 1. Nach der fünften Potenzierung beginnen sich diese Werte zu wiederholen.

Wir können nun eine zyklische Gruppe als jede Gruppe mit mindestens einem Generator definieren. Das heißt, es gibt mindestens ein Gruppenelement, aus dem man alle anderen Gruppenelemente durch Potenzierung erzeugen kann.

In unserem obigen Beispiel haben Sie vielleicht bemerkt, dass sowohl 2^{10} als auch 3^{10} gleich 1 \mod 11 sind. Tatsächlich ergibt die Potenzierung durch 10 eines beliebigen Elements der Gruppe \langle \mathbb{Z}^* \mod 11, \cdot \rangle 1 \mod 11, auch wenn wir die Berechnungen nicht durchführen werden. Warum ist dies der Fall?

Dies ist eine wichtige Frage, deren Beantwortung jedoch einige Arbeit erfordert.

Nehmen wir zu Beginn zwei positive ganze Zahlen a und N an. Ein wichtiger Satz in der Zahlentheorie besagt, dass a einen multiplikativen Kehrwert modulo N hat (d.h. eine ganze Zahl b, so dass a \cdot b = 1 \mod N), und zwar nur dann, wenn der größte gemeinsame Teiler von a und N gleich 1 ist. Das heißt, wenn a und N Koprimzahlen sind.

Für jede Gruppe ganzer Zahlen, die mit der Multiplikation modulo N ausgestattet ist, sind also nur die kleineren Koprimzahlen mit N in der Menge enthalten. Wir können diese Menge mit \mathbb{Z}^c \mod N bezeichnen.

Nehmen wir zum Beispiel an, dass N gleich 10 ist. Nur die ganzen Zahlen 1, 3, 7 und 9 sind Koprimzahlen von 10. Die Menge \mathbb{Z}^c \mod 10 enthält also nur \{1, 3, 7, 9\}. Man kann keine Gruppe mit ganzzahliger Multiplikation modulo 10 mit anderen ganzen Zahlen zwischen 1 und 10 bilden. Für diese spezielle Gruppe sind die Inversen die Paare 1 und 9 sowie 3 und 7.

Für den Fall, dass N selbst prim ist, sind alle ganzen Zahlen von 1 bis N - 1 Koprimzahlen von N. Eine solche Gruppe hat also eine Ordnung von N - 1. Unter Verwendung unserer früheren Notation ist \mathbb{Z}^c \mod N gleich \mathbb{Z}^* \mod N, wenn N prim ist. Die Gruppe, die wir für unser früheres Beispiel ausgewählt haben, \langle \mathbb{Z}^* \mod 11, \cdot \rangle, ist ein besonderes Beispiel für diese Klasse von Gruppen.

Anschließend berechnet die Funktion \phi(N) die Anzahl der Koprimzahlen bis zu einer Zahl N und ist als Eulersche Phi-Funktion bekannt. [1] Nach dem Eulerschen Lehrsatz gilt, dass immer dann, wenn zwei ganze Zahlen a und N Koprimzahlen sind, Folgendes gilt:

Dies hat eine wichtige Auswirkung auf die Klasse der Gruppen \langle \mathbb{Z}^* \mod N, \cdot \rangle, bei denen N eine Primzahl ist. Für diese Gruppen ist die Potenzierung der Gruppenelemente die arithmetische Potenzierung. Das heißt, a^{\phi(N)} \mod N entspricht der arithmetischen Operation a^{\phi(N)} \mod N. Da jedes Element a in diesen multiplikativen Gruppen koprim mit N ist, bedeutet dies, dass a^{\phi(N)} \mod N = a^{N - 1} \mod N = 1 \mod N.

Das Eulersche Theorem ist ein wirklich wichtiges Ergebnis. Er besagt zunächst, dass alle Elemente in \langle \mathbb{Z}^* \mod N, \cdot \rangle nur eine Anzahl von Werten durch Potenzierung durchlaufen können, die sich durch N - 1 teilt. Im Fall von \langle \mathbb{Z}^* \mod 11, \cdot \rangle bedeutet dies, dass jedes Element nur 2, 5 oder 10 Elemente durchlaufen kann. Die Gruppenwerte, die ein Element bei der Potenzierung durchläuft, werden als Ordnung des Elements bezeichnet. Ein Element mit einer Ordnung, die der Ordnung einer Gruppe entspricht, ist ein Generator.

Außerdem impliziert der Satz von Euler, dass wir immer das Ergebnis von a^{N - 1} \mod N für jede Gruppe \langle \mathbb{Z}^* \mod N, \cdot \rangle, bei der N eine Primzahl ist. Dies gilt unabhängig davon, wie kompliziert die eigentlichen Berechnungen sein mögen.

Nehmen wir zum Beispiel an, unsere Gruppe sei \mathbb{Z}^* \mod 160,481,182 (wobei 160,481,182 tatsächlich eine Primzahl ist). Wir wissen, dass alle ganzen Zahlen von 1 bis 160.481.181 Elemente dieser Gruppe sein müssen, und dass \phi(n) = 160.481.181. Obwohl wir nicht alle Rechenschritte durchführen können, wissen wir, dass Ausdrücke wie 514^{160,481,181}, 2,005^{160,481,181} und 256,212^{160,481,181} alle zu 1 \mod 160,481,182 auswerten müssen.

Anmerkungen:

[1] Die Funktion funktioniert folgendermaßen. Jede ganze Zahl N kann in ein Produkt von Primzahlen zerlegt werden. Angenommen, ein bestimmtes N wird wie folgt faktorisiert: p_1^{e1} \cdot p_2^{e2} \cdot \ldots \cdot p_m^{em}, wobei alle p Primzahlen und alle e ganze Zahlen größer oder gleich 1 sind:

\phi(N) = \sum_{i=1}^m \left[p_i^{e_i} - p_i^{e_i - 1}\right]

Eulers Phi-Funktionsformel für die Primfaktorzerlegung von N.

Felder

Eine Gruppe ist die grundlegende algebraische Struktur in der abstrakten Algebra, aber es gibt noch viele weitere. Die einzige andere algebraische Struktur, mit der Sie vertraut sein müssen, ist die eines Feldes, insbesondere die eines unendlichen Feldes. Diese Art von algebraischer Struktur wird häufig in der Kryptographie verwendet, z. B. im Advanced Encryption Standard. Letzterer ist das wichtigste symmetrische Verschlüsselungsverfahren, dem Sie in der Praxis begegnen werden.

Ein Feld ist vom Begriff der Gruppe abgeleitet. Genauer gesagt ist ein Feld eine Menge von Elementen S, die mit zwei binären Operatoren \circ und \diamond ausgestattet ist und die folgenden Bedingungen erfüllt:

  1. Die mit \circ ausgestattete Menge S ist eine abelsche Gruppe.

  2. Die mit \diamond ausgestattete Menge S ist eine abelsche Gruppe für die "Nicht-Null"-Elemente.

  3. Die Menge S mit den beiden Operatoren erfüllt die so genannte Distributivbedingung: Nehmen wir an, dass a, b und c Elemente von S sind. Dann erfüllt S mit den beiden Operatoren die distributive Eigenschaft, wenn a \circ (b \diamond c) = (a \circ b) \diamond (a \circ c).

Beachten Sie, dass die Definition eines Feldes wie bei Gruppen sehr abstrakt ist. Sie macht keine Aussagen über die Arten der Elemente in S oder über die Operationen \circ und \diamond. Sie besagt lediglich, dass ein Feld eine beliebige Menge von Elementen mit zwei Operationen ist, für die die drei oben genannten Bedingungen gelten. (Das "Null"-Element in der zweiten abelschen Gruppe kann abstrakt interpretiert werden.)

Was könnte also ein Beispiel für ein Feld sein? Ein gutes Beispiel ist die Menge \mathbb{Z} \mod 7, oder \{0, 1, \ldots, 7\}, definiert über Standardaddition (anstelle von \circ oben) und Standardmultiplikation (anstelle von \diamond oben).

Erstens: \mathbb{Z} \mod 7 die Bedingung, eine abelsche Gruppe über Addition zu sein, und sie erfüllt die Bedingung, eine abelsche Gruppe über Multiplikation zu sein, wenn man nur die Nicht-Null-Elemente betrachtet. Zweitens erfüllt die Kombination der Menge mit den beiden Operatoren die Distributivbedingung.

Es ist didaktisch sinnvoll, diese Behauptungen anhand einiger besonderer Werte zu untersuchen. Nehmen wir die Versuchswerte 5, 2 und 3, einige zufällig ausgewählte Elemente aus der Menge \mathbb{Z} \mod 7, zur Untersuchung des Feldes \langle \mathbb{Z} \mod 7, +, \cdot \rangle. Wir werden diese drei Werte in der Reihenfolge verwenden, wie sie für die Untersuchung bestimmter Bedingungen erforderlich sind.

Wir wollen zunächst untersuchen, ob \mathbb{Z} \mod 7, ausgestattet mit Addition, eine abelsche Gruppe ist.

  1. Abschlussbedingung: Nehmen wir 5 und 2 als unsere Werte an. In diesem Fall ist [5 + 2] \mod 7 = 7 \mod 7 = 0. Dies ist tatsächlich ein Element von \mathbb{Z} \mod 7, so dass das Ergebnis mit der Abschlussbedingung vereinbar ist.

  2. Assoziativitätsbedingung: Nehmen wir 5, 2 und 3 als unsere Werte an. In diesem Fall ist [(5 + 2) + 3] \mod 7 = [5 + (2 + 3)] \mod 7 = 10 \mod 7 = 3. Dies ist mit der Assoziativitätsbedingung vereinbar.

  3. Eigenschaftsbedingung: Nehmen wir 5 als unseren Wert an. In diesem Fall ist [5 + 0] \mod 7 = [0 + 5] \mod 7 = 5. 0 scheint also das Identitätselement für die Addition zu sein.

  4. Inverse Bedingung: Betrachten Sie den Kehrwert von 5. Es muss der Fall sein, dass [5 + d] \mod 7 = 0, für irgendeinen Wert von d. In diesem Fall ist der einzige Wert aus \mathbb{Z} \mod 7, der diese Bedingung erfüllt, 2.

  5. Kommutativitätsbedingung: Nehmen wir 5 und 3 als unsere Werte an. In diesem Fall ist [5 + 3] \mod 7 = [3 + 5] \mod 7 = 1. Dies ist mit der Kommutativitätsbedingung vereinbar.

Die Menge \mathbb{Z} \mod 7, die mit Addition ausgestattet ist, scheint eindeutig eine abelsche Gruppe zu sein. Wir wollen nun untersuchen, ob \mathbb{Z} \mod 7 mit Multiplikation eine abelsche Gruppe für alle Nicht-Null-Elemente ist.

  1. Abschlussbedingung: Nehmen wir 5 und 2 als unsere Werte an. In diesem Fall ist [5 \cdot 2] \mod 7 = 10 \mod 7 = 3. Dies ist auch ein Element von \mathbb{Z} \mod 7, so dass das Ergebnis mit der Schließungsbedingung vereinbar ist.

  2. Assoziativitätsbedingung: Nehmen wir 5, 2 und 3 als unsere Werte. In diesem Fall ist [(5 \cdot 2) \cdot 3] \mod 7 = [5 \cdot (2 \cdot 3)] \mod 7 = 30 \mod 7 = 2. Dies ist mit der Assoziativitätsbedingung vereinbar.

  3. Eigenschaftsbedingung: Nehmen wir 5 als unseren Wert an. In diesem Fall ist [5 \cdot 1] \mod 7 = [1 \cdot 5] \mod 7 = 5. 1 scheint also das Identitätselement für die Multiplikation zu sein.

  4. Inverse Bedingung: Betrachten Sie den Kehrwert von 5. Es muss der Fall sein, dass [5 \cdot d] \mod 7 = 1, für irgendeinen Wert von d. Der einzige Wert aus \mathbb{Z} \mod 7, der diese Bedingung erfüllt, ist 3. Dies ist konsistent mit der inversen Bedingung.

  5. Kommutativitätsbedingung: Nehmen wir 5 und 3 als unsere Werte an. In diesem Fall ist [5 \cdot 3] \mod 7 = [3 \cdot 5] \mod 7 = 15 \mod 7 = 1. Dies ist mit der Kommutativitätsbedingung vereinbar.

Die Menge \mathbb{Z} \mod 7 scheint eindeutig die Regeln für eine abelsche Gruppe zu erfüllen, wenn sie entweder mit Addition oder Multiplikation über die Nicht-Null-Elemente verbunden ist.

Schließlich scheint diese Menge in Kombination mit beiden Operatoren die Distributionsbedingung zu erfüllen. Nehmen wir 5, 2 und 3 als unsere Werte. Wir können sehen, dass [5 \cdot (2 + 3)] \mod 7 = [5 \cdot 2 + 5 \cdot 3] \mod 7 = 25 \mod 7 = 4.

Wir haben nun gesehen, dass \mathbb{Z} \mod 7, ausgestattet mit Addition und Multiplikation, die Axiome für ein endliches Feld erfüllt, wenn es mit bestimmten Werten getestet wird. Natürlich können wir das auch allgemein zeigen, aber das werden wir hier nicht tun.

Eine wichtige Unterscheidung ist die zwischen zwei Arten von Feldern: endliche und unendliche Felder.

Ein unendliches Feld ist ein Feld, bei dem die Menge S unendlich groß ist. Die Menge der reellen Zahlen \mathbb{R}, die mit Addition und Multiplikation ausgestattet ist, ist ein Beispiel für ein unendliches Feld. Ein endliches Feld, auch Galoisfeld genannt, ist ein Feld, bei dem die Menge S endlich ist. Unser obiges Beispiel von \langle \mathbb{Z} \mod 7, +, \cdot \rangle ist ein endliches Feld.

In der Kryptographie sind wir hauptsächlich an endlichen Feldern interessiert. Im Allgemeinen kann gezeigt werden, dass ein endliches Feld für eine Menge von Elementen S dann und nur dann existiert, wenn es p^m Elemente hat, wobei p eine Primzahl und m eine positive ganze Zahl größer oder gleich eins ist. Mit anderen Worten: Wenn die Ordnung einer Menge S eine Primzahl (p^m mit m = 1) oder eine Primzahlpotenz (p^m mit m > 1) ist, dann kann man zwei Operatoren \circ und \diamond finden, die die Bedingungen für ein Feld erfüllen.

Hat ein endliches Feld eine Primzahl von Elementen, so nennt man es ein Primzahlfeld. Ist die Anzahl der Elemente des endlichen Feldes eine Primzahlpotenz, so nennt man das Feld ein Erweiterungsfeld. In der Kryptographie sind wir sowohl an Primzahl- als auch an Erweiterungsfeldern interessiert. [2]

Die wichtigsten Primzahlfelder, die für die Kryptographie von Interesse sind, sind solche, bei denen die Menge aller ganzen Zahlen durch eine Primzahl moduliert wird und die Operatoren Standardaddition und -multiplikation sind. Zu dieser Klasse von endlichen Feldern gehören \mathbb{Z} \mod 2, \mathbb{Z} \mod 3, \mathbb{Z} \mod 5, \mathbb{Z} \mod 7, \mathbb{Z} \mod 11, \mathbb{Z} \mod 13, und so weiter. Für jedes Primzahlfeld \mathbb{Z} \mod p ist die Menge der ganzen Zahlen des Feldes wie folgt: \{0, 1, \ldots, p - 2, p - 1\}.

In der Kryptographie sind wir auch an Erweiterungsfeldern interessiert, insbesondere an Feldern mit 2^m Elementen, wobei m > 1 ist. Solche endlichen Felder werden z. B. in der Rijndael-Chiffre verwendet, die die Grundlage des Advanced Encryption Standard bildet. Während Primzahlfelder relativ intuitiv sind, sind diese Erweiterungsfelder zur Basis 2 wahrscheinlich nichts für jemanden, der mit abstrakter Algebra nicht vertraut ist.

Zunächst einmal ist es tatsächlich so, dass jeder Menge ganzer Zahlen mit 2^m Elementen zwei Operatoren zugeordnet werden können, die ihre Kombination zu einem Feld machen (solange m eine positive ganze Zahl ist). Doch nur weil es ein Feld gibt, heißt das nicht unbedingt, dass es leicht zu entdecken oder für bestimmte Anwendungen besonders praktisch ist.

Wie sich herausstellt, sind die in der Kryptographie besonders anwendbaren Erweiterungsfelder von 2^m solche, die über bestimmte Mengen von Polynomausdrücken definiert sind, und nicht über eine Menge von ganzen Zahlen.

Nehmen wir zum Beispiel an, wir wollten ein Erweiterungsfeld mit 2^3 (d.h. 8) Elementen in der Menge. Es gibt zwar viele verschiedene Mengen, die für Felder dieser Größe verwendet werden können, aber eine dieser Mengen enthält alle eindeutigen Polynome der Form a_2x^2 + a_1x + a_0, wobei jeder Koeffizient a_i entweder 0 oder 1 ist. Diese Menge S enthält also die folgenden Elemente:

  1. 0: Der Fall, in dem a_2 = 0, a_1 = 0, und a_0 = 0.

  2. 1: Der Fall, in dem a_2 = 0, a_1 = 0, und a_0 = 1.

  3. x: Der Fall, in dem a_2 = 0, a_1 = 1, und a_0 = 0.

  4. x + 1: Der Fall, in dem a_2 = 0, a_1 = 1, und a_0 = 1.

  5. x^2: Der Fall, in dem a_2 = 1, a_1 = 0, und a_0 = 0.

  6. x^2 + 1: Der Fall, in dem a_2 = 1, a_1 = 0 und a_0 = 1.

  7. x^2 + x: Der Fall, in dem a_2 = 1, a_1 = 1, und a_0 = 0.

  8. x^2 + x + 1: Der Fall, in dem a_2 = 1, a_1 = 1, und a_0 = 1.

S wäre also die Menge \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}. Welche zwei Operationen können über dieser Menge von Elementen definiert werden, um sicherzustellen, dass ihre Kombination ein Feld ist?

Die erste Operation an der Menge S (\circ) kann als Standard-Polynomaddition modulo 2 definiert werden. Alles, was Sie tun müssen, ist, die Polynome wie gewohnt zu addieren und dann den Modulo 2 auf jeden der Koeffizienten des resultierenden Polynoms anzuwenden. Hier sind einige Beispiele:

Die zweite Operation auf der Menge S (\diamond), die für die Erstellung des Feldes benötigt wird, ist komplizierter. Es handelt sich um eine Art Multiplikation, aber nicht um die Standardmultiplikation aus der Arithmetik. Stattdessen muss man jedes Element als Vektor betrachten und die Operation als Multiplikation dieser beiden Vektoren modulo eines irreduziblen Polynoms verstehen.

Wenden wir uns zunächst dem Begriff des irreduziblen Polynoms zu. Ein irrreduzierbares Polynom ist ein Polynom, das nicht faktorisiert werden kann (so wie eine Primzahl nicht in andere Komponenten als 1 und die Primzahl selbst zerlegt werden kann). Für unsere Zwecke sind wir an Polynomen interessiert, die in Bezug auf die Menge aller ganzen Zahlen irreduzibel sind. (Beachten Sie, dass Sie bestimmte Polynome z. B. mit den reellen oder komplexen Zahlen faktorisieren können, auch wenn Sie sie nicht mit ganzen Zahlen faktorisieren können)

Betrachten wir zum Beispiel das Polynom x^2 - 3x + 2. Dieses kann als (x - 1)(x - 2) umgeschrieben werden. Es ist also nicht irreduzibel. Betrachten wir nun das Polynom x^2 + 1. Wenn man nur ganze Zahlen verwendet, gibt es keine Möglichkeit, diesen Ausdruck weiter zu faktorisieren. Daher ist dies ein irreduzibles Polynom in Bezug auf die ganzen Zahlen.

Als nächstes wollen wir uns dem Konzept der Vektormultiplikation zuwenden. Wir werden dieses Thema nicht in die Tiefe gehen, aber Sie müssen nur eine Grundregel verstehen: Jede Vektordivision kann durchgeführt werden, solange der Dividend einen höheren oder gleichen Grad wie der Divisor hat. Hat der Dividend einen niedrigeren Grad als der Divisor, so kann der Dividend nicht mehr durch den Divisor dividiert werden.

Betrachten wir zum Beispiel den Ausdruck x^6 + x + 1 \mod x^5 + x^2. Dieser reduziert sich eindeutig weiter, da der Grad des Dividenden, 6, höher ist als der Grad des Divisors, 5. Betrachten Sie nun den Ausdruck x^5 + x + 1 \mod x^5 + x^2. Auch dieser reduziert sich weiter, da der Grad des Dividenden, 5, und des Divisors, 5, gleich sind.

Betrachten wir nun aber den Ausdruck x^4 + x + 1 \mod x^5 + x^2. Dieser lässt sich nicht weiter reduzieren, da der Grad des Dividenden, 4, niedriger ist als der Grad des Divisors, 5.

Auf der Grundlage dieser Informationen sind wir nun bereit, unsere zweite Operation für die Menge \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\} zu finden.

Ich habe bereits gesagt, dass die zweite Operation als Vektormultiplikation modulo eines irreduziblen Polynoms verstanden werden sollte. Dieses irreduzible Polynom sollte sicherstellen, dass die zweite Operation eine abelsche Gruppe über S definiert und mit der Distributivbedingung vereinbar ist. Was sollte dieses irreduzible Polynom also sein?

Da alle Vektoren in der Menge vom Grad 2 oder niedriger sind, sollte das irreduzible Polynom vom Grad 3 sein. Wenn jede Multiplikation zweier Vektoren in der Menge ein Polynom vom Grad 3 oder höher ergibt, wissen wir, dass modulo ein Polynom vom Grad 3 immer ein Polynom vom Grad 2 oder niedriger ergibt. Dies ist der Fall, weil jedes Polynom vom Grad 3 oder höher immer durch ein Polynom vom Grad 3 teilbar ist. Außerdem muss das Polynom, das als Divisor fungiert, irreduzibel sein.

Es stellt sich heraus, dass es mehrere irreduzible Polynome vom Grad 3 gibt, die wir als Divisor verwenden können. Jedes dieser Polynome definiert in Verbindung mit unserer Menge S und der Addition modulo 2 ein anderes Feld. Das bedeutet, dass man mehrere Optionen hat, wenn man Erweiterungsfelder 2^m in der Kryptographie verwendet.

Für unser Beispiel nehmen wir an, dass wir das Polynom x^3 + x + 1 wählen. Dieses ist in der Tat irreduzibel, weil man es nicht mit ganzen Zahlen faktorisieren kann. Außerdem stellt es sicher, dass jede Multiplikation von zwei Elementen ein Polynom vom Grad 2 oder weniger ergibt.

Um die Funktionsweise der zweiten Operation zu verdeutlichen, wollen wir ein Beispiel mit dem Polynom x^3 + x + 1 als Divisor durchspielen. Angenommen, man multipliziert die Elemente x^2 + 1 mit x^2 + x in unserer Menge S. Wir müssen dann den Ausdruck [(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1 berechnen. Dies kann wie folgt vereinfacht werden:

Wir wissen, dass [x^4 + x^3 + x^2 + x] \mod x^3 + x + 1 reduziert werden kann, da der Dividend einen höheren Grad (4) hat als der Divisor (3).

Zunächst kann man sehen, dass der Ausdruck x^3 + x + 1 insgesamt x mal in x^4 + x^3 + x^2 + x übergeht. Man kann dies überprüfen, indem man x^3 + x + 1 mit x multipliziert, was x^4 + x^2 + x ergibt. Da der letztgenannte Term den gleichen Grad wie der Dividend hat, nämlich 4, wissen wir, dass dies funktioniert. Den Rest dieser Division durch x kann man wie folgt berechnen:

Nachdem wir also x^4 + x^3 + x^2 + x durch x^3 + x + 1 insgesamt x mal geteilt haben, haben wir einen Rest von x^3. Kann dieser weiter durch x^3 + x + 1 geteilt werden?

Intuitiv mag es verlockend sein, zu sagen, dass x^3 nicht mehr durch x^3 + x + 1 geteilt werden kann, weil der letztere Term größer erscheint. Erinnern Sie sich jedoch an unsere Diskussion über die Vektordivision. Solange der Dividend einen Grad größer oder gleich dem Divisor hat, kann der Ausdruck weiter reduziert werden. Genauer gesagt kann der Ausdruck x^3 + x + 1 genau 1 Mal in x^3 eingehen. Der Rest wird wie folgt berechnet:

[(x^3) - (x^3 + x + 1)] \mod x^3 + x + 1 = [x + 1] \mod x^3 + x + 1 = x + 1

Sie fragen sich vielleicht, warum (x^3) - (x^3 + x + 1) x + 1ergibt und nicht-x - 1$. Erinnern Sie sich, dass die erste Operation unseres Feldes modulo 2 definiert ist. Daher ergibt die Subtraktion zweier Vektoren genau das gleiche Ergebnis wie die Addition zweier Vektoren.

Die Multiplikation von x^2 + 1 und x^2 + x zusammenfassen: Wenn man diese beiden Terme multipliziert, erhält man ein Polynom vom Grad 4, x^4 + x^3 + x^2 + x, das modulo x^3 + x + 1 reduziert werden muss. Das Polynom vom Grad 4 ist durch x^3 + x + 1 genau x + 1 mal teilbar. Der Rest nach der Division von x^4 + x^3 + x^2 + x durch x^3 + x + 1 genau x + 1 mal ist x + 1. Dies ist in der Tat ein Element in unserer Menge \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.

Warum sollten Erweiterungsfelder zur Basis 2 über Mengen von Polynomen, wie im obigen Beispiel, für die Kryptographie nützlich sein? Der Grund dafür ist, dass man die Koeffizienten in den Polynomen solcher Mengen, die entweder 0 oder 1 sind, als Elemente von binären Zeichenketten mit einer bestimmten Länge betrachten kann. Die Menge S in unserem obigen Beispiel könnte zum Beispiel stattdessen als eine Menge S betrachtet werden, die alle binären Zeichenketten der Länge 3 (000 bis 111) enthält. Die Operationen auf S können dann auch verwendet werden, um Operationen auf diesen binären Zeichenketten durchzuführen und eine binäre Zeichenkette derselben Länge zu erzeugen.

Anmerkungen:

[2] Erweiterungsfelder sind sehr kontraintuitiv. Anstatt Elemente aus ganzen Zahlen zu haben, haben sie Mengen von Polynomen. Darüber hinaus werden alle Operationen modulo eines irreduziblen Polynoms durchgeführt.

Abstrakte Algebra in der Praxis

Trotz der formalen Sprache und der Abstraktheit der Diskussion sollte das Konzept einer Gruppe nicht allzu schwer zu begreifen sein. Es ist einfach eine Menge von Elementen zusammen mit einer binären Operation, wobei die Durchführung dieser binären Operation auf diesen Elementen vier allgemeine Bedingungen erfüllt. Eine abelsche Gruppe hat lediglich eine zusätzliche Bedingung, die Kommutativität. Eine zyklische Gruppe wiederum ist eine spezielle Art von abelscher Gruppe, nämlich eine, die einen Generator hat. Ein Feld ist lediglich ein komplexeres Konstrukt aus dem Grundbegriff der Gruppe.

Aber wenn Sie ein praktisch veranlagter Mensch sind, werden Sie sich an dieser Stelle vielleicht fragen: Wen interessiert das? Hat das Wissen, dass eine Menge von Elementen mit einem Operator eine Gruppe ist, oder sogar eine abelsche oder zyklische Gruppe, irgendeine Bedeutung in der realen Welt? Ist es wichtig zu wissen, dass etwas ein Feld ist?

Ohne zu sehr ins Detail gehen zu wollen, lautet die Antwort "ja". Gruppen wurden erstmals im 19. Jahrhundert von dem französischen Mathematiker Evariste Galois geschaffen. Er benutzte sie, um Schlussfolgerungen für die Lösung von Polynomgleichungen höheren Grades als fünf zu ziehen.

Seitdem hat das Konzept einer Gruppe dazu beigetragen, Licht in eine Reihe von Problemen in der Mathematik und anderswo zu bringen. Auf ihrer Grundlage konnte beispielsweise der Physiker Murray-Gellman die Existenz eines Teilchens vorhersagen, bevor es in Experimenten tatsächlich beobachtet wurde. [3] Ein weiteres Beispiel: Chemiker verwenden die Gruppentheorie, um die Formen von Molekülen zu klassifizieren. Mathematiker haben das Konzept einer Gruppe sogar benutzt, um Schlussfolgerungen über etwas so Konkretes wie eine Tapete zu ziehen!

Der Nachweis, dass eine Menge von Elementen mit einem bestimmten Operator eine Gruppe ist, bedeutet im Wesentlichen, dass das, was Sie beschreiben, eine bestimmte Symmetrie aufweist. Nicht eine Symmetrie im üblichen Sinne des Wortes, sondern in einer abstrakteren Form. Und das kann wesentliche Erkenntnisse über bestimmte Systeme und Probleme liefern. Die komplexeren Begriffe aus der abstrakten Algebra liefern uns lediglich zusätzliche Informationen.

Am wichtigsten ist, dass Sie die Bedeutung von zahlentheoretischen Gruppen und Feldern in der Praxis durch ihre Anwendung in der Kryptographie, insbesondere der Kryptographie mit öffentlichen Schlüsseln, sehen werden. Wir haben in unserer Diskussion über Felder bereits gesehen, wie Erweiterungsfelder in der Rijndael-Chiffre verwendet werden. Wir werden dieses Beispiel in Kapitel 5 ausarbeiten.

Zur weiteren Erörterung der abstrakten Algebra empfehle ich die ausgezeichnete Videoserie über abstrakte Algebra von Socratica. [4] Ich würde insbesondere die folgenden Videos empfehlen: "Was ist abstrakte Algebra?", "Gruppendefinition (erweitert)", "Ringdefinition (erweitert)", und "Felddefinition (erweitert)" Diese vier Videos werden Ihnen einen zusätzlichen Einblick in einen Großteil der obigen Diskussion geben. (Wir haben nicht über Ringe gesprochen, aber ein Feld ist nur eine spezielle Art von Ring)

Für weitere Diskussionen über die moderne Zahlentheorie können Sie viele fortgeschrittene Diskussionen über Kryptographie konsultieren. Ich würde Jonathan Katz und Yehuda Lindell's Introduction to Modern Cryptography oder Christof Paar und Jan Pelzl's Understanding Cryptography zur weiteren Diskussion vorschlagen. [5]

Anmerkungen:

[3] Siehe YouTube Video

[4] Socratica, Abstrakte Algebra

[5] Katz und Lindell, Introduction to Modern Cryptography, 2nd edn, 2015 (CRC Press: Boca Raton, FL). Paar und Pelzl, Understanding Cryptography, 2010 (Springer-Verlag: Berlin).

Symmetrische Kryptographie

Alice und Bob

Einer der beiden Hauptzweige der Kryptographie ist die symmetrische Kryptographie. Sie umfasst sowohl Verschlüsselungsverfahren als auch Verfahren zur Authentifizierung und Integrität. Bis in die 1970er Jahre bestand die gesamte Kryptografie aus symmetrischen Verschlüsselungsverfahren.

Die Hauptdiskussion beginnt mit der Betrachtung symmetrischer Verschlüsselungssysteme und der Unterscheidung zwischen Stromchiffren und Blockchiffren. Anschließend werden wir uns den Nachrichtenauthentifizierungscodes zuwenden, bei denen es sich um Verfahren zur Gewährleistung der Integrität und Authentizität von Nachrichten handelt. Schließlich untersuchen wir, wie symmetrische Verschlüsselungsverfahren und Nachrichtenauthentifizierungscodes kombiniert werden können, um eine sichere Kommunikation zu gewährleisten.

In diesem Kapitel werden verschiedene symmetrische kryptographische Verfahren aus der Praxis beiläufig besprochen. Das nächste Kapitel bietet eine detaillierte Darstellung der Verschlüsselung mit einer Stromchiffre und einer Blockchiffre aus der Praxis, nämlich RC4 bzw. AES.

Bevor wir mit der Diskussion über symmetrische Kryptographie beginnen, möchte ich kurz einige Bemerkungen zu den Abbildungen von Alice und Bob in diesem und den folgenden Kapiteln machen.

Zur Veranschaulichung der Grundsätze der Kryptografie werden häufig Beispiele mit Alice und Bob herangezogen. Ich werde das auch tun.

Besonders wenn Sie neu in der Kryptographie sind, ist es wichtig zu wissen, dass diese Beispiele von Alice und Bob nur zur Veranschaulichung der kryptographischen Prinzipien und Konstruktionen in einer vereinfachten Umgebung dienen sollen. Die Prinzipien und Konstruktionen sind jedoch auf eine viel breitere Palette von realen Kontexten anwendbar.

Nachfolgend finden Sie fünf wichtige Punkte, die Sie bei Beispielen mit Alice und Bob in der Kryptografie beachten sollten:

  1. Sie lassen sich leicht auf Beispiele mit anderen Akteuren wie Unternehmen oder Regierungsorganisationen übertragen.

  2. Sie können leicht auf drei oder mehr Akteure erweitert werden.

  3. In den Beispielen sind Bob und Alice in der Regel aktiv an der Erstellung jeder Nachricht und an der Anwendung kryptografischer Verfahren auf diese Nachricht beteiligt. In der Realität ist die elektronische Kommunikation jedoch weitgehend automatisiert. Wenn Sie z. B. eine Website besuchen, die Transport Layer Security verwendet, wird die Kryptografie in der Regel vollständig von Ihrem Computer und dem Webserver übernommen.

  4. Im Rahmen der elektronischen Kommunikation sind die "Nachrichten", die über einen Kommunikationskanal gesendet werden, in der Regel TCP/IP-Pakete. Diese können zu einer E-Mail, einer Facebook-Nachricht, einem Telefongespräch, einer Dateiübertragung, einer Website, einem Software-Upload usw. gehören. Sie sind keine Nachrichten im herkömmlichen Sinne. Dennoch vereinfachen Kryptographen diese Realität oft, indem sie sagen, dass es sich bei der Nachricht beispielsweise um eine E-Mail handelt.

  5. Die Beispiele beziehen sich in der Regel auf die elektronische Kommunikation, lassen sich aber auch auf traditionelle Kommunikationsformen wie Briefe übertragen.

Symmetrische Verschlüsselungsverfahren

Wir können ein symmetrisches Verschlüsselungsverfahren grob als jedes kryptografische Verfahren mit drei Algorithmen definieren:

  1. Ein Schlüsselgenerierungsalgorithmus, der einen privaten Schlüssel erzeugt.

  2. Ein Verschlüsselungsalgorithmus, der den privaten Schlüssel und einen Klartext als Eingaben nimmt und einen Chiffretext ausgibt.

  3. Ein Entschlüsselungsalgorithmus, der den privaten Schlüssel und den Chiffretext als Eingaben nimmt und den ursprünglichen Klartext ausgibt.

Normalerweise bietet ein Verschlüsselungsschema - ob symmetrisch oder asymmetrisch - eher eine Vorlage für die Verschlüsselung auf der Grundlage eines Kernalgorithmus als eine genaue Spezifikation.

Nehmen wir zum Beispiel Salsa20, ein symmetrisches Verschlüsselungsverfahren. Es kann sowohl mit 128- als auch mit 256-Bit-Schlüssellängen verwendet werden. Die Wahl der Schlüssellänge wirkt sich auf einige kleinere Details des Algorithmus aus (die Anzahl der Runden im Algorithmus, um genau zu sein).

Man kann aber nicht sagen, dass die Verwendung von Salsa20 mit einem 128-Bit-Schlüssel ein anderes Verschlüsselungsverfahren ist als Salsa20 mit einem 256-Bit-Schlüssel. Der Kernalgorithmus bleibt derselbe. Nur wenn sich der Kernalgorithmus ändert, würde man wirklich von zwei verschiedenen Verschlüsselungsverfahren sprechen.

Symmetrische Verschlüsselungssysteme sind typischerweise in zwei Arten von Fällen nützlich: (1) in denen zwei oder mehr Agenten aus der Ferne kommunizieren und den Inhalt ihrer Kommunikation geheim halten wollen; und (2) in denen ein Agent den Inhalt einer Nachricht über die Zeit geheim halten will.

Eine Darstellung der Situation (1) ist in Abbildung 1 unten zu sehen. Bob möchte eine Nachricht M über eine bestimmte Entfernung an Alice senden, möchte aber nicht, dass andere diese Nachricht lesen können.

Bob verschlüsselt zunächst die Nachricht M mit dem privaten Schlüssel K. Anschließend sendet er den Chiffretext C an Alice. Sobald Alice den verschlüsselten Text erhalten hat, kann sie ihn mit dem Schlüssel K entschlüsseln und den Klartext lesen. Bei einem guten Verschlüsselungsverfahren sollte ein Angreifer, der den Chiffretext C abfängt, nichts wirklich Wichtiges über die Nachricht M in Erfahrung bringen können.

Eine Darstellung der Situation (2) sehen Sie in Abbildung 2 unten. Bob möchte verhindern, dass andere bestimmte Informationen einsehen können. Eine typische Situation könnte sein, dass Bob ein Angestellter ist, der sensible Daten auf seinem Computer speichert, die weder Außenstehende noch seine Kollegen lesen sollen.

Bob verschlüsselt die Nachricht M zum Zeitpunkt T_0 mit dem Schlüssel K, um den Chiffretext C zu erzeugen. Zum Zeitpunkt T_1 benötigt er die Nachricht erneut und entschlüsselt den Chiffretext C mit dem Schlüssel K. Jeder Angreifer, der in der Zwischenzeit auf den Chiffretext C gestoßen ist, sollte nicht in der Lage gewesen sein, daraus irgendetwas Signifikantes über M abzuleiten.

Abbildung 1: Raumübergreifende Geheimhaltung

Figure 1: Secrecy across space

Abbildung 2: Geheimhaltung im Zeitverlauf

Figure 2: Secrecy across time

Ein Beispiel: Die Shift-Chiffre

In Kapitel 2 haben wir die Shift-Chiffre kennengelernt, die ein Beispiel für ein sehr einfaches symmetrisches Verschlüsselungsverfahren ist. Schauen wir sie uns hier noch einmal an.

Nehmen wir ein Wörterbuch D an, das alle Buchstaben des englischen Alphabets der Reihe nach mit der Menge der Zahlen \{0,1,2,\dots,25\} gleichsetzt. Angenommen, es gibt eine Menge möglicher Nachrichten M. Die Shift-Chiffre ist dann ein Verschlüsselungsverfahren, das wie folgt definiert ist:

Was die Shift-Chiffre zu einem symmetrischen Verschlüsselungsverfahren macht, ist, dass derselbe Schlüssel sowohl für die Verschlüsselung als auch für die Entschlüsselung verwendet wird. Nehmen wir zum Beispiel an, dass Sie die Nachricht "DOG" mit der Shift-Chiffre verschlüsseln wollen und als Schlüssel zufällig "24" gewählt haben. Die Verschlüsselung der Nachricht mit diesem Schlüssel würde "BME" ergeben. Die einzige Möglichkeit, die ursprüngliche Nachricht wiederherzustellen, ist die Verwendung desselben Schlüssels, nämlich "24", für die Entschlüsselung.

Diese Shift-Chiffre ist ein Beispiel für eine monoalphabetische Substitutions-Chiffre: ein Verschlüsselungsverfahren, bei dem das Alphabet des Geheimtextes feststeht (d. h. es wird nur ein Alphabet verwendet). Unter der Annahme, dass der Entschlüsselungsalgorithmus deterministisch ist, kann jedes Symbol im Substitutions-Chiffretext höchstens zu einem Symbol im Klartext gehören.

Bis in die 1700er Jahre stützten sich viele Verschlüsselungsanwendungen auf monoalphabetische Substitutions-Chiffren, obwohl diese oft viel komplexer waren als die Shift-Chiffre. Man könnte zum Beispiel für jeden Buchstaben des Originaltextes einen Buchstaben aus dem Alphabet zufällig auswählen, wobei jeder Buchstabe nur einmal im Alphabet des Geheimtextes vorkommen darf. Das bedeutet, dass man faktoriell 26 mögliche private Schlüssel hätte, was im Vorcomputerzeitalter sehr viel war.

Beachten Sie, dass Sie in der Kryptographie häufig auf den Begriff Cipher stoßen werden. Seien Sie sich bewusst, dass dieser Begriff verschiedene Bedeutungen hat. Tatsächlich kenne ich mindestens fünf verschiedene Bedeutungen des Begriffs in der Kryptographie.

In einigen Fällen bezieht er sich auf ein Verschlüsselungsverfahren, wie bei der Shift-Chiffre und der monoalphabetischen Substitutions-Chiffre. Der Begriff kann sich jedoch auch speziell auf den Verschlüsselungsalgorithmus, den privaten Schlüssel oder einfach nur auf den Chiffretext eines solchen Verschlüsselungsverfahrens beziehen.

Schließlich kann sich der Begriff Chiffre auch auf einen Kernalgorithmus beziehen, aus dem man kryptografische Schemata konstruieren kann. Dazu können verschiedene Verschlüsselungsalgorithmen, aber auch andere Arten von kryptografischen Verfahren gehören. Diese Bedeutung des Begriffs wird im Zusammenhang mit Blockchiffren relevant (siehe den Abschnitt "Blockchiffren" weiter unten).

Vielleicht stoßen Sie auch auf die Begriffe verschlüsseln oder entschlüsseln. Diese Begriffe sind lediglich Synonyme für Verschlüsselung und Entschlüsselung.

Brute-Force-Angriffe und das Kerckhoffsche Prinzip

Die Shift-Chiffre ist ein sehr unsicheres symmetrisches Verschlüsselungsverfahren, zumindest in der modernen Welt. [1] Ein Angreifer könnte einfach versuchen, jeden beliebigen Chiffretext mit allen 26 möglichen Schlüsseln zu entschlüsseln, um zu sehen, welches Ergebnis sinnvoll ist. Diese Art von Angriff, bei dem der Angreifer einfach alle Schlüssel durchprobiert, um zu sehen, was funktioniert, ist als Brute-Force-Angriff oder exhaustive Schlüsselsuche bekannt.

Damit ein Verschlüsselungsverfahren einem Minimalbegriff von Sicherheit entspricht, muss es über eine Menge möglicher Schlüssel, den Schlüsselraum, verfügen, die so groß ist, dass Brute-Force-Angriffe nicht durchführbar sind. Alle modernen Verschlüsselungsverfahren erfüllen diesen Standard. Dieser Grundsatz ist als Prinzip des ausreichenden Schlüsselraums bekannt. Ein ähnliches Prinzip gilt in der Regel für verschiedene Arten von kryptografischen Verfahren.

Um ein Gefühl für die enorme Größe des Schlüsselraums in modernen Verschlüsselungsverfahren zu bekommen, nehmen wir an, dass eine Datei mit einem 128-Bit-Schlüssel nach dem fortgeschrittenen Verschlüsselungsstandard verschlüsselt wurde. Dies bedeutet, dass ein Angreifer einen Satz von 2^{128} Schlüsseln hat, die er für einen Brute-Force-Angriff durchgehen muss. Bei einer Erfolgschance von 0,78% mit dieser Strategie müsste der Angreifer etwa 2,65 \times 10^{36} Schlüssel durchprobieren.

Nehmen wir optimistisch an, dass ein Angreifer 10^{16} Schlüssel pro Sekunde testen kann (d.h. 10 Billiarden Schlüssel pro Sekunde). Um 0,78 % aller Schlüssel im Schlüsselraum zu testen, müsste ihr Angriff 2,65 \times 10^{20} Sekunden dauern. Das sind etwa 8,4 Billionen Jahre. Selbst ein Brute-Force-Angriff eines absurd mächtigen Gegners ist also bei einem modernen 128-Bit-Verschlüsselungssystem nicht realistisch. Hier kommt das Prinzip des ausreichenden Schlüsselraums zum Tragen.

Ist die Shift-Chiffre sicherer, wenn der Angreifer den Verschlüsselungsalgorithmus nicht kennt? Vielleicht, aber nicht viel.

In jedem Fall geht die moderne Kryptografie immer davon aus, dass die Sicherheit eines symmetrischen Verschlüsselungsverfahrens nur auf der Geheimhaltung des privaten Schlüssels beruht. Es wird immer davon ausgegangen, dass der Angreifer alle anderen Details kennt, einschließlich des Nachrichtenraums, des Schlüsselraums, des Chiffretextraums, des Schlüsselauswahlalgorithmus, des Verschlüsselungsalgorithmus und des Entschlüsselungsalgorithmus.

Der Gedanke, dass die Sicherheit eines symmetrischen Verschlüsselungsverfahrens nur auf der Geheimhaltung des privaten Schlüssels beruhen kann, ist als Kerckhoffs' Prinzip bekannt.

Wie ursprünglich von Kerckhoffs beabsichtigt, gilt das Prinzip nur für symmetrische Verschlüsselungsverfahren. Eine allgemeinere Version des Prinzips gilt jedoch auch für alle anderen modernen Arten von kryptografischen Verfahren: Der Entwurf eines kryptografischen Verfahrens muss nicht geheim sein, damit es sicher ist; die Geheimhaltung kann sich nur auf einige Informationsketten erstrecken, in der Regel auf einen privaten Schlüssel.

Das Kerckhoffsche Prinzip ist für die moderne Kryptographie aus vier Gründen von zentraler Bedeutung. [2] Erstens gibt es nur eine begrenzte Anzahl von kryptografischen Verfahren für bestimmte Arten von Anwendungen. Zum Beispiel verwenden die meisten modernen symmetrischen Verschlüsselungsanwendungen die Rijndael-Chiffre. Die Geheimhaltung des Designs eines Schemas ist also nur sehr begrenzt. Die Geheimhaltung eines privaten Schlüssels für die Rijndael-Chiffre bietet jedoch wesentlich mehr Flexibilität.

Zweitens ist es einfacher, eine Informationskette zu ersetzen als ein ganzes kryptografisches System. Nehmen wir an, die Mitarbeiter eines Unternehmens haben alle dieselbe Verschlüsselungssoftware und jeder zweite Mitarbeiter hat einen privaten Schlüssel, um vertraulich zu kommunizieren. Schlüsselkompromittierungen sind in diesem Szenario lästig, aber zumindest könnte das Unternehmen die Software bei solchen Sicherheitsverletzungen behalten. Würde sich das Unternehmen auf die Geheimhaltung des Systems verlassen, müsste bei einer Verletzung dieser Geheimhaltung die gesamte Software ausgetauscht werden.

Drittens ermöglicht das Kerckhoffsche Prinzip die Standardisierung und Kompatibilität zwischen den Nutzern kryptographischer Verfahren. Dies hat enorme Vorteile für die Effizienz. Es ist zum Beispiel schwer vorstellbar, wie Millionen von Menschen jeden Tag eine sichere Verbindung zu den Webservern von Google herstellen könnten, wenn diese Sicherheit die Geheimhaltung kryptografischer Verfahren erfordern würde.

Viertens ermöglicht das Kerckhoff-Prinzip die öffentliche Prüfung kryptographischer Verfahren. Diese Art der Prüfung ist absolut notwendig, um sichere kryptografische Verfahren zu entwickeln. Ein Beispiel: Der wichtigste Kernalgorithmus der symmetrischen Kryptografie, die Rijndael-Chiffre, war das Ergebnis eines Wettbewerbs, der zwischen 1997 und 2000 vom National Institute of Standards and Technology veranstaltet wurde.

Jedes System, das versucht, Sicherheit durch Unklarheit zu erreichen, beruht darauf, dass die Einzelheiten seines Entwurfs und/oder seiner Implementierung geheim gehalten werden. In der Kryptographie wäre dies insbesondere ein System, das sich auf die Geheimhaltung der Konstruktionsdetails des kryptographischen Verfahrens stützt. Sicherheit durch Geheimhaltung steht also in direktem Gegensatz zu Kerckhoffs' Prinzip.

Die Fähigkeit der Offenheit, die Qualität und Sicherheit zu verbessern, erstreckt sich auch auf die digitale Welt im weiteren Sinne als nur auf die Kryptographie. Freie und quelloffene Linux-Distributionen wie Debian beispielsweise haben im Allgemeinen mehrere Vorteile gegenüber ihren Windows- und MacOS-Pendants in Bezug auf Datenschutz, Stabilität, Sicherheit und Flexibilität. Auch wenn dies mehrere Ursachen haben mag, so ist der wichtigste Grundsatz wohl, wie Eric Raymond es in seinem berühmten Essay "The Cathedral and the Bazaar" formulierte, dass "given enough eyeballs, all bugs are shallow" [3] Es ist dieses Prinzip der Weisheit der Massen, das Linux seinen größten Erfolg beschert hat.

Man kann nie eindeutig sagen, dass ein kryptographisches Verfahren "sicher" oder "unsicher" ist Stattdessen gibt es verschiedene Vorstellungen von Sicherheit für kryptografische Verfahren. Jede Definition der kryptographischen Sicherheit muss (1) Sicherheitsziele und (2) die Fähigkeiten eines Angreifers spezifizieren. Die Analyse kryptographischer Verfahren anhand eines oder mehrerer spezifischer Sicherheitsbegriffe gibt Aufschluss über ihre Anwendungen und Grenzen.

Wir werden hier nicht auf alle Einzelheiten der verschiedenen kryptografischen Sicherheitsbegriffe eingehen, aber Sie sollten wissen, dass zwei Annahmen für alle modernen kryptografischen Sicherheitsbegriffe im Zusammenhang mit symmetrischen und asymmetrischen Verfahren (und in gewisser Form auch für andere kryptografische Primitive) allgegenwärtig sind:

Anmerkungen:

[1] Laut Seutonius wurde von Julius Cäsar in seiner militärischen Kommunikation eine Shift-Chiffre mit einem konstanten Schlüsselwert von 3 verwendet. So wurde A immer zu D, B immer zu E, C immer zu F und so weiter. Diese spezielle Version der Shift-Chiffre ist daher als Caesar-Chiffre bekannt geworden (obwohl es sich nicht wirklich um eine Chiffre im modernen Sinne des Wortes handelt, da der Schlüsselwert konstant ist). Die Caesar-Chiffre mag im ersten Jahrhundert v. Chr. sicher gewesen sein, wenn die Feinde Roms mit Verschlüsselung wenig vertraut waren. Aber in der heutigen Zeit wäre sie eindeutig kein sehr sicheres Verfahren.

[2] Jonathan Katz und Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), S. 7f.

[3] Eric Raymond, "The Cathedral and the Bazaar" (Die Kathedrale und der Basar), Vortrag auf dem Linux Kongress, Würzburg, Deutschland (27. Mai 1997). Es gibt eine Reihe von Folgeversionen sowie ein Buch. Meine Zitate stammen von Seite 30 des Buches: Eric Raymond, The Cathedral and the Bazaar: Musings on Linux and Open Source by an Accidental Revolutionary, überarbeitete Ausgabe. (2001), O'Reilly: Sebastopol, CA.

Stromchiffren

Symmetrische Verschlüsselungsverfahren werden standardmäßig in zwei Arten unterteilt: Stromchiffren und Blockchiffren. Diese Unterscheidung ist jedoch nicht ganz unproblematisch, da die Leute diese Begriffe nicht einheitlich verwenden. In den nächsten Abschnitten werde ich die Unterscheidung so darlegen, wie ich es für richtig halte. Sie sollten sich jedoch darüber im Klaren sein, dass viele Leute diese Begriffe etwas anders verwenden werden, als ich es darlege.

Wenden wir uns zunächst den Stromchiffren zu. Eine Stromchiffre ist ein symmetrisches Verschlüsselungsverfahren, bei dem die Verschlüsselung aus zwei Schritten besteht.

Zunächst wird mit Hilfe eines privaten Schlüssels eine Zeichenfolge in der Länge des Klartextes erzeugt. Diese Zeichenfolge wird Keystream genannt.

Anschließend wird der Schlüsselstrom mathematisch mit dem Klartext kombiniert, um einen Chiffretext zu erzeugen. Diese Kombination ist in der Regel eine XOR-Operation. Zur Entschlüsselung kann man die Operation einfach umkehren. (Man beachte, dass A \oplus B = B \oplus A ist, wenn A und B Bit-Strings sind. Die Reihenfolge einer XOR-Operation in einer Stromchiffre spielt also keine Rolle für das Ergebnis. Diese Eigenschaft ist als Kommutativität bekannt)

Eine typische XOR-Stromchiffre ist in Abbildung 3 dargestellt. Zunächst wird ein privater Schlüssel K verwendet, um einen Keystream zu erzeugen. Der Keystream wird dann mit dem Klartext durch eine XOR-Operation kombiniert, um den Chiffriertext zu erzeugen. Jeder Agent, der den Chiffriertext erhält, kann ihn leicht entschlüsseln, wenn er den Schlüssel K besitzt. Alles, was er tun muss, ist, einen Keystream zu erzeugen, der so lang ist wie der Chiffretext, und ihn mit dem Chiffretext zu XOR-verknüpfen.

Abbildung 3: Eine XOR-Stromchiffre

Figure 3: An XOR stream cipher

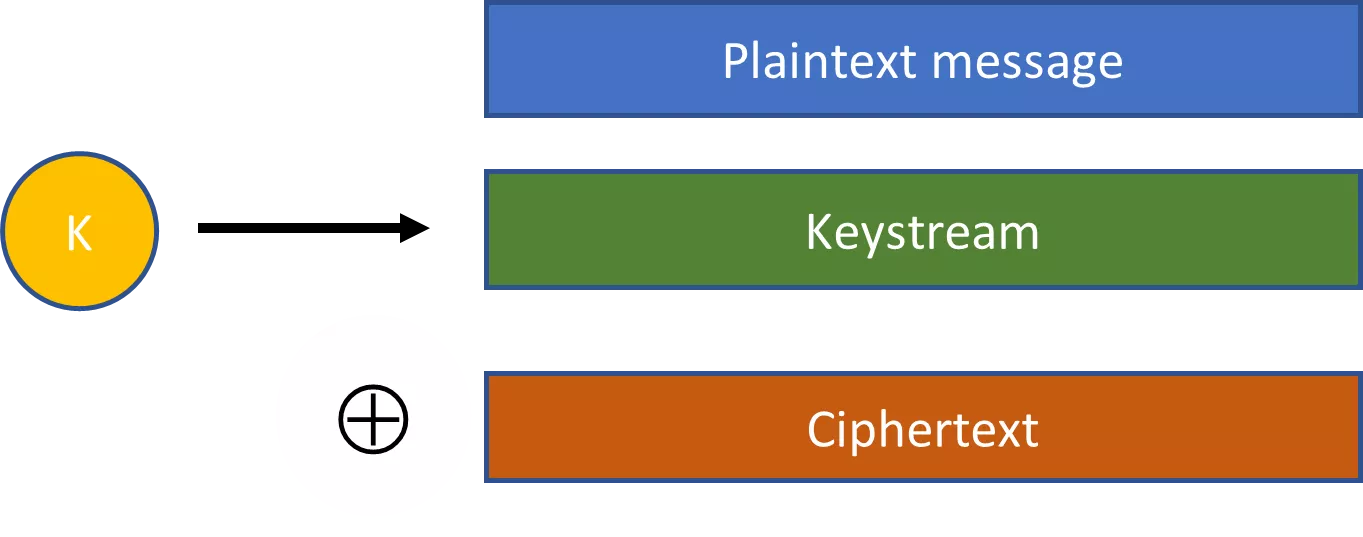
Denken Sie daran, dass ein Verschlüsselungsschema in der Regel eine Vorlage für eine Verschlüsselung mit demselben Kernalgorithmus ist und keine genaue Spezifikation. So ist auch eine Stromchiffre in der Regel eine Vorlage für eine Verschlüsselung, bei der Sie Schlüssel unterschiedlicher Länge verwenden können. Die Schlüssellänge kann sich zwar auf einige kleinere Details des Schemas auswirken, hat aber keinen Einfluss auf seine grundlegende Form.

Die Shift-Chiffre ist ein Beispiel für eine sehr einfache und unsichere Stromchiffre. Mit einem einzigen Buchstaben (dem privaten Schlüssel) kann man eine Buchstabenfolge in der Länge der Nachricht (den Schlüsselstrom) erzeugen. Dieser Keystream wird dann mit dem Klartext durch eine Modulo-Operation kombiniert, um einen Chiffretext zu erzeugen. (Diese Modulo-Operation kann zu einer XOR-Operation vereinfacht werden, wenn die Buchstaben in Bits dargestellt werden).

Ein weiteres berühmtes Beispiel für eine Stromchiffre ist die Vigenere-Chiffre, die nach Blaise de Vigenere benannt ist, der sie Ende des 16. Jahrhunderts vollständig entwickelt hat (auch wenn andere bereits viel Vorarbeit geleistet hatten). Sie ist ein Beispiel für eine polyalphabetische Substitutions-Chiffre: ein Verschlüsselungsverfahren, bei dem sich das Alphabet des Geheimtextes für ein Klartextsymbol je nach dessen Position im Text ändert. Im Gegensatz zu einer monoalphabetischen Substitutions-Chiffre können Chiffretext-Symbole mit mehr als einem Klartext-Symbol verknüpft werden.

Als die Verschlüsselung im Europa der Renaissance an Popularität gewann, wurde auch die Kryptoanalyse, d. h. das Brechen von Chiffretexten, populär, insbesondere durch die Häufigkeitsanalyse. Letztere nutzt statistische Regelmäßigkeiten in unserer Sprache, um Chiffretexte zu knacken, und wurde von arabischen Gelehrten bereits im neunten Jahrhundert entdeckt. Es handelt sich um eine Technik, die besonders gut bei längeren Texten funktioniert. Und selbst die ausgeklügeltsten monoalphabetischen Substitutions-Chiffren reichten um 1700 in Europa nicht mehr aus, um der Häufigkeitsanalyse zu widerstehen, insbesondere in militärischen und sicherheitsrelevanten Bereichen. Da die Vigenere-Chiffre einen bedeutenden Fortschritt in der Sicherheit bot, wurde sie in dieser Zeit populär und war gegen Ende des 17. Jahrhunderts weit verbreitet.

Informell ausgedrückt, funktioniert das Verschlüsselungsverfahren wie folgt:

  1. Wählen Sie ein Wort mit mehreren Buchstaben als privaten Schlüssel.

  2. Wenden Sie für eine beliebige Nachricht die Shift-Chiffre auf jeden Buchstaben der Nachricht an, indem Sie den entsprechenden Buchstaben des Schlüsselworts als Shift verwenden.

  3. Wenn Sie das Schlüsselwort durchgegangen sind, den Klartext aber immer noch nicht vollständig verschlüsselt haben, wenden Sie die Buchstaben des Schlüsselworts erneut als Shift-Chiffre auf die entsprechenden Buchstaben im Rest des Textes an.

  4. Setzen Sie diesen Vorgang fort, bis die gesamte Nachricht verschlüsselt ist.

Zur Veranschaulichung: Nehmen wir an, Ihr privater Schlüssel ist "GOLD" und Sie wollen die Nachricht "CRYPTOGRAPHIE" verschlüsseln. In diesem Fall würden Sie nach der Vigenère-Chiffre wie folgt vorgehen:

Somit ist der Chiffretext c = "IFJSZCRUGDSB".

Ein weiteres berühmtes Beispiel für eine Stromchiffre ist das One-Time-Pad. Beim One-Time-Pad erstellt man einfach eine Kette von Zufallsbits, die so lang ist wie die Klartextnachricht, und erzeugt den Chiffretext durch die XOR-Operation. Daher sind der private Schlüssel und der Schlüsselstrom mit einem One-Time-Pad gleichwertig.

Während die Shift-Chiffre und die Vigenere-Chiffre im modernen Zeitalter sehr unsicher sind, ist das One-Time-Pad bei richtiger Anwendung sehr sicher. Die wohl berühmteste Anwendung des One-Time-Pad war, zumindest bis in die 1980er Jahre, für die Washington-Moskau-Hotline. [4]

Die Hotline ist eine direkte Kommunikationsverbindung zwischen Washington und Moskau für dringende Angelegenheiten, die nach der Kuba-Krise eingerichtet wurde. Die Technologie für die Hotline hat sich im Laufe der Jahre verändert. Derzeit umfasst sie ein direktes Glasfaserkabel sowie zwei Satellitenverbindungen (zur Redundanz), die E-Mail und Textnachrichten ermöglichen. Die Verbindung endet an verschiedenen Orten in den USA. Das Pentagon, das Weiße Haus und der Raven Rock Mountain sind bekannte Endpunkte. Entgegen der landläufigen Meinung war die Hotline nie mit Telefonen verbunden.

Im Wesentlichen funktionierte das One-Time-Pad-Verfahren folgendermaßen. Sowohl Washington als auch Moskau verfügten über zwei Sätze von Zufallszahlen. Ein Satz von Zufallszahlen, der von den Russen erstellt wurde, betraf die Ver- und Entschlüsselung von Nachrichten in russischer Sprache. Ein Satz von Zufallszahlen, der von den Amerikanern erstellt wurde, betraf die Ver- und Entschlüsselung von Nachrichten in englischer Sprache. Von Zeit zu Zeit wurden weitere Zufallszahlen durch vertrauenswürdige Kuriere an die andere Seite geliefert.

Washington und Moskau konnten also heimlich kommunizieren, indem sie diese Zufallszahlen für die Erstellung von einmaligen Pads verwendeten. Jedes Mal, wenn Sie kommunizieren mussten, verwendeten Sie den nächsten Teil der Zufallszahlen für Ihre Nachricht.

Obwohl das One-Time-Pad sehr sicher ist, stößt es in der Praxis auf erhebliche Einschränkungen: Der Schlüssel muss so lang sein wie die Nachricht, und kein Teil eines One-Time-Pads kann wiederverwendet werden. Das bedeutet, dass Sie den Überblick darüber behalten müssen, wo Sie sich im One-Time-Pad befinden, eine riesige Anzahl von Bits speichern und von Zeit zu Zeit Zufallsbits mit Ihren Gesprächspartnern austauschen müssen. Aus diesem Grund wird der One-Time-Pad in der Praxis nicht häufig verwendet.

Stattdessen werden in der Praxis überwiegend pseudozufällige Stromchiffren verwendet. Salsa20 und eine eng verwandte Variante namens ChaCha sind Beispiele für häufig verwendete Pseudozufallsstromchiffren.

Bei diesen pseudozufälligen Stromchiffren wählen Sie zunächst einen Zufallsschlüssel K, der kürzer ist als die Länge des Klartextes. Ein solcher Zufallsschlüssel K wird in der Regel von unserem Computer auf der Grundlage von unvorhersehbaren Daten erstellt, die er im Laufe der Zeit sammelt, wie z. B. die Zeit zwischen Netzwerknachrichten, Mausbewegungen und so weiter.

Dieser Zufallsschlüssel K wird dann in einen Expansionsalgorithmus eingefügt, der einen pseudozufälligen Schlüsselstrom erzeugt, der so lang ist wie die Nachricht. Sie können genau angeben, wie lang der Schlüsselstrom sein muss (z. B. 500 Bits, 1000 Bits, 1200 Bits, 29.117 Bits usw.).

Ein pseudozufälliger Schlüsselstrom sieht so aus, als ob er völlig zufällig aus der Menge aller Zeichenketten mit der gleichen Länge ausgewählt wurde. Die Verschlüsselung mit einem pseudozufälligen Schlüsselstrom sieht also so aus, als ob sie mit einem One-Time-Pad durchgeführt worden wäre. Aber das ist natürlich nicht der Fall.

Da unser privater Schlüssel kürzer ist als der Schlüsselstrom und unser Expansionsalgorithmus deterministisch sein muss, damit der Verschlüsselungs-/Entschlüsselungsprozess funktioniert, hätte nicht jeder Schlüsselstrom dieser Länge als Ergebnis unserer Expansionsoperation ausgegeben werden können.

Nehmen wir zum Beispiel an, dass unser privater Schlüssel eine Länge von 128 Bit hat und wir ihn in einen Expansionsalgorithmus einfügen können, um einen viel längeren Schlüsselstrom zu erzeugen, z. B. von 2.500 Bit. Da unser Expansionsalgorithmus deterministisch sein muss, kann unser Algorithmus höchstens 1/2^{128} Zeichenfolgen mit einer Länge von 2.500 Bits auswählen. Ein solcher Schlüsselstrom könnte also niemals völlig zufällig aus allen Zeichenketten derselben Länge ausgewählt werden.

Unsere Definition einer Stromchiffre hat zwei Aspekte: (1) ein Schlüsselstrom, der so lang ist wie der Klartext, wird mit Hilfe eines privaten Schlüssels erzeugt; und (2) dieser Schlüsselstrom wird mit dem Klartext kombiniert, typischerweise über eine XOR-Operation, um den Chiffretext zu erzeugen.

Manchmal wird die Bedingung (1) strenger definiert, indem behauptet wird, dass der Schlüsselstrom ausdrücklich pseudozufällig sein muss. Das bedeutet, dass weder die Shift-Chiffre noch das One-Time-Pad als Stromchiffre betrachtet werden können.

Meiner Meinung nach bietet die Definition von Bedingung (1) eine einfachere Möglichkeit, Verschlüsselungssysteme zu organisieren. Darüber hinaus bedeutet dies, dass wir nicht aufhören müssen, ein bestimmtes Verschlüsselungsverfahren als Stromchiffre zu bezeichnen, nur weil wir erfahren, dass es nicht auf pseudozufälligen Schlüsselströmen beruht.

Anmerkungen:

[4] Krypto-Museum, "Washington-Moskau-Hotline", 2013, verfügbar unter https://www.cryptomuseum.com/crypto/hotline/index.htm.

Blockchiffren

Eine Blockchiffre wird im Allgemeinen zunächst als etwas Primitiveres als eine Stromchiffre verstanden: Ein Kernalgorithmus, der mit Hilfe eines Schlüssels eine längenerhaltende Transformation an einer Zeichenkette geeigneter Länge durchführt. Dieser Algorithmus kann für die Erstellung von Verschlüsselungsschemata und vielleicht auch für andere Arten von kryptografischen Schemata verwendet werden.

Häufig kann eine Blockchiffre Eingabestrings unterschiedlicher Länge (z. B. 64, 128 oder 256 Bit) sowie Schlüssel unterschiedlicher Länge (z. B. 128, 192 oder 256 Bit) verarbeiten. Obwohl sich einige Details des Algorithmus in Abhängigkeit von diesen Variablen ändern können, ändert sich der Kernalgorithmus nicht. Wäre dies der Fall, würde man von zwei verschiedenen Blockchiffren sprechen. Beachten Sie, dass die Terminologie des Kernalgorithmus hier dieselbe ist wie bei den Verschlüsselungsverfahren.

Eine Darstellung der Funktionsweise einer Blockchiffre ist in Abbildung 4 unten zu sehen. Eine Nachricht M der Länge L und ein Schlüssel K dienen als Eingabe für die Blockchiffre. Sie gibt eine Nachricht M' der Länge L aus. Der Schlüssel muss bei den meisten Blockchiffren nicht unbedingt die gleiche Länge wie M und M' haben.

Abbildung 4: Eine Blockchiffre

Figure 4: A block cipher

Eine Blockchiffre ist für sich genommen kein Verschlüsselungsverfahren. Eine Blockchiffre kann jedoch mit verschiedenen Arbeitsmodi verwendet werden, um verschiedene Verschlüsselungsverfahren zu erzeugen. Eine Betriebsart fügt einfach einige zusätzliche Operationen außerhalb der Blockchiffre hinzu.

Um zu veranschaulichen, wie dies funktioniert, nehmen wir eine Blockchiffre (BC) an, die eine 128-Bit-Eingabezeichenfolge und einen 128-Bit-Privatschlüssel erfordert. Abbildung 5 unten zeigt, wie diese Blockchiffre mit dem elektronischen Codebuchmodus (ECB-Modus) verwendet werden kann, um ein Verschlüsselungsschema zu erstellen. (Die Ellipsen auf der rechten Seite zeigen an, dass Sie dieses Muster so lange wie nötig wiederholen können).

Abbildung 5: Eine Blockchiffre mit ECB-Modus

Figure 5: A block cipher with ECB mode

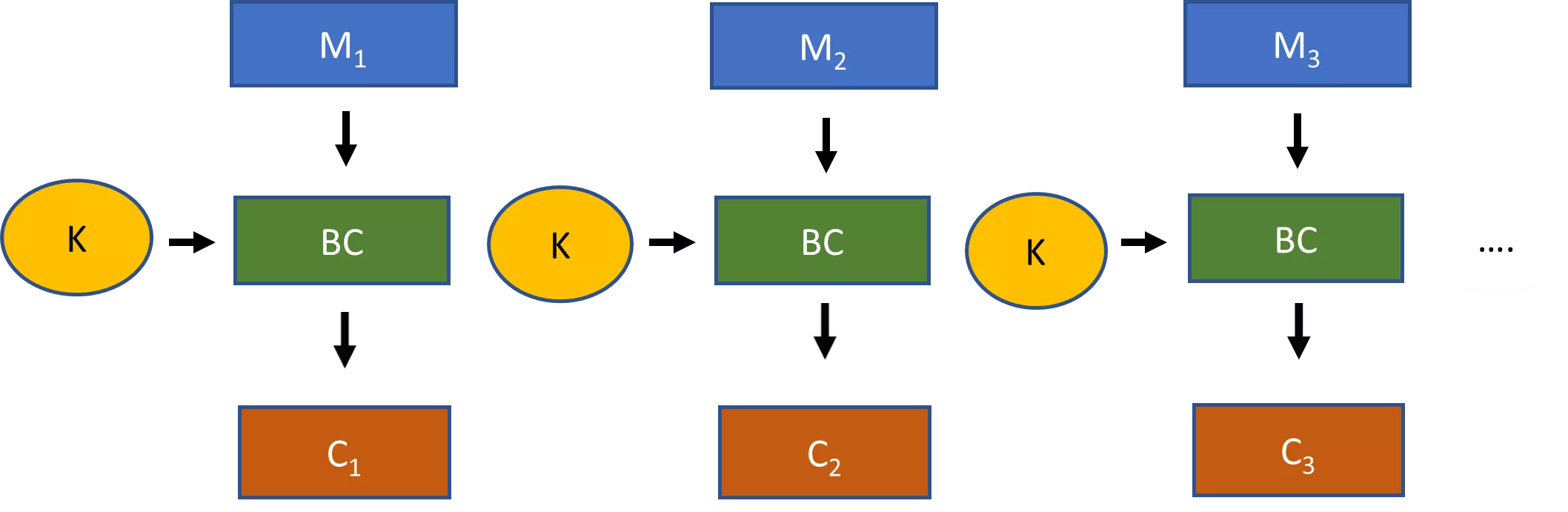
Das Verfahren zur Verschlüsselung von elektronischen Codebüchern mit der Blockchiffre ist wie folgt. Prüfen Sie, ob Sie Ihre Klartextnachricht in 128-Bit-Blöcke unterteilen können. Wenn nicht, fügen Sie Padding zu der Nachricht hinzu, so dass das Ergebnis gleichmäßig durch die Blockgröße von 128 Bit geteilt werden kann. Dies sind Ihre Daten, die für den Verschlüsselungsprozess verwendet werden.

Teilen Sie nun die Daten in 128-Bit-Strings auf (M_1, M_2, M_3, usw.). Lassen Sie jede 128-Bit-Zeichenkette mit Ihrem 128-Bit-Schlüssel durch die Blockchiffre laufen, um 128-Bit-Teile des Chiffriertextes zu erzeugen (C_1, C_2, C_3 usw.). Diese Teile bilden, wenn sie neu kombiniert werden, den vollständigen Chiffretext.

Die Entschlüsselung erfolgt in umgekehrter Weise, wobei der Empfänger jedoch eine erkennbare Möglichkeit benötigt, um die entschlüsselten Daten zu entschärfen und den ursprünglichen Klartext wiederherzustellen.

Eine Blockchiffre mit elektronischem Codebuchmodus ist zwar relativ einfach, aber nicht sicher. Dies liegt daran, dass sie zu einer deterministischen Verschlüsselung führt. Zwei identische 128-Bit-Datenstrings werden auf genau dieselbe Weise verschlüsselt. Diese Information kann ausgenutzt werden.

Stattdessen sollte jedes aus einer Blockchiffre konstruierte Verschlüsselungsverfahren probabilistisch sein: Das heißt, die Verschlüsselung einer beliebigen Nachricht M oder eines bestimmten Teils von M sollte im Allgemeinen jedes Mal ein anderes Ergebnis liefern. [5]

Der Cipher-Block-Chaining-Modus (CBC-Modus) ist wahrscheinlich der am häufigsten mit einer Blockchiffre verwendete Modus. Die richtige Kombination ergibt ein probabilistisches Verschlüsselungsverfahren. Eine Darstellung dieser Funktionsweise sehen Sie in Abbildung 6 unten.

Abbildung 6: Eine Blockchiffre mit CBC-Modus

Figure 6: A block cipher with CBC mode

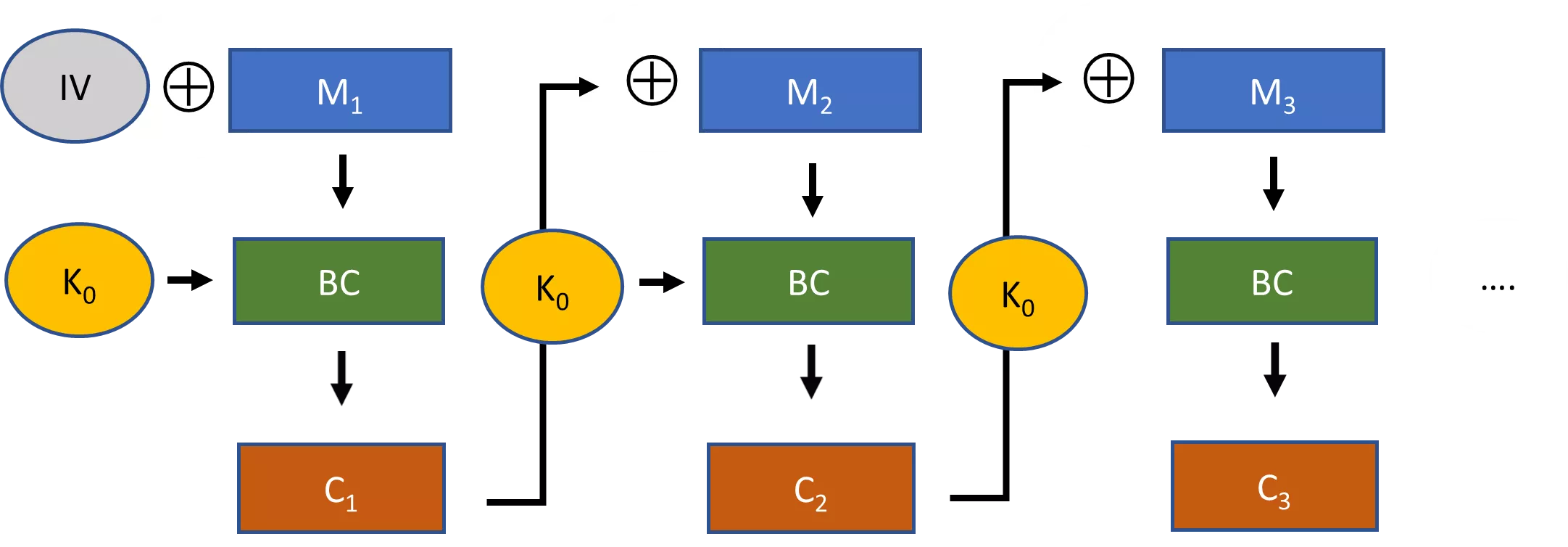
Nehmen wir an, die Blockgröße beträgt wieder 128 Bit. Sie müssten also zunächst wieder sicherstellen, dass Ihre ursprüngliche Klartextnachricht die erforderliche Auffüllung erhält.

Dann wird der erste 128-Bit-Teil des Klartextes mit einem Initialisierungsvektor von 128 Bits XOR-verknüpft. Das Ergebnis wird in die Blockchiffre eingegeben, um einen Chiffriertext für den ersten Block zu erzeugen. Für den zweiten 128-Bit-Block wird zunächst der Klartext mit dem Chiffretext des ersten Blocks XOR-verknüpft, bevor er in die Blockchiffre eingefügt wird. Diesen Vorgang setzen Sie fort, bis Sie die gesamte Klartextnachricht verschlüsselt haben.

Wenn Sie fertig sind, senden Sie die verschlüsselte Nachricht zusammen mit dem unverschlüsselten Initialisierungsvektor an den Empfänger. Der Empfänger muss den Initialisierungsvektor kennen, sonst kann er den Chiffretext nicht entschlüsseln.

Diese Konstruktion ist bei richtiger Anwendung wesentlich sicherer als der elektronische Codebuchmodus. Sie sollten zunächst sicherstellen, dass der Initialisierungsvektor eine zufällige oder pseudozufällige Zeichenfolge ist. Darüber hinaus sollten Sie jedes Mal, wenn Sie dieses Verschlüsselungsverfahren verwenden, einen anderen Initialisierungsvektor verwenden.

Mit anderen Worten: Ihr Initialisierungsvektor sollte ein zufälliger oder pseudozufälliger Nonce sein, wobei Nonce für "eine Zahl, die nur einmal verwendet wird" steht Wenn Sie diese Praxis beibehalten, gewährleistet der CBC-Modus mit einer Blockchiffre, dass zwei identische Klartextblöcke im Allgemeinen jedes Mal anders verschlüsselt werden.

Wenden wir uns nun dem Ausgangsrückkopplungsmodus (OFB-Modus) zu. Eine Darstellung dieses Modus finden Sie in Abbildung 7.

Abbildung 7: Eine Blockchiffre mit OFB-Modus

Figure 7: A block cipher with OFB mode

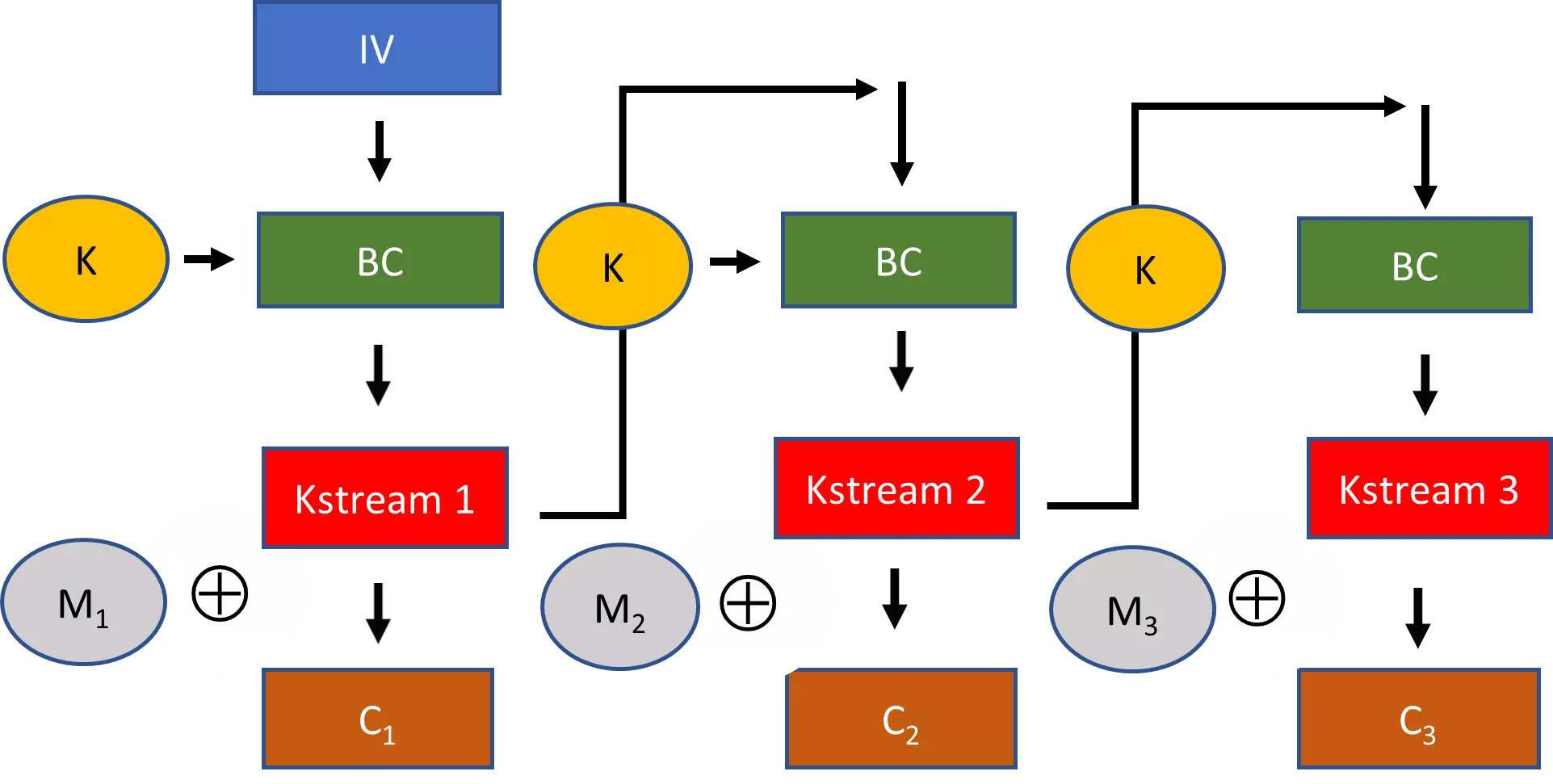
Im OFB-Modus wählen Sie ebenfalls einen Initialisierungsvektor. Aber hier wird der Initialisierungsvektor für den ersten Block direkt in die Blockchiffre mit Ihrem Schlüssel eingefügt. Die sich daraus ergebenden 128 Bits werden dann als Schlüsselstrom (Keystream) behandelt. Dieser Keystream wird mit dem Klartext XOR-verknüpft, um den Chiffriertext für den Block zu erzeugen. Für nachfolgende Blöcke verwenden Sie den Schlüsselstrom des vorherigen Blocks als Eingabe für die Blockchiffre und wiederholen die Schritte.

Wenn man genau hinsieht, ist das, was hier aus der Blockchiffre mit OFB-Modus entstanden ist, eigentlich eine Stromchiffre. Sie erzeugen Schlüsselstromteile von 128 Bit, bis Sie die Länge des Klartextes haben (wobei Sie die nicht benötigten Bits des letzten 128-Bit-Schlüsselstromteils verwerfen). Anschließend wird der Schlüsselstrom mit der Klartextnachricht XOR-verknüpft, um den Chiffriertext zu erhalten.

Im vorigen Abschnitt über Stromchiffren habe ich erklärt, dass man einen Schlüsselstrom mit Hilfe eines privaten Schlüssels erzeugt. Um genau zu sein, muss er nicht nur mit einem privaten Schlüssel erstellt werden. Wie Sie im OFB-Modus sehen können, wird der Keystream sowohl mit Hilfe eines privaten Schlüssels als auch eines Initialisierungsvektors erzeugt.

Beachten Sie, dass es wie beim CBC-Modus wichtig ist, jedes Mal, wenn Sie eine Blockchiffre im OFB-Modus verwenden, eine pseudozufällige oder zufällige Nonce für den Initialisierungsvektor auszuwählen. Andernfalls wird die gleiche 128-Bit-Nachrichtenkette, die in verschiedenen Kommunikationen gesendet wird, auf die gleiche Weise verschlüsselt. Dies ist eine Möglichkeit, eine probabilistische Verschlüsselung mit einer Stromchiffre zu erzeugen.

Einige Stromchiffren verwenden nur einen privaten Schlüssel zur Erstellung eines Schlüsselstroms. Bei diesen Stromchiffren ist es wichtig, dass Sie eine zufällige Nonce verwenden, um den privaten Schlüssel für jeden Kommunikationsvorgang auszuwählen. Andernfalls werden die Ergebnisse der Verschlüsselung mit diesen Stromchiffren ebenfalls deterministisch sein, was zu Sicherheitsproblemen führt.

Die bekannteste moderne Blockchiffre ist die Rijndael-Chiffre. Sie war der Gewinner eines Wettbewerbs, den das National Institute of Standards and Technology (NIST) zwischen 1997 und 2000 ausgeschrieben hatte, um einen älteren Verschlüsselungsstandard, den Datenverschlüsselungsstandard (DES), zu ersetzen.

Die Rijndael-Chiffre kann mit verschiedenen Spezifikationen für Schlüssellängen und Blockgrößen sowie in verschiedenen Betriebsmodi verwendet werden. Das Komitee für den NIST-Wettbewerb hat eine eingeschränkte Version der Rijndael-Chiffre - nämlich eine, die 128-Bit-Blockgrößen und Schlüssellängen von entweder 128 Bit, 192 Bit oder 256 Bit erfordert - als Teil des advanced encryption standard (AES) angenommen. Dies ist eigentlich der Hauptstandard für symmetrische Verschlüsselungsanwendungen. Er ist so sicher, dass sogar die NSA bereit ist, ihn mit 256-Bit-Schlüsseln für streng geheime Dokumente zu verwenden. [6]

Die AES-Blockchiffre wird in Kapitel 5 ausführlich erklärt.

Anmerkungen:

[5] Die Bedeutung der probabilistischen Verschlüsselung wurde erstmals von Shafi Goldwasser und Silvio Micali, "Probabilistic encryption", Journal of Computer and System Sciences, 28 (1984), 270-99 hervorgehoben.

[6] Siehe NSA, "Commercial National Security Algorithm Suite", https://apps.nsa.gov/iaarchive/programs/iad-initiatives/cnsa-suite.cfm.

Klärung der Verwirrung

Die Verwirrung über die Unterscheidung zwischen Blockchiffren und Stromchiffren rührt daher, dass der Begriff Blockchiffre manchmal so verstanden wird, dass er sich speziell auf eine Blockchiffre mit einem Blockmodus der Verschlüsselung bezieht.

Betrachten Sie die Modi ECB und CBC aus dem vorherigen Abschnitt. Bei diesen Modi müssen die zu verschlüsselnden Daten durch die Blockgröße teilbar sein (d. h., Sie müssen möglicherweise die ursprüngliche Nachricht auffüllen). Außerdem werden die Daten in diesen Modi direkt von der Blockchiffre bearbeitet (und nicht nur mit dem Ergebnis einer Blockchiffre-Operation kombiniert wie im OFB-Modus).

Daher kann man alternativ eine Blockchiffre als ein beliebiges Verschlüsselungsverfahren definieren, das jeweils auf Blöcken fester Länge der Nachricht arbeitet (wobei jeder Block länger als ein Byte sein muss, da er sonst in eine Stromchiffre zerfällt). Sowohl die zu verschlüsselnden Daten als auch der Chiffretext müssen sich gleichmäßig auf diese Blockgröße verteilen. Normalerweise ist die Blockgröße 64, 128, 192 oder 256 Bit lang. Im Gegensatz dazu kann eine Stromchiffre beliebige Nachrichten in Abschnitten von jeweils einem Bit oder Byte verschlüsseln.

Mit diesem spezifischeren Verständnis von Blockchiffre können Sie tatsächlich behaupten, dass moderne Verschlüsselungssysteme entweder Strom- oder Blockchiffren sind. Von nun an werde ich den Begriff Blockchiffre im allgemeineren Sinne verwenden, sofern nicht anders angegeben.

Die Diskussion über den OFB-Modus im vorherigen Abschnitt wirft noch einen weiteren interessanten Punkt auf. Einige Stromchiffren sind aus Blockchiffren aufgebaut, wie Rijndael mit OFB. Andere wie Salsa20 und ChaCha sind nicht aus Blockchiffren entstanden. Letztere könnte man als primitive Stromchiffren bezeichnen. (Es gibt keinen wirklich standardisierten Begriff für solche Stromchiffren)

Wenn von den Vor- und Nachteilen von Stromchiffren und Blockchiffren die Rede ist, werden in der Regel primitive Stromchiffren mit Verschlüsselungsverfahren auf der Grundlage von Blockchiffren verglichen.

Während man eine Stromchiffre immer leicht aus einer Blockchiffre konstruieren kann, ist es in der Regel sehr schwierig, aus einer primitiven Stromchiffre eine Art Konstrukt mit einem Blockmodus der Verschlüsselung (wie z. B. mit dem CBC-Modus) zu bauen.

Nach dieser Diskussion sollten Sie jetzt Abbildung 8 verstehen. Sie gibt einen Überblick über symmetrische Verschlüsselungsverfahren. Wir verwenden drei Arten von Verschlüsselungsverfahren: primitive Stromchiffren, blockchiffrierte Stromchiffren und Blockchiffren im Blockmodus (im Diagramm auch "Blockchiffren" genannt).

Abbildung 8: Übersicht über die symmetrischen Verschlüsselungsverfahren

Figure 8: Overview of symmetric encryption schemes

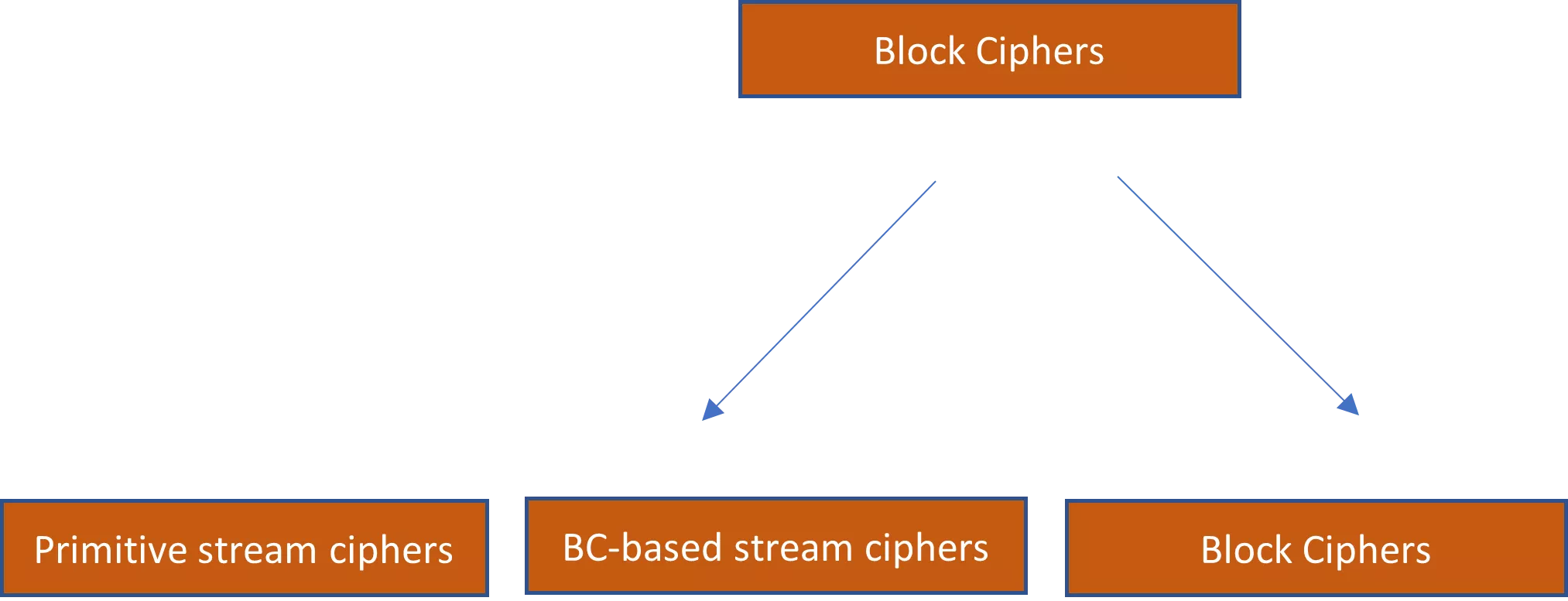
Authentifizierungscodes für Nachrichten

Bei der Verschlüsselung geht es um die Geheimhaltung. Die Kryptografie befasst sich aber auch mit allgemeineren Themen wie der Integrität, Authentizität und Nichtabstreitbarkeit von Nachrichten. Sogenannte Message Authentication Codes (MACs) sind kryptografische Verfahren mit symmetrischem Schlüssel, die Authentizität und Integrität in der Kommunikation unterstützen.

Warum ist bei der Kommunikation etwas anderes als Geheimhaltung erforderlich? Nehmen wir an, Bob schickt Alice eine Nachricht mit einer praktisch unknackbaren Verschlüsselung. Ein Angreifer, der diese Nachricht abfängt, wird keine wesentlichen Erkenntnisse über den Inhalt gewinnen können. Allerdings stehen dem Angreifer noch mindestens zwei weitere Angriffsmöglichkeiten zur Verfügung:

  1. Sie könnte den Chiffretext abfangen, seinen Inhalt ändern und den geänderten Chiffretext an Alice weiterleiten.

  2. Sie könnte Bobs Nachricht vollständig blockieren und ihren eigenen Chiffriertext senden.

In beiden Fällen könnte der Angreifer keinen Einblick in den Inhalt der Chiffretexte (1) und (2) haben. Aber er könnte auf diese Weise trotzdem erheblichen Schaden anrichten. An dieser Stelle werden Nachrichtenauthentifizierungscodes wichtig.

Nachrichtenauthentifizierungscodes sind frei definiert als symmetrische kryptografische Verfahren mit drei Algorithmen: einem Algorithmus zur Schlüsselgenerierung, einem Algorithmus zur Tag-Generierung und einem Verifikationsalgorithmus. Ein sicherer MAC stellt sicher, dass die Tags für jeden Angreifer existentiell fälschungssicher sind, d. h., er kann nur dann erfolgreich ein Tag für die zu verifizierende Nachricht erstellen, wenn er den privaten Schlüssel besitzt.

Bob und Alice können die Manipulation einer bestimmten Nachricht mit einem MAC bekämpfen. Nehmen wir einmal an, dass sie sich nicht um die Geheimhaltung kümmern. Sie wollen nur sicherstellen, dass die von Alice empfangene Nachricht tatsächlich von Bob stammt und nicht in irgendeiner Weise verändert wurde.

Der Vorgang ist in Abbildung 9 dargestellt. Um einen MAC (Message Authentication Code) zu verwenden, wird zunächst ein privater Schlüssel K erzeugt, der von beiden gemeinsam genutzt wird. Bob erstellt mit dem privaten Schlüssel K eine Markierung T für die Nachricht. Anschließend sendet er die Nachricht sowie das Nachrichten-Tag an Alice. Sie kann dann überprüfen, ob Bob die Markierung tatsächlich vorgenommen hat, indem sie den privaten Schlüssel, die Nachricht und die Markierung durch einen Verifikationsalgorithmus laufen lässt.

Abbildung 9: Übersicht über die symmetrischen Verschlüsselungsverfahren

Figure 9: Overview of symmetric encryption schemes

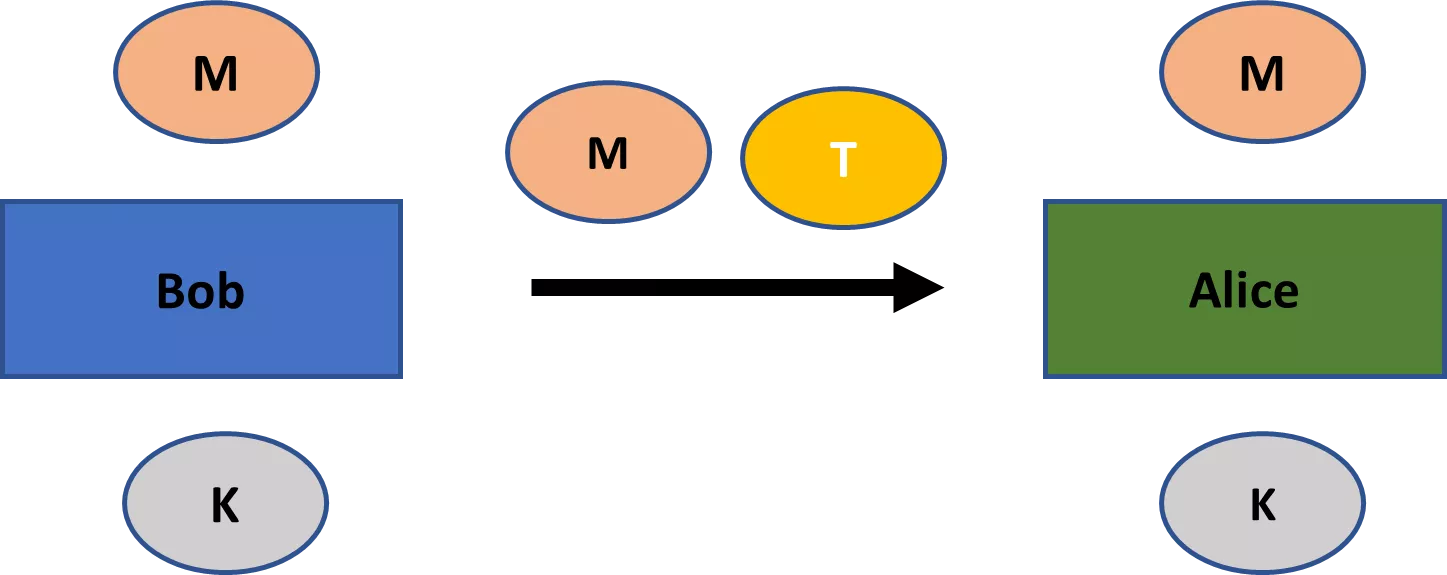
Aufgrund der existentiellen Fälschungssicherheit kann ein Angreifer die Nachricht M in keiner Weise verändern oder eine eigene Nachricht mit einem gültigen Tag erstellen. Dies gilt selbst dann, wenn der Angreifer die Tags vieler Nachrichten zwischen Bob und Alice beobachtet, die denselben privaten Schlüssel verwenden. Ein Angreifer könnte allenfalls verhindern, dass Alice die Nachricht M erhält (ein Problem, das die Kryptographie nicht lösen kann).

Ein MAC garantiert, dass eine Nachricht tatsächlich von Bob erstellt wurde. Diese Authentizität impliziert automatisch die Integrität der Nachricht, d. h. wenn Bob eine Nachricht erstellt hat, dann wurde sie ipso facto nicht von einem Angreifer verändert. Von nun an sollte jedes Bemühen um Authentifizierung automatisch auch ein Bemühen um Integrität bedeuten.

Obwohl ich in meinen Ausführungen zwischen der Authentizität und der Integrität von Nachrichten unterschieden habe, ist es auch üblich, diese Begriffe als Synonyme zu verwenden. Sie beziehen sich also auf Nachrichten, die von einem bestimmten Absender erstellt und in keiner Weise verändert wurden. In diesem Sinne werden Nachrichtenauthentifizierungscodes häufig auch Nachrichtenintegritätscodes genannt.

Authentifizierte Verschlüsselung

Normalerweise möchte man bei der Kommunikation sowohl die Geheimhaltung als auch die Authentizität gewährleisten, weshalb Verschlüsselungs- und MAC-Schemata in der Regel gemeinsam verwendet werden.

Ein authentifiziertes Verschlüsselungsverfahren ist ein Verfahren, das Verschlüsselung mit einem MAC auf hochsichere Weise kombiniert. Insbesondere muss es die Standards für existentielle Fälschungssicherheit sowie eine sehr starke Vorstellung von Geheimhaltung erfüllen, nämlich eine, die resistent gegen Chiphertext-Angriffe ist. [7]

Damit ein Verschlüsselungsverfahren gegen chosen-ciphertext-Angriffe resistent ist, muss es die Standards für Nicht-Malleabilität erfüllen: Das heißt, jede Veränderung eines Chiffretextes durch einen Angreifer sollte entweder einen ungültigen Chiffretext ergeben oder einen, der zu einem Klartext entschlüsselt wird, der keine Beziehung zum Originaltext hat. [8]

Da ein authentifiziertes Verschlüsselungsverfahren sicherstellt, dass ein von einem Angreifer erstellter Chiffretext immer ungültig ist (da das Tag nicht verifiziert wird), erfüllt es die Standards für die Resistenz gegen chosen-ciphertext-Angriffe. Interessanterweise kann man beweisen, dass ein authentifiziertes Verschlüsselungsverfahren immer aus der Kombination eines existentiell fälschungssicheren MAC und eines Verschlüsselungsverfahrens erstellt werden kann, das einen weniger strengen Sicherheitsbegriff erfüllt, der als Wahl-Plaintext-Angriffssicherheit bekannt ist.

Wir werden uns nicht mit allen Einzelheiten der Konstruktion authentifizierter Verschlüsselungssysteme befassen. Aber es ist wichtig, zwei Details ihrer Konstruktion zu kennen.

Bei einem authentifizierten Verschlüsselungsverfahren wird zunächst die Verschlüsselung durchgeführt und dann eine Markierung für den Chiffretext erstellt. Es hat sich gezeigt, dass andere Ansätze - wie die Kombination des Chiffriertextes mit einer Markierung des Klartextes oder die Erstellung einer Markierung und die anschließende Verschlüsselung des Klartextes und der Markierung - unsicher sind. Außerdem verfügen beide Verfahren über einen eigenen, zufällig ausgewählten privaten Schlüssel, da sonst die Sicherheit stark beeinträchtigt wird.

Der vorgenannte Grundsatz gilt ganz allgemein: bei der Kombination grundlegender kryptographischer Verfahren sollten Sie immer getrennte Schlüssel verwenden.

Ein authentifiziertes Verschlüsselungsverfahren ist in Abbildung 10 dargestellt. Bob erstellt zunächst einen Chiffretext C aus der Nachricht M unter Verwendung eines zufällig ausgewählten Schlüssels K_C. Dann erstellt er ein Nachrichten-Tag T, indem er den Chiffretext und einen anderen zufällig ausgewählten Schlüssel K_T durch den Tag-Generierungsalgorithmus laufen lässt. Sowohl der Chiffriertext als auch das Nachrichten-Tag werden an Alice gesendet.

Alice prüft nun zunächst, ob die Markierung mit dem Chiffretext C und dem Schlüssel K_T gültig ist. Ist sie gültig, kann sie die Nachricht mit dem Schlüssel K_C entschlüsseln. Sie hat nicht nur die Gewissheit, dass ihre Kommunikation streng geheim ist, sondern sie weiß auch, dass die Nachricht von Bob erstellt wurde.

Abbildung 10: Ein authentifiziertes Verschlüsselungsverfahren

Figure 10: An authenticated encryption scheme

Wie werden MACs erstellt? MACs können zwar mit verschiedenen Methoden erstellt werden, eine gängige und effiziente Methode ist jedoch die kryptografische Hash-Funktion.

Wir werden kryptographische Hash-Funktionen in Kapitel 6 genauer vorstellen. Für den Moment genügt es zu wissen, dass eine Hash-Funktion eine effizient berechenbare Funktion ist, die Eingaben beliebiger Größe annimmt und Ausgaben fester Länge liefert. Die beliebte Hash-Funktion SHA-256 (Secure Hash Algorithm 256) beispielsweise erzeugt unabhängig von der Größe der Eingabe immer eine 256-Bit-Ausgabe. Einige Hash-Funktionen, wie SHA-256, haben nützliche Anwendungen in der Kryptographie.

Der gebräuchlichste Typ von Kennzeichen, der mit einer kryptografischen Hash-Funktion erzeugt wird, ist der hashbasierte Nachrichtenauthentifizierungscode (HMAC). Das Verfahren ist in Abbildung 11 dargestellt. Eine Partei erzeugt zwei verschiedene Schlüssel aus einem privaten Schlüssel K, den inneren Schlüssel K_1 und den äußeren Schlüssel K_2. Der Klartext M oder Chiffretext C wird dann mit dem inneren Schlüssel gehasht. Das Ergebnis T' wird dann mit dem äußeren Schlüssel gehasht, um das Nachrichtenkennzeichen T zu erzeugen.

Es gibt eine Reihe von Hash-Funktionen, die zur Erstellung eines HMAC verwendet werden können. Die am häufigsten verwendete Hash-Funktion ist SHA-256.

Abbildung 11: HMAC

Figure 11: HMAC

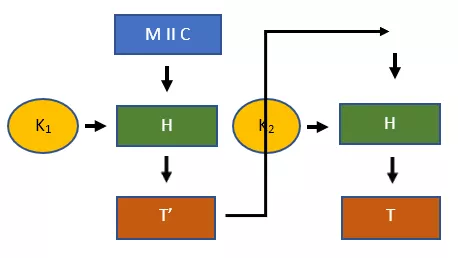
Anmerkungen:

[7] Die in diesem Abschnitt diskutierten spezifischen Ergebnisse stammen aus Katz und Lindell, S. 131-47.

[8] Technisch gesehen ist die Definition von Angriffen auf ausgewählte Chiffretexte anders als der Begriff der Nicht-Malleabilität. Aber man kann zeigen, dass diese beiden Sicherheitsbegriffe äquivalent sind.

Sichere Kommunikationssitzungen

Angenommen, zwei Parteien befinden sich in einer Kommunikationssitzung und senden mehrere Nachrichten hin und her.

Ein authentifiziertes Verschlüsselungsverfahren ermöglicht es dem Empfänger einer Nachricht zu überprüfen, ob sie von seinem Partner in der Kommunikationssitzung erstellt wurde (solange der private Schlüssel nicht durchgesickert ist). Dies funktioniert gut genug für eine einzelne Nachricht. Normalerweise senden jedoch zwei Parteien in einer Kommunikationssitzung Nachrichten hin und her. In diesem Fall bietet ein einfaches authentifiziertes Verschlüsselungsverfahren, wie es im vorherigen Abschnitt beschrieben wurde, keine ausreichende Sicherheit.

Der Hauptgrund dafür ist, dass ein authentifiziertes Verschlüsselungsverfahren keine Garantie dafür bietet, dass die Nachricht tatsächlich auch von dem Agenten gesendet wurde, der sie innerhalb einer Kommunikationssitzung erstellt hat. Betrachten Sie die folgenden drei Angriffsvektoren:

  1. Wiederholungsangriff: Ein Angreifer sendet einen Chiffretext und eine Markierung, die er zu einem früheren Zeitpunkt zwischen zwei Parteien abgefangen hat, erneut.

  2. Umstellungsangriff: Ein Angreifer fängt zwei Nachrichten zu unterschiedlichen Zeitpunkten ab und sendet sie in umgekehrter Reihenfolge an den Empfänger.

  3. Reflexionsangriff: Ein Angreifer beobachtet eine von A nach B gesendete Nachricht und sendet diese Nachricht auch an A.

Obwohl der Angreifer keine Kenntnis vom Chiffretext hat und keine gefälschten Chiffretexte erstellen kann, können die oben genannten Angriffe dennoch erheblichen Schaden in der Kommunikation anrichten.

Nehmen wir zum Beispiel an, dass eine bestimmte Nachricht zwischen den beiden Parteien die Überweisung von Geldmitteln beinhaltet. Ein Wiederholungsangriff könnte die Gelder ein zweites Mal überweisen. Ein einfaches authentifiziertes Verschlüsselungsverfahren bietet keinen Schutz gegen solche Angriffe.

Glücklicherweise können diese Arten von Angriffen in einer Kommunikationssitzung mit Hilfe von Kennungen und relativen Zeitindikatoren leicht entschärft werden.

Der Klartextnachricht können vor der Verschlüsselung Kennungen hinzugefügt werden. Dies würde jegliche Reflexionsangriffe verhindern. Ein relativer Zeitindikator kann z. B. eine Sequenznummer in einer bestimmten Kommunikationssitzung sein. Jede Partei fügt vor der Verschlüsselung eine Sequenznummer zu einer Nachricht hinzu, so dass der Empfänger weiß, in welcher Reihenfolge die Nachrichten gesendet wurden. Dadurch wird die Möglichkeit von Umordnungsangriffen ausgeschlossen. Auch Wiederholungsangriffe werden so verhindert. Jede Nachricht, die ein Angreifer über die Leitung sendet, hat eine alte Sequenznummer, und der Empfänger weiß, dass er die Nachricht nicht noch einmal verarbeiten soll.

Um zu veranschaulichen, wie sichere Kommunikationssitzungen funktionieren, nehmen wir wieder an, dass Alice und Bob miteinander kommunizieren. Sie senden insgesamt vier Nachrichten hin und her. In Abbildung 11 sehen Sie, wie ein authentifiziertes Verschlüsselungsverfahren mit Identifikatoren und Sequenznummern funktionieren würde.

Die Kommunikationssitzung beginnt damit, dass Bob einen Chiffretext C_{0,B} an Alice mit einem Nachrichten-Tag T_{0,B} sendet. Der Chiffriertext enthält die Nachricht sowie einen Identifikator (BOB) und eine Sequenznummer (0). Die Markierung T_{0,B} wird über den gesamten Chiffretext vorgenommen. In ihren nachfolgenden Kommunikationen behalten Alice und Bob dieses Protokoll bei und aktualisieren die Felder nach Bedarf.

Abbildung 12: Eine sichere Kommunikationssitzung

Figure 12: A secure communication session

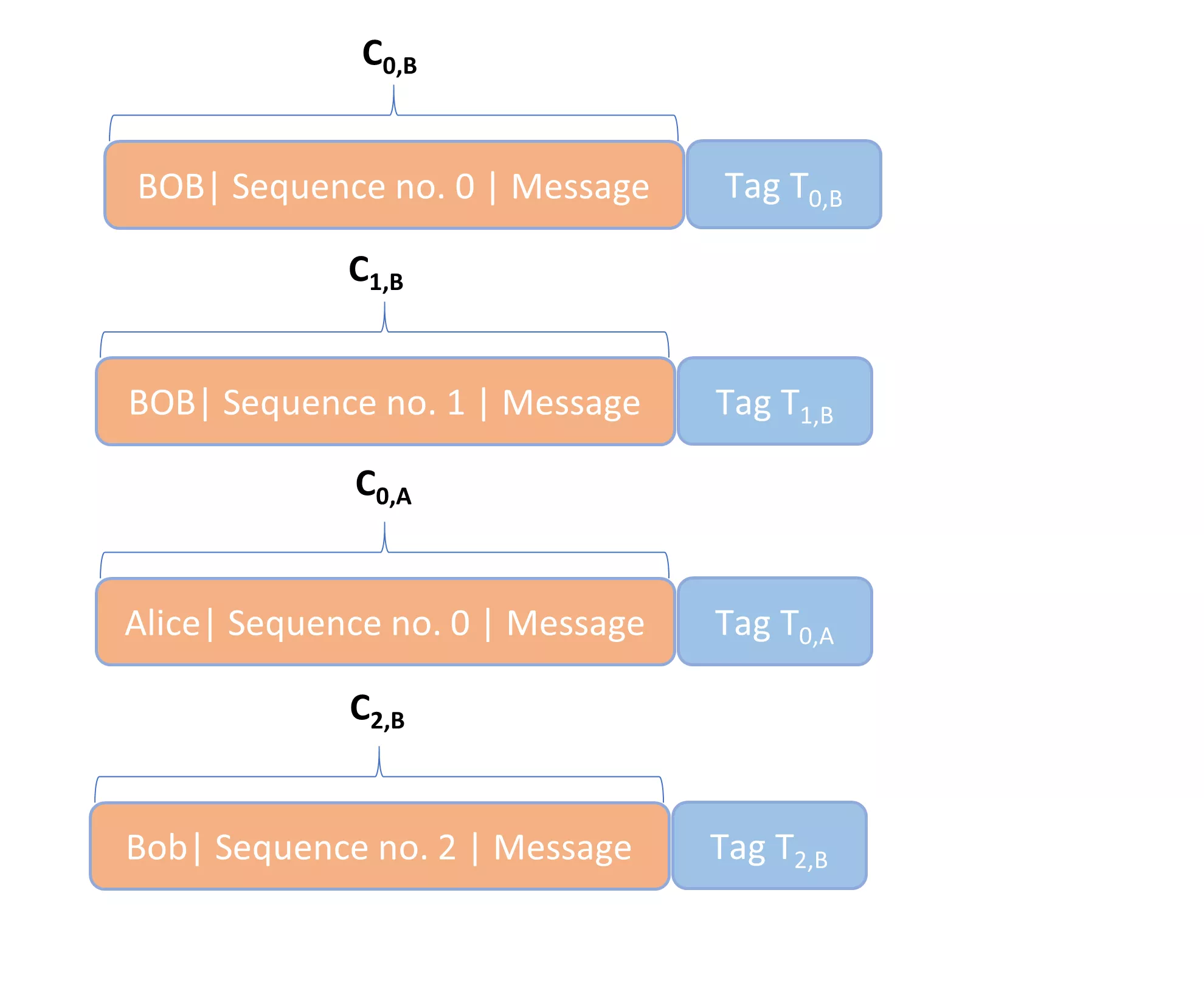
RC4 und AES

Die RC4-Stromchiffre

In diesem Kapitel werden wir die Details eines Verschlüsselungsschemas mit einer modernen primitiven Stromchiffre, RC4 (oder "Rivest-Chiffre 4"), und einer modernen Blockchiffre, AES, besprechen. Während die RC4-Chiffre als Verschlüsselungsmethode in Ungnade gefallen ist, ist AES der Standard für moderne symmetrische Verschlüsselung. Diese beiden Beispiele sollen eine bessere Vorstellung davon vermitteln, wie die symmetrische Verschlüsselung unter der Haube funktioniert.

Um ein Gefühl dafür zu bekommen, wie moderne pseudozufällige Stromchiffren funktionieren, werde ich mich auf die RC4-Stromchiffre konzentrieren. Es handelt sich um eine pseudozufällige Stromchiffre, die in den Sicherheitsprotokollen WEP und WAP für drahtlose Zugangspunkte sowie in TLS verwendet wurde. Da RC4 nachweislich viele Schwächen hat, ist es in Ungnade gefallen. Tatsächlich verbietet die Internet Engineering Task Force jetzt die Verwendung von RC4-Suiten durch Client- und Serveranwendungen in allen TLS-Instanzen. Dennoch eignet er sich gut als Beispiel für die Funktionsweise einer primitiven Stromchiffre.

Zu Beginn zeige ich, wie man eine Klartextnachricht mit einer Baby-RC4-Chiffre verschlüsselt. Nehmen wir an, unsere Klartextnachricht lautet "SOUP" Die Verschlüsselung mit unserer Baby-RC4-Chiffre erfolgt dann in vier Schritten.

Schritt 1

Definieren Sie zunächst ein Array S mit S[0] = 0 bis S[7] = 7. Ein Array bedeutet hier einfach eine veränderbare Sammlung von Werten, die nach einem Index geordnet sind, in manchen Programmiersprachen (z.B. Python) auch Liste genannt. In diesem Fall geht der Index von 0 bis 7, und die Werte gehen ebenfalls von 0 bis 7. S ist also wie folgt:

Die Werte hier sind keine ASCII-Zahlen, sondern die dezimale Darstellung von 1-Byte-Zeichenketten. Der Wert 2 würde also 0000 \ 0011 entsprechen. Die Länge des Arrays S beträgt also 8 Byte.

Schritt 2

Zweitens definieren Sie ein Schlüssel-Array K von 8 Byte Länge, indem Sie einen Schlüssel zwischen 1 und 8 Byte wählen (wobei keine Bruchteile von Bytes zulässig sind). Da jedes Byte aus 8 Bits besteht, können Sie für jedes Byte Ihres Schlüssels eine beliebige Zahl zwischen 0 und 255 wählen.

Angenommen, wir wählen unseren Schlüssel k als [14, 48, 9], so dass er eine Länge von 3 Byte hat. Jeder Index unseres Schlüsselarrays wird dann entsprechend dem Dezimalwert für das jeweilige Element des Schlüssels gesetzt, und zwar der Reihe nach. Wenn Sie den gesamten Schlüssel durchgehen, fangen Sie wieder am Anfang an, bis Sie die 8 Slots des Schlüsselarrays gefüllt haben. Unser Schlüssel-Array sieht also wie folgt aus:

Schritt 3

Drittens wird das Array S mit Hilfe des Schlüssel-Arrays K umgewandelt, ein Prozess, der als Schlüssel-Scheduling bekannt ist. Der Prozess sieht im Pseudocode wie folgt aus:

Die Transformation des Feldes S ist in Tabelle 1 dargestellt.

Der Anfangszustand von S ist [0, 1, 2, 3, 4, 5, 6, 7] mit einem Anfangswert von 0 für j. Dies wird mit Hilfe des Schlüsselarrays [14, 48, 9, 14, 48, 9, 14, 48] transformiert.

Die for-Schleife beginnt mit i = 0. Nach unserem obigen Pseudocode wird der neue Wert von j 6 (j = (j + S[0] + K[0]) \mod 8 = (0 + 0 + 14) \mod 8 = 6 \mod 8). Durch Vertauschen von S[0] und S[6] wird der Zustand von S nach einer Runde zu [6, 1, 2, 3, 4, 5, 0, 7].

In der nächsten Zeile ist i = 1. Wenn man die for-Schleife erneut durchläuft, erhält j einen Wert von 7 (j = (j + S[1] + K[1]) \mod 8 = (6 + 1 + 48) \mod 8 = 55 \mod 8 = 7 \mod 8). Das Vertauschen von S[1] und S[7] aus dem aktuellen Zustand von S, [6, 1, 2, 3, 4, 5, 0, 7], ergibt nach Runde 2 [6, 7, 2, 3, 4, 5, 0, 1].

Wir fahren mit diesem Vorgang fort, bis wir die letzte Zeile am unteren Rand für das Feld S, [6, 4, 1, 0, 3, 7, 5, 2], erhalten.

Tabelle 1: Schlüsseldispositionstabelle

RoundijS[0]S[1]S[2]S[3]S[4]S[5]S[6]S[7]
Initial001234567
10661234507
21767234501
32267234501
43367234501
54367203541
65664203751
76164203752
87264103752

Schritt 4

In einem vierten Schritt wird der Keystream erzeugt. Dabei handelt es sich um eine pseudozufällige Zeichenfolge mit einer Länge, die der zu übermittelnden Nachricht entspricht. Diese wird zur Verschlüsselung der ursprünglichen Nachricht "SOUP" verwendet Da der Keystream so lang wie die Nachricht sein muss, brauchen wir einen, der 4 Bytes lang ist.

Der Keystream wird mit dem folgenden Pseudocode erzeugt:

Sie können die Berechnungen in Tabelle 2 nachvollziehen.

Der Anfangszustand von S ist S = [6, 4, 1, 0, 3, 7, 5, 2]. Setzt man i = 1, so wird der Wert von j 4 (j = (j + S[i]) \mod 8 = (0 + 4) \mod 8 = 4). Dann vertauschen wir S[1] und S[4], um die Transformation von S in der zweiten Zeile zu erhalten, [6, 3, 1, 0, 4, 7, 5, 2]. Der Wert von t ist dann 7 (t = (S[i] + S[j]) \mod 8 = (3 + 4) \mod 8 = 7). Das Byte für den Keystream ist schließlich S[7], also 2.

Wir fahren dann fort, die anderen Bytes zu erzeugen, bis wir die folgenden vier Bytes haben: 2, 6, 3 und 7. Jedes dieser Bytes kann dann verwendet werden, um jeden Buchstaben des Klartextes "SOUP" zu verschlüsseln.

Anhand einer ASCII-Tabelle können wir zunächst sehen, dass "SOUP", kodiert durch die Dezimalwerte der zugrunde liegenden Byte-Strings, "83 79 85 80" ist. In Kombination mit dem Schlüsselstrom "2 6 3 7" ergibt sich "85 85 88 87", was nach einer Modulo-256-Operation gleich bleibt. In ASCII entspricht der Chiffriertext "85 85 88 87" dem Wert "UUXW".

Was passiert, wenn das zu verschlüsselnde Wort länger wäre als das Array S? In diesem Fall verwandelt sich das Feld S für jedes Byte i des Klartextes auf die oben dargestellte Weise, bis die Anzahl der Bytes im Schlüsselstrom der Anzahl der Buchstaben im Klartext entspricht.

Tabelle 2: Keystream-Erzeugung

ijtKeystreamS[0]S[1]S[2]S[3]S[4]S[5]S[6]S[7]
064103752
147263104752
250663704152
351363714052
417264713052

Das Beispiel, das wir gerade besprochen haben, ist nur eine verwässerte Version der RC4-Stromchiffre. Die eigentliche RC4-Stromchiffre hat ein S-Array mit einer Länge von 256 Byte, nicht 8 Byte, und einen Schlüssel, der zwischen 1 und 256 Byte und nicht zwischen 1 und 8 Byte lang sein kann. Das Schlüssel-Array und die Schlüsselströme werden dann alle unter Berücksichtigung der 256-Byte-Länge des S-Arrays erzeugt. Die Berechnungen werden immens komplexer, aber die Prinzipien bleiben dieselben. Unter Verwendung desselben Schlüssels, 14,48,9, mit der Standard-RC4-Chiffre wird die Klartextnachricht "SOUP" als 67 02 ed df im Hexadezimalformat verschlüsselt.

Eine Stromchiffre, bei der der Schlüsselstrom unabhängig von der Klartextnachricht oder dem Chiffretext aktualisiert wird, ist eine synchrone Stromchiffre. Der Keystream ist nur vom Schlüssel abhängig. RC4 ist eindeutig ein Beispiel für eine synchrone Stromchiffre, da der Schlüsselstrom keine Beziehung zum Klartext oder zum Chiffretext hat. Alle unsere im vorigen Kapitel erwähnten primitiven Stromchiffren, einschließlich der Shift-Chiffre, der Vigenère-Chiffre und des One-Time-Pad, waren ebenfalls synchroner Natur.

Im Gegensatz dazu hat eine asynchrone Stromchiffre einen Schlüsselstrom, der sowohl aus dem Schlüssel als auch aus den vorherigen Elementen des Chiffretextes erzeugt wird. Diese Art von Chiffre wird auch selbstsynchronisierende Chiffre genannt.

Wichtig ist, dass der mit RC4 erzeugte Schlüsseldatenstrom als einmaliges Pad behandelt werden sollte, und Sie können den Schlüsseldatenstrom nicht beim nächsten Mal auf genau dieselbe Weise erzeugen. Anstatt den Schlüssel jedes Mal zu ändern, besteht die praktische Lösung darin, den Schlüssel mit einem nonce zu kombinieren, um den Bytestream zu erzeugen.

AES mit einem 128-Bit-Schlüssel

Wie im vorigen Kapitel erwähnt, veranstaltete das National Institute of Standards and Technology (NIST) zwischen 1997 und 2000 einen Wettbewerb zur Festlegung eines neuen symmetrischen Verschlüsselungsstandards. Die Rijndael-Chiffre ging dabei als Sieger hervor. Der Name ist ein Wortspiel mit den Namen der belgischen Erfinder, Vincent Rijmen und Joan Daemen.

Die Rijndael-Chiffre ist eine Blockchiffre, d. h. es gibt einen Kernalgorithmus, der mit verschiedenen Spezifikationen für Schlüssellängen und Blockgrößen verwendet werden kann. Sie können ihn dann mit verschiedenen Betriebsarten verwenden, um Verschlüsselungsschemata zu konstruieren.

Der Ausschuss für den NIST-Wettbewerb hat eine eingeschränkte Version der Rijndael-Chiffre - nämlich eine, die 128-Bit-Blockgrößen und Schlüssellängen von entweder 128 Bit, 192 Bit oder 256 Bit erfordert - als Teil des Advanced Encryption Standard (AES) angenommen. Diese eingeschränkte Version der Rijndael-Chiffre kann auch in mehreren Betriebsmodi verwendet werden. Die Spezifikation für den Standard ist der so genannte Advanced Encryption Standard (AES).

Um zu zeigen, wie die Rijndael-Chiffre, der Kern von AES, funktioniert, werde ich den Prozess der Verschlüsselung mit einem 128-Bit-Schlüssel veranschaulichen. Die Schlüsselgröße wirkt sich auf die Anzahl der Runden aus, die für jeden Verschlüsselungsblock durchgeführt werden. Bei 128-Bit-Schlüsseln sind 10 Runden erforderlich. Bei 192 Bit und 256 Bit wären es 12 bzw. 14 Runden gewesen.

Außerdem werde ich davon ausgehen, dass AES im ECB-Modus verwendet wird. Das macht die Darstellung etwas einfacher und spielt für den Rijndael-Algorithmus keine Rolle. Allerdings ist der ECB-Modus in der Praxis nicht sicher, da er zu einer deterministischen Verschlüsselung führt. Der am häufigsten verwendete sichere Modus bei AES ist CBC (Cipher Block Chaining).

Nennen wir den Schlüssel K_0. Die Konstruktion mit den obigen Parametern sieht dann wie in Abbildung 1 aus, wobei M_i für einen Teil der Klartextnachricht von 128 Bit und C_i für einen Teil des Chiffretextes von 128 Bit steht. Für den letzten Block wird dem Klartext ein Padding hinzugefügt, wenn der Klartext nicht gleichmäßig durch die Blockgröße geteilt werden kann.

Abbildung 1: AES-ECB mit einem 128-Bit-Schlüssel

Figure 1: AES-ECB with a 128-bit key

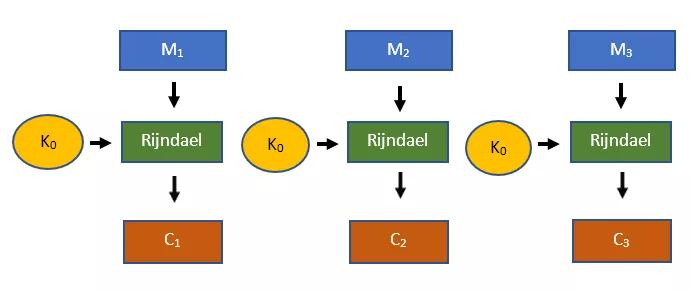
Jeder 128-Bit-Textblock durchläuft beim Rijndael-Verschlüsselungsverfahren zehn Runden. Dies erfordert einen separaten Rundenschlüssel für jede Runde (K_1 bis K_{10}). Diese werden für jede Runde aus dem ursprünglichen 128-Bit-Schlüssel K_0 mithilfe eines Schlüsselerweiterungsalgorithmus erzeugt. Für jeden zu verschlüsselnden Textblock werden also sowohl der ursprüngliche Schlüssel K_0 als auch zehn separate Rundenschlüssel verwendet. Für jeden 128-Bit-Klartextblock, der verschlüsselt werden muss, werden dieselben 11 Schlüssel verwendet.

Der Schlüsselerweiterungsalgorithmus ist lang und komplex. Ihn durchzuarbeiten hat wenig didaktischen Nutzen. Sie können den Schlüsselexpansionsalgorithmus auf eigene Faust durchgehen, wenn Sie möchten. Sobald die runden Schlüssel erzeugt sind, wird die Rijndael-Chiffre den ersten 128-Bit-Block des Klartextes, M_1, wie in Abbildung 2 zu sehen, manipulieren. Wir werden nun diese Schritte durchgehen.

Abbildung 2: Die Manipulation von M_1 mit der Rijndael-Chiffre:

Runde 0:

Runde n für n = {1,...,9}:

Runde 10:

Runde 0

Runde 0 der Rijndael-Chiffre ist einfach. Ein Array S_0 wird durch eine XOR-Operation zwischen dem 128-Bit-Klartext und dem privaten Schlüssel erzeugt. Das heißt,

Runde 1

In Runde 1 wird zunächst das Array S_0 mit dem Rundenschlüssel K_1 durch eine XOR-Operation kombiniert. Dadurch wird ein neuer Zustand von S erzeugt.

Zweitens wird die Operation Bytesubstitution mit dem aktuellen Zustand von S durchgeführt. Dabei wird jedes Byte des 16-Byte-Arrays S durch ein Byte aus einem Array namens Rijndael's S-box ersetzt. Jedes Byte hat eine eindeutige Transformation, und als Ergebnis wird ein neuer Zustand von S erzeugt. Rijndaels S-Box ist in Abbildung 3 dargestellt.

Abbildung 3: Rijndaels S-Box

000102030405060708090A0B0C0D0E0F
00637C777BF26B6FC53001672BFED7AB76
10CA82C97DFA5947F0ADD4A2AF9CA472C0
20B7FD9326363FF7CC34A5E5F171D83115
3004C723C31896059A071280E2EB27B275
4009832C1A1B6E5AA0523BD6B329E32F84
5053D100ED20FCB15B6ACBBE394A4C58CF
60D0EFAAFB434D338545F9027F503C9FA8
7051A3408F929D38F5BCB6DA2110FFF3D2
80CD0C13EC5F974417C4A77E3D645D1973
9060814FDC222A908846EEB814DE5E0BDB
A0E0323A0A4906245CC2D3AC629195E479
B0E7C8376D8DD54EA96C56F4EA657AAE08
C0BA78252E1CA6B4C6E8DD741F4BBD8B8A
D0703EB5664803F60E613557B986C11D9E
E0E1F8981169D98E949B1E87E9CE5528DF
F08CA1890DBFE6426841992D0FB054BB16

Diese S-Box ist ein Ort, an dem abstrakte Algebra in der Rijndael-Chiffre ins Spiel kommt, insbesondere Galois-Felder.

Zunächst definieren Sie jedes mögliche Byte-Element 00 bis FF als 8-Bit-Vektor. Jeder dieser Vektoren ist ein Element des Galois-Feldes GF(2^8), wobei das irreduzible Polynom für die Modulo-Operation x^8 + x^4 + x^3 + x + 1 ist. Das Galois-Feld mit diesen Spezifikationen wird auch Rijndael's Finite Field genannt.

Als Nächstes erstellen wir für jedes mögliche Element des Feldes die so genannte Nyberg S-Box. In dieser Box wird jedes Byte auf seinen multiplikativen Kehrwert abgebildet (d. h., dass ihr Produkt gleich 1 ist). Anschließend werden die Werte aus der Nyberg-S-Box mit Hilfe der affinen Transformation auf die S-Box von Rijndael übertragen.

Die dritte Operation auf dem Feld S ist die Operation Zeilen verschieben. Sie nimmt den Zustand von S und listet alle sechzehn Bytes in einer Matrix auf. Das Füllen der Matrix beginnt oben links und arbeitet sich von oben nach unten vor, wobei jedes Mal, wenn eine Spalte gefüllt ist, eine Spalte nach rechts und nach oben verschoben wird.

Nachdem die Matrix S erstellt wurde, werden die vier Zeilen verschoben. Die erste Zeile bleibt unverändert. Die zweite Zeile wird um eine Zeile nach links verschoben. Die dritte verschiebt zwei nach links. Die vierte verschiebt drei nach links. Ein Beispiel für diesen Vorgang ist in Abbildung 4 dargestellt. Oben ist der ursprüngliche Zustand von S zu sehen, darunter der Zustand, der sich nach dem Verschieben der Zeilen ergibt.

Abbildung 4: Zeilenverschiebung

F1A0B123
59EF0982
9701B0CC
D4720421
F1A0B123
EF098259
B0CC9701
21D47204

Im vierten Schritt treten die Galoisfelder wieder in Erscheinung. Zu Beginn wird jede Spalte der S-Matrix mit der Spalte der 4 x 4-Matrix aus Abbildung 5 multipliziert. Aber statt einer normalen Matrixmultiplikation handelt es sich um eine Vektormultiplikation modulo eines irreduziblen Polynoms, x^8 + x^4 + x^3 + x + 1. Die resultierenden Vektorkoeffizienten stellen die einzelnen Bits eines Bytes dar.

Abbildung 5: Matrix der Mischspalten

02030101
01020301
01010203
03010102

Die Multiplikation der ersten Spalte der S-Matrix mit der obigen 4 x 4-Matrix ergibt das Ergebnis in Abbildung 6.

Abbildung 6: Multiplikation der ersten Spalte:

\begin{matrix}
02 \cdot F1 + 03 \cdot EF + 01 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 02 \cdot EF + 03 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 01 \cdot EF + 02 \cdot B0 + 03 \cdot 21 \\
03 \cdot F1 + 01 \cdot EF + 01 \cdot B0 + 02 \cdot 21
\end{matrix}

In einem nächsten Schritt müssten alle Terme in der Matrix in Polynome umgewandelt werden. Zum Beispiel steht F1 für 1 Byte und würde zu x^7 + x^6 + x^5 + x^4 + 1, und 03 steht für 1 Byte und würde zu x + 1.

Alle Multiplikationen werden dann modulo x^8 + x^4 + x^3 + x + 1 durchgeführt. Das Ergebnis ist die Addition von vier Polynomen in jeder der vier Zellen der Spalte. Nachdem man diese Additionen modulo 2 durchgeführt hat, erhält man vier Polynome. Jedes dieser Polynome repräsentiert eine 8-Bit-Zeichenkette oder 1 Byte von S. Wir werden hier nicht alle diese Berechnungen mit der Matrix in Abbildung 6 durchführen, da sie sehr umfangreich sind.

Sobald die erste Spalte verarbeitet wurde, werden die anderen drei Spalten der S-Matrix auf die gleiche Weise verarbeitet. Das Ergebnis ist eine Matrix mit sechzehn Bytes, die in ein Array umgewandelt werden kann.

In einem letzten Schritt wird das Array S wieder mit dem Rundschlüssel in einer XOR-Operation kombiniert. Dies ergibt den Zustand S_1. Das heißt,

Runden 2 bis 10

Die Runden 2 bis 9 sind lediglich eine Wiederholung von Runde 1, mutatis mutandis. Die letzte Runde sieht sehr ähnlich aus wie die vorherigen Runden, außer dass der Schritt Spalten mischen entfällt. Das heißt, Runde 10 wird wie folgt ausgeführt:

Der Zustand S_{10} ist nun auf C_1, die ersten 128 Bits des Chiffretextes, gesetzt. Wenn man die restlichen 128-Bit-Klartextblöcke durchgeht, erhält man den vollständigen Chiffretext C.

Die Operationen der Rijndael-Chiffre

Was ist der Grund für die verschiedenen Operationen in der Rijndael-Chiffre?

Ohne auf die Einzelheiten einzugehen, werden Verschlüsselungssysteme danach beurteilt, inwieweit sie Verwirrung und Verbreitung stiften. Wenn das Verschlüsselungsverfahren einen hohen Grad an Verwirrung aufweist, bedeutet dies, dass der Chiffretext drastisch anders aussieht als der Klartext. Wenn das Verschlüsselungsverfahren einen hohen Grad an Diffusion aufweist, bedeutet dies, dass jede kleine Änderung des Klartextes einen drastisch anderen Chiffretext erzeugt.

Der Grund für die Operationen hinter der Rijndael-Chiffre ist, dass sie sowohl ein hohes Maß an Konfusion als auch an Diffusion erzeugen. Die Verwirrung wird durch die Byte-Substitutionsoperation erzeugt, während die Diffusion durch die Operationen "Zeilen verschieben" und "Spalten mischen" erzeugt wird.

Asymmetrische Kryptographie

Das Problem der Schlüsselverteilung und -verwaltung

Wie bei der symmetrischen Kryptografie können auch asymmetrische Verfahren verwendet werden, um sowohl Geheimhaltung als auch Authentifizierung zu gewährleisten. Im Gegensatz dazu werden bei diesen Verfahren jedoch nicht nur ein, sondern zwei Schlüssel verwendet: ein privater und ein öffentlicher Schlüssel.

Wir beginnen unsere Untersuchung mit der Entdeckung der asymmetrischen Kryptographie, insbesondere mit den Problemen, die ihr den Anstoß gaben. Als Nächstes erörtern wir, wie asymmetrische Verschlüsselungs- und Authentifizierungsverfahren auf hohem Niveau funktionieren. Anschließend stellen wir Hash-Funktionen vor, die für das Verständnis asymmetrischer Authentifizierungsverfahren von zentraler Bedeutung sind und auch in anderen kryptographischen Zusammenhängen eine Rolle spielen, etwa für die in Kapitel 4 besprochenen hashbasierten Nachrichtenauthentifizierungscodes.

Angenommen, Bob möchte bei Jim's Sporting Goods, einem Online-Sportartikelhändler mit Millionen von Kunden in Nordamerika, eine neue Regenjacke kaufen. Dies ist sein erster Kauf bei diesem Unternehmen, und er möchte seine Kreditkarte verwenden. Bob muss also zunächst ein Konto bei Jim's Sporting Goods einrichten, wozu er persönliche Daten wie seine Adresse und Kreditkarteninformationen übermitteln muss. Dann kann er die für den Kauf des Regenmantels erforderlichen Schritte durchführen.

Da das Internet ein offenes Kommunikationssystem ist, wollen Bob und Jim's Sporting Goods sicherstellen, dass ihre Kommunikation während dieses Prozesses sicher ist. Sie werden beispielsweise sicherstellen wollen, dass kein potenzieller Angreifer Bobs Kreditkarten- und Adressdaten in Erfahrung bringen kann und dass kein potenzieller Angreifer seine Einkäufe wiederholen oder in seinem Namen gefälschte Einkäufe tätigen kann.

Ein fortschrittliches authentifiziertes Verschlüsselungsverfahren, wie es im vorigen Kapitel besprochen wurde, könnte die Kommunikation zwischen Bob und Jim's Sporting Goods sicherlich sicher machen. Aber es gibt eindeutig praktische Hindernisse bei der Umsetzung eines solchen Verfahrens.

Um diese praktischen Hindernisse zu veranschaulichen, nehmen wir an, wir lebten in einer Welt, in der es nur die Werkzeuge der symmetrischen Kryptographie gäbe. Was könnten Jim's Sporting Goods und Bob dann tun, um eine sichere Kommunikation zu gewährleisten?

Unter diesen Umständen wäre eine sichere Kommunikation für sie mit erheblichen Kosten verbunden. Da das Internet ein offenes Kommunikationssystem ist, können sie nicht einfach einen Satz von Schlüsseln darüber austauschen. Daher müssen Bob und ein Vertreter von Jim's Sporting Goods den Schlüsselaustausch persönlich vornehmen.

Eine Möglichkeit wäre, dass Jim's Sporting Goods spezielle Schlüsselaustauschstellen einrichtet, an denen Bob und andere neue Kunden einen Schlüsselsatz für die sichere Kommunikation abrufen können. Dies wäre natürlich mit erheblichen organisatorischen Kosten verbunden und würde die Effizienz, mit der neue Kunden ihre Einkäufe tätigen können, stark verringern.

Alternativ kann Jim's Sporting Goods Bob ein Paar Schlüssel mit einem sehr vertrauenswürdigen Kurier schicken. Dies ist wahrscheinlich effizienter als die Organisation von Schlüsselaustauschstellen. Allerdings wäre dies immer noch mit erheblichen Kosten verbunden, insbesondere wenn viele Kunden nur einen oder wenige Einkäufe tätigen.

Außerdem zwingt ein symmetrisches Verfahren für die authentifizierte Verschlüsselung Jim's Sporting Goods dazu, für alle seine Kunden getrennte Schlüsselsätze zu speichern. Dies wäre eine erhebliche praktische Herausforderung für Tausende von Kunden, ganz zu schweigen von Millionen.

Um diesen letzten Punkt zu verstehen, nehmen wir an, dass Jim's Sporting Goods jedem Kunden das gleiche Schlüsselpaar zur Verfügung stellt. Dies würde es jedem Kunden - oder jedem anderen, der dieses Schlüsselpaar erhalten könnte - ermöglichen, die gesamte Kommunikation zwischen Jim's Sporting Goods und seinen Kunden zu lesen und sogar zu manipulieren. Sie könnten also genauso gut überhaupt keine Kryptographie in Ihrer Kommunikation verwenden.

Selbst die Wiederholung eines Schlüsselsatzes für nur einige Kunden ist eine schreckliche Sicherheitspraxis. Jeder potenzielle Angreifer könnte versuchen, diese Eigenschaft des Systems auszunutzen (es sei daran erinnert, dass man davon ausgeht, dass Angreifer alles über ein System wissen, außer den Schlüsseln, gemäß dem Kerckhoffschen Prinzip)

Jim's Sporting Goods müsste also für jeden Kunden ein Schlüsselpaar speichern, unabhängig davon, wie diese Schlüsselpaare verteilt werden. Dies wirft natürlich mehrere praktische Probleme auf.

Diese beiden soeben beschriebenen Hauptprobleme waren bis Ende der 1970er Jahre ein sehr grundlegendes Problem. Sie wurden als das Schlüsselverteilungsproblem bzw. das Schlüsselverwaltungsproblem bezeichnet.

Diese Probleme gab es natürlich schon immer, und sie haben in der Vergangenheit oft Kopfzerbrechen bereitet. So mussten die Streitkräfte beispielsweise ständig Bücher mit Schlüsseln für die sichere Kommunikation an das Personal im Feld verteilen, was mit großen Risiken und Kosten verbunden war. Diese Probleme verschärften sich jedoch in dem Maße, in dem sich die Welt zunehmend zu einer Welt der digitalen Fernkommunikation entwickelte, insbesondere für nichtstaatliche Einrichtungen.

Wären diese Probleme in den 1970er Jahren nicht gelöst worden, hätte es den effizienten und sicheren Einkauf bei Jim's Sporting Goods wahrscheinlich nicht gegeben. Tatsächlich wäre der größte Teil unserer modernen Welt mit praktischem und sicherem E-Mail-Verkehr, Online-Banking und Einkaufen wahrscheinlich nur eine ferne Fantasie. Etwas, das auch nur annähernd mit Bitcoin vergleichbar ist, hätte es vielleicht gar nicht gegeben.

Was geschah also in den 1970er Jahren? Wie ist es möglich, dass wir sofort online einkaufen und sicher im World Wide Web surfen können? Wie ist es möglich, dass wir von unseren Smartphones aus sofort Bitcoins in die ganze Welt verschicken können?

Neue Wege in der Kryptographie

In den 1970er Jahren hatten die Probleme der Schlüsselverteilung und -verwaltung die Aufmerksamkeit einer Gruppe amerikanischer akademischer Kryptographen geweckt: Whitfield Diffie, Martin Hellman und Ralph Merkle. Angesichts der großen Skepsis der meisten ihrer Kollegen wagten sie es, eine Lösung zu entwickeln.

Zumindest eine der Hauptmotivationen für ihr Vorhaben war die Voraussicht, dass die offene Computerkommunikation unsere Welt tiefgreifend beeinflussen würde. Wie Diffie und Helmann 1976 feststellten,

Die Entwicklung computergesteuerter Kommunikationsnetze verspricht mühelose und kostengünstige Kontakte zwischen Menschen oder Computern auf entgegengesetzten Seiten der Welt und ersetzt die meiste Post und viele Ausflüge durch Telekommunikation. Für viele Anwendungen müssen diese Kontakte sowohl gegen Abhören als auch gegen das Einschleusen unzulässiger Nachrichten gesichert werden. Die Lösung von Sicherheitsproblemen hinkt derzeit jedoch weit hinter anderen Bereichen der Kommunikationstechnologie hinterher. Die gegenwärtige Kryptographie ist nicht in der Lage, den Anforderungen gerecht zu werden, da ihre Anwendung den Systembenutzern so große Unannehmlichkeiten auferlegen würde, dass viele der Vorteile der Telekommunikation zunichte gemacht würden. [1]

Die Hartnäckigkeit von Diffie, Hellman und Merkle zahlte sich aus. Die erste Veröffentlichung ihrer Ergebnisse war ein Papier von Diffie und Helmann aus dem Jahr 1976 mit dem Titel "New Directions in Cryptography" Darin präsentierten sie zwei originelle Wege, um das Problem der Schlüsselverteilung und der Schlüsselverwaltung zu lösen.

Die erste Lösung, die sie anboten, war ein entferntes Schlüsselaustauschprotokoll, d. h. eine Reihe von Regeln für den Austausch eines oder mehrerer symmetrischer Schlüssel über einen unsicheren Kommunikationskanal. Dieses Protokoll ist heute als Diffie-Helmann-Schlüsselaustausch oder Diffie-Helmann-Merkle-Schlüsselaustausch bekannt. [2]

Beim Diffie-Helmann-Schlüsselaustausch tauschen zwei Parteien zunächst einige Informationen öffentlich über einen unsicheren Kanal wie das Internet aus. Auf der Grundlage dieser Informationen erstellen sie dann unabhängig voneinander einen symmetrischen Schlüssel (oder ein Paar symmetrischer Schlüssel) für eine sichere Kommunikation. Während beide Parteien ihre Schlüssel unabhängig voneinander erstellen, stellen die öffentlich ausgetauschten Informationen sicher, dass dieser Schlüsselerstellungsprozess für beide das gleiche Ergebnis liefert.

Wichtig ist, dass die Informationen, die von den Parteien über den unsicheren Kanal öffentlich ausgetauscht werden, zwar von jedermann eingesehen werden können, aber nur die beiden Parteien, die am Informationsaustausch beteiligt sind, können daraus symmetrische Schlüssel erstellen.

Das klingt natürlich völlig kontraintuitiv. Wie könnten zwei Parteien öffentlich Informationen austauschen, die es nur ihnen ermöglichen, daraus symmetrische Schlüssel zu erstellen? Warum sollte eine andere Person, die den Informationsaustausch beobachtet, nicht in der Lage sein, die gleichen Schlüssel zu erstellen?

Es beruht natürlich auf einer schönen Mathematik. Der Diffie-Helmann-Schlüsselaustausch funktioniert über eine Einwegfunktion mit einer Falltür. Erläutern wir die Bedeutung dieser beiden Begriffe nacheinander.

Angenommen, man erhält eine Funktion f(x) und das Ergebnis f(a) = y, wobei a ein bestimmter Wert für x ist. Wir sagen, dass f(x) eine Einwegfunktion ist, wenn es einfach ist, den Wert y zu berechnen, wenn a und f(x) gegeben sind, aber es rechnerisch undurchführbar ist, den Wert a zu berechnen, wenn y und f(x) gegeben sind. Der Name Einwegfunktion rührt natürlich daher, dass die Berechnung einer solchen Funktion nur in einer Richtung sinnvoll ist.

Einige Einwegfunktionen haben eine so genannte Falltür. Während es praktisch unmöglich ist, a nur aus y und f(x) zu berechnen, gibt es eine bestimmte Information Z, die die Berechnung von a aus y rechnerisch möglich macht. Diese Information Z wird als Falltür bezeichnet. Einwegfunktionen, die eine Falltür haben, nennt man Falltürfunktionen.

Wir werden hier nicht auf die Einzelheiten des Diffie-Helmann-Schlüsselaustauschs eingehen. Aber im Wesentlichen erstellt jeder Teilnehmer einige Informationen, von denen ein Teil öffentlich freigegeben wird und ein Teil geheim bleibt. Jede Partei nimmt dann ihre geheimen Informationen und die von der anderen Partei freigegebenen öffentlichen Informationen, um einen privaten Schlüssel zu erstellen. Und wie durch ein Wunder haben beide Parteien am Ende denselben privaten Schlüssel.

Jede Partei, die nur die öffentlich geteilten Informationen zwischen den beiden Parteien in einem Diffie-Helmann-Schlüsselaustausch beobachtet, ist nicht in der Lage, diese Berechnungen zu replizieren. Dazu bräuchte er die privaten Informationen von einer der beiden Parteien.

Obwohl die 1976 vorgestellte Grundversion des Diffie-Helmann-Schlüsselaustauschs nicht sehr sicher ist, werden ausgefeilte Versionen des Grundprotokolls sicherlich auch heute noch verwendet. Vor allem ist jedes Schlüsselaustauschprotokoll in der neuesten Version des Sicherheitsprotokolls für die Transportschicht (Version 1.3) im Wesentlichen eine angereicherte Version des 1976 von Diffie und Hellman vorgestellten Protokolls. Das Transport Layer Security Protocol ist das vorherrschende Protokoll für den sicheren Austausch von Informationen, die gemäß dem Hypertext Transfer Protocol (http), dem Standard für den Austausch von Webinhalten, formatiert sind.

Wichtig ist, dass es sich beim Diffie-Helmann-Schlüsselaustausch nicht um ein asymmetrisches Verfahren handelt. Streng genommen gehört er wohl in den Bereich der symmetrischen Kryptographie. Da aber sowohl der Diffie-Helmann-Schlüsselaustausch als auch die asymmetrische Kryptographie auf einseitigen zahlentheoretischen Funktionen mit Falltüren beruhen, werden sie in der Regel zusammen behandelt.

Der zweite Weg, den Diffie und Helmann in ihrem Papier von 1976 zur Lösung des Problems der Schlüsselverteilung und -verwaltung anboten, war natürlich die asymmetrische Kryptographie.

Im Gegensatz zu ihrer Darstellung des Diffie-Hellman-Schlüsselaustauschs lieferten sie nur die allgemeinen Konturen dessen, wie asymmetrische kryptografische Systeme plausibel konstruiert werden könnten. Sie boten keine Einwegfunktion an, die speziell die Bedingungen erfüllen könnte, die für eine angemessene Sicherheit in solchen Schemata erforderlich sind.

Eine praktische Umsetzung eines asymmetrischen Verfahrens wurde jedoch ein Jahr später von drei verschiedenen akademischen Kryptographen und Mathematikern gefunden: Ronald Rivest, Adi Shamir und Leonard Adleman. [3] Das von ihnen vorgestellte Kryptosystem wurde als RSA-Kryptosystem (nach ihren Nachnamen) bekannt.

Die in der asymmetrischen Kryptographie (und beim Diffie-Helmann-Schlüsselaustausch) verwendeten Falltürfunktionen sind alle mit zwei rechnerisch schwierigen Problemen verbunden: der Primfaktorzerlegung und der Berechnung von diskreten Logarithmen.

bei der Primfaktorzerlegung muss, wie der Name schon sagt, eine ganze Zahl in ihre Primfaktoren zerlegt werden. Das RSA-Problem ist bei weitem das bekannteste Beispiel für ein Kryptosystem, das mit der Primfaktorzerlegung zusammenhängt.

Das Diskrete Logarithmusproblem ist ein Problem, das in zyklischen Gruppen auftritt. Bei einem Generator in einer bestimmten zyklischen Gruppe muss der eindeutige Exponent berechnet werden, der erforderlich ist, um aus dem Generator ein anderes Element der Gruppe zu erzeugen.

Auf dem diskreten Logarithmus basierende Verfahren stützen sich im Wesentlichen auf zwei Arten von zyklischen Gruppen: multiplikative Gruppen von ganzen Zahlen und Gruppen, die die Punkte auf elliptischen Kurven enthalten. Der ursprüngliche Diffie-Helmann-Schlüsselaustausch, der in "New Directions in Cryptography" vorgestellt wurde, arbeitet mit einer zyklischen multiplikativen Gruppe von ganzen Zahlen. Der digitale Signaturalgorithmus von Bitcoin und das kürzlich eingeführte Schnorr-Signaturverfahren (2021) basieren beide auf dem Problem des diskreten Logarithmus für eine bestimmte zyklische Gruppe elliptischer Kurven.

Als Nächstes werden wir einen Überblick über die Geheimhaltung und Authentifizierung im asymmetrischen Umfeld geben. Zuvor müssen wir jedoch noch eine kurze historische Anmerkung machen.

Es scheint nun plausibel, dass eine Gruppe britischer Kryptographen und Mathematiker, die für das Government Communications Headquarters (GCHQ) arbeiteten, einige Jahre zuvor unabhängig voneinander die oben genannten Entdeckungen gemacht hatten. Diese Gruppe bestand aus James Ellis, Clifford Cocks und Malcolm Williamson.

Nach eigenen Angaben und denen des GCHQ war es James Ellis, der 1969 als Erster das Konzept der Kryptographie mit öffentlichen Schlüsseln entwickelte. Angeblich entdeckte Clifford Cocks dann 1973 das RSA-Kryptosystem und Malcolm Williamson 1974 das Konzept des Diffie-Helmann-Schlüsselaustauschs. [4] Ihre Entdeckungen wurden jedoch angeblich erst 1997 bekannt gegeben, da die Arbeit des GCHQ geheim war.

Anmerkungen:

[1] Whitfield Diffie und Martin Hellman, "New directions in cryptography", IEEE Transactions on Information Theory IT-22 (1976), S. 644-654, hier S. 644.

[2] Ralph Merkle erörtert ebenfalls ein Schlüsselaustauschprotokoll in "Secure communications over insecure channels", Communications of the Association for Computing Machinery, 21 (1978), 294-99. Merkle reichte diese Arbeit zwar vor der Arbeit von Diffie und Hellman ein, sie wurde jedoch später veröffentlicht. Merkles Lösung ist im Gegensatz zu der von Diffie-Hellman nicht exponentiell sicher.

[3] Ron Rivest, Adi Shamir, und Leonard Adleman, "A method for obtaining digital signatures and public-key cryptosystems", Communications of the Association for Computing Machinery, 21 (1978), S. 120-26.

[4] Eine gute Geschichte dieser Entdeckungen findet sich in Simon Singh, The Code Book, Fourth Estate (London, 1999), Kapitel 6.

Asymmetrische Verschlüsselung und Authentifizierung

Einen Überblick über die asymmetrische Verschlüsselung mit Hilfe von Bob und Alice gibt Abbildung 1.

Alice erstellt zunächst ein Schlüsselpaar, bestehend aus einem öffentlichen Schlüssel (K_P) und einem privaten Schlüssel (K_S), wobei das "P" in K_P für "öffentlich" und das "S" in K_S für "geheim" steht. Diesen öffentlichen Schlüssel gibt sie dann frei an andere weiter. Wir werden auf die Einzelheiten dieses Verteilungsprozesses etwas später zurückkommen. Nehmen wir aber zunächst an, dass jeder, auch Bob, Alices öffentlichen Schlüssel K_P sicher erhalten kann.

Zu einem späteren Zeitpunkt möchte Bob eine Nachricht M an Alice schreiben. Da sie sensible Informationen enthält, möchte er, dass der Inhalt für alle außer Alice geheim bleibt. Also verschlüsselt Bob zunächst seine Nachricht M mit K_P. Den daraus resultierenden Chiffretext C schickt er an Alice, die C mit K_S entschlüsselt, um die ursprüngliche Nachricht M zu erhalten.

Abbildung 1: Asymmetrische Verschlüsselung

Figure 1: Asymmetric encryption

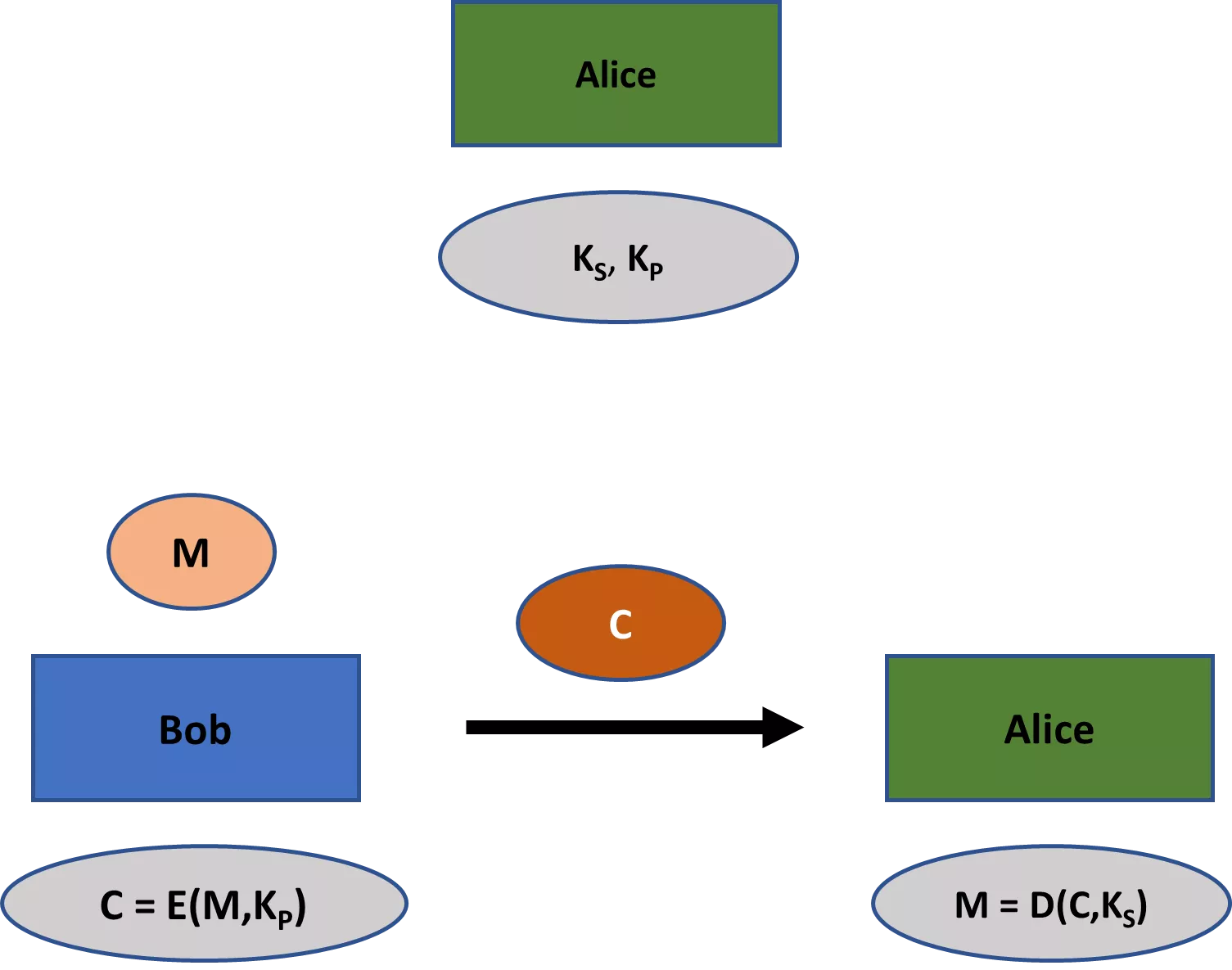
Jeder Gegner, der die Kommunikation von Bob und Alice abhört, kann C beobachten. Sie kennt auch K_P und den Verschlüsselungsalgorithmus E(\cdot). Wichtig ist jedoch, dass diese Informationen es dem Angreifer nicht ermöglichen, den Chiffretext C zu entschlüsseln. Die Entschlüsselung erfordert nämlich K_S, das der Angreifer nicht besitzt.

Symmetrische Verschlüsselungssysteme müssen im Allgemeinen gegen einen Angreifer sicher sein, der Klartextnachrichten gültig verschlüsseln kann (bekannt als Sicherheit bei Chiffrierangriffen). Sie sind jedoch nicht mit dem ausdrücklichen Ziel entwickelt worden, die Erstellung solcher gültigen Chiffretexte durch einen Angreifer oder eine andere Person zu ermöglichen.

Dies steht in krassem Gegensatz zu einem asymmetrischen Verschlüsselungsverfahren, bei dem der Zweck darin besteht, dass jeder, auch Angreifer, gültige Chiffretexte erzeugen kann. Asymmetrische Verschlüsselungsverfahren können daher als Mehrfachzugriffs-Chiffren bezeichnet werden.

Um besser zu verstehen, was hier passiert, stellen Sie sich vor, dass Bob statt einer elektronischen Nachricht einen physischen Brief unter Geheimhaltung versenden möchte. Eine Möglichkeit, die Geheimhaltung zu gewährleisten, bestünde darin, dass Alice ein sicheres Vorhängeschloss an Bob schickt, aber den Schlüssel zum Aufschließen behält. Nachdem er seinen Brief geschrieben hat, könnte er ihn in eine Schachtel legen und diese mit dem Vorhängeschloss von Alice verschließen. Dann könnte er die verschlossene Schachtel mit der Nachricht an Alice schicken, die den Schlüssel zum Aufschließen hat.

Bob kann das Vorhängeschloss zwar abschließen, aber weder er noch eine andere Person, die das Kästchen abfängt, kann das Vorhängeschloss aufschließen, wenn es tatsächlich gesichert ist. Nur Alice kann es aufschließen und den Inhalt von Bobs Brief sehen, weil sie den Schlüssel hat.

Ein asymmetrisches Verschlüsselungsverfahren ist, grob gesagt, eine digitale Version dieses Prozesses. Das Vorhängeschloss entspricht dem öffentlichen Schlüssel und der Schlüssel des Vorhängeschlosses entspricht dem privaten Schlüssel. Da das Vorhängeschloss jedoch digital ist, ist es für Alice viel einfacher und weniger kostspielig, es an jeden weiterzugeben, der ihr geheime Nachrichten schicken möchte.

Für die Authentifizierung im asymmetrischen Bereich verwenden wir digitale Signaturen. Diese haben also die gleiche Funktion wie die Nachrichtenauthentifizierungscodes im symmetrischen Bereich. Eine Übersicht über digitale Signaturen ist in Abbildung 2 dargestellt.

Bob erstellt zunächst ein Schlüsselpaar, bestehend aus dem öffentlichen Schlüssel (K_P) und dem privaten Schlüssel (K_S), und gibt seinen öffentlichen Schlüssel weiter. Wenn er eine authentifizierte Nachricht an Alice senden will, nimmt er zunächst seine Nachricht M und seinen privaten Schlüssel, um eine digitale Signatur D zu erstellen. Bob schickt dann Alice seine Nachricht zusammen mit der digitalen Signatur.

Alice gibt die Nachricht, den öffentlichen Schlüssel und die digitale Signatur in einen Prüfalgorithmus ein. Dieser Algorithmus liefert entweder true für eine gültige Signatur oder false für eine ungültige Signatur.

Eine digitale Signatur ist, wie der Name schon sagt, das digitale Äquivalent einer schriftlichen Unterschrift auf Briefen, Verträgen usw. In der Tat ist eine digitale Unterschrift in der Regel viel sicherer. Eine schriftliche Unterschrift lässt sich mit einigem Aufwand fälschen; ein Vorgang, der dadurch erleichtert wird, dass schriftliche Unterschriften häufig nicht genau überprüft werden. Eine sichere digitale Signatur ist jedoch, genau wie ein sicherer Nachrichtenauthentifizierungscode, existentiell fälschungssicher: Das heißt, bei einem sicheren digitalen Signaturschema kann niemand eine Signatur für eine Nachricht erstellen, die das Prüfverfahren besteht, es sei denn, er verfügt über den privaten Schlüssel.

Abbildung 2: Asymmetrische Authentifizierung

Figure 2: Asymmetric authentication

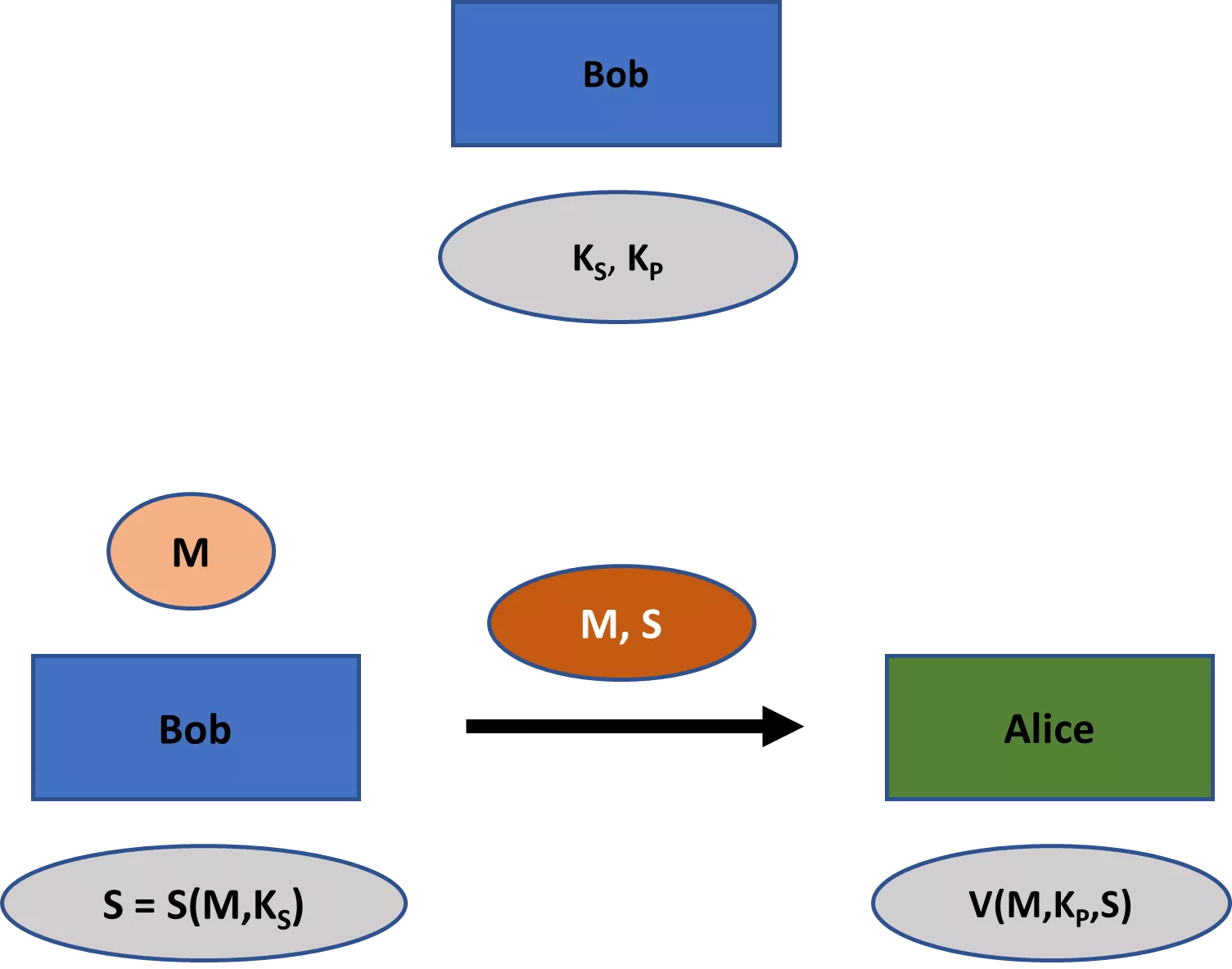
Wie bei der asymmetrischen Verschlüsselung gibt es einen interessanten Unterschied zwischen digitalen Signaturen und Nachrichtenauthentifizierungscodes. Bei letzteren kann der Verifizierungsalgorithmus nur von einer der in die sichere Kommunikation eingeweihten Parteien verwendet werden. Dies liegt daran, dass er einen privaten Schlüssel benötigt. Bei der asymmetrischen Verschlüsselung hingegen kann jeder eine von Bob geleistete digitale Signatur S verifizieren.

All dies macht digitale Signaturen zu einem äußerst leistungsfähigen Instrument. Es bildet beispielsweise die Grundlage für die Erstellung von Unterschriften auf Verträgen, die für rechtliche Zwecke überprüft werden können. Wenn Bob im obigen Austausch eine Signatur auf einem Vertrag erstellt hat, kann Alice die Nachricht M, den Vertrag und die Signatur S einem Gericht vorlegen. Das Gericht kann dann die Signatur mit Bobs öffentlichem Schlüssel überprüfen. [5]

Ein weiteres Beispiel: Digitale Signaturen sind ein wichtiger Aspekt der sicheren Verteilung von Software und Software-Updates. Diese Art der öffentlichen Verifizierbarkeit könnte niemals nur mit Nachrichtenauthentifizierungscodes erreicht werden.

Als letztes Beispiel für die Leistungsfähigkeit digitaler Signaturen sei Bitcoin genannt. Eines der häufigsten Missverständnisse über Bitcoin, insbesondere in den Medien, ist, dass die Transaktionen verschlüsselt sind: Das ist nicht der Fall. Stattdessen arbeiten Bitcoin-Transaktionen mit digitalen Signaturen, um die Sicherheit zu gewährleisten.

Bitcoins existieren in Stapeln, die als unverbrauchte Transaktionsausgaben (oder UTXOs) bezeichnet werden. Angenommen, Sie erhalten drei Zahlungen auf eine bestimmte Bitcoin-Adresse für jeweils 2 Bitcoins. Technisch gesehen haben Sie jetzt nicht 6 Bitcoins auf dieser Adresse. Stattdessen haben Sie drei Stapel von 2 Bitcoins, die durch ein kryptografisches Problem im Zusammenhang mit dieser Adresse gesperrt sind. Für jede Zahlung, die Sie tätigen, können Sie einen, zwei oder alle drei dieser Stapel verwenden, je nachdem, wie viel Sie für die Transaktion benötigen.

Der Eigentumsnachweis für nicht ausgegebene Transaktionsergebnisse wird normalerweise durch eine oder mehrere digitale Signaturen erbracht. Bitcoin funktioniert genau deshalb, weil gültige digitale Signaturen für nicht ausgegebene Transaktionsergebnisse rechnerisch nicht machbar sind, es sei denn, man ist im Besitz der geheimen Informationen, die für die Erstellung erforderlich sind.

Derzeit enthalten Bitcoin-Transaktionen transparent alle Informationen, die von den Teilnehmern des Netzwerks verifiziert werden müssen, wie z. B. die Herkunft der in der Transaktion verwendeten nicht verbrauchten Transaktionsausgaben. Es ist zwar möglich, einige dieser Informationen zu verbergen und trotzdem eine Verifizierung zu ermöglichen (wie es einige alternative Kryptowährungen wie Monero tun), aber dies schafft auch besondere Sicherheitsrisiken.

Manchmal kommt es zu Verwechslungen zwischen digitalen Unterschriften und schriftlichen Unterschriften, die digital erfasst werden. Im letzteren Fall nehmen Sie ein Bild Ihrer schriftlichen Unterschrift auf und fügen es in ein elektronisches Dokument ein, beispielsweise in einen Arbeitsvertrag. Dabei handelt es sich jedoch nicht um eine digitale Signatur im kryptografischen Sinne. Letztere ist lediglich eine lange Zahl, die nur durch den Besitz eines privaten Schlüssels erzeugt werden kann.

Wie bei den symmetrischen Schlüsseln können Sie auch asymmetrische Verschlüsselungs- und Authentifizierungsverfahren zusammen verwenden. Es gelten ähnliche Grundsätze. Zunächst einmal sollten Sie unterschiedliche Paare von privaten und öffentlichen Schlüsseln für die Verschlüsselung und die Erstellung digitaler Signaturen verwenden. Darüber hinaus sollten Sie eine Nachricht zuerst verschlüsseln und dann authentifizieren.

Wichtig ist, dass in vielen Anwendungen die asymmetrische Kryptographie nicht während des gesamten Kommunikationsprozesses verwendet wird. Stattdessen wird sie in der Regel nur zum Austausch von symmetrischen Schlüsseln zwischen den Parteien verwendet, über die sie tatsächlich kommunizieren.

Dies ist zum Beispiel der Fall, wenn Sie Waren online kaufen. Wenn Sie den öffentlichen Schlüssel des Verkäufers kennen, kann er Ihnen digital signierte Nachrichten schicken, die Sie auf ihre Echtheit überprüfen können. Auf dieser Grundlage können Sie eines von mehreren Protokollen für den Austausch von symmetrischen Schlüsseln verwenden, um sicher zu kommunizieren.

Der Hauptgrund für die Häufigkeit des oben genannten Ansatzes ist, dass die asymmetrische Kryptografie bei der Herstellung eines bestimmten Sicherheitsniveaus viel weniger effizient ist als die symmetrische Kryptografie. Dies ist ein Grund, warum wir neben der öffentlichen Kryptographie immer noch die symmetrische Kryptographie benötigen. Darüber hinaus ist die symmetrische Kryptografie für bestimmte Anwendungen, wie z. B. die Verschlüsselung der eigenen Daten durch einen Computernutzer, viel natürlicher.

Wie genau lösen digitale Signaturen und die Verschlüsselung mit öffentlichen Schlüsseln die Probleme der Schlüsselverteilung und Schlüsselverwaltung?

Hier gibt es nicht nur eine Antwort. Asymmetrische Kryptographie ist ein Werkzeug, und es gibt nicht nur einen Weg, dieses Werkzeug einzusetzen. Aber nehmen wir unser früheres Beispiel von Jim's Sporting Goods, um zu zeigen, wie die Probleme in diesem Beispiel typischerweise angegangen werden würden.

Zunächst würde sich Jim's Sporting Goods wahrscheinlich an eine Zertifizierungsstelle wenden, eine Organisation, die sich mit der Verteilung öffentlicher Schlüssel befasst. Die Zertifizierungsstelle würde einige Details über Jim's Sporting Goods registrieren und ihm einen öffentlichen Schlüssel zuweisen. Anschließend würde sie Jim's Sporting Goods ein Zertifikat, ein so genanntes TLS/SSL-Zertifikat, zusenden, in dem der öffentliche Schlüssel von Jim's Sporting Goods mit dem eigenen öffentlichen Schlüssel der Zertifizierungsstelle digital signiert ist. Auf diese Weise bestätigt die Zertifizierungsstelle, dass ein bestimmter öffentlicher Schlüssel tatsächlich zu Jim's Sporting Goods gehört.

Der Schlüssel zum Verständnis dieses Vorgangs bei TLS/SSL-Zertifikaten liegt darin, dass der öffentliche Schlüssel von Jim's Sporting Goods zwar in der Regel nicht auf Ihrem Computer gespeichert ist, die öffentlichen Schlüssel anerkannter Zertifizierungsstellen jedoch tatsächlich in Ihrem Browser oder in Ihrem Betriebssystem gespeichert sind. Diese sind in so genannten Wurzelzertifikaten gespeichert.

Wenn Jim's Sporting Goods Ihnen also sein TLS/SSL-Zertifikat zur Verfügung stellt, können Sie die digitale Signatur der Zertifizierungsstelle über ein Stammzertifikat in Ihrem Browser oder Betriebssystem überprüfen. Wenn die Signatur gültig ist, können Sie relativ sicher sein, dass der öffentliche Schlüssel des Zertifikats tatsächlich zu Jim's Sporting Goods gehört. Auf dieser Grundlage ist es einfach, ein Protokoll für die sichere Kommunikation mit Jim's Sporting Goods einzurichten.

Die Schlüsselverteilung ist für Jim's Sporting Goods nun wesentlich einfacher geworden. Es ist unschwer zu erkennen, dass sich auch die Schlüsselverwaltung stark vereinfacht hat. Anstatt Tausende von Schlüsseln speichern zu müssen, muss Jim's Sporting Goods lediglich einen privaten Schlüssel speichern, der es ihm ermöglicht, Signaturen für den öffentlichen Schlüssel auf seinem SSL-Zertifikat zu erstellen. Jedes Mal, wenn ein Kunde die Website von Jim's Sporting Goods besucht, kann er mit diesem öffentlichen Schlüssel eine sichere Kommunikationssitzung aufbauen. Die Kunden müssen auch keine anderen Informationen speichern (außer den öffentlichen Schlüsseln der anerkannten Zertifizierungsstellen in ihrem Betriebssystem und Browser).

Anmerkungen:

[5] Alle Systeme, die versuchen, Nichtabstreitbarkeit zu erreichen, das andere Thema, das wir in Kapitel 1 erörtert haben, muss als Grundlage digitale Signaturen beinhalten.

Hash-Funktionen

Hash-Funktionen sind in der Kryptographie allgegenwärtig. Sie gehören weder zu den symmetrischen noch zu den asymmetrischen Verfahren, sondern sind eine eigenständige kryptografische Kategorie.

Wir haben Hash-Funktionen bereits in Kapitel 4 bei der Erstellung von hashbasierten Authentifizierungsnachrichten kennengelernt. Sie sind auch im Zusammenhang mit digitalen Signaturen wichtig, wenn auch aus einem etwas anderen Grund: Digitale Signaturen werden nämlich in der Regel über den Hash-Wert einer (verschlüsselten) Nachricht erstellt, und nicht über die eigentliche (verschlüsselte) Nachricht. In diesem Abschnitt werde ich eine gründlichere Einführung in Hash-Funktionen geben.

Beginnen wir mit der Definition einer Hash-Funktion. Eine Hash-Funktion ist eine effizient berechenbare Funktion, die Eingaben beliebiger Größe annimmt und Ausgaben fester Länge liefert.

Eine kryptografische Hash-Funktion ist einfach eine Hash-Funktion, die für Anwendungen in der Kryptografie nützlich ist. Die Ausgabe einer kryptografischen Hash-Funktion wird in der Regel als Hash, Hash-Wert oder Message Digest bezeichnet.

Im Kontext der Kryptographie bezieht sich eine "Hash-Funktion" in der Regel auf eine kryptographische Hash-Funktion. Ich werde diese Praxis von hier an übernehmen.

Ein Beispiel für eine beliebte Hash-Funktion ist SHA-256 (Secure Hash Algorithm 256). Unabhängig von der Größe der Eingabe (z. B. 15 Bit, 100 Bit oder 10.000 Bit) ergibt diese Funktion einen 256-Bit-Hash-Wert. Nachfolgend sehen Sie einige Beispielausgaben der SHA-256-Funktion.

"Hallo": 185f8db32271fe25f561a6fc938b2e264306ec304eda518007d1764826381969

"52398": a3b14d2bf378c1bd47e7f8eaec63b445150a3d7a80465af16dd9fd319454ba90

"Kryptographie macht Spaß": 3cee2a5c7d2cc1d62db4893564c34ae553cc88623992d994e114e344359b146c

Alle Ausgaben sind genau 256 Bits im Hexadezimalformat (jede Hex-Ziffer kann durch vier Binärziffern dargestellt werden). Selbst wenn Sie also Tolkiens Buch Der Herr der Ringe in die SHA-256-Funktion eingegeben hätten, würde die Ausgabe immer noch 256 Bits betragen.

Hash-Funktionen wie SHA-256 werden in der Kryptographie zu verschiedenen Zwecken eingesetzt. Welche Eigenschaften von einer Hash-Funktion verlangt werden, hängt vom Kontext einer bestimmten Anwendung ab. Es gibt zwei Haupteigenschaften, die von Hash-Funktionen in der Kryptographie allgemein gewünscht werden: [6]

  1. Aufprallschutz

  2. Verstecken

Eine Hash-Funktion H ist kollisionssicher, wenn es nicht möglich ist, zwei Werte x und y zu finden, so dass x \neq y ist, aber H(x) = H(y).

Kollisionssichere Hash-Funktionen sind z. B. für die Überprüfung von Software wichtig. Angenommen, Sie möchten die Windows-Version von Bitcoin Core 0.21.0 (eine Serveranwendung zur Verarbeitung des Bitcoin-Netzwerkverkehrs) herunterladen. Die wichtigsten Schritte, die Sie unternehmen müssten, um die Legitimität der Software zu überprüfen, sind die folgenden:

  1. Sie müssen zunächst die öffentlichen Schlüssel eines oder mehrerer Mitwirkender von Bitcoin Core herunterladen und in eine Software importieren, die digitale Signaturen überprüfen kann (z. B. Kleopetra). Sie können diese öffentlichen Schlüssel hier finden. Es wird empfohlen, die Bitcoin Core Software mit den öffentlichen Schlüsseln von mehreren Mitwirkenden zu verifizieren.

  2. Als nächstes müssen Sie die von Ihnen importierten öffentlichen Schlüssel überprüfen. Zumindest ein Schritt sollte darin bestehen, dass Sie überprüfen, ob die gefundenen öffentlichen Schlüssel mit den an verschiedenen anderen Stellen veröffentlichten übereinstimmen. Sie können zum Beispiel die persönlichen Webseiten, Twitter-Seiten oder Github-Seiten der Personen konsultieren, deren öffentliche Schlüssel Sie importiert haben. In der Regel erfolgt dieser Vergleich öffentlicher Schlüssel durch den Vergleich eines kurzen Hashwerts des öffentlichen Schlüssels, des sogenannten Fingerabdrucks.

  3. Als nächstes müssen Sie die ausführbare Datei für Bitcoin Core von der Website herunterladen. Es werden Pakete für die Betriebssysteme Linux, Windows und MAC verfügbar sein.

  4. Als nächstes müssen Sie zwei Veröffentlichungsdateien finden. Die erste Datei enthält den offiziellen SHA-256-Hash für die heruntergeladene ausführbare Datei zusammen mit den Hashes aller anderen Pakete, die veröffentlicht wurden. Eine weitere Freigabedatei enthält die Signaturen von verschiedenen Mitwirkenden über die Freigabedatei mit den Paket-Hashes. Diese beiden Freigabedateien sollten auf der Bitcoin Core Website zu finden sein.

  5. Als nächstes müssen Sie den SHA-256-Hash der ausführbaren Datei, die Sie von der Bitcoin Core-Website heruntergeladen haben, auf Ihrem eigenen Computer berechnen. Dieses Ergebnis vergleichen Sie dann mit dem Hash des offiziellen Pakets für die ausführbare Datei. Sie sollten identisch sein.

  6. Schließlich müssen Sie überprüfen, ob eine oder mehrere der digitalen Signaturen über der Veröffentlichungsdatei mit den offiziellen Paket-Hashes tatsächlich einem oder mehreren öffentlichen Schlüsseln entsprechen, die Sie importiert haben (Veröffentlichungen von Bitcoin Core werden nicht immer von allen signiert). Sie können dies mit einer Anwendung wie Kleopetra tun.

Dieser Prozess der Softwareüberprüfung hat zwei Hauptvorteile. Erstens stellt es sicher, dass beim Herunterladen von der Bitcoin Core-Website keine Übertragungsfehler aufgetreten sind. Zweitens wird sichergestellt, dass kein Angreifer Sie dazu gebracht hat, modifizierten, bösartigen Code herunterzuladen, entweder durch Hacken der Bitcoin Core Website oder durch Abfangen des Datenverkehrs.

Wie genau schützt der oben beschriebene Softwareüberprüfungsprozess vor diesen Problemen?

Wenn Sie die öffentlichen Schlüssel, die Sie importiert haben, sorgfältig überprüft haben, dann können Sie ziemlich sicher sein, dass diese Schlüssel tatsächlich ihnen gehören und nicht kompromittiert wurden. Da digitale Signaturen existenziell fälschungssicher sind, wissen Sie, dass nur diese Mitwirkenden eine digitale Signatur über die offiziellen Paket-Hashes in der Veröffentlichungsdatei erstellt haben können.

Angenommen, die Signaturen der heruntergeladenen Freigabedatei sind korrekt. Sie können nun den Hash-Wert, den Sie lokal für die heruntergeladene ausführbare Windows-Datei berechnet haben, mit dem in der ordnungsgemäß signierten Freigabedatei enthaltenen Wert vergleichen. Wie Sie wissen, ist die SHA-256-Hash-Funktion kollisionssicher. Eine Übereinstimmung bedeutet, dass Ihre ausführbare Datei genau mit der offiziellen ausführbaren Datei übereinstimmt.

Wenden wir uns nun der zweiten gemeinsamen Eigenschaft von Hash-Funktionen zu: Hiding. Eine beliebige Hashfunktion H hat die Eigenschaft des Versteckens, wenn es für ein beliebiges, zufällig ausgewähltes x aus einem sehr großen Bereich nicht möglich ist, x zu finden, wenn nur H(x) gegeben ist.

Unten sehen Sie die SHA-256-Ausgabe einer von mir geschriebenen Nachricht. Um eine ausreichende Zufälligkeit zu gewährleisten, enthielt die Nachricht am Ende eine zufällig generierte Zeichenfolge. Da SHA-256 die Eigenschaft hat, sich zu verstecken, wäre niemand in der Lage, diese Nachricht zu entschlüsseln.

Aber ich werde Sie nicht im Ungewissen lassen, bis SHA-256 schwächer wird. Die ursprüngliche Nachricht, die ich schrieb, lautete wie folgt:

Hash-Funktionen mit der Eigenschaft des Versteckens werden häufig bei der Verwaltung von Passwörtern verwendet (Kollisionssicherheit ist auch für diese Anwendung wichtig). Jeder anständige kontobasierte Online-Dienst wie Facebook oder Google speichert Ihre Passwörter nicht direkt, um den Zugriff auf Ihr Konto zu verwalten. Stattdessen wird nur ein Hash des Passworts gespeichert. Jedes Mal, wenn Sie Ihr Passwort in einen Browser eingeben, wird zunächst ein Hash berechnet. Nur dieser Hash wird an den Server des Dienstanbieters gesendet und mit dem in der Backend-Datenbank gespeicherten Hash verglichen. Die Eigenschaft des Versteckens kann dazu beitragen, dass Angreifer das Passwort nicht aus dem Hash-Wert wiederherstellen können.

Die Passwortverwaltung über Hashes funktioniert natürlich nur, wenn die Benutzer tatsächlich schwierige Passwörter wählen. Die Eigenschaft des Versteckens setzt voraus, dass x zufällig aus einem sehr großen Bereich gewählt wird. Die Wahl von Passwörtern wie "1234", "mypassword" oder das Datum Ihres Geburtstags bietet keine wirkliche Sicherheit. Es gibt lange Listen mit gängigen Kennwörtern und ihren Hashes, die Angreifer ausnutzen können, wenn sie den Hash Ihres Kennworts in Erfahrung bringen. Diese Art von Angriffen wird als Wörterbuchangriff bezeichnet. Wenn Angreifer einige Ihrer persönlichen Daten kennen, könnten sie auch versuchen, diese in Kenntnis der Sachlage zu erraten. Daher brauchen Sie immer lange, sichere Passwörter (vorzugsweise lange, zufällige Zeichenfolgen aus einem Passwort-Manager).

Manchmal benötigt eine Anwendung eine Hash-Funktion, die sowohl kollisionssicher als auch versteckt ist. Aber sicherlich nicht immer. Bei dem von uns besprochenen Software-Verifizierungsverfahren ist es beispielsweise nur erforderlich, dass die Hash-Funktion kollisionssicher ist, Verstecken ist nicht wichtig.

Während Kollisionssicherheit und Verbergen die wichtigsten Eigenschaften sind, die von Hash-Funktionen in der Kryptographie verlangt werden, können in bestimmten Anwendungen auch andere Eigenschaften wünschenswert sein.

Anmerkungen:

[6] Die Terminologie des "Versteckens" ist nicht gebräuchlich, sondern stammt speziell aus Arvind Narayanan, Joseph Bonneau, Edward Felten, Andrew Miller und Steven Goldfeder, Bitcoin and Cryptocurrency Technologies, Princeton University Press (Princeton, 2016), Kapitel 1.

Das RSA-Kryptosystem

Das Factoring-Problem

Während die symmetrische Kryptographie für die meisten Menschen ziemlich intuitiv ist, ist dies bei der asymmetrischen Kryptographie in der Regel nicht der Fall. Obwohl Sie wahrscheinlich mit der allgemeinen Beschreibung in den vorangegangenen Abschnitten vertraut sind, fragen Sie sich wahrscheinlich, was genau Einwegfunktionen sind und wie genau sie verwendet werden, um asymmetrische Verfahren zu konstruieren.

In diesem Kapitel werde ich einige der Geheimnisse der asymmetrischen Kryptographie lüften, indem ich ein spezifisches Beispiel, nämlich das RSA-Kryptosystem, genauer untersuche. Im ersten Abschnitt stelle ich das Faktorisierungsproblem vor, auf dem das RSA-Problem beruht. Anschließend werden einige Schlüsselergebnisse aus der Zahlentheorie behandelt. Im letzten Abschnitt werden wir diese Informationen zusammenführen, um das RSA-Problem zu erklären und zu zeigen, wie es für die Erstellung asymmetrischer kryptografischer Systeme verwendet werden kann.

Es ist keine leichte Aufgabe, unserer Diskussion diese Tiefe zu verleihen. Sie erfordert die Einführung zahlreicher zahlentheoretischer Theoreme und Sätze. Aber lassen Sie sich von der Mathematik nicht abschrecken. Wenn Sie diese Diskussion durcharbeiten, werden Sie deutlich besser verstehen, was der asymmetrischen Kryptographie zugrunde liegt, und es ist eine lohnende Investition.

Wenden wir uns nun zunächst dem Faktorisierungsproblem zu.

Bei der Multiplikation zweier Zahlen, z. B. a und b, bezeichnet man die Zahlen a und b als Faktoren und das Ergebnis als Produkt. Der Versuch, eine Zahl N in die Multiplikation zweier oder mehrerer Faktoren zu schreiben, wird Faktorisierung oder Faktorisierung genannt. [1] Man kann jedes Problem, das dies erfordert, ein Faktorisierungsproblem nennen.

Vor etwa 2.500 Jahren entdeckte der griechische Mathematiker Euklid von Alexandria einen wichtigen Satz über die Faktorisierung ganzer Zahlen. Er wird gemeinhin als Einzelfaktorisierungssatz bezeichnet und besagt Folgendes:

Theorem 1. Jede ganze Zahl N, die größer als 1 ist, ist entweder eine Primzahl oder kann als Produkt von Primfaktoren ausgedrückt werden.

Der letzte Teil dieser Aussage bedeutet lediglich, dass man jede nicht-primzahlige ganze Zahl N, die größer als 1 ist, als Multiplikation von Primzahlen ausschreiben kann. Im Folgenden finden Sie einige Beispiele für nicht-primzahlige ganze Zahlen, die als Produkt von Primfaktoren geschrieben werden.

Für alle drei der oben genannten ganzen Zahlen ist die Berechnung ihrer Primfaktoren relativ einfach, auch wenn man nur N hat. Man beginnt mit der kleinsten Primzahl, nämlich 2, und schaut, wie oft die ganze Zahl N durch sie teilbar ist. Dann geht man dazu über, die Teilbarkeit von N durch 3, 5, 7 und so weiter zu testen. So geht es weiter, bis die ganze Zahl N nur noch als Produkt von Primzahlen geschrieben wird.

Nehmen wir zum Beispiel die ganze Zahl 84. Unten sehen Sie das Verfahren zur Bestimmung ihrer Primfaktoren. Bei jedem Schritt wird der kleinste verbleibende Primfaktor (links) herausgenommen und der zu faktorisierende Restterm bestimmt. Wir fahren fort, bis der Restterm ebenfalls eine Primzahl ist. Bei jedem Schritt wird die aktuelle Faktorisierung von 84 ganz rechts angezeigt.

Nehmen wir nun an, dass N sehr groß ist. Wie schwierig wäre es, N in seine Primfaktoren zu zerlegen?

Das hängt wirklich von N ab. Nehmen wir zum Beispiel an, dass N 50.450.400 ist. Obwohl diese Zahl einschüchternd aussieht, sind die Berechnungen nicht so kompliziert und können leicht von Hand durchgeführt werden. Wie oben beginnen Sie einfach mit 2 und arbeiten sich weiter vor. Unten sehen Sie das Ergebnis dieses Prozesses auf ähnliche Weise wie oben.

Dieses Problem von Hand zu lösen, dauert einige Zeit. Ein Computer könnte all dies natürlich in einem Bruchteil einer Sekunde erledigen. In der Tat kann ein Computer häufig sogar extrem große ganze Zahlen in einem Bruchteil einer Sekunde faktorisieren.

Es gibt jedoch einige Ausnahmen. Nehmen wir an, wir wählen zunächst zufällig zwei sehr große Primzahlen aus. Es ist üblich, diese mit p und q zu bezeichnen, und ich werde diese Konvention hier übernehmen.

Nehmen wir an, dass p und q beides 1024-Bit-Primzahlen sind, und dass sie tatsächlich mindestens 1024 Bits benötigen, um dargestellt werden zu können (das erste Bit muss also 1 sein). So kann z.B. 37 keine Primzahl sein. Man kann 37 sicherlich mit 1024 Bits darstellen. Aber offensichtlich braucht man nicht so viele Bits, um sie darzustellen. Man kann 37 durch eine beliebige Zeichenkette darstellen, die 6 Bits oder mehr hat. (In 6 Bits würde 37 als 100101 dargestellt werden).

Es ist wichtig zu wissen, wie groß p und q sind, wenn sie unter den obigen Bedingungen ausgewählt werden. Als Beispiel habe ich eine zufällige Primzahl gewählt, die mindestens 1024 Bits zur Darstellung benötigt.

Nehmen wir nun an, dass wir nach der zufälligen Auswahl der Primzahlen p und q diese multiplizieren, um eine ganze Zahl N zu erhalten. Diese letzte Zahl ist also eine 2048-Bit-Zahl, die mindestens 2048 Bits für ihre Darstellung benötigt. Sie ist viel, viel größer als p oder q.

Angenommen, man gibt einem Computer nur N und bittet ihn, die beiden 1024-Bit-Primfaktoren von N zu finden. Die Wahrscheinlichkeit, dass der Computer p und q herausfindet, ist extrem gering. Man kann sagen, dass es für alle praktischen Zwecke unmöglich ist. Das gilt selbst dann, wenn Sie einen Supercomputer oder sogar ein Netzwerk von Supercomputern einsetzen würden.

Nehmen wir an, dass der Computer versucht, das Problem zu lösen, indem er 1024 Bit-Zahlen durchläuft und jeweils prüft, ob sie Primzahlen sind und ob sie Faktoren von N sind. Die Menge der zu prüfenden Primzahlen ist dann etwa 1.265 \cdot 10^{305}. [2]

Selbst wenn man alle Computer der Welt auf diese Weise versuchen ließe, 1024-Bit-Primzahlen zu finden und zu testen, würde eine Chance von 1 zu einer Milliarde, einen Primfaktor von N zu finden, eine Rechenzeit erfordern, die viel länger ist als das Alter des Universums.

Nun kann ein Computer in der Praxis besser arbeiten als das soeben beschriebene grobe Verfahren. Es gibt mehrere Algorithmen, die der Computer anwenden kann, um schneller zu einer Faktorisierung zu kommen. Der Punkt ist jedoch, dass selbst mit diesen effizienteren Algorithmen die Aufgabe des Computers immer noch rechnerisch undurchführbar ist. [3]

Wichtig ist, dass die Schwierigkeit der Faktorisierung unter den eben beschriebenen Bedingungen auf der Annahme beruht, dass es keine rechnerisch effizienten Algorithmen zur Berechnung von Primfaktoren gibt. Wir können zwar nicht beweisen, dass ein effizienter Algorithmus nicht existiert. Dennoch ist diese Annahme sehr plausibel: Trotz umfangreicher Bemühungen über Hunderte von Jahren hinweg haben wir noch keinen solchen recheneffizienten Algorithmus gefunden.

Daher kann das Faktorisierungsproblem unter bestimmten Umständen plausibel als ein schweres Problem angenommen werden. Insbesondere, wenn p und q sehr große Primzahlen sind, ist ihr Produkt N nicht schwer zu berechnen; aber eine Faktorisierung nur bei N ist praktisch unmöglich.

Anmerkungen:

[1] Die Faktorisierung kann auch für die Arbeit mit anderen Arten von mathematischen Objekten als Zahlen wichtig sein. Zum Beispiel kann es nützlich sein, Polynomausdrücke wie x^2 - 2x + 1 zu faktorisieren. In unserer Diskussion werden wir uns nur auf die Faktorisierung von Zahlen, insbesondere von ganzen Zahlen, konzentrieren.

[2] Nach dem Primzahlentheorem ist die Anzahl der Primzahlen kleiner oder gleich N ungefähr N/\ln(N). Das bedeutet, dass man die Anzahl der Primzahlen der Länge 1024 Bits annähernd berechnen kann, indem man:

\frac{2^{1024}}{\ln(2^{1024})} - \frac{2^{1023}}{\ln(2^{1023})}

...was ungefähr 1,265 \times 10^{305} entspricht.

[3] Das Gleiche gilt für diskrete Logarithmusprobleme. Daher funktionieren asymmetrische Konstruktionen mit viel größeren Schlüsseln als symmetrische kryptografische Konstruktionen.

Zahlentheoretische Ergebnisse

Leider kann das Faktorisierungsproblem nicht direkt für asymmetrische kryptografische Verfahren verwendet werden. Wir können jedoch ein komplexeres, aber verwandtes Problem für diesen Zweck verwenden: das RSA-Problem.

Um das RSA-Problem zu verstehen, müssen wir eine Reihe von Theoremen und Sätzen aus der Zahlentheorie verstehen. Diese werden in diesem Abschnitt in drei Unterabschnitten vorgestellt: (1) die Ordnung von N, (2) die Invertierbarkeit modulo N und (3) das Eulersche Theorem.

Ein Teil des Materials in den drei Unterabschnitten wurde bereits in Kapitel 3 vorgestellt. Der Einfachheit halber werde ich dieses Material jedoch hier wiedergeben.

Die Reihenfolge von N

Eine ganze Zahl a ist Koprim oder eine relative Primzahl mit einer ganzen Zahl N, wenn der größte gemeinsame Teiler zwischen ihnen 1 ist. 1 ist zwar vereinbarungsgemäß keine Primzahl, aber sie ist ein Koprim jeder ganzen Zahl (ebenso wie -1).

Betrachten wir zum Beispiel den Fall, dass a = 18 und N = 37. Dies sind eindeutig Koprimzahlen. Die größte ganze Zahl, die sich sowohl durch 18 als auch durch 37 teilt, ist 1. Betrachten wir dagegen den Fall, dass a = 42 und N = 16. Dies sind eindeutig keine Koprimzahlen. Beide Zahlen sind durch 2 teilbar, was größer als 1 ist.

Wir können nun die Ordnung von N wie folgt definieren. Nehmen wir an, dass N eine ganze Zahl größer als 1 ist. Die Ordnung von N ist dann die Anzahl aller Koprimzahlen mit N, so dass für jede Koprimzahl a die folgende Bedingung gilt: 1 \leq a < N.

Wenn zum Beispiel N = 12, dann sind 1, 5, 7 und 11 die einzigen Primzahlen, die die obige Bedingung erfüllen. Folglich ist die Ordnung von 12 gleich 4.

Nehmen wir an, dass N eine Primzahl ist. Dann ist jede ganze Zahl, die kleiner als N, aber größer oder gleich 1 ist, koprimal zu ihr. Dazu gehören alle Elemente der folgenden Menge: \{1,2,3,....,N - 1\}. Wenn N prim ist, ist die Ordnung von N also N - 1. Dies ist in Satz 1 festgelegt, wobei \phi(N) die Ordnung von N bezeichnet.

Proposition 1. \phi(N) = N - 1 wenn N prim ist

Nehmen wir an, dass N nicht prim ist. Dann kann man seine Ordnung mit der Eulerschen Phi-Funktion berechnen. Während die Berechnung der Ordnung einer kleinen ganzen Zahl relativ einfach ist, wird die Eulersche Phi-Funktion für größere ganze Zahlen besonders wichtig. Der Satz der Eulerschen Phi-Funktion ist unten aufgeführt.

Theorem 2. Sei N gleich p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot p_i^{e_i} \cdot \ldots \cdot p_n^{e_n}, wobei die Menge \{p_i\} aus allen verschiedenen Primfaktoren von N besteht und jedes e_i angibt, wie oft der Primfaktor p_i für N vorkommt. Dann,

\phi(N) = p_1^{e_1 - 1} \cdot (p_1 - 1) \cdot p_2^{e_2 - 1} \cdot (p_2 - 1) \cdot (p_2 - 1) \cdot p_n^{e_n - 1} \cdot (p_n - 1)

Theorem 2 zeigt, dass es einfach ist, die Ordnung von N zu berechnen, wenn man jedes nicht-prime N in seine verschiedenen Primfaktoren zerlegt hat.

Nehmen wir zum Beispiel an, dass N = 270 ist. Dies ist eindeutig keine Primzahl. Zerlegt man N in seine Primfaktoren, so erhält man den Ausdruck: 2 \cdot 3^3 \cdot 5. Nach der Eulerschen Phi-Funktion ist die Ordnung von N dann wie folgt:

\phi(N) = 2^{1 - 1} \cdot (2 - 1) + 3^{3 - 1} \cdot (3 - 1) + 5^{1 - 1} \cdot (5 - 1) = 1 \cdot 1 + 9 \cdot 2 + 1 \cdot 4 = 1 + 18 + 4 = 23

Nehmen wir weiter an, dass N ein Produkt aus zwei Primzahlen p und q ist. **Der obige Satz 2 besagt dann, dass die Ordnung von N wie folgt ist:

p^{1 - 1} \cdot (p - 1) \cdot q^{1 - 1} \cdot (q - 1) = (p - 1) \cdot (q - 1)

Dies ist ein Schlüsselergebnis insbesondere für das RSA-Problem und wird in Proposition 2 unten dargelegt.

Proposition 2. Ist N das Produkt von zwei Primzahlen p und q, so ist die Ordnung von N das Produkt (p - 1) \cdot (q - 1).

Zur Veranschaulichung: Nehmen wir an, dass N = 119 ist. Diese ganze Zahl kann in zwei Primzahlen zerlegt werden, nämlich 7 und 17. Die Eulersche Phi-Funktion legt also nahe, dass die Ordnung von 119 wie folgt ist:

\phi(119) = (7 - 1) \cdot (17 - 1) = 6 \cdot 16 = 96

Mit anderen Worten: Die ganze Zahl 119 hat 96 Koprimzahlen im Bereich von 1 bis 119. Tatsächlich umfasst diese Menge alle ganzen Zahlen von 1 bis 119, die keine Vielfachen von 7 oder 17 sind.

Von nun an bezeichnen wir die Menge der Koprimzahlen, die die Ordnung von N bestimmt, als C_N. Für unser Beispiel mit N = 119 ist die Menge C_{119} viel zu groß, um sie vollständig aufzulisten. Aber einige der Elemente sind wie folgt:

C_{119} = \{1, 2, \dots, 6, 8, \dots, 13, 15, 16, 18, \dots, 33, 35, \dots, 96\}

Invertierbarkeit modulo N

Man kann sagen, dass eine ganze Zahl a invertierbar modulo N ist, wenn es mindestens eine ganze Zahl b gibt, so dass a \cdot b \mod N = 1 \mod N. Jede solche ganze Zahl b wird als Inverse (oder multiplikative Inverse) von a bei Reduktion durch modulo N bezeichnet.

Nehmen wir zum Beispiel an, dass a = 5 und N = 11. Es gibt viele ganze Zahlen, mit denen man 5 multiplizieren kann, so dass 5 \cdot b \mod 11 = 1 \mod 11. Betrachten wir zum Beispiel die ganzen Zahlen 20 und 31. Es ist leicht zu sehen, dass diese beiden ganzen Zahlen Inversionen von 5 bei der Reduktion modulo 11 sind.

Während 5 viele Inverse hat, die modulo 11 reduzieren, kann man zeigen, dass es nur eine einzige positive Inverse von 5 gibt, die kleiner als 11 ist. Tatsächlich ist dies nicht nur für unser spezielles Beispiel, sondern ein allgemeines Ergebnis.

Proposition 3. Ist die ganze Zahl a invertierbar modulo N, so muss genau eine positive Inverse von a kleiner als N sein. (Diese einzige Inverse von a muss also aus der Menge \{1, \dots, N - 1\} stammen).

Bezeichnen wir die eindeutige Inverse von a aus Proposition 3 als a^{-1}. Für den Fall, dass a = 5 und N = 11 ist, kann man sehen, dass a^{-1} = 9 ist, da 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11.

Beachten Sie, dass Sie den Wert 9 für a^{-1} in unserem Beispiel auch erhalten können, indem Sie einfach jeden anderen Kehrwert von a durch Modulo 11 reduzieren. Zum Beispiel: 20 \mod 11 = 31 \mod 11 = 9 \mod 11. Wenn also eine ganze Zahl a > N invertierbar modulo N ist, dann muss auch a \mod N invertierbar modulo N sein.

Es ist nicht notwendigerweise der Fall, dass eine Inverse von a als Reduktion modulo N existiert. Nehmen wir zum Beispiel an, dass a = 2 und N = 8 ist. Es gibt kein b, oder speziell kein a^{-1}, so dass 2 \cdot b \mod 8 = 1 \mod 8. Das liegt daran, dass jeder Wert von b immer ein Vielfaches von 2 ergibt, so dass keine Division durch 8 jemals einen Rest ergeben kann, der gleich 1 ist.

Wie genau weiß man, ob eine ganze Zahl a für ein gegebenes N eine Inverse hat? Wie Sie im obigen Beispiel vielleicht bemerkt haben, ist der größte gemeinsame Teiler zwischen 2 und 8 größer als 1, nämlich 2. Und das ist eigentlich ein Beispiel für das folgende allgemeine Ergebnis:

Proposition 4. Es gibt eine Inverse einer ganzen Zahl a bei gegebener Reduktion modulo N, und zwar eine eindeutige positive Inverse kleiner als N, wenn und nur wenn der größte gemeinsame Teiler zwischen a und N 1 ist (d.h. wenn sie Koprimzahlen sind).

Für den Fall, dass a = 5 und N = 11 ist, haben wir festgestellt, dass a^{-1} = 9 ist, da 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11. Es ist wichtig zu beachten, dass der umgekehrte Fall ebenfalls zutrifft. Das heißt, wenn a = 9 und N = 11, ist es der Fall, dass a^{-1} = 5 ist.

Eulers Theorem

Bevor wir uns dem RSA-Problem zuwenden, müssen wir ein weiteres wichtiges Theorem verstehen, nämlich das Eulersche Theorem. Er besagt Folgendes:

Theorem 3. Angenommen, zwei ganze Zahlen a und N sind Koprimzahlen. Dann ist a^{\phi(N)} \mod N = 1 \mod N.

Dies ist ein bemerkenswertes Ergebnis, das aber zunächst etwas verwirrend ist. Wenden wir uns einem Beispiel zu, um es zu verstehen.

Nehmen wir an, dass a = 5 und N = 7. Dies sind in der Tat Koprimzahlen, wie es der Eulersche Satz verlangt. Wir wissen, dass die Ordnung von 7 gleich 6 ist, da 7 eine Primzahl ist (siehe Proposition 1).

Das Eulersche Theorem besagt nun, dass 5^6 \mod 7 gleich 1 \mod 7 sein muss. Im Folgenden finden Sie die Berechnungen, die zeigen, dass dies tatsächlich der Fall ist.

Die ganze Zahl 7 teilt sich insgesamt 2.233 Mal durch 15.624. Der Rest der Division von 16.625 durch 7 ist also 1.

Mit Hilfe der Eulerschen Phi-Funktion, Theorem 2, kann man dann die Proposition 5 ableiten.

Proposition 5. \phi(a \cdot b) = \phi(a) \cdot \phi(b) für beliebige positive ganze Zahlen a und b.

Wir werden nicht zeigen, warum dies der Fall ist. Wir wollen nur darauf hinweisen, dass wir den Beweis für diesen Satz bereits gesehen haben, und zwar durch die Tatsache, dass \phi(p \cdot q) = \phi(p) \cdot \phi(q) = (p - 1) \cdot (q - 1) ist, wenn p und q Primzahlen sind, wie in Proposition 2 angegeben.

Der Satz von Euler in Verbindung mit Proposition 5 hat wichtige Auswirkungen. Sehen Sie sich an, was zum Beispiel in den folgenden Ausdrücken passiert, in denen a und N Koprimzahlen sind.

Die Kombination aus dem Euler'schen Lehrsatz und Vorschlag 5 erlaubt es uns also, eine Reihe von Ausdrücken einfach zu berechnen. Im Allgemeinen können wir die Erkenntnis wie in Proposition 6 zusammenfassen.

Proposition 6. a^x \mod N = a^{x \mod \phi(N)}

Jetzt müssen wir alles in einem letzten, kniffligen Schritt zusammenfügen.

So wie N eine Ordnung \phi(N) hat, die die Elemente der Menge C_N einschließt, wissen wir, dass die ganze Zahl \phi(N) ihrerseits auch eine Ordnung und eine Menge von Koprimzahlen haben muss. Setzen wir \phi(N) = R. Dann wissen wir, dass es auch einen Wert für \phi(R) und eine Menge von Koprimzahlen C_R gibt.

Wir wählen nun eine ganze Zahl e aus der Menge C_R. Wir wissen aus Proposition 3, dass diese ganze Zahl e nur eine einzige positive Inverse kleiner als R hat. Das heißt, e hat eine einzige Inverse aus der Menge C_R. Nennen wir diese Inverse d. Nach der Definition einer Inversen bedeutet dies, dass e \cdot d = 1 \mod R.

Wir können dieses Ergebnis nutzen, um eine Aussage über unsere ursprüngliche ganze Zahl N zu treffen. Dies ist in Proposition 7 zusammengefasst.

Proposition 7. Angenommen, e \cdot d \mod \phi(N) = 1 \mod \phi(N). Dann muss für jedes Element a der Menge C_N gelten, dass a^{e \cdot d \mod \phi(N)} = a^{1 \mod \phi(N)} = a \mod N.

Wir haben nun alle zahlentheoretischen Ergebnisse, die wir brauchen, um das RSA-Problem klar zu formulieren.

Das RSA-Kryptosystem

Wir sind nun bereit, das RSA-Problem zu formulieren. Nehmen wir an, Sie erstellen eine Menge von Variablen, bestehend aus p, q, N, \phi(N), e, d und y. Nennen Sie diese Menge \Pi. Sie wird wie folgt gebildet:

  1. Erzeuge zwei zufällige Primzahlen p und q von gleicher Größe und berechne ihr Produkt N.

  2. Berechnen Sie die Ordnung von N, \phi(N), durch das folgende Produkt: (p - 1) \cdot (q - 1).

  3. Wählen Sie ein e > 2 so, dass es kleiner und koprim zu \phi(N) ist.

  4. Berechnen Sie d, indem Sie e \cdot d \mod \phi(N) = 1 setzen.

  5. Wählen Sie einen Zufallswert y, der kleiner und koprimal zu N ist.

Das RSA-Problem besteht darin, ein x so zu finden, dass x^e = y ist, wobei nur eine Teilmenge der Informationen über \Pi, nämlich die Variablen N, e und y, gegeben ist. Wenn p und q sehr groß sind, typischerweise wird empfohlen, dass sie 1024 Bit groß sind, gilt das RSA-Problem als schwierig. Sie können jetzt sehen, warum dies der Fall ist, wenn man die vorangegangene Diskussion betrachtet.

Ein einfacher Weg, x zu berechnen, wenn x^e \mod N = y \mod N ist, ist die Berechnung von y^d \mod N. Wir wissen durch die folgenden Berechnungen, dass y^d \mod N = x \mod N ist:

y^d \mod N = x^{e \cdot d} \mod N = x^{e \cdot d \mod \phi(N)} \mod N = x^{1 \mod \phi(N)} \mod N = x \mod N.

Das Problem ist, dass wir den Wert d nicht kennen, da er in der Aufgabe nicht angegeben ist. Daher können wir y^d \mod N nicht direkt berechnen, um x \mod N zu erzeugen.

Wir könnten jedoch d indirekt aus der Ordnung von N, \phi(N), berechnen, da wir wissen, dass e \cdot d \mod \phi(N) = 1 \mod \phi(N). Aber auch für \phi(N) gibt das Problem keinen Wert vor.

Schließlich könnte die Ordnung indirekt mit den Primfaktoren p und q berechnet werden, so dass wir schließlich d berechnen können. Allerdings wurden uns die Werte p und q auch nicht zur Verfügung gestellt.

Selbst wenn das Faktorisierungsproblem innerhalb eines RSA-Problems schwer ist, können wir streng genommen nicht beweisen, dass das RSA-Problem ebenfalls schwer ist. Es kann nämlich andere Wege geben, das RSA-Problem zu lösen als durch Faktorisierung. Es wird jedoch allgemein akzeptiert und angenommen, dass, wenn das Faktorisierungsproblem innerhalb des RSA-Problems schwer ist, auch das RSA-Problem selbst schwer ist.

Wenn das RSA-Problem tatsächlich schwer ist, dann ergibt es eine Einwegfunktion mit einer Falltür. Die Funktion ist hier f(g) = g^e \mod N. Mit der Kenntnis von f(g) könnte jeder leicht einen Wert y für ein bestimmtes g = x berechnen. Es ist jedoch praktisch unmöglich, einen bestimmten Wert x zu berechnen, nur weil man den Wert y und die Funktion f(g) kennt. Die Ausnahme ist, wenn man eine Information d, die Falltür, erhält. In diesem Fall kann man einfach y^d berechnen, um x zu erhalten.

Gehen wir ein konkretes Beispiel durch, um das RSA-Problem zu veranschaulichen. Ich kann kein RSA-Problem auswählen, das unter den oben genannten Bedingungen als schwer gelten würde, da die Zahlen unhandlich wären. Stattdessen soll dieses Beispiel nur veranschaulichen, wie das RSA-Problem im Allgemeinen funktioniert.

Nehmen wir an, Sie wählen zwei zufällige Primzahlen 13 und 31. Also p = 13 und q = 31. Das Produkt N dieser beiden Primzahlen ist gleich 403. Wir können die Ordnung von 403 leicht berechnen. Sie ist äquivalent zu (13 - 1) \cdot (31 - 1) = 360.

Als Nächstes müssen wir, wie in Schritt 3 des RSA-Problems vorgeschrieben, einen Koprimus für 360 auswählen, der größer als 2 und kleiner als 360 ist. Wir müssen diesen Wert nicht zufällig wählen. Nehmen wir an, wir wählen 103. Dies ist ein Koprimus von 360, da sein größter gemeinsamer Teiler mit 103 gleich 1 ist.

Schritt 4 erfordert nun, dass wir einen Wert d berechnen, der so beschaffen ist, dass 103 \cdot d \mod 360 = 1. Dies ist keine einfache Aufgabe, wenn der Wert für N groß ist. Dazu müssen wir ein Verfahren verwenden, das erweiterter euklidischer Algorithmus genannt wird.

Obwohl ich das Verfahren hier nicht zeige, ergibt es den Wert 7, wenn e = 103. Dass das Wertepaar 103 und 7 tatsächlich die allgemeine Bedingung e \cdot d \mod \phi(n) = 1 erfüllt, können Sie anhand der folgenden Berechnungen überprüfen.

Wichtig ist, dass wir aufgrund von Proposition 4 wissen, dass keine andere ganze Zahl zwischen 1 und 360 für d das Ergebnis liefert, dass 103 \cdot d = 1 \mod 360. Außerdem impliziert der Satz, dass die Wahl eines anderen Wertes für e einen anderen eindeutigen Wert für d ergibt.

In Schritt 5 des RSA-Problems müssen wir eine positive ganze Zahl y wählen, die ein kleinerer Koprimus von 403 ist. Nehmen wir an, wir setzen y = 2^{103}. Die Potenzierung von 2 durch 103 ergibt das folgende Ergebnis.

Das RSA-Problem in diesem speziellen Beispiel lautet nun wie folgt: Sie haben N = 403, e = 103 und y = 349 \mod 403. Sie müssen nun x so berechnen, dass x^{103} = 349 \mod 403. Das heißt, Sie müssen herausfinden, dass der ursprüngliche Wert vor der Potenzierung durch 103 2 war.

Es wäre (zumindest für einen Computer) einfach, x zu berechnen, wenn wir wüssten, dass d = 7 ist. In diesem Fall könnte man x einfach wie folgt bestimmen.

Das Problem ist, dass Sie nicht die Information erhalten haben, dass d = 7 ist. Sie könnten natürlich d aus der Tatsache berechnen, dass 103 \cdot d = 1 \mod 360. Das Problem ist, dass man auch nicht die Information hat, dass die Ordnung von N = 360 ist. Schließlich könnte man auch die Ordnung von 403 berechnen, indem man das folgende Produkt berechnet: (p - 1) \cdot (q - 1). Aber auch hier wird nicht gesagt, dass p = 13 und q = 31 ist.

Natürlich könnte ein Computer das RSA-Problem für dieses Beispiel noch relativ leicht lösen, weil die beteiligten Primzahlen nicht groß sind. Aber wenn die Primzahlen sehr groß werden, steht er vor einer praktisch unlösbaren Aufgabe.

Wir haben nun das RSA-Problem, eine Reihe von Bedingungen, unter denen es schwierig ist, und die zugrunde liegende Mathematik vorgestellt. Wie hilft das alles bei der asymmetrischen Kryptographie? Wie können wir insbesondere die Schwierigkeit des RSA-Problems unter bestimmten Bedingungen in ein Verschlüsselungsverfahren oder ein digitales Signaturverfahren umsetzen?

Ein Ansatz besteht darin, das RSA-Problem zu nehmen und auf unkomplizierte Weise Schemata zu entwickeln. Nehmen wir zum Beispiel an, dass Sie einen Satz von Variablen \Pi wie im RSA-Problem beschrieben erzeugt haben und sicherstellen, dass p und q ausreichend groß sind. Sie setzen Ihren öffentlichen Schlüssel gleich (N, e) und teilen diese Information mit der Welt. Wie oben beschrieben, halten Sie die Werte für p, q, \phi(n) und d geheim. In der Tat ist d Ihr privater Schlüssel.

Jeder, der Ihnen eine Nachricht m schicken will, die ein Element von C_N ist, könnte sie einfach wie folgt verschlüsseln: c = m^e \mod N. (Der Chiffretext c entspricht hier dem Wert y aus dem RSA-Problem.) Sie können diese Nachricht leicht entschlüsseln, indem Sie einfach c^d \mod N berechnen.

Auf die gleiche Weise könnte man versuchen, ein digitales Signaturschema zu erstellen. Angenommen, Sie wollen jemandem eine Nachricht m mit einer digitalen Signatur S schicken. Sie könnten einfach S = m^d \mod N setzen und das Paar (m,S) an den Empfänger senden. Jeder kann die digitale Signatur verifizieren, indem er einfach prüft, ob S^e \mod N = m \mod N ist. Ein Angreifer hätte es jedoch sehr schwer, ein gültiges S für eine Nachricht zu erstellen, da er nicht im Besitz von d ist.

Leider ist es nicht so einfach, ein an sich schwieriges Problem, das RSA-Problem, in ein kryptographisches Schema umzuwandeln. Bei einem einfachen Verschlüsselungsschema kann man nur Koprimzahlen von N als Nachrichten auswählen. Damit bleiben nicht viele mögliche Nachrichten übrig, jedenfalls nicht genug für eine Standardkommunikation. Außerdem müssen diese Nachrichten zufällig ausgewählt werden. Das erscheint etwas unpraktisch. Schließlich wird jede Nachricht, die zweimal ausgewählt wird, genau den gleichen Chiffretext ergeben. Dies ist in jedem Verschlüsselungsverfahren äußerst unerwünscht und entspricht nicht den strengen modernen Standardvorstellungen von Sicherheit in der Verschlüsselung.

Die Probleme werden für unser einfaches digitales Unterschriftsverfahren noch größer. So wie es aussieht, kann jeder Angreifer digitale Signaturen leicht fälschen, indem er zunächst einen Koprimus von N als Signatur wählt und dann die entsprechende Originalnachricht berechnet. Dies verstößt eindeutig gegen die Anforderung der existenziellen Unfälschbarkeit.

Dennoch kann das RSA-Problem mit ein wenig cleverer Komplexität verwendet werden, um ein sicheres Verschlüsselungsverfahren mit öffentlichem Schlüssel sowie ein sicheres digitales Signaturverfahren zu schaffen. Wir werden hier nicht auf die Details solcher Konstruktionen eingehen. [4] Wichtig ist jedoch, dass diese zusätzliche Komplexität nichts an dem grundlegenden RSA-Problem ändert, auf dem diese Verfahren beruhen.

Anmerkungen:

[4] Siehe z. B. Jonathan Katz und Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), S. 410-32 zur RSA-Verschlüsselung und S. 444-41 für digitale RSA-Signaturen.

Abschließender Abschnitt

Bewertung & Beurteilung

366d6fd0-ceb2-4299-bf37-8c6dfcb681d5 true

Abschlussprüfung

44882d2b-63cd-4fde-8485-f76f14d8b2fe true

Schlussfolgerung

f1905f78-8cf7-5031-949a-dfa8b76079b4 true