name: Die inneren Mechanismen von Bitcoin-Wallets goal: Tauchen Sie ein in die kryptografischen Prinzipien, die Bitcoin-Wallets antreiben. objectives:
- Definieren Sie die theoretischen Konzepte, die für das Verständnis der in Bitcoin verwendeten kryptografischen Algorithmen notwendig sind.
- Verstehen Sie vollständig den Aufbau einer deterministischen und hierarchischen Wallet.
- Wissen, wie man die mit der Verwaltung einer Wallet verbundenen Risiken identifiziert und reduziert.
- Verstehen Sie die Prinzipien von Hash-Funktionen, kryptografischen Schlüsseln und digitalen Signaturen.
Eine Reise ins Herz der Bitcoin-Wallets
Entdecken Sie die Geheimnisse deterministischer und hierarchischer Bitcoin-Wallets mit unserem CYP201-Kurs! Egal, ob Sie ein regelmäßiger Nutzer sind oder ein Enthusiast, der sein Wissen vertiefen möchte, dieser Kurs bietet eine vollständige Eintauchung in die Funktionsweise dieser Werkzeuge, die wir alle täglich nutzen.
Lernen Sie die Mechanismen von Hash-Funktionen, digitalen Signaturen (ECDSA und Schnorr), mnemonischen Phrasen, kryptografischen Schlüsseln und die Erstellung von Empfangsadressen kennen, während Sie fortgeschrittene Sicherheitsstrategien erkunden.
Dieses Training wird Sie nicht nur mit dem Wissen ausstatten, um die Struktur einer Bitcoin-Wallet zu verstehen, sondern wird Sie auch darauf vorbereiten, tiefer in die aufregende Welt der Kryptografie einzutauchen.
Mit klarer Pädagogik, über 60 erläuternden Diagrammen und konkreten Beispielen wird CYP201 es Ihnen ermöglichen, von A bis Z zu verstehen, wie Ihre Wallet funktioniert, sodass Sie das Bitcoin-Universum mit Vertrauen navigieren können. Nehmen Sie heute die Kontrolle über Ihre UTXOs, indem Sie verstehen, wie HD-Wallets funktionieren!
Einführung
Kurseinführung
Willkommen zum CYP201-Kurs, in dem wir die Funktionsweise von HD Bitcoin-Wallets ausführlich erkunden werden. Dieser Kurs ist für jeden gedacht, der die technischen Grundlagen der Nutzung von Bitcoin verstehen möchte, egal ob es sich um Gelegenheitsnutzer, aufgeklärte Enthusiasten oder zukünftige Experten handelt.
Das Ziel dieses Trainings ist es, Ihnen die Schlüssel zu geben, um die Werkzeuge, die Sie täglich verwenden, zu beherrschen. HD Bitcoin-Wallets, die im Mittelpunkt Ihrer Benutzererfahrung stehen, basieren auf manchmal komplexen Konzepten, die wir zugänglich machen werden. Gemeinsam werden wir sie entmystifizieren!
Bevor wir in die Details des Aufbaus und der Funktionsweise von
Bitcoin-Wallets eintauchen, beginnen wir mit einigen Kapiteln über die
kryptografischen Grundlagen, die für das Folgende zu wissen sind. Wir
beginnen mit kryptografischen Hash-Funktionen, die sowohl für Wallets als
auch für das Bitcoin-Protokoll selbst grundlegend sind. Sie werden ihre
Hauptmerkmale entdecken, die spezifischen Funktionen, die in Bitcoin
verwendet werden, und in einem technischeren Kapitel werden Sie im Detail
über die Funktionsweise der Königin der Hash-Funktionen lernen: SHA256. 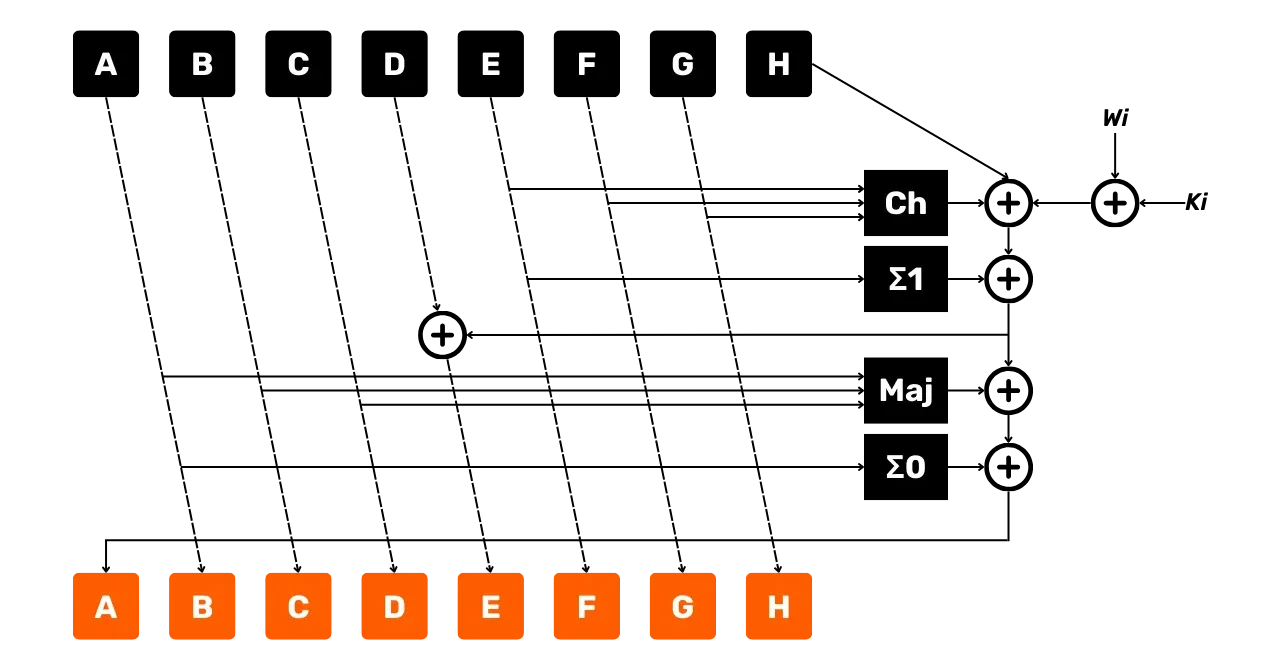
Als Nächstes werden wir die Funktionsweise von digitalen Signaturalgorithmen besprechen, die Sie jeden Tag verwenden, um Ihre UTXOs zu sichern. Bitcoin verwendet zwei: ECDSA und das Schnorr-Protokoll. Sie werden erfahren, welche mathematischen Grundlagen diesen Algorithmen zugrunde liegen und wie sie die Sicherheit von Transaktionen gewährleisten.
Sobald wir ein gutes Verständnis dieser Elemente der Kryptografie haben, werden wir schließlich zum Kern des Trainings übergehen: deterministische und hierarchische Wallets! Zuerst gibt es einen Abschnitt, der den mnemonischen Phrasen gewidmet ist, diesen Sequenzen von 12 oder 24 Wörtern, die es Ihnen ermöglichen, Ihre Wallets zu erstellen und wiederherzustellen. Sie werden entdecken, wie diese Wörter aus einer Quelle der Entropie generiert werden und wie sie die Nutzung von Bitcoin erleichtern.
 Das Training wird mit dem Studium des BIP39-Passphrases, des Seeds (nicht zu
verwechseln mit der mnemonischen Phrase), des Master Chain Codes und des Master-Schlüssels
fortgesetzt. Wir werden im Detail sehen, was diese Elemente sind, ihre jeweiligen
Rollen und wie sie berechnet werden.
Das Training wird mit dem Studium des BIP39-Passphrases, des Seeds (nicht zu
verwechseln mit der mnemonischen Phrase), des Master Chain Codes und des Master-Schlüssels
fortgesetzt. Wir werden im Detail sehen, was diese Elemente sind, ihre jeweiligen
Rollen und wie sie berechnet werden. 
Schließlich werden wir vom Master-Schlüssel aus entdecken, wie kryptografische Schlüsselpaare auf eine deterministische und hierarchische Weise bis zu den Empfangsadressen abgeleitet werden.

Dieses Training wird es Ihnen ermöglichen, Ihre Wallet-Software mit Vertrauen zu nutzen, während Sie Ihre Fähigkeiten verbessern, Risiken zu identifizieren und zu mindern. Bereiten Sie sich darauf vor, ein wahrer Experte für Bitcoin-Wallets zu werden!
Hash-Funktionen
Einführung in Hash-Funktionen
Die erste Art von kryptografischen Algorithmen, die bei Bitcoin verwendet werden, umfasst Hash-Funktionen. Sie spielen eine wesentliche Rolle auf verschiedenen Ebenen des Protokolls, aber auch innerhalb von Bitcoin-Wallets. Lassen Sie uns gemeinsam entdecken, was eine Hash-Funktion ist und wofür sie bei Bitcoin verwendet wird.
Definition und Prinzip des Hashings
Hashing ist ein Prozess, der Informationen beliebiger Länge in ein anderes Stück Information fester Länge durch eine kryptografische Hash-Funktion transformiert. Mit anderen Worten, eine Hash-Funktion nimmt eine Eingabe beliebiger Größe und wandelt sie in einen Fingerabdruck fester Größe um, der als "Hash" bezeichnet wird. Der Hash kann manchmal auch als "Digest", "Kondensat", "verdichtet" oder "gehasht" bezeichnet werden.
Zum Beispiel erzeugt die SHA256-Hash-Funktion einen Hash fester Länge von 256 Bit. Wenn wir also die Eingabe "PlanB", eine Nachricht beliebiger Länge, verwenden, wird der erzeugte Hash der folgende 256-Bit-Fingerabdruck sein:
24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688

Eigenschaften von Hash-Funktionen
Diese kryptografischen Hash-Funktionen haben mehrere wesentliche Eigenschaften, die sie besonders nützlich im Kontext von Bitcoin und anderen Computersystemen machen:
- Unumkehrbarkeit (oder Preimage-Resistenz)
- Manipulationssicherheit (Lawineneffekt)
- Kollisionsresistenz
- Zweite Preimage-Resistenz
1. Unumkehrbarkeit (Preimage-Resistenz):
Unumkehrbarkeit bedeutet, dass es einfach ist, den Hash aus der Eingabeinformation zu berechnen, aber die umgekehrte Berechnung, also das Auffinden der Eingabe aus dem Hash, praktisch unmöglich ist. Diese Eigenschaft macht Hash-Funktionen perfekt für die Erstellung einzigartiger digitaler Fingerabdrücke, ohne die ursprünglichen Informationen zu gefährden.
Im gegebenen Beispiel ist es einfach und schnell, den Hash 24f1b9… zu erhalten, wenn man die Eingabe "PlanB" kennt. Jedoch ist es
unmöglich, die Nachricht "PlanB" zu finden, wenn man nur 24f1b9… kennt.

Daher ist es unmöglich, ein Preimage m für einen Hash h zu finden,
so dass h = \text{HASH}(m),
wobei \text{HASH} eine
kryptografische Hash-Funktion ist.
2. Manipulationssicherheit (Lawineneffekt)
Das zweite Merkmal ist die Manipulationssicherheit, auch bekannt als der Lawineneffekt. Dieses Merkmal wird bei einer Hash-Funktion beobachtet, wenn eine kleine Änderung in der Eingangsnachricht eine radikale Änderung im Ausgabe-Hash bewirkt. Wenn wir zu unserem Beispiel mit der Eingabe "PlanB" und der SHA256-Funktion zurückkehren, haben wir gesehen, dass der generierte Hash wie folgt ist:
24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688
Wenn wir eine sehr geringfügige Änderung an der Eingabe vornehmen, indem wir dieses Mal "Planb" verwenden, dann ändert das einfache Wechseln von einem Großbuchstaben "B" zu einem Kleinbuchstaben "b" den SHA256-Ausgabe-Hash komplett:
bb038b4503ac5d90e1205788b00f8f314583c5e22f72bec84b8735ba5a36df3f

Diese Eigenschaft stellt sicher, dass selbst eine geringfügige Änderung der ursprünglichen Nachricht sofort erkennbar ist, da sich nicht nur ein kleiner Teil des Hashs ändert, sondern der gesamte Hash. Dies kann in verschiedenen Bereichen von Interesse sein, um die Integrität von Nachrichten, Software oder sogar Bitcoin-Transaktionen zu überprüfen.
3. Kollisionsresistenz
Das dritte Merkmal ist die Kollisionsresistenz. Eine Hash-Funktion ist
kollisionsresistent, wenn es rechnerisch unmöglich ist, 2 verschiedene
Nachrichten zu finden, die denselben Hash-Ausgang von der Funktion
produzieren. Formal ist es schwierig, zwei unterschiedliche Nachrichten m_1 und m_2 zu finden, so dass:
\text{HASH}(m_1) = \text{HASH}(m_2)
In der Realität ist es mathematisch unvermeidlich, dass Kollisionen für
Hash-Funktionen existieren, da die Größe der Eingaben größer sein kann als
die Größe der Ausgaben. Dies ist bekannt als das
Dirichlet-Schubladenprinzip: Wenn n Objekte in m Schubladen
verteilt werden, mit m < n, dann wird
mindestens eine Schublade notwendigerweise zwei oder mehr Objekte enthalten.
Für eine Hash-Funktion gilt dieses Prinzip, weil die Anzahl der möglichen
Nachrichten (fast) unendlich ist, während die Anzahl der möglichen Hashes
endlich ist (2^{256} im Fall von SHA256).
Daher bedeutet dieses Merkmal nicht, dass es keine Kollisionen für
Hash-Funktionen gibt, sondern dass eine gute Hash-Funktion die
Wahrscheinlichkeit, eine Kollision zu finden, vernachlässigbar macht. Dieses
Merkmal wird beispielsweise bei den SHA-0 und SHA-1 Algorithmen, den
Vorgängern von SHA-2, nicht mehr verifiziert, da für diese Kollisionen
gefunden wurden. Diese Funktionen werden daher nun abgeraten und oft als
veraltet betrachtet. Für eine Hash-Funktion von n Bits ist die Kollisionsresistenz in der Größenordnung von 2^{\frac{n}{2}}, in Übereinstimmung mit dem Geburtstagsangriff. Zum Beispiel, für SHA256 (n = 256), ist die Komplexität, eine Kollision zu finden, in der Größenordnung von 2^{128} Versuchen. Praktisch bedeutet dies, dass wenn man 2^{128} verschiedene
Nachrichten durch die Funktion laufen lässt, man wahrscheinlich eine Kollision
finden wird.
4. Resistenz gegen Second Preimage
Die Resistenz gegen Second Preimage ist ein weiteres wichtiges Merkmal von
Hash-Funktionen. Es besagt, dass es rechnerisch unpraktikabel ist, gegeben
eine Nachricht m_1 und ihren
Hash h, eine andere Nachricht m_2 \neq m_1 zu finden, so dass:
\text{HASH}(m_1) = \text{HASH}(m_2)Daher ist die Resistenz gegen Second Preimage in gewisser Weise ähnlich zur
Kollisionsresistenz, außer hier ist der Angriff schwieriger, weil der
Angreifer m_1 nicht frei wählen
kann.

Anwendungen von Hash-Funktionen in Bitcoin
Die am häufigsten verwendete Hash-Funktion in Bitcoin ist SHA256 ("Secure Hash Algorithm 256 bits"). Entwickelt Anfang der 2000er Jahre vom NSA und standardisiert durch das NIST, erzeugt sie einen 256-Bit-Hash-Ausgang.
Diese Funktion wird in vielen Aspekten von Bitcoin verwendet. Auf Protokollebene ist sie am Proof-of-Work-Mechanismus beteiligt, wo sie in einer doppelten Hashing-Prozedur angewendet wird, um eine partielle Kollision zwischen dem Header eines Kandidatenblocks, der von einem Miner erstellt wurde, und dem Schwierigkeitsziel zu suchen. Wenn diese partielle Kollision gefunden wird, wird der Kandidatenblock gültig und kann zur Blockchain hinzugefügt werden.
SHA256 wird auch beim Aufbau eines Merkle-Baums verwendet, der insbesondere der Akkumulator ist, der für die Aufzeichnung von Transaktionen in Blöcken verwendet wird. Diese Struktur findet sich auch im Utreexo-Protokoll, das die Größe des UTXO-Sets reduziert. Zusätzlich wird mit der Einführung von Taproot im Jahr 2021 SHA256 im MAST (Merkelised Alternative Script Tree) ausgenutzt, der es ermöglicht, nur die tatsächlich in einem Skript verwendeten Ausgabebedingungen zu offenbaren, ohne die anderen möglichen Optionen offenzulegen. Es wird auch bei der Berechnung von Transaktionsidentifikatoren, bei der Übertragung von Paketen über das P2P-Netzwerk, bei elektronischen Signaturen... verwendet. Schließlich, und das ist in dieser Schulung von besonderem Interesse, wird SHA256 auf Anwendungsebene für den Aufbau von Bitcoin-Wallets und die Ableitung von Adressen verwendet.
Meistens, wenn man in Bitcoin auf die Verwendung von SHA256 stößt, wird es tatsächlich ein doppelter Hash SHA256 sein, notiert als "HASH256", der einfach darin besteht, SHA256 zweimal hintereinander anzuwenden:
\text{HASH256}(m) = \text{SHA256}(\text{SHA256}(m))Diese Praxis des doppelten Hashings fügt eine zusätzliche Sicherheitsebene gegen bestimmte potenzielle Angriffe hinzu, obwohl ein einzelnes SHA256 heute als kryptografisch sicher gilt.
Eine weitere in der Script-Sprache verfügbare Hash-Funktion, die für die Ableitung von Empfangsadressen verwendet wird, ist die RIPEMD160-Funktion. Diese Funktion erzeugt einen 160-Bit-Hash (also kürzer als SHA256). Sie wird in der Regel mit SHA256 kombiniert, um die HASH160-Funktion zu bilden:
\text{HASH160}(m) = \text{RIPEMD160}(\text{SHA256}(m))Diese Kombination wird verwendet, um kürzere Hashes zu erzeugen, insbesondere bei der Erstellung bestimmter Bitcoin-Adressen, die Hashes von Schlüsseln oder Skript-Hashes darstellen, sowie zur Erzeugung von Schlüsselfingerabdrücken.
Schließlich wird auf Anwendungsebene manchmal auch die SHA512-Funktion verwendet, die indirekt eine Rolle bei der Schlüsselableitung für Wallets spielt. Diese Funktion ist in ihrer Arbeitsweise SHA256 sehr ähnlich; beide gehören zur gleichen SHA2-Familie, aber SHA512 erzeugt, wie der Name schon sagt, einen 512-Bit-Hash, verglichen mit 256 Bits für SHA256. Wir werden ihre Verwendung in den folgenden Kapiteln detailliert beschreiben.
Sie kennen nun die wesentlichen Grundlagen über Hash-Funktionen für das Folgende. Im nächsten Kapitel schlage ich vor, die Funktionsweise der Funktion, die im Herzen von Bitcoin steht: SHA256, detaillierter zu entdecken. Wir werden sie analysieren, um zu verstehen, wie sie die hier beschriebenen Eigenschaften erreicht. Das nächste Kapitel ist ziemlich lang und technisch, aber es ist nicht wesentlich, um dem Rest der Schulung zu folgen. Wenn Sie also Schwierigkeiten haben, es zu verstehen, machen Sie sich keine Sorgen und gehen Sie direkt zum folgenden Kapitel über, das viel zugänglicher sein wird.
Die Funktionsweise von SHA256
905eb320-f15b-5fb6-8d2d-5bb447337deb Wir haben zuvor gesehen, dass Hashing-Funktionen wichtige Eigenschaften besitzen, die ihren Einsatz bei Bitcoin rechtfertigen. Lassen Sie uns nun die internen Mechanismen dieser Hashing-Funktionen untersuchen, die ihnen diese Eigenschaften verleihen, und dazu schlage ich vor, die Funktionsweise von SHA256 zu analysieren.
Die Funktionen SHA256 und SHA512 gehören zur gleichen SHA2-Familie. Ihr Mechanismus basiert auf einer spezifischen Konstruktion, der Merkle-Damgård-Konstruktion. RIPEMD160 verwendet ebenfalls diesen Typ von Konstruktion.
Zur Erinnerung: Wir haben eine Nachricht beliebiger Größe als Eingabe für SHA256, und wir werden sie durch die Funktion leiten, um einen 256-Bit-Hash als Ausgabe zu erhalten.
Vorverarbeitung der Eingabe
Zu Beginn müssen wir unsere Eingabenachricht m so vorbereiten, dass sie eine standardisierte Länge hat, die ein Vielfaches
von 512 Bits ist. Dieser Schritt ist entscheidend für das ordnungsgemäße
Funktionieren des Algorithmus im weiteren Verlauf. Dazu beginnen wir mit dem
Schritt der Padding-Bits. Wir fügen zuerst ein Trennbit 1 zur
Nachricht hinzu, gefolgt von einer bestimmten Anzahl von 0 Bits. Die Anzahl der hinzugefügten 0 Bits wird so berechnet,
dass die Gesamtlänge der Nachricht nach dieser Ergänzung kongruent zu 448
modulo 512 ist. Somit ist die Länge L der Nachricht mit den Padding-Bits
gleich:
L \equiv 448 \mod 512\text{mod}, für
modulo, ist eine mathematische Operation, die zwischen zwei Ganzzahlen den
Rest der euklidischen Division des Ersten durch den Zweiten zurückgibt. Zum
Beispiel: 16 \mod 5 = 1. Es
ist eine Operation, die in der Kryptographie weit verbreitet ist.
Hier stellt der Padding-Schritt sicher, dass nach dem Hinzufügen der 64 Bits
im nächsten Schritt die Gesamtlänge der angeglichenen Nachricht ein
Vielfaches von 512 Bits sein wird. Wenn die ursprüngliche Nachricht eine
Länge von M Bits hat, ist die
Anzahl (N) der
hinzuzufügenden 0 Bits also:
N = (448 - (M + 1) \mod 512) \mod 512Zum Beispiel, wenn die ursprüngliche Nachricht 950 Bits lang ist, wäre die Berechnung wie folgt:
\begin{align*}
M & = 950 \\
M + 1 & = 951 \\
(M + 1) \mod 512 & = 951 \mod 512 \\
& = 951 - 512 \cdot \left\lfloor \frac{951}{512} \right\rfloor \\
& = 951 - 512 \cdot 1 \\
& = 951 - 512 \\
& = 439 \\
\\
448 - (M + 1) \mod 512 & = 448 - 439 \\
& = 9 \\
\\
N & = (448 - (M + 1) \mod 512) \mod 512 \\
N & = 9 \mod 512 \\
& = 9
\end{align*}Somit hätten wir 9 0en zusätzlich zum Trennbit 1.
Unsere direkt nach unserer Nachricht M hinzuzufügenden Padding-Bits
wären also:
1000 0000 00
Nachdem wir die Padding-Bits zu unserer Nachricht M hinzugefügt haben, fügen wir auch eine 64-Bit-Darstellung der ursprünglichen
Länge der Nachricht M hinzu,
ausgedrückt in Binär. Dies ermöglicht es der Hash-Funktion, empfindlich auf
die Bitreihenfolge und die Länge der Nachricht zu reagieren. Wenn wir zu
unserem Beispiel mit einer anfänglichen Nachricht von 950 Bits zurückkehren,
konvertieren wir die Dezimalzahl 950 in Binär, was uns 1110 1101 10 ergibt. Wir ergänzen diese Zahl an der Basis mit Nullen,
um insgesamt 64 Bits zu erhalten. In unserem Beispiel ergibt das:
0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0011 1011 0110
Diese Padding-Größe wird nach dem Bit-Padding hinzugefügt. Daher besteht die Nachricht nach unserer Vorverarbeitung aus drei Teilen:
- Die ursprüngliche Nachricht
M; - Ein Bit
1gefolgt von mehreren Bits0, um das Bit-Padding zu bilden; - Eine 64-Bit-Darstellung der Länge von
M, um das Padding mit der Größe zu bilden.

Initialisierung der Variablen
SHA256 verwendet acht Anfangszustandsvariablen, bezeichnet mit A bis H, jede mit 32 Bits.
Diese Variablen werden mit spezifischen Konstanten initialisiert, die die
Bruchteile der Quadratwurzeln der ersten acht Primzahlen sind. Wir werden
diese Werte im Laufe des Hashing-Prozesses verwenden:
A = 0x6a09e667B = 0xbb67ae85C = 0x3c6ef372D = 0xa54ff53aE = 0x510e527fF = 0x9b05688cG = 0x1f83d9abH = 0x5be0cd19
SHA256 verwendet auch 64 andere Konstanten, bezeichnet mit K_0 bis K_{63}, die die
Bruchteile der Kubikwurzeln der ersten 64 Primzahlen sind:
K[0 \ldots 63] = \begin{pmatrix}
0x428a2f98, & 0x71374491, & 0xb5c0fbcf, & 0xe9b5dba5, \\
0x3956c25b, & 0x59f111f1, & 0x923f82a4, & 0xab1c5ed5, \\
0xd807aa98, & 0x12835b01, & 0x243185be, & 0x550c7dc3, \\
0x72be5d74, & 0x80deb1fe, & 0x9bdc06a7, & 0xc19bf174, \\
0xe49b69c1, & 0xefbe4786, & 0x0fc19dc6, & 0x240ca1cc, \\
0x2de92c6f, & 0x4a7484aa, & 0x5cb0a9dc, & 0x76f988da, \\
0x983e5152, & 0xa831c66d, & 0xb00327c8, & 0xbf597fc7, \\
0xc6e00bf3, & 0xd5a79147, & 0x06ca6351, & 0x14292967, \\
0x27b70a85, & 0x2e1b2138, & 0x4d2c6dfc, & 0x53380d13, \\
0x650a7354, & 0x766a0abb, & 0x81c2c92e, & 0x92722c85, \\
0xa2bfe8a1, & 0xa81a664b, & 0xc24b8b70, & 0xc76c51a3, \\
0xd192e819, & 0xd6990624, & 0xf40e3585, & 0x106aa070, \\
0x19a4c116, & 0x1e376c08, & 0x2748774c, & 0x34b0bcb5, \\
0x391c0cb3, & 0x4ed8aa4a, & 0x5b9cca4f, & 0x682e6ff3, \\
0x748f82ee, & 0x78a5636f, & 0x84c87814, & 0x8cc70208, \\
0x90befffa, & 0xa4506ceb, & 0xbef9a3f7, & 0xc67178f2
\end{pmatrix}Aufteilung der Eingabe
Nachdem wir nun eine ausgeglichene Eingabe haben, werden wir nun zur Hauptverarbeitungsphase des SHA256-Algorithmus übergehen: die Kompressionsfunktion. Dieser Schritt ist sehr wichtig, da er hauptsächlich die kryptografischen Eigenschaften der Hash-Funktion verleiht, die wir im vorherigen Kapitel untersucht haben.
Zuerst beginnen wir damit, unsere ausgeglichene Nachricht (Ergebnis der
Vorverarbeitungsschritte) in mehrere Blöcke P von jeweils 512 Bits aufzuteilen. Wenn unsere ausgeglichene Nachricht eine
Gesamtgröße von n \times 512 Bits hat, werden wir daher n Blöcke haben, jeder davon mit 512 Bits. Jeder 512-Bit-Block wird einzeln von
der Kompressionsfunktion verarbeitet, die aus 64 Runden aufeinanderfolgender
Operationen besteht. Nennen wir diese Blöcke P_1, P_2, P_3...
Logische Operationen
Bevor wir die Kompressionsfunktion im Detail erkunden, ist es wichtig, die grundlegenden logischen Operationen zu verstehen, die darin verwendet werden. Diese Operationen, basierend auf der Booleschen Algebra, arbeiten auf Bit-Ebene. Die grundlegenden logischen Operationen, die verwendet werden, sind:
- Konjunktion (UND): bezeichnet mit
\land, entspricht einem logischen "UND". - Disjunktion (ODER): bezeichnet mit
\lor, entspricht einem logischen "ODER". - Negation (NICHT): bezeichnet mit
\lnot, entspricht einem logischen "NICHT".
Aus diesen grundlegenden Operationen können wir komplexere Operationen
definieren, wie das "Exklusive ODER" (XOR) bezeichnet mit \oplus, das in der Kryptografie weit verbreitet ist. Jede logische Operation kann
durch eine Wahrheitstabelle dargestellt werden, die das Ergebnis für alle
möglichen Kombinationen von binären Eingabewerten (zwei Operanden p und q) angibt.
Für XOR (\oplus):
p | q | p \oplus q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Für AND (\land):
p | q | p \land q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Für NOT (\lnot p):
p | \lnot p |
|---|---|
| 0 | 1 |
| 1 | 0 |
Nehmen wir ein Beispiel, um die Operation von XOR auf Bit-Ebene zu verstehen. Wenn wir zwei Binärzahlen mit 6 Bits haben:
a = 101100b = 001000
Dann:
a \oplus b = 101100 \oplus 001000 = 100100
Durch Anwendung von XOR Bit für Bit:
| Bit Position | a | b | a \oplus b |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 1 | 0 | 1 |
| 5 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 |
Das Ergebnis ist daher 100100.
Zusätzlich zu logischen Operationen verwendet die Kompressionsfunktion Bit-Schiebeoperationen, die eine wesentliche Rolle bei der Diffusion von Bits im Algorithmus spielen werden.
Zuerst gibt es die logische Rechtsverschiebung, bezeichnet mit ShR_n(x), die alle Bits von x um n Positionen nach rechts verschiebt
und die freien Bits links mit Nullen füllt.
Zum Beispiel, für x = 101100001 (auf 9 Bits) und n = 4:
ShR_4(101100001) = 000010110
Schematisch könnte die Rechtsverschiebung so aussehen:
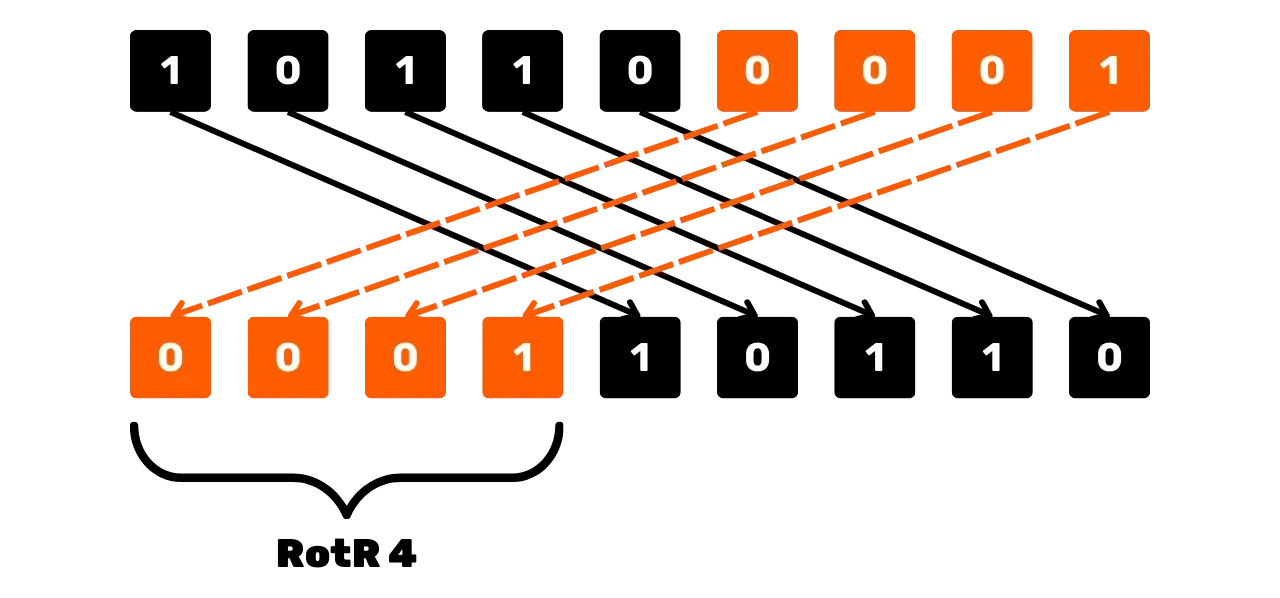
 Eine weitere in SHA256 für die Bitmanipulation verwendete Operation ist die rechte
zirkuläre Rotation, bezeichnet mit
Eine weitere in SHA256 für die Bitmanipulation verwendete Operation ist die rechte
zirkuläre Rotation, bezeichnet mit RotR_n(x), die die Bits von x um n Positionen nach rechts
verschiebt und die verschobenen Bits am Anfang der Zeichenkette wieder
einfügt. Zum Beispiel, für x = 101100001 (über 9 Bits) und n = 4:
RotR_4(101100001) = 000110110
Schematisch könnte die rechte zirkuläre Verschiebung so aussehen:
Kompressionsfunktion
Jetzt, da wir die grundlegenden Operationen verstanden haben, betrachten wir die SHA256-Kompressionsfunktion im Detail.
Im vorherigen Schritt haben wir unsere Eingabe in mehrere 512-Bit-Teile P unterteilt. Für jeden 512-Bit-Block P haben wir:
- Die Nachrichtenwörter
W_i: fürivon 0 bis 63. - Die Konstanten
K_i: fürivon 0 bis 63, definiert im vorherigen Schritt. - Die Zustandsvariablen
A, B, C, D, E, F, G, H: initialisiert mit den Werten aus dem vorherigen Schritt.
Die ersten 16 Wörter, W_0 bis W_{15}, werden
direkt aus dem verarbeiteten 512-Bit-Block P extrahiert. Jedes Wort W_i besteht aus 32 aufeinanderfolgenden Bits des Blocks. So nehmen wir zum
Beispiel unser erstes Stück Eingabe P_1 und teilen es weiter in kleinere 32-Bit-Stücke auf, die wir Wörter nennen.
Die nächsten 48 Wörter (W_{16} bis W_{63}) werden
mit der folgenden Formel generiert:
W_i = W_{i-16} + \sigma_0(W_{i-15}) + W_{i-7} + \sigma_1(W_{i-2}) \mod 2^{32}
Mit:
\sigma_0(x) = RotR_7(x) \oplus RotR_{18}(x) \oplus ShR_3(x)\sigma_1(x) = RotR_{17}(x) \oplus RotR_{19}(x) \oplus ShR_{10}(x)
In diesem Fall entspricht x W_{i-15} für \sigma_0(x) und W_{i-2} für \sigma_1(x).
Sobald wir alle Wörter W_i für
unser 512-Bit-Stück bestimmt haben, können wir zur Kompressionsfunktion übergehen,
die aus 64 Runden besteht.
 Für jede Runde
Für jede Runde i von 0 bis 63
haben wir drei verschiedene Arten von Eingaben. Zuerst die W_i, die wir gerade bestimmt
haben, teilweise bestehend aus unserem Nachrichtenstück P_n. Als Nächstes die 64
Konstanten K_i. Schließlich
verwenden wir die Zustandsvariablen A, B, C, D, E, F, G und H, die sich im Laufe des
Hashing-Prozesses entwickeln und mit jeder Kompressionsfunktion modifiziert
werden. Jedoch verwenden wir für das erste Stück P_1 die zuvor gegebenen Anfangskonstanten.
Wir führen dann die folgenden Operationen mit unseren Eingaben durch:
- Funktion
\Sigma_0:
\Sigma_0(A) = RotR_2(A) \oplus RotR_{13}(A) \oplus RotR_{22}(A)
- Funktion
\Sigma_1:
\Sigma_1(E) = RotR_6(E) \oplus RotR_{11}(E) \oplus RotR_{25}(E)$$
- **Funktion $Ch$ ("*Wählen*"):**
Ch(E, F, G) = (E \land F) \oplus (\lnot E \land G)
- **Funktion $Maj$ ("*Mehrheit*"):**
Maj(A, B, C) = (A \land B) \oplus (A \land C) \oplus (B \land C)
Dann berechnen wir 2 temporäre Variablen:
- $temp1$:
temp1 = H + \Sigma_1(E) + Ch(E, F, G) + K_i + W_i \mod 2^{32}
- $temp2$:
temp2 = \Sigma_0(A) + Maj(A, B, C) \mod 2^{32}
Anschließend aktualisieren wir die Zustandsvariablen wie folgt:
\begin{cases} H = G \ G = F \ F = E \ E = D + temp1 \mod 2^{32} \ D = C \ C = B \ B = A \ A = temp1 + temp2 \mod 2^{32} \end{cases}
Das folgende Diagramm stellt eine Runde der SHA256-Kompressionsfunktion dar, wie wir sie gerade beschrieben haben:

- Die Pfeile zeigen den Datenfluss an;
- Die Kästen repräsentieren die durchgeführten Operationen;
- Das $+$ in einem Kreis repräsentiert die Addition modulo $2^{32}$.
Wir können bereits beobachten, dass diese Runde neue Zustandsvariablen $A$, $B$, $C$, $D$, $E$, $F$, $G$ und $H$ ausgibt. Diese neuen Variablen dienen als Eingabe für die nächste Runde, die wiederum neue Variablen $A$, $B$, $C$, $D$, $E$, $F$, $G$ und $H$ produziert, die für die folgende Runde verwendet werden. Dieser Prozess setzt sich bis zur 64. Runde fort.
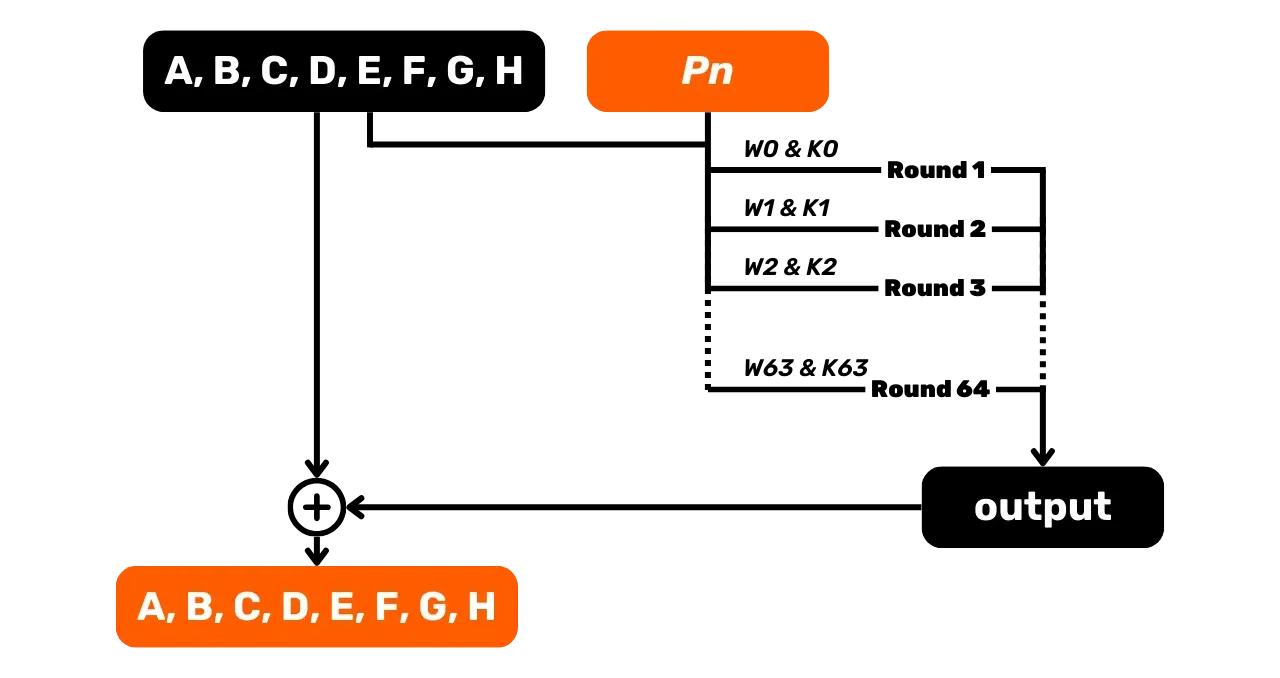
Nach den 64 Runden aktualisieren wir die Anfangswerte der Zustandsvariablen, indem wir sie zu den Endwerten am Ende der 64. Runde addieren:
\begin{cases} A = A_{\text{initial}} + A \mod 2^{32} \ B = B_{\text{initial}} + B \mod 2^{32} \ C = C_{\text{initial}} + C \mod 2^{32} \ D = D_{\text{initial}} + D \mod 2^{32} \ E = E_{\text{initial}} + E \mod 2^{32} \ F = F_{\text{initial}} + F \mod 2^{32} \ G = G_{\text{initial}} + G \mod 2^{32} \ H = H_{\text{initial}} + H \mod 2^{32} \end{cases}
Diese neuen Werte von $A$, $B$, $C$, $D$, $E$, $F$, $G$ und $H$ dienen als die Anfangswerte für den nächsten Block, $P_2$. Für diesen Block $P_2$ replizieren wir denselben Kompressionsprozess mit 64 Runden, dann aktualisieren wir die Variablen für Block $P_3$ und so weiter bis zum letzten Block unseres ausgeglichenen Inputs.
Nach der Verarbeitung aller Nachrichtenblöcke fügen wir die Endwerte der Variablen $A$, $B$, $C$, $D$, $E$, $F$, $G$ und $H$ zusammen, um den endgültigen 256-Bit-Hash unserer Hashing-Funktion zu bilden:
\text{Hash} = A \Vert B \Vert C \Vert D \Vert E \Vert F \Vert G \Vert H
Jede Variable ist ein 32-Bit-Integer, daher ergibt ihre Verkettung immer ein 256-Bit-Ergebnis, unabhängig von der Größe unserer Nachrichteneingabe in die Hashing-Funktion.
### Begründung der kryptografischen Eigenschaften
Aber wie ist diese Funktion irreversibel, kollisionsresistent und manipulationssicher?
Die Manipulationssicherheit ist recht einfach zu verstehen. Es werden so viele Berechnungen in Kaskade durchgeführt, die sowohl von der Eingabe als auch von den Konstanten abhängen, dass die geringste Modifikation der Anfangsnachricht den genommenen Pfad vollständig ändert und somit den Ausgabe-Hash komplett verändert. Dies wird als Lawineneffekt bezeichnet. Diese Eigenschaft wird teilweise durch das Mischen der Zwischenzustände mit den Anfangszuständen für jedes Stück sichergestellt.
Als Nächstes, wenn wir über eine kryptographische Hashfunktion sprechen, wird der Begriff "Irreversibilität" normalerweise nicht verwendet. Stattdessen sprechen wir über "Preimage-Resistenz", was spezifiziert, dass es für ein gegebenes $y$ schwierig ist, ein $x$ zu finden, so dass $h(x) = y$. Diese Preimage-Resistenz wird durch die algebraische Komplexität und die starke Nichtlinearität der Operationen, die in der Kompressionsfunktion durchgeführt werden, sowie durch den Verlust bestimmter Informationen im Prozess garantiert. Zum Beispiel gibt es für ein gegebenes Ergebnis einer Addition modulo mehrere mögliche Operanden:
3+2 \mod 10 = 5 \ 7+8 \mod 10 = 5 \ 5+10 \mod 10 = 5
In diesem Beispiel kann man, wenn nur das verwendete Modulo (10) und das Ergebnis (5) bekannt sind, nicht mit Sicherheit bestimmen, welche die korrekten Operanden bei der Addition waren. Es wird gesagt, dass es mehrere Kongruenzen modulo 10 gibt.
Beim XOR-Betrieb stehen wir vor demselben Problem. Erinnern wir uns an die Wahrheitstabelle für diese Operation: Jedes 1-Bit-Ergebnis kann durch zwei verschiedene Eingangskonfigurationen bestimmt werden, die genau die gleiche Wahrscheinlichkeit haben, die richtigen Werte zu sein. Daher kann man die Operanden eines XOR nicht mit Sicherheit bestimmen, wenn nur sein Ergebnis bekannt ist. Wenn wir die Größe der XOR-Operanden erhöhen, steigt die Anzahl der möglichen Eingaben, die nur das Ergebnis kennen, exponentiell. Darüber hinaus wird XOR oft zusammen mit anderen bitweisen Operationen verwendet, wie der $\text{RotR}$-Operation, die noch mehr mögliche Interpretationen zum Ergebnis hinzufügen.
Die Kompressionsfunktion verwendet auch die $\text{ShR}$-Operation. Diese Operation entfernt einen Teil der grundlegenden Informationen, die später unmöglich wiederhergestellt werden können. Auch hier gibt es kein algebraisches Mittel, um diese Operation umzukehren. Alle diese Einweg- und Informationsverlustoperationen werden sehr häufig in Kompressionsfunktionen verwendet. Die Anzahl der möglichen Eingaben für ein gegebenes Ausgabe ist somit fast unendlich, und jeder Versuch einer Rückberechnung würde zu Gleichungen mit einer sehr hohen Anzahl von Unbekannten führen, die bei jedem Schritt exponentiell ansteigen würden.
Schließlich, für das Merkmal der Kollisionsresistenz, kommen mehrere Parameter ins Spiel. Die Vorverarbeitung der ursprünglichen Nachricht spielt eine wesentliche Rolle. Ohne diese Vorverarbeitung könnte es einfacher sein, Kollisionen in der Funktion zu finden. Obwohl theoretisch Kollisionen existieren (aufgrund des Schubfachprinzips), macht die Struktur der Hashfunktion, kombiniert mit den zuvor genannten Eigenschaften, die Wahrscheinlichkeit, eine Kollision zu finden, extrem niedrig.
Damit eine Hashfunktion kollisionsresistent ist, ist es wesentlich, dass:
- Das Ergebnis unvorhersehbar ist: Jede Vorhersehbarkeit kann ausgenutzt werden, um Kollisionen schneller als mit einem Brute-Force-Angriff zu finden. Die Funktion stellt sicher, dass jedes Bit des Ausgangs auf eine nicht-triviale Weise vom Eingang abhängt. Mit anderen Worten, die Funktion ist so konzipiert, dass jedes Bit des Endergebnisses eine unabhängige Wahrscheinlichkeit hat, 0 oder 1 zu sein, auch wenn diese Unabhängigkeit in der Praxis nicht absolut ist.
- Die Verteilung der Hashes ist pseudo-zufällig: Dies stellt sicher, dass die Hashes gleichmäßig verteilt sind.
- Die Größe des Hashs ist erheblich: je größer der mögliche Raum für Ergebnisse, desto schwieriger ist es, eine Kollision zu finden.
Kryptographen entwerfen diese Funktionen, indem sie die bestmöglichen Angriffe zur Findung von Kollisionen bewerten und dann die Parameter anpassen, um diese Angriffe unwirksam zu machen.
### Merkle-Damgård-Konstruktion
Die Struktur von SHA256 basiert auf der Merkle-Damgård-Konstruktion, die es ermöglicht, eine Kompressionsfunktion in eine Hashfunktion umzuwandeln, die Nachrichten beliebiger Länge verarbeiten kann. Genau das haben wir in diesem Kapitel gesehen.
Allerdings sind einige alte Hash-Funktionen wie SHA1 oder MD5, die diese spezifische Konstruktion verwenden, anfällig für Length-Extension-Angriffe. Dies ist eine Technik, die es einem Angreifer, der den Hash eines Nachricht $M$ und die Länge von $M$ kennt (ohne die Nachricht selbst zu kennen), ermöglicht, den Hash einer Nachricht $M'$ zu berechnen, die durch das Anhängen von zusätzlichem Inhalt an $M$ gebildet wird.
SHA256, obwohl es denselben Typ von Konstruktion verwendet, ist theoretisch resistent gegen diesen Typ von Angriff, im Gegensatz zu SHA1 und MD5. Dies könnte das Geheimnis des doppelten Hashings erklären, das in Bitcoin von Satoshi Nakamoto implementiert wurde. Um diesen Typ von Angriff zu vermeiden, könnte Satoshi es bevorzugt haben, ein doppeltes SHA256 zu verwenden:
\text{HASH256}(m) = \text{SHA256}(\text{SHA256}(m))
Dies erhöht die Sicherheit gegen potenzielle Angriffe, die mit der Merkle-Damgård-Konstruktion zusammenhängen, erhöht jedoch nicht die Sicherheit des Hashing-Prozesses in Bezug auf Kollisionsresistenz. Darüber hinaus hätte selbst wenn SHA256 für diesen Typ von Angriff anfällig gewesen wäre, dies keinen ernsthaften Einfluss gehabt, da alle Anwendungsfälle von Hash-Funktionen in Bitcoin öffentliche Daten betreffen. Der Length-Extension-Angriff könnte jedoch nur für einen Angreifer nützlich sein, wenn die gehashten Daten privat sind und der Benutzer die Hash-Funktion als Authentifizierungsmechanismus für diese Daten verwendet hat, ähnlich einem MAC. Daher bleibt die Implementierung des doppelten Hashings ein Geheimnis im Design von Bitcoin.
Jetzt, da wir uns im Detail mit der Funktionsweise von Hash-Funktionen, insbesondere SHA256, das in Bitcoin umfangreich verwendet wird, beschäftigt haben, werden wir uns spezifischer auf die kryptografischen Ableitungsalgorithmen konzentrieren, die auf Anwendungsebene verwendet werden, insbesondere für die Ableitung der Schlüssel für Ihre Wallet.
## Die für die Ableitung verwendeten Algorithmen
<chapterId>cc668121-7789-5e99-bf5e-1ba085f4f5f2</chapterId>
In Bitcoin auf Anwendungsebene werden neben Hash-Funktionen kryptografische Ableitungsalgorithmen verwendet, um sichere Daten aus anfänglichen Eingaben zu generieren. Obwohl diese Algorithmen auf Hash-Funktionen basieren, dienen sie unterschiedlichen Zwecken, insbesondere in Bezug auf Authentifizierung und Schlüsselgenerierung. Diese Algorithmen behalten einige der Eigenschaften von Hash-Funktionen bei, wie Irreversibilität, Manipulationssicherheit und Kollisionsresistenz.
In Bitcoin-Wallets werden hauptsächlich 2 Ableitungsalgorithmen verwendet:
- **HMAC (*Hash-based Message Authentication Code*)**
- **PBKDF2 (*Password-Based Key Derivation Function 2*)**
Wir werden gemeinsam die Funktionsweise und Rolle jedes von ihnen erkunden.
### HMAC-SHA512
HMAC ist ein kryptografischer Algorithmus, der einen Authentifizierungscode basierend auf einer Kombination aus einer Hash-Funktion und einem geheimen Schlüssel berechnet. Bitcoin verwendet HMAC-SHA512, die Variante von HMAC, die die SHA512-Hash-Funktion verwendet. Wir haben bereits im vorherigen Kapitel gesehen, dass SHA512 zur gleichen Familie von Hash-Funktionen wie SHA256 gehört, aber eine 512-Bit-Ausgabe produziert.
Hier ist sein allgemeines Betriebsschema mit $m$ als Eingangsnachricht und $K$ als geheimem Schlüssel:
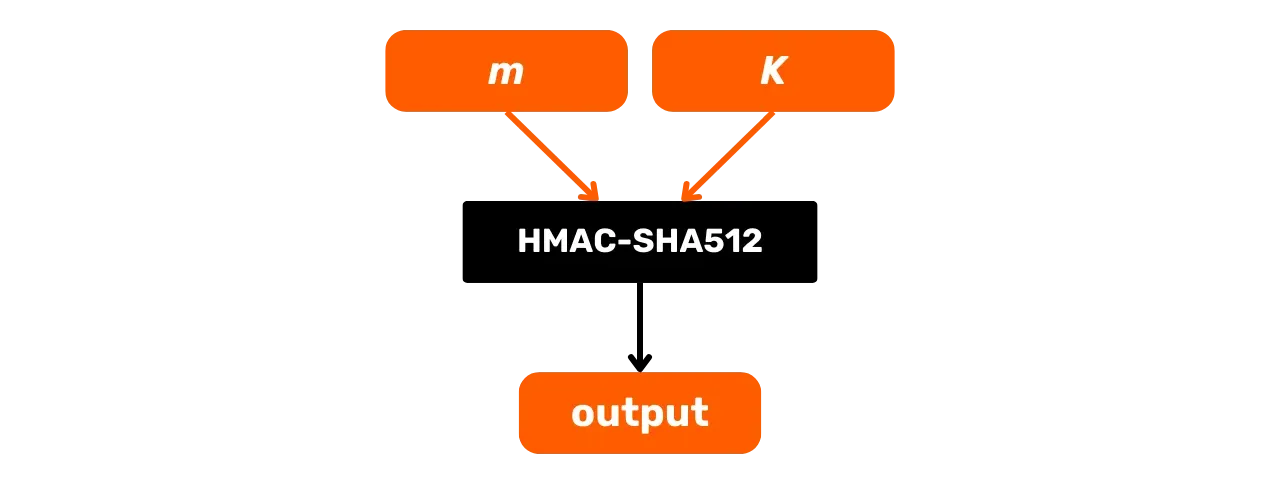
Lassen Sie uns im Detail untersuchen, was in dieser HMAC-SHA512-Blackbox passiert. Die HMAC-SHA512-Funktion mit:
- $m$: die beliebig große Nachricht, die vom Benutzer gewählt wird (erster Eingang);
- $K$: der beliebige geheime Schlüssel, der vom Benutzer gewählt wird (zweiter Eingang);
- $K'$: der Schlüssel $K$, angepasst an die Größe $B$ der Hash-Funktionsblöcke (1024 Bits für SHA512, oder 128 Bytes);
- $\text{SHA512}$: die SHA512-Hash-Funktion;
- $\oplus$: die XOR (exklusives Oder) Operation;
- $\Vert$: der Verkettungsoperator, der Bitstrings Ende-zu-Ende verbindet;
- $\text{opad}$: Konstante, bestehend aus dem Byte $0x5c$, das 128 Mal wiederholt wird
- $\text{ipad}$: Konstante, bestehend aus dem Byte $0x36$, das 128 Mal wiederholt wird
Bevor der HMAC berechnet wird, ist es notwendig, den Schlüssel und die Konstanten entsprechend der Blockgröße $B$ anzugleichen. Wenn zum Beispiel der Schlüssel $K$ kürzer als 128 Bytes ist, wird er mit Nullen aufgefüllt, um die Größe $B$ zu erreichen. Ist $K$ länger als 128 Bytes, wird er mit SHA512 komprimiert und dann mit Nullen aufgefüllt, bis er 128 Bytes erreicht. Auf diese Weise wird ein angeglichener Schlüssel namens $K'$ erhalten.
Die Werte von $\text{opad}$ und $\text{ipad}$ werden erhalten, indem ihr Basisbyte ($0x5c$ für $\text{opad}$, $0x36$ für $\text{ipad}$) wiederholt wird, bis die Größe $B$ erreicht ist. Somit haben wir mit $B = 128$ Bytes:
\text{opad} = \underbrace{0x5c5c\ldots5c}_{128 , \text{bytes}}
Sobald die Vorverarbeitung abgeschlossen ist, wird der HMAC-SHA512-Algorithmus durch die folgende Gleichung definiert:
\text {HMAC-SHA512}_K(m) = \text{SHA512} \left( (K' \oplus \text{opad}) \parallel \text{SHA512} \left( (K' \oplus \text{ipad}) \parallel m \right) \right)
Diese Gleichung wird in die folgenden Schritte unterteilt:
- XOR des angeglichenen Schlüssels $K'$ mit $\text{ipad}$, um $\text{iKpad}$ zu erhalten;
- XOR des angeglichenen Schlüssels $K'$ mit $\text{opad}$, um $\text{oKpad}$ zu erhalten;
- Verkettung von $\text{iKpad}$ mit der Nachricht $m$.
- Hashen dieses Ergebnisses mit SHA512, um einen Zwischenhash $H_1$ zu erhalten.
- Verkettung von $\text{oKpad}$ mit $H_1$.
- Hashen dieses Ergebnisses mit SHA512, um das endgültige Ergebnis $H_2$ zu erhalten.
Diese Schritte können schematisch wie folgt zusammengefasst werden:
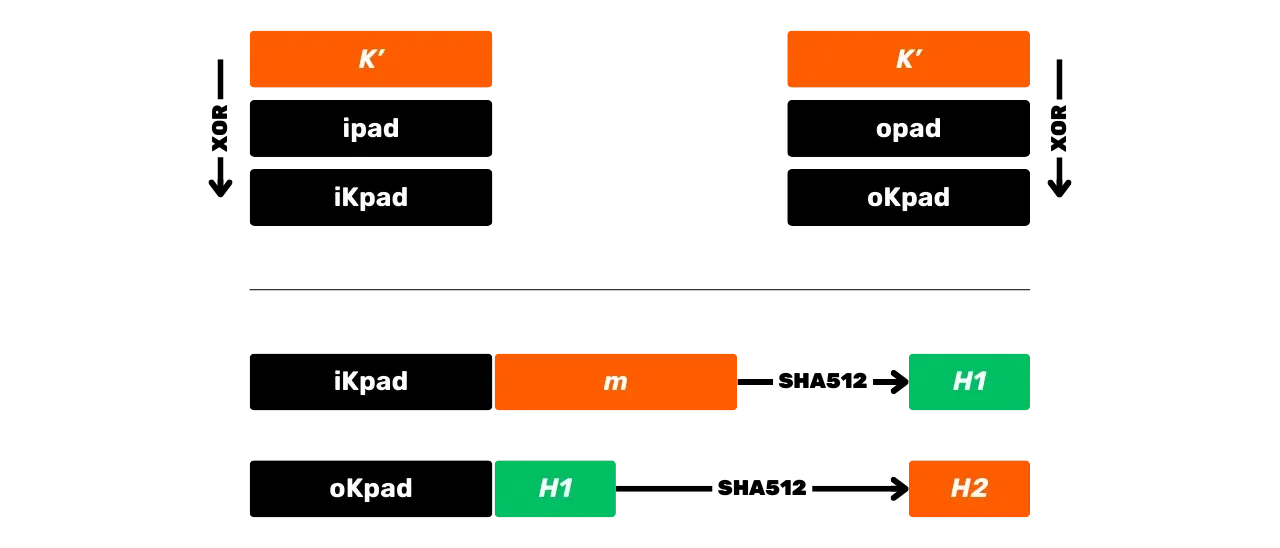
HMAC wird insbesondere in Bitcoin für die Schlüsselableitung in HD (Hierarchisch Deterministischen) Wallets verwendet (wir werden dies in den kommenden Kapiteln genauer besprechen) und als Komponente von PBKDF2.
### PBKDF2
PBKDF2 (*Password-Based Key Derivation Function 2*) ist ein Schlüsselableitungsalgorithmus, der entwickelt wurde, um die Sicherheit von Passwörtern zu erhöhen. Der Algorithmus wendet eine Pseudozufallsfunktion (hier HMAC-SHA512) auf ein Passwort und ein kryptografisches Salt an und wiederholt diese Operation eine bestimmte Anzahl von Malen, um einen Ausgabeschlüssel zu erzeugen.
In Bitcoin wird PBKDF2 verwendet, um den Seed eines HD-Wallets aus einer mnemonischen Phrase und einer Passphrase zu generieren (aber wir werden dies in den kommenden Kapiteln genauer besprechen).
Der PBKDF2-Prozess ist wie folgt, mit:
- $m$: die mnemonische Phrase des Benutzers;
- $s$: die optionale Passphrase zur Erhöhung der Sicherheit (leeres Feld, wenn keine Passphrase);
- $n$: die Anzahl der Iterationen der Funktion, in unserem Fall sind es 2048.
Die PBKDF2-Funktion ist iterativ definiert. Jede Iteration nimmt das Ergebnis der vorherigen, leitet es durch HMAC-SHA512 und kombiniert die aufeinanderfolgenden Ergebnisse, um den endgültigen Schlüssel zu produzieren:
\text{PBKDF2}(m, s) = \text{HMAC-SHA512}^{2048}(m, s)
Schematisch kann PBKDF2 wie folgt dargestellt werden:
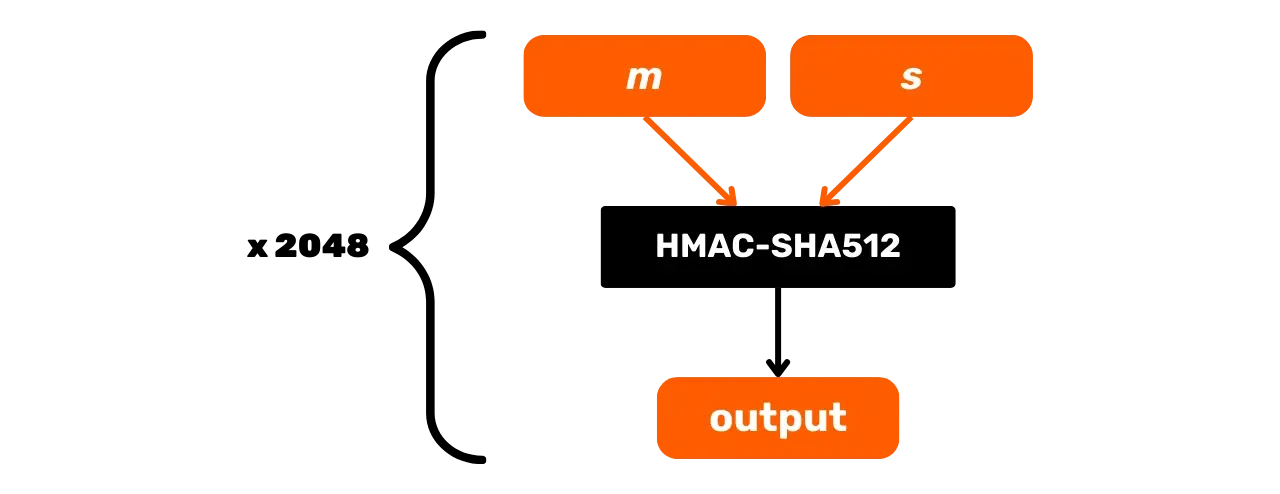
In diesem Kapitel haben wir die HMAC-SHA512- und PBKDF2-Funktionen erkundet, die Hashing-Funktionen verwenden, um die Integrität und Sicherheit von Schlüsselableitungen im Bitcoin-Protokoll zu gewährleisten. Im nächsten Teil werden wir uns mit digitalen Signaturen befassen, einer weiteren kryptografischen Methode, die in Bitcoin weit verbreitet ist.
# Digitale Signaturen
<partId>76b58a00-0c18-54b9-870d-6b7e34029db8</partId>
## Digitale Signaturen und elliptische Kurven
<chapterId>c9dd9672-6da1-57f8-9871-8b28994d4c1a</chapterId>
Die zweite kryptografische Methode, die in Bitcoin verwendet wird, umfasst Algorithmen für digitale Signaturen. Lassen Sie uns erkunden, was dies beinhaltet und wie es funktioniert.
### Bitcoins, UTXOs und Ausgabebedingungen
Der Begriff "*Wallet*" in Bitcoin kann für Anfänger ziemlich verwirrend sein. Tatsächlich ist das, was als Bitcoin-Wallet bezeichnet wird, Software, die Ihre Bitcoins nicht direkt hält, im Gegensatz zu einem physischen Wallet, das Münzen oder Scheine halten kann. Bitcoins sind einfach Recheneinheiten. Diese Recheneinheit wird durch **UTXO** (*Unspent Transaction Outputs*), also unverbrauchte Transaktionsausgänge, dargestellt. Wenn diese Ausgänge unverbraucht sind, bedeutet das, dass sie einem Benutzer gehören. UTXOs sind gewissermaßen Bitcoin-Stücke variabler Größe, die einem Benutzer gehören.
Das Bitcoin-Protokoll ist verteilt und funktioniert ohne zentrale Autorität. Daher ist es nicht wie traditionelle Bankaufzeichnungen, bei denen die Euros, die Ihnen gehören, einfach mit Ihrer persönlichen Identität verknüpft sind. Bei Bitcoin gehören Ihre UTXOs Ihnen, weil sie durch Ausgabebedingungen geschützt sind, die in der Script-Sprache angegeben sind. Vereinfacht gesagt gibt es zwei Arten von Scripts: das Sperrscript (*scriptPubKey*), das ein UTXO schützt, und das Entsperrscript (*scriptSig*), das das Entsperren eines UTXO ermöglicht und somit die darin vertretenen Bitcoin-Einheiten ausgibt.
Die ursprüngliche Operation von Bitcoin mit P2PK-Scripts beinhaltet die Verwendung eines öffentlichen Schlüssels, um Gelder zu sperren, indem in einem *scriptPubKey* angegeben wird, dass die Person, die dieses UTXO ausgeben möchte, eine gültige Signatur mit dem privaten Schlüssel vorlegen muss, der zu diesem öffentlichen Schlüssel gehört. Um dieses UTXO zu entsperren, ist es daher notwendig, eine gültige Signatur im *scriptSig* bereitzustellen. Wie ihre Namen andeuten, ist der öffentliche Schlüssel allen bekannt, da er in der Blockchain übertragen wird, während der private Schlüssel nur dem legitimen Besitzer der Gelder bekannt ist.
Dies ist die grundlegende Funktionsweise von Bitcoin, aber im Laufe der Zeit ist diese Operation komplexer geworden. Zuerst führte Satoshi auch P2PKH-Scripts ein, die eine Empfangsadresse im *scriptPubKey* verwenden, die den Hash des öffentlichen Schlüssels darstellt. Dann wurde das System noch komplexer mit der Ankunft von SegWit und dann Taproot. Das allgemeine Prinzip bleibt jedoch grundsätzlich dasselbe: Ein öffentlicher Schlüssel oder eine Darstellung dieses Schlüssels wird verwendet, um UTXOs zu sperren, und ein entsprechender privater Schlüssel ist erforderlich, um sie zu entsperren und somit auszugeben.
Ein Nutzer, der eine Bitcoin-Transaktion durchführen möchte, muss daher eine digitale Signatur mit seinem privaten Schlüssel für die betreffende Transaktion erstellen. Die Signatur kann von anderen Netzwerkteilnehmern überprüft werden. Wenn sie gültig ist, bedeutet dies, dass der Nutzer, der die Transaktion initiiert, tatsächlich der Besitzer des privaten Schlüssels und somit der Besitzer der Bitcoins ist, die er ausgeben möchte. Andere Nutzer können dann die Transaktion akzeptieren und weiterleiten.
Folglich muss ein Nutzer, der Bitcoins besitzt, die mit einem öffentlichen Schlüssel gesperrt sind, einen Weg finden, um das, was das Entsperren seiner Mittel ermöglicht: den privaten Schlüssel, sicher aufzubewahren. Ein Bitcoin-Wallet ist genau ein Gerät, das es Ihnen ermöglicht, alle Ihre Schlüssel einfach zu behalten, ohne dass andere Personen Zugang dazu haben. Es ist daher eher wie ein Schlüsselbund als wie eine Brieftasche.
Die mathematische Verbindung zwischen einem öffentlichen Schlüssel und einem privaten Schlüssel sowie die Fähigkeit, eine Signatur zu leisten, um den Besitz eines privaten Schlüssels zu beweisen, ohne ihn zu offenbaren, werden durch einen digitalen Signaturalgorithmus ermöglicht. Im Bitcoin-Protokoll werden 2 Signaturalgorithmen verwendet: **ECDSA** (*Elliptic Curve Digital Signature Algorithm*) und das **Schnorr-Signaturschema**. ECDSA ist das digitale Signaturprotokoll, das seit den Anfängen von Bitcoin verwendet wird. Schnorr ist in Bitcoin neuer, da es im November 2021 mit dem Taproot-Update eingeführt wurde.
Diese beiden Algorithmen sind in ihren Mechanismen recht ähnlich. Sie basieren beide auf elliptischer Kurvenkryptografie. Der Hauptunterschied zwischen diesen beiden Protokollen liegt in der Struktur der Signatur und einigen spezifischen mathematischen Eigenschaften. Wir werden daher die Funktionsweise dieser Algorithmen untersuchen, beginnend mit dem ältesten: ECDSA.
### Elliptische Kurvenkryptografie
Die elliptische Kurvenkryptografie (ECC) ist eine Reihe von Algorithmen, die eine elliptische Kurve für ihre verschiedenen mathematischen und geometrischen Eigenschaften zu kryptografischen Zwecken nutzen. Die Sicherheit dieser Algorithmen beruht auf der Schwierigkeit des diskreten Logarithmusproblems auf elliptischen Kurven. Elliptische Kurven werden insbesondere für Schlüsselaustausche, asymmetrische Verschlüsselung oder zur Erstellung digitaler Signaturen verwendet.
Eine wichtige Eigenschaft dieser Kurven ist, dass sie symmetrisch bezüglich der x-Achse sind. So wird jede nicht-vertikale Linie, die die Kurve an zwei unterschiedlichen Punkten schneidet, immer einen dritten Schnittpunkt mit der Kurve haben. Außerdem wird jede Tangente an die Kurve an einem nicht-singulären Punkt die Kurve an einem weiteren Punkt schneiden. Diese Eigenschaften werden nützlich sein, um Operationen auf der Kurve zu definieren.
Hier ist eine Darstellung einer elliptischen Kurve über dem Feld der reellen Zahlen:
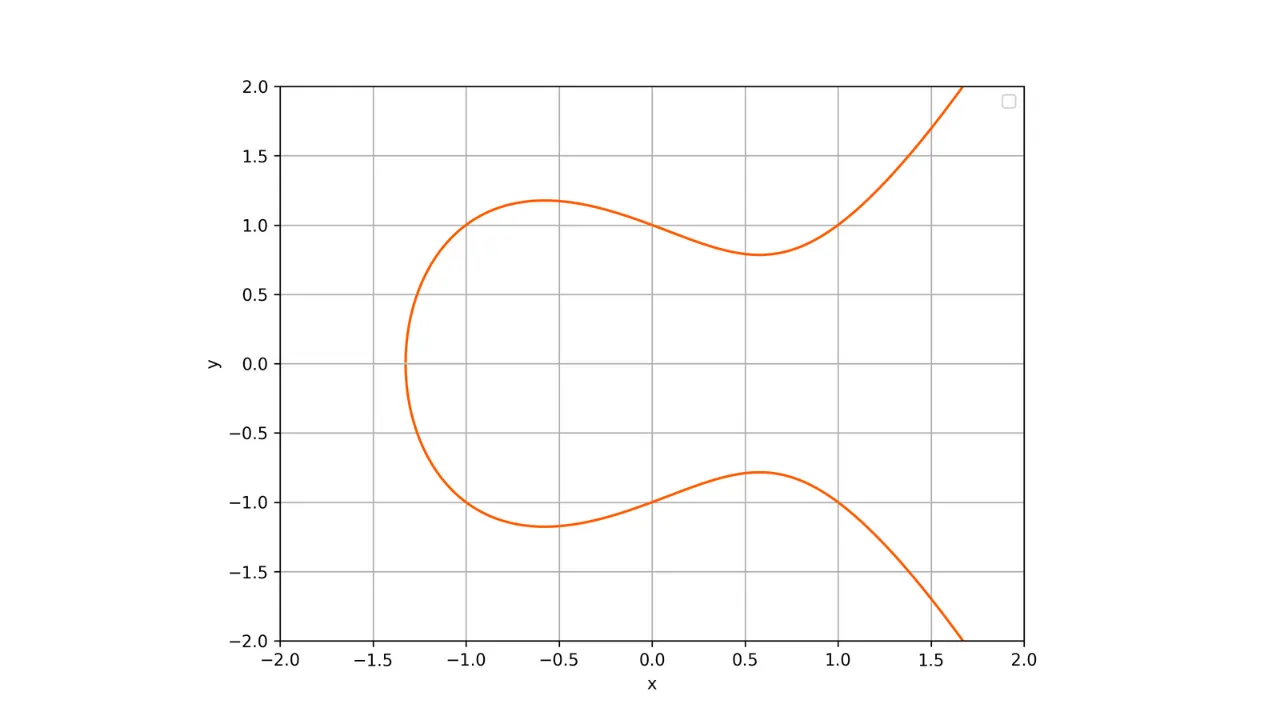
Jede elliptische Kurve wird durch eine Gleichung der Form definiert:
y^2 = x^3 + ax + b
### secp256k1
Um ECDSA oder Schnorr zu verwenden, muss man die Parameter der elliptischen Kurve wählen, das heißt, die Werte von $a$ und $b$ in der Kurvengleichung. Es gibt verschiedene Standards elliptischer Kurven, die als kryptografisch sicher gelten. Der bekannteste ist die *secp256r1*-Kurve, die vom NIST (*National Institute of Standards and Technology*) definiert und empfohlen wird.
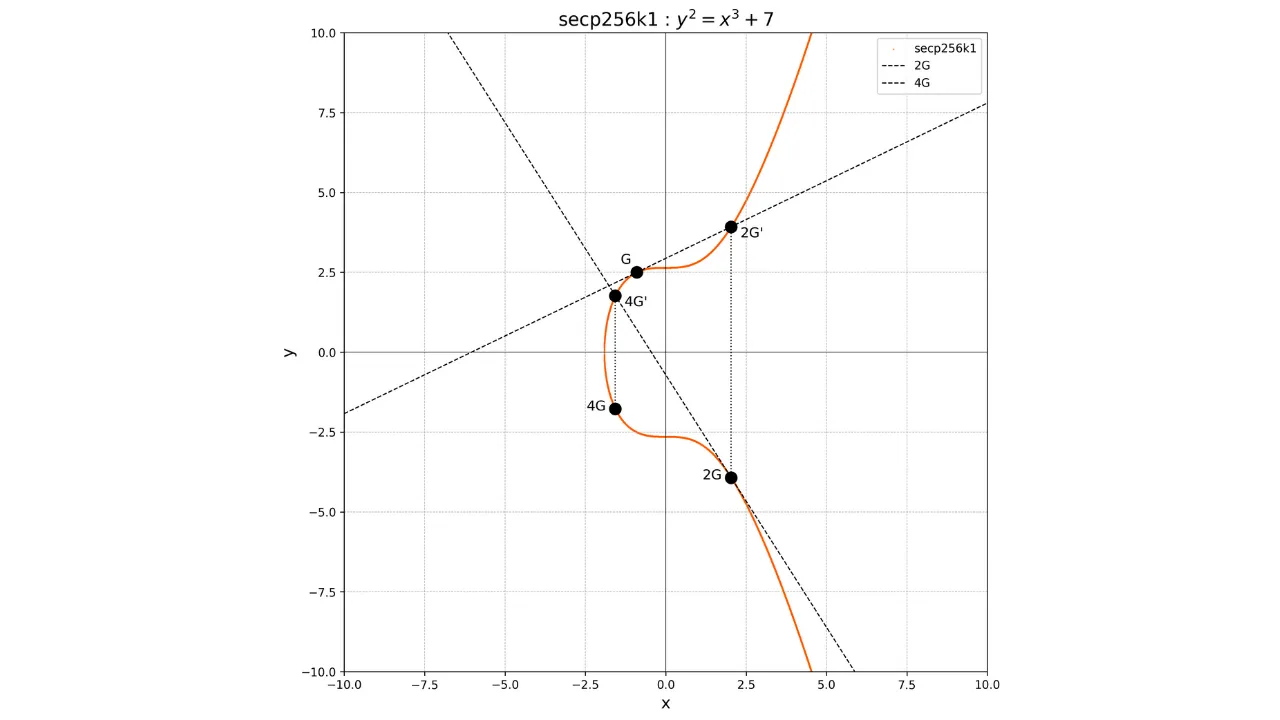
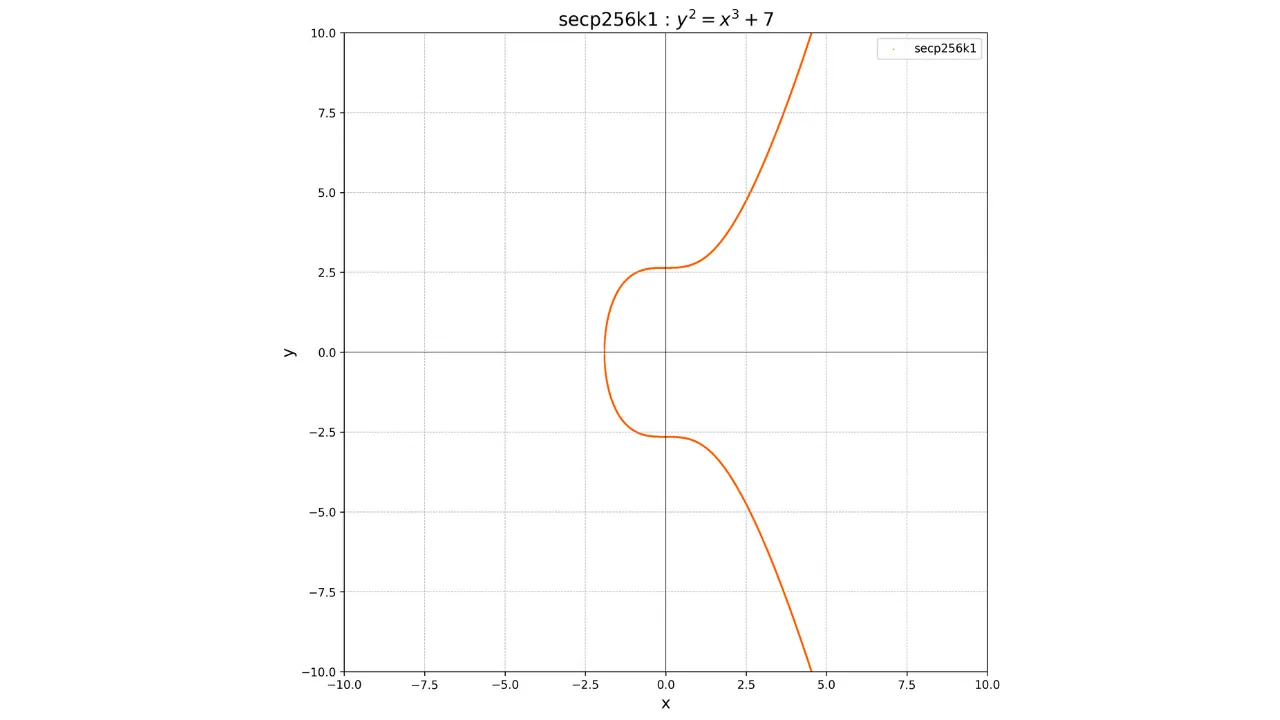
Trotzdem entschied sich Satoshi Nakamoto, der Erfinder von Bitcoin, diese Kurve nicht zu verwenden. Der Grund für diese Wahl ist unbekannt, aber einige glauben, er bevorzugte eine Alternative, weil die Parameter dieser Kurve potenziell einen Hintertür enthalten könnten. Stattdessen verwendet das Bitcoin-Protokoll den Standard ***secp256k1***. Diese Kurve ist durch die Parameter $a = 0$ und $b = 7$ definiert. Ihre Gleichung ist daher:
y^2 = x^3 + 7
Ihre grafische Darstellung über dem Feld der reellen Zahlen sieht folgendermaßen aus:
In der Kryptographie arbeiten wir jedoch mit endlichen Zahlenmengen. Genauer gesagt arbeiten wir im endlichen Feld $\mathbb{F}_p$, welches das Feld der ganzen Zahlen modulo einer Primzahl $p$ ist.
**Definition**: Eine Primzahl ist eine natürliche ganze Zahl, die größer oder gleich 2 ist und nur zwei verschiedene positive ganze Zahlenteiler hat: 1 und sich selbst. Zum Beispiel ist die Zahl 7 eine Primzahl, da sie nur durch 1 und 7 geteilt werden kann. Andererseits ist die Zahl 8 keine Primzahl, weil sie durch 1, 2, 4 und 8 geteilt werden kann.
Bei Bitcoin wird die Primzahl $p$, die verwendet wird, um das endliche Feld zu definieren, sehr groß gewählt. Sie wird so ausgewählt, dass die Ordnung des Feldes (d.h. die Anzahl der Elemente in $\mathbb{F}_p$) ausreichend groß ist, um kryptografische Sicherheit zu gewährleisten.
Die verwendete Primzahl $p$ ist:
```text
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
```
In Dezimalschreibweise entspricht dies:
p = 2^{256} - 2^{32} - 977
Daher ist die Gleichung unserer elliptischen Kurve tatsächlich:
y^2 \equiv x^3 + 7 \mod p
Da diese Kurve über das endliche Feld $\mathbb{F}_p$ definiert ist, ähnelt sie nicht mehr einer kontinuierlichen Kurve, sondern eher einer diskreten Menge von Punkten. Zum Beispiel sieht hier die in Bitcoin verwendete Kurve für ein sehr kleines $p = 17$ so aus:
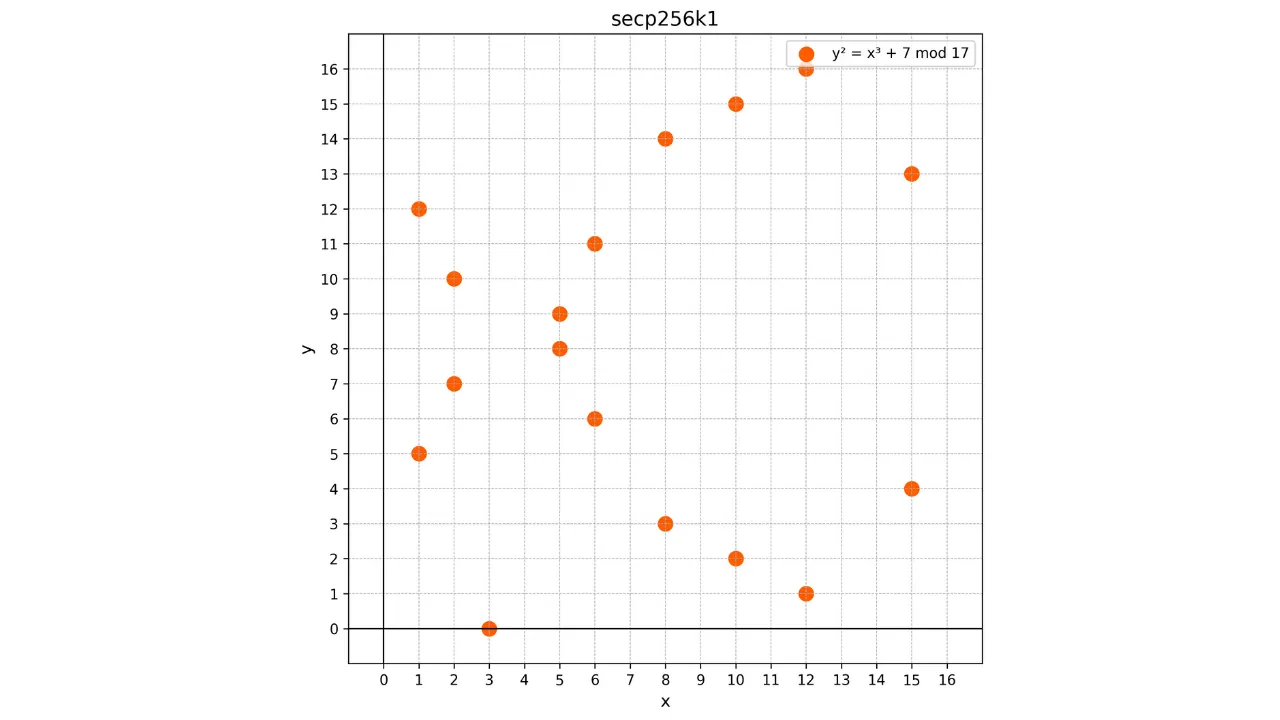
In diesem Beispiel habe ich das endliche Feld absichtlich auf $p = 17$ beschränkt, aus pädagogischen Gründen, aber man muss sich vorstellen, dass das in Bitcoin verwendete um ein Vielfaches größer ist, fast $2^{256}$.
Wir verwenden ein endliches Feld ganzer Zahlen modulo $p$, um die Genauigkeit der Operationen auf der Kurve zu gewährleisten. Tatsächlich sind elliptische Kurven über dem Feld der reellen Zahlen aufgrund von Rundungsfehlern bei Berechnungen ungenau. Werden zahlreiche Operationen auf der Kurve durchgeführt, sammeln sich diese Fehler an und das Endergebnis kann falsch oder schwer zu reproduzieren sein. Die ausschließliche Verwendung positiver ganzer Zahlen gewährleistet eine perfekte Genauigkeit der Berechnungen und somit die Reproduzierbarkeit des Ergebnisses.
Die Mathematik der elliptischen Kurven über endlichen Feldern ist analog zu der über dem Feld der reellen Zahlen, mit der Anpassung, dass alle Operationen modulo $p$ durchgeführt werden. Um die Erklärungen zu vereinfachen, werden wir in den folgenden Kapiteln weiterhin Konzepte anhand einer Kurve, die über reelle Zahlen definiert ist, veranschaulichen, während wir im Hinterkopf behalten, dass die Kurve in der Praxis über ein endliches Feld definiert ist.
Wenn Sie mehr über die mathematischen Grundlagen der modernen Kryptographie erfahren möchten, empfehle ich auch, diesen anderen Kurs im Plan ₿ Network zu konsultieren:
https://planb.network/courses/d2fd9fc0-d9ed-4a87-9fa3-0fdbb3937e28
## Berechnung des öffentlichen Schlüssels aus dem privaten Schlüssel
<chapterId>fcb2bd58-5dda-5ecf-bb8f-ad1a0561ab4a</chapterId>
Wie zuvor gesehen, basieren die digitalen Signaturalgorithmen bei Bitcoin auf einem Paar von privaten und öffentlichen Schlüsseln, die mathematisch miteinander verknüpft sind. Lassen Sie uns gemeinsam erkunden, was diese mathematische Verknüpfung ist und wie sie generiert werden.
### Der private Schlüssel
Der private Schlüssel ist einfach eine zufällige oder pseudozufällige Zahl. Im Fall von Bitcoin ist diese Zahl 256 Bit groß. Die Anzahl der Möglichkeiten für einen Bitcoin-privaten Schlüssel ist daher theoretisch $2^{256}$.
**Hinweis**: Eine "pseudo-zufällige Zahl" ist eine Zahl, die Eigenschaften aufweist, die denen einer wirklich zufälligen Zahl nahekommen, aber durch einen deterministischen Algorithmus erzeugt wird.
In der Praxis gibt es jedoch nur $n$ unterschiedliche Punkte auf unserer elliptischen Kurve secp256k1, wobei $n$ die Ordnung des Generatorpunkts $G$ der Kurve ist. Wir werden später sehen, was diese Zahl bedeutet, aber merken Sie sich einfach, dass ein gültiger privater Schlüssel eine ganze Zahl zwischen $1$ und $n-1$ ist, wobei $n$ eine Zahl ist, die nahe, aber etwas weniger als $2^{256}$ ist. Daher gibt es einige 256-Bit-Zahlen, die nicht gültig sind, um ein privater Schlüssel in Bitcoin zu werden, speziell alle Zahlen zwischen $n$ und $2^{256}$. Wenn die Erzeugung der Zufallszahl (der private Schlüssel) einen Wert $k$ ergibt, sodass $k \geq n$ ist, wird er als ungültig betrachtet, und ein neuer Zufallswert muss generiert werden.
Die Anzahl der Möglichkeiten für einen Bitcoin-privaten Schlüssel beträgt daher etwa $n$, was einer Zahl nahe $1.158 \times 10^{77}$ entspricht. Diese Zahl ist so groß, dass es statistisch fast unmöglich ist, zufällig auf den privaten Schlüssel eines anderen Benutzers zu stoßen, wenn Sie einen privaten Schlüssel zufällig wählen. Um Ihnen eine Vorstellung von der Größenordnung zu geben, die Anzahl der möglichen privaten Schlüssel bei Bitcoin liegt in einer Größenordnung nahe der geschätzten Atome im beobachtbaren Universum.
Wie wir in den kommenden Kapiteln sehen werden, werden heute die meisten privaten Schlüssel bei Bitcoin nicht zufällig generiert, sondern sind das Ergebnis einer deterministischen Ableitung aus einer mnemonischen Phrase, die selbst pseudo-zufällig ist (dies ist die berühmte Phrase aus 12 oder 24 Wörtern). Diese Information ändert nichts an der Verwendung von Signaturalgorithmen wie ECDSA, hilft aber, unseren Popularisierungsansatz auf Bitcoin zu fokussieren.
Für die Fortsetzung der Erklärung wird der private Schlüssel durch den Kleinbuchstaben $k$ dargestellt.
### Der öffentliche Schlüssel
Der öffentliche Schlüssel ist ein Punkt auf der elliptischen Kurve, dargestellt durch den Großbuchstaben $K$, und wird aus dem privaten Schlüssel $k$ berechnet. Dieser Punkt $K$ wird durch ein Paar von Koordinaten $(x, y)$ auf der elliptischen Kurve repräsentiert, wobei jede Koordinate eine ganze Zahl modulo $p$ ist, der Primzahl, die das endliche Feld $\mathbb{F}_p$ definiert.
In der Praxis wird ein unkomprimierter öffentlicher Schlüssel durch 512 Bits (oder 64 Bytes) dargestellt, die zwei 256-Bit-Zahlen ($x$ und $y$) entsprechen, die hintereinander platziert sind. Diese Zahlen sind die Abszisse ($x$) und die Ordinate ($y$) unseres Punktes auf secp256k1. Wenn wir das Präfix hinzufügen, summiert sich der öffentliche Schlüssel auf 520 Bits.
Es ist jedoch auch möglich, den öffentlichen Schlüssel in einer komprimierten Form darzustellen, die nur 33 Bytes (264 Bits) verwendet, indem nur die Abszisse $x$ unseres Punktes auf der Kurve und ein Byte, das die Parität von $y$ angibt, beibehalten wird. Dies ist als komprimierter öffentlicher Schlüssel bekannt. Ich werde in den letzten Kapiteln dieses Trainings mehr darüber sprechen. Aber was Sie sich merken müssen, ist, dass ein öffentlicher Schlüssel $K$ ein Punkt ist, der durch $x$ und $y$ beschrieben wird.
Um den Punkt $K$ zu berechnen, der unserem öffentlichen Schlüssel entspricht, verwenden wir die Operation der skalaren Multiplikation auf elliptischen Kurven, definiert als eine wiederholte Addition ($k$-mal) des Generatorpunkts $G$:
K = k \cdot G
wo:
- $k$ ist der private Schlüssel (eine zufällige ganze Zahl zwischen $1$ und $n-1$);
- $G$ ist der Generatorpunkt der elliptischen Kurve, der von allen Teilnehmern des Bitcoin-Netzwerks verwendet wird; - $\cdot$ repräsentiert die skalare Multiplikation auf der elliptischen Kurve, was dem Hinzufügen des Punktes $G$ zu sich selbst $k$ Mal entspricht.
Die Tatsache, dass dieser Punkt $G$ allen öffentlichen Schlüsseln auf Bitcoin gemeinsam ist, ermöglicht es uns sicherzustellen, dass der gleiche private Schlüssel $k$ uns immer den gleichen öffentlichen Schlüssel $K$ geben wird:
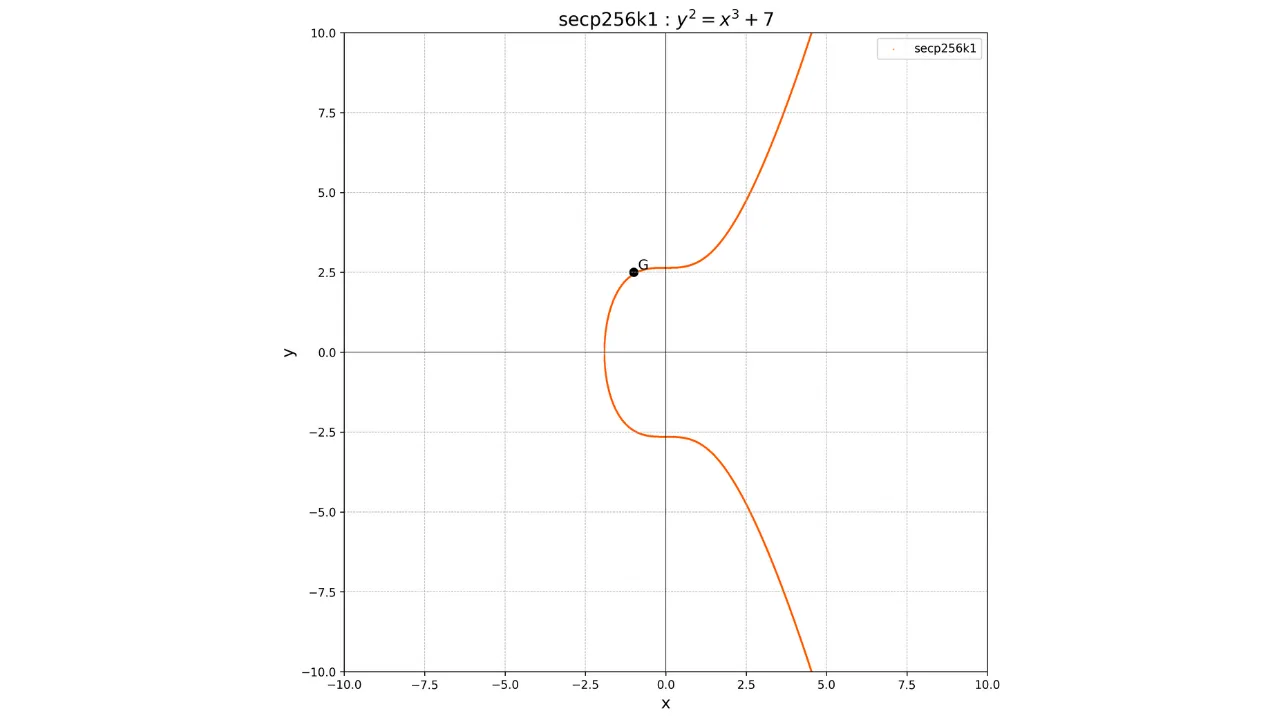
Die Hauptcharakteristik dieser Operation ist, dass sie eine Einwegfunktion ist. Es ist einfach, den öffentlichen Schlüssel $K$ zu berechnen, wenn man den privaten Schlüssel $k$ und den Generatorpunkt $G$ kennt, aber es ist praktisch unmöglich, den privaten Schlüssel $k$ zu berechnen, wenn man nur den öffentlichen Schlüssel $K$ und den Generatorpunkt $G$ kennt. $k$ aus $K$ und $G$ zu finden, entspricht der Lösung des diskreten Logarithmusproblems auf elliptischen Kurven, ein mathematisch schwieriges Problem, für das kein effizienter Algorithmus bekannt ist. Selbst die leistungsfähigsten aktuellen Rechner sind nicht in der Lage, dieses Problem in einer vernünftigen Zeit zu lösen.

### Addition und Verdopplung von Punkten auf elliptischen Kurven
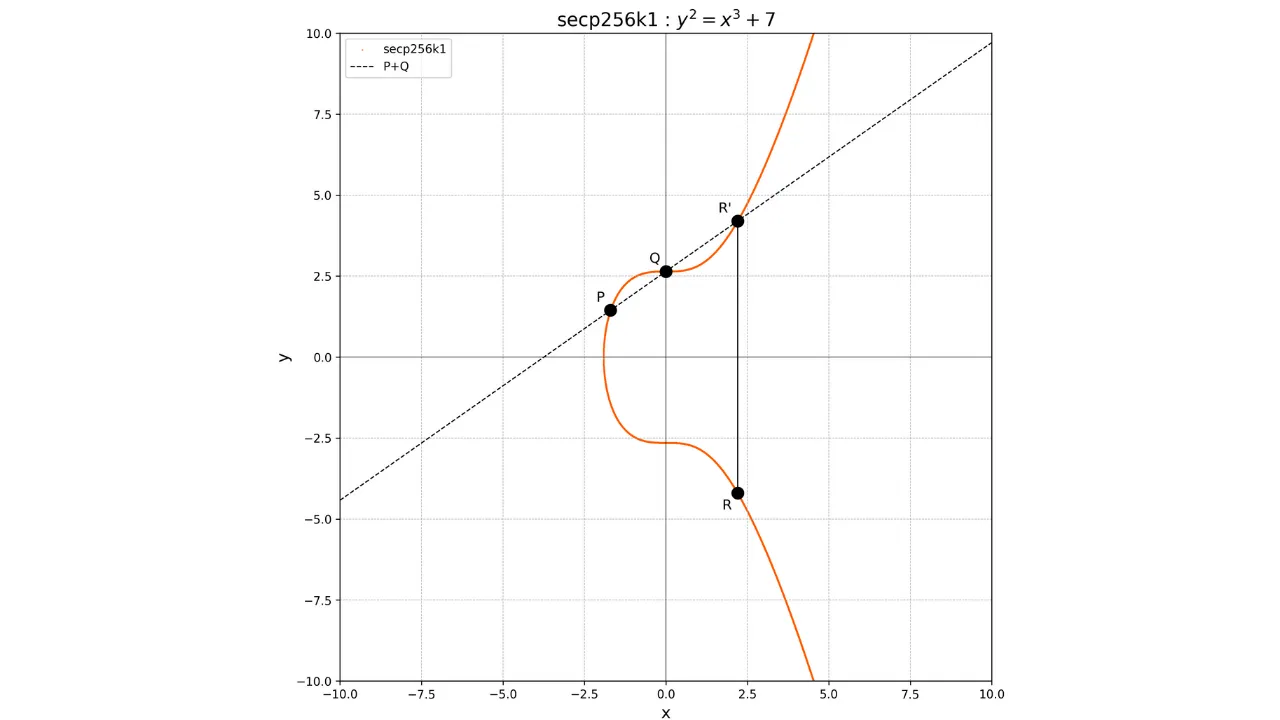
Das Konzept der Addition auf elliptischen Kurven ist geometrisch definiert. Wenn wir zwei Punkte $P$ und $Q$ auf der Kurve haben, wird die Operation $P + Q$ berechnet, indem eine Linie gezeichnet wird, die durch $P$ und $Q$ verläuft. Diese Linie wird die Kurve notwendigerweise an einem dritten Punkt $R'$ schneiden. Wir nehmen dann das Spiegelbild dieses Punktes bezüglich der x-Achse, um den Punkt $R$ zu erhalten, der das Ergebnis der Addition ist:
P + Q = R
Grafisch kann dies wie folgt dargestellt werden:
Für die Verdopplung eines Punktes, also die Operation $P + P$, zeichnen wir die Tangente an die Kurve am Punkt $P$. Diese Tangente schneidet die Kurve an einem anderen Punkt $S'$. Wir nehmen dann das Spiegelbild dieses Punktes bezüglich der x-Achse, um den Punkt $S$ zu erhalten, der das Ergebnis der Verdopplung ist:
2P = S
Grafisch wird dies gezeigt als:
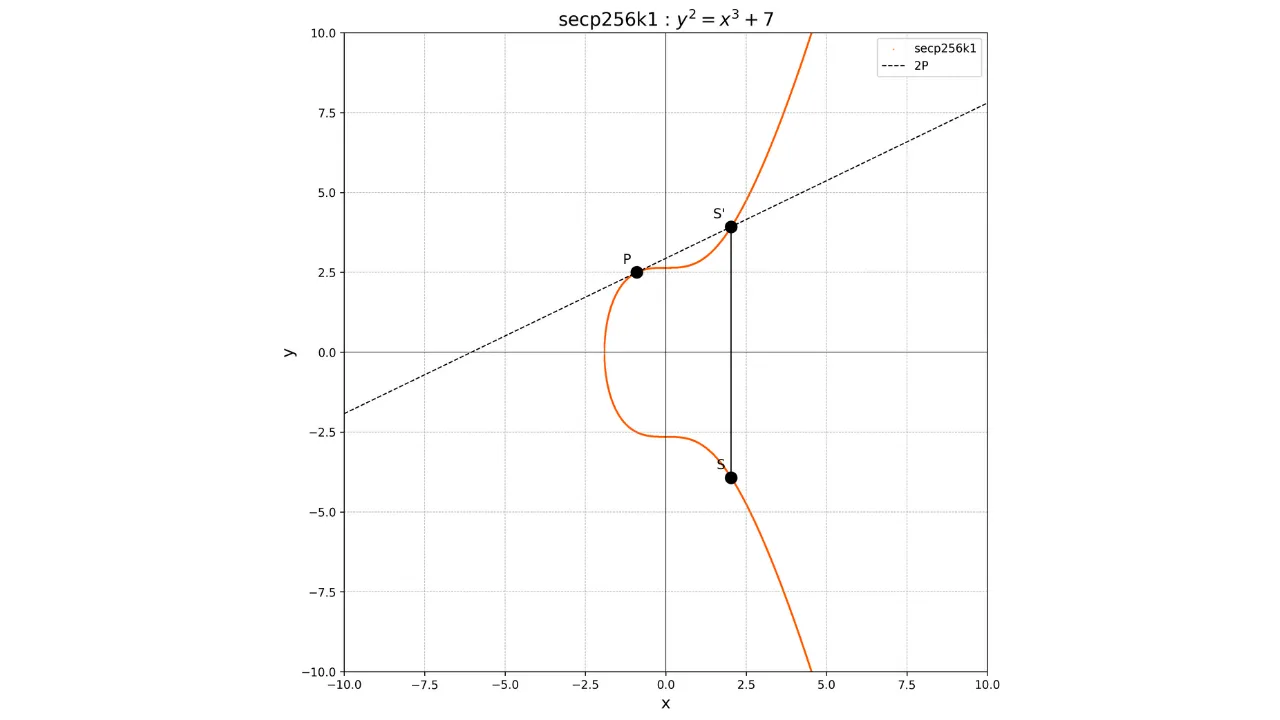
Durch die Verwendung dieser Operationen der Addition und Verdopplung können wir die skalare Multiplikation eines Punktes mit einer ganzen Zahl $k$, bezeichnet als $kP$, durchführen, indem wiederholte Verdopplungen und Additionen durchgeführt werden.
Nehmen wir zum Beispiel an, wir haben einen privaten Schlüssel $k = 4$ gewählt. Um den zugehörigen öffentlichen Schlüssel zu berechnen, führen wir aus:
K = k \cdot G = 4G
Grafisch entspricht dies der Durchführung einer Reihe von Additionen und Verdopplungen:
- Berechne $2G$ durch Verdopplung von $G$.
- Berechne $4G$ durch Verdopplung von $2G$.

Wenn wir zum Beispiel den Punkt $3G$ berechnen möchten, müssen wir zuerst den Punkt $2G$ durch Verdopplung des Punktes $G$ berechnen, dann $G$ und $2G$ addieren. Um $G$ und $2G$ zu addieren, zeichnen wir einfach die Linie, die diese beiden Punkte verbindet, holen den einzigartigen Punkt $-3G$ am Schnittpunkt zwischen dieser Linie und der elliptischen Kurve und bestimmen dann $3G$ als das Gegenteil von $-3G$.
Wir werden haben:
G + G = 2G
2G + G = 3G
Grafisch würde dies wie folgt dargestellt:
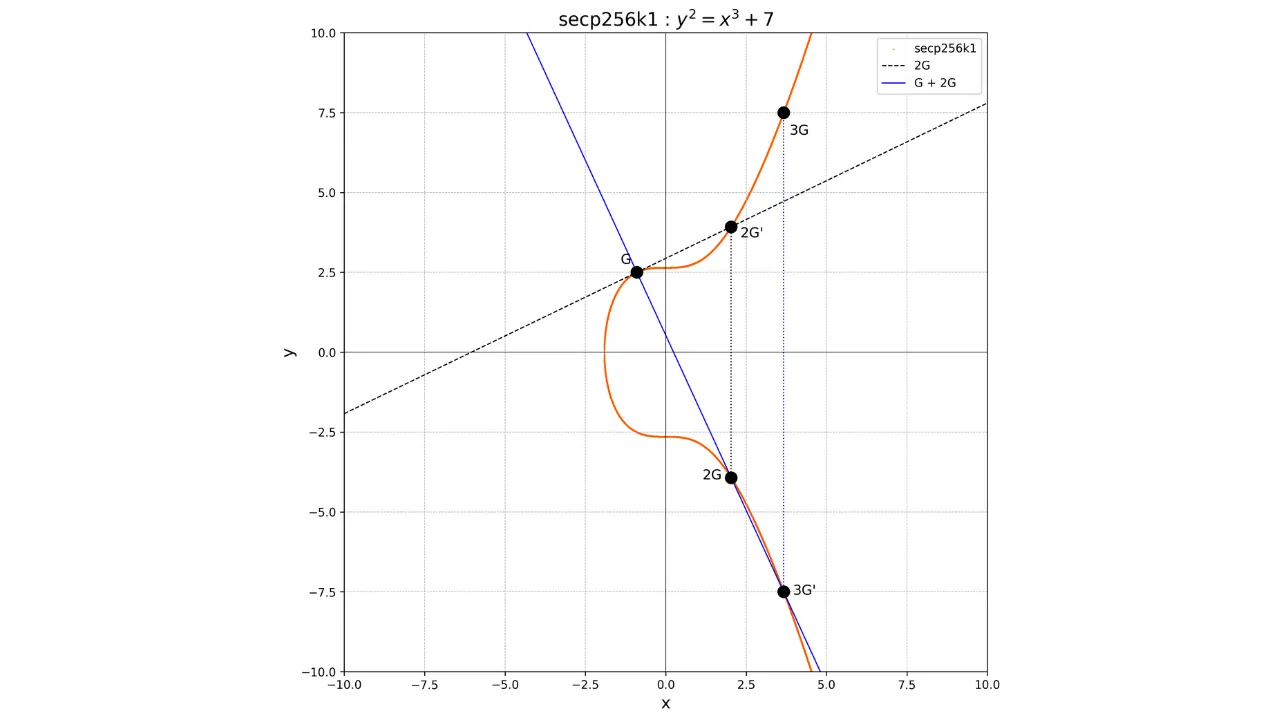
### Einwegfunktion
Dank dieser Operationen können wir verstehen, warum es einfach ist, einen öffentlichen Schlüssel aus einem privaten Schlüssel abzuleiten, aber das Umgekehrte praktisch unmöglich ist.
Kehren wir zu unserem vereinfachten Beispiel zurück. Mit einem privaten Schlüssel $k = 4$. Um den zugehörigen öffentlichen Schlüssel zu berechnen, führen wir aus:
K = k \cdot G = 4G
Wir haben somit den öffentlichen Schlüssel $K$ leicht berechnen können, indem wir $k$ und $G$ kannten.
Wenn jemand jedoch nur den öffentlichen Schlüssel $K$ kennt, steht er vor dem Problem des diskreten Logarithmus: das Finden von $k$ so, dass $K = k \cdot G$. Dieses Problem gilt als schwierig, weil es keinen effizienten Algorithmus gibt, um es auf elliptischen Kurven zu lösen. Dies gewährleistet die Sicherheit der ECDSA- und Schnorr-Algorithmen.
Natürlich wäre es in diesem vereinfachten Beispiel mit $k = 4$ möglich, $k$ durch Ausprobieren zu finden, da die Anzahl der Möglichkeiten gering ist. In der Praxis bei Bitcoin ist $k$ jedoch eine 256-Bit-Ganzzahl, was die Anzahl der Möglichkeiten astronomisch groß macht (ungefähr $1.158 \times 10^{77}$). Daher ist es undurchführbar, $k$ durch Brute-Force zu finden.
## Signieren mit dem privaten Schlüssel
<chapterId>bb07826f-826e-5905-b307-3d82001fb778</chapterId>
Jetzt, da Sie wissen, wie man einen öffentlichen Schlüssel aus einem privaten Schlüssel ableitet, können Sie bereits Bitcoins empfangen, indem Sie dieses Schlüsselpaar als Ausgabebedingung verwenden. Aber wie gibt man sie aus? Um Bitcoins auszugeben, müssen Sie das _scriptPubKey_ entsperren, das an Ihr UTXO angehängt ist, um zu beweisen, dass Sie tatsächlich dessen legitimer Besitzer sind. Dazu müssen Sie eine Signatur $s$ erzeugen, die zum öffentlichen Schlüssel $K$ passt, der im _scriptPubKey_ vorhanden ist, indem Sie den privaten Schlüssel $k$ verwenden, der ursprünglich verwendet wurde, um $K$ zu berechnen. Die digitale Signatur ist somit ein unwiderlegbarer Beweis dafür, dass Sie im Besitz des privaten Schlüssels sind, der mit dem öffentlichen Schlüssel verbunden ist, den Sie beanspruchen.
### Elliptische Kurvenparameter
Um eine digitale Signatur durchzuführen, müssen alle Teilnehmer zunächst die Parameter der verwendeten elliptischen Kurve vereinbaren. Im Fall von Bitcoin sind die Parameter von **secp256k1** wie folgt:
Das endliche Feld $\mathbb{Z}_p$ definiert durch:
p = 2^{256} - 2^{32} - 977
```text
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
```
$p$ ist eine sehr große Primzahl, die etwas kleiner als $2^{256}$ ist.
Die elliptische Kurve $y^2 = x^3 + ax + b$ über $\mathbb{Z}_p$ definiert durch:
a = 0, \quad b = 7
Der Generatorpunkt oder Ursprungspunkt $G$:
```text
G = 0x0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
```
Diese Zahl ist die komprimierte Form, die nur die Abszisse des Punktes $G$ angibt. Das Präfix `02` am Anfang bestimmt, welche der beiden Werte mit dieser Abszisse $x$ als Erzeugungspunkt verwendet werden soll.
Die Ordnung $n$ von $G$ (die Anzahl der existierenden Punkte) und der Kofaktor $h$:
```text
n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
```
$n$ ist eine sehr große Zahl, die etwas kleiner als $p$ ist.
h=1
$h$ ist der Kofaktor oder die Anzahl der Untergruppen. Ich werde hier nicht näher darauf eingehen, was dies repräsentiert, da es ziemlich komplex ist, und im Fall von Bitcoin müssen wir dies nicht berücksichtigen, da es gleich $1$ ist.
Alle diese Informationen sind öffentlich und allen Teilnehmern bekannt. Dank ihnen können Benutzer eine digitale Signatur erstellen und verifizieren.
### Signatur mit ECDSA
Der ECDSA-Algorithmus ermöglicht es einem Benutzer, eine Nachricht mit seinem privaten Schlüssel zu signieren, sodass jeder, der den entsprechenden öffentlichen Schlüssel kennt, die Gültigkeit der Signatur überprüfen kann, ohne dass der private Schlüssel jemals offenbart wird. Im Kontext von Bitcoin hängt die zu signierende Nachricht vom _sighash_ ab, den der Benutzer wählt. Dieser _sighash_ bestimmt, welche Teile der Transaktion von der Signatur abgedeckt werden. Ich werde im nächsten Kapitel näher darauf eingehen.
Hier sind die Schritte zur Erzeugung einer ECDSA-Signatur:
Zuerst berechnen wir den Hash ($e$) der zu signierenden Nachricht. Die Nachricht $m$ wird also durch eine kryptografische Hash-Funktion geleitet, im Allgemeinen SHA256 oder doppeltes SHA256 im Fall von Bitcoin:
e = \text{HASH}(m)
Als Nächstes berechnen wir einen Nonce. In der Kryptografie ist ein Nonce einfach eine Zahl, die auf zufällige oder pseudozufällige Weise generiert wird und nur einmal verwendet wird. Das heißt, jedes Mal, wenn eine neue digitale Signatur mit diesem Schlüsselpaar erstellt wird, ist es sehr wichtig, einen anderen Nonce zu verwenden, da sonst die Sicherheit des privaten Schlüssels gefährdet wird. Es reicht daher aus, eine zufällige und einzigartige ganze Zahl $r$ zu bestimmen, sodass $1 \leq r \leq n-1$, wobei $n$ die Ordnung des erzeugenden Punkts $G$ der elliptischen Kurve ist.
Dann berechnen wir den Punkt $R$ auf der elliptischen Kurve mit den Koordinaten $(x_R, y_R)$, sodass:
R = r \cdot G
Wir extrahieren den Wert der Abszisse des Punkts $R$ ($x_R$). Dieser Wert stellt den ersten Teil der Signatur dar. Und schließlich berechnen wir den zweiten Teil der Signatur $s$ auf folgende Weise:
s = r^{-1} \left( e + k \cdot x_R \right) \mod n
wobei:
- $r^{-1}$ das modulare Inverse von $r$ modulo $n$ ist, das heißt, eine ganze Zahl, sodass $r \cdot r^{-1} \equiv 1 \mod n$;
- $k$ ist der private Schlüssel des Benutzers;
- $e$ ist der Hash der Nachricht;
- $n$ ist die Ordnung des Generatorpunkts $G$ der elliptischen Kurve.
Die Signatur ist dann einfach die Verkettung von $x_R$ und $s$:
\text{SIG} = x_R \Vert s
### Überprüfung der ECDSA-Signatur
Um eine Signatur $(x_R, s)$ zu überprüfen, kann jeder, der den öffentlichen Schlüssel $K$ und die Parameter der elliptischen Kurve kennt, auf folgende Weise vorgehen:
Zuerst überprüfen Sie, ob $x_R$ und $s$ im Intervall $[1, n-1]$ liegen. Dies stellt sicher, dass die Signatur die mathematischen Einschränkungen der elliptischen Gruppe respektiert. Ist dies nicht der Fall, lehnt der Verifizierer die Signatur sofort als ungültig ab.
Berechnen Sie dann den Hash des Nachricht:
e = \text{HASH}(m)
Berechnen Sie das modulare Inverse von $s$ modulo $n$:
s^{-1} \mod n
Berechnen Sie zwei Skalarwerte $u_1$ und $u_2$ auf diese Weise:
\begin{align*} u_1 &= e \cdot s^{-1} \mod n \ u_2 &= x_R \cdot s^{-1} \mod n \end{align*}
Und schließlich berechnen Sie den Punkt $V$ auf der elliptischen Kurve, so dass:
V = u_1 \cdot G + u_2 \cdot K
Die Signatur ist nur gültig, wenn $x_V \equiv x_R \mod n$, wobei $x_V$ die $x$-Koordinate des Punktes $V$ ist. Tatsächlich erhält man durch die Kombination von $u_1 \cdot G$ und $u_2 \cdot K$ einen Punkt $V$, der, wenn die Signatur gültig ist, dem Punkt $R$ entsprechen muss, der während der Signatur verwendet wurde (modulo $n$).
### Signatur mit dem Schnorr-Protokoll
Das Schnorr-Signaturschema ist eine Alternative zu ECDSA, die viele Vorteile bietet. Seit 2021 und der Einführung von Taproot mit den P2TR-Skriptmustern ist es möglich, es bei Bitcoin zu verwenden. Wie ECDSA ermöglicht das Schnorr-Schema das Signieren einer Nachricht mit einem privaten Schlüssel, sodass die Signatur von jedem überprüft werden kann, der den entsprechenden öffentlichen Schlüssel kennt.
Im Fall von Schnorr wird genau dieselbe Kurve wie bei ECDSA mit denselben Parametern verwendet. Öffentliche Schlüssel werden jedoch im Vergleich zu ECDSA etwas anders dargestellt. Tatsächlich werden sie nur durch die $x$-Koordinate des Punktes auf der elliptischen Kurve bezeichnet. Im Gegensatz zu ECDSA, wo komprimierte öffentliche Schlüssel durch 33 Bytes dargestellt werden (mit dem Präfixbyte, das die Parität von $y$ angibt), verwendet Schnorr 32-Byte öffentliche Schlüssel, die nur der $x$-Koordinate des Punktes $K$ entsprechen, und es wird standardmäßig angenommen, dass $y$ gerade ist. Diese vereinfachte Darstellung reduziert die Größe der Signaturen und erleichtert bestimmte Optimierungen in den Verifizierungsalgorithmen.
Der öffentliche Schlüssel ist dann die $x$-Koordinate des Punktes $K$:
\text{pk} = K_x
Der erste Schritt zur Generierung einer Signatur besteht darin, die Nachricht zu hashen. Aber im Gegensatz zu ECDSA wird dies mit anderen Werten gemacht und eine beschriftete Hash-Funktion wird verwendet, um Kollisionen in verschiedenen Kontexten zu vermeiden. Eine beschriftete Hash-Funktion beinhaltet einfach das Hinzufügen eines willkürlichen Labels zu den Eingaben der Hash-Funktion neben den Nachrichtendaten.
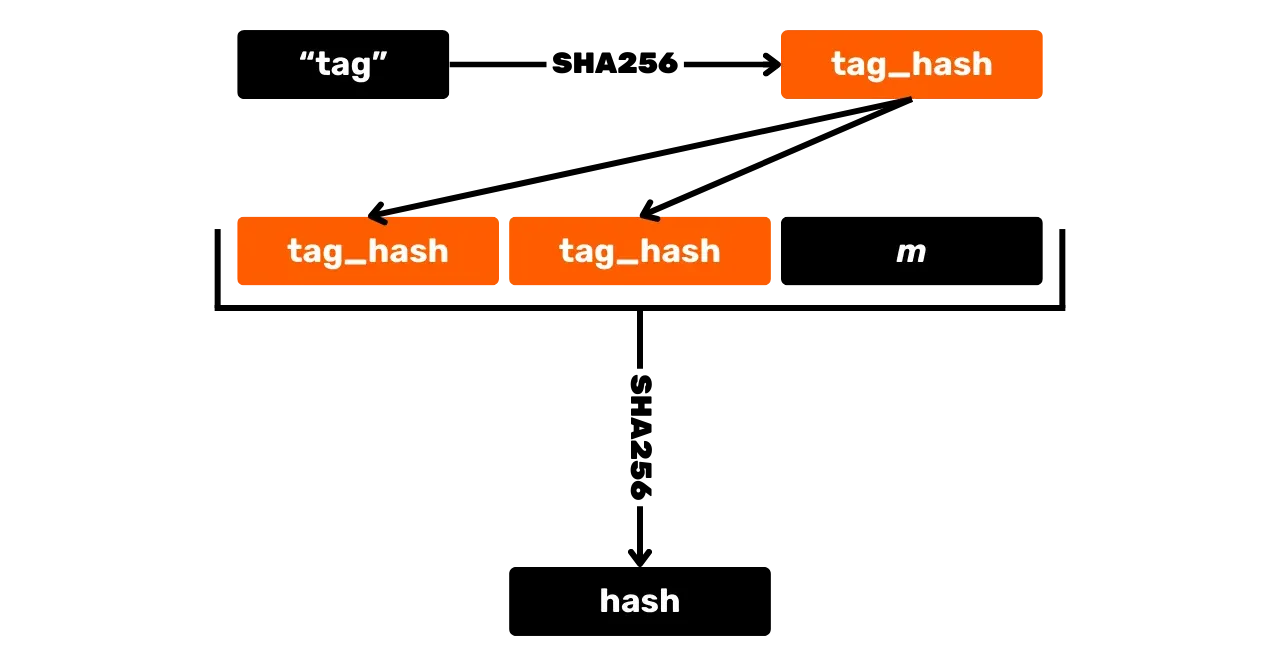
Zusätzlich zur Nachricht werden die $x$-Koordinate des öffentlichen Schlüssels $K_x$ sowie ein Punkt $R$, der aus dem Nonce $r$ ($R=r \cdot G$) berechnet wird, der selbst eine einzigartige Ganzzahl für jede Signatur ist, berechnet deterministisch aus dem privaten Schlüssel und der Nachricht, um Schwachstellen im Zusammenhang mit der Wiederverwendung von Nonces zu vermeiden, ebenfalls in die beschriftete Funktion eingegeben. Wie beim öffentlichen Schlüssel wird nur die $x$-Koordinate des Nonce-Punktes $R_x$ beibehalten, um den Punkt zu beschreiben.
Das Ergebnis dieses Hashings, notiert $e$, wird als "Herausforderung" bezeichnet:
e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod n
Hierbei ist $\text{HASH}$ die SHA256-Hashfunktion, und $\text{``BIP0340/challenge''}$ ist das spezifische Tag für das Hashing.
Schließlich wird der Parameter $s$ auf diese Weise aus dem privaten Schlüssel $k$, dem Nonce $r$ und der Herausforderung $e$ berechnet:
s = (r + e \cdot k) \mod n
Die Signatur ist dann einfach das Paar $Rx$ und $s$.
\text{SIG} = R_x \Vert s
### Verifizierung der Schnorr-Signatur
Die Verifizierung einer Schnorr-Signatur ist einfacher als die einer ECDSA-Signatur. Hier sind die Schritte zur Verifizierung der Signatur $(R_x, s)$ mit dem öffentlichen Schlüssel $K_x$ und der Nachricht $m$:
Zuerst überprüfen wir, ob $K_x$ eine gültige Ganzzahl und kleiner als $p$ ist. Wenn dies der Fall ist, holen wir den entsprechenden Punkt auf der Kurve mit $K_y$ als gerade. Wir extrahieren auch $R_x$ und $s$, indem wir die Signatur $\text{SIG}$ trennen. Dann prüfen wir, ob $R_x < p$ und $s < n$ (die Ordnung der Kurve) ist.
Als Nächstes berechnen wir die Herausforderung $e$ auf die gleiche Weise wie der Aussteller der Signatur:
e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod n
Dann berechnen wir einen Referenzpunkt auf der Kurve auf diese Weise:
R' = s \cdot G - e \cdot K
Schließlich überprüfen wir, ob $R'_x = R_x$. Wenn die beiden x-Koordinaten übereinstimmen, dann ist die Signatur $(R_x, s)$ tatsächlich gültig mit dem öffentlichen Schlüssel $K_x$.
### Warum funktioniert das?
Der Unterzeichner hat $s = r + e \cdot k \mod n$ berechnet, also sollte $R' = s \cdot G - e \cdot K$ gleich dem ursprünglichen Punkt $R$ sein, weil:
s \cdot G = (r + e \cdot k) \cdot G = r \cdot G + e \cdot k \cdot G
Da $K = k \cdot G$ ist, haben wir $e \cdot k \cdot G = e \cdot K$. Somit:
R' = r \cdot G = R
Daher haben wir:
R'_x = R_x
### Die Vorteile von Schnorr-Signaturen
Das Schnorr-Signaturschema bietet mehrere Vorteile für Bitcoin gegenüber dem ursprünglichen ECDSA-Algorithmus. Zuerst ermöglicht Schnorr die Aggregation von Schlüsseln und Signaturen. Das bedeutet, dass mehrere öffentliche Schlüssel zu einem einzigen Schlüssel kombiniert werden können.
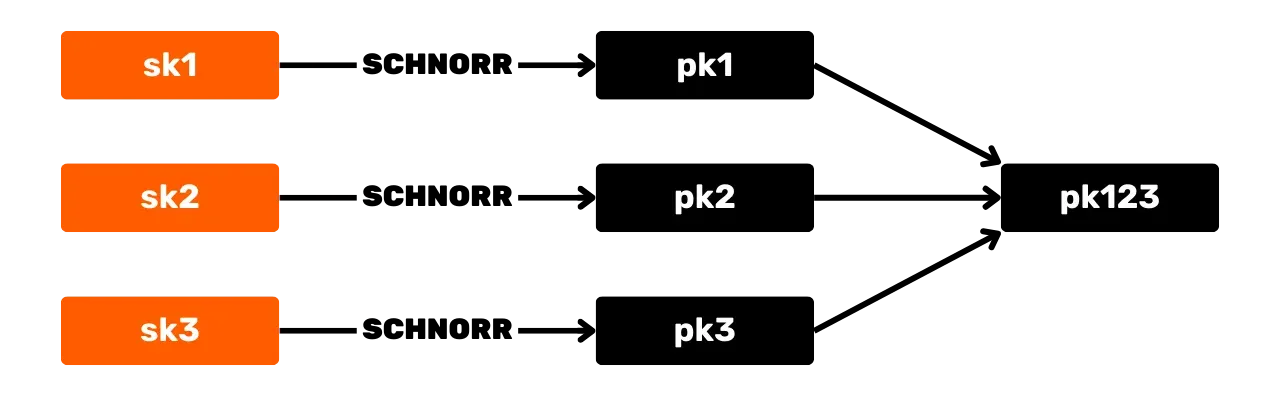
Und ähnlich können mehrere Signaturen zu einer einzigen gültigen Signatur aggregiert werden. Somit kann bei einer Multisignatur-Transaktion eine Gruppe von Teilnehmern mit einer einzigen Signatur und einem einzigen aggregierten öffentlichen Schlüssel unterschreiben. Dies reduziert die Speicher- und Rechenkosten für das Netzwerk erheblich, da jede Node nur eine einzige Signatur verifizieren muss.

Darüber hinaus verbessert die Signaturaggregation die Privatsphäre. Mit Schnorr wird es unmöglich, eine Multisignatur-Transaktion von einer Standard-Einzelsignatur-Transaktion zu unterscheiden. Diese Homogenität erschwert die Kettenanalyse, da sie die Fähigkeit einschränkt, Wallet-Fingerabdrücke zu identifizieren.
Schließlich bietet Schnorr auch die Möglichkeit der Stapelverifizierung. Durch die gleichzeitige Überprüfung mehrerer Signaturen können Knoten Effizienz gewinnen, insbesondere bei Blöcken, die viele Transaktionen enthalten. Diese Optimierung reduziert die Zeit und Ressourcen, die benötigt werden, um einen Block zu validieren. Außerdem sind Schnorr-Signaturen im Gegensatz zu mit ECDSA erzeugten Signaturen nicht verformbar. Das bedeutet, dass ein Angreifer eine gültige Signatur nicht so modifizieren kann, dass eine andere gültige Signatur für dieselbe Nachricht und denselben öffentlichen Schlüssel erstellt wird. Diese Schwachstelle war zuvor bei Bitcoin vorhanden und verhinderte insbesondere die sichere Implementierung des Lightning-Netzwerks. Sie wurde für ECDSA mit dem SegWit-Softfork im Jahr 2017 gelöst, der die Signaturen in eine separate Datenbank von den Transaktionen verschiebt, um deren Verformbarkeit zu verhindern.
### Warum hat Satoshi sich für ECDSA entschieden?
Wie wir gesehen haben, entschied sich Satoshi zunächst dafür, ECDSA für digitale Signaturen bei Bitcoin zu implementieren. Doch haben wir auch gesehen, dass Schnorr in vielen Aspekten ECDSA überlegen ist, und dieses Protokoll wurde 1989 von Claus-Peter Schnorr, 20 Jahre vor der Erfindung von Bitcoin, geschaffen.
Nun, wir wissen nicht wirklich, warum Satoshi es nicht gewählt hat, aber eine wahrscheinliche Hypothese ist, dass dieses Protokoll bis 2008 unter Patent stand. Obwohl Bitcoin ein Jahr später, im Januar 2009, erschaffen wurde, gab es zu diesem Zeitpunkt keine Open-Source-Standardisierung für Schnorr-Signaturen. Vielleicht hielt es Satoshi für sicherer, ECDSA zu verwenden, das bereits weit verbreitet und in Open-Source-Software getestet war und mehrere anerkannte Implementierungen hatte (insbesondere die bis 2015 bei Bitcoin Core verwendete OpenSSL-Bibliothek, die dann in Version 0.10.0 durch libsecp256k1 ersetzt wurde). Oder vielleicht war ihm nicht bewusst, dass dieses Patent im Jahr 2008 auslaufen würde. In jedem Fall scheint die wahrscheinlichste Hypothese mit diesem Patent und der Tatsache zusammenzuhängen, dass ECDSA eine bewährte Geschichte hatte und einfacher zu implementieren war.
## Die sighash flags
<chapterId>231c41a2-aff2-4655-9048-47b6d2d83d64</chapterId>
Wie wir in vorherigen Kapiteln gesehen haben, werden digitale Signaturen oft verwendet, um das Skript eines Eingangs zu entsperren. Im Signaturprozess ist es notwendig, die signierten Daten in die Berechnung einzubeziehen, in unseren Beispielen durch die Nachricht $m$ bezeichnet. Diese Daten, einmal signiert, können nicht modifiziert werden, ohne die Signatur ungültig zu machen. Tatsächlich muss, egal ob für ECDSA oder Schnorr, der Signaturprüfer dieselbe Nachricht $m$ in seine Berechnung einbeziehen. Unterscheidet sie sich von der Nachricht $m$, die ursprünglich vom Unterzeichner verwendet wurde, wird das Ergebnis falsch sein und die Signatur wird als ungültig angesehen. Es wird dann gesagt, dass eine Signatur bestimmte Daten abdeckt und sie gewissermaßen vor unbefugten Modifikationen schützt.
### Was ist ein sighash flag?
Im spezifischen Fall von Bitcoin haben wir gesehen, dass die Nachricht $m$ der Transaktion entspricht. In Wirklichkeit ist es jedoch etwas komplexer. Tatsächlich ist es dank der sighash flags möglich, spezifische Daten innerhalb der Transaktion auszuwählen, die von der Signatur abgedeckt werden oder nicht.
Der "sighash flag" ist also ein Parameter, der jedem Eingang hinzugefügt wird und die Bestimmung der Komponenten einer Transaktion erlaubt, die von der zugehörigen Signatur abgedeckt sind. Diese Komponenten sind die Eingänge und die Ausgänge. Die Wahl des sighash flags bestimmt also, welche Eingänge und welche Ausgänge der Transaktion durch die Signatur fixiert werden und welche noch modifiziert werden können, ohne sie zu invalidieren. Dieser Mechanismus ermöglicht es Signaturen, Transaktionsdaten gemäß den Absichten des Unterzeichners zu verpflichten.
Offensichtlich wird eine Transaktion, sobald sie auf der Blockchain bestätigt ist, unveränderlich, unabhängig von den verwendeten Sighash-Flags. Die Möglichkeit einer Modifikation über die Sighash-Flags ist auf den Zeitraum zwischen der Signierung und der Bestätigung beschränkt.
Generell bieten Wallet-Softwareprogramme nicht die Option, das Sighash-Flag Ihrer Eingaben manuell zu modifizieren, wenn Sie eine Transaktion erstellen. Standardmäßig ist `SIGHASH_ALL` eingestellt. Persönlich kenne ich nur Sparrow Wallet, das diese Modifikation über die Benutzeroberfläche erlaubt.
### Welche Sighash-Flags gibt es bei Bitcoin?
Bei Bitcoin gibt es vor allem 3 grundlegende Sighash-Flags:
- `SIGHASH_ALL` (`0x01`): Die Signatur gilt für alle Eingaben und alle Ausgaben der Transaktion. Die Transaktion ist somit vollständig durch die Signatur abgedeckt und kann nicht mehr modifiziert werden. `SIGHASH_ALL` ist das am häufigsten verwendete Sighash bei alltäglichen Transaktionen, wenn man einfach eine Transaktion durchführen möchte, ohne dass sie modifiziert werden kann.

In allen Diagrammen dieses Kapitels repräsentiert die orangefarbene Farbe die Elemente, die von der Signatur abgedeckt sind, während die schwarze Farbe jene angibt, die nicht abgedeckt sind.
- `SIGHASH_NONE` (`0x02`): Die Signatur deckt alle Eingaben ab, aber keine der Ausgaben, und ermöglicht somit die Modifikation der Ausgaben nach der Signatur. Konkret ist dies vergleichbar mit einem Blankoscheck. Der Unterzeichner entsperrt die UTXOs in den Eingaben, lässt aber das Feld der Ausgaben vollständig modifizierbar. Jeder, der diese Transaktion kennt, kann somit die Ausgabe seiner Wahl hinzufügen, indem er beispielsweise eine Empfangsadresse angibt, um die durch die Eingaben verbrauchten Mittel zu sammeln, und dann die Transaktion überträgt, um die Bitcoins zu erhalten. Die Signatur des Besitzers der Eingaben wird nicht ungültig, da sie nur die Eingaben abdeckt.

- `SIGHASH_SINGLE` (`0x03`): Die Signatur deckt alle Eingaben sowie eine einzelne Ausgabe ab, die dem Index der signierten Eingabe entspricht. Wenn beispielsweise die Signatur das _scriptPubKey_ der Eingabe #0 entsperrt, dann deckt sie auch die Ausgabe #0 ab. Die Signatur schützt auch alle anderen Eingaben, die nicht mehr modifiziert werden können. Jedoch kann jeder eine zusätzliche Ausgabe hinzufügen, ohne die Signatur zu invalidieren, vorausgesetzt, dass Ausgabe #0, die die einzige von ihr abgedeckte ist, nicht modifiziert wird.

Zusätzlich zu diesen drei Sighash-Flags gibt es auch den Modifikator `SIGHASH_ANYONECANPAY` (`0x80`). Dieser Modifikator kann mit einem grundlegenden Sighash-Flag kombiniert werden, um drei neue Sighash-Flags zu erstellen:
- `SIGHASH_ALL | SIGHASH_ANYONECANPAY` (`0x81`): Die Signatur deckt eine einzelne Eingabe ab, während sie alle Ausgaben der Transaktion einschließt. Dieses kombinierte Sighash-Flag ermöglicht beispielsweise die Erstellung einer Crowdfunding-Transaktion. Der Organisator bereitet die Ausgabe mit seiner Adresse und dem Zielbetrag vor, und jeder Investor kann dann Eingaben hinzufügen, um diese Ausgabe zu finanzieren. Sobald ausreichend Mittel in den Eingaben gesammelt sind, um die Ausgabe zu befriedigen, kann die Transaktion übertragen werden.

- `SIGHASH_NONE | SIGHASH_ANYONECANPAY` (`0x82`): Die Signatur deckt eine einzelne Eingabe ab, ohne sich auf eine Ausgabe festzulegen;

- `SIGHASH_SINGLE | SIGHASH_ANYONECANPAY` (`0x83`): Die Signatur deckt einen einzelnen Eingang sowie den Ausgang ab, der denselben Index wie dieser Eingang hat. Zum Beispiel, wenn die Signatur das _scriptPubKey_ des Eingangs #3 entsperrt, wird sie auch den Ausgang #3 abdecken. Der Rest der Transaktion bleibt modifizierbar, sowohl in Bezug auf andere Eingänge als auch andere Ausgänge.

### Projekte zur Hinzufügung neuer Sighash-Flags
Derzeit (2024) sind nur die im vorherigen Abschnitt vorgestellten Sighash-Flags in Bitcoin verwendbar. Einige Projekte erwägen jedoch die Einführung neuer Sighash-Flags. Zum Beispiel führt BIP118, vorgeschlagen von Christian Decker und Anthony Towns, zwei neue Sighash-Flags ein: `SIGHASH_ANYPREVOUT` und `SIGHASH_ANYPREVOUTANYSCRIPT` (_AnyPrevOut = "Jeder vorherige Ausgang"_).
Diese beiden Sighash-Flags würden eine zusätzliche Möglichkeit in Bitcoin bieten: das Erstellen von Signaturen, die keinen spezifischen Eingang der Transaktion abdecken.

Diese Idee wurde ursprünglich von Joseph Poon und Thaddeus Dryja im Lightning-Whitepaper formuliert. Bevor es umbenannt wurde, hieß dieses Sighash-Flag `SIGHASH_NOINPUT`.
Wenn dieses Sighash-Flag in Bitcoin integriert wird, ermöglicht es die Verwendung von Covenants, ist aber auch eine zwingende Voraussetzung für die Implementierung von Eltoo, einem allgemeinen Protokoll für zweite Schichten, das definiert, wie das Eigentum an einem UTXO gemeinsam verwaltet wird. Eltoo wurde speziell entwickelt, um die Probleme zu lösen, die mit den Mechanismen zur Aushandlung des Zustands von Lightning-Kanälen verbunden sind, das heißt, zwischen Öffnen und Schließen.
Um Ihr Wissen über das Lightning-Netzwerk zu vertiefen, empfehle ich nach dem CYP201-Kurs den LNP201-Kurs von Fanis Michalakis, der das Thema detailliert behandelt:
https://planb.network/courses/34bd43ef-6683-4a5c-b239-7cb1e40a4aeb
Im nächsten Teil schlage ich vor, zu entdecken, wie die mnemonische Phrase, die die Basis Ihrer Bitcoin-Wallet bildet, funktioniert.
# Die mnemonische Phrase
<partId>4070af16-c8a2-58b5-9871-a22c86c07458</partId>
## Entwicklung von Bitcoin-Wallets
<chapterId>9d9acd5d-a0e5-5dfd-b544-f043fae8840f</chapterId>
Jetzt, da wir die Funktionsweise von Hash-Funktionen und digitalen Signaturen erkundet haben, können wir untersuchen, wie Bitcoin-Wallets funktionieren. Das Ziel wird sein, sich vorzustellen, wie eine Wallet auf Bitcoin konstruiert ist, wie sie zerlegt wird und wofür die verschiedenen Informationen, die sie konstituieren, verwendet werden. Dieses Verständnis der Wallet-Mechanismen wird es Ihnen ermöglichen, Ihre Nutzung von Bitcoin in Bezug auf Sicherheit und Privatsphäre zu verbessern.
Bevor wir in die technischen Details eintauchen, ist es wesentlich zu klären, was unter "Bitcoin-Wallet" verstanden wird und deren Nutzen zu verstehen.
### Was ist eine Bitcoin-Wallet?
Im Gegensatz zu traditionellen Geldbörsen, die es Ihnen ermöglichen, physische Scheine und Münzen zu speichern, "enthält" eine Bitcoin-Wallet per se keine Bitcoins. Tatsächlich existieren Bitcoins nicht in einer physischen oder digitalen Form, die gespeichert werden kann, sondern werden durch Kontoeinheiten dargestellt, die im System in Form von **UTXOs** (_Unspent Transaction Output_) abgebildet sind.
UTXOs repräsentieren also Fragmente von Bitcoins in unterschiedlichen Größen, die ausgegeben werden können, vorausgesetzt, ihr _scriptPubKey_ wird erfüllt. Um seine Bitcoins auszugeben, muss ein Benutzer ein _scriptSig_ bereitstellen, das den _scriptPubKey_ entsperrt, der mit seinem UTXO verbunden ist. Dieser Nachweis erfolgt in der Regel durch eine digitale Signatur, die aus dem privaten Schlüssel generiert wird, der dem im _scriptPubKey_ vorhandenen öffentlichen Schlüssel entspricht. Somit ist das entscheidende Element, das der Benutzer sichern muss, der private Schlüssel. Die Rolle einer Bitcoin-Wallet besteht genau darin, diese privaten Schlüssel sicher zu verwalten. In Wirklichkeit ist ihre Rolle eher mit der eines Schlüsselbunds als mit einer Geldbörse im traditionellen Sinne vergleichbar.
### JBOK Wallets (_Just a Bunch Of Keys_)
Die ersten auf Bitcoin verwendeten Wallets waren JBOK (_Just a Bunch Of Keys_) Wallets, die privat generierte Schlüssel unabhängig voneinander und ohne jegliche Verbindung zwischen ihnen zusammenfassten. Diese Wallets funktionierten nach einem einfachen Modell, bei dem jeder private Schlüssel eine einzigartige Bitcoin-Empfangsadresse entsperren konnte.
Wenn man mehrere private Schlüssel verwenden wollte, war es dann notwendig, ebenso viele Backups zu machen, um im Falle von Problemen mit dem Gerät, das die Wallet hostet, Zugang zu den Mitteln zu gewährleisten. Bei Verwendung eines einzigen privaten Schlüssels könnte diese Wallet-Struktur ausreichen, da ein einzelnes Backup genügt. Dies stellt jedoch ein Problem dar: Bei Bitcoin wird dringend davon abgeraten, immer denselben privaten Schlüssel zu verwenden. Tatsächlich ist ein privater Schlüssel mit einer einzigartigen Adresse verbunden, und Bitcoin-Empfangsadressen sind normalerweise für den einmaligen Gebrauch konzipiert. Jedes Mal, wenn Sie Gelder erhalten, sollten Sie eine neue leere Adresse generieren.
Diese Einschränkung ergibt sich aus dem Datenschutzmodell von Bitcoin. Durch die Wiederverwendung derselben Adresse wird es externen Beobachtern leichter gemacht, alle meine Bitcoin-Transaktionen nachzuverfolgen. Deshalb wird dringend davon abgeraten, eine Empfangsadresse wiederzuverwenden. Um jedoch mehrere Adressen zu haben und unsere Transaktionen öffentlich zu trennen, ist es notwendig, mehrere private Schlüssel zu verwalten. Im Falle von JBOK-Wallets impliziert dies, so viele Backups zu erstellen, wie es neue Schlüsselpaare gibt, eine Aufgabe, die schnell komplex und für die Benutzer schwer zu pflegen werden kann.
Um mehr über das Datenschutzmodell von Bitcoin zu erfahren und Methoden zum Schutz Ihrer Privatsphäre zu entdecken, empfehle ich auch, meinem BTC204-Kurs im Plan ₿ Network zu folgen:
https://planb.network/courses/65c138b0-4161-4958-bbe3-c12916bc959c
### HD Wallets (_Hierarchical Deterministic_)
Um die Einschränkung von JBOK-Wallets zu adressieren, wurde später eine neue Wallet-Struktur genutzt. Im Jahr 2012 führte Pieter Wuille mit BIP32 eine Verbesserung ein, die hierarchische deterministische Wallets einführt. Das Prinzip einer HD-Wallet besteht darin, alle privaten Schlüssel von einer einzigen Informationsquelle, genannt Seed, auf eine deterministische und hierarchische Weise abzuleiten. Dieser Seed wird zufällig beim Erstellen der Wallet generiert und stellt ein einzigartiges Backup dar, das die Wiederherstellung aller privaten Schlüssel der Wallet ermöglicht. So kann der Benutzer eine sehr große Anzahl von privaten Schlüsseln generieren, um die Wiederverwendung von Adressen zu vermeiden und ihre Privatsphäre zu bewahren, während nur ein einziges Backup ihrer Wallet über den Seed benötigt wird.
In HD-Wallets wird die Schlüsselableitung gemäß einer hierarchischen Struktur durchgeführt, die es ermöglicht, Schlüssel in Ableitungssubräume zu organisieren, die weiter unterteilbar sind, um die Verwaltung von Mitteln und die Interoperabilität zwischen verschiedenen Wallet-Software zu erleichtern. Heutzutage wird dieser Standard von der überwiegenden Mehrheit der Bitcoin-Benutzer angenommen. Aus diesem Grund werden wir ihn in den folgenden Kapiteln detailliert untersuchen.
### Der BIP39-Standard: Die Mnemonische Phrase
Neben BIP32 standardisiert BIP39 das Seed-Format als eine mnemonische Phrase, um die Sicherung und Lesbarkeit durch Benutzer zu erleichtern. Die mnemonische Phrase, auch Wiederherstellungsphrase oder 24-Wort-Phrase genannt, ist eine Abfolge von Wörtern aus einer vordefinierten Liste, die den Seed der Wallet sicher kodiert.
Die mnemonische Phrase vereinfacht die Sicherung für den Benutzer erheblich. Im Falle eines Verlusts, Schadens oder Diebstahls des Geräts, das die Wallet hostet, ermöglicht das einfache Wissen dieser mnemonischen Phrase die Wiederherstellung der Wallet und die Wiedererlangung des Zugriffs auf alle durch sie gesicherten Geldmittel.
In den kommenden Kapiteln werden wir die internen Arbeitsweisen von HD-Wallets erforschen, einschließlich der Schlüsselableitungsmechanismen und der verschiedenen möglichen hierarchischen Strukturen. Dies wird Ihnen helfen, die kryptografischen Grundlagen, auf denen die Sicherheit von Geldern auf Bitcoin basiert, besser zu verstehen. Und um zu beginnen, schlage ich im nächsten Kapitel vor, wir entdecken die Rolle der Entropie an der Basis Ihrer Wallet.
## Entropie und Zufallszahl
<chapterId>b43c715d-affb-56d8-a697-ad5bc2fffd63</chapterId>
Moderne HD-Wallets (deterministisch und hierarchisch) stützen sich auf ein einzelnes anfängliches Informationsstück, genannt "Entropie", um das gesamte Set von Wallet-Schlüsseln deterministisch zu generieren. Diese Entropie ist eine pseudozufällige Zahl, deren Chaosgrad teilweise die Sicherheit der Wallet bestimmt.
### Definition von Entropie
Entropie ist im Kontext der Kryptografie und Information eine quantitative Messung der Unsicherheit oder Unvorhersehbarkeit, die mit einer Datenquelle oder einem zufälligen Prozess verbunden ist. Sie spielt eine wichtige Rolle in der Sicherheit kryptografischer Systeme, insbesondere bei der Generierung von Schlüsseln und Zufallszahlen. Hohe Entropie stellt sicher, dass die generierten Schlüssel ausreichend unvorhersehbar und widerstandsfähig gegen Brute-Force-Angriffe sind, bei denen ein Angreifer alle möglichen Kombinationen ausprobiert, um den Schlüssel zu erraten.
Im Kontext von Bitcoin wird Entropie verwendet, um den Seed zu generieren. Bei der Erstellung einer deterministischen und hierarchischen Wallet wird die Konstruktion der mnemonischen Phrase aus einer Zufallszahl durchgeführt, die selbst von einer Entropiequelle abgeleitet ist. Die Phrase wird dann verwendet, um mehrere private Schlüssel auf eine deterministische und hierarchische Weise zu generieren, um Ausgabebedingungen für UTXOs zu erstellen.
### Methoden zur Generierung von Entropie
Die anfängliche Entropie, die für eine HD-Wallet verwendet wird, beträgt in der Regel 128 Bits oder 256 Bits, wobei:
- **128 Bits Entropie** einer mnemonischen Phrase von **12 Wörtern** entsprechen;
- **256 Bits Entropie** einer mnemonischen Phrase von **24 Wörtern** entsprechen.
In den meisten Fällen wird diese Zufallszahl automatisch von der Wallet-Software unter Verwendung eines PRNG (_Pseudo-Random Number Generator_) generiert. PRNGs sind eine Kategorie von Algorithmen, die verwendet werden, um Sequenzen von Zahlen aus einem Anfangszustand zu generieren, die Eigenschaften aufweisen, die denen einer Zufallszahl nahekommen, ohne tatsächlich eine zu sein. Ein guter PRNG muss Eigenschaften wie Ausgabeuniformität, Unvorhersehbarkeit und Widerstandsfähigkeit gegen vorhersagende Angriffe aufweisen. Im Gegensatz zu echten Zufallszahlengeneratoren (TRNG) sind PRNGs deterministisch und reproduzierbar.
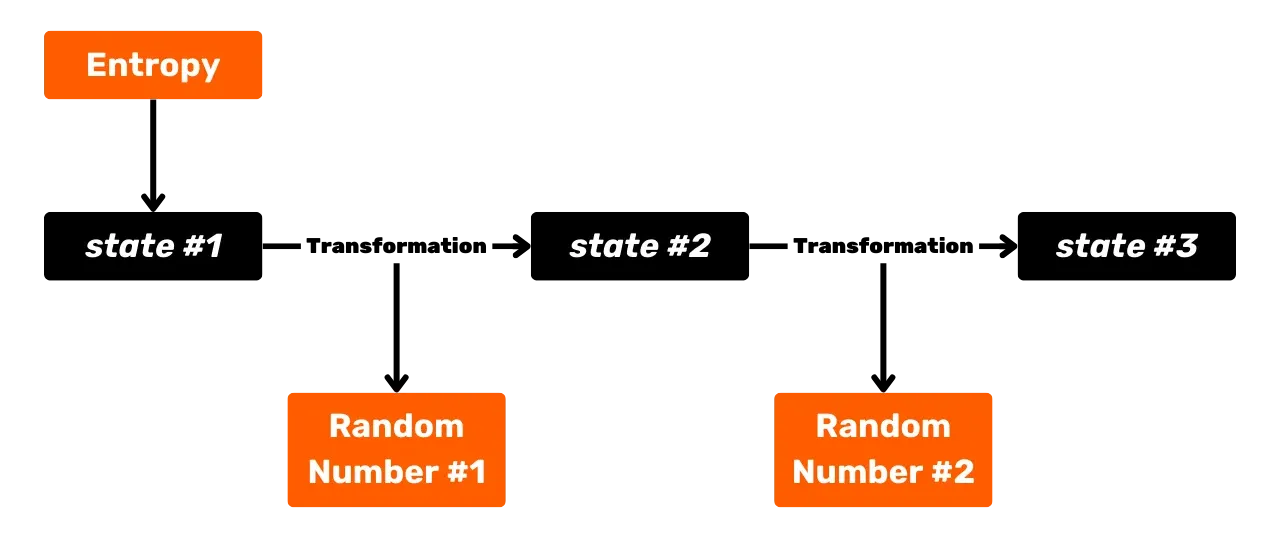
Eine Alternative ist die manuelle Generierung der Entropie, die eine bessere Kontrolle bietet, aber auch viel riskanter ist. Ich rate dringend davon ab, die Entropie für Ihre HD-Wallet selbst zu generieren.
Im nächsten Kapitel werden wir sehen, wie wir von einer Zufallszahl zu einer mnemonischen Phrase von 12 oder 24 Wörtern kommen.
## Die mnemonische Phrase
<chapterId>8f9340c1-e6dc-5557-a2f2-26c9669987d5</chapterId>
Die mnemonische Phrase, auch bekannt als "Seed-Phrase", "Wiederherstellungsphrase", "Geheimphrase" oder "24-Wort-Phrase", ist eine Sequenz, die üblicherweise aus 12 oder 24 Wörtern besteht und aus Entropie generiert wird. Sie wird verwendet, um deterministisch alle Schlüssel eines HD-Wallets abzuleiten. Das bedeutet, dass aus dieser Phrase alle privaten und öffentlichen Schlüssel des Bitcoin-Wallets deterministisch generiert und rekonstruiert werden können und somit Zugang zu den damit geschützten Geldern ermöglicht wird. Der Zweck der mnemonischen Phrase besteht darin, ein Mittel zur Sicherung und Wiederherstellung von Bitcoins zu bieten, das sowohl sicher als auch einfach zu verwenden ist. Sie wurde 2013 mit BIP39 in Standards eingeführt.
Lassen Sie uns gemeinsam entdecken, wie man von Entropie zu einer mnemonischen Phrase gelangt.
### Die Prüfsumme
Um Entropie in eine mnemonische Phrase umzuwandeln, muss zunächst eine Prüfsumme (oder "Kontrollsumme") am Ende der Entropie hinzugefügt werden. Diese Prüfsumme ist eine kurze Bitsequenz, die die Integrität der Daten sicherstellt, indem sie überprüft, ob keine zufällige Modifikation eingeführt wurde.
Um die Prüfsumme zu berechnen, wird die SHA256-Hashfunktion einmalig auf die Entropie angewendet (dies ist einer der seltenen Fälle bei Bitcoin, in denen ein einzelner SHA256-Hash anstelle eines doppelten Hashs verwendet wird). Diese Operation produziert einen 256-Bit-Hash. Die Prüfsumme besteht aus den ersten Bits dieses Hashs, und ihre Länge hängt von der Länge der Entropie ab, gemäß der folgenden Formel:
\text{CS} = \frac{\text{ENT}}{32}
wobei $\text{ENT}$ die Länge der Entropie in Bits und $\text{CS}$ die Länge der Prüfsumme in Bits darstellt.
Beispielsweise wird für eine Entropie von 256 Bits die ersten 8 Bits des Hashs genommen, um die Prüfsumme zu bilden:
\text{CS} = \frac{256}{32} = 8 \text{ bits}
Sobald die Prüfsumme berechnet ist, wird sie mit der Entropie verkettet, um eine erweiterte Bitsequenz zu erhalten, notiert als $\text{ENT} \Vert \text{CS}$ ("verketten" bedeutet, Ende an Ende zu setzen).

### Entsprechung zwischen der Entropie und der mnemonischen Phrase
Die Anzahl der Wörter in der mnemonischen Phrase hängt von der Größe der anfänglichen Entropie ab, wie in der folgenden Tabelle dargestellt mit:
- $\text{ENT}$: die Größe in Bits der Entropie;
- $\text{CS}$: die Größe in Bits der Prüfsumme;
- $w$: die Anzahl der Wörter in der endgültigen mnemonischen Phrase.
\begin{array}{|c|c|c|c|} \hline \text{ENT} & \text{CS} & \text{ENT} \Vert \text{CS} & w \ \hline 128 & 4 & 132 & 12 \ 160 & 5 & 165 & 15 \ 192 & 6 & 198 & 18 \ 224 & 7 & 231 & 21 \ 256 & 8 & 264 & 24 \ \hline \end{array}
Beispielsweise ergibt eine 256-Bit-Entropie das Ergebnis $\text{ENT} \Vert \text{CS}$ von 264 Bits und führt zu einer mnemonischen Phrase von 24 Wörtern.
### Umwandlung der Binärsequenz in eine mnemonische Phrase
Die Bitsequenz $\text{ENT} \Vert \text{CS}$ wird dann in Segmente von 11 Bits unterteilt. Jedes 11-Bit-Segment, einmal in Dezimal umgewandelt, entspricht einer Zahl zwischen 0 und 2047, die die Position eines Wortes [in einer Liste von 2048 durch BIP39 standardisierten Wörtern](https://github.com/Planb-Network/bitcoin-educational-content/blob/dev/resources/bet/bip39-wordlist//courses/cyp201/assets/BIP39-WORDLIST.pdf) bezeichnet.
Zum Beispiel beträgt bei einer 128-Bit-Entropie die Prüfsumme 4 Bits, und somit misst die gesamte Sequenz 132 Bits. Sie wird in 12 Segmente zu je 11 Bits unterteilt (die orangefarbenen Bits bezeichnen die Prüfsumme):

Jedes Segment wird dann in eine Dezimalzahl umgewandelt, die ein Wort in der Liste repräsentiert. Zum Beispiel ist das binäre Segment `01011010001` in Dezimalzahl `721` äquivalent. Indem man 1 hinzufügt, um sich an die Indexierung der Liste anzupassen (die bei 1 und nicht bei 0 beginnt), ergibt dies den Wortrang `722`, welcher "*focus*" in der Liste ist.

Diese Entsprechung wird für jedes der 12 Segmente wiederholt, um eine 12-Wort-Phrase zu erhalten.

### Merkmale der BIP39-Wortliste
Eine Besonderheit der BIP39-Wortliste ist, dass kein Wort die gleichen ersten vier Buchstaben in derselben Reihenfolge wie ein anderes Wort teilt. Das bedeutet, dass es ausreicht, nur die ersten vier Buchstaben jedes Wortes zu notieren, um die mnemonische Phrase zu speichern. Dies kann interessant sein, um Platz zu sparen, insbesondere für diejenigen, die sie auf einem Metallträger eingravieren möchten.
Diese Liste von 2048 Wörtern existiert in mehreren Sprachen. Es handelt sich dabei nicht um einfache Übersetzungen, sondern um unterschiedliche Wörter für jede Sprache. Es wird jedoch dringend empfohlen, bei der englischen Version zu bleiben, da Versionen in anderen Sprachen im Allgemeinen nicht von Wallet-Software unterstützt werden.
### Welche Länge sollte man für seine mnemonische Phrase wählen?
Um die optimale Länge Ihrer mnemonischen Phrase zu bestimmen, muss man die tatsächliche Sicherheit berücksichtigen, die sie bietet. Eine 12-Wort-Phrase gewährleistet 128 Bits an Sicherheit, während eine 24-Wort-Phrase 256 Bits bietet.
Allerdings verbessert dieser Unterschied in der Phrasen-Sicherheit nicht die Gesamtsicherheit eines Bitcoin-Wallets, da die daraus abgeleiteten privaten Schlüssel nur von 128 Bits an Sicherheit profitieren. Tatsächlich, wie wir zuvor gesehen haben, werden Bitcoin-Private-Keys aus Zufallszahlen (oder von einer zufälligen Quelle abgeleitet) generiert, die zwischen $1$ und $n-1$ liegen, wobei $n$ die Ordnung des Generatorpunkts $G$ der secp256k1-Kurve darstellt, eine Zahl, die etwas weniger als $2^{256}$ beträgt. Man könnte daher denken, dass diese privaten Schlüssel 256 Bits an Sicherheit bieten. Ihre Sicherheit liegt jedoch in der Schwierigkeit, einen privaten Schlüssel aus seinem zugehörigen öffentlichen Schlüssel zu finden, eine Schwierigkeit, die durch das mathematische Problem des diskreten Logarithmus auf elliptischen Kurven (*ECDLP*) festgelegt ist. Bis heute ist der bekannteste Algorithmus zur Lösung dieses Problems Pollards Rho-Algorithmus, der die Anzahl der Operationen, die benötigt werden, um einen Schlüssel zu brechen, auf die Quadratwurzel seiner Größe reduziert.
Für 256-Bit-Schlüssel, wie sie bei Bitcoin verwendet werden, reduziert Pollards Rho-Algorithmus die Komplexität somit auf $2^{128}$ Operationen:
O(\sqrt{2^{256}}) = O(2^{128})
Daher wird angenommen, dass ein privater Schlüssel, der bei Bitcoin verwendet wird, 128 Bits an Sicherheit bietet.
Folglich bietet die Wahl einer 24-Wort-Phrase keinen zusätzlichen Schutz für das Wallet, da 256 Bits an Sicherheit bei der Phrase sinnlos sind, wenn die daraus abgeleiteten Schlüssel nur 128 Bits an Sicherheit bieten. Um dieses Prinzip zu veranschaulichen, ist es, als hätte man ein Haus mit zwei Türen: eine alte Holztür und eine verstärkte Tür. Im Falle eines Einbruchs wäre die verstärkte Tür nutzlos, da der Eindringling durch die Holztür gehen würde. Hier liegt eine analoge Situation vor.
Ein 12-Wort-Phrase, die auch 128 Bit an Sicherheit bietet, ist daher derzeit ausreichend, um Ihre Bitcoins gegen jeden Diebstahlversuch zu schützen. Solange der digitale Signaturalgorithmus nicht geändert wird, um größere Schlüssel zu verwenden oder sich auf ein anderes mathematisches Problem als das ECDLP zu stützen, bleibt eine 24-Wort-Phrase überflüssig. Darüber hinaus erhöht eine längere Phrase das Risiko eines Verlusts während der Sicherung: Eine Sicherung, die halb so lang ist, ist immer einfacher zu verwalten.
Um weiter zu gehen und konkret zu lernen, wie man manuell eine Test-Mnemonic-Phrase generiert, rate ich Ihnen, dieses Tutorial zu entdecken:
https://planb.network/tutorials/wallet/backup/generate-mnemonic-phrase-47507d90-e6af-4cac-b01b-01a14d7a8228
Bevor wir mit der Ableitung des Wallets aus dieser Mnemonic-Phrase fortfahren, werde ich Ihnen im folgenden Kapitel die BIP39-Passphrase vorstellen, da sie eine Rolle im Ableitungsprozess spielt und sie sich auf derselben Ebene wie die Mnemonic-Phrase befindet.
## Die Passphrase
<chapterId>6a51b397-f3b5-5084-b151-cef94bc9b93f</chapterId>
Wie wir gerade gesehen haben, werden HD-Wallets aus einer Mnemonic-Phrase generiert, die typischerweise aus 12 oder 24 Wörtern besteht. Diese Phrase ist sehr wichtig, da sie die Wiederherstellung aller Schlüssel eines Wallets ermöglicht, falls dessen physisches Gerät (wie zum Beispiel ein Hardware-Wallet) verloren geht. Allerdings stellt sie einen einzigen Ausfallpunkt dar, denn wenn sie kompromittiert wird, könnte ein Angreifer alle Bitcoins stehlen. Hier kommt die BIP39-Passphrase ins Spiel.
### Was ist eine BIP39-Passphrase?
Die Passphrase ist ein optionales Passwort, das Sie frei wählen können, das zur Mnemonic-Phrase im Schlüsselableitungsprozess hinzugefügt wird, um die Sicherheit des Wallets zu erhöhen.
Achten Sie darauf, die Passphrase nicht mit dem PIN-Code Ihres Hardware-Wallets oder dem Passwort zu verwechseln, das verwendet wird, um den Zugang zu Ihrem Wallet auf Ihrem Computer freizuschalten. Im Gegensatz zu all diesen Elementen spielt die Passphrase eine Rolle in der Ableitung der Schlüssel Ihres Wallets. **Das bedeutet, dass Sie ohne sie niemals in der Lage sein werden, Ihre Bitcoins wiederherzustellen.**
Die Passphrase arbeitet zusammen mit der Mnemonic-Phrase und modifiziert den Seed, aus dem die Schlüssel generiert werden. So kann selbst, wenn jemand Ihre 12- oder 24-Wort-Phrase erhält, ohne die Passphrase nicht auf Ihre Gelder zugreifen. Die Verwendung einer Passphrase erstellt im Wesentlichen ein neues Wallet mit unterschiedlichen Schlüsseln. Eine Modifikation (selbst eine geringfügige) der Passphrase wird ein anderes Wallet generieren.

### Warum sollten Sie eine Passphrase verwenden?
Die Passphrase ist willkürlich und kann jede vom Benutzer gewählte Zeichenkombination sein. Die Verwendung einer Passphrase bietet somit mehrere Vorteile. Zunächst reduziert sie alle Risiken, die mit dem Kompromittieren der Mnemonic-Phrase verbunden sind, indem sie einen zweiten Faktor zum Zugriff auf die Gelder erfordert (Einbruch, Zugang zu Ihrem Zuhause usw.).
Weiterhin kann sie strategisch verwendet werden, um ein Köder-Wallet zu erstellen, um physischen Zwängen zum Stehlen Ihrer Gelder wie dem berüchtigten "_$5 Schraubenschlüssel-Angriff_" zu begegnen. In diesem Szenario besteht die Idee darin, ein Wallet ohne Passphrase zu haben, das nur eine kleine Menge an Bitcoins enthält, genug, um einen potenziellen Aggressor zufriedenzustellen, während man ein verstecktes Wallet hat. Dieses letztere verwendet dieselbe Mnemonic-Phrase, ist aber mit einer zusätzlichen Passphrase gesichert.
Schließlich ist die Verwendung einer Passphrase interessant, wenn man die Zufälligkeit der Generierung des Seeds des HD-Wallets kontrollieren möchte.
### Wie wählt man eine gute Passphrase?
Damit die Passphrase wirksam ist, muss sie ausreichend lang und zufällig sein. Wie bei einem starken Passwort empfehle ich, eine Passphrase zu wählen, die so lang und zufällig wie möglich ist, mit einer Vielfalt an Buchstaben, Zahlen und Symbolen, um jeden Brute-Force-Angriff unmöglich zu machen.
Es ist ebenfalls wichtig, diese Passphrase ordnungsgemäß zu speichern, genauso wie die mnemonische Phrase. **Der Verlust bedeutet den Verlust des Zugangs zu Ihren Bitcoins**. Ich rate dringend davon ab, sie sich nur zu merken, da dies das Risiko eines Verlusts unangemessen erhöht. Das Ideal ist, sie auf einem physischen Medium (Papier oder Metall) getrennt von der mnemonischen Phrase niederzuschreiben. Diese Sicherungskopie muss offensichtlich an einem anderen Ort als Ihre mnemonische Phrase aufbewahrt werden, um zu verhindern, dass beide gleichzeitig kompromittiert werden.
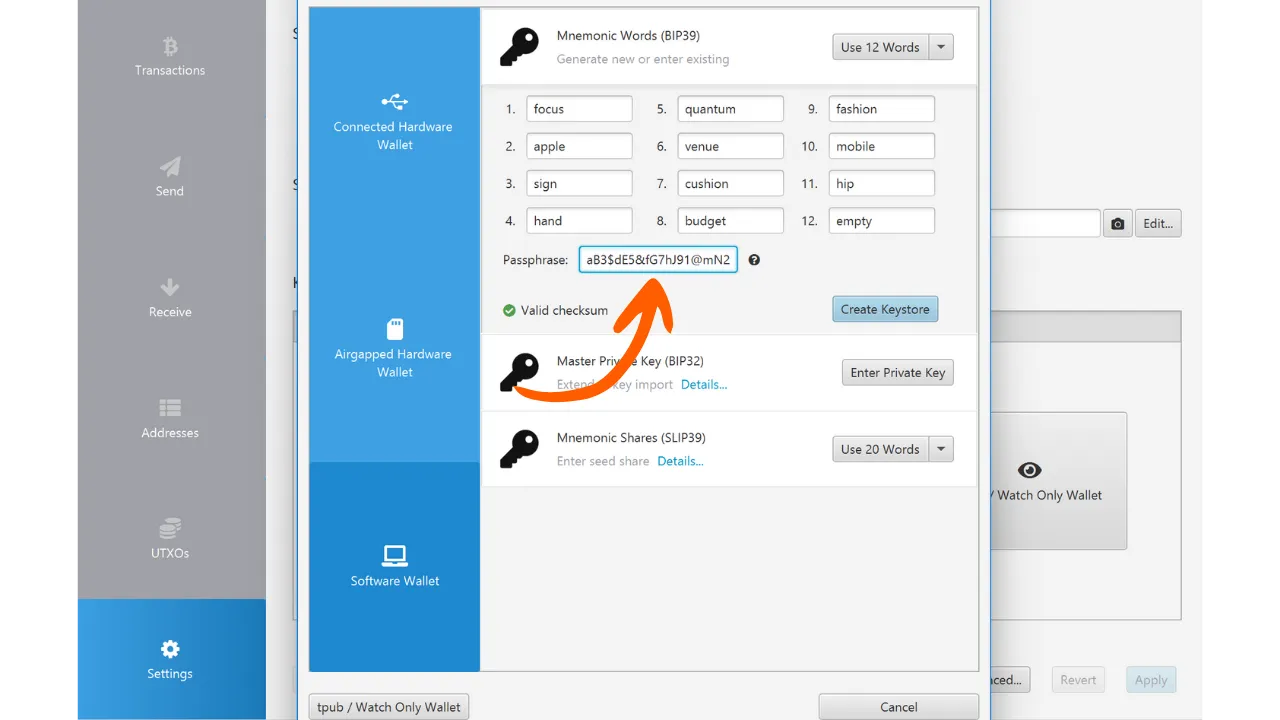
Im folgenden Abschnitt werden wir entdecken, wie diese beiden Elemente an der Basis Ihrer Wallet – die mnemonische Phrase und die Passphrase – verwendet werden, um die Schlüsselpaare abzuleiten, die in dem *scriptPubKey* verwendet werden, um Ihre UTXOs zu sperren.
# Erstellung von Bitcoin-Wallets
<partId>9c25e767-7eae-50b8-8c5f-679d8fc83bab</partId>
## Erstellung des Seeds und des Master-Schlüssels
<chapterId>63093760-2010-5691-8d0e-9a04732ae557</chapterId>
Sobald die mnemonische Phrase und die optionale Passphrase generiert sind, kann der Prozess der Ableitung einer Bitcoin-HD-Wallet beginnen. Die mnemonische Phrase wird zunächst in einen Seed umgewandelt, der die Basis aller Schlüssel der Wallet bildet.
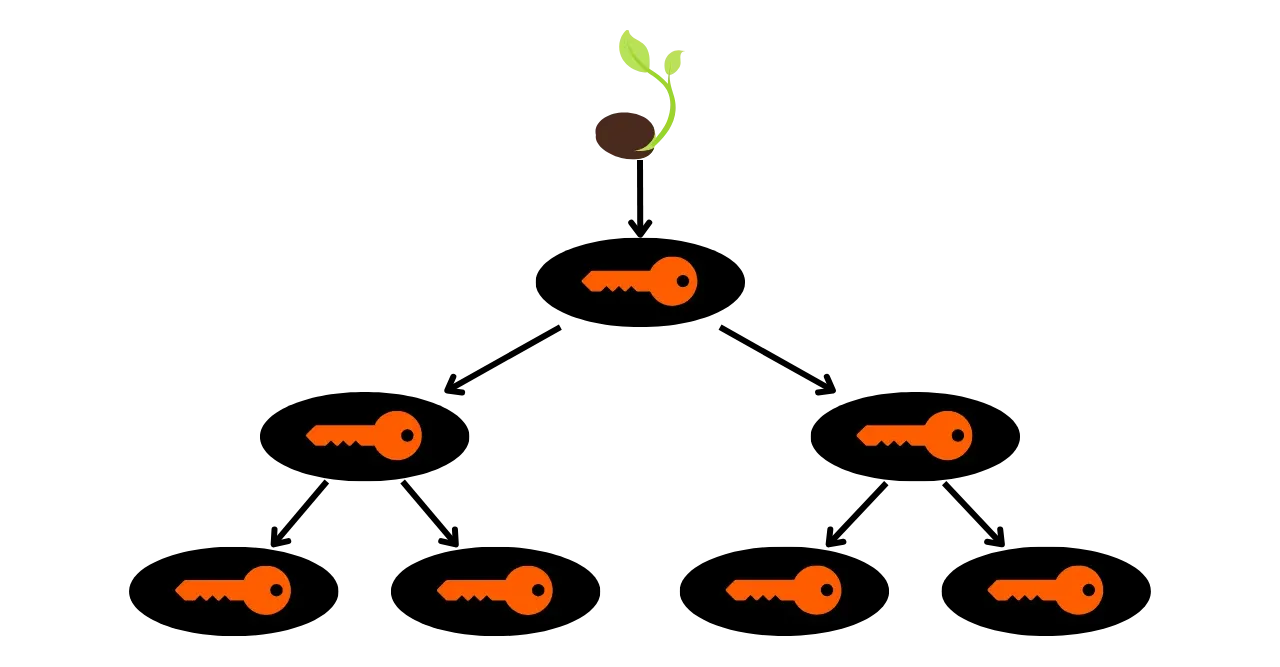
### Der Seed einer HD-Wallet
Der BIP39-Standard definiert den Seed als eine 512-Bit-Sequenz, die als Ausgangspunkt für die Ableitung aller Schlüssel einer HD-Wallet dient. Der Seed wird aus der mnemonischen Phrase und der möglichen Passphrase unter Verwendung des **PBKDF2**-Algorithmus (*Password-Based Key Derivation Function 2*) abgeleitet, den wir bereits in Kapitel 3.3 besprochen haben. In dieser Ableitungsfunktion werden wir die folgenden Parameter verwenden:
- $m$ : die mnemonische Phrase;
- $p$ : eine optionale Passphrase, die vom Benutzer gewählt wird, um die Sicherheit des Seeds zu erhöhen. Wenn keine Passphrase vorhanden ist, bleibt dieses Feld leer;
- $\text{PBKDF2}$ : die Ableitungsfunktion mit $\text{HMAC-SHA512}$ und $2048$ Iterationen;
- $s$: der 512-Bit-Wallet-Seed.
Unabhängig von der gewählten Länge der mnemonischen Phrase (132 Bits oder 264 Bits) wird die PBKDF2-Funktion immer ein 512-Bit-Ergebnis produzieren, und der Seed wird daher immer diese Größe haben.
### Seed-Ableitungsschema mit PBKDF2
Die folgende Gleichung veranschaulicht die Ableitung des Seeds aus der mnemonischen Phrase und der Passphrase:
s = \text{PBKDF2}_{\text{HMAC-SHA512}}(m, p, 2048)

Der Wert des Seeds wird also durch den Wert der mnemonischen Phrase und der Passphrase beeinflusst. Durch Ändern der Passphrase wird ein anderer Seed erhalten. Jedoch wird mit derselben mnemonischen Phrase und Passphrase immer derselbe Seed generiert, da PBKDF2 eine deterministische Funktion ist. Dies stellt sicher, dass dieselben Schlüsselpaare über unsere Sicherungen abgerufen werden können.
**Hinweis:** Im allgemeinen Sprachgebrauch bezieht sich der Begriff "Seed" oft, durch Sprachmissbrauch, auf die mnemonische Phrase. Tatsächlich ist in Abwesenheit einer Passphrase das eine einfach die Kodierung des anderen. Wie wir jedoch gesehen haben, sind in der technischen Realität von Wallets der Seed und die mnemonische Phrase tatsächlich zwei unterschiedliche Elemente.
Jetzt, da wir unseren Seed haben, können wir mit der Ableitung unserer Bitcoin-Wallet fortfahren.
### Der Master-Schlüssel und der Master-Chain-Code
Sobald der Seed erhalten wurde, besteht der nächste Schritt bei der Ableitung eines HD-Wallets darin, den Master-Privatschlüssel und den Master-Chain-Code zu berechnen, die die Tiefe 0 unseres Wallets darstellen werden.
Um den Master-Privatschlüssel und den Master-Chain-Code zu erhalten, wird die HMAC-SHA512-Funktion auf den Seed angewendet, unter Verwendung eines festen Schlüssels "*Bitcoin Seed*", der für alle Bitcoin-Nutzer identisch ist. Diese Konstante wird gewählt, um sicherzustellen, dass die Schlüsselableitungen spezifisch für Bitcoin sind. Hier sind die Elemente:
- $\text{HMAC-SHA512}$: die Ableitungsfunktion;
- $s$: der 512-Bit-Wallet-Seed;
- $\text{"Bitcoin Seed"}$: die gemeinsame Ableitungskonstante für alle Bitcoin-Wallets.
\text{output} = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)
Der Output dieser Funktion ist daher 512 Bit lang. Er wird dann in 2 Teile geteilt:
- Die linken 256 Bit bilden den **Master-Privatschlüssel**;
- Die rechten 256 Bit bilden den **Master-Chain-Code**.
Mathematisch können diese beiden Werte wie folgt mit $k_M$ als dem Master-Privatschlüssel und $C_M$ als dem Master-Chain-Code notiert werden:
k_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[:256]}
C_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[256:]}

### Rolle des Master-Schlüssels und des Chain-Codes
Der Master-Privatschlüssel wird als Elternschlüssel betrachtet, von dem alle abgeleiteten Privatschlüssel — Kinder, Enkelkinder, Urenkel usw. — generiert werden. Er repräsentiert die Null-Ebene in der Hierarchie der Ableitung.
Der Master-Chain-Code führt andererseits eine zusätzliche Quelle der Entropie in den Schlüsselableitungsprozess für Kinder ein, um bestimmten potenziellen Angriffen entgegenzuwirken. Darüber hinaus hat im HD-Wallet jedes Schlüsselpaar einen einzigartigen Chain-Code, der ebenfalls verwendet wird, um Kinderschlüssel aus diesem Paar abzuleiten, aber wir werden dies in den kommenden Kapiteln genauer besprechen.
Bevor wir mit der Ableitung des HD-Wallets mit den folgenden Elementen fortfahren, möchte ich im nächsten Kapitel erweiterte Schlüssel vorstellen, die oft mit dem Master-Schlüssel verwechselt werden. Wir werden sehen, wie sie konstruiert sind und welche Rolle sie im Bitcoin-Wallet spielen.
## Erweiterte Schlüssel
<chapterId>8dcffce1-31bd-5e0b-965b-735f5f9e4602</chapterId>
Ein erweiterter Schlüssel ist einfach die Verkettung eines Schlüssels (egal ob privat oder öffentlich) und seines zugehörigen Chain-Codes. Dieser Chain-Code ist wesentlich für die Ableitung von Kinderschlüsseln, denn ohne ihn ist es unmöglich, Kinderschlüssel von einem Elternschlüssel abzuleiten, aber wir werden diesen Prozess im nächsten Kapitel genauer entdecken. Diese erweiterten Schlüssel ermöglichen es also, alle notwendigen Informationen zur Ableitung von Kinderschlüsseln zu aggregieren und dadurch die Kontenverwaltung innerhalb eines HD-Wallets zu vereinfachen.
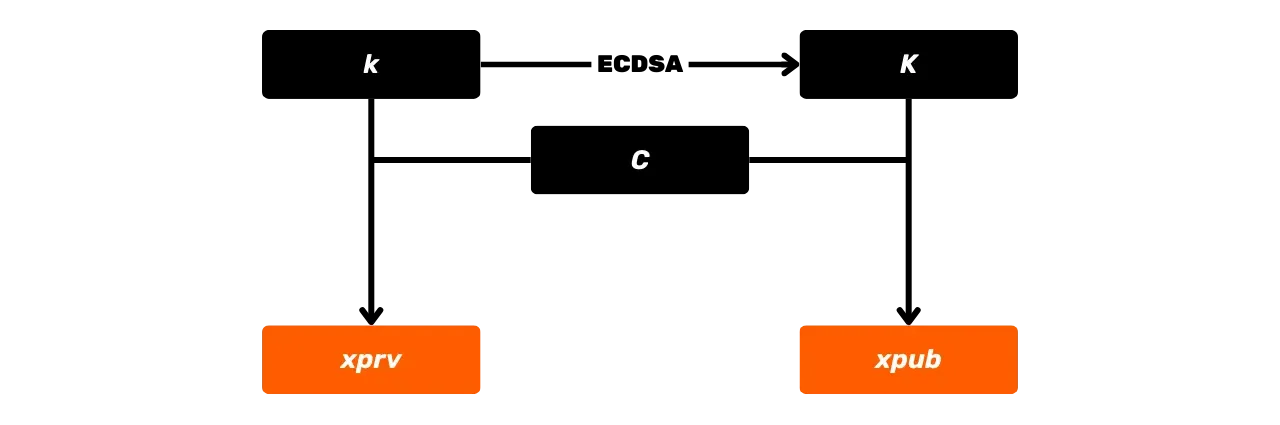
Der erweiterte Schlüssel besteht aus zwei Teilen:
- Der Nutzlast, die den privaten oder öffentlichen Schlüssel sowie den zugehörigen Chain-Code enthält;
- Den Metadaten, die verschiedene Informationen zur Erleichterung der Interoperabilität zwischen Software und zur Verbesserung des Verständnisses für den Benutzer enthalten.
### Wie erweiterte Schlüssel funktionieren
Wenn der erweiterte Schlüssel einen privaten Schlüssel enthält, wird er als erweiterter privater Schlüssel bezeichnet. Er ist an seinem Präfix erkennbar, das die Bezeichnung `prv` enthält. Zusätzlich zum privaten Schlüssel enthält der erweiterte private Schlüssel auch den zugehörigen Chain-Code. Mit dieser Art von erweitertem Schlüssel ist es möglich, alle Arten von Kind-privaten Schlüsseln abzuleiten, und daher durch Addition und Verdopplung von Punkten auf elliptischen Kurven ermöglicht es auch die Ableitung der Gesamtheit von Kind-öffentlichen Schlüsseln.
Wenn der erweiterte Schlüssel keinen privaten Schlüssel enthält, sondern stattdessen einen öffentlichen Schlüssel, wird er als erweiterter öffentlicher Schlüssel bezeichnet. Er ist an seinem Präfix erkennbar, das die Bezeichnung `pub` enthält. Offensichtlich enthält er zusätzlich zum Schlüssel auch den zugehörigen Chain-Code. Im Gegensatz zum erweiterten privaten Schlüssel ermöglicht der erweiterte öffentliche Schlüssel die Ableitung von nur "normalen" Kind-öffentlichen Schlüsseln (was bedeutet, dass er keine "gehärteten" Kind-Schlüssel ableiten kann). Wir werden im folgenden Kapitel sehen, was diese Bezeichnungen "normal" und "gehärtet" bedeuten.
Aber in jedem Fall erlaubt der erweiterte öffentliche Schlüssel nicht die Ableitung von Kind-privaten Schlüsseln. Daher kann selbst, wenn jemand Zugang zu einem `xpub` hat, nicht die zugehörigen Mittel ausgeben, da er keinen Zugang zu den entsprechenden privaten Schlüsseln hat. Sie können nur Kind-öffentliche Schlüssel ableiten, um die zugehörigen Transaktionen zu beobachten.
Für das Folgende werden wir die folgende Notation anwenden:
- $K_{\text{PAR}}$: ein Eltern-öffentlicher Schlüssel;
- $k_{\text{PAR}}$: ein Eltern-privater Schlüssel;
- $C_{\text{PAR}}$: ein Eltern-Chain-Code;
- $C_{\text{CHD}}$: ein Kind-Chain-Code;
- $K_{\text{CHD}}^n$: ein normaler Kind-öffentlicher Schlüssel;
- $k_{\text{CHD}}^n$: ein normaler Kind-privater Schlüssel;
- $K_{\text{CHD}}^h$: ein gehärteter Kind-öffentlicher Schlüssel;
- $k_{\text{CHD}}^h$: ein gehärteter Kind-privater Schlüssel.

### Aufbau eines erweiterten Schlüssels
Ein erweiterter Schlüssel ist wie folgt strukturiert:
- **Version**: Versionscode zur Identifizierung der Art des Schlüssels (`xprv`, `xpub`, `yprv`, `ypub`...). Am Ende dieses Kapitels werden wir sehen, was die Buchstaben `x`, `y` und `z` entsprechen.
- **Tiefe**: Hierarchische Ebene im HD-Wallet relativ zum Master-Schlüssel (0 für den Master-Schlüssel).
- **Eltern-Fingerabdruck**: Die ersten 4 Bytes des HASH160-Hashs des Eltern-öffentlichen Schlüssels, der zur Ableitung des im Payload vorhandenen Schlüssels verwendet wurde.
- **Indexnummer**: Kennzeichnung des Kindes unter Geschwisterschlüsseln, das heißt, unter allen Schlüsseln auf derselben Ableitungsebene, die dieselben Elternschlüssel haben.
- **Chain-Code**: Ein einzigartiger 32-Byte-Code zur Ableitung von Kind-Schlüsseln.
- **Schlüssel**: Der private Schlüssel (gekennzeichnet durch 1 Byte für die Größe) oder der öffentliche Schlüssel.
- **Prüfsumme**: Eine mit der HASH256-Funktion (doppeltes SHA256) berechnete Prüfsumme wird ebenfalls hinzugefügt, was die Überprüfung der Integrität des erweiterten Schlüssels während seiner Übertragung oder Speicherung ermöglicht.
Das vollständige Format eines erweiterten Schlüssels beträgt daher 78 Bytes ohne die Prüfsumme und 82 Bytes mit der Prüfsumme. Es wird dann in Base58 konvertiert, um eine Darstellung zu erzeugen, die für Benutzer leicht lesbar ist. Das Base58-Format ist dasselbe wie das für *Legacy*-Empfangsadressen (vor *SegWit*).
| Element | Beschreibung | Größe |
| ----------------- | ------------------------------------------------------------------------------------------------------------------ | --------- |
| Version | Gibt an, ob der Schlüssel öffentlich (`xpub`, `ypub`) oder privat (`xprv`, `zprv`) ist, sowie die Version des erweiterten Schlüssels | 4 Bytes |
| Depth | Ebene in der Hierarchie relativ zum Master-Schlüssel | 1 Byte |
| Parent Fingerprint| Die ersten 4 Bytes von HASH160 des öffentlichen Elternschlüssels | 4 Bytes |
| Index Number | Position des Schlüssels in der Reihenfolge der Kinder | 4 Bytes |
| Chain Code | Wird verwendet, um Kind-Schlüssel abzuleiten | 32 Bytes |
| Key | Der private Schlüssel (mit einem 1-Byte-Präfix) oder der öffentliche Schlüssel | 33 Bytes |
| Checksum | Prüfsumme zur Überprüfung der Integrität | 4 Bytes |
Wenn ein Byte nur zum privaten Schlüssel hinzugefügt wird, liegt das daran, dass der komprimierte öffentliche Schlüssel um ein Byte länger ist als der private Schlüssel. Dieses zusätzliche Byte, das am Anfang des privaten Schlüssels als `0x00` hinzugefügt wird, gleicht ihre Größe aus und stellt sicher, dass die Nutzlast des erweiterten Schlüssels dieselbe Länge hat, egal ob es sich um einen öffentlichen oder einen privaten Schlüssel handelt.
### Erweiterte Schlüsselpräfixe
Wie wir gerade gesehen haben, enthalten erweiterte Schlüssel ein Präfix, das sowohl die Version des erweiterten Schlüssels als auch seine Natur angibt. Die Notation `pub` zeigt an, dass es sich um einen erweiterten öffentlichen Schlüssel handelt, und die Notation `prv` zeigt einen erweiterten privaten Schlüssel an. Der zusätzliche Buchstabe an der Basis des erweiterten Schlüssels hilft anzugeben, ob der Standard Legacy, SegWit v0, SegWit v1 usw. folgt.
Hier ist eine Zusammenfassung der verwendeten Präfixe und ihrer Bedeutungen:
| Base 58 Prefix | Base 16 Prefix | Network | Purpose | Associated Scripts | Derivation | Key Type |
| --------------- | --------------- | ------- | ------------------- | ------------------- | --------------------- | ------------ |
| `xpub` | `0488b21e` | Mainnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/0'`, `m/86'/0'` | public |
| `xprv` | `0488ade4` | Mainnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/0'`, `m/86'/0'` | private |
| `tpub` | `043587cf` | Testnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/1'`, `m/86'/1'` | public |
| `tprv` | `04358394` | Testnet | Legacy and SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/1'`, `m/86'/1'` | private |
| `ypub` | `049d7cb2` | Mainnet | Nested SegWit | P2WPKH in P2SH | `m/49'/0'` | public |
| `yprv` | `049d7878` | Mainnet | Nested SegWit | P2WPKH in P2SH | `m/49'/0'` | private |
| `upub` | `049d7cb2` | Testnet | Nested SegWit | P2WPKH in P2SH | `m/49'/1'` | public |
| `uprv` | `044a4e28` | Testnet | Nested SegWit | P2WPKH in P2SH | `m/49'/1'` | private |
| `zpub` | `04b24746` | Mainnet | SegWit V0 | P2WPKH | `m/84'/0'` | public |
| `zprv` | `04b2430c` | Mainnet | SegWit V0 | P2WPKH | `m/84'/0'` | private |
| `vpub` | `045f1cf6` | Testnet | SegWit V0 | P2WPKH | `m/84'/1'` | public |
| `vprv` | `045f18bc` | Testnet | SegWit V0 | P2WPKH | `m/84'/1'` | private |
### Details der Elemente eines erweiterten Schlüssels
Um die interne Struktur eines erweiterten Schlüssels besser zu verstehen, nehmen wir einen als Beispiel und zerlegen ihn. Hier ist ein erweiterter Schlüssel:
- **In Base58**:
```text
xpub6CTNzMUkzpurBWaT4HQoYzLP4uBbGJuWY358Rj7rauiw4rMHCyq3Rfy9w4kyJXJzeFfyrKLUar2rUCukSiDQFa7roTwzjiAhyQAdPLEjqHT
```
- **In Hexadezimal**:
```text
0488B21E036D5601AD80000000C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A89303772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF50658051F067C3A
```
Dieser erweiterte Schlüssel zerfällt in mehrere unterschiedliche Elemente:
- **Version**: `0488B21E`
Die ersten 4 Bytes sind die Version. Hier entspricht sie einem erweiterten öffentlichen Schlüssel im Mainnet mit einem Ableitungszweck von entweder *Legacy* oder *SegWit v1*.
- **Tiefe**: `03`
Dieses Feld gibt die hierarchische Ebene des Schlüssels innerhalb der HD-Wallet an. In diesem Fall bedeutet eine Tiefe von `03`, dass dieser Schlüssel drei Ableitungsebenen unterhalb des Master-Schlüssels liegt.
- **Eltern-Fingerabdruck**: `6D5601AD`
Diese sind die ersten 4 Bytes des HASH160-Hashes des übergeordneten öffentlichen Schlüssels, der verwendet wurde, um diesen `xpub` abzuleiten.
- **Indexnummer**: `80000000`
Dieser Index gibt die Position des Schlüssels unter den Kindern seines Elternteils an. Das Präfix `0x80` zeigt an, dass der Schlüssel auf eine gehärtete Weise abgeleitet wurde, und da der Rest mit Nullen gefüllt ist, zeigt es an, dass dieser Schlüssel der erste unter seinen möglichen Geschwistern ist.
- **Chain-Code**: `C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A893`
- **Öffentlicher Schlüssel**: `03772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF5065805`
- **Prüfsumme**: `1F067C3A`
Die Prüfsumme entspricht den ersten 4 Bytes des Hashes (doppelter SHA256) von allem anderen.
In diesem Kapitel haben wir entdeckt, dass es zwei verschiedene Arten von Kinderschlüsseln gibt. Wir haben auch gelernt, dass die Ableitung dieser Kinderschlüssel einen Schlüssel (entweder privat oder öffentlich) und seinen Chain-Code erfordert. Im nächsten Kapitel werden wir die Natur dieser verschiedenen Arten von Schlüsseln im Detail untersuchen und wie sie aus ihrem Elternschlüssel und Chain-Code abgeleitet werden können.
## Ableitung von Kinderschlüsselpaaren
<chapterId>61c0807c-845b-5076-ad06-7f395b36adfd</chapterId>
Die Ableitung von Kinderschlüsselpaaren in Bitcoin HD-Wallets basiert auf einer hierarchischen Struktur, die es ermöglicht, eine große Anzahl von Schlüsseln zu generieren, während diese Paare durch Zweige in verschiedene Gruppen organisiert werden. Jedes von einem Elternpaar abgeleitete Kindpaar kann entweder direkt in einem *scriptPubKey* verwendet werden, um Bitcoins zu sperren, oder als Ausgangspunkt, um mehr Kinderschlüssel zu generieren, und so weiter, um einen Baum von Schlüsseln zu erstellen.
Alle diese Ableitungen beginnen mit dem Master-Schlüssel und dem Master-Chain-Code, die die ersten Eltern auf der Tiefeebene 0 sind. Sie sind gewissermaßen der Adam und Eva der Schlüssel Ihrer Wallet, die gemeinsamen Vorfahren aller abgeleiteten Schlüssel.
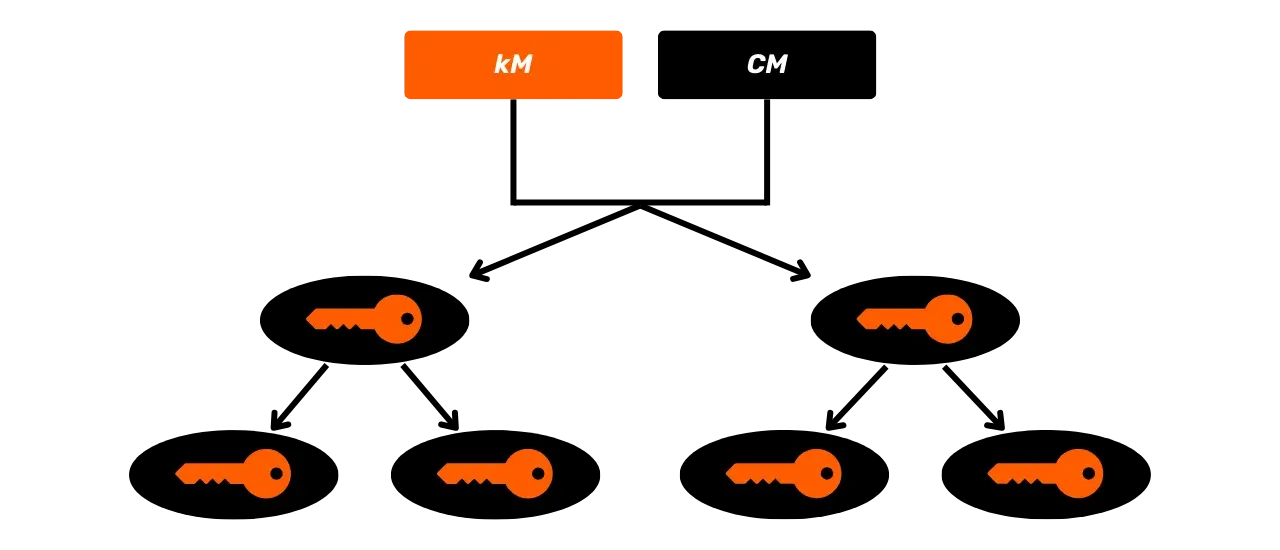
Lassen Sie uns erkunden, wie diese deterministische Ableitung funktioniert.
### Die verschiedenen Arten von Kinderschlüsselableitungen
Wie wir im vorherigen Kapitel kurz angesprochen haben: Kinderschlüssel sind in zwei Haupttypen unterteilt:
- **Normale Kinderschlüssel** ($k_{\text{CHD}}^n, K_{\text{CHD}}^n$): Diese werden vom erweiterten öffentlichen Schlüssel ($K_{\text{PAR}}$) oder dem erweiterten privaten Schlüssel ($k_{\text{PAR}}$) abgeleitet, indem zuerst der öffentliche Schlüssel abgeleitet wird.
- **Gehärtete Kinderschlüssel** ($k_{\text{CHD}}^h, K_{\text{CHD}}^h$): Diese können nur vom erweiterten privaten Schlüssel ($k_{\text{PAR}}$) abgeleitet werden und sind daher für Beobachter, die nur den erweiterten öffentlichen Schlüssel haben, unsichtbar.
Jedes Kind-Schlüsselpaar wird durch einen 32-Bit **Index** (benannt $i$ in unseren Berechnungen) identifiziert. Die Indizes für normale Schlüssel reichen von $0$ bis $2^{31}-1$, während die für gehärtete Schlüssel von $2^{31}$ bis $2^{32}-1$ reichen. Diese Zahlen werden verwendet, um Geschwister-Schlüsselpaare während der Ableitung zu unterscheiden. Tatsächlich muss jedes Eltern-Schlüsselpaar in der Lage sein, mehrere Kind-Schlüsselpaare abzuleiten. Würden wir dieselbe Berechnung systematisch von den Elternschlüsseln aus anwenden, wären alle erhaltenen Geschwisterschlüssel identisch, was nicht wünschenswert ist. Der Index führt somit eine Variable ein, die die Ableitungsberechnung modifiziert und es ermöglicht, jedes Geschwisterpaar zu differenzieren. Außer für spezifische Verwendungen in bestimmten Protokollen und Ableitungsstandards beginnen wir in der Regel damit, das erste Kind-Schlüsselpaar mit dem Index `0`, das zweite mit dem Index `1` usw. abzuleiten.
### Ableitungsprozess mit HMAC-SHA512
Die Ableitung jedes Kind-Schlüssels basiert auf der HMAC-SHA512-Funktion, die wir in Abschnitt 2 über Hash-Funktionen besprochen haben. Sie nimmt zwei Eingaben: den Eltern-Chain-Code $C_{\text{PAR}}$ und die Verkettung des Elternschlüssels (entweder des öffentlichen Schlüssels $K_{\text{PAR}}$ oder des privaten Schlüssels $k_{\text{PAR}}$, abhängig von der Art des gewünschten Kind-Schlüssels) und des Index. Die Ausgabe des HMAC-SHA512 ist eine 512-Bit-Sequenz, aufgeteilt in zwei Teile:
- **Die ersten 32 Bytes** (oder $h_1$) werden verwendet, um das neue Kind-Paar zu berechnen.
- **Die letzten 32 Bytes** (oder $h_2$) dienen als neuer Chain-Code $C_{\text{CHD}}$ für das Kind-Paar.
In all unseren Berechnungen werde ich $\text{hash}$ die Ausgabe der HMAC-SHA512-Funktion nennen.
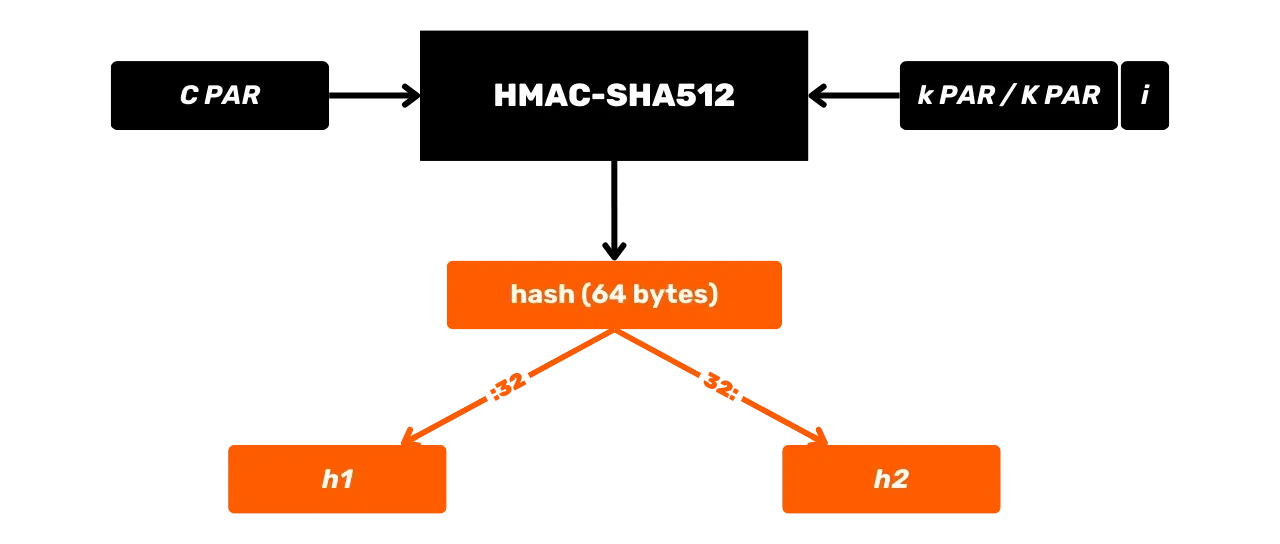
#### Ableitung eines Kind-Privatschlüssels von einem Eltern-Privatschlüssel
Um einen Kind-Privatschlüssel $k_{\text{CHD}}$ von einem Eltern-Privatschlüssel $k_{\text{PAR}}$ abzuleiten, sind zwei Szenarien möglich, abhängig davon, ob ein gehärteter oder normaler Schlüssel gewünscht ist.
Für einen **normalen Kind-Schlüssel** ($i < 2^{31}$) erfolgt die Berechnung von $\text{hash}$ wie folgt:
\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, G \cdot k_{\text{PAR}} \Vert i)
In dieser Berechnung beobachten wir, dass unsere HMAC-Funktion zwei Eingaben nimmt: zuerst den Eltern-Chain-Code und dann die Verkettung des Index mit dem öffentlichen Schlüssel, der mit dem Eltern-Privatschlüssel assoziiert ist. Der Eltern-Öffentliche-Schlüssel wird hier verwendet, weil wir einen normalen Kind-Schlüssel ableiten möchten, keinen gehärteten.
Wir haben jetzt einen 64-Byte $\text{hash}$, den wir in 2 Teile zu je 32 Bytes aufteilen: $h_1$ und $h_2$:
\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}{[:32]} \quad, \quad h_2 = \text{hash}{[32:]}
Der Kind-Privatschlüssel $k_{\text{CHD}}^n$ wird dann wie folgt berechnet:
k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n
Bei dieser Berechnung besteht die Operation $\text{parse256}(h_1)$ darin, die ersten 32 Bytes des $\text{hash}$ als eine 256-Bit-Ganzzahl zu interpretieren. Diese Zahl wird dann zum übergeordneten privaten Schlüssel hinzugefügt, alles modulo $n$ genommen, um innerhalb der Ordnung der elliptischen Kurve zu bleiben, wie wir in Abschnitt 3 über digitale Signaturen gesehen haben. Um also einen normalen Kind-Privatschlüssel abzuleiten, obwohl der öffentliche Schlüssel des Elternteils als Basis für die Berechnung in den Eingaben der HMAC-SHA512-Funktion verwendet wird, ist es immer notwendig, den privaten Schlüssel des Elternteils zu haben, um die Berechnung abzuschließen.
Von diesem Kind-Privatschlüssel aus ist es möglich, den entsprechenden öffentlichen Schlüssel abzuleiten, indem ECDSA oder Schnorr angewendet wird. Auf diese Weise erhalten wir ein vollständiges Schlüsselpaar.
Dann wird der zweite Teil des $\text{hash}$ einfach als der Kettenkode für das Kind-Schlüsselpaar interpretiert, das wir gerade abgeleitet haben:
C_{\text{CHD}} = h_2
Hier ist eine schematische Darstellung der gesamten Ableitung:
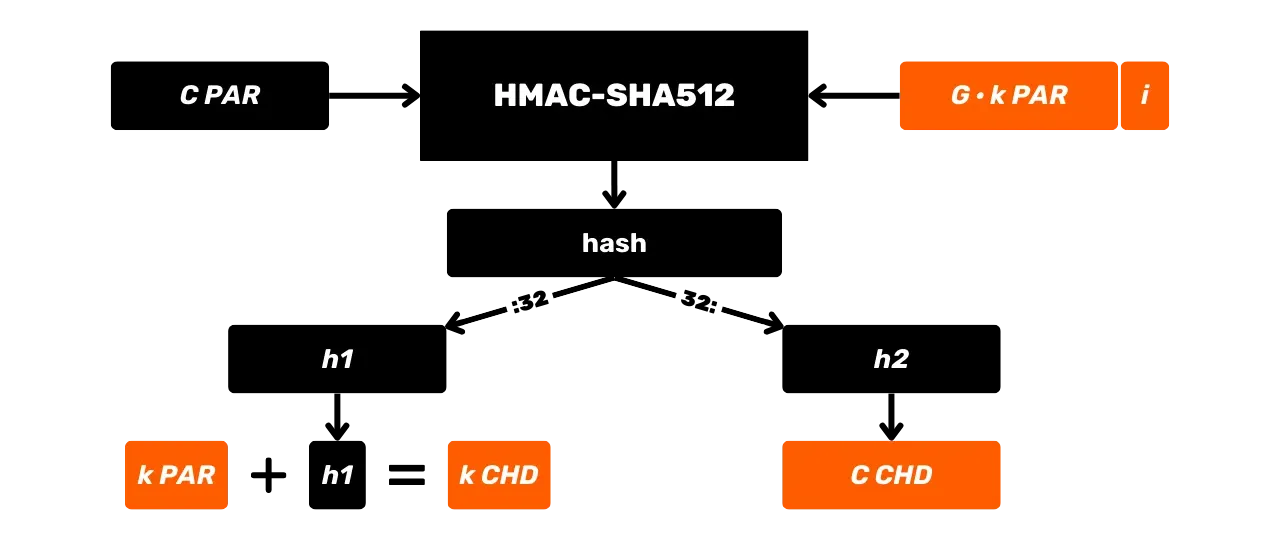
Für einen **verstärkten Kind-Schlüssel** ($i \geq 2^{31}$) erfolgt die Berechnung des $\text{hash}$ wie folgt:
hash = \text{HMAC-SHA512}(C_{\text{PAR}}, 0x00 \Vert k_{\text{PAR}} \Vert i)
In dieser Berechnung beobachten wir, dass unsere HMAC-Funktion zwei Eingaben nimmt: zuerst den Eltern-Kettenkode und dann die Verkettung des Index mit dem privaten Schlüssel des Elternteils. Der private Schlüssel des Elternteils wird hier verwendet, weil wir darauf abzielen, einen verstärkten Kind-Schlüssel abzuleiten. Außerdem wird am Anfang des Schlüssels ein Byte gleich `0x00` hinzugefügt. Diese Operation gleicht seine Länge an, um der eines komprimierten öffentlichen Schlüssels zu entsprechen.
So haben wir jetzt einen 64-Byte $\text{hash}$, den wir in 2 Teile von je 32 Bytes aufteilen werden: $h_1$ und $h_2$:\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}[:32] \quad, \quad h_2 = \text{hash}[32:]
Der Kind-Privatschlüssel $k_{\text{CHD}}^h$ wird dann wie folgt berechnet:
k_{\text{CHD}}^h = \text{parse256}(h_1) + k_{\text{PAR}} \mod n
Als Nächstes interpretieren wir einfach den zweiten Teil des $\text{hash}$ als den Kettenkode für das Paar von Kind-Schlüsseln, das wir gerade abgeleitet haben:
C_{\text{CHD}} = h_2
Hier ist eine schematische Darstellung der gesamten Ableitung:

Wir können sehen, dass die normale Ableitung und die verstärkte Ableitung auf die gleiche Weise funktionieren, mit diesem Unterschied: Die normale Ableitung verwendet den öffentlichen Schlüssel des Elternteils als Eingabe für die HMAC-Funktion, während die verstärkte Ableitung den privaten Schlüssel des Elternteils verwendet.
#### Ableitung eines Kind-öffentlichen Schlüssels aus einem Eltern-öffentlichen Schlüssel
Wenn wir nur den öffentlichen Schlüssel des Elternteils $K_{\text{PAR}}$ und den zugehörigen Ketten-Code $C_{\text{PAR}}$ kennen, also einen erweiterten öffentlichen Schlüssel, ist es möglich, Kind-öffentliche Schlüssel $K_{\text{CHD}}^n$ abzuleiten, aber nur für normale (nicht verstärkte) Kind-Schlüssel. Dieses Prinzip ermöglicht es insbesondere, die Bewegungen eines Kontos in einer Bitcoin-Wallet vom `xpub` (*nur-beobachten*) zu überwachen.
Um diese Berechnung durchzuführen, werden wir den $\text{hash}$ mit einem Index $i < 2^{31}$ (normale Ableitung) berechnen:
\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, K_{\text{PAR}} \Vert i)
In dieser Berechnung beobachten wir, dass unsere HMAC-Funktion zwei Eingaben nimmt: zuerst den Ketten-Code des Elternteils, dann die Verkettung des Indexes mit dem öffentlichen Schlüssel des Elternteils.
So haben wir jetzt einen $hash$ von 64 Bytes, den wir in 2 Teile von je 32 Bytes aufteilen werden: $h_1$ und $h_2$:
\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}{[:32]} \quad, \quad h_2 = \text{hash}{[32:]}
Der Kind-öffentliche Schlüssel $K_{\text{CHD}}^n$ wird dann wie folgt berechnet:
K_{\text{CHD}}^n = G \cdot \text{parse256}(h_1) + K_{\text{PAR}}
Wenn $\text{parse256}(h_1) \geq n$ (Ordnung der elliptischen Kurve) ist oder wenn $K_{\text{CHD}}^n$ der Punkt im Unendlichen ist, ist die Ableitung ungültig, und ein anderer Index muss gewählt werden.
In dieser Berechnung beinhaltet die Operation $\text{parse256}(h_1)$, die ersten 32 Bytes des $\text{hash}$ als eine 256-Bit-Ganzzahl zu interpretieren. Diese Zahl wird verwendet, um einen Punkt auf der elliptischen Kurve durch Addition und Verdopplung vom Generatorpunkt $G$ zu berechnen. Dieser Punkt wird dann zum öffentlichen Schlüssel des Elternteils addiert, um den normalen Kind-öffentlichen Schlüssel zu erhalten. Somit ist zur Ableitung eines normalen Kind-öffentlichen Schlüssels nur der öffentliche Schlüssel des Elternteils und der Ketten-Code des Elternteils notwendig; der private Schlüssel des Elternteils kommt in diesem Prozess im Gegensatz zur Berechnung des Kind-privaten Schlüssels, die wir zuvor gesehen haben, nie ins Spiel.
Als Nächstes ist der Ketten-Code des Kindes einfach:
C_{\text{CHD}} = h_2
Hier ist eine schematische Darstellung der gesamten Ableitung:
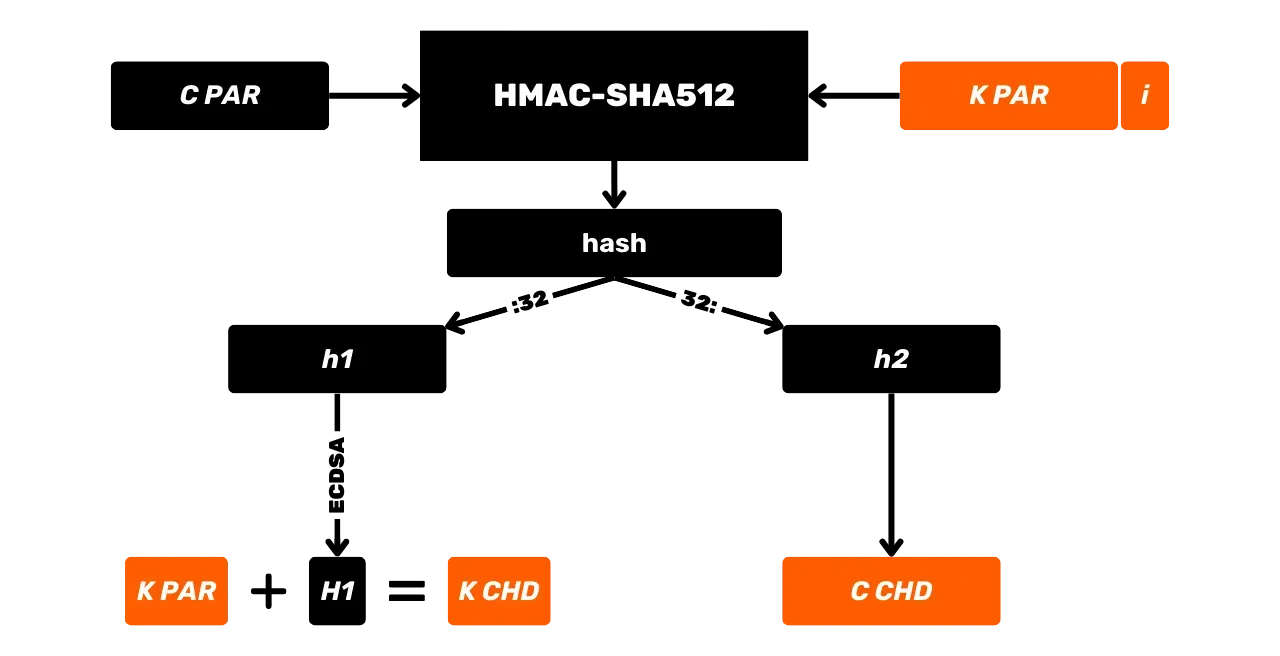
### Entsprechung zwischen Kind-öffentlichen und privaten Schlüsseln
Eine Frage, die aufkommen könnte, ist, wie ein normaler Kind-öffentlicher Schlüssel, der von einem Eltern-öffentlichen Schlüssel abgeleitet wurde, einem normalen Kind-privaten Schlüssel entsprechen kann, der vom entsprechenden Eltern-privaten Schlüssel abgeleitet wurde. Diese Verbindung wird genau durch die Eigenschaften elliptischer Kurven sichergestellt. Tatsächlich wird zur Ableitung eines normalen Kind-öffentlichen Schlüssels HMAC-SHA512 auf die gleiche Weise angewendet, aber sein Ausgang wird anders verwendet:
- **Normaler Kind-privater Schlüssel**: $k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n$
- **Normaler Kind-öffentlicher Schlüssel**: $K_{\text{CHD}}^n = G \cdot \text{parse256}(h_1) + K_{\text{PAR}}$
Dank der Addition und Verdopplungsoperationen auf der elliptischen Kurve liefern beide Methoden konsistente Ergebnisse: Der vom Kind-Privatschlüssel abgeleitete öffentliche Schlüssel ist identisch mit dem Kind-Öffentlichen Schlüssel, der direkt vom Eltern-Öffentlichen Schlüssel abgeleitet wurde.
### Zusammenfassung der Ableitungstypen
Zusammengefasst gibt es hier die verschiedenen möglichen Typen von Ableitungen:
\begin{array}{|c|c|c|c|} \hline \rightarrow & \text{PAR} & \text{CHD} & \text{n/h} \ \hline k_{\text{PAR}} \rightarrow k_{\text{CHD}} & k_{\text{PAR}} & { k_{\text{CHD}}^n, k_{\text{CHD}}^h } & { n, h } \ k_{\text{PAR}} \rightarrow K_{\text{CHD}} & k_{\text{PAR}} & { K_{\text{CHD}}^n, K_{\text{CHD}}^h } & { n, h } \ K_{\text{PAR}} \rightarrow k_{\text{CHD}} & K_{\text{PAR}} & \times & \times \ K_{\text{PAR}} \rightarrow K_{\text{CHD}} & K_{\text{PAR}} & K_{\text{CHD}}^n & n \ \hline \end{array}
Zusammengefasst haben Sie bisher gelernt, die grundlegenden Elemente des HD-Wallets zu erstellen: die mnemonische Phrase, den Seed und dann den Master-Schlüssel und den Master-Chain-Code. Sie haben auch entdeckt, wie man in diesem Kapitel Kind-Schlüsselpaare ableitet. Im nächsten Kapitel werden wir erforschen, wie diese Ableitungen in Bitcoin-Wallets organisiert sind und welche Struktur zu befolgen ist, um konkret die Empfangsadressen sowie die Schlüsselpaare, die im *scriptPubKey* und *scriptSig* verwendet werden, zu erhalten.
## Wallet-Struktur und Ableitungspfade
<chapterId>34e1bbda-67de-5493-b268-1fded8d67689</chapterId>
Die hierarchische Struktur von HD-Wallets bei Bitcoin ermöglicht die Organisation von Schlüsselpaaren auf verschiedene Weisen. Die Idee besteht darin, von dem Master-Privatschlüssel und dem Master-Chain-Code aus mehrere Tiefenebenen abzuleiten. Jede hinzugefügte Ebene entspricht der Ableitung eines Kind-Schlüsselpaares von einem Eltern-Schlüsselpaar.
Im Laufe der Zeit haben verschiedene BIPs (*Bitcoin Improvement Proposals*) Standards für diese Ableitungspfade eingeführt, um deren Nutzung über verschiedene Software hinweg zu standardisieren. In diesem Kapitel werden wir also die Bedeutung jeder Ableitungsebene in HD-Wallets gemäß diesen Standards entdecken.
### Die Tiefen der Ableitung eines HD-Wallets
Ableitungspfade sind in Tiefenebenen organisiert, die von Tiefe 0, die den Master-Schlüssel und den Master-Chain-Code repräsentiert, bis zu Unter-Ebenen für die Ableitung von Adressen reichen, die verwendet werden, um UTXOs zu sperren. Die BIPs definieren die Standards für jede Ebene, was hilft, Praktiken über verschiedene Wallet-Management-Software hinweg zu harmonisieren.
Ein Ableitungspfad bezieht sich daher auf die Sequenz von Indizes, die verwendet werden, um Kind-Schlüssel von einem Master-Schlüssel abzuleiten.
**Tiefe 0: Master-Schlüssel (BIP32)**
Diese Tiefe entspricht dem Master-Privatschlüssel und dem Master-Chain-Code des Wallets. Sie wird durch die Notation $m/$ dargestellt.
**Tiefe 1: Zweck (BIP43)**
Das Ziel bestimmt die logische Struktur der Ableitung. Zum Beispiel wird eine P2WPKH-Adresse auf der Tiefe 1 den Index $/84'/$ haben (gemäß BIP84), während eine P2TR-Adresse den Index $/86'/$ haben wird (gemäß BIP86). Diese Schicht erleichtert die Kompatibilität zwischen Wallets, indem sie Indexnummern angibt, die den BIP-Nummern entsprechen.
Anders gesagt, sobald Sie den Master-Schlüssel und den Master-Chain-Code haben, dienen diese als Elternschlüsselpaar, um ein Kind-Schlüsselpaar abzuleiten. Der in dieser Ableitung verwendete Index kann zum Beispiel $/84'/$ sein, wenn das Wallet vorgesehen ist, SegWit v0 Typ-Skripte zu verwenden. Dieses Schlüsselpaar befindet sich dann auf Tiefe 1. Seine Rolle ist es nicht, Bitcoins zu sperren, sondern einfach als Wegpunkt in der Ableitungshierarchie zu dienen.
**Tiefe 2: Währungstyp (BIP44)**
Vom Schlüsselpaar auf Tiefe 1 wird eine neue Ableitung durchgeführt, um das Schlüsselpaar auf Tiefe 2 zu erhalten. Diese Tiefe ermöglicht es, Bitcoin-Konten von anderen Kryptowährungen innerhalb derselben Wallet zu unterscheiden.
Jede Währung hat einen einzigartigen Index, um Kompatibilität über Multi-Währungs-Wallets hinweg zu gewährleisten. Zum Beispiel ist für Bitcoin der Index $/0'/$ (oder `0x80000000` in hexadezimaler Notation). Währungsindizes werden im Bereich von $2^{31}$ bis $2^{32}-1$ gewählt, um eine gehärtete Ableitung zu gewährleisten.
Um Ihnen andere Beispiele zu geben, hier sind die Indizes einiger Währungen:
- $1'$ (`0x80000001`) für Testnet-Bitcoins;
- $2'$ (`0x80000002`) für Litecoin;
- $60'$ (`0x8000003c`) für Ethereum...
**Tiefe 3: Konto (BIP32)**
Jede Wallet kann in mehrere Konten unterteilt werden, nummeriert ab $2^{31}$, und auf Tiefe 3 durch $/0'/$ für das erste Konto, $/1'/$ für das zweite usw. dargestellt. Allgemein, wenn auf einen erweiterten Schlüssel `xpub` Bezug genommen wird, bezieht es sich auf Schlüssel auf dieser Ableitungstiefe.
Diese Unterteilung in verschiedene Konten ist optional. Sie zielt darauf ab, die Organisation der Wallet für Benutzer zu vereinfachen. In der Praxis wird oft nur ein Konto verwendet, üblicherweise das erste standardmäßig. Jedoch kann es in einigen Fällen, wenn man Schlüsselpaare für unterschiedliche Verwendungen klar unterscheiden möchte, nützlich sein. Zum Beispiel ist es möglich, aus demselben Seed ein persönliches und ein berufliches Konto zu erstellen, mit völlig unterschiedlichen Schlüsselgruppen ab dieser Ableitungstiefe.
**Tiefe 4: Kette (BIP32)**
Jedes auf Tiefe 3 definierte Konto wird dann in zwei Ketten strukturiert:
- **Die externe Kette**: In dieser Kette werden sogenannte "öffentliche" Adressen abgeleitet. Diese Empfangsadressen sind dazu bestimmt, UTXOs zu sperren, die von externen Transaktionen kommen (das heißt, von der Verwendung von UTXOs, die nicht Ihnen gehören). Einfach ausgedrückt, wird diese externe Kette immer dann verwendet, wenn man Bitcoins erhalten möchte. Wenn Sie in Ihrer Wallet-Software auf "*empfangen*" klicken, wird Ihnen immer eine Adresse aus der externen Kette angeboten. Diese Kette wird durch ein Paar von Schlüsseln dargestellt, die mit dem Index $/0/$ abgeleitet werden.
- **Die interne Kette (Wechsel)**: Diese Kette ist für Empfangsadressen reserviert, die Bitcoins sperren, die von der Verwendung von UTXOs kommen, die Ihnen gehören, mit anderen Worten, Wechseladressen. Sie wird durch den Index $/1/$ identifiziert.
**Tiefe 5: Adressindex (BIP32)**
Schließlich stellt Tiefe 5 den letzten Schritt der Ableitung im Wallet dar. Obwohl es technisch möglich ist, unendlich fortzufahren, stoppen die aktuellen Standards hier. Auf dieser letzten Tiefe werden die Paare von Schlüsseln abgeleitet, die tatsächlich verwendet werden, um die UTXOs zu sperren und zu entsperren. Jeder Index ermöglicht die Unterscheidung zwischen Geschwisterschlüsselpaaren: so wird die erste Empfangsadresse den Index $/0/$ verwenden, die zweite den Index $/1/$ und so weiter.
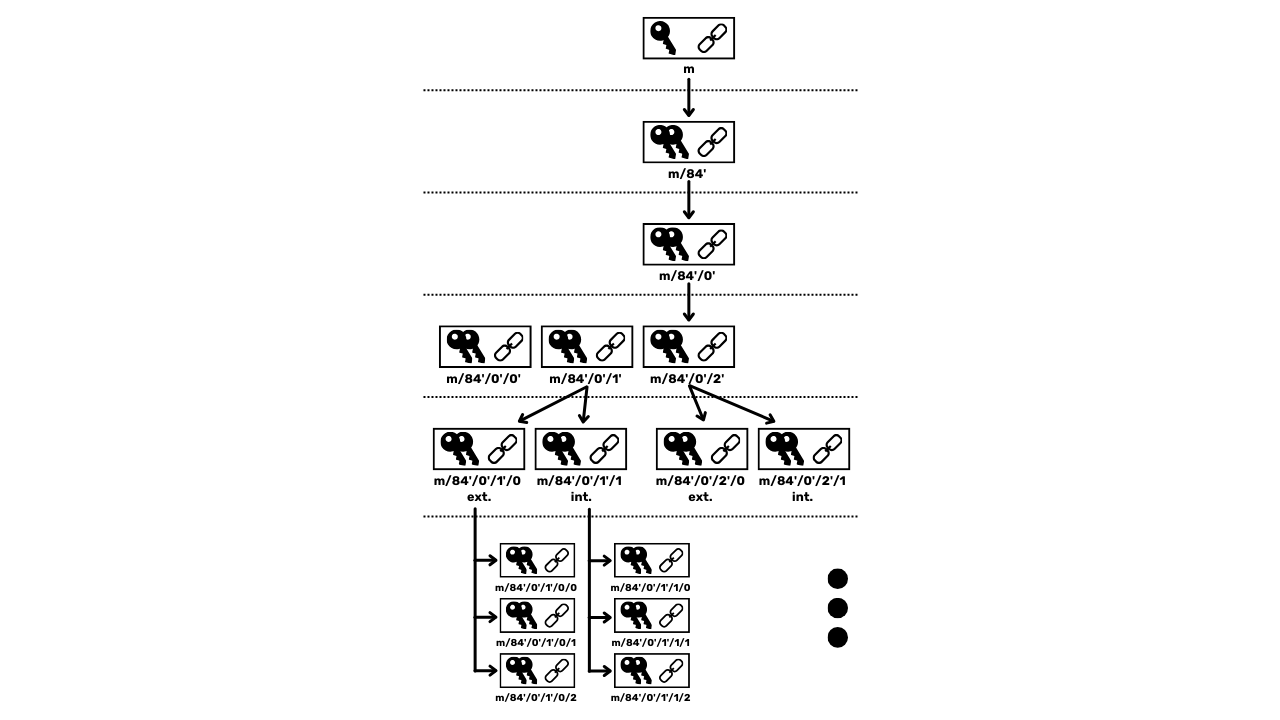
### Notation von Ableitungspfaden
Der Ableitungspfad wird geschrieben, indem jede Ebene mit einem Schrägstrich ($/$) getrennt wird. Jeder Schrägstrich zeigt somit eine Ableitung eines Elternschlüsselpaares ($k_{\text{PAR}}$, $K_{\text{PAR}}$, $C_{\text{PAR}}$) zu einem Kinderschlüsselpaar ($k_{\text{CHD}}$, $K_{\text{CHD}}$, $C_{\text{CHD}}$) an. Die bei jeder Tiefe notierte Zahl entspricht dem Index, der verwendet wird, um diesen Schlüssel von seinen Eltern abzuleiten. Das Apostroph ($'$), das manchmal rechts vom Index platziert wird, zeigt eine gehärtete Ableitung ($k_{\text{CHD}}^h$, $K_{\text{CHD}}^h$) an. Manchmal wird dieses Apostroph durch ein $h$ ersetzt. In Abwesenheit eines Apostrophs oder $h$ handelt es sich daher um eine normale Ableitung ($k_{\text{CHD}}^n$, $K_{\text{CHD}}^n$).
Wie wir in den vorherigen Kapiteln gesehen haben, beginnen gehärtete Schlüsselindizes bei $2^{31}$ oder `0x80000000` in Hexadezimal. Daher muss, wenn ein Index in einem Ableitungspfad von einem Apostroph gefolgt wird, $2^{31}$ zu der angegebenen Zahl addiert werden, um den tatsächlichen Wert zu erhalten, der in der HMAC-SHA512-Funktion verwendet wird. Zum Beispiel, wenn der Ableitungspfad $/44'/$ angibt, wird der tatsächliche Index sein:i = 44 + 2^{31} = 2,147,483,692
In Hexadezimal ist dies `0x8000002C`.
Jetzt, da wir die Hauptprinzipien der Ableitungspfade verstanden haben, nehmen wir ein Beispiel! Hier ist der Ableitungspfad für eine Bitcoin-Empfangsadresse:
m / 84' / 0' / 1' / 0 / 7
In diesem Beispiel:
- $84'$ zeigt den P2WPKH (SegWit v0) Standard an;
- $0'$ zeigt die Bitcoin-Währung im Hauptnetz an;
- $1'$ entspricht dem zweiten Konto im Wallet;
- $0$ zeigt an, dass die Adresse auf der externen Kette ist;
- $7$ zeigt die 8. externe Adresse dieses Kontos an.
### Zusammenfassung der Ableitungsstruktur
| Tiefe | Beschreibung | Standardbeispiel |
| ----- | ------------------ | --------------------------------- |
| 0 | Master-Schlüssel | $m/$ |
| 1 | Zweck | $/86'/$ (P2TR) |
| 2 | Währung | $/0'/$ (Bitcoin) |
| 3 | Konto | $/0'/$ (Erstes Konto) |
| 4 | Kette | $/0/$ (extern) oder $/1/$ (Wechsel)|
| 5 | Adressindex | $/0/$ (erste Adresse) |
Im nächsten Kapitel werden wir entdecken, was "*Output Script Descriptors*" sind, eine kürzlich eingeführte Innovation in Bitcoin Core, die das Backup eines Bitcoin-Wallets vereinfacht.
## Output Script Descriptors
<chapterId>e4f1c2d3-9b8a-4d3e-8f2a-7b6c5d4e3f2a</chapterId>
Oft wird gesagt, dass die mnemonische Phrase allein ausreicht, um den Zugang zu einem Wallet wiederherzustellen. In Wirklichkeit sind die Dinge ein wenig komplexer. Im vorherigen Kapitel haben wir uns die Ableitungsstruktur des HD-Wallets angesehen, und Sie haben vielleicht bemerkt, dass dieser Prozess ziemlich komplex ist. Ableitungspfade zeigen der Software, welche Richtung sie verfolgen soll, um die Schlüssel des Benutzers abzuleiten. Wenn man jedoch ein Bitcoin-Wallet wiederherstellen möchte und diese Pfade nicht kennt, reicht die mnemonische Phrase allein nicht aus. Sie ermöglicht es, den Master-Schlüssel und den Master-Chain-Code zu erhalten, aber es ist dann notwendig, die Indizes zu kennen, die verwendet wurden, um die Kind-Schlüssel zu erreichen.
Theoretisch wäre es notwendig, nicht nur die mnemonische Phrase unseres Wallets zu speichern, sondern auch die Pfade zu den Konten, die wir verwenden. In der Praxis ist es oft möglich, ohne diese Informationen wieder Zugang zu den Kind-Schlüsseln zu erhalten, vorausgesetzt, die Standards wurden eingehalten. Indem man jeden Standard einzeln testet, ist es im Allgemeinen möglich, wieder Zugang zu den Bitcoins zu erhalten. Dies ist jedoch nicht garantiert und besonders kompliziert für Anfänger. Auch mit der Diversifizierung der Skripttypen und dem Aufkommen komplexerer Konfigurationen könnten diese Informationen schwer zu extrapolieren sein, wodurch diese Daten zu privaten Informationen werden und schwer durch Brute-Force zu erholen sind. Deshalb wurde kürzlich eine Innovation eingeführt und beginnt, in Ihre bevorzugte Wallet-Software integriert zu werden: die *Output Script Descriptors*.
### Was ist ein "Descriptor"?
Die "*Output Script Descriptors*", oder einfach "*Descriptors*", sind strukturierte Ausdrücke, die ein Ausgabeskript (*scriptPubKey*) vollständig beschreiben und alle notwendigen Informationen liefern, um den Transaktionen zu folgen, die mit einem bestimmten Skript verbunden sind. Sie erleichtern die Verwaltung von Schlüsseln in HD-Wallets, indem sie eine standardisierte und vollständige Beschreibung der Wallet-Struktur und der verwendeten Adresstypen bieten.
Der Hauptvorteil von Descriptors liegt in ihrer Fähigkeit, alle wesentlichen Informationen zur Wiederherstellung eines Wallets in einer einzigen Zeichenfolge (zusätzlich zur Wiederherstellungsphrase) zu kapseln. Indem man einen Descriptor mit den zugehörigen mnemonischen Phrasen speichert, wird es möglich, die privaten Schlüssel genau in ihrer Position in der Hierarchie wiederherzustellen. Für Multisig-Wallets, deren Backup ursprünglich komplexer war, beinhaltet der Descriptor die `xpub` jedes Faktors und gewährleistet so die Möglichkeit, die Adressen im Falle eines Problems neu zu generieren.
### Aufbau eines Descriptors
Ein Descriptor besteht aus mehreren Elementen:
* Skriptfunktionen wie `pk` (*Pay-to-PubKey*), `pkh` (*Pay-to-PubKey-Hash*), `wpkh` (*Pay-to-Witness-PubKey-Hash*), `sh` (*Pay-to-Script-Hash*), `wsh` (*Pay-to-Witness-Script-Hash*), `tr` (*Pay-to-Taproot*), `multi` (*Multisignatur*), und `sortedmulti` (*Multisignatur mit sortierten Schlüsseln*);
* Ableitungspfade, zum Beispiel `[d34db33f/44h/0h/0h]`, die einen abgeleiteten Kontopfad und einen spezifischen Master-Schlüssel-Fingerabdruck anzeigen;
* Schlüssel in verschiedenen Formaten wie hexadezimale öffentliche Schlüssel oder erweiterte öffentliche Schlüssel (`xpub`);
* Eine Prüfsumme, vorangestellt von einem Hash-Zeichen, um die Integrität des Descriptors zu überprüfen.
Zum Beispiel könnte ein Deskriptor für eine P2WPKH (SegWit v0) Wallet so aussehen:
```text
wpkh([cdeab12f/84h/0h/0h]xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U/<0;1>/*)#jy0l7nr4
```
In diesem Deskriptor zeigt die Ableitungsfunktion `wpkh` auf einen Skripttyp *Pay-to-Witness-Public-Key-Hash*. Es folgt der Ableitungspfad, der enthält:
* `cdeab12f`: der Fingerabdruck des Master-Schlüssels;
* `84h`: was die Verwendung eines BIP84-Zwecks anzeigt, vorgesehen für SegWit v0 Adressen;
* `0h`: was darauf hinweist, dass es sich um eine BTC-Währung im Hauptnetz handelt;
* `0h`: was sich auf die spezifische Kontonummer bezieht, die im Wallet verwendet wird.
Der Deskriptor beinhaltet auch den erweiterten öffentlichen Schlüssel, der in diesem Wallet verwendet wird:
```text
xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U
```
Als Nächstes gibt die Notation `/<0;1>/*` an, dass der Deskriptor Adressen von der externen Kette (`0`) und internen Kette (`1`) generieren kann, mit einem Platzhalter (`*`), der die sequenzielle Ableitung mehrerer Adressen in einer konfigurierbaren Weise erlaubt, ähnlich der Verwaltung eines "Gap-Limits" in traditioneller Wallet-Software.
Schließlich repräsentiert `#jy0l7nr4` die Prüfsumme zur Verifizierung der Integrität des Deskriptors.
Nun wissen Sie alles über die Funktionsweise des HD-Wallets bei Bitcoin und den Prozess der Ableitung von Schlüsselpaaren. Allerdings haben wir uns in den letzten Kapiteln auf die Generierung von privaten und öffentlichen Schlüsseln beschränkt, ohne die Konstruktion von Empfangsadressen anzusprechen. Dies wird genau das Thema des nächsten Kapitels sein!
## Empfangsadressen
<chapterId>ca80a89d-f8da-4e09-8c35-43179b65bced</chapterId>
Empfangsadressen sind Informationen, die in *scriptPubKey* eingebettet sind, um neu erstellte UTXOs zu sperren. Einfach ausgedrückt, dient eine Adresse dazu, Bitcoins zu empfangen. Lassen Sie uns ihre Funktionsweise im Zusammenhang mit dem untersuchen, was wir in den vorherigen Kapiteln studiert haben.
### Die Rolle von Bitcoin-Adressen in Skripten
Wie zuvor erklärt, besteht die Rolle einer Transaktion darin, das Eigentum an Bitcoins von Eingängen zu Ausgängen zu übertragen. Dieser Prozess beinhaltet das Verbrauchen von UTXOs als Eingänge, während neue UTXOs als Ausgänge erstellt werden. Diese UTXOs werden durch Skripte gesichert, die die notwendigen Bedingungen definieren, um die Mittel freizugeben.
Wenn ein Benutzer Bitcoins erhält, erstellt der Sender ein Ausgabe-UTXO und sperrt es mit einem *scriptPubKey*. Dieses Skript enthält die Regeln, die typischerweise die erforderlichen Signaturen und öffentlichen Schlüssel angeben, um dieses UTXO freizuschalten. Um dieses UTXO in einer neuen Transaktion auszugeben, muss der Benutzer die angeforderten Informationen über ein *scriptSig* bereitstellen. Die Ausführung von *scriptSig* in Kombination mit *scriptPubKey* muss "true" oder `1` zurückgeben. Wenn diese Bedingung erfüllt ist, kann das UTXO ausgegeben werden, um ein neues UTXO zu erstellen, das selbst durch ein neues *scriptPubKey* gesperrt ist, und so weiter.

Genau im *scriptPubKey* befinden sich die Empfangsadressen. Ihre Verwendung variiert jedoch je nach dem angenommenen Skriptstandard. Hier ist eine Zusammenfassungstabelle der Informationen, die im *scriptPubKey* enthalten sind, entsprechend dem verwendeten Standard, sowie der Informationen, die im *scriptSig* erwartet werden, um das *scriptPubKey* freizuschalten.
| Standard | *scriptPubKey* | *scriptSig* | *Erlösungsskript* | *Zeuge* |
| ------------------ | ----------------------------------------------------------- | ------------------------------- | ------------------- | ---------------------------------------- |
| P2PK | `<pubkey> OP_CHECKSIG` | `<Signatur>` | | |
| P2PKH | `OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG` | `<Signatur> <öffentlicher Schlüssel>` | | |
| P2SH | `OP_HASH160 <scriptHash> OP_EQUAL` | `<Datenübertragungen> <Erlösungsskript>` | Beliebige Daten | |
| P2WPKH | `0 <pubKeyHash>` | | | `<Signatur> <öffentlicher Schlüssel>` |
| P2WSH | `0 <witnessScriptHash>` | | | `<Datenübertragungen> <Zeugenskript>` |
| P2SH-P2WPKH | `OP_HASH160 <ErlösungsskriptHash> OP_EQUAL` | `<Erlösungsskript>` | `0 <pubKeyHash>` | `<Signatur> <öffentlicher Schlüssel>` |
| P2SH-P2WSH | `OP_HASH160 <ErlösungsskriptHash> OP_EQUAL` | `<Erlösungsskript>` | `0 <scriptHash>` | `<Datenübertragungen> <Zeugenskript>` |
| P2TR (Schlüsselpfad) | `1 <öffentlicher Schlüssel>` | | | `<Signatur>` |
| P2TR (Skriptpfad) | `1 <öffentlicher Schlüssel>` | | | `<Datenübertragungen> <Skript> <Kontrollblock>` |
*Quelle: Bitcoin Core PR Review Club, 7. Juli 2021 - Gloria Zhao*
Die in einem Skript verwendeten Opcodes sind dazu ausgelegt, Informationen zu manipulieren und, falls notwendig, diese zu vergleichen oder zu testen. Nehmen wir das Beispiel eines P2PKH-Skripts, das wie folgt lautet:
```text
OP_DUP OP_HASH160 OP_PUSHBYTES_20 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG
```
Wie wir in diesem Kapitel sehen werden, stellt `<pubKeyHash>` tatsächlich die Nutzlast der Empfangsadresse dar, die verwendet wird, um das UTXO zu sperren. Um dieses *scriptPubKey* freizuschalten, ist es notwendig, ein *scriptSig* bereitzustellen, das enthält:
```text
<Signatur> <öffentlicher Schlüssel>
```
Im Skriptsprachenkontext ist der "Stack" eine "*LIFO*" ("*Last In, First Out*") Datenstruktur, die dazu verwendet wird, Elemente während der Ausführung eines Skripts temporär zu speichern. Jede Skriptoperation manipuliert diesen Stack, wobei Elemente hinzugefügt (*push*) oder entfernt (*pop*) werden können. Skripte nutzen diese Stacks, um Ausdrücke zu evaluieren, temporäre Variablen zu speichern und Bedingungen zu verwalten.
Die Ausführung des Skripts, das ich gerade als Beispiel gegeben habe, folgt diesem Prozess:
- Wir haben das *scriptSig*, das *ScriptPubKey* und den Stack:

- Das *scriptSig* wird auf den Stack gelegt:

- `OP_DUP` dupliziert den im *scriptSig* bereitgestellten öffentlichen Schlüssel auf dem Stack:

- `OP_HASH160` gibt den Hash des gerade duplizierten öffentlichen Schlüssels zurück:
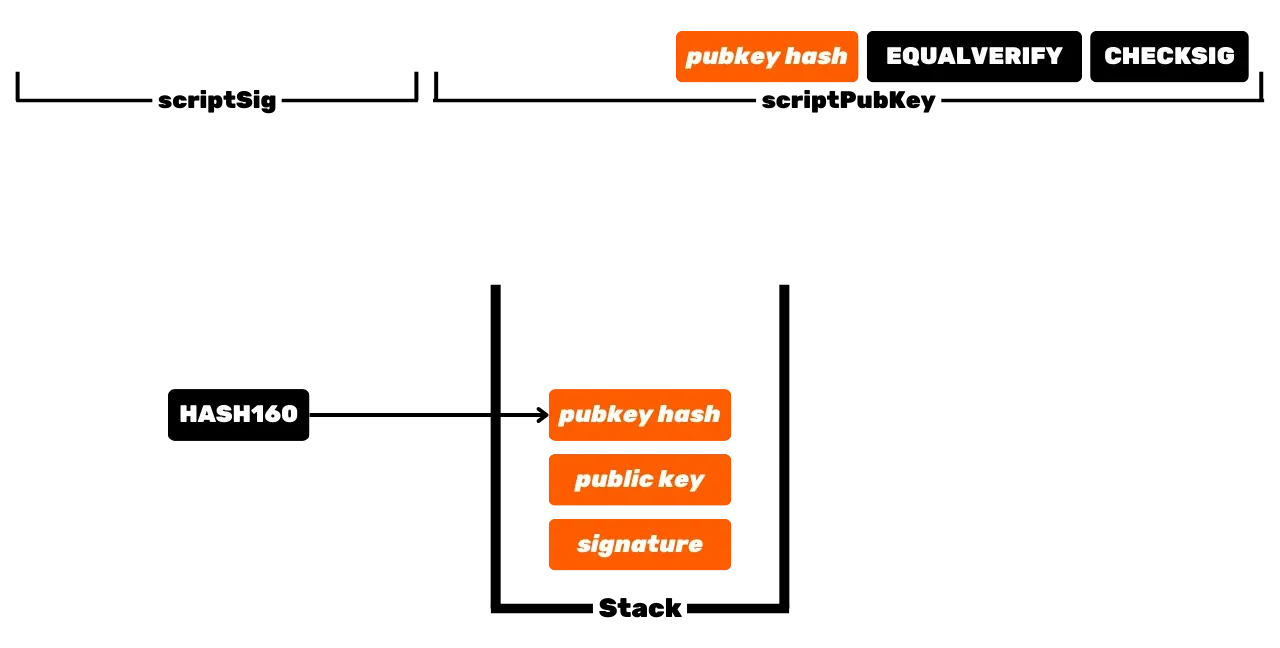
- `OP_PUSHBYTES_20 <pubKeyHash>` legt die im *scriptPubKey* enthaltene Bitcoin-Adresse auf den Stack:

- `OP_EQUALVERIFY` überprüft, ob der gehashte öffentliche Schlüssel mit der angegebenen Empfangsadresse übereinstimmt:

`OP_CHECKSIG` überprüft die im *scriptSig* enthaltene Signatur mit dem öffentlichen Schlüssel. Dieser Opcode führt im Wesentlichen eine Signaturverifikation durch, wie wir in Teil 3 dieses Trainings beschrieben haben:

- Wenn `1` auf dem Stack verbleibt, dann ist das Skript gültig:
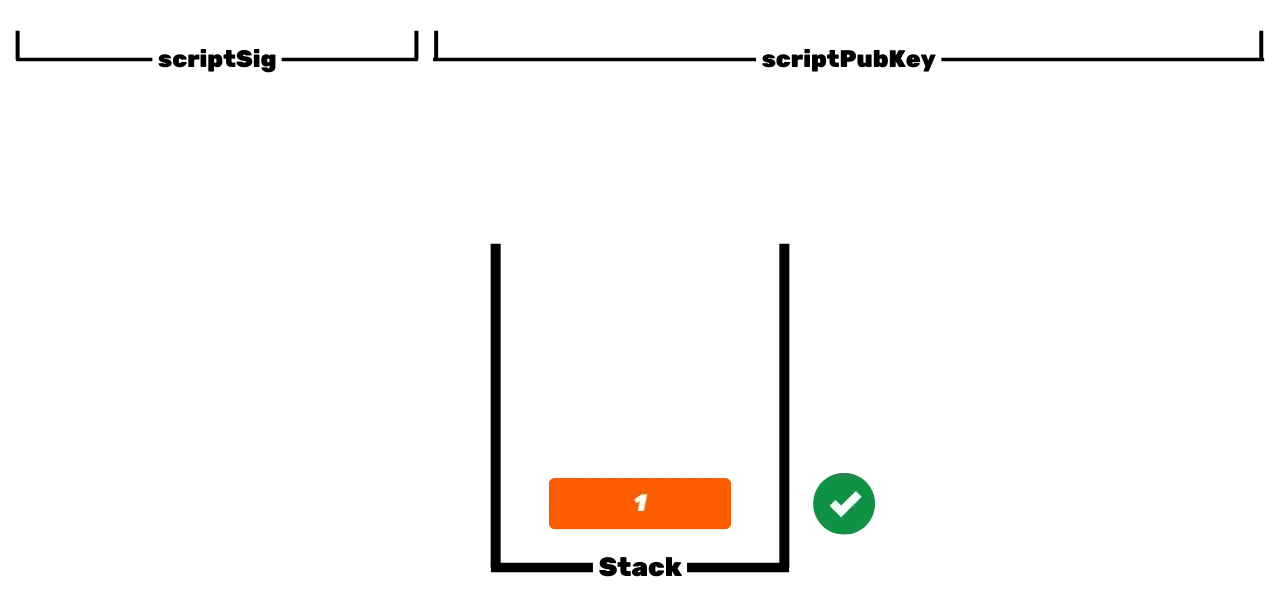
Zusammenfassend ermöglicht dieses Skript also, mit Hilfe der digitalen Signatur zu überprüfen, dass der Benutzer, der behauptet, Eigentümer dieses UTXO zu sein und es ausgeben zu wollen, tatsächlich den privaten Schlüssel besitzt, der mit der Empfangsadresse verbunden ist, die bei der Erstellung dieses UTXO verwendet wurde.
### Die verschiedenen Typen von Bitcoin-Adressen
Im Laufe der Entwicklung von Bitcoin wurden mehrere Standard-Skriptmodelle hinzugefügt. Jedes davon verwendet einen bestimmten Typ von Empfangsadresse. Hier ist ein Überblick über die wichtigsten derzeit verfügbaren Skriptmodelle:
**P2PK (*Pay-to-PubKey*)**:
Dieses Skriptmodell wurde in der ersten Version von Bitcoin von Satoshi Nakamoto eingeführt. Das P2PK-Skript sperrt Bitcoins direkt unter Verwendung eines rohen öffentlichen Schlüssels (somit wird bei diesem Modell keine Empfangsadresse verwendet). Seine Struktur ist einfach: es enthält einen öffentlichen Schlüssel und erfordert eine entsprechende digitale Signatur, um die Mittel freizugeben. Dieses Skript ist Teil des "*Legacy*" Standards.
**P2PKH (*Pay-to-PubKey-Hash*)**:
Wie P2PK wurde das P2PKH-Skript beim Start von Bitcoin eingeführt. Im Gegensatz zu seinem Vorgänger sperrt es die Bitcoins unter Verwendung des Hashs des öffentlichen Schlüssels, anstatt direkt den rohen öffentlichen Schlüssel zu verwenden. Das *scriptSig* muss dann den öffentlichen Schlüssel, der mit der Empfangsadresse verbunden ist, sowie eine gültige Signatur bereitstellen. Die Adressen, die diesem Modell entsprechen, beginnen mit `1` und sind in *base58check* kodiert. Dieses Skript gehört ebenfalls zum "*Legacy*" Standard.
**P2SH (*Pay-to-Script-Hash*)**:
Eingeführt im Jahr 2012 mit BIP16, ermöglicht das P2SH-Modell die Verwendung des Hashs eines beliebigen Skripts im *scriptPubKey*. Dieses gehashte Skript, genannt "*redeemScript*", enthält die Bedingungen zum Entsperren der Mittel. Um ein UTXO, das mit P2SH gesperrt ist, auszugeben, ist es notwendig, ein *scriptSig* bereitzustellen, das das ursprüngliche *redeemScript* sowie die notwendigen Daten zu dessen Validierung enthält. Dieses Modell wird insbesondere für alte Multisigs verwendet. Die mit P2SH assoziierten Adressen beginnen mit `3` und sind in *base58check* kodiert. Dieses Skript gehört auch zum "*Legacy*" Standard.
**P2WPKH (*Pay-to-Witness-PubKey-Hash*)**:
Dieses Skript ähnelt P2PKH, da es ebenfalls Bitcoins mittels des Hashs eines öffentlichen Schlüssels sperrt. Im Gegensatz zu P2PKH wird jedoch das *scriptSig* in einen separaten Abschnitt namens "*Witness*" verschoben. Dies wird manchmal als "*scriptWitness*" bezeichnet, um das Set, bestehend aus der Signatur und dem öffentlichen Schlüssel, zu benennen. Jeder SegWit-Eingang hat sein eigenes *scriptWitness*, und die Sammlung von *scriptWitnesses* bildet das *Witness*-Feld der Transaktion. Diese Verlagerung der Signaturdaten ist eine Innovation, die durch das SegWit-Update eingeführt wurde, insbesondere um die Veränderbarkeit von Transaktionen aufgrund von ECDSA-Signaturen zu verhindern.
P2WPKH-Adressen verwenden *bech32*-Kodierung und beginnen immer mit `bc1q`. Dieser Typ von Skript entspricht den Version-0-SegWit-Ausgängen.
**P2WSH (*Pay-to-Witness-Script-Hash*)**:
Das P2WSH-Modell wurde ebenfalls mit dem SegWit-Update im August 2017 eingeführt. Ähnlich wie das P2SH-Modell sperrt es Bitcoins mittels des Hashs eines Skripts. Der Hauptunterschied liegt darin, wie Signaturen und Skripte in die Transaktion eingebunden werden. Um Bitcoins, die mit diesem Typ von Skript gesperrt sind, auszugeben, muss der Empfänger das Originalskript, genannt *witnessScript* (entspricht dem *redeemScript* in P2SH), zusammen mit den notwendigen Daten zur Validierung dieses *witnessScript* bereitstellen. Dieser Mechanismus ermöglicht die Implementierung komplexerer Ausgabebedingungen, wie z.B. Multisigs.
P2WSH-Adressen verwenden *bech32*-Kodierung und beginnen immer mit `bc1q`. Dieses Skript entspricht ebenfalls den Version-0-SegWit-Ausgängen.
**P2TR (*Pay-to-Taproot*)**:
Das P2TR-Modell wurde mit der Implementierung von Taproot im November 2021 eingeführt. Es basiert auf dem Schnorr-Protokoll zur kryptografischen Schlüsselaggregation sowie auf einem Merkle-Baum für alternative Skripte, genannt MAST (*Merkelized Alternative Script Tree*). Im Gegensatz zu anderen Skripttypen, bei denen die Ausgabebedingungen öffentlich ausgestellt werden (entweder beim Empfang oder bei der Ausgabe), ermöglicht P2TR das Verbergen komplexer Skripte hinter einem einzigen, scheinbaren öffentlichen Schlüssel.
Technisch gesehen sperrt ein P2TR-Skript Bitcoins auf einem einzigartigen Schnorr-öffentlichen Schlüssel, bezeichnet als $Q$. Dieser Schlüssel $Q$ ist tatsächlich eine Aggregation eines öffentlichen Schlüssels $P$ und eines öffentlichen Schlüssels $M$, wobei letzterer aus der Merkle-Wurzel einer Liste von *scriptPubKey* berechnet wird. Bitcoins, die mit diesem Typ von Skript gesperrt sind, können auf zwei Arten ausgegeben werden:
- Durch Veröffentlichung einer Signatur für den öffentlichen Schlüssel $P$ (*key path*).
- Durch Erfüllung eines der Skripte im Merkle-Baum (*script path*).
P2TR bietet somit eine große Flexibilität, da es das Sperren von Bitcoins entweder mit einem einzigartigen öffentlichen Schlüssel, mit mehreren Skripten nach Wahl oder beidem gleichzeitig ermöglicht. Der Vorteil dieser Merkle-Baum-Struktur ist, dass nur das verwendete Ausgabeskript während der Transaktion offenbart wird, aber alle anderen alternativen Skripte geheim bleiben. 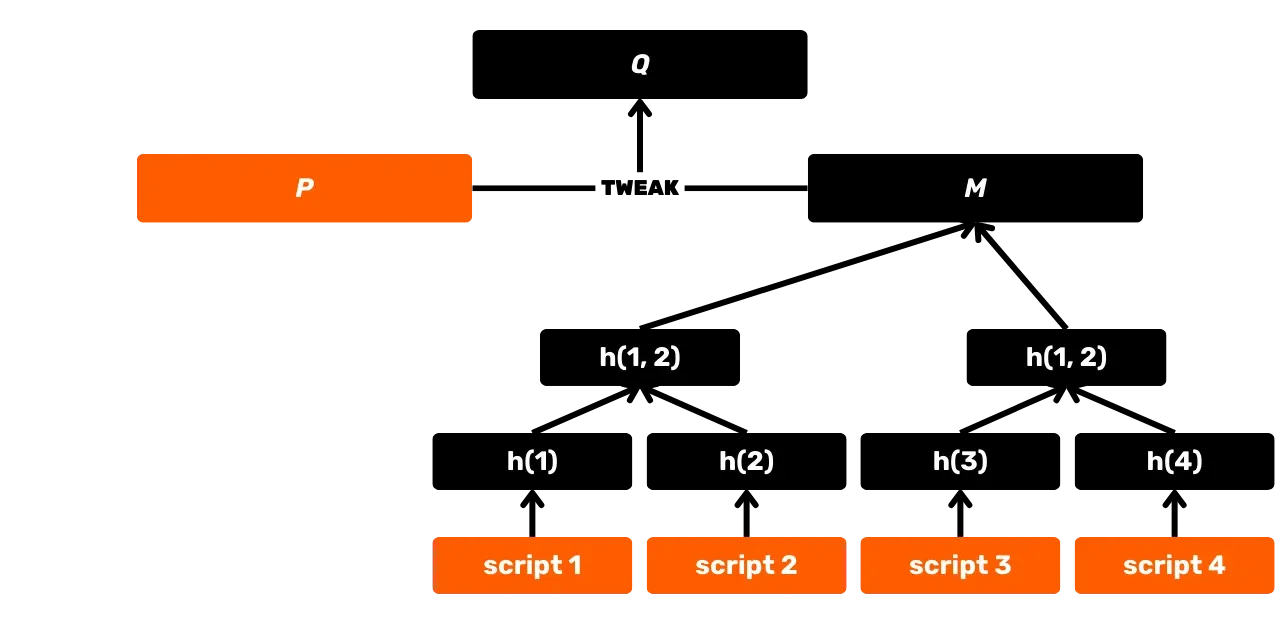
P2TR entspricht den SegWit-Ausgaben der Version 1, was bedeutet, dass die Signaturen für P2TR-Eingaben im *Witness*-Abschnitt der Transaktion gespeichert sind und nicht im *scriptSig*. P2TR-Adressen verwenden die *bech32m*-Kodierung und beginnen mit `bc1p`, aber sie sind ziemlich einzigartig, da sie keine Hash-Funktion für ihre Konstruktion verwenden. Tatsächlich repräsentieren sie direkt den öffentlichen Schlüssel $Q$, der einfach mit Metadaten formatiert ist. Es handelt sich daher um ein Skriptmodell, das dem P2PK nahe kommt.
Nachdem wir die Theorie behandelt haben, gehen wir zur Praxis über! Im folgenden Kapitel schlage ich vor, sowohl eine SegWit v0-Adresse als auch eine SegWit v1-Adresse aus einem Schlüsselpaar abzuleiten.
## Adressableitung
<chapterId>3ebdc750-4135-4881-b07e-08965941b93e</chapterId>
Lassen Sie uns gemeinsam erkunden, wie man eine Empfangsadresse aus einem Schlüsselpaar generiert, das sich beispielsweise in der Tiefe 5 eines HD-Wallets befindet. Diese Adresse kann dann in einer Wallet-Software verwendet werden, um ein UTXO zu sperren.
Da der Prozess der Adressgenerierung vom angenommenen Skriptmodell abhängt, konzentrieren wir uns auf zwei spezifische Fälle: die Generierung einer SegWit v0-Adresse in P2WPKH und einer SegWit v1-Adresse in P2TR. Diese beiden Adresstypen decken heute die überwiegende Mehrheit der Anwendungen ab.
### Komprimierung des öffentlichen Schlüssels
Nachdem alle Ableitungsschritte vom Master-Schlüssel bis zur Tiefe 5 unter Verwendung der entsprechenden Indizes durchgeführt wurden, erhalten wir ein Schlüsselpaar ($k$, $K$) mit $K = k \cdot G$. Obwohl es möglich ist, diesen öffentlichen Schlüssel so zu verwenden, um Mittel mit dem P2PK-Standard zu sperren, ist das nicht unser Ziel hier. Stattdessen zielen wir darauf ab, in erster Instanz eine Adresse in P2WPKH zu erstellen und dann in P2TR für ein weiteres Beispiel.
Der erste Schritt ist die Komprimierung des öffentlichen Schlüssels $K$. Um diesen Prozess gut zu verstehen, erinnern wir uns zunächst an einige Grundlagen, die in Teil 3 behandelt wurden.
Ein öffentlicher Schlüssel bei Bitcoin ist ein Punkt $K$, der sich auf einer elliptischen Kurve befindet. Er wird in der Form $(x, y)$ dargestellt, wobei $x$ und $y$ die Koordinaten des Punktes sind. In seiner unkomprimierten Form misst dieser öffentliche Schlüssel 520 Bits: 8 Bits für ein Präfix (Anfangswert von `0x04`), 256 Bits für die $x$-Koordinate und 256 Bits für die $y$-Koordinate.
Elliptische Kurven haben jedoch eine Symmetrieeigenschaft bezüglich der x-Achse: Für eine gegebene $x$-Koordinate gibt es nur zwei mögliche Werte für $y$: $y$ und $-y$. Diese beiden Punkte befinden sich auf beiden Seiten der x-Achse. Mit anderen Worten, wenn wir $x$ kennen, reicht es aus, anzugeben, ob $y$ gerade oder ungerade ist, um den genauen Punkt auf der Kurve zu identifizieren.
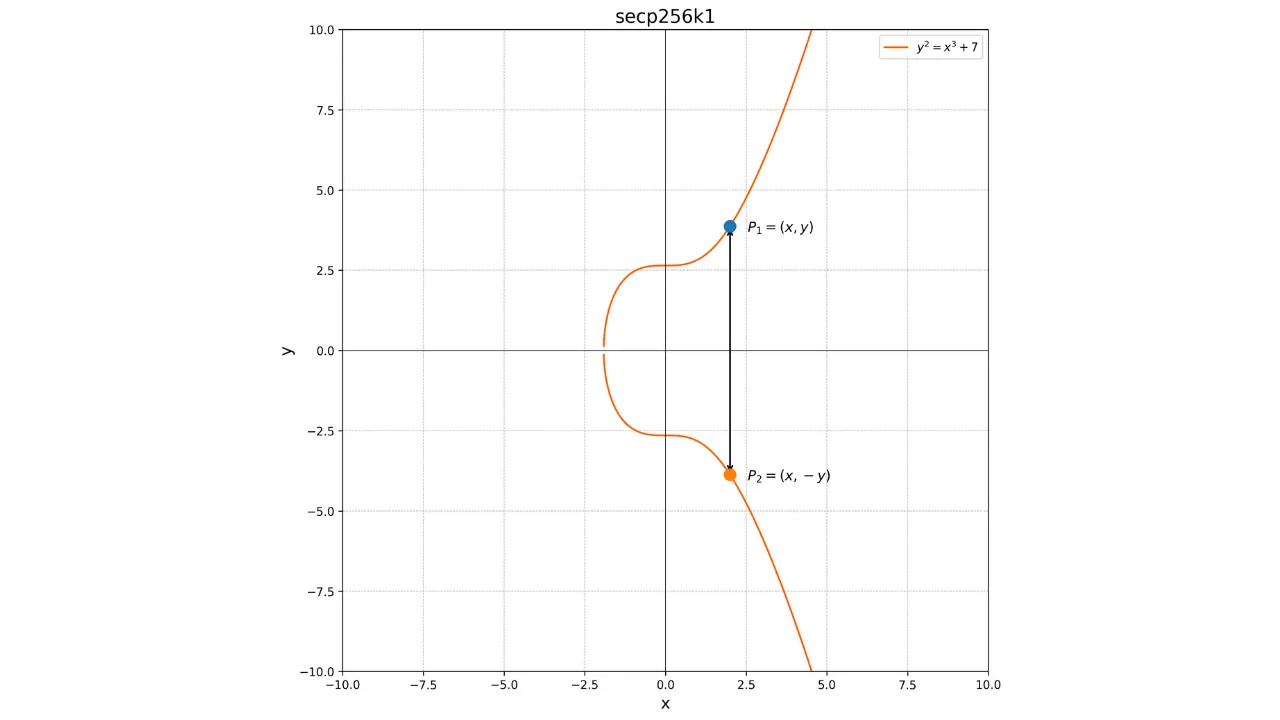
Um einen öffentlichen Schlüssel zu komprimieren, wird nur $x$ kodiert, was 256 Bits belegt, und ein Präfix wird hinzugefügt, um die Parität von $y$ anzugeben. Diese Methode reduziert die Größe des öffentlichen Schlüssels auf 264 Bits statt der ursprünglichen 520. Das Präfix `0x02` zeigt an, dass $y$ gerade ist, und das Präfix `0x03` zeigt an, dass $y$ ungerade ist.
Nehmen wir ein Beispiel, um dies gut zu verstehen, mit einem rohen öffentlichen Schlüssel in unkomprimierter Darstellung:
```text
K = 04678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f
```
Wenn wir diesen Schlüssel zerlegen, haben wir:
- Das Präfix: `04`;
- $x$: `678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6`;
- $y$: `49f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f`
Das letzte hexadezimale Zeichen von $y$ ist `f`. In Basis 10 entspricht `f = 15`, was einer ungeraden Zahl entspricht. Daher ist $y$ ungerade, und das Präfix wird `0x03` sein, um dies anzuzeigen.
Der komprimierte öffentliche Schlüssel wird zu:
```text
K = 03678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6
```
Diese Operation gilt für alle Skriptmodelle, die auf ECDSA basieren, das heißt, alle außer P2TR, das Schnorr verwendet. Im Fall von Schnorr, wie in Teil 3 erklärt, behalten wir nur den Wert von $x$ bei, ohne ein Präfix hinzuzufügen, um die Parität von $y$ anzugeben, im Gegensatz zu ECDSA. Dies wird dadurch ermöglicht, dass eine einzigartige Parität willkürlich für alle Schlüssel gewählt wird. Dies ermöglicht eine leichte Reduzierung des für öffentliche Schlüssel benötigten Speicherplatzes.
### Ableitung einer SegWit v0 (bech32) Adresse
Jetzt, da wir unseren komprimierten öffentlichen Schlüssel erhalten haben, können wir daraus eine SegWit v0 Empfangsadresse ableiten.
Der erste Schritt besteht darin, die HASH160-Hashfunktion auf den komprimierten öffentlichen Schlüssel anzuwenden. HASH160 ist eine Zusammensetzung von zwei aufeinanderfolgenden Hashfunktionen: SHA256, gefolgt von RIPEMD160:
\text{HASH160}(K) = \text{RIPEMD160}(\text{SHA256}(K))
Zuerst führen wir den Schlüssel durch SHA256:
```text
SHA256(K) = C489EBD66E4103B3C4B5EAFF462B92F5847CA2DCE0825F4997C7CF57DF35BF3A
```
Dann führen wir das Ergebnis durch RIPEMD160:
```text
RIPEMD160(SHA256(K)) = 9F81322CC88622CA4CCB2A52A21E2888727AA535
```
Wir haben einen 160-Bit-Hash des öffentlichen Schlüssels erhalten, der das darstellt, was als Payload der Adresse bezeichnet wird. Dieser Payload repräsentiert den zentralen und wichtigsten Teil der Adresse. Er wird auch im *scriptPubKey* verwendet, um die UTXOs zu sperren.
Um diesen Payload jedoch für Menschen leichter nutzbar zu machen, werden ihm Metadaten hinzugefügt. Der nächste Schritt beinhaltet die Kodierung dieses Hashs in Gruppen von 5 Bits in Dezimalzahlen. Diese dezimale Transformation wird für die Umwandlung in *bech32* nützlich sein, das von Post-SegWit-Adressen verwendet wird. Der 160-Bit-Binärhash wird somit in 32 Gruppen von 5 Bits aufgeteilt:
\begin{array}{|c|c|} \hline \text{5 bits} & \text{Decimal} \ \hline 10011 & 19 \ 11110 & 30 \ 00000 & 0 \ 10011 & 19 \ 00100 & 4 \ 01011 & 11 \ 00110 & 6 \ 01000 & 8 \ 10000 & 16 \ 11000 & 24 \ 10001 & 17 \ 01100 & 12 \ 10100 & 20 \ 10011 & 19 \ 00110 & 6 \ 01011 & 11 \ 00101 & 5 \ 01001 & 9 \ 01001 & 9 \ 01010 & 10 \ 00100 & 4 \ 00111 & 7 \ 10001 & 17 \ 01000 & 8 \ 10001 & 17 \ 00001 & 1 \ 11001 & 25 \ 00111 & 7 \ 10101 & 21 \ 00101 & 5 \ 00101 & 5 \ 10101 & 21 \ \hline \end{array}
Also haben wir:
```text
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
```
Sobald der Hash in Gruppen von 5 Bits kodiert ist, wird der Adresse eine Prüfsumme hinzugefügt. Diese Prüfsumme wird verwendet, um zu verifizieren, dass der Payload der Adresse während seiner Speicherung oder Übertragung nicht verändert wurde. Zum Beispiel ermöglicht es eine Wallet-Software sicherzustellen, dass Sie keinen Tippfehler gemacht haben, als Sie eine Empfangsadresse eingegeben haben. Ohne diese Überprüfung könnten Sie versehentlich Bitcoins an eine falsche Adresse senden, was zu einem dauerhaften Verlust von Geldern führen würde, da Sie den zugehörigen öffentlichen oder privaten Schlüssel nicht besitzen. Daher ist die Prüfsumme ein Schutz gegen menschliche Fehler.
Für die alten Bitcoin *Legacy*-Adressen wurde die Prüfsumme einfach vom Anfang des Adresshashs mit der HASH256-Funktion berechnet. Mit der Einführung von SegWit und dem *bech32*-Format werden nun BCH-Codes (*Bose, Ray-Chaudhuri und Hocquenghem*) verwendet. Diese fehlerkorrigierenden Codes werden verwendet, um Fehler in Datenfolgen zu erkennen und zu korrigieren. Sie stellen sicher, dass die übermittelten Informationen intakt an ihrem Ziel ankommen, selbst im Falle von geringfügigen Änderungen. BCH-Codes werden in vielen Bereichen verwendet, wie z.B. SSDs, DVDs und QR-Codes. Zum Beispiel können dank dieser BCH-Codes teilweise verdeckte QR-Codes immer noch gelesen und dekodiert werden.
Im Kontext von Bitcoin bieten BCH-Codes einen besseren Kompromiss zwischen Größe und Fehlererkennungsfähigkeit im Vergleich zu den einfachen Hash-Funktionen, die für *Legacy*-Adressen verwendet werden. Allerdings werden auf Bitcoin BCH-Codes nur zur Fehlererkennung, nicht zur Korrektur verwendet. Daher wird Wallet-Software eine inkorrekte Empfangsadresse signalisieren, aber nicht automatisch korrigieren. Diese Einschränkung ist absichtlich: Die Ermöglichung einer automatischen Korrektur würde die Fehlererkennungsfähigkeit verringern.
Um die Prüfsumme mit BCH-Codes zu berechnen, müssen wir mehrere Elemente vorbereiten:
- **Der HRP (*Human Readable Part*)**: Für das Bitcoin-Hauptnetz ist der HRP `bc`;
Der HRP muss erweitert werden, indem jeder Buchstabe in zwei Teile getrennt wird:
- Die Zeichen des HRP in ASCII nehmen:
- `b`: `01100010`
- `c`: `01100011`
- Die 3 signifikantesten Bits und die 5 am wenigsten signifikanten Bits extrahieren:
- 3 signifikanteste Bits: `011` (3 im Dezimal)
- 3 signifikanteste Bits: `011` (3 im Dezimal)
- 5 am wenigsten signifikante Bits: `00010` (2 im Dezimal)
- 5 am wenigsten signifikante Bits: `00011` (3 im Dezimal)
Mit dem Trennzeichen `0` zwischen den beiden Zeichen ist die HRP-Erweiterung daher:
```text
03 03 00 02 03
```
- **Die Witness-Version**: Für SegWit Version 0 ist es `00`;
- **Die Nutzlast**: Die Dezimalwerte des öffentlichen Schlüssel-Hashs;
- **Die Reservierung für die Prüfsumme**: Wir fügen am Ende der Sequenz 6 Nullen `[0, 0, 0, 0, 0, 0]` hinzu.
Alle Daten, die kombiniert werden, um in das Programm zur Berechnung der Prüfsumme eingegeben zu werden, sind wie folgt:
```text
HRP = 03 03 00 02 03
SEGWIT v0 = 00
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
PRÜFSUMME = 00 00 00 00 00 00
EINGABE = 03 03 00 02 03 00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 00 00 00 00 00 00
```
Die Berechnung der Prüfsumme ist ziemlich komplex. Sie beinhaltet polynomiale endliche Feldarithmetik. Wir werden diese Berechnung hier nicht im Detail erläutern und direkt zum Ergebnis übergehen. In unserem Beispiel ist die erhaltene Prüfsumme in Dezimal:
```text
10 16 11 04 13 18
```
Wir können nun die Empfangsadresse konstruieren, indem wir der Reihe nach die folgenden Elemente zusammenfügen:
- **Die SegWit-Version**: `00`
- **Die Nutzlast**: Der öffentliche Schlüssel-Hash
- **Die Prüfsumme**: Die im vorherigen Schritt erhaltenen Werte (`10 16 11 04 13 18`)
Das ergibt in Dezimal:
```text
00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 10 16 11 04 13 18
```
Anschließend muss jeder Dezimalwert anhand der folgenden Konvertierungstabelle in seinen *bech32*-Zeichen abgebildet werden:
\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \ \hline +0 & q & p & z & r & y & 9 & x & 8 \ \hline +8 & g & f & 2 & t & v & d & w & 0 \ \hline +16 & s & 3 & j & n & 5 & 4 & k & h \ \hline +24 & c & e & 6 & m & u & a & 7 & l \ \hline \end{array}
Um einen Wert in einen _bech32_-Zeichen mithilfe dieser Tabelle umzuwandeln, suchen Sie einfach die Werte in der ersten Spalte und der ersten Reihe, die zusammenaddiert das gewünschte Ergebnis ergeben. Dann holen Sie sich den entsprechenden Buchstaben. Zum Beispiel wird die Dezimalzahl `19` in den Buchstaben `n` umgewandelt, weil $19 = 16 + 3$.
Durch das Abbilden all unserer Werte erhalten wir die folgende Adresse:
```
qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj
```
Es bleibt nur noch, das HRP `bc` hinzuzufügen, was anzeigt, dass es sich um eine Adresse für das Bitcoin-Hauptnetz handelt, sowie den Separator `1`, um die vollständige Empfangsadresse zu erhalten:
```
bc1qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj
```
Die Besonderheit dieses _bech32_-Alphabets ist, dass es alle alphanumerischen Zeichen außer `1`, `b`, `i` und `o` umfasst, um visuelle Verwechslungen zwischen ähnlichen Zeichen zu vermeiden, insbesondere während ihrer Eingabe oder beim Lesen durch Menschen.
Zusammengefasst sieht der Ableitungsprozess so aus:
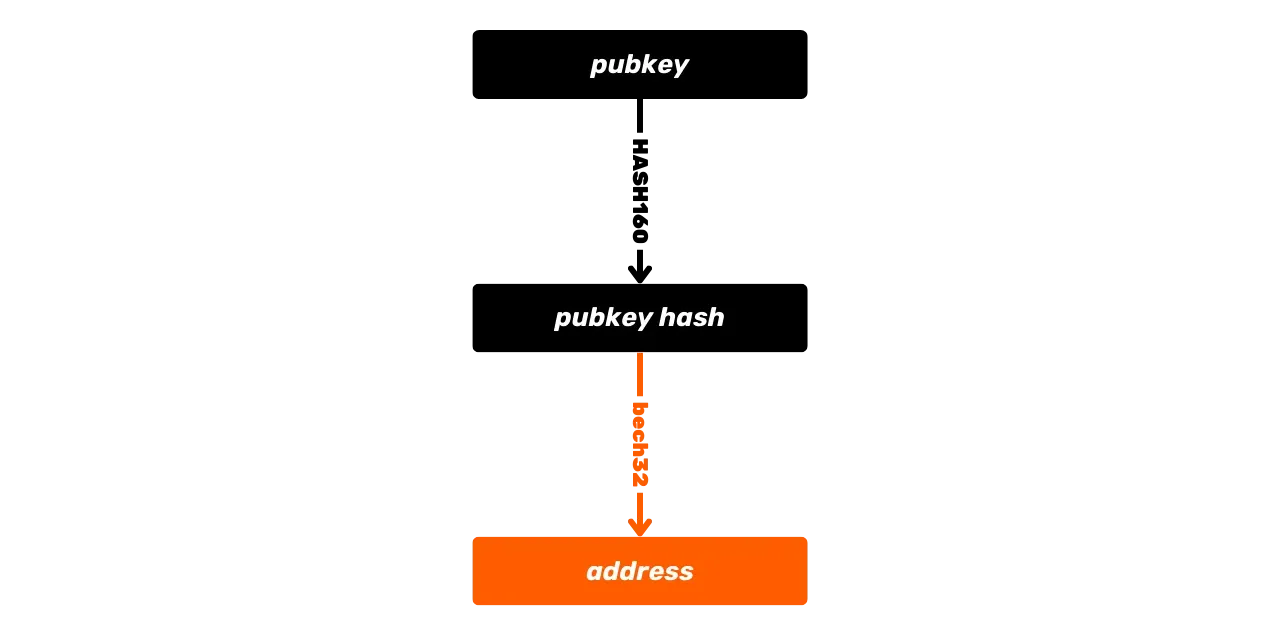
So leitet man eine P2WPKH (SegWit v0) Empfangsadresse aus einem Schlüsselpaar ab. Lassen Sie uns nun zu P2TR (SegWit v1 / Taproot) Adressen übergehen und deren Generierungsprozess entdecken.
### Ableitung einer SegWit v1 (bech32m) Adresse
Für Taproot-Adressen unterscheidet sich der Generierungsprozess leicht. Lassen Sie uns dies gemeinsam betrachten!
Vom Schritt der öffentlichen Schlüsselkompression erscheint eine erste Unterscheidung im Vergleich zu ECDSA: Die für Schnorr auf Bitcoin verwendeten öffentlichen Schlüssel werden nur durch ihre Abszisse ($x$) dargestellt. Daher gibt es kein Präfix, und der komprimierte Schlüssel misst genau 256 Bits.
Wie wir im vorherigen Kapitel gesehen haben, sperrt ein P2TR-Skript Bitcoins auf einem einzigartigen Schnorr-öffentlichen Schlüssel, der durch $Q$ bezeichnet wird. Dieser Schlüssel $Q$ ist eine Aggregation von zwei öffentlichen Schlüsseln: $P$, einem Haupt-internen öffentlichen Schlüssel, und $M$, einem öffentlichen Schlüssel, der aus der Merkle-Wurzel einer Liste von _scriptPubKey_ abgeleitet wird. Die mit diesem Typ von Skript gesperrten Bitcoins können auf zwei Arten ausgegeben werden:
- Durch Veröffentlichung einer Signatur für den öffentlichen Schlüssel $P$ (_key path_);
- Durch Erfüllung eines der Skripte im Merkle-Baum (_script path_).
In Wirklichkeit sind diese beiden Schlüssel nicht wirklich "aggregiert". Der Schlüssel $P$ wird stattdessen durch den Schlüssel $M$ modifiziert. In der Kryptographie bedeutet das "Modifizieren" eines öffentlichen Schlüssels, diesen Schlüssel zu ändern, indem ein additiver Wert namens "Tweak" angewendet wird. Diese Operation ermöglicht es, dass der modifizierte Schlüssel mit dem ursprünglichen privaten Schlüssel und dem Tweak kompatibel bleibt. Technisch ist ein Tweak ein Skalarwert $t$, der zum ursprünglichen öffentlichen Schlüssel hinzugefügt wird. Wenn $P$ der ursprüngliche öffentliche Schlüssel ist, wird der modifizierte Schlüssel zu:
P' = P + tG
Wobei $G$ der Generator der verwendeten elliptischen Kurve ist. Diese Operation erzeugt einen neuen öffentlichen Schlüssel, der vom ursprünglichen Schlüssel abgeleitet ist, während sie kryptografische Eigenschaften beibehält, die seine Verwendung ermöglichen.
Wenn Sie keine alternativen Skripte hinzufügen müssen (ausschließlich über den _key path_ ausgeben), können Sie eine Taproot-Adresse generieren, die ausschließlich auf dem öffentlichen Schlüssel basiert, der in der Tiefe 5 Ihrer Wallet vorhanden ist. In diesem Fall ist es notwendig, ein nicht-ausgabefähiges Skript für den _script path_ zu erstellen, um die Anforderungen der Struktur zu erfüllen. Die Anpassung $t$ wird dann berechnet, indem eine getaggte Hash-Funktion, **`TapTweak`**, auf den internen öffentlichen Schlüssel $P$ angewendet wird:
t = \text{H}_{\text{TapTweak}}(P)
wo:
- **$\text{H}_{\text{TapTweak}}$** ist eine SHA256-Hash-Funktion, getaggt mit dem Tag `TapTweak`. Wenn Sie nicht vertraut sind, was eine getaggte Hash-Funktion ist, lade ich Sie ein, Kapitel 3.3 zu konsultieren;
- $P$ ist der interne öffentliche Schlüssel, dargestellt in seinem komprimierten 256-Bit-Format, unter Verwendung nur der $x$-Koordinate.
Der Taproot-öffentliche Schlüssel $Q$ wird dann berechnet, indem die Anpassung $t$, multipliziert mit dem Generator der elliptischen Kurve $G$, zum internen öffentlichen Schlüssel $P$ hinzugefügt wird:
Q = P + t \cdot G
Sobald der Taproot-öffentliche Schlüssel $Q$ erhalten ist, können wir die entsprechende Empfangsadresse generieren. Anders als bei anderen Formaten basieren Taproot-Adressen nicht auf einem Hash des öffentlichen Schlüssels. Daher wird der Schlüssel $Q$ direkt in die Adresse eingefügt, auf rohe Weise.
Zunächst extrahieren wir die $x$-Koordinate des Punktes $Q$, um einen komprimierten öffentlichen Schlüssel zu erhalten. Auf diese Nutzlast wird eine Prüfsumme berechnet, die BCH-Codes verwendet, wie bei SegWit v0-Adressen. Das für Taproot-Adressen verwendete Programm unterscheidet sich jedoch leicht. Tatsächlich wurde nach der Einführung des _bech32_-Formats mit SegWit ein Fehler entdeckt: Wenn der letzte Buchstabe einer Adresse ein `p` ist, macht das Einfügen oder Entfernen von `q`s direkt vor diesem `p` die Prüfsumme nicht ungültig. Obwohl dieser Fehler bei SegWit v0 keine Konsequenzen hat (dank einer Größenbeschränkung), könnte er in Zukunft ein Problem darstellen. Dieser Fehler wurde daher für Taproot-Adressen korrigiert, und das neue korrigierte Format wird "_bech32m_" genannt.
Die Taproot-Adresse wird generiert, indem die $x$-Koordinate von $Q$ im _bech32m_-Format kodiert wird, mit den folgenden Elementen:
- **Der HRP (_Human Readable Part_)**: `bc`, um das Haupt-Bitcoin-Netzwerk anzugeben;
- **Die Version**: `1`, um Taproot / SegWit v1 anzugeben;
- **Die Prüfsumme**.
Die endgültige Adresse wird daher das Format haben:
```
bc1p[Qx][Prüfsumme]
```
Andererseits, wenn Sie zusätzlich zum Ausgeben mit dem internen öffentlichen Schlüssel (_script path_) alternative Skripte hinzufügen möchten, wird die Berechnung der Empfangsadresse leicht unterschiedlich sein. Sie müssen den Hash der alternativen Skripte in die Berechnung der Anpassung einbeziehen. In Taproot wird jedes alternative Skript, das sich am Ende des Merkle-Baums befindet, als "Blatt" bezeichnet.
Sobald die verschiedenen alternativen Skripte geschrieben sind, müssen Sie sie einzeln durch eine getaggte Hash-Funktion `TapLeaf` führen, begleitet von einigen Metadaten:
\text{h}{\text{leaf}} = \text{H}{\text{TapLeaf}} (v \Vert sz \Vert S)
Mit:
- $v$: die Skriptversionsnummer (Standard `0xC0` für Taproot);
- $sz$: die Größe des Skripts kodiert im _CompactSize_-Format;
- $S$: das Skript.
Die verschiedenen Skripthashes ($\text{h}_{\text{leaf}}$) werden zunächst in lexikographischer Reihenfolge sortiert. Dann werden sie paarweise zusammengefügt und durch die getaggte Hashfunktion `TapBranch` geleitet. Dieser Prozess wird iterativ wiederholt, um Schritt für Schritt den Merkle-Baum aufzubauen:
\text{h}{\text{branch}} = \text{H}{\text{TapBranch}}(\text{h}{\text{leaf1}} \Vert \text{h}{\text{leaf2}})
Wir fahren dann fort, indem wir die Ergebnisse zwei zu zwei zusammenfügen und sie in jedem Schritt durch die getaggte Hashfunktion `TapBranch` leiten, bis wir die Wurzel des Merkle-Baums erhalten:
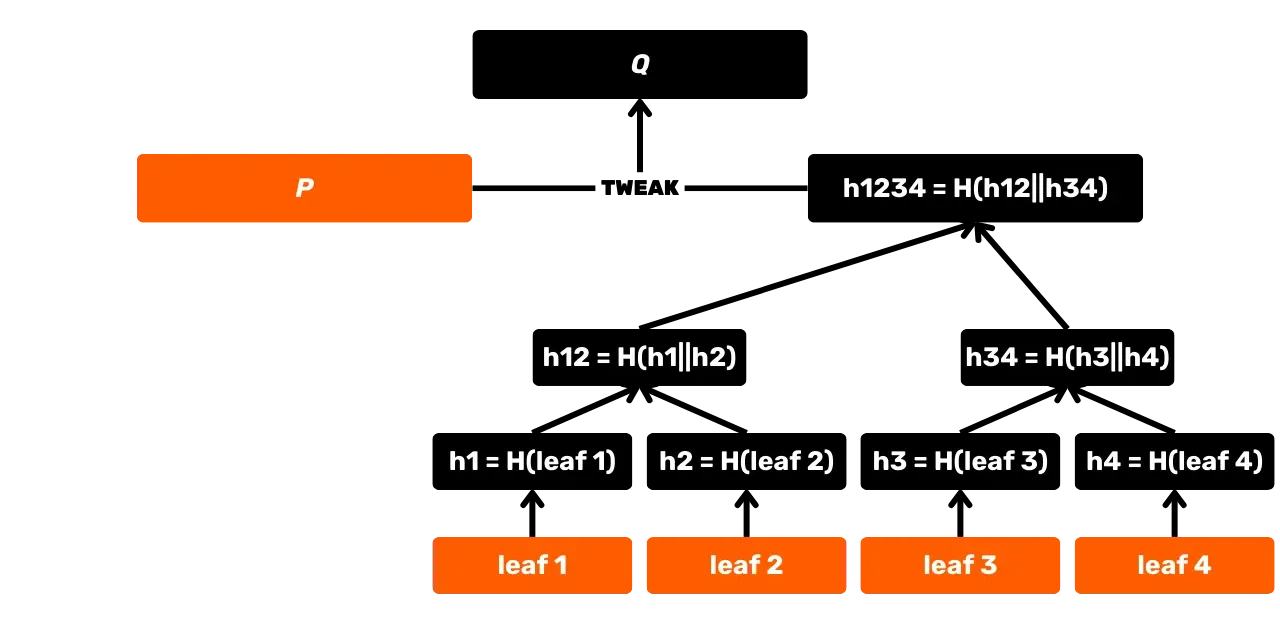
Sobald die Merkle-Wurzel $h_{\text{root}}$ berechnet ist, kann der Tweak berechnet werden. Dazu wird der interne öffentliche Schlüssel der Wallet $P$ mit der Wurzel $h_{\text{root}}$ verkettet und dann durch die markierte Hash-Funktion `TapTweak` geführt:
t = \text{H}{\text{TapTweak}}(P \Vert h{\text{root}})
Schließlich wird, wie zuvor, der Taproot-öffentliche Schlüssel $Q$ durch Hinzufügen des internen öffentlichen Schlüssels $P$ zum Produkt des Tweaks $t$ und des Generatorpunkts $G$ erhalten:
Q = P + t \cdot G
Die Adressgenerierung folgt dann demselben Prozess, wobei der rohe öffentliche Schlüssel $Q$ als Nutzlast zusammen mit einigen zusätzlichen Metadaten verwendet wird.
Und damit haben wir das Ende dieses CYP201-Kurses erreicht. Wenn Sie diesen Kurs hilfreich fanden, wäre ich Ihnen sehr dankbar, wenn Sie sich ein paar Momente Zeit nehmen könnten, um ihm in dem folgenden Bewertungskapitel eine gute Bewertung zu geben. Fühlen Sie sich auch frei, ihn mit Ihren Liebsten oder in Ihren sozialen Netzwerken zu teilen. Schließlich, wenn Sie Ihr Diplom für diesen Kurs erhalten möchten, können Sie direkt nach dem Bewertungskapitel die Abschlussprüfung ablegen.
# Abschluss
<partId>58111408-b734-54db-9ea7-0d5b67f99f99</partId>
## Bewertungen & Noten
<chapterId>0cd71541-a7fd-53db-b66a-8611b6a28b04</chapterId>
<isCourseReview>true</isCourseReview>
## Abschlussprüfung
<chapterId>a53ea27d-0f84-56cd-b37c-a66210a4b31d</chapterId>
<isCourseExam>true</isCourseExam>
## Fazit
<chapterId>d291428b-3cfa-5394-930e-4b514be82d5a</chapterId>
<isCourseConclusion>true</isCourseConclusion>