name: Úvod do formální kryptografie goal: Hloubkový úvod do vědy a praxe kryptografie. objectives:
- Prozkoumejte Bealovy šifry a moderní kryptografické metody a pochopte základní a historické koncepty kryptografie.
- Pronikněte do teorie čísel, grup a polí a osvojte si klíčové matematické pojmy, které jsou základem kryptografie.
- Prostudujte si proudovou šifru RC4 a AES se 128bitovým klíčem a seznamte se se symetrickými kryptografickými algoritmy.
- Prozkoumejte kryptosystém RSA, distribuci klíčů a hašovací funkce a prozkoumejte asymetrickou kryptografii.
Hluboký ponor do kryptografie
Je obtížné najít mnoho materiálů, které by ve výuce kryptografie nabízely dobrou střední cestu.
Na jedné straně existují dlouhá, formální pojednání, která jsou přístupná opravdu jen těm, kdo mají silné zázemí v matematice, logice nebo jiné formální disciplíně. Na druhé straně existují úvody na velmi vysoké úrovni, které skutečně skrývají příliš mnoho detailů pro každého, kdo je alespoň trochu zvědavý.
Tento úvod do kryptografie se snaží zachytit střední cestu. Ačkoli by měl být poměrně náročný a podrobný pro každého, kdo s kryptografií začíná, není to králičí nora typického základního pojednání.
Úvod
Přehled kurzu
bb8a8b73-7fb2-50da-bf4e-98996d79887b Vítejte v kurzu CYP302!
Tato kniha nabízí hluboký úvod do vědy a praxe kryptografie. Tam, kde je to možné, se zaměřuje spíše na koncepční než formální výklad látky.
Tento vzdělávací obsah je adaptován z knihy a repo JWBurgers. Přestože autor laskavě povolil jeho vzdělávací využití, veškerá práva duševního vlastnictví zůstávají původnímu tvůrci.
Motivace a cíle
Je obtížné najít mnoho materiálů, které by ve výuce kryptografie nabízely dobrou střední cestu.
Na jedné straně existují dlouhá, formální pojednání, která jsou přístupná opravdu jen těm, kdo mají silné zázemí v matematice, logice nebo jiné formální disciplíně. Na druhé straně existují úvody na velmi vysoké úrovni, které skutečně skrývají příliš mnoho detailů pro každého, kdo je alespoň trochu zvědavý.
Tento úvod do kryptografie se snaží zachytit střední cestu. Ačkoli by měl být pro každého, kdo se s kryptografií teprve seznamuje, poměrně náročný a podrobný, není to králičí nora typického základního pojednání.
Cílová skupina
Tato kniha je užitečná pro všechny, kteří chtějí kryptografii porozumět více než jen povrchně, a to od vývojářů až po intelektuály. Pokud je vaším cílem ovládnout oblast kryptografie, pak je tato kniha také dobrým výchozím bodem.
Pokyny pro čtení
Kniha v současné době obsahuje sedm kapitol: "Co je kryptografie?" (kapitola 1), "Matematické základy kryptografie I" (kapitola 2), "Matematické základy kryptografie II" (kapitola 3), "Symetrická kryptografie" (kapitola 4), "RC4 a AES" (kapitola 5), "Asymetrická kryptografie" (kapitola 6) a "Kryptosystém RSA" (kapitola 7). Závěrečná kapitola "Kryptografie v praxi" bude ještě doplněna. Zaměřuje se na různé kryptografické aplikace, včetně zabezpečení transportní vrstvy, cibulového směrování a systému výměny hodnot Bitcoin.
Pokud nemáte silné matematické vzdělání, je teorie čísel pravděpodobně nejobtížnějším tématem této knihy. Její přehled nabízím ve 3. kapitole a objevuje se také ve výkladu šifry AES v 5. kapitole a kryptosystému RSA v 7. kapitole.
Pokud máte s formálními detaily v těchto částech knihy opravdu potíže, doporučuji vám, abyste se napoprvé spokojili s jejich přečtením na vysoké úrovni.
Poděkování
Nejvlivnější knihou, která se podílela na formování tohoto tématu, byla kniha Jonathana Katze a Yehudy Lindella Introduction to Modern Cryptography, CRC Press (Boca Raton, FL), 2015. Na serveru Coursera je k dispozici doprovodný kurz s názvem "Cryptography"
Hlavními dalšími zdroji, které byly užitečné při vytváření přehledu v této knize, jsou Simon Singh, The Code Book, Fourth Estate (London, 1999); Christof Paar a Jan Pelzl, Understanding Cryptography, Springer (Heidelberg, 2010) a kurz založený na Paarově knize s názvem "Introduction to Cryptography"; a Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons).
Z těchto zdrojů budu citovat pouze velmi konkrétní informace a výsledky, které jsem převzal, ale chci zde přiznat, že jsem jim obecně zavázán.
Těm čtenářům, kteří chtějí po tomto úvodu hledat pokročilejší znalosti o kryptografii, vřele doporučuji knihu Katze a Lindella. Katzův kurz na Coursera je o něco přístupnější než kniha.
Příspěvky
Podívejte se prosím na soubor s příspěvky v úložišti, kde najdete pokyny, jak projekt podpořit.
Notový zápis
Klíčové pojmy:
Klíčové pojmy jsou v úvodnících uvedeny tučným písmem. Například uvedení šifry Rijndael jako klíčového termínu by vypadalo následovně: Šifra Rijndael.
Klíčové pojmy jsou výslovně definovány, pokud se nejedná o vlastní jména nebo pokud jejich význam není zřejmý z diskuse.
Definice se obvykle uvádí při uvedení klíčového pojmu, i když někdy je vhodnější ponechat definici na pozdější dobu.
Zvýrazněná slova a slovní spojení:
Slova a slovní spojení jsou zvýrazněna kurzívou. Například věta "Zapamatujte si heslo" by vypadala takto: Pamatujte si své heslo.
Formální zápis:
Formální zápis se týká především proměnných, náhodných veličin a množin.
- Proměnné: Obvykle se označují pouze malým písmenem (např. "x" nebo "y"). Někdy se pro přehlednost píší velkými písmeny (např. "M" nebo "K").
- Náhodné proměnné: Jsou vždy označeny velkým písmenem (např. "X" nebo "Y")
- Sady: Jsou vždy označeny tučnými velkými písmeny (např. S)
Připraveni prozkoumat fascinující svět kryptografie? Jdeme na to!
Co je to kryptografie?
Šifry Beale
Začněme naše pátrání v oblasti kryptografie jednou z nejpůvabnějších a nejzábavnějších epizod v její historii: epizodou Bealeových šifer. [1]
Příběh o Bealeových šifrách je podle mého názoru spíše fikcí než skutečností. Údajně se však odehrál takto.
V zimě 1820 a 1822 se v hostinci Roberta Morrisse v Lynchburgu (Virginie) ubytoval muž jménem Thomas J. Beale. Na konci druhého pobytu předal Beale Morrissovi do úschovy železnou skříňku s cennými dokumenty.
O několik měsíců později obdržel Morriss od Beala dopis z 9. května 1822. Zdůrazňoval v něm velkou hodnotu obsahu železné schránky a sděloval Morrissovi několik pokynů: pokud si Beale ani nikdo z jeho společníků nikdy nepřijde pro schránku, měl by ji otevřít přesně za deset let od data dopisu (tj. 9. května 1832). Některé z listin uvnitř by byly napsány běžným textem. Několik dalších by však bylo "bez pomoci klíče nesrozumitelných" Tento "klíč" by tedy Morrissovi doručil nejmenovaný Bealeův přítel v červnu 1832.
Navzdory jasným instrukcím Morriss v květnu 1832 schránku neotevřel a Bealův tajemný přítel se v červnu téhož roku neobjevil. Teprve v roce 1845 se hostinský konečně rozhodl skříňku otevřít. Morriss v ní našel vzkaz, který vysvětloval, jak Beale a jeho společníci objevili na Západě zlato a stříbro a pro jistotu je spolu s několika šperky zakopali. Kromě toho schránka obsahovala tři šifrové texty: tj. texty napsané v kódu, k jejichž odemčení je zapotřebí šifrový klíč neboli tajemství a doprovodný algoritmus. Tento proces odemknutí šifrového textu se nazývá dešifrování, zatímco proces uzamčení se nazývá šifrování. (Jak je vysvětleno v kapitole 3, pojem šifra může nabývat různých významů. V názvu "Bealeovy šifry" je to zkratka pro šifry.)
Tři šifry, které Morriss našel v železné skříňce, se skládají z řady čísel oddělených čárkami. Podle Bealeovy poznámky tyto šifry samostatně uvádějí polohu pokladu, obsah pokladu a seznam jmen s právoplatnými dědici pokladu a jejich podíly (poslední informace jsou důležité pro případ, že by si Beale a jeho společníci nikdy nepřišli pro schránku).
Morris se pokoušel dešifrovat tři šifry dvacet let. S klíčem by to bylo snadné. Morriss však klíč neměl a při pokusech o obnovení původních textů, neboli plaintextů, jak se obvykle nazývají v kryptografii, byl neúspěšný.
Na sklonku života předal Morriss v roce 1862 skříňku svému příteli. Tento přítel následně v roce 1885 vydal brožuru pod pseudonymem J. B. Ward. Obsahovala popis (údajné) historie skříňky, tři šifry a řešení, které našel pro druhou šifru. (Podle všeho existuje pro každý šifrový text jeden klíč, a nikoli jeden klíč, který funguje na všechny tři šifry, jak Beale původně zřejmě navrhoval v dopise Morrissovi)
Druhý šifrový text vidíte na obrázku 2 níže. [2] Klíčem k tomuto šifrovému textu je Deklarace nezávislosti Spojených států. Postup dešifrování spočívá v použití následujících dvou pravidel:
- Pro libovolné číslo n v šifrovém textu najděte n-té slovo v Deklaraci nezávislosti Spojených států amerických
- Nahraďte číslo n prvním písmenem nalezeného slova
Obrázek 1: Bealeova šifra č. 2

Například první číslo druhého šifrového textu je 115. 115. slovo Deklarace nezávislosti je "instituted", takže první písmeno otevřeného textu je "i" Šifrový text přímo neuvádí rozestupy mezi slovy a psaní velkých písmen. Po dešifrování několika prvních slov však lze logicky odvodit, že první slovo otevřeného textu bylo jednoduše "i" (Otevřený text začíná větou "I have deposited in the county of Bedford.")
Po rozluštění druhá zpráva uvádí podrobný obsah pokladu (zlato, stříbro a šperky) a naznačuje, že byl zakopán v železných nádobách a zasypán kamením v Bedford County (Virginie). Lidé mají rádi dobré záhady, a tak bylo vynaloženo velké úsilí na dešifrování dalších dvou Bealových šifer, zejména té, která popisuje umístění pokladu. Dokonce se o ně pokoušeli různí významní kryptografové. Zatím se však nikomu nepodařilo dešifrovat zbylé dvě šifry.
Poznámky:
[1] Dobré shrnutí příběhu viz Simon Singh, The Code Book, Fourth Estate (Londýn, 1999), str. 82-99. Krátký film o příběhu natočil Andrew Allen v roce 2010. Film najdete pod názvem "Šifra Thomase Beala" na jeho webových stránkách.
[2] Tento obrázek je k dispozici na stránce Bealeovy šifry na Wikipedii.
Moderní kryptografie
S kryptografií si většina z nás spojuje barvité příběhy, jako je ten o Bealeových šifrách. Moderní kryptografie se však od těchto typů historických příkladů liší nejméně ve čtyřech důležitých ohledech.
Za prvé, historicky se kryptografie zabývala pouze tajností (nebo důvěrností). [3] Šifrové texty by byly vytvořeny tak, aby bylo zajištěno, že informace v otevřených textech budou moci být zpřístupněny pouze určitým stranám, jako v případě Bealeových šifer. Aby šifrovací schéma dobře sloužilo tomuto účelu, mělo by být dešifrování šifrového textu proveditelné pouze tehdy, pokud máte klíč.
Moderní kryptografie se zabývá širší škálou témat než jen utajením. Mezi tato témata patří především (1) integrita zprávy - tj. zajištění, že zpráva nebyla změněna; (2) autentičnost zprávy - tj. zajištění, že zpráva skutečně pochází od konkrétního odesílatele; a (3) neodmítnutí - tj. zajištění, že odesílatel nemůže později falešně popřít, že zprávu odeslal. [4]
Důležité je tedy rozlišovat mezi šifrovacím schématem a šifrovacím schématem. Šifrovací schéma se zabývá pouze utajením. Zatímco šifrovací schéma je kryptografické schéma, opak není pravdou. Kryptografické schéma může sloužit i dalším hlavním tématům kryptografie, včetně integrity, autenticity a nepopiratelnosti.
Témata integrity a autenticity jsou stejně důležitá jako utajení. Naše moderní komunikační systémy by nemohly fungovat bez záruk týkajících se integrity a autenticity komunikace. Neodmítnutí je také důležitým problémem, například u digitálních smluv, ale v kryptografických aplikacích je méně všudypřítomné než utajení, integrita a autenticita.
Za druhé, klasická šifrovací schémata, jako jsou Bealeovy šifry, vždy zahrnují jeden klíč, který byl sdílen mezi všemi příslušnými stranami. Mnoho moderních kryptografických schémat však nezahrnuje pouze jeden, ale dva klíče: soukromý a veřejný klíč. Zatímco první z nich by měl při jakémkoli použití zůstat soukromý, druhý je obvykle veřejně známý (odtud jejich příslušné názvy). V rámci šifrování lze veřejný klíč použít k zašifrování zprávy, zatímco soukromý klíč lze použít k dešifrování.
Odvětví kryptografie, které se zabývá schématy, kde všechny strany sdílejí jeden klíč, se nazývá symetrická kryptografie. Jediný klíč v takovém schématu se obvykle nazývá soukromý klíč (nebo tajný klíč). Odvětví kryptografie, které se zabývá schématy vyžadujícími dvojici soukromý a veřejný klíč, je známé jako asymetrická kryptografie. Tato odvětví se někdy označují také jako kryptografie se soukromým klíčem, respektive kryptografie s veřejným klíčem (i když to může vyvolat zmatek, protože kryptografická schémata s veřejným klíčem mají také soukromé klíče).
Nástup asymetrické kryptografie na konci 70. let 20. století byl jednou z nejdůležitějších událostí v historii kryptografie. Bez ní by většina našich moderních komunikačních systémů, včetně Bitcoinu, nebyla možná, nebo by byla přinejmenším velmi nepraktická.
Důležité je, že moderní kryptografie není výhradně studiem kryptografických schémat se symetrickým a asymetrickým klíčem (i když to pokrývá velkou část oboru). Kryptografie se zabývá například také hashovacími funkcemi a generátory pseudonáhodných čísel a na těchto primitivech lze postavit aplikace, které se symetrickou nebo asymetrickou klíčovou kryptografií nesouvisejí.
Zatřetí, klasická šifrovací schémata, jako byla Bealeova šifra, byla spíše uměním než vědou. Jejich vnímaná bezpečnost byla do značné míry založena na intuici ohledně jejich složitosti. Obvykle se opravovala, když se zjistil nový útok na ně, nebo se od nich zcela upustilo, pokud byl útok obzvláště závažný. Moderní kryptografie je však přísnou vědou s formálním, matematickým přístupem k vývoji i analýze kryptografických schémat. [5]
Moderní kryptografie se zaměřuje na formální důkazy bezpečnosti. Každý důkaz bezpečnosti kryptografického schématu probíhá ve třech krocích:
Vyjádření kryptografické definice bezpečnosti, tj. souboru bezpečnostních cílů a hrozby, kterou představuje útočník.
Uvedení všech matematických předpokladů týkajících se výpočetní složitosti schématu. Kryptografické schéma může například obsahovat generátor pseudonáhodných čísel. I když nemůžeme dokázat, že existují, můžeme předpokládat, že existují.
Výklad matematického důkazu bezpečnosti schématu na základě formálního pojmu bezpečnosti a případných matematických předpokladů.
Začtvrté, zatímco v minulosti se kryptografie využívala především ve vojenském prostředí, v digitálním věku pronikla do našich každodenních činností. Ať už používáte internetové bankovnictví, zveřejňujete příspěvky na sociálních sítích, kupujete zboží na Amazonu pomocí kreditní karty nebo dáváte kamarádovi spropitné v bitcoinech, kryptografie je nezbytnou podmínkou našeho digitálního věku.
Vzhledem k těmto čtyřem aspektům moderní kryptografie bychom mohli moderní kryptografii charakterizovat jako vědu zabývající se formálním vývojem a analýzou kryptografických schémat pro zabezpečení digitálních informací proti útokům protivníka. [6] Bezpečnost by zde měla být chápána široce jako prevence útoků, které poškozují utajení, integritu, autentizaci a/nebo nepopiratelnost komunikace.
Kryptografie je nejlépe chápána jako dílčí disciplína kybernetické bezpečnosti, která se zabývá prevencí krádeží, poškození a zneužití počítačových systémů. Všimněte si, že mnoho problémů kybernetické bezpečnosti má s kryptografií jen malou nebo jen částečnou souvislost.
Například pokud má firma drahé servery umístěné na místě, může se zajímat o zabezpečení tohoto hardwaru před krádeží a poškozením. To je sice problém kybernetické bezpečnosti, ale s kryptografií má jen málo společného.
Dalším příkladem jsou phishingové útoky, které jsou v dnešní době běžným problémem. Tyto útoky se pokoušejí oklamat lidi prostřednictvím e-mailu nebo jiného média, aby se vzdali citlivých informací, jako jsou hesla nebo čísla kreditních karet. Kryptografie sice může do jisté míry pomoci řešit phishingové útoky, ale komplexní přístup vyžaduje více než jen použití nějaké kryptografie.
Poznámky:
[3] Přesněji řečeno, důležité aplikace kryptografických schémat se týkaly utajení. Například děti často používají jednoduchá kryptografická schémata pro "zábavu". V těchto případech se o utajení příliš nejedná.
[4] Bruce Schneier, Applied Cryptography, 2nd edn, 2015 (Indianapolis, IN: John Wiley & Sons), s. 2.
[5] Dobrý popis viz Jonathan Katz a Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), zejména str. 16-23.
[6] Srov. Katz a Lindell, tamtéž, s. 3. Domnívám se, že jejich charakteristika je poněkud problematická, a proto zde uvádím poněkud odlišnou verzi jejich výroku.
Otevřená komunikace
Moderní kryptografie je navržena tak, aby poskytovala bezpečnostní záruky v prostředí otevřené komunikace. Pokud je náš komunikační kanál tak dobře chráněn, že odposlouchávači nemají šanci manipulovat s našimi zprávami nebo je dokonce jen pozorovat, pak je kryptografie zbytečná. Většina našich komunikačních kanálů však takto dobře chráněna není.
Páteří komunikace v moderním světě je rozsáhlá síť optických kabelů. Telefonování, sledování televize a prohlížení webu v moderních domácnostech se zpravidla spoléhá na tuto síť optických kabelů (malé procento se může spoléhat výhradně na satelity). Je pravda, že v domácnosti můžete mít různá datová připojení, například koaxiální kabel, (asymetrickou) digitální účastnickou linku a optický kabel. Ale přinejmenším ve vyspělém světě se tato různá datová média rychle připojují mimo váš dům k uzlu v masivní síti optických kabelů, která propojuje celou zeměkouli. Výjimkou jsou některé odlehlé oblasti vyspělého světa, například ve Spojených státech a Austrálii, kde může datový provoz stále ještě překonávat značné vzdálenosti i po tradičních měděných telefonních drátech.
Případným útočníkům by nebylo možné zabránit ve fyzickém přístupu k této síti kabelů a její podpůrné infrastruktuře. Ve skutečnosti již víme, že většina našich dat je zachycována různými národními zpravodajskými agenturami na klíčových křižovatkách internetu [7], což zahrnuje vše od zpráv na Facebooku až po adresy webových stránek, které navštěvujete.
Zatímco sledování dat v masovém měřítku vyžaduje silného protivníka, například národní zpravodajskou agenturu, útočníci s malými zdroji se mohou snadno pokusit o slídění v lokálnějším měřítku. Ačkoli k tomu může dojít na úrovni odposlechu kabelů, mnohem snazší je pouze zachytit bezdrátovou komunikaci.
Většina dat v místní síti - ať už v našich domácnostech, kancelářích nebo kavárnách - se nyní přenáší prostřednictvím rádiových vln do bezdrátových přístupových bodů na univerzálních směrovačích, nikoli prostřednictvím fyzických kabelů. Útočník tedy nepotřebuje mnoho prostředků k tomu, aby zachytil jakýkoli váš místní provoz. To je obzvláště znepokojující, protože většina lidí dělá jen velmi málo pro ochranu dat, která putují přes jejich místní sítě. Kromě toho se potenciální útočníci mohou zaměřit také na naše mobilní širokopásmová připojení, jako jsou 3G, 4G a 5G. Všechny tyto bezdrátové komunikace jsou pro útočníky snadným cílem.
Proto je myšlenka utajení komunikace prostřednictvím ochrany komunikačního kanálu pro většinu moderního světa beznadějně iluzorní. Vše, co víme, opravňuje k těžké paranoie: vždy byste měli předpokládat, že vás někdo poslouchá. A kryptografie je hlavním nástrojem, který máme k dispozici, abychom v tomto moderním prostředí dosáhli jakéhokoli zabezpečení.
Poznámky:
[7] Viz například Olga Khazan, "The creepy, long-standing practice of undersea cable tapping", The Atlantic, 16. července 2013 (dostupné na The Atlantic).
Matematické základy kryptografie 1
Náhodné proměnné
Kryptografie se opírá o matematiku. A pokud chcete kryptografii porozumět více než jen povrchně, musíte se s touto matematikou dobře vyrovnat.
V této kapitole se seznámíte s většinou základních matematických poznatků, se kterými se při výuce kryptografie setkáte. Témata zahrnují náhodné veličiny, operace modulo, operace XOR a pseudonáhodnost. Materiál v těchto kapitolách byste měli zvládnout pro jakékoli jiné než povrchní pochopení kryptografie.
Další část se zabývá teorií čísel, která je mnohem náročnější.
Náhodné proměnné
Náhodná veličina se obvykle označuje velkým písmenem, které není tučné.
Můžeme tedy například hovořit o náhodné veličině X, náhodné veličině Y nebo
náhodné veličině Z. Tento
zápis budu od této chvíle používat i já.
Náhodná proměnná** může nabývat dvou nebo více možných hodnot, z nichž každá má určitou kladnou pravděpodobnost. Možné hodnoty jsou uvedeny v souboru výsledků.
Při každém vzorkování náhodné veličiny se podle definovaných pravděpodobností vybere určitá hodnota z její výsledné množiny.
Podívejme se na jednoduchý příklad. Předpokládejme proměnnou X, která je definována takto:
- X má množinu výsledků
\{1,2\}
Pr[X = 1] = 0.5Pr[X = 2] = 0.5Je snadné zjistit, že X je
náhodná veličina. Za prvé, existují dvě nebo více možných hodnot, kterých
může X nabývat, a to 1 a 2. Za druhé, každá z
možných hodnot má kladnou pravděpodobnost výskytu, kdykoli vyberete vzorek X, a to 0,5.
Jediné, co náhodná veličina vyžaduje, je množina výsledků se dvěma nebo více možnostmi, přičemž každá možnost má při výběru kladnou pravděpodobnost výskytu. V zásadě lze tedy náhodnou veličinu definovat abstraktně, bez jakéhokoli kontextu. V tomto případě si lze "výběr vzorku" představit jako provedení nějakého přirozeného experimentu, jehož cílem je určit hodnotu náhodné veličiny.
Výše uvedená proměnná X byla
definována abstraktně. Výše uvedený výběr proměnné X si tedy můžete představit jako hod spravedlivou mincí a přiřazení hodnoty
"2" v případě hlavy a "1" v případě ořechu. Pro každý vzorek X si hodíte mincí znovu.
Alternativně si můžete výběr vzorku X představit také jako hod spravedlivou kostkou a přiřazení hodnoty "2" v
případě, že kostka padne na 1, 3 nebo 4, a přiřazení hodnoty "1" v případě,
že kostka padne na 2, 5 nebo 6. Pokaždé, když vyberete vzorek X, hodíte kostkou znovu.
Skutečně si lze představit jakýkoli přirozený experiment, který by umožnil
definovat pravděpodobnosti výše uvedených možných hodnot X s ohledem na kresbu.
Často se však náhodné veličiny nezavádějí jen abstraktně. Místo toho má množina možných výsledných hodnot explicitní význam v reálném světě (nikoliv jen jako čísla). Kromě toho mohou být tyto výsledné hodnoty definovány na pozadí nějakého konkrétního typu experimentu (spíše než jako jakýkoli přirozený experiment s těmito hodnotami).
Uvažujme nyní příklad proměnné X, která není definována abstraktně. X je definována takto, aby bylo možné
určit, který ze dvou týmů začne fotbalový zápas:
Xmá výslednou množinu {červená vykopává,modrá vykopává}- Hod konkrétní mincí
C: orel = "červená vyrazí"; hlava = "modrá vyrazí"
Pr [X = \text{red kicks off}] = 0.5Pr [X = \text{blue kicks off}] = 0.5V tomto případě má množina výsledků X konkrétní význam, a to který tým začne
fotbalový zápas. Kromě toho jsou možné výsledky a s nimi spojené
pravděpodobnosti určeny konkrétním experimentem, a to házením konkrétní
mincí C.
V rámci diskusí o kryptografii se náhodné veličiny obvykle zavádějí na pozadí množiny výsledků s reálným významem. Může to být množina všech zpráv, které lze zašifrovat, známá jako prostor zpráv, nebo množina všech klíčů, z nichž si strany používající šifrování mohou vybrat, známá jako prostor klíčů.
Náhodné veličiny v diskusích o kryptografii se však obvykle nedefinují na základě nějakého konkrétního přirozeného experimentu, ale na základě jakéhokoli experimentu, který by mohl přinést správné rozdělení pravděpodobnosti.
Náhodné veličiny mohou mít diskrétní nebo spojité rozdělení
pravděpodobnosti. Náhodné veličiny s diskrétním rozdělením pravděpodobnosti - tedy diskrétní náhodné veličiny - mají konečný počet možných výsledků.
Náhodná veličina X v obou dosud
uvedených příkladech byla diskrétní.
Spojité náhodné veličiny mohou místo toho nabývat hodnot v jednom nebo více intervalech. Můžete například říci, že náhodná veličina při výběru nabývá libovolné reálné hodnoty mezi 0 a 1 a že každé reálné číslo v tomto intervalu je stejně pravděpodobné. V tomto intervalu existuje nekonečně mnoho možných hodnot.
Pro kryptografické diskuse vám stačí porozumět diskrétním náhodným veličinám. Veškeré diskuse o náhodných veličinách od této chvíle by proto měly být chápány jako diskrétní náhodné veličiny, pokud není výslovně uvedeno jinak.
Grafické znázornění náhodných veličin
Možné hodnoty a související pravděpodobnosti náhodné veličiny lze snadno
vizualizovat pomocí grafu. Uvažujme například náhodnou veličinu X z předchozí části s množinou výsledků \{1, 2\} a Pr [X = 1] = 0,5 a Pr [X = 2] = 0,5. Takovou
náhodnou veličinu bychom obvykle zobrazili ve formě sloupcového grafu jako
na obrázku 1.
Obrázek 1: Náhodná proměnná X
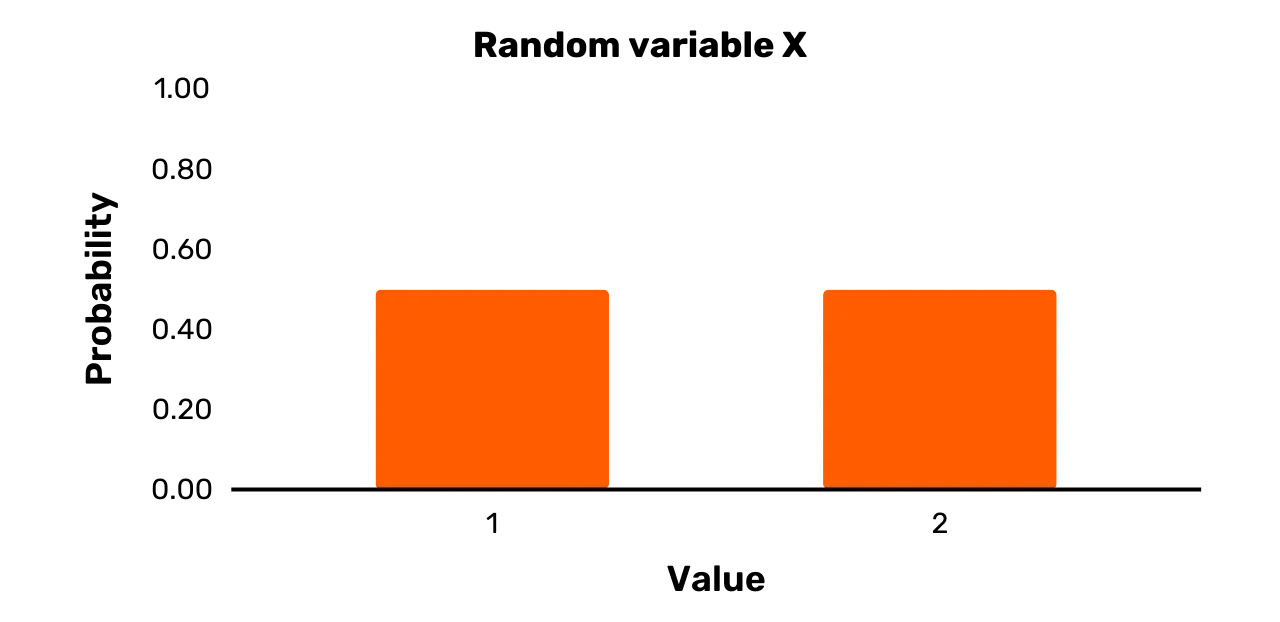
Široké sloupce na obrázku 1 samozřejmě neznamenají, že náhodná
veličina X je skutečně spojitá.
Místo toho jsou sloupce široké, aby byly vizuálně přitažlivější (pouhá přímka
rovně nahoru poskytuje méně intuitivní vizualizaci).
Jednotné proměnné
Ve výrazu "náhodná veličina" znamená výraz "náhodný" pouze "pravděpodobný". Jinými slovy znamená pouze to, že dva nebo více možných výsledků proměnné se vyskytují s určitou pravděpodobností. Tyto výsledky však nemusí být nutně stejně pravděpodobné (i když výraz "náhodný" může mít v jiných kontextech skutečně tento význam).
Jednotná proměnná je speciálním případem náhodné proměnné.
Může nabývat dvou nebo více hodnot se stejnou pravděpodobností. Náhodná
veličina X zobrazená na obrázku 1 je jednoznačně rovnoměrná veličina, protože oba možné výsledky se vyskytují
s pravděpodobností 0,5.
Existuje však mnoho náhodných veličin, které nejsou případy rovnoměrných
veličin.
Uvažujme například náhodnou veličinu Y. Má množinu výsledků {1, 2, 3, 8, 10} a následující
rozdělení pravděpodobnosti:
\Pr[Y = 1] = 0.25\Pr[Y = 2] = 0.35\Pr[Y = 3] = 0.1\Pr[Y = 8] = 0.25\Pr[Y = 10] = 0.05Zatímco dva možné výsledky mají skutečně stejnou pravděpodobnost výskytu, a
to 1 a 8, Y může při výběru nabývat i určitých hodnot s jinou pravděpodobností než 0,25. Ačkoli je tedy Y skutečně náhodná veličina, není
to veličina rovnoměrná.
Grafické znázornění Y je na obrázku 2.
Obrázek 2: Náhodná proměnná Y
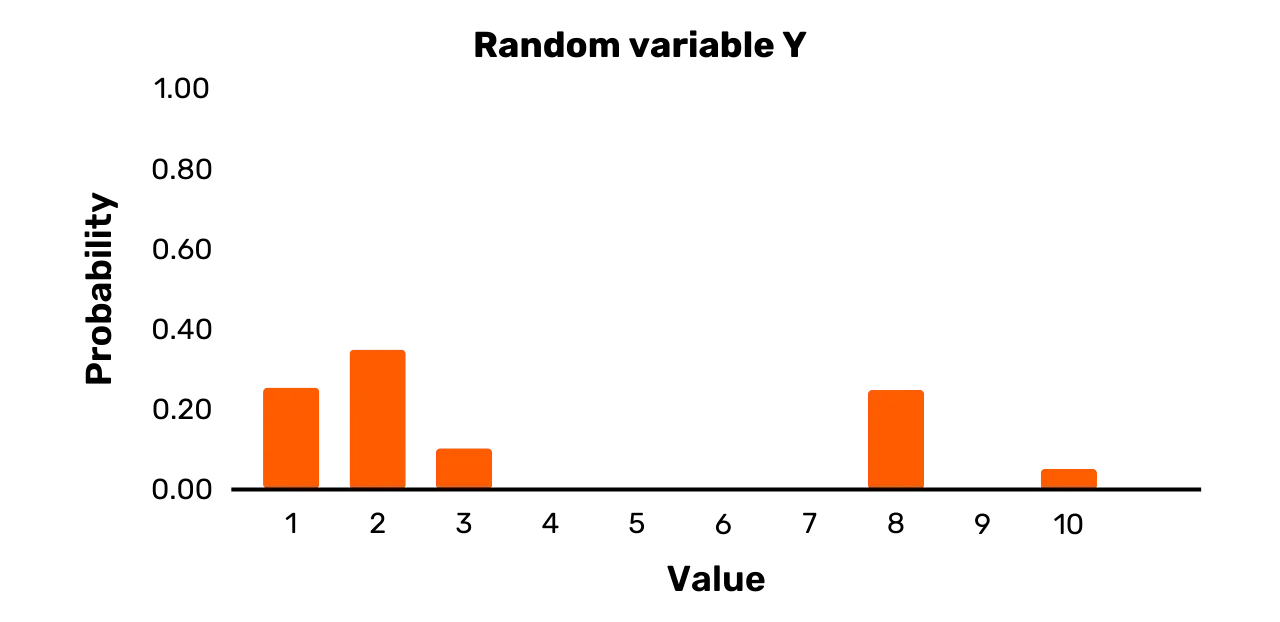
Jako poslední příklad uvažujme náhodnou veličinu Z. Má množinu výsledků {1,3,7,11,12} a následující rozdělení pravděpodobnosti:
\Pr[Z = 2] = 0.2\Pr[Z = 3] = 0.2\Pr[Z = 9] = 0.2\Pr[Z = 11] = 0.2\Pr[Z = 12] = 0.2Můžete si ji prohlédnout na obrázku 3. Náhodná veličina Z je na rozdíl od Y rovnoměrná veličina, protože všechny pravděpodobnosti možných hodnot při výběru jsou stejné.
Obrázek 3: Náhodná proměnná Z
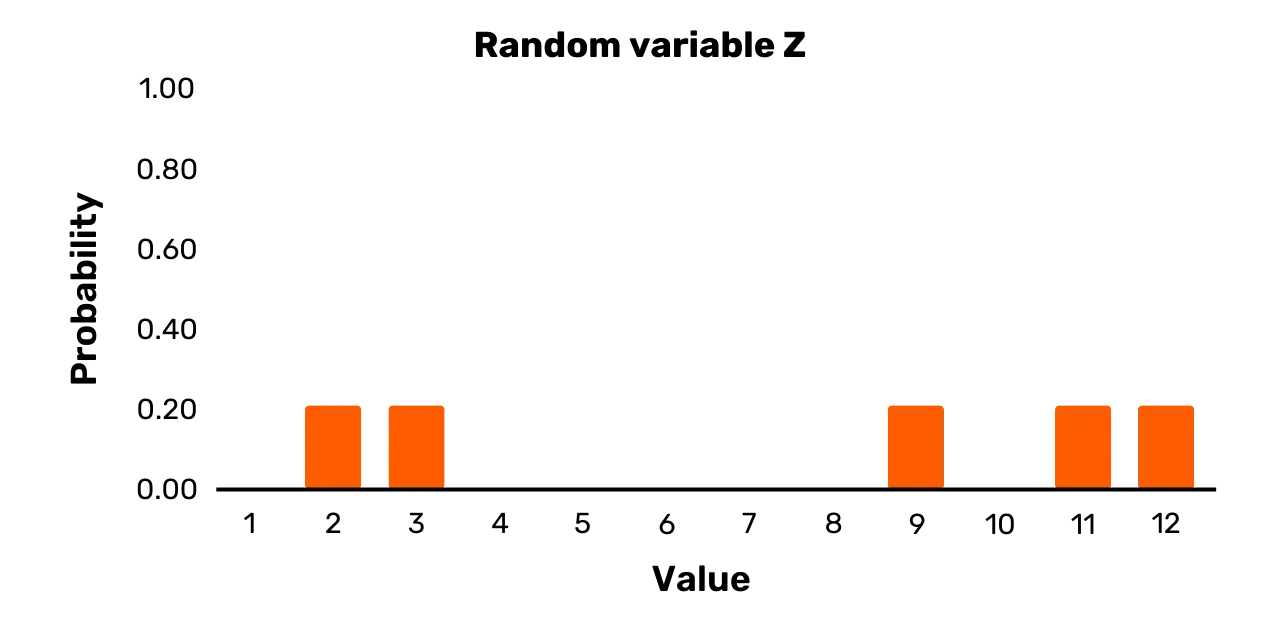
Podmíněná pravděpodobnost
Předpokládejme, že Bob hodlá rovnoměrně vybrat den z posledního kalendářního roku. Jaká je pravděpodobnost, že vybraný den bude v létě?
Pokud si myslíme, že Bobův proces bude skutečně rovnoměrný, měli bychom dojít k závěru, že existuje 1/4 pravděpodobnost, že Bob vybere den v létě. To je nepodmíněná pravděpodobnost, že náhodně vybraný den bude v létě.
Předpokládejme nyní, že Bob místo rovnoměrného losování kalendářního dne vybírá rovnoměrně pouze z těch dnů, kdy byla polední teplota v Crystal Lake (New Jersey) 21 stupňů Celsia nebo vyšší. Co můžeme vzhledem k této dodatečné informaci vyvodit o pravděpodobnosti, že Bob vybere den v létě?
I bez dalších konkrétních informací (např. teplota v poledne každého dne v minulém kalendářním roce) bychom skutečně měli dojít k jinému závěru než dosud.
Vzhledem k tomu, že Crystal Lake leží v New Jersey, určitě bychom neočekávali, že teplota v poledne bude v zimě 21 stupňů Celsia nebo vyšší. Mnohem pravděpodobnější je naopak teplý den na jaře nebo na podzim, případně den někde v létě. Pokud tedy víme, že polední teplota u jezera Crystal Lake ve vybraný den byla 21 stupňů Celsia nebo vyšší, je pravděpodobnost, že Bobem vybraný den je v létě, mnohem vyšší. To je podmíněná pravděpodobnost, že náhodně vybraný den bude v létě, pokud víme, že polední teplota u jezera Crystal Lake byla 21 stupňů Celsia nebo vyšší.
Na rozdíl od předchozího příkladu mohou být pravděpodobnosti dvou událostí také zcela nesouvisející. V takovém případě říkáme, že jsou nezávislé.
Předpokládejme například, že na určité minci padla hlava. Jaká je tedy pravděpodobnost, že zítra bude pršet? Podmíněná pravděpodobnost by v tomto případě měla být stejná jako nepodmíněná pravděpodobnost, že zítra bude pršet, protože hod mincí obecně nemá na počasí žádný vliv.
Pro zápis podmíněných pravděpodobnostních výroků používáme symbol "|".
Například pravděpodobnost události A za předpokladu, že nastala událost B, lze zapsat takto:
Pr[A|B]Jsou-li tedy dvě události A a B nezávislé, pak:
Pr[A|B] = Pr[A] \text{ and } Pr[B|A] = Pr[B]Podmínku nezávislosti lze zjednodušit takto:
Pr[A, B] = Pr[A] \cdot Pr[B]Klíčový výsledek teorie pravděpodobnosti je známý jako Bayesova věta. V podstatě říká, že Pr[A|B] lze přepsat takto:
Pr[A|B] = \frac{Pr[B|A] \cdot Pr[A]}{Pr[B]}Namísto podmíněných pravděpodobností u konkrétních událostí se můžeme
zabývat podmíněnými pravděpodobnostmi u dvou nebo více náhodných veličin v
souboru možných událostí. Předpokládejme dvě náhodné veličiny, X a Y. Jakoukoli možnou hodnotu
pro X můžeme označit x a jakoukoli možnou hodnotu pro Y y. Můžeme tedy říci, že dvě
náhodné veličiny jsou nezávislé, pokud platí následující tvrzení:
Pr[X = x, Y = y] = Pr[X = x] \cdot Pr[Y = y]pro všechny x a y.
Ujasněme si, co toto tvrzení znamená.
Předpokládejme, že množiny výsledků pro X a Y jsou definovány takto: X = \{x_1, x_2, \ldots, x_i, \ldots, x_n\} a Y = \{y_1, y_2, \ldots, y_i, \ldots, y_m\}. (Typické je označovat množiny hodnot tučným písmem a velkými písmeny.)
Nyní předpokládejme, že vybereme vzorek Y a pozorujeme y_1. Výše
uvedené tvrzení nám říká, že pravděpodobnost, že nyní získáme x_1 z výběru vzorku X, je přesně
stejná, jako kdybychom nikdy nepozorovali y_1. To platí pro libovolné y_i, které jsme mohli získat
z našeho původního výběru vzorku Y. A konečně to platí nejen
pro x_1. Pro libovolné x_i není pravděpodobnost výskytu ovlivněna výsledkem výběru vzorku Y. To vše platí i pro případ,
kdy je nejprve vybrán vzorek X.
Ukončeme naši diskusi trochu filozofičtěji. V každé reálné situaci se pravděpodobnost nějaké události vždy posuzuje na základě určitého souboru informací. Neexistuje žádná "nepodmíněná pravděpodobnost" ve velmi striktním slova smyslu.
Předpokládejme například, že se vás zeptám na pravděpodobnost, že v roce 2030 budou létat prasata. Ačkoli vám neposkytnu žádné další informace, je zřejmé, že o světě víte mnoho, co může ovlivnit váš úsudek. Nikdy jste neviděli létat prasata. Víte, že většina lidí nebude očekávat, že budou létat. Víte, že ve skutečnosti nejsou na létání stavěná. A tak dále.
Proto když v reálném světě hovoříme o "nepodmíněné pravděpodobnosti" nějaké události, může mít tento termín smysl pouze tehdy, pokud jím rozumíme něco jako "pravděpodobnost bez dalších explicitních informací". Jakékoli chápání "podmíněné pravděpodobnosti" by tedy mělo být vždy chápáno na pozadí nějaké konkrétní informace.
Mohl bych se vás například zeptat, jaká je pravděpodobnost, že do roku 2030 budou létat prasata, poté, co vám předložím důkaz, že některé kozy na Novém Zélandu se po několika letech výcviku naučily létat. V takovém případě pravděpodobně upravíte svůj úsudek o pravděpodobnosti, že prasata budou létat do roku 2030. Pravděpodobnost, že prasata budou létat do roku 2030, je tedy podmíněna tímto důkazem o kozách na Novém Zélandu.
Operace modulo
Modulo
Nejzákladnější výraz s operací modulo má následující tvar: x \mod y.
Proměnná x se nazývá
dividenda a proměnná y dělitel.
Chcete-li provést operaci modulo s kladnou dividendou a kladným dělitelem, stačí
určit zbytek dělení.
Vezměme například výraz 25 \mod 4. Číslo 4 přechází do čísla 25 celkem šestkrát. Zbytek tohoto dělení je 1.
Proto se 25 \mod 4 rovná 1. Podobným
způsobem můžeme vyhodnotit níže uvedené výrazy:
29 \mod 30 = 29(protože 30 přechází do 29 celkem 0krát a zbytek je 29)42 \mod 2 = 0(protože 2 přechází do 42 celkem 21krát a zbytek je 0)12 \mod 5 = 2(protože 5 přechází do 12 celkem 2krát a zbytek je 2)20 \mod 8 = 4(protože 8 přechází do 20 celkem 2krát a zbytek je 4)
Pokud je dividenda nebo dělitel záporný, mohou programovací jazyky s operacemi modulo zacházet odlišně.
V kryptografii se určitě setkáte s případy s negativní dividendou. V těchto případech je typický následující postup:
- Nejprve určete nejbližší hodnotu menší nebo rovnou dividendě, na
kterou se dělitel dělí se zbytkem nula. Tuto hodnotu nazvěte
p. - Je-li dividenda
x, pak výsledkem operace modulo je hodnotax - p.
Předpokládejme například, že dividenda je -20 a dělitel 3. Nejbližší hodnota menší nebo rovna -20, na kterou se 3
rovnoměrně dělí, je -21.
Hodnota x - p je v tomto
případě -20 - (-21). Tato
hodnota je rovna 1, a proto se -20 \mod 3 rovná 1. Podobným způsobem
můžeme vyhodnotit následující výrazy:
-8 \mod 5 = 2-19 \mod 16 = 13-14 \mod 6 = 4
Pokud jde o zápis, obvykle se setkáte s následujícími typy výrazů: x = [y \mod z]. Vzhledem k závorkám se operace modulo v tomto případě vztahuje pouze na
pravou stranu výrazu. Pokud je například y rovno 25 a z rovno 4, pak se x vyhodnotí jako 1.
Bez závorek působí operace modulo na obě strany výrazu.
Předpokládejme například následující výraz: x = y \mod z. Pokud se y rovná 25 a z se rovná 4, pak
víme jen to, že x \mod 4 se
vyhodnotí jako 1. To je v souladu s libovolnou hodnotou pro x z množiny \{\ldots,-7, -3, 1, 5, 9,\ldots\}.
Odvětví matematiky, které zahrnuje modulové operace s čísly a výrazy, se označuje jako modulární aritmetika. Tento obor si můžete představit jako aritmetiku pro případy, kdy číselná řada není nekonečně dlouhá. Ačkoli se v rámci kryptografie obvykle setkáváme s modulo operacemi pro (kladná) celá čísla, modulo operace můžete provádět i s libovolnými reálnými čísly.
Posunovací šifra
Operace modulo se v kryptografii vyskytuje často. Pro ilustraci uveďme jedno z nejznámějších historických šifrovacích schémat: šifru s posunem.
Nejprve si ji definujme. Předpokládejme slovník D, který přirovnává
všechna písmena anglické abecedy v pořadí k množině čísel \{0, 1, 2, \ldots, 25\}. Předpokládejme prostor zpráv M. Šifra shift je tedy šifrovací schéma definované takto:
- Z prostoru klíčů K vyberte rovnoměrně klíč
k, kde K =\{0, 1, 2, \ldots, 25\}[1] - Zašifrujte zprávu
m \in \mathbf{M}takto:- Rozdělte
mna jednotlivá písmenam_0, m_1, \ldots, m_i, \ldots, m_l - Převeďte každé
m_ina číslo podle D - Pro každé
m_iplatíc_i = [(m_i + k) \mod 26] - Převeďte každé
c_ina písmeno podle D - Pak zkombinujte
c_0, c_1, \ldots, c_la získáte šifrový textc
- Rozdělte
- Dešifrování šifrového textu
cnásledujícím způsobem:- Převeďte každé
c_ina číslo podle D - Pro každé
c_iplatím_i = [(c_i - k) \mod 26] - Převeďte každé
m_ina písmeno podle D - Pak zkombinujte
m_0, m_1, \ldots, m_la získáte původní zprávum
- Převeďte každé
Operátor modulo v šifře shift zajišťuje, že se písmena obtékají, takže jsou definována všechna písmena šifrového textu. Pro ilustraci uvažujme použití šifry shift na slovo "DOG".
Předpokládejme, že jste jednotně vybrali klíč, který má hodnotu 17. Písmeno
"O" odpovídá hodnotě 15. Bez operace modulo by součet tohoto čísla
otevřeného textu s klíčem znamenal číslo šifrového textu 32. Toto číslo
šifrového textu však nelze změnit na písmeno šifrového textu, protože
anglická abeceda má pouze 26 písmen. Operace modulo zajistí, že číslo
šifrového textu je ve skutečnosti 6 (výsledek 32 \mod 26), což odpovídá písmenu šifrového textu "G".
Celé šifrování slova "DOG" s hodnotou klíče 17 je následující:
- Zpráva = DOG = D,O,G = 3,15,6
c_0 = [(3 + 17) \mod 26] = [(20) \mod 26] = 20 = Uc_1 = [(15 + 17) \mod 26] = [(32) \mod 26] = 6 = Gc_2 = [(6 + 17) \mod 26] = [(23) \mod 26] = 23 = Xc = UGX
Každý intuitivně chápe, jak šifra shift funguje, a pravděpodobně ji sám používá. Pro prohloubení znalostí kryptografie je však důležité začít se lépe orientovat ve formalizaci, protože schémata budou mnohem složitější. Proto byly kroky pro posunovací šifru formalizovány.
Poznámky:
[1] Toto tvrzení můžeme přesně definovat pomocí terminologie z předchozí
části. Nechť jednotná proměnná K má jako množinu možných výsledků K. Tedy:
Pr[K = 0] = \frac{1}{26}Pr[K = 1] = \frac{1}{26}...a tak dále. Pro získání konkrétního klíče se jednou vybere jednotná
proměnná K.
Operace XOR
Všechna počítačová data se zpracovávají, ukládají a posílají po sítích na úrovni bitů. Veškerá kryptografická schémata, která se používají na počítačová data, pracují rovněž na úrovni bitů.
Předpokládejme například, že jste do e-mailové aplikace napsali e-mail. Jakékoli šifrování, které použijete, se neprojeví přímo na znacích ASCII vašeho e-mailu. Místo toho se použije na bitovou reprezentaci písmen a dalších symbolů v e-mailu.
Pro moderní kryptografii je kromě operace modulo klíčová matematická operace XOR neboli operace "exkluzivní nebo". Tato operace přijímá jako vstupy dva bity
a jako výstup dává další bit. Operaci XOR budeme jednoduše označovat jako
"XOR". Výsledkem je 0, pokud jsou oba bity stejné, a 1, pokud se oba bity
liší. Níže si můžete prohlédnout čtyři možnosti. Symbol \oplus představuje "XOR" :
0 \oplus 0 = 00 \oplus 1 = 11 \oplus 0 = 11 \oplus 1 = 0
Pro ilustraci předpokládejme, že máte zprávu m_1 (01111001) a zprávu m_2 (01011001).
Operaci XOR těchto dvou zpráv si můžete prohlédnout níže.
m_1 \oplus m_2 = 01111001 \oplus 01011001 = 00100000
Postup je jednoduchý. Nejprve zkontrolujete XOR nejlevějších bitů m_1 a m_2. V tomto případě je to 0 \oplus 0 = 0. Poté XORujete
druhou dvojici bitů zleva. V tomto případě je to 1 \oplus 1 = 0. V tomto
postupu pokračujete, dokud neprovedete operaci XOR na nejpravějších bitech.
Snadno zjistíme, že operace XOR je komutativní, tedy že m_1 \oplus m_2 = m_2 \oplus m_1. Kromě toho je operace XOR také asociativní. To znamená, že (m_1 \oplus m_2) \oplus m_3 = m_1 \oplus (m_2 \oplus m_3).
Operace XOR na dvou řetězcích různých délek může mít v závislosti na kontextu různou interpretaci. Operacemi XOR na řetězcích různých délek se zde zabývat nebudeme.
Operace XOR je ekvivalentní speciálnímu případu provedení operace modulo na sčítání bitů, kdy dělitel je 2. Ekvivalenci můžete vidět v následujících výsledcích:
(0 + 0) \mod 2 = 0 \oplus 0 = 0(1 + 0) \mod 2 = 1 \oplus 0 = 1(0 + 1) \mod 2 = 0 \oplus 1 = 1(1 + 1) \mod 2 = 1 \oplus 1 = 0
Pseudonáhodnost
V naší diskusi o náhodných a rovnoměrných proměnných jsme rozlišovali mezi "náhodnými" a "rovnoměrnými" proměnnými. Toto rozlišení se v praxi při popisu náhodných veličin obvykle zachovává. V našem současném kontextu je však třeba od tohoto rozlišení upustit a slova "náhodný" a "rovnoměrný" používat jako synonyma. Proč, to vysvětlím na konci této části.
Na začátku můžeme binární řetězec délky n nazvat náhodným (nebo jednotným), pokud
vznikl výběrem jednotné proměnné S, která dává každému
binárnímu řetězci takové délky n stejnou pravděpodobnost výběru.
Předpokládejme například množinu všech binárních řetězců o délce 8: \{0000\ 0000, 0000\ 0001, \ldots, 1111\ 1111\}. (Typické je zapsat 8bitový řetězec ve dvou čtveřicích, z nichž každá se
nazývá nibble.) Nazvěme tuto množinu řetězců S_8.
Podle výše uvedené definice pak můžeme určitý binární řetězec délky 8 nazvat
náhodným (nebo rovnoměrným), pokud byl výsledkem výběru rovnoměrné proměnné S, která dává každému řetězci v S_8 stejnou pravděpodobnost výběru. Vzhledem k tomu, že množina S_8 obsahuje 2^8 prvků, musela by
být pravděpodobnost výběru při vzorkování pro každý řetězec v množině 1/2^8.
Klíčovým aspektem náhodnosti binárního řetězce je to, že je definován s ohledem na proces, kterým byl vybrán. Tvar konkrétního binárního řetězce sám o sobě tedy neprozrazuje nic o jeho náhodnosti při výběru.
Mnoho lidí má například intuitivní představu, že řetězec jako 1111\ 1111 nemohl být vybrán náhodně. To je však zjevně nepravdivé.
Definujeme-li jednotnou proměnnou S nad všemi binárními řetězci délky 8, je pravděpodobnost výběru 1111\ 1111 z množiny S_8 stejná jako pravděpodobnost výběru řetězce 0111\ 0100. O náhodnosti
řetězce tedy nelze nic říci pouhou analýzou samotného řetězce.
Můžeme také mluvit o náhodných řetězcích, aniž bychom měli na mysli
konkrétně binární řetězce. Můžeme například mluvit o náhodném hexadecimálním
řetězci AF\ 02\ 82. V tomto
případě by byl řetězec náhodně vybrán z množiny všech hexadecimálních
řetězců délky 6. To je ekvivalentní náhodnému výběru binárního řetězce délky
24, protože každá hexadecimální číslice představuje 4 bity.
Obvykle se výraz "náhodný řetězec" bez upřesnění vztahuje na řetězec náhodně
vybraný z množiny všech řetězců stejné délky. Takto jsem to popsal výše.
Řetězec o délce n lze
samozřejmě náhodně vybrat i z jiné množiny. Například takového, který tvoří
pouze podmnožinu všech řetězců délky n, nebo třeba množiny, která
obsahuje řetězce různé délky. V těchto případech bychom však o něm nemluvili
jako o "náhodném řetězci", ale spíše jako o "řetězci, který je náhodně
vybrán z nějaké množiny S".
Klíčovým pojmem v kryptografii je pseudonáhodnost. Pseudonáhodný řetězec**
délky n se jeví, jako by byl
výsledkem vzorkování jednotné proměnné S, která dává každému řetězci
v S_n stejnou pravděpodobnost výběru. Ve skutečnosti je však tento řetězec
výsledkem vzorkování rovnoměrné proměnné S', která pouze definuje
rozdělení pravděpodobnosti - ne nutně s rovnými pravděpodobnostmi pro
všechny možné výsledky - na podmnožině S_n. Zásadní
je, že ve skutečnosti nikdo nedokáže rozlišit mezi vzorky z S a S', i když jich odeberete
mnoho.
Předpokládejme například náhodnou veličinu S. Její výsledná množina je S_{256}, což je množina všech binárních řetězců délky 256. Tato množina má 2^{256} prvků. Každý prvek má při výběru stejnou pravděpodobnost výběru, 1/2^{256}.
Dále předpokládejme náhodnou veličinu S'. Její množina výsledků obsahuje pouze 2^{128} binárních řetězců
o délce 256. Má nějaké rozdělení pravděpodobnosti nad těmito řetězci, ale toto
rozdělení nemusí být nutně rovnoměrné.
Předpokládejme, že jsem nyní vzal 1000 vzorků z S a 1000 vzorků z S' a dal vám
tyto dvě sady výsledků. Řeknu vám, který soubor výsledků je spojen s kterou
náhodnou veličinou. Dále vezmu vzorek z jedné z obou náhodných veličin.
Tentokrát vám však neřeknu, ze které náhodné veličiny vzorek odebírám. Pokud
by S' byla pseudonáhodná, pak
jde o to, že vaše pravděpodobnost správného odhadu, kterou náhodnou veličinu
jsem vybral, není prakticky lepší než 1/2.
Pseudonáhodný řetězec délky n se obvykle vytváří náhodným výběrem řetězce o velikosti n - x, kde x je celé kladné číslo, a jeho použitím jako vstupu pro rozšiřující
algoritmus. Tento náhodný řetězec o velikosti n - x se nazývá semeno.
Pseudonáhodné řetězce jsou klíčovým konceptem pro praktické využití kryptografie. Vezměme si například proudové šifry. U proudové šifry se náhodně vybraný klíč zapojí do rozšiřujícího algoritmu, aby vznikl mnohem větší pseudonáhodný řetězec. Tento pseudonáhodný řetězec se pak kombinuje s otevřeným textem pomocí operace XOR, čímž vznikne šifrový text.
Pokud bychom nebyli schopni vytvořit tento typ pseudonáhodného řetězce pro proudovou šifru, pak bychom pro její zabezpečení potřebovali klíč, který by byl stejně dlouhý jako zpráva. To ve většině případů není příliš praktická možnost.
Pojem pseudonáhodnosti, o kterém se hovoří v této části, lze definovat formálněji. Rozšiřuje se i na další souvislosti. Do této diskuse se zde však nemusíme pouštět. Pro většinu kryptografie skutečně stačí intuitivně pochopit rozdíl mezi náhodným a pseudonáhodným řetězcem. [2]
Důvod, proč jsme v naší diskusi upustili od rozlišování mezi "náhodným" a
"rovnoměrným", by měl být nyní také jasný. V praxi všichni používají termín
pseudonáhodný pro označení řetězce, který se jeví jako by byl výsledkem vzorkování jednotné proměnné S. Přísně vzato bychom takový
řetězec měli nazývat "pseudouniformní", přičemž bychom měli převzít náš
jazyk z dřívějška. Protože termín "pseudouniformní" je jednak těžkopádný a
jednak ho nikdo nepoužívá, nebudeme ho zde pro přehlednost zavádět. Místo
toho v současném kontextu prostě upustíme od rozlišování mezi "náhodným" a
"rovnoměrným".
Poznámky
[2] Pokud máte zájem o formálnější výklad těchto otázek, můžete si přečíst knihu Introduction to Modern Cryptography od Katze a Lindella, zejména kapitolu 3.
Matematické základy kryptografie 2
Co je to teorie čísel?
Tato kapitola se zabývá pokročilejším tématem matematických základů kryptografie: teorií čísel. Ačkoli je teorie čísel důležitá pro symetrickou kryptografii (například v šifře Rijndael), je obzvláště důležitá v prostředí kryptografie s veřejným klíčem.
Pokud se vám zdají detaily teorie čísel těžkopádné, doporučuji napoprvé číst na vysoké úrovni. Vždy se k ní můžete později vrátit.
Teorii čísel** lze charakterizovat jako studium vlastností celých čísel a matematických funkcí, které s celými čísly pracují.
Uvažujte například, že jakákoli dvě čísla a a N jsou koprimena (nebo relativní prvočísla), pokud je jejich největší
společný dělitel roven 1. Předpokládejme nyní konkrétní celé číslo N. Kolik celých čísel menších
než N je koprimem N? Můžeme o odpovědích na
tuto otázku vyslovit obecné tvrzení? To jsou typické typy otázek, na které
se snaží odpovědět teorie čísel.
Moderní teorie čísel se opírá o nástroje abstraktní algebry. Obor abstraktní algebry je dílčí disciplínou matematiky, kde jsou hlavními objekty analýzy abstraktní objekty známé jako algebraické struktury. Algebraická struktura je množina prvků spojená s jednou nebo více operacemi, která splňuje určité axiomy. Prostřednictvím algebraických struktur mohou matematici získat vhled do konkrétních matematických problémů tím, že abstrahují od jejich detailů.
Obor abstraktní algebry se někdy nazývá také moderní algebra. Můžete se také setkat s pojmem abstraktní matematika (nebo čistá matematika). Tento druhý termín není odkazem na abstraktní algebru, ale spíše znamená studium matematiky pro ni samotnou, nikoliv pouze s ohledem na možné aplikace.
Množiny z abstraktní algebry se mohou zabývat mnoha typy objektů, od transformací zachovávajících tvar rovnostranného trojúhelníku až po vzory tapet. Pro teorii čísel uvažujeme pouze množiny prvků, které obsahují celá čísla, nebo funkce, které pracují s celými čísly.
Skupiny
Základním pojmem v matematice je množina prvků. Množina se obvykle označuje znaky akuzativu, přičemž prvky se oddělují čárkami.
Například množina všech celých čísel je \{..., -2, -1, 0, 1, 2, ...\}. Elipsy zde znamenají, že určitý vzorec pokračuje v určitém směru. Do
množiny všech celých čísel tedy patří také 3, 4, 5, 6 a tak dále, stejně jako -3, -4, -5, -6 a tak dále. Tuto množinu všech celých čísel obvykle označujeme \mathbb{Z}.
Dalším příkladem množiny je \mathbb{Z} \mod 11, neboli množina všech celých čísel modulo 11. Na rozdíl od celé množiny \mathbb{Z} obsahuje tato množina pouze konečný počet prvků, a to \{0, 1, \ldots, 9, 10\}.
Častým omylem je domnívat se, že množina \mathbb{Z} \mod 11 je ve skutečnosti \{-10, -9, \ldots, 0, \ldots, 9, 10\}. To však není pravda, vzhledem k tomu, jak jsme operaci modulo definovali
dříve. Jakákoli záporná celá čísla redukovaná pomocí modulo 11 se nabalí na \{0, 1, \ldots, 9, 10\}. Například výraz -2 \mod 11 se zabalí na 9, zatímco výraz -27 \mod 11 se zabalí na 5.
Dalším základním pojmem v matematice je binární operace. Jedná se o jakoukoli operaci, při které se ze dvou prvků získá třetí prvek. Například ze základů aritmetiky a algebry znáte čtyři základní binární operace: sčítání, odčítání, násobení a dělení.
Tyto dva základní matematické pojmy, množiny a binární operace, slouží k definici pojmu grupy, nejpodstatnější struktury abstraktní algebry.
Konkrétně předpokládejme nějakou binární operaci \circ. Dále předpokládejme nějakou množinu prvků S vybavenou
touto operací. Vše, co zde znamená "vybaven", je, že operaci \circ lze provést mezi libovolnými dvěma prvky v množině S.
Kombinace \langle \mathbf{S}, \circ \rangle je tedy grupou, pokud splňuje čtyři specifické podmínky,
známé jako axiomy grupy.
Pro libovolné
aab, které jsou prvky\mathbf{S}, jea \circ brovněž prvkem\mathbf{S}. To je známé jako uzavřená podmínka.Pro libovolné
a,bac, které jsou prvky\mathbf{S}, platí, že(a \circ b) \circ c = a \circ (b \circ c). To je známé jako podmínka asociativity.Existuje jedinečný prvek
ev\mathbf{S}, který pro každý prvekav\mathbf{S}platí následující rovnice:e \circ a = a \circ e = a. Protože existuje pouze jeden takový prveke, nazývá se identitní prvek. Tato podmínka je známá jako podmínka identity.Pro každý prvek
av\mathbf{S}existuje prvekbv\mathbf{S}takový, že platí následující rovnice:a \circ b = b \circ a = e, kdeeje prvek identity. Prvekbse zde nazývá inverzní prvek a běžně se označuje jakoa^{-1}. Tato podmínka je známá jako inverzní podmínka nebo podmínka invertibility.
Prozkoumejme skupiny trochu podrobněji. Množinu všech celých čísel označme \mathbb{Z}. Tato množina v kombinaci se standardním sčítáním, neboli \langle \mathbb{Z}, + \rangle, jasně odpovídá definici grupy, protože splňuje čtyři výše uvedené axiomy.
Pro libovolné
xay, které jsou prvky\mathbb{Z}, jex + ytaké prvkem\mathbb{Z}. Takže\langle \mathbb{Z}, + \ranglesplňuje podmínku uzavření.Pro libovolné
x,yaz, které jsou prvky\mathbb{Z}, platí(x + y) + z = x + (y + z). Takže\langle \mathbb{Z}, + \ranglesplňuje podmínku asociativity.V
\langle \mathbb{Z}, + \rangleexistuje prvek identity, a to 0. Pro libovolnéxv\mathbb{Z}totiž platí, že:0 + x = x + 0 = x. Takže\langle \mathbb{Z}, + \ranglesplňuje podmínku identity.Konečně pro každý prvek
xv\mathbb{Z}existujeytak, žex + y = y + x = 0. Pokud by napříkladxbylo 10,yby bylo-10(v případě, žexje 0,yje také 0). Takže\langle \mathbb{Z}, + \ranglesplňuje inverzní podmínku.
Důležité je, že to, že množina celých čísel se sčítáním tvoří grupu,
neznamená, že tvoří grupu s násobením. To si můžete ověřit testováním \langle \mathbb{Z}, \cdot \rangle proti čtyřem grupovým axiomům (kde \cdot znamená standardní násobení).
První dva axiomy samozřejmě platí. Navíc při násobení může prvek 1 sloužit
jako prvek identity. Jakékoli celé číslo x vynásobené 1 totiž dává x.
Avšak \langle \mathbb{Z}, \cdot \rangle nesplňuje inverzní podmínku. To znamená, že v \mathbb{Z} neexistuje jedinečný prvek y pro každé x v \mathbb{Z}, takže x \cdot y = 1.
Předpokládejme například, že x = 22. Jaká hodnota y z množiny \mathbb{Z} vynásobená s x by dala prvek
identity 1? Vyhovovala by hodnota 1/22, ale ta se v množině \mathbb{Z} nenachází. Ve skutečnosti narazíte na tento problém pro jakékoli celé číslo x, kromě hodnot 1 a -1 (kde
by y muselo být 1, resp. -1).
Pokud bychom pro naši množinu připustili reálná čísla, naše problémy by z
velké části zmizely. Pro libovolný prvek x v množině dává násobení 1/x hodnotu
1. Protože do množiny reálných čísel patří i zlomky, lze pro každé reálné číslo
najít inverzní hodnotu. Výjimkou je nula, protože jakékoliv násobení nulou nikdy
nedá identitní prvek 1. Proto je množina nenulových reálných čísel vybavená násobením
skutečně grupou.
Některé grupy splňují pátou obecnou podmínku, známou jako podmínka komutativity. Tato podmínka je následující:
- Předpokládejme grupu
Gs množinou S a binárním operátorem\circ. Předpokládejme, žeaabjsou prvky S. Pokud platí, žea \circ b = b \circ apro libovolné dva prvkyaabv S, pakGsplňuje podmínku komutativity.
Každá grupa, která splňuje podmínku komutativity, se nazývá komutativní grupa nebo Abelova grupa (podle Nielse Henrika Abela). Je snadné ověřit, že jak množina reálných čísel nad sčítáním, tak množina celých čísel nad sčítáním jsou abelovské grupy. Množina celých čísel nad násobením vůbec není grupa, takže ipso facto nemůže být abelovskou grupou. Naproti tomu množina nenulových reálných čísel nad násobením je rovněž abelovskou grupou.
Měli byste dodržovat dvě důležité konvence týkající se zápisu. Zaprvé, znaménka "+" nebo "×" budou často používána k označení skupinových operací, i když prvky ve skutečnosti nejsou čísla. V těchto případech byste neměli tato znaménka interpretovat jako standardní aritmetické sčítání nebo násobení. Místo toho se jedná o operace, které se těmto aritmetickým operacím podobají pouze abstraktně.
Pokud nemáte na mysli konkrétně aritmetické sčítání nebo násobení, je
jednodušší používat pro skupinové operace symboly jako \circ a \diamond, protože nemají
příliš kulturně zakořeněné konotace.
Za druhé, ze stejného důvodu, proč se znaky "+" a "×" často používají pro
označení nearitmetických operací, se prvky identity grup často symbolizují
znaky "0" a "1", i když prvky těchto grup nejsou čísla. Pokud se nejedná o
prvek identity grupy s čísly, je jednodušší použít pro označení prvku
identity neutrálnější symbol, například "e".
Mnoho různých a velmi důležitých množin hodnot v matematice vybavených určitými binárními operacemi jsou skupiny. Kryptografické aplikace však pracují pouze s množinami celých čísel nebo alespoň prvků, které jsou popsány celými čísly, tedy v rámci oboru teorie čísel. Proto se množiny s jinými reálnými čísly než celými čísly v kryptografických aplikacích nepoužívají.
Na závěr uveďme příklad prvků, které lze "popsat celými čísly", i když to nejsou celá čísla. Dobrým příkladem jsou body eliptických křivek. Ačkoli jakýkoli bod na eliptické křivce zjevně není celé číslo, takový bod je skutečně popsán dvěma celými čísly.
Eliptické křivky jsou například pro Bitcoin klíčové. Jakýkoli standardní pár soukromého a veřejného klíče Bitcoinu je vybrán z množiny bodů, která je definována následující eliptickou křivkou:
x^3 + 7 = y^2 \mod 2^{256} – 2^{32} – 29 – 28 – 27 – 26 - 24 - 1(největší prvočíslo menší než 2^{256}). Souřadnice x je soukromý
klíč a souřadnice y je váš veřejný
klíč.
Transakce v bitcoinech obvykle zahrnují nějakým způsobem uzamčení výstupů k jednomu nebo více veřejným klíčům. Hodnotu z těchto transakcí pak lze odemknout pomocí digitálních podpisů s odpovídajícími soukromými klíči.
Cyklické skupiny
Hlavní rozdíl, který můžeme učinit, je mezi konečnou a nekonečnou skupinou. První má konečný počet prvků, zatímco druhá má nekonečný počet prvků. Počet prvků v každé konečné grupě se nazývá pořadí grupy. Veškerá praktická kryptografie, která zahrnuje použití grup, se opírá o konečné (číselně-teoretické) grupy.
V rámci kryptografie s veřejným klíčem je obzvláště důležitá určitá třída konečných abelovských grup, známá jako cyklické grupy. Abychom porozuměli cyklickým grupám, musíme nejprve pochopit pojem exponencializace prvků grupy.
Předpokládejme grupu G s
grupovou operací \circ a že a je prvkem G. Výraz a^n bychom pak měli interpretovat jako prvek a kombinovaný sám se sebou celkem n - 1krát. Například a^2 znamená a \circ a, a^3 znamená a \circ a \circ a a tak
dále. (Všimněte si, že exponencializace zde nemusí nutně znamenat exponencializaci
ve standardním aritmetickém smyslu.)
Podívejme se na příklad. Předpokládejme, že G = \langle \mathbb{Z} \mod 7, + \rangle a že naše hodnota pro a je
rovna 4. V tomto případě je a^2 = [4 + 4 \mod 7] = [8 \mod 7] = 1 \mod 7. Alternativně by a^4 představovalo [4 + 4 + 4 + 4 + 4 \mod 7] = [16 \mod 7] = 2 \mod 7.
Některé abelovské grupy mají jeden nebo více prvků, z nichž lze pomocí pokračující exponenciály získat všechny ostatní prvky grupy. Tyto prvky se nazývají generátory nebo primitivní prvky.
Důležitou třídou takových grup je \langle \mathbb{Z}^* \mod N, \cdot \rangle, kde N je prvočíslo. Zápis \mathbb{Z}^* zde znamená, že grupa obsahuje všechna nenulová kladná celá čísla menší než N. Taková grupa má tedy vždy N - 1 prvků.
Uvažujme například G = \langle \mathbb{Z}^* \mod 11, \cdot \rangle. Tato grupa má následující prvky: \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. Řád této grupy je 10 (což je skutečně rovno 11 - 1).
Prozkoumejme exponenciální prvek 2 z této skupiny. Výpočty až do 2^{12} jsou uvedeny níže. Všimněte si, že na levé straně rovnice se exponent vztahuje
k exponencializaci prvku grupy. V našem konkrétním příkladu se skutečně jedná
o aritmetické exponenciování na pravé straně rovnice (ale mohlo by se jednat
například i o sčítání). Pro upřesnění jsem vypsal opakovanou operaci, nikoliv
tvar exponentu na pravé straně.
2^1 = 2 \mod 112^2 = 2 \cdot 2 \mod 11 = 4 \mod 112^3 = 2 \cdot 2 \cdot 2 \mod 11 = 8 \mod 112^4 = 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 16 \mod 11 = 5 \mod 112^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 32 \mod 11 = 10 \mod 112^6 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 64 \mod 11 = 9 \mod 112^7 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 128 \mod 11 = 7 \mod 112^8 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 256 \mod 11 = 3 \mod 112^9 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 512 \mod 11 = 6 \mod 112^{10} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 1024 \mod 11 = 1 \mod 112^{11} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 2048 \mod 11 = 2 \mod 112^{12} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \mod 11 = 4096 \mod 11 = 4 \mod 11
Pokud se pozorně podíváte, zjistíte, že při exponenciování prvku 2
procházíme všechny prvky \langle \mathbb{Z}^* \mod 11, \cdot \rangle v následujícím pořadí: po 2^{10} pokračujeme v exponenciování prvku 2 opět přes všechny prvky a ve stejném
pořadí: 2, 4, 8, 5, 10, 9, 7, 3, 6, 1. Proto je prvek 2 generátorem v \langle \mathbb{Z}^* \mod 11, \cdot \rangle.
Ačkoli \langle \mathbb{Z}^* \mod 11, \cdot \rangle má více generátorů, ne všechny prvky této grupy jsou generátory. Vezměme si
například prvek 3. Projdeme-li prvních 10 exponenciál, aniž bychom ukazovali
těžkopádné výpočty, získáme následující výsledky:
3^1 = 3 \mod 113^2 = 9 \mod 113^3 = 5 \mod 113^4 = 4 \mod 113^5 = 1 \mod 113^6 = 3 \mod 113^7 = 9 \mod 113^8 = 5 \mod 113^9 = 4 \mod 113^{10} = 1 \mod 11
Namísto procházení všech hodnot v \langle \mathbb{Z}^* \mod 11, \cdot \rangle vede exponencializace prvku 3 pouze k podmnožině těchto hodnot: po páté exponenciaci
se tyto hodnoty začnou opakovat.
Nyní můžeme definovat cyklickou grupu jako jakoukoli grupu s alespoň jedním generátorem. To znamená, že existuje alespoň jeden prvek grupy, z něhož lze exponováním získat všechny ostatní prvky grupy.
Možná jste si v našem příkladu výše všimli, že 2^{10} i 3^{10} se rovnají 1 \mod 11. Ve skutečnosti,
ačkoli to nebudeme počítat, exponenciování 10 libovolného prvku v grupě \langle \mathbb{Z}^* \mod 11, \cdot \rangle dá 1 \mod 11. Proč tomu tak
je?
To je důležitá otázka, ale její zodpovězení vyžaduje určitou práci.
Pro začátek předpokládejme dvě celá kladná čísla a a N. Důležitá věta v teorii
čísel říká, že a má
multiplikativní inverzní modulo N (tj. celé číslo b, takže a \cdot b = 1 \mod N) tehdy a
jen tehdy, když největší společný dělitel mezi a a N je roven 1. To znamená,
že a a N jsou koprimena.
Pro libovolnou skupinu celých čísel vybavenou násobením modulo N jsou tedy do množiny zahrnuta pouze menší koprimena s N. Tuto množinu můžeme
označit \mathbb{Z}^c \mod N.
Předpokládejme například, že N je 10. Pouze celá čísla 1, 3, 7 a 9 jsou koprimem 10. Množina \mathbb{Z}^c \mod 10 tedy obsahuje pouze \{1, 3, 7, 9\}.
Skupinu s celočíselným násobením modulo 10 nelze vytvořit pomocí žádných
jiných celých čísel mezi 1 a 10. Pro tuto konkrétní skupinu jsou inverzemi
dvojice 1 a 9 a 3 a 7.
V případě, že N je samo
prvočíslo, jsou všechna celá čísla od 1 do N - 1 koprimoly s N. Taková skupina
má tedy řád N - 1.
Použijeme-li náš dřívější zápis, \mathbb{Z}^c \mod N se rovná \mathbb{Z}^* \mod N, když je N prvočíslo.
Grupa, kterou jsme vybrali pro náš předchozí příklad, \langle \mathbb{Z}^* \mod 11, \cdot \rangle, je konkrétním případem této třídy grup.
Dále funkce \phi(N) vypočítává počet koprimátů až do čísla N a je známá jako Eulerova funkce Phi. [1] Podle Eulerovy věty platí, že kdykoli jsou dvě celá čísla a a N koprimena, platí následující:
a^{\phi(N)} \mod N = 1 \mod N
To má důležitý důsledek pro třídu grup \langle \mathbb{Z}^* \mod N, \cdot \rangle, kde N je prvočíslo. Pro
tyto grupy představuje exponencializace prvků grupy aritmetickou
exponencializaci. To znamená, že a^{\phi(N)} \mod N představuje aritmetickou operaci a^{\phi(N)} \mod N.
Protože každý prvek a v
těchto multiplikativních grupách je koprimovaný s N, znamená to, že a^{\phi(N)} \mod N = a^{N - 1} \mod N = 1 \mod N.
Eulerova věta je opravdu důležitý výsledek. Na začátek z ní vyplývá, že
všechny prvky v \langle \mathbb{Z}^* \mod N, \cdot \rangle mohou procházet pouze takovým počtem hodnot exponenciálním dělením, které se
dělí na N - 1. V případě \langle \mathbb{Z}^* \mod 11, \cdot \rangle to znamená, že každý prvek může procházet pouze 2, 5 nebo 10 prvky. Hodnoty
skupiny, kterými každý prvek prochází při exponenciální exponenciále, se
nazývají pořadí prvku. Prvek s pořadím odpovídajícím pořadí
grupy je generátor.
Z Eulerovy věty navíc vyplývá, že vždy můžeme znát výsledek a^{N - 1} \mod N pro libovolnou skupinu \langle \mathbb{Z}^* \mod N, \cdot \rangle, kde N je prvočíslo. To platí
bez ohledu na to, jak složité mohou být skutečné výpočty.
Předpokládejme například, že naše skupina je \mathbb{Z}^* \mod 160,481,182 (kde 160,481,182 je skutečně prvočíslo). Víme, že všechna celá čísla 1 až
160 481 181 musí být prvky této grupy a že \phi(n) = 160 481 181. I když
nemůžeme provést všechny kroky výpočtu, víme, že výrazy jako 514^{160,481,181}, 2,005^{160,481,181} a 256,212^{160,481,181} se všechny musí vyhodnotit jako 1 \mod 160,481,182.
Poznámky:
[1] Funkce funguje následovně. Libovolné celé číslo N lze rozložit na součin prvočísel. Předpokládejme, že konkrétní N je vynásobeno následujícím způsobem: p_1^{e1} \cdot p_2^{e2} \cdot \ldots \cdot
p_m^{em}, kde všechna p jsou
prvočísla a všechna e jsou celá
čísla větší nebo rovna 1. Potom:
\phi(N) = \sum_{i=1}^m \left[p_i^{e_i} - p_i^{e_i - 1}\right]Eulerův vzorec funkce Phi pro prvočíselnou faktorizaci N.
Pole
Základní algebraickou strukturou v abstraktní algebře je grupa, ale existuje jich mnohem více. Jedinou další algebraickou strukturou, kterou je třeba znát, je pole, konkrétně konečné pole. Tento typ algebraické struktury se často používá v kryptografii, například v Advanced Encryption Standard. Ten je hlavním symetrickým šifrovacím schématem, se kterým se v praxi setkáte.
Pole je odvozeno od pojmu grupy. Konkrétně pole je množina
prvků S vybavená dvěma binárními operátory \circ a \diamond, která splňuje
následující podmínky:
Množina S vybavená
\circje abelovská grupa.Množina S vybavená
\diamondje abelovskou grupou pro "nenulové" prvky.Množina S vybavená těmito dvěma operátory splňuje tzv. distributivní podmínku: Předpokládejme, že
a,bacjsou prvky S. Pak množina S vybavená těmito dvěma operátory splňuje distributivní vlastnost, kdyža \circ (b \diamond c) = (a \circ b) \diamond (a \circ c).
Všimněte si, že stejně jako u skupin je definice pole velmi abstraktní.
Nevyjadřuje žádné nároky na typy prvků v S ani na operace \circ a \diamond. Pouze uvádí, že
pole je jakákoli množina prvků se dvěma operacemi, pro které platí tři výše
uvedené podmínky. (Nulový prvek v druhé abelovské grupě lze interpretovat
abstraktně.)
Co může být příkladem pole? Dobrým příkladem je množina \mathbb{Z} \mod 7, neboli \{0, 1, \ldots, 7\} definovaná standardním sčítáním (místo výše uvedeného \circ) a standardním
násobením (místo výše uvedeného \diamond).
Za prvé, \mathbb{Z} \mod 7 splňuje podmínku abelovské grupy nad sčítáním a splňuje podmínku abelovské
grupy nad násobením, pokud uvažujeme pouze nenulové prvky. Za druhé, kombinace
množiny s oběma operátory splňuje distributivní podmínku.
Z didaktického hlediska je vhodné prozkoumat tato tvrzení pomocí některých
konkrétních hodnot. Vezměme experimentální hodnoty 5, 2 a 3, náhodně vybrané
prvky z množiny \mathbb{Z} \mod 7, abychom prozkoumali pole \langle \mathbb{Z} \mod 7, +, \cdot \rangle. Tyto tři hodnoty budeme používat v pořadí podle potřeby zkoumání
konkrétních podmínek.
Nejprve prozkoumejme, zda \mathbb{Z} \mod 7 vybavený sčítáním je abelovská grupa.
Podmínka uzavření: Vezměme jako hodnoty 5 a 2. V tom případě platí
[5 + 2] \mod 7 = 7 \mod 7 = 0. To je skutečně prvek\mathbb{Z} \mod 7, takže výsledek je v souladu s podmínkou uzavření.Podmínka asociativnosti: Vezměme jako hodnoty 5, 2 a 3. V tom případě platí
[(5 + 2) + 3] \mod 7 = [5 + (2 + 3)] \mod 7 = 10 \mod 7 = 3. To je v souladu s podmínkou asociativity.Podmínka identity: Vezměme jako hodnotu 5. V tom případě platí
[5 + 0] \mod 7 = [0 + 5] \mod 7 = 5. Zdá se tedy, že 0 je identitní prvek pro sčítání.Inverzní stav: Uvažujme inverzní hodnotu 5. Musí platit, že
[5 + d] \mod 7 = 0pro nějakou hodnotud. V tomto případě je jedinečná hodnota z\mathbb{Z}_7, která tuto podmínku splňuje, je 2.Podmínka komutativity: Vezměme si za hodnoty 5 a 3. V tom případě platí
[5 + 3] \mod 7 = [3 + 5] \mod 7 = 1. To je v souladu s podmínkou komutativity.
Množina \mathbb{Z} \mod 7 vybavená sčítáním se zjevně jeví jako abelovská grupa. Nyní prozkoumejme,
zda \mathbb{Z} \mod 7 vybavená
násobením je abelovskou grupou pro všechny nenulové prvky.
Podmínka uzavření: Vezměme jako hodnoty 5 a 2. V tom případě platí
[5 \cdot 2] \mod 7 = 10 \mod 7 = 3. To je také prvek\mathbb{Z} \mod 7, takže výsledek je v souladu s podmínkou uzavření.Podmínka asociativnosti: Vezměme jako hodnoty 5, 2 a 3. V tom případě platí
[(5 \cdot 2) \cdot 3] \mod 7 = [5 \cdot (2 \cdot 3)] \mod 7 = 30 \mod 7 = 2. To je v souladu s podmínkou asociativity.Podmínka identity: Vezměme jako hodnotu 5. V tomto případě platí
[5 \cdot 1] \mod 7 = [1 \cdot 5] \mod 7 = 5. Zdá se tedy, že 1 je identitní prvek pro násobení.Inverzní stav: Uvažujme inverzní hodnotu 5. Musí platit, že
[5 \cdot d] \mod 7 = 1pro nějakou hodnotud. Jedinečná hodnota z\mathbb{Z}_7, která tuto podmínku splňuje, je 3. To je v souladu s inverzní podmínkou.Podmínka komutativity: Vezměme si za hodnoty 5 a 3. V tom případě platí
[5 \cdot 3] \mod 7 = [3 \cdot 5] \mod 7 = 15 \mod 7 = 1. To je v souladu s podmínkou komutativity.
Množina \mathbb{Z} \mod 7 zjevně splňuje pravidla pro abelovskou grupu, pokud je spojena se sčítáním
nebo násobením nad nenulovými prvky.
Nakonec se zdá, že tato množina v kombinaci s oběma operátory splňuje
distributivní podmínku. Vezměme jako hodnoty 5, 2 a 3. Vidíme, že [5 \cdot (2 + 3)] \mod 7 = [5 \cdot 2 + 5 \cdot 3] \mod 7 = 25 \mod 7 = 4.
Nyní jsme viděli, že \mathbb{Z} \mod 7 vybavený sčítáním a násobením splňuje axiomy pro konečné pole při testování
s konkrétními hodnotami. Samozřejmě to můžeme ukázat i obecně, ale zde to nebudeme
dělat.
Klíčový rozdíl je mezi dvěma typy polí: konečnými a nekonečnými poli.
Konečné pole zahrnuje pole, jehož množina S je nekonečně velká. Příkladem nekonečného pole je množina reálných čísel \mathbb{R} vybavená sčítáním a násobením. Konečné pole, známé také
jako Galoisovo pole, je pole, kde je množina S konečná. Náš výše uvedený příklad \langle \mathbb{Z} \mod 7, +, \cdot \rangle je konečné pole.
V kryptografii nás zajímají především konečná pole. Obecně lze ukázat, že
konečné pole existuje pro nějakou množinu prvků S tehdy a
jen tehdy, když má p^m prvků,
kde p je prvočíslo a m kladné celé číslo větší nebo rovno jedné. Jinými slovy, je-li řád nějaké
množiny S prvočíslo (p^m, kde m = 1) nebo nějaká
prvočíselná mocnina (p^m, kde m > 1), pak lze najít dva
operátory \circ a \diamond takové, že jsou splněny
podmínky pro pole.
Má-li nějaké konečné pole prvočíselný počet prvků, pak se nazývá prvočíselné pole. Pokud je počet prvků v konečném poli prvočíselný, pak se pole nazývá rozšířené pole. V kryptografii nás zajímají jak prvočíselná, tak rozšiřující pole. [2]
V kryptografii jsou zajímavá především pole prvočísel, kde je množina všech
celých čísel modulována nějakým prvočíslem a operátory jsou standardní
sčítání a násobení. Do této třídy konečných polí patří \mathbb{Z} \mod 2, \mathbb{Z} \mod 3, \mathbb{Z} \mod 5, \mathbb{Z} \mod 7, \mathbb{Z} \mod 11, \mathbb{Z} \mod 13 a tak dále. Pro libovolné prvočíselné pole \mathbb{Z} \mod p je množina celých čísel tohoto pole následující: \{0, 1, \ldots, p - 2, p - 1\}.
V kryptografii nás také zajímají rozšiřující pole, zejména pole s 2^m prvky, kde m > 1. Taková
konečná pole se používají například v šifře Rijndael, která tvoří základ
šifrovacího standardu Advanced Encryption Standard. Zatímco pole prvočísel
jsou poměrně intuitivní, tato rozšiřující pole báze 2 pravděpodobně nejsou
pro nikoho, kdo nezná abstraktní algebru.
Pro začátek je skutečně pravda, že každé množině celých čísel s 2^m prvky lze přiřadit dva operátory, které z jejich kombinace vytvoří pole
(pokud je m kladné celé číslo).
Přesto to, že pole existuje, nemusí nutně znamenat, že je snadné ho objevit nebo
že je obzvláště praktické pro určité aplikace.
Ukazuje se, že v kryptografii jsou použitelná zejména pole rozšíření 2^m definovaná nad určitými množinami polynomických výrazů, nikoli nad nějakou
množinou celých čísel.
Předpokládejme například, že bychom chtěli rozšiřující pole s 2^3 (tj. 8) prvky v množině. Ačkoli může existovat mnoho různých množin, které
lze pro pole této velikosti použít, jedna taková množina obsahuje všechny
unikátní polynomy tvaru a_2x^2 + a_1x + a_0, kde
každý koeficient a_i je buď
0, nebo 1. Tato množina S tedy obsahuje následující prvky:
0: Případ, kdya_2 = 0,a_1 = 0aa_0 = 0.1: Případ, kdya_2 = 0,a_1 = 0aa_0 = 1.x: Případ, kdya_2 = 0,a_1 = 1aa_0 = 0.x + 1: Případ, kdya_2 = 0,a_1 = 1aa_0 = 1.x^2: Případ, kdya_2 = 1,a_1 = 0aa_0 = 0.x^2 + 1: Případ, kdya_2 = 1,a_1 = 0aa_0 = 1.x^2 + x: Případ, kdya_2 = 1,a_1 = 1aa_0 = 0.x^2 + x + 1: Případ, kdya_2 = 1,a_1 = 1aa_0 = 1.
Takže S by byla množina \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}. Jaké dvě operace lze nad touto množinou prvků definovat, aby jejich
kombinace byla polem?
První operaci na množině S (\circ) lze definovat jako standardní polynomické sčítání modulo 2. Stačí
polynomy sečíst jako obvykle a pak na každý z koeficientů výsledného
polynomu aplikovat modulo 2. Zde je několik příkladů:
[(x^2) + (x^2 + x + 1)] \mod 2 = [2x^2 + x + 1] \mod 2 = x + 1[(x^2 + x) + (x)] \mod 2 = [x^2 + 2x] \mod 2 = x^2[(x + 1) + (x^2 + x + 1)] \mod 2 = [x^2 + 2x + 2] \mod 2 = x^2 + 1
Druhá operace s množinou S (\diamond), která je nutná pro vytvoření pole, je složitější. Je to druh násobení,
ale ne standardní násobení z aritmetiky. Místo toho je třeba vnímat každý
prvek jako vektor a operaci chápat jako násobení těchto dvou vektorů modulem
neredukovatelného polynomu.
Nejprve se věnujme myšlence neredukovatelného polynomu. Neredukovatelný polynom** je takový, který nelze rozložit na jiné složky (stejně jako prvočíslo nelze rozložit na jiné složky než 1 a prvočíslo samotné). Pro naše účely nás zajímají polynomy, které jsou neredukovatelné vzhledem k množině všech celých čísel. (Všimněte si, že některé polynomy můžete vydělit například pomocí reálných nebo komplexních čísel, i když je nemůžete vydělit pomocí celých čísel.)
Vezměme si například polynom x^2 - 3x + 2. Ten lze přepsat jako (x - 1)(x - 2). Není tedy
neredukovatelný. Nyní uvažujme polynom x^2 + 1. Použijeme-li pouze
celá čísla, není možné tento výraz dále dělit. Jedná se tedy o
neredukovatelný polynom vzhledem k celým číslům.
Dále se věnujme pojmu násobení vektorů. Nebudeme se tímto tématem zabývat do hloubky, ale stačí pochopit základní pravidlo: Dělení vektorů může probíhat libovolně, pokud má dividenda vyšší nebo stejný stupeň jako dělitel. Pokud má dividenda nižší stupeň než dělitel, pak již dividendu nelze dělit dělitelem.
Vezměme například výraz x^6 + x + 1 \mod x^5 + x^2. Ten se zjevně dále redukuje, protože stupeň dividendy 6 je vyšší než
stupeň dělitele 5. Nyní uvažujme výraz x^5 + x + 1 \mod x^5 + x^2.
Ten se také dále redukuje, protože stupeň dividendy 5 a dělitele 5 je
stejný.
Nyní však uvažujme výraz x^4 + x + 1 \mod x^5 + x^2. Ten se dále neredukuje, protože stupeň dividendy 4 je nižší než stupeň
dělitele 5.
Na základě těchto informací jsme nyní připraveni najít druhou operaci pro
množinu \{0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1\}.
Již jsem řekl, že druhou operaci je třeba chápat jako násobení vektorů modulo nějakého neredukovatelného polynomu. Tento neredukovatelný polynom by měl zajistit, že druhá operace definuje abelovskou grupu nad S a je v souladu s distributivní podmínkou. Jaký by tedy měl být tento neredukovatelný polynom?
Protože všechny vektory v množině jsou stupně 2 nebo nižšího, měl by být neredukovatelný polynom stupně 3. Jestliže jakékoliv násobení dvou vektorů v množině dává polynom stupně 3 nebo vyššího, víme, že modulo polynomu stupně 3 dává vždy polynom stupně 2 nebo nižšího. Je tomu tak proto, že každý polynom stupně 3 nebo vyšší je vždy dělitelný polynomem stupně 3. Navíc polynom, který funguje jako dělitel, musí být neredukovatelný.
Ukázalo se, že existuje několik neredukovatelných polynomů stupně 3, které
bychom mohli použít jako dělitele. Každý z těchto polynomů definuje ve
spojení s naší množinou S a sčítáním modulo 2 jiné pole. To
znamená, že při použití rozšiřujících polí 2^m v kryptografii máte více možností.
Pro náš příklad předpokládejme, že vybereme polynom x^3 + x + 1. Ten je skutečně neredukovatelný, protože jej nelze vydělit pomocí celých
čísel. Navíc zajistí, že při jakémkoli násobení dvou prvků získáme polynom
stupně 2 nebo méně.
Pro ilustraci si ukážeme příklad druhé operace s polynomem x^3 + x + 1 jako dělitelem. Předpokládejme, že v naší množině S vynásobíme prvky x^2 + 1 s x^2 + x. Potřebujeme tedy
vypočítat výraz [(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1. To lze zjednodušit následujícím způsobem:
[(x^2 + 1) \cdot (x^2 + x)] \mod x^3 + x + 1 =[x^2 \cdot x^2 + x^2 \cdot x + 1 \cdot x^2 + 1 \cdot x] \mod x^3 + x + 1 =[x^4 + x^3 + x^2 + x] \mod x^3 + x + 1
Víme, že [x^4 + x^3 + x^2 + x] \mod x^3 + x + 1 lze redukovat, protože dividenda má vyšší stupeň (4) než dělitel (3).
Pro začátek si můžete všimnout, že výraz x^3 + x + 1 přechází v x^4 + x^3 + x^2 + x celkem xkrát. To si můžete
ověřit vynásobením x^3 + x + 1 částkou x, což je x^4 + x^2 + x. Protože druhý
člen je stejného stupně jako dividenda, tedy 4, víme, že to funguje. Zbytek
tohoto dělení číslem x můžeme
vypočítat následujícím způsobem:
[(x^4 + x^3 + x^2 + x) - (x^4 + x^2 + x)] \mod x^3 + x + 1 =[x^3] \mod x^3 + x + 1 =x^3
Takže po dělení x^4 + x^3 + x^2 + x číslem x^3 + x + 1 celkem x krát dostaneme zbytek x^3.
Lze tento zbytek dále dělit číslem x^3 + x + 1?
Intuitivně by mohlo být lákavé říci, že x^3 již nelze dělit x^3 + x + 1,
protože druhý člen se zdá být větší. Vzpomeňte si však na naši dřívější
diskusi o dělení vektorů. Pokud má dividenda stupeň větší nebo stejný jako
dělitel, lze výraz dále redukovat. Konkrétně výraz x^3 + x + 1 může přejít do x^3 přesně 1krát.
Zbytek se vypočítá následujícím způsobem:
[(x^3) - (x^3 + x + 1)] \mod x^3 + x + 1 = [x + 1] \mod x^3 + x + 1 = x + 1Možná vás zajímá, proč se (x^3) - (x^3 + x + 1) vyhodnotí jako x + 1 a ne
jako -x - 1. Nezapomeňte, že
první operace našeho pole je definována modulo 2. Proto odčítání dvou
vektorů dává přesně stejný výsledek jako sčítání dvou vektorů.
Součet násobení x^2 + 1 a x^2 + x: Po vynásobení těchto
dvou členů dostaneme polynom 4. stupně x^4 + x^3 + x^2 + x, který je
třeba redukovat modulo x^3 + x + 1. Polynom 4.
stupně je dělitelný x^3 + x + 1 přesně x + 1 krát. Zbytek po
dělení x^4 + x^3 + x^2 + x prvkem x^3 + x + 1 přesně x + 1 krát je x + 1. To je skutečně
prvek naší množiny {0, 1, x, x + 1, x^2, x^2 + 1, x^2 + x, x^2 + x + 1}.
Proč by měla být rozšiřující pole se základem 2 nad množinami polynomů, jako ve výše uvedeném příkladu, užitečná pro kryptografii? Důvodem je to, že na koeficienty v polynomech takových množin, buď 0, nebo 1, lze pohlížet jako na prvky binárních řetězců o určité délce. Na množinu S z našeho příkladu výše lze například místo toho pohlížet jako na množinu S, která obsahuje všechny binární řetězce délky 3 (000 až 111). Operace nad množinou S pak lze použít i k provádění operací nad těmito binárními řetězci a k vytvoření binárního řetězce stejné délky.
Poznámky:
[2] Rozšiřující pole se stávají velmi neintuitivními. Místo prvků celých čísel mají množiny polynomů. Kromě toho se veškeré operace provádějí modulo některého neredukovatelného polynomu.
Abstraktní algebra v praxi
Navzdory formálnímu jazyku a abstraktnosti diskuse by nemělo být příliš obtížné pochopit pojem skupiny. Je to prostě množina prvků spolu s binární operací, přičemž provedení této binární operace na těchto prvcích splňuje čtyři obecné podmínky. Abeliánská grupa má pouze další podmínku známou jako komutativita. Cyklická grupa je zase speciální druh abelovské grupy, a to taková, která má generátor. Pole je pouze složitější konstrukce ze základního pojmu grupy.
Pokud jste však prakticky založený člověk, možná se v tuto chvíli zamyslíte: Koho to zajímá? Má vědomí, že nějaká množina prvků s operátorem je grupa, nebo dokonce abelovská či cyklická grupa, nějaký reálný význam? Má vědomí, že něco je pole?
Aniž bychom zabíhali do přílišných podrobností, odpověď zní "ano". Skupiny poprvé vytvořil v 19. století francouzský matematik Evariste Galois. Použil je k vyvození závěrů o řešení polynomiálních rovnic vyššího stupně než pět.
Od té doby pomohl pojem skupiny objasnit řadu problémů v matematice i jinde. Na jejich základě byl například fyzik Murray-Gellman schopen předpovědět existenci částice dříve, než byla skutečně pozorována při experimentech. [3] Dalším příkladem je chemik, který teorii grup používá ke klasifikaci tvarů molekul. Matematici dokonce použili koncept grupy k vyvození závěrů o něčem tak konkrétním, jako je nástěnný papír!
Ukázat, že množina prvků s nějakým operátorem je grupa, v podstatě znamená, že to, co popisujete, má určitou symetrii. Ne symetrii v běžném slova smyslu, ale v abstraktnější podobě. A to může poskytnout podstatné poznatky o konkrétních systémech a problémech. Složitější pojmy z abstraktní algebry nám pouze poskytují další informace.
Nejdůležitější je, že se seznámíte s významem teoretických grup a polí čísel v praxi prostřednictvím jejich použití v kryptografii, zejména v kryptografii s veřejným klíčem. V diskusi o polích jsme již viděli, jak se například rozšiřující pole používají v šifře Rijndael. Tento příklad zpracujeme v Kapitole 5.
Pro další diskusi o abstraktní algebře bych doporučil vynikající sérii videí o abstraktní algebře od společnosti Socratica. [4] Doporučuji zejména následující videa: "Co je abstraktní algebra?", "Definice grupy (rozšířená)", "Definice kruhu (rozšířená)" a "Definice pole (rozšířená)" Tato čtyři videa vám poskytnou další vhled do většiny výše uvedených diskusí. (O kruzích jsme nehovořili, ale pole je jen speciální typ kruhu.)
Další informace o moderní teorii čísel najdete v mnoha pokročilých diskusích o kryptografii. Jako návrhy pro další diskusi bych nabídl knihu Jonathana Katze a Yehudy Lindella Introduction to Modern Cryptography nebo knihu Christofa Paara a Jana Pelzla Understanding Cryptography. [5]
Poznámky:
[3] Viz YouTube Video
[4] Socratica, Abstract Algebra
[5] Katz a Lindell, Introduction to Modern Cryptography, 2. vydání, 2015 (CRC Press: Boca Raton, FL). Paar a Pelzl, Understanding Cryptography, 2010 (Springer-Verlag: Berlin).
Symetrická kryptografie
Alice a Bob
Jedním ze dvou hlavních odvětví kryptografie je symetrická kryptografie. Zahrnuje šifrovací schémata i schémata zabývající se autentizací a integritou. Až do 70. let 20. století by veškerá kryptografie tvořena symetrickými šifrovacími schématy.
Hlavní diskuse začíná pohledem na symetrická šifrovací schémata a zásadním rozlišením mezi proudovými a blokovými šiframi. Poté se zaměříme na autentizační kódy zpráv, což jsou schémata pro zajištění integrity a pravosti zpráv. Nakonec prozkoumáme, jak lze symetrická šifrovací schémata a kódy pro ověřování zpráv kombinovat k zajištění bezpečné komunikace.
V této kapitole jsou zběžně probrána různá symetrická kryptografická schémata z praxe. Další kapitola nabízí podrobný výklad šifrování pomocí proudové šifry a blokové šifry z praxe, konkrétně RC4 a AES.
Než začneme diskutovat o symetrické kryptografii, chtěl bych v této a následujících kapitolách stručně uvést několik poznámek k ilustracím Alice a Boba.
Při vysvětlování principů kryptografie se lidé často opírají o příklady zahrnující Alici a Boba. Udělám to také.
Zejména pokud s kryptografií začínáte, je důležité si uvědomit, že tyto příklady Alice a Boba mají sloužit pouze jako ilustrace kryptografických principů a konstrukcí ve zjednodušeném prostředí. Tyto principy a konstrukce jsou však použitelné v mnohem širší škále reálných souvislostí.
Následuje pět klíčových bodů, které je třeba mít na paměti u příkladů zahrnujících Alici a Boba v kryptografii:
Lze je snadno převést na příklady s jinými typy aktérů, jako jsou společnosti nebo vládní organizace.
Lze je snadno rozšířit na tři nebo více aktérů.
V příkladech jsou Bob a Alice obvykle aktivními účastníky při vytváření každé zprávy a při aplikaci kryptografických schémat na tuto zprávu. Ve skutečnosti je však elektronická komunikace z velké části automatizovaná. Například při návštěvě webové stránky, která využívá zabezpečení transportní vrstvy, se o kryptografii obvykle stará váš počítač a webový server.
V kontextu elektronické komunikace jsou "zprávami", které se posílají přes komunikační kanál, obvykle pakety TCP/IP. Ty mohou patřit k e-mailu, zprávě na Facebooku, telefonické konverzaci, přenosu souborů, webové stránce, nahrání softwaru atd. Nejsou to zprávy v tradičním smyslu. Nicméně kryptografové tuto skutečnost často zjednodušují tím, že uvádějí, že se jedná například o e-mailovou zprávu.
Příklady se obvykle zaměřují na elektronickou komunikaci, ale lze je rozšířit i na tradiční formy komunikace, jako jsou dopisy.
Symetrická šifrovací schémata
Volně můžeme definovat symetrické šifrovací schéma jako jakékoli kryptografické schéma se třemi algoritmy:
Algoritmus generování klíče, který generuje soukromý klíč.
šifrovací algoritmus, který na vstupu přijímá soukromý klíč a otevřený text a na výstupu má šifrovaný text.
dešifrovací algoritmus, který jako vstupy přijímá soukromý klíč a šifrový text a na výstupu získá původní otevřený text.
Šifrovací schéma - ať už symetrické nebo asymetrické - obvykle nabízí spíše šablonu pro šifrování založenou na základním algoritmu než přesnou specifikaci.
Vezměme si například symetrické šifrovací schéma Salsa20. Lze jej použít s klíči o délce 128 i 256 bitů. Volba délky klíče ovlivňuje některé drobné detaily algoritmu (přesněji počet kol v algoritmu).
Nelze však říci, že použití Salsa20 se 128bitovým klíčem je jiné šifrovací schéma než Salsa20 s 256bitovým klíčem. Jádro algoritmu zůstává stejné. Pouze v případě, že by se základní algoritmus změnil, bychom skutečně hovořili o dvou různých šifrovacích schématech.
Symetrická šifrovací schémata jsou obvykle užitečná ve dvou typech případů: (1) v případech, kdy dva nebo více agentů komunikují na dálku a chtějí utajit obsah své komunikace, a (2) v případech, kdy jeden agent chce utajit obsah zprávy v čase.
Zobrazení situace (1) je na obrázku 1 níže. Bob chce poslat zprávu M Alici na dálku, ale nechce,
aby si tuto zprávu mohli přečíst ostatní.
Bob nejprve zašifruje zprávu M soukromým klíčem K. Poté
pošle zašifrovaný text C Alici. Jakmile Alice šifrový text obdrží, může jej dešifrovat pomocí klíče K a přečíst otevřený text. Při dobrém šifrovacím schématu by žádný útočník,
který zachytí šifrový text C,
neměl být schopen zjistit nic skutečně významného o zprávě M.
Zobrazení situace (2) je na obrázku 2 níže. Bob chce ostatním zabránit v zobrazení určitých informací. Typickou situací může být, že Bob je zaměstnanec, který na svém počítači ukládá citlivá data, která nemají číst ani cizí osoby, ani jeho kolegové.
Bob zašifruje zprávu M v čase T_0 klíčem K a získá šifrový text C. V čase T_1 potřebuje zprávu znovu a dešifruje šifrový text C klíčem K. Jakýkoli útočník,
který by mezitím mohl narazit na šifrový text C, by z něj neměl být schopen
odvodit nic podstatného o M.
Obrázek 1: Utajení v prostoru

Obrázek 2: Utajení v čase

Příklad: Posunovací šifra
V kapitole 2 jsme se setkali s posunovací šifrou, která je příkladem velmi jednoduchého symetrického šifrovacího schématu. Podívejme se na ni znovu zde.
Předpokládejme slovník D, který přirovnává všechna písmena anglické
abecedy v pořadí k množině čísel \{0,1,2,\dots,25\}.
Předpokládejme množinu možných zpráv M. Posunovací šifra je
tedy šifrovací schéma definované takto:
- Náhodně vyberte klíč
kz množiny možných klíčů K, kde K =\{0,1,2,\dots,25\} - Zašifrujte zprávu
m \vM takto:- Rozdělte
mna jednotlivá písmenam_0, m_1,\dots, m_i, \dots, m_l - Převeďte každé
m_ina číslo podle D - Pro každé
m_iplatíc_i = [(m_i + k) \mod 26] - Převeďte každé
c_ina písmeno podle D - Pak zkombinujte
c_0, c_1,\dots, c_la získáte šifrový textc
- Rozdělte
- Dešifrování šifrového textu
cnásledujícím způsobem:- Převeďte každé
c_ina číslo podle D - Pro každé
c_iplatím_i = [(c_i - k) \mod 26] - Převeďte každé
m_ina písmeno podle D - Pak zkombinujte
m_0, m_1,\dots, m_la získáte původní zprávum
- Převeďte každé
Posunovací šifra je symetrické šifrovací schéma, protože pro šifrování i dešifrování se používá stejný klíč. Předpokládejme například, že chcete zašifrovat zprávu "DOG" pomocí shiftové šifry a že jste jako klíč náhodně zvolili "24". Zašifrováním zprávy tímto klíčem získáte "BME". Jediný způsob, jak získat původní zprávu, je použít stejný klíč "24" pro dešifrování.
Tato šifra Shift je příkladem monoalfabetické substituční šifry: šifrovacího schématu, kde je abeceda šifrového textu pevně daná (tj. používá se pouze jedna abeceda). Za předpokladu, že dešifrovací algoritmus je deterministický, může každý symobl v substituční šifře odpovídat nejvýše jednomu symbolu v otevřeném textu.
Až do roku 1700 se mnoho aplikací šifrování opíralo o monoalfabetické substituční šifry, které však byly často mnohem složitější než šifra Shift. Mohli jste například náhodně vybrat písmeno z abecedy pro každé písmeno původního textu s omezením, že každé písmeno se v abecedě šifrového textu vyskytuje pouze jednou. To znamená, že byste měli faktoriál 26 možných soukromých klíčů, což bylo v předpočítačovém věku obrovské množství.
Všimněte si, že v kryptografii se často setkáte s pojmem cipher. Uvědomte si, že tento termín má různé významy. Ve skutečnosti znám nejméně pět různých významů tohoto termínu v rámci kryptografie.
V některých případech se vztahuje k šifrovacímu schématu, jako je tomu v případě šifry Shift a monoalfabetické substituční šifry. Tento termín však může také odkazovat konkrétně na šifrovací algoritmus, soukromý klíč nebo jen na šifrový text takového šifrovacího schématu.
A konečně, pojem šifra může také označovat základní algoritmus, ze kterého lze sestavit kryptografická schémata. Ta mohou zahrnovat různé šifrovací algoritmy, ale také další typy kryptografických schémat. Tento význam pojmu nabývá na významu v souvislosti s blokovými šiframi (viz níže část "Blokové šifry").
Můžete se také setkat s termíny encipher nebo decipher. Tyto výrazy jsou pouze synonyma pro šifrování a dešifrování.
Útoky hrubou silou a Kerckhoffův princip
Posunovací šifra je velmi nejisté symetrické šifrovací schéma, alespoň v moderním světě. [1] Útočník se může jednoduše pokusit dešifrovat libovolný šifrový text všemi 26 možnými klíči a zjistit, který výsledek dává smysl. Tento typ útoku, při kterém útočník pouze cyklicky prochází klíče, aby zjistil, co funguje, je znám jako útok hrubou silou nebo vyčerpávající hledání klíčů.
Aby šifrovací schéma splňovalo minimální představu o bezpečnosti, musí mít množinu možných klíčů neboli prostor klíčů, která je tak velká, že útoky hrubou silou jsou neproveditelné. Tento standard splňují všechna moderní šifrovací schémata. Je to známé jako princip dostatečného prostoru klíčů. Podobný princip se obvykle uplatňuje v různých typech kryptografických schémat.
Pro představu o obrovské velikosti prostoru pro klíč v moderních šifrovacích
schématech předpokládejme, že soubor byl zašifrován 128bitovým klíčem pomocí
pokročilého šifrovacího standardu. To znamená, že útočník má k dispozici
sadu 2^{128} klíčů,
které musí projít při útoku hrubou silou. Při 0,78% šanci na úspěch s touto strategií
by útočník musel projít zhruba 2,65 \krát 10^{36}$ klíčů.
Předpokládejme optimisticky, že útočník se může pokusit o 10^{16} klíčů za sekundu (tj. 10 kvadrilionů klíčů za sekundu). Aby otestoval 0,78 %
všech klíčů v prostoru klíčů, musel by jeho útok trvat 2,65 \times 10^{20} sekund. To je přibližně 8,4 bilionu let. Takže ani útok hrubou silou absurdně
silného protivníka není u moderního 128bitového šifrovacího schématu reálný.
To je princip dostatečného klíčového prostoru.
Je posunovací šifra bezpečnější, pokud útočník nezná šifrovací algoritmus? Možná ano, ale ne o mnoho.
V každém případě moderní kryptografie vždy předpokládá, že bezpečnost jakéhokoli symetrického šifrovacího schématu závisí pouze na zachování soukromého klíče v tajnosti. Vždy se předpokládá, že útočník zná všechny ostatní podrobnosti, včetně prostoru zprávy, prostoru klíče, prostoru šifrového textu, algoritmu výběru klíče, šifrovacího algoritmu a dešifrovacího algoritmu.
Myšlenka, že bezpečnost symetrického šifrovacího schématu může záviset pouze na utajení soukromého klíče, je známá jako Kerckhoffův princip.
Jak Kerckhoff původně zamýšlel, platí tento princip pouze pro symetrická šifrovací schémata. Obecnější verze tohoto principu se však vztahuje i na všechny ostatní moderní typy kryptografických schémat: Aby bylo kryptografické schéma bezpečné, nesmí být jeho konstrukce tajná; utajení se může vztahovat pouze na některé řetězce informací, typicky na soukromý klíč.
Kerckhoffův princip je pro moderní kryptografii klíčový ze čtyř důvodů. [2] Zaprvé, existuje pouze omezený počet kryptografických schémat pro určité typy aplikací. Například většina moderních aplikací symetrického šifrování používá šifru Rijndael. Takže vaše utajení ohledně návrhu schématu je jen velmi omezené. Existuje však mnohem větší flexibilita při utajování určitého soukromého klíče pro šifru Rijndael.
Za druhé je snazší nahradit určitý řetězec informací než celé kryptografické schéma. Předpokládejme, že všichni zaměstnanci firmy mají stejný šifrovací software a že každý ze dvou zaměstnanců má soukromý klíč pro důvěrnou komunikaci. Kompromitace klíčů je v tomto scénáři nepříjemná, ale společnost by si mohla alespoň ponechat software s takovým narušením bezpečnosti. Pokud by se společnost spoléhala na utajení schématu, pak by jakékoli narušení tohoto utajení vyžadovalo výměnu celého softwaru.
Za třetí, Kerckhoffův princip umožňuje standardizaci a kompatibilitu mezi uživateli kryptografických schémat. To má obrovský přínos pro efektivitu. Je například obtížné si představit, jak by se miliony lidí mohly denně bezpečně připojovat k webovým serverům společnosti Google, kdyby toto zabezpečení vyžadovalo utajení kryptografických schémat.
Za čtvrté, Kerckhoffův princip umožňuje veřejnou kontrolu kryptografických schémat. Tento typ kontroly je naprosto nezbytný pro dosažení bezpečných kryptografických schémat. Jako příklad lze uvést hlavní klíčový algoritmus symetrické kryptografie, šifru Rijndael, který byl výsledkem soutěže pořádané Národním institutem pro standardy a technologie v letech 1997 až 2000.
Každý systém, který se pokouší dosáhnout bezpečnosti prostřednictvím utajení, je systém, který se spoléhá na utajení podrobností o svém návrhu a/nebo implementaci. V kryptografii by to byl konkrétně systém, který se spoléhá na utajení podrobností návrhu kryptografického schématu. Zabezpečení prostřednictvím utajení je tedy v přímém rozporu s Kerckhoffovým principem.
Schopnost otevřenosti posílit kvalitu a bezpečnost se vztahuje i na širší oblast digitálního světa než jen na kryptografii. Svobodné a otevřené distribuce Linuxu, jako je například Debian, mají oproti svým protějškům se systémy Windows a MacOS obecně několik výhod, pokud jde o soukromí, stabilitu, bezpečnost a flexibilitu. I když to může mít více příčin, nejdůležitějším principem je pravděpodobně to, jak to formuloval Eric Raymond ve své slavné eseji "Katedrála a bazar", že "při dostatku očí jsou všechny chyby povrchní" [3] Právě tento princip typu moudrosti davů přinesl Linuxu největší úspěch.
Nikdy nelze jednoznačně prohlásit, že kryptografické schéma je "bezpečné" nebo "nezabezpečené" Namísto toho existují různá pojetí bezpečnosti kryptografických schémat. Každá definice kryptografické bezpečnosti musí specifikovat (1) bezpečnostní cíle a také (2) možnosti útočníka. Analýza kryptografických schémat na základě jednoho nebo více specifických pojetí bezpečnosti umožňuje nahlédnout do jejich aplikací a omezení.
I když se nebudeme zabývat všemi podrobnostmi různých pojetí kryptografické bezpečnosti, měli byste vědět, že dva předpoklady jsou všudypřítomné ve všech moderních kryptografických pojetích bezpečnosti týkajících se symetrických a asymetrických schémat (a v určité podobě i dalších kryptografických primitiv):
- Útočníkova znalost schématu odpovídá Kerckhoffovu principu.
- Útočník nemůže provést útok hrubou silou na toto schéma. Konkrétně modely hrozeb kryptografických pojetí bezpečnosti obvykle nepřipouštějí ani útoky hrubou silou, protože předpokládají, že tyto útoky nepřicházejí v úvahu.
Poznámky:
[1] Podle Seutonia používal Julius Caesar ve své vojenské komunikaci šifru s konstantní hodnotou klíče 3. A by se tedy vždy stalo D, B vždy E, C vždy F atd. Tato konkrétní verze posunovací šifry se proto stala známou jako Caesarova šifra (i když ve skutečnosti nejde o šifru v moderním slova smyslu, protože hodnota klíče je konstantní). Caesarova šifra mohla být bezpečná již v prvním století před naším letopočtem, pokud nepřátelé Říma šifrování příliš neznali. V moderní době by však zjevně nešlo o příliš bezpečné schéma.
[2] Jonathan Katz a Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), str. 7f.
[3] Eric Raymond, "The Cathedral and the Bazaar", příspěvek byl přednesen na konferenci Linux Kongress, Würzburg, Německo (27. května 1997). K dispozici je řada následných verzí i kniha. Mé citace pocházejí ze strany 30 v knize: Eric Raymond, _The Cathedral and the Bazaar: Vydání: Brána a bazar, revidované vydání. (2001), O'Reilly: Sebastopol, Kalifornie.
Proudové šifry
Symetrická šifrovací schémata se standardně dělí na dva typy: proudové šifry a blokové šifry. Toto rozdělení je však poněkud problematické, protože lidé používají tyto termíny nejednotně. V několika následujících částech uvedu toto rozlišení způsobem, který považuji za nejlepší. Měli byste si však uvědomit, že mnoho lidí bude tyto pojmy používat poněkud jinak, než jsem je uvedl.
Nejprve se věnujme proudovým šifrám. Proudová šifra** je symetrické šifrovací schéma, kde se šifrování skládá ze dvou kroků.
Nejprve se pomocí soukromého klíče vytvoří řetězec o délce otevřeného textu. Tento řetězec se nazývá keystream.
Poté se klíčový proud matematicky zkombinuje s otevřeným textem a vytvoří se
šifrový text. Tato kombinace je obvykle operace XOR. Pro dešifrování stačí
tuto operaci obrátit. (Všimněte si, že A \oplus B = B \oplus A, v případě, že A a B jsou bitové řetězce. Na pořadí operace XOR v proudové šifře tedy pro
výsledek nezáleží. Tato vlastnost se nazývá komutativita.)
Typická proudová šifra XOR je znázorněna na obrázku 3. Nejprve se
vezme soukromý klíč K a
použije se k vygenerování proudu klíčů. Poté se tento proud klíčů zkombinuje
s otevřeným textem pomocí operace XOR a vznikne šifrový text. Každý agent,
který šifrový text obdrží, jej může snadno dešifrovat, pokud má klíč K. Stačí, když vytvoří stejně
dlouhý proud klíčů jako šifrový text podle stanoveného postupu schématu a
provede operaci XOR s šifrovým textem.
Obrázek 3: Proudová šifra XOR
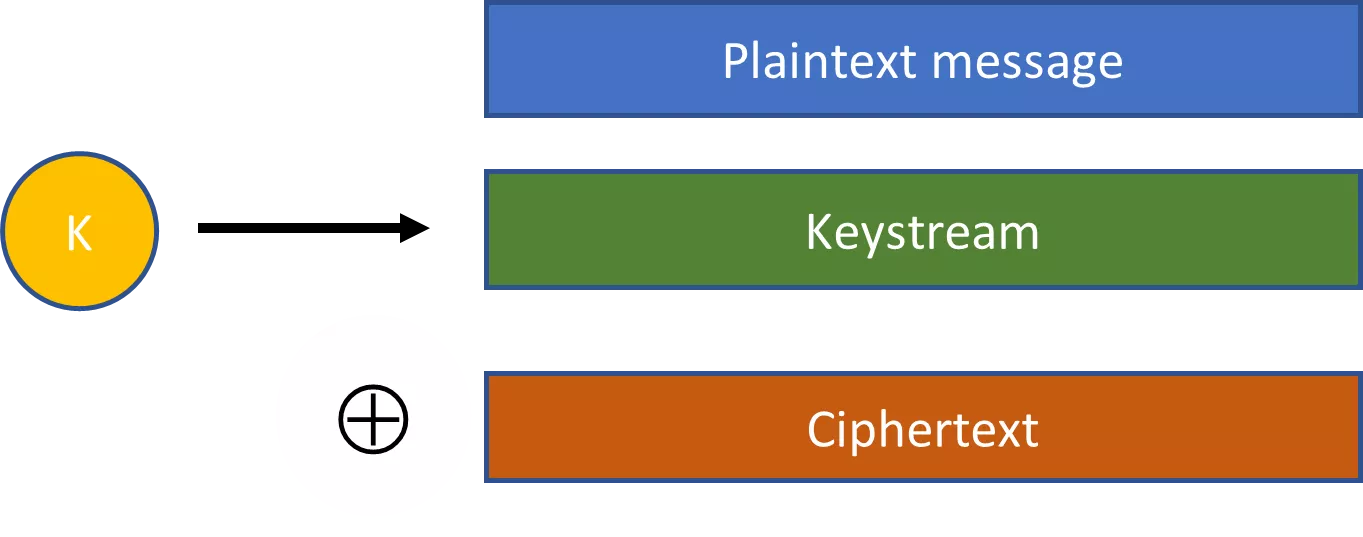
Připomeňme, že šifrovací schéma je obvykle šablona pro šifrování se stejným základním algoritmem, nikoli přesná specifikace. V důsledku toho je proudová šifra typicky šablonou pro šifrování, ve kterém můžete použít klíče různých délek. Ačkoli délka klíče může ovlivnit některé drobné detaily schématu, neovlivní jeho základní podobu.
Posunovací šifra je příkladem velmi jednoduché a nezabezpečené proudové šifry. Pomocí jediného písmene (soukromého klíče) lze vytvořit řetězec písmen o délce zprávy (proud klíčů). Tento proud klíčů se pak kombinuje s otevřeným textem pomocí operace modulo, čímž se získá šifrový text. (Tuto operaci modulo lze při reprezentaci písmen v bitech zjednodušit na operaci XOR).
Dalším známým příkladem proudové šifry je Vigenereova šifra podle Blaise de Vigenere, který ji plně vyvinul na konci 16. století (ačkoli mnoho práce předtím odvedli jiní). Jedná se o příklad polyalfabetické substituční šifry: šifrovací schéma, v němž se abeceda šifrového textu pro symbol otevřeného textu mění v závislosti na jeho pozici v textu. Na rozdíl od monoalfabetické substituční šifry mohou být symboly šifrového textu spojeny s více než jedním symbolem otevřeného textu.
S tím, jak v renesanční Evropě získávalo šifrování na popularitě, rozvíjela se i šifrovací analýza, tedy luštění šifrových textů, zejména pomocí frekvenční analýzy. Ta využívá k prolomení šifrových textů statistické zákonitosti našeho jazyka a byla objevena arabskými učenci již v 9. století. Jedná se o techniku, která se osvědčuje zejména u delších textů. A ani ty nejdokonalejší monoalfabetické substituční šifry už v Evropě v roce 1700 nestačily proti frekvenční analýze, zejména ve vojenském a bezpečnostním prostředí. Protože Vigenereho šifra nabízela výrazný pokrok v zabezpečení, stala se v tomto období populární a koncem 17. století byla velmi rozšířená.
Neformálně řečeno, šifrovací schéma funguje takto:
Jako soukromý klíč vyberte vícepísmenné slovo.
Pro každou zprávu použijte šifru posunu na každé písmeno zprávy, přičemž jako posun použijete odpovídající písmeno klíčového slova.
Pokud jste klíčové slovo prošli, ale stále jste otevřený text zcela nerozluštili, použijte písmena klíčového slova jako šifru posunu na odpovídající písmena ve zbytku textu.
V tomto postupu pokračujte, dokud nebude zašifrována celá zpráva.
Pro ilustraci předpokládejme, že váš soukromý klíč je "GOLD" a chcete zašifrovat zprávu "CRYPTOGRAPHY". V takovém případě byste postupovali podle Vigenèrovy šifry:
c_0 = [(2 + 6) \mod 26] = 8 = Ic_1 = [(17 + 14) \mod 26] = 5 = Fc_2 = [(24 + 11) \mod 26] = 9 = Jc_3 = [(15 + 3) \mod 26] = 18 = Sc_4 = [(19 + 6) \mod 26] = 25 = Zc_5 = [(14 + 14) \mod 26] = 2 = Cc_6 = [(6 + 11) \mod 26] = 17 = Rc_7 = [(17 + 3) \mod 26] = 20 = Uc_8 = [(0 + 6) \mod 26] = 6 = Gc_9 = [(15 + 14) \mod 26] = 3 = Dc_{10} = [(7 + 11) \mod 26] = 18 = Sc_{11} = [(24 + 3) \mod 26] = 1 = B
Šifrový text c = "IFJSZCRUGDSB".
Dalším známým příkladem proudové šifry je one-time pad. Při použití jednorázové podložky jednoduše vytvoříte řetězec náhodných bitů dlouhý jako otevřený text zprávy a pomocí operace XOR vytvoříte šifrový text. Soukromý klíč a proud klíčů jsou tedy s jednorázovou podložkou ekvivalentní.
Zatímco šifry Shift a Vigenere jsou v moderní době velmi nezabezpečené, jednorázová podložka je při správném použití velmi bezpečná. Pravděpodobně nejznámějším použitím jednorázové podložky bylo, přinejmenším do 80. let 20. století, použití pro horkou linku Washington-Moskva. [4]
Horká linka je přímé komunikační spojení mezi Washingtonem a Moskvou pro naléhavé záležitosti, které bylo zavedeno po kubánské krizi. Technologie pro tuto linku se v průběhu let proměnila. V současné době zahrnuje přímý optický kabel a také dvě satelitní spojení (kvůli redundanci), která umožňují zasílání e-mailů a textových zpráv. Spojení končí na různých místech v USA. Známými koncovými body jsou Pentagon, Bílý dům a hora Raven Rock. Navzdory rozšířenému názoru se horká linka nikdy netýkala telefonů.
Schéma jednorázových bloků fungovalo v podstatě takto. Washington i Moskva měly k dispozici dvě sady náhodných čísel. Jedna sada náhodných čísel, vytvořená Rusy, se týkala šifrování a dešifrování všech zpráv v ruském jazyce. Jedna sada náhodných čísel vytvořená Američany se týkala šifrování a dešifrování zpráv v anglickém jazyce. Čas od času dodávali důvěryhodní kurýři druhé straně další náhodná čísla.
Washington a Moskva pak mohly tajně komunikovat pomocí těchto náhodných čísel pro vytvoření jednorázových bloků. Pokaždé, když jste potřebovali komunikovat, použili jste pro svou zprávu další část náhodných čísel.
Ačkoli je jednorázový blok vysoce bezpečný, naráží na značná praktická omezení: klíč musí být stejně dlouhý jako zpráva a žádnou část jednorázového bloku nelze použít opakovaně. To znamená, že je třeba sledovat, kde se v jednorázové podložce nacházíte, ukládat obrovské množství bitů a čas od času si s protistranami vyměňovat náhodné bity. V důsledku toho se jednorázová podložka v praxi nepoužívá často.
Místo toho se v praxi používají převážně pseudonáhodné proudové šifry. Příkladem běžně používaných pseudonáhodných proudových šifer je Salsa20 a její úzce související varianta ChaCha.
U těchto pseudonáhodných proudových šifer se nejprve náhodně vybere klíč K, který je kratší než délka otevřeného textu. Takový náhodný klíč K obvykle vytvoří náš počítač na základě nepředvídatelných údajů, které shromažďuje v průběhu času, jako jsou například časy mezi síťovými zprávami, pohyby myši apod.
Tento náhodný klíč K je poté vložen
do rozšiřujícího algoritmu, který vytvoří pseudonáhodný proud klíčů dlouhý jako
zpráva. Můžete přesně určit, jak dlouhý má být proud klíčů (např. 500 bitů, 1000
bitů, 1200 bitů, 29 117 bitů atd.).
Pseudonáhodný proud klíčů se jeví, jako by byl vybrán zcela náhodně z množiny všech řetězců stejné délky. Šifrování pomocí pseudonáhodného proudu klíčů se tedy jeví, jako by bylo provedeno pomocí jednorázové podložky. Tak tomu ale samozřejmě není.
Protože náš soukromý klíč je kratší než proud klíčů a náš expanzní algoritmus musí být deterministický, aby proces šifrování/dešifrování fungoval, nemohl být výstupem naší expanzní operace každý proud klíčů dané délky.
Předpokládejme například, že náš soukromý klíč má délku 128 bitů a že jej
můžeme vložit do rozšiřujícího algoritmu a vytvořit tak mnohem delší proud
klíčů, řekněme 2500 bitů. Protože náš expanzní algoritmus musí být
deterministický, může náš algoritmus vybrat nanejvýš 1/2^{128} řetězce o délce 2 500 bitů. Takový řetězec klíčů by tedy nikdy nemohl být vybrán
zcela náhodně ze všech řetězců stejné délky.
Naše definice proudové šifry má dva aspekty: (1) pomocí soukromého klíče se generuje proud klíčů dlouhý jako otevřený text a (2) tento proud klíčů se kombinuje s otevřeným textem, obvykle pomocí operace XOR, aby se získal šifrový text.
Někdy se podmínka (1) definuje přísněji a tvrdí se, že proud klíčů musí být konkrétně pseudonáhodný. To znamená, že posunovací šifra ani jednorázová podložka by nebyly považovány za proudové šifry.
Podle mého názoru poskytuje širší definice podmínky (1) snazší způsob organizace šifrovacích schémat. Navíc to znamená, že nemusíme přestat nazývat určité šifrovací schéma proudovou šifrou jen proto, že se dozvíme, že ve skutečnosti nespoléhá na pseudonáhodné proudy klíčů.
Poznámky:
[4] Crypto Museum, "Washington-Moskva hotline", 2013, dostupné na https://www.cryptomuseum.com/crypto/hotline/index.htm.
Blokové šifry
První způsob, jakým je bloková šifra běžně chápána, je něco primitivnějšího než proudová šifra: Jde o základní algoritmus, který pomocí klíče provádí transformaci řetězce vhodné délky se zachováním délky. Tento algoritmus lze použít pro vytváření šifrovacích schémat a možná i jiných typů kryptografických schémat.
Bloková šifra může často přijímat vstupní řetězce různé délky, například 64, 128 nebo 256 bitů, a klíče různé délky, například 128, 192 nebo 256 bitů. I když se některé detaily algoritmu mohou v závislosti na těchto proměnných měnit, jádro algoritmu se nemění. Pokud by se tak stalo, hovořili bychom o dvou různých blokových šifrách. Všimněte si, že terminologie základního algoritmu se zde používá stejně jako u šifrovacích schémat.
Princip blokové šifry je znázorněn na obrázku 4 níže. Jako vstupy
blokové šifry slouží zpráva M o délce L a klíč K. Jejím výstupem je zpráva M' délky L. U většiny blokových
šifer nemusí být klíč nutně stejně dlouhý jako M a M'.
Obrázek 4: Bloková šifra

Bloková šifra sama o sobě není šifrovacím schématem. Blokovou šifru však lze použít s různými režimy činnosti k vytvoření různých šifrovacích schémat. Režim operace jednoduše přidává některé další operace mimo blokovou šifru.
Pro ilustraci, jak to funguje, předpokládejme blokovou šifru (BC), která vyžaduje 128bitový vstupní řetězec a 128bitový soukromý klíč. Na obrázku 5 níže je zobrazeno, jak lze tuto blokovou šifru použít v režimu elektronické kódové knihy (režim ECB) k vytvoření šifrovacího schématu. (Elipsy vpravo naznačují, že tento vzorec můžete opakovat tak dlouho, jak je potřeba).
Obrázek 5: Bloková šifra s režimem ECB
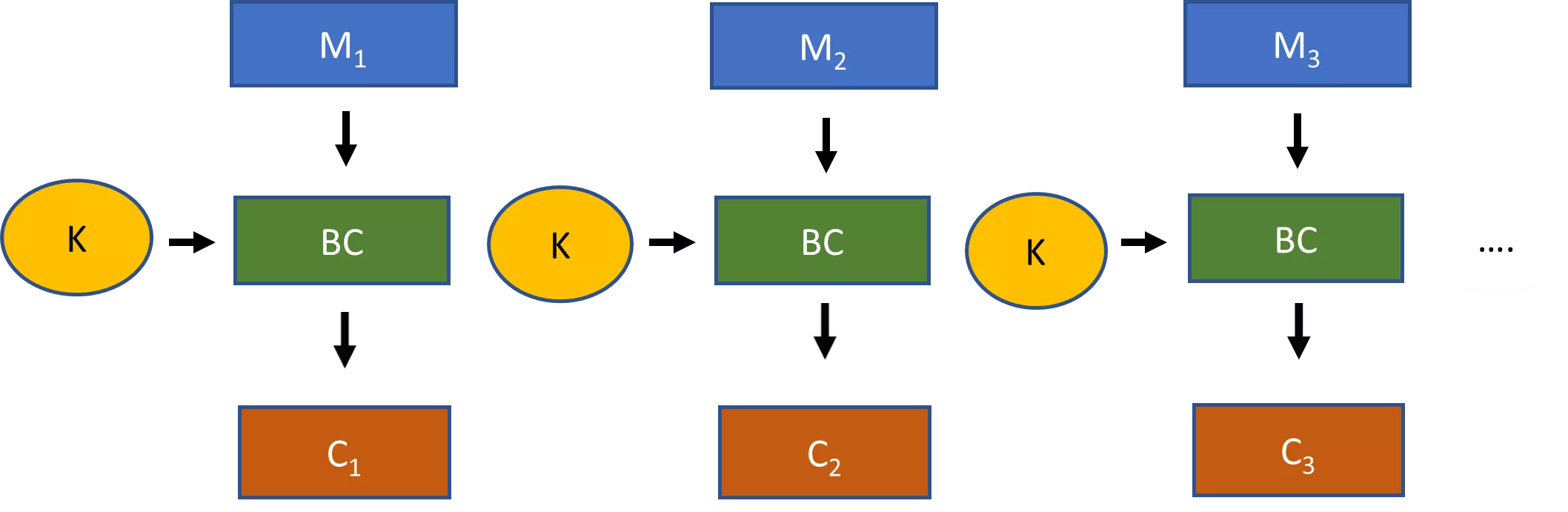
Postup šifrování elektronické kódové knihy pomocí blokové šifry je následující. Zjistěte, zda můžete zprávu s otevřeným textem rozdělit do 128bitových bloků. Pokud ne, přidejte ke zprávě padding tak, aby se výsledek dal rovnoměrně rozdělit na blok o velikosti 128 bitů. To jsou vaše data použitá pro proces šifrování.
Nyní rozdělte data na části 128bitových řetězců (M_1, M_2, M_3 atd.). Proveďte každý 128bitový řetězec blokovou šifrou s vaším 128bitovým
klíčem, abyste získali 128bitové kousky šifrového textu (C_1, C_2, C_3 atd.). Tyto části po opětovném
zkombinování vytvoří celý šifrový text.
Dešifrování je pouze opačný proces, ačkoli příjemce potřebuje nějaký rozpoznatelný způsob, jak z dešifrovaných dat odstranit případnou výplň, aby získal původní zprávu s otevřeným textem.
Bloková šifra s režimem elektronické kódové knihy je sice relativně jednoduchá, ale nemá dostatečnou bezpečnost. To proto, že vede k deterministickému šifrování. Jakékoli dva identické 128bitové řetězce dat jsou zašifrovány naprosto stejně. Tuto informaci lze zneužít.
Místo toho by mělo být každé šifrovací schéma vytvořené z blokové šifry pravděpodobnostní: to znamená, že šifrování libovolné zprávy M nebo libovolného konkrétního úseku M by mělo obecně pokaždé přinést
jiný výsledek. [5]
Režim cipher block chaining (CBC režim) je pravděpodobně nejběžnějším režimem používaným s blokovou šifrou. Správně provedená kombinace vytváří pravděpodobnostní šifrovací schéma. Vyobrazení tohoto režimu práce můžete vidět na obrázku 6 níže.
Obrázek 6: Bloková šifra s režimem CBC
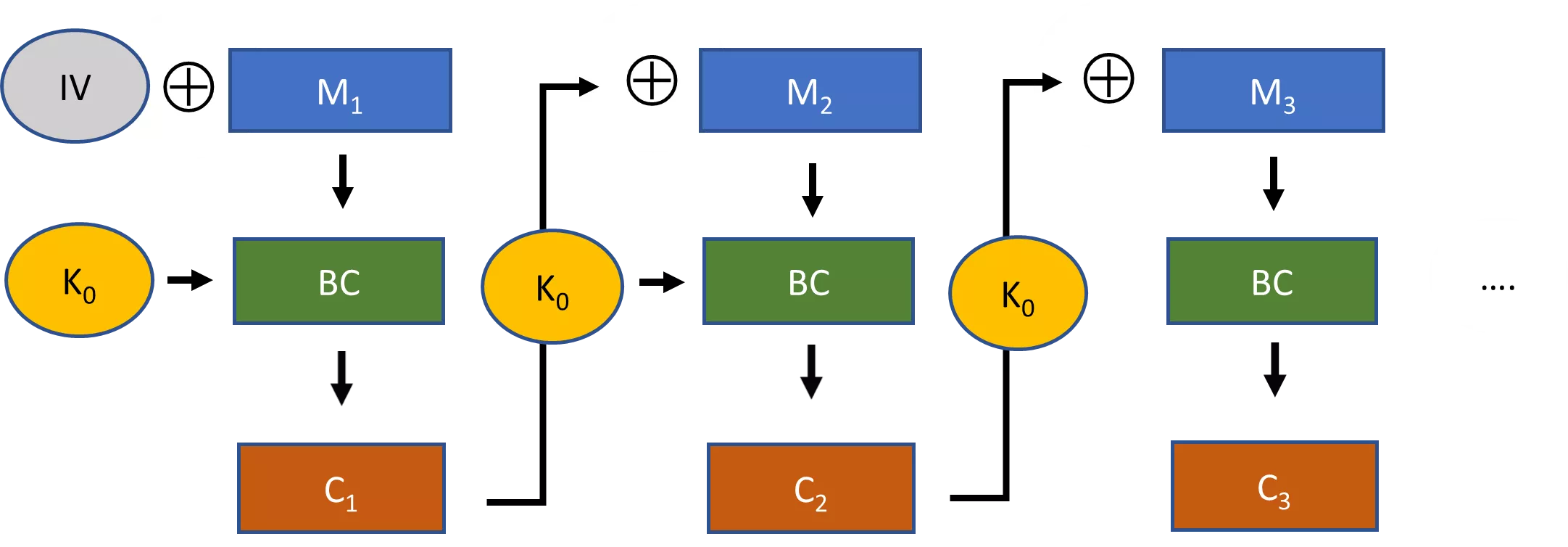
Předpokládejme, že velikost bloku je opět 128 bitů. Pro začátek je tedy opět třeba zajistit, aby původní zpráva s otevřeným textem dostala potřebnou výplň.
Poté XORujete první 128bitovou část otevřeného textu s inicializačním vektorem o 128 bitech. Výsledek se vloží do blokové šifry a vytvoří se šifrový text pro první blok. Pro druhý blok o 128 bitech nejprve XORujete otevřený text se šifrovým textem z prvního bloku a teprve poté jej vložíte do blokové šifry. V tomto procesu pokračujete, dokud nezašifrujete celý otevřený text zprávy.
Po dokončení odešlete zašifrovanou zprávu spolu s nezašifrovaným inicializačním vektorem příjemci. Příjemce musí znát inicializační vektor, jinak nemůže dešifrovat zašifrovaný text.
Tato konstrukce je při správném použití mnohem bezpečnější než režim elektronické kódové knihy. Nejprve byste měli zajistit, aby inicializační vektor byl náhodný nebo pseudonáhodný řetězec. Kromě toho byste měli při každém použití tohoto šifrovacího schématu použít jiný inicializační vektor.
Jinými slovy, váš inicializační vektor by měl být náhodný nebo pseudonáhodný nonce, kde nonce znamená "číslo, které se použije pouze jednou" Pokud tento postup dodržíte, pak režim CBC s blokovou šifrou zajistí, že jakékoli dva identické bloky otevřeného textu budou zpravidla pokaždé zašifrovány jinak.
Nakonec se zaměříme na režim výstupní zpětné vazby (OFB režim). Zobrazení tohoto režimu je na obrázku 7.
Obrázek 7: Bloková šifra s režimem OFB
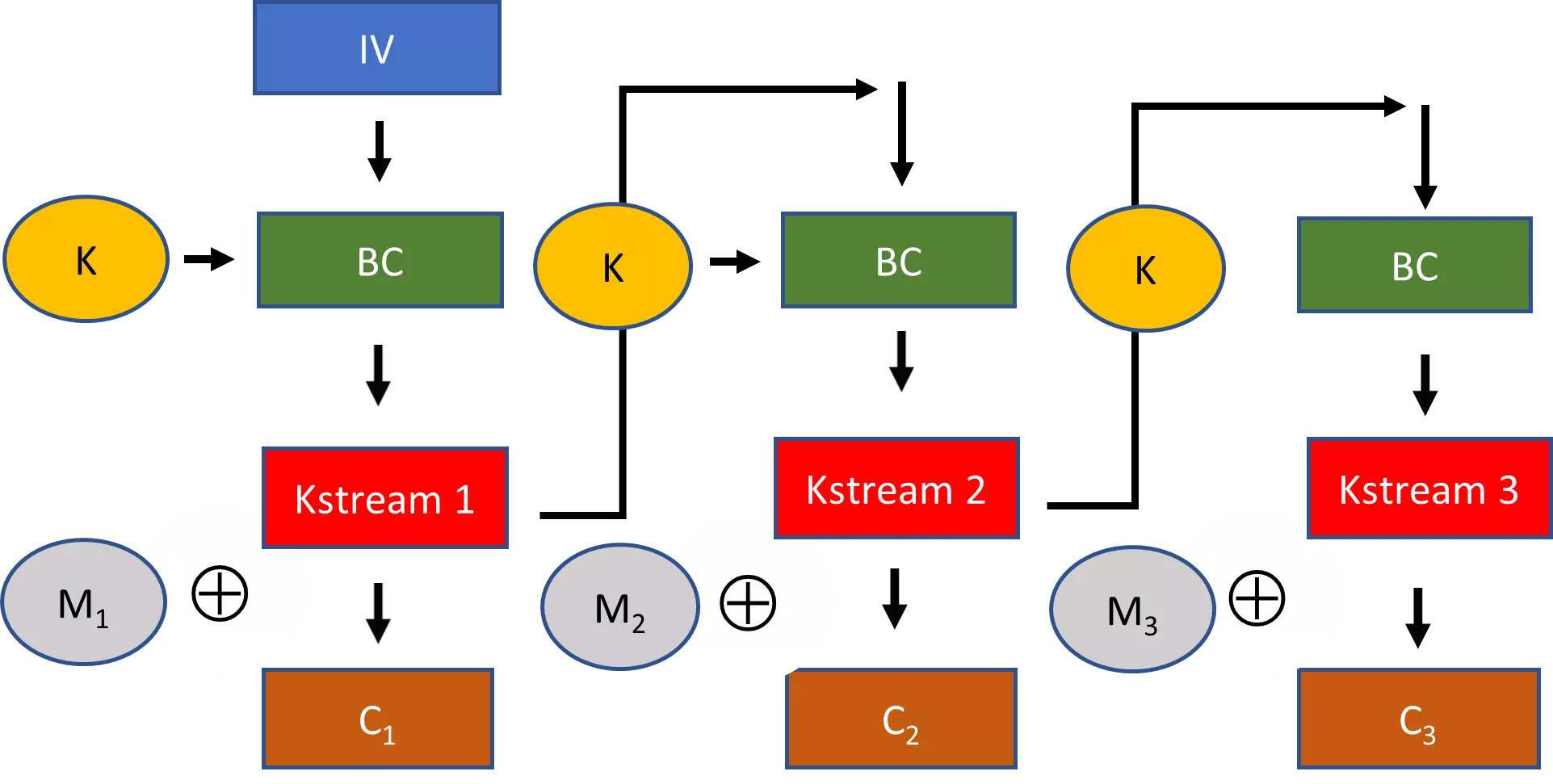
V režimu OFB můžete také vybrat inicializační vektor. Zde je však pro první blok inicializační vektor vložen přímo do blokové šifry s vaším klíčem. Výsledných 128 bitů se pak považuje za proud klíčů. Tento proud klíčů se XORuje s otevřeným textem, čímž se získá šifrový text pro daný blok. Pro následující bloky použijete jako vstup do blokové šifry proud klíčů z předchozího bloku a postup opakujete.
Pokud se podíváte pozorně, zjistíte, že z blokové šifry s režimem OFB zde byla vytvořena proudová šifra. Generujete 128bitové části proudu klíčů, dokud nezískáte délku otevřeného textu (přičemž z poslední 128bitové části proudu klíčů vyřadíte nepotřebné bity). Poté XORujete proud klíčů se zprávou otevřeného textu, abyste získali šifrový text.
V předchozí části o proudových šifrách jsem uvedl, že proud klíčů vytváříte pomocí soukromého klíče. Přesněji řečeno, nemusí být vytvořen pouze pomocí soukromého klíče. Jak vidíte v režimu OFB, keystream se vytváří s pomocí soukromého klíče i inicializačního vektoru.
Všimněte si, že stejně jako v režimu CBC je při každém použití blokové šifry v režimu OFB důležité zvolit pseudonáhodnou nebo náhodnou nonce pro inicializační vektor. Jinak bude stejný 128bitový řetězec zpráv odeslaný v různých komunikacích zašifrován stejným způsobem. To je jeden ze způsobů, jak vytvořit pravděpodobnostní šifrování pomocí proudové šifry.
Některé proudové šifry používají k vytvoření proudu klíčů pouze soukromý klíč. U těchto proudových šifer je důležité, abyste pro výběr soukromého klíče pro každý případ komunikace použili náhodnou nonce. Jinak budou výsledky šifrování pomocí těchto proudových šifer také deterministické, což povede k problémům se zabezpečením.
Nejpopulárnější moderní blokovou šifrou je Šifra Rijndael. Zvítězila z patnácti přihlášek do soutěže pořádané Národním institutem pro standardy a technologie (NIST) v letech 1997 až 2000 s cílem nahradit starší šifrovací standard, standard šifrování dat (DES).
Šifru Rijndael lze používat s různými specifikacemi délky klíče a velikosti bloku a také v různých režimech provozu. Výbor pro soutěž NIST přijal zúženou verzi šifry Rijndael - konkrétně takovou, která vyžaduje 128bitové velikosti bloků a délky klíčů buď 128 bitů, 192 bitů, nebo 256 bitů - jako součást pokročilého šifrovacího standardu (AES). Jedná se skutečně o hlavní standard pro symetrické šifrovací aplikace. Je natolik bezpečný, že jej zřejmě i NSA je ochotna používat s 256bitovými klíči pro přísně tajné dokumenty. [6]
Bloková šifra AES bude podrobně vysvětlena v kapitole 5.
Poznámky:
[5] Význam pravděpodobnostního šifrování poprvé zdůraznili Shafi Goldwasser a Silvio Micali, "Probabilistic encryption," Journal of Computer and System Sciences, 28 (1984), 270-99.
[6] Viz NSA, "Commercial National Security Algorithm Suite", https://apps.nsa.gov/iaarchive/programs/iad-initiatives/cnsa-suite.cfm.
Vyjasnění nejasností
Zmatek ohledně rozdílu mezi blokovými a proudovými šiframi vzniká proto, že někdy lidé chápou pojem bloková šifra jako označení pro blokovou šifru s blokovým způsobem šifrování.
Vezměme v úvahu režimy ECB a CBC v předchozí části. Ty konkrétně vyžadují, aby data pro šifrování byla dělitelná velikostí bloku (což znamená, že možná budete muset použít výplň pro původní zprávu). Kromě toho se s daty v těchto režimech pracuje také přímo blokovou šifrou (a ne pouze v kombinaci s výsledkem operace blokové šifry jako v režimu OFB).
Proto lze alternativně definovat blokovou šifru jako libovolné šifrovací schéma, které pracuje s bloky zprávy pevné délky najednou (přičemž každý blok musí být delší než bajt, jinak se rozpadá na proudovou šifru). Data pro šifrování i šifrový text se musí rovnoměrně rozdělit do tohoto bloku. Obvykle je velikost bloku dlouhá 64, 128, 192 nebo 256 bitů. Naproti tomu proudová šifra může šifrovat libovolné zprávy po částech o délce jednoho bitu nebo bajtu.
S tímto konkrétnějším chápáním blokové šifry lze skutečně tvrdit, že moderní šifrovací schémata jsou buď proudové, nebo blokové šifry. Od této chvíle budu pojem bloková šifra používat v obecnějším smyslu, pokud nebude uvedeno jinak.
Diskuse o režimu OFB v předchozí části přináší také další zajímavý bod. Některé proudové šifry jsou postaveny z blokových šifer, jako například Rijndael s OFB. Některé jako Salsa20 a ChaCha nejsou vytvořeny z blokových šifer. Ty druhé by se daly nazvat primitivními proudovými šiframi. (Ve skutečnosti neexistuje žádný standardizovaný termín, který by takové proudové šifry označoval.)
Když se hovoří o výhodách a nevýhodách proudových a blokových šifer, obvykle se porovnávají primitivní proudové šifry se šifrovacími schématy založenými na blokových šifrách.
Zatímco z blokové šifry lze vždy snadno sestavit proudovou šifru, z primitivní proudové šifry je obvykle velmi obtížné sestavit nějaký typ konstrukce s blokovým režimem šifrování (například s režimem CBC).
Na základě této diskuse byste nyní měli pochopit obrázek 8. Poskytuje přehled o symetrických šifrovacích schématech. Používáme tři druhy šifrovacích schémat: primitivní proudové šifry, blokové proudové šifry a blokové šifry v blokovém režimu (ve schématu nazývané také "blokové šifry").
Obrázek 8: Přehled symetrických šifrovacích schémat
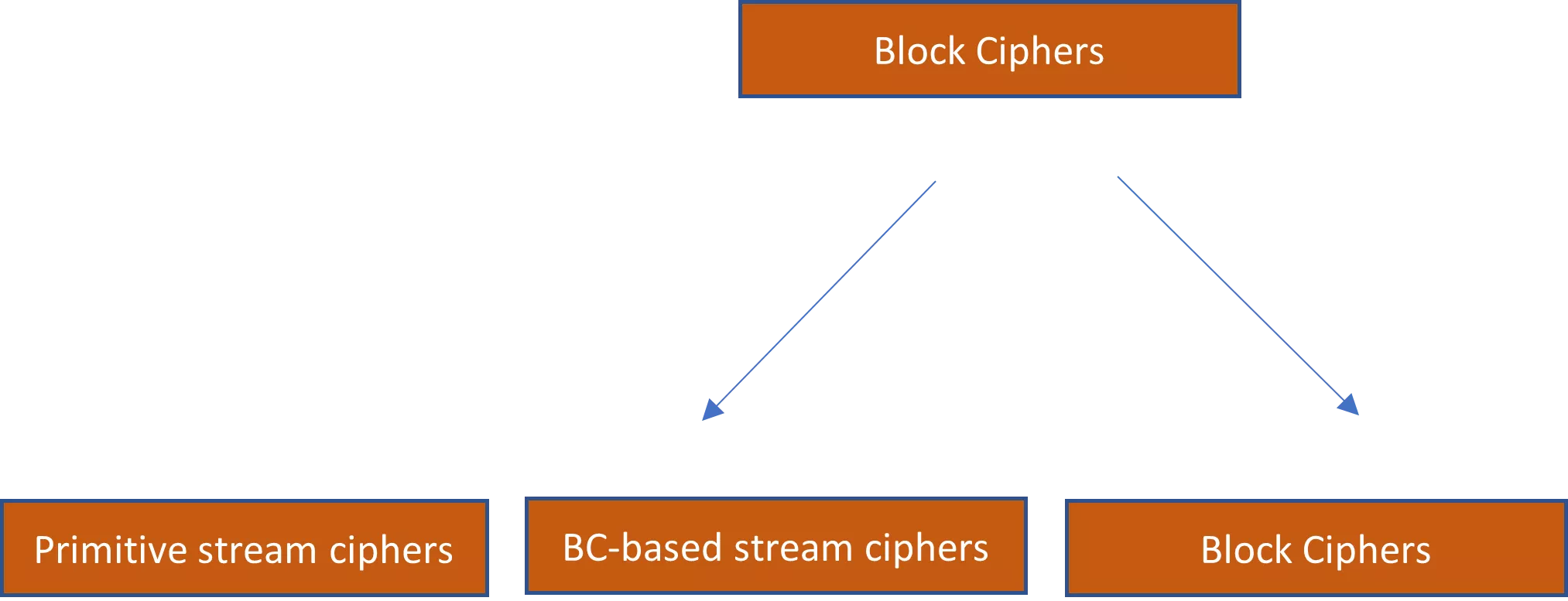
Kódy pro ověřování zpráv
Šifrování se týká utajení. Kryptografie se však zabývá i širšími tématy, jako je integrita, autenticita a nepopiratelnost zpráv. Takzvané autentizační kódy zpráv (MAC) jsou kryptografická schémata se symetrickým klíčem, která podporují autenticitu a integritu komunikace.
Proč je v komunikaci zapotřebí něco jiného než tajemství? Předpokládejme, že Bob pošle Alici zprávu s použitím prakticky neprolomitelného šifrování. Útočník, který tuto zprávu zachytí, nebude schopen zjistit žádné významné informace o jejím obsahu. Útočník má však stále k dispozici nejméně dva další vektory útoku:
Mohla by zachytit šifrový text, změnit jeho obsah a poslat jej Alici.
Mohla by zcela zablokovat Bobovu zprávu a poslat svůj vlastní vytvořený šifrový text.
V obou těchto případech nemusí mít útočník žádné informace o obsahu ze šifrových textů (1) a (2). Přesto však může tímto způsobem způsobit značné škody. V tomto případě nabývají na významu kódy pro ověřování zpráv.
Autentizační kódy zpráv jsou volně definovány jako symetrická kryptografická schémata se třemi algoritmy: algoritmem generování klíče, algoritmem generování značky a algoritmem ověřování. Bezpečný MAC zajišťuje, že značky jsou existenčně nezfalšovatelné pro jakéhokoli útočníka - to znamená, že nemůže úspěšně vytvořit značku na zprávě, která se ověřuje, pokud nemá soukromý klíč.
Bob a Alice mohou bojovat proti manipulaci s konkrétní zprávou pomocí MAC. Předpokládejme, že jim na utajení nezáleží. Chtějí se pouze ujistit, že zpráva, kterou Alice obdržela, byla skutečně od Boba a nebyla nijak pozměněna.
Postup je znázorněn na obrázku 9. Aby mohli použít MAC (Message Authentication Code), musí nejprve vygenerovat soukromý klíč K, který je sdílen mezi nimi.
Bob vytvoří značku T pro
zprávu pomocí soukromého klíče K. Poté odešle zprávu i
značku zprávy Alici. Ta si pak může ověřit, že Bob značku skutečně vytvořil,
a to tak, že soukromý klíč, zprávu a značku prověří ověřovacím algoritmem.
Obrázek 9: Přehled symetrických šifrovacích schémat
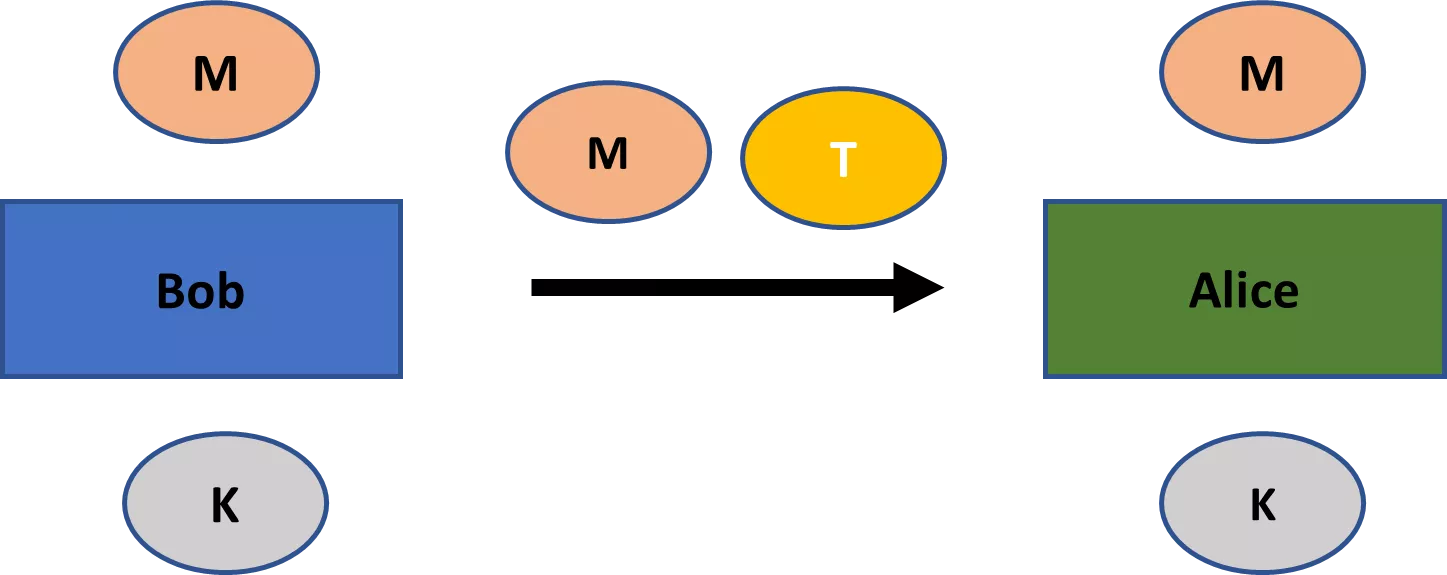
Vzhledem k existenciální nezfalšovatelnosti nemůže útočník
zprávu M nijak změnit ani
vytvořit vlastní zprávu s platnou značkou. To platí, i když útočník pozoruje
značky mnoha zpráv mezi Bobem a Alicí, které používají stejný soukromý klíč.
Útočník může nanejvýš zablokovat Alici příjem zprávy M (což je problém, který kryptografie
nedokáže řešit).
MAC zaručuje, že zprávu skutečně vytvořil Bob. Z této pravosti automaticky vyplývá integrita zprávy - to znamená, že pokud Bob vytvořil nějakou zprávu, pak ji útočník ipso facto nijak nezměnil. Od této chvíle by tedy jakákoli starost o autentičnost měla být automaticky chápána jako starost o integritu.
I když jsem ve své diskusi rozlišoval mezi autenticitou a integritou zprávy, je běžné používat tyto pojmy jako synonyma. Vztahují se tedy k myšlence zpráv, které byly vytvořeny konkrétním odesílatelem a nebyly nijak pozměněny. V tomto duchu se kódy pro ověření pravosti zpráv často nazývají také kódy pro integritu zpráv.
Ověřené šifrování
Obvykle je třeba zaručit utajení i autenticitu komunikace, a proto se šifrovací schémata a schémata MAC obvykle používají společně.
Ověřené šifrovací schéma je schéma, které kombinuje šifrování s MAC vysoce bezpečným způsobem. Konkrétně musí splňovat standardy pro existenční neprolomitelnost a také velmi silné pojetí utajení, konkrétně takové, které je odolné proti útoku vybraným šifrovým textem. [7]
Aby bylo šifrovací schéma odolné proti útokům na vybraný šifrový text, musí splňovat normy pro nemalleabilitu: to znamená, že jakákoli modifikace šifrového textu útočníkem by měla vést buď k neplatnému šifrovému textu, nebo k dešifrování na otevřený text, který nemá žádný vztah k původnímu textu. [8]
Protože autentizované šifrovací schéma zajišťuje, že šifrový text vytvořený útočníkem je vždy neplatný (protože značka nebude ověřena), splňuje normy pro odolnost proti útokům vybraným šifrovým textem. Zajímavé je, že lze dokázat, že autentizované šifrovací schéma lze vždy vytvořit z kombinace existenčně nezfalšovatelného MAC a šifrovacího schématu, které splňuje méně silnější pojetí bezpečnosti, známé jako bezpečnost proti útokům na vybraný text.
Nebudeme se zabývat všemi podrobnostmi konstrukce ověřených šifrovacích schémat. Je však důležité znát dva detaily jejich konstrukce.
Nejdříve se šifrovací schéma s ověřenou identitou postará o šifrování a poté vytvoří na šifrovaném textu značku zprávy. Ukazuje se, že jiné přístupy - například kombinace šifrového textu se značkou na otevřeném textu nebo nejprve vytvoření značky a poté zašifrování otevřeného textu i značky - jsou nezabezpečené. Obě operace mají navíc svůj vlastní náhodně vybraný soukromý klíč, jinak je vaše bezpečnost vážně ohrožena.
Výše uvedená zásada platí obecněji: při kombinování základních kryptografických schémat byste měli vždy používat odlišné klíče.
Schéma ověřeného šifrování je znázorněno na obrázku 10. Bob nejprve
vytvoří šifrový text C ze
zprávy M pomocí náhodně
zvoleného klíče K_C. Poté
vytvoří značku zprávy T tak,
že šifrový text a jiný náhodně zvolený klíč K_T projde algoritmem pro generování
značek. Šifrový text i značka zprávy jsou odeslány Alici.
Alice nyní nejprve ověří, zda je značka platná vzhledem k šifrovému textu C a klíči K_T. Pokud je platný,
může zprávu dešifrovat pomocí klíče K_C. Nejenže má jistotu velmi
silné představy o utajení jejich komunikace, ale také ví, že zprávu vytvořil
Bob.
Obrázek 10: Ověřené šifrovací schéma

Jak se vytvářejí kódy MAC? Přestože MAC lze vytvořit různými způsoby, běžným a efektivním způsobem jejich vytváření jsou kryptografické hashovací funkce.
S kryptografickými hašovacími funkcemi se podrobněji seznámíme v kapitole 6. Prozatím jen vězte, že heslová funkce je efektivně vypočitatelná funkce, která přijímá vstupy libovolné velikosti a dává výstupy pevné délky. Například populární hašovací funkce SHA-256 (secure hash algorithm 256) vždy generuje 256bitový výstup bez ohledu na velikost vstupu. Některé hashovací funkce, jako například SHA-256, mají užitečné využití v kryptografii.
Nejběžnějším typem značky vytvořené pomocí kryptografické hashovací funkce
je autentizační kód zprávy založený na hashi (HMAC). Postup
je znázorněn na obrázku 11. Strana vytvoří ze soukromého klíče K dva různé klíče, vnitřní klíč K_1 a vnější klíč K_2. Otevřený
text M nebo šifrový text C je pak hashován spolu s vnitřním klíčem. Výsledek T' je pak hashován vnějším klíčem, čímž vznikne značka zprávy T.
Existuje paleta hašovacích funkcí, které lze použít k vytvoření HMAC. Nejčastěji používanou hašovací funkcí je SHA-256.
Obrázek 11: HMAC
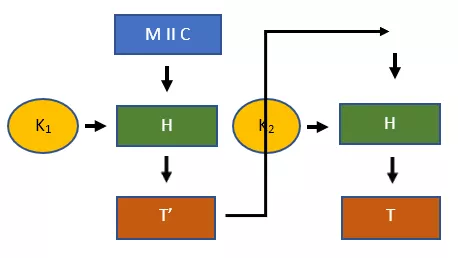
Poznámky:
[7] Konkrétní výsledky diskutované v této části jsou převzaty z Katz a Lindell, str. 131-47.
[8] Z technického hlediska se definice útoků na vybraný šifrový text liší od pojmu nemalebnosti. Lze však ukázat, že tyto dva pojmy bezpečnosti jsou ekvivalentní.
Zabezpečené komunikační relace
Předpokládejme, že dvě strany jsou v komunikační relaci a posílají si několik zpráv tam a zpět.
Ověřené šifrovací schéma umožňuje příjemci zprávy ověřit, že ji vytvořil jeho partner v komunikační relaci (pokud nedošlo k úniku soukromého klíče). To funguje dostatečně dobře pro jednu zprávu. Obvykle si však dvě strany v komunikační relaci posílají zprávy tam a zpět. A v tomto prostředí prosté šifrovací schéma s ověřením, jak je popsáno v předchozí části, nedokáže zajistit bezpečnost.
Hlavním důvodem je, že autentizované šifrovací schéma neposkytuje žádné záruky, že zprávu skutečně odeslal také agent, který ji v rámci komunikační relace vytvořil. Uvažujme následující tři vektory útoku:
Útok při přehrávání: Útočník znovu odešle šifrový text a značku, které zachytil mezi dvěma stranami v dřívějším okamžiku.
Útok na změnu pořadí: Útočník zachytí dvě zprávy v různém čase a odešle je příjemci v opačném pořadí.
Odrazový útok: Útočník pozoruje zprávu odeslanou z A do B a také ji odešle do A.
Ačkoli útočník nezná šifrový text a nemůže vytvářet podvržené šifrové texty, výše uvedené útoky mohou přesto způsobit značné škody v komunikaci.
Předpokládejme například, že konkrétní zpráva mezi dvěma stranami zahrnuje převod finančních prostředků. Opakovaný útok by mohl tyto prostředky převést podruhé. Autentické šifrovací schéma nemá proti takovým útokům žádnou obranu.
Naštěstí lze tyto druhy útoků snadno zmírnit v komunikační relaci pomocí identifikátorů a indikátorů relativního času.
Identifikátory lze přidat do zprávy s otevřeným textem před šifrováním. To by znemožnilo jakékoliv útoky odrazem. Relativním časovým indikátorem může být například pořadové číslo v konkrétní komunikační relaci. Každá strana přidá do zprávy před šifrováním pořadové číslo, takže příjemce ví, v jakém pořadí byly zprávy odeslány. Tím se vyloučí možnost útoků na změnu pořadí. Eliminuje také útoky typu replay. Každá zpráva, kterou útočník odešle po lince, bude mít staré sekvenční číslo a příjemce bude vědět, že nemá zprávu znovu zpracovávat.
Pro ilustraci fungování zabezpečených komunikačních relací předpokládejme opět Alici a Boba. Pošlou si celkem čtyři zprávy tam a zpět. Jak by fungovalo autentizované šifrovací schéma s identifikátory a sekvenčními čísly, můžete vidět níže na obrázku 11.
Komunikace začíná tím, že Bob pošle Alici šifrovaný text C_{0,B} se značkou zprávy T_{0,B}. Šifrový
text obsahuje zprávu a také identifikátor (BOB) a pořadové číslo (0). Značka T_{0,B} je vytvořena
nad celým šifrovým textem. Při následné komunikaci Alice a Bob tento protokol
dodržují a podle potřeby aktualizují pole.
Obrázek 12: Zabezpečená komunikační relace
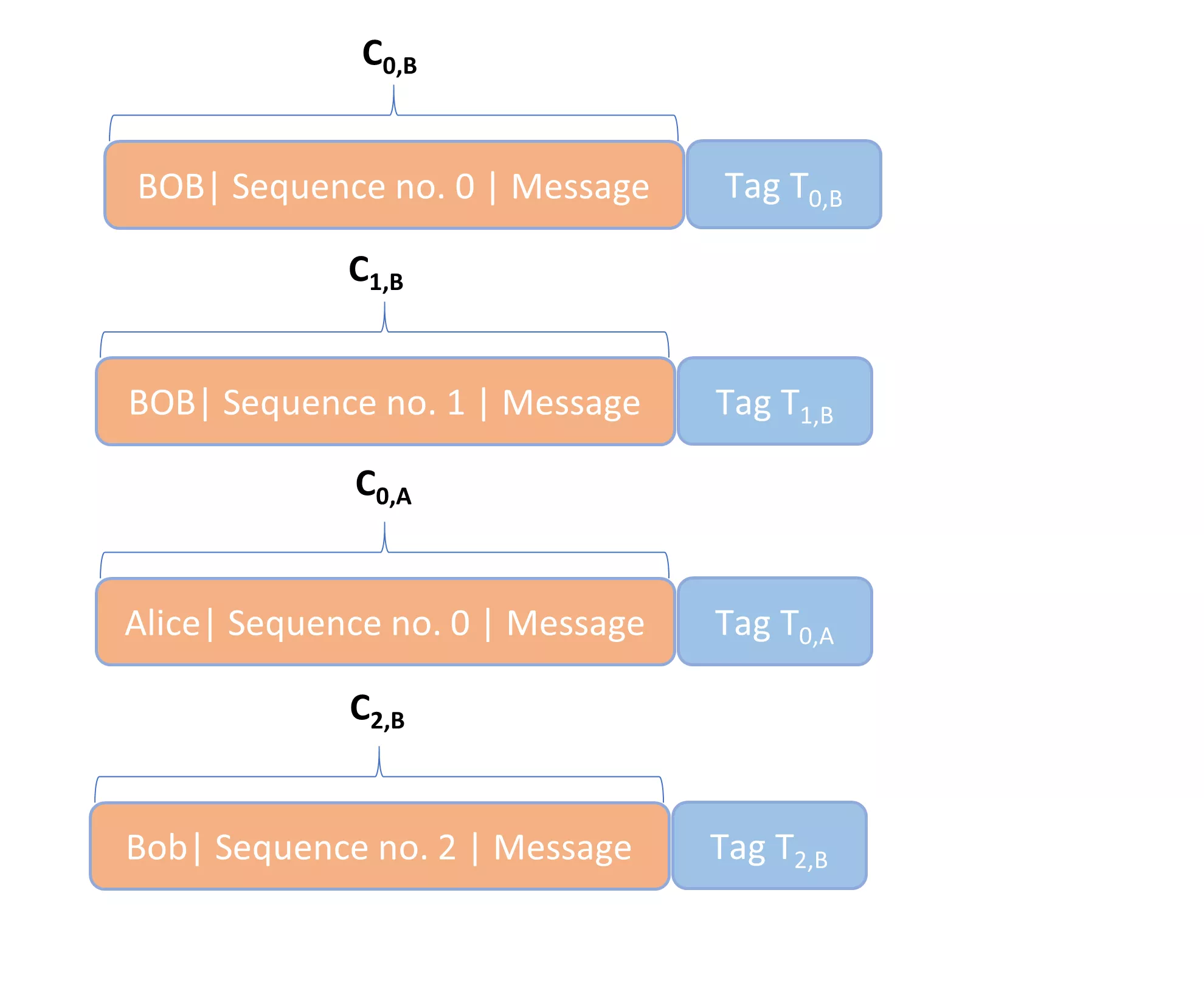
RC4 a AES
Proudová šifra RC4
V této kapitole se budeme zabývat podrobnostmi šifrovacího schématu s moderní primitivní proudovou šifrou RC4 (neboli "Rivestovou šifrou 4") a moderní blokovou šifrou AES. Zatímco šifra RC4 upadla jako metoda šifrování v nemilost, AES je standardem moderního symetrického šifrování. Tyto dva příklady by měly poskytnout lepší představu o tom, jak symetrické šifrování funguje pod kapotou.
Abychom měli představu o tom, jak fungují moderní pseudonáhodné proudové šifry, zaměřím se na proudovou šifru RC4. Jedná se o pseudonáhodnou proudovou šifru, která byla použita v bezpečnostních protokolech bezdrátových přístupových bodů WEP a WAP a také v protokolu TLS. Protože RC4 má mnoho prokázaných slabin, upadla v nemilost. Organizace Internet Engineering Task Force nyní zakazuje používání sad RC4 klientskými a serverovými aplikacemi ve všech případech protokolu TLS. Přesto dobře slouží jako příklad pro ilustraci fungování primitivní proudové šifry.
Na úvod nejprve ukážu, jak zašifrovat zprávu s otevřeným textem pomocí dětské šifry RC4. Předpokládejme, že naše zpráva s otevřeným textem je "SOUP" Šifrování naší dětskou šifrou RC4 tedy probíhá ve čtyřech krocích.
Krok 1
Nejprve definujte pole S s hodnotami S[0] = 0 až S[7] = 7. Pole zde
jednoduše znamená proměnlivou kolekci hodnot uspořádanou podle indexu, v
některých programovacích jazycích (např. Pythonu) nazývanou také seznam. V
tomto případě je index od 0 do 7 a hodnoty jsou také od 0 do 7. Takže S je následující:
S = [0, 1, 2, 3, 4, 5, 6, 7]
Hodnoty zde nejsou čísla ASCII, ale reprezentace 1bajtových řetězců v
desítkové soustavě. Hodnota 2 by se tedy rovnala 0000 \ 0011. Délka pole S je tedy 8 bajtů.
Krok 2
Za druhé definujte pole klíčů K o délce 8 bajtů výběrem klíče v rozsahu 1 až 8 bajtů (bez přípustných zlomků bajtů). Protože každý bajt má 8 bitů, můžete pro každý bajt klíče zvolit libovolné číslo v rozsahu 0 až 255.
Předpokládejme, že náš klíč k je [14, 48, 9], takže má délku 3
bajty. Každý index našeho pole klíčů je pak nastaven podle desetinné hodnoty
pro daný prvek klíče, a to v pořadí. Pokud projdete celý klíč, začněte znovu
od začátku, dokud nezaplníte 8 míst pole klíčů. Naše pole klíčů je tedy
následující:
K = [14, 48, 9, 14, 48, 9, 14, 48]
Krok 3
Zatřetí transformujeme pole S pomocí pole klíčů K v procesu známém jako plánování klíčů. Postup je v pseudokódu následující:
- Vytvoření proměnných j a i
- Nastavení proměnné
j = 0 - Pro každé
iod 0 do 7:- Nastavte
j = (j + S[i] + K[i]) \mod 8 - Výměna
S[i]aS[j]
- Nastavte
Transformaci pole S zachycuje Tabulka 1.
Na začátku si můžete prohlédnout počáteční stav S jako [0, 1, 2, 3, 4, 5, 6, 7] s počáteční hodnotou 0 pro j. Ta bude transformována pomocí
pole klíčů [14, 48, 9, 14, 48, 9, 14, 48].
Smyčka for začíná hodnotou i = 0. Podle našeho výše uvedeného pseudokódu se nová hodnota j stane 6 (j = (j + S[0] + K[0]) \mod 8 = (0 + 0 + 14) \mod 8 = 6 \mod 8). Výměnou S[0] a S[6] se stav S po jednom kole stane [6, 1, 2, 3, 4, 5, 0, 7].
V dalším řádku je i = 1. Při
dalším průchodu smyčkou for získá j hodnotu 7 (j = (j + S[1] + K[1]) \mod 8 = (6 + 1 + 48) \mod 8 = 55 \mod 8 = 7 \mod 8). Prohozením S[1] a S[7] z aktuálního stavu S, [6, 1, 2, 3, 4, 5, 0, 7],
získáme po 2. kole [6, 7, 2, 3, 4, 5, 0, 1].
V tomto postupu pokračujeme, dokud nevytvoříme poslední řádek na konci pole S, [6, 4, 1, 0, 3, 7, 5, 2].
Tabulka 1: Tabulka klíčových plánů
| Round | i | j | S[0] | S[1] | S[2] | S[3] | S[4] | S[5] | S[6] | S[7] | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 1 | 0 | 6 | 6 | 1 | 2 | 3 | 4 | 5 | 0 | 7 | |
| 2 | 1 | 7 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 3 | 2 | 2 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 4 | 3 | 3 | 6 | 7 | 2 | 3 | 4 | 5 | 0 | 1 | |
| 5 | 4 | 3 | 6 | 7 | 2 | 0 | 3 | 5 | 4 | 1 | |
| 6 | 5 | 6 | 6 | 4 | 2 | 0 | 3 | 7 | 5 | 1 | |
| 7 | 6 | 1 | 6 | 4 | 2 | 0 | 3 | 7 | 5 | 2 | |
| 8 | 7 | 2 | 6 | 4 | 1 | 0 | 3 | 7 | 5 | 2 |
Krok 4
Ve čtvrtém kroku vytvoříme keystream. Jedná se o pseudonáhodný řetězec o délce rovnající se zprávě, kterou chceme odeslat. Ten bude použit k zašifrování původní zprávy "SOUP" Protože klíčový proud musí být stejně dlouhý jako zpráva, potřebujeme takový, který má 4 bajty.
Klíčový proud je vytvořen následujícím pseudokódem:
- Vytvořte proměnné j, i a t.
- Nastavte
j = 0. - Pro každé
iotevřeného textu, počínajei = 1až doi = 4, se každý bajt klíčového proudu vytvoří takto:j = (j + S[i]) \mod 8- Vyměňte
S[i]aS[j]. t = (S[i] + S[j]) \mod 8i^{th}bajt klíčového proudu =S[t]
Výpočty můžete sledovat v Tabulce 2.
Počáteční stav S je S = [6, 4, 1, 0, 3, 7, 5, 2].
Nastavíme-li i = 1, hodnota j se stane 4 (j = (j + S[i]) \mod 8 = (0 + 4) \mod 8 = 4). Poté prohodíme S[1] a S[4], čímž získáme
transformaci S ve druhém řádku: [6, 3, 1, 0, 4, 7, 5, 2].
Hodnota t je pak 7 (t = (S[i] + S[j]) \mod 8 = (3 + 4) \mod 8 = 7). Nakonec je bajt pro klíčový proud S[7] nebo 2.
Poté pokračujeme ve vytváření dalších bajtů, dokud nezískáme následující čtyři bajty: 2, 6, 3 a 7. Každý z těchto bajtů pak můžeme použít k zašifrování každého písmene otevřeného textu "SOUP".
Pro začátek můžeme pomocí tabulky ASCII zjistit, že "SOUP" zakódovaný pomocí desítkových hodnot základních řetězců bajtů je "83 79 85 80". Kombinací s klíčovým řetězcem "2 6 3 7" získáme "85 85 88 87", který zůstane stejný i po operaci modulo 256. V ASCII se šifrový text "85 85 88 87" rovná "UUXW".
Co by se stalo, kdyby slovo k zašifrování bylo delší než pole S? V takovém případě se pole S prostě bude transformovat výše uvedeným způsobem pro každý bajt i otevřeného textu, dokud nebudeme mít v proudu klíčů počet bajtů rovný počtu písmen v otevřeném textu.
Tabulka 2: Generování klíčového proudu
| i | j | t | Keystream | S[0] | S[1] | S[2] | S[3] | S[4] | S[5] | S[6] | S[7] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 4 | 1 | 0 | 3 | 7 | 5 | 2 | |||
| 1 | 4 | 7 | 2 | 6 | 3 | 1 | 0 | 4 | 7 | 5 | 2 |
| 2 | 5 | 0 | 6 | 6 | 3 | 7 | 0 | 4 | 1 | 5 | 2 |
| 3 | 5 | 1 | 3 | 6 | 3 | 7 | 1 | 4 | 0 | 5 | 2 |
| 4 | 1 | 7 | 2 | 6 | 4 | 7 | 1 | 3 | 0 | 5 | 2 |
Příklad, který jsme právě probrali, je pouze oslabenou verzí proudové šifry RC4. Skutečná proudová šifra RC4 má pole S o délce 256 bajtů, nikoli 8 bajtů, a klíč může mít délku 1 až 256 bajtů, nikoli 1 až 8 bajtů. Pole klíčů a proudy klíčů se pak vytvářejí s ohledem na délku 256 bajtů pole S. Výpočty se stávají nesmírně složitějšími, ale principy zůstávají stejné. Při použití stejného klíče [14,48,9] se standardní šifrou RC4 se zpráva s otevřeným textem "SOUP" zašifruje jako 67 02 ed df v šestnáctkovém formátu.
Proudová šifra, ve které se proud klíčů aktualizuje nezávisle na zprávě otevřeného textu nebo šifrovém textu, je synchronní proudová šifra. Tok klíčů závisí pouze na klíči. Je zřejmé, že RC4 je příkladem synchronní proudové šifry, protože proud klíčů nemá žádný vztah k otevřenému textu nebo šifrovému textu. Všechny naše primitivní proudové šifry zmíněné v předchozí kapitole, včetně šifry posunu, Vigenèrovy šifry a jednorázové podložky, byly také synchronní.
Naproti tomu asynchronní proudová šifra má proud klíčů, který je tvořen klíčem i předchozími prvky šifrového textu. Tento typ šifry se také nazývá samosynchronizující šifra.
Důležité je, že proud klíčů vytvořený pomocí RC4 je třeba považovat za jednorázový blok a příště jej nelze vytvořit přesně stejným způsobem. Místo toho, aby se klíč pokaždé měnil, je praktickým řešením spojit klíč s nonce a vytvořit tak bytestream.
AES se 128bitovým klíčem
Jak bylo zmíněno v předchozí kapitole, Národní institut pro standardy a technologie (NIST) uspořádal v letech 1997 až 2000 soutěž o nový standard symetrického šifrování. Vítězem se stala šifra Rijndael. Název je slovní hříčkou se jmény belgických tvůrců, Vincenta Rijmena a Joana Daemena.
Šifra Rijndael je bloková šifra, což znamená, že existuje základní algoritmus, který lze použít s různými specifikacemi délky klíče a velikosti bloku. Můžete jej tedy použít s různými režimy práce pro konstrukci šifrovacích schémat.
Výbor pro soutěž NIST přijal zúženou verzi šifry Rijndael - konkrétně takovou, která vyžaduje 128bitové velikosti bloků a délky klíčů 128, 192 nebo 256 bitů - jako součást pokročilého šifrovacího standardu (AES). Tuto zúženou verzi šifry Rijndael lze také používat ve více pracovních režimech. Specifikace tohoto standardu je známá jako Pokročilý šifrovací standard (AES).
Abych ukázal, jak funguje šifra Rijndael, která je jádrem AES, ukážu postup šifrování se 128bitovým klíčem. Velikost klíče má vliv na počet kol pro každý blok šifrování. Pro 128bitový klíč je zapotřebí 10 kol. U 192bitového a 256bitového klíče by to bylo 12, resp. 14 kol.
Kromě toho budu předpokládat, že AES se používá v režimu ECB. To poněkud usnadňuje výklad a pro algoritmus Rijndael to nehraje roli. Pro jistotu dodejme, že režim ECB není v praxi bezpečný, protože vede k deterministickému šifrování. Nejčastěji používaným bezpečným režimem u AES je CBC (Cipher Block Chaining).
Klíč nazvěme K_0. Konstrukce
s výše uvedenými parametry pak vypadá jako na obrázku 1, kde M_i znamená část zprávy otevřeného textu o délce 128 bitů a C_i část šifrového textu o délce
128 bitů. Pokud nelze otevřený text rovnoměrně rozdělit velikostí bloku, přidá
se k němu pro poslední blok padding.
Obrázek 1: AES-ECB se 128bitovým klíčem
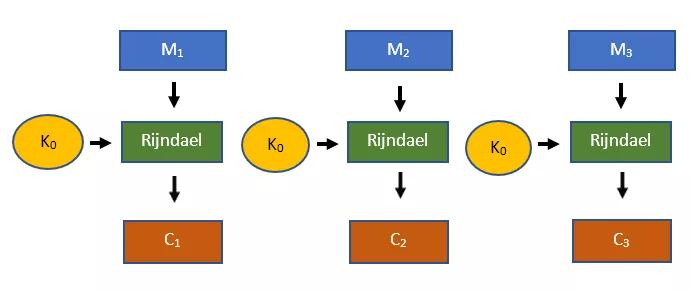
Každý 128bitový blok textu prochází v šifrovacím schématu Rijndael deseti
koly. To vyžaduje pro každé kolo samostatný klíč (K_1 až K_{10}). Ty se
pro každé kolo vytvářejí z původního 128bitového klíče K_0 pomocí algoritmu pro expanzi klíče. Proto pro každý blok
textu, který má být zašifrován, použijeme původní klíč K_0 a deset samostatných kruhových
klíčů. Všimněte si, že pro každý 128bitový blok otevřeného textu, který vyžaduje
šifrování, se použije stejných 11 klíčů.
Algoritmus expanze klíče je dlouhý a složitý. Jeho zpracování má jen malý
didaktický přínos. Pokud chcete, můžete si algoritmus expanze klíče projít
sami. Po vytvoření kruhových klíčů bude šifra Rijndael manipulovat s prvním
128bitovým blokem otevřeného textu M_1, jak je vidět na obrázku 2. Nyní si tyto kroky projdeme.
Obrázek 2: Manipulace s M_1 pomocí šifry Rijndael:
Kolo 0:
- XOR
M_1aK_0pro vytvořeníS_0
Kruh n pro n = {1,...,9}:
- XOR
S_{n-1}aK_n - Substituce bajtů
- Řádky posunu
- Mix sloupců
- XOR
SaK_npro vytvořeníS_n
Kolo 10:
- XOR
S_9aK_{10} - Substituce bajtů
- Řádky posunu
- XOR
SaK_{10}pro vytvořeníS_{10} S_{10}=C_1
0. kolo
- kolo šifry Rijndael je jednoduché. Pole
S_0se vytvoří operací XOR mezi 128bitovým otevřeným textem a soukromým klíčem. To znamená,
S_0 = M_1 \oplus K_0
1. kolo
V 1. kole se pole S_0 nejprve
spojí s kruhovým klíčem K_1 pomocí operace XOR. Tím vznikne nový stav S.
Zadruhé se provede operace záměna bajtů na aktuálním stavu S. Funguje tak, že se vezme
každý bajt 16bajtového pole S a nahradí se bajtem z pole zvaného Rijndaelovo S-box. Každý
bajt má jedinečnou transformaci a výsledkem je nový stav S. Rijndaelův S-box je
zobrazen na obrázku 3.
Obrázek 3: Rijndaelův S-Box
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 0A | 0B | 0C | 0D | 0E | 0F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 63 | 7C | 77 | 7B | F2 | 6B | 6F | C5 | 30 | 01 | 67 | 2B | FE | D7 | AB | 76 |
| 10 | CA | 82 | C9 | 7D | FA | 59 | 47 | F0 | AD | D4 | A2 | AF | 9C | A4 | 72 | C0 |
| 20 | B7 | FD | 93 | 26 | 36 | 3F | F7 | CC | 34 | A5 | E5 | F1 | 71 | D8 | 31 | 15 |
| 30 | 04 | C7 | 23 | C3 | 18 | 96 | 05 | 9A | 07 | 12 | 80 | E2 | EB | 27 | B2 | 75 |
| 40 | 09 | 83 | 2C | 1A | 1B | 6E | 5A | A0 | 52 | 3B | D6 | B3 | 29 | E3 | 2F | 84 |
| 50 | 53 | D1 | 00 | ED | 20 | FC | B1 | 5B | 6A | CB | BE | 39 | 4A | 4C | 58 | CF |
| 60 | D0 | EF | AA | FB | 43 | 4D | 33 | 85 | 45 | F9 | 02 | 7F | 50 | 3C | 9F | A8 |
| 70 | 51 | A3 | 40 | 8F | 92 | 9D | 38 | F5 | BC | B6 | DA | 21 | 10 | FF | F3 | D2 |
| 80 | CD | 0C | 13 | EC | 5F | 97 | 44 | 17 | C4 | A7 | 7E | 3D | 64 | 5D | 19 | 73 |
| 90 | 60 | 81 | 4F | DC | 22 | 2A | 90 | 88 | 46 | EE | B8 | 14 | DE | 5E | 0B | DB |
| A0 | E0 | 32 | 3A | 0A | 49 | 06 | 24 | 5C | C2 | D3 | AC | 62 | 91 | 95 | E4 | 79 |
| B0 | E7 | C8 | 37 | 6D | 8D | D5 | 4E | A9 | 6C | 56 | F4 | EA | 65 | 7A | AE | 08 |
| C0 | BA | 78 | 25 | 2E | 1C | A6 | B4 | C6 | E8 | DD | 74 | 1F | 4B | BD | 8B | 8A |
| D0 | 70 | 3E | B5 | 66 | 48 | 03 | F6 | 0E | 61 | 35 | 57 | B9 | 86 | C1 | 1D | 9E |
| E0 | E1 | F8 | 98 | 11 | 69 | D9 | 8E | 94 | 9B | 1E | 87 | E9 | CE | 55 | 28 | DF |
| F0 | 8C | A1 | 89 | 0D | BF | E6 | 42 | 68 | 41 | 99 | 2D | 0F | B0 | 54 | BB | 16 |
Tento S-Box je jedním z míst, kde v šifře Rijndael vstupuje do hry abstraktní algebra, konkrétně Galoisova pole.
Na začátku definujete každý možný prvek bajtu 00 až FF jako 8bitový vektor.
Každý takový vektor je prvkem Galoisova pole GF(2^8), kde
neredukovatelný polynom pro operaci modulo je x^8 + x^4 + x^3 + x + 1.
Galoisovo pole s těmito specifikacemi se také nazývá Rijndaelovo konečné pole.
Dále pro každý možný prvek v poli vytvoříme takzvaný Nybergův S-Box. V tomto poli je každý bajt namapován na svou multiplikativní inverzi (tj. tak, aby se jejich součin rovnal 1). Tyto hodnoty pak mapujeme z Nybergova S-boxu do Rijndaelova S-boxu pomocí afinní transformace.
Třetí operací na poli S je operace posun řádků. Vezme stav pole S a vypíše všech šestnáct bajtů do matice. Naplňování matice začíná vlevo nahoře a postupuje shora dolů a pak se při každém naplnění sloupce posune o jeden sloupec doprava a nahoru.
Po sestavení matice S se posunou čtyři řádky. První řádek zůstává stejný. Druhý řádek se posune o jeden doleva. Třetí řádek se posune o dva doleva. Čtvrtý řádek přesune tři doleva. Příklad tohoto postupu je uveden na obrázku 4. Původní stav S je zobrazen nahoře a výsledný stav po operaci posunu řádků je zobrazen pod ním.
Obrázek 4: Operace posunutí řádků
| F1 | A0 | B1 | 23 |
|---|---|---|---|
| 59 | EF | 09 | 82 |
| 97 | 01 | B0 | CC |
| D4 | 72 | 04 | 21 |
| F1 | A0 | B1 | 23 |
|---|---|---|---|
| EF | 09 | 82 | 59 |
| B0 | CC | 97 | 01 |
| 21 | D4 | 72 | 04 |
Ve čtvrtém kroku se opět objeví Galoisova pole. Na začátku
se každý sloupec matice S vynásobí sloupcem matice 4 x 4,
která je vidět na obrázku 5. Místo běžného násobení matic se však
jedná o násobení vektorů modulo neredukovatelného polynomu, x^8 + x^4 + x^3 + x + 1.
Výsledné koeficienty vektoru představují jednotlivé bity bajtu.
Obrázek 5: Matice sloupců směsi
| 02 | 03 | 01 | 01 |
|---|---|---|---|
| 01 | 02 | 03 | 01 |
| 01 | 01 | 02 | 03 |
| 03 | 01 | 01 | 02 |
Vynásobením prvního sloupce matice S s výše uvedenou maticí 4 x 4 získáme výsledek na obrázku 6.
Obrázek 6: Násobení prvního sloupce:
\begin{matrix}
02 \cdot F1 + 03 \cdot EF + 01 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 02 \cdot EF + 03 \cdot B0 + 01 \cdot 21 \\
01 \cdot F1 + 01 \cdot EF + 02 \cdot B0 + 03 \cdot 21 \\
03 \cdot F1 + 01 \cdot EF + 01 \cdot B0 + 02 \cdot 21
\end{matrix}V dalším kroku by bylo třeba všechny členy matice převést na polynomy.
Například F1 představuje 1 bajt a stal by se z něj x^7 + x^6 + x^5 + x^4 + 1 a 03 představuje 1 bajt a stal by se z něj x + 1.
Všechna násobení se pak provedou modulo x^8 + x^4 + x^3 + x + 1.
Výsledkem je sčítání čtyř polynomů v každém ze čtyř políček sloupce. Po
provedení těchto sčítání modulo 2 získáme čtyři polynomy.
Každý z těchto polynomů představuje osmibitový řetězec neboli 1 bajt S. Všechny tyto výpočty zde nebudeme provádět na matici na obrázku 6, protože jsou rozsáhlé.
Po zpracování prvního sloupce se stejným způsobem zpracují další tři sloupce matice S. Nakonec se získá matice o šestnácti bajtech, kterou lze transformovat do pole.
V posledním kroku se pole S opět spojí s kulatým klíčem v
operaci XOR. Tím vznikne stav S_1. To znamená,
S_1 = S \oplus K_0
2. až 10. kolo
- až 9. kolo jsou jen opakováním 1. kola, mutatis mutandis. Závěrečné kolo vypadá velmi podobně jako předchozí kola s tím rozdílem, že odpadá krok smíchání sloupců. To znamená, že 10. kolo se provede takto:
S_9 \oplus K_{10}- Substituce bajtů
- Řádky posunu
S_{10} = S \oplus K_{10}
Stav S_{10} je nyní
nastaven na C_1, prvních 128
bitů šifrového textu. Postupem přes zbývající 128bitové bloky otevřeného
textu získáme celý šifrový text C.
Operace šifry Rijndael
Jaký je důvod různých operací v šifře Rijndael?
Aniž bychom zacházeli do podrobností, šifrovací schémata se hodnotí na základě míry, v jaké způsobují zmatek a šíření. Pokud šifrovací schéma vykazuje vysoký stupeň zmatení, znamená to, že šifrový text vypadá dramaticky jinak než otevřený text. Pokud má šifrovací schéma vysoký stupeň difuze, znamená to, že jakákoli malá změna otevřeného textu vede k drasticky odlišnému šifrovému textu.
Důvodem operací, které stojí za šifrou Rijndael, je vysoký stupeň zmatení i rozptylu. Zmatení je způsobeno operací záměny bajtů, zatímco rozptyl je způsoben operacemi posunu řádků a míchání sloupců.
Asymetrická kryptografie
Problém distribuce a správy klíčů
Stejně jako v případě symetrické kryptografie lze asymetrická schémata použít k zajištění utajení i autentizace. Na rozdíl od nich však tato schémata nepoužívají jeden, ale dva klíče: soukromý a veřejný.
Naše zkoumání začneme objevem asymetrické kryptografie, zejména problémy, které ji podnítily. Dále se budeme zabývat tím, jak asymetrická schémata pro šifrování a autentizaci fungují na vysoké úrovni. Poté představíme hašovací funkce, které jsou klíčové pro pochopení asymetrických autentizačních schémat a mají význam i v jiných kryptografických souvislostech, například pro hašovací kódy pro ověřování zpráv, o nichž jsme hovořili v kapitole 4.
Předpokládejme, že si Bob chce koupit nový plášť do deště u firmy Jim's Sporting Goods, online prodejce sportovního zboží s miliony zákazníků v Severní Americe. Bude to jeho první nákup u nich a chce použít svou kreditní kartu. Bob si tedy nejprve bude muset u společnosti Jim's Sporting Goods vytvořit účet, což vyžaduje zaslání osobních údajů, jako je adresa a informace o kreditní kartě. Poté může provést kroky potřebné k nákupu pláštěnky.
Bob a Jim's Sporting Goods budou chtít zajistit, aby jejich komunikace byla během tohoto procesu bezpečná, vzhledem k tomu, že internet je otevřený komunikační systém. Budou chtít například zajistit, aby žádný potenciální útočník nemohl zjistit údaje o Bobově kreditní kartě a adrese a aby žádný potenciální útočník nemohl opakovat jeho nákupy nebo jeho jménem vytvářet falešné nákupy.
Pokročilé autentizované šifrovací schéma, o kterém jsme hovořili v předchozí kapitole, by jistě mohlo zajistit bezpečnost komunikace mezi Bobem a společností Jim's Sporting Goods. Implementace takového schématu však zjevně naráží na praktické překážky.
Pro ilustraci těchto praktických překážek předpokládejme, že žijeme ve světě, kde existují pouze nástroje symetrické kryptografie. Co by tedy mohli Jim's Sporting Goods a Bob udělat pro zajištění bezpečné komunikace?
Za těchto okolností by jim vznikly značné náklady na bezpečnou komunikaci. Protože internet je otevřený komunikační systém, nemohou si přes něj jednoduše vyměnit sadu klíčů. Proto budou muset Bob a zástupce společnosti Jim's Sporting Goods provést výměnu klíčů osobně.
Jednou z možností je, že společnost Jim's Sporting Goods vytvoří speciální místa pro výměnu klíčů, kde si Bob a další noví zákazníci mohou vyzvednout sadu klíčů pro bezpečnou komunikaci. To by samozřejmě bylo spojeno se značnými organizačními náklady a výrazně by to snížilo efektivitu, s níž mohou noví zákazníci nakupovat.
Společnost Jim's Sporting Goods může Bobovi poslat pár klíčů prostřednictvím důvěryhodného kurýra. To je pravděpodobně efektivnější než organizovat místa výměny klíčů. Stále by to však bylo spojeno se značnými náklady, zejména pokud mnoho zákazníků provede pouze jeden nebo několik málo nákupů.
Dále symetrické schéma pro ověřené šifrování nutí společnost Jim's Sporting Goods ukládat oddělené sady klíčů pro všechny své zákazníky. To by pro tisíce zákazníků, natož pro miliony, představovalo značný praktický problém.
Pro pochopení tohoto posledního bodu předpokládejme, že společnost Jim's Sporting Goods poskytne každému zákazníkovi stejný pár klíčů. To by umožnilo každému zákazníkovi - nebo komukoli jinému, kdo by mohl tento pár klíčů získat - číst a dokonce manipulovat s veškerou komunikací mezi společností Jim's Sporting Goods a jejími zákazníky. To byste pak mohli ve své komunikaci rovnou nepoužívat kryptografii vůbec.
Dokonce i opakování sady klíčů pouze pro některé zákazníky je špatný bezpečnostní postup. Každý potenciální útočník by se mohl pokusit tuto vlastnost schématu zneužít (nezapomeňte, že podle Kerckhoffova principu se předpokládá, že útočníci znají o schématu vše kromě klíčů)
Společnost Jim's Sporting Goods by tedy musela uložit pár klíčů pro každého zákazníka bez ohledu na to, jak jsou tyto páry klíčů distribuovány. To zjevně představuje několik praktických problémů.
- Společnost Jim's Sporting Goods by musela skladovat miliony párů klíčů, jednu sadu pro každého zákazníka.
- Tyto klíče by musely být řádně zabezpečeny, protože by byly jistým cílem hackerů. Jakékoli narušení bezpečnosti by vyžadovalo opakování nákladných výměn klíčů, a to buď na speciálních místech pro výměnu klíčů, nebo prostřednictvím kurýra.
- Každý zákazník společnosti Jim's Sporting Goods by si měl doma bezpečně uložit pár klíčů. Dochází ke ztrátám a krádežím, což vyžaduje opakovanou výměnu klíčů. Tímto procesem by museli zákazníci projít i u všech ostatních internetových obchodů nebo jiných typů subjektů, se kterými chtějí komunikovat a provádět transakce přes internet.
Tyto dva hlavní problémy, které jsme právě popsali, byly až do konce 70. let 20. století velmi zásadní. Byly známy jako problém distribuce klíčů a problém správy klíčů.
Tyto problémy samozřejmě existovaly vždy a v minulosti často způsobovaly bolesti hlavy. Například vojenské jednotky musely neustále distribuovat knihy s klíči pro bezpečnou komunikaci personálu v terénu, což představovalo velké riziko a náklady. Tyto problémy se však zhoršovaly s tím, jak svět stále více přecházel na dálkovou digitální komunikaci, zejména pro nevládní subjekty.
Pokud by tyto problémy nebyly vyřešeny v 70. letech 20. století, efektivní a bezpečné nakupování v prodejnách Jim's Sporting Goods by pravděpodobně neexistovalo. Ve skutečnosti by většina našeho moderního světa s praktickým a bezpečným e-mailingem, online bankovnictvím a nakupováním byla pravděpodobně jen vzdálenou fantazií. Cokoli, co by se byť jen podobalo Bitcoinu, by vůbec nemohlo existovat.
Co se stalo v 70. letech? Jak je možné, že můžeme okamžitě nakupovat online a bezpečně procházet celosvětovou síť? Jak je možné, že můžeme okamžitě posílat bitcoiny po celém světě z našich chytrých telefonů?
Nové směry v kryptografii
V 70. letech 20. století upoutala pozornost skupiny amerických akademických kryptografů problematika distribuce a správy klíčů: Whitfield Diffie, Martin Hellman a Ralph Merkle. Tváří v tvář velké skepsi většiny svých kolegů se odhodlali navrhnout řešení.
Přinejmenším jednou z hlavních motivací pro jejich podnikání byla předvídavost, že otevřená počítačová komunikace zásadně ovlivní náš svět. Diffie a Helmann v roce 1976 poznamenávají,
Rozvoj počítačem řízených komunikačních sítí slibuje snadný a levný kontakt mezi lidmi nebo počítači na opačných koncích světa, který nahradí většinu pošty a mnoho výletů telekomunikací. Pro mnoho aplikací musí být tyto kontakty zabezpečeny jak proti odposlechu, tak proti vnášení nelegitimních zpráv. V současné době však řešení bezpečnostních problémů značně zaostává za jinými oblastmi komunikačních technologií. Současná kryptografie není schopna splnit požadavky v tom smyslu, že její použití by pro uživatele systému znamenalo tak závažné nepříjemnosti, že by eliminovalo mnohé výhody teleprocesingu [1]
Vytrvalost Diffieho, Hellmana a Merkleho se vyplatila. První publikací jejich výsledků byl článek Diffieho a Helmanna z roku 1976 s názvem "Nové směry v kryptografii" V něm představili dva originální způsoby řešení problémů distribuce a správy klíčů.
Prvním řešením, které nabídli, byl vzdálený protokol výměny klíčů, tj. soubor pravidel pro výměnu jednoho nebo více symetrických klíčů přes nezabezpečený komunikační kanál. Tento protokol je nyní znám jako Diffie-Helmannova výměna klíčů nebo Diffie-Helmann-Merkleova výměna klíčů. [2]
Při Diffieho-Helmannově výměně klíčů si dvě strany nejprve veřejně vymění určité informace na nezabezpečeném kanálu, například na internetu. Na základě těchto informací pak nezávisle vytvoří symetrický klíč (nebo dvojici symetrických klíčů) pro bezpečnou komunikaci. Ačkoli obě strany vytvářejí své klíče nezávisle, veřejně sdílené informace zajišťují, že tento proces vytváření klíčů vede ke stejnému výsledku pro obě strany.
Důležité je, že zatímco každý může sledovat informace, které si strany veřejně vyměňují přes nezabezpečený kanál, pouze dvě strany, které se účastní výměny informací, z nich mohou vytvořit symetrické klíče.
To samozřejmě zní naprosto neintuitivně. Jak by si dvě strany mohly veřejně vyměnit nějaké informace, které by umožnily vytvořit z nich symetrické klíče pouze jim? Proč by kdokoli jiný, kdo sleduje výměnu informací, nemohl vytvořit stejné klíče?
Samozřejmě se opírá o krásnou matematiku. Diffie-Helmannova výměna klíčů funguje prostřednictvím jednosměrné funkce s trapdoor. Pojďme si postupně probrat význam těchto dvou pojmů.
Předpokládejme, že je dána nějaká funkce f(x) a výsledek f(a) = y, kde a je konkrétní hodnota pro x.
Říkáme, že f(x) je jednosměrná funkce, jestliže je snadné vypočítat hodnotu y, když jsou dány a a f(x), ale výpočetně je
nemožné vypočítat hodnotu a,
když jsou dány y a f(x). Název jednosměrná funkce samozřejmě vychází ze skutečnosti, že takovou
funkci je praktické počítat pouze v jednom směru.
Některé jednosměrné funkce mají tzv. trapdoor. I když je
prakticky nemožné vypočítat a pouze na základě y a f(x), existuje určitá
informace Z, díky které je
výpočet a z y výpočetně proveditelný. Tato informace Z je známá jako trapdoor. Jednosměrné funkce, které mají
trapdoor, se nazývají trapdoor funkce.
Nebudeme se zde zabývat podrobnostmi Diffie-Helmannovy výměny klíčů. V podstatě však každý účastník vytvoří určitou informaci, jejíž část je veřejně sdílena a část zůstává tajná. Každý účastník pak vezme svou tajnou část informace a veřejnou informaci sdílenou druhým účastníkem a vytvoří soukromý klíč. A poněkud zázračně obě strany nakonec získají stejný soukromý klíč.
Žádná strana, která sleduje pouze veřejně sdílené informace mezi dvěma stranami při výměně Diffie Helmannova klíče, nemůže tyto výpočty zopakovat. K tomu by potřebovala soukromé informace jedné ze stran.
Ačkoli základní verze Diffieho-Helmannovy výměny klíčů, která byla představena v článku z roku 1976, není příliš bezpečná, sofistikované verze základního protokolu se jistě používají i dnes. Nejdůležitější je, že každý protokol výměny klíčů v nejnovější verzi protokolu zabezpečení transportní vrstvy (verze 1.3) je v podstatě obohacenou verzí protokolu, který Diffie a Hellman představili v roce 1976. Protokol zabezpečení transportní vrstvy je převládajícím protokolem pro bezpečnou výměnu informací formátovaných podle hypertextového přenosového protokolu (http), který je standardem pro výměnu obsahu webu.
Důležité je, že Diffie-Helmannova výměna klíčů není asymetrické schéma. Přísně vzato patří pravděpodobně do oblasti kryptografie se symetrickým klíčem. Ale protože jak Diffieho-Helmannova výměna klíčů, tak asymetrická kryptografie se opírají o jednosměrné číselně-teoretické funkce s trapdoory, obvykle se o nich hovoří společně.
Druhým způsobem, který Diffie a Helmann ve svém článku z roku 1976 nabídli k řešení problému distribuce a správy klíčů, byla samozřejmě asymetrická kryptografie.
Na rozdíl od jejich prezentace Diffieho-Hellmanovy výměny klíčů uvedli pouze obecné obrysy toho, jak by bylo možné asymetrická kryptografická schémata pravděpodobně zkonstruovat. Nenabídli žádnou jednosměrnou funkci, která by konkrétně splňovala podmínky potřebné pro rozumnou bezpečnost takových schémat.
Praktickou implementaci asymetrického schématu však našli o rok později tři různí akademičtí kryptografové a matematici: Ronald Rivest, Adi Shamir a Leonard Adleman. [3] Kryptosystém, který představili, se stal známým jako RSA kryptosystém (podle jejich příjmení).
Funkce trapdoor používané v asymetrické kryptografii (a Diffie Helmannově výměně klíčů) souvisejí se dvěma hlavními výpočetně obtížnými problémy: faktorizací prvočísel a výpočtem diskrétních logaritmů.
Primární faktorizace vyžaduje, jak název napovídá, rozklad celého čísla na jeho prvočinitele. Problém RSA je zdaleka nejznámějším příkladem kryptosystému souvisejícího s prvočiniteli.
Problém diskrétního logaritmu je problém, který se vyskytuje v cyklických grupách. Je dán generátor v určité cyklické grupě a je třeba vypočítat jedinečný exponent potřebný k tomu, aby z generátoru vznikl další prvek v grupě.
Diskrétní logaritmická schémata se opírají o dva hlavní druhy cyklických grup: multiplikativní grupy celých čísel a grupy, které zahrnují body na eliptických křivkách. Původní Diffieho Helmannova výměna klíčů, jak byla představena v knize "Nové směry v kryptografii", pracuje s cyklickou multiplikativní grupou celých čísel. Algoritmus digitálního podpisu Bitcoinu a nedávno představené Schnorrovo podpisové schéma (2021) jsou oba založeny na problému diskrétního logaritmu pro konkrétní cyklickou grupu eliptických křivek.
Dále se zaměříme na přehled utajení a autentizace v asymetrickém prostředí. Ještě předtím však musíme učinit krátkou historickou poznámku.
Nyní se zdá být pravděpodobné, že skupina britských kryptografů a matematiků pracujících pro Vládní komunikační ústřednu (GCHQ) učinila výše uvedené objevy nezávisle na sobě o několik let dříve. Tuto skupinu tvořili James Ellis, Clifford Cocks a Malcolm Williamson.
Podle jejich vlastního vyjádření a vyjádření GCHQ to byl James Ellis, kdo v roce 1969 poprvé navrhl koncept kryptografie s veřejným klíčem. Clifford Cocks pak údajně v roce 1973 objevil kryptografický systém RSA a Malcolm Williamson v roce 1974 koncept Diffie Helmannovy výměny klíčů. [4] Jejich objevy však byly údajně odhaleny až v roce 1997, a to vzhledem k tajné povaze práce prováděné v GCHQ.
Poznámky:
[1] Whitfield Diffie a Martin Hellman, "New directions in cryptography", IEEE Transactions on Information Theory IT-22 (1976), str. 644-654, na str. 644.
[2] Ralph Merkle se také zabývá protokolem výměny klíčů v článku "Secure communications over insecure channels", Communications of the Association for Computing Machinery, 21 (1978), 294-99. Ačkoli Merkle tento článek ve skutečnosti předložil ještě před článkem Diffieho a Hellmana, byl publikován později. Merkleho řešení není na rozdíl od Diffieho-Hellmanova řešení exponenciálně bezpečné.
[3] Ron Rivest, Adi Shamir a Leonard Adleman, "A method for obtaining digital signatures and public-key cryptosystems", Communications of the Association for Computing Machinery, 21 (1978), s. 120-26.
[4] Dobrou historii těchto objevů podává Simon Singh, The Code Book, Fourth Estate (London, 1999), kapitola 6.
Asymetrické šifrování a ověřování
Přehled asymetrického šifrování pomocí Boba a Alice je uveden na obrázku 1.
Alice nejprve vytvoří dvojici klíčů, která se skládá z jednoho veřejného
klíče (K_P) a jednoho
soukromého klíče (K_S), kde
"P" ve slově K_P znamená
"veřejný" a "S" ve slově K_S znamená "tajný". Tento veřejný klíč pak volně šíří mezi ostatní. K
podrobnostem tohoto distribučního procesu se vrátíme o něco později.
Prozatím však předpokládejme, že kdokoli, včetně Boba, může bezpečně získat
Alicin veřejný klíč K_P.
Později chce Bob napsat Alici zprávu M. Protože obsahuje citlivé informace, chce, aby její obsah zůstal tajný pro
všechny kromě Alice. Bob tedy nejprve zašifruje svou zprávu M pomocí K_P. Výsledný
šifrovaný text C pak pošle
Alici, která dešifruje C pomocí K_S a získá původní
zprávu M.
Obrázek 1: Asymetrické šifrování
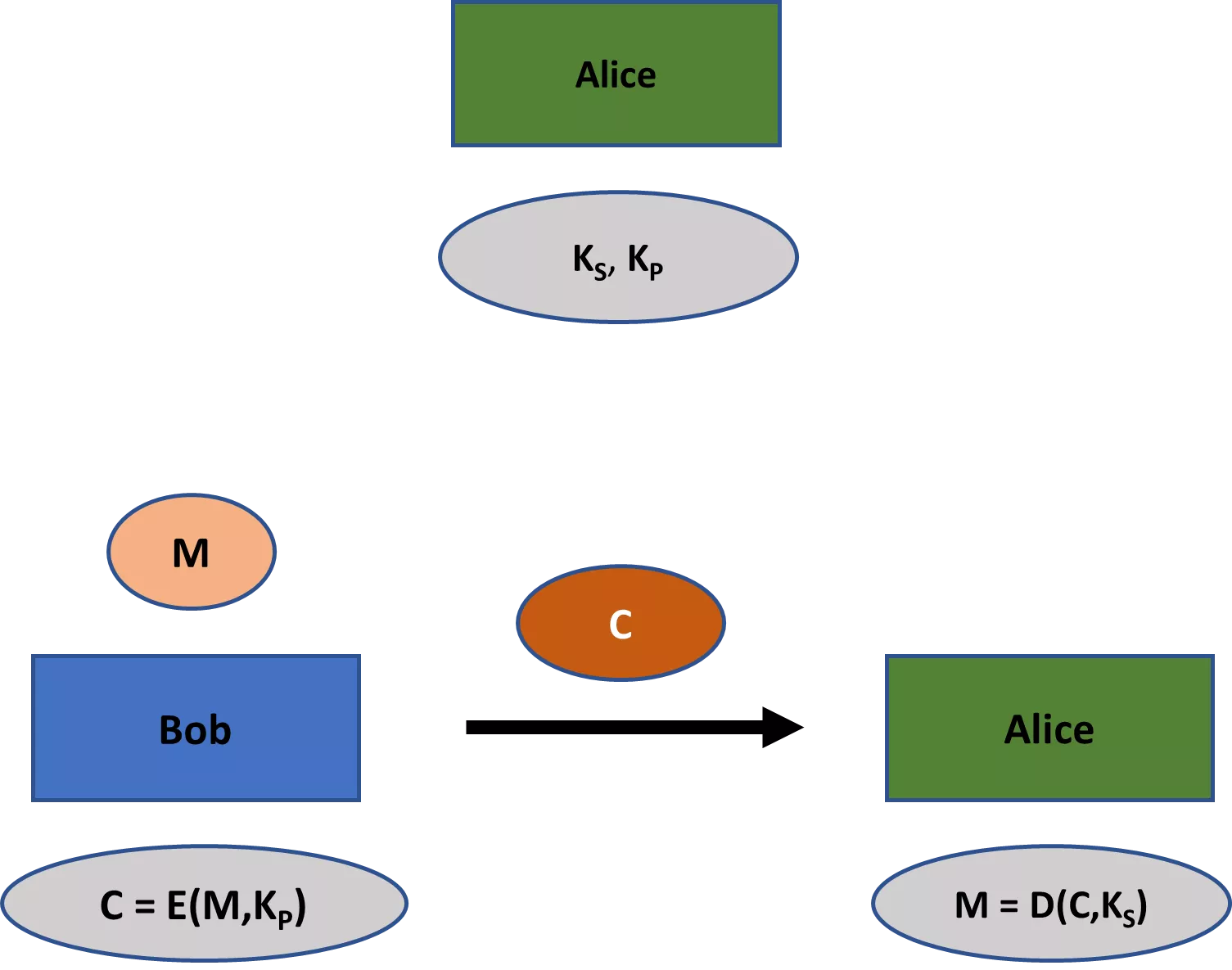
Každý protivník, který odposlouchává komunikaci Boba aAlice, může pozorovat C. Zná také K_P a šifrovací
algoritmus E(\cdot). Důležité
však je, že tyto informace neumožňují útočníkovi dešifrovat šifrový text C. Dešifrování vyžaduje
konkrétně K_S, které útočník
nemá.
Symetrická šifrovací schémata musí být obecně zabezpečena proti útočníkovi, který může platně zašifrovat zprávy s otevřeným textem (tzv. zabezpečení proti útoku vybraným šifrovaným textem). Není však navržena s výslovným cílem umožnit vytvoření takových platných šifrových textů útočníkem nebo kýmkoli jiným.
To je v příkrém rozporu s asymetrickým šifrovacím schématem, jehož smyslem je umožnit komukoli, včetně útočníků, vytvořit platné šifrové texty. Asymetrická šifrovací schémata lze proto označit jako šifry s vícenásobným přístupem.
Abychom lépe pochopili, co se děje, představme si, že by Bob místo elektronické zprávy chtěl poslat tajný fyzický dopis. Jedním ze způsobů, jak zajistit utajení, by bylo, kdyby Alice poslala Bobovi zabezpečený visací zámek, ale klíč k jeho odemčení by si ponechala. Po napsání dopisu by Bob mohl dopis vložit do schránky a uzavřít ji Aliciným visacím zámkem. Poté by mohl uzamčenou schránku se zprávou poslat Alici, která má klíč k jejímu odemčení.
Bob je sice schopen visací zámek zamknout, ale ani on, ani žádná jiná osoba, která schránku zachytí, nemůže visací zámek odemknout, pokud je skutečně zabezpečený. Odemknout jej a prohlédnout si obsah Bobova dopisu může pouze Alice, protože má klíč.
Asymetrické šifrovací schéma je zhruba řečeno digitální verzí tohoto procesu. Visací zámek je podobný veřejnému klíči a klíč visacího zámku je podobný soukromému klíči. Protože je však visací zámek digitální, je pro Alici mnohem snazší a ne tak nákladné jej distribuovat komukoli, kdo by jí chtěl posílat tajné zprávy.
Pro ověřování v asymetrickém prostředí používáme digitální podpisy. Ty tedy mají stejnou funkci jako kódy pro ověřování zpráv v symetrickém prostředí. Přehled digitálních podpisů je uveden na obrázku 2.
Bob nejprve vytvoří dvojici klíčů, která se skládá z veřejného klíče (K_P) a soukromého klíče (K_S),
a rozešle svůj veřejný klíč. Když chce poslat ověřenou zprávu Alici, vezme
nejprve svou zprávu M a svůj
soukromý klíč a vytvoří digitální podpis D. Bob pak pošle Alici svou
zprávu spolu s digitálním podpisem.
Alice vloží zprávu, veřejný klíč a digitální podpis do ověřovacího algoritmu. Výsledkem tohoto algoritmu je buď pravdivý platný podpis, nebo nepravdivý neplatný podpis.
Digitální podpis je, jak už název jasně napovídá, digitální obdobou písemného podpisu na dopisech, smlouvách apod. Ve skutečnosti je digitální podpis obvykle mnohem bezpečnější. S jistým úsilím lze zfalšovat i písemný podpis; tento proces je usnadněn tím, že písemné podpisy často nejsou důkladně ověřovány. Bezpečný digitální podpis je však, stejně jako bezpečný kód pro ověřování zpráv, existenčně nezfalšovatelný: to znamená, že u schématu bezpečného digitálního podpisu nemůže nikdo reálně vytvořit podpis pro zprávu, která projde ověřovacím postupem, pokud nemá soukromý klíč.
Obrázek 2: Asymetrické ověřování
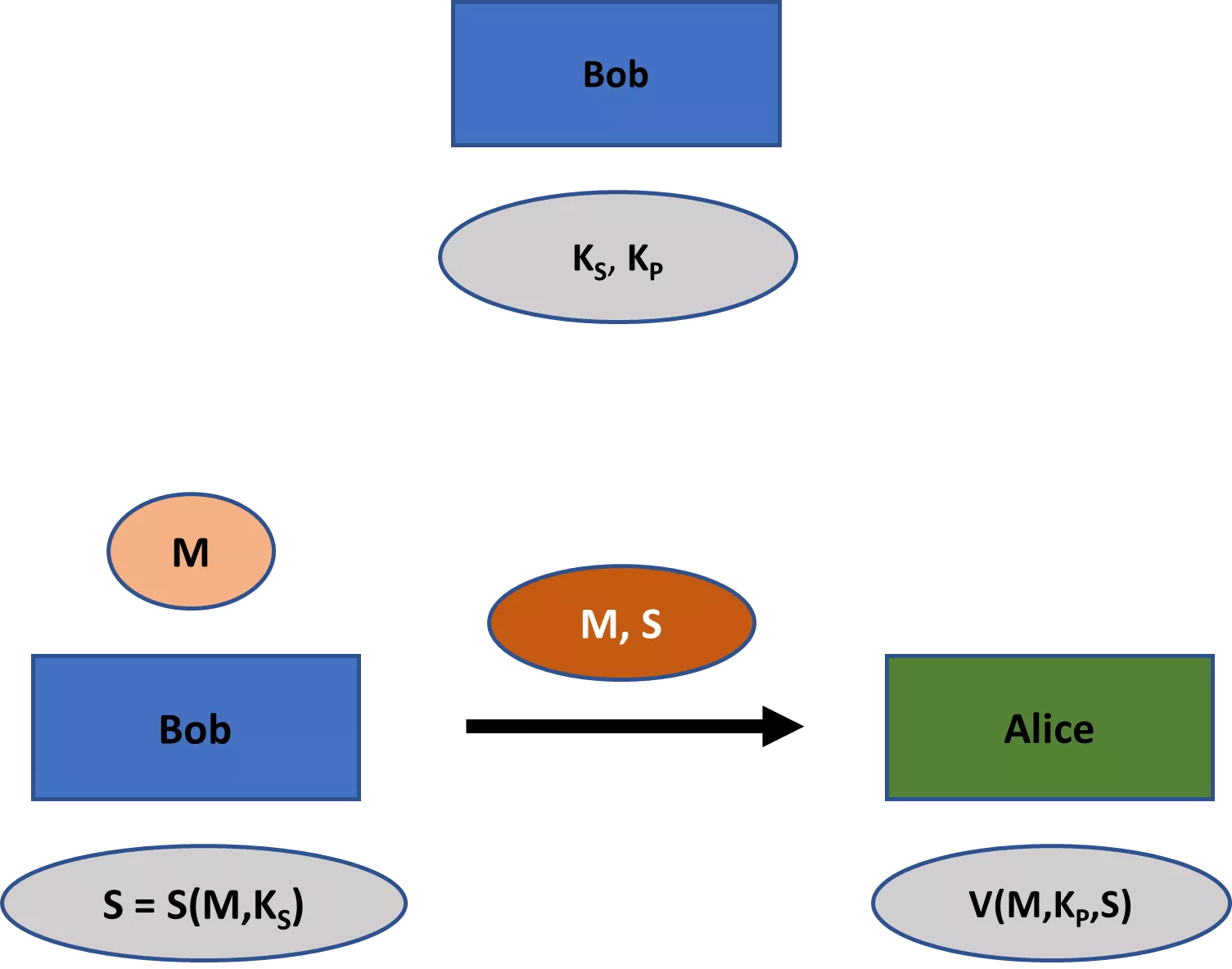
Stejně jako u asymetrického šifrování vidíme zajímavý kontrast mezi
digitálními podpisy a kódy pro ověřování zpráv. V druhém případě může
ověřovací algoritmus použít pouze jedna ze stran, která je do zabezpečené
komunikace zasvěcena. To proto, že vyžaduje soukromý klíč. V asymetrickém
nastavení však může digitální podpis S vytvořený Bobem ověřit kdokoli.
To vše dělá z digitálních podpisů mimořádně mocný nástroj. Tvoří například
základ pro vytváření podpisů na smlouvách, které lze ověřit pro právní
účely. Pokud by Bob ve výše uvedené výměně vytvořil podpis na smlouvě, může
Alice soudu ukázat zprávu M,
smlouvu a podpis S. Soud pak
může podpis ověřit pomocí Bobova veřejného klíče. [5]
Dalším příkladem jsou digitální podpisy, které jsou důležitým aspektem bezpečné distribuce softwaru a aktualizací softwaru. Tento typ veřejné ověřitelnosti nelze nikdy vytvořit pouze pomocí kódů pro ověřování zpráv.
Jako poslední příklad síly digitálních podpisů uveďme Bitcoin. Jednou z nejčastějších mylných představ o Bitcoinu, zejména v médiích, je, že transakce jsou šifrované: nejsou. Místo toho transakce v Bitcoinech pracují s digitálními podpisy pro zajištění bezpečnosti.
Bitcoiny existují v dávkách, které se nazývají nespotřebované transakční výstupy (neboli UTXO). Předpokládejme, že na určitou bitcoinovou adresu obdržíte tři platby po 2 bitcoinech. Technicky vzato nyní nemáte na této adrese 6 bitcoinů. Místo toho máte tři dávky po 2 bitcoinech, které jsou uzamčeny kryptografickým problémem spojeným s touto adresou. Pro jakoukoli platbu, kterou provedete, můžete použít jednu, dvě nebo všechny tři tyto dávky, podle toho, kolik pro danou transakci potřebujete.
Důkaz vlastnictví nad nevyčerpanými výstupy transakcí se obvykle prokazuje jedním nebo více digitálními podpisy. Bitcoin funguje právě proto, že platné digitální podpisy na nespotřebovaných výstupech transakcí je výpočetně nemožné vytvořit, pokud nevlastníte tajné informace potřebné k jejich vytvoření.
V současné době transakce Bitcoinu transparentně obsahují všechny informace, které musí být ověřeny účastníky sítě, jako je původ nespotřebovaných výstupů transakcí použitých v transakci. Některé z těchto informací je sice možné skrýt, a přesto umožnit jejich ověření (jak to dělají některé alternativní kryptoměny, například Monero), to však zároveň vytváří určitá bezpečnostní rizika.
Někdy dochází k záměně digitálních podpisů a písemných podpisů zachycených digitálně. V druhém případě zachytíte obrázek svého písemného podpisu a vložíte jej do elektronického dokumentu, např. pracovní smlouvy. To však není digitální podpis v kryptografickém smyslu. Ten je pouze dlouhým číslem, které lze vytvořit pouze tehdy, pokud vlastníte soukromý klíč.
Stejně jako v případě symetrického klíče můžete použít i asymetrické šifrování a ověřování společně. Platí zde podobné principy. Především byste měli používat různé páry soukromých a veřejných klíčů pro šifrování a vytváření digitálních podpisů. Kromě toho byste měli zprávu nejprve zašifrovat a poté ji ověřit.
Důležité je, že v mnoha aplikacích se asymetrická kryptografie nepoužívá v celém procesu komunikace. Místo toho se obvykle používá pouze k výměně symetrických klíčů mezi stranami, které spolu budou skutečně komunikovat.
Tak je tomu například při nákupu zboží online. Když znáte veřejný klíč prodejce, může vám posílat digitálně podepsané zprávy, jejichž pravost si můžete ověřit. Na tomto základě můžete pro bezpečnou komunikaci použít jeden z několika protokolů pro výměnu symetrických klíčů.
Hlavním důvodem četnosti výše uvedeného přístupu je skutečnost, že asymetrická kryptografie je při vytváření určité úrovně bezpečnosti mnohem méně účinná než symetrická kryptografie. To je jeden z důvodů, proč vedle veřejné kryptografie stále potřebujeme kryptografii se symetrickým klíčem. Kromě toho je kryptografie se symetrickým klíčem mnohem přirozenější v konkrétních aplikacích, například když uživatel počítače šifruje svá vlastní data.
Jak přesně tedy digitální podpisy a šifrování s veřejným klíčem řeší problémy s distribucí a správou klíčů?
Neexistuje jediná odpověď. Asymetrická kryptografie je nástroj a neexistuje jediný způsob, jak tento nástroj použít. Vezměme si však náš dřívější příklad z Jim's Sporting Goods, abychom si ukázali, jak by se v tomto příkladu typicky řešily problémy.
Pro začátek by se společnost Jim's Sporting Goods pravděpodobně obrátila na certifikační autoritu, organizaci, která podporuje distribuci veřejných klíčů. Certifikační autorita by zaregistrovala některé údaje o společnosti Jim's Sporting Goods a udělila by jí veřejný klíč. Poté by společnosti Jim's Sporting Goods zaslala certifikát, známý jako TLS/SSL certifikát, s veřejným klíčem společnosti Jim's Sporting Goods digitálně podepsaným pomocí vlastního veřejného klíče certifikační autority. Tímto způsobem certifikační autorita potvrdí, že konkrétní veřejný klíč skutečně patří společnosti Jim's Sporting Goods.
Klíčem k pochopení tohoto procesu u certifikátů TLS/SSL je skutečnost, že ačkoli veřejný klíč společnosti Jim's Sporting Goods zpravidla nemáte uložen nikde ve svém počítači, veřejné klíče uznávaných certifikačních autorit jsou skutečně uloženy ve vašem prohlížeči nebo v operačním systému. Jsou uloženy v takzvaných kořenových certifikátech.
Pokud vám tedy společnost Jim's Sporting Goods poskytne svůj certifikát TLS/SSL, můžete si digitální podpis certifikační autority ověřit prostřednictvím kořenového certifikátu v prohlížeči nebo operačním systému. Pokud je podpis platný, můžete si být relativně jisti, že veřejný klíč v certifikátu skutečně patří společnosti Jim's Sporting Goods. Na tomto základě lze snadno nastavit protokol pro bezpečnou komunikaci se společností Jim's Sporting Goods.
Distribuce klíčů je nyní pro společnost Jim's Sporting Goods mnohem jednodušší. Není těžké si všimnout, že se výrazně zjednodušila i správa klíčů. Namísto ukládání tisíců klíčů stačí společnosti Jim's Sporting Goods ukládat pouze soukromý klíč, který jí umožňuje vytvářet podpisy pro veřejný klíč na jejím certifikátu SSL. Pokaždé, když zákazník přijde na stránky společnosti Jim's Sporting Goods, může z tohoto veřejného klíče navázat zabezpečenou komunikační relaci. Zákazníci také nemusí ukládat žádné informace (kromě veřejných klíčů uznávaných certifikačních autorit ve svém operačním systému a prohlížeči).
Poznámky:
[5] Jakékoli schéma, které se snaží dosáhnout nepopiratelnosti, což je další téma, které jsme probírali v kapitole 1, bude muset ve svém základu zahrnovat digitální podpisy.
Funkce Hash
Hašovací funkce jsou v kryptografii všudypřítomné. Nejsou ani symetrickými, ani asymetrickými schématy, ale patří do samostatné kryptografické kategorie.
S hashovacími funkcemi jsme se již setkali v kapitole 4 při vytváření autentizačních zpráv založených na hashování. Jsou důležité i v souvislosti s digitálními podpisy, i když z trochu jiného důvodu: Digitální podpisy se totiž obvykle vytvářejí nad hodnotou hashe nějaké (zašifrované) zprávy, nikoli nad skutečnou (zašifrovanou) zprávou. V této části nabídnu důkladnější úvod do hashovacích funkcí.
Začněme definicí hashovací funkce. Hašovací funkce** je jakákoli efektivně vypočitatelná funkce, která přijímá vstupy libovolné velikosti a dává výstupy pevné délky.
Kryptografická hashovací funkce je pouze hashovací funkce, která je užitečná pro aplikace v kryptografii. Výstup kryptografické hashovací funkce se obvykle nazývá hash, hash-value nebo message digest.
V kontextu kryptografie se "hashovací funkcí" obvykle rozumí kryptografická hashovací funkce. Od této chvíle se budu řídit touto praxí.
Příkladem oblíbené hašovací funkce je SHA-256 (secure hash algorithm 256). Bez ohledu na velikost vstupu (např. 15 bitů, 100 bitů nebo 10 000 bitů) poskytne tato funkce 256bitovou hodnotu hash. Níže si můžete prohlédnout několik příkladů výstupů funkce SHA-256.
"Dobrý den": 185f8db32271fe25f561a6fc938b2e264306ec304eda518007d1764826381969
"52398": a3b14d2bf378c1bd47e7f8eaec63b445150a3d7a80465af16dd9fd319454ba90
"Kryptografie je zábava": 3cee2a5c7d2cc1d62db4893564c34ae553cc88623992d994e114e344359b146c
Všechny výstupy jsou přesně 256 bitů zapsaných v hexadecimálním formátu (každou hexadecimální číslici lze reprezentovat čtyřmi binárními číslicemi). Takže i kdybyste do funkce SHA-256 vložili Tolkienovu knihu Pán prstenů, výstup by byl stále 256 bitů.
Hašovací funkce, jako je SHA-256, se používají k různým účelům v kryptografii. Které vlastnosti jsou od hašovací funkce vyžadovány, závisí na kontextu konkrétní aplikace. V kryptografii jsou obecně požadovány dvě hlavní vlastnosti hashovacích funkcí: [6]
Odolnost proti nárazu
Skrývání
O hašovací funkci H se říká,
že je odolná proti kolizi, jestliže je nemožné najít dvě
hodnoty x a y tak, aby x \neq y, ale H(x) = H(y).
Hashovací funkce odolné proti kolizím jsou důležité například při ověřování softwaru. Předpokládejme, že si chcete stáhnout verzi Bitcoin Core 0.21.0 (serverová aplikace pro zpracování síťového provozu Bitcoinu) pro systém Windows. Hlavní kroky, které byste museli provést, abyste ověřili legitimitu softwaru, jsou následující:
Nejprve je třeba stáhnout a importovat veřejné klíče jednoho nebo více přispěvatelů Bitcoin Core do softwaru, který umí ověřovat digitální podpisy (např. Kleopetra). Tyto veřejné klíče najdete zde. Doporučujeme ověřit software Bitcoin Core pomocí veřejných klíčů od více přispěvatelů.
Dále je třeba ověřit importované veřejné klíče. Alespoň jedním z kroků, které byste měli udělat, je ověřit, že nalezené veřejné klíče jsou stejné jako ty, které jsou zveřejněny na různých jiných místech. Můžete se například podívat na osobní webové stránky, stránky Twitteru nebo Githubu lidí, jejichž veřejné klíče jste importovali. Obvykle se toto porovnání veřejných klíčů provádí porovnáním krátkého hashe veřejného klíče známého jako otisk prstu.
Dále je třeba stáhnout spustitelný soubor pro jádro bitcoinu z jejich webové stránky. K dispozici budou balíčky pro operační systémy Linux, Windows a MAC.
Dále je třeba vyhledat dva soubory pro vydání. První z nich obsahuje oficiální hash SHA-256 pro stažený spustitelný soubor spolu s hashi všech ostatních vydaných balíčků. Druhý soubor s vydáním bude obsahovat podpisy různých přispěvatelů nad souborem s vydáním spolu s hashi balíčků. Oba tyto soubory vydání by měly být umístěny na webových stránkách Bitcoin Core.
Dále je třeba vypočítat hash SHA-256 spustitelného souboru staženého z webu Bitcoin Core na vlastním počítači. Tento výsledek pak porovnáte s hashem oficiálního balíčku pro daný spustitelný soubor. Měly by se shodovat.
Nakonec byste museli ověřit, zda jeden nebo více digitálních podpisů nad souborem s oficiálními hashi balíčků skutečně odpovídá jednomu nebo více importovaným veřejným klíčům (vydání jádra Bitcoin nejsou vždy podepsána všemi). To můžete provést pomocí aplikace, jako je Kleopetra.
Tento proces ověřování softwaru má dvě hlavní výhody. Zaprvé zajišťuje, že při stahování z webových stránek Bitcoin Core nedošlo k chybám v přenosu. Zadruhé zajišťuje, že vás žádný útočník nemohl přimět ke stažení upraveného, škodlivého kódu, ať už hacknutím webových stránek Bitcoin Core, nebo zachycením provozu.
Jak přesně výše uvedený proces ověřování softwaru chrání před těmito problémy?
Pokud jste pečlivě ověřili importované veřejné klíče, můžete si být jisti, že tyto klíče jsou skutečně jejich a nebyly kompromitovány. Vzhledem k tomu, že digitální podpisy mají existenční nezfalšovatelnost, víte, že pouze tito přispěvatelé mohli vytvořit digitální podpis nad oficiálními hashi balíčku v souboru s vydáním.
Předpokládejme, že podpisy na staženém souboru s verzí jsou správné. Nyní můžete porovnat hodnotu hash, kterou jste vypočítali lokálně pro stažený spustitelný soubor systému Windows, s hodnotou obsaženou ve správně podepsaném souboru vydání. Jak víte, hashovací funkce SHA-256 je odolná proti kolizím, shoda znamená, že váš spustitelný soubor je přesně stejný jako oficiální spustitelný soubor.
Přejděme nyní k druhé společné vlastnosti hashovacích funkcí: skrývání. O jakékoli hašovací funkci H se říká, že má vlastnost skrývání, jestliže pro libovolné náhodně vybrané x z velmi velkého rozsahu je nemožné najít x, pokud je dáno pouze H(x).
Níže vidíte výstup SHA-256 zprávy, kterou jsem napsal. Aby byla zajištěna dostatečná náhodnost, obsahovala zpráva na konci náhodně vygenerovaný řetězec znaků. Vzhledem k tomu, že SHA-256 má vlastnost skrývání, nikdo by tuto zprávu nedokázal rozluštit.
b194221b37fa4cd1cfce15aaef90351d70de17a98ee6225088b523b586c32ded
Ale nenechám vás v napětí, dokud SHA-256 nebude slabší. Původní zpráva, kterou jsem napsal, byla následující:
- "Tohle je velmi náhodná zpráva, nebo spíš tak trochu náhodná. Tato počáteční část není, ale ukončím ji několika relativně náhodnými znaky, abych zajistil velmi nepředvídatelnou zprávu. XLWz4dVG3BxUWm7zQ9qS".
Běžným způsobem, jak se hashovací funkce s vlastností skrývání používají, je správa hesel (pro tuto aplikaci je důležitá také odolnost proti kolizím). Každá slušná online služba založená na účtu, jako je Facebook nebo Google, neukládá hesla přímo pro správu přístupu k účtu. Místo toho ukládají pouze hash tohoto hesla. Při každém vyplnění hesla v prohlížeči se nejprve vypočítá hash. Teprve tento hash je odeslán na server poskytovatele služby a porovnán s hashem uloženým v koncové databázi. Vlastnost skrývání může pomoci zajistit, aby útočníci nemohli z hodnoty hash obnovit.
Správa hesel pomocí hashů samozřejmě funguje pouze tehdy, pokud si uživatelé skutečně vybírají složitá hesla. Vlastnost skrývání předpokládá, že x je vybráno náhodně z velmi širokého rozsahu. Výběr hesel jako "1234", "mypassword" nebo datum narozenin nezajistí žádnou skutečnou bezpečnost. Existují dlouhé seznamy běžných hesel a jejich hashů, které mohou útočníci využít, pokud někdy získají hash vašeho hesla. Tyto typy útoků se označují jako slovníkové útoky. Pokud útočníci znají některé vaše osobní údaje, mohou se také pokusit o informovaný odhad. Proto vždy potřebujete dlouhá a bezpečná hesla (nejlépe dlouhé náhodné řetězce ze správce hesel).
Někdy může aplikace potřebovat hašovací funkci, která je odolná proti kolizím i proti skrývání. Ale určitě ne vždy. Například proces ověřování softwaru, o kterém jsme hovořili, vyžaduje pouze to, aby hašovací funkce vykazovala odolnost proti kolizím, skrývání není důležité.
Zatímco odolnost proti kolizím a skrývání jsou hlavními vlastnostmi, které se u hašovacích funkcí v kryptografii hledají, v některých aplikacích mohou být žádoucí i jiné typy vlastností.
Poznámky:
[6] Terminologie "skrývání" není běžná, ale je převzata z knihy Arvind Narayanan, Joseph Bonneau, Edward Felten, Andrew Miller a Steven Goldfeder, Bitcoin and Cryptocurrency Technologies, Princeton University Press (Princeton, 2016), kapitola 1.
Kryptosystém RSA
Problém faktoringu
Zatímco symetrická kryptografie je pro většinu lidí obvykle poměrně intuitivní, u asymetrické kryptografie tomu tak není. Ačkoli vám pravděpodobně vyhovuje popis na vysoké úrovni, který jsme vám nabídli v předchozích částech, pravděpodobně vás zajímá, co přesně jsou jednosměrné funkce a jak přesně se používají při konstrukci asymetrických schémat.
V této kapitole se pokusím odstranit část tajemství, které obklopuje asymetrickou kryptografii, a to tím, že se budu hlouběji zabývat konkrétním příkladem, konkrétně kryptosystémem RSA. V první části představím problém faktorizace, na němž je problém RSA založen. Poté se budu zabývat řadou klíčových výsledků z teorie čísel. V posledním oddíle dáme tyto informace dohromady a vysvětlíme si problém RSA a způsob, jak jej lze využít při vytváření asymetrických kryptografických schémat.
Přidat tuto hloubku do naší diskuse není snadné. Vyžaduje to zavedení poměrně velkého počtu teoretických tvrzení a propozic. Nenechte se však odradit matematikou. Práce na této diskusi výrazně zlepší vaše chápání toho, co je základem asymetrické kryptografie, a je to investice, která se vyplatí.
Nyní se nejprve věnujme problému faktoringu.
Kdykoli násobíte dvě čísla, například a a b, označujeme čísla a a b jako faktory a výsledek jako součin. Pokus o zápis čísla N do součinu dvou nebo více činitelů se nazývá faktorizace nebo faktorizace. [1] Každou úlohu, která to vyžaduje,
můžete nazvat faktorizační úlohou.
Přibližně před 2 500 lety objevil řecký matematik Euklides z Alexandrie klíčovou větu o faktorizaci celých čísel. Běžně se nazývá jediná věta o faktorizaci a říká následující:
Věta 1. Každé celé číslo N, které je větší než 1, je
buď prvočíslo, nebo je lze vyjádřit jako součin prvočinitelů.
Jediné, co druhá část tohoto tvrzení znamená, je, že můžete vzít libovolné
celé číslo, které není prvočíslo N větší než 1, a zapsat ho jako násobení prvočísel. Níže uvádíme několik příkladů
celých čísel, která nejsou prvočísla, zapsaných jako součin prvočinitelů.
18 = 2 \cdot 3 \cdot 3 = 2 \cdot 3^284 = 2 \cdot 2 \cdot 3 \cdot 7 = 2^2 \cdot 3 \cdot 7144 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 = 2^4 \cdot 3^2
U všech tří výše uvedených celých čísel je výpočet jejich prvočinitelů
poměrně snadný, i když máte k dispozici pouze N. Začněte nejmenším prvočíslem, tedy 2, a zjistěte, kolikrát je jím celé
číslo N dělitelné. Poté
přejdete k testování dělitelnosti N čísly 3, 5, 7 atd. V tomto postupu pokračujete, dokud vaše celé číslo N není zapsáno jako součin pouze
prvočísel.
Vezměme si například celé číslo 84. Níže vidíte postup pro určení jeho prvočinitelů. V každém kroku vyjmeme nejmenší zbývající prvočinitel (vlevo) a určíme zbytkový člen, který je třeba vynásobit. Pokračujeme tak dlouho, dokud zbytkový člen není také prvočíslo. V každém kroku se vpravo zobrazí aktuální faktorizace čísla 84.
- Prvočinitel = 2: zbytkový člen = 42 (
84 = 2 \cdot 42) - Prvočinitel = 2: zbytkový člen = 21 (
84 = 2 \cdot 2 \cdot 21) - Prvočinitel = 3: zbytkový člen = 7 (
84 = 2 \cdot 2 \cdot 3 \cdot 7) - Protože 7 je prvočíslo, výsledek je
2 \cdot 2 \cdot 3 \cdot 7nebo2^2 \cdot 3 \cdot 7.
Předpokládejme nyní, že N je
velmi velké. Jak obtížné by bylo redukovat N na jeho prvočinitele?
To skutečně závisí na N.
Předpokládejme například, že N je 50 450 400. I když toto číslo
vypadá hrozivě, výpočty nejsou tak složité a lze je snadno provést ručně. Stejně
jako výše stačí začít od čísla 2 a postupovat dále. Níže si můžete prohlédnout
výsledek tohoto postupu podobným způsobem jako výše.
- 2:
25,225,200(50,450,400 =2 \cdot 25,225,200USD) - 2:
12,612,600(50,450,400 =2^2 \cdot 12,612,600) - 2:
6,306,300(50,450,400 =2^3 \cdot 6,306,300) - 2:
3,153,150(50,450,400 =2^4 \cdot 3,153,150) - 2:
1,576,575(50,450,400 =2^5 \cdot 1,576,575) - 3:
525,525(50,450,400 =2^5 \cdot 3 \cdot 525,525) - 3:
175,175(50,450,400 =2^5 \cdot 3^2 \cdot 175,175) - 5:
35,035(50,450,400 =2^5 \cdot 3^2 \cdot 5 \cdot 35,035) - 5:
7,007(50,450,400 =2^5 \cdot 3^2 \cdot 5^2 \cdot 7,007) - 7:
1,001(50,450,400 =2^5 \cdot 3^2 \cdot 5^2 \cdot 7 \cdot 1,001) - 7:
143(50,450,400 =2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 143) - 11:
13(50,450,400 =2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13) - Protože 13 je prvočíslo, výsledek je
2^5 \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11 \cdot 13.
Ruční řešení tohoto problému zabere nějaký čas. Počítač to samozřejmě zvládne za zlomek sekundy. Ve skutečnosti počítač často dokáže faktorizovat i extrémně velká celá čísla za zlomek sekundy.
Existují však určité výjimky. Předpokládejme, že nejprve náhodně vybereme
dvě velmi velká prvočísla. Je typické označovat je p a q a tuto konvenci zde převezmu.
Pro konkrétnost řekněme, že p a q jsou 1024bitová prvočísla
a že k jejich reprezentaci je skutečně potřeba alespoň 1024 bitů (první bit
tedy musí být 1). Takže například číslo 37 nemůže být jedním z prvočísel.
Určitě lze 37 reprezentovat pomocí 1024 bitů. Ale je zřejmé, že k jeho reprezentaci nepotřebujete tolik bitů. Číslo 37 můžete reprezentovat libovolným řetězcem, který má 6
nebo více bitů. (V 6 bitech by 37 bylo reprezentováno jako 100101).
Je důležité si uvědomit, jak velké jsou p a q, pokud jsou zvoleny za
výše uvedených podmínek. Jako příklad jsem vybral náhodné prvočíslo, které
potřebuje pro reprezentaci níže alespoň 1024 bitů.
- 14,752,173,874,503,595,484,930,006,383,670,759,559,764,562,721,397,166,747,289,220,945,457,932,666,751,048,198,854,920,097,085,690,793,755,254,946,188,163,753,506,778,089,706,699,671,722,089,715,624,760,049,594,106,189,662,669,156,149,028,900,805,928,183,585,427,782,974,951,355,515,394,807,209,836,870,484,558,332,897,443,152,653,214,483,870,992,618,171,825,921,582,253,023,974,514,209,142,520,026,807,636,589
Předpokládejme, že po náhodném výběru prvočísel p a q je vynásobíme a získáme
celé číslo N. Toto poslední
celé číslo je tedy 2048bitové číslo, které pro svou reprezentaci potřebuje
alespoň 2048 bitů. Je mnohem, mnohem větší než p nebo q.
Předpokládejme, že počítači zadáte pouze N a požádáte ho, aby našel dva 1024bitové prvočinitele N. Pravděpodobnost, že
počítač objeví p a q, je extrémně malá. Lze
říci, že je to pro všechny praktické účely nemožné. Je tomu tak, i kdybyste
použili superpočítač nebo dokonce síť superpočítačů.
Pro začátek předpokládejme, že se počítač pokusí vyřešit problém tak, že
prochází 1024 bitových čísel a v každém případě testuje, zda jsou prvočísla
a zda jsou činiteli N.
Množina testovaných prvočísel je pak přibližně 1,265 \cdot 10^{305}. [2]
I kdybyste vzali všechny počítače na planetě a nechali je tímto způsobem
najít a otestovat 1024bitová prvočísla, šance 1 ku miliardě na úspěšné
nalezení prvočinitele N by vyžadovala
dobu výpočtu mnohem delší, než je stáří vesmíru.
V praxi si počítač poradí lépe než s právě popsaným hrubým postupem. Existuje několik algoritmů, které může počítač použít k rychlejšímu dosažení faktorizace. Jde však o to, že i při použití těchto efektivnějších algoritmů je úloha počítače stále výpočetně nesplnitelná. [3]
Důležité je, že obtížnost faktorizace za právě popsaných podmínek vychází z předpokladu, že neexistují žádné výpočetně efektivní algoritmy pro výpočet prvočinitelů. Ve skutečnosti nemůžeme dokázat, že efektivní algoritmus neexistuje. Nicméně tento předpoklad je velmi pravděpodobný: navzdory rozsáhlému úsilí trvajícímu stovky let jsme takový výpočetně efektivní algoritmus dosud nenašli.
Proto lze za určitých okolností předpokládat, že problém faktorizace je
těžký problém. Konkrétně, když p a q jsou velmi velká
prvočísla, jejich součin N není obtížné vypočítat; ale faktorizace pouze za předpokladu N je prakticky nemožná.
Poznámky:
[1] Faktorizace může být důležitá i pro práci s jinými typy matematických
objektů, než jsou čísla. Může být například užitečná pro faktorizaci
polynomických výrazů, jako je x^2 - 2x + 1. V naší diskusi se zaměříme pouze na faktorizaci čísel, konkrétně celých
čísel.
[2] Podle věty o prvočíslech je počet prvočísel menších
nebo rovných N přibližně N/\ln(N). To znamená, že
počet prvočísel o délce 1024 bitů lze přibližně určit takto:
\frac{2^{1024}}{\ln(2^{1024})} -
\frac{2^{1023}}{\ln(2^{1023})}
...což je přibližně 1,265 \krát 10^{305}$.
[3] Totéž platí pro úlohy diskrétního logaritmu. Proto asymetrické konstrukce pracují s mnohem většími klíči než symetrické kryptografické konstrukce.
Výsledky teorie čísel
Problém faktoringu bohužel nelze přímo použít pro asymetrická kryptografická schémata. Můžeme však k tomuto účelu použít složitější, ale příbuzný problém: problém RSA.
Abychom pochopili problém RSA, musíme porozumět řadě tvrzení a výroků z teorie čísel. Ty jsou v této části uvedeny ve třech podkapitolách: (1) řád N, (2) invertibilita modulo N a (3) Eulerova věta.
Některé materiály v těchto třech podkapitolách již byly představeny v Kapitole 3. Zde však tento materiál pro větší pohodlí zopakuji.
Pořadí N
Celé číslo a je prvočíslem nebo relativním prvočíslem s celým číslem N, pokud je jejich největší
společný dělitel roven 1. I když 1 není podle konvence prvočíslo, je
prvočíslem každého celého čísla (stejně jako -1).
Uvažujme například případ, kdy a = 18 a N = 37. To jsou jednoznačně
koprimena. Největší celé číslo, které se dělí jak 18, tak 37, je 1. Naproti
tomu uvažujme případ, kdy a = 42 a N = 16. Je zřejmé, že se
nejedná o koprimata. Obě čísla jsou dělitelná číslem 2, které je větší než
1.
Nyní můžeme definovat pořadí N takto. Předpokládejme, že N je celé číslo větší než 1. Řád N je tedy počet všech
koprimátů s N takový, že pro
každý koprimát a platí
následující podmínka: 1 \leq a < N.
Například pokud N = 12, pak
1, 5, 7 a 11 jsou jediná koprimena, která splňují výše uvedený požadavek.
Řád 12 je tedy roven 4.
Předpokládejme, že N je
prvočíslo. Pak každé celé číslo menší než N, ale větší nebo rovno 1, je
jeho koprimátem. To zahrnuje všechny prvky následující množiny: \{1,2,3,....,N - 1\}. Je-li tedy N prvočíslo, je
řád N roven N - 1. To je uvedeno ve větě
1, kde \phi(N) označuje řád N.
Návrh 1. \phi(N) = N - 1, když N je prvočíslo
Předpokládejme, že N není
prvočíslo. Pak můžete vypočítat jeho řád pomocí Eulerovy funkce Phi. Zatímco výpočet řádu malého celého
čísla je poměrně jednoduchý, Eulerova funkce Phi nabývá na významu zejména u
větších celých čísel. Věta o Eulerově funkci Phi je uvedena níže.
Věta 2. Nechť N je rovno p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot
p_i^{e_i} \cdot \ldots \cdot p_n^{e_n}, kde množina \{p_i\} obsahuje všechny různé prvočinitele N a každé e_i udává, kolikrát
se prvočinitel p_i vyskytuje
pro N. Potom,
\phi(N) = p_1^{e_1 - 1} \cdot (p_1 - 1) \cdot p_2^{e_2 -
1} \cdot (p_2 - 1) \cdot \ldots \cdot p_n^{e_n - 1} \cdot
(p_n - 1)
Věta 2 ukazuje, že po rozkladu libovolného neprimárního
čísla N na jeho jednotlivé
prvočinitele lze snadno vypočítat pořadí N.
Předpokládejme například, že N = 270. To zjevně není prvočíslo. Rozložením N na prvočinitele získáme výraz: 2 \cdot 3^3 \cdot 5. Podle
Eulerovy funkce Phi je pak pořadí N následující:
\phi(N) = 2^{1 - 1} \cdot (2 - 1) + 3^{3 - 1} \cdot
(3 - 1) + 5^{1 - 1} \cdot (5 - 1) = 1 \cdot 1 + 9 \cdot 2 + 1
\cdot 4 = 1 + 18 + 4 = 23
Dále předpokládejme, že N je
součinem dvou prvočísel p a q. Výše uvedená věta 2 pak říká, že pořadí N je následující:
p^{1 - 1} \cdot (p - 1) \cdot q^{1 - 1} \cdot (q - 1)
= (p - 1) \cdot (q - 1)
To je klíčový výsledek zejména pro problém RSA, který je uveden v následujícím Propozici 2.
Návrh 2. Je-li N součinem dvou prvočísel p a q, je řád N součinem (p - 1) \cdot (q - 1).
Pro ilustraci předpokládejme, že N = 119. Toto celé číslo lze rozložit na dvě prvočísla, a to 7 a 17. Z Eulerovy
funkce Phi tedy vyplývá, že pořadí čísla 119 je následující:
\phi(119) = (7 - 1) \cdot (17 - 1) = 6 \cdot 16 = 96
Jinými slovy, celé číslo 119 má 96 koprimů vrozsahu od 1 do 119. Ve skutečnosti tato množina zahrnuje všechna celá čísla od 1 do 119, která nejsou násobky 7 ani 17.
Od této chvíle označujme množinu koprimů, která určuje pořadí N, jako C_N. Pro náš příklad,
kdy N = 119, je množina C_{119} příliš velká
na to, abychom ji mohli kompletně vypsat. Některé prvky jsou však následující:
C_{119} = \{1, 2, \dots, 6, 8, \dots, 13, 15, 16, 18,
\dots, 33, 35, \dots, 96\}
Invertibilita modulo N
Můžeme říci, že celé číslo a je neobrácené modulo N, jestliže existuje alespoň jedno
celé číslo b takové, že a \cdot b \mod N = 1 \mod N.
Každé takové celé číslo b se
označuje jako inverzní (nebo multiplikativní inverzní) a vzhledem k redukci modulem N.
Předpokládejme například, že a = 5 a N = 11. Existuje mnoho
celých čísel, kterými lze vynásobit 5, takže 5 \cdot b \mod 11 = 1 \mod 11. Uvažujme například celá čísla 20 a 31. Je snadné zjistit, že obě tato
celá čísla jsou inverzí čísla 5 pro redukci modulo 11.
5 \cdot 20 \mod 11 = 100 \mod 11 = 1 \mod 115 \cdot 31 \mod 11 = 155 \mod 11 = 1 \mod 11
Zatímco číslo 5 má mnoho inverzí redukujících modulo 11, můžete ukázat, že existuje pouze jediná kladná inverze čísla 5, která je menší než 11. Ve skutečnosti se nejedná o jedinečný příklad, ale o obecný výsledek.
Návrh 3. Je-li celé číslo a inverzní modulo N, musí
platit, že přesně jedna kladná inverze a je menší než N. (Tato
jedinečná inverze a tedy musí
pocházet z množiny \{1, \dots, N - 1\}).
Označme jedinečnou inverzní hodnotu a z Výroku 3 jako a^{-1}. Pro případ,
kdy a = 5 a N = 11, vidíme, že a^{-1} = 9, protože 5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11.
Všimněte si, že hodnotu 9 pro a^{-1} v našem příkladu získáte také prostou redukcí jakékoli jiné inverzní hodnoty a modulem 11. Například 20 \mod 11 = 31 \mod 11 = 9 \mod 11. Kdykoli je tedy celé číslo a > N inverzní modulo N, pak a \mod N musí být také inverzní modulo N.
Nemusí nutně platit, že existuje inverzní redukce a modulo N. Předpokládejme
například, že a = 2 a N = 8. Neexistuje žádné b, nebo konkrétně a^{-1}, takové, aby 2 \cdot b \mod 8 = 1 \mod 8.
Je to proto, že jakákoli hodnota b vždy dává násobek 2, takže žádné
dělení 8 nikdy nemůže dát zbytek rovný 1.
Jak přesně poznáme, že nějaké celé číslo a má inverzní hodnotu pro dané N? Jak jste si mohli všimnout
v příkladu výše, největší společný dělitel mezi 2 a 8 je větší než 1,
konkrétně 2. A to je vlastně ilustrace následujícího obecného výsledku:
Návrh 4. Existuje inverzní číslo k celému číslu a danému redukcí modulo N,
konkrétně jedinečná kladná inverzní hodnota menší než N, tehdy a jen tehdy, je-li
největší společný dělitel mezi a a N roven 1 (tj. jsou-li koprimem).
Pro případ, kdy a = 5 a N = 11, jsme dospěli k
závěru, že a^{-1} = 9, protože
5 \cdot 9 \mod 11 = 45 \mod 11 = 1 \mod 11. Je důležité poznamenat, že platí i opačný postup. To znamená, že kdyža = 9aN = 11, platí, žea^{-1} = 5$.
Eulerova věta
Než přejdeme k problému RSA, musíme pochopit ještě jednu zásadní větu, a to Eulerovu větu. Ta říká následující:
Věta 3. Předpokládejme, že dvě celá čísla a a N jsou koprimena. Pak a^{\phi(N)} \mod N = 1 \mod N.
To je pozoruhodný výsledek, ale zpočátku trochu matoucí. Podívejme se na příklad, abychom ho pochopili.
Předpokládejme, že a = 5 a N = 7. To jsou skutečně
koprimena, jak vyžaduje Eulerova věta. Víme, že řád 7 je roven 6, vzhledem k
tomu, že 7 je prvočíslo (viz Výrok 1).
Eulerova věta nyní říká, že 5^6 \mod 7 se musí rovnat 1 \mod 7. Níže
jsou uvedeny výpočty, které ukazují, že to skutečně platí.
5^6 \mod 7 = 15,625 \mod 7 = 1 \mod N
Celé číslo 7 se dělí na 15 624 celkem 2233krát. Zbytek po dělení 16 625 číslem 7 je tedy 1.
Dále lze pomocí Eulerovy funkce Phi, Věty 2, odvodit Větu 5 níže.
Návrh 5. \phi(a \cdot b) = \phi(a) \cdot \phi(b) pro libovolná celá kladná čísla a a b.
Nebudeme ukazovat, proč tomu tak je. Pouze si všimněte, že jste již viděli
důkaz této věty v tom, že \phi(p \cdot q) = \phi(p) \cdot \phi(q) = (p - 1) \cdot (q - 1), když p a q jsou prvočísla, jak je uvedeno v Věta 2.
Eulerova věta ve spojení s Výrokem 5 má důležité důsledky.
Podívejte se například, co se stane v níže uvedených výrazech, kde a a N jsou koprimena.
a^{2 \cdot \phi(N)} \mod N = a^{\phi(N)} \cdot a^{\phi(N)} \mod N = 1 \cdot 1 \mod N = 1 \mod Na^{\phi(N) + 1} \mod N = a^{\phi(N)} \cdot a^1 \mod N = 1 \cdot a^1 \mod N = a \mod Na^{8 \cdot \phi(N) + 3} \mod N = a^{8 \cdot \phi(N)} \cdot a^3 \mod N = 1 \cdot a^3 \mod N = a^3 \mod N
Kombinace Eulerovy věty a Výroku 5 nám tedy umožňuje jednoduše vypočítat řadu výrazů. Obecně můžeme poznatek shrnout jako v Výroku 6.
Návrh 6. a^x \mod N = a^{x \mod \phi(N)}
Nyní musíme vše spojit v posledním složitém kroku.
Stejně jako N má řád \phi(N), který zahrnuje prvky
množiny C_N, víme, že celé
číslo \phi(N) musí mít také
řád a množinu koprimů. Nastavme \phi(N) = R. Pak víme, že
existuje také hodnota \phi(R) a množina koprimů C_R.
Předpokládejme, že nyní vybereme celé číslo e z množiny C_R. Z Věty 3 víme, že toto celé číslo e má
pouze jednu jedinečnou kladnou inverzi menší než R. To znamená, že e má jednu jedinečnou inverzní hodnotu z množiny C_R. Nazvěme tuto inverzi d. Vzhledem k definici
inverze to znamená, že e \cdot d = 1 \mod R.
Tento výsledek můžeme použít k vyjádření našeho původního celého čísla N. To je shrnuto v Propozici 7.
Propozice 7. Předpokládejme, že e \cdot d \mod \phi(N) = 1 \mod \phi(N). Pak pro libovolný prvek a množiny C_N musí platit, že a^{e \cdot d \mod \phi(N)} = a^{1 \mod \phi(N)} = a
\mod N.
Nyní máme k dispozici všechny výsledky teorie čísel potřebné k jasnému vyjádření problému RSA.
Kryptosystém RSA
Nyní jsme připraveni uvést problém RSA. Předpokládejme, že vytvoříte sadu
proměnných, která se skládá z p, q, N, \phi(N), e, d a y. Tuto množinu nazvěte \Pi. Vytvoříme ji takto:
Vygenerujte dvě náhodná prvočísla
paqstejné velikosti a vypočítejte jejich součinN.Vypočítejte řád
N,\phi(N), následujícím součinem:(p - 1) \cdot (q - 1).Zvolte
e > 2tak, aby bylo menší a koprimované s\phi(N).Vypočítejte
dnastaveníme \cdot d \mod \phi(N) = 1.Zvolte náhodnou hodnotu
y, která je menší a koprimovaná sN.
Problém RSA spočívá v nalezení takového x, aby x^e = y, přičemž je
dána pouze podmnožina informací o \Pi, konkrétně proměnné N, e a y. Pokud jsou p a q velmi velké, obvykle se doporučuje,
aby měly velikost 1024 bitů, je problém RSA považován za obtížný. Vzhledem k
výše uvedené diskusi nyní vidíte, proč tomu tak je.
Jednoduchý způsob, jak vypočítat x, když x^e \mod N = y \mod N, je
jednoduše vypočítat y^d \mod N. Následujícím
výpočtem zjistíme, že y^d \mod N = x \mod N:
y^d \mod N = x^{e \cdot d} \mod N = x^{e \cdot d \mod
\phi(N)} \mod N = x^{1 \mod \phi(N)} \mod N = x \mod N.
Problém je v tom, že neznáme hodnotu d, protože není v úloze uvedena. Proto nemůžeme přímo vypočítat y^d \mod N a získat x \mod N.
Mohli bychom však být schopni nepřímo vypočítat d z řádu N, \phi(N), protože víme, že e \cdot d \mod \phi(N) = 1 \mod \phi(N). Ale podle předpokladu tato úloha neudává ani hodnotu pro \phi(N).
Nakonec lze pořadí vypočítat nepřímo pomocí prvočinitelů p a q, takže nakonec můžeme
vypočítat d. Podle
předpokladu nám však hodnoty p a q rovněž nebyly poskytnuty.
Přísně vzato, i když je problém faktoringu v rámci problému RSA těžký, nemůžeme dokázat, že problém RSA je také těžký. Mohou totiž existovat i jiné způsoby řešení problému RSA než pomocí faktoringu. Obecně se však přijímá a předpokládá, že pokud je problém faktoringu v rámci problému RSA těžký, je těžký i samotný problém RSA.
Pokud je problém RSA skutečně těžký, pak vytváří jednosměrnou funkci s
trapdoor. Tato funkce je f(g) = g^e \mod N. Se znalostí f(g) může
kdokoli snadno vypočítat hodnotu y pro konkrétní g = x. Je však
prakticky nemožné vypočítat konkrétní hodnotu x pouze na základě znalosti hodnoty y a funkce f(g). Výjimkou je
situace, kdy je vám dána informace d, tzv. trapdoor. V takovém
případě můžete jednoduše vypočítat y^d a získat tak x.
Pro ilustraci problému RSA si uvedeme konkrétní příklad. Nemohu vybrat problém RSA, který by byl za výše uvedených podmínek považován za obtížný, protože čísla by byla nepřehledná. Místo toho tento příklad slouží pouze k ilustraci toho, jak problém RSA obecně funguje.
Pro začátek předpokládejme, že si vyberete dvě náhodná prvočísla 13 a 31.
Takže p = 13 a q = 31. Součin N těchto dvou prvočísel se rovná 403. Řád čísla 403 můžeme snadno vypočítat.
Je to ekvivalent (13 - 1) \cdot (31 - 1) = 360.
Dále, jak vyplývá z kroku 3 úlohy RSA, musíme zvolit koprimát pro 360, který je větší než 2 a menší než 360. Tuto hodnotu nemusíme volit náhodně. Předpokládejme, že vybereme 103. To je koprimát 360, protože jeho největší společný dělitel se 103 je 1.
Krok 4 nyní vyžaduje, abychom vypočítali takovou hodnotu d, že 103 \cdot d \mod 360 = 1. To
není snadný ruční úkol, pokud je hodnota N velká. Je třeba použít postup zvaný rozšířený euklidovský algoritmus.
Ačkoli zde neuvádím postup, při e = 103 získáme hodnotu 7. O tom, že dvojice hodnot 103 a 7 skutečně splňuje obecnou
podmínku e \cdot d \mod \phi(n) = 1,
se můžete přesvědčit pomocí následujících výpočtů.
103 \cdot 7 \mod 360 = 721 \mod 360 = 1 \mod 360
Důležité je, že vzhledem k Výroku 4 víme, že žádné jiné celé číslo
mezi 1 a 360 pro d nedá
výsledek, že 103 \cdot d = 1 \mod 360.
Navíc z věty vyplývá, že volba jiné hodnoty pro e dá jinou jedinečnou hodnotu pro d.
V 5. kroku úlohy RSA musíme vybrat nějaké kladné celé číslo y, které je menším koprimem čísla 403. Předpokládejme, že nastavíme y = 2^{103}.
Exponentizací 2 číslem 103 získáme následující výsledek.
2^{103} \mod 403 = 10,141,204,801,825,835,211,973,625,643,008 \mod 403 = 349 \mod 403
Problém RSA v tomto konkrétním příkladu je nyní následující: Máme k
dispozici N = 403, e = 103 a y = 349 \mod 403. Nyní
musíte vypočítat x tak, aby x^{103} = 349 \mod 403. To znamená, že musíte zjistit, že původní hodnota před exponencializací
číslem 103 byla 2.
Bylo by snadné (alespoň pro počítač) vypočítat x, kdybychom věděli, že d = 7. V takovém případě by
stačilo určit x následujícím způsobem.
x = y^7 \mod 403 = 349^7 \mod 403 = 630,634,881,591,804,949 \mod 403 = 2 \mod 403
Problém je v tom, že vám nebyla poskytnuta informace, že d = 7. Mohli byste samozřejmě vypočítat d z toho, že 103 \cdot d = 1 \mod 360.
Problém je v tom, že vám také nebyla poskytnuta informace, že řád N = 360. Nakonec byste také
mohli vypočítat řád 403 výpočtem následujícího součinu: (p - 1) \cdot (q - 1). Ale
také vám není řečeno, že p = 13 a q = 31.
Počítač by samozřejmě mohl problém RSA pro tento příklad vyřešit poměrně snadno, protože se nejedná o velká prvočísla. Když se však prvočísla stanou velmi velkými, stojí před prakticky nemožným úkolem.
Nyní jsme představili problém RSA, soubor podmínek, za kterých je obtížný, a základní matematiku. Jak to pomůže při řešení asymetrické kryptografie? Konkrétně, jak můžeme tvrdost problému RSA za určitých podmínek proměnit v šifrovací schéma nebo schéma digitálního podpisu?
Jedním z přístupů je vzít problém RSA a vytvořit schémata jednoduchým
způsobem. Předpokládejte například, že jste vygenerovali sadu proměnných \Pi, jak je popsáno v problému RSA, a zajistili, že p a q jsou dostatečně velké.
Nastavíte svůj veřejný klíč na hodnotu (N, e) a tuto informaci sdělíte světu. Jak je popsáno výše, hodnoty p, q, \phi(n) a d uchováte v tajnosti. Ve
skutečnosti je d váš soukromý
klíč.
Každý, kdo vám chce poslat zprávu m, která je prvkem C_N, ji
může jednoduše zašifrovat následujícím způsobem: (Šifrový text c je zde ekvivalentní hodnotě y v problému RSA.) Tuto zprávu můžete snadno dešifrovat pouhým výpočtem c^d \mod N.
Stejným způsobem se můžete pokusit vytvořit schéma digitálního podpisu.
Předpokládejme, že chcete někomu poslat zprávu m s digitálním podpisem S.
Stačí nastavit S = m^d \mod N a poslat dvojici (m,S) příjemci. Kdokoli může digitální podpis ověřit pouhou kontrolou, zda S^e \mod N = m \mod N. Pro
každého útočníka by však bylo velmi obtížné vytvořit platný S pro zprávu, vzhledem k tomu, že nevlastní d.
Bohužel přeměna problému RSA, který je sám o sobě těžkým problémem, na
kryptografické schéma není tak jednoduchá. U přímočarého šifrovacího
schématu můžete jako zprávy zvolit pouze koprimata N. To nám nedává mnoho možných zpráv, rozhodně ne dost pro standardní
komunikaci. Navíc tyto zprávy musí být vybrány náhodně. To se zdá poněkud
nepraktické. A konečně, každá zpráva, která je vybrána dvakrát, poskytne
úplně stejný šifrový text. To je v jakémkoli šifrovacím schématu krajně
nežádoucí a neodpovídá to žádnému přísnému modernímu standardnímu pojetí
bezpečnosti v šifrování.
Problémy se ještě zhoršují u našeho jednoduchého schématu digitálního
podpisu. Za současného stavu může jakýkoli útočník snadno zfalšovat
digitální podpis pouhým výběrem koprimátu N jako podpisu a následným výpočtem odpovídající původní zprávy. Tím je jasně
porušen požadavek existenční nezfalšovatelnosti.
Nicméně s přidáním trochu chytré složitosti lze problém RSA použít k vytvoření bezpečného schématu šifrování s veřejným klíčem i bezpečného schématu digitálního podpisu. Do podrobností takových konstrukcí se zde nebudeme pouštět. [4] Důležité však je, že tato dodatečná složitost nemění základní základní problém RSA, na kterém jsou tato schémata založena.
Poznámky:
[4] Viz například Jonathan Katz a Yehuda Lindell, Introduction to Modern Cryptography, CRC Press (Boca Raton, FL: 2015), str. 410-32 o šifrování RSA a str. 444-41 o digitálních podpisech RSA.
Sekce finále
Hodnocení & Recenze
366d6fd0-ceb2-4299-bf37-8c6dfcb681d5 true
Závěrečná Zkouška
44882d2b-63cd-4fde-8485-f76f14d8b2fe true
Závěr
f1905f78-8cf7-5031-949a-dfa8b76079b4 true