name: Vnitřní fungování Bitcoinových peněženek goal: Ponořte se do kryptografických principů, které stojí za Bitcoinovými peněženkami. objectives:
- Definovat teoretické pojmy nezbytné pro pochopení kryptografických algoritmů používaných v Bitcoinu.
- Plně pochopit konstrukci deterministické a hierarchické peněženky.
- Znát způsoby, jak identifikovat a snížit rizika spojená se správou peněženky.
- Porozumět principům hašovacích funkcí, kryptografických klíčů a digitálních podpisů.
Cesta do srdce Bitcoinových peněženek
Objevte tajemství deterministických a hierarchických Bitcoinových peněženek s naším kurzem CYP201! Ať už jste pravidelný uživatel nebo nadšenec, který si chce prohloubit své znalosti, tento kurz nabízí kompletní ponoření do fungování těchto nástrojů, které všichni používáme každý den.
Naučte se o mechanismech hašovacích funkcí, digitálních podpisů (ECDSA a Schnorr), mnemonických frázích, kryptografických klíčích a vytváření přijímacích adres, a to vše při prozkoumávání pokročilých bezpečnostních strategií.
Tento trénink vás nejen vybaví znalostmi potřebnými k pochopení struktury Bitcoinové peněženky, ale také vás připraví na hlubší ponoření do vzrušujícího světa kryptografie.
S jasnou pedagogikou, více než 60 vysvětlujícími diagramy a konkrétními příklady vás CYP201 umožní pochopit od A do Z, jak vaše peněženka funguje, abyste mohli s důvěrou navigovat vesmírem Bitcoinu. Vezměte kontrolu nad svými UTXOs dnes tím, že porozumíte, jak fungují HD peněženky!
Úvod
Úvod do kurzu
Vítejte v kurzu CYP201, kde se podrobně seznámíme s fungováním HD Bitcoinových peněženek. Tento kurz je určen každému, kdo chce pochopit technické základy používání Bitcoinu, ať už jde o příležitostné uživatele, osvícené nadšence nebo budoucí odborníky.
Cílem tohoto školení je dát vám klíče k ovládnutí nástrojů, které používáte každý den. HD Bitcoinové peněženky, které jsou v srdci vašeho uživatelského zážitku, jsou založeny na někdy složitých konceptech, které se pokusíme zpřístupnit. Společně je odhalíme!
Než se ponoříme do detailů konstrukce a fungování Bitcoinových peněženek,
začneme několika kapitolami o kryptografických primitivách, které je třeba
znát pro následující. Začneme hašovacími funkcemi, zásadními jak pro
peněženky, tak pro samotný protokol Bitcoinu. Objevíte jejich hlavní
charakteristiky, specifické funkce používané v Bitcoinu a v techničtější
kapitole se dozvíte podrobně o fungování královny hašovacích funkcí: SHA256. 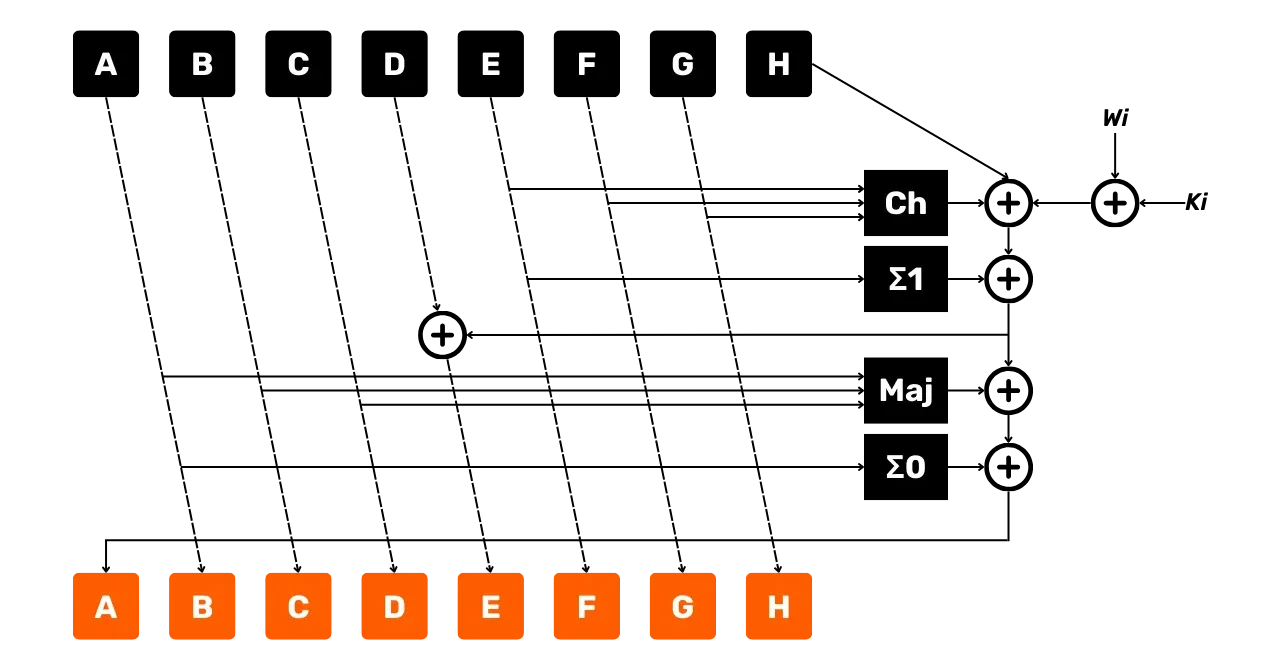
Dále budeme diskutovat o fungování algoritmů digitálního podpisu, které každý den používáte k zabezpečení vašich UTXOs. Bitcoin používá dva: ECDSA a protokol Schnorr. Naučíte se, které matematické primitivy leží v základu těchto algoritmů a jak zajišťují bezpečnost transakcí.
Jakmile budeme mít dobré porozumění těmto prvkům kryptografie, konečně přejdeme k srdci školení: deterministické a hierarchické peněženky! Nejprve je sekce věnovaná mnemonickým frázím, těmto sekvencím 12 nebo 24 slov, které vám umožňují vytvořit a obnovit vaše peněženky. Objevíte, jak jsou tato slova generována zdrojem entropie a jak usnadňují používání Bitcoinu.
 Školení bude pokračovat studiem BIP39 hesla, seedu (nesmí být zaměňován s mnemonickou
frází), hlavního řetězového kódu a hlavního klíče. Podrobně si probereme, co
tyto prvky jsou, jaké mají role a jak jsou vypočítány.
Školení bude pokračovat studiem BIP39 hesla, seedu (nesmí být zaměňován s mnemonickou
frází), hlavního řetězového kódu a hlavního klíče. Podrobně si probereme, co
tyto prvky jsou, jaké mají role a jak jsou vypočítány. 
Nakonec, z hlavního klíče, objevíme, jak jsou odvozeny kryptografické klíčové páry deterministickým a hierarchickým způsobem až po přijímací adresy.

Toto školení vám umožní používat vaše peněženkové software s důvěrou, zatímco si rozšíříte dovednosti v identifikaci a minimalizaci rizik. Připravte se stát se pravým expertem na Bitcoinové peněženky!
Hašovací Funkce
Úvod do Hašovacích Funkcí
První typ kryptografických algoritmů používaných na Bitcoinu zahrnuje hašovací funkce. Hrají zásadní roli na různých úrovních protokolu, ale také uvnitř Bitcoinových peněženek. Pojďme společně objevit, co je hašovací funkce a k čemu se používá v Bitcoinu.
Definice a Princip Hašování
Hašování je proces, který transformuje informace libovolné délky na jinou informaci pevné délky prostřednictvím kryptografické hašovací funkce. Jinými slovy, hašovací funkce přijme vstup jakékoli velikosti a převede jej na otisk pevné velikosti, nazývaný "hash". Hash může být také někdy označován jako "digest", "condensate", "condensed" nebo "hashed".
Například hašovací funkce SHA256 produkuje hash pevné délky 256 bitů. Takže pokud použijeme vstup "PlanB", zprávu libovolné délky, vygenerovaný hash bude následující 256bitový otisk:
24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688

Charakteristiky Hašovacích Funkcí
Tyto kryptografické hašovací funkce mají několik zásadních charakteristik, které je činí obzvláště užitečnými v kontextu Bitcoinu a dalších počítačových systémů:
- Nezvratnost (nebo odolnost proti zpětnému zjištění)
- Odolnost proti manipulaci (lavina efekt)
- Odolnost proti kolizím
- Odolnost proti druhému zpětnému zjištění
1. Nezvratnost (odolnost proti zpětnému zjištění):
Nezvratnost znamená, že je snadné vypočítat hash z vstupní informace, ale opačný výpočet, tedy nalezení vstupu z hashe, je prakticky nemožný. Tato vlastnost činí hashovací funkce ideálními pro vytváření jedinečných digitálních otisků, aniž by byla ohrožena původní informace.
V daném příkladu, získání hash 24f1b9… znalostí vstupu "PlanB" je jednoduché a rychlé. Nicméně, nalezení zprávy "PlanB" pouze
znalostí 24f1b9… je nemožné.

Proto je nemožné najít preimage m pro hash h tak, že h = \text{HASH}(m),
kde \text{HASH} je kryptografická
hašovací funkce.
2. Odolnost proti manipulaci (lavina efekt)
Druhá charakteristika je odolnost proti manipulaci, známá také jako lavina efekt. Tato charakteristika je pozorována u hašovací funkce, pokud malá změna ve vstupní zprávě způsobí radikální změnu ve výstupním haši. Pokud se vrátíme k našemu příkladu se vstupem "PlanB" a funkcí SHA256, viděli jsme, že generovaný haš je následující:
24f1b93b68026bfc24f5c8265f287b4c940fb1664b0d75053589d7a4f821b688
Pokud uděláme velmi malou změnu ve vstupu použitím "Planb" tentokrát, pak jednoduchá změna z velkého "B" na malé "b" zcela změní výstupní haš SHA256:
bb038b4503ac5d90e1205788b00f8f314583c5e22f72bec84b8735ba5a36df3f

Tato vlastnost zajišťuje, že i malá úprava původní zprávy je okamžitě zjistitelná, protože se nezmění jen malá část haše, ale celý haš. To může být zajímavé v různých oblastech pro ověření integrity zpráv, softwaru nebo dokonce Bitcoinových transakcí.
3. Odolnost proti kolizím
Třetí charakteristika je odolnost proti kolizím. Hašovací funkce je odolná
proti kolizím, pokud je výpočetně nemožné najít 2 různé zprávy, které
produkují stejný hašovací výstup z funkce. Formálně je obtížné najít dvě
odlišné zprávy m_1 a m_2 tak, že:
\text{HASH}(m_1) = \text{HASH}(m_2)
Ve skutečnosti je matematicky nevyhnutelné, že pro hašovací funkce existují
kolize, protože velikost vstupů může být větší než velikost výstupů. To je
známé jako Dirichletův princip šuplíku: pokud jsou n objekty rozděleny do m šuplíků, přičemž m < n,
pak alespoň jeden šuplík nutně obsahuje dva nebo více objektů. Pro hašovací
funkci se tento princip uplatňuje, protože počet možných zpráv je (téměř)
nekonečný, zatímco počet možných hašů je konečný (2^{256} v případě SHA256).
Takže tato charakteristika neznamená, že pro hašovací funkce neexistují
žádné kolize, ale spíše, že dobrá hašovací funkce činí pravděpodobnost
nalezení kolize zanedbatelnou. Tato charakteristika například již není
ověřena u algoritmů SHA-0 a SHA-1, předchůdců SHA-2, u kterých byly nalezeny
kolize. Tyto funkce jsou proto nyní často nedoporučovány a považovány za
zastaralé. Pro hašovací funkci o n bitech je odolnost proti kolizím řádu 2^{\frac{n}{2}}, v souladu s útokem narozenin. Například pro SHA256 (n = 256) je složitost nalezení kolize řádu 2^{128} pokusů. V praktickém smyslu to znamená, že pokud se přes funkci převede 2^{128} různých zpráv,
je pravděpodobné, že se najde kolize.
4. Odolnost proti druhému preobrazu
Odolnost proti druhému preobrazu je další důležitou charakteristikou
hašovacích funkcí. Tvrzení, že pokud je dána zpráva m_1 a její haš h, je výpočetně
nemožné najít jinou zprávu m_2 \neq m_1 tak, že:
\text{HASH}(m_1) = \text{HASH}(m_2)Tedy odolnost proti druhému preobrazu je do jisté míry podobná odolnosti
proti kolizím, kromě toho, že zde je útok obtížnější, protože útočník nemůže
volně vybírat m_1.

Aplikace hašovacích funkcí v Bitcoinu
Nejpoužívanější hašovací funkcí v Bitcoinu je SHA256 ("Secure Hash Algorithm 256 bits"). Navržena na začátku 2000s NSA a standardizována NIST, produkuje 256-bitový hašovací výstup.
Tato funkce je používána v mnoha aspektech Bitcoinu. Na úrovni protokolu se podílí na mechanismu Proof-of-Work, kde je aplikována dvojité hašování pro hledání částečné kolize mezi hlavičkou kandidátního bloku, vytvořeného těžařem, a cílem obtížnosti. Pokud je tato částečná kolize nalezena, kandidátní blok se stává platným a může být přidán do blockchainu.
SHA256 je také používána při konstrukci Merkleova stromu, který je významným akumulátorem používaným pro zaznamenávání transakcí v blocích. Tato struktura je také nalezena v protokolu Utreexo, který umožňuje snížení velikosti UTXO Setu. Kromě toho, s představením Taprootu v roce 2021, je SHA256 využívána v MAST (Merkelised Alternative Script Tree), což umožňuje odhalit pouze skutečně použité podmínky výdaje ve skriptu, aniž by byly odhaleny ostatní možné možnosti. Je také používána při výpočtu identifikátorů transakcí, při přenosu paketů přes P2P síť, v elektronických podpisech... Nakonec, a to je zvláště zajímavé v tomto školení, SHA256 je používána na aplikační úrovni pro konstrukci Bitcoinových peněženek a derivaci adres.
Většinou, když narazíte na použití SHA256 v Bitcoinu, bude to ve skutečnosti dvojité hašování SHA256, označované jako "HASH256", které jednoduše spočívá v dvakrát po sobě jdoucím aplikování SHA256: HASH256(m) = SHA256(SHA256(m))
Tato praxe dvojitého hašování přidává další vrstvu zabezpečení proti určitým potenciálním útokům, i když je dnes jednoduché SHA256 považováno za kryptograficky bezpečné.
Další hašovací funkcí dostupnou v jazyce Script a používanou pro derivaci přijímacích adres je funkce RIPEMD160. Tato funkce produkuje 160-bitový haš (tedy kratší než SHA256). Obvykle je kombinována s SHA256 pro vytvoření funkce HASH160:
\text{HASH160}(m) = \text{RIPEMD160}(\text{SHA256}(m))Tato kombinace je používána pro generování kratších hašů, zejména při vytváření určitých Bitcoinových adres, které představují haše klíčů nebo haše skriptů, stejně jako pro výrobu otisků klíčů.
Nakonec, pouze na aplikační úrovni, je někdy používána také funkce SHA512, která nepřímo hraje roli v derivaci klíčů pro peněženky. Tato funkce je velmi podobná SHA256 ve svém fungování; obě patří do stejné rodiny SHA2, ale SHA512 produkuje, jak už název napovídá, 512-bitový haš, ve srovnání s 256 bity pro SHA256. Její použití podrobně rozebereme v následujících kapitolách.
Nyní znáte základní informace o hašovacích funkcích pro to, co následuje. V další kapitole navrhuji podrobněji prozkoumat fungování funkce, která je jádrem Bitcoinu: SHA256. Rozklíčujeme ji, abychom pochopili, jak dosahuje charakteristik, které jsme zde popisovali. Tato další kapitola je poměrně dlouhá a technická, ale není nezbytná pro pokračování v školení. Takže, pokud máte s jejím pochopením potíže, nebojte se a přejděte přímo na následující kapitolu, která bude mnohem přístupnější.
Vnitřní fungování SHA256
905eb320-f15b-5fb6-8d2d-5bb447337deb Dříve jsme viděli, že hashovací funkce mají důležité charakteristiky, které ospravedlňují jejich použití v Bitcoinu. Nyní se podíváme na vnitřní mechanismy těchto hashovacích funkcí, které jim dávají tyto vlastnosti, a k tomu navrhuji rozebrat fungování SHA256. Funkce SHA256 a SHA512 patří do stejné rodiny SHA2. Jejich mechanismus je založen na specifické konstrukci nazvané Merkle-Damgårdova konstrukce. RIPEMD160 také využívá tento stejný typ konstrukce.
Jako připomínku, máme na vstupu do SHA256 zprávu libovolné velikosti a převedeme ji funkcí, abychom získali 256bitový hash na výstupu.
Předzpracování vstupu
Začneme tím, že připravíme naši vstupní zprávu m tak, aby měla standardní délku, která je násobkem 512 bitů. Tento krok je
zásadní pro správné fungování algoritmu následně. K tomu začneme krokem
přidání bitů pro zarovnání. Nejprve přidáme k zprávě oddělovací bit 1, následovaný určitým počtem bitů 0. Počet
přidaných bitů 0 je vypočítán tak, aby celková délka zprávy po
tomto přidání byla kongruentní s 448 modulo 512. Tedy délka L zprávy s bitů pro zarovnání
je rovna:
L \equiv 448 \mod 512\text{mod}, pro
modulo, je matematická operace, která mezi dvěma celými čísly vrací zbytek
po Euklidovském dělení prvního číslem druhým. Například: 16 \mod 5 = 1. Je to operace
široce používaná v kryptografii.
Zde krok zarovnání zajišťuje, že po přidání 64 bitů v dalším kroku bude
celková délka zarovnané zprávy násobkem 512 bitů. Pokud má původní zpráva
délku M bitů, počet (N) bitů 0, které mají být přidány, je tedy:
N = (448 - (M + 1) \mod 512) \mod 512Například, pokud je původní zpráva 950 bitů, výpočet by byl následující:
\begin{align*}
M & = 950 \\
M + 1 & = 951 \\
(M + 1) \mod 512 & = 951 \mod 512 \\
& = 951 - 512 \cdot \left\lfloor \frac{951}{512} \right\rfloor \\
& = 951 - 512 \cdot 1 \\
& = 951 - 512 \\
& = 439 \\
\\
448 - (M + 1) \mod 512 & = 448 - 439 \\
& = 9 \\
\\
N & = (448 - (M + 1) \mod 512) \mod 512 \\
N & = 9 \mod 512 \\
& = 9
\end{align*}Takže bychom měli 9 0 navíc k oddělovací 1. Naše
bity pro zarovnání, které mají být přidány přímo po naší zprávě M, by tedy byly:
1000 0000 00
Po přidání bitů pro zarovnání k naší zprávě M přidáme také 64bitovou reprezentaci původní délky zprávy M, vyjádřenou v binární
formě. To umožňuje hashovací funkci být citlivou na pořadí bitů a délku
zprávy. Pokud se vrátíme k našemu příkladu s počáteční zprávou o 950 bitech,
převedeme desítkové číslo 950 na binární, což nám dá 1110 1101 10. Toto číslo doplníme nulami na základně, aby
celkem dosáhlo 64 bitů. V našem příkladu to dává:
0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0011 1011 0110
Tato velikost doplnění je přidána podle pravidel doplnění bitů. Proto zpráva po našem předzpracování se skládá ze tří částí:
- Původní zpráva
M; - Bit
1následovaný několika bity0pro formování doplnění bitů; - 64-bitová reprezentace délky
Mpro formování doplnění s velikostí.

Inicializace proměnných
SHA256 používá osm počátečních stavových proměnných, označených A až H, každá o velikosti 32
bitů. Tyto proměnné jsou inicializovány specifickými konstantami, které jsou
desetinnými částmi odmocnin prvních osmi prvočísel. Tyto hodnoty budeme
následně používat během hashovacího procesu:
A = 0x6a09e667B = 0xbb67ae85C = 0x3c6ef372D = 0xa54ff53aE = 0x510e527fF = 0x9b05688cG = 0x1f83d9abH = 0x5be0cd19
SHA256 také používá dalších 64 konstant, označených K_0 až K_{63}, které
jsou desetinnými částmi odmocnin třetích mocnin prvních 64 prvočísel:
K[0 \ldots 63] = \begin{pmatrix}
0x428a2f98, & 0x71374491, & 0xb5c0fbcf, & 0xe9b5dba5, \\
0x3956c25b, & 0x59f111f1, & 0x923f82a4, & 0xab1c5ed5, \\
0xd807aa98, & 0x12835b01, & 0x243185be, & 0x550c7dc3, \\
0x72be5d74, & 0x80deb1fe, & 0x9bdc06a7, & 0xc19bf174, \\
0xe49b69c1, & 0xefbe4786, & 0x0fc19dc6, & 0x240ca1cc, \\
0x2de92c6f, & 0x4a7484aa, & 0x5cb0a9dc, & 0x76f988da, \\
0x983e5152, & 0xa831c66d, & 0xb00327c8, & 0xbf597fc7, \\
0xc6e00bf3, & 0xd5a79147, & 0x06ca6351, & 0x14292967, \\
0x27b70a85, & 0x2e1b2138, & 0x4d2c6dfc, & 0x53380d13, \\
0x650a7354, & 0x766a0abb, & 0x81c2c92e, & 0x92722c85, \\
0xa2bfe8a1, & 0xa81a664b, & 0xc24b8b70, & 0xc76c51a3, \\
0xd192e819, & 0xd6990624, & 0xf40e3585, & 0x106aa070, \\
0x19a4c116, & 0x1e376c08, & 0x2748774c, & 0x34b0bcb5, \\
0x391c0cb3, & 0x4ed8aa4a, & 0x5b9cca4f, & 0x682e6ff3, \\
0x748f82ee, & 0x78a5636f, & 0x84c87814, & 0x8cc70208, \\
0x90befffa, & 0xa4506ceb, & 0xbef9a3f7, & 0xc67178f2
\end{pmatrix}Dělení vstupu
Nyní, když máme vyrovnán vstup, přejdeme k hlavní fázi zpracování algoritmu SHA256: kompresní funkce. Tento krok je velmi důležitý, protože je to primárně to, co dává hašovací funkci její kryptografické vlastnosti, které jsme studovali v předchozí kapitole.
Nejprve začneme dělením naší vyrovnáné zprávy (výsledek předzpracovatelských
kroků) na několik bloků P o
velikosti 512 bitů každý. Pokud má naše vyrovnáná zpráva celkovou velikost n \times 512 bitů, budeme mít tedy n bloků, každý o velikosti 512 bitů. Každý 512-bitový blok bude zpracován
individuálně kompresní funkcí, která se skládá ze 64 kol postupných operací.
Pojmenujme tyto bloky P_1, P_2, P_3...
Logické operace
Před prozkoumáním kompresní funkce detailně je důležité porozumět základním logickým operacím používaným v ní. Tyto operace, založené na Booleově algebře, pracují na úrovni bitů. Základní logické operace používané jsou:
- Konjunkce (AND): označená
\land, odpovídá logickému "A". - Disjunkce (OR): označená
\lor, odpovídá logickému "NEBO". - Negace (NOT): označená
\lnot, odpovídá logickému "NE".
Z těchto základních operací můžeme definovat složitější operace, jako je
"Exkluzivní NEBO" (XOR) označené \oplus, které je široce používáno v kryptografii. Každou logickou operaci lze
reprezentovat pravdivostní tabulkou, která udává výsledek pro všechny možné
kombinace binárních vstupních hodnot (dva operandy p a q). Pro XOR (\oplus):
p | q | p \oplus q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Pro AND (\land):
p | q | p \land q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Pro NOT (\lnot p):
p | \lnot p |
|---|---|
| 0 | 1 |
| 1 | 0 |
Pojďme si na příkladu vysvětlit operaci XOR na úrovni bitů. Máme-li dva binární čísla na 6 bitech:
a = 101100b = 001000
Pak:
a \oplus b = 101100 \oplus 001000 = 100100Aplikací XOR bit po bitu:
| Pozice bitu | a | b | a \oplus b |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 1 | 0 | 1 |
| 5 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 |
Výsledek je tedy 100100.
Kromě logických operací kompresní funkce využívá operace bitového posunu, které budou hrát zásadní roli v rozptylu bitů v algoritmu.
Nejprve je tu logická operace posunu doprava, označovaná ShR_n(x), která posune všechny bity x o n pozic doprava, přičemž prázdné
bity vlevo se vyplní nulami.
Například pro x = 101100001 (na 9 bitech) a n = 4:
ShR_4(101100001) = 000010110Schématicky lze operaci posunu doprava vidět takto:
 Další operací používanou v SHA256 pro manipulaci s bity je pravá kruhová rotace,
označovaná
Další operací používanou v SHA256 pro manipulaci s bity je pravá kruhová rotace,
označovaná RotR_n(x), která
posune bity x o n pozic doprava, přičemž posunuté bity se znovu vloží na začátek řetězce.
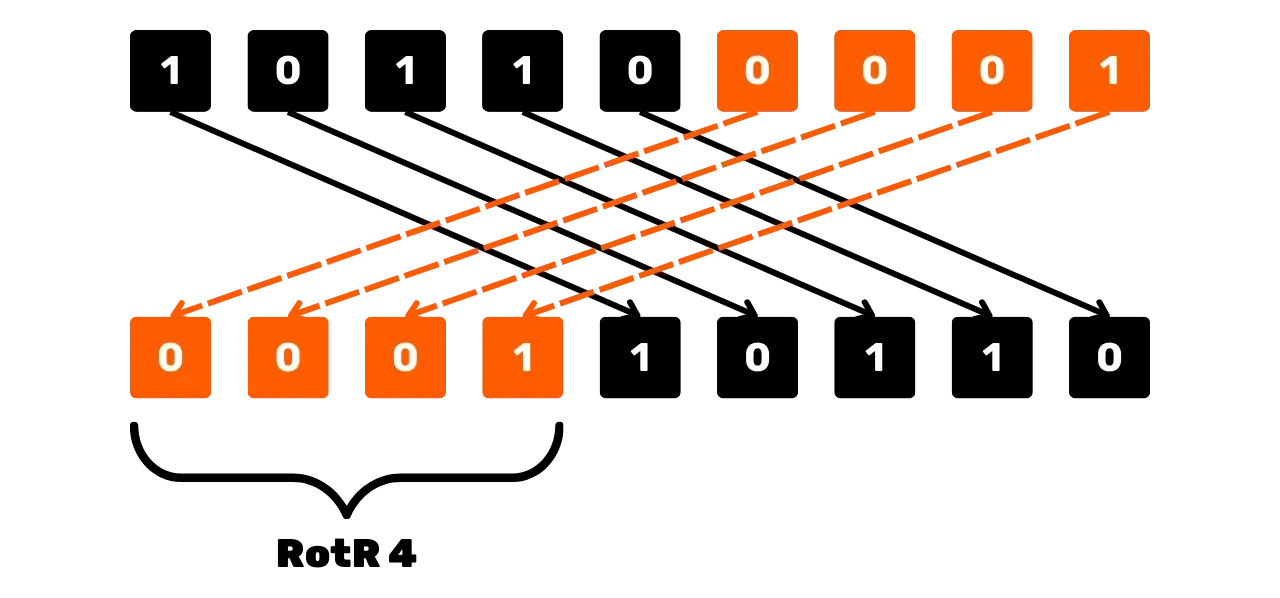
Například pro x = 101100001 (na 9 bitech) a n = 4:
RotR_4(101100001) = 000110110Schématicky lze pravou kruhovou rotaci vidět takto:
Kompresní funkce
Nyní, když jsme pochopili základní operace, pojďme si podrobně prohlédnout kompresní funkci SHA256.
V předchozím kroku jsme náš vstup rozdělili na několik 512bitových částí P. Pro každý 512bitový blok P máme:
- Slova zprávy
W_i: proiod 0 do 63. - Konstanty
K_i: proiod 0 do 63, definované v předchozím kroku. - Stavové proměnné
A, B, C, D, E, F, G, H: inicializované hodnotami z předchozího kroku. Prvních 16 slov,W_0ažW_{15}, je přímo extrahováno z zpracovaného 512-bitového blokuP. Každé slovoW_ise skládá z 32 po sobě jdoucích bitů z bloku. Takže například vezmeme naši první část vstupuP_1a dále ji rozdělíme na menší 32-bitové části, které nazýváme slova. Dalších 48 slov (W_{16}ažW_{63}) je generováno použitím následujícího vzorce:
W_i = W_{i-16} + \sigma_0(W_{i-15}) + W_{i-7} + \sigma_1(W_{i-2}) \mod 2^{32}S:
\sigma_0(x) = RotR_7(x) \oplus RotR_{18}(x) \oplus ShR_3(x)\sigma_1(x) = RotR_{17}(x) \oplus RotR_{19}(x) \oplus ShR_{10}(x)
V tomto případě x se rovná W_{i-15} pro \sigma_0(x) a W_{i-2} pro \sigma_1(x).
Jakmile určíme všechna slova W_i pro naši 512-bitovou část, můžeme přejít k funkci komprese, která se skládá
z provedení 64 kol.
 Pro každé kolo
Pro každé kolo i od 0 do 63
máme tři různé typy vstupů. Nejprve W_i, které jsme právě určili,
částečně se skládající z naší části zprávy P_n. Dále 64 konstant K_i. Nakonec používáme
stavové proměnné A, B, C, D, E, F, G a H, které se během
hashovacího procesu budou vyvíjet a s každou kompresní funkcí upravovat.
Nicméně pro první část P_1 používáme
původně dané konstanty. Poté provedeme následující operace na našich vstupech:
- Funkce
\Sigma_0:
\Sigma_0(A) = RotR_2(A) \oplus RotR_{13}(A) \oplus RotR_{22}(A)- Funkce
\Sigma_1:
\Sigma_1(E) = RotR_6(E) \oplus RotR_{11}(E) \oplus RotR_{25}(E)- Funkce
Ch("Vybrat"):
Ch(E, F, G) = (E \land F) \oplus (\lnot E \land G)- Funkce
Maj("Většina"):
Maj(A, B, C) = (A \land B) \oplus (A \land C) \oplus (B \land C)Poté vypočítáme 2 dočasné proměnné:
temp1:
temp1 = H + \Sigma_1(E) + Ch(E, F, G) + K_i + W_i \mod 2^{32}temp2:
temp2 = \Sigma_0(A) + Maj(A, B, C) \mod 2^{32}Dále aktualizujeme stavové proměnné následovně:
\begin{cases}
H = G \\
G = F \\
F = E \\
E = D + temp1 \mod 2^{32} \\
D = C \\
C = B \\
B = A \\
A = temp1 + temp2 \mod 2^{32}
\end{cases}Následující diagram představuje jedno kolo kompresní funkce SHA256, jak jsme právě popisovali:

- Šipky ukazují tok dat;
- Boxíky reprezentují prováděné operace;
+obklopené reprezentuje sčítání modulo2^{32}.
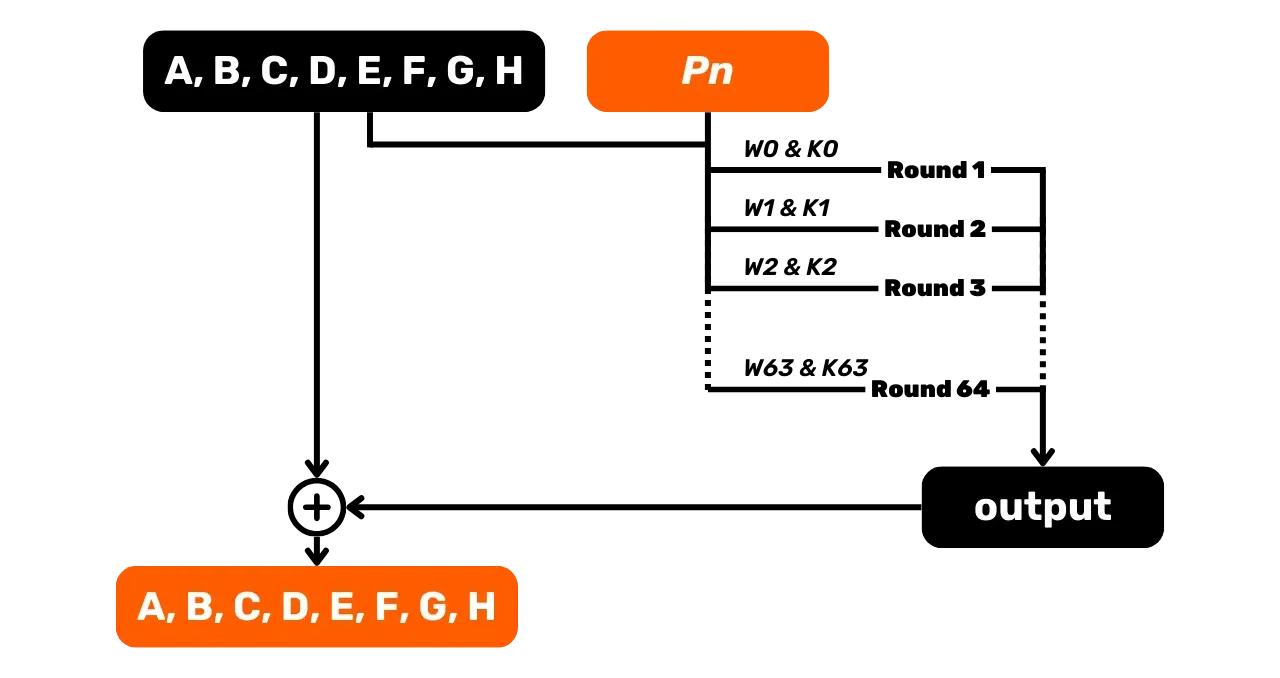
Už nyní můžeme pozorovat, že toto kolo výstupuje nové stavové proměnné A, B, C, D, E, F, G a H. Tyto nové proměnné budou
sloužit jako vstup pro další kolo, které zase produkuje nové proměnné A, B, C, D, E, F, G a H, jež budou použity pro
následující kolo. Tento proces pokračuje až do 64. kola. Po 64 kolech
aktualizujeme počáteční hodnoty stavových proměnných jejich přičtením k
konečným hodnotám na konci 64. kola:
\begin{cases}
A = A_{\text{initial}} + A \mod 2^{32} \\
B = B_{\text{initial}} + B \mod 2^{32} \\
C = C_{\text{initial}} + C \mod 2^{32} \\
D = D_{\text{initial}} + D \mod 2^{32} \\
E = E_{\text{initial}} + E \mod 2^{32} \\
F = F_{\text{initial}} + F \mod 2^{32} \\
G = G_{\text{initial}} + G \mod 2^{32} \\
H = H_{\text{initial}} + H \mod 2^{32}
\end{cases}Tyto nové hodnoty A, B, C, D, E, F, G a H budou sloužit jako
počáteční hodnoty pro další blok, P_2. Pro tento blok P_2 replikujeme stejný kompresní proces s 64 koly, poté aktualizujeme proměnné
pro blok P_3 a tak dále až do
posledního bloku našeho vyrovnávaného vstupu.
Po zpracování všech bloků zprávy konkatenací konečných hodnot proměnných A, B, C, D, E, F, G a H vytvoříme konečný 256bitový
hash naší hašovací funkce:
\text{Hash} = A \Vert B \Vert C \Vert D \Vert E \Vert F \Vert G \Vert H
Každá proměnná je 32bitové celé číslo, takže jejich konkatenace vždy vede k 256bitovému výsledku, bez ohledu na velikost našeho vstupu zprávy do hašovací funkce.
Odůvodnění kryptografických vlastností
Ale jak je tato funkce nevratná, odolná vůči kolizím a odolná vůči manipulaci?
Pro odolnost vůči manipulaci je to poměrně snadné pochopit. Provádí se tolik
výpočtů v kaskádě, které závisí jak na vstupu, tak na konstantách, že
nejmenší modifikace počáteční zprávy zcela změní cestu, kterou se výpočet
ubírá, a tím pádem zcela změní výstupní hash. To je to, co se nazývá
lavinový efekt. Tato vlastnost je částečně zajištěna mícháním
meziprostorových stavů s počátečními stavy pro každý kus. Dále, při diskusi
o kryptografické hašovací funkci se termín "nevrátitelnost" obvykle
nepoužívá. Místo toho mluvíme o "odolnosti vůči nalezení původního obrazu",
což specifikuje, že pro libovolné dané y je obtížné najít x takové, že h(x) = y. Tato odolnost vůči
nalezení původního obrazu je zaručena algebraickou složitostí a silnou
nelinearitou operací prováděných ve funkci komprese, stejně jako ztrátou
určitých informací v procesu. Například pro daný výsledek sčítání modulo
existuje několik možných operandů:$$ 3+2 \mod 10 = 5 \ 7+8 \mod 10 = 5 \
5+10 \mod 10 = 5
V tomto příkladu, znaje pouze použité modulo (10) a výsledek (5), nelze s jistotou určit, které jsou správné operandy použité při sčítání. Říká se, že existuje několik kongruencí modulo 10.
Pro operaci XOR se setkáváme se stejným problémem. Pamatujte na pravdivostní tabulku pro tuto operaci: jakýkoliv 1-bitový výstup lze určit dvěma různými konfiguracemi vstupů, které mají přesně stejnou pravděpodobnost, že jsou správnými hodnotami. Proto nelze s jistotou určit operandy XORu, znaje pouze jeho výsledek. Pokud zvětšíme velikost operandů XORu, počet možných vstupů znaje pouze výsledek exponenciálně roste. Navíc je XOR často používán společně s dalšími operacemi na úrovni bitů, jako je operace $\text{RotR}$, které přidávají ještě více možných interpretací výsledku.
Komprese také využívá operaci $\text{ShR}$. Tato operace odstraní část základních informací, které je pak nemožné později získat zpět. Opět neexistuje algebraický způsob, jak tuto operaci obrátit. Všechny tyto jednosměrné operace a operace vedoucí ke ztrátě informací jsou velmi často používány ve funkcích komprese. Počet možných vstupů pro daný výstup je tedy téměř nekonečný a každý pokus o obrácený výpočet by vedl k rovnicím s velmi vysokým počtem neznámých, který by exponenciálně narůstal v každém kroku.
Nakonec, pro charakteristiku odolnosti vůči kolizím, hrají roli několik parametrů. Předzpracování původní zprávy hraje zásadní roli. Bez tohoto předzpracování by mohlo být snazší najít kolize na funkci. Ačkoliv teoreticky kolize existují (kvůli principu holubníku), struktura hašovací funkce, kombinovaná s výše zmíněnými vlastnostmi, činí pravděpodobnost nalezení kolize extrémně nízkou.
Pro to, aby byla hašovací funkce odolná vůči kolizím, je zásadní, že:
- Výstup je nepředvídatelný: Jakákoli předvídatelnost může být využita k rychlejšímu nalezení kolizí než pomocí útoku hrubou silou. Funkce zajišťuje, že každý bit výstupu závisí na vstupu netriviálním způsobem. Jinými slovy, funkce je navržena tak, aby každý bit konečného výsledku měl nezávislou pravděpodobnost být 0 nebo 1, i když tato nezávislost v praxi není absolutní.
- Distribuce hašů je pseudonáhodná: To zajišťuje, že haše jsou rovnoměrně distribuovány.
- Velikost haše je značná: čím větší možný prostor pro výsledky, tím je obtížnější najít kolizi.
Kryptografové tyto funkce navrhují tak, že hodnotí nejlepší možné útoky pro nalezení kolizí, a poté upravují parametry tak, aby tyto útoky byly neúčinné.
### Konstrukce Merkle-Damgård
Struktura SHA256 je založena na konstrukci Merkle-Damgård, která umožňuje transformovat kompresní funkci na hašovací funkci, která může zpracovávat zprávy libovolné délky. To je přesně to, co jsme viděli v této kapitole.
Nicméně některé staré hašovací funkce jako SHA1 nebo MD5, které používají tuto specifickou konstrukci, jsou zranitelné vůči útokům typu prodloužení délky. Jedná se o techniku, která umožňuje útočníkovi, který zná hash zprávy $M$ a délku $M$ (aniž by znal samotnou zprávu), vypočítat hash zprávy $M'$ vytvořené konkatenací $M$ s dodatečným obsahem.
SHA256, i když používá stejný typ konstrukce, je teoreticky odolná vůči tomuto typu útoku, na rozdíl od SHA1 a MD5. To by mohlo vysvětlovat záhadu dvojitého hašování implementovaného v Bitcoinu Satoshi Nakamotem. Aby se vyhnul tomuto typu útoku, Satoshi mohl dát přednost použití dvojitého SHA256:
\text{HASH256}(m) = \text{SHA256}(\text{SHA256}(m))
To zvyšuje bezpečnost proti potenciálním útokům souvisejícím s konstrukcí Merkle-Damgård, ale nezvyšuje bezpečnost procesu hašování z hlediska odolnosti proti kolizím. Navíc, i kdyby SHA256 bylo zranitelné vůči tomuto typu útoku, nemělo by to vážný dopad, jelikož všechny případy použití hašovacích funkcí v Bitcoinu zahrnují veřejná data. Nicméně útok typu prodloužení délky by mohl být pro útočníka užitečný pouze v případě, že hašovaná data jsou soukromá a uživatel použil hašovací funkci jako autentizační mechanismus pro tato data, podobně jako MAC. Implementace dvojitého hašování tak zůstává záhadou v návrhu Bitcoinu.
Nyní, když jsme se podrobně podívali na fungování hašovacích funkcí, zejména SHA256, které se v Bitcoinu používá rozsáhle, zaměříme se konkrétněji na kryptografické algoritmy derivace používané na aplikační úrovni, zejména pro odvozování klíčů pro vaši peněženku.
## Algoritmy používané pro derivaci
<chapterId>cc668121-7789-5e99-bf5e-1ba085f4f5f2</chapterId>
V Bitcoinu na aplikační úrovni, kromě hašovacích funkcí, se používají kryptografické algoritmy derivace k generování bezpečných dat z počátečních vstupů. Ačkoli tyto algoritmy spoléhají na hašovací funkce, slouží k jiným účelům, zejména co se týče autentizace a generování klíčů. Tyto algoritmy si zachovávají některé charakteristiky hašovacích funkcí, jako je nevratnost, odolnost vůči manipulaci a odolnost proti kolizím.
V peněženkách Bitcoinu se hlavně používají 2 algoritmy derivace:
- **HMAC (_Hash-based Message Authentication Code_)**
- **PBKDF2 (_Password-Based Key Derivation Function 2_)**
Společně prozkoumáme fungování a roli každého z nich.
### HMAC-SHA512
HMAC je kryptografický algoritmus, který vypočítává autentizační kód na základě kombinace hašovací funkce a tajného klíče. Bitcoin používá HMAC-SHA512, variantu HMAC, která používá hašovací funkci SHA512. Již jsme viděli v předchozí kapitole, že SHA512 je součástí stejné rodiny hašovacích funkcí jako SHA256, ale produkuje 512bitový výstup.
Zde je jeho obecné schéma fungování s $m$ jako vstupní zprávou a $K$ tajným klíčem:
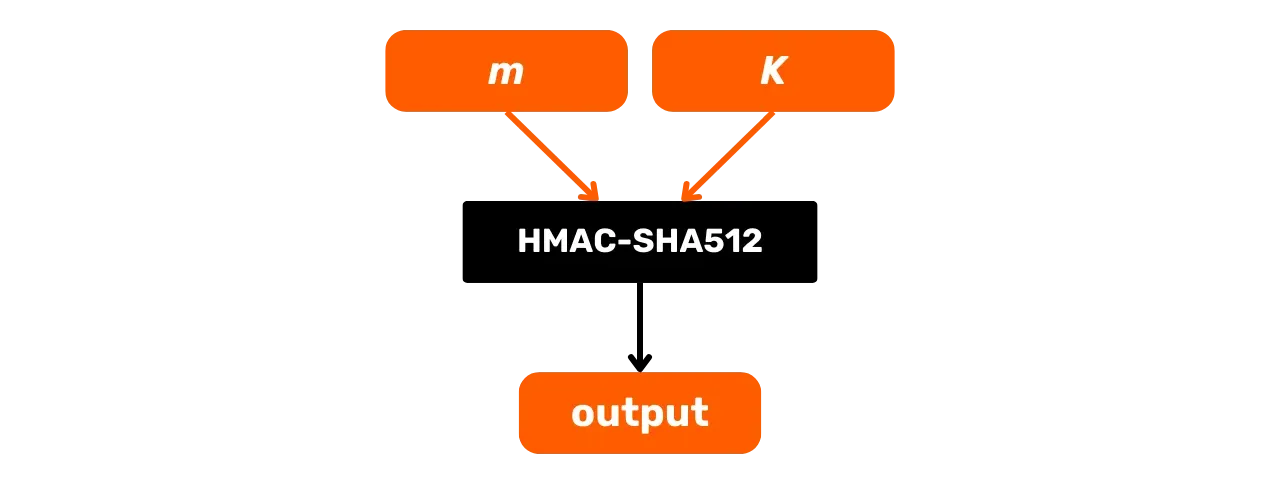
Podívejme se podrobněji na to, co se děje v této černé skříňce HMAC-SHA512. Funkce HMAC-SHA512 s:
- $m$: libovolně velká zpráva zvolená uživatelem (první vstup);
- $K$: libovolný tajný klíč zvolený uživatelem (druhý vstup);
- $K'$: klíč $K$ upravený na velikost $B$ bloků hašovací funkce (1024 bitů pro SHA512, nebo 128 bajtů);
- $\text{SHA512}$: hašovací funkce SHA512;
- $\oplus$: operace XOR (exkluzivní nebo);
- $\Vert$: operátor konkatenace, spojující řetězce bitů konec s koncem;
- $\text{opad}$: konstanta složená z bytu $0x5c$ opakovaného 128krát
- $\text{ipad}$: konstanta složená z bytu $0x36$ opakovaného 128krát
Před výpočtem HMAC je nutné sladit klíč a konstanty podle velikosti bloku $B$. Například, pokud je klíč $K$ kratší než 128 bytů, je doplněn nulami, aby dosáhl velikosti $B$. Pokud je $K$ delší než 128 bytů, je komprimován pomocí SHA512 a poté jsou přidány nuly, dokud nedosáhne 128 bytů. Tímto způsobem je získán sladěný klíč pojmenovaný $K'$.
Hodnoty $\text{opad}$ a $\text{ipad}$ jsou získány opakováním jejich základního bytu ($0x5c$ pro $\text{opad}$, $0x36$ pro $\text{ipad}$) dokud není dosaženo velikosti $B$. Tedy s $B = 128$ byty máme:
\text{opad} = \underbrace{0x5c5c\ldots5c}_{128 , \text{bytes}}
Jakmile je předzpracování dokončeno, algoritmus HMAC-SHA512 je definován následující rovnicí:
\text {HMAC-SHA512}_K(m) = \text{SHA512} \left( (K' \oplus \text{opad}) \parallel \text{SHA512} \left( (K' \oplus \text{ipad}) \parallel m \right) \right)
Tato rovnice je rozložena na následující kroky:
- XOR upraveného klíče $K'$ s $\text{ipad}$ pro získání $\text{iKpad}$;
- XOR upraveného klíče $K'$ s $\text{opad}$ pro získání $\text{oKpad}$;
- Konkatenace $\text{iKpad}$ s zprávou $m$.
- Hashování tohoto výsledku pomocí SHA512 pro získání mezivýsledku $H_1$.
- Konkatenace $\text{oKpad}$ s $H_1$.
- Hashování tohoto výsledku pomocí SHA512 pro získání konečného výsledku $H_2$.
Tyto kroky lze shrnout schématicky následovně:
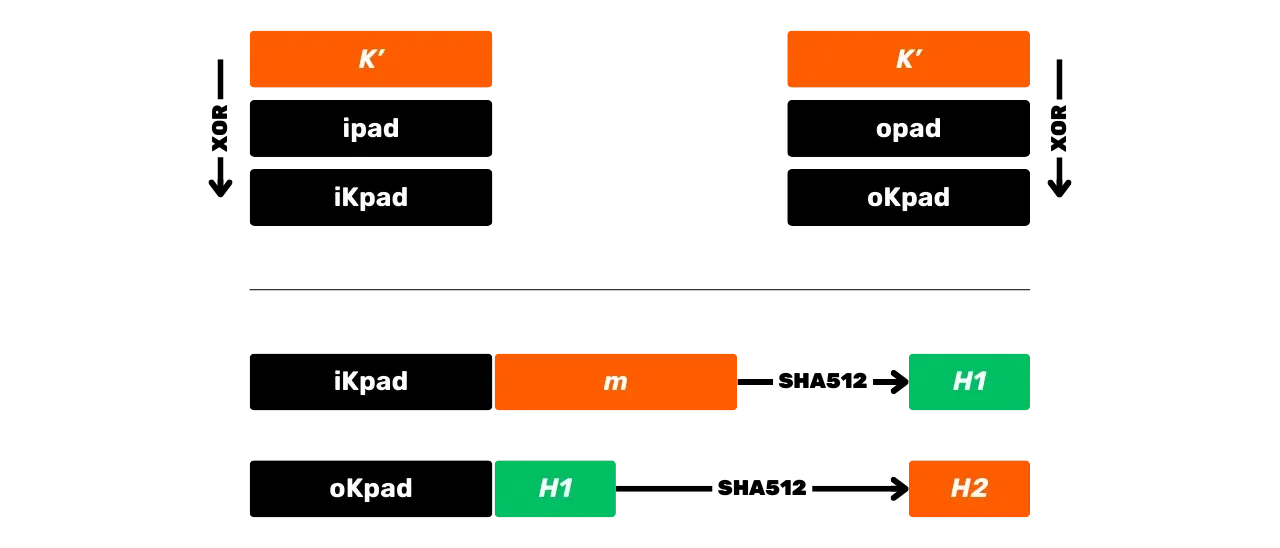
HMAC se v Bitcoinu používá zejména pro derivaci klíčů v HD (Hierarchických Deterministických) peněženkách (o tomto budeme mluvit podrobněji v nadcházejících kapitolách) a jako součást PBKDF2.
### PBKDF2
PBKDF2 (_Password-Based Key Derivation Function 2_) je algoritmus derivace klíčů navržený pro zvýšení bezpečnosti hesel. Algoritmus aplikuje pseudo-náhodnou funkci (zde HMAC-SHA512) na heslo a kryptografickou sůl, a poté tuto operaci opakuje určitý počet krát, aby vyprodukoval výstupní klíč.
V Bitcoinu se PBKDF2 používá k generování seedu HD peněženky z mnemonické fráze a heslové fráze (ale o tomto budeme mluvit podrobněji v nadcházejících kapitolách).
Proces PBKDF2 je následující, s:
- $m$: mnemonická fráze uživatele;
- $s$: volitelná heslová fráze pro zvýšení bezpečnosti (prázdné pole, pokud není heslová fráze);
- $n$: počet iterací funkce, v našem případě je to 2048.
Funkce PBKDF2 je definována iterativně. Každá iterace vezme výsledek předchozí, projde jej přes HMAC-SHA512 a kombinuje postupné výsledky k vytvoření finálního klíče:\text{PBKDF2}(m, s) = \text{HMAC-SHA512}^{2048}(m, s)
Schématicky lze PBKDF2 reprezentovat takto:
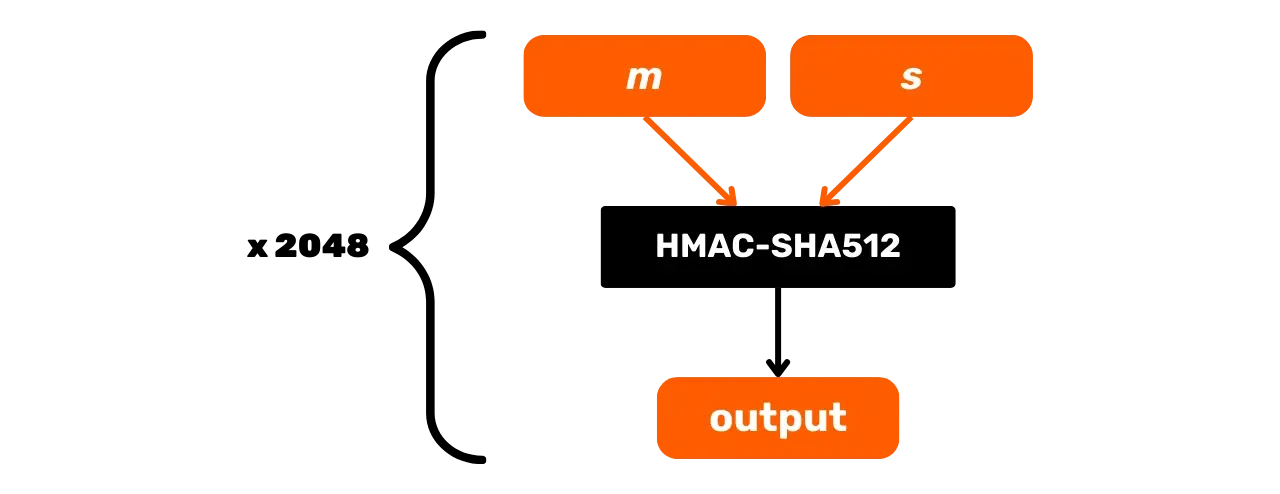
V této kapitole jsme prozkoumali funkce HMAC-SHA512 a PBKDF2, které používají hashovací funkce k zajištění integrity a bezpečnosti odvození klíčů v protokolu Bitcoinu. V další části se podíváme na digitální podpisy, další kryptografickou metodu široce používanou v Bitcoinu.
# Digitální Podpisy
<partId>76b58a00-0c18-54b9-870d-6b7e34029db8</partId>
## Digitální Podpisy a Eliptické Křivky
<chapterId>c9dd9672-6da1-57f8-9871-8b28994d4c1a</chapterId>
Druhou kryptografickou metodou používanou v Bitcoinu jsou algoritmy digitálních podpisů. Pojďme prozkoumat, co to znamená a jak to funguje.
### Bitcoiny, UTXO a Podmínky Výdaje
Pojem "_peněženka_" v Bitcoinu může být pro začátečníky matoucí. Skutečně, to, co se nazývá Bitcoinová peněženka, je software, který přímo neobsahuje vaše bitcoiny, na rozdíl od fyzické peněženky, která může obsahovat mince nebo bankovky. Bitcoiny jsou prostě jednotky účtu. Tato jednotka účtu je reprezentována **UTXO** (_Unspent Transaction Outputs_), což jsou nevyužité transakční výstupy. Pokud jsou tyto výstupy nevyužité, znamená to, že patří uživateli. UTXO jsou, jakýmsi způsobem, kusy bitcoinů, proměnné velikosti, patřící uživateli.
Protokol Bitcoinu je distribuovaný a funguje bez centrální autority. Proto to není jako tradiční bankovní záznamy, kde eura, která vám patří, jsou jednoduše spojena s vaší osobní identitou. V Bitcoinu vaše UTXO patří vám, protože jsou chráněna podmínkami výdaje specifikovanými v jazyce Script. Zjednodušeně řečeno, existují dva typy skriptů: uzamykací skript (_scriptPubKey_), který chrání UTXO, a odemykací skript (_scriptSig_), který umožňuje odemknout UTXO a tím utratit bitcoinové jednotky, které reprezentuje.
Počáteční operace Bitcoinu s P2PK skripty zahrnuje použití veřejného klíče k uzamčení prostředků, specifikující v _scriptPubKey_, že osoba, která si přeje utratit toto UTXO, musí poskytnout platný podpis s privátním klíčem odpovídajícím tomuto veřejnému klíči. K odemčení tohoto UTXO je tedy nutné poskytnout platný podpis v _scriptSig_. Jak názvy napovídají, veřejný klíč je znám všem, protože je vysílán na blockchainu, zatímco privátní klíč zná pouze legitimní vlastník prostředků.
To je základní operace Bitcoinu, ale časem se tato operace stala složitější. Nejprve Satoshi také představil P2PKH skripty, které používají přijímací adresu v _scriptPubKey_, což představuje hash veřejného klíče. Poté se systém stal ještě složitějším s příchodem SegWitu a poté Taprootu. Nicméně, obecný princip zůstává zásadně stejný: veřejný klíč nebo reprezentace tohoto klíče je použita k uzamčení UTXO, a odpovídající privátní klíč je vyžadován k jejich odemčení a tím k jejich utracení.
Uživatel, který si přeje provést transakci s Bitcoinem, musí proto vytvořit digitální podpis pomocí svého soukromého klíče k dané transakci. Tento podpis mohou ověřit ostatní účastníci sítě. Pokud je platný, znamená to, že uživatel iniciující transakci je skutečně vlastníkem soukromého klíče a tedy i vlastníkem bitcoinů, které si přeje utratit. Ostatní uživatelé mohou poté transakci přijmout a dále šířit.
V důsledku toho musí uživatel, který vlastní bitcoiny uzamčené veřejným klíčem, najít způsob, jak bezpečně uložit to, co umožňuje odemknout jejich prostředky: soukromý klíč. Bitcoinová peněženka je přesně zařízení, které vám umožní snadno uchovávat všechny vaše klíče bez přístupu ostatních lidí. Je tedy spíše jako svazek klíčů než jako peněženka.
Matematická vazba mezi veřejným a soukromým klíčem, stejně jako schopnost provést podpis k prokázání držení soukromého klíče bez jeho odhalení, jsou umožněny algoritmem digitálního podpisu. V protokolu Bitcoinu jsou použity 2 algoritmy pro podpis: **ECDSA** (_Elliptic Curve Digital Signature Algorithm_) a **Schnorrův schéma podpisu**. ECDSA je digitální podpisový protokol používaný v Bitcoinu od jeho počátků. Schnorr je v Bitcoinu novější, protože byl zaveden v listopadu 2021 s aktualizací Taproot.
Tyto dva algoritmy jsou si ve svých mechanismech poměrně podobné. Oba jsou založeny na kryptografii eliptických křivek. Hlavní rozdíl mezi těmito dvěma protokoly spočívá ve struktuře podpisu a některých specifických matematických vlastnostech. Proto se budeme zabývat fungováním těchto algoritmů, začínající nejstarším: ECDSA.
### Kryptografie eliptických křivek
Kryptografie eliptických křivek (ECC) je soubor algoritmů, které pro kryptografické účely využívají eliptickou křivku a její různé matematické a geometrické vlastnosti. Bezpečnost těchto algoritmů spočívá v obtížnosti problému diskrétního logaritmu na eliptických křivkách. Eliptické křivky se významně používají pro výměnu klíčů, asymetrické šifrování nebo pro vytváření digitálních podpisů.
Důležitou vlastností těchto křivek je, že jsou symetrické vzhledem k ose x. Tedy každá nevertikální čára, která křivku protne ve dvou různých bodech, vždy protne křivku v třetím bodu. Navíc každá tečna k křivce v bodě, který není singulární, protne křivku v dalším bodě. Tyto vlastnosti budou užitečné pro definování operací na křivce.
Zde je reprezentace eliptické křivky nad polem reálných čísel:
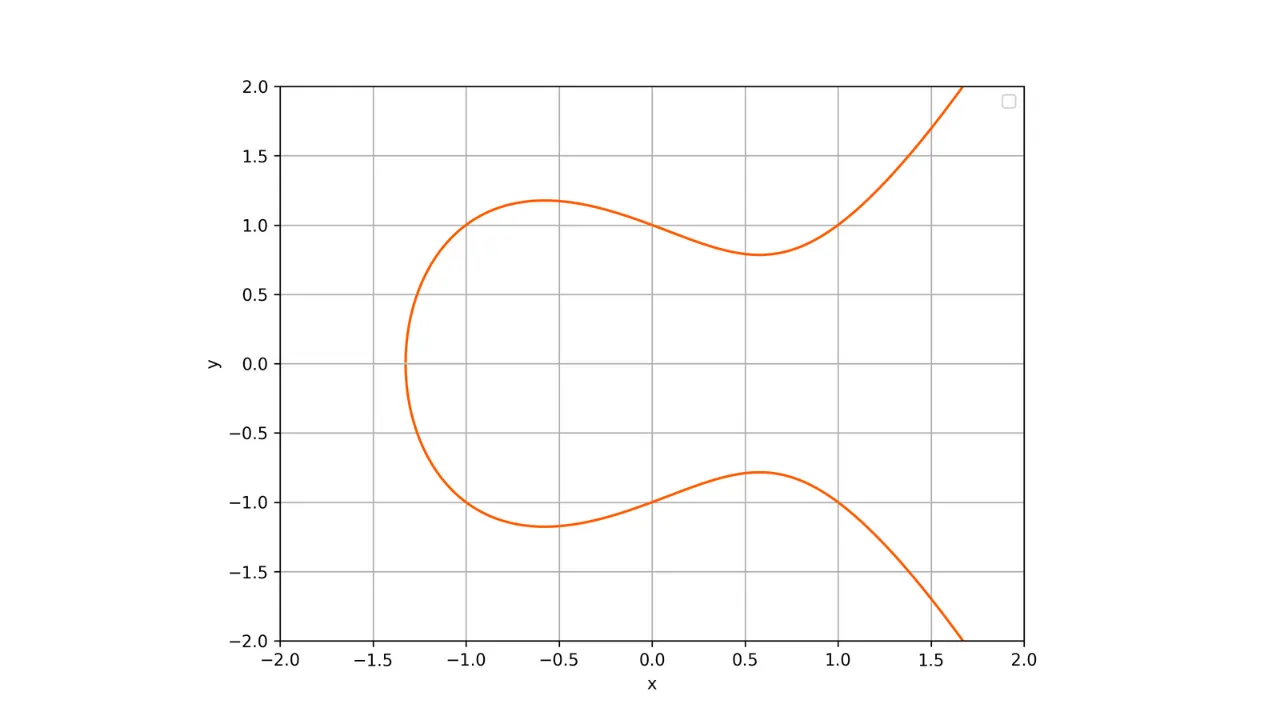
Každá eliptická křivka je definována rovnicí ve tvaru:
y^2 = x^3 + ax + b
### secp256k1
Pro použití ECDSA nebo Schnorra je nutné zvolit parametry eliptické křivky, tj. hodnoty $a$ a $b$ v rovnici křivky. Existují různé standardy eliptických křivek, které jsou považovány za kryptograficky bezpečné. Nejznámější je křivka _secp256r1_, definovaná a doporučená NIST (_National Institute of Standards and Technology_).
Přesto se Satoshi Nakamoto, tvůrce Bitcoinu, rozhodl tuto křivku nepoužít. Důvod tohoto rozhodnutí není znám, ale někteří se domnívají, že upřednostnil hledání alternativy, protože parametry této křivky by mohly potenciálně obsahovat zadní vrátka. Místo toho protokol Bitcoinu používá standardní křivku **_secp256k1_**. Tato křivka je definována parametry $a = 0$ a $b = 7$. Její rovnice je tedy:
y^2 = x^3 + 7
Její grafická reprezentace nad polem reálných čísel vypadá takto:
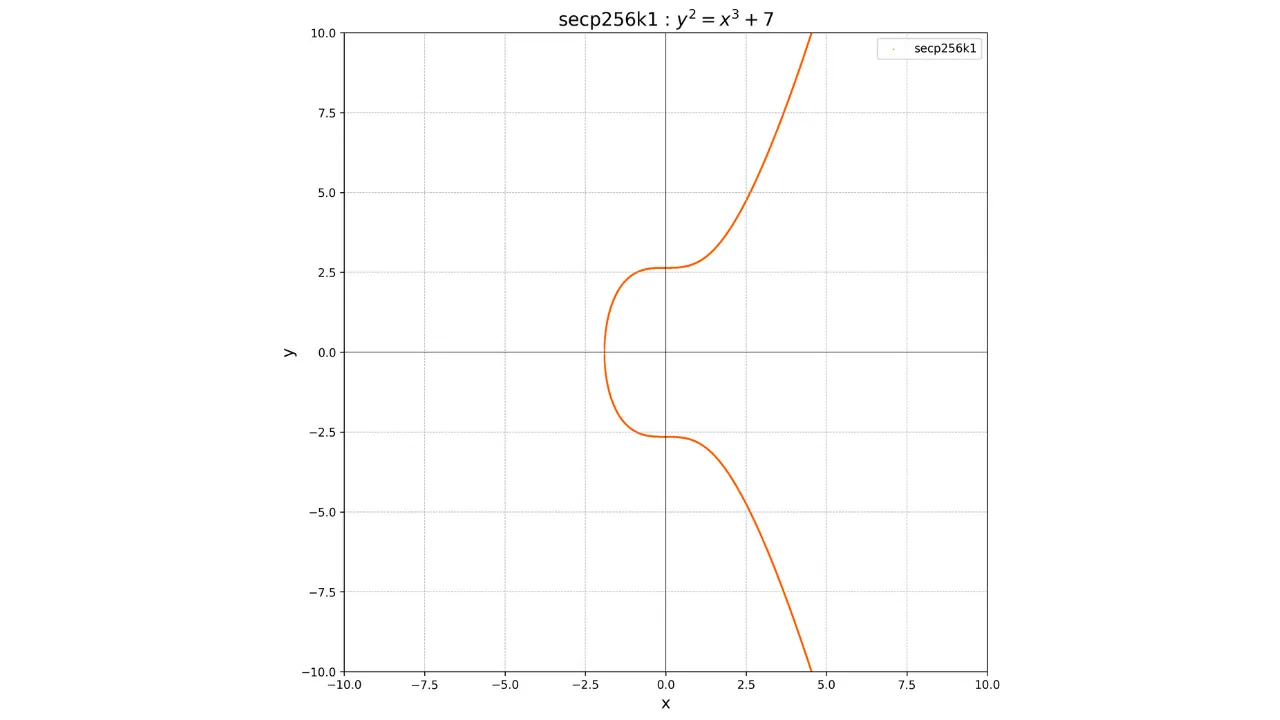
Nicméně v kryptografii pracujeme s konečnými množinami čísel. Konkrétně pracujeme na konečném tělese $\mathbb{F}_p$, které je tělesem celých čísel modulo prvočíslo $p$.
**Definice**: Prvočíslo je přirozené celé číslo větší nebo rovno 2, které má pouze dva různé kladné celočíselné dělitele: 1 a samo sebe. Například číslo 7 je prvočíslo, protože je dělitelné pouze 1 a 7. Na druhou stranu, číslo 8 prvočíslem není, protože je dělitelné 1, 2, 4 a 8.
V Bitcoinu je prvočíslo $p$ použité k definici konečného tělesa velmi velké. Je vybráno tak, aby řád tělesa (tj. počet prvků v $\mathbb{F}_p$) byl dostatečně velký, aby zajistil kryptografickou bezpečnost.
Použité prvočíslo $p$ je:
```text
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
```
V desítkové notaci to odpovídá:
p = 2^{256} - 2^{32} - 977
Takže rovnice naší eliptické křivky je ve skutečnosti:
y^2 \equiv x^3 + 7 \mod p
Vzhledem k tomu, že tato křivka je definována nad konečným tělesem $\mathbb{F}_p$, již nevypadá jako spojitá křivka, ale spíše jako diskrétní množina bodů. Například zde je, jak vypadá křivka používaná v Bitcoinu pro velmi malé $p = 17$:
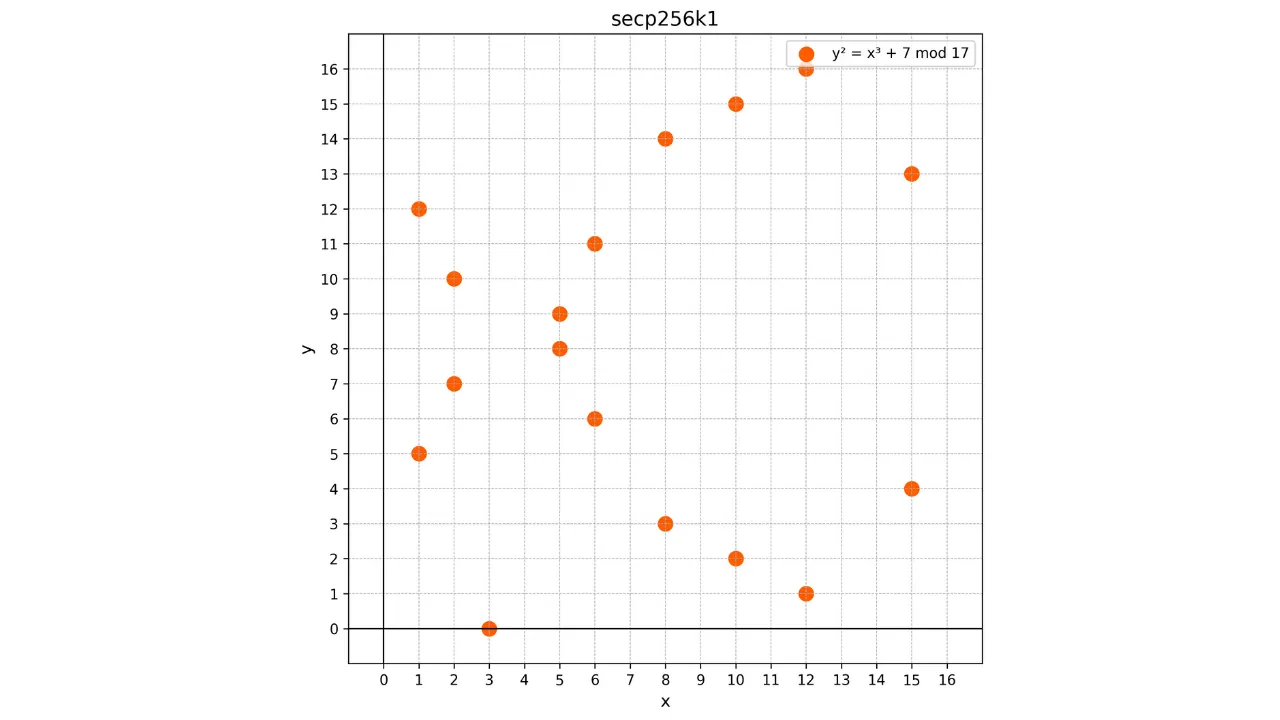
V tomto příkladu jsem záměrně omezil konečné těleso na $p = 17$ z vzdělávacích důvodů, ale musíme si představit, že to používané v Bitcoinu je nesmírně větší, téměř $2^{256}$.
Používáme konečné těleso celých čísel modulo $p$, abychom zajistili přesnost operací na křivce. Skutečně, eliptické křivky nad tělesem reálných čísel jsou předmětem nepřesností kvůli zaokrouhlovacím chybám během výpočetních výpočtů. Pokud se na křivce provede mnoho operací, tyto chyby se hromadí a konečný výsledek může být nesprávný nebo obtížně reprodukovatelný. Exkluzivní použití kladných celých čísel zajišťuje dokonalou přesnost výpočtů a tím i reprodukovatelnost výsledku.
Matematika eliptických křivek nad konečnými tělesy je analogická té nad tělesem reálných čísel, s adaptací, že všechny operace se provádějí modulo $p$. Abychom zjednodušili vysvětlení, budeme v následujících kapitolách pokračovat v ilustraci konceptů pomocí křivky definované nad reálnými čísly, přičemž si budeme pamatovat, že v praxi je křivka definována nad konečným tělesem.
Pokud se chcete dozvědět více o matematických základech moderní kryptografie, doporučuji také konzultovat tento další kurz na Plan ₿ Network:
https://planb.network/courses/d2fd9fc0-d9ed-4a87-9fa3-0fdbb3937e28
## Výpočet veřejného klíče z privátního klíče
<chapterId>fcb2bd58-5dda-5ecf-bb8f-ad1a0561ab4a</chapterId>
Jak bylo dříve viděno, algoritmy digitálního podpisu v Bitcoinu jsou založeny na páru privátních a veřejných klíčů, které jsou matematicky propojeny. Pojďme společně prozkoumat, jaký je tento matematický vztah a jak jsou generovány.
### Privátní klíč
Privátní klíč je jednoduše náhodné nebo pseudonáhodné číslo. V případě Bitcoinu je toto číslo 256 bitů velké. Počet možností pro privátní klíč Bitcoinu je tedy teoreticky $2^{256}$.
**Poznámka**: "Pseudo-náhodné číslo" je číslo, které má vlastnosti blízké skutečně náhodnému číslu, ale je generováno deterministickým algoritmem.
Nicméně, v praxi existuje na naší eliptické křivce secp256k1 pouze $n$ rozlišitelných bodů, kde $n$ je řád generátorového bodu $G$ křivky. Později uvidíme, co toto číslo odpovídá, ale jednoduše si zapamatujte, že platný soukromý klíč je celé číslo mezi $1$ a $n-1$, vědě, že $n$ je číslo blízké, ale mírně menší než $2^{256}$. Proto existují některá 256-bitová čísla, která nejsou platná pro stání se soukromým klíčem v Bitcoinu, konkrétně všechna čísla mezi $n$ a $2^{256}$. Pokud generování náhodného čísla (soukromý klíč) produkuje hodnotu $k$ takovou, že $k \geq n$, je považováno za neplatné a musí být vygenerována nová náhodná hodnota.
Počet možností pro soukromý klíč Bitcoinu je tedy přibližně $n$, což je číslo blízké $1.158 \times 10^{77}$. Toto číslo je tak velké, že pokud si vyberete soukromý klíč náhodně, je statisticky téměř nemožné narazit na soukromý klíč jiného uživatele. Abych vám dal představu o měřítku, počet možných soukromých klíčů na Bitcoinu je řádově blízký odhadovanému počtu atomů ve viditelném vesmíru.
Jak uvidíme v nadcházejících kapitolách, dnes většina soukromých klíčů používaných na Bitcoinu není generována náhodně, ale je výsledkem deterministické derivace z mnemonické fráze, sama o sobě pseudo-náhodná (to je ta slavná fráze 12 nebo 24 slov). Tato informace nic nemění na používání algoritmů digitálního podpisu jako ECDSA, ale pomáhá nám zaměřit se znovu na popularizaci Bitcoinu.
Pro pokračování vysvětlení bude soukromý klíč označen malým písmenem $k$.
### Veřejný klíč
Veřejný klíč je bod na eliptické křivce, označený velkým písmenem $K$, a je vypočítán z soukromého klíče $k$. Tento bod $K$ je reprezentován párem souřadnic $(x, y)$ na eliptické křivce, přičemž každá souřadnice je celé číslo modulo $p$, prvočíslo definující konečné pole $\mathbb{F}_p$.
V praxi je nekomprimovaný veřejný klíč reprezentován 512 bity (nebo 64 byty), což odpovídá dvěma 256-bitovým číslům ($x$ a $y$) umístěným vedle sebe. Tato čísla jsou souřadnice abscisy ($x$) a ordináty ($y$) našeho bodu na secp256k1. Pokud přidáme prefix, veřejný klíč má celkem 520 bitů.
Je však také možné reprezentovat veřejný klíč v komprimované formě použitím pouze 33 bytů (264 bitů) tím, že zachováme pouze abscisu $x$ našeho bodu na křivce a byte indikující paritu $y$. To je známé jako komprimovaný veřejný klíč. O tomto budu více mluvit v posledních kapitolách tohoto školení. Ale co si potřebujete zapamatovat, je, že veřejný klíč $K$ je bod popsaný $x$ a $y$.
Pro výpočet bodu $K$, který odpovídá našemu veřejnému klíči, používáme operaci skalárního násobení na eliptických křivkách, definovanou jako opakované sčítání ($k$-krát) generátorového bodu $G$:
K = k \cdot G
kde:
- $k$ je soukromý klíč (náhodné celé číslo mezi $1$ a $n-1$);
- $G$ je generátorový bod eliptické křivky používaný všemi účastníky Bitcoinové sítě; - $\cdot$ reprezentuje skalární násobení na eliptické křivce, což je ekvivalentní k přidání bodu $G$ k sobě samému $k$-krát.
Fakt, že tento bod $G$ je společný pro všechny veřejné klíče na Bitcoinu, nám umožňuje být si jisti, že stejný soukromý klíč $k$ nám vždy dá stejný veřejný klíč $K$:
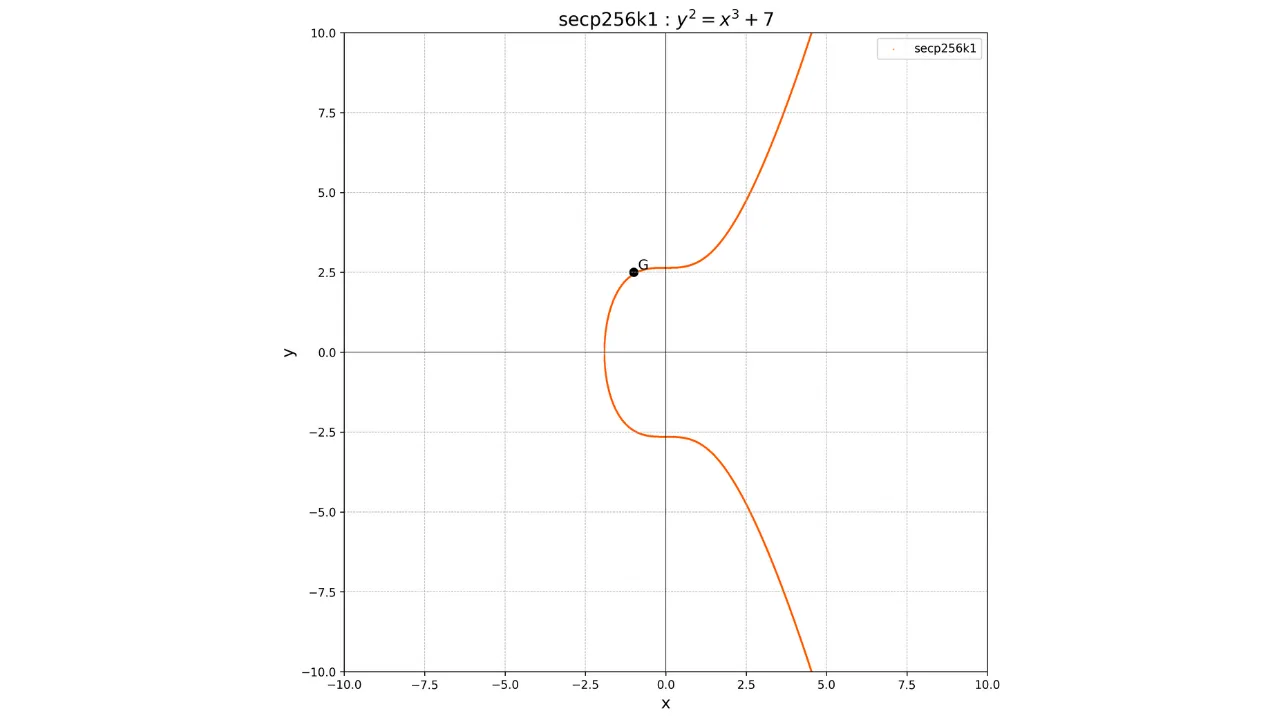
Hlavní charakteristikou této operace je, že jde o jednosměrnou funkci. Je snadné vypočítat veřejný klíč $K$ znalostí soukromého klíče $k$ a generátorového bodu $G$, ale je prakticky nemožné vypočítat soukromý klíč $k$ znalostí pouze veřejného klíče $K$ a generátorového bodu $G$. Najít $k$ z $K$ a $G$ znamená řešit problém diskrétního logaritmu na eliptických křivkách, matematicky obtížný problém, pro který není znám žádný efektivní algoritmus. Ani nejsilnější současné kalkulačky nejsou schopny tento problém vyřešit v rozumném čase.

### Sčítání a zdvojení bodů na eliptických křivkách
Koncept sčítání na eliptických křivkách je definován geometricky. Pokud máme na křivce dva body $P$ a $Q$, operace $P + Q$ se vypočítá tak, že nakreslíme čáru procházející body $P$ a $Q$. Tato čára nutně protne křivku ve třetím bodě $R'$. Poté vezmeme zrcadlový obraz tohoto bodu vzhledem k ose x, abychom získali bod $R$, který je výsledkem sčítání:
P + Q = R
Graficky to lze znázornit takto:
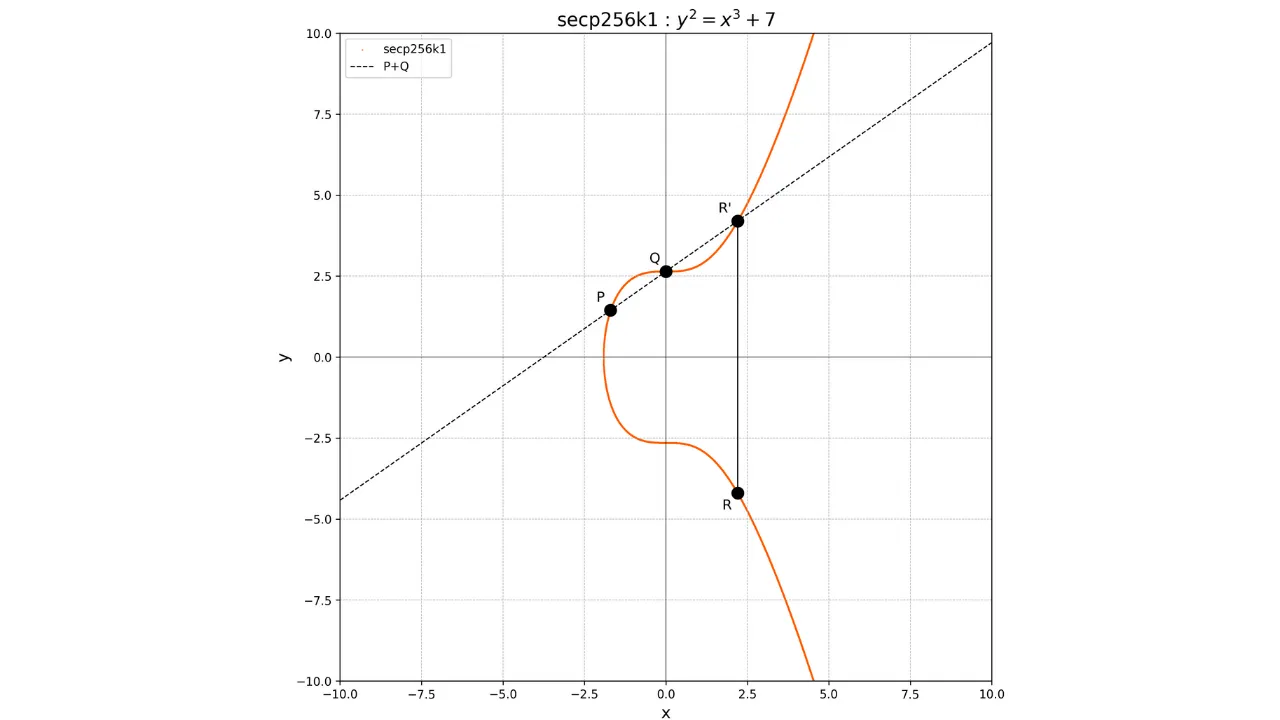
Pro zdvojení bodu, tj. operaci $P + P$, nakreslíme tečnu k křivce v bodě $P$. Tato tečna protne křivku v dalším bodě $S'$. Poté vezmeme zrcadlový obraz tohoto bodu vzhledem k ose x, abychom získali bod $S$, který je výsledkem zdvojení:
2P = S
Graficky je to znázorněno takto:
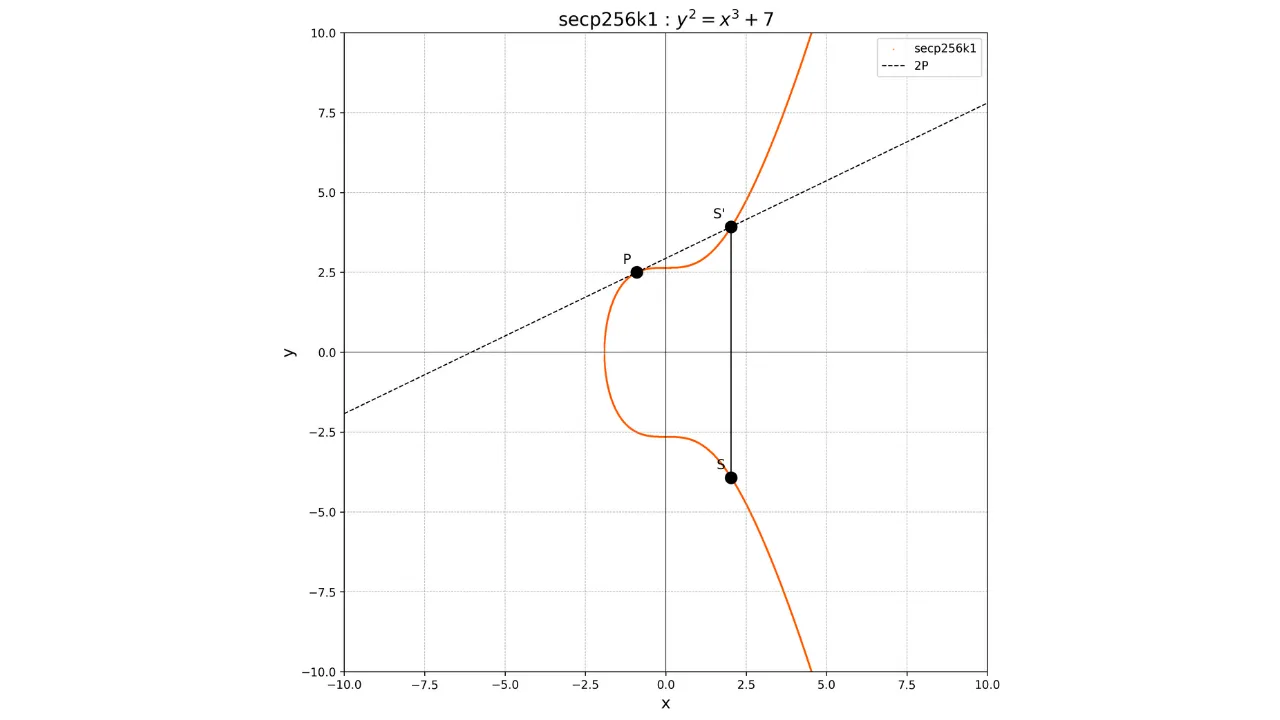
Použitím těchto operací sčítání a zdvojení můžeme provést skalární násobení bodu celým číslem $k$, označené $kP$, opakovaným zdvojením a sčítáním.
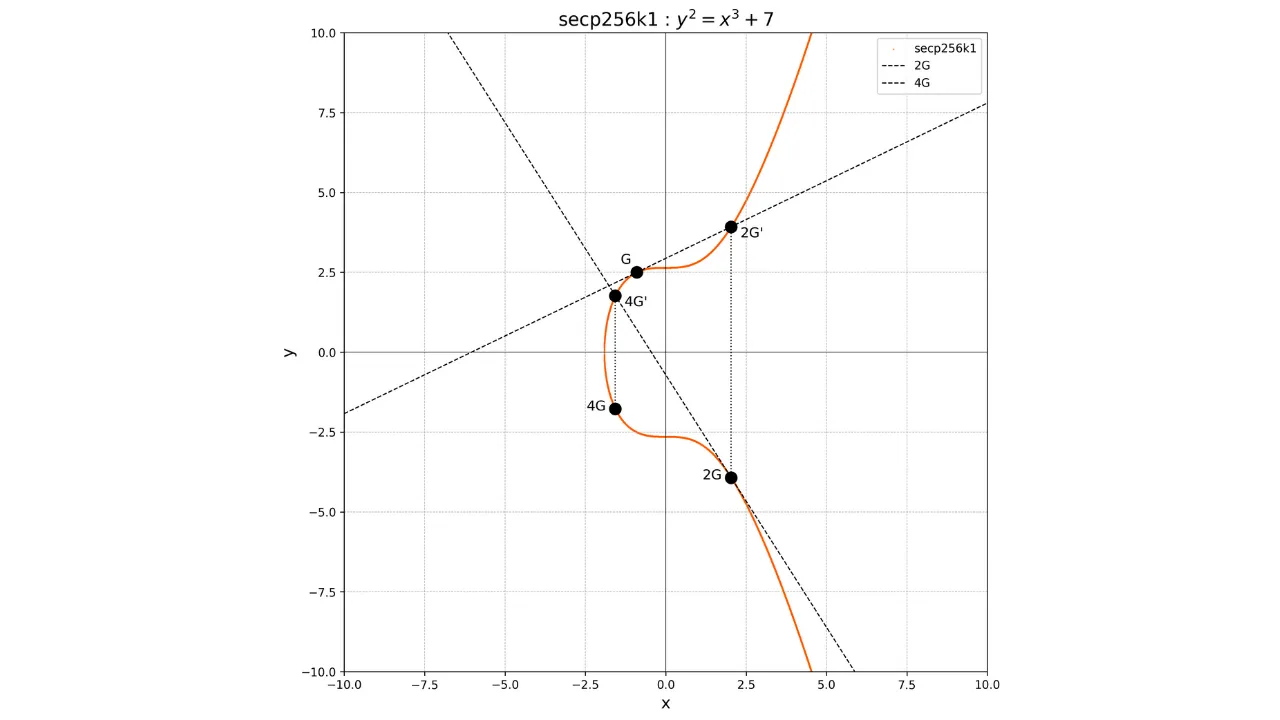
Například, předpokládejme, že jsme si vybrali soukromý klíč $k = 4$. Pro výpočet přidruženého veřejného klíče provedeme:
K = k \cdot G = 4G
Graficky to odpovídá provádění série sčítání a zdvojení:
- Vypočítáme $2G$ zdvojením $G$.
- Vypočítáme $4G$ zdvojením $2G$.

Pokud bychom chtěli například vypočítat bod $3G$, musíme nejprve vypočítat bod $2G$ zdvojením bodu $G$, poté přidat $G$ a $2G$. Pro přidání $G$ a $2G$ jednoduše nakreslíme čáru spojující tyto dva body, získáme jedinečný bod $-3G$ na průsečíku této čáry a eliptické křivky, a poté určíme $3G$ jako opak $-3G$.
Budeme mít:
G + G = 2G
2G + G = 3G
Graficky by to bylo znázorněno takto:
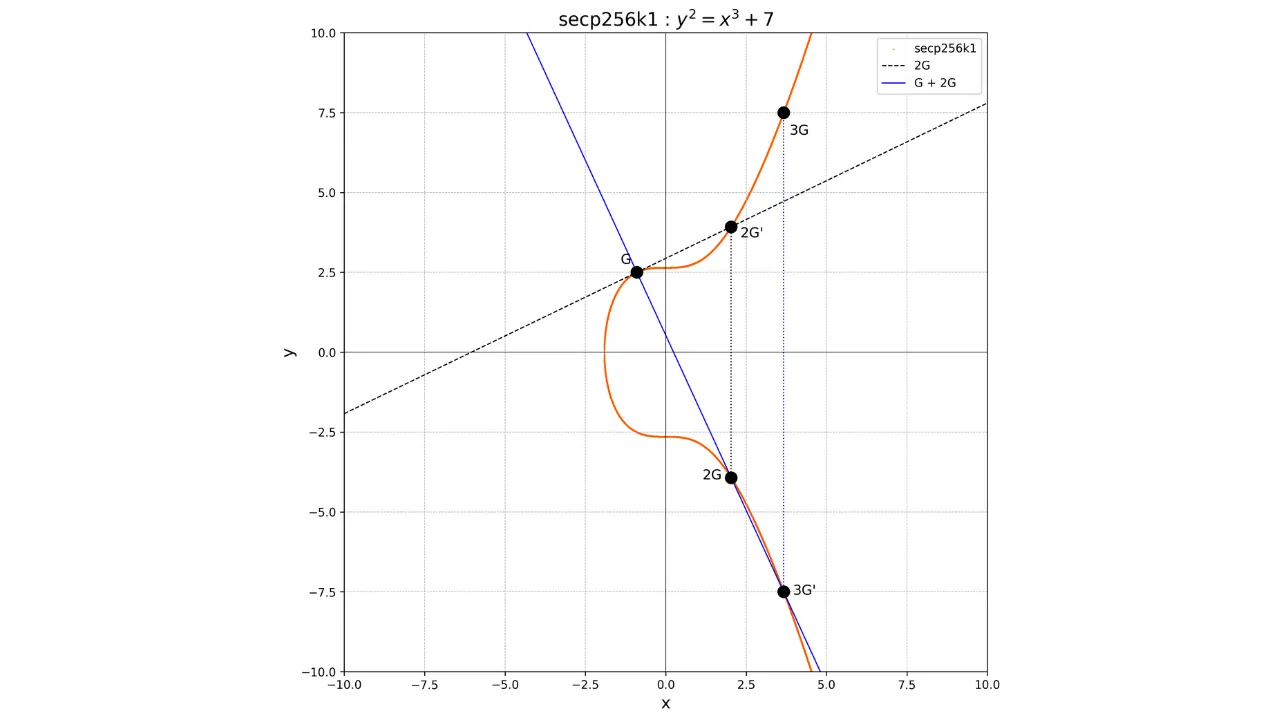
### Jednosměrná funkce
Díky těmto operacím můžeme pochopit, proč je snadné odvodit veřejný klíč z privátního klíče, ale opak je prakticky nemožný.
Vraťme se k našemu zjednodušenému příkladu. S privátním klíčem $k = 4$. Pro výpočet přidruženého veřejného klíče provedeme:
K = k \cdot G = 4G
Takto jsme snadno vypočítali veřejný klíč $K$ znalostí $k$ a $G$.
Nyní, pokud někdo zná pouze veřejný klíč $K$, setká se s problémem diskrétního logaritmu: najít $k$ tak, aby $K = k \cdot G$. Tento problém je považován za obtížný, protože neexistuje efektivní algoritmus pro jeho řešení na eliptických křivkách. To zajišťuje bezpečnost algoritmů ECDSA a Schnorr.
Samozřejmě, v tomto zjednodušeném příkladu s $k = 4$, by bylo možné najít $k$ metodou pokus-omyl, protože počet možností je nízký. Avšak v praxi na Bitcoinu je $k$ 256-bitové celé číslo, což činí počet možností astronomicky velký (přibližně $1.158 \times 10^{77}$). Proto je nemožné najít $k$ hrubou silou.
## Podpis privátním klíčem
<chapterId>bb07826f-826e-5905-b307-3d82001fb778</chapterId>
Nyní, když víte, jak odvodit veřejný klíč z privátního klíče, můžete již přijímat bitcoiny použitím této dvojice klíčů jako podmínky pro utrácení. Ale jak je utratit? Pro utrácení bitcoinů budete muset odemknout _scriptPubKey_ připojený k vašemu UTXO, abyste dokázali, že jste skutečně jeho legitimním vlastníkem. K tomu musíte vyprodukovat podpis $s$, který odpovídá veřejnému klíči $K$ přítomnému ve _scriptPubKey_ pomocí privátního klíče $k$, který byl původně použit pro výpočet $K$. Digitální podpis je tak nezpochybnitelným důkazem, že máte v držení privátní klíč spojený s veřejným klíčem, který tvrdíte.
### Parametry eliptické křivky
Pro provedení digitálního podpisu se všichni účastníci musí nejprve dohodnout na parametrech použité eliptické křivky. V případě Bitcoinu jsou parametry **secp256k1** následující:
Konečné pole $\mathbb{Z}_p$ definované:
p = 2^{256} - 2^{32} - 977
```text
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
```
$p$ je velmi velké prvočíslo o něco menší než $2^{256}$.
Eliptická křivka $y^2 = x^3 + ax + b$ nad $\mathbb{Z}_p$ definovaná:
a = 0, \quad b = 7
Generující bod nebo počáteční bod $G$:
```text
G = 0x0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
```
Toto číslo je komprimovaná forma, která udává pouze souřadnici bodu $G$. Předpona `02` na začátku určuje, která ze dvou hodnot majících tuto souřadnici $x$ má být použita jako generující bod.
Řád $n$ bodu $G$ (počet existujících bodů) a kofaktor $h$:
```text
n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
```
$n$ je velmi velké číslo, které je o něco menší než $p$.
h=1
$h$ je kofaktor nebo počet podskupin. Zde nebudu podrobně vysvětlovat, co to představuje, protože je to poměrně složité a v případě Bitcoinu to nemusíme brát v úvahu, protože je rovno $1$.
Všechny tyto informace jsou veřejné a známé všem účastníkům. Díky nim mohou uživatelé vytvářet digitální podpis a ověřovat jej.
### Podpis s ECDSA
Algoritmus ECDSA umožňuje uživateli podepsat zprávu pomocí svého soukromého klíče takovým způsobem, že kdokoli zná odpovídající veřejný klíč, může ověřit platnost podpisu, aniž by byl soukromý klíč kdy odhalen. V kontextu Bitcoinu závisí zpráva, která má být podepsána, na _sighash_ vybraném uživatelem. Právě tento _sighash_ určí, které části transakce jsou podpisem pokryty. O tomto budu hovořit více v další kapitole.
Zde jsou kroky pro generování podpisu ECDSA:
Nejprve vypočítáme hash ($e$) zprávy, která má být podepsána. Zpráva $m$ je tedy prošla kryptografickou hashovací funkcí, obvykle SHA256 nebo dvojitým SHA256 v případě Bitcoinu:
e = \text{HASH}(m)
Dále vypočítáme nonce. V kryptografii je nonce jednoduše číslo generované náhodně nebo pseudonáhodně, které se použije pouze jednou. To znamená, že pokaždé, když je s tímto párem klíčů vytvořen nový digitální podpis, bude velmi důležité použít jiný nonce, jinak to ohrozí bezpečnost soukromého klíče. Je tedy dostatečné určit náhodné a unikátní celé číslo $r$ tak, aby $1 \leq r \leq n-1$, kde $n$ je řád generujícího bodu $G$ eliptické křivky.
Poté vypočítáme bod $R$ na eliptické křivce s koordináty $(x_R, y_R)$ tak, že:
R = r \cdot G
Extrahujeme hodnotu abscisy bodu $R$ ($x_R$). Tato hodnota představuje první část podpisu. A nakonec vypočítáme druhou část podpisu $s$ tímto způsobem:
s = r^{-1} \left( e + k \cdot x_R \right) \mod n
kde:
- $r^{-1}$ je modulární inverze $r$ modulo $n$, tj. celé číslo takové, že $r \cdot r^{-1} \equiv 1 \mod n$;
- $k$ je soukromý klíč uživatele;
- $e$ je hash zprávy;
- $n$ je řád generujícího bodu $G$ eliptické křivky.
Podpis je pak jednoduše konkatenace $x_R$ a $s$:
\text{SIG} = x_R \Vert s
### Ověření podpisu ECDSA
Pro ověření podpisu $(x_R, s)$ může kdokoli, kdo zná veřejný klíč $K$ a parametry eliptické křivky, postupovat tímto způsobem:
Nejprve ověřte, že $x_R$ a $s$ jsou v intervalu $[1, n-1]$. To zajistí, že podpis respektuje matematické omezení eliptické skupiny. Pokud to není splněno, verifikátor okamžitě odmítne podpis jako neplatný.
Poté vypočítejte hash zprávy:
e = \text{HASH}(m)
Vypočítejte modulární inverzi $s$ modulo $n$:
s^{-1} \mod n
Vypočítejte dvě skalární hodnoty $u_1$ a $u_2$ následovně:
\begin{align*} u_1 &= e \cdot s^{-1} \mod n \ u_2 &= x_R \cdot s^{-1} \mod n \end{align*}
A nakonec vypočítejte bod $V$ na eliptické křivce tak, že:
V = u_1 \cdot G + u_2 \cdot K
Podpis je platný pouze pokud $x_V \equiv x_R \mod n$, kde $x_V$ je $x$ souřadnice bodu $V$. Skutečně, kombinací $u_1 \cdot G$ a $u_2 \cdot K$ se získá bod $V$, který, pokud je podpis platný, musí odpovídat bodu $R$ použitému během podpisu (modulo $n$).
### Podpis s protokolem Schnorr
Schnorrův schéma podpisu je alternativou k ECDSA, která nabízí mnoho výhod. Od roku 2021 je možné jej používat na Bitcoinu díky zavedení Taprootu s P2TR skriptovacími vzory. Stejně jako ECDSA umožňuje Schnorrův schéma podepisovat zprávu pomocí soukromého klíče tak, že podpis může být ověřen kýmkoli, kdo zná odpovídající veřejný klíč.
V případě Schnorra se používá přesně stejná křivka jako u ECDSA se stejnými parametry. Veřejné klíče jsou však reprezentovány mírně odlišně ve srovnání s ECDSA. Skutečně, jsou označeny pouze $x$ souřadnicí bodu na eliptické křivce. Na rozdíl od ECDSA, kde jsou komprimované veřejné klíče reprezentovány 33 bajty (s předponovým bajtem udávajícím paritu $y$), Schnorr používá 32-bajtové veřejné klíče, odpovídající pouze $x$ souřadnici bodu $K$, a předpokládá se, že $y$ je ve výchozím stavu sudé. Toto zjednodušené znázornění snižuje velikost podpisů a usnadňuje určité optimalizace v algoritmech ověřování.
Veřejný klíč je poté $x$ souřadnice bodu $K$:
\text{pk} = K_x
Prvním krokem k vygenerování podpisu je hashování zprávy. Ale na rozdíl od ECDSA, je to provedeno s dalšími hodnotami a používá se označená hashovací funkce, aby se zabránilo kolizím v různých kontextech. Označená hashovací funkce jednoduše zahrnuje přidání libovolného štítku k vstupům hashovací funkce společně s daty zprávy.
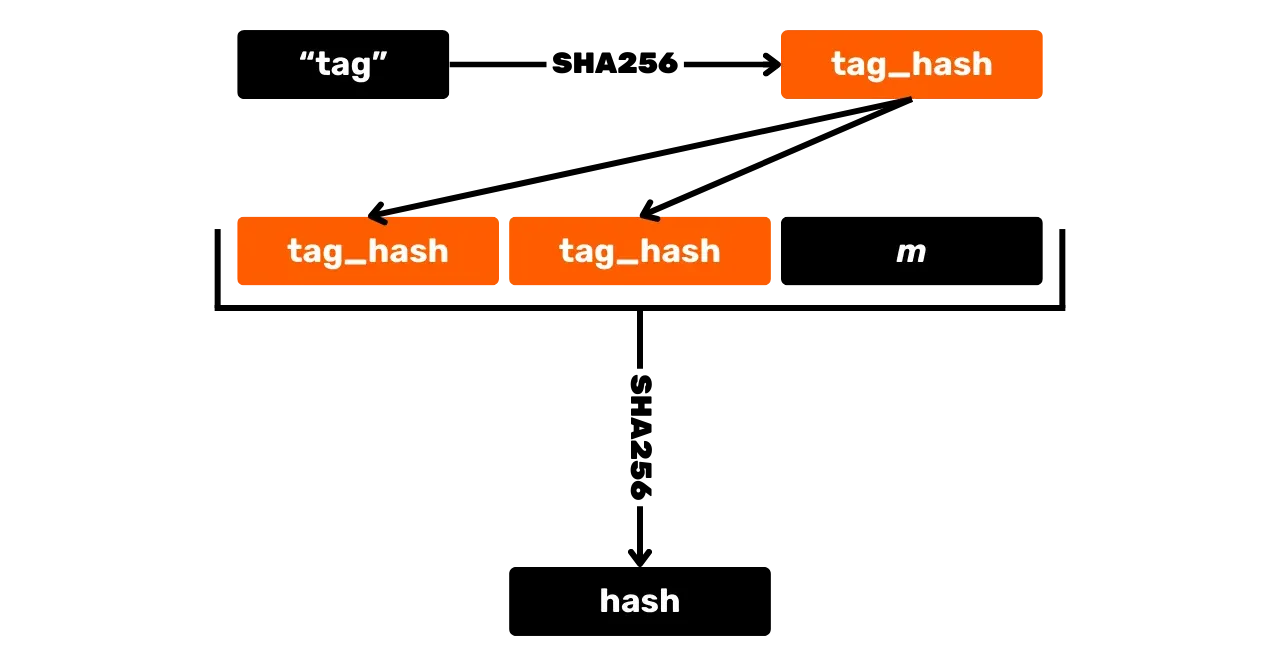
Kromě zprávy jsou do označené funkce předány také $x$ souřadnice veřejného klíče $K_x$, stejně jako bod $R$ vypočítaný z nonce $r$ ($R=r \cdot G$), který je sám o sobě unikátní celé číslo pro každý podpis, vypočítané deterministicky z soukromého klíče a zprávy, aby se předešlo zranitelnostem souvisejícím s opětovným použitím nonce. Stejně jako pro veřejný klíč, je zachována pouze $x$ souřadnice nonce bodu $R_x$ pro popis bodu.
Výsledek tohoto hashování označený $e$ se nazývá "výzva":
e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod n
Zde $\text{HASH}$ je hashovací funkce SHA256 a $\text{``BIP0340/challenge''}$ je specifický tag pro hashování.
Nakonec se parametr $s$ vypočítá z privátního klíče $k$, nonce $r$ a výzvy $e$ takto:
s = (r + e \cdot k) \mod n
Podpis je pak jednoduše pár $Rx$ a $s$.
\text{SIG} = R_x \Vert s
### Ověření Schnorr podpisu
Ověření Schnorr podpisu je jednodušší než ověření podpisu ECDSA. Zde jsou kroky pro ověření podpisu $(R_x, s)$ s veřejným klíčem $K_x$ a zprávou $m$:
Nejprve ověříme, že $K_x$ je platné celé číslo a menší než $p$. Pokud to platí, získáme odpovídající bod na křivce s $K_y$ jako sudým. Také extrahujeme $R_x$ a $s$ oddělením podpisu $\text{SIG}$. Poté zkontrolujeme, že $R_x < p$ a $s < n$ (řád křivky).
Dále vypočítáme výzvu $e$ stejným způsobem jako vydavatel podpisu:
e = \text{HASH}(\text{``BIP0340/challenge''}, R_x \Vert K_x \Vert m) \mod n
Poté vypočítáme referenční bod na křivce takto:
R' = s \cdot G - e \cdot K
Nakonec ověříme, že $R'_x = R_x$. Pokud se dvě x-souřadnice shodují, pak je podpis $(R_x, s)$ skutečně platný s veřejným klíčem $K_x$.
### Proč to funguje?
Podpisovatel vypočítal $s = r + e \cdot k \mod n$, takže $R' = s \cdot G - e \cdot K$ by měl být roven původnímu bodu $R$, protože:
s \cdot G = (r + e \cdot k) \cdot G = r \cdot G + e \cdot k \cdot G
Vzhledem k tomu, že $K = k \cdot G$, máme $e \cdot k \cdot G = e \cdot K$. Tedy:
R' = r \cdot G = R
Takže máme:
R'_x = R_x
### Výhody Schnorr podpisů
Schnorrův podpisový schéma nabízí pro Bitcoin několik výhod oproti původnímu algoritmu ECDSA. První výhodou je, že Schnorr umožňuje agregaci klíčů a podpisů. To znamená, že více veřejných klíčů lze kombinovat do jednoho klíče.
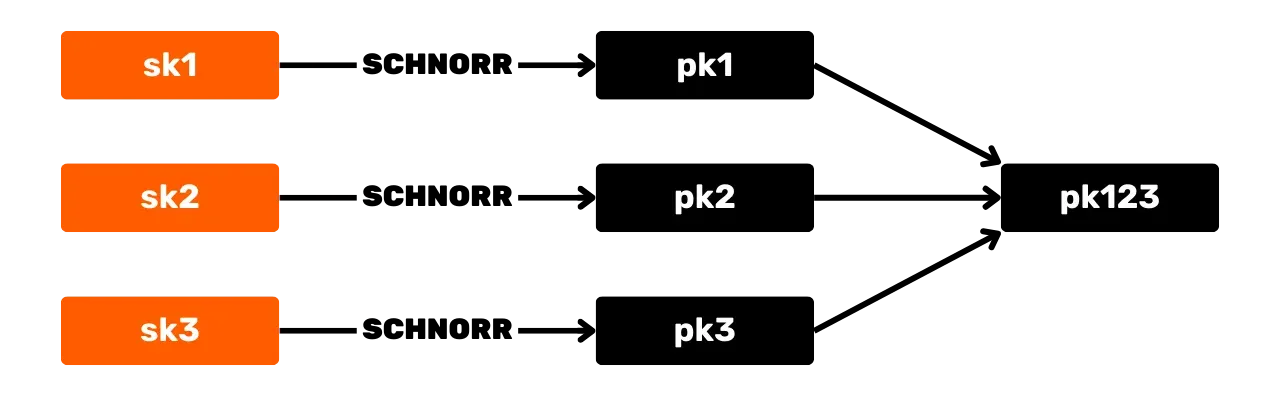
A podobně, více podpisů lze agregovat do jednoho platného podpisu. Tedy v případě transakce s více podpisy může sada účastníků podepsat jediným podpisem a jedním agregovaným veřejným klíčem. To výrazně snižuje náklady na úložiště a výpočty pro síť, protože každý uzel musí ověřit pouze jeden podpis.

Navíc agregace podpisů zlepšuje soukromí. S Schnorrem se stává nemožným rozlišit transakci s více podpisy od standardní transakce s jedním podpisem. Tato homogenita činí analýzu řetězce obtížnější, protože omezuje schopnost identifikovat otisky peněženek.
Nakonec Schnorr také nabízí možnost hromadného ověřování. Ověřováním více podpisů současně mohou uzly získat efektivitu, zejména pro bloky obsahující mnoho transakcí. Tato optimalizace snižuje čas a zdroje potřebné k ověření bloku. Navíc Schnorrovy podpisy nejsou měnitelné, na rozdíl od podpisů vytvořených pomocí ECDSA. To znamená, že útočník nemůže upravit platný podpis tak, aby vytvořil další platný podpis pro stejnou zprávu a stejný veřejný klíč. Tato zranitelnost byla dříve přítomna na Bitcoinu a významně bránila bezpečné implementaci Lightning Network. Pro ECDSA byla tato zranitelnost vyřešena softforkem SegWit v roce 2017, který zahrnoval přesun podpisů do samostatné databáze od transakcí, aby se zabránilo jejich měnitelnosti.
### Proč si Satoshi vybral ECDSA?
Jak jsme viděli, Satoshi původně zvolil pro digitální podpisy na Bitcoinu implementaci ECDSA. Přestože jsme také viděli, že Schnorr je v mnoha aspektech lepší než ECDSA, a tento protokol byl vytvořen Claus-Peterem Schnorrem v roce 1989, 20 let před vynálezem Bitcoinu.
Ve skutečnosti nevíme, proč si Satoshi jej nevybral, ale pravděpodobná hypotéza je, že tento protokol byl do roku 2008 pod patentem. Ačkoli byl Bitcoin vytvořen o rok později, v lednu 2009, v té době nebyla k dispozici žádná otevřená standardizace pro Schnorrovy podpisy. Možná Satoshi považoval za bezpečnější použít ECDSA, která byla již široce používána a testována v open-source software a měla několik uznávaných implementací (zejména knihovna OpenSSL používaná do roku 2015 na Bitcoin Core, poté nahrazená libsecp256k1 ve verzi 0.10.0). Nebo možná nevěděl, že tento patent vyprší v roce 2008. Každopádně nejpravděpodobnější hypotéza se zdá být spojena s tímto patentem a skutečností, že ECDSA měla prokázanou historii a byla snazší k implementaci.
## The sighash flags
<chapterId>231c41a2-aff2-4655-9048-47b6d2d83d64</chapterId>
Jak jsme viděli v předchozích kapitolách, digitální podpisy jsou často používány k odemčení skriptu vstupu. Při procesu podepisování je nutné zahrnout podepsaná data do výpočtu, označená v našich příkladech jako zpráva $m$. Tato data, jakmile jsou podepsána, nemohou být změněna bez zneplatnění podpisu. Skutečně, ať už pro ECDSA nebo Schnorr, musí verifikátor podpisu zahrnout do svého výpočtu stejnou zprávu $m$. Pokud se liší od zprávy $m$ původně použité signatářem, výsledek bude nesprávný a podpis bude považován za neplatný. Říká se, že podpis pokrývá určitá data a chrání je tak nějakým způsobem proti neoprávněným úpravám.
### Co je to sighash flag?
Ve specifickém případě Bitcoinu jsme viděli, že zpráva $m$ odpovídá transakci. Ve skutečnosti je to ale trochu složitější. Díky sighash flagům je možné vybrat specifická data v rámci transakce, která budou nebo nebudou podpisem pokryta.
"Sighash flag" je tedy parametr přidaný ke každému vstupu, který umožňuje určit komponenty transakce, které jsou pokryty přidruženým podpisem. Tyto komponenty jsou vstupy a výstupy. Volba sighash flagu tedy určuje, které vstupy a výstupy transakce jsou podpisem fixovány a které je možné stále měnit bez zneplatnění. Tento mechanismus umožňuje podpisům zavázat data transakce podle záměrů signatáře.
Je zřejmé, že jakmile je transakce potvrzena na blockchainu, stává se neměnnou, bez ohledu na použité příznaky sighash. Možnost úpravy prostřednictvím příznaků sighash je omezena na období mezi podepsáním a potvrzením.
Obecně peněženkový software nenabízí možnost ručně upravit příznak sighash vašich vstupů při konstrukci transakce. Ve výchozím nastavení je nastaven `SIGHASH_ALL`. Osobně znám pouze Sparrow Wallet, který umožňuje tuto úpravu z uživatelského rozhraní.
### Jaké existují příznaky sighash na Bitcoinu?
Na Bitcoinu existují především 3 základní příznaky sighash:
- `SIGHASH_ALL` (`0x01`): Podpis se vztahuje na všechny vstupy a všechny výstupy transakce. Transakce je tedy úplně pokryta podpisem a již nemůže být upravena. `SIGHASH_ALL` je nejčastěji používaný sighash v běžných transakcích, když někdo jednoduše chce provést transakci, aniž by mohla být upravena.

Ve všech diagramech této kapitoly oranžová barva reprezentuje prvky pokryté podpisem, zatímco černá barva označuje ty, které nejsou.
- `SIGHASH_NONE` (`0x02`): Podpis pokrývá všechny vstupy, ale žádné výstupy, což umožňuje úpravu výstupů po podpisu. Konkrétně je to podobné jako vystavit prázdný šek. Signatář odemkne UTXO na vstupech, ale nechá pole výstupů zcela upravitelné. Kdokoli, kdo zná tuto transakci, může tedy přidat výstup dle svého výběru, například zadáním přijímací adresy pro shromáždění prostředků spotřebovaných vstupy, a poté transakci vysílat, aby získal bitcoiny. Podpis vlastníka vstupů nebude zneplatněn, protože pokrývá pouze vstupy.

- `SIGHASH_SINGLE` (`0x03`): Podpis pokrývá všechny vstupy stejně jako jeden výstup, který odpovídá indexu podepsaného vstupu. Například, pokud podpis odemkne _scriptPubKey_ vstupu č. 0, pak také pokrývá výstup č. 0. Podpis také chrání všechny ostatní vstupy, které již nemohou být upraveny. Nicméně, kdokoli může přidat další výstup bez zneplatnění podpisu, za předpokladu, že výstup č. 0, který je jediný jím pokrytý, není upraven.

Kromě těchto tří základních příznaků sighash existuje také modifikátor `SIGHASH_ANYONECANPAY` (`0x80`). Tento modifikátor lze kombinovat se základním příznakem sighash a vytvořit tak tři nové příznaky sighash:
- `SIGHASH_ALL | SIGHASH_ANYONECANPAY` (`0x81`): Podpis pokrývá jediný vstup, zahrnující všechny výstupy transakce. Tento kombinovaný příznak sighash umožňuje například vytvoření transakce pro crowdfunding. Organizátor připraví výstup s jejich adresou a cílovou částkou, a každý investor může poté přidat vstupy k financování tohoto výstupu. Jakmile jsou ve vstupech shromážděny dostatečné prostředky pro uspokojení výstupu, může být transakce vysílána.

- `SIGHASH_NONE | SIGHASH_ANYONECANPAY` (`0x82`): Podpis pokrývá jediný vstup, aniž by se zavazoval k jakémukoli výstupu;

- `SIGHASH_SINGLE | SIGHASH_ANYONECANPAY` (`0x83`): Podpis pokrývá jediný vstup stejně jako výstup, který má stejný index jako tento vstup. Například, pokud podpis odemyká _scriptPubKey_ vstupu č. 3, bude také pokrývat výstup č. 3. Zbytek transakce zůstává modifikovatelný, a to jak z hlediska ostatních vstupů, tak i ostatních výstupů.

### Projekty na přidání nových Sighash příznaků
V současnosti (2024) jsou na Bitcoinu použitelné pouze příznaky sighash prezentované v předchozí sekci. Nicméně, některé projekty zvažují přidání nových příznaků sighash. Například, BIP118, navržený Christianem Deckerem a Anthonym Townsem, představuje dva nové příznaky sighash: `SIGHASH_ANYPREVOUT` a `SIGHASH_ANYPREVOUTANYSCRIPT` (_AnyPrevOut = "Jakýkoliv Předchozí Výstup"_).
Tyto dva příznaky sighash by nabídly na Bitcoinu další možnost: vytváření podpisů, které nepokrývají žádný konkrétní vstup transakce.

Tento nápad byl původně formulován Josephem Poonem a Thaddeem Dryjou v bílé knize Lightning Network. Před přejmenováním byl tento příznak sighash nazván `SIGHASH_NOINPUT`.
Pokud bude tento příznak sighash integrován do Bitcoinu, umožní použití covenants, ale je také nezbytným předpokladem pro implementaci Eltoo, obecného protokolu pro druhé vrstvy, který definuje, jak společně spravovat vlastnictví UTXO. Eltoo bylo speciálně navrženo k řešení problémů spojených s mechanismy pro vyjednávání o stavu Lightning kanálů, tj. mezi otevřením a zavřením.
Pro prohloubení vašich znalostí o Lightning Network, po kurzu CYP201, vřele doporučuji kurz LNP201 od Fanise Michalakise, který téma podrobně pokrývá:
https://planb.network/courses/34bd43ef-6683-4a5c-b239-7cb1e40a4aeb
V další části navrhuji objevit, jak funguje mnemonická fráze, která je základem vaší Bitcoin peněženky.
# Mnemonická fráze
<partId>4070af16-c8a2-58b5-9871-a22c86c07458</partId>
## Vývoj Bitcoin peněženek
<chapterId>9d9acd5d-a0e5-5dfd-b544-f043fae8840f</chapterId>
Nyní, když jsme prozkoumali fungování hašovacích funkcí a digitálních podpisů, můžeme studovat, jak fungují Bitcoin peněženky. Cílem bude představit si, jak je peněženka na Bitcoinu konstruována, jak je dekomponována a jaké různé informace, které ji tvoří, se používají. Toto porozumění mechanismům peněženky vám umožní zlepšit vaše používání Bitcoinu z hlediska bezpečnosti a soukromí.
Před ponořením do technických detailů je nezbytné objasnit, co se myslí pojmem "Bitcoin peněženka" a pochopit její užitečnost.
### Co je Bitcoin peněženka?
Na rozdíl od tradičních peněženek, které vám umožňují ukládat fyzické bankovky a mince, Bitcoin peněženka jako taková neobsahuje bitcoiny. Ve skutečnosti bitcoiny neexistují ve fyzické nebo digitální formě, která by mohla být uložena, ale jsou reprezentovány jednotkami účtu zobrazenými v systému ve formě **UTXO** (_Unspent Transaction Output_ - Nevyužitý Transakční Výstup).
UTXO tak představují fragmenty bitcoinů různých velikostí, které lze utratit, pokud je splněn jejich _scriptPubKey_. Aby uživatel mohl utratit své bitcoiny, musí poskytnout _scriptSig_, který odemkne _scriptPubKey_ spojený s jeho UTXO. Tento důkaz je obvykle poskytnut prostřednictvím digitálního podpisu, generovaného z privátního klíče odpovídajícího veřejnému klíči přítomnému v _scriptPubKey_. Tím pádem je klíčovým prvkem, který musí uživatel zabezpečit, privátní klíč. Úlohou Bitcoinové peněženky je právě bezpečně spravovat tyto privátní klíče. Ve skutečnosti je její role více podobná té klíčenky než peněženky v tradičním smyslu.
### JBOK Peněženky (_Just a Bunch Of Keys_)
První peněženky používané na Bitcoinu byly JBOK (_Just a Bunch Of Keys_) peněženky, které seskupovaly soukromě generované klíče nezávisle a bez jakéhokoli vzájemného propojení. Tyto peněženky fungovaly na jednoduchém modelu, kde každý soukromý klíč mohl odemknout unikátní přijímací adresu Bitcoinu.
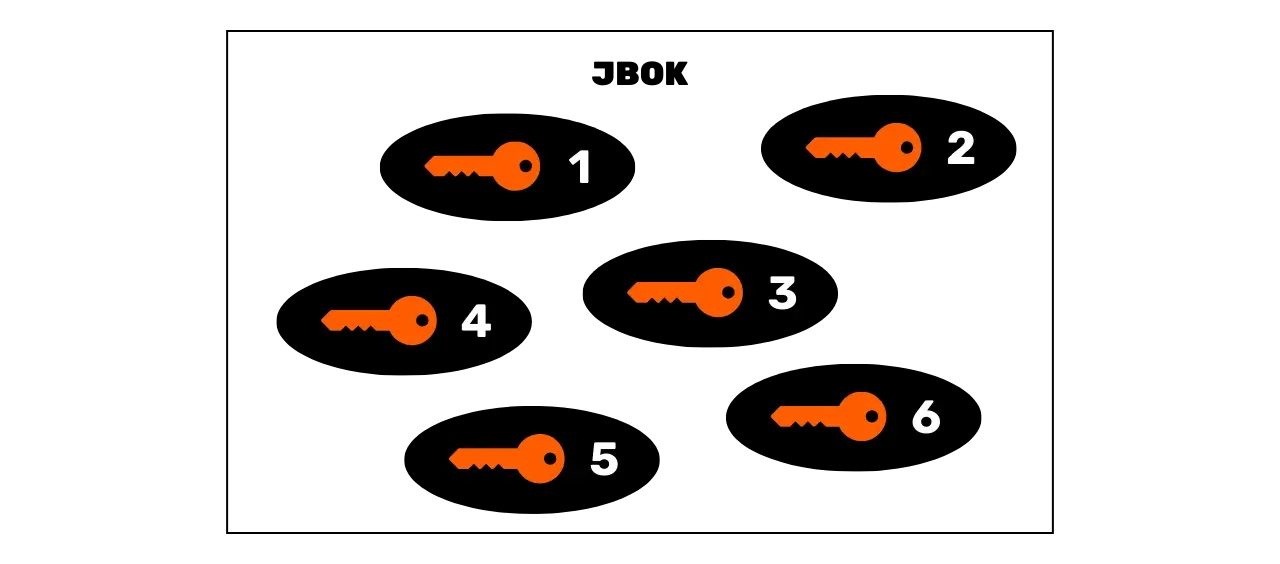
Pokud by člověk chtěl použít více soukromých klíčů, bylo poté nutné udělat tolik záloh, aby se zajistil přístup k finančním prostředkům v případě problémů se zařízením, které peněženku hostuje. Pokud se používá jediný soukromý klíč, tato struktura peněženky může postačovat, protože stačí jediná záloha. To však představuje problém: na Bitcoinu se důrazně nedoporučuje vždy používat stejný soukromý klíč. Skutečně, soukromý klíč je spojen s unikátní adresou a přijímací adresy Bitcoinu jsou normálně navrženy pro jednorázové použití. Při každém přijetí finančních prostředků byste měli generovat novou prázdnou adresu.
Toto omezení vyplývá z modelu soukromí Bitcoinu. Opakovaným používáním stejné adresy usnadňujete externím pozorovatelům sledování všech mých transakcí s Bitcoinem. To je důvod, proč se důrazně nedoporučuje opakovaně používat přijímací adresu. Nicméně, abychom měli více adres a veřejně oddělili naše transakce, je nutné spravovat více soukromých klíčů. V případě JBOK peněženek to znamená vytvářet tolik záloh, kolik je nových párů klíčů, úkol, který se může rychle stát složitým a obtížně udržitelným pro uživatele.
Pro více informací o modelu soukromí Bitcoinu a objevení metod, jak chránit vaše soukromí, doporučuji také sledovat můj kurz BTC204 na Plan ₿ Network:
https://planb.network/courses/65c138b0-4161-4958-bbe3-c12916bc959c
### HD Peněženky (_Hierarchical Deterministic_)
Aby se překonalo omezení JBOK peněženek, byla následně využita nová struktura peněženky. V roce 2012 Pieter Wuille představil vylepšení s BIP32, které zavádí hierarchické deterministické peněženky. Princip HD peněženky spočívá v odvození všech soukromých klíčů z jediného zdroje informací, nazývaného semínko, deterministickým a hierarchickým způsobem. Toto semínko je generováno náhodně při vytvoření peněženky a představuje unikátní zálohu, která umožňuje rekreaci všech soukromých klíčů peněženky. Tímto způsobem může uživatel generovat velmi velké množství soukromých klíčů, aby se vyhnul opakovanému používání adres a zachoval své soukromí, zatímco potřebuje udělat jedinou zálohu své peněženky prostřednictvím semínka.
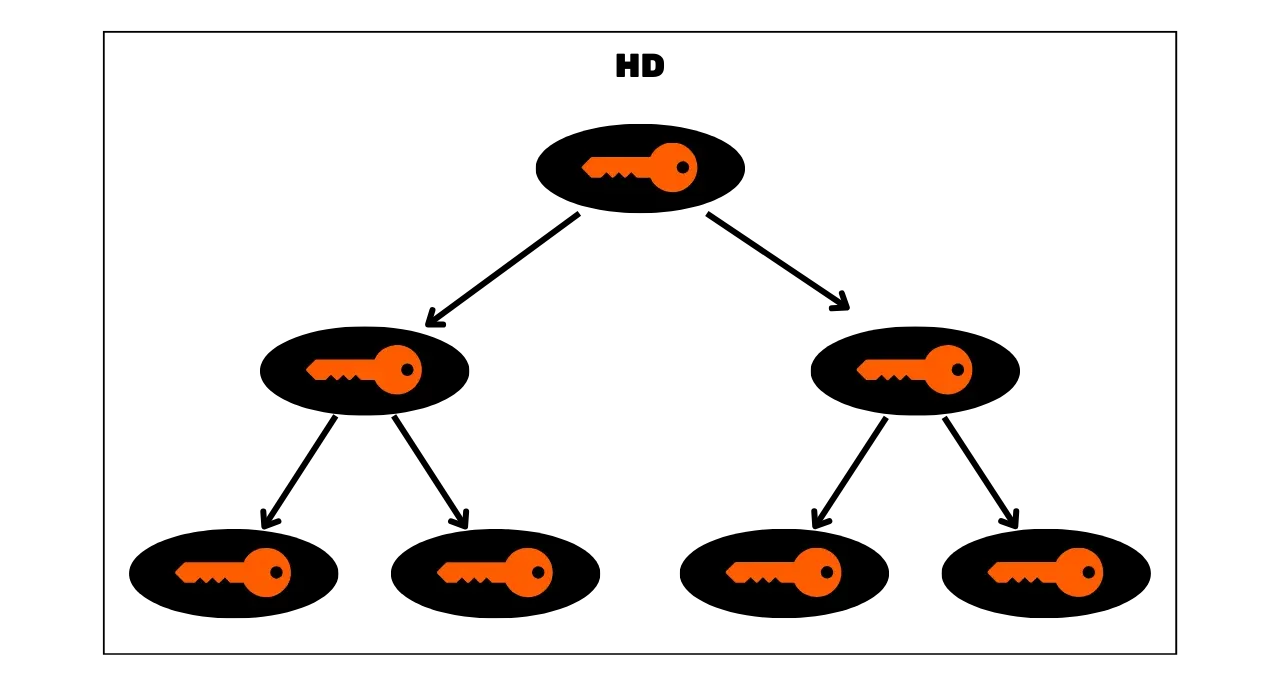
V HD peněženkách se odvození klíčů provádí podle hierarchické struktury, která umožňuje klíče organizovat do odvozovacích podprostorů, přičemž každý podprostor je dále dělitelný, aby se usnadnilo správa finančních prostředků a interoperabilita mezi různými softwary peněženek. Dnes je tento standard přijat většinou uživatelů Bitcoinu. Z tohoto důvodu se mu budeme v následujících kapitolách podrobně věnovat.
### Standard BIP39: Mnemonická Fráze
Kromě BIP32 standardizuje BIP39 formát seedu jako mnemonickou frázi, aby usnadnil zálohování a čitelnost uživateli. Mnemonická fráze, také nazývaná obnovovací fráze nebo 24-slovní fráze, je sekvence slov vybraných z předdefinovaného seznamu, která bezpečně kóduje seed peněženky.
Mnemonická fráze výrazně zjednodušuje zálohování pro uživatele. V případě ztráty, poškození nebo krádeže zařízení hostícího peněženku umožňuje pouhé znalosti této mnemonické fráze obnovit peněženku a získat zpět přístup ke všem finančním prostředkům, které jsou jí zajištěny.
V nadcházejících kapitolách prozkoumáme vnitřní fungování HD peněženek, včetně mechanismů derivace klíčů a různých možných hierarchických struktur. To vám umožní lépe pochopit kryptografické základy, na kterých je založena bezpečnost finančních prostředků na Bitcoinu. A začneme v další kapitole, kde navrhuji objevit roli entropie v základu vaší peněženky.
## Entropie a náhodné číslo
<chapterId>b43c715d-affb-56d8-a697-ad5bc2fffd63</chapterId>
Moderní HD peněženky (deterministické a hierarchické) spoléhají na jediný počáteční kus informace nazývaný "entropie" pro deterministické generování celé sady klíčů peněženky. Tato entropie je pseudo-náhodné číslo, jehož úroveň chaosu částečně určuje bezpečnost peněženky.
### Definice Entropie
Entropie, v kontextu kryptografie a informací, je kvantitativní míra nejistoty nebo nepředvídatelnosti spojená se zdrojem dat nebo náhodným procesem. Hraje důležitou roli v bezpečnosti kryptografických systémů, zejména při generování klíčů a náhodných čísel. Vysoká entropie zajišťuje, že generované klíče jsou dostatečně nepředvídatelné a odolné vůči útokům hrubou silou, kdy útočník zkouší všechny možné kombinace, aby uhodl klíč.
V kontextu Bitcoinu se entropie používá k generování seedu. Při vytváření deterministické a hierarchické peněženky se konstrukce mnemonické fráze provádí z náhodného čísla, které je samo odvozeno ze zdroje entropie. Fráze se pak používá k generování více soukromých klíčů, deterministickým a hierarchickým způsobem, pro vytváření podmínek pro výdaje na UTXO.
### Metody generování entropie
Počáteční entropie použitá pro HD peněženku je obvykle 128 bitů nebo 256 bitů, kde:
- **128 bitů entropie** odpovídá mnemonické frázi **12 slov**;
- **256 bitů entropie** odpovídá mnemonické frázi **24 slov**.
Ve většině případů je toto náhodné číslo generováno automaticky softwarovou peněženkou pomocí PRNG (_Pseudo-Random Number Generator_). PRNG jsou kategorie algoritmů používaných k generování sekvencí čísel z počátečního stavu, které mají vlastnosti přibližující se náhodnému číslu, aniž by byly skutečně náhodné. Dobrý PRNG musí mít vlastnosti jako je uniformita výstupu, nepředvídatelnost a odolnost vůči prediktivním útokům. Na rozdíl od skutečných generátorů náhodných čísel (TRNG) jsou PRNG deterministické a reprodukovatelné.
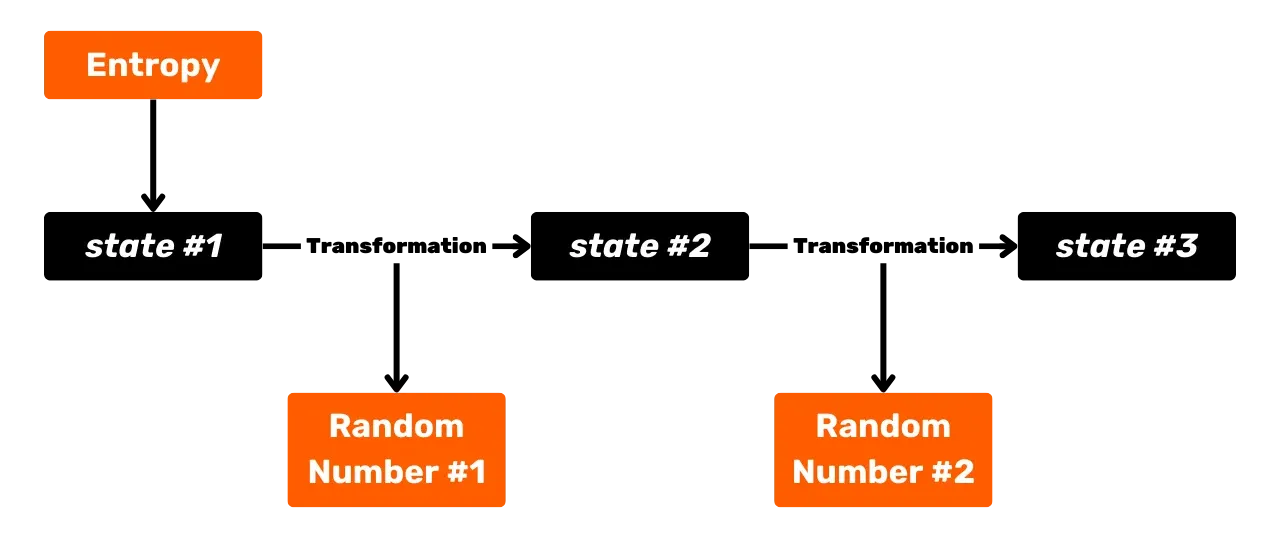
Alternativou je manuální generování entropie, které nabízí lepší kontrolu, ale je také mnohem riskantnější. Silně doporučuji negenerovat entropii pro vaši HD peněženku sami.
V další kapitole uvidíme, jak přejdeme od náhodného čísla k mnemonické frázi 12 nebo 24 slov.
## Mnemonická fráze
<chapterId>8f9340c1-e6dc-5557-a2f2-26c9669987d5</chapterId>
Mnemonická fráze, také nazývaná "seed fráze", "recovery fráze", "tajná fráze" nebo "24-slovní fráze", je sekvence obvykle složená ze 12 nebo 24 slov, která je generována z entropie. Používá se k deterministickému odvození všech klíčů HD peněženky. To znamená, že z této fráze je možné deterministicky generovat a znovu vytvořit všechny soukromé a veřejné klíče Bitcoinové peněženky a tím pádem přistupovat k fondům, které jsou s ní chráněny. Účelem mnemonické fráze je poskytnout prostředek pro zálohování a obnovu bitcoinů, který je zároveň bezpečný a snadno použitelný. Do standardů byla zavedena v roce 2013 s BIP39.
Pojďme společně objevit, jak přejít od entropie k mnemonické frázi.
### Kontrolní součet
Pro přeměnu entropie na mnemonickou frázi je nejprve nutné přidat na konec entropie kontrolní součet (nebo "kontrolní suma"). Tento kontrolní součet je krátká sekvence bitů, která zajišťuje integritu dat ověřením, že nebyla zavedena žádná náhodná modifikace.
Pro výpočet kontrolního součtu se na entropii aplikuje hašovací funkce SHA256 (pouze jednou; to je jeden z mála případů v Bitcoinu, kdy se používá jediný SHA256 hash místo dvojitého hash). Tato operace produkuje 256bitový hash. Kontrolní součet se skládá z prvních bitů tohoto hash a jeho délka závisí na délce entropie podle následujícího vzorce:
\text{CS} = \frac{\text{ENT}}{32}
kde $\text{ENT}$ představuje délku entropie v bitech a $\text{CS}$ délku kontrolního součtu v bitech.
Například pro entropii 256 bitů se bere prvních 8 bitů hash pro vytvoření kontrolního součtu:
\text{CS} = \frac{256}{32} = 8 \text{ bitů}
Jakmile je kontrolní součet vypočítán, je konkatenován s entropií, aby se získala rozšířená bitová sekvence označená $\text{ENT} \Vert \text{CS}$ ("konkatenace" znamená spojit konec s koncem).

### Korespondence mezi Entropií a Mnemonickou Frází
Počet slov v mnemonické frázi závisí na velikosti počáteční entropie, jak je ilustrováno v následující tabulce s:
- $\text{ENT}$: velikost entropie v bitech;
- $\text{CS}$: velikost kontrolního součtu v bitech;
- $w$: počet slov v konečné mnemonické frázi.
\begin{array}{|c|c|c|c|} \hline \text{ENT} & \text{CS} & \text{ENT} \Vert \text{CS} & w \ \hline 128 & 4 & 132 & 12 \ 160 & 5 & 165 & 15 \ 192 & 6 & 198 & 18 \ 224 & 7 & 231 & 21 \ 256 & 8 & 264 & 24 \ \hline \end{array}
Například pro entropii 256 bitů je výsledek $\text{ENT} \Vert \text{CS}$ 264 bitů a vede k mnemonické frázi o 24 slovech.
### Převod Binární Sekvence na Mnemonickou Frázi
Bitová sekvence $\text{ENT} \Vert \text{CS}$ je poté rozdělena na segmenty po 11 bitech. Každý 11bitový segment, jednou převedený na desítkové číslo, odpovídá číslu mezi 0 a 2047, které určuje pozici slova [v seznamu 2048 slov standardizovaném BIP39](https://github.com/Planb-Network/bitcoin-educational-content/blob/dev/resources/bet/bip39-wordlist//courses/cyp201/assets/BIP39-WORDLIST.pdf).
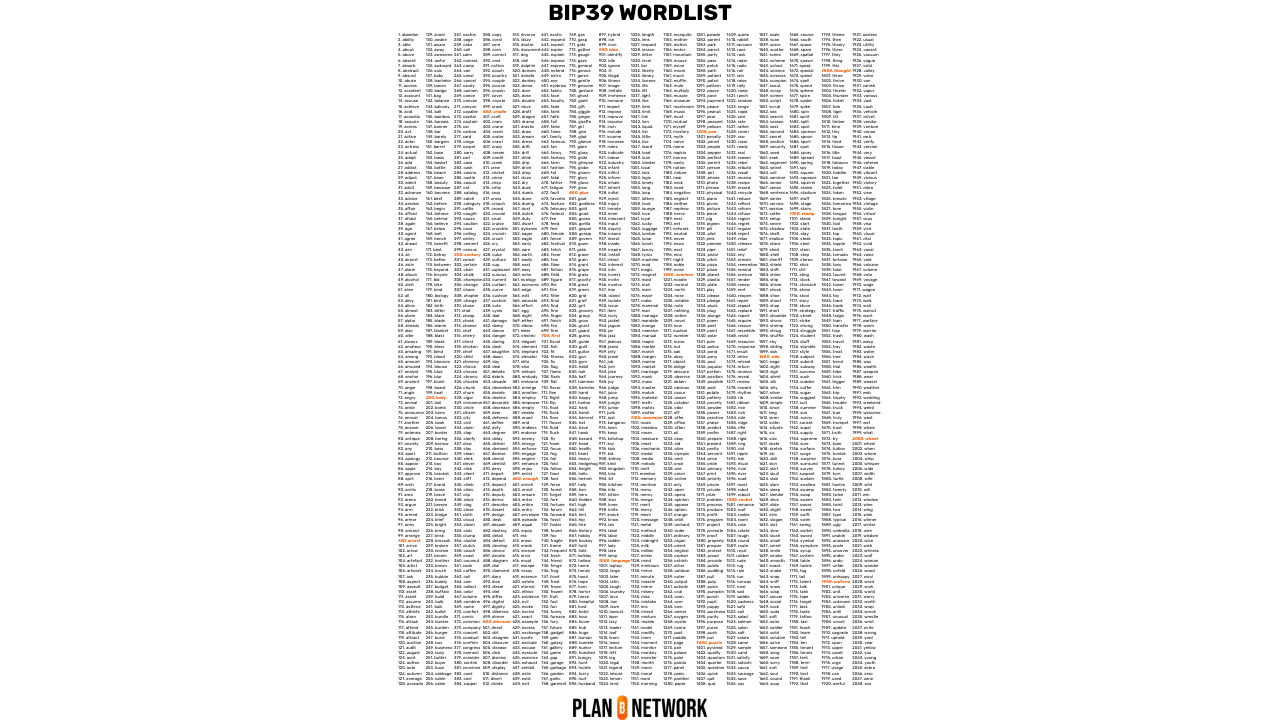
Například pro 128bitovou entropii je kontrolní součet 4 bity, a celková sekvence tak měří 132 bitů. Je rozdělena na 12 segmentů po 11 bitech (oranžové bity označují kontrolní součet):

Každý segment je poté převeden na desítkové číslo, které reprezentuje slovo ze seznamu. Například binární segment `01011010001` je v desítkové soustavě ekvivalentní číslu `721`. Přidáním 1 pro zarovnání s indexací seznamu (která začíná na 1, nikoli na 0), dostaneme pořadové číslo slova `722`, což je v seznamu "*focus*".

Tato korespondence se opakuje pro každý z 12 segmentů, aby se získala 12slovní fráze.

### Charakteristiky seznamu slov BIP39
Zvláštností seznamu slov BIP39 je, že žádné slovo nesdílí stejné první čtyři písmena ve stejném pořadí s jiným slovem. To znamená, že zaznamenání pouze prvních čtyř písmen každého slova je dostatečné pro uložení mnemonické fráze. To může být zajímavé pro úsporu místa, zejména pro ty, kteří si ji přejí vyryt do kovového nosiče.
Tento seznam 2048 slov existuje v několika jazycích. Nejedná se o jednoduché překlady, ale o odlišná slova pro každý jazyk. Nicméně, je silně doporučeno držet se anglické verze, protože verze v jiných jazycích obecně nejsou podporovány softwary peněženek.
### Jakou délku si vybrat pro vaši mnemonickou frázi?
Pro určení optimální délky vaší mnemonické fráze je nutné zvážit skutečnou bezpečnost, kterou poskytuje. 12slovní fráze zajišťuje 128bitovou bezpečnost, zatímco 24slovní fráze nabízí 256 bitů.
Tento rozdíl v bezpečnosti na úrovni fráze však nezlepšuje celkovou bezpečnost Bitcoinové peněženky, protože soukromé klíče odvozené z této fráze mají prospěch pouze z 128bitové bezpečnosti. Jak jsme již dříve viděli, soukromé klíče Bitcoinu jsou generovány z náhodných čísel (nebo odvozeny z náhodného zdroje) v rozmezí od $1$ do $n-1$, kde $n$ představuje řád generátorového bodu $G$ křivky secp256k1, číslo o něco menší než $2^{256}$. Mohlo by se tedy zdát, že tyto soukromé klíče nabízejí 256bitovou bezpečnost. Nicméně, jejich bezpečnost spočívá v obtížnosti najít soukromý klíč z jeho přidruženého veřejného klíče, obtížnosti založené na matematickém problému diskrétního logaritmu na eliptických křivkách (*ECDLP*). K dnešnímu dni je nejznámějším algoritmem pro řešení tohoto problému Pollardův rho algoritmus, který snižuje počet operací potřebných k prolomení klíče na odmocninu jeho velikosti.
Pro 256bitové klíče, jako jsou ty používané na Bitcoinu, tak Pollardův rho algoritmus snižuje složitost na $2^{128}$ operací:
O(\sqrt{2^{256}}) = O(2^{128})
Proto se považuje, že soukromý klíč používaný na Bitcoinu nabízí 128bitovou bezpečnost.
Výsledkem je, že výběr 24slovní fráze neposkytuje peněžence další ochranu, protože 256bitová bezpečnost na frázi je zbytečná, pokud odvozené klíče nabízejí pouze 128bitovou bezpečnost. Abychom ilustrovali tento princip, je to jako mít dům se dvěma dveřmi: starými dřevěnými dveřmi a zpevněnými dveřmi. V případě vloupání by zpevněné dveře byly zbytečné, protože zloděj by prošel dřevěnými dveřmi. Zde je situace analogická.
Fáze o 12 slovech, která také nabízí 128 bitů zabezpečení, je proto v současnosti dostatečná k ochraně vašich bitcoinů proti jakémukoli pokusu o krádež. Pokud se algoritmus digitálního podpisu nezmění tak, aby používal větší klíče nebo spoléhal na matematický problém jiný než ECDLP, zůstává fráze o 24 slovech nadbytečná. Navíc delší fráze zvyšuje riziko ztráty během zálohování: záloha, která je dvakrát kratší, je vždy snazší spravovat.
Pokud chcete jít dále a konkrétně se naučit, jak ručně generovat testovací mnemonickou frázi, doporučuji vám objevit tento tutoriál:
https://planb.network/tutorials/wallet/backup/generate-mnemonic-phrase-47507d90-e6af-4cac-b01b-01a14d7a8228
Před pokračováním v odvození peněženky z této mnemonické fráze vám v následující kapitole představím BIP39 heslo, protože hraje roli v procesu odvození a je na stejné úrovni jako mnemonická fráze.
## Heslo
<chapterId>6a51b397-f3b5-5084-b151-cef94bc9b93f</chapterId>
Jak jsme právě viděli, HD peněženky jsou generovány z mnemonické fráze, která obvykle sestává z 12 nebo 24 slov. Tato fráze je velmi důležitá, protože umožňuje obnovit všechny klíče peněženky v případě, že je její fyzické zařízení (jako například hardware peněženka) ztraceno. Nicméně představuje jediný bod selhání, protože pokud je kompromitována, útočník by mohl ukrást všechny bitcoiny. Zde přichází na řadu BIP39 heslo.
### Co je BIP39 heslo?
Heslo je volitelné heslo, které si můžete svobodně zvolit, a které je přidáno k mnemonické frázi v procesu odvození klíče, aby se zvýšilo zabezpečení peněženky.
Buďte opatrní, heslo by nemělo být zaměňováno s PIN kódem vaší hardware peněženky nebo heslem používaným k odemčení přístupu k vaší peněžence na počítači. Na rozdíl od všech těchto prvků hraje heslo roli v odvození klíčů vaší peněženky. **To znamená, že bez něj nikdy nebudete moci obnovit své bitcoiny.**
Heslo pracuje v tandemu s mnemonickou frází, mění semeno, ze kterého jsou generovány klíče. Takže i když někdo získá vaši frázi o 12 nebo 24 slovech, bez hesla nemůže přistupovat k vašim prostředkům. Použití hesla v podstatě vytváří novou peněženku s odlišnými klíči. Modifikace (i mírná) hesla vygeneruje jinou peněženku.

### Proč byste měli používat heslo?
Heslo je libovolné a může být jakoukoli kombinací znaků zvolenou uživatelem. Použití hesla tak nabízí několik výhod. Především snižuje všechna rizika spojená s kompromitací mnemonické fráze tím, že vyžaduje druhý faktor pro přístup k prostředkům (vloupání, přístup do vašeho domova atd.).
Dále může být strategicky použito k vytvoření návnadové peněženky, aby čelilo fyzickým omezením krádeže vašich prostředků, jako je proslulý "_útok klíčem za 5 dolarů_". V tomto scénáři je myšlenka mít peněženku bez hesla obsahující pouze malé množství bitcoinů, dostatečné k uspokojení potenciálního agresora, zatímco máte skrytou peněženku. Tato poslední používá stejnou mnemonickou frázi, ale je zabezpečena dodatečným heslem.
Nakonec je použití hesla zajímavé, když si přejete kontrolovat náhodnost generování semene HD peněženky.
### Jak vybrat dobré heslo?
Aby bylo heslo účinné, musí být dostatečně dlouhé a náhodné. Stejně jako u silného hesla doporučuji vybrat heslo, které je co nejdelší a nejnáhodnější, s rozmanitostí písmen, čísel a symbolů, aby byl jakýkoli pokus o hrubou sílu nemožný.
Je také důležité správně uložit tuto heslovou frázi, stejně jako mnemonickou frázi. **Ztráta znamená ztrátu přístupu k vašim bitcoinům**. Důrazně nedoporučuji ji pamatovat si pouze nazpaměť, protože to neracionálně zvyšuje riziko ztráty. Ideální je zapsat ji na fyzické médium (papír nebo kov) odděleně od mnemonické fráze. Tato záloha musí být samozřejmě uložena na jiném místě než vaše mnemonická fráze, aby se zabránilo jejich současnému ohrožení.
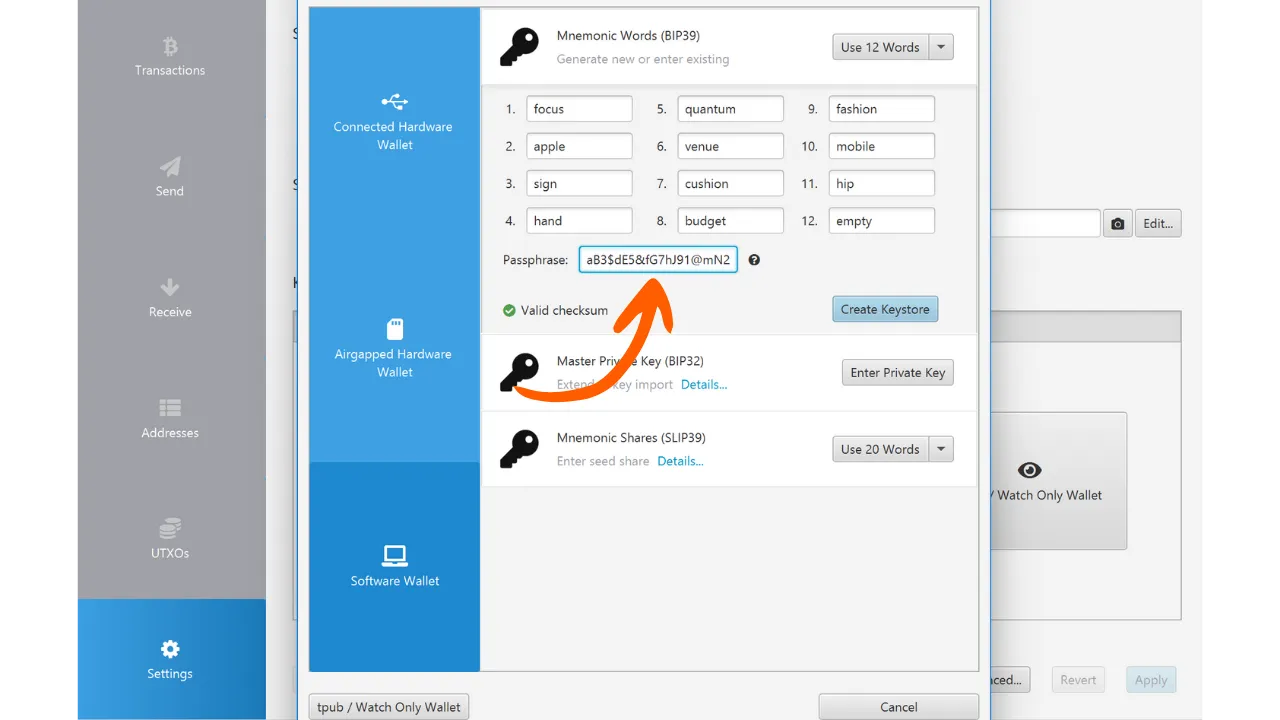
V následující části se dozvíme, jak jsou tyto dva prvky na základě vaší peněženky - mnemonická fráze a heslová fráze - použity k odvození klíčových párů používaných ve *scriptPubKey*, které zamykají vaše UTXO.
# Vytváření Bitcoinových Peněženek
<partId>9c25e767-7eae-50b8-8c5f-679d8fc83bab</partId>
## Vytváření Semene a Hlavního Klíče
<chapterId>63093760-2010-5691-8d0e-9a04732ae557</chapterId>
Jakmile jsou mnemonická fráze a volitelná heslová fráze vygenerovány, může začít proces odvozování Bitcoinové HD peněženky. Mnemonická fráze je nejprve převedena na semeno, které tvoří základ všech klíčů peněženky.
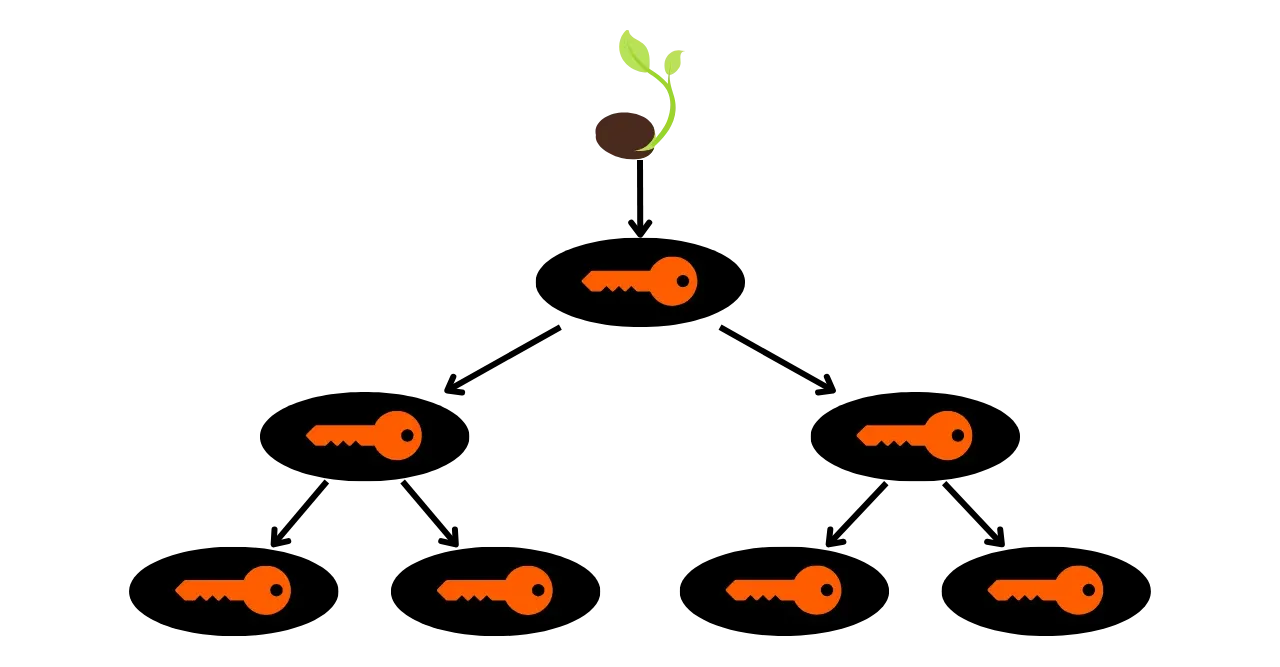
### Semeno HD Peněženky
Standard BIP39 definuje semeno jako 512bitovou sekvenci, která slouží jako výchozí bod pro odvození všech klíčů HD peněženky. Semeno je odvozeno z mnemonické fráze a možné heslové fráze pomocí algoritmu **PBKDF2** (*Password-Based Key Derivation Function 2*), o kterém jsme již hovořili v kapitole 3.3. V této odvozovací funkci použijeme následující parametry:
- $m$ : mnemonická fráze;
- $p$ : volitelná heslová fráze zvolená uživatelem pro zvýšení bezpečnosti semene. Pokud heslová fráze není, toto pole zůstává prázdné;
- $\text{PBKDF2}$ : odvozovací funkce s $\text{HMAC-SHA512}$ a $2048$ iteracemi;
- $s$: 512bitové semeno peněženky.
Bez ohledu na délku zvolené mnemonické fráze (132 bitů nebo 264 bitů), funkce PBKDF2 vždy produkuje 512bitový výstup a semeno bude tedy vždy této velikosti.
### Schéma Odvození Semene s PBKDF2
Následující rovnice ilustruje odvození semene z mnemonické fráze a heslové fráze:
s = \text{PBKDF2}_{\text{HMAC-SHA512}}(m, p, 2048)

Hodnota semene je tedy ovlivněna hodnotou mnemonické fráze a heslové fráze. Změnou heslové fráze se získá odlišné semeno. Nicméně, s tou samou mnemonickou frází a heslovou frází je vždy generováno stejné semeno, protože PBKDF2 je deterministická funkce. To zajišťuje, že stejné páry klíčů lze získat prostřednictvím našich záloh.
**Poznámka:** V běžném jazyce se termín "semeno" často používá, nesprávně, pro mnemonickou frázi. Ve skutečnosti, v případě absence heslové fráze, je jedno jednoduše kódováním druhého. Jak jsme však viděli, v technické realitě peněženek jsou semeno a mnemonická fráze skutečně dva odlišné prvky.
Nyní, když máme naše semeno, můžeme pokračovat v odvozování naší Bitcoinové peněženky.
### Hlavní klíč a hlavní řetězový kód
Jakmile je získáno semínko, dalším krokem při odvozování HD peněženky je výpočet hlavního soukromého klíče a hlavního řetězového kódu, které budou reprezentovat hloubku 0 naší peněženky.
Pro získání hlavního soukromého klíče a hlavního řetězového kódu se na semínko aplikuje funkce HMAC-SHA512, s použitím pevného klíče "*Bitcoin Seed*", který je identický pro všechny uživatele Bitcoinu. Tato konstanta je zvolena, aby se zajistilo, že odvození klíčů je specifické pro Bitcoin. Zde jsou prvky:
- $\text{HMAC-SHA512}$: funkce odvození;
- $s$: 512-bitové semínko peněženky;
- $\text{"Bitcoin Seed"}$: společná konstanta odvození pro všechny Bitcoinové peněženky.
\text{output} = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)
Výstup této funkce je tedy 512 bitů. Poté je rozdělen na 2 části:
- Levých 256 bitů tvoří **hlavní soukromý klíč**;
- Pravých 256 bitů tvoří **hlavní řetězový kód**.
Matematicky lze tyto dvě hodnoty označit následovně s $k_M$ jako hlavním soukromým klíčem a $C_M$ jako hlavním řetězovým kódem:
k_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[:256]}
C_M = \text{HMAC-SHA512}(\text{"Bitcoin Seed"}, s)_{[256:]}

### Role hlavního klíče a řetězového kódu
Hlavní soukromý klíč je považován za rodičovský klíč, z něhož budou generovány všechny odvozené soukromé klíče — děti, vnoučata, pravnoučata atd. Reprezentuje nultou úroveň v hierarchii odvození.
Hlavní řetězový kód na druhou stranu přináší do procesu odvození klíčů pro potomky další zdroj entropie, aby se předešlo určitým potenciálním útokům. Navíc v HD peněžence má každý pár klíčů spojený unikátní řetězový kód, který se také používá k odvození dětských klíčů z tohoto páru, ale o tomto budeme hovořit podrobněji v nadcházejících kapitolách.
Před pokračováním v odvození HD peněženky s následujícími prvky si přeji v další kapitole představit rozšířené klíče, které jsou často zaměňovány s hlavním klíčem. Uvidíme, jak jsou konstruovány a jakou roli hrají v Bitcoinové peněžence.
## Rozšířené klíče
<chapterId>8dcffce1-31bd-5e0b-965b-735f5f9e4602</chapterId>
Rozšířený klíč je jednoduše spojení klíče (ať už soukromého nebo veřejného) a jeho přidruženého řetězového kódu. Tento řetězový kód je zásadní pro odvození dětských klíčů, protože bez něj je nemožné odvodit dětské klíče z rodičovského klíče, ale tento proces objevíme přesněji v další kapitole. Tyto rozšířené klíče tak umožňují agregovat veškeré informace nezbytné pro odvození dětských klíčů, čímž se zjednodušuje správa účtů v rámci HD peněženky.
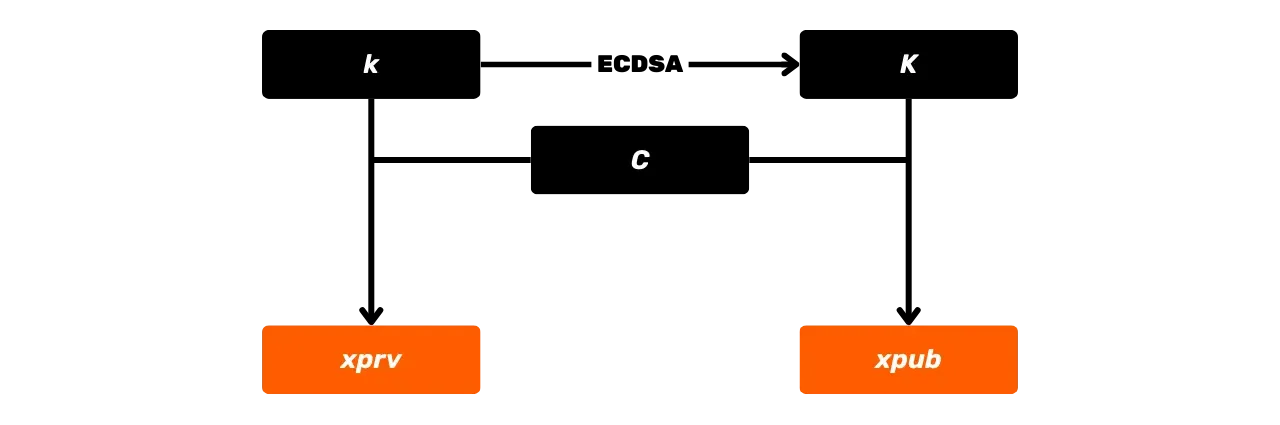
Rozšířený klíč se skládá ze dvou částí:
- Užitečná zátěž, která obsahuje soukromý nebo veřejný klíč spolu s přidruženým řetězovým kódem;
- Metadata, která jsou různé informace usnadňující interoperabilitu mezi softwary a zlepšující pochopení pro uživatele.
### Jak rozšířené klíče fungují
Když rozšířený klíč obsahuje soukromý klíč, označuje se jako rozšířený soukromý klíč. Pozná se podle své předpony, která obsahuje označení `prv`. Kromě soukromého klíče rozšířený soukromý klíč obsahuje také přidružený řetězový kód. S tímto typem rozšířeného klíče je možné odvodit všechny typy dětských soukromých klíčů a tedy přidáním a zdvojením bodů na eliptických křivkách umožňuje také odvození celého souboru dětských veřejných klíčů.
Když rozšířený klíč neobsahuje soukromý klíč, ale místo toho veřejný klíč, označuje se jako rozšířený veřejný klíč. Pozná se podle své předpony, která obsahuje označení `pub`. Samozřejmě, kromě klíče, obsahuje také přidružený řetězový kód. Na rozdíl od rozšířeného soukromého klíče umožňuje rozšířený veřejný klíč odvození pouze "normálních" dětských veřejných klíčů (což znamená, že nemůže odvodit "pevné" dětské klíče). V následující kapitole uvidíme, co tyto kvalifikátory "normální" a "pevný" znamenají.
Ale v každém případě rozšířený veřejný klíč neumožňuje odvození dětských soukromých klíčů. Proto, i když někdo má přístup k `xpub`, nebude moci utratit přidružené prostředky, protože nebude mít přístup k odpovídajícím soukromým klíčům. Mohou pouze odvodit dětské veřejné klíče a sledovat přidružené transakce.
Pro následující budeme používat následující notaci:
- $K_{\text{PAR}}$: rodičovský veřejný klíč;
- $k_{\text{PAR}}$: rodičovský soukromý klíč;
- $C_{\text{PAR}}$: rodičovský řetězový kód;
- $C_{\text{CHD}}$: dětský řetězový kód;
- $K_{\text{CHD}}^n$: normální dětský veřejný klíč;
- $k_{\text{CHD}}^n$: normální dětský soukromý klíč;
- $K_{\text{CHD}}^h$: pevný dětský veřejný klíč;
- $k_{\text{CHD}}^h$: pevný dětský soukromý klíč.

### Konstrukce rozšířeného klíče
Rozšířený klíč je strukturován následovně:
- **Verze**: Kód verze pro identifikaci povahy klíče (`xprv`, `xpub`, `yprv`, `ypub`...). Na konci této kapitoly uvidíme, co písmena `x`, `y` a `z` odpovídají.
- **Hloubka**: Hierarchická úroveň v HD peněžence vzhledem k hlavnímu klíči (0 pro hlavní klíč).
- **Otisk rodiče**: První 4 bajty HASH160 hash rodičovského veřejného klíče použitého pro odvození klíče přítomného v payloadu.
- **Číslo indexu**: Identifikátor dítěte mezi sourozeneckými klíči, to jest mezi všemi klíči na stejné úrovni odvození, které mají stejné rodičovské klíče.
- **Řetězový kód**: Unikátní 32bajtový kód pro odvození dětských klíčů.
- **Klíč**: Soukromý klíč (předpona o 1 bajtu pro velikost) nebo veřejný klíč.
- **Kontrolní součet**: Kontrolní součet vypočítaný funkcí HASH256 (dvojitý SHA256) je také přidán, což umožňuje ověření integrity rozšířeného klíče během jeho přenosu nebo uložení.
Celkový formát rozšířeného klíče je tedy 78 bajtů bez kontrolního součtu a 82 bajtů s kontrolním součtem. Poté je převeden do formátu Base58, aby se vyprodukovala reprezentace, která je snadno čitelná uživateli. Formát Base58 je stejný jako ten, který se používá pro *Legacy* přijímací adresy (před *SegWit*).
| Element | Popis | Velikost |
| ----------------- | ------------------------------------------------------------------------------------------------------------------ | --------- |
| Verze | Udává, zda je klíč veřejný (`xpub`, `ypub`) nebo soukromý (`xprv`, `zprv`), stejně jako verzi rozšířeného klíče | 4 bajty |
| Hloubka | Úroveň v hierarchii vzhledem k hlavnímu klíči | 1 bajt |
| Odtisk rodiče | První 4 bajty z HASH160 veřejného klíče rodiče | 4 bajty |
| Číslo indexu | Pozice klíče v pořadí potomků | 4 bajty |
| Řetězový kód | Používá se k odvození dětských klíčů | 32 bajtů |
| Klíč | Soukromý klíč (s 1-bajtovým prefixem) nebo veřejný klíč | 33 bajtů |
| Kontrolní součet | Kontrolní součet pro ověření integrity | 4 bajty |
Pokud je k soukromému klíči přidán jeden bajt, je to proto, že komprimovaný veřejný klíč je o jeden bajt delší než soukromý klíč. Tento dodatečný bajt, přidaný na začátek soukromého klíče jako `0x00`, vyrovnává jejich velikost a zajišťuje, že náklad rozšířeného klíče je stejně dlouhý, ať už jde o veřejný nebo soukromý klíč.
### Předpony rozšířených klíčů
Jak jsme právě viděli, rozšířené klíče zahrnují předponu, která udává jak verzi rozšířeného klíče, tak jeho povahu. Označení `pub` ukazuje, že se jedná o rozšířený veřejný klíč, a označení `prv` ukazuje rozšířený soukromý klíč. Dodatečné písmeno na základně rozšířeného klíče pomáhá určit, zda se jedná o standard Legacy, SegWit v0, SegWit v1 atd.
Zde je souhrn použitých předpon a jejich významů:
| Prefix Base 58 | Prefix Base 16 | Síť | Účel | Související skripty | Odvození | Typ klíče |
| --------------- | --------------- | ------- | ------------------ | ------------------- | --------------------- | ------------ |
| `xpub` | `0488b21e` | Mainnet | Legacy a SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/0'`, `m/86'/0'` | veřejný |
| `xprv` | `0488ade4` | Mainnet | Legacy a SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/0'`, `m/86'/0'` | soukromý |
| `tpub` | `043587cf` | Testnet | Legacy a SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/1'`, `m/86'/1'` | veřejný |
| `tprv` | `04358394` | Testnet | Legacy a SegWit V1 | P2PK / P2PKH / P2TR | `m/44'/1'`, `m/86'/1'` | soukromý |
| `ypub` | `049d7cb2` | Mainnet | Nested SegWit | P2WPKH in P2SH | `m/49'/0'` | veřejný |
| `yprv` | `049d7878` | Mainnet | Nested SegWit | P2WPKH in P2SH | `m/49'/0'` | soukromý |
| `upub` | `049d7cb2` | Testnet | Nested SegWit | P2WPKH in P2SH | `m/49'/1'` | veřejný |
| `uprv` | `044a4e28` | Testnet | Nested SegWit | P2WPKH in P2SH | `m/49'/1'` | soukromý |
| `zpub` | `04b24746` | Mainnet | SegWit V0 | P2WPKH | `m/84'/0'` | veřejný |
| `zprv` | `04b2430c` | Mainnet | SegWit V0 | P2WPKH | `m/84'/0'` | soukromý |
| `vpub` | `045f1cf6` | Testnet | SegWit V0 | P2WPKH | `m/84'/1'` | veřejný |
| `vprv` | `045f18bc` | Testnet | SegWit V0 | P2WPKH | `m/84'/1'` | soukromý |
### Detaily prvků rozšířeného klíče
Pro lepší pochopení vnitřní struktury rozšířeného klíče si vezměme jeden jako příklad a rozeberme ho. Zde je rozšířený klíč:
- **V Base58**:
```text
xpub6CTNzMUkzpurBWaT4HQoYzLP4uBbGJuWY358Rj7rauiw4rMHCyq3Rfy9w4kyJXJzeFfyrKLUar2rUCukSiDQFa7roTwzjiAhyQAdPLEjqHT
```
- **V hexadecimálním formátu**:
```text
0488B21E036D5601AD80000000C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A89303772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF50658051F067C3A
```
Tento rozšířený klíč se rozkládá na několik odlišných prvků:
- **Verze**: `0488B21E`
První 4 bajty jsou verze. Zde odpovídá rozšířenému veřejnému klíči na Mainnetu s účelem derivace buď *Legacy* nebo *SegWit v1*.
- **Hloubka**: `03`
Toto pole udává hierarchickou úroveň klíče v rámci HD peněženky. V tomto případě hloubka `03` znamená, že tento klíč je tři úrovně derivace pod hlavním klíčem.
- **Otisk rodiče**: `6D5601AD`
Tyto jsou první 4 bajty HASH160 hashe rodičovského veřejného klíče, který byl použit k odvození tohoto `xpub`.
- **Číslo indexu**: `80000000`
Tento index označuje pozici klíče mezi jeho rodičovskými potomky. Předpona `0x80` naznačuje, že klíč je odvozen tvrdě (hardened způsobem), a protože zbytek je vyplněn nulami, naznačuje to, že tento klíč je první mezi jeho možnými sourozenci.
- **Chain code**: `C605DF9FBD77FD6965BD02B77831EC5C78646AD3ACA14DC3984186F72633A893`
- **Veřejný klíč**: `03772CCB99F4EF346078D167065404EED8A58787DED31BFA479244824DF5065805`
- **Kontrolní součet**: `1F067C3A`
Kontrolní součet odpovídá prvním 4 bajtům hashe (dvojitý SHA256) všeho ostatního.
V této kapitole jsme zjistili, že existují dva různé typy dětských klíčů. Také jsme se dozvěděli, že odvození těchto dětských klíčů vyžaduje klíč (buď soukromý nebo veřejný) a jeho chain code. V další kapitole podrobně prozkoumáme povahu těchto různých typů klíčů a jak je odvodit od jejich rodičovského klíče a chain code.
## Odvození Párů Dětských Klíčů
<chapterId>61c0807c-845b-5076-ad06-7f395b36adfd</chapterId>
Odvození párů dětských klíčů v Bitcoin HD peněženkách spoléhá na hierarchickou strukturu, která umožňuje generování velkého počtu klíčů, zatímco tyto páry jsou organizovány do různých skupin prostřednictvím větví. Každý dětský pár odvozený od rodičovského páru může být použit přímo v *scriptPubKey* k uzamčení bitcoinů, nebo jako výchozí bod pro generování dalších dětských klíčů, a tak dále, k vytvoření stromu klíčů.
Všechna tato odvození začínají hlavním klíčem a hlavním chain code, které jsou prvními rodiči na úrovni hloubky 0. Jsou, jakýmsi způsobem, Adamem a Evou klíčů vaší peněženky, společnými předky všech odvozených klíčů.
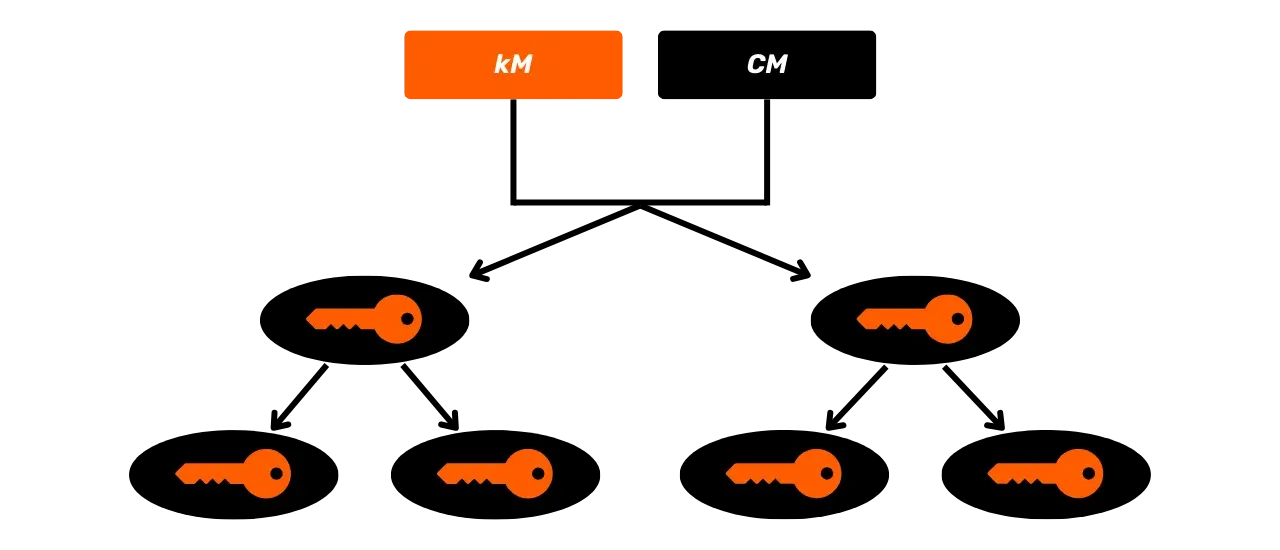
Pojďme prozkoumat, jak toto deterministické odvození funguje.
### Různé Typy Odvození Dětských Klíčů
Jak jsme se již dotkli v předchozí kapitole: dětské klíče jsou rozděleny do dvou hlavních typů:
- **Normální dětské klíče** ($k_{\text{CHD}}^n, K_{\text{CHD}}^n$): Tyto jsou odvozeny z rozšířeného veřejného klíče ($K_{\text{PAR}}$), nebo rozšířeného soukromého klíče ($k_{\text{PAR}}$), nejprve odvozením veřejného klíče.
- **Tvrdě odvozené dětské klíče** ($k_{\text{CHD}}^h, K_{\text{CHD}}^h$): Tyto mohou být odvozeny pouze z rozšířeného soukromého klíče ($k_{\text{PAR}}$) a jsou proto neviditelné pro pozorovatele, kteří mají pouze rozšířený veřejný klíč.
Každý dětský klíčový pár je identifikován 32-bitovým **indexem** (v našich výpočtech označeným jako $i$). Indexy pro normální klíče se pohybují od $0$ do $2^{31}-1$, zatímco ty pro zpevněné (hardened) klíče se pohybují od $2^{31}$ do $2^{32}-1$. Tyto čísla se používají k rozlišení sourozeneckých klíčových párů během derivace. Skutečně, každý rodičovský klíčový pár musí být schopen derivovat několik dětských klíčových párů. Pokud bychom aplikovali stejný výpočet systematicky od rodičovských klíčů, všechny získané sourozenecké klíče by byly identické, což není žádoucí. Index tedy zavádí proměnnou, která modifikuje výpočet derivace, což umožňuje rozlišit každý pár sourozenců. Kromě specifického použití v určitých protokolech a standardech derivace obvykle začínáme derivací prvního dětského klíče s indexem `0`, druhého s indexem `1` a tak dále.
### Proces derivace s HMAC-SHA512
Derivace každého dětského klíče je založena na funkci HMAC-SHA512, o které jsme diskutovali v sekci 2 na téma hašovací funkce. Přijímá dva vstupy: rodičovský řetězec kódů $C_{\text{PAR}}$ a konkatenaci rodičovského klíče (buď veřejného klíče $K_{\text{PAR}}$ nebo soukromého klíče $k_{\text{PAR}}$, v závislosti na typu požadovaného dětského klíče) a indexu. Výstupem funkce HMAC-SHA512 je 512-bitová sekvence, rozdělená na dvě části:
- **Prvních 32 bajtů** (nebo $h_1$) se používá k výpočtu nového dětského páru.
- **Posledních 32 bajtů** (nebo $h_2$) slouží jako nový řetězec kódů $C_{\text{CHD}}$ pro dětský pár.
Ve všech našich výpočtech budu označovat $\text{hash}$ výstup funkce HMAC-SHA512.
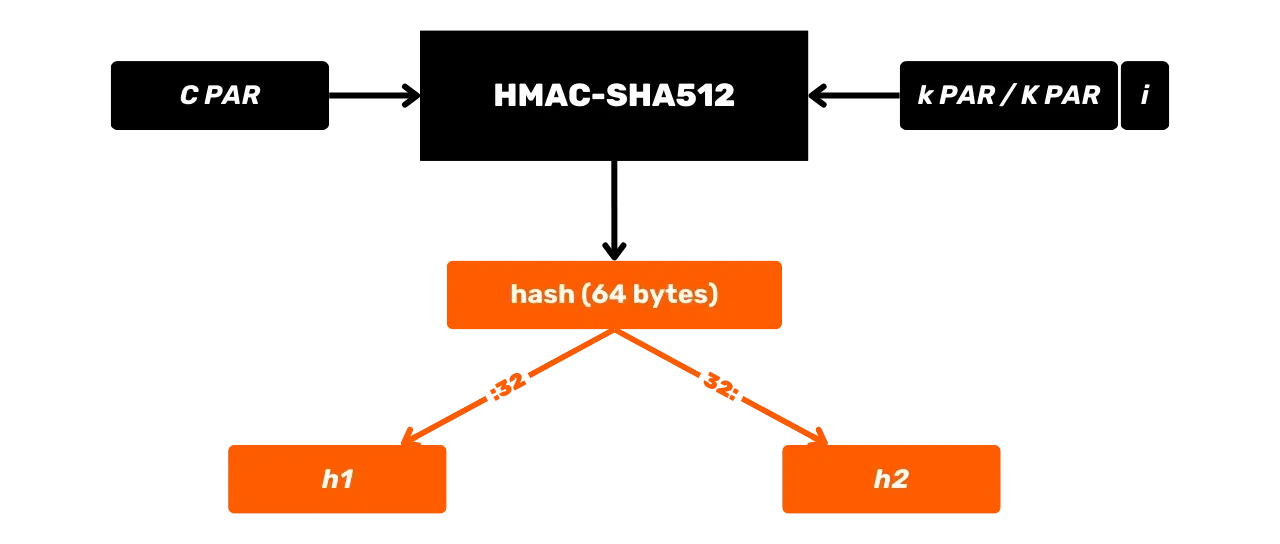
#### Derivace dětského soukromého klíče z rodičovského soukromého klíče
Pro derivaci dětského soukromého klíče $k_{\text{CHD}}$ z rodičovského soukromého klíče $k_{\text{PAR}}$ jsou možné dva scénáře v závislosti na tom, zda je požadován zpevněný nebo normální klíč.
Pro **normální dětský klíč** ($i < 2^{31}$) je výpočet $\text{hash}$ následující:
\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, G \cdot k_{\text{PAR}} \Vert i)
V tomto výpočtu pozorujeme, že naše HMAC funkce přijímá dva vstupy: nejprve rodičovský řetězec kódů a poté konkatenaci indexu s veřejným klíčem spojeným s rodičovským soukromým klíčem. Rodičovský veřejný klíč je zde použit, protože hledáme derivaci normálního dětského klíče, nikoli zpevněného.
Nyní máme 64-bajtový $\text{hash}$, který rozdělíme na 2 části po 32 bajtech: $h_1$ a $h_2$:
\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}{[:32]} \quad, \quad h_2 = \text{hash}{[32:]}
Dětský soukromý klíč $k_{\text{CHD}}^n$ je poté vypočítán následovně:
k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n
V této kalkulaci operace $\text{parse256}(h_1)$ spočívá v interpretaci prvních 32 bajtů $\text{hash}$ jako 256-bitového celého čísla. Toto číslo je poté přičteno k rodičovskému soukromému klíči, vše modulo $n$ pro zachování v rámci řádu eliptické křivky, jak jsme viděli v sekci 3 o digitálních podpisech. Takto, pro odvození normálního dětského soukromého klíče, ačkoliv je jako základ pro výpočet vstupů funkce HMAC-SHA512 použit rodičovský veřejný klíč, je vždy nutné mít rodičovský soukromý klíč pro dokončení výpočtu.
Z tohoto dětského soukromého klíče je možné odvodit odpovídající veřejný klíč aplikací ECDSA nebo Schnorr. Tímto způsobem získáme kompletní pár klíčů.
Poté je druhá část $\text{hash}$ jednoduše interpretována jako řetězový kód pro právě odvozený pár dětských klíčů:
C_{\text{CHD}} = h_2
Zde je schématické znázornění celkové derivace:
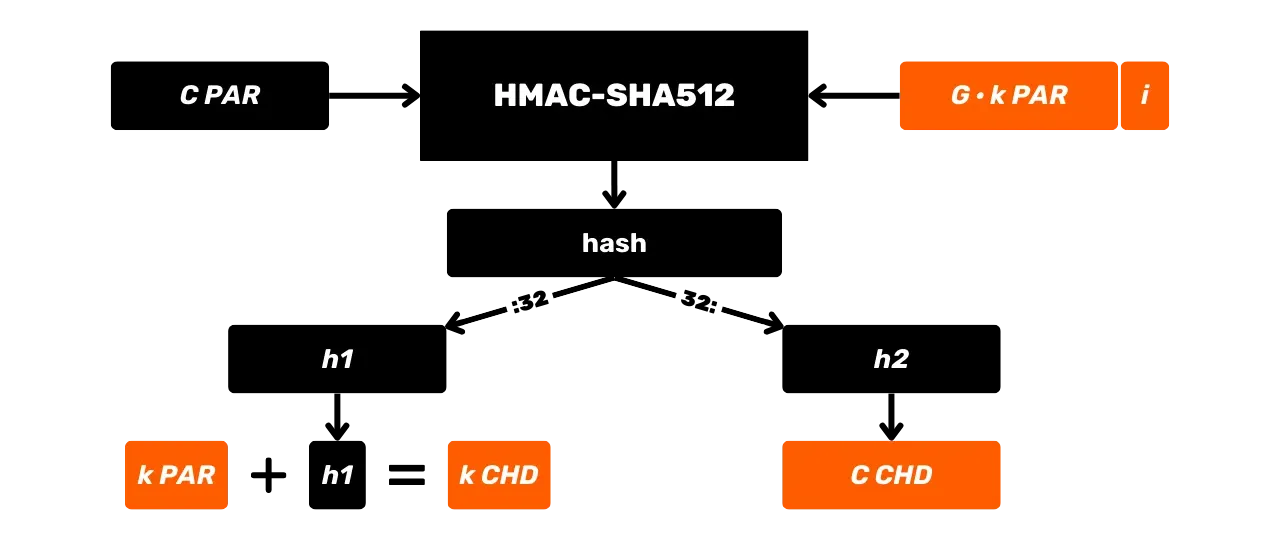
Pro **zpevněný dětský klíč** ($i \geq 2^{31}$) je výpočet $\text{hash}$ následující:
hash = \text{HMAC-SHA512}(C_{\text{PAR}}, 0x00 \Vert k_{\text{PAR}} \Vert i)
V tomto výpočtu pozorujeme, že naše funkce HMAC bere dva vstupy: prvně, rodičovský řetězový kód, a poté konkatenaci indexu s rodičovským soukromým klíčem. Rodičovský soukromý klíč je zde použit, protože se snažíme odvodit zpevněný dětský klíč. Navíc, na začátek klíče je přidán bajt rovný `0x00`. Tato operace vyrovnává jeho délku tak, aby odpovídala délce komprimovaného veřejného klíče.
Takže nyní máme 64-bajtový $\text{hash}$, který rozdělíme na 2 části po 32 bajtech: $h_1$ a $h_2$:\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}[:32] \quad, \quad h_2 = \text{hash}[32:]
Dětský soukromý klíč $k_{\text{CHD}}^h$ je poté vypočítán následovně:
k_{\text{CHD}}^h = \text{parse256}(h_1) + k_{\text{PAR}} \mod n
Dále jednoduše interpretujeme druhou část $\text{hash}$ jako řetězový kód pro právě odvozený pár dětských klíčů:
C_{\text{CHD}} = h_2
Zde je schématické znázornění celkové derivace:

Vidíme, že normální derivace a zpevněná derivace fungují stejným způsobem, s tím rozdílem, že normální derivace používá jako vstup do funkce HMAC rodičovský veřejný klíč, zatímco zpevněná derivace používá rodičovský soukromý klíč.
#### Odvození dětského veřejného klíče z rodičovského veřejného klíče
Pokud známe pouze veřejný klíč rodiče $K_{\text{PAR}}$ a přidružený řetězový kód $C_{\text{PAR}}$, to znamená rozšířený veřejný klíč, je možné odvodit dětské veřejné klíče $K_{\text{CHD}}^n$, ale pouze pro normální (nepevněné) dětské klíče. Tento princip umožňuje zejména sledování pohybů na účtu v Bitcoinové peněžence z `xpub` (*pouze pro sledování*).
Pro provedení tohoto výpočtu vypočítáme $\text{hash}$ s indexem $i < 2^{31}$ (normální odvození):
\text{hash} = \text{HMAC-SHA512}(C_{\text{PAR}}, K_{\text{PAR}} \Vert i)
V tomto výpočtu pozorujeme, že naše funkce HMAC bere dva vstupy: nejprve řetězový kód rodiče, poté konkatenaci indexu s veřejným klíčem rodiče.
Nyní tedy máme $hash$ o velikosti 64 bajtů, který rozdělíme na 2 části po 32 bajtech: $h_1$ a $h_2$:
\text{hash} = h_1 \Vert h_2
h_1 = \text{hash}[:32] \quad, \quad h_2 = \text{hash}[32:]
Dětský veřejný klíč $K_{\text{CHD}}^n$ je poté vypočítán následovně:
K_{\text{CHD}}^n = G \cdot \text{parse256}(h_1) + K_{\text{PAR}}
Pokud $\text{parse256}(h_1) \geq n$ (řád eliptické křivky) nebo pokud $K_{\text{CHD}}^n$ je bod v nekonečnu, odvození je neplatné a musí být vybrán jiný index.
V tomto výpočtu operace $\text{parse256}(h_1)$ zahrnuje interpretaci prvních 32 bajtů $\text{hash}$ jako 256-bitového celého čísla. Toto číslo se používá k výpočtu bodu na eliptické křivce prostřednictvím sčítání a zdvojení od generátorového bodu $G$. Tento bod je poté přičten k veřejnému klíči rodiče, aby se získal normální dětský veřejný klíč. Takže pro odvození normálního dětského veřejného klíče jsou nutné pouze veřejný klíč rodiče a řetězový kód rodiče; soukromý klíč rodiče do tohoto procesu nikdy nevstupuje, na rozdíl od výpočtu dětského soukromého klíče, který jsme viděli dříve.
Následně je dětský řetězový kód jednoduše:
C_{\text{CHD}} = h_2
Zde je schématické znázornění celkového odvození:
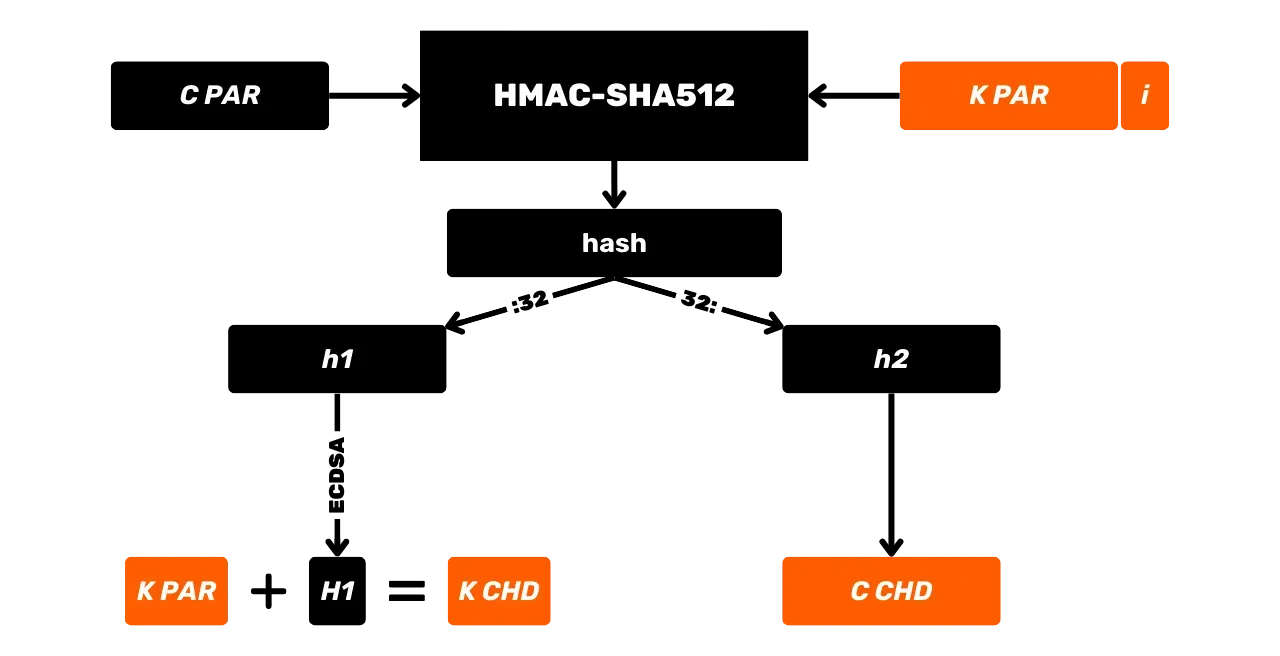
### Korespondence mezi dětskými veřejnými a soukromými klíči
Otázka, která se může vynořit, je, jak může normální dětský veřejný klíč odvozený z veřejného klíče rodiče odpovídat normálnímu dětskému soukromému klíči odvozenému z odpovídajícího soukromého klíče rodiče. Tento vztah je přesně zajištěn vlastnostmi eliptických křivek. Skutečně, pro odvození normálního dětského veřejného klíče se aplikuje HMAC-SHA512 stejným způsobem, ale jeho výstup se používá jinak:
- **Normální dětský soukromý klíč**: $k_{\text{CHD}}^n = \text{parse256}(h_1) + k_{\text{PAR}} \mod n$
- **Normální dětský veřejný klíč**: $K_{\text{CHD}}^n = G \cdot \text{parse256}(h_1) + K_{\text{PAR}}$
Díky operacím sčítání a zdvojení na eliptické křivce obě metody produkují konzistentní výsledky: veřejný klíč odvozený z dětského soukromého klíče je identický s dětským veřejným klíčem přímo odvozeným z rodičovského veřejného klíče.
### Shrnutí typů derivací
Shrnutí různých možných typů derivací:
\begin{array}{|c|c|c|c|} \hline \rightarrow & \text{PAR} & \text{CHD} & \text{n/h} \ \hline k_{\text{PAR}} \rightarrow k_{\text{CHD}} & k_{\text{PAR}} & { k_{\text{CHD}}^n, k_{\text{CHD}}^h } & { n, h } \ k_{\text{PAR}} \rightarrow K_{\text{CHD}} & k_{\text{PAR}} & { K_{\text{CHD}}^n, K_{\text{CHD}}^h } & { n, h } \ K_{\text{PAR}} \rightarrow k_{\text{CHD}} & K_{\text{PAR}} & \times & \times \ K_{\text{PAR}} \rightarrow K_{\text{CHD}} & K_{\text{PAR}} & K_{\text{CHD}}^n & n \ \hline \end{array}
Shrnutí, dosud jste se naučili vytvářet základní prvky HD peněženky: mnemonickou frázi, seed a poté hlavní klíč a hlavní řetězový kód. Také jste objevili, jak odvozovat dětské páry klíčů v této kapitole. V další kapitole prozkoumáme, jak jsou tyto derivace organizovány v Bitcoinových peněženkách a jakou strukturu sledovat, abychom konkrétně získali přijímací adresy stejně jako páry klíčů používané v *scriptPubKey* a *scriptSig*.
## Struktura peněženky a cesty derivace
<chapterId>34e1bbda-67de-5493-b268-1fded8d67689</chapterId>
Hierarchická struktura HD peněženek na Bitcoinu umožňuje organizaci párů klíčů různými způsoby. Myšlenka spočívá v odvození několika úrovní hloubky z hlavního soukromého klíče a hlavního řetězového kódu. Každá přidaná úroveň odpovídá derivaci dětského páru klíčů z rodičovského páru klíčů.
Časem různé BIPy (Bitcoin Improvement Proposals) představily standardy pro tyto cesty derivace s cílem standardizovat jejich používání napříč různým softwarem. V této kapitole tedy objevíme význam každé úrovně derivace v HD peněženkách podle těchto standardů.
### Hloubky derivace HD peněženky
Cesty derivace jsou organizovány do vrstev hloubky, počínaje hloubkou 0, která představuje hlavní klíč a hlavní řetězový kód, až po vrstvy podúrovní pro odvození adres používaných k uzamčení UTXO. BIPy definují standardy pro každou vrstvu, což pomáhá harmonizovat praxe napříč různým softwarem pro správu peněženek.
Cesta derivace se tedy vztahuje k sekvenci indexů použitých k odvození dětských klíčů z hlavního klíče.
**Hloubka 0: Hlavní klíč (BIP32)**
Tato hloubka odpovídá hlavnímu soukromému klíči a hlavnímu řetězovému kódu peněženky. Je reprezentována notací $m/$.
**Hloubka 1: Účel (BIP43)**
Cíl určuje logickou strukturu odvození. Například adresa P2WPKH bude mít na hloubce 1 $/84'/$ (podle BIP84), zatímco adresa P2TR bude mít $/86'/$ (podle BIP86). Tato vrstva usnadňuje kompatibilitu mezi peněženkami tím, že udává indexová čísla odpovídající číslům BIP.
Jinými slovy, jakmile máte hlavní klíč a hlavní řetězec kódů, slouží tyto jako rodičovský pár klíčů pro odvození dětského páru klíčů. Index použitý v tomto odvození může být například $/84'/$, pokud je peněženka určena k použití skriptů typu SegWit v0. Tento pár klíčů je pak na hloubce 1. Jeho úlohou není uzamknout bitcoiny, ale sloužit pouze jako orientační bod v hierarchii odvození.
**Hloubka 2: Typ měny (BIP44)**
Z páru klíčů na hloubce 1 se provádí nové odvození, aby se získal pár klíčů na hloubce 2. Tato hloubka umožňuje rozlišení účtů Bitcoinu od ostatních kryptoměn ve stejné peněžence.
Každá měna má jedinečný index, aby se zajistila kompatibilita napříč peněženkami s více měnami. Například pro Bitcoin je index $/0'/$ (nebo `0x80000000` v hexadecimální notaci). Indexy měn jsou vybrány v rozmezí od $2^{31}$ do $2^{32}-1$, aby se zajistilo zpevněné odvození.
Pro další příklady, zde jsou indexy některých měn:
- $1'$ (`0x80000001`) pro testnetové bitcoiny;
- $2'$ (`0x80000002`) pro Litecoin;
- $60'$ (`0x8000003c`) pro Ethereum...
**Hloubka 3: Účet (BIP32)**
Každou peněženku lze rozdělit do několika účtů, číslovaných od $2^{31}$, a reprezentovaných na hloubce 3 $/0'/$ pro první účet, $/1'/$ pro druhý a tak dále. Obecně, když se mluví o rozšířeném klíči `xpub`, odkazuje se na klíče na této hloubce odvození.
Toto rozdělení do různých účtů je volitelné. Jeho cílem je zjednodušit organizaci peněženky pro uživatele. V praxi se často používá pouze jeden účet, obvykle ten první jako výchozí. Nicméně, v některých případech, pokud si přeje někdo jasně rozlišit páry klíčů pro různé účely, může to být užitečné. Například je možné vytvořit osobní a profesionální účet ze stejného seedu, s úplně odlišnými skupinami klíčů z této hloubky odvození.
**Hloubka 4: Řetězec (BIP32)**
Každý účet definovaný na hloubce 3 je poté strukturován do dvou řetězců:
- **Vnější řetězec**: V tomto řetězci jsou odvozeny takzvané "veřejné" adresy. Tyto přijímací adresy jsou určeny k uzamčení UTXO pocházejících z externích transakcí (to znamená, pocházejících z konzumace UTXO, které vám nepatří). Jednoduše řečeno, tento vnější řetězec se používá vždy, když si přejete přijímat bitcoiny. Když v softwaru vaší peněženky kliknete na "*přijmout*", je vám vždy nabídnuta adresa z vnějšího řetězce. Tento řetězec je reprezentován párem klíčů odvozených s indexem $/0/$.
- **Vnitřní řetězec (změna)**: Tento řetězec je vyhrazen pro přijímací adresy, které uzamknou bitcoiny pocházející z konzumace UTXO, které vám patří, jinými slovy, adresy pro změnu. Je identifikován indexem $/1/$.
**Hloubka 5: Index adresy (BIP32)**
Nakonec, hloubka 5 představuje poslední krok odvození v peněžence. Ačkoliv je technicky možné pokračovat neomezeně, současné standardy zde končí. Na této konečné hloubce jsou odvozeny páry klíčů, které budou skutečně použity pro uzamčení a odemčení UTXO. Každý index umožňuje rozlišení mezi sourozeneckými páry klíčů: tak první přijímací adresa použije index $/0/$, druhá index $/1/$ a tak dále.
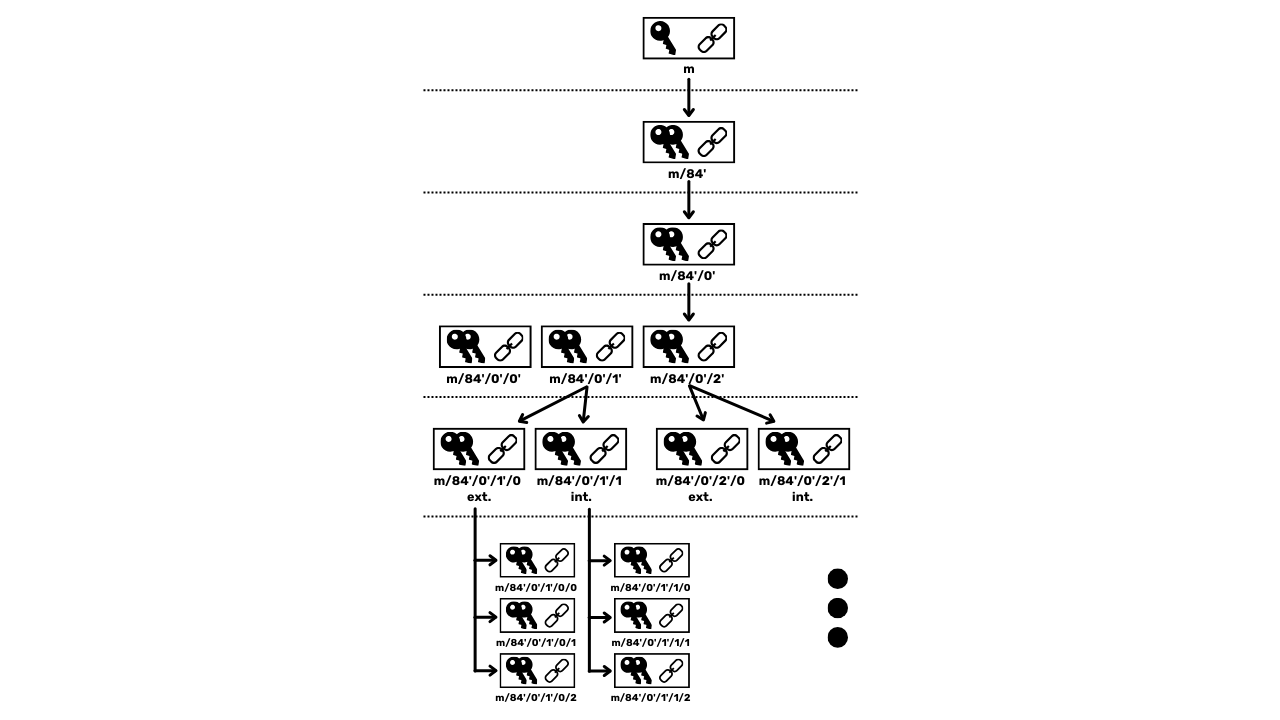
### Notace cest odvození
Cesta odvození je zapsána oddělením každé úrovně lomítkem ($/$). Každé lomítko tak indikuje odvození rodičovského páru klíčů ($k_{\text{PAR}}$, $K_{\text{PAR}}$, $C_{\text{PAR}}$) na dětský pár klíčů ($k_{\text{CHD}}$, $K_{\text{CHD}}$, $C_{\text{CHD}}$). Číslo uvedené na každé hloubce odpovídá indexu použitému k odvození tohoto klíče od jeho rodičů. Apostrof ($'$) někdy umístěný vpravo od indexu označuje zpevněné odvození ($k_{\text{CHD}}^h$, $K_{\text{CHD}}^h$). Někdy je tento apostrof nahrazen písmenem $h$. V případě absence apostrofu nebo $h$ se jedná tedy o normální odvození ($k_{\text{CHD}}^n$, $K_{\text{CHD}}^n$).
Jak jsme viděli v předchozích kapitolách, indexy zpevněných klíčů začínají od $2^{31}$, nebo `0x80000000` v hexadecimálním zápisu. Proto, když je index následován apostrofem v cestě odvození, musí být k uvedenému číslu přidáno $2^{31}$, aby byla získána skutečná hodnota použitá ve funkci HMAC-SHA512. Například, pokud cesta odvození specifikuje $/44'/$, skutečný index bude:i = 44 + 2^{31} = 2,147,483,692
V hexadecimálním zápisu je to `0x8000002C`.
Nyní, když jsme pochopili hlavní principy cest odvození, pojďme si dát příklad! Zde je cesta odvození pro přijímací adresu Bitcoinu:
m / 84' / 0' / 1' / 0 / 7
V tomto příkladu:
- $84'$ označuje standard P2WPKH (SegWit v0);
- $0'$ označuje měnu Bitcoin na hlavní síti;
- $1'$ odpovídá druhému účtu v peněžence;
- $0$ označuje, že adresa je na vnější řetězci;
- $7$ označuje 8. vnější adresu tohoto účtu.
### Souhrn struktury odvození
| Hloubka | Popis | Standardní příklad |
| ------- | ------------------ | --------------------------------- |
| 0 | Hlavní klíč | $m/$ |
| 1 | Účel | $/86'/$ (P2TR) |
| 2 | Měna | $/0'/$ (Bitcoin) |
| 3 | Účet | $/0'/$ (První účet) |
| 4 | Řetězec | $/0/$ (externí) nebo $/1/$ (změna)|
| 5 | Index adresy | $/0/$ (první adresa) |
V následující kapitole objevíme, co jsou to "*output script descriptors*", což je nedávno představená inovace v Bitcoin Core, která zjednodušuje zálohování Bitcoinové peněženky.
## Output script descriptors
<chapterId>e4f1c2d3-9b8a-4d3e-8f2a-7b6c5d4e3f2a</chapterId>
Často se říká, že mnemonická fráze sama o sobě stačí k obnovení přístupu k peněžence. Ve skutečnosti jsou věci trochu složitější. V předchozí kapitole jsme se podívali na strukturu derivace HD peněženky a možná jste si všimli, že tento proces je poměrně složitý. Derivační cesty říkají softwaru, kterým směrem se má ubírat k odvození klíčů uživatele. Při obnově Bitcoinové peněženky však, pokud tyto cesty neznáme, není mnemonická fráze sama o sobě dostatečná. Umožňuje získat hlavní klíč a hlavní řetězový kód, ale je pak nutné znát indexy použité k dosažení dětských klíčů.
Teoreticky by bylo nutné uložit nejen mnemonickou frázi naší peněženky, ale také cesty k účtům, které používáme. V praxi je často možné znovu získat přístup k dětským klíčům bez těchto informací, pokud byly dodrženy standardy. Testováním každého standardu po jednom je obecně možné znovu získat přístup k bitcoinům. Nicméně to není zaručené a je to zejména pro začátečníky složité. Také s diverzifikací typů skriptů a vznikem složitějších konfigurací by se tyto informace mohly stát obtížně extrapolovatelnými, čímž by se tyto údaje proměnily v soukromé informace a obtížně obnovitelné hrubou silou. To je důvod, proč byla nedávno představena inovace, která začíná být integrována do vašeho oblíbeného softwaru pro peněženky: *output script descriptors*.
### Co je "descriptor"?
"*Output script descriptors*", nebo jednoduše "*descriptors*", jsou strukturované výrazy, které plně popisují výstupní skript (*scriptPubKey*) a poskytují veškeré informace potřebné k sledování transakcí spojených s konkrétním skriptem. Ulehčují správu klíčů v HD peněženkách tím, že nabízejí standardizovaný a úplný popis struktury peněženky a typů použitých adres.
Hlavní výhodou descriptorů je jejich schopnost zahrnout veškeré zásadní informace pro obnovu peněženky do jediného řetězce (kromě obnovovací fráze). Uložením descriptoru spolu s přidruženými mnemonickými frázemi se stává možné obnovit soukromé klíče s přesným vědomím jejich pozice v hierarchii. Pro multisig peněženky, jejichž záloha byla původně složitější, descriptor zahrnuje `xpub` každého faktoru, čímž zajišťuje možnost regenerace adres v případě problému.
### Konstrukce descriptoru
Descriptor se skládá z několika prvků:
* Skriptové funkce jako `pk` (*Pay-to-PubKey*), `pkh` (*Pay-to-PubKey-Hash*), `wpkh` (*Pay-to-Witness-PubKey-Hash*), `sh` (*Pay-to-Script-Hash*), `wsh` (*Pay-to-Witness-Script-Hash*), `tr` (*Pay-to-Taproot*), `multi` (*Multisignature*), a `sortedmulti` (*Multisignature s řazenými klíči*);
* Derivační cesty, například `[d34db33f/44h/0h/0h]`, které označují odvozenou cestu účtu a specifický otisk hlavního klíče;
* Klíče v různých formátech, jako jsou hexadecimální veřejné klíče nebo rozšířené veřejné klíče (`xpub`);
* Kontrolní součet, předcházený hash znakem, pro ověření integrity descriptoru.
Například popisovač pro peněženku P2WPKH (SegWit v0) by mohl vypadat takto:
```text
wpkh([cdeab12f/84h/0h/0h]xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U/<0;1>/*)#jy0l7nr4
```
V tomto popisovači funkce derivace `wpkh` označuje typ skriptu *Pay-to-Witness-Public-Key-Hash*. Následuje cesta derivace, která obsahuje:
* `cdeab12f`: otisk hlavního klíče;
* `84h`: což značí použití účelu BIP84, určeného pro adresy SegWit v0;
* `0h`: což ukazuje, že se jedná o měnu BTC na hlavní síti;
* `0h`: což odkazuje na konkrétní číslo účtu použité v peněžence.
Popisovač také zahrnuje rozšířený veřejný klíč použitý v této peněžence:
```text
xpub6CUGRUonZSQ4TWtTMmzXdrXDtyPWKiKbERr4d5qkSmh5h17C1TjvMt7DJ9Qve4dRxm91CDv6cNfKsq2mK1rMsJKhtRUPZz7MQtp3y6atC1U
```
Dále, notace `/<0;1>/*` specifikuje, že popisovač může generovat adresy z externího řetězce (`0`) a interního řetězce (`1`), s použitím zástupného symbolu (`*`), což umožňuje sekvenční derivaci více adres v konfigurovatelný způsob, podobně jako správa "mezery limitu" v tradičním softwaru peněženky.
Nakonec, `#jy0l7nr4` představuje kontrolní součet pro ověření integrity popisovače.
Nyní víte vše o fungování HD peněženky na Bitcoinu a procesu derivace klíčových párů. Nicméně, v posledních kapitolách jsme se omezili na generování soukromých a veřejných klíčů, aniž bychom se zabývali konstrukcí přijímacích adres. To bude přesně předmětem následující kapitoly!
## Přijímací Adresy
<chapterId>ca80a89d-f8da-4e09-8c35-43179b65bced</chapterId>
Přijímací adresy jsou informace vložené do *scriptPubKey* pro uzamčení nově vytvořených UTXO. Jednoduše řečeno, adresa slouží k přijímání bitcoinů. Pojďme prozkoumat jejich fungování v souvislosti s tím, co jsme studovali v předchozích kapitolách.
### Role Bitcoinových Adres ve Skriptech
Jak bylo vysvětleno dříve, úlohou transakce je převést vlastnictví bitcoinů z vstupů na výstupy. Tento proces zahrnuje spotřebování UTXO jako vstupy při vytváření nových UTXO jako výstupy. Tyto UTXO jsou zabezpečeny skripty, které definují nezbytné podmínky pro odemčení prostředků.
Když uživatel obdrží bitcoiny, odesílatel vytvoří výstupní UTXO a zamkne jej pomocí *scriptPubKey*. Tento skript obsahuje pravidla, která typicky specifikují požadované podpisy a veřejné klíče potřebné k odemčení tohoto UTXO. Aby uživatel mohl toto UTXO utratit v nové transakci, musí poskytnout požadované informace prostřednictvím *scriptSig*. Spuštění *scriptSig* ve spojení se *scriptPubKey* musí vrátit "true" nebo `1`. Pokud je tato podmínka splněna, UTXO lze utratit k vytvoření nového UTXO, které je samo zamčeno novým *scriptPubKey*, a tak dále.

Je právě v *scriptPubKey*, kde se nacházejí přijímací adresy. Nicméně jejich použití se liší v závislosti na přijatém standardu skriptu. Zde je shrnutí tabulka informací obsažených v *scriptPubKey* podle použitého standardu, stejně jako informace očekávané v *scriptSig* k odemčení *scriptPubKey*.
| Standard | *scriptPubKey* | *scriptSig* | *redeem script* | *witness* |
| ------------------ | ----------------------------------------------------------- | ------------------------------- | ------------------- | ---------------------------------------- |
| P2PK | `<pubkey> OP_CHECKSIG` | `<signature>` | | |
| P2PKH | `OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG` | `<signature> <public key>` | | |
| P2SH | `OP_HASH160 <scriptHash> OP_EQUAL` | `<data pushes> <redeem script>` | Libovolná data | |
| P2WPKH | `0 <pubKeyHash>` | | | `<signature> <public key>` |
| P2WSH | `0 <witnessScriptHash>` | | | `<data pushes> <witness script>` |
| P2SH-P2WPKH | `OP_HASH160 <redeemScriptHash> OP_EQUAL` | `<redeem script>` | `0 <pubKeyHash>` | `<signature> <public key>` |
| P2SH-P2WSH | `OP_HASH160 <redeemScriptHash> OP_EQUAL` | `<redeem script>` | `0 <scriptHash>` | `<data pushes> <witness script>` |
| P2TR (key path) | `1 <public key>` | | | `<signature>` |
| P2TR (script path) | `1 <public key>` | | | `<data pushes> <script> <control block>` |
*Zdroj: Bitcoin Core PR review club, 7. července 2021 - Gloria Zhao*
Opcodes použité ve skriptu jsou navrženy k manipulaci s informacemi a v případě potřeby k jejich porovnání nebo testování. Vezměme si příklad skriptu P2PKH, který vypadá takto:
```text
OP_DUP OP_HASH160 OP_PUSHBYTES_20 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG
```
Jak uvidíme v této kapitole, `<pubKeyHash>` ve skutečnosti představuje náklad přijímací adresy použité k zamčení UTXO. K odemčení *scriptPubKey* je nutné poskytnout *scriptSig* obsahující:
```text
<signature> <public key>
```
Ve skriptovacím jazyce je "zásobník" datová struktura typu "*LIFO*" ("*Last In, First Out*"), která se používá k dočasnému ukládání prvků během vykonávání skriptu. Každá operace ve skriptu manipuluje s tímto zásobníkem, kde mohou být prvky přidávány (*push*) nebo odebírány (*pop*). Skripty využívají tyto zásobníky k vyhodnocení výrazů, ukládání dočasných proměnných a řízení podmínek.
Vykonání skriptu, který jsem právě dal jako příklad, sleduje tento proces:
- Máme *scriptSig*, *ScriptPubKey* a zásobník:

- *scriptSig* je vložen na zásobník:

- `OP_DUP` duplikuje veřejný klíč poskytnutý v *scriptSig* na zásobníku:

- `OP_HASH160` vrátí hash veřejného klíče, který byl právě duplikován:
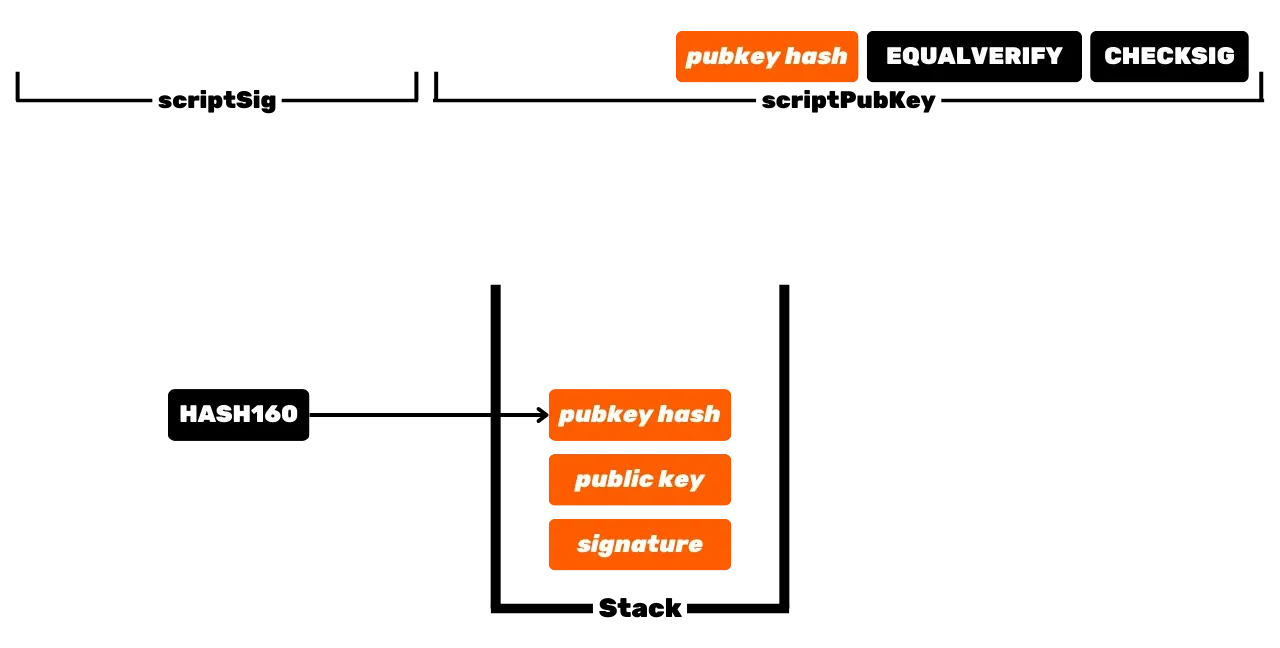
- `OP_PUSHBYTES_20 <pubKeyHash>` vloží Bitcoinovou adresu obsaženou v *scriptPubKey* na zásobník:

- `OP_EQUALVERIFY` ověří, že hashovaný veřejný klíč odpovídá poskytnuté přijímací adrese:

`OP_CHECKSIG` zkontroluje podpis obsažený v *scriptSig* pomocí veřejného klíče. Tento opcode v podstatě provádí ověření podpisu, jak jsme popisovali v části 3 tohoto školení:

- Pokud na zásobníku zůstane `1`, pak je skript platný:
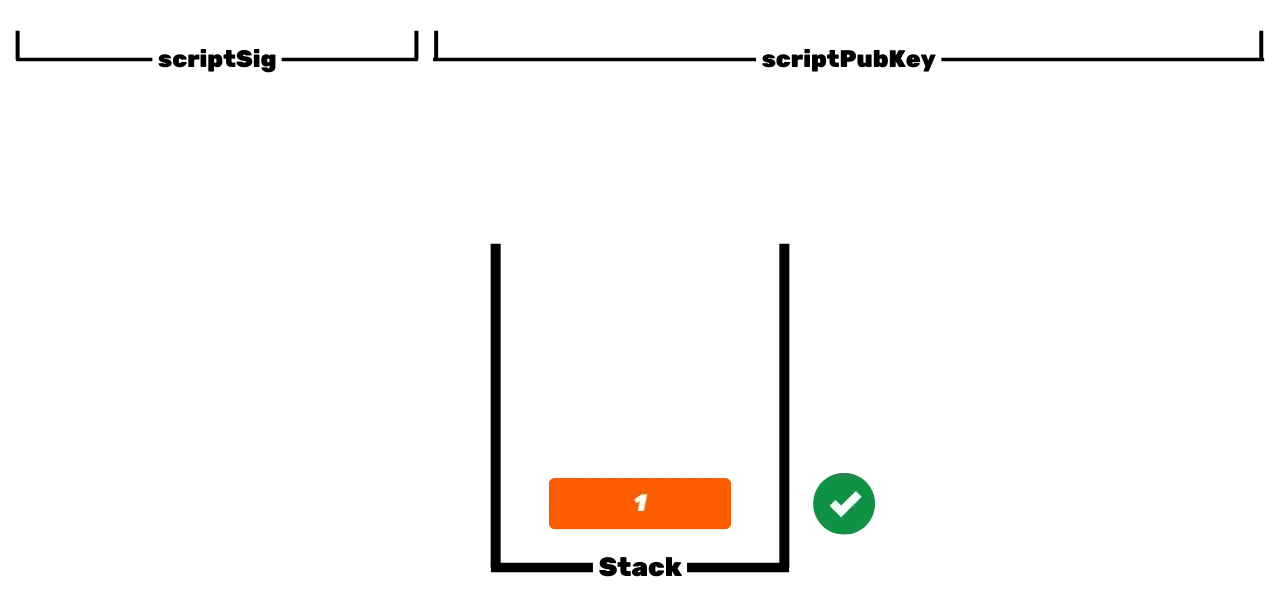
Shrnutí, tento skript umožňuje ověřit, s pomocí digitálního podpisu, že uživatel, který tvrdí, že vlastní toto UTXO a chce jej utratit, skutečně vlastní soukromý klíč spojený s přijímací adresou použitou při vytváření tohoto UTXO.
### Různé typy Bitcoinových adres
Během vývoje Bitcoinu bylo přidáno několik standardních modelů skriptů. Každý z nich používá odlišný typ přijímací adresy. Zde je přehled hlavních dostupných modelů skriptů:
**P2PK (*Pay-to-PubKey*)**:
Tento model skriptu byl představen v první verzi Bitcoinu Satoshi Nakamotem. Skript P2PK uzamkne bitcoiny přímo pomocí surového veřejného klíče (takže s tímto modelem není používána žádná přijímací adresa). Jeho struktura je jednoduchá: obsahuje veřejný klíč a vyžaduje odpovídající digitální podpis k odemčení prostředků. Tento skript je součástí standardu "*Legacy*".
**P2PKH (*Pay-to-PubKey-Hash*)**:
Stejně jako P2PK, skript P2PKH byl představen při spuštění Bitcoinu. Na rozdíl od svého předchůdce uzamkne bitcoiny pomocí hashe veřejného klíče, namísto přímého použití surového veřejného klíče. *scriptSig* musí poté poskytnout veřejný klíč spojený s přijímací adresou, stejně jako platný podpis. Adresy odpovídající tomuto modelu začínají číslem `1` a jsou kódovány v *base58check*. Tento skript také patří do standardu "*Legacy*".
**P2SH (*Pay-to-Script-Hash*)**:
Zavedený v roce 2012 s BIP16, model P2SH umožňuje použití hash hodnoty libovolného skriptu v *scriptPubKey*. Tento zahašovaný skript, nazývaný "*redeemScript*", obsahuje podmínky pro odemčení prostředků. Pro utrácení UTXO zamčeného pomocí P2SH je nutné poskytnout *scriptSig* obsahující původní *redeemScript* a také nezbytná data pro jeho validaci. Tento model je významně používán pro staré multisigy. Adresy spojené s P2SH začínají na `3` a jsou kódovány v *base58check*. Tento skript také patří do standardu "*Legacy*".
**P2WPKH (*Pay-to-Witness-PubKey-Hash*)**:
Tento skript je podobný P2PKH, protože také zamyká bitcoiny pomocí hash hodnoty veřejného klíče. Na rozdíl od P2PKH je však *scriptSig* přesunut do samostatné sekce nazývané "*Witness*". Někdy se tomu říká "*scriptWitness*", aby se označila sada obsahující podpis a veřejný klíč. Každý SegWit vstup má svůj vlastní *scriptWitness*, a sbírka *scriptWitnesses* tvoří pole *Witness* transakce. Tento přesun dat o podpisu je inovace zavedená aktualizací SegWit, zaměřená zejména na prevenci manipulovatelnosti transakcí kvůli podpisům ECDSA.
Adresy P2WPKH používají kódování *bech32* a vždy začínají `bc1q`. Tento typ skriptu odpovídá výstupům SegWit verze 0.
**P2WSH (*Pay-to-Witness-Script-Hash*)**:
Model P2WSH byl také zaveden s aktualizací SegWit v srpnu 2017. Podobně jako model P2SH zamyká bitcoiny pomocí hash hodnoty skriptu. Hlavní rozdíl spočívá v tom, jak jsou podpisy a skripty začleněny do transakce. Pro utrácení bitcoinů zamčených tímto typem skriptu musí příjemce poskytnout původní skript, nazývaný *witnessScript* (ekvivalent k *redeemScript* v P2SH), spolu s nezbytnými daty pro validaci tohoto *witnessScript*. Tento mechanismus umožňuje implementaci složitějších podmínek utrácení, jako jsou multisigy.
Adresy P2WSH používají kódování *bech32* a vždy začínají `bc1q`. Tento skript také odpovídá výstupům SegWit verze 0.
**P2TR (*Pay-to-Taproot*)**:
Model P2TR byl zaveden s implementací Taproot v listopadu 2021. Je založen na protokolu Schnorr pro agregaci kryptografických klíčů, stejně jako na Merkleově stromu pro alternativní skripty, nazývaný MAST (*Merkelized Alternative Script Tree*). Na rozdíl od ostatních typů skriptů, kde jsou podmínky utrácení veřejně vystaveny (buď při přijetí nebo při utrácení), P2TR umožňuje skrýt složité skripty za jediným, zdánlivě veřejným klíčem.
Technicky skript P2TR zamyká bitcoiny na unikátním veřejném klíči Schnorr, označeném jako $Q$. Tento klíč $Q$ je ve skutečnosti agregátem veřejného klíče $P$ a veřejného klíče $M$, přičemž posledně jmenovaný je vypočítán z Merkleova kořene seznamu *scriptPubKey*. Bitcoiny zamčené tímto typem skriptu lze utratit dvěma způsoby:
- Publikováním podpisu pro veřejný klíč $P$ (*key path*).
- Splněním jednoho ze skriptů obsažených v Merkleově stromu (*script path*).
P2TR tedy nabízí velkou flexibilitu, protože umožňuje uzamknout bitcoiny buď s unikátním veřejným klíčem, s několika vybranými skripty, nebo s obojím současně. Výhodou této struktury Merkleova stromu je, že během transakce je odhalen pouze použitý výdajový skript, ale všechny ostatní alternativní skripty zůstávají tajné.
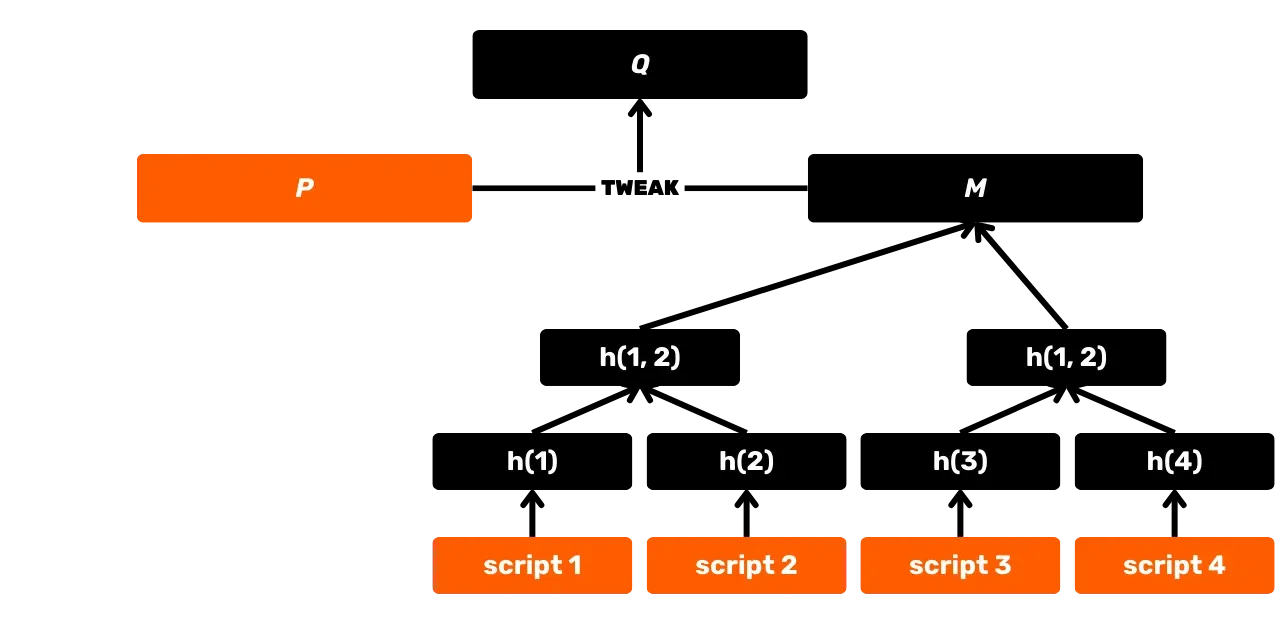
P2TR odpovídá výstupům SegWit verze 1, což znamená, že podpisy pro vstupy P2TR jsou uloženy v sekci *Witness* transakce, a ne v *scriptSig*. Adresy P2TR používají kódování *bech32m* a začínají na `bc1p`, ale jsou poměrně unikátní tím, že pro jejich konstrukci nepoužívají hashovací funkci. Skutečně přímo reprezentují veřejný klíč $Q$, který je jednoduše formátován s metadaty. Je to tedy model skriptu blízký P2PK.
Nyní, když jsme probrali teorii, pojďme přejít k praxi! V následující kapitole navrhuji odvození jak adresy SegWit v0, tak adresy SegWit v1 z páru klíčů.
## Odvození adresy
<chapterId>3ebdc750-4135-4881-b07e-08965941b93e</chapterId>
Pojďme společně prozkoumat, jak generovat přijímací adresu z páru klíčů umístěných například na hloubce 5 v HD peněžence. Tato adresa pak může být použita v softwaru peněženky k uzamčení UTXO.
Protože proces generování adresy závisí na přijatém modelu skriptu, zaměřme se na dva konkrétní případy: generování adresy SegWit v0 v P2WPKH a adresy SegWit v1 v P2TR. Tyto dva typy adres pokrývají dnes velkou většinu použití.
### Komprese veřejného klíče
Po provedení všech kroků odvození od hlavního klíče k hloubce 5 pomocí vhodných indexů získáme pár klíčů ($k$, $K$) s $K = k \cdot G$. Ačkoli je možné tento veřejný klíč použít tak, jak je, k uzamčení prostředků se standardem P2PK, to není náš cíl zde. Místo toho je naším cílem v první řadě vytvořit adresu v P2WPKH a poté v P2TR pro další příklad.
Prvním krokem je komprese veřejného klíče $K$. Abychom tento proces dobře pochopili, připomeňme si nejprve některé základy, které byly pokryty v části 3.
Veřejný klíč v Bitcoinu je bod $K$ umístěný na eliptické křivce. Je reprezentován ve formě $(x, y)$, kde $x$ a $y$ jsou souřadnice bodu. Ve své neskomprimované formě má tento veřejný klíč 520 bitů: 8 bitů pro prefix (počáteční hodnota `0x04`), 256 bitů pro souřadnici $x$ a 256 bitů pro souřadnici $y$.
Eliptické křivky však mají vlastnost symetrie vzhledem k ose x: pro danou souřadnici $x$ existují pouze dvě možné hodnoty pro $y$: $y$ a $-y$. Tyto dva body se nacházejí na obou stranách osy x. Jinými slovy, pokud známe $x$, stačí specifikovat, zda je $y$ sudé nebo liché, abychom identifikovali přesný bod na křivce.
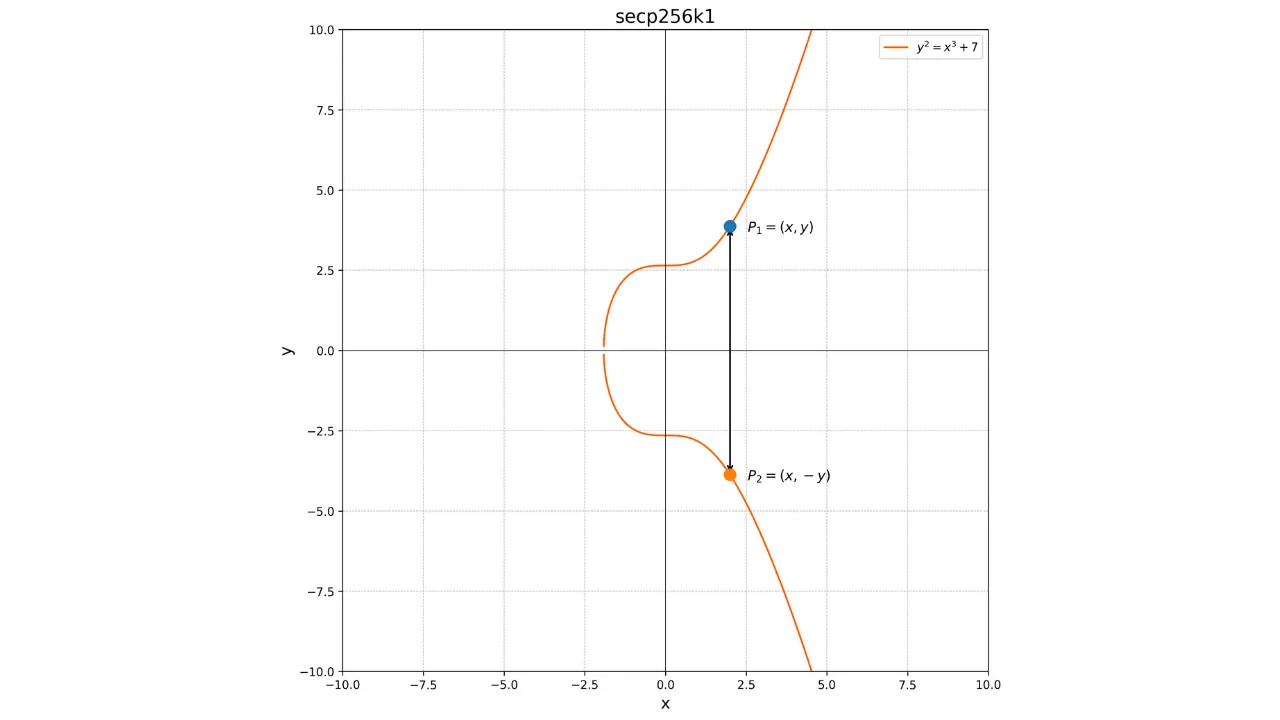
Pro kompresi veřejného klíče se kóduje pouze $x$, které zabírá 256 bitů, a přidá se prefix, který specifikuje paritu $y$. Tato metoda redukuje velikost veřejného klíče na 264 bitů namísto původních 520. Prefix `0x02` indikuje, že $y$ je sudé, a prefix `0x03` indikuje, že $y$ je liché.
Pojďme si vzít příklad pro lepší pochopení, s nekomprimovanou reprezentací veřejného klíče:
```text
K = 04678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f
```
Pokud tento klíč rozložíme, máme:
- Prefix: `04`;
- $x$: `678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6`;
- $y$: `49f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f`
Poslední hexadecimální znak $y$ je `f`. V desítkové soustavě `f = 15`, což odpovídá lichému číslu. Proto je $y$ liché, a prefix bude `0x03`, aby toto indikoval.
Kompresovaný veřejný klíč se stává:
```text
K = 03678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb6
```
Tato operace se aplikuje na všechny modely skriptů založené na ECDSA, to znamená na všechny kromě P2TR, který používá Schnorr. V případě Schnorra, jak je vysvětleno v části 3, si ponecháváme pouze hodnotu $x$, bez přidání prefixu k indikaci parity $y$, na rozdíl od ECDSA. To je umožněno tím, že pro všechny klíče je libovolně zvolena jedinečná parita. To umožňuje mírné snížení potřebného úložného prostoru pro veřejné klíče.
### Odvození adresy SegWit v0 (bech32)
Nyní, když jsme získali náš komprimovaný veřejný klíč, můžeme z něj odvodit přijímací adresu SegWit v0.
Prvním krokem je aplikovat hashovací funkci HASH160 na komprimovaný veřejný klíč. HASH160 je kompozice dvou po sobě jdoucích hashovacích funkcí: SHA256, následovaná RIPEMD160:
\text{HASH160}(K) = \text{RIPEMD160}(\text{SHA256}(K))
Nejprve klíč projde SHA256:
```text
SHA256(K) = C489EBD66E4103B3C4B5EAFF462B92F5847CA2DCE0825F4997C7CF57DF35BF3A
```
Poté výsledek projde RIPEMD160:
```text
RIPEMD160(SHA256(K)) = 9F81322CC88622CA4CCB2A52A21E2888727AA535
```
Získali jsme 160bitový hash veřejného klíče, který tvoří to, co se nazývá payload adresy. Tento payload představuje centrální a nejdůležitější část adresy. Používá se také ve *scriptPubKey* k uzamčení UTXO.
Avšak, aby byl tento payload snadněji použitelný pro lidi, je k němu přidána metadata. Dalším krokem je zakódování tohoto hashe do skupin po 5 bitech v desítkové soustavě. Tato desítková transformace bude užitečná pro konverzi do *bech32*, která je používána u adres po SegWit. 160bitový binární hash je tak rozdělen do 32 skupin po 5 bitech:
\begin{array}{|c|c|} \hline \text{5 bits} & \text{Decimal} \ \hline 10011 & 19 \ 11110 & 30 \ 00000 & 0 \ 10011 & 19 \ 00100 & 4 \ 01011 & 11 \ 00110 & 6 \ 01000 & 8 \ 10000 & 16 \ 11000 & 24 \ 10001 & 17 \ 01100 & 12 \ 10100 & 20 \ 10011 & 19 \ 00110 & 6 \ 01011 & 11 \ 00101 & 5 \ 01001 & 9 \ 01001 & 9 \ 01010 & 10 \ 00100 & 4 \ 00111 & 7 \ 10001 & 17 \ 01000 & 8 \ 10001 & 17 \ 00001 & 1 \ 11001 & 25 \ 00111 & 7 \ 10101 & 21 \ 00101 & 5 \ 00101 & 5 \ 10101 & 21 \ \hline \end{array}
Takže máme:
```text
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
```
Jakmile je hash zakódován do skupin po 5 bitech, je k adrese přidán kontrolní součet. Tento kontrolní součet se používá k ověření, že payload adresy nebyl během jeho ukládání nebo přenosu změněn. Například to umožňuje softwaru peněženky zajistit, že jste při zadávání přijímací adresy neudělali překlep. Bez této verifikace byste mohli omylem poslat bitcoiny na nesprávnou adresu, což by vedlo k trvalé ztrátě finančních prostředků, protože nevlastníte přidružený veřejný nebo soukromý klíč. Kontrolní součet je tedy ochranou proti lidským chybám.
Pro staré Bitcoinové *Legacy* adresy byl kontrolní součet jednoduše vypočítán od začátku hash adresy funkcí HASH256. S příchodem SegWit a formátem *bech32* se nyní používají BCH kódy (*Bose, Ray-Chaudhuri a Hocquenghem*). Tyto kódy pro opravu chyb se používají k detekci a opravě chyb v datových sekvencích. Zajišťují, že přenášené informace dorazí na místo určení neporušené, i v případě menších změn. BCH kódy se používají v mnoha oblastech, jako jsou SSD, DVD a QR kódy. Například díky těmto BCH kódům lze částečně zakrytý QR kód stále přečíst a dekódovat.
V kontextu Bitcoinu nabízejí BCH kódy lepší kompromis mezi velikostí a schopností detekce chyb ve srovnání s jednoduchými hash funkcemi používanými pro *Legacy* adresy. Nicméně, na Bitcoinu se BCH kódy používají pouze pro detekci chyb, nikoli pro jejich opravu. Tedy, software peněženky signalizuje nesprávnou přijímací adresu, ale automaticky ji neopraví. Toto omezení je záměrné: umožnění automatické opravy by snížilo schopnost detekce chyb.
Pro výpočet kontrolního součtu s BCH kódy potřebujeme připravit několik prvků:
- **HRP (*Human Readable Part*)**: Pro hlavní síť Bitcoinu je HRP `bc`;
HRP musí být rozšířeno oddělením každého znaku na dvě části:
- Převzetí znaků HRP v ASCII:
- `b`: `01100010`
- `c`: `01100011`
- Extrakce 3 nejvýznamnějších bitů a 5 nejméně významných bitů:
- 3 nejvýznamnější bity: `011` (3 v desítkové soustavě)
- 3 nejvýznamnější bity: `011` (3 v desítkové soustavě)
- 5 nejméně významných bitů: `00010` (2 v desítkové soustavě)
- 5 nejméně významných bitů: `00011` (3 v desítkové soustavě)
S oddělovačem `0` mezi dvěma znaky je tedy rozšíření HRP:
```text
03 03 00 02 03
```
- **Verze witness**: Pro SegWit verzi 0 je to `00`;
- **Payload**: Desítkové hodnoty hash veřejného klíče;
- **Rezervace pro kontrolní součet**: Na konec sekvence přidáme 6 nul `[0, 0, 0, 0, 0, 0]`.
Všechna data kombinovaná pro vstup do programu pro výpočet kontrolního součtu jsou následující:
```text
HRP = 03 03 00 02 03
SEGWIT v0 = 00
HASH = 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21
CHECKSUM = 00 00 00 00 00 00
INPUT = 03 03 00 02 03 00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 00 00 00 00 00 00
```
Výpočet kontrolního součtu je poměrně složitý. Zahrnuje aritmetiku konečných polynomů. Tento výpočet zde podrobněji rozebírat nebudeme a přejdeme přímo k výsledku. V našem příkladu je získaný kontrolní součet v desítkové soustavě:
```text
10 16 11 04 13 18
```
Nyní můžeme sestavit přijímací adresu spojením následujících prvků v pořadí:
- **Verze SegWit**: `00`
- **Payload**: Hash veřejného klíče
- **Kontrolní součet**: Hodnoty získané v předchozím kroku (`10 16 11 04 13 18`)
To nám v desítkové soustavě dává:
```text
00 19 30 00 19 04 11 06 08 16 24 17 12 20 19 06 11 05 09 09 10 04 07 17 08 17 01 25 07 21 09 09 21 10 16 11 04 13 18
```
Poté musí být každá desítková hodnota převedena na její *bech32* znak pomocí následující konverzní tabulky:
\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \ \hline +0 & q & p & z & r & y & 9 & x & 8 \ \hline +8 & g & f & 2 & t & v & d & w & 0 \ \hline +16 & s & 3 & j & n & 5 & 4 & k & h \ \hline +24 & c & e & 6 & m & u & a & 7 & l \ \hline \end{array}
Pro převedení hodnoty na znak _bech32_ pomocí této tabulky jednoduše najděte hodnoty v prvním sloupci a prvním řádku, které po sečtení dávají požadovaný výsledek. Poté získejte odpovídající znak. Například desítkové číslo `19` bude převedeno na písmeno `n`, protože $19 = 16 + 3$.
Mapováním všech našich hodnot získáme následující adresu:
```
qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj
```
Zbývá již jen přidat HRP `bc`, což naznačuje, že se jedná o adresu pro Bitcoin mainnet, stejně jako oddělovač `1`, abychom získali kompletní přijímací adresu:
```
bc1qn7qnytxgsc3v5nxt9ff2y83g3pe84ff42stydj
```
Zvláštností této abecedy _bech32_ je, že zahrnuje všechny alfanumerické znaky kromě `1`, `b`, `i` a `o`, aby se zabránilo vizuálnímu zmatení mezi podobnými znaky, zejména při jejich zadávání nebo čtení lidmi.
Shrnutí, zde je proces derivace:
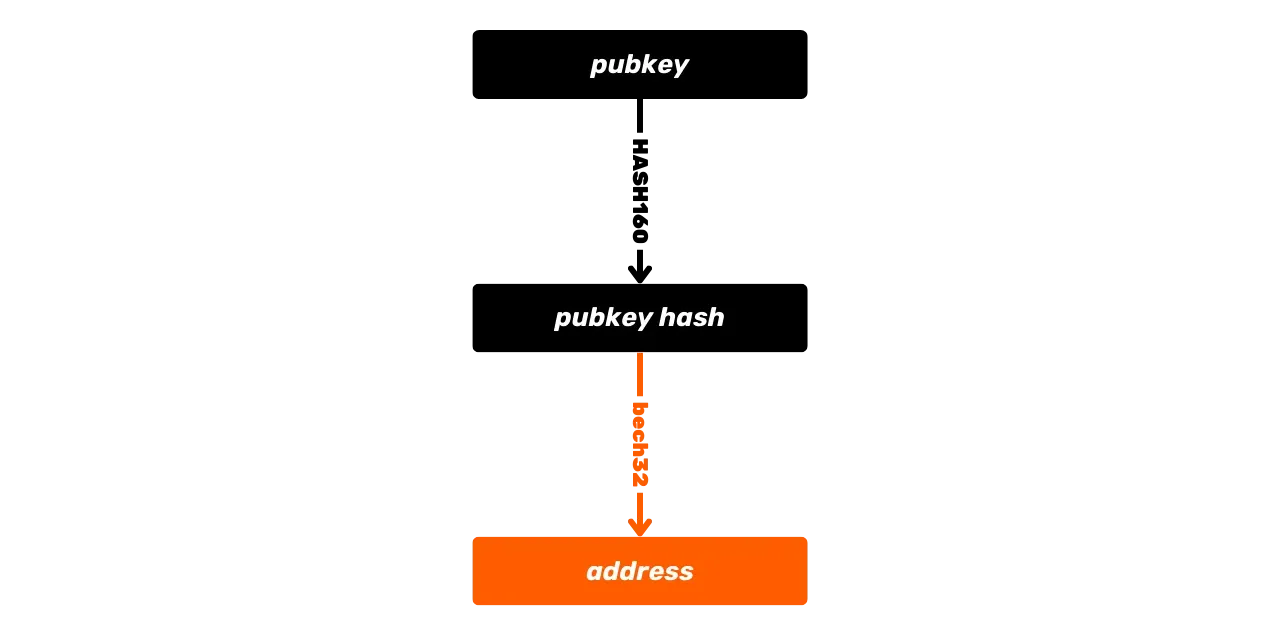
Takto se odvozuje P2WPKH (SegWit v0) přijímací adresa z páru klíčů. Nyní přejděme na adresy P2TR (SegWit v1 / Taproot) a objevme jejich proces generování.
### Odvození adresy SegWit v1 (bech32m)
Pro adresy Taproot se proces generování mírně liší. Podívejme se na to společně!
Od kroku komprese veřejného klíče se objevuje první rozdíl ve srovnání s ECDSA: veřejné klíče používané pro Schnorr na Bitcoinu jsou reprezentovány pouze jejich abscisou ($x$). Proto není žádná předpona a komprimovaný klíč má přesně 256 bitů.
Jak jsme viděli v předchozí kapitole, skript P2TR uzamkne bitcoiny na unikátním veřejném klíči Schnorr, označeném jako $Q$. Tento klíč $Q$ je agregátem dvou veřejných klíčů: $P$, hlavní interní veřejný klíč, a $M$, veřejný klíč odvozený z kořenového Merkle stromu seznamu _scriptPubKey_. Bitcoiny uzamčené s tímto typem skriptu lze utratit dvěma způsoby:
- Zveřejněním podpisu pro veřejný klíč $P$ (_cesta klíče_);
- Splněním jednoho ze skriptů zahrnutých v Merkle stromu (_cesta skriptu_).
Ve skutečnosti tyto dva klíče nejsou skutečně "agregovány". Klíč $P$ je místo toho upraven klíčem $M$. V kryptografii znamená "upravit" veřejný klíč modifikaci tohoto klíče aplikací aditivní hodnoty nazývané "tweak". Tato operace umožňuje modifikovanému klíči zůstat kompatibilní s původním soukromým klíčem a tweakem. Technicky je tweak skalární hodnota $t$, která je přidána k původnímu veřejnému klíči. Pokud je $P$ původní veřejný klíč, upravený klíč se stává:
P' = P + tG
Kde $G$ je generátor eliptické křivky použité. Tato operace produkuje nový veřejný klíč odvozený z původního klíče, přičemž si zachovává kryptografické vlastnosti umožňující jeho použití.
Pokud nepotřebujete přidávat alternativní skripty (výdaje výhradně prostřednictvím _klíčové cesty_), můžete vygenerovat Taproot adresu založenou pouze na veřejném klíči přítomném na hloubce 5 vaší peněženky. V tomto případě je nutné vytvořit nespotřebitelný skript pro _skriptovou cestu_, aby byly splněny požadavky struktury. Úprava $t$ je poté vypočítána aplikací značkované hašovací funkce, **`TapTweak`**, na interní veřejný klíč $P$:
t = \text{H}_{\text{TapTweak}}(P)
kde:
- **$\text{H}_{\text{TapTweak}}$** je SHA256 hašovací funkce označená značkou `TapTweak`. Pokud nejste obeznámeni s tím, co je značkovaná hašovací funkce, doporučuji vám konzultovat kapitolu 3.3;
- $P$ je interní veřejný klíč, reprezentovaný ve svém komprimovaném 256-bitovém formátu, používající pouze souřadnici $x$.
Taproot veřejný klíč $Q$ je poté vypočítán přičtením úpravy $t$, vynásobené generátorem eliptické křivky $G$, k internímu veřejnému klíči $P$:
Q = P + t \cdot G
Jakmile je získán Taproot veřejný klíč $Q$, můžeme vygenerovat odpovídající přijímací adresu. Na rozdíl od jiných formátů nejsou Taproot adresy založeny na haši veřejného klíče. Klíč $Q$ je proto vložen přímo do adresy, v surové formě.
Začneme extrakcí souřadnice $x$ bodu $Q$ k získání komprimovaného veřejného klíče. Na tuto nákladovou část je vypočítán kontrolní součet pomocí BCH kódů, stejně jako u adres SegWit v0. Program použitý pro Taproot adresy se však mírně liší. Skutečně, po zavedení formátu _bech32_ s SegWit byla objevena chyba: když je poslední znak adresy `p`, vkládání nebo odstraňování `q` těsně před tímto `p` nezpůsobí neplatnost kontrolního součtu. Ačkoli tato chyba nemá důsledky na SegWit v0 (díky omezení velikosti), v budoucnu by mohla představovat problém. Tato chyba byla proto pro Taproot adresy opravena a nový opravený formát se nazývá "_bech32m_".
Taproot adresa je generována kódováním souřadnice $x$ $Q$ ve formátu _bech32m_, s následujícími prvky:
- **HRP (_Human Readable Part_)**: `bc`, k označení hlavní sítě Bitcoinu;
- **Verze**: `1` k označení Taproot / SegWit v1;
- **Kontrolní součet**.
Konečná adresa bude mít tedy formát:
```
bc1p[Qx][kontrolní součet]
```
Na druhou stranu, pokud si přejete přidat alternativní skripty kromě výdajů s interním veřejným klíčem (_skriptová cesta_), výpočet přijímací adresy bude mírně odlišný. Budete muset zahrnout haš alternativních skriptů do výpočtu úpravy. V Taprootu je každý alternativní skript, umístěný na konci Merkleova stromu, nazýván "list".
Jakmile jsou napsány různé alternativní skripty, musíte je jednotlivě projít značkovanou hašovací funkcí `TapLeaf`, doprovázenou některými metadaty:
\text{h}{\text{leaf}} = \text{H}{\text{TapLeaf}} (v \Vert sz \Vert S)
S:
- $v$: číslo verze skriptu (výchozí `0xC0` pro Taproot);
- $sz$: velikost skriptu zakódovaná ve formátu _CompactSize_;
- $S$: skript.
Různé hashe skriptů ($\text{h}_{\text{leaf}}$) jsou nejprve seřazeny v lexikografickém pořadí. Poté jsou spojeny po dvojicích a procházejí funkcí značeného hashování `TapBranch`. Tento proces se opakuje iterativně, aby se krok za krokem budoval Merkleův strom:
\text{h}{\text{branch}} = \text{H}{\text{TapBranch}}(\text{h}{\text{leaf1}} \Vert \text{h}{\text{leaf2}})
Pokračujeme spojováním výsledků po dvou, přičemž je na každém kroku procházíme funkcí značeného hashování `TapBranch`, dokud nezískáme kořen Merkleova stromu:
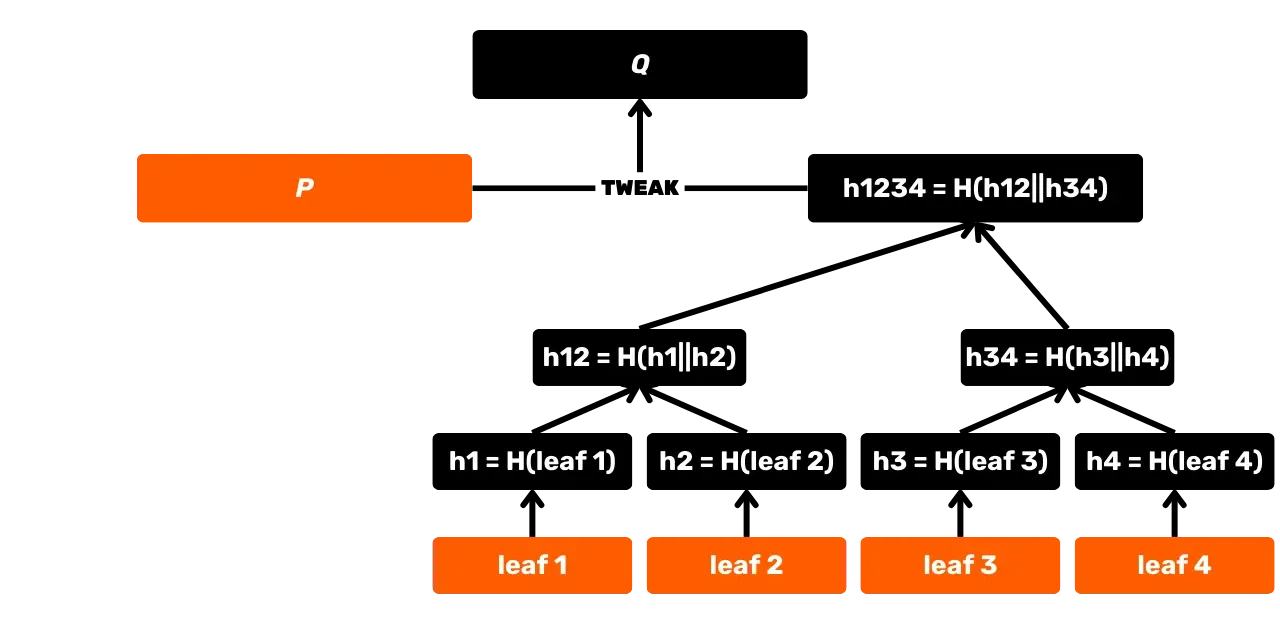
Jakmile je vypočten kořen Merkle $h_{\text{root}}$, můžeme vypočítat tweak. Za tímto účelem zkombinujeme interní veřejný klíč peněženky $P$ s kořenem $h_{\text{root}}$ a celé to proženeme značkovou hashovací funkcí `TapTweak`:
t = \text{H}{\text{TapTweak}}(P \Vert h{\text{root}})
Nakonec, stejně jako dříve, je veřejný klíč Taproot $Q$ získán přidáním interního veřejného klíče $P$ k produktu tweaku $t$ s generátorovým bodem $G$:
Q = P + t \cdot G
Generování adresy pak pokračuje stejným procesem, přičemž surový veřejný klíč $Q$ je použit jako užitečný náklad spolu s několika dalšími metadata.
A to je vše! Dospěli jsme ke konci tohoto kurzu CYP201. Pokud jste tento kurz považovali za užitečný, byl bych velmi vděčný, pokud byste si našli chvilku na to, abyste mu dali dobré hodnocení v následující kapitole hodnocení. Neváhejte jej také sdílet s vašimi blízkými nebo na sociálních sítích. Nakonec, pokud si přejete získat diplom za tento kurz, můžete po kapitole hodnocení absolvovat závěrečnou zkoušku.
# Sekce finále
<partId>58111408-b734-54db-9ea7-0d5b67f99f99</partId>
## Recenze & Hodnocení
<chapterId>0cd71541-a7fd-53db-b66a-8611b6a28b04</chapterId>
<isCourseReview>true</isCourseReview>
## Závěrečná zkouška
<chapterId>a53ea27d-0f84-56cd-b37c-a66210a4b31d</chapterId>
<isCourseExam>true</isCourseExam>
## Závěr
<chapterId>d291428b-3cfa-5394-930e-4b514be82d5a</chapterId>
<isCourseConclusion>true</isCourseConclusion>